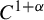1 Introduction
We start by recalling the terminology introduced by Gromov [Reference Gromov6]. Given a finitely generated group
![]() $\Gamma $
, we fix a finite system of generators, and we denote
$\Gamma $
, we fix a finite system of generators, and we denote
![]() $\| \cdot \|$
the corresponding word length. An element
$\| \cdot \|$
the corresponding word length. An element
![]() $f \in \Gamma $
is said to be distorted if
$f \in \Gamma $
is said to be distorted if
(Notice that this condition does not depend on the choice of the finite generating system.) Given an arbitrary group G, an element
![]() $f \in G$
is said to be distorted if there exists a finitely generated subgroup
$f \in G$
is said to be distorted if there exists a finitely generated subgroup
![]() $\Gamma \subset G$
containing f so that f is distorted in
$\Gamma \subset G$
containing f so that f is distorted in
![]() $\Gamma $
in the sense above.
$\Gamma $
in the sense above.
Examples of ‘large’ groups for which this notion becomes interesting are groups of diffeomorphisms of compact manifolds M. Very little is known about distorted elements therein. In particular, the following question from [Reference Navas14] is widely open: Given
![]() $r < s$
, does there exist an undistorted element
$r < s$
, does there exist an undistorted element
![]() $f \in \mathrm {Diff}^{s}_+ (M)$
that is distorted when considered as an element of
$f \in \mathrm {Diff}^{s}_+ (M)$
that is distorted when considered as an element of
![]() $\mathrm {Diff}^{r}_+ (M)$
? In [Reference Navas14], Andrés Navas proves that this is the case for M the closed interval,
$\mathrm {Diff}^{r}_+ (M)$
? In [Reference Navas14], Andrés Navas proves that this is the case for M the closed interval,
![]() $r = 1$
and
$r = 1$
and
![]() $s=2$
. Actually, undistortion holds in the larger group
$s=2$
. Actually, undistortion holds in the larger group
![]() $\mathrm {Diff}^{1+bv}_+([0,1])$
of
$\mathrm {Diff}^{1+bv}_+([0,1])$
of
![]() $C^1$
diffeomorphisms with derivative of bounded variation.
$C^1$
diffeomorphisms with derivative of bounded variation.
In this Note, we give an extension of this result from
![]() $C^1$
to
$C^1$
to
![]() $C^{1+\alpha }$
regularity.
$C^{1+\alpha }$
regularity.
Theorem 1.1. There exist
![]() $C^{\infty }$
diffeomorphisms of
$C^{\infty }$
diffeomorphisms of
![]() $[0,1]$
that are distorted in
$[0,1]$
that are distorted in
![]() $\mathrm {Diff}^{1+\alpha }_+([0,1])$
for all
$\mathrm {Diff}^{1+\alpha }_+([0,1])$
for all
![]() $\alpha \in (0,1)$
yet undistorted in
$\alpha \in (0,1)$
yet undistorted in
![]() $\mathrm {Diff}^{1+bv}_+([0,1])$
.
$\mathrm {Diff}^{1+bv}_+([0,1])$
.
The groups we consider are variations of those introduced in [Reference Navas14]. One of the new contributions consists in improving the regularity of some elements, which is not at all straightforward. Indeed, the construction of [Reference Navas14] uses a well-known lemma that ensures
![]() $C^1$
regularity of maps built by pasting together infinitely many diffeomorphisms that are defined on disjoint intervals and satisfy certain equivariance relations. This idea comes from the thesis of Kopell [Reference Kopell9], and has been systematically used in the study of codimension-1 foliations [Reference Druck and Firmo4] and centralizers of diffeomorphisms [Reference Bonatti and Farinelli1]. Nevertheless, such a lemma is unavailable in
$C^1$
regularity of maps built by pasting together infinitely many diffeomorphisms that are defined on disjoint intervals and satisfy certain equivariance relations. This idea comes from the thesis of Kopell [Reference Kopell9], and has been systematically used in the study of codimension-1 foliations [Reference Druck and Firmo4] and centralizers of diffeomorphisms [Reference Bonatti and Farinelli1]. Nevertheless, such a lemma is unavailable in
![]() $C^{1+\alpha }$
regularity and, as we show in the Appendix, it cannot hold without imposing extra hypotheses. Hence we are forced to go into more explicit constructions and very long computations, which are however interesting by themselves. To do this, we use a classical technique of Dennis Pixton (later extended by Tsuboi [Reference Tsuboi17]) to produce commuting diffeomorphisms and control their
$C^{1+\alpha }$
regularity and, as we show in the Appendix, it cannot hold without imposing extra hypotheses. Hence we are forced to go into more explicit constructions and very long computations, which are however interesting by themselves. To do this, we use a classical technique of Dennis Pixton (later extended by Tsuboi [Reference Tsuboi17]) to produce commuting diffeomorphisms and control their
![]() $C^{1+\alpha }$
norms.
$C^{1+\alpha }$
norms.
To close this Introduction, let us point out that our main result is a step forward in the understanding of the large-scale structure of the groups
![]() $\mathrm {Diff}^s_+([0,1])$
with respect to the regularity parameter s [Reference Rosendal16]. This may be compared with a recent result of Kim and Koberda [Reference Kim and Koberda7] (see also [Reference Mann and Wolff10]), who showed that the local algebraic structure of such groups is sensibly different. It seems reasonable to expect for a general theory that combines these two approaches and (hopefully) extends to higher dimensional manifolds.
$\mathrm {Diff}^s_+([0,1])$
with respect to the regularity parameter s [Reference Rosendal16]. This may be compared with a recent result of Kim and Koberda [Reference Kim and Koberda7] (see also [Reference Mann and Wolff10]), who showed that the local algebraic structure of such groups is sensibly different. It seems reasonable to expect for a general theory that combines these two approaches and (hopefully) extends to higher dimensional manifolds.
2 On a family of
 $C^{1+bv}$
-undistorted diffeomorphisms
$C^{1+bv}$
-undistorted diffeomorphisms
Here and in what follows, all maps we consider are supposed to preserve the orientation.
Recall that for a
![]() $C^{1+bv}$
diffeomorphism f of a compact 1-manifold, the asymptotic distortion was defined by Navas in [Reference Navas13] as
$C^{1+bv}$
diffeomorphism f of a compact 1-manifold, the asymptotic distortion was defined by Navas in [Reference Navas13] as
By the subadditivity of
![]() $\mathrm {var} (\log D(\cdot ))$
, if f is a distorted element of the group of
$\mathrm {var} (\log D(\cdot ))$
, if f is a distorted element of the group of
![]() $C^{1+bv}$
diffeomorphisms, then
$C^{1+bv}$
diffeomorphisms, then
![]() $\mathrm {dist}_{\infty } (f) = 0$
.
$\mathrm {dist}_{\infty } (f) = 0$
.
The family of diffeomorphisms with positive asymptotic distortion studied in [Reference Navas14] is as follows: Start with a
![]() $C^{1+bv}$
diffeomorphism of
$C^{1+bv}$
diffeomorphism of
![]() $[0,1]$
with vanishing asymptotic distortion and no fixed point in
$[0,1]$
with vanishing asymptotic distortion and no fixed point in
![]() $]0,1[$
. Let I be a fundamental domain for the action of f, that is, an open interval with endpoints
$]0,1[$
. Let I be a fundamental domain for the action of f, that is, an open interval with endpoints
![]() $x_0$
and
$x_0$
and
![]() $x_1 := f (x_0)$
for a certain
$x_1 := f (x_0)$
for a certain
![]() $x_0 \in \, ]0,1[$
. Let g be any non-trivial
$x_0 \in \, ]0,1[$
. Let g be any non-trivial
![]() $C^{1+bv}$
diffeomorphism of
$C^{1+bv}$
diffeomorphism of
![]() $]0,1[$
supported on I. Then the diffeomorphism
$]0,1[$
supported on I. Then the diffeomorphism
![]() $\bar {f} := fg$
has positive asymptotic distortion and, in particular, it is undistorted in
$\bar {f} := fg$
has positive asymptotic distortion and, in particular, it is undistorted in
![]() $\mathrm {Diff}_+^{1+bv} ([0,1])$
(hence in
$\mathrm {Diff}_+^{1+bv} ([0,1])$
(hence in
![]() $\mathrm {Diff}_+^2([0,1])$
if f and g are of class
$\mathrm {Diff}_+^2([0,1])$
if f and g are of class
![]() $C^2$
). This fact follows from [Reference Eynard-Bontemps and Navas5] (see Lemmas 2.2 and 7.2 therein) by using the relation between the asymptotic distortion and the Mather invariant. For the reader’s convenience, below we present a short and direct argument based on Kopell’s like estimates [Reference Kopell9, Reference Navas11].
$C^2$
). This fact follows from [Reference Eynard-Bontemps and Navas5] (see Lemmas 2.2 and 7.2 therein) by using the relation between the asymptotic distortion and the Mather invariant. For the reader’s convenience, below we present a short and direct argument based on Kopell’s like estimates [Reference Kopell9, Reference Navas11].

Let us consider the product
![]() $\bar {f}^n f^{-n}$
. Since f has vanishing asymptotic distortion, if we show that
$\bar {f}^n f^{-n}$
. Since f has vanishing asymptotic distortion, if we show that
![]() $\mathrm {var} (\log D (\bar {f}^n f^{-n}) )$
has linear growth, the same will hold for
$\mathrm {var} (\log D (\bar {f}^n f^{-n}) )$
has linear growth, the same will hold for
![]() $\mathrm {var} (\log D \bar {f}^n)$
. Now, notice that
$\mathrm {var} (\log D \bar {f}^n)$
. Now, notice that
has support in the union of the intervals
![]() $f(I), f^2(I), \ldots , f^n (I)$
, and equals
$f(I), f^2(I), \ldots , f^n (I)$
, and equals
![]() $f^k g f^{-k}$
on each such interval
$f^k g f^{-k}$
on each such interval
![]() $f^k (I)$
. In particular, its derivative at the endpoints
$f^k (I)$
. In particular, its derivative at the endpoints
![]() $x_k,x_{k+1}$
of each of these intervals equals 1. We claim that there is a constant
$x_k,x_{k+1}$
of each of these intervals equals 1. We claim that there is a constant
![]() $\lambda> 1$
such that, for all
$\lambda> 1$
such that, for all
![]() $k \geq 1$
, there is a point
$k \geq 1$
, there is a point
![]() $y_k \in f^k (I)$
satisfying
$y_k \in f^k (I)$
satisfying
![]() $D (f^k g f^{-k}) (y_k) \geq \lambda $
. Assuming this, we conclude
$D (f^k g f^{-k}) (y_k) \geq \lambda $
. Assuming this, we conclude
 $$ \begin{align*}\mathrm{var} (\log D (\bar{f}^n f^{-n}) ) \geq \sum_{k=1}^{n} |\!\log D(f^kgf^{-k}) (y_k) - \log D (f^kgf^{-k}) (x_k)| \geq n \, \log (\lambda),\end{align*} $$
$$ \begin{align*}\mathrm{var} (\log D (\bar{f}^n f^{-n}) ) \geq \sum_{k=1}^{n} |\!\log D(f^kgf^{-k}) (y_k) - \log D (f^kgf^{-k}) (x_k)| \geq n \, \log (\lambda),\end{align*} $$
which yields the desired linear growth.
Now, to check the existence of
![]() $\lambda $
and the points
$\lambda $
and the points
![]() $y_k$
, let
$y_k$
, let
![]() $V := \mathrm {var} (\log Df)$
, and let
$V := \mathrm {var} (\log Df)$
, and let
![]() $N \geq 1$
be such that
$N \geq 1$
be such that
![]() $Dg^N (z)> e^{2V}$
holds for some
$Dg^N (z)> e^{2V}$
holds for some
![]() $z \!\in \! I$
. We claim that
$z \!\in \! I$
. We claim that
![]() $\lambda := e^{V/N}$
works. Assume otherwise. Then, for a certain
$\lambda := e^{V/N}$
works. Assume otherwise. Then, for a certain
![]() $K \geq 0$
, one would have
$K \geq 0$
, one would have
![]() $ \| D (f^K g f^{-K} ) \|_{\infty } \leq e^{V / N}$
, which by the chain rule would yield
$ \| D (f^K g f^{-K} ) \|_{\infty } \leq e^{V / N}$
, which by the chain rule would yield
![]() $ \| D (f^K g^N f^{-K} ) \|_{\infty } \leq e^{V}$
. However, at the point
$ \| D (f^K g^N f^{-K} ) \|_{\infty } \leq e^{V}$
. However, at the point
![]() $z_K \!:=\! f^K (z)$
, we have
$z_K \!:=\! f^K (z)$
, we have
![]() $D (f^K g^N f^{-K}) (z_K)> e^V$
. Indeed,
$D (f^K g^N f^{-K}) (z_K)> e^V$
. Indeed,
 $$ \begin{align*} \log (D (f^K g^N f^{-K}) (z_K)) &= \log Df^K (g^N (z) ) + \log Dg^N (z) - \log Df^K (z) \\ &\geq \log Dg^N (z) - |\!\log Df^K (g^N (z) ) - \log Df^K (z) | \\ &> 2V - \sum^{K-1}_{k=0} |\!\log Df (f^k (g^N (z))) - \log Df (f^k (z)) |. \end{align*} $$
$$ \begin{align*} \log (D (f^K g^N f^{-K}) (z_K)) &= \log Df^K (g^N (z) ) + \log Dg^N (z) - \log Df^K (z) \\ &\geq \log Dg^N (z) - |\!\log Df^K (g^N (z) ) - \log Df^K (z) | \\ &> 2V - \sum^{K-1}_{k=0} |\!\log Df (f^k (g^N (z))) - \log Df (f^k (z)) |. \end{align*} $$
Since both z and
![]() $g^N (z)$
lie in the fundamental domain I of f,
$g^N (z)$
lie in the fundamental domain I of f,
 $$ \begin{align*}\sum^{K-1}_{k=0} |\!\log Df (f^k (g^N (z))) - \log Df (f^k(z)) | \leq \mathrm{var} (\log Df) \leq V.\end{align*} $$
$$ \begin{align*}\sum^{K-1}_{k=0} |\!\log Df (f^k (g^N (z))) - \log Df (f^k(z)) | \leq \mathrm{var} (\log Df) \leq V.\end{align*} $$
We thus conclude that
![]() $\log (D (f^K g^N f^{-K}) (z_K))> V,$
as announced.
$\log (D (f^K g^N f^{-K}) (z_K))> V,$
as announced.
3 Distortion in class
 $C^{1+\alpha }$
for
$C^{1+\alpha }$
for
 $\alpha < 1/2$
$\alpha < 1/2$
In this section, we start by briefly recalling the construction of the group
![]() $\Gamma $
with a distorted element
$\Gamma $
with a distorted element
![]() $\bar {f}$
considered in [Reference Navas14]. Next, we proceed to smooth the action of
$\bar {f}$
considered in [Reference Navas14]. Next, we proceed to smooth the action of
![]() $\Gamma $
in order to achieve any differentiability class
$\Gamma $
in order to achieve any differentiability class
![]() $C^{1+\alpha }$
for
$C^{1+\alpha }$
for
![]() $\alpha < 1/2$
. Upgrading
$\alpha < 1/2$
. Upgrading
![]() $\alpha $
to any number less than 1 will require the introduction of an extra element plus a tricky new computation, and will be carried out in the next section.
$\alpha $
to any number less than 1 will require the introduction of an extra element plus a tricky new computation, and will be carried out in the next section.
Start with the vector fields
![]() $\hat {\mathcal {X}}$
and
$\hat {\mathcal {X}}$
and
![]() $\mathcal {X}$
on the real line whose time-1 maps are, respectively,
$\mathcal {X}$
on the real line whose time-1 maps are, respectively,
Let
![]() $\varphi \! : \mathbb {R} \to \, ]0,1[$
be a
$\varphi \! : \mathbb {R} \to \, ]0,1[$
be a
![]() $C^{\infty }$
diffeomorphism such that
$C^{\infty }$
diffeomorphism such that
![]() $\hat {\mathcal {Y}} := \varphi _* (\hat {\mathcal {X}})$
and
$\hat {\mathcal {Y}} := \varphi _* (\hat {\mathcal {X}})$
and
![]() $\mathcal {Y} := \varphi _* (\mathcal {X})$
extend to the endpoints of
$\mathcal {Y} := \varphi _* (\mathcal {X})$
extend to the endpoints of
![]() $[0,1]$
as infinitely flat vector fields. Denote
$[0,1]$
as infinitely flat vector fields. Denote
![]() $\hat {f} := \hat {\mathcal {Y}}^1$
and
$\hat {f} := \hat {\mathcal {Y}}^1$
and
![]() $f := \mathcal {Y}^1$
, which we view as diffeomorphisms of
$f := \mathcal {Y}^1$
, which we view as diffeomorphisms of
![]() $[-1,2]$
that coincide with the identity outside
$[-1,2]$
that coincide with the identity outside
![]() $[0,1]$
. The affine relation
$[0,1]$
. The affine relation
![]() $\hat {f} f \hat {f}^{-1} = f^2$
yields that
$\hat {f} f \hat {f}^{-1} = f^2$
yields that
![]() $\| f^n \| = O (\log (n))$
; in particular, f has vanishing asymptotic distortion.
$\| f^n \| = O (\log (n))$
; in particular, f has vanishing asymptotic distortion.
Let
![]() $x_0 := \varphi (0)$
and, for each
$x_0 := \varphi (0)$
and, for each
![]() $k \!\in \! \mathbb {Z}$
, let
$k \!\in \! \mathbb {Z}$
, let
![]() $x_k := f^k (x_0) = \varphi (k)$
. Denote also
$x_k := f^k (x_0) = \varphi (k)$
. Denote also
![]() $x_{-1/2} := \varphi (-1/2)$
and
$x_{-1/2} := \varphi (-1/2)$
and
![]() $x_{-3/4} := \varphi (-3/4)$
. Let
$x_{-3/4} := \varphi (-3/4)$
. Let
![]() $\varphi _0$
be the affine diffeomorphism sending
$\varphi _0$
be the affine diffeomorphism sending
![]() $I := [x_0,x_1]$
onto
$I := [x_0,x_1]$
onto
![]() $[0,1]$
, and let
$[0,1]$
, and let
![]() $g := \varphi _0^{-1} f \varphi _0$
. This can be extended to
$g := \varphi _0^{-1} f \varphi _0$
. This can be extended to
![]() $[-1,2]$
by the identity outside I.
$[-1,2]$
by the identity outside I.
We next define two diffeomorphisms
![]() $\hat {h}$
and h as follows.
$\hat {h}$
and h as follows.
-
(i) They act by the identity outside
 $[0,1]$
.
$[0,1]$
. -
(ii) On each interval
 $I_k := f^k (I)$
, the diffeomorphism
$I_k := f^k (I)$
, the diffeomorphism
 $\hat {h}$
(respectively h) coincides with the
$\hat {h}$
(respectively h) coincides with the
 $s_k$
-time map (respectively
$s_k$
-time map (respectively
 $t_k$
-time map) of the flow of the vector field
$t_k$
-time map) of the flow of the vector field
 $f^k_* (\varphi _0^* (\hat {\mathcal {Y}} ) )$
(respectively
$f^k_* (\varphi _0^* (\hat {\mathcal {Y}} ) )$
(respectively
 $f^k_* (\varphi _0^* (\mathcal {Y})) $
).
$f^k_* (\varphi _0^* (\mathcal {Y})) $
).Here,
 $s_k$
and
$s_k$
and
 $t_k$
are sequences of real numbers such that as follows.
$t_k$
are sequences of real numbers such that as follows. -
(iii) If
 $2^{i-1} \leq k < 2^{i}$
for a certain positive even integer i, then where
$2^{i-1} \leq k < 2^{i}$
for a certain positive even integer i, then where $$ \begin{align*}s_k := \log_2 \bigg( 1 - \frac{1}{\sqrt{\ell_{i/2}}} \bigg) \quad \mbox{ and } \quad t_k := \frac{1}{ \sqrt{\ell_{i/2}} },\end{align*} $$
$$ \begin{align*}s_k := \log_2 \bigg( 1 - \frac{1}{\sqrt{\ell_{i/2}}} \bigg) \quad \mbox{ and } \quad t_k := \frac{1}{ \sqrt{\ell_{i/2}} },\end{align*} $$
 $\ell _j$
is a prescribed sequence of positive integers diverging to infinity to be fixed below.
$\ell _j$
is a prescribed sequence of positive integers diverging to infinity to be fixed below.
-
(iv) Otherwise,
 $s_k = t_k := 0$
.
$s_k = t_k := 0$
.Finally, we let
 $\psi $
be a
$\psi $
be a
 $C^{\infty }$
diffeomorphism of
$C^{\infty }$
diffeomorphism of
 $[-1,2]$
such that:
$[-1,2]$
such that: -
(v)
 $\psi $
coincides with the identity on
$\psi $
coincides with the identity on
 $[x_{-1/2} , x_0];$
$[x_{-1/2} , x_0];$
-
(vi)
 $\psi (x_{-3/4}) = 0$
and
$\psi (x_{-3/4}) = 0$
and
 $\psi (x_1) = 1$
.
$\psi (x_1) = 1$
.
The group we consider is
![]() $\Gamma := \langle \hat {f}, f, g, \hat {h}, h, \psi \rangle $
. The computations of [Reference Navas14] show the following relation for certain powers of
$\Gamma := \langle \hat {f}, f, g, \hat {h}, h, \psi \rangle $
. The computations of [Reference Navas14] show the following relation for certain powers of
![]() $\bar {f} := fg$
(which justifies the construction):
$\bar {f} := fg$
(which justifies the construction):
where i is an even (positive) integer and
![]() $n:= 2^i$
. Roughly, this works as follows: set
$n:= 2^i$
. Roughly, this works as follows: set
One easily checks that
 $$ \begin{align*}&\text{supp} (a_n) \subset[0,x_{-3/2}]\cup[x_{-1/2},x_0]\cup[x_1,1] \quad \mbox{ and }\\ &\text{supp} (b_n) \subset[-1,0]\cup[x_{-1/2},x_0]\cup[1,2].\end{align*} $$
$$ \begin{align*}&\text{supp} (a_n) \subset[0,x_{-3/2}]\cup[x_{-1/2},x_0]\cup[x_1,1] \quad \mbox{ and }\\ &\text{supp} (b_n) \subset[-1,0]\cup[x_{-1/2},x_0]\cup[1,2].\end{align*} $$
Thus, the commutator
![]() $c_n:=[a_n,b_n] = a_n b_n a_n^{-1} b_n^{-1}$
is supported on
$c_n:=[a_n,b_n] = a_n b_n a_n^{-1} b_n^{-1}$
is supported on
![]() $[x_{-1/2},x_0]$
, so the conjugate
$[x_{-1/2},x_0]$
, so the conjugate
![]() $\hat {f}^{i}c_n\hat {f}^{-i}$
is supported on
$\hat {f}^{i}c_n\hat {f}^{-i}$
is supported on
![]() $ [x_{-2^{i-1}},x_0] $
. Besides, on each
$ [x_{-2^{i-1}},x_0] $
. Besides, on each
![]() $[x_k,x_{k+1}]\subset [x_{-2^{i-1}},x_0]$
, this conjugate
$[x_k,x_{k+1}]\subset [x_{-2^{i-1}},x_0]$
, this conjugate
![]() $\hat {f}^{i}c_n\hat {f}^{-i}$
coincides with the time-
$\hat {f}^{i}c_n\hat {f}^{-i}$
coincides with the time-
![]() ${1}/{\ell _{i/2}}$
map of the flow of
${1}/{\ell _{i/2}}$
map of the flow of
![]() $f^k_\ast (\varphi _0^\ast (\mathcal {Y}))$
. Moreover, the restriction of the map
$f^k_\ast (\varphi _0^\ast (\mathcal {Y}))$
. Moreover, the restriction of the map
to each
![]() $[x_k,x_{k+1}]\subset [x_{-2^{i-1}},x_0]$
equals the time-1 map of the flow of
$[x_k,x_{k+1}]\subset [x_{-2^{i-1}},x_0]$
equals the time-1 map of the flow of
![]() $f^k_\ast (\varphi _0^\ast (\mathcal {Y}))$
. This implies that
$f^k_\ast (\varphi _0^\ast (\mathcal {Y}))$
. This implies that
which corresponds to identity (3.1).
Since
![]() $\| f^n \| = O (\log (n))$
, identity (3.1) implies that
$\| f^n \| = O (\log (n))$
, identity (3.1) implies that
![]() $\| (\bar {f})^{2^{i-1}}\| = O (i \, \ell _{i/2})$
. Therefore,
$\| (\bar {f})^{2^{i-1}}\| = O (i \, \ell _{i/2})$
. Therefore,
![]() $\bar {f}$
is distorted provided
$\bar {f}$
is distorted provided
![]() $\ell _{j}$
grows to infinity in such a way that
$\ell _{j}$
grows to infinity in such a way that
The maps
![]() $\hat {f}, f, g, \psi $
above are obviously smooth. However, regularity for
$\hat {f}, f, g, \psi $
above are obviously smooth. However, regularity for
![]() $\hat {h}, h$
is more subtler. Indeed, their
$\hat {h}, h$
is more subtler. Indeed, their
![]() $C^1$
smoothness is ensured by the conditions
$C^1$
smoothness is ensured by the conditions
![]() $s_n \to 0$
and
$s_n \to 0$
and
![]() $t_n \to 0$
as
$t_n \to 0$
as
![]() $|n| \to \infty $
(which are equivalent to
$|n| \to \infty $
(which are equivalent to
![]() $\ell _j \to \infty $
as
$\ell _j \to \infty $
as
![]() $j \to \infty $
) together with the next lemma. This is strongly inspired on the work of Kopell (a proof together with a discussion appears in the Appendix of [Reference Navas14]). Below, by
$j \to \infty $
) together with the next lemma. This is strongly inspired on the work of Kopell (a proof together with a discussion appears in the Appendix of [Reference Navas14]). Below, by
![]() $C^{1+\mathrm {Lip}}$
we refer to maps with Lipschitz derivative.
$C^{1+\mathrm {Lip}}$
we refer to maps with Lipschitz derivative.
Lemma 3.1. Let
![]() $f \in \mathrm {Diff}^{1+\mathrm {Lip}}_+([0,1])$
be such that
$f \in \mathrm {Diff}^{1+\mathrm {Lip}}_+([0,1])$
be such that
![]() $f(x) \neq x$
for all
$f(x) \neq x$
for all
![]() $x \in (0,1)$
. Fix
$x \in (0,1)$
. Fix
![]() $x_0\in (0,1)$
, and let
$x_0\in (0,1)$
, and let
![]() $x_n := f^n(x_0)$
. Let
$x_n := f^n(x_0)$
. Let
![]() $(g_n)_{n \in \mathbb {Z}}$
be a sequence of
$(g_n)_{n \in \mathbb {Z}}$
be a sequence of
![]() $C^1$
diffeomorphisms of the interval of endpoints
$C^1$
diffeomorphisms of the interval of endpoints
![]() $x_0,x_1$
such that
$x_0,x_1$
such that
![]() $Dg_n(x_0) = Dg_n(x_1)=1$
for all
$Dg_n(x_0) = Dg_n(x_1)=1$
for all
![]() $n \in \mathbb {Z}$
. Let
$n \in \mathbb {Z}$
. Let
![]() $g: (0,1)\rightarrow (0,1)$
be the diffeomorphism whose restriction to each interval of endpoints
$g: (0,1)\rightarrow (0,1)$
be the diffeomorphism whose restriction to each interval of endpoints
![]() $x_n , x_{n+1}$
coincides with
$x_n , x_{n+1}$
coincides with
![]() $f^ng_nf^{-n}$
. If
$f^ng_nf^{-n}$
. If
![]() $g_n \rightarrow \mathrm {Id}$
in
$g_n \rightarrow \mathrm {Id}$
in
![]() $C^1$
topology as
$C^1$
topology as
![]() $n \to \infty $
, then g extends to a
$n \to \infty $
, then g extends to a
![]() $C^1$
diffeomorphism of
$C^1$
diffeomorphism of
![]() $[0,1]$
by letting
$[0,1]$
by letting
![]() $f(0) = 0$
and
$f(0) = 0$
and
![]() $f(1)=1$
.
$f(1)=1$
.
Unfortunately, as we will see in the Appendix, this fails to extend to class
![]() $C^{1+\alpha }$
. Because of this, we need to go into more explicit computations for our example. Although these are difficult to handle, the following key elementary lemma taken from the work of Pixton [Reference Pixton15] and Tsuboi [Reference Tsuboi17] will be enough for us.
$C^{1+\alpha }$
. Because of this, we need to go into more explicit computations for our example. Although these are difficult to handle, the following key elementary lemma taken from the work of Pixton [Reference Pixton15] and Tsuboi [Reference Tsuboi17] will be enough for us.
Lemma 3.2. Given a
![]() $C^2$
vector field
$C^2$
vector field
![]() $\mathcal {X}$
on an interval
$\mathcal {X}$
on an interval
![]() $[0,a]$
, denote
$[0,a]$
, denote
![]() $C_1 := \| D \mathcal {X} \|$
and
$C_1 := \| D \mathcal {X} \|$
and
![]() $C_2 := \| D^2 \mathcal {X} \| $
. If
$C_2 := \| D^2 \mathcal {X} \| $
. If
![]() $f^t$
denotes its flow, then, for all
$f^t$
denotes its flow, then, for all
![]() $t \geq 0$
,
$t \geq 0$
,
Proof Taking derivatives on the equality
![]() $d f^t / dt = \mathcal {X} \circ f^t$
, we deduce
$d f^t / dt = \mathcal {X} \circ f^t$
, we deduce
so
 $$ \begin{align*}\frac{d}{dt} \log Df^t = \frac{({d}/{dt}) Df^t}{Df^t} = D \mathcal{X} (f^t).\end{align*} $$
$$ \begin{align*}\frac{d}{dt} \log Df^t = \frac{({d}/{dt}) Df^t}{Df^t} = D \mathcal{X} (f^t).\end{align*} $$
Since
![]() $f^0 = \mathrm {Id}$
, we conclude
$f^0 = \mathrm {Id}$
, we conclude
 $$\begin{align*}\log Df^t = \int_0^t D \mathcal{X} (f^s) \, ds. \end{align*}$$
$$\begin{align*}\log Df^t = \int_0^t D \mathcal{X} (f^s) \, ds. \end{align*}$$
Since
![]() $\| D \mathcal {X} \| \leq C_1$
, this yields
$\| D \mathcal {X} \| \leq C_1$
, this yields
![]() $|\!\log Df^t | \leq C_1 t$
, so
$|\!\log Df^t | \leq C_1 t$
, so
![]() $|D f^t| \leq e^{C_1 t}$
. Moreover,
$|D f^t| \leq e^{C_1 t}$
. Moreover,
 $$ \begin{align*}D \log Df^t = D \bigg( \int_0^t D \mathcal{X} (f^s) \, ds \bigg) = \int_0^t D^2 \mathcal{X} (f^s) \cdot Df^s \, ds.\end{align*} $$
$$ \begin{align*}D \log Df^t = D \bigg( \int_0^t D \mathcal{X} (f^s) \, ds \bigg) = \int_0^t D^2 \mathcal{X} (f^s) \cdot Df^s \, ds.\end{align*} $$
Since
![]() $\| D^2 \mathcal {X} \| \leq C_2$
, we conclude
$\| D^2 \mathcal {X} \| \leq C_2$
, we conclude
 $$ \begin{align*}| D \log Df^t | \leq C_2 \int_0^t |Df^s| \, ds \leq C_2 \int_0^t e^{C_1 s} ds = \frac{C_2}{C_1} \, ( e^{C_1 t} -1 ),\end{align*} $$
$$ \begin{align*}| D \log Df^t | \leq C_2 \int_0^t |Df^s| \, ds \leq C_2 \int_0^t e^{C_1 s} ds = \frac{C_2}{C_1} \, ( e^{C_1 t} -1 ),\end{align*} $$
as announced.
We now turn to very long computations that will allow us to ensure that the resulting maps
![]() $h, \hat {h}$
built via the procedure above are
$h, \hat {h}$
built via the procedure above are
![]() $C^{1+\alpha }$
diffeomorphisms for well chosen
$C^{1+\alpha }$
diffeomorphisms for well chosen
![]() $\varphi $
and
$\varphi $
and
![]() $\ell _i$
that respect all the properties we have imposed. This will close the proof of our theorem.
$\ell _i$
that respect all the properties we have imposed. This will close the proof of our theorem.
In order to simplify these computations, let us remind the chain rules for different derivatives of maps between one-dimensional spaces, namely logarithmic (L), affine (A), and Schwarzian (S):
 $$ \begin{align*}L (f) &:= \log Df, \quad A(f) := DL(f) = \frac{D^2 f}{D f} ,\\ S (f) &:= DA(f) - \frac{A(f)^2}{2} = \frac{D^3 f}{D f} - \frac{3}{2} \bigg( \frac{D^2 f}{D f} \bigg)^2.\end{align*} $$
$$ \begin{align*}L (f) &:= \log Df, \quad A(f) := DL(f) = \frac{D^2 f}{D f} ,\\ S (f) &:= DA(f) - \frac{A(f)^2}{2} = \frac{D^3 f}{D f} - \frac{3}{2} \bigg( \frac{D^2 f}{D f} \bigg)^2.\end{align*} $$
These are listed below:
We let
![]() $\varphi \! : (0,1) \to \mathbb {R}$
be a
$\varphi \! : (0,1) \to \mathbb {R}$
be a
![]() $C^{\infty }$
diffeomorphism such that, for a sufficiently small
$C^{\infty }$
diffeomorphism such that, for a sufficiently small
![]() $\delta> 0$
,
$\delta> 0$
,
 $$ \begin{align*}\varphi(x)= \begin{cases} - \text{exp}{(\text{exp}{(1/x)})} \quad & \mbox{if } 0<x\leqslant \delta, \\ \text{exp}{(\text{exp}{(1/(1-x))})}\quad & \mbox{if } 1-\delta \leqslant x <1. \end{cases} \end{align*} $$
$$ \begin{align*}\varphi(x)= \begin{cases} - \text{exp}{(\text{exp}{(1/x)})} \quad & \mbox{if } 0<x\leqslant \delta, \\ \text{exp}{(\text{exp}{(1/(1-x))})}\quad & \mbox{if } 1-\delta \leqslant x <1. \end{cases} \end{align*} $$
If we denote
![]() $\mathcal {Z} := \varphi _0^* (\hat {\mathcal {Y}} )$
, then we need to control
$\mathcal {Z} := \varphi _0^* (\hat {\mathcal {Y}} )$
, then we need to control
![]() $f^n_* (\mathcal {Z})$
.
$f^n_* (\mathcal {Z})$
.
3.1 An estimate for lengths of fundamental domains
Let us come back to the group
![]() $\Gamma = \langle \hat {f}, f, g, \hat {h}, h, \psi \rangle $
. Recall that I denotes the interval
$\Gamma = \langle \hat {f}, f, g, \hat {h}, h, \psi \rangle $
. Recall that I denotes the interval
![]() $[x_0,x_1]$
. We claim that, for a certain constant
$[x_0,x_1]$
. We claim that, for a certain constant
![]() ${C> 0}$
,
${C> 0}$
,
 $$ \begin{align} |f^n (I)| = O \bigg( \frac{C}{n \log(n) \, (\log (\log (n)))^2} \bigg). \end{align} $$
$$ \begin{align} |f^n (I)| = O \bigg( \frac{C}{n \log(n) \, (\log (\log (n)))^2} \bigg). \end{align} $$
This is checked via a direct computation. Namely, for a sufficiently large n,
Since the derivative of
![]() $x \mapsto 1/\log \log (x)$
is
$x \mapsto 1/\log \log (x)$
is
![]() $1 / [x \, \log (x) \, (\log \log (x))^2]$
, a direct application of the mean value theorem yields the desired estimate (3.6).
$1 / [x \, \log (x) \, (\log \log (x))^2]$
, a direct application of the mean value theorem yields the desired estimate (3.6).
3.2 Estimates for the vector field and its derivative
Notice that
Taking derivatives, we obtain
 $$ \begin{align*}D (f^n_\ast(\mathcal{Z}))(x) = \frac{D^2f^n(f^{-n}(x))}{Df^{n}(f^{-n}(x))} \, \mathcal{Z}(f^{-n}(x)) + D \mathcal{Z}(f^{-n}(x)).\end{align*} $$
$$ \begin{align*}D (f^n_\ast(\mathcal{Z}))(x) = \frac{D^2f^n(f^{-n}(x))}{Df^{n}(f^{-n}(x))} \, \mathcal{Z}(f^{-n}(x)) + D \mathcal{Z}(f^{-n}(x)).\end{align*} $$
Now, using the chain rule (3.4), this yields
 $$ \begin{align*}D (f^n_\ast(\mathcal{Z}))(x) = \sum_{i=0}^{n-1}\bigg( \frac{D^2f(f^{i-n}(x))}{Df(f^{i-n}(x))}\bigg)Df^{i}(f^{-n}(x)) \, \mathcal{Z}(f^{-n}(x)) + D \mathcal{Z}(f^{-n}(x)).\end{align*} $$
$$ \begin{align*}D (f^n_\ast(\mathcal{Z}))(x) = \sum_{i=0}^{n-1}\bigg( \frac{D^2f(f^{i-n}(x))}{Df(f^{i-n}(x))}\bigg)Df^{i}(f^{-n}(x)) \, \mathcal{Z}(f^{-n}(x)) + D \mathcal{Z}(f^{-n}(x)).\end{align*} $$
Thus, letting
 $$ \begin{align*}C' := \bigg\| \frac{D^2 f}{Df} \bigg\| \| \mathcal{Z} \|, \quad C" := \| D \mathcal{Z} \|,\end{align*} $$
$$ \begin{align*}C' := \bigg\| \frac{D^2 f}{Df} \bigg\| \| \mathcal{Z} \|, \quad C" := \| D \mathcal{Z} \|,\end{align*} $$
we obtain
 $$ \begin{align*}| D (f^n_\ast (\mathcal{Z}))(x) | \leq C' \sum_{i=0}^{n-1} Df^{i}(f^{-n}(x)) + C".\end{align*} $$
$$ \begin{align*}| D (f^n_\ast (\mathcal{Z}))(x) | \leq C' \sum_{i=0}^{n-1} Df^{i}(f^{-n}(x)) + C".\end{align*} $$
We claim that the sum above is uniformly bounded (independently of n and
![]() $x \in I_n$
), so that
$x \in I_n$
), so that
for a certain constant C. Indeed, a standard control of distortion argument yields that
![]() $Df^{i}(f^{-n}(x))$
is of the order of
$Df^{i}(f^{-n}(x))$
is of the order of
![]() $|I_i| / |I_0|$
, so
$|I_i| / |I_0|$
, so
 $$ \begin{align*}\sum_{i=0}^{n-1} Df^{i}(f^{-n}(x)) \sim \sum_{i=0}^{n-1} |I_i| \leq 1.\end{align*} $$
$$ \begin{align*}\sum_{i=0}^{n-1} Df^{i}(f^{-n}(x)) \sim \sum_{i=0}^{n-1} |I_i| \leq 1.\end{align*} $$
3.3 Estimates for the second derivative
We now claim that, for a certain constant
![]() ${C>0}$
and all
${C>0}$
and all
![]() $x \in I_n$
,
$x \in I_n$
,
To show this, notice that, from
we obtain
which is equal to
Let us analyze each term entering in this expression. First, by equation (3.6) and the control of distortion argument above,
We next claim that
![]() $A(f^n)$
is uniformly bounded on
$A(f^n)$
is uniformly bounded on
![]() $I_0$
. Indeed, letting
$I_0$
. Indeed, letting
![]() $C:= \| A (f) \|$
, the chain rule (3.4) yields
$C:= \| A (f) \|$
, the chain rule (3.4) yields
 $$ \begin{align*}A (f^n) = \sum_{i=0}^{n-1} A (f) \circ f^i \cdot Df^i \leq C \sum_{i=0}^{n-1} Df^i.\end{align*} $$
$$ \begin{align*}A (f^n) = \sum_{i=0}^{n-1} A (f) \circ f^i \cdot Df^i \leq C \sum_{i=0}^{n-1} Df^i.\end{align*} $$
The control of distortion argument above shows that the last sum is bounded from above by a constant, which is the claim.
Since
![]() $\mathcal {Z}$
,
$\mathcal {Z}$
,
![]() $D \mathcal {Z}$
and
$D \mathcal {Z}$
and
![]() $D^2 \mathcal {Z}$
are obviously uniformly bounded, to show equation (3.8), it remains to check that
$D^2 \mathcal {Z}$
are obviously uniformly bounded, to show equation (3.8), it remains to check that
![]() $S (f^n) (f^{-n} (x))$
is uniformly bounded. To see this, we use the chain rule (3.5) to obtain
$S (f^n) (f^{-n} (x))$
is uniformly bounded. To see this, we use the chain rule (3.5) to obtain
 $$ \begin{align*}Sf^n(f^{-n}(x)) = \sum_{i=0}^{n-1}Sf(f^{i-n}(x))(Df^{i}(f^{-n}(x)))^2.\end{align*} $$
$$ \begin{align*}Sf^n(f^{-n}(x)) = \sum_{i=0}^{n-1}Sf(f^{i-n}(x))(Df^{i}(f^{-n}(x)))^2.\end{align*} $$
This implies
 $$ \begin{align*}| Sf^n(f^{-n}(x)) | \leq C \, \sum_{i=0}^{n-1} ( Df^i (f^{-n}(x)) )^2,\end{align*} $$
$$ \begin{align*}| Sf^n(f^{-n}(x)) | \leq C \, \sum_{i=0}^{n-1} ( Df^i (f^{-n}(x)) )^2,\end{align*} $$
and the last sum can be estimated as it was done before. (The sum here is even smaller since it involves the squares of the derivatives.)
3.4 Estimates for the maps
We are now in a position to check that the group
![]() $\Gamma $
is made of
$\Gamma $
is made of
![]() $C^{1+\alpha }$
diffeomorphisms for
$C^{1+\alpha }$
diffeomorphisms for
![]() $\alpha < 1/2$
and
$\alpha < 1/2$
and
![]() $\ell _i$
of order
$\ell _i$
of order
![]() $n / \log (n)^2$
. (Notice that, according to equation (3.2), the element
$n / \log (n)^2$
. (Notice that, according to equation (3.2), the element
![]() $\bar {f}$
is distorted in
$\bar {f}$
is distorted in
![]() $\Gamma $
for this choice.) Notice that this is obvious for all the generators except h and
$\Gamma $
for this choice.) Notice that this is obvious for all the generators except h and
![]() $\hat {h}$
. The estimates for these two elements are similar, so that we only deal with h. Besides, we may deal with
$\hat {h}$
. The estimates for these two elements are similar, so that we only deal with h. Besides, we may deal with
![]() $\log Dh$
instead of
$\log Dh$
instead of
![]() $Dh$
, since the condition ‘
$Dh$
, since the condition ‘
![]() $Dh$
is of class
$Dh$
is of class
![]() $C^{\alpha }$
’ is equivalent to that ‘
$C^{\alpha }$
’ is equivalent to that ‘
![]() $\log Dh$
is of class
$\log Dh$
is of class
![]() $C^{\alpha }$
’.
$C^{\alpha }$
’.
We need to check that there exists a uniform bound B for expressions of type
for all points
![]() $x< y$
in the same interval
$x< y$
in the same interval
![]() $I_n$
. Indeed, having such an estimate, one can easily treat the case of arbitrary pairs
$I_n$
. Indeed, having such an estimate, one can easily treat the case of arbitrary pairs
![]() $x < y$
just by noticing that at each endpoint of an interval of the form above, the derivative of h equals 1. Namely, letting
$x < y$
just by noticing that at each endpoint of an interval of the form above, the derivative of h equals 1. Namely, letting
![]() $z_1$
(respectively
$z_1$
(respectively
![]() $z_2$
) be such an endpoint that is immediately to the right of x (respectively to the left of y), one has
$z_2$
) be such an endpoint that is immediately to the right of x (respectively to the left of y), one has
 $$ \begin{align*} \frac{|Dh(y) - Dh(x)|}{|y-x|^{\alpha}} &\leq \frac{|Dh(y) - Dh(z)|}{|y-x|^{\alpha}} + \frac{|Dh(z) - Dh(x)|}{|y-x|^{\alpha}} \\ &\leq \frac{|Dh(y) - Dh(z)|}{|y-z|^{\alpha}} + \frac{|Dh(z) - Dh(x)|}{|z-x|^{\alpha}} \\ &\leq 2 \, B. \end{align*} $$
$$ \begin{align*} \frac{|Dh(y) - Dh(x)|}{|y-x|^{\alpha}} &\leq \frac{|Dh(y) - Dh(z)|}{|y-x|^{\alpha}} + \frac{|Dh(z) - Dh(x)|}{|y-x|^{\alpha}} \\ &\leq \frac{|Dh(y) - Dh(z)|}{|y-z|^{\alpha}} + \frac{|Dh(z) - Dh(x)|}{|z-x|^{\alpha}} \\ &\leq 2 \, B. \end{align*} $$
Now, for all
![]() $ z \in I_n$
(with
$ z \in I_n$
(with
![]() $n \geq 0$
), Lemma 3.2 and estimate (3.7) yield, for
$n \geq 0$
), Lemma 3.2 and estimate (3.7) yield, for
![]() $t_n$
small enough,
$t_n$
small enough,
By estimate (3.8), this implies, for a certain constant
![]() $C>0$
,
$C>0$
,
Moreover, for
![]() $x,y$
in
$x,y$
in
![]() $I_n$
,
$I_n$
,
 $$ \begin{align*}\frac{ |\!\log Dh (y) - \log Dh (x)| }{|y-x|^{\alpha}} &= \frac{ |\!\log Dh (y) - \log Dh (x)| }{|y-x|} \, |y-x|^{1-\alpha}\\ &= D (\log Dh (z)) \, |y-x|^{1-\alpha}\end{align*} $$
$$ \begin{align*}\frac{ |\!\log Dh (y) - \log Dh (x)| }{|y-x|^{\alpha}} &= \frac{ |\!\log Dh (y) - \log Dh (x)| }{|y-x|} \, |y-x|^{1-\alpha}\\ &= D (\log Dh (z)) \, |y-x|^{1-\alpha}\end{align*} $$
for a certain point
![]() $z \in I_n$
. By equation (3.9), this yields
$z \in I_n$
. By equation (3.9), this yields
 $$ \begin{align} &\frac{ |\!\log Dh (y) - \log Dh (x)| }{|y-x|^{\alpha}}\nonumber\\ &\quad\leq 2 \, C \, n \log (n) \, (\log(\log(n)))^2 \, t_n \, \bigg[ \frac{C}{ n \log (n) (\log (\log (n)))^2}, \bigg] ^{1-\alpha}. \end{align} $$
$$ \begin{align} &\frac{ |\!\log Dh (y) - \log Dh (x)| }{|y-x|^{\alpha}}\nonumber\\ &\quad\leq 2 \, C \, n \log (n) \, (\log(\log(n)))^2 \, t_n \, \bigg[ \frac{C}{ n \log (n) (\log (\log (n)))^2}, \bigg] ^{1-\alpha}. \end{align} $$
Since
![]() $t_n = 1/ \sqrt {\ell _{i/2}} \leq C \, \log (n) / \sqrt {n}$
, we finally obtain
$t_n = 1/ \sqrt {\ell _{i/2}} \leq C \, \log (n) / \sqrt {n}$
, we finally obtain
 $$ \begin{align*}&\frac{ |\!\log Dh (y) - \log Dh (x)| }{|y-x|^{\alpha}}\\ &\quad\leq 2 \, C' \, n \log (n) \, (\log(\log(n)))^2 \, \frac{\log(n)}{n^{1/2}} \, \frac{1}{[n \log (n) (\log(\log(n)))^2]^{1-\alpha}}.\end{align*} $$
$$ \begin{align*}&\frac{ |\!\log Dh (y) - \log Dh (x)| }{|y-x|^{\alpha}}\\ &\quad\leq 2 \, C' \, n \log (n) \, (\log(\log(n)))^2 \, \frac{\log(n)}{n^{1/2}} \, \frac{1}{[n \log (n) (\log(\log(n)))^2]^{1-\alpha}}.\end{align*} $$
To get the desired upper bound B, it suffices that the total exponent of n in the expression above is negative. Since this exponent equals
![]() $1 - 1/2 - (1-\alpha ) = \alpha - 1/2$
, this condition reduces to
$1 - 1/2 - (1-\alpha ) = \alpha - 1/2$
, this condition reduces to
![]() $\alpha < 1/2$
, which is our hypothesis.
$\alpha < 1/2$
, which is our hypothesis.
4 Distortion in class
 $C^{1+\alpha }$
for
$C^{1+\alpha }$
for
 $\alpha < 1$
$\alpha < 1$
It is unclear whether the previous action can be smoothed beyond the class
![]() $C^{3/2}$
(compare [Reference Castro, Jorquera and Navas2, Reference Deroin, Kleptsyn and Navas3, Reference Kleptsyn and Navas8, Reference Navas12]). To achieve a larger differentiability class, we will need to accelerate the distorted behavior of
$C^{3/2}$
(compare [Reference Castro, Jorquera and Navas2, Reference Deroin, Kleptsyn and Navas3, Reference Kleptsyn and Navas8, Reference Navas12]). To achieve a larger differentiability class, we will need to accelerate the distorted behavior of
![]() $\bar {f}$
, which will allow us to consider smaller integration times for the flows of vector fields (in concrete terms, we will increase the sequence
$\bar {f}$
, which will allow us to consider smaller integration times for the flows of vector fields (in concrete terms, we will increase the sequence
![]() $\ell _i$
). This will be crucial to improve the regularity from
$\ell _i$
). This will be crucial to improve the regularity from
![]() $\alpha < 1/2$
to any
$\alpha < 1/2$
to any
![]() $\alpha < 1$
.
$\alpha < 1$
.
4.1 Adding an extra element
We consider the map
![]() $\tilde {h}$
acts by the identity outside the intervals
$\tilde {h}$
acts by the identity outside the intervals
![]() $I_k$
, and that each such interval coincides with the
$I_k$
, and that each such interval coincides with the
![]() $r_k$
-time of the time flow of the vector field
$r_k$
-time of the time flow of the vector field
![]() $f^k_* (\varphi _0^* (\hat {\mathcal {Y}}))$
, where
$f^k_* (\varphi _0^* (\hat {\mathcal {Y}}))$
, where
![]() $r_k := 1 / \sqrt {\ell _{i/2}}$
for
$r_k := 1 / \sqrt {\ell _{i/2}}$
for
![]() $2^{i-1} \leq k < 2^{i}$
and
$2^{i-1} \leq k < 2^{i}$
and
![]() $r_k := 0$
otherwise. Notice that
$r_k := 0$
otherwise. Notice that
![]() $\tilde {h}$
is very similar to
$\tilde {h}$
is very similar to
![]() $\hat {h}$
. (Actually, we could perform the computations that follow using
$\hat {h}$
. (Actually, we could perform the computations that follow using
![]() $\hat {h}$
instead of
$\hat {h}$
instead of
![]() $\tilde {h}$
, but this would become much harder.)
$\tilde {h}$
, but this would become much harder.)
Then we let
![]() $d_n := \hat {f}^{-i}f^{-n}\tilde {h}f^n\hat {f}^{i}$
for
$d_n := \hat {f}^{-i}f^{-n}\tilde {h}f^n\hat {f}^{i}$
for
![]() $n = 2^i$
, where i is an even integer. We have
$n = 2^i$
, where i is an even integer. We have
![]() $\mathrm {supp} (d_n) \subset [0,x_{-3/2}]\cup [x_{-1/2},x_0]\cup [x_1,1]$
. Since
$\mathrm {supp} (d_n) \subset [0,x_{-3/2}]\cup [x_{-1/2},x_0]\cup [x_1,1]$
. Since
![]() $\mathrm {supp} (c_n) \subset [x_{-1/2},x_0]$
, for every integer
$\mathrm {supp} (c_n) \subset [x_{-1/2},x_0]$
, for every integer
![]() $L_i \geq 1$
, the support of
$L_i \geq 1$
, the support of
![]() $d_n^{L_i} c_n d_n^{-L_i}$
is also contained in
$d_n^{L_i} c_n d_n^{-L_i}$
is also contained in
![]() $[x_{-1/2}, x_0]$
, thus the support of
$[x_{-1/2}, x_0]$
, thus the support of
is contained in
![]() $[x_{-2^{i-1}},x_0]$
.
$[x_{-2^{i-1}},x_0]$
.
Now recall that, on each
![]() $[x_k,x_{k+1}]\subset [x_{-2^{i-1}},x_0]$
, the conjugate
$[x_k,x_{k+1}]\subset [x_{-2^{i-1}},x_0]$
, the conjugate
![]() $\hat {f}^{i}c_n\hat {f}^{-i}$
coincides with the time-
$\hat {f}^{i}c_n\hat {f}^{-i}$
coincides with the time-
![]() ${1}/{\ell _{i/2}}$
map of the flow of
${1}/{\ell _{i/2}}$
map of the flow of
![]() $f^k_\ast (\varphi _0^\ast (\mathcal {Y}))$
. Moreover, by construction, on the same interval, the conjugate
$f^k_\ast (\varphi _0^\ast (\mathcal {Y}))$
. Moreover, by construction, on the same interval, the conjugate
![]() $\hat {f}^{i} d_n\hat {f}^{-i}$
coincides with the time-
$\hat {f}^{i} d_n\hat {f}^{-i}$
coincides with the time-
![]() ${1}/{\sqrt {\ell _{i/2}}}$
map of the flow of
${1}/{\sqrt {\ell _{i/2}}}$
map of the flow of
![]() $f^k_\ast (\varphi _0^\ast (\hat {\mathcal {Y}}))$
. By the affine relation, still on the same interval, the map
$f^k_\ast (\varphi _0^\ast (\hat {\mathcal {Y}}))$
. By the affine relation, still on the same interval, the map
![]() $\hat {f}^{-i} d_n^{L_i} c_n d_n^{-L_i} \hat {f}^i$
lies in the flow of
$\hat {f}^{-i} d_n^{L_i} c_n d_n^{-L_i} \hat {f}^i$
lies in the flow of
![]() $f^k_\ast (\varphi _0^\ast (\mathcal {Y}))$
, and arises at time
$f^k_\ast (\varphi _0^\ast (\mathcal {Y}))$
, and arises at time
 $$ \begin{align*}\frac{2^{({L_i}/{\sqrt{\ell_{i/2}}})}}{\ell_{i/2}}.\end{align*} $$
$$ \begin{align*}\frac{2^{({L_i}/{\sqrt{\ell_{i/2}}})}}{\ell_{i/2}}.\end{align*} $$
If
![]() $L_i := \sqrt {\ell _{i/2}} \, \log _2 (\ell _{i/2})$
(which will be chosen to be an integer number), then this quantity equals 1. Therefore, for this choice,
$L_i := \sqrt {\ell _{i/2}} \, \log _2 (\ell _{i/2})$
(which will be chosen to be an integer number), then this quantity equals 1. Therefore, for this choice,
![]() $\hat {f}^{-i} d_n^{L_i} c_n d_n^{-L_i} \hat {f}^i$
coincides with
$\hat {f}^{-i} d_n^{L_i} c_n d_n^{-L_i} \hat {f}^i$
coincides with
![]() $h_{n/2}$
.
$h_{n/2}$
.
4.2 The distortion estimate
The identity
![]() $h_{n/2} = \hat {f}^{-i} d_n^{L_i} c_n d_n^{-L_i} \hat {f}^i$
implies that, in the new group
$h_{n/2} = \hat {f}^{-i} d_n^{L_i} c_n d_n^{-L_i} \hat {f}^i$
implies that, in the new group
![]() $\tilde {\Gamma } := \langle \hat {f}, f, g, \hat {h}, h, \tilde {h}, \psi \rangle $
, we have the estimate
$\tilde {\Gamma } := \langle \hat {f}, f, g, \hat {h}, h, \tilde {h}, \psi \rangle $
, we have the estimate
Since
![]() $\| f^n \| = O (\log (n)) = O (i)$
, we conclude that
$\| f^n \| = O (\log (n)) = O (i)$
, we conclude that
Since
![]() $h_{n/2} = f^{-n/2} (f^{-1} \bar {f}^{n/2} f) $
and
$h_{n/2} = f^{-n/2} (f^{-1} \bar {f}^{n/2} f) $
and
![]() $\| f^{n/2} \| = O (\log (n))$
, this yields
$\| f^{n/2} \| = O (\log (n))$
, this yields
Notice that the last estimate is much better than what we had in the group
![]() $\Gamma $
of the previous section. There,
$\Gamma $
of the previous section. There,
![]() $\| \bar {f}^{n/2}\|$
was of the order
$\| \bar {f}^{n/2}\|$
was of the order
![]() $O (i \, \ell _{i/2})$
, so
$O (i \, \ell _{i/2})$
, so
![]() $\bar {f}$
was distorted provided the growth of
$\bar {f}$
was distorted provided the growth of
![]() $\ell _j$
was smaller than exponential. In the new setting, that is, in the modified group
$\ell _j$
was smaller than exponential. In the new setting, that is, in the modified group
![]() $\tilde {\Gamma }$
, the diffeomorphism
$\tilde {\Gamma }$
, the diffeomorphism
![]() $\bar {f}$
is distorted whenever the condition below is satisfied (recall that
$\bar {f}$
is distorted whenever the condition below is satisfied (recall that
![]() $n = 2^i$
):
$n = 2^i$
):
4.3 Checking regularity
We thus choose a new sequence
![]() $\ell _i$
so that condition (4.1) holds and
$\ell _i$
so that condition (4.1) holds and
![]() $\sqrt {\ell _{i/2}} \, \log _2 (\ell _{i/2})$
is an integer number. This can be achieved for a sequence of type
$\sqrt {\ell _{i/2}} \, \log _2 (\ell _{i/2})$
is an integer number. This can be achieved for a sequence of type
that we fix from now on. With such a choice, we claim that
![]() $\tilde {\Gamma }$
is a group of
$\tilde {\Gamma }$
is a group of
![]() $C^{1+\alpha }$
diffeomorphisms. Again, this is obvious for all generators except
$C^{1+\alpha }$
diffeomorphisms. Again, this is obvious for all generators except
![]() $h,\hat {h},\tilde {h}$
, and for these three elements the computations are the exact same, because each of the sequences
$h,\hat {h},\tilde {h}$
, and for these three elements the computations are the exact same, because each of the sequences
![]() $r_n, s_n, t_n$
is equivalent to
$r_n, s_n, t_n$
is equivalent to
![]() $1/ \sqrt {\ell _{i/2}}$
. We thus write everything only for h. Remind estimate (3.10):
$1/ \sqrt {\ell _{i/2}}$
. We thus write everything only for h. Remind estimate (3.10):
 $$ \begin{align*}&\frac{ |\!\log Dh (y) - \log Dh (x)| }{|y-x|^{\alpha}}\\ &\quad\leq 2 \, C \, n \log (n) \, (\log(\log(n)))^2 \, t_n \, \bigg[ \frac{C}{ n \log (n) (\log (\log (n)))^2}, \bigg] ^{1-\alpha}.\end{align*} $$
$$ \begin{align*}&\frac{ |\!\log Dh (y) - \log Dh (x)| }{|y-x|^{\alpha}}\\ &\quad\leq 2 \, C \, n \log (n) \, (\log(\log(n)))^2 \, t_n \, \bigg[ \frac{C}{ n \log (n) (\log (\log (n)))^2}, \bigg] ^{1-\alpha}.\end{align*} $$
With the new estimate for
![]() $t_n$
, this becomes
$t_n$
, this becomes
 $$ \begin{align*}&\frac{ |\!\log Dh (y) - \log Dh (x)| }{|y-x|^{\alpha}}\\ &\quad\leq 2 \, C \, n \log (n) \, (\log(\log(n)))^2 \, \frac{\log (n)^{3}}{n} \, \bigg[ \frac{C}{ n \log (n) (\log (\log (n)))^2}, \bigg] ^{1-\alpha}.\end{align*} $$
$$ \begin{align*}&\frac{ |\!\log Dh (y) - \log Dh (x)| }{|y-x|^{\alpha}}\\ &\quad\leq 2 \, C \, n \log (n) \, (\log(\log(n)))^2 \, \frac{\log (n)^{3}}{n} \, \bigg[ \frac{C}{ n \log (n) (\log (\log (n)))^2}, \bigg] ^{1-\alpha}.\end{align*} $$
The expression on the right is of order
 $$ \begin{align*}O \bigg( \frac{\log(n)^{3+\alpha} \, (\log \log(n))^{2\alpha}}{n^{1-\alpha}} \bigg),\end{align*} $$
$$ \begin{align*}O \bigg( \frac{\log(n)^{3+\alpha} \, (\log \log(n))^{2\alpha}}{n^{1-\alpha}} \bigg),\end{align*} $$
which converges to
![]() $0$
as n goes to infinity. This allows us to show that h is a
$0$
as n goes to infinity. This allows us to show that h is a
![]() $C^{1+\alpha }$
diffeomorphism as it was done in the previous section.
$C^{1+\alpha }$
diffeomorphism as it was done in the previous section.
Acknowledgments
Both authors would like to gratefully acknowledge the guidance of Andrés Navas during this work. They also thank Cristóbal Rivas for organizing the seminar on group actions where the problem treated in the paper was presented, as well as all the participants of the seminar. The first author was funded by the Fondecyt Project 1200114, and the second author by the Fondecyt Project 1181548.
Appendix. No Strong Kopell’s Lemma in Class
![]() $C^{1+\alpha }$
$C^{1+\alpha }$
The goal of this appendix is to give an example of the phenomenon announced just after Lemma 3.1. Namely, there exist:
-
• a
 $C^{\infty }$
diffeomorphism of
$C^{\infty }$
diffeomorphism of
 $[0,1]$
such that
$[0,1]$
such that
 $f(x)> x$
for all
$f(x)> x$
for all
 $x \in (0,1)$
with a fundamental domain
$x \in (0,1)$
with a fundamental domain
 $[x_0,x_1]$
(where
$[x_0,x_1]$
(where
 $x_1 := f(x_0)$
);
$x_1 := f(x_0)$
);
and
-
• a sequence
 $(g_n)_{n \in \mathbb {Z}}$
of
$(g_n)_{n \in \mathbb {Z}}$
of
 $C^{\infty }$
diffeomorphisms of
$C^{\infty }$
diffeomorphisms of
 $[x_0,x_1]$
;
$[x_0,x_1]$
;
such that
![]() $Dg_n (x_0) = Dg_n (x_1) = 1$
for all n, one has the convergence
$Dg_n (x_0) = Dg_n (x_1) = 1$
for all n, one has the convergence
![]() $g_n \to \mathrm {Id}$
as
$g_n \to \mathrm {Id}$
as
![]() $|n| \to \infty $
in
$|n| \to \infty $
in
![]() $C^{\infty }$
topology, but the
$C^{\infty }$
topology, but the
![]() $C^1$
diffeomorphism
$C^1$
diffeomorphism
![]() $g \! : [0,1]\rightarrow [0,1]$
defined as
$g \! : [0,1]\rightarrow [0,1]$
defined as
is not
![]() $C^{1+\alpha }$
for any
$C^{1+\alpha }$
for any
![]() $\alpha \in (0,1)$
.
$\alpha \in (0,1)$
.
Our diffeomorphism f is
Notice that
Hence, for all
![]() $x,y$
,
$x,y$
,
 $$ \begin{align*}| f^n (x) - f^n (y) | &= \bigg| \frac{2^n x}{(2^{n}-1)x+1} - \frac{2^n y}{(2^{n}-1)y + 1} \bigg| \\ &= \frac{2^n |x-y|}{[(2^{n}-1)x+1] \cdot [(2^{n}-1)y+1]},\end{align*} $$
$$ \begin{align*}| f^n (x) - f^n (y) | &= \bigg| \frac{2^n x}{(2^{n}-1)x+1} - \frac{2^n y}{(2^{n}-1)y + 1} \bigg| \\ &= \frac{2^n |x-y|}{[(2^{n}-1)x+1] \cdot [(2^{n}-1)y+1]},\end{align*} $$
which yields
for a certain universal constant
![]() $C> 0$
provided that
$C> 0$
provided that
![]() $x,y$
are uniformly bounded away from zero.
$x,y$
are uniformly bounded away from zero.
Now consider the points
![]() $x_0 := 1/2$
and
$x_0 := 1/2$
and
![]() $x_1 := f (x_0) = 2/3$
. Notice that
$x_1 := f (x_0) = 2/3$
. Notice that
![]() $x_1-x_0 = 1/6$
. Then let
$x_1-x_0 = 1/6$
. Then let
 $$ \begin{align*}&a:= \frac{1}{2} + \frac{1}{30} = \frac{8}{15}, \quad b := \frac{1}{2} + \frac{2}{30} = \frac{17}{30}, \\ &b' := \frac{1}{2} + \frac{3}{30} = \frac{3}{5}, \quad b" := \frac{1}{2} + \frac{4}{30} = \frac{19}{30}.\end{align*} $$
$$ \begin{align*}&a:= \frac{1}{2} + \frac{1}{30} = \frac{8}{15}, \quad b := \frac{1}{2} + \frac{2}{30} = \frac{17}{30}, \\ &b' := \frac{1}{2} + \frac{3}{30} = \frac{3}{5}, \quad b" := \frac{1}{2} + \frac{4}{30} = \frac{19}{30}.\end{align*} $$
Let
![]() $\varrho \! : [a,2/3] \to [-1/2,1/2]$
be a
$\varrho \! : [a,2/3] \to [-1/2,1/2]$
be a
![]() $C^{\infty }$
function such that
$C^{\infty }$
function such that
Assume also that
![]() $\varrho $
is strictly increasing on
$\varrho $
is strictly increasing on
![]() $[a,b]$
and
$[a,b]$
and
![]() $[b",3/2]$
, strictly decreasing on
$[b",3/2]$
, strictly decreasing on
![]() $[b,b"]$
, infinitely flat at a and
$[b,b"]$
, infinitely flat at a and
![]() $3/2$
, and its graph is symmetric with respect to the point
$3/2$
, and its graph is symmetric with respect to the point
![]() $(b',0)$
. Let
$(b',0)$
. Let
![]() $\rho _n \! : [1/2,2/3] \to \mathbb {R}$
be the function that is identically equal to
$\rho _n \! : [1/2,2/3] \to \mathbb {R}$
be the function that is identically equal to
![]() $1$
on
$1$
on
![]() $[1/2,a]$
and whose restriction to
$[1/2,a]$
and whose restriction to
![]() $[a,2/3]$
coincides with
$[a,2/3]$
coincides with
![]() $1 + \varrho / n$
See Figure A.1.
$1 + \varrho / n$
See Figure A.1.

Figure A.1 The construction of ρ n .
By the symmetry property of
![]() $\varrho $
, we have
$\varrho $
, we have
 $$ \begin{align*}\int_{x_0}^{x_1} \rho_n (s)\, ds = x_1 - x_0,\end{align*} $$
$$ \begin{align*}\int_{x_0}^{x_1} \rho_n (s)\, ds = x_1 - x_0,\end{align*} $$
so
![]() $\rho _n$
is the derivative of a diffeomorphism
$\rho _n$
is the derivative of a diffeomorphism
![]() $g_n$
of
$g_n$
of
![]() $[x_0,x_1]$
. Since
$[x_0,x_1]$
. Since
![]() $\rho _n$
is
$\rho _n$
is
![]() $C^{\infty }$
, the diffeomorphism
$C^{\infty }$
, the diffeomorphism
![]() $g_n$
is of class
$g_n$
is of class
![]() $C^{\infty }$
. We claim that
$C^{\infty }$
. We claim that
![]() $g_n$
converges to the identity in the
$g_n$
converges to the identity in the
![]() $C^k$
topology for every integer k. (Hence, by definition, the convergence holds in
$C^k$
topology for every integer k. (Hence, by definition, the convergence holds in
![]() $C^{\infty }$
topology.) Indeed, for
$C^{\infty }$
topology.) Indeed, for
![]() $k \geq 2$
, as n goes to infinity, we have
$k \geq 2$
, as n goes to infinity, we have
We will next show that the corresponding diffeomorphism g obtained via equation (A.1) is not
![]() $C^{1+\alpha }$
for any
$C^{1+\alpha }$
for any
![]() $\alpha> 0$
.
$\alpha> 0$
.
Since
![]() $g_n (a) = a$
and
$g_n (a) = a$
and
![]() $D g_n (a) =1$
, we have
$D g_n (a) =1$
, we have
To compute
![]() $Dg (f^n (b))$
, first notice that
$Dg (f^n (b))$
, first notice that
We compute
 $$ \begin{align*}Dg (f^n(b)) = \frac{Df^n (g_n(b))}{Df^n (b)}\cdot Dg_n (b) = \bigg[ \frac{(2^n-1)b+1}{(2^n-1)g_n(b)+1} \bigg] \cdot \bigg( 1+\frac{1}{n}\bigg).\end{align*} $$
$$ \begin{align*}Dg (f^n(b)) = \frac{Df^n (g_n(b))}{Df^n (b)}\cdot Dg_n (b) = \bigg[ \frac{(2^n-1)b+1}{(2^n-1)g_n(b)+1} \bigg] \cdot \bigg( 1+\frac{1}{n}\bigg).\end{align*} $$
Since
 $$ \begin{align*}g_n (b) &= g_n (a) + \int_a^b \rho_n (s) \, ds = g_n (a) + \int_a^b \bigg( 1 + \frac{\varrho}{n} \bigg) (s) \, ds\\ &= a + (b-a) + \int_a^b \frac{\varrho}{n} \, ds = b + \frac{I}{n},\end{align*} $$
$$ \begin{align*}g_n (b) &= g_n (a) + \int_a^b \rho_n (s) \, ds = g_n (a) + \int_a^b \bigg( 1 + \frac{\varrho}{n} \bigg) (s) \, ds\\ &= a + (b-a) + \int_a^b \frac{\varrho}{n} \, ds = b + \frac{I}{n},\end{align*} $$
where
 $$ \begin{align*}I:= \int_a^b \varrho (s) \, ds> 0,\end{align*} $$
$$ \begin{align*}I:= \int_a^b \varrho (s) \, ds> 0,\end{align*} $$
this yields
 $$ \begin{align*}Dg (f^n(b)) = \bigg[ \frac{(2^n-1)b + 1}{(2^n-1)(b + I/n) + 1} \bigg] \cdot \bigg( 1+\frac{1}{n}\bigg),\end{align*} $$
$$ \begin{align*}Dg (f^n(b)) = \bigg[ \frac{(2^n-1)b + 1}{(2^n-1)(b + I/n) + 1} \bigg] \cdot \bigg( 1+\frac{1}{n}\bigg),\end{align*} $$
so
 $$ \begin{align*}| Dg (f^n (b)) - Dg (f^n (a))| &= \frac{1}{n} \bigg[ \frac{(2^n-1)b + 1}{(2^n-1)(b + I/n) + 1} \bigg] \\ &\quad - \bigg[ \frac{I}{n \, (2^n-1)(b + I/n) + 1} \bigg].\end{align*} $$
$$ \begin{align*}| Dg (f^n (b)) - Dg (f^n (a))| &= \frac{1}{n} \bigg[ \frac{(2^n-1)b + 1}{(2^n-1)(b + I/n) + 1} \bigg] \\ &\quad - \bigg[ \frac{I}{n \, (2^n-1)(b + I/n) + 1} \bigg].\end{align*} $$
Therefore, for a certain constant
![]() $C'> 0$
,
$C'> 0$
,
Finally, putting equations (A.2) and (A.3) together, we obtain
 $$ \begin{align*}\frac{|Dg (f^n(b) - Dg (f^n (a)))|}{|f^n(b)-f^n(a)|^{\alpha}} \geq \frac{C'}{C^{\alpha}} \cdot \frac{2^{n\alpha}}{n},\end{align*} $$
$$ \begin{align*}\frac{|Dg (f^n(b) - Dg (f^n (a)))|}{|f^n(b)-f^n(a)|^{\alpha}} \geq \frac{C'}{C^{\alpha}} \cdot \frac{2^{n\alpha}}{n},\end{align*} $$
which diverges to infinite as
![]() $n \to \infty $
provided
$n \to \infty $
provided
![]() $\alpha> 0$
. This shows that g is not of class
$\alpha> 0$
. This shows that g is not of class
![]() $C^{1+\alpha }$
.
$C^{1+\alpha }$
.
Remark A.1. It is not hard to modify the preceding example so that the map f has a parabolic fixed point. In this framework, the divergence in the last step above is much slower, but still holds.