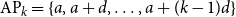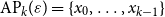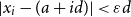1. Introduction
For a natural number N we set
$[N]=\{1,2\ldots,N\}$
. Assume that [N] is coloured by r colours. We denote by
\begin{align*} N \rightarrow (\mathrm{AP}_k)_r\end{align*}
the fact that any such r-colouring yields a monochromatic arithmetic progression
$\mathrm{AP}_k$
of length k. With this notation the well known Van der Waerden’s theorem can be stated as follows.
Theorem 1.1. For every positive integers r and k, there exists a positive integer N such that
$N \rightarrow (\mathrm{AP}_k)_r$
.
The minimum N with the property of Theorem 1.1 is called the Van der Waerden number of r, k and is denoted by W(k, r). In other words, W(k, r) is the minimum integer N such that any r-colouring of [N] contains a monochromatic arithmetic progression of length k. Much effort was put to determine lower and upper bounds for W(k, r), but the problem remains widely open. As an illustration, the best known bounds for W(k, 2) are
\begin{align*} \frac{2^k}{k^{o(1)}}\leq W(k,2) \leq 2^{2^{2^{2^{2^{k+9}}}}},\end{align*}
where
$o(1)\rightarrow 0$
as
$k\rightarrow \infty$
. The lower bound is due to Szabo [Reference Szabo25] while the upper bound is a celebrated result of Gowers on Szemerédi’s theorem [Reference Gowers10]. It is good to remark that when k is a prime the lower bound can be improved to
$W(k+1,2)\geq k2^k$
by a construction of Berlekamp [Reference Berlekamp2].
Ron Graham was keenly interested in the research leading to improvements of the upper bound of W(k, 2) and motivated it by monetary prizes. Currently open is his
$\$1000$
award for the proof that
$W(k,2)<2^{k^2}$
(see [Reference Graham14]). During his career he also contributed to related problems in the area (see [Reference Brown, Graham and Landman3, Reference Graham and Nešetřil12, Reference Graham13]). For instance, together with Erdös [Reference Erdös and Graham6], Graham proved a canonical version of Van der Waerden: Every colouring of
$\mathbb{N}$
, not necessarily with finitely many colours, contains either an monochromatic arithmetic progression or a rainbow arithmetic progression, i.e., a progression with every element of distinct colour.
Inspired by the works of [4] and [Reference Han, Kohayakawa, Sales and Stagni16], we are interested in the related problem where we replace an arithmetic progression by an perturbation of it.
Definition 1.2. Given
$\varepsilon>0$
, a set
$X=\{x_0,\ldots,x_{k-1}\}\subseteq [N]$
is an
$\varepsilon$
-approximate
$\mathrm{AP}_k(\varepsilon)$
of an arithmetic progression of length k if there exists
$a \in \mathbb{R}$
and
$d>0$
such that
$|x_i-(a+id)|<\varepsilon d$
.
In other words, an
$\mathrm{AP}_k(\varepsilon)$
is just a transversal of
$\bigcup_{i=0}^{k-1}B(a+id; \varepsilon d)$
, where
$B(a+id; \varepsilon d)$
is the open ball centred at
$a+id$
of radius
$\varepsilon d$
. Depending on the choice of
$\varepsilon$
, an
$\mathrm{AP}_k(\varepsilon)$
can be different from an
$\mathrm{AP}_k$
. For example, if
$\varepsilon=1/3$
, then
$a=0.8$
and
$d=2.4$
testifies that
$\{1,3,6\}$
is an
$\varepsilon$
-approximate arithmetic progression of length 3, but it is not an arithmetic progression itself.
For integers r, k and
$\varepsilon>0$
, let
\begin{align*} W_{\varepsilon}(k,r)=\min\{N\,:\, N\rightarrow (\mathrm{AP}_k(\varepsilon))_r\}.\end{align*}
That is,
$W_{\varepsilon}(k,r)$
is the smallest N with the property that any colouring of [N] by r colours yields a monochromatic
$\mathrm{AP}_k(\varepsilon)$
. Our first result shows that one can obtain sharper bounds to the Van der Waerden problem by replacing
$\mathrm{AP}_k$
to
$\mathrm{AP}_k(\varepsilon)$
.
Theorem 1.3. Let
$r\geq 1$
. There exists a positive constant
$\varepsilon_0$
and a real number
$c_r$
depending on r such that the following holds. If
$0<\varepsilon\leq \varepsilon_0$
and
$k\geq 2^rr!\varepsilon^{-1}\log^r(1/5\varepsilon)$
, then
\begin{align*}c_r\frac{k^r}{\varepsilon^{r-1}\log(1/\varepsilon)^{\binom{r+1}{2}-1}}\leq W_{\varepsilon}(k,r) \leq \frac{2k^r}{\varepsilon^{r-1}}.\end{align*}
Similar as in the previous discussion we will write
$N\rightarrow_{\alpha} \mathrm{AP}_k$
(or
$N\rightarrow_{\alpha} \mathrm{AP}_k(\varepsilon)$
) to denote that any subset
$S\subseteq [N]$
with
$|S|\geq \alpha N$
necessarily contains an arithmetic progression
$\mathrm{AP}_k$
(or
$\mathrm{AP}_k(\varepsilon)$
, respectively). Answering a question of Erdös and Turan [Reference Erdös and Turán7], Szemerédi proved the following celebrated result:
Theorem 1.4. For any
$\alpha>0$
and a positive integer k, there exists an integer
$N_0$
such that for every
$N\geq N_0$
the relation
$N\rightarrow_{\alpha} \mathrm{AP}_k$
holds.
Basically Szemerédi theorem states that any positive proportion of
$\mathbb{N}$
contains an arithmetic progression of length k. Not much later Furstenberg [Reference Furstenberg9] gave an alternative proof of Theorem 1.4 using Ergodic theory. Extending [Reference Furstenberg9], Furstenberg and Katznelson [Reference Furstenberg and Katznelson8] were able to prove a multidimensional version of Szemerédi’s theorem:
An m-dimensional cube C(m, k) is a set of
$k^m$
points in m-dimensional Euclidean lattice
$\mathbb{Z}^m$
such that
\begin{align*} C(m,k)=\{\vec{a}+d\vec{v}\,:\, \vec{a}=(a_1,\ldots,a_m) \in \mathbb{Z}^m \text{ and } \vec{v}=(v_1,\ldots,v_m) \in \{0,1,\ldots,k-1\}^m\}.\end{align*}
That is, C(m, k) is a homothetic translation of
$[k]^m$
. As in the one dimensional case, for
$\alpha>0$
and integers m, k and N we will write
$[N]^m \rightarrow_{\alpha} C(m,k)$
to mean that any subset
$S \subseteq [N]^m$
with
$|S|\geq \alpha N^m$
contains a cube C(m, k). The following is the multidimensional version of Theorem 1.4 proved in [Reference Furstenberg and Katznelson8].
Theorem 1.5. For any
$\alpha>0$
and positive integers k and m, there exists an integer
$N_0$
such that for every
$N\geq N_0$
the relation
$[N]^m \rightarrow_{\alpha} C(m,k)$
holds
Define f(N, m, k) as the maximum size of a subset
$A \subseteq [N]^m$
without a cube C(m, k). Note that f(N, 1, k) corresponds to the maximal size of a subset
$A\subseteq [N]$
without an arithmetic progression
$\mathrm{AP}_k$
. Theorems 1.4 and 1.5 give us that
$f(N,m,k)=o(N^m)$
. Determining bounds for f(N, m, k) is a long standing problem in additive combinatorics. For
$m=1$
the best current bounds are
\begin{align*}N \exp\left(-c_k(\log N)^{1/\lceil\log_2 k \rceil}\right) \leq f(N,1,k)\leq\frac{N}{(\log \log N)^{2^{-2^{k+9}}}}\end{align*}
where
$c_k$
is a positive constant depending only on k. The upper bound is due to Gowers [Reference Gowers10], while the lower bound with best constant
$c_k$
is due to O’Bryant [Reference O’Bryant21].
For larger m it is worth mentioning that Furstenberg–Katznelson proof of Theorem 1.5 uses Ergodic theory and gives us no quantitative bounds on f(N, m, K). Purely combinatorial proofs were given later based on the hypergraph regularity lemma in [Reference Gowers11] and [Reference Nagle, Rodl and Schacht20, Reference Rodl and Skokan23]. Those proofs give quantitative bounds which are incomparably weaker than the one for
$m=1$
. For instance, in [Reference Moshkovitz and Shapira19] Moshkovitz and Shapira proved that the hypergraph regularity lemma gives a bound of the order of the k-th Ackermann function.
Now we consider
$\varepsilon$
-approximate versions of Theorems 1.4 and 1.5.
Definition 1.6. Given
$\varepsilon>0$
, a set
$X=\{x_{\vec{v}}\,:\, \vec{v} \in \{0,1,\ldots,k-1\}^m\}\subseteq [N]^m$
is an
$\varepsilon$
-approximate cube
$C_{\varepsilon}(m,k)$
if there exists
$\vec{a} \in \mathbb{R}^m$
and
$d>0$
such that
$||x_{\vec{v}}-(\vec{a}+d\vec{v})||<\varepsilon d.$
For integers N, m, k and
$\varepsilon>0$
, let
$f_{\varepsilon}(N,m,k)$
be the maximal size of a subset
$A \subseteq [N]^m$
without an
$C_{\varepsilon}(m,k)$
. Dimitrescu showed an upper bound for
$f_{\varepsilon}(N,m,k)$
in [4]. We complement his result by also providing a lower bound to the problem.
Theorem 1.7. Let
$m\geq 1$
and
$k\geq 3$
be integers and
$0<\varepsilon<1/125$
. Then there exists an integer
$N_0\,:\!=\,N_0(k,\varepsilon)$
and positive constants
$c_1$
and
$c_2$
depending only on k and m such that
\begin{align*} N^{m-c_1(\log(1/\varepsilon))^{\frac{1}{\ell}-1}}\leq f_{\varepsilon}(N,m,k)\leq N^{m-c_2(\log(1/\varepsilon))^{-1}},\end{align*}
for
$N\geq N_0$
and
$\ell=\lceil \log_2 k \rceil$
.
The paper is organised as follows. In Section 2, we present a proof of Theorem 1.3. The upper bound is an iterated blow-up construction, while the lower bound is given by an ad-hoc inductive colouring. We prove Theorem 1.7 in Section 3. The lower bound uses the current lower bounds for f(N, 1, k), while the upper bound is given by an iterated blow-up construction combined with an averaging argument.
2. Proof of Theorem 1.3
2.1 Upper bound
We start with the upper bound. Given
$r\geq 1$
colours, we consider the following r-iterated blow-up of an
$\mathrm{AP}_k$
given by the set of integers
\begin{align*} B_r=\left\{b_0+tb_1+\ldots+t^{r-1}b_{r-1}\,:\, (b_0,\ldots,b_{r-1})\in \{0,1\ldots,k-1\}^r,\, t=\lceil k/\varepsilon \rceil \right\}.\end{align*}
Note that
$B_r$
is a set of size
$|B_r|=k^r$
and
$\mathrm{diam}(B_r)\leq (k-1)(1+t+\ldots+t^{r-1})<2(k-1)t^{r-1}$
. It turns out that any r-colouring of
$B_r$
contains a monochromatic
$\mathrm{AP}_k(\varepsilon)$
. In particular, this implies that
$W_{\varepsilon}(k,r)\leq \mathrm{diam}(B_r)+1\leq 2k^r/\varepsilon^{r-1}$
.
Proposition 2.1. Any r-colouring of
$B_r$
has a monochromatic
$\mathrm{AP}_k(\varepsilon)$
.
Proof. We prove the proposition by induction on the number of colours r. For
$r=1$
, one can see that
$B_1=[k]$
, which is an arithmetic progression of length k and in particular a
$\mathrm{AP}_k(\varepsilon)$
. Now suppose that any
$(r-1)$
-colouring of
$B_{r-1}$
contains a monochromatic
$\mathrm{AP}_k(\varepsilon)$
. Consider an r-colouring of
$B_r$
. Note that we can partition
$B_r=\bigcup_{i=0}^{k-1} B_{r,i}$
where
\begin{align*} B_{r,i}=\left\{b_0+\ldots+t^{r-2}b_{r-2}+it^{r-1}\,:\, (b_0,\ldots,b_{r-2})\in \{0,1,\ldots,k-1\}^{r-1},\, t=\lceil k/\varepsilon \rceil \right\}.\end{align*}
That is, for every
$0\leq i \leq k-1$
, the set
$B_{r,i}$
is a translation of
$B_{r-1}$
by
$it^{r-1}$
.
Consider a transversal
$X=\{x_0,\ldots,x_{k-1}\}$
of
$B_r=\bigcup_{i=0}^{k-1} B_{r,i}$
with
$x_i \in B_{r,i}$
for every
$0\leq i \leq$
$k-1$
. Let
$a=\mathrm{diam}(B_{r-1})/2$
and
$d=t^{r-1}$
. Since
$x_i \in B_{r,i}$
implies that
$it^{r-1}\leq x_i \leq it^{r-1}+ \mathrm{diam}(B_{r-1})$
, we obtain that
\begin{align*} |x_i-(a+id)|\leq \frac{\mathrm{diam}(B_{r-1})}{2} \leq \frac{k^{r-1}}{\varepsilon^{r-2}} \leq \varepsilon d\end{align*}
and X is an
$\varepsilon$
-approximate
$\mathrm{AP}_k(\varepsilon)$
. Therefore, if some colour c is present in each of the sets
$B_{r,i}$
for
$0\leq i \leq r-1$
, we could select X to be a monochromatic
$\mathrm{AP}_k(\varepsilon)$
. Consequently we may assume that there is no monochromatic transversal in
$B_r$
, which means that there exists an index i such that
$B_{r,i}$
is coloured with at most
$(r-1)$
colours. Since
$B_{r,i}$
is just a translation of
$B_{r-1}$
, by induction hypothesis we conclude that there exists a monochromatic
$\mathrm{AP}_k(\varepsilon)$
inside
$B_{r,i}$
.
2.2 Lower bound
In order to construct a large set avoiding
$\varepsilon$
-approximate
$\mathrm{AP}_k(\varepsilon)$
we need some preliminary results. Given a real number
$D>0$
, we define an
$(r-1,1;\,D)$
-alternate labelling of
$\mathbb{R}$
to be an labelling
$\chi\,:\, \mathbb{R} \rightarrow \{-1,+1\}$
such that
\begin{align*}\chi(x)=\begin{cases}+1,& \quad \text{if } x\in \bigcup_{i\in\mathbb{Z}}\left(irD+mD,\left(i+\frac{r-1}{r}\right)rD+mD\right],\\[5pt]
-1,& \quad \text{if } x\in\bigcup_{i\in \mathbb{Z}}\left(\left(i+\frac{r-1}{r}\right)rD+mD, (i+1)rD+mD\right],\end{cases}\end{align*}
for some
$m \in \mathbb{Z}$
. That is,
$\chi$
is a periodic labelling of
$\mathbb{R}$
with period rD, where we partition
$\mathbb{R}$
into disjoint intervals of length D and label them alternating between
$r-1$
consecutive intervals of label
$+1$
and one of label
$-1$
. The restriction of an
$(r-1,1;\,D)$
-alternate labelling to
$\mathbb{Z}$
will be of great importance for us. The following lemma roughly characterises the common difference of any large monochromatic approximate arithmetic progression in such a labelling.
Lemma 2.2. Let
$D,\delta>0$
, m be a positive integer with
$\delta\leq \frac{1}{2r(r+1)}$
and
$\chi\,:\, \mathbb{R} \rightarrow \{-1,+1\}$
be an
$(r-1,1;\,D)$
-alternate labelling of
$\mathbb{R}$
. If there exist
$a, d\in \mathbb{R}$
and an integer
$\ell$
such that
\begin{align*} d\not \in \bigcup_{i\in \mathbb{Z}}\bigcup_{q=1}^{r}\left(\left(\frac{i}{q}-\delta\right)rD, \left(\frac{i}{q}+\delta\right)rD\right),\end{align*}
and that
$B=\bigcup_{i=0}^{\ell-1}B(a+id,\delta r D)$
has a monochromatic transversal of label
$+1$
, then
$\ell\leq 3r/\delta$
.
Proof. We may assume without loss of generality that
$\chi$
is the following labelling of
$\mathbb{R}$
:
\begin{align*} \chi(x)=\begin{cases}+1,& \quad \text{if } x\in \bigcup_{i\in\mathbb{Z}}\left(irD,\left(i+\frac{r-1}{r}\right)rD\right],\\[5pt]
-1,& \quad \text{if } x\in\bigcup_{i\in \mathbb{Z}}\left(\left(i+\frac{r-1}{r}\right)rD, (i+1)rD\right],\end{cases}\end{align*}
That is, we may assume that
$m=0$
in the definition of an alternate labelling. Also, during the proof we shall write
$\overline{x}$
to be the representative of x modulo rD in the interval (0, rD], i.e., the number
$0<\overline{x}\leq rD$
such that
$x-\overline{x}=brD$
for some integer
$b\in \mathbb{Z}$
.
We start by claiming that there exists
$1\leq s \leq r$
such that
\begin{align} \overline{sd} \in \left[\delta rD, \frac{rD}{r+1}\right] \cup \left[\left(1-\frac{1}{r+1}\right)rD, (1-\delta)rD\right].\end{align}
First note by our hypothesis that
\begin{align*} d\notin \left(\left(\frac{i}{q}-\delta\right)rD, \left(\frac{i}{q}+\delta\right)rD\right)\end{align*}
for every
$i \in \mathbb{Z}$
and
$1\leq q \leq r$
. Therefore,
\begin{align} qd \notin ((i-\delta)rD, (i+\delta)rD) \subseteq ((i-q\delta)rD, (i+q\delta)rD)\end{align}
for every
$i \in \mathbb{Z}$
and
$1\leq q \leq r$
.
Now consider the partition
$(0,rD]=\bigcup_{j=0}^r\left(\frac{jrD}{r+1},\frac{(j+1)rD}{r+1}\right]$
. If there exists
$1\leq s \leq r$
such that
$\overline{sd}$
is in the two outer intervals above, i.e., in either
$\left(0,\frac{rD}{r+1}\right]$
or
$\left(\left(1-\frac{1}{r+1}\right)rD,rD\right]$
, then by (2) we obtain that s satisfies (1). Otherwise, assume that there is no
$1\leq s \leq r$
with
$\overline{sd}$
in the two outer intervals. Then by the pigeonhole principle there exist
$1\leq p<q \leq r$
and an index j such that
$\overline{pd}, \overline{qd}\in \left(\frac{jrD}{r+1},\frac{(j+1)rD}{r+1}\right]$
. Consequently, we have that
$\overline{qd}-\overline{pd}\in \left(-\frac{rD}{r+1}, \frac{rD}{r+1}\right)$
. By letting
$s=q-p$
we obtain that
\begin{align*} \overline{sd} \in \left(0,\frac{rD}{r+1}\right] \cup \left(\left(1-\frac{1}{r+1}\right)rD,rD\right],\end{align*}
for
$1\leq s \leq r$
, which is a contradiction. Therefore, condition (1) is always satisfied for some s.
Let
$1\leq s \leq r$
be the number satisfying (1) and consider the subset
\begin{align*} B'=\bigcup_{i=0}^{\ell'}B(a+isd,\delta r D) \subseteq B,\end{align*}
where
$\ell'=\lfloor(\ell-1)/s \rfloor$
. That is, if we see B as the arithmetic progression of intervals of length
$\delta rD$
, size
$\ell$
and common difference d, then B
′ is a subarithmetic progression of B with common difference sd. Since B has a monochromatic transversal labeled
$+1$
, then B
′ also has a monochromatic transversal labeled
$+1$
. Hence, because
$\bigcup_{i\in \mathbb{Z}}\left(irD,(i+\frac{r-1}{r})rD\right]$
are the elements of label
$+1$
in our
$(r-1,1;\,D)$
-alternate labelling, we have that
\begin{align*} \{a,a+sd,\ldots,a+\ell' sd\} \subseteq \bigcup_{i \in \mathbb{Z}} \left((i-\delta)rD, \left(i+\frac{r-1}{r}+\delta\right) rD\right).\end{align*}
Suppose that
$\overline{sd} \in \big[\delta rD,\frac{1}{r+1}rD\big]$
. Since the colouring
$\chi$
is periodic modulo rD, we may assume without loss of generality that
$sd \in \big[\delta rD,\frac{rD}{r+1}\big]$
. We claim that there exists an integer p such that
$\{a,a+sd,\ldots,a+\ell' sd\} \subseteq \left((p-\delta)rD, \left(p+\frac{r-1}{r}+\delta\right) rD\right)$
. Suppose that this is not the case. Because
$sd>0$
there exist integers
$p<q$
and
$0\leq i\leq \ell'-1$
such that
$a+isd \in \left((p-\delta)rD, \left(p+\frac{r-1}{r}+\delta\right) rD\right)$
and
$a+(i+1)sd \in \left((q-\delta)rD, \left(q+\frac{r-1}{r}+\delta\right) rD\right)$
. A computation shows that
\begin{align*} sd=a+(i+1)sd-(a+isd)> (q-\delta)rD-\left(p+\frac{r-1}{r}+\delta\right)rD\geq (1-2\delta r)D \geq \frac{rD}{r+1}\end{align*}
for
$\delta\leq \frac{1}{2r(r+1)}$
, which contradicts our assumption on sd.
Hence, there exists p such that
$a, a+\ell'sd \in \left((p-\delta)rD, \left(p+\frac{r-1}{r}+\delta\right) rD\right)$
, which implies that
\begin{align*} \ell' sd= (a+\ell' sd)-a\leq \left(p+\frac{r-1}{r}+\delta\right) rD-(p-\delta)rD=(r-1)D+2\delta r D.\end{align*}
Since
$sd \geq \delta r D$
, we obtain that
\begin{align*} \ell'sd \geq \left\lfloor\frac{\ell-1}{s}\right\rfloor\delta r D \geq \frac{\ell\delta r D}{2s} \geq \frac{\delta \ell D}{2}\end{align*}
for
$\ell>r\geq s$
. The last two computations combined with the fact that
$\delta\leq \frac{1}{2r(r+1)} \leq \frac{1}{4}$
gives us that
\begin{align*} \ell\leq \frac{2(r-1)D+4\delta rD}{\delta D}\leq \frac{2(r-1)}{\delta}+4r\leq\left(\frac{2}{\delta}+4\right)r \leq \frac{3r}{\delta}\end{align*}
Now assume that
$\overline{sd} \in \left[\left(1-\frac{1}{r+1}\right)rD,(1-\delta)rD\right]$
. By the periodicity of
$\chi$
, we may assume without loss of generality that
$sd \in [-\frac{rD}{r+1},-\delta rD]$
. By rewriting
$\{a,a+sd,\ldots,a+\ell' sd\}$
as
$\{a',a'+sd',\ldots,a'+\ell' sd'\}$
with
$a'=a+\ell' sd$
and
$d'=-d$
, we are back to the previous case and again
$\ell\leq 3r/\delta$
.
Although it is convenient to prove Lemma 2.2 using an alternate labelling of
$\mathbb{R}$
, the lower bound construction will use alternate labellings of set of integers. With this in mind, we give the following companion definition.
Given positive integers D, r and t, an
$(r-1,1;\, D)$
-alternate labelling of the set [rtD] is a labelling
$\chi'\,:\,[rtD] \rightarrow \{-1,+1\}$
such that
$\chi'(x)=\chi(x)$
, where
$\chi$
is an
$(r-1,1;\,D)$
-alternate labelling of
$\mathbb{R}$
. In other words, an alternate labelling of a set of integers is just the restriction of an alternate labelling of
$\mathbb{R}$
to the set. Note that by this definition, there exists r distinct
$(r-1,1;\,D)$
-alternate labellings of [rtD]. A D-block of [rtD] is a block of D consecutive integers of the form
$[iD+1,(i+1)D]$
. One can note that the D-blocks form a partition of [rtD] and each D-block is monochromatic in an
$(r-1,1;\,D)$
-alternate labelling of [rtD].
Finally, note that given an alternate labelling
$\chi'$
of a set [rtD] we can extend back to a an alternate labelling of (0, rtD] by labelling the entire interval
$(iD,(i+1)D]$
with the same label as the D-block of integers
$[iD+1,(i+1)D]$
. Since the labelling is periodic, it is now easy to extend back to a labelling
$\chi$
of
$\mathbb{R}$
.
The next result is a consequence of the proof of Lemma 2.2.
Proposition 2.3. Let D, r, t and
$\ell$
be positive integers with
$\ell\geq t(r+1)+2$
and
$0<\varepsilon<1/2r$
be a real number. If [rtD] is coloured by an
$(r-1, 1;\, D)$
-alternate labelling and
$X\subseteq [rtD]$
is a monochromatic
$\mathrm{AP}_{\ell}(\varepsilon)$
of label
$+1$
, then there exists
$0\leq i \leq rt-1$
such that the D-block
$[iD+1,(i+1)D]$
satisfies
$|X\cap [iD+1,(i+1)D]|\geq \ell/(r-1)$
.
Proof. Write
$X=\{x_0,\ldots,x_{\ell-1}\}$
. Since X is an
$\mathrm{AP}_{\ell}(\varepsilon)$
, there exists
$a\in \mathbb{R}$
,
$d>0$
such that
$|x_i-(a+id)|<\varepsilon d$
. Therefore, a computation shows that
\begin{align*} rtD>|x_{\ell-1}-x_0|\geq a+(\ell-1)d-a-2\varepsilon d=(\ell-1-2\varepsilon)d,\end{align*}
which implies that
\begin{align} d\leq \frac{rtD}{\ell-2} \leq \frac{rD}{r+1}\end{align}
for
$\ell\geq t(r+1)+2$
.
Similarly as in the proof of Lemma 2.2, we will show that all the elements of X are inside an interval of
$(r-1)$
consecutive D-blocks of label
$+1$
.
Suppose that this was not the case. Since non-consecutive D-blocks of label
$+1$
are at a distance of at least D elements, then there exists
$x_i$
and
$x_{i+1}$
such that
$|x_{i+1}-x_i|\geq D$
. However, in view of
$\varepsilon<1/2r$
and (3), we obtain
\begin{align*} |x_{i+1}-x_i|\leq |x_{i+1}-(a+(i+1)d)|+|a+(i+1)d-(a+id)|+|x_{i}-(a+id)|\leq (1+2\varepsilon)d
< D,\end{align*}
which is a contradiction. The result now follows by an application of the pigeonhole principle.
Note that Proposition 2.3 already gives us a lower bound for the case
$r=2$
. Indeed, we will prove that an
$(1,1;\,k-1)$
-alternate labelling of
$\left[\frac{2(k-1)(k-2)}{3}\right]$
Footnote 1 does not contain a monochromatic
$\mathrm{AP}_k(\varepsilon)$
for
$\varepsilon<1/4$
and sufficiently large k.
Suppose that this is not the case. Since an
$(1,1;\,k-1)$
-alternate labelling is symmetric, we may assume that there is a monochromatic
$\mathrm{AP}_k(\varepsilon)$
of label
$+1$
. Applying Proposition 2.3 with
$r=2$
,
$t=(k-2)/3$
,
$D=k-1$
and
$\ell=k$
gives us that there exists a
$(k-1)$
-block of the form
$[i(k-1)+1,(i+1)(k-1)]$
such that
$|X\cap [i(k-1)+1,(i+1)(k-1)]|\geq k$
, which contradicts the size of the block.
Unfortunately, the argument above does not give a lower bound depending on
$\varepsilon$
. To achieve such a bound we will need to refine the previous construction, but first we need one more preliminary result.
The second Chebyshev function
$\psi(x)$
is defined to be the logarithm of the least common multiple of all positive integers less or equal than x. The following bound on
$\psi(x)$
will be useful for us.
Theorem 2.4. ([Reference Rosser and Schoenfeld24], Theorem 7). If
$x\geq 10^8$
, then
$|\psi(x)-x|<cx/\log x$
for some positive constant c.
In particular, Theorem 2.4 asserts that for sufficiently large n we have
\begin{align} \mathrm{lcm}(1,\ldots,n)=e^{n+O(n/\log n)}.\end{align}
We are now ready to prove the lower bound of Theorem 1.3.
Theorem 2.5. Let
$r\geq 1$
. There exists a positive constant
$\varepsilon_0$
and a real number
$c_r$
depending on r such that the following holds. If
$0<\varepsilon\leq \varepsilon_0$
and
$k\geq 2^rr!\varepsilon^{-1}\log^r(1/5\varepsilon)$
is a integer, then there exist an integer
$N\,:\!=\,N(\varepsilon,k,r)$
satisfying
\begin{align*} N\geq c_r\frac{k^r}{\varepsilon^{r-1} \log(1/\varepsilon)^{\binom{r+1}{2}-1}},\end{align*}
so that [N] admits an r-colouring without monochromatic
$\mathrm{AP}_k(\varepsilon)$
.
Proof. The proof is by induction on the number of colours r. For
$r=1$
, the result clearly holds for
$N(\varepsilon,k,1)=k-1$
since there is no
$\mathrm{AP}_k(\varepsilon)$
, or even
$\mathrm{AP}_k$
, on
$(k-1)$
terms. Now suppose that for any
$\varepsilon$
and k such that
$0<\varepsilon\leq \varepsilon_0$
and
$k\geq 2^{r-1}(r-1)!\varepsilon^{-1}\log^{r-1}(1/5\varepsilon)$
, there exists
$N(\varepsilon,k,r-1)$
and a
$(r-1)$
-colouring of
$[N(\varepsilon,k,r-1)]$
satisfying the conclusion of the statement. We want to find an integer
$N_1$
so that
$[N_1]$
has a r-colouring without monochromatic
$\mathrm{AP}_k(\varepsilon)$
.
To do that we start with some choice of variables. Let
\begin{align} N_0=N\left(\varepsilon, \frac{k}{rs}, r-1\right), \quad s=\frac{1}{0.9}\log(1/5\varepsilon), \quad w=\frac{e^{0.9s}}{s(r-1)!}, \quad t=\frac{k}{2rs}, \quad D_j=\frac{s-j+1}{s}N_0\end{align}
be integers for
$1\leq j \leq s/2$
. Note that although s, w, t and
$\{D_j\}_{1\leq j\leq s/2}$
might not be integers, we prefer to write in this way, since it simplifies the exposition and has no significant effect on the arguments. Moreover, the integer
$N_0$
always exists since by hypothesis
\begin{align*}\frac{k}{rs}\geq \frac{2^rr!\varepsilon^{-1}\log^r (1/5\varepsilon)}{rs}\geq 2^{r-1}(r-1)!\varepsilon^{-1}\log^{r-1}(1/5\varepsilon).\end{align*}
Let
$N_1=rwt(D_1+\ldots+D_{s/2})$
. We are going to define a colouring
$\varphi: [N_1]\rightarrow [r]$
not admitting monochromatic
$\mathrm{AP}_k(\varepsilon)$
. To this end we partition
$[N_1]$
into consecutive intervals following the four steps below:
-
• First we partition
$[N_1]$
into
$[N_1]=Y_1\cup \ldots \cup Y_w$
, where
$Y_i$
are consecutive intervals and
$|Y_i|=rt(D_1+\ldots+D_{s/2})$
for every
$i=1,\ldots,w$
. -
• Each
$Y_i$
is partitioned into
$Y_i=Y_{i,1}\cup \ldots \cup Y_{i,s/2}$
, where
$Y_{i,j}$
’s are consecutive intervals and
$|Y_{i,j}|=rtD_j$
for every
$j=1,\ldots,s/2$
. -
• Each
$Y_{i,j}$
is partitioned into
$Y_{i,j}=Z_{1}^{i,j}\cup\ldots \cup Z_{t}^{i,j}$
, where
$Z_{u}^{i,j}$
’s are consecutive intervals and
$|Z_{u}^{i,j}|=rD_j$
for every
$u=1,\ldots,t$
. -
• Each
$Z_u^{i,j}$
is partitioned into
$Z_u^{i,j}=Z_{u,1}^{i,j}\cup \ldots \cup Z_{u,r}^{i,j}$
, where
$Z_{u,v}^{i,j}$
’s are consecutive intervals and
$|Z_{u,v}^{i,j}|=D_j$
for every
$v=1,\ldots,r$
.
More explicitly, we define
\begin{align*} \alpha_i&=(i-1)rt(D_1+\ldots+D_{s/2}), \quad i\in [w]\\[3pt]
\beta_{i,1}&=\alpha_i, \quad i\in[w]\\[3pt]
\beta_{i,j}&=rt(D_1+\ldots+D_{j-1})+\alpha_i, \quad (i,j)\in[w]\times[2,s/2]\\[3pt]
\gamma_{i,j,u}&=(u-1)rD_j+\beta_{i,j}, \quad (i,j,u)\in [w]\times[s/2]\times [t]\\[3pt]
\sigma_{i,j,u,v}&=(v-1)D_j+\gamma_{i,j,u}\quad (i,j,u,w)\in [w]\times[s/2]\times [t] \times [r].\end{align*}
Therefore, our intervals can be written as:
\begin{align*} Y_i&=[\alpha_i+1,\alpha_i+rt(D_1+\ldots+D_{s/2})], \quad i\in [w]\\[3pt]
Y_{i,j}&=[\beta_{i,j}+1,\beta_{i,j}+rtD_j], \quad (i,j)\in[w]\times [s/2]\\[3pt]
Z_{u}^{i,j}&=[\gamma_{i,j,u}+1,\gamma_{i,j,u}+rD_j], \quad (i,j,u)\in [w]\times[s/2]\times[t]\\[3pt]
Z_{u,v}^{i,j}&=[\sigma_{i,j,u,v}+1,\sigma_{i,j,u,v}+D_j], \quad (i,j,u,v)\in [w]\times[s/2]\times[t]\times [r]\end{align*}
Finally, we describe the colouring
$\varphi:[N_1]\rightarrow [r]$
on the intervals
$Z_{u,v}^{i,j}$
. By induction hypothesis, given any set C of
$r-1$
colours there exists a colouring
$\varphi_C: [N_0]\rightarrow C$
with no monochromatic
$\mathrm{AP}_{k/rs}(\varepsilon)$
. Fix
$Z_{u,v}^{i,j}$
with
$(i,j,u,v)\in [w]\times [s/2] \times [t] \times [r]$
. We colour
$Z_{u,v}^{i,j}$
by the same colouring as the first
$D_j$
elements of
$[N_0]$
when
$[N_0]$
is coloured by
$\varphi_{[r]\setminus \{v\}}$
. That is, the colouring
$\varphi$
restricted to
$Z_{u,v}^{i,j}$
only uses
$r-1$
colours and does not contain a monochromatic
$\mathrm{AP}_{k/rs}(\varepsilon)$
.
To prove that the colouring
$\varphi$
is free of
$\mathrm{AP}_k(\varepsilon)$
we are going to show that there is no
$a \in \mathbb{R}$
and
$d>0$
such that
$\bigcup_{i=0}^{k-1}B(a+id, \varepsilon d)$
has a monochromatic transversal in
$[N_1]$
. Suppose the opposite and assume that there exists a and d such that
$\bigcup_{i=0}^{k-1}B(a+id, \varepsilon d)$
has a monochromatic transversal
$X=\{x_0,\ldots,x_{k-1}\} \subseteq [N_1]$
of colour
$c\in [r]$
. Since all the balls have radius
$\varepsilon d$
, we obtain that
$\{a,a+d,\ldots,a+(k-1)d\}\subseteq (1-\varepsilon d, N_1+\varepsilon d)$
, which gives that
$(k-1)d\leq (N_1-1)+2\varepsilon d$
. By (5) and by the fact that
$\varepsilon\leq \varepsilon_0$
we have that
\begin{align} d\leq \frac{N_1-1}{k-1-2\varepsilon}\leq \frac{2N_1}{k}=\frac{2rwt(D_1+\ldots+D_{s/2})}{k}=\frac{w N_0}{s^2}\left(s+\ldots+\left(\frac{s}{2}+1\right)\right)\leq \frac{w N_0}{2},\end{align}
for sufficiently small
$\varepsilon_0$
.
For a fixed
$Y_{i,j}=\bigcup_{u=1}^t\bigcup_{v=1}^rZ_{u,v}^{i,j}$
we define an auxiliary labelling
$\chi_{i,j}\,:\,Y_{i,j} \rightarrow \{-1,+1\}$
of
$Y_{i,j}$
such that every
$D_j$
-block
$Z_{u,v}^{i,j}$
is monochromatic and
\begin{align*}\chi_{i,j}(Z_{u,v}^{i,j})=\begin{cases}+1,& \quad \text{if } v\neq c,\\[3pt]
-1,& \quad \text{if } v=c.\end{cases}.\end{align*}
In other words, every element of a
$D_j$
-block
$Z_{u,v}^{i,j}$
is of label
$-1$
if the colouring
$\varphi$
restricted to
$Z_{u,v}^{i,j}$
has the same colouring of the first
$D_j$
elements of
$\varphi_C\,:\,[N_0]\rightarrow C$
, where
$C=[r]\setminus\{c\}$
, i.e., the set of colours missing the colour c. Otherwise, we label all the elements in
$Z_{u,v}^{i,j}$
by
$+1$
. It is not difficult to check that
$\chi_{i,j}$
is an
$(r-1,1;\,D_j)$
-alternate labelling of
$Y_{i,j}$
. Moreover, since X is monochromatic of colour c and
$Z_{u,c}^{i,j}$
is coloured by
$\varphi_{[r]\setminus\{c\}}$
, we obtain that
$X\cap Z_{u,c}^{i,j}=\emptyset$
. This implies that every element of
$X\cap Y_{i,j}$
is labeled
$+1$
. Finally, in order to apply Lemma 2.2, we extend the labelling
$\chi_{i,j}$
to the set of real numbers
$(\beta_{i,j},\beta_{i,j}+rtD_j]$
by labelling the entire interval
$(\sigma_{i,j,u,v},\sigma_{i,j,u,v}+D_j]$
by colour
$\chi_{i,j}(Z_{u,v}^{i,j})$
for every
${u,v}\in [t]\times[r]$
.
The main idea of the proof is based on the fact that for d not too small, there exists an index
$j_0$
such that d is far from certain fractions involving
$D_{j_0}$
. We will then imply by Lemma 2.2 that the number of elements of X in
$Y_{i,j_0}$
is ‘small’. It turns out that this fact is enough to restrict the entire location of X to just a few
$Y_{i,j}$
’s. Then by the pigeonhole principle and Proposition 2.3 we can show that there exists a
$D_j$
-block
$Z_{u,v}^{i,j}$
with large intersection with X, which contradicts the inductive colouring of
$Z_{u,v}^{i,j}$
.
The next proposition elaborates more on the existence of such a
$j_0$
.
Proposition 2.6. If
$d>\frac{N_0}{s(r-1)!}$
, then there exists index
$1\leq j_0\leq s/2$
such that
\begin{align*} \left|d-\frac{mD_{j_0}}{(r-1)!}\right|\geq \frac{N_0}{2s(r-1)!}\end{align*}
for every
$m \in \mathbb{Z}$
.
Proof. Let
$M_0=\frac{N_0}{s(r-1)!}$
. Note that by (5) we can write
\begin{align*} \frac{D_j}{(r-1)!}=(s-j+1)\frac{N_0}{s(r-1)!}=(s-j+1)M_0,\end{align*}
for every
$1\leq j \leq s/2$
. Therefore, every number of the form
$\frac{mD_j}{(r-1)!}$
for
$m\in \mathbb{Z}^+$
and
$1\leq j\leq s/2$
is a multiple of
$M_0$
. Moreover, the least non-zero common term among the sequences
$\left\{\frac{mD_j}{(r-1)!}\right\}_{m\in \mathbb{Z}^+}$
for
$1\leq j \leq s/2$
, i.e.,
\begin{align*} \min\bigcap_{1\leq j \leq s/2}\left\{\frac{mD_j}{(r-1)!}\,:\, m\in \mathbb{Z}^+\right\}=\min\bigcap_{1\leq j \leq s/2}\left\{m(s-j+1)M_0\,:\, m\in \mathbb{Z}^+\right\}\end{align*}
is equal to
$LM_0$
, where
$L=\mathrm{lcm}(s/2+1,\ldots,s)$
.
Since every number in
$\{1,\ldots,s/2\}$
has a non-trivial multiple inside
$\{s/2+1,\ldots,s\}$
we obtain by (4) that
\begin{align*} L=\mathrm{lcm}(s/2+1,\ldots, s)=\mathrm{lcm}(1,\ldots,s)=e^{s+O(s/\log s)}\geq e^{0.9s},\end{align*}
for
$s=\frac{1}{0.9}\log(1/5\varepsilon)\geq \frac{1}{0.9}\log(1/5\varepsilon_0)$
and
$\varepsilon_0$
sufficiently small. Hence, by (5) and (6) we have
\begin{align*} d\leq \frac{wN_0}{2}= \frac{N_0e^{0.9s}}{2s(r-1)!}\leq \frac{LN_0}{2s(r-1)!}=\frac{L}{2}M_0.\end{align*}
Let
$pM_0$
be the multiple of
$M_0$
closest to d. Since
$d>M_0$
, we clearly have that
$p\neq 0$
. By definition,
\begin{align*} pM_0=\frac{pN_0}{s(r-1)!}\leq d +\left|\frac{pN_0}{s(r-1)!}-d\right|\leq d+ \frac{M_0}{2}
< LM_0.\end{align*}
Therefore, by the minimality of
$LM_0$
, there exists an index
$1\leq j_0 \leq s/2$
such that
$pM_0$
is not a multiple of
$\frac{D_{j_0}}{(r-1)!}=(s-j_0+1)M_0$
. Since, by the definition of p, all the other numbers of the form
$mM_0$
have distance at least
$\frac{M_0}{2}=\frac{N_0}{2s(r-1)!}$
to d, Proposition 2.6 follows.
We now prove that there exists a set
$Y_{i,j}$
with a large proportion of elements of X.
Proposition 2.7. There exist indices
$(i_1,j_1)\in [w]\times [s/2]$
such that
$|X\cap Y_{i_1,j_1}|\geq k/s.$
Proof. Let
$I\subseteq [w]\times [s/2]$
be set of pair of indices defined by
\begin{align*} I=\left\{(i,j)\in [w]\times [s/2]\,:\,X\cap Y_{i,j}\neq \emptyset\right\},\end{align*}
and let
$\mathcal{Y}=\bigcup_{(i,j)\in I}Y_{i,j}$
. By (5) and (6) we obtain that the difference between two consecutive terms of X is bounded by
\begin{align*} |x_{h+1}-x_h|\leq (1+2\varepsilon)d \leq (1+2\varepsilon)\frac{e^{0.9s}N_0}{2s(r-1)!}
< \frac{kN_0}{4s}\leq \frac{k(s-j+1)N_0}{2s^2}=rtD_{j}=|Y_{i,j}|,\end{align*}
for
$k\geq 2^rr!\varepsilon^{-1}\log^r(1/5\varepsilon)\geq \varepsilon^{-1}/(r-1)!$
. That is, the difference between two consecutive terms of X is smaller than the size of an interval
$Y_{i,j}$
for
$(i,j)\in [w]\times [s/2]$
. This implies that all intervals in
$\mathcal{Y}$
must be consecutive. Recall that by construction two intervals
$Y_{i,j}$
and
$Y_{i',j'}$
are consecutive if (i, j) and (i
′, j
′) are consecutive in the lexicographical ordering of
$[w]\times [s/2]$
.
If
$|I|\leq 2$
, then by the pigeonhole principle there exist indices
$(i_1,j_1)$
such that
$|X\cap Y_{i_1,j_1}|\geq k/2\geq k/s$
for
$\varepsilon_0$
sufficiently small. Thus we may assume that
$|I|>3$
. This implies that there exists at least one pair of indices (i
′, j
′) such that
$Y_{i',j'}$
is neither the first or last interval of
$\mathcal{Y}$
.
Let
$X\cap Y_{i',j'}=\{x_h,\ldots,x_{h+b-1}\}$
, where
$b=|X\cap Y_{i',j'}|$
. Since
$Y_{i',j'}$
is not one of intervals in the extreme of
$\mathcal{Y}$
, we obtain that
$2\leq h\leq h+b-1\leq k-1$
and in particular there exists points
$x_{h-1}$
and
$x_{h+b}$
outside of
$Y_{i',j'}$
. Then a simple computation gives us that
\begin{align*} |Y_{i',j'}|\leq |x_{h+b}-x_{h-1}|\leq (b+1+2\varepsilon)d
< 2bd\end{align*}
and consequently
\begin{align} |X\cap Y_{i',j'}|=b > \frac{|Y_{i',j'}|}{2d}\end{align}
for any
$Y_{i',j'}$
not on the extremes of
$\mathcal{Y}$
.
We split the proof into two cases depending on the size of d. If
$d\leq \frac{N_0}{s(r-1)!}$
, then (5) and (7) give that
\begin{align*} |X\cap Y_{i',j'}| > \frac{|Y_{i',j'}|}{2d}=\frac{rtD_{j'}}{2d}\geq \frac{k(s-j'+1)(r-1)!}{4s}\geq\frac{k(r-1)!}{8}\geq \frac{k}{s}\end{align*}
for every
$Y_{i',j'}$
not on the extremes and sufficiently large s. Taking
$(i_1,j_1)$
as one such (i
′, j
′) gives the desired result.
Now suppose that
$d>\frac{N_0}{s(r-1)!}$
. Let
$j_0$
be the index provided by Proposition 2.6. In particular, it holds that
\begin{align} \left|d-\frac{mrD_{j_0}}{q}\right|\geq \frac{N_0}{2s(r-1)!}\end{align}
for every
$m\in \mathbb{Z}$
and
$1\leq q \leq r$
. Suppose that
$X\cap Y_{i,j_0}\neq \emptyset$
for some
$1\leq i \leq w$
. Our goal is to apply Lemma 2.2 with
$D=D_{j_0}$
,
$\delta=1/4sr!$
to the interval
$(\min(Y_{i,j_0})-1,\max(Y_{i,j_0})]=(\beta_{i,j_0},\beta_{i,j_0}+rtD_j]$
labeled with our extension of
$\chi_{i,j_0}$
. In order to verify the assumptions of the lemma note that
\begin{align*} \frac{N_0}{2s(r-1)!}=\frac{D_{j_0}}{2(s-j_0+1)(r-1)!}\geq \frac{D_{j_0}}{2s(r-1)!}>\delta r D_{j_0}\end{align*}
and therefore by
$(8)$
we have
\begin{align*} d\notin \bigcup_{m \in \mathbb{Z}}\bigcup_{q=1}^r\left(\left(\frac{m}{q}-\delta\right)rD_{j_0},\left(\frac{m}{q}+\delta\right)rD_{j_0}\right).\end{align*}
Consequently, the conclusion of the lemma gives to us that any arithmetic progression of intervals of radius
$\delta r D_{j_0}$
with common difference d and a monochromatic transversal of label
$+1$
inside the interval
$(\min(Y_{i,j_0})-1,\max(Y_{i,j_0})]$
has length bounded by
$3r/\delta$
. This is true in particular for
$\bigcup_{i=0}^{k-1}B(a+id,\varepsilon d)$
, since by (5) and (6) we have
\begin{align*} \varepsilon d\leq \frac{\varepsilon w N_0}{2}=\frac{N_0}{10s(r-1)!}= \frac{D_{j_0}}{10(s-j_0+1)(r-1)!}\leq \frac{D_{j_0}}{5s(r-1)!}<\delta r D_{j_0}.\end{align*}
Hence, because X is transversal of label
$+1$
of
$\bigcup_{i=0}^{k-1}B(a+id,\varepsilon d)$
, the conclusion of Lemma 2.2 gives for
$k\geq 2^rr!\varepsilon^{-1}\log^r(1/5\varepsilon)> \frac{32}{3}r^2\varepsilon^{-1}\log(1/5\varepsilon)$
that
\begin{align}|X\cap Y_{i,j_0}|\leq \frac{3r}{\delta}=12sr! r=\frac{40}{3}r!r\log(1/5\varepsilon)<\frac{5}{4}\varepsilon(r-1)!k.\end{align}
However, by (5), (6) and (7) we have
\begin{align} |X\cap Y_{i',j'}| > \frac{|Y_{i',j'}|}{2d}=\frac{rtD_{j'}}{2d}\geq \frac{1}{w N_0} \cdot \frac{k(s-j'+1)N_0}{2s^2} \geq \frac{k}{4w s}=\frac{5}{4}\varepsilon(r-1)!k\end{align}
for any
$Y_{i',j'}$
in the middle of
$\mathcal{Y}$
. Comparing (9) and (10) yields that
$|X\cap Y_{i,j_0}|<|X\cap Y_{i',j'}|$
for any interval
$Y_{i',j'}$
in the middle of
$\mathcal{Y}$
. Thus
$Y_{i,j_0}$
cannot be a middle interval and we obtain that if
$(i,j_0)\in I$
, then
$Y_{i,j_0}$
is either the first or last interval of
$\mathcal{Y}$
. Therefore, we can have at most two occurrences of
$j_0$
in I and consequently the entire location of I is contained between those two occurrences, i.e.,
$I \subseteq \{(i,j_0),(i,j_0+1),\ldots,(i+1,j_0-1),(i+1,j_0)\}$
for some
$1\leq i \leq w-1$
. Hence, the set I has at most
$s/2+1$
elements and by the pigeonhole principle there exists a pair of indices
$(i_1,j_1)\in I$
such that
$|X\cap Y_{i_1,j_1}|\geq k/(s/2+1) \geq k/s$
.
Let
$(i_1,j_1)$
be the indices given by Proposition 2.7. Next we apply Proposition 2.3 to the set
$Y_{i_1,j_1}$
labeled by
$\chi_{i_1,j_1}$
with
$D=D_{j_1}$
,
$\ell=k/s$
and
$\varepsilon$
-approximate arithmetic progression
$X\cap Y_{i_1,j_1}$
. Note that by (5) the hypothesis concerning r, t and
$\ell$
in the statement holds since
\begin{align*}t(r+1)+2=\frac{(r+1)k}{2rs}+2<\frac{k}{s}=\ell\end{align*}
for
$r\geq 2$
and
$k\geq 2^rr!\varepsilon^{-1}\log^r(1/5\varepsilon)\geq 80\log(1/5\varepsilon)/9$
. Also a
$D_j$
-block of
$Y_{i_1,j_1}$
is an interval of the form
$Z_{u,v}^{i_1,j_1}$
. Hence, by the conclusion of the proposition, there exists
$Z_{u,v}^{i_1,j_1}$
such that
$|X\cap Z_{u,v}^{i_1,j_1}|\geq \ell/(r-1)>k/rs$
. Since each set
$Z_{u,v}^{i,j}$
was
$(r-1)$
-coloured inductively not to contain an
$AP_{k/rs}(\varepsilon)$
, we reach a contradiction. Thus there is no monochromatic
$AP_k(\varepsilon)$
in
$[N_1]$
. In view of (5) we have
\begin{align*} N_1=rwt(D_1+\ldots+D_{s/2})&=\frac{ke^{0.9s}N_0}{2s^3(r-1)!}\left(s+\ldots+\left(\frac{s}{2}+1\right)\right)\\[5pt]
&\geq \frac{kN_0}{40\varepsilon s(r-1)!}\geq \frac{kN_0}{50(r-1)!\varepsilon\log(1/\varepsilon)}.\end{align*}
Consequently, in view of
$s=O(\log(1/5\varepsilon))$
we obtain by induction that
\begin{align*} \qquad\qquad N_1\geq \frac{k}{50(r-1)!\varepsilon \log(1/\varepsilon)}\cdot\frac{c^{\prime}_r\left(\frac{k}{rs}\right)^{r-1}}{\varepsilon^{r-2}\log(1/\varepsilon)^{\binom{r}{2}-1}}\geq c_r\frac{k^r}{\varepsilon^{r-1}\log(1/\varepsilon)^{\binom{r+1}{2}-1}}.\end{align*}
3. Proof of Theorem 1.7
3.1 Lower bound
For positive integers k and N, recall that f(N, 1, k), sometimes denoted by
$r_k(N)$
, is defined to be the size of the largest set
$A \subseteq [N]$
without an arithmetic progression of length k. A classical result of Behrend [Reference Behrend1] shows that,
\begin{align*} f(N,1,3)> N\exp\left(-c\sqrt{\log N}\right),\end{align*}
for a positive constant c (see [Reference Elkin5, Reference Green and Wolf15] for slightly improvements). In [Reference Rankin22] (See also [Reference Laba and Lacey18]) the argument was generalised to yield that
\begin{align} f(N,1,k) > N\exp\left(-c(\log N)^{1/\ell}\right),\end{align}
where
$\ell=\lceil \log_2 k \rceil$
and
$k\geq 3$
and c is a constant depending only on k. We will use the last result as a building block for our construction.
Before we turn our attention to the lower bound construction, we will state a preliminary result about
$\varepsilon$
-approximate arithmetic progressions. Given a set of k integers, one can identify them as an
$AP_k$
by the common difference between the elements. Unfortunately, the same is not true for an
$AP_k(\varepsilon)$
. On the positive side, the next result shows that if a set of k elements is an
$AP_k(\varepsilon)$
, then the differences of consecutive terms are almost equal.
Proposition 3.1. Given
$0<\varepsilon<1/10$
, let
$X=\left\{x_0,\ldots, x_{k-1}\right\}$
be an
$\mathrm{AP}_k(\varepsilon)$
. Then for every pair of indices
$0\leq i, j \leq k-2$
the following holds
\begin{align*} \left|\frac{|x_{j+1}-x_j|}{|x_{i+1}-x_i|}-1\right|
< 5\varepsilon.\end{align*}
Proof. Since X is an
$\mathrm{AP}_k(\varepsilon)$
, there exist a and d such that
$|x_i-(a+id)|<\varepsilon d$
for
$0\leq i \leq k-1$
. Therefore, a simple computation shows that
\begin{align*} 1-5\varepsilon<\frac{(1-2\varepsilon)d}{(1+2\varepsilon)d}<\frac{|x_{j+1}-x_j|}{|x_{i+1}-x_i|}<\frac{(1+2\varepsilon)d}{(1-2\varepsilon)d}<1+5\varepsilon\end{align*}
for
$0<\varepsilon<1/10$
and
$0\leq i,j \leq k-2$
.
We now prove the lower bound of Theorem 1.3 for one dimension.
Lemma 3.2. Let
$k\geq 3$
and
$0<\varepsilon\leq 1/125$
. Then there exists a positive constant
$c_1$
depending only on k and an integer
$N_0\,:\!=\,N_0(k,\varepsilon)$
such that the following holds. If
$N\geq N_0$
, then there exists a set
$A\subseteq [N]$
without
$AP_k(\varepsilon)$
such that
\begin{align*} |A|\geq N^{1-c_1(\log(1/\varepsilon))^{\frac{1}\ell-1}}\end{align*}
for
$\ell=\lceil \log_2 k\rceil$
.
Proof. For integers a, b, let
$S_k([a,b])$
be the largest subset in the interval [a, b] without any arithmetic progression
$\mathrm{AP}_k$
of length k. By a simple translation, one can note that
$S_k([a,b])$
has the same size as
$S_k([b-a+1])$
and by (11) we have
\begin{align} |S_k([a,b])|=f(b-a+1,1,k)\geq (b-a+1)\exp\left(-c(\log(b-a+1))^{1/\ell}\right),\end{align}
for a positive constant c and
$\ell=\lceil \log_2 k \rceil$
.
Let
$q=\frac{1}{25\varepsilon}\geq 5$
be an integer and h be largest exponent such that
$q^h\leq N < q^{h+1}$
. For such a choice of q and h, we construct the set
\begin{align*} A=\left\{s\in [N]\,:\, a=s_0+s_1q+\ldots+s_{h-1}q^{h-1}\right\},\end{align*}
where
$s_{h-1}\in S_k([0,q-1])$
and
$s_i \in S_k\left(\left[2q/5,3q/5\right]\right)$
for
$0\leq i \leq h-2$
. Our goal is to show that A satisfies the conclusion of Lemma 3.2.
First note by (12) that
\begin{align*} |A|&= |S_k([0,q-1])|\cdot \left|S_k\left(\left[2q/5,3q/5\right]\right)\right|^{h-1}\\[5pt]
&\geq \frac{q}{\exp(c(\log q)^{1/\ell})}\cdot \left(\frac{q}{5\exp(c(\log q/5)^{1/\ell})}\right)^{h-1}\\[5pt]
&\geq \frac{q^h}{\exp(c(\log q)^{1/\ell})(5\exp(c(\log q)^{1/\ell}))^{h-1}}\\[5pt]
&\geq \frac{N}{5^{h-1}q\exp(c(\log q)^{1/\ell})^h}\geq \frac{N}{q\exp(c'h(\log q)^{1/\ell})},\end{align*}
and in view of
$h\leq \frac{\log N}{\log q}$
and our choice of q we obtain that
\begin{align*} |A|\geq \frac{20\varepsilon N}{\exp\left(c'\log N(\log q)^{1/\ell-1}\right)} \geq N^{1-c_1\log (1/\varepsilon)^{1/\ell-1}}\end{align*}
for sufficiently large N and appropriate constant
$c_1$
depending only on k. Therefore the set A has the desired size. It remains to prove that A is
$\mathrm{AP}_k(\varepsilon)$
-free.
Suppose that there exists an
$\varepsilon$
-approximate arithmetic progression
$X=\{x_0,\ldots,x_{k-1}\}$
in A. For each
$0\leq i \leq k-1$
, write
$x_i=\sum_{j=0}^{h-1}x_{i,j}q^j$
. Since all
$x_i$
’s are distinct, there exists a maximal index
$j_0$
such that the elements of
$X_{j_0}=\{x_{i,j_0}\}_{0\leq i \leq k-1}$
are not all equal. By construction of A the set
$X_{j_0}$
fails to be an
$\mathrm{AP}_k$
. Therefore there exists two indices
$0\leq i_1, i_2 \leq k-2$
such that
\begin{align} |x_{i_1+1,j_0}-x_{i_1,j_0}|\neq |x_{i_2+1,j_0}-x_{i_2,j_0}|.\end{align}
For
$0\leq i \leq k-1$
, note that
\begin{align*} |x_{i+1}-x_i|=\left|\sum_{j=0}^{h-1}(x_{i+1,j}-x_{i,j})q^j\right|=\left|\sum_{j=0}^{j_0}(x_{i+1,j}-x_{i,j})q^j\right|\end{align*}
by the maximality of
$j_0$
. Thus by the triangle inequality we obtain that
\begin{align} \left||x_{i+1}-x_i|-|x_{i+1,j_0}-x_{i,j_0}|q^{j_0}\right|\leq \sum_{j=0}^{j_0-1}|x_{i+1,j}-x_{i,j}|q^j.\end{align}
Moreover, recalling that
$x_{i,j} \in \left[2q/5,3q/5\right]$
for
$0\leq j \leq h-2$
we infer that
\begin{align*} \sum_{j=0}^{j_0-1}|x_{i+1,j}-x_{i,j}|q^j\leq \sum_{j=0}^{j_0-1}\frac{q^{j+1}}{5} \leq \frac{2q^{j_0}}{5}\end{align*}
for
$q\geq 2$
. The last inequality combined with (14) gives us that
\begin{align} \left||x_{i+1}-x_i|-|x_{i+1,j_0}-x_{i,j_0}|q^{j_0}\right|\leq \frac{2}{5}q^{j_0},\end{align}
for
$0\leq i \leq k-2$
. Hence by (13) we have that
\begin{align} \big||x_{i_2+1}-x_{i_2}|-|x_{i_1+1}-x_{i_1}|\big|&\geq \big||x_{i_2+1,j_0}-x_{i_2,j_0}|-|x_{i_1+1,j_0}-x_{i_1,j_0}|\big|q^{j_0}-\frac{4}{5}q^{j_0}\nonumber\\ &\geq q^{j_0}-\frac{4}{5}q^{j_0}=\frac{q^{j_0}}{5}\end{align}
On the other hand, Proposition 3.1 for
$i_1$
and
$i_2$
together with (15) gives us that
\begin{align*} \big||x_{i_2+1}-x_{i_2}|-|x_{i_1+1}-x_{i_1}|\big| <5\varepsilon|x_{i_1+1}-x_{i_1}|<5\varepsilon\left(|x_{i_1+1,j_0}-x_{i_1,j_0}|+\frac{2}{5}\right)q^{j_0}.\end{align*}
Since
$x_{i,j_0} \in [0,q-1]$
for every
$0\leq i \leq k-1$
and
$\varepsilon q=1/25$
we have
\begin{align*} \big||x_{i_2+1}-x_{i_2}|-|x_{i_1+1}-x_{i_1}|\big|<5\varepsilon q^{j_0+1}=\frac{q^{j_0}}{5},\end{align*}
which contradicts (16).
For higher dimensions the result follow as a corollary of Lemma 3.2. Recall by Definition 1.6 that an
$\varepsilon$
-approximate cube
$C_\varepsilon(m,k)$
is just an multidimensional version of an
$\mathrm{AP}_k(\varepsilon)$
Corollary 3.3. Let
$k\geq 3$
and
$m\geq 1$
be integers and
$0<\varepsilon\leq 1/125$
. Then there exists an integer
$N_0\,:\!=\,N_0(k,\varepsilon)$
and a positive constant
$c_1$
depending on k such that the following holds. If
$N\geq N_0$
, then there exists a set
$S\subseteq [N]^m$
without
$C_{\varepsilon}(m,k)$
such that
\begin{align*} |S|\geq N^{m-c(\log(1/\varepsilon))^{\frac{1}\ell-1}}\end{align*}
for
$\ell=\lceil \log_2(k-1)\rceil$
.
Proof. Let
$N_0$
be the integer given by Lemma 3.2 and let
$A\subseteq [N]$
be the set such that A has no
$\mathrm{AP}_k(\varepsilon)$
for
$N\geq N_0$
. Set
$S=A\times [N]^{m-1}$
, i.e.,
$S=\left\{(s_1,\ldots,s_m)\,:\, s_1\in A,\, s_2,\ldots,s_m \in [N]\right\}$
. Note that S has the desired size since
\begin{align*} |S|=N^{m-1}|A|\geq N^{m-c(\log(1/\varepsilon))^{\frac{1}\ell-1}}.\end{align*}
We claim that S is free of
$C_{\varepsilon}(m,k)$
.
Suppose that the claim is not true and let
$X=\{x_{\vec{v}}\,:\, \vec{v}\in \{0,\ldots,k-1\}^m\}$
be an
$C_{\varepsilon}(m,k)$
in S. By definition there exists
$\vec{a} \in \mathbb{R}^m$
and
$d>0$
such that
$||x_{\vec{v}}-(\vec{a}+d\vec{v})||<\varepsilon d$
for every
$\vec{v} \in \{0,\ldots,$
$k-1\}^m$
. In particular, when applied to
$\{te_1=(t,0,\ldots,0)\,:\, 0\leq t \leq k-1\}$
the observation gives us that
\begin{align*} |x_{te_1,1}-(a_1+td)| \leq \left((x_{te_1,1}-(a_1+dt))^2+\sum_{i=2}^m(x_{te_1,i}-a_i)^2\right)^{1/2}=||x_{te_1}-(\vec{a}+dte_1)||<\varepsilon d\end{align*}
Therefore, the set
$\{x_{te_1,1}\}_{0\leq t \leq k-1}\subseteq A$
is an
$\mathrm{AP}_k(\varepsilon)$
, which contradicts our choice of A.
3.2 Upper bound
As in the upper bound of
$W_\varepsilon(k,r)$
, our proof of the upper bound of
$f_\varepsilon(N,m,k)$
will use an iterative blow-up construction. It is worth to point out that a similar proof was obtained independently by Dumitrescu in [4]. While both proofs use a blow-up construction, the author of [4] finishes the proof with a packing argument. Here we will follow the approach of [Reference Han, Kohayakawa, Sales and Stagni16, Reference Han, Kohayakawa, Sales and Stagni17], which uses an iterative blow-up construction combined with an average argument to estimate the largest subset of a grid without a class of configurations of a given size. This approach allows us to slightly improve the constants in the result.
The proof is split into two auxiliary lemmas.
Lemma 3.4. Given positive real numbers
$\alpha$
,
$\varepsilon>0$
and integers
$m\geq 1$
and
$k\geq 3$
, there exists
$N_0\,:\!=\,N_0(\alpha,\varepsilon,m,k)\leq \left(k\sqrt{m}/\varepsilon\right)^{2k^m\log(1/\alpha)}$
and a subset
$A \subseteq [N]^m$
with the property that any
$X\subseteq A$
,
$|X|\geq \alpha|A|$
contains a
$C_{\varepsilon}(m,k)$
.
Proof. For m and k, let
$\Delta$
be the standard cube C(m, k) of dimension m over
$\{0,\ldots,k-1\}$
, i.e.,
$\Delta$
is the set of all m-tuples
$\vec{v}=\{v_1,\ldots,v_m\}\in \{0,\ldots,k-1\}^m$
. Viewing
$\Delta$
as an m-dimensional lattice in the Euclidean space, we note that
$\mathrm{diam}(\Delta)=(k-1)\sqrt{m}$
, while the minimum distance between two vertices in
$\Delta$
is one.
Similarly as in the proof of the upper bound of Theorem 1.3, we consider an iterated blow-up of the cube. For integers r and
$t=k\sqrt{m}/\varepsilon$
, let
$A_r$
be the following r-iterated blow-up of a cube
\begin{align*} A_r=\left\{ \vec{v}_0+t\vec{v}_1+\ldots+t^{r-1}\vec{v}_{r-1}\,:\, \vec{v}_0,\ldots,\vec{v}_{r-1}\in \Delta,\, t=\frac{k\sqrt{m}}{\varepsilon}\right\}.\end{align*}
Alternatively, we can view
$A_r$
as the product
$\prod_{i=1}^mB_r^{(i)}$
of m identical copies of
\begin{align*} B_r=\left\{b_0+tb_1+\ldots+t^{r-1}b_{r-1}\,:\, (b_0,\ldots,b_{r-1})\in \{0,1\ldots,k-1\}^r,\, t=\frac{k\sqrt{m}}{\varepsilon} \right\},\end{align*}
an r-iterated blow-up of the standard
$\mathrm{AP}_k$
. Note by the construction that
$|A_r|=k^{rm}$
. The next proposition shows that fixed
$\alpha>0$
, for a sufficiently large r any
$\alpha$
-proportion of
$A_r$
will contain a
$C_{\varepsilon}(m,k)$
.
Proposition 3.5. Let
$0<\alpha<1$
be a real number and r a positive integer such that
$\alpha> \left(\frac{k^m-1}{k^m}\right)^r$
. Then every
$X\subseteq A_r$
with
$|X|\geq \alpha|A_r|$
contains a
$C_{\varepsilon}(m,k)$
.
Proof. The proof is by induction on r. If
$r=1$
, then
$A_1=\Delta$
and
$\alpha>\frac{k^m-1}{k^m}$
. Let
$X\subseteq A_1$
with
$|X|\geq \alpha |A_1|$
. Thus
\begin{align*} |X|\geq \alpha |A_1| >\frac{k^m-1}{k^m}\cdot k^m=k^m-1,\end{align*}
which implies that
$X=\Delta$
. So X contains a cube C(k, m) and in particular an
$\varepsilon$
-approximate cube.
Now suppose that the proposition is true for
$r-1$
and we want to prove it for r. First, we partition
$A_r$
into
$\bigcup_{\vec{u}\in \Delta} A_{r,\vec{u}}$
, where
\begin{align*} A_{r,\vec{u}}=\left\{\vec{v}_0+t\vec{v}_1+\ldots+t^{r-2}\vec{v}_{r-2}+t^{r-1}\vec{u}\,:\,\vec{v_0},\ldots,\vec{v}_{r-2}\in \Delta,\, t=\frac{k\sqrt{m}}{\varepsilon}\right\}.\end{align*}
Note that by definition
$A_{r,\vec{u}}$
is a translation of
$A_{r-1}$
by
$t^{r-1}\vec{u}$
. In particular, this implies that
$|A_{r,\vec{v}}|=k^{(r-1)m}$
. Let
$X\subseteq A_r$
with
$|X|\geq \alpha |A_r|$
be given. We will distinguish two cases:
Case 1:
$X\cap A_{r,\vec{u}}\neq \emptyset$
for all
$\vec{u}\in \Delta$
.
For each
$\vec{u}\in \Delta$
choose an arbitrary vector
$w(\vec{u}) \in X\cap A_{r,\vec{u}}$
. We will observe that
$\{w(\vec{u})\}_{\vec{u}\in \Delta}$
forms a
$C_{\varepsilon}(m,k)$
. To testify that, set
$\vec{a}=(0,\ldots,0)$
and
$d=t^{r-1}$
. Write
$w(\vec{u})=\sum_{i=0}^{r-2}t^i\vec{w}_i+t^{r-1}\vec{u}$
with
$\vec{w}_i \in \Delta$
. Thus, a computation shows that
\begin{align*} ||w(\vec{u})-(\vec{a}+d\vec{u})||=||w(\vec{u})-t^{r-1}\vec{u}||=\left|\left|\sum_{i=0}^{r-2}t^i\vec{w}_i\right|\right|\leq \sum_{i=0}^{r-2}t^i||\vec{w}_i||\end{align*}
for
$\vec{w}_0,\ldots,\vec{w}_{r-2} \in \Delta$
. Since
$\mathrm{diam}(\Delta)=(k-1)\sqrt{m}$
, it follows that
\begin{align*} ||w(\vec{u})-(\vec{a}+d\vec{u})||\leq (k-1)\sqrt{m}\left(\sum_{i=0}^{r-2}t^i\right)\leq kt^{r-2}\sqrt{m}<\varepsilon t^{r-1}=\varepsilon d,\end{align*}
by our choice of t. Since
$\{w(\vec{u})\}_{\vec{u}\in \Delta}\subseteq X$
, we conclude that X contains an
$C_{\varepsilon}(m,k)$
.
Case 2: There exists
$\vec{u_0} \in \Delta$
with
$X\cap A_{r,\vec{u}_0}=\emptyset$
.
Since
$|X|\geq \alpha |A_r|$
and
$|\Delta|=k^m$
, by an average argument there exists
$\vec{u}_1\in \Delta$
such that
\begin{align*} |X\cap A_{r,\vec{u}_1}|\geq \frac{\alpha|A_r|}{k^m-1}=\frac{\alpha k^m|A_{r-1}|}{k^m-1}.\end{align*}
Set
$X'=X\cap A_{r,\vec{u}_1}$
and
$\alpha'=\frac{\alpha k^m}{k^m-1}$
. Note that
\begin{align*} \alpha'=\frac{\alpha k^m}{k^m-1}>\left(\frac{k^m-1}{k^m} \right)^r\cdot \frac{k^m}{k^m-1}=\left(\frac{k^m-1}{k^m} \right)^{r-1}.\end{align*}
Therefore, viewing
$A_{r,\vec{u}}$
as a copy of
$A_{r-1}$
by the induction assumption we obtain that
$X'\subseteq X$
contains an
$C_{\varepsilon}(m,k)$
.
Let r be the smallest integer such that
$\left(\frac{k^m-1}{k^m}\right)^r< \alpha$
and set
$A=A_r$
. A computation shows that
\begin{align*} r=\left\lceil \frac{\log(1/\alpha)}{\log \frac{k^m}{k^m-1}} \right\rceil
< 2k^m\log(1/\alpha).\end{align*}
Therefore by Proposition 3.5 we have that any set
$X\subseteq A$
with
$|X|\geq \alpha|A|$
contains an
$C_{\varepsilon}(m,k)$
. Finally, by the construction of A we have that
$A\subseteq [N_0]^m$
for
\begin{align*} \qquad N_0\leq \mathrm{diam}(B_r)+1 =(k-1)(1+t+\ldots+t^{r-1})+1 \leq kt^{r-1}\leq \left(\frac{k\sqrt{m}}{\varepsilon}\right)^{2k^m\log(1/\alpha)}.\end{align*}
Lemma 3.4 gives us a set
$A\subseteq [N]^m$
such that any
$\alpha$
-proportion contains a
$C_{\varepsilon}(m,k)$
. However, this is still not good enough, since to obtain an upper bound we need a similar result for
$[N]^m$
. The next lemma shows by an average argument that the property of A can be extended to
$[N]^m$
by losing a factor of a power of two in the proportion
$\alpha$
.
Lemma 3.6. Let
$A \subseteq [N]^m$
be a configuration in the grid. For any
$X\subseteq [N]^m$
with
$|X|\geq \alpha N^m$
, there exists a translation A′ of A such that
$|X\cap A'|\geq \frac{\alpha}{2^m} |A'|$
.
Proof. Consider a random translation
$A'=A+\vec{u}$
, where
$\vec{u}=(u_1,\ldots,u_m)$
is an integer vector chosen uniformly inside
$[-N+1,N]^m$
. For every vector
$\vec{x} \in X$
, there exists exactly
$|A|$
elements
$\vec{v} \in [-N+1,N]^m$
such that
$\vec{x}-\vec{v}\in A$
. This means that
$\mathbb{P}(\vec{x} \in A')=\mathbb{P}(\vec{x}-\vec{u}\in A)=\frac{|A|}{(2N)^m}$
. Therefore
\begin{align*} \mathbb{E}(|X\cap A'|)=\sum_{\vec{x} \in X}\mathbb{P}(\vec{x} \in A')=\frac{|X||A|}{(2N)^m}\geq \frac{\alpha}{2^m}|A|=\frac{\alpha}{2^m}|A'|\end{align*}
Consequently, by the first moment method, there is
$\vec{u}$
and A
′ satisfying our conclusion.
We finish the section putting everything together.
Proposition 3.7. Let N, m and k be integers and
$\varepsilon>0$
. Then there exists a positive constant
$c_2$
depending only on k and m such that the following holds. If
$S\subseteq [N]^m$
is such that
\begin{align*} |S|> N^{m-c_2(\log(1/\varepsilon))^{-1}},\end{align*}
then S contains an
$C_{\varepsilon}(m,k)$
.
Proof. Set
$\alpha_0=2^mN^{-c'(\log(1/\varepsilon))^{-1}}$
where
$c'=(4k^m\log(k\sqrt{m}))^{-1}$
. Let
$N_0=N_0(\alpha_0/2^m,\varepsilon,m,k)$
be the integer obtained by Lemma 3.4 and
$A\subseteq [N_0]$
be the set such that any
$X\subseteq A$
with
$|X|\geq \frac{\alpha_0}{2^m}|A|$
contains an
$C_{\varepsilon}(m,k)$
. Note that
\begin{align*} N_0&\leq \left(\frac{k\sqrt{m}}{\varepsilon}\right)^{2k^m\log(2^m/\alpha_0)} = \exp\left(\frac{2c'k^m\log N \log(k\sqrt{m}/\varepsilon)}{\log(1/\varepsilon)} \right)\\ &\leq \exp\left(4c'k^m\log N \log(k\sqrt{m}) \right)=N,\end{align*}
which implies that
$A\subseteq [N]$
.
Let
$S \subseteq [N]$
with
$|S|\geq \alpha_0 N^m$
. Then by Lemma 3.6, there exists a translation A
′ of A such that
$|S\cap A'|\geq \frac{\alpha_0}{2^m}|A'|$
. Hence, by Lemma 3.4, the set S contains a
$C_{\varepsilon}(m,k)$
. The result now follows since
\begin{align*} |S|\geq \alpha_0 N^m=2^mN^{m-c'(\log(1/\varepsilon))^{-1}}>N^{m-c_2(\log(1/\varepsilon))^{-1}}\end{align*}
for appropriate
$c_2$
.
Acknowledgement
We would like to thank the anonymous referee for the valuable comments including pointing out an omitted case in the original version of the manuscript.
