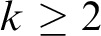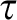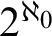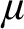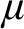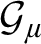1 Introduction
Zilber conjectured that every strongly minimal set was (essentially) bi-interpretable either with a strongly minimal set whose associated acl-geometry was trivial or locally modular, or with an algebraically closed field. Hrushovski [Reference Hrushovski16] refuted that conjecture by a seminal extension of the Fraïssé construction of
$\aleph _0$
-categorical theories as ‘limits’ of finite structures to construct strongly minimal (and so
$\aleph _1$
-categorical) theories. In this paper we modify Hrushovski’s method to construct
$2^{\aleph _0}$
-many strongly minimal Steiner systems that also violate Zilber’s conjecture. The examples arising from Hrushovski’s construction have been seen as pathological, and there has been little work exploring the actual theories. The new examples that we construct here are infinite analogs of concepts that have been central to combinatorics for 150 years.
Our construction of strongly minimal linear spaces via a Hrushovski construction might lead in two directions: (i) explore infinite Steiner systems investigating combinatorial notions appearing in such papers as [Reference Cameron5, Reference Cameron and Webb6, Reference Ganter and Werner11, Reference Stein24]; (ii) search for further mathematically interesting strongly minimal sets with exotic geometries. This paper is an essential prerequisite for the sequel [Reference Baldwin and Shi2], where we address both issues by showing the examples here admit no parameter-free definable binary function, expand the techniques used here to construct strongly minimal quasigroups, and extend the combinatorial analysis of [Reference Cameron and Webb6] to those quasigroups.
Our construction combines methods from the theory of linear spaces/combinatorics and model theory. A linear space (Definition 2.2) is a system of points and lines such that any two points determine a unique line. A Steiner k-system is a linear space such that all lines have size k. We explain strong minimality below and explore its connection with Steiner systems in Section 2.2.
The key ingredient of our construction is the development in [Reference Paolini22] of a new model theoretic rank function inspired by Mason’s
$\alpha $
-function [Reference Mason20], which arose in matroid theory. Using this new rank to produce a strongly minimal set requires a variant on the Hrushovski construction [Reference Hrushovski16] with several new features. This is the first of a series of papers exploring these examples. Here are the main results of this paper; they depend on definitions explained below.
-
• Theorem 2.5: The one-sorted (Definition 2.1) and two-sorted (Definition 2.2) notions of linear space are bi-interpretable.
-
• Theorem 2.9(2): For each k, with
$3 \leq k < \omega $
, there are
$2^{\aleph _0}$
-many strongly minimal theories
$T_\mu $
(dependingFootnote
1
on an integer valued function
$\mu $
) of infinite linear spaces in the one-sorted vocabulary
$\tau $
that are Steiner k-systems. -
• Conclusion 5.26: Each theory
$T_\mu $
admits weakFootnote
2
elimination of imaginaries, its geometry is not locally modular, but it is CM-trivial and so it does not interpret a field. Thus, it violates Zilber’s conjecture.
The last two results make sense only in the one-sorted vocabulary
$\tau $
(see below for a more detailed explanation of this). This phenomena is symptomatic of the interplay among model theory, finite geometries and matroid theory. Notions in these areas are ‘almost’ the same. Sometimes ‘almost’ is good enough and sometimes not. The same intuitive structures are formalized in different vocabularies and in different logics depending on the field. Theorem 2.5 addresses this issue; further refinements on bi-interpretability appear in Section 2.1 and even more in [Reference Baldwin and Shi2].
Much of the current research on strongly minimal theories (as opposed for example to the strongly minimal sets discovered in differentially closed fields) focuses on classifying the attached
$\mathrm {acl}$
-geometry. Work of Evans, Ferreira, Hasson, and Mermelstein [Reference Evans and Ferreira9, Reference Evans and Ferreira10, Reference Hasson and Mermelstein14, Reference Mermelstein21] suggests that up to arity or more precisely, purity, (and modulo some apparently natural conditionsFootnote
3
) any two
$\mathrm {acl}$
-geometries associated with strongly minimal Hrushovski constructions are locally isomorphic. This analysis is orthogonal to our program, which focuses on the particular strongly minimal theories constructed.
A key difference from the finite situation is that k-Steiner systems of finite cardinality v occur only under strict number theoretic conditions on v and k. In contrast, for every k, we construct theories with countably many models in
$\aleph _0$
and one in each uncountable power that are all Steiner k-systems. But the number theory reappears when we attempt to find algebraic structures associated with these geometries. One goal is to coordinatize the Steiner systems by nicely behaved algebras. A substantial literature [Reference Stein25, Reference Stein24, Reference Ganter and Werner11, Reference Ganter, Werner, Lindner and Rosa12] builds a correspondence between k-Steiner systems and certain varieties of universal algebras. But while this correspondence is a bi-interpretation for
$k =3$
, it does not rise to that level in general. Indeed, for
$k>3$
, we show [Reference Baldwin and Shi2] that none of the strongly minimal Steiner systems constructed here interpret a quasi-groupFootnote
4
. We also prove there that for q a prime power, and V an appropriate variety, for each of our theories
$T_\mu $
there is a theory
$T_{\mu ,V}$
of a strongly minimal quasigroup in V that interprets a q-strongly minimal Steiner system.
Section 2 provides background on strong minimality and linear spaces, and proves the bi-interpretability between the one and two-sorted approach. Sections 3 and 4 lay out the distinctions in the basic theory between the general Hrushovski approach and the specific dimension function for linear spaces studied here. In Section 5 we prove the main existence theorem for strongly minimal Steiner systems and discuss the connection with recent work on the model theory of Steiner systems. For space reasons, this paper has been substantially shortened from a version at https://arxiv.org/abs/1903.03541 that contains a few proofs hinted at here and much more extensive discussion of the background for the results. We thank the referee for a very helpful report.
2 Linear spaces
In this section firstly we explore the relationships between the one-sorted approach to linear spaces (Definition 2.1) and the two-sorted approach (Definition 2.2), and show that the two approaches are bi-interpretable (Theorem 2.5). We then show how the assumption of strong minimality imposes very strong conditions on a linear space (Fact 2.7): all lines are finite and of bounded length.
2.1 One and two-sorted formalization
Definition 2.1 (Linear Spaces in
$\tau $
)
Let
$\tau $
contain a single ternary relation symbol R which holds of sets of
$3$
distinct elements in any order.
${\boldsymbol {K}}^{\ast }$
, the class of linear spaces, consists of the
$\tau $
-structures that satisfy: any two distinct points determine a unique line when R is interpreted as collinearity. That is,
$R(x,y,z) \wedge R(x,y,w) \rightarrow R(x,w,z)$
. Each pair of elements is regarded as lying on a (trivial) line; each nontrivial line is a maximal R-clique.
${\boldsymbol K}^*_0$
denotes the collection of finite structures in
${\boldsymbol {K}}^{\ast }$
.
Definition 2.2 (Linear Spaces in
$\tau ^+$
)
A linear space is a structure S for a vocabulary
$\tau ^+$
with unary predicates P (points) and L (lines) and a binary relation I (incidence) satisfying the following properties:
-
(A) any two distinct points lie on at exactly one line;
-
(B) each line contains at least two points.
${\boldsymbol {K}}^+$
denotes the collection of
$\tau ^+$
-structures that are linear spaces.
Remark 2.3. We omit in Definition 2.2 the usual nontrivality condition that there are at least three points not on a common line. It will of course be true of the infinite structures that we construct, but allowing even the empty structure is technically convenient.
The switch from a
$2$
-sorted to a
$1$
-sorted formalism leads to some peculiar notation. In the two-sorted world, a line in
$(M; P^M, L^M)$
can gain points when M is extended. In the one-sorted context a line is a subset of the universe which is definable from any two points lying on it. But this definition is nonuniform. If the line is trivial (only two points) the definition is
$x=a \vee x = b$
; if the line is nontrivial the definition is
$R(a,b,x)$
. As a model M is extended, not only may a line gain points, but the correct such definition can change.
In the next definitions, we regard a linear space in the vocabulary
$\tau ^+$
(cf. Definition 2.2) as a
$\tau $
-structure (cf. Definition 2.1); this is easily done. Given a
$\tau ^+$
-structure B as in Definition 2.2, define a
$\tau $
-structure A by letting A be
$P(B)$
,the points of B, and define
$R(a,b,c)$
to hold if and only there is line
$\ell $
in B such that each of
$a,b,c$
is on
$\ell $
.
Remark 2.4. We now show that the class
$\boldsymbol {K}^{\ast }$
(Definition 2.1) of single-sorted linear spaces is bi-interpretable with the class
$\boldsymbol {K}^+$
of linear spaces in the two-sorted vocabulary
$\tau ^+$
(cf. Definition 2.2). Notice that conditions (A) and (B) of Definition 2.2 imply that every pair of distinct lines intersects in at most one point. Also, recall that we allow models with no points or lines.
We now define a pair of mutually inverse bijections from the models of a class of
$\tau $
-structures to a class of
$\tau ^+$
-structures and back that are uniformly definable, respect isomorphism, and preserve substructure.
Theorem 2.5.
-
(1) There is an interpretation F of
${\boldsymbol {K}}^+$
into
${\boldsymbol {K}}^{\ast }$
. That is, for every
$A \in {\boldsymbol {K}}^{\ast }$
there is a
$\tau ^+$
-structure
$F(A) \in {\boldsymbol {K}}^+$
definable without parameters in A. -
(2) There is an interpretation G of
${\boldsymbol {K}}^{\ast }$
into
${\boldsymbol {K}}^+$
. That is, for every
$B\in {\boldsymbol {K}}^+$
there is a
$\tau $
-structure
$G(B) \in {\boldsymbol {K}}^{\ast }$
definable without parameters in B. -
(3) For any
$A\in {\boldsymbol {K}}^{\ast }$
,
$G(F(A))$
is definably isomorphic to A and for any
$B\in {\boldsymbol {K}}^+$
,
$F(G(B))$
is definably isomorphic to B. Thus we have a bi-interpretation.
Proof We prove (1). Let
$A \in {\boldsymbol {K}}^{\ast }$
. Set
$P = \{ (a, a) \colon a \in A \}$
as the set of points of the
$\tau ^+$
-structure
$F(A)$
. Towards describing the lines, define the following equivalence relation E on
$A^2 - P$
by declaring
$(a, b) \mathbin{E} (c, d)$
if and only if the following condition is met:
$$ \begin{align} \{ a, b \} = \{ c, d \} \text{ or } \{ a, b \} \cup \{ c, d \} \text{ is an }R\text{-clique}. \end{align} $$
We verify that E is transitive. To this end, suppose that
$(a, b) \mathbin{E} (c, d)$
and
$(c, d) \mathbin{E} (e, f)$
,
$e \neq f$
,
$\{ a, b \} \neq \{ c, d \}$
and
$\{ c, d \} \neq \{ e, f \}$
. Since each pair is of distinct elements both
$\{a,b,c,d\}$
and
$\{c,d,e,f\}$
are R-cliques and since two points determine a line
$\{a,b,c,d,e,f\}$
is an R-clique and transitivity is established. Now, let
$$ \begin{align*}L = \{ [(a, b )]_E : (a, b) \in A^2 \text{ such that } a \neq b \}\end{align*} $$
be the set of lines of
$F(A)$
. For
$(p,p) \in P$
and
$[(a, b)]_E \in L$
define the following point-line incidence relation:
$$ \begin{align*}(p,p) \mathbin{I} [(a, b)]_E \Leftrightarrow \exists (c, d) \in [(a, b)]_E \text{ such that } p \in \{ c, d \}.\end{align*} $$
Clearly,
$F(A)$
is definable in the
$\tau $
-structure
$(A,R)$
. We show that
$F(A)\in {\boldsymbol {K}}^+$
, that is, Definition 2.2 is satisfied. Obviously, Axiom (B) is satisfied. We prove axiom (A). Towards this goal, let
$\ell _1$
and
$\ell _2$
be two distinct lines of
$F(A)$
that intersect (via the definition of I) in two distinct points
$(b_1,b_1)$
and
$(b_2,b_2)$
. By hypothesis
$\ell _1 \neq \ell _2$
and so, we can assume
$\ell _1 = [(b_1,b_2)]_E$
and there is
$(c, d) \in A^2$
such that
$c \neq d$
,
$\neg E((b_1, b_2), (c, d))$
and
$(c, d) \in \ell _2$
. Note that any E-equivalence class of element with more than 3 elements consists of an R-clique and distinct R-cliques can intersect in only one point; so, we finish.
We prove (2). Let
$B\in {\boldsymbol {K}}^+$
. Define the
$\tau $
-structure
$G(B) =(A,R)$
by letting A be the points of B and defining
$R(a,b,c)$
if and only if
$a,b,c$
are distinct and there is a line
$\ell $
in B such that each of
$a,b,c$
is on
$\ell $
. Since B is a linear space the axioms of
${\boldsymbol {K}}^{\ast }$
are immediate.
We prove (3) by showing that up to definable isomorphism G is
$F^{-1}$
. Fix A and
$F(A)$
from (1). We analyze the composition
$G(F(A))$
and show the image is definably isomorphic to A. The set of points,
$P^{F(A)}$
, is the diagonal
$\Delta (A^2)$
of
$A^2$
. Map
$(a,a)$
to a. The set of lines of
$F(A)$
is
$L^{F(A)}=(A^2- \Delta (A^2))/E$
. Let
$m \in L^{F(A)}$
and suppose
$ (a_0,a_0), (a_1,a_1), (a_2,a_2)$
are on m, where the
$a_i$
are distinct. By the definition of I in
$F(A)$
, for each
$i<3$
there exists an
$a^{\prime }_i$
such that for
$i\neq j$
,
$[(a_i,a^{\prime }_i)]_E = [(a_j,a^{\prime }_j)]_E$
. By
$(*)$
this implies the
$a_i, a^{\prime }_i$
for
$i< 3$
(some may be repeated) form an R-clique in A. Thus
$G(F(A))$
is definably isomorphic to A. Now we reverse the procedure and show that for
$B \in {\boldsymbol {K}}^+$
,
$F(G(B))$
is definably isomorphic to B. This is even easier. If
$a,b,c$
are collinear in B, then
$G(B) \models R(a,b,c)$
(Note
$P^B$
is the domain of
$G(B)$
). For this, recall the argument in part (1) showing
$F(A) \in {\boldsymbol {K}}^{\ast }$
takes collinear points of A into a clique composed of elements of the diagonal of
$G(B)$
, which correspond to a clique in B. Applying this argument to
$G(B)$
completes the proof. Finally, this shows, in the case at hand, the essential point of [Reference Makowsky19], that F is onto from
${\boldsymbol {K}}^{\ast }$
to
${\boldsymbol {K}}^+$
.⊣
2.2 Strongly minimal linear spaces
Strong minimality imposes significant restrictions due to the following easy consequence of the compactness theorem:
Fact 2.6. If M is strongly minimal, then for every formula
$\varphi (x,\overline {y})$
, there is an integer
$k = k_\varphi $
such that for any
$\overline {a} \in M$
,
$(\exists {{\hspace {-0.0001pt}}}^{>k_\varphi } x) \varphi (x,\overline {a})$
implies that there are infinitely many solutions of
$\varphi (x,\overline {a})$
, and thus finitely many solutions of
$\neg \varphi (x,\overline {a})$
.
Fact 2.6 has an immediate consequence for any strongly minimal linear space,
$(M,R)\in {\boldsymbol {K}}^{\ast }$
(cf. Definition 2.1), where all lines have at least 3 points: there can be no infinite lines. Suppose
$\ell $
is an infinite line. Choose A not on
$\ell $
. For each
$B_i, B_j$
on
$\ell $
the lines
$AB_i$
and
$AB_j$
intersect only in A. But each line
$AB_i$
has a point not on
$\ell $
and not equal to A. Thus
$\ell $
has an infinite definable complement, contradicting strong minimality. More strongly, we observe:
Fact 2.7. If
$(M,R)$
is a strongly minimal linear space, then there exists an integer k such that all lines have length at most k.
As,
$R(x,y,z)$
meansFootnote
5
$x,y,z$
are collinear, that is, x is on the line determined by
$y,z$
, applying Fact 2.6 we see that there is
$k = k_R$
such that
$(\exists {{\hspace {-0.0001pt}}}^{>k_R} x) R(x,a,b )$
implies the line through
$a,b$
is infinite, which contradicts the preceding paragraph. In particular, there can be no strongly minimal affine or projective plane, since in such planes the number points on a line must equal the number of lines through a point (
$+1$
in the finite affine case).
Definition 2.8. Let
$K \subseteq \omega $
. We say that the linear space S is a K-Steiner system if any line of S is finite and its size is in K. When
$K = \{k\}$
we simply write k-Steiner system instead of
$\{k\}$
-Steiner system.
The main goal of our paper is to prove item (2) of the next theorem, where item (1) is just a reformulation of Fact 2.7.
Theorem 2.9.
-
(1) A strongly minimal infinite linear space in the vocabulary
$\tau $
(cf. Definition 2.1
) is a K-Steiner system for some finite set
$K \subseteq \omega $
. -
(2) For each
$3 \leq k < \omega $
, we construct continuum-many strongly minimal infinite linear spaces in the vocabulary
$\tau $
that are k-Steiner systems.
3 The specific context
We develop in this section the basic properties of the essential ingredient in the construction of our strongly minimal Steiner systems, a new predimension function
$\delta $
(cf. Definition 3.3), introduced in [Reference Paolini22]. It was inspired by Mason’s
$\alpha $
-function [Reference Mason20], a well-known measure of complexity for matroids. We define this function explicitly without exploring the
$\alpha $
-function. For the connection see [Reference Paolini22, Section 3].
-
(1) For any class
${\boldsymbol {L}}_0$
of finite structures for a vocabulary
$\sigma $
that is closed under substructure,
$\hat {\boldsymbol {L}}_0$
denotes the class of all
$\sigma $
-structures M such that every finite substructure of M is in
${\boldsymbol {L}}_0$
. -
(2) Given an arbitrary class of structures
${\boldsymbol {L}}$
for a vocabulary
$\sigma $
we denote by
${\boldsymbol {L}}_0$
the class of finite structures in
${\boldsymbol {L}}$
. (For convenience, we allow the empty structure.) -
(3) We write
$\backsimeq $
for isomorphism and
$X\subseteq _\omega Y$
for finite subset.
The following notation will clarify the distinction between 2-element lines (a.k.a. trivial lines) which are understood to hold of arbitrary pairs of elements from models in
${{\boldsymbol K}}^{\ast }$
and lines where the relation symbol R is explicit (cf. Definition 2.1).
Definition 3.2. Let
$A, B \in {\boldsymbol {K}}^{\ast }$
(cf. Definition 2.1).
-
(1) The subspace closure
$\mathrm {cl}_R(X)$
in A, is the smallest subset B of A containing X such that if
$a\in A$
satsfies
$R(b_1,b_2,a)$
with the
$b_i \in B$
, then
$a \in B$
. -
(2) A line of A is an R-closed subset X of A such that all the points from X are collinear. In particular, if two points
$a \neq b \in A$
and there is no
$c \in A$
with
$R(a,b,c)$
, then
$\{a,b\}$
is a line. We call such lines ‘trivial’. -
(3) We denote the cardinality of a line
$\ell \subseteq A$
by
$|\ell |$
, and, for
$B \subseteq A$
, we denote by
$|\ell |_B$
the cardinality of
$\ell \cap B$
. -
(4) We say that a line
$\ell $
contained in A is based in
$B \subseteq A$
if
$|\ell \cap B| \geq 2$
, in this case we write
$\ell \in L(B)$
. -
(5) The nullity of a line
$\ell $
contained in a structure
$A \in {\boldsymbol {K}}^{\ast }$
is:
$$ \begin{align*}\mathbf{n}_A(\ell) = |\ell| - 2.\end{align*} $$
Note that if
$ B\subseteq A$
are both in
${\boldsymbol {K}}^{\ast }$
, and
$\ell \subseteq A$
is a line then
$\ell \cap B$
may be in
$L(B)$
(if it has at least two points) but may not be R-closed in B (i.e.,if
$\ell -B \neq \emptyset $
). We introduce the new rank
$\delta $
that is central to this paperFootnote
6
. It has two key features: (i) it is based on the notion of ‘dimension’ of a line; (ii) the associated geometry is flat, and so we get counterexamples to Zilber’s conjecture.
Definition 3.3. For
$A \in {\boldsymbol {K}}^{*}_0$
(recall Definitions 2.1 and 3.1(2)), let:
$$ \begin{align*}\delta(A) = |A| - \sum\limits_{\ell \in L(A)} \mathbf{n}_A(\ell).\end{align*} $$
Definition 3.4.
-
(1) Let:
and
$$ \begin{align*}{\boldsymbol{K}}_0 = \{ A \in {\boldsymbol {K}}^{*}_0 \text{ such that for any } A' \subseteq A,\delta(A') \geq 0\},\end{align*} $$
$({\boldsymbol {K}}_0, \leq )$
be as in [Reference Baldwin3, Definition 3.11], that is,we let
$A \leq B$
if and only if:
$$ \begin{align*}A \subseteq B \wedge \forall X (A \subseteq X \subseteq B \Rightarrow \delta(X) \geq \delta(A)).\end{align*} $$
-
(2) We write
$A < B$
to mean that
$A \leq B$
and A is a proper subset of B. -
(3) For any X, the least subset of A containing X that is strong in A is called the intrinsic or self-sufficient closure of X in A and denoted by
$\mathrm {icl}_A(X)$
or
$\overline {X}$
.
Since in the current situation we are dealing with integer coefficients, for our
$\delta $
the intrinsic closure of every finite set is finite. Note that
${\boldsymbol {K}}_0$
has many fewer structures that
${\boldsymbol {K}}^*_0$
. In particular, no projective plane (except the Fano plane, Example 4.3) or space A over a finite field is in
${\boldsymbol {K}}_0$
; as, for each such A,
$\delta (A)<0$
.
We give a general conceptual analysis for submodularityFootnote
7
and flatness of
$\delta $
that clarifies the proofs of Lemmas 3.7 and 5.26 (flatness of d).
Definition 3.5.
-
(1) Let f be a function from a set
${\boldsymbol {K}}_0$
of finite structures to the non-negative integers. For S with
$\emptyset \subsetneq S \subseteq \{1,\ldots, s\} =I$
and a sequence
$F_1,\ldots,F_s$
of elements of
${\boldsymbol {K}}_0$
, we let
$F_S = \bigcap _{i\in S} F_i$
and
$F_{\emptyset } = \bigcup _{1\leq i \leq s} F_i$
. We say that f is flat if for all
$F_1,\ldots,F_s \in {\boldsymbol {K}}_0$
we have:
$$ \begin{align*}(*) \hspace{.1in} f(\bigcup\limits_{1\leq i \leq s} F_i) \leq \sum\limits_{\emptyset \neq S} (-1)^{|S|+1} f(F_S).\end{align*} $$
-
(2) Suppose
$(A, \text {cl})$
is a pregeometry on a structure M with dimension function d and
$F_1,\ldots,F_s$
are finite-dimensional d-closed subsets of A. Then
$(A, \text {cl})$
is flat if d satisfies equation
$(*)$
.
In the basic Hrushovski case,
$\delta $
is flat because it is the difference between two functions, the cardinality of each set, which satisfies inclusion–exclusion, and counting the number of occurrences of R in each set, which undercounts. We now note our
$\delta $
is similarly represented and that
$\delta $
is modular on the appropriate notion of free amalgam:
$A \oplus _C B$
in
${\boldsymbol {K}}_0$
.
Definition 3.6. Let
$A \cap B =C$
with
$A,B,C \in {\boldsymbol {K}}_0$
. We define
$D:= A \oplus _{C} B$
as follows:
-
(1) the domain of D is
$A \cup B$
; -
(2) a pair of points
$a \in A - C$
and
$b \in B - C$
are on a nontrivial line
$\ell '$
in D if and only if there is a line
$\ell $
based in C such that
$a \in \ell $
(in A) and
$b \in \ell $
(in B). Thus, in this case,
$\ell '=\ell $
(in D).
Lemma 3.7.3 follows from submodularity and the particular definition of free amalgam which is driven by ‘two points determine a line’.
Lemma 3.7.
-
(2) Let
$A, B, C \subseteq D \in {\boldsymbol {K}}^{*}_0$
, with
$A \cap C = B$
. Then: which an easy calculation shows is equivalent to submodularity:
$$ \begin{align*}\delta(A/B) \geq \delta(A/C),\end{align*} $$
$$ \begin{align*}\delta(A\cup C) \leq \delta(A) + \delta(C) - \delta(B).\end{align*} $$
-
(3) If
$E \cap F = D$
,
$D\leq E$
and
$E,F, D \in {\boldsymbol {K}}_0$
then
$G = F \oplus _D E$
is in
$ {\boldsymbol {K}}_0$
. Moreover,
$\delta (F \oplus _{D} E)= \delta (F) +\delta (E) - \delta (D)$
and any P with
$D \subseteq P \subseteq F \oplus _{D} E$
is also free. Thus,
$F \leq G$
.
Proof (1) Recall
$\delta (A) = |A| - \Sigma _{\ell \subseteq A} (|\ell | -2$
). Observe that if
$A,B$
are sets and
$\ell $
is a line in
$A\cup B$
, then:
$$ \begin{align*}|\ell|=|\ell \cap A| + |\ell \cap B| - |\ell \cap (A\cap B)|.\end{align*} $$
But in computing
$\delta (\bigcup _{1\leq i \leq s} F_i)$
on the right hand of (*) one must sum for each S only over those lines based in
$F_S$
. Thus for example, in the case of two sets
$A,B$
, if a line is based in
$A-B$
and has a single point in
$C-B$
(and none in B) that point will not be counted on the right-hand-side but will be on the left. So the subtracted term of
$\delta (F_S)$
is under-counted and
$\delta (F_S)$
is overcounted. This is not corrected at the next step because no
$\ell $
is based there. Thus,
$\delta $
is flat.
(2) Since
$\delta $
is a difference of two counting functions, submodularity is just the notion of flat for two sets.
(3) We need to check that each pair of points
$a_0,a_1$
determine a unique line in G. Without loss of generality, one is in
$F-D$
and the other in E. Suppose for contradiction there are two distinct lines on which both of
$a_0,a_1$
are incident. If both lines are contained in F, the claim is obvious. But, if not, Definition 3.6 guarantees that both of
$a_0,a_1$
are on a unique line based in D.
By the general submodularity argument,
$\delta (F\oplus _{D} E)\leq \delta (F) +\delta (E) - \delta (D)$
. But the definition of the free amalgamation guarantees that each line that intersects
$F-D$
and
$E-D$
in based on two points in D. There is no undercount as there may be in (2) so we have equality.⊣
Reference [Reference Baldwin3] provides a set of axioms for strong substructure. These axioms can be seen to hold in our situation using Lemma 3.7.
Fact 3.8.
$({\boldsymbol {K}}_0, \leq )$
satisfies Axiom A1–A6 from [Reference Baldwin3, Axioms Group A], that is,
-
(1) if
$A \in {\boldsymbol {K}}_0$
, then
$A \leq A$
; -
(2) if
$A \leq B \in {\boldsymbol {K}}_0$
, then A is a substructure of B; -
(3) if
$A, B, C \in {\boldsymbol {K}}_0$
and
$A \leq B \leq C$
, then
$A \leq C$
; -
(4) if
$A, B, C \in {\boldsymbol {K}}_0$
,
$A \leq C$
, B is a substructure of C, and A is a substructure of B, then
$A \leq B$
; -
(5)
$\emptyset \in {\boldsymbol {K}}_0$
and
$\emptyset \leq A$
, for all
$A \in {\boldsymbol {K}}_0$
; -
(6) if
$A, B, C \in {\boldsymbol {K}}_0$
,
$A \leq B$
, and C is a substructure of B, then
$A \cap C \leq C$
.
We use the following notion of genericity:
Definition 3.9. The countable model
$M\in \hat {\boldsymbol {K}}_0$
is
$({{\boldsymbol {K}}_0}, \leq )$
-generic when:
-
(1) if
$A\leq M, A\leq B\in {\boldsymbol {K}}_{0}$
, then there exists
$B'\leq M $
such that
$ B\backsimeq _{A} B'$
; -
(2) M is a union of finite substructures from
${\boldsymbol {K}}_0$
.
4 Primitive extensions and good pairs
Using only the
$\delta $
function one can build up models in
${\boldsymbol {K}}_0$
from well-defined building blocks: primitive extensions and good pairs (Definition 4.1). This section is an analysis of these foundations. In the next section we use them to study the complete theories we are constructing.
Definition 4.1. Let
$A, B \in {\boldsymbol {K}}_0$
.
-
(1) We say that A is a primitive extension of B if
$B \leq A$
and there is no
$A_0$
with
$B \subsetneq A_0 \subsetneq A$
such that
$B \leq A_0 \leq A$
. Equivalently, we may describe a primitive pair as
$(B,A)$
where B and A are disjoint (and so
$BA$
is the set in the initial description). -
(2) If
$\delta (A/B) =0$
, we write
$0$
-primitive. We stress that in this definition while B may be empty, A cannot be. -
(3) We say that the
$0$
-primitive pair
$A/B$
is good if there is no
$B' \subsetneq B$
such that
$(A/B')$
is
$0$
-primitive. When discussing good pairs, usually A and B are disjoint; for ease of notation, sometimes A is confused with
$A \cup B$
. -
(4) If A is
$0$
-primitive over B and
$B' \subseteq B$
is such that we have that
$A/B'$
is good, then we say that
$B'$
is a base for A (or sometimes for
$AB$
). -
(5) If the pair
$A/B$
is good, then we also write
$(B,A)$
is a good pair.
Remark 4.2. Note that if C is primitive over the empty set then the unique base for C is
$\emptyset $
. For, if there is
$B\neq \emptyset $
with
$B \subsetneq C$
with C based on B, then
$\emptyset \leq B$
and
$B \subsetneq C$
contradicting that C is primitive over the empty set. This does not forbid the existence of
$C \in {\boldsymbol {K}}_0$
such that
$\delta (C/\emptyset ) = 0$
but C is not primitive over
$\emptyset $
; on this see Lemma 5.25.
Example 4.3. Some sets are based on the empty set. In particular, if C is the
$\tau $
-structure representing the unique 7 point projective plane (often called the Fano plane), then
$\delta (C)= 0$
. And it is easy to see
$(\emptyset ,C)$
is a good pair.
In earlier variants of the Hrushovski’s construction one could prove the existence of a unique base
$B'$
for any given
$0$
-primitive extension
$A/B$
. Unfortunately, this assertion is false in the current situation; cf. Example 4.4. We make up for this with a careful examination of the structure of good pairs that almost regains uniqueness.
Example 4.4. For
$A \in {\boldsymbol {K}}_0$
containing
$m + 2$
points
$p_1,\ldots,p_{m+2}$
on a line
$\ell $
and for some c such that
$c \not \in \{ p_1,\ldots,p_{m+2} \}$
but c is on
$\ell $
in
$A \cup \{c\}$
; we have that c is
$0$
-primitive over A, and any pair of points in
$\ell \cap A$
constitutes a base for
$c/A$
.
The following preparatory results allow us to characterize primitive extensions and eventually prove amalgamation for
$({\boldsymbol {K}}_{\mu }, \leq )$
(cf. Conclusion 5.13).
Proposition 4.5. Let
$B \in {\boldsymbol {K}}_0$
and
$b \in B$
such that b does not occur in any R-tuple from B, then
$\delta (B) = \delta (B - \{ b \}) + 1$
.
Using the above proposition, we can see:
Proposition 4.6. Let
$A, B \in {\boldsymbol {K}}_0$
with
$A \cap B = \emptyset $
,
$AB \in {\boldsymbol {K}}_0$
and
$B \leq AB$
. Then:
-
(1) if there exists
$b \in B$
such that b does not occur in any R-tuple from
$AB$
, and
$B'$
denotes
$B - \{ b \}$
, then
$\delta (A/B) = \delta (A/B')$
. -
(2) if the
$0$
-primitive pair
$A/B$
is good (cf. Definition 4.1(2)), then for every
$b \in B$
we have that b occurs in an R-tuple from
$AB$
.
Proof It suffices to prove (1), and (1) is clear by applying Proposition 4.5 to
$AB$
as follows:
$$ \begin{align*}\delta(A/B) = \delta(AB) - \delta(B) = (\delta(AB') + 1) - (\delta(B') + 1) = \delta(AB') - \delta(B').\\[-5.5pc] \end{align*} $$
⊣
We omit the short proof, using Proposition 4.5, of Lemma 4.7.
Lemma 4.7. Suppose C is a primitive extension of B such that
$|(C-B)| \geq 2$
, then every nontrivial line
$\ell $
with
$\ell \cap C \neq \emptyset $
intersects B in at most one point. Furthermore, if C is
$0$
-primitive, then any point in
$(C-B)$
lies on two lines based in
$(C-B)$
.
The next lemma is the fundamental tool for our analysis of primitive extensions.
Lemma 4.8. Let
$B \leq C \in {\boldsymbol {K}}_0$
be a primitive extension. Then there are two cases:
-
(1)
$\delta (C/B) = 1$
and
$C = B \cup \{ c \}$
; -
(2)
$\delta (C/B) = 0$
.-
(2.1) There is
$c \in (C-B)$
incident with a line
$\ell $
based in B if and only if
$|(C-B)| = 1$
. In that case, any
$B' \subseteq B$
with
$B'\subseteq \ell $
and such that
$|B'|=2$
yields a good pair
$(B',c)$
. Furthermore, c is in the relation R with an element
$b \in B$
if and only if b is on the unique line based in
$B'$
.
-
(2.2) If
$|(C-B)| \geq 2$
then there is a unique base
$B_0$
in B for C. Moreover, suppose
$b \in B$
and
$c \in (C-B)$
. If b and c lie on a nontrivial line, then
$b\in B_0$
. And every
$b\in B_0$
lies on such a line, which must be based in
$(C-B)$
.
-
Proof We follow the case distinction of the statement of the lemma:
-
Case 1. Suppose
$\delta (C/B)>0$
and there are distinct elements in
$(C-B)$
that are not on lines based in B, then any one of them gives a proper intermediate strong extension of B that is strong in C. Thus C must add only one element to B yielding Case 1. -
Case 2. Suppose
$\delta (C/B) =0$
.-
Case 2.1. Suppose there is an element
$c \in (C-B)$
which is on a line with two points in B, say
$b_1,b_2$
, and
$|(C-B)| \geq 2$
. Then clearly
$Bc$
is a primitive extension of B and
$Bc \lneq BC$
. Thus,
$(C-B)$
must be
$ \{c\}$
. Furthermore,
$(\{b_1,b_2\},c)$
is a good pair. So C is based on
$\{b_1,b_2\}$
and for any
$b \in B$
, b is R-related to c if and if
$R(b_1,b_2,b)$
; otherwise c would be on two lines based in B (contradicting
$B \leq C$
). Conversely, if
$|(C-B)| = 1$
then c must be on a line based in B since
$\delta (C/B) = 0$
. -
Case 2.2.
$|(C-B)| \geq 2$
and
$\delta (C/B) =0$
. By Lemma 4.7, each line
$\ell \in L((C-B))$
intersects B in at most one point
$b_{\ell }$
. If there is no such
$b_\ell $
, then there is no R-relation between
$(C-B)$
and B, so by Proposition 4.6(2),
$B = \emptyset $
and C is based on
$\emptyset $
. As argued in Remark 4.2, that base must be unique. If there is such a
$b_\ell $
, let
$B_0$
be the collection of all the
$b_\ell $
,
$\ell \in L((C-B))$
. By Lemma 4.6.(1),
$\delta (C/B_0)=\delta (C/B)$
, and so
$(B_0,C)$
is a good pair. Further
$B_0$
is the unique base for C as these are the only elements of B on lines that intersect
$(C-B)$
.⊣
-
Omer Mermelstein provided us with an example showing there are infinitely many primitives based on a single three element set. But the study of
$(a,b)$
cycles in [Reference Baldwin and Shi2] led to stronger and simpler examples over smaller base sets. Recall that any linear space with
$3$
-point lines is an example of Steiner triple system (Definition 2.8.2). In the next definition, used to prove Lemma 4.10, we generalize the notion from [Reference Cameron and Webb6] of an
$(a,b)$
-cycle graph in a Steiner triple system.
Definition 4.9. Fix any two points
$a,b$
of a Steiner m-system
${\mathcal {S}} = (P,L)$
. An
$(a,b)$
-cycle,
$C_k$
is a sequence
$c_1, c_2, \ldots , c_{4k}$
of length
$4k$
such that
$R(a,c_{2n+1}, c_{2n+2})$
for
$0\leq n \leq 2k$
,
$R(b, c_{2n+2},c_{2n+3})$
for
$0\leq n < 2k$
, and
$R(b, c_{1},c_{4k})$
.
In the Steiner triple system case a triple
$a,b,c_1$
with
$c_1$
not on
$(a,b)$
determines a unique cycle as described in Definition 4.9. For m-Steiner systems with
$m>3$
, we can choose such cycles but not uniquely. Note that the lines determined by the pairs of points
$c_n,c_{n+1}$
in Definition 4.9 must be distinct.
Lemma 4.10. There are infinitely many mutually nonembeddable primitives in
${\boldsymbol {K}}_0$
over a two-element set. In fact, there are infinitely many mutually nonembeddable primitives in
${\boldsymbol {K}}_0$
over the empty set and similarly over a
$1$
-element set.
Proof Over any
$a,b$
for each k build an
$(a,b)$
-cycle
$C_k$
, as in Definition 4.9.
$C_k$
has
$4k$
points and
$(\{a,b\} \cup C_k)\in {\boldsymbol {K}}_0$
has
$4k$
3-element lines. So
$\delta (\{a,b\}\cup C_k))= 2 = \delta (\{a,b\})$
. Primitivity easily follows since if the cycle is broken, the
$\delta $
-rank goes up. So
$(\{a,b\},C_k))$
is a good pair whose isomorphism type we denote by
$\boldsymbol {\gamma }_k$
.
To get primitives over
$\emptyset $
, let c be on
$ab$
and add the relations
$R(c,c_1,c_{2k+1}$
) and
$R(c,c_{k+1},c_{3k+1})$
. Now the entire structure
$D_k$
has
$4k+3$
points and
$4k+3$
lines and can easily be seen to be
$0$
-primitive over the empty set. (Note that for
$k=1$
, this is another avatar of the Fano plane.)
Remove one of the last two instances of R and the result is primitive over a or b. ⊣
5 The class
${\boldsymbol {K}}_\mu $
We now introduce the new classes of structures needed to obtain strong minimality. Recall that we have two classes: (i)
${\boldsymbol {K}}_0$
is a class of finite structures; (ii)
$\hat {\boldsymbol {K}}_0$
is the universal class generated by
${\boldsymbol {K}}_0$
. The new class
${\boldsymbol {K}}_\mu \subseteq {\boldsymbol {K}}_0$
adds additional restrictions so that the generic model for
${\boldsymbol {K}}_\mu $
is a strongly minimal linear space, and, in fact, a Steiner k-system for some k. Using Definition 5.6, we axiomatize the subclass
${\boldsymbol {K}}^\mu _d$
of
$\hat {\boldsymbol {K}}_\mu $
(the universal class generated by
${\boldsymbol {K}}_\mu $
) of those models that are elementarily equivalent to the generic for
${\boldsymbol {K}}_\mu $
.
The following notation singles out the effect of the fact that our rank depends on line length rather than the number of occurrences of a relation.
Notation 5.1 (Line length)
We write
$\boldsymbol {\alpha }$
for the isomorphism type of the good pair
$(\{b_1,b_2\},a)$
with
$R(b_1,b_2,a)$
(cf. Lemma 4.8(2.1)).
Definition 5.2. Recall the characterization of primitive extensions from Lemma 4.8.
-
(1) Let
${\mathcal {U}}$
be the collection of functions
$\mu $
assigning to every isomorphism type
$\beta $
of a good pair
$(B,C)$
in
${\boldsymbol {K}}_0$
(we write
$\mu (B,C)$
instead of
$\mu ((B,C))$
):-
(i) an integer
$\mu (\beta ) = \mu (B,C) \geq \delta (B)$
, if
$|C-B|\geq 2$
; -
(ii) an integer
$\mu (\beta ) \geq 1$
, if
$\beta = \boldsymbol {\alpha }$
(cf. Notation 5.1).
-
-
(2) For any good pair
$(B,C)$
with
$B \subseteq M$
and
$M \in \hat {\boldsymbol {K}}_0$
,
$\chi _M(B,C)$
denotes the number of disjoint copies of C over B in M. Of course,
$\chi _M(B,C)$
may be
$0$
. -
(3) Let
${\boldsymbol {K}}_{\mu }$
be the class of structures M in
$ {\boldsymbol {K}}_{0}$
such that if
$(B,C)$
is a good pair, then
$\chi _M(B,C) \leq \mu (B,C)$
. -
(4)
$\hat {\boldsymbol {K}}_\mu $
is the universal class generated by
${\boldsymbol {K}}_\mu $
(cf. Notation 3.1(1)).
In [Reference Baldwin and Shi2], we change the set
${\mathcal {U}}$
in various ways (and explore the combinatorial consequences of this change in the resulting generic model). In this paper, we assume
$\mu \in {\mathcal {U}}$
unless specified otherwise.
The value of
$\mu (\boldsymbol {\alpha })$
is a fundamental invariant in determining the possible complete theories of generic structures; in particular we will see that it determines the length of every line in the generic and thus in any model elementary equivalent to it.
Remark 5.3. We analyze the structure of extensions governed by good pairs with isomorphism type
$\boldsymbol {\alpha }$
from Notation 5.1. Suppose
$\{b_1,b_2,a\} \subseteq F \in {\boldsymbol {K}}_{\mu }$
with
$R(b_1, b_2, a)$
. The
$0$
-primitive extensions C of
$B= \{b_1,b_2\}$
with
$|(C-B)|=1$
are exactly the points on the line
$\ell $
through
$b_1,b_2$
. Any pair of points
$e_1, e_2$
from F that are on
$\ell $
form a base witnessed by
$(\{e_1,e_2\},a)$
with
$R(e_1,e_2,a)\wedge R(b_1,b_2,a) $
.
Most arguments for amalgamation in Hrushovski constructions (e.g., [Reference Baldwin1, Reference Holland15, Reference Hrushovski16, Reference Ziegler26]) depend on a careful analysis of the location of the unique base of a good pair. Here, when
$|(C-B)| =1$
, the uniqueness disappears and one must focus on the line rather than a particular base for it.
There are two general approaches to showing existence of complete strongly minimal theories by the Hrushovki construction. One divides the construction into two pieces, free and collapsed [Reference Goode, Dahn and Wolter13, Reference Ziegler26]. The final theory is taken as the sentences true in the generic model. The second, as the original [Reference Hrushovski16], provides a direct construction of the strongly minimal set. We choose here to follow Holland’s version of this approachFootnote
8
. She insightfully emphasised axiomatizing the theory of the class
${\boldsymbol {K}}^{\mu }_{d}$
of d-closed structures [Reference Holland15], which we now define, by clearly identifiable
$\pi _2$
-sentences. This established the model completeness that was left open in [Reference Hrushovski16]. In fact, we axiomatize the theory
$T_\mu $
of the class
${\boldsymbol {K}}^{\mu }_{d}$
, prove it is strongly minimal, and then observe that the generic satisfies
$T_\mu $
.
Definition 5.4. Fix the class
$({\boldsymbol {K}}_0,\leq )$
of
$\tau $
-structures as defined in Definition 3.4.
-
(1) For
$A\in \hat {{\boldsymbol {K}}}_0$
,
$X \subseteq _\omega A$
and
$a \in A$
, we let: and
$$ \begin{align*}d_A(X) = \min\{\delta(Y): X \subseteq Y \subseteq_\omega A\},\end{align*} $$
$$ \begin{align*}d_A(a/X) = d_A(aX) -d_A(X).\end{align*} $$
-
(2) [d-closure] For
$M\in \hat {{\boldsymbol {K}}}_\mu $
, and
$X \subseteq _\omega M$
: For infinite X,
$$ \begin{align*}\operatorname{\mathrm{cl^d_M}}(X) = \{a \in M: d_M(aX) = d_M(X)\}.\end{align*} $$
$a \in \operatorname {\mathrm {cl^d_M}}(X)$
if
$a \in \operatorname {\mathrm {cl^d_M}}(X_0)$
for some
$X_0\subseteq _\omega X$
.
-
(3) [d-closed] For
$M\in \hat {{\boldsymbol {K}}}_\mu $
and
$X \subseteq M$
, X is d-closed in M if
$d(a/X)= 0$
implies
$a \in X$
(equivalently, for all
$Y \subseteq _{\omega } M-X$
,
$d(Y/X)>0$
). -
(4) Let
${\boldsymbol {K}}^{\mu }_{d}$
consist of those
$M\in \hat {{\boldsymbol {K}}}_\mu $
such that
$M \leq N$
and
$N \in \hat {\boldsymbol {K}}_\mu $
imply M is d-closed in N.
The switch from
$\delta $
to d is designed to ensure that
$X \subseteq Y $
implies
$d(X) \leq d(Y)$
; the submodularity of d is verified as in, for example, [Reference Baldwin3, Reference Holland15, Reference Hrushovski16, Reference Ziegler26], and so the function d is truly a dimension function, thus inducing a matroid structure.
Fact 5.5. The d-closure operator
$ \operatorname {\mathrm {cl^d_M}}$
(cf. Definition 5.4(2)) induces a combinatorial pregeometry on any
$M \in \hat {\boldsymbol {K}}_\mu $
.
We use good pairs to build our axiomatization,
$\Sigma _\mu $
, of the theory of the class
${\boldsymbol {K}}^{\mu }_{d}$
. We write
$\Sigma _\mu $
as the union of four sets of first-order
$\tau $
-sentences:
$\Sigma ^0_\mu $
,
$\Sigma ^1_\mu $
,
$\Sigma ^2_\mu $
and
$\Sigma ^3_\mu $
. Before listing them, we explain the origin of the third group:
$\Sigma ^2_\mu $
. We would like to just assert the collection of universal-existential sentences: for all good pairs
$(B,C)$
with
$B \subseteq M$
,
$\chi _M(B,C) = \mu (B,C)$
. Unfortunately, some good pairs may conflict with each others, and so, as far as we know, the equality may fail for some good pairs when the base B is not strong in the model. Basically, this could happen because if
$(P,G)$
and
$(Q,F)$
are good pairs with
$QF$
contained in
$PG$
then realizing
$(P,G)$
implies that
$(Q,F)$
is automatically realized. In particular, note that the C of the good pair
$(B,C)$
of Example 5.7 contains a new good pair
$(B',C')$
.
The distinguishing property of models
$M \in {\boldsymbol {K}}^{\mu }_{d}$
is that since every
$0$
-primitive extension over a finite strong subset of M can be embedded in M, by Lemma 5.17, no proper
$0$
-primitive extension of M is in
$\hat {{\boldsymbol {K}}}_\mu $
. In fact, this property characterizes the models that are elementarily equivalent to the generic. A salient point about the generic for
${\boldsymbol {K}}_\mu $
, denoted
$\mathcal {G}_\mu $
(Notation 5.14), is that
$\mathcal {G}_\mu \in {\boldsymbol {K}}^{\mu }_{d}$
. This fact is not used directly in the proof of strong minimality of
$T_\mu $
; we will observe it in Proposition 5.16.
One reason for the difficulty in the axiomatization is that the function
$\mu $
is defined on arbitrary substructures, not strong substructures. Restricting to strong substructure would inhibit if not prevent the
$\pi _2$
-axiomatization as the strong substructure relation (
$A \leq M$
) is only type-definable. Thus, in Lemma 5.10, we cannot assume D is strong in both E and F. In the following definition we rely on the terminology introduced in Definitions 4.1 and 5.2.
Definition 5.6.
$\Sigma _\mu $
is the union of the following four sets of sentences:
-
(1)
$\Sigma ^0_\mu $
is the collection of universal sentences axiomatizing
${\boldsymbol {K}}_0$
as in Definition 3.4. -
(2)
$\Sigma ^1_\mu $
is the collection of universal sentences that assert:
$$ \begin{align*}B \subseteq M \;\; \Rightarrow \;\; \chi_M(B,C) \leq \mu(B,C).\end{align*} $$
-
(3)
$\Sigma ^2_\mu $
is a collection of universal-existential sentences
$\psi _{B,C}$
, depending on the good pair
$(B,C)$
, such that for every occurrence of B if
$M \models \psi _{B,C} $
then for some good pair
$(A,D)$
with
$AD \subseteq BC$
, any structure
$N $
containing
$MC$
satisfies
$\chi _N(A,D)> \mu (A,D)$
and so violates
$\Sigma ^1_\mu $
. See Lemma 5.18 for the explicit formulation of these sentences -
(4)
$\Sigma ^3_\mu $
is the sentence asserting every nontrivial line has length
$\mu (\boldsymbol {\alpha }) +2$
.
$\Sigma ^3_\mu $
implies that every model is infinite. The argument in Lemma 5.10 that underlies both the axiomatization of
${\boldsymbol {K}}^{\mu }_{d}$
and the amalgamation for
$({\boldsymbol {K}}_\mu , \leq )$
differs from a mere amalgamation argument in one significant way:
$D \subseteq F$
but
$D \leq F$
is not assumed (on the other hand,
$D \leq E$
is assumed). We require several technical lemmas to address the difficulties arising from this fact. We will see that models that satisfy
$\Sigma _\mu $
are in
$ {\boldsymbol {K}}^{\mu }_{d}$
by showing that if a model M satisfies
$\Sigma _\mu $
, then we can find sentences to prevent extensions in which M is not d-closed. The following example shows the necessity for the complications in proving Lemma 5.10: new primitives can occur in many ways.
Example 5.7. Construct the isomorphism type
$\boldsymbol {\beta }$
of a good pair
$(B,C)$
defined as follows. Let B be two points
$d_1,d_2$
and C consists of six points
$c_i$
for
$i = 1, \dots, 6$
. Let the nontrivial lines be
$\{d_1, c_1,c_2, c_3\}$
,
$\{d_2, c_4,c_5, c_3\}$
,
$\{c_4,c_1,c_6\}$
and
$\{c_5,c_2,c_6\}$
. So C has 6 points and 4 lines each of nullity 1 so rank 2. And
$BC$
has 8 points and 4 lines, 2 of nullity 1 and 2 of nullity 2 so
$BC$
also has rank 2. Check primitivity by inspection.
Now turn this example on its head. Consider the following example of the setting of Lemma 5.10. Set
$\mu (\boldsymbol {\alpha }) =4$
and
$\mu (\boldsymbol {\beta }) =2$
Let
$D = \{c_1,c_2\}$
,
$F = D \cup \{c_3,c_4, c_5,c_6, d_2\}$
and
$E = D \cup \{d_1\}$
.
$(D,E)$
is a good pair. Amalgamating F and E over D we get a new realization
$(B',C')$
of the isomorphism type
$\boldsymbol {\beta }$
of the good pair
$(B,C)$
, which is not contained in either D or E, but in
$F \cup E$
. This example does not violate Lemma 5.10 as
$\mu (\boldsymbol {\alpha }) =2$
(and has to be since there are
$4$
-element lines in F).
Remark 5.8. Example 5.7 shows that good pairs can conflict so we don’t know in general that a model M of
$T_\mu $
will satisfy
$\chi _M(B,C) = \mu (B,C)$
for all good pairs
$(B,C)$
that appear in M. We first prove in Lemma 5.10 that each good pair
$(B,C)$
can only conflict with finitely many pairs
$(B',C')$
and that that can happen only if one pair is included in the other. Following [Reference Holland15], to guarantee that
$M \in {\boldsymbol {K}}^{\mu }_{d}$
, we assert by the formula
$\psi _{B,C}$
(cf. Definition 5.6(3)) that each conflicting pair
$(A,D)$
is ‘almost realized’ in M so that adding points from C contradicts
$\Sigma ^1_\mu $
.
Lemma 5.9 is a variant on [Reference Ziegler26, Lemma 5.1] that is proved by replacing the phrase ‘adds a relation to B’ in Ziegler’s proof by careful consideration of the lines involved. See the archive version for details.
Lemma 5.9. Suppose
$F \leq G$
and F satisfies
$\Sigma ^0_\mu $
. Suppose
$\chi _G(B,C) \geq n$
with
$n \geq \delta (B)$
, witnessed by
${\mathcal {C}} =\langle C_1,\ldots,C_m\rangle $
, for
$m = \mu (B,C)+1$
. Then at least one of the following holds.
-
1.
$B \subseteq F.$
-
2. Some
$C_i\in {\mathcal {C}}$
lies in
$G-F$
.
Notice that by Lemma 3.7 in the following lemma we have that
$F \leq G$
.
Lemma 5.10. Let
$F, E \models \Sigma ^i_\mu $
, for
$i< 2$
,
$D \subseteq F$
, and suppose that
$(D,{E})$
is a good pair (and so in particular
$D \leq E$
). Now, if
$G = E \oplus _{{D}} F$
and for some good pair
$(B,C) \subseteq G$
we have
$\chi _G(B,C)> \mu (B,C)$
, then:
-
(A) if
$|C| = 1$
,
$C = \{c\}$
and c is on a line based on some
$B'\subseteq D$
; -
(B) if
$|C| \geq 2$
then
$B\subseteq E$
and there exists
$C'$
with
$BC' \backsimeq BC$
, with
$C' \subseteq (E-D)$
. Further, if
$D\leq F$
, there is a copy
$C''$
of C over B with
$C'' =(E-D)$
, and
$B \subseteq D$
.
Proof Since
$G = E \oplus _{{D}} F$
we can use the notation and results of 3.6 and 3.7(3). Note that
$F, D, E$
are in
${\boldsymbol {K}}_\mu $
by the definition of the axioms
$\Sigma _\mu $
. Let
${\mathcal {C}}$
be a set of
$\mu (B,C)+1$
disjoint copies of C over B in G, and list
${\mathcal {C}}$
as
$\langle C_1,\ldots,C_m\rangle $
, for
$m = \mu (B,C)+1$
.
-
Case A.
$|C| = 1$
. Then
$(B,C)$
witnesses the isomorphism type
$\boldsymbol {\alpha }$
from Definition 5.1. So, there must be a line
$\ell $
of size
$\mu (B,C)+3$
in G. Since E and F satisfy
$\Sigma ^1_\mu $
, there must be
$d \in F-D$
and
$c \in E-D$
that lie on
$\ell $
. By Definition 3.6(2) of free almalgam
$\ell $
must contain two points (say, comprising
$B'$
) in
${D}$
that are connected to
$c \in E-D$
. Since
$\{c\}$
is then primitive over D,
$E-D $
must be
$ \{c\}$
. We finish the first claim. Note
$\chi _F(B',C)=\mu (B,C)$
as
$\ell $
has
$\mu ({\boldsymbol {\alpha }})+2$
points in F. -
Case B.
$|C| \geq 2$
.
Claim 5.11. If some
$C_j\in {\mathcal {C}}$
satisfies
$C_j\subseteq E-D$
is good over
$B \subseteq F$
, then
$B \subseteq E$
.
Proof We show
$B \subseteq E$
. If not, there is a
$b_1 \in B \cap (F-E)$
and since
$C_j \subseteq (E-D)$
a line from
$b_1$
to some
$c\in C_j$
. Thus c is on a line based on D and so
$C_j = E-D = \{c\}$
. This contradicts
$|C_j| \geq 2$
so
$B \subseteq E$
.⊣
We split into two cases depending on the location of B. Each cases relies on Lemma 3to show
$F\leq G$
and the second on Lemma 5.9.
-
Case B.1. Suppose
$B \subseteq F$
. Since
$\chi _F (B,C) \leq \mu (B,C)$
, there must be a
$C_i \in {\mathcal {C}}$
that intersects
$G-F = E-D$
. So, since
$F\leq G$
and
$C/B$
is primitive,
$C_i \subseteq G-F = E-D$
. But, since E is primitive over D,
$FE$
is primitive over F, so
$C_i = E-D$
. By Case 2.2 of Lemma 4.8, B is the only subset of F on which
$C_i$
is based. Hence, as
$BC_i \subseteq E$
, we finish Case B.1 without using the supplemental hypothesis for the ‘further’ of Case (B). -
Case B.2. Suppose
$B \not \subseteq F$
. By Lemma 5.9, we have the main claim; some
$C_j$
lies in
$E-D$
. We prove the further. There must be a
$C'\in {\mathcal {C}}$
that intersects
$F-D$
, since
$E \in {\boldsymbol {K}}_\mu $
. But
$C'$
cannot split over E since,
$B \subseteq E$
by Claim 5.11. As we now assume
$D\leq F$
,
$E \leq G$
; so
$C' \subseteq (F-D)$
. But then
$C'$
is based on a unique
$B' \subseteq D$
since
$D\leq F$
. So
$B = B'\subseteq D$
. But then
$C_j$
is primitive over D and based on
$B\subseteq D$
, and so
$C_j = E-D$
. Hence,
$C_j$
is the required
$C''$
.
The argument for Lemma 5.12 differs from the standard only in requiring a special case for extending a line.
Lemma 5.12. Suppose A and
$A'$
are primitive over Y with
$\delta (A/Y) = \delta (A'/Y) = 0$
and both are based on
$B \subseteq Y$
with isomorphic good pairs
$(B,\hat A)$
and
$(B,\hat A')$
, where
$\hat A = A-Y$
and
$\hat A' = A'-Y$
. Then the map fixing Y and taking A to
$A'$
is an isomorphism.
We now show that any element of
$\hat {\boldsymbol {K}}_\mu $
(not just
${\boldsymbol {K}}_\mu $
) can be amalgamated (possibly with identifications) over a (necessarily finite) strong substructure D of F with a strong extension of D to a member E of
$\hat {\boldsymbol {K}}_\mu $
. Conclusion 5.13 follows from Lemma 5.12, breaking into cases given by Lemma 5.10 A) and B).
Conclusion 5.13. If
$D \leq F \in \hat {\boldsymbol {K}}_\mu $
and
$D \leq E \in {\boldsymbol {K}}_\mu $
then there is
$G\in \hat {\boldsymbol {K}}_\mu $
that embeds (possibly with identifications) both F and E over D. Moreover, if
$F \in {\boldsymbol {K}}^\mu _d$
, then
$F = G$
. In particular,
$({\boldsymbol {K}}_\mu , \leq )$
has the amalgamation property, and there is a generic structure
$\mathcal {G}_\mu \in \hat {\boldsymbol {K}}_\mu $
for
$({\boldsymbol {K}}_\mu , \leq )$
.
Notation 5.14. Let
${\mathcal {G}}_\mu $
denote the generic for
$({\boldsymbol {K}}_{\mu } \leq )$
(cf. Conclusion 5.13
).
Notice that it follows from Corollary 5.13 that every member of
${\boldsymbol {K}}_\mu $
is strongly embeddable in
${\mathcal {G}}_\mu $
.
Definition 5.15. Let
$({\boldsymbol {K}}_0, \leq )$
be as in the context of Fact 3.8. The structure M is rich for the class
$(\hat {{\boldsymbol {K}}_0}, \leq )$
(or
$(\hat {{\boldsymbol {K}}_0}, \leq )$
-rich) if for any finite
$A,B \in {\boldsymbol {K}}_0$
with
$A \leq M$
and
$A\leq B$
there is a strong embedding of B into M over A.
Clearly, a generic is rich. Even more, since the definition of
${\boldsymbol {K}}^{\mu }_{d}$
requires the embedding only of finite extensions with dimension
$0$
, we have:
Proposition 5.16. Every rich model, and so in particular
$\mathcal {G}_\mu $
, is in
${\boldsymbol {K}}^{\mu }_{d}$
.
Proof We show that every
$({\boldsymbol {K}}_\mu ,\leq )$
-rich model M is in
${\boldsymbol {K}}^{\mu }_{d}$
. Suppose for contradiction that there is an
$N \in \hat {\boldsymbol {K}}_\mu $
with
$M \leq N$
and there is a
$C \subseteq (N-M)$
such that C is
$0$
-primitive over M. By Lemma 4.8, C is based on some finite
$B \subseteq M$
. Since
$M \leq N$
, C is also primitive over
$B_0 = \mathrm {icl}_M(B)$
. Since M is rich there is a copy
$C_1\subseteq M$
of C over
$B_0$
. Now let
$B_1 = \mathrm {icl}_M(C_1)$
. Applying richness again we can choose another embedding
$C_2$
of C into M over
$B_1$
. Continuing in this fashion, after less than
$\mu (B,C) + 1$
steps we have contradicted
$M \in \hat {\boldsymbol {K}}_\mu $
.⊣
We provide two sufficient condition for
$\mu (B,C)$
to be realized in a d-closed model.
Corollary 5.17. Suppose
$M \in {\boldsymbol {K}}^\mu _d$
. If either
-
1.
$(B,C)$
represents
$\boldsymbol {\alpha }$
or -
2.
$(B,C)$
is a good pair with
$|C|> 1$
and
$B\leq M$
then
$$ \begin{align*}\chi_M(B,C) =\mu(B,C).\end{align*} $$
In particular, if
$\mu (\boldsymbol {\alpha }) = m$
, then the length of every line in M is
$m+2$
.
Proof In either case, since M is d-closed,
$M \oplus _B C \not \in \hat {\boldsymbol {K}}_\mu $
(Definition 5.4.3). In the first case this obviously implies the conclusion. In the second, By the ‘further’ of Lemma 5.10(B).2, the violation of
$\Sigma _1$
is given by the new copy of the pair
$(B,C)$
, and so
$\chi _M(B,C) =\mu (B,C)$
.⊣
The requirement in (2) that
$B\leq M$
guarantees that the obstruction is exactly the extension we are trying to make. Without that requirement the corollary seems unlikely.
Now we explain the interaction between the axioms
$\Sigma ^1_\mu $
and
$\Sigma ^2_\mu $
. No extension of a model of
$\Sigma ^2_\mu $
by a good pair is in
$\hat {\boldsymbol {K}}_\mu $
. This will yield the axiomatization of the theory of the d-closed structures and thus of the generic (by Proposition 5.16). We proved Lemma 5.10 without assuming
$D \leq F$
(given by a type), precisely so we could quantifier over a definable set
$\rho $
in equation (3) in the proof of Lemma 5.18.
Lemma 5.18. The family of first-order sentences
$\Sigma _\mu $
(Definition 5.6) defines the class of d-closed models.
Proof We use the notation of Lemma 5.10. For
$M \in \hat {{\boldsymbol {K}}}_\mu $
, we say
$M \oplus _D E$
is bad if for some good pair
$(B,C)$
with
$BC \subseteq DE$
,
$\chi _{M \oplus _D E}(B,C)> \mu (B,C)$
.
We first define for each good pair
$(D,E)$
the formula
$\psi _{(D,E)}$
described in Definition 5.6. For each duo of good pairs
$(D,E)$
and
$(B,C)$
with
$BC \subseteq DE$
define the formula
$\varphi _{(D,E),(B,C)}$
as follows. Fix a model
$M_0 \in \hat {{\boldsymbol {K}}}_\mu $
; choose a copy of
$D\subseteq M_0$
such that
$M_0 \oplus _D E$
is bad witnessed by
$(B,C)$
. If
$|C|>1$
choose by Lemma 5.10.B
$C_1,\ldots , C_r$
(where
$r =\mu (B,C)+1$
) that are disjoint copies of C over B contained in
$M_0 \oplus _D E$
and let
$\overline {s}$
enumerate
$H =(\bigcup _i C_i)-D) \cap M_0$
. Let
$\chi (\overline {v},\overline {x})$
be a possible atomic diagram of
$H \cup D \subseteq M$
, where
$\lg (\overline {v}) = \lg (\overline {s})$
, for pairs
$(M_0,D)$
as
$M_0$
varies over
$\hat {{\boldsymbol {K}}}_\mu $
and D varies over possible embeddings into
$M_0$
. Let
$$ \begin{align}\varphi_{(D,E),(B,C)}: \bigvee\limits_i (\exists \overline{v})\chi_i(\overline{v},\overline{x}),\end{align} $$
where the
$\chi _i$
are the finitely many possible such diagrams
$\chi $
. We have chosen
$\psi _{(D,E)(B,C)}$
so that for any
$M \in \hat {{\boldsymbol {K}}}_\mu $
if
$M \oplus _D E$
is a bad extension witnessed by
$(B,C)$
then
$M\models \psi _{(D,E)(B,C)}$
.
Let
$\rho (\overline {x})$
be the atomic diagram of D. Now we define
$\Sigma ^2_\mu $
and
$\Sigma ^3_\mu $
to assert a) each line has cardinality
$\mu (\boldsymbol {\alpha })+2$
and b) each of the following (countable) collection of sentences (for all good pairs
$(D,E)$
), where
$\rho (\overline {x})$
is the atomic diagram of D.
$$ \begin{align}\psi_{(D,E)}: \hskip .1in (\forall \overline{x}) [\rho(\overline{x}) \rightarrow \bigvee\limits_{BC \subseteq DE}\varphi_{(D,E),(B,C)}(\overline{x})]. \end{align} $$
Now, if
$M\models \Sigma _\mu $
then M is d-closed. Since if not, there is an
$N \in \hat {{\boldsymbol {K}}}_\mu $
such that for some
$(D,E)$
,
$M \oplus _D E \subseteq N$
. If
$|E|=1$
then condition a) is violated.
Suppose
$M\models \psi _{(D,E)}$
witnessed by
$(B,C)$
. If
$|C| =1$
condition a) is again violated by Lemma 5.10.A. But, if
$|C|>1$
some
$\chi _i$
from Equation 2 will be satisfied in M. And, by Definition 3.7. 3,
$\chi (\overline {v},\overline {x}) \cup \text {diag}_{\text {qf}}(E) \models \text {diag}_{\text {qf}}(HE)$
where H is, as before, the interpretation of
$\overline {v}$
. This implies
$\chi _{M \oplus _D E}(B,C)\geq \chi _{HE}(B,C)> \mu (B,C)$
and we finish.⊣
Recall (Definition 5.4) that a finite set X is d-independent when each
$x \not \in \operatorname {\mathrm {cl^d}}(X -\{x\})$
, that is,
$d(X)> d(X -\{x\})$
for each
$x \in X$
. It is then easy to establish the first of the following assertions by induction and the others follow.
Lemma 5.19. Let
$M \in \hat {{\boldsymbol {K}}}_\mu $
and let Y be d-independent in M. For every finite
$X \subseteq Y$
we have:
-
(i)
$d(X) = |X|$
; -
(ii)
$X\leq M$
, and so
$\mathrm {icl}_M(X) =X$
; -
(iii) there are no R-relations among elements of X.
We follow Holland’s proof to show
$\Sigma _\mu $
axiomatizes the complete theory of
${\boldsymbol {K}}^{\mu }_d$
.
Lemma 5.20. Moreover,
$\Sigma _\mu $
is an axiomatization of the complete theory
$T_\mu $
of the class
${\boldsymbol {K}}^\mu _d$
.
Proof By Lemma 5.18, it suffices to show
${\boldsymbol {K}}^\mu _d$
is
$\kappa $
-categorical for
$\kappa> \aleph _0$
. This follows by Lemmas 5.19 and 5.13 as each model is the algebraic closure of a basis. (See Lemma 25 of [Reference Holland15] or the archive version of this article for details.)⊣
Having followed the outline of her proof, we have the analog to Holland’s result [Reference Holland15] that the strongly minimal Hrushovski constructions are model complete.
Remark 5.21. Since the axioms
$\Sigma _\mu $
are universal-existential and
$T_\mu $
is
$\aleph _1$
-categorical, it is model complete by Lindstroms’s ‘little theorem’: that
$\pi _2$
-axiomatizable theories that are categorical in some infinite power are model complete [Reference Lindström18].
Our theories
$T_\mu $
uniformize the result that there are only finitely many finite line lengths in any strongly minimal linear space (cf. Fact 2.7). We show in Corollary 5.22 using Lemma 4.10 that there are continuum-many strongly minimal theories
$T_\mu $
such that in each of them all lines have fixed length
$\mu (\boldsymbol {\alpha }) +2$
.
Corollary 5.22. There are continuum-many
$\mu \in {\mathcal {U}}$
(cf. Definition 5.2(1)) which give distinct first-order theories of Steiner systems. That is, there is
$\mathcal {V} \subseteq {\mathcal {U}}$
such that
$|\mathcal {V}| = 2^{\aleph _0}$
and
$\mu \neq \nu \in \mathcal {V}$
implies that
$Th(G_\mu ) \neq Th(G_{\nu })$
(recall Notation 5.14
).
Proof For any
$X \subseteq \omega $
, let
$\mu _X$
assert that
$\mu (\boldsymbol {\gamma }_k)$
(from the proof of Lemma 4.10) is
$3$
if
$k\in X$
and
$2$
if not (recall that it must be at least
$2$
). Then, if
$k\in X\setminus Y$
, then
$T_{\mu _X} \not \equiv T_{\mu _Y}$
(cf. Notation 5.14), since there are three extensions in the isomorphism type
$\mu (\boldsymbol {\gamma }_k)$
of some pairs
$\{a,b\}$
in models of
$T_{\mu _X}$
but not in models of
$T_{\mu _Y}$
. ⊣
Lemma 5.23. If
$M \in {\boldsymbol {K}}^{\mu }_{d}$
, then for every
$X \subseteq M$
,
$ \operatorname {\mathrm {cl^d}}(X) = \mathrm {\mathrm{acl}}_M(X)$
. Thus,
$T_\mu $
is strongly minimal.
Proof We first show that for
$M \in \hat {\boldsymbol {K}}_\mu $
,
$ \operatorname {\mathrm {cl^d}}(X) = \mathrm {\mathrm{acl}}_M(X)$
. If Y is a finite subset of M,
$\delta (Y/X) =0$
, Y is a union of a finite chain with length
$k< \omega $
of extensions by good pairs
$(B_i,C_i)$
; each is realized by at most
$\mu (B_i,C_i)$
copies, and so:
$$ \begin{align*}|Y|\leq \sum\limits_{i<k}\ \mu(B_i,C_i) \times |C_i|.\end{align*} $$
Thus,
$Y \subseteq \mathrm{acl}_M(X)$
.
Concerning the other containment, let
$M \in {\boldsymbol {K}}^\mu _d$
,
$a \in M$
and
$X \subseteq _\omega M$
. If
$d(a/X)> 0$
and
$X_0$
is a maximal d-independent subset of X, then
$X_0 \cup \{a\}$
extends to a d-basis for M. Furthermore, a detailed proof of Lemma 5.20 shows that any permutation of a d-basis extends to an automorphism of M. Thus, if
$a\notin \operatorname {\mathrm {cl^d}}(X)$
, then
$a \notin \mathrm{acl}_M(X)$
. Hence,
$ \operatorname {\mathrm {cl^d}}(X) = \mathrm {acl}_M(X)$
, as desired.
Strong minimality follows, since for any finite A there is a unique nonalgebraic
$1$
-type over A, namely the type p of a point a such that: (i) a is not on any line based in A (and so
$\delta (a/A) =1$
); (ii)
$Aa$
is strong in any model. Clause (ii) is given by the collection of universal sentences forbidding any
$B \supseteq Aa$
with
$\delta (B) <\delta (Aa)$
. Thus, in
${\mathcal {G}}_\mu $
we have that
$d(a/A) = 1$
for any a realizing p. Hence, any two realizations a and b of p are such that
$Aa \leq {\mathcal {G}}_\mu $
and
$Ab \leq {\mathcal {G}}_\mu $
, and thus they are automorphic by the genericity of
${\mathcal {G}}_\mu $
(cf. Conclusion 5.13). Hence, p is a complete type. ⊣
Notation 5.24. Let F be the Fano plane and
${\mathcal {F}}$
be the set of
$\mu \in \mathcal {U}$
such that:
$$ \begin{align*}\mu(\emptyset, F)> 0.\end{align*} $$
Lemma 5.25 shows that for any
$\mu \in {\mathcal {F}}$
and
$M \models T_\mu $
, we have that
$\mathrm{acl}_M(\emptyset )$
is infinite; by Ryll-Nardjewski,
$T_\mu $
is not
$\aleph _0$
-categorical. In view of Lemma 5.23, the countable models correspond exactly to the models of dimension
$\alpha $
for
$\alpha \leq \aleph _0$
.
Lemma 5.25. Let
$\mu \in {\mathcal {F}}$
. Neither the generic,
${\mathcal {G}}_\mu $
, nor any model of
$T_\mu $
is locally finite with respect to
$ \operatorname {\mathrm {cl^d}} = \mathrm{acl}$
(cf. Lemma 5.23
). Thus,
$T_\mu $
is not
$\aleph _0$
-categorical and has
$\aleph _0$
countable models. Since the generic has infinite dimension, it is
$\omega $
-saturated.
Proof We show that the algebraic closure of the empty set is infinite. Construct a sequence
$(A_i : i<\omega )$
in
${\mathcal {G}}_\mu $
by letting
$A_0$
to be the Fano plane, which (Example 4.3) is easily seen to be
$0$
- primitive over the empty set. Notice that there can only be finitely many realizations of the Fano plane in any model of
$T_\mu $
, and so
$A_0$
is in the algebraic closure of the empty set. Now let
$a_0,b_0,c_0$
be the vertices of the triangle in the standard picture of the Fano plane. Choose
$a_1,b_1,c_1$
disjoint from
$A_0$
so that
$(a_0,a_1,c_1)$
,
$(b_0,b_1,c_1)$
, and
$(a_1,b_1,c_0)$
are triples of collinear points. Then, letting
$A_1 = \{a_0,b_0,c_0,a_1,b_1,c_1 \}$
, it is to see that
$A_1$
is a primitive extension of
$A_0$
. Now build
$A_2$
by taking
$a_1,b_1,c_1$
as the base and adding
$a_2,b_2,c_2$
as in the construction of
$A_1$
from
$A_0$
; and then iterate. Each stage (and hence the union) can be strongly embedded as
$A^{\prime }_i$
in the generic. But then
$\delta (A^{\prime }_{i+1}/A^{\prime }_i) = d(A_{i+1}/A_i) = 0$
. By transitivity, with
$A_\omega $
denoting
$\bigcup _{i < \omega } A_i$
, we have that for any finite
$X\subseteq A_\omega $
,
$d(X/A_0) = 0$
. Since
$ \operatorname {\mathrm {cl^d}} = \mathrm {acl}$
(Lemma 5.23), we finish. We constructed this sequence in the algebraic closure of the empty set, and so it occurs in the prime model of T. Thus,
$\mathrm {acl}_M(\emptyset )$
is infinite for any model M of
$T_\mu $
. By Ryll-Nardjewski,
$T_\mu $
is not
$\aleph _0$
-categorical. In view of Lemma 5.23, as in any strongly minimal theory, these models correspond exactly to models of dimension
$\alpha $
for
$\alpha \leq \aleph _0$
. ⊣
We modify [Reference Hrushovski16, Lemma 15] to show our examples have the characteristic properties of the ab initio Hrushovski construction.
Conclusion 5.26. For any
$\mu \in \mathcal {U}$
, the
$\mathrm {acl}$
-pregeometry associated with
$T_\mu $
is flat (Definition 3.5). Thus, we have:
-
(1)
$T_\mu $
does not interpret an infinite group and T is CM-trivial. -
(2) If
$\mu \in {\mathcal {F}}$
,
$T_\mu $
admits weak elimination of imaginaries.
Proof Fix
$M \models T_\mu $
. By Lemma 5.23,
$\mathrm {acl}$
is the same as
$\text {cl}_d$
. We use the notation of Definition 3.5 and start with
$\mathrm {acl}$
-closed subsets
$E_i\leq M$
of finite dimension for i in the finite set I. For flatness, for each
$\emptyset \neq S\subseteq I$
, let
$E_S = \bigcap _{i\in S} E_i$
; let
$\check E_S$
, be a finite base for
$E_S$
. That is,
$\check E_S \leq E_S \leq M$
and
$\mathrm {cl}_d(\check E_S) = E_S$
. For
$i\in I$
, let
$F_i = \text {icl}(\bigcup _{i \in S\subseteq I } \check E_S)$
. Then, as usual, for
$S \subseteq I$
let
$F_S = \bigcap _{i\in S} F_i$
and
$F_{\emptyset } = \bigcup _{i\in I} F_i$
. Now we have the following
$$ \begin{align*}E_S = \bigcap\limits_{i\in S} E_i = \mathrm{acl}(\check E_S) = \mathrm{acl}(F_S).\end{align*} $$
The first two equalities are immediate from the definitions.
$\check E_S$
is clearly a subset of
$F_S$
since
$i\in S$
implies
$\check E_S \subseteq F_i$
. Finally examination of the definitions of
$F_i$
and
$F_S$
shows
$E_S \subseteq \mathrm {acl}(F_S)$
for each
$\emptyset \neq S \subseteq I$
. Since
$\delta (F_S) =d(F_S)$
and
$\delta $
is flat by Lemma 3.7.1 applied to the
$F_i$
and
$F_S$
, lifting by
$d(F_S) = d(E_S)$
, we have that d is flat. Finally, (1) follows as in [Reference Hrushovski16], and (2) from [Reference Pillay and Bouscaren23, Lemma 1.6].⊣
We place our work in the context of a number of papers that use model theoretic techniques and, in at least one case, the Hrushovski construction, to investigate linear spaces and Steiner systems. Our approach differs by invoking a predimension function inspired by Mason’s
$\alpha $
-function, and focusing on the combinatorial consequences of strong minimality by investigating the family of similar (elementarily equivalent) structures of arbitrary cardinality arising from a particular strongly minimal k-Steiner system. In contrast, Evans [Reference Evans8] constructs Steiner triple systems using a variant of the Hrushovski construction without discussing their stability class. Between these extremes, Hytinnen and Paolini [Reference Hyttinen and Paolini17] show that the Hall construction of free projective planes yields a strictly stable theory. Conant and Kruckman [Reference Conant and Kruckman7] find an existentially closed projective plane and prove it is
$NSOP_1$
but not simple. Their construction involves a generalized Fraïssé construction for the existential completeness as well as the Hall construction.
Remark 5.27. We compare our examples with the construction by Barbina and Casanovas in [Reference Barbina and Casanovas4] of structures existentially closed for the class of all Steiner quasigroups. At the opposite end of the stability spectra from our result, Barbina and Casanovas [Reference Barbina and Casanovas4] find existentially closed Steiner triple systems that are
$TP2$
and
$NSOP_1$
by a traditional Fraïssé construction. Note that Steiner quasigroups are the quasigroups associated with Steiner triple systems in [Reference Barbina and Casanovas4].
-
(i) Their generic, denoted
$\mathbb {M}_{\text {sq}}$
, has continuum many types over the empty set, satisfies
$TP_2$
and
$NSOP_1$
, and it is locally finite (but not uniformly locally finite) as a quasigroup. If
$\mu \in {\mathcal {U}}$
, then it is obvious that
$T_\mu $
fails the first three of these properties since it is strongly minimal. Furthermore, we showed in Lemma 5.25 that our examples with
$\mu \in {\mathcal {F}}$
are not locally finite for
$\mathrm {acl} = \operatorname {\mathrm {cl^d}}$
. Strikingly, in
$\mathbb {M}_{\text {sq}}$
, the definable closure is equal to the algebraic closure (
$\text {dcl} = \mathrm {acl}$
). In [Reference Baldwin and Shi2] we show that this equality fails drastically in any
$T_\mu $
with
$\mu \in {\mathcal {U}}$
. -
(ii) The structure
$\mathbb {M}_{\text {sq}}$
is the prime model of its theory; our
${\mathcal {G}}_\mu $
is saturated. While the example in [Reference Barbina and Casanovas4] is quantifier eliminable, ours is only model complete. The first is the model completion of the universal theory of Steiner quasigroups. Since each
$M \in {\boldsymbol {K}}_\mu $
can be extended to
$N \in {\boldsymbol {K}}^\mu _d$
, the second is the model completion of the universal theory of
$\hat {\boldsymbol {K}}_\mu $
for the relevant
$\mu $
. Quantifier elimination does not follow since, despite the limited amalgamation in Conclusion 5.13,
$\hat {\boldsymbol {K}}_\mu $
does not have amalgamation.
Thus, there are four techniques that construct infinite linear spaces in a range of stability classes: taking all extensions in a given universal class but insisting on finite amalgamation in a standard Fraïssé construction [Reference Barbina and Casanovas4], building one chain of models carefully [Reference Hyttinen and Paolini17], combining these two methods but allowing the amalgam of finite structures to be countable [Reference Conant and Kruckman7], and, as here, restricting the amalgamation class to guarantee a well-behaved
$\mathrm {acl}$
-geometry.
The first author was partially supported (during a 2018 visit to Jerusalem) by European Research Council grant 338821 and by Simons travel grant G5402. The second author was partially supported by European Research Council grant 338821.
