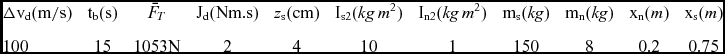NOMENCLATURE
- Δv
-
velocity change increment
- xsyszs
-
body-fixed coordinate frame
- xnynzn
-
nozzle-fixed coordinate frame
- XIYIZI
-
inertial coordinate system
- ω s
-
body angular velocity
- τ s
-
body external torque
- Gs
-
body CM location
- Gn
-
nozzle CM location
- ω n
-
nozzle angular velocity
- τ n
-
nozzle external torque
- FT
-
thrust force
- α
-
gimbal angle
- ω r
-
angular velocity of the nozzle with respect to the body
-
${\bm{\dot{\omega }}_r}$
-
angular acceleration of the nozzle with respect to the body
-
${\bm{\dot{\omega }}_s}$
-
spacecraft body angular acceleration
- ms
-
body mass
- mn
-
nozzle mass
- θ
-
body attitude angle
- Jd
-
jet damping coefficient
- zs
-
uncertainty in the body CM location
- xs
-
half of the body length
- xn
-
half of the nozzle length
- Δvd
-
desired velocity change
- tb
-
burning time
- I s2
-
body moment of inertia
- I n2
-
nozzle moment of inertia
- αgimb
-
maximum gimbal angle
- δ FT
-
thrust vector deviation from the XI
- u
-
control input
- K
-
linear controller gain
- P
-
closed-loop system poles
- Δvw
-
wasted velocity change
- τ d
-
exogenous disturbance
- u com
-
combined controller input
- u lin
-
linear controller input
- u nonl
-
nonlinear controller input
1.0 INTRODUCTION
Attitude control of a spacecraft during an impulsive thrusting manoeuvre has been a difficult problem since the early days of space missions. An impulsive orbital manoeuvre (i.e., retrofiring before an atmospheric re-entry) is used to generate a velocity increment Δv by using a large thrust force. During the burning of a rocket, thrust vector misalignment from the CM always exists and is inescapable(Reference Orr and Shtessel1). This misalignment produces a large disturbance torque that tends to divert the orientation of spacecraft and thrust vector from the desired inertial direction. It is obvious that a high-capacity attitude control system is needed to compensate for the mentioned large exogenous disturbance. Since the spacecraft attitude during a thrusting manoeuvre is naturally unstable, desired values of Δv components cannot be achieved in practice. A review study about the effects of thrust vector misalignments on orbit transfers has been addressed in Reference SouzaRef. 2. The main control methods are classified in the NASA report(Reference Noll3) which are (1) spin-stabilisation for a small spacecraft (i.e. Biosatellite), (2) RCSs (in Mercury and Gemini), and (3) a combination of a RCS and TVC for large spacecraft (Apollo and Viking). In addition to the methods presented in Reference NollRef. 3, a novel method is proposed in Reference KouhiRef. 4 where the combination of the TVC scheme and spin-stabilisation is formulated and investigated.
A simple and low-cost method which is used in orbital manoeuvres of small satellites and spacecraft is spin stabilisation(Reference Oldenburg and Tragesser5-Reference Hu and Gong7). But it has some disadvantages and limitations:
-
1. Due to the flexibility and energy dissipation sources in a spacecraft, only the spin about the axis of maximum moment of inertia is stable for a spin-stabilised-only spacecraft.
-
2. Nutational or coning instability has happened in several spacecraft therefore, a nutation control system equipped with a RCS is needed(Reference Meyer8-Reference Martin and Longuski10).
-
3. Some equipment such as thrusters and fuel tanks are needed for spin-up and spin-down(Reference Noll3).
-
4. In some works such as in Reference CloutierRefs 11-13, the resonance in the spacecraft devices created by the nutation is addressed.
-
5. Spin-axis stabilisation (thrust vector stabilisation) with respect to the desired inertial direction is not possible for a spin-stabilised-only spacecraft. In the some works such as Reference Tsiotras and LonguskiRefs 14-17, it is shown that for the spin-axis stabilisation, an active control system with extra actuators (such as RCSs) is needed.
-
6. Spin stabilisation may not be a suitable choice for a spacecraft with solar panels, directional antennae and sensors which are sensitive to angular motions, especially in a lengthy mission.
An RCS is able to provide a high level of active control torque to reject exogenous disturbances and perform fast attitude manoeuvres. Although RCSs have many advantages, in practice they have many weaknesses and limitations such as:
-
1. They include several pieces of equipment that increase the complexity and cost of a spacecraft
-
2. Because RCSs use liquid propellants, fuel sloshing occurs due to rotational and lateral motions of propellant tanks; in the presence of sloshing, attitude control of spacecraft will be very difficult. There are several works such as Reference Reyhanoglu and HervasRefs 18-21 on the interaction of spacecraft dynamics and slosh dynamics and their control. In Reference Reyhanoglu and HervasRefs 18 and Reference Hervas and Reyhanoglu22-Reference Kishore24, the TVC for the rocket engine is addressed, including the fuel slosh dynamics in which many external torques are needed in the control system.
-
3. RCSs are inherently nonlinear actuators with complex control logic(Reference Hall25). Although for large spacecraft and upper-stage vehicles (see Reference Orr and ShtesselRefs 1, Reference Reyhanoglu and Hervas18 and Reference Yeh26-Reference Wang28) a combination of RCSs and TVC has been employed, RCSs are not suitable to be used in a small spacecraft mission.
The TVC method with all its advantages is a powerful technique in control of spacecraft and launchers which can be actuated by a servo actuator (without fuel consumption). For instance, terminal guidance and landing capability of the Falcon 9 rocket with new TVC system technology is being provided by the company SpaceX. Although during an impulsive manoeuvre, a high-level disturbance torque is created proportional to the thrust vector misalignment, a gimbaled TVC can generate an active control torque larger than the disturbance level. When the disturbance level is larger than the attitude control capacity, a fixed thrust system is not efficient (Apollo, Cassini(Reference Rizvi and Weitl29), (Reference Millard and Reed30) and rockets). TVC methods such as moving plates(Reference Kong, Jin and Kim31) are accompanied by a highly nonlinear behaviour in comparison with the gimbaled thruster. A gimbaled TVC can be also employed for a solar-sail spacecraft(Reference Sperber, Fu and Eke32). The gimbaled nozzle (gimbaled thruster) can be very useful in preserving weight, simplifying the attitude control system and reducing the requirements of the CM positioning accuracy(Reference Noll3,Reference Kouhi4,Reference Wang28) . It should be noted that in large and massive spacecraft or launchers with a liquid propellant rocket, several heavy and complex components as well as fuel tanks are located in the body not presented (or attached) at the rotatable nozzle. Therefore, the mass properties of the liquid propellant rocket are negligible in comparison with the body's, and as a result, the dynamical interaction between the movable nozzle and body will be very small(Reference Orr and Shtessel1,Reference Reyhanoglu and Hervas18,Reference Hervas and Reyhanoglu22,Reference Rubio Hervas and Reyhanoglu23). It is obvious that using a liquid propellant rocket is not efficient or possible for a small spacecraft for which a SRM (solid rocket motor) is used where all mass properties of the SRM (including solid fuel) will be added to the nozzle mass properties. Therefore, for a small spacecraft equipped with a SRM, the aforementioned interaction cannot be neglected and leads to nonlinear two-body dynamics(Reference Kouhi4,Reference Wang28,Reference Kouhi, Mansour, Fani Saberi and Shahravi33) . Note that for large spacecraft, a TVC was used together with RCSs(Reference Orr and Shtessel1,Reference Reyhanoglu and Hervas18,Reference Yeh26,Reference Widnall27) and for a small spacecraft, it has been combined with the spin-stabilisation method(Reference Kouhi4). Although in Felicetti et al(Reference Felicetti34), an adaptive thrust vector control during on-orbit servicing is addressed, the interaction dynamics between the nozzle and the body is not considered as well, because it is not applicable for an impulsive orbital manoeuvre. In Wang et al(Reference Wang28), a nonlinear control law based on a two-axis gimbaled thruster is proposed for an upper-stage launcher where the launcher is equipped with eight RCSs on the body and two gimbal actuators by which the nonlinear dynamics is over-actuated. In contrast to Wang(Reference Wang28), the control of an underactuated system is investigated in this paper.
The use of momentum exchange devices such as reaction wheels and control moment gyros for attitude control is very attractive because, they do not require any fuel consumption. The external disturbance rejection is not possible for an attitude control system based only on these devises. In study(Reference Kouhi, Mansour, Fani Saberi and Shahravi33), a large control torque has been produced by the interaction between the reaction wheels angular momentum and the spacecraft spin rate, but in this paper the use of these devices is deficient.
Some major assumptions and goals that establish the control problem of this paper are considering of 1) a small spacecraft 2) the nonlinear two-body dynamics model 3) an impulsive orbital manoeuvre (high velocity change in a short time) with a high level exogenous disturbance 4) using only gimbal actuator and 5) not using of the RCS and spin-stabilisation (because of their limitations). Although attitude control during thrusting manoeuvre has received a large attention, it is clear that up to now, only TVC method has not been used to solve the mature problem in hand. The exogenous disturbance torque originates from the CM location uncertainty, is much more than the other orbital disturbance sources such as drag, solar pressure, and earth oblate disturbance. The difficulty of the present control problem is that for the two-body nonlinear plant, both attitude and thrust vector stabilisation (with respect to the desired inertial direction ZI) must be performed using only a gimbal actuator while rejecting the exogenous disturbance torque. According to the previous literatures, these performances need some thrusters (RCSs) and fuel consumption which are not efficient for a small spacecraft. Similar to(Reference Kouhi, Mansour, Fani Saberi and Shahravi33), in this paper a small spacecraft equipped with a gimbaled-SRM is considered in which the nozzle mass properties are not negligible with respect to the body's. Although orbital manoeuvres are performed in a three dimensional space, in some papers such as Reyhanoglu and Hervas(Reference Reyhanoglu and Hervas18), a planar manoeuvre is considered in order to facilitate the stability analysis. In this paper, a planar manoeuvre is also considered. To achieve some performance goals in transient and steady-state modes, a new control scheme is derived based on combination of two linear and nonlinear controllers. The proposed method ensures attitude and thrust vector stability during an impulsive orbital manoeuvre while eliminating and rejecting the exogenous disturbance torque. The important control object which is considered for the transient mode is to stabilise the body attitude angle very fast and in an under-damped behaviour without any overshoot and oscillation. The damped behaviour of the body attitude is very useful and effective for a flexible spacecraft (i.e., one equipped with solar panels).
The remainder of the paper is organised as follows. In Section 2 the planar dynamics model of a small spacecraft equipped with a gimbaled-nozzle is achieved. In Section 3, the proposed control system including linear, nonlinear and combined controllers is designed along with its simulation results. In Section 4, the important findings are discussed, and the conclusion is reported in Section 5.
2.0 MODEL FORMULATION
As discussed before, in the modelling of the spacecraft, the dynamical interaction between the nozzle and body must be considered. As indicated in Fig. 1, the spacecraft is composed of the three main parts: the body, the nozzle and the gimbal where the nozzle can rotate by means of a gimbal actuator at the pivot o. Subscripts s, n, o and T denote the body, nozzle, gimbal pivot and point of acting the thrust force, respectively. xsyszs is the body-fixed coordinate frame (xs is parallel to the body longitudinal axis), Gs denotes the body CM location, τ s ∈ R 3 and ω s ∈ R 3 express the body external torque and the angular velocity respectively, ρ so ∈ R 3 is the vector from Gs to the gimbal pivot, Gn is the nozzle CM position, xnynzn is the nozzle-fixed coordinate frame, and τ n ∈ R 3 and ω n ∈ R 3 represent the nozzle external torque and the angular velocity, respectively. The control input is defined by the gimbal angles of a non-throttable thrust engine (FT ) without any other moment source. The gimbal deflects the thrust vector with respect to the spacecraft's CM and then the attitude control torque is produced in proportion to the thrust vector misalignment.
Figure 1. A small spacecraft composed of body (a), nozzle (b) and a gimbal actuator at the pivot o.
2.1 Nonlinear dynamics of the planar manoeuvre
In the planar manoeuvre, the rotations are around the ys (yn) axis. The nozzle rotation with respect to the body and inertial coordinate system is shown in Fig. 2 with gimbal angle α. Thus, the relative angular velocity and acceleration of the nozzle with respect to the body will be
${\bm{\omega }_r} = {[ {\begin{array}{*{20}{c}} 0&{\dot{\alpha }}&0 \end{array}} ]^T},\,\,{\bm{\dot{\omega }}_r} = {[ {\begin{array}{*{20}{c}} 0&{\ddot{\alpha }}&0 \end{array}} ]^T}$
.
Figure 2. The gimbal rotation at the pivot o and the body, nozzle and inertial coordinate system.
The corresponding rotation matrix that transforms a vector in the nozzle frame to a vector in the body frame is
$$\begin{equation}
\bm{R}_n^s\,(\alpha ) = \left[ {\begin{array}{@{}*{3}{c}@{}} {\cos (\alpha )}&0&{\sin (\alpha )}\\ 0&1&0\\ { - \sin (\alpha )}&0&{\cos (\alpha )} \end{array}} \right]\,\,
\end{equation}$$
The three-dimensional mathematical modelling of a two-body spacecraft is derived in Reference Kouhi, Mansour, Fani Saberi and ShahraviRef. 33 by which
${\bm{\dot{\omega }}_s}$
as the spacecraft body angular acceleration can be calculated as
$$\begin{equation}
\begin{array}{@{}l@{}} {{\bm{\dot{\omega }}}_s} = {\left[ {{\bm{I}_{ns,T}}} \right]^{ - 1}}\left[ {{\bm{\tau }_{ns}} + \bm{\rho }_T^{} \times \bm{F}_T^{} - {\bm{I}_r}({{\bm{\dot{\omega }}}_r} + \,{\bm{\omega }_s} \times {\bm{\omega }_r})} \right.\\[3pt] \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + M\bm{\rho }_{ns}^{} \times \left( {{\bm{\omega }_s} \times ({\bm{\omega }_s} \times {\bm{\rho }_{so}}) - {\bm{\omega }_n} \times ({\bm{\omega }_n} \times {\bm{\rho }_{no}})} \right)\\[3pt]
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left. {\,\,\,\,\,\,\,\,\,\, - {\bm{\omega }_s} \times ({\bm{I}_s}{\bm{\omega }_s}) - \bm{\omega }_n^{} \times (\bm{I}_n^{}\bm{\omega }_n^{})\,} \right] \end{array}
\end{equation}$$
where
$\bm{\omega }_s^{} = {[ {\begin{array}{*{20}{c}} {\omega _{sx}^{}}&{\omega _{sy}^{}}&{\omega _{sz}^{}} \end{array}} ]^T}$
,
ω
n
=
ω
s
+
ω
r
,
τ
ns
=
τ
s
+
τ
n
,
ρ
ns
=
ρ
no
−
ρ
so
,
ρ
sn
= −
ρ
ns
.
I
s
∈
R
3 × 3 and
I
n
n
∈
R
3 × 3 are the body and the nozzle moment of inertia, respectively. ms
and mn
are the body and the nozzle mass, by which
$M = {{({m_n}{m_s})}
/ {({m_n} + {m_s})}}$
,
I
ns, T
=
I
ns
− M[
ρ
ns
× ]2,
I
r
=
I
n
− M[
ρ
ns
× ][
ρ
no
× ],
$\bm{\rho }_T^{} = \bm{\rho }_{nT}^{} + \bm{\rho }_{sn}^{}\,({M
/ {{m_n}}})$
,
I
ns
=
I
s
+
I
n
. All vectors and moment of inertias are presented in the s frame. For a vector
$\bm{s} = {[ {\begin{array}{*{20}{c}} {{s_1}}&{{s_2}}&{{s_3}} \end{array}} ]^T}$
, the operator [
s
× ] is defined by
$$\begin{equation*}
\left[ {\bm{s} \times } \right] = \left[ {\begin{array}{@{}*{3}{c}@{}} 0&{ - {s_3}}&{{s_2}}\\ {{s_3}}&0&{ - {s_1}}\\ { - {s_2}}&{{s_1}}&0 \end{array}} \right]
\end{equation*}$$
Some assumptions and definitions are made to summarise and extract the planar manoeuvre mathematical model from the three-dimensional modelling of Equation (2).
The attitude of the body is the rotation angle θ around the ys axis with angular velocity
$\omega _{sy}^{} = \dot{\theta }$
that results in
$\bm{\omega }_s^{} = {[ {\begin{array}{*{20}{c}} 0&{\dot{\theta }}&0 \end{array}} ]^T}$
. As assumed before, there is no external control torque (
τ
s
= 0
3 × 1) and the only active control input is
$\ddot{\alpha }$
(in
${{{\bm{\dot{\omega}}}}_r}$
); no attitude control torque exists that directly controls the spacecraft attitude. Some parameters and inputs are given in Equation (3) where
${J_d}(\dot{\alpha } + \dot{\theta })$
denotes the passive torque created by the jet damping effect and Jd
is the damping coefficient. The jet-damping torque originates from the Coriolis forces due to the outflow of SRM gases; a detailed discussion on the jet damping can be found in Reference Van Der Ha and JanssensRefs 35 and Reference van der Ha36. In vector
${{{\bm \rho }}_{so}}$
, zs represents the uncertainty in the CM location that leads to thrust vector misalignment (offset) and produces the exogenous disturbance torque.
$$\begin{equation}
\begin{array}{@{}l@{}} {{\bm \rho }}_{no}^n = {\left[ {\begin{array}{*{20}{c}} {{x_n}}&0&0 \end{array}} \right]^T},\,\,{{\bm \rho }}_{nT}^n = {0_{3 \times 1}},\,\,\,{{{\bm \rho }}_{so}} = {\left[ {\begin{array}{*{20}{c}} { - {x_s}}&0&{{z_s}} \end{array}} \right]^T},\,\\[2pt] \,\bm{I}_n^n = diag(I_{n,11}^{}\,,\,I_{n,22}^{},\,I_{n,33}^{}),\,\,\bm{I}_s^{} = diag(I_{s,11}^{}\,,\,I_{s,22}^{},\,I_{s,33}^{}),\\[2pt] {{\bf F}}_T^n = {\left[ {\begin{array}{*{20}{c}} {{{\bar{F}}_T}}&0&0 \end{array}} \right]^T},\,\,\,{{\bm \tau }}_n^{} = {\left[ {\begin{array}{*{20}{c}} 0&{ - {J_d}(\dot{\alpha } + \dot{\theta })}&0 \end{array}} \right]^T} \end{array}
\end{equation}$$
Actually, the magnitude of the thrust offset z s is so much smaller than the dimensions of the spacecraft's body and nozzle, it then can be assumed that
$$\begin{equation}
{z_s} < < \,\,{x_n},\,\,{z_s} < < \,\,{x_s}
\end{equation}$$
Thus, under the indicated assumptions and considerations, the nonlinear dynamics of the planar manoeuvre in the y axis is given in Equation (5) where d X zs and u denote the disturbance acceleration and the control input, respectively. During the engine burn, the undesired transverse acceleration d X zs , produces the undesired velocity. The details of the nonlinear terms f X and d X and the two moments of inertia Ir (α) and Iyy (α) are given in Equations (6) and (7), respectively.
$$\begin{equation}
\begin{array}{@{}l@{}} \ddot{\theta } = {f_{\bm{X}}} - {\raise0.7ex\hbox{${{I_r}(\alpha )}$} \!
/ \!\lower0.7ex\hbox{${{I_{yy}}(\alpha )}$}}\,\,u + {d_X}{z_s},\\ \ddot{\alpha } = u. \end{array}
\end{equation}$$
$$\begin{equation}
\left\{ \begin{array}{@{}l@{}} {f_{\bm{X}}} = - \frac{{{{\bar{F}}_T}M}}{{{m_n}{I_{yy}}(\alpha )}}{x_s}\sin (\alpha ) + \frac{{M{x_s}{x_n}}}{{{I_{yy}}(\alpha )}}\sin (\alpha )({{\dot{\alpha }}^2} + 2\dot{\alpha }\dot{\theta }) - \frac{{{J_d}(\dot{\alpha } + \dot{\theta })}}{{{I_{yy}}(\alpha )}},\\[3pt] {d_{\bm{X}}} = \frac{M}{{{I_{yy}}(\alpha )}}(\frac{{{{\bar{F}}_T}}}{{{m_n}}} - {x_n}({{\dot{\alpha }}^2} + 2\dot{\alpha }\dot{\theta }))cos(\alpha ). \end{array} \right.
\end{equation}$$
$$\begin{equation}
\begin{array}{@{}l@{}} {I_r}(\alpha ) = {I_{n,\,\,22}} + Mx_n^2 + M{x_s}{x_n}\cos (\alpha ) + M{x_n}{z_s}sin(\alpha ),\\[2pt] {I_{yy}}(\alpha ) = {I_{n,\,\,22}} + {I_{s,\,\,22}} + M{({x_s} + {x_n}cos(\alpha ))^2} + M{({z_s} + {x_n}sin(\alpha ))^2} \end{array}
\end{equation}$$
2.2 Mission requirements and parameters
The purpose of this section is to define the spacecraft mission requirements and parameters. Since the aim is to show the specifications of the proposed method and compare it with the other thrusting methods, a typical mission is considered here which is similar to the deorbiting manoeuvre of some small spacecraft. The goal of this mission is to generate a large Δ v in a short time for performing an impulsive orbital manoeuvre. Based on this mission, the specifications of the proposed method are obtained, and its merits and weaknesses will then be compared with the other methods. Because a comparative study will be done here, it is not necessary to define an absolute accuracy for the orbital mission. Moreover, in space engineering, one cannot generally say that one method is better than another method; based on various mission requirements and criteria, design procedures should be passed and finally the better case may be determined. Therefore, in this paper according to some special criteria (not generally), the proposed method is compared with the other thrusting method. Moreover, the attempt is to show that the proposed method is able to satisfy the objectives of this paper.
The impulsive orbital transfer mission is defined by the desired velocity change Δvd
and a short burning time tb. Similar to deorbiting missions of some spacecraft, a large Δvd
= 100m/s is selected and the short burning time is chosen to be tb= 15s. The small spacecraft body parameters selected are m
s
= 150kg, xs = 0.75m and I
s2 = 10 kgm2. Based on an SRM burning specification, the nozzle's mass is approximately mn = 8kg and finally the thrust force can be calculated as
${\bar{F}_T} = {{( {{{\rm{m}}_{\rm{n}}}{\rm{ + }}{{\rm{m}}_{\rm{s}}}} )\,(\Delta {{\rm{v}}_d}}
/ {{{\rm{t}}_{\rm{b}}}}}) = {\rm{1}}0{\rm{53N}}$
. The other nozzle parameters selected are xn =0.2 m and I
n2 = 1kgm
2. Maximum offset in the CM location is considered as z
s = 4 cm (more than the value in Reference Martin and LonguskiRef. 10). Finally, the jet damping coefficient is considered as Jd = 2Nms. The parameters are listed in Table 1.
Table 1 The spacecraft parameters
Due to the mechanical limitation and necessity for a good thrusting manoeuvre performance, the nozzle deviation should not be larger than an inappropriate value. The maximum value of gimbal angle is considered to be bounded by
$$\begin{equation}
\left| {\alpha (t)} \right| < {\alpha _{gimb}}\,,
\end{equation}$$
by which the following approximation can be concluded:
$$\begin{equation}
\begin{array}{@{}l@{}} {{\bar{I}}_r} \approx {I_{n,\,\,22}} + M{x_n}({x_n} + {x_s}),\\ {{\bar{I}}_{yy}} \approx {I_{n,\,\,22}} + {I_{s,\,\,22}} + M{({x_s} + {x_n})^2} \end{array}
\end{equation}$$
It should be noted that the closed-loop control system must meet and satisfy the condition (8).
3.0 CONTROLLER DESIGN
This section presents a detailed development of three types feedback control law through the nonlinear model obtained in Equation (5). First, the control problem statement is presented and then a linear controller with controllability analysis is designed. Next, in order to modify some weaknesses of the linear controller in transient mode, a nonlinear control law is proposed in which the stability of the nonlinear closed-loop system is proved. Finally, both linear and nonlinear controllers are combined together in order to achieve an efficient controller which is better than the two aforementioned controllers.
3.1 Control problem statement
For the planar manoeuvre, the linear acceleration components of the spacecraft CM in the inertial coordinate system (XIYIZI in Fig. 2), is given in Equation (10) where δ
FT
= α + θ is the thrust vector deviation from the desired inertial direction XI; v
x
,v
z
are the axial and transverse components, respectively, of the velocity change of the CM; and
${a_{\max }} = {{{{\bar{F}}_T}}
/ {({m_s} + {m_n})}}$
represents the maximum acceleration.
$$\begin{equation}
\begin{array}{@{}l@{}} {{{\rm{\dot{v}}}}_x} = {a_{\max }}\cos ({\delta _{FT}}),\\ {{{\rm{\dot{v}}}}_z} = - {a_{\max }}\sin ({\delta _{FT}}) \end{array}
\end{equation}$$
As discussed before, the control object is to eliminate the undesired acceleration component (
${{\rm{\dot{v}}}_z} \to 0$
) in order to maximise the velocity change in the XI direction (
${{\rm{\dot{v}}}_x} \to {a_{\max }}$
). Therefore, in addition to the attitude stabilisation, the important consideration is to direct the thrust vector FT
toward the inertial XI direction or to achieve δ
FT, eq
= θ
eq
+ α
eq
→ 0 as time tends to infinity. If there is the offset zs
in the CM location, then the desired equilibrium condition of the spacecraft can be shown in Fig. 3. The control system must align the thrust vector through the spacecraft CM (G) and desired velocity change
$\Delta {\bf v}_{\bm d}$
direction (XI) simultaneously. To reach these objects, the stabilised state variables will be
$$\begin{equation}
{\theta _{eq}} = - {\alpha _{eq}},\,\,\,{\dot{\theta }_{eq}} = {\dot{\alpha }_{eq}} = 0\,\,
\end{equation}$$
Figure 3. The desired equilibrium condition of the spacecraft in presence of CM uncertainty.
Figure 4. Spacecraft body attitude (θ) and gimbal angle (α) without active control.
Using Equations (5), (6) and (4), θ eq and α eq are obtained in Equation (12).
$$\begin{equation}
\begin{array}{@{}l@{}}
\ddot{\theta } = 0,\,\,\dot{\theta } = 0,\,\,\dot{\alpha } = 0,\,\,u = 0,\\
\,\, \Rightarrow {f_{\bm X}} + {d_X}{z_s} = 0,\\
\,\, \Rightarrow - \frac{{{{\bar{F}}_T}M}}{{{m_n}{I_{yy}}({\alpha _{eq}})}}{x_s}\sin ({\alpha _{eq}}) + \frac{M}{{{I_{yy}}({\alpha _{eq}})}}(\frac{{{{\bar{F}}_T}}}{{{m_n}}})cos({\alpha _{eq}})\,{z_s} = 0\,\,\,\, \Rightarrow \tan ({\alpha _{eq}}) = \frac{{{z_s}}}{{{x_s}}}\,\,\,,\\ \Rightarrow \,\,{\alpha _{eq}} \approx {{{z_s}}
/ {{x_s}}}\,\,\,\& \,\,\,{\theta _{eq}} \approx - {{{z_s}}
/ {{x_s}}}. \end{array}
\end{equation}$$
Thrust vector misalignment must be completely rejected by the proper gimbal deflection (see Fig. 3). In what follows, it is assumed that zs is constant(Reference Kishore24) and can be estimated by a nonlinear disturbance observer(Reference Chen37,Reference Wu and Meng38) .
To obtain a stabilisation control problem, the error dynamics are needed, for which new variables are defined as
$$\begin{equation}
\bar{\theta } = \theta - {\theta _{eq}}\,,\,\,\,\bar{\alpha } = \alpha - {\alpha _{eq}}
\end{equation}$$
Using Equations (4), (12), (9) and (13), the form of the nonlinear plant in Equations (5) and (6) are changed into Equation (14).
$$\begin{equation}
\begin{array}{@{}l@{}} \ddot{\bar{\theta }} = {{\bar{f}}_{\bm X}} - ({{{{\bar{I}}_r}}
/ {{{\bar{I}}_{yy}}}})u,\\ \ddot{\bar{\alpha }} = u, \end{array}
\end{equation}$$
where
${\bar{f}_{\bm X}} = - \frac{{{{\bar{F}}_T}M}}{{{m_n}{{\bar{I}}_{yy}}}}{x_s}\sin (\bar{\alpha }) + \frac{{M{x_s}{x_n}}}{{{{\bar{I}}_{yy}}}}\sin (\bar{\alpha })({\dot{\bar{\alpha }}^2} + 2\dot{\bar{\alpha }}\dot{\bar{\theta }}) - \frac{{{J_d}(\dot{\bar{\alpha }} + \dot{\bar{\theta }})}}{{{{\bar{I}}_{yy}}}}$
3.2 Linear controller design
In this section, at first controllability of the proposed method near the equilibrium point will be investigated and then a linear controller will be designed to result in a steady-state response.
3.2.1 Controllability of the linearised system
Before designing a linear or nonlinear control law, the controllability analysis of the linearised system is important to show the behaviour of the nonlinear system near the equilibrium point. By linearising the plant (Equation 14) about
$\bar{\theta } = 0$
and
$\bar{\alpha } = 0$
, the linear model is derived and given by
$$\begin{equation}
\begin{array}{@{}l@{}} \ddot{\bar{\theta }} = - \frac{{{{\bar{F}}_T}M}}{{{m_n}\,{{\bar{I}}_{yy}}}}{x_s}\,\bar{\alpha } - \frac{{{J_d}(\dot{\bar{\alpha }} + \dot{\bar{\theta }})}}{{{{\bar{I}}_{yy}}}} - \frac{{{{\bar{I}}_r}}}{{{{\bar{I}}_{yy}}}}u,\\ \ddot{\bar{\alpha }} = u. \end{array}
\end{equation}$$
By introducing
${\bm X} = {[ {\begin{array}{*{20}{c}} {\bar{\theta }}&{\dot{\bar{\theta }}}&{\bar{\alpha }}&{\dot{\bar{\alpha }}} \end{array}} ]^T}$
as the vector of state variables, the linear state space model is given as
$$\begin{equation}
{\bm{\dot{X}}} = {\bm{AX}} + {\bm B}\,u,
\end{equation}$$
where
${\bm A} = \left[ {\begin{array}{@{}*{4}{c}@{}} 0&1&0&0\\ 0&{ - \frac{{{J_d}}}{{{{\bar{I}}_{yy}}}}}&{ - \frac{{{{\bar{F}}_T}M}}{{{m_n}\,{{\bar{I}}_{yy}}}}{x_s}}&{ - \frac{{{J_d}}}{{{{\bar{I}}_{yy}}}}}\\ 0&0&0&1\\ 0&0&0&0 \end{array}} \right],\,\,{\bm B} = \left[ \begin{array}{@{}l@{}} 0\\ - \frac{{{{\bar{I}}_r}}}{{{{\bar{I}}_{yy}}}}\\ 0\\ 1 \end{array} \right]$
The controllability matrix Co is formed here in which the rank condition | Co | ≠ 0 is guaranteed. Therefore, the origin of the linearised system can be made uniformly asymptotically stable by a linear state feedback.
$$\begin{equation*}
{\bm{Co}} = [\bm{B},\bm{AB}, {\bm{A}^{\bm{2}}}\bm{B}, {\bm{A}^{\bm{3}}}\bm{B}],\,\,\left| {\bm{Co}} \right| = \frac{{{{\bar{F}}_T}M{x_s}({{\bar{F}}_T}\bar{I}_{yy}^2M{x_s} + {m_n}J_d^2({{\bar{I}}_r} - {{\bar{I}}_{yy}}))}}{{{{(\bar{I}_{yy}^2{m_n})}^2}}}
\end{equation*}$$
If the pair (A, B) be controllable, then the following controller can guarantee the stability of the above system:
$$\begin{equation}
u\left( t \right) = - \bm{KX}\left( t \right),\bm{K}\,\, \in \,\,{R^{1\, \times \,n}}
\end{equation}$$
This type of controller is the preferred for many industrial applications. By using a proper gain
K
,
$\bm{\tilde{A}} = \bm{A} - \bm{BK}$
can be stable. To have a good response at first, poles location are selected then MATLAB place function is used to compute gain
K
from the mentioned poles.
3.2.2 Numerical simulation
In this subsection, the simulation results of the nonlinear plant with a linear controller are carried out. The objects are to show the merits and weaknesses of using the linear controller in the proposed method. The time response specifications which are studied here are transient and steady-state responses of the body and the gimbal angles and the overshoot of the body attitude. The set of parameters which are used in the simulations are listed in Table 1. The disturbance torque is τ d = FTzs = 42.13Nm . The poles location of the linearised closed-loop system is selected as P = (–1 + 0.5i, –1 –0.5i, –2 –0.8i, –2 + 0.8i) that results in the control gain K = (–0.138, –0.304, 13.182, 5.846). Simulations are done using MATLB/ Simulink.
From Equation (10) Δvx as the actual velocity change along the desired inertial direction XI can be calculated as follows. The ideal condition at the thrusting manoeuvre is that δ FT (t) = 0 for 0 ⩽ t ⩽ tb (or Δvx=Δvd).
$$\begin{equation*}
\Delta {v_x} = \int\limits_0^{{t_b}} {{a_{\max }}\cos ({\delta _{FT}}(t))\,} dt\,\end{equation*}$$
Δvz as the undesired velocity change component in the inertial direction ZI can be calculated as
$$\begin{equation*}
\Delta {v_z} = - \int\limits_0^{{t_b}} {{a_{\max }}\sin ({\delta _{FT}}(t))\,} dt\,
\end{equation*}$$
However, the actual wasted velocity change is computed as
$$\begin{equation*}
\Delta {v_w} = {(\Delta v_d^2 - \Delta v_x^2)^{0.5}}\,
\end{equation*}$$
The following two numerical simulations are carried out, which are the simulations of the open-loop system (without active control system) and the nonlinear system with the linear controller, respectively.
Case 1
In this case, the gimbal actuator is inactivated and fixed at α(t) = 0. The attitude instability is obvious under the thrust vector misalignment (z s = 4 cm or α eq = 30). This simulation shows that without an active controller, the disturbance τ d = 42.13Nm can rotate the thrust vector direction more than 1500° in the first 5 s. In the open loop mode, the orbital manoeuvre cannot be performed correctly. This simulation shows that a high-capacity control system (a high-level control torque during the burning time) is needed for an impulsive orbital manoeuvre.
Case 2
The simulation results of the closed-loop system with the linear controller are given in this case. In Fig. 5, the time response of the body and gimbal angle are presented while they are converging to θeq = –3.055° and α eq = 3.0550, respectively. This result confirms the desired equilibrium condition in Fig. 3 where the thrust vector is pointed to the CM. Thrust vector stabilisation can be observed in Fig. 6 that converges to zero. Spacecraft velocity change along the two inertial directions is shown in Fig. 7. The velocity change along the axis XI is Δvx = 95.27m/s and the wasted velocity change is become Δvw = 30.38m/s.
Figure 5. Spacecraft body attitude (θ) and gimbal angle (α) when using a linear controller.
Figure 6. Thrust vector deviation (δ FT ) from the desired inertial direction (XI) when using a linear controller.
Figure 7. Spacecraft velocity change along the two inertial directions XI and ZI.
The advantages of using the linear controller are:
-
1. After the transient time or in steady-state mode, thrust vector deviation is completely eliminated.
-
2. The control action in steady-state mode is zero while a high-level exogenous disturbance torque (τ d = 42.13Nm) is completely rejected.
-
3. Near the equilibrium point (where a linearised model is a good approximation,) the closed-loop system has a fast response to reach the steady-state mode.
The weaknesses of using the linear controller are:
-
1. High overshoot of the body attitude during the transient response (the damped behaviour is not achieved).
-
2. Duo to high deviation of the body attitude and consequently a high deviation of the thrust vector, much velocity change is wasted.
-
3. In the presence of the nonlinear terms (far from the equilibrium point), there is no stability analysis for the nonlinear closed-loop system.
3.3 Nonlinear controller design
In the previous section, a linear controller is designed and its weaknesses and merits are discussed. Here the object is to design a nonlinear controller that lacks the shortcomings of the linear controller. The purposes of the nonlinear control law are 1) a damped (or under-damped) behaviour without an overshoot can be achieved for the body attitude in the transient mode, and 2) to show the stability of the nonlinear closed-loop system.
At the following, at first a nonlinear control law is proposed next, the stability of the nonlinear closed-loop system is proven and then by using the numerical simulations, its lack and merits are explained.
3.3.1 Nonlinear control law
By introducing the scalars η, γ and ξ, and using
${\bar{f}_{\bm{X}}}$
, Equation (14) is reformed to Equation (18)
$$\begin{equation}
\begin{array}{@{}l@{}} {{({{\bar{I}}_{yy}}}
/ {{{\bar{I}}_r}}})\ddot{\bar{\theta }} = \left( { - \eta + \gamma ({{\dot{\bar{\alpha }}}^2} + 2\dot{\bar{\alpha }}\dot{\bar{\theta }})} \right)\sin (\bar{\alpha }) - \xi (\dot{\bar{\alpha }} + \dot{\bar{\theta }}) - u,\\ \ddot{\bar{\alpha }} = u, \end{array}
\end{equation}$$
where
$\eta = {{({{\bar{F}}_T}M{x_s})}
/ {({m_n}{{\bar{I}}_r}}})\,,\,\,\gamma = {{(M{x_s}{x_n})}
/ {{{\bar{I}}_r}}},\,\,\xi = {{{J_d}}
/ {{{\bar{I}}_r}}}.$
As noticed before, in addition to guarantee the stability of the nonlinear closed-loop system, the important goal is to achieve a smooth or damped behaviour for the body attitude θ. Therefore, first a compensator is design for regulating the angle θ in a damped manner and then the nonlinear stability of the gimbal angle α will be proven. By proposing the nonlinear control law in Equation (19), the nonlinear closed-loop system is achieved in Equation (20):
$$\begin{equation}
u = \left( { - \eta + \gamma ({{\dot{\bar{\alpha }}}^2} + 2\dot{\bar{\alpha }}\dot{\bar{\theta }})} \right)\sin (\bar{\alpha }) - \xi (\dot{\bar{\alpha }} + \dot{\bar{\theta }}) - {{({{\bar{I}}_{yy}}}
/ {{{\bar{I}}_r}}}){\ddot{\bar{\theta }}_r}
\end{equation}$$
$$\begin{equation}
\left\{ \begin{array}{@{}l@{}} \ddot{\bar{\theta }} = {{\ddot{\bar{\theta }}}_r}\,,\\ \ddot{\bar{\alpha }} = \left( { - \eta + \gamma ({{\dot{\bar{\alpha }}}^2} + 2\dot{\bar{\alpha }}\dot{\bar{\theta }})} \right)\sin (\bar{\alpha }) - \xi (\dot{\bar{\alpha }} + \dot{\bar{\theta }}) - {{({{\bar{I}}_{yy}}}
/ {{{\bar{I}}_r}}}){{\ddot{\bar{\theta }}}_r}\,\,, \end{array} \right.
\end{equation}$$
where
$$\begin{equation}
{\ddot{\bar{\theta }}_r} = - 2\lambda \,\dot{\bar{\theta }} - {\lambda ^2}\,\bar{\theta }
\end{equation}$$
Putting Equation (21) into (Equation 20), the stable error dynamics of the
$\bar{\theta }(t)$
are obtained in Equation (22) as
$$\begin{equation}
\ddot{\bar{\theta }} + 2\lambda \,\dot{\bar{\theta }} + {\lambda ^2}\,\bar{\theta } = 0\,\,,
\end{equation}$$
where the constant and positive parameter λis employed for tuning the convergence rate in a damped manner. Then the following result can be easily concluded:
$$\begin{equation}
\bar{\theta }(t) \to 0,\,\,\dot{\bar{\theta }}(t) \to 0\,\,\,\& \,\,\,\,{\ddot{\bar{\theta }}_r} \to 0\,\,\,\,\,\,\,\,as\,\,\,\,\,t \to \infty
\end{equation}$$
According to the outcomes of (23), some terms in Equation (20) can be neglected for t > Tss
where Tss
is the settling time of the body attitude, which depends on the magnitude of λ. For t = Tss
, we have
$\bar{\theta }({T_{ss}}) \approx 0$
and
$\dot{\bar{\theta }}({T_{ss}}) \approx 0$
; therefore, the stability of the following system remains to be proved.
$$\begin{equation}
\begin{array}{@{}l@{}} \ddot{\bar{\alpha }}(t) \approx ( - \eta + \gamma {{\dot{\bar{\alpha }}}^2}(t))\sin (\bar{\alpha }(t)) - \xi \dot{\bar{\alpha }}(t)\,\,\,for\,\,t > {T_{ss}},\\ \bar{\alpha }({T_{ss}}) \ne 0\,,\,\,\dot{\bar{\alpha }}({T_{ss}}) \ne 0 \end{array}
\end{equation}$$
At first, to understand the behaviour of the dynamics (24), it is supposed that there is no damping ratio (ξ = 0). The approximate relation between the peak value of gimbal angle
${\bar{\alpha }_m}$
(at
$\dot{\bar{\alpha }} = 0$
) and its maximum angular velocity
${\dot{\bar{\alpha }}_m}$
(at
$\bar{\alpha } = 0$
) are formulated here. Using the transformation
$\ddot{\bar{\alpha }} = {{\dot{\bar{\alpha }}d\dot{\bar{\alpha }}}
/ {d\bar{\alpha }}} = {{d{{\dot{\bar{\alpha }}}^2}}
/ {2d\bar{\alpha }}}$
and by integrating Equation (24) from point
$(\bar{\alpha } = 0,\,\,\dot{\bar{\alpha }} = {\dot{\bar{\alpha }}_m})$
to
$(\bar{\alpha } = {\bar{\alpha }_m},\,\,\dot{\bar{\alpha }} = 0)$
the mentioned relation between
${\bar{\alpha }_m}$
and
${\dot{\bar{\alpha }}_m}$
is obtained in Equation (25).
$$\begin{equation}
\begin{array}{@{}l@{}}\frac{{ - 1}}{2}\frac{{d{{\dot{\bar{\alpha }}}^2}}}{{\eta - \gamma {{\dot{\bar{\alpha }}}^2}(t)}} \approx \sin (\bar{\alpha }(t))d\bar{\alpha }\mathop \Rightarrow \limits^{\int {} } \frac{1}{{2\gamma }}\left. {Ln(\eta - \gamma {{\dot{\bar{\alpha }}}^2})} \right|_{{{\dot{\bar{\alpha }}}_m}}^0 \approx - \left. {\cos (\bar{\alpha })} \right|_0^{{{\bar{\alpha }}_m}}\,\\\,\,\,\,\,\,\,\,\,\,\,\, \Rightarrow \dot{\bar{\alpha }}_m^2 \approx \frac{\eta }{\gamma }(1 - \exp \left[ {2\gamma (\cos ({{\bar{\alpha }}_m}) - 1)} \right])
\end{array}
\end{equation}$$
In the absence of the jet damping effect, Equation (25) gives the relation between the amplitude of gimbal angle
${\bar{\alpha }_m}$
and its rate amplitude
${\dot{\bar{\alpha }}_m}$
for the oscillatory behaviour of the dynamics Equation (24). In the other words, for ξ = 0 the maximum rates
${\dot{\bar{\alpha }}_m}$
(at
$\bar{\alpha } = 0$
) is only a function of maximum amplitude
${\bar{\alpha }_m}$
(at
$\dot{\bar{\alpha }} = 0$
) and does not converge to zero as time tends to infinity. Note that the condition (8) and the mission parameters can hold the condition
$\gamma \dot{\bar{\alpha }}_m^2 < \eta $
.
Theorem 1: in the presence of the jet damping (ξ ≠ 0), the dynamics in Equation (24) is stable and
$\bar{\alpha }(t) \to 0$
and
$\dot{\bar{\alpha }}(t) \to 0$
as t → ∞.
Proof: at first, three sequential points are defined in Equation (26) in order to be used as the bounds in the integrating of Equation (24). The aim is to show that
${| {\dot{\bar{\alpha }}(t)} |_{\bar{\alpha } = 0}}$
will be decreased for each oscillation (or
$| {{{\dot{\bar{\alpha }}}_3}} | < \,| {{{\dot{\bar{\alpha }}}_1}} |$
)
$$\begin{equation}
{P_1}({t_1},\,\,{\bar{\alpha }_1} = 0,\,\,{\dot{\bar{\alpha }}_1}),\,\,{P_2}({t_2},\,\,{\bar{\alpha }_2},\,\,{\dot{\bar{\alpha }}_2} = 0),\,\,{P_3}({t_3},\,\,{\bar{\alpha }_3} = 0,\,\,{\dot{\bar{\alpha }}_3})\,\,for\,\,{t_1} < {t_2} < {t_3}
\end{equation}$$
Using the transformations
$\ddot{\bar{\alpha }} = {{\dot{\bar{\alpha }}d\dot{\bar{\alpha }}}
/ {d\bar{\alpha }}} = {{d{{\dot{\bar{\alpha }}}^2}}
/ {2d\bar{\alpha }}}$
and
$\dot{\bar{\alpha }}d\bar{\alpha } = {\dot{\bar{\alpha }}^2}dt$
, and integrating of Equation (24) from P
1 to P
3, the following result is obtained in which reduction of the magnitude of
${| {\dot{\bar{\alpha }}(t)} |_{\bar{\alpha } = 0}}$
is shown as time tends to infinity.
$$\begin{equation}
\begin{array}{@{}l@{}} \frac{1}{{2\gamma }}\left. {Ln(\eta - \gamma {{\dot{\bar{\alpha }}}^2})} \right|_{{{\dot{\bar{\alpha }}}_1}}^{{{\dot{\bar{\alpha }}}_3}} = - \left. {\cos (\bar{\alpha })} \right|_{{{\bar{\alpha }}_1}}^{{{\bar{\alpha }}_3}} + {\sigma ^2} \Rightarrow Ln(\frac{{\eta - \gamma \dot{\bar{\alpha }}_3^2}}{{\eta - \gamma \dot{\bar{\alpha }}_1^2}}) = 2\gamma {\sigma ^2}\,\,\,\,\\[2pt] \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Rightarrow \frac{{\eta - \gamma \dot{\bar{\alpha }}_3^2}}{{\eta - \gamma \dot{\bar{\alpha }}_1^2}} = \exp (2\gamma {\sigma ^2}) > 1\,\,\, \Rightarrow {\left| {{{\dot{\bar{\alpha }}}_3}({t_3})} \right|_{\bar{\alpha } = 0}} < {\left| {{{\dot{\bar{\alpha }}}_1}({t_1})} \right|_{\bar{\alpha } = 0}}\,\,for\,\,{t_1} < {t_3}, \end{array}
\end{equation}$$
where
${\sigma ^2} = \xi \int\limits_{{t_1}}^{{t_3}} {\frac{{{{\dot{\bar{\alpha }}}^2}}}{{\eta - \gamma {{\dot{\bar{\alpha }}}^2}}}dt} > 0.$
Therefore, it can be claimed that by increasing the time t > tn
the
${| {\dot{\bar{\alpha }}(t)} |_{\bar{\alpha } = 0}}$
will be small enough to conclude
$ - \eta + \gamma {\dot{\bar{\alpha }}^2}(t) \approx - \eta $
, then the approximate form of the dynamics in Equation (24) is achieved as
$$\begin{equation}
\ddot{\bar{\alpha }}(t) \approx - \eta \sin (\bar{\alpha }(t)) - \xi \dot{\bar{\alpha }}(t)\,\,\,for\,\,t > {t_n}\,
\end{equation}$$
The candidate Lyapunov function is introduced as
$$\begin{equation}
V = \eta (1 - \cos (\bar{\alpha }(t))) + \frac{{\dot{\bar{\alpha }}{{(t)}^2}}}{2}\,.
\end{equation}$$
The time derivative of V along the dynamics (28) is
$$\begin{equation}
\dot{V} \approx - \xi {\dot{\bar{\alpha }}^2}(t)\, < 0\,
\end{equation}$$
Because the set
$(\dot{\bar{\alpha }} = 0\,,\,\,\bar{\alpha } \ne 0)$
is not a stable set for the dynamics (28), then from Equation (30), the stability of the error dynamics (28) can be easily concluded.
3.3.2 Numerical simulation
In this subsection, the performance of the nonlinear closed-loop system proven previously is illustrated. In addition to the parameters used in subsection 3.2.2, the parameters which are needed here are selected as Tss
= 3s and
$\lambda = {{{2.5}/ T}_{ss}} = {{0.83}/ s}$
.
The body and the gimbal angle are presented in Fig. 8 while they are converging to θeq = –3.0550 and α eq = 3.0550, respectively. Convergence of the thrust vector deviation can be observed in Fig. 9. Spacecraft velocity change along the two inertial directions is shown in Fig. 10. The velocity change along the axis XI is Δvx = 99.97m/s and the wasted velocity change is Δv w =2.0m/s.
Figure 8. Spacecraft body attitude (θ) and gimbal angle (α) when using a nonlinear controller.
Figure 9. Thrust vector deviation (δ FT ) from the desired inertial direction (XI) when using a nonlinear controller.
Figure 10. Spacecraft velocity change along the two inertial directions XI and ZI.
The advantages of using the proposed nonlinear controller in comparison with using the linear controller are:
-
1. Smaller overshoot of the body attitude during the transient response (the damped behaviour) is achieved.
-
2. Due to smaller deviation of the body attitude and consequently a smaller deviation of the thrust vector, the wasted velocity change is become smaller.
-
3. The stability of the nonlinear closed-loop system is illustrated.
Although there are advantages, some weaknesses can be seen in this method: 1) in the steady-state response of the body attitude, gimbal angle deviation is not completely eliminated and is oscillating during the burning time, and 2) the control action in steady-state mode is not zero while it is also oscillating.
The important idea presented in the next subsection is to derive a control law based on the combination of the linear and nonlinear controllers in which only the advantages of the two mentioned controllers are included and their shortcomings are excluded.
3.4 Combined linear and nonlinear controller
The purpose of this subsection is to combine the mentioned linear and nonlinear controllers with the aim of utilising their advantages and excluding their weaknesses. The expectation is to have a better controller than the two others. Moreover, the control effort in the steady-state mode is an important criterion that will be compared with the other thrusting methods.
3.4.1 Controller design
There are many complex methods to combine two or more control laws, but in this paper a simple combination law is employed. The combined control logic works according to the following model:
$$\begin{equation}
{u_{com}} = (1 - \exp ( - {a_c}t))\,{u_{lin}} + \exp ( - {a_c}t)\,{u_{nonl}}\,\,,
\end{equation}$$
where ucom denotes the combined control input, and ulin and unonl are the linear and nonlinear control law in Equations (17) and (19), respectively. ac is a constant to tune the switching rate between the two controllers; here it is chosen as 0.25. During the burning, for t < 1.2 Tss, only unonl acts as the control input and for t > 1.2 Tss, ucom is applied.
3.4.2 Numerical simulation
The time response specifications are illustrated in Figs. 11 and 12. The velocity change along the axis XI is Δvx = 99.97m/s and the wasted velocity change is Δv w =2.0m/s. It can be easily seen that the nonlinear controller generates the transient response and the linear controller is working well in steady-state mode; in other words, the combined controller includes the advantages of the two aforementioned controllers. It should be noted that these results are for the misalignment z s = 4 cm (α eq = 30); it is obvious that by decreasing the magnitude of the misalignment, all errors will be decreased and Δvx converges to Δvd.
Figure 11. Spacecraft body attitude (θ) and gimbal angle (α) when using a combined controller.
Figure 12. Spacecraft velocity change along the two inertial directions XI and ZI when using a combined controller.
In the following, closed-loop system performance is investigated in presence of high deviation in initial condition.
Based on the definition of the state-variables
$$\begin{equation*}
\bm{X}(t) = {\left[ {\begin{array}{*{20}{c}} {\bar{\theta }(t)}&{\dot{\bar{\theta }}(t)}&{\bar{\alpha }(t)}&{\dot{\bar{\alpha }}(t)} \end{array}} \right]^T} = {\left[ {\begin{array}{*{20}{c}} {\theta (t) - {\theta _{eq}}}&{\dot{\bar{\theta }}(t)}&{\alpha (t) - {\alpha _{eq}}}&{\dot{\alpha }(t)} \end{array}} \right]^T},
\end{equation*}$$
the vector of initial condition is
$$\begin{equation*}
\bm{X}{\rm{(0)}} = {\left[ {\begin{array}{*{20}{c}} {{\theta _0}}&{{{\dot{\theta }}_0}}&{{\alpha _0}}&{{{\dot{\alpha }}_0}} \end{array}} \right]^T} - {\left[ {\begin{array}{*{20}{c}} {{\theta _{eq}}}&0&{{\alpha _{eq}}}&0 \end{array}} \right]^T}\,
\end{equation*}$$
In practice, before thrusting manoeuvre the attitude can be stabilised by using the simple control methods by which
${\theta _0} = 0,\,\,{\dot{\theta }_0} = 0,\,\,{\alpha _0} = 0$
and
$\,{\dot{\alpha }_0} = 0$
can be achieved. Then using
${\alpha _{eq}} = {{{z_s}}
/ {{x_s}}}$
and
${\theta _{eq}} = - {{{z_s}}
/ {{x_s}}}$
the initial condition will be
$$\begin{equation*}
\bm{X}{\rm{(0)}} = {\left[ {\begin{array}{*{20}{c}} 1&0&{ - 1}&0 \end{array}} \right]^T}{{{z_s}}
/ {{x_s}}}\,\,,
\end{equation*}$$
which is used in the previous simulations.
Against previous simulations, there is a simulation in Fig. 13 that shows the ability of the proposed method in presence of high deviation in initial condition (initial attitude deviation). To show this ability, in addition to the disturbance, a large deviation is considered for the body attitude as θ0 = 300. A well transient and steady-state response can be clearly seen in this simulation.
Figure 13. Spacecraft body attitude (θ) and gimbal angle (α) in the presence of high initial attitude deviation.
4.0 DISCUSSION
The proposed thrusting method has some important merits in comparison with the RCS method. As shown before, in the steady-state mode of the proposed method, the large exogenous disturbance torque (τ
d
= 42.13Nm) is completely eliminated and rejected by a proper gimbal deflection while, in RCS method the mentioned disturbance always exist and should be rejected by a large active control torque that needs fuel consumption. It is assumed that four RCSs are located at the z = ±30cm to create the control torque about the ± ys
axis, then the force of each RCS is calculated as
${F_{RCS}} = ({{{\tau _d}}
/ {0.3}}{\rm{)/2 = }}70.2{\rm{N}}$
. Using the Isp=260s, the needed fuel is calculated about 0.8kg. As discussed in introduction section, in addition to the fuel consumption there are many disadvantages and limitations for using a RCS in a small spacecraft. It is obvious that for a longer time mission the more fuel consumption is needed but in the steady-state mode of the proposed method, control effort is zero because disturbances are successfully eliminated.
Many weaknesses and limitations of the basic (common) methods such as: spin-stabilisation and RCS are discussed in introduction section. At the following some major advantages of the proposed method in comparison with the spin-stabilisation, RCS, spin-stabilisation/RCS and TVC/RCS are summarised as:
-
1) Spin-stabilisation is just able to attenuate the exogenous disturbance effects but is not able to reject the disturbance caused by thrust vector misalignment, while in the proposed method the mentioned disturbance can be completely eliminated and rejected by a proper gimbal deflection at the steady-state mode.
-
2) When only the RCS method is employed, the disturbance torque rejection is accompanied by high control effort and fuel consumption during all of the burning time. But in the proposed method the control effort is zero in steady-state mode.
-
3) The proposed method does not need fuel consumption, stabilising spin and many complex components.
-
4) The combined TVC and RCS method is a powerful and accurate method but, for using in a small spacecraft it is not efficient and has many structural limitations.
-
5) Like as combined TVC and RCS, the combined spin-stabilisation and RCS is not suitable for a small spacecraft.
5.0 CONCLUSION
Although during an impulsive orbital manoeuvre a thrust vector misalignment generates a high level disturbance torque, an active control torque larger than the disturbance level can be obtained by using the TVC scheme. Based on some assumptions and criteria the subject of this paper is defined and then the weaknesses and limitations of the previous thrusting methods are well discussed to show they are not the proper choices for satisfying the objects of this paper. The structure of the proposed method is based on only the gimbaled-TVC where, the other control systems such as RCSs and spin-stabilisation are not employed moreover, a gimbal actuator does not need fuel consumption.
The major objects of the proposed underactuated control system are considered as 1) a damped (or under-damped) behaviour without an overshoot can be achieved for the body attitude in the transient mode 2) show the stability of the nonlinear closed-loop system 3) after the transient time or in the steady-state mode, thrust vector deviation should be completely eliminated 4) The control action in the steady-state mode remains zero while a high level exogenous disturbance can be completely rejected 5) near the equilibrium point, the closed-loop system converges to the steady-state mode very fast. To satisfy the mentioned objects, a linear controller is designed which has a good performance in the steady-state mode and then a nonlinear controller is proposed which is efficient to satisfy the transient mode objects. Since each of the linear and nonlinear controllers are just suitable for one mode (transient or steady-state), a new control law based on the combination of them is derived to satisfy both of the transient and steady-state modes objects, simultaneously. In the combined controller, the lacks of the linear and nonlinear controllers are excluded in a good manner. The attitude and thrust vector stabilisation along with full disturbance rejection are achieved where the maximum amplitude of the gimbal angle remains bounded in an acceptable range. Moreover, the good performance of the proposed method in presence of the high initial attitude deviation is illustrated.
A quantitative comparison to the RCS method is given to show the ability and effectiveness of the proposed method in sustained operation. It is shown that the proposed method has some advantages in comparison with the spin-stabilisation, RCS, spin-stabilisation/RCS and TVC/RCS. Considering the disadvantages of the other control methods, the proposed method can be very useful for an impulsive orbital manoeuvre of a small spacecraft, especially for missions with a long burning time.
An important application of the proposed method can be transferring the space debris (junk) to the deep space because; the other methods (such as spin-stabilisation and RCS) are not efficient and applicable for this mission.
