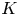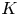1. Introduction
For a symplectic resolutions ![]() $X$ with symplectic form
$X$ with symplectic form ![]() $\omega$ in the sense of [Reference KaledinKal09], the stable basis defined in [Reference Maulik and OkounkovMO19] has found more and more applications. It is the crucial ingredient in the work of Maulik and Okounkov in constructing geometrical
$\omega$ in the sense of [Reference KaledinKal09], the stable basis defined in [Reference Maulik and OkounkovMO19] has found more and more applications. It is the crucial ingredient in the work of Maulik and Okounkov in constructing geometrical ![]() $R$-matrices, satisfying the Yang–Baxter equations. These
$R$-matrices, satisfying the Yang–Baxter equations. These ![]() $R$-matrices induce a Yangian action on the cohomology of Nakajima quiver varieties, so that the quantum connection of the quiver variety is identified with the trigonometric Casimir connection for the Yangian. In the case when
$R$-matrices induce a Yangian action on the cohomology of Nakajima quiver varieties, so that the quantum connection of the quiver variety is identified with the trigonometric Casimir connection for the Yangian. In the case when ![]() $X$ is the cotangent bundle of the flag variety (the Springer resolution) the stable basis is computed by the first-named author in [Reference SuSu17]. Using this, he computed the quantum connection of the cotangent bundle of partial flag varieties [Reference SuSu16] and generalized the result in [Reference Braverman, Maulik and OkounkovBMO11]. Pulling back the stable basis of the Springer resolution to the flag variety, one gets the Chern–Schwartz–MacPherson classes [Reference MacPhersonMac74] of the Schubert cells, see [Reference Aluffi, Mihalcea, Schürmann and SuAMSS17, Reference Rimanyi and VarchenkoRV18]. Combining this with the fact that the stable basis are the characteristic cycles of certain
$X$ is the cotangent bundle of the flag variety (the Springer resolution) the stable basis is computed by the first-named author in [Reference SuSu17]. Using this, he computed the quantum connection of the cotangent bundle of partial flag varieties [Reference SuSu16] and generalized the result in [Reference Braverman, Maulik and OkounkovBMO11]. Pulling back the stable basis of the Springer resolution to the flag variety, one gets the Chern–Schwartz–MacPherson classes [Reference MacPhersonMac74] of the Schubert cells, see [Reference Aluffi, Mihalcea, Schürmann and SuAMSS17, Reference Rimanyi and VarchenkoRV18]. Combining this with the fact that the stable basis are the characteristic cycles of certain ![]() $\mathcal {D}$-modules on the flag variety, the authors in [Reference Aluffi, Mihalcea, Schürmann and SuAMSS17] proved the non-equivariant version of the positivity conjecture in [Reference Aluffi and MihalceaAM16].
$\mathcal {D}$-modules on the flag variety, the authors in [Reference Aluffi, Mihalcea, Schürmann and SuAMSS17] proved the non-equivariant version of the positivity conjecture in [Reference Aluffi and MihalceaAM16].
The ![]() $K$-theoretic generalization of the stable basis is also undergoing significant developments, a survey of which can be found in [Reference OkounkovOko18a, Reference OkounkovOko18b].
$K$-theoretic generalization of the stable basis is also undergoing significant developments, a survey of which can be found in [Reference OkounkovOko18a, Reference OkounkovOko18b].
The definition of the ![]() $K$-theory stable bases for a symplectic resolution
$K$-theory stable bases for a symplectic resolution ![]() $(X, \omega )$ depends on a choice of a chamber in the Lie algebra of a maximal torus
$(X, \omega )$ depends on a choice of a chamber in the Lie algebra of a maximal torus ![]() $A$ in
$A$ in ![]() $\operatorname {Aut}(X, \omega )$, an alcove in
$\operatorname {Aut}(X, \omega )$, an alcove in ![]() $\operatorname {Pic}(X)_\mathbb {Q}$, as well as an orientation of the tangent bundle
$\operatorname {Pic}(X)_\mathbb {Q}$, as well as an orientation of the tangent bundle ![]() $TX$ (see e.g. § 2). Here a hyperplane configuration in
$TX$ (see e.g. § 2). Here a hyperplane configuration in ![]() $\operatorname {Pic}(X)_\mathbb {Q}$ naturally occurs.
$\operatorname {Pic}(X)_\mathbb {Q}$ naturally occurs.
It is an interesting question to find the change of bases matrices for stable bases associated to different choice of chambers or alcoves. The case when ![]() $X=\operatorname {Hilb}_n(\mathbb {C}^2)$ is studied in [Reference Gorsky and NegutGN17]. If
$X=\operatorname {Hilb}_n(\mathbb {C}^2)$ is studied in [Reference Gorsky and NegutGN17]. If ![]() $X$ is a Nakajima quiver variety, such change of bases matrices are certain trigonometric
$X$ is a Nakajima quiver variety, such change of bases matrices are certain trigonometric ![]() $R$-matrices, and induced an action of certain quantum loop algebra on the
$R$-matrices, and induced an action of certain quantum loop algebra on the ![]() $K$-theory of Nakajima quiver varieties [Reference Okounkov and SmirnovOS16, Reference Rimanyi, Tarasov and VarchenkoRTV15], generalizing the construction by Nakajima [Reference NakajimaNak01]. These played a crucial role in calculations of quantum
$K$-theory of Nakajima quiver varieties [Reference Okounkov and SmirnovOS16, Reference Rimanyi, Tarasov and VarchenkoRTV15], generalizing the construction by Nakajima [Reference NakajimaNak01]. These played a crucial role in calculations of quantum ![]() $K$-theory of Nakajima quiver varieties [Reference OkounkovOko17, Reference Okounkov and SmirnovOS16]. For example, they fully determined the two sets of the difference equations in the quantum
$K$-theory of Nakajima quiver varieties [Reference OkounkovOko17, Reference Okounkov and SmirnovOS16]. For example, they fully determined the two sets of the difference equations in the quantum ![]() $K$-theory of Nakajima quiver varieties.
$K$-theory of Nakajima quiver varieties.
In the case when ![]() $X=T^*\mathcal {B}$, the Springer resolution, the chamber structure is given by the Weyl chambers, and the alcove structure is given by the affine Weyl alcoves in
$X=T^*\mathcal {B}$, the Springer resolution, the chamber structure is given by the Weyl chambers, and the alcove structure is given by the affine Weyl alcoves in ![]() $\Lambda _\mathbb {Q}:=\operatorname {Pic}(T^*\mathcal {B})_\mathbb {Q}$ in the dual of the Cartan Lie algebra. That is, the hyperplane configuration occurring in the definition of stable bases are the affine coroot hyperplanes
$\Lambda _\mathbb {Q}:=\operatorname {Pic}(T^*\mathcal {B})_\mathbb {Q}$ in the dual of the Cartan Lie algebra. That is, the hyperplane configuration occurring in the definition of stable bases are the affine coroot hyperplanes ![]() $H_{\alpha ^\vee , n}$ for some coroot
$H_{\alpha ^\vee , n}$ for some coroot ![]() $\alpha ^\vee$ and
$\alpha ^\vee$ and ![]() $n\in {\mathbb {Z}}$, with the affine Weyl group
$n\in {\mathbb {Z}}$, with the affine Weyl group ![]() $W_{\operatorname {aff}}$ being the group generated by reflections.
$W_{\operatorname {aff}}$ being the group generated by reflections.
In [Reference Su, Zhao and ZhongSZZ20] we calculated the stable bases of ![]() $T^*\mathcal {B}$ associated to the fundamental alcove using the affine Hecke algebra actions via convolution [Reference Chriss and GinzburgCG97]. We identified the stable basis (respectively the fixed point basis) with the standard basis (respectively the Casselman basis) in the Iwahori-invariants of unramified principal series for the
$T^*\mathcal {B}$ associated to the fundamental alcove using the affine Hecke algebra actions via convolution [Reference Chriss and GinzburgCG97]. We identified the stable basis (respectively the fixed point basis) with the standard basis (respectively the Casselman basis) in the Iwahori-invariants of unramified principal series for the ![]() $p$-adic Langlands dual groups. With this, in [Reference Su, Zhao and ZhongSZZ20] we provided a
$p$-adic Langlands dual groups. With this, in [Reference Su, Zhao and ZhongSZZ20] we provided a ![]() $K$-theoretic interpretation of the Macdonald's formula for the spherical function [Reference CasselmanCas80] and the Casselman–Shalika formula for the spherical Whittaker function [Reference Casselman and ShalikaCS80]. Pulling back the stable basis to the flag variety from its cotangent bundle, we get the motivic Chern classes [Reference Brasselet, Schürmann and YokuraBSY10] of the Schubert cells [Reference Aluffi, Mihalcea, Schürmann and SuAMSS19, Reference Feher, Rimanyi and WeberFRW21]. This connection is used to prove a series of conjectures about the Casselman basis, see [Reference Aluffi, Mihalcea, Schürmann and SuAMSS19, Reference Bump and NakasujiBN11, Reference Bump and NakasujiBN19].
$K$-theoretic interpretation of the Macdonald's formula for the spherical function [Reference CasselmanCas80] and the Casselman–Shalika formula for the spherical Whittaker function [Reference Casselman and ShalikaCS80]. Pulling back the stable basis to the flag variety from its cotangent bundle, we get the motivic Chern classes [Reference Brasselet, Schürmann and YokuraBSY10] of the Schubert cells [Reference Aluffi, Mihalcea, Schürmann and SuAMSS19, Reference Feher, Rimanyi and WeberFRW21]. This connection is used to prove a series of conjectures about the Casselman basis, see [Reference Aluffi, Mihalcea, Schürmann and SuAMSS19, Reference Bump and NakasujiBN11, Reference Bump and NakasujiBN19].
The goal of the present paper is to calculate the bases associated to an arbitrary choice of alcove, and find the change of bases operators for the bases associated to two different alcoves. We also determine the effect of changing the chambers.
As applications, we prove that the ![]() $K$-theory stable basis is categorified by the Verma modules of the quantization of
$K$-theory stable basis is categorified by the Verma modules of the quantization of ![]() $T^*\mathcal {B}$ in positive characteristic [Reference Bezrukavnikov, Mirković and RumyninBMR08]. Consequently, we prove that the change of bases operators induced by two different choices of alcoves coincide with the monodromy matrices of the quantum cohomology. These facts have been conjectured by Bezrukavnikov and Okounkov to hold for a general symplectic resolution
$T^*\mathcal {B}$ in positive characteristic [Reference Bezrukavnikov, Mirković and RumyninBMR08]. Consequently, we prove that the change of bases operators induced by two different choices of alcoves coincide with the monodromy matrices of the quantum cohomology. These facts have been conjectured by Bezrukavnikov and Okounkov to hold for a general symplectic resolution ![]() $(X,\omega )$ [Reference OkounkovOko18a]. The case when
$(X,\omega )$ [Reference OkounkovOko18a]. The case when ![]() $X$ is the Nakajima quiver variety is proved in unpublished work of Bezrukavnikov and Okounkov via a different method. However, to the best of our knowledge, the present paper provides one of the first examples where a connection between
$X$ is the Nakajima quiver variety is proved in unpublished work of Bezrukavnikov and Okounkov via a different method. However, to the best of our knowledge, the present paper provides one of the first examples where a connection between ![]() $K$-theory stable bases and quantizations in positive characteristic is established.
$K$-theory stable bases and quantizations in positive characteristic is established.
We now state our main result on the wall-crossings, without introducing too many notations and technicalities. For simplicity we fix the choice of the Weyl chamber to be the positive Weyl chamber ![]() $+$, and the orientation to be a canonical one given by the tangent bundle § 2. For each choice of alcove
$+$, and the orientation to be a canonical one given by the tangent bundle § 2. For each choice of alcove ![]() $\nabla$, the basis elements are labelled by the torus fixed points on
$\nabla$, the basis elements are labelled by the torus fixed points on ![]() $T^*\mathcal {B}$, which in turn are labelled by elements of the Weyl group
$T^*\mathcal {B}$, which in turn are labelled by elements of the Weyl group ![]() $W$. Hence the stable basis is denoted by
$W$. Hence the stable basis is denoted by ![]() $\{\operatorname {stab}^{+,T\mathcal {B},\nabla }_w\mid w\in W\}$.
$\{\operatorname {stab}^{+,T\mathcal {B},\nabla }_w\mid w\in W\}$.
Let ![]() $A$ be the maximal torus of
$A$ be the maximal torus of ![]() $G$, and
$G$, and ![]() $A^\vee$ its Langlands dual. We use subindex reg to denote the open complement to the coroot hyperplanes. Let
$A^\vee$ its Langlands dual. We use subindex reg to denote the open complement to the coroot hyperplanes. Let ![]() $B'_{\operatorname {aff}}=\pi _1(A^\vee _\textit {reg}/W)$. There is a quotient
$B'_{\operatorname {aff}}=\pi _1(A^\vee _\textit {reg}/W)$. There is a quotient ![]() $\mathbb {C}[q^{\pm 1/2}][B'_{\operatorname {aff}}]\to {\mathbb {H}}$ from the group algebra to the affine Hecke algebra, and an action of
$\mathbb {C}[q^{\pm 1/2}][B'_{\operatorname {aff}}]\to {\mathbb {H}}$ from the group algebra to the affine Hecke algebra, and an action of ![]() ${\mathbb {H}}$ on
${\mathbb {H}}$ on ![]() $K_{A\times \mathbb {C}^*}(T^*\mathcal {B})$, constructed by Kazhdan and Lusztig [Reference Kazhdan and LusztigKL87] and Ginzburg [Reference Chriss and GinzburgCG97]. This action describes the wall-crossings of stable bases completely. This is the first main result in the present paper. See Theorem 5.4 for a precise statement.
$K_{A\times \mathbb {C}^*}(T^*\mathcal {B})$, constructed by Kazhdan and Lusztig [Reference Kazhdan and LusztigKL87] and Ginzburg [Reference Chriss and GinzburgCG97]. This action describes the wall-crossings of stable bases completely. This is the first main result in the present paper. See Theorem 5.4 for a precise statement.
Theorem 1.1 Assume two alcoves ![]() $\nabla _1, \nabla _2$ are adjacent and separated by
$\nabla _1, \nabla _2$ are adjacent and separated by ![]() $H_{\alpha ^\vee , n}$ for some positive coroot
$H_{\alpha ^\vee , n}$ for some positive coroot ![]() $\alpha ^\vee$ and
$\alpha ^\vee$ and ![]() $n\in {\mathbb {Z}}$, and that
$n\in {\mathbb {Z}}$, and that ![]() $(\lambda _1, \alpha ^\vee )<(\lambda _2, \alpha ^\vee )$ for any
$(\lambda _1, \alpha ^\vee )<(\lambda _2, \alpha ^\vee )$ for any ![]() $\lambda _i\in \nabla _i$. Let
$\lambda _i\in \nabla _i$. Let ![]() $b_{\nabla _1,\nabla _2}$ be the element in
$b_{\nabla _1,\nabla _2}$ be the element in ![]() $\pi _1({\frak h}^*_{{\mathbb {C}},\textit {reg}}/W_{\operatorname {aff}})\subseteq B'_{\operatorname {aff}}$ represented by a positive path going from
$\pi _1({\frak h}^*_{{\mathbb {C}},\textit {reg}}/W_{\operatorname {aff}})\subseteq B'_{\operatorname {aff}}$ represented by a positive path going from ![]() $\nabla _1$ to
$\nabla _1$ to ![]() $\nabla _2$. Then, the image of
$\nabla _2$. Then, the image of ![]() $b_{\nabla _2,\nabla _1}^{-1}$ in
$b_{\nabla _2,\nabla _1}^{-1}$ in ![]() ${\mathbb {H}}$ sends the set
${\mathbb {H}}$ sends the set ![]() $\{\mathcal {L}_{-\rho }\otimes \operatorname {stab}^{+,T\mathcal {B},\nabla _1}_w\mid w\in W\}$ to
$\{\mathcal {L}_{-\rho }\otimes \operatorname {stab}^{+,T\mathcal {B},\nabla _1}_w\mid w\in W\}$ to ![]() $\{\mathcal {L}_{-\rho }\otimes \operatorname {stab}^{+,T\mathcal {B},\nabla _2}_w\mid w\in W\}$, up to some (explicitly determined) scalars.
$\{\mathcal {L}_{-\rho }\otimes \operatorname {stab}^{+,T\mathcal {B},\nabla _2}_w\mid w\in W\}$, up to some (explicitly determined) scalars.
As an immediate consequence of Theorem 1.1, we proved that the standard objects in the quantizations of ![]() $T^*\mathcal {B}$ in positive characteristic categorify the stable bases. More precisely, we have a categorification of the stable basis, well defined for the Springer resolution
$T^*\mathcal {B}$ in positive characteristic categorify the stable bases. More precisely, we have a categorification of the stable basis, well defined for the Springer resolution ![]() $T^*\mathcal {B}_{{\mathbb {Z}}}$ over
$T^*\mathcal {B}_{{\mathbb {Z}}}$ over ![]() ${\mathbb {Z}}$. When base changing to characteristic zero and passing to the Grothendieck group, we get the usual stable basis. When base changing to positive characteristic, we get localization of Verma modules via the equivalence [Reference Bezrukavnikov and MirkovićBM13, Reference Bezrukavnikov, Mirković and RumyninBMR08, Reference Bezrukavnikov, Mirković and RumyninBMR06].
${\mathbb {Z}}$. When base changing to characteristic zero and passing to the Grothendieck group, we get the usual stable basis. When base changing to positive characteristic, we get localization of Verma modules via the equivalence [Reference Bezrukavnikov and MirkovićBM13, Reference Bezrukavnikov, Mirković and RumyninBMR08, Reference Bezrukavnikov, Mirković and RumyninBMR06].
Theorem 1.2 (Theorems 6.4 and 7.5)
For any ![]() $\lambda \in \Lambda _\mathbb {Q}$ not on any hyperplanes
$\lambda \in \Lambda _\mathbb {Q}$ not on any hyperplanes ![]() $H_{\alpha ^\vee , n}$, we define the set of objects
$H_{\alpha ^\vee , n}$, we define the set of objects ![]() $\{{\frak s}{\frak t}{\frak a}{\frak b}^{{\mathbb {Z}}}_{\lambda }(w)\mid w\in W\}$ in the derived category
$\{{\frak s}{\frak t}{\frak a}{\frak b}^{{\mathbb {Z}}}_{\lambda }(w)\mid w\in W\}$ in the derived category ![]() $D^b_{A_{\mathbb {Z}}\times (\mathbb {G}_m)_{{\mathbb {Z}}}}(T^*\mathcal {B}_{{\mathbb {Z}}})$.
$D^b_{A_{\mathbb {Z}}\times (\mathbb {G}_m)_{{\mathbb {Z}}}}(T^*\mathcal {B}_{{\mathbb {Z}}})$.
(1) Applying the derived base change functor
 $\otimes ^L_{{\mathbb {Z}}}\mathbb {C}$ and then taking classes in the Grothendieck group, these objects become the
$\otimes ^L_{{\mathbb {Z}}}\mathbb {C}$ and then taking classes in the Grothendieck group, these objects become the  $K$-theory stable basis for the alcove containing
$K$-theory stable basis for the alcove containing  $\lambda$.
$\lambda$.(2) Applying the base change functor
 $\otimes ^L_{{\mathbb {Z}}}k$ for an algebraically closed field
$\otimes ^L_{{\mathbb {Z}}}k$ for an algebraically closed field  $k$ of characteristic
$k$ of characteristic  $p$ greater than the Coxeter number, up to
$p$ greater than the Coxeter number, up to  $\lambda =-({\lambda '+\rho })/{p}$, these objects become the image of Verma modules over
$\lambda =-({\lambda '+\rho })/{p}$, these objects become the image of Verma modules over  $U({\frak g}_k)$ with Harish-Chandra central character
$U({\frak g}_k)$ with Harish-Chandra central character  $\lambda '+2\rho$, under the localization functor
$\lambda '+2\rho$, under the localization functor  $\gamma ^{\lambda '}$ of [Reference Bezrukavnikov, Mirković and RumyninBMR06] (recalled in § 7.1).
$\gamma ^{\lambda '}$ of [Reference Bezrukavnikov, Mirković and RumyninBMR06] (recalled in § 7.1).
In particular, under the duality between ![]() $A\times \mathbb {G}_m$-equivariant
$A\times \mathbb {G}_m$-equivariant ![]() $K$-theory of
$K$-theory of ![]() $T^*\mathcal {B}$ and the Iwahori-invariants of the principal series representation of the
$T^*\mathcal {B}$ and the Iwahori-invariants of the principal series representation of the ![]() $p$-adic Langlands dual group, the standard objects, which are the Verma modules, are mapped to the standard objects, i.e. the characteristic functions. The restriction formula of [Reference Su, Zhao and ZhongSZZ20, Theorem 7.5] gives a formula of the graded Ext between Verma modules and baby Verma modules with respect to the Koszul grading on [Reference Bezrukavnikov and MirkovićBM13].
$p$-adic Langlands dual group, the standard objects, which are the Verma modules, are mapped to the standard objects, i.e. the characteristic functions. The restriction formula of [Reference Su, Zhao and ZhongSZZ20, Theorem 7.5] gives a formula of the graded Ext between Verma modules and baby Verma modules with respect to the Koszul grading on [Reference Bezrukavnikov and MirkovićBM13].
It has been well known that the ![]() $K$-theory lift of the monodromy of quantum connection of
$K$-theory lift of the monodromy of quantum connection of ![]() $T^*\mathcal {B}$ defines an affine Hecke algebra action on the equivariant
$T^*\mathcal {B}$ defines an affine Hecke algebra action on the equivariant ![]() $K$-theory of
$K$-theory of ![]() $T^*\mathcal {B}$ [Reference Braverman, Maulik and OkounkovBMO11], which coincides with the one coming from [Reference Bezrukavnikov, Mirković and RumyninBMR06]. An immediate consequence of Theorem 7.5 is that the change of bases operator, induced by
$T^*\mathcal {B}$ [Reference Braverman, Maulik and OkounkovBMO11], which coincides with the one coming from [Reference Bezrukavnikov, Mirković and RumyninBMR06]. An immediate consequence of Theorem 7.5 is that the change of bases operator, induced by ![]() $K$-theory stable bases associated to different alcove, agrees with the monodromy operator in
$K$-theory stable bases associated to different alcove, agrees with the monodromy operator in ![]() $\pi _1(A^\vee _\textit {reg}/W)$ of the quantum connection of
$\pi _1(A^\vee _\textit {reg}/W)$ of the quantum connection of ![]() $T^*\mathcal {B}$ (see Theorem 8.1 for a precise statement).
$T^*\mathcal {B}$ (see Theorem 8.1 for a precise statement).
Organization of the paper
In § 2 we recall the definition and basic facts of stable bases, and in § 3 we recall some basic facts of wall-crossings. In § 4 we compute the formula of crossing walls determined by simple roots, which is generalized in § 5 to non-simple walls. In § 6 we recall affine braid group actions on the derived categories of Springer resolutions, and use them to define categorified version of the stable basis. In § 7, we show such basis coincides with Verma modules under the localization of Lie algebras in positive characteristic. As another consequence, we deduce in § 8 that wall-crossing of the stable basis agree with monodromy of quantum cohomology. In the appendix we compute the wall-crossing matrix in the case of ![]() $\operatorname {SL}(3,\mathbb {C})$.
$\operatorname {SL}(3,\mathbb {C})$.
2. Recollection of stable bases and the affine Hecke algebra
2.1 Notations
Let ![]() $G$ be a connected, semisimple, simply connected, complex linear algebraic group with a Borel subgroup
$G$ be a connected, semisimple, simply connected, complex linear algebraic group with a Borel subgroup ![]() $B$, whose roots are positive. Let
$B$, whose roots are positive. Let ![]() $A\subset B$ be a maximal torus of
$A\subset B$ be a maximal torus of ![]() $G$,
$G$, ![]() ${\frak h}$ be the Lie algebra of
${\frak h}$ be the Lie algebra of ![]() $A$, and
$A$, and ![]() $\Lambda$ (respectively
$\Lambda$ (respectively ![]() $\Lambda ^\vee$) the group of characters (respectively cocharacters) of
$\Lambda ^\vee$) the group of characters (respectively cocharacters) of ![]() $A$. Let
$A$. Let ![]() $\rho$ denote the half sum of the positive roots. Let
$\rho$ denote the half sum of the positive roots. Let ![]() $\pm :={\frak C}_\pm \subset \Lambda ^\vee \otimes _{\mathbb {Z}}{\mathbb {R}}$ denote the dominant/anti-dominant Weyl chambers in
$\pm :={\frak C}_\pm \subset \Lambda ^\vee \otimes _{\mathbb {Z}}{\mathbb {R}}$ denote the dominant/anti-dominant Weyl chambers in ![]() ${\frak h}$. For any coroot
${\frak h}$. For any coroot ![]() $\alpha ^\vee$, define the hyperplanes in
$\alpha ^\vee$, define the hyperplanes in ![]() $\mathfrak {h}^*_{\mathbb {R}}$ by
$\mathfrak {h}^*_{\mathbb {R}}$ by
We refer the connected components of
as the alcoves of this hyperplane arrangement. The walls of an alcove are the codimension-![]() $1$ facets in the boundary of this alcove. The following alcove will be referred to as the fundamental alcove
$1$ facets in the boundary of this alcove. The following alcove will be referred to as the fundamental alcove
In other words, it contains ![]() $\epsilon \rho$ for small
$\epsilon \rho$ for small ![]() $\epsilon >0$. Write
$\epsilon >0$. Write ![]() $\nabla _-=-\nabla _+$. We say two alcoves
$\nabla _-=-\nabla _+$. We say two alcoves ![]() $\nabla _1,\nabla _2$ are adjacent if they share a wall on some hyperplane
$\nabla _1,\nabla _2$ are adjacent if they share a wall on some hyperplane ![]() $H_{\alpha ^\vee , n}$.
$H_{\alpha ^\vee , n}$.
We will use the same terminologies of alcoves, walls, and fundamental alcoves for their intersections with ![]() $\Lambda _\mathbb {Q}\subseteq {\frak h}^*_{{\mathbb {R}}}$.
$\Lambda _\mathbb {Q}\subseteq {\frak h}^*_{{\mathbb {R}}}$.
Denote by ![]() $\mathcal {B}\simeq G/B$, the variety of all the Borel groups of
$\mathcal {B}\simeq G/B$, the variety of all the Borel groups of ![]() $G$, and
$G$, and ![]() $T^*\mathcal {B}$ (respectively
$T^*\mathcal {B}$ (respectively ![]() $T\mathcal {B}$) its cotangent bundle (respectively tangent bundle). For each
$T\mathcal {B}$) its cotangent bundle (respectively tangent bundle). For each ![]() $\lambda \in \Lambda$, there is an associated line bundle
$\lambda \in \Lambda$, there is an associated line bundle ![]() $\mathcal {L}_\lambda$ on
$\mathcal {L}_\lambda$ on ![]() $\mathcal {B}$ independent on the choice of
$\mathcal {B}$ independent on the choice of ![]() $B$ [Reference Chriss and GinzburgCG97, §6.1.11]. Pulling it back onto
$B$ [Reference Chriss and GinzburgCG97, §6.1.11]. Pulling it back onto ![]() $T^*\mathcal {B}$, we still denote it by
$T^*\mathcal {B}$, we still denote it by ![]() $\mathcal {L}_\lambda$. Therefore, we have identity
$\mathcal {L}_\lambda$. Therefore, we have identity
Let ![]() $\mathbb {C}^*$ act on
$\mathbb {C}^*$ act on ![]() $T^*\mathcal {B}$ by
$T^*\mathcal {B}$ by ![]() $z\cdot (B', x)=(B', z^{-2}x)$, where
$z\cdot (B', x)=(B', z^{-2}x)$, where ![]() $z\in \mathbb {C}^*$ and
$z\in \mathbb {C}^*$ and ![]() $(B', x)\in T^*\mathcal {B}$. Let
$(B', x)\in T^*\mathcal {B}$. Let ![]() $q^{-1}$ denote the character of cotangent fiber under this action. We refer the readers to [Reference Chriss and GinzburgCG97] for a beautiful account of the equivariant K-theory. Let
$q^{-1}$ denote the character of cotangent fiber under this action. We refer the readers to [Reference Chriss and GinzburgCG97] for a beautiful account of the equivariant K-theory. Let ![]() $T=A\times \mathbb {C}^*$, and
$T=A\times \mathbb {C}^*$, and ![]() $K_{T}(\operatorname {pt})\cong {\mathbb {Z}}[q^{1/2},q^{-1/2}][\Lambda ]$. In this paper, we will consider
$K_{T}(\operatorname {pt})\cong {\mathbb {Z}}[q^{1/2},q^{-1/2}][\Lambda ]$. In this paper, we will consider ![]() $K_T(T^*\mathcal {B})$, which is a module over
$K_T(T^*\mathcal {B})$, which is a module over ![]() $K_T(\operatorname {pt})$. The
$K_T(\operatorname {pt})$. The ![]() $A$-fixed points of
$A$-fixed points of ![]() $T^*\mathcal {B}$ are indexed by
$T^*\mathcal {B}$ are indexed by ![]() $W$; each
$W$; each ![]() $w\in W$ determines the fixed point
$w\in W$ determines the fixed point ![]() $wB\in \mathcal {B}\subset T^*\mathcal {B}$. We will just use
$wB\in \mathcal {B}\subset T^*\mathcal {B}$. We will just use ![]() $w$ to denote the corresponding fixed point
$w$ to denote the corresponding fixed point ![]() $wB$. For each
$wB$. For each ![]() $w \in W$, denote by
$w \in W$, denote by ![]() $1_w\in K_{T}((T^*\mathcal {B})^A)\cong \oplus _{v\in W}K_T(\operatorname {pt})$ the basis corresponding to
$1_w\in K_{T}((T^*\mathcal {B})^A)\cong \oplus _{v\in W}K_T(\operatorname {pt})$ the basis corresponding to ![]() $w$, and by
$w$, and by ![]() $\iota _w$ its image via the push-forward of the embedding
$\iota _w$ its image via the push-forward of the embedding ![]() $i:w\to T^*\mathcal {B}$, that is,
$i:w\to T^*\mathcal {B}$, that is, ![]() $\iota _w=i_*(1)\in K_T(T^*\mathcal {B})$. It follows from the localization theorem [Reference Chriss and GinzburgCG97] that
$\iota _w=i_*(1)\in K_T(T^*\mathcal {B})$. It follows from the localization theorem [Reference Chriss and GinzburgCG97] that ![]() $\{\iota _w|w\in W\}$ forms a basis for the localized equivariant K-theory
$\{\iota _w|w\in W\}$ forms a basis for the localized equivariant K-theory ![]() $K_T(T^*\mathcal {B})_{{loc}}:= K_T(T^*\mathcal {B})\otimes _{K_T(\operatorname {pt})}\operatorname {Frac} K_T(\operatorname {pt})$, where
$K_T(T^*\mathcal {B})_{{loc}}:= K_T(T^*\mathcal {B})\otimes _{K_T(\operatorname {pt})}\operatorname {Frac} K_T(\operatorname {pt})$, where ![]() $\operatorname {Frac} K_T(\operatorname {pt})$ denotes the fraction field of
$\operatorname {Frac} K_T(\operatorname {pt})$ denotes the fraction field of ![]() $K_T(\operatorname {pt})$. For any vector space
$K_T(\operatorname {pt})$. For any vector space ![]() $V$ with a
$V$ with a ![]() $T$-action, write
$T$-action, write
where the last product is over all the ![]() $T$-weights in
$T$-weights in ![]() $V$, counted with multiplicities. Note that this is not the standard notation for the wedge product because of the dual
$V$, counted with multiplicities. Note that this is not the standard notation for the wedge product because of the dual ![]() $^\vee$.
$^\vee$.
Recall there is a non-degenerate pairing ![]() $\langle \cdot , \cdot \rangle$ on
$\langle \cdot , \cdot \rangle$ on ![]() $K_T(T^*\mathcal {B})$ defined via localization:
$K_T(T^*\mathcal {B})$ defined via localization:
where ![]() $\mathcal {F}, \mathcal {G}\in K_T(T^*\mathcal {B})$, and
$\mathcal {F}, \mathcal {G}\in K_T(T^*\mathcal {B})$, and ![]() $\mathcal {F}|_w$ denotes the pullback of
$\mathcal {F}|_w$ denotes the pullback of ![]() $\mathcal {F}$ to the fixed point
$\mathcal {F}$ to the fixed point ![]() $wB\in \mathcal {B}\subset T^*\mathcal {B}$.
$wB\in \mathcal {B}\subset T^*\mathcal {B}$.
2.2 Definition of stable bases
We recall the definition of stable bases of Maulik and Okounkov.
Let ![]() ${\frak C}$ be a chamber in
${\frak C}$ be a chamber in ![]() $\Lambda ^\vee _{\mathbb {R}}$. For any cocharacter
$\Lambda ^\vee _{\mathbb {R}}$. For any cocharacter ![]() $\sigma \in {\frak C}$, the stable leaf (also called the attracting set) of the fixed point
$\sigma \in {\frak C}$, the stable leaf (also called the attracting set) of the fixed point ![]() $w$ is
$w$ is
It defines a partial order on ![]() $W$ as follows:
$W$ as follows:
For example, with ![]() ${\frak C}_+$ (respectively
${\frak C}_+$ (respectively ![]() ${\frak C}_-$) denoting the dominant chamber (respectively the anti-dominant chamber) where all the positive roots take positive (respectively negative) values, then
${\frak C}_-$) denoting the dominant chamber (respectively the anti-dominant chamber) where all the positive roots take positive (respectively negative) values, then
where ![]() $\le$ is the usual Bruhat order of
$\le$ is the usual Bruhat order of ![]() $W$. In this case,
$W$. In this case, ![]() $\operatorname {Attr}_{{\frak C}_+}(w)$ (respectively
$\operatorname {Attr}_{{\frak C}_+}(w)$ (respectively ![]() $\operatorname {Attr}_{{\frak C}_-}(w)$) is equal to the conormal bundle of the Schubert cell
$\operatorname {Attr}_{{\frak C}_-}(w)$) is equal to the conormal bundle of the Schubert cell ![]() $BwB/B$ (respectively opposite Schubert cell
$BwB/B$ (respectively opposite Schubert cell ![]() $B^-wB/B$, where
$B^-wB/B$, where ![]() $B^-$ is the opposite Borel subgroup) inside the flag variety
$B^-$ is the opposite Borel subgroup) inside the flag variety ![]() $\mathcal {B}$. Denote the full attracting set by
$\mathcal {B}$. Denote the full attracting set by
Define a polarization ![]() $T^{1/2}\in K_T(T^*\mathcal {B})$ to be an equivariant K-theory class such that the following identity holds,
$T^{1/2}\in K_T(T^*\mathcal {B})$ to be an equivariant K-theory class such that the following identity holds,
Write ![]() $T^{1/2}_{\operatorname {opp}}=q^{-1}(T^{1/2})^\vee$. We will mostly use the following two mutually opposite polarizations:
$T^{1/2}_{\operatorname {opp}}=q^{-1}(T^{1/2})^\vee$. We will mostly use the following two mutually opposite polarizations: ![]() $T\mathcal {B}$ and
$T\mathcal {B}$ and ![]() $T^*\mathcal {B}$, which lie in
$T^*\mathcal {B}$, which lie in ![]() $K_{G\times \mathbb {C}^*}(T^*\mathcal {B})$.
$K_{G\times \mathbb {C}^*}(T^*\mathcal {B})$.
Let ![]() $N_w:=T_w(T^*\mathcal {B})$ be the tangent space of
$N_w:=T_w(T^*\mathcal {B})$ be the tangent space of ![]() $T^*\mathcal {B}$ at the torus fixed point
$T^*\mathcal {B}$ at the torus fixed point ![]() $wB$, and
$wB$, and ![]() $T^{1/2}_w:=T^{1/2}|_w$. Each chamber
$T^{1/2}_w:=T^{1/2}|_w$. Each chamber ![]() ${\frak C}$ determines a decomposition
${\frak C}$ determines a decomposition ![]() $N_w=N_{w,+}\oplus N_{w,-}$ of
$N_w=N_{w,+}\oplus N_{w,-}$ of ![]() $N_w$ into
$N_w$ into ![]() $A$-weight spaces which are positive and negative with respect to
$A$-weight spaces which are positive and negative with respect to ![]() ${\frak C}$, and similarly
${\frak C}$, and similarly ![]() $T^{1/2}_w=T^{1/2}_{w,+}\oplus T^{1/2}_{w,-}$. Then
$T^{1/2}_w=T^{1/2}_{w,+}\oplus T^{1/2}_{w,-}$. Then
and
Thus,
 \[ \bigg(\frac{\det N_{w,-}}{\det T^{1/2}_w}\bigg)^{1/2} =q^{-{\operatorname{rank} T^{1/2}_{w,+}}/{2}}\det (T^{1/2}_{w,+})^\vee{\in} K_T(\operatorname{pt}). \]
\[ \bigg(\frac{\det N_{w,-}}{\det T^{1/2}_w}\bigg)^{1/2} =q^{-{\operatorname{rank} T^{1/2}_{w,+}}/{2}}\det (T^{1/2}_{w,+})^\vee{\in} K_T(\operatorname{pt}). \]
For any Laurent polynomial ![]() $f=\sum _{\mu \in \Lambda }f_\mu e^\mu \in K_T(\operatorname {pt})$ with
$f=\sum _{\mu \in \Lambda }f_\mu e^\mu \in K_T(\operatorname {pt})$ with ![]() $f_\mu \in K_{\mathbb {C}^*}(\operatorname {pt})$, define its Newton polygon to be
$f_\mu \in K_{\mathbb {C}^*}(\operatorname {pt})$, define its Newton polygon to be
Definition 2.1 [Reference Okounkov and SmirnovOS16, Reference OkounkovOko17]
For any chamber ![]() ${\frak C}$, polarization
${\frak C}$, polarization ![]() $T^{1/2}$, alcove
$T^{1/2}$, alcove ![]() $\nabla$, there is a unique map of
$\nabla$, there is a unique map of ![]() $K_T(\operatorname {pt})$-modules (called the stable envelope),
$K_T(\operatorname {pt})$-modules (called the stable envelope),
satisfying the following three conditions. Write ![]() $\operatorname {stab}^{{\frak C},T^{1/2}, \nabla }_w=\operatorname {stab}(1_w)$. Then we have:
$\operatorname {stab}^{{\frak C},T^{1/2}, \nabla }_w=\operatorname {stab}(1_w)$. Then we have:
(i) (Support)
 $\operatorname {supp}( \operatorname {stab}^{{\frak C}, T^{1/2},\nabla }_w)\subset \operatorname {FAttr}_{ {\frak C}}(w)$;
$\operatorname {supp}( \operatorname {stab}^{{\frak C}, T^{1/2},\nabla }_w)\subset \operatorname {FAttr}_{ {\frak C}}(w)$;(ii) (Normalization)
 $\operatorname {stab}^{{\frak C},T^{1/2}, \nabla }_w|_w=(-1)^{\operatorname {rank} T^{1/2}_{w, +}}({\det N_{w,-}}/{\det T_w^{1/2}})^{1/2} \mathcal {O}_{\operatorname {Attr} _{\frak C}(w)}|_w$;
$\operatorname {stab}^{{\frak C},T^{1/2}, \nabla }_w|_w=(-1)^{\operatorname {rank} T^{1/2}_{w, +}}({\det N_{w,-}}/{\det T_w^{1/2}})^{1/2} \mathcal {O}_{\operatorname {Attr} _{\frak C}(w)}|_w$;(iii) (Degree)
 $\deg _A(\operatorname {stab}^{{\frak C}, T^{1/2},\nabla }_w|_v)\subset \deg _A(\operatorname {stab}^{{\frak C},T^{1/2}, \nabla }_v|_v)+\mathcal {L}|_v- \mathcal {L}|_w$ for any
$\deg _A(\operatorname {stab}^{{\frak C}, T^{1/2},\nabla }_w|_v)\subset \deg _A(\operatorname {stab}^{{\frak C},T^{1/2}, \nabla }_v|_v)+\mathcal {L}|_v- \mathcal {L}|_w$ for any  $v\prec _{\frak C} w, \mathcal {L}\in \nabla$.
$v\prec _{\frak C} w, \mathcal {L}\in \nabla$.
Remark 2.2 (a) Using the identification in (1), ![]() $\mathcal {L}\in \nabla$ is the same as a fractional line bundle.
$\mathcal {L}\in \nabla$ is the same as a fractional line bundle.
(b) The degree condition only depends on the choice of ![]() $\nabla$, not the fractional line bundle
$\nabla$, not the fractional line bundle ![]() $\mathcal {L}\in \nabla$ itself. Moreover, the normalization condition does not depend on the alcove
$\mathcal {L}\in \nabla$ itself. Moreover, the normalization condition does not depend on the alcove ![]() $\nabla$.
$\nabla$.
(c) We have duality [Reference Okounkov and SmirnovOS16, Proposition 1]
(d) The existence of the K-theory stable bases also follows from the existence of the elliptic stable envelopes, see [Reference Aganagic and OkounkovAO21, Reference OkounkovOko20a, Reference OkounkovOko20b].
It follows immediately from the definition that we have the following lemma.
Lemma 2.3 For any ![]() $w\in W$, we have
$w\in W$, we have
We will mostly consider the following two cases:
From [Reference Su, Zhao and ZhongSZZ20, Lemma 3.2], which follows immediately from Definition 2.1(ii), we have
Moreover, it is easy to see from definition that
where ![]() $w_0\in W$ is the longest element in the Weyl group.
$w_0\in W$ is the longest element in the Weyl group.
2.3 The affine Hecke algebra
We give a brief reminder on the Hecke algebra and Demazure–Lusztig operators.
Let ![]() ${\mathbb {H}}$ be the affine Hecke algebra, see [Reference Chriss and GinzburgCG97, § 7.1]. Then we have the following well-known Kazhdan–Lusztig and Ginzburg isomorphism [Reference Kazhdan and LusztigKL87, Reference Chriss and GinzburgCG97]
${\mathbb {H}}$ be the affine Hecke algebra, see [Reference Chriss and GinzburgCG97, § 7.1]. Then we have the following well-known Kazhdan–Lusztig and Ginzburg isomorphism [Reference Kazhdan and LusztigKL87, Reference Chriss and GinzburgCG97]
where ![]() $Z=T^*\mathcal {B}\times _\mathcal {N} T^*\mathcal {B}$ is the Steinberg variety and
$Z=T^*\mathcal {B}\times _\mathcal {N} T^*\mathcal {B}$ is the Steinberg variety and ![]() $\mathcal {N}\subset \mathfrak {g}$ is the nilpotent cone. The right-hand side
$\mathcal {N}\subset \mathfrak {g}$ is the nilpotent cone. The right-hand side ![]() $K_{G\times \mathbb {C}^*}(Z)$ has a convolution algebra structure. Let us recall one construction of this isomorphism [Reference RicheRic08, Reference LusztigLus98].
$K_{G\times \mathbb {C}^*}(Z)$ has a convolution algebra structure. Let us recall one construction of this isomorphism [Reference RicheRic08, Reference LusztigLus98].
Let ![]() $\triangle (T^*\mathcal {B})\subset T^*\mathcal {B}\times _{\mathcal {N}} T^*\mathcal {B}$ denote the diagonal copy of
$\triangle (T^*\mathcal {B})\subset T^*\mathcal {B}\times _{\mathcal {N}} T^*\mathcal {B}$ denote the diagonal copy of ![]() $T^*\mathcal {B}$ inside the Steinberg variety
$T^*\mathcal {B}$ inside the Steinberg variety ![]() $Z$. For any torus weight
$Z$. For any torus weight ![]() $\lambda$, let
$\lambda$, let ![]() $\mathcal {O}_\triangle (\lambda ):=\mathcal {L}_\lambda$, where
$\mathcal {O}_\triangle (\lambda ):=\mathcal {L}_\lambda$, where ![]() $\mathcal {L}_\lambda$ is the line bundle on
$\mathcal {L}_\lambda$ is the line bundle on ![]() $T^*\mathcal {B}$ introduced in § 2.1. For any simple root
$T^*\mathcal {B}$ introduced in § 2.1. For any simple root ![]() $\alpha$, let
$\alpha$, let ![]() $P_\alpha$ be the corresponding minimal parabolic subgroup and
$P_\alpha$ be the corresponding minimal parabolic subgroup and ![]() $\mathcal {P}_\alpha =G/P_\alpha$. Let
$\mathcal {P}_\alpha =G/P_\alpha$. Let
On ![]() $Y_\alpha$, the
$Y_\alpha$, the ![]() $A$-fixed points are of the form either
$A$-fixed points are of the form either ![]() $(w, w)$ or
$(w, w)$ or ![]() $(w, ws_\alpha )$ with
$(w, ws_\alpha )$ with ![]() $w\in W$. Let
$w\in W$. Let ![]() $T^*_{Y_\alpha }:=N^*_{\mathcal {B}\times \mathcal {B}/Y_\alpha }$ be the conormal bundle of
$T^*_{Y_\alpha }:=N^*_{\mathcal {B}\times \mathcal {B}/Y_\alpha }$ be the conormal bundle of ![]() $Y_\alpha$ inside
$Y_\alpha$ inside ![]() $\mathcal {B}\times \mathcal {B}$. Let
$\mathcal {B}\times \mathcal {B}$. Let ![]() $\mathcal {O}_{T_{Y_{\alpha }}^*}(\lambda ,\mu )=\pi _1^*\mathcal {L}_\lambda \otimes \pi _2^*\mathcal {L}_\mu$, where
$\mathcal {O}_{T_{Y_{\alpha }}^*}(\lambda ,\mu )=\pi _1^*\mathcal {L}_\lambda \otimes \pi _2^*\mathcal {L}_\mu$, where ![]() $\pi _i:T^*_{Y_\alpha }\to T^*\mathcal {B}$ are the two projections. Let
$\pi _i:T^*_{Y_\alpha }\to T^*\mathcal {B}$ are the two projections. Let ![]() $T_\alpha$ be the usual generator of
$T_\alpha$ be the usual generator of ![]() ${\mathbb {H}}$ that satisfies
${\mathbb {H}}$ that satisfies ![]() $(T_\alpha +1)(T_\alpha -q)=0$. For the purpose of this paper, let us choose the isomorphism (7) as follows:
$(T_\alpha +1)(T_\alpha -q)=0$. For the purpose of this paper, let us choose the isomorphism (7) as follows:
This is conjugate to the one in [Reference RicheRic08, Proposition 6.1.5] by ![]() $\mathcal {L}_\rho$, since our
$\mathcal {L}_\rho$, since our ![]() $q$ and
$q$ and ![]() $T_\alpha$ are the same as
$T_\alpha$ are the same as ![]() $v^2$ and
$v^2$ and ![]() $vT_\alpha$ in [Reference RicheRic08], respectively.
$vT_\alpha$ in [Reference RicheRic08], respectively.
The convolution algebra ![]() $K_{G\times \mathbb {C}^*}(Z)$ is a subalgebra of
$K_{G\times \mathbb {C}^*}(Z)$ is a subalgebra of ![]() $K_{A\times \mathbb {C}^*}(Z)$, and hence defines two actions of
$K_{A\times \mathbb {C}^*}(Z)$, and hence defines two actions of ![]() ${\mathbb {H}}$ on
${\mathbb {H}}$ on ![]() $K_{A\times \mathbb {C}^*}(T^*\mathcal {B})$, namely, by convolution from the left, or from the right (which therefore is a right action). The operators on
$K_{A\times \mathbb {C}^*}(T^*\mathcal {B})$, namely, by convolution from the left, or from the right (which therefore is a right action). The operators on ![]() $K_{A\times \mathbb {C}^*}(T^*\mathcal {B})$ corresponding to these two convolutions with
$K_{A\times \mathbb {C}^*}(T^*\mathcal {B})$ corresponding to these two convolutions with ![]() $T_\alpha$ will then be denoted by
$T_\alpha$ will then be denoted by ![]() $T_\alpha$ and
$T_\alpha$ and ![]() $T'_\alpha$ respectively, following the notations used in [Reference Su, Zhao and ZhongSZZ20].Footnote 1 That is, for any
$T'_\alpha$ respectively, following the notations used in [Reference Su, Zhao and ZhongSZZ20].Footnote 1 That is, for any ![]() $\mathcal {F}\in K_{A\times \mathbb {C}^*}(T^*\mathcal {B})$,
$\mathcal {F}\in K_{A\times \mathbb {C}^*}(T^*\mathcal {B})$,
Let ![]() $D_\alpha :=-T_\alpha -1$ and
$D_\alpha :=-T_\alpha -1$ and ![]() $D'_\alpha :=-T'_\alpha -1$. Then we have adjointness [Reference Su, Zhao and ZhongSZZ20, Lemma 4.4]
$D'_\alpha :=-T'_\alpha -1$. Then we have adjointness [Reference Su, Zhao and ZhongSZZ20, Lemma 4.4]
The relation between these two operators ![]() $T_\alpha$ and
$T_\alpha$ and ![]() $T'_\alpha$ can be deduced as follows. Since
$T'_\alpha$ can be deduced as follows. Since ![]() $[\mathcal {O}_{T_{Y_\alpha }^*}(\rho ,-\rho +\alpha )]=[\mathcal {O}_{T_{Y_\alpha }^*}(-\rho +\alpha ,\rho )]$ (see [Reference RicheRic08, Lemma 1.5.1]), the two operators on
$[\mathcal {O}_{T_{Y_\alpha }^*}(\rho ,-\rho +\alpha )]=[\mathcal {O}_{T_{Y_\alpha }^*}(-\rho +\alpha ,\rho )]$ (see [Reference RicheRic08, Lemma 1.5.1]), the two operators on ![]() $K_{A\times \mathbb {C}^*}(T^*\mathcal {B})$, given by left and right convolutions with this sheaf, are equal to each other. In other words, for any
$K_{A\times \mathbb {C}^*}(T^*\mathcal {B})$, given by left and right convolutions with this sheaf, are equal to each other. In other words, for any ![]() $\mathcal {F}\in K_{A\times \mathbb {C}^*}(T^*\mathcal {B})$,
$\mathcal {F}\in K_{A\times \mathbb {C}^*}(T^*\mathcal {B})$,
Therefore, we get the following equality as operators on ![]() $K_{A\times \mathbb {C}^*}(T^*\mathcal {B})$:
$K_{A\times \mathbb {C}^*}(T^*\mathcal {B})$:
The operator of the left action is denoted by ![]() $T^L_\alpha :=\mathcal {L}_{\rho }T_\alpha \mathcal {L}_{-\rho }$ and the right action is denoted by
$T^L_\alpha :=\mathcal {L}_{\rho }T_\alpha \mathcal {L}_{-\rho }$ and the right action is denoted by ![]() $T^{\operatorname {R}}_\alpha :=\mathcal {L}_{-\rho } T'_\alpha \mathcal {L}_{\rho }$.
$T^{\operatorname {R}}_\alpha :=\mathcal {L}_{-\rho } T'_\alpha \mathcal {L}_{\rho }$.
Remark 2.4 In the present paper, compositions of operators are read from right to left, even for right action operators. So for any ![]() $K$-theory class
$K$-theory class ![]() $\mathcal {F}\in K_{A\times \mathbb {C}^*}(T^*(G/B))$,
$\mathcal {F}\in K_{A\times \mathbb {C}^*}(T^*(G/B))$, ![]() $\mathcal {L}_\rho (T_{\alpha }(\mathcal {L}_{-\rho }\otimes \mathcal {F}))= \mathcal {L}_{-\rho }T'_{\alpha }(\mathcal {L}_{\rho }\otimes \mathcal {F})$. For any reduced decomposition
$\mathcal {L}_\rho (T_{\alpha }(\mathcal {L}_{-\rho }\otimes \mathcal {F}))= \mathcal {L}_{-\rho }T'_{\alpha }(\mathcal {L}_{\rho }\otimes \mathcal {F})$. For any reduced decomposition ![]() $w=s_1\cdots s_k$, we define
$w=s_1\cdots s_k$, we define ![]() $T_w^L:=T^L_{s_1}\cdots T^L_{s_k}$ and
$T_w^L:=T^L_{s_1}\cdots T^L_{s_k}$ and ![]() $T^{\operatorname {R}}_w:=T^{\operatorname {R}}_{s_k}\cdots T^{\operatorname {R}}_{s_1}$. On the other hand, in [Reference Su, Zhao and ZhongSZZ20] a left action of the affine Hecke algebra through right convolution operators were used. In particular, under the notations of [Reference Su, Zhao and ZhongSZZ20] we have
$T^{\operatorname {R}}_w:=T^{\operatorname {R}}_{s_k}\cdots T^{\operatorname {R}}_{s_1}$. On the other hand, in [Reference Su, Zhao and ZhongSZZ20] a left action of the affine Hecke algebra through right convolution operators were used. In particular, under the notations of [Reference Su, Zhao and ZhongSZZ20] we have ![]() $T'_{s_1\cdots s_k}:=T'_{s_1}\cdots T'_{s_k}$. Compared to the notations in the present paper we have, for any
$T'_{s_1\cdots s_k}:=T'_{s_1}\cdots T'_{s_k}$. Compared to the notations in the present paper we have, for any ![]() $x\in W$,
$x\in W$,
The following is one of the main results in [Reference Su, Zhao and ZhongSZZ20].
Theorem 2.5 [Reference Su, Zhao and ZhongSZZ20, Theorem 4.5]
Let ![]() $\alpha$ be a simple root. Then
$\alpha$ be a simple root. Then
 \begin{align} T_\alpha(\operatorname{stab}^{-,{\nabla_+}}_{w})&=\left\{ \begin{array}{@{}ll} (q-1)\operatorname{stab}^{-,{\nabla_+}}_{w}+q^{1/2}\operatorname{stab}^{-,{\nabla_+}}_{ws_\alpha} & \text{if }ws_\alpha< w,\\ q^{1/2}\operatorname{stab}^{-,{\nabla_+}}_{ws_\alpha} & \text{if }ws_\alpha>w.\end{array}\right. \end{align}
\begin{align} T_\alpha(\operatorname{stab}^{-,{\nabla_+}}_{w})&=\left\{ \begin{array}{@{}ll} (q-1)\operatorname{stab}^{-,{\nabla_+}}_{w}+q^{1/2}\operatorname{stab}^{-,{\nabla_+}}_{ws_\alpha} & \text{if }ws_\alpha< w,\\ q^{1/2}\operatorname{stab}^{-,{\nabla_+}}_{ws_\alpha} & \text{if }ws_\alpha>w.\end{array}\right. \end{align} \begin{align} T'_\alpha(\operatorname{stab}^{+, {\nabla_-}}_{w})&=\left\{\begin{array}{@{}ll}(q-1)\operatorname{stab}^{+, {\nabla_-}}_{w}+q^{1/2}\operatorname{stab}^{+, {\nabla_-}}_{ws_\alpha} & \text{if }ws_\alpha< w,\\ q^{1/2}\operatorname{stab}^{+, {\nabla_-}}_{ws_\alpha} & \text{if }ws_\alpha>w.\end{array}\right. \end{align}
\begin{align} T'_\alpha(\operatorname{stab}^{+, {\nabla_-}}_{w})&=\left\{\begin{array}{@{}ll}(q-1)\operatorname{stab}^{+, {\nabla_-}}_{w}+q^{1/2}\operatorname{stab}^{+, {\nabla_-}}_{ws_\alpha} & \text{if }ws_\alpha< w,\\ q^{1/2}\operatorname{stab}^{+, {\nabla_-}}_{ws_\alpha} & \text{if }ws_\alpha>w.\end{array}\right. \end{align}In particular,
3. General facts on the wall-crossing formulas
The definition of a stable basis depends on a choice of a chamber and an alcove. In this section, we collect some general facts about how the stable basis changes according to the change of these two choices involved.
When the choice of the chamber is fixed, the formula giving the change of bases associated to two different choices of alcove is called a wall-crossing formula.
3.1 Duality of coherent sheaves
Since ![]() $T^*\mathcal {B}$ is smooth,
$T^*\mathcal {B}$ is smooth, ![]() $K_{T}(T^*\mathcal {B})$ is generated by vector bundles. For each vector bundle
$K_{T}(T^*\mathcal {B})$ is generated by vector bundles. For each vector bundle ![]() $\mathcal {F}$, there is a dual vector bundle
$\mathcal {F}$, there is a dual vector bundle ![]() $\mathcal {F}^\vee$. This operation is well defined on
$\mathcal {F}^\vee$. This operation is well defined on ![]() $K_{T}(T^*\mathcal {B})$, and gives the duality operation
$K_{T}(T^*\mathcal {B})$, and gives the duality operation
which sends ![]() $q$ to
$q$ to ![]() $q^{-1}$. Then we have the following relations.
$q^{-1}$. Then we have the following relations.
Lemma 3.1 Let ![]() $w\in W$. Then
$w\in W$. Then
Remark 3.2 See [Reference Aluffi, Mihalcea, Schürmann and SuAMSS19, Lemma 11.1(b)] or [Reference Okounkov and SmirnovOS16, Equation (15)] for related statements. In our lemma, the polarizations on both sides of the equalities are unchanged, while those in [Reference Aluffi, Mihalcea, Schürmann and SuAMSS19, Lemma 11.1(b)] or [Reference Okounkov and SmirnovOS16, Equation (15)] are changed to the opposite polarizations.
Proof. We first show that (12) implies (13). Indeed, by duality (3) and (12), we have
 \begin{align*} \delta_{w,z}&=\langle ({-}q)^{\dim \mathcal{B}}\mathcal{L}_{{-}2\rho}\otimes(\operatorname{stab}^{-,{\nabla}}_{w})^\vee, \operatorname{stab}^{+, {\nabla}}_{z}\rangle\\ &=({-}q)^{\dim \mathcal{B}}\sum_{y\in W}\frac{e^{{-}2y\rho}\ast(\operatorname{stab}^{-,{\nabla}}_{w}|_y) \operatorname{stab}^{+, {\nabla}}_{z}|_y}{\prod_{\alpha>0}(1-e^{y\alpha})(1-qe^{{-}y\alpha})}, \end{align*}
\begin{align*} \delta_{w,z}&=\langle ({-}q)^{\dim \mathcal{B}}\mathcal{L}_{{-}2\rho}\otimes(\operatorname{stab}^{-,{\nabla}}_{w})^\vee, \operatorname{stab}^{+, {\nabla}}_{z}\rangle\\ &=({-}q)^{\dim \mathcal{B}}\sum_{y\in W}\frac{e^{{-}2y\rho}\ast(\operatorname{stab}^{-,{\nabla}}_{w}|_y) \operatorname{stab}^{+, {\nabla}}_{z}|_y}{\prod_{\alpha>0}(1-e^{y\alpha})(1-qe^{{-}y\alpha})}, \end{align*}
where ![]() $\ast$ in the second line acts on
$\ast$ in the second line acts on ![]() $K_T(pt)$ by sending
$K_T(pt)$ by sending ![]() $e^\lambda$ to
$e^\lambda$ to ![]() $e^{-\lambda }$ and
$e^{-\lambda }$ and ![]() $q$ to
$q$ to ![]() $q^{-1}$. Applying
$q^{-1}$. Applying ![]() $\ast$ to the above identity, we get
$\ast$ to the above identity, we get
 \begin{align*} \delta_{w,z}&=({-}q)^{-\dim \mathcal{B}}\sum_{y\in W}\frac{e^{2y\rho}\operatorname{stab}^{-,{\nabla}}_{w}|_y \ast(\operatorname{stab}^{+, {\nabla}}_{z}|_y)}{\prod_{\alpha>0}(1-e^{{-}y\alpha})(1-q^{{-}1}e^{y\alpha})}\\ &=({-}1)^{\dim \mathcal{B}}\sum_{y\in W}\frac{e^{2y\rho}\operatorname{stab}^{-,{\nabla}}_{w}|_y \ast(\operatorname{stab}^{+, {\nabla}}_{z}|_y)}{\prod_{\alpha>0}(1-e^{y\alpha})(1-qe^{{-}y\alpha})}\\ &=\langle \operatorname{stab}^{-,{\nabla}}_{w}, ({-}1)^{\dim \mathcal{B}}\mathcal{L}_{2\rho}\otimes(\operatorname{stab}^{+, {\nabla}}_{z})^\vee\rangle. \end{align*}
\begin{align*} \delta_{w,z}&=({-}q)^{-\dim \mathcal{B}}\sum_{y\in W}\frac{e^{2y\rho}\operatorname{stab}^{-,{\nabla}}_{w}|_y \ast(\operatorname{stab}^{+, {\nabla}}_{z}|_y)}{\prod_{\alpha>0}(1-e^{{-}y\alpha})(1-q^{{-}1}e^{y\alpha})}\\ &=({-}1)^{\dim \mathcal{B}}\sum_{y\in W}\frac{e^{2y\rho}\operatorname{stab}^{-,{\nabla}}_{w}|_y \ast(\operatorname{stab}^{+, {\nabla}}_{z}|_y)}{\prod_{\alpha>0}(1-e^{y\alpha})(1-qe^{{-}y\alpha})}\\ &=\langle \operatorname{stab}^{-,{\nabla}}_{w}, ({-}1)^{\dim \mathcal{B}}\mathcal{L}_{2\rho}\otimes(\operatorname{stab}^{+, {\nabla}}_{z})^\vee\rangle. \end{align*}Again by duality (3), we then get (13).
Now we prove (12). It suffices to show that ![]() $(-q)^{\dim \mathcal {B}}\mathcal {L}_{-2\rho }\otimes (\operatorname {stab}^{-,{\nabla }}_{w})^\vee$ satisfies the defining properties of
$(-q)^{\dim \mathcal {B}}\mathcal {L}_{-2\rho }\otimes (\operatorname {stab}^{-,{\nabla }}_{w})^\vee$ satisfies the defining properties of ![]() $\operatorname {stab}^{-,{-\nabla }}_{w}$. The support condition is obvious. The normalization condition is checked as follows:
$\operatorname {stab}^{-,{-\nabla }}_{w}$. The support condition is obvious. The normalization condition is checked as follows:
 \begin{align*} \big(({-}q)^{\dim \mathcal{B}}\mathcal{L}_{{-}2\rho}\otimes(\operatorname{stab}^{-,{\nabla}}_{w})^\vee\big)|_w &= ({-}q)^{\dim \mathcal{B}}e^{{-}2w\rho}\ast(\operatorname{stab}^{-,{\nabla}}_{w}|_w)\\ & \overset{5}= ({-}q)^{\dim \mathcal{B}}q^{-({\ell(w)}/{2})}e^{{-}2w\rho} \prod_{\beta>0, w\beta<0}(1-e^{w\beta})\prod_{\beta>0, w\beta>0}(1-q^{{-}1}e^{w\beta}) \\ &= q^{{\ell(w)}/{2}}\prod_{\beta>0, w\beta<0}(1-e^{{-}w\beta})\prod_{\beta>0, w\beta>0}(1-qe^{{-}w\beta})\\ & \overset{5}= \operatorname{stab}^{-,{-\nabla}}_{w}|_w. \end{align*}
\begin{align*} \big(({-}q)^{\dim \mathcal{B}}\mathcal{L}_{{-}2\rho}\otimes(\operatorname{stab}^{-,{\nabla}}_{w})^\vee\big)|_w &= ({-}q)^{\dim \mathcal{B}}e^{{-}2w\rho}\ast(\operatorname{stab}^{-,{\nabla}}_{w}|_w)\\ & \overset{5}= ({-}q)^{\dim \mathcal{B}}q^{-({\ell(w)}/{2})}e^{{-}2w\rho} \prod_{\beta>0, w\beta<0}(1-e^{w\beta})\prod_{\beta>0, w\beta>0}(1-q^{{-}1}e^{w\beta}) \\ &= q^{{\ell(w)}/{2}}\prod_{\beta>0, w\beta<0}(1-e^{{-}w\beta})\prod_{\beta>0, w\beta>0}(1-qe^{{-}w\beta})\\ & \overset{5}= \operatorname{stab}^{-,{-\nabla}}_{w}|_w. \end{align*}Therefore, the normalization condition is verified.
Finally, we check the degree condition. Pick ![]() $\mathcal {L}\in -\nabla$. We need to check that for any
$\mathcal {L}\in -\nabla$. We need to check that for any ![]() $y> w$ the following is true:
$y> w$ the following is true:
Indeed, this in turn is equivalent to
Since ![]() $\mathcal {L}^{-1}\in \nabla$, the above identity is precisely the degree condition for the stable basis
$\mathcal {L}^{-1}\in \nabla$, the above identity is precisely the degree condition for the stable basis ![]() $\operatorname {stab}^{-,{\nabla }}_{w}$. Therefore, the degree condition also follows.
$\operatorname {stab}^{-,{\nabla }}_{w}$. Therefore, the degree condition also follows.
3.2 Weyl group action
Recall on ![]() $K_T(T^*\mathcal {B})$, we have a left Weyl group action induced from the
$K_T(T^*\mathcal {B})$, we have a left Weyl group action induced from the ![]() $G$-action on
$G$-action on ![]() $T^*\mathcal {B}$. Using equivariant localization,
$T^*\mathcal {B}$. Using equivariant localization, ![]() $w(\mathcal {F})$ for
$w(\mathcal {F})$ for ![]() $\mathcal {F}\in K_T(T^*\mathcal {B})$ and
$\mathcal {F}\in K_T(T^*\mathcal {B})$ and ![]() $w\in W$ is determined by its restrictions to the fixed points, which is given by
$w\in W$ is determined by its restrictions to the fixed points, which is given by
Moreover, the action by ![]() $w$ also acts on the base field
$w$ also acts on the base field ![]() $K_T(pt)$ by the usual Weyl group action. From the above formula, it is easy to get
$K_T(pt)$ by the usual Weyl group action. From the above formula, it is easy to get
 \[ w(\iota_{y})|_{v}=\left\{\begin{array}{@{}ll} w(\iota_{y}|_y) & \text{if }v=wy,\\ 0 & \text{otherwise}.\end{array} \right. \]
\[ w(\iota_{y})|_{v}=\left\{\begin{array}{@{}ll} w(\iota_{y}|_y) & \text{if }v=wy,\\ 0 & \text{otherwise}.\end{array} \right. \]
That is, ![]() $w(\iota _{y})=\iota _{wy}$. This action agrees with the
$w(\iota _{y})=\iota _{wy}$. This action agrees with the ![]() $\odot$-action defined in [Reference Lenart, Zainoulline and ZhongLZZ20, Definition 3.2]. The effect of this group action on a stable basis is the following, which can be proved in exactly the same way as the proof of (12) in Lemma 3.1 above.
$\odot$-action defined in [Reference Lenart, Zainoulline and ZhongLZZ20, Definition 3.2]. The effect of this group action on a stable basis is the following, which can be proved in exactly the same way as the proof of (12) in Lemma 3.1 above.
Lemma 3.3 [Reference Aluffi, Mihalcea, Schürmann and SuAMSS19, Lemma 11.1(a)]
For any ![]() $w, y\in W$, we have
$w, y\in W$, we have
Remark 3.4 (a) If the polarization ![]() $T^{1/2}=T\mathcal {B}$ or
$T^{1/2}=T\mathcal {B}$ or ![]() $T^{1/2}=T^*\mathcal {B}$, then
$T^{1/2}=T^*\mathcal {B}$, then ![]() $w(T^{1/2})=T^{1/2}$ as it lies in the
$w(T^{1/2})=T^{1/2}$ as it lies in the ![]() $G$-equivariant K-theory, which are fixed by the left Weyl group action.
$G$-equivariant K-theory, which are fixed by the left Weyl group action.
(b) A priori, the alcove on the right-hand side should be ![]() $w(\nabla )$. i.e. for any
$w(\nabla )$. i.e. for any ![]() $\lambda \in \nabla$, the fractional line bundle
$\lambda \in \nabla$, the fractional line bundle ![]() $\mathcal {L}_\lambda$ should be changed to
$\mathcal {L}_\lambda$ should be changed to ![]() $w(\mathcal {L}_\lambda )$. But since
$w(\mathcal {L}_\lambda )$. But since ![]() $\mathcal {L}_\lambda$ is
$\mathcal {L}_\lambda$ is ![]() $G$-equivariant,
$G$-equivariant, ![]() $w(\mathcal {L}_\lambda )=\mathcal {L}_\lambda$. Thus, the alcove stays the same.
$w(\mathcal {L}_\lambda )=\mathcal {L}_\lambda$. Thus, the alcove stays the same.
3.3 Wall-crossing matrix
Our computation of wall-crossings for the K-theoretic stable bases is based on the following.
Lemma 3.5 [Reference Okounkov and SmirnovOS16, Theorem 1]
Suppose the alcoves ![]() $\nabla _1$ and
$\nabla _1$ and ![]() $\nabla _2$ are adjacent and separated by
$\nabla _2$ are adjacent and separated by ![]() $H_{\alpha ^\vee ,n}$. For any
$H_{\alpha ^\vee ,n}$. For any ![]() $y\in W$, we have
$y\in W$, we have
 \[ \operatorname{stab}^{{\frak C}, T^{1/2}, \nabla_1}_y=\left\{\begin{array}{@{}ll}\operatorname{stab}^{{\frak C}, T^{1/2}, \nabla_2}_y+f^{\nabla_1\leftarrow \nabla_2}_y\operatorname{stab}_{ys_\alpha}^{{\frak C}, T^{1/2}, \nabla_2} & \text{if }ys_\alpha\prec_{\frak C} y,\\ \operatorname{stab}^{{\frak C}, T^{1/2}, \nabla_2}_y & \text{if } ys_\alpha \succ_{\frak C} y, \end{array}\right. \]
\[ \operatorname{stab}^{{\frak C}, T^{1/2}, \nabla_1}_y=\left\{\begin{array}{@{}ll}\operatorname{stab}^{{\frak C}, T^{1/2}, \nabla_2}_y+f^{\nabla_1\leftarrow \nabla_2}_y\operatorname{stab}_{ys_\alpha}^{{\frak C}, T^{1/2}, \nabla_2} & \text{if }ys_\alpha\prec_{\frak C} y,\\ \operatorname{stab}^{{\frak C}, T^{1/2}, \nabla_2}_y & \text{if } ys_\alpha \succ_{\frak C} y, \end{array}\right. \]
where ![]() $f_y^{\nabla _1\leftarrow \nabla _2}\in K_{T}(\operatorname {pt})$. If
$f_y^{\nabla _1\leftarrow \nabla _2}\in K_{T}(\operatorname {pt})$. If ![]() $n=0$,
$n=0$, ![]() $f_y^{\nabla _1\leftarrow \nabla _2}\in K_{\mathbb {C}^*}(\operatorname {pt})$, i.e. it does not depend on the equivariant parameters of
$f_y^{\nabla _1\leftarrow \nabla _2}\in K_{\mathbb {C}^*}(\operatorname {pt})$, i.e. it does not depend on the equivariant parameters of ![]() $A$. In particular,
$A$. In particular,
Proof. Let us first recall the moment map ![]() $\mu :(T^*\mathcal {B})^A\to H_2(T^*\mathcal {B}, {\mathbb {Z}})\otimes \Lambda$ defined in [Reference Okounkov and SmirnovOS16, § 2.1.7]. It is characterized by the following condition. If
$\mu :(T^*\mathcal {B})^A\to H_2(T^*\mathcal {B}, {\mathbb {Z}})\otimes \Lambda$ defined in [Reference Okounkov and SmirnovOS16, § 2.1.7]. It is characterized by the following condition. If ![]() $p$ and
$p$ and ![]() $q$ are two fixed points connected by a torus invariant curve
$q$ are two fixed points connected by a torus invariant curve ![]() $C$, then
$C$, then
This is also closely related to the Goresky–Kottwitz–MacPherson (GKM) condition in equivariant cohomology, see [Reference Maulik and OkounkovMO19, § 4.8.5].
Identifying ![]() $H_2(T^*\mathcal {B}, {\mathbb {Z}})$ with the coroot lattice, we get
$H_2(T^*\mathcal {B}, {\mathbb {Z}})$ with the coroot lattice, we get
For any other ![]() $z$ different from
$z$ different from ![]() $y$ and
$y$ and ![]() $ys_\alpha$,
$ys_\alpha$, ![]() $\mu (y)-\mu (z)$ will not be a multiple of
$\mu (y)-\mu (z)$ will not be a multiple of ![]() $\alpha ^\vee$.Footnote 2 The conclusion then follows from [Reference Okounkov and SmirnovOS16, Theorem 1].
$\alpha ^\vee$.Footnote 2 The conclusion then follows from [Reference Okounkov and SmirnovOS16, Theorem 1].
We are interested in computing these wall-crossing coefficients ![]() $f_y^{\nabla _1\leftarrow \nabla _2}$, which form the entries of the so-called wall R-matrix [Reference Okounkov and SmirnovOS16, § 2.2.3]. Similarly as stable bases, these matrices depend on the choice of the alcove, the chamber, and the polarization. For simplicity of notations, we omit the last two choices whenever they are clear from the context.
$f_y^{\nabla _1\leftarrow \nabla _2}$, which form the entries of the so-called wall R-matrix [Reference Okounkov and SmirnovOS16, § 2.2.3]. Similarly as stable bases, these matrices depend on the choice of the alcove, the chamber, and the polarization. For simplicity of notations, we omit the last two choices whenever they are clear from the context.
From the definition, those wall-crossing coefficients depend on the wall of the alcove lying on the hyperplane ![]() $H_{\alpha ^\vee ,n}$. However, it follows from Theorem 5.1 below, that the coefficients do not depend on the wall where we cross the hyperplane
$H_{\alpha ^\vee ,n}$. However, it follows from Theorem 5.1 below, that the coefficients do not depend on the wall where we cross the hyperplane ![]() $H_{\alpha ^\vee ,n}$.
$H_{\alpha ^\vee ,n}$.
Example 3.6 We consider the case ![]() $\operatorname {SL}(2,\mathbb {C})$.Footnote 3 Then
$\operatorname {SL}(2,\mathbb {C})$.Footnote 3 Then ![]() $\mathcal {B}\cong {\mathbb {P}}^1$, and
$\mathcal {B}\cong {\mathbb {P}}^1$, and ![]() $\operatorname {Pic}(T^*{\mathbb {P}}^1)\otimes _{\mathbb {Z}} \mathbb {Q}=\mathbb {Q}\alpha$. The two
$\operatorname {Pic}(T^*{\mathbb {P}}^1)\otimes _{\mathbb {Z}} \mathbb {Q}=\mathbb {Q}\alpha$. The two ![]() $A$-fixed points on
$A$-fixed points on ![]() $T^*{\mathbb {P}}^1$ are denoted by
$T^*{\mathbb {P}}^1$ are denoted by ![]() $0$ and
$0$ and ![]() $\infty$, corresponding to
$\infty$, corresponding to ![]() $e$ and
$e$ and ![]() $s_\alpha$ in the Weyl group, respectively. The alcoves are
$s_\alpha$ in the Weyl group, respectively. The alcoves are ![]() $(({n}/{2})\alpha ,(({n+1})/{2})\alpha ), n\in {\mathbb {Z}}$. The wall
$(({n}/{2})\alpha ,(({n+1})/{2})\alpha ), n\in {\mathbb {Z}}$. The wall ![]() $H_{\alpha ^\vee , 0}$ is the origin
$H_{\alpha ^\vee , 0}$ is the origin ![]() $0$. We have
$0$. We have ![]() $\nabla _+= (0,\frac {1}{2}\alpha )$ and
$\nabla _+= (0,\frac {1}{2}\alpha )$ and ![]() $\nabla _-=(\frac {1}{2}\alpha , 0)=\nabla _+-({\alpha }/{2})$. Using the translation formula of Lemma 3.7, we compute
$\nabla _-=(\frac {1}{2}\alpha , 0)=\nabla _+-({\alpha }/{2})$. Using the translation formula of Lemma 3.7, we compute ![]() $f_{s_\alpha }^{\nabla _-\leftarrow \nabla _+}$ for the dominant chamber and the polarization
$f_{s_\alpha }^{\nabla _-\leftarrow \nabla _+}$ for the dominant chamber and the polarization ![]() $T{\mathbb {P}}^1$, in which case
$T{\mathbb {P}}^1$, in which case ![]() $0\prec _{{\frak C}_+}\infty$. The stable basis is given by the following formulas [Reference Su, Zhao and ZhongSZZ20, Example 2.4]:
$0\prec _{{\frak C}_+}\infty$. The stable basis is given by the following formulas [Reference Su, Zhao and ZhongSZZ20, Example 2.4]:
 \begin{gather*} \operatorname{stab}^{+, {\nabla_-}}_{e}=[\mathcal{O}_{T_0^*{\mathbb{P}}^1}],\\ \operatorname{stab}^{+, {\nabla_-}}_{s_\alpha}={-}q^{-{1/2}}e^{-\alpha}[\mathcal{O}_{{\mathbb{P}}^1}]+ \big({-}q^{{1/2}}e^{{-}2\alpha}+(q^{-{1/2}}-q^{{1/2}})e^{-\alpha}\big)[\mathcal{O}_{T_0^*{\mathbb{P}}^1}]. \end{gather*}
\begin{gather*} \operatorname{stab}^{+, {\nabla_-}}_{e}=[\mathcal{O}_{T_0^*{\mathbb{P}}^1}],\\ \operatorname{stab}^{+, {\nabla_-}}_{s_\alpha}={-}q^{-{1/2}}e^{-\alpha}[\mathcal{O}_{{\mathbb{P}}^1}]+ \big({-}q^{{1/2}}e^{{-}2\alpha}+(q^{-{1/2}}-q^{{1/2}})e^{-\alpha}\big)[\mathcal{O}_{T_0^*{\mathbb{P}}^1}]. \end{gather*}So their localizations are given by
 \begin{gather*} \operatorname{stab}^{+, {\nabla_-}}_{e}|_e=1-e^{\alpha}, \\ \operatorname{stab}^{+, {\nabla_-}}_{s_\alpha}|_e=q^{{1/2}}-q^{-{1/2}}, \quad \operatorname{stab}^{+, {\nabla_-}}_{s_\alpha}|_{s_\alpha}=q^{{1/2}}-q^{-{1/2}}e^{-\alpha}. \end{gather*}
\begin{gather*} \operatorname{stab}^{+, {\nabla_-}}_{e}|_e=1-e^{\alpha}, \\ \operatorname{stab}^{+, {\nabla_-}}_{s_\alpha}|_e=q^{{1/2}}-q^{-{1/2}}, \quad \operatorname{stab}^{+, {\nabla_-}}_{s_\alpha}|_{s_\alpha}=q^{{1/2}}-q^{-{1/2}}e^{-\alpha}. \end{gather*}
By (15), for any ![]() $y,w\in W$,
$y,w\in W$,
Therefore,
 \begin{gather*} \operatorname{stab}^{+, {\nabla_+}}_{e}|_e=1-e^{\alpha},\\ \operatorname{stab}^{+, {\nabla_+}}_{s_\alpha}|_e =(q^{{1/2}}-q^{-{1/2}})e^\alpha, \quad \operatorname{stab}^{+, {\nabla_+}}_{s_\alpha}|_{s_\alpha}=q^{{1/2}}-q^{-{1/2}}e^{-\alpha}. \end{gather*}
\begin{gather*} \operatorname{stab}^{+, {\nabla_+}}_{e}|_e=1-e^{\alpha},\\ \operatorname{stab}^{+, {\nabla_+}}_{s_\alpha}|_e =(q^{{1/2}}-q^{-{1/2}})e^\alpha, \quad \operatorname{stab}^{+, {\nabla_+}}_{s_\alpha}|_{s_\alpha}=q^{{1/2}}-q^{-{1/2}}e^{-\alpha}. \end{gather*}By Lemma 3.5,
Restricting both sides to the fixed point ![]() $e$, we get
$e$, we get
Hence
3.4 Translations
We consider the effect of translation by an integral weight ![]() $\mu \in \Lambda$ on a stable basis. By the uniqueness of stable basis, we have (see [Reference Aluffi, Mihalcea, Schürmann and SuAMSS19, Lemma 8.2.(c)])
$\mu \in \Lambda$ on a stable basis. By the uniqueness of stable basis, we have (see [Reference Aluffi, Mihalcea, Schürmann and SuAMSS19, Lemma 8.2.(c)])
An immediate corollary of this fact is the following.
Lemma 3.7 Let ![]() $\nabla _1,\nabla _2$ are adjacent alcoves separated by
$\nabla _1,\nabla _2$ are adjacent alcoves separated by ![]() $H_{\alpha ^\vee , n}$. For any integral weight
$H_{\alpha ^\vee , n}$. For any integral weight ![]() $\mu \in \Lambda$, we let
$\mu \in \Lambda$, we let ![]() $\nabla +\mu$ be the alcove obtained by translating
$\nabla +\mu$ be the alcove obtained by translating ![]() $\nabla$ by
$\nabla$ by ![]() $\mu$. Then
$\mu$. Then
Hence the conclusion follows from the identity ![]() $\mu -s_\alpha \mu =(\mu , \alpha ^\vee )\alpha$.
$\mu -s_\alpha \mu =(\mu , \alpha ^\vee )\alpha$.
With this lemma, we can reduce the wall-crossing for ![]() $H_{\alpha ^\vee , n}$ to
$H_{\alpha ^\vee , n}$ to ![]() $H_{\alpha ^\vee , 0}$ as follows. Let
$H_{\alpha ^\vee , 0}$ as follows. Let ![]() $\nabla _1,\nabla _2$ be adjacent alcoves separated by
$\nabla _1,\nabla _2$ be adjacent alcoves separated by ![]() $H_{\alpha ^\vee , n}$. If
$H_{\alpha ^\vee , n}$. If ![]() $\alpha$ is simple, then
$\alpha$ is simple, then ![]() $\nabla _1-n\varpi _\alpha ,\nabla _2-n\varpi _\alpha$ are adjacent alcoves separated by
$\nabla _1-n\varpi _\alpha ,\nabla _2-n\varpi _\alpha$ are adjacent alcoves separated by ![]() $H_{\alpha ^\vee , 0}$, where
$H_{\alpha ^\vee , 0}$, where ![]() $\varpi _\alpha$ is the corresponding fundamental weight. Otherwise,
$\varpi _\alpha$ is the corresponding fundamental weight. Otherwise, ![]() $\alpha =w\beta$ for some
$\alpha =w\beta$ for some ![]() $w\in W$ and simple root
$w\in W$ and simple root ![]() $\beta$. Then we can shift the alcoves
$\beta$. Then we can shift the alcoves ![]() $\nabla _i$ by
$\nabla _i$ by ![]() $-nw(\varpi _\beta )$ to get adjacent alcoves separated by
$-nw(\varpi _\beta )$ to get adjacent alcoves separated by ![]() $H_{\alpha ^\vee , 0}$.
$H_{\alpha ^\vee , 0}$.
Therefore, we only need to cross the walls on the root hyperplanes ![]() $H_{\alpha ^\vee , 0}$. These are divided into two cases depending on whether
$H_{\alpha ^\vee , 0}$. These are divided into two cases depending on whether ![]() $\alpha$ is simple or not.
$\alpha$ is simple or not.
4. Crossing the simple walls
In this section, we compute the formula for crossing the simple walls.
4.1 The formulas
The following is the main result of this section.
Theorem 4.1 Let ![]() $\alpha ^\vee$ be a simple coroot. Suppose
$\alpha ^\vee$ be a simple coroot. Suppose ![]() $\nabla$ has a wall on
$\nabla$ has a wall on ![]() $H_{\alpha ^\vee , 0}$, and
$H_{\alpha ^\vee , 0}$, and ![]() $(\lambda , \alpha ^\vee )>0$,
$(\lambda , \alpha ^\vee )>0$, ![]() $\forall \, \lambda \in \nabla$. Then
$\forall \, \lambda \in \nabla$. Then
 \begin{align} \operatorname{stab}^{+, {s_\alpha\nabla}}_{y}&= \left\{ \begin{array}{@{}ll} \operatorname{stab}^{+, {\nabla}}_{y}+(q^{{1/2}}-q^{-{1/2}})\cdot\operatorname{stab}^{+, {\nabla}}_{ys_{\alpha}} & \text{if } ys_{\alpha}< y,\\ \operatorname{stab}^{+, {\nabla}}_{y} & \text{if } ys_{\alpha}>y, \end{array}\right.\end{align}
\begin{align} \operatorname{stab}^{+, {s_\alpha\nabla}}_{y}&= \left\{ \begin{array}{@{}ll} \operatorname{stab}^{+, {\nabla}}_{y}+(q^{{1/2}}-q^{-{1/2}})\cdot\operatorname{stab}^{+, {\nabla}}_{ys_{\alpha}} & \text{if } ys_{\alpha}< y,\\ \operatorname{stab}^{+, {\nabla}}_{y} & \text{if } ys_{\alpha}>y, \end{array}\right.\end{align} \begin{align} \operatorname{stab}^{-,{s_\alpha\nabla}}_{y}&= \left\{ \begin{array}{@{}ll} \operatorname{stab}^{-,{\nabla}}_{y}+(q^{{1/2}}-q^{-{1/2}})\cdot\operatorname{stab}^{-,{\nabla}}_{ys_{\alpha}} & \text{if } ys_{\alpha}> y,\\ \operatorname{stab}^{-,{\nabla}}_{y} & \text{if } ys_{\alpha}< y. \end{array}\right. \end{align}
\begin{align} \operatorname{stab}^{-,{s_\alpha\nabla}}_{y}&= \left\{ \begin{array}{@{}ll} \operatorname{stab}^{-,{\nabla}}_{y}+(q^{{1/2}}-q^{-{1/2}})\cdot\operatorname{stab}^{-,{\nabla}}_{ys_{\alpha}} & \text{if } ys_{\alpha}> y,\\ \operatorname{stab}^{-,{\nabla}}_{y} & \text{if } ys_{\alpha}< y. \end{array}\right. \end{align}Proof. We first show that (16) follows from (17) via duality (3). By Lemma 3.5, we can assume ![]() $ys_\alpha < y$ and it suffices to compute
$ys_\alpha < y$ and it suffices to compute
 \begin{align*} &\langle \operatorname{stab}^{+, {s_\alpha\nabla}}_{y}, \operatorname{stab}^{-,{-\nabla}}_{ys_{\alpha}}\rangle\\ &\quad = \langle \operatorname{stab}^{+, {s_\alpha\nabla}}_{y}, \operatorname{stab}^{-,{-s_\alpha\nabla}}_{ys_{\alpha}} +(q^{{1/2}}-q^{-{1/2}})\operatorname{stab}^{-,{-s_\alpha\nabla}}_{y}\rangle\\ &\quad = q^{{1/2}}-q^{-{1/2}}, \end{align*}
\begin{align*} &\langle \operatorname{stab}^{+, {s_\alpha\nabla}}_{y}, \operatorname{stab}^{-,{-\nabla}}_{ys_{\alpha}}\rangle\\ &\quad = \langle \operatorname{stab}^{+, {s_\alpha\nabla}}_{y}, \operatorname{stab}^{-,{-s_\alpha\nabla}}_{ys_{\alpha}} +(q^{{1/2}}-q^{-{1/2}})\operatorname{stab}^{-,{-s_\alpha\nabla}}_{y}\rangle\\ &\quad = q^{{1/2}}-q^{-{1/2}}, \end{align*}
where the first equality follows from (17) with the alcove being ![]() $s_\alpha (-\nabla )$ satisfying the condition of theorem.
$s_\alpha (-\nabla )$ satisfying the condition of theorem.
Now we prove (17). From Lemma 3.5 it suffices to assume that ![]() $ys_\alpha >y$. Applying the operator
$ys_\alpha >y$. Applying the operator ![]() $D_\alpha$ from § 2.3 to the identity
$D_\alpha$ from § 2.3 to the identity
and use (18) and (19) below, we get
 \begin{align*} &-\operatorname{stab}^{-,{\nabla}}_{y}-q^{1/2}\operatorname{stab}^{-,{\nabla}}_{ys_\alpha}+\sum_{w\not< ys_\alpha }a_w\operatorname{stab}^{-,{\nabla}}_{w}\\ &\qquad +f^{s_\alpha\nabla\leftarrow\nabla}_y\bigg({-}q\operatorname{stab}^{-,{\nabla}}_{ys_\alpha}-q^{1/2}\operatorname{stab}^{-,{\nabla}}_{y} +\sum_{w\not< ys_\alpha }a_w\operatorname{stab}^{-,{\nabla}}_{w}\bigg)\\ &\quad ={-}q\operatorname{stab}^{-,{s_\alpha\nabla}}_{y}-q^{1/2}\operatorname{stab}^{-,{s_\alpha\nabla}}_{ys_\alpha}+\sum_{w\not< ys_\alpha}a_w\operatorname{stab}^{-,{s_\alpha\nabla}}_{w}\\ &\quad \overset{\text{Lemma 3.5}}={-}q(\operatorname{stab}^{-,{\nabla}}_{y}+f^{s_\alpha\nabla \leftarrow\nabla}_y\operatorname{stab}^{-,{\nabla}}_{ys_\alpha})-q^{1/2}\operatorname{stab}^{-,{\nabla}}_{ys_\alpha}+\sum_{w \not< ys_\alpha}a_w\operatorname{stab}^{-,{s_\alpha\nabla}}_{w}, \end{align*}
\begin{align*} &-\operatorname{stab}^{-,{\nabla}}_{y}-q^{1/2}\operatorname{stab}^{-,{\nabla}}_{ys_\alpha}+\sum_{w\not< ys_\alpha }a_w\operatorname{stab}^{-,{\nabla}}_{w}\\ &\qquad +f^{s_\alpha\nabla\leftarrow\nabla}_y\bigg({-}q\operatorname{stab}^{-,{\nabla}}_{ys_\alpha}-q^{1/2}\operatorname{stab}^{-,{\nabla}}_{y} +\sum_{w\not< ys_\alpha }a_w\operatorname{stab}^{-,{\nabla}}_{w}\bigg)\\ &\quad ={-}q\operatorname{stab}^{-,{s_\alpha\nabla}}_{y}-q^{1/2}\operatorname{stab}^{-,{s_\alpha\nabla}}_{ys_\alpha}+\sum_{w\not< ys_\alpha}a_w\operatorname{stab}^{-,{s_\alpha\nabla}}_{w}\\ &\quad \overset{\text{Lemma 3.5}}={-}q(\operatorname{stab}^{-,{\nabla}}_{y}+f^{s_\alpha\nabla \leftarrow\nabla}_y\operatorname{stab}^{-,{\nabla}}_{ys_\alpha})-q^{1/2}\operatorname{stab}^{-,{\nabla}}_{ys_\alpha}+\sum_{w \not< ys_\alpha}a_w\operatorname{stab}^{-,{s_\alpha\nabla}}_{w}, \end{align*}
where the ![]() $a_w$ are some coefficients. These coefficients are determined by (18) and (19) in Lemma 4.4 below. By comparing the coefficients of
$a_w$ are some coefficients. These coefficients are determined by (18) and (19) in Lemma 4.4 below. By comparing the coefficients of ![]() $\operatorname {stab}^{-,{\nabla }}_{y}$, we see that
$\operatorname {stab}^{-,{\nabla }}_{y}$, we see that ![]() $f^{s_\alpha \nabla \leftarrow \nabla }_y=q^{1/2}-q^{-1/2}$. Note that the sums in the above identity will have no contribution to such coefficients. The first two are obvious since
$f^{s_\alpha \nabla \leftarrow \nabla }_y=q^{1/2}-q^{-1/2}$. Note that the sums in the above identity will have no contribution to such coefficients. The first two are obvious since ![]() $ys_\alpha >y$. The reason for the last one is that
$ys_\alpha >y$. The reason for the last one is that ![]() $\operatorname {stab}^{-,{s_\alpha} \nabla }_w$ is a linear combination of
$\operatorname {stab}^{-,{s_\alpha} \nabla }_w$ is a linear combination of ![]() $\operatorname {stab}^{-,\nabla }_{w}$ and
$\operatorname {stab}^{-,\nabla }_{w}$ and ![]() $\operatorname {stab}^{-,{\nabla }}_{ws_\alpha }$, and both will not be equal to
$\operatorname {stab}^{-,{\nabla }}_{ws_\alpha }$, and both will not be equal to ![]() $\operatorname {stab}^{-,{\nabla }}_{y}$ when
$\operatorname {stab}^{-,{\nabla }}_{y}$ when ![]() $w\not < ys_\alpha$.
$w\not < ys_\alpha$.
4.2 Some technical lemmas
In this subsection we prove Lemma 4.4, which is used in the proof of Theorem 4.1. First we recall a well-known fact.
Lemma 4.2 [Reference DeodharDeo77, Theorem 1.1]
Let ![]() $w_1, w_2\in W$, and
$w_1, w_2\in W$, and ![]() $\alpha$ be a simple root. Assume
$\alpha$ be a simple root. Assume ![]() $w_1s_\alpha < w_1$ and
$w_1s_\alpha < w_1$ and ![]() $w_2s_\alpha < w_2$. Then
$w_2s_\alpha < w_2$. Then
In preparation for the proof of Lemma 4.4, we have the following lemma.
Lemma 4.3 Let ![]() $w, y\in W$.
$w, y\in W$.
(1) Assume
 $y\le z\le w$.
$y\le z\le w$.
(a) If
 $ys_\alpha < y$,
$ys_\alpha < y$,  $w\le y$, and
$w\le y$, and  $w\not \in \{y, ys_\alpha \}$, then there is no such
$w\not \in \{y, ys_\alpha \}$, then there is no such  $z$.
$z$.(b) If
 $ys_\alpha >y$,
$ys_\alpha >y$,  $w\le ys_\alpha$, and
$w\le ys_\alpha$, and  $w\not \in \{y, ys_\alpha \}$, then there is no such
$w\not \in \{y, ys_\alpha \}$, then there is no such  $z$.
$z$.(c) If
 $w=y$, then
$w=y$, then  $z=w=y$.
$z=w=y$.(d) If
 $ys_\alpha < y$ and
$ys_\alpha < y$ and  $w=ys_\alpha$, then there is no such
$w=ys_\alpha$, then there is no such  $z$.
$z$.(e) If
 $ys_\alpha >y$ and
$ys_\alpha >y$ and  $w=ys_\alpha$, then
$w=ys_\alpha$, then  $z=y$ or
$z=y$ or  $z=ys_\alpha$.
$z=ys_\alpha$.
(2) Assume
 $y\le z$ and
$y\le z$ and  $w\ge zs_\alpha$.
$w\ge zs_\alpha$.
(a) If
 $ys_\alpha < y$,
$ys_\alpha < y$,  $w\le y$, and
$w\le y$, and  $w\not \in \{y, ys_\alpha \}$, then there is no such
$w\not \in \{y, ys_\alpha \}$, then there is no such  $z$.
$z$.(b) If
 $ys_\alpha >y$,
$ys_\alpha >y$,  $w\le ys_\alpha$, and
$w\le ys_\alpha$, and  $w\not \in \{y, ys_\alpha \}$, then there is no such
$w\not \in \{y, ys_\alpha \}$, then there is no such  $z$.
$z$.(c) If
 $ys_\alpha < y$ and
$ys_\alpha < y$ and  $w=y$, then
$w=y$, then  $z=y$.
$z=y$.(d) If
 $ys_\alpha >y$ and
$ys_\alpha >y$ and  $w=y$, then
$w=y$, then  $z=ys_\alpha$.
$z=ys_\alpha$.(e) If
 $ys_\alpha < y$ and
$ys_\alpha < y$ and  $w=ys_\alpha$, then
$w=ys_\alpha$, then  $z=y$.
$z=y$.(f) If
 $ys_\alpha >y$ and
$ys_\alpha >y$ and  $w=ys_\alpha$, then
$w=ys_\alpha$, then  $z=y$ or
$z=y$ or  $z=ys_\alpha$.
$z=ys_\alpha$.
(3) If
 $w>\min \{y, ys_\alpha \}$ and
$w>\min \{y, ys_\alpha \}$ and  $w\neq y, ys_\alpha$, then
$w\neq y, ys_\alpha$, then  $y<\max \{w, ws_\alpha \}$.
$y<\max \{w, ws_\alpha \}$.
Proof. (1a)–(1d) are obvious. For (1e), we have ![]() $ys_\alpha =w\ge z\ge y$. So
$ys_\alpha =w\ge z\ge y$. So ![]() $z=y$ or
$z=y$ or ![]() $z=ys_\alpha$.
$z=ys_\alpha$.
(2a) ![]() $w< y$ and
$w< y$ and ![]() $w\neq ys_\alpha$ imply that
$w\neq ys_\alpha$ imply that ![]() $z\ge y>w\ge zs_\alpha$, so
$z\ge y>w\ge zs_\alpha$, so
So ![]() $\ell (z)=\ell (y)$ and
$\ell (z)=\ell (y)$ and ![]() $\ell (w)=\ell (zs_\alpha )$. That is,
$\ell (w)=\ell (zs_\alpha )$. That is, ![]() $z=y$ and
$z=y$ and ![]() $w=zs_\alpha$. Hence,
$w=zs_\alpha$. Hence, ![]() $w=ys_\alpha$, which is a contradiction. So no such
$w=ys_\alpha$, which is a contradiction. So no such ![]() $z$ exists.
$z$ exists.
(2b) If ![]() $z=y$, then
$z=y$, then ![]() $w\ge ys_\alpha$, which contradicts
$w\ge ys_\alpha$, which contradicts ![]() $ys_\alpha >w$. So
$ys_\alpha >w$. So ![]() $y< z$.
$y< z$.
If ![]() $zs_\alpha >z$, then
$zs_\alpha >z$, then ![]() $\ell (y)+1=\ell (ys_\alpha )> \ell (w)\geq \ell (zs_\alpha )=\ell (z)+1$. So
$\ell (y)+1=\ell (ys_\alpha )> \ell (w)\geq \ell (zs_\alpha )=\ell (z)+1$. So ![]() $\ell (y)>\ell (z)$. This contradicts the assumption that
$\ell (y)>\ell (z)$. This contradicts the assumption that ![]() $y\le z$.
$y\le z$.
If ![]() $zs_\alpha < z$, then
$zs_\alpha < z$, then ![]() $\ell (y)+1=\ell (ys_\alpha )>\ell (w)\geq \ell (zs_\alpha )=\ell (z)-1$. So
$\ell (y)+1=\ell (ys_\alpha )>\ell (w)\geq \ell (zs_\alpha )=\ell (z)-1$. So ![]() $\ell (y)+2>\ell (z)> \ell (y)$ which forces
$\ell (y)+2>\ell (z)> \ell (y)$ which forces ![]() $\ell (z)=\ell (y)+1$, i.e.
$\ell (z)=\ell (y)+1$, i.e. ![]() $z=ys_\beta$ for some positive root
$z=ys_\beta$ for some positive root ![]() $\beta$ such that
$\beta$ such that ![]() $y\beta >0$. We claim
$y\beta >0$. We claim ![]() $\alpha =\beta$. If not, then
$\alpha =\beta$. If not, then ![]() $s_\alpha \beta >0$. But
$s_\alpha \beta >0$. But ![]() $\ell (ys_\alpha )=\ell (y)+1=\ell (z)>\ell (zs_\alpha )=\ell (ys_\beta s_\alpha )=\ell (ys_\alpha s_{s_\alpha \beta })$, which implies
$\ell (ys_\alpha )=\ell (y)+1=\ell (z)>\ell (zs_\alpha )=\ell (ys_\beta s_\alpha )=\ell (ys_\alpha s_{s_\alpha \beta })$, which implies ![]() $ys_\alpha (s_\alpha (\beta ))=y\beta <0$. This contradicts the assumption that
$ys_\alpha (s_\alpha (\beta ))=y\beta <0$. This contradicts the assumption that ![]() $y\beta >0$. Therefore
$y\beta >0$. Therefore ![]() $\alpha =\beta$, and
$\alpha =\beta$, and ![]() $z=ys_\alpha$.
$z=ys_\alpha$.
Then ![]() $ys_\alpha >w\geq zs_\alpha =y$. Since
$ys_\alpha >w\geq zs_\alpha =y$. Since ![]() $w\neq y$, such
$w\neq y$, such ![]() $w$ does not exist.
$w$ does not exist.
(2c) We have ![]() $z\ge y\ge zs_\alpha$. So
$z\ge y\ge zs_\alpha$. So ![]() $z=y$ or
$z=y$ or ![]() $z=ys_\alpha$. Since
$z=ys_\alpha$. Since ![]() $z\geq y$,
$z\geq y$, ![]() $z$ must be equal to
$z$ must be equal to ![]() $y$.
$y$.
(2d) The proof is similar as that of (2c).
(2e) Since ![]() $zs_\alpha \le ys_\alpha < y\le z$,
$zs_\alpha \le ys_\alpha < y\le z$, ![]() $z=y$.
$z=y$.
(2f) It is easy to see that ![]() $z=y$ and
$z=y$ and ![]() $z=ys_\alpha$ satisfy the conditions. Now assume that
$z=ys_\alpha$ satisfy the conditions. Now assume that ![]() $ys_\alpha >y, z>y$ and
$ys_\alpha >y, z>y$ and ![]() $ys_\alpha >zs_\alpha$. Then
$ys_\alpha >zs_\alpha$. Then ![]() $\ell (y)+1=\ell (ys_\alpha )>\ell (zs_\alpha )\ge \ell (z)-1$. Hence,
$\ell (y)+1=\ell (ys_\alpha )>\ell (zs_\alpha )\ge \ell (z)-1$. Hence, ![]() $\ell (y)+2>\ell (z)>\ell (y)$, which implies that
$\ell (y)+2>\ell (z)>\ell (y)$, which implies that ![]() $\ell (z)=\ell (y)+1$. It follows similarly as the proof of (2b) that
$\ell (z)=\ell (y)+1$. It follows similarly as the proof of (2b) that ![]() $z=ys_\alpha$.
$z=ys_\alpha$.
(3) This follows from a case-by-case study, using Lemma 4.2.
Now we are ready to prove the following technical lemma, which has been used in the proof of Theorem 4.1.
Lemma 4.4 Let ![]() $\alpha$ be a simple root, and
$\alpha$ be a simple root, and ![]() $\nabla$ be an alcove whose closure intersects with
$\nabla$ be an alcove whose closure intersects with ![]() $H_{\alpha ^\vee , 0}$ non-trivially.
$H_{\alpha ^\vee , 0}$ non-trivially.
(1) If
 $(\lambda , \alpha ^\vee )>0, \forall \, \lambda \in \nabla$, then
(18)
$(\lambda , \alpha ^\vee )>0, \forall \, \lambda \in \nabla$, then
(18) \begin{equation} D_\alpha(\operatorname{stab}^{-,{\nabla}}_{y})=\left\{\begin{array}{@{}ll} \displaystyle -q\operatorname{stab}^{-,{\nabla}}_{y} -q^{{1/2}}\operatorname{stab}^{-,{\nabla}}_{ys_{\alpha}}+\sum_{w\not< y}a_w\operatorname{stab}^{-,{\nabla}}_{w} & \text{if }ys_\alpha< y,\\ \displaystyle -\operatorname{stab}^{-,{\nabla}}_{y}-q^{1/2}\operatorname{stab}^{-,{\nabla}}_{ys_\alpha}+\sum_{w\not< ys_\alpha}a_w \operatorname{stab}^{-,{\nabla}}_{w} & \text{if } ys_\alpha>y.\end{array}\right. \end{equation}
\begin{equation} D_\alpha(\operatorname{stab}^{-,{\nabla}}_{y})=\left\{\begin{array}{@{}ll} \displaystyle -q\operatorname{stab}^{-,{\nabla}}_{y} -q^{{1/2}}\operatorname{stab}^{-,{\nabla}}_{ys_{\alpha}}+\sum_{w\not< y}a_w\operatorname{stab}^{-,{\nabla}}_{w} & \text{if }ys_\alpha< y,\\ \displaystyle -\operatorname{stab}^{-,{\nabla}}_{y}-q^{1/2}\operatorname{stab}^{-,{\nabla}}_{ys_\alpha}+\sum_{w\not< ys_\alpha}a_w \operatorname{stab}^{-,{\nabla}}_{w} & \text{if } ys_\alpha>y.\end{array}\right. \end{equation}(2) If
 $(\lambda , \alpha ^\vee )<0, \forall \, \lambda \in \nabla$, then
(19)Here
$(\lambda , \alpha ^\vee )<0, \forall \, \lambda \in \nabla$, then
(19)Here \begin{equation} D_\alpha(\operatorname{stab}^{-,{\nabla}}_{y})=\left\{\begin{array}{@{}ll} \displaystyle -\operatorname{stab}^{-,{\nabla}}_{y} -q^{{1/2}}\operatorname{stab}^{-,{\nabla}}_{ys_{\alpha}}+\sum_{w\not< y}a_w\operatorname{stab}^{-,{\nabla}}_{w} & \text{if }ys_\alpha< y,\\ \displaystyle -q\operatorname{stab}^{-,{\nabla}}_{y}-q^{1/2}\operatorname{stab}^{-,{\nabla}}_{ys_\alpha}+\sum_{w\not< ys_\alpha}a_w \operatorname{stab}^{-,{\nabla}}_{w} & \text{if } ys_\alpha>y.\end{array}\right. \end{equation}
\begin{equation} D_\alpha(\operatorname{stab}^{-,{\nabla}}_{y})=\left\{\begin{array}{@{}ll} \displaystyle -\operatorname{stab}^{-,{\nabla}}_{y} -q^{{1/2}}\operatorname{stab}^{-,{\nabla}}_{ys_{\alpha}}+\sum_{w\not< y}a_w\operatorname{stab}^{-,{\nabla}}_{w} & \text{if }ys_\alpha< y,\\ \displaystyle -q\operatorname{stab}^{-,{\nabla}}_{y}-q^{1/2}\operatorname{stab}^{-,{\nabla}}_{ys_\alpha}+\sum_{w\not< ys_\alpha}a_w \operatorname{stab}^{-,{\nabla}}_{w} & \text{if } ys_\alpha>y.\end{array}\right. \end{equation} $a_w\in K_T(\operatorname {pt})$. Note that we have been sloppy about the coefficients
$a_w\in K_T(\operatorname {pt})$. Note that we have been sloppy about the coefficients  $a_w$, since they clearly depend on
$a_w$, since they clearly depend on  $\nabla$,
$\nabla$,  $y$, and
$y$, and  $\alpha$.
$\alpha$.
Proof. The proof is similar to that for [Reference Su, Zhao and ZhongSZZ20, Proposition 4.3].
Step 1. By duality (3),
By the support condition of the stable basis, ![]() $a_w=\langle D_\alpha (\operatorname {stab}^{-,{\nabla }}_{y}), \operatorname {stab}^{+, {-\nabla }}_{w}\rangle$ is a proper integral. Hence
$a_w=\langle D_\alpha (\operatorname {stab}^{-,{\nabla }}_{y}), \operatorname {stab}^{+, {-\nabla }}_{w}\rangle$ is a proper integral. Hence ![]() $a_w\in K_T(\operatorname {pt})$. By localization formula and the support condition (see the first several lines in the proof of [Reference Su, Zhao and ZhongSZZ20, Proposition 4.3]),
$a_w\in K_T(\operatorname {pt})$. By localization formula and the support condition (see the first several lines in the proof of [Reference Su, Zhao and ZhongSZZ20, Proposition 4.3]),
 \begin{align} a_w=\sum_{y\leq z\leq w}\frac{\operatorname{stab}^{+, {-\nabla}}_{w}|_z\operatorname{stab}^{-,{\nabla}}_{y}|_z}{\bigwedge^\bullet T_z(T^*\mathcal{B})}\frac{e^{z\alpha}-q}{1-e^{z\alpha}} +\sum_{w\geq zs_\alpha\text{ and } y\leq z}\frac{\operatorname{stab}^{+, {-\nabla}}_{w}|_{zs_\alpha}\operatorname{stab}^{-,{\nabla}}_{y}|_z}{\bigwedge^\bullet T_z(T^*\mathcal{B})}\frac{1-qe^{{-}z\alpha}}{1-e^{{-}z\alpha}}e^{z\alpha}. \end{align}
\begin{align} a_w=\sum_{y\leq z\leq w}\frac{\operatorname{stab}^{+, {-\nabla}}_{w}|_z\operatorname{stab}^{-,{\nabla}}_{y}|_z}{\bigwedge^\bullet T_z(T^*\mathcal{B})}\frac{e^{z\alpha}-q}{1-e^{z\alpha}} +\sum_{w\geq zs_\alpha\text{ and } y\leq z}\frac{\operatorname{stab}^{+, {-\nabla}}_{w}|_{zs_\alpha}\operatorname{stab}^{-,{\nabla}}_{y}|_z}{\bigwedge^\bullet T_z(T^*\mathcal{B})}\frac{1-qe^{{-}z\alpha}}{1-e^{{-}z\alpha}}e^{z\alpha}. \end{align} From Lemma 4.3 above, we know that if ![]() $ys_\alpha < y$,
$ys_\alpha < y$, ![]() $w< y$ and
$w< y$ and ![]() $w\not \in \{y, ys_\alpha \}$, or if
$w\not \in \{y, ys_\alpha \}$, or if ![]() $ys_\alpha >y$,
$ys_\alpha >y$, ![]() $w< ys_\alpha$ and
$w< ys_\alpha$ and ![]() $w\not \in \{y, ys_\alpha \}$, then the two sums are empty, so
$w\not \in \{y, ys_\alpha \}$, then the two sums are empty, so ![]() $a_w=0$. Therefore, we just need to consider
$a_w=0$. Therefore, we just need to consider ![]() $a_y$ and
$a_y$ and ![]() $a_{ys_\alpha }$.
$a_{ys_\alpha }$.
In the following Steps 2–5, we assume ![]() $ys_\alpha < y$, and starting from Step 6, we assume
$ys_\alpha < y$, and starting from Step 6, we assume ![]() $ys_\alpha >y$.
$ys_\alpha >y$.
Step 2. We compute ![]() $a_{ys_\alpha }$, assuming
$a_{ys_\alpha }$, assuming ![]() $ys_\alpha < y$. By Lemma 4.3, there is only one term in the second sum with
$ys_\alpha < y$. By Lemma 4.3, there is only one term in the second sum with ![]() $z=y$, then
$z=y$, then
 \begin{align*} a_{ys_\alpha}&=\frac{\operatorname{stab}^{+, {-\nabla}}_{ys_\alpha}|_{ys_\alpha}\operatorname{stab}^{-,{\nabla}}_{y}|_y}{\bigwedge^\bullet T_y(T^*\mathcal{B})}\frac{1-qe^{{-}y\alpha}}{1-e^{{-}y\alpha}}e^{y\alpha}\\ &\overset{\text{Lemma 2.3}}=\frac{\operatorname{stab}^{+, {-\nabla}}_{ys_\alpha}|_{ys_\alpha}}{\operatorname{stab}^{+, {-\nabla}}_{y}|_y} \frac{1-qe^{{-}y\alpha}}{1-e^{{-}y\alpha}}e^{y\alpha}\\ &\overset{(4)}=\frac{q^{-\ell(ys_\alpha)/2}\prod_{\beta>0, ys_\alpha\beta<0}(q-e^{ys_\alpha\beta})\prod_{\beta>0, ys_\alpha\beta>0}(1-e^{ys_\alpha \beta})}{q^{-\ell(y)/2}\prod_{\beta>0, y\beta<0}(q-e^{y\beta})\prod_{\beta>0, y\beta>0}(1-e^{y\beta})} \frac{1-qe^{{-}y\alpha}}{1-e^{{-}y\alpha}}e^{y\alpha}\\ &\overset{\sharp}=q^{1/2}\frac{1-e^{{-}y\alpha}}{q-e^{y\alpha}} \frac{1-qe^{{-}y\alpha}}{1-e^{{-}y\alpha}}e^{y\alpha}\\ &={-}q^{{1/2}}, \end{align*}
\begin{align*} a_{ys_\alpha}&=\frac{\operatorname{stab}^{+, {-\nabla}}_{ys_\alpha}|_{ys_\alpha}\operatorname{stab}^{-,{\nabla}}_{y}|_y}{\bigwedge^\bullet T_y(T^*\mathcal{B})}\frac{1-qe^{{-}y\alpha}}{1-e^{{-}y\alpha}}e^{y\alpha}\\ &\overset{\text{Lemma 2.3}}=\frac{\operatorname{stab}^{+, {-\nabla}}_{ys_\alpha}|_{ys_\alpha}}{\operatorname{stab}^{+, {-\nabla}}_{y}|_y} \frac{1-qe^{{-}y\alpha}}{1-e^{{-}y\alpha}}e^{y\alpha}\\ &\overset{(4)}=\frac{q^{-\ell(ys_\alpha)/2}\prod_{\beta>0, ys_\alpha\beta<0}(q-e^{ys_\alpha\beta})\prod_{\beta>0, ys_\alpha\beta>0}(1-e^{ys_\alpha \beta})}{q^{-\ell(y)/2}\prod_{\beta>0, y\beta<0}(q-e^{y\beta})\prod_{\beta>0, y\beta>0}(1-e^{y\beta})} \frac{1-qe^{{-}y\alpha}}{1-e^{{-}y\alpha}}e^{y\alpha}\\ &\overset{\sharp}=q^{1/2}\frac{1-e^{{-}y\alpha}}{q-e^{y\alpha}} \frac{1-qe^{{-}y\alpha}}{1-e^{{-}y\alpha}}e^{y\alpha}\\ &={-}q^{{1/2}}, \end{align*}
where ![]() $\sharp$ follows from the facts
$\sharp$ follows from the facts ![]() $y\alpha <0$ and
$y\alpha <0$ and ![]() $s_\alpha \{\beta >0|\beta \neq \alpha \}=\{\beta >0|\beta \neq \alpha \}$, since
$s_\alpha \{\beta >0|\beta \neq \alpha \}=\{\beta >0|\beta \neq \alpha \}$, since ![]() $\alpha$ is simple.
$\alpha$ is simple.
Step 3. We consider ![]() $a_y$, assuming
$a_y$, assuming ![]() $ys_\alpha < y$. By Lemma 4.3 above, there is only one term in each sum with both
$ys_\alpha < y$. By Lemma 4.3 above, there is only one term in each sum with both ![]() $z=y$, and we have
$z=y$, and we have
 \begin{align*} a_y&=\frac{\operatorname{stab}^{+, {-\nabla}}_{y}|_y\operatorname{stab}^{-,{\nabla}}_{y}|_y}{\bigwedge^\bullet T_y(T^*\mathcal{B})}\frac{e^{y\alpha}-q}{1-e^{y\alpha}} +\frac{\operatorname{stab}^{+, {-\nabla}}_{y}|_{ys_\alpha}\operatorname{stab}^{-,{\nabla}}_{y}|_y}{\bigwedge^\bullet T_y(T^*\mathcal{B})}\frac{1-qe^{{-}y\alpha}}{1-e^{{-}y\alpha}}e^{y\alpha}\\ &\overset{\text{Lemma 2.3}}=\frac{e^{y\alpha}-q}{1-e^{y\alpha}}+ \frac{\operatorname{stab}^{+, {-\nabla}}_{y}|_{ys_\alpha}\operatorname{stab}^{-,{\nabla}}_{y}|_y}{\bigwedge^\bullet T_y(T^*\mathcal{B})} \frac{1-qe^{{-}y\alpha}}{1-e^{{-}y\alpha}}e^{y\alpha}\\ &=\frac{e^{y\alpha}-q}{1-e^{y\alpha}}\bigg(1-\frac{\operatorname{stab}^{+, {-\nabla}}_{y}|_{ys_\alpha}\operatorname{stab}^{-,{\nabla}}_{y}|_y\cdot e^{y\alpha}}{\bigwedge^\bullet T_y(T^*\mathcal{B})}\bigg). \end{align*}
\begin{align*} a_y&=\frac{\operatorname{stab}^{+, {-\nabla}}_{y}|_y\operatorname{stab}^{-,{\nabla}}_{y}|_y}{\bigwedge^\bullet T_y(T^*\mathcal{B})}\frac{e^{y\alpha}-q}{1-e^{y\alpha}} +\frac{\operatorname{stab}^{+, {-\nabla}}_{y}|_{ys_\alpha}\operatorname{stab}^{-,{\nabla}}_{y}|_y}{\bigwedge^\bullet T_y(T^*\mathcal{B})}\frac{1-qe^{{-}y\alpha}}{1-e^{{-}y\alpha}}e^{y\alpha}\\ &\overset{\text{Lemma 2.3}}=\frac{e^{y\alpha}-q}{1-e^{y\alpha}}+ \frac{\operatorname{stab}^{+, {-\nabla}}_{y}|_{ys_\alpha}\operatorname{stab}^{-,{\nabla}}_{y}|_y}{\bigwedge^\bullet T_y(T^*\mathcal{B})} \frac{1-qe^{{-}y\alpha}}{1-e^{{-}y\alpha}}e^{y\alpha}\\ &=\frac{e^{y\alpha}-q}{1-e^{y\alpha}}\bigg(1-\frac{\operatorname{stab}^{+, {-\nabla}}_{y}|_{ys_\alpha}\operatorname{stab}^{-,{\nabla}}_{y}|_y\cdot e^{y\alpha}}{\bigwedge^\bullet T_y(T^*\mathcal{B})}\bigg). \end{align*} Step 4. In this step we compute ![]() $a_y$, assuming
$a_y$, assuming ![]() $(\lambda , \alpha ^\vee )>0, \lambda \in \nabla$. For any Laurent polynomial
$(\lambda , \alpha ^\vee )>0, \lambda \in \nabla$. For any Laurent polynomial ![]() $g=\sum _{\mu \in I}c_\mu e^\mu$ and
$g=\sum _{\mu \in I}c_\mu e^\mu$ and ![]() $\xi \in {\frak h}$, write
$\xi \in {\frak h}$, write
For example, for any ![]() $y\in W$,
$y\in W$,
 \begin{equation} \operatorname{Max}_\xi\Big(\bigwedge\nolimits^\bullet T_y(T^*\mathcal{B})\Big)={-}\operatorname{Min}_\xi\Big(\bigwedge\nolimits^\bullet T_y(T^*\mathcal{B})\Big)=\left\{\begin{array}{@{}ll} (2\rho, \xi) & \text{if }\xi\in {\frak C}_+,\\ -(2\rho, \xi) & \text{if }\xi\in {\frak C}_-. \end{array}\right. \end{equation}
\begin{equation} \operatorname{Max}_\xi\Big(\bigwedge\nolimits^\bullet T_y(T^*\mathcal{B})\Big)={-}\operatorname{Min}_\xi\Big(\bigwedge\nolimits^\bullet T_y(T^*\mathcal{B})\Big)=\left\{\begin{array}{@{}ll} (2\rho, \xi) & \text{if }\xi\in {\frak C}_+,\\ -(2\rho, \xi) & \text{if }\xi\in {\frak C}_-. \end{array}\right. \end{equation}Write
Here ![]() $I\subset X^*(T)$ is a finite subset. Following [Reference Su, Zhao and ZhongSZZ20, Lemma 3.1], let
$I\subset X^*(T)$ is a finite subset. Following [Reference Su, Zhao and ZhongSZZ20, Lemma 3.1], let ![]() $\xi$ be in
$\xi$ be in ![]() ${\frak C}_+$ (so that
${\frak C}_+$ (so that ![]() $(2\rho , \xi )>0$) such that
$(2\rho , \xi )>0$) such that
Since ![]() $ys_\alpha < y$,
$ys_\alpha < y$, ![]() $y\alpha <0$, so
$y\alpha <0$, so ![]() $(y\alpha , \xi )<0$. Since
$(y\alpha , \xi )<0$. Since ![]() $(\lambda , \alpha ^\vee )>0$, we adjust
$(\lambda , \alpha ^\vee )>0$, we adjust ![]() $\lambda \in \nabla$ close to
$\lambda \in \nabla$ close to ![]() $H_{\alpha ^\vee , 0}$ so that
$H_{\alpha ^\vee , 0}$ so that
The degree condition together with [Reference Su, Zhao and ZhongSZZ20, (9)] implies that
 \begin{align*} \operatorname{Max}_\xi(f)&\le \operatorname{Max}_\xi(\operatorname{stab}^{+, {-\nabla}}_{ys_\alpha}|_{ys_\alpha})+( \mathcal{L}_{-\lambda}|_{ys_\alpha}-\mathcal{L}_{-\lambda}|_y, \xi)+\operatorname{Max}_\xi(\operatorname{stab}^{-,{\nabla}}_{y}|_y)+(y\alpha, \xi)\\ &=(2\rho, \xi)+(\lambda, \alpha^\vee)(y\alpha, \xi). \end{align*}
\begin{align*} \operatorname{Max}_\xi(f)&\le \operatorname{Max}_\xi(\operatorname{stab}^{+, {-\nabla}}_{ys_\alpha}|_{ys_\alpha})+( \mathcal{L}_{-\lambda}|_{ys_\alpha}-\mathcal{L}_{-\lambda}|_y, \xi)+\operatorname{Max}_\xi(\operatorname{stab}^{-,{\nabla}}_{y}|_y)+(y\alpha, \xi)\\ &=(2\rho, \xi)+(\lambda, \alpha^\vee)(y\alpha, \xi). \end{align*}
Since ![]() $\operatorname {Max}_\xi (f)\in {\mathbb {Z}}$,
$\operatorname {Max}_\xi (f)\in {\mathbb {Z}}$, ![]() $\operatorname {Max}_\xi (f)\le (2\rho , \xi )-1$. Therefore, by using (21), we have
$\operatorname {Max}_\xi (f)\le (2\rho , \xi )-1$. Therefore, by using (21), we have
So
Similarly, we have [Reference Su, Zhao and ZhongSZZ20, (10)]
 \begin{align*} \operatorname{Min} _\xi(f)&\ge \operatorname{Min}_\xi(\operatorname{stab}^{+, {-\nabla}}_{ys_\alpha}|_{ys_\alpha})+(\mathcal{L}_{-\lambda}|_{ys_\alpha} -\mathcal{L}_{-\lambda}|_{y},\xi)+\operatorname{Min}_\xi(\operatorname{stab}^{-,{\nabla}}_{y}|_y)+(y\alpha, \xi)\\ &={-}(2\rho, \xi)+(\lambda, \alpha^\vee)(y\alpha, \xi). \end{align*}
\begin{align*} \operatorname{Min} _\xi(f)&\ge \operatorname{Min}_\xi(\operatorname{stab}^{+, {-\nabla}}_{ys_\alpha}|_{ys_\alpha})+(\mathcal{L}_{-\lambda}|_{ys_\alpha} -\mathcal{L}_{-\lambda}|_{y},\xi)+\operatorname{Min}_\xi(\operatorname{stab}^{-,{\nabla}}_{y}|_y)+(y\alpha, \xi)\\ &={-}(2\rho, \xi)+(\lambda, \alpha^\vee)(y\alpha, \xi). \end{align*}
Since ![]() $\operatorname {Min}_\xi (f_1)\in {\mathbb {Z}}$, so
$\operatorname {Min}_\xi (f_1)\in {\mathbb {Z}}$, so ![]() $\operatorname {Min}_\xi (f_1)\ge -(2\rho , \xi )$. From (21), we get that
$\operatorname {Min}_\xi (f_1)\ge -(2\rho , \xi )$. From (21), we get that
Therefore,
which is bounded. Since ![]() $a_y\in K_T(\operatorname {pt})$,
$a_y\in K_T(\operatorname {pt})$, ![]() $a_y(t\xi )$ is a Laurent polynomial in variable
$a_y(t\xi )$ is a Laurent polynomial in variable ![]() $e^t$. The above two limits show that
$e^t$. The above two limits show that ![]() $a_y=-q$ is a constant Laurent polynomial.
$a_y=-q$ is a constant Laurent polynomial.
Step 5. In this step we compute ![]() $a_y$ assuming
$a_y$ assuming ![]() $(\lambda , \alpha ^\vee )<0, \lambda \in \nabla$. We can pick
$(\lambda , \alpha ^\vee )<0, \lambda \in \nabla$. We can pick ![]() $\xi \in {\frak C}_-$ (so that
$\xi \in {\frak C}_-$ (so that ![]() $(2\rho , \xi )<0$) satisfying (22). In this case,
$(2\rho , \xi )<0$) satisfying (22). In this case, ![]() $(y\alpha , \xi )>0$, and we adjust
$(y\alpha , \xi )>0$, and we adjust ![]() $\lambda \in \nabla$ close to
$\lambda \in \nabla$ close to ![]() $H_{\alpha ^\vee , 0}$ so that
$H_{\alpha ^\vee , 0}$ so that
Then similarly as in Step 4, we can show that
and ![]() $\lim _{t\to -\infty } a_y(t\xi )$ is bounded. Hence,
$\lim _{t\to -\infty } a_y(t\xi )$ is bounded. Hence, ![]() $a_y=-1$.
$a_y=-1$.
Step 6. We now consider the case ![]() $ys_\alpha >y$. For
$ys_\alpha >y$. For ![]() $a_y$ with
$a_y$ with ![]() $ys_\alpha >y$, then in (20),
$ys_\alpha >y$, then in (20), ![]() $z=y$ in the first sum and
$z=y$ in the first sum and ![]() $z=ys_\alpha$ in the second, so
$z=ys_\alpha$ in the second, so
 \begin{align*} a_y&=\frac{\operatorname{stab}^{+, {-\nabla}}_{y}|_y\operatorname{stab}^{-,{\nabla}}_{y}|_y}{\bigwedge^\bullet T_y(T^*\mathcal{B})}\frac{e^{y\alpha}-q}{1-e^{y\alpha}}+ \frac{\operatorname{stab}^{+, {-\nabla}}_{y}|_{y}\operatorname{stab}^{-,{\nabla}}_{y}|_{ys_\alpha}}{\bigwedge^\bullet T_{ys_\alpha}(T^*\mathcal{B})}\frac{1-qe^{y\alpha}}{1-e^{y\alpha}}e^{{-}y\alpha}\\ &=\frac{e^{y\alpha}-q}{1-e^{y\alpha}}+\frac{\operatorname{stab}^{+, {-\nabla}}_{y}|_{y} \operatorname{stab}^{-,{\nabla}}_{y}|_{ys_\alpha}}{\bigwedge^\bullet T_{ys_\alpha}(T^*\mathcal{B})}\frac{1-qe^{y\alpha}}{1-e^{y\alpha}}e^{{-}y\alpha}. \end{align*}
\begin{align*} a_y&=\frac{\operatorname{stab}^{+, {-\nabla}}_{y}|_y\operatorname{stab}^{-,{\nabla}}_{y}|_y}{\bigwedge^\bullet T_y(T^*\mathcal{B})}\frac{e^{y\alpha}-q}{1-e^{y\alpha}}+ \frac{\operatorname{stab}^{+, {-\nabla}}_{y}|_{y}\operatorname{stab}^{-,{\nabla}}_{y}|_{ys_\alpha}}{\bigwedge^\bullet T_{ys_\alpha}(T^*\mathcal{B})}\frac{1-qe^{y\alpha}}{1-e^{y\alpha}}e^{{-}y\alpha}\\ &=\frac{e^{y\alpha}-q}{1-e^{y\alpha}}+\frac{\operatorname{stab}^{+, {-\nabla}}_{y}|_{y} \operatorname{stab}^{-,{\nabla}}_{y}|_{ys_\alpha}}{\bigwedge^\bullet T_{ys_\alpha}(T^*\mathcal{B})}\frac{1-qe^{y\alpha}}{1-e^{y\alpha}}e^{{-}y\alpha}. \end{align*}
Now let ![]() $k=\operatorname {stab}^{+, {-\nabla }}_{y}|_{y}\operatorname {stab}^{-,{\nabla }}_{y}|_{ys_\alpha }e^{-y\alpha }$.
$k=\operatorname {stab}^{+, {-\nabla }}_{y}|_{y}\operatorname {stab}^{-,{\nabla }}_{y}|_{ys_\alpha }e^{-y\alpha }$.
Step 7. Suppose ![]() $(\lambda , \alpha ^\vee )>0, \forall \, \lambda \in \nabla$. We choose
$(\lambda , \alpha ^\vee )>0, \forall \, \lambda \in \nabla$. We choose ![]() $\xi \in {\frak C}_+$ (so that
$\xi \in {\frak C}_+$ (so that ![]() $(2\rho , \xi )>0$ and
$(2\rho , \xi )>0$ and ![]() $(y\alpha , \xi )>0$) satisfying properties similar as (22). We pick
$(y\alpha , \xi )>0$) satisfying properties similar as (22). We pick ![]() $\lambda \in \nabla$, so that
$\lambda \in \nabla$, so that
Then
 \begin{align*} \operatorname{Max}_\xi(k)&\le \operatorname{Max}_\xi(\operatorname{stab}^{+, {-\nabla}}_{y}|_y)+\operatorname{Max}_\xi(\operatorname{stab}^{-,{\nabla}}_{ys_\alpha}|_{ys_\alpha}) +(\mathcal{L}_\lambda|_{ys_\alpha}-\mathcal{L}_\lambda|_y, \xi)-(y\alpha, \xi)\\ &=(2\rho, \xi)-(\lambda,\alpha^\vee)(y\alpha, \xi).\end{align*}
\begin{align*} \operatorname{Max}_\xi(k)&\le \operatorname{Max}_\xi(\operatorname{stab}^{+, {-\nabla}}_{y}|_y)+\operatorname{Max}_\xi(\operatorname{stab}^{-,{\nabla}}_{ys_\alpha}|_{ys_\alpha}) +(\mathcal{L}_\lambda|_{ys_\alpha}-\mathcal{L}_\lambda|_y, \xi)-(y\alpha, \xi)\\ &=(2\rho, \xi)-(\lambda,\alpha^\vee)(y\alpha, \xi).\end{align*}So
On the other hand, we have
 \begin{align*} \operatorname{Min}_\xi(k)&\ge \operatorname{Min}_\xi(\operatorname{stab}^{+, {-\nabla}}_{y}|_y)+\operatorname{Min}_\xi(\operatorname{stab}^{-,{\nabla}}_{ys_\alpha}|_{ys_\alpha}) +(\mathcal{L}_\lambda|_{ys_\alpha}-\mathcal{L}_\lambda|_y, \xi)-(y\alpha, \xi) \\ &\ge ({-}2\rho, \xi)-(\lambda, \alpha^\vee)(y\alpha, \xi). \end{align*}
\begin{align*} \operatorname{Min}_\xi(k)&\ge \operatorname{Min}_\xi(\operatorname{stab}^{+, {-\nabla}}_{y}|_y)+\operatorname{Min}_\xi(\operatorname{stab}^{-,{\nabla}}_{ys_\alpha}|_{ys_\alpha}) +(\mathcal{L}_\lambda|_{ys_\alpha}-\mathcal{L}_\lambda|_y, \xi)-(y\alpha, \xi) \\ &\ge ({-}2\rho, \xi)-(\lambda, \alpha^\vee)(y\alpha, \xi). \end{align*}
Since ![]() $\operatorname {Min}_\xi (k)\in {\mathbb {Z}}$, so
$\operatorname {Min}_\xi (k)\in {\mathbb {Z}}$, so ![]() $\operatorname {Min}_\xi (k)\ge (-2\rho , \xi )$, therefore,
$\operatorname {Min}_\xi (k)\ge (-2\rho , \xi )$, therefore,
So ![]() $a_y=-1$.
$a_y=-1$.
Step 8. If ![]() $(\lambda , \alpha ^\vee )<0, \forall \, \lambda \in \nabla$, then we can mimic Step 7 by picking
$(\lambda , \alpha ^\vee )<0, \forall \, \lambda \in \nabla$, then we can mimic Step 7 by picking ![]() $\xi \in {\frak C}_-$ (so that
$\xi \in {\frak C}_-$ (so that ![]() $(2\rho , \xi )<0$ and
$(2\rho , \xi )<0$ and ![]() $(y\alpha , \xi )<0$), and pick
$(y\alpha , \xi )<0$), and pick ![]() $\lambda \in \nabla$ so that
$\lambda \in \nabla$ so that ![]() $-1<-(\lambda , \alpha ^\vee )(y\alpha , \xi )<0$; then
$-1<-(\lambda , \alpha ^\vee )(y\alpha , \xi )<0$; then
So ![]() $a_y=-q.$
$a_y=-q.$
Step 9. We then compute ![]() $a_{ys_\alpha }$ assuming
$a_{ys_\alpha }$ assuming ![]() $ys_\alpha >y$. In (20),
$ys_\alpha >y$. In (20), ![]() $z=y$ and
$z=y$ and ![]() $z=ys_\alpha$ in both sums, so we have
$z=ys_\alpha$ in both sums, so we have
 \begin{align*} a_{ys_\alpha}&=\frac{\operatorname{stab}^{+, {-\nabla}}_{ys_\alpha}|_y\operatorname{stab}^{-,{\nabla}}_{y}|_y}{\bigwedge^\bullet T_y(T^*\mathcal{B})}\frac{e^{y\alpha}-q}{1-e^{y\alpha}}+\frac{\operatorname{stab}^{+, {-\nabla}}_{ys_\alpha}|_{ys_\alpha} \operatorname{stab}^{-,{\nabla}}_{y}|_{ys_\alpha}}{\bigwedge^\bullet T_{ys_\alpha}(T^*\mathcal{B})} \frac{e^{{-}y\alpha}-q}{1-e^{{-}y\alpha}}\\ &\quad+\frac{\operatorname{stab}^{+, {-\nabla}}_{ys_\alpha}|_{ys_\alpha}\operatorname{stab}^{-,{\nabla}}_{y}|_{y}}{\bigwedge^\bullet T_{y}(T^*\mathcal{B})}\frac{1-qe^{{-}y\alpha}}{1-e^{{-}y\alpha}}e^{y\alpha}+ \frac{\operatorname{stab}^{+, {-\nabla}}_{ys_\alpha}|_{y}\operatorname{stab}^{-,{\nabla}}_{y}|_{ys_\alpha}}{\bigwedge^\bullet T_{ys_\alpha}T^*\mathcal{B}}\frac{1-qe^{y\alpha}}{1-e^{y\alpha}}e^{{-}y\alpha}. \end{align*}
\begin{align*} a_{ys_\alpha}&=\frac{\operatorname{stab}^{+, {-\nabla}}_{ys_\alpha}|_y\operatorname{stab}^{-,{\nabla}}_{y}|_y}{\bigwedge^\bullet T_y(T^*\mathcal{B})}\frac{e^{y\alpha}-q}{1-e^{y\alpha}}+\frac{\operatorname{stab}^{+, {-\nabla}}_{ys_\alpha}|_{ys_\alpha} \operatorname{stab}^{-,{\nabla}}_{y}|_{ys_\alpha}}{\bigwedge^\bullet T_{ys_\alpha}(T^*\mathcal{B})} \frac{e^{{-}y\alpha}-q}{1-e^{{-}y\alpha}}\\ &\quad+\frac{\operatorname{stab}^{+, {-\nabla}}_{ys_\alpha}|_{ys_\alpha}\operatorname{stab}^{-,{\nabla}}_{y}|_{y}}{\bigwedge^\bullet T_{y}(T^*\mathcal{B})}\frac{1-qe^{{-}y\alpha}}{1-e^{{-}y\alpha}}e^{y\alpha}+ \frac{\operatorname{stab}^{+, {-\nabla}}_{ys_\alpha}|_{y}\operatorname{stab}^{-,{\nabla}}_{y}|_{ys_\alpha}}{\bigwedge^\bullet T_{ys_\alpha}T^*\mathcal{B}}\frac{1-qe^{y\alpha}}{1-e^{y\alpha}}e^{{-}y\alpha}. \end{align*}Write
 \begin{gather*} f_1 =\operatorname{stab}^{+, {-\nabla}}_{ys_\alpha}|_y\operatorname{stab}^{-,{\nabla}}_{y}|_y, \quad f_2=\operatorname{stab}^{+, {-\nabla}}_{ys_\alpha}|_{ys_\alpha}\operatorname{stab}^{-,{\nabla}}_{y}|_{ys_\alpha}, \\ f_3 =\operatorname{stab}^{+, {-\nabla}}_{ys_\alpha}|_{ys_\alpha}\operatorname{stab}^{-,{\nabla}}_{y}|_{y}e^{y\alpha}, \quad f_4=\operatorname{stab}^{+, {-\nabla}}_{ys_\alpha}|_{y}\operatorname{stab}^{-,{\nabla}}_{y}|_{ys_\alpha}e^{{-}y\alpha}. \end{gather*}
\begin{gather*} f_1 =\operatorname{stab}^{+, {-\nabla}}_{ys_\alpha}|_y\operatorname{stab}^{-,{\nabla}}_{y}|_y, \quad f_2=\operatorname{stab}^{+, {-\nabla}}_{ys_\alpha}|_{ys_\alpha}\operatorname{stab}^{-,{\nabla}}_{y}|_{ys_\alpha}, \\ f_3 =\operatorname{stab}^{+, {-\nabla}}_{ys_\alpha}|_{ys_\alpha}\operatorname{stab}^{-,{\nabla}}_{y}|_{y}e^{y\alpha}, \quad f_4=\operatorname{stab}^{+, {-\nabla}}_{ys_\alpha}|_{y}\operatorname{stab}^{-,{\nabla}}_{y}|_{ys_\alpha}e^{{-}y\alpha}. \end{gather*} Step 10. If ![]() $(\lambda , \alpha ^\vee )>0, \forall \,\lambda \in \nabla$, then we can choose
$(\lambda , \alpha ^\vee )>0, \forall \,\lambda \in \nabla$, then we can choose ![]() $\xi \in {\frak C}_+$ satisfying (22) and
$\xi \in {\frak C}_+$ satisfying (22) and ![]() $(y\alpha , \xi )>0$, and pick
$(y\alpha , \xi )>0$, and pick ![]() $\lambda \in \nabla$ satisfying
$\lambda \in \nabla$ satisfying ![]() $-1<-2(\lambda , \alpha ^\vee )(y\alpha , \xi )<0$; then
$-1<-2(\lambda , \alpha ^\vee )(y\alpha , \xi )<0$; then
and it is easy to calculate from (5) and (4) that
Therefore,
Similarly, if ![]() $(\lambda , \alpha ^\vee )<0, \forall \, \lambda \in \nabla$, then we can choose
$(\lambda , \alpha ^\vee )<0, \forall \, \lambda \in \nabla$, then we can choose ![]() $\xi \in {\frak C}_-$ (so that
$\xi \in {\frak C}_-$ (so that ![]() $(y\alpha , \xi )<0$), and
$(y\alpha , \xi )<0$), and ![]() $\lambda \in \nabla$ satisfying
$\lambda \in \nabla$ satisfying ![]() $-1<-2(\lambda , \alpha ^\vee )(y\alpha , \xi )<0$; then
$-1<-2(\lambda , \alpha ^\vee )(y\alpha , \xi )<0$; then
Therefore, ![]() $a_{ys_\alpha }=-q^{1/2}$.
$a_{ys_\alpha }=-q^{1/2}$.
4.3 Arbitrary chamber
We generalize Theorem 4.1 to the setting of an arbitrary chamber. The choice of a chamber ![]() ${\frak C}$ determines a set of simple roots. Replacing the positive chamber
${\frak C}$ determines a set of simple roots. Replacing the positive chamber ![]() $+$ in Theorem 4.1 by the chamber
$+$ in Theorem 4.1 by the chamber ![]() ${\frak C}$, we get the following result.
${\frak C}$, we get the following result.
Theorem 4.5 Let ![]() $\alpha ^\vee$ be a simple coroot determined by the chamber
$\alpha ^\vee$ be a simple coroot determined by the chamber ![]() ${\frak C}$. Suppose
${\frak C}$. Suppose ![]() $\nabla$ has a wall on
$\nabla$ has a wall on ![]() $H_{\alpha ^\vee , 0}$, and
$H_{\alpha ^\vee , 0}$, and ![]() $(\lambda , \alpha ^\vee )>0, \forall \, \lambda \in \nabla$. Then
$(\lambda , \alpha ^\vee )>0, \forall \, \lambda \in \nabla$. Then
 \begin{align*} \operatorname{stab}^{{\frak C}, T\mathcal{B}, s_\alpha\nabla}_{y}&= \left\{ \begin{array}{@{}ll} \operatorname{stab}^{{\frak C}, T\mathcal{B}, \nabla}_{y}+(q^{{1/2}}-q^{-{1/2}})\cdot\operatorname{stab}^{{\frak C}, T\mathcal{B}, \nabla}_{ys_{\alpha}} & \text{if } ys_{\alpha}\prec_{\frak C} y,\\ \operatorname{stab}^{{\frak C}, T\mathcal{B},\nabla}_{y} & \text{if } ys_{\alpha}\succ_{\frak C} y. \end{array}\right. \\ \operatorname{stab}^{-{\frak C}, T^*\mathcal{B}, s_\alpha\nabla}_{y}&= \left\{ \begin{array}{@{}ll} \operatorname{stab}^{-{\frak C}, T^*\mathcal{B}, \nabla}_{y}+(q^{{1/2}}-q^{-{1/2}})\cdot\operatorname{stab}^{-{\frak C}, T^*\mathcal{B}, \nabla}_{ys_{\alpha}} & \text{if } ys_{\alpha}\succ_{\frak C} y,\\ \operatorname{stab}^{-{\frak C}, T^*\mathcal{B}, \nabla}_{y} & \text{if } ys_{\alpha}\prec_{\frak C} y. \end{array}\right. \end{align*}
\begin{align*} \operatorname{stab}^{{\frak C}, T\mathcal{B}, s_\alpha\nabla}_{y}&= \left\{ \begin{array}{@{}ll} \operatorname{stab}^{{\frak C}, T\mathcal{B}, \nabla}_{y}+(q^{{1/2}}-q^{-{1/2}})\cdot\operatorname{stab}^{{\frak C}, T\mathcal{B}, \nabla}_{ys_{\alpha}} & \text{if } ys_{\alpha}\prec_{\frak C} y,\\ \operatorname{stab}^{{\frak C}, T\mathcal{B},\nabla}_{y} & \text{if } ys_{\alpha}\succ_{\frak C} y. \end{array}\right. \\ \operatorname{stab}^{-{\frak C}, T^*\mathcal{B}, s_\alpha\nabla}_{y}&= \left\{ \begin{array}{@{}ll} \operatorname{stab}^{-{\frak C}, T^*\mathcal{B}, \nabla}_{y}+(q^{{1/2}}-q^{-{1/2}})\cdot\operatorname{stab}^{-{\frak C}, T^*\mathcal{B}, \nabla}_{ys_{\alpha}} & \text{if } ys_{\alpha}\succ_{\frak C} y,\\ \operatorname{stab}^{-{\frak C}, T^*\mathcal{B}, \nabla}_{y} & \text{if } ys_{\alpha}\prec_{\frak C} y. \end{array}\right. \end{align*}Thanks to this result, in the rest of the paper we focus on stable bases associated to the positive/negative chamber.
5. Wall-crossings and the affine Hecke algebra action
In this section we compute the formula when crossing a wall of a non-simple root, and also study the relation between wall-crossing and the affine Hecke algebra action.
5.1 Crossing the non-simple walls
Theorem 5.1 Suppose ![]() $\nabla$ has a wall on
$\nabla$ has a wall on ![]() $H_{\alpha ^\vee , 0}$ (so that
$H_{\alpha ^\vee , 0}$ (so that ![]() $\nabla$ and
$\nabla$ and ![]() $s_\alpha \nabla$ share a wall on
$s_\alpha \nabla$ share a wall on ![]() $H_{\alpha ^\vee , 0}$), and
$H_{\alpha ^\vee , 0}$), and ![]() $(\lambda ,\alpha ^\vee )>0, \forall \, \lambda \in \nabla$. Then
$(\lambda ,\alpha ^\vee )>0, \forall \, \lambda \in \nabla$. Then
 \begin{align*} \operatorname{stab}^{{\frak C}, T\mathcal{B},s_\alpha\nabla}_{y}&= \left\{ \begin{array}{@{}ll} \operatorname{stab}^{{\frak C}, T\mathcal{B},\nabla}_{y}+(q^{{1/2}}-q^{-{1/2}})\cdot\operatorname{stab}^{{\frak C}, T\mathcal{B}, \nabla}_{ys_{\alpha}} & \text{if } ys_{\alpha}\prec_{\frak C} y,\\ \operatorname{stab}^{{\frak C}, T\mathcal{B}, \nabla}_{y} & \text{if } ys_{\alpha}\succ_{\frak C} y. \end{array}\right. \\ \operatorname{stab}^{-{\frak C}, T^*\mathcal{B}, s_\alpha\nabla}_{y}&= \left\{ \begin{array}{@{}ll} \operatorname{stab}^{-{\frak C}, T^*\mathcal{B}, \nabla}_{y}+(q^{{1/2}}-q^{-{1/2}})\cdot\operatorname{stab}^{-{\frak C}, T^*\mathcal{B}, \nabla}_{ys_{\alpha}} & \text{if } ys_{\alpha}\succ_{\frak C} y,\\ \operatorname{stab}^{-{\frak C}, T^*\mathcal{B}, \nabla}_{y} & \text{if } ys_{\alpha}\prec_{\frak C} y. \end{array}\right. \end{align*}
\begin{align*} \operatorname{stab}^{{\frak C}, T\mathcal{B},s_\alpha\nabla}_{y}&= \left\{ \begin{array}{@{}ll} \operatorname{stab}^{{\frak C}, T\mathcal{B},\nabla}_{y}+(q^{{1/2}}-q^{-{1/2}})\cdot\operatorname{stab}^{{\frak C}, T\mathcal{B}, \nabla}_{ys_{\alpha}} & \text{if } ys_{\alpha}\prec_{\frak C} y,\\ \operatorname{stab}^{{\frak C}, T\mathcal{B}, \nabla}_{y} & \text{if } ys_{\alpha}\succ_{\frak C} y. \end{array}\right. \\ \operatorname{stab}^{-{\frak C}, T^*\mathcal{B}, s_\alpha\nabla}_{y}&= \left\{ \begin{array}{@{}ll} \operatorname{stab}^{-{\frak C}, T^*\mathcal{B}, \nabla}_{y}+(q^{{1/2}}-q^{-{1/2}})\cdot\operatorname{stab}^{-{\frak C}, T^*\mathcal{B}, \nabla}_{ys_{\alpha}} & \text{if } ys_{\alpha}\succ_{\frak C} y,\\ \operatorname{stab}^{-{\frak C}, T^*\mathcal{B}, \nabla}_{y} & \text{if } ys_{\alpha}\prec_{\frak C} y. \end{array}\right. \end{align*}Remark 5.2 This theorem shows that the wall-crossing coefficients ![]() $f_y^{s_\alpha \nabla \leftarrow \nabla }$ do not depend on where we cross the root hyperplane
$f_y^{s_\alpha \nabla \leftarrow \nabla }$ do not depend on where we cross the root hyperplane ![]() $H_{\alpha ^\vee , 0}$, which is not obvious from the definitions. In other words, for any
$H_{\alpha ^\vee , 0}$, which is not obvious from the definitions. In other words, for any ![]() $\nabla$ having a wall on
$\nabla$ having a wall on ![]() $H_{\alpha ^\vee ,0}$, the coefficient
$H_{\alpha ^\vee ,0}$, the coefficient ![]() $f_y^{s_\alpha \nabla \leftarrow \nabla }$ does not depend on the choice of
$f_y^{s_\alpha \nabla \leftarrow \nabla }$ does not depend on the choice of ![]() $\nabla$.
$\nabla$.
Proof. It suffices to prove the first one, since the other one will follow from it via duality as in Theorem 4.1. Assume first that ![]() ${\frak C}={\frak C}_+$, then we just need to consider the case when
${\frak C}={\frak C}_+$, then we just need to consider the case when ![]() $ys_\alpha < y$ due to Lemma 3.5. We have
$ys_\alpha < y$ due to Lemma 3.5. We have
where ![]() $f^{s_\alpha \nabla \leftarrow \nabla }\in K_{\mathbb {C}^*}(pt)$ due to Lemma 3.5. Suppose
$f^{s_\alpha \nabla \leftarrow \nabla }\in K_{\mathbb {C}^*}(pt)$ due to Lemma 3.5. Suppose ![]() $\alpha ^\vee =w\beta ^\vee$ for some simple coroot
$\alpha ^\vee =w\beta ^\vee$ for some simple coroot ![]() $\beta ^\vee$ and
$\beta ^\vee$ and ![]() $w\in W$. Applying
$w\in W$. Applying ![]() $w$ to the above identity and using Lemma 3.3, we get
$w$ to the above identity and using Lemma 3.3, we get
Here we have used the fact that ![]() $w(T\mathcal {B})=T\mathcal {B}$ and
$w(T\mathcal {B})=T\mathcal {B}$ and ![]() $w(f_y^{s_\alpha \nabla \leftarrow \nabla })=f_y^{s_\alpha \nabla \leftarrow \nabla }$. From definition, we see that
$w(f_y^{s_\alpha \nabla \leftarrow \nabla })=f_y^{s_\alpha \nabla \leftarrow \nabla }$. From definition, we see that ![]() $ys_\alpha < y$ implies that
$ys_\alpha < y$ implies that ![]() $wys_\alpha \prec _{w{\frak C}_+}wy$. Moreover, since
$wys_\alpha \prec _{w{\frak C}_+}wy$. Moreover, since ![]() $\beta ^\vee$ is a simple coroot with respect to
$\beta ^\vee$ is a simple coroot with respect to ![]() ${\frak C}_+$,
${\frak C}_+$, ![]() $\alpha ^\vee =w\beta ^\vee$ is a simple coroot with respect to
$\alpha ^\vee =w\beta ^\vee$ is a simple coroot with respect to ![]() $w{\frak C}_+$, and
$w{\frak C}_+$, and ![]() $s_\alpha \nabla , \nabla$ are separated by the simple wall
$s_\alpha \nabla , \nabla$ are separated by the simple wall ![]() $H_{\alpha ^\vee , 0}$. Therefore, Theorem 4.5 implies that
$H_{\alpha ^\vee , 0}$. Therefore, Theorem 4.5 implies that ![]() $f_y^{s_\alpha \nabla \leftarrow \nabla }=q^{1/2}-q^{-1/2}$.
$f_y^{s_\alpha \nabla \leftarrow \nabla }=q^{1/2}-q^{-1/2}$.
Now if ![]() ${\frak C}$ is general, we need to compute
${\frak C}$ is general, we need to compute ![]() $f^{s_\alpha \nabla \leftarrow \nabla }_y\in K_{\mathbb {C}^*}(\operatorname {pt})$ in
$f^{s_\alpha \nabla \leftarrow \nabla }_y\in K_{\mathbb {C}^*}(\operatorname {pt})$ in
Write ![]() ${\frak C}_+=v{\frak C}$; then
${\frak C}_+=v{\frak C}$; then ![]() $ys_\alpha \prec _{\frak C} y$ implies
$ys_\alpha \prec _{\frak C} y$ implies ![]() $vys_\alpha < vy$. Applying
$vys_\alpha < vy$. Applying ![]() $v$ to the above identity, we get
$v$ to the above identity, we get
By using the first part of the proof, we see that ![]() $f_{y}^{s_\alpha \nabla \leftarrow \nabla }=q^{1/2}-q^{-1/2}$.
$f_{y}^{s_\alpha \nabla \leftarrow \nabla }=q^{1/2}-q^{-1/2}$.
By translation, we can compute the wall-crossing coefficients for any wall ![]() $H_{\alpha ^\vee , n}$.
$H_{\alpha ^\vee , n}$.
Corollary 5.3 Suppose ![]() $\nabla _1, \nabla _2$ are adjacent and separated by the hyperplane
$\nabla _1, \nabla _2$ are adjacent and separated by the hyperplane ![]() $H_{\alpha ^\vee , n}$. Moreover, assume that
$H_{\alpha ^\vee , n}$. Moreover, assume that ![]() $(\lambda _1,\alpha ^\vee )< n<(\lambda _2, \alpha ^\vee ), \forall \, \lambda _i\in \nabla _i$. Then for any chamber
$(\lambda _1,\alpha ^\vee )< n<(\lambda _2, \alpha ^\vee ), \forall \, \lambda _i\in \nabla _i$. Then for any chamber ![]() ${\frak C}$, the polarization
${\frak C}$, the polarization ![]() $T\mathcal {B}$ or
$T\mathcal {B}$ or ![]() $T^*\mathcal {B}$, the coefficient
$T^*\mathcal {B}$, the coefficient ![]() $f^{\nabla _1\leftarrow \nabla _2}_y$ in Lemma 3.5 is equal to
$f^{\nabla _1\leftarrow \nabla _2}_y$ in Lemma 3.5 is equal to ![]() $e^{-ny\alpha }(q^{1/2}-q^{-1/2})$.
$e^{-ny\alpha }(q^{1/2}-q^{-1/2})$.
Proof. There exists an integral weight ![]() $\varpi _\alpha \in \Lambda$ such that,
$\varpi _\alpha \in \Lambda$ such that, ![]() $(\varpi _\alpha , \alpha ^\vee )=1$. Indeed, if
$(\varpi _\alpha , \alpha ^\vee )=1$. Indeed, if ![]() $\alpha$ is simple, take
$\alpha$ is simple, take ![]() $\varpi _\alpha$ to be the corresponding fundamental weight. If
$\varpi _\alpha$ to be the corresponding fundamental weight. If ![]() $\alpha$ is not simple, there exists
$\alpha$ is not simple, there exists ![]() $v\in W$ such that
$v\in W$ such that ![]() $v\alpha$ is simple. We can take
$v\alpha$ is simple. We can take ![]() $\varpi _\alpha =v^{-1}\varpi _{v\alpha }$, where
$\varpi _\alpha =v^{-1}\varpi _{v\alpha }$, where ![]() $\varpi _{v\alpha }$ is the fundamental weight corresponding to the simple root
$\varpi _{v\alpha }$ is the fundamental weight corresponding to the simple root ![]() $v\alpha$. Then
$v\alpha$. Then ![]() $\nabla _1':=\nabla _1-n\varpi _\alpha$ and
$\nabla _1':=\nabla _1-n\varpi _\alpha$ and ![]() $\nabla _2'=\nabla _2-n\varpi _\alpha$ are adjacent and separated by
$\nabla _2'=\nabla _2-n\varpi _\alpha$ are adjacent and separated by ![]() $H_{\alpha ^\vee , 0}$. Lemma 3.7 and Theorem 5.1 imply that
$H_{\alpha ^\vee , 0}$. Lemma 3.7 and Theorem 5.1 imply that
5.2 The affine Hecke algebra action
We can further express the wall-crossing formulas in terms of the affine Hecke algebra action. Let ![]() $q_y=q^{\ell (y)}, \epsilon _y=(-1)^{\ell (y)}$.
$q_y=q^{\ell (y)}, \epsilon _y=(-1)^{\ell (y)}$.
Theorem 5.4 For any ![]() $x, y\in W$, we have
$x, y\in W$, we have
Remark 5.5 This, together with (6), (15), and Theorem 2.5 completely determines the stable basis for the positive and negative chambers. The stable basis associated to other chambers are determined by § 3.2, on top of those for the positive or negative chambers.
Proof. We first show that (23) implies (24). By the duality of stable bases (3) and the adjointness between ![]() $T_\alpha$ and
$T_\alpha$ and ![]() $T'_\alpha$ (8), we get
$T'_\alpha$ (8), we get
 \begin{align*} q_x^{1/2}(T_{x^{{-}1}}')^{{-}1}(\operatorname{stab}^{+, {\nabla_-}}_{yx})&=\sum_{v\in W}\langle q_x^{1/2}(T_{x^{{-}1}}')^{{-}1}(\operatorname{stab}^{+, {\nabla_-}}_{yx}), \operatorname{stab}^{-,{x\nabla_+}}_{v}\rangle \operatorname{stab}^{+, {x\nabla_-}}_{v}\\ &=\sum_{v\in W} \langle \operatorname{stab}^{+, {\nabla_-}}_{yx}, q_x^{1/2}T_{x}^{{-}1}(\operatorname{stab}^{-,{x\nabla_+}}_{v})\rangle\operatorname{stab}^{+, {x\nabla_-}}_{v}\\ &\overset{(23)}=\sum_{v\in W}\langle \operatorname{stab}^{+, {\nabla_-}}_{yx}, \operatorname{stab}^{-,{\nabla_+}}_{vx}\rangle\operatorname{stab}^{+, {x\nabla_-}}_{v}\\ &=\operatorname{stab}^{+, {x\nabla_-}}_{y}. \end{align*}
\begin{align*} q_x^{1/2}(T_{x^{{-}1}}')^{{-}1}(\operatorname{stab}^{+, {\nabla_-}}_{yx})&=\sum_{v\in W}\langle q_x^{1/2}(T_{x^{{-}1}}')^{{-}1}(\operatorname{stab}^{+, {\nabla_-}}_{yx}), \operatorname{stab}^{-,{x\nabla_+}}_{v}\rangle \operatorname{stab}^{+, {x\nabla_-}}_{v}\\ &=\sum_{v\in W} \langle \operatorname{stab}^{+, {\nabla_-}}_{yx}, q_x^{1/2}T_{x}^{{-}1}(\operatorname{stab}^{-,{x\nabla_+}}_{v})\rangle\operatorname{stab}^{+, {x\nabla_-}}_{v}\\ &\overset{(23)}=\sum_{v\in W}\langle \operatorname{stab}^{+, {\nabla_-}}_{yx}, \operatorname{stab}^{-,{\nabla_+}}_{vx}\rangle\operatorname{stab}^{+, {x\nabla_-}}_{v}\\ &=\operatorname{stab}^{+, {x\nabla_-}}_{y}. \end{align*} Now we prove (23) by induction on ![]() $\ell (x)$. If
$\ell (x)$. If ![]() $x$ is a simple reflection, it follows from (17) and (10). Now assume it holds for
$x$ is a simple reflection, it follows from (17) and (10). Now assume it holds for ![]() $x$. Let
$x$. Let ![]() $\alpha$ be a simple root such that
$\alpha$ be a simple root such that ![]() $xs_\alpha >x$. Then
$xs_\alpha >x$. Then ![]() $\beta :=x\alpha >0$ and
$\beta :=x\alpha >0$ and ![]() $s_\beta =x s_\alpha x^{-1}$. Notice that the two alcoves
$s_\beta =x s_\alpha x^{-1}$. Notice that the two alcoves ![]() $x\nabla _+$ and
$x\nabla _+$ and ![]() $xs_\alpha \nabla _+=s_{\beta }x\nabla _+$ are adjacent alcoves separated by a wall on
$xs_\alpha \nabla _+=s_{\beta }x\nabla _+$ are adjacent alcoves separated by a wall on ![]() $H_{\beta ^\vee ,0}$, and for any
$H_{\beta ^\vee ,0}$, and for any ![]() $\lambda \in \nabla _+$,
$\lambda \in \nabla _+$,
So we can use Theorem 5.1 with respect to the wall-crossing ![]() $xs_\alpha \nabla _+\leftarrow x\nabla _+$, which corresponds to
$xs_\alpha \nabla _+\leftarrow x\nabla _+$, which corresponds to ![]() $s_\beta x\nabla _+\leftarrow x\nabla _+.$
$s_\beta x\nabla _+\leftarrow x\nabla _+.$
If ![]() $y\beta <0$, then
$y\beta <0$, then ![]() $ys_\beta < y$, and
$ys_\beta < y$, and ![]() $ys_\beta \succ _{{\frak C}_-} y$. Since
$ys_\beta \succ _{{\frak C}_-} y$. Since ![]() $yx \alpha =y\beta <0$,
$yx \alpha =y\beta <0$, ![]() $yxs_\alpha \succ _{{\frak C}_-}yx$. Then
$yxs_\alpha \succ _{{\frak C}_-}yx$. Then
 \begin{align*} \operatorname{stab}^{-,{xs_\alpha\nabla_+}}_{y} &\overset{\text{Theorem 5.1}}=\operatorname{stab}^{-,{x\nabla_+}}_{y}\\ &\overset{\text{induction}}=q_x^{{-}1/2}T_x(\operatorname{stab}^{-,{\nabla_+}}_{yx})\\ &\overset{\text{Theorem 2.5}}=q_x^{{-}1/2}T_x \big(q^{{-}1/2}T_\alpha(\operatorname{stab}^{-,{\nabla_+}}_{yxs_\alpha})\big)\\ &=q_{xs_\alpha}^{{-}1/2}T_{x s_\alpha}(\operatorname{stab}^{-,{\nabla_+}}_{yxs_\alpha}). \end{align*}
\begin{align*} \operatorname{stab}^{-,{xs_\alpha\nabla_+}}_{y} &\overset{\text{Theorem 5.1}}=\operatorname{stab}^{-,{x\nabla_+}}_{y}\\ &\overset{\text{induction}}=q_x^{{-}1/2}T_x(\operatorname{stab}^{-,{\nabla_+}}_{yx})\\ &\overset{\text{Theorem 2.5}}=q_x^{{-}1/2}T_x \big(q^{{-}1/2}T_\alpha(\operatorname{stab}^{-,{\nabla_+}}_{yxs_\alpha})\big)\\ &=q_{xs_\alpha}^{{-}1/2}T_{x s_\alpha}(\operatorname{stab}^{-,{\nabla_+}}_{yxs_\alpha}). \end{align*} If ![]() $y\beta >0$, then
$y\beta >0$, then ![]() $ys_\beta \prec _{{\frak C}_-}y$, and
$ys_\beta \prec _{{\frak C}_-}y$, and ![]() $yxs_\alpha \prec _{{\frak C}_-}yx$. We have
$yxs_\alpha \prec _{{\frak C}_-}yx$. We have
 \begin{align*} q_{xs_\alpha}^{{-}1/2}T_{xs_\alpha}(\operatorname{stab}^{-,{\nabla_+}}_{yxs_\alpha}) &=q_{xs_\alpha}^{{-}1/2}T_xT_\alpha(\operatorname{stab}^{-,{\nabla_+}}_{yxs_\alpha})\\ &\overset{\text{Theorem 2.5}}=q_{xs_\alpha}^{{-}1/2} T_xT_\alpha[q^{{-}1/2}T_\alpha(\operatorname{stab}^{-,{\nabla_+}}_{yx})]\\ &=q_{xs_\alpha}^{{-}1/2}T_x\big(q^{1/2}+(q^{1/2}-q^{{-}1/2})T_\alpha \big)(\operatorname{stab}^{-,{\nabla_+}}_{yx})\\ &\overset{\text{Theorem 2.5}}=q_{xs_\alpha}^{{-}1/2}T_x \big(q^{1/2}\operatorname{stab}^{-,{\nabla_+}}_{yx}+(q^{1/2}-q^{{-}1/2})q^{1/2}\operatorname{stab}^{-,{\nabla_+}}_{yxs_\alpha}\big)\\ &=q_x^{{-}1/2}\big(T_x(\operatorname{stab}^{-,{\nabla_+}}_{yx})+(q^{1/2}-q^{{-}1/2})T_x(\operatorname{stab}^{-,{\nabla_+}}_{yxs_\alpha})\big) \\ &\overset{\text{induction}}=\operatorname{stab}^{-,{x\nabla_+}}_{y}+(q^{{1/2}}-q^{-{1/2}}) \operatorname{stab}^{-,{x\nabla_+}}_{yxs_\alpha x^{{-}1}}\\ &\overset{\text{Theorem 5.1}}=\operatorname{stab}^{-,{xs_\alpha\nabla_+}}_{y}. \end{align*}
\begin{align*} q_{xs_\alpha}^{{-}1/2}T_{xs_\alpha}(\operatorname{stab}^{-,{\nabla_+}}_{yxs_\alpha}) &=q_{xs_\alpha}^{{-}1/2}T_xT_\alpha(\operatorname{stab}^{-,{\nabla_+}}_{yxs_\alpha})\\ &\overset{\text{Theorem 2.5}}=q_{xs_\alpha}^{{-}1/2} T_xT_\alpha[q^{{-}1/2}T_\alpha(\operatorname{stab}^{-,{\nabla_+}}_{yx})]\\ &=q_{xs_\alpha}^{{-}1/2}T_x\big(q^{1/2}+(q^{1/2}-q^{{-}1/2})T_\alpha \big)(\operatorname{stab}^{-,{\nabla_+}}_{yx})\\ &\overset{\text{Theorem 2.5}}=q_{xs_\alpha}^{{-}1/2}T_x \big(q^{1/2}\operatorname{stab}^{-,{\nabla_+}}_{yx}+(q^{1/2}-q^{{-}1/2})q^{1/2}\operatorname{stab}^{-,{\nabla_+}}_{yxs_\alpha}\big)\\ &=q_x^{{-}1/2}\big(T_x(\operatorname{stab}^{-,{\nabla_+}}_{yx})+(q^{1/2}-q^{{-}1/2})T_x(\operatorname{stab}^{-,{\nabla_+}}_{yxs_\alpha})\big) \\ &\overset{\text{induction}}=\operatorname{stab}^{-,{x\nabla_+}}_{y}+(q^{{1/2}}-q^{-{1/2}}) \operatorname{stab}^{-,{x\nabla_+}}_{yxs_\alpha x^{{-}1}}\\ &\overset{\text{Theorem 5.1}}=\operatorname{stab}^{-,{xs_\alpha\nabla_+}}_{y}. \end{align*}Corollary 5.6 If ![]() $\alpha$ is a simple root and
$\alpha$ is a simple root and ![]() $s_\alpha x>x$, then we have
$s_\alpha x>x$, then we have
Proof. We have ![]() $(T_{s_\alpha x})^{-1}=(T_x)^{-1}T_\alpha ^{-1}$. By Theorem 5.4, we have
$(T_{s_\alpha x})^{-1}=(T_x)^{-1}T_\alpha ^{-1}$. By Theorem 5.4, we have
 \begin{align*} q_x^{1/2}(T_x)^{{-}1}\operatorname{stab}^{-,{x\nabla_+}}_{yx^{{-}1}}&=\operatorname{stab}^{-,{\nabla_+}}_{y}=q_{s_\alpha x}^{1/2}(T_{s_\alpha x})^{{-}1}(\operatorname{stab}^{-,{s_\alpha x\nabla_+}}_{yx^{{-}1}s_\alpha})\\&=q_{ x}^{1/2}q^{1/2}(T_{ x})^{{-}1}T_\alpha^{{-}1}(\operatorname{stab}^{-,{s_\alpha x\nabla_+}}_{yx^{{-}1}s_\alpha}). \end{align*}
\begin{align*} q_x^{1/2}(T_x)^{{-}1}\operatorname{stab}^{-,{x\nabla_+}}_{yx^{{-}1}}&=\operatorname{stab}^{-,{\nabla_+}}_{y}=q_{s_\alpha x}^{1/2}(T_{s_\alpha x})^{{-}1}(\operatorname{stab}^{-,{s_\alpha x\nabla_+}}_{yx^{{-}1}s_\alpha})\\&=q_{ x}^{1/2}q^{1/2}(T_{ x})^{{-}1}T_\alpha^{{-}1}(\operatorname{stab}^{-,{s_\alpha x\nabla_+}}_{yx^{{-}1}s_\alpha}). \end{align*}
Cancelling ![]() $q_x^{1/2}(T_x)^{-1}$, we get the first identity. The second one can be proved similarly.
$q_x^{1/2}(T_x)^{-1}$, we get the first identity. The second one can be proved similarly.
6. Affine braid group action and categorification of stable basis
In this section we give a quick review of the affine braid group action on ![]() $D^{\operatorname {b}}_{T}(T^*\mathcal {B})$, following [Reference Bezrukavnikov and RicheBR13, Reference Bezrukavnikov, Mirković and RumyninBMR06], and then use it to define an integral lift of the stable basis
$D^{\operatorname {b}}_{T}(T^*\mathcal {B})$, following [Reference Bezrukavnikov and RicheBR13, Reference Bezrukavnikov, Mirković and RumyninBMR06], and then use it to define an integral lift of the stable basis ![]() $\{\operatorname {stab}^{+,T\mathcal {B},\nabla }_{w}\mid w\in W\}$.
$\{\operatorname {stab}^{+,T\mathcal {B},\nabla }_{w}\mid w\in W\}$.
6.1 The affine braid group
We first recall the level-![]() $p$ affine Weyl group action. In
$p$ affine Weyl group action. In ![]() $\Lambda$, we consider the level-
$\Lambda$, we consider the level-![]() $p$ configuration of
$p$ configuration of ![]() $\rho$-shifted affine hyperplanes. That is, for a coroot
$\rho$-shifted affine hyperplanes. That is, for a coroot ![]() $\alpha ^\vee$ and
$\alpha ^\vee$ and ![]() $n\in \mathbb {Z}$, let the hyperplanes
$n\in \mathbb {Z}$, let the hyperplanes ![]() $H^p_{\alpha ^\vee ,n}$ be
$H^p_{\alpha ^\vee ,n}$ be ![]() $\{\lambda \in \Lambda \mid {\langle \alpha ^\vee ,\lambda +\rho \rangle }= np\}$. The open facets are called
$\{\lambda \in \Lambda \mid {\langle \alpha ^\vee ,\lambda +\rho \rangle }= np\}$. The open facets are called ![]() $p$-alcoves, and the codimension one facets are called faces.
$p$-alcoves, and the codimension one facets are called faces.
There is a special alcove, denoted by ![]() $A_0$, which is the alcove containing
$A_0$, which is the alcove containing ![]() $(\epsilon -1)\rho$ for small
$(\epsilon -1)\rho$ for small ![]() $\epsilon >0$. It consists of those weights
$\epsilon >0$. It consists of those weights ![]() $\lambda$ such that
$\lambda$ such that ![]() $0< {\langle \lambda +\rho ,\alpha ^\vee \rangle }< p$ for all
$0< {\langle \lambda +\rho ,\alpha ^\vee \rangle }< p$ for all ![]() $\alpha \in \Phi ^+$. This alcove is referred as the fundamental alcove in [Reference Bezrukavnikov, Mirković and RumyninBMR06], which, to avoid confusion, will not be called the fundamental alcove in the present paper.
$\alpha \in \Phi ^+$. This alcove is referred as the fundamental alcove in [Reference Bezrukavnikov, Mirković and RumyninBMR06], which, to avoid confusion, will not be called the fundamental alcove in the present paper.
Let ![]() $Q$ be the root lattice. We consider the level-
$Q$ be the root lattice. We consider the level-![]() $p$ affine Weyl group. It is the usual affine Weyl group
$p$ affine Weyl group. It is the usual affine Weyl group ![]() $W_{\operatorname {aff}}:= W\ltimes Q$ as an abstract group, with a different action on the lattice
$W_{\operatorname {aff}}:= W\ltimes Q$ as an abstract group, with a different action on the lattice ![]() $\Lambda$, the level-
$\Lambda$, the level-![]() $p$ dot-action, recalled as follows. Elements in
$p$ dot-action, recalled as follows. Elements in ![]() $W$ acts via the usual dot-action
$W$ acts via the usual dot-action ![]() $w:\lambda \mapsto w\bullet \lambda :=w(\lambda +\rho )-\rho$. Elements
$w:\lambda \mapsto w\bullet \lambda :=w(\lambda +\rho )-\rho$. Elements ![]() $\nu$ in the lattice act by
$\nu$ in the lattice act by ![]() $\lambda \mapsto \lambda +p\nu$. The group
$\lambda \mapsto \lambda +p\nu$. The group ![]() $W_{\operatorname {aff}}$ is generated by reflections in affine hyperplanes
$W_{\operatorname {aff}}$ is generated by reflections in affine hyperplanes ![]() $H_{\alpha ^\vee ,n}^p$. The set of faces in the closure of
$H_{\alpha ^\vee ,n}^p$. The set of faces in the closure of ![]() $A_0$ will be denoted by
$A_0$ will be denoted by ![]() $I_{\operatorname {aff}}$. The
$I_{\operatorname {aff}}$. The ![]() $(W_{\operatorname {aff}},\bullet )$-orbits in the set of faces are canonically identified with
$(W_{\operatorname {aff}},\bullet )$-orbits in the set of faces are canonically identified with ![]() $I_{\operatorname {aff}}$. Via this identification, the (Coxeter) generators of the group
$I_{\operatorname {aff}}$. Via this identification, the (Coxeter) generators of the group ![]() $W_{\operatorname {aff}}$ can be chosen to be the reflections in the faces of the alcove
$W_{\operatorname {aff}}$ can be chosen to be the reflections in the faces of the alcove ![]() $A_0$.
$A_0$.
We will consider the extended affine Weyl group Footnote 4 ![]() $W_{\operatorname {aff}}':=W\ltimes \Lambda$. Let
$W_{\operatorname {aff}}':=W\ltimes \Lambda$. Let ![]() $\Omega$ denote the stabilizer subgroup of
$\Omega$ denote the stabilizer subgroup of ![]() $W'_{\operatorname {aff}}$ that fixes
$W'_{\operatorname {aff}}$ that fixes ![]() $A_0$. The group
$A_0$. The group ![]() $W_{\operatorname {aff}}'$ is the semi-direct product
$W_{\operatorname {aff}}'$ is the semi-direct product ![]() $\Omega \ltimes W_{\operatorname {aff}}$ [Reference CartierCar79, § 3.5(a)]. For example, for type
$\Omega \ltimes W_{\operatorname {aff}}$ [Reference CartierCar79, § 3.5(a)]. For example, for type ![]() $A_2$ root system (see Figure A.1 below) the subgroup
$A_2$ root system (see Figure A.1 below) the subgroup ![]() $\Omega$ is a cyclic group of order 3, cyclically permuting the 3 walls of the fundamental alcove. A fundamental domain of
$\Omega$ is a cyclic group of order 3, cyclically permuting the 3 walls of the fundamental alcove. A fundamental domain of ![]() $\Lambda$ can be chosen to be
$\Lambda$ can be chosen to be ![]() $(W,\bullet )$-orbit of
$(W,\bullet )$-orbit of ![]() $A_0$. This means, for any
$A_0$. This means, for any ![]() $\lambda \in \Lambda$, there exists
$\lambda \in \Lambda$, there exists ![]() $\mu \in \Lambda$ and a Weyl group element
$\mu \in \Lambda$ and a Weyl group element ![]() $w\in W,$ such that
$w\in W,$ such that ![]() $\lambda -\mu \in w\bullet A_0$.
$\lambda -\mu \in w\bullet A_0$.
Note that in the definition above, as abstract groups, ![]() $W_{\operatorname {aff}}$ and
$W_{\operatorname {aff}}$ and ![]() $W'_{\operatorname {aff}}$ do not depend on the level
$W'_{\operatorname {aff}}$ do not depend on the level ![]() $p$. When
$p$. When ![]() $p$ is equal to 1, this action is the
$p$ is equal to 1, this action is the ![]() $\rho$-shift of the action used in § 2, that is,
$\rho$-shift of the action used in § 2, that is, ![]() $H^{p=1}_{\alpha ^\vee ,n}$ is the
$H^{p=1}_{\alpha ^\vee ,n}$ is the ![]() $\rho$-shift of
$\rho$-shift of ![]() $H_{\alpha ^\vee ,n}$. In §§ 6.2 and 6.3 below, we will focus on the
$H_{\alpha ^\vee ,n}$. In §§ 6.2 and 6.3 below, we will focus on the ![]() $p=1$ case. The case when
$p=1$ case. The case when ![]() $p$ is a prime number will be relevant in § 7.
$p$ is a prime number will be relevant in § 7.
We refer the readers to [Reference LusztigLus80, § 1.1] for the local action of ![]() $W_{\operatorname {aff}}$, where for each
$W_{\operatorname {aff}}$, where for each ![]() $\alpha \in I_{\operatorname {aff}}$ and on each alcove
$\alpha \in I_{\operatorname {aff}}$ and on each alcove ![]() $s_\alpha$ acts via reflection along the wall labelled by
$s_\alpha$ acts via reflection along the wall labelled by ![]() $\alpha$. We follow [Reference Bezrukavnikov, Mirković and RumyninBMR06, § 2.1.2] to define the local action of
$\alpha$. We follow [Reference Bezrukavnikov, Mirković and RumyninBMR06, § 2.1.2] to define the local action of ![]() $W_{\operatorname {aff}}'$. This depends on the choice of a character
$W_{\operatorname {aff}}'$. This depends on the choice of a character ![]() $\lambda _0\in A_0$, so that
$\lambda _0\in A_0$, so that ![]() $W_{\operatorname {aff}}' \bullet \lambda _0$ is a free
$W_{\operatorname {aff}}' \bullet \lambda _0$ is a free ![]() $W_{\operatorname {aff}}' \bullet$-orbit. Given
$W_{\operatorname {aff}}' \bullet$-orbit. Given ![]() $v\in W'_{\operatorname {aff}}$ and
$v\in W'_{\operatorname {aff}}$ and ![]() $\lambda '=w\bullet \lambda _0\in W_{\operatorname {aff}}' \bullet \lambda _0$ with
$\lambda '=w\bullet \lambda _0\in W_{\operatorname {aff}}' \bullet \lambda _0$ with ![]() $w\in W'_{\operatorname {aff}}$, define
$w\in W'_{\operatorname {aff}}$, define ![]() $\lambda '\star v:=wv \bullet \lambda _0$. Note that
$\lambda '\star v:=wv \bullet \lambda _0$. Note that ![]() $\bullet$ is a left action of
$\bullet$ is a left action of ![]() $W_{\operatorname {aff}}'$ on
$W_{\operatorname {aff}}'$ on ![]() $\Lambda$, and
$\Lambda$, and ![]() $\star$ is a right action of
$\star$ is a right action of ![]() $W_{\operatorname {aff}}'$ only on the subset
$W_{\operatorname {aff}}'$ only on the subset ![]() $W_{\operatorname {aff}}' \bullet \lambda _0$. For
$W_{\operatorname {aff}}' \bullet \lambda _0$. For ![]() $\lambda \in W_{\operatorname {aff}}' \bullet \lambda _0$ and
$\lambda \in W_{\operatorname {aff}}' \bullet \lambda _0$ and ![]() $w\in W'_{\operatorname {aff}}$, we say
$w\in W'_{\operatorname {aff}}$, we say ![]() $w$ increases
$w$ increases ![]() $\lambda$ if the following holds. Write
$\lambda$ if the following holds. Write ![]() $w=s_1\cdots s_n \omega$, with
$w=s_1\cdots s_n \omega$, with ![]() $s_i\in I_{\operatorname {aff}}$ and
$s_i\in I_{\operatorname {aff}}$ and ![]() $\omega \in \Omega$. Then,
$\omega \in \Omega$. Then, ![]() $\lambda \star (s_1\cdots s_{i-1})<\lambda \star (s_1\cdots s_{i})$ in the standard order of
$\lambda \star (s_1\cdots s_{i-1})<\lambda \star (s_1\cdots s_{i})$ in the standard order of ![]() $\Lambda$ for any
$\Lambda$ for any ![]() $i=1,\ldots , n$ [Reference Bezrukavnikov, Mirković and RumyninBMR06, § 2.1.3].
$i=1,\ldots , n$ [Reference Bezrukavnikov, Mirković and RumyninBMR06, § 2.1.3].
Remark 6.1 (a) We note the difference between ![]() $A_0$ and
$A_0$ and ![]() $\nabla _+$. We consider the map
$\nabla _+$. We consider the map ![]() $\Lambda \to \Lambda \otimes _{{\mathbb {Z}}}\mathbb {Q}$, sending
$\Lambda \to \Lambda \otimes _{{\mathbb {Z}}}\mathbb {Q}$, sending ![]() $\lambda \in \Lambda$ to
$\lambda \in \Lambda$ to ![]() $({\lambda +\rho })/{p}$. Note that
$({\lambda +\rho })/{p}$. Note that ![]() $\lambda$ being in
$\lambda$ being in ![]() $A_0$ is equivalent to
$A_0$ is equivalent to ![]() $({\lambda +\rho })/{p}$ being in the fundamental alcove
$({\lambda +\rho })/{p}$ being in the fundamental alcove ![]() $\nabla _+$ in the present sense. In turn, this is equivalent to
$\nabla _+$ in the present sense. In turn, this is equivalent to ![]() $-({\lambda +\rho })/{p}\in \nabla _-$. Note that the map
$-({\lambda +\rho })/{p}\in \nabla _-$. Note that the map ![]() $\Lambda \to \Lambda \otimes _{{\mathbb {Z}}}\mathbb {Q}$, sending
$\Lambda \to \Lambda \otimes _{{\mathbb {Z}}}\mathbb {Q}$, sending ![]() $\lambda \in \Lambda$ to
$\lambda \in \Lambda$ to ![]() $-({\lambda +\rho })/{p}$ intertwines the natural action of
$-({\lambda +\rho })/{p}$ intertwines the natural action of ![]() $\Lambda$ on
$\Lambda$ on ![]() $\Lambda _\mathbb {Q}$ and the level-
$\Lambda _\mathbb {Q}$ and the level-![]() $p$ action of
$p$ action of ![]() $\Lambda$ on itself, composed with the abelian group automorphism
$\Lambda$ on itself, composed with the abelian group automorphism ![]() $\Lambda \to \Lambda$,
$\Lambda \to \Lambda$, ![]() $\lambda \mapsto -\lambda$.
$\lambda \mapsto -\lambda$.
(b) Moreover, we have ![]() $x(({\lambda +\rho })/{p})=({x\bullet \lambda +\rho })/{p}$ for any
$x(({\lambda +\rho })/{p})=({x\bullet \lambda +\rho })/{p}$ for any ![]() $\lambda$ and
$\lambda$ and ![]() $x\in W$.
$x\in W$.
(c) For ![]() $\lambda _0\in A_0$ and
$\lambda _0\in A_0$ and ![]() $x\in W_{\operatorname {aff}}$, with
$x\in W_{\operatorname {aff}}$, with ![]() $\lambda =\lambda _0\star x$, we have equivalently
$\lambda =\lambda _0\star x$, we have equivalently ![]() $\lambda =x\bullet \lambda _0$ and
$\lambda =x\bullet \lambda _0$ and ![]() $x^{-1}\bullet \lambda =\lambda _0$.
$x^{-1}\bullet \lambda =\lambda _0$.
To be consistent with [Reference Su, Zhao and ZhongSZZ20] and § 2, the roots of the Borel subalgebra ![]() ${\frak b}$ are positive roots
${\frak b}$ are positive roots ![]() $\Delta ^+$. Note that this is the opposite of the convention used in [Reference Bezrukavnikov, Mirković and RumyninBMR06, § 1.1.1], and hence results in an opposite lifting of the affine Weyl group into the affine braid group, as will be discussed in detail in Remark 6.3(a).
$\Delta ^+$. Note that this is the opposite of the convention used in [Reference Bezrukavnikov, Mirković and RumyninBMR06, § 1.1.1], and hence results in an opposite lifting of the affine Weyl group into the affine braid group, as will be discussed in detail in Remark 6.3(a).
Now we recall the affine braid group. The group ![]() $B_{\operatorname {aff}}$ is generated by
$B_{\operatorname {aff}}$ is generated by ![]() $\widetilde {w}$ for
$\widetilde {w}$ for ![]() $w\in W_{\operatorname {aff}}$ subject to the relation
$w\in W_{\operatorname {aff}}$ subject to the relation ![]() $\widetilde {wu}=\widetilde {w}\widetilde {u}$ when
$\widetilde {wu}=\widetilde {w}\widetilde {u}$ when ![]() $l(wu)=l(w)+l(u)$ [Reference MacDonaldMac96, § 3]. There is a set theoretical lifting
$l(wu)=l(w)+l(u)$ [Reference MacDonaldMac96, § 3]. There is a set theoretical lifting ![]() $C :W_{\operatorname {aff}}\to B_{\operatorname {aff}}$, sending the simple reflection
$C :W_{\operatorname {aff}}\to B_{\operatorname {aff}}$, sending the simple reflection ![]() $s_\alpha$ for
$s_\alpha$ for ![]() $\alpha \in I_{\operatorname {aff}}$ to
$\alpha \in I_{\operatorname {aff}}$ to ![]() $\tilde {s}_\alpha$, and any reduced decomposition
$\tilde {s}_\alpha$, and any reduced decomposition ![]() $w=s_{\alpha _1}\cdots s_{\alpha _{k}}$ to
$w=s_{\alpha _1}\cdots s_{\alpha _{k}}$ to ![]() $\widetilde {w}=\tilde {s}_{\alpha _1}\cdots \tilde {s}_{\alpha _{k}}$.
$\widetilde {w}=\tilde {s}_{\alpha _1}\cdots \tilde {s}_{\alpha _{k}}$.
On the extended affine Weyl group ![]() $W_{\operatorname {aff}}'$, the length function is given by
$W_{\operatorname {aff}}'$, the length function is given by ![]() $l(w\omega )=l(w)$ for
$l(w\omega )=l(w)$ for ![]() $\omega \in \Omega$. The extended affine Braid group
$\omega \in \Omega$. The extended affine Braid group ![]() $B_{\operatorname {aff}}'$ is generated by
$B_{\operatorname {aff}}'$ is generated by ![]() $\widetilde {w}$ for
$\widetilde {w}$ for ![]() $w\in W_{\operatorname {aff}}'$, subject to the relation
$w\in W_{\operatorname {aff}}'$, subject to the relation ![]() $\widetilde {wu}=\widetilde {w}\widetilde {u}$ when
$\widetilde {wu}=\widetilde {w}\widetilde {u}$ when ![]() $l(wu)=l(w)+l(u)$. As
$l(wu)=l(w)+l(u)$. As ![]() $\Omega$ permutes
$\Omega$ permutes ![]() $I_{\operatorname {aff}}$, we have
$I_{\operatorname {aff}}$, we have ![]() $B_{\operatorname {aff}}'=B_{\operatorname {aff}}\rtimes \Omega$. A smaller set of generators of
$B_{\operatorname {aff}}'=B_{\operatorname {aff}}\rtimes \Omega$. A smaller set of generators of ![]() $B_{\operatorname {aff}}'$ can be chosen to be
$B_{\operatorname {aff}}'$ can be chosen to be ![]() $\{\widetilde {s}_\alpha \mid \alpha \in I_{\operatorname {aff}}\}$ and
$\{\widetilde {s}_\alpha \mid \alpha \in I_{\operatorname {aff}}\}$ and ![]() $\Omega$.
$\Omega$.
The set of finite simple roots ![]() $\Sigma$ can be naturally identified with a subset of
$\Sigma$ can be naturally identified with a subset of ![]() $I_{\operatorname {aff}}$ via their corresponding simple reflections. Alternatively, the group
$I_{\operatorname {aff}}$ via their corresponding simple reflections. Alternatively, the group ![]() $B_{\operatorname {aff}}'$ is generated by simple finite reflections
$B_{\operatorname {aff}}'$ is generated by simple finite reflections ![]() $\widetilde {s}_\alpha$ for
$\widetilde {s}_\alpha$ for ![]() $\alpha \in \Sigma$ and translations
$\alpha \in \Sigma$ and translations ![]() $\Lambda ^+\subset \Lambda$ consisting of
$\Lambda ^+\subset \Lambda$ consisting of ![]() $\lambda \in \Lambda$ with
$\lambda \in \Lambda$ with ![]() $\langle \alpha ^\vee ,\lambda \rangle >0$ for all positive coroots
$\langle \alpha ^\vee ,\lambda \rangle >0$ for all positive coroots ![]() $\alpha ^\vee$.
$\alpha ^\vee$.
For any ![]() $w\in W$, let
$w\in W$, let ![]() $w=s_1\dots s_k$ be a reduced decomposition of
$w=s_1\dots s_k$ be a reduced decomposition of ![]() $w$. Then, in
$w$. Then, in ![]() $B_{\operatorname {aff}}'$ we have the element
$B_{\operatorname {aff}}'$ we have the element ![]() $\tilde {s}_1\dots \tilde {s}_k$ via
$\tilde {s}_1\dots \tilde {s}_k$ via ![]() $\Sigma \subseteq I_{\operatorname {aff}}$. This element is independent of the reduced word decomposition, hence is a well-defined lifting
$\Sigma \subseteq I_{\operatorname {aff}}$. This element is independent of the reduced word decomposition, hence is a well-defined lifting ![]() $\widetilde {w}\in B'_{\operatorname {aff}}$. Sending
$\widetilde {w}\in B'_{\operatorname {aff}}$. Sending ![]() $w\in W$ to
$w\in W$ to ![]() $\widetilde {w}$ defines a set-theoretical lifting
$\widetilde {w}$ defines a set-theoretical lifting ![]() $W\to B_{\operatorname {aff}}\subseteq B'_{\operatorname {aff}}$. Since
$W\to B_{\operatorname {aff}}\subseteq B'_{\operatorname {aff}}$. Since ![]() $w^{-1}=s_k\dots s_1$, we have
$w^{-1}=s_k\dots s_1$, we have ![]() $\widetilde {w^{-1}}=\tilde {s}_k\dots \tilde {s}_1$, which is different from
$\widetilde {w^{-1}}=\tilde {s}_k\dots \tilde {s}_1$, which is different from ![]() $(\widetilde {w})^{-1}=(\tilde {s}_k)^{-1}\dots (\tilde {s}_1)^{-1}$. On the other hand, the lifting of
$(\widetilde {w})^{-1}=(\tilde {s}_k)^{-1}\dots (\tilde {s}_1)^{-1}$. On the other hand, the lifting of ![]() $\Lambda \subseteq W'_{\operatorname {aff}}$ is a subgroup of
$\Lambda \subseteq W'_{\operatorname {aff}}$ is a subgroup of ![]() $B_{\operatorname {aff}}'$ [Reference MacDonaldMac96, § 3]. Therefore for any
$B_{\operatorname {aff}}'$ [Reference MacDonaldMac96, § 3]. Therefore for any ![]() $\lambda \in A$, we will not distinguish between the group inverse taken in
$\lambda \in A$, we will not distinguish between the group inverse taken in ![]() $\Lambda$ and the group inverse taken in
$\Lambda$ and the group inverse taken in ![]() $B_{\operatorname {aff}}'$. For this reason, we will denote the lifting of
$B_{\operatorname {aff}}'$. For this reason, we will denote the lifting of ![]() $\lambda$ still by
$\lambda$ still by ![]() $\lambda$. A similar property holds for the subgroup
$\lambda$. A similar property holds for the subgroup ![]() $\Omega \subseteq W'_{\operatorname {aff}}$.
$\Omega \subseteq W'_{\operatorname {aff}}$.
6.2 A categorical affine braid group action
Let ![]() $G_{\mathbb {Z}}$ be a split
$G_{\mathbb {Z}}$ be a split ![]() ${\mathbb {Z}}$-form of the complex algebraic group
${\mathbb {Z}}$-form of the complex algebraic group ![]() $G$. Let
$G$. Let ![]() $A_{\mathbb {Z}}\subseteq B_{\mathbb {Z}}\subseteq G_{\mathbb {Z}}$ be a maximal torus and a Borel subgroup, which we assume to have base changes
$A_{\mathbb {Z}}\subseteq B_{\mathbb {Z}}\subseteq G_{\mathbb {Z}}$ be a maximal torus and a Borel subgroup, which we assume to have base changes ![]() $A\subset B\subset G$. Let
$A\subset B\subset G$. Let ![]() ${\frak h}_{\mathbb {Z}}\subset {\frak b}_{\mathbb {Z}}\subset {\frak g}_{\mathbb {Z}}$ be the corresponding Lie algebras. Similar to the setup of § 2, we have the integral forms
${\frak h}_{\mathbb {Z}}\subset {\frak b}_{\mathbb {Z}}\subset {\frak g}_{\mathbb {Z}}$ be the corresponding Lie algebras. Similar to the setup of § 2, we have the integral forms ![]() $\mathcal {B}_{\mathbb {Z}}$ and
$\mathcal {B}_{\mathbb {Z}}$ and ![]() $T^*\mathcal {B}_{\mathbb {Z}}$, etc.
$T^*\mathcal {B}_{\mathbb {Z}}$, etc.
In [Reference Bezrukavnikov and RicheBR13], an action of the extended affine braid group on the category ![]() $D^{\operatorname {b}}_{T_{\mathbb {Z}}}(T^*\mathcal {B}_{\mathbb {Z}})$ is constructed, where elements of
$D^{\operatorname {b}}_{T_{\mathbb {Z}}}(T^*\mathcal {B}_{\mathbb {Z}})$ is constructed, where elements of ![]() $B'_{\operatorname {aff}}$ act by Fourier–Mukai transforms. Moreover, for any algebraically closed field
$B'_{\operatorname {aff}}$ act by Fourier–Mukai transforms. Moreover, for any algebraically closed field ![]() $k$, this affine braid group action can be base changed to
$k$, this affine braid group action can be base changed to ![]() $k$. More precisely, we have the following. The base change of the groups and varieties from
$k$. More precisely, we have the following. The base change of the groups and varieties from ![]() ${\mathbb {Z}}$ to
${\mathbb {Z}}$ to ![]() $k$ are denoted by
$k$ are denoted by ![]() $A_k\subseteq B_k\subseteq G_k$,
$A_k\subseteq B_k\subseteq G_k$, ![]() $T^*\mathcal {B}_k$, etc. When
$T^*\mathcal {B}_k$, etc. When ![]() $k=\mathbb {C}$, we will omit the subscripts. This is consistent with the notations introduced in § 2.
$k=\mathbb {C}$, we will omit the subscripts. This is consistent with the notations introduced in § 2.
Theorem 6.2 [Reference Bezrukavnikov and RicheBR13, Theorem 1.3.1, Proposition 1.4.3, Theorem 1.6.1]
There exists a right action of ![]() $B_{\operatorname {aff}}'$ on the category
$B_{\operatorname {aff}}'$ on the category ![]() $D^{\operatorname {b}}_{T_{\mathbb {Z}}}(T^*\mathcal {B}_{\mathbb {Z}})$, denoted by
$D^{\operatorname {b}}_{T_{\mathbb {Z}}}(T^*\mathcal {B}_{\mathbb {Z}})$, denoted by ![]() $J_b^{\mathbb {Z}}$ with
$J_b^{\mathbb {Z}}$ with ![]() $b \in B_{\operatorname {aff}}'$, such that the generator
$b \in B_{\operatorname {aff}}'$, such that the generator ![]() $J_s^{\mathbb {Z}}$ for
$J_s^{\mathbb {Z}}$ for ![]() $s\in \Sigma$ acts via a Fourier–Mukai transform with kernel the structure sheaf of a certain subvariety of
$s\in \Sigma$ acts via a Fourier–Mukai transform with kernel the structure sheaf of a certain subvariety of ![]() $T^*\mathcal {B}_{\mathbb {Z}}\times T^*\mathcal {B}_{\mathbb {Z}}$ (given explicitly in [Reference Bezrukavnikov and RicheBR13, § 1.3]), and the generator
$T^*\mathcal {B}_{\mathbb {Z}}\times T^*\mathcal {B}_{\mathbb {Z}}$ (given explicitly in [Reference Bezrukavnikov and RicheBR13, § 1.3]), and the generator ![]() $J_\lambda ^{\mathbb {Z}}$ for
$J_\lambda ^{\mathbb {Z}}$ for ![]() $\lambda \in \Lambda$ acts via tensoring by the line bundle
$\lambda \in \Lambda$ acts via tensoring by the line bundle ![]() $\mathcal {L}_\lambda$.
$\mathcal {L}_\lambda$.
Similarly, for any algebraically closed field ![]() $k$, applying
$k$, applying ![]() $\_\otimes ^L_{\mathbb {Z}} k$ to the action above, we have a right action of
$\_\otimes ^L_{\mathbb {Z}} k$ to the action above, we have a right action of ![]() $B_{\operatorname {aff}}'$ on the category
$B_{\operatorname {aff}}'$ on the category ![]() $D^{\operatorname {b}}_{T_k}(T^*\mathcal {B}_k)$, denoted by
$D^{\operatorname {b}}_{T_k}(T^*\mathcal {B}_k)$, denoted by ![]() $J^k_b$ with
$J^k_b$ with ![]() $b\in B_{\operatorname {aff}}'$, such that the generator
$b\in B_{\operatorname {aff}}'$, such that the generator ![]() $J_s^k$ for
$J_s^k$ for ![]() $s\in \Sigma$ acts via a Fourier–Mukai transform with kernel the structure sheaf of certain subvariety of
$s\in \Sigma$ acts via a Fourier–Mukai transform with kernel the structure sheaf of certain subvariety of ![]() $T^*\mathcal {B}_k\times T^*\mathcal {B}_k$, and the generator
$T^*\mathcal {B}_k\times T^*\mathcal {B}_k$, and the generator ![]() $J_\lambda ^k$ for
$J_\lambda ^k$ for ![]() $\lambda \in \Lambda$ acts via tensoring by the line bundle
$\lambda \in \Lambda$ acts via tensoring by the line bundle ![]() $\mathcal {L}_\lambda$.
$\mathcal {L}_\lambda$.
Remark 6.3 (a) Using the local affine Weyl group action, the order on ![]() $\Lambda$, which is determined by a choice of a dominant dual Weyl chamber
$\Lambda$, which is determined by a choice of a dominant dual Weyl chamber ![]() $\Lambda ^+$, identifies the abstractly defined
$\Lambda ^+$, identifies the abstractly defined ![]() $B_{\operatorname {aff}}$ above with the topologically defined
$B_{\operatorname {aff}}$ above with the topologically defined ![]() $\pi _1({\frak h}^*_{\mathbb {C},\textit {reg}}/(W_{\operatorname {aff}},\bullet ))$. Then the lifting
$\pi _1({\frak h}^*_{\mathbb {C},\textit {reg}}/(W_{\operatorname {aff}},\bullet ))$. Then the lifting ![]() $C:W_{\operatorname {aff}}\to B_{\operatorname {aff}}$ here is characterized as the set of positive paths going from any alcove to an alcove above it in the natural order [Reference Bezrukavnikov and MirkovićBM13, Lemma 1.8.1(c)].
$C:W_{\operatorname {aff}}\to B_{\operatorname {aff}}$ here is characterized as the set of positive paths going from any alcove to an alcove above it in the natural order [Reference Bezrukavnikov and MirkovićBM13, Lemma 1.8.1(c)].
As mentioned above, the choice of positive roots in the present paper is opposite to that in [Reference Bezrukavnikov, Mirković and RumyninBMR06, Reference Bezrukavnikov and RicheBR13], and hence the anti-dominant chamber ![]() $-\Lambda ^+$ in our setting consists of ample line bundles. Consequently, the order on
$-\Lambda ^+$ in our setting consists of ample line bundles. Consequently, the order on ![]() $\Lambda$ considered here is opposite to that of [Reference Bezrukavnikov, Mirković and RumyninBMR06, Reference Bezrukavnikov and RicheBR13]. For comparison, denote the order of [Reference Bezrukavnikov, Mirković and RumyninBMR06, Reference Bezrukavnikov and RicheBR13] by
$\Lambda$ considered here is opposite to that of [Reference Bezrukavnikov, Mirković and RumyninBMR06, Reference Bezrukavnikov and RicheBR13]. For comparison, denote the order of [Reference Bezrukavnikov, Mirković and RumyninBMR06, Reference Bezrukavnikov and RicheBR13] by ![]() $>^{BMR}$. Then, for any
$>^{BMR}$. Then, for any ![]() $s\in I_{\operatorname {aff}}$,
$s\in I_{\operatorname {aff}}$, ![]() $\lambda \star s>\lambda$ is equivalent to
$\lambda \star s>\lambda$ is equivalent to ![]() $\lambda \star s<^{BMR}\lambda \star s\star s=\lambda$. Taking the corresponding lifting of
$\lambda \star s<^{BMR}\lambda \star s\star s=\lambda$. Taking the corresponding lifting of ![]() $s$ to
$s$ to ![]() $B_{\operatorname {aff}}'$, which is denoted by
$B_{\operatorname {aff}}'$, which is denoted by ![]() $\tilde {s}$ in the present notation, we have that the lifting taken in [Reference Bezrukavnikov, Mirković and RumyninBMR06, Reference Bezrukavnikov and RicheBR13] is
$\tilde {s}$ in the present notation, we have that the lifting taken in [Reference Bezrukavnikov, Mirković and RumyninBMR06, Reference Bezrukavnikov and RicheBR13] is ![]() $(\widetilde s)^{-1}$.
$(\widetilde s)^{-1}$.
(b) The action of ![]() $B_{\operatorname {aff}}$ in [Reference Bezrukavnikov and RicheBR13] is a left action. As we will not be considering any left actions in this section, we use [Reference Bezrukavnikov and RicheBR13, Remark 2.5.2] and the paragraph after [Reference Bezrukavnikov and RicheBR13, Corollary 2.5.3] to translate the left action therein to a right action. The effect coincides with taking the opposite lifting as in part (a) above. Therefore, when
$B_{\operatorname {aff}}$ in [Reference Bezrukavnikov and RicheBR13] is a left action. As we will not be considering any left actions in this section, we use [Reference Bezrukavnikov and RicheBR13, Remark 2.5.2] and the paragraph after [Reference Bezrukavnikov and RicheBR13, Corollary 2.5.3] to translate the left action therein to a right action. The effect coincides with taking the opposite lifting as in part (a) above. Therefore, when ![]() $k=\mathbb {C}$, taking the Grothendieck group, the above actions of the generators
$k=\mathbb {C}$, taking the Grothendieck group, the above actions of the generators ![]() $J_{\widetilde {s}_\alpha }$ and
$J_{\widetilde {s}_\alpha }$ and ![]() $J_\lambda$ for
$J_\lambda$ for ![]() $\alpha \in \Sigma$ and
$\alpha \in \Sigma$ and ![]() $\lambda \in \Lambda$ of
$\lambda \in \Lambda$ of ![]() $B'_{\operatorname {aff}}$ on
$B'_{\operatorname {aff}}$ on ![]() $K_T(T^*\mathcal {B})$ from Theorem 6.2 are equal to the operators
$K_T(T^*\mathcal {B})$ from Theorem 6.2 are equal to the operators ![]() $q^{-1/2}T^{\operatorname {R}}_\alpha$ and
$q^{-1/2}T^{\operatorname {R}}_\alpha$ and ![]() $\mathcal {L}_\lambda$ in § 2.3, respectively. In particular, the action factors through the action of the affine Hecke algebra
$\mathcal {L}_\lambda$ in § 2.3, respectively. In particular, the action factors through the action of the affine Hecke algebra ![]() ${\mathbb {H}}$ considered in § 2.
${\mathbb {H}}$ considered in § 2.
(c) To remind ourselves that this is a right action, and also to be consistent with the notations in § 2, we will also write the operator ![]() $J_b$ as
$J_b$ as ![]() $J_b^{\operatorname {R}}$. By our convention of a right action, for any
$J_b^{\operatorname {R}}$. By our convention of a right action, for any ![]() $w\in W$, via the lifting
$w\in W$, via the lifting ![]() $W\to B_{\operatorname {aff}}$, we have
$W\to B_{\operatorname {aff}}$, we have ![]() $J^{\operatorname {R}}_{\widetilde {w}}=J^{\operatorname {R}}_{\tilde {s}_k}\circ \cdots \circ J^{\operatorname {R}}_{\tilde {s}_1}$ if
$J^{\operatorname {R}}_{\widetilde {w}}=J^{\operatorname {R}}_{\tilde {s}_k}\circ \cdots \circ J^{\operatorname {R}}_{\tilde {s}_1}$ if ![]() $w=s_1\dots s_k$ is a reduced decomposition of
$w=s_1\dots s_k$ is a reduced decomposition of ![]() $w$.
$w$.
6.3 Integral form of stable bases
Now we define the objects ![]() ${\frak s}{\frak t}{\frak a}{\frak b}^{\mathbb {Z}}_{\lambda }(y)\in D^{\operatorname {b}}_{T_{\mathbb {Z}}}(T^*\mathcal {B}_{\mathbb {Z}}), y\in W, \lambda \in \Lambda _\mathbb {Q}$ in the interior of an alcove, inductively as follows:
${\frak s}{\frak t}{\frak a}{\frak b}^{\mathbb {Z}}_{\lambda }(y)\in D^{\operatorname {b}}_{T_{\mathbb {Z}}}(T^*\mathcal {B}_{\mathbb {Z}}), y\in W, \lambda \in \Lambda _\mathbb {Q}$ in the interior of an alcove, inductively as follows:
According to 6.2, the functor ![]() $J^{\operatorname {R}}_{\mu }$ in (28) is twisting by
$J^{\operatorname {R}}_{\mu }$ in (28) is twisting by ![]() $\mathcal {L}_\mu$. From the definitions,
$\mathcal {L}_\mu$. From the definitions, ![]() ${\frak s}{\frak t}{\frak a}{\frak b}^{\mathbb {Z}}_{\lambda }(y)$ only depends on the alcove
${\frak s}{\frak t}{\frak a}{\frak b}^{\mathbb {Z}}_{\lambda }(y)$ only depends on the alcove ![]() $\nabla$ containing
$\nabla$ containing ![]() $\lambda$, so sometimes it is also denoted by
$\lambda$, so sometimes it is also denoted by ![]() ${\frak s}{\frak t}{\frak a}{\frak b}^{\mathbb {Z}}_{\nabla }(y)$.
${\frak s}{\frak t}{\frak a}{\frak b}^{\mathbb {Z}}_{\nabla }(y)$.
Now we are ready to state the main result of this section.
Theorem 6.4 Applying ![]() $-\otimes ^L_{{\mathbb {Z}}}\mathbb {C}$ to
$-\otimes ^L_{{\mathbb {Z}}}\mathbb {C}$ to ![]() ${\frak s}{\frak t}{\frak a}{\frak b}^{\mathbb {Z}}_{\nabla }(w)\in D^{\operatorname {b}}_{T_{\mathbb {Z}}}(T^*\mathcal {B}_{\mathbb {Z}})$, and taking the class in the Grothendieck group, we get
${\frak s}{\frak t}{\frak a}{\frak b}^{\mathbb {Z}}_{\nabla }(w)\in D^{\operatorname {b}}_{T_{\mathbb {Z}}}(T^*\mathcal {B}_{\mathbb {Z}})$, and taking the class in the Grothendieck group, we get ![]() $\mathcal {L}_{-\rho }\otimes \operatorname {stab}^{+,T\mathcal {B},\nabla }_w\in K_T(T^*\mathcal {B})$.
$\mathcal {L}_{-\rho }\otimes \operatorname {stab}^{+,T\mathcal {B},\nabla }_w\in K_T(T^*\mathcal {B})$.
Proof. We need to verify (25)–(28) inductively. The first equation is a direct consequence of (6). Keeping in mind Theorem 6.2 and the relations ![]() $[J_{\widetilde {s}_\alpha }^\mathbb {C}]=q^{-1/2}T^{\operatorname {R}}_\alpha$ and
$[J_{\widetilde {s}_\alpha }^\mathbb {C}]=q^{-1/2}T^{\operatorname {R}}_\alpha$ and ![]() $T^{\operatorname {R}}_\alpha =\mathcal {L}_{-\rho }T'_\alpha \mathcal {L}_{\rho }$, then the second equation follows directly from Theorem 2.5. The third one follows from Theorem 5.4, and the last one follows from (15).
$T^{\operatorname {R}}_\alpha =\mathcal {L}_{-\rho }T'_\alpha \mathcal {L}_{\rho }$, then the second equation follows directly from Theorem 2.5. The third one follows from Theorem 5.4, and the last one follows from (15).
7. Verma modules in prime characteristic
In this section, we prove that, when base changed to a field ![]() $k$ of positive characteristic, the integral form of stable basis defined in § 6.3 agrees with the Verma modules of
$k$ of positive characteristic, the integral form of stable basis defined in § 6.3 agrees with the Verma modules of ![]() $U({\frak g}_k)$ under the localization equivalence of [Reference Bezrukavnikov and MirkovićBM13, Reference Bezrukavnikov, Mirković and RumyninBMR08].
$U({\frak g}_k)$ under the localization equivalence of [Reference Bezrukavnikov and MirkovićBM13, Reference Bezrukavnikov, Mirković and RumyninBMR08].
7.1 Reminder on localization in prime characteristic
We start by a brief review of [Reference Bezrukavnikov, Mirković and RumyninBMR08]. Now we assume ![]() $k$ is an algebraically closed field of characteristic
$k$ is an algebraically closed field of characteristic ![]() $p$ greater than the Coxeter number of
$p$ greater than the Coxeter number of ![]() $G$. For any
$G$. For any ![]() $k$-variety
$k$-variety ![]() $X$, its Frobenius twist is denoted by
$X$, its Frobenius twist is denoted by ![]() $X^{(1)}$. If
$X^{(1)}$. If ![]() $X$ is defined over
$X$ is defined over ![]() ${\mathbb {F}}_p$, then
${\mathbb {F}}_p$, then ![]() $X^{(1)}\cong X$ as abstract
$X^{(1)}\cong X$ as abstract ![]() $k$-varieties. However, the natural map
$k$-varieties. However, the natural map ![]() $X\to X^{(1)}$ is not an isomorphism. Below we will take
$X\to X^{(1)}$ is not an isomorphism. Below we will take ![]() $X$ to be
$X$ to be ![]() $\mathcal {B}_k$,
$\mathcal {B}_k$, ![]() $T^*\mathcal {B}_k$, etc. We will often omit the subscript
$T^*\mathcal {B}_k$, etc. We will often omit the subscript ![]() $k$, when there is a Frobenius twist. For example,
$k$, when there is a Frobenius twist. For example, ![]() ${\mathcal {B}_k}^{(1)}$ will be simply denoted by
${\mathcal {B}_k}^{(1)}$ will be simply denoted by ![]() $\mathcal {B}^{(1)}$.
$\mathcal {B}^{(1)}$.
Differentiating a character of ![]() $A_k$ defines a map
$A_k$ defines a map ![]() $d:\Lambda \to {\frak h}_k^*$. We call a character
$d:\Lambda \to {\frak h}_k^*$. We call a character ![]() $\lambda \in {\frak h}^*_k$ integral if it lies in the image of
$\lambda \in {\frak h}^*_k$ integral if it lies in the image of ![]() $d:\Lambda \to {\frak h}^*_k$. An integral character is said to be regular if it does not lie on any walls
$d:\Lambda \to {\frak h}^*_k$. An integral character is said to be regular if it does not lie on any walls ![]() $H^p_{\alpha ^\vee ,n}$. For
$H^p_{\alpha ^\vee ,n}$. For ![]() $\lambda \in \Lambda$, on the flag variety
$\lambda \in \Lambda$, on the flag variety ![]() $\mathcal {B}_k$, consider the ring of
$\mathcal {B}_k$, consider the ring of ![]() $\mathcal {L}_\lambda$-twisted differential operators
$\mathcal {L}_\lambda$-twisted differential operators ![]() $\mathcal {D}^\lambda$, which is a sheaf of algebras. Its central subalgebra, i.e. the sheaf of functions on
$\mathcal {D}^\lambda$, which is a sheaf of algebras. Its central subalgebra, i.e. the sheaf of functions on ![]() $T^*\mathcal {B}^{(1)}$, makes any coherent
$T^*\mathcal {B}^{(1)}$, makes any coherent ![]() $\mathcal {D}^\lambda$-module naturally a coherent sheaf on
$\mathcal {D}^\lambda$-module naturally a coherent sheaf on ![]() $T^*\mathcal {B}^{(1)}$, and moreover,
$T^*\mathcal {B}^{(1)}$, and moreover, ![]() $\mathcal {D}^\lambda$ is an Azumaya algebra on
$\mathcal {D}^\lambda$ is an Azumaya algebra on ![]() $T^*\mathcal {B}^{(1)}_k$ [Reference Bezrukavnikov, Mirković and RumyninBMR08, § 2.3].
$T^*\mathcal {B}^{(1)}_k$ [Reference Bezrukavnikov, Mirković and RumyninBMR08, § 2.3].
There exists a vector bundle ![]() $\mathcal {E}^s$ with the following properties.
$\mathcal {E}^s$ with the following properties.
(1)
 $\mathcal {E} nd_{T^*\mathcal {B}^{(1)\wedge }}(\mathcal {E}^s)\cong \mathcal {D}^{\lambda _0}|_{T^*\mathcal {B}^{(1)\wedge }}$, where
$\mathcal {E} nd_{T^*\mathcal {B}^{(1)\wedge }}(\mathcal {E}^s)\cong \mathcal {D}^{\lambda _0}|_{T^*\mathcal {B}^{(1)\wedge }}$, where  $T^*\mathcal {B}^{(1)\wedge }$ is the formal neighbourhood of the zero-section
$T^*\mathcal {B}^{(1)\wedge }$ is the formal neighbourhood of the zero-section  $\mathcal {B}^{(1)}$. That is, the Azumaya algebra
$\mathcal {B}^{(1)}$. That is, the Azumaya algebra  $\mathcal {D}^{\lambda _0}$ splits on this formal neighbourhood [Reference Bezrukavnikov, Mirković and RumyninBMR08, Theorem 5.1.1].
$\mathcal {D}^{\lambda _0}$ splits on this formal neighbourhood [Reference Bezrukavnikov, Mirković and RumyninBMR08, Theorem 5.1.1].(2)
 $\mathcal {E}^s$ is
$\mathcal {E}^s$ is  $T_k$-equivariant [Reference Bezrukavnikov and MirkovićBM13, § 5.2.4], where
$T_k$-equivariant [Reference Bezrukavnikov and MirkovićBM13, § 5.2.4], where  $T_k=A_k\times k^*.$
$T_k=A_k\times k^*.$(3) Define
 $\mathcal {A}^{\lambda _0}$ to be
$\mathcal {A}^{\lambda _0}$ to be  $End_{T^*\mathcal {B}^{(1)}}(\mathcal {E}^s)$, a
$End_{T^*\mathcal {B}^{(1)}}(\mathcal {E}^s)$, a  $\mathcal {O}({\mathcal {N}^{(1)}})$-algebra endowed with a compatible
$\mathcal {O}({\mathcal {N}^{(1)}})$-algebra endowed with a compatible  $A_k\times (\mathbb {G}_m)_k$-action. Then there exists a localization functor
$A_k\times (\mathbb {G}_m)_k$-action. Then there exists a localization functor  $\gamma ^{\lambda _0}: D^{\operatorname {b}}\operatorname {Mod}^{\operatorname {gr}}(\mathcal {A}^{\lambda _0},A_k)\cong D^{\operatorname {b}}_{T_k}\operatorname {Coh}(T^*\mathcal {B}^{(1)}_k)$ [Reference Bezrukavnikov and MirkovićBM13, Theorem 5.1.1].Footnote 5
$\gamma ^{\lambda _0}: D^{\operatorname {b}}\operatorname {Mod}^{\operatorname {gr}}(\mathcal {A}^{\lambda _0},A_k)\cong D^{\operatorname {b}}_{T_k}\operatorname {Coh}(T^*\mathcal {B}^{(1)}_k)$ [Reference Bezrukavnikov and MirkovićBM13, Theorem 5.1.1].Footnote 5(4) The completion
 $(\mathcal {A}^{\lambda _0})^\wedge _0$ is related to the Lie algebra
$(\mathcal {A}^{\lambda _0})^\wedge _0$ is related to the Lie algebra  ${\frak g}_k$ (see (29) below).
${\frak g}_k$ (see (29) below).
The algebra ![]() $U({\frak g}_k)$ has two central subalgebras: the Frobenius center, which is naturally identified with
$U({\frak g}_k)$ has two central subalgebras: the Frobenius center, which is naturally identified with ![]() $\mathcal {O}({\frak g}^{*(1)})$; and the Harish-Chandra center, which is identified with
$\mathcal {O}({\frak g}^{*(1)})$; and the Harish-Chandra center, which is identified with ![]() $\mathcal {O}({\frak h}^*_k/(W,\bullet ))$ under the choice of the Borel subgroup
$\mathcal {O}({\frak h}^*_k/(W,\bullet ))$ under the choice of the Borel subgroup ![]() $B_k$ and the maximal torus
$B_k$ and the maximal torus ![]() $A_k$. A point
$A_k$. A point ![]() $W\bullet d\lambda \in {\frak h}_k^*/(W,\bullet )$ defines a maximal ideal in
$W\bullet d\lambda \in {\frak h}_k^*/(W,\bullet )$ defines a maximal ideal in ![]() $\mathcal {O}({\frak h}^*_k/(W,\bullet ))$, which is a central subalgebra of
$\mathcal {O}({\frak h}^*_k/(W,\bullet ))$, which is a central subalgebra of ![]() $U({\frak g}_k)$. The quotient of
$U({\frak g}_k)$. The quotient of ![]() $U({\frak g}_k)$ by the central ideal is denote by
$U({\frak g}_k)$ by the central ideal is denote by ![]() $U({\frak g}_k)^\lambda$, that is
$U({\frak g}_k)^\lambda$, that is ![]() $U({\frak g}_k)^\lambda :=U({\frak g}_k)\otimes _{\mathcal {O}({\frak h}^*_k/(W,\bullet ))}k_\lambda$. Similarly
$U({\frak g}_k)^\lambda :=U({\frak g}_k)\otimes _{\mathcal {O}({\frak h}^*_k/(W,\bullet ))}k_\lambda$. Similarly ![]() $\chi \in \mathcal {N}^{(1)}$ defines a central ideal, and the completion of
$\chi \in \mathcal {N}^{(1)}$ defines a central ideal, and the completion of ![]() $U({\frak g}_k)^{\lambda _0}$ at this ideal is denoted by
$U({\frak g}_k)^{\lambda _0}$ at this ideal is denoted by ![]() $U({\frak g}_k)^{\lambda _0}_\chi$. Then
$U({\frak g}_k)^{\lambda _0}_\chi$. Then
The vector bundle ![]() $\mathcal {E}^s$ above is not unique. Different choices are related by
$\mathcal {E}^s$ above is not unique. Different choices are related by ![]() $\mathcal {D}^\lambda$ [Reference Bezrukavnikov, Mirković and RumyninBMR08, Remark 5.2.2]. Nevertheless, as has been done in [Reference Bezrukavnikov and RicheBR13, Reference Bezrukavnikov and MirkovićBM13], the property (30) below about baby Verma modules fixes the choice [Reference Bezrukavnikov, Mirković and RumyninBMR06, Remark 1.3.5].
$\mathcal {D}^\lambda$ [Reference Bezrukavnikov, Mirković and RumyninBMR08, Remark 5.2.2]. Nevertheless, as has been done in [Reference Bezrukavnikov and RicheBR13, Reference Bezrukavnikov and MirkovićBM13], the property (30) below about baby Verma modules fixes the choice [Reference Bezrukavnikov, Mirković and RumyninBMR06, Remark 1.3.5].
For the Borel subalgebra ![]() ${\frak b}_k$ and for any
${\frak b}_k$ and for any ![]() $\chi \in \mathcal {N}^{(1)}$ and
$\chi \in \mathcal {N}^{(1)}$ and ![]() $\lambda \in \Lambda$, consider the
$\lambda \in \Lambda$, consider the ![]() $U({\frak b}_k)$-character
$U({\frak b}_k)$-character ![]() $k_\lambda$ obtained via the projection
$k_\lambda$ obtained via the projection ![]() ${\frak b}\to {\frak h}$ composing with the
${\frak b}\to {\frak h}$ composing with the ![]() ${\frak h}$-character
${\frak h}$-character ![]() $k_\lambda$. Recall that the Verma module of
$k_\lambda$. Recall that the Verma module of ![]() $U({\frak g}_k)$ associated to the Borel
$U({\frak g}_k)$ associated to the Borel ![]() ${\frak b}$ and
${\frak b}$ and ![]() $\lambda \in \Lambda$ is
$\lambda \in \Lambda$ is ![]() $Z^{{\frak b}}(\lambda ):=U({\frak g}_k)\otimes _{U({\frak b}_k)}k_\lambda$, and the baby Verma module is
$Z^{{\frak b}}(\lambda ):=U({\frak g}_k)\otimes _{U({\frak b}_k)}k_\lambda$, and the baby Verma module is ![]() $Z^{{\frak b}}_\chi (\lambda ):=U_\chi ({\frak g}_k)\otimes _{U({\frak b}_k)}k_{\lambda }$, where
$Z^{{\frak b}}_\chi (\lambda ):=U_\chi ({\frak g}_k)\otimes _{U({\frak b}_k)}k_{\lambda }$, where ![]() $U_\chi ({\frak g}_k)$ is the quotient of
$U_\chi ({\frak g}_k)$ is the quotient of ![]() $U({\frak g}_k)$ by the central ideal
$U({\frak g}_k)$ by the central ideal ![]() $\chi \in \mathcal {N}^{(1)}\subseteq {\frak g}^{*(1)}$.
$\chi \in \mathcal {N}^{(1)}\subseteq {\frak g}^{*(1)}$.
Recall that under the identification ![]() $\mathcal {B}_k\cong G_k/B_k$, the
$\mathcal {B}_k\cong G_k/B_k$, the ![]() $T_k$-fixed points on
$T_k$-fixed points on ![]() $T^*\mathcal {B}^{(1)}$ are identified with the Weyl group elements, with
$T^*\mathcal {B}^{(1)}$ are identified with the Weyl group elements, with ![]() $B_k$ corresponding to
$B_k$ corresponding to ![]() $id$, whose skyscraper sheaf is denoted by
$id$, whose skyscraper sheaf is denoted by ![]() $k_{id}$. Then [Reference Bezrukavnikov, Mirković and RumyninBMR08, Example 5.3.3.(0)]
$k_{id}$. Then [Reference Bezrukavnikov, Mirković and RumyninBMR08, Example 5.3.3.(0)]
The isomorphism (29) defines a ![]() $T_k$-action on
$T_k$-action on ![]() $U({\frak g}_k)^{\lambda _0}_0$ making it an equivariant isomorphism. Taking completion of
$U({\frak g}_k)^{\lambda _0}_0$ making it an equivariant isomorphism. Taking completion of ![]() $Z^{{\frak b}}(\lambda _0+2\rho )$ with respect to the maximal ideal
$Z^{{\frak b}}(\lambda _0+2\rho )$ with respect to the maximal ideal ![]() $W\bullet d\lambda \in {\frak h}_k^*/(W,\bullet )$ of the central subalgebra
$W\bullet d\lambda \in {\frak h}_k^*/(W,\bullet )$ of the central subalgebra ![]() $\mathcal {O}({\frak h}_k^*/(W,\bullet ))$ defines a module over
$\mathcal {O}({\frak h}_k^*/(W,\bullet ))$ defines a module over ![]() $U({\frak g}_k)^{\lambda _0}_0$. The
$U({\frak g}_k)^{\lambda _0}_0$. The ![]() $T_k$-action on
$T_k$-action on ![]() $U({\frak g}_k)^{\lambda _0}_0$ provides
$U({\frak g}_k)^{\lambda _0}_0$ provides ![]() $T_k$-actions on
$T_k$-actions on ![]() $Z_0^{{\frak b}}(\lambda _0+2\rho )$ and
$Z_0^{{\frak b}}(\lambda _0+2\rho )$ and ![]() $Z^{{\frak b}}(\lambda _0+2\rho )$, making (30) equivariant. Taking
$Z^{{\frak b}}(\lambda _0+2\rho )$, making (30) equivariant. Taking ![]() $\mathbb {G}_m$-finite vectors in
$\mathbb {G}_m$-finite vectors in ![]() $Z^{{\frak b}}(\lambda _0+2\rho )$, we get an
$Z^{{\frak b}}(\lambda _0+2\rho )$, we get an ![]() $A_k$-Koszul graded module of
$A_k$-Koszul graded module of ![]() $\mathcal {A}^{\lambda _0}$, which, without causing confusions, will still be denoted by
$\mathcal {A}^{\lambda _0}$, which, without causing confusions, will still be denoted by ![]() $Z^{{\frak b}}(\lambda _0+2\rho )$. Then, under the equivalence in property (3) of § 7.1 above, we have the isomorphism
$Z^{{\frak b}}(\lambda _0+2\rho )$. Then, under the equivalence in property (3) of § 7.1 above, we have the isomorphism
7.2 Localization and the affine braid group action
We collect a few preliminary results, which are direct consequences of [Reference Bezrukavnikov, Mirković and RumyninBMR06] reviewed above. Let us consider the category ![]() $\operatorname {Mod}_0 U({\frak g}_k)^\lambda$ of finitely generated modules of
$\operatorname {Mod}_0 U({\frak g}_k)^\lambda$ of finitely generated modules of ![]() $U({\frak g}_k)^\lambda$ on which the Frobenius center
$U({\frak g}_k)^\lambda$ on which the Frobenius center ![]() $\mathcal {O}({\frak g}^{*(1)})$ acts by the generalized character
$\mathcal {O}({\frak g}^{*(1)})$ acts by the generalized character ![]() $0\in {\frak g}^{*(1)}$. For
$0\in {\frak g}^{*(1)}$. For ![]() $\lambda$,
$\lambda$, ![]() $\mu \in \Lambda$, we define
$\mu \in \Lambda$, we define ![]() $T_\lambda ^\mu :\operatorname {Mod}_0 U({\frak g}_k)^\lambda \to \operatorname {Mod}_0 U({\frak g}_k)^\mu$ sending
$T_\lambda ^\mu :\operatorname {Mod}_0 U({\frak g}_k)^\lambda \to \operatorname {Mod}_0 U({\frak g}_k)^\mu$ sending ![]() $M$ to
$M$ to ![]() $[V_{\mu -\lambda }\otimes M]_\mu$. Here
$[V_{\mu -\lambda }\otimes M]_\mu$. Here ![]() $V_{\mu -\lambda }$ is a finite-dimensional representation with extremal weight
$V_{\mu -\lambda }$ is a finite-dimensional representation with extremal weight ![]() $\mu -\lambda$, and
$\mu -\lambda$, and ![]() $[-]_\mu$ means taking the component supported on the point
$[-]_\mu$ means taking the component supported on the point ![]() $\mu$ in
$\mu$ in ![]() ${\frak h}^*//W$. Assume
${\frak h}^*//W$. Assume ![]() $\nu$ lies in a codimension-
$\nu$ lies in a codimension-![]() $1$ wall of the facet of the alcove containing
$1$ wall of the facet of the alcove containing ![]() $\mu$. Define
$\mu$. Define
Indeed, ![]() $R_{\mu |\nu }$ depends only on the wall, not the character
$R_{\mu |\nu }$ depends only on the wall, not the character ![]() $\nu$ itself. Taking mapping cone of the adjunction, we define
$\nu$ itself. Taking mapping cone of the adjunction, we define
When ![]() $\mu$ is in the alcove
$\mu$ is in the alcove ![]() $A_0$, then the wall on which
$A_0$, then the wall on which ![]() $\nu$ lies is labelled by some
$\nu$ lies is labelled by some ![]() $\alpha \in I_{\operatorname {aff}}$, therefore we will also denote
$\alpha \in I_{\operatorname {aff}}$, therefore we will also denote ![]() $\Theta _{\mu |\nu }$ by
$\Theta _{\mu |\nu }$ by ![]() $\Theta _\alpha$ in this case. For
$\Theta _\alpha$ in this case. For ![]() $\omega \in \Omega$, we write
$\omega \in \Omega$, we write ![]() $T_{\lambda _0}^{\lambda _0\star \omega }:\operatorname {Mod}_0 U({\frak g}_k)^{\lambda _0}\to \operatorname {Mod}_0 U({\frak g}_k)^{\lambda _0}$ simply as
$T_{\lambda _0}^{\lambda _0\star \omega }:\operatorname {Mod}_0 U({\frak g}_k)^{\lambda _0}\to \operatorname {Mod}_0 U({\frak g}_k)^{\lambda _0}$ simply as ![]() $\Theta _{\omega }$. Note that this is possible due to the fact that
$\Theta _{\omega }$. Note that this is possible due to the fact that ![]() $\lambda _0$ and
$\lambda _0$ and ![]() $\lambda _0\star \omega$ have the same central character in
$\lambda _0\star \omega$ have the same central character in ![]() ${\frak h}^*_k/(W,\bullet )$.
${\frak h}^*_k/(W,\bullet )$.
Remark 7.1 For ![]() $\alpha \in I_{\operatorname {aff}}$, the functor
$\alpha \in I_{\operatorname {aff}}$, the functor ![]() $\Theta _\alpha$ is the same as that in [Reference Bezrukavnikov, Mirković and RumyninBMR06], and is equal to
$\Theta _\alpha$ is the same as that in [Reference Bezrukavnikov, Mirković and RumyninBMR06], and is equal to ![]() $\mathbf {I}_{\alpha }^{-1}$ in [Reference Bezrukavnikov and RicheBR13]. Similarly, for
$\mathbf {I}_{\alpha }^{-1}$ in [Reference Bezrukavnikov and RicheBR13]. Similarly, for ![]() $\omega \in \Omega$,
$\omega \in \Omega$, ![]() $\Theta _\omega$ in the present paper is
$\Theta _\omega$ in the present paper is ![]() ${\mathbf {I}}_{\omega ^{-1}}$ in [Reference Bezrukavnikov and RicheBR13]. This inversion is also noticed in [Reference Bezrukavnikov and RicheBR13, Remark 2.5.2]. In the present paper, we adopt the notation from [Reference Bezrukavnikov, Mirković and RumyninBMR06] so as to consider right actions throughout. This is consistent with Remark 6.3.
${\mathbf {I}}_{\omega ^{-1}}$ in [Reference Bezrukavnikov and RicheBR13]. This inversion is also noticed in [Reference Bezrukavnikov and RicheBR13, Remark 2.5.2]. In the present paper, we adopt the notation from [Reference Bezrukavnikov, Mirković and RumyninBMR06] so as to consider right actions throughout. This is consistent with Remark 6.3.
The following is essentially [Reference Bezrukavnikov, Mirković and RumyninBMR06, Theorem 2.1.4] and [Reference Bezrukavnikov and RicheBR13, Theorem 2.5.4], taking into account the correction in [Reference Bezrukavnikov and RicheBR13, Remark 2.5.2] and the translation between the left and right actions in Remark 6.3.
Theorem 7.2 Let ![]() $\lambda _0$ be in the alcove
$\lambda _0$ be in the alcove ![]() $A_0$.
$A_0$.
(i) The functors
 $\Theta _\alpha$ for
$\Theta _\alpha$ for  $\alpha \in I_{\operatorname {aff}}$ and
$\alpha \in I_{\operatorname {aff}}$ and  $R_\omega$ for
$R_\omega$ for  $\omega \in \Omega$ induce right actions of the group
$\omega \in \Omega$ induce right actions of the group  $B_{\operatorname {aff}}'$ on the categories
$B_{\operatorname {aff}}'$ on the categories  $D^{\operatorname {b}}\operatorname {Mod}_{0}U({\frak g}_k)^{\lambda _0}$,
$D^{\operatorname {b}}\operatorname {Mod}_{0}U({\frak g}_k)^{\lambda _0}$,  $D^{\operatorname {b}}\operatorname {Mod}_0^{\operatorname {gr}}(U({\frak g}_k)^{\lambda _0},A_k)$,
$D^{\operatorname {b}}\operatorname {Mod}_0^{\operatorname {gr}}(U({\frak g}_k)^{\lambda _0},A_k)$,  $D^{\operatorname {b}}\operatorname {Mod}^{\operatorname {gr}}(U({\frak g}_k)^{\lambda _0}_0,A_k)$, and
$D^{\operatorname {b}}\operatorname {Mod}^{\operatorname {gr}}(U({\frak g}_k)^{\lambda _0}_0,A_k)$, and  $D^{\operatorname {b}}\operatorname {Mod}^{\operatorname {gr}}(\mathcal {A}^{\lambda _0},A_k)$.
$D^{\operatorname {b}}\operatorname {Mod}^{\operatorname {gr}}(\mathcal {A}^{\lambda _0},A_k)$.(ii) For any
 $b\in B_{\operatorname {aff}}'$, write the corresponding auto-equivalence as
$b\in B_{\operatorname {aff}}'$, write the corresponding auto-equivalence as  $\Theta _b^{\operatorname {R}}$. The localization functor
$\Theta _b^{\operatorname {R}}$. The localization functor  $\gamma ^{\lambda _0}$ intertwines these two
$\gamma ^{\lambda _0}$ intertwines these two  $B_{\operatorname {aff}}'$-actions. That is, for any
$B_{\operatorname {aff}}'$-actions. That is, for any  $b\in B_{\operatorname {aff}}'$, the following diagram commutes.
Similar conclusions hold for the completed or graded versions:
$b\in B_{\operatorname {aff}}'$, the following diagram commutes.
Similar conclusions hold for the completed or graded versions:
 \[ D^{\operatorname{b}}\operatorname{Mod}_0^{\operatorname{gr}}(U({\frak g}_k)^{\lambda_0},A_k), \quad D^{\operatorname{b}}\operatorname{Mod}^{\operatorname{gr}}(U({\frak g}_k)^{\lambda_0}_0,A_k), \quad \text{and} \quad D^{\operatorname{b}}\operatorname{Mod}^{\operatorname{gr}}(\mathcal{A}^{\lambda_0},A_k). \]
\[ D^{\operatorname{b}}\operatorname{Mod}_0^{\operatorname{gr}}(U({\frak g}_k)^{\lambda_0},A_k), \quad D^{\operatorname{b}}\operatorname{Mod}^{\operatorname{gr}}(U({\frak g}_k)^{\lambda_0}_0,A_k), \quad \text{and} \quad D^{\operatorname{b}}\operatorname{Mod}^{\operatorname{gr}}(\mathcal{A}^{\lambda_0},A_k). \]
Note that under this identification of the two affine braid group actions, ![]() $\operatorname {Pic}(T^*\mathcal {B})\cong \Lambda$ acts on
$\operatorname {Pic}(T^*\mathcal {B})\cong \Lambda$ acts on ![]() $\Lambda$ as in the level-
$\Lambda$ as in the level-![]() $p$ affine Weyl group action
$p$ affine Weyl group action ![]() $\bullet$.
$\bullet$.
The un-graded version of the following has been well known (see, e.g. [Reference JanztenJan00, Lemma 4.7]). Here we give a different proof, which also holds in the ![]() $A_k$-Koszul-bigraded setting.
$A_k$-Koszul-bigraded setting.
Lemma 7.3 Assuming ![]() $\mu$ is regular. Let
$\mu$ is regular. Let ![]() $\alpha \in I_{\operatorname {aff}}$ be such that
$\alpha \in I_{\operatorname {aff}}$ be such that ![]() $\dot {\mu }:=\mu \star s_\alpha >\mu$, then we have as objects in
$\dot {\mu }:=\mu \star s_\alpha >\mu$, then we have as objects in ![]() $D^{\operatorname {b}}\operatorname {Mod}^{\operatorname {gr}}(\mathcal {A}^{\lambda _0},A_k)$
$D^{\operatorname {b}}\operatorname {Mod}^{\operatorname {gr}}(\mathcal {A}^{\lambda _0},A_k)$
 \begin{align*} \Theta_{\widetilde{s}_\alpha}^{{-}1}(Z^{{\frak b}}_0(\mu+2\rho))&\cong Z^{{\frak b}}_0(\dot{\mu}+2\rho),\\ \Theta_{\widetilde{s}_\alpha}^{{-}1}(Z^{{\frak b}}(\mu+2\rho))&\cong Z^{{\frak b}}(\dot{\mu}+2\rho). \end{align*}
\begin{align*} \Theta_{\widetilde{s}_\alpha}^{{-}1}(Z^{{\frak b}}_0(\mu+2\rho))&\cong Z^{{\frak b}}_0(\dot{\mu}+2\rho),\\ \Theta_{\widetilde{s}_\alpha}^{{-}1}(Z^{{\frak b}}(\mu+2\rho))&\cong Z^{{\frak b}}(\dot{\mu}+2\rho). \end{align*}Proof. The usual equivariant D-module calculation as in [Reference Beilinson and BernsteinBB81] (see also [Reference Ben-Zvi and FrenkelBF04, § 11.2.11]) yields that the global section of the delta-D-module at ![]() $id\in \mathcal {B}_k$ gives the Verma module over
$id\in \mathcal {B}_k$ gives the Verma module over ![]() $U({\frak g}_k)$. More precisely, for any
$U({\frak g}_k)$. More precisely, for any ![]() $\lambda$ regular and integral, let
$\lambda$ regular and integral, let ![]() $\delta _{\frak b}^\lambda$ be the module of
$\delta _{\frak b}^\lambda$ be the module of ![]() $\mathcal {D}^\lambda$ given by the
$\mathcal {D}^\lambda$ given by the ![]() $\delta$-distributions at
$\delta$-distributions at ![]() $id\in \mathcal {B}_k$. Under the equivalence
$id\in \mathcal {B}_k$. Under the equivalence ![]() $R\Gamma _{\mathcal {D}^\lambda ,0}:D^{\operatorname {b}}(\operatorname {Coh}_{0}\mathcal {D}^\lambda ) \overset {\cong }\longrightarrow D^{\operatorname {b}}(\operatorname {Mod}_{0}U({\frak g}_k)^\lambda )$ [Reference Bezrukavnikov, Mirković and RumyninBMR08, Theorem 3.2],
$R\Gamma _{\mathcal {D}^\lambda ,0}:D^{\operatorname {b}}(\operatorname {Coh}_{0}\mathcal {D}^\lambda ) \overset {\cong }\longrightarrow D^{\operatorname {b}}(\operatorname {Mod}_{0}U({\frak g}_k)^\lambda )$ [Reference Bezrukavnikov, Mirković and RumyninBMR08, Theorem 3.2],
Similarly, let ![]() $\delta ^\lambda _{{\frak b},0}$ be the central reduction of
$\delta ^\lambda _{{\frak b},0}$ be the central reduction of ![]() $\delta _{\frak b}^\lambda$ with respect to the sheaf of ideals corresponding to
$\delta _{\frak b}^\lambda$ with respect to the sheaf of ideals corresponding to ![]() $\mathcal {B}^{(1)}\subseteq T^*\mathcal {B}^{(1)}$ in the center of
$\mathcal {B}^{(1)}\subseteq T^*\mathcal {B}^{(1)}$ in the center of ![]() $\mathcal {D}^\lambda$. Then we have [Reference Bezrukavnikov, Mirković and RumyninBMR08, § 3.1.4]
$\mathcal {D}^\lambda$. Then we have [Reference Bezrukavnikov, Mirković and RumyninBMR08, § 3.1.4]
By [Reference Bezrukavnikov, Mirković and RumyninBMR06, Theorem 2.2.8] (taking into account the correction in [Reference Bezrukavnikov and RicheBR13] in Remark 2.5.2 and the paragraph afterwards), the following diagram commutes.

Here we have used the assumption that ![]() $\dot {\mu }=\mu \star s_\alpha >\mu$. By definition,
$\dot {\mu }=\mu \star s_\alpha >\mu$. By definition,
By (33), ![]() $R\Gamma _{\mathcal {D}^\mu ,0}(\delta _{{\frak b}, 0}^{{\mu }})=Z^{\frak b}_0(\mu +2\rho )$, and
$R\Gamma _{\mathcal {D}^\mu ,0}(\delta _{{\frak b}, 0}^{{\mu }})=Z^{\frak b}_0(\mu +2\rho )$, and ![]() $R\Gamma _{\mathcal {D}^{\dot {\mu }},0}(\delta _{{\frak b}, 0}^{\dot {\mu }})=Z^{\frak b}_0(\dot {\mu }+2\rho )$. Therefore, we have
$R\Gamma _{\mathcal {D}^{\dot {\mu }},0}(\delta _{{\frak b}, 0}^{\dot {\mu }})=Z^{\frak b}_0(\dot {\mu }+2\rho )$. Therefore, we have ![]() $\Theta _{\alpha }^{-1}(Z^{{\frak b}}_0(\mu +2\rho ))\cong Z^{{\frak b}}_0(\dot {\mu }+2\rho )$. Note that this isomorphism is equivariant with respect to the
$\Theta _{\alpha }^{-1}(Z^{{\frak b}}_0(\mu +2\rho ))\cong Z^{{\frak b}}_0(\dot {\mu }+2\rho )$. Note that this isomorphism is equivariant with respect to the ![]() $A_k$ and Koszul gradings.
$A_k$ and Koszul gradings.
About the assertion on Verma modules, we follow the same argument using (32), with the commutative square above replaced by their counterparts for the completed algebras. We get an isomorphism between the completions of ![]() $\Theta _{\alpha }^{-1}(Z^{{\frak b}}(\mu +2\rho ))$ and
$\Theta _{\alpha }^{-1}(Z^{{\frak b}}(\mu +2\rho ))$ and ![]() $Z^{{\frak b}}(\dot {\mu }+2\rho )$, which is equivariant with respect to the
$Z^{{\frak b}}(\dot {\mu }+2\rho )$, which is equivariant with respect to the ![]() $A_k$ and Koszul gradings. Then, taking the subspaces of finite vectors with respect to the Koszul grading gives the required isomorphism.
$A_k$ and Koszul gradings. Then, taking the subspaces of finite vectors with respect to the Koszul grading gives the required isomorphism.
The following is a direct consequence of the existence of the affine braid group action on the representation category.
Corollary 7.4 If ![]() $\lambda _0\in A_0$; then for any
$\lambda _0\in A_0$; then for any ![]() $w\in W$ we have
$w\in W$ we have ![]() $\Theta _{\widetilde {w^{^{-1}}}}^{\operatorname {R}}(Z^{{\frak b}}(\lambda _0+2\rho )) =Z^{{\frak b}}(\lambda _0\star w^{-1}+2\rho )$. A similar conclusion holds for the baby Verma modules.
$\Theta _{\widetilde {w^{^{-1}}}}^{\operatorname {R}}(Z^{{\frak b}}(\lambda _0+2\rho )) =Z^{{\frak b}}(\lambda _0\star w^{-1}+2\rho )$. A similar conclusion holds for the baby Verma modules.
Proof. We have ![]() $\lambda _0=\lambda _0\star w^{-1}\star w$. Clearly
$\lambda _0=\lambda _0\star w^{-1}\star w$. Clearly ![]() $w$ increases
$w$ increases ![]() $\lambda _0\star w^{-1}$ by assumption. Then, the statement follows directly by applying Lemma 7.3 iteratively to
$\lambda _0\star w^{-1}$ by assumption. Then, the statement follows directly by applying Lemma 7.3 iteratively to ![]() $\Theta _{\widetilde {w^{^{-1}}}}^{\operatorname {R}}=\Theta ^{\operatorname {R}}_{\tilde {s}_1}\circ \cdots \circ \Theta ^{\operatorname {R}}_{\tilde {s}_k}$ for any reduced decomposition
$\Theta _{\widetilde {w^{^{-1}}}}^{\operatorname {R}}=\Theta ^{\operatorname {R}}_{\tilde {s}_1}\circ \cdots \circ \Theta ^{\operatorname {R}}_{\tilde {s}_k}$ for any reduced decomposition ![]() $w=s_1\dots s_k$ of
$w=s_1\dots s_k$ of ![]() $w$, similar to the calculation done in Remark 6.3(c). We get
$w$, similar to the calculation done in Remark 6.3(c). We get ![]() $(\Theta _{\widetilde {w^{^{-1}}}}^{\operatorname {R}})^{-1}Z^{\frak b}(\lambda _0\star w^{-1})=(\Theta ^{\operatorname {R}}_{\tilde {s}_1}\circ \cdots \circ \Theta ^{\operatorname {R}}_{\tilde {s}_k})^{-1}Z^{\frak b}(\lambda _0\star w^{-1})$
$(\Theta _{\widetilde {w^{^{-1}}}}^{\operatorname {R}})^{-1}Z^{\frak b}(\lambda _0\star w^{-1})=(\Theta ^{\operatorname {R}}_{\tilde {s}_1}\circ \cdots \circ \Theta ^{\operatorname {R}}_{\tilde {s}_k})^{-1}Z^{\frak b}(\lambda _0\star w^{-1})$ ![]() $=(\Theta ^{\operatorname {R}}_{\tilde {s}_k})^{-1}\circ \cdots \circ (\Theta ^{\operatorname {R}}_{\tilde {s}_1})^{-1}Z^{\frak b}(\lambda _0\star w^{-1})=Z^{\frak b}(\lambda _0\star w^{-1}\star w)$.
$=(\Theta ^{\operatorname {R}}_{\tilde {s}_k})^{-1}\circ \cdots \circ (\Theta ^{\operatorname {R}}_{\tilde {s}_1})^{-1}Z^{\frak b}(\lambda _0\star w^{-1})=Z^{\frak b}(\lambda _0\star w^{-1}\star w)$.
Motivated by [Reference Bezrukavnikov and MirkovićBM13, p.870], for any ![]() $\lambda$ in the
$\lambda$ in the ![]() $W_{\operatorname {aff}}'$-orbit of
$W_{\operatorname {aff}}'$-orbit of ![]() $\lambda _0$, we define the localization functor
$\lambda _0$, we define the localization functor
which is determined by the property that ![]() $\gamma ^{\lambda \star w}=\gamma ^{\lambda }\circ \Theta _{\widetilde {w^{^{-1}}}}^{\operatorname {R}}$ for
$\gamma ^{\lambda \star w}=\gamma ^{\lambda }\circ \Theta _{\widetilde {w^{^{-1}}}}^{\operatorname {R}}$ for ![]() $w\in W'_{\operatorname {aff}}$, as long as
$w\in W'_{\operatorname {aff}}$, as long as ![]() $w$ increases
$w$ increases ![]() $\lambda$. Localization functor associated to singular
$\lambda$. Localization functor associated to singular ![]() $\lambda$ has also been studied in [Reference Bezrukavnikov, Mirković and RumyninBMR06], although we will not explicitly use this. In particular, if
$\lambda$ has also been studied in [Reference Bezrukavnikov, Mirković and RumyninBMR06], although we will not explicitly use this. In particular, if ![]() $\lambda _0\in A_0$, and
$\lambda _0\in A_0$, and ![]() $w\in W$ such that
$w\in W$ such that ![]() $\lambda =\lambda _0\star w$, then using the fact that
$\lambda =\lambda _0\star w$, then using the fact that ![]() $\lambda _0=\lambda _0\star w\star w^{-1}$ and that
$\lambda _0=\lambda _0\star w\star w^{-1}$ and that ![]() $w^{-1}$ increases
$w^{-1}$ increases ![]() $\lambda _0\star w$, we get
$\lambda _0\star w$, we get
7.3 A categorification of the stable basis via the Verma modules
Now we are ready to state and prove the main theorem of this section.
Theorem 7.5 Let ![]() $k$ be an algebraically closed field of characteristic
$k$ be an algebraically closed field of characteristic ![]() $p$, and
$p$, and ![]() $p$ is greater than the Coxeter number. Assume
$p$ is greater than the Coxeter number. Assume ![]() $\lambda$ is regular and integral, then in
$\lambda$ is regular and integral, then in ![]() $D^{\operatorname {b}}_{T_k}(T^*\mathcal {B}_k^{(1)})$, we have isomorphisms
$D^{\operatorname {b}}_{T_k}(T^*\mathcal {B}_k^{(1)})$, we have isomorphisms
The left-hand side is the base changed integral form of the stable basis defined in § 6.3, not to be confused with the complex one. The relation between these two is given by Theorem 6.4. Using the isomorphism of ![]() $k$-varieties
$k$-varieties ![]() $T^*\mathcal {B}_k\cong T^*\mathcal {B}^{(1)}$, we consider
$T^*\mathcal {B}_k\cong T^*\mathcal {B}^{(1)}$, we consider ![]() $T^*\mathcal {B}^{(1)}$ as the base-change of
$T^*\mathcal {B}^{(1)}$ as the base-change of ![]() $T^*\mathcal {B}_{\mathbb {Z}}$ to the field
$T^*\mathcal {B}_{\mathbb {Z}}$ to the field ![]() $k$.
$k$.
Proof. As the objects ![]() ${\frak s}{\frak t}{\frak a}{\frak b}^k_{-({\lambda +\rho })/{p}}(y)$ are defined inductively, we prove this theorem inductively.
${\frak s}{\frak t}{\frak a}{\frak b}^k_{-({\lambda +\rho })/{p}}(y)$ are defined inductively, we prove this theorem inductively.
First, we prove the case when ![]() $\lambda =\lambda _0\in A_0$. We have
$\lambda =\lambda _0\in A_0$. We have ![]() $\gamma ^{\lambda _0}Z^{\frak b}(\lambda _0+2\rho )=\mathcal {O}_{T^*_{id}\mathcal {B}}= \mathcal {L}_\rho \otimes {\frak s}{\frak t}{\frak a}{\frak b}^k_{-({\lambda _0+\rho })/{p}}(id)=e^\rho {\frak s}{\frak t}{\frak a}{\frak b}^k_{-({\lambda _0+\rho })/{p}}(id)$. Here
$\gamma ^{\lambda _0}Z^{\frak b}(\lambda _0+2\rho )=\mathcal {O}_{T^*_{id}\mathcal {B}}= \mathcal {L}_\rho \otimes {\frak s}{\frak t}{\frak a}{\frak b}^k_{-({\lambda _0+\rho })/{p}}(id)=e^\rho {\frak s}{\frak t}{\frak a}{\frak b}^k_{-({\lambda _0+\rho })/{p}}(id)$. Here ![]() $id\in \mathcal {B}_k$ corresponds to the Borel subalgebra
$id\in \mathcal {B}_k$ corresponds to the Borel subalgebra ![]() ${\frak b}$ that has been used to define the Verma modules. For
${\frak b}$ that has been used to define the Verma modules. For ![]() $w\in W$, Remark 6.1(c) yields that
$w\in W$, Remark 6.1(c) yields that ![]() $Z^{\frak b}(w\bullet \lambda _0+2\rho )=Z^{\frak b}(\lambda _0\star w+2\rho )$, so
$Z^{\frak b}(w\bullet \lambda _0+2\rho )=Z^{\frak b}(\lambda _0\star w+2\rho )$, so
 \begin{align*} \gamma^{\lambda_0}Z^{\frak b}(\lambda_0\star w+2\rho) &\overset{\text{Corollary 7.4}}= \gamma^{\lambda_0}\Theta^{\operatorname{R}}_{\widetilde w}Z^{\frak b}(\lambda_0+2\rho) \overset{\text{Theorem 7.2 (ii)}}=J^{\operatorname{R}}_{\widetilde w} \gamma^{\lambda_0}Z^{\frak b}(\lambda_0+2\rho)\\ & = J^{\operatorname{R}}_{\widetilde w}e^\rho{\frak s}{\frak t}{\frak a}{\frak b}^k_{-({\lambda_0+\rho})/{p}}(id) \overset{(26)}=e^{\rho}{\frak s}{\frak t}{\frak a}{\frak b}^k_{-({\lambda_0+\rho})/{p}}(w). \end{align*}
\begin{align*} \gamma^{\lambda_0}Z^{\frak b}(\lambda_0\star w+2\rho) &\overset{\text{Corollary 7.4}}= \gamma^{\lambda_0}\Theta^{\operatorname{R}}_{\widetilde w}Z^{\frak b}(\lambda_0+2\rho) \overset{\text{Theorem 7.2 (ii)}}=J^{\operatorname{R}}_{\widetilde w} \gamma^{\lambda_0}Z^{\frak b}(\lambda_0+2\rho)\\ & = J^{\operatorname{R}}_{\widetilde w}e^\rho{\frak s}{\frak t}{\frak a}{\frak b}^k_{-({\lambda_0+\rho})/{p}}(id) \overset{(26)}=e^{\rho}{\frak s}{\frak t}{\frak a}{\frak b}^k_{-({\lambda_0+\rho})/{p}}(w). \end{align*}Here the third equality follows from the initial case above.
Second, we prove this for general ![]() $\lambda \in W\bullet A_0$, a fundamental domain of the action of the Picard group. We assume
$\lambda \in W\bullet A_0$, a fundamental domain of the action of the Picard group. We assume ![]() $\lambda =x\bullet \lambda _0$ with
$\lambda =x\bullet \lambda _0$ with ![]() $\lambda _0\in A_0$ and
$\lambda _0\in A_0$ and ![]() $x\in W$. We have
$x\in W$. We have
 \begin{align*} {\frak s}{\frak t}{\frak a}{\frak b}^k_{-({\lambda+\rho})/{p}}(y) &\overset{\text{Remark 6.1(b)}}= {\frak s}{\frak t}{\frak a}{\frak b}^k_{{-}x(({\lambda_0+\rho})/{p})}(y) \overset{(27)}=(J^{\operatorname{R}}_{\widetilde{x}})^{{-}1} {\frak s}{\frak t}{\frak a}{\frak b}_{-({\lambda_0+\rho})/{p}}(yx)\\ &= (J^{\operatorname{R}}_{\widetilde x})^{{-}1}e^{-\rho}\gamma^{\lambda_0} Z^{{\frak b}}((yx)\bullet\lambda_0+2\rho)\\ &\overset{(34)}=e^{-\rho}\gamma^{\lambda}Z^{{\frak b}}((yx) \bullet\lambda_0+2\rho) =e^{-\rho}\gamma^{\lambda}Z^{{\frak b}}(y\bullet \lambda+2\rho). \end{align*}
\begin{align*} {\frak s}{\frak t}{\frak a}{\frak b}^k_{-({\lambda+\rho})/{p}}(y) &\overset{\text{Remark 6.1(b)}}= {\frak s}{\frak t}{\frak a}{\frak b}^k_{{-}x(({\lambda_0+\rho})/{p})}(y) \overset{(27)}=(J^{\operatorname{R}}_{\widetilde{x}})^{{-}1} {\frak s}{\frak t}{\frak a}{\frak b}_{-({\lambda_0+\rho})/{p}}(yx)\\ &= (J^{\operatorname{R}}_{\widetilde x})^{{-}1}e^{-\rho}\gamma^{\lambda_0} Z^{{\frak b}}((yx)\bullet\lambda_0+2\rho)\\ &\overset{(34)}=e^{-\rho}\gamma^{\lambda}Z^{{\frak b}}((yx) \bullet\lambda_0+2\rho) =e^{-\rho}\gamma^{\lambda}Z^{{\frak b}}(y\bullet \lambda+2\rho). \end{align*}
Here the third equality follows from the first step above; The last equality follows from ![]() $(yx)\bullet \lambda _0=y\bullet \lambda$.
$(yx)\bullet \lambda _0=y\bullet \lambda$.
Finally, we consider the case of general ![]() $\lambda$. There is an
$\lambda$. There is an ![]() $\mu \in \Lambda$, and
$\mu \in \Lambda$, and ![]() $\lambda _1\in W\bullet A_0$ so that
$\lambda _1\in W\bullet A_0$ so that ![]() $\lambda =\lambda _1\star (-\mu )$. If
$\lambda =\lambda _1\star (-\mu )$. If ![]() $\lambda _1=x\bullet \lambda _0$ for
$\lambda _1=x\bullet \lambda _0$ for ![]() $x\in W$ and
$x\in W$ and ![]() $\lambda _0\in A_0$, the above is equivalent to
$\lambda _0\in A_0$, the above is equivalent to
Without loss of generality, we assume ![]() $-\mu$ increases
$-\mu$ increases ![]() $\lambda _1$. That is,
$\lambda _1$. That is, ![]() $-x\mu \in \Lambda ^+$. We have
$-x\mu \in \Lambda ^+$. We have
 \begin{align*} {\frak s}{\frak t}{\frak a}{\frak b}^k_{-({\lambda+\rho})/{p}}(y)&= {\frak s}{\frak t}{\frak a}{\frak b}^k_{x(\mu)-({\lambda_1+\rho})/{p}}(y)\\ &\overset{(28)}= e^{{-}yx(\mu)}\mathcal{L}_{x(\mu)}\otimes{\frak s}{\frak t}{\frak a}{\frak b}^k_{-({\lambda_1+\rho})/{p}}(y)\\ &\overset{\text{Theorem 6.2}}= e^{{-}yx(\mu)}J_{x(\mu)}^{\operatorname{R}}e^{-\rho}\gamma^{\lambda_1}Z^{\frak b}(y\bullet\lambda_1 +2\rho)\\ &\overset{(34)}= e^{{-}yx(\mu)}e^{-\rho}J_{x(\mu)}^{\operatorname{R}} \gamma^{\lambda_0}(\Theta_{\widetilde x}^{\operatorname{R}})^{{-}1}Z^{\frak b}(y\bullet\lambda_1+2\rho)\\ &\overset{\text{Theorem 7.2(ii)}}= e^{{-}yx(\mu)}e^{-\rho}\gamma^{\lambda_0}\Theta^{\operatorname{R}}_{x(\mu)}(\Theta_{\widetilde x}^{\operatorname{R}})^{{-}1}Z^{\frak b}(y\bullet\lambda_1+2\rho)\\ &= e^{{-}yx(\mu)}e^{-\rho}\gamma^{\lambda_0-px(\mu)}(\Theta_{\widetilde x}^{\operatorname{R}})^{{-}1}Z^{\frak b}(y\bullet\lambda_1+2\rho)\\ &= e^{{-}yx(\mu)}e^{-\rho}\gamma^{\lambda}Z^{\frak b}(y\bullet\lambda_1+2\rho). \end{align*}
\begin{align*} {\frak s}{\frak t}{\frak a}{\frak b}^k_{-({\lambda+\rho})/{p}}(y)&= {\frak s}{\frak t}{\frak a}{\frak b}^k_{x(\mu)-({\lambda_1+\rho})/{p}}(y)\\ &\overset{(28)}= e^{{-}yx(\mu)}\mathcal{L}_{x(\mu)}\otimes{\frak s}{\frak t}{\frak a}{\frak b}^k_{-({\lambda_1+\rho})/{p}}(y)\\ &\overset{\text{Theorem 6.2}}= e^{{-}yx(\mu)}J_{x(\mu)}^{\operatorname{R}}e^{-\rho}\gamma^{\lambda_1}Z^{\frak b}(y\bullet\lambda_1 +2\rho)\\ &\overset{(34)}= e^{{-}yx(\mu)}e^{-\rho}J_{x(\mu)}^{\operatorname{R}} \gamma^{\lambda_0}(\Theta_{\widetilde x}^{\operatorname{R}})^{{-}1}Z^{\frak b}(y\bullet\lambda_1+2\rho)\\ &\overset{\text{Theorem 7.2(ii)}}= e^{{-}yx(\mu)}e^{-\rho}\gamma^{\lambda_0}\Theta^{\operatorname{R}}_{x(\mu)}(\Theta_{\widetilde x}^{\operatorname{R}})^{{-}1}Z^{\frak b}(y\bullet\lambda_1+2\rho)\\ &= e^{{-}yx(\mu)}e^{-\rho}\gamma^{\lambda_0-px(\mu)}(\Theta_{\widetilde x}^{\operatorname{R}})^{{-}1}Z^{\frak b}(y\bullet\lambda_1+2\rho)\\ &= e^{{-}yx(\mu)}e^{-\rho}\gamma^{\lambda}Z^{\frak b}(y\bullet\lambda_1+2\rho). \end{align*}
Here the third equality follows from Theorem 6.2 and the second step. The second to last equality follows from the fact that ![]() $-x\mu$ increases
$-x\mu$ increases ![]() $\lambda _0$, since
$\lambda _0$, since ![]() $x\mu \in \Lambda ^-$ and that the inverse of
$x\mu \in \Lambda ^-$ and that the inverse of ![]() $x\mu$ is
$x\mu$ is ![]() $-x\mu$. The last equality follows from the fact that
$-x\mu$. The last equality follows from the fact that ![]() $\lambda \star x^{-1}=\lambda _0-px(\mu )$, and that
$\lambda \star x^{-1}=\lambda _0-px(\mu )$, and that ![]() $x^{-1}$ increases
$x^{-1}$ increases ![]() $\lambda$, which in turn is equivalent to
$\lambda$, which in turn is equivalent to ![]() $x^{-1}$ increases
$x^{-1}$ increases ![]() $\lambda _0\star x$. Finally, note that the definition of the Verma modules only depends on an element in
$\lambda _0\star x$. Finally, note that the definition of the Verma modules only depends on an element in ![]() ${\frak h}^*_k$, which in particular is invariant under shifting by
${\frak h}^*_k$, which in particular is invariant under shifting by ![]() $p\lambda '$ for any
$p\lambda '$ for any ![]() $\lambda '\in \Lambda$. Hence ,
$\lambda '\in \Lambda$. Hence , ![]() $Z^{\frak b}(y\bullet \lambda _1+2\rho )$ and
$Z^{\frak b}(y\bullet \lambda _1+2\rho )$ and ![]() $Z^{\frak b}(y\bullet \lambda +2\rho )$ only differ by a
$Z^{\frak b}(y\bullet \lambda +2\rho )$ only differ by a ![]() $A_k$-grading, namely,
$A_k$-grading, namely, ![]() $e^{yx(\mu )}$. Therefore, the proof is finished.
$e^{yx(\mu )}$. Therefore, the proof is finished.
7.4 Restriction formula and Lie algebra cohomology
In general, for any variety ![]() $X$, let
$X$, let ![]() $a\in X$ be a closed point with residue field
$a\in X$ be a closed point with residue field ![]() $k_a$ and embedding
$k_a$ and embedding ![]() $i:\{a\}\hookrightarrow X$, and
$i:\{a\}\hookrightarrow X$, and ![]() $\mathcal {F}\in D^{\operatorname {b}}\operatorname {Coh}(X)$. Then
$\mathcal {F}\in D^{\operatorname {b}}\operatorname {Coh}(X)$. Then ![]() $\mathcal {F}|_a^\vee \cong \operatorname {Hom}_{k_a}(i^*\mathcal {F},k_a)\cong \operatorname {Hom}_X(\mathcal {F},i_*k_a)=\operatorname {Hom}_X(\mathcal {F},\mathcal {O}_a)$.
$\mathcal {F}|_a^\vee \cong \operatorname {Hom}_{k_a}(i^*\mathcal {F},k_a)\cong \operatorname {Hom}_X(\mathcal {F},i_*k_a)=\operatorname {Hom}_X(\mathcal {F},\mathcal {O}_a)$.
We have ![]() $k_{x{\frak b}}={\frak L}^{\lambda } Z_0^{x{\frak b}}(\lambda +2\rho )$ for any
$k_{x{\frak b}}={\frak L}^{\lambda } Z_0^{x{\frak b}}(\lambda +2\rho )$ for any ![]() $x\in W$. Recall that here
$x\in W$. Recall that here ![]() ${\frak b}$ is labelled by
${\frak b}$ is labelled by ![]() $id\in W$. Putting these together with Theorems 6.4 and 7.5, we get
$id\in W$. Putting these together with Theorems 6.4 and 7.5, we get
Here the ![]() $\operatorname {Ext}$ is taken in the Grothendieck group of the category
$\operatorname {Ext}$ is taken in the Grothendieck group of the category ![]() $\operatorname {Mod}^{\operatorname {gr}}(U({\frak g}_k)_0^{\lambda _0},A_k)$.
$\operatorname {Mod}^{\operatorname {gr}}(U({\frak g}_k)_0^{\lambda _0},A_k)$.
Remark 7.6 This is a reinterpretation of the restriction formula of stable bases in terms of Lie algebra cohomologies. Therefore, the formula [Reference Su, Zhao and ZhongSZZ20, Theorem 7.5] gives the a formula for ![]() $\operatorname {Ext}^*(Z^{{\frak b}}(y\bullet \lambda +2\rho ), Z_0^{x{\frak b}}(\lambda +2\rho ))^\vee$. In particular, this yields an explicit expression of the Koszul gradings on the Verma modules in terms of those on the baby Verma modules.
$\operatorname {Ext}^*(Z^{{\frak b}}(y\bullet \lambda +2\rho ), Z_0^{x{\frak b}}(\lambda +2\rho ))^\vee$. In particular, this yields an explicit expression of the Koszul gradings on the Verma modules in terms of those on the baby Verma modules.
Remark 7.7 Let ![]() $\omega \in \Omega$, and
$\omega \in \Omega$, and ![]() $\dot {\mu }:=\mu \star \omega$; then
$\dot {\mu }:=\mu \star \omega$; then
 \begin{align*} \Theta_{\omega}^{{-}1}(Z^{{\frak b}}_0(\mu+2\rho))&\cong Z^{{\frak b}}_0(\dot{\mu}+2\rho),\\ \Theta_{\omega}^{{-}1}(Z^{{\frak b}}(\mu+2\rho))&\cong Z^{{\frak b}}(\dot{\mu}+2\rho). \end{align*}
\begin{align*} \Theta_{\omega}^{{-}1}(Z^{{\frak b}}_0(\mu+2\rho))&\cong Z^{{\frak b}}_0(\dot{\mu}+2\rho),\\ \Theta_{\omega}^{{-}1}(Z^{{\frak b}}(\mu+2\rho))&\cong Z^{{\frak b}}(\dot{\mu}+2\rho). \end{align*}
The proof is similar to that of Lemma 7.3, using [Reference Bezrukavnikov, Mirković and RumyninBMR06, § 2.3.1(1)] in place of [Reference Bezrukavnikov, Mirković and RumyninBMR06, Theorem 2.2.8], again taking into account the correction in [Reference Bezrukavnikov and RicheBR13] in Remark 2.5.2 and the paragraph afterwards. Together with Lemma 7.3, one can see that these localization functors have the properties that ![]() $\gamma ^\lambda Z_0^{\frak b}(\lambda +2\rho )\cong k_{id}$, the latter being the skyscraper sheaf, and
$\gamma ^\lambda Z_0^{\frak b}(\lambda +2\rho )\cong k_{id}$, the latter being the skyscraper sheaf, and ![]() $\gamma ^\lambda Z^{\frak b}(\lambda +2\rho )\cong \mathcal {O}_{T^*_{id}\mathcal {B}^{(1)}}$.
$\gamma ^\lambda Z^{\frak b}(\lambda +2\rho )\cong \mathcal {O}_{T^*_{id}\mathcal {B}^{(1)}}$.
The right-hand side of Theorem 7.5 is the standard object in the ![]() $t$-structure associated to the alcove containing
$t$-structure associated to the alcove containing ![]() $\lambda$ [Reference Bezrukavnikov and MirkovićBM13, § 1.8.2].
$\lambda$ [Reference Bezrukavnikov and MirkovićBM13, § 1.8.2].
7.5 Other chambers
For an arbitrary chamber ![]() ${\frak C}$, let
${\frak C}$, let ![]() $B'_{{\mathbb {Z}}}$ be the Borel subgroup whose roots are in
$B'_{{\mathbb {Z}}}$ be the Borel subgroup whose roots are in ![]() ${\frak C}$. Then, identifying the maximal torus
${\frak C}$. Then, identifying the maximal torus ![]() $A_{\mathbb {Z}}$ with the abstract Cartan group using
$A_{\mathbb {Z}}$ with the abstract Cartan group using ![]() $B'_{\mathbb {Z}}$, and defining the Verma modules of
$B'_{\mathbb {Z}}$, and defining the Verma modules of ![]() $U({\frak g}_k)$ using
$U({\frak g}_k)$ using ![]() $B'_k$, these Verma modules under localization functor give the categorification of stable basis associated to the chamber
$B'_k$, these Verma modules under localization functor give the categorification of stable basis associated to the chamber ![]() ${\frak C}$.
${\frak C}$.
The change of chambers are controlled by the Weyl group as usual. More precisely, for any Weyl group element ![]() $w\in W$, taking a representative of it in
$w\in W$, taking a representative of it in ![]() $N_{G_{{\mathbb {Z}}}}(A_{\mathbb {Z}})$, we get an automorphism
$N_{G_{{\mathbb {Z}}}}(A_{\mathbb {Z}})$, we get an automorphism ![]() $w:T_{{\mathbb {Z}}}\to T_{{\mathbb {Z}}}$ of groups together with an automorphism
$w:T_{{\mathbb {Z}}}\to T_{{\mathbb {Z}}}$ of groups together with an automorphism ![]() $w:T^*\mathcal {B}_{{\mathbb {Z}}}\to T^*\mathcal {B}_{{\mathbb {Z}}}$ of varieties. These two automorphisms intertwine the two actions of
$w:T^*\mathcal {B}_{{\mathbb {Z}}}\to T^*\mathcal {B}_{{\mathbb {Z}}}$ of varieties. These two automorphisms intertwine the two actions of ![]() $T_{{\mathbb {Z}}}$ on
$T_{{\mathbb {Z}}}$ on ![]() $T^*\mathcal {B}_{{\mathbb {Z}}}$, hence induces an auto-equivalence of categories
$T^*\mathcal {B}_{{\mathbb {Z}}}$, hence induces an auto-equivalence of categories ![]() $w:D^{\operatorname {b}}_{T_{\mathbb {Z}}}\operatorname {Coh}(T^*\mathcal {B}_{\mathbb {Z}})\to D^{\operatorname {b}}_{T_{\mathbb {Z}}}\operatorname {Coh}(T^*\mathcal {B}_{\mathbb {Z}})$. Applying this functor to the objects
$w:D^{\operatorname {b}}_{T_{\mathbb {Z}}}\operatorname {Coh}(T^*\mathcal {B}_{\mathbb {Z}})\to D^{\operatorname {b}}_{T_{\mathbb {Z}}}\operatorname {Coh}(T^*\mathcal {B}_{\mathbb {Z}})$. Applying this functor to the objects ![]() $\{{\frak s}{\frak t}{\frak a}{\frak b}_\lambda ^{\mathbb {Z}}(y)\mid y\in W\}$ for
$\{{\frak s}{\frak t}{\frak a}{\frak b}_\lambda ^{\mathbb {Z}}(y)\mid y\in W\}$ for ![]() $\lambda \in \Lambda$ regular, according to § 3.2, we obtain integral forms of the categorification of the stable basis associated to the chamber
$\lambda \in \Lambda$ regular, according to § 3.2, we obtain integral forms of the categorification of the stable basis associated to the chamber ![]() $w{\frak C}_+$ and the polarization
$w{\frak C}_+$ and the polarization ![]() $w(T\mathcal {B})=T\mathcal {B}\in K_{T_{{\mathbb {Z}}}}(T^*\mathcal {B}_{{\mathbb {Z}}})$.
$w(T\mathcal {B})=T\mathcal {B}\in K_{T_{{\mathbb {Z}}}}(T^*\mathcal {B}_{{\mathbb {Z}}})$.
8. Monodromy of the quantum cohomology
The action of the affine braid group discussed in the previous section is one of the many incarnations of the same representation. In this section we briefly review some of the other incarnations, with emphasis on its appearance as the monodromy of the ![]() $G\times \mathbb {C}^*$-equivariant quantum connection of
$G\times \mathbb {C}^*$-equivariant quantum connection of ![]() $T^*\mathcal {B}$.
$T^*\mathcal {B}$.
8.1 Other incarnations of the braid group action
(1) As has been reviewed in detail, in [Reference Bezrukavnikov, Mirković and RumyninBMR06] an action of ![]() $B_{\operatorname {aff}}'$ on
$B_{\operatorname {aff}}'$ on ![]() $D^{\operatorname {b}}(\operatorname {Mod}_{A\times \mathbb {C}^*}{\frak g}_{\overline {\mathbb {F}}_p})$ has been constructed.
$D^{\operatorname {b}}(\operatorname {Mod}_{A\times \mathbb {C}^*}{\frak g}_{\overline {\mathbb {F}}_p})$ has been constructed.
(2) Via the localization of [Reference Bezrukavnikov and MirkovićBM13, Reference Bezrukavnikov, Mirković and RumyninBMR08], ![]() $D^{\operatorname {b}}(\operatorname {Mod}_{A\times \mathbb {C}^*}{\frak g}_{\overline {\mathbb {F}}_p})\cong D^{\operatorname {b}}_{A\times \mathbb {C}^*}(T^*\mathcal {B})$, the above affine braid group action lifts to an action on
$D^{\operatorname {b}}(\operatorname {Mod}_{A\times \mathbb {C}^*}{\frak g}_{\overline {\mathbb {F}}_p})\cong D^{\operatorname {b}}_{A\times \mathbb {C}^*}(T^*\mathcal {B})$, the above affine braid group action lifts to an action on ![]() $D^{\operatorname {b}}_{A\times \mathbb {C}^*}(T^*\mathcal {B})$.
$D^{\operatorname {b}}_{A\times \mathbb {C}^*}(T^*\mathcal {B})$.
(3) In [Reference Bezrukavnikov and RicheBR13] the Fourier–Mukai kernels on ![]() $D^{\operatorname {b}}_{A\times \mathbb {C}^*}(T^*\mathcal {B})$ on which the generators of
$D^{\operatorname {b}}_{A\times \mathbb {C}^*}(T^*\mathcal {B})$ on which the generators of ![]() $B_{\operatorname {aff}}'$ acts has been determined. Hence, taking Grothendieck group, this action agrees with the affine Hecke algebra
$B_{\operatorname {aff}}'$ acts has been determined. Hence, taking Grothendieck group, this action agrees with the affine Hecke algebra ![]() ${\mathbb {H}}$ action on
${\mathbb {H}}$ action on ![]() $K_{A\times \mathbb {C}^*}(T^*\mathcal {B})$ of Kazhdan-Lusztig and Ginzburg.
$K_{A\times \mathbb {C}^*}(T^*\mathcal {B})$ of Kazhdan-Lusztig and Ginzburg.
(4) In [Reference Braverman, Maulik and OkounkovBMO11], building up on earlier work of Cherednik [Reference CherednikChe05], the monodromy of the quantum connection of ![]() $T^*\mathcal {B}$, which a priori is an action of the affine braid group on
$T^*\mathcal {B}$, which a priori is an action of the affine braid group on ![]() $H^*_{G\times \mathbb {C}^*}(T^*\mathcal {B})$, also agrees with the action of
$H^*_{G\times \mathbb {C}^*}(T^*\mathcal {B})$, also agrees with the action of ![]() ${\mathbb {H}}$ on
${\mathbb {H}}$ on ![]() $K_{A\times \mathbb {C}^*}(T^*\mathcal {B})$ via proper identifications. More details will be recalled below.
$K_{A\times \mathbb {C}^*}(T^*\mathcal {B})$ via proper identifications. More details will be recalled below.
(5) Were the category ![]() $D^{\operatorname {b}}_{A\times \mathbb {C}^*}(T^*\mathcal {B})$ replaced by
$D^{\operatorname {b}}_{A\times \mathbb {C}^*}(T^*\mathcal {B})$ replaced by ![]() $D^{\operatorname {b}}_{G\times \mathbb {C}^*}(T^*\mathcal {B})$, then the equivalences of [Reference BezrukavnikovBez16, Reference Arkhipov and BezrukavnikovAB09] give
$D^{\operatorname {b}}_{G\times \mathbb {C}^*}(T^*\mathcal {B})$, then the equivalences of [Reference BezrukavnikovBez16, Reference Arkhipov and BezrukavnikovAB09] give ![]() $D^{\operatorname {b}}_{G\times \mathbb {C}^*}(T^*\mathcal {B})\cong D^I_{const}(G^L_K/G^L_\mathcal {O})$, where
$D^{\operatorname {b}}_{G\times \mathbb {C}^*}(T^*\mathcal {B})\cong D^I_{const}(G^L_K/G^L_\mathcal {O})$, where ![]() $K={\mathbb {F}}_p(\!(t)\!)$,
$K={\mathbb {F}}_p(\!(t)\!)$, ![]() $\mathcal {O}={\mathbb {F}}_p[[t]]$ is the ring of integers,
$\mathcal {O}={\mathbb {F}}_p[[t]]$ is the ring of integers, ![]() $G^L$ is the dual group, and
$G^L$ is the dual group, and ![]() $I$ is the Iwahori subgroup. The category
$I$ is the Iwahori subgroup. The category ![]() $D^I_{const}(G^L_K/G^L_\mathcal {O})$ categorifies the action of the Iwahori–Matsumoto Hecke algebra on its (anti)spherical module. For
$D^I_{const}(G^L_K/G^L_\mathcal {O})$ categorifies the action of the Iwahori–Matsumoto Hecke algebra on its (anti)spherical module. For ![]() $D^{\operatorname {b}}_{A\times \mathbb {C}^*}(T^*\mathcal {B})$, the corresponding Langlands dual should be
$D^{\operatorname {b}}_{A\times \mathbb {C}^*}(T^*\mathcal {B})$, the corresponding Langlands dual should be ![]() $D^I_{const}(G^L_K/A^L_\mathcal {O} N^L_K)$, which is beyond our present method. Nevertheless, in [Reference Su, Zhao and ZhongSZZ20] we considered its decategorification, which is the Iwahori-invariants
$D^I_{const}(G^L_K/A^L_\mathcal {O} N^L_K)$, which is beyond our present method. Nevertheless, in [Reference Su, Zhao and ZhongSZZ20] we considered its decategorification, which is the Iwahori-invariants ![]() $\Pi ^I$ in the principal series representation of
$\Pi ^I$ in the principal series representation of ![]() $G^L_K$. This is the periodic module of the Iwahori–Matsumoto Hecke algebra. Under the isomorphism
$G^L_K$. This is the periodic module of the Iwahori–Matsumoto Hecke algebra. Under the isomorphism ![]() $K_{A\times \mathbb {C}^*}(T^*\mathcal {B})\cong \Pi ^I$ of Hecke-modules, we proved that the
$K_{A\times \mathbb {C}^*}(T^*\mathcal {B})\cong \Pi ^I$ of Hecke-modules, we proved that the ![]() $K$-theory stable basis goes to the normalized characteristic functions of the orbits, and the basis of
$K$-theory stable basis goes to the normalized characteristic functions of the orbits, and the basis of ![]() $A$-fixed points goes to the Casselman basis [Reference CasselmanCas80].
$A$-fixed points goes to the Casselman basis [Reference CasselmanCas80].
The result in the present paper can be seen as a contribution to yet another realization of the same affine braid group action, i.e. it comes from wall-crossings of the ![]() $K$-theory stable bases of
$K$-theory stable bases of ![]() $T^*\mathcal {B}$. Consequently, wall-crossings of the
$T^*\mathcal {B}$. Consequently, wall-crossings of the ![]() $K$-theory stable bases of
$K$-theory stable bases of ![]() $T^*\mathcal {B}$ are equal to the monodromy of the quantum connections. This is in line with the results of [Reference Aganagic and OkounkovAO21] that the monodromy of the quantum difference equations of Nakajima quiver varieties is equal to the wall-crossing of the elliptic stable envelope.
$T^*\mathcal {B}$ are equal to the monodromy of the quantum connections. This is in line with the results of [Reference Aganagic and OkounkovAO21] that the monodromy of the quantum difference equations of Nakajima quiver varieties is equal to the wall-crossing of the elliptic stable envelope.
Now we recall the details of (4) from the above list, following [Reference Braverman, Maulik and OkounkovBMO11].
The quantum connection of ![]() $T^*\mathcal {B}$ is a flat connection on the trivial bundle
$T^*\mathcal {B}$ is a flat connection on the trivial bundle ![]() $H_{G\times \mathbb {C}^*}^*(T^*\mathcal {B})\times A^\vee _\textit {reg}$ on the dual torus
$H_{G\times \mathbb {C}^*}^*(T^*\mathcal {B})\times A^\vee _\textit {reg}$ on the dual torus ![]() $A^\vee$ with the root hyperplanes removed. This connection is equivariant with respect to the Weyl group action, hence descents to a flat connection on
$A^\vee$ with the root hyperplanes removed. This connection is equivariant with respect to the Weyl group action, hence descents to a flat connection on ![]() $A^\vee _\textit {reg}/W$.
$A^\vee _\textit {reg}/W$.
On the other hand, by the work of Lusztig [Reference LusztigLus88], ![]() $H^*_{G\times \mathbb {C}^*}(T^*\mathcal {B})$ can be realized as the polynomial representation
$H^*_{G\times \mathbb {C}^*}(T^*\mathcal {B})$ can be realized as the polynomial representation ![]() $\mathcal {M}_{\xi ,t}$ of the graded affine Hecke algebra, where
$\mathcal {M}_{\xi ,t}$ of the graded affine Hecke algebra, where ![]() $\xi$ is the
$\xi$ is the ![]() $\mathbb {C}^*$-equivariant parameter and
$\mathbb {C}^*$-equivariant parameter and ![]() $t\in {\frak h}^*$ is the
$t\in {\frak h}^*$ is the ![]() $A$-equivariant parameter. For any module of the graded affine Hecke algebra, there is an associated affine Knizhnik–Zamolodchikov connection on the trivial bundle on
$A$-equivariant parameter. For any module of the graded affine Hecke algebra, there is an associated affine Knizhnik–Zamolodchikov connection on the trivial bundle on ![]() $A^\vee _\textit {reg}$, so that derivatives with respect to
$A^\vee _\textit {reg}$, so that derivatives with respect to ![]() $\operatorname {Lie}(A^\vee )={\frak h}^\vee$ are expressed in terms of operators in the graded affine Hecke algebra. Cherednik has studied the monodromy of such a flat connection [Reference CherednikChe05]. For any module
$\operatorname {Lie}(A^\vee )={\frak h}^\vee$ are expressed in terms of operators in the graded affine Hecke algebra. Cherednik has studied the monodromy of such a flat connection [Reference CherednikChe05]. For any module ![]() $M$ of the graded affine Hecke algebra, the monodromy
$M$ of the graded affine Hecke algebra, the monodromy ![]() $\mathcal {I} M$, which a priori is a representation of
$\mathcal {I} M$, which a priori is a representation of ![]() $\pi _1(A^\vee _\textit {reg}/W)\cong B_{\operatorname {aff}}'$ on the fiber of
$\pi _1(A^\vee _\textit {reg}/W)\cong B_{\operatorname {aff}}'$ on the fiber of ![]() $M$, factors through the affine Hecke algebra
$M$, factors through the affine Hecke algebra ![]() ${\mathbb {H}}$.
${\mathbb {H}}$.
In [Reference Braverman, Maulik and OkounkovBMO11], these two flat connections have been identified. In other words, quantum multiplication by a divisor class in ![]() $H^2(T^*\mathcal {B},\mathbb {C})\cong {\frak h}^\vee$ is expressed as taking derivatives with respect to the affine Knizhnik–Zamolodchikov connection. Consequently, it follows from the work of Cherednik that the monodromy
$H^2(T^*\mathcal {B},\mathbb {C})\cong {\frak h}^\vee$ is expressed as taking derivatives with respect to the affine Knizhnik–Zamolodchikov connection. Consequently, it follows from the work of Cherednik that the monodromy ![]() $\mathcal {I} (\mathcal {M}_{\xi ,t})$ is the polynomial representation
$\mathcal {I} (\mathcal {M}_{\xi ,t})$ is the polynomial representation ![]() $M_{q,z}$ of the affine Hecke algebra
$M_{q,z}$ of the affine Hecke algebra ![]() ${\mathbb {H}}$ with
${\mathbb {H}}$ with ![]() $q=\exp (\xi )$ and
$q=\exp (\xi )$ and ![]() $z=\exp (t)$. Moreover, under the natural isomorphism
$z=\exp (t)$. Moreover, under the natural isomorphism ![]() $M_{q,z}\cong K_{G\times \mathbb {C}^*}(T^*\mathcal {B})$, the action of
$M_{q,z}\cong K_{G\times \mathbb {C}^*}(T^*\mathcal {B})$, the action of ![]() ${\mathbb {H}}$ on
${\mathbb {H}}$ on ![]() $M_{q,z}$ coming from the monodromy is further identified with the action on
$M_{q,z}$ coming from the monodromy is further identified with the action on ![]() $K_{G\times \mathbb {C}^*}(T^*\mathcal {B})$ of Kazhdan–Lusztig [Reference Kazhdan and LusztigKL87] and Ginzburg [Reference Chriss and GinzburgCG97]. Extending scalars of the module
$K_{G\times \mathbb {C}^*}(T^*\mathcal {B})$ of Kazhdan–Lusztig [Reference Kazhdan and LusztigKL87] and Ginzburg [Reference Chriss and GinzburgCG97]. Extending scalars of the module ![]() $M_{q,z}$ via the map
$M_{q,z}$ via the map ![]() $K_{G\times \mathbb {C}^*}(\operatorname {pt})\to K_{A\times \mathbb {C}^*}(\operatorname {pt})$, we get an action of
$K_{G\times \mathbb {C}^*}(\operatorname {pt})\to K_{A\times \mathbb {C}^*}(\operatorname {pt})$, we get an action of ![]() $B'_{\operatorname {aff}}$ on
$B'_{\operatorname {aff}}$ on ![]() $K_{A\times \mathbb {C}}(T*\mathcal {B})$, which factors through the
$K_{A\times \mathbb {C}}(T*\mathcal {B})$, which factors through the ![]() ${\mathbb {H}}$-action considered in § 2. In other words, for any
${\mathbb {H}}$-action considered in § 2. In other words, for any ![]() $b\in \pi _1(A^\vee _\textit {reg}/W)\cong B_{\operatorname {aff}}'$, the monodromy operator
$b\in \pi _1(A^\vee _\textit {reg}/W)\cong B_{\operatorname {aff}}'$, the monodromy operator ![]() $b:\mathcal {I} (\mathcal {M}_{\xi ,t})\to \mathcal {I} (\mathcal {M}_{\xi ,t})$ is given by
$b:\mathcal {I} (\mathcal {M}_{\xi ,t})\to \mathcal {I} (\mathcal {M}_{\xi ,t})$ is given by ![]() $\mathcal {I} (\mathcal {M}_{\xi ,t})\cong K_{G\times \mathbb {C}^*}(T^*\mathcal {B})\to K_{G\times \mathbb {C}^*}(T^*\mathcal {B})\cong \mathcal {I} (\mathcal {M}_{\xi ,t})$, the image of
$\mathcal {I} (\mathcal {M}_{\xi ,t})\cong K_{G\times \mathbb {C}^*}(T^*\mathcal {B})\to K_{G\times \mathbb {C}^*}(T^*\mathcal {B})\cong \mathcal {I} (\mathcal {M}_{\xi ,t})$, the image of ![]() $b$ under the projection
$b$ under the projection ![]() $\mathbb {C}[q^\pm ][B'_{\operatorname {aff}}]\to {\mathbb {H}}$.
$\mathbb {C}[q^\pm ][B'_{\operatorname {aff}}]\to {\mathbb {H}}$.
8.2 K-theory wall-crossing  $=$ cohomological monodromy
$=$ cohomological monodromy
Note that ![]() ${\frak h}^\vee _{\mathbb {C},\textit {reg}}/(W_{\operatorname {aff}},\bullet )$ is naturally a covering space of
${\frak h}^\vee _{\mathbb {C},\textit {reg}}/(W_{\operatorname {aff}},\bullet )$ is naturally a covering space of ![]() $A^\vee _\textit {reg}/W$. Let
$A^\vee _\textit {reg}/W$. Let ![]() $\nabla _1$ and
$\nabla _1$ and ![]() $\nabla _2$ be two alcoves in
$\nabla _2$ be two alcoves in ![]() ${\frak h}^\vee _{\mathbb {C},\textit {reg}}$, which are separated by a wall, and
${\frak h}^\vee _{\mathbb {C},\textit {reg}}$, which are separated by a wall, and ![]() $\nabla _1$ is below
$\nabla _1$ is below ![]() $\nabla _2$ in the natural order determined by that on
$\nabla _2$ in the natural order determined by that on ![]() $\Lambda$. Note that this order has been used in Remark 6.3(a), and is an extension of the order used in Theorem 5.1 for
$\Lambda$. Note that this order has been used in Remark 6.3(a), and is an extension of the order used in Theorem 5.1 for ![]() ${\frak C}_+$. Then, the homotopy class of a positive path in
${\frak C}_+$. Then, the homotopy class of a positive path in ![]() ${\frak h}^\vee _{\mathbb {C},\textit {reg}}$, going from a point in
${\frak h}^\vee _{\mathbb {C},\textit {reg}}$, going from a point in ![]() $\nabla _1$ to a point in
$\nabla _1$ to a point in ![]() $\nabla _2$ in the same
$\nabla _2$ in the same ![]() $W_{\operatorname {aff}}$ orbit, determines a unique element [Reference Bezrukavnikov and MirkovićBM13, Lemma 1.8.1]
$W_{\operatorname {aff}}$ orbit, determines a unique element [Reference Bezrukavnikov and MirkovićBM13, Lemma 1.8.1]
Note that we have ![]() $b_{\nabla _3,\nabla _1}=b_{\nabla _3,\nabla _2}b_{\nabla _2,\nabla _1}$,
$b_{\nabla _3,\nabla _1}=b_{\nabla _3,\nabla _2}b_{\nabla _2,\nabla _1}$, ![]() $b_{x\nabla _-, \nabla _-}=\tilde {x}$ for any
$b_{x\nabla _-, \nabla _-}=\tilde {x}$ for any ![]() $x\in W$, and
$x\in W$, and ![]() $b_{x\nabla _-+\lambda ,\nabla _-}=\lambda \widetilde {x}$ for any
$b_{x\nabla _-+\lambda ,\nabla _-}=\lambda \widetilde {x}$ for any ![]() $\lambda \in \Lambda$ and
$\lambda \in \Lambda$ and ![]() $x\in W$ [Reference Bezrukavnikov and MirkovićBM13, Lemma 1.8.1]. The subscripts of
$x\in W$ [Reference Bezrukavnikov and MirkovićBM13, Lemma 1.8.1]. The subscripts of ![]() $b$ here we use are again different from that of [Reference Bezrukavnikov and MirkovićBM13] for the same reason as explained Remark 6.3(a).
$b$ here we use are again different from that of [Reference Bezrukavnikov and MirkovićBM13] for the same reason as explained Remark 6.3(a).
To relate the affine braid group action of Bezrukavnikov and Riche with the monodromy braid group action, we first define the automorphism ![]() $\tau :B'_{\operatorname {aff}}\to B'_{\operatorname {aff}}$,
$\tau :B'_{\operatorname {aff}}\to B'_{\operatorname {aff}}$, ![]() $\widetilde {s_\alpha }\mapsto \widetilde {s_\alpha }$ for
$\widetilde {s_\alpha }\mapsto \widetilde {s_\alpha }$ for ![]() $\alpha \in \Sigma$, and
$\alpha \in \Sigma$, and ![]() $\lambda \mapsto -\lambda$ for
$\lambda \mapsto -\lambda$ for ![]() $\lambda \in \Lambda$. Recall that the action of
$\lambda \in \Lambda$. Recall that the action of ![]() $B_{\operatorname {aff}}$, denoted by
$B_{\operatorname {aff}}$, denoted by ![]() $J^{\operatorname {R}}$, is such that
$J^{\operatorname {R}}$, is such that ![]() $J^{\operatorname {R}}_{ab}=J^{\operatorname {R}}_b\circ J^{\operatorname {R}}_a$. Hence, in case
$J^{\operatorname {R}}_{ab}=J^{\operatorname {R}}_b\circ J^{\operatorname {R}}_a$. Hence, in case ![]() $b_{x\nabla _-+\lambda , \nabla _-}=\lambda \widetilde {x}$,
$b_{x\nabla _-+\lambda , \nabla _-}=\lambda \widetilde {x}$,
 \begin{align*} (J^{\operatorname{R}}_{\tau(b_{x\nabla_-{+}\lambda,\nabla_-})})^{{-}1} &=(J^{\operatorname{R}}_{\tau(\lambda\widetilde{x})})^{{-}1}\\ &=(J^{\operatorname{R}}_{\widetilde{x}}\circ J^{\operatorname{R}}_{-\lambda})^{{-}1}\\ &=J^{\operatorname{R}}_{\lambda}\circ(J^{\operatorname{R}}_{\widetilde{x}})^{{-}1}. \end{align*}
\begin{align*} (J^{\operatorname{R}}_{\tau(b_{x\nabla_-{+}\lambda,\nabla_-})})^{{-}1} &=(J^{\operatorname{R}}_{\tau(\lambda\widetilde{x})})^{{-}1}\\ &=(J^{\operatorname{R}}_{\widetilde{x}}\circ J^{\operatorname{R}}_{-\lambda})^{{-}1}\\ &=J^{\operatorname{R}}_{\lambda}\circ(J^{\operatorname{R}}_{\widetilde{x}})^{{-}1}. \end{align*} For simplicity, the class in the Grothendieck group of the auto-equivalence ![]() $J^{\operatorname {R}}_{\tau (b)}:D^{\operatorname {b}}_{T_{\mathbb {Z}}}(T^*\mathcal {B}_{\mathbb {Z}})\to D^{\operatorname {b}}_{T_{\mathbb {Z}}}(T^*\mathcal {B}_{\mathbb {Z}})$ for
$J^{\operatorname {R}}_{\tau (b)}:D^{\operatorname {b}}_{T_{\mathbb {Z}}}(T^*\mathcal {B}_{\mathbb {Z}})\to D^{\operatorname {b}}_{T_{\mathbb {Z}}}(T^*\mathcal {B}_{\mathbb {Z}})$ for ![]() $b\in \ B_{\operatorname {aff}}$ is denoted by
$b\in \ B_{\operatorname {aff}}$ is denoted by ![]() $[b]$.
$[b]$.
Theorem 8.1 Notations as above. For each pair of alcoves ![]() $\nabla _1$ and
$\nabla _1$ and ![]() $\nabla _2$, the monodromy action of
$\nabla _2$, the monodromy action of ![]() $b_{\nabla _2,\nabla _1}\in \pi _1(A^\vee _\textit {reg}/W)\cong B_{\operatorname {aff}}'$:
$b_{\nabla _2,\nabla _1}\in \pi _1(A^\vee _\textit {reg}/W)\cong B_{\operatorname {aff}}'$:
 \begin{align*} [b_{\nabla_2,\nabla_1}^{{-}1}]:\mathcal{I}(\mathcal{M}_{\xi,t}) \otimes_{K_{G\times\mathbb{C}^*}(pt)}K_{A\times\mathbb{C}^*}(pt)&\cong K_{A\times\mathbb{C}^*}(T^*\mathcal{B})\to K_{A\times\mathbb{C}^*}(T^*\mathcal{B})\\ &\cong\mathcal{I}(\mathcal{M}_{\xi,t})\otimes_{K_{G\times\mathbb{C}^*}(pt)}K_{A\times\mathbb{C}^*}(pt), \end{align*}
\begin{align*} [b_{\nabla_2,\nabla_1}^{{-}1}]:\mathcal{I}(\mathcal{M}_{\xi,t}) \otimes_{K_{G\times\mathbb{C}^*}(pt)}K_{A\times\mathbb{C}^*}(pt)&\cong K_{A\times\mathbb{C}^*}(T^*\mathcal{B})\to K_{A\times\mathbb{C}^*}(T^*\mathcal{B})\\ &\cong\mathcal{I}(\mathcal{M}_{\xi,t})\otimes_{K_{G\times\mathbb{C}^*}(pt)}K_{A\times\mathbb{C}^*}(pt), \end{align*}
sends the set ![]() $\{\mathcal {L}_{-\rho }\otimes \operatorname {stab}^{+,T\mathcal {B},\nabla _1}_w\mid w\in W\}$ to
$\{\mathcal {L}_{-\rho }\otimes \operatorname {stab}^{+,T\mathcal {B},\nabla _1}_w\mid w\in W\}$ to ![]() $\{\mathcal {L}_{-\rho }\otimes \operatorname {stab}^{+,T\mathcal {B},\nabla _2}_w\mid w\in W\}$, up to (explicitly determined) scalars.
$\{\mathcal {L}_{-\rho }\otimes \operatorname {stab}^{+,T\mathcal {B},\nabla _2}_w\mid w\in W\}$, up to (explicitly determined) scalars.
More precisely, assume ![]() $\nabla _1=x\nabla _-+\lambda$ and
$\nabla _1=x\nabla _-+\lambda$ and ![]() $\nabla _2=y\nabla _-+\mu$, with
$\nabla _2=y\nabla _-+\mu$, with ![]() $x,y\in W$ and
$x,y\in W$ and ![]() $\lambda ,\mu \in Q$. Then,
$\lambda ,\mu \in Q$. Then, ![]() $[b_{\nabla _2,\nabla _1}^{-1}]$ sends
$[b_{\nabla _2,\nabla _1}^{-1}]$ sends ![]() $\mathcal {L}_{-\rho }\otimes \operatorname {stab}^{+,T\mathcal {B},\nabla _1}_w$ to
$\mathcal {L}_{-\rho }\otimes \operatorname {stab}^{+,T\mathcal {B},\nabla _1}_w$ to ![]() $e^{w\lambda -wxy^{-1}\mu }\mathcal {L}_{-\rho }\otimes \operatorname {stab}^{+,T\mathcal {B},\nabla _1}_{wxy^{-1}}$.
$e^{w\lambda -wxy^{-1}\mu }\mathcal {L}_{-\rho }\otimes \operatorname {stab}^{+,T\mathcal {B},\nabla _1}_{wxy^{-1}}$.
For example, in the case when alcoves ![]() $\nabla _1$ and
$\nabla _1$ and ![]() $\nabla _2$ are adjacent and separated by a wall
$\nabla _2$ are adjacent and separated by a wall ![]() $H_{x\dot \alpha ^\vee ,0}$ for some
$H_{x\dot \alpha ^\vee ,0}$ for some ![]() $x\in W$ and
$x\in W$ and ![]() $\alpha \in \Sigma$, i.e. there exists
$\alpha \in \Sigma$, i.e. there exists ![]() $\lambda \in \Lambda$ and
$\lambda \in \Lambda$ and ![]() $x\in W$, such that
$x\in W$, such that ![]() $\nabla _1=x\nabla _-$ and
$\nabla _1=x\nabla _-$ and ![]() $\nabla _2=xs_\alpha \nabla _-$. Then
$\nabla _2=xs_\alpha \nabla _-$. Then ![]() $b_{\nabla _2, \nabla _1}=\widetilde {xs_\alpha }\widetilde {x}^{-1}$, and the corresponding operator is
$b_{\nabla _2, \nabla _1}=\widetilde {xs_\alpha }\widetilde {x}^{-1}$, and the corresponding operator is
Proof. Let ![]() $\nabla _1=x\nabla _-+\lambda$. Then, a direct consequence of the definition in § 6.3 is that
$\nabla _1=x\nabla _-+\lambda$. Then, a direct consequence of the definition in § 6.3 is that ![]() ${\frak s}{\frak t}{\frak a}{\frak b}_{\nabla _1}^{\mathbb {Z}}(w)=e^{-w\lambda }J^{\operatorname {R}}_\lambda (J^{\operatorname {R}}_{\tilde {x}})^{-1}{\frak s}{\frak t}{\frak a}{\frak b}_{\nabla _-}^{\mathbb {Z}}(wx)$. Hence, induced K-theory map of the functor
${\frak s}{\frak t}{\frak a}{\frak b}_{\nabla _1}^{\mathbb {Z}}(w)=e^{-w\lambda }J^{\operatorname {R}}_\lambda (J^{\operatorname {R}}_{\tilde {x}})^{-1}{\frak s}{\frak t}{\frak a}{\frak b}_{\nabla _-}^{\mathbb {Z}}(wx)$. Hence, induced K-theory map of the functor ![]() $(J^{\operatorname {R}}_{\tau (b_{x\nabla _-+\lambda ,\nabla _-})})^{-1}$ sends
$(J^{\operatorname {R}}_{\tau (b_{x\nabla _-+\lambda ,\nabla _-})})^{-1}$ sends ![]() $\mathcal {L}_{-\rho }\otimes \operatorname {stab}^{+,T\mathcal {B},\nabla _-}_{wx}$ to
$\mathcal {L}_{-\rho }\otimes \operatorname {stab}^{+,T\mathcal {B},\nabla _-}_{wx}$ to ![]() $e^{-w\lambda }\mathcal {L}_{-\rho }\otimes \operatorname {stab}^{+,T\mathcal {B},\nabla _1}_w$ by Theorem 6.4.
$e^{-w\lambda }\mathcal {L}_{-\rho }\otimes \operatorname {stab}^{+,T\mathcal {B},\nabla _1}_w$ by Theorem 6.4.
The analysis above implies that ![]() $[b_{\nabla _1,\nabla _-}^{-1}]$, which is the induced K-theory map of the functor
$[b_{\nabla _1,\nabla _-}^{-1}]$, which is the induced K-theory map of the functor ![]() $(J^{\operatorname {R}}_{\tau (b_{x\nabla _-+\lambda ,\nabla _-})})^{-1}$, sends
$(J^{\operatorname {R}}_{\tau (b_{x\nabla _-+\lambda ,\nabla _-})})^{-1}$, sends ![]() $\mathcal {L}_{-\rho }\otimes \operatorname {stab}^{+,T\mathcal {B},\nabla _-}_{wx}$ to
$\mathcal {L}_{-\rho }\otimes \operatorname {stab}^{+,T\mathcal {B},\nabla _-}_{wx}$ to ![]() $e^{-w\lambda }\mathcal {L}_{-\rho }\otimes \operatorname {stab}^{+,T\mathcal {B},\nabla _1}_w$. Similarly,
$e^{-w\lambda }\mathcal {L}_{-\rho }\otimes \operatorname {stab}^{+,T\mathcal {B},\nabla _1}_w$. Similarly, ![]() $[b_{\nabla _2,\nabla _-}^{-1}]$ which is the induced K-theory map of the functor
$[b_{\nabla _2,\nabla _-}^{-1}]$ which is the induced K-theory map of the functor ![]() $(J^{\operatorname {R}}_{\tau (b_{y\nabla _-+\mu ,\nabla _-})})^{-1}$, sends
$(J^{\operatorname {R}}_{\tau (b_{y\nabla _-+\mu ,\nabla _-})})^{-1}$, sends ![]() $\mathcal {L}_{-\rho }\otimes \operatorname {stab}^{+,T\mathcal {B},\nabla _-}_{vy}$ to
$\mathcal {L}_{-\rho }\otimes \operatorname {stab}^{+,T\mathcal {B},\nabla _-}_{vy}$ to ![]() $e^{-v\mu }\mathcal {L}_{-\rho }\otimes \operatorname {stab}^{+,T\mathcal {B},\nabla _2}_v$. Hence,
$e^{-v\mu }\mathcal {L}_{-\rho }\otimes \operatorname {stab}^{+,T\mathcal {B},\nabla _2}_v$. Hence, ![]() $[b_{\nabla _2,\nabla _1}^{-1}]=[b_{\nabla _2,\nabla _-}^{-1}][b_{\nabla _1,\nabla _-}]$ sends
$[b_{\nabla _2,\nabla _1}^{-1}]=[b_{\nabla _2,\nabla _-}^{-1}][b_{\nabla _1,\nabla _-}]$ sends ![]() $\mathcal {L}_{-\rho }\otimes \operatorname {stab}^{+,T\mathcal {B},\nabla _1}_w$ to
$\mathcal {L}_{-\rho }\otimes \operatorname {stab}^{+,T\mathcal {B},\nabla _1}_w$ to ![]() $e^{w\lambda -wxy^{-1}\mu }\mathcal {L}_{-\rho }\otimes \operatorname {stab}^{+,T\mathcal {B},\nabla _1}_{wxy^{-1}}$.
$e^{w\lambda -wxy^{-1}\mu }\mathcal {L}_{-\rho }\otimes \operatorname {stab}^{+,T\mathcal {B},\nabla _1}_{wxy^{-1}}$.
A much more general phenomenon has been expected for symplectic resolutions. Namely, for a symplectic resolution ![]() $X$, there are derived auto-equivalences of
$X$, there are derived auto-equivalences of ![]() $D^{\operatorname {b}}(X)$ that come from quantizations of
$D^{\operatorname {b}}(X)$ that come from quantizations of ![]() $X$ [Reference KaledinKal08]. These derived auto-equivalences are expected to be related to the monodromy of the quantum connection of
$X$ [Reference KaledinKal08]. These derived auto-equivalences are expected to be related to the monodromy of the quantum connection of ![]() $X$ [Reference OkounkovOko18a]. For quiver varieties, such results are proven in unpublished work of Bezrukavnikov and Okounkov. In future works we will explore in more examples of symplectic resolutions the categorification of the
$X$ [Reference OkounkovOko18a]. For quiver varieties, such results are proven in unpublished work of Bezrukavnikov and Okounkov. In future works we will explore in more examples of symplectic resolutions the categorification of the ![]() $K$-theoretic stable bases in terms of standard objects of the quantizations.
$K$-theoretic stable bases in terms of standard objects of the quantizations.
Acknowledgements
C.S. benefited a lot from various discussions with R. Bezrukavnikov, A. Okounkov, S. Riche and E. Vasserot. He would also like to thank the I.H.E.S. for providing excellent research environment. C.Z. would like to thank C. Lenart for helpful conversations. A part of the paper was prepared when G.Z. was affiliated to the Institute of Science and Technology Austria, Hausel Group, supported by the Advanced Grant Arithmetic and Physics of Higgs moduli spaces No. 320593 of the European Research Council. Another part was prepared when G.Z. was under the support of the Australian Research Council via the award DE190101222. We thank the anonymous referee for many useful suggestions.
Appendix A. Wall-crossings in the example of  $\operatorname {SL}(3,\mathbb {C})$
$\operatorname {SL}(3,\mathbb {C})$
In this appendix, we compute some wall-crossing matrix coefficients when ![]() $G=\operatorname {SL}(3,\mathbb {C})$.
$G=\operatorname {SL}(3,\mathbb {C})$.

Figure A.1. Alcoves of ![]() ${\rm SL}(3,\mathbb {C})$.
${\rm SL}(3,\mathbb {C})$.
A.1 Crossing a simple wall
There are two simple roots ![]() $\alpha _1, \alpha _2$ and another positive root
$\alpha _1, \alpha _2$ and another positive root ![]() $\alpha _3=\alpha _1+\alpha _2$. Let
$\alpha _3=\alpha _1+\alpha _2$. Let ![]() $s_i=s_{\alpha _i}$. The identity element of
$s_i=s_{\alpha _i}$. The identity element of ![]() $W$ is denoted by
$W$ is denoted by ![]() $e$. The fundamental weights
$e$. The fundamental weights ![]() $\omega _i$ are noted by the arrows. Let
$\omega _i$ are noted by the arrows. Let ![]() $\nabla _1=s_{1}\nabla _+, \nabla _2=\nabla _+-\varpi _1$, and
$\nabla _1=s_{1}\nabla _+, \nabla _2=\nabla _+-\varpi _1$, and ![]() $\nabla _3=\nabla _2+\varpi _2$. See Figure A.1.
$\nabla _3=\nabla _2+\varpi _2$. See Figure A.1.
We consider the dominant chamber ![]() ${\frak C}_+$ and polarization
${\frak C}_+$ and polarization ![]() $T\mathcal {B}$, and compute
$T\mathcal {B}$, and compute ![]() $f_y^{\nabla _1\leftarrow \nabla _+}$.
$f_y^{\nabla _1\leftarrow \nabla _+}$.
We first cross ![]() $H_{\alpha _3^\vee , 0}$, i.e.
$H_{\alpha _3^\vee , 0}$, i.e. ![]() $\nabla _1\rightarrow \nabla _2$. There are two ways to do this:
$\nabla _1\rightarrow \nabla _2$. There are two ways to do this: ![]() $\nabla _1\rightarrow \nabla _+\rightarrow \nabla _2$ and
$\nabla _1\rightarrow \nabla _+\rightarrow \nabla _2$ and ![]() $\nabla _1\rightarrow \nabla _3\rightarrow \nabla _2$. The second steps of both ways are done by translations. Then by Lemma 3.5 and (15), we have the following formulas corresponding to the two ways:
$\nabla _1\rightarrow \nabla _3\rightarrow \nabla _2$. The second steps of both ways are done by translations. Then by Lemma 3.5 and (15), we have the following formulas corresponding to the two ways:
 \begin{align} \operatorname{stab}^{+, {\nabla_1}}_{y}&=\left\{\begin{array}{@{}ll} \operatorname{stab}^{+, {\nabla_+}}_{y}+f_y^{\nabla_1\leftarrow \nabla_+}\operatorname{stab}^{+, {\nabla_+}}_{ys_{1}} & \text{if } ys_{1}< y,\\ \operatorname{stab}^{+, {\nabla_+}}_{y} & \text{if } ys_{1}>y, \end{array}\right.\nonumber\\ &=\left\{\begin{array}{@{}ll} e^{{-}y\varpi_1}\mathcal{L}_{\varpi_1}\otimes\operatorname{stab}^{+, {\nabla_2}}_{y}+e^{{-}ys_{1}\varpi_1}f^{\nabla_1\leftarrow \nabla_+}_y\mathcal{L}_{\varpi_1}\otimes\operatorname{stab}^{+, {\nabla_2}}_{ys_{1}} & \text{if } ys_{1}< y,\\ e^{{-}y\varpi_1}\mathcal{L}_{\varpi_1}\otimes\operatorname{stab}^{+, {\nabla_2}}_{y} & \text{if } ys_{1}>y, \end{array}\right.\end{align}
\begin{align} \operatorname{stab}^{+, {\nabla_1}}_{y}&=\left\{\begin{array}{@{}ll} \operatorname{stab}^{+, {\nabla_+}}_{y}+f_y^{\nabla_1\leftarrow \nabla_+}\operatorname{stab}^{+, {\nabla_+}}_{ys_{1}} & \text{if } ys_{1}< y,\\ \operatorname{stab}^{+, {\nabla_+}}_{y} & \text{if } ys_{1}>y, \end{array}\right.\nonumber\\ &=\left\{\begin{array}{@{}ll} e^{{-}y\varpi_1}\mathcal{L}_{\varpi_1}\otimes\operatorname{stab}^{+, {\nabla_2}}_{y}+e^{{-}ys_{1}\varpi_1}f^{\nabla_1\leftarrow \nabla_+}_y\mathcal{L}_{\varpi_1}\otimes\operatorname{stab}^{+, {\nabla_2}}_{ys_{1}} & \text{if } ys_{1}< y,\\ e^{{-}y\varpi_1}\mathcal{L}_{\varpi_1}\otimes\operatorname{stab}^{+, {\nabla_2}}_{y} & \text{if } ys_{1}>y, \end{array}\right.\end{align} \begin{align} \operatorname{stab}^{+, {\nabla_1}}_{y}&=\left\{\begin{array}{@{}ll} \operatorname{stab}^{+, {\nabla_3}}_{y}+f_y^{\nabla_1\leftarrow \nabla_3}\operatorname{stab}^{+, {\nabla_3}}_{ys_{2}} & \text{if } ys_{2}< y,\\ \operatorname{stab}^{+, {\nabla_3}}_{y} & \text{if } ys_{2}>y, \end{array}\right.\nonumber\\ &=\left\{\begin{array}{@{}ll} e^{{-}y\varpi_2}\mathcal{L}_{\varpi_2}\otimes\operatorname{stab}^{+, {\nabla_2}}_{y}+e^{{-}ys_{2}\varpi_2}f_y^{\nabla_1\leftarrow \nabla_3}\mathcal{L}_{\varpi_2}\otimes\operatorname{stab}^{+, {\nabla_2}}_{ys_{2}} & \text{if } ys_{2}< y,\\ e^{{-}y\varpi_2}\mathcal{L}_{\varpi_2}\otimes\operatorname{stab}^{+, {\nabla_2}}_{y} & \text{if } ys_{2}>y. \end{array}\right. \end{align}
\begin{align} \operatorname{stab}^{+, {\nabla_1}}_{y}&=\left\{\begin{array}{@{}ll} \operatorname{stab}^{+, {\nabla_3}}_{y}+f_y^{\nabla_1\leftarrow \nabla_3}\operatorname{stab}^{+, {\nabla_3}}_{ys_{2}} & \text{if } ys_{2}< y,\\ \operatorname{stab}^{+, {\nabla_3}}_{y} & \text{if } ys_{2}>y, \end{array}\right.\nonumber\\ &=\left\{\begin{array}{@{}ll} e^{{-}y\varpi_2}\mathcal{L}_{\varpi_2}\otimes\operatorname{stab}^{+, {\nabla_2}}_{y}+e^{{-}ys_{2}\varpi_2}f_y^{\nabla_1\leftarrow \nabla_3}\mathcal{L}_{\varpi_2}\otimes\operatorname{stab}^{+, {\nabla_2}}_{ys_{2}} & \text{if } ys_{2}< y,\\ e^{{-}y\varpi_2}\mathcal{L}_{\varpi_2}\otimes\operatorname{stab}^{+, {\nabla_2}}_{y} & \text{if } ys_{2}>y. \end{array}\right. \end{align}
Comparing (A.1) and (A.2) with ![]() $y=s_{1}$, and restricting to the fixed point
$y=s_{1}$, and restricting to the fixed point ![]() $e$, we get
$e$, we get
By the normalization formula (4),
Due to Lemma 3.1 and [Reference Su, Zhao and ZhongSZZ20, Proposition 3.6(3)], if ![]() $ws_{\alpha _i}>w$, we have the following recursion for any
$ws_{\alpha _i}>w$, we have the following recursion for any ![]() $u\in W$:
$u\in W$:
 \begin{equation} q^{{1/2}}\operatorname{stab}^{+, {\nabla_-}}_{ws_{\alpha_i}}|_u=\frac{q-1}{1-e^{u\alpha_i}} \operatorname{stab}^{+, {\nabla_-}}_{w}\bigg|_u-\frac{e^{u\alpha_i}-q}{1-e^{{-}u\alpha_i}} \operatorname{stab}^{+, {\nabla_-}}_{w}\bigg|_{us_{\alpha_i}}. \end{equation}
\begin{equation} q^{{1/2}}\operatorname{stab}^{+, {\nabla_-}}_{ws_{\alpha_i}}|_u=\frac{q-1}{1-e^{u\alpha_i}} \operatorname{stab}^{+, {\nabla_-}}_{w}\bigg|_u-\frac{e^{u\alpha_i}-q}{1-e^{{-}u\alpha_i}} \operatorname{stab}^{+, {\nabla_-}}_{w}\bigg|_{us_{\alpha_i}}. \end{equation}
Let ![]() $w=u=e$ and
$w=u=e$ and ![]() $\alpha _i=\alpha _1$. We get
$\alpha _i=\alpha _1$. We get
Therefore,
Hence, solving from (A.3), we get
By Lemma 3.7, we also have ![]() $f_{y}^{\nabla _-\leftarrow s_1\nabla _-}=f_y^{\nabla _1\leftarrow \nabla _+}$.
$f_{y}^{\nabla _-\leftarrow s_1\nabla _-}=f_y^{\nabla _1\leftarrow \nabla _+}$.
A.2 Crossing a non-simple wall
We calculate the constants ![]() $f_{s_1s_2}^{\nabla _2\leftarrow \nabla _1}$,
$f_{s_1s_2}^{\nabla _2\leftarrow \nabla _1}$, ![]() $f_{s_2s_1}^{\nabla _2\leftarrow \nabla _1}$ and
$f_{s_2s_1}^{\nabla _2\leftarrow \nabla _1}$ and ![]() $f_{s_3}^{\nabla _2\leftarrow \nabla _1}$. Let
$f_{s_3}^{\nabla _2\leftarrow \nabla _1}$. Let ![]() $y=s_1s_2$ in (A.1). We get
$y=s_1s_2$ in (A.1). We get
By Lemma 3.5 and the identity ![]() $f_{s_1s_2}^{\nabla _2\leftarrow \nabla _1}=-f_{s_1s_2}^{\nabla _1\leftarrow \nabla _2}$, we have
$f_{s_1s_2}^{\nabla _2\leftarrow \nabla _1}=-f_{s_1s_2}^{\nabla _1\leftarrow \nabla _2}$, we have
Comparing the two identities and restricting to the fixed point ![]() $s_2$, we get
$s_2$, we get
So we just need to compute ![]() $\operatorname {stab}^{+, {\nabla _2}}_{s_2}|_{s_2}$ and
$\operatorname {stab}^{+, {\nabla _2}}_{s_2}|_{s_2}$ and ![]() $\operatorname {stab}^{+, {\nabla _2}}_{s_1s_2}|_{s_2}$. By (A.4) with
$\operatorname {stab}^{+, {\nabla _2}}_{s_1s_2}|_{s_2}$. By (A.4) with ![]() $w=s_1, i=2, u=s_2$, we get
$w=s_1, i=2, u=s_2$, we get
By Lemma 3.1,
By the translation formula (15),
By the normalization formula (4),
Therefore, by using (A.5)
By symmetry of ![]() $\alpha _1$ and
$\alpha _1$ and ![]() $\alpha _2$, we have
$\alpha _2$, we have
Let us compute ![]() $f_{s_1s_2s_1}^{\nabla _2\leftarrow \nabla _1}$. By Lemma 3.5, we have
$f_{s_1s_2s_1}^{\nabla _2\leftarrow \nabla _1}$. By Lemma 3.5, we have
Hence, we only need to know ![]() $\operatorname {stab}^{+, {\nabla _1}}_{s_1s_2s_1}|_{e}$ and
$\operatorname {stab}^{+, {\nabla _1}}_{s_1s_2s_1}|_{e}$ and ![]() $\operatorname {stab}^{+, {\nabla _2}}_{s_1s_2s_1}|_{e}$. We compute
$\operatorname {stab}^{+, {\nabla _2}}_{s_1s_2s_1}|_{e}$. We compute ![]() $\operatorname {stab}^{+, {\nabla _-}}_{s_1s_2s_1}|_{e}$ first. By (A.4) with
$\operatorname {stab}^{+, {\nabla _-}}_{s_1s_2s_1}|_{e}$ first. By (A.4) with ![]() $w=s_{1}s_2, \alpha _i=\alpha _2,u=e$, we get
$w=s_{1}s_2, \alpha _i=\alpha _2,u=e$, we get
 \begin{align*} q^{{1/2}}\operatorname{stab}^{+, {\nabla_-}}_{s_1s_2s_1}|_e&=\frac{q-1}{1-e^{\alpha_1}}\operatorname{stab}^{+, {\nabla_-}}_{s_1s_2}\bigg|_e- \frac{e^{\alpha_1}-q}{1-e^{-\alpha_1}}\operatorname{stab}^{+, {\nabla_-}}_{s_1s_2s_1}\bigg|_{s_1}\\ &=\frac{q-1}{1-e^{\alpha_1}}q^{{-}1}(q-1)^2(1-e^{\alpha_3})-\frac{e^{\alpha_1}-q}{1-e^{-\alpha_1}}(1-q^{{-}1})(1-e^{\alpha_2})(q-e^{-\alpha_1})\\ &=(1-q^{{-}1})(q^2+1+qe^{\alpha_3}-qe^{\alpha_2}-q-1e^{\alpha_1}). \end{align*}
\begin{align*} q^{{1/2}}\operatorname{stab}^{+, {\nabla_-}}_{s_1s_2s_1}|_e&=\frac{q-1}{1-e^{\alpha_1}}\operatorname{stab}^{+, {\nabla_-}}_{s_1s_2}\bigg|_e- \frac{e^{\alpha_1}-q}{1-e^{-\alpha_1}}\operatorname{stab}^{+, {\nabla_-}}_{s_1s_2s_1}\bigg|_{s_1}\\ &=\frac{q-1}{1-e^{\alpha_1}}q^{{-}1}(q-1)^2(1-e^{\alpha_3})-\frac{e^{\alpha_1}-q}{1-e^{-\alpha_1}}(1-q^{{-}1})(1-e^{\alpha_2})(q-e^{-\alpha_1})\\ &=(1-q^{{-}1})(q^2+1+qe^{\alpha_3}-qe^{\alpha_2}-q-1e^{\alpha_1}). \end{align*}
By Lemma 3.1, we can compute ![]() $\operatorname {stab}^{+, {\nabla _+}}_{s_1s_2s_1}|_e$, which, together with the formula
$\operatorname {stab}^{+, {\nabla _+}}_{s_1s_2s_1}|_e$, which, together with the formula ![]() $\nabla _2=\nabla _+-\omega _1$, can be used to get
$\nabla _2=\nabla _+-\omega _1$, can be used to get
Finally, from ![]() $\nabla _1=\nabla _-+\omega _2$, we can get
$\nabla _1=\nabla _-+\omega _2$, we can get
Therefore,
 \begin{align*} f_{s_2s_1s_2}^{\nabla_2\leftarrow \nabla_1}&=\frac{\operatorname{stab}^{+, {\nabla_2}}_{s_1s_2s_1}|_e-\operatorname{stab}^{+, {\nabla_1}}_{s_1s_2s_1}|_e}{\operatorname{stab}^{+, {\nabla_1}}_{e}|_e}\\ &=(q^{{1/2}}-q^{-{1/2}})\frac{e^{\alpha_3}(e^{-\alpha_3}-e^{-\alpha_2}-e^{-\alpha_1}-e^{\alpha_3}+e^{\alpha_2}+e^{\alpha_1})}{(1-e^{\alpha_1})(1-e^{\alpha_2})(1-e^{\alpha_3})}\\ &=(q^{{1/2}}-q^{-{1/2}}). \end{align*}
\begin{align*} f_{s_2s_1s_2}^{\nabla_2\leftarrow \nabla_1}&=\frac{\operatorname{stab}^{+, {\nabla_2}}_{s_1s_2s_1}|_e-\operatorname{stab}^{+, {\nabla_1}}_{s_1s_2s_1}|_e}{\operatorname{stab}^{+, {\nabla_1}}_{e}|_e}\\ &=(q^{{1/2}}-q^{-{1/2}})\frac{e^{\alpha_3}(e^{-\alpha_3}-e^{-\alpha_2}-e^{-\alpha_1}-e^{\alpha_3}+e^{\alpha_2}+e^{\alpha_1})}{(1-e^{\alpha_1})(1-e^{\alpha_2})(1-e^{\alpha_3})}\\ &=(q^{{1/2}}-q^{-{1/2}}). \end{align*}