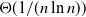1. Introduction
1.1. Motivation and history
The jigsaw percolation process was introduced by Brummitt et al. Reference Brummitt, Chatterjee, Dey and Sivakoff[7] as a model for how a group of people might collectively solve a problem which would be insurmountable individually. The premise is that each person has a piece of a puzzle (or some knowledge, idea, or expertise) and the pieces must be combined in a certain way to solve the puzzle.
This is modelled using two graphs on a common vertex set: a red people graph with an edge if the two people know or collaborate with each other; and a blue puzzle graph if the two corresponding pieces of the puzzle can be combined. If a pair of vertices are connected by both a red and a blue edge, the two corresponding people share their information—modelled in the graphs by merging the two vertices into one cluster. Subsequently, two clusters are merged if a red and a blue edge runs between them. Thus, once parts of the puzzle have already been assembled, they become easier to merge. The process continues until no additional merges are possible. If it ends with one single cluster this indicates that the puzzle has been solved, in which case we say that the process percolates. The process is formally defined in Section 1.4.
This process was first studied by Brummitt et al. Reference Brummitt, Chatterjee, Dey and Sivakoff[7] and subsequently by Gravner and Sivakoff Reference Gravner and Sivakoff[11]. They considered various deterministic possibilities for the blue graph and random possibilities for the red graph, and determined some necessary and some sufficient conditions for the process to percolate with high probability (w.h.p.), meaning with probability tending to 1 as the number of vertices n tends to ![]() $\infty.$
$\infty.$
Bollobás et al. Reference Bollobás, Riordan, Slivken and Smith[5] then considered the case when both the red and blue graphs are random. Given a natural number n and a real number ![]() $p\in [0,1]$, the Erdös–Rényi binomial random graph G(n,p) is a graph on vertex set
$p\in [0,1]$, the Erdös–Rényi binomial random graph G(n,p) is a graph on vertex set ![]() $[n] :\!=\{1,2,\ldots,n\}$ in which each pair of vertices forms an edge with probability p independently. Consider the binomial random graphs
$[n] :\!=\{1,2,\ldots,n\}$ in which each pair of vertices forms an edge with probability p independently. Consider the binomial random graphs ![]() $G_1=G(n,p_1)$ and independently
$G_1=G(n,p_1)$ and independently ![]() $G_2=G(n,p_2)$ on the same vertex set. The random double graph created in this way is denoted by
$G_2=G(n,p_2)$ on the same vertex set. The random double graph created in this way is denoted by ![]() $G(n,p_1,p_2)$. For brevity, we refer to the jigsaw process rather than the jigsaw percolation process.
$G(n,p_1,p_2)$. For brevity, we refer to the jigsaw process rather than the jigsaw percolation process.
Theorem 1.1. ([5].) There exists a constant c such that the following statements hold.
(i) If
 $p_1p_2 \lt {1}/{(cn\ln n)}$ then w.h.p. the jigsaw process on
$p_1p_2 \lt {1}/{(cn\ln n)}$ then w.h.p. the jigsaw process on  $G(n,p_1,p_2)$ does not percolate.
$G(n,p_1,p_2)$ does not percolate.(ii) If
 $p_1p_2 > {c}/{(n\ln n)}$ and
$p_1p_2 > {c}/{(n\ln n)}$ and  $p_1,p_2\ge {c\ln n}/{n}$, then w.h.p. the jigsaw process on
$p_1,p_2\ge {c\ln n}/{n}$, then w.h.p. the jigsaw process on  $G(n,p_1, p_2)$ percolates.
$G(n,p_1, p_2)$ percolates.
In other words, percolation of the jigsaw process undergoes a phase transition when the product ![]() $p_1p_2$ has order
$p_1p_2$ has order ![]() ${1}/{(n\ln n)}$. Note that connectedness of each graph is a necessary condition for percolation, which is the reason for the additional assumption in the supercritical case (statement (ii)): both
${1}/{(n\ln n)}$. Note that connectedness of each graph is a necessary condition for percolation, which is the reason for the additional assumption in the supercritical case (statement (ii)): both ![]() $p_1$ and
$p_1$ and ![]() $p_2$ must be larger than
$p_2$ must be larger than ![]() ${\ln n}/{n}$, which is the threshold for connectedness, as first proved by Erdös and Rényi Reference Erdös and Rényi[10].
${\ln n}/{n}$, which is the threshold for connectedness, as first proved by Erdös and Rényi Reference Erdös and Rényi[10].
Indeed Buldyrev et al. Reference Buldyrev, Parshani, Paul, Stanley and Havlin[8] considered a related process, in which a set of vertices percolates if the graph spanned by these vertices is connected both in the red and the blue graph.
Theorem 1.1 has subsequently been extended in various directions. Bollobás et al. Reference Bollobás, Cooley, Kang and Koch[4] proved a generalisation to k-uniform hypergraphs and a jigsaw percolation process on the j-sets for each ![]() $1\le j \le k-1$. In another direction, Cooley and Gutiérrez Reference Cooley and Gutiérrez[9] proved an analogous result for a set of r graphs on a common vertex set, where
$1\le j \le k-1$. In another direction, Cooley and Gutiérrez Reference Cooley and Gutiérrez[9] proved an analogous result for a set of r graphs on a common vertex set, where ![]() $2\le r =o(\sqrt{\ln \ln n})$.
$2\le r =o(\sqrt{\ln \ln n})$.
1.2. Main theorem
All of the results previously described (except for two special cases in Reference Gravner and Sivakoff[11]) determine their thresholds only up to a multiplicative constant. In this paper we strengthen the result of Bollobás et al. Reference Bollobás, Riordan, Slivken and Smith[5] by determining the precise location of the threshold.
Theorem 1.2. Let ![]() $\varepsilon>0$ be any constant.
$\varepsilon>0$ be any constant.
(i) If
 $p_1p_2\le {(1-\varepsilon)}/{(4n\ln n)}$ then w.h.p. the jigsaw process on
$p_1p_2\le {(1-\varepsilon)}/{(4n\ln n)}$ then w.h.p. the jigsaw process on  $G(n,p_1,p_2)$ does not percolate.
$G(n,p_1,p_2)$ does not percolate.(ii) If
 $p_1p_2\ge {(1+\varepsilon)}/{(4n\ln n)}$ and
$p_1p_2\ge {(1+\varepsilon)}/{(4n\ln n)}$ and  $p_1,p_2 \geq {\ln n}/{n}$, then conditioned on
$p_1,p_2 \geq {\ln n}/{n}$, then conditioned on  $G_1,G_2$ being connected, w.h.p. the jigsaw process on
$G_1,G_2$ being connected, w.h.p. the jigsaw process on  $G(n,p_1,p_2)$ percolates.
$G(n,p_1,p_2)$ percolates.
Let us observe that the jigsaw process has a natural generalisation to any number of graphs on a common vertex set (see Reference Cooley and Gutiérrez[9]), and, in particular, the analogous process on just one graph would percolate if and only if the graph is connected. Thus, we may view jigsaw percolation as a measure of whether two graphs on a common vertex set are jointly connected. In this way, Theorem 1.2 may be considered a double-graph analogue of the classical result of Erdös and Rényi Reference Erdös and Rényi[10] on the threshold for connectedness of a random graph.
1.3. Proof strategy
For random graphs, the famous hitting time result of Bollobás and Thomason Reference Bollobás and Thomason[3] relates the threshold for connectedness of a random graph to the disappearance of the last isolated vertex, implying that the critical obstruction for connectedness of random graphs is the minimal one, and, in particular, whether a random graph is connected or not is essentially determined by local conditions. In contrast, the critical obstructions for jigsaw percolation on at least two graphs are not local ones—in fact they are of size ![]() $\Theta({\ln}\ n)$. This makes determining the threshold, and the proofs of both subcritical and supercritical cases, significantly more complex.
$\Theta({\ln}\ n)$. This makes determining the threshold, and the proofs of both subcritical and supercritical cases, significantly more complex.
The proof strategies for both the subcritical and supercritical cases of Theorem 1.2 are influenced by the fact that there is a bottleneck in the jigsaw process. More precisely, if any cluster reaches size around ![]() ${1}/{(2np_1p_2)}$, then it is large enough that w.h.p. it will go on to incorporate all vertices. However, for small
${1}/{(2np_1p_2)}$, then it is large enough that w.h.p. it will go on to incorporate all vertices. However, for small ![]() $p_1p_2$, no cluster will reach this size. In fact, the size of the largest cluster is approximately the smallest positive solution of the implicit equation
$p_1p_2$, no cluster will reach this size. In fact, the size of the largest cluster is approximately the smallest positive solution of the implicit equation ![]() $2xN \mathrm{e}^{-xN}=n^{-1/x}$, where
$2xN \mathrm{e}^{-xN}=n^{-1/x}$, where ![]() $N=np_1p_2$, which reaches
$N=np_1p_2$, which reaches ![]() ${1}/{(2np_1p_2)}$ when
${1}/{(2np_1p_2)}$ when ![]() $p_1p_2$ is
$p_1p_2$ is ![]() ${1}/{(4n\ln n)}$, i.e. at the threshold for percolation. Thus, there is a bottleneck in the process at size around
${1}/{(4n\ln n)}$, i.e. at the threshold for percolation. Thus, there is a bottleneck in the process at size around ![]() $2\ln n$. Therefore, in the subcritical case we will prove that w.h.p. no percolating set has size at least
$2\ln n$. Therefore, in the subcritical case we will prove that w.h.p. no percolating set has size at least ![]() $2\ln n$. On the other hand, in the supercritical case, the main difficulty is to show that w.h.p. some percolating sets reach size slightly larger than
$2\ln n$. On the other hand, in the supercritical case, the main difficulty is to show that w.h.p. some percolating sets reach size slightly larger than ![]() $2\ln n$, after which it is relatively straightforward to show that, in fact, w.h.p. one of these sets will also percolate with all remaining vertices.
$2\ln n$, after which it is relatively straightforward to show that, in fact, w.h.p. one of these sets will also percolate with all remaining vertices.
1.4. The jigsaw process
We now formally introduce the jigsaw process. A double graph is a triple ![]() $(V,E_1,E_2)$, where V is a set of vertices and, for
$(V,E_1,E_2)$, where V is a set of vertices and, for ![]() $i=1,2,$ we have
$i=1,2,$ we have ![]() ${E_i} \subset \left( {_2^V} \right)$. In other words,
${E_i} \subset \left( {_2^V} \right)$. In other words, ![]() $(V,E_1)$ and
$(V,E_1)$ and ![]() $(V,E_2)$ are both graphs on a common vertex set.
$(V,E_2)$ are both graphs on a common vertex set.
Algorithm 1.1. (Jigsaw process.)
Input: Double graph ![]() $(V,E_1,E_2)$.
$(V,E_1,E_2)$.
Set ![]() $i=0$,
$i=0$, ![]() $V^{(0)}=V$,
$V^{(0)}=V$, ![]() $E_1^{(0)}=E_1$ and
$E_1^{(0)}=E_1$ and ![]() $E_2^{(0)}=E_2$.
$E_2^{(0)}=E_2$.
Set ![]() $H^{(0)}$ to be the auxiliary graph
$H^{(0)}$ to be the auxiliary graph ![]() $(V^{(0)},E_1^{(0)}\cap
E_2^{(0)})$.
$(V^{(0)},E_1^{(0)}\cap
E_2^{(0)})$.
while ![]() $E\left( {{H^{\left( i \right)}}} \right) \ne \emptyset$ do
$E\left( {{H^{\left( i \right)}}} \right) \ne \emptyset$ do
Set ![]() $V^{(i+1)}$ to be the set of components of
$V^{(i+1)}$ to be the set of components of ![]() $H^{(i)}$.
$H^{(i)}$.
For ![]() $C,D\in V^{(i+1)}$ and
$C,D\in V^{(i+1)}$ and ![]() $j=1,2$ let
$j=1,2$ let ![]() $\{C,D\}\in E_j^{(i+1)}$ if and only if there is at least one edge between C and D in
$\{C,D\}\in E_j^{(i+1)}$ if and only if there is at least one edge between C and D in ![]() $E_j^{(i)}$.
$E_j^{(i)}$.
Set ![]() $H^{(i+1)}$ to be the auxiliary graph
$H^{(i+1)}$ to be the auxiliary graph ![]() $(V^{(i+1)},E_1^{(i+1)}\cap
E_2^{(i+1)})$.
$(V^{(i+1)},E_1^{(i+1)}\cap
E_2^{(i+1)})$.
Proceed to step ![]() $i+1$.
$i+1$.
end
Output: ![]() $V^{(i)}$.
$V^{(i)}$.
Note that the process always terminates since ![]() $|V^{(i)}|$ is always positive, but strictly decreasing with i. We say that the jigsaw process percolates if at the end of the process
$|V^{(i)}|$ is always positive, but strictly decreasing with i. We say that the jigsaw process percolates if at the end of the process ![]() $V^{(i)}$ contains exactly one vertex.
$V^{(i)}$ contains exactly one vertex.
1.5. Paper overview
The proofs of both the subcritical and supercritical cases are based on showing that, for k in a suitable range, the probability that there exists a percolating set of size ![]() $k+1$ is approximately
$k+1$ is approximately
Very roughly, ![]() ${\left( {2kn} \right)^{k + 1}}$ is the number of configurations on
${\left( {2kn} \right)^{k + 1}}$ is the number of configurations on ![]() $k+1$ vertices (within a set of n vertices) that can make these k vertices a percolating set,
$k+1$ vertices (within a set of n vertices) that can make these k vertices a percolating set, ![]() ${\left( {{p_1}{p_2}} \right)^k}$ is the probability that the relevant edges are present, while
${\left( {{p_1}{p_2}} \right)^k}$ is the probability that the relevant edges are present, while ![]() $\mathrm{e}^{-k^2np_1p_2}$ is the probability that this percolating set would actually be obtained (with an appropriate algorithm) without other vertices also being added.
$\mathrm{e}^{-k^2np_1p_2}$ is the probability that this percolating set would actually be obtained (with an appropriate algorithm) without other vertices also being added.
The main difficulty in each of the proofs is rigorously proving that this approximation is valid, as a lower bound for the supercritical case and as an upper bound for the subcritical case.
Some preliminary results and notation are established in Section 2. This is followed by the proof of the subcritical regime in Section 3 and by the proof of the supercritical regime in Section 4. Finally, in Section 5 we discuss some further results and open problems.
2. Preliminaries
We first collect various auxiliary results and definitions that we will need throughout the paper. First note that since the jigsaw process is symmetric in the two graphs, we may assume, without loss of generality, that ![]() $p_2\leq p_1\le 1$. Furthermore, since percolation of the jigsaw process is a monotone property of double graphs, we may also assume that
$p_2\leq p_1\le 1$. Furthermore, since percolation of the jigsaw process is a monotone property of double graphs, we may also assume that
i.e. we assume, for the subcritical case, that ![]() $p_1p_2=(1-
\varepsilon)/{(4n\ln{n})}$ and, for the supercritical case, that
$p_1p_2=(1-
\varepsilon)/{(4n\ln{n})}$ and, for the supercritical case, that ![]() $p_1p_2=(1+
\varepsilon)/{(4n\ln{n})}$. Furthermore, since connectedness of both graphs is a necessary condition for the double graph to percolate, in both subcritical and supercritical cases we may assume that
$p_1p_2=(1+
\varepsilon)/{(4n\ln{n})}$. Furthermore, since connectedness of both graphs is a necessary condition for the double graph to percolate, in both subcritical and supercritical cases we may assume that
This is already true by assumption in the supercritical case. In the subcritical case, if ![]() $p_2$ does not satisfy this condition then w.h.p.
$p_2$ does not satisfy this condition then w.h.p. ![]() $G(n,p_2)$ is not connected by the classical result of Erdös and Rényi Reference Erdös and Rényi[10], and, therefore, the conclusion of Theorem 1.2(i) certainly holds.
$G(n,p_2)$ is not connected by the classical result of Erdös and Rényi Reference Erdös and Rényi[10], and, therefore, the conclusion of Theorem 1.2(i) certainly holds.
Note that (2.1) and (2.2) imply an upper bound on the individual probabilities, namely,
Furthermore, observe that
and
We will need to bound various random variables from above and below, which we do by means of stochastic domination.
Definition 2.1. Let X and Y be two positive integer-valued random variables. We say that X stochastically dominates Y, and write ![]() $X \succ Y$ if
$X \succ Y$ if ![]() $ \mathbb{P} [X\geq r] \geq \mathbb{P} [Y\geq r] $ for all
$ \mathbb{P} [X\geq r] \geq \mathbb{P} [Y\geq r] $ for all ![]() $r\in \mathbb{N}.$
$r\in \mathbb{N}.$
We will often use the following form of the Chernoff bound (see, e.g. Reference Janson, uczak and Ruciski[12]).
Lemma 2.1. For any binomial random variable X, we have
and
Throughout the paper we will ignore floors and ceilings when this does not significantly affect the argument. We will use the following bounds on factorials which hold for every positive integer (see, e.g. Reference Robbins[14]):
The following will be a central definition in the paper.
Definition 2.2. A percolating set in a double graph ![]() $(V,E_1,E_2)$ is a set of vertices
$(V,E_1,E_2)$ is a set of vertices ![]() $U\subset V$ such that given the two edge sets
$U\subset V$ such that given the two edge sets ![]() $E_i'=E_i \cap
\binom{U}{2}$ for
$E_i'=E_i \cap
\binom{U}{2}$ for ![]() $i=1,2$, the jigsaw process on the double graph
$i=1,2$, the jigsaw process on the double graph ![]() $(U,E_1',E_2')$ percolates.
$(U,E_1',E_2')$ percolates.
Whenever we talk about a cluster of vertices, in particular this is always a percolating set.
3. Subcritical case: proof of Theorem 1.2(i)
3.1. Outline
As previously mentioned, to prove Theorem 1.2(i) we will show that w.h.p. there is no percolating set of size at least ![]() $2\ln n$. The key idea is to bound the number of configurations which can cause a set of vertices to percolate.
$2\ln n$. The key idea is to bound the number of configurations which can cause a set of vertices to percolate.
Definition 3.1. A minimal percolating configuration is a percolating double-graph ![]() $(U,E_1,E_2)$, where
$(U,E_1,E_2)$, where ![]() $U\subset [n]$ and
$U\subset [n]$ and ![]() $E_i\subset E(G_i)$ for
$E_i\subset E(G_i)$ for ![]() $i=1,2$, and each
$i=1,2$, and each ![]() $E_i$ forms a spanning tree in U.
$E_i$ forms a spanning tree in U.
In other words, a minimal percolating configuration contains only the edges which are needed for it to percolate. Note that we do not forbid additional edges in the host double graph ![]() $G(n,p_1,p_2)$, but they are not part of the minimal percolating configuration.
$G(n,p_1,p_2)$, but they are not part of the minimal percolating configuration.
It is easy to see by induction that any percolating set admits a minimal percolating configuration, since for two clusters to merge it is enough that there is just one red edge and one blue edge between them.
In order to bound the number of minimal percolating configurations, we will analyse how the jigsaw process might evolve on them by introducing the absorption process in Section 3.2. In Section 3.3 we will characterise minimal percolating configurations according to certain parameters related to their corresponding absorption processes, and state bounds on the number of possibilities for configurations based on these parameters (Theorem 3.1 and Lemma 3.2). These bounds will be proved in Section 3.5 and 3.6, after some technical preliminaries have been proved in Section 3.4. Finally, in Section 3.7 we show how these bounds prove Theorem 1.2(i).
3.2. The absorption process
We need a variant of the jigsaw process, which we call an absorption process. In this process we gradually construct a percolating set ![]() $S_i=\{v_1,\ldots, v_{t(i)}\}$.
$S_i=\{v_1,\ldots, v_{t(i)}\}$.
Algorithm 3.1. (Absorption process.)
Input: Double graph ![]() $(V,E_1,E_2)$, vertex
$(V,E_1,E_2)$, vertex ![]() $v_1\in V$ and a set of clusters
$v_1\in V$ and a set of clusters ![]() $\mathcal{C}$ partitioning
$\mathcal{C}$ partitioning ![]() $V\setminus \{v_1\}$.
$V\setminus \{v_1\}$.
Set ![]() $i=1$,
$i=1$, ![]() $t(i)=1$,
$t(i)=1$, ![]() $\mathcal{C}_1=\mathcal{C}$ and
$\mathcal{C}_1=\mathcal{C}$ and ![]() $S_1=\{v_1\}$.
$S_1=\{v_1\}$.
while ![]() $t(i)\ge i$ do Set
$t(i)\ge i$ do Set ![]() $\mathcal{C}'_i\subset \mathcal{C}_i$ be the set of clusters of size at most t(i) which are adjacent to
$\mathcal{C}'_i\subset \mathcal{C}_i$ be the set of clusters of size at most t(i) which are adjacent to ![]() $v_i$ in one colour and to some vertex from
$v_i$ in one colour and to some vertex from ![]() $\{v_1,\ldots,v_i\}$ in the other colour.
$\{v_1,\ldots,v_i\}$ in the other colour.
Set ![]() $S_{i+1}=S_i\cup (\bigcup_{C\in \mathcal{C}_i'}C)$.
$S_{i+1}=S_i\cup (\bigcup_{C\in \mathcal{C}_i'}C)$.
Set ![]() $t(i+1)=|S_{i+1}|$.
$t(i+1)=|S_{i+1}|$.
Set ![]() $v_{t(i)+1},\ldots,v_{t(i+1)}$ to be the vertices of
$v_{t(i)+1},\ldots,v_{t(i+1)}$ to be the vertices of ![]() $S_{i+1}\setminus
S_i$ in any order.
$S_{i+1}\setminus
S_i$ in any order.
Set ![]() $\mathcal{C}_{i+1}=\mathcal{C}_{i}\setminus \mathcal{C}_{i}'$.
$\mathcal{C}_{i+1}=\mathcal{C}_{i}\setminus \mathcal{C}_{i}'$.
Proceed to step ![]() $i+1$.
$i+1$.
end
Output: ![]() $S_i$.
$S_i$.
If at the end of this algorithm we have ![]() $S_i=V$, we say that the absorption process percolates. If the double graph
$S_i=V$, we say that the absorption process percolates. If the double graph ![]() $(V,E_1,E_2)$ is clear from the context then we sometimes abuse terminology slightly by referring to
$(V,E_1,E_2)$ is clear from the context then we sometimes abuse terminology slightly by referring to ![]() $(v_1,\mathcal{C})$ as the input of the algorithm.
$(v_1,\mathcal{C})$ as the input of the algorithm.
Lemma 3.1. For every percolating double-graph ![]() $\left( {V,{E_1},{E_2}} \right),$ there exists a vertex
$\left( {V,{E_1},{E_2}} \right),$ there exists a vertex ![]() $v_1$ and a set of disjoint clusters
$v_1$ and a set of disjoint clusters ![]() $\mathcal{C}$ such that the absorption process with input
$\mathcal{C}$ such that the absorption process with input ![]() $(v_1,\mathcal{C})$ percolates.
$(v_1,\mathcal{C})$ percolates.
Proof. We prove this statement by induction on the size of V. Clearly, if ![]() $|V|=1$ the statement holds, so assume that it holds for every set of size at most k and that
$|V|=1$ the statement holds, so assume that it holds for every set of size at most k and that ![]() $|V|=k+1$.
$|V|=k+1$.
Since ![]() $(V,E_1,E_2)$ percolates, in the final step of the jigsaw process, a connected auxiliary graph
$(V,E_1,E_2)$ percolates, in the final step of the jigsaw process, a connected auxiliary graph ![]() $H^{(i)}$ was merged into one cluster. Consider a vertex of
$H^{(i)}$ was merged into one cluster. Consider a vertex of ![]() $H^{(i)}$ which is not a cut vertex. This vertex corresponds to a set X of vertices in V, and let
$H^{(i)}$ which is not a cut vertex. This vertex corresponds to a set X of vertices in V, and let ![]() $Y :\!= V\setminus X$. Then we have partitioned V into two nonempty percolating sets.
$Y :\!= V\setminus X$. Then we have partitioned V into two nonempty percolating sets.
Fix edges ![]() $e_1=x_1y_1\in E_1$ and
$e_1=x_1y_1\in E_1$ and ![]() $e_2=x_2y_2\in E_2$ such that
$e_2=x_2y_2\in E_2$ such that ![]() $x_1,x_2\in X$ and
$x_1,x_2\in X$ and ![]() $y_1,y_2\in Y$. Note that since
$y_1,y_2\in Y$. Note that since ![]() $(V,E_1,E_2)$ percolates, such edges must exist.
$(V,E_1,E_2)$ percolates, such edges must exist.
By the induction hypothesis, there exists a vertex ![]() $v_X\in X$ and a set of clusters
$v_X\in X$ and a set of clusters ![]() $\mathcal{C}_X$ within X such that the absorption process on X with input
$\mathcal{C}_X$ within X such that the absorption process on X with input ![]() $(v_X,\mathcal{C}_X)$ percolates. Let us denote by
$(v_X,\mathcal{C}_X)$ percolates. Let us denote by ![]() $X_{i}$ the percolating set constructed within X after i steps of this absorption process. Let i′ be the first step in which
$X_{i}$ the percolating set constructed within X after i steps of this absorption process. Let i′ be the first step in which ![]() $X_{i'}$ contains both
$X_{i'}$ contains both ![]() $x_1$ and
$x_1$ and ![]() $x_2$. We define
$x_2$. We define ![]() $v_Y, \mathcal{C}_Y, j',$ and
$v_Y, \mathcal{C}_Y, j',$ and ![]() $Y_{j'}$ analogously within Y.
$Y_{j'}$ analogously within Y.
Without loss of generality, we have ![]() $|X_{i'}|\ge |Y_{j'}|$. Recall that the vertices of
$|X_{i'}|\ge |Y_{j'}|$. Recall that the vertices of ![]() $X_{i'}$ are ordered in the absorption process, and let i″ be the index of the later of
$X_{i'}$ are ordered in the absorption process, and let i″ be the index of the later of ![]() $x_1,x_2$, without loss of generality
$x_1,x_2$, without loss of generality ![]() $x_2$. Then when we reach
$x_2$. Then when we reach ![]() $x_2$ at step i″, we have
$x_2$ at step i″, we have ![]() $|X_{i''}|\ge
|X_{i'}|\ge |Y_{j'}|$ and, therefore, at step i″, the cluster
$|X_{i''}|\ge
|X_{i'}|\ge |Y_{j'}|$ and, therefore, at step i″, the cluster ![]() $Y_{j'}$ can be merged with
$Y_{j'}$ can be merged with ![]() $X_{i''}$. Thus, the absorption process on V with input vertex
$X_{i''}$. Thus, the absorption process on V with input vertex ![]() $v_X$ and with input of clusters
$v_X$ and with input of clusters ![]() $\mathcal{C}_X, Y_{j'}$ and
$\mathcal{C}_X, Y_{j'}$ and ![]() $\{C\in \mathcal{C}_Y \ \,\,|\, \ \, C\cap Y_{j'}= \emptyset\}$ percolates.
$\{C\in \mathcal{C}_Y \ \,\,|\, \ \, C\cap Y_{j'}= \emptyset\}$ percolates.
Lemma 3.1 tells us that any percolating set can be discovered via an absorption process with some input of starting vertex and clusters. Note that this is slightly nonconstructive, since some percolating clusters are already in the input of the algorithm.
3.3. Bounding configurations
Our aim is to bound the number of possible minimal percolating configurations by analysing how the absorption process evolves on them. For this analysis, we will need to define the order in which clusters are added, which is primarily determined by the step in which a cluster is added, but there may be more than one cluster added in a single step. In such a case we order the clusters added in a single step according to the order of their smallest vertices (recall that the vertices of ![]() $G(n,p_1,p_2)$ are labelled
$G(n,p_1,p_2)$ are labelled ![]() $1,\ldots,n$).
$1,\ldots,n$).
Definition 3.2. Given integers ![]() $k,\ell,$ and r, let
$k,\ell,$ and r, let ![]() $M_{k,\ell,r}$ be the number of possible minimal percolating configurations on vertex set
$M_{k,\ell,r}$ be the number of possible minimal percolating configurations on vertex set ![]() $[k+r]$ for which there exists some input of starting vertex and clusters such that the absorption process with this input percolates in
$[k+r]$ for which there exists some input of starting vertex and clusters such that the absorption process with this input percolates in ![]() $\ell$ steps, and which adds a cluster of size exactly r in the
$\ell$ steps, and which adds a cluster of size exactly r in the ![]() $\ell$th step (and, therefore, has a percolating set of size at most k after
$\ell$th step (and, therefore, has a percolating set of size at most k after ![]() $\ell-1$ steps).
$\ell-1$ steps).
Note that Definition 3.2 allows the possibility that, as well as the cluster of size r, there are some further clusters which are also added in the ![]() $\ell$th step.
$\ell$th step.
The main difficulty in the subcritical case is to prove the following.
Theorem 3.1. Given integers ![]() $1\le r,\ell\le k$, we have
$1\le r,\ell\le k$, we have
In order to prove this we first approximate a slightly different parameter.
Definition 3.3. Let ![]() $M'_{k,\ell}$ be the number of possible minimal percolating configurations on vertex set [k] for which there exists some input of starting vertex and clusters such that the absorption process with this input percolates in at most
$M'_{k,\ell}$ be the number of possible minimal percolating configurations on vertex set [k] for which there exists some input of starting vertex and clusters such that the absorption process with this input percolates in at most ![]() $\ell$ steps.
$\ell$ steps.
Note that there are two crucial differences between this and the definition of ![]() $M_{k,\ell,r}$. First, we do not consider the final cluster on r vertices and, second, we do not demand that the process takes exactly
$M_{k,\ell,r}$. First, we do not consider the final cluster on r vertices and, second, we do not demand that the process takes exactly ![]() $\ell$ steps to percolate.
$\ell$ steps to percolate.
Let us observe that
since a configuration which contributes to ![]() $M_{k,\ell,r}$ can be partitioned into a minimal percolating set on k vertices whose absorption process takes at most
$M_{k,\ell,r}$ can be partitioned into a minimal percolating set on k vertices whose absorption process takes at most ![]() $\ell$ steps to percolate and a minimal percolating set on r vertices, for which
$\ell$ steps to percolate and a minimal percolating set on r vertices, for which ![]() $r-1\le r$ is certainly an upper bound on the number of steps required for an absorption process on r vertices to percolate. There are
$r-1\le r$ is certainly an upper bound on the number of steps required for an absorption process on r vertices to percolate. There are ![]() $\binom{k+r}{r}$ possible ways of partitioning the vertices and
$\binom{k+r}{r}$ possible ways of partitioning the vertices and ![]() $M'_{k,\ell} M_{r,r}'$ possible minimal percolating configurations on the two resulting parts. There must also be an edge of each colour between the two vertex sets, one of which has the last vertex of the set of size k as a neighbour, which leaves
$M'_{k,\ell} M_{r,r}'$ possible minimal percolating configurations on the two resulting parts. There must also be an edge of each colour between the two vertex sets, one of which has the last vertex of the set of size k as a neighbour, which leaves ![]() $2r^2\ell$ choices as claimed. Thus, in order to prove Theorem 3.1 it is enough to bound
$2r^2\ell$ choices as claimed. Thus, in order to prove Theorem 3.1 it is enough to bound ![]() $M'_{k,\ell}$.
$M'_{k,\ell}$.
Lemma 3.2. Given integers ![]() $1 \le \ell \le k$, we have
$1 \le \ell \le k$, we have
We will prove Lemma 3.2 in Section 3.5. Subsequently, in Section 3.6 we will use Lemma 3.2 to prove Theorem 3.1. Finally, we will show how Theorem 1.2(i) follows from Theorem 3.1 in Section 3.7. But first in Section 3.4 we will collect a few auxiliary results that we will need for the proof of Lemma 3.2.
3.4. Auxiliary results
Our aim in Lemma 3.2 is to bound ![]() $M'_{k,\ell}$, and we will need the following basic bound on
$M'_{k,\ell}$, and we will need the following basic bound on ![]() $M'_{j,j}$, i.e. the number of minimal percolating configurations on j vertices, with no restrictions on the number of steps they take to percolate in an absorption process (since certainly
$M'_{j,j}$, i.e. the number of minimal percolating configurations on j vertices, with no restrictions on the number of steps they take to percolate in an absorption process (since certainly ![]() $j-1\le j$ is an upper bound on the number of steps an absorption process on j vertices can take to percolate). The following result was already proved in Reference Bollobás, Riordan, Slivken and Smith[5], but since the proof is easy, we include it here for completeness.
$j-1\le j$ is an upper bound on the number of steps an absorption process on j vertices can take to percolate). The following result was already proved in Reference Bollobás, Riordan, Slivken and Smith[5], but since the proof is easy, we include it here for completeness.
Claim 3.2. ([5]) For any integer ![]() $j\ge 1$, we have
$j\ge 1$, we have ![]() $M_{j,j}' \le j^{2\,j-4}$.
$M_{j,j}' \le j^{2\,j-4}$.
Proof. Recall that in a minimal percolating configuration, the red and blue edge sets each form a spanning tree. By Cayley’s formula there are ![]() $j^{\,j-2}$ spanning trees on j vertices and the result follows. □
$j^{\,j-2}$ spanning trees on j vertices and the result follows. □
In the proof of Lemma 3.2 we also use the following technical proposition.
Proposition 3.1. For every ![]() $j\geq 3$, we have
$j\geq 3$, we have
 $$\begin{equation*}
\sum_{i=j}^\infty \frac{1}{(i+1)(i+2)\cdots(i+j-1)}=\frac{1}{(j-2)}
\frac{j!}{(2\,j-2)!}.
\end{equation*}$$
$$\begin{equation*}
\sum_{i=j}^\infty \frac{1}{(i+1)(i+2)\cdots(i+j-1)}=\frac{1}{(j-2)}
\frac{j!}{(2\,j-2)!}.
\end{equation*}$$
In particular,
 $$\begin{equation*}
\sum_{i=j}^\infty \frac{1}{(i+1)(i+2)\cdots(i+j-1)}\leq \mathrm{e}^2
\frac{j!}{j-2} \bigg(\frac{\mathrm{e}}{2\,j}\bigg)^{2\,j-2}.
\end{equation*}$$
$$\begin{equation*}
\sum_{i=j}^\infty \frac{1}{(i+1)(i+2)\cdots(i+j-1)}\leq \mathrm{e}^2
\frac{j!}{j-2} \bigg(\frac{\mathrm{e}}{2\,j}\bigg)^{2\,j-2}.
\end{equation*}$$
Proof. The Chu–Vandermonde identity, which can be easily verified combinatorially, states that, for nonnegative integers a,b, and c, we have
In fact this equality also holds if a is negative, where we interpret ![]() $\binom{a}{\ell}$ as
$\binom{a}{\ell}$ as
(see, e.g. Corollary 2.2.3 of Reference Andrews, Askey and Roy[1]). Setting ![]() $a=-i-1$,
$a=-i-1$, ![]() $b=i+j-1$, and
$b=i+j-1$, and ![]() $c\,{=}\,j-2$ leads to
$c\,{=}\,j-2$ leads to
 $$\begin{align*}\\[-18pt]
1&=\sum_{\ell=0}^{j-2}({-}1)^{\ell}\frac{(i+1)(i+2)\cdots (i+\ell)}{\ell!}
\frac{(i+j-1)!}{(j-2-\ell)!\, (i+\ell+1)!}
\\
&=\sum_{\ell=0}^{j-2}({-}1)^{\ell}\frac{(i+\ell)!}{\ell!}
\frac{(i+1)(i+2)\cdots (i+j-1)}{(j-2-\ell)!\, (i+\ell+1)!}
\\
&=\frac{1}{(\,j-2)!}\sum_{\ell=0}^{j-2}({-}1)^{\ell}\frac{(\,j-2)!}{\ell!
(\,j-2-\ell)!} \frac{(i+1)(i+2)\cdots (i+j-1)}{i+\ell+1},
\end{align*}$$
$$\begin{align*}\\[-18pt]
1&=\sum_{\ell=0}^{j-2}({-}1)^{\ell}\frac{(i+1)(i+2)\cdots (i+\ell)}{\ell!}
\frac{(i+j-1)!}{(j-2-\ell)!\, (i+\ell+1)!}
\\
&=\sum_{\ell=0}^{j-2}({-}1)^{\ell}\frac{(i+\ell)!}{\ell!}
\frac{(i+1)(i+2)\cdots (i+j-1)}{(j-2-\ell)!\, (i+\ell+1)!}
\\
&=\frac{1}{(\,j-2)!}\sum_{\ell=0}^{j-2}({-}1)^{\ell}\frac{(\,j-2)!}{\ell!
(\,j-2-\ell)!} \frac{(i+1)(i+2)\cdots (i+j-1)}{i+\ell+1},
\end{align*}$$
implying that
 $$\begin{equation}
\frac{1}{(i+1)(i+2)\cdots(i+j-1)}=\frac{1}{(j-2)!}\sum_{\ell=0}^{j-2}
(-1)^{\ell}\binom{j-2}{\ell}\frac{1}{i+1+\ell}.
\label{eqn7}
\end{equation}$$
$$\begin{equation}
\frac{1}{(i+1)(i+2)\cdots(i+j-1)}=\frac{1}{(j-2)!}\sum_{\ell=0}^{j-2}
(-1)^{\ell}\binom{j-2}{\ell}\frac{1}{i+1+\ell}.
\label{eqn7}
\end{equation}$$
Summing this for ![]() $j \le i \le m$ leads to
$j \le i \le m$ leads to
 $$\begin{align*}
&\sum_{i=j}^{m}\frac{1}{(i+1)(i+2)\cdots(i+j-1)}
\\
&\qquad=\frac{1}{(j-2)!}\sum_{i=j}^{m}\sum_{\ell=0}^{j-2}({-}1)^{\ell}
\binom{j-2} {\ell}\frac{1}{i+1+\ell}
\\
&\qquad=\frac{1}{(j-2)!}\sum_{i=j}^{m}\bigg(\frac{1}{i+1} +
\frac{({-}1)^{\,j-2}}{i+j-1}
+\sum_{\ell=1}^{j-3}({-}1)^{\ell}\bigg(\binom{j-3}{\ell}+\binom{j-3}
{\ell-1}\bigg)\frac{1}{i+1+\ell}\bigg)
\\
&\qquad=\frac{1}{(j-2)!}\sum_{i=j}^{m}\sum_{\ell=0}^{j-3}({-}1)^{\ell}\binom{j-3}
{\ell}\bigg(\frac{1}{i+1+\ell}-\frac{1}{i+2+\ell}\bigg)
\\
&\qquad=\frac{1}{(j-2)!}\bigg(\sum_{\ell=0}^{j-3}({-}1)^{\ell}\binom{j-3}{\ell}
\frac{1}{j+1+\ell}-\sum_{\ell=0}^{j-3}({-}1)^{\ell}\binom{j-3}{\ell}
\frac{1}{m+2+\ell}\bigg),
\end{align*}$$
$$\begin{align*}
&\sum_{i=j}^{m}\frac{1}{(i+1)(i+2)\cdots(i+j-1)}
\\
&\qquad=\frac{1}{(j-2)!}\sum_{i=j}^{m}\sum_{\ell=0}^{j-2}({-}1)^{\ell}
\binom{j-2} {\ell}\frac{1}{i+1+\ell}
\\
&\qquad=\frac{1}{(j-2)!}\sum_{i=j}^{m}\bigg(\frac{1}{i+1} +
\frac{({-}1)^{\,j-2}}{i+j-1}
+\sum_{\ell=1}^{j-3}({-}1)^{\ell}\bigg(\binom{j-3}{\ell}+\binom{j-3}
{\ell-1}\bigg)\frac{1}{i+1+\ell}\bigg)
\\
&\qquad=\frac{1}{(j-2)!}\sum_{i=j}^{m}\sum_{\ell=0}^{j-3}({-}1)^{\ell}\binom{j-3}
{\ell}\bigg(\frac{1}{i+1+\ell}-\frac{1}{i+2+\ell}\bigg)
\\
&\qquad=\frac{1}{(j-2)!}\bigg(\sum_{\ell=0}^{j-3}({-}1)^{\ell}\binom{j-3}{\ell}
\frac{1}{j+1+\ell}-\sum_{\ell=0}^{j-3}({-}1)^{\ell}\binom{j-3}{\ell}
\frac{1}{m+2+\ell}\bigg),
\end{align*}$$
implying that
 $$\begin{equation*}
\sum_{i=j}^{\infty}\frac{1}{(i+1)(i+2)\cdots(i+j-1)}=\frac{1}{(j-2)!}
\sum_{\ell=0}^{j-3}({-}1)^{\ell}\binom{j-3}{\ell}\frac{1}{j+1+\ell}.
\end{equation*}$$
$$\begin{equation*}
\sum_{i=j}^{\infty}\frac{1}{(i+1)(i+2)\cdots(i+j-1)}=\frac{1}{(j-2)!}
\sum_{\ell=0}^{j-3}({-}1)^{\ell}\binom{j-3}{\ell}\frac{1}{j+1+\ell}.
\end{equation*}$$
We now apply (3.2) again, with j replaced by ![]() $j-1$ and i replaced by j, to obtain
$j-1$ and i replaced by j, to obtain
 $$\begin{align*}
\frac{1}{(\,j-2)!}\sum_{\ell=0}^{j-3}({-}1)^{\ell}\binom{j-3}{\ell}
\frac{1}{j+1+\ell} & =\frac{1}{j-2}\frac{1}{(\,j+1)(j+2)\cdots (2\,j-2)}
\\
& =\frac{1}{j-2}\frac{j!}{(2\,j-2)!}
\end{align*}$$
$$\begin{align*}
\frac{1}{(\,j-2)!}\sum_{\ell=0}^{j-3}({-}1)^{\ell}\binom{j-3}{\ell}
\frac{1}{j+1+\ell} & =\frac{1}{j-2}\frac{1}{(\,j+1)(j+2)\cdots (2\,j-2)}
\\
& =\frac{1}{j-2}\frac{j!}{(2\,j-2)!}
\end{align*}$$
as required.
For the second statement, we simply apply (2.5) to obtain
and the result follows.
3.5. Proof of Lemma 3.2
We aim to prove Lemma 3.2, i.e. that ![]() $M'_{k,\ell}\le
k (k!)^2 2^{k-1} \mathrm{e}^{\ell+291} $ for
$M'_{k,\ell}\le
k (k!)^2 2^{k-1} \mathrm{e}^{\ell+291} $ for ![]() $\ell\le k$. Recall that when a cluster C is added in step i of the absorption process, the vertex
$\ell\le k$. Recall that when a cluster C is added in step i of the absorption process, the vertex ![]() $v_i$ will be joined to a vertex
$v_i$ will be joined to a vertex ![]() $w_C$ of C in one colour, and, for some
$w_C$ of C in one colour, and, for some ![]() $i'\le i$, the vertex
$i'\le i$, the vertex ![]() $v_{i'}$ will be joined to a vertex
$v_{i'}$ will be joined to a vertex ![]() $w_C'$ of C in the other colour.
$w_C'$ of C in the other colour.
For ![]() $1\le j \le k/2$, let
$1\le j \le k/2$, let ![]() $c_j$ be the number of clusters of size j which are added in the process and set
$c_j$ be the number of clusters of size j which are added in the process and set ![]() ${{\boldsymbol{c}}}=(c_1,\ldots,c_{k/2})$. Observe that no clusters of size larger than
${{\boldsymbol{c}}}=(c_1,\ldots,c_{k/2})$. Observe that no clusters of size larger than ![]() $k/2$ can be added, since clusters can only be added to a percolating set which is at least as large as the cluster, and we have only k vertices in total. Note also that the first vertex
$k/2$ can be added, since clusters can only be added to a percolating set which is at least as large as the cluster, and we have only k vertices in total. Note also that the first vertex ![]() $v_1$ does not count towards
$v_1$ does not count towards ![]() $c_1$ (recall that it is not considered a cluster), and so
$c_1$ (recall that it is not considered a cluster), and so
 $$\begin{equation}
\sum_{j=1}^{k/2} j\ c_j=k-1.
\label{eqn8}
\end{equation}$$
$$\begin{equation}
\sum_{j=1}^{k/2} j\ c_j=k-1.
\label{eqn8}
\end{equation}$$
Initially, we order the clusters ![]() $C_1,\ldots,C_d$, where
$C_1,\ldots,C_d$, where ![]() $d :\!=\sum_{j=1}^{k/2} c_j$ is the total number of clusters, according to the order of their smallest vertices. Recall that the absorption process gives us a new order on the clusters according to the order in which they are added, so we have a permutation
$d :\!=\sum_{j=1}^{k/2} c_j$ is the total number of clusters, according to the order of their smallest vertices. Recall that the absorption process gives us a new order on the clusters according to the order in which they are added, so we have a permutation ![]() $\sigma$ on [d] such that
$\sigma$ on [d] such that ![]() $C_{\sigma(s)}$ is the sth cluster to be added.
$C_{\sigma(s)}$ is the sth cluster to be added.
We further define the following parameters:
let
 $i_s$ denote the step in which
$i_s$ denote the step in which  $C_s$ is added;
$C_s$ is added;let
 $j_s$ denote the size of
$j_s$ denote the size of  $C_s$;
$C_s$;let
 $m_s :\!=\max(i_s,j_s)$.
$m_s :\!=\max(i_s,j_s)$.
In particular, this gives a vector ![]() ${{\boldsymbol{i}}}=(i_1,\ldots,i_{d})$. Let
${{\boldsymbol{i}}}=(i_1,\ldots,i_{d})$. Let ![]() $I :\!= I({{\boldsymbol{c}}})$ denote the set of permissible vectors, meaning that
$I :\!= I({{\boldsymbol{c}}})$ denote the set of permissible vectors, meaning that
(P1)
 $i_{\sigma(s)}\le 1+\sum_{t=1}^{s-1}j_{\sigma(t)}$ for all
$i_{\sigma(s)}\le 1+\sum_{t=1}^{s-1}j_{\sigma(t)}$ for all  $1\le s \le
d$, i.e. we do not run out of vertices before adding the next cluster;
$1\le s \le
d$, i.e. we do not run out of vertices before adding the next cluster;(P2)
 $j_{\sigma(s)}\le 1+\sum_{t=1}^{s-1}j_{\sigma(t)}$ for all
$j_{\sigma(s)}\le 1+\sum_{t=1}^{s-1}j_{\sigma(t)}$ for all  $1\le s \le
d$, i.e. we do not add a cluster larger than the current percolating set;
$1\le s \le
d$, i.e. we do not add a cluster larger than the current percolating set;(P3)
 $i_s\le \ell$ for all
$i_s\le \ell$ for all  $1\le s \le d$.
$1\le s \le d$.
Note that conditions (P1) and (P2) are implicitly dependent on the vector ![]() ${{\boldsymbol{i}}}$ because
${{\boldsymbol{i}}}$ because ![]() $\sigma$ is dependent on
$\sigma$ is dependent on ![]() ${{\boldsymbol{i}}}$. Note also that while (P2) is necessary to ensure that we do not add a cluster larger than the current percolating set, it is not quite sufficient as if we add multiple clusters to a percolating set in a single step, this condition would allow for all but the first of these clusters to be too large. However, since we are concerned with upper bounds, this is not a problem.
${{\boldsymbol{i}}}$. Note also that while (P2) is necessary to ensure that we do not add a cluster larger than the current percolating set, it is not quite sufficient as if we add multiple clusters to a percolating set in a single step, this condition would allow for all but the first of these clusters to be too large. However, since we are concerned with upper bounds, this is not a problem.
We may now bound ![]() $M_{k,\ell}'$ by considering how many choices we have for various parameters for each fixed
$M_{k,\ell}'$ by considering how many choices we have for various parameters for each fixed ![]() ${{\boldsymbol{c}}}=(c_1,\ldots,c_{k/2})$ and
${{\boldsymbol{c}}}=(c_1,\ldots,c_{k/2})$ and ![]() ${{\boldsymbol{i}}}=(i_1,\ldots,i_d)$ and summing over all possibilities for
${{\boldsymbol{i}}}=(i_1,\ldots,i_d)$ and summing over all possibilities for ![]() ${{\boldsymbol{c}}},{{\boldsymbol{i}}}$. Given vectors
${{\boldsymbol{c}}},{{\boldsymbol{i}}}$. Given vectors ![]() ${{\boldsymbol{c}}}$ and
${{\boldsymbol{c}}}$ and ![]() ${{\boldsymbol{i}}}$:
${{\boldsymbol{i}}}$:
we have k choices for the first vertex
 $v_1$;
$v_1$;there are
 ${(k-1)!}/{\big(\!\prod_{j=1}^{k/2} (\,j!)^{c_j} c_j!\big)}$ distinct ways of assigning the remaining vertices to clusters;
${(k-1)!}/{\big(\!\prod_{j=1}^{k/2} (\,j!)^{c_j} c_j!\big)}$ distinct ways of assigning the remaining vertices to clusters;for each cluster
 $C_s$ of size
$C_s$ of size  $j_s$ which is to be added in step
$j_s$ which is to be added in step  $i_s$ we have at most:
$i_s$ we have at most: $j_s^2$ choices for the two vertices
$j_s^2$ choices for the two vertices  $w_C$ and
$w_C$ and  $w'_C$;
$w'_C$;two choices for the colour of the edge from
 $v_{i_s}$ to
$v_{i_s}$ to  $w_C$;
$w_C$; $M_{j_s,j_s}' \le j_s^{2\,j_s-4}$ possible minimal percolating configurations within C (by Claim 1);
$M_{j_s,j_s}' \le j_s^{2\,j_s-4}$ possible minimal percolating configurations within C (by Claim 1); $i_s$ choices for
$i_s$ choices for  $i_s'\le i_s$.
$i_s'\le i_s$.
Thus, we obtain
 $$\begin{equation}
M'_{k,\ell} \le \sum_{{{\boldsymbol{c}}}} \bigg\{k \frac{(k-1)!}{\prod_{j=1}^{k/2}
(\,j!)^{c_j} c_j!} \bigg(\prod_{j=1}^{k/2} (2 j^2 j^{2\,j-4})^{c_j}\bigg)
\sum_{{{\boldsymbol{i}}}\in I} \prod_{s=1}^{d} i_s \bigg\}.
\label{eqn9}
\end{equation}$$
$$\begin{equation}
M'_{k,\ell} \le \sum_{{{\boldsymbol{c}}}} \bigg\{k \frac{(k-1)!}{\prod_{j=1}^{k/2}
(\,j!)^{c_j} c_j!} \bigg(\prod_{j=1}^{k/2} (2 j^2 j^{2\,j-4})^{c_j}\bigg)
\sum_{{{\boldsymbol{i}}}\in I} \prod_{s=1}^{d} i_s \bigg\}.
\label{eqn9}
\end{equation}$$
We first consider the terms involving ![]() $i_s$, which require the most care. We have
$i_s$, which require the most care. We have
 $$\begin{equation}
\sum_{{{\boldsymbol{i}}}\in I} \prod_{s=1}^{d} i_s \le \sum_{{{\boldsymbol{i}}}\in I}
\prod_{s=1}^{d} m_s = \sum_{{{\boldsymbol{i}}}\in I} \frac{\prod_{s=1}^{d}
m_s(m_s+1)\cdots (m_s+j_s-1)}{\prod_{s=1}^{d}(m_s+1)\cdots (m_s+j_s-1)}.
\label{eqn10}
\end{equation}$$
$$\begin{equation}
\sum_{{{\boldsymbol{i}}}\in I} \prod_{s=1}^{d} i_s \le \sum_{{{\boldsymbol{i}}}\in I}
\prod_{s=1}^{d} m_s = \sum_{{{\boldsymbol{i}}}\in I} \frac{\prod_{s=1}^{d}
m_s(m_s+1)\cdots (m_s+j_s-1)}{\prod_{s=1}^{d}(m_s+1)\cdots (m_s+j_s-1)}.
\label{eqn10}
\end{equation}$$
Here we use the convention that an empty product is interpreted as 1. We bound the numerator in (3.5) with the following claim.
Claim 3.3. It holds that ![]() $\prod_{s=1}^{d} m_s(m_s+1)\cdots (m_s+j_s-1)\le (k-1)!$
$\prod_{s=1}^{d} m_s(m_s+1)\cdots (m_s+j_s-1)\le (k-1)!$
Proof. The conditions (P1) and (P2) together imply that ![]() $m_{\sigma(s)}\le
1+\sum_{t=1}^{s-1}j_{\sigma(t)}$, and, therefore,
$m_{\sigma(s)}\le
1+\sum_{t=1}^{s-1}j_{\sigma(t)}$, and, therefore,
 $$\begin{align*}\\[-24pt]
&\prod_{s=1}^d \{m_s(m_s+1)\cdots (m_s+j_s-1)\}
\\
&\qquad = \prod_{s=1}^d \{m_{\sigma(s)}(m_{\sigma(s)}+1)\cdots
(m_{\sigma(s)}+j_{\sigma(s)}-1)\}
\\
&\qquad \le \prod_{s=1}^d \bigg\{\bigg(\sum_{t=1}^{s-1}j_{\sigma(t)}+1\bigg)
\bigg(\sum_{t=1}^{s-1}j_{\sigma(t)}+2\bigg)\cdots
\bigg(\sum_{t=1}^{s-1}j_{\sigma(t)}+j_{\sigma(s)}\bigg)\bigg\}
\\
&\qquad = \bigg(\sum_{s=1}^d j_{\sigma(s)}\bigg)!
\\
&\qquad = (k-1)!
\end{align*}$$
$$\begin{align*}\\[-24pt]
&\prod_{s=1}^d \{m_s(m_s+1)\cdots (m_s+j_s-1)\}
\\
&\qquad = \prod_{s=1}^d \{m_{\sigma(s)}(m_{\sigma(s)}+1)\cdots
(m_{\sigma(s)}+j_{\sigma(s)}-1)\}
\\
&\qquad \le \prod_{s=1}^d \bigg\{\bigg(\sum_{t=1}^{s-1}j_{\sigma(t)}+1\bigg)
\bigg(\sum_{t=1}^{s-1}j_{\sigma(t)}+2\bigg)\cdots
\bigg(\sum_{t=1}^{s-1}j_{\sigma(t)}+j_{\sigma(s)}\bigg)\bigg\}
\\
&\qquad = \bigg(\sum_{s=1}^d j_{\sigma(s)}\bigg)!
\\
&\qquad = (k-1)!
\end{align*}$$
as claimed. □
We handle the denominator and sum in (3.5) with the following claim.
Claim 3.4. It holds that
 $$\begin{align*}
&\sum_{{{\boldsymbol{i}}}\in I} \frac{1}{\prod_{s=1}^{d} (m_s+1)(m_s+2)\cdots
(m_s+j_s-1)}
\\
&\qquad\le \ell^{c_1}(2 \ln (\ell+1))^{c_2} \prod_{j=3}^{k/2} \bigg(3
\mathrm{e}^2\,j!\bigg(\frac{\mathrm{e}}{2\,j}\bigg)^{2\,j-2}\bigg)^{c_j}.
\end{align*}$$
$$\begin{align*}
&\sum_{{{\boldsymbol{i}}}\in I} \frac{1}{\prod_{s=1}^{d} (m_s+1)(m_s+2)\cdots
(m_s+j_s-1)}
\\
&\qquad\le \ell^{c_1}(2 \ln (\ell+1))^{c_2} \prod_{j=3}^{k/2} \bigg(3
\mathrm{e}^2\,j!\bigg(\frac{\mathrm{e}}{2\,j}\bigg)^{2\,j-2}\bigg)^{c_j}.
\end{align*}$$
Proof. Let us note that we first fixed the assignment of vertices to clusters, which in particular determines the ![]() $j_s$, and then chose the vector
$j_s$, and then chose the vector ![]() ${{\boldsymbol{i}}}$, so in particular
${{\boldsymbol{i}}}$, so in particular ![]() $j_s$ is not dependent on
$j_s$ is not dependent on ![]() $i_s$ (although which values of
$i_s$ (although which values of ![]() $i_s$ are permissible does depend on the
$i_s$ are permissible does depend on the ![]() $j_s$). Therefore, we have
$j_s$). Therefore, we have
 $$\begin{align*}
&\sum_{{{\boldsymbol{i}}}\in I} \frac{1}{\prod_{s=1}^{d} (m_s+1)(m_s+2)\cdots
(m_s+j_s-1)}
\\
&\qquad \le \sum_{i_1=1}^\ell\cdots \sum_{i_d=1}^\ell \prod_{s=1}^{d}
\frac{1}{ (m_s+1)(m_s+2)\cdots (m_s+j_s-1)}[0]
\\
&\qquad \le \sum_{i_1=\min(\,j_1,\ell)}^\ell\cdots
\sum_{i_d=\min(\,j_d,\ell)}^\ell \prod_{s=1}^{d} \frac{j_s}{
(m_s+1)(m_s+2)\cdots (m_s+j_s-1)}
\\
&\qquad \le \prod_{j=1}^{\ell}
\bigg(\sum_{i=j}^\ell\frac{j}{(i+1)\cdots(i+j-1)}\bigg)^{c_j}
\prod_{j=\ell+1}^{ k/2} \bigg(\frac{j}{(\,j+1)\cdots(2\,j-1)}\bigg)^{c_j}
\\
&\qquad \le \prod_{j=1}^{ k/2 } \bigg(\sum_{i=j}^{\ell+j-1}\frac{j}{(i+1)
\cdots(i+j-1)}\bigg)^{c_j}.
\end{align*}$$
$$\begin{align*}
&\sum_{{{\boldsymbol{i}}}\in I} \frac{1}{\prod_{s=1}^{d} (m_s+1)(m_s+2)\cdots
(m_s+j_s-1)}
\\
&\qquad \le \sum_{i_1=1}^\ell\cdots \sum_{i_d=1}^\ell \prod_{s=1}^{d}
\frac{1}{ (m_s+1)(m_s+2)\cdots (m_s+j_s-1)}[0]
\\
&\qquad \le \sum_{i_1=\min(\,j_1,\ell)}^\ell\cdots
\sum_{i_d=\min(\,j_d,\ell)}^\ell \prod_{s=1}^{d} \frac{j_s}{
(m_s+1)(m_s+2)\cdots (m_s+j_s-1)}
\\
&\qquad \le \prod_{j=1}^{\ell}
\bigg(\sum_{i=j}^\ell\frac{j}{(i+1)\cdots(i+j-1)}\bigg)^{c_j}
\prod_{j=\ell+1}^{ k/2} \bigg(\frac{j}{(\,j+1)\cdots(2\,j-1)}\bigg)^{c_j}
\\
&\qquad \le \prod_{j=1}^{ k/2 } \bigg(\sum_{i=j}^{\ell+j-1}\frac{j}{(i+1)
\cdots(i+j-1)}\bigg)^{c_j}.
\end{align*}$$
In the third inequality we have used ![]() $m_s \ge i_s,j_s$. In the last inequality we have used the fact that
$m_s \ge i_s,j_s$. In the last inequality we have used the fact that ![]() $\ell+j-1\ge \ell,j$.
$\ell+j-1\ge \ell,j$.
The ![]() $j=1$ term in the product is simply
$j=1$ term in the product is simply
 $$\begin{equation}
\bigg(\sum_{i=1}^\ell 1\bigg)^{c_1}= \ell^{c_1}.
\label{eqn11}
\end{equation}$$
$$\begin{equation}
\bigg(\sum_{i=1}^\ell 1\bigg)^{c_1}= \ell^{c_1}.
\label{eqn11}
\end{equation}$$
We bound the term ![]() $j=2$ as follows:
$j=2$ as follows:
 $$\begin{equation}
\bigg(\sum_{i=2}^{\ell+1}\frac{2}{i+1}\bigg)^{c_2} \le
\bigg(\int_{1}^{\ell+1} \frac{2}{x} \,\mathrm{d} x\bigg)^{c_2} = ( 2 \ln (\ell+1)
)^{c_2}.
\label{eqn12}
\end{equation}$$
$$\begin{equation}
\bigg(\sum_{i=2}^{\ell+1}\frac{2}{i+1}\bigg)^{c_2} \le
\bigg(\int_{1}^{\ell+1} \frac{2}{x} \,\mathrm{d} x\bigg)^{c_2} = ( 2 \ln (\ell+1)
)^{c_2}.
\label{eqn12}
\end{equation}$$
For ![]() $j\ge 3$, we apply Proposition 3.1 to obtain
$j\ge 3$, we apply Proposition 3.1 to obtain
 $$\begin{equation*}
\sum_{i=j}^{\infty}\frac{j}{(i+1)\cdots (i+j-1)} \le j\mathrm{e}^2
\frac{j!}{j-2}\bigg(\frac{\mathrm{e}}{2\,j}\bigg)^{2\,j-2} \leq 3 \mathrm{e}^2
j!\bigg(\frac{\mathrm{e}}{2\,j}\bigg)^{2\,j-2},
\end{equation*}$$
$$\begin{equation*}
\sum_{i=j}^{\infty}\frac{j}{(i+1)\cdots (i+j-1)} \le j\mathrm{e}^2
\frac{j!}{j-2}\bigg(\frac{\mathrm{e}}{2\,j}\bigg)^{2\,j-2} \leq 3 \mathrm{e}^2
j!\bigg(\frac{\mathrm{e}}{2\,j}\bigg)^{2\,j-2},
\end{equation*}$$
which gives
 $$\begin{equation}
\prod_{j=3}^{ k/2} \bigg(\sum_{i=j}^{\ell+j-1}\frac{j}{(i+1)\cdots
(i+j-1)}\bigg)^{c_j} \leq \prod_{j=3}^{ k/2 }\bigg( 3 \mathrm{e}^2
j!\bigg(\frac{\mathrm{e}}{2\,j}\bigg)^{2\,j-2}\bigg)^{c_j}.
\label{eqn13}
\end{equation}$$
$$\begin{equation}
\prod_{j=3}^{ k/2} \bigg(\sum_{i=j}^{\ell+j-1}\frac{j}{(i+1)\cdots
(i+j-1)}\bigg)^{c_j} \leq \prod_{j=3}^{ k/2 }\bigg( 3 \mathrm{e}^2
j!\bigg(\frac{\mathrm{e}}{2\,j}\bigg)^{2\,j-2}\bigg)^{c_j}.
\label{eqn13}
\end{equation}$$
Combining the bounds from (3.6) (3.7), and (3.8) proves the claim. □
Substituting the bounds from Claims 3.3 and 3.4 into (3.5), we have
 $$\begin{equation*}
\sum_{{{\boldsymbol{i}}}\in I} \prod_{s=1}^{d} i_s \le (k-1)!\,\ell^{c_1}(2 \ln
(\ell+1))^{c_2} \prod_{j=3}^{k/2} \bigg(3
\mathrm{e}^2\,j!\bigg(\frac{\mathrm{e}}{2\,j}\bigg)^{2\,j-2}\bigg)^{c_j},
\end{equation*}$$
$$\begin{equation*}
\sum_{{{\boldsymbol{i}}}\in I} \prod_{s=1}^{d} i_s \le (k-1)!\,\ell^{c_1}(2 \ln
(\ell+1))^{c_2} \prod_{j=3}^{k/2} \bigg(3
\mathrm{e}^2\,j!\bigg(\frac{\mathrm{e}}{2\,j}\bigg)^{2\,j-2}\bigg)^{c_j},
\end{equation*}$$
and therefore (3.4) gives
 $$\begin{align*}
M'_{k,\ell} & \le \sum_{{{\boldsymbol{c}}}} {\bigg\{ } \frac{k!}{\prod_{j=1}^{k/2}
(\,j!)^{c_j} c_j!} \bigg(\prod_{j=1}^{k/2} (2 j^2 j^{2\,j-4})^{c_j}\bigg)
(k-1)!
\\
& \times \bigg( \ell^{c_1}(2\ln (\ell+1))^{c_2} \prod_{j=
3}^{k/2} \bigg(3 \mathrm{e}^2 j!\bigg(\frac{\mathrm{e}}{2\,j}\bigg)^{2\,j-2}
\bigg)^{c_j}\bigg){\bigg\} }
\\
& = k!\,(k-1)!\, \sum_{{\boldsymbol{c}}} \bigg\{ \frac{(2\ell)^{c_1}}{c_1!}
\frac{(16\ln (\ell+1))^{c_2}}{2^{c_2}c_2!} \prod_{j= 3}^{k/2}
\frac{(2\,j^{2\,j-2} 3\mathrm{e}^2 j!\,({\mathrm{e}}/{2\,j})^{2\,j-2})^{c_j} }{(\,j!)^{c_j}c_j!}
\bigg\}[0]
\\
& \stackrel{\tiny\ref{eqn8}}{=} k!\,(k-1)!\,2^{k-1} \sum_{{\boldsymbol{c}}} \bigg\{ \frac{\ell^{c_1}}{c_1!} \frac{(2 \ln (\ell+1))^{c_2}}{c_2!}
\prod_{j= 3}^{k/2} \frac{1}{c_j!}\bigg(\frac{3\mathrm{e}^2 ({\mathrm{e}}/{2})^{2\,j-2}
}{2^{j-1}}\bigg)^{c_j} \bigg\}
%\quad\text{(\ref{eqn8})}
\\
& \le k!\,(k-1)!\,2^{k-1} \bigg\{ \sum_{c_1=0}^\infty
\frac{\ell^{c_1}}{c_1!} \bigg\} \bigg\{ \sum_{c_2=0}^\infty \frac{(2 \ln
(\ell+1))^{c_2}}{c_2!} \bigg\}
\\
& \quad\,\times \bigg\{ \prod_{j= 3}^{k/2} \sum_{c_j=0}^\infty
\frac{1}{c_j!}\bigg(3\mathrm{e}^2 \bigg(\frac{\mathrm{e}^2}{8}\bigg)^{j-1}\bigg)^{c_j}
\bigg\}
\\
& = k!\,(k-1)!\,2^{k-1}\ {\exp}(\ell)\ {\exp}( 2 \ln (\ell+1) ) \prod_{j=
3}^{k/2}\ {\exp}\bigg( 3\mathrm{e}^2 \bigg(\frac{\mathrm{e}^2}{8}\bigg)^{j-1}\bigg)
\\
& \le k (k!)^2 2^{k-1} \mathrm{e}^{\ell}\ {\exp}\bigg( \sum_{j= 3}^{k/2} 3\mathrm{e}^2
\bigg(\frac{\mathrm{e}^2}{8}\bigg)^{j-1} \bigg).
\end{align*}$$
$$\begin{align*}
M'_{k,\ell} & \le \sum_{{{\boldsymbol{c}}}} {\bigg\{ } \frac{k!}{\prod_{j=1}^{k/2}
(\,j!)^{c_j} c_j!} \bigg(\prod_{j=1}^{k/2} (2 j^2 j^{2\,j-4})^{c_j}\bigg)
(k-1)!
\\
& \times \bigg( \ell^{c_1}(2\ln (\ell+1))^{c_2} \prod_{j=
3}^{k/2} \bigg(3 \mathrm{e}^2 j!\bigg(\frac{\mathrm{e}}{2\,j}\bigg)^{2\,j-2}
\bigg)^{c_j}\bigg){\bigg\} }
\\
& = k!\,(k-1)!\, \sum_{{\boldsymbol{c}}} \bigg\{ \frac{(2\ell)^{c_1}}{c_1!}
\frac{(16\ln (\ell+1))^{c_2}}{2^{c_2}c_2!} \prod_{j= 3}^{k/2}
\frac{(2\,j^{2\,j-2} 3\mathrm{e}^2 j!\,({\mathrm{e}}/{2\,j})^{2\,j-2})^{c_j} }{(\,j!)^{c_j}c_j!}
\bigg\}[0]
\\
& \stackrel{\tiny\ref{eqn8}}{=} k!\,(k-1)!\,2^{k-1} \sum_{{\boldsymbol{c}}} \bigg\{ \frac{\ell^{c_1}}{c_1!} \frac{(2 \ln (\ell+1))^{c_2}}{c_2!}
\prod_{j= 3}^{k/2} \frac{1}{c_j!}\bigg(\frac{3\mathrm{e}^2 ({\mathrm{e}}/{2})^{2\,j-2}
}{2^{j-1}}\bigg)^{c_j} \bigg\}
%\quad\text{(\ref{eqn8})}
\\
& \le k!\,(k-1)!\,2^{k-1} \bigg\{ \sum_{c_1=0}^\infty
\frac{\ell^{c_1}}{c_1!} \bigg\} \bigg\{ \sum_{c_2=0}^\infty \frac{(2 \ln
(\ell+1))^{c_2}}{c_2!} \bigg\}
\\
& \quad\,\times \bigg\{ \prod_{j= 3}^{k/2} \sum_{c_j=0}^\infty
\frac{1}{c_j!}\bigg(3\mathrm{e}^2 \bigg(\frac{\mathrm{e}^2}{8}\bigg)^{j-1}\bigg)^{c_j}
\bigg\}
\\
& = k!\,(k-1)!\,2^{k-1}\ {\exp}(\ell)\ {\exp}( 2 \ln (\ell+1) ) \prod_{j=
3}^{k/2}\ {\exp}\bigg( 3\mathrm{e}^2 \bigg(\frac{\mathrm{e}^2}{8}\bigg)^{j-1}\bigg)
\\
& \le k (k!)^2 2^{k-1} \mathrm{e}^{\ell}\ {\exp}\bigg( \sum_{j= 3}^{k/2} 3\mathrm{e}^2
\bigg(\frac{\mathrm{e}^2}{8}\bigg)^{j-1} \bigg).
\end{align*}$$
Note that in the last line we have used the fact that ![]() $\ell \le k-1$, since this is an upper bound on the number of steps it can take for the absorption process on k vertices to percolate. We bound the remaining sum by
$\ell \le k-1$, since this is an upper bound on the number of steps it can take for the absorption process on k vertices to percolate. We bound the remaining sum by
 $$\begin{equation*}
\sum_{j= 3}^{k/2} 3\mathrm{e}^2 \bigg(\frac{\mathrm{e}^2}{8}\bigg)^{j-1}\leq
\frac{3\mathrm{e}^2}{1-\mathrm{e}^2/8}\leq 291,
\end{equation*}$$
$$\begin{equation*}
\sum_{j= 3}^{k/2} 3\mathrm{e}^2 \bigg(\frac{\mathrm{e}^2}{8}\bigg)^{j-1}\leq
\frac{3\mathrm{e}^2}{1-\mathrm{e}^2/8}\leq 291,
\end{equation*}$$
since ![]() $\le^2/8\lt1$. Thus, we obtain
$\le^2/8\lt1$. Thus, we obtain
which completes the proof of Lemma 3.2.
3.6. Proof of Theorem 3.1
We can now prove Theorem 3.1. Observe that Lemma 3.2 gives a bound on ![]() $M_{j,j}'$ which is better than Claim 3.2 for large j,
$M_{j,j}'$ which is better than Claim 3.2 for large j,
We use (3.9) and Lemma 3.2 to obtain
 $$\begin{align*}
M_{k,\ell,r} & \stackrel{\tiny\ref{eqn6}}{\le}
\binom{k+r}{r} M'_{k,\ell} 2r^2\ell M_{r,r}'
\\
& \le \binom{k+r}{r} \bigg((k!)^2
2^{k}\mathrm{e}^{\ell}\frac{k\mathrm{e}^{291}}{2}\bigg) 2r^2\ell \bigg((r!)^2
2^{r}\mathrm{e}^{r}\frac{r\mathrm{e}^{291}}{2}\bigg)
\\
& = \binom{k+r}{r} (k!)^2 (r!)^2 2^{k+r} \mathrm{e}^{r+\ell} \frac{k\ell r^3
\mathrm{e}^{582}}{2},
\end{align*}$$
$$\begin{align*}
M_{k,\ell,r} & \stackrel{\tiny\ref{eqn6}}{\le}
\binom{k+r}{r} M'_{k,\ell} 2r^2\ell M_{r,r}'
\\
& \le \binom{k+r}{r} \bigg((k!)^2
2^{k}\mathrm{e}^{\ell}\frac{k\mathrm{e}^{291}}{2}\bigg) 2r^2\ell \bigg((r!)^2
2^{r}\mathrm{e}^{r}\frac{r\mathrm{e}^{291}}{2}\bigg)
\\
& = \binom{k+r}{r} (k!)^2 (r!)^2 2^{k+r} \mathrm{e}^{r+\ell} \frac{k\ell r^3
\mathrm{e}^{582}}{2},
\end{align*}$$
as claimed in Theorem 3.1.
3.7. Proof of Theorem 1.2(i)
To prove the subcritical case of Theorem 1.2, we need the following strengthening of the notion of a minimal percolating configuration.
Definition 3.4. An optimal configuration in a double graph ![]() $(V,E_1,E_2)$ is a minimal percolating configuration
$(V,E_1,E_2)$ is a minimal percolating configuration ![]() $(U,E_1',E_2')$, where
$(U,E_1',E_2')$, where ![]() $U\subset V$ and
$U\subset V$ and ![]() $E_i' \subset E_i$ for
$E_i' \subset E_i$ for ![]() $i=1,2$, together with a vertex
$i=1,2$, together with a vertex ![]() $v\in U$ and a set of clusters partitioning
$v\in U$ and a set of clusters partitioning ![]() $U\setminus \{v\}$ such that an absorption process with this input will percolate, and, furthermore, the following holds. Let
$U\setminus \{v\}$ such that an absorption process with this input will percolate, and, furthermore, the following holds. Let ![]() $\ell$ be the number of steps it takes for this absorption process to percolate, and let
$\ell$ be the number of steps it takes for this absorption process to percolate, and let ![]() $v=v_1,\ldots,v_{|U|}$ be the vertices of U in the order that they are added to the percolating set in the absorption process. Then no vertex in
$v=v_1,\ldots,v_{|U|}$ be the vertices of U in the order that they are added to the percolating set in the absorption process. Then no vertex in ![]() $V\setminus U$ has an edge to
$V\setminus U$ has an edge to ![]() $\{v_1,\ldots,v_{\ell-1}\}$ in both
$\{v_1,\ldots,v_{\ell-1}\}$ in both ![]() $E_1$ and
$E_1$ and ![]() $E_2$.
$E_2$.
In other words, an optimal configuration is a minimal percolating configuration which allows the absorption process to percolate and includes all of the vertices which could be added as clusters in the process before step ![]() $\ell$. Note that it is not necessarily a maximal percolating set, since it is still possible that some clusters of size larger than one could have been added to the process, that more single vertices could have been added in step
$\ell$. Note that it is not necessarily a maximal percolating set, since it is still possible that some clusters of size larger than one could have been added to the process, that more single vertices could have been added in step ![]() $\ell$, or indeed that the absorption process could have continued beyond
$\ell$, or indeed that the absorption process could have continued beyond ![]() $\ell$ steps.
$\ell$ steps.
Set
If ![]() $G(n,p_1,p_2)$ percolates then, by Lemma 3.1, there exists an input of starting vertex and clusters such that running an absorption process with this input will lead to an optimal configuration (and, in particular, a minimal percolating configuration) of size greater than
$G(n,p_1,p_2)$ percolates then, by Lemma 3.1, there exists an input of starting vertex and clusters such that running an absorption process with this input will lead to an optimal configuration (and, in particular, a minimal percolating configuration) of size greater than ![]() $k_0$. Let us consider the first time at which this process becomes larger than
$k_0$. Let us consider the first time at which this process becomes larger than ![]() $k_0$, in step
$k_0$, in step ![]() $\ell$, say. Then it reached size
$\ell$, say. Then it reached size ![]() $k\le k_0$ in either the
$k\le k_0$ in either the ![]() $(\ell-1)$th or the
$(\ell-1)$th or the ![]() $\ell$th step, and we next added a cluster of size r in the
$\ell$th step, and we next added a cluster of size r in the ![]() $\ell$th step such that
$\ell$th step such that ![]() $k+r> k_0$. We aim to bound the number of optimal configurations with parameters
$k+r> k_0$. We aim to bound the number of optimal configurations with parameters ![]() $k,\ell,$ and r, and sum over all
$k,\ell,$ and r, and sum over all ![]() $k,\ell,$ and r, observing that
$k,\ell,$ and r, observing that
For ![]() $0\le i \le \ell$, define
$0\le i \le \ell$, define ![]() $X_{i}$ to be the set of vertices in the percolating set after i steps of the absorption process, which is terminated the moment we reach size larger than
$X_{i}$ to be the set of vertices in the percolating set after i steps of the absorption process, which is terminated the moment we reach size larger than ![]() $k_0$, so, in particular, we have
$k_0$, so, in particular, we have ![]() $|X_\ell|=k+r$, and, furthermore,
$|X_\ell|=k+r$, and, furthermore, ![]() $\ell \le
|X_{\ell-1}|\le k$.
$\ell \le
|X_{\ell-1}|\le k$.
Since we have an optimal configuration, none of the vertices outside ![]() $X_\ell$ may have both a red and a blue neighbour within the first
$X_\ell$ may have both a red and a blue neighbour within the first ![]() $\ell-1$ vertices
$\ell-1$ vertices ![]() $\{x_1,x_2,\ldots,x_{\ell-1}\}$ of
$\{x_1,x_2,\ldots,x_{\ell-1}\}$ of ![]() $X_{\ell-1}$. Note that this holds for a given vertex with probability at most
$X_{\ell-1}$. Note that this holds for a given vertex with probability at most
By (2.3), we have ![]() $p_1(\ell-1)\le p_1 k_0 =o(1)$ and, similarly,
$p_1(\ell-1)\le p_1 k_0 =o(1)$ and, similarly, ![]() $p_2 (\ell-1)=o(1)$. Therefore,
$p_2 (\ell-1)=o(1)$. Therefore,
Thus, the probability that none of the vertices outside ![]() $X_\ell$ has both a red and a blue neighbour within
$X_\ell$ has both a red and a blue neighbour within ![]() $\{x_1,\ldots,x_{\ell-1}\}$ is at most
$\{x_1,\ldots,x_{\ell-1}\}$ is at most
where ![]() $\varepsilon_0 :\!=\varepsilon/3$.
$\varepsilon_0 :\!=\varepsilon/3$.
Therefore, the expected number of optimal configurations with parameters ![]() $k,\ell,$ and r is at most
$k,\ell,$ and r is at most
Let us define S to be the set of triples ![]() $(k,\ell,r)$ satisfying (3.10). We need to bound the expression
$(k,\ell,r)$ satisfying (3.10). We need to bound the expression
 $$\begin{align}
&\sum_{(k,\ell,r)\in S}\binom{n}{k+r} M_{k,\ell,r}(p_1p_2)^{k+r-1}\,
{\exp}({-}(1-\varepsilon_0)(\ell-1)^2 np_1p_2)\nonumber
\\[4pt]
&\qquad \le \sum_{(k,\ell,r)\in S} \frac{n^{k+r}}{(k+r)!}\binom{k+r}{r}
(k!)^2 (r!)^2 2^{k+r} \mathrm{e}^{r+\ell} \frac{k\ell r^3 \mathrm{e}^{582}}{2}\nonumber
\\[4pt]
& \times \bigg(\frac{1-\varepsilon}{4n\ln n}\bigg)^{k+r-1}\,
{\exp}({-}(1-\varepsilon_0)(\ell-1)^2 np_1p_2)\nonumber
\\[4pt]
&\qquad \le \frac{ \mathrm{e}^{582} \cdot n\cdot 2\ln n}{1-\varepsilon} \bigg(\sum_{k=k_0/2}^{k_0}k\cdot
k!\, \bigg(\frac{1-\varepsilon}{2\ln n}\bigg)^{k} \sum_{r=k_0-k}^{k} r!\,
r^3\bigg(\frac{\mathrm{e}(1-\varepsilon)}{2\ln n}\bigg)^r \bigg)\nonumber
\\[4pt]
&\qquad\quad\, \times \sum_{\ell=1}^{k_0}\ell {\exp}\bigg(\ell
-(1-\varepsilon_0)(\ell-1)^2 \frac{1-\varepsilon}{4\ln n}\bigg).
\label{eqn16}\end{align}$$
$$\begin{align}
&\sum_{(k,\ell,r)\in S}\binom{n}{k+r} M_{k,\ell,r}(p_1p_2)^{k+r-1}\,
{\exp}({-}(1-\varepsilon_0)(\ell-1)^2 np_1p_2)\nonumber
\\[4pt]
&\qquad \le \sum_{(k,\ell,r)\in S} \frac{n^{k+r}}{(k+r)!}\binom{k+r}{r}
(k!)^2 (r!)^2 2^{k+r} \mathrm{e}^{r+\ell} \frac{k\ell r^3 \mathrm{e}^{582}}{2}\nonumber
\\[4pt]
& \times \bigg(\frac{1-\varepsilon}{4n\ln n}\bigg)^{k+r-1}\,
{\exp}({-}(1-\varepsilon_0)(\ell-1)^2 np_1p_2)\nonumber
\\[4pt]
&\qquad \le \frac{ \mathrm{e}^{582} \cdot n\cdot 2\ln n}{1-\varepsilon} \bigg(\sum_{k=k_0/2}^{k_0}k\cdot
k!\, \bigg(\frac{1-\varepsilon}{2\ln n}\bigg)^{k} \sum_{r=k_0-k}^{k} r!\,
r^3\bigg(\frac{\mathrm{e}(1-\varepsilon)}{2\ln n}\bigg)^r \bigg)\nonumber
\\[4pt]
&\qquad\quad\, \times \sum_{\ell=1}^{k_0}\ell {\exp}\bigg(\ell
-(1-\varepsilon_0)(\ell-1)^2 \frac{1-\varepsilon}{4\ln n}\bigg).
\label{eqn16}\end{align}$$
We first show that the summand involving ![]() $\ell$ is increasing. Certainly the multiplicative factor of
$\ell$ is increasing. Certainly the multiplicative factor of ![]() $\ell$ is increasing, so let us define
$\ell$ is increasing, so let us define ![]() $x_\ell :\!={\exp}(\ell -(1-\varepsilon_0)(\ell-1)^2 (1-\varepsilon)/{(4\ln n)})$. Then, for
$x_\ell :\!={\exp}(\ell -(1-\varepsilon_0)(\ell-1)^2 (1-\varepsilon)/{(4\ln n)})$. Then, for ![]() $\ell \le k_0=2\ln n,$ we have
$\ell \le k_0=2\ln n,$ we have
Therefore, the sum over ![]() $\ell$ in (3.11) can be bounded from above by replacing each summand by the summand with
$\ell$ in (3.11) can be bounded from above by replacing each summand by the summand with ![]() $\ell=k_0$, i.e.
$\ell=k_0$, i.e.
 $$\begin{align}
&\sum_{\ell=1}^{k_0}\ell{\exp}\bigg(\ell -(1-\varepsilon_0)(\ell-1)^2 (1-\varepsilon)
\frac{1}{4\ln n}\bigg) \nonumber
\\
&\qquad \le k_0^2\, {\exp}\bigg(k_0 -(1-\varepsilon_0)(k_0-1)^2
(1-\varepsilon)\frac{1}{2k_0}\bigg)\nonumber
\\
&\qquad = k_0^2\,
{\exp}\bigg(k_0\bigg(1-\frac{(1-\varepsilon_0)(1-\varepsilon)}{2}\bigg)\bigg)\,
{\exp}\bigg(\frac{(2k_0-1)(1-\varepsilon_0)(1-\varepsilon)}{2k_0}\bigg)\nonumber
\\
&\qquad \le k_0^2\,{\exp}\bigg(k_0\bigg(\frac{1 +\varepsilon +\varepsilon_0}{2}\bigg)\bigg)
\mathrm{e}.
\label{eqn17}\end{align}$$
$$\begin{align}
&\sum_{\ell=1}^{k_0}\ell{\exp}\bigg(\ell -(1-\varepsilon_0)(\ell-1)^2 (1-\varepsilon)
\frac{1}{4\ln n}\bigg) \nonumber
\\
&\qquad \le k_0^2\, {\exp}\bigg(k_0 -(1-\varepsilon_0)(k_0-1)^2
(1-\varepsilon)\frac{1}{2k_0}\bigg)\nonumber
\\
&\qquad = k_0^2\,
{\exp}\bigg(k_0\bigg(1-\frac{(1-\varepsilon_0)(1-\varepsilon)}{2}\bigg)\bigg)\,
{\exp}\bigg(\frac{(2k_0-1)(1-\varepsilon_0)(1-\varepsilon)}{2k_0}\bigg)\nonumber
\\
&\qquad \le k_0^2\,{\exp}\bigg(k_0\bigg(\frac{1 +\varepsilon +\varepsilon_0}{2}\bigg)\bigg)
\mathrm{e}.
\label{eqn17}\end{align}$$
On the other hand, considering the sum over r in (3.11), we approximate as follows. Since ![]() $r\le k \le k_0$ and
$r\le k \le k_0$ and ![]() $k_0\ge \mathrm{e}^2$, by (2.5), we have
$k_0\ge \mathrm{e}^2$, by (2.5), we have ![]() $r!\le \mathrm{e} \sqrt{r} (r/\mathrm{e})^r \leq k_0
(r/\mathrm{e})^r$, implying that
$r!\le \mathrm{e} \sqrt{r} (r/\mathrm{e})^r \leq k_0
(r/\mathrm{e})^r$, implying that
 $$\begin{align}
\sum_{r=k_0-k}^{k} r!\,r^3 \bigg(\frac{\mathrm{e}(1-\varepsilon)}{2\ln n}\bigg)^r &\le
k_0^4\sum_{r=k_0-k}^{k}
\bigg(\frac{r}{\mathrm{e}}\bigg)^r\bigg(\frac{\mathrm{e}(1-\varepsilon)}{k_0}\bigg)^r
\nonumber
\\
&= k_0^4\sum_{r=k_0-k}^{k} \bigg(\frac{(1-\varepsilon)r}{k_0}\bigg)^r\nonumber[0]
\\
&\le k_0^4 \bigg(\frac{1-\varepsilon}{k_0}\bigg)^{k_0-k}\sum_{r=k_0-k}^{k}
\frac{r^r}{k_0^{r-k_0+k}}\nonumber
\\
&\le k_0^4 \bigg(\frac{1-\varepsilon}{k_0}\bigg)^{k_0-k} \sum_{r=k_0-k}^{k}
\frac{k_0^{k_0}}{k^k} \bigg(\frac{k}{k_0}\bigg)^{r+k}.
\label{eqn18}\end{align}$$
$$\begin{align}
\sum_{r=k_0-k}^{k} r!\,r^3 \bigg(\frac{\mathrm{e}(1-\varepsilon)}{2\ln n}\bigg)^r &\le
k_0^4\sum_{r=k_0-k}^{k}
\bigg(\frac{r}{\mathrm{e}}\bigg)^r\bigg(\frac{\mathrm{e}(1-\varepsilon)}{k_0}\bigg)^r
\nonumber
\\
&= k_0^4\sum_{r=k_0-k}^{k} \bigg(\frac{(1-\varepsilon)r}{k_0}\bigg)^r\nonumber[0]
\\
&\le k_0^4 \bigg(\frac{1-\varepsilon}{k_0}\bigg)^{k_0-k}\sum_{r=k_0-k}^{k}
\frac{r^r}{k_0^{r-k_0+k}}\nonumber
\\
&\le k_0^4 \bigg(\frac{1-\varepsilon}{k_0}\bigg)^{k_0-k} \sum_{r=k_0-k}^{k}
\frac{k_0^{k_0}}{k^k} \bigg(\frac{k}{k_0}\bigg)^{r+k}.
\label{eqn18}\end{align}$$
Note that since ![]() $k_0-k \leq r \leq k,$ we have
$k_0-k \leq r \leq k,$ we have
Since ![]() $0 \leq {(k_0-k)}/{k} \leq 1,$ the Taylor expansion of
$0 \leq {(k_0-k)}/{k} \leq 1,$ the Taylor expansion of ![]() $\ln(1+x)$ leads to
$\ln(1+x)$ leads to
 $$\begin{align*}
(k+r) \ln{\bigg(1+\frac{k_0-k}{k}\bigg)} & \geq (k+r)
\frac{k_0-k}{k}-\frac{k+r}{2}\bigg(\frac{k_0-k}{k}\bigg)^2
\\
& = (k_0-k)\bigg( \frac{k+r}{k}-\frac{k_0-k}{k}\cdot \frac{k+r}{2k} \bigg)
\\
&\geq k_0-k.
\end{align*}$$
$$\begin{align*}
(k+r) \ln{\bigg(1+\frac{k_0-k}{k}\bigg)} & \geq (k+r)
\frac{k_0-k}{k}-\frac{k+r}{2}\bigg(\frac{k_0-k}{k}\bigg)^2
\\
& = (k_0-k)\bigg( \frac{k+r}{k}-\frac{k_0-k}{k}\cdot \frac{k+r}{2k} \bigg)
\\
&\geq k_0-k.
\end{align*}$$
Therefore, by (2.5), we conclude that
Thus (3.13) gives
 $$\begin{equation*}
\sum_{r=k_0-k}^{k} r!\,r^3 \bigg(\frac{\mathrm{e}(1-\varepsilon)}{2\ln n}\bigg)^r\le
k_0^6 \bigg(\frac{1-\varepsilon}{k_0}\bigg)^{k_0-k}\frac{k_0!}{k!}.
\end{equation*}$$
$$\begin{equation*}
\sum_{r=k_0-k}^{k} r!\,r^3 \bigg(\frac{\mathrm{e}(1-\varepsilon)}{2\ln n}\bigg)^r\le
k_0^6 \bigg(\frac{1-\varepsilon}{k_0}\bigg)^{k_0-k}\frac{k_0!}{k!}.
\end{equation*}$$
Hence, the sum over k in (3.11) can be bounded by
 $$\begin{align}
&\sum_{k=k_0/2}^{k_0}k\cdot k!\, \bigg(\frac{1-\varepsilon}{2\ln n}\bigg)^{k}
\sum_{r=k_0-k}^{k} r!\, r^3\bigg(\frac{\mathrm{e}(1-\varepsilon)}{2\ln n}\bigg)^r\nonumber
\\
&\qquad\le \sum_{k=k_0/2}^{k_0}k \cdot k!\, \bigg(\frac{1-\varepsilon}{k_0}\bigg)^{k}
k_0^6 \bigg(\frac{1-\varepsilon}{k_0}\bigg)^{k_0-k} \frac{k_0!}{k!}\nonumber
\\
&\qquad\le k_0^8 \bigg(\frac{1-\varepsilon}{k_0}\bigg)^{k_0} k_0!
\label{eqn19}\end{align}$$
$$\begin{align}
&\sum_{k=k_0/2}^{k_0}k\cdot k!\, \bigg(\frac{1-\varepsilon}{2\ln n}\bigg)^{k}
\sum_{r=k_0-k}^{k} r!\, r^3\bigg(\frac{\mathrm{e}(1-\varepsilon)}{2\ln n}\bigg)^r\nonumber
\\
&\qquad\le \sum_{k=k_0/2}^{k_0}k \cdot k!\, \bigg(\frac{1-\varepsilon}{k_0}\bigg)^{k}
k_0^6 \bigg(\frac{1-\varepsilon}{k_0}\bigg)^{k_0-k} \frac{k_0!}{k!}\nonumber
\\
&\qquad\le k_0^8 \bigg(\frac{1-\varepsilon}{k_0}\bigg)^{k_0} k_0!
\label{eqn19}\end{align}$$
Substituting (3.12) and (3.14) into (3.11), we find that the expected number of optimal configurations with parameters ![]() $\left( {k,\ell ,r} \right) \in S$ is at most
$\left( {k,\ell ,r} \right) \in S$ is at most
 $$\begin{align*}
&\frac{ \mathrm{e}^{582}nk_0}{1-\varepsilon} \bigg(k_0^8
\bigg(\frac{1-\varepsilon}{k_0}\bigg)^{k_0} k_0!\bigg)
k_0^2\,{\exp}\bigg(k_0\bigg(\frac{1 +\varepsilon +\varepsilon_0}{2}\bigg)\bigg) \mathrm{e}
\\
&\qquad \le nk_0^{12} \bigg(\bigg(\frac{1-\varepsilon}{k_0}\bigg)^{k_0}k_0
\bigg(\frac{k_0}{\mathrm{e}}\bigg)^{k_0}\bigg)\,
{\exp}\bigg(k_0\bigg(\frac{1+\varepsilon+\varepsilon_0}{2}\bigg)\bigg)
\\
&\qquad \le nk_0^{13} \bigg(\frac{1-\varepsilon}{\mathrm{e}}\, {\exp}
\bigg(\frac{1+\varepsilon+\varepsilon_0}{2}\bigg)\bigg)^{k_0}[0]
\\
&\qquad \le nk_0^{13} \bigg(\mathrm{e}^{-1-\varepsilon}\,
{\exp}\bigg(\frac{1+\varepsilon+\varepsilon_0}{2}\bigg)\bigg)^{k_0}
\\
&\qquad = n (2\ln n)^{13}\,
{\exp}\bigg(\bigg({-}\frac{1}{2}-\frac{\varepsilon}{2}+\frac{\varepsilon_0}{2}\bigg)2\ln
n\bigg)
\\
&\qquad = n (2\ln n)^{13} n^{({-}1-\varepsilon+\varepsilon_0)}
\\
&\qquad = (2\ln n)^{13} n^{-\varepsilon+\varepsilon_0}.
\end{align*}$$
$$\begin{align*}
&\frac{ \mathrm{e}^{582}nk_0}{1-\varepsilon} \bigg(k_0^8
\bigg(\frac{1-\varepsilon}{k_0}\bigg)^{k_0} k_0!\bigg)
k_0^2\,{\exp}\bigg(k_0\bigg(\frac{1 +\varepsilon +\varepsilon_0}{2}\bigg)\bigg) \mathrm{e}
\\
&\qquad \le nk_0^{12} \bigg(\bigg(\frac{1-\varepsilon}{k_0}\bigg)^{k_0}k_0
\bigg(\frac{k_0}{\mathrm{e}}\bigg)^{k_0}\bigg)\,
{\exp}\bigg(k_0\bigg(\frac{1+\varepsilon+\varepsilon_0}{2}\bigg)\bigg)
\\
&\qquad \le nk_0^{13} \bigg(\frac{1-\varepsilon}{\mathrm{e}}\, {\exp}
\bigg(\frac{1+\varepsilon+\varepsilon_0}{2}\bigg)\bigg)^{k_0}[0]
\\
&\qquad \le nk_0^{13} \bigg(\mathrm{e}^{-1-\varepsilon}\,
{\exp}\bigg(\frac{1+\varepsilon+\varepsilon_0}{2}\bigg)\bigg)^{k_0}
\\
&\qquad = n (2\ln n)^{13}\,
{\exp}\bigg(\bigg({-}\frac{1}{2}-\frac{\varepsilon}{2}+\frac{\varepsilon_0}{2}\bigg)2\ln
n\bigg)
\\
&\qquad = n (2\ln n)^{13} n^{({-}1-\varepsilon+\varepsilon_0)}
\\
&\qquad = (2\ln n)^{13} n^{-\varepsilon+\varepsilon_0}.
\end{align*}$$
Note that since we chose ![]() $\varepsilon_0=\varepsilon/3$ and
$\varepsilon_0=\varepsilon/3$ and ![]() $\varepsilon$ is constant, this term tends to 0.
$\varepsilon$ is constant, this term tends to 0.
Thus, by Markov’s inequality, with high probability there is no such percolating set and, therefore, the double-graph does not percolate.
4. Supercritical case: proof of Theorem 1.2(ii)
In this section we prove Theorem 1.2(ii). Recall that we assume that ![]() $p_1 \ge p_2 \ge {\ln n}/{n}$ and the statement says that, conditioned on the individual graphs
$p_1 \ge p_2 \ge {\ln n}/{n}$ and the statement says that, conditioned on the individual graphs ![]() $G_1 \sim G(n,p_1)$ and
$G_1 \sim G(n,p_1)$ and ![]() $G_2 \sim
G(n,p_2)$ being connected, with high probability, the jigsaw process percolates on the double graph
$G_2 \sim
G(n,p_2)$ being connected, with high probability, the jigsaw process percolates on the double graph ![]() $G(n,p_1,p_2)$.
$G(n,p_1,p_2)$.
We first note that, for ![]() $p_1,p_2 \ge {\ln n}/{n}$, the probability of
$p_1,p_2 \ge {\ln n}/{n}$, the probability of ![]() $G_1$ and
$G_1$ and ![]() $G_2$ being connected is bounded below by a (nonzero) constant. Thus, any event that holds with high probability also holds with high probability in the probability space conditioned on
$G_2$ being connected is bounded below by a (nonzero) constant. Thus, any event that holds with high probability also holds with high probability in the probability space conditioned on ![]() $G_1$ and
$G_1$ and ![]() $G_2$ being connected. Therefore, for simplicity, in the following arguments we will suppress this conditioning.
$G_2$ being connected. Therefore, for simplicity, in the following arguments we will suppress this conditioning.
The proof consists of three stages in which we construct a nested sequence of percolating sets ![]() $U_1 \subset U_2 \subset U_3 = V,$ growing in size as we reveal more edges. In Section 4.1 we define and analyse a construction algorithm (Algorithm 4.1) which constructs percolating sets, and show in Lemma 4.2 that w.h.p. it constructs at least one percolating set of a reasonably large size. Subsequently, in Section 4.2 we show that this percolating set expands to cover almost all its red neighbours (Lemma 4.7). Finally, we use a sprinkling argument to extend this percolating set until it eventually covers all vertices and so prove the supercritical case.
$U_1 \subset U_2 \subset U_3 = V,$ growing in size as we reveal more edges. In Section 4.1 we define and analyse a construction algorithm (Algorithm 4.1) which constructs percolating sets, and show in Lemma 4.2 that w.h.p. it constructs at least one percolating set of a reasonably large size. Subsequently, in Section 4.2 we show that this percolating set expands to cover almost all its red neighbours (Lemma 4.7). Finally, we use a sprinkling argument to extend this percolating set until it eventually covers all vertices and so prove the supercritical case.
We will reveal the red graph with two rounds of exposure. To this end, set
and
Consider the double graphs ![]() $G(n,p_1^{(i)},p_2^{(i)})$ for
$G(n,p_1^{(i)},p_2^{(i)})$ for ![]() $i=1,2$. For
$i=1,2$. For ![]() $i=1, 2$, we denote by
$i=1, 2$, we denote by ![]() $N_1^{(i)} (U)$ the neighbourhood of U within
$N_1^{(i)} (U)$ the neighbourhood of U within ![]() $G(n,p_1^{(i)})$.
$G(n,p_1^{(i)})$.
Let us note that ![]() $G(n,p_1^{(1)},p_2^{(1)})\cup G(n,p_1^{(2)},p_2^{(2)})
\sim G(n,p_1^*,p_2)$, where
$G(n,p_1^{(1)},p_2^{(1)})\cup G(n,p_1^{(2)},p_2^{(2)})
\sim G(n,p_1^*,p_2)$, where
Since percolation is a monotone increasing property, the probability that ![]() $G(n,p_1,p_2)$ percolates is at least the probability that
$G(n,p_1,p_2)$ percolates is at least the probability that ![]() $G(n,p_1^{(1)},p_2^{(1)})\cup G(n,p_1^{(2)},p_2^{(2)})$ percolates.
$G(n,p_1^{(1)},p_2^{(1)})\cup G(n,p_1^{(2)},p_2^{(2)})$ percolates.
4.1. Getting past the bottleneck
We set
Our aim is to construct a percolating set of size ![]() $k_1$ by means of an algorithm. Refining an algorithm in Reference Bollobás, Riordan, Slivken and Smith[5], we grow a percolating set
$k_1$ by means of an algorithm. Refining an algorithm in Reference Bollobás, Riordan, Slivken and Smith[5], we grow a percolating set ![]() $X_t$ by adding vertices in each step t.
$X_t$ by adding vertices in each step t.
We first describe the algorithm informally, suppressing the index t for simplicity. We begin with X being a single vertex. At the start of step t, the set X will consist of vertices ![]() $x_1,\ldots,x_{s}$ which form a percolating set, with
$x_1,\ldots,x_{s}$ which form a percolating set, with ![]() $s\ge t$. In addition, the set R consists of vertices which are adjacent to at least one of
$s\ge t$. In addition, the set R consists of vertices which are adjacent to at least one of ![]() $x_1,\ldots,x_{t-1}$ in red, but not in blue.
$x_1,\ldots,x_{t-1}$ in red, but not in blue.
In step t, we will reveal the red neighbours Q of ![]() $x_t$ (outside of
$x_t$ (outside of ![]() $X\cup R$). We will also reveal any blue edges between Q and
$X\cup R$). We will also reveal any blue edges between Q and ![]() $x_1,\ldots,x_t$—vertices incident to such a blue edge will be added to X, while the remaining vertices of Q are added to R. We also reveal any blue edges between R and
$x_1,\ldots,x_t$—vertices incident to such a blue edge will be added to X, while the remaining vertices of Q are added to R. We also reveal any blue edges between R and ![]() $x_t$, and vertices incident to such an edge will be moved from R to X.
$x_t$, and vertices incident to such an edge will be moved from R to X.
There are two main differences between our algorithm and the algorithm described by Bollobás et al. Reference Bollobás, Riordan, Slivken and Smith[5]: first, in their algorithm they only add one vertex to X in each step, and second, they did not keep track of the set R and reveal blue edges between ![]() $x_t$ and R, but simply discarded it along with any other vertices that could have been added to X. In order to prove the sharper version of the theorem with the exact threshold, we require this more detailed algorithm and significantly more precise analysis until it passes the bottleneck.
$x_t$ and R, but simply discarded it along with any other vertices that could have been added to X. In order to prove the sharper version of the theorem with the exact threshold, we require this more detailed algorithm and significantly more precise analysis until it passes the bottleneck.
We will run the algorithm several times. Each attempt is called a round, indexed by ![]() $\ell$. At the end of each round, we will discard the percolating set generated in the round—this ensures independence between rounds. In order to make the analysis of each round identical, we will artificially exclude some vertices from each round to ensure that we always have the same number of vertices available.
$\ell$. At the end of each round, we will discard the percolating set generated in the round—this ensures independence between rounds. In order to make the analysis of each round identical, we will artificially exclude some vertices from each round to ensure that we always have the same number of vertices available.
Algorithm 4.1. (The construction algorithm.)
Input: Double graph ![]() $(V,E_1,E_2)$.
$(V,E_1,E_2)$.
Set ![]() $\ell = 1$ and
$\ell = 1$ and ![]() $V_1'=V.$
$V_1'=V.$
while ![]() $|V_\ell'|\ge n-n^{1-\delta}$ do
$|V_\ell'|\ge n-n^{1-\delta}$ do
Fix an arbitrary set ![]() $V_\ell \subset V_\ell'$ of size
$V_\ell \subset V_\ell'$ of size ![]() $ n-n^{1-\delta}$.
$ n-n^{1-\delta}$.
Pick an arbitrary vertex ![]() $x_1=x_1(\ell)\in V_\ell$ and set
$x_1=x_1(\ell)\in V_\ell$ and set ![]() $X_0=X_0(\ell) :\!=\{x_1\}$ and
$X_0=X_0(\ell) :\!=\{x_1\}$ and ![]() $s_0=s_0(\ell) :\!= 1$.
$s_0=s_0(\ell) :\!= 1$.
Also set ![]() $R_0=R_0(\ell) :\!=\varnothing$ and
$R_0=R_0(\ell) :\!=\varnothing$ and ![]() $t=1$.
$t=1$.
while ![]() $t\le s_{t-1}\lt k_1$ do Set
$t\le s_{t-1}\lt k_1$ do Set ![]() $Q_t=Q_t(\ell)=N_1^{(1)}(x_t)\cap (V_\ell\setminus (X_{t-1}\cup
R_{t-1}))$.
$Q_t=Q_t(\ell)=N_1^{(1)}(x_t)\cap (V_\ell\setminus (X_{t-1}\cup
R_{t-1}))$.
Set ![]() $B_t=B_t(\ell)=N_2(x_1,\ldots,x_t) \cap Q_t$.
$B_t=B_t(\ell)=N_2(x_1,\ldots,x_t) \cap Q_t$.
Set ![]() $C_t=C_t(\ell)=N_2(x_t) \cap R_t$.
$C_t=C_t(\ell)=N_2(x_t) \cap R_t$.
Set ![]() $X_{t}=X_{t}(\ell)=X_{t-1}\cup B_t \cup C_t$ and
$X_{t}=X_{t}(\ell)=X_{t-1}\cup B_t \cup C_t$ and ![]() $s_t=s_t(\ell) :\!=|X_t|$.
$s_t=s_t(\ell) :\!=|X_t|$.
Set ![]() $R_{t}=R_{t}(\ell)=(R_{t-1}\cup Q_t)\setminus (B_t \cup C_t)$.
$R_{t}=R_{t}(\ell)=(R_{t-1}\cup Q_t)\setminus (B_t \cup C_t)$.
Proceed to step ![]() $t+1$.
$t+1$.
end
Set ![]() $T= T(\ell)=t-1$.
$T= T(\ell)=t-1$.
Set ![]() $V_{\ell+1}'=V_{\ell}'\setminus X_{T(\ell)}$ and proceed to round
$V_{\ell+1}'=V_{\ell}'\setminus X_{T(\ell)}$ and proceed to round ![]() $\ell+1$.
$\ell+1$.
end
Set ![]() $L=\ell-1$.
$L=\ell-1$.
Output: ![]() $X_{T(1)},X_{T(2)},\ldots,X_{T(\ell-1)}$.
$X_{T(1)},X_{T(2)},\ldots,X_{T(\ell-1)}$.
Note that ![]() $T(\ell)$ is the number of steps in round
$T(\ell)$ is the number of steps in round ![]() $\ell$, while L is the number of rounds run by the construction algorithm.
$\ell$, while L is the number of rounds run by the construction algorithm.
We will apply the construction algorithm to ![]() $G(n,p_1^{(1)},p_2)$ and reveal edges only as they are required by the algorithm. The following lemma shows that the construction algorithm is well defined and builds a percolating set.
$G(n,p_1^{(1)},p_2)$ and reveal edges only as they are required by the algorithm. The following lemma shows that the construction algorithm is well defined and builds a percolating set.
Lemma 4.1. Algorithm 4.1 satisfies the following conditions:
(i) the algorithm terminates after a finite number of steps;
(ii) the rounds of the algorithm are mutually independent;
(iii) the set
 $X_{T(\ell)}$ forms a percolating set for
$X_{T(\ell)}$ forms a percolating set for  $1 \le \ell \leq L.$
$1 \le \ell \leq L.$
Proof. (i) For each round ![]() $\ell$ of the algorithm, we perform
$\ell$ of the algorithm, we perform ![]() $T(\ell)$ steps and
$T(\ell)$ steps and ![]() $|X_{T(\ell)}|\ge T(\ell)$ vertices are discarded, so the algorithm terminates after at most
$|X_{T(\ell)}|\ge T(\ell)$ vertices are discarded, so the algorithm terminates after at most ![]() $n^{1-\delta}$ steps.
$n^{1-\delta}$ steps.
(ii) Within a round, any edge is revealed at most once and every queried pair is incident to ![]() $X_{T(\ell)}.$ When the algorithm proceeds to the next round, it removes all the vertices of
$X_{T(\ell)}.$ When the algorithm proceeds to the next round, it removes all the vertices of ![]() $X_{T(\ell)}$ from the vertex pool
$X_{T(\ell)}$ from the vertex pool ![]() $V_\ell'$. Thus, the algorithm queries every edge at most once.
$V_\ell'$. Thus, the algorithm queries every edge at most once.
(iii) Assume that ![]() $X_{t-1}$ forms a percolating set. Every element in
$X_{t-1}$ forms a percolating set. Every element in ![]() $B_t$ has a red edge to
$B_t$ has a red edge to ![]() $x_t$ and a blue edge into
$x_t$ and a blue edge into ![]() $\{
x_1, \dots, x_{t}\} \subset X_{t-1}$. Similarly, the elements of
$\{
x_1, \dots, x_{t}\} \subset X_{t-1}$. Similarly, the elements of ![]() $C_t$ have a blue edge to
$C_t$ have a blue edge to ![]() $x_t$ and a red edge into
$x_t$ and a red edge into ![]() $\{ x_1, \dots, x_{t-1}\}$. Consequently,
$\{ x_1, \dots, x_{t-1}\}$. Consequently, ![]() $X_t$ also forms a percolating set and the assertion follows by induction over t. □
$X_t$ also forms a percolating set and the assertion follows by induction over t. □
The heart of the supercritical case is the following result.
Lemma 4.2. Running the construction algorithm on ![]() $G(n,p_1^{(1)},p_2),$ with high probability there is a round
$G(n,p_1^{(1)},p_2),$ with high probability there is a round ![]() $\ell$ such that
$\ell$ such that ![]() $X_{T(\ell)}(\ell)$ has size at least
$X_{T(\ell)}(\ell)$ has size at least ![]() $k_1$ and
$k_1$ and ![]() $|R_{T(\ell)}{(\ell)}|\ge T(\ell)np_1^{(1)}/2$.
$|R_{T(\ell)}{(\ell)}|\ge T(\ell)np_1^{(1)}/2$.
The proof of Lemma 4.2 will be given in Section 4.1.3. As preparation, we first approximate the sizes of various sets in the construction algorithm.
4.1.1. Poisson approximation
By Lemma 4.1 the rounds of the construction algorithm are independent. Thus, the following results hold uniformly for all ![]() $1\leq \ell \leq L$ and we will therefore lighten the notation by dropping
$1\leq \ell \leq L$ and we will therefore lighten the notation by dropping ![]() $\ell$. Moreover, we use the notation
$\ell$. Moreover, we use the notation ![]() $a = b \pm c$ to mean that
$a = b \pm c$ to mean that ![]() $b-c \leq a \leq b+c$, and, similarly,
$b-c \leq a \leq b+c$, and, similarly, ![]() $a = (b \pm c)d$ to mean
$a = (b \pm c)d$ to mean ![]() $(b-c)d
\leq a \leq (b+c)d$.
$(b-c)d
\leq a \leq (b+c)d$.
We aim to simplify the analysis of the algorithm by approximating the sizes of the various sets constructed. In particular, our main aim is Lemma 4.4, in which we approximate the distribution of the number of vertices added to the percolating set in each step. In order to achieve this, we first need to know that various other sets are about as large as we expect.
Definition 4.1. Set ![]() ${\varepsilon^*} :\!= {\varepsilon}/{10}$ and define the events
${\varepsilon^*} :\!= {\varepsilon}/{10}$ and define the events
 $$\begin{gather*}
\mathcal{Q}_t :\!= \bigg\{|Q_t| = \bigg(1\pm \frac{\varepsilon^*} 2\bigg)np_1^{(1)}\bigg\},
\qquad \mathcal{B}_t :\!=\bigg\{ |B_t| \lt \frac {\varepsilon^*} 4np_1^{(1)}\bigg\},
\\
\mathcal{C}_t :\!=\bigg\{ |C_t| \lt \frac {\varepsilon^*} 4np_1^{(1)}\bigg\}, \qquad \mathcal{R}_t
:\!=\bigg\{ |R_t| = (1\pm {\varepsilon^*})tnp_1^{(1)}\bigg\},
\\
\mathcal{H} :\!=\bigcap_{t\leq T} \mathcal{H}_t :\!=\bigcap_{t\leq T} \mathcal{Q}_t \cap \mathcal{B}_t\cap \mathcal{C}_t
\cap \mathcal{R}_t.
\end{gather*}$$
$$\begin{gather*}
\mathcal{Q}_t :\!= \bigg\{|Q_t| = \bigg(1\pm \frac{\varepsilon^*} 2\bigg)np_1^{(1)}\bigg\},
\qquad \mathcal{B}_t :\!=\bigg\{ |B_t| \lt \frac {\varepsilon^*} 4np_1^{(1)}\bigg\},
\\
\mathcal{C}_t :\!=\bigg\{ |C_t| \lt \frac {\varepsilon^*} 4np_1^{(1)}\bigg\}, \qquad \mathcal{R}_t
:\!=\bigg\{ |R_t| = (1\pm {\varepsilon^*})tnp_1^{(1)}\bigg\},
\\
\mathcal{H} :\!=\bigcap_{t\leq T} \mathcal{H}_t :\!=\bigcap_{t\leq T} \mathcal{Q}_t \cap \mathcal{B}_t\cap \mathcal{C}_t
\cap \mathcal{R}_t.
\end{gather*}$$
The events ![]() $\mathcal{Q}_t$ and
$\mathcal{Q}_t$ and ![]() $\mathcal{R}_t$ state that
$\mathcal{R}_t$ state that ![]() $|Q_t|$ and
$|Q_t|$ and ![]() $|R_t|$ are concentrated around their means. Conditioned on
$|R_t|$ are concentrated around their means. Conditioned on ![]() $\mathcal{Q}_t$ and
$\mathcal{Q}_t$ and ![]() $\mathcal{R}_t$, the expected sizes of
$\mathcal{R}_t$, the expected sizes of ![]() $B_t$ and
$B_t$ and ![]() $C_t$ are about
$C_t$ are about ![]() $tnp_1^{(1)}p_2$ and
$tnp_1^{(1)}p_2$ and ![]() ${(t-1) np_1^{(1)}p_2,}$ respectively. Thus, observing that
${(t-1) np_1^{(1)}p_2,}$ respectively. Thus, observing that ![]() $tp_2 \le k_1
p_1 = o(1)$, the events
$tp_2 \le k_1
p_1 = o(1)$, the events ![]() $\mathcal{B}_t$ and
$\mathcal{B}_t$ and ![]() $\mathcal{C}_t$ only require the corresponding random variables to be below a very crude upper bound. As a preliminary, we show that these events are very likely to hold in every round of the algorithm.
$\mathcal{C}_t$ only require the corresponding random variables to be below a very crude upper bound. As a preliminary, we show that these events are very likely to hold in every round of the algorithm.
Lemma 4.3. During one round of the construction algorithm on ![]() $G(n,p_1^{(1)},p_2),$ the event
$G(n,p_1^{(1)},p_2),$ the event ![]() $\mathcal{H}$ holds with probability at least
$\mathcal{H}$ holds with probability at least ![]() $1-{\exp}({-}\Omega (
n^{1/3} ) )$.
$1-{\exp}({-}\Omega (
n^{1/3} ) )$.
Proof. We have
 $$\begin{equation*}
\mathbb{P} [\mathcal{H}] = \prod_{t=1}^T \mathbb{P} [\mathcal{H}_t \ \,\,|\, \ \, \mathcal{H}_1, \dots, \mathcal{H}_{t-1} ]=
\prod_{t=1}^T \mathbb{P} [\mathcal{Q}_t,\mathcal{B}_t, \mathcal{C}_t,\mathcal{R}_t \ \,\,|\, \ \, \mathcal{H}_1, \dots,
\mathcal{H}_{t-1}].
\end{equation*}$$
$$\begin{equation*}
\mathbb{P} [\mathcal{H}] = \prod_{t=1}^T \mathbb{P} [\mathcal{H}_t \ \,\,|\, \ \, \mathcal{H}_1, \dots, \mathcal{H}_{t-1} ]=
\prod_{t=1}^T \mathbb{P} [\mathcal{Q}_t,\mathcal{B}_t, \mathcal{C}_t,\mathcal{R}_t \ \,\,|\, \ \, \mathcal{H}_1, \dots,
\mathcal{H}_{t-1}].
\end{equation*}$$
We will give a uniform lower bound for each of these terms. Recalling the definitions of ![]() $R_t,Q_t,B_t,$ and
$R_t,Q_t,B_t,$ and ![]() $C_t$ from the construction algorithm, conditional on
$C_t$ from the construction algorithm, conditional on ![]() $\mathcal{Q}_t,\mathcal{B}_t, \mathcal{C}_t,$ and
$\mathcal{Q}_t,\mathcal{B}_t, \mathcal{C}_t,$ and ![]() $\mathcal{R}_{t-1}\,{\subset}\, \mathcal{H}_{t-1},$ we have
$\mathcal{R}_{t-1}\,{\subset}\, \mathcal{H}_{t-1},$ we have
 $$\begin{align*}
|R_t|& =|R_{t-1}|+|Q_t|-|B_t|-|C_t|
\\
& =(1\pm {\varepsilon^*})(t-1)np_1^{(1)}+\bigg(1\pm \frac{{\varepsilon^*}}{2}\bigg)
np_1^{(1)}\pm \frac{{\varepsilon^*}}{4} np_1^{(1)} \pm \frac{{\varepsilon^*}}{4} np_1^{(1)}
\\
&=(1\pm {\varepsilon^*})tnp_1^{(1)},
\end{align*}$$
$$\begin{align*}
|R_t|& =|R_{t-1}|+|Q_t|-|B_t|-|C_t|
\\
& =(1\pm {\varepsilon^*})(t-1)np_1^{(1)}+\bigg(1\pm \frac{{\varepsilon^*}}{2}\bigg)
np_1^{(1)}\pm \frac{{\varepsilon^*}}{4} np_1^{(1)} \pm \frac{{\varepsilon^*}}{4} np_1^{(1)}
\\
&=(1\pm {\varepsilon^*})tnp_1^{(1)},
\end{align*}$$
i.e. ![]() $\mathcal{R}_t$ holds deterministically, implying that
$\mathcal{R}_t$ holds deterministically, implying that
 $$\begin{align}
&\mathbb{P} [\mathcal{Q}_t,\mathcal{B}_t, \mathcal{C}_t,\mathcal{R}_t \ \,\,|\, \ \, \mathcal{H}_1, \dots, \mathcal{H}_{t-1}]\nonumber
\\
&\qquad=\mathbb{P} [\mathcal{Q}_t,\mathcal{B}_t, \mathcal{C}_t \ \,\,|\, \ \, \mathcal{H}_1, \dots, \mathcal{H}_{t-1}]\nonumber
\\
&\qquad=\mathbb{P} [\mathcal{Q}_t \ \,\,|\, \ \, \mathcal{H}_1, \dots, \mathcal{H}_{t-1}] \mathbb{P} [\mathcal{B}_t \ \,\,|\, \ \, \mathcal{Q}_t,
\mathcal{H}_1, \dots, \mathcal{H}_{t-1}] \mathbb{P} [ \mathcal{C}_t \ \,\,|\, \ \, \mathcal{Q}_t, \mathcal{B}_t, \mathcal{H}_1, \dots,
\mathcal{H}_{t-1}].
\label{eqn20}\end{align}$$
$$\begin{align}
&\mathbb{P} [\mathcal{Q}_t,\mathcal{B}_t, \mathcal{C}_t,\mathcal{R}_t \ \,\,|\, \ \, \mathcal{H}_1, \dots, \mathcal{H}_{t-1}]\nonumber
\\
&\qquad=\mathbb{P} [\mathcal{Q}_t,\mathcal{B}_t, \mathcal{C}_t \ \,\,|\, \ \, \mathcal{H}_1, \dots, \mathcal{H}_{t-1}]\nonumber
\\
&\qquad=\mathbb{P} [\mathcal{Q}_t \ \,\,|\, \ \, \mathcal{H}_1, \dots, \mathcal{H}_{t-1}] \mathbb{P} [\mathcal{B}_t \ \,\,|\, \ \, \mathcal{Q}_t,
\mathcal{H}_1, \dots, \mathcal{H}_{t-1}] \mathbb{P} [ \mathcal{C}_t \ \,\,|\, \ \, \mathcal{Q}_t, \mathcal{B}_t, \mathcal{H}_1, \dots,
\mathcal{H}_{t-1}].
\label{eqn20}\end{align}$$
Our goal is to show that each of these terms has probability ![]() $1-{\exp}({-}\Omega(n^{1/3}))$. We will repeatedly use the fact that
$1-{\exp}({-}\Omega(n^{1/3}))$. We will repeatedly use the fact that
First note that
Since ![]() $|X_{t-1}|\le k_1=o(n)$, and conditional on
$|X_{t-1}|\le k_1=o(n)$, and conditional on ![]() $\mathcal{H}_{t-1}$, we have
$\mathcal{H}_{t-1}$, we have ![]() $|R_{t-1}|=(1\pm {\varepsilon^*})(t-1)np_1^{(1)}=O(k_1 n p_1^{(1)})=o(n)$; thus,
$|R_{t-1}|=(1\pm {\varepsilon^*})(t-1)np_1^{(1)}=O(k_1 n p_1^{(1)})=o(n)$; thus,
Together with the Chernoff bound (Lemma 2.1), this implies that
 $$\begin{align*}
\mathbb{P} [\overline{\mathcal{Q}}_t \ \,\,|\, \ \, \mathcal{H}_1, \dots, \mathcal{H}_{t-1}] & \le \mathbb{P}\bigg[
||Q_t|-\mathbb{E}[|Q_t|]|\ge \frac{{\varepsilon^*}}{4}np_1^{(1)}\bigg]
\\
& \le {\exp}({-}\Omega (np_1^{(1)}))
\\
&={\exp}({-}\Omega(n^{1/3})).
\end{align*}$$
$$\begin{align*}
\mathbb{P} [\overline{\mathcal{Q}}_t \ \,\,|\, \ \, \mathcal{H}_1, \dots, \mathcal{H}_{t-1}] & \le \mathbb{P}\bigg[
||Q_t|-\mathbb{E}[|Q_t|]|\ge \frac{{\varepsilon^*}}{4}np_1^{(1)}\bigg]
\\
& \le {\exp}({-}\Omega (np_1^{(1)}))
\\
&={\exp}({-}\Omega(n^{1/3})).
\end{align*}$$
Next we consider ![]() $\mathcal{B}_t$. Clearly,
$\mathcal{B}_t$. Clearly,
therefore, conditional on ![]() $\mathcal{Q}_t$ we have
$\mathcal{Q}_t$ we have
and, thus, Lemma 2.1 implies that
Finally,
and conditional on ![]() $\mathcal{R}_{t-1}\subset \mathcal{H}_{t-1}$ we have
$\mathcal{R}_{t-1}\subset \mathcal{H}_{t-1}$ we have
and again Lemma 2.1 implies that
Taking a union bound and substituting into (4.1), we have
The statement follows by applying the union bound over all steps in the round of the algorithm, of which there are at most ![]() $k_1$, and observing that
$k_1$, and observing that
□
It will be convenient in future analysis to condition on ![]() $\mathcal{H}$. Lemma 4.3 tells us that this is reasonable. In order to compare binomials with Poisson random variables, we need the following notation. For a nonnegative integer-valued random variable X and
$\mathcal{H}$. Lemma 4.3 tells us that this is reasonable. In order to compare binomials with Poisson random variables, we need the following notation. For a nonnegative integer-valued random variable X and ![]() $r\in \mathbb{N},$ let
$r\in \mathbb{N},$ let ![]() $X_{\le r}$ be the cutoff transform of X, i.e. the random variable with
$X_{\le r}$ be the cutoff transform of X, i.e. the random variable with
 $$\begin{equation*}
\mathbb{P} [X_{\le r} = t] =
\begin{cases}
\displaystyle\frac{\mathbb{P} [X=t]}{\mathbb{P} [X\le r]} & \text{for } t\leq r,
\\
0 & \text{otherwise.}
\end{cases}
\end{equation*}$$
$$\begin{equation*}
\mathbb{P} [X_{\le r} = t] =
\begin{cases}
\displaystyle\frac{\mathbb{P} [X=t]}{\mathbb{P} [X\le r]} & \text{for } t\leq r,
\\
0 & \text{otherwise.}
\end{cases}
\end{equation*}$$
The following claim shows how binomials dominate Poisson variables with suitable cutoff.
Claim 4.1. Let ![]() $X\sim \mathrm{Bi} ( N, p) $ and
$X\sim \mathrm{Bi} ( N, p) $ and ![]() $Y \sim \mathrm{Po}_{\le r} ((1-\theta)Np)$, with
$Y \sim \mathrm{Po}_{\le r} ((1-\theta)Np)$, with ![]() $N>0$ and
$N>0$ and ![]() $r/N \lt \theta\lt1$. Then
$r/N \lt \theta\lt1$. Then ![]() $ X \succ Y.$
$ X \succ Y.$
Proof. Clearly, for every ![]() $i>r,$ we have
$i>r,$ we have ![]() $\mathbb{P}[X\geq i]\ge \mathbb{P}[Y\ge i]=0$. For
$\mathbb{P}[X\geq i]\ge \mathbb{P}[Y\ge i]=0$. For ![]() $0{\le} i{\lt}r,$ we have
$0{\le} i{\lt}r,$ we have
implying that
Now suppose for a contradiction that, for some ![]() $\ell \le r,$ we have
$\ell \le r,$ we have ![]() $\mathbb{P}[Y\ge \ell] > \mathbb{P}[X\ge \ell]$. It follows that
$\mathbb{P}[Y\ge \ell] > \mathbb{P}[X\ge \ell]$. It follows that ![]() $\mathbb{P}[Y= \ell] > \mathbb{P}[X=
\ell]$ and, hence, it also follows that
$\mathbb{P}[Y= \ell] > \mathbb{P}[X=
\ell]$ and, hence, it also follows that ![]() $\mathbb{P}[Y=i] > \mathbb{P}[X=i]$ for all
$\mathbb{P}[Y=i] > \mathbb{P}[X=i]$ for all ![]() $0
\le i \le \ell$. But then we have
$0
\le i \le \ell$. But then we have
 $$\begin{equation*}
1=\mathbb{P}[Y\ge 0] = \sum_{i=1}^{\ell-1} \mathbb{P}[Y=i] + \mathbb{P}[Y\ge \ell] >
\sum_{i=1}^{\ell-1} \mathbb{P}[X=i] + \mathbb{P}[X\ge \ell] = \mathbb{P}[X\ge 0]=1,
\end{equation*}$$
$$\begin{equation*}
1=\mathbb{P}[Y\ge 0] = \sum_{i=1}^{\ell-1} \mathbb{P}[Y=i] + \mathbb{P}[Y\ge \ell] >
\sum_{i=1}^{\ell-1} \mathbb{P}[X=i] + \mathbb{P}[X\ge \ell] = \mathbb{P}[X\ge 0]=1,
\end{equation*}$$
which is a contradiction.
It is well known that the sum of Poisson variables is also Poisson, but we will need a similar result for Poisson variables with a cutoff.
Claim 4.2. For every ![]() $r\ge 0,$ we have
$r\ge 0,$ we have
Proof. Note that, for ![]() $i\le r,$ we have
$i\le r,$ we have
 $$\begin{align*}
\mathbb{P}[\mathrm{Po}_{\le r}(\lambda)+\mathrm{Po}_{\le r}(\mu)=i]&=\frac{\mathbb{P}[\mathrm{Po}(\lambda+\mu)
=i]}{\mathbb{P} [\mathrm{Po}(\lambda)\le r] \mathbb{P} [\mathrm{Po}(\mu)\le r]}
\\
& \le \frac{\mathbb{P}[\mathrm{Po}(\lambda+\mu)=i]}{\mathbb{P} [\mathrm{Po}(\lambda+\mu)\le r]}
\\
& =
\mathbb{P}[\mathrm{Po}_{\le r}(\lambda+\mu)=i]
\end{align*}$$
$$\begin{align*}
\mathbb{P}[\mathrm{Po}_{\le r}(\lambda)+\mathrm{Po}_{\le r}(\mu)=i]&=\frac{\mathbb{P}[\mathrm{Po}(\lambda+\mu)
=i]}{\mathbb{P} [\mathrm{Po}(\lambda)\le r] \mathbb{P} [\mathrm{Po}(\mu)\le r]}
\\
& \le \frac{\mathbb{P}[\mathrm{Po}(\lambda+\mu)=i]}{\mathbb{P} [\mathrm{Po}(\lambda+\mu)\le r]}
\\
& =
\mathbb{P}[\mathrm{Po}_{\le r}(\lambda+\mu)=i]
\end{align*}$$
as required. □
Our cutoff point will be at ![]() $\rho :\!=\omega^{-1}np_1^{(1)}$.
$\rho :\!=\omega^{-1}np_1^{(1)}$.
Lemma 4.4. For any round and any step ![]() $t\leq T$ of the construction algorithm on
$t\leq T$ of the construction algorithm on ![]() $G(n,p_1^{(1)},p_2),$ conditional on
$G(n,p_1^{(1)},p_2),$ conditional on ![]() $\mathcal{H},$ we have
$\mathcal{H},$ we have
Proof. Conditional on ![]() $\mathcal{H}$, the increment
$\mathcal{H}$, the increment ![]() $|X_{t}|-|X_{t-1}| = |B_t| + |C_t|$ dominates the sum of two independent binomials
$|X_{t}|-|X_{t-1}| = |B_t| + |C_t|$ dominates the sum of two independent binomials ![]() $ B_t^- \sim \mathrm{Bi}((1-
{\varepsilon^*}/2)np_1^{(1)},(1-{{\varepsilon^*}}/{2})tp_2)$ and
$ B_t^- \sim \mathrm{Bi}((1-
{\varepsilon^*}/2)np_1^{(1)},(1-{{\varepsilon^*}}/{2})tp_2)$ and ![]() $C_t^- \sim \mathrm{Bi} ((1-
{\varepsilon^*}) (t-1)np_1^{(1)},p_2).$
$C_t^- \sim \mathrm{Bi} ((1-
{\varepsilon^*}) (t-1)np_1^{(1)},p_2).$
Set ![]() $\theta = {\varepsilon^*}$ and, for
$\theta = {\varepsilon^*}$ and, for ![]() $t>1$, we have
$t>1$, we have
and
Hence, Claim 4.1, together with ![]() $C_1^-=\mathrm{Po}_{\le
\rho}(0)=0$, and Claim 4.2 yield
$C_1^-=\mathrm{Po}_{\le
\rho}(0)=0$, and Claim 4.2 yield
 $$\begin{align*}
B_t^- + C_t^- & \succ \mathrm{Po}_{\le \rho} ((1-{\varepsilon^*})^2tnp_1^{(1)} p_2) +
\mathrm{Po}_{\le \rho} ((1-{\varepsilon^*})^2(t-1)np_1^{(1)}p_2)
\\
& \succ \mathrm{Po}_{\le \rho} ((1-{\varepsilon^*})^2(2t-1)np_1^{(1)}p_2).
\end{align*}$$
$$\begin{align*}
B_t^- + C_t^- & \succ \mathrm{Po}_{\le \rho} ((1-{\varepsilon^*})^2tnp_1^{(1)} p_2) +
\mathrm{Po}_{\le \rho} ((1-{\varepsilon^*})^2(t-1)np_1^{(1)}p_2)
\\
& \succ \mathrm{Po}_{\le \rho} ((1-{\varepsilon^*})^2(2t-1)np_1^{(1)}p_2).
\end{align*}$$
Now Lemma 4.4 follows immediately, since
□
4.1.2. Two-stage analysis
We break the proof of Lemma 4.2 into two stages. To this end, for ![]() $k \in \mathbb{N},$ define
$k \in \mathbb{N},$ define
i.e. ![]() $\mathcal{E}_k$ is the event that the current round of the construction algorithm finds a percolating set of size at least
$\mathcal{E}_k$ is the event that the current round of the construction algorithm finds a percolating set of size at least ![]() $k+1$, or, equivalently, that it survives for at least k steps. First we show that percolating sets of size
$k+1$, or, equivalently, that it survives for at least k steps. First we show that percolating sets of size ![]() $k_0 :\!= 2 \ln n$ (just above the bottleneck) are not too unlikely. Recall that
$k_0 :\!= 2 \ln n$ (just above the bottleneck) are not too unlikely. Recall that ![]() $\delta = {\varepsilon}/{20}$.
$\delta = {\varepsilon}/{20}$.
Lemma 4.5. We have ![]() $ \mathbb{P}[\mathcal{E}_{k_0}\ \,\,|\, \ \, \mathcal{H}] \geq n^{-1+2\delta}. $
$ \mathbb{P}[\mathcal{E}_{k_0}\ \,\,|\, \ \, \mathcal{H}] \geq n^{-1+2\delta}. $
Proof. Let ![]() $Z_1,Z_2,\ldots$ be a family of independent random variables with distribution
$Z_1,Z_2,\ldots$ be a family of independent random variables with distribution
A sufficient condition for the construction algorithm to survive k steps in a round is that the sum of increments ![]() $|X_t|-1= \sum_{1\le s
\leq t} (|X_s|-|X_{s-1}|)$ never drops below t for
$|X_t|-1= \sum_{1\le s
\leq t} (|X_s|-|X_{s-1}|)$ never drops below t for ![]() $1\le t \le k$. Due to Lemma 4.4, it holds that
$1\le t \le k$. Due to Lemma 4.4, it holds that
 $$\begin{align}
\mathbb{P} [\mathcal{E}_k \ \,\,|\, \ \, \mathcal{H}] \geq \mathbb{P}\bigg[ \bigwedge_{t=1}^k
\sum_{s=1}^t Z_s \geq t \bigg].
\label{eqn21}
\end{align}$$
$$\begin{align}
\mathbb{P} [\mathcal{E}_k \ \,\,|\, \ \, \mathcal{H}] \geq \mathbb{P}\bigg[ \bigwedge_{t=1}^k
\sum_{s=1}^t Z_s \geq t \bigg].
\label{eqn21}
\end{align}$$
We write ![]() ${\boldsymbol{i}}$ for a vector
${\boldsymbol{i}}$ for a vector ![]() $ (i_1, \dots, i_k) \in [k]^k $ and set
$ (i_1, \dots, i_k) \in [k]^k $ and set
 $$\begin{equation*}
\mathcal{A}_k :\!=\biggl\{{\boldsymbol{i}} \in [k]^k\colon \sum_{t=1}^k i_t=k \biggr\}
\quad\text{and}\quad \mathcal{A}_k^* :\!=\biggl\{{\boldsymbol{i}} \in \mathcal{A}_k\colon
\bigwedge_{t=1}^k \sum_{s=1}^t i_s \geq t\biggr\}.
\end{equation*}$$
$$\begin{equation*}
\mathcal{A}_k :\!=\biggl\{{\boldsymbol{i}} \in [k]^k\colon \sum_{t=1}^k i_t=k \biggr\}
\quad\text{and}\quad \mathcal{A}_k^* :\!=\biggl\{{\boldsymbol{i}} \in \mathcal{A}_k\colon
\bigwedge_{t=1}^k \sum_{s=1}^t i_s \geq t\biggr\}.
\end{equation*}$$
Consequently, it holds that ![]() $ \mathbb{P}[ \bigwedge_{t=1}^k \sum_{s=1}^t Z_s
\geq t ] \ge \sum_{{\boldsymbol{i}} \in \mathcal{A}_k^*} \prod_{t=1}^k \mathbb{P} [Z_t=i_t]$. The additional, seemingly arbitrary restriction that the entries
$ \mathbb{P}[ \bigwedge_{t=1}^k \sum_{s=1}^t Z_s
\geq t ] \ge \sum_{{\boldsymbol{i}} \in \mathcal{A}_k^*} \prod_{t=1}^k \mathbb{P} [Z_t=i_t]$. The additional, seemingly arbitrary restriction that the entries ![]() $i_t$ sum up to k will turn out to be very useful for the following analysis. Set
$i_t$ sum up to k will turn out to be very useful for the following analysis. Set
 $$\begin{equation*}
S_{k_0} :\!=\sum_{{\boldsymbol{i}} \in \mathcal{A}_{k_0}^*}\prod_{t=1}^{k_0}
\frac{(2t-1)^{i_t}}{i_t!}.
\end{equation*}$$
$$\begin{equation*}
S_{k_0} :\!=\sum_{{\boldsymbol{i}} \in \mathcal{A}_{k_0}^*}\prod_{t=1}^{k_0}
\frac{(2t-1)^{i_t}}{i_t!}.
\end{equation*}$$
Since ![]() $k_0\le \rho,$ we have
$k_0\le \rho,$ we have
 $$\begin{align}
\mathbb{P}\bigg[ \bigwedge_{t=1}^{k_0} \sum_{s=1}^t Z_s \geq t \bigg] \nonumber
& \geq \sum_{{\boldsymbol{i}} \in \mathcal{A}_{k_0}^*} \prod_{t=1}^{k_0} \exp
\bigg(-\bigg(1+\frac \varepsilon 5\bigg)\frac {2t-1}{4\ln{n}}\bigg)
\frac{( (1+\varepsilon/5)({2t-1})/{(4\ln{n})})^{i_t}}{i_t!}\nonumber
\\
&\hskip4.7em\times
\frac{1}{\mathbb{P}[\mathrm{Po}((1+{\varepsilon}/{5})({2t-1})/{(4\ln n)}\le \rho )]} \nonumber
\\
&\ge \exp\bigg(-\frac{1+ \varepsilon/5}{4\ln{n}}k_0^2\bigg) S_{k_0}
\bigg(\frac{1+\varepsilon/5}{4\ln{n}}\bigg)^{k_0} \cdot 1.
\label{eqn22}\end{align}$$
$$\begin{align}
\mathbb{P}\bigg[ \bigwedge_{t=1}^{k_0} \sum_{s=1}^t Z_s \geq t \bigg] \nonumber
& \geq \sum_{{\boldsymbol{i}} \in \mathcal{A}_{k_0}^*} \prod_{t=1}^{k_0} \exp
\bigg(-\bigg(1+\frac \varepsilon 5\bigg)\frac {2t-1}{4\ln{n}}\bigg)
\frac{( (1+\varepsilon/5)({2t-1})/{(4\ln{n})})^{i_t}}{i_t!}\nonumber
\\
&\hskip4.7em\times
\frac{1}{\mathbb{P}[\mathrm{Po}((1+{\varepsilon}/{5})({2t-1})/{(4\ln n)}\le \rho )]} \nonumber
\\
&\ge \exp\bigg(-\frac{1+ \varepsilon/5}{4\ln{n}}k_0^2\bigg) S_{k_0}
\bigg(\frac{1+\varepsilon/5}{4\ln{n}}\bigg)^{k_0} \cdot 1.
\label{eqn22}\end{align}$$
Moreover, defining ![]() $m :\!= k_0^{2/3}$ and
$m :\!= k_0^{2/3}$ and
 $$\begin{equation*}
\tilde{\mathcal{A}}_{k_0} :\!= \bigg\{{\boldsymbol{i}} \in \mathcal{A}_k\colon
\bigwedge_{t=1}^k \sum_{s=1}^t i_s \lt t +m\bigg\},
\end{equation*}$$
$$\begin{equation*}
\tilde{\mathcal{A}}_{k_0} :\!= \bigg\{{\boldsymbol{i}} \in \mathcal{A}_k\colon
\bigwedge_{t=1}^k \sum_{s=1}^t i_s \lt t +m\bigg\},
\end{equation*}$$
we observe that, for ![]() ${\boldsymbol{i}} \in \mathcal{A}_{k_0}^* \cap \tilde{\mathcal{A}}_{k_0}, $ the product
${\boldsymbol{i}} \in \mathcal{A}_{k_0}^* \cap \tilde{\mathcal{A}}_{k_0}, $ the product ![]() $\prod_{t=1}^{k_0}(2t-1)^{i_t}$ is bounded below by
$\prod_{t=1}^{k_0}(2t-1)^{i_t}$ is bounded below by ![]() $1^{m+1}\cdot 3\cdot 5\cdots (2(k_0-m)-1) = (2k_0-2m-1)!!.$ Hence,
$1^{m+1}\cdot 3\cdot 5\cdots (2(k_0-m)-1) = (2k_0-2m-1)!!.$ Hence,
 $$\begin{align}
S_{k_0} & \ge (2k_0-2m-1)!! \sum_{{\boldsymbol{i}} \in \mathcal{A}_{k_0}^* \cap
\tilde{\mathcal{A}}_{k_0}} \prod_{t=1}^{k_0}\frac{1}{i_t!}\nonumber
\\
& = \frac{(2k_0-2m)!}{2^{k_0-m}(k_0-m)!} \frac{k_0^{k_0}}{k_0!}
\biggl(\frac{1}{k_0^{k_0}}\sum_{{\boldsymbol{i}} \in \mathcal{A}_{k_0}^* \cap
\tilde{\mathcal{A}}_{k_0}} \binom{k_0}{i_1, \dots, i_{k_0}} \biggr).
\label{eqn23}\end{align}$$
$$\begin{align}
S_{k_0} & \ge (2k_0-2m-1)!! \sum_{{\boldsymbol{i}} \in \mathcal{A}_{k_0}^* \cap
\tilde{\mathcal{A}}_{k_0}} \prod_{t=1}^{k_0}\frac{1}{i_t!}\nonumber
\\
& = \frac{(2k_0-2m)!}{2^{k_0-m}(k_0-m)!} \frac{k_0^{k_0}}{k_0!}
\biggl(\frac{1}{k_0^{k_0}}\sum_{{\boldsymbol{i}} \in \mathcal{A}_{k_0}^* \cap
\tilde{\mathcal{A}}_{k_0}} \binom{k_0}{i_1, \dots, i_{k_0}} \biggr).
\label{eqn23}\end{align}$$
Let ![]() ${\boldsymbol{U}} = (U_1, \dots, U_{k_0})\in \mathcal{A}_{k_0}$ be a random vector created by independently assigning
${\boldsymbol{U}} = (U_1, \dots, U_{k_0})\in \mathcal{A}_{k_0}$ be a random vector created by independently assigning ![]() $k_0$ labelled balls into
$k_0$ labelled balls into ![]() $k_0$ labelled bins, where
$k_0$ labelled bins, where ![]() $U_s$ denotes the number of balls in bin s. Then the term in brackets describes the probability that
$U_s$ denotes the number of balls in bin s. Then the term in brackets describes the probability that ![]() ${\boldsymbol{U}} \in \mathcal{A}_{k_0}^* \cap
\tilde{\mathcal{A}}_{k_0}.$ Clearly,
${\boldsymbol{U}} \in \mathcal{A}_{k_0}^* \cap
\tilde{\mathcal{A}}_{k_0}.$ Clearly,
and, thus, we need a lower bound on ![]() $\mathbb{P} [{\boldsymbol{U}} \in \mathcal{A}_{k_0}^*]$ and an upper bound on
$\mathbb{P} [{\boldsymbol{U}} \in \mathcal{A}_{k_0}^*]$ and an upper bound on ![]() $\mathbb{P}[{\boldsymbol{U}} \notin \tilde{\mathcal{A}}_{k_0} ]$.
$\mathbb{P}[{\boldsymbol{U}} \notin \tilde{\mathcal{A}}_{k_0} ]$.
First let ![]() $t^*$ be the largest index such that
$t^*$ be the largest index such that
 $$\begin{equation*}
\sum_{s=1}^{t^*}U_{s} - t^* = z :\!=\min_{1\le t \le k_0}
\sum_{s=1}^{t}U_{s} - t.
\end{equation*}$$
$$\begin{equation*}
\sum_{s=1}^{t^*}U_{s} - t^* = z :\!=\min_{1\le t \le k_0}
\sum_{s=1}^{t}U_{s} - t.
\end{equation*}$$
We claim that ![]() $ ( U_{t^*+1}, \dots, U_{k_0}, U_1, \dots U_{t^*}) \in
\mathcal{A}_{k_0}^* $ implying that
$ ( U_{t^*+1}, \dots, U_{k_0}, U_1, \dots U_{t^*}) \in
\mathcal{A}_{k_0}^* $ implying that ![]() $\mathbb{P} [{\boldsymbol{U}} \in \mathcal{A}_{k_0}^*]\geq 1/k_0$. We observe that certainly
$\mathbb{P} [{\boldsymbol{U}} \in \mathcal{A}_{k_0}^*]\geq 1/k_0$. We observe that certainly ![]() $U_{t^*+1}+ \cdots + U_i \ge i-t^*$ for
$U_{t^*+1}+ \cdots + U_i \ge i-t^*$ for ![]() $t^*+1\le
i \le k_0$ by the definition of
$t^*+1\le
i \le k_0$ by the definition of ![]() $t^*$. Furthermore,
$t^*$. Furthermore,
 $$\begin{equation*}
U_{t^*+1}+ \cdots + U_{k_0} = k_0-\sum_{s=1}^{t^*}U_s=k_0-t^*-z,
\end{equation*}$$
$$\begin{equation*}
U_{t^*+1}+ \cdots + U_{k_0} = k_0-\sum_{s=1}^{t^*}U_s=k_0-t^*-z,
\end{equation*}$$
and so, for ![]() $1 \le i \le t^*$, we have
$1 \le i \le t^*$, we have
by the definition of z, as required. Secondly, since ![]() $\sum_{s=1}^t U_s
\sim \mathrm{Bi} (k_0, t/k_0),$ by Lemma 2.1 and a union bound, we obtain
$\sum_{s=1}^t U_s
\sim \mathrm{Bi} (k_0, t/k_0),$ by Lemma 2.1 and a union bound, we obtain
 $$\begin{align*}
\mathbb{P}[{\boldsymbol{U}} \notin \tilde{\mathcal{A}}_{k_0} ] &= \mathbb{P} \bigg[ \bigcup_{t=1}^{k_0}
\bigg\{ \sum_{s=1}^t U_s > t + m \bigg \} \bigg]
\\
& \leq \sum_{t=1}^{k_0} \mathbb{P} \bigg[ \sum_{s=1}^t U_s > t + m\bigg]
\\
& \leq k_0\, {\exp}\bigg( - \frac{m^2}{3k_0}\bigg)
\\
&\leq k_0\, {\exp}\biggl({-}\frac{k_0^{1/3}}{3}\biggr).
\end{align*}$$
$$\begin{align*}
\mathbb{P}[{\boldsymbol{U}} \notin \tilde{\mathcal{A}}_{k_0} ] &= \mathbb{P} \bigg[ \bigcup_{t=1}^{k_0}
\bigg\{ \sum_{s=1}^t U_s > t + m \bigg \} \bigg]
\\
& \leq \sum_{t=1}^{k_0} \mathbb{P} \bigg[ \sum_{s=1}^t U_s > t + m\bigg]
\\
& \leq k_0\, {\exp}\bigg( - \frac{m^2}{3k_0}\bigg)
\\
&\leq k_0\, {\exp}\biggl({-}\frac{k_0^{1/3}}{3}\biggr).
\end{align*}$$
Consequently,
 $$\begin{equation*}
\frac{1}{k_0^{k_0}}\sum_{{\boldsymbol{i}} \in \tilde{\mathcal{A}}_{k_0}}
\binom{k_0}{i_1, \dots, i_{k_0}} = \mathbb{P} [{\boldsymbol{U}} \in \mathcal{A}_{k_0}^* \cap
\tilde{\mathcal{A}}_{k_0}] \geq \frac{1}{k_0}-k_0\, {\exp}({-}k_0^{1/3}) \geq k_0^{-2}.
\end{equation*}$$
$$\begin{equation*}
\frac{1}{k_0^{k_0}}\sum_{{\boldsymbol{i}} \in \tilde{\mathcal{A}}_{k_0}}
\binom{k_0}{i_1, \dots, i_{k_0}} = \mathbb{P} [{\boldsymbol{U}} \in \mathcal{A}_{k_0}^* \cap
\tilde{\mathcal{A}}_{k_0}] \geq \frac{1}{k_0}-k_0\, {\exp}({-}k_0^{1/3}) \geq k_0^{-2}.
\end{equation*}$$
 $$\begin{align}
S_{k_0} &\ge \frac{(2(k_0-m))^{2(k_0-m)}}{2^{k_0-m}(k_0-m)^{k_0-m}}
\frac{\mathrm{e}^{m-1}}{k_0(k_0-m)} \frac{1}{k_0^2} \nonumber
\\
& \geq (2k_0-2m)^{k_0-m}\frac{\mathrm{e}^{m-1}}{k_0^4}\nonumber
\\
& = {\exp}(k_0 \ln (2k_0) - o(k_0)).
\label{eqn24}\end{align}$$
$$\begin{align}
S_{k_0} &\ge \frac{(2(k_0-m))^{2(k_0-m)}}{2^{k_0-m}(k_0-m)^{k_0-m}}
\frac{\mathrm{e}^{m-1}}{k_0(k_0-m)} \frac{1}{k_0^2} \nonumber
\\
& \geq (2k_0-2m)^{k_0-m}\frac{\mathrm{e}^{m-1}}{k_0^4}\nonumber
\\
& = {\exp}(k_0 \ln (2k_0) - o(k_0)).
\label{eqn24}\end{align}$$
Combining (4.2) (4.3), and (4.5) gives us
 $$\begin{align*}
\mathbb{P}[\mathcal{E}_{k_0} \ \,\,|\, \ \, \mathcal{H}] &\ge {\exp}\bigg( k_0 \bigg({-}\frac{1+ \varepsilon/5
}{4\ln{n}}k_0 + \ln (2k_0) - o(1)\bigg)\bigg) \bigg(\frac{1+
\varepsilon/5}{4\ln{n}}\bigg)^{k_0}
\\
&= {\exp}\bigg(2\ln n\bigg({-}\frac 12 \bigg(1+\frac \varepsilon 5\bigg) +\ln \bigg(
1+\frac \varepsilon 5 \bigg) - o(1) \bigg) \bigg)
\\
&= n^{-1}\, {\exp}\bigg(2\ln n\bigg({-}\frac \varepsilon {10} +\ln \bigg( 1+\frac \varepsilon
5 \bigg) - o(1) \bigg) \bigg)
\\
& \ge n^{-1+2\delta},
\end{align*}$$
$$\begin{align*}
\mathbb{P}[\mathcal{E}_{k_0} \ \,\,|\, \ \, \mathcal{H}] &\ge {\exp}\bigg( k_0 \bigg({-}\frac{1+ \varepsilon/5
}{4\ln{n}}k_0 + \ln (2k_0) - o(1)\bigg)\bigg) \bigg(\frac{1+
\varepsilon/5}{4\ln{n}}\bigg)^{k_0}
\\
&= {\exp}\bigg(2\ln n\bigg({-}\frac 12 \bigg(1+\frac \varepsilon 5\bigg) +\ln \bigg(
1+\frac \varepsilon 5 \bigg) - o(1) \bigg) \bigg)
\\
&= n^{-1}\, {\exp}\bigg(2\ln n\bigg({-}\frac \varepsilon {10} +\ln \bigg( 1+\frac \varepsilon
5 \bigg) - o(1) \bigg) \bigg)
\\
& \ge n^{-1+2\delta},
\end{align*}$$
where the last line holds since
for sufficiently small ![]() $\varepsilon$. □
$\varepsilon$. □
Lemma 4.5 gave a lower bound on the probability of constructing a percolating set of size ![]() $k_0$ in one round of the construction algorithm. Subsequently, there is a small but constant probability of growing a percolating set of size
$k_0$ in one round of the construction algorithm. Subsequently, there is a small but constant probability of growing a percolating set of size ![]() $k_1$ from a percolating set of size of
$k_1$ from a percolating set of size of ![]() $k_0$.
$k_0$.
Lemma 4.6. If we run a round of the construction algorithm in ![]() $G(n,p_1^{(1)},p_2),$ then we have
$G(n,p_1^{(1)},p_2),$ then we have ![]() $\mathbb{P} [ \mathcal{E}_{k_1} \ \,\,|\, \ \, \mathcal{E}_{k_0},\mathcal{H} ] = \Theta (\varepsilon) .$
$\mathbb{P} [ \mathcal{E}_{k_1} \ \,\,|\, \ \, \mathcal{E}_{k_0},\mathcal{H} ] = \Theta (\varepsilon) .$
Proof. We view the percolating set constructed in Algorithm 4.1 as a graph branching process, in which the vertex ![]() $x_t$ gives birth to the vertices in
$x_t$ gives birth to the vertices in ![]() $B_t\cup C_t$. (Note that in fact while they are certainly each adjacent to
$B_t\cup C_t$. (Note that in fact while they are certainly each adjacent to ![]() $x_t$ in one colour, they may not be adjacent in both, so we are constructing an auxiliary graph.) It follows from Lemma 4.4 that, conditional on
$x_t$ in one colour, they may not be adjacent in both, so we are constructing an auxiliary graph.) It follows from Lemma 4.4 that, conditional on ![]() $\mathcal{H}$, the branching process up to termination of the round, i.e. until it dies out or reaches size
$\mathcal{H}$, the branching process up to termination of the round, i.e. until it dies out or reaches size ![]() $k_1$, dominates a branching process with offspring distribution
$k_1$, dominates a branching process with offspring distribution ![]() $\mathrm{Po}_{\le \rho}(1+\varepsilon/5)$. Since the expected number of offspring is
$\mathrm{Po}_{\le \rho}(1+\varepsilon/5)$. Since the expected number of offspring is ![]() $1+\Theta(\varepsilon)$, this branching process survives forever with probability
$1+\Theta(\varepsilon)$, this branching process survives forever with probability ![]() $\Theta(\varepsilon)$. Therefore, conditioned on the percolating set constructed by Algorithm 4.1 reaching size
$\Theta(\varepsilon)$. Therefore, conditioned on the percolating set constructed by Algorithm 4.1 reaching size ![]() $k_0$, with probability
$k_0$, with probability ![]() $\Theta(\varepsilon)$ it will also reach size
$\Theta(\varepsilon)$ it will also reach size ![]() $k_1$. □
$k_1$. □
4.1.3. Proof of Lemma 4.2
With regard to the first statement of Lemma 4.2, i.e. that w.h.p. there exists a round ![]() $\ell$ in which
$\ell$ in which ![]() $|X_{T(\ell)}(\ell)|\ge
k_1$, define the event
$|X_{T(\ell)}(\ell)|\ge
k_1$, define the event ![]() $\mathcal{D}=\bigcap_{\ell \le
L}\overline{\mathcal{E}_{k_1-1}(\ell)}$. Then the assertion is simply
$\mathcal{D}=\bigcap_{\ell \le
L}\overline{\mathcal{E}_{k_1-1}(\ell)}$. Then the assertion is simply ![]() $\mathbb{P}[\mathcal{D}
]=o(1)$. Let
$\mathbb{P}[\mathcal{D}
]=o(1)$. Let ![]() $\mathcal{H}^*$ denote the event that
$\mathcal{H}^*$ denote the event that ![]() $\mathcal{H}(\ell)$ holds for every
$\mathcal{H}(\ell)$ holds for every ![]() $1\le \ell \le L$. By Lemma 4.3,
$1\le \ell \le L$. By Lemma 4.3, ![]() $\mathbb{P}[\mathcal{D} ]=o(1)$ follows from
$\mathbb{P}[\mathcal{D} ]=o(1)$ follows from ![]() $\mathbb{P}[\mathcal{D} \ \,\,|\, \ \, \mathcal{H}^*]=o(1)$. Observe that if
$\mathbb{P}[\mathcal{D} \ \,\,|\, \ \, \mathcal{H}^*]=o(1)$. Observe that if ![]() $\mathcal{D}$ holds then we discarded at most
$\mathcal{D}$ holds then we discarded at most ![]() $k_1$ vertices in each round of the algorithm. Now let
$k_1$ vertices in each round of the algorithm. Now let ![]() $L_0$ be the number of rounds in which
$L_0$ be the number of rounds in which ![]() $\mathcal{E}_{k_0}(\ell)$ does not hold, and let
$\mathcal{E}_{k_0}(\ell)$ does not hold, and let ![]() $L_1$ be the number of rounds in which
$L_1$ be the number of rounds in which ![]() $\mathcal{E}_{k_0}(\ell)$ does hold. Thus,
$\mathcal{E}_{k_0}(\ell)$ does hold. Thus, ![]() $L_0+L_1=L$. Furthermore, if
$L_0+L_1=L$. Furthermore, if ![]() $\mathcal{D}$ holds then we have deleted at most
$\mathcal{D}$ holds then we have deleted at most ![]() $k_0L_0+k_1L_1$ vertices during the algorithm, and, therefore,
$k_0L_0+k_1L_1$ vertices during the algorithm, and, therefore,
We show that this is very unlikely by observing that by Lemma 4.6, ![]() $\mathbb{P}[\mathcal{D} \ \,\,|\, \ \, L_1,\mathcal{H}^*]\leq
(1-c\varepsilon)^{L_1}$ for some constant
$\mathbb{P}[\mathcal{D} \ \,\,|\, \ \, L_1,\mathcal{H}^*]\leq
(1-c\varepsilon)^{L_1}$ for some constant ![]() $c>0$, while by Lemma 4.5, conditional on
$c>0$, while by Lemma 4.5, conditional on ![]() $\mathcal{H}^*$, we have
$\mathcal{H}^*$, we have ![]() $L_1\succ
\mathrm{Bi}(L,n^{-1+2\delta})$.
$L_1\succ
\mathrm{Bi}(L,n^{-1+2\delta})$.
We analyse
We split into various cases. Firstly, if ![]() $L_1$ is large, then
$L_1$ is large, then ![]() $\mathcal{D}$ is very unlikely:
$\mathcal{D}$ is very unlikely:
 $$\begin{align*}
\sum_{\ell_0} \sum_{\ell_1\ge \ln n} \mathbb{P}[L_0=\ell_0,\, L_1=\ell_1, \mathcal{D}
\ \,\,|\, \ \, \mathcal{H}^*] & \le \sum_{\ell_1\ge \ln n} \mathbb{P}[\mathcal{D}\ \,\,|\, \ \, L_1=\ell_1,\mathcal{H}^*]
\\
& \le \sum_{\ell_1\ge \ln n} (1-c\varepsilon)^{\ell_1}
\\
&\le \frac{{\exp}({-}c\varepsilon \ln n)}{c\varepsilon}
\\
&= o(1).
\end{align*}$$
$$\begin{align*}
\sum_{\ell_0} \sum_{\ell_1\ge \ln n} \mathbb{P}[L_0=\ell_0,\, L_1=\ell_1, \mathcal{D}
\ \,\,|\, \ \, \mathcal{H}^*] & \le \sum_{\ell_1\ge \ln n} \mathbb{P}[\mathcal{D}\ \,\,|\, \ \, L_1=\ell_1,\mathcal{H}^*]
\\
& \le \sum_{\ell_1\ge \ln n} (1-c\varepsilon)^{\ell_1}
\\
&\le \frac{{\exp}({-}c\varepsilon \ln n)}{c\varepsilon}
\\
&= o(1).
\end{align*}$$
On the other hand, we show that it is very unlikely that ![]() $L_0$ is large, but
$L_0$ is large, but ![]() $L_1$ is small:
$L_1$ is small:
 $$\begin{align*}
&\sum_{\ell_0\ge n^{1-3\delta/2}} \sum_{\ell_1 \lt \ln n} \mathbb{P} [L_0=\ell_0,\,
L_1=\ell_1, \mathcal{D} \ \,\,|\, \ \, \mathcal{H}^*]
\\
&\qquad \le \sum_{\ell_0\ge n^{1-3\delta/2}} \sum_{\ell_1 \lt \ln n} \mathbb{P} [
L_1=\ell_1 \ \,\,|\, \ \, L_0=\ell_0, \mathcal{H}^*][0]
\\
&\qquad \le \sum_{\ell_0\ge n^{1-3\delta/2}}
\mathbb{P}[\mathrm{Bi}(\ell_0,n^{-1+2\delta})\le \ln n]
\\
&\qquad \le n \mathbb{P}[\mathrm{Bi}(n^{1-3\delta/2},n^{-1+2\delta})\le \ln n].
\end{align*}$$
$$\begin{align*}
&\sum_{\ell_0\ge n^{1-3\delta/2}} \sum_{\ell_1 \lt \ln n} \mathbb{P} [L_0=\ell_0,\,
L_1=\ell_1, \mathcal{D} \ \,\,|\, \ \, \mathcal{H}^*]
\\
&\qquad \le \sum_{\ell_0\ge n^{1-3\delta/2}} \sum_{\ell_1 \lt \ln n} \mathbb{P} [
L_1=\ell_1 \ \,\,|\, \ \, L_0=\ell_0, \mathcal{H}^*][0]
\\
&\qquad \le \sum_{\ell_0\ge n^{1-3\delta/2}}
\mathbb{P}[\mathrm{Bi}(\ell_0,n^{-1+2\delta})\le \ln n]
\\
&\qquad \le n \mathbb{P}[\mathrm{Bi}(n^{1-3\delta/2},n^{-1+2\delta})\le \ln n].
\end{align*}$$
Using Lemma 2.1, we obtain
 $$\begin{align*}
\mathbb{P}[\mathrm{Bi}(n^{1-3\delta/2},n^{-1+2\delta}) \le \ln n ] & \leq
\mathbb{P}[\mathrm{Bi}(n^{1-3\delta/2},n^{-1+2\delta}) \le ( 1-\delta) n^{\delta /2} ]
\\
& \leq {\exp}\bigg[ - \frac{n^{\delta /2} \delta^2}{2} \bigg]
\end{align*}$$
$$\begin{align*}
\mathbb{P}[\mathrm{Bi}(n^{1-3\delta/2},n^{-1+2\delta}) \le \ln n ] & \leq
\mathbb{P}[\mathrm{Bi}(n^{1-3\delta/2},n^{-1+2\delta}) \le ( 1-\delta) n^{\delta /2} ]
\\
& \leq {\exp}\bigg[ - \frac{n^{\delta /2} \delta^2}{2} \bigg]
\end{align*}$$
and, consequently,
Finally, observe that if both ![]() $L_0$ and
$L_0$ and ![]() $L_1$ are small, but
$L_1$ are small, but ![]() $\mathcal{D}$ holds, then we cannot have terminated the algorithm because we have not deleted enough vertices. If
$\mathcal{D}$ holds, then we cannot have terminated the algorithm because we have not deleted enough vertices. If ![]() $\mathcal{D}$ holds,
$\mathcal{D}$ holds, ![]() $\ell_0 \lt n^{1-3\delta/2},$ and
$\ell_0 \lt n^{1-3\delta/2},$ and ![]() $\ell_1 \lt
\ln n,$ then
$\ell_1 \lt
\ln n,$ then
which is clearly a contradiction. Thus, we have ![]() $\mathbb{P}[\mathcal{D} \ \,\,|\, \ \, \mathcal{H}^*] =
o(1)$.
$\mathbb{P}[\mathcal{D} \ \,\,|\, \ \, \mathcal{H}^*] =
o(1)$.
Moreover, from Lemma 4.3 we obtain that, conditional on ![]() $\mathcal{H}^*$,
$\mathcal{H}^*$,
Finally, due to Lemma 4.3 this yields
 $$\begin{align*}
\mathbb{P} \biggl[ \bigcup_{\ell \leq L} {\mathcal{E}}_{k_1-1}(\ell) \cap \bigg\{
\bigg|R_{T(\ell)}\bigg| \geq \frac{1}{2}n p_1^{(1)} T(\ell)\bigg\}
\biggr] & \ge \mathbb{P} [\overline{\mathcal{D}} \cap {\mathcal{H}}^*]
\\
& \ge \mathbb{P} [\overline{\mathcal{D}} \ \,\,|\, \ \, {\mathcal{H}}^*]- \mathbb{P} [\bar{{\mathcal{H}}^*}]
\\
&= 1-o(1)
\end{align*}$$
$$\begin{align*}
\mathbb{P} \biggl[ \bigcup_{\ell \leq L} {\mathcal{E}}_{k_1-1}(\ell) \cap \bigg\{
\bigg|R_{T(\ell)}\bigg| \geq \frac{1}{2}n p_1^{(1)} T(\ell)\bigg\}
\biggr] & \ge \mathbb{P} [\overline{\mathcal{D}} \cap {\mathcal{H}}^*]
\\
& \ge \mathbb{P} [\overline{\mathcal{D}} \ \,\,|\, \ \, {\mathcal{H}}^*]- \mathbb{P} [\bar{{\mathcal{H}}^*}]
\\
&= 1-o(1)
\end{align*}$$
as required.
4.2. Final stages
In the previous section we found a step ![]() $\ell$ such that
$\ell$ such that ![]() $|X_{T(\ell)}|\ge k_1$ and
$|X_{T(\ell)}|\ge k_1$ and ![]() $|R_{T(\ell)}|\ge T(\ell) n p_1^{(1)}/2$. Once again we drop the
$|R_{T(\ell)}|\ge T(\ell) n p_1^{(1)}/2$. Once again we drop the ![]() $\ell$ from our notation.
$\ell$ from our notation.
We now show that ![]() $X_T$ grows into a larger percolating set by examining the red neighbourhood of
$X_T$ grows into a larger percolating set by examining the red neighbourhood of ![]() $X_T$. Note that until this point no edge between
$X_T$. Note that until this point no edge between ![]() $x_{k_1}$ and
$x_{k_1}$ and ![]() $R_T$ has been revealed. In addition, any blue edge we have revealed so far is incident to a vertex of
$R_T$ has been revealed. In addition, any blue edge we have revealed so far is incident to a vertex of ![]() $D_1:=(V\setminus
V_L')$.
$D_1:=(V\setminus
V_L')$.
Lemma 4.7. With high probability ![]() $G(n,p_1^{(1)},p_2^{(1)})$ contains a percolating set of size
$G(n,p_1^{(1)},p_2^{(1)})$ contains a percolating set of size ![]() $n/(4\omega)$.
$n/(4\omega)$.
Proof. By Lemma 4.2, w.h.p. we have ![]() $|X_T|\ge k_1$ and
$|X_T|\ge k_1$ and ![]() $|R_T|\ge
T np_1^{(1)}/2$. Until this point, we have only exposed the (partial) red neighbourhood of
$|R_T|\ge
T np_1^{(1)}/2$. Until this point, we have only exposed the (partial) red neighbourhood of ![]() $\{x_1,\ldots,x_T\}$. Now we expose the red neighbourhood in
$\{x_1,\ldots,x_T\}$. Now we expose the red neighbourhood in ![]() $V_L'$ of
$V_L'$ of ![]() $\{x_{T+1},\ldots,x_{k_1}\}$, and denote this red neighbourhood by R’. Clearly,
$\{x_{T+1},\ldots,x_{k_1}\}$, and denote this red neighbourhood by R’. Clearly,
and since ![]() $\mathbb{E}[|R'|] \ge (1-o(1))n(k_1-T)p_1^{(1)}\to \infty$, Lemma 2.1 implies that w.h.p.
$\mathbb{E}[|R'|] \ge (1-o(1))n(k_1-T)p_1^{(1)}\to \infty$, Lemma 2.1 implies that w.h.p. ![]() $|R'|\ge
(k_1-T)np_1^{(1)}/2$. Therefore, for
$|R'|\ge
(k_1-T)np_1^{(1)}/2$. Therefore, for ![]() $R=(R_T\cup R')\setminus D_1,$ we have
$R=(R_T\cup R')\setminus D_1,$ we have
Now ![]() $X_T$ forms a percolating set and every vertex in R has a red neighbour in
$X_T$ forms a percolating set and every vertex in R has a red neighbour in ![]() $X_T$, and, therefore, the (blue) component of
$X_T$, and, therefore, the (blue) component of ![]() $G_2[\{x_{k_1}\}\cup R]$ containing
$G_2[\{x_{k_1}\}\cup R]$ containing ![]() $x_{k_1}$ can be added to the percolating set. Recall that no blue edges have been exposed in
$x_{k_1}$ can be added to the percolating set. Recall that no blue edges have been exposed in ![]() $\{x_{k_1}\}\cup R$, and, therefore,
$\{x_{k_1}\}\cup R$, and, therefore, ![]() $G_2[\{x_{k_1}\}\cup R]\sim
G(|R|+1,p_2)$. This graph has an expected average degree
$G_2[\{x_{k_1}\}\cup R]\sim
G(|R|+1,p_2)$. This graph has an expected average degree ![]() $|R|p_2 \ge
np_2/(3\omega)=\omega(1)$ and, therefore, w.h.p. has a giant component covering all but
$|R|p_2 \ge
np_2/(3\omega)=\omega(1)$ and, therefore, w.h.p. has a giant component covering all but ![]() $o(|R|)$ vertices, and in particular containing
$o(|R|)$ vertices, and in particular containing ![]() $x_{k_1}$, and the result follows. □
$x_{k_1}$, and the result follows. □
We can now complete the proof of the supercritical case
Proof of Theorem 1.2(ii). Recall that since we assume that ![]() $p_2 \ge {\ln n}/{n}$, the probability that
$p_2 \ge {\ln n}/{n}$, the probability that ![]() $G_2\sim G(n,p_2)$ is connected is at least a positive constant. Therefore, any event that occurs with high probability also occurs with high probability in the probability space conditioned on
$G_2\sim G(n,p_2)$ is connected is at least a positive constant. Therefore, any event that occurs with high probability also occurs with high probability in the probability space conditioned on ![]() $G_2$ being connected. (Note that this is the only point in the argument at which we need to condition on
$G_2$ being connected. (Note that this is the only point in the argument at which we need to condition on ![]() $G_2$ being connected. We also no longer need to assume that
$G_2$ being connected. We also no longer need to assume that ![]() $G_1$ is connected since we assumed (without loss of generality) that
$G_1$ is connected since we assumed (without loss of generality) that ![]() $p_1\ge p_2$, and it follows from (2.4) that
$p_1\ge p_2$, and it follows from (2.4) that ![]() $G_1$ is connected with high probability.)
$G_1$ is connected with high probability.)
In particular, let ![]() $U_2$ be the percolating set provided with high probability by Lemma 4.7. For all
$U_2$ be the percolating set provided with high probability by Lemma 4.7. For all ![]() $v\notin
U_2,$ we have
$v\notin
U_2,$ we have
where we have used (2.4) and the fact that ![]() $\omega = \ln
\ln n$ is subpolynomial. Hence, a union bound over all at most n vertices of
$\omega = \ln
\ln n$ is subpolynomial. Hence, a union bound over all at most n vertices of ![]() $V\setminus U_2$ shows that w.h.p. all are in
$V\setminus U_2$ shows that w.h.p. all are in ![]() $
N^{(2)}_1(U_2)$. On the other hand, since the blue graph is connected by assumption, it is easy to see that the jigsaw process will percolate. □
$
N^{(2)}_1(U_2)$. On the other hand, since the blue graph is connected by assumption, it is easy to see that the jigsaw process will percolate. □
5. Concluding remarks
5.1. The critical window
We have proved that Theorem 1.2 for ![]() $\varepsilon >0$ an arbitrarily small constant. However, we note that for connectedness, of which jigsaw percolation may be considered the double-graph analogue, a much stronger result is true. Namely, the classical result of Erdös and Rényi Reference Erdös and Rényi[10] implies that if
$\varepsilon >0$ an arbitrarily small constant. However, we note that for connectedness, of which jigsaw percolation may be considered the double-graph analogue, a much stronger result is true. Namely, the classical result of Erdös and Rényi Reference Erdös and Rényi[10] implies that if ![]() $p= {({\ln}\ n + c_n)}/{n}$ then w.h.p. G(n,p) is not connected if
$p= {({\ln}\ n + c_n)}/{n}$ then w.h.p. G(n,p) is not connected if ![]() $c_n \to -\infty$ and w.h.p. G(n,p) is connected if
$c_n \to -\infty$ and w.h.p. G(n,p) is connected if ![]() $c_n \to \infty$. In other words, setting
$c_n \to \infty$. In other words, setting ![]() $p=(1-
\varepsilon){\ln n}/{n}$ in the subcritical case, or
$p=(1-
\varepsilon){\ln n}/{n}$ in the subcritical case, or ![]() $p=(1+\varepsilon){\ln n}/{n}$, w.h.p. we have G(n,p) being disconnected or connected, respectively, provided that
$p=(1+\varepsilon){\ln n}/{n}$, w.h.p. we have G(n,p) being disconnected or connected, respectively, provided that ![]() $\varepsilon \gg ({\ln}\ {n})^{-1}$.
$\varepsilon \gg ({\ln}\ {n})^{-1}$.
Similarly, it would be interesting to know for which ![]() $\varepsilon = o(1)$ the statement of Theorem 1.2 is still true. With a little more care, our proof would show that
$\varepsilon = o(1)$ the statement of Theorem 1.2 is still true. With a little more care, our proof would show that ![]() $\varepsilon \gg ({\ln}\ {n})^{-1/4}$ is sufficient, but it seems likely that this is not best possible.
$\varepsilon \gg ({\ln}\ {n})^{-1/4}$ is sufficient, but it seems likely that this is not best possible.
The key step required to understand the critical window seems to be the number of minimal percolating sets on k vertices. We provide upper and lower bounds on the asymptotics of this value, which differ by a factor of ![]() $\mathrm{e}^{o(k)}$. More precise estimates on this value translate into sharper bounds on the threshold.
$\mathrm{e}^{o(k)}$. More precise estimates on this value translate into sharper bounds on the threshold.
5.2. Generalisations
It would also be interesting to determine the exact threshold for the various generalisations of Theorem 1.1, including the analogous results for multiple graphs Reference Cooley and Gutiérrez[9] and for hypergraphs Reference Bollobás, Cooley, Kang and Koch[4]. The latter would be a particular challenge since the proof of the supercritical case in Reference Bollobás, Cooley, Kang and Koch[4] simply involved a reduction to the graph case, i.e. Theorem 1.1. Since Theorem 1.2 is a strengthening of Theorem 1.1, it also makes the hypergraph result stronger; however, the reduction step is not optimal, and it seems likely that significant new ideas would be required.
5.3. Other random graph models
Real world graphs, in particular social networks, tend to have a power-law degree distribution. The binomial random graph does not have this property; however several other random graph models do, for example, the preferential attachment model (introduced in Reference Barabási and Albert[2] and rigorously defined in Reference Bollobás, Riordan, Spencer and Tusnády[6]) and random graphs on the hyperbolic plane (introduced in Reference Krioukov, Papadopoulos, Kitsak, Vahdat and Boguñá[13]). The threshold for jigsaw percolation when the people graph is modelled by such a random graph and for any random or deterministic choice of the puzzle graph is still unknown. Indeed, apart from a brief one-directional result in Reference Brummitt, Chatterjee, Dey and Sivakoff[7], jigsaw percolation involving random graphs with a power-law degree distribution have not been studied.
5.4. Speed of percolation
One might also ask how many steps it takes for the jigsaw process to percolate in the supercritical case, i.e. how often we have to construct an auxiliary graph and merge the components in Algorithm 1.1. With a little care, the arguments in this paper could be adapted to show that, for ![]() $p_1p_2={(1+\varepsilon)}/{(4n\ln n)},$ where
$p_1p_2={(1+\varepsilon)}/{(4n\ln n)},$ where ![]() $\varepsilon >0$ is constant, w.h.p. at most
$\varepsilon >0$ is constant, w.h.p. at most ![]() $O({\ln}\ n)$ steps are required, and indeed this can even be improved to
$O({\ln}\ n)$ steps are required, and indeed this can even be improved to ![]() $(1+o(1))2\ln n$. It would be interesting to know whether this upper bound is in fact tight w.h.p.
$(1+o(1))2\ln n$. It would be interesting to know whether this upper bound is in fact tight w.h.p.
Acknowledgement
The authors would like to thank Kathrin Skubch for helpful discussions in the early stages of this project.