1. INTRODUCTION
Nonlinear wave mixing was first considered in optics by Boembergen
and others (Armstrong et al., 1962)
in the early 1960s and imported into plasma physics soon afterward,
especially by Russian researchers. It was soon realized that, in
contrast to optics, where the laser frequencies were well-defined
quantities and the spectral bandwidth was negligible, in plasma physics
we usually deal with broadband spectra. Photon kinetic theory is
appropriate to deal with waves having a large spectral bandwidth, and
the early versions of this theory can be found in books on plasma
turbulence published in the late 1960s (Kadomtsev,
1965; Sagdeev & Galeev, 1969).
This theory was derived in the framework of the random phase
approximation, which is well justified for plasma turbulence problems,
in contrast with the fixed phase approximation (or monochromatic wave
approach) more fitted to optical problems. The main feature of this
early work was that nonlinear effects are much stronger in the fixed
phase approximation than in the random phase one, where they appear at
a higher order of the nonlinear coupling parameters. In recent years,
we have returned to the photon kinetic theory by using a different
perspective and a better understanding of the physical meaning of the
photon kinetic equations (Silva &
Mendonça, 1998; Tsintsadze &
Mendonça, 1998; Mendonça &
Tsintsadze, 2000). The result of this new approach is that many
of the effects associated with the fixed phase approximation can also
be described by the kinetic equations, which provide a general view of
nonlinear effects in plasmas and in optics. Thus, the previous
distinction between the two regimes (random and fixed phase) loses its
sense, the rule played by the field phase is better understood, and
intermediate cases can be treated as well. Finally, the resonant
collective processes associated with Landau damping by quasi-particles
become extremely relevant in a large variety of domains (Bingham et al., 1997; Mendonça & Bingham, 2002). On the other
hand, with the recent advent of very short laser pulses, the discovery
of phase modulation effects and of supercontinuum radiation (Alfano, 1989), the study of broadband spectra
became also very useful and important in nonlinear optics. The more
recent versions of the photon kinetic theory are thus very appropriate
to provide a unified description of nonlinear wave phenomena both in
plasma physics and in optics. Here, we will briefly describe the
contents of the photon kinetic equations and apply them to a specific
problem in plasma physics (the Raman forward scattering process) and
another similar problem in optics (self-phase modulation and the
generation of a supercontinuum).
2. PHOTON KINETIC EQUATIONS
It is well known that a quantum system described by a wave function
ψ(r,t) can be represented in the classical phase
space (r,p) if we use the Wigner function (Wigner, 1932):
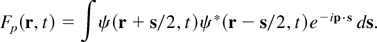
This function behaves in many cases as a density distribution of
point particles and, for that reason, is usually called a
quasi-distribution. Similarly, an electromagnetic wave spectrum
described by the electric field E(r,t) can
be represented in terms of particles, evolving along ray trajectories
with momentum k, if we introduce the corresponding Wigner
function (Mendonça, 2001):
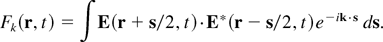
From Maxwell's equations it is possible to derive an evolution
equation for this Wigner function, for waves propagating in a space and
time varying medium, with dielectric constant ε, in the form (Tsintsadze & Mendonça, 1998; Mendonça & Tsintsadze, 2000; Hall et al., 2002):
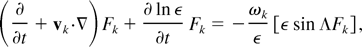
where vk and ωk
are the group velocity and the frequency of the field mode k,
and Λ is a differential operator, acting backwards on ε and
forward on Fk: Λ = (1 /2) ←
(∂/∂r·∂/∂k)
→.
This is similar to the Wigner–Moyal equation of quantum
mechanics (Hillary et al., 1984) and
it has been discussed for the case of a dispersive dielectric medium
(Mendonça & Tsintsadze, 2000), and
more specifically for a plasma (Tsintsadze &
Mendonça, 1998). This equation can be seen as a kinetic
equation for the field quasi-distribution
Fk. It should be noticed that it is
exactly equivalent to the propagation equation for the electric field
E, but it is of little use because of its complexity. It is
then more convenient to introduce some simplifying assumptions, namely
that the medium is slowly varying in space and time in comparison with
the space and time scales of the field. We are now left with a much
simpler form of kinetic equation, where diffraction effects are
completely neglected:
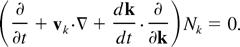
The quantity Nk is the photon number
density, defined in terms of the Wigner function as
Nk = (ε0
/8)(∂R/∂ω)kFk, where R(ω,k) =
0 denotes the linear dispersion relation of the medium. The
electromagnetic energy density can then be simply written as the
product of the photon frequency with the number density
Wk = ωkNk. This equation is nothing but the
photon number conservation, valid in the geometric optics limit. Here
we should stress the physical meaning of the third term, which was
mostly ignored in the past and represents the photon acceleration
effects leading to frequency shift and energy nonconservation. These
effects are associated with the force
dk/dt =
−∂ωk /∂r, acting
on the photon field. This new kinetic equation will then be applied to
two illustrative examples in the following two sections.
3. FORWARD RAMAN SCATTERING IN A PLASMA
If a laser beam, described here as a bunch of photons, propagates in
a plasma, electron plasma waves can be excited that modulate the
propagating medium and induce a perturbation in the photon population,
which in turn increase the electron plasma wave perturbation, thus
leading to an instability process. The electron plasma oscillations are
driven by the ponderomotive force associated with the laser beam
inhomogeneities. The electron plasma density perturbations
ñ are then described by the following propagation
equation:
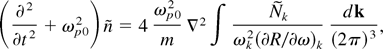
where the right-hand side represents the ponderomotive force effect.
On the other hand, the perturbed photon number density
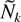
is determined by the kinetic Eq. (3), where the force term is determined
by the electron density perturbation
,
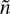
according to:
.
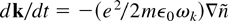
For electron and photon density perturbations,
,
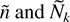
of the form exp(ik·r −
iωt), we can derive the dispersion relation: 1 +
χe + χph = 0, where
χe is the usual electron susceptibility and
χph is the new term associated with the photon
field. If we consider the simplest case of a mono-energetic photon
beam, such that the unperturbed distribution is
Nk0 =
(2π)2N0δ(k⊥)δ(k
− k0), the dispersion relation reduces to
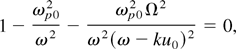
where u0 = ω0
/k0 ≃ c is the laser group
velocity, and Ω2 =
(k4c2/mn0)(ωp0
/ω0)2N0. For
ku0 ≤ ωp0 we can have
an instability at a frequency ω = ku0, with a
growth rate γ ∼
(Ω/ωp0)ku0. This
means that we can recover the usual growth rate of the forward Raman
scattering, proportional to the field amplitude,
N01/2. However, the above dispersion
relation shows that the maximum growth rate is attained at ω
≃ ku0 = ωp0, with a
growth rate proportional to
N01/3:
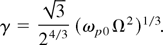
Our kinetic approach could also be used to study the photon beam
instabilities created by laser beams with a frequency or an angular
spread (Silvo et al., 2000; Mendonça, 2001), thus allowing for a global
description of instabilities created by spectra with arbitrary
shape.
4. SELF-PHASE MODULATION IN OPTICAL MEDIA
Let us now apply the photon kinetic theory to one of the most
paradigmatic effects of nonlinear optics, which is usually associated
with phase modulation. Here, in contrast, the field phase will be
completely ignored (Silva & Mendonça,
2001). We will now use the kinetic Eq. (4), with the photon
acceleration force determined by: dk/dt
= −∇[kc/n0 +
n2I(r,t)] , where
n0 and n2 are the linear and
the nonlinear refractive indices of the medium (e.g., an optical fiber
or a piece of common glass) and I(r,t) =
∫ωkNk(r,t)
dk/(2π)3 is the intensity of the
laser beam. The beam spectrum will change along propagation, due to the
local gradient of the nonlinear refractive index, as determined by
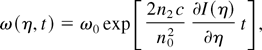
where we have assumed propagation along Ox and used η =
x − ct/n0. For a
Gaussian laser pulse of width σ, as determined by the intensity
profile I(η) = I0
exp(−η2/σ2), we can obtain two
maxima of the up-shifted and the down-shifted spectra, which grow
exponentially with time:
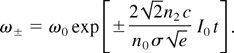
For small time durations, this can be simplified to:
.
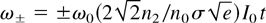
This is the usual result for the optical theory of
self-phase modulation, which gives a frequency shift proportional to
the time of propagation of the laser pulse inside the nonlinear medium.
We can see from here that the photon kinetic theory can not only lead
to more exact expression for the frequency shifts, but also show that
the same effects remain when we completely ignore the field phase. This
process can then be more appropriately described as a nonlinear photon
acceleration process in the optical medium.
5. CONCLUSION
Here we have given a brief description of the photon kinetic theory.
Photon kinetic equations can be derived from Maxwell's equations
and, in their more rigorous versions, they are formally identical to
the Wigner–Moyal of quantum mechanics. If diffraction effects are
neglected, they can take the simpler and more suggestive form of an
equation of conservation for the photon number density.
Examples of application in plasmas and in other optical media were
discussed. We have shown that beamed photon distributions propagating
in a plasma can drive electron plasma waves, by a process known as
forward Raman scattering. We can say that our photon kinetic approach
has the ability to describe forward scattering instabilities, not only
for mono-energetic photon beams, but also for laser beams with an
arbitrary spectral width. When applied to optics, the photon kinetic
theory can provide a very accurate description of the processes known
as phase modulation, thus showing that the field phase (absent in the
photon kinetic description) is not an essential ingredient. We can then
conclude that the photon kinetic theory provides a very powerful method
to understand the spectral changes in plasma physics and in optics, and
can provide a unified view of a large variety of physical processes.
