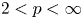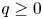1. Introduction
The present paper is concerned with a new class of solutions to the stationary nonlinear Schrödinger equation
\begin{equation} -\Delta v +q v =|v|^{p-2} v \qquad \text{in}\,{{\mathbb{R}^{N}},} \end{equation}
where 
$p > 2$ and 
$q \ge 0$ is a constant. Since the case 
$q > 0$ is equivalent to 
$q=1$ by rescaling, we only consider the cases 
$q=1$ and 
$q=0$ in the following.
For subcritical exponents 
$p$ (i.e., 
$p < \frac {2N}{N-2}$, if 
$N \ge 3$) and 
$q=1$, there is a vast literature on solutions of (1.1) in 
$H^{1}(\mathbb {R}^{N})$, which decay expontially at infinity, see e.g. the monographs [Reference Ambrosetti and Malchiodi1, Reference Kuzin and Pohozaev18, Reference Struwe24, Reference Sulem and Sulem25, Reference Willem28] and the references therein.
In the present paper, we focus on solutions with only partial decay. These solutions are less understood but have attracted considerable attention in recent years.
To be more precise, let us write 
$\bar x=(x,t) \in \mathbb {R}^{N}$ with 
$x \in \mathbb {R}^{N-1}$ and 
$t\in \mathbb {R}$. We shall consider solutions 
$v: \mathbb {R}^{N} \to \mathbb {R}$ satisfying the condition
\begin{equation} \lim \limits_{|x| \to \infty}v(x,t) =0 \quad \text{uniformly in } t. \end{equation}
A trivial class of solutions satisfying (1.2) is the class of solutions that are axially symmetric with respect to the axis 
$\{(0_{\mathbb {R}^{N-1}},t): \ t \in \mathbb {R} \} \subset \mathbb {R}^{N}$ and that in addition are 
$t$-invariant, i.e., solutions having the form 
$v(x,t)= \tilde v(x)$, where 
$\tilde v$ is a radial solution of (1.1) in 
$\mathbb {R}^{N-1}$ satisfying 
$\tilde v(x) \to 0$ as 
$|x| \to \infty$. Here and in the following, axial symmetry is always understood with respect to the 
$t$-axis.
In a seminal paper, Dancer [Reference Dancer11] constructed, for 
$q=1$, nontrivial, 
$t$-periodic axially symmetric solutions of (1.1) by means of bifurcation theory. The solutions found in [Reference Dancer11] are positive, and they bifurcate from the unique family of 
$t$-invariant axially symmetric positive solutions of (1.1).
It is natural to ask whether, for a given positive solution of (1.1), the decay property (1.2) enforces axial symmetry up to translations. As shown in the following theorem by Farina, Malchiodi and Rizzi in [Reference Farina, Malchiodi and Rizzi15], this is true for positive solutions which are periodic in 
$t$.
Theorem 1.1 [15, Special case of Theorem 2] Let 
$p>2$, 
$q=1$, and let 
$v \in C^{2}(\mathbb {R}^{N})$ be a bounded positive solution of (1.1) satisfying the uniform decay property (1.2). Suppose moreover that 
$v$ is periodic in 
$t$, i.e., there exists 
$\tau \in \mathbb {R}$ with
\[ v(x,t+ \tau)= v(x,t) \qquad \text{for all}\ (x,t) \in {\mathbb{R}}^{N} \hbox{with some constant}\ \tau >0. \]
Then, up to translations in the 
$x$-variable, 
$v$ is axially symmetric.
Let us also briefly discuss the case 
$q=0$ in (1.1). In this case, for subcritical 
$p$, it is known that (1.1) does not admit positive solutions (see [Reference Gidas and Spruck16, Theorem 1.1]), and it also does not admit solutions of any sign in 
$H^{1}(\mathbb {R}^{N})$ (by Pohozaev's identity, see e.g. [Reference Willem28, Appendix B]). The latter property is related to the fact that, in this case, equation (1.1) remains invariant under the rescaling transformation 
$v \mapsto \kappa ^{\frac {2}{p-2}}v(\kappa \,\cdot \,)$.
In the present paper, we discuss solutions of (1.1)–(1.2) with periodicity in 
$t$, but without axial symmetry. By Theorem 1.1 and the remarks above, such solutions have to change sign. As far as we know, solutions of this type have not been studied yet with the exception of the 
$t$-independent case where 
$v(x,t)= \tilde v(x)$ for some nonradial sign-changing solution 
$\tilde v$ of (1.1) in 
$\mathbb {R}^{N-1}$ with 
$\tilde v(x) \to 0$ as 
$|x| \to \infty$.
In this context, we briefly recall some existence results on nonradial sign-changing solutions of (1.1) in 
$\mathbb {R}^{N}$ for 
$q=1$ with exponential decay in all variables. In the work of Bartsch and Willem [Reference Bartsch and Willem3], solutions of this type were found for 
$N=4$ or 
$N \ge 6$ by a careful application of the Fountain Theorem within the space of functions in 
$H^{1}(\mathbb {R}^{N})$ that are invariant under the action of the group 
$O(m)\times O(m)\times O(N-2\,m)$, with 
$N\geq 2m+1$. The case 
$N=5$ was considered subsequently by a related argument in [Reference Lorca and Ubilla21]. More recently, in [Reference Ao, Musso, Pacard and Wei2, Reference Musso, Pacard and Wei22], nonradial sign-changing solutions to (1.1) with no symmetry and with dihedral symmetry, respectively, have been constructed with the Lyapunov–Schmidt reduction method in any dimension 
$N \ge 2$.
In the following, we restrict our attention to the case 
$N =3$ and consider the special class of spiraling solutions of the nonlinear Schrödinger equation
\begin{equation} -\Delta v +q v =|v|^{p-2} v \qquad \text{in} \mathbb{R}^{3}, \end{equation}i.e., solutions that are invariant under the action of a screw motion.
To be more precise, let 
$\lambda >0$. We call a function 
$v: \mathbb {R}^{3} \to \mathbb {R}$ 
$\lambda$-spiraling if for any 
$\theta \in \mathbb {R}$,
\begin{equation} v(R_{\theta} x,t + \lambda \theta)= v(x,t) \qquad \text{for} \,{{x \in \mathbb{R}^{2}}, {t\in \mathbb{R}},} \end{equation}
where 
$R_\theta : \mathbb {R}^{2} \to \mathbb {R}^{2}$ denotes the counter-clockwise rotation with angle 
$\theta$ in 
$\mathbb {R}^{2}$. Notice that 
$\lambda$-spiraling functions are 
$2 \lambda \pi$-periodic in 
$t$. Hence, the parameter 
$\lambda$ represents the rotational slope of the underlying screw motion, and 
$2 \lambda \pi$ is the associated turn-around shift.
Our work is partly inspired by the papers [Reference del Pino, Musso and Pacard12] resp. [Reference Cinti, Davila and Del Pino9], where spiraling solutions have been constructed for the classical and fractional Allen–Cahn equation, respectively. Without going into detail, we mention the well-known fact that, despite its similar-looking form, the Allen–Cahn equation 
$-\Delta u = u - u^{3}$ differs significantly from the nonlinear Schrödinger equation (1.3) with regard to the variational framework and the shape of solutions.
In cylindrical coordinates 
$(x,t)= (r \cos \varphi , r \sin \varphi , t)$ with 
$(r, \varphi ,t) \in [0,\infty ) \times \mathbb {R} \times \mathbb {R}$, 
$\lambda$-spiraling functions have the form
\[ v(r,\varphi, t) = u \left(r,\varphi- \frac{t}{\lambda} \right) \]
with a function 
$u: [0,\infty ) \times \mathbb {R} \to \mathbb {R}$ which is 
$2 \pi$-periodic in the second variable. Also, in these coordinates the equation (1.3) reads as
\[{-}v_{rr}-\frac{v_r}{r} - \frac{v_{\varphi \varphi }}{r^{2}} - v_{tt} +q\,v = |v|^{p-2} v \]
so that the equation for 
$u$ has the form
\begin{equation} -u_{rr} -\frac{u_r}{r} - \Bigl(\frac{1}{\lambda^{2}}+ \frac{1}{r^{2}} \Bigr)u_{\theta\theta} + q\,u= |u|^{p-2} u . \end{equation} It is convenient to transform equation (1.5) further to planar euclidean coordinates 
$x=(x_1,x_2)$, where 
$r= |x|$ and 
$\theta = \arcsin \frac {x_2}{|x|}$. This leads to the problem
\begin{equation} \left \{ \begin{aligned} -\Delta u - \frac{1}{\lambda^{2}} [x_1 \partial_{x_2} - x_2 \partial_{x_1}]^{2} u + q\, u & = |u|^{p-2} u & & \qquad \text{on} \,{\,{\mathbb{R}^{2}},} \\ u(x) & \to 0 & & \qquad \text{as} \,{\,{|x| \to \infty}.} \end{aligned} \right. \end{equation} Observe that radial solutions of (1.6) correspond to axially symmetric and 
$t$-invariant solutions of (1.3). By Theorem 1.1, every positive solution of (1.6) is radial. On the other hand, nonradial solutions of (1.6) correspond to solutions of (1.3) which are 
$2 \lambda \pi$-periodic in 
$t$ but neither axially symmetric nor 
$t$-invariant. We, therefore, restrict our attention to nodal (i.e., sign changing) solutions of (1.6).
We study problem (1.6) using variational methods, and hence we first introduce some notation related to its variational structure.
We write 
$\partial _\theta := x_1 \partial _{x_2} - x_2 \partial _{x_1}$ for the angular derivative and consider the space
\begin{equation} H:= \left\{u \in H^{1}(\mathbb{R}^{2})\::\: \int_{\mathbb{R}^{2}} |\partial _\theta u|^{2} \textrm{d}x <\infty \right\}. \end{equation}
For 
$\lambda >0$, we endow 
$H$ with the 
$\lambda$-dependent scalar product
\begin{equation} \langle u,v \rangle_{\lambda} := \int_{\mathbb{R}^{2}} \Bigl(\nabla u \cdot \nabla v + \frac{1}{\lambda^{2}} (\partial _\theta u)(\partial _\theta v) + \,uv \Bigr) \textrm{d}x \end{equation}
and consider the Hilbert space 
$(H,\langle \cdot ,\cdot \rangle _{\lambda })$.
Let 
$E_\lambda : H \to \mathbb {R}$ be the energy functional associated to (1.6) in the case 
$q=1$, defined by
\begin{equation} E_\lambda(u) := \frac{1}{2} \int_{\mathbb{R}^{2}} \Bigl(|\nabla u|^{2} + \frac{1}{\lambda^{2}} |\partial _\theta u|^{2} + |u|^{2} \Bigr) \textrm{d}x - \frac{1}{p}\int_{\mathbb{R}^{2}} |u|^{p} \,\textrm{d}x. \end{equation}
By standard arguments, 
$E_\lambda$ is of class 
$C^{1}$, and critical points of 
$E_\lambda$ are weak solutions of (1.6).
By definition, a least energy nodal solution of (1.6) is a minimizer of 
$E_\lambda$ within the class of sign-changing solutions of (1.6). Our first main result is concerned with the least energy nodal solutions and reads as follows.
Theorem 1.2 Let 
$p > 2$ and 
$q=1$. For every 
$\lambda >0$ there exists a least energy nodal solution of (1.6). Furthermore, there exist 
$0<\lambda _0 \leq \Lambda _0 < \infty$ with the following properties:
Theorem 1.2 establishes a symmetry breaking phenomenon for least energy nodal solutions, which occurs within a finite range of parameters 
$\lambda \in [\lambda _0,\Lambda _0]$. We are not aware of any other setting where such a transition from radiality to nonradiality has been observed for least energy nodal solutions. The main difficulty when dealing with least energy radial nodal solutions of the equation 
$-\Delta u + u = |u|^{p-2}u$ in 
$\mathbb {R}^{2}$ is given by the fact that so far neither uniqueness (up to sign) nor nondegeneracy is known. Hence, in order to prove the first part of Theorem 1.2, we have to follow an approach, which does not rely on these properties. In fact, a more general radiality result for solutions of (1.6) with small 
$\lambda >0$ can be obtained by combining uniform elliptic 
$L^{\infty }$-estimates with Poincaré type inequalities in the angular variable. More precisely, we have the following.
Theorem 1.3 Let 
$p >2$ and 
$q=1$.
i. If
$u \in H$ is a nontrivial weak solution of (1.6) for some $\lambda >0$ satisfying $\lambda < \Bigl (\frac {1}{(p-1)|u|_\infty ^{p-2}}\Bigr )^{\frac {1}{2}}$, then $u$ is a radial function.ii. For every
$c>0$, there exists $\lambda _c>0$ with the property that every weak solution $u \in H$ of (1.6) for some $\lambda \in (0,\lambda _c)$ with $E_\lambda (u) \le c$ is radial.
The first part of Theorem 1.2 turns out to be a consequence of Theorem 1.3(ii) and uniform (in 
$\lambda$) energy estimates for least energy nodal solutions of (1.6) in the case 
$p>2$, 
$q=1$, see § 5 below.
While least energy nodal solutions are particularly interesting from a variational point of view, Theorem 1.2(i) and Theorem 1.3(ii) show that, in order to detect nonradial sign-changing solutions of (1.6) for small values 
$\lambda >0$, we have to pass to higher energy levels. A natural class of nonradial nodal solutions of (1.6) is the class of odd solutions with respect to a hyperplane reflection.
If we consider the hyperplane 
$\{x_1=0\}$, then any such solution corresponds to a solution of the boundary value problem
\begin{equation} \left \{ \begin{aligned} -\Delta u - \frac{1}{\lambda^{2}} [x_1 \partial_{x_2} - x_2 \partial_{x_1}]^{2} u + q\,u & = |u|^{p-2}u & & \qquad \text{on} \ {{\mathbb{R}^{2}_+},}\\ u & =0 & & \qquad \text{on} \ {{\partial \mathbb{R}^{2}_+}} \end{aligned} \right.\end{equation}
in the half space 
$\mathbb {R}^{2}_+:= \{x \in \mathbb {R}^{2}\::\: x_1>0\}$. Moreover, by odd reflection and transformation of coordinates, any such solution 
$u$ gives rise to a 
$\lambda$-spiraling nodal solution 
$v: \mathbb {R}^{3} \to \mathbb {R}$ of (1.3) with the property that
\[ v(0,t)=0= v(R_{t}(0,x_2), \lambda t) \qquad \text{for all} \ {{t, x_2 \in \mathbb{R}}.} \]
Consequently, 
$v$ vanishes on a helicoid, i.e. the condition 
$u =0$ on 
$\partial \mathbb {R}_+^{2}$ implies that 
$v$ is zero on the set 
$\left \{ (x \sin t, x \cos t, \lambda t): t,x \in \mathbb {R} \right \}$.
Weak solutions of (1.10) correspond to critical points of the 
$C^{1}$-functional 
$E_{\lambda }^{+}: H^{+} \to \mathbb {R}$ defined by
\begin{equation} E_{\lambda}^{+}(u) := \frac{1}{2} \int_{\mathbb{R}^{2}_+} (|\nabla u|^{2} + \frac{1}{\lambda^{2}} |\partial _\theta u|^{2} + q u^{2} )\textrm{d}x- \frac{1}{p} \int_{\mathbb{R}^{2}_+} |u|^{p} \,\textrm{d}x , \end{equation}where
\begin{equation} H^{+}:= \left\{u \in H^{1}_0(\mathbb{R}^{2}_+)\::\: \int_{\mathbb{R}^{2}_+} |\partial _\theta u|^{2} \textrm{d}x <\infty \right\}. \end{equation}
By trivial extension, we regard 
$H^{+}$ as a closed subspace of 
$H$, see § 3 below for details.
Our main result for (1.10) reads as follows.
Theorem 1.4 Let 
$p>2$, 
$q \in \{0,1\}$ and 
$\lambda >0$.
(i) (Existence) Problem (1.10) admits a positive least energy solution.
(ii) (Symmetry) Any positive solution
$u$ of (1.10) is symmetric with respect to reflection at the $x_1$-axis and decreasing in the angle $|\theta |$ from the $x_1$-axis. In particular, $u$ takes its maximum on the $x_1$-axis.(iii) (Asymptotics) If
$q=1$ and $\lambda _k \ge 1$ are given with $\lambda _k \to + \infty$ as $k \to \infty$ and $u_k$ is a positive least energy solution of (1.10) with $\lambda = \lambda _k$, then, after passing to a subsequence, there exists a sequence of numbers $\tau _k >0$ with
such that the translated functions\[ \tau_k \to + \infty, \qquad \frac{\tau_k}{\lambda_k} \to 0 \qquad \text{as} \,{{k \to \infty}} \]$w_k \in H^{1}(\mathbb {R}^{2})$, $w_k(x)= u_k(x_1+ \tau _k,x_2)$ satisfy
where\[ w_k \to w_\infty \qquad \text{strongly in} \,{{H^{1}(\mathbb{R}^{2})},} \]$w_\infty$ is the unique positive radial solution of
(1.13)\begin{equation} -\Delta w_\infty + w_\infty = |w_\infty|^{p-2}w_\infty, \qquad w_\infty \in H^{1}(\mathbb{R}^{2}). \end{equation}
Similarly, as defined for the equation (1.6), a least energy solution of (1.10) is, by definition, an energy minimizer within the class of nontrivial solutions of (1.10). More specifically, least energy solutions will be characterized as minimizers of 
$E_{\lambda }^{+}$ w.r.t. the associated Nehari manifold and attain the mountain pass level
\begin{equation} c_{\lambda}=\inf_{u \in H^{+} \setminus \{ 0\}} \sup_{t \geq 0} E_{\lambda}^{+}(tu), \end{equation}see § 3 below. We also point out that the uniqueness of a positive radial solution to (1.13) was shown by Kwong [Reference Kwong17].
Remark 1.5
(i) Let
$p>2$ and $q=1$. As a consequence of Theorem 1.4, the energy of the least energy nodal solution of (1.6), as considered in Theorem 1.2, tends to $2 c_\infty$ as $\lambda \to \infty$, where $c_\infty$ is the least energy of nontrivial solutions of the limit problem (1.13). This fact is the key ingredient in the proof of Theorem 1.2(ii).(ii) The existence result for (1.10) for
$p>2$ and $q \in \{0,1\}$ relies on compact embeddings. More precisely, we will prove in § 2 below that the space $H$ is compactly embedded into $L^{\rho }(\mathbb {R}^{2})$ for $\rho \in (2,\infty )$, which readily implies that the space $H^{+}$ is compactly embedded in $L^{\rho }(\mathbb {R}^{2}_+)$ for $\rho \in (2,\infty )$. With the help of these embeddings and by applying the symmetric mountain pass theorem (see Theorem 6.5 in [Reference Struwe24]), we may also prove, for any $\lambda >0$, the existence of a sequence of pairs of solutions $\pm u_j$ whose sequence of energies is unbounded.
The existence and symmetry parts of Theorem 1.4 extend to a larger class of semilinear equations, see § 3 below. Next, we shall see that the case 
$q=0$ in (1.10) arises naturally when considering the asymptotics of positive least energy solutions of (1.10) in the case 
$q=1$ when 
$\lambda \to 0$. We shall see that these solutions concentrate at the origin as 
$\lambda \to 0$. More precisely, we have the following.
Theorem 1.6 Let 
$(\lambda _k)_k$ be sequence of numbers 
$\lambda _k \le 1$ such that 
$\lambda _k \to 0$ as 
$k \to \infty$. Moreover, let 
$u_k \in H^{+}$ be a positive least energy solution of (1.10) with 
$q=1$, and let 
$v_k \in H^{+}$ be defined by 
$v_k(x)= \lambda _k^{\frac {2}{p-2}}u_k(\lambda _k x).$
Then, after passing to a subsequence, we have 
$v_k \to v^{*}$ in 
$H^{+}$, where 
$v$ is a positive least energy solution of the problem
\begin{equation} \left \{ \begin{aligned} -\Delta v^{*} - [x_1 \partial_{x_2} - x_2 \partial_{x_1}]^{2} v^{*} & = |v^{*}|^{p-2}v^{*} & & \qquad \text{on} \ {{\mathbb{R}^{2}_+},}\\ v & =0 & & \qquad \text{on} \ {{\partial \mathbb{R}^{2}_+}} \end{aligned} \right. \end{equation}Remark 1.7 The statements given in Theorems 1.4(i) and 1.6 remain valid when the underlying half space 
$\mathbb {R}^{2}_+$ is replaced by the cone
\[ C_{\alpha}:= \{x \in \mathbb{R}^{2}\::\: x_1>0, \quad \arcsin \frac{x_2}{|x|} < \alpha\}. \]
In particular, in the case where 
$\alpha = \frac {\pi }{2 j}$ for some positive integer 
$j$, successive reflection yields solutions with precisely 
$2j$ nodal domains.
The paper is organized as follows. Section 2 sets up the functional analytic framework and provides some preliminary results. In particular, we shall prove the compactness of the embedding 
$H \hookrightarrow L^{\rho }(\mathbb {R}^{2})$ for 
$\rho \in (2,\infty )$, and we establish the existence of least energy nodal solutions for problem (1.6). In § 3, we study the symmetry and existence of ground state solutions for a generalization of problem (1.10). In § 4 we discuss the asymptotics of least energy solutions to (1.10) as 
$\lambda \to \infty$ and as 
$\lambda \to 0$ and prove Theorems 1.4 and 1.6. Finally, § 5 is devoted to the proofs of Theorems 1.2 and 1.3. In the appendix, we prove a result on uniform 
$L^{\infty }$-bounds for weak solutions of (1.6) in the case 
$q=1$.
2. Preliminary results
In the following, all functions are assumed to be real-valued. We consider the space 
$H$ defined in (1.7) with the 
$\lambda$-dependent scalar product defined in (1.8) with 
$\|\cdot \|_\lambda$ denoting the corresponding norm. The space 
$(H, \langle \cdot , \cdot \rangle _\lambda )$ is a Hilbert space and clearly, all the norms 
$\|\cdot \|_\lambda$, 
$\lambda >0$, are equivalent.
For easier distinction from the norms on 
$H$, for 
$\rho \in [1,\infty ]$, we will use the notation 
$|\cdot |_{\rho }$ to denote the standard norm on 
$L^{\rho }(\mathbb {R}^{2})$.
Recall also that we have set 
$\partial _\theta :=[x_1 \partial _{x_2} - x_2 \partial _{x_1}]$ for the angular derivative operator. We first note the following.
Lemma 2.1 For any 
$\lambda >0$, the space 
$C_c^{\infty }(\mathbb {R}^{2})$ of test functions is dense in 
$(H,\langle \cdot ,\cdot \rangle _{\lambda })$.
Proof. The argument is essentially the same as the one proving the density of 
$C_c^{\infty }(\mathbb {R}^{2})$ in 
$H^{1}(\mathbb {R}^{2})$, see e.g. the proof of Theorem 9.2 in [Reference Brezis7]. We only sketch it briefly. Let 
$W$ denote the subspace of functions in 
$H$ which vanish outside a bounded subset of 
$\mathbb {R}^{2}$. By a straightforward cut-off argument, 
$W$ is dense in 
$H$. Moreover, for a given function 
$u \in W$, it is well known that a sequence of mollifications 
$u_n \in C_c^{\infty }(\mathbb {R}^{2})$ of 
$u$ converges to 
$u$ in the 
$H^{1}$-norm. Moreover, since there is a compact set 
$K \subset \mathbb {R}^{2}$ with the property that every 
$u_n$, 
$n \in \mathbb {N}$ vanishes in 
$\mathbb {R}^{2} \setminus K$, the convergence in the 
$H^{1}$-norm also implies convergence in 
$\|\cdot \|_\lambda$. This shows the claim.
Next, we consider the radial averaging operator
\begin{align} &L^{1}_{loc}(\mathbb{R}^{2}) \to L^{1}_{loc}(\mathbb{R}^{2}), \quad u \mapsto u^\#, \qquad \text{with}\notag\\ &u^\# (x) := \frac{1}{2\pi}\int_{S^{1}} u(|x|\omega) \, \textrm{d}\omega \quad \text{for a.e.} \,{{x \in \mathbb{R}^{2}}.} \end{align}
We note that, as a consequence of Jensen's inequality, the averaging operator extends to a continuous linear map 
$L^{\rho }(\mathbb {R}^{2}) \to L^{\rho }(\mathbb {R}^{2})$ for every 
$\rho \in [1,\infty ]$ with
\begin{equation} |u^\#|_{\rho} \le |u|_{\rho} \qquad \text{for every} \,{{u \in L^{\rho}(\mathbb{R}^{2})}.} \end{equation}
Moreover, since 
$u^\# \in C_c^{1}(\mathbb {R}^{2})$ for 
$u \in C_c^{1}(\mathbb {R}^{2})$ and
\[ \|u^\#\|_{\lambda}=\|u^\#\|_{H^{1}(\mathbb{R}^{2})} \leq \|u\|_{H^{1}(\mathbb{R}^{2})} \leq \|u\|_{\lambda} \quad \text{for} \,{{\lambda>0},} \]
the operator 
$u \mapsto u^\#$ extends to a continuous linear map 
$H \to H$.
We need the following angular Poincaré type estimates.
Lemma 2.2
(i) For any
$u \in H$,
In particular, any\[ |u|_{2}^{2} \le |\partial _\theta u|_2^{2} + |u^\#|_{2}^{2} . \]$u \in H$ with $u^\# \equiv 0$ satisfies $|u|_{2}^{2} \le |\partial _\theta u|_2^{2}.$(ii) Let
$\theta _0 \in (0,\pi )$, and consider the cone
If\[ C_{\theta_0} := \{ (r\cos \theta,r \sin \theta) \in \mathbb{R}^{2}\::\: r>0, |\theta| < \theta_0 \}. \]$u \equiv 0$ on $\mathbb {R}^{2} \setminus C_{\theta _0}$, then we have
\[ |u|_{2} \le \frac{2\theta_0}{\pi}|\partial_\theta u|_{2}. \]
Proof. (i) By lemma 2.1, it suffices to prove the claim for 
$u \in C^{\infty }_c(\mathbb {R}^{2})$.
We first assume that 
$u^\# \equiv 0$. In this case, we have, in polar coordinates,
\[ |u|_{2}^{2} = \int_{0}^{\infty} r \int_0^{2\pi} |u (r,\theta)|^{2}\,\textrm{d}\theta \,\textrm{d}r, \]
where the function 
$\theta \mapsto u(r,\theta )$ is 
$2\pi$-periodic and satisfies 
$\int _0^{2\pi } u(r,\theta )\,\textrm {d}\theta = 0$ for every 
$r>0$. Consequently, by Wirtinger's inequality for periodic functions,
\[ \int_0^{2\pi} |u (r,\theta)|^{2}\,\textrm{d}\theta \le \int_0^{2\pi} |\partial_\theta u (r,\theta)|^{2}\,\textrm{d}\theta \qquad \text{for every} \,{{r > 0},} \]which implies that
\[ |u|_{2}^{2} \le \int_{0}^{\infty} r \int_0^{2\pi} |\partial_\theta u (r,\theta)|^{2}\,\textrm{d}\theta \,\textrm{d}r = |\partial_\theta u|_2^{2}. \]
If 
$u \in C^{\infty }_c(\mathbb {R}^{2})$ is arbitrary, we may apply the above argument to the function 
$u-u^\#$. Since 
$(u- u^\#)^\#=0$ and 
$\langle u- u^\#, u^\# \rangle _{L^{2}(\mathbb {R}^{2})} =0$, we get that
\[ |u|_2^{2} -|u^\#|_2^{2} = |u-u^\#|_2^{2} \le |\partial_\theta (u-u^\#)|_2^{2} = |\partial_\theta u|_2^{2}, \]as claimed.
(ii) Let 
$u \in H$ with 
$u \equiv 0$ on 
$\mathbb {R}^{2} \setminus C_{\theta _0}$. By lemma 2.1, there exists a sequence 
$(u_n)_n$ in 
$C^{\infty }_c(\mathbb {R}^{2})$ with 
$u_n \to u$.
We fix 
$r_0>0$ and we let 
$\rho \in C^{\infty }([0,\infty ))$ be a function with 
$0 \le \rho \le 1$, 
$\rho \equiv 0$ on 
$[0,r_0]$ and 
$\rho \equiv 1$ on 
$[2r_0,\infty )$. Moreover, we let 
$\theta ' \in (\theta _0,\pi )$ and 
$\psi \in C^{\infty }_c(\mathbb {R})$ be a function with 
$0 \le \psi \le 1$, 
$\psi \equiv 1$ in 
$[-\theta _0, \theta _0]$ and 
$\psi \equiv 0$ in 
$\mathbb {R} \setminus [-\theta ',\theta ']$. Next we define, in polar coordinates,
\[ \varphi_0,\varphi_1 \in L^{\infty}(\mathbb{R}^{2}) \cap C^{\infty}(\mathbb{R}^{2}), \qquad \varphi_0(r,\theta)= \rho(r), \quad \varphi_1(r,\theta) = \rho(r) \psi(\theta). \]
Setting 
$v_n:= u_n \varphi _1$ for 
$n \in \mathbb {N}$, it is then easy to see that
\begin{equation} v_n \to u \varphi_1 = u \varphi_0 \qquad \text{in} \,{{H},} \end{equation}
where the last equality follows since 
$u \equiv 0$ on 
$\mathbb {R}^{2} \setminus C_{\theta _0}$. Moreover, we have, in polar coordinates,
\[ |v_n|_{2}^{2} = \int_{0}^{\infty} r \int_{-\pi}^{\pi} |v_n (r,\theta)|^{2}\,\textrm{d}\theta \textrm{d}r, \]
where the function 
$\theta \mapsto v_n(r,\theta )$ is of class 
$C^{1}$ and satisfies 
$v_n(r,\theta )=0$ for 
$\theta \not \in [-\theta ', \theta ']$, 
$r>0$. Using again a classical Wirtinger type inequality (see § 1.7 in [Reference Dym and McKean13]),
\[ \int_{-\pi}^{\pi} |v_n (r,\theta)|^{2}\,\textrm{d}\theta \le \Bigl(\frac{2 \theta'}{\pi}\Bigr)^{2} \int_{-\pi}^{\pi} |\partial_\theta v_n|^{2} (r,\theta)\,\textrm{d}\theta \qquad \text{for every} \,{ {r>0},} \]which implies that
\begin{equation} |v_n|_{2}^{2} \le \Bigl(\frac{2 \theta'}{\pi}\Bigr)^{2} \int_{0}^{\infty} r \int_{-\pi}^{\pi} |\partial_\theta v_n|^{2} (r,\theta)\,\textrm{d}\theta \textrm{d}r = \Bigl(\frac{2 \theta'}{\pi}\Bigr)^{2} |\partial_\theta v_n|_2^{2} \end{equation}
for every 
$n \in \mathbb {N}$.
Using (2.3), we may thus pass to the limit in (2.4) to obtain the inequality
\[ |u \varphi_0 |_{2}^{2} \le \Bigl(\frac{2 \theta'}{\pi}\Bigr)^{2} |\varphi_0 \partial_\theta u |_2^{2}, \]which yields that
\[ \|u\|_{L^{2}(\mathbb{R}^{2} \setminus B_{2r_0}(0))} \le \frac{2\theta'}{\pi} \|\partial_\theta u\|_{L^{2}(\mathbb{R}^{2})}. \]
Since 
$r_0> 0$ and 
$\theta ' >\theta _0$ were chosen arbitrarily, the claim follows.
Next, we note embedding properties of the space 
$H$.
Lemma 2.3 For every 
$\lambda >0$, 
$(H,\langle \cdot , \cdot \rangle _\lambda )$ is a Hilbert space canonically embedded in 
$H^{1}(\mathbb {R}^{2})$. Moreover, 
$H$ is compactly embedded in 
$L^{\rho }(\mathbb {R}^{2})$ for all 
$\rho \in (2,\infty )$.
Proof. We have
\[ \|u\|_{H^{1}(\mathbb{R}^{2})} \le \|u\|_\lambda \qquad \text{for all} \,{{\lambda>0}, {v \in H},} \]
which implies that 
$H$ is a Hilbert space contained in 
$H^{1}(\mathbb {R}^{2})$. By standard Sobolev embeddings, 
$H$ is thus embedded in 
$L^{\rho }(\mathbb {R}^{2})$ for all 
$\rho \in [2,\infty )$. It remains to show that these embeddings are compact for 
$\rho >2$.
Let 
$(u_n)_n$ be a sequence in 
$H$ with 
$u_n \rightharpoonup 0$ in 
$H$, and suppose by contradiction that 
$u_n \not \to 0$ in 
$L^{\rho }(\mathbb {R}^{2})$ for some 
$\rho >2$.
Since, 
$u_n \rightharpoonup 0$ in 
$H^{1}(\mathbb {R}^{2})$, it follows from Lions’ Lemma [Reference Lions19, Lemma I.1] and Rellich's Theorem that, after passing to a subsequence, there exists a sequence 
$x^{n} \in \mathbb {R}^{2}$ with 
$|x^{n}| \to \infty$ and such that
\begin{equation} v_n \rightharpoonup v \not = 0 \qquad \text{in} \,{{H^{1}(\mathbb{R}^{2})}} \end{equation}
for the functions 
$v_n \in H^{1}(\mathbb {R}^{2})$, 
$v_n= u_n( \cdot + x^{n})$.
Let 
$r_n := |x^{n}|$. Passing to a subsequence, we may assume that the limits
\[ a := \lim \limits_{n \to \infty} \frac{x_1^{n}}{r_n}, \qquad b: = \lim \limits_{n \to \infty} \frac{x_2^{n}}{r_n} \]
exist, whereas 
$a^{2}+b^{2}=1$. For every 
$R>0$, we then have
\begin{align*} \lambda^{2} \|u_n\|_{\lambda}^{2} &\ge \int_{\mathbb{R}^{2}_+}|x_1 \partial_{x_2}u_n- x_2 \partial_{x_1}u_n|^{2} \textrm{d}x\\ & = \int_{\mathbb{R}^{2}}|(x_1+x_1^{n}) \partial_{x_2}v_n- (x_2+x_2^{n}) \partial_{x_1}v_n|^{2} \textrm{d}x\\ &\ge \int_{B_{R}(0)}|(x_1+x_1^{n}) \partial_{x_2}v_n- (x_2+x_2^{n}) \partial_{x_1}v_n|^{2} \,\textrm{d}x\\ & = r_n^{2} \int_{B_{R}(0)}\left|\frac{x_1+x_1^{n}}{r_n} \partial_{x_2}v_n - \frac{x_2+x_2^{n}}{r_n} \partial_{x_1}v_n\right|^{2} \textrm{d}x\\ &\ge r_n^{2} \left( \int_{B_{R}(0)}|a \partial_{x_2}v_n - b\partial_{x_1}v_n|^{2} \textrm{d}x\right.\\ &\quad - \sup_{x \in B_R(0)}\Bigl|\frac{x_1+x_1^{n}}{r_n}-a\Bigr| \|\partial_{x_2}v_n\|_{L^{2}(B_R(0))}^{2}\\ &\quad -\left. \sup_{x \in B_R(0)}\Bigl|\frac{x_2+x_1^{n}}{r_n}-b\Bigr| \|\partial_{x_1}v_n\|_{L^{2}(B_R(0))}^{2} \right)\\ &\ge r_n^{2} \left( \int_{B_{R}(0)}|a \partial_{x_2}v_n - b\partial_{x_1}v_n|^{2} \textrm{d}x +o(1) \right)\\ & \ge r_n^{2} \left( \int_{B_{R}(0)}|a \partial_{x_2}v - b\partial_{x_1}v|^{2} \,\textrm{d}x + o(1)\right), \end{align*}where in the last step we used the fact that
\[ a \partial_{x_2}v_n - b\partial_{x_1}v_n \;\rightharpoonup \; a \partial_{x_2}v - b\partial_{x_1}v \qquad \text{in} \,{{L^{2}(B_R(0))}} \]
and the weak lower semicontinuity of the 
$L^{2}$-norm. The boundedness of 
$(u_n)_n$ in 
$H$ now implies that
\[ \int_{B_{R}(0)}[a \partial_{x_2}v - b\partial_{x_1}v]^{2} \textrm{d}x = 0 \qquad \text{for every} \,{{R>0},} \]and thus
\begin{equation} \int_{\mathbb{R}^{2}}|a \partial_{x_2}v - b\partial_{x_1}v|^{2} \textrm{d}x =0 . \end{equation}
Since 
$a^{2} + b^{2} = 1$, if we had 
$a=0$ or 
$b=0$ it would follow that
\[ \int_{\mathbb{R}^{2}} |\partial_{x_2}v|^{2}\,\textrm{d}x = 0\quad \text{or}\quad \int_{\mathbb{R}^{2}} |\partial_{x_1}v|^{2}\,\textrm{d}x. \]
The fact that 
$v\in L^{2}(\mathbb {R}^{2})$ would imply 
$v \equiv 0$, contradicting (2.5). If, on the other hand, 
$a,b\neq 0$, (2.6) implies that 
$\partial _{x_1} v = \frac {a}{b} \partial _{x_2} v$ in 
$L^{2}(\mathbb {R}^{2})$. Thus 
$v$ satisfies 
$\partial _\beta v =0$ with 
$\beta = (1, - \frac {a}{b})$, which again implies 
$v \equiv 0$ and thus contradicts (2.5). The proof is finished.
Lemma 2.4 The embedding 
$H \hookrightarrow L^{2}(\mathbb {R}^{2})$ is not compact.
Proof. Let 
$\psi \in C^{\infty }_c((1,2)) \setminus \{ 0\}$. After trivially extending 
$\psi$ to 
$\mathbb {R}$, for 
$n \in \mathbb {N}$ consider the functions
\[ u_n(r,s)=\frac{1}{\sqrt{r}} \psi(r-n) \]so that
\[ {\textrm{supp}} \, u_n \subset \left\{ x \in \mathbb{R}_+^{2}: n+1 < |x| < n + 2 \right\} . \]
Clearly, 
$u_n \rightharpoonup 0$ in 
$H$, but
\begin{align*} |u_n|_2^{2} & = 2\pi \int_0^{\infty} \psi(r-n)^{2} \, \textrm{d}r = 2\pi \int_0^{\infty} \psi(r)^{2} \, \textrm{d}r >0 \end{align*}
so 
$u_n \not \to 0$ in 
$L^{2}(\mathbb {R}^{2})$.
In the following, we fix 
$p >2$ and 
$q=1$ in (1.6), i.e., we consider the equation
\begin{equation} \left \{ \begin{aligned} -\Delta u - \frac{1}{\lambda^{2}} [x_1 \partial_{x_2} - x_2 \partial_{x_1}]^{2} u + u & = |u|^{p-2} u & & \qquad \text{on} \,{{\mathbb{R}^{2}},}\\ u(x) & \to 0 & & \qquad \text{as} \,{{|x| \to \infty}.} \end{aligned} \right. \end{equation}
Here and in what follows, for a given 
$\lambda >0$, a function 
$u \in H$ will be called a weak solution of (2.7) if
\[ \langle u,v \rangle_\lambda = \int_{\mathbb{R}^{2}}|u|^{p-2}u v \,\textrm{d}x \qquad \text{for all} \,{{v \in H}.} \]
As a consequence of lemma 2.3 and standard arguments in the calculus of variations, we see that for 
$\lambda >0$, the energy functional
\[ E_\lambda: H \to \mathbb{R}, \quad E_\lambda(u) := \frac{1}{2}\|u\|_\lambda^{2}- \frac{1}{p}\int_{\mathbb{R}^{2}} |u|^{p} \,\textrm{d}x \]
is of class 
$C^{1}$ and critical points of 
$E_\lambda$ are weak solutions of (2.7).
We note the following uniform boundedness property of weak solutions of (1.6).
Lemma 2.5 Fix 
$\lambda >0$ and let 
$u \in H$ be a weak solution of
\begin{equation} -\Delta u - \frac{1}{\lambda^{2}} \partial _\theta^{2} u + u = |u|^{p-2} u \quad \text{in} \,{{\mathbb{R}^{2}}}. \end{equation}
Then 
$u \in L^{\infty }(\mathbb {R}^{2})$. Moreover, there exist constants 
$\sigma , C>0$, depending on 
$p>2$ but not on 
$u$ and 
$\lambda$, such that
\begin{equation} |u|_\infty \leq C \|u\|_{H^{1}(\mathbb{R}^{2})}^{\sigma} . \end{equation} The fact that the constants 
$C$ and 
$\sigma$ in (2.9) do not depend on 
$\lambda$ is of key importance in the proofs of Theorems 1.2(i) and Theorem 1.3(ii). The proof of lemma 2.5 follows by a Moser iteration scheme based on uniform estimates which do not depend on 
$\lambda >0$. We include the details in the appendix, see lemma A.1 below.
Remark 2.6 If 
$f: \mathbb {R} \to \mathbb {R}$ is a 
$C^{1}$-function with 
$f(0)=0$ and 
$u \in H \cap L^{\infty }(\mathbb {R}^{2})$, it is easy to see that also 
$f(u)= f \circ u \in H \cap L^{\infty }(\mathbb {R}^{2})$ with 
$\nabla f(u) = f'(u) \nabla u$ and 
$\partial _\theta f(u) = f'(u) \partial _\theta u$.
By lemma 2.5, this observation applies, in particular, to weak solutions 
$u \in H$ of (2.8).
Next we note that every nontrivial solution of (2.7) is contained in the Nehari manifold
\[ {{\mathcal{N}}}_{\lambda} := \{ u \in H \setminus \{ 0 \} : E_\lambda'(u) u = 0 \} . \]Let
\begin{equation} \alpha_\lambda := \inf \limits_{u \in {{\mathcal{N}}}_{\lambda}} E_\lambda(u)>0 , \end{equation}
then every minimizer is a critical point and hence a solution (cf. [Reference Szulkin and Weth26] and Theorem 3.5 below). It is easy to see that such a minimizer is positive and thus radial by Theorem 1.1. Therefore, 
$\alpha =\alpha _{\lambda }$ does not depend on 
$\lambda$.
Hence we now focus on sign-changing solutions. Consider
\begin{align*} {{\mathcal{M}}}_\lambda & := \left\{ u \in H: u^{+} \not \equiv 0, u^{-} \not \equiv 0, \ E_\lambda'(u)u^{+}=E_\lambda'(u)u^{-}=0 \right\} \\ & = \left\{ u \in H\setminus\{0\}: u^{+}, u^{-} \in {{\mathcal{N}}}_{\lambda}\right\} \end{align*}and set
\begin{equation} \beta_\lambda := \inf_{ u \in {{\mathcal{M}}}_\lambda} E_\lambda(u) . \end{equation}Proposition 2.7 The value 
$\beta _\lambda$ is positive. Moreover, every minimizer 
$u \in {{\mathcal {M}}}_\lambda$ of (2.11) is a critical point of 
$E_\lambda$ and hence a sign-changing solution of (2.7).
The proof of proposition 2.7 follows the same argument as in the proof of proposition 3.1 in [Reference Bartsch, Weth and Willem4].
We also remark that 
$\beta _\lambda \geq 2\alpha > 0$ in view of (2.10) and the fact that for any 
$u\in H$,
\[ E_{\lambda}(u)=E_{\lambda}(u^{+}) + E_{\lambda}(u^{-}) \quad \hbox{and} \quad E'_{\lambda}(u)u=E'_{\lambda}(u^{+})u^{+} + E'_{\lambda}(u^{-}) u^{-}. \]
We say that a function 
$u \in H$ is a least energy nodal solution of (2.7) if 
$u$ is a sign-changing solution of (2.7) such that 
$E_\lambda (u)=\beta _\lambda$. The following lemma yields the existence of a least energy nodal solution.
Lemma 2.8 There exists 
$u \in {{\mathcal {M}}}_\lambda$ such that 
$E_\lambda (u)=\beta _\lambda$.
Proof. We proceed similarly as in [Reference Castro, Cossio and Neuberger8]. Let 
$(u_n)_n \subset {{\mathcal {M}}}_\lambda$ be a minimizing sequence. Note that for any 
$u \in {{\mathcal {M}}}_\lambda$ we have
\[ E_\lambda(u_n)= \left( \frac{1}{2} - \frac{1}{p} \right) \int_{\mathbb{R}^{2}} \left( |\nabla u|^{2} + \frac{1}{\lambda^{2}} |\partial _\theta u|^{2} + u^{2} \right) \, \textrm{d}x, \]
which implies that 
$E_\lambda$ is coercive on 
${{\mathcal {M}}}_\lambda$. This yields that 
$(u_n)_n$ is bounded and we may, therefore, pass to a subsequence such that
\[ u_n \rightharpoonup u \quad \text{in} \,{{H}} . \]
We then also have 
$u_n^{\pm } \rightharpoonup u^{\pm }$ in 
$H$, and the compact embedding 
$H \hookrightarrow L^{p}$ implies
\[ \int_{\mathbb{R}^{2}} |u^{{\pm}}|^{p} \, \textrm{d}x= \lim \limits_{n\to \infty} \int_{\mathbb{R}^{2}} |u_n^{{\pm}}|^{p} \, \textrm{d}x = C \| u_n^{{\pm}} \|_{\lambda}^{2} \geq C'>0. \]
Hence 
$u^{\pm } \not \equiv 0$. Next, we show that 
$u_n^{\pm } \to u^{\pm }$ in 
$H$. Arguing by contradiction, assume first that 
$\|u^{+}\|_{\lambda }^{2} < \liminf \limits _{n \to \infty } \|u_n^{+}\|_{\lambda }^{2}$. Then
\[ E_\lambda'(u^{+})u^{+} = \|u^{+}\|_{\lambda}^{2} - \|u^{+}\|_p^{p} < \liminf \limits_{n\to \infty}\left( \|u_n^{+}\|_{\lambda}^{2} - \|u_n^{+}\|_p^{p} \right) =0 . \]
Hence the characterization of 
${{\mathcal {N}}}_{\lambda }$ yields the existence of 
$a\in (0,1)$ such that 
$a u^{+} \in {{\mathcal {N}}}_{\lambda }$. A similar argument yields 
$b u^{-} \in {{\mathcal {N}}}_{\lambda }$ for some 
$0< b \leq 1$. Thus, 
$au^{+} +bu^{-}\in {{\mathcal {M}}}_\lambda$ and we estimate
\begin{align*} \beta_{\lambda} &\leq E_\lambda(a u^{+} + b u^{-}) < \liminf \limits_{n\to \infty} E_\lambda(a u_n^{+} + b u_n^{-}) = \liminf \limits_{n\to \infty}\left( E_\lambda(a u_n^{+}) + E_\lambda(b u_n^{-}) \right) \\ &\leq \liminf \limits_{n\to \infty}(E_\lambda(u_n^{+}) + E_\lambda(u_n^{-})) = \liminf \limits_{n\to \infty}E_\lambda(u_n) = \beta_{\lambda}, \end{align*}
which is a contradiction. Thus, after passing to a subsequence if necessary and using the uniform convexity of 
$(H,\|\cdot \|_{\lambda })$, we conclude that 
$u_n^{+} \to u^{+}$ strongly in 
$H$. In particular, 
$u^{+} \in {{\mathcal {N}}}_\lambda$. Proceeding similarly, we prove that 
$u_n^{-} \to u^{-}$ strongly in 
$H$ and that 
$u^{-}\in {{\mathcal {N}}}_{\lambda }$ and consequently, 
$u \in {{\mathcal {M}}}_\lambda$ with 
$E_\lambda (u)=\beta _\lambda$.
Summarizing the previous results, we have the following.
Corollary 2.9 Let 
$p>2$. For every 
$\lambda > 0$ there exists a least energy nodal solution to (2.7), i.e. a sign-changing solution 
$u \in H$ such that 
$E_\lambda (u)=\beta _\lambda$.
Remark 2.10 We may also consider the more general equation
\begin{equation} \left \{ \begin{aligned} -\Delta u - \frac{1}{\lambda^{2}} [x_1 \partial_{x_2} - x_2 \partial_{x_1}]^{2} u + u & = f(u) & & \qquad \text{on} \,{{\mathbb{R}^{2}},}\\ u(x) & \to 0 & & \qquad \text{for} \,{{|x| \to \infty},} \end{aligned} \right. \end{equation}
where 
$f: \mathbb {R} \to \mathbb {R}$ is a continuous function. In order to extend our results, consider the following conditions:
\begin{align*} (A_1) & \ \text{There exists} \,{{C > 0} {\rm such\, that} {|f(t)| \le C (|t| + |t|^{p})} for {t \in \mathbb{R}}} \\ (A_2) & t \mapsto \frac{f(t)}{t} \hbox{ is strictly increasing on}\ {\mathbb{R}} {\setminus} \{0\} and \lim_{t \to 0}\frac{f(t)}{t}\le 0, \ \lim_{t \to \pm \infty }\frac{f(t)}{t} = \infty. \end{align*}Under these assumptions, it can be shown that the results of this section, concerned with problem (2.7), continue to hold true for (2.12).
3. Existence and symmetry of odd solutions
This section is devoted to the study of solutions of the problem (1.10), which correspond, by odd reflection, to solutions of (1.6) with hyperplane antisymmetry. In particular, we shall prove Parts (i) and (ii) of Theorem 1.4.
Consider the space 
$H^{+}$ defined in (1.12). For fixed 
$\lambda >0$ and 
$q \in \{0,1\}$, we endow 
$H^{+}$ with the 
$\lambda$-dependent scalar product
\[ \langle u,v \rangle_{\lambda,q} \mapsto \int_{\mathbb{R}^{2}_+} \Bigl(\nabla u \cdot \nabla v + \frac{1}{\lambda^{2}} (\partial _\theta u)(\partial _\theta v)+ q\, u v \Bigr) \textrm{d}x, \]
and we let 
$\|\cdot \|_{\lambda ,q}$ denote the corresponding norm. Observe that any 
$u \in H^{+}$ can be extended to an element of 
$H$ either trivially or by odd reflection. Therefore, lemmas 2.2 and 2.3 immediately yield the following.
Corollary 3.1
(i) Any
$u \in H^{+}$ satisfies
(3.1)In particular, the norms\begin{equation} |u|_{2}^{2} \le \int_{\mathbb{R}^{2}_+}|\partial _\theta u|^{2} \textrm{d}x . \end{equation}$\|\cdot \|_{\lambda ,0}$ and $\|\cdot \|_{\lambda ,1}$ are equivalent on $H^{+}$, and $H^{+}$ is a Hilbert space with either of these norms. Moreover, we have a continuous embedding $H^{+} \hookrightarrow H^{1}(\mathbb {R}^{2}_+)$.(ii) The space
$H^{+}$ is compactly embedded in $L^{\rho }(\mathbb {R}^{2}_+)$ for $\rho > 2$.
Remark 3.2 (i) Similar statements are also true, when the underlying space is the cone 
$C_{\theta _0}$ described in lemma 2.2. (ii) As in lemma 2.4, we see that the embedding 
$H^{+} \hookrightarrow L^{2}(\mathbb {R}^{2}_+)$ is not compact.
First, we establish the symmetry of positive weak solutions of (1.10) as a consequence of the following.
Theorem 3.3 Let 
$\lambda >0$, and let 
$f \in C^{1}([0,\infty ))$ satisfy
\begin{equation} f'(t) \le C \Bigl(t^{\sigma_1}+t^{\sigma_2}\Bigr) \quad \hbox{for} \quad t \ge 0 \end{equation}
with constants 
$\sigma _1,\sigma _2>0$. Moreover, let 
$u \in H^{+} \cap L^{\infty }(\mathbb {R}^{2})$ be a positive weak solution of the problem
\begin{equation} \left\{ \begin{aligned} -\Delta u - \frac{1}{\lambda^{2}} \partial _\theta^{2} u & =f(u) & & \qquad \text{on}\ {\mathbb{R}^{2}_+},\\ u & =0 & & \qquad \text{on} \ {\partial \mathbb{R}^{2}_+}. \end{aligned} \right. \end{equation}
Then 
$u$ is symmetric with respect to the 
$x_1$-axis and decreasing with respect to the angle 
$|\theta |$ from the 
$x_1$-axis.
Remark 3.4 Theorem 3.3 in particular applies in the case where the nonlinearity 
$f$ is given by 
$f(t)=-q t + |t|^{p-2}t$ for some 
$p \in (2,\infty )$, 
$q \in \{0,1\}$. In this case, lemma 2.5 and remark A.2 below imply that every weak solution 
$u \in H^{+}$ of (3.2) is bounded. Hence we deduce the statement of Theorem 1.4(ii).
Proof of Theorem 3.3. For simplicity, we assume 
$\lambda =1$. We shall argue by the method of rotating planes. For 
$\theta \in [-\frac {\pi }{2},0) \cup (0,\frac {\pi }{2}]$, set 
$e_\theta := (\cos \theta , \sin \theta )$,
\[ T_\theta := \{x \in \mathbb{R}^{2}: x \cdot e_\theta =0\} \quad \hbox{and}\quad \Sigma_\theta := \{ x \in \mathbb{R}_+^{2}: x \cdot e_\theta < 0 \} . \]
Given a positive solution 
$u\in H^{+}\cap L^{\infty }(\mathbb {R}^{2}_+)$ of (3.3), consider the functions 
$u_\theta , w_\theta :\Sigma _\theta \to \mathbb {R}$ defined by
\[ u_\theta(x) = u(x-2 (x \cdot e_\theta)e_\theta) \quad \hbox{and} \quad w_\theta := u_\theta - u \]
and extend them trivially outside 
$\Sigma _{\theta }$. A direct calculation shows that 
$w_\theta$ satisfies
\begin{equation} \begin{aligned} -\Delta w_\theta - \partial _\theta^{2} w_\theta & = c_\theta(x) w_\theta \quad & & \text{in} \,{{\Sigma_\theta}} \\ w_\theta & = 0 \quad \quad & & \text{on} \,{{T_\theta}} \\ w_\theta & > 0 \quad \quad & & \text{on} \,{{\partial \Sigma_\theta \setminus T_\theta},} \end{aligned} \end{equation}where
\[ c_\theta(x)=\int_0^{1} f'((1-t)u(x)+t u_\theta(x))\,dt. \]Consider the set
\[ \Theta^{+} := \left\{ \theta \in \left(0,\frac{\pi}{2} \right): w_{\theta} \geq 0 \text{ in} \,{{\Sigma_{\theta}}} \right\} \]
which is clearly a closed set in 
$(0,\frac {\pi }{2})$.
We claim that 
$\Theta ^{+}$ is non-empty. To prove this claim, we proceed as follows. Observe first that 
$w_\theta ^{-} := \min \{w_\theta ,0\} \in H^{+}$. Moreover, using (3.2), we have that for 
$x \in \Sigma _\theta$ with 
$w_\theta ^{-}(x)<0$,
\begin{equation} \begin{aligned} c_\theta(x) \le & C \int_0^{1} \Bigl[((1-t)u(x)+t u_\theta(x))^{\sigma_1}+ ((1-t)u(x)+t u_\theta(x))^{\sigma_2} \Bigr]dt \\ \le & C \Bigl[u^{\sigma_1}(x)+u^{\sigma_2}(x)\Bigr]. \end{aligned} \end{equation} Also, the boundary conditions imply 
$w_\theta ^{-} \equiv 0$ on 
$\partial \Sigma _\theta$, and testing the equation (3.4) against 
$w_\theta ^{-}$ yields
\begin{equation} \begin{aligned} |\nabla w_\theta^{-}|_2^{2} + |\partial _\theta w_\theta^{-}|_2^{2} = & \int_{\mathbb{R}^{2}} c_\theta(x) (w_\theta^{-})^{2} \, \textrm{d}x\\ \leq & C \int_{\mathbb{R}^{2}}\Bigl[u^{\sigma_1}+u^{\sigma_2}\Bigr] (w_\theta^{-})^{2}\,\textrm{d}x\\ \le & C_0 |w_\theta^{-}|_2^{2} \end{aligned} \end{equation}
with 
$C_0 = C (|u|_\infty ^{\sigma _1} +|u|_\infty ^{\sigma _2} )$. Therefore, by lemma 2.2(ii),
\[ \frac{\pi}{2\theta}|w_\theta^{-}|_2 \le |\partial _\theta w_\theta^{-}|_2 \le \sqrt{C_0}|w_\theta^{-}|_2. \]
Consequently, 
$w_\theta ^{-} \equiv 0$ provided that 
$0 < |\theta | < \frac {\sqrt {C_0} \pi }{2}$ and this proves the claim.
Next, we claim that 
$\Theta ^{+}$ is also open in 
$(0,\frac {\pi }{2})$. To see this, let 
$\theta _0 \in \Theta ^{+}$. Since 
$w_{\theta _0} \not \equiv 0$ by (3.4), the strong maximum principle implies that 
$w_{\theta _0} > 0$ in 
$\Sigma _{\theta _0}$.
Fix 
$\rho > 2$ such that 
$\tau _i:= \frac {\sigma _i \rho }{\rho -2}>2$ for 
$i=1,2$. By lemma 2.3, there exists 
$\kappa _\rho >0$ such that
\[ |w|_\rho^{2} \le \kappa_\rho \Bigl(|\nabla w|_2^{2} + |\partial _\theta w|_2^{2}\Bigr) \qquad \text{for all} \,{{w \in H^{+}}.} \]
Moreover, we may choose a compact set 
$D \subset \Sigma _{\theta _0}$ such that
\[ \|u\|_{L^{\tau_1}(\Sigma_{\theta_0} \setminus D)}^{\sigma_1}+\|u\|_{L^{\tau_2}(\Sigma_{\theta_0} \setminus D)}^{\sigma_2}< \frac{1}{2\kappa_\rho C}, \]
where 
$C>0$ is the constant in (3.5).
On the other hand, by continuity of the family 
$w_{\theta }$ w.r.t. 
$\theta$ there exists a neighborhood 
$N \subset (0,\frac {\pi }{2})$ of 
$\theta _0$ with the property that for all 
$\theta \in N$,
\[ w_\theta>0\quad \text{in} \,{{D}}\quad \text{and}\quad \|u\|_{L^{\tau_1}(\Sigma_{\theta} \setminus D)}^{\sigma_1}+\|u\|_{L^{\tau_2}(\Sigma_{\theta} \setminus D)}^{\sigma_2} < \frac{1}{2\kappa_\rho C}. \]From (3.6) and Hölder's inequality, it follows that
\begin{align*} |w_\theta^{-}|_{\rho}^{2} &\leq \kappa_\rho \Bigl(|\nabla w_\theta^{-}|_2^{2} + |\partial _\theta w_\theta^{-}|_2^{2}\Bigr)\le \kappa_\rho C \int_{\mathbb{R}^{2}}\Bigl[u^{\sigma_1}+u^{\sigma_2}\Bigr](w_\theta^{-})^{2}\,\textrm{d}x\\ &\le \kappa_\rho C \Bigl(\|u\|_{L^{\tau_1}(\Sigma_{\theta_0} \setminus D)}^{\sigma_1}+\|u\|_{L^{\tau_2}(\Sigma_{\theta_0} \setminus D)}^{\sigma_2}\Bigr)|w_\theta^{-}|_{\rho}^{2} \le \frac{1}{2}|w_\theta^{-}|_{\rho}^{2} \end{align*}
for any 
$\theta \in N$.
Consequently, 
$w_\theta ^{-} \equiv 0$ for 
$\theta \in N$ and this proves the claim.
Since 
$\Theta ^{+}$ is an open, closed and nonempty subset of 
$(0,\frac {\pi }{2})$, we conclude that 
$\Theta ^{+} = (0,\frac {\pi }{2})$. In the same manner, we see that
\[ \Theta^{-} := \left\{ \theta \in \left(-\frac{\pi}{2},0 \right): w_{\theta} \geq 0 \text{ in} \,{{\Sigma_{\theta}}} \right\} = (-\frac{\pi}{2},0) \]
Consequently, 
$u$ is decreasing with respect to the angle 
$|\theta |$ from the 
$x_1$-axis.
Finally, a continuity argument also shows that 
$w_\theta \ge 0$ in 
$\Sigma _\theta$ for 
$\theta \in \{\pm \frac {\pi }{2}\}$, which, in particular, forces the symmetry of 
$u$ with respect to reflection at the 
$x_1$-axis.
Next, let 
$f: \mathbb {R} \to \mathbb {R}$ be a continuous function satisfying 
$(A_1)$ and 
$(A_2)$ as in remark 2.10 and set 
$F(t)=\int _0^{t} f(s) \, ds$. We consider the energy functional
\[ E_{\lambda}^{+}: H^{+} \to \mathbb{R}, \quad E_{\lambda}^{+}(u) := \frac{1}{2} \|u\|_{\lambda,0}^{2}- \int_{\mathbb{R}^{2}_+} F(u) \,\textrm{d}x \]
Again, standard arguments in the calculus of variations show that 
$E_{\lambda }^{+}$ is of class 
$C^{1}$, and critical points of 
$E_{\lambda }^{+}$ are solutions of the associated Euler–Lagrange equation
\begin{equation} \left \{ \begin{aligned} -\Delta u - \frac{1}{\lambda^{2}} \partial _\theta^{2} u & =f(u) & & \qquad \text{on} \,{{\mathbb{R}^{2}_+},}\\ u & =0 & & \qquad \text{on} \,{{\partial \mathbb{R}^{2}_+}.} \end{aligned} \right. \end{equation}As in § 2 we consider the associated Nehari manifold
\[ {{\mathcal{N}}}_{\lambda}^{+} := \left\{ u \in H^{+} \setminus \{0\}: [E_{\lambda}^{+}]'(u)u=0 \right\} \]and set
\begin{equation} c_{\lambda}:=\inf_{u \in {{\mathcal{N}}}^{+}} E_{\lambda}^{+}(u) . \end{equation}
This is the ground state energy in the sense that 
$E_{\lambda }^{+}(u) \ge c_{\lambda }$ for every nontrivial solution of (3.7).
Theorem 3.5 Let 
$p > 2$, 
$\lambda > 0$, and assume that 
$f: \mathbb {R} \to \mathbb {R}$ is a continuous function satisfying the assumptions 
$(A_1)$ and 
$(A_2)$ listed in remark 2.10. Then
\begin{equation} c_{\lambda} = \inf_{u \in H^{+} \setminus \{0\}} \sup_{t \ge 0} E_{\lambda}^{+}(t u). \end{equation}
Moreover, problem (3.7) admits a ground state solution, i.e., a solution 
$v \in H^{+} \setminus \{0\}$ such that 
$E_{\lambda }^{+}(v)=c_{\lambda }$.
Proof. The proof essentially follows the lines of the proof of [Reference Szulkin and Weth26, Theorem 20], see also [Reference Liu and Wang20, Section 4]. We note here that 
$(A_1)$ and 
$(A_2)$ ensure that the assumptions in [Reference Szulkin and Weth26, Theorem 20] are satisfied. Indeed, 
$(A_2)$ implies that for any 
$R > 0$ there exists 
$t_R > 0$ such that 
$f(t) \geq Rt$ for 
$t \geq t_R$. Thus
\[ F(t)=\int_0^{t} f(s) \, ds \geq \int_{t_R}^{t} Rs \, ds = \frac{R}{2} (t^{2} - t_R^{2}) \]
for 
$t \geq t_R$. It follows that
\[ \lim_{t \to \infty} \frac{F(t)}{t^{2}} = \infty , \]
i.e. assumption (iv) in [Reference Szulkin and Weth26, Theorem 20] is satisfied. Consequently, the proof given there can be carried through similarly, with some simplifications because the compact embedding 
$H^{+} \hookrightarrow L^{p}(\mathbb {R}^{2}_+)$ replaces arguments based on compactness modulo translations in the periodic setting of [Reference Szulkin and Weth26, Theorem 20].
Remark 3.6 (i) The statement of Theorem 1.4(i) is a special case of Theorem 3.5, since the nonlinearity 
$t \mapsto f(t)=-q t + |t|^{p-2}t$ satisfies conditions 
$(A_1)$ and 
$(A_2)$ if 
$q \in \{0,1\}$ and 
$p \in (2,\infty )$.
(ii) Under the assumptions of Theorem 3.5, it can be shown that ground state solutions cannot change sign, see [Reference Szulkin and Weth26, Remark 17].
4. Asymptotics of least energy odd solutions
In this section we fix 
$p \in (2,\infty )$, 
$q=1$, and we study the asymptotics of least energy solutions to (1.10) in the case 
$q=1$ as 
$\lambda \to \infty$ and as 
$\lambda \to 0$. In particular, we shall complete the proofs of Theorem 1.4(iii) and of Theorem 1.6. We will use the notation introduced in the previous section in the special case of the nonlinearity 
$t \mapsto f(t)=-t + |t|^{p-2}t$, which satisfies conditions 
$(A_1)$ and 
$(A_2)$. By the definition of the mountain pass value in (3.8) and the fact that 
$E_{\lambda _1}^{+} \ge E_{\lambda _2}^{+}$ for 
$0 <\lambda _1 < \lambda _2 < \infty$, we infer that the function
\[ (0,\infty) \to (0,\infty), \qquad \lambda \mapsto c_{\lambda} \]is decreasing, and therefore, the limits
\begin{equation} c_0 := \lim_{\lambda \to 0} c_{\lambda} \qquad \text{and} \qquad c_\infty := \lim_{\lambda \to \infty} c_{\lambda} \end{equation}
exist in 
$[0,\infty ]$. Next we note that
\begin{equation} \sup_{t \ge 0}E_{\lambda}^{+} (tv) = E_{\lambda}^{+}(t_v^{\lambda} v)= \Bigl(\frac{1}{2}-\frac{1}{p}\Bigr)\frac{ \|v\|_{\lambda,1}^{\frac{2p}{p-2}}}{|v|_{p}^{\frac{2p}{p-2}}} \quad \text{for every} \,{{v \in H^{+} \setminus \{0\}}} \end{equation}with
\[ t_v^{\lambda} = \left(\frac{\|v\|_{\lambda,1}^{2}}{|v|_{p}^{p}}\right)^{\frac{1}{p-2}}. \]
We start by considering the asymptotics of least energy solutions to (1.10) as 
$\lambda \to \infty$.
4.1 The limit $\lambda \to \infty$
Consider the limit energy functional
\[ E_*: H^{1}(\mathbb{R}^{2}) \to \mathbb{R}, \qquad E_*(v)= \frac{1}{2} \int_{\mathbb{R}^{2}} \left( |\nabla v|^{2} + v^{2} \right) \,\textrm{d}x - \frac{1}{p} \int_{\mathbb{R}^{2}} |v|^{p} \,\textrm{d}x. \]
Similarly as in (4.2), for 
$v \in H^{1}(\mathbb {R}^{2}) \setminus \{0\}$ we have
\begin{equation} \sup_{t \ge 0}E_*(t v) = E_*(t_v v)= \Bigl(\frac{1}{2}-\frac{1}{p}\Bigr)\frac{\|v\|_{H^{1}(\mathbb{R}^{2})}^{\frac{2p}{p-2}}}{|v|_{p}^{\frac{2p}{p-2}}} \end{equation}
with 
$t_v =(\frac {\|v\|_{H^{1}(\mathbb {R}^{2})}^{2}}{|v|_{p}^{p}})^{\frac {1}{p-2}}$.
Observe that for every 
$v\in H^{1}(\mathbb {R}^{2})$ with 
$E_*'(v)v=0$ we have 
$t_{v}=1$ and hence
\[ \sup_{t \ge 0} E_*(t v)= E_*(v). \]Define
\begin{equation} \hat{c}_\infty := \inf_{v \in H^{1}(\mathbb{R}^{2}) \setminus \{0\}} \sup_{t \ge 0} E_*(t v) \end{equation}
and let 
$w_\infty$ denote the unique positive radial solution (see [Reference Kwong17]) of the problem
\begin{equation} -\Delta w_\infty + w_\infty = |w_\infty|^{p-2}w_\infty, \qquad w_{\infty} \in C^{2}(\mathbb{R}^{2}) \cap H^{1}(\mathbb{R}^{2}). \end{equation} Since 
$E_*'(w_{\infty })w_{\infty }=0$, 
$t_{w_{\infty }}=1$ and hence
\begin{equation} \sup \limits_{t\geq 0}E_*(tw_{\infty})=E_*(w_{\infty}). \end{equation}
The following result provides a variational characterization of the limit 
$c_\infty$, defined in (4.1), in terms of 
$\hat {c}_{\infty }$ and 
$w_{\infty }$.
Lemma 4.1
\begin{equation} c_\infty = \hat{c}_{\infty}= E_*(w_\infty). \end{equation}Proof. We first prove the second equality in (4.7). Since the proof is standard, we only sketch the argument. By (4.6), we have 
$\hat {c}_{\infty }\leq E_*(w_{\infty })$. On the other hand, using Schwarz symmetrization and (4.3), it is easy to see that
\[ \hat{c}_\infty = \inf_{v \in H^{1}_{rad}(\mathbb{R}^{2}) \setminus \{0\}} \sup_{t \ge 0} E_*(t v). \]
Proceeding as in Theorem 20 and remark 17 in [Reference Szulkin and Weth26] and using the compactness of the embedding 
$H^{1}_{rad}(\mathbb {R}^{2})\hookrightarrow L^{p}(\mathbb {R}^{2})$, one can prove that 
$\hat {c}_{\infty }$ is attained at a positive radial solution of (4.5). By uniqueness, we then deduce that 
$\hat {c}_{\infty }=E_*(w_{\infty })$.
Next, we prove the first equality in (4.7). Identifying 
$v \in H^{+}$ with its trivial extension in 
$H$, we see that 
$E_{\lambda }^{+}(v)= E_{\lambda }(v) \ge E_*(v)$ for any 
$v \in H^{+}$ and any 
$\lambda > 0$. Hence 
$c_{\lambda }\geq \hat {c}_{\infty }$ for any 
$\lambda > 0$ by (3.9) and (4.4). Taking the limit as 
$\lambda \to \infty$, we obtain that 
$c_{\infty }\geq \hat {c}_{\infty }$.
To see the opposite inequality, we let 
$v \in H^{1}(\mathbb {R}^{2}) \setminus \{0\}$ be arbitrary. Let 
$t_v > 0$ be as in (4.3), which implies that
\[ 0 = \frac{\partial_t \big|_{t_v} E_*(t v)}{t_v} = \|v\|_{H^{1}(\mathbb{R}^{2})}^{2}- t_v^{p-2} \int_{\mathbb{R}^{2}} |v|^{p} \,\textrm{d}x. \]From this, we find that
\[ \|v\|^{2}_{H^{1}(\mathbb{R}^{2})} < (2t_v)^{p-2} \int_{\mathbb{R}^{2}} |v|^{p} \,\textrm{d}x. \]
Since 
$C_c^{\infty }(\mathbb {R}^{2})$ is dense in 
$H^{1}(\mathbb {R}^{2})$, there exists a sequence 
$\psi _n \in C_c^{\infty }(\mathbb {R}^{2})$ such that 
$\|v-\psi _n\|_{H^{1}(\mathbb {R}^{2})} \to 0$ as 
$n \to \infty$, and
\[ \|\psi_n\|^{2}_{H^{1}(\mathbb{R}^{2})} < (2t_v)^{p-2} \int_{\mathbb{R}^{2}} | \psi_n|^{p} \,\textrm{d}x \qquad \text{for all} \,{{n \in \mathbb{N}}.} \]This implies that
\begin{equation} \sup_{t \ge 0} E_*(t \psi_n)= \sup_{0 \le t \le 2t_v} E_*(t \psi_n) \to \sup_{0 \le t \le 2t_v} E_*(t v)= E_*(t_v v) \qquad \text{as} \,{{n \to \infty}.} \end{equation}
Next, we fix 
$n \in \mathbb {N}$ and choose 
$y_n \in \mathbb {R}^{2}$ such that 
$\tilde \psi _n \in C^{\infty }_c(\mathbb {R}^{2}_+) \subset H^{+}$ for the function 
$\tilde \psi _n: \mathbb {R}^{2}_+ \to \mathbb {R}$, 
$\tilde \psi _n(x)= \psi _n(x-y_n)$. Then there exists 
${t}_n>2t_v$ such that
\[ \|\psi_n\|^{2}_{\lambda,1} = \|\psi_n\|_{H^{1}(\mathbb{R}^{2}_+)}^{2} +\frac{1}{\lambda^{2}} \|\partial _\theta \psi_n\|_{L^{2}(\mathbb{R}^{2}_+)}^{2} < (2{t}_n)^{p-2} \int_{\mathbb{R}^{2}} |\psi_n|^{p} \,\textrm{d}x \quad \text{for all} \ {{\lambda \ge 1}.} \]Using the fact that
\[ \frac{t^{2}}{\lambda^{2}} \int_{\mathbb{R}^{2}_+}|\partial _\theta \psi_n|^{2} \, \textrm{d}x \to 0 \quad \text{as} \,{{\lambda \to \infty} uniformly in {t \in [0,t_n]},} \]we find that
\begin{align} c_\infty &= \lim_{\lambda \to \infty} c_{\lambda} \le \lim_{\lambda \to \infty} \sup_{t \ge 0} E_{\lambda}^{+}(t \tilde \psi_n) = \lim_{\lambda \to \infty} \sup_{0 \le t \le t_n} E_{\lambda}^{+}(t \tilde \psi_n) \nonumber\\ &= \sup_{0 \le t \le t_n} E_*(t \tilde \psi_n)=\sup_{t \ge 0} E_*(t \tilde \psi_n)=\sup_{t \ge 0} E_*(t \psi_n), \end{align}Combining (4.8) and (4.9), it follows that
\[ c_\infty \le E_*(t_v v) = \sup_{t \ge 0} E_*(t v). \]
Since 
$v \in H^{1}(\mathbb {R}^{2}) \setminus \{0\}$ was arbitrary, we conclude that 
$c_{\infty }\leq \hat {c}_{\infty }$. This completes the proof of the theorem.
Now we are in a position to prove Theorem 1.4.
Proof of Theorem 1.4. The existence statement in (i) is a direct consequence of Theorem 3.5, whereas the symmetry property stated in Theorem 1.4 (ii) is a special case of Theorem 3.3.
Next, we prove the asymptotics in (iii). In what follows, the functions in 
$H^{+}$ are extended trivially outside 
$\mathbb {R}^{2}_+$. Assume that 
$1\leq \lambda _{k} \to \infty$ and, for every 
$k\in \mathbb {N}$, let 
$u_{k}\in H^{+}$ denote a positive least energy solution of (1.10) for 
$\lambda =\lambda _k$. Observe that for 
$k \in \mathbb {N}$,
\[ \|u_k\|_{\lambda_k,1}^{2}= |u_k|_{p}^{p} \]and
\begin{align*} c_{1} \ge c_{\lambda_k} = E_{\lambda_k}^{+}(u_k) &= \Bigl(\frac{1}{2}-\frac{1}{p}\Bigr)\|u_k\|_{\lambda_k,1}^{2} = \Bigl(\frac{1}{2}-\frac{1}{p}\Bigr) |u_k|_{p}^{p} \ge c_\infty>0. \end{align*}Since
\[ \|u_k\|_{H^{1}_0(\mathbb{R}^{2}_+)}^{2} \le \|u_k\|_{\lambda_k,1}^{2} \qquad \text{for every} \,{{k \in \mathbb{N}},} \]
we conclude that 
$(u_k)_k$ is bounded in 
$H^{1}_0(\mathbb {R}^{2}_+) \subset H^{1}(\mathbb {R}^{2})$. Moreover, 
$|u_k|_{p}$ remains bounded away from zero. From Lions’ Lemma [Reference Lions19, Lemma I.1] and Theorem 3.3, it thus follows that, after passing to a subsequence, there exists a sequence of numbers 
$\tau _k \in (0,\infty )$ such that 
$w_k \rightharpoonup w \not = 0$ in 
$H^{1}(\mathbb {R}^{2})$ for the functions 
$w_k:= u_k( \cdot + (\tau _k,0))$. Observe that 
$w\geq 0$ a.e. in 
$\mathbb {R}^{2}$.
We first claim that
\begin{equation} \tau_k \to \infty \qquad \text{as} \,{{k \to \infty}.} \end{equation}
Indeed, suppose by contradiction that 
$(\tau _k)_k$ contains a bounded subsequence. Then we may again pass to a subsequence with the property that
\[ u_k \rightharpoonup u \not =0 \qquad \text{in} \,{{H^{1}_0(\mathbb{R}^{2}_+)},} \]
where 
$u\geq 0$ a.e. in 
$\mathbb {R}^{2}_+$. For 
$\varphi \in C^{\infty }_c(\mathbb {R}^{2}_+)$ and 
$R > 0$ with 
${\textrm {supp}} \, \varphi \subset B_R(0)$ we then have
\[ \frac{1}{\lambda_k^{2}} \int_{\mathbb{R}^{2}_+} (\partial _\theta u_k)(\partial _\theta \varphi) \textrm{d}x \le \frac{R^{2}}{\lambda_k^{2}} \|\nabla u_k\|_{L^{2}(R^{2}_+)} \| \nabla \varphi\|_{L^{2}(R^{2}_+)} \to 0 \qquad \text{as} \,{{k \to \infty}} \]and thus
\[ \int_{\mathbb{R}^{2}_+} \Bigl( \nabla u \cdot \nabla \varphi + u \varphi -u^{p-1} \varphi\Bigr)\textrm{d}x = \lim_{k \to \infty}\Bigl(\langle u_k,\varphi \rangle_{\lambda_k,1} - \int_{\mathbb{R}^{2}_+} u_k^{p-1} \varphi\, \textrm{d}x\Bigr)= 0. \]
Hence 
$u \in H^{1}_0(\mathbb {R}^{2}_+)$ is a nontrivial nonnegative weak solution of the problem
\[ -\Delta u + u = u^{p-1}\quad \text{in} \,{{\mathbb{R}^{2}_+}},\qquad u = 0 \quad \text{on} \,{{\partial \mathbb{R}^{2}_+}} \]which contradicts a classical nonexistence result of Esteban and Lions in [Reference Esteban and Lions14]. Thus (4.10) is true.
We now claim that
\begin{equation} \frac{\tau_k}{\lambda_k} \to 0 \qquad \text{as} \,{{k \to \infty}.} \end{equation}Before proving the claim, observe that by weak lower semicontinuity,
\begin{align} \tau_k^{{-}2} \int_{\mathbb{R}^{2}_+}|\partial _\theta u_k|^{2}\textrm{d}x &= \tau_k^{{-}2} \int_{\mathbb{R}^{2}_+}|x_1 \partial_{x_2}u_k- x_2 \partial_{x_1}u_k|^{2} \textrm{d}x \notag\\ & = \tau_k^{{-}2} \int_{\mathbb{R}^{2}}|(x_1+\tau_k) \partial_{x_2}w_k- x_2 \partial_{x_1}w_k|^{2} \textrm{d}x \nonumber\\ & \ge \int_{B_{R}(0)}|\frac{x_1+\tau_k}{\tau_k} \partial_{x_2}w_k - \frac{x_2}{\tau_k} \partial_{x_1}w_k|^{2} \textrm{d}x\nonumber\\ &\ge \int_{B_{R}(0)} |\partial_{x_2}w|^{2} \,\textrm{d}x + o(1) \qquad \text{for every} \ {{R > 0},} \end{align}
whereas for 
$R>0$ large enough,
\[ \int_{B_{R}(0)} |\partial_{x_2}w|^{2} \textrm{d}x > 0 \]
since 
$w \in H^{1}_0(\mathbb {R}^{2}_+)$ is not identically zero.
Now, in order to prove (4.11), assume by contradiction that, passing to a subsequence,
\[ \frac{\tau_k}{\lambda_k} \to d \in (0,\infty] \qquad \text{as} \,{{k \to \infty}.} \]
In the case where 
$d=\infty$ the estimate (4.12) implies that
\[ \frac{1}{\lambda_k^{2}} \int_{\mathbb{R}^{2}_+}|\partial _\theta u_k|^{2} \textrm{d}x \to \infty \qquad \text{as} \,{{k \to \infty}} \]and therefore
\[ \|u_k\|_{\lambda_k,1} \to \infty \qquad \text{as} \,{{k \to \infty}} \]
which contradicts the fact that 
$\|u_k\|_{\lambda _k,1}$ is bounded in 
$k$.
Therefore, we have 
$d < \infty$ and from (4.12),
\begin{equation} \liminf \limits_{k \to \infty} \frac{1}{\lambda_k^{2}} \int_{\mathbb{R}^{2}_+}|\partial _\theta u_k|^{2}\textrm{d}x \ge d^{2} \int_{\mathbb{R}^{2}} |\partial_{x_2}w|^{2} \textrm{d}x. \end{equation}
Notice that in this case, 
$w \in H^{1}(\mathbb {R}^{2})$ is a weak solution of
\begin{equation} -\Delta w + d^{2} \partial_{x_2 x_2} w + w = w^{p-1} \qquad \text{on} \,{{\mathbb{R}^{2}}.} \end{equation}
Indeed, let 
$\varphi \in C^{\infty }_c(\mathbb {R}^{2})$ and let 
$\varphi _k \in C^{\infty }_c(\mathbb {R}^{2}_+)$ be defined by
\[ \varphi_k(x_1,x_2) = \varphi(x_1- \tau_k,x_2) \]
for 
$k$ sufficiently large. We then have
\begin{align*} &\frac{1}{\lambda_k^{2}} \int_{\mathbb{R}^{2}_+} (\partial _\theta u_k)(\partial _\theta \varphi_k) \textrm{d}x \\ &\quad=\frac{(d^{2}+o(1))}{\tau_k^{2}} \int_{\mathbb{R}^{2}_+} (x_1 \partial_{x_2} u_k- x_2 \partial_{x_1} u_k)(x_1 \partial_{x_2} \varphi_k-x_2 \partial_{x_1} \varphi_k) \textrm{d}x\\ &\quad =(d^{2}+o(1)) \int_{\mathbb{R}^{2}} \Bigl(\frac{x_1+\tau_k}{\tau_k} \partial_{x_2} w_k- \frac{x_2}{\tau_k} \partial_{x_1} w_k\Bigr)\Bigl(\frac{x_1+\tau_k}{\tau_k} \partial_{x_2} \varphi-\frac{x_2}{\tau_k} \partial_{x_1} \varphi\Bigr) \textrm{d}x\\ &\quad=d^{2} \int_{\mathbb{R}^{2}} \partial_{x_2} w \partial_{x_2} \varphi \textrm{d}x + o(1) \qquad \text{as} \ {{k \to \infty}} \end{align*}and therefore
\begin{align*} &\int_{\mathbb{R}^{2}_+} \Bigl( \nabla w \cdot \nabla \varphi + d^{2} \partial_{x_2} w \partial_{x_2} \varphi + w \varphi -w^{p-1} \varphi\Bigr)\textrm{d}x\\ &\quad = \lim_{k \to \infty} \int_{\mathbb{R}^{2}_+} \Bigl( \nabla u_k \cdot \nabla \varphi_k + \frac{1}{\lambda_k^{2}}(\partial _\theta u_k)(\partial _\theta \varphi_k)+ u_k \varphi_k -u_k^{p-1} \varphi_k \Bigr)\textrm{d}x\\ &\quad = \lim_{k \to \infty}\Bigl( \langle u_k,\varphi \rangle_{\lambda_k,1} - \int_{\mathbb{R}^{2}_+} u_k^{p-1} \varphi_k \textrm{d}x\Bigr)= 0. \end{align*}
Hence 
$w$ satisfies (4.14) in this case. By (4.13) and weak lower semicontinuity, this implies that
\begin{align*} \sup_{t \ge 0}&\Bigl( E_*(t w) + \frac{t^{2} d^{2}}{2} \int_{\mathbb{R}^{2}}|\partial_{x_2} w|^{2}\textrm{d}x \Bigr)= \Bigl(\frac{1}{2}-\frac{1}{p}\Bigr) \Bigl( \|w\|_{H^{1}(\mathbb{R}^{2})}^{2} +d^{2} \int_{\mathbb{R}^{2}}|\partial_{x_2} w|^{2} \textrm{d}x\Bigr) \\ &\le \Bigl(\frac{1}{2}-\frac{1}{p}\Bigr) \lim_{k \to \infty} \|u_k\|_{\lambda_k,1}^{2}= \lim_{k \to \infty} E_{\lambda_k}(u_k) = \lim_{k \to \infty} c_{\lambda_k,1} = c_\infty. \end{align*}On the other hand, we have
\[ c_\infty \le \sup_{t \ge 0} E_*(t w) < \sup_{t \ge 0}\Bigl( E_*(t w) + t^{2} d^{2} \int_{\mathbb{R}^{2}}|\partial_{x_2} w|^{2}\textrm{d}x \Bigr). \]Combining these inequalities yields a contradiction. Hence (4.11) holds.
The same argument as above with 
$d=0$ yields that 
$w \geq 0$ is a solution of the limit problem
\[ -\Delta w + w = w^{p-1} \qquad \text{in} \,{{\mathbb{R}^{2}}} \]
and by uniqueness, we have 
$w = w_\infty$ after adding a finite translation to the sequence 
$\tau _k$ if necessary.
We finish the proof by showing that 
$w_k \to w$ strongly in 
$H^{1}(\mathbb {R}^{2})$. Indeed, by weak lower semicontinuity,
\begin{align*} c_\infty &= \Bigl(\frac{1}{2}-\frac{1}{p}\Bigr) \|w\|_{H^{1}(\mathbb{R}^{2})}^{2} \le \Bigl(\frac{1}{2}-\frac{1}{p}\Bigr) \liminf_{k \to \infty} \|w_k\|_{H^{1}(\mathbb{R}^{2})}^{2}\\ &= \Bigl(\frac{1}{2}-\frac{1}{p}\Bigr) \liminf_{k \to \infty} \|u_k\|_{H^{1}(\mathbb{R}^{2}_+)}^{2} \le \Bigl(\frac{1}{2}-\frac{1}{p}\Bigr) \lim_{k \to \infty} \Bigl(\|u_k\|_{\lambda_k,1}^{2}\Bigr)\\ &= \lim_{k \to \infty}c_{\lambda_k}= c_\infty. \end{align*}
Hence equality holds in all steps. Since 
$H^{1}(\mathbb {R}^{2})$ is uniformly convex, this shows that 
$w_k \to w$ strongly in 
$H^{1}(\mathbb {R}^{2})$, as claimed and this completes the proof of the theorem.
4.2 The limit $\lambda \to 0$
Next we consider the asymptotics of least energy solutions to (1.10) in the case 
$q=1$ as 
$\lambda \to 0$. To find a suitable limit problem, we consider the transformed Dirichlet problem
\begin{equation} \left \{ \begin{aligned} -\Delta v - \partial _\theta^{2} v + \lambda^{2} v & = |v|^{p-2} v & & \qquad \text{in} \,{{\mathbb{R}^{2}_+},}\\ v & = 0 & & \qquad \text{on} \,{{\partial \mathbb{R}^{2}_+}.} \end{aligned} \right. \end{equation}
Weak solutions 
$v \in H^{+}$ of (4.15) are critical points of the associated energy functional given by
\[ J_\lambda: H^{+} \to \mathbb{R}, \quad J_\lambda(v)= \frac{1}{2} \left( | \nabla v|_2^{2} + | \partial _\theta v|_2^{2} + \lambda^{2} |v|_2^{2} \right) - \frac{1}{p} \|v\|_p^{p} . \]
These notions can be related to the original problem as follows: For 
$\lambda > 0$, consider the transformation
\[ H^{+} \ni u \mapsto v \in H^{+}, \quad v(x)=\lambda^{\frac{2}{p-2}} u(\lambda x) \]so that
\begin{equation} J_\lambda (v) = \lambda^{\frac{4}{p-2}} E_{\lambda}^{+}(u). \end{equation}
Moreover, 
$u$ is a (least energy) solution of (1.10) if and only if 
$v$ is a (least energy) solution of (4.15).
In order to prove Theorem 1.6, let 
$(\lambda _k)_k$ be sequence of numbers 
$\lambda _k \le 1$ such that 
$\lambda _k \to 0$ as 
$k \to \infty$ and let 
$u_k \in H^{+}$ be positive least energy solutions of (1.10) for 
$\lambda =\lambda _k$.
For any 
$k\in \mathbb {N}$, set
\[ v_k(x)= \lambda_k^{\frac{2}{p-2}}u_k(\lambda_k x), \quad v_k \in H^{+}. \]Lemma 4.2 The sequence 
$(v_k)_k$ is bounded in 
$H^{+}$.
Proof. By Corollary 3.1, it suffices to show that there exists 
$C > 0$ such that
\[ \|v_k\|_{1,0} \leq C \qquad \text{for all} {k \in \mathbb{N}}.\]
By the remarks above, 
$v_k$ is a least energy solution of the transformed problem (4.15) with 
$\lambda =\lambda _k$. Multiplying this equation with 
$v_k$ and integrating by parts yields
\begin{equation} \|v_k\|_{1,0}^{2} +\lambda_k^{2} |v_k|_2^{2} = |v_k|_p^{p} \qquad \text{for all} \,{ {k \in \mathbb{N}}.} \end{equation}Moreover, we have
\[ J_{\lambda_k}(v_k) = \inf_{v \in H^{+} \setminus \{0\}} \sup_{t \geq 0} J_{\lambda_k}(tv). \]
Fix 
$\varphi \in C_c^{\infty }(\mathbb {R}_+^{2}) \setminus \{ 0\}$. Since 
$v_{k}$ is a least energy solution of (4.15) for 
$\lambda =\lambda _k \le 1$, we have
\[ J_{\lambda_k}(v_k) \leq \sup_{t \geq 0} J_{\lambda_k}(t \varphi) \leq \sup_{t \geq 0} J_1(t \varphi) =: C_0 \]
where, clearly, 
$C_0$ is independent of 
$k$. We can then use (4.17) to get
\[ J_{\lambda_k}(v_k) = \left(\frac{1}{2} - \frac{1}{p} \right)\Bigl(\|v_k\|_{1,0}^{2} +\lambda_k^{2} |v_k|_2^{2}\Bigr) \geq \left(\frac{1}{2} - \frac{1}{p} \right) \|v_k\|_{1,0}^{2} \]and hence
\[ \|v_k\|_{1,0}^{2} \leq \frac{C_0}{\frac{1}{2} - \frac{1}{p}} \qquad \text{for all} \,{ {k \in \mathbb{N}}.} \]As a consequence of lemma 4.2, we can pass to a subsequence and assume
\[ v_k \rightharpoonup v^{*} \quad \text{in} \,{ {H^{+}}.} \]Lemma 4.3 The weak limit 
$v^{*}$ is a nontrivial weak solution of (1.15).
Proof. Since every 
$v_k$ is a weak solutions of (1.10), for any test function 
$\varphi \in C^{\infty }_c(\mathbb {R}^{2}_+)$ we have
\[ \int_{\mathbb{R}^{2}_+} \left( \nabla v_k \cdot \nabla \varphi + \partial _\theta v_k \partial _\theta \varphi \right) \, \textrm{d}x = \int_{\mathbb{R}^{2}_+} |v_k|^{p-2} v_k \varphi \, \textrm{d}x - \lambda_k^{2} \int_{\mathbb{R}^{2}_+} v_k \varphi \, \textrm{d}x. \]
Besides, since 
$v_k \rightharpoonup v^{*}$ weakly in 
$H^{+}$ and 
$\lambda _k \to 0^{+}$ as 
$k \to \infty$,
\[ \int_{\mathbb{R}^{2}_+} \left( \nabla v_k \cdot \nabla \varphi + \partial _\theta v_k \partial _\theta \varphi \right) \, \textrm{d}x - \lambda_k^{2} \int_{\mathbb{R}^{2}_+} v_k \varphi \, \textrm{d}x\to \int_{\mathbb{R}^{2}_+} \left( \nabla v^{*} \cdot \nabla \varphi + \partial _\theta v^{*} \partial _\theta \varphi \right) \, \textrm{d}x, \]and
\[ \int_{\mathbb{R}^{2}_+} |v_k|^{p-2} v_k \varphi \, \textrm{d}x \to \int_{\mathbb{R}^{2}+} |v^{*}|^{p-2} v^{*} \varphi \, \textrm{d}x \]
as a consequence of the compact embedding 
$H^{+} \hookrightarrow L^{p}(\mathbb {R}^{2}_+)$. It then follows that 
$v^{*} \in H^{+}$ is a weak solution of
\[ -\Delta v^{*} - \partial _\theta^{2} v^{*} = |v^{*}|^{p-2} v^{*} \quad \text{in} \,{{\mathbb{R}_+^{2}}.} \]
Next, we prove that 
$v^{*} \not \equiv 0$. To do so, first, observe that the embedding 
$H^{+} \hookrightarrow L^{p}$ yields
\[ C:=\inf_{u \in H^{+} \setminus \{0\}} \frac{\|u\|_{1,0}}{|u|_p}\in (0,\infty). \]
Thus, the above comments, together with the fact that 
$|u|_2^{2} \leq | \partial _\theta u |_2^{2} \leq \|u\|_{1,0}^{2}$ for 
$u \in H^{+}$ (see Corollary 3.1), imply that
\[ C^{2} = \inf_{u\in H^{+}\setminus \{0\}} \frac{\|u\|_{1,0}^{2}}{|u|_p^{2}} \leq \inf_{u\in H^{+}\setminus \{0\}} \frac{\|u\|_{1,0}^{2} + \lambda_k^{2} |u|_2^{2}}{|u|_p^{2}} \leq 2 \inf_{u\in H^{+}\setminus \{0\}} \frac{\|u\|_{1,0}^{2}}{|u|_p^{2}} = 2 C^{2} . \]Recalling also that
\[ J_{\lambda_k}(v_k) = \inf_{u\in H^{+}\setminus \{0\}} \left(\frac{1}{2} - \frac{1}{p} \right) \left( \frac{\|u\|_{1,0}^{2} + \lambda_k^{2} |u|_2^{2}}{|u|_p^{2}}\right)^{\frac{p}{p-2}}, \]we thus have
\begin{equation} \left(\frac{1}{2}-\frac{1}{p} \right)C^{\frac{2p}{p-2}} \leq J_{\lambda_k}(v_k) \leq \left(\frac{1}{2}-\frac{1}{p}\right) (2 C^{2})^{\frac{p}{p-2}} \qquad \text{for all} \,{ {k \in \mathbb{N}}.} \end{equation}
Now assume by contradiction that 
$v^{*}= 0$, i.e., 
$v_k \rightharpoonup 0$ weakly in 
$H^{+}$. The compact embedding 
$H^{+} \hookrightarrow L^{p}$ implies 
$v_k \to 0$ in 
$L^{p}$, and therefore 
$\|v_k\|_{1,0} \to 0$ by (4.17). Hence also 
$|v_k|_2 \to 0$ by Corollary 3.1. We then deduce that
\[ J_{\lambda_k}(v_k) = \left(\frac{1}{2} - \frac{1}{p} \right) (\|v_k\|_{1,0}^{2} + \lambda_k^{2} |v_k|_2^{2}) \to 0, \]
which contradicts (4.18). We conclude that 
$v^{*} \not = 0$, as claimed.
We will now use 
$\Gamma$-convergence to finish the proof of Theorem 1.6:
Proof of Theorem 1.6. It remains to prove that 
$v^{*}$ is a least energy solution of (1.15), and that 
$v_k \to v^{*}$ strongly in 
$H^{+}$ as 
$k \to \infty$.
To deduce these properties from 
$\Gamma$-convergence theory, we consider the space 
$X:=H^{+} \setminus \{ 0\}$ endowed with the weak topology (induced by 
$\|\cdot \|_{1,0}$). Consider the functionals 
$F_k,F:X \to [0,\infty ]$ defined by
\[ F_k(u) := \frac{(\|u\|_{1,0}^{2} + \lambda_k^{2} |u|_2^{2})^{\frac{p}{p-2}}}{|u|_p^{\frac{2p}{p-2}}} \quad \hbox{and}\quad F(u) := \frac{\|u\|_{1,0}^{\frac{2p}{p-2}}}{|u|_p^{\frac{2p}{p-2}}}. \]Then we have
\[ F(u) \leq F_k(u) \qquad \text{for every} \ { {k\in \mathbb{N}}\hbox{ and }{u\in H^{+}}.} \]
Let 
$(\tilde {u}_k)_k \subset X$ be an arbitrary sequence such that 
$\tilde {u}_k \to \tilde {u}$ in 
$X$ (recall that 
$X$ has the weak topology of 
$H^{+}$). The compact embedding 
$H^{+}\hookrightarrow L^{p}(\mathbb {R}^{2}_+)$ and the weak lower semicontinuity of 
$\|\cdot \|_{1,0}$ imply
\[ F(\tilde{u}) \leq \liminf_{k \to \infty} F(\tilde{u}_k) \leq \liminf_{k \to \infty} F_k(\tilde{u}_k) . \]
On the other hand, for any 
$\tilde {u} \in X$, the constant sequence 
$\tilde {u}_k :=\tilde {u}$ satisfies that 
$\tilde {u}_k \to \tilde {u}$ in 
$X$ and
\[ F(\tilde{u})=\lim \limits_{k \to \infty} F_k(\tilde{u}_k) . \]
We conclude that 
$F_k\overset {\Gamma }{\to }F$. Since,
\[ F_k(v_k) = \inf_{u \in X} F_k(u) \]
and 
$v_k \to v$ in 
$X$, it follows from [Reference Dal Maso10, Corollary 7.20] that
\begin{equation} F(v)=\inf_{u \in X} F(u) = \lim \limits_{k \to \infty}F_k(v_k). \end{equation}Consequently,
\begin{align*} \left(\frac{1}{2}-\frac{1}{p} \right) \frac{\|v\|_{1,0}^{\frac{2p}{p-2}}}{|v|_p^{\frac{2p}{p-2}}} &= \inf_{u \in H^{+} \setminus \{0\}} \left(\frac{1}{2}-\frac{1}{p} \right) \frac{\|u\|_{1,0}^{\frac{2p}{p-2}}}{|u|_p^{\frac{2p}{p-2}}} \\ &= \inf_{u \in H^{+} \setminus \{0\}} \sup_{t \geq 0} \left( \frac{t^{2}}{2}\|u\|_{1,0}^{2} - \frac{t^{p}}{p} |u|_p^{p} \right) , \end{align*}
and this implies that 
$v$ is a least energy solution of (1.15). Moreover, since 
$v_k \to v$ in 
$L^{p}(\mathbb {R}^{2}_+)$ by the compact embedding 
$H^{+} \hookrightarrow L^{p}(\mathbb {R}^{2}_+)$, it follows from (4.19) and the definition of the functionals 
$F_k$ and 
$F$ that
\[ \|v\|_{1,0}^{2} = \lim_{k\to \infty}\Bigl(\|v_k\|_{1,0}^{2} + \lambda_k^{2} |v_k|_2^{2}\Bigr) \ge \limsup_{k \to \infty}\|v_k\|_{1,0}^{2} \ge \liminf_{k \to \infty}\|v_k\|_{1,0}^{2} \ge \|v\|_{1,0}^{2}. \]Consequently, we have
\[ \|v_k\|_{1,0} \to \|v\|_{1,0} \qquad \text{as} \,{ {k \to \infty},} \]
and the uniform convexity of 
$(H^{+},\|\cdot \|_{1,0})$ implies that 
$v_k \to v$ strongly in 
$H^{+}$ as 
$k \to \infty$.
5. Radial versus nonradial least energy nodal solutions
In this section we complete the proofs of Theorem 1.2 and Theorem 1.3. Given the assumptions of Theorem 1.2, the existence of a least energy nodal solution of (1.6) for every 
$\lambda > 0$ is a direct consequence of Corollary 2.9.
We will now first prove Theorem 1.2(ii), which will be a consequence of lemma 4.1 and a result in [Reference Weth27].
We recall that, as in § 4.1 and § 2, the energy functionals 
$E_*,E_{\lambda }: H \to \mathbb {R}$ are defined by
\[ E_*(v):= \frac{1}{2}\int_{\mathbb{R}^{2}}\Bigl(|\nabla v|^{2} + |v|^{2}\Bigr)\textrm{d}x -\frac{1}{p}\int_{\mathbb{R}^{2}}|v|^{p}\textrm{d}x \]and
\[ E_{\lambda}(v)=E_*(v) + \frac{1}{\lambda^{2}}\int_{\mathbb{R}^{2}}|\partial _\theta v|^{2}\textrm{d}x \]
for 
$v\in H$. Moreover, as in § 2, we consider the 
$\lambda$-dependent scalar product 
$\langle \cdot , \cdot \rangle _\lambda$ defined in (1.8) on 
$H$ and the corresponding norm 
$\|\cdot \|_\lambda$. In particular, we shall use 
$\|\cdot \|_1$ given by
\[ \|u\|_1^{2} = \int_{\mathbb{R}^{2}}(|\nabla u|^{2}+ |\partial _\theta u|^{2} + |u|^{2})\,\textrm{d}x \qquad \text{for} \,{ {u \in H}.} \]Proposition 5.1 There exists 
$\varepsilon _*> 0$ such that for every 
$\lambda > 0$ and every radial nodal solution 
$u \in H$ of (1.6) we have
\[ E_*(u) = E_\lambda(u) > 2c_\infty + \varepsilon_*, \]
where 
$c_\infty$ is given in (4.1).
Proof. First observe that 
$E_*(u) = E_\lambda (u)$ for every radial function 
$u \in H$. Moreover, if 
$u$ is a radial nodal solution of (1.6), then 
$u$ also solves the limit problem (1.13). By [Reference Weth27, Theorem 1.5], and the variational characterization of 
$c_\infty$ given (4.4) and (4.7), there exists 
$\varepsilon _* > 0$ with the property that 
$E_*(u) > 2c_\infty + \varepsilon _*$ for every nodal solution of (1.13). This proves the claim.
Proof of Theorem 1.2(ii) (completed). Let 
$\varepsilon _*>0$ be given by proposition 5.1. By (4.1), there exists 
$\Lambda _0 > 0$ with the property that
\[ c_{\lambda} < c_\infty + \frac{\varepsilon_*}{2} \qquad \text{for every} \,{ {\lambda> \Lambda_0}.} \]
Consequently, for 
$\lambda >\Lambda _0$, problem (1.10) admits a nontrivial solution 
$u \in H^{+}$ with 
$E_\lambda ^{+}(u)< c_\infty + \frac {\varepsilon _*}{2}$. By odd reflection, we may extend 
$u$ to a nodal solution of (1.6) with 
$E_\lambda (u) < 2c_\infty + \varepsilon _*$. Proposition 5.1, therefore, implies that the least energy nodal solutions of (1.6) cannot be radial.
Next, we complete the proof of Theorem 1.3, which we restate here for the reader's convenience.
Theorem 5.2 Let 
$p > 2$.
(i) If
$u \in H$ is a nontrivial weak solution of
(5.1)for some\begin{equation} -\Delta u - \frac{1}{\lambda^{2}} \partial _\theta^{2} u + u = |u|^{p-2} u \quad \text{in} \,{ {\mathbb{R}^{2}}} \end{equation}$\lambda >0$ satisfying $\lambda < \Bigl (\frac {1}{(p-1)|u|_\infty ^{p-2}}\Bigr )^{\frac {1}{2}}$, then $u$ is a radial function.(ii) For every
$c > 0$, there exists $\lambda _c > 0$ with the property that every weak solution $u \in H$ of (5.1) for some $\lambda \in (0,\lambda _c)$ with $E_\lambda (u) \le c$ is radial.
Proof. (i) Let 
$u \in H$ be a nontrivial weak solution of (5.1) for some 
$\lambda > 0$, and let, as before, 
$u^\#$ denote the radial average of 
$u$ as defined in (2.1). It is easy to see that, for every 
$k \in \mathbb {N}$, the function 
$u^\# \in H$ is a weak solution of
\[ -\Delta u^\# + u^\# = \left(|u|^{p-2} u \right)^\# \quad \text{in} \,{ {\mathbb{R}^{2}}}. \]Consequently we have, in weak sense,
\[ -\Delta (u-u^\#) - \frac{1}{\lambda^{2}} \partial _\theta^{2} (u-u^\#) + (u- u^\#) = |u|^{p-2} u - \left(|u|^{p-2} u \right)^\# \quad \text{in} \ { {\mathbb{R}^{2}}.} \]
Testing this equation against 
$u-u^\#$ yields
\begin{align} \frac{1}{\lambda^{2}} |\partial _\theta u |_2^{2}&= \frac{1}{\lambda^{2}} |\partial _\theta (u-u^\#) |_2^{2} \le |\nabla(u-u^\#)|_2^{2} + \frac{1}{\lambda^{2}} |\partial _\theta (u-u^\#) |_2^{2} + |u-u^\#|_2^{2} \nonumber\\ & = \int_{\mathbb{R}^{2}} \left( |u|^{p-2} u - \left(|u|^{p-2} u \right)^\# \right) (u-u^\#) \, \textrm{d}x\notag\\ & \leq \left| |u|^{p-2} u - \left(|u|^{p-2} u \right)^\# \right|_2 \, |u-u^\#|_2 \nonumber\\ &\leq \left| |u|^{p-2} u - \left(|u|^{p-2} u \right)^\# \right|_2 \, |\partial _\theta u|_2 , \end{align}
where we used lemma 2.2 in the last step. Moreover, 
$|u|^{p-2} u \in H$ by remark 2.6, and therefore
\begin{align} \left| |u|^{p-2} u - \left(|u|^{p-2} u \right)^\# \right|_2 &\le |\partial _\theta (|u|^{p-2} u)|_2 = (p-1) | |u|^{p-2} \partial _\theta u |_2\notag\\ & \le (p-1)|u|_\infty^{p-2}|\partial _\theta u |_2 , \end{align}again by lemma 2.2. Combining (5.2) and (5.3), we obtain that
\[ \frac{1}{\lambda^{2}} |\partial _\theta u |_2^{2} \le (p-1)|u|_\infty^{p-2 } |\partial _\theta u |_2^{2} \]
which implies that 
$\partial _\theta u \equiv 0$ if 
$\lambda < \Bigl (\frac {1}{(p-1)|u|_\infty ^{p-2}}\Bigr )^{\frac {1}{2}}$. The proof of (i) is thus finished.
(ii) Let 
$c > 0$ be given, and let 
$u \in H$ be a nontrivial weak solution of (5.1) for some 
$\lambda >0$ with 
$E_\lambda (u) \le c$. Since 
$E_\lambda (u) =\Bigl (\frac {1}{2}-\frac {1}{p}\Bigr )\|u\|_\lambda ^{2}$, it then follows that
\[ \|u\|_{H^{1}(\mathbb{R}^{2})}^{2} \le \|u\|_\lambda^{2} = \frac{2p}{p-2}E_\lambda (u) \leq \frac{2p c}{p-2} \]and therefore
\[ |u|_\infty \le C \|u\|_{H^{1}(\mathbb{R}^{2})}^{\sigma} \le C \Bigl(\frac{2p c}{p-2} \Bigr)^{\frac{\sigma}{2}} =:\mu_c \]
by lemma 2.5 with the constants 
$C,\sigma >0$ given there. Hence, if
\[ \lambda < \lambda_c:= \Bigl(\frac{1}{(p-1)\mu_c^{p-2}}\Bigr)^{\frac{1}{2}}, \]
then also 
$\lambda < \Bigl (\frac {1}{(p-1)|u|_\infty ^{p-2}}\Bigr )^{\frac {1}{2}}$ and therefore, 
$u$ is radial by (i). The proof is finished.
Next we provide uniform energy estimates for least energy nodal solutions of (5.1).
Lemma 5.3 Let 
$p > 2$. There exist constants 
$c,C > 0$ with the property that
\begin{equation} c \leq E_\lambda(u) \leq C \end{equation}
for every 
$\lambda > 0$ and every least energy nodal solution 
$u \in H$ of (5.1).
Proof. The lower bound is obtained by choosing 
$c = \hat c_\infty$ as defined in (4.4), since
\[ E_\lambda(u) = \sup_{t \ge 0} E_\lambda(tu) \ge \sup_{t \ge 0} E_*(tu) \ge \hat c_\infty \]
for every 
$\lambda >0$ and every nontrivial solution 
$u \in H$ of (5.1).
For the upper bound, we first remark that the existence of radial nodal solutions of (1.13) is well known, see for instance Theorems 4 and 5 in [Reference Strauss23]. Let 
$\hat {u} \in H^{1}(\mathbb {R}^{2})$ be a fixed radial nodal solution of (1.13) and set 
$C= E_*(\hat {u})$. For every 
$\lambda > 0$, the function 
$\hat {u} \in H$ is then also a nodal solution of (5.1), and therefore
\[ E_\lambda(u) \le E_\lambda(\hat{u}) = E_*(\hat{u})= C \]
for every least energy nodal solution 
$u \in H$ of (5.1).
The proof of Theorem 1.2 is now completed by deriving Part (i) of this theorem as follows:
Let 
$C>0$ be given by lemma 5.3, and let 
$u \in H$ be a least energy solution of (5.1) for some 
$\lambda > 0$. Then we have 
$E_\lambda (u) \le C$. Applying Theorem 5.2 with 
$c=C$ and considering 
$\lambda _0:= \min \{\lambda _c, \Lambda _0\}$ with 
$\Lambda _0>0$ given as in Theorem 1.2(ii), we then deduce that 
$0 < \lambda _0 \le \Lambda _0$, and 
$u$ is radial if 
$\lambda < \lambda _0$. The proof of Theorem 1.2(i) is thus finished.
Appendix A.
We give the proof of lemma 2.5, which we restate here for the reader's convenience.
Lemma A.1 Let 
$\lambda >0$ and let 
$u \in H$ be a weak solution of
\begin{equation} -\Delta u - \frac{1}{\lambda^{2}} \partial _\theta^{2} u + u = |u|^{p-2} u \quad \text{in} \,{ {\mathbb{R}^{2}}}. \end{equation}
Then 
$u \in L^{\infty }(\mathbb {R}^{2})$. Furthermore, there exist constants 
$C,\sigma >0$, depending on 
$p > 2$ but not on 
$u$ and 
$\lambda$, such that
\begin{equation} |u|_\infty \leq C \|u\|_{H^{1}(\mathbb{R}^{2})}^{\sigma} . \end{equation}Proof. The proof is based on Moser iteration, cf. Appendix B in [Reference Struwe24] and the references therein. We fix 
$L,s \geq 2$ and consider auxiliary functions 
$h, g \in C^{1}([0,\infty ))$ defined by
\[ h(t) := s \int_0^{t} \min \{\tau^{s-1},L^{s-1}\}\,\textrm{d}\tau \qquad \text{and}\qquad g(t) := \int_0^{t} [h'(\tau)]^{2} \, \textrm{d}\tau \]We note that
\begin{equation} h(t)= t^{s}\quad \text{for} \,{ {t \le L}}\qquad \text{and}\qquad g(t) \leq t g'(t)= t(h'(t))^{2} \quad \text{for} \,{ {t \geq 0},} \end{equation}
since the function 
$t \mapsto h'(t) = s \min \{t^{s-1},L^{s-1}\}$ is nondecreasing. We shall now show that 
$w := u^{+} \in L^{\infty }(\mathbb {R}^{2})$, and that 
$\|w\|_\infty$ is bounded by the r.h.s. of (A.2). Since we may replace 
$u$ with 
$-u$, the claim will then follow. We note that 
$w \in H$ and 
$\varphi := g(w) \in H$ with
\[ \nabla w = \mathbf{1}_{\{u>0\}} \nabla u, \quad \nabla \varphi= g'(w) \nabla w , \quad \partial _\theta w = \mathbf{1}_{\{u > 0\}} \partial _\theta u, \quad \partial _\theta \varphi= g'(w) \partial _\theta w . \]
This follows from the boundedness of 
$g'$ and the estimate 
$g(t) \leq s^{2} t^{2s-1}$ for 
$t \ge 0$. Testing (A.1) with 
$\varphi$ gives
\[ \int_{\mathbb{R}^{2}} \Bigl(\nabla u \cdot \nabla \varphi + \frac{1}{\lambda^{2}} (\partial _\theta u \ \partial _\theta \varphi) + u \varphi\Bigr)\textrm{d}x = \int_{\mathbb{R}^{2}} |u|^{p-2} u \varphi \, \textrm{d}x , \]from where we estimate,
\begin{align} &\int_{\mathbb{R}^{2}} \Bigl(|\nabla h(w) |^{2} + \frac{1}{\lambda^{2}}(\partial _\theta h(w))^{2} + w g(w)\Bigr) \textrm{d}x\notag\\ &\quad =\int_{\mathbb{R}^{2}} \Bigl(g'(w) \Bigl(|\nabla w |^{2} + \frac{1}{\lambda^{2}}(\partial _\theta w)^{2} \Bigr) + u g(w)\Bigr) \textrm{d}x \nonumber\\ &\quad = \int_{\mathbb{R}^{2}} |u|^{p-2} u g(w) \, \textrm{d}x \nonumber\\ & \quad \leq \int_{\mathbb{R}^{2}} w^{p} (h'(w))^{2} \, \textrm{d}x. \end{align} Here we used (A.3) in the last step. We now fix 
$r >1$ with 
$\frac {(p-2)r}{r-1} \geq 2$ and 
$q > 4r$. Combining (A.4) with Sobolev embeddings, we obtain the inequality
\begin{equation} \frac{1}{c_0} |h(w)|_q^{2} - |h(w)|_2^{2} + \int_{\mathbb{R}^{2}} w g(w) \, \textrm{d}x \leq \int_{\mathbb{R}^{2}} w^{p} (h'(w))^{2} \, \textrm{d}x \end{equation}
with a constant 
$c_0= c_0(q)>0$. Since
\begin{align*} &h(t)= t^{s},\quad h'(t) = st^{s-1}\quad \text{and}\\ &g(t)= s^{2} \int_0^{t} \tau^{2s-2}\,\textrm{d}\tau = \frac{s^{2}}{2s-1} t^{2s-1}\qquad \text{for} \,{ {t \le L},} \end{align*}
we may let 
$L \to \infty$ in (A.5) and apply Lebesgue's theorem to obtain
\[ \frac{1}{c_0} |w^{s}|_q^{2} +\Bigl(\frac{s^{2}}{2s-1}-1\Bigr)|w^{s}|_2^{2} \leq s^{2} \int_{\mathbb{R}^{2}} w^{p+2s-2} \, \textrm{d}x \le s^{2} |w|_{ \frac{(p-2)r}{r-1}}^{p-2}|w|_{2rs}^{2s} \]
Since 
$s \ge 2$, we have 
$\frac {s^{2}}{2s-1}\ge 1$, and we thus obtain the inequality
\begin{equation} |w|_{sq} \le (c_1s)^{\frac{1}{s}} |w|_{2rs}\qquad \text{with} \,{ {c_1:= \Bigl(c_0 |w|_{ \frac{r(p-2)}{r-1}}^{p-2}\Bigr)^{\frac{1}{2}}}.} \end{equation}
Next we note that the choice of 
$r$ and 
$q$ only depends on 
$p$ but not on 
$s\ge 2$. We may, therefore, consider 
$s=s_n= \rho ^{n}$ for 
$n \in \mathbb {N}$ with 
$\rho := \frac {q}{2r} >2$, so that
\[ 2s_1 r = q \qquad \text{and}\qquad 2s_{n+1} r = q s_n \quad \text{for} \,{ {n \in \mathbb{N}}.} \]Iteration of (A.6) then gives
\begin{align*} &|w|_{\rho^{n} q} = |w|_{s_n q} \leq |w|_q \prod_{j=1}^{n} (c_1 \rho^{j})^{\rho^{{-}j}} \leq c_1^{\frac{\rho}{\rho-1}} c_2 |w|_q \quad \text{for all} \ { {n}}\quad \text{with}\\ &c_2 : = \rho^{\sum_{j=1}^{\infty} j \rho^{{-}j}} < \infty. \end{align*}It follows that
\begin{equation} |w|_\infty = \lim_{n \to \infty} |w|_{ \rho^{n} q} \leq c_1^{\frac{\rho}{\rho-1}} c_2 |w|_q . \end{equation}Moreover, by Sobolev embeddings, we have
\[ c_1 \leq c_1' \|w\|_{H^{1}(\mathbb{R}^{2})}^{\frac{p-2}{2}} \le c_1' \|u\|_{H^{1}(\mathbb{R}^{2})}^{\frac{p-2}{2}}\qquad \text{and}\qquad |w|_q\le \tilde c \|w\|_{H^{1}} \le \tilde c \|u\|_{H^{1}(\mathbb{R}^{2})} \]
with constants 
$c_1', \tilde c > 0$ depending only on 
$p,r$ and 
$q$. It thus follows from (A.7) that
\[ |w|_\infty \leq C \|u\|_{H^{1}(\mathbb{R}^{2})}^{\frac{(p-2)\rho}{2(\rho-1)} +1}\qquad \text{with}\qquad C:= c_2 (c_1')^{\frac{\rho}{\rho-1}}\tilde c. \]The proof is thus finished.
Remark A.2 Let 
$\lambda > 0$ and 
$p \in (2,\infty )$. By a variant of the Moser iteration argument given above, we can also show that every weak solution 
$u \in H^{+}$ of
\begin{equation} -\Delta u - \frac{1}{\lambda^{2}} \partial _\theta^{2} u = |u|^{p-2} u \quad \text{in} \,{ {\mathbb{R}^{2}_+},}\qquad u = 0 \quad \text{on} \,{ {\partial \mathbb{R}^{2}_+}} \end{equation}
satisfies 
$u \in L^{\infty }(\mathbb {R}^{2}_+)$. To see this, we replace, with the help of Corollary 3.1 and (A.8), the inequalities (A.4) and (A.5) by
\[ \frac{1}{c}|h(w)|^{2}_q \le \|h(w)\|_{\lambda,0}^{2} = \int_{\mathbb{R}^{2}_+} |u|^{p-2}u g(w)\,\textrm{d}x \le \int_{\mathbb{R}^{2}_+} w^{p} (h'(w))^{2}\,\textrm{d}x \]
with a constant 
$c > 0$ depending on 
$q$ and 
$\lambda$. We can then complete the argument as above, noting that in this case, the constants depend on 
$\lambda >0$.
Acknowledgments
The first author, Oscar Agudelo, was supported by the Grant 18-03253S of the Grant Agency of the Czech Republic and also by the Project LO1506 of the Ministry of Education, Youth and Sports of the Czech Republic. The authors would like to thank the referee for his/her comments and for pointing out relevant references.
