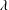1 Introduction
Since Plateau’s experiments involving toroidal drops in a rotating fluid (Plateau Reference Plateau1857), the formation and evolution of toroidal structures in fluid dynamics have attracted much interest. Furthermore, such structures are not restricted to a single phase. Some ubiquitous occurrences (but not limited to) in daily life include the toroidal cloud of small bubbles emitted by dolphins and the toroidal-shaped smoke exhaled by cigarette smokers into the air. An interesting phenomenon is the evolution of spherical swarms of particles in a viscous fluid into toroidal shapes under the influence of gravity (Machu et al. Reference Machu, Meile, Nitsche and Schaflinger2001a ,Reference Machu, Meile, Nitsche and Schaflinger b ; Bosse et al. Reference Bosse, Kleiser, Härtel and Meiburg2005). It has been found to be important in the characterization of rising mantle plumes and flows of bubbles in molten rock. Although these swarms have practically zero surface tension, they behave dynamically as drops composed of an immiscible different phase.
One significant characteristic of toroidal, as compared to spherical drops, is the relatively large surface to volume ratio for the former. This has led to recent interest in non-trivial forms of fluid particles. Sparked by novel applications of non-spherical microparticles, they were found to have potential as building blocks for self-assembled materials, including clustering of cells, imaging probes for therapy, drug carriers (Champion, Katare & Mitragotri Reference Champion, Katare and Mitragotri2007; Dean et al. Reference Dean, Napolitano, Youssef and Morgan2007; Nurse, Freund & Youseff Reference Nurse, Freund and Youseff2012) and more.
One of the advanced methods to produce microparticles of complex shapes is solidification of drops deformed by the flow in microfluidic devices (Chen et al. Reference Chen, Shah, Abate and Weitz2009; Shum et al. Reference Shum, Abate, Lee, Studart, Wang, Chen, Thiele, Shah, Krummel and Weitz2010; Szymusiak et al. Reference Szymusiak, Sharma, Nitsche and Liu2012). Another method of mass production of toroidal forms with sizes in the micrometre to millimetre range via vortex ring freezing was most recently demonstrated by An et al. (Reference An, Warning, Yancey, Chang, Kern, Datta, Steen, Luo and Ma2016), with particular potential for encapsulating DNA segments, cells and bacteria – an application that was also proposed by Chang et al. (Reference Chang, Fragkopoulos, Marquez, Kim, Angelini and Fernandes-Nieves2015).
Toroidal drop formation has also been generated and observed in a variety of contexts. One of the earliest seminal works we wish to highlight in this area was conducted by Kojima, Hinch & Acrivos (Reference Kojima, Hinch and Acrivos1984). They investigated the deformation of drops settling in a quiescent fluid and obtained analytical solutions for toroidal-shaped drops, upon the application of interfacial instability induced by a finite surface perturbation. We next mention a few works here to highlight the significance of studying such phenomena and their wide applicability: evolution of the free fall of a drop in an immiscible fluid (Baumann et al. Reference Baumann, Josef, Mohr and Renardy1992; Sostarecz & Belmonte Reference Sostarecz and Belmonte2003), splashing in an immiscible medium (Sharma et al. Reference Sharma, Szymusiak, Shen, Nitsche and Liu2012), impact of a droplet with a superhydrophobic surface (Renardy et al. Reference Renardy, Popinet, Duchemin, Renardy, Zaleski, Josserand, Drumright-Clarke, Richard, Clanet and Quéré2003), head-on collision of two drops (Menchaca-Rocha et al. Reference Menchaca-Rocha, Borunda, Hidalgo, Huidobro, Michaelian, Pérez and Rodríguez1996), and deformation of a drop in electric (Deshmukh & Thaokar Reference Deshmukh and Thaokar2013; Ghazian, Adamiak & Castle Reference Ghazian, Adamiak and Castle2013) and magnetic fields (Texier et al. Reference Texier, Piroird, Quere and Clanet2013).
Stone & Leal (Reference Stone and Leal1989), followed by Zabarankin et al. (Reference Zabarankin, Smagin, Lavrenteva and Nir2013), reported numerical simulations of the deformation of a drop embedded in an ambient bi-axial (compressional) flow of an immiscible viscous fluid. The drop shape is governed by the viscosity ratio and by a capillary number Ca, the latter characterizing the ratio of viscous to surface tension forces (see definition in § 2). It was shown that if the capillary number does not exceed a certain critical value, the drop obtains a flattened form. At supercritical capillary numbers, such a drop becomes unstable and continues to deform until the width of the centre flat layer becomes so small that it can break up by centre pinching and a liquid torus is formed. Such tori, embedded in viscous compressional flow, are the focus of our paper.
Pairam & Fernández-Nieves (Reference Pairam and Fernández-Nieves2009) performed an experimental study of the breakup of glycerol tori suspended in silicone oil and observed that a torus can either shrink to a single droplet or break down into multiple droplets, depending on the thickness of the torus relative to its circumference. Mehrabian & Feng (Reference Mehrabian and Feng2013) suggested a theoretical model of the capillary breakup of liquid toroidal drops.
Zabarankin, Lavrenteva & Nir (Reference Zabarankin, Lavrenteva and Nir2015) investigated the deformation of an immiscible toroidal drop embedded in axisymmetric compressional Stokes flow in the case of equal viscosity. Analytic solutions were obtained using conformal mapping methods when the cross-section of the torus was nearly circular. Numerical simulations via the boundary integral formulation were performed for the evolution of the deforming toroidal drop with a circular cross-section as the initial condition. Quasistationary dynamic simulations demonstrated that when the viscous forces are relatively weak compared with the surface tension, three different scenarios of drop evolution are possible: indefinite expansion of the liquid torus, contraction towards the centre, and a stationary toroidal shape.
When the intensity of the ambient flow is low, the stationary shapes were shown to be close to circular tori. Once the outer flow strengthens, the cross-section of the stationary torus assumes an almost elliptic shape. As the flow further intensifies, the cross-section deforms to an egg-like shape. For capillary number greater than a critical value, toroidal stationary shapes were not found. In the equal viscosity case, the stationary shapes obtained are all unstable. Any infinitesimal disturbance will cause the torus either to collapse or expand indefinitely.
Recently, Zabarankin (Reference Zabarankin2016) studied toroidal drops in compressional flow with an arbitrary viscosity ratio using conformal mapping methods. The fundamental assumption employed in this work is that the stationary toroidal shapes are restricted to having circular toroidal cross-sections. This assumption allows the solution via conformal mapping and the transformation of this complicated problem to an inverse optimization problem involving two parameters: capillary number
![]() $Ca$
and the initial toroidal radius
$Ca$
and the initial toroidal radius
![]() $R$
, making it more mathematically tractable. However, this assumption is restrictive, and exists in practice only in the limiting case of extremely highly expanded tori, as was also reported by Zabarankin et al. (Reference Zabarankin, Lavrenteva and Nir2015) for the case of equal viscosity.
$R$
, making it more mathematically tractable. However, this assumption is restrictive, and exists in practice only in the limiting case of extremely highly expanded tori, as was also reported by Zabarankin et al. (Reference Zabarankin, Lavrenteva and Nir2015) for the case of equal viscosity.
The purpose of this work is to study the deformation of an immiscible toroidal drop embedded in an axisymmetric compressional Stokes flow with an arbitrary viscosity ratio, thus generalizing the work done in Zabarankin et al. (Reference Zabarankin, Lavrenteva and Nir2015). In § 2, the problem of the dynamic and stationary deformation of a drop in linear compressional viscous flow is formulated, and the numerical method is described and validated. Section 3 outlines numerical results showing the dynamic evolution of the toroidal drops, and the conditions in which stationary drops are obtained for the various viscosity ratios. A detailed study of stationary states is presented in § 4. A discussion of the results is given in § 5.
2 Problem formulation and method of solution
Consider a drop of volume
![]() $4\unicode[STIX]{x03C0}a^{3}/3$
(equal to that of a sphere with radius
$4\unicode[STIX]{x03C0}a^{3}/3$
(equal to that of a sphere with radius
![]() $a$
) and viscosity
$a$
) and viscosity
![]() $\unicode[STIX]{x1D707}$
that is embedded in an unbounded compressional viscous flow of viscosity
$\unicode[STIX]{x1D707}$
that is embedded in an unbounded compressional viscous flow of viscosity
![]() $\unicode[STIX]{x1D707}^{\ast }$
. The ratio
$\unicode[STIX]{x1D707}^{\ast }$
. The ratio
![]() $\unicode[STIX]{x1D707}/\unicode[STIX]{x1D707}^{\ast }$
will be denoted by
$\unicode[STIX]{x1D707}/\unicode[STIX]{x1D707}^{\ast }$
will be denoted by
![]() $\unicode[STIX]{x1D706}$
. The surrounding fluid, in the absence of the drop, is subject to an undisturbed flow
$\unicode[STIX]{x1D706}$
. The surrounding fluid, in the absence of the drop, is subject to an undisturbed flow
where the shear rate tensor
![]() $\unicode[STIX]{x1D640}$
is given by
$\unicode[STIX]{x1D640}$
is given by
![]() $\unicode[STIX]{x1D60C}_{11}=\unicode[STIX]{x1D60C}_{22}=G,\unicode[STIX]{x1D60C}_{33}=-2G$
and
$\unicode[STIX]{x1D60C}_{11}=\unicode[STIX]{x1D60C}_{22}=G,\unicode[STIX]{x1D60C}_{33}=-2G$
and
![]() $\unicode[STIX]{x1D60C}_{ij}=0$
for
$\unicode[STIX]{x1D60C}_{ij}=0$
for
![]() $i\,\neq j$
, with
$i\,\neq j$
, with
![]() $G$
being a constant characterizing the flow intensity.
$G$
being a constant characterizing the flow intensity.
Let
![]() $V$
denote the closed domain occupied by the drop and
$V$
denote the closed domain occupied by the drop and
![]() $V^{\ast }$
the open domain occupied by the ambient fluid, with
$V^{\ast }$
the open domain occupied by the ambient fluid, with
![]() $S$
being the interface between them. Let the velocity and pressure in
$S$
being the interface between them. Let the velocity and pressure in
![]() $V$
and
$V$
and
![]() $V^{\ast }$
be denoted as
$V^{\ast }$
be denoted as
![]() $\boldsymbol{u},p$
and
$\boldsymbol{u},p$
and
![]() $\boldsymbol{u}^{\ast },p^{\ast }$
, respectively. As we assume creeping flow conditions, these fields satisfy the stationary Stokes equations
$\boldsymbol{u}^{\ast },p^{\ast }$
, respectively. As we assume creeping flow conditions, these fields satisfy the stationary Stokes equations
and
where
![]() $\unicode[STIX]{x1D70E}_{ij}=-p\unicode[STIX]{x1D6FF}_{ij}+\unicode[STIX]{x1D707}((\unicode[STIX]{x2202}u_{i}/\unicode[STIX]{x2202}x_{j})+(\unicode[STIX]{x2202}u_{j}/\unicode[STIX]{x2202}x_{i}))$
, with a similar expression in
$\unicode[STIX]{x1D70E}_{ij}=-p\unicode[STIX]{x1D6FF}_{ij}+\unicode[STIX]{x1D707}((\unicode[STIX]{x2202}u_{i}/\unicode[STIX]{x2202}x_{j})+(\unicode[STIX]{x2202}u_{j}/\unicode[STIX]{x2202}x_{i}))$
, with a similar expression in
![]() $V^{\ast }$
.
$V^{\ast }$
.
The velocity is continuous at the interface
while
![]() $u_{i}^{\ast }=u_{i}^{\infty }$
and
$u_{i}^{\ast }=u_{i}^{\infty }$
and
![]() $p^{\ast }=0$
at infinity.
$p^{\ast }=0$
at infinity.
The stress balance across the interface is of the form
with the interfacial tension
![]() $\unicode[STIX]{x1D6FE}$
being constant.
$\unicode[STIX]{x1D6FE}$
being constant.
![]() $\boldsymbol{n}$
is a unit normal pointing outwards into the ambient phase and
$\boldsymbol{n}$
is a unit normal pointing outwards into the ambient phase and
![]() $\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{n}$
is the surface curvature. The kinematic condition denoting the surface deformation is given by
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{n}$
is the surface curvature. The kinematic condition denoting the surface deformation is given by
with
![]() $U_{n}$
denoting the velocity of the interface in the normal direction.
$U_{n}$
denoting the velocity of the interface in the normal direction.
In what follows, throughout the paper, length, time, and the velocity and pressure fields are scaled with
![]() $a$
,
$a$
,
![]() $1/G,Ga$
and
$1/G,Ga$
and
![]() $\unicode[STIX]{x1D707}^{\ast }G$
, respectively and the capillary number,
$\unicode[STIX]{x1D707}^{\ast }G$
, respectively and the capillary number,
![]() $Ca$
, is formally defined to be
$Ca$
, is formally defined to be
Note that, for the purpose of brevity, the same notation is used henceforth for scaled variables.
For a given shape of the drop, the stationary Stokes equations (2.2) with boundary conditions (2.3) and (2.4) can be reduced to a system of integral equations for the surface of the viscous drop,
![]() $S$
, given by:
$S$
, given by:
 $$\begin{eqnarray}\displaystyle u_{i}\left(\boldsymbol{x}\right) & = & \displaystyle \left(\frac{2}{\unicode[STIX]{x1D706}+1}\right)u_{i}^{\infty }\left(\boldsymbol{x}\right)+\frac{2(1-\unicode[STIX]{x1D706})}{\unicode[STIX]{x1D706}+1}\unicode[STIX]{x0222F}_{S_{y}}K_{ijk}\left(\boldsymbol{x}-\boldsymbol{y}\right)u_{j}\left(\boldsymbol{y}\right)n_{k}\left(\boldsymbol{y}\right)\,\text{d}S_{y}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{1}{Ca(\unicode[STIX]{x1D706}+1)}\unicode[STIX]{x0222F}_{S_{y}}J_{ij}(\boldsymbol{x}-\boldsymbol{y})n_{j}(\boldsymbol{y})\frac{\unicode[STIX]{x2202}n_{k}}{\unicode[STIX]{x2202}x_{k}}(\boldsymbol{y})\,\text{d}S_{y},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle u_{i}\left(\boldsymbol{x}\right) & = & \displaystyle \left(\frac{2}{\unicode[STIX]{x1D706}+1}\right)u_{i}^{\infty }\left(\boldsymbol{x}\right)+\frac{2(1-\unicode[STIX]{x1D706})}{\unicode[STIX]{x1D706}+1}\unicode[STIX]{x0222F}_{S_{y}}K_{ijk}\left(\boldsymbol{x}-\boldsymbol{y}\right)u_{j}\left(\boldsymbol{y}\right)n_{k}\left(\boldsymbol{y}\right)\,\text{d}S_{y}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{1}{Ca(\unicode[STIX]{x1D706}+1)}\unicode[STIX]{x0222F}_{S_{y}}J_{ij}(\boldsymbol{x}-\boldsymbol{y})n_{j}(\boldsymbol{y})\frac{\unicode[STIX]{x2202}n_{k}}{\unicode[STIX]{x2202}x_{k}}(\boldsymbol{y})\,\text{d}S_{y},\end{eqnarray}$$
where the kernels are given by
Given the axial symmetry of the toroidal drop under consideration, we can employ a cylindrical coordinate system (
![]() $r$
,
$r$
,
![]() $\unicode[STIX]{x1D711}$
,
$\unicode[STIX]{x1D711}$
,
![]() $z$
) with basis (
$z$
) with basis (
![]() $\boldsymbol{e}_{r}$
,
$\boldsymbol{e}_{r}$
,
![]() $\boldsymbol{e}_{\unicode[STIX]{x1D711}}$
,
$\boldsymbol{e}_{\unicode[STIX]{x1D711}}$
,
![]() $\boldsymbol{e}_{z}$
) and note that the
$\boldsymbol{e}_{z}$
) and note that the
![]() $z$
-axis is the same as the
$z$
-axis is the same as the
![]() $x_{3}$
-axis defined earlier. In this coordinate system, the undisturbed flow velocity is
$x_{3}$
-axis defined earlier. In this coordinate system, the undisturbed flow velocity is
![]() $\boldsymbol{u}^{\infty }=r\boldsymbol{e}_{r}-2z\boldsymbol{e}_{z}$
, and
$\boldsymbol{u}^{\infty }=r\boldsymbol{e}_{r}-2z\boldsymbol{e}_{z}$
, and
![]() $G=1$
can be assumed without loss of generality. In the axisymmetric case, i.e. when velocity and pressure are independent of the angular coordinate
$G=1$
can be assumed without loss of generality. In the axisymmetric case, i.e. when velocity and pressure are independent of the angular coordinate
![]() $\unicode[STIX]{x1D711}$
, the integral equations (2.7) can be integrated over the angular coordinate and reduced to expressions containing curvilinear integrals over the cross-section of the drop interface
$\unicode[STIX]{x1D711}$
, the integral equations (2.7) can be integrated over the angular coordinate and reduced to expressions containing curvilinear integrals over the cross-section of the drop interface
![]() $S$
. The resulting expressions for the kernels can be found, for example, in Pozrikidis (Reference Pozrikidis1992) [29].
$S$
. The resulting expressions for the kernels can be found, for example, in Pozrikidis (Reference Pozrikidis1992) [29].

Figure 1. An axisymmetric toroidal drop.
In this paper, we present numerical simulations of the quasistationary dynamic deformation of a drop starting from a certain set of initial shapes, in the form of tori with circular cross-section with various major radii (see figure 1). Here, we briefly summarize the general scheme for the quasistationary deformations as follows.
-
(1) At time
 $\unicode[STIX]{x1D70F}$
the initial shape is given by
$\unicode[STIX]{x1D70F}$
the initial shape is given by
 $S_{\unicode[STIX]{x1D70F}}$
.
$S_{\unicode[STIX]{x1D70F}}$
. -
(2) Divide
 $S_{\unicode[STIX]{x1D70F}}$
into
$S_{\unicode[STIX]{x1D70F}}$
into
 $N$
(evenly distributed) boundary elements and represent each element by a cubic spline parametrized by the arclength. Typically,
$N$
(evenly distributed) boundary elements and represent each element by a cubic spline parametrized by the arclength. Typically,
 $N=200$
on a half cross-section yielded sufficient accuracy and was adopted.
$N=200$
on a half cross-section yielded sufficient accuracy and was adopted. -
(3) Express the normal unit vector
 $\boldsymbol{n}$
and the curvature in terms of the cubic spline coefficients explicitly.
$\boldsymbol{n}$
and the curvature in terms of the cubic spline coefficients explicitly. -
(4) The integral equation (2.7) is solved iteratively with numerical evaluation of the boundary integrals based on Gauss–Legendre quadrature with singularity subtraction (Pozrikidis Reference Pozrikidis1992).
-
(5) Evaluation of
 $\Vert u_{n}\Vert$
, where (2.9)
$\Vert u_{n}\Vert$
, where (2.9) $$\begin{eqnarray}\Vert u_{n}\Vert =\frac{1}{S}\unicode[STIX]{x0222F}_{S}|u_{n}|\,\text{d}S.\end{eqnarray}$$
$$\begin{eqnarray}\Vert u_{n}\Vert =\frac{1}{S}\unicode[STIX]{x0222F}_{S}|u_{n}|\,\text{d}S.\end{eqnarray}$$
If
![]() $\Vert u_{n}\Vert \leqslant \unicode[STIX]{x1D700}$
, with a specified accuracy
$\Vert u_{n}\Vert \leqslant \unicode[STIX]{x1D700}$
, with a specified accuracy
![]() $\unicode[STIX]{x1D700}$
, then terminate the routine. Otherwise, for a given time step
$\unicode[STIX]{x1D700}$
, then terminate the routine. Otherwise, for a given time step
![]() $\text{d}\unicode[STIX]{x1D70F}$
update the position of the interface, making use of the kinematic condition (2.5): the point
$\text{d}\unicode[STIX]{x1D70F}$
update the position of the interface, making use of the kinematic condition (2.5): the point
![]() $\boldsymbol{x}$
at the interface is moved to the position
$\boldsymbol{x}$
at the interface is moved to the position
![]() $\boldsymbol{x}+\boldsymbol{u}\,\text{d}\unicode[STIX]{x1D70F}$
and the new time is set as
$\boldsymbol{x}+\boldsymbol{u}\,\text{d}\unicode[STIX]{x1D70F}$
and the new time is set as
![]() $\unicode[STIX]{x1D70F}+\text{d}\unicode[STIX]{x1D70F}$
. Go to step (2) above.
$\unicode[STIX]{x1D70F}+\text{d}\unicode[STIX]{x1D70F}$
. Go to step (2) above.
As mentioned earlier, the initial shape of the toroidal drop in this procedure is a circular cross-section with major radius
![]() $R$
. In the scaled variables introduced above, the volume of the torus equals
$R$
. In the scaled variables introduced above, the volume of the torus equals
![]() $4\unicode[STIX]{x03C0}/3$
and this gives a minor radius of
$4\unicode[STIX]{x03C0}/3$
and this gives a minor radius of
![]() $\sqrt{2/(3\unicode[STIX]{x03C0}R)}$
.
$\sqrt{2/(3\unicode[STIX]{x03C0}R)}$
.
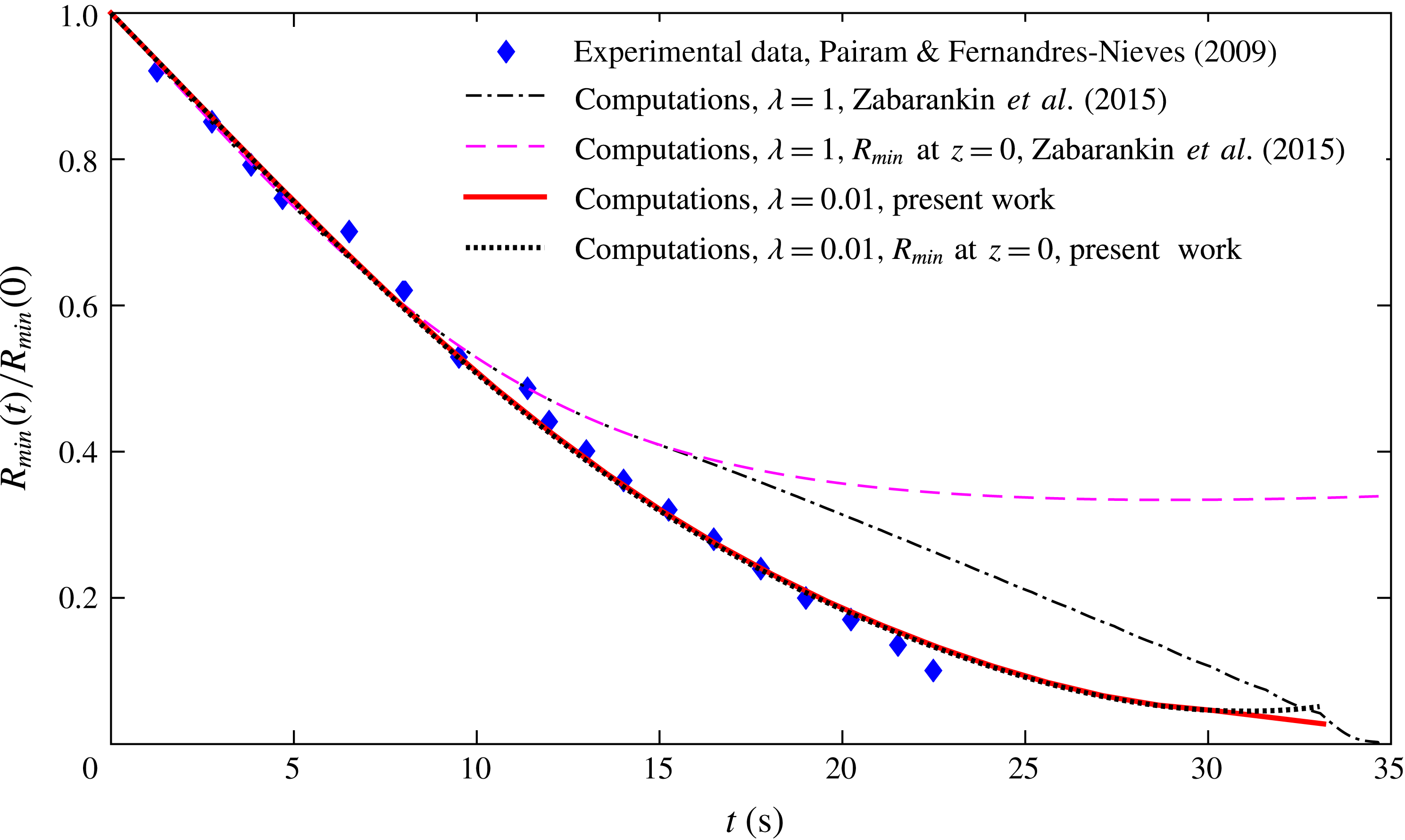
Figure 2. The dynamic collapse of an axisymmetric toroidal drop in the absence of external flow. Experimental data (diamonds) are quoted from Pairam & Fernández-Nieves (Reference Pairam and Fernández-Nieves2009). Solid and dotted curves obtained numerically in this work with
![]() $\unicode[STIX]{x1D706}=0.01$
, denote deformation with
$\unicode[STIX]{x1D706}=0.01$
, denote deformation with
![]() $R_{min}$
calculated at
$R_{min}$
calculated at
![]() $|z|\geqslant 0$
and
$|z|\geqslant 0$
and
![]() $z=0$
, respectively. Dashed–dotted and dashed curves were reported by Zabarankin et al. (Reference Zabarankin, Lavrenteva and Nir2015) for the above-mentioned calculation of
$z=0$
, respectively. Dashed–dotted and dashed curves were reported by Zabarankin et al. (Reference Zabarankin, Lavrenteva and Nir2015) for the above-mentioned calculation of
![]() $R_{min}$
.
$R_{min}$
.
There are only very limited experimental results to which a simulation of toroidal drop dynamics at these viscous conditions can be compared. Pairam & Fernández-Nieves (Reference Pairam and Fernández-Nieves2009) followed the collapse dynamics of a low-viscosity torus with initial circular cross-section in a quiescent viscous fluid. Zabarankin et al. (Reference Zabarankin, Lavrenteva and Nir2015) presented a comparison of these experimental data with the results of their calculation at
![]() $\unicode[STIX]{x1D706}=1$
, after an appropriate time rescaling, and obtained good agreement for the initial stages of the process. Here we present the results of a new calculation with low viscosity ratio. In figure 2, the inner radius of the droplet normalized by its initial value is plotted versus dimensional time. The initial ratio of the torus major and minor radii was chosen to be 1.4. It should be noted that this was the only condition that exhibited axisymmetric dynamics in the experiment (Pairam & Fernández-Nieves Reference Pairam and Fernández-Nieves2009). The experimental data points taken from Pairam & Fernández-Nieves (Reference Pairam and Fernández-Nieves2009) are presented by diamond symbols. Two definitions of the inner radius are used: minimum distance of the toroidal surface to the
$\unicode[STIX]{x1D706}=1$
, after an appropriate time rescaling, and obtained good agreement for the initial stages of the process. Here we present the results of a new calculation with low viscosity ratio. In figure 2, the inner radius of the droplet normalized by its initial value is plotted versus dimensional time. The initial ratio of the torus major and minor radii was chosen to be 1.4. It should be noted that this was the only condition that exhibited axisymmetric dynamics in the experiment (Pairam & Fernández-Nieves Reference Pairam and Fernández-Nieves2009). The experimental data points taken from Pairam & Fernández-Nieves (Reference Pairam and Fernández-Nieves2009) are presented by diamond symbols. Two definitions of the inner radius are used: minimum distance of the toroidal surface to the
![]() $z$
-axis (solid curve
$z$
-axis (solid curve
![]() $\unicode[STIX]{x1D706}=0.01$
, dashed curve
$\unicode[STIX]{x1D706}=0.01$
, dashed curve
![]() $\unicode[STIX]{x1D706}=1$
with time rescaled) and minimum distance of the cross-section at the plane
$\unicode[STIX]{x1D706}=1$
with time rescaled) and minimum distance of the cross-section at the plane
![]() $z=0$
to the origin (dotted curve
$z=0$
to the origin (dotted curve
![]() $\unicode[STIX]{x1D706}=0.01$
, dashed–dotted curve
$\unicode[STIX]{x1D706}=0.01$
, dashed–dotted curve
![]() $\unicode[STIX]{x1D706}=1$
with time rescaled). These two definitions coincide for circular tori and also during the period of torus deformation before the region of converted curvature is formed. It is evident that, during the initial period, when none of the computed shapes exhibit a dimple, all the curves agree well. As the torus contracts, the results computed with
$\unicode[STIX]{x1D706}=1$
with time rescaled). These two definitions coincide for circular tori and also during the period of torus deformation before the region of converted curvature is formed. It is evident that, during the initial period, when none of the computed shapes exhibit a dimple, all the curves agree well. As the torus contracts, the results computed with
![]() $\unicode[STIX]{x1D706}=1$
deviate from the data of Pairam & Fernández-Nieves (Reference Pairam and Fernández-Nieves2009), while those computed with
$\unicode[STIX]{x1D706}=1$
deviate from the data of Pairam & Fernández-Nieves (Reference Pairam and Fernández-Nieves2009), while those computed with
![]() $\unicode[STIX]{x1D706}=0.01$
are in excellent agreement with the experimental measurement during the entire period that these are available. However, since the numerical procedure does not allow for drop coalescence, the computations demonstrate that a slow deformation proceeds, relatively a long time after the collapse is seen in the experiment, and a belated small region of converted curvature appears following this deformation. Note that the earlier appearance of a dimple reported by Zabarankin et al. (Reference Zabarankin, Lavrenteva and Nir2015), when using the time scaling at
$\unicode[STIX]{x1D706}=0.01$
are in excellent agreement with the experimental measurement during the entire period that these are available. However, since the numerical procedure does not allow for drop coalescence, the computations demonstrate that a slow deformation proceeds, relatively a long time after the collapse is seen in the experiment, and a belated small region of converted curvature appears following this deformation. Note that the earlier appearance of a dimple reported by Zabarankin et al. (Reference Zabarankin, Lavrenteva and Nir2015), when using the time scaling at
![]() $\unicode[STIX]{x1D706}=1$
, is not supported by the experimental observations.
$\unicode[STIX]{x1D706}=1$
, is not supported by the experimental observations.
Before proceeding, we need to define the parameters that are used to characterize the drop deformation throughout this paper. The major radius
![]() $R$
(
$R$
(
![]() $\unicode[STIX]{x1D70F}$
) and the Taylor deformation factor of the torus
$\unicode[STIX]{x1D70F}$
) and the Taylor deformation factor of the torus
![]() $D$
(
$D$
(
![]() $\unicode[STIX]{x1D70F}$
) are defined to be
$\unicode[STIX]{x1D70F}$
) are defined to be
where
![]() $R_{min}$
and
$R_{min}$
and
![]() $R_{max}$
are the minimum and maximum distances of the drop interface from the
$R_{max}$
are the minimum and maximum distances of the drop interface from the
![]() $z$
-axis, respectively, and
$z$
-axis, respectively, and
![]() $z_{max}=\max _{x\in S}z$
. Also following Zabarankin et al. (Reference Zabarankin, Lavrenteva and Nir2015), we define the Taylor deformation factor for the torus cross-section
$z_{max}=\max _{x\in S}z$
. Also following Zabarankin et al. (Reference Zabarankin, Lavrenteva and Nir2015), we define the Taylor deformation factor for the torus cross-section
3 Dynamics
In this section we study the dynamics and evolution of axisymmetric toroidal drops at various capillary numbers, Ca, and viscosity ratios,
![]() $\unicode[STIX]{x1D706}$
. The initial structure is a torus with a circular cross-section, and at time
$\unicode[STIX]{x1D706}$
. The initial structure is a torus with a circular cross-section, and at time
![]() $\unicode[STIX]{x1D70F}=0$
it is subject to the axisymmetric compressional viscous flow.
$\unicode[STIX]{x1D70F}=0$
it is subject to the axisymmetric compressional viscous flow.
The dynamic deformation of the initially circular viscous toroidal drop in a compressional flow is governed by three types of forcing: the external flow tends to expand the torus; the surface tension tends to shrink the torus and to make its cross-section circular; the viscosity of the drop slows down its deformation. Since the external flow is linear,
![]() $u_{r}=r$
, its dragging effect grows with the radius of torus. The shrinking effect of the surface tension is inversely proportional to the major radius of the torus,
$u_{r}=r$
, its dragging effect grows with the radius of torus. The shrinking effect of the surface tension is inversely proportional to the major radius of the torus,
![]() $R$
. Thus, it can be anticipated that the tori with high
$R$
. Thus, it can be anticipated that the tori with high
![]() $R$
will expand indefinitely, while those with small
$R$
will expand indefinitely, while those with small
![]() $R$
will collapse. For a certain critical value,
$R$
will collapse. For a certain critical value,
![]() $R_{c}$
(Ca,
$R_{c}$
(Ca,
![]() $\unicode[STIX]{x1D706}$
), a third type of evolution is expected where, after initial limited deformation, a relatively long period of almost stationary state is conceivable. These dynamic evolutions patterns were reported by Zabarankin et al. (Reference Zabarankin, Lavrenteva and Nir2015) for the case of equal viscosity,
$\unicode[STIX]{x1D706}$
), a third type of evolution is expected where, after initial limited deformation, a relatively long period of almost stationary state is conceivable. These dynamic evolutions patterns were reported by Zabarankin et al. (Reference Zabarankin, Lavrenteva and Nir2015) for the case of equal viscosity,
![]() $\unicode[STIX]{x1D706}=1$
, and are observed also for
$\unicode[STIX]{x1D706}=1$
, and are observed also for
![]() $\unicode[STIX]{x1D706}\neq 1$
as long as Ca is not too large.
$\unicode[STIX]{x1D706}\neq 1$
as long as Ca is not too large.
Examples of the dynamic evolution at
![]() $Ca=0.08$
are shown in figure 3 for relatively low and high viscosity ratio. The case
$Ca=0.08$
are shown in figure 3 for relatively low and high viscosity ratio. The case
![]() $\unicode[STIX]{x1D706}=0.1$
is demonstrated in figure 3(a,b). In panel (a), where the initial radius is
$\unicode[STIX]{x1D706}=0.1$
is demonstrated in figure 3(a,b). In panel (a), where the initial radius is
![]() $R=1.1$
(see figure 1), we observe the torus collapsing towards the centre. Its radius,
$R=1.1$
(see figure 1), we observe the torus collapsing towards the centre. Its radius,
![]() $R$
, is shrinking while its cross-section area is growing. In the initial stages, the circular cross-section deforms and becomes oval. When collapse progresses and the centre gap, occupied by the external fluid, narrows, the inner part of the cross-section of the torus flattens. As the torus approaches the final stages of collapse, the squeezing of the external viscous fluid from the ever-narrowing centre gap results in high local normal stresses, thereby inducing a circular interfacial dimple in the vicinity of the plane
$R$
, is shrinking while its cross-section area is growing. In the initial stages, the circular cross-section deforms and becomes oval. When collapse progresses and the centre gap, occupied by the external fluid, narrows, the inner part of the cross-section of the torus flattens. As the torus approaches the final stages of collapse, the squeezing of the external viscous fluid from the ever-narrowing centre gap results in high local normal stresses, thereby inducing a circular interfacial dimple in the vicinity of the plane
![]() $z=0$
. As a result, the first interfacial collapse may either occur at
$z=0$
. As a result, the first interfacial collapse may either occur at
![]() $z=0$
or at some vertical distance,
$z=0$
or at some vertical distance,
![]() $|z|>0$
, with a finite volume of the external fluid being trapped. Similar patterns are obtained for smaller initial toroidal radii. However, when the initial
$|z|>0$
, with a finite volume of the external fluid being trapped. Similar patterns are obtained for smaller initial toroidal radii. However, when the initial
![]() $R$
is increased there is a critical value,
$R$
is increased there is a critical value,
![]() $R_{c}$
(Ca,
$R_{c}$
(Ca,
![]() $\unicode[STIX]{x1D706}$
) beyond which the evolution is different. In panel (b), we see an example of an evolution that starts when the torus initial radius is somewhat higher,
$\unicode[STIX]{x1D706}$
) beyond which the evolution is different. In panel (b), we see an example of an evolution that starts when the torus initial radius is somewhat higher,
![]() $R=1.4$
. Here the dynamics evolves in an opposite manner. The torus radius,
$R=1.4$
. Here the dynamics evolves in an opposite manner. The torus radius,
![]() $R$
, expands while the area of the cross-section becomes smaller. The initial deformation of the circular cross-section into an oval shape is again evident. However, as the dynamic evolution progresses and the interfacial forces become more and more dominant over the deforming viscous stresses, the circularity of the cross-section is gradually regained. Indeed, if the axisymmetric stability of the toroidal shape is maintained it is expected that the cross-section becomes circular as
$R$
, expands while the area of the cross-section becomes smaller. The initial deformation of the circular cross-section into an oval shape is again evident. However, as the dynamic evolution progresses and the interfacial forces become more and more dominant over the deforming viscous stresses, the circularity of the cross-section is gradually regained. Indeed, if the axisymmetric stability of the toroidal shape is maintained it is expected that the cross-section becomes circular as
![]() $R\rightarrow \infty$
.
$R\rightarrow \infty$
.

Figure 3. Dynamic deformation of toroidal drop, initially with circular cross-section.
![]() $Ca=0.08$
. (a)
$Ca=0.08$
. (a)
![]() $\unicode[STIX]{x1D706}=0.1$
,
$\unicode[STIX]{x1D706}=0.1$
,
![]() $R=1.1$
; (b)
$R=1.1$
; (b)
![]() $\unicode[STIX]{x1D706}=0.1$
,
$\unicode[STIX]{x1D706}=0.1$
,
![]() $R=1.4$
; (c)
$R=1.4$
; (c)
![]() $\unicode[STIX]{x1D706}=10,R=1.1$
; (d)
$\unicode[STIX]{x1D706}=10,R=1.1$
; (d)
![]() $\unicode[STIX]{x1D706}=10$
,
$\unicode[STIX]{x1D706}=10$
,
![]() $R=1.4$
. The origin of the abscissa coincides with the axis of symmetry.
$R=1.4$
. The origin of the abscissa coincides with the axis of symmetry.

Figure 4. Evolution of
![]() $R_{max}$
(a) and
$R_{max}$
(a) and
![]() $R_{min}$
(b) in the process of indefinite expansion for various values of the viscosity ratio.
$R_{min}$
(b) in the process of indefinite expansion for various values of the viscosity ratio.
![]() $Ca=0.08$
, initial radius
$Ca=0.08$
, initial radius
![]() $R=1.4$
.
$R=1.4$
.
In the case
![]() $\unicode[STIX]{x1D706}=10$
, depicted in figure 3(c,d), similar evolution patterns are evident, i.e. collapse towards the centre for the smaller initial value of
$\unicode[STIX]{x1D706}=10$
, depicted in figure 3(c,d), similar evolution patterns are evident, i.e. collapse towards the centre for the smaller initial value of
![]() $R$
and an indefinite expansion when the dynamic starts at the higher value of
$R$
and an indefinite expansion when the dynamic starts at the higher value of
![]() $R$
. As in the previous case, a critical initial torus radius,
$R$
. As in the previous case, a critical initial torus radius,
![]() $R_{c}$
, is anticipated, where transition from the collapse mode to the expansion mode occurs. There are differences in the evolution dynamics between the cases of low and high drop viscosity. The collapse time in the
$R_{c}$
, is anticipated, where transition from the collapse mode to the expansion mode occurs. There are differences in the evolution dynamics between the cases of low and high drop viscosity. The collapse time in the
![]() $\unicode[STIX]{x1D706}=10$
case is longer, the radius of the interfacial dimple is smaller, and the cross-section at collapse is more elongated in the
$\unicode[STIX]{x1D706}=10$
case is longer, the radius of the interfacial dimple is smaller, and the cross-section at collapse is more elongated in the
![]() $r$
direction. During the expanding dynamics, the cross-section of both high- and low-viscosity tori deform to an oval, and thereafter regain the circular shape. However, in contrast to the contraction case, the low-viscosity torus (
$r$
direction. During the expanding dynamics, the cross-section of both high- and low-viscosity tori deform to an oval, and thereafter regain the circular shape. However, in contrast to the contraction case, the low-viscosity torus (
![]() $\unicode[STIX]{x1D706}=0.1$
) expands more slowly than the high-viscosity one.
$\unicode[STIX]{x1D706}=0.1$
) expands more slowly than the high-viscosity one.
In order to understand this unexpected behaviour, consider the dynamic change of characteristic geometric parameters during the toroidal expansion at
![]() $Ca=0.08$
and various value of
$Ca=0.08$
and various value of
![]() $\unicode[STIX]{x1D706}$
that is shown in figures 4 and 5. All tori start at an initial radius
$\unicode[STIX]{x1D706}$
that is shown in figures 4 and 5. All tori start at an initial radius
![]() $R=1.4$
which is higher than
$R=1.4$
which is higher than
![]() $R_{c}$
for the depicted
$R_{c}$
for the depicted
![]() $\unicode[STIX]{x1D706}$
cases. In figure 4(a) we plot the evolution of the outer radius of the torus,
$\unicode[STIX]{x1D706}$
cases. In figure 4(a) we plot the evolution of the outer radius of the torus,
![]() $R_{max}$
, with time for the various viscosity ratios. Naturally,
$R_{max}$
, with time for the various viscosity ratios. Naturally,
![]() $R_{max}$
monotonically increases with time for all the cases. For short time shown, in the inset, it grows faster for a lower viscosity ratio, as can be anticipated. However, for the low-viscosity torus, the increase of
$R_{max}$
monotonically increases with time for all the cases. For short time shown, in the inset, it grows faster for a lower viscosity ratio, as can be anticipated. However, for the low-viscosity torus, the increase of
![]() $R_{max}$
first slows down and then accelerates again. In contrast to this, for higher viscosity ratios no deceleration is observed:
$R_{max}$
first slows down and then accelerates again. In contrast to this, for higher viscosity ratios no deceleration is observed:
![]() $R_{max}$
initially increases at an almost constant rate and then accelerates. As a result, with the passage of time the curves corresponding to lower
$R_{max}$
initially increases at an almost constant rate and then accelerates. As a result, with the passage of time the curves corresponding to lower
![]() $\unicode[STIX]{x1D706}$
(
$\unicode[STIX]{x1D706}$
(
![]() $\unicode[STIX]{x1D706}\leqslant O(1)$
) and higher
$\unicode[STIX]{x1D706}\leqslant O(1)$
) and higher
![]() $\unicode[STIX]{x1D706}$
intersect and high-viscosity tori become more extended than low-viscosity tori, as is evident also in figure 3. Note again that for
$\unicode[STIX]{x1D706}$
intersect and high-viscosity tori become more extended than low-viscosity tori, as is evident also in figure 3. Note again that for
![]() $\unicode[STIX]{x1D706}>O(1)$
, the extension does not slow down and these curves retain their initial order. Thus, at advanced stages,
$\unicode[STIX]{x1D706}>O(1)$
, the extension does not slow down and these curves retain their initial order. Thus, at advanced stages,
![]() $R_{max}$
becomes a non-monotonic function of the viscosity ratio that is determined by the capillary number and the initial torus radius. For example, for the case presented in figures 3 and 4 (
$R_{max}$
becomes a non-monotonic function of the viscosity ratio that is determined by the capillary number and the initial torus radius. For example, for the case presented in figures 3 and 4 (
![]() $Ca=0.08$
,
$Ca=0.08$
,
![]() $R(0)=1.4$
), the torus with
$R(0)=1.4$
), the torus with
![]() $\unicode[STIX]{x1D706}=2$
appears to be the most extended one.
$\unicode[STIX]{x1D706}=2$
appears to be the most extended one.

Figure 5. Evolution of the Taylor deformation parameters in the process of indefinite expansion for various values of the viscosity ratio.
![]() $Ca=0.08$
,
$Ca=0.08$
,
![]() $R=1.4$
. (a) Toroidal deformation parameter. (b) Cross-section deformation parameter.
$R=1.4$
. (a) Toroidal deformation parameter. (b) Cross-section deformation parameter.
In figure 4(b) we plot the evolution of the inner radius of the torus,
![]() $R_{min}$
, with time for various viscosity ratios. For short time, there is a different dynamics for cases of low and high viscosity ratio. This is depicted in the inset. When
$R_{min}$
, with time for various viscosity ratios. For short time, there is a different dynamics for cases of low and high viscosity ratio. This is depicted in the inset. When
![]() $\unicode[STIX]{x1D706}\leqslant O(1)$
there is a short transition stage where
$\unicode[STIX]{x1D706}\leqslant O(1)$
there is a short transition stage where
![]() $R_{min}$
first diminishes since the inward motion of the deforming inner surface due to capillary force overrides the outward motion of the torus cross-section induced by the outer flow. The viscosity slows down this motion, and for lower-
$R_{min}$
first diminishes since the inward motion of the deforming inner surface due to capillary force overrides the outward motion of the torus cross-section induced by the outer flow. The viscosity slows down this motion, and for lower-
![]() $\unicode[STIX]{x1D706}$
cases, the initial motion of the interface towards the axis of symmetry is more pronounced.
$\unicode[STIX]{x1D706}$
cases, the initial motion of the interface towards the axis of symmetry is more pronounced.
For the higher-viscosity-ratio cases, with
![]() $\unicode[STIX]{x1D706}\geqslant O(10)$
, the deformation is not fast enough to exhibit such a transition stage with inward motion. Nevertheless, the viscosity slows down the outward motion as well. As a result, the curve corresponding to
$\unicode[STIX]{x1D706}\geqslant O(10)$
, the deformation is not fast enough to exhibit such a transition stage with inward motion. Nevertheless, the viscosity slows down the outward motion as well. As a result, the curve corresponding to
![]() $\unicode[STIX]{x1D706}=20$
is located below the one corresponding to
$\unicode[STIX]{x1D706}=20$
is located below the one corresponding to
![]() $\unicode[STIX]{x1D706}=$
10. Note that, initially, the outer part of the interface (
$\unicode[STIX]{x1D706}=$
10. Note that, initially, the outer part of the interface (
![]() $R_{max}$
) moves outwards and at high
$R_{max}$
) moves outwards and at high
![]() $\unicode[STIX]{x1D706}$
it moves faster than the inner part (
$\unicode[STIX]{x1D706}$
it moves faster than the inner part (
![]() $R_{min}$
). As a result, at the initial stage of the process, the torus cross-section assumes the form of an oval shape elongated in the
$R_{min}$
). As a result, at the initial stage of the process, the torus cross-section assumes the form of an oval shape elongated in the
![]() $r$
direction (see figure 3). As time progresses and all tori are expanded, the growth of
$r$
direction (see figure 3). As time progresses and all tori are expanded, the growth of
![]() $R_{min}$
and
$R_{min}$
and
![]() $R_{max}$
becomes exponential for all
$R_{max}$
becomes exponential for all
![]() $\unicode[STIX]{x1D706}$
cases, thus, reflecting the convective dominance of the ambient linear flow,
$\unicode[STIX]{x1D706}$
cases, thus, reflecting the convective dominance of the ambient linear flow,
![]() $u_{r}=r$
.
$u_{r}=r$
.
Figure 5(a,b) shows the evolution of the Taylor deformation parameter of the torus, D, defined by (2.10) for various values of the viscosity ratio. In all of the presented cases,
![]() $D$
grows monotonically with time, exhibiting four distinct periods. During the initial period shown in the inset of figure 5(a), the lower is
$D$
grows monotonically with time, exhibiting four distinct periods. During the initial period shown in the inset of figure 5(a), the lower is
![]() $\unicode[STIX]{x1D706}$
, the faster is the deformation. Then the deformation slows down, with this effect being more pronounced for low-viscosity cases. Further on, the deformation rate increases again, and finally it slows down as the torus radius grows indefinitely and the deformation factor approaches 1. Figure 5(b) shows the evolution of the Taylor deformation parameter of the torus cross-section,
$\unicode[STIX]{x1D706}$
, the faster is the deformation. Then the deformation slows down, with this effect being more pronounced for low-viscosity cases. Further on, the deformation rate increases again, and finally it slows down as the torus radius grows indefinitely and the deformation factor approaches 1. Figure 5(b) shows the evolution of the Taylor deformation parameter of the torus cross-section,
![]() $D_{1}$
, defined by (2.11), for various values of the viscosity ratio. Evidently,
$D_{1}$
, defined by (2.11), for various values of the viscosity ratio. Evidently,
![]() $D_{1}(0)=0$
for all cases, reflecting the initially circular form of the cross-section. Then it grows, with the deformation rate being higher for lower
$D_{1}(0)=0$
for all cases, reflecting the initially circular form of the cross-section. Then it grows, with the deformation rate being higher for lower
![]() $\unicode[STIX]{x1D706}$
. After reaching maximum values, it decreases and tends to zero as the cross-section regains its circular shape with
$\unicode[STIX]{x1D706}$
. After reaching maximum values, it decreases and tends to zero as the cross-section regains its circular shape with
![]() $\unicode[STIX]{x1D70F}\rightarrow \infty$
. The maximum deformation is higher and it is achieved faster for lower values of the viscosity ratio. Nevertheless, the non-monotonic dependence of the deformation process on
$\unicode[STIX]{x1D70F}\rightarrow \infty$
. The maximum deformation is higher and it is achieved faster for lower values of the viscosity ratio. Nevertheless, the non-monotonic dependence of the deformation process on
![]() $\unicode[STIX]{x1D706}$
is retained.
$\unicode[STIX]{x1D706}$
is retained.
A somewhat different evolution is found when Ca is significantly larger. An example is shown in figure 6 for
![]() $Ca=0.5$
. When the torus inner circle is initially very close to the axis of symmetry, the torus deforms until a total collapse occurs, with or without a centre dimple, as is depicted in figure 6(a,c), for the low- and high-
$Ca=0.5$
. When the torus inner circle is initially very close to the axis of symmetry, the torus deforms until a total collapse occurs, with or without a centre dimple, as is depicted in figure 6(a,c), for the low- and high-
![]() $\unicode[STIX]{x1D706}$
cases, where the initial radius is
$\unicode[STIX]{x1D706}$
cases, where the initial radius is
![]() $R=0.64$
. Recall that this value is close to the minimum
$R=0.64$
. Recall that this value is close to the minimum
![]() $R$
for a torus, of volume
$R$
for a torus, of volume
![]() $4\unicode[STIX]{x03C0}/3$
, having a circular cross-section, which is
$4\unicode[STIX]{x03C0}/3$
, having a circular cross-section, which is
![]() $R=0.5965$
. If such a collapse during the initial deformation does not occur, the torus expands without bound, as is shown in panels (b) and (d), where the initial radius is
$R=0.5965$
. If such a collapse during the initial deformation does not occur, the torus expands without bound, as is shown in panels (b) and (d), where the initial radius is
![]() $R=0.68$
. Thus, in such cases, no critical initial radius exhibiting some stationarity was found.
$R=0.68$
. Thus, in such cases, no critical initial radius exhibiting some stationarity was found.
The evolution during the expansion at
![]() $Ca=0.5$
is demonstrated in figure 6 for the cases
$Ca=0.5$
is demonstrated in figure 6 for the cases
![]() $\unicode[STIX]{x1D706}=0.1$
and
$\unicode[STIX]{x1D706}=0.1$
and
![]() $\unicode[STIX]{x1D706}=10$
(see also Zabarankin et al.
Reference Zabarankin, Lavrenteva and Nir2015 for
$\unicode[STIX]{x1D706}=10$
(see also Zabarankin et al.
Reference Zabarankin, Lavrenteva and Nir2015 for
![]() $\unicode[STIX]{x1D706}=1$
). In these examples it is evident that, during the expansion, the oval shapes lose their fore-and-aft symmetry about the cross-section middle point,
$\unicode[STIX]{x1D706}=1$
). In these examples it is evident that, during the expansion, the oval shapes lose their fore-and-aft symmetry about the cross-section middle point,
![]() $r=R$
, with the region pointing towards
$r=R$
, with the region pointing towards
![]() $R_{min}$
becoming sharper. Furthermore, in cases where
$R_{min}$
becoming sharper. Furthermore, in cases where
![]() $\unicode[STIX]{x1D706}\leqslant O(1)$
, when the torus is at this expanding mode of evolution there are stages where the cross-section width reduces to a slender shape that is susceptible to possible local capillary disturbances endangering the toroidal structure (see, e.g. Mehrabian & Feng Reference Mehrabian and Feng2013). Nevertheless, if the torus prevails, the circular cross-section is slowly regained as the expansion continues towards
$\unicode[STIX]{x1D706}\leqslant O(1)$
, when the torus is at this expanding mode of evolution there are stages where the cross-section width reduces to a slender shape that is susceptible to possible local capillary disturbances endangering the toroidal structure (see, e.g. Mehrabian & Feng Reference Mehrabian and Feng2013). Nevertheless, if the torus prevails, the circular cross-section is slowly regained as the expansion continues towards
![]() $R\rightarrow \infty$
. Similar patterns are expected to occur at all
$R\rightarrow \infty$
. Similar patterns are expected to occur at all
![]() $\unicode[STIX]{x1D706}$
. For these initial conditions, the expansion of low-viscosity torus is considerably faster than the high-viscosity one.
$\unicode[STIX]{x1D706}$
. For these initial conditions, the expansion of low-viscosity torus is considerably faster than the high-viscosity one.

Figure 6. Dynamic deformation of toroidal drop, initially with circular cross-section at relatively high capillary number
![]() $Ca=0.5$
. (a)
$Ca=0.5$
. (a)
![]() $\unicode[STIX]{x1D706}=0.1$
,
$\unicode[STIX]{x1D706}=0.1$
,
![]() $R=0.64$
; (b)
$R=0.64$
; (b)
![]() $\unicode[STIX]{x1D706}=0.1$
,
$\unicode[STIX]{x1D706}=0.1$
,
![]() $R=0.68$
; (c)
$R=0.68$
; (c)
![]() $\unicode[STIX]{x1D706}=10$
,
$\unicode[STIX]{x1D706}=10$
,
![]() $R=0.64$
; (d)
$R=0.64$
; (d)
![]() $\unicode[STIX]{x1D706}=10$
,
$\unicode[STIX]{x1D706}=10$
,
![]() $R=0.68$
. The origin of the abscissa coincides with the axis of symmetry.
$R=0.68$
. The origin of the abscissa coincides with the axis of symmetry.
The dynamic behaviour presented above suggests that, for all viscosity ratios, there are basically two patterns of motion and deformation. If the initial radius of the torus is small enough, the toroidal drop deforms and collapses towards a closed shape. If the initial radius is large enough, the torus deforms and expands indefinitely. This behaviour occurs at capillary numbers that are smaller than some critical value for each viscosity ratio,
![]() $Ca_{cr}$
(
$Ca_{cr}$
(
![]() $\unicode[STIX]{x1D706}$
). When this critical state is surpassed the intact torus only expands. Hence, it is expected that, in the finite range
$\unicode[STIX]{x1D706}$
). When this critical state is surpassed the intact torus only expands. Hence, it is expected that, in the finite range
![]() $0<Ca<Ca_{cr}$
(
$0<Ca<Ca_{cr}$
(
![]() $\unicode[STIX]{x1D706}$
), for each Ca and
$\unicode[STIX]{x1D706}$
), for each Ca and
![]() $\unicode[STIX]{x1D706}$
there will be a value of
$\unicode[STIX]{x1D706}$
there will be a value of
![]() $R=R_{c}$
(Ca,
$R=R_{c}$
(Ca,
![]() $\unicode[STIX]{x1D706}$
) at which the transition between the two patterns of dynamics occurs. A collection of calculated
$\unicode[STIX]{x1D706}$
) at which the transition between the two patterns of dynamics occurs. A collection of calculated
![]() $R_{c}$
values is given in table 1.
$R_{c}$
values is given in table 1.
Table 1. Critical initial radius of the torus.

It is interesting to examine these cases and observe if they can indicate a map of possible stationary states in which the torus cross-section only deforms, but the torus does not collapse or expand, and the drop maintains its position with the deformed cross-section indefinitely. This is addressed in the next section.
4 Stationary states
The search for
![]() $R_{c}$
(Ca,
$R_{c}$
(Ca,
![]() $\unicode[STIX]{x1D706}$
) in cases of a dynamically deforming interface is a tedious process involving multiple evaluation of numerical solutions of the boundary integral equation (2.7) for each choice of the parameters
$\unicode[STIX]{x1D706}$
) in cases of a dynamically deforming interface is a tedious process involving multiple evaluation of numerical solutions of the boundary integral equation (2.7) for each choice of the parameters
![]() $\unicode[STIX]{x1D706}$
and Ca. Indeed, when it is assumed that the cross-section shape is given – as it is in Zabarankin (Reference Zabarankin2016), who considered a family of circular cross-sections throughout the dynamic evolution – it is possible to define an inverse problem by searching for
$\unicode[STIX]{x1D706}$
and Ca. Indeed, when it is assumed that the cross-section shape is given – as it is in Zabarankin (Reference Zabarankin2016), who considered a family of circular cross-sections throughout the dynamic evolution – it is possible to define an inverse problem by searching for
![]() $Ca=Ca(R_{c})$
where the boundary integral equation (2.7) assumes some criterion of stationarity. However, such an approach is not applicable in the general case. Thus, the procedure adopted here is as follows: for given
$Ca=Ca(R_{c})$
where the boundary integral equation (2.7) assumes some criterion of stationarity. However, such an approach is not applicable in the general case. Thus, the procedure adopted here is as follows: for given
![]() $\unicode[STIX]{x1D706}$
and Ca choose
$\unicode[STIX]{x1D706}$
and Ca choose
![]() $R$
and follow the dynamic change of the parameters
$R$
and follow the dynamic change of the parameters
![]() $R$
,
$R$
,
![]() $R_{min}$
and
$R_{min}$
and
![]() $D_{1}$
. The search is accepted as a stationary result, i.e.
$D_{1}$
. The search is accepted as a stationary result, i.e.
![]() $R=R_{c}$
if the three parameters assume constant asymptotic values.
$R=R_{c}$
if the three parameters assume constant asymptotic values.

Figure 7. Evolution of
![]() $R,R_{min}$
and cross-section deformation parameter
$R,R_{min}$
and cross-section deformation parameter
![]() $D_{1}$
to a stationary torus, initially with circular cross-section and
$D_{1}$
to a stationary torus, initially with circular cross-section and
![]() $R\sim R_{c},Ca=0.15$
,
$R\sim R_{c},Ca=0.15$
,
![]() $\unicode[STIX]{x1D706}=10$
.
$\unicode[STIX]{x1D706}=10$
.
An example is depicted in figure 7, where
![]() $\unicode[STIX]{x1D706}=10$
,
$\unicode[STIX]{x1D706}=10$
,
![]() $Ca=0.15$
. The value of
$Ca=0.15$
. The value of
![]() $R_{min}$
decreases, while the values of
$R_{min}$
decreases, while the values of
![]() $R$
and the deformation parameter increase as the cross-section deforms to an oval shape. It then assumes constant values for a relatively long stretch of dimensionless time. Nevertheless, after that time it is evident that
$R$
and the deformation parameter increase as the cross-section deforms to an oval shape. It then assumes constant values for a relatively long stretch of dimensionless time. Nevertheless, after that time it is evident that
![]() $R_{min}$
and
$R_{min}$
and
![]() $R$
either grow or reduce, indicating that the torus starts expanding or collapsing, respectively. The deformation parameter follows a similar evolution dynamics but lags somewhat behind. As the cross-section flattens, the deformation parameter increases until it achieves a constant value that lasts a similar considerable time, beyond which the deformation proceeds. We conclude that the torus in this period with no observed evolution is a stationary state. Indeed, the stretch of time exhibiting stationary parameters can be extended by calculating
$R$
either grow or reduce, indicating that the torus starts expanding or collapsing, respectively. The deformation parameter follows a similar evolution dynamics but lags somewhat behind. As the cross-section flattens, the deformation parameter increases until it achieves a constant value that lasts a similar considerable time, beyond which the deformation proceeds. We conclude that the torus in this period with no observed evolution is a stationary state. Indeed, the stretch of time exhibiting stationary parameters can be extended by calculating
![]() $R_{c}$
to more significant figures. However, it was found that, no matter what accuracy of
$R_{c}$
to more significant figures. However, it was found that, no matter what accuracy of
![]() $R_{c}$
is approached, the torus eventually either collapses or expands. It follows that the numerically calculated stationary shape is sensitive to any small disturbance. Thus, we conclude that the calculated tori have stationary but unstable states.
$R_{c}$
is approached, the torus eventually either collapses or expands. It follows that the numerically calculated stationary shape is sensitive to any small disturbance. Thus, we conclude that the calculated tori have stationary but unstable states.

Figure 8. The dependence of
![]() $R_{c}$
on the capillary number (a) and on the viscosity ratio (b).
$R_{c}$
on the capillary number (a) and on the viscosity ratio (b).
![]() $Ca<Ca_{cr}$
for all
$Ca<Ca_{cr}$
for all
![]() $\unicode[STIX]{x1D706}$
.
$\unicode[STIX]{x1D706}$
.
The length of the time stretch during which a stationary torus exists depends also on the capillary number and on the viscosity ratio. In the previous section we demonstrated that there exist relatively high capillary numbers for which there is no critical
![]() $R_{c}$
(see figure 6). Thus, for each value of
$R_{c}$
(see figure 6). Thus, for each value of
![]() $\unicode[STIX]{x1D706}$
, there is a limiting value of the capillary number,
$\unicode[STIX]{x1D706}$
, there is a limiting value of the capillary number,
![]() $Ca_{cr}(\unicode[STIX]{x1D706})$
, for which the existence of a stationary, yet unstable, shape can be anticipated. However, the numerical detection of a transition point at
$Ca_{cr}(\unicode[STIX]{x1D706})$
, for which the existence of a stationary, yet unstable, shape can be anticipated. However, the numerical detection of a transition point at
![]() $Ca_{cr}$
is inaccurate; thus, only sub- and near-critical data are reported in this work. The existence of a critical capillary number,
$Ca_{cr}$
is inaccurate; thus, only sub- and near-critical data are reported in this work. The existence of a critical capillary number,
![]() $Ca_{cr}$
, which is a bifurcation point where a stable solution and unstable solution diverge from each other, has been shown and discussed for drops embedded in extensional and bi-extensional viscous flows (e.g. Acrivos & Lo Reference Acrivos and Lo1978, Zabarankin et al.
Reference Zabarankin, Smagin, Lavrenteva and Nir2013) or for drops in a linear electrical field (Karyappa, Deshmukh & Thaokar (Reference Karyappa, Deshmukh and Thaokar2014) and others cited therein). However, the dynamics studied here is somewhat more complex. In this case each value of
$Ca_{cr}$
, which is a bifurcation point where a stable solution and unstable solution diverge from each other, has been shown and discussed for drops embedded in extensional and bi-extensional viscous flows (e.g. Acrivos & Lo Reference Acrivos and Lo1978, Zabarankin et al.
Reference Zabarankin, Smagin, Lavrenteva and Nir2013) or for drops in a linear electrical field (Karyappa, Deshmukh & Thaokar (Reference Karyappa, Deshmukh and Thaokar2014) and others cited therein). However, the dynamics studied here is somewhat more complex. In this case each value of
![]() $Ca<Ca_{cr}$
presents a supercritical bifurcation point in which the unstable solution can separate to either a collapsing dynamics or an indefinite expansion.
$Ca<Ca_{cr}$
presents a supercritical bifurcation point in which the unstable solution can separate to either a collapsing dynamics or an indefinite expansion.
A summary of the dependence of
![]() $R_{c}$
on the parameters
$R_{c}$
on the parameters
![]() $\unicode[STIX]{x1D706}$
and Ca is given in figure 8 (see also table 1). In panel (a) the change with Ca is depicted for various values of
$\unicode[STIX]{x1D706}$
and Ca is given in figure 8 (see also table 1). In panel (a) the change with Ca is depicted for various values of
![]() $\unicode[STIX]{x1D706}$
and in panel (b) the change with
$\unicode[STIX]{x1D706}$
and in panel (b) the change with
![]() $\unicode[STIX]{x1D706}$
is depicted for various values of Ca. Note that for all Ca the changes between
$\unicode[STIX]{x1D706}$
is depicted for various values of Ca. Note that for all Ca the changes between
![]() $\unicode[STIX]{x1D706}=2$
and
$\unicode[STIX]{x1D706}=2$
and
![]() $\unicode[STIX]{x1D706}=10$
are relatively small.
$\unicode[STIX]{x1D706}=10$
are relatively small.

Figure 9. Taylor deformation factor of unstable stationary state toroidal drops.
![]() $0<Ca<Ca_{cr}(\unicode[STIX]{x1D706})$
.
$0<Ca<Ca_{cr}(\unicode[STIX]{x1D706})$
.

Figure 10. Cross-section shapes of unstable stationary tori. (a) Near-circular cross-sections,
![]() $Ca=0.04$
. (b) Oval cross-section,
$Ca=0.04$
. (b) Oval cross-section,
![]() $Ca=0.14$
. (c) Highly deformed cross-section at near-critical Ca,
$Ca=0.14$
. (c) Highly deformed cross-section at near-critical Ca,
![]() $D\sim 0.72$
. The origin of the abscissa coincides with the axis of symmetry.
$D\sim 0.72$
. The origin of the abscissa coincides with the axis of symmetry.
A collection of results showing stationary states for various values of
![]() $\unicode[STIX]{x1D706}$
is depicted in figure 9, where the Taylor deformation parameter of the torus,
$\unicode[STIX]{x1D706}$
is depicted in figure 9, where the Taylor deformation parameter of the torus,
![]() $D$
, (see equation (2.10)) is plotted against Ca. In general, in all cases of
$D$
, (see equation (2.10)) is plotted against Ca. In general, in all cases of
![]() $\unicode[STIX]{x1D706}$
, all the curves start from
$\unicode[STIX]{x1D706}$
, all the curves start from
![]() $D=1$
when
$D=1$
when
![]() $Ca=0$
, indicating that in this limit the radius of the torus is infinitely extended and that the cross-section has a vanishingly small circular area. As Ca increases, the torus radius decreases and the cross-section area becomes slightly deformed, but it still can be approximated by a circle in the region
$Ca=0$
, indicating that in this limit the radius of the torus is infinitely extended and that the cross-section has a vanishingly small circular area. As Ca increases, the torus radius decreases and the cross-section area becomes slightly deformed, but it still can be approximated by a circle in the region
![]() $Ca\ll 1$
. This change is reflected by
$Ca\ll 1$
. This change is reflected by
![]() $D$
reducing in value. Depending on
$D$
reducing in value. Depending on
![]() $\unicode[STIX]{x1D706}$
, at various intermediate values of the capillary number,
$\unicode[STIX]{x1D706}$
, at various intermediate values of the capillary number,
![]() $0.1\lesssim Ca\lesssim 0.17$
, the decrease in
$0.1\lesssim Ca\lesssim 0.17$
, the decrease in
![]() $D$
reaches a minimum. In this region the cross-sections of the various tori are oval, with fore-and-aft symmetry about the centre, and the shape can be approximated as ellipsoidal. At further increase of Ca, towards the limiting value for each
$D$
reaches a minimum. In this region the cross-sections of the various tori are oval, with fore-and-aft symmetry about the centre, and the shape can be approximated as ellipsoidal. At further increase of Ca, towards the limiting value for each
![]() $\unicode[STIX]{x1D706}$
,
$\unicode[STIX]{x1D706}$
,
![]() $D$
is increasing, indicating a decrease in the cross-section thickness. Note that due to the growing numerical inaccuracy that is encountered as
$D$
is increasing, indicating a decrease in the cross-section thickness. Note that due to the growing numerical inaccuracy that is encountered as
![]() $Ca\rightarrow Ca_{cr}(\unicode[STIX]{x1D706})$
, in all
$Ca\rightarrow Ca_{cr}(\unicode[STIX]{x1D706})$
, in all
![]() $\unicode[STIX]{x1D706}$
cases, the plotted curves are truncated when the inner circle radius,
$\unicode[STIX]{x1D706}$
cases, the plotted curves are truncated when the inner circle radius,
![]() $R_{min}$
, is very small, short of reporting exact values for the various
$R_{min}$
, is very small, short of reporting exact values for the various
![]() $Ca_{cr}$
(
$Ca_{cr}$
(
![]() $\unicode[STIX]{x1D706}$
). It is remarkable that the near-critical values of
$\unicode[STIX]{x1D706}$
). It is remarkable that the near-critical values of
![]() $D$
are very similar for all
$D$
are very similar for all
![]() $\unicode[STIX]{x1D706}$
,
$\unicode[STIX]{x1D706}$
,
![]() $D\sim 0.72$
.
$D\sim 0.72$
.
Typical cross-section shapes in these three regions are shown in figure 10. In figure 10(a) we show the close to circular cross-section of drops having various
![]() $\unicode[STIX]{x1D706}$
values at
$\unicode[STIX]{x1D706}$
values at
![]() $Ca=0.04$
. Note that the more viscous the drop is, the shorter is the torus major radius and the larger is the cross-section radius (which is approximately its minor radius). At high
$Ca=0.04$
. Note that the more viscous the drop is, the shorter is the torus major radius and the larger is the cross-section radius (which is approximately its minor radius). At high
![]() $\unicode[STIX]{x1D706}$
values, the viscous drag induced by the ambient flow is larger than at lower
$\unicode[STIX]{x1D706}$
values, the viscous drag induced by the ambient flow is larger than at lower
![]() $\unicode[STIX]{x1D706}$
values. Thus, a shorter torus radius is needed to increase a stronger portion of surface tension force that resists the drag. This difference is reflected in the order deformation values depicted in figure 9 for small Ca – where the smaller is
$\unicode[STIX]{x1D706}$
values. Thus, a shorter torus radius is needed to increase a stronger portion of surface tension force that resists the drag. This difference is reflected in the order deformation values depicted in figure 9 for small Ca – where the smaller is
![]() $\unicode[STIX]{x1D706}$
, the larger is
$\unicode[STIX]{x1D706}$
, the larger is
![]() $D$
. In figure 10(b) we show cross-sections typical to the intermediate Ca values,
$D$
. In figure 10(b) we show cross-sections typical to the intermediate Ca values,
![]() $Ca=0.14$
, where evidently all have an almost perfect ellipsoidal shape with similar thickness and with centres ‘crowded’ in a small range of distances
$Ca=0.14$
, where evidently all have an almost perfect ellipsoidal shape with similar thickness and with centres ‘crowded’ in a small range of distances
![]() $r\sim 0.9$
from the axis of symmetry. At this intermediate-Ca region, all deformation factors, depicted in figure 9, are close to their minima. In figure 10(c) we assembled the cross-sections of tori at capillary numbers close to the upper limit ones. It is evident that the tori are not at complete collapse, as their values of the various
$r\sim 0.9$
from the axis of symmetry. At this intermediate-Ca region, all deformation factors, depicted in figure 9, are close to their minima. In figure 10(c) we assembled the cross-sections of tori at capillary numbers close to the upper limit ones. It is evident that the tori are not at complete collapse, as their values of the various
![]() $R_{min}$
are still of
$R_{min}$
are still of
![]() $O$
(0.01). There are several structural phenomena to signify in this region. The symmetric elliptic shapes are lost and the sections assume oval forms that resemble egg shapes. When
$O$
(0.01). There are several structural phenomena to signify in this region. The symmetric elliptic shapes are lost and the sections assume oval forms that resemble egg shapes. When
![]() $\unicode[STIX]{x1D706}\gtrsim O(1)$
, the sharper portion of the oval form is directed towards the centre of the torus, reflecting the reaction to the squeezing effect of the relatively higher viscous drag in these cases. When
$\unicode[STIX]{x1D706}\gtrsim O(1)$
, the sharper portion of the oval form is directed towards the centre of the torus, reflecting the reaction to the squeezing effect of the relatively higher viscous drag in these cases. When
![]() $\unicode[STIX]{x1D706}\ll 1$
, the form is reversed, as the viscous drag is grossly diminished, and the surface shapes are mainly dictated by competition of opposing normal forces, i.e. pressure and capillary. Note that the values of
$\unicode[STIX]{x1D706}\ll 1$
, the form is reversed, as the viscous drag is grossly diminished, and the surface shapes are mainly dictated by competition of opposing normal forces, i.e. pressure and capillary. Note that the values of
![]() $R_{max}$
and the torus thickness in all the cases are almost identical, as is reflected in similar near-critical values of
$R_{max}$
and the torus thickness in all the cases are almost identical, as is reflected in similar near-critical values of
![]() $D$
. This effect is opposite to that shown in figure 9(a) when
$D$
. This effect is opposite to that shown in figure 9(a) when
![]() $Ca\ll 1$
. In this region, at constant Ca, the deformation parameter increases with an increase of the viscosity ratio, opposite to what is shown in figure 9 when
$Ca\ll 1$
. In this region, at constant Ca, the deformation parameter increases with an increase of the viscosity ratio, opposite to what is shown in figure 9 when
![]() $Ca\ll 1$
.
$Ca\ll 1$
.
The change of shape near the critical conditions, which depends on the viscosity ratio, raises the question if a related effect can be observed in the streamlines structure in the ambient fluid or within the torus. In particular, one can expect the formation of close streamline regions near the axis of symmetry, as reported in Zabarankin (Reference Zabarankin2016) for ‘stationary’ tori with circular cross-section. Should this be the case, stagnation points would appear on the cross-section profile other than the two along the
![]() $r$
axis at
$r$
axis at
![]() $z=0$
. We have calculated the tangential velocity along the surface for high and low values of
$z=0$
. We have calculated the tangential velocity along the surface for high and low values of
![]() $\unicode[STIX]{x1D706}$
, and found no such stagnation points, irrespective of the deformation pattern. Several examples, spanning a wide range of the viscosity ratio, are shown in figure 11. Thus, we conclude that the stationary external flow fields contain only open streamlines, as is the undisturbed flow in the absence of the drop.
$\unicode[STIX]{x1D706}$
, and found no such stagnation points, irrespective of the deformation pattern. Several examples, spanning a wide range of the viscosity ratio, are shown in figure 11. Thus, we conclude that the stationary external flow fields contain only open streamlines, as is the undisturbed flow in the absence of the drop.
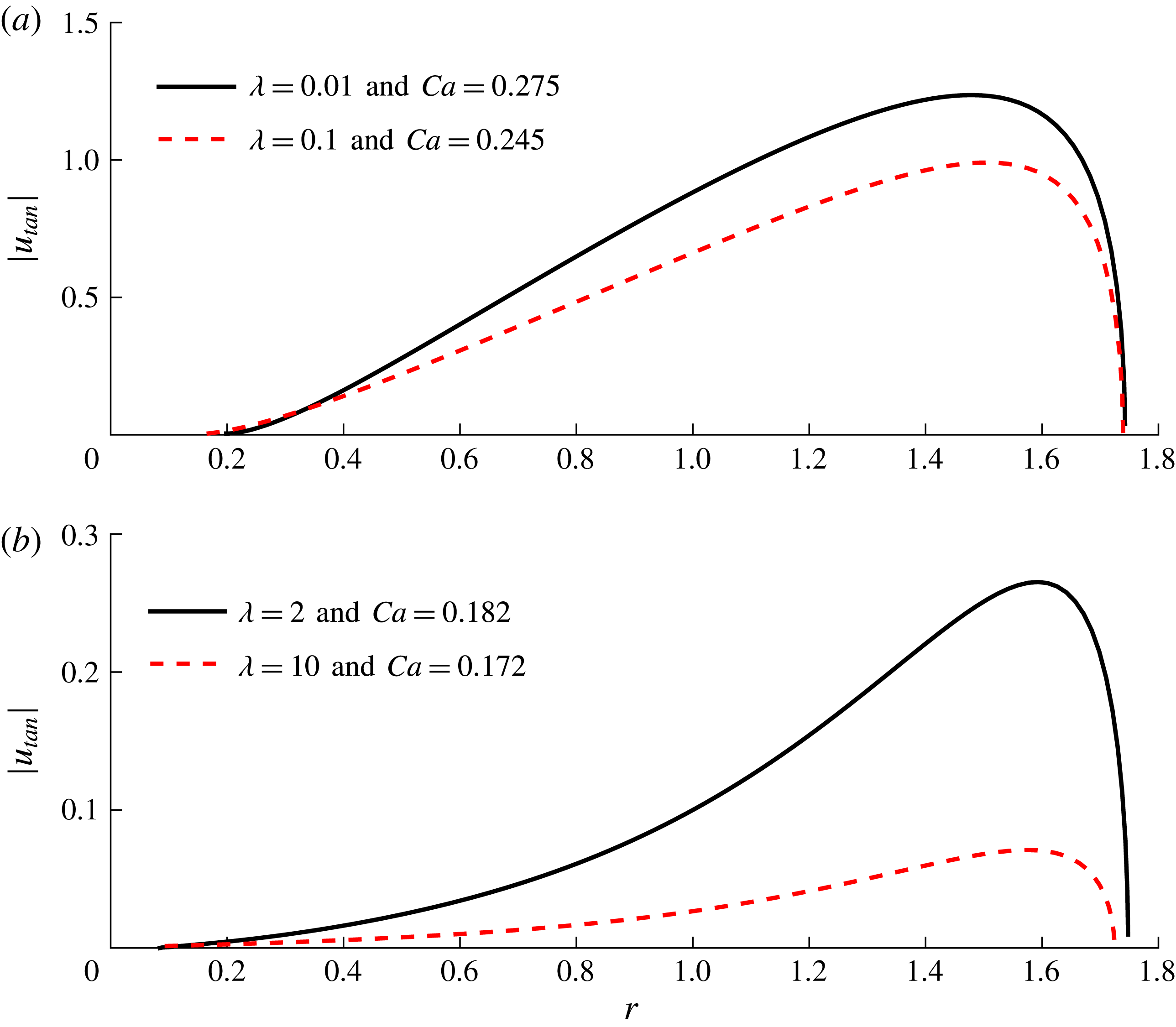
Figure 11. Tangential velocity component on the interface of deformed tori at near-critical Ca. The origin of the abscissa coincides with the axis of symmetry.
This observation is supported by the patterns of open and close streamlines that are depicted in figure 12. Here, it is clearly evident that the outer streamlines are open for low and high
![]() $\unicode[STIX]{x1D706}$
, as was also reported earlier by Zabarankin et al. (Reference Zabarankin, Lavrenteva and Nir2015) for the case
$\unicode[STIX]{x1D706}$
, as was also reported earlier by Zabarankin et al. (Reference Zabarankin, Lavrenteva and Nir2015) for the case
![]() $\unicode[STIX]{x1D706}=1$
. Furthermore, the stationarity is also demonstrated, where both outer open lines and inner closed vortices become tangent to the deformed cross-section and the surface is a streamline as well. Note that the inner region of the torus contains two vortices, moving in opposite directions, in contrast to the single vortex that exists when the torus translates along the line of axial symmetry (e.g. as is shown in Machu et al.
Reference Machu, Meile, Nitsche and Schaflinger2001a
).
$\unicode[STIX]{x1D706}=1$
. Furthermore, the stationarity is also demonstrated, where both outer open lines and inner closed vortices become tangent to the deformed cross-section and the surface is a streamline as well. Note that the inner region of the torus contains two vortices, moving in opposite directions, in contrast to the single vortex that exists when the torus translates along the line of axial symmetry (e.g. as is shown in Machu et al.
Reference Machu, Meile, Nitsche and Schaflinger2001a
).

Figure 12. Streamlines patterns of unsteady stationary tori at intermediate and high (near collapse) capillary numbers. (a)
![]() $\unicode[STIX]{x1D706}=0.1$
,
$\unicode[STIX]{x1D706}=0.1$
,
![]() $Ca=0.14$
; (b)
$Ca=0.14$
; (b)
![]() $\unicode[STIX]{x1D706}=0.1$
,
$\unicode[STIX]{x1D706}=0.1$
,
![]() $Ca=0.245$
; (c)
$Ca=0.245$
; (c)
![]() $\unicode[STIX]{x1D706}=10$
,
$\unicode[STIX]{x1D706}=10$
,
![]() $Ca=0.14$
; (d)
$Ca=0.14$
; (d)
![]() $\unicode[STIX]{x1D706}=10$
,
$\unicode[STIX]{x1D706}=10$
,
![]() $Ca=0.172$
.
$Ca=0.172$
.
It is interesting to compare our stationary tori results with those obtained recently by Zabarankin (Reference Zabarankin2016) for tori having a circular cross-section. Of course, only relevant parameters should be compared as the tori in Zabarankin (Reference Zabarankin2016) are not permitted to deform, and therefore they exist as stationary only in the limit
![]() $Ca\rightarrow 0$
. Recall the procedure described above and illustrated in figure 7, where the stationary tori were determined numerically from tori with circular cross-section that deform but do not collapse or expand. The initial radius of such a torus
$Ca\rightarrow 0$
. Recall the procedure described above and illustrated in figure 7, where the stationary tori were determined numerically from tori with circular cross-section that deform but do not collapse or expand. The initial radius of such a torus
![]() $R_{c}$
can be compared to the radius of Zabarankin’s ’stationary’ torus, which is taken from his table 1. The comparison is depicted in figure 13 for several values of the viscosity ratio
$R_{c}$
can be compared to the radius of Zabarankin’s ’stationary’ torus, which is taken from his table 1. The comparison is depicted in figure 13 for several values of the viscosity ratio
![]() $\unicode[STIX]{x1D706}$
. In this figure the results of Zabarankin (Reference Zabarankin2016) are shown as full circles and our numerical results include both
$\unicode[STIX]{x1D706}$
. In this figure the results of Zabarankin (Reference Zabarankin2016) are shown as full circles and our numerical results include both
![]() $R_{c}$
and
$R_{c}$
and
![]() $R$
, the actual radius of the centre of the deformed cross-section.
$R$
, the actual radius of the centre of the deformed cross-section.

Figure 13. A comparison of stationary tori with deformed cross-section with ‘stationary’ tori having circular cross-section (dots, Zabarankin Reference Zabarankin2016).
![]() $R_{c}$
, solid lines,
$R_{c}$
, solid lines,
![]() $R$
, dashed lines.
$R$
, dashed lines.
It is clearly evident that in the region of very small capillary number,
![]() $Ca<0.05$
, there is an agreement, implying that the almost perfect circular cross-sections, obtained via the numerical algorithm used in this work, are in good agreement with those obtained analytically via conformal mapping. However, as Ca increases, the results predicted by the two methods diverge, reflecting the shape difference between the deformed and circular cross-section in the respective cases. As the torus deforms from its initial circular cross-section shape, both
$Ca<0.05$
, there is an agreement, implying that the almost perfect circular cross-sections, obtained via the numerical algorithm used in this work, are in good agreement with those obtained analytically via conformal mapping. However, as Ca increases, the results predicted by the two methods diverge, reflecting the shape difference between the deformed and circular cross-section in the respective cases. As the torus deforms from its initial circular cross-section shape, both
![]() $R_{c}$
and
$R_{c}$
and
![]() $R$
deviate from the ideal case as well as from each other. The actual
$R$
deviate from the ideal case as well as from each other. The actual
![]() $R$
of the deformed stationary torus always exceeds
$R$
of the deformed stationary torus always exceeds
![]() $R_{c}$
(see also figure 7). Note, that Zabarankin (Reference Zabarankin2016) ‘stationary’ torus
$R_{c}$
(see also figure 7). Note, that Zabarankin (Reference Zabarankin2016) ‘stationary’ torus
![]() $R$
provides a very good approximation of
$R$
provides a very good approximation of
![]() $R_{c}$
, especially for
$R_{c}$
, especially for
![]() $\unicode[STIX]{x1D706}\geqslant O(1)$
.
$\unicode[STIX]{x1D706}\geqslant O(1)$
.

Figure 14. Critical capillary number as a function of the viscosity ratio.
Another comparison can be made between the near-critical Ca obtained in this work for the deforming tori and the critical Ca estimated by Zabarankin (Reference Zabarankin2016) for tori with circular cross-section. This comparison is given in figure 14, where three cases are depicted. The near-critical Ca and Zabarankin’s critical Ca for the existence of stationary tori are shown by solid and dashed–dotted curves, respectively. In addition we show the critical capillary number for the simply connected flat drop under a similar compressional flow reported by Zabarankin et al. (Reference Zabarankin, Smagin, Lavrenteva and Nir2013) (dashed line).
The difference between the critical condition which applies to tori with circular cross-section and tori with deformed cross-section is evident. At small viscosity ratio the stationary deformed tori exist for higher Ca values, while at high
![]() $\unicode[STIX]{x1D706}$
the order is reversed, and the transition occurs at some
$\unicode[STIX]{x1D706}$
the order is reversed, and the transition occurs at some
![]() $\unicode[STIX]{x1D706}$
of
$\unicode[STIX]{x1D706}$
of
![]() $O(1)$
. In addition, the similarity of near-critical stationary deformed tori and the critical flat simply connected drops, that emerge from the same problem, defined by equations (2.2)–(2.4) subject to
$O(1)$
. In addition, the similarity of near-critical stationary deformed tori and the critical flat simply connected drops, that emerge from the same problem, defined by equations (2.2)–(2.4) subject to
![]() $u_{n}=0$
, is striking. They are separated by a small gap, which deserves separate special attention.
$u_{n}=0$
, is striking. They are separated by a small gap, which deserves separate special attention.
5 Concluding remarks
In this communication we report on a study of the dynamic behaviour and stationary states of toroidal drops embedded in a viscous fluid under a slow compressional flow. The study employed numerical evaluation via a boundary integral representation and the main focus was on the effect of the viscosity ratio,
![]() $\unicode[STIX]{x1D706}$
, of the two immiscible fluids. The case of equal viscosity,
$\unicode[STIX]{x1D706}$
, of the two immiscible fluids. The case of equal viscosity,
![]() $\unicode[STIX]{x1D706}=1$
, studied earlier by Zabarankin et al. (Reference Zabarankin, Lavrenteva and Nir2015), is incorporated as a particular case of the general results. The dynamic deformation of drops initiated from tori with circular cross-section, was studied for short and long time. For relatively large initial radius the torus expands to infinity and the cross-section first deforms to an oval or flattened shape, before eventually regaining a circular form. In the initial stages, more viscous tori expand faster than less viscous tori. However, an interplay of viscous and surface tension forcing on the drop of complex toroidal geometry may result in a non-monotonic dependence on the expansion level at advanced stages.
$\unicode[STIX]{x1D706}=1$
, studied earlier by Zabarankin et al. (Reference Zabarankin, Lavrenteva and Nir2015), is incorporated as a particular case of the general results. The dynamic deformation of drops initiated from tori with circular cross-section, was studied for short and long time. For relatively large initial radius the torus expands to infinity and the cross-section first deforms to an oval or flattened shape, before eventually regaining a circular form. In the initial stages, more viscous tori expand faster than less viscous tori. However, an interplay of viscous and surface tension forcing on the drop of complex toroidal geometry may result in a non-monotonic dependence on the expansion level at advanced stages.
Increasing the inner viscosity increases
![]() $\unicode[STIX]{x1D706}$
with no change in Ca. As the drop becomes more ‘solid like’, higher resistance and slower deformation can be expected. One of the most interesting findings of the paper is that this is not always the case. An example is shown in figure 5, and a possible explanation is as follows: there are stationary states in the system. Naturally, close to a steady state the dynamic shape-changes slow down (at the steady state the shape does not change at all). A change of the viscosity ratio affects also the stationary shape. Thus, a shape that is close to a steady one for a certain
$\unicode[STIX]{x1D706}$
with no change in Ca. As the drop becomes more ‘solid like’, higher resistance and slower deformation can be expected. One of the most interesting findings of the paper is that this is not always the case. An example is shown in figure 5, and a possible explanation is as follows: there are stationary states in the system. Naturally, close to a steady state the dynamic shape-changes slow down (at the steady state the shape does not change at all). A change of the viscosity ratio affects also the stationary shape. Thus, a shape that is close to a steady one for a certain
![]() $\unicode[STIX]{x1D706}$
, can be further off stationarity and deform faster when
$\unicode[STIX]{x1D706}$
, can be further off stationarity and deform faster when
![]() $\unicode[STIX]{x1D706}$
increases. When a certain shape is far from stationarity for two values of
$\unicode[STIX]{x1D706}$
increases. When a certain shape is far from stationarity for two values of
![]() $\unicode[STIX]{x1D706}$
, the deformations changes are slower for a higher viscosity ratio, as is evident in the case presented in figure 3.
$\unicode[STIX]{x1D706}$
, the deformations changes are slower for a higher viscosity ratio, as is evident in the case presented in figure 3.
For small initial
![]() $R$
the torus collapses towards the axis of symmetry and the cross-section deforms, and in some cases the interface develops a circular dimple around the axis. Our general viscosity model is also compared with the experimental results of Pairam & Fernández-Nieves (Reference Pairam and Fernández-Nieves2009), and it is shown that the collapse of axisymmetric low-viscosity tori, after quenching the flow, is modelled correctly by applying the numerical model at small viscosity ratio.
$R$
the torus collapses towards the axis of symmetry and the cross-section deforms, and in some cases the interface develops a circular dimple around the axis. Our general viscosity model is also compared with the experimental results of Pairam & Fernández-Nieves (Reference Pairam and Fernández-Nieves2009), and it is shown that the collapse of axisymmetric low-viscosity tori, after quenching the flow, is modelled correctly by applying the numerical model at small viscosity ratio.
At relatively low capillary number, in between these two zones, there exists a critical radius,
![]() $R_{c}$
, at which the torus initially deforms and maintains a constant position and deformation for a considerable duration of time before deviating from it towards expansion or collapse. This dynamic behaviour applies to all viscosity ratios.
$R_{c}$
, at which the torus initially deforms and maintains a constant position and deformation for a considerable duration of time before deviating from it towards expansion or collapse. This dynamic behaviour applies to all viscosity ratios.
The dynamic behaviour initiated at
![]() $R_{c}$
suggested the existence of stationary yet absolutely unstable tori. A summary of such unstable stationary states spanning a wide range of low to high viscosity ratio is depicted in figures 9 and 10. For each viscosity ratio there is a critical capillary number
$R_{c}$
suggested the existence of stationary yet absolutely unstable tori. A summary of such unstable stationary states spanning a wide range of low to high viscosity ratio is depicted in figures 9 and 10. For each viscosity ratio there is a critical capillary number
![]() $Ca_{cr}$
beyond which a stationary state does not exist. For such supercritical values of Ca, the torus either experiences collapse during the initial deformation or, if it does not collapse, it departs to expansion and a critical radius,
$Ca_{cr}$
beyond which a stationary state does not exist. For such supercritical values of Ca, the torus either experiences collapse during the initial deformation or, if it does not collapse, it departs to expansion and a critical radius,
![]() $R_{c}$
, is not found.
$R_{c}$
, is not found.
The stationary deformation patterns of the toroidal cross-section are similar to those obtained in the particular case of
![]() $\unicode[STIX]{x1D706}=1$
– i.e. at relatively small Ca the cross-section is nearly circular, at intermediate Ca it is nearly oval, while at higher capillary numbers it resembles egg shapes. It is also demonstrated that in all
$\unicode[STIX]{x1D706}=1$
– i.e. at relatively small Ca the cross-section is nearly circular, at intermediate Ca it is nearly oval, while at higher capillary numbers it resembles egg shapes. It is also demonstrated that in all
![]() $\unicode[STIX]{x1D706}$
cases there exists no stagnation point on the interface except on the plane
$\unicode[STIX]{x1D706}$
cases there exists no stagnation point on the interface except on the plane
![]() $z=0$
and, hence, the external and internal flows contain no separation of the streamlines patterns.
$z=0$
and, hence, the external and internal flows contain no separation of the streamlines patterns.
It should be stressed that the numerical study shows that, at all viscosity ratios, stationary tori always deform from the circular shape and that circular cross-sections exist only as the tori are expanded to infinity. Indeed, the comparison with the theoretical results, obtained by Zabarankin (Reference Zabarankin2016) via conformal mapping techniques, shows an interesting agreement when the numerical evaluation of the cross-section deformation is nearly circular, i.e. at small Ca, while deviations are evident as the capillary number increases, when the cross-section shapes deviate as well.
Finally, it should be noted that the near-critical capillary numbers reported in this study are very similar to the critical capillary number reported by Zabarankin et al. (Reference Zabarankin, Smagin, Lavrenteva and Nir2013) for steady deformation of a singly connected flat drop in the same forcing compressional flow. Indeed, the two cases result from the same problem, i.e. equations (2.2a
)–(2.4) subject to
![]() $u_{n}=0$
at S, and thus comprise two branches separated only by the pattern of deformation. The connectivity between these branches and the possible existence of yet a third branch is currently under investigation.
$u_{n}=0$
at S, and thus comprise two branches separated only by the pattern of deformation. The connectivity between these branches and the possible existence of yet a third branch is currently under investigation.
Acknowledgements
This work is supported by the Israel Science Foundation (grant no. ISF 327/14). O.M.L. also acknowledges the support of the Israel Ministry of Immigrant Absorption.