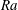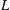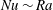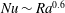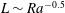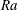1. Introduction
Porous medium convection is a key environmental process that has been extensively studied since the 1940s (Horton & Rogers Reference Horton and Rogers1945; Lapwood Reference Lapwood1948) due to its numerous geoscientific applications including oil recovery, groundwater flow and geothermal energy extraction (Phillips Reference Phillips1991, Reference Phillips2009; Nield & Bejan Reference Nield and Bejan2006). More fundamentally, as a paradigm for forced-dissipative infinite-dimensional nonlinear dynamical systems, buoyancy-driven convection in a fluid-saturated porous layer retains much of the rich dynamics of Rayleigh–Bénard convection in a pure fluid layer yet provides a simpler physical and mathematical setting for studying instabilities, bifurcations, pattern formation and spatiotemporally chaotic dynamics. Recently, this system has again become the subject of intense scrutiny due to applications in carbon dioxide sequestration in terrestrial aquifers, one promising means of reducing the emission of greenhouse gases into the atmosphere (Metz et al. Reference Metz, Davidson, de Coninck, Loos and Meyer2005).
The flow in a horizontal porous layer uniformly heated from below undergoes a sequence of bifurcations as the Rayleigh number
![]() $\mathit{Ra}$
, the normalised temperature drop across the layer, is increased. When
$\mathit{Ra}$
, the normalised temperature drop across the layer, is increased. When
![]() $\mathit{Ra}>4{\rm\pi}^{2}$
, the simple conduction solution becomes linearly unstable (Nield & Bejan Reference Nield and Bejan2006) and steady
$\mathit{Ra}>4{\rm\pi}^{2}$
, the simple conduction solution becomes linearly unstable (Nield & Bejan Reference Nield and Bejan2006) and steady
![]() $O(1)$
aspect-ratio large-scale convection rolls emerge. In a two-dimensional (2D) domain, the steady rolls strengthen but remain stable as
$O(1)$
aspect-ratio large-scale convection rolls emerge. In a two-dimensional (2D) domain, the steady rolls strengthen but remain stable as
![]() $\mathit{Ra}$
is increased up to
$\mathit{Ra}$
is increased up to
![]() $\mathit{Ra}\approx 400$
(Schubert & Straus Reference Schubert and Straus1982). For
$\mathit{Ra}\approx 400$
(Schubert & Straus Reference Schubert and Straus1982). For
![]() $\mathit{Ra}$
slightly greater than 400, instabilities within the upper and lower thermal boundary layers generate small-scale features that are advected around the cell by the large-scale rolls. In this moderate-
$\mathit{Ra}$
slightly greater than 400, instabilities within the upper and lower thermal boundary layers generate small-scale features that are advected around the cell by the large-scale rolls. In this moderate-
![]() $\mathit{Ra}$
parameter regime,
$\mathit{Ra}$
parameter regime,
![]() $400\lesssim \mathit{Ra}\lesssim 1300$
, the resulting flow exhibits a series of transitions between periodic and quasi-periodic roll motions, as discussed in considerable detail by Kimura, Schubert & Straus (Reference Kimura, Schubert and Straus1986, Reference Kimura, Schubert and Straus1987), Aidun & Steen (Reference Aidun and Steen1987) and Graham & Steen (Reference Graham and Steen1992, Reference Graham and Steen1994). However, the rolls do not completely lose coherence until
$400\lesssim \mathit{Ra}\lesssim 1300$
, the resulting flow exhibits a series of transitions between periodic and quasi-periodic roll motions, as discussed in considerable detail by Kimura, Schubert & Straus (Reference Kimura, Schubert and Straus1986, Reference Kimura, Schubert and Straus1987), Aidun & Steen (Reference Aidun and Steen1987) and Graham & Steen (Reference Graham and Steen1992, Reference Graham and Steen1994). However, the rolls do not completely lose coherence until
![]() $\mathit{Ra}\gtrsim 1300$
. The overall dynamics is then better characterised as spatiotemporally chaotic plume shedding from the boundaries rather than quasi-coherent cellular flow (Otero et al.
Reference Otero, Dontcheva, Johnston, Worthing, Kurganov, Petrova and Doering2004; Hewitt, Neufeld & Lister Reference Hewitt, Neufeld and Lister2012). This marks the transition to the ‘turbulent’ high-
$\mathit{Ra}\gtrsim 1300$
. The overall dynamics is then better characterised as spatiotemporally chaotic plume shedding from the boundaries rather than quasi-coherent cellular flow (Otero et al.
Reference Otero, Dontcheva, Johnston, Worthing, Kurganov, Petrova and Doering2004; Hewitt, Neufeld & Lister Reference Hewitt, Neufeld and Lister2012). This marks the transition to the ‘turbulent’ high-
![]() $\mathit{Ra}$
regime.
$\mathit{Ra}$
regime.
The direct numerical simulations (DNS) of Hewitt et al. (Reference Hewitt, Neufeld and Lister2012) reveal that at large
![]() $\mathit{Ra}$
porous medium convection exhibits a three-region asymptotic structure: adjacent to the upper and lower walls are extremely thin thermal boundary layers, with a thickness that scales as
$\mathit{Ra}$
porous medium convection exhibits a three-region asymptotic structure: adjacent to the upper and lower walls are extremely thin thermal boundary layers, with a thickness that scales as
![]() $O(\mathit{Ra}^{-1})$
; the interior region is dominated by a nearly vertical columnar exchange flow (‘mega-plumes’) spanning the height of the domain; and the transition zone between these regions is characterised by a series of small ‘proto-plumes’ that grow from the boundaries and merge with the interior mega-plumes. Remarkably, as
$O(\mathit{Ra}^{-1})$
; the interior region is dominated by a nearly vertical columnar exchange flow (‘mega-plumes’) spanning the height of the domain; and the transition zone between these regions is characterised by a series of small ‘proto-plumes’ that grow from the boundaries and merge with the interior mega-plumes. Remarkably, as
![]() $\mathit{Ra}$
is increased, the interior columnar exchange flow becomes increasingly well organised. Hewitt et al. (Reference Hewitt, Neufeld and Lister2012) model this interior flow analytically using a single horizontal Fourier-mode ‘heat-exchanger’ solution, and extract a
$\mathit{Ra}$
is increased, the interior columnar exchange flow becomes increasingly well organised. Hewitt et al. (Reference Hewitt, Neufeld and Lister2012) model this interior flow analytically using a single horizontal Fourier-mode ‘heat-exchanger’ solution, and extract a
![]() $\mathit{Ra}^{-0.4}$
scaling for the time-mean inter-plume spacing from their simulation data. In a subsequent investigation, Hewitt, Neufeld & Lister (Reference Hewitt, Neufeld and Lister2013) show that the vertical columnar exchange flow is unstable for horizontal wavenumbers
$\mathit{Ra}^{-0.4}$
scaling for the time-mean inter-plume spacing from their simulation data. In a subsequent investigation, Hewitt, Neufeld & Lister (Reference Hewitt, Neufeld and Lister2013) show that the vertical columnar exchange flow is unstable for horizontal wavenumbers
![]() $k$
greater than
$k$
greater than
![]() $k\sim \mathit{Ra}^{5/14}$
as
$k\sim \mathit{Ra}^{5/14}$
as
![]() $\mathit{Ra}\rightarrow \infty$
, in evident agreement with their DNS results. However, their stability analysis employs the analytical heat-exchanger model – in which the upper and lower boundaries are ignored – as the pertinent base flow on the grounds that
$\mathit{Ra}\rightarrow \infty$
, in evident agreement with their DNS results. However, their stability analysis employs the analytical heat-exchanger model – in which the upper and lower boundaries are ignored – as the pertinent base flow on the grounds that
![]() $k$
is not controlled directly by the small-scale dynamics of proto-plumes near the boundary, since these have a lateral scale of
$k$
is not controlled directly by the small-scale dynamics of proto-plumes near the boundary, since these have a lateral scale of
![]() $\mathit{Ra}^{-1}$
. Nevertheless, the relevance of their stability analysis remains an open question, since the influence of the boundaries is ignored. Our view is that it is preferable to analyse the stability of (numerically) exact solutions of the complete dynamical system (i.e. in which the base flow exactly satisfies the governing equations and all boundary conditions) that also exhibit certain flow structures observed in the time-dependent simulations. Specifically, the objective of our investigation is to determine the structure and secondary stability of steady cellular solutions in porous medium convection at large Rayleigh number. Although our study is restricted to 2D configurations, we note that recent DNS of Rayleigh–Bénard convection in a three-dimensional (3D) porous layer at large Rayleigh number clearly exhibit the emergence of a three-region asymptotic structure, with an interior flow that is increasingly well described by an extension of the heat-exchanger model that consists of mega-plumes whose spacing decreases approximately as
$\mathit{Ra}^{-1}$
. Nevertheless, the relevance of their stability analysis remains an open question, since the influence of the boundaries is ignored. Our view is that it is preferable to analyse the stability of (numerically) exact solutions of the complete dynamical system (i.e. in which the base flow exactly satisfies the governing equations and all boundary conditions) that also exhibit certain flow structures observed in the time-dependent simulations. Specifically, the objective of our investigation is to determine the structure and secondary stability of steady cellular solutions in porous medium convection at large Rayleigh number. Although our study is restricted to 2D configurations, we note that recent DNS of Rayleigh–Bénard convection in a three-dimensional (3D) porous layer at large Rayleigh number clearly exhibit the emergence of a three-region asymptotic structure, with an interior flow that is increasingly well described by an extension of the heat-exchanger model that consists of mega-plumes whose spacing decreases approximately as
![]() $\mathit{Ra}^{-0.5}$
(Hewitt, Neufeld & Lister Reference Hewitt, Neufeld and Lister2014). Thus, we may reasonably expect the results of our 2D investigation to provide at least partial insight into 3D porous medium convection, too.
$\mathit{Ra}^{-0.5}$
(Hewitt, Neufeld & Lister Reference Hewitt, Neufeld and Lister2014). Thus, we may reasonably expect the results of our 2D investigation to provide at least partial insight into 3D porous medium convection, too.
The structure and stability of steady 2D porous medium convection at small to moderate Rayleigh number has been discussed in detail in many previous studies (Elder Reference Elder1967; Palm, Weber & Kvernvold Reference Palm, Weber and Kvernvold1972; Horne & O’Sullivan Reference Horne and O’Sullivan1974; Schubert & Straus Reference Schubert and Straus1982; Aidun & Steen Reference Aidun and Steen1987; Kimura et al.
Reference Kimura, Schubert and Straus1987; Graham & Steen Reference Graham and Steen1992, Reference Graham and Steen1994). The study of high-Rayleigh-number steady solutions, however, has been rather limited, in part because these solutions are unstable and exhibit fine-scale spatial structure. In the present work, we overcome these difficulties by numerically solving the steady governing equations using a Newton–Kantorovich iteration scheme (Boyd Reference Boyd2000). By investigating the dependence of the steady solutions on the domain aspect ratio
![]() $L$
, we find that there exist two qualitatively distinct types of steady convective states at large
$L$
, we find that there exist two qualitatively distinct types of steady convective states at large
![]() $\mathit{Ra}$
: for small
$\mathit{Ra}$
: for small
![]() $L$
, the flow has the heat-exchanger structure in the interior identified by Hewitt et al. (Reference Hewitt, Neufeld and Lister2012); however, as
$L$
, the flow has the heat-exchanger structure in the interior identified by Hewitt et al. (Reference Hewitt, Neufeld and Lister2012); however, as
![]() $L$
is increased, the steady convection develops a stably stratified core with a horizontal structure involving multiple Fourier modes. Comparison of the steady solutions with the long-time-averaged columnar flow observed in the DNS reveals that the latter is neither a heat exchanger nor a stably stratified core solution but instead combines certain attributes of both types of steady solutions.
$L$
is increased, the steady convection develops a stably stratified core with a horizontal structure involving multiple Fourier modes. Comparison of the steady solutions with the long-time-averaged columnar flow observed in the DNS reveals that the latter is neither a heat exchanger nor a stably stratified core solution but instead combines certain attributes of both types of steady solutions.
After characterising these steady convective states as a function of
![]() $\mathit{Ra}$
and
$\mathit{Ra}$
and
![]() $L$
, we assess their stability to small-amplitude disturbances using Floquet theory. The Floquet technique was first introduced as a tool for secondary stability analysis in fluid dynamics by Kelly (Reference Kelly1967), who applied this method to inviscid shear flows. Since then, Floquet analysis has been applied to numerous other shear and convective flows, including thermal convection (Busse Reference Busse1967, Reference Busse1972; Clever & Busse Reference Clever and Busse1974), viscous shear flows (Herbert Reference Herbert1983, Reference Herbert1988; Orszag & Patera Reference Orszag and Patera1983) and Langmuir circulation (Tandon & Leibovich Reference Tandon and Leibovich1995; Chini, Julien & Knobloch Reference Chini, Julien and Knobloch2009). In this paper, we follow Chini et al. (Reference Chini, Julien and Knobloch2009) by employing a Fourier–Chebyshev spectral method to discretise the differential eigenvalue problem derived from linearising the governing equations of porous medium convection about the fully nonlinear steady states. Our analysis reveals the existence of two types of instability for different
$L$
, we assess their stability to small-amplitude disturbances using Floquet theory. The Floquet technique was first introduced as a tool for secondary stability analysis in fluid dynamics by Kelly (Reference Kelly1967), who applied this method to inviscid shear flows. Since then, Floquet analysis has been applied to numerous other shear and convective flows, including thermal convection (Busse Reference Busse1967, Reference Busse1972; Clever & Busse Reference Clever and Busse1974), viscous shear flows (Herbert Reference Herbert1983, Reference Herbert1988; Orszag & Patera Reference Orszag and Patera1983) and Langmuir circulation (Tandon & Leibovich Reference Tandon and Leibovich1995; Chini, Julien & Knobloch Reference Chini, Julien and Knobloch2009). In this paper, we follow Chini et al. (Reference Chini, Julien and Knobloch2009) by employing a Fourier–Chebyshev spectral method to discretise the differential eigenvalue problem derived from linearising the governing equations of porous medium convection about the fully nonlinear steady states. Our analysis reveals the existence of two types of instability for different
![]() $L$
at large
$L$
at large
![]() $\mathit{Ra}$
: a bulk instability in which the most unstable disturbance spans the convective layer, and a wall instability in which the most unstable disturbance is strongly localised near the hot and cold boundaries.
$\mathit{Ra}$
: a bulk instability in which the most unstable disturbance spans the convective layer, and a wall instability in which the most unstable disturbance is strongly localised near the hot and cold boundaries.
We explore the nonlinear evolution of these secondary instabilities using high-resolution DNS. Both the bulk and the wall instability modes are shown to influence the mean inter-plume spacing at large
![]() $\mathit{Ra}$
. To obtain a reliable estimate of this mean spacing the aspect ratio of the computational domain must be sufficiently large to capture long-wavelength secondary instabilities. We quantify this inter-plume spacing by performing DNS at extreme values of
$\mathit{Ra}$
. To obtain a reliable estimate of this mean spacing the aspect ratio of the computational domain must be sufficiently large to capture long-wavelength secondary instabilities. We quantify this inter-plume spacing by performing DNS at extreme values of
![]() $\mathit{Ra}$
, up to
$\mathit{Ra}$
, up to
![]() $O(10^{5})$
, in large-
$O(10^{5})$
, in large-
![]() $L$
domains containing more than 15 pairs of plumes. The simulations show that the interior columnar exchange flow becomes very well organised for
$L$
domains containing more than 15 pairs of plumes. The simulations show that the interior columnar exchange flow becomes very well organised for
![]() $\mathit{Ra}\geqslant 39\,716$
, and that, at a given large
$\mathit{Ra}\geqslant 39\,716$
, and that, at a given large
![]() $\mathit{Ra}$
, there exists a small range of preferred plume spacings for which the bulk and wall instabilities are balanced so that the interior columnar exchange flow is statistically steady.
$\mathit{Ra}$
, there exists a small range of preferred plume spacings for which the bulk and wall instabilities are balanced so that the interior columnar exchange flow is statistically steady.
The reminder of this paper is organised as follows. In the next section, we formulate the standard mathematical model of porous medium convection and recall the key results of linear stability theory for this system. In § 3, we outline the numerical method used to find (generally unstable) steady high-
![]() $\mathit{Ra}$
solutions, describe the structure of these solutions for different aspect ratios, document the variation of heat transport with aspect ratio, identify the steady flows that maximise the heat transport as a function of both
$\mathit{Ra}$
solutions, describe the structure of these solutions for different aspect ratios, document the variation of heat transport with aspect ratio, identify the steady flows that maximise the heat transport as a function of both
![]() $\mathit{Ra}$
and
$\mathit{Ra}$
and
![]() $L$
, and quantitatively compare the mean interior columnar exchange flow manifested in DNS with the interior structure of the steady solutions. Using Floquet theory, we analyse the stability of these steady convective states in § 4. In § 5, we perform DNS strategically initialised with a superposition of the steady solutions and a small-amplitude contribution of the most unstable secondary instability eigenfunction to investigate how these steady states evolve into the statistically steady but spatiotemporally chaotic (turbulent) convective flow. Moreover, new results for the mean inter-plume spacing in porous medium convection for
$L$
, and quantitatively compare the mean interior columnar exchange flow manifested in DNS with the interior structure of the steady solutions. Using Floquet theory, we analyse the stability of these steady convective states in § 4. In § 5, we perform DNS strategically initialised with a superposition of the steady solutions and a small-amplitude contribution of the most unstable secondary instability eigenfunction to investigate how these steady states evolve into the statistically steady but spatiotemporally chaotic (turbulent) convective flow. Moreover, new results for the mean inter-plume spacing in porous medium convection for
![]() $\mathit{Ra}=O(10^{5})$
are also presented. Our conclusions are given in § 6.
$\mathit{Ra}=O(10^{5})$
are also presented. Our conclusions are given in § 6.
2. Problem formulation
We consider a 2D fluid-saturated porous layer in a domain of aspect ratio
![]() $L$
that is heated from below at
$L$
that is heated from below at
![]() $z=0$
and cooled from above at
$z=0$
and cooled from above at
![]() $z=1$
. For simplicity as well as for consistency with the numerous prior stability, dynamical systems and computational investigations of porous medium convection in a Rayleigh–Bénard configuration referenced in § 1, the evolution of the 2D velocity
$z=1$
. For simplicity as well as for consistency with the numerous prior stability, dynamical systems and computational investigations of porous medium convection in a Rayleigh–Bénard configuration referenced in § 1, the evolution of the 2D velocity
![]() $\boldsymbol{u}(\boldsymbol{x},t)=(u,w)$
, temperature
$\boldsymbol{u}(\boldsymbol{x},t)=(u,w)$
, temperature
![]() $T(\boldsymbol{x},t)$
and pressure
$T(\boldsymbol{x},t)$
and pressure
![]() $p(\boldsymbol{x},t)$
fields is presumed to be governed by the non-dimensional Darcy–Oberbeck–Boussinesq equations (Nield & Bejan Reference Nield and Bejan2006) in the infinite Darcy–Prandtl number limit:
$p(\boldsymbol{x},t)$
fields is presumed to be governed by the non-dimensional Darcy–Oberbeck–Boussinesq equations (Nield & Bejan Reference Nield and Bejan2006) in the infinite Darcy–Prandtl number limit:
Equations (2.1)–(2.3) are solved subject to the boundary conditions
and
![]() $L$
-periodicity of all fields in
$L$
-periodicity of all fields in
![]() $x$
. The Rayleigh number
$x$
. The Rayleigh number
![]() $\mathit{Ra}$
appearing in (2.2) is a dimensionless parameter quantifying the ratio of driving to damping forces:
$\mathit{Ra}$
appearing in (2.2) is a dimensionless parameter quantifying the ratio of driving to damping forces:
where
![]() ${\it\alpha}$
is the thermal expansion coefficient,
${\it\alpha}$
is the thermal expansion coefficient,
![]() $g$
is the gravitational acceleration,
$g$
is the gravitational acceleration,
![]() $T_{bot}-T_{top}$
is the dimensional temperature difference across the layer,
$T_{bot}-T_{top}$
is the dimensional temperature difference across the layer,
![]() $K$
is the Darcy permeability coefficient,
$K$
is the Darcy permeability coefficient,
![]() $H$
is the layer depth,
$H$
is the layer depth,
![]() ${\it\nu}$
is the kinematic viscosity and
${\it\nu}$
is the kinematic viscosity and
![]() ${\it\kappa}$
is the thermal diffusivity. A second control parameter governing the behaviour of this system is the domain aspect ratio
${\it\kappa}$
is the thermal diffusivity. A second control parameter governing the behaviour of this system is the domain aspect ratio
![]() $L$
. One of the key quantities of interest in convection is the Nusselt number
$L$
. One of the key quantities of interest in convection is the Nusselt number
![]() $\mathit{Nu}$
, the ratio of the heat transport in the presence of convective motion to the conductive heat transport when
$\mathit{Nu}$
, the ratio of the heat transport in the presence of convective motion to the conductive heat transport when
![]() $\boldsymbol{u}=\mathbf{0}$
:
$\boldsymbol{u}=\mathbf{0}$
:
where the angle brackets denote a long-time average; i.e. for some function
![]() $f$
$f$
From the equations of motion an alternative but equivalent expression for the Nusselt number can be derived,
where
![]() $\overline{f}=1/L\int _{0}^{L}f\,\text{d}x$
and
$\overline{f}=1/L\int _{0}^{L}f\,\text{d}x$
and
![]() $\Vert f\Vert =(\int |f|^{2}\,\text{d}x\,\text{d}z)^{1/2}$
.
$\Vert f\Vert =(\int |f|^{2}\,\text{d}x\,\text{d}z)^{1/2}$
.
One elementary solution of this system is the conduction state:
![]() $T=1-z$
,
$T=1-z$
,
![]() $\boldsymbol{u}=\mathbf{0}$
and
$\boldsymbol{u}=\mathbf{0}$
and
![]() $p=\mathit{Ra}(z-z^{2}/2)$
. A linear stability analysis can be performed by setting
$p=\mathit{Ra}(z-z^{2}/2)$
. A linear stability analysis can be performed by setting
![]() $T=(1-z)+{\it\theta}^{\star }(x,z,t)$
and
$T=(1-z)+{\it\theta}^{\star }(x,z,t)$
and
![]() $\boldsymbol{u}=(u^{\star },w^{\star })$
, where
$\boldsymbol{u}=(u^{\star },w^{\star })$
, where
![]() ${\it\theta}^{\star }$
,
${\it\theta}^{\star }$
,
![]() $u^{\star }$
and
$u^{\star }$
and
![]() $w^{\star }$
are small perturbations, and linearising (2.1)–(2.3) about the conduction solution. As first shown by Horton & Rogers (Reference Horton and Rogers1945) and Lapwood (Reference Lapwood1948), the resulting (normalised) eigenfunctions are
$w^{\star }$
are small perturbations, and linearising (2.1)–(2.3) about the conduction solution. As first shown by Horton & Rogers (Reference Horton and Rogers1945) and Lapwood (Reference Lapwood1948), the resulting (normalised) eigenfunctions are
with the corresponding eigenvalue
representing the growth rate of the given eigenmode. The eigenvalues for different
![]() $\mathit{Ra}$
, vertical mode number
$\mathit{Ra}$
, vertical mode number
![]() $m\geqslant 1$
and (continuous) horizontal wavenumber
$m\geqslant 1$
and (continuous) horizontal wavenumber
![]() $k$
(in an infinitely wide domain) are strictly real, implying that the onset of convection is to steady cells, and the largest growth rates occur for
$k$
(in an infinitely wide domain) are strictly real, implying that the onset of convection is to steady cells, and the largest growth rates occur for
![]() $m=1$
. By setting
$m=1$
. By setting
![]() ${\it\lambda}^{\star }=0$
with
${\it\lambda}^{\star }=0$
with
![]() $m=1$
, an expression for the marginal stability boundary of the conduction state can be obtained:
$m=1$
, an expression for the marginal stability boundary of the conduction state can be obtained:
![]() $\mathit{Ra}=({\rm\pi}^{2}+k^{2})^{2}/k^{2}$
. We denote the high-wavenumber branch of marginal modes by
$\mathit{Ra}=({\rm\pi}^{2}+k^{2})^{2}/k^{2}$
. We denote the high-wavenumber branch of marginal modes by
and we define
![]() $L_{c}=2{\rm\pi}/k_{c}$
as the corresponding wavelength of these marginal modes. At a given
$L_{c}=2{\rm\pi}/k_{c}$
as the corresponding wavelength of these marginal modes. At a given
![]() $\mathit{Ra}>4{\rm\pi}^{2}$
, the conduction solution will become linearly unstable for aspect ratios
$\mathit{Ra}>4{\rm\pi}^{2}$
, the conduction solution will become linearly unstable for aspect ratios
![]() $L>L_{c}$
. Alternatively, by setting
$L>L_{c}$
. Alternatively, by setting
![]() $\partial {\it\lambda}^{\star }/\partial k=0$
, we find that the wavenumber
$\partial {\it\lambda}^{\star }/\partial k=0$
, we find that the wavenumber
![]() $k_{f}$
of the fastest-growing linear mode is given by
$k_{f}$
of the fastest-growing linear mode is given by
We define
![]() $L_{f}=2{\rm\pi}/k_{f}$
as the corresponding wavelength of this fastest-growing linear mode. In the limit
$L_{f}=2{\rm\pi}/k_{f}$
as the corresponding wavelength of this fastest-growing linear mode. In the limit
![]() $\mathit{Ra}\rightarrow \infty$
,
$\mathit{Ra}\rightarrow \infty$
,
![]() $k_{f}\sim \sqrt{{\rm\pi}}\mathit{Ra}^{1/4}$
while
$k_{f}\sim \sqrt{{\rm\pi}}\mathit{Ra}^{1/4}$
while
![]() $k_{c}\sim \mathit{Ra}^{1/2}$
.
$k_{c}\sim \mathit{Ra}^{1/2}$
.
3. Steady convective states
3.1. Newton–Kantorovich method
Following Corson (Reference Corson2011), we solve the steady version of the governing equations (2.1)–(2.3) numerically using a Newton–Kantorovich (NK) iterative scheme (Boyd Reference Boyd2000). It is convenient to first introduce a stream function
![]() ${\it\psi}$
to describe the fluid velocity, so that
${\it\psi}$
to describe the fluid velocity, so that
![]() $(u,w)=(\partial _{z}{\it\psi},-\partial _{x}{\it\psi})$
. Then the time-independent dimensionless equations can be written as
$(u,w)=(\partial _{z}{\it\psi},-\partial _{x}{\it\psi})$
. Then the time-independent dimensionless equations can be written as
where
![]() $k_{s}=2{\rm\pi}/L_{s}$
is the fundamental wavenumber of the spatially periodic steady solution,
$k_{s}=2{\rm\pi}/L_{s}$
is the fundamental wavenumber of the spatially periodic steady solution,
![]() $M$
is the vertical truncation mode number,
$M$
is the vertical truncation mode number,
![]() $N$
is the horizontal truncation mode number and
$N$
is the horizontal truncation mode number and
![]() $T_{m}(z)$
is the
$T_{m}(z)$
is the
![]() $m$
th Chebyshev polynomial. In each
$m$
th Chebyshev polynomial. In each
![]() $L_{s}\times 1$
computational domain we seek steady solutions with reflection symmetry about
$L_{s}\times 1$
computational domain we seek steady solutions with reflection symmetry about
![]() $x=L_{s}/2$
and centrosymmetry within each of the two
$x=L_{s}/2$
and centrosymmetry within each of the two
![]() $L_{s}/2\times 1$
subdomains which contain a single convection cell. These symmetry constraints require
$L_{s}/2\times 1$
subdomains which contain a single convection cell. These symmetry constraints require
To employ the NK algorithm, we rearrange (3.1) and (3.2) into the following form:
where, for example,
![]() $F_{{\it\psi}_{x}}^{{\it\theta}}$
denotes the Frechet derivative of the function
$F_{{\it\psi}_{x}}^{{\it\theta}}$
denotes the Frechet derivative of the function
![]() $F^{{\it\theta}}({\it\psi}_{x},{\it\psi}_{z},{\it\theta}_{x},{\it\theta}_{z})$
with respect to
$F^{{\it\theta}}({\it\psi}_{x},{\it\psi}_{z},{\it\theta}_{x},{\it\theta}_{z})$
with respect to
![]() ${\it\psi}_{x}$
. After defining the correction terms
${\it\psi}_{x}$
. After defining the correction terms
and evaluating the Frechet derivatives, the linear differential equations for the corrections can be expressed as
where
![]() $\hat{{\it\phi}}_{n}\equiv \text{Im}\{\hat{{\it\psi}}_{n}\}$
is real. Then, for a given horizontal wavenumber
$\hat{{\it\phi}}_{n}\equiv \text{Im}\{\hat{{\it\psi}}_{n}\}$
is real. Then, for a given horizontal wavenumber
![]() $nk_{s}$
, (3.10) and (3.11) become
$nk_{s}$
, (3.10) and (3.11) become
![]() $D_{zz}$
is the second partial derivative operator with respect to
$D_{zz}$
is the second partial derivative operator with respect to
![]() $z$
,
$z$
,
![]() $g_{n}^{i}$
and
$g_{n}^{i}$
and
![]() $h_{n}^{i}$
can be obtained by calculating the convolution of the non-constant coefficient terms on the left-hand side of (3.11) for each iterate and
$h_{n}^{i}$
can be obtained by calculating the convolution of the non-constant coefficient terms on the left-hand side of (3.11) for each iterate and
![]() $\hat{f}_{n}^{i}$
represents the coefficients of the right-hand side of (3.11) in Fourier space at the
$\hat{f}_{n}^{i}$
represents the coefficients of the right-hand side of (3.11) in Fourier space at the
![]() $i$
th iterate. We solve (3.13) and (3.14) numerically using a Chebyshev spectral collocation method.
$i$
th iterate. We solve (3.13) and (3.14) numerically using a Chebyshev spectral collocation method.
Although the NK method is only locally convergent, the basin of attraction (in the space of initial iterates) can be expanded by updating the variables for each iterate using
where
![]() $0\leqslant a\leqslant 1$
. The step-length coefficient
$0\leqslant a\leqslant 1$
. The step-length coefficient
![]() $a$
is reduced whenever
$a$
is reduced whenever
![]() $F_{res}^{i+1}>bF_{res}^{i}$
, where
$F_{res}^{i+1}>bF_{res}^{i}$
, where
![]() $F_{res}^{i}$
is the norm of the residual of the steady governing equations at the
$F_{res}^{i}$
is the norm of the residual of the steady governing equations at the
![]() $i$
th iterate and
$i$
th iterate and
![]() $b\approx 1$
is an adjustable parameter. The iteration is continued until
$b\approx 1$
is an adjustable parameter. The iteration is continued until
![]() $F_{res}^{i+1}<10^{-7}$
, and then the spatial resolution is increased until the relative error in
$F_{res}^{i+1}<10^{-7}$
, and then the spatial resolution is increased until the relative error in
![]() $\mathit{Nu}$
is less than
$\mathit{Nu}$
is less than
![]() $10^{-5}$
.
$10^{-5}$
.
Computations are performed for a discrete set of
![]() $\mathit{Ra}=50\times 10^{(\hat{\jmath }-1)/10}$
from
$\mathit{Ra}=50\times 10^{(\hat{\jmath }-1)/10}$
from
![]() $\mathit{Ra}=50$
to
$\mathit{Ra}=50$
to
![]() $\mathit{Ra}=31\,548$
and
$\mathit{Ra}=31\,548$
and
![]() $L_{s}=0.01\times 10^{(\hat{k}-1)/10}$
(for integer
$L_{s}=0.01\times 10^{(\hat{k}-1)/10}$
(for integer
![]() $\hat{\jmath }$
and
$\hat{\jmath }$
and
![]() $\hat{k}$
). For each
$\hat{k}$
). For each
![]() $\mathit{Ra}$
, we first solve the steady governing equations for a small aspect ratio
$\mathit{Ra}$
, we first solve the steady governing equations for a small aspect ratio
![]() $L_{s}$
that is slightly greater than
$L_{s}$
that is slightly greater than
![]() $L_{c}$
, and then use that solution as the initial guess for a case with larger
$L_{c}$
, and then use that solution as the initial guess for a case with larger
![]() $L_{s}$
.
$L_{s}$
.

Figure 1. Temperature and stream function fields at
![]() $\mathit{Ra}=9976~(L_{c}=0.063)$
: (a)
$\mathit{Ra}=9976~(L_{c}=0.063)$
: (a)
![]() $L_{s}=0.1$
; (b)
$L_{s}=0.1$
; (b)
![]() $L_{s}=0.1585$
; (c)
$L_{s}=0.1585$
; (c)
![]() $L_{s}=0.3162$
; (d)
$L_{s}=0.3162$
; (d)
![]() $L_{s}=0.5012$
. The aspect ratio in (c) is close to the mean inter-plume spacing
$L_{s}=0.5012$
. The aspect ratio in (c) is close to the mean inter-plume spacing
![]() $L_{m}=0.319$
from DNS performed in a domain with
$L_{m}=0.319$
from DNS performed in a domain with
![]() $L=5.01$
. At small
$L=5.01$
. At small
![]() $L_{s}$
(a,b) the interior streamlines are independent of
$L_{s}$
(a,b) the interior streamlines are independent of
![]() $z$
. However, as
$z$
. However, as
![]() $L_{s}$
is increased (c,d) the interior streamlines become
$L_{s}$
is increased (c,d) the interior streamlines become
![]() $z$
-dependent.
$z$
-dependent.
3.2. Solution structure
The structure of steady convection at large
![]() $\mathit{Ra}$
depends on
$\mathit{Ra}$
depends on
![]() $L_{s}$
. When
$L_{s}$
. When
![]() $L_{s}<L_{c}$
, the only steady solution is the conduction state. As
$L_{s}<L_{c}$
, the only steady solution is the conduction state. As
![]() $L_{s}$
is increased, the conduction solution becomes linearly unstable, and two thin thermal boundary layers arise near the upper and lower walls (figure 1). Unlike the unsteady flow observed in DNS, the proto-plumes are absent in the steady solution. Near the walls there exists a boundary layer in the temperature field and a thicker boundary layer in the stream function field. Away from these nested boundary layers, the interior structure for small
$L_{s}$
is increased, the conduction solution becomes linearly unstable, and two thin thermal boundary layers arise near the upper and lower walls (figure 1). Unlike the unsteady flow observed in DNS, the proto-plumes are absent in the steady solution. Near the walls there exists a boundary layer in the temperature field and a thicker boundary layer in the stream function field. Away from these nested boundary layers, the interior structure for small
![]() $L_{s}$
is quite simple: the temperature deviation from the horizontal mean
$L_{s}$
is quite simple: the temperature deviation from the horizontal mean
![]() ${\it\theta}^{\prime }=T-\overline{T}$
and the stream function
${\it\theta}^{\prime }=T-\overline{T}$
and the stream function
![]() ${\it\psi}$
are almost independent of
${\it\psi}$
are almost independent of
![]() $z$
, so their
$z$
, so their
![]() $z$
-derivatives are small (figure 1
a,b; figure 2
a,b), and there exists only a single non-zero horizontal Fourier mode (figure 2
a,b). Indeed, this type of steady interior flow is well approximated using the analytical heat-exchanger solution
$z$
-derivatives are small (figure 1
a,b; figure 2
a,b), and there exists only a single non-zero horizontal Fourier mode (figure 2
a,b). Indeed, this type of steady interior flow is well approximated using the analytical heat-exchanger solution

Figure 2. The
![]() $z$
-dependent Fourier components of the temperature field for steady convective states at
$z$
-dependent Fourier components of the temperature field for steady convective states at
![]() $\mathit{Ra}=9976$
: (a)
$\mathit{Ra}=9976$
: (a)
![]() $L_{s}=0.1$
; (b)
$L_{s}=0.1$
; (b)
![]() $L_{s}=0.1585$
; (c)
$L_{s}=0.1585$
; (c)
![]() $L_{s}=0.3162$
; (d)
$L_{s}=0.3162$
; (d)
![]() $L_{s}=0.5012$
. At small
$L_{s}=0.5012$
. At small
![]() $L_{s}$
(a,b) the horizontal-mean temperature in the interior agrees closely with the analytical heat-exchanger solution; in the core, only a single (non-mean) Fourier mode is active and the temperature fluctuations are nearly independent of
$L_{s}$
(a,b) the horizontal-mean temperature in the interior agrees closely with the analytical heat-exchanger solution; in the core, only a single (non-mean) Fourier mode is active and the temperature fluctuations are nearly independent of
![]() $z$
. However, as
$z$
. However, as
![]() $L_{s}$
is increased (c,d) more Fourier modes arise and the structure of the steady solutions departs from that of the analytical heat-exchanger solution even in the interior.
$L_{s}$
is increased (c,d) more Fourier modes arise and the structure of the steady solutions departs from that of the analytical heat-exchanger solution even in the interior.
Perhaps not surprisingly, as
![]() $L_{s}$
is increased the steady large-
$L_{s}$
is increased the steady large-
![]() $\mathit{Ra}$
numerical solutions do not retain the heat-exchanger structure in the interior. Instead, the streamlines deviate from the vertical (figure 1
c,d), and multiple horizontal Fourier modes are excited, although the fundamental mode still dominates the flow (figure 2
c,d). Moreover, when
$\mathit{Ra}$
numerical solutions do not retain the heat-exchanger structure in the interior. Instead, the streamlines deviate from the vertical (figure 1
c,d), and multiple horizontal Fourier modes are excited, although the fundamental mode still dominates the flow (figure 2
c,d). Moreover, when
![]() $L_{s}$
is sufficiently large, the numerically computed
$L_{s}$
is sufficiently large, the numerically computed
![]() $\overline{T}$
clearly deviates from that predicted by the heat-exchanger solution. In fact, the slope of
$\overline{T}$
clearly deviates from that predicted by the heat-exchanger solution. In fact, the slope of
![]() $\overline{T}$
at the mid-plane
$\overline{T}$
at the mid-plane
![]() $z=0.5$
becomes positive, implying that hotter fluid overlies colder fluid in the interior. We refer to this class of numerically computed steady states as stably stratified core solutions.
$z=0.5$
becomes positive, implying that hotter fluid overlies colder fluid in the interior. We refer to this class of numerically computed steady states as stably stratified core solutions.
To quantify the proximity of a given numerically computed steady solution to the analytical heat-exchanger solution in the interior we introduce the parameter
measuring the ratio of the numerically computed mean temperature gradient at the mid-plane to the analytically predicted (constant) vertical temperature gradient. The solutions are identical when
![]() ${\it\gamma}=1$
, and so we quantitatively (but arbitrarily) define the steady convective state as a numerical heat-exchanger solution when
${\it\gamma}=1$
, and so we quantitatively (but arbitrarily) define the steady convective state as a numerical heat-exchanger solution when
![]() $0.99\leqslant {\it\gamma}\leqslant 1$
.
$0.99\leqslant {\it\gamma}\leqslant 1$
.
Figure 3 shows how the structure of the steady solution changes as
![]() $\mathit{Ra}$
and
$\mathit{Ra}$
and
![]() $L_{s}$
are varied. For small
$L_{s}$
are varied. For small
![]() $L_{s}>L_{c}$
, we observe that
$L_{s}>L_{c}$
, we observe that
![]() $0.99\leqslant {\it\gamma}\leqslant 1$
, so these solutions belong to the class of numerical heat-exchanger solutions. However,
$0.99\leqslant {\it\gamma}\leqslant 1$
, so these solutions belong to the class of numerical heat-exchanger solutions. However,
![]() ${\it\gamma}$
decreases appreciably as
${\it\gamma}$
decreases appreciably as
![]() $L_{s}$
increases, and the steady solutions assume a transitional form for
$L_{s}$
increases, and the steady solutions assume a transitional form for
![]() $0\leqslant {\it\gamma}<0.99$
. When
$0\leqslant {\it\gamma}<0.99$
. When
![]() $L_{s}$
is sufficiently large,
$L_{s}$
is sufficiently large,
![]() ${\it\gamma}$
changes sign, yielding a family of stably stratified core solutions. It should be noted that the wavelength
${\it\gamma}$
changes sign, yielding a family of stably stratified core solutions. It should be noted that the wavelength
![]() $L_{h}$
of solutions with
$L_{h}$
of solutions with
![]() ${\it\gamma}=0.99$
(see figure 3
b), which separates the heat-exchanger and non-heat-exchanger solutions, is approximately half the mean inter-plume spacing (
${\it\gamma}=0.99$
(see figure 3
b), which separates the heat-exchanger and non-heat-exchanger solutions, is approximately half the mean inter-plume spacing (
![]() $L_{m}$
in figure 3
b) measured from the DNS of Hewitt et al. (Reference Hewitt, Neufeld and Lister2012).
$L_{m}$
in figure 3
b) measured from the DNS of Hewitt et al. (Reference Hewitt, Neufeld and Lister2012).

Figure 3. (a) Proximity of numerical solutions to the heat-exchanger solution:
![]() ${\it\gamma}=-(\mathit{Ra}/k_{s}^{2})\partial _{z}\overline{T}|_{z=0.5}$
versus
${\it\gamma}=-(\mathit{Ra}/k_{s}^{2})\partial _{z}\overline{T}|_{z=0.5}$
versus
![]() $L_{s}\mathit{Ra}$
. As
$L_{s}\mathit{Ra}$
. As
![]() $L_{s}$
is increased,
$L_{s}$
is increased,
![]() ${\it\gamma}$
eventually departs from unity and the interior structure of the numerical solution changes from that of the heat-exchanger solution to that of the stably stratified core solution. (b) Variation with
${\it\gamma}$
eventually departs from unity and the interior structure of the numerical solution changes from that of the heat-exchanger solution to that of the stably stratified core solution. (b) Variation with
![]() $\mathit{Ra}$
of
$\mathit{Ra}$
of
![]() $L_{h}$
, the wavelength of steady solutions with
$L_{h}$
, the wavelength of steady solutions with
![]() ${\it\gamma}=0.99$
(i.e. numerical heat-exchanger solutions). Also plotted for comparison are
${\it\gamma}=0.99$
(i.e. numerical heat-exchanger solutions). Also plotted for comparison are
![]() $L_{c}\sim 2{\rm\pi}\mathit{Ra}^{-0.5}$
, the wavelength of the marginal stability boundary,
$L_{c}\sim 2{\rm\pi}\mathit{Ra}^{-0.5}$
, the wavelength of the marginal stability boundary,
![]() $L_{m}\approx (2{\rm\pi}/0.47)\mathit{Ra}^{-0.4}$
, the mean inter-plume spacing measured from the DNS of Hewitt et al. (Reference Hewitt, Neufeld and Lister2012), and
$L_{m}\approx (2{\rm\pi}/0.47)\mathit{Ra}^{-0.4}$
, the mean inter-plume spacing measured from the DNS of Hewitt et al. (Reference Hewitt, Neufeld and Lister2012), and
![]() $L_{f}\sim 2\sqrt{{\rm\pi}}\mathit{Ra}^{-0.25}$
, the wavelength of the fastest-growing linear mode. Interestingly, at large
$L_{f}\sim 2\sqrt{{\rm\pi}}\mathit{Ra}^{-0.25}$
, the wavelength of the fastest-growing linear mode. Interestingly, at large
![]() $\mathit{Ra}$
,
$\mathit{Ra}$
,
![]() $L_{m}\approx 2L_{h}$
.
$L_{m}\approx 2L_{h}$
.
3.3. Maximising
 $\mathit{Nu}$
$\mathit{Nu}$
Of particular physical importance is the relationship between the Nusselt number
![]() $\mathit{Nu}$
and the two control parameters
$\mathit{Nu}$
and the two control parameters
![]() $\mathit{Ra}$
and
$\mathit{Ra}$
and
![]() $L$
. Wen et al. (Reference Wen, Chini, Dianati and Doering2013) systematically studied the influence of the domain aspect ratio on the heat transport in turbulent porous medium convection using upper bound theory and DNS. At large
$L$
. Wen et al. (Reference Wen, Chini, Dianati and Doering2013) systematically studied the influence of the domain aspect ratio on the heat transport in turbulent porous medium convection using upper bound theory and DNS. At large
![]() $\mathit{Ra}$
the turbulent flow in porous medium convection was found to be self-sustaining with a
$\mathit{Ra}$
the turbulent flow in porous medium convection was found to be self-sustaining with a
![]() $\mathit{Ra}$
-dependent lateral scale, identified as a ‘minimal flow unit’, above which the heat transport is effectively independent of
$\mathit{Ra}$
-dependent lateral scale, identified as a ‘minimal flow unit’, above which the heat transport is effectively independent of
![]() $L$
. The dependence of
$L$
. The dependence of
![]() $\mathit{Nu}$
on
$\mathit{Nu}$
on
![]() $\mathit{Ra}$
and
$\mathit{Ra}$
and
![]() $L_{s}$
in steady porous medium convection, however, differs both qualitatively and quantitatively from that characterising turbulent heat transport in a porous layer. Figure 4 shows the variation of
$L_{s}$
in steady porous medium convection, however, differs both qualitatively and quantitatively from that characterising turbulent heat transport in a porous layer. Figure 4 shows the variation of
![]() $\mathit{Nu}$
with
$\mathit{Nu}$
with
![]() $\mathit{Ra}$
and
$\mathit{Ra}$
and
![]() $L_{s}$
for steady convective states (see also Corson Reference Corson2011). There is no convection when the domain aspect ratio is smaller than the wavelength
$L_{s}$
for steady convective states (see also Corson Reference Corson2011). There is no convection when the domain aspect ratio is smaller than the wavelength
![]() $L_{c}$
of the marginal stability mode, so
$L_{c}$
of the marginal stability mode, so
![]() $\mathit{Nu}=1$
in this regime. Unlike time-dependent convection, for which the value of
$\mathit{Nu}=1$
in this regime. Unlike time-dependent convection, for which the value of
![]() $\mathit{Nu}$
asymptotes when the domain aspect ratio exceeds the size of the minimal flow unit, the heat transport in steady convection is maximised along a particular path in (
$\mathit{Nu}$
asymptotes when the domain aspect ratio exceeds the size of the minimal flow unit, the heat transport in steady convection is maximised along a particular path in (
![]() $\mathit{Ra},L_{s}$
) parameter space (the solid black curve in figure 4).
$\mathit{Ra},L_{s}$
) parameter space (the solid black curve in figure 4).

Figure 4. Contour plot of the Nusselt number in
![]() $(\mathit{Ra},L_{s})$
parameter space for steady convective states. The solid line (
$(\mathit{Ra},L_{s})$
parameter space for steady convective states. The solid line (
![]() $L_{max\;Nu}$
) marks the path along which
$L_{max\;Nu}$
) marks the path along which
![]() $\mathit{Nu}$
is maximised. Here,
$\mathit{Nu}$
is maximised. Here,
![]() $L_{c}$
,
$L_{c}$
,
![]() $L_{m}$
and
$L_{m}$
and
![]() $L_{f}$
are as in figure 3.
$L_{f}$
are as in figure 3.
To accurately extract the scalings associated with the steady heat-flux-maximising solutions, we employed greater resolution in parameter space for (
![]() $\mathit{Ra},L_{s}$
) pairs near the ridge along which
$\mathit{Ra},L_{s}$
) pairs near the ridge along which
![]() $\mathit{Nu}$
is maximised. We also continued the computations to
$\mathit{Nu}$
is maximised. We also continued the computations to
![]() $\mathit{Ra}=31\,548$
, as shown in figures 4 and 5. When
$\mathit{Ra}=31\,548$
, as shown in figures 4 and 5. When
![]() $\mathit{Nu}$
is maximum and
$\mathit{Nu}$
is maximum and
![]() $\mathit{Ra}$
is less than roughly 100,
$\mathit{Ra}$
is less than roughly 100,
![]() $L_{s}$
scales as
$L_{s}$
scales as
![]() $\mathit{Ra}^{-1/4}$
, the scaling for the wavelength
$\mathit{Ra}^{-1/4}$
, the scaling for the wavelength
![]() $L_{f}$
of the fastest-growing linear mode. As
$L_{f}$
of the fastest-growing linear mode. As
![]() $\mathit{Ra}$
is increased, the ridge of maximum
$\mathit{Ra}$
is increased, the ridge of maximum
![]() $\mathit{Nu}$
shifts to the right and for
$\mathit{Nu}$
shifts to the right and for
![]() $10^{3}<\mathit{Ra}<10^{4}$
,
$10^{3}<\mathit{Ra}<10^{4}$
,
![]() $L_{s}\sim \mathit{Ra}^{-0.52}$
. As is evident in figure 5(a), the heat-flux-maximising solutions at large
$L_{s}\sim \mathit{Ra}^{-0.52}$
. As is evident in figure 5(a), the heat-flux-maximising solutions at large
![]() $\mathit{Ra}$
are, in fact, numerical heat-exchanger states. Figure 5(b) shows the variation of
$\mathit{Ra}$
are, in fact, numerical heat-exchanger states. Figure 5(b) shows the variation of
![]() $\mathit{Nu}$
with
$\mathit{Nu}$
with
![]() $\mathit{Ra}$
for high-
$\mathit{Ra}$
for high-
![]() $\mathit{Ra}$
steady solutions on the ridge (Corson Reference Corson2011), along with results from upper bound analysis and DNS. Both the upper bound calculation and the DNS predict
$\mathit{Ra}$
steady solutions on the ridge (Corson Reference Corson2011), along with results from upper bound analysis and DNS. Both the upper bound calculation and the DNS predict
![]() $\mathit{Nu}\sim \mathit{Ra}$
for the unsteady flow. Steady convection at large
$\mathit{Nu}\sim \mathit{Ra}$
for the unsteady flow. Steady convection at large
![]() $\mathit{Ra}$
is thus seen to transport less heat than the realised turbulent flow, with
$\mathit{Ra}$
is thus seen to transport less heat than the realised turbulent flow, with
![]() $\mathit{Nu}\sim \mathit{Ra}^{0.6}$
for the equilibrium states (Corson Reference Corson2011). Like the real flow, however, the heat transported by the steady heat-flux-maximising solutions increases substantially as the inter-plume spacing (i.e.
$\mathit{Nu}\sim \mathit{Ra}^{0.6}$
for the equilibrium states (Corson Reference Corson2011). Like the real flow, however, the heat transported by the steady heat-flux-maximising solutions increases substantially as the inter-plume spacing (i.e.
![]() $L_{s}$
) decreases from
$L_{s}$
) decreases from
![]() $O(1)$
to asymptotically small values; in contrast, the matched asymptotic analysis of Fowler (Reference Fowler1997) suggests that in steady porous medium convection at fixed aspect ratio
$O(1)$
to asymptotically small values; in contrast, the matched asymptotic analysis of Fowler (Reference Fowler1997) suggests that in steady porous medium convection at fixed aspect ratio
![]() $\mathit{Nu}\sim \mathit{Ra}^{1/3}=o(\mathit{Ra}^{0.6})$
.
$\mathit{Nu}\sim \mathit{Ra}^{1/3}=o(\mathit{Ra}^{0.6})$
.

Figure 5. (a) Rayleigh-number scaling of the inverse wavelength associated with heat-flux-maximising steady convective states (dots). It should be noted that at sufficiently large
![]() $\mathit{Ra}$
multiple states yield nearly the same (maximum) heat flux. The dashed line is the best fit curve
$\mathit{Ra}$
multiple states yield nearly the same (maximum) heat flux. The dashed line is the best fit curve
![]() $1/L_{s}=0.070\mathit{Ra}^{0.52}$
for
$1/L_{s}=0.070\mathit{Ra}^{0.52}$
for
![]() $\mathit{Ra}\leqslant 12\,559$
. For reference,
$\mathit{Ra}\leqslant 12\,559$
. For reference,
![]() $1/L_{h}$
and
$1/L_{h}$
and
![]() $1/L_{c}$
are also plotted as functions of
$1/L_{c}$
are also plotted as functions of
![]() $\mathit{Ra}$
. (b) Rayleigh-number scaling of the Nusselt number for steady convective solutions (dots). The dashed line is the best fit curve
$\mathit{Ra}$
. (b) Rayleigh-number scaling of the Nusselt number for steady convective solutions (dots). The dashed line is the best fit curve
![]() $\mathit{Nu}=0.155\mathit{Ra}^{0.60}+1.213$
. For reference, data from upper bound analysis and various DNS are also shown.
$\mathit{Nu}=0.155\mathit{Ra}^{0.60}+1.213$
. For reference, data from upper bound analysis and various DNS are also shown.
3.4. Statistical structure of the columnar flow in DNS
As described above, the spatial structure of steady convection varies appreciably with
![]() $L_{s}$
. A natural question concerns the difference between the structure of the steady convective states and that of the time-averaged flow observed in DNS. As
$L_{s}$
. A natural question concerns the difference between the structure of the steady convective states and that of the time-averaged flow observed in DNS. As
![]() $\mathit{Ra}$
increases, DNS indicate that the interior flow becomes more organised and is dominated by persistent vertical columnar flow across the domain, driven by the chaotic mixing of small proto-plumes at the upper and lower boundaries (Otero et al.
Reference Otero, Dontcheva, Johnston, Worthing, Kurganov, Petrova and Doering2004; Hewitt et al.
Reference Hewitt, Neufeld and Lister2012). The columnar flow has been modelled using the heat-exchanger solution in Hewitt et al. (Reference Hewitt, Neufeld and Lister2012, Reference Hewitt, Neufeld and Lister2013). As discussed in § 3.2, the heat-exchanger solution is well represented by the interior part of steady solutions only for convective states with sufficiently small aspect ratios; of course, the time-averaged columnar flow in DNS need not satisfy the steady governing equations. To further investigate the differences between the time-averaged columnar flow and the strictly steady convective states, we performed DNS in the high-
$\mathit{Ra}$
increases, DNS indicate that the interior flow becomes more organised and is dominated by persistent vertical columnar flow across the domain, driven by the chaotic mixing of small proto-plumes at the upper and lower boundaries (Otero et al.
Reference Otero, Dontcheva, Johnston, Worthing, Kurganov, Petrova and Doering2004; Hewitt et al.
Reference Hewitt, Neufeld and Lister2012). The columnar flow has been modelled using the heat-exchanger solution in Hewitt et al. (Reference Hewitt, Neufeld and Lister2012, Reference Hewitt, Neufeld and Lister2013). As discussed in § 3.2, the heat-exchanger solution is well represented by the interior part of steady solutions only for convective states with sufficiently small aspect ratios; of course, the time-averaged columnar flow in DNS need not satisfy the steady governing equations. To further investigate the differences between the time-averaged columnar flow and the strictly steady convective states, we performed DNS in the high-
![]() $\mathit{Ra}$
regime, extending previous results to
$\mathit{Ra}$
regime, extending previous results to
![]() $\mathit{Ra}\approx 10^{5}$
. The unsteady version of the system (3.1) and (3.2) was solved numerically using a Fourier–Chebyshev-tau pseudospectral algorithm. Temporal discretisation was achieved using the Crank–Nicolson method for the linear terms and a two-step Adams–Bashforth method for the nonlinear terms, yielding second-order accuracy in time. The code was thoroughly validated and gives
$\mathit{Ra}\approx 10^{5}$
. The unsteady version of the system (3.1) and (3.2) was solved numerically using a Fourier–Chebyshev-tau pseudospectral algorithm. Temporal discretisation was achieved using the Crank–Nicolson method for the linear terms and a two-step Adams–Bashforth method for the nonlinear terms, yielding second-order accuracy in time. The code was thoroughly validated and gives
![]() $\mathit{Nu}$
values quantitatively matching those of previous DNS, as shown in figure 5(b).
$\mathit{Nu}$
values quantitatively matching those of previous DNS, as shown in figure 5(b).
Figure 6 shows snapshots of the temperature fields and corresponding long-time-averaged magnitudes of the (complex) Fourier amplitudes of the temperature fluctuations (i.e. deviations from the horizontal mean) as functions of
![]() $z$
from our DNS at
$z$
from our DNS at
![]() $\mathit{Ra}=50\,000$
conducted in two different domains. As is evident in figure 6(a), there exist 17 very well organised columnar flows, each consisting of a single rising and descending mega-plume, at the given parameter values. The time-averaged amplitudes of the temperature fluctuations,
$\mathit{Ra}=50\,000$
conducted in two different domains. As is evident in figure 6(a), there exist 17 very well organised columnar flows, each consisting of a single rising and descending mega-plume, at the given parameter values. The time-averaged amplitudes of the temperature fluctuations,
![]() $\langle |\hat{{\it\theta}}_{n}|\rangle$
, in figure 6(c) reveal that the interior flow is a composite of a few low-wavenumber Fourier modes but is dominated by one mode, features shared by the strictly steady stably stratified core solutions. Indeed, we recall that steady convective states with
$\langle |\hat{{\it\theta}}_{n}|\rangle$
, in figure 6(c) reveal that the interior flow is a composite of a few low-wavenumber Fourier modes but is dominated by one mode, features shared by the strictly steady stably stratified core solutions. Indeed, we recall that steady convective states with
![]() $L_{s}=L_{m}$
, the mean inter-plume spacing observed in DNS, are stably stratified core solutions (figures 1
c, 2
c and 3
b). Furthermore, at high wavenumber, the Fourier amplitudes
$L_{s}=L_{m}$
, the mean inter-plume spacing observed in DNS, are stably stratified core solutions (figures 1
c, 2
c and 3
b). Furthermore, at high wavenumber, the Fourier amplitudes
![]() $\hat{{\it\theta}}_{n}$
are strongly localised near the upper and lower walls, where they superpose to comprise the small rolls and proto-plumes within the thermal and vorticity boundary layers. Figure 6(b,d) shows corresponding results for DNS performed in a narrower domain, confirming that the flow has a structure similar to that in the larger domain. In particular, the time-averaged interior flow is well represented by only six Fourier modes.
$\hat{{\it\theta}}_{n}$
are strongly localised near the upper and lower walls, where they superpose to comprise the small rolls and proto-plumes within the thermal and vorticity boundary layers. Figure 6(b,d) shows corresponding results for DNS performed in a narrower domain, confirming that the flow has a structure similar to that in the larger domain. In particular, the time-averaged interior flow is well represented by only six Fourier modes.

Figure 6. Snapshots of the temperature fields (a,b) and corresponding time-averaged Fourier amplitudes (c,d) of the temperature fluctuations (i.e. deviations from the horizontal mean) from DNS at
![]() $\mathit{Ra}=50\,000$
. In (a,c)
$\mathit{Ra}=50\,000$
. In (a,c)
![]() $L=2.39$
, while in (b,d)
$L=2.39$
, while in (b,d)
![]() $L=2.39/17$
.
$L=2.39/17$
.
Nevertheless, the DNS indicate that the interior slope of the time- and horizontal-mean temperature field is not positive (figure 7
a); i.e. the core is not stably stratified. Furthermore, although the interior mean temperature profile is roughly linear in
![]() $z$
with negative slope for large
$z$
with negative slope for large
![]() $\mathit{Ra}$
, this slope is not well predicted by the heat-exchanger solution either: compared with the slope of
$\mathit{Ra}$
, this slope is not well predicted by the heat-exchanger solution either: compared with the slope of
![]() $\overline{T}$
for the heat-exchanger solution, the mean temperature gradient from the DNS is more negative (figure 7
a). On the other hand, figure 7 does confirm that the mean temperature gradient approaches zero as
$\overline{T}$
for the heat-exchanger solution, the mean temperature gradient from the DNS is more negative (figure 7
a). On the other hand, figure 7 does confirm that the mean temperature gradient approaches zero as
![]() $\mathit{Ra}$
is increased and that the mean amplitude of the dominant Fourier mode in the interior is almost independent of
$\mathit{Ra}$
is increased and that the mean amplitude of the dominant Fourier mode in the interior is almost independent of
![]() $\mathit{Ra}$
at large
$\mathit{Ra}$
at large
![]() $\mathit{Ra}$
(figure 7
b), consistent with the measurements in Hewitt et al. (Reference Hewitt, Neufeld and Lister2012) and the form of the heat-exchanger solution. In short, the statistical structure of the turbulent columnar flow at large
$\mathit{Ra}$
(figure 7
b), consistent with the measurements in Hewitt et al. (Reference Hewitt, Neufeld and Lister2012) and the form of the heat-exchanger solution. In short, the statistical structure of the turbulent columnar flow at large
![]() $\mathit{Ra}$
resembles the heat-exchanger solution in the interior, but with a modified mean temperature gradient and more than one Fourier mode to adequately represent the fluctuations.
$\mathit{Ra}$
resembles the heat-exchanger solution in the interior, but with a modified mean temperature gradient and more than one Fourier mode to adequately represent the fluctuations.

Figure 7. Statistical structure of turbulent convection obtained from DNS. (a) Comparison of the long-time- and horizontally averaged temperature profile
![]() $\langle \overline{T}\rangle$
from DNS with
$\langle \overline{T}\rangle$
from DNS with
![]() $\overline{T}$
from the analytical heat-exchanger model. (b) Time-averaged amplitude
$\overline{T}$
from the analytical heat-exchanger model. (b) Time-averaged amplitude
![]() $A_{d}$
of the dominant Fourier mode (after subtraction of the horizontal mean) at
$A_{d}$
of the dominant Fourier mode (after subtraction of the horizontal mean) at
![]() $z=0.5$
. For each
$z=0.5$
. For each
![]() $\mathit{Ra}$
, DNS was performed in a domain with
$\mathit{Ra}$
, DNS was performed in a domain with
![]() $L=10L_{f}$
so that 17 columnar flows were captured. In (a), only half of the mean temperature profile (i.e. for
$L=10L_{f}$
so that 17 columnar flows were captured. In (a), only half of the mean temperature profile (i.e. for
![]() $0\leqslant z\leqslant 0.5$
) is plotted due to statistical antisymmetry about the mid-plane.
$0\leqslant z\leqslant 0.5$
) is plotted due to statistical antisymmetry about the mid-plane.
4. Secondary stability analysis
4.1. Floquet theory
To investigate the stability properties of the steady convective states described in the previous section, we next perform a secondary stability analysis using spatial Floquet theory. First, all fields are expressed as the sum of the steady nonlinear base flow (denoted with a subscript ‘
![]() $s$
’) and a time-varying perturbation,
$s$
’) and a time-varying perturbation,
and
![]() $L$
-periodicity (not generally
$L$
-periodicity (not generally
![]() $L_{s}$
-periodicity) in
$L_{s}$
-periodicity) in
![]() $x$
. Floquet theory implies that solutions may be sought having the following form:
$x$
. Floquet theory implies that solutions may be sought having the following form:
where
![]() ${\it\lambda}$
is the temporal growth rate,
${\it\lambda}$
is the temporal growth rate,
![]() $\text{i}{\it\beta}k_{s}$
is the Floquet exponent, with the real Floquet parameter
$\text{i}{\it\beta}k_{s}$
is the Floquet exponent, with the real Floquet parameter
![]() ${\it\beta}$
providing the freedom to modify the fundamental horizontal wavenumber of the perturbation (i.e. for
${\it\beta}$
providing the freedom to modify the fundamental horizontal wavenumber of the perturbation (i.e. for
![]() ${\it\beta}\neq 0$
,
${\it\beta}\neq 0$
,
![]() ${\it\beta}k_{s}$
is the wavenumber of the largest horizontal scale), and c.c. denotes complex conjugate. Since (4.6) is invariant under integer shifts in
${\it\beta}k_{s}$
is the wavenumber of the largest horizontal scale), and c.c. denotes complex conjugate. Since (4.6) is invariant under integer shifts in
![]() ${\it\beta}$
and under reflections
${\it\beta}$
and under reflections
![]() ${\it\beta}\rightarrow -{\it\beta}$
, we can restrict attention to
${\it\beta}\rightarrow -{\it\beta}$
, we can restrict attention to
![]() $0\leqslant {\it\beta}\leqslant 0.5$
without loss of generality. Substitution of (4.6) into (4.3) and (4.4) yields
$0\leqslant {\it\beta}\leqslant 0.5$
without loss of generality. Substitution of (4.6) into (4.3) and (4.4) yields
where
![]() $\unicode[STIX]{x1D63C}$
and
$\unicode[STIX]{x1D63C}$
and
![]() $\unicode[STIX]{x1D63D}$
are real matrices due to the symmetries (3.4) of the base flow, and the vector
$\unicode[STIX]{x1D63D}$
are real matrices due to the symmetries (3.4) of the base flow, and the vector
![]() $\boldsymbol{V}=(\cdots \hat{\widetilde{{\it\theta}}}_{n-1},\hat{\widetilde{{\it\theta}}}_{n},\hat{\widetilde{{\it\theta}}}_{n+1}\cdots \hat{\widetilde{{\it\phi}}}_{n-1},\hat{\widetilde{{\it\phi}}}_{n},\hat{\widetilde{{\it\phi}}}_{n+1}\cdots \!)^{\text{T}}$
. The eigenvalue
$\boldsymbol{V}=(\cdots \hat{\widetilde{{\it\theta}}}_{n-1},\hat{\widetilde{{\it\theta}}}_{n},\hat{\widetilde{{\it\theta}}}_{n+1}\cdots \hat{\widetilde{{\it\phi}}}_{n-1},\hat{\widetilde{{\it\phi}}}_{n},\hat{\widetilde{{\it\phi}}}_{n+1}\cdots \!)^{\text{T}}$
. The eigenvalue
![]() ${\it\lambda}$
and the corresponding eigenvector
${\it\lambda}$
and the corresponding eigenvector
![]() $\boldsymbol{V}$
can be obtained by numerically solving this differential eigenvalue problem. It should be noted that in the following sections, the convective rather than diffusive time,
$\boldsymbol{V}$
can be obtained by numerically solving this differential eigenvalue problem. It should be noted that in the following sections, the convective rather than diffusive time,
![]() ${\it\tau}\equiv t\mathit{Ra}$
, will be utilised, so that the corresponding convective growth rate
${\it\tau}\equiv t\mathit{Ra}$
, will be utilised, so that the corresponding convective growth rate
![]() ${\it\sigma}\equiv {\it\lambda}/\mathit{Ra}$
.
${\it\sigma}\equiv {\it\lambda}/\mathit{Ra}$
.
4.2. Secondary stability results
The eigensystem (4.9) is discretised using a Chebyshev collocation method and the infinite-dimensional system is truncated to
![]() $0\leqslant m\leqslant M$
vertically and
$0\leqslant m\leqslant M$
vertically and
![]() $-N/2\leqslant n\leqslant N/2$
horizontally. Arnoldi iteration is used to solve the resulting algebraic eigenvalue problem to obtain the leading eigenvalues and eigenfunctions. The numerical resolution is increased until the relative error in the eigenvalue with the largest real part,
$-N/2\leqslant n\leqslant N/2$
horizontally. Arnoldi iteration is used to solve the resulting algebraic eigenvalue problem to obtain the leading eigenvalues and eigenfunctions. The numerical resolution is increased until the relative error in the eigenvalue with the largest real part,
![]() ${\it\sigma}_{m}$
, is less than
${\it\sigma}_{m}$
, is less than
![]() $10^{-4}$
.
$10^{-4}$
.
Figure 8 shows the contours of maximum growth rate,
![]() $\text{Re}\{{\it\sigma}_{m}\}$
, as a function of
$\text{Re}\{{\it\sigma}_{m}\}$
, as a function of
![]() ${\it\beta}$
and
${\it\beta}$
and
![]() $L_{s}$
for various
$L_{s}$
for various
![]() $\mathit{Ra}$
. At a given
$\mathit{Ra}$
. At a given
![]() $\mathit{Ra}$
, the steady solution at small
$\mathit{Ra}$
, the steady solution at small
![]() $L_{s}$
(specifically,
$L_{s}$
(specifically,
![]() $L_{c}<L_{s}<L_{b}$
, where
$L_{c}<L_{s}<L_{b}$
, where
![]() $L_{b}$
is a stability boundary defined in figures 10 and 11) is marginally stable for
$L_{b}$
is a stability boundary defined in figures 10 and 11) is marginally stable for
![]() ${\it\beta}=0$
– corresponding to disturbances that simply translate the steady base flow in
${\it\beta}=0$
– corresponding to disturbances that simply translate the steady base flow in
![]() $x$
– although there is insufficient resolution around
$x$
– although there is insufficient resolution around
![]() ${\it\beta}=0$
to observe this clearly in the contour plots. However, the solution is unstable for a range of long-wavelength perturbations (
${\it\beta}=0$
to observe this clearly in the contour plots. However, the solution is unstable for a range of long-wavelength perturbations (
![]() $0<{\it\beta}\leqslant 0.5$
, see figure 8). The Floquet parameter
$0<{\it\beta}\leqslant 0.5$
, see figure 8). The Floquet parameter
![]() ${\it\beta}$
of the fastest-growing perturbation is approximately 0.2–0.3, implying that the most unstable disturbance has a wavelength 3–5 times the wavelength of the base flow. At
${\it\beta}$
of the fastest-growing perturbation is approximately 0.2–0.3, implying that the most unstable disturbance has a wavelength 3–5 times the wavelength of the base flow. At
![]() $\mathit{Ra}=1581$
and 3155, the growth rate of the most unstable mode decreases as
$\mathit{Ra}=1581$
and 3155, the growth rate of the most unstable mode decreases as
![]() $L_{s}$
is increased and, in fact, the steady solution becomes linearly stable for a finite range of
$L_{s}$
is increased and, in fact, the steady solution becomes linearly stable for a finite range of
![]() $L_{s}$
. However, as
$L_{s}$
. However, as
![]() $L_{s}$
is further increased, the steady state becomes unstable, exhibiting a growth rate that is essentially independent of
$L_{s}$
is further increased, the steady state becomes unstable, exhibiting a growth rate that is essentially independent of
![]() ${\it\beta}$
. Similar phenomena are observed at larger
${\it\beta}$
. Similar phenomena are observed at larger
![]() $\mathit{Ra}$
except that the linearly stable region shrinks nearly to a point at
$\mathit{Ra}$
except that the linearly stable region shrinks nearly to a point at
![]() $\mathit{Ra}=5000$
and vanishes completely at larger
$\mathit{Ra}=5000$
and vanishes completely at larger
![]() $\mathit{Ra}$
.
$\mathit{Ra}$
.

Figure 8. Contours of the maximum growth rate
![]() $\text{Re}\{{\it\sigma}_{m}\}$
as a function of
$\text{Re}\{{\it\sigma}_{m}\}$
as a function of
![]() ${\it\beta}$
and
${\it\beta}$
and
![]() $L_{s}$
for various
$L_{s}$
for various
![]() $\mathit{Ra}$
: (a)
$\mathit{Ra}$
: (a)
![]() $\mathit{Ra}=1581$
; (b)
$\mathit{Ra}=1581$
; (b)
![]() $\mathit{Ra}=3155$
; (c)
$\mathit{Ra}=3155$
; (c)
![]() $\mathit{Ra}=5000$
; (d)
$\mathit{Ra}=5000$
; (d)
![]() $\mathit{Ra}=9976$
. At small
$\mathit{Ra}=9976$
. At small
![]() $L_{s}~(L_{c}<L_{s}<L_{b})$
, the base state is stable within small domains of size
$L_{s}~(L_{c}<L_{s}<L_{b})$
, the base state is stable within small domains of size
![]() $L_{s}\times 1$
(since
$L_{s}\times 1$
(since
![]() $L=L_{s}$
for
$L=L_{s}$
for
![]() ${\it\beta}=0$
), but unstable to certain long-wavelength perturbations (
${\it\beta}=0$
), but unstable to certain long-wavelength perturbations (
![]() $0<{\it\beta}\leqslant 0.5$
); at large
$0<{\it\beta}\leqslant 0.5$
); at large
![]() $L_{s}$
, the base state is unstable even for
$L_{s}$
, the base state is unstable even for
![]() ${\it\beta}=0$
, and has the same growth rate for different
${\it\beta}=0$
, and has the same growth rate for different
![]() ${\it\beta}$
. It should be noted that the contour plot in (
${\it\beta}$
. It should be noted that the contour plot in (
![]() $d$
) has been annotated to indicate the parameters corresponding to the bulk (‘B’) and wall (‘W’) mode eigenfunctions displayed in figure 9.
$d$
) has been annotated to indicate the parameters corresponding to the bulk (‘B’) and wall (‘W’) mode eigenfunctions displayed in figure 9.

Figure 9. The fastest-growing 2D temperature eigenfunctions at
![]() $\mathit{Ra}=9976$
shown in a domain with aspect ratio
$\mathit{Ra}=9976$
shown in a domain with aspect ratio
![]() $L=5L_{s}$
(where
$L=5L_{s}$
(where
![]() $L_{s}$
is the wavelength of the steady base state): (a)
$L_{s}$
is the wavelength of the steady base state): (a)
![]() $L_{s}=0.1$
,
$L_{s}=0.1$
,
![]() ${\it\beta}=0.2$
; (b)
${\it\beta}=0.2$
; (b)
![]() $L_{s}=0.1585$
,
$L_{s}=0.1585$
,
![]() ${\it\beta}=0$
; (c)
${\it\beta}=0$
; (c)
![]() $L_{s}=0.1585$
,
$L_{s}=0.1585$
,
![]() ${\it\beta}=0.2$
. At small
${\it\beta}=0.2$
. At small
![]() $L_{s}$
, a bulk mode controls the instability, and at large
$L_{s}$
, a bulk mode controls the instability, and at large
![]() $L_{s}$
, a wall mode dominates. It should be noted that at large
$L_{s}$
, a wall mode dominates. It should be noted that at large
![]() $L_{s}$
the spatial structure of the fastest-growing (wall) mode is nearly independent of
$L_{s}$
the spatial structure of the fastest-growing (wall) mode is nearly independent of
![]() ${\it\beta}$
.
${\it\beta}$
.

Figure 10. The leading eigenvalues at
![]() $\mathit{Ra}=9976$
: (a)
$\mathit{Ra}=9976$
: (a)
![]() $L_{s}=0.1$
,
$L_{s}=0.1$
,
![]() ${\it\beta}=0.2$
; (b)
${\it\beta}=0.2$
; (b)
![]() $L_{s}=0.1585$
,
$L_{s}=0.1585$
,
![]() ${\it\beta}=0$
; (c)
${\it\beta}=0$
; (c)
![]() $L_{s}=0.1585$
,
$L_{s}=0.1585$
,
![]() ${\it\beta}=0.2$
;
${\it\beta}=0.2$
;
![]() $\text{Re}\,{\it\sigma}~(\text{Im}~{\it\sigma})$
is the real (imaginary) part of
$\text{Re}\,{\it\sigma}~(\text{Im}~{\it\sigma})$
is the real (imaginary) part of
![]() ${\it\sigma}$
. In each case, the inset shows a magnification of the region near the origin, with the asterisk denoting the most unstable bulk mode(s). Here,
${\it\sigma}$
. In each case, the inset shows a magnification of the region near the origin, with the asterisk denoting the most unstable bulk mode(s). Here,
![]() $L_{b}$
is defined such that when
$L_{b}$
is defined such that when
![]() $L_{s}<L_{b}$
(as in a) only bulk modes exist. As
$L_{s}<L_{b}$
(as in a) only bulk modes exist. As
![]() $L_{s}$
is increased (b,c), an increasing number of wall modes are destabilised. One should note the similarity of the eigenspectra in (b) and (c) for the same (large)
$L_{s}$
is increased (b,c), an increasing number of wall modes are destabilised. One should note the similarity of the eigenspectra in (b) and (c) for the same (large)
![]() $L_{s}$
.
$L_{s}$
.

Figure 11. Schematic identifying distinct steady states and the associated secondary instability regimes at large
![]() $\mathit{Ra}$
. DNS are performed for six steady base states with aspect ratios
$\mathit{Ra}$
. DNS are performed for six steady base states with aspect ratios
![]() $L_{s1}{-}L_{s6}$
to study the fully nonlinear evolution of the fastest-growing instability modes. Here,
$L_{s1}{-}L_{s6}$
to study the fully nonlinear evolution of the fastest-growing instability modes. Here,
![]() $L_{o}$
is the aspect ratio for which the normalised horizontal-mean temperature gradient
$L_{o}$
is the aspect ratio for which the normalised horizontal-mean temperature gradient
![]() ${\it\gamma}=0$
.
${\it\gamma}=0$
.
Figure 9 shows, for
![]() $\mathit{Ra}=9976$
, the 2D eigenfunctions corresponding to these two families of secondary instabilities. At small
$\mathit{Ra}=9976$
, the 2D eigenfunctions corresponding to these two families of secondary instabilities. At small
![]() $L_{s}$
, e.g.
$L_{s}$
, e.g.
![]() $L_{s}=0.1$
, when the growth rate depends on the horizontal wavenumber
$L_{s}=0.1$
, when the growth rate depends on the horizontal wavenumber
![]() ${\it\beta}k_{s}$
, the most unstable perturbation (occurring for
${\it\beta}k_{s}$
, the most unstable perturbation (occurring for
![]() ${\it\beta}\approx 0.2$
) is a bulk mode that spans the layer (figure 9
a). However, for larger
${\it\beta}\approx 0.2$
) is a bulk mode that spans the layer (figure 9
a). However, for larger
![]() $L_{s}$
, e.g.
$L_{s}$
, e.g.
![]() $L_{s}=0.1585$
, the most unstable perturbation for each
$L_{s}=0.1585$
, the most unstable perturbation for each
![]() ${\it\beta}$
has nearly the same growth rate and a very similar spatial structure, which is strongly localised near the upper and lower walls (figure 9
b,c). Figure 10 shows the eigenspectrum for three different (
${\it\beta}$
has nearly the same growth rate and a very similar spatial structure, which is strongly localised near the upper and lower walls (figure 9
b,c). Figure 10 shows the eigenspectrum for three different (
![]() ${\it\beta},L_{s}$
) combinations. We note that the bulk mode, as shown in figure 9(a), occurs for certain long-wavelength (e.g.
${\it\beta},L_{s}$
) combinations. We note that the bulk mode, as shown in figure 9(a), occurs for certain long-wavelength (e.g.
![]() ${\it\beta}=0.2$
) disturbances and exhibits comparably small growth rates (
${\it\beta}=0.2$
) disturbances and exhibits comparably small growth rates (
![]() ${\it\sigma}_{m}=O(0.1)$
). At small
${\it\sigma}_{m}=O(0.1)$
). At small
![]() $L_{s}$
, the bulk modes control the instability. As
$L_{s}$
, the bulk modes control the instability. As
![]() $L_{s}$
is increased, however, an increasing number of wall modes become unstable. These wall modes, which are born in a Hopf bifurcation associated with the advection of small-scale disturbances within the thermal boundary layers (see Aidun & Steen (Reference Aidun and Steen1987) and Graham & Steen (Reference Graham and Steen1992, Reference Graham and Steen1994)), ultimately dominate the secondary instability with growth rates 10–50 times larger than those associated with the bulk modes. For sufficiently large
$L_{s}$
is increased, however, an increasing number of wall modes become unstable. These wall modes, which are born in a Hopf bifurcation associated with the advection of small-scale disturbances within the thermal boundary layers (see Aidun & Steen (Reference Aidun and Steen1987) and Graham & Steen (Reference Graham and Steen1992, Reference Graham and Steen1994)), ultimately dominate the secondary instability with growth rates 10–50 times larger than those associated with the bulk modes. For sufficiently large
![]() $L_{s}$
, the eigenspectra for disturbances with distinct fundamental horizontal wavenumbers are very similar. We conclude this section by contrasting our secondary stability results with those of Hewitt et al. (Reference Hewitt, Neufeld and Lister2013). Not only do we find two modes of instability rather than one, but in the presence of walls the bulk modes are found to have much reduced growth rates: specifically,
$L_{s}$
, the eigenspectra for disturbances with distinct fundamental horizontal wavenumbers are very similar. We conclude this section by contrasting our secondary stability results with those of Hewitt et al. (Reference Hewitt, Neufeld and Lister2013). Not only do we find two modes of instability rather than one, but in the presence of walls the bulk modes are found to have much reduced growth rates: specifically,
![]() $O(0.1)$
rather than
$O(0.1)$
rather than
![]() $O(1)$
.
$O(1)$
.
5. Nonlinear evolution of the instability
In this section we use strategically initialised high-resolution DNS in wide domains to investigate the nonlinear evolution of the fastest-growing secondary instability mode for various steady convective states distinguished by their wavelength
![]() $L_{s}$
. Our aim is to gain insight into the mechanisms by which the base flow, with plume spacing
$L_{s}$
. Our aim is to gain insight into the mechanisms by which the base flow, with plume spacing
![]() $L_{s}$
, evolves to the final columnar flow, with mean inter-plume spacing
$L_{s}$
, evolves to the final columnar flow, with mean inter-plume spacing
![]() $L_{m}$
(in the bulk). The steady state at a given
$L_{m}$
(in the bulk). The steady state at a given
![]() $L_{s}$
plus a small-amplitude contribution of the most unstable secondary instability mode is chosen as the initial condition, and then DNS is performed in a large domain with
$L_{s}$
plus a small-amplitude contribution of the most unstable secondary instability mode is chosen as the initial condition, and then DNS is performed in a large domain with
![]() $L=10L_{s}{-}20L_{s}$
.
$L=10L_{s}{-}20L_{s}$
.
As shown in figure 11, for a specific large
![]() $\mathit{Ra}=O(10^{4})$
, with increasing
$\mathit{Ra}=O(10^{4})$
, with increasing
![]() $L$
, generally
$L$
, generally
![]() $L_{c}<L_{b}<L_{max\,Nu}<L_{h}<L_{o}<L_{m}$
, where
$L_{c}<L_{b}<L_{max\,Nu}<L_{h}<L_{o}<L_{m}$
, where
![]() $L_{c}$
is the wavelength of the neutral mode on the right-hand marginal stability boundary of the conduction state,
$L_{c}$
is the wavelength of the neutral mode on the right-hand marginal stability boundary of the conduction state,
![]() $L_{b}$
is the largest aspect ratio at which only the bulk instability mode exists,
$L_{b}$
is the largest aspect ratio at which only the bulk instability mode exists,
![]() $L_{max\,Nu}$
is the wavelength of the steady cellular flow that maximises the heat transport,
$L_{max\,Nu}$
is the wavelength of the steady cellular flow that maximises the heat transport,
![]() $L_{h}$
is the largest aspect ratio at which the heat-exchanger solution is relevant and
$L_{h}$
is the largest aspect ratio at which the heat-exchanger solution is relevant and
![]() $L_{o}$
is the aspect ratio at which the parameter
$L_{o}$
is the aspect ratio at which the parameter
![]() ${\it\gamma}$
vanishes (implying a steady base flow with zero mean stratification in the centre of the cell). In the following sections, six different steady convective states, five at
${\it\gamma}$
vanishes (implying a steady base flow with zero mean stratification in the centre of the cell). In the following sections, six different steady convective states, five at
![]() $\mathit{Ra}=9976$
and one at
$\mathit{Ra}=9976$
and one at
![]() $\mathit{Ra}=50\,000$
, are considered:
$\mathit{Ra}=50\,000$
, are considered:
![]() $L_{s1}$
is less than
$L_{s1}$
is less than
![]() $L_{c}$
so that the base state is the conduction solution;
$L_{c}$
so that the base state is the conduction solution;
![]() $L_{s2}$
is greater than
$L_{s2}$
is greater than
![]() $L_{c}$
but within the aspect-ratio range for which the bulk mode controls the instability;
$L_{c}$
but within the aspect-ratio range for which the bulk mode controls the instability;
![]() $L_{s3}$
is greater than
$L_{s3}$
is greater than
![]() $L_{b}$
but is within the numerical heat-exchanger solution regime;
$L_{b}$
but is within the numerical heat-exchanger solution regime;
![]() $L_{s4}$
is between
$L_{s4}$
is between
![]() $L_{h}$
and
$L_{h}$
and
![]() $L_{m}$
, within the stably stratified core solution regime;
$L_{m}$
, within the stably stratified core solution regime;
![]() $L_{s5}$
is close to the final mean inter-plume spacing
$L_{s5}$
is close to the final mean inter-plume spacing
![]() $L_{m}$
; and
$L_{m}$
; and
![]() $L_{s6}$
is much larger than
$L_{s6}$
is much larger than
![]() $L_{m}$
. Thus, for
$L_{m}$
. Thus, for
![]() $\mathit{Ra}=9976$
, for example,
$\mathit{Ra}=9976$
, for example,
![]() $L_{c}=0.063$
,
$L_{c}=0.063$
,
![]() $L_{b}=0.106$
,
$L_{b}=0.106$
,
![]() $L_{h}=0.172$
,
$L_{h}=0.172$
,
![]() $L_{m}=0.319$
(measured from DNS in
$L_{m}=0.319$
(measured from DNS in
![]() $L=5.012$
) and
$L=5.012$
) and
![]() $L_{f}=0.36$
.
$L_{f}=0.36$
.
5.1.
 $L_{s2}~(\mathit{Ra}=9976)$
$L_{s2}~(\mathit{Ra}=9976)$
For
![]() $\mathit{Ra}=9976$
, we first perform DNS to investigate the dynamics ensuing from unstable steady states with
$\mathit{Ra}=9976$
, we first perform DNS to investigate the dynamics ensuing from unstable steady states with
![]() $L_{s}=L_{s2}$
, which is within the bulk instability parameter regime. The initial condition comprises 20 replicas of the steady convective state at
$L_{s}=L_{s2}$
, which is within the bulk instability parameter regime. The initial condition comprises 20 replicas of the steady convective state at
![]() $L_{s}=0.1$
plus a small-amplitude contribution of the corresponding fastest-growing perturbation at
$L_{s}=0.1$
plus a small-amplitude contribution of the corresponding fastest-growing perturbation at
![]() ${\it\beta}=0.2$
. Figure 12 depicts the nonlinear evolution from this initial state to the final turbulent columnar flow. Initially, the dominant horizontal mode number in the interior is
${\it\beta}=0.2$
. Figure 12 depicts the nonlinear evolution from this initial state to the final turbulent columnar flow. Initially, the dominant horizontal mode number in the interior is
![]() $n_{d}=20$
. In accord with the stability analysis in § 4 and as is evident in figure 12(b,c), the base state is unstable to a bulk mode. As the secondary mode grows in amplitude, the pattern coarsens to an unsteady convective state at
$n_{d}=20$
. In accord with the stability analysis in § 4 and as is evident in figure 12(b,c), the base state is unstable to a bulk mode. As the secondary mode grows in amplitude, the pattern coarsens to an unsteady convective state at
![]() ${\it\tau}=87.29$
(figure 12
d) with five times the wavelength of the initial steady cellular solution. The resulting mean inter-plume spacing, however, is larger than the final
${\it\tau}=87.29$
(figure 12
d) with five times the wavelength of the initial steady cellular solution. The resulting mean inter-plume spacing, however, is larger than the final
![]() $L_{m}$
. Subsequently, some plumes growing from the upper and lower boundary layers split the wider plumes into narrower ones (figure 12
e). These proto-plumes appear to be generated by a localised instability that closely resembles the wall-mode secondary instability of strictly steady base states having a wavelength greater than
$L_{m}$
. Subsequently, some plumes growing from the upper and lower boundary layers split the wider plumes into narrower ones (figure 12
e). These proto-plumes appear to be generated by a localised instability that closely resembles the wall-mode secondary instability of strictly steady base states having a wavelength greater than
![]() $L_{b}$
(figure 12
d). Ultimately, the system converges to a statistically steady turbulent state (figure 12
f). Thus, there exist two stages of evolution: initially, the bulk instability controls the evolution of the flow so that the background plumes merge forming a convective flow with smaller interior wavenumber; then, as the plume spacing becomes too wide, a variant of the boundary instability intensifies so that small plumes generated from the upper and lower walls are able to split the wider plumes into narrower ones until the flow settles into a statistically steady state. We note that the first stage of this process is loosely similar to the instability and predicted nonlinear evolution of the analytical heat-exchanger flow described in Hewitt et al. (Reference Hewitt, Neufeld and Lister2013), in which only the bulk instability mode is found.
$L_{b}$
(figure 12
d). Ultimately, the system converges to a statistically steady turbulent state (figure 12
f). Thus, there exist two stages of evolution: initially, the bulk instability controls the evolution of the flow so that the background plumes merge forming a convective flow with smaller interior wavenumber; then, as the plume spacing becomes too wide, a variant of the boundary instability intensifies so that small plumes generated from the upper and lower walls are able to split the wider plumes into narrower ones until the flow settles into a statistically steady state. We note that the first stage of this process is loosely similar to the instability and predicted nonlinear evolution of the analytical heat-exchanger flow described in Hewitt et al. (Reference Hewitt, Neufeld and Lister2013), in which only the bulk instability mode is found.

Figure 12. Snapshots of the temperature field from DNS showing the nonlinear evolution of the fastest-growing secondary instability mode for
![]() $L_{s2}=0.1$
,
$L_{s2}=0.1$
,
![]() $L=20L_{s2}$
,
$L=20L_{s2}$
,
![]() $\mathit{Ra}=9976$
: (a)
$\mathit{Ra}=9976$
: (a)
![]() ${\it\tau}=0$
; (b)
${\it\tau}=0$
; (b)
![]() ${\it\tau}=49.38$
; (c)
${\it\tau}=49.38$
; (c)
![]() ${\it\tau}=54.37$
; (d)
${\it\tau}=54.37$
; (d)
![]() ${\it\tau}=87.29$
; (e)
${\it\tau}=87.29$
; (e)
![]() ${\it\tau}=93.28$
; (f)
${\it\tau}=93.28$
; (f)
![]() ${\it\tau}=446.94$
. (g) The time evolution of the dominant horizontal mode number
${\it\tau}=446.94$
. (g) The time evolution of the dominant horizontal mode number
![]() $n_{d}$
at
$n_{d}$
at
![]() $z=0.5$
(solid line). The dashed line shows the time-average dominant mode number and the circles correspond to the times highlighted in (a–f).
$z=0.5$
(solid line). The dashed line shows the time-average dominant mode number and the circles correspond to the times highlighted in (a–f).

Figure 13. Snapshots of the temperature field from DNS showing the nonlinear evolution of the fastest-growing secondary instability mode for
![]() $L_{s3}=0.1585$
,
$L_{s3}=0.1585$
,
![]() $L=16L_{s3}$
,
$L=16L_{s3}$
,
![]() $\mathit{Ra}=9976$
: (a)
$\mathit{Ra}=9976$
: (a)
![]() ${\it\tau}=0$
; (b)
${\it\tau}=0$
; (b)
![]() ${\it\tau}=2.49$
; (c)
${\it\tau}=2.49$
; (c)
![]() ${\it\tau}=42.90$
; (d)
${\it\tau}=42.90$
; (d)
![]() ${\it\tau}=57.86$
; (e)
${\it\tau}=57.86$
; (e)
![]() ${\it\tau}=82.30$
; (f)
${\it\tau}=82.30$
; (f)
![]() ${\it\tau}=349.17$
. (g) The time evolution of the dominant horizontal mode number
${\it\tau}=349.17$
. (g) The time evolution of the dominant horizontal mode number
![]() $n_{d}$
at
$n_{d}$
at
![]() $z=0.5$
(solid line). The dashed line shows the time-average dominant mode number and the circles correspond to the times highlighted in (a–f).
$z=0.5$
(solid line). The dashed line shows the time-average dominant mode number and the circles correspond to the times highlighted in (a–f).
5.2.
 $L_{s3}~(\mathit{Ra}=9976)$
$L_{s3}~(\mathit{Ra}=9976)$
Next, we consider a wider base flow with
![]() $L_{s}=L_{s3}=0.1585$
, which also is a member of the numerical heat-exchanger family but which is (most) unstable to wall modes. From the stability analysis, the growth rate and spatial structure of the most unstable perturbation are nearly independent of
$L_{s}=L_{s3}=0.1585$
, which also is a member of the numerical heat-exchanger family but which is (most) unstable to wall modes. From the stability analysis, the growth rate and spatial structure of the most unstable perturbation are nearly independent of
![]() ${\it\beta}$
(figures 8
d and 9
b,c). The initial condition for the DNS consists of 16 copies of this steady state plus a small-amplitude contribution of the most unstable perturbation at
${\it\beta}$
(figures 8
d and 9
b,c). The initial condition for the DNS consists of 16 copies of this steady state plus a small-amplitude contribution of the most unstable perturbation at
![]() ${\it\beta}=0$
. Figure 13 shows the nonlinear evolution from this initial condition to the final state. By construction, the dominant horizontal mode number in the interior is
${\it\beta}=0$
. Figure 13 shows the nonlinear evolution from this initial condition to the final state. By construction, the dominant horizontal mode number in the interior is
![]() $n_{d}=16$
at
$n_{d}=16$
at
![]() ${\it\tau}=0$
. At early times (
${\it\tau}=0$
. At early times (
![]() ${\it\tau}=2.49$
, figure 13
b), proto-plumes generated in the upper and lower boundary layers because of the wall instability are continually swept into and thus merge with the mega-plumes in the interior. However, the resulting quasi-time-periodic flow itself evidently is unstable to a variant of the bulk mode (figure 13
c), causing a coarsening of the convective pattern (figure 13
d,e), in rough correspondence with the first stage of the evolution for the base flow with
${\it\tau}=2.49$
, figure 13
b), proto-plumes generated in the upper and lower boundary layers because of the wall instability are continually swept into and thus merge with the mega-plumes in the interior. However, the resulting quasi-time-periodic flow itself evidently is unstable to a variant of the bulk mode (figure 13
c), causing a coarsening of the convective pattern (figure 13
d,e), in rough correspondence with the first stage of the evolution for the base flow with
![]() $L_{s}=L_{s2}$
. The plumes generated from the walls then split the wider plumes before the flow reaches a statistically steady state (figure 13
f), similar to the second stage of the evolution for the case for which
$L_{s}=L_{s2}$
. The plumes generated from the walls then split the wider plumes before the flow reaches a statistically steady state (figure 13
f), similar to the second stage of the evolution for the case for which
![]() $L_{s}=L_{s2}$
. Interestingly, the final state is not dominated by a unique horizontal wavenumber in the interior. In short, there exist three evolutionary stages for the scenario with
$L_{s}=L_{s2}$
. Interestingly, the final state is not dominated by a unique horizontal wavenumber in the interior. In short, there exist three evolutionary stages for the scenario with
![]() $L_{s}=L_{s3}$
. In the linear instability regime, the wall mode dominates the evolution of the flow so that a series of proto-plumes rising from the walls merge with the background mega-plumes; this process leaves the mean inter-plume spacing unchanged from its initial value
$L_{s}=L_{s3}$
. In the linear instability regime, the wall mode dominates the evolution of the flow so that a series of proto-plumes rising from the walls merge with the background mega-plumes; this process leaves the mean inter-plume spacing unchanged from its initial value
![]() $L_{s}$
. However, the modified roughly time-periodic flow appears to be susceptible to a bulk instability, causing the merger of some mega-plumes. Finally, as the inter-plume spacing increases, a wall-like mode is again activated and some of the nascent proto-plumes split the wider plumes, yielding the final turbulent convective state. This scenario suggests that a generalisation of the bulk instability may occur for unsteady flow, and that this instability intensifies as the inter-plume spacing is reduced.
$L_{s}$
. However, the modified roughly time-periodic flow appears to be susceptible to a bulk instability, causing the merger of some mega-plumes. Finally, as the inter-plume spacing increases, a wall-like mode is again activated and some of the nascent proto-plumes split the wider plumes, yielding the final turbulent convective state. This scenario suggests that a generalisation of the bulk instability may occur for unsteady flow, and that this instability intensifies as the inter-plume spacing is reduced.
5.3.
 $L_{s4}$
and
$L_{s4}$
and
 $L_{s5}~(\mathit{Ra}=9976)$
$L_{s5}~(\mathit{Ra}=9976)$
Figure 14 shows the time evolution of the dominant horizontal mode number in the interior for the cases
![]() $L_{s}=L_{s4}$
and
$L_{s}=L_{s4}$
and
![]() $L_{s}=L_{s5}$
. For
$L_{s}=L_{s5}$
. For
![]() $L_{s}=L_{s4}=0.224$
, the steady state belongs to the family of stably stratified core solutions, but the inter-plume spacing is still less than that of the final state. From figure 14(a), it can be ascertained that the evolution for the case
$L_{s}=L_{s4}=0.224$
, the steady state belongs to the family of stably stratified core solutions, but the inter-plume spacing is still less than that of the final state. From figure 14(a), it can be ascertained that the evolution for the case
![]() $L_{s4}$
is similar to that for the case
$L_{s4}$
is similar to that for the case
![]() $L_{s3}$
. In figure 14(b),
$L_{s3}$
. In figure 14(b),
![]() $L_{s5}=0.316$
is very close to
$L_{s5}=0.316$
is very close to
![]() $L_{m}$
so that the base state evolves directly to the final state, with the dominant interior horizontal wavenumber fluctuating within a small range.
$L_{m}$
so that the base state evolves directly to the final state, with the dominant interior horizontal wavenumber fluctuating within a small range.

Figure 14. The time evolution of the dominant horizontal mode number
![]() $n_{d}$
at
$n_{d}$
at
![]() $z=0.5$
for the temperature field from DNS at
$z=0.5$
for the temperature field from DNS at
![]() $\mathit{Ra}=9976$
(solid line); the dashed line shows the time-average dominant mode number: (a)
$\mathit{Ra}=9976$
(solid line); the dashed line shows the time-average dominant mode number: (a)
![]() $L_{s4}=0.224$
,
$L_{s4}=0.224$
,
![]() $L=12L_{s4}$
; (b)
$L=12L_{s4}$
; (b)
![]() $L_{s5}=0.316$
,
$L_{s5}=0.316$
,
![]() $L=10L_{s5}$
.
$L=10L_{s5}$
.

Figure 15. Snapshots of the temperature field from DNS showing the nonlinear evolution of the fastest-growing secondary instability mode for
![]() $L_{s6}=0.5012$
,
$L_{s6}=0.5012$
,
![]() $L=10L_{s6}$
,
$L=10L_{s6}$
,
![]() $\mathit{Ra}=9976$
: (a)
$\mathit{Ra}=9976$
: (a)
![]() ${\it\tau}=0$
; (b)
${\it\tau}=0$
; (b)
![]() ${\it\tau}=1.50$
; (c)
${\it\tau}=1.50$
; (c)
![]() ${\it\tau}=40.40$
; (d)
${\it\tau}=40.40$
; (d)
![]() ${\it\tau}=573.64$
. (e) The time evolution of the dominant horizontal mode number
${\it\tau}=573.64$
. (e) The time evolution of the dominant horizontal mode number
![]() $n_{d}$
at
$n_{d}$
at
![]() $z=0.5$
(solid line). The dashed line shows the time-average dominant mode number and the circles correspond to the times highlighted in (a–d).
$z=0.5$
(solid line). The dashed line shows the time-average dominant mode number and the circles correspond to the times highlighted in (a–d).
5.4.
 $L_{s6}~(\mathit{Ra}=9976)$
$L_{s6}~(\mathit{Ra}=9976)$
Figure 15 shows the evolution for the case
![]() $L_{s}=L_{s6}=0.501$
, which is much larger than
$L_{s}=L_{s6}=0.501$
, which is much larger than
![]() $L_{m}$
. As demonstrated using secondary stability analysis, this wide-aspect-ratio convective state is strongly unstable to a wall mode. At early times, a series of proto-plumes generated from the upper and lower boundary layers continually feed the background mega-plumes (figure 15
b,c), creating a quasi-periodic flow state. Moreover, for a short time, the dominant interior horizontal wavenumber for this unsteady flow remains constant at
$L_{m}$
. As demonstrated using secondary stability analysis, this wide-aspect-ratio convective state is strongly unstable to a wall mode. At early times, a series of proto-plumes generated from the upper and lower boundary layers continually feed the background mega-plumes (figure 15
b,c), creating a quasi-periodic flow state. Moreover, for a short time, the dominant interior horizontal wavenumber for this unsteady flow remains constant at
![]() $L_{s6}$
, hence the inter-plume spacing remains much larger than
$L_{s6}$
, hence the inter-plume spacing remains much larger than
![]() $L_{m}$
. However, due to the strong boundary instability some proto-plumes grow and split the wider mega-plumes into narrower ones. This process continues until the flow converges to the final state. Thus, there is only a single stage of evolution for this case: the strong boundary instability dominates the evolution of both the initial steady state and the ensuing unsteady flow with large
$L_{m}$
. However, due to the strong boundary instability some proto-plumes grow and split the wider mega-plumes into narrower ones. This process continues until the flow converges to the final state. Thus, there is only a single stage of evolution for this case: the strong boundary instability dominates the evolution of both the initial steady state and the ensuing unsteady flow with large
![]() $L_{s}$
, generating boundary plumes that ultimately split the wide-aspect-ratio interior mega-plumes. This boundary instability becomes much stronger as
$L_{s}$
, generating boundary plumes that ultimately split the wide-aspect-ratio interior mega-plumes. This boundary instability becomes much stronger as
![]() $L_{s}$
increases.
$L_{s}$
increases.
As noted above, only a fraction of the growing proto-plumes successfully split the wide mega-plumes. Figure 16 shows this plume splitting process. Initially, a small (warm) proto-plume is generated near the lower wall because of the boundary-localised instability (figure 16 a). Shortly thereafter, many smaller proto-plumes generated around its root merge with the primary proto-plume, accelerating its growth (figure 16 b,c). Meanwhile, another (cold) proto-plume is generated near the upper wall and grows downward (figure 16 c,d). The upward growing plume soon reaches the upper wall, forming a mega-plume (figure 16 e). Near the bottom wall, this mega-plume begins to merge with its neighbouring warm mega-plume; however, the growing cold plume disrupts this merging process by splitting the wider root into two narrower roots (figure 16 f). Finally, the cold plume reaches the bottom wall, forming another downwelling mega-plume (figure 16 g). Hence, the wider plume is successfully split into two narrower ones (figure 16 h).

Figure 16. The splitting process from a wider plume to a narrower one,
![]() $L_{s6}=0.5012$
,
$L_{s6}=0.5012$
,
![]() $L=10L_{s6}$
,
$L=10L_{s6}$
,
![]() $\mathit{Ra}=9976$
: (a)
$\mathit{Ra}=9976$
: (a)
![]() ${\it\tau}=40.4$
; (b)
${\it\tau}=40.4$
; (b)
![]() ${\it\tau}=43.4$
; (c)
${\it\tau}=43.4$
; (c)
![]() ${\it\tau}=47.9$
; (d)
${\it\tau}=47.9$
; (d)
![]() ${\it\tau}=51.4$
; (e)
${\it\tau}=51.4$
; (e)
![]() ${\it\tau}=56.4$
; (f)
${\it\tau}=56.4$
; (f)
![]() ${\it\tau}=59.9$
; (g)
${\it\tau}=59.9$
; (g)
![]() ${\it\tau}=61.9$
; (h)
${\it\tau}=61.9$
; (h)
![]() ${\it\tau}=68.8$
. The solid ellipse marks the growing process for the hot plume and the dashed ellipse marks the growing process for the cold plume. Only the portion of the domain
${\it\tau}=68.8$
. The solid ellipse marks the growing process for the hot plume and the dashed ellipse marks the growing process for the cold plume. Only the portion of the domain
![]() $0\leqslant x\leqslant 0.69$
is shown to highlight the plume splitting process.
$0\leqslant x\leqslant 0.69$
is shown to highlight the plume splitting process.

Figure 17. Snapshots of the temperature field from DNS showing the nonlinear evolution of the fastest-growing linear instability mode for any
![]() $L_{s1}\leqslant L_{c}$
,
$L_{s1}\leqslant L_{c}$
,
![]() $L=10L_{f}~(L_{f}=0.2387)$
,
$L=10L_{f}~(L_{f}=0.2387)$
,
![]() $\mathit{Ra}=50\,000$
: (a)
$\mathit{Ra}=50\,000$
: (a)
![]() ${\it\tau}=0$
; (b)
${\it\tau}=0$
; (b)
![]() ${\it\tau}=6$
; (c)
${\it\tau}=6$
; (c)
![]() ${\it\tau}=8.25$
; (d)
${\it\tau}=8.25$
; (d)
![]() ${\it\tau}=9.5$
; (e)
${\it\tau}=9.5$
; (e)
![]() ${\it\tau}=10.5$
; (f)
${\it\tau}=10.5$
; (f)
![]() ${\it\tau}=16.5$
; (g)
${\it\tau}=16.5$
; (g)
![]() ${\it\tau}=28$
; (h)
${\it\tau}=28$
; (h)
![]() ${\it\tau}=227$
. (i) The time evolution of the dominant horizontal mode number
${\it\tau}=227$
. (i) The time evolution of the dominant horizontal mode number
![]() $n_{d}$
at
$n_{d}$
at
![]() $z=0.5$
(solid line). The circles correspond to the times highlighted in (a–h).
$z=0.5$
(solid line). The circles correspond to the times highlighted in (a–h).
5.5.
 $L_{s1}~(\mathit{Ra}=50\,000)$
$L_{s1}~(\mathit{Ra}=50\,000)$
As described in § 2, the conduction solution is linearly stable in domains of sufficiently small aspect ratio (
![]() $L<L_{c}$
). This solution is, of course, linearly unstable at larger
$L<L_{c}$
). This solution is, of course, linearly unstable at larger
![]() $L$
. We note that since the wavenumber of the fastest-growing mode
$L$
. We note that since the wavenumber of the fastest-growing mode
![]() $k_{f}=\pm ({\rm\pi}\sqrt{\mathit{Ra}}-{\rm\pi}^{2})^{1/2}$
, the corresponding wavelength
$k_{f}=\pm ({\rm\pi}\sqrt{\mathit{Ra}}-{\rm\pi}^{2})^{1/2}$
, the corresponding wavelength
![]() $2{\rm\pi}/k_{f}$
is larger than the mean inter-plume spacing measured from DNS at large
$2{\rm\pi}/k_{f}$
is larger than the mean inter-plume spacing measured from DNS at large
![]() $\mathit{Ra}$
, e.g. at
$\mathit{Ra}$
, e.g. at
![]() $\mathit{Ra}=50\,000$
. To illustrate the nonlinear evolution of a non-convective base flow with very small
$\mathit{Ra}=50\,000$
. To illustrate the nonlinear evolution of a non-convective base flow with very small
![]() $L_{s}=L_{s1}\leqslant L_{c}$
in the high-
$L_{s}=L_{s1}\leqslant L_{c}$
in the high-
![]() $\mathit{Ra}$
regime, the conduction solution plus its most unstable perturbation at
$\mathit{Ra}$
regime, the conduction solution plus its most unstable perturbation at
![]() $\mathit{Ra}=50\,000$
is used as the initial condition for DNS in a larger domain with
$\mathit{Ra}=50\,000$
is used as the initial condition for DNS in a larger domain with
![]() $L=10L_{f}$
. From figure 17, we see that at early times the flow evolves in accord with the predictions of linear theory (see (2.9) and figure 17
b,c). However, after a short while, thermal boundary layers form near the upper and lower walls, and in the interior the flow develops a stably stratified structure (with hot/lighter fluid above cold/heavier fluid, figure 17
d). This structure is similar to that of the steady stably stratified core solution at large
$L=10L_{f}$
. From figure 17, we see that at early times the flow evolves in accord with the predictions of linear theory (see (2.9) and figure 17
b,c). However, after a short while, thermal boundary layers form near the upper and lower walls, and in the interior the flow develops a stably stratified structure (with hot/lighter fluid above cold/heavier fluid, figure 17
d). This structure is similar to that of the steady stably stratified core solution at large
![]() $L_{s}$
. Since the inter-plume spacing is comparably large, a boundary instability dominates the subsequent evolution, with many small proto-plumes generated near the walls (figure 17
e). Unlike the previous cases in which the proto-plumes merge into the background mega-plumes, the strong stable stratification in the core prevents the warm and cold plumes from penetrating across the domain. Instead, these proto-plumes impact near the mid-plane (figure 17
f). After a series of plume merging and splitting events, the flow evolves to the final state (figure 17
g,h). Figure 17(i) shows the evolution of the dominant interior mode number for this scenario.
$L_{s}$
. Since the inter-plume spacing is comparably large, a boundary instability dominates the subsequent evolution, with many small proto-plumes generated near the walls (figure 17
e). Unlike the previous cases in which the proto-plumes merge into the background mega-plumes, the strong stable stratification in the core prevents the warm and cold plumes from penetrating across the domain. Instead, these proto-plumes impact near the mid-plane (figure 17
f). After a series of plume merging and splitting events, the flow evolves to the final state (figure 17
g,h). Figure 17(i) shows the evolution of the dominant interior mode number for this scenario.

Figure 18. Variation of mean inter-plume spacing with
![]() $\mathit{Ra}$
. The points have been computed from the DNS reported here; the solid line marks the fitted mean inter-plume spacing measured from the DNS of Hewitt et al. (Reference Hewitt, Neufeld and Lister2012). The DNS performed in this study were carried out in a domain with aspect ratio
$\mathit{Ra}$
. The points have been computed from the DNS reported here; the solid line marks the fitted mean inter-plume spacing measured from the DNS of Hewitt et al. (Reference Hewitt, Neufeld and Lister2012). The DNS performed in this study were carried out in a domain with aspect ratio
![]() $L=10L_{f}$
for
$L=10L_{f}$
for
![]() $39\,716\leqslant \mathit{Ra}\leqslant 99\,763$
; a domain with
$39\,716\leqslant \mathit{Ra}\leqslant 99\,763$
; a domain with
![]() $L=11L_{f}$
was also used for
$L=11L_{f}$
was also used for
![]() $\mathit{Ra}=39\,716$
. For
$\mathit{Ra}=39\,716$
. For
![]() $\mathit{Ra}\leqslant 19\,905$
, the dominant interior horizontal mode varies (in time) within a small range so that
$\mathit{Ra}\leqslant 19\,905$
, the dominant interior horizontal mode varies (in time) within a small range so that
![]() $L_{m}$
can be determined by taking a long-time average of the inter-plume spacing. However, for
$L_{m}$
can be determined by taking a long-time average of the inter-plume spacing. However, for
![]() $\mathit{Ra}\geqslant 39\,716$
, the interior flow becomes very well organised and (apparently) can be statistically steady for a band of wavelengths (the dash-dotted box).
$\mathit{Ra}\geqslant 39\,716$
, the interior flow becomes very well organised and (apparently) can be statistically steady for a band of wavelengths (the dash-dotted box).
5.6. Statistical inter-plume spacing up to
 $\mathit{Ra}=O(10^{5})$
$\mathit{Ra}=O(10^{5})$
From the preceding discussion, we conclude that for large
![]() $\mathit{Ra}$
the final mean inter-plume spacing is determined by a balance between (suitably generalised) bulk-mode and wall-mode instabilities. When the inter-plume spacing is small, the bulk mode controls the instability, causing plume merger and coarsening of the convective pattern; when the inter-plume spacing is large, the wall-mode instability dominates, causing small plumes generated from the walls to split the wider plumes into narrower ones. To find the mean inter-plume spacing at which the effects of these two instabilities balance, we performed DNS up to
$\mathit{Ra}$
the final mean inter-plume spacing is determined by a balance between (suitably generalised) bulk-mode and wall-mode instabilities. When the inter-plume spacing is small, the bulk mode controls the instability, causing plume merger and coarsening of the convective pattern; when the inter-plume spacing is large, the wall-mode instability dominates, causing small plumes generated from the walls to split the wider plumes into narrower ones. To find the mean inter-plume spacing at which the effects of these two instabilities balance, we performed DNS up to
![]() $\mathit{Ra}=O(10^{5})$
and measured
$\mathit{Ra}=O(10^{5})$
and measured
![]() $L_{m}$
by taking a long-time average of the inter-plume spacing. Our results are plotted in figure 18. Interestingly, for
$L_{m}$
by taking a long-time average of the inter-plume spacing. Our results are plotted in figure 18. Interestingly, for
![]() $\mathit{Ra}\geqslant 39\,716$
, the interior flow becomes very well organised and appears to be metastable within a band of wavelengths. For instance, at
$\mathit{Ra}\geqslant 39\,716$
, the interior flow becomes very well organised and appears to be metastable within a band of wavelengths. For instance, at
![]() $\mathit{Ra}=50\,000$
, given different initial conditions, there can exist 14, 16, 17 or 18 plumes in a domain with
$\mathit{Ra}=50\,000$
, given different initial conditions, there can exist 14, 16, 17 or 18 plumes in a domain with
![]() $L=10L_{f}$
. These numerical experiments suggest that very long averaging times and very wide domains are required to firmly establish the nonlinear scale selection manifested in turbulent porous medium convection. In particular, our data arguably could be fitted by scaling relations of the form
$L=10L_{f}$
. These numerical experiments suggest that very long averaging times and very wide domains are required to firmly establish the nonlinear scale selection manifested in turbulent porous medium convection. In particular, our data arguably could be fitted by scaling relations of the form
![]() $L_{m}\sim \mathit{Ra}^{{\it\alpha}}$
with
$L_{m}\sim \mathit{Ra}^{{\it\alpha}}$
with
![]() ${\it\alpha}\neq -0.4$
, the exponent proposed by Hewitt et al. (Reference Hewitt, Neufeld and Lister2012).
${\it\alpha}\neq -0.4$
, the exponent proposed by Hewitt et al. (Reference Hewitt, Neufeld and Lister2012).
6. Conclusion
We have examined the form, stability and nonlinear evolution of initially steady cellular porous medium convection in the high-
![]() $\mathit{Ra}$
regime as a function of the domain aspect ratio. Our results show that the steady solutions capture certain features characterising the turbulent columnar flows observed in DNS. For steady states with small aspect ratio
$\mathit{Ra}$
regime as a function of the domain aspect ratio. Our results show that the steady solutions capture certain features characterising the turbulent columnar flows observed in DNS. For steady states with small aspect ratio
![]() $L_{s}$
(but for which
$L_{s}$
(but for which
![]() $L_{s}>L_{c}$
, the linear stability boundary), the steady flow has a heat-exchanger structure in the interior: the vertical advection of the horizontal-mean temperature is precisely balanced by the lateral diffusion of the fluctuation temperature field associated with a single horizontal Fourier mode. However, as
$L_{s}>L_{c}$
, the linear stability boundary), the steady flow has a heat-exchanger structure in the interior: the vertical advection of the horizontal-mean temperature is precisely balanced by the lateral diffusion of the fluctuation temperature field associated with a single horizontal Fourier mode. However, as
![]() $L_{s}$
increases, the interior flow develops a stably stratified core involving many Fourier modes; moreover, the interior fluctuation fields are not depth-independent, also unlike their heat-exchanger counterparts. By comparing these equilibrium solutions with the time-averaged columnar flow in DNS, we find that the interior part of the mean columnar convection is neither a heat exchanger nor a stably stratified core flow, but rather blends certain features of these two steady solutions. Our results indicate that
$L_{s}$
increases, the interior flow develops a stably stratified core involving many Fourier modes; moreover, the interior fluctuation fields are not depth-independent, also unlike their heat-exchanger counterparts. By comparing these equilibrium solutions with the time-averaged columnar flow in DNS, we find that the interior part of the mean columnar convection is neither a heat exchanger nor a stably stratified core flow, but rather blends certain features of these two steady solutions. Our results indicate that
![]() $L_{h}$
, the maximum
$L_{h}$
, the maximum
![]() $L_{s}$
at which the strictly steady heat-exchanger solution exists, is almost half of the mean inter-plume spacing
$L_{s}$
at which the strictly steady heat-exchanger solution exists, is almost half of the mean inter-plume spacing
![]() $L_{m}$
measured from the DNS. Furthermore, heat transport in steady porous medium convection is confirmed to be less efficient than that occurring in turbulent convection. Specifically, steady convection has a ridge of maximum
$L_{m}$
measured from the DNS. Furthermore, heat transport in steady porous medium convection is confirmed to be less efficient than that occurring in turbulent convection. Specifically, steady convection has a ridge of maximum
![]() $\mathit{Nu}$
in (
$\mathit{Nu}$
in (
![]() $\mathit{Ra},L_{s}$
) parameter space along the curve
$\mathit{Ra},L_{s}$
) parameter space along the curve
![]() $L_{s}\sim \mathit{Ra}^{-0.52}$
, with
$L_{s}\sim \mathit{Ra}^{-0.52}$
, with
![]() $\mathit{Nu}\sim \mathit{Ra}^{0.6}$
along this ridge.
$\mathit{Nu}\sim \mathit{Ra}^{0.6}$
along this ridge.
Linear stability analysis of these fully nonlinear steady states indicates that the steady solutions are most unstable at large
![]() $\mathit{Ra}$
to one of two types of secondary modes. For small
$\mathit{Ra}$
to one of two types of secondary modes. For small
![]() $L_{s}$
, the most unstable disturbance is a bulk mode having roughly three to five times the wavelength of the steady convective state. The bulk instability intensifies as
$L_{s}$
, the most unstable disturbance is a bulk mode having roughly three to five times the wavelength of the steady convective state. The bulk instability intensifies as
![]() $L_{s}$
is reduced. For large
$L_{s}$
is reduced. For large
![]() $L_{s}$
, the most unstable disturbance has a growth rate that is essentially independent of horizontal scale and a vertical structure that is strongly localised near the walls. The growth rate of this wall mode increases as
$L_{s}$
, the most unstable disturbance has a growth rate that is essentially independent of horizontal scale and a vertical structure that is strongly localised near the walls. The growth rate of this wall mode increases as
![]() $L_{s}$
increases and is generally an order of magnitude larger than that of the bulk mode. The nonlinear evolution of unstable steady convective states suggests that these two types of secondary instability play a primary role in determining the mean inter-plume spacing realised in turbulent porous medium convection. When the inter-plume spacing is small, the bulk mode drives the instability, causing plume merging and coarsening of the convective pattern; when the inter-plume spacing is large, the wall-mode instability dominates, causing small plumes generated from the walls to split the wider plumes into narrower ones. For generic initial conditions, this to-and-fro process continues until there is a balance between the effects of these two types of instability. We note that for the particular case in which a conduction solution is established at large
$L_{s}$
increases and is generally an order of magnitude larger than that of the bulk mode. The nonlinear evolution of unstable steady convective states suggests that these two types of secondary instability play a primary role in determining the mean inter-plume spacing realised in turbulent porous medium convection. When the inter-plume spacing is small, the bulk mode drives the instability, causing plume merging and coarsening of the convective pattern; when the inter-plume spacing is large, the wall-mode instability dominates, causing small plumes generated from the walls to split the wider plumes into narrower ones. For generic initial conditions, this to-and-fro process continues until there is a balance between the effects of these two types of instability. We note that for the particular case in which a conduction solution is established at large
![]() $\mathit{Ra}$
and then subjected to a broad spectrum of small-amplitude disturbances, the fastest-growing linear mode will dominate the early evolution. As shown in § 5.5, the flow evolves towards a steady convective state that necessarily has a lateral scale
$\mathit{Ra}$
and then subjected to a broad spectrum of small-amplitude disturbances, the fastest-growing linear mode will dominate the early evolution. As shown in § 5.5, the flow evolves towards a steady convective state that necessarily has a lateral scale
![]() ${\approx}L_{f}$
(the wavelength of the fastest-growing linear mode) that is larger than the final mean inter-plume spacing. In this scenario, too, the dominant secondary instability by which the resulting quasi-steady flow initially approaches the final mean inter-plume spacing
${\approx}L_{f}$
(the wavelength of the fastest-growing linear mode) that is larger than the final mean inter-plume spacing. In this scenario, too, the dominant secondary instability by which the resulting quasi-steady flow initially approaches the final mean inter-plume spacing
![]() $L_{m}$
observed in statistically steady turbulent porous medium convection is the wall mode rather than the bulk mode identified in Hewitt et al. (Reference Hewitt, Neufeld and Lister2013).
$L_{m}$
observed in statistically steady turbulent porous medium convection is the wall mode rather than the bulk mode identified in Hewitt et al. (Reference Hewitt, Neufeld and Lister2013).
Our DNS show that, in sufficiently wide domains, for
![]() $\mathit{Ra}\leqslant 19\,976$
the dominant wavelength of the interior columnar flow may vary with time within a small range (figure 15
e). In contrast, for
$\mathit{Ra}\leqslant 19\,976$
the dominant wavelength of the interior columnar flow may vary with time within a small range (figure 15
e). In contrast, for
![]() $\mathit{Ra}\geqslant 39\,716$
, the dominant interior wavelength remains constant at sufficiently large times (figure 17
i). Interestingly, our simulations suggest that this final inter-plume spacing is not unique but may itself fall within some small band. Although more simulations are required to determine the boundaries of this band, it is clear that the precise high-
$\mathit{Ra}\geqslant 39\,716$
, the dominant interior wavelength remains constant at sufficiently large times (figure 17
i). Interestingly, our simulations suggest that this final inter-plume spacing is not unique but may itself fall within some small band. Although more simulations are required to determine the boundaries of this band, it is clear that the precise high-
![]() $\mathit{Ra}$
scaling of the mean interior inter-plume spacing in statistically steady porous medium convection remains to be firmly established and will require extremely long simulations in very wide computational domains.
$\mathit{Ra}$
scaling of the mean interior inter-plume spacing in statistically steady porous medium convection remains to be firmly established and will require extremely long simulations in very wide computational domains.
Acknowledgements
We thank C. Doering, D. Hewitt and K. Shao for helpful discussions. This work was supported in part by NSF Award DMS-0928098 (G.P.C.). All of the authors are grateful for the hospitality of the Geophysical Fluid Dynamics Program at Woods Hole Oceanographic Institution, supported by NSF and ONR, where some of this work was completed.