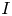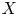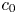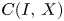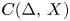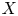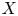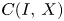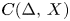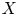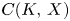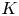The paper alluded to in the title contains the following striking result [Reference Kalton8, Theorem 6.4]: Let $I$![]() be the unit interval and $\Delta$
be the unit interval and $\Delta$![]() the Cantor set. If $X$
the Cantor set. If $X$![]() is a quasi Banach space containing no copy of $c_0$
is a quasi Banach space containing no copy of $c_0$![]() which is isomorphic to a closed subspace of a space with a basis and $C(I,\,X)$
which is isomorphic to a closed subspace of a space with a basis and $C(I,\,X)$![]() is linearly homeomorphic to $C(\Delta ,\, X)$
is linearly homeomorphic to $C(\Delta ,\, X)$![]() , then $X$
, then $X$![]() is locally convex, i.e., a Banach space.
is locally convex, i.e., a Banach space.
Here $C(K,\,X)$![]() denotes the space of continuous functions $F:K \longrightarrow X$
denotes the space of continuous functions $F:K \longrightarrow X$![]() . When $K$
. When $K$![]() is a compact space and $X$
is a compact space and $X$![]() a quasi Banach space $C(K,\,X)$
a quasi Banach space $C(K,\,X)$![]() is also a quasi Banach space under the quasinorm $\|F\|=\sup \{\|F(t)\|: t\in K\}$
is also a quasi Banach space under the quasinorm $\|F\|=\sup \{\|F(t)\|: t\in K\}$![]() .
.
When $X$![]() is a Banach space, the isomorphic theory of the spaces $C(K,\,X)$
is a Banach space, the isomorphic theory of the spaces $C(K,\,X)$![]() is somehow oversimplified by Miljutin theorem (the spaces $C(K)=C(K,\,\mathbb {R})$
is somehow oversimplified by Miljutin theorem (the spaces $C(K)=C(K,\,\mathbb {R})$![]() for $K$
for $K$![]() uncountable and metrizable are all mutually isomorphic) and, above all, by Grothendieck's identity $C(K,\,X)=C(K)\check {\otimes }_{\varepsilon } X$
uncountable and metrizable are all mutually isomorphic) and, above all, by Grothendieck's identity $C(K,\,X)=C(K)\check {\otimes }_{\varepsilon } X$![]() which implies that the isomorphic type of the Banach space $C(K,\,X)$
which implies that the isomorphic type of the Banach space $C(K,\,X)$![]() depends only on those of $C(K)$
depends only on those of $C(K)$![]() and $X$
and $X$![]() . The situation for quasi Banach spaces is more thrilling and actually some seemingly innocent questions remain open: Is $C(I,\,\ell _p)$
. The situation for quasi Banach spaces is more thrilling and actually some seemingly innocent questions remain open: Is $C(I,\,\ell _p)$![]() isomorphic to $C(I^{2},\,\ell _p)$
isomorphic to $C(I^{2},\,\ell _p)$![]() ? Is $C(I,\,L_p)$
? Is $C(I,\,L_p)$![]() isomorphic to $C(\Delta ,\,L_p)$
isomorphic to $C(\Delta ,\,L_p)$![]() ? These appear as Problems 7.2 and 7.3 at the end of [Reference Kalton8]. Problem 7.1, namely if $C(K)\otimes X$
? These appear as Problems 7.2 and 7.3 at the end of [Reference Kalton8]. Problem 7.1, namely if $C(K)\otimes X$![]() (the subspace of functions whose range is contained in some finite-dimensional subspace of $X$
(the subspace of functions whose range is contained in some finite-dimensional subspace of $X$![]() ) is always dense in $C(K,\,X)$
) is always dense in $C(K,\,X)$![]() , was posed by Klee and is connected with quite serious mathematics. While it seems to be widely open for quasi Banach spaces $X$
, was posed by Klee and is connected with quite serious mathematics. While it seems to be widely open for quasi Banach spaces $X$![]() , the answer is negative for $F$
, the answer is negative for $F$![]() -spaces (complete linear metric spaces) as shown by Cauty's celebrated example [Reference Cauty4] (see also [Reference Kalton and Dobrowolski9]) and affirmative for locally convex spaces. See Waelbroeck [Reference Waelbroeck13, Section 8] for a discussion on Klee's density problem.
-spaces (complete linear metric spaces) as shown by Cauty's celebrated example [Reference Cauty4] (see also [Reference Kalton and Dobrowolski9]) and affirmative for locally convex spaces. See Waelbroeck [Reference Waelbroeck13, Section 8] for a discussion on Klee's density problem.
The aim of this short note is much more modest: we will show that Kalton's result is sharp by exhibiting non-locally convex quasi Banach spaces $X$![]() with a basis for which $C(I,\,X)$
with a basis for which $C(I,\,X)$![]() and $C(\Delta ,\, X)$
and $C(\Delta ,\, X)$![]() are isomorphic. Our examples are rather specific and actually, in all cases, $X$
are isomorphic. Our examples are rather specific and actually, in all cases, $X$![]() is isomorphic to $C(K,\,X)$
is isomorphic to $C(K,\,X)$![]() if $K$
if $K$![]() is a metric compactum of finite covering dimension.
is a metric compactum of finite covering dimension.
Recall that the (Lebesgue) covering dimension of a (not necessarily compact) topological space $K$![]() is the smallest number $n\geq 0$
is the smallest number $n\geq 0$![]() such that every open cover admits a refinement in which every point of $K$
such that every open cover admits a refinement in which every point of $K$![]() lies in the intersection of no more than $n+1$
lies in the intersection of no more than $n+1$![]() sets of the refinement.
sets of the refinement.
A quasi Banach space $X$![]() has the $\lambda$
has the $\lambda$![]() -approximation property ($\lambda$
-approximation property ($\lambda$![]() -AP) if for every $x_1,\,\ldots ,\, x_n\in X$
-AP) if for every $x_1,\,\ldots ,\, x_n\in X$![]() (or in some dense subset) there is a finite-rank operator $T$
(or in some dense subset) there is a finite-rank operator $T$![]() on $X$
on $X$![]() such that $\|T\|\leq \lambda$
such that $\|T\|\leq \lambda$![]() and $\|x_i-Tx_i\|<\varepsilon$
and $\|x_i-Tx_i\|<\varepsilon$![]() . We say that $X$
. We say that $X$![]() has the bounded approximation property (BAP) if it has the $\lambda$
has the bounded approximation property (BAP) if it has the $\lambda$![]() -AP for some $\lambda \geq 1$
-AP for some $\lambda \geq 1$![]() .
.
We end these preliminaries by recalling that a $p$![]() -norm, where $0< p\leq 1$
-norm, where $0< p\leq 1$![]() , is a quasinorm satisfying the inequality $\|x+y\|^{p}\leq \|x\|^{p}+\|y\|^{p}$
, is a quasinorm satisfying the inequality $\|x+y\|^{p}\leq \|x\|^{p}+\|y\|^{p}$![]() and that every quasinormed space has an equivalent $p$
and that every quasinormed space has an equivalent $p$![]() -norm for some $0< p\leq 1$
-norm for some $0< p\leq 1$![]() , so says the Aoki–Rolewicz theorem.
, so says the Aoki–Rolewicz theorem.
Lemma If $K$![]() has finite covering dimension and $X$
has finite covering dimension and $X$![]() has the BAP, then $C(K,\,X)$
has the BAP, then $C(K,\,X)$![]() has the BAP.
has the BAP.
Proof. We first observe that if $K$![]() has finite covering dimension or $X$
has finite covering dimension or $X$![]() has the BAP, then $C(K)\otimes X$
has the BAP, then $C(K)\otimes X$![]() is dense in $C(K,\,X)$
is dense in $C(K,\,X)$![]() . The part concerning the BAP is obvious; the other part is a result by Shuchat [Reference Shuchat12, Theorem 1].
. The part concerning the BAP is obvious; the other part is a result by Shuchat [Reference Shuchat12, Theorem 1].
Given $g\in C(K)$![]() and $x\in X$
and $x\in X$![]() , we denote by $g\otimes x$
, we denote by $g\otimes x$![]() the function $t\longmapsto g(t)x$
the function $t\longmapsto g(t)x$![]() . Since every function in $C(K)\otimes X$
. Since every function in $C(K)\otimes X$![]() can be written as a finite sum $\sum \nolimits _{i} g_i\otimes x_i$
can be written as a finite sum $\sum \nolimits _{i} g_i\otimes x_i$![]() with $g_i\in C(K),\, x_i\in X$
with $g_i\in C(K),\, x_i\in X$![]() (which justifies our notation, see [Reference Shuchat12, Proposition 1]), it suffices to see that there is a constant $\Lambda$
(which justifies our notation, see [Reference Shuchat12, Proposition 1]), it suffices to see that there is a constant $\Lambda$![]() such that, given $f_1,\,\ldots ,\,f_m\in C(K),\, y_1,\,\ldots ,\,y_m\in X$
such that, given $f_1,\,\ldots ,\,f_m\in C(K),\, y_1,\,\ldots ,\,y_m\in X$![]() and $\varepsilon >0$
and $\varepsilon >0$![]() , there is a finite-rank operator $T$
, there is a finite-rank operator $T$![]() on $C(K,\,X)$
on $C(K,\,X)$![]() such that $\|T\|\leq \Lambda$
such that $\|T\|\leq \Lambda$![]() and $\|f_i\otimes y_i - T(f_i\otimes y_i)\|<\varepsilon$
and $\|f_i\otimes y_i - T(f_i\otimes y_i)\|<\varepsilon$![]() . As $\varepsilon$
. As $\varepsilon$![]() is arbitrary, there is no loss of generality in assuming that $\|f_i\|=\|y_i\|=1$
is arbitrary, there is no loss of generality in assuming that $\|f_i\|=\|y_i\|=1$![]() for $1\leq i\leq m$
for $1\leq i\leq m$![]() .
.
Take an open cover $U_1,\,\ldots ,\,U_r$![]() of $K$
of $K$![]() such that for every $i,\,j$
such that for every $i,\,j$![]() , one has $|f_i(s)-f_i(t)|<\varepsilon$
, one has $|f_i(s)-f_i(t)|<\varepsilon$![]() for all $s,\,t\in U_j$
for all $s,\,t\in U_j$![]() . Put $n=\dim (K)$
. Put $n=\dim (K)$![]() and take a refinement $V_1,\,\ldots ,\, V_k$
and take a refinement $V_1,\,\ldots ,\, V_k$![]() so that each point of $K$
so that each point of $K$![]() lies in no more than $n+1$
lies in no more than $n+1$![]() of those sets. Finally, let $\phi _1,\, \ldots ,\, \phi _k$
of those sets. Finally, let $\phi _1,\, \ldots ,\, \phi _k$![]() be a partition of unity of $K$
be a partition of unity of $K$![]() subordinate to $V_1,\,\ldots ,\, V_k$
subordinate to $V_1,\,\ldots ,\, V_k$![]() .
.
For each $j$![]() , pick $t_j\in V_j$
, pick $t_j\in V_j$![]() and define an operator $L$
and define an operator $L$![]() on $C(K,\,X)$
on $C(K,\,X)$![]() by letting $L(F)=\sum \nolimits _{j\leq k} \phi _j\otimes F(t_j)$
by letting $L(F)=\sum \nolimits _{j\leq k} \phi _j\otimes F(t_j)$![]() , that is, $(LF)(t)=\sum \nolimits _{j\leq k} \phi _j(t) F(t_j)$
, that is, $(LF)(t)=\sum \nolimits _{j\leq k} \phi _j(t) F(t_j)$![]() . Let us estimate $\|L\|$
. Let us estimate $\|L\|$![]() assuming $X$
assuming $X$![]() is $p$
is $p$![]() -normed: one has
-normed: one has

but for each $t\in K$![]() the sum has no more than $n+1$
the sum has no more than $n+1$![]() nonzero summands, so
nonzero summands, so

We claim that $\|f_i\otimes y_i - L(f_i\otimes y_i)\|\le \varepsilon$![]() for all $i$
for all $i$![]() . We have $L(f_i\otimes y_i)(t)=\sum \nolimits _{j\leq k}f_i(t_j)\phi _j(t) y_i$
. We have $L(f_i\otimes y_i)(t)=\sum \nolimits _{j\leq k}f_i(t_j)\phi _j(t) y_i$![]() , hence
, hence

For each $j$![]() and each $t\in K$
and each $t\in K$![]() one has $|f_i(t)\phi _j(t)-f_i(t_j)\phi _j(t)|\le \varepsilon \phi _j(t)$
one has $|f_i(t)\phi _j(t)-f_i(t_j)\phi _j(t)|\le \varepsilon \phi _j(t)$![]() : this is obvious if $t\notin V_j$
: this is obvious if $t\notin V_j$![]() since in this case $\phi _j(t)=0$
since in this case $\phi _j(t)=0$![]() , while for $t\in V_j$
, while for $t\in V_j$![]() we have $|f_i(t)-f_i(t_j)|\le \varepsilon$
we have $|f_i(t)-f_i(t_j)|\le \varepsilon$![]() by our choice of $V_1,\,\ldots ,\, V_k$
by our choice of $V_1,\,\ldots ,\, V_k$![]() and thus
and thus

holds for all $t\in K$![]() ; consequently, we have
; consequently, we have

Let $R$![]() be a finite-rank operator on $X$
be a finite-rank operator on $X$![]() such that $\|y_i-R(y_i)\|<\varepsilon$
such that $\|y_i-R(y_i)\|<\varepsilon$![]() , with $\|R\|\leq \lambda$
, with $\|R\|\leq \lambda$![]() , where $\lambda$
, where $\lambda$![]() is the ‘approximation constant’ of $X$
is the ‘approximation constant’ of $X$![]() , and define $T$
, and define $T$![]() on $C(K,\,X)$
on $C(K,\,X)$![]() by $(TF)(t)=R((LF)(t))$
by $(TF)(t)=R((LF)(t))$![]() . Clearly, $T$
. Clearly, $T$![]() has finite-rank since for an elementary tensor $f\otimes x$
has finite-rank since for an elementary tensor $f\otimes x$![]() one has
one has
Finally, let us estimate $\|f_i\otimes y_i - T(f_i\otimes y_i)\|$![]() . Write
. Write
and then

so that $C(K,\,X)$![]() has the BAP with constant at most $\lambda (n+1)^{1/p -1}$
has the BAP with constant at most $\lambda (n+1)^{1/p -1}$![]() .
.
The proof raises the question of whether the lemma is true for, say, the Hilbert cube $I^{\omega }$![]() .
.
The other ingredient we need is a complementably universal space for the BAP. A separable $p$![]() -Banach space is complementably universal for the BAP if it has the BAP and contains a complemented copy of each separable $p$
-Banach space is complementably universal for the BAP if it has the BAP and contains a complemented copy of each separable $p$![]() -Banach space with the BAP. The existence of such spaces (one for each $0< p<1$
-Banach space with the BAP. The existence of such spaces (one for each $0< p<1$![]() ) was first mentioned by Kalton himself in [Reference Kalton6, Theorem 4.1(b)]. A complete proof appears in the related issues of [Reference Cabello Sánchez, Castillo and Moreno1]. In any case, it easily follows from the Pełczyński decomposition method that any two separable $p$
) was first mentioned by Kalton himself in [Reference Kalton6, Theorem 4.1(b)]. A complete proof appears in the related issues of [Reference Cabello Sánchez, Castillo and Moreno1]. In any case, it easily follows from the Pełczyński decomposition method that any two separable $p$![]() -Banach spaces complementably universal for the BAP are isomorphic, so let us denote by $\mathscr K_p$
-Banach spaces complementably universal for the BAP are isomorphic, so let us denote by $\mathscr K_p$![]() the isomorphic type of such specimens and observe that since each separable $p$
the isomorphic type of such specimens and observe that since each separable $p$![]() -Banach space with the BAP is complemented in one with a basis, it follows that $\mathscr K_p$
-Banach space with the BAP is complemented in one with a basis, it follows that $\mathscr K_p$![]() does have a basis. Needless to say, $\mathscr K_p$
does have a basis. Needless to say, $\mathscr K_p$![]() is not locally convex since it contains a complemented copy of $\ell _p$
is not locally convex since it contains a complemented copy of $\ell _p$![]() .
.
Corollary If $K$![]() is a (non-empty) metrizable compactum of finite covering dimension, then $C(K,\,\mathscr K_p)$
is a (non-empty) metrizable compactum of finite covering dimension, then $C(K,\,\mathscr K_p)$![]() is linearly homeomorphic to $\mathscr K_p$
is linearly homeomorphic to $\mathscr K_p$![]() . In particular, $C(I,\,\mathscr K_p)$
. In particular, $C(I,\,\mathscr K_p)$![]() and $C(\Delta ,\,\mathscr K_p)$
and $C(\Delta ,\,\mathscr K_p)$![]() are linearly homeomorphic although $\mathscr K_p$
are linearly homeomorphic although $\mathscr K_p$![]() is not locally convex.
is not locally convex.
Proof. This clearly follows from the lemma since $C(K,\,\mathscr K_p)$![]() is separable, has the BAP and contains $\mathscr K_p$
is separable, has the BAP and contains $\mathscr K_p$![]() complemented as the subspace of constant functions.
complemented as the subspace of constant functions.
We do not know of any other non-locally convex quasi Banach space $X$![]() for which $C(I,\,X)$
for which $C(I,\,X)$![]() and $C(\Delta ,\, X)$
and $C(\Delta ,\, X)$![]() are isomorphic, apart from the obvious ones arising as direct sums of $\mathscr K_p$
are isomorphic, apart from the obvious ones arising as direct sums of $\mathscr K_p$![]() and Banach spaces lacking the BAP. An obvious candidate is the $p$
and Banach spaces lacking the BAP. An obvious candidate is the $p$![]() -Gurariy space, introduced by Kalton in [Reference Kalton7, Theorem 4.3] and further studied in [Reference Cabello Sánchez, Garbulińska-Wȩgrzyn and Kubiś2]. Note that if $X$
-Gurariy space, introduced by Kalton in [Reference Kalton7, Theorem 4.3] and further studied in [Reference Cabello Sánchez, Garbulińska-Wȩgrzyn and Kubiś2]. Note that if $X$![]() is a quasi Banach space isomorphic to $X\oplus F$
is a quasi Banach space isomorphic to $X\oplus F$![]() , with $F$
, with $F$![]() finite dimensional and $C(I,\,X)$
finite dimensional and $C(I,\,X)$![]() and $C(\Delta ,\, X)$
and $C(\Delta ,\, X)$![]() are not isomorphic then neither are $C(I,\,X\oplus c_0)$
are not isomorphic then neither are $C(I,\,X\oplus c_0)$![]() and $C(\Delta ,\, X\oplus c_0)$
and $C(\Delta ,\, X\oplus c_0)$![]() .
.
It's time to leave. Perhaps the most important question regarding the general topological properties of quasi Banach spaces is to know whether every quotient operator $Q:Z \longrightarrow X$![]() (acting between quasi Banach spaces) admits a continuous section, namely a continuous $\sigma : X \longrightarrow Z$
(acting between quasi Banach spaces) admits a continuous section, namely a continuous $\sigma : X \longrightarrow Z$![]() such that $Q\circ \sigma =\textbf {I}_X$
such that $Q\circ \sigma =\textbf {I}_X$![]() . More generally, let us say that $f\in C(K,\,X)$
. More generally, let us say that $f\in C(K,\,X)$![]() lifts through $Q$
lifts through $Q$![]() if there is $F\in C(K,\,Z)$
if there is $F\in C(K,\,Z)$![]() such that $f=F\circ Q$
such that $f=F\circ Q$![]() . Now, given $0< p<1$
. Now, given $0< p<1$![]() , a quotient operator between $p$
, a quotient operator between $p$![]() -Banach spaces $Q:Z \longrightarrow X$
-Banach spaces $Q:Z \longrightarrow X$![]() and a compactum $K$
and a compactum $K$![]() , consider the following statements:
, consider the following statements:
(1) $Q$
 admits a continuous section.
admits a continuous section.(2) Every continuous $f:K \longrightarrow X$
 has a lifting to $Z$
has a lifting to $Z$ .
.(3) $C(K)\otimes X$
 is dense in $C(K,\,X)$
is dense in $C(K,\,X)$ .
.
Clearly, (1)$\implies$![]() (2): set $F=\sigma \circ f$
(2): set $F=\sigma \circ f$![]() , where $\sigma$
, where $\sigma$![]() is the hypothesized section of $Q$
is the hypothesized section of $Q$![]() . Besides, if (1) is true for some quotient map $\ell _p(J) \longrightarrow X$
. Besides, if (1) is true for some quotient map $\ell _p(J) \longrightarrow X$![]() then so it is for every $Q$
then so it is for every $Q$![]() . Similarly, if (2) is true for a given $K$
. Similarly, if (2) is true for a given $K$![]() for some quotient map $\ell _p(J) \longrightarrow X$
for some quotient map $\ell _p(J) \longrightarrow X$![]() , then it is true for any quotient map onto $X$
, then it is true for any quotient map onto $X$![]() and (3) holds.
and (3) holds.
Following (badly) Klee [Reference Klee10, Section 2], let us say that the pair $(K,\,X)$![]() is admissible if (3) holds, that $K$
is admissible if (3) holds, that $K$![]() is admissible if (3) holds for every quasi Banach space $X$
is admissible if (3) holds for every quasi Banach space $X$![]() and that $X$
and that $X$![]() is admissible if (3) holds for every compact $K$
is admissible if (3) holds for every compact $K$![]() . We do not know whether the $p$
. We do not know whether the $p$![]() -Gurariy spaces are admissible or not.
-Gurariy spaces are admissible or not.
We have mentioned Shuchat's result that every compactum of finite covering dimension is admissible. Actually one can prove that (2) holds for any $Q$![]() if $\dim (K)<\infty$
if $\dim (K)<\infty$![]() . This indeed follows from Michael's [Reference Michael11, Theorem 1.2] but a simpler proof can be given using Shuchat's result, the argument of the proof of the lemma, and the open mapping theorem. Since every metrizable compactum is the continuous image of $\Delta$
. This indeed follows from Michael's [Reference Michael11, Theorem 1.2] but a simpler proof can be given using Shuchat's result, the argument of the proof of the lemma, and the open mapping theorem. Since every metrizable compactum is the continuous image of $\Delta$![]() , this implies that for every compact subset $S\subset X$
, this implies that for every compact subset $S\subset X$![]() , there is a compact subset $T\subset Z$
, there is a compact subset $T\subset Z$![]() such that $Q[T]=S$
such that $Q[T]=S$![]() .
.
Long time ago, Riedrich proved that the spaces $L_p$![]() are admissible for $0\leq p<1$
are admissible for $0\leq p<1$![]() ; see [Reference Caponetti and Lewicki3, Reference Ishii5] for more general results that cover all modular function spaces. We do not know if the quotient map $\ell _p \longrightarrow L_p$
; see [Reference Caponetti and Lewicki3, Reference Ishii5] for more general results that cover all modular function spaces. We do not know if the quotient map $\ell _p \longrightarrow L_p$![]() has a continuous section or satisfies (2) for arbitrary compact $K$
has a continuous section or satisfies (2) for arbitrary compact $K$![]() and $0< p<1$
and $0< p<1$![]() .
.
Acknowledgements
Research supported in part by MICIN Project PID2019-103961GB-C21 and Junta de Extremadura Project IB-20038.