2.1 Axisymmetric menisci in and around a cylinder

Consider a vertical circular cylinder partially immersed in an infinite water bath in a downward gravity field. The meniscus in or around the cylinder is determined uniquely by its contact angle $\unicode[STIX]{x1D703}$ and the cylinder radius $r_{0}$ , as mentioned above. The configurations of the tube and cylinder can be unified by the signed curvature $k_{r}\equiv \pm 1/r_{0}$ of the cylinder cross-section, shown by $u_{c}(k_{r})$ the height of the contact line as a function of $k_{r}$ (figure 1). It is assumed that $k_{r}<0$ ( ${>}0$ ) if the cylinder cross-section is convex towards (away from) the liquid. Therefore, the case of $k_{r}=0$ (i.e. $r_{0}\rightarrow \infty$ ) corresponds to the configuration of a vertical flat plate (inset of figure 1 b). For the vertical flat plate, the meniscus shape is described by (see e.g. Finn (Reference Finn2010), Bhatnagar & Finn (Reference Bhatnagar and Finn2016))

(2.1a ) $$\begin{eqnarray}\displaystyle & \displaystyle u=\frac{2}{\sqrt{\unicode[STIX]{x1D705}}}\sin \frac{\unicode[STIX]{x1D713}}{2}, & \displaystyle\end{eqnarray}$$

(2.1b ) $$\begin{eqnarray}\displaystyle & \displaystyle x-x_{0}=\frac{1}{\sqrt{\unicode[STIX]{x1D705}}}\left[2\cos \frac{\unicode[STIX]{x1D713}}{2}-2\cos \frac{\unicode[STIX]{x1D713}_{0}}{2}+\ln \left(\frac{\tan {\displaystyle \frac{\unicode[STIX]{x1D713}}{4}}}{\tan {\displaystyle \frac{\unicode[STIX]{x1D713}_{0}}{4}}}\right)\right], & \displaystyle\end{eqnarray}$$

$\unicode[STIX]{x1D713}$

$\unicode[STIX]{x1D705}=\unicode[STIX]{x1D70C}g/\unicode[STIX]{x1D70E}$

$\unicode[STIX]{x1D70C}$

$g$

$\unicode[STIX]{x1D70E}$

$k_{r}\gg 0$

(2.2) $$\begin{eqnarray}\displaystyle u_{c}=2k_{r}\cos \unicode[STIX]{x1D703}/\unicode[STIX]{x1D705}, & & \displaystyle\end{eqnarray}$$

where $u_{c}$ and $k_{r}$ are proportional. However, $u_{c}$ and $k_{r}$ for $k_{r}\ll 0$ (figure 1 a) are not inversely proportional, confirmed by Hildebrand, Hildebrand & Tallmadge (Reference Hildebrand, Hildebrand and Tallmadge1971).

These results are calculated numerically, based on the Young–Laplace equation in cylindrical coordinates ( $r$ , $u$ ) with the $u$ -axis passing through the axis of the cylinder and $u=0$ located at the undisturbed surface (Concus Reference Concus1968):

(2.3) $$\begin{eqnarray}\displaystyle \left[\frac{ru^{\prime }}{(1+u^{^{\prime }2})^{1/2}}\right]^{\prime }=\unicode[STIX]{x1D705}ru, & & \displaystyle\end{eqnarray}$$

where the prime refers to the derivative with respect to $r$ . The boundary conditions are

(2.4a ) $$\begin{eqnarray}\displaystyle & \displaystyle u^{\prime }=\tan (\unicode[STIX]{x03C0}/2-\unicode[STIX]{x1D703})\quad \text{at }r=1/k_{r}, & \displaystyle\end{eqnarray}$$

(2.4b ) $$\begin{eqnarray}\displaystyle & \displaystyle u^{\prime }=0\quad \text{as }r\rightarrow -\infty ,\text{ for }k_{r}<0, & \displaystyle\end{eqnarray}$$

(2.4c ) $$\begin{eqnarray}\displaystyle & \displaystyle u^{\prime }=0\quad \text{at }r=0,\text{ for }k_{r}>0. & \displaystyle\end{eqnarray}$$

$\unicode[STIX]{x1D713}$

$R$

$U$

$1/\sqrt{\unicode[STIX]{x1D705}}$

(2.5a,b ) $$\begin{eqnarray}\displaystyle \frac{\text{d}R}{\text{d}\unicode[STIX]{x1D713}}=\frac{R\cos \unicode[STIX]{x1D713}}{RU-\sin \unicode[STIX]{x1D713}},\quad \frac{\text{d}U}{\text{d}\unicode[STIX]{x1D713}}=\frac{R\sin \unicode[STIX]{x1D713}}{RU-\sin \unicode[STIX]{x1D713}}, & & \displaystyle\end{eqnarray}$$

with the boundary conditions

(2.6a ) $$\begin{eqnarray}\displaystyle & \displaystyle R=1/K_{r}\quad \text{at }\unicode[STIX]{x1D713}=\unicode[STIX]{x03C0}/2-\unicode[STIX]{x1D703}, & \displaystyle\end{eqnarray}$$

(2.6b ) $$\begin{eqnarray}\displaystyle & \displaystyle U\rightarrow 0\quad \text{and}\quad R\rightarrow -\infty \quad \text{as }\unicode[STIX]{x1D713}\rightarrow 0,\text{ for }K_{r}<0, & \displaystyle\end{eqnarray}$$

(2.6c ) $$\begin{eqnarray}\displaystyle & \displaystyle R=0\quad \text{at }\unicode[STIX]{x1D713}=0,\text{ for }K_{r}>0, & \displaystyle\end{eqnarray}$$

$K_{r}$

$k_{r}/\sqrt{\unicode[STIX]{x1D705}}$

The system of (2.5) with (2.6) can be solved numerically by the shooting method for solving a boundary-value problem by reducing it to the solution of an initial-value problem (Concus Reference Concus1968; Rapacchietta & Neumann Reference Rapacchietta and Neumann1977). Because of the singularity of (2.5) at $\unicode[STIX]{x1D713}=0$ , the asymptotic solutions of the system as $\unicode[STIX]{x1D713}\rightarrow 0$ are taken as the initial conditions for the numerical integration of (2.5), given by (see Concus Reference Concus1968; Huh & Scriven Reference Huh and Scriven1969)

(2.7a ) $$\begin{eqnarray}\displaystyle & \displaystyle U^{\ast }=\tan \unicode[STIX]{x1D713}^{\ast }\text{K}_{0}(-R^{\ast })/\text{K}_{1}(-R^{\ast }),\quad \text{for }K_{r}<0, & \displaystyle\end{eqnarray}$$

(2.7b ) $$\begin{eqnarray}\displaystyle & \displaystyle U^{\ast }=\tan \unicode[STIX]{x1D713}^{\ast }\text{I}_{0}(R^{\ast })/\text{I}_{1}(R^{\ast }),\quad \text{for }K_{r}>0, & \displaystyle\end{eqnarray}$$

$\text{I}$

$\text{K}$

$\unicode[STIX]{x1D713}^{\ast }$

$R^{\ast }$

$\pm 0.01^{\circ }$

$\unicode[STIX]{x1D703}<\unicode[STIX]{x03C0}/2$

$({>}\unicode[STIX]{x03C0}/2)$

$R^{\ast }$

Figure 2. Two families of solution curves for $\unicode[STIX]{x1D713}\in [-\unicode[STIX]{x03C0},\unicode[STIX]{x03C0}]$ (see also figure 2 in Huh & Scriven (Reference Huh and Scriven1969) and figure 1 in Wente (Reference Wente2011)): (a) $K_{r}<0$ and (b)  $K_{r}>0$ . The thick red lines represent the envelopes of the solution curves, which divide the solution curves into two parts: $F(\unicode[STIX]{x1D713},t)<0$ for generating the shape of the exotic cylinder (solid lines) and $F(\unicode[STIX]{x1D713},t)>0$ (dashed lines). The dot-dashed lines represent the solution curves of $K_{r}=0$ (i.e. the two-dimensional case), given by the dimensionless form of (2.1) with $\unicode[STIX]{x1D713}_{0}=\unicode[STIX]{x03C0}$ .

2.2 Shapes of the exotic cylinders

Based on the above considerations, a mathematic model is formulated for determining the exotic cylinder with a given contact angle $\unicode[STIX]{x1D703}$ and an initial curvature $K_{in}=K_{r}$ at $U=0$ . Wente (Reference Wente2011) has shown that the exotic tube ( $K_{r}>0$ ) can be determined by integrating the vector field $\langle \cos (\unicode[STIX]{x1D713}+\unicode[STIX]{x1D703}),\sin (\unicode[STIX]{x1D713}+\unicode[STIX]{x1D703})\rangle$ , constructed from the scalar field $\unicode[STIX]{x1D713}=\unicode[STIX]{x1D713}(R,U)$ with the Jacobian determinant $F(\unicode[STIX]{x1D713},t)$ of $(R(\unicode[STIX]{x1D713},t),U(\unicode[STIX]{x1D713},t))$ being non-zero and remaining the same sign. Substituting (2.5) for the Jacobian determinant gives

(2.8) $$\begin{eqnarray}\displaystyle F(\unicode[STIX]{x1D713},t)=\frac{(-{\dot{R}}\sin \unicode[STIX]{x1D713}+\dot{U}\cos \unicode[STIX]{x1D713})R}{RU-\sin \unicode[STIX]{x1D713}}, & & \displaystyle\end{eqnarray}$$

where the overdot refers to the derivative with respect to the parameter $t$ . Two families of solution curves of (2.5) with (2.6) are defined in parametric form by $(R(\unicode[STIX]{x1D713},t),U(\unicode[STIX]{x1D713},t))$ (see figure 2). Here the parameter $t$ is chosen as $R^{\ast }$ in (2.7) with $\unicode[STIX]{x1D713}^{\ast }$ remaining unchanged. The region of $\unicode[STIX]{x1D713}(R,U)$ is bounded by the coordinate axes and the envelopes of the family curves in the $R$ – $U$ plane. The envelopes are found by solving $F(\unicode[STIX]{x1D713},t)=0$ numerically. In these cases, the numerical results show that the Jacobian determinant $F(\unicode[STIX]{x1D713},t)$ is negative in the region (solid lines in figure 2) for generating the shape of the exotic cylinder while the Jacobian determinant in Wente (Reference Wente2011) is positive in the same region, because the parameter $t$ is chosen as $R^{\ast }$ in our cases while $t$ is $U/2$ at $\unicode[STIX]{x1D713}=0$ in Wente (Reference Wente2011).

Figure 2 shows two families of solution curves with $\unicode[STIX]{x1D713}\in [-\unicode[STIX]{x03C0},\unicode[STIX]{x03C0}]$ for the axisymmetric menisci satisfying (2.5) with the conditions (2.6b ) and (2.6c ), respectively. In figure 2(a), the axisymmetric menisci with the condition (2.6b ) extend outward to infinity and do not meet the axis of revolution. These menisci are called the axisymmetric fluid interfaces of unbounded extent by Huh & Scriven (Reference Huh and Scriven1969). The envelope in figure 2(a) has a right endpoint $(R,U)\rightarrow (0,0)$ and the height of the envelope is asymptotic to $2$ as $R\rightarrow -\infty$ . The height of the solution curve $K_{r}=0$ equals 2 according to the dimensionless form of (2.1) with $\unicode[STIX]{x1D713}_{0}=\unicode[STIX]{x03C0}$ . Therefore, the envelope appears to transversally cross the curve $K_{r}=0$ for the two-dimensional case in figure 2(a). In figure 2(b), the axisymmetric menisci with the condition (2.6c ) are simply connected and are perpendicular to the axis of revolution at $R=0$ . The envelope in figure 2(b) is asymptotic to $RU=2$ as $U\rightarrow +\infty$ and the height of the envelope decreases to $2$ as $R\rightarrow +\infty$ and hence the envelope appears to miss the curve $K_{r}=0$ in figure 2(b). Both the envelopes divide the solution curves into two parts: $F(\unicode[STIX]{x1D713},t)<0$ (solid lines) and $F(\unicode[STIX]{x1D713},t)>0$ (dashed lines). The first parts of the solution curves form the region of $\unicode[STIX]{x1D713}(R,U)$ for generating the shape of the exotic cylinder.

We make a natural extension of the cases of $K_{r}>0$ studied by Wente (Reference Wente2011) to $K_{r}<0$ , where the menisci are formed around the cylinders. Then the shapes of the exotic cylinders (see figure 3) can be obtained by the above method of Wente (Reference Wente2011). The equations for determining the exotic cylinders are

(2.9a ) $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}X}{\text{d}Y}=\cot (\unicode[STIX]{x1D713}+\unicode[STIX]{x1D703}), & \displaystyle\end{eqnarray}$$

(2.9b ) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D713}=\unicode[STIX]{x1D713}(X,Y),\quad \text{for }F(\unicode[STIX]{x1D713},R^{\ast })<0, & \displaystyle\end{eqnarray}$$

(2.10a,b ) $$\begin{eqnarray}\displaystyle X=\mp R_{0},\quad \unicode[STIX]{x1D713}=0\quad \text{at }Y=0, & & \displaystyle\end{eqnarray}$$

where the upper (lower) sign is taken if the cylinder cross-section is convex towards (away from) the liquid, $(X(Y),Y)$ denotes a point on the generatrix of the exotic cylinder and $R_{0}$ is the radius of the exotic cylinder at $U=0$ . As discussed above, the envelope in figure 2 bounds the region of $\unicode[STIX]{x1D713}(R,U)$ so that the exotic cylinder is also bounded by the corresponding envelope.

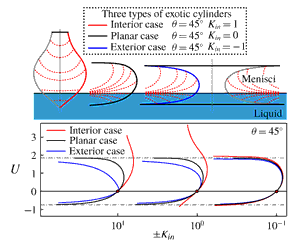
The system of (2.9) with (2.10) is solved numerically to generate the shapes of the exotic cylinders. The Runge–Kutta method is used to integrate (2.9a ). Similar to the cases shown in figure 1, the interior, planar and exterior cases of the exotic cylinders shown in figure 3 are classified by the sign of the signed curvature $K_{in}=\pm 1/R_{0}$ (with the same sign rule as $K_{r}$ ) of the cross-section at the height $U=0$ , where the planar and exterior cases are new. Figure 3(a) shows three types of exotic cylinders with $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/4$ and $K_{in}=1$ , 0 and $-1$ , and figure 3(b,c) compares the generatrices of exotic cylinders for different values of $K_{in}$ .

Figure 3. (a) Three types of exotic cylinders with $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/4$ and $K_{in}=1$ , 0 and $-1$ (from left to right), and (b,c) comparison between the shapes of the exotic cylinders with $K_{in}=10^{1}$ , $10^{0}$ and $10^{-1}$ for (b) $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/4$ and (c) $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/2$ . The thick solid red (thin blue) lines represent cases of $K_{in}>0$ $({<}0)$ , where the menisci are formed in (around) the exotic cylinders. In (a), the dotted lines represent the central axes and the dashed red lines represent the equilibrium menisci. The cases of $K_{in}=0$ (dashed black lines) are determined by (2.12). The abscissa $K_{in}$ indicates the reciprocal of $R_{0}$ , where the central axis of the exotic cylinder is located at $R=0$ . The exotic cylinders with $K_{in}<0$ are bounded by two horizontal (dot-dashed) lines $U=2\cos (\unicode[STIX]{x1D703}/2)$ and $U=-2\sin (\unicode[STIX]{x1D703}/2)$ .

For the interior cases ( $K_{in}>0$ ), as shown by Wente (Reference Wente2011), the exotic tube (thick red lines in figure 3) with $\unicode[STIX]{x1D703}\in (0,\unicode[STIX]{x03C0}/2)$ has a bottom tip at $Y=Y_{m}<0$ and is asymptotic to $XY=2\cos \unicode[STIX]{x1D703}$ as $Y\rightarrow +\infty$ . For the case of $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/2$ , the tube is asymptotic to $\lim XY=0$ as $Y\rightarrow \pm \infty$ at both extremes.

For the exterior cases ( $K_{in}<0$ ), the exotic cylinder (thin blue lines in figure 3) is bounded by two horizontal lines $U=2\cos (\unicode[STIX]{x1D703}/2)$ and $U=-2\sin (\unicode[STIX]{x1D703}/2)$ , because the height of the meniscus is asymptotic to $2\sin (\unicode[STIX]{x1D713}/2)$ as $X\rightarrow -\infty$ with $\unicode[STIX]{x1D713}\rightarrow \unicode[STIX]{x03C0}-\unicode[STIX]{x1D703}$ $(-\unicode[STIX]{x1D703})$ for $Y>0$ $({<}0)$ at the contact point. Thus, the height of the exotic cylinder with $K_{in}<0$ is finite, given by $H<2\sqrt{2}\sin \;[(2\unicode[STIX]{x1D703}+\unicode[STIX]{x03C0})/4]$ .

For the planar cases ( $K_{in}=0$ ), equation (2.9b ) is given as $\unicode[STIX]{x1D713}=2\sin ^{-1}(Y/2)$ . Then the exotic cylinder with $K_{in}=0$ is described by

(2.11) $$\begin{eqnarray}\displaystyle X(Y)=\int \cot [2\sin ^{-1}(Y/2)+\unicode[STIX]{x1D703}]\,\text{d}Y, & & \displaystyle\end{eqnarray}$$

with $X(0)=X_{0}$ . The indefinite integral (2.11) can be given explicitly as (see the dashed lines in figure 3)

(2.12) $$\begin{eqnarray}\displaystyle X-X_{0} & = & \displaystyle \sqrt{4-Y^{2}}-\cos \frac{\unicode[STIX]{x1D703}}{2}\ln \frac{\sqrt{4-Y^{2}}+2\cos {\displaystyle \frac{\unicode[STIX]{x1D703}}{2}}}{2\cos {\displaystyle \frac{\unicode[STIX]{x1D703}}{2}}(\sqrt{2-2\cos \unicode[STIX]{x1D703}}+Y)}\nonumber\\ \displaystyle & & \displaystyle -\,\sin \frac{\unicode[STIX]{x1D703}}{2}\ln \frac{\sqrt{4-Y^{2}}+2\sin {\displaystyle \frac{\unicode[STIX]{x1D703}}{2}}}{2\sin {\displaystyle \frac{\unicode[STIX]{x1D703}}{2}}(\sqrt{2+2\cos \unicode[STIX]{x1D703}}-Y)}-G(\unicode[STIX]{x1D703}),\end{eqnarray}$$

where

(2.13) $$\begin{eqnarray}\displaystyle G(\unicode[STIX]{x1D703})=2-\cos \frac{\unicode[STIX]{x1D703}}{2}\ln \frac{1+\cos {\displaystyle \frac{\unicode[STIX]{x1D703}}{2}}}{\sin \unicode[STIX]{x1D703}}-\sin \frac{\unicode[STIX]{x1D703}}{2}\ln \frac{1+\sin {\displaystyle \frac{\unicode[STIX]{x1D703}}{2}}}{\sin \unicode[STIX]{x1D703}}. & & \displaystyle\end{eqnarray}$$

In particular for $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/2$ , the exotic wall (i.e. $K_{in}=0$ ) is described by

(2.14) $$\begin{eqnarray}\displaystyle X-X_{0}=\sqrt{4-Y^{2}}-\sqrt{2}\ln \frac{\sqrt{4-Y^{2}}+\sqrt{2}}{\sqrt{4-2Y^{2}}}-G\left(\frac{\unicode[STIX]{x03C0}}{2}\right). & & \displaystyle\end{eqnarray}$$

Additionally, compared to the case of $K_{in}=0$ (dashed black lines), the difference between the cases of $K_{in}=0$ and $K_{in}\neq 0$ becomes less with the decrease of $|K_{in}|$ . Because of the symmetry of the solution curves in figure 2 with respect to the water line, the exotic cylinder with contact angle $\unicode[STIX]{x1D703}\in (\unicode[STIX]{x03C0}/2,\unicode[STIX]{x03C0})$ is the inverse of that with contact angle $\unicode[STIX]{x03C0}-\unicode[STIX]{x1D703}\in (0,\unicode[STIX]{x03C0}/2)$ for all $K_{in}$ . Thus, the exotic cylinder with contact angle $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/2$ is symmetric with respect to the $R$ -axis. It is noted that the envelopes in figure 2 are tangent to all of the solution curves. Therefore, these envelopes can be regarded as the exotic cylinders with zero contact angle, but they do not intersect with the $R$ -axis. In summary, we extend the exotic tube (Wente Reference Wente2011) to the planar and exterior cases and the three cases are unified by the signed curvatures $K_{in}$ of their cross-sections at $U=0$ , as shown in figure 3.

3.1 Axisymmetric case

We consider axisymmetric unperturbed menisci (in or around the exotic cylinders with $K_{in}\neq 0$ ) that can be described by the parametric dimensionless arclength variable $S$ , which gives a parametric representation $R=R(S)$ , $U=U(S)$ for the meniscus. The above parametric representation can be determined by the integration of (2.5) together with

(3.1) $$\begin{eqnarray}\displaystyle \frac{\text{d}S}{\text{d}\unicode[STIX]{x1D713}}=\frac{R}{RU-\sin \unicode[STIX]{x1D713}}, & & \displaystyle\end{eqnarray}$$

with the initial conditions (2.7) and $S(\unicode[STIX]{x1D713}^{\ast })=0$ with $\unicode[STIX]{x1D713}^{\ast }=0.01^{\circ }$ (to avoid the singularity at $R=0$ ). According to the approach of Myshkis et al. (Reference Myshkis, Babskii, Kopachevskii, Slobozhanin, Tyuptsov and Wadhwa1987), the perturbations are given by

(3.2) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D711}=\unicode[STIX]{x1D711}_{0}(S)+\mathop{\sum }_{n=1}^{\infty }[\unicode[STIX]{x1D711}_{n}(S)\cos n\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D719}_{n}(S)\sin n\unicode[STIX]{x1D6FC}]. & & \displaystyle\end{eqnarray}$$

It is known that axisymmetric perturbations without a fixed volume constraint are more dangerous than non-axisymmetric ones (Myshkis et al. Reference Myshkis, Babskii, Kopachevskii, Slobozhanin, Tyuptsov and Wadhwa1987; Slobozhanin & Alexander Reference Slobozhanin and Alexander2003). Because the perturbations for the exotic cylinders are unconstrained, only the axisymmetric perturbation needs to be analysed in the study of stability, which leads to an eigenvalue problem (Myshkis et al. Reference Myshkis, Babskii, Kopachevskii, Slobozhanin, Tyuptsov and Wadhwa1987)

(3.3) $$\begin{eqnarray}\displaystyle & \displaystyle L_{0}\unicode[STIX]{x1D711}_{0}\equiv -\unicode[STIX]{x1D711}_{0}^{\prime \prime }-\frac{R^{\prime }}{R}\unicode[STIX]{x1D711}_{0}^{\prime }+a(S)\unicode[STIX]{x1D711}_{0}=\unicode[STIX]{x1D706}\unicode[STIX]{x1D711}_{0},\quad \text{for }0\leqslant S\leqslant S_{1}, & \displaystyle\end{eqnarray}$$

(3.4) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D711}_{0}^{\prime }(S_{1})+\unicode[STIX]{x1D712}_{1}\unicode[STIX]{x1D711}_{0}(S_{1})=0, & \displaystyle\end{eqnarray}$$

with

(3.5a,b ) $$\begin{eqnarray}\displaystyle a(S)\equiv \cos \unicode[STIX]{x1D713}-\tilde{K}_{1}^{2}-\tilde{K}_{2}^{2}\quad \text{and}\quad \unicode[STIX]{x1D712}_{1}\equiv \frac{\tilde{K}_{1}(S_{1})\cos \unicode[STIX]{x1D703}-\bar{K}}{\sin \unicode[STIX]{x1D703}}, & & \displaystyle\end{eqnarray}$$

where the prime refers to the derivative with respect to $S$ and $\bar{K}$ is the dimensionless curvature of the generatrix of the exotic cylinder at the contact point ( $\bar{K}<0$ if the solid is convex to the liquid). Here, $S=S_{1}$ is the arc length of the profile where the meniscus meets the solid. The two dimensionless principal curvatures $\tilde{K}_{1}$ and $\tilde{K}_{2}$ of the fluid interface have the forms

(3.6a,b ) $$\begin{eqnarray}\displaystyle \tilde{K}_{1}=\frac{\text{d}\unicode[STIX]{x1D713}}{\text{d}S}=U-\frac{\sin \unicode[STIX]{x1D713}}{R}\quad \text{and}\quad \tilde{K}_{2}=\frac{\sin \unicode[STIX]{x1D713}}{R}. & & \displaystyle\end{eqnarray}$$

It is noted that the boundary conditions at $S=0$ are not given here, because the meniscus at $S=0$ does not meet a solid. The boundary conditions at $S=0$ need to be determined by the condition that the solution $\unicode[STIX]{x1D711}_{0}$ is bounded at the symmetry axis for the case of $K_{in}>0$ or at infinity for the case of $K_{in}<0$ .

The eigenvalues $\unicode[STIX]{x1D706}_{1}$ , $\unicode[STIX]{x1D706}_{2}$ , $\unicode[STIX]{x1D706}_{3},\ldots$ of the Sturm–Liouville problem (3.3)–(3.4) are real and can be ordered such that $\unicode[STIX]{x1D706}_{1}<\unicode[STIX]{x1D706}_{2}<\unicode[STIX]{x1D706}_{3}<\cdots <\unicode[STIX]{x1D706}_{n}<\cdots \rightarrow \infty$ . The smallest eigenvalue $\unicode[STIX]{x1D706}_{1}$ of the above problem (3.3) with (3.4) corresponds to the minimum value of the second variation of the potential energy of the system. Thus the equilibrium is stable if $\unicode[STIX]{x1D706}_{1}>0$ , and is unstable if $\unicode[STIX]{x1D706}_{1}<0$ (Alexander & Slobozhanin Reference Alexander and Slobozhanin2004).

For a fixed meniscus wetting a solid, the smallest eigenvalue $\unicode[STIX]{x1D706}_{1}$ depends only on the boundary parameter $\unicode[STIX]{x1D712}_{1}$ , which is related to the contact angle and the dimensionless curvature of the generatrix of the solid (3.5b ). The function $\unicode[STIX]{x1D706}_{1}(\unicode[STIX]{x1D712}_{1})$ is monotonically increasing (Myshkis et al. Reference Myshkis, Babskii, Kopachevskii, Slobozhanin, Tyuptsov and Wadhwa1987). The eigenvalue $\unicode[STIX]{x1D706}_{n}$ varies monotonically with $\unicode[STIX]{x1D712}_{1}$ for fixed mode $n$ and this relation between $\unicode[STIX]{x1D706}_{n}$ and $\unicode[STIX]{x1D712}_{1}$ is called modal monotonicity by Bostwick & Steen (Reference Bostwick and Steen2015). The value of the boundary parameter $\unicode[STIX]{x1D712}_{1}$ letting $\unicode[STIX]{x1D706}_{1}(\unicode[STIX]{x1D712}_{1})=0$ is termed the critical value $\unicode[STIX]{x1D712}_{1}^{\ast }$ .

Therefore, this problem can be further simplified by solving (3.3) with $\unicode[STIX]{x1D706}=0$ and then substituting the solution of the simplified problem $L_{0}\unicode[STIX]{x1D711}_{0}=0$ into (3.4) to obtain the critical value $\unicode[STIX]{x1D712}_{1}^{\ast }=-\unicode[STIX]{x1D711}_{0}^{\prime }/\unicode[STIX]{x1D711}_{0}$ . For the problem $L_{0}\unicode[STIX]{x1D711}_{0}=0$ , the solution $\unicode[STIX]{x1D711}_{0}$ also needs to satisfy the boundary conditions at $S=0$ mentioned above. Based on the modal monotonicity, the equilibrium meniscus under pressure disturbances will be stable if $\unicode[STIX]{x1D712}_{1}>\unicode[STIX]{x1D712}_{1}^{\ast }$ , and unstable if $\unicode[STIX]{x1D712}_{1}<\unicode[STIX]{x1D712}_{1}^{\ast }$ (Slobozhanin & Tyuptsov Reference Slobozhanin and Tyuptsov1974). The existence of $\unicode[STIX]{x1D712}_{1}^{\ast }$ requires the meniscus ( $0\leqslant S\leqslant S_{1}$ ) to be within the maximal stable profiles (i.e. $S_{1}<S_{1}^{\ast }$ ), where the maximal stable profiles ( $0\leqslant S\leqslant S_{1}^{\ast }$ ) denote the maximal possible profiles of stable equilibrium menisci. This means that a meniscus with $S_{1}>S_{1}^{\ast }$ is always unstable under pressure disturbances in any container and at any wetting angle (Slobozhanin & Alexander Reference Slobozhanin and Alexander2003).

The Sturm–Liouville problem $L_{0}\unicode[STIX]{x1D711}_{0}=0$ on a finite interval $[0,S_{1}]$ can be solved numerically by the SPPS method (Kravchenko & Porter Reference Kravchenko and Porter2010), which expresses the general solution of the Sturm–Liouville equation as a SPPS. In order to apply this method, the equation $L_{0}\unicode[STIX]{x1D711}_{0}=0$ is transformed to the Sturm–Liouville form

(3.7) $$\begin{eqnarray}\displaystyle (p\unicode[STIX]{x1D711}_{0}^{\prime })^{\prime }=r\unicode[STIX]{x1D711}_{0}, & & \displaystyle\end{eqnarray}$$

where $S_{0}$ is an arbitrary point in $[0,S_{1}]$ , $p=\exp (\int _{S_{0}}^{x}(R^{\prime }/R)\text{d}x)$ and $r=p(x)a(x)$ .

We assume that the general solution is $\unicode[STIX]{x1D711}_{0}=c_{1}\unicode[STIX]{x1D711}_{1}+c_{2}\unicode[STIX]{x1D711}_{2}$ , where $c_{1}$ and $c_{2}$ are arbitrary constants. Based on the SPPS method, the two linearly independent regular solutions $\unicode[STIX]{x1D711}_{1}$ and $\unicode[STIX]{x1D711}_{2}$ can be calculated numerically by

(3.8a,b ) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D711}_{1}=\unicode[STIX]{x1D711}_{00}\mathop{\sum }_{k=0}^{\infty }\tilde{X}^{(2k)}\quad \text{and}\quad \unicode[STIX]{x1D711}_{2}=\unicode[STIX]{x1D711}_{00}\mathop{\sum }_{k=0}^{\infty }X^{(2k+1)}, & & \displaystyle\end{eqnarray}$$

with $\tilde{X}^{(n)}$ and $X^{(n)}$ being defined by the recursive relations

(3.9a,b ) $$\begin{eqnarray}\displaystyle \tilde{X}^{(0)}\equiv 1,\quad X^{(0)}\equiv 1, & & \displaystyle\end{eqnarray}$$

(3.9c ) $$\begin{eqnarray}\displaystyle \tilde{X}^{(n)}(S)=\left\{\begin{array}{@{}l@{}}\displaystyle \int _{S_{0}}^{S}\tilde{X}^{(n-1)}(x)\unicode[STIX]{x1D711}_{00}^{2}(x)r(x)\,\text{d}x,\quad n\text{ odd},\\[12.0pt] \displaystyle \int _{S_{0}}^{S}\tilde{X}^{(n-1)}(x)\frac{1}{\unicode[STIX]{x1D711}_{00}^{2}(x)p(x)}\text{d}x,\quad n\text{ even},\end{array}\right. & & \displaystyle\end{eqnarray}$$

(3.9d ) $$\begin{eqnarray}\displaystyle X^{(n)}(S)=\left\{\begin{array}{@{}l@{}}\displaystyle \int _{S_{0}}^{S}X^{(n-1)}(x)\frac{1}{\unicode[STIX]{x1D711}_{00}^{2}p(x)}\text{d}x,\quad n\text{ odd},\\[12.0pt] \displaystyle \int _{S_{0}}^{S}X^{(n-1)}(x)\unicode[STIX]{x1D711}_{00}^{2}r(x)\,\text{d}x,\quad n\text{ even},\end{array}\right. & & \displaystyle\end{eqnarray}$$

where $\unicode[STIX]{x1D711}_{00}$ is a non-vanishing solution of $(p\unicode[STIX]{x1D711}_{0}^{\prime })^{\prime }=0$ , typically chosen as the constant function $\unicode[STIX]{x1D711}_{00}=1$ .

3.1.1 $K_{in}>0$

The stability of an axisymmetric meniscus (simply connected) restricted by a constant-pressure constraint has been well studied by Slobozhanin & Alexander (Reference Slobozhanin and Alexander2003). They have shown that the maximal stable profiles with $S\in [-R^{\ast },S_{1}^{\ast }]$ can be determined from the first zero point of $\unicode[STIX]{x1D711}_{0}(S)$ , which is the solution of (3.7) with the condition that $\unicode[STIX]{x1D711}_{0}$ is bounded at $S=-R^{\ast }$ (i.e. at the symmetry axis). To obtain the appropriate coefficients $c_{1}$ and $c_{2}$ for $\unicode[STIX]{x1D711}_{0}=c_{1}\unicode[STIX]{x1D711}_{1}+c_{2}\unicode[STIX]{x1D711}_{2}$ , the initial conditions need to be given at the point $S=0$ corresponding to $\unicode[STIX]{x1D713}=\unicode[STIX]{x1D713}^{\ast }$ , because the numerical calculation is conducted for $S\in [0,S_{1}]$ . The initial conditions at $S=0$ can be determined by the asymptotic solution of $L_{0}\unicode[STIX]{x1D711}_{0}=0$ with $S\in [-R^{\ast },0]$ for small inclination angles.

For $S\in [-R^{\ast },0]$ , $L_{0}\unicode[STIX]{x1D711}_{0}=0$ simplifies to

(3.10) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D711}_{0}^{\prime \prime }+\frac{1}{S+R^{\ast }}\unicode[STIX]{x1D711}_{0}^{\prime }+\left(\frac{U^{\ast 2}}{2}-1\right)\unicode[STIX]{x1D711}_{0}=0 & & \displaystyle\end{eqnarray}$$

using the relations $R^{\prime }/R\approx 1/(S+R^{\ast })$ and $a\approx c=1-U^{\ast 2}/2$ at small inclination angles, where $U^{\ast }$ is given by (2.7). Equation (3.10) has the solution

(3.11a ) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D711}_{0}=\text{I}_{0}((S+R^{\ast })\sqrt{c}),\quad \text{for }U^{\ast 2}<2, & \displaystyle\end{eqnarray}$$

(3.11b ) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D711}_{0}=1,\quad \text{for }U^{\ast 2}=2, & \displaystyle\end{eqnarray}$$

(3.11c ) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D711}_{0}=\text{J}_{0}((S+R^{\ast })\sqrt{-c}),\quad \text{for }U^{\ast 2}>2, & \displaystyle\end{eqnarray}$$

which satisfies the condition that $\unicode[STIX]{x1D711}_{0}$ is bounded at $S=-R^{\ast }$ , where $\text{J}$ is the Bessel function of the first kind. Differentiating (3.8) gives the expressions of $\unicode[STIX]{x1D711}_{1}^{\prime }$ and $\unicode[STIX]{x1D711}_{2}^{\prime }$ :

(3.12a,b ) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D711}_{1}^{\prime }=\frac{1}{p}\mathop{\sum }_{k=1}^{\infty }\tilde{X}^{(2k-1)}\quad \text{and}\quad \unicode[STIX]{x1D711}_{2}^{\prime }=\frac{1}{p}\mathop{\sum }_{k=0}^{\infty }X^{(2k)}. & & \displaystyle\end{eqnarray}$$

If $S_{0}=0$ is chosen for (3.9), from the definitions of $\unicode[STIX]{x1D711}_{1}$ and $\unicode[STIX]{x1D711}_{2}$ we have $\unicode[STIX]{x1D711}_{1}(0)=1$ , $\unicode[STIX]{x1D711}_{1}^{\prime }(0)=0$ , $\unicode[STIX]{x1D711}_{2}(0)=0$ and $\unicode[STIX]{x1D711}_{2}^{\prime }(0)=1$ . Then the coefficients $c_{1}$ and $c_{2}$ can be given by $c_{1}=\unicode[STIX]{x1D711}_{0}(0)$ and $c_{2}=\unicode[STIX]{x1D711}_{0}^{\prime }(0)$ , both of which are determined by (3.11). Last, the critical values $\unicode[STIX]{x1D712}_{1}^{\ast }(S)$ within the maximal stable profiles can be calculated by (3.4) together with (3.8) and (3.12), and further the stability of the meniscus is determined.

3.1.2 $K_{in}<0$

Because the solution curves for $K_{in}<0$ are infinitely long, the solution curves are divided into two parts: $S\in (-\infty ,0]$ and $S\in (0,S_{1}^{\ast }]$ . The point $S=0$ corresponds to the initial conditions (2.7a ) for the integration of (2.5). The part $S\in (-\infty ,0]$ is solved asymptotically due to small inclination angles, and the part $S\in (0,S_{1}^{\ast }]$ is solved numerically by integrating (2.5) with (2.7a ). Two linearly independent solutions $\unicode[STIX]{x1D711}_{1}$ and $\unicode[STIX]{x1D711}_{2}$ for $S\in (0,S_{1}^{\ast }]$ are determined by the mathematical model described in § 3.1. This model is suitable for both the axisymmetric cases $K_{in}>0$ and $K_{in}<0$ .

Similar to the case of $K_{in}>0$ , the coefficients $c_{1}$ and $c_{2}$ for $\unicode[STIX]{x1D711}_{0}=c_{1}\unicode[STIX]{x1D711}_{1}+c_{2}\unicode[STIX]{x1D711}_{2}$ also need to be determined from the conditions $\unicode[STIX]{x1D711}_{0}(0)$ and $\unicode[STIX]{x1D711}_{0}^{\prime }(0)$ , which are determined by the asymptotic solution for $S\in (-\infty ,0]$ . The only difference is that the meniscus is formed around the cylinder and thus the condition for the solution of (3.7) is that $\unicode[STIX]{x1D711}_{0}$ is bounded at $S\rightarrow -\infty$ (i.e. at $R\rightarrow -\infty$ ). For $S\in (-\infty ,0]$ , the Sturm–Liouville problem $L_{0}\unicode[STIX]{x1D711}_{0}=0$ simplifies to $\unicode[STIX]{x1D711}_{0}^{\prime \prime }+\unicode[STIX]{x1D711}_{0}^{\prime }/(S+R^{\ast })-\unicode[STIX]{x1D711}_{0}=0$ due to the small inclination angles. This equation has the solution

(3.13) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D711}_{0}=\text{K}_{0}(-S-R^{\ast }), & & \displaystyle\end{eqnarray}$$

which satisfies the condition that $\unicode[STIX]{x1D711}_{0}$ is bounded at $S\rightarrow -\infty$ . Then $c_{1}=\unicode[STIX]{x1D711}_{0}(0)$ and $c_{2}=\unicode[STIX]{x1D711}_{0}^{\prime }(0)$ are determined by (3.13) and the appropriate solution $\unicode[STIX]{x1D711}_{0}=c_{1}\unicode[STIX]{x1D711}_{1}+c_{2}\unicode[STIX]{x1D711}_{2}$ is obtained. Finally, the critical values $\unicode[STIX]{x1D712}_{1}^{\ast }(S)$ within the maximal stable profiles are calculated by $\unicode[STIX]{x1D712}_{1}^{\ast }=-\unicode[STIX]{x1D711}_{0}^{\prime }/\unicode[STIX]{x1D711}_{0}$ and further the determination of stability is the same as before.

3.1.3 Numerical results

Using the SPPS method, the two linearly independent regular solutions $\unicode[STIX]{x1D711}_{1}$ and $\unicode[STIX]{x1D711}_{2}$ of the equation $L_{0}\unicode[STIX]{x1D711}_{0}=0$ are determined. The appropriate solution is $\unicode[STIX]{x1D711}_{0}=c_{1}\unicode[STIX]{x1D711}_{1}+c_{2}\unicode[STIX]{x1D711}_{2}$ , where the coefficients $c_{1}$ and $c_{2}$ need to be determined. Then, the asymptotic solution of $L_{0}\unicode[STIX]{x1D711}_{0}=0$ is determined by the condition that the appropriate solution $\unicode[STIX]{x1D711}_{0}$ is bounded at the symmetry axis for the case of $K_{in}>0$ or at infinity for the case of $K_{in}<0$ , and the initial conditions at $S=0$ (i.e. $\unicode[STIX]{x1D711}_{0}(0)$ and $\unicode[STIX]{x1D711}_{0}^{\prime }(0)$ ) can be given by the asymptotic solution. The coefficients $c_{1}$ and $c_{2}$ are determined from the initial conditions $\unicode[STIX]{x1D711}_{0}(0)$ and $\unicode[STIX]{x1D711}_{0}^{\prime }(0)$ . Finally, the appropriate solution $\unicode[STIX]{x1D711}_{0}=c_{1}\unicode[STIX]{x1D711}_{1}+c_{2}\unicode[STIX]{x1D711}_{2}$ is determined.

After determining the appropriate solutions $\unicode[STIX]{x1D711}_{0}$ of (3.7) for different values of $R^{\ast }$ , the critical values $\unicode[STIX]{x1D712}_{1}^{\ast }$ within the maximal stable profiles can be easily determined, as shown in figure 4. In figure 4(a), we reproduce the diagram of stability to pressure disturbances by fixing the left-hand tip points of the meniscus profiles to the origin (see also figure 3 in Slobozhanin & Alexander (Reference Slobozhanin and Alexander2003)). In these cases, the value of meniscus height at the axis of symmetry is approximately equal to $U^{\ast }$ because of the small value $\unicode[STIX]{x1D713}^{\ast }=0.01^{\circ }$ .

Figure 4. Stability to pressure disturbances for axisymmetric menisci: (a) the solution curves fixed at the origin for $K_{in}>0$ (see also figure 3 in Slobozhanin & Alexander (Reference Slobozhanin and Alexander2003)) and (b,c) the solution curves with $U=0$ located at the water line for (b) $K_{in}>0$ and (c) $K_{in}<0$ . Panel (b) is essentially the same as panel (a) except for the different choices of the ordinates. The thick black lines denote the maximal stable profiles to pressure disturbances and the thin red lines denote the contour lines of $\unicode[STIX]{x1D712}_{1}^{\ast }$ . The end point of the maximal stable profile corresponds to $\unicode[STIX]{x1D712}_{1}^{\ast }=\infty$ . In these calculations, the order $k$ for (3.8) is given as $k=12$ .

To clearly illustrate the stability diagrams, two families of solution curves (figure 2) are contoured with a set of values of $\unicode[STIX]{x1D712}_{1}^{\ast }$ , as shown in figure 4(b,c). Figures 4(b) and 4(c) give the critical values $\unicode[STIX]{x1D712}_{1}^{\ast }$  for the two families of solution curves in figures 2(b) and 2(a), respectively. As mentioned above, the equilibrium meniscus under pressure disturbances will be stable if $\unicode[STIX]{x1D712}_{1}>\unicode[STIX]{x1D712}_{1}^{\ast }$ , and unstable if $\unicode[STIX]{x1D712}_{1}<\unicode[STIX]{x1D712}_{1}^{\ast }$ , where $\unicode[STIX]{x1D712}_{1}$ is the boundary parameter related to the contact angle and the dimensionless curvature of the generatrix of the solid (3.5b ). Any meniscus for the exotic cylinders has an end point $(R,U)$ and the critical value $\unicode[STIX]{x1D712}_{1}^{\ast }$ at $(R,U)$ in figure 4 is applied for the stability analysis. The contour lines $\unicode[STIX]{x1D712}_{1}^{\ast }=\infty$ divide the solution curves (figure 2) into two parts, and only the lower curves corresponding to the maximal stable profiles (thick black lines in figure 4) are plotted.

We found that there are two regions $-1<\unicode[STIX]{x1D712}_{1}^{\ast }<0$ and $\unicode[STIX]{x1D712}_{1}^{\ast }>0$ separated by the contour line $\unicode[STIX]{x1D712}_{1}^{\ast }=0$ in figure 4(b). The line $\unicode[STIX]{x1D712}_{1}^{\ast }=0$ only intersects with the solution curves with $U^{\ast 2}\leqslant 2$ and there is only one intersection point for each of the solution curves. In the region $-1<\unicode[STIX]{x1D712}_{1}^{\ast }<0$ , the contour line intersects with the abscissa at $(R_{c},0)$ which satisfies the relation (Slobozhanin & Alexander Reference Slobozhanin and Alexander2003)

(3.14) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D712}_{1}^{\ast }=-\text{I}_{1}(R_{c})/\text{I}_{0}(R_{c}). & & \displaystyle\end{eqnarray}$$

We can see that $\unicode[STIX]{x1D712}_{1}^{\ast }\rightarrow -1$ as $R_{c}\rightarrow \infty$ . In the region $\unicode[STIX]{x1D712}_{1}^{\ast }>0$ , the contour lines will intersect with all solution curves, and there is only one intersection point for each of the solution curves. In particular, the line $\unicode[STIX]{x1D712}_{1}^{\ast }=\infty$ is the boundary line of the maximal stable profiles. In figure 4(c), the stability diagram is also divided into two regions $\unicode[STIX]{x1D712}_{1}^{\ast }>-1$ and $\unicode[STIX]{x1D712}_{1}^{\ast }<-1$ by the contour line $\unicode[STIX]{x1D712}_{1}^{\ast }=-1$ . In the region $\unicode[STIX]{x1D712}_{1}^{\ast }<-1$ , the contour line intersects with the abscissa at $(\bar{R}_{c},0)$ which satisfies the relation

(3.15) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D712}_{1}^{\ast }=-\text{K}_{1}(-\bar{R}_{c})/\text{K}_{0}(-\bar{R}_{c}). & & \displaystyle\end{eqnarray}$$

Most interestingly, the numerical results show that the contour lines $\unicode[STIX]{x1D712}_{1}^{\ast }=\infty$ (figure 4 b,c) are in good agreement with the envelopes of solution curves (figure 2). We will discuss these results in § 3.3.

3.2 Two-dimensional case

Similar to the approach taken for the stability for $K_{in}\neq 0$ , the stability of the two-dimensional meniscus ( $K_{in}=0$ ) can be determined by solving the problem

(3.16) $$\begin{eqnarray}\displaystyle L_{0}\unicode[STIX]{x1D711}_{0}\equiv -\unicode[STIX]{x1D711}_{0}^{\prime \prime }+a(S)\unicode[STIX]{x1D711}_{0}=0,\quad \text{for }0\leqslant S\leqslant S_{1}, & & \displaystyle\end{eqnarray}$$

where $a(S)=3\cos \unicode[STIX]{x1D713}-2$ is derived from (3.5a ). We assume $S=0$ at a small inclination angle $\unicode[STIX]{x1D713}_{0}=0.01^{\circ }$ . Then the parametric representation $S(\unicode[STIX]{x1D713})$ is given by

(3.17) $$\begin{eqnarray}\displaystyle S(\unicode[STIX]{x1D713})=\int _{\unicode[STIX]{x1D713}_{0}}^{\unicode[STIX]{x1D713}}\frac{1}{U(\unicode[STIX]{x1D713})}\text{d}\unicode[STIX]{x1D713}=\ln \left(\tan \frac{\unicode[STIX]{x1D713}}{4}\left/\tan \frac{\unicode[STIX]{x1D713}_{0}}{4}\right.\right). & & \displaystyle\end{eqnarray}$$

The inverse of (3.17) is

(3.18) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D713}(S)=4\tan ^{-1}(\exp (S+S_{0})), & & \displaystyle\end{eqnarray}$$

where $S_{0}=\ln (\tan (\unicode[STIX]{x1D713}_{0}/4))$ . Then

(3.19) $$\begin{eqnarray}\displaystyle a(S)=\frac{\exp (4S+4S_{0})-22\exp (2S+2S_{0})+1}{\exp (4S+4S_{0})+2\exp (2S+2S_{0})+1}. & & \displaystyle\end{eqnarray}$$

To apply the SPPS method to this problem, equation (3.16) is transformed to the form of $(p\unicode[STIX]{x1D711}_{0}^{\prime })^{\prime }=r\unicode[STIX]{x1D711}_{0}$ , where $p=1$ and $r=a(S)$ . Then two independent solutions $\unicode[STIX]{x1D711}_{1}$ and $\unicode[STIX]{x1D711}_{2}$ are given by (3.8). The boundary condition at $S=0$ can be obtained from the solution of $\unicode[STIX]{x1D711}_{0}^{\prime \prime }=a\unicode[STIX]{x1D711}_{0}$ for $S\leqslant 0$ (corresponding to $\unicode[STIX]{x1D713}\in (0,\unicode[STIX]{x1D713}_{0}]$ ), where $a\approx 1$ at small inclination angles or $a=1$ for flat menisci. The solution that satisfies that $\unicode[STIX]{x1D711}_{0}$ is bounded as $S\rightarrow -\infty$ is $\exp (S)$ . Thus the conditions at $S=0$ are $\unicode[STIX]{x1D711}_{0}(0)=1$ and $\unicode[STIX]{x1D711}_{0}^{\prime }(0)=1$ , and hence $\unicode[STIX]{x1D711}_{0}=\unicode[STIX]{x1D711}_{1}+\unicode[STIX]{x1D711}_{2}$ with $S_{0}=0$ . Then the critical values $\unicode[STIX]{x1D712}_{1}^{\ast }$ are determined.

Figure 5(a) shows the numerical solution $\unicode[STIX]{x1D711}_{0}$ calculated by the SPPS method, where the boundary conditions at $S=0$ are given by the solution $\unicode[STIX]{x1D711}_{0}=\exp (S)$ (see the left-hand inset). The first zero point of $\unicode[STIX]{x1D711}_{0}$ (the yellow point) corresponds to the maximal stable profile, as shown in the right-hand inset. The numerical result indicates that the end point of the maximal stable profile is the point with $U\approx 2$ ( $|U-2|=4.3\times 10^{-10}$ ), corresponding to an inclination angle $\unicode[STIX]{x1D713}=\unicode[STIX]{x03C0}$ , where the order of the SPPS method is $k=12$ . Similar to the axisymmetric case, the stability can be determined by the critical values $\unicode[STIX]{x1D712}_{1}^{\ast }$ , as shown in figure 5(b). The critical values $\unicode[STIX]{x1D712}_{1}^{\ast }$ can be uniquely determined by the inclination angle $\unicode[STIX]{x1D713}$ . It is known that this meniscus is invariant under translation in $R$ . Thus the contour lines for $\unicode[STIX]{x1D712}_{1}^{\ast }$ are the horizontal straight lines. Specifically, the lines $U=\pm 2$ are the contour lines $\unicode[STIX]{x1D712}_{1}^{\ast }=\infty$ , and also the envelopes of the two-dimensional menisci.

Figure 5. (a) Numerical result of (3.16) calculated by the SPPS method and (b) relation between $\unicode[STIX]{x1D712}_{1}^{\ast }$ and $\unicode[STIX]{x1D713}$ .

Figure 6. Comparison between the critical values $\unicode[STIX]{x1D712}_{1}^{\ast }$ and the boundary parameters of $\unicode[STIX]{x1D712}_{1}$ of the exotic cylinders with contact angle $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/2$ and parameters $K_{in}=1$ (a), $0$ (b) and $-1$ (c). The abscissa $Y$ denotes the height of the exotic cylinder.

3.3 Stability analysis of exotic cylinders and ‘exotic’ property

The profiles of the menisci in or around the exotic cylinder are the parts of the solution curves in figure 4(b,c), each of which meets the exotic cylinder at a prescribed contact angle $\unicode[STIX]{x1D703}$ . Then, the stabilities of the menisci are determined by comparing the boundary parameters $\unicode[STIX]{x1D712}_{1}$ of the exotic cylinder and the critical values $\unicode[STIX]{x1D712}_{1}^{\ast }$ . The meniscus under pressure disturbances will be stable if $\unicode[STIX]{x1D712}_{1}>\unicode[STIX]{x1D712}_{1}^{\ast }$ , and unstable if $\unicode[STIX]{x1D712}_{1}<\unicode[STIX]{x1D712}_{1}^{\ast }$ .

For the exotic cylinders with $K_{in}>0$ , Wente (Reference Wente2011) has shown that any (equilibrium) meniscus in the exotic cylinder is a minimiser of energy. This means that the second variation of energy is zero to pressure disturbances. This case can be extended to the cases of $K_{in}<0$ and $K_{in}=0$ (see appendix A). Therefore, the boundary parameter $\unicode[STIX]{x1D712}_{1}$ of the exotic cylinder is expected to be equal to the critical value $\unicode[STIX]{x1D712}_{1}^{\ast }$ . This observation is validated in our numerical experiments. Figure 6 shows that, as expected, there is a good agreement between the critical values $\unicode[STIX]{x1D712}_{1}^{\ast }$ and the boundary parameters $\unicode[STIX]{x1D712}_{1}$ of the exotic cylinders for $K_{in}=1$ , $0$ and $-1$ . This means that the smallest eigenvalue of the Sturm–Liouville problem for the meniscus in or around the exotic cylinders is equal to zero under pressure disturbances. Although these results may seem not surprising at first, they provide another way to determine stability, because the critical values $\unicode[STIX]{x1D712}_{1}^{\ast }$ are equal to the boundary parameters $\unicode[STIX]{x1D712}_{1}$ of the exotic cylinders. Namely, the critical values $\unicode[STIX]{x1D712}_{1}^{\ast }$ can be determined by calculating the boundary parameters $\unicode[STIX]{x1D712}_{1}$ of the exotic cylinders by (3.5b ), not by solving the Sturm–Liouville problem $L_{0}\unicode[STIX]{x1D711}_{0}=0$ .

3.3.1 Two-dimensional case

For $K_{in}=0$ , substituting (2.11) into $\bar{K}=-X^{\prime \prime }/(1+X^{^{\prime }2})^{3/2}$ with $Y=2\sin (\unicode[STIX]{x1D713}/2)$ gives

(3.20) $$\begin{eqnarray}\displaystyle \bar{K}=\frac{\sin (\unicode[STIX]{x1D713}+\unicode[STIX]{x1D703})}{\cos {\displaystyle \frac{\unicode[STIX]{x1D713}}{2}}}, & & \displaystyle\end{eqnarray}$$

where $\bar{K}$ is the signed curvature of the exotic cylinder. Substituting (3.20) into (3.5b ) with $\tilde{K}_{1}=2\sin (\unicode[STIX]{x1D713}/2)$ and $\unicode[STIX]{x1D712}_{1}^{\ast }=\unicode[STIX]{x1D712}_{1}$ , we have

(3.21) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D712}_{1}^{\ast }=-\frac{\cos \unicode[STIX]{x1D713}}{\cos {\displaystyle \frac{\unicode[STIX]{x1D713}}{2}}}. & & \displaystyle\end{eqnarray}$$

To verify this equation, substituting (3.21) into (3.4) gives

(3.22) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D711}_{0}^{\prime }=\frac{\cos \unicode[STIX]{x1D713}}{\cos {\displaystyle \frac{\unicode[STIX]{x1D713}}{2}}}\unicode[STIX]{x1D711}_{0}. & & \displaystyle\end{eqnarray}$$

Then the differential equation (3.22) is solved using the ‘dsolve’ program in MATLAB for the analytical solution

(3.23) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D711}_{0}=\frac{\exp (S)[\exp (2S+2S_{0})-1]}{[\exp (2S+2S_{0})+1]^{2}}, & & \displaystyle\end{eqnarray}$$

which satisfies (3.16). Thus (3.21) is verified and provides an analytical expression for the critical value $\unicode[STIX]{x1D712}_{1}^{\ast }$ for the two-dimensional meniscus.

Interestingly, the property of the exotic cylinder is related to the floating phenomenon. It is known that the meridional curvature of the exotic cylinder with $K_{in}=0$ is given by (3.20). This expression can also be deduced from the relation between the variations $\unicode[STIX]{x1D6FF}H$ and $\unicode[STIX]{x1D6FF}U$ (see appendix B in Zhang, Zhou & Zhu (Reference Zhang, Zhou and Zhu2018)):

(3.24) $$\begin{eqnarray}\displaystyle \left[\cos \frac{\unicode[STIX]{x1D713}}{2}-\frac{1}{\bar{K}}\sin (\unicode[STIX]{x1D713}+\unicode[STIX]{x1D703})\right]\unicode[STIX]{x1D6FF}U=\cos \frac{\unicode[STIX]{x1D713}}{2}\unicode[STIX]{x1D6FF}H, & & \displaystyle\end{eqnarray}$$

where all the quantities are dimensionless, $\bar{K}$ denotes the curvature of solid at the contact point, $\unicode[STIX]{x1D713}$ denotes the inclination angle of the meniscus at the contact point and $\unicode[STIX]{x1D6FF}U$ and $\unicode[STIX]{x1D6FF}H$ denote the variations of the contact point height and the vertical displacement of floating body, respectively. This equation provides quantitative relations between the infinitesimal vertical displacement $\unicode[STIX]{x1D6FF}H$ of a two-dimensional floating body and the change $\unicode[STIX]{x1D6FF}U$ of the contact point height. This means that in response to an infinitesimal vertical displacement $\unicode[STIX]{x1D6FF}H$ of the floating body, the equilibrium meniscus will adjust itself, leading to a change of the contact point height $\unicode[STIX]{x1D6FF}U$ . For the exotic cylinders with $K_{in}=0$ , the coefficient $[\cos (\unicode[STIX]{x1D713}/2)-(1/\bar{K})\sin (\unicode[STIX]{x1D713}+\unicode[STIX]{x1D703})]$ for $\unicode[STIX]{x1D6FF}U$ will be zero, because $\unicode[STIX]{x1D6FF}U$ can be arbitrary when the exotic cylinder is fixed ( $\unicode[STIX]{x1D6FF}H=0$ ). Then (3.20) is derived. This finding seems to provide a useful way to calculate the curvature of the exotic cylinder and then to determine stability without solving the Sturm–Liouville problem $L_{0}\unicode[STIX]{x1D711}_{0}=0$ .

Additionally, it is noted that the envelopes can be regarded as exotic cylinders with $\unicode[STIX]{x1D703}=0$ , because the envelopes are tangent to all menisci. Seen from (3.5b ), we have $\unicode[STIX]{x1D712}_{1}=\infty$ for the exotic cylinders with $\unicode[STIX]{x1D703}=0$ . Therefore, it is not surprising that the envelopes are in good agreement with the contour lines $\unicode[STIX]{x1D712}_{1}^{\ast }=\infty$ in figure 4. Therefore, the maximal stable profiles can be determined by solving $F(\unicode[STIX]{x1D713},t)=0$ .

3.3.2 Axisymmetric case

The exotic cylinder with $K_{in}<0$ can also be regarded as a special floating body with a fixed position in which the contact point is allowed to move continuously on the solid. This idea also applies to the case of $K_{in}>0$ . Suppose that $U(R,\unicode[STIX]{x1D713})$ determines the families of curves in figure 2. Then the signed curvature of the generatrix of the exotic cylinder at the contact point satisfies the relation

(3.25) $$\begin{eqnarray}\displaystyle \bar{K}\equiv \left.\frac{\text{d}\bar{\unicode[STIX]{x1D713}}}{\text{d}\bar{S}}\right|_{S}=\frac{\sin \bar{\unicode[STIX]{x1D713}}}{\left.{\displaystyle \frac{\text{d}U}{\text{d}\unicode[STIX]{x1D713}}}\right|_{S}}, & & \displaystyle\end{eqnarray}$$

where the inclination angle of the solid satisfies $\bar{\unicode[STIX]{x1D713}}=\unicode[STIX]{x1D713}+\unicode[STIX]{x1D703}$ (the ‘exotic’ property), $\bar{S}$ denotes the arc length of the solid and the subscript ‘ $S$ ’ denotes that the total derivative is constrained to the solid. Then we obtain

(3.26) $$\begin{eqnarray}\displaystyle \left.\frac{\text{d}U}{\text{d}\unicode[STIX]{x1D713}}\right|_{S}=\frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}+\frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}R}\left.\frac{\text{d}R}{\text{d}U}\right|_{S}\left.\frac{\text{d}U}{\text{d}\unicode[STIX]{x1D713}}\right|_{S}, & & \displaystyle\end{eqnarray}$$

where $\text{d}R/\text{d}U|_{S}=\cot \bar{\unicode[STIX]{x1D713}}$ . This gives

(3.27) $$\begin{eqnarray}\displaystyle \bar{K}=\frac{\sin \bar{\unicode[STIX]{x1D713}}}{{\displaystyle \frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}}}\left(1-\cot \bar{\unicode[STIX]{x1D713}}\frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}R}\right). & & \displaystyle\end{eqnarray}$$

It is noted that another expression for $\bar{K}$ has been proposed in Huh & Mason (Reference Huh and Mason1974) using the relation between $\unicode[STIX]{x1D6FF}H$ and $\unicode[STIX]{x1D6FF}U$ , similar to (3.24). For the curvature of the meniscus at the contact point, a similar derivation gives

(3.28) $$\begin{eqnarray}\displaystyle \tilde{K}_{1}=\frac{\sin \unicode[STIX]{x1D713}}{{\displaystyle \frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}}}\left(1-\cot \unicode[STIX]{x1D713}\frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}R}\right). & & \displaystyle\end{eqnarray}$$

The curvature of the meniscus is also represented by (3.6a ), and therefore the relation between $\unicode[STIX]{x2202}U/\unicode[STIX]{x2202}\unicode[STIX]{x1D713}$ and $\unicode[STIX]{x2202}U/\unicode[STIX]{x2202}R$ is

(3.29) $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}=\frac{R\sin \unicode[STIX]{x1D713}}{RU-\sin \unicode[STIX]{x1D713}}\left(1-\cot \unicode[STIX]{x1D713}\frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}R}\right). & & \displaystyle\end{eqnarray}$$

Then substituting (3.27), (3.28) and (3.29) into (3.5b ) gives the boundary parameter of the exotic cylinder:

(3.30) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D712}_{1}=\unicode[STIX]{x1D712}_{1}^{\ast }=-\frac{(RU-\sin \unicode[STIX]{x1D713})\left(\cos \unicode[STIX]{x1D713}+\sin \unicode[STIX]{x1D713}{\displaystyle \frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}R}}\right)}{R\left(\sin \unicode[STIX]{x1D713}-\cos \unicode[STIX]{x1D713}{\displaystyle \frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}R}}\right)}, & & \displaystyle\end{eqnarray}$$

which is independent of $\unicode[STIX]{x1D703}$ . The critical value $\unicode[STIX]{x1D712}_{1}^{\ast }$ can be determined as long as $\unicode[STIX]{x2202}U/\unicode[STIX]{x2202}R$ is determined. The partial derivative $\unicode[STIX]{x2202}U/\unicode[STIX]{x2202}R$ can be determined by integrating (2.5) together with

(3.31) $$\begin{eqnarray}\displaystyle \frac{\text{d}(\unicode[STIX]{x2202}U/\unicode[STIX]{x2202}R)}{\text{d}\unicode[STIX]{x1D713}}=\frac{\unicode[STIX]{x2202}(\unicode[STIX]{x2202}U/\unicode[STIX]{x2202}R)}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}+\frac{\unicode[STIX]{x2202}(\unicode[STIX]{x2202}U/\unicode[STIX]{x2202}R)}{\unicode[STIX]{x2202}R}\frac{\text{d}R}{\text{d}\unicode[STIX]{x1D713}}. & & \displaystyle\end{eqnarray}$$

Suppose that $U$ is a new variable. We have

(3.32) $$\begin{eqnarray}\displaystyle \left.\frac{\text{d}(\text{d}U/\text{d}\unicode[STIX]{x1D713})}{\text{d}R}\right|_{\unicode[STIX]{x1D713}=\text{const.}}=\frac{\unicode[STIX]{x2202}(\text{d}U/\text{d}\unicode[STIX]{x1D713})}{\unicode[STIX]{x2202}R}+\frac{\unicode[STIX]{x2202}(\text{d}U/\text{d}\unicode[STIX]{x1D713})}{\unicode[STIX]{x2202}U}\frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}R}, & & \displaystyle\end{eqnarray}$$

where $\unicode[STIX]{x2202}(\text{d}U/\text{d}\unicode[STIX]{x1D713})/\unicode[STIX]{x2202}R$ and $\unicode[STIX]{x2202}(\text{d}U/\text{d}\unicode[STIX]{x1D713})/\unicode[STIX]{x2202}U$ are the partial derivatives of (2.5). On the other hand, (3.32) can also be written as

(3.33) $$\begin{eqnarray}\displaystyle \left.\frac{\text{d}(\text{d}U/\text{d}\unicode[STIX]{x1D713})}{\text{d}R}\right|_{\unicode[STIX]{x1D713}=\text{const.}} & = & \displaystyle \frac{\unicode[STIX]{x2202}(\unicode[STIX]{x2202}U/\unicode[STIX]{x2202}R)}{\unicode[STIX]{x2202}R}\frac{\text{d}R}{\text{d}\unicode[STIX]{x1D713}}+\frac{\unicode[STIX]{x2202}(\unicode[STIX]{x2202}U/\unicode[STIX]{x2202}\unicode[STIX]{x1D713})}{\unicode[STIX]{x2202}R}\nonumber\\ \displaystyle & & \displaystyle +\,\left[\frac{\unicode[STIX]{x2202}(\text{d}R/\text{d}\unicode[STIX]{x1D713})}{\unicode[STIX]{x2202}R}+\frac{\unicode[STIX]{x2202}(\text{d}R/\text{d}\unicode[STIX]{x1D713})}{\unicode[STIX]{x2202}U}\frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}R}\right]\frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}R},\end{eqnarray}$$

where $\unicode[STIX]{x2202}(\text{d}R/\text{d}\unicode[STIX]{x1D713})/\unicode[STIX]{x2202}R$ and $\unicode[STIX]{x2202}(\text{d}R/\text{d}\unicode[STIX]{x1D713})/\unicode[STIX]{x2202}U$ are the partial derivatives of (2.5). Comparing (3.31), (3.32) and (3.33), we find

(3.34) $$\begin{eqnarray}\displaystyle \frac{\text{d}(\unicode[STIX]{x2202}U/\unicode[STIX]{x2202}R)}{\text{d}\unicode[STIX]{x1D713}} & = & \displaystyle \frac{\unicode[STIX]{x2202}(\text{d}U/\text{d}\unicode[STIX]{x1D713})}{\unicode[STIX]{x2202}R}+\frac{\unicode[STIX]{x2202}(\text{d}U/\text{d}\unicode[STIX]{x1D713})}{\unicode[STIX]{x2202}U}\frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}R}\nonumber\\ \displaystyle & & \displaystyle -\,\left[\frac{\unicode[STIX]{x2202}(\text{d}R/\text{d}\unicode[STIX]{x1D713})}{\unicode[STIX]{x2202}R}+\frac{\unicode[STIX]{x2202}(\text{d}R/\text{d}\unicode[STIX]{x1D713})}{\unicode[STIX]{x2202}U}\frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}R}\right]\frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}R}.\end{eqnarray}$$

By integrating (3.34) together with (2.5) and then substituting the value of $\unicode[STIX]{x2202}U/\unicode[STIX]{x2202}R$ for (3.30), the critical value $\unicode[STIX]{x1D712}_{1}^{\ast }$ is obtained, where the initial condition for $\unicode[STIX]{x2202}U/\unicode[STIX]{x2202}R$ is given by the partial derivatives of (2.7). Figure 7 shows a good agreement between the contour lines $\unicode[STIX]{x1D712}_{1}^{\ast }=0$ calculated by solving the Sturm–Liouville problem $L_{0}\unicode[STIX]{x1D711}_{0}=0$ and by (3.30). Thus, by utilising the property of the exotic cylinder we find a convenient alternative for calculating the critical value $\unicode[STIX]{x1D712}_{1}^{\ast }$ and then determining the stability of the axisymmetric meniscus under pressure disturbances.

Figure 7. Comparison between the contour lines $\unicode[STIX]{x1D712}_{1}^{\ast }=0$ by solving the Sturm–Liouville problem $L_{0}\unicode[STIX]{x1D711}_{0}=0$ and by (3.30) for (a) $K_{in}>0$ and (b) $K_{in}<0$ .

For (3.30), we make the following simple observations. (i) For $\unicode[STIX]{x1D712}_{1}^{\ast }\rightarrow \infty$ (i.e. $\sin \unicode[STIX]{x1D713}-\cos \unicode[STIX]{x1D713}(\unicode[STIX]{x2202}U/\unicode[STIX]{x2202}R)=0$ ), this equation determines the maximal stable profiles (see figure 4), and also the envelopes of menisci (see figure 2), and therefore the equation is equivalent to $F(\unicode[STIX]{x1D713},t)=0$ when $t$ is chosen as $R$ with $\unicode[STIX]{x1D713}$ held constant. (ii) Equation (3.30) can be written in a generalised form:

(3.35) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D712}_{1}=\unicode[STIX]{x1D712}_{1}^{\ast }=-\frac{\cos \unicode[STIX]{x1D713}+\sin \unicode[STIX]{x1D713}{\displaystyle \frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}R}}}{{\displaystyle \frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}}}, & & \displaystyle\end{eqnarray}$$

which can degenerate to (3.21) when $U=2\sin (\unicode[STIX]{x1D713}/2)$ for the two-dimensional case.