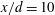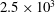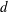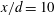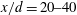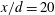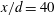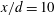1 Introduction
It is of fundamental importance to understand the relationship that exists between the organized motions of a turbulent flow and its ability to influence the momentum and heat transfer characteristics of the flow. One flow that has received a great deal of attention, in the context of both the different types of organizations or coherent large-scale structures that prevail in different regions of the flow as well as the contribution these structures make to momentum and heat fluxes, is the turbulent wake generated by a circular cylinder. In particular, the near (
$0<x/d<10$
where
$x$
is the streamwise distance from the cylinder axis and
$d$
is the cylinder diameter) and intermediate
$(10\lesssim x/d\lesssim 100)$
regions of the wake have been studied extensively because of the dominance of the Kármán vortex street immediately downstream of the cylinder, its gradual weakening and eventual disappearance.
Meaningful research into the organized motion first requires the development of a reliable procedure for identifying this motion and reducing its features (e.g. Cantwell & Coles Reference Cantwell and Coles1983; Hayakawa & Hussain Reference Hayakawa and Hussain1985, Reference Hayakawa and Hussain1989; Hussain & Hayakawa Reference Hussain and Hayakawa1987; Kiya & Matsumura Reference Kiya and Matsumura1988; Matsumura & Antonia Reference Matsumura and Antonia1993; Zhou et al. Reference Zhou, Zhou, Yiu and Chua2003). We single out here the work of Hayakawa & Hussain (Reference Hayakawa and Hussain1989), which confirmed the three-dimensional (3-D) nature of the organization in the intermediate wake. These authors found that the typical spanwise extent of two-dimensionality of the primary vortices or spanwise vortex rollers (hereafter referred to as ‘rollers’) is comparable to the local half-width of the wake. They were also able to identify the structure of ribs, aligned mainly along the diverging separatrix, although they could not distinguish unambiguously between distorted rollers and ribs. Scarano & Poelma (Reference Scarano and Poelma2009) studied the 3-D vorticity patterns in the near wake of a circular cylinder and captured the ribs in the flow based on their tomographic particle image velocimetry (PIV) measurements and confirmed that the Kármán rollers are locally distorted at the inception of the ribs.
The first major investigation into the combined momentum and heat transport characteristics associated with the organization of the intermediate wake is that of Matsumura & Antonia (Reference Matsumura and Antonia1993), hereafter referred to as MA. A probe consisting of an X-wire and a cold wire was traversed in the
$y$
direction at three
$x/d$
locations in the intermediate wake of a slightly heated circular cylinder. A major conclusion of the study was that the Kármán vortex street transports heat more effectively than momentum. In particular, the difference between the contribution from the coherent motion to the lateral heat flux and Reynolds shear stress was reflected in the different topologies of the temperature and velocity fields. MA’s study addressed only two-dimensional (2-D) aspects of the flow, with the authors recognizing that it would be ‘of interest in the future to examine momentum and heat transfer characteristics in the context of the three-dimensional organization’. We address this specific issue here by essentially repeating the MA experiment using a probe that provides all three components of the velocity and vorticity vectors as well as the temperature derivative vector, at nominally the same location. Since the probe is only traversed in the
$y$
direction, the flow topology is known only in the (
$x$
,
$y$
) plane. The topology does, however, contain information about
$\unicode[STIX]{x1D714}_{x}$
,
$\unicode[STIX]{x1D714}_{y}$
and
$\unicode[STIX]{x1D714}_{z}$
, the components of the vorticity vector in the
$x$
,
$y$
and
$z$
directions respectively. The information from
$\unicode[STIX]{x1D714}_{x}$
and
$\unicode[STIX]{x1D714}_{y}$
reflects the signatures of the ribs, while
$\unicode[STIX]{x1D714}_{z}$
is linked primarily to the rollers. In other words, the topology should now indicate the spatial relationship between the ribs and rollers, as well as the manner in which the two types of structure are associated with the Reynolds stresses and the heat flux vector. Specifically, the availability of
$w$
, the spanwise velocity fluctuation, is expected to provide some insight into the motion induced by the ribs and distorted rollers. Overall, this should lead to a more complete picture of the way in which the 3-D aspects of the flow affect the momentum and heat transport than what could possibly be obtained by MA.
This paper is organized as follows. Experimental details are provided in § 2, while the phase-averaging technique is described briefly in § 3. Conventionally time-averaged and phase-averaged results are presented in §§ 4 and 5 respectively. Conclusions are summarized in § 6.
2 Experimental details
Experiments were conducted in an open-loop wind tunnel with a working section of 1.2 m
$\times$
0.8 m and 2.0 m long. The free-stream longitudinal turbulence intensity was less than 0.5 %. A circular stainless steel cylinder with a diameter of
$d=12.7$
mm was used to generate the wake. A heating wire with a diameter of approximately 0.5 mm was wrapped and inserted in a ceramic tube, which was placed inside the stainless steel cylinder as a heating element. The free-stream velocity
$U_{1}$
was 3 m s
$^{-1}$
, corresponding to a Reynolds number
$Re(\equiv U_{1}d/\unicode[STIX]{x1D708})$
of
$2.5\times 10^{3}$
, where
$\unicode[STIX]{x1D708}$
is the kinematic viscosity. Measurements were conducted at
$x/d=10$
, 20 and 40. Assuming symmetry, measurements were made mainly only on one side of the centreline, i.e.
$y/d=-0.2$
to 2.8 at
$x/d=10$
and 20 and
$-0.2$
to 4.3 at
$x/d=40$
, with a transverse measurement increment of approximately
$0.2d$
for all
$x/d$
stations, except for the region near free stream at
$x/d=40$
where the increment was
$0.4d$
. The coordinate system and some symbols are defined in figure 1(a). The maximum mean temperature excess
$\unicode[STIX]{x1D6E9}_{0}$
, relative to the ambient, was approximately
$1.6\,^{\circ }\text{C}$
,
$1.5\,^{\circ }\text{C}$
and
$1.3\,^{\circ }\text{C}$
on the centreline of the wake for
$x/d=10$
, 20 and 40 respectively. The Richardson number,
$Ri$
(
$\equiv g\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6E9}_{0}d/U_{1}^{2}$
, where
$g$
is the gravitational acceleration,
$\unicode[STIX]{x1D6FD}$
is the thermal expansion coefficient, and the other symbols are defined in figure 1
a), which reflects the relative contributions from buoyancy and inertia forces (e.g. Boirlaud, Couton & Plourde Reference Boirlaud, Couton and Plourde2012), was estimated to be
$7.6\times 10^{-5}$
at the centreline for
$x^{\ast }=10$
of the present flow, and even smaller for
$x^{\ast }=20$
and 40. Hereinafter, an asterisk indicates normalization by
$U_{1}$
,
$d$
, and
$\unicode[STIX]{x1D6E9}_{0}$
(see figure 1). This normalization is used only for convenience since the velocity and temperature fields in the wake region considered here are not self-preserving. Antonia & Mi (Reference Antonia and Mi1993) and Antonia & Smalley (Reference Antonia and Smalley2000) noted that heat may be considered to be a passive scalar when
$Ri\leqslant 0.003$
; for the present flow, the temperature may thus be safely considered as passive.
Figure 1. (a) Experimental arrangement, coordinate system and definition sketch; (b) and (c) side and front views of the vorticity probe.
A probe consisting of four X-wires and four cold wires (figure 1
b,c) was used to measure the velocity and temperature fluctuations simultaneously. Two of the X-wires,
$b$
and
$d$
, were aligned in the (
$x,y$
) plane and separated by
$\unicode[STIX]{x0394}z=2.7~\text{mm}$
in the
$z$
direction; the other two,
$a$
and
$c$
, were in the (
$x$
,
$z$
) plane and separated by
$\unicode[STIX]{x0394}y=2.0~\text{mm}$
in the
$y$
direction. The separation between the two wires of each X-probe was approximately 0.6 mm. Four cold wires whose diameter
$d_{cold}$
was
$1.27~\unicode[STIX]{x03BC}\text{m}$
were orthogonally orientated to the plane of the cross-wire and placed approximately 1 mm upstream of the vorticity probe, at approximately
$800d_{cold}$
, which is a sufficiently large distance to ensure that the influence on the X-wire from the ‘wake’ of the cold wire is negligible. This was confirmed by the good agreement of the root-mean-square (r.m.s.) values of the present velocity fluctuations
$u$
,
$v$
and
$w$
at the centreline of
$x^{\ast }=10$
with those reported in Ong & Wallace (Reference Ong and Wallace1996) and Zhou et al. (Reference Zhou, Zhou, Yiu and Chua2003) (shown later in figure 5), which were measured without the cold wires. The separations
$\unicode[STIX]{x0394}y$
and
$\unicode[STIX]{x0394}z$
between the opposite cold wires were 2.5 mm and 2.2 mm respectively. The fluctuations
$u$
,
$v$
,
$w$
and
$\unicode[STIX]{x1D703}$
captured by this probe may be considered to be obtained at nominally the same point in space.
All three components of the vorticity vector can be calculated using the measured signals
$u$
,
$v$
,
$w$
from the probe, namely
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D714}_{x}=\frac{\unicode[STIX]{x2202}w}{\unicode[STIX]{x2202}y}-\frac{\unicode[STIX]{x2202}v}{\unicode[STIX]{x2202}z}\approx \frac{\unicode[STIX]{x0394}w}{\unicode[STIX]{x0394}y}-\frac{\unicode[STIX]{x0394}v}{\unicode[STIX]{x0394}z}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D714}_{y}=\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}z}-\frac{\unicode[STIX]{x2202}w}{\unicode[STIX]{x2202}x}\approx \frac{\unicode[STIX]{x0394}u}{\unicode[STIX]{x0394}z}-\frac{\unicode[STIX]{x0394}w}{\unicode[STIX]{x0394}x}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D714}_{z}=\frac{\unicode[STIX]{x2202}v}{\unicode[STIX]{x2202}x}-\frac{\unicode[STIX]{x2202}(\bar{U}+u)}{\unicode[STIX]{x2202}y}\approx \frac{\unicode[STIX]{x0394}v}{\unicode[STIX]{x0394}x}-\frac{\unicode[STIX]{x0394}(\bar{U}+u)}{\unicode[STIX]{x0394}y}, & \displaystyle\end{eqnarray}$$
$u$
,
$v$
and
$w$
are the velocity fluctuations in the
$x$
,
$y$
and
$z$
directions respectively. The symbols
$\unicode[STIX]{x0394}w$
and
$\unicode[STIX]{x0394}u$
in (2.1) and (2.3) denote the differences in velocities between cross-wires
$a$
and
$c$
, and
$\unicode[STIX]{x0394}\unicode[STIX]{x1D708}$
and
$\unicode[STIX]{x0394}u$
in (2.1) and (2.2) are the differences in velocities between cross-wires
$b$
and
$d$
. The velocity gradients in the streamwise direction in (2.2) and (2.3) are obtained by applying a central difference scheme to the time series of the measured velocity signals. The spatial separation
$\unicode[STIX]{x0394}x$
is inferred from Taylor’s hypothesis, i.e.
$\unicode[STIX]{x0394}x\equiv -2U_{c}\unicode[STIX]{x0394}t$
, where
$U_{c}$
is the averaged convection velocity of vortices (table 1), estimated from Zhou & Antonia (Reference Zhou and Antonia1992), and
$\unicode[STIX]{x0394}t=1/f_{samp}$
, where
$f_{samp}$
is the sampling frequency, is the time interval between consecutive points in the time series of the velocity signals. Previous studies (e.g. Zaman & Hussain Reference Zaman and Hussain1981; Mi & Antonia Reference Mi and Antonia2010; Geng et al.
Reference Geng, He, Wang, Xu, Lozano-Durán and Wallace2015) have demonstrated that Taylor’s hypothesis for the transformation between time and space derivatives works well, especially when the turbulent intensity (
$u_{rms}/U_{1}$
) is small. In the present study, the largest
$u_{rms}/U_{1}$
(approximately 0.18 at
$x^{\ast }=10$
) is quite comparable to that (0.16 at
$x^{\ast }=10$
) reported in Mi & Antonia (Reference Mi and Antonia2010), in which Taylor’s hypothesis is validated by comparing simultaneously measured temporal and streamwise spatial derivatives of the temperature fluctuation.
Table 1. Maximum mean velocity defect, mean temperature excess, mean velocity half-width, mean temperature half-width and vortex convection velocity.
Table 2 provides the information on the separation distances between the hot wires (
$\unicode[STIX]{x0394}x$
,
$\unicode[STIX]{x0394}y$
,
$\unicode[STIX]{x0394}z$
) in terms of the Kolmogorov length scale
$\unicode[STIX]{x1D702}\equiv (\unicode[STIX]{x1D708}^{3}/\bar{\unicode[STIX]{x1D700}})^{1/4}$
at the wake centreline. The estimation of
$\bar{\unicode[STIX]{x1D700}}$
, the mean energy dissipation rate, is based on the assumption of local homogeneity in the transverse plane (equation (9) in Lefeuvre et al.
Reference Lefeuvre, Thiesset, Djenidi and Antonia2014), which, according to the latter authors, should be more accurate in the intermediate wake than by assuming isotropy. In order to assess the minimum resolution of the probe, we compare our
$\unicode[STIX]{x1D714}_{y}$
and
$\unicode[STIX]{x1D714}_{z}$
spectra with those in Antonia & Mi (Reference Antonia and Mi1998) in figure 2; the spatial resolution of their probe is
$\unicode[STIX]{x0394}y=\unicode[STIX]{x0394}z\approx 8\unicode[STIX]{x1D702}$
at
$x^{\ast }=10$
, which is better than ours (
$11\unicode[STIX]{x1D702}$
for
$\unicode[STIX]{x0394}y$
and
$15\unicode[STIX]{x1D702}$
for
$\unicode[STIX]{x0394}z$
). The present distributions fall below those of Antonia & Mi (Reference Antonia and Mi1998) over the higher-wavenumber range, reflecting the larger attenuation in our experiment. Nevertheless, scales one order smaller than that corresponding to the Strouhal number (with a non-dimensional frequency
$f^{\ast }$
of 0.2) can be resolved reliably. Since this work aims to study the spatial structures of the vorticity, heat and momentum fluxes, which are associated with scales of the order of the Kármán vortex, the probe resolution should be adequate. In fact, as is shown in figure 6, the r.m.s. value of the vorticity is comparable to that measured in previous studies (Mi & Antonia’s (Reference Mi and Antonia1996) data were corrected for the effect of probe attenuation). The results indicate that the attenuation in the vorticity measurement is acceptable even for the vorticity variance, which is equal to the integral of the vorticity spectrum.
Figure 2. Comparison between the present spectra (solid lines) of (a)
$\unicode[STIX]{x1D714}_{z}$
and (b)
$\unicode[STIX]{x1D714}_{y}$
on the centreline and those of Antonia & Mi (Reference Antonia and Mi1998) (dashed lines) at
$x^{\ast }=10$
, where
$k_{1}$
is the streamwise wavenumber, ‘
$+$
’ denotes normalization by the Kolmogorov scale and
$f^{\ast }$
is the non-dimensional frequency.
Table 2. The mean energy dissipation rate, the Kolmogorov length scale and the probe resolution in the context of the vorticity measurements.
Both the hot and the cold wires were etched from Wollaston (Pt–10 %Rh) wires, with active lengths of approximately
$200d_{hot}$
and
$800d_{cold}$
respectively, where
$d_{hot}$
is the diameter of the wires,
$2.5~\unicode[STIX]{x03BC}\text{m}$
. The hot wires were operated with constant-temperature circuits, built in-house, at an overheat ratio of 1.5. The cold wires were operated with in-house constant-current (0.1 mA) circuits. The hot wires were calibrated at the centreline of the tunnel using a Pitot static tube connected to an MKS Baratron pressure transducer. Yaw calibration was performed over
$\pm 20^{\circ }$
. The output signals from the anemometers were passed through buck and gain circuits and low-pass filtered at a cutoff frequency
$f_{c}$
of 1250 Hz at three locations. The filtered signals were subsequently sampled at a frequency of
$f_{samp}=2f_{c}$
(2500 Hz) using a 16 bit analogue-to-digital converter. The duration of each digital record was approximately 45 s.
3 Phase-averaging technique
A phase-averaging technique is used to extract the coherent structures from the flow field. The technique is an improvement over that used by Zhou, Zhang & Yiu (Reference Zhou, Zhang and Yiu2002) and Zhou & Yiu (Reference Zhou and Yiu2006). Briefly, the transverse velocity fluctuation signals
$\unicode[STIX]{x1D708}$
from the probe are filtered using a fourth-order Butterworth filter with the centre frequency set at the vortex shedding frequency
$f_{s}$
, as identified from the most pronounced peak in the
$\unicode[STIX]{x1D708}$
spectrum. A cross-correlation between the measured signal
$\unicode[STIX]{x1D708}$
and the filtered signal
$\unicode[STIX]{x1D708}_{f}$
is carried out to determine the average phase shift between
$\unicode[STIX]{x1D708}_{f}$
and the measured
$\unicode[STIX]{x1D708}$
. This shift is then applied to
$\unicode[STIX]{x1D708}_{f}$
and a new reference signal
$\unicode[STIX]{x1D708}_{f}^{\prime }$
is formed. A similar technique was also adopted by Li, Balaras & Wallace (Reference Li, Balaras and Wallace2010) in their phase-average study of a turbulent shear layer. Figure 3 illustrates the
$\unicode[STIX]{x1D708}$
signals at three typical lateral locations at
$x^{\ast }=10$
and the corresponding shifted
$\unicode[STIX]{x1D708}_{f}^{\prime }$
signals.
Figure 3. Comparison of a measured signal
$v$
(the thin line) and the shifted filtered signal
$\unicode[STIX]{x1D708}_{f}^{\prime }$
(the thicker line) at
$x^{\ast }=10$
.
Two phases of particular interest are identified on
$\unicode[STIX]{x1D708}_{f}^{\prime }$
, namely
$$\begin{eqnarray}\displaystyle \text{phase A: }\unicode[STIX]{x1D708}_{f}^{\prime }=0\quad \text{and}\quad \frac{\text{d}\unicode[STIX]{x1D708}_{f}^{\prime }}{\text{d}t}>0 & & \displaystyle\end{eqnarray}$$
and
$$\begin{eqnarray}\displaystyle \text{phase B: }\unicode[STIX]{x1D708}_{f}^{\prime }=0\quad \text{and}\quad \frac{\text{d}\unicode[STIX]{x1D708}_{f}^{\prime }}{\text{d}t}<0. & & \displaystyle\end{eqnarray}$$
The two phases correspond to instants
$t_{A,i}$
and
$t_{B,i}$
(figure 3) respectively. The origin of time is arbitrary. The phase of the measured fluctuation signals is then determined as
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}=\unicode[STIX]{x03C0}\frac{t-t_{A,i}}{t_{B,i}-t_{A,i}},\quad t_{A,i}<t<t_{B,i} & & \displaystyle\end{eqnarray}$$
and
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}=\unicode[STIX]{x03C0}\frac{t-t_{B,i}}{t_{A,i+1}-t_{B,i}}+\unicode[STIX]{x03C0},\quad t_{B,i}<t<t_{A,i+1}. & & \displaystyle\end{eqnarray}$$
The interval between phases A and B is made equal to
$0.5T_{s}=0.5/f_{s}$
by compressing or stretching and is further divided into 20 equal intervals. Phase averaging is then applied to the measured rather than the filtered signals. The phase average of an instantaneous quantity
$\unicode[STIX]{x1D6E4}$
is given by
$\langle \unicode[STIX]{x1D6E4}\rangle _{k}=(1/N)\sum _{i=1}^{N}\unicode[STIX]{x1D6E4}_{k,i}$
, where
$k$
represents the phase and
$N$
is the number of detections, which is approximately 1980, 1700, and 1050 at
$x^{\ast }=10$
, 20 and 40 respectively.
Based on the triple decomposition (Hussain Reference Hussain1983), an instantaneous quantity
$\unicode[STIX]{x1D6E4}$
may be viewed as the sum of the time-averaged component
$\bar{\unicode[STIX]{x1D6E4}}$
and the fluctuating component
$\unicode[STIX]{x1D6FD}$
, which can be further decomposed into a coherent fluctuation
$\tilde{\unicode[STIX]{x1D6FD}}$
and a remainder
$\unicode[STIX]{x1D6FD}_{r}$
, namely
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FD}=\tilde{\unicode[STIX]{x1D6FD}}+\unicode[STIX]{x1D6FD}_{r}. & & \displaystyle\end{eqnarray}$$
The coherent component
$\tilde{\unicode[STIX]{x1D6FD}}\equiv \langle \unicode[STIX]{x1D6FD}\rangle$
reflects the effect from the large-scale coherent structures, while
$\unicode[STIX]{x1D6FD}_{r}$
is referred to as the remainder fluctuation. After multiplying (3.5) with
$\unicode[STIX]{x1D6FE}=\tilde{\unicode[STIX]{x1D6FE}}+\unicode[STIX]{x1D6FE}_{r}$
, we obtain
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}=\tilde{\unicode[STIX]{x1D6FD}}\tilde{\unicode[STIX]{x1D6FE}}+\tilde{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FE}_{r}+\tilde{\unicode[STIX]{x1D6FE}}\unicode[STIX]{x1D6FD}_{r}+\unicode[STIX]{x1D6FD}_{r}\unicode[STIX]{x1D6FE}_{r}. & & \displaystyle\end{eqnarray}$$
By phase averaging (3.6) and assuming a zero correlation between coherent and remainder fluctuations, i.e.
$\langle \tilde{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FE}_{r}\rangle =0$
and
$\langle \tilde{\unicode[STIX]{x1D6FE}}\unicode[STIX]{x1D6FD}_{r}\rangle =0$
, we obtain
$$\begin{eqnarray}\displaystyle \langle \unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\rangle =\tilde{\unicode[STIX]{x1D6FD}}\tilde{\unicode[STIX]{x1D6FE}}+\langle \unicode[STIX]{x1D6FD}_{r}\unicode[STIX]{x1D6FE}_{r}\rangle , & & \displaystyle\end{eqnarray}$$
where
$\unicode[STIX]{x1D6FD}$
and
$\unicode[STIX]{x1D6FE}$
represent either
$u$
,
$v$
,
$w$
or
$\unicode[STIX]{x1D703}$
.
4 Time-averaged flow and temperature fields
Distributions of the time-averaged streamwise velocity
$\bar{U}^{\ast }$
and temperature
$\bar{\unicode[STIX]{x1D6E9}}^{\ast }$
in the
$y$
direction are shown in figure 4. In this paper, a single overbar denotes conventional time averaging. It should be noted that the imperfect symmetry of the curve of
$\bar{U}^{\ast }$
at
$x^{\ast }=40$
is mainly caused by the third point, which could be due to the experimental uncertainty, approximately
$\pm$
2 % in the mean velocity. For example, the curve could appear quite symmetrical if this point were adjusted by only approximately 0.7 %. Table 1 summarizes the maximum mean velocity defect
$U_{0}^{\ast }$
,
$\unicode[STIX]{x1D6E9}_{0}$
, mean velocity half-widths
$L^{\ast }$
and mean temperature half-width
$L_{\unicode[STIX]{x1D703}}^{\ast }$
extracted from figure 4, along with
$U_{c}^{\ast }$
. The value of
$U_{c}^{\ast }$
is 0.27, 0.22 and 0.18 at
$x^{\ast }=10$
, 20 and 40 respectively. These values are slightly larger than their counterparts (0.22, 0.19, 0.16) reported by Antonia & Mi (Reference Antonia and Mi1998) at
$Re=3000$
. The value of
$\unicode[STIX]{x1D6E9}_{0}$
diminishes downstream as a result of heat transported from the wake to the free stream. The value of
$L^{\ast }$
is smaller than that of
$L_{\unicode[STIX]{x1D703}}^{\ast }$
, suggesting a more efficient transport of heat than momentum in the lateral direction. The ratio
$L^{\ast }/L_{\unicode[STIX]{x1D703}}^{\ast }$
is 0.68, 0.58 and 0.60 at
$x^{\ast }=10$
, 20 and 40 respectively, in reasonable agreement with Zhou et al. (Reference Zhou, Zhang and Yiu2002).
Figure 4. Distributions of mean streamwise velocity and temperature at
$x^{\ast }=10$
, 20 and 40.
Figure 5. Comparison of the r.m.s. values of velocity and temperature fluctuations from different wires of the probe at
$x^{\ast }=10$
, 20 and 40. Comparison of
$u_{rms}$
,
$v_{rms}$
and
$w_{rms}$
with those from Ong & Wallace (Reference Ong and Wallace1996) and Zhou et al. (Reference Zhou, Zhou, Yiu and Chua2003) is made at
$x^{\ast }=10$
.
Since the vorticity components are calculated from velocity fluctuation signals from the four X-wires, it is important to ensure that the interference between these X-wires is negligible. Figure 5 compares
$u_{rms}$
,
$v_{rms}$
,
$w_{rms}$
and
$\unicode[STIX]{x1D703}_{rms}$
from different X-wires and cold wires at three
$x^{\ast }$
locations. The values of
$u_{rms}$
,
$v_{rms}$
and
$w_{rms}$
reported in Ong & Wallace (Reference Ong and Wallace1996) and Zhou et al. (Reference Zhou, Zhou, Yiu and Chua2003) at
$x^{\ast }=10$
are also included. The subscript ‘rms’ denotes the r.m.s. value of the fluctuating quantity. Several observations can be made. First, the values of
$u_{rms}$
,
$v_{rms}$
,
$w_{rms}$
and
$\unicode[STIX]{x1D703}_{rms}$
from different wires are in good agreement with each other, suggesting a negligible interference between wires. Second, the reasonable agreement between the present data and those of Zhou et al. (Reference Zhou, Zhou, Yiu and Chua2003) (
$Re=2500$
) and Ong & Wallace (Reference Ong and Wallace1996) (
$Re=3900$
) is such as to exclude the possibility that the agreement between the different wires results from similar interference at each of the four measurement locations. Third, at
$x^{\ast }=10$
,
$v_{rms}^{\ast }$
is larger than
$u_{rms}^{\ast }$
, which is larger than
$w_{rms}^{\ast }$
. This result indicates the strong anisotropy of the flow, which is attributed to the presence of the Kármán vortices. As
$x^{\ast }$
increases,
$v_{rms}$
drops faster than
$u_{rms}$
and
$w_{rms}$
. By
$x^{\ast }=40$
,
$v_{rms}$
is approximately equal to
$w_{rms}$
and even smaller than
$u_{rms}$
. This suggests a preferential transfer of turbulent kinetic energy to the
$u$
component rather than to the
$v$
or
$w$
components with increasing
$x^{\ast }$
. This axisymmetric trend of the streamwise evolution of
$u_{rms}$
,
$v_{rms}$
and
$w_{rms}$
was also observed by Djenidi & Antonia (Reference Djenidi and Antonia2009) in their direct numerical simulation (DNS) study of the transitional wake of a heated square cylinder (
$Re=200$
) and by Mi & Antonia (Reference Mi and Antonia2010) in their experiment (
$Re=3000$
). The lateral position of the peak in
$\unicode[STIX]{x1D703}_{rms}^{\ast }$
approximately corresponds to the path or most likely position of the Kármán vortices. This is not unreasonable since heat is mostly retained by the Kármán vortex in the near and intermediate wake (e.g. MA; Djenidi & Antonia Reference Djenidi and Antonia2009). As
$x^{\ast }$
increases, the peak of
$\unicode[STIX]{x1D703}_{rms}^{\ast }$
drifts away from the centreline towards the free stream, reflecting the movement of the Kármán vortices. In fact, the peak of
$\unicode[STIX]{x1D703}_{rms}^{\ast }$
is nearer at
$x^{\ast }=40$
to the free stream than the vortex path; this will be discussed in detail in § 5. In summary, the above comparison indicates that the measurements of
$u$
,
$v$
,
$w$
and
$\unicode[STIX]{x1D703}$
are quite reasonable.
Figure 6. Comparison of the normalized r.m.s. values of vorticity components between the present and previously reported measurements at
$x^{\ast }=20$
. Here,
$L$
is the mean velocity half-width and
$U_{0}$
is the maximum mean velocity deficit.
Figure 6 compares
$(\unicode[STIX]{x1D714}_{x})_{rms}$
,
$(\unicode[STIX]{x1D714}_{y})_{rms}$
and
$(\unicode[STIX]{x1D714}_{z})_{rms}$
measured at
$x^{\ast }=20$
with those reported by Marasli, Nguyen & Wallace (Reference Marasli, Nguyen and Wallace1993), Mi & Antonia (Reference Mi and Antonia1996), Zhang, Zhou & Antonia (Reference Zhang, Zhou and Antonia2000) and Zhou et al. (Reference Zhou, Zhou, Yiu and Chua2003). The fluctuating vorticity, normalized by
$L$
and
$U_{0}$
, is multiplied by
$(U_{0}L/\unicode[STIX]{x1D708})^{-1/2}$
to account for the Reynolds number effect (Antonia, Rajagopalan & Zhu Reference Antonia, Rajagopalan and Zhu1996). The magnitudes reported by Zhang et al. (Reference Zhang, Zhou and Antonia2000) are the smallest, due to the poor spatial resolution (approximately 20 Kolmogorov length scales) of the hot wires. Mi & Antonia (Reference Mi and Antonia1996) perhaps provide the most accurate data since they used two X-wire probes with a resolution of approximately 6 Kolmogorov length scales and further applied a spectral correction to account for the high wavenumber attenuation of vorticity, resulting in larger
$(\unicode[STIX]{x1D714}_{y})_{rms}$
and
$(\unicode[STIX]{x1D714}_{z})_{rms}$
than for the present data. The data of Zhou et al. (Reference Zhou, Zhou, Yiu and Chua2003) agree well with the present values of
$(\unicode[STIX]{x1D714}_{x})_{rms}$
and
$(\unicode[STIX]{x1D714}_{z})_{rms}$
, but are slightly larger than the present
$(\unicode[STIX]{x1D714}_{y})_{rms}$
values. This may be attributed to the better resolution of the probe used by Zhou et al. (Reference Zhou, Zhou, Yiu and Chua2003) in the
$z$
direction (
$\unicode[STIX]{x0394}z\approx 1.9$
mm in their probe, while
$\unicode[STIX]{x0394}z\approx 2.7$
mm in our present probe), which will affect the velocity gradient
$\text{d}u/\text{d}z$
(and hence
$\unicode[STIX]{x1D714}_{y}$
). Marasli et al. (Reference Marasli, Nguyen and Wallace1993) obtained smaller values of
$(\unicode[STIX]{x1D714}_{y})_{rms}$
and
$(\unicode[STIX]{x1D714}_{z})_{rms}$
than the present study and the experiments of Mi & Antonia (Reference Mi and Antonia1996) and Zhou et al. (Reference Zhou, Zhou, Yiu and Chua2003). It should be noted that Marasli et al. (Reference Marasli, Nguyen and Wallace1993) measured at
$x^{\ast }=30$
, while all of the other experiments were at
$x^{\ast }=20$
. Considering that some departure is not unexpected in view of the different experimental facilities and uncertainties, the comparison in figure 5 can be considered as providing reasonable validation of the present vorticity data.
5 Phase-averaged flow and temperature field
5.1 Phase-averaged vorticity
Rib-like structures, which are located in the alleyway between successive Kármán vortices and oriented mostly along the diverging separatrix, have been identified in both experiments (e.g. Hayakawa & Hussain Reference Hayakawa and Hussain1989; Bays-muchmore & Ahmed Reference Bays-muchmore and Ahmed1993; Mi & Antonia Reference Mi and Antonia1996; Scarano & Poelma Reference Scarano and Poelma2009) and numerical simulations (Jeong, Grinstein & Hussain Reference Jeong, Grinstein and Hussain1994; Brede, Eckelmann & Rockwell Reference Brede, Eckelmann and Rockwell1996). However, the streamwise evolution of the ribs, their interaction with the rollers and their effect on the heat and momentum transport are, probably for the first time, captured in the present experiment. In this section, the capture of the ribs will be verified in terms of both the coherent vorticity topology and the spectral correlation of
$\unicode[STIX]{x1D714}_{x}$
and
$\unicode[STIX]{x1D714}_{y}$
. The interaction between ribs and rollers and their effect on the heat and momentum transport will be discussed in detail in § 5.7.
The isocontours of the three phase-averaged coherent vorticity components, i.e.
$\tilde{\unicode[STIX]{x1D714}}_{x}^{\ast }$
,
$\tilde{\unicode[STIX]{x1D714}}_{y}^{\ast }$
and
$\tilde{\unicode[STIX]{x1D714}}_{z}^{\ast }$
, are presented in figure 7. The phase
$\unicode[STIX]{x1D719}$
, ranging from
$-2\unicode[STIX]{x03C0}$
to
$+2\unicode[STIX]{x03C0}$
, can be interpreted as a longitudinal distance based on Taylor’s hypothesis,
$\unicode[STIX]{x1D719}=0$
to
$2\unicode[STIX]{x03C0}$
corresponding to the averaged vortex wavelength. To avoid any distortion of the physical space, the same scales are used in the
$\unicode[STIX]{x1D719}$
and
$y^{\ast }$
directions in this and subsequent figures. The positions of the centres and saddle points (e.g. Zhou & Antonia Reference Zhou and Antonia1994), identified from the phase-averaged sectional streamlines (not shown), are marked by ‘
$+$
’ and ‘
$\times$
’ respectively. The thicker broken line denotes the outermost vorticity contour of
$\tilde{\unicode[STIX]{x1D714}}_{z}^{\ast }$
, which is approximately 25 % of the maximum magnitude
$|\tilde{\unicode[STIX]{x1D714}}_{z,max}^{\ast }|$
. This contour provides a reference for the periphery of the Kármán vortex. The broken line passing through the saddle point is the diverging separatrix, i.e. the braid connecting the consecutive roller structures (Hussain & Hayakawa Reference Hussain and Hayakawa1987). The contours of vorticity are similar to those in Zhou et al. (Reference Zhou, Zhou, Yiu and Chua2003), in which a similar experimental arrangement was employed. Because of the improved phase-average method used in this work, the organized motion is more accurately extracted at all stations, providing a clearer picture of the streamwise evolution of the coherent structures, especially the rib structures, which could hardly be identified in Zhou et al. (Reference Zhou, Zhou, Yiu and Chua2003).
Figure 7. Phase-averaged vorticity isocontours: (a–c)
$\tilde{\unicode[STIX]{x1D714}}_{x}^{\ast }$
, contour increment
$=$
0.042, 0.013 and 0.012 respectively; (d–f)
$\tilde{\unicode[STIX]{x1D714}}_{y}^{\ast }$
, 0.031, 0.020 and 0.016; (g–i)
$\tilde{\unicode[STIX]{x1D714}}_{z}^{\ast }$
, 0.102, 0.051 and 0.019. Here and in subsequent figures, upstanding crosses
$+$
and
$\times$
represent the locations of the vortex centre and saddle points respectively. The thick broken contour corresponds to the contour of 25 % of the maximum spanwise vorticity and the broken line through the saddle point indicates the diverging separatrix.
The
$\tilde{\unicode[STIX]{x1D714}}_{z}^{\ast }$
contours display the well-known Kármán vortex street from
$x^{\ast }=10$
to 40 (figure 7
g–i). The vortices decay rapidly, and the maximum concentration of
$\tilde{\unicode[STIX]{x1D714}}_{z}^{\ast }$
at
$x^{\ast }=40$
drops to only 26 % of that at
$x^{\ast }=10$
. However, its size grows considerably, and the vortex centre shifts away from the centreline, increasing from
$y^{\ast }=0.39$
at
$x^{\ast }=10$
to
$y^{\ast }=1.38$
at
$x^{\ast }=40$
. This observation is consistent with the downstream growth in the wake width. It should be noted that the
$\tilde{\unicode[STIX]{x1D714}}_{z}^{\ast }$
concentrations at
$x^{\ast }=40$
are hardly identifiable in Zhou et al. (Reference Zhou, Zhou, Yiu and Chua2003) but are easily discernible in figure 7(i) because of the improved phase averaging.
In figure 7(a–f), the contours of
$\tilde{\unicode[STIX]{x1D714}}_{x}^{\ast }$
and
$\tilde{\unicode[STIX]{x1D714}}_{y}^{\ast }$
display concentrations along the diverging separatrix and wrap around the consecutive opposite-signed rollers, as also observed in Williamson (Reference Williamson1996) and Scarano & Poelma (Reference Scarano and Poelma2009), thus highlighting the signature of the rib-like structures. The organized structures at
$x^{\ast }=10$
are more complicated than and quite different from those at
$x^{\ast }=20$
and 40. As shown in figure 7(g), rollers of opposite sign are closely arranged near the centreline, resulting in the vigorous vorticity transport between them (this is discussed in the next section) and subsequently causing the rollers to contort, as delineated by the opposite-signed
$\tilde{\unicode[STIX]{x1D714}}_{z}^{\ast }$
contours that lean against each other. The deformed rollers can make an extra contribution to
$\unicode[STIX]{x1D714}_{x}$
and
$\unicode[STIX]{x1D714}_{y}$
in addition to that resulting from the rib structures, which is why both the
$\tilde{\unicode[STIX]{x1D714}}_{x}^{\ast }$
and
$\tilde{\unicode[STIX]{x1D714}}_{y}^{\ast }$
contours within the Kármán vortex (figure 7
a,d) exhibit a similarity to those of
$\tilde{\unicode[STIX]{x1D714}}_{z}^{\ast }$
. The concentration of
$\tilde{\unicode[STIX]{x1D714}}_{x}^{\ast }$
within the vortex at
$x^{\ast }=10$
is much larger than that of
$\tilde{\unicode[STIX]{x1D714}}_{y}^{\ast }$
(figure 7
a,d), indicating that the interactions between the opposite-signed vortices occur mostly in the streamwise direction, as observed from the instantaneous isocontours of
$\unicode[STIX]{x1D714}_{z}$
from the DNS data of Djenidi & Antonia (Reference Djenidi and Antonia2009) (their figure 17c). At
$x^{\ast }=10$
, the additional
$\tilde{\unicode[STIX]{x1D714}}_{x}^{\ast }$
from the deformed rollers smears the
$\tilde{\unicode[STIX]{x1D714}}_{x}^{\ast }$
contours linked to the ribs. As a result, the
$\tilde{\unicode[STIX]{x1D714}}_{x}^{\ast }$
contours are not concentrated along the diverging separatrix (figure 7
a). At
$x^{\ast }=20$
and 40, the opposite-signed vortices drift away from the centreline, and the braid region between them expands. Consequently, both
$\tilde{\unicode[STIX]{x1D714}}_{x}^{\ast }$
and
$\tilde{\unicode[STIX]{x1D714}}_{y}^{\ast }$
resulting from the longitudinal rib structures show comparable maximum concentrations in the braid region. As such, although the roller distortion may be further enhanced by the spanwise instability (Williamson Reference Williamson1996), the presence of the ribs is clearly identifiable from the distributions of
$\tilde{\unicode[STIX]{x1D714}}_{x}^{\ast }$
and
$\tilde{\unicode[STIX]{x1D714}}_{y}^{\ast }$
along the diverging separatrix. The capture of the ribs is further confirmed by comparing the cospectra between
$\unicode[STIX]{x1D714}_{x}$
and
$\unicode[STIX]{x1D714}_{y}$
at the centre and saddle point locations at
$x^{\ast }=20$
and 40 (figure 8). The cospectra corresponding to the saddle point display a pronounced peak at
$St(\equiv \,fd/U_{1})=0.2$
, indicating a strong correlation between
$\unicode[STIX]{x1D714}_{x}$
and
$\unicode[STIX]{x1D714}_{y}$
at
$f_{s}$
, which is expected given the presence of the rib-like structures. On the other hand, such a peak is absent in the cospectra corresponding to the vortex centre at
$x^{\ast }=20$
and 40, as
$\unicode[STIX]{x1D714}_{x}$
and
$\unicode[STIX]{x1D714}_{y}$
are unlikely to be correlated within the spanwise vortices. The same sign of
$\tilde{\unicode[STIX]{x1D714}}_{x}^{\ast }$
and
$\tilde{\unicode[STIX]{x1D714}}_{y}^{\ast }$
as
$\tilde{\unicode[STIX]{x1D714}}_{z}^{\ast }$
within the spanwise vortex is connected to how the rollers are distorted in the (
$x,z$
) and (
$y,z$
) planes, which will be discussed in § 5.3.
Figure 8. Cospectral density functions of
$\unicode[STIX]{x1D714}_{x}$
and
$\unicode[STIX]{x1D714}_{y}$
at (a)
$x^{\ast }=20$
,
$y^{\ast }=0.79$
and (c) 40, 1.38, i.e. the most likely positions of vortex centres, and (b) 20, 1.38 and (d) 40, 1.77, i.e. the most likely positions of saddle points.
Figure 9. The vorticity flux density vector
$\boldsymbol{J}$
(
$J_{x},J_{y}$
) at (a,b)
$x^{\ast }=10$
and (c,d) 20. The vectors in (a,c) are calculated from the 3-D data with the
$w$
component included, and those in (b,d) from the 2-D data without
$w$
.
5.2 Vorticity transport
As discussed in § 5.1, the vigorous interactions between the neighbouring opposite-signed vortices may be responsible for the distortion of the spanwise rollers at
$x^{\ast }=10$
. One way to evaluate the interactions between the vortices is to examine the turbulent vorticity flux density vector,
$\boldsymbol{J}=(J^{x},J^{y})$
, which provides a measure for the transport of vorticity, as defined by (Kolar, Lyn & Rodi Reference Kolar, Lyn and Rodi1997)
$$\begin{eqnarray}\displaystyle & \displaystyle J^{x}=\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}y}\left[\frac{\langle v_{r}^{2}\rangle -\langle u_{r}^{2}\rangle -\langle w_{r}^{2}\rangle }{2}\right]+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}\langle u_{r}v_{r}\rangle , & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle J^{y}=\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}\left[\frac{\langle v_{r}^{2}\rangle -\langle u_{r}^{2}\rangle +\langle w_{r}^{2}\rangle }{2}\right]-\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}y}\langle u_{r}v_{r}\rangle . & \displaystyle\end{eqnarray}$$
$\langle w_{r}^{2}\rangle$
in (5.1) and (5.2), since the spanwise velocity component was not measured. In fact, Kolar et al. (Reference Kolar, Lyn and Rodi1997) noted that the ‘total’ turbulent vorticity flux should include gradients in
$\langle w_{r}^{2}\rangle$
. The present data, which include all of the terms in (5.1) and (5.2), should lead to a more accurate picture of the vorticity transport. The full flux density vector has been calculated and compared with the estimation from the 2-D data in figure 9. The correspondence between the magnitude and length of the vectors is given in the upper left corner of each plot. In the 2-D case (figure 9
b,d and also figure 18b in Kolar et al. (Reference Kolar, Lyn and Rodi1997)), the vorticity transport appears to be very weak especially at
$x^{\ast }=20$
in the downstream half, away from the centreline, of the spanwise roller at
$\unicode[STIX]{x1D719}=0$
. However, the full flux density vectors (figure 9
a,c) show an unequivocally strong activity. There is another important difference that emerges from the comparison. While the vectors calculated from the 2-D data appear to cross the border downstream of the vortex, implying a vorticity exchange or vorticity cancellation between neighbouring opposite-signed vortices, this is not the case if the vectors are calculated from the 3-D data. Instead, the vorticity flux vectors are now predominantly linked to the rotational motion of the vortex. That is, the 2-D data could be misleading. A close examination of figure 9(a,c) points to the vorticity transport between the neighbouring vortices on the downstream side of the vortex (
$\unicode[STIX]{x1D719}=0$
) being ‘blocked’, at least partially, by the engulfed non-turbulent fluid from the free stream immediately downstream of the rollers. This inference is corroborated by the maximum negative concentrations of
$\tilde{\unicode[STIX]{x1D703}}^{\ast }$
in figure 10(j,k), i.e. the engulfed non-turbulent cold fluid from the free stream, which occurs downstream close to the vortex at
$\unicode[STIX]{x1D719}=0$
. Consequently, the intense vorticity exchange or cancellation between neighbouring vortices occurs mostly on the upstream half of the vortex (
$\unicode[STIX]{x1D719}=0$
) and below the diverging separatrix. One should note the small magnitude of the negative
$\tilde{\unicode[STIX]{x1D703}}^{\ast }$
contours below the diverging separatrix between
$\unicode[STIX]{x1D719}=1$
and 0 in figure 10(j,k).
Figure 10. Isocontours of phase-averaged velocity and temperature fluctuations at
$x^{\ast }=10$
, 20 and 40: (a–c) contour intervals
$=$
0.020, 0.008, 0.004; (d–f) 0.041, 0.017, 0.007; (g–i) 0.0066, 0.0038, 0.0052; (j–l) 0.089, 0.018, 0.020.
Previous studies (Cantwell & Coles Reference Cantwell and Coles1983; Hussain & Hayakawa Reference Hussain and Hayakawa1987; Williamson Reference Williamson1996) have highlighted the importance, in the context of the flow dynamics, of the saddle region where turbulence production occurs and the contact region between the ribs and the spanwise rollers where turbulent mixing takes place. The present data shown in figure 9(a,c) point to the fact that the upstream half of the vortex is also of great importance, as it is where most of the vorticity cancellation occurs, thus contributing greatly to the decay of the vortex strength, at least in the near wake (
$x^{\ast }\leqslant 20$
). At
$x^{\ast }=40$
(not shown), this vorticity cancellation becomes quite weak, mainly due to the consecutive positive and negative vortices drifting away from each other. As a result, the vorticity decay downstream is mainly dominated by the vortex breakdown process (Hussain & Hayakawa Reference Hussain and Hayakawa1987).
5.3 Phase-averaged velocity and temperature fluctuations
All three phase-averaged components,
$\tilde{u} ^{\ast }$
,
$\tilde{v}^{\ast }$
and
$\tilde{w}^{\ast }$
, of the velocity fluctuation and their evolution from
$x^{\ast }=10$
to 40 are presented in figure 10, along with the phase-averaged temperature fluctuation
$\tilde{\unicode[STIX]{x1D703}}^{\ast }$
. In contrast, MA showed only
$\tilde{u} ^{\ast }$
,
$\tilde{v}^{\ast }$
and
$\tilde{\unicode[STIX]{x1D703}}^{\ast }$
at
$x^{\ast }=10$
. The contours of
$\tilde{u} ^{\ast }$
,
$\tilde{v}^{\ast }$
and
$\tilde{\unicode[STIX]{x1D703}}^{\ast }$
at
$x^{\ast }=10$
resemble those in MA. For example, the
$\tilde{u} ^{\ast }$
contours display approximate up–down antisymmetry about the vortex centre, while the
$\tilde{v}^{\ast }$
contours are antisymmetric about
$\unicode[STIX]{x1D719}=0$
, the maximum occurring in the alleyways between opposite-signed vortices. The positive contours of
$\tilde{\unicode[STIX]{x1D703}}^{\ast }$
show a concentric distribution within the spanwise roller and the negative contours occur between adjacent rollers, indicating that heat is contained within the Kármán vortex and cold fluid is entrained from free stream into the wake. The resemblance between the two sets of data provides a validation for the present phase-averaged results.
It is
$\tilde{w}^{\ast }$
, missing in MA, that is most interesting in the evolving coherent velocity fluctuations. At
$x^{\ast }=10$
, the contours of
$\tilde{w}^{\ast }$
(figure 10
g) exhibit markedly different features from those of either
$\tilde{u} ^{\ast }$
or
$\tilde{v}^{\ast }$
, with the opposite-signed contours almost evenly distributed along the two sides of the diverging separatrix. At
$x^{\ast }=20$
and 40, however, the contours of
$\tilde{w}^{\ast }$
evolve into a distribution similar to those of
$\tilde{v}^{\ast }$
. The distinct behaviours of
$\tilde{w}^{\ast }$
at
$x^{\ast }=10$
from those at
$x^{\ast }=20$
and 40 imply that the mechanism of inducing
$\tilde{w}^{\ast }$
changes from
$x^{\ast }=10$
to
$x^{\ast }=20$
and 40. Djenidi & Antonia (Reference Djenidi and Antonia2009) studied the momentum and heat transport in a transitional wake (
$Re=200$
) via DNS. They found that, while the structures of
$u$
and
$v$
are both related with the spanwise rollers, the structures of
$w$
result from the induction of ribs as well as the contorted rollers. The present distribution of
$\tilde{w}^{\ast }$
along the diverging separatrix at
$x^{\ast }=10$
, also observed by Djenidi & Antonia (Reference Djenidi and Antonia2009), is clearly a signature of ribs, with a caveat that the small
$\tilde{w}^{\ast }$
concentrations near the vortex centre should result from the distorted rollers. With increasing
$x^{\ast }$
, the ribs decay rapidly, as is evident in figure 7 and also in previous measurements, e.g. Brede et al. (Reference Brede, Eckelmann and Rockwell1996) and Huang, Zhou & Zhou (Reference Huang, Zhou and Zhou2006); also, the distortion of the spanwise rollers is enhanced (Williamson Reference Williamson1996; Zdravkovich Reference Zdravkovich1997). A possible scenario of the distorted spanwise rollers is sketched in figure 11. Without distortion (figure 11
a), the measurement plane (
$x$
,
$y$
) is perpendicular to the axis of the rollers, and the coherent velocities
$\tilde{v}_{1}$
and
$\tilde{v}_{2}$
induced by rollers will stay in the measurement plane, making no contribution to the spanwise velocity component. However, in reality, the spanwise rollers are in general distorted. One possible scenario for the distortion is illustrated in figure 11(b): the axis of the roller is non-perpendicular to the measurement plane,
$\tilde{v}_{1}$
and
$\tilde{v}_{2}$
producing velocity components in both the
$y$
and
$z$
directions. Specifically,
$\tilde{v}_{1}$
can be decomposed into a positive lateral component
$\tilde{v}_{+}^{m}$
and a negative spanwise component
$\tilde{w}_{-}^{m}$
, where the superscript
$m$
denotes measured quantities and the subscript ‘
$+$
’ or ‘
$-$
’ indicates the sign of the measured quantities. The scenario is consistent with the positive
$\tilde{v}^{\ast }$
and negative
$\tilde{w}^{\ast }$
contours between
$\unicode[STIX]{x1D719}=1$
and 0 at
$x^{\ast }=20$
and 40 (figure 10
e,f,h,i). Further,
$\tilde{v}_{2}$
can be decomposed into a negative lateral component
$\tilde{v}_{-}^{m}$
and a positive spanwise component
$\tilde{w}_{+}^{m}$
, which is in agreement with the negative
$\tilde{v}^{\ast }$
and positive
$\tilde{w}^{\ast }$
contours between
$\unicode[STIX]{x1D719}=0$
and
$-1$
in figure 10(e,f,h,i). All of the observations point to the strong likelihood that
$\tilde{w}^{\ast }$
results mainly from the distorted spanwise rollers at
$x^{\ast }=20$
and 40. It should be noted that the roller in figure 11(b) can also result in a negative lateral vorticity component (
$\tilde{\unicode[STIX]{x1D714}}_{y}<0$
) within the roller, as evidenced by the negative
$\tilde{\unicode[STIX]{x1D714}}_{y}^{\ast }$
contours within the spanwise vortex in figure 7(e,f).
Figure 11. Sketch of (a) non-distorted and (b) distorted spanwise vortex rollers in the
$y$
–
$z$
plane. Superscript ‘
$m$
’ denotes the measured velocity and subscripts ‘
$+$
’ and ‘
$-$
’ indicate the positive and negative signs respectively of the measured quantities; ‘A–A’ and ‘B–B’ represent the sectional views of the vortex roller.
The evolution of the
$\tilde{\unicode[STIX]{x1D703}}^{\ast }$
contours exhibits a close correlation with the variation in the strength of the spanwise vortex. At
$x^{\ast }=10$
and 20, the positive contours of
$\tilde{\unicode[STIX]{x1D703}}^{\ast }$
due to heat separated along with the vortex from the electrically heated cylinder coincide well with the
$\tilde{\unicode[STIX]{x1D714}}_{z}^{\ast }$
concentrations, indicating that the Kármán vortex retains heat effectively with its strong rotational motion. This changes dramatically at
$x^{\ast }=40$
. Heat is transferred out of the periphery of the vortex, the main trend being towards the free stream. This is directly connected to the fact that the spanwise vortex becomes quite weak at
$x^{\ast }=40$
, with its maximum magnitude of
$\tilde{\unicode[STIX]{x1D714}}_{z}^{\ast }$
dropping to only approximately 26 % of that at
$x^{\ast }=10$
(figure 7
g,i), and hence cannot retain heat as effectively as at
$x^{\ast }=10$
and 20.
5.4 Coherent momentum and heat fluxes and remainders
The topologies of the heat and momentum transport are examined in this section, including both large-scale coherent quantities and relatively small-scale remainders. In contrast to only two components (
$u\unicode[STIX]{x1D703}$
and
$v\unicode[STIX]{x1D703}$
) available in MA, all three components (
$u\unicode[STIX]{x1D703}$
,
$v\unicode[STIX]{x1D703}$
,
$w\unicode[STIX]{x1D703}$
) of the heat flux vector are examined here, thus providing a more complete picture of 3-D momentum and heat transport.
Figure 12. Isocontours of phase-averaged coherent momentum and heat fluxes. Contour intervals: (a–c) 0.0026, 0.0005, 0.00016; (d–f) 0.0076, 0.0006, 0.00047; (g–i) 0.015, 0.0016, 0.00088; (j–l) 0.0015, 0.0005, 0.00034.
Figure 12 presents the coherent Reynolds shear stress
$\tilde{u} ^{\ast }\tilde{v}^{\ast }$
and the three components, i.e.
$\tilde{u} ^{\ast }\tilde{\unicode[STIX]{x1D703}}^{\ast }$
,
$\tilde{v}^{\ast }\tilde{\unicode[STIX]{x1D703}}^{\ast }$
and
$\tilde{w}^{\ast }\tilde{\unicode[STIX]{x1D703}}^{\ast }$
, of the heat flux vector at the three stations. The structures of
$\tilde{u} ^{\ast }\tilde{v}^{\ast }$
,
$\tilde{u} ^{\ast }\tilde{\unicode[STIX]{x1D703}}^{\ast }$
and
$\tilde{v}^{\ast }\tilde{\unicode[STIX]{x1D703}}^{\ast }$
are similar to those reported by MA, and need not be discussed individually. Similarly to the behaviours of
$\tilde{w}^{\ast }$
, the
$\tilde{w}^{\ast }\tilde{\unicode[STIX]{x1D703}}^{\ast }$
contours exhibit quite different features between
$x^{\ast }=10$
and the other two
$x^{\ast }$
positions. At
$x^{\ast }=10$
, the oppositely signed
$\tilde{w}^{\ast }\tilde{\unicode[STIX]{x1D703}}^{\ast }$
concentrations occur on the two sides of the diverging separatrix, opposite to each other, apparently resulting from the motion of ribs. It should be noted that, due to the high concentration of
$\tilde{\unicode[STIX]{x1D703}}^{\ast }$
within the roller, a high concentration of
$\tilde{w}^{\ast }\tilde{\unicode[STIX]{x1D703}}^{\ast }$
occurs near the vortex centre, though with a weak
$\tilde{w}^{\ast }$
(figure 10
g), at
$x^{\ast }=10$
. At
$x^{\ast }=20$
and 40, the high-level contours of
$\tilde{w}^{\ast }\tilde{\unicode[STIX]{x1D703}}^{\ast }$
do not seem to show any correlation with the diverging separatrix and, instead, exhibit a great resemblance to those of
$\tilde{v}^{\ast }\tilde{\unicode[STIX]{x1D703}}^{\ast }$
at the same
$x^{\ast }$
. This difference in
$\tilde{w}^{\ast }\tilde{\unicode[STIX]{x1D703}}^{\ast }$
is consistent with that in
$\tilde{w}^{\ast }$
(figure 10
g–i) between
$x^{\ast }=10$
and the other two
$x^{\ast }$
positions. The similarity between the contours of
$\tilde{w}^{\ast }\tilde{\unicode[STIX]{x1D703}}^{\ast }$
and
$\tilde{v}^{\ast }\tilde{\unicode[STIX]{x1D703}}^{\ast }$
at
$x^{\ast }=20$
and 40 is connected to that between the contours of
$\tilde{w}^{\ast }$
and
$\tilde{v}^{\ast }$
(figure 10
e,h,f,i). The
$\tilde{v}\tilde{\unicode[STIX]{x1D703}}$
and
$\tilde{w}\tilde{\unicode[STIX]{x1D703}}$
contours are of opposite sign, as are the
$\tilde{v}$
and
$\tilde{\unicode[STIX]{x1D714}}$
contours, due to the spatial contortion of the spanwise rollers as seen in figure 11. The evolution of
$\tilde{w}^{\ast }\tilde{\unicode[STIX]{x1D703}}^{\ast }$
reflects the fact that both rollers and ribs influence the coherent part of the heat transport at
$x^{\ast }=10$
. However, the ribs appear to be weakened at
$x^{\ast }=20$
and 40; so does their ability to induce the spanwise motion and heat flux. Consequently, the coherent heat transport is overwhelmingly dominated by the distorted spanwise rollers at
$x^{\ast }=20$
and 40. The result is in agreement with the observation of Huang et al. (Reference Huang, Zhou and Zhou2006), from PIV data (
$Re=2000$
), that the ribs become weak and less organized from
$x^{\ast }=4$
to 12.
Interestingly, the ribs seem to play a role that is increasingly important downstream in both momentum and heat flux of the remainders (figure 13). At
$x^{\ast }=10$
, the high-level
$\langle u_{r}^{\ast }v_{r}^{\ast }\rangle$
contours tend to run along the diverging separatrix. The concentration of positive
$\langle u_{r}^{\ast }v_{r}^{\ast }\rangle$
near the vortex centre is the footprint of the shear stress that is associated with the diverging separatrix below the centreline (
$y^{\ast }<0$
). Because the positive and negative vortices are close to each other near the centreline at
$x^{\ast }=10$
, the contours of the shear stress generated in the saddle region have actually protruded into the Kármán vortex on the other side of the centreline, as also observed by Hussain & Hayakawa (Reference Hussain and Hayakawa1987) and Matsumura & Antonia (Reference Matsumura and Antonia1993). As
$x^{\ast }$
increases, the maximum of
$\langle u_{r}^{\ast }v_{r}^{\ast }\rangle$
is gradually shifted to the saddle point. This change is correlated with the observation that the vortices drift away from the centreline. It should be noted that the saddle region at
$y^{\ast }>0$
corresponds laterally to the positive vortex roller at
$y^{\ast }<0$
. As a result, the influence of the rollers at
$y^{\ast }<0$
on the saddle region at
$y^{\ast }>0$
diminishes as both positive and negative vortices move away from the centreline and the contours of
$\langle u_{r}^{\ast }v_{r}^{\ast }\rangle$
are predominantly concentrated along the diverging separatrix, with a maximum at the saddle point at
$x^{\ast }=40$
(figure 13
c). Hussain & Hayakawa (Reference Hussain and Hayakawa1987) observed that the turbulent production occurs mostly at approximately the same location as the peak of
$\langle u_{r}^{\ast }v_{r}^{\ast }\rangle$
. The shift of the location in the maximum
$\langle u_{r}^{\ast }v_{r}^{\ast }\rangle$
implies the improved importance of the saddle region in the turbulence production. On the other hand, while the maximum
$\langle v_{r}^{\ast }\unicode[STIX]{x1D703}_{r}^{\ast }\rangle$
is also near the vortex centre at
$x^{\ast }=10$
, the
$\langle w_{r}^{\ast }\unicode[STIX]{x1D703}_{r}^{\ast }\rangle$
concentrations occur between spanwise vortices. However, at
$x^{\ast }=20$
and 40 the concentrations of both
$\langle v_{r}^{\ast }\unicode[STIX]{x1D703}_{r}^{\ast }\rangle$
and
$\langle w_{r}^{\ast }\unicode[STIX]{x1D703}_{r}^{\ast }\rangle$
occur about the diverging separatrix. Hussain & Hayakawa (Reference Hussain and Hayakawa1987) asserted, without providing the experimental evidence, that the most effective turbulence mixing occurs where ribs and spanwise vortices are in contact with each other as a result of the small-scale fluctuations produced by the direct interaction between the streamwise vorticity and the spanwise vorticity. The present observation from the
$\langle v_{r}^{\ast }\unicode[STIX]{x1D703}_{r}^{\ast }\rangle$
and
$\langle w_{r}^{\ast }\unicode[STIX]{x1D703}_{r}^{\ast }\rangle$
contours at
$x^{\ast }=20$
and 40 (figure 13
h,i,k,l) seems consistent with their assertion, given that the remainder is composed mainly of small scales responsible for turbulent diffusion and mixing (Tennekes & Lumley Reference Tennekes and Lumley1972). Generally,
$\langle u_{r}^{\ast }\unicode[STIX]{x1D703}_{r}^{\ast }\rangle$
and
$\langle v_{r}^{\ast }\unicode[STIX]{x1D703}_{r}^{\ast }\rangle$
are of opposite sign above the centreline, reflecting the negative correlation between
$u$
and
$v$
in the region where
$\text{d}\bar{U}/\text{d}y>0$
(e.g. Li et al.
Reference Li, Balaras and Wallace2010, also figure 13
c). The interesting exception is that the
$\langle w_{r}^{\ast }\unicode[STIX]{x1D703}_{r}^{\ast }\rangle$
concentrations are of opposite sign on either side of the diverging separatrix at
$x^{\ast }=20$
and 40 (figure 13
k,l), again confirming the claim that the ribs are dynamically important in these
$x^{\ast }$
positions.
Figure 13. Isocontours of momentum and heat fluxes associated with the remainder motion. Contour intervals: (a–c) 0.001, 0.0007, 0.00034; (d–f) 0.0048, 0.0021, 0.0029; (g–i) 0.0037, 0.0015, 0.0015; (j–l) 0.0014, 0.0011, 0.0013.
5.5 Productions of turbulent kinetic energy and temperature variance
The turbulence energy production
$\langle P_{e}\rangle ^{\ast }$
plays the role of an energy sink for the mean flow and an energy source for the fluctuating velocities, defined by (e.g. Cantwell & Coles Reference Cantwell and Coles1983; Pope Reference Pope2001)
$$\begin{eqnarray}\displaystyle \langle P_{e}\rangle ^{\ast } & = & \displaystyle -\langle u_{ir}u_{jr}\rangle ^{\ast }\frac{\unicode[STIX]{x2202}\langle \bar{U}_{i}+\tilde{u} _{i}\rangle ^{\ast }}{\unicode[STIX]{x2202}x_{j}^{\ast }}\nonumber\\ \displaystyle & = & \displaystyle -\langle u_{r}^{2}\rangle ^{\ast }\frac{\unicode[STIX]{x2202}\langle \bar{U}+\tilde{u} \rangle ^{\ast }}{\unicode[STIX]{x2202}x^{\ast }}-\langle v_{r}^{2}\rangle ^{\ast }\frac{\unicode[STIX]{x2202}\langle \bar{V}+\tilde{v}\rangle ^{\ast }}{\unicode[STIX]{x2202}y^{\ast }}\nonumber\\ \displaystyle & & \displaystyle -\,\langle w_{r}^{2}\rangle ^{\ast }\frac{\unicode[STIX]{x2202}\langle \bar{W}+\tilde{w}\rangle ^{\ast }}{\unicode[STIX]{x2202}z^{\ast }}-\langle u_{r}v_{r}\rangle ^{\ast }\left(\frac{\unicode[STIX]{x2202}\langle \bar{U}+\tilde{u} \rangle ^{\ast }}{\unicode[STIX]{x2202}y^{\ast }}+\frac{\unicode[STIX]{x2202}\langle \bar{V}+\tilde{v}\rangle ^{\ast }}{\unicode[STIX]{x2202}x^{\ast }}\right)\nonumber\\ \displaystyle & & \displaystyle -\,\langle u_{r}w_{r}\rangle ^{\ast }\left(\frac{\unicode[STIX]{x2202}\langle \bar{U}+\tilde{u} \rangle ^{\ast }}{\unicode[STIX]{x2202}z^{\ast }}+\frac{\unicode[STIX]{x2202}\langle \bar{W}+\tilde{w}\rangle ^{\ast }}{\unicode[STIX]{x2202}x^{\ast }}\right)-\langle v_{r}w_{r}\rangle ^{\ast }\left(\frac{\unicode[STIX]{x2202}\langle \bar{V}+\tilde{v}\rangle ^{\ast }}{\unicode[STIX]{x2202}z^{\ast }}+\frac{\unicode[STIX]{x2202}\langle \bar{W}+\tilde{w}\rangle ^{\ast }}{\unicode[STIX]{x2202}y^{\ast }}\right)\nonumber\\ \displaystyle & {\approx} & \displaystyle \underbrace{-\langle u_{r}^{2}\rangle ^{\ast }\frac{\unicode[STIX]{x2202}\langle \bar{U}+\tilde{u} \rangle ^{\ast }}{\unicode[STIX]{x2202}x^{\ast }}-\langle v_{r}^{2}\rangle ^{\ast }\frac{\unicode[STIX]{x2202}\langle \tilde{v}\rangle ^{\ast }}{\unicode[STIX]{x2202}y^{\ast }}-\langle u_{r}v_{r}\rangle ^{\ast }\left(\frac{\unicode[STIX]{x2202}\langle \bar{U}+\tilde{u} \rangle ^{\ast }}{\unicode[STIX]{x2202}y^{\ast }}+\frac{\unicode[STIX]{x2202}\langle \tilde{v}\rangle ^{\ast }}{\unicode[STIX]{x2202}x^{\ast }}\right)}_{\text{I}}\nonumber\\ \displaystyle & & \displaystyle \underbrace{-\langle w_{r}^{2}\rangle ^{\ast }\frac{\unicode[STIX]{x2202}\langle \tilde{w}\rangle ^{\ast }}{\unicode[STIX]{x2202}z^{\ast }}-\langle u_{r}w_{r}\rangle ^{\ast }\left(\frac{\unicode[STIX]{x2202}\langle \bar{U}+\tilde{u} \rangle ^{\ast }}{\unicode[STIX]{x2202}z^{\ast }}+\frac{\unicode[STIX]{x2202}\langle \tilde{w}\rangle ^{\ast }}{\unicode[STIX]{x2202}x^{\ast }}\right)-\langle v_{r}w_{r}\rangle ^{\ast }\left(\frac{\unicode[STIX]{x2202}\langle \tilde{v}\rangle ^{\ast }}{\unicode[STIX]{x2202}z^{\ast }}+\frac{\unicode[STIX]{x2202}\langle \tilde{w}\rangle ^{\ast }}{\unicode[STIX]{x2202}y^{\ast }}\right)}_{\text{II}}.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
Previous calculations (e.g. Cantwell & Coles Reference Cantwell and Coles1983; Antonia et al.
Reference Antonia, Browne, Bisset and Fulachier1987; Hussain & Hayakawa Reference Hussain and Hayakawa1987) of
$\langle P_{e}\rangle ^{\ast }$
were based on only
$u$
and
$v$
, so that only part I in (5.3) was estimated. However, even in the intermediate wake, the three-dimensionality of the flow (e.g. Williamson Reference Williamson1996) cannot be ignored. Here, both parts I and II in (5.3) are measured directly with the vorticity probe, thus providing a more complete picture of the turbulence energy production and its streamwise evolution.
Figure 14 shows the isocontours of
$\langle P_{e}\rangle ^{\ast }$
at
$x^{\ast }=10$
and 40. For comparison, both part I and parts I
$+$
II in (5.3) are presented. The topological features of part I (figure 14
a,b) resemble, in general, those reported in Hussain & Hayakawa (Reference Hussain and Hayakawa1987), who studied
$\langle P_{e}\rangle ^{\ast }$
in a turbulent intermediate wake (
$x^{\ast }=10$
and 40) at
$Re=1.3\times 10^{4}$
. For example, the concentrations of
$\langle P_{e}\rangle ^{\ast }$
at both
$x^{\ast }=10$
and 40 occur largely in the saddle region and along the divergent separatrix; there are insignificant negative concentrations mainly within the vortex. These similarities provide a validation of the present data. Not surprisingly, the isocontours of parts I
$+$
II of
$\langle P_{e}\rangle ^{\ast }$
(figure 14
c,d) exhibit a similar pattern to part I (figure 14
a,b). However, the maximum concentrations of parts I
$+$
II at
$x^{\ast }=10$
and 40 are 16 % and 22 % larger than their counterparts of part I respectively; that is, the contribution from part II cannot be neglected especially at
$x^{\ast }=40$
. The larger contribution from part II to the full
$\langle P_{e}\rangle ^{\ast }$
at
$x^{\ast }=40$
is associated with the more pronounced three-dimensionality of the flow than at
$x^{\ast }=10$
. One can expect that the contribution from part II to the full quantity of
$\langle P_{e}\rangle ^{\ast }$
will increase further downstream where the three-dimensionality of the flow will be enhanced with increasing
$x^{\ast }$
(e.g. Williamson Reference Williamson1996).
Figure 14. Isocontours of the production
$\langle P_{e}\rangle ^{\ast }$
of turbulent kinetic energies: (a,b) part I in (5.3), i.e. without
$w$
-related terms; (c,d) parts I
$+$
II. Contour intervals: (a) 0.00083, (b) 0.000033, (c) 0.00107, (d) 0.000054.
It is worth noting that the negative concentration of parts I
$+$
II (figure 14
c,d) is much larger than that of part I (figure 14
a,b). An examination of the contours of the individual terms of part I and part II (not shown) indicates that this negative production is mainly from the contribution of the normal stress terms, i.e. the terms related to
$\langle u_{r}^{2}\rangle ^{\ast }$
,
$\langle v_{r}^{2}\rangle ^{\ast }$
and
$\langle w_{r}^{2}\rangle ^{\ast }$
. Both Antonia et al. (Reference Antonia, Browne, Bisset and Fulachier1987) and Hussain & Hayakawa (Reference Hussain and Hayakawa1987) also noted, based on 2-D data, the small negative concentrations of
$\langle P_{e}\rangle ^{\ast }$
within the vortex, as figure 14(a,b) indicates; Hussain & Hayakawa (Reference Hussain and Hayakawa1987) confirmed that the negative contribution to the production is from the normal stress terms by studying the normal stress and shear stress terms separately. The present data further reveal that this contribution to the full
$\langle P_{e}\rangle ^{\ast }$
comes mainly from the spanwise normal stress.
The production of the temperature variance associated with small-scale motions,
$\langle P_{\unicode[STIX]{x1D703}}\rangle ^{\ast }$
, is given by (Tennekes & Lumley Reference Tennekes and Lumley1972; Antonia et al.
Reference Antonia, Browne, Bisset and Fulachier1987)
$$\begin{eqnarray}\displaystyle \langle P_{\unicode[STIX]{x1D703}}\rangle ^{\ast }=-\langle u_{r}\unicode[STIX]{x1D703}_{r}\rangle ^{\ast }\frac{\unicode[STIX]{x2202}\langle \bar{\unicode[STIX]{x1D6E9}}+\tilde{\unicode[STIX]{x1D703}}\rangle ^{\ast }}{\unicode[STIX]{x2202}x^{\ast }}-\langle v_{r}\unicode[STIX]{x1D703}_{r}\rangle ^{\ast }\frac{\unicode[STIX]{x2202}\langle \bar{\unicode[STIX]{x1D6E9}}+\tilde{\unicode[STIX]{x1D703}}\rangle ^{\ast }}{\unicode[STIX]{x2202}y^{\ast }}-\langle w_{r}\unicode[STIX]{x1D703}_{r}\rangle ^{\ast }\frac{\unicode[STIX]{x2202}\langle \bar{\unicode[STIX]{x1D6E9}}+\tilde{\unicode[STIX]{x1D703}}\rangle ^{\ast }}{\unicode[STIX]{x2202}z^{\ast }}. & & \displaystyle\end{eqnarray}$$
To the best of our knowledge, no attempt has yet been made to determine the topological features of
$\langle P_{\unicode[STIX]{x1D703}}\rangle ^{\ast }$
in the intermediate wake. The isocontours of
$\langle P_{\unicode[STIX]{x1D703}}\rangle ^{\ast }$
at all three
$x^{\ast }$
stations are shown in figure 15. The contours of the three individual terms on the right-hand side of (5.4) are also studied, though not shown. At
$x^{\ast }=10$
, the first two terms occur mainly within the Kármán vortex and make a dominant contribution to
$\langle P_{\unicode[STIX]{x1D703}}\rangle ^{\ast }$
; on the other hand, the third term occurs mostly between neighbouring vortices with a maximum concentration of approximately 7 % of the total
$\langle P_{\unicode[STIX]{x1D703}}\rangle ^{\ast }$
, i.e. the sum of all three terms. That is,
$\langle P_{\unicode[STIX]{x1D703}}\rangle ^{\ast }$
at
$x^{\ast }=10$
is mainly due to the contribution from the first two terms. This is also reflected in the relatively low magnitudes of the
$\langle w_{r}\unicode[STIX]{x1D703}\rangle ^{\ast }$
contours compared with those of
$\langle u_{r}\unicode[STIX]{x1D703}\rangle ^{\ast }$
and
$\langle v_{r}\unicode[STIX]{x1D703}\rangle ^{\ast }$
at
$x^{\ast }=10$
(figure 13
d,g,j). However, as
$x^{\ast }$
increases, the third term gradually increases in magnitude. At
$x^{\ast }=40$
, the maximum contour levels of the three terms are quite comparable, along with the topological similarity in the contours of
$\langle u_{r}\unicode[STIX]{x1D703}_{r}\rangle ^{\ast }$
,
$\langle v_{r}\unicode[STIX]{x1D703}_{r}\rangle ^{\ast }$
and
$\langle w_{r}\unicode[STIX]{x1D703}\rangle ^{\ast }$
(figure 13
f,i,l). The maximum concentration of the
$w$
-related term is 13 % of that of the total
$\langle P_{\unicode[STIX]{x1D703}}\rangle ^{\ast }$
. The
$w$
-related term is expected to contribute more to
$\langle P_{\unicode[STIX]{x1D703}}\rangle ^{\ast }$
beyond
$x^{\ast }=40$
as the flow and hence heat transport become more 3-D.
Figure 15. Isocontours of the production of temperature variance associated with the small-scale motions: (a)
$x^{\ast }=10$
, (b) 20, (c) 40. Contour intervals: (a) 0.0039, (b) 0.00051, (c) 0.00049.
Figure 16. Distributions of the r.m.s. values of the three components of the heat flux vector across the wake: (a)
$x^{\ast }=10$
, (b) 20, (c) 40. The symbol
$\unicode[STIX]{x1D6FC}$
denotes
$u,v$
or
$w$
.
5.6 Evolution of the heat flux components
Since the instantaneous heat transport is highly 3-D and
$w\unicode[STIX]{x1D703}$
plays a role in transporting heat, it is of fundamental interest to understand the streamwise evolution characteristics of the three components of the heat flux vector. Figure 16 compares the distributions of
$(u^{\ast }\unicode[STIX]{x1D703}^{\ast })_{rms}$
,
$(v^{\ast }\unicode[STIX]{x1D703}^{\ast })_{rms}$
and
$(w^{\ast }\unicode[STIX]{x1D703}^{\ast })_{rms}$
across the wake for the three stations. At
$x^{\ast }=10$
,
$(v^{\ast }\unicode[STIX]{x1D703}^{\ast })_{rms}$
is the largest of the three and
$(w^{\ast }\unicode[STIX]{x1D703}^{\ast })_{rms}$
is the smallest. The difference is especially evident for
$y^{\ast }<1$
. Nonetheless,
$(u^{\ast }\unicode[STIX]{x1D703}^{\ast })_{rms}$
,
$(v^{\ast }\unicode[STIX]{x1D703}^{\ast })_{rms}$
and
$(w^{\ast }\unicode[STIX]{x1D703}^{\ast })_{rms}$
are certainly of comparable magnitude. The magnitude of
$(v^{\ast }\unicode[STIX]{x1D703}^{\ast })_{rms}$
drops rapidly with increasing
$x^{\ast }$
, as does
$(u^{\ast }\unicode[STIX]{x1D703}^{\ast })_{rms}$
. These decreases are correlated with the rapidly decaying spanwise vortices (figure 7). On the other hand,
$(w^{\ast }\unicode[STIX]{x1D703}^{\ast })_{rms}$
declines slowly even though the rib structures also decay downstream. As a result, the difference between
$(u^{\ast }\unicode[STIX]{x1D703}^{\ast })_{rms}$
,
$(v^{\ast }\unicode[STIX]{x1D703}^{\ast })_{rms}$
and
$(w^{\ast }\unicode[STIX]{x1D703}^{\ast })_{rms}$
shrinks. As a matter of fact, by
$x^{\ast }=40$
,
$(w^{\ast }\unicode[STIX]{x1D703}^{\ast })_{rms}$
even exceeds
$(v^{\ast }\unicode[STIX]{x1D703}^{\ast })_{rms}$
, and
$(u^{\ast }\unicode[STIX]{x1D703}^{\ast })_{rms}$
is now slightly larger than the other two components. Further, the downstream evolution of
$(u^{\ast }\unicode[STIX]{x1D703}^{\ast })_{rms}$
,
$(v^{\ast }\unicode[STIX]{x1D703}^{\ast })_{rms}$
and
$(w^{\ast }\unicode[STIX]{x1D703}^{\ast })_{rms}$
suggests an approach to axisymmetry of the flow. Mi & Antonia (Reference Mi and Antonia2010) observed that both global and local axisymmetry, i.e. the axisymmetry of large and small scales respectively, is approximately satisfied at
$x^{\ast }=40$
. It should be noted that axisymmetry implies invariance of properties with respect to rotation about a preferred axis; it is therefore much less constraining than isotropy, which implies spherical symmetry. George & Hussein (Reference George and Hussein1991) examined previously discussed data and found that local axisymmetry was more adequate than local isotropy in many turbulent shear flows, including the turbulent jet, the far wake and also regions of the boundary layer. A possible explanation for the onset of axisymmetry at
$x^{\ast }\geqslant 40$
is that the coherent structures are quite weak in this region and the strong directional characteristics of the mean flow dominate. As such, the turbulent kinetic energy extracted from the mean flow is preferentially allocated to the streamwise velocity fluctuation. The similar behaviour of the r.m.s. values of the fluctuating velocity and heat flux indicates a close association between
$(u^{\ast }\unicode[STIX]{x1D703}^{\ast })_{rms}$
,
$(v^{\ast }\unicode[STIX]{x1D703}^{\ast })_{rms}$
,
$(w^{\ast }\unicode[STIX]{x1D703}^{\ast })_{rms}$
and the corresponding relative behaviour of the fluctuating velocity components.
5.7 Discussion: topologies of heat transport and production
The characteristics of heat transport can be examined by means of the coherent heat flux vectors
$\tilde{\boldsymbol{q}}^{\ast }\equiv (\tilde{u} ^{\ast }\tilde{\unicode[STIX]{x1D703}}^{\ast },\tilde{v}^{\ast }\tilde{\unicode[STIX]{x1D703}}^{\ast },\tilde{w}^{\ast }\tilde{\unicode[STIX]{x1D703}}^{\ast })$
and the remainder vectors
$\langle \boldsymbol{q}_{r}^{\ast }\rangle$
$\equiv$
(
$\langle u_{r}^{\ast }\unicode[STIX]{x1D703}_{r}^{\ast }\rangle$
,
$\langle v_{r}^{\ast }\unicode[STIX]{x1D703}_{r}^{\ast }\rangle$
,
$\langle w_{r}^{\ast }\unicode[STIX]{x1D703}_{r}^{\ast }\rangle$
), along with the phase-averaged vorticity vector
$\tilde{\unicode[STIX]{x1D74E}}^{\ast }\equiv (\tilde{\unicode[STIX]{x1D714}}_{x}^{\ast },\tilde{\unicode[STIX]{x1D714}}_{y}^{\ast },\tilde{\unicode[STIX]{x1D714}}_{z}^{\ast })$
, as shown in figure 17. The 3-D vectors are presented in terms of 2-D vectors (streamwise and lateral components) and the isocontours of the spanwise component, which are represented by colour for clarity.
Figure 17. Phase-averaged vorticity, coherent and incoherent heat flux vectors. In (a–c),
$\tilde{\unicode[STIX]{x1D74E}}^{\ast }:(\tilde{\unicode[STIX]{x1D714}}_{x}^{\ast }:\tilde{\unicode[STIX]{x1D714}}_{y}^{\ast })$
is given by vectors and
$\tilde{\unicode[STIX]{x1D714}}_{z}^{\ast }$
is given by the isocontours; in (d–f),
$\tilde{\boldsymbol{q}}^{\ast }$
: (
$\tilde{u} ^{\ast }\tilde{\unicode[STIX]{x1D703}}^{\ast },\tilde{v}^{\ast }\tilde{\unicode[STIX]{x1D703}}^{\ast }$
) is given by vectors and
$\tilde{w}^{\ast }\tilde{\unicode[STIX]{x1D703}}^{\ast }$
is given by the isocontours; in (g–i),
$\langle \boldsymbol{q}_{r}^{\ast }\rangle$
: (
$\langle u_{r}^{\ast }\unicode[STIX]{x1D703}_{r}^{\ast }\rangle$
,
$\langle v_{r}^{\ast }\unicode[STIX]{x1D703}_{r}^{\ast }\rangle$
) is given by vectors and
$\langle w_{r}^{\ast }\unicode[STIX]{x1D703}_{r}^{\ast }\rangle$
is given by the isocontours.
At
$x^{\ast }=10$
, the vorticity vectors
$(\tilde{\unicode[STIX]{x1D714}}_{x}^{\ast },\tilde{\unicode[STIX]{x1D714}}_{y}^{\ast })$
of relatively large magnitude occur largely within the spanwise vortices and appear to be nearly parallel to the centreline (figure 17
a). Presumably, the opposite-signed spanwise rollers are closely separated with respect to each other such that the deformation of the rollers in the (
$x$
,
$z$
) plane can lead to additionally produced
$\tilde{\unicode[STIX]{x1D714}}_{x}^{\ast }$
in addition to
$\tilde{\unicode[STIX]{x1D714}}_{x}^{\ast }$
originated from the predominantly longitudinal rib-like structures (cf. § 5.1 and also Hayakawa & Hussain Reference Hayakawa and Hussain1989; Hammache & Gharib Reference Hammache and Gharib1991). The ensuing
$\tilde{\unicode[STIX]{x1D714}}_{x}^{\ast }$
is naturally substantially larger than the lateral component
$\tilde{\unicode[STIX]{x1D714}}_{y}^{\ast }$
, resulting in almost horizontally oriented vectors
$(\tilde{\unicode[STIX]{x1D714}}_{x}^{\ast },\tilde{\unicode[STIX]{x1D714}}_{y}^{\ast })$
within the Kármán vortex. With increasing
$x^{\ast }$
, the opposite-signed rollers drift away from the centreline and hence from each other, and the braid region between two neighbouring rollers grows so that the ribs are more readily identifiable with the vectors
$(\tilde{\unicode[STIX]{x1D714}}_{x}^{\ast },\tilde{\unicode[STIX]{x1D714}}_{y}^{\ast })$
, which are oriented along the diverging separatrix (figure 17
b,c).
The coherent heat flux vectors
$\tilde{\boldsymbol{q}}^{\ast }$
exhibit a marked change from
$x^{\ast }=10$
to the other two
$x^{\ast }$
positions. At
$x^{\ast }=10$
, the vectors
$(\tilde{u} ^{\ast }\tilde{\unicode[STIX]{x1D703}}^{\ast },\tilde{v}^{\ast }\tilde{\unicode[STIX]{x1D703}}^{\ast })$
within the spanwise rollers indicate unambiguously the rotational motion about the vortex centre. The vectors immediately downstream of the negative rollers point upwards, almost perpendicularly to the centreline, reflecting the arrival of cooler fluid engulfed from the free stream. The concentration of the
$\tilde{w}^{\ast }\tilde{\unicode[STIX]{x1D703}}^{\ast }$
contours on one side of the diverging separatrix is opposite in sign to that on the other side of the separatrix. The observation that the maximum
$\tilde{w}^{\ast }\tilde{\unicode[STIX]{x1D703}}^{\ast }$
occurs at a location different from that of the maximum magnitude of (
$\tilde{u} ^{\ast }\tilde{\unicode[STIX]{x1D703}}^{\ast },\tilde{v}^{\ast }\tilde{\unicode[STIX]{x1D703}}^{\ast }$
) corroborates the conclusion in § 5.4, i.e. the coherent flow structures that induce the heat fluxes (
$\tilde{u} ^{\ast }\tilde{\unicode[STIX]{x1D703}}^{\ast },\tilde{v}^{\ast }\tilde{\unicode[STIX]{x1D703}}^{\ast }$
) are different from those responsible for
$\tilde{w}^{\ast }\tilde{\unicode[STIX]{x1D703}}^{\ast }$
. While (
$\tilde{u} ^{\ast }\tilde{\unicode[STIX]{x1D703}}^{\ast },\tilde{v}^{\ast }\tilde{\unicode[STIX]{x1D703}}^{\ast }$
) result mainly from the spanwise vortices,
$\tilde{w}^{\ast }\tilde{\unicode[STIX]{x1D703}}^{\ast }$
is mostly attributed to the predominantly longitudinal ribs. In contrast, at
$x^{\ast }=20$
and 40, the maximum concentration of
$\tilde{w}^{\ast }\tilde{\unicode[STIX]{x1D703}}^{\ast }$
occurs at almost the same location as that of
$\tilde{u} ^{\ast }\tilde{\unicode[STIX]{x1D703}}^{\ast }$
and
$\tilde{v}^{\ast }\tilde{\unicode[STIX]{x1D703}}^{\ast }$
, an indication that the same coherent structures, i.e. the contorted spanwise rollers (cf. § 5.4), account for (
$\tilde{u} ^{\ast }\tilde{\unicode[STIX]{x1D703}}^{\ast },\tilde{v}^{\ast }\tilde{\unicode[STIX]{x1D703}}^{\ast }$
) and
$\tilde{w}^{\ast }\tilde{\unicode[STIX]{x1D703}}^{\ast }$
. It should be noted that at
$x^{\ast }=40$
, the vectors (
$\tilde{u} ^{\ast }\tilde{\unicode[STIX]{x1D703}}^{\ast },\tilde{v}^{\ast }\tilde{\unicode[STIX]{x1D703}}^{\ast }$
) no longer show any rotational motion within the spanwise vortex; rather, they appear to drift out of the periphery of the vortex, moving towards the free stream. The result reflects the greatly weakened strength, due to decaying and breaking up, of the spanwise vortices. The weakened vortices are unable to retain heat as well as at
$x^{\ast }=10$
and 20.
The behaviour of
$\langle q_{r}^{\ast }\rangle$
differs markedly from that of
$\tilde{q}^{\ast }$
. The vectors (
$\langle u_{r}^{\ast }\unicode[STIX]{x1D703}_{r}^{\ast }\rangle$
,
$\langle v_{r}^{\ast }\unicode[STIX]{x1D703}_{r}^{\ast }\rangle$
) point, in general, upstream and are characterized by a large magnitude at the upstream half of the rollers near the centreline. Concentrations of
$\langle w_{r}^{\ast }\unicode[STIX]{x1D703}_{r}^{\ast }\rangle$
occur mostly between neighbouring rollers, where the ribs are connected to the spanwise rollers (figure 13
j–l). They result from direct interactions between the ribs and the rollers, which act to produce large random velocity fluctuations (Hussain & Hayakawa Reference Hussain and Hayakawa1987).
Knowing all three components of the vorticity and heat flux vectors, we can now propose a 3-D picture of the heat and momentum transport. The conceptual sketch in figure 18(a) is based on the present experimental data at
$x^{\ast }=10$
. Compared with the 2-D model (see the inset of figure 18) in MA, the present model highlights the roles played by the rib structures in transporting heat and momentum in the braid region and also the vorticity flux density between neighbouring opposite-signed rollers. This model also underlines the importance of the upstream half of the spanwise rollers, rather than only one quadrant of the roller, as in the MA model, in diffusing heat out of the vortex. For simplicity, the spanwise rollers are drawn as 2-D structures, i.e. the spanwise contortion of the rollers is not shown. This simplification is reasonable since the roller at the beginning of the intermediate wake is less distorted compared with that downstream (Williamson Reference Williamson1996; Zdravkovich Reference Zdravkovich1997). The ribs are drawn conceptually as counter-rotating longitudinal vortices, which wrap around the spanwise vortices on the basis of the present coherent vorticity data (figures 7
a–f and 17
a–c) and previous reports (e.g. Brede et al.
Reference Brede, Eckelmann and Rockwell1996; Huang et al.
Reference Huang, Zhou and Zhou2006).
Figure 18. (a) Conceptual model of momentum and 3-D heat transport at
$x^{\ast }=10$
; the 2-D model of Matsumura & Antonia (Reference Matsumura and Antonia1993) (MA) is shown in the inset to the figure. Thick and thin red arrows denote the coherent and remainder heat fluxes respectively. (b) Evolution of the topological features of turbulent energy and temperature variance productions from
$x^{\ast }=10$
to 40 (structures are not to scale).
For clarity, we consider only one vortex shedding period. The cooler fluid from the free stream engulfed by the Kármán vortex can be largely divided into three parts. The first is entrained immediately downstream of vortex A towards the centreline, resulting in a strong heat transport from the centreline to the free stream, as indicated by the large arrows between
$\unicode[STIX]{x1D719}=-1$
and 0 in figure 17(d). The second is drawn into the saddle region between vortices B and C and further bifurcated into two branches, due to the combined induced motion of the adjacent opposite-signed rolls, which lead to the opposite-signed spanwise velocities (figure 10
g) and heat fluxes (figure 12
j) on the two sides of the diverging separatrix. Although only one branch of the bifurcated flow is detected, the existence of the bifurcated flow near the saddle region has been demonstrated by the observation of Wu et al. (Reference Wu, Sheridan, Welsh and Hourigan1996) from the PIV data. The third (and last) part of the entrained flow is engulfed into the wake by vortex C. While the heat flux associated with the first part of the engulfed flow, as in the MA model, occurs mainly in the (
$x$
–
$y$
) plane and makes a predominant contribution to heat transport from the wake region to the free stream, the heat flux due to the second part should generally account for the heat transport in the spanwise direction.
The coherent motions play an important role in large-scale heat and momentum transport by entraining the cooler potential fluid from the free stream to the heated turbulent wake, while the small-scale random motions are crucial for heat diffusion and mixing between the warm wake and entrained cooler fluid. At
$x^{\ast }=10$
, heat is mostly contained within the Kármán vortex (figure 10
j). Both the present (figure 17
g) and the MA results indicate that the remainder heat flux occurs mostly in quadrant II of vortex B and quadrant III of vortex C. The vectors pointing in the upstream centrifugal direction suggest that the remainder heat flux
$(\langle u_{r}^{\ast }\unicode[STIX]{x1D703}_{r}^{\ast }\rangle ,\langle v_{r}^{\ast }\unicode[STIX]{x1D703}_{r}^{\ast }\rangle )$
serves to diffuse heat out of the vortex. However, what is overlooked by MA is the importance of quadrant II of vortex C (also quadrant III of vortex B), which contains the contact region between the rib and the roller, where effective turbulent mixing occurs (Hussain & Hayakawa Reference Hussain and Hayakawa1987). The heat flux
$\langle v_{r}^{\ast }\unicode[STIX]{x1D703}_{r}^{\ast }\rangle$
in quadrant II of vortex C is opposite in sign to
$\langle v_{r}^{\ast }\unicode[STIX]{x1D703}_{r}^{\ast }\rangle$
in quadrant III and points in the centrifugal direction (figure 17
g), implying a heat transport out of the vortex. Although relatively small at
$x^{\ast }=10$
compared with that in quadrant III, the heat flux
$(\langle u_{r}^{\ast }\unicode[STIX]{x1D703}_{r}^{\ast }\rangle ,\langle v_{r}^{\ast }\unicode[STIX]{x1D703}_{r}^{\ast }\rangle )$
in quadrant II of vortex C gains importance and in fact overwhelms that of quadrant III at
$x^{\ast }=20{-}40$
where the maximum
$\langle v_{r}^{\ast }\unicode[STIX]{x1D703}_{r}^{\ast }\rangle$
(and also
$\langle w_{r}^{\ast }\unicode[STIX]{x1D703}_{r}^{\ast }\rangle$
at
$x^{\ast }=40$
) is shifted towards quadrant II (cf. figure 13
h,i,l).
Some comments regarding the downstream evolution of the proposed model are appropriate. As the rib structures decay and the distortion of the spanwise rollers intensifies with increasing
$x^{\ast }$
, the large-scale heat and momentum transport is caused predominantly by the deformed rollers. This is why the coherent momentum flux and three heat fluxes are characterized by almost the same topologies at
$x^{\ast }=40$
(figure 12
c,f,i,l). On the other hand, the most important heat diffusion region is gradually shifted from quadrant III to quadrant II of vortex C. This is consistent with the observations by Cantwell & Coles (Reference Cantwell and Coles1983) and Hussain (Reference Hussain1986) that the saddle region becomes more important as
$x^{\ast }$
increases. Although based on the data at
$x^{\ast }=10$
, the model is certainly expected to apply upstream of this location where the ribs are greater in strength and more organized (Huang et al.
Reference Huang, Zhou and Zhou2006).
Figure 18(b) compares the streamwise evolution of the topologies associated with
$\langle P_{e}\rangle ^{\ast }$
and
$\langle P_{\unicode[STIX]{x1D703}}\rangle ^{\ast }$
. While Hussain & Hayakawa (Reference Hussain and Hayakawa1987) have shown the typical topology of the turbulence production for
$x^{\ast }=10{-}40$
based on their 2-D data, the topology of the temperature variance and a comparison with that of the turbulent energy production have not been reported hitherto. As indicated in figure 14(c),
$\langle P_{e}\rangle ^{\ast }$
at
$x^{\ast }=10$
is largely concentrated along the diverging separatrix below the saddle point; while exhibiting a similar distribution to
$\langle P_{e}\rangle ^{\ast }$
,
$\langle P_{\unicode[STIX]{x1D703}}\rangle ^{\ast }$
occurs nearer to the centreline (figure 15
a). At
$x^{\ast }=40$
,
$\langle P_{e}\rangle ^{\ast }$
spreads along the diverging separatrix and has a maximum overlap with the saddle point (figure 14
d), but the concentration of
$\langle P_{\unicode[STIX]{x1D703}}\rangle ^{\ast }$
is located further away from the centreline than
$\langle P_{e}\rangle ^{\ast }$
with a maximum above the saddle point. The more rapid lateral shift exhibited by
$\langle P_{\unicode[STIX]{x1D703}}\rangle ^{\ast }$
than by
$\langle P_{e}\rangle ^{\ast }$
as
$x^{\ast }$
increases is quite similar to the difference between
$\langle v_{r}\unicode[STIX]{x1D703}_{r}\rangle ^{\ast }$
(figure 13
g–i) and
$\langle u_{r}v_{r}\rangle ^{\ast }$
(figure 12
a–c). This is reasonable since
$\langle v_{r}\unicode[STIX]{x1D703}_{r}\rangle ^{\ast }$
and
$\langle u_{r}v_{r}\rangle ^{\ast }$
together with their interactions with the temperature and velocity gradients are the dominant terms of
$\langle P_{\unicode[STIX]{x1D703}}\rangle ^{\ast }$
and
$\langle P_{e}\rangle ^{\ast }$
respectively.
6 Conclusions
The transport of momentum and heat has been experimentally investigated in a slightly heated turbulent wake based on data captured from a three-component vorticity probe combined with four cold wires. Compared with MA, the present study provides a more complete and systematic study of the vorticity, momentum and heat transport in the turbulent intermediate wake. Apart from the kinematic topological features, this work also examines the vorticity dynamics (e.g. transport and cancellation), production of the turbulent energy and temperature variance, interactions between vorticity and momentum flux or heat flux, and the streamwise evolution of these dynamical processes, none of which were studied by MA. As a matter of fact, many physical aspects such as the vorticity flux density vector, the production of turbulence energy and temperature variance are, to the best of our knowledge, studied for the first time with the most complete set of experimental data. Five major conclusions can be drawn from this study.
(1) Both rollers and predominantly streamwise rib structures are captured by the present probe. The former are represented by
$\tilde{\unicode[STIX]{x1D714}}_{z}^{\ast }$
, while the latter are associated with
$\tilde{\unicode[STIX]{x1D714}}_{x}^{\ast }$
and
$\tilde{\unicode[STIX]{x1D714}}_{y}^{\ast }$
. The presence of ribs is confirmed both in the flow structures of the coherent
$\tilde{\unicode[STIX]{x1D714}}_{x}^{\ast }$
and
$\tilde{\unicode[STIX]{x1D714}}_{y}^{\ast }$
and in the cospectra between
$\unicode[STIX]{x1D714}_{x}$
and
$\unicode[STIX]{x1D714}_{y}$
. Both
$\tilde{\unicode[STIX]{x1D714}}_{x}^{\ast }$
and
$\tilde{\unicode[STIX]{x1D714}}_{y}^{\ast }$
exhibit distributions along the diverging separatrix at all
$x^{\ast }$
positions, except for
$\tilde{\unicode[STIX]{x1D714}}_{x}^{\ast }$
at
$x^{\ast }=10$
due to the smearing of the
$\tilde{\unicode[STIX]{x1D714}}_{x}^{\ast }$
from the deformed rollers. The capture of ribs at
$x^{\ast }=20$
and 40 is also indirectly corroborated by the observation that the cospectra between
$\unicode[STIX]{x1D714}_{x}$
and
$\unicode[STIX]{x1D714}_{y}$
at the saddle points show an evident peak at
$St=0.2$
. This peak is absent in the cospectra at the vortex centres of the corresponding
$x^{\ast }$
positions. Vorticity transport between neighbouring vortices can be partly responsible for the distortion of the rollers, especially for
$x^{\ast }\leqslant 20$
. The vorticity flux density vectors are for the first time determined experimentally from all three velocity components. It is found that information on vectors extracted from the 2-D data can be misleading in the downstream half of the vortices where vorticity transport between neighbouring vortices is interrupted by the engulfed non-turbulent fluid from the free stream, and vorticity cancellation takes place mainly on the upstream side of the vortices below the divergent separatrix.
(2) The streamwise evolutions of the coherent velocity fluctuations
$\tilde{u} ^{\ast }$
,
$\tilde{v}^{\ast }$
and
$\tilde{w}^{\ast }$
exhibit quite different characteristics. The concentrations of
$\tilde{u} ^{\ast }$
and
$\tilde{v}^{\ast }$
are always linked to the spanwise rollers, while that of
$\tilde{w}^{\ast }$
may be associated with both rollers and ribs. It is found that
$\tilde{w}^{\ast }$
is mostly induced by the ribs at
$x^{\ast }=10$
but results mainly from the deformation of the spanwise rollers in the (
$y$
–
$z$
) plane at
$x^{\ast }=20$
and 40, where the ribs become weak. Consequently, the
$\tilde{w}^{\ast }$
contours resemble those of
$\tilde{v}^{\ast }$
at
$x^{\ast }=20$
and 40. The contours of
$\tilde{u} ^{\ast }$
,
$\tilde{v}^{\ast }$
and
$\tilde{w}^{\ast }$
are quite similar to each other at
$x^{\ast }=40$
, implying an enhanced distortion of the spanwise rollers. The concentrations of
$\tilde{\unicode[STIX]{x1D703}}^{\ast }$
coincide well with those of
$\tilde{\unicode[STIX]{x1D714}}_{z}^{\ast }$
at
$x^{\ast }=10$
and 20, indicating that heat is contained within the periphery of the spanwise vortex. However, at
$x^{\ast }=40$
, the vortices are greatly weakened, releasing heat to the free stream. Consequently, the high-level
$\tilde{\unicode[STIX]{x1D703}}^{\ast }$
contours move out of the periphery of the spanwise vortex and drift to larger
$y^{\ast }$
.
(3) In the context of the production of both turbulent kinetic energy and temperature variance associated with the small-scale motions, the present results demonstrate unequivocally that the quantitative contribution from the
$w$
-related terms to the total
$\langle P_{e}\rangle ^{\ast }$
cannot be neglected, especially at
$x^{\ast }=40$
where the maximum concentration of the full
$\langle P_{e}\rangle ^{\ast }$
is approximately 22 % larger than that calculated based only on the 2-D data. It is further found that the negative concentration of the production at the vortex centre is mainly from the contribution of the spanwise normal stress. The contribution to
$\langle P_{\unicode[STIX]{x1D703}}\rangle ^{\ast }$
at
$x^{\ast }=10$
comes largely from the
$u$
- and
$v$
-related terms in (5.4). However, the
$w$
-related term becomes significant downstream. At
$x^{\ast }=40$
, the maximum concentration of the
$w$
-related term is 13 % of that of the total
$\langle P_{\unicode[STIX]{x1D703}}\rangle ^{\ast }$
. It is expected that the significance of the terms related to the spanwise velocity in both
$\langle P_{e}\rangle ^{\ast }$
and
$\langle P_{\unicode[STIX]{x1D703}}\rangle ^{\ast }$
will continue to increase further downstream, as the three-dimensionality of the flow is more prominent, and thus the heat transport should also be enhanced with increasing
$x^{\ast }$
. A comparison between the topologies of
$\langle P_{e}\rangle ^{\ast }$
and
$\langle P_{\unicode[STIX]{x1D703}}\rangle ^{\ast }$
reveals that
$\langle P_{\unicode[STIX]{x1D703}}\rangle ^{\ast }$
drifts laterally away from the centreline more rapidly than
$\langle P_{e}\rangle ^{\ast }$
, which is closely linked to the behaviours of
$\langle v_{r}\unicode[STIX]{x1D703}_{r}\rangle ^{\ast }$
and
$\langle u_{r}v_{r}\rangle ^{\ast }$
.
(4) The evolution of both momentum and heat fluxes is closely associated with the evolution of the vorticity structures (spanwise vortices and ribs) for both the coherent structures and the remainder motion. At
$x^{\ast }=10$
,
$\tilde{w}^{\ast }\tilde{\unicode[STIX]{x1D703}}^{\ast }$
is mostly due to the ribs, whereas
$\tilde{u} ^{\ast }\tilde{\unicode[STIX]{x1D703}}^{\ast }$
and
$\tilde{v}^{\ast }\tilde{\unicode[STIX]{x1D703}}^{\ast }$
are induced by the spanwise rollers. A conceptual model is proposed, which summarizes the 3-D features of the heat and momentum transport at this
$x^{\ast }$
location. Compared with that proposed in MA, this model provides more details on the role the rib structures play in transporting the heat and momentum and also highlights the importance of the upstream half of the spanwise rollers, instead of only one quadrant of the rollers as in the MA model, in terms of diffusion heat out of the vortex. At
$x^{\ast }=20$
and 40, the strength of the ribs decreases. At the same time, the deformation of the spanwise rollers is intensified. Consequently, the distortion of the rollers becomes exceedingly important in inducing
$\tilde{w}^{\ast }\tilde{\unicode[STIX]{x1D703}}^{\ast }$
, as well as
$\tilde{u} ^{\ast }\tilde{\unicode[STIX]{x1D703}}^{\ast }$
and
$\tilde{v}^{\ast }\tilde{\unicode[STIX]{x1D703}}^{\ast }$
, and the remainder motions undertake a more important role in diffusing heat out of the Kármán vortices. One very important feature of the remainder motion is that the predominant heat diffusion is gradually shifted from the upstream near-centreline quadrant of the spanwise rollers to the region where the ribs wrap around the rollers. This is essentially a reflection of the improved importance of the saddle region with increasing
$x^{\ast }$
(Cantwell & Coles Reference Cantwell and Coles1983).
(5) The present study contains a rather complete set of experimental data for the turbulent cylinder wake, including the simultaneously measured three components of the velocity vector, the three components of the vorticity vector and the three components of the heat flux vector, which may be used for validating numerical codes as well as gaining insight into various aspects of the flow.
Acknowledgements
The authors wish to acknowledge support given to them from NSFC through grant 51421063 and from Scientific Research Fund of Shenzhen Government through grants KQCX2014052114430139, JCYJ20130329154125496.
