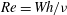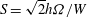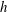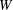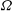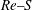1. Introduction
Any review of studies of the flow between rotating disks must commence with the work of Lance & Rogers (Reference Lance and Rogers1962), who considered both co-rotation and counter-rotation. Continuing work on this problem in the absence of wall transpiration, Mellor, Chapple & Stokes (Reference Mellor, Chapple and Stokes1968) and Holodniok, Kubicek & Hlavacek (Reference Holodniok, Kubicek and Hlavacek1981) reported multiple cell solutions, and a review of the large body of work in this area has been given by Zandbergen & Dijkstra (Reference Zandbergen and Dijkstra1987).
Of particular interest here is the effect of transpiration though one porous disk to another impermeable disk. Terrill & Cornish (Reference Terrill and Cornish1973) looked at the limit of small blowing and suction between stationary disks and also considered various large suction limits. Hinch & Lemaître (Reference Hinch and Lemaître1994) studied blowing through a stationary disk in order to predict the float height of levitated disks. Their similarity analysis, valid under the assumption of uniform blowing velocity
$W$
along the stationary lower plate, assumes the flow is steady and governed by the Reynolds number
$Re=Wh/{\it\nu}$
, where
$h$
is the plate separation distance and
${\it\nu}$
is the kinematic viscosity of the fluid. For application to finite levitated disks, the uniform blowing assumption fails for reservoir pressures near to that necessary for lift-off, and an important contribution of their study is a lubrication analysis for the float height at near-lift-off reservoir pressures. In figure 2 of Hinch & Lemaître (Reference Hinch and Lemaître1994), experimental and theoretical float heights of disks of diameter 7.9 cm and 11.9 cm are compared with some success. In a subsequent theoretical study, Cox (Reference Cox2002) showed that non-axisymmetric flows levitating stationary disks are possible based on Howarth’s (Reference Howarth1951) three-dimensional stagnation point flow ansatz; Cox finds the interesting feature that disks so levitated can float at heights greater than for axisymmetrically levitated disks.
The initial motivation for this present investigation was an attempt to find the fluid analogue of results presented by Farkas et al. (Reference Farkas, Bartels, Unger and Wolf2003) concerning the terminal motion of a disk spinning and sliding on a horizontal table under the action of uniform Coulomb friction. In that rigid body mechanics problem the coupling between the frictional force and torque results in a terminal motion for which sliding and spinning stop simultaneously, with a terminal value of
$v/R{\it\omega}=0.643$
, where
$v$
is the translational speed,
$R$
is the disk radius and
${\it\omega}$
is the rotation rate. Weidman & Malhotra (Reference Weidman and Malhotra2005, Reference Weidman and Malhotra2007) extended this work to study the motion of composite disks, and thereby discovered situations for which (i) sliding stops first and the disk spins down to rest, or (ii) spinning stops first and the disk slides to rest. These studies piqued our interest in the sliding and spinning motion of an air hockey disk, where the Coulomb friction force is replaced by aerodynamic resistance. Wang (Reference Wang1974) showed that a similarity reduction of the Navier–Stokes equations exists for a circular porous slider moving laterally on a flat plate, and the current study shows that a similarity reduction exists for a disk rotating above an air hockey table. Unfortunately, however, no similarity reduction of the Navier–Stokes equation for a disk both translating and spinning above an air hockey table is available, and therefore studies of this problem would require full numerical simulation of the governing partial differential equations.
Nevertheless, we consider the problem of a disk rotating at angular velocity
${\it\Omega}$
above an air hockey table to be inherently interesting. Such flows have been considered, to varying degrees, by Dorfman (Reference Dorfman1966), Jawa (Reference Jawa1971), Nguyen, Ribault & Florent (Reference Nguyen, Ribault and Florent1975), and Wang & Watson (Reference Wang and Watson1979). Nguyen et al. (Reference Nguyen, Ribault and Florent1975) reported multiple solutions for this configuration. While a few specific results have been presented in these papers, particularly in Dorfman (Reference Dorfman1966) and in Wang & Watson (Reference Wang and Watson1979), no complete survey of the steady similarity solutions for an upper rotating plate has been reported. It is important to note that all these similarity reductions of the Navier–Stokes equations assume the flow to be steady.
For infinite horizontal plates we now, in addition to
$Re$
, include the effect of rotation through the dimensionless parameter
$S=\sqrt{2}{\it\Omega}h/W$
. The ultimate goal of the paper is to use the similarity results to model a disk of finite radius levitated above an air hockey table. As noted by Hinch & Lemaître (Reference Hinch and Lemaître1994), this model for a disk of radius
$a$
is expected to be a good approximation under the proviso
$h/2a\ll 1$
, with the further assumption that the pressure at the edge and on top of the disk is atmospheric.
However, we understand that the interaction of the radial jet, emanating from the gap, with the wall transpiration probably renders the flow unsteady in the outer ambient flow field. This possibility is of concern, and we therefore implement direct numerical simulation (DNS) of the unsteady, axisymmetric, incompressible Navier–Stokes equations with the ability to model fluid–structure interaction (FSI). We examine solutions for an air hockey disk rotating at fixed angular velocity that is either at a fixed height or free to move axially. Our limited results indeed show that the flow outside the gap is weakly unsteady for the reason cited above, and this imparts small axial oscillations of the disk, from which we can estimate the statistical-steady-state disk float height to compare with the steady flow model.
The presentation is as follows. Section 2 gives the formulation and numerical solution of the steady problem along with low-
$Re$
series solutions and high-
$Re$
asymptotics and other solution results. An outline of the unsteady DNS code and results derived therefrom are given in § 3. A summary and discussion of results are given in § 4.
2. Steady-problem formulation and asymptotics
Dimensional cylindrical coordinates (
$r^{\ast }$
,
${\it\theta}$
,
$z^{\ast }$
) with corresponding dimensional velocities (
$u^{\ast }$
,
$v^{\ast }$
,
$w^{\ast }$
) are employed to study the steady axisymmetric flow between a porous stationary disk at
$z^{\ast }=0$
and a rotating disk at
$z^{\ast }=h$
. The lower disk has spatially uniform transpiration velocity
$W$
and the upper disk rotates at angular velocity
${\it\Omega}$
. Axisymmetry implies that the flow depends only on coordinates (
$r^{\ast }$
,
$z^{\ast }$
) which are scaled with the fixed plate separation distance
$h$
to obtain dimensionless meridional coordinates
$r=r^{\ast }/h$
and
${\it\eta}=z^{\ast }/h$
. Inserting the similarity ansatz of von Kármán (Reference von Kármán1921) satisfying the continuity equation
$$\begin{eqnarray}u^{\ast }(r,{\it\eta})=\frac{W}{2}rf^{\prime }({\it\eta}),\quad v^{\ast }(r,{\it\eta})=h{\it\Omega}rg({\it\eta}),\quad w^{\ast }({\it\eta})=-Wf({\it\eta})\end{eqnarray}$$
into the Navier–Stokes equations yields the coupled pair of ordinary differential equations
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{1}{2}f^{\prime 2}-ff^{\prime \prime }-S^{2}g^{2}=\frac{{\it\alpha}}{2}+Re^{-1}f^{\prime \prime \prime }, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & f^{\prime }g-fg^{\prime }=Re^{-1}g^{\prime \prime }, & \displaystyle\end{eqnarray}$$
${\it\eta}$
. Note that
$w^{\ast }(0)>0$
corresponds to blowing, which is the case of interest in this investigation. The pressure field for this flow is 
$$\begin{eqnarray}p^{\ast }=p_{0}^{\ast }-{\it\rho}W^{2}\left(\frac{1}{8}r^{2}{\it\alpha}+\frac{1}{2}f^{2}+\frac{1}{Re}f^{\prime }\right)\end{eqnarray}$$
and the dimensionless parameters appearing in (2.2) are
$$\begin{eqnarray}Re=\frac{Wh}{{\it\nu}},\quad S=\frac{\sqrt{2}{\it\Omega}h}{W}.\end{eqnarray}$$
While
$Re$
is the Reynolds number based on the transpiration velocity through the stationary lower plate, we shall have recourse to the Reynolds number
$Re_{{\it\Omega}}=ReS/\sqrt{2}={\it\Omega}h^{2}/{\it\nu}$
based on the rotation rate of the upper spinning plate. Here
$S$
denotes the rotation parameter.
As usual in problems of this type, the radial pressure gradient parameter
${\it\alpha}$
is an eigenvalue that must be determined during the course of solution. The boundary conditions prescribing blowing through the lower plate and rotation of the upper impermeable plate are
$$\begin{eqnarray}\displaystyle & f(0)=-1,\quad f^{\prime }(0)=0,\quad g(0)=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & f(1)=0,\quad f^{\prime }(1)=0,\quad g(1)=1. & \displaystyle\end{eqnarray}$$
Numerical integration of (2.2) obtained by shooting from the upper to the lower plate requires variation of
$f^{\prime \prime }(1)$
,
$g^{\prime }(1)$
and
${\it\alpha}$
to satisfy the three conditions in (2.5a
). Following Cox (Reference Cox2002),
${\it\alpha}$
may be eliminated by differentiating (2.2a
) to obtain
$$\begin{eqnarray}-ff^{\prime \prime \prime }-2S^{2}gg^{\prime }=Re^{-1}f^{\prime \prime \prime \prime }.\end{eqnarray}$$
Integration of this fourth-order equation requires a guess for
$f^{\prime \prime \prime }(1)$
in lieu of
${\it\alpha}$
; evaluation of (2.2a
) at
${\it\eta}=1$
shows that the two parameters are related via the equation
$$\begin{eqnarray}f^{\prime \prime \prime }(1)=-Re\left(\frac{{\it\alpha}}{2}+S^{2}\right).\end{eqnarray}$$
Numerical solutions are facilitated by accurate initial guesses for the shooting parameters. These are obtained using the small-
$Re$
and large-
$Re$
behaviours determined in the following sections.
2.1. Low-Reynolds-number behaviour
Extending the analysis of Hinch & Lemaître (Reference Hinch and Lemaître1994) to include the effect of upper disk rotation, we seek the low-Reynolds-number solution behaviour of (2.2) in the form
$$\begin{eqnarray}\displaystyle & f({\it\eta})=f_{0}({\it\eta})+Ref_{1}({\it\eta})+\cdots \,, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & g({\it\eta})=g_{0}({\it\eta})+Reg_{1}({\it\eta})+\cdots \,, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\alpha}=\frac{1}{Re}{\it\alpha}_{0}+{\it\alpha}_{1}+\cdots & \displaystyle\end{eqnarray}$$
$O(Re^{-1})$
problem 
$$\begin{eqnarray}\displaystyle & f_{0}^{\prime \prime \prime }+{\textstyle \frac{1}{2}}{\it\alpha}_{0}=0,\quad g_{0}^{\prime \prime }=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & f_{0}(0)=-1,\quad f_{0}^{\prime }(0)=0,\quad g_{0}(0)=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & f_{0}(1)=0,\quad f_{0}^{\prime }(1)=0,\quad g_{0}(1)=1, & \displaystyle\end{eqnarray}$$
$O(1)$
problem 
$$\begin{eqnarray}\displaystyle & f_{1}^{\prime \prime \prime }+{\textstyle \frac{1}{2}}{\it\alpha}_{1}=\frac{1}{2}f_{0}^{\prime 2}-f_{0}\,f_{0}^{\prime \prime }-S^{2}g_{0}^{2}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & g_{1}^{\prime \prime }=f_{0}^{\prime }g_{0}-f_{0}g_{0}^{\prime }, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & f_{1}(0)=0,\quad f_{1}^{\prime }(0)=0,\quad g_{1}(0)=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & f_{1}(1)=0,\quad f_{1}^{\prime }(1)=0,\quad g_{1}(1)=0. & \displaystyle\end{eqnarray}$$
The solution to boundary-value problem (2.9)
$$\begin{eqnarray}f_{0}({\it\eta})=-(1-{\it\eta})^{2}(2{\it\eta}+1),\quad g_{0}({\it\eta})={\it\eta},\quad {\it\alpha}_{0}=24\end{eqnarray}$$
gives a linear azimuthal shear flow superposed on the stationary disk solution. At this leading order there is no dependence on the rotation parameter
$S$
. Inserting solutions
$f_{0}({\it\eta})$
and
$g_{0}({\it\eta})$
into boundary-value problem (2.10) and solving the
$O(1)$
system gives
$$\begin{eqnarray}\displaystyle & \displaystyle f_{1}({\it\eta})=-\frac{1}{70}{\it\eta}^{2}(1-{\it\eta})^{2}(2{\it\eta}^{3}-3{\it\eta}^{2}-8{\it\eta}+22)-\frac{S^{2}}{60}(2-{\it\eta})(1-{\it\eta}){\it\eta}^{2}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & g_{1}({\it\eta})={\textstyle \frac{1}{20}}{\it\eta}(1-{\it\eta})(4{\it\eta}^{3}-{\it\eta}^{2}-{\it\eta}-11), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & {\it\alpha}_{1}={\textstyle \frac{3}{5}}\left({\textstyle \frac{36}{7}}-S^{2}\right). & \displaystyle\end{eqnarray}$$
The results for
$f_{0}({\it\eta})$
,
$g_{0}({\it\eta})$
,
$f_{1}({\it\eta})$
and
$g_{1}({\it\eta})$
are in agreement with Wang & Watson (Reference Wang and Watson1979). The above results are used to obtain the low-Reynolds-number behaviours of the relevant shear stress parameters and the radial pressure gradient given by
$$\begin{eqnarray}\displaystyle & \displaystyle f^{\prime \prime }(1)\sim -6-\frac{1}{5}\left(\frac{13}{7}+\frac{S^{2}}{2}\right)Re+O(Re^{2}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle f^{\prime \prime }(0)\sim 6-\frac{1}{5}\left(\frac{22}{7}+\frac{S^{2}}{3}\right)Re+O(Re^{2}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & g^{\prime }(1)\sim 1+{\textstyle \frac{9}{20}}Re+O(Re^{2}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\alpha}\sim \frac{24}{Re}+\frac{3}{5}\left(\frac{36}{7}-S^{2}\right)+O(Re). & \displaystyle\end{eqnarray}$$
$S$
on the radial pressure gradient parameter is now apparent in (2.13d
). For
$S=0$
, the above results agree with the stationary disk results of Hinch & Lemaître (Reference Hinch and Lemaître1994) and Cox (Reference Cox2002). We note that Dorfman (Reference Dorfman1966) normalized his variables differently to obtain an expansion in terms of
$Re_{{\it\Omega}}$
, so a direct comparison with his low-
$Re_{{\it\Omega}}$
expansion results is not readily made.
2.2. High-Reynolds-number asymptotics
At large
$Re$
we are faced with matching the boundary layer flow on the rotating disk to the outer inviscid flow which appears since the bottom plate does not rotate; see Wang & Watson (Reference Wang and Watson1979). The boundary layer is intensified by the rotating disk which centrifuges fluid radially outward, in what would be a von Kármán type boundary layer of thickness
$O(Re_{{\it\Omega}}^{-1/2})$
if there were no transpiration through the lower boundary.
Both Dorfman (Reference Dorfman1966) and Wang & Watson (Reference Wang and Watson1979) performed the leading-order matching of solutions between the boundary layer and the outer flow, but in a manner different from Hinch & Lemaître (Reference Hinch and Lemaître1994) which is followed here. We anticipate that the solution outside the boundary layer will take the form
$$\begin{eqnarray}\displaystyle & f({\it\eta})=f_{0}({\it\eta})+Re^{-1/2}f_{1}({\it\eta})+\cdots \,, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & g({\it\eta})=g_{0}({\it\eta})+Re^{-1/2}g_{1}({\it\eta})+\cdots \,, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & {\it\alpha}={\it\alpha}_{0}+Re^{-1/2}{\it\alpha}_{1}+\cdots \,. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{1}{2}f_{0}^{\prime 2}-f_{0}f_{0}^{\prime \prime }-S^{2}g_{0}^{2}=\frac{{\it\alpha}_{0}}{2}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & f_{0}^{\prime }g_{0}-f_{0}g_{0}^{\prime }=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & f_{0}(0)=-1,\quad f_{0}^{\prime }(0)=0,\quad g(0)=0,\quad f_{0}(1)=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle f_{0}^{\prime }f_{1}^{\prime }-f_{0}f_{1}^{\prime \prime }-f_{1}f_{0}^{\prime \prime }-2S^{2}g_{0}g_{1}=\frac{{\it\alpha}_{1}}{2}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle f_{0}^{\prime }g_{1}+f_{1}^{\prime }g_{0}-f_{0}g_{1}^{\prime }-f_{1}g_{0}^{\prime }=0, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}f_{1}(0)=0,\quad f_{1}^{\prime }(0)=0,\quad g_{1}(0)=0.\quad\end{eqnarray}$$
The solution of (2.15) is readily obtained as
$$\begin{eqnarray}f_{0}({\it\eta})={\it\eta}^{2}-1,\quad g_{0}({\it\eta})=0,\quad {\it\alpha}_{0}=4.\end{eqnarray}$$
Equation (2.17) gives
$f_{0}^{\prime }(1)=2$
and
$g_{0}(1)=0$
, so in order to satisfy the no-slip conditions in (2.5b
) we need an inner solution adjacent to the upper wall. With stretched coordinate
${\it\xi}$
pointing downward from the upper wall, leading-order inner expansions
$$\begin{eqnarray}{\it\xi}=Re^{1/2}(1-{\it\eta}),\quad f\sim Re^{-1/2}F({\it\xi}),\quad g\sim G({\it\xi})\end{eqnarray}$$
are inserted into (2.2), using
${\it\alpha}_{0}=4$
. One thereby obtains the boundary-value problem
$$\begin{eqnarray}\displaystyle & F_{{\it\xi}{\it\xi}{\it\xi}}=-{\textstyle \frac{1}{2}}F_{{\it\xi}}^{2}+FF_{{\it\xi}{\it\xi}}+S^{2}G^{2}+2, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & G_{{\it\xi}{\it\xi}}=FG_{{\it\xi}}-F_{{\it\xi}}G, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F(0)=0,\quad F_{{\it\xi}}(0)=0,\quad G(0)=1, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{{\it\xi}}\sim -2,\quad G\rightarrow 0,\quad {\it\xi}\rightarrow \infty . & & \displaystyle\end{eqnarray}$$
Behaviours (2.19f−h
) are used to match the inner boundary layer solution to the outer inviscid solution. Numerical solutions of (2.19) at selected values of
$S$
in the range
$0\leqslant S\leqslant 50$
have been obtained using a fourth-order Runge–Kutta shooting routine, details of which are given in § 2.3. This furnishes numerical values of
$F_{{\it\xi}{\it\xi}}(0)$
and
$G_{{\it\xi}}(0)$
and further provides the far-field behaviour
$$\begin{eqnarray}F({\it\xi})\sim -2{\it\xi}+{\it\delta}(S).\end{eqnarray}$$
Plots of the variation of
$F_{{\it\xi}{\it\xi}}(0)$
,
$G_{{\it\xi}}(0)$
and
${\it\delta}$
with
$S$
are provided in figure 1. The
$S=0$
values are
$F_{{\it\xi}{\it\xi}}(0)=-2.623875$
,
$G_{{\it\xi}}(0)=-1.074496$
and
${\it\delta}=1.137804$
, the first and last of which are in agreement with the stationary disk results of Hinch & Lemaître (Reference Hinch and Lemaître1994). Matching the outer solution
$f({\it\eta})$
as
${\it\eta}\rightarrow 1$
to the inner solution
$F({\it\xi})$
as
${\it\xi}\rightarrow \infty$
gives
$f_{1}(1)={\it\delta}$
. Now inserting the solutions for
$f_{0}({\it\eta})$
and
$g_{0}({\it\eta})$
into (2.16a,c
), we find the boundary-value problem for
$f_{1}({\it\eta})$
as
$$\begin{eqnarray}\displaystyle ({\it\eta}^{2}-1)f_{1}^{\prime \prime }-2{\it\eta}f_{1}^{\prime }+2f_{1}=-\frac{{\it\alpha}_{1}}{2} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & f_{1}(0)=0,\quad f_{1}^{\prime }(0)=0,\quad f_{1}(1)={\it\delta}. & \displaystyle\end{eqnarray}$$
It is evident from (2.16b
) that
$g_{1}({\it\eta})=Kf_{0}({\it\eta})$
which must vanish in order to satisfy (2.16e
) so that
$K=0$
. The solution of (2.21) is
$$\begin{eqnarray}f_{1}({\it\eta})={\it\delta}\,{\it\eta}^{2},\quad {\it\alpha}_{1}=4\,{\it\delta}\end{eqnarray}$$
where
${\it\delta}={\it\delta}(S)$
. Summarizing results to this point we have
$$\begin{eqnarray}\displaystyle & f({\it\eta})\sim ({\it\eta}^{2}-1)+Re^{-1/2}{\it\delta}\,{\it\eta}^{2}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & g({\it\eta})=o(Re^{-1/2}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & {\it\alpha}\sim 4(1+Re^{-1/2}{\it\delta}), & \displaystyle\end{eqnarray}$$
$F_{{\it\xi}{\it\xi}}(0)$
,
$G_{{\it\xi}}(0)$
and
${\it\delta}$
are functions of
$S$
.
Figure 1. Values of (a)
$F_{{\it\xi}{\it\xi}}(0)$
, (b)
$G_{{\it\xi}}(0)$
, and (c)
${\it\delta}$
as a function of rotation parameter
$S$
for asymptotic matching to the outer flow.
The radial pressure gradient and shear stress parameters are then found to possess the following asymptotic behaviours as
$Re\rightarrow \infty$
:
$$\begin{eqnarray}\displaystyle & f^{\prime \prime }(1)\sim Re^{1/2}F_{{\it\xi}{\it\xi}}(0)+o(Re^{1/2}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & f^{\prime \prime }(0)\sim 2(1+Re^{-1/2}{\it\delta}(S))+O(Re^{-1}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & g^{\prime }(1)\sim -Re^{1/2}G_{{\it\xi}}(0)+o(Re^{1/2}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & {\it\alpha}\sim 4(1+Re^{-1/2}{\it\delta}(S))+O(Re^{-1}). & \displaystyle\end{eqnarray}$$
2.3. Steady solutions
Numerical solutions of (2.6) and (2.2b
) are obtained using multiple parameter shooting of the Numerical Recipes (Press et al.
Reference Press, Flannery, Teukolosky and Vetterling1989) code ODEINT for integration and MNEWT for updating successive values of the initial guesses, setting TOLX and TOLF in MNEWT at
$10^{-6}$
and accuracy in ODEINT to
$10^{-6}$
. Values of the shooting parameters
$f^{\prime \prime }(1)$
,
$f^{\prime \prime \prime }(1)$
and
$g^{\prime }(1)$
were estimated from the results derived in the previous section and varied until boundary conditions (2.5a
) were attained to better than six decimal places. Decreasing the above tolerance parameters to
$10^{-7}$
affected final shear stress and
${\it\alpha}$
values to only one part in
$10^{5}$
or less. At low values of
$Re$
for fixed values of
$S$
, convergence is readily obtained, even if the initial guesses are not accurate. At high Reynolds numbers, however, it is imperative to have an accurate initial guess for the shooting parameters. Note that estimates of
$f^{\prime \prime \prime }(1)$
are readily calculated, at each value of
$S$
, using (2.7) and the high-
$Re$
asymptotic behaviour for
${\it\alpha}$
given in (2.24d
).
Solutions have been obtained over a range of Reynolds numbers sufficient to exhibit matching to the low-
$Re$
and high-
$Re$
asymptotics for rotation parameters in the range
$0\leqslant S\leqslant 12$
. In addition, we have calculated solutions for two special values of
$S$
. The first is the Dorfman (Reference Dorfman1966) value
$S_{d}=5\sqrt{2}$
and the second is the critical value
$S_{c}=7.6399$
, for which the
${\it\alpha}$
curve first touches down to zero at
$Re_{c}=1.950$
. In the plots to be displayed, some solution curves at low and high
$S$
are omitted for clarity of presentation. Figure 2 displays the radial pressure gradient parameter in which it may be seen, at sufficiently high
$S$
, that regions of
${\it\alpha}<0$
develop. The upper curve for
$S=0$
is equivalent to that found by Hinch & Lemaître (Reference Hinch and Lemaître1994) in the absence of disk rotation. Results for the radial shear stress
$f^{\prime \prime }(0)$
on the bottom wall are shown in figure 3 along with its low-
$Re$
and high-
$Re$
behaviours. Here again, for sufficiently large
$S$
, regions of
$f^{\prime \prime }(0)<0$
develop. Results for the radial shear stress
$f^{\prime \prime }(1)$
at the upper wall are shown in figure 4 along with its low-
$Re$
and high-
$Re$
behaviours. Of particular importance for studying the spin-down behaviour of a rotating disk is the azimuthal shear stress
$g^{\prime }(1)$
at the upper plate displayed in figure 5, again with corresponding low-
$Re$
and high-
$Re$
behaviours.
Figure 2. Variation of radial pressure gradient parameter
${\it\alpha}$
with Reynolds number
$Re$
for selected values of
$S$
.
$S_{d}=5\sqrt{2}$
is the value considered by Dorfman (Reference Dorfman1966) and the solid circles are his computed results. The critical value
$S_{c}=7.6399$
is that for which
${\it\alpha}$
first becomes zero at
$Re_{c}=1.950$
.
Figure 3. Variation of lower-wall radial shear stress parameter
$f^{\prime \prime }(0)$
with Reynolds number for selected values of
$S$
. Asymptotics at low and high values of
$Re$
are shown as dashed lines.
Figure 4. Variation of upper-wall radial shear stress parameter
$f^{\prime \prime }(1)$
with Reynolds number for selected values of
$S$
. The low-
$Re$
and high-
$Re$
behaviours are shown as dashed lines.
Figure 5. Variation of upper-wall azimuthal shear stress parameter
$g^{\prime }(1)$
with Reynolds number for selected values of
$S$
. The low-
$Re$
and high-
$Re$
behaviours are shown as dashed lines.
All solutions have
$g({\it\eta})\geqslant 0$
. Hence, in the nomenclature of Mellor et al. (Reference Mellor, Chapple and Stokes1968), these are regions of positive
$Re$
. In their parlance, regions of
$Re$
negative are those for which
$g({\it\eta})$
has a change of sign somewhere between the disks. Thus one cannot expect to find the effect of blowing on the 2-cell and 3-cell solutions found by Mellor et al. (Reference Mellor, Chapple and Stokes1968) since they occur only when
$g({\it\eta})$
exhibits a change in sign. An investigation into these flows would be best undertaken using another normalization of the governing equations that would have
$Re_{{\it\Omega}}$
appearing in (2.2) in lieu of
$Re$
, which would account for the blowing only through the wall transpiration boundary condition. However, exploration of multiple solutions of this problem, though certainly interesting, is not the goal of this investigation.
The regions of negative
${\it\alpha}$
and
$f^{\prime \prime }(0)$
obtained from the similarity solution have interesting implications. Lift-off is not possible for
${\it\alpha}\leqslant 0$
. For
$f^{\prime \prime }(0)<0$
there is radial inflow near the lower boundary, whilst for
$f^{\prime \prime }(0)>0$
the flow is everywhere radially outward; these will be called regions of counter-flow and outward flow, respectively. Of course, this is just the motion in a meridional section, and one must bear in mind that the flow is fully three-dimensional.
Additional computations were performed to accurately depict the boundaries
${\it\alpha}=0$
and
$f^{\prime \prime }(0)=0$
. Numerical solutions in these regions were carried out at smaller increments of
$S$
and the exploration was extended up to
$S=20$
. The two boundaries in question are shown in the
$Re{-}S$
plane in figure 6(a). The turning point of the
${\it\alpha}=0$
boundary lies at
$Re=1.950$
,
$S=7.6399$
and that for the
$f^{\prime \prime }(0)=0$
boundary is at
$Re=2.625$
,
$S=9.603$
. It is a simple exercise to find the low-
$Re$
behaviours of the lower branches of these curves by setting the expressions for
${\it\alpha}$
and
$f^{\prime \prime }(0)$
in (2.13b,d
) equal to zero to obtain
$$\begin{eqnarray}Re=\frac{280}{7S^{2}-36}\quad ({\it\alpha}=0)\end{eqnarray}$$
and
$$\begin{eqnarray}Re=\frac{630}{7S^{2}+66}\quad (f^{\prime \prime }(0)=0).\end{eqnarray}$$
These are shown as the dashed and dot-dashed lines in figure 6(a). Both of these boundaries emanate from the origin in
$Re_{{\it\Omega}}$
–
$Re$
parameter space. This is readily seen by substituting
$S^{2}=2Re_{{\it\Omega}}^{2}/Re^{2}$
in the above relations and solving for
$Re_{{\it\Omega}}$
, an exercise that leads to the expressions
$$\begin{eqnarray}Re_{{\it\Omega}}=\sqrt{2Re\left({\textstyle \frac{9}{7}}Re+10\right)}\quad ({\it\alpha}=0)\end{eqnarray}$$
and
$$\begin{eqnarray}Re_{{\it\Omega}}=\sqrt{3Re\left(15-{\textstyle \frac{11}{7}}Re\right)}\quad (f^{\prime \prime }(0)=0).\end{eqnarray}$$
These results are compared with the numerically determined boundaries in figure 6(b).
Figure 6. Boundaries separating (i) positive and negative radial pressure gradient parameter
${\it\alpha}$
and (ii) outward flow and counter-flow regions of radial velocity shown in (a) the
$Re{-}S$
and (b) the
$Re_{{\it\Omega}}{-}Re$
planes; the small-
$Re$
asymptotics are shown as dashed and dot-dashed lines, respectively. The turning point in (a) for boundary (i) is
$Re=1.9225$
,
$S=7.631$
and that for boundary (ii) is
$Re=2.607$
,
$S=9.594$
.
The dimensionless meridional streamfunction
${\it\psi}={\it\psi}^{\ast }/Wa^{2}$
for the similarity flow is
$$\begin{eqnarray}{\it\psi}=-{\textstyle \frac{1}{2}}r^{2}f({\it\eta}),\end{eqnarray}$$
from which one can compute the non-dimensional radial and axial velocities (
$-r^{-1}{\it\psi}_{z}$
,
$r^{-1}{\it\psi}_{r}$
), respectively. In our variables, Mellor et al. (Reference Mellor, Chapple and Stokes1968) define a ‘cell’ as the flow bounded by planes of constant
${\it\eta}$
where
$f=0$
, and therefore includes only recirculating fluid. Thus all the flows determined here are not ‘cells’ but rather may be considered as ‘half-cells’, since when the flow is reflected about
${\it\eta}=0$
one obtains a full cell. However, these half-cells may or may not have reverse meridional flow as shown in the two example streamline plots in figure 7. Figure 7(a) exhibits an outward flow at
$Re=2$
and
$S=5$
while figure 7(b) shows a counter-flow at
$Re=2$
and
$S=15$
. The horizontal dashed line in figure 7(b) is the height
${\it\eta}=0.390$
of zero radial velocity, concomitant with the interior points of vertical streamline tangents.
Figure 7. Meridional streamline plots at selected values of
${\it\psi}$
showing examples of (a) outward flow at
$Re=2$
for
$S=5$
and (b) counter-flow at
$Re=2$
for
$S=15$
; the dashed line at
${\it\eta}=0.390$
is the height of zero radial velocity.
3. Unsteady-flow numerical simulations
The steady theory is now tested with numerical computation of the axisymmetric unsteady flow for hockey disks rotating at a fixed angular rotation rate. We begin with the float height obtained from the steady flow model in § 3.1. The numerical method described in § 3.2 is followed by a presentation of results in § 3.3 for a disk floating at a fixed height. These results motivate our study in § 3.4 for a freely floating disk.
3.1. Steady float height
Using steady theory assuming
$h/2a\ll 1$
so that the flow under a finite disk of radius
$a$
approximates that under an infinite plate, the pressure (2.3) on the underside (
${\it\eta}=1$
) of the rotating disk where
$f(1)=f^{\prime }(1)=0$
is given as
$$\begin{eqnarray}p^{\ast }=p_{0}^{\ast }-\frac{{\it\rho}W^{2}}{8}r^{2}{\it\alpha}.\end{eqnarray}$$
Evaluating this pressure at the corner of the disk
$r^{\ast }=a$
where the pressure is assumed to be atmospheric,
$p_{a}^{\ast }$
, and subtracting from (3.1) gives
$$\begin{eqnarray}p^{\ast }-p_{a}^{\ast }=-\frac{{\it\rho}W^{2}}{8}\left[\left(\frac{r^{\ast }}{h}\right)^{2}-\left(\frac{a}{h}\right)^{2}\right]{\it\alpha}.\end{eqnarray}$$
Assuming atmospheric pressure in the steady von Kármán layer above the disk furnishes the pressure drop across the disk as
$$\begin{eqnarray}{\rm\Delta}p^{\ast }=-\frac{{\it\rho}W^{2}}{8h^{2}}({r^{\ast }}^{2}-a^{2}){\it\alpha}.\end{eqnarray}$$
Integration of this pressure drop over the surface of the spinning disk provides the aerodynamic lift; setting this equal to the disk weight
$mg$
furnishes the steady float height
$$\begin{eqnarray}h=\sqrt{\frac{{\rm\pi}{\it\rho}W^{2}a^{4}}{16mg}}\,{\it\alpha}^{1/2}.\end{eqnarray}$$
Numerical computations are compared with some of the steady model results listed in table 1 for a lightweight Lexan disk of mass
$m=18~\text{g}$
and radius
$a=6~\text{cm}$
levitated in air of density
${\it\rho}=0.001225~\text{g}~\text{cm}^{-3}$
and kinematic viscosity
${\it\nu}=0.145~\text{cm}^{2}~\text{s}^{-1}$
using gravitational constant
$g=980~\text{cm}~\text{s}^{-2}$
.
Table 1. For fixed
$Re=40$
and selected integer values of
$S$
, the values of
${\it\alpha}$
are computed. From these dimensionless parameters the values of
$W$
,
${\it\Omega}$
and
$h$
at the chosen values of
$m$
,
$a$
,
${\it\rho}$
,
${\it\nu}$
and
$g$
are determined.
3.2. Numerical method
For an investigation of unsteady flow in the gap and surrounding the disk, we performed direct numerical solutions of the axisymmetric incompressible-flow Navier–Stokes equations. For these computations, the disk thickness was taken as 0.12 cm. Simulations were performed with the open-source Nek5000 computational fluid dynamics program, which is based on the spectral finite element method and is described in detail elsewhere (Fischer Reference Fischer1997). The so-called PN/PN-2 formulation was employed, where the pressure field was solved with polynomial basis functions that are two orders lower than those used for the velocity field. Time integration was second-order accurate and semi-implicit.
For direct numerical solutions with FSI, the disk was modelled as a rigid body with constant rotation rate but was free to move in the axial direction. An arbitrary Eulerian–Lagrangian (ALE) approach was used in the fluid for the deforming mesh. Axial motion of the disk was calculated with forward Euler time integration. The total vertical force acting on the disk was calculated as that due to gravity plus the integrated pressure over the top and bottom surfaces, and includes the vertical shear force on the edge.
The computational domain was
$0\leqslant r^{\ast }\leqslant 20~\text{cm}$
,
$0\leqslant z^{\ast }\leqslant 20~\text{cm}$
. Mesh refinement was chosen to provide grid-independent solutions. Figure 8 shows the fluid elements in the vicinity of the edge of the disk. The spectral elements were employed basis functions of 19th order, i.e. each element had
$20\times 20$
nodes. The entire model had about
$3.9\times 10^{5}$
nodes.
Figure 8. Mesh in the neighbourhood of the edge of the disk. Each element is composed of
$20\times 20$
nodes, and element boundaries are indicated by clustering of horizontal and vertical lines.
All simulations were initialized with disk height
$h=0.2317~\text{cm}$
, which corresponds to the predicted steady-state height of the
$S=1$
case as described above. The fluid and disk were initialized under quiescent conditions. The disk rotation velocity and the bottom-boundary transpiration velocity were ramped up to their steady values over the initial
$10^{-3}~\text{s}$
period. An outflow boundary condition was employed at the top boundary. The lateral boundary had a vertical velocity condition. Table 2 shows the time-step sizes employed in each calculation. For increasing values of
$S$
, the time-step size must decrease in order to achieve numerically stable solutions. As discussed below, the FSI calculations need to be evolved to at least
$t=0.5~\text{s}$
for good statistics. The small time steps required by the fluid solver can thus require millions of time steps, which makes these simulations computationally expensive.
Table 2. DNS time step sizes employed for calculations at the indicated values of
$S$
.
3.3. Unsteady results with fixed disk height
We first compare solutions from the unsteady DNS code with the steady-flow model, taking the nominal case
$Re=40$
and
$S=1$
and keeping the disk height fixed at the value obtained from the steady model shown in table 1. A comparison of steady and DNS radial and azimuthal velocity distributions across the gap at mid-radius
$r^{\ast }=3.0~\text{cm}$
is shown in figure 9; here the steady solutions are plotted as continuous lines and DNS results are plotted as solid dots corresponding to nodal values. The velocity distributions as calculated by the DNS code are steady over about 95 % of the gap region. The excellent agreement between the solutions serves to verify our methodology. A comparison of the radial pressure distributions on the bottom and top surfaces of the rotating disk is given in figure 10, where the solid lines are the steady-model pressures and the dot-dashed lines are a snapshot of the unsteady DNS results. It is clear that the DNS pressures lie above those of the steady model both underneath and on top of the floating disk. However, while the DNS pressure distribution over the upper disk surface (lower dot-dashed line) is unsteady, the corresponding pressure distribution over the lower disk surface (upper dot-dashed line) is virtually time-independent, as verified by examining pressure snapshots at multiple time instances. Further, the DNS lower-surface pressure distribution is identical in shape to the pressure distribution obtained from the steady model. To effect a comparison between these two pressure distributions, we have shifted the steady-model pressure distribution up to match the DNS pressure distribution at
$r^{\ast }=0$
and plotted only the outer half of that shifted distribution. These two pressures are identical up to
$r^{\ast }\simeq 5.7~\text{cm}$
, beyond which the DNS pressure tends steeply to its edge value of
$-13.4~\text{dyn}~\text{cm}^{-1}$
(not easily visible in figure 10). These comparisons support the conclusion that over 95 % of the gap the flow is accurately given by the steady flow model.
Figure 9. Comparison of radial and azimuthal velocities at
$r^{\ast }=3.0~\text{cm}$
for
$S=1$
obtained from the steady theoretical analysis (solid lines) and those computed from the DNS code with disk height fixed (solid dots).
Figure 10. Comparison of pressures under and above the disk at
$S=1$
for fixed disk height corresponding to
$Re=40$
obtained from the steady theoretical analysis (solid lines) and those captured from the DNS code (dot-dashed lines). The solid line superimposed on the DNS pressure distribution on the lower disk surface is the steady pressure distribution shifted up to match pressures at
$r^{\ast }=0$
.
Figure 11 shows the history of total lift
$L(t)$
on the disk for the
$Re=40$
,
$S=1$
configuration (with fixed height) and is compared with the disk weight plotted as the dashed line. The lift force reaches a statistically steady state (SST) of about 20 000 dyn – significantly greater than the disk weight. This disparity motivates our DNS–FSI study to determine the correct disk height in unsteady flow.
Figure 11. Evolution of the lift computed from the DNS code at
$Re=40$
and
$S=1$
for fixed disk height. The simulation is compared with the disk weight (17 640 dyn) shown by the dashed line.
Figure 12. Evolution of floating-disk heights at
$Re=40$
for spin-rate parameters (a)
$S=0$
, (b)
$S=1$
, (c)
$S=3$
and (d)
$S=5$
showing estimates for the statistically steady-state heights as dashed lines. All computations were initiated with zero axial velocity at height
$h_{0}=0.2317~\text{cm}$
shown by the solid dots at
$t=0$
.
3.4. Unsteady fluid–structure interaction results
FSI direct numerical solutions were performed for
$S=0,1,3,5$
. The associated time histories of disk heights are shown in figure 12. As described above, all computations were initiated with zero axial velocity at the initial height
$h=0.2317~\text{cm}$
corresponding to the initial steady disk height for
$Re=40$
,
$S=1$
. After strong initial rapid deviations from this initial height, the disk is seen to reach an SST. The horizontal lines plotted in each panel in figure 12 are the average height and the period over which the averaging was performed. The computational demands associated with small time steps as described above, which increase with increasing
$S$
, have limited the maximum simulated time in each case. However, in the four cases shown, the maximum simulated time was deemed sufficient for capturing an accurate average disk height.
These SST heights estimated from the FSI simulations are compared with the float heights obtained from the steady model in figure 13. Error bars for the unsteady results are
$\pm$
one standard deviation of the heights calculated during the periods indicated by the horizontal lines in figure 12. The unsteady results from the FSI computations give SST heights consistently above the steady-model heights with deviations ranging from 6.6 % at
$S=0$
to 7.5 % at
$S=5$
.
Figure 13. Comparison of the steady float heights (solid diamonds) with the statistically steady-state heights (solid dots) found using the FSI code. Error bars for the unsteady results are
$\pm$
one standard deviation of the heights calculated during the periods indicated by the horizontal lines in figure 12.
Colour snapshots of the flow are provided in figure 14 at times
$t=0.2,0.3,0.4,0.5~\text{s}$
. The heights at these times are in the statistical steady-state region beyond the start-up from the given initial height. A movie of the flow reveals the ejection of a vortex ring on start-up composed primarily of vorticity in the jet shed from the lower disk surface, but there is also a weak component of opposite-sign vorticity shed from the von Kármán boundary layer that develops on the upper surface. A movie of the flow shows that the start-up vortex propagates around to impact with the now developed radial jet, thereby forming a vortex ring pair. As time evolves, other vortex–vortex and vortex–jet interactions have occurred to produce the complicated flow field seen at
$t=0.2~\text{s}$
in figure 14(a). As the flow field evolves further, one has the impression that the mean flow in the meridional plane resembles an anticlockwise circulatory motion above the outer half of the disk.
4. Summary and discussion
A complete survey of steady solutions for an infinite disk rotating above an air-bearing table is obtained using a similarity reduction of the Navier–Stokes equations. Numerical integration of the coupled pair of ordinary differential equations yields the radial pressure gradient and wall shear stress parameters as a function of the Reynolds number
$Re$
for selected values of the rotation parameter
$S$
, which are compared with their low-
$Re$
series approximations and high-
$Re$
asymptotics. It is interesting to find that the present numerical values of the pressure gradient parameter
${\it\alpha}$
compare remarkably well with three solution values on the curve
$S=5\sqrt{2}$
in figure 2 computed long ago by Dorfman (Reference Dorfman1966).
Figure 14. Snapshots of the meridional-velocity magnitude as calculated using the fluid–structure interaction code at four times after the disc height has developed to statistically steady state: (a)
$t=0.2$
, (b)
$t=0.3$
, (c)
$t=0.4$
, (d)
$t=0.5$
.
A detailed analysis of the
$Re{-}S$
boundaries separating lift from no lift and regions of outward flow and counter-flow is given. Meridional streamlines exhibiting an outward flow solution and a counter-flow solution are presented. For application of these results to a finite-radius air hockey disk, the
$Re{-}S$
region in which
${\it\alpha}\leqslant 0$
would imply that the disk does not lift off. We speculate on the flow field in this event that the disk remains attached to the lower wall: the upward propagating stream passing by the rim of the disk would form successive like-sign vortex rings, which themselves interact with each other and the top of the disk in a complicated manner.
The steady model for the float height of a finite-radius disk rotating at constant angular velocity is predicated on four assumptions: (i) the float height is small compared to the disk diameter so that the similarity solution is a good approximation to the flow in the gap, (ii) the pressures at the edge of the gap and above the disk are atmospheric, (iii) the flow is everywhere laminar and (iv) steady.
Concerning assumption (iii), whether the flow is laminar or turbulent above the disk is rather a moot point for this study, where the disk is presumed to rotate at constant angular velocity, since turbulence in the von Kármán boundary layer would not seriously affect the pressure distribution there. According to experiments reported in Schlichting (Reference Schlichting1960), the flow in a steady von Kármán boundary layer, presumed to reside above the rotating disk, remains stable for Reynolds numbers
$\mathit{Re}<\mathit{Re}_{c}$
where
$\mathit{Re}=a^{2}{\it\Omega}/{\it\nu}$
and
$\mathit{Re}_{c}=3\times 10^{5}$
.
Turbulent flow in the gap, however, is a concern and, although much is known about the transition to turbulence in rotor–stator configurations, we are not aware of studies of the transition to turbulence beneath freely floating disks. We believe that the gap flow in the present numerical simulations the flow is laminar since the gap Reynolds number
$Re=40$
is relatively small. Moreover, while turbulent flow in the gap is expected to be important for determining the float height of a disk under constant rotation, it is deemed even more important for studies of the spin-down of a disk from some initial rotation rate
${\it\Omega}_{0}$
where one must take into account the unsteady disk torque due to azimuthal friction both underneath and above the disk.
We now analyse the flow physics as deduced from the direct numerical simulations of the unsteady axisymmetric Navier–Stokes equations performed for a finite-radius disk rotating at constant angular velocity
${\it\Omega}$
. We examined in detail a DNS solution where the disk was held at a fixed height at
$Re=40$
,
$S=1$
as well as DNS solutions from FSI calculations for
$S=0,1,3,5$
where the disk is free to move axially. (Note that at the highest rotation rate considered,
${\it\Omega}\simeq 406~\text{rad}~\text{s}^{-1}$
at
$S=5$
, one finds
$\mathit{Re}\approxeq 1\times 10^{5}<\mathit{Re}_{c}$
so the flow in a steady von Kármán boundary layer remains laminar.)
The DNS fixed-height calculations indeed exhibit unsteady flow, which results in the average unsteady lift force being somewhat greater than the height (equal to the disk weight) predicted by steady theory; see figure 11. However, the velocity distributions in the gap matched the infinite-disk steady-flow predictions over 95 % of the disk radius. The same agreement in this region of flow in the gap was found between the unsteady and steady pressure distributions to within a constant.
Fluid–structure interaction simulations were performed to understand the true evolution of disk height in axisymmetric flow. While the unsteady vortical nature of the flow causes the disk to undergo relatively small axial oscillations, the SST height is found to be, on average, about 7 % greater than that predicted for steady flow in each of the four cases considered. Snapshots of this flow obtained from a movie for
$Re=40$
,
$S=1$
(URL http://michaelasprague.com/s1_movie.avi) reveal a complicated interaction of counter-rotating vortex rings with the upper surface of the disk and the radial jet emanating from the exit of the gap. As shown by Saffman (Reference Saffman1978), the assumption of axisymmetry of the vortex rings will break down when the vortex-ring Reynolds number (dependent on parameters forming a vortex ring by the piston-in-cylinder method) is sufficiently large. In these instances, the ring will break up into an integer number of waves around the ring circumference. This ring instability feature, though perhaps an interesting detail of the flow, is not expected to significantly change the SST heights calculated in the FSI numerical simulations.
The above numerical FSI calculations lead to the conclusion that the discord between the SST float heights and the steady-model float heights owes its existence to the disparity in pressure at the edge of the gap. We saw excellent agreement, to within a constant, between the steady-flow similarity solution and unsteady DNS calculation over a range of
$S$
. However, the vortex generation that occurs as the jet impinges on the upward flow outside the gap induces a departure from the steady-flow assumption of atmospheric pressure at the gap exit.
Acknowledgements
Discussion of the asymptotics of this problem with Professor D. Kassoy are gratefully acknowledged. The authors are grateful to Professor K. Julien for providing a code to iteratively determine the dimensional values
$W$
,
${\it\Omega}$
and
$h$
for given dimensionless values of
$Re$
,
$S$
and
${\it\alpha}$
, and for a careful reading of the manuscript. The authors enthusiastically thank Professor P. Fischer for his assistance with the Nek5000 spectral finite element program. A portion of the research was performed using computational resources sponsored by the US Department of Energy’s Office of Energy Efficiency and Renewable Energy and located at the National Renewable Energy Laboratory. The work by MAS was supported by the US Department of Energy under contract DE-AC36-08-GO28308 with the National Renewable Energy Laboratory. The US Government and the publisher, by accepting the article for publication, acknowledges that the US Government retains a non-exclusive, paid-up, irrevocable, worldwide license to publish or reproduce the published form of this work, or allow others to do so, for US Government purposes.
