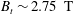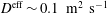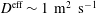1 Introduction
Generally, the temperature of fusion plasmas is sustained by the external heating. The heatings are achieved by the kinetic energy transfer from fast particles to the bulk plasma through Coulomb collisions. Additionally, in future fusion power plants, fusion plasmas will mainly be sustained by fusion-born 
$\unicode[STIX]{x1D6FC}$ particles, which have 3.5 MeV kinetic energy. Therefore, fast particles should be confined until their velocities are decelerated to the plasma thermal velocity. For this reason, the fast particle confinement is one of the most important issues (Heidbrink & Sadler Reference Heidbrink and Sadler1994; Gorelenkov, Pinches & Toi Reference Gorelenkov, Pinches and Toi2014) for magnetically confined fusion devices.
There are several diagnostics systems to investigate the fast particle physics (Gorelenkov et al. Reference Gorelenkov, Pinches and Toi2014), such as the neutral particle analyser (Medley & Roquemore Reference Medley and Roquemore1998; Osakabe et al. Reference Osakabe, Yamamoto, Toi, Takeiri, Sakakibara, Nagaoka, Tanaka and Narihara2006; Kamio et al. Reference Kamio, Fujiwara, Ogawa, Isobe, Seki, Nuga, Nishitani and Osakabe2019), fast ion 
$\text{D}_{\unicode[STIX]{x1D6FC}}$ spectroscopy (FIDA) (Luo, Heidbrink & Burrell Reference Luo, Heidbrink and Burrell2004; Heidbrink et al. Reference Heidbrink, Luo, Burrell, Harvey, Pinsker and Ruskov2007), fast ion loss detector (Darrow et al. Reference Darrow, Herrmann, Johnson, Marsala, Palladino, Zweben and Tuszewski1995; Ogawa et al. Reference Ogawa, Isobe, Toi, Watanabe, Spong, Shimizu, Osakabe, Ohdachi and Sakakibara2010) and neutron spectroscopy (Adams et al. Reference Adams, Jarvis, Sadler, Syme and Watkins1993; Ishikawa et al. Reference Ishikawa, Takechi, Shinohara, Cheng, Matsunaga, Kusama, Fukuyama, Nishitani, Morioka and Sasao2007). Because the deuterium plasma experiment campaign began in the Large Helical Device (LHD) (Osakabe et al. Reference Osakabe, Takeiri, Morisaki, Motojima, Ogawa, Isobe, Tanaka, Murakami, Shimizu and Nagaoka2017, Reference Osakabe, Isobe, Tanaka, Motojima, Tsumori, Yokoyama, Morisaki and Takeiri2018; Takeiri Reference Takeiri2018a,Reference Takeirib) from March 2017, the investigation of fast ion behaviour using neutron diagnostics (Isobe et al. Reference Isobe, Ogawa, Nishitani, Miyake, Kobuchi, Pu, Kawase, Takada, Tanaka and Li2018; Ogawa et al. Reference Ogawa, Isobe, Nishitani, Murakami, Seki, Nuga, Kamio, Fujiwara, Yamaguchi and Saito2019) and FIDA (Fujiwara et al. Reference Fujiwara, Kamio, Yamaguchi, Garcia, Stagner, Nuga, Seki, Ogawa, Isobe and Yokoyama2019) have been enabled in LHD.
In LHD deuterium plasmas, 
${\sim}2.45~\text{MeV}$ fast neutrons are yielded owing to the deuterium–deuterium (DD) fusion reaction. Because of the high injection energy of neutral beams of up to 
$E_{b}\sim 180~\text{keV}$, most of the neutrons are generated by the fusion reaction between fast deuteron and thermal deuteron instead of the reaction between thermal ions (Osakabe et al. Reference Osakabe, Takeiri, Morisaki, Motojima, Ogawa, Isobe, Tanaka, Murakami, Shimizu and Nagaoka2017). This is the so-called ‘beam-thermal’ fusion reaction. In such cases, we can study the fast ion global confinement from the neutron emission rate 
$S_{n}$. This is because the DD fusion reactivity increases monotonically with their relative kinetic energy up to 
$E\sim 2~\text{MeV}$. If the plasma temperature and density are constant in time, the decrement of the neutron emission rate comes from the decrement of the fusion cross-section due to the fast ion deceleration and the decrement of the fast ion density. Because the fast ion deceleration can be estimated by simulations, we can estimate the fast ion confinement from the neutron measurement without simulating the fast ion transport, which is usually too complex to estimate accurately.
We have studied the effective confinement time of NB fast ions in LHD using neutron measurement in this paper. There are several previous works that investigated fast ion confinement through the neutron diagnostics. Earliest works in tokamaks (Strachan et al. Reference Strachan, Colestock, Davis, Eames, Efthimion, Eubank, Goldston, Grisham, Hawryluk and Hosea1981; Heidbrink, Kim & Groebner Reference Heidbrink, Kim and Groebner1988; Heidbrink et al. Reference Heidbrink, Barnes, Hammett, Kusama, Scott, Zarnstorff, Johnson, McCune, Medley and Park1991) showed that the classical collisional slowing down model can explain the neutron emission with good agreement. The following investigation in the JT-60U tokamak (Tobita et al. Reference Tobita, Tani, Nishitani, Nagashima and Kusama1994) reported a deviation from the classical collisional slowing down model due to the toroidal field ripple for perpendicular NB. Anomalous fast ion losses, which cannot be explained by the toroidal field ripple, were observed on TFTR (Ruskov et al. Reference Ruskov, Bell, Budny, McCune, Medley, Redi, Scott, Synakowski, von Goeler and White1999). Moreover, fast ion confinement was investigated by using neutron measurement also in various types of magnetically confinement device, such as the reversed field pinch devices (Fiksel et al. Reference Fiksel, Hudson, Den Hartog, Magee, O’Connell, Prager, Beklemishev, Davydenko, Ivanov and Tsidulko2005; Anderson et al. Reference Anderson, Capecchi, Eilerman, Koliner, Nornberg, Reusch, Sarff and Lin2014), the spherical tokamak (Heidbrink et al. Reference Heidbrink, Miah, Darrow, LeBlanc, Medley, Roquemore and Cecil2003), the tokamak (Zhang et al. Reference Zhang, Isobe, Liu, Yuan, Yang, Song, Song, Cao, Lei and Wei2012) and the stellarator and heliotron (Isobe et al. Reference Isobe, Sasao, Okamura, Kondo, Murakami, Minami, Kado, Ida, Shimizu and Osakabe2001; Nuga et al. Reference Nuga, Seki, Ogawa, Kamio, Fujiwara, Osakabe, Isobe, Nishitani and Yokoyama2019), In our previous work (Nuga et al. Reference Nuga, Seki, Ogawa, Kamio, Fujiwara, Osakabe, Isobe, Nishitani and Yokoyama2019), we have reported the NB fast ion confinement time by using neutron measurement for a single magnetic configuration in LHD. In this paper, we investigate the dependence of the fast ion confinement on the magnetic configuration and discuss the contribution of the charge exchange loss to the fast ion confinement, especially in low electron density plasmas.
The rest of this paper consists of the following. The detail of the experimental scenario and devices are provided in § 2. Simulation tools and models used in this paper are introduced in § 3. The results of the analyses to estimate the fast ion confinement time are shown in §§ 4 and 5. The dilution effect of the deuteron density due to the presence of impurity ions is discussed in § 6. Section 7 concludes this paper.
2 Experimental set-up
2.1 Experimental scenario
A series of experiments which use short-pulse NB injection have been performed in LHD to investigate the fast ion confinement time. The decay time of 
$S_{n}$, yielded by the DD fusion reaction has been observed after short-pulse NBs have been turned off. In the previous work (Nuga et al. Reference Nuga, Seki, Ogawa, Kamio, Fujiwara, Osakabe, Isobe, Nishitani and Yokoyama2019), we performed the short-pulse NB experiment in a single magnetic configuration (
$R_{\text{ax}}=3.6~\text{m}$, 
$B_{t}=2.75~\text{T}$), where 
$R_{\text{ax}}$ and 
$B_{t}$ indicate the position of the magnetic axis and the strength of the magnetic field on the magnetic axis. The direction of the magnetic field is counter-clockwise in the top view. In this paper, we have performed the short-pulse NB experiment in five magnetic configurations, 
$(R_{\text{ax}},B_{t})=(3.53~\text{m},2.80~\text{T})$, (3.55 m, 2.79 T), (3.60 m, 2.75 T), (3.75 m, 2.64 T) and (3.90 m, 2.54 T), respectively. A typical waveform of this series of experiments is shown in figure 1. The NB pulse width is 
${\sim}40~\text{ms}$ in each beam.
Figure 1. Typical waveform of this series of experiments (SN148442) is displayed. The NB port through power in each beam, the plasma temperature and density at the position where the normalized minor radius, 
$\unicode[STIX]{x1D70C}=0.5$, and the neutron emission rate are shown.
In this series of experiments, the fast ion confinement time, 
$\unicode[STIX]{x1D70F}_{c}$, is assumed to be
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70F}_{c}^{-1}=\unicode[STIX]{x1D70F}_{n}^{-1}-(\unicode[STIX]{x1D70F}_{n}^{\text{cl}})^{-1}, & & \displaystyle\end{eqnarray}$$ where 
$\unicode[STIX]{x1D70F}_{n}$ is the neutron decay time after NB has been turned off and 
$\unicode[STIX]{x1D70F}_{n}^{\text{cl}}$ is the 
$e$-folding time of the neutron decay rate due to the classical fast ion deceleration. This is because the reduction of the neutron emission rate is caused by the decrease of the fusion cross-section due to the deceleration and the decrease of the fast ion density due to the fast ion loss. Because the contribution of the fast ion loss is ignored in the estimation of 
$\unicode[STIX]{x1D70F}_{n}^{\text{cl}}$, 
$\unicode[STIX]{x1D70F}_{c}$ can be estimated from 
$\unicode[STIX]{x1D70F}_{n}$ and 
$\unicode[STIX]{x1D70F}_{n}^{\text{cl}}$. In this paper, 
$\unicode[STIX]{x1D70F}_{n}$ can be obtained from the experimental results and 
$\unicode[STIX]{x1D70F}_{n}^{\text{cl}}$ can be obtained from the simulation results instead of the analytical solution given by Strachan et al. (Reference Strachan, Colestock, Davis, Eames, Efthimion, Eubank, Goldston, Grisham, Hawryluk and Hosea1981). The method of simulation will be introduced in § 3.
2.2 Experiment apparatus
Figure 2. Top view of NBI system in LHD. There are three tangential beams, NB#1, NB#2 and NB#3, and there are two perpendicular beams, NB#4 and NB#5. Because the direction of the magnetic field line is counter-clockwise, NB#1 and NB#3 are the co-directions to the magnetic field line.
In this series of experiments, two external heating systems, electron cyclotron heating (ECH) and neutral beam injection (NBI), are used. Plasmas are sustained by 3.5 MW ECH.
The top view of the NBI system in LHD (Takeiri et al. Reference Takeiri, Kaneko, Tsumori, Osakabe, Ikeda, Nagaoka, Nakano, Asano, Kondo and Sato2010) is shown in figure 2. The typical injection energy and power in each beam is also displayed. In LHD, there are three negative ion-based tangential NBs and two positive ion-based perpendicular NBs. The directions of NB#1 and NB#3 are co-directions to the magnetic field and the direction of NB#2 is counter-direction to the magnetic field. It is noted that the injection energy of NB#4 is set to the untypically low energy, 
$E_{b}\sim 35~\text{keV}$, to investigate the dependence of the perpendicular NBs on the injection energy.
Experiments have been performed with five magnetic configurations as noted in § 2.1. The averaged plasma minor radius, which depends on the position of the magnetic axis, is approximately 
$0.58{-}0.63~\text{m}$.
LHD is equipped with several diagnostic systems (Kawahata et al. Reference Kawahata, Peterson, Akiyama, Ashikawa, Emoto, Funaba, Hamada, Ida, Inagaki and Ido2010). In this paper, we have mainly used electron temperature and density profiles, the ion ratio among protons, deuterons and helium ions, and the time evolution of the neutron emission rate. The Thomson scattering diagnostic is used for the measurement of the electron density and temperature (Narihara et al. Reference Narihara, Yamada, Hayashi and Yamauchi2001; Yamada et al. Reference Yamada, Narihara, Funaba, Minami, Hayashi and Kohmoto2010). A fast-response wide dynamic range neutron flux monitor (NFM) (Isobe et al. Reference Isobe, Ogawa, Nishitani, Miyake, Kobuchi, Pu, Kawase, Takada, Tanaka and Li2018) is equipped in LHD to measure the neutron emission rate.
3 Simulation tools
Estimation of 
$\unicode[STIX]{x1D70F}_{n}^{\text{cl}}$ is required to evaluate 
$\unicode[STIX]{x1D70F}_{c}$ as shown in (2.1). Although there is an analytical expression for 
$\unicode[STIX]{x1D70F}_{n}^{\text{cl}}$ (Strachan et al. Reference Strachan, Colestock, Davis, Eames, Efthimion, Eubank, Goldston, Grisham, Hawryluk and Hosea1981), we use the following simulations to include the plasma profiles, plasma volume and NB birth profile for the estimation of 
$\unicode[STIX]{x1D70F}_{n}^{\text{cl}}$.
Figure 3. Flow of the simulations to obtain the time evolution of the neutron emission rate.
In this paper, the neutron emission simulations have been performed by the combination among VMEC (Hirshman & Whitson Reference Hirshman and Whitson1983), FIT3D (HFREYA and MCNBI) (Murakami, Nakajima & Okamoto Reference Murakami, Nakajima and Okamoto1995; Sato et al. Reference Sato, Murakami, Fukuyama, Nakamura, Watanabe, Toda, Yokoyama, Funaba, Yamada and Nakajima2008; Vincenzi et al. Reference Vincenzi, Bolzonella, Murakami, Osakabe, Seki and Yokoyama2016; Seki et al. Reference Seki, Ogawa, Isobe, Yokoyama, Murakami, Nuga, Kamio, Fujiwara and Osakabe2019) and CONV_FIT3D (Nuga et al. Reference Nuga, Seki, Ogawa, Kamio, Fujiwara, Osakabe, Isobe, Nishitani and Yokoyama2019), which are included in the integrated transport analysis suite TASK3D-a (Yokoyama et al. Reference Yokoyama, Seki, Suzuki, Sato, Emoto, Murakami, Osakabe, Tsujimura, Yoshimura and Ido2017). The flow of the simulations are displayed in figure 3. Three-dimensional magnetic equilibrium is calculated by the VMEC code. According to the obtained magnetic configuration, FIT3D calculates the NB fast ion birth profile. At this step, NB fast ion orbits are followed for a few tens of micro-seconds by using the Monte Carlo method to consider the NB fast ion prompt loss effect. In this process, the effect of the birth profile broadening owing to the deviation of the NB fast ion drift orbit from the magnetic surface is also considered. Moreover, for positive ion-based NBs, the full, half and one-third energy fractions of injected neutral particles are assumed to be 0.78, 0.16 and 0.06, respectively. Although these values are the typical values of perpendicular NBI systems in LHD, they are not reliable for NB#4. This is because NB#4 has an untypically low injection energy in the following analyses. CONV_FIT3D solves the NB fast ion slowing down equation to obtain the energy distribution of NB fast ions. Here, the fast ion transport across the magnetic surface during the slowing down process is neglected. In LHD, the beam-thermal fusion reaction is dominant instead of the reaction between thermal ions due to the insufficient plasma temperature. Additionally, in this paper, the fusion reaction between NB fast ions is also negligible. Therefore, it is enough to consider the fusion reaction between NB fast ions and thermal ions in this paper. Because it can be considered that the velocity distribution of thermal ions is isotropic, the velocity direction of NB fast ions is not necessary for the estimation of the fusion reaction rate. For this reason, CONV_FIT3D, which can obtain the energy distribution of NB fast ions, can estimate the neutron emission rate. The details of CONV_FIT3D are introduced in § 3.1.
3.1 CONV_FIT3D
CONV_FIT3D is a code solving the fast ion slowing down equation based on the classical Coulomb collision theory. In the previous work (Nuga et al. Reference Nuga, Seki, Ogawa, Kamio, Fujiwara, Osakabe, Isobe, Nishitani and Yokoyama2019), we had chosen the model which assumes the NB fast ion velocity 
$v_{\text{EP}}$ is sufficiently faster than the thermal ion velocity 
$v_{\text{th}}$. However, in this paper, we have a perpendicular NB#4, which has an injection energy of 
$E_{b}=35~\text{keV}$. NB fast ions, whose kinetic energy is 35 keV, cannot satisfy the assumption 
$v_{\text{EP}}\gg v_{\text{th}}$ because the typical temperature of this series of experiments is a few keV. Therefore, we have refined the slowing down equation based on equation (30c) in Karney (Reference Karney1986). This model assumes a background Maxwellian. The refined equations are expressed as below
$$\begin{eqnarray}\displaystyle \frac{\text{d}E}{\text{d}t} & = & \displaystyle -\frac{2}{\unicode[STIX]{x1D70F}_{se}}Z_{\text{EP}}^{2}E\nonumber\\ \displaystyle & & \displaystyle \times \left[1+\frac{3\unicode[STIX]{x03C0}^{1/2}m_{\text{EP}}^{3/2}T_{e}^{3/2}}{4m_{e}^{1/2}}\left(\mathop{\sum }_{i}\frac{n_{i}Z_{i}^{2}}{n_{e}m_{i}}g(u_{i})\right)\frac{1}{E^{3/2}}\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle g(u_{i})=\text{erf}(u_{i})-u_{i}\text{erf}^{\prime }(u_{i}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D70F}_{se}=\frac{3(2\unicode[STIX]{x03C0})^{3/2}\unicode[STIX]{x1D716}_{0}^{2}m_{\text{EP}}T_{e}^{3/2}}{n_{e}e^{4}m_{e}^{1/2}\ln \unicode[STIX]{x1D6EC}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \text{erf}(u)=\frac{2}{\unicode[STIX]{x03C0}}\int _{0}^{u}\exp (-x^{2})\,\text{d}x, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \text{erf}^{\prime }(u)=\frac{2}{\unicode[STIX]{x03C0}}\exp (-u^{2}), & \displaystyle\end{eqnarray}$$ where 
$\unicode[STIX]{x1D70F}_{se}$ is the Spitzer slowing down time on electrons, 
$u_{i}=v/\sqrt{2}v_{\text{th},i}$ and 
$v_{\text{th}}=\sqrt{T_{i}/m_{i}}$. In the following calculation, we assume that the ion temperature 
$T_{i}$ is equal to the electron temperature 
$T_{e}$. In actuality, however, it is expected that 
$T_{e}$ is greater than 
$T_{i}$ because the plasmas are sustained by ECH.
As noted above, in LHD, the beam-thermal fusion reaction is dominant. In this case, the fusion reaction rate can be expressed as
$$\begin{eqnarray}\displaystyle {\mathcal{R}}_{bt}=n_{D}\int \langle \unicode[STIX]{x1D70E}v\rangle _{bt}(T_{i},E_{EP})f_{EP}(\boldsymbol{v}_{EP})\,\text{d}\boldsymbol{v}_{EP}, & & \displaystyle\end{eqnarray}$$ where 
$n_{D}$ is the deuteron density in the bulk plasma. The beam-thermal reactivity 
$\langle \unicode[STIX]{x1D70E}v\rangle _{bt}$, which is derived by Mikkelsen (Mikkelsen Reference Mikkelsen1989), is implemented in CONV_FIT3D. The fitting coefficients used in the expression of 
$\langle \unicode[STIX]{x1D70E}v\rangle _{bt}$ are chosen from Bosch & Hale (Reference Bosch and Hale1992).
4 Analysis results for tangential beams
Figure 4. Example of the neutron emission simulation assuming 
$n_{D}=n_{e}$ and 
$\unicode[STIX]{x1D70F}_{c}=\infty$.
In figure 4, the example of the simulated neutron emission rate is shown with the measured neutron emission rate. The solid curve is the measured neutron emission rate and the dashed curve is the simulated neutron emission rate. The simulation over-estimates the neutron emission rate due to the assumptions that 
$n_{D}=n_{e}$ and 
$\unicode[STIX]{x1D70F}_{c}=\infty$. From measured and simulated neutron emission rates, we can estimate 
$\unicode[STIX]{x1D70F}_{n}$ and 
$\unicode[STIX]{x1D70F}_{n}^{\text{cl}}$ by using the least mean square fitting. The fitting functions are 
$f(t)=S_{n}^{\text{p},\text{exp}}\exp (-t/\unicode[STIX]{x1D70F}_{n})$ for the measured decay rate and 
$f(t)=S_{n}^{\text{p},\text{sim}}\exp (-t/\unicode[STIX]{x1D70F}_{n}^{\text{cl}})$ for the simulated decay rate, where 
$S_{n}^{\text{p},\text{exp}}$ and 
$S_{n}^{\text{p},\text{sim}}$ are the peak values of the measured and simulated neutron emission rates. The durations used for these fittings are defined as the times when the neutron emission rates decay to 
$S_{n}^{\text{p},\text{exp}}/e$ and 
$S_{n}^{\text{p},\text{sim}}/e$, respectively.
Figure 5. The experimentally measured neutron decay times are plotted against the simulated neutron decay time for tangential NBs in the configuration of 
$R_{\text{ax}}=3.53~\text{m}$. Dashed guide curve is 
$\unicode[STIX]{x1D70F}_{n}=\unicode[STIX]{x1D70F}_{c}\unicode[STIX]{x1D70F}_{n}^{\text{cl}}/(\unicode[STIX]{x1D70F}_{n}^{\text{cl}}+\unicode[STIX]{x1D70F}_{c})$, 
$\unicode[STIX]{x1D70F}_{c}=0.53~\text{s}$.
Similar experiments have been performed with the same magnetic configuration (
$R_{\text{ax}}=3.53~\text{m}$, 
$B_{t}=2.8045~\text{T}$) and different plasma parameters to survey the dependence of 
$\unicode[STIX]{x1D70F}_{n}$ on 
$\unicode[STIX]{x1D70F}_{n}^{\text{cl}}$. It is noted that the control parameter is the electron density 
$n_{e}$ in these experiments. Additionally, because the plasma heating power is constant in each shot, the electron temperature 
$T_{e}$ also changes with the electron density. Figure 5 is obtained from experiment and simulation results for three tangential NBs. Their injection energies are also displayed in figure 5. In this figure, the 
$x$ axis denotes the simulated neutron decay time 
$\unicode[STIX]{x1D70F}_{n}^{\text{cl}}$ and the 
$y$ axis denotes the experimental neutron decay time 
$\unicode[STIX]{x1D70F}_{n}$. The 
$y$ error-bars shown in figure 5 denote the standard deviation of 
$\unicode[STIX]{x1D70F}_{n}$. The solid guideline indicates 
$y=x$. If the NB fast ions are confined perfectly, plots obey this guide line. Actually, because the NB fast ion loss is not ignorable, plots separate from the guide line as shown in figure 5. Additionally, in figure 5, there is a dashed guide curve which indicates 
$\unicode[STIX]{x1D70F}_{n}=0.53\unicode[STIX]{x1D70F}_{n}^{\text{cl}}/(\unicode[STIX]{x1D70F}_{n}^{\text{cl}}+0.53)$. The reason for the value 
$\unicode[STIX]{x1D70F}_{c}=0.53~\text{s}$ is explained later. From figure 5, it is found that a different trend, which does not obey the dashed guide curve, appears in the 
$\unicode[STIX]{x1D70F}_{n}^{\text{cl}}>0.4~\text{s}$ region. This means that the dominant transport mechanism is different between the 
$\unicode[STIX]{x1D70F}_{n}^{\text{cl}}<0.4~\text{s}$ region and the 
$\unicode[STIX]{x1D70F}_{n}^{\text{cl}}>0.4~\text{s}$ region. It is noted that the high frequency (
${>}10~\text{kHz}$) magneto-hydro-dynamics (MHD) instabilities triggered by NBI hardly appeared in the short 
$\unicode[STIX]{x1D70F}_{n}^{\text{cl}}$ region. On the contrary, in the long 
$\unicode[STIX]{x1D70F}_{n}^{\text{cl}}$ region, NB fast ion driven instabilities were observed in several discharges. Therefore, we can ignore the anomalous transport due to fast ion driven instabilities in the short 
$\unicode[STIX]{x1D70F}_{n}^{\text{cl}}$ region. The following analyses in the long 
$\unicode[STIX]{x1D70F}_{n}^{\text{cl}}$ region may include the anomalous transport. The low frequency (
${<}10~\text{kHz}$) MHD instabilities excited by bulk plasma pressure were observed through this series of experiments. The typical amplitude of the low frequency magnetic fluctuation, which is detected by a magnetic probe set on the vacuum vessel, was 
$\unicode[STIX]{x1D6FF}B/B_{t}<2\times 10^{-5}$. This value is sufficiently low compared to the case where the low frequency magnetic fluctuation plays an important role in the NB fast ion loss (Ogawa et al. Reference Ogawa, Isobe, Toi, Watanabe, Spong, Shimizu, Osakabe, Ohdachi and Sakakibara2010). Therefore, it can be considered that the NB fast ion loss due to the low frequency fluctuation is negligible.
4.1 Long 
$\unicode[STIX]{x1D70F}_{n}^{\text{cl}}$ region ($\unicode[STIX]{x1D70F}_{n}^{\text{cl}}>0.4~\text{s}$)
In LHD plasmas, it is known that the neutral atom density in the plasma core region has a negative 
$n_{e}$ dependence (Goto et al. Reference Goto, Sawada, Fujii, Hasuo and Morita2011, Reference Goto, Sawada, Oishi and Morita2016; Fujii et al. Reference Fujii, Goto and Morita2015) because the penetration of neutral atoms into the plasma core increases with the decrease of the plasma density. Therefore, it can be considered that the neutral atom density in the plasma core region in 
$\unicode[STIX]{x1D70F}_{n}^{\text{cl}}>0.4~\text{s}$ region is higher than that in 
$\unicode[STIX]{x1D70F}_{n}^{\text{cl}}<0.4~\text{s}$ region. Here we focus on the 
$\unicode[STIX]{x1D70F}_{n}^{\text{cl}}>0.4~\text{s}$ region to investigate the contribution of the charge exchange loss to the fast ion loss.
Figure 6. The dependence of the inverse of the charge exchange reactivity 
$1/\langle \unicode[STIX]{x1D70E}v\rangle _{cx}$ on beam energy is shown. Here, it is assumed that the velocity of neutral atoms is negligible.
From figure 5, it is found that the values of 
$\unicode[STIX]{x1D70F}_{n}$ for NB#1, NB#2 and NB#3 are approximately 
$\unicode[STIX]{x1D70F}_{n}\sim 0.25~\text{s}$, 
$0.2~\text{s}$ and 
$0.2~\text{s}$ at 
$\unicode[STIX]{x1D70F}_{n}^{\text{cl}}=1~\text{s}$. Here we assume that the separation from the dashed guide curve in the long 
$\unicode[STIX]{x1D70F}_{n}^{\text{cl}}$ region can be described only by the charge exchange loss. In this assumption, the neutron decay time 
$\unicode[STIX]{x1D70F}_{n}$ can be expressed as
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70F}_{n}^{-1}=(\unicode[STIX]{x1D70F}_{n}^{\text{cl}})^{-1}+(\unicode[STIX]{x1D70F}_{c}^{\text{eff}})^{-1}+\unicode[STIX]{x1D70F}_{\text{cx}}^{-1}, & & \displaystyle\end{eqnarray}$$ where 
$\unicode[STIX]{x1D70F}_{c}^{\text{eff}}$ is the effective confinement time in the short 
$\unicode[STIX]{x1D70F}_{n}^{\text{cl}}$ region and 
$\unicode[STIX]{x1D70F}_{\text{cx}}$ is the charge exchange time. In this configuration, the value of 
$\unicode[STIX]{x1D70F}_{c}^{\text{eff}}$, which will be obtained in § 4.2, is 
$\unicode[STIX]{x1D70F}_{c}^{\text{eff}}=0.53~\text{s}$. For these assumptions and estimations, the charge exchange times for NB#1, NB#2 and NB#3 are approximately 
$\unicode[STIX]{x1D70F}_{\text{cx}}=0.90~\text{s}$, 
$0.47~\text{s}$ and 
$0.47~\text{s}$, respectively.
The dependence of the charge exchange reactivity on the beam energy is shown in figure 6. Although fast ions in plasmas have a velocity distribution, we estimate the charge exchange reactivity 
$\langle \unicode[STIX]{x1D70E}v\rangle _{\text{cx}}$ in each beam from the beam injection energy. This is because that we have discussed the fast ion confinement through the measurement of the neutron emission rate, which exponentially depends on the beam energy within the range of the NB injection energy. Accordingly, the charge exchange time can be expressed as 
$\unicode[STIX]{x1D70F}_{\text{cx}}^{-1}=n_{0}\langle \unicode[STIX]{x1D70E}v\rangle _{\text{cx}}(E_{b})$, where 
$n_{0}$ is the neutral atom density. From this expression, we can estimate the values of 
$n_{0}$ in each beam. The neutral atom densities, which are felt by fast ions from NB#1, NB#2 and NB#3, are 
$n_{0}=1.7\times 10^{14}~\text{m}^{-3}$, 
$1.9\times 10^{14}~\text{m}^{-3}$ and 
$2.1\times 10^{14}~\text{m}^{-3}$, respectively. In Goto et al. (Reference Goto, Sawada, Oishi and Morita2016), the neutral atom density in the LHD plasma, whose electron density is 
${\sim}2\times 10^{19}~\text{m}^{-3}$, is measured as approximately 
$10^{14}~\text{m}^{-3}$. Because the plasmas in the long 
$\unicode[STIX]{x1D70F}_{n}^{\text{cl}}$ region have an electron density of approximately 
$n_{e}\lesssim 0.5\times 10^{19}~\text{m}^{-3}$, it can be expected that the neutral density is larger than 
$10^{14}~\text{m}^{-3}$ in these plasmas. Therefore, it can be considered that the estimation of 
$n_{0}$ is a realistic value and the charge exchange loss is not negligible in the long 
$\unicode[STIX]{x1D70F}_{n}^{\text{cl}}$ region.
Figure 7. The short 
$\unicode[STIX]{x1D70F}_{n}^{\text{cl}}$ region (
$\unicode[STIX]{x1D70F}_{n}^{\text{cl}}<0.4~\text{s}$) of figure 5 is focused.
4.2 Short $\unicode[STIX]{x1D70F}_{n}^{\text{cl}}$ region ($\unicode[STIX]{x1D70F}_{n}^{\text{cl}}<0.4~\text{s}$)
Here, we focus on the region 
$\unicode[STIX]{x1D70F}_{n}^{\text{cl}}<0.4~\text{s}$ of figure 5 to exclude the cases where the charge exchange loss is significant. The dashed guide curve in figure 7 is obtained by the weighted least mean square fitting in 
$\unicode[STIX]{x1D70F}_{n}=\unicode[STIX]{x1D70F}_{n}^{\text{cl}}\unicode[STIX]{x1D70F}_{c}^{\text{eff}}/(\unicode[STIX]{x1D70F}_{n}^{\text{cl}}+\unicode[STIX]{x1D70F}_{c}^{\text{eff}})$. In this fitting, data in 
$\unicode[STIX]{x1D70F}_{n}^{\text{cl}}>0.4~\text{s}$ region are omitted. It is noted that because three tangential NBs have a similar trend, they are fitted in a single curve. For this fitting, the effective fast confinement time in this region is obtained as 
$\unicode[STIX]{x1D70F}_{c}^{\text{eff}}=0.53~\text{s}$.
Similar analyses are performed for the different configurations shown in § 2.1. To compare the confinement among different magnetic configurations, the effective fast ion confinement time 
$\unicode[STIX]{x1D70F}_{c}^{\text{eff}}$ is converted into the effective particle diffusion coefficient 
$D^{\text{eff}}$. The relation between 
$\unicode[STIX]{x1D70F}_{c}^{\text{eff}}$ and 
$D^{\text{eff}}$ is expressed as
$$\begin{eqnarray}\displaystyle D^{\text{eff}}=\frac{a^{2}}{5.8\unicode[STIX]{x1D70F}_{c}^{\text{eff}}}, & & \displaystyle\end{eqnarray}$$ where 
$a$ is the plasma minor radius. Here it is assumed that 
$D^{\text{eff}}$ is uniform in the plasma and the plasma poloidal cross-section is not elongated. The 
$R_{\text{ax}}$ dependence of 
$D^{\text{eff}}$ is shown in figure 8. It is found that the fast ion confinement becomes poor when the plasma is shifted outward. Additionally, the absolute value of 
$D^{\text{eff}}$ obtained in this paper is larger than that obtained in tokamaks (Tobita et al. Reference Tobita, Tani, Nishitani, Nagashima and Kusama1994; Heidbrink et al. Reference Heidbrink, Kim and Groebner1988).
Figure 8. The effective particle diffusion coefficients are plotted against the position of the magnetic axis.
5 Analysis results for perpendicular beams
Perpendicular beams are analysed by a method similar to the tangential beams. Figure 9 shows the relation between 
$\unicode[STIX]{x1D70F}_{n}$ and 
$\unicode[STIX]{x1D70F}_{n}^{\text{cl}}$ for perpendicular NBs. The dashed guide curve indicates 
$\unicode[STIX]{x1D70F}_{n}=0.057\unicode[STIX]{x1D70F}_{n}^{\text{cl}}/(\unicode[STIX]{x1D70F}_{n}^{\text{cl}}+0.057)$. In figure 9, the different trends appear at approximately 
$\unicode[STIX]{x1D70F}_{n}^{\text{cl}}=0.1~\text{s}$.
Figure 9. The experimentally measured neutron decay times are plotted against the simulated neutron decay time for perpendicular NBs in the configuration of 
$R_{\text{ax}}=3.53~\text{m}$. Dashed guide curve is 
$\unicode[STIX]{x1D70F}_{n}=\unicode[STIX]{x1D70F}_{c}\unicode[STIX]{x1D70F}_{n}^{\text{cl}}/(\unicode[STIX]{x1D70F}_{n}^{\text{cl}}+\unicode[STIX]{x1D70F}_{c})$, 
$\unicode[STIX]{x1D70F}_{c}=0.057~\text{s}$.
5.1 Long $\unicode[STIX]{x1D70F}_{n}^{\text{cl}}$ region ($\unicode[STIX]{x1D70F}_{n}^{\text{cl}}>0.1~\text{s}$)
Similar to § 4.1, we investigate the contribution of the charge exchange loss to the fast ion confinement. From figure 9, the neutron decay times of NB#4 and NB#5 at 
$\unicode[STIX]{x1D70F}_{n}^{\text{cl}}=0.2~\text{s}$ are approximately 
$\unicode[STIX]{x1D70F}_{n}=0.025~\text{s}$ and 
$0.035~\text{s}$, respectively. From these values and (4.1), the charge exchange times of NB#4 and NB#5 can be estimated as 
$\unicode[STIX]{x1D70F}_{\text{cx}}=0.057~\text{s}$ and 
$0.17~\text{s}$, respectively. The neutral atom densities evaluated from 
$\unicode[STIX]{x1D70F}_{\text{cx}}$ are 
$n_{0}=2.1\times 10^{14}~\text{m}^{-3}$, and 
$1.3\times 10^{14}~\text{m}^{-3}$, respectively. These values of density are within the range of realistic values as noted in § 4.2. Therefore, it can be also considered that the charge exchange losses are not negligible for perpendicular beams in the long 
$\unicode[STIX]{x1D70F}_{n}^{\text{cl}}$ region.
5.2 Short $\unicode[STIX]{x1D70F}_{n}^{\text{cl}}$ region ($\unicode[STIX]{x1D70F}_{n}^{\text{cl}}<0.1~\text{s}$)
Figure 10. The short 
$\unicode[STIX]{x1D70F}_{n}^{\text{cl}}$ region (
$\unicode[STIX]{x1D70F}_{n}^{\text{cl}}<0.1~\text{s}$) of figure 9 is focused on.
Figure 11. The effective particle diffusion coefficients for perpendicular beams are plotted against the position of the magnetic axis.
Owing to the above discussion, we focus on the 
$\unicode[STIX]{x1D70F}_{n}^{\text{cl}}<0.1~\text{s}$ region to exclude the cases that the charge exchange loss is significant. In figure 10, the short 
$\unicode[STIX]{x1D70F}_{n}^{\text{cl}}$ region 
$\unicode[STIX]{x1D70F}_{n}^{\text{cl}}<0.1~\text{s}$ of figure 9 is focused on. The guide curve indicates 
$\unicode[STIX]{x1D70F}_{c}^{\text{eff}}\unicode[STIX]{x1D70F}_{n}^{\text{cl}}/(\unicode[STIX]{x1D70F}_{n}^{\text{cl}}+\unicode[STIX]{x1D70F}_{c}^{\text{eff}})$, 
$\unicode[STIX]{x1D70F}_{c}^{\text{eff}}=0.057~\text{s}$. The value of 
$\unicode[STIX]{x1D70F}_{c}^{\text{eff}}$ is obtained by the weighted least mean square fitting in 
$\unicode[STIX]{x1D70F}_{n}=\unicode[STIX]{x1D70F}_{c}^{\text{eff}}\unicode[STIX]{x1D70F}_{n}^{\text{cl}}/(\unicode[STIX]{x1D70F}_{n}^{\text{cl}}+\unicode[STIX]{x1D70F}_{c}^{\text{eff}})$.
Similar to the discussion in § 4.2, the effective particle diffusion coefficient 
$D^{\text{eff}}$ for a perpendicular beam is estimated for the five magnetic configurations. In figure 11, the dependence of 
$D^{\text{eff}}$ on 
$R_{\text{ax}}$ for perpendicular beams is shown. It is found that the perpendicular beams have a poorer confinement than the tangential beams. As with tangential beams, the confinement of the perpendicular beams becomes poor when the plasmas are shifted outward.
It is noted that the perpendicular beam injection energy is not uniform in each configuration due to experimental constraints. In the cases of 
$R_{\text{ax}}=3.75~\text{m}$ and 
$3.9~\text{m}$, the perpendicular beam injection energy is 
$E_{b}=60~\text{keV}$. The data of the 
$R_{\text{ax}}=3.6~\text{m}$ configuration consist of the data with 
$E_{b}=35~\text{keV}$, 60 keV and 80 keV. In the remaining configurations (
$R_{\text{ax}}=3.53~\text{m}$ and 
$3.55~\text{m}$), the data consist of those with 
$E_{b}=35~\text{keV}$ and 
$80~\text{keV}$. These data are fitted in a single curve as shown in figure 10.
6 Discussion regarding the deuteron dilution
In this paper, in order to estimate the fast ion confinement time, we have focused on the neutron decay time instead of the absolute value of the neutron emission rate itself. This is because there are some ambiguities in estimating the absolute value of the neutron emission rate. The fusion reaction rate in beam-thermal reaction dominant plasmas is described by (3.6). Our simulation over-estimates the neutron emission rate due to the assumptions of 
$n_{D}=n_{e}$ and 
$\unicode[STIX]{x1D70F}_{c}=\infty$ as shown in figure 4. In actual plasmas, however, deuterons are diluted due to the presence of impurity ions. Because the evaluation of the impurity density profile is difficult, the ambiguity cannot be reduced to estimate the neutron emission rate. On the other hand, the estimation of the neutron decay time has fewer ambiguities. This is because the fast ion slowing down process mainly depends on the measurable values, which are electron density 
$n_{e}$ and temperature 
$T_{e}$. Since we have estimated the fast ion confinement time 
$\unicode[STIX]{x1D70F}_{c}$ in the previous section, the diluted deuteron density can be evaluated by a comparison between the peak values of the measured and simulated neutron emission rates.
The relation between two neutron emission rate peak values, measured peak value 
$S_{n}^{\text{p},\text{exp}}$ and simulated peak value 
$S_{n}^{\text{p},\text{sim}}$, can be expressed as (Nuga et al. Reference Nuga, Seki, Ogawa, Kamio, Fujiwara, Osakabe, Isobe, Nishitani and Yokoyama2019)
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \frac{S_{n}^{\text{p},\text{exp}}}{S_{n}^{\text{p},\text{sim}}}=\frac{n_{D}}{n_{e}}{\mathcal{F}},\\ \displaystyle {\mathcal{F}}\equiv \frac{\unicode[STIX]{x1D70F}_{c}}{\unicode[STIX]{x1D70F}_{n}^{\text{cl}}+\unicode[STIX]{x1D70F}_{c}}\frac{1-\exp (-t_{0}/[\unicode[STIX]{x1D70F}_{n}^{\text{cl}}\unicode[STIX]{x1D70F}_{c}/(\unicode[STIX]{x1D70F}_{n}^{\text{cl}}+\unicode[STIX]{x1D70F}_{c})])}{1-\exp (-t_{0}/\unicode[STIX]{x1D70F}_{n}^{\text{cl}})},\end{array}\right\} & & \displaystyle\end{eqnarray}$$ where 
$t_{0}$ is the beam injection duration 
$t_{0}\sim 40~\text{ms}$. Here, we assume that the plasma parameters and the fast ion birth rate are constant during beam injection.
Figure 12. The relation between 
$S_{n}^{\text{p},\text{exp}}$ and 
${\mathcal{F}}S_{n}^{\text{p},\text{sim}}$ is shown for the 
$R_{\text{ax}}=3.53~\text{m}$ configuration. The solid line indicates 
$y=x$ and the dashed line indicates 
$y=0.42x$.
Figure 12 shows the relation between 
$S_{n}^{\text{p},\text{exp}}$ and 
${\mathcal{F}}S_{n}^{\text{p},\text{sim}}$ for the 
$R_{\text{ax}}=3.53~\text{m}$ configuration. It is noted that, in this figure, data in the long 
$\unicode[STIX]{x1D70F}_{n}^{\text{cl}}$ region (
$\unicode[STIX]{x1D70F}_{n}^{\text{cl}}>0.4~\text{s}$ for tangential beams and 
$\unicode[STIX]{x1D70F}_{n}^{\text{cl}}>0.1~\text{s}$ for perpendicular beams) are omitted. From equation (6.1), the slope of dashed line in figure 12 indicates the ratio of the deuteron density to the electron density 
$n_{D}/n_{e}$. The value is obtained by the weighted least mean square fitting in 
$y=\unicode[STIX]{x1D6FC}x$, where 
$\unicode[STIX]{x1D6FC}$ is the fitting parameter. For this reason, here we assume the deuteron density ratio to the electron density is approximately 
$n_{D}/n_{e}=0.42$.
It is noted that this fitting is performed by using only tangential NBs. This is because the full energy fraction of perpendicular NBs is unclear. From figure 12, the plot of NB#5 has a good agreement with the fitting line. This indicates that the assumption of the full energy fraction, 0.78 used in the simulation is valid. On the contrary, results of NB#4 are separated from the fitting line. One of the reasons of this deviation is that the assumption of the full energy fraction is invalid. If the deviation can be explained only by the full energy fraction, the fraction becomes 1.2. Therefore, it seems that there are the other factors separating the results from the fitting. In this paper, NB#4 has a low injection energy, whose value is out of the typical range of injection energy. Because of this unusual operation of NB#4, the 
$S_{n}$ peak value estimation of NB#4 is not reliable.
The deuterium ion ratio and the helium ion ratio in this series of experiment are approximately 
$n_{\text{D}}/(n_{\text{H}}+n_{\text{D}})\sim 1$ and 
$(n_{\text{D}}+n_{\text{H}})/(n_{\text{D}}+n_{\text{H}}+n_{\text{He}})\sim 0.9$. Here, we assume that there are only three ion species, deuterons, helium ions and carbon ions in the plasmas. This assumption indicates 
$n_{e}=n_{\text{D}}+2n_{\text{He}}+6n_{\text{C}}$. We can estimate the typical ion ratios from the deuteron ratio estimation, two measured ratios and this assumption. These ratios are 
$n_{\text{D}}/n_{e}=0.42$, 
$n_{\text{He}}/n_{e}=0.047$ and 
$n_{\text{C}}/n_{e}=0.081$. The effective charge of the plasma, which consists of these ion ratios, is approximately 
$Z_{\text{eff}}=3.5$. From Zhou et al. (Reference Zhou, Morita, Goto, Dong, Yanagibayashi and Hasuo2010) and Huang et al. (Reference Huang, Morita, Oishi, Goto and Zhang2015), the typical value of the effective charge in LHD plasmas measured by an extreme ultraviolet (EUV) spectrometer is approximately 
$Z_{\text{eff}}=2{-}4$. Therefore, this estimation is within the range of the realistic value.
Additionally, the carbon density profile, 
$n_{\text{C}}$, is measured by the charge exchange spectroscopy of CVI using the neutral beam (Chen et al. Reference Chen, Ida, Yoshinuma, Murakami, Kobayashi, Ye and Lyu2019; Ida et al. Reference Ida, Yoshinuma, Kobayashi, Fujiwara, Chen, Murakami, Kisaki and Osakabe2019) in LHD. Unlike 
$n_{\text{D}}/(n_{\text{H}}+n_{\text{D}})$ and 
$(n_{\text{D}}+n_{\text{H}})/(n_{\text{D}}+n_{\text{H}}+n_{\text{He}})$, the carbon density ratio to the electron density changes widely shot-by-shot as shown in figure 13. In most of the discharges, the value of 
$n_{C}/n_{e}$ has changed around 
${\lesssim}0.1$ and it does not exceed 0.2. Therefore, it can be considered that the value 
$n_{\text{D}}/n_{e}=0.42$ is reasonable.
Figure 13. The carbon density ratio to the electron density 
$n_{\text{C}}/n_{e}$ is shown for three discharges. The horizontal axis indicates the normalized minor radius 
$\unicode[STIX]{x1D70C}$. The minus value of 
$\unicode[STIX]{x1D70C}$ means the position inside the magnetic axis.
Here we can recalculate the neutron emission rate by using estimated 
$\unicode[STIX]{x1D70F}_{c}$ and ion ratios. Figure 14 shows the time evolutions of the measured and simulated neutron emission rate. In this simulation, the dilution effect of deuteron density and the fast ion loss effect are included. As compared to figure 4, it is found that a consistent result for the measured neutron emission rate can be obtained by this simulation.
Figure 14. Time evolutions of the measured and simulated neutron emission rates are shown. The bulk deuteron density is assumed to be 
$n_{\text{D}}/n_{e}=0.42$ and the fast ion confinement times are assumed to be 
$\unicode[STIX]{x1D70F}_{c}=0.6~\text{s}$ for tangential beams and 
$\unicode[STIX]{x1D70F}_{c}=0.06~\text{s}$ for perpendicular beams.
7 Conclusion
We have investigated the NB fast ion confinement in LHD deuterium plasmas in five magnetic configurations. The effective confinement time of NB fast ions has been estimated from the decay time of the neutron emission rate after short-pulse NBs are turned off. It can be considered that the decay of the neutron emission rate can be expressed by a combination of a reduction of the fusion cross-section due to the fast ions slowing down and the reduction of the fast ion density due to the fast ion loss. Therefore, the comparison between the simulated neutron decay time 
$\unicode[STIX]{x1D70F}_{n}^{\text{cl}}$, which ignores the fast ion loss, and the measured neutron decay time 
$\unicode[STIX]{x1D70F}_{n}$ clarifies the fast ion confinement time.
As shown in figures 5 and 9, the relation between 
$\unicode[STIX]{x1D70F}_{n}$ and 
$\unicode[STIX]{x1D70F}_{n}^{\text{cl}}$ has two trends. In the short 
$\unicode[STIX]{x1D70F}_{n}^{\text{cl}}$ region, 
$\unicode[STIX]{x1D70F}_{n}$ obeys the curve, 
$f(\unicode[STIX]{x1D70F}_{n}^{\text{cl}})=\unicode[STIX]{x1D70F}_{c}\unicode[STIX]{x1D70F}_{n}^{\text{cl}}/(\unicode[STIX]{x1D70F}_{n}^{\text{cl}}+\unicode[STIX]{x1D70F}_{c})$, where 
$\unicode[STIX]{x1D70F}_{c}$ is constant. In other words, this region is the high electron density region. On the other hand, 
$\unicode[STIX]{x1D70F}_{n}$ separates from the guide curve as 
$\unicode[STIX]{x1D70F}_{n}^{\text{cl}}$ increases. This indicates that the dominant fast ion loss mechanism is different in each region. As shown in §§ 4 and 5, in the long 
$\unicode[STIX]{x1D70F}_{n}^{\text{cl}}$ region, the charge exchange loss cannot be negligible because low electron density plasmas include many neutral particles. To reduce the charge exchange loss in the estimation of 
$\unicode[STIX]{x1D70F}_{c}$, we have focused on the short 
$\unicode[STIX]{x1D70F}_{n}^{\text{cl}}$ region. Here the short 
$\unicode[STIX]{x1D70F}_{n}^{\text{cl}}$ region indicates 
$\unicode[STIX]{x1D70F}_{n}^{\text{cl}}<0.4~\text{s}$ for tangential beams and 
$\unicode[STIX]{x1D70F}_{n}^{\text{cl}}<0.1~\text{s}$ for perpendicular beams, respectively. In this region, we can estimate the effective confinement time 
$\unicode[STIX]{x1D70F}_{c}^{\text{eff}}$ by the weighted least mean square fitting in 
$f(\unicode[STIX]{x1D70F}_{n}^{\text{cl}})$. In addition, similar analyses have been performed for the other magnetic configurations. In figures 8 and 11, the effective NB fast ion diffusion coefficient 
$D^{\text{eff}}$ is plotted against the position of the magnetic axis. It is clear that the tangential NBs have good confinement rather than the perpendicular NBs. Additionally, inward shifted plasmas have a good confinement of NB fast ions in both injection directions.
The dependence of the neo-classical diffusion coefficient on the position of the magnetic axis in LHD have been discussed numerically in Murakami et al. (Reference Murakami, Wakasa, Maaßberg, Beidler, Yamada and Watanabe2002). This reference showed that the neo-classical diffusion coefficient in the 
$1/\unicode[STIX]{x1D708}$ regime decreases as the plasma shifts inward. Because the neo-classical diffusion is dominated by trapped particles in usual, it can be considered that the dependence of 
$D^{\text{eff}}$ on 
$R_{\text{ax}}$ for perpendicular beam ions has same trend as the reference result. For tangential beam ions, it can be roughly explained that the orbit deviation from the magnetic surface becomes larger as the plasma shifts outward because the toroidal curvature component of the magnetic field, 
$B_{1,0}$ (poloidal mode number 
$=1$, toroidal mode number 
$=0$), increases as the plasma shifts outward. Obviously, however, the sensitivity of 
$D^{\text{eff}}$ to 
$R_{\text{ax}}$ is different from the reference results. Since the detailed discussion of this issue requires orbit simulations, this is future work.
We have focused on the decay time of the neutron emission rate to estimate 
$\unicode[STIX]{x1D70F}_{c}^{\text{eff}}$ instead of the absolute value of the neutron emission rate 
$S_{n}$. The absolute value of 
$S_{n}$ linearly depends on the bulk deuteron density, which is difficult to measure in the plasma core region. In actual plasmas, the deuteron density is diluted by the presence of the impurity ions. This dilution effect can be estimated by the obtained 
$\unicode[STIX]{x1D70F}_{c}^{\text{eff}}$ and by the difference of the peak values of the measured and simulated neutron emission rates. From figure 12, the ratio of the deuteron density to the electron density is roughly estimated as 
$n_{\text{D}}/n_{e}=0.42$. This estimation suffers no significant contradictions with impurity measurements as shown in § 6. According to the obtained 
$\unicode[STIX]{x1D70F}_{c}$ and 
$n_{\text{D}}/n_{e}$, we can simulate a consistent neutron emission rate to the measured neutron emission rate.
Although we have estimated quantitatively the fast ion confinement time 
$\unicode[STIX]{x1D70F}_{c}$ in LHD plasmas, the transport mechanism itself is still unclear. The clarification of the transport mechanism dominant in the short 
$\unicode[STIX]{x1D70F}_{n}^{\text{cl}}$ region is future work.
Acknowledgements
This work is supported partly by LHD project budgets (NIFS07KLPH004 and NIFS14KNTT025). It is performed on ‘Plasma Simulator’ (FUJITSU FX100) of NIFS with the support and under the auspices of the NIFS Collaboration Research program (NIFS18KNSR007).
