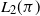1. Introduction
The use of Markov chain Monte Carlo (MCMC) arises from the need to sample from probabilistic models when simple Monte Carlo is not possible. The procedure is to simulate a positive recurrent Markov process where the stationary distribution is the measure one intends to sample, so that the dynamics of the process converge to the distribution required. Temporally correlated samples may then be used to approximate various expectations; see e.g. [Reference Brooks, Gelmand, Jones and Meng7] and the many references therein. Examples of common applications may be found in hierarchical models, spatio-temporal models, random networks, finance, bioinformatics, etc.
Often, however, the transition dynamics of the Markov chain required to run this process exactly are too computationally expensive because of prohibitively large datasets, intractable likelihoods, etc. In such cases it is tempting to instead approximate the transition dynamics of the Markov process in question, either deterministically as in the low-rank Gaussian approximation of [Reference Johndrow, Mattingly, Mukherjee and Dunson18], or stochastically as in the noisy Metropolis–Hastings procedure of [Reference Alquier, Friel, Everitt and Boland1]. It is important then to understand whether these approximations will yield stable and reliable results. This paper aims to provide quantitative tools for the analysis of these algorithms. Since the use of approximation for the transition dynamics may be interpreted as a perturbation of the transition kernel of the exact MCMC algorithm, we focus on bounds on the convergence of perturbations of Markov chains.
The primary purpose of this paper is to extend existing quantitative bounds on the errors of approximate Markov chains from the uniformly ergodic case in [Reference Johndrow, Mattingly, Mukherjee and Dunson18] to the geometrically ergodic case (a weaker condition, for which multiple equivalent definitions may be found in [Reference Roberts and Rosenthal29]). Our work will extend the theoretical results of [Reference Johndrow, Mattingly, Mukherjee and Dunson18] in the case that the exact chain is reversible, replacing the total variation metric with ![]() $L_2$ distances, and relaxing the uniform contraction condition to
$L_2$ distances, and relaxing the uniform contraction condition to ![]() $L_2(\pi)$-geometric ergodicity.
$L_2(\pi)$-geometric ergodicity.
1.1. Geometric ergodicity
When analyzing the performance of exact MCMC algorithms, it is natural to decompose the error in approximation of expectations into a component for the transient phase error of the process and one for the Monte Carlo approximation error. The former may be interpreted as the bias due to not having started the process in the stationary distribution. A Markov chain is geometrically ergodic if, from a suitable initial distribution ![]() $\nu$, the marginal distribution of the nth iterate of the chain converges to the stationary distribution, with an error that decays as
$\nu$, the marginal distribution of the nth iterate of the chain converges to the stationary distribution, with an error that decays as ![]() $C(\nu) \rho^n$ for some
$C(\nu) \rho^n$ for some ![]() $\rho\in(0,1)$ and some constant depending on the initial distribution
$\rho\in(0,1)$ and some constant depending on the initial distribution ![]() $C(\nu)$, in some suitable metric on the space of probability measures. The geometric ergodicity condition essentially dictates that the transient phase error of the nth sample decays exponentially quickly in n. The chain is uniformly (geometrically) ergodic if C can be chosen independently of the initial distribution. Geometric ergodicity is a desirable property as it ensures that the cumulative transient phase error asymptotically does not dominate the Monte Carlo error, while still being less restrictive than the uniform ergodicity condition, which often fails when the state space is not finite or compact (for example, an AR(1) process is geometrically ergodic but not uniformly ergodic).
$C(\nu)$, in some suitable metric on the space of probability measures. The geometric ergodicity condition essentially dictates that the transient phase error of the nth sample decays exponentially quickly in n. The chain is uniformly (geometrically) ergodic if C can be chosen independently of the initial distribution. Geometric ergodicity is a desirable property as it ensures that the cumulative transient phase error asymptotically does not dominate the Monte Carlo error, while still being less restrictive than the uniform ergodicity condition, which often fails when the state space is not finite or compact (for example, an AR(1) process is geometrically ergodic but not uniformly ergodic).
When using approximate MCMC methods, one desires the approximation to preserve geometric ergodicity, so that convergence to stationarity is still fast and the transient phase error goes to zero quickly. This is an important issue, especially since Medina-Aguayo et al. [Reference Medina-Aguayo, Lee and Roberts25] have shown that intuitive approximations such as Monte Carlo within Metropolis may lead to transient approximating chains.
1.2. Outline of the paper
The outline of this paper is as follows. Section 2 reviews related work. Then Section 3 contains our main theoretical results and their proofs. Theorem 1 therein provides bounds on the distance between stationary distributions, and gives a sufficient condition for the perturbed chain to be geometrically ergodic in ![]() $L_2(\pi)$, where
$L_2(\pi)$, where ![]() $\pi$ is the stationary distribution of the unperturbed chain. Theorem 2 and Theorem 3 give sufficient conditions for the perturbed chain to be geometrically ergodic according to several other variants of the definition of geometric ergodicity (for different metrics and families of initial distributions), and provide quantitative rates when possible. The remainder of Section 3 establishes bounds on autocorrelations and mean squared error for Monte Carlo estimates of expected values computed with the perturbed chain.
$\pi$ is the stationary distribution of the unperturbed chain. Theorem 2 and Theorem 3 give sufficient conditions for the perturbed chain to be geometrically ergodic according to several other variants of the definition of geometric ergodicity (for different metrics and families of initial distributions), and provide quantitative rates when possible. The remainder of Section 3 establishes bounds on autocorrelations and mean squared error for Monte Carlo estimates of expected values computed with the perturbed chain.
Finally, Section 4 considers noisy and/or approximate Metropolis–Hastings algorithms. It provides sufficient conditions that one can check in order for our results from Section 3 to be applied. We use this to study Metropolis–Hastings with deterministic approximations to the target density, as well as the Monte Carlo within Metropolis algorithm, as in [Reference Medina-Aguayo, Rudolf and Schweizer24], and provide some examples of how these types of approximations might arise in practice.
2. Related work
This section presents a brief review of related work, discussing convergence of perturbed Markov chains in the uniformly ergodic and geometrically ergodic cases with varying metrics and additional assumptions. The results in the literature require a wide range of assumptions and have a wide range of scopes. The results for uniformly ergodic chains have a simpler aesthetic, in line with what intuition for finite-state-space chains might inspire, as they do not require drift and minorization conditions to state. Our results cover the geometrically ergodic and reversible case, and use properties of reversibility to match the simpler aesthetic found in the literature for the uniformly ergodic case.
In close relation to the present paper, Johndrow et al. [Reference Johndrow, Mattingly, Mukherjee and Dunson18] derive perturbation bounds to assess the robustness of approximate MCMC algorithms. The assumptions upon which their results rely are as follows: the original chain is uniformly contractive in the total variation norm (this implies uniform ergodicity), and the perturbation is sufficiently small (in the operator norm induced by the total variation norm). The main results of their paper are as follows:
• The perturbed kernel is uniformly contractive in the total variation norm.
-
• The perturbed stationary distribution is close to the original stationary distribution in total variation.
-
• Explicit bounds are proved on the total variation distance between finite-time approximate sampling distributions and the original stationary distribution.
-
• Explicit bounds are proved on the total variation difference between the original stationary distribution and the mixture of finite-time approximate sampling distributions.
-
• Explicit bounds are proved on the mean squared error for integral approximation using the approximate kernel and the true kernel.
The results derived by [Reference Johndrow, Mattingly, Mukherjee and Dunson18] are applied within the same paper to a wide variety of approximate MCMC problems, including low-rank approximation to Gaussian processes and sub-sampling approximations. In other work, Johndrow and Mattingly [Reference Johndrow and Mattingly16] use intuitive coupling arguments to establish similar results under the same uniform contractivity assumption.
Further results on perturbations for uniformly ergodic chains may be found in [Reference Mitrophanov26]. This work is motivated in part by numerical rounding errors. Various applications of these results may be found in [Reference Alquier, Friel, Everitt and Boland1]. The only assumption of [Reference Mitrophanov26] is that the original chain is uniformly ergodic. The paper is unique in that it makes no assumption regarding the proximity of the original and perturbed kernel, though the level of approximation error does still scale linearly with the total variation distance of the original and perturbed kernels. The main results are explicit bounds on the total variation distance between finite-time sampling distributions, and explicit bounds on the total variation distance between stationary distributions.
The work of Roberts et al. [Reference Roberts, Rosenthal and Schwartz31] (see also [Reference Breyer, Roberts and Rosenthal6]) is also motivated by numerical rounding errors. The perturbed kernel is assumed to be derived from the original kernel by a round-off function, which e.g. maps the input to the nearest multiple of ![]() $2^{-31}$. In such cases, the new state space is at most countable while the old state space may have been uncountable, and so the resulting chains have mutually singular marginal distributions at all finite times and mutually singular stationary distributions (if they have stationary distributions at all). The results of [Reference Roberts, Rosenthal and Schwartz31] require the analysis of Lyapunov drift conditions and drift functions (which we will avoid by working in an appropriate
$2^{-31}$. In such cases, the new state space is at most countable while the old state space may have been uncountable, and so the resulting chains have mutually singular marginal distributions at all finite times and mutually singular stationary distributions (if they have stationary distributions at all). The results of [Reference Roberts, Rosenthal and Schwartz31] require the analysis of Lyapunov drift conditions and drift functions (which we will avoid by working in an appropriate ![]() $L_2$ space). The key assumptions in [Reference Roberts, Rosenthal and Schwartz31] are as follows: the original kernel is geometrically ergodic, and V is a Lyapunov drift function for the original kernel; the original and perturbed transition kernels are close in the V-norm; the perturbed kernel is defined via a round-off function with round-off error uniformly sufficiently small; and
$L_2$ space). The key assumptions in [Reference Roberts, Rosenthal and Schwartz31] are as follows: the original kernel is geometrically ergodic, and V is a Lyapunov drift function for the original kernel; the original and perturbed transition kernels are close in the V-norm; the perturbed kernel is defined via a round-off function with round-off error uniformly sufficiently small; and ![]() $\log V$ is uniformly continuous. The main results of the paper include the following:
$\log V$ is uniformly continuous. The main results of the paper include the following:
• If the perturbed kernel is sufficiently close in the V-norm, then geometric ergodicity is preserved.
-
• If the drift function, V, can be chosen so that
 $\log V$ is uniformly continuous, and if the round-off errors can be made arbitrarily small, then the kernels can be made arbitrarily close in the V-norm.
$\log V$ is uniformly continuous, and if the round-off errors can be made arbitrarily small, then the kernels can be made arbitrarily close in the V-norm. -
• Explicit bounds are proved on the total variation distance between the approximate finite-time sampling distribution and the true stationary distribution.
-
• Sufficient conditions are given for the approximating stationary distribution to be arbitrarily close in total variation to the true stationary distribution.
Roberts et al. [Reference Roberts, Rosenthal and Schwartz31] also prove results that do not require closeness in the V-norm, or even absolute continuity of the perturbed transitions; in such cases they show that a suitable drift condition on the original chain together with a uniformly small round-off error yields perturbed chains which are geometrically ergodic, and that the stationary measure varies continuously under such perturbations in the topology of weak convergence.
Pillai and Smith [Reference Pillai and Smith28] provide bounds in terms of the Wasserstein topology (cf. [Reference Gibbs11]). Their main focus is on approximate MCMC algorithms, especially approximation due to sub-sampling from a large dataset (e.g., when computing the posterior density). Their underlying assumptions are as follows:
• The original and perturbed kernels satisfy a series of drift-like conditions with shared parameters.
-
• The original kernel has finite eccentricity for all states (where eccentricity of a state is defined as the expected distance between the state and a sample from the stationary distribution).
-
• The Ricci curvature of the original kernel has a non-trivial uniform lower bound on a positive measure subset of the state space.
-
• The transition kernels are close in the Wasserstein metric, uniformly on the mentioned subset.
Their main results under these assumptions are as follows:
• Explicit bounds on the Wasserstein distance between the approximate sampling distribution and the original stationary distribution.
-
• Explicit bounds on the total variation distance of the original and perturbed stationary distributions and bounds on the mixing times of each chain.
-
• Explicit bounds on the bias and
 $L_1$ error of Monte Carlo approximations.
$L_1$ error of Monte Carlo approximations. -
• Decomposition of the error from approximate MCMC estimation into components from burn-in, asymptotic bias, and variance.
-
• Rigorous discussion of the trade-off between the above error components.
Rudolf and Schweizer [Reference Rudolf and Schweizer35] also use the Wasserstein topology. They focus on approximate MCMC algorithms, with applications to auto-regressive processes and stochastic Langevin algorithms for Gibbs random fields. Their results use the following assumptions: the original kernel is Wasserstein ergodic; a Lyapunov drift condition for perturbed kernel is given, with drift function ![]() $\tilde{V}$;
$\tilde{V}$; ![]() $\tilde{V}$ has finite expectation under the initial distribution; and the perturbation operator is uniformly bounded in a
$\tilde{V}$ has finite expectation under the initial distribution; and the perturbation operator is uniformly bounded in a ![]() $\tilde{V}$-normalized Wasserstein norm. Their main results are explicit bounds on the Wasserstein distance and weighted total variation distance between the original and perturbed finite-time sampling distributions, and explicit bounds on the Wasserstein distance between stationary distributions.
$\tilde{V}$-normalized Wasserstein norm. Their main results are explicit bounds on the Wasserstein distance and weighted total variation distance between the original and perturbed finite-time sampling distributions, and explicit bounds on the Wasserstein distance between stationary distributions.
Ferré et al. [Reference Ferré, Hervé and Ledoux10] build upon the work of Keller and Liverani [Reference Keller and Liverani20] to provide perturbation results for V-geometrically ergodic Markov chains using a simultaneous drift condition. They show that any perturbation to the transition kernel which shares its drift condition has a stationary distribution, that such a perturbation is also V-geometrically ergodic, and that the perturbed stationary distribution is close to the original one. The assumption of a shared drift condition may be difficult to verify or may not hold in some cases of interest related to approximate or noisy MCMC. Hervé and Ledoux [Reference Hervé and Ledoux12] consider finite-rank approximations to a transition kernel. That work gives sufficient conditions for approximations to inherit V-geometric ergodicity; it provides a quantitative relationship between the rates of convergence and bounds the total variation distance between stationary measures. It also provides sufficient conditions for V-geometric ergodicity of a family of finite-rank approximations to a transition kernel to guarantee geometric ergodicity of the kernel, and provides quantitative rates of convergence. In both of these results, as in [Reference Ferré, Hervé and Ledoux10], the results depend on a simultaneous drift condition for the approximations and the original kernel.
Each of the above papers demonstrate bounds on various measures of error from using approximate finite-time sampling distributions and approximate ergodic distributions to calculate expectations of functions. On the other hand, the assumptions underlying the results vary dramatically. The results for uniformly ergodic chains are based on simpler and more intuitive assumptions than those for geometrically ergodic chains. Our work extends these results to geometrically ergodic chains and perturbations while preserving essentially the same level of simplicity in the assumptions. In particular we avoid the need to identify a Lyapunov drift condition, and our assumptions are expressed directly in terms of transition kernels, rather than in terms of a relationship between drift conditions which they satisfy.
3. Perturbation bounds
This section extends the main results from [Reference Johndrow, Mattingly, Mukherjee and Dunson18] to the ![]() $L_2(\pi)$-geometrically ergodic case, assuming the perturbation
$L_2(\pi)$-geometrically ergodic case, assuming the perturbation ![]() $P-P_{\epsilon}$ has bounded
$P-P_{\epsilon}$ has bounded ![]() $L_{2}(\pi)$ operator norm.
$L_{2}(\pi)$ operator norm.
3.1. Definitions and notation
Let ![]() $\pi$ be a probability measure on a measurable space
$\pi$ be a probability measure on a measurable space ![]() $({\mathcal{X}}, \Sigma)$. We make considerable use of the following norms on signed measures and their corresponding Banach spaces:
$({\mathcal{X}}, \Sigma)$. We make considerable use of the following norms on signed measures and their corresponding Banach spaces:
 \begin{align*} { \Vert {\lambda} \Vert_{\text{TV}}} & = \sup\limits_{A\in\Sigma} \vert {{\lambda(A)}} \vert , & \mathcal{M}(\Sigma) & = \{ {\text{bounded signed measures on }({\mathcal{X}}, \Sigma)} \}, \\
\Vert {{\lambda}}\Vert_{L_2(\pi)} & = \left( {\int\left({{\frac{{\textrm{d}}\lambda}{{\textrm{d}}\pi}}}\right)^2 {\textrm{d}}\pi} \right)^{1/2}, & L_2(\pi) & = \{ {{\nu\ll\pi \,{:}\, \Vert {{\nu}}\Vert_{L_2(\pi)} <\infty }} \},\\
\Vert {{\cdot}}\Vert_{L_{2,0}(\pi)} & = \Vert {{\cdot}}\Vert_{L_2(\pi)} \vert_{{L_{2,0}(\pi)}}, & L_{2,0}(\pi) & = \{ {\nu\in L_2(\pi) \,{:}\,\nu({\mathcal{X}}) = 0} \},\\
\Vert {{\lambda}}\Vert_{L_1(\pi)} & = \int \vert {{{\frac{{\textrm{d}}\lambda}{{\textrm{d}}\pi}}}} \vert {\textrm{d}}\pi, & L_{1}(\pi) & = \{ {\nu\ll\pi \,{:}\, \Vert {{\nu}}\Vert_{L_1(\pi)} <\infty} \},\\
\Vert {\lambda} \Vert_{L_{\infty}(\pi)} & =\text{ess}\sup\limits_{X\sim\pi}{\frac{{\textrm{d}}\lambda}{{\textrm{d}}\pi}}(X), & L_{\infty}(\pi) & = \left\{ {{\nu\ll\pi \,{:}\, (\exists b>0)\left({ \vert {{{\frac{{\textrm{d}}\nu}{{\textrm{d}}\pi}}}} \vert < b \quad \pi\text{a.e.}}\right)}} \right\}.
\end{align*}
\begin{align*} { \Vert {\lambda} \Vert_{\text{TV}}} & = \sup\limits_{A\in\Sigma} \vert {{\lambda(A)}} \vert , & \mathcal{M}(\Sigma) & = \{ {\text{bounded signed measures on }({\mathcal{X}}, \Sigma)} \}, \\
\Vert {{\lambda}}\Vert_{L_2(\pi)} & = \left( {\int\left({{\frac{{\textrm{d}}\lambda}{{\textrm{d}}\pi}}}\right)^2 {\textrm{d}}\pi} \right)^{1/2}, & L_2(\pi) & = \{ {{\nu\ll\pi \,{:}\, \Vert {{\nu}}\Vert_{L_2(\pi)} <\infty }} \},\\
\Vert {{\cdot}}\Vert_{L_{2,0}(\pi)} & = \Vert {{\cdot}}\Vert_{L_2(\pi)} \vert_{{L_{2,0}(\pi)}}, & L_{2,0}(\pi) & = \{ {\nu\in L_2(\pi) \,{:}\,\nu({\mathcal{X}}) = 0} \},\\
\Vert {{\lambda}}\Vert_{L_1(\pi)} & = \int \vert {{{\frac{{\textrm{d}}\lambda}{{\textrm{d}}\pi}}}} \vert {\textrm{d}}\pi, & L_{1}(\pi) & = \{ {\nu\ll\pi \,{:}\, \Vert {{\nu}}\Vert_{L_1(\pi)} <\infty} \},\\
\Vert {\lambda} \Vert_{L_{\infty}(\pi)} & =\text{ess}\sup\limits_{X\sim\pi}{\frac{{\textrm{d}}\lambda}{{\textrm{d}}\pi}}(X), & L_{\infty}(\pi) & = \left\{ {{\nu\ll\pi \,{:}\, (\exists b>0)\left({ \vert {{{\frac{{\textrm{d}}\nu}{{\textrm{d}}\pi}}}} \vert < b \quad \pi\text{a.e.}}\right)}} \right\}.
\end{align*}
Note that ![]() $L_{2,0}(\pi)$ is a complete subspace of
$L_{2,0}(\pi)$ is a complete subspace of ![]() $L_2(\pi)$. Let
$L_2(\pi)$. Let
be the set of probability measures on ![]() $({\mathcal{X}}, \Sigma )$. Note that for any probability measure
$({\mathcal{X}}, \Sigma )$. Note that for any probability measure ![]() $\pi$,
$\pi$, ![]() $L_\infty(\pi)\subset L_2(\pi) \subset L_1(\pi) \subset \mathcal{M}(\Sigma)$, though in general they are not complete subspaces of each other when their corresponding norms are not equivalent. For a norm
$L_\infty(\pi)\subset L_2(\pi) \subset L_1(\pi) \subset \mathcal{M}(\Sigma)$, though in general they are not complete subspaces of each other when their corresponding norms are not equivalent. For a norm ![]() $ \Vert {\cdot} \Vert$ on a vector space, we also write
$ \Vert {\cdot} \Vert$ on a vector space, we also write ![]() $ \Vert {\cdot} \Vert$ for the corresponding operator norm on the space of bounded linear operators from V to itself,
$ \Vert {\cdot} \Vert$ for the corresponding operator norm on the space of bounded linear operators from V to itself, ![]() $\mathcal{B}(V)$.
$\mathcal{B}(V)$.
Definition 1. (Geometric ergodicity) Let P be the kernel of a positive recurrent Markov chain with invariant measure ![]() $\pi$. Let
$\pi$. Let ![]() $\lambda$ be any measure with
$\lambda$ be any measure with ![]() $\pi\ll\lambda$. Suppose that
$\pi\ll\lambda$. Suppose that ![]() $\rho_{\text{TV}},\rho_1,\rho_2 \in (0,1)$.
$\rho_{\text{TV}},\rho_1,\rho_2 \in (0,1)$.
(i) P is
 $\pi$-a.e.-TV geometrically ergodic with factor
$\pi$-a.e.-TV geometrically ergodic with factor  $\rho_{\text{TV}}$ if there exists
$\rho_{\text{TV}}$ if there exists  $C_{\text{TV}}\,{:}\,{\mathcal{X}}\to\mathbb{R}_+$ such that for
$C_{\text{TV}}\,{:}\,{\mathcal{X}}\to\mathbb{R}_+$ such that for  $\pi$-almost every (
$\pi$-almost every ( $\pi$-a.e.)
$\pi$-a.e.)  $x\in{\mathcal{X}}$ and for all
$x\in{\mathcal{X}}$ and for all  $n\in\mathbb{N}$,
The optimal rate for
$n\in\mathbb{N}$,
The optimal rate for \begin{align*} { \Vert {\delta_x P^n - \pi} \Vert_{\text{TV}}} \leq C_{\text{TV}}(x) \rho_{\text{TV}}^n \ .\end{align*}
\begin{align*} { \Vert {\delta_x P^n - \pi} \Vert_{\text{TV}}} \leq C_{\text{TV}}(x) \rho_{\text{TV}}^n \ .\end{align*}
 $\pi$-a.e.-TV geometric ergodicity is the infimum over factors for which the above definition holds:
(1)
$\pi$-a.e.-TV geometric ergodicity is the infimum over factors for which the above definition holds:
(1) \begin{equation}\begin{aligned} \rho^\star_{\text{TV}} = \textrm{inf}\bigg\{{\rho>0 \ \text{s.t.}\ }.&\exists C\,{:}\,{\mathcal{X}}\to\mathbb{R}_+ \text{ with } \pi( \{ {x\,{:}\,C(x)<\infty} \})=1 \ \text{and}\
\\ & {\forall n\in\mathbb{N}, \pi\text{-a.e. }x\in{\mathcal{X}} \quad { \Vert {\delta_x P^n - \pi} \Vert_{\text{TV}}} \leq C(x) \rho^n} \bigg\}. \end{aligned}\end{equation}
\begin{equation}\begin{aligned} \rho^\star_{\text{TV}} = \textrm{inf}\bigg\{{\rho>0 \ \text{s.t.}\ }.&\exists C\,{:}\,{\mathcal{X}}\to\mathbb{R}_+ \text{ with } \pi( \{ {x\,{:}\,C(x)<\infty} \})=1 \ \text{and}\
\\ & {\forall n\in\mathbb{N}, \pi\text{-a.e. }x\in{\mathcal{X}} \quad { \Vert {\delta_x P^n - \pi} \Vert_{\text{TV}}} \leq C(x) \rho^n} \bigg\}. \end{aligned}\end{equation}
-
(ii) P is
 $L_2(\lambda)$-geometrically ergodic with factor
$L_2(\lambda)$-geometrically ergodic with factor  $\rho_2$ if
$\rho_2$ if  $P\,{:}\, L_2(\lambda)\to L_2(\lambda)$ and there exists
$P\,{:}\, L_2(\lambda)\to L_2(\lambda)$ and there exists  $C_2\,{:}\, L_2(\lambda)\cap\mathcal{M}_{+,1}\to\mathbb{R}_+$ such that for every
$C_2\,{:}\, L_2(\lambda)\cap\mathcal{M}_{+,1}\to\mathbb{R}_+$ such that for every  $\nu\in L_2(\lambda)\cap\mathcal{M}_{+,1}$ and for all
$\nu\in L_2(\lambda)\cap\mathcal{M}_{+,1}$ and for all  $n\in\mathbb{N}$,
The optimal rate for
$n\in\mathbb{N}$,
The optimal rate for \begin{align*} \Vert {\nu P^n - \pi} \Vert_{L_2(\lambda)} \leq C_2(\nu) \rho_2^n \ .\end{align*}
\begin{align*} \Vert {\nu P^n - \pi} \Vert_{L_2(\lambda)} \leq C_2(\nu) \rho_2^n \ .\end{align*}
 $L_2(\lambda)$-geometric ergodicity is the infimum over factors for which the above definition holds:
$L_2(\lambda)$-geometric ergodicity is the infimum over factors for which the above definition holds:
 \begin{align*} \rho^\star_2 & = \textrm{inf}\{{\rho>0 \ \text{s.t.}\ \exists C\,{:}\,L_2(\lambda)\cap\mathcal{M}_{+,1}\to\mathbb{R}_+ \text{ with } } \\ &\qquad \qquad {\forall n\in\mathbb{N}, \nu\in L_2(\lambda)\cap\mathcal{M}_{+,1} \quad \Vert {\nu P^n - \pi} \Vert_{L_2(\lambda)} \leq C(\nu) \rho^n}\} \ .\end{align*}
\begin{align*} \rho^\star_2 & = \textrm{inf}\{{\rho>0 \ \text{s.t.}\ \exists C\,{:}\,L_2(\lambda)\cap\mathcal{M}_{+,1}\to\mathbb{R}_+ \text{ with } } \\ &\qquad \qquad {\forall n\in\mathbb{N}, \nu\in L_2(\lambda)\cap\mathcal{M}_{+,1} \quad \Vert {\nu P^n - \pi} \Vert_{L_2(\lambda)} \leq C(\nu) \rho^n}\} \ .\end{align*}
Remark 1. If P is ![]() $\pi$-reversible and aperiodic, then P is
$\pi$-reversible and aperiodic, then P is ![]() $L_2(\pi)$-geometrically ergodic if and only if it is
$L_2(\pi)$-geometrically ergodic if and only if it is ![]() $\pi$-a.e.-TV geometrically ergodic, as per [Reference Roberts and Rosenthal29]. In this case the optimal rate of
$\pi$-a.e.-TV geometrically ergodic, as per [Reference Roberts and Rosenthal29]. In this case the optimal rate of ![]() $L_2(\pi)$-geometric ergodicity,
$L_2(\pi)$-geometric ergodicity, ![]() $\rho_2^\star$, is equal to the spectral radius of
$\rho_2^\star$, is equal to the spectral radius of ![]() $P\vert_{{L_{2,0}(\pi)}}$. In this case, the spectrum of P is a subset of
$P\vert_{{L_{2,0}(\pi)}}$. In this case, the spectrum of P is a subset of ![]() $[-\rho_2^\star,\rho_2^\star]\cup \{ {1} \}$, and P is
$[-\rho_2^\star,\rho_2^\star]\cup \{ {1} \}$, and P is ![]() $L_2(\pi)$-geometrically ergodic with factor
$L_2(\pi)$-geometrically ergodic with factor ![]() $\rho_2^\star$ and
$\rho_2^\star$ and ![]() $C(\mu) = \Vert {{\mu-\pi}}\Vert_{L_2(\pi)} $. For more details see Proposition 2 and [Reference Roberts and Rosenthal29].
$C(\mu) = \Vert {{\mu-\pi}}\Vert_{L_2(\pi)} $. For more details see Proposition 2 and [Reference Roberts and Rosenthal29].
We abbreviate geometric ergodicity and geometrically ergodic as ‘GE’ for brevity going forward.
3.2. Assumptions
We assume throughout that P is the transition kernel for a Markov chain on a countably generated state space ![]() $\mathcal{X}$ with
$\mathcal{X}$ with ![]() $\sigma$-algebra
$\sigma$-algebra ![]() $\Sigma$, which is reversible with respect to a stationary probability measure
$\Sigma$, which is reversible with respect to a stationary probability measure ![]() $\pi$, and is
$\pi$, and is ![]() $\pi$-irreducible and aperiodic. We call the Markov chain induced by P the ‘original’ chain. The
$\pi$-irreducible and aperiodic. We call the Markov chain induced by P the ‘original’ chain. The ![]() $\pi$-reversibility of P makes it natural to work in
$\pi$-reversibility of P makes it natural to work in ![]() $L_2(\pi)$, since in this case P is a self-adjoint linear operator on a Hilbert space. This allows us access to the rich, elegant, and mature spectral theory of such operators. See for example [33, Chapter 12] and [9, Chapter 22]. We further assume that P is
$L_2(\pi)$, since in this case P is a self-adjoint linear operator on a Hilbert space. This allows us access to the rich, elegant, and mature spectral theory of such operators. See for example [33, Chapter 12] and [9, Chapter 22]. We further assume that P is ![]() $L_2(\pi)$-GE with factor
$L_2(\pi)$-GE with factor ![]() $0<(1-\alpha)<1$. Equivalent definitions of
$0<(1-\alpha)<1$. Equivalent definitions of ![]() $L_2(\pi)$-GE are given in Proposition 2. This assumption is weaker than the Doeblin condition used by [Reference Johndrow, Mattingly, Mukherjee and Dunson18], which implies uniform ergodicity.
$L_2(\pi)$-GE are given in Proposition 2. This assumption is weaker than the Doeblin condition used by [Reference Johndrow, Mattingly, Mukherjee and Dunson18], which implies uniform ergodicity.
Next, we assume that ![]() $P_\epsilon$ is a second, ‘perturbed’ transition kernel, such that
$P_\epsilon$ is a second, ‘perturbed’ transition kernel, such that
for some fixed ![]() $\epsilon>0$, and that
$\epsilon>0$, and that
i.e. that the perturbed transition kernel maps ![]() $L_2(\pi)$ measures to
$L_2(\pi)$ measures to ![]() $L_2(\pi)$ measures. The norm condition quantifies the intuition that the perturbation is ‘small’. We assume that
$L_2(\pi)$ measures. The norm condition quantifies the intuition that the perturbation is ‘small’. We assume that ![]() $P_\epsilon$ is
$P_\epsilon$ is ![]() $\pi$-irreducible and aperiodic. We demonstrate (in Theorem 1) that under these assumptions
$\pi$-irreducible and aperiodic. We demonstrate (in Theorem 1) that under these assumptions ![]() $P_\epsilon$ has a unique stationary distribution, denoted by
$P_\epsilon$ has a unique stationary distribution, denoted by ![]() $\pi_\epsilon$, with
$\pi_\epsilon$, with ![]() $\pi_\epsilon\in L_2(\pi)$.
$\pi_\epsilon\in L_2(\pi)$.
Note that when ![]() $\mu\in L_1(\pi)$ we have
$\mu\in L_1(\pi)$ we have
On the other hand, ![]() ${ \Vert {\cdot} \Vert_{\text{TV}}}$ applies to all bounded measures, while
${ \Vert {\cdot} \Vert_{\text{TV}}}$ applies to all bounded measures, while ![]() $ \Vert {{\cdot}}\Vert_{L_1(\pi)} $ applies only to the subspace of
$ \Vert {{\cdot}}\Vert_{L_1(\pi)} $ applies only to the subspace of ![]() $L_1(\pi)$ measures. Note also that if
$L_1(\pi)$ measures. Note also that if ![]() $\pi \sim \pi_\epsilon$ (the two measures are mutually absolutely continuous), then
$\pi \sim \pi_\epsilon$ (the two measures are mutually absolutely continuous), then ![]() $L_1(\pi)$ and
$L_1(\pi)$ and ![]() $L_1(\pi_\epsilon)$ are equal as spaces and their norms are always equal, so in this case we need not distinguish between them.
$L_1(\pi_\epsilon)$ are equal as spaces and their norms are always equal, so in this case we need not distinguish between them.
To summarize, we assume the following.
Assumption 1. (Assumptions of Section 3.2.)
• P is a Markov kernel that is
–
 $\pi$-reversible for a probability measure
$\pi$-reversible for a probability measure  $\pi$,
$\pi$,– irreducible and aperiodic,
–
 $L_2(\pi)$-GE with factor
$L_2(\pi)$-GE with factor  $(1-\alpha)$;
$(1-\alpha)$;
•
 $P_\epsilon$ is a Markov kernel that is
$P_\epsilon$ is a Markov kernel that is
– irreducible and aperiodic,
–
 $P_\epsilon : L_2(\pi) \to L_2(\pi)$, and
$P_\epsilon : L_2(\pi) \to L_2(\pi)$, and–
 $ \Vert {{P-P_\epsilon}}\Vert_{L_2(\pi)} <\epsilon$.
$ \Vert {{P-P_\epsilon}}\Vert_{L_2(\pi)} <\epsilon$.
The assumption that ![]() $P_\epsilon: L_2(\pi)\to L_2(\pi)$ and that
$P_\epsilon: L_2(\pi)\to L_2(\pi)$ and that ![]() $ \Vert {{P_\epsilon}}\Vert_{L_2(\pi)} <\infty$ may seem difficult to verify. However, the following proposition shows us that it is satisfied for
$ \Vert {{P_\epsilon}}\Vert_{L_2(\pi)} <\infty$ may seem difficult to verify. However, the following proposition shows us that it is satisfied for ![]() $P_\epsilon$ constructed based on the Metropolis–Hastings algorithm with suitable jump kernels. As long as the jump kernel, J, has
$P_\epsilon$ constructed based on the Metropolis–Hastings algorithm with suitable jump kernels. As long as the jump kernel, J, has ![]() $ \Vert {{J}}\Vert_{L_2(\pi)} <\infty$, the assumption will be satisfied. Therefore, this assumption is not excessively restrictive for MCMC applications. The jump kernel J describes the conditional distribution of a new point in the chain proposed from x given that the proposal is accepted; it is related to the proposal kernel, Q, by
$ \Vert {{J}}\Vert_{L_2(\pi)} <\infty$, the assumption will be satisfied. Therefore, this assumption is not excessively restrictive for MCMC applications. The jump kernel J describes the conditional distribution of a new point in the chain proposed from x given that the proposal is accepted; it is related to the proposal kernel, Q, by ![]() $\alpha(x) J(x,A) = \int_A a(x,y) Q(x, dy), $ where a(x, y) is the Metropolis–Hastings acceptance ratio and
$\alpha(x) J(x,A) = \int_A a(x,y) Q(x, dy), $ where a(x, y) is the Metropolis–Hastings acceptance ratio and ![]() $\alpha(x) = \int_{\mathcal{X}} a(x,y) Q(x, dy)$ is the implied local jump-intensity.
$\alpha(x) = \int_{\mathcal{X}} a(x,y) Q(x, dy)$ is the implied local jump-intensity.
Proposition 1. If ![]() $P_\epsilon(x,\cdot) = (1-\alpha(x))\delta_x +\alpha(x)J(x,\cdot)$ with
$P_\epsilon(x,\cdot) = (1-\alpha(x))\delta_x +\alpha(x)J(x,\cdot)$ with ![]() $\alpha\,{:}{\mathcal{X}}\to[0,1]$ measurable, and
$\alpha\,{:}{\mathcal{X}}\to[0,1]$ measurable, and ![]() $J \,{:}\, L_2(\pi)\to L_2(\pi)$ and
$J \,{:}\, L_2(\pi)\to L_2(\pi)$ and ![]() $ \Vert {{J}}\Vert_{L_2(\pi)} <\infty$, then
$ \Vert {{J}}\Vert_{L_2(\pi)} <\infty$, then
Proof of Proposition 1. Consider the operator A on ![]() $L_2(\pi)$ given by the formula
$L_2(\pi)$ given by the formula ![]() $[\nu A](C) = \int_C \alpha(x)\nu(dx)$ for all measurable sets C. Its adjoint,
$[\nu A](C) = \int_C \alpha(x)\nu(dx)$ for all measurable sets C. Its adjoint, ![]() $A'$, is given by the formula
$A'$, is given by the formula ![]() $[A' f] (x) = \alpha(x) f(x)$ for all
$[A' f] (x) = \alpha(x) f(x)$ for all ![]() $x \in {\mathcal{X}}$ and
$x \in {\mathcal{X}}$ and ![]() $f\in L_2^{\prime}(\pi)$. Since
$f\in L_2^{\prime}(\pi)$. Since ![]() $\alpha \,{:}\, {\mathcal{X}} \to [0,1]$, we have
$\alpha \,{:}\, {\mathcal{X}} \to [0,1]$, we have ![]() $A'\,{:}\,L_2^{\prime}(\pi)\to L_2^{\prime}(\pi)$ with
$A'\,{:}\,L_2^{\prime}(\pi)\to L_2^{\prime}(\pi)$ with ![]() $ \Vert {{A'}}\Vert_{L^{\prime}_2(\pi)} \leq 1$. Thus
$ \Vert {{A'}}\Vert_{L^{\prime}_2(\pi)} \leq 1$. Thus ![]() $A \,{:}\, L_2(\pi)\to L_2(\pi)$ with
$A \,{:}\, L_2(\pi)\to L_2(\pi)$ with ![]() $ \Vert {{A}}\Vert_{L_2(\pi)} \leq 1 $. The same also holds for
$ \Vert {{A}}\Vert_{L_2(\pi)} \leq 1 $. The same also holds for ![]() $I-A$. Now,
$I-A$. Now, ![]() $P_\epsilon = A + (I-A) J$, so
$P_\epsilon = A + (I-A) J$, so
Verifying that ![]() $ \Vert {P-P_\epsilon}\Vert_{L_2(\pi)} $ is finite and sufficiently small will be the main analytic burden faced when trying to apply our results to more general settings. The development of further tools to determine whether
$ \Vert {P-P_\epsilon}\Vert_{L_2(\pi)} $ is finite and sufficiently small will be the main analytic burden faced when trying to apply our results to more general settings. The development of further tools to determine whether ![]() $ \Vert {P-P_\epsilon}\Vert_{L_2(\pi)} $ is finite and to bound it quantitatively would be an interesting line of future research.
$ \Vert {P-P_\epsilon}\Vert_{L_2(\pi)} $ is finite and to bound it quantitatively would be an interesting line of future research.
3.3. Convergence rates and closeness of stationary distributions
Theorem 1. (Geometric ergodicity of the perturbed chain and closeness of the stationary distributions in original norm, ![]() $L_2(\pi)$) Under the assumptions of Section 3.2, if in addition
$L_2(\pi)$) Under the assumptions of Section 3.2, if in addition ![]() $\epsilon<\alpha$, then
$\epsilon<\alpha$, then ![]() $\pi_\epsilon\in L_2(\pi)$,
$\pi_\epsilon\in L_2(\pi)$,
![]() $P_\epsilon$ is
$P_\epsilon$ is ![]() $L_2(\pi)$-geometrically ergodic with factor
$L_2(\pi)$-geometrically ergodic with factor ![]() $1-(\alpha-\epsilon)$, and for any initial probability measure
$1-(\alpha-\epsilon)$, and for any initial probability measure ![]() $\mu\in L_2(\pi)$,
$\mu\in L_2(\pi)$,
The proof of this result is the content of Appendix A.1. We follow the derivation in [Reference Johndrow, Mattingly, Mukherjee and Dunson18] with minimal structural modification, though the technicalities must be handled differently and additional theoretical machinery is required. We use the fact that the existence of a spectral gap for the restriction of P to ![]() $L_{2,0}(\pi)$ yields an inequality of the same form as the uniform contractivity condition, but in the
$L_{2,0}(\pi)$ yields an inequality of the same form as the uniform contractivity condition, but in the ![]() $L_{2}(\pi)$-norm as opposed to the total variation norm (cf. Theorem 2.1 of [Reference Roberts and Rosenthal29]).
$L_{2}(\pi)$-norm as opposed to the total variation norm (cf. Theorem 2.1 of [Reference Roberts and Rosenthal29]).
Remark 2. Bounds on the differences between measures in ![]() $L_2(\pi)$-norm can be converted into bounds on the total variation distance, since, by Cauchy–Schwarz, for any measure
$L_2(\pi)$-norm can be converted into bounds on the total variation distance, since, by Cauchy–Schwarz, for any measure ![]() $\lambda$ and any signed measure
$\lambda$ and any signed measure ![]() $\nu \in L_2(\lambda)$, we have
$\nu \in L_2(\lambda)$, we have
Thus, for example, under the assumptions of Theorem 1,
Similarly, under the assumptions of Theorem 1, we find that ![]() $P_\epsilon$ is
$P_\epsilon$ is ![]() $(L_2(\pi),{ \Vert {\cdot} \Vert_{\text{TV}}})$-GE with factor
$(L_2(\pi),{ \Vert {\cdot} \Vert_{\text{TV}}})$-GE with factor ![]() $1-(\alpha-\epsilon)$ (see Definition 2 below).
$1-(\alpha-\epsilon)$ (see Definition 2 below).
In some situations, such as the computation of mean squared errors in Theorem 5, it may be inconvenient or impossible to use the ![]() $L_2(\pi)$ norm when studying some aspects of
$L_2(\pi)$ norm when studying some aspects of ![]() $P_\epsilon$. The next theorem will allow us to ‘switch’ to other norms which may be more natural for a given task. First, however, we need to introduce one more notion of geometric ergodicity.
$P_\epsilon$. The next theorem will allow us to ‘switch’ to other norms which may be more natural for a given task. First, however, we need to introduce one more notion of geometric ergodicity.
Definition 2. (![]() $(V, \vert{\kern-0.25ex{ \vert{\kern-0.25ex{ \vert {\cdot} \vert}\kern-0.25ex}\vert}\kern-0.25ex}\vert)$-geometric ergodicity.) Let P be the kernel of a positive recurrent Markov chain with invariant measure
$(V, \vert{\kern-0.25ex{ \vert{\kern-0.25ex{ \vert {\cdot} \vert}\kern-0.25ex}\vert}\kern-0.25ex}\vert)$-geometric ergodicity.) Let P be the kernel of a positive recurrent Markov chain with invariant measure ![]() $\pi$. Let V be a vector space of signed measures on
$\pi$. Let V be a vector space of signed measures on ![]() $({\mathcal{X}},\Sigma)$ containing
$({\mathcal{X}},\Sigma)$ containing ![]() $\pi$, and let
$\pi$, and let ![]() $ \vert{\kern-0.25ex{ \vert{\kern-0.25ex{ \vert {\cdot} \vert}\kern-0.25ex}\vert}\kern-0.25ex}\vert$ be a norm on V (for which V may not be complete).
$ \vert{\kern-0.25ex{ \vert{\kern-0.25ex{ \vert {\cdot} \vert}\kern-0.25ex}\vert}\kern-0.25ex}\vert$ be a norm on V (for which V may not be complete).
P is ![]() $(V, \vert{\kern-0.25ex{ \vert{\kern-0.25ex{ \vert {\cdot} \vert}\kern-0.25ex}\vert}\kern-0.25ex}\vert)$-geometrically ergodic with factor
$(V, \vert{\kern-0.25ex{ \vert{\kern-0.25ex{ \vert {\cdot} \vert}\kern-0.25ex}\vert}\kern-0.25ex}\vert)$-geometrically ergodic with factor ![]() $\rho$ if there exists
$\rho$ if there exists ![]() $C\,{:}\, V\cap \mathcal{M}_{+,1}\to\mathbb{R}_+$ such that for every
$C\,{:}\, V\cap \mathcal{M}_{+,1}\to\mathbb{R}_+$ such that for every ![]() $\nu\in V\cap \mathcal{M}_{+,1}$ and for all
$\nu\in V\cap \mathcal{M}_{+,1}$ and for all ![]() $n\in\mathbb{N}$,
$n\in\mathbb{N}$,
The optimal rate for ![]() $(V, \vert{\kern-0.25ex{ \vert{\kern-0.25ex{ \vert {\cdot} \vert}\kern-0.25ex}\vert}\kern-0.25ex}\vert)$-geometric ergodicity is the infimum over factors for which the above definition holds:
$(V, \vert{\kern-0.25ex{ \vert{\kern-0.25ex{ \vert {\cdot} \vert}\kern-0.25ex}\vert}\kern-0.25ex}\vert)$-geometric ergodicity is the infimum over factors for which the above definition holds:
We will be interested in this definition for the cases that ![]() $V = L_\infty(\pi)$ and
$V = L_\infty(\pi)$ and ![]() $ \vert{\kern-0.25ex{ \vert{\kern-0.25ex{ \vert {\cdot} \vert}\kern-0.25ex}\vert}\kern-0.25ex}\vert$ is either
$ \vert{\kern-0.25ex{ \vert{\kern-0.25ex{ \vert {\cdot} \vert}\kern-0.25ex}\vert}\kern-0.25ex}\vert$ is either ![]() $ \Vert {\cdot}\Vert_{L_2(\pi)} $ or
$ \Vert {\cdot}\Vert_{L_2(\pi)} $ or ![]() $ \Vert {{\cdot}}\Vert_{L_1(\pi)} $.
$ \Vert {{\cdot}}\Vert_{L_1(\pi)} $.
Remark 3. (Relationships between ![]() $(L_\infty(\lambda), \Vert {\cdot} \Vert_{L_p(\lambda)})$-GE, a.e.-TV-GE, and
$(L_\infty(\lambda), \Vert {\cdot} \Vert_{L_p(\lambda)})$-GE, a.e.-TV-GE, and ![]() $L_2(\lambda)$-GE.) Clearly if P is
$L_2(\lambda)$-GE.) Clearly if P is ![]() $L_2(\lambda)$-GE with factor
$L_2(\lambda)$-GE with factor ![]() $\rho_2$ then it is also
$\rho_2$ then it is also ![]() $(L_\infty(\lambda), \Vert {\cdot} \Vert_{L_2(\lambda)})$-GE with factor
$(L_\infty(\lambda), \Vert {\cdot} \Vert_{L_2(\lambda)})$-GE with factor ![]() $\rho_2$. Conversely, Roberts and Tweedie [Reference Roberts and Tweedie32] show that if P is
$\rho_2$. Conversely, Roberts and Tweedie [Reference Roberts and Tweedie32] show that if P is ![]() $(L_\infty(\pi), \Vert {\cdot} \Vert_{L_2(\pi)})$-GE with factor
$(L_\infty(\pi), \Vert {\cdot} \Vert_{L_2(\pi)})$-GE with factor ![]() $\rho_2$, then it is also a.e.-TV-GE with some factor
$\rho_2$, then it is also a.e.-TV-GE with some factor ![]() $\rho_{\text{TV}}\in(0,1)$. However, the factor for a.e.-TV-GE may in fact be worse than the factor for
$\rho_{\text{TV}}\in(0,1)$. However, the factor for a.e.-TV-GE may in fact be worse than the factor for ![]() $(L_\infty(\pi), \Vert {\cdot} \Vert_{L_2(\pi)})$-GE or
$(L_\infty(\pi), \Vert {\cdot} \Vert_{L_2(\pi)})$-GE or ![]() $(L_\infty(\pi), \Vert {\cdot} \Vert_{L_1(\pi)})$-GE. Baxendale [Reference Baxendale3] gives a detailed exposition on the barriers to the comparison of factors for geometric ergodicity given by different equivalent definitions.
$(L_\infty(\pi), \Vert {\cdot} \Vert_{L_1(\pi)})$-GE. Baxendale [Reference Baxendale3] gives a detailed exposition on the barriers to the comparison of factors for geometric ergodicity given by different equivalent definitions.
In Appendix C we give an example where the optimal rates for ![]() $L_2(\pi)$-GE and
$L_2(\pi)$-GE and ![]() $(L_\infty(\pi), \Vert {\cdot} \Vert_{L_2(\pi)})$-GE are distinct when P is not reversible. If P is
$(L_\infty(\pi), \Vert {\cdot} \Vert_{L_2(\pi)})$-GE are distinct when P is not reversible. If P is ![]() $\pi$-reversible then the factors for
$\pi$-reversible then the factors for ![]() $L_2(\pi)$-GE,
$L_2(\pi)$-GE, ![]() $(L_\infty(\pi), \Vert {\cdot} \Vert_{L_2(\pi)})$-GE, and
$(L_\infty(\pi), \Vert {\cdot} \Vert_{L_2(\pi)})$-GE, and ![]() $(L_\infty(\pi), \Vert {\cdot} \Vert_{L_1(\pi)})$-GE must be the same. This result combines a comment and Theorem 3 of [Reference Roberts and Tweedie32], both stated but not proved. The formal statement of that result and its proof may be found in Appendix D.
$(L_\infty(\pi), \Vert {\cdot} \Vert_{L_1(\pi)})$-GE must be the same. This result combines a comment and Theorem 3 of [Reference Roberts and Tweedie32], both stated but not proved. The formal statement of that result and its proof may be found in Appendix D.
Finally, note that by definition ![]() $L_2(\pi)$-GE is equivalent to
$L_2(\pi)$-GE is equivalent to ![]() $(L_2(\pi), \Vert {\cdot}\Vert_{L_2(\pi)} )$ with the same coefficient functions and factors, and that a.e.-TV-GE is equivalent to
$(L_2(\pi), \Vert {\cdot}\Vert_{L_2(\pi)} )$ with the same coefficient functions and factors, and that a.e.-TV-GE is equivalent to ![]() $(D,{ \Vert {\cdot} \Vert_{\text{TV}}})$-GE where we can take
$(D,{ \Vert {\cdot} \Vert_{\text{TV}}})$-GE where we can take ![]() $D = \text{span} ( { \{ {\pi} \}\cup \{ {\delta_x\,{:}\, x\in {\mathcal{X}}\setminus{N}, r\in\mathbb{R}} \}} ) $ for some
$D = \text{span} ( { \{ {\pi} \}\cup \{ {\delta_x\,{:}\, x\in {\mathcal{X}}\setminus{N}, r\in\mathbb{R}} \}} ) $ for some ![]() $\pi$-null set N. The null set N can be taken to be the same for all factors
$\pi$-null set N. The null set N can be taken to be the same for all factors ![]() $\rho$ by taking the union over the null sets for factors
$\rho$ by taking the union over the null sets for factors ![]() $\rho\in\mathbb{Q}$ (since a countable union of null sets is still null).
$\rho\in\mathbb{Q}$ (since a countable union of null sets is still null).
Lemma 1. (Characterization of optimal rates for ![]() $(V, \vert{\kern-0.25ex{ \vert{\kern-0.25ex{ \vert {\cdot} \vert}\kern-0.25ex}\vert}\kern-0.25ex}\vert)$-GE chains) If P is
$(V, \vert{\kern-0.25ex{ \vert{\kern-0.25ex{ \vert {\cdot} \vert}\kern-0.25ex}\vert}\kern-0.25ex}\vert)$-GE chains) If P is ![]() $(V, \vert{\kern-0.25ex{ \vert{\kern-0.25ex{ \vert {\cdot} \vert}\kern-0.25ex}\vert}\kern-0.25ex}\vert)$-GE with stationary measure
$(V, \vert{\kern-0.25ex{ \vert{\kern-0.25ex{ \vert {\cdot} \vert}\kern-0.25ex}\vert}\kern-0.25ex}\vert)$-GE with stationary measure ![]() $\pi$, then the optimal rate for
$\pi$, then the optimal rate for ![]() $(V, \vert{\kern-0.25ex{ \vert{\kern-0.25ex{ \vert {\cdot} \vert}\kern-0.25ex}\vert}\kern-0.25ex}\vert)$-GE is equal to
$(V, \vert{\kern-0.25ex{ \vert{\kern-0.25ex{ \vert {\cdot} \vert}\kern-0.25ex}\vert}\kern-0.25ex}\vert)$-GE is equal to
The proof of this result is found in Appendix D.
Remark 4. The quantity ![]() $\limsup_{n\to\infty} \vert{\kern-0.25ex{ \vert{\kern-0.25ex{ \vert {\mu P^n -\pi} \vert}\kern-0.25ex}\vert}\kern-0.25ex}\vert^{1/n}$ is the local spectral radius of
$\limsup_{n\to\infty} \vert{\kern-0.25ex{ \vert{\kern-0.25ex{ \vert {\mu P^n -\pi} \vert}\kern-0.25ex}\vert}\kern-0.25ex}\vert^{1/n}$ is the local spectral radius of ![]() $P-\Pi$ at
$P-\Pi$ at ![]() $\mu$ with respect to
$\mu$ with respect to ![]() $ \vert{\kern-0.25ex{ \vert{\kern-0.25ex{ \vert {\cdot} \vert}\kern-0.25ex}\vert}\kern-0.25ex}\vert$, where
$ \vert{\kern-0.25ex{ \vert{\kern-0.25ex{ \vert {\cdot} \vert}\kern-0.25ex}\vert}\kern-0.25ex}\vert$, where ![]() $\Pi$ is the rank-1 kernel defined by
$\Pi$ is the rank-1 kernel defined by ![]() $\Pi(x,A) = \pi(A)$ for all
$\Pi(x,A) = \pi(A)$ for all ![]() $x\in{\mathcal{X}}$ and
$x\in{\mathcal{X}}$ and ![]() $A\in \Sigma$.
$A\in \Sigma$.
Lemma 2. (![]() $L_2(\pi)$-GE,
$L_2(\pi)$-GE, ![]() $(L_\infty(\pi), \Vert {\cdot} \Vert_{L_2(\pi)})$-GE, and
$(L_\infty(\pi), \Vert {\cdot} \Vert_{L_2(\pi)})$-GE, and ![]() $(L_\infty(\pi), \Vert {\cdot} \Vert_{L_1(\pi)})$-GE are equivalent for
$(L_\infty(\pi), \Vert {\cdot} \Vert_{L_1(\pi)})$-GE are equivalent for ![]() $\pi$-reversible chains, with equal optimal rates) Let
$\pi$-reversible chains, with equal optimal rates) Let ![]() $\rho\in[0,1)$. The following are equivalent for a
$\rho\in[0,1)$. The following are equivalent for a ![]() $\pi$-reversible Markov chain P:
$\pi$-reversible Markov chain P:
(i) P is
 $(L_\infty(\pi), \Vert {\cdot} \Vert_{L_1(\pi)})$-GE with optimal rate
$(L_\infty(\pi), \Vert {\cdot} \Vert_{L_1(\pi)})$-GE with optimal rate  $\rho$.
$\rho$.-
(ii) P is
 $(L_\infty(\pi), \Vert {\cdot} \Vert_{L_2(\pi)})$-GE with optimal rate
$(L_\infty(\pi), \Vert {\cdot} \Vert_{L_2(\pi)})$-GE with optimal rate  $\rho$.
$\rho$. -
(iii) P is
 $L_2(\pi)$-GE with optimal rate
$L_2(\pi)$-GE with optimal rate  $\rho$.
$\rho$. -
(iv) The spectral radius of
 $P\vert_{{L_{2,0}(\pi)}}$ is equal to
$P\vert_{{L_{2,0}(\pi)}}$ is equal to  $\rho$.
$\rho$.
Remark 5. Since either of (iii) or (iv) is equivalent to all the conditions listed in [Reference Roberts and Rosenthal29, Theorem 2.1], indeed all the items listed above are equivalent to all the items listed in their result. We only included (iii) and (iv) here for brevity, since these are the conditions most relevant to the present paper. Moreover, all of these conditions are implied by any of the equivalent conditions for ![]() $\pi$-a.e.-TV-GE in [Reference Roberts and Rosenthal29, Proposition 2.1] (though with possibly different optimal rates for each condition therein). The proof of this result is found in Appendix D.
$\pi$-a.e.-TV-GE in [Reference Roberts and Rosenthal29, Proposition 2.1] (though with possibly different optimal rates for each condition therein). The proof of this result is found in Appendix D.
Theorem 1 controls the convergence of the perturbed chain ![]() $P_\epsilon$ in terms of the ‘original’ norm (from
$P_\epsilon$ in terms of the ‘original’ norm (from ![]() $L_2(\pi)$). We also demonstrate that
$L_2(\pi)$). We also demonstrate that ![]() $P_\epsilon$ is geometrically ergodic in the
$P_\epsilon$ is geometrically ergodic in the ![]() $L_2(\pi_\epsilon)$ norm, as this would also allow us to use the equivalences in [Reference Roberts and Rosenthal29]. The following two results allow us to transfer the geometric ergodicity of
$L_2(\pi_\epsilon)$ norm, as this would also allow us to use the equivalences in [Reference Roberts and Rosenthal29]. The following two results allow us to transfer the geometric ergodicity of ![]() $P_\epsilon$ in
$P_\epsilon$ in ![]() $L_2(\pi)$ to other notions of geometric ergodicity. Theorem 3 handles the case that the perturbed kernel is reversible, while Theorem 2 handles both the case that the perturbed kernel is reversible and the case that it is non-reversible.
$L_2(\pi)$ to other notions of geometric ergodicity. Theorem 3 handles the case that the perturbed kernel is reversible, while Theorem 2 handles both the case that the perturbed kernel is reversible and the case that it is non-reversible.
Theorem 2. (Geometric ergodicity of the perturbed chain in the other norms: ![]() $L_1(\pi_\epsilon)$,
$L_1(\pi_\epsilon)$, ![]() $L_2(\pi_\epsilon)$, total variation) Under the assumptions of Section 3.2, if
$L_2(\pi_\epsilon)$, total variation) Under the assumptions of Section 3.2, if ![]() $\epsilon<\alpha$, then the following hold:
$\epsilon<\alpha$, then the following hold:
(i)
 $P_\epsilon$ is a.e.-TV-GE with some factor
$P_\epsilon$ is a.e.-TV-GE with some factor  $\rho_{\text{TV}} \in (0,1)$.
$\rho_{\text{TV}} \in (0,1)$.-
(ii)
 $P_\epsilon$ is
$P_\epsilon$ is  $(L_\infty(\pi_\epsilon), \Vert {\cdot} \Vert_{L_1(\pi_\epsilon)})$-GE with factor
$(L_\infty(\pi_\epsilon), \Vert {\cdot} \Vert_{L_1(\pi_\epsilon)})$-GE with factor  $\rho_1=(1-(\alpha-\epsilon))$ and with
$\rho_1=(1-(\alpha-\epsilon))$ and with  $C_1(\mu) = \Vert {\mu-\pi_\epsilon}\Vert_{L_2(\pi)} $.
$C_1(\mu) = \Vert {\mu-\pi_\epsilon}\Vert_{L_2(\pi)} $. -
(iii) If
 $\pi\in L_\infty(\pi_\epsilon)$ then
$\pi\in L_\infty(\pi_\epsilon)$ then  $P_\epsilon$ is
$P_\epsilon$ is  $L_2(\pi_\epsilon)$-GE with factor
$L_2(\pi_\epsilon)$-GE with factor  $\rho_2=(1-(\alpha-\epsilon))$ and with
$\rho_2=(1-(\alpha-\epsilon))$ and with
 \begin{align*}C_2(\mu) = \Vert {\pi} \Vert_{L_\infty(\pi_\epsilon)}^{1/2} \Vert {\mu-\pi}\Vert_{L_2(\pi)} \ .\end{align*}
\begin{align*}C_2(\mu) = \Vert {\pi} \Vert_{L_\infty(\pi_\epsilon)}^{1/2} \Vert {\mu-\pi}\Vert_{L_2(\pi)} \ .\end{align*}
The proof of this result is found in Appendix A.2.
Example 1. For example, consider perturbations of a Gaussian ![]() $\text{AR}(1)$ process. Let
$\text{AR}(1)$ process. Let ![]() $Z_i{\stackrel{{iid}}{\sim{\mathcal{N}}}}(0,\sigma^2)$ and let
$Z_i{\stackrel{{iid}}{\sim{\mathcal{N}}}}(0,\sigma^2)$ and let ![]() $W_i{\stackrel{{iid}}\sim{\mu}}$. Take
$W_i{\stackrel{{iid}}\sim{\mu}}$. Take
Then the original chain ![]() $ \{ {X_t} \}_{t\in\mathbb{N}}$ is not uniformly ergodic, but it is geometrically ergodic. Hence, the results of [Reference Alquier, Friel, Everitt and Boland1,Reference Johndrow, Mattingly, Mukherjee and Dunson18] do not apply. The stationary measure of the exact chain is
$ \{ {X_t} \}_{t\in\mathbb{N}}$ is not uniformly ergodic, but it is geometrically ergodic. Hence, the results of [Reference Alquier, Friel, Everitt and Boland1,Reference Johndrow, Mattingly, Mukherjee and Dunson18] do not apply. The stationary measure of the exact chain is
it is reversible, and the rate of geometric ergodicity is ![]() $(1-\alpha)$. Note that the perturbed chain, which we will call a
$(1-\alpha)$. Note that the perturbed chain, which we will call a ![]() $\mu\text{AR}(1)$ process, may not be reversible, and whether it is geometrically ergodic generally depends on the distribution
$\mu\text{AR}(1)$ process, may not be reversible, and whether it is geometrically ergodic generally depends on the distribution ![]() $\mu$.
$\mu$.
Now, letting ![]() $\phi_{\sigma^2}$ be the
$\phi_{\sigma^2}$ be the ![]() $\mathcal{N}(0,\sigma^2)$ density, for any
$\mathcal{N}(0,\sigma^2)$ density, for any ![]() $\mu$ with
$\mu$ with ![]() ${\frac{{\textrm{d}}\mu}{\textrm{d} \phi_{\sigma^2}}}\in [1-\epsilon,1+\epsilon]$,
${\frac{{\textrm{d}}\mu}{\textrm{d} \phi_{\sigma^2}}}\in [1-\epsilon,1+\epsilon]$,
 \begin{equation}\begin{aligned} \Vert {P - P_\epsilon}\Vert_{L_2(\pi)} ^2 & = \int_{-\infty}^\infty \int_{-\infty}^\infty \left( { \frac{\mu(y-(1-\alpha)x)}{\pi(y)} - \frac{\phi_{\sigma^2}(y-(1-\alpha)x)}{\pi(y)}} \right)^2 \pi(y)dy\ \pi(x)dx \\[3pt] & \leq \int_{-\infty}^\infty\int_{-\infty}^\infty \epsilon^2 \left( {\frac{\phi_{\sigma^2}(y-(1-\alpha)x)}{\pi(y)} dy} \right)^2 \pi(y)dy\ \pi(x)dx \\[3pt] & = \epsilon^2 \Vert {P}\Vert_{L_2(\pi)} \\[3pt] & = \epsilon^2. \end{aligned}\end{equation}
\begin{equation}\begin{aligned} \Vert {P - P_\epsilon}\Vert_{L_2(\pi)} ^2 & = \int_{-\infty}^\infty \int_{-\infty}^\infty \left( { \frac{\mu(y-(1-\alpha)x)}{\pi(y)} - \frac{\phi_{\sigma^2}(y-(1-\alpha)x)}{\pi(y)}} \right)^2 \pi(y)dy\ \pi(x)dx \\[3pt] & \leq \int_{-\infty}^\infty\int_{-\infty}^\infty \epsilon^2 \left( {\frac{\phi_{\sigma^2}(y-(1-\alpha)x)}{\pi(y)} dy} \right)^2 \pi(y)dy\ \pi(x)dx \\[3pt] & = \epsilon^2 \Vert {P}\Vert_{L_2(\pi)} \\[3pt] & = \epsilon^2. \end{aligned}\end{equation}
Therefore, when ![]() $\epsilon<\alpha$ we can extend the geometric ergodicity of the Gaussian AR process to the
$\epsilon<\alpha$ we can extend the geometric ergodicity of the Gaussian AR process to the ![]() $\mu-\text{AR}(1)$ process using Theorem 2. We can also bound the discrepancy of the stationary measure of the perturbed chain from that
$\mu-\text{AR}(1)$ process using Theorem 2. We can also bound the discrepancy of the stationary measure of the perturbed chain from that ![]() $\mathcal{N}(0,\frac{\sigma^2}{\alpha(2-\alpha)})$ using Theorem 1. The subsequent results, Corollary 1 and Theorem 4 of this section, may also be applied to this example to bound the discrepancy between the marginal distributions of the
$\mathcal{N}(0,\frac{\sigma^2}{\alpha(2-\alpha)})$ using Theorem 1. The subsequent results, Corollary 1 and Theorem 4 of this section, may also be applied to this example to bound the discrepancy between the marginal distributions of the ![]() $\mu\hbox{-}\text{AR}(1)$ from an
$\mu\hbox{-}\text{AR}(1)$ from an ![]() $\mathcal{N}(0,\frac{\sigma^2}{\alpha(2-\alpha)})$ at any time, as well as the approximation error of the time-averaged law of the
$\mathcal{N}(0,\frac{\sigma^2}{\alpha(2-\alpha)})$ at any time, as well as the approximation error of the time-averaged law of the ![]() $\mu\hbox{-}\text{AR}(1)$ from
$\mu\hbox{-}\text{AR}(1)$ from ![]() $\mathcal{N}(0,\frac{\sigma^2}{\alpha(2-\alpha)})$.
$\mathcal{N}(0,\frac{\sigma^2}{\alpha(2-\alpha)})$.
Theorem 3. (![]() $L_2(\pi_\epsilon)$-GE of the perturbed chain, reversible case.) Under the assumptions of Section 3.2, if
$L_2(\pi_\epsilon)$-GE of the perturbed chain, reversible case.) Under the assumptions of Section 3.2, if ![]() $\epsilon<\alpha$ and
$\epsilon<\alpha$ and ![]() $P_\epsilon$ is
$P_\epsilon$ is ![]() $\pi_\epsilon$-reversible, then
$\pi_\epsilon$-reversible, then ![]() $P_\epsilon$ is
$P_\epsilon$ is ![]() $L_2(\pi_\epsilon)$-GE with factor
$L_2(\pi_\epsilon)$-GE with factor ![]() $\rho_2 = (1 - \alpha + \epsilon)$ and coefficient function
$\rho_2 = (1 - \alpha + \epsilon)$ and coefficient function ![]() $C(\nu) = \Vert {{\nu}}\Vert_{L_2(\pi_\epsilon)} $. The proof of this result is found in Appendix A.2.
$C(\nu) = \Vert {{\nu}}\Vert_{L_2(\pi_\epsilon)} $. The proof of this result is found in Appendix A.2.
Corollary 1. (Closeness of stationary distributions in ![]() $L_2(\pi_\epsilon)$.) If
$L_2(\pi_\epsilon)$.) If ![]() $\epsilon < \alpha$ and
$\epsilon < \alpha$ and ![]() $ \Vert {P-P_\epsilon} \Vert_{L_2(\pi_\epsilon)} \leq \varphi$, then the following hold:
$ \Vert {P-P_\epsilon} \Vert_{L_2(\pi_\epsilon)} \leq \varphi$, then the following hold:
(i) If
 $P_\epsilon$ is
$P_\epsilon$ is  $\pi_\epsilon$ reversible and
$\pi_\epsilon$ reversible and  $\varphi<\alpha-\epsilon$, then
and for any
$\varphi<\alpha-\epsilon$, then
and for any \begin{align*} \Vert {{\pi-\pi_\epsilon}}\Vert_{L_2(\pi_\epsilon)} \leq \frac{\varphi}{\sqrt{(\alpha-\epsilon)^2-\varphi^2}} \ ,\end{align*}
\begin{align*} \Vert {{\pi-\pi_\epsilon}}\Vert_{L_2(\pi_\epsilon)} \leq \frac{\varphi}{\sqrt{(\alpha-\epsilon)^2-\varphi^2}} \ ,\end{align*}
 $\mu\in L_2(\pi_\epsilon)$,
$\mu\in L_2(\pi_\epsilon)$,
 \begin{align*} \Vert {{ \mu P_\epsilon^n -\pi}}\Vert_{L_2(\pi_\epsilon)} & \leq (1-(\alpha-\epsilon))^n \Vert {{\mu-\pi_\epsilon}}\Vert_{L_2(\pi_\epsilon)} + \frac{\varphi}{\sqrt{(\alpha-\epsilon)^2-\varphi^2}} \ .\end{align*}
\begin{align*} \Vert {{ \mu P_\epsilon^n -\pi}}\Vert_{L_2(\pi_\epsilon)} & \leq (1-(\alpha-\epsilon))^n \Vert {{\mu-\pi_\epsilon}}\Vert_{L_2(\pi_\epsilon)} + \frac{\varphi}{\sqrt{(\alpha-\epsilon)^2-\varphi^2}} \ .\end{align*}
-
(ii) If
 $\pi\in L_\infty(\pi_\epsilon)$ and
$\pi\in L_\infty(\pi_\epsilon)$ and  $\varphi<1$, then
and for any
$\varphi<1$, then
and for any \begin{align*} \Vert {{\pi-\pi_\epsilon}}\Vert_{L_2(\pi_\epsilon)} \leq \frac{\varphi + \Vert {\pi} \Vert_{L_\infty(\pi_\epsilon)}^{1/2}\frac{\epsilon}{\sqrt{\alpha^2-\epsilon^2}}(1-(\alpha-\epsilon))}{1-\varphi} \ ,\end{align*}
\begin{align*} \Vert {{\pi-\pi_\epsilon}}\Vert_{L_2(\pi_\epsilon)} \leq \frac{\varphi + \Vert {\pi} \Vert_{L_\infty(\pi_\epsilon)}^{1/2}\frac{\epsilon}{\sqrt{\alpha^2-\epsilon^2}}(1-(\alpha-\epsilon))}{1-\varphi} \ ,\end{align*}
 $\mu\in L_\infty(\pi_\epsilon)$,
$\mu\in L_\infty(\pi_\epsilon)$,
 \begin{align*} \Vert {{ \mu P_\epsilon^n -\pi}}\Vert_{L_2(\pi_\epsilon)} & \leq (1-(\alpha-\epsilon))^n \Vert {\pi} \Vert_{L_\infty(\pi_\epsilon)}^{1/2} \Vert {{\mu-\pi_\epsilon}}\Vert_{L_2(\pi_\epsilon)} \\[3pt] &\qquad + \frac{\varphi + \Vert {\pi} \Vert_{L_\infty(\pi_\epsilon)}^{1/2}\frac{\epsilon}{\sqrt{\alpha^2-\epsilon^2}}(1-(\alpha-\epsilon))}{1-\varphi} \ .\end{align*}
\begin{align*} \Vert {{ \mu P_\epsilon^n -\pi}}\Vert_{L_2(\pi_\epsilon)} & \leq (1-(\alpha-\epsilon))^n \Vert {\pi} \Vert_{L_\infty(\pi_\epsilon)}^{1/2} \Vert {{\mu-\pi_\epsilon}}\Vert_{L_2(\pi_\epsilon)} \\[3pt] &\qquad + \frac{\varphi + \Vert {\pi} \Vert_{L_\infty(\pi_\epsilon)}^{1/2}\frac{\epsilon}{\sqrt{\alpha^2-\epsilon^2}}(1-(\alpha-\epsilon))}{1-\varphi} \ .\end{align*}
The proof of this result is found in Appendix A.2. We turn our attention to bounds on the error of estimation measures of the form ![]() $\frac{1}{t} \sum_{k=0}^{t-1} \mu P^k$, and estimates of the form
$\frac{1}{t} \sum_{k=0}^{t-1} \mu P^k$, and estimates of the form ![]() $\frac{1}{t} \sum_{k=0}^{t-1} f(X_k)$. Firstly, when computing Monte Carlo estimates, the bias is controlled by a time-averaged marginal distribution of the form
$\frac{1}{t} \sum_{k=0}^{t-1} f(X_k)$. Firstly, when computing Monte Carlo estimates, the bias is controlled by a time-averaged marginal distribution of the form ![]() $\frac{1}{t}\sum_{k=0}^{t-1} \mu P_\epsilon^k $. This leads us to the following result.
$\frac{1}{t}\sum_{k=0}^{t-1} \mu P_\epsilon^k $. This leads us to the following result.
Theorem 4. (Convergence of time-averaged marginal distributions) Under the assumptions of Section 3.2, suppose ![]() $\epsilon<\alpha$ and
$\epsilon<\alpha$ and ![]() $\pi_\epsilon\in L_2(\pi)$. Then for any probability distribution
$\pi_\epsilon\in L_2(\pi)$. Then for any probability distribution ![]() $\mu\in L_2(\pi)$,
$\mu\in L_2(\pi)$,
 \begin{align*} \bigg\Vert {\pi -\frac{1}{t}\sum_{k=0}^{t-1} \mu P_\epsilon^k}\bigg\Vert_{L_2(\pi)} & \leq \frac{1-(1-(\alpha-\epsilon))^t}{t(\alpha-\epsilon)} \Vert { \pi_\epsilon-\mu}\Vert_{L_2(\pi)} +\frac{\epsilon}{\sqrt{\alpha^2-\epsilon^2}}.\end{align*}
\begin{align*} \bigg\Vert {\pi -\frac{1}{t}\sum_{k=0}^{t-1} \mu P_\epsilon^k}\bigg\Vert_{L_2(\pi)} & \leq \frac{1-(1-(\alpha-\epsilon))^t}{t(\alpha-\epsilon)} \Vert { \pi_\epsilon-\mu}\Vert_{L_2(\pi)} +\frac{\epsilon}{\sqrt{\alpha^2-\epsilon^2}}.\end{align*}
If additionally ![]() $ \Vert {P-P_\epsilon} \Vert_{L_2(\pi_\epsilon)} \leq \varphi$, then the following hold:
$ \Vert {P-P_\epsilon} \Vert_{L_2(\pi_\epsilon)} \leq \varphi$, then the following hold:
(i) If
 $P_\epsilon$ is
$P_\epsilon$ is  $\pi_\epsilon$-reversible and
$\pi_\epsilon$-reversible and  $\varphi<\alpha-\epsilon$, then
$\varphi<\alpha-\epsilon$, then
 \begin{align*} \bigg\Vert {{\pi -\frac{1}{t}\sum_{k=0}^{t-1} \mu P_\epsilon^k}}\bigg\Vert_{L_2(\pi_\epsilon)} &\leq \frac{1-(1-(\alpha-\epsilon))^t}{t(\alpha-\epsilon)} \Vert {{ \pi_\epsilon-\mu}}\Vert_{L_2(\pi_\epsilon)} +\frac{\varphi}{\sqrt{(\alpha-\epsilon)^2-\varphi^2}} \ .\end{align*}
\begin{align*} \bigg\Vert {{\pi -\frac{1}{t}\sum_{k=0}^{t-1} \mu P_\epsilon^k}}\bigg\Vert_{L_2(\pi_\epsilon)} &\leq \frac{1-(1-(\alpha-\epsilon))^t}{t(\alpha-\epsilon)} \Vert {{ \pi_\epsilon-\mu}}\Vert_{L_2(\pi_\epsilon)} +\frac{\varphi}{\sqrt{(\alpha-\epsilon)^2-\varphi^2}} \ .\end{align*}
-
(ii) If
 $\pi\in L_\infty(\pi_\epsilon)$ and
$\pi\in L_\infty(\pi_\epsilon)$ and  $\varphi<1$, and if
$\varphi<1$, and if  $\mu\in L_\infty(\pi_\epsilon)$, then
$\mu\in L_\infty(\pi_\epsilon)$, then
 \begin{align*} \bigg\Vert {{\pi -\frac{1}{t}\sum_{k=0}^{t-1} \mu P_\epsilon^k}}\bigg\Vert_{L_2(\pi_\epsilon)} &\leq \frac{1-(1-(\alpha-\epsilon))^t}{t(\alpha-\epsilon)} \Vert {\pi} \Vert_{L_\infty(\pi_\epsilon)}^{1/2} \Vert {{ \pi_\epsilon-\mu}}\Vert_{L_2(\pi_\epsilon)} \\[3pt] &\qquad +\frac{\varphi + \Vert {\pi} \Vert_{L_\infty(\pi_\epsilon)}^{1/2}\frac{\epsilon}{\sqrt{\alpha^2-\epsilon^2}}(1-(\alpha-\epsilon))}{1-\varphi}.\end{align*}
\begin{align*} \bigg\Vert {{\pi -\frac{1}{t}\sum_{k=0}^{t-1} \mu P_\epsilon^k}}\bigg\Vert_{L_2(\pi_\epsilon)} &\leq \frac{1-(1-(\alpha-\epsilon))^t}{t(\alpha-\epsilon)} \Vert {\pi} \Vert_{L_\infty(\pi_\epsilon)}^{1/2} \Vert {{ \pi_\epsilon-\mu}}\Vert_{L_2(\pi_\epsilon)} \\[3pt] &\qquad +\frac{\varphi + \Vert {\pi} \Vert_{L_\infty(\pi_\epsilon)}^{1/2}\frac{\epsilon}{\sqrt{\alpha^2-\epsilon^2}}(1-(\alpha-\epsilon))}{1-\varphi}.\end{align*}
The proof of this result is found in Appendix A.3.1. Relative to the uniform closeness of kernels (in total variation) required in [Reference Johndrow, Mattingly, Mukherjee and Dunson18], our assumption that the approximating kernel is close in the operator norm induced by ![]() $L_2(\pi)$ is non-comparable. This is because our bound is in terms of the
$L_2(\pi)$ is non-comparable. This is because our bound is in terms of the ![]() $L_2$ distance, which always upper-bounds the total variation distance (up to a constant factor of
$L_2$ distance, which always upper-bounds the total variation distance (up to a constant factor of ![]() $1/2$), but our assumption also does not require spatial uniformity, which that of [Reference Johndrow, Mattingly, Mukherjee and Dunson18] does. Thus, this paper’s assumptions are neither weaker nor stronger than those in [Reference Johndrow, Mattingly, Mukherjee and Dunson18]. Comparing the above results to the corresponding
$1/2$), but our assumption also does not require spatial uniformity, which that of [Reference Johndrow, Mattingly, Mukherjee and Dunson18] does. Thus, this paper’s assumptions are neither weaker nor stronger than those in [Reference Johndrow, Mattingly, Mukherjee and Dunson18]. Comparing the above results to the corresponding ![]() $L_1$ result of [Reference Johndrow, Mattingly, Mukherjee and Dunson18], we see that the transient phase bias part of our
$L_1$ result of [Reference Johndrow, Mattingly, Mukherjee and Dunson18], we see that the transient phase bias part of our ![]() $L_2$ bounds differ from the
$L_2$ bounds differ from the ![]() $L_1$ transient phase bias bound of [Reference Johndrow, Mattingly, Mukherjee and Dunson18] only by a factor which is constant in time, but varies with the initial distribution (as is to be expected when moving from uniform ergodicity to geometric ergodicity).
$L_1$ transient phase bias bound of [Reference Johndrow, Mattingly, Mukherjee and Dunson18] only by a factor which is constant in time, but varies with the initial distribution (as is to be expected when moving from uniform ergodicity to geometric ergodicity).
3.4. Mean squared error bounds for Monte Carlo estimates
Suppose that ![]() $ ( {X^\epsilon_k} )_{k\in{\mathbb{N}\cup{\{0\}}}}$ is a realization of the Markov chain with transition kernel
$ ( {X^\epsilon_k} )_{k\in{\mathbb{N}\cup{\{0\}}}}$ is a realization of the Markov chain with transition kernel ![]() $P_\epsilon$ and initial distribution
$P_\epsilon$ and initial distribution ![]() $\mu$. The mean squared error of a Monte Carlo estimate of
$\mu$. The mean squared error of a Monte Carlo estimate of ![]() $\pi f$ made using
$\pi f$ made using ![]() $ ( {X^\epsilon_k} )_{k\leq t}$ is given by
$ ( {X^\epsilon_k} )_{k\leq t}$ is given by
 \begin{equation}\begin{aligned} {MSE}^{{\epsilon}}_{{t}} ( {{\mu},{f}} ) & = \mathbb{E}\left[\left(\pi(f) - \frac{1}{t}\sum_{k=0}^{t-1} f(X^\epsilon_k)\right)^2\right].\end{aligned}\end{equation}
\begin{equation}\begin{aligned} {MSE}^{{\epsilon}}_{{t}} ( {{\mu},{f}} ) & = \mathbb{E}\left[\left(\pi(f) - \frac{1}{t}\sum_{k=0}^{t-1} f(X^\epsilon_k)\right)^2\right].\end{aligned}\end{equation}
Theorem 5. (Mean squared error of Monte Carlo estimates from the perturbed chain) Under the assumptions of Section 3.2, if ![]() $\epsilon<\alpha$,
$\epsilon<\alpha$, ![]() $X^\epsilon_0\sim\mu$,
$X^\epsilon_0\sim\mu$, ![]() $P_\epsilon$ is
$P_\epsilon$ is ![]() $\pi_\epsilon$-reversible, and
$\pi_\epsilon$-reversible, and ![]() $\rho_2 = (1-(\alpha-\epsilon))$, then for
$\rho_2 = (1-(\alpha-\epsilon))$, then for ![]() $f\in L^{\prime}_4(\pi_\epsilon)$,
$f\in L^{\prime}_4(\pi_\epsilon)$,
(i) if
 $f\in L_2^{\prime}(\pi)$ as well, then
and
$f\in L_2^{\prime}(\pi)$ as well, then
and \begin{align*} {MSE}^{{\epsilon}}_{{t}} ( {{\mu},{f}} ) &\leq \frac{2 \Vert {{ f - \pi_\epsilon f}}\Vert_{L^{\prime}_2(\pi_\epsilon)} ^2}{(1-\rho_2) t} + \frac{2^{7/2} \Vert {{ \mu -\pi_\epsilon}}\Vert_{L_2(\pi_\epsilon)} \Vert {f -\pi_\epsilon f } \Vert_{L_4^{\prime}(\pi_\epsilon)}^2}{(1-\rho_2)^2 t^2} \\ & \qquad + \Vert {{f-\pi_\epsilon f}}\Vert_{L^{\prime}_2(\pi)} ^2\left({\frac{\epsilon^2}{\alpha^2 - \epsilon^2} + 2\frac{\epsilon}{\sqrt{\alpha^2 - \epsilon^2}}\frac{1}{t(\alpha-\epsilon)} \Vert {\pi_\epsilon-\mu}\Vert_{L_2(\pi)} } \right) \end{align*}
\begin{align*} {MSE}^{{\epsilon}}_{{t}} ( {{\mu},{f}} ) &\leq \frac{2 \Vert {{ f - \pi_\epsilon f}}\Vert_{L^{\prime}_2(\pi_\epsilon)} ^2}{(1-\rho_2) t} + \frac{2^{7/2} \Vert {{ \mu -\pi_\epsilon}}\Vert_{L_2(\pi_\epsilon)} \Vert {f -\pi_\epsilon f } \Vert_{L_4^{\prime}(\pi_\epsilon)}^2}{(1-\rho_2)^2 t^2} \\ & \qquad + \Vert {{f-\pi_\epsilon f}}\Vert_{L^{\prime}_2(\pi)} ^2\left({\frac{\epsilon^2}{\alpha^2 - \epsilon^2} + 2\frac{\epsilon}{\sqrt{\alpha^2 - \epsilon^2}}\frac{1}{t(\alpha-\epsilon)} \Vert {\pi_\epsilon-\mu}\Vert_{L_2(\pi)} } \right) \end{align*}
 \begin{align*} {MSE}^{{\epsilon}}_{{t}} ( {{\mu},{f}} ) &\leq \frac{4 \Vert {{ f - \pi_\epsilon f}}\Vert_{L^{\prime}_2(\pi_\epsilon)} ^2}{(1-\rho_2) t} + \frac{2^{9/2} \Vert {{ \mu -\pi_\epsilon}}\Vert_{L_2(\pi_\epsilon)} \Vert {f -\pi_\epsilon f } \Vert_{L_4^{\prime}(\pi_\epsilon)}^2}{(1-\rho_2)^2 t^2} \\ &\qquad+ 2 \Vert {{f-\pi_\epsilon f}}\Vert_{L^{\prime}_2(\pi)} ^2\frac{\epsilon^2}{\alpha^2 - \epsilon^2} \ ; \end{align*}
\begin{align*} {MSE}^{{\epsilon}}_{{t}} ( {{\mu},{f}} ) &\leq \frac{4 \Vert {{ f - \pi_\epsilon f}}\Vert_{L^{\prime}_2(\pi_\epsilon)} ^2}{(1-\rho_2) t} + \frac{2^{9/2} \Vert {{ \mu -\pi_\epsilon}}\Vert_{L_2(\pi_\epsilon)} \Vert {f -\pi_\epsilon f } \Vert_{L_4^{\prime}(\pi_\epsilon)}^2}{(1-\rho_2)^2 t^2} \\ &\qquad+ 2 \Vert {{f-\pi_\epsilon f}}\Vert_{L^{\prime}_2(\pi)} ^2\frac{\epsilon^2}{\alpha^2 - \epsilon^2} \ ; \end{align*}
-
(ii) if
 $ \Vert {{P-P_\epsilon}}\Vert_{L_2(\pi_\epsilon)} \leq \varphi < (1-\rho_2)$, then
and
$ \Vert {{P-P_\epsilon}}\Vert_{L_2(\pi_\epsilon)} \leq \varphi < (1-\rho_2)$, then
and \begin{align*}{MSE}^{{\epsilon}}_{{t}} ( {{\mu},{f}} ) &\leq \frac{2^{7/2} \Vert {{ \mu -\pi_\epsilon}}\Vert_{L_2(\pi_\epsilon)} \Vert {f -\pi_\epsilon f } \Vert_{L_4^{\prime}(\pi_\epsilon)}^2}{(1-\rho_2)^2 t^2} \\
& \quad + { \Vert {{f-\pi_\epsilon f}}\Vert_{L^{\prime}_2(\pi_\epsilon)} ^2} .\!\bigg(\!{\frac{\varphi^2}{(1-\rho_2)^2 - \varphi^2}{+} 2\frac{1+\frac{\varphi}{\sqrt{(1-\rho_2)^2 {-} \varphi^2}}} {t(1-\rho_2)} \Vert {{ \pi_\epsilon{-}\mu}}\Vert_{L_2(\pi_\epsilon)} } \!\bigg)\!,\end{align*}
\begin{align*}{MSE}^{{\epsilon}}_{{t}} ( {{\mu},{f}} ) &\leq \frac{2^{7/2} \Vert {{ \mu -\pi_\epsilon}}\Vert_{L_2(\pi_\epsilon)} \Vert {f -\pi_\epsilon f } \Vert_{L_4^{\prime}(\pi_\epsilon)}^2}{(1-\rho_2)^2 t^2} \\
& \quad + { \Vert {{f-\pi_\epsilon f}}\Vert_{L^{\prime}_2(\pi_\epsilon)} ^2} .\!\bigg(\!{\frac{\varphi^2}{(1-\rho_2)^2 - \varphi^2}{+} 2\frac{1+\frac{\varphi}{\sqrt{(1-\rho_2)^2 {-} \varphi^2}}} {t(1-\rho_2)} \Vert {{ \pi_\epsilon{-}\mu}}\Vert_{L_2(\pi_\epsilon)} } \!\bigg)\!,\end{align*}
 \begin{align*}{MSE}^{{\epsilon}}_{{t}} ( {{\mu},{f}} ) &\leq \frac{2^{9/2} \Vert {{ \mu -\pi_\epsilon}}\Vert_{L_2(\pi_\epsilon)} \Vert {f -\pi_\epsilon f } \Vert_{L_4^{\prime}(\pi_\epsilon)}^2}{(1-\rho_2)^2 t^2} \\ & \quad + { \Vert {{f-\pi_\epsilon f}}\Vert_{L^{\prime}_2(\pi_\epsilon)} ^2}. \!\left(\!{\frac{2\varphi^2}{(1-\rho_2)^2 - \varphi^2}+ \frac{4} {t(1-\rho_2)} \Vert {{ \pi_\epsilon-\mu}}\Vert_{L_2(\pi_\epsilon)} }\!\right)\!.\end{align*}
\begin{align*}{MSE}^{{\epsilon}}_{{t}} ( {{\mu},{f}} ) &\leq \frac{2^{9/2} \Vert {{ \mu -\pi_\epsilon}}\Vert_{L_2(\pi_\epsilon)} \Vert {f -\pi_\epsilon f } \Vert_{L_4^{\prime}(\pi_\epsilon)}^2}{(1-\rho_2)^2 t^2} \\ & \quad + { \Vert {{f-\pi_\epsilon f}}\Vert_{L^{\prime}_2(\pi_\epsilon)} ^2}. \!\left(\!{\frac{2\varphi^2}{(1-\rho_2)^2 - \varphi^2}+ \frac{4} {t(1-\rho_2)} \Vert {{ \pi_\epsilon-\mu}}\Vert_{L_2(\pi_\epsilon)} }\!\right)\!.\end{align*}
The proof of this result is found in Appendix A.3.3. Perturbation bounds based upon drift and minorization conditions could provide similar mean squared error bounds for functions in ![]() $L_2(\pi_\epsilon)$ with
$L_2(\pi_\epsilon)$ with
(where V is the function appearing in the drift condition), as in [Reference Johndrow and Mattingly17]. While that may be a larger class of functions than ![]() $L_4^{\prime}(\pi_\epsilon)$ (depending on what V happens to be), the class
$L_4^{\prime}(\pi_\epsilon)$ (depending on what V happens to be), the class ![]() $L_4^{\prime}(\pi_\epsilon)$ is quite rich, making this bound still useful. Moreover, the class of functions to which our mean squared error bounds apply, and the value of the bound itself, depend only on intrinsic features of the Markov chains under consideration. In contrast, bounds based on drift and minorization conditions include extrinsic features—introduced by the user for analytic purposes (such as the drift function, V)—for which many choices might exist, each leading to different function classes and different bounds.
$L_4^{\prime}(\pi_\epsilon)$ is quite rich, making this bound still useful. Moreover, the class of functions to which our mean squared error bounds apply, and the value of the bound itself, depend only on intrinsic features of the Markov chains under consideration. In contrast, bounds based on drift and minorization conditions include extrinsic features—introduced by the user for analytic purposes (such as the drift function, V)—for which many choices might exist, each leading to different function classes and different bounds.
4. Applications to Markov chain Monte Carlo
In this section we apply our theoretical results to some specific variants of MCMC algorithms to obtain guarantees for noisy and/or approximate variants of MCMC algorithms. MCMC is used to generate (correlated) samples approximately from a target distribution for which the (unnormalized) density can be evaluated. The key insight is to construct a (typically reversible) Markov chain for which the stationary distribution is the target distribution. This is possible since the reversibility condition is readily verified locally (without integration).
The most commonly used family of MCMC methods is the Metropolis–Hastings (MH) algorithm. The chain is initialized from some distribution ![]() $X_0\sim \mu_0$. At each step a proposal is drawn from some transition kernel,
$X_0\sim \mu_0$. At each step a proposal is drawn from some transition kernel, ![]() $Y_t \sim Q(X_{t-1},\cdot)$. Suppose that the kernel
$Y_t \sim Q(X_{t-1},\cdot)$. Suppose that the kernel ![]() $Q(x,\cdot)$ has density
$Q(x,\cdot)$ has density ![]() $q(\cdot\vert x)$. The proposal is accepted with probability
$q(\cdot\vert x)$. The proposal is accepted with probability
If the proposal is accepted then ![]() $X_t = Y_t$, and if it is rejected (not accepted) then
$X_t = Y_t$, and if it is rejected (not accepted) then ![]() $X_t = X_{t-1}$. The combination of proposal and accept/reject steps yields a
$X_t = X_{t-1}$. The combination of proposal and accept/reject steps yields a ![]() $\pi$-reversible Markov kernel, and reversibility guarantees that the stationary distribution is the target distribution. The user has freedom in selecting the proposal kernel, Q, and some choices lead to better performance than others. The accept/reject step requires evaluating the target density,
$\pi$-reversible Markov kernel, and reversibility guarantees that the stationary distribution is the target distribution. The user has freedom in selecting the proposal kernel, Q, and some choices lead to better performance than others. The accept/reject step requires evaluating the target density, ![]() $\pi$, twice on each step.
$\pi$, twice on each step.
A large body of research exists guaranteeing that specific MCMC algorithms will be geometrically ergodic (see for example [Reference Hobert and Geyer13,Reference Livingstone, Betancourt, Byrne and Girolami22,Reference Roberts and Rosenthal30], and many more.). These typically verify geometric ergodicity for a collection of target distributions, ![]() $\pi$, and for a small family of proposal kernels, Q.
$\pi$, and for a small family of proposal kernels, Q.
If the target likelihood involves some integral which is computed numerically or by simple Monte Carlo, then the numerical and/or stochastic approximation introduces a perturbation to the idealized MCMC scheme. This occurs even in standard and widely used statistical models such as generalized linear mixed effect models (GLMMs), since the random effects are nuisance variables which need to be integrated away, either using Laplace or Gaussian quadrature schemes, or by simple Monte Carlo, in order to evaluate the likelihood. Since the MH algorithm requires evaluation of the density, these each introduce a perturbation in the acceptance ratio, and hence in the actual transition kernel of the MH scheme. We now consider the extent to which our results from Section 3 can be applied to prove geometric ergodicity for certain approximate MCMC algorithms.
4.1. Noisy and approximate MCMC
The noisy (or approximate) Metropolis–Hastings (nMH) algorithm, as found in [Reference Alquier, Friel, Everitt and Boland1] (see also [Reference Medina-Aguayo, Lee and Roberts25]), was briefly described above. The algorithm is defined exactly the same way as the MH algorithm, except that the acceptance ratio, ![]() $a(Y_t|X_{t-1})$, is replaced by a (possibly stochastic) approximation
$a(Y_t|X_{t-1})$, is replaced by a (possibly stochastic) approximation ![]() $\widehat a(Y_t|X_{t-1}, Z_t)$. Here
$\widehat a(Y_t|X_{t-1}, Z_t)$. Here ![]() $Z_t$ denotes some random element providing an additional source of randomness, so that
$Z_t$ denotes some random element providing an additional source of randomness, so that ![]() $a(Y_t|X_{t-1}, Z_t)$ is not
$a(Y_t|X_{t-1}, Z_t)$ is not ![]() $\sigma(Y_t, X_{t-1})$-measurable when the approximation
$\sigma(Y_t, X_{t-1})$-measurable when the approximation ![]() $\widehat a(Y_t|X_{t-1}, Z_t)$ is stochastic. In the case of a deterministic approximation,
$\widehat a(Y_t|X_{t-1}, Z_t)$ is stochastic. In the case of a deterministic approximation, ![]() $Z_t$ can be ignored or treated as a constant. The approximation can typically be thought of as replacing the target density in the acceptance ratio with some approximation. This includes most approximate MCMC algorithms which preserve the state space and the Markov property, such as those replacing
$Z_t$ can be ignored or treated as a constant. The approximation can typically be thought of as replacing the target density in the acceptance ratio with some approximation. This includes most approximate MCMC algorithms which preserve the state space and the Markov property, such as those replacing ![]() $\pi$ with a deterministic approximation or an independent stochastic approximation at each step (as in Monte Carlo within Metropolis). It does not include algorithms which retain the Markov property only for an augmented state space, such as the pseudo-marginal approach of [Reference Andrieu and Roberts2].
$\pi$ with a deterministic approximation or an independent stochastic approximation at each step (as in Monte Carlo within Metropolis). It does not include algorithms which retain the Markov property only for an augmented state space, such as the pseudo-marginal approach of [Reference Andrieu and Roberts2].
For our analysis of these algorithms, P will represent the transition kernel for the MH algorithm, while ![]() $\widehat P$ will represent the kernel for the corresponding nMH chain. The key step in applying our results from Section 3 will be to show the
$\widehat P$ will represent the kernel for the corresponding nMH chain. The key step in applying our results from Section 3 will be to show the ![]() $L_2(\pi)$ closeness of the nMH transition kernel to the MH transition kernel. Again,
$L_2(\pi)$ closeness of the nMH transition kernel to the MH transition kernel. Again, ![]() $ \Vert {\cdot}\Vert_{L_2(\pi)} $ is the norm on
$ \Vert {\cdot}\Vert_{L_2(\pi)} $ is the norm on ![]() $L_2(\pi)$ and the corresponding operator norm. We will assume that
$L_2(\pi)$ and the corresponding operator norm. We will assume that ![]() $\pi$ and
$\pi$ and ![]() $\{Q(x,\cdot)\}_{x\in {\mathcal{X}}}$ are all absolutely continuous with respect to the Lebesgue measure and have densities
$\{Q(x,\cdot)\}_{x\in {\mathcal{X}}}$ are all absolutely continuous with respect to the Lebesgue measure and have densities ![]() $\pi$ and
$\pi$ and ![]() $ \{ {q(\cdot\vert x)} \}_{x\in{\mathcal{X}}}$ respectively. All arguments used would still apply if there were an arbitrary dominating measure in place of the Lebesgue measure. Let
$ \{ {q(\cdot\vert x)} \}_{x\in{\mathcal{X}}}$ respectively. All arguments used would still apply if there were an arbitrary dominating measure in place of the Lebesgue measure. Let ![]() $F_{y\vert x}$ be the regular conditional distribution for Z given
$F_{y\vert x}$ be the regular conditional distribution for Z given ![]() $X=x$ and
$X=x$ and ![]() $Y=y$, and let
$Y=y$, and let ![]() $f_{y\vert x}$ be its Lebesgue density. Define the perturbation function for the nMH algorithm as
$f_{y\vert x}$ be its Lebesgue density. Define the perturbation function for the nMH algorithm as
Theorem 6. (Geometric ergodicity and closeness of stationary distributions for nMH) Let P be the transition kernel for an MH algorithm with proposal distribution Q, target distribution ![]() $\pi$, and acceptance ratio
$\pi$, and acceptance ratio ![]() $a(\cdot\vert \cdot)$. Let
$a(\cdot\vert \cdot)$. Let ![]() $\widehat P$ be the transition kernel for a corresponding nMH algorithm with approximate/noisy acceptance ratio
$\widehat P$ be the transition kernel for a corresponding nMH algorithm with approximate/noisy acceptance ratio ![]() $\widehat a(\cdot\vert \cdot, \cdot)$. Let
$\widehat a(\cdot\vert \cdot, \cdot)$. Let ![]() $r(\cdot\vert \cdot)$ be the corresponding perturbation function.
$r(\cdot\vert \cdot)$ be the corresponding perturbation function.
If ![]() $ \Vert {Q}\Vert_{L_2(\pi)} <\infty$ and
$ \Vert {Q}\Vert_{L_2(\pi)} <\infty$ and ![]() $\sup_{x,y} \vert {{r(y|x)}} \vert \leq R$, then
$\sup_{x,y} \vert {{r(y|x)}} \vert \leq R$, then
Furthermore, if P is reversible and ![]() $L_2(\pi)$-GE with geometric contraction factor
$L_2(\pi)$-GE with geometric contraction factor ![]() $(1-\alpha)$, and
$(1-\alpha)$, and ![]() $\epsilon = R (1+ \Vert {{Q}}\Vert_{L_2(\pi)} ) <\alpha$, then
$\epsilon = R (1+ \Vert {{Q}}\Vert_{L_2(\pi)} ) <\alpha$, then ![]() $\widehat P$ has a stationary distribution
$\widehat P$ has a stationary distribution ![]() $\widehat\pi$, and the assumptions outlined in Section 3.2 hold with
$\widehat\pi$, and the assumptions outlined in Section 3.2 hold with ![]() $P_\epsilon = \widehat P$ and
$P_\epsilon = \widehat P$ and ![]() $\pi_\epsilon =\widehat\pi$.
$\pi_\epsilon =\widehat\pi$.
Therefore, Theorems 1 to 5 and Corollary 1 can all be applied. In particular, ![]() $\widehat P$ is
$\widehat P$ is ![]() $L_2(\pi)$-GE with factor
$L_2(\pi)$-GE with factor ![]() $1-(\alpha-R (1+ \Vert {{Q}}\Vert_{L_2(\pi)} ))$, it is a.e.-TV-GE, and
$1-(\alpha-R (1+ \Vert {{Q}}\Vert_{L_2(\pi)} ))$, it is a.e.-TV-GE, and
 \begin{equation}\begin{aligned} \Vert {\widehat \pi - \pi}\Vert_{L_2(\pi)} \leq \frac{R (1+ \Vert {{Q}}\Vert_{L_2(\pi)} )}{\sqrt{\alpha^2 - R^2 (1+ \Vert {{Q}}\Vert_{L_2(\pi)} )^2}} \ ;\end{aligned}\end{equation}
\begin{equation}\begin{aligned} \Vert {\widehat \pi - \pi}\Vert_{L_2(\pi)} \leq \frac{R (1+ \Vert {{Q}}\Vert_{L_2(\pi)} )}{\sqrt{\alpha^2 - R^2 (1+ \Vert {{Q}}\Vert_{L_2(\pi)} )^2}} \ ;\end{aligned}\end{equation}
furthermore, if ![]() $\widehat P$ is reversible, then it is
$\widehat P$ is reversible, then it is ![]() $L_2(\widehat\pi)$-GE with factor
$L_2(\widehat\pi)$-GE with factor ![]() $(1-(\alpha-R (1+ \Vert {{Q}}\Vert_{L_2(\pi)} )))$.
$(1-(\alpha-R (1+ \Vert {{Q}}\Vert_{L_2(\pi)} )))$.
The above theorem provides an alternative to the analogous result of Corollary 2.3 from [Reference Alquier, Friel, Everitt and Boland1], relaxing the uniform ergodicity assumption. In particular, it requires that ![]() $Q\in\mathcal{B}(L_2(\pi))$ and that
$Q\in\mathcal{B}(L_2(\pi))$ and that ![]() $R(1+ \Vert {{Q}}\Vert_{L_2(\pi)} )<\alpha$. The first of these requirements is not dramatically limiting since the user has control over the choice of Q. The second requirement is also not dramatically limiting, as control over R may be interpreted as limiting the amount of noise in the nMH algorithm, and such control is required regardless in order to ensure the accuracy of approximation in both the geometrically ergodic and uniformly ergodic cases.
$R(1+ \Vert {{Q}}\Vert_{L_2(\pi)} )<\alpha$. The first of these requirements is not dramatically limiting since the user has control over the choice of Q. The second requirement is also not dramatically limiting, as control over R may be interpreted as limiting the amount of noise in the nMH algorithm, and such control is required regardless in order to ensure the accuracy of approximation in both the geometrically ergodic and uniformly ergodic cases.
4.2. Application to fixed deterministic approximations
Suppose we run a fixed MH algorithm, but replace the target density with one which is close everywhere. Perhaps this alternative density is easier to compute (e.g. replacing an integral with a Laplace approximation as in [Reference Kass, Tierney and Kadane19], or replacing a full sample with a coreset for sub-sampled Bayesian inference as in [Reference Campbell and Broderick8]). By construction we would know that the approximate target distribution is close to the ideal target distribution. The question still remains whether geometric ergodicity is preserved. We resolve this question in the case that the approximation has constant relative error.
Corollary 2. Suppose we can approximate the unnormalized target density, ![]() $C\pi$, by
$C\pi$, by ![]() $\widehat \pi$, with a
$\widehat \pi$, with a ![]() $\theta$-bounded relative error:
$\theta$-bounded relative error:
 \begin{equation}\begin{aligned} \sup\limits_{x\in{\mathcal{X}}} \vert {{\log\frac{C\pi(x)}{\widehat\pi(x)}}} \vert \leq \theta \ . \end{aligned}\end{equation}
\begin{equation}\begin{aligned} \sup\limits_{x\in{\mathcal{X}}} \vert {{\log\frac{C\pi(x)}{\widehat\pi(x)}}} \vert \leq \theta \ . \end{aligned}\end{equation}
If the MH algorithm with proposal kernel Q is ![]() $L_2(\pi)$-GE with factor
$L_2(\pi)$-GE with factor ![]() $(1-\alpha)$, and if
$(1-\alpha)$, and if
then the corresponding approximate transition kernel, ![]() $\hat P$, is
$\hat P$, is ![]() $L_2(\widehat \pi)$-GE, and
$L_2(\widehat \pi)$-GE, and
 \begin{equation}\begin{aligned} \Vert {{\widehat \pi - \pi}}\Vert_{L_2(\pi)} \leq \frac{2\theta (1+ \Vert {{Q}}\Vert_{L_2(\pi)} )}{\sqrt{\alpha^2 - 4\theta^2 (1+ \Vert {{Q}}\Vert_{L_2(\pi)} )^2}} \ . \end{aligned}\end{equation}
\begin{equation}\begin{aligned} \Vert {{\widehat \pi - \pi}}\Vert_{L_2(\pi)} \leq \frac{2\theta (1+ \Vert {{Q}}\Vert_{L_2(\pi)} )}{\sqrt{\alpha^2 - 4\theta^2 (1+ \Vert {{Q}}\Vert_{L_2(\pi)} )^2}} \ . \end{aligned}\end{equation}
Proof. Since the function ![]() $x\mapsto 1\wedge \exp(x)$ is 1-Lipschitz, we have
$x\mapsto 1\wedge \exp(x)$ is 1-Lipschitz, we have
 \begin{equation}\begin{aligned} \vert {{r(y\vert x)}} \vert & = \left\vert {{a(y\vert x) - \widehat a(y\vert x)}} \right\vert \\[3pt]
& \leq \left\vert {\log\frac{\pi(y)q(x\vert y)}{\pi(x)q(y\vert x)} - \log\frac{\widehat \pi(y)q(x\vert y)}{\widehat\pi(x)q(y\vert x)} } \right\vert \\[3pt]
& = \left\vert {{\log\frac{C\pi(y)}{\widehat \pi(y)} - \log\frac{C\pi(x)}{\widehat\pi(x) }}} \right\vert \\[3pt]
& \leq 2 \theta. \end{aligned}\end{equation}
\begin{equation}\begin{aligned} \vert {{r(y\vert x)}} \vert & = \left\vert {{a(y\vert x) - \widehat a(y\vert x)}} \right\vert \\[3pt]
& \leq \left\vert {\log\frac{\pi(y)q(x\vert y)}{\pi(x)q(y\vert x)} - \log\frac{\widehat \pi(y)q(x\vert y)}{\widehat\pi(x)q(y\vert x)} } \right\vert \\[3pt]
& = \left\vert {{\log\frac{C\pi(y)}{\widehat \pi(y)} - \log\frac{C\pi(x)}{\widehat\pi(x) }}} \right\vert \\[3pt]
& \leq 2 \theta. \end{aligned}\end{equation}
So ![]() $\widehat P$ will be
$\widehat P$ will be ![]() $L_2(\pi)$-GE as long as P was geometrically ergodic with some factor
$L_2(\pi)$-GE as long as P was geometrically ergodic with some factor ![]() $0\leq(1-\alpha)<1$ and
$0\leq(1-\alpha)<1$ and
 \begin{equation}\begin{aligned} \theta
< \frac{\alpha}{2(1+ \Vert {{Q}}\Vert_{L_2(\pi)} )} \ . \end{aligned}\end{equation}
\begin{equation}\begin{aligned} \theta
< \frac{\alpha}{2(1+ \Vert {{Q}}\Vert_{L_2(\pi)} )} \ . \end{aligned}\end{equation}
Moreover, in this case, ![]() $\widehat P$ is reversible. Thus, we can use Theorem 3 to obtain
$\widehat P$ is reversible. Thus, we can use Theorem 3 to obtain ![]() $L_2(\widehat \pi)$-GE of
$L_2(\widehat \pi)$-GE of ![]() $\widehat P$, with factor
$\widehat P$, with factor ![]() $1- \alpha + 2\theta(1+ \Vert {{Q}}\Vert_{L_2(\pi)} )$.
$1- \alpha + 2\theta(1+ \Vert {{Q}}\Vert_{L_2(\pi)} )$.
In this scenario, we can also use Theorem 5 to get quantitative bounds for the mean squared error of any Monte Carlo estimates made using ![]() $\widehat P$, or any of our other results in Theorems 1 to 4 and Corollary 1 as needed.
$\widehat P$, or any of our other results in Theorems 1 to 4 and Corollary 1 as needed.
Example 2. (Independence sampler.) The previous result also immediately gives that if ![]() ${\frac{{\textrm{d}}\widehat \pi}{\textrm{d} \pi}}$ is bounded above by
${\frac{{\textrm{d}}\widehat \pi}{\textrm{d} \pi}}$ is bounded above by ![]() $C<\exp(1/4)$ and below by
$C<\exp(1/4)$ and below by ![]() $c>\exp(-1/4)$, then the independence sampler for
$c>\exp(-1/4)$, then the independence sampler for ![]() $\widehat \pi$ with proposals from
$\widehat \pi$ with proposals from ![]() $\pi$ is geometrically ergodic with factor
$\pi$ is geometrically ergodic with factor ![]() $4\textrm{max}(\log C, -\log(c))$. This is, however, sub-optimal when compared to [Reference Smith and Tierney36], which only requires a finite upper bound on
$4\textrm{max}(\log C, -\log(c))$. This is, however, sub-optimal when compared to [Reference Smith and Tierney36], which only requires a finite upper bound on ![]() ${\frac{{\textrm{d}}\widehat \pi}{\textrm{d} \pi}}$ to establish uniform ergodicity.
${\frac{{\textrm{d}}\widehat \pi}{\textrm{d} \pi}}$ to establish uniform ergodicity.
Example 3. (Laplace approximation for GLMMs.) Generalized linear mixed models (GLMMs) (see [Reference Breslow and Clayton5,Reference McCulloch, Neuhaus, Armitage, Colton, Wiley and York23], etc.) are widely used in the modelling of non-normal response variables under repeated or correlated measurements. They are the natural common extension of generalized linear models and linear mixed effects models. They handle dependence between observations by introducing Gaussian latent variables. These random effects are nuisance variables for the purpose of inference. In order to perform Bayesian inference for GLMMs, one requires samples from the marginal posterior distribution of the parameters given the data. The marginal posterior, here, is the posterior for the parameters given the observations, in contrast to the joint posterior of the random effects and the parameters given the data.
This can be approached in two ways. One option is to obtain samples for the random effects and parameters jointly given the data, and discard the random effects to get marginal posterior samples for the parameters. The second option is to approximate the likelihood by integrating (numerically) over the random effects, and using the resulting approximate likelihood in the calculations involving the unnormalized posterior for the parameters.
In the second case, when the prior for the parameters is compactly supported, if one had established a result saying that a particular MH procedure for the exact posterior distribution of the parameters would be geometrically ergodic, then one could directly transfer this result to the approximate posterior computed using a Laplace approximation, at least for large enough samples. This is valid since the Laplace approximation has constant relative error on compact sets, and the relative error decreases with sample size (see [Reference Tierney and Kadane37]). Hence, for a large enough sample size, Equation (12) will be satisfied regardless of what the proposal kernel Q was (as long as ![]() $ \Vert {{Q}}\Vert_{L_2(\pi)} $ was finite).
$ \Vert {{Q}}\Vert_{L_2(\pi)} $ was finite).
Example 4. (Uniform coresets.) In Bayesian inference with large samples, an approach to reducing the computational burden of evaluating the likelihood in the unnormalized posterior for MCMC accept/reject steps is to select a representative subsample of the data and to up-weight the contributions of each of the selected samples in such a way as to best approximate the original likelihood. These up-weighted subsamples are called coresets. They naturally give rise to approximate MCMC methods in which the true posterior is replaced by an approximation based upon a coreset. Several methods for coreset construction exist; however, relatively little work has been done to assess their impact upon approximate MCMC methods. We will consider the uniform coreset construction of [Reference Huggins, Campbell, Broderick and Lee14] (so named in [Reference Campbell and Broderick8]).
Theorem 3.2 of [Reference Campbell and Broderick8] provides the guarantee that, with probability ![]() $(1-\delta)$, the unnormalized approximate posterior
$(1-\delta)$, the unnormalized approximate posterior ![]() $\hat C \hat \pi$ based on a uniform coreset of size M will satisfy
$\hat C \hat \pi$ based on a uniform coreset of size M will satisfy
 \begin{equation}\begin{aligned} \sup\limits_{x\in {\mathcal{X}}}\frac{1}{ \vert {{\mathcal{L}(x)}} \vert } \left\vert {{\log \frac{\hat C \hat \pi(x)}{C\pi(x)}}} \right\vert \leq \frac{\sigma }{\sqrt{M}} \left( {\frac{3}{2}D +\overline \eta\sqrt{2\log({1/\delta}})} \right), \end{aligned}\end{equation}
\begin{equation}\begin{aligned} \sup\limits_{x\in {\mathcal{X}}}\frac{1}{ \vert {{\mathcal{L}(x)}} \vert } \left\vert {{\log \frac{\hat C \hat \pi(x)}{C\pi(x)}}} \right\vert \leq \frac{\sigma }{\sqrt{M}} \left( {\frac{3}{2}D +\overline \eta\sqrt{2\log({1/\delta}})} \right), \end{aligned}\end{equation}
where ![]() $\sigma = \sum_{n=1}^N \sigma_n$, N is the number of observations,
$\sigma = \sum_{n=1}^N \sigma_n$, N is the number of observations,
![]() $\mathcal{L}_i(x)$ is the log-likelihood of parameter x at the ith observation,
$\mathcal{L}_i(x)$ is the log-likelihood of parameter x at the ith observation, ![]() $\mathcal{L}(x) = \sum_{i=1}^N \mathcal{L}_i(x)$ is the log-likelihood of the dataset
$\mathcal{L}(x) = \sum_{i=1}^N \mathcal{L}_i(x)$ is the log-likelihood of the dataset
 \begin{equation}\begin{aligned} \overline \eta = \max_{i,j\in \{ {1,\dots,N} \}} \sup\limits_{x\in {\mathcal{X}}}\frac{1}{ \vert {\mathcal{L}(x)} \vert } \vert {\frac{\mathcal{L}_i(x)}{\sigma_i} - \frac{\mathcal{L}_j(x)}{\sigma_j}} \vert , \end{aligned}\end{equation}
\begin{equation}\begin{aligned} \overline \eta = \max_{i,j\in \{ {1,\dots,N} \}} \sup\limits_{x\in {\mathcal{X}}}\frac{1}{ \vert {\mathcal{L}(x)} \vert } \vert {\frac{\mathcal{L}_i(x)}{\sigma_i} - \frac{\mathcal{L}_j(x)}{\sigma_j}} \vert , \end{aligned}\end{equation}
and D is the approximate dimension of ![]() $ \{ {\mathcal{L}_i} \}_{i=1}^n$ ([Reference Campbell and Broderick8, Definition 3.1]).
$ \{ {\mathcal{L}_i} \}_{i=1}^n$ ([Reference Campbell and Broderick8, Definition 3.1]).
If, in addition to assuming that ![]() $ \{ {\sigma_i} \}_{i=1}^N$ are all finite as in [8, Section 3], one were to assume that
$ \{ {\sigma_i} \}_{i=1}^N$ are all finite as in [8, Section 3], one were to assume that ![]() $ \vert {\mathcal{L}(x)} \vert $ is bounded as a function of x, then the uniform coreset result would imply the conditions of our Corollary 2, namely that
$ \vert {\mathcal{L}(x)} \vert $ is bounded as a function of x, then the uniform coreset result would imply the conditions of our Corollary 2, namely that
 \begin{equation}\begin{aligned} \sup\limits_{x\in{\mathcal{X}}} \left\vert {\log\frac{C\pi(x)}{\widehat\pi(x)}} \right\vert & \leq \frac{\sigma \Vert {\mathcal{L}} \Vert_\infty}{\sqrt{M}} \left( {\frac{3}{2}D +\overline \eta\sqrt{2\log({1/\delta}})} \right), \end{aligned}\end{equation}
\begin{equation}\begin{aligned} \sup\limits_{x\in{\mathcal{X}}} \left\vert {\log\frac{C\pi(x)}{\widehat\pi(x)}} \right\vert & \leq \frac{\sigma \Vert {\mathcal{L}} \Vert_\infty}{\sqrt{M}} \left( {\frac{3}{2}D +\overline \eta\sqrt{2\log({1/\delta}})} \right), \end{aligned}\end{equation}
with high probability. Consequently, for any proposal kernel ![]() $Q\,{:}\,L_2(\pi)\to L_2(\pi)$ we should be able to choose M sufficiently large so that with high probability
$Q\,{:}\,L_2(\pi)\to L_2(\pi)$ we should be able to choose M sufficiently large so that with high probability
 \begin{equation}\begin{aligned} \frac{\sigma \Vert {\mathcal{L}} \Vert_\infty}{\sqrt{M}} \left( {\frac{3}{2}D +\overline \eta\sqrt{2\log({1/\delta}})} \right)
< \frac{\alpha}{2(1+ \Vert {{Q}}\Vert_{L_2(\pi)} )}. \end{aligned}\end{equation}
\begin{equation}\begin{aligned} \frac{\sigma \Vert {\mathcal{L}} \Vert_\infty}{\sqrt{M}} \left( {\frac{3}{2}D +\overline \eta\sqrt{2\log({1/\delta}})} \right)
< \frac{\alpha}{2(1+ \Vert {{Q}}\Vert_{L_2(\pi)} )}. \end{aligned}\end{equation}
Hence the approximating Markov chain will be geometrically ergodic with high probability.
4.3. Application to Monte Carlo within Metropolis
Following [Reference Medina-Aguayo, Rudolf and Schweizer24], we can get bounds for the simple Monte Carlo within Metropolis algorithm (MCwM). This is the special case of nMH where we approximate the likelihood ratio
by
 \begin{equation*}\widehat{\left ({\frac{\pi(y)}{\pi(x)}} \right)} = \frac{\sum_{i=1}^N \Pi(y,Z_{i})}{\sum_{i=N+1}^{2N} \Pi(x,Z_{i})}\end{equation*}
\begin{equation*}\widehat{\left ({\frac{\pi(y)}{\pi(x)}} \right)} = \frac{\sum_{i=1}^N \Pi(y,Z_{i})}{\sum_{i=N+1}^{2N} \Pi(x,Z_{i})}\end{equation*}
using a new independent sample taken each time the likelihood is evaluated. In the notation of the previous section,
 \begin{equation}\begin{aligned} \widehat a(y\vert x,z) = 1 \wedge \frac{q(x\vert y)\sum_{i=1}^N \Pi(y,z_{i})}{q(y\vert x)\sum_{i=N+1}^{2N} \Pi(x,z_{i})}.\end{aligned}\end{equation}
\begin{equation}\begin{aligned} \widehat a(y\vert x,z) = 1 \wedge \frac{q(x\vert y)\sum_{i=1}^N \Pi(y,z_{i})}{q(y\vert x)\sum_{i=N+1}^{2N} \Pi(x,z_{i})}.\end{aligned}\end{equation}
Let
 \begin{equation}\begin{aligned} W_k(x) & = \frac{1}{k \pi(x)} \sum_{i=1}^k \Pi(x,Z_{i}), \\[3pt] i_{k}(x)^2 & = {\mathbb{E}}[W_k(x)^{-2}],\\[3pt] s(x) & = \frac{1}{\sqrt{\pi(x)}} \textrm{StdDev}(\Pi(x,Z_1)). \\\end{aligned}\end{equation}
\begin{equation}\begin{aligned} W_k(x) & = \frac{1}{k \pi(x)} \sum_{i=1}^k \Pi(x,Z_{i}), \\[3pt] i_{k}(x)^2 & = {\mathbb{E}}[W_k(x)^{-2}],\\[3pt] s(x) & = \frac{1}{\sqrt{\pi(x)}} \textrm{StdDev}(\Pi(x,Z_1)). \\\end{aligned}\end{equation}
Lemma 14 of [Reference Medina-Aguayo, Rudolf and Schweizer24] tells us that if there is a ![]() $k\in {\mathbb{N}}$ such that
$k\in {\mathbb{N}}$ such that ![]() $i_{k}(x)<\infty$ for all
$i_{k}(x)<\infty$ for all ![]() $x\in{\mathcal{X}}$, then for
$x\in{\mathcal{X}}$, then for ![]() $N\geq k$,
$N\geq k$,
 \begin{equation}\begin{aligned} \vert {{r(y\vert x)}} \vert & \leq a(y\vert x) \frac{1}{\sqrt{N}} i_k(y)\left ({s(x)+s(y)} \right) \\ &\leq \frac{1}{\sqrt{N}} i_k(y)\left ({s(x)+s(y)} \right).\end{aligned}\end{equation}
\begin{equation}\begin{aligned} \vert {{r(y\vert x)}} \vert & \leq a(y\vert x) \frac{1}{\sqrt{N}} i_k(y)\left ({s(x)+s(y)} \right) \\ &\leq \frac{1}{\sqrt{N}} i_k(y)\left ({s(x)+s(y)} \right).\end{aligned}\end{equation}
Corollary 3. Let P be the MH transition kernel for the target density ![]() $\pi$ and proposal kernel Q. Let
$\pi$ and proposal kernel Q. Let ![]() $\widehat P_N$ be the corresponding MCwM transition kernel when
$\widehat P_N$ be the corresponding MCwM transition kernel when ![]() $\pi(\cdot)$ is approximated by
$\pi(\cdot)$ is approximated by ![]() $\frac{1}{N} \sum_{i=1}^N \Pi(\cdot,Z_{i})$.
$\frac{1}{N} \sum_{i=1}^N \Pi(\cdot,Z_{i})$.
Assume that s and the ![]() $i_k$ as defined above are uniformly bounded for some
$i_k$ as defined above are uniformly bounded for some ![]() $k\in\mathbb{N}$. Suppose further that
$k\in\mathbb{N}$. Suppose further that
and ![]() $N\geq \lfloor {N_0} \rfloor+1$.
$N\geq \lfloor {N_0} \rfloor+1$.
Then ![]() $\widehat P_N$ is reversible and
$\widehat P_N$ is reversible and ![]() $L_2(\pi)$-GE with factor
$L_2(\pi)$-GE with factor
and it has a stationary distribution
 \begin{equation*}\widehat{\pi}_N(x) \propto \frac{\pi(x)}{N\ {\mathbb{E}} \left[{\left({\sum_{i=1}^N \Pi(x,Z_i)} \right)^{-1}} \right]}\end{equation*}
\begin{equation*}\widehat{\pi}_N(x) \propto \frac{\pi(x)}{N\ {\mathbb{E}} \left[{\left({\sum_{i=1}^N \Pi(x,Z_i)} \right)^{-1}} \right]}\end{equation*}
with
 \begin{equation}\begin{aligned} \Vert {{\pi - \widehat \pi_N}}\Vert_{L_2(\pi)} \leq \sqrt{\frac{N_0}{N\alpha^2 -N_0}}. \end{aligned}\end{equation}
\begin{equation}\begin{aligned} \Vert {{\pi - \widehat \pi_N}}\Vert_{L_2(\pi)} \leq \sqrt{\frac{N_0}{N\alpha^2 -N_0}}. \end{aligned}\end{equation}
Proof. Suppose that ![]() $N\geq \lfloor {N_0} \rfloor+1$. From Theorem 1, we know that the perturbed chain
$N\geq \lfloor {N_0} \rfloor+1$. From Theorem 1, we know that the perturbed chain ![]() $\widehat P_N$ is
$\widehat P_N$ is ![]() $L_2(\pi)$-GE with factor
$L_2(\pi)$-GE with factor ![]() $ 1- \alpha + \frac{1}{\sqrt{N/N_0}}$ and has a stationary distribution
$ 1- \alpha + \frac{1}{\sqrt{N/N_0}}$ and has a stationary distribution ![]() $\widehat\pi_N$ with
$\widehat\pi_N$ with
 \begin{equation}\begin{aligned} \Vert {{\pi - \widehat \pi_N}}\Vert_{L_2(\pi)} \leq \sqrt{\frac{N_0}{N\alpha^2 -N_0}} \ .\end{aligned}\end{equation}
\begin{equation}\begin{aligned} \Vert {{\pi - \widehat \pi_N}}\Vert_{L_2(\pi)} \leq \sqrt{\frac{N_0}{N\alpha^2 -N_0}} \ .\end{aligned}\end{equation}
Moreover, by inspection, ![]() $\widehat P_N$ is reversible with respect to
$\widehat P_N$ is reversible with respect to
 \begin{align*}\widehat{\pi}_N(x) \propto \frac{\pi(x)}{N\ {\mathbb{E}} \left [{\left ({\sum_{i=1}^N \Pi(x,Z_i)}\right) ^{-1}} \right]}.\end{align*}
\begin{align*}\widehat{\pi}_N(x) \propto \frac{\pi(x)}{N\ {\mathbb{E}} \left [{\left ({\sum_{i=1}^N \Pi(x,Z_i)}\right) ^{-1}} \right]}.\end{align*}
Thus, we can use Theorem 3 to obtain ![]() $L_2(\widehat \pi_N)$-GE of
$L_2(\widehat \pi_N)$-GE of ![]() $\widehat P_N$, with factor
$\widehat P_N$, with factor ![]() $1- \alpha + \frac{1}{\sqrt{N/N_0}}$.
$1- \alpha + \frac{1}{\sqrt{N/N_0}}$.
Remark 6. A simple scenario under which these ![]() $i_k$ and s are uniformly bounded is when the joint density of x and Z is bounded above and below by a multiple of the marginal of x, so that
$i_k$ and s are uniformly bounded is when the joint density of x and Z is bounded above and below by a multiple of the marginal of x, so that
 \begin{equation}\begin{aligned} \frac{\Pi(x,z)}{\pi(x)} \in [c,C] \end{aligned}\end{equation}
\begin{equation}\begin{aligned} \frac{\Pi(x,z)}{\pi(x)} \in [c,C] \end{aligned}\end{equation}
for all ![]() $(x,z)\in{\mathcal{X}}\times\mathcal{Z}$. This condition is essentially tight if we wish to take
$(x,z)\in{\mathcal{X}}\times\mathcal{Z}$. This condition is essentially tight if we wish to take ![]() $k=1$ and take the base measure to be the Lebesgue measure restricted to
$k=1$ and take the base measure to be the Lebesgue measure restricted to ![]() $U\subset\mathbb{R}^d$; in this case the condition
$U\subset\mathbb{R}^d$; in this case the condition ![]() $ \Vert {i_k(x)} \Vert_{L_\infty}<\infty$ implies that
$ \Vert {i_k(x)} \Vert_{L_\infty}<\infty$ implies that
 \begin{equation}\begin{aligned} \int_{U} \frac{\pi(x)}{\Pi(x,z)} dz = {\mathbb{E}}_{Z\sim\frac{\Pi(x,\cdot)}{\pi(x)}} \frac{\pi(x)^2}{\Pi(x,\cdot)^2} <\infty \end{aligned}\end{equation}
\begin{equation}\begin{aligned} \int_{U} \frac{\pi(x)}{\Pi(x,z)} dz = {\mathbb{E}}_{Z\sim\frac{\Pi(x,\cdot)}{\pi(x)}} \frac{\pi(x)^2}{\Pi(x,\cdot)^2} <\infty \end{aligned}\end{equation}
for all x. That is, the reciprocal of the conditional density of Z given ![]() $X=x$ has a finite integral for each x.
$X=x$ has a finite integral for each x.
Remark 7. More generally, [Reference Medina-Aguayo, Rudolf and Schweizer24, Lemma 23] tells us that if ![]() ${\mathbb{E}}[W_{k_0}(x)^{-p}]<\infty$ for some
${\mathbb{E}}[W_{k_0}(x)^{-p}]<\infty$ for some ![]() $k_0\in\mathbb{N}$ and
$k_0\in\mathbb{N}$ and ![]() $p>0$, then for
$p>0$, then for ![]() $k\geq k_0 \lceil {\frac{2}{p}} \rceil$,
$k\geq k_0 \lceil {\frac{2}{p}} \rceil$, ![]() $i_{k}(x)^2 < {\mathbb{E}}[W_{k_0}(x)^{-p}]$. Therefore, in order to uniformly bound
$i_{k}(x)^2 < {\mathbb{E}}[W_{k_0}(x)^{-p}]$. Therefore, in order to uniformly bound ![]() $i_k(x)$, it is sufficient to bound
$i_k(x)$, it is sufficient to bound ![]() ${\mathbb{E}}[W_{k_0}(x)^{-p}]$ uniformly in x for some
${\mathbb{E}}[W_{k_0}(x)^{-p}]$ uniformly in x for some ![]() $k_0\in\mathbb{N}$,
$k_0\in\mathbb{N}$, ![]() $p>0$. This is much less restrictive than trying to bound
$p>0$. This is much less restrictive than trying to bound ![]() $i_1(x)$. In the case that
$i_1(x)$. In the case that ![]() $p<1$,
$p<1$, ![]() $k_0=1$, this is much less restrictive than when
$k_0=1$, this is much less restrictive than when ![]() $p=2$,
$p=2$, ![]() $k_0=1$; it is equivalent to requiring that tempered versions of the conditional distribution
$k_0=1$; it is equivalent to requiring that tempered versions of the conditional distribution
can be normalized by uniformly bounded normalizing constants. This would be true if, for example, ![]() $(Z| X=x)\sim\mathcal{N}(\mu(x),\sigma^2(x))$ with
$(Z| X=x)\sim\mathcal{N}(\mu(x),\sigma^2(x))$ with ![]() $\sigma^2(x)$ uniformly bounded in x. More generally, using
$\sigma^2(x)$ uniformly bounded in x. More generally, using ![]() $0<p<1$ instead of
$0<p<1$ instead of ![]() $p=2$, whenever the conditional law of Z has uniform exp-poly tails, i.e.
$p=2$, whenever the conditional law of Z has uniform exp-poly tails, i.e.
with ![]() $\alpha>0$, the p-version of the condition would hold.
$\alpha>0$, the p-version of the condition would hold.
We could also use Theorem 5 to get quantitative bounds for the mean squared error of any Monte Carlo estimates made using ![]() $\widehat P_N$, or any of our other results in Theorems 1 to 4 and Corollary 1 as needed.
$\widehat P_N$, or any of our other results in Theorems 1 to 4 and Corollary 1 as needed.
Medina-Aguayo et al. [Reference Medina-Aguayo, Rudolf and Schweizer24] also consider a case where the assumption that s and the ![]() $i_k$ are uniformly bounded is dropped, and instead, the perturbed kernel is restricted to a bounded region. We do not address this case here.
$i_k$ are uniformly bounded is dropped, and instead, the perturbed kernel is restricted to a bounded region. We do not address this case here.
Appendix A. Proofs
A.1 Proof of Theorem 1
The following lemma is contained in the remark after Theorem 2.1 of [Reference Roberts and Rosenthal29]; we prove it here as well since the proof is so simple.
Lemma 3. (Remark in [Reference Roberts and Rosenthal29].) For any probability measure ![]() $\mu\in L_2(\pi)$,
$\mu\in L_2(\pi)$,
Proof.
 \begin{align*}0\leq \Vert {{\mu-\pi}}\Vert_{L_2(\pi)} ^2 &=\int \left ({{\frac{{\textrm{d}}\mu}{{\textrm{d}}\pi}} -1}\right)^2 {\textrm{d}}\pi =\int \left ({\left ({{\frac{{\textrm{d}}\mu}{{\textrm{d}}\pi}}}\right)^2 -2 {\frac{{\textrm{d}}\mu}{{\textrm{d}}\pi}} +1 }\right) \textrm{d}\pi\\ &=\int \left ({{\frac{{\textrm{d}}\mu}{{\textrm{d}}\pi}}}\right)^2\textrm{d}\pi-2\int \textrm{d}\mu +\int \textrm{d}\pi = \Vert {\mu^2-1}\Vert_{L_2(\pi)} .\end{align*}
\begin{align*}0\leq \Vert {{\mu-\pi}}\Vert_{L_2(\pi)} ^2 &=\int \left ({{\frac{{\textrm{d}}\mu}{{\textrm{d}}\pi}} -1}\right)^2 {\textrm{d}}\pi =\int \left ({\left ({{\frac{{\textrm{d}}\mu}{{\textrm{d}}\pi}}}\right)^2 -2 {\frac{{\textrm{d}}\mu}{{\textrm{d}}\pi}} +1 }\right) \textrm{d}\pi\\ &=\int \left ({{\frac{{\textrm{d}}\mu}{{\textrm{d}}\pi}}}\right)^2\textrm{d}\pi-2\int \textrm{d}\mu +\int \textrm{d}\pi = \Vert {\mu^2-1}\Vert_{L_2(\pi)} .\end{align*}
We will make use of the following simplified version of Theorem 2.1 from [Reference Roberts and Rosenthal29] as well.
Proposition 2. (Equivalent definitions of ![]() $L_2(\pi)$-GE from [Reference Roberts and Rosenthal29].) For a reversible Markov chain with kernel P and stationary distribution
$L_2(\pi)$-GE from [Reference Roberts and Rosenthal29].) For a reversible Markov chain with kernel P and stationary distribution ![]() $\pi$ on state space
$\pi$ on state space ![]() ${\mathcal{X}}$, the following are equivalent (and
${\mathcal{X}}$, the following are equivalent (and ![]() $\rho$ is equal in both cases):
$\rho$ is equal in both cases):
(i) P is
 $L_2(\pi)$-GE with optimal rate
$L_2(\pi)$-GE with optimal rate  $\rho$ and coefficient function
$\rho$ and coefficient function  $C(\mu) = \Vert {{\mu-\pi}}\Vert_{L_2(\pi)} $.
$C(\mu) = \Vert {{\mu-\pi}}\Vert_{L_2(\pi)} $.-
(ii) P has
 $L_{2,0}(\pi)$-spectral radius and norm both equal to
$L_{2,0}(\pi)$-spectral radius and norm both equal to  $\rho$:
where
$\rho$:
where \begin{align*} \sup\limits_{\nu \in L_{2,0}(\pi)\setminus \{ {0} \}}\frac{ \Vert {{\nu P}}\Vert_{L_2(\pi)} }{ \Vert {{\nu}}\Vert_{L_2(\pi)} } = \rho = r(P\vert_{{L_{2,0}(\pi)}}) \ ,\end{align*}
(24)
\begin{align*} \sup\limits_{\nu \in L_{2,0}(\pi)\setminus \{ {0} \}}\frac{ \Vert {{\nu P}}\Vert_{L_2(\pi)} }{ \Vert {{\nu}}\Vert_{L_2(\pi)} } = \rho = r(P\vert_{{L_{2,0}(\pi)}}) \ ,\end{align*}
(24) \begin{equation}\begin{aligned}r(P\vert_{{L_{2,0}(\pi)}})\,{:\!=}\,\sup\limits \{ { \vert {\rho} \vert \,{:}\, \rho\in{\mathbb{C}} \ \text{and}\ ( {P\vert_{{L_{2,0}(\pi)}}-\rho I_{L_{2,0}(\pi)}} ) \textit{ is\ not\ invertible}} \}.\end{aligned}\end{equation}
\begin{equation}\begin{aligned}r(P\vert_{{L_{2,0}(\pi)}})\,{:\!=}\,\sup\limits \{ { \vert {\rho} \vert \,{:}\, \rho\in{\mathbb{C}} \ \text{and}\ ( {P\vert_{{L_{2,0}(\pi)}}-\rho I_{L_{2,0}(\pi)}} ) \textit{ is\ not\ invertible}} \}.\end{aligned}\end{equation}
Note that while when the kernel is reversible we may take ![]() $C(\mu) = \Vert {{\mu-\pi}}\Vert_{L_2(\pi)} $ in the bound corresponding to
$C(\mu) = \Vert {{\mu-\pi}}\Vert_{L_2(\pi)} $ in the bound corresponding to ![]() $L_2(\pi)$-GE with optimal rate
$L_2(\pi)$-GE with optimal rate ![]() $\rho$, this is not true for non-reversible chains. By applying the above theorem in our context we have the following.
$\rho$, this is not true for non-reversible chains. By applying the above theorem in our context we have the following.
Lemma 4. Under the assumptions of Section 3.2,
for any probability distributions ![]() $\nu_1,\nu_2\in L_2(\pi)$. In particular, taking
$\nu_1,\nu_2\in L_2(\pi)$. In particular, taking ![]() $\nu_2=\pi$,
$\nu_2=\pi$,
and applying Cauchy–Schwarz yields
We begin with a first result giving sufficient conditions under which the stationary distribution ![]() $\pi_\epsilon$ of the perturbed chain is in
$\pi_\epsilon$ of the perturbed chain is in ![]() $L_2(\pi)$.
$L_2(\pi)$.
Lemma 5. Under the assumptions of Section 3.2, if in addition ![]() $\epsilon<\alpha$, then
$\epsilon<\alpha$, then ![]() $P_\epsilon$ has a unique stationary distribution,
$P_\epsilon$ has a unique stationary distribution, ![]() $\pi_\epsilon\in L_2(\pi)$, and
$\pi_\epsilon\in L_2(\pi)$, and ![]() $ \Vert {{\pi_\epsilon-\pi}}\Vert_{L_2(\pi)} \leq \frac{\epsilon}{\alpha-\epsilon}$.
$ \Vert {{\pi_\epsilon-\pi}}\Vert_{L_2(\pi)} \leq \frac{\epsilon}{\alpha-\epsilon}$.
Proof. Since ![]() $P_\epsilon$ is
$P_\epsilon$ is ![]() $\pi$-irreducible and aperiodic, it has at most one stationary distribution,
$\pi$-irreducible and aperiodic, it has at most one stationary distribution, ![]() $\pi_\epsilon$, with
$\pi_\epsilon$, with ![]() $\pi_\epsilon\ll \pi$ (see for example [Reference Douc, Moulines, Priouret and Soulier9, Corollary 9.2.16]).
$\pi_\epsilon\ll \pi$ (see for example [Reference Douc, Moulines, Priouret and Soulier9, Corollary 9.2.16]).
Suppose for now that ![]() $\pi P_\epsilon^n$ has an
$\pi P_\epsilon^n$ has an ![]() $L_2(\pi)$ limit,
$L_2(\pi)$ limit, ![]() $\pi_\epsilon$. Then, using the triangle inequality, the contraction property (
$\pi_\epsilon$. Then, using the triangle inequality, the contraction property (![]() ${ \Vert {P_\epsilon} \Vert_{\text{TV}}} = 1$), and Cauchy–Schwarz, we have
${ \Vert {P_\epsilon} \Vert_{\text{TV}}} = 1$), and Cauchy–Schwarz, we have
 \begin{align*} { \Vert {\pi_\epsilon P_\epsilon - \pi_\epsilon} \Vert_{\text{TV}}} & \leq { \Vert {\pi_\epsilon P_\epsilon - \pi P_\epsilon^{n}}\Vert_{\text{TV}}} + { \Vert {\pi P_\epsilon^{n} - \pi_\epsilon} \Vert_{\text{TV}}}\\[3pt]
& \leq { \Vert {\pi_\epsilon - \pi P_\epsilon^{n-1}} \Vert_{\text{TV}}} + { \Vert {\pi P_\epsilon^{n} - \pi_\epsilon} \Vert_{\text{TV}}}\\[3pt] &
\leq \Vert {{\pi_\epsilon - \pi P_\epsilon^{n-1}}}\Vert_{L_2(\pi)} + \Vert {{\pi P_\epsilon^{n} - \pi_\epsilon}}\Vert_{L_2(\pi)} {\stackrel{{n\to\infty}}{\to}}{0};\end{align*}
\begin{align*} { \Vert {\pi_\epsilon P_\epsilon - \pi_\epsilon} \Vert_{\text{TV}}} & \leq { \Vert {\pi_\epsilon P_\epsilon - \pi P_\epsilon^{n}}\Vert_{\text{TV}}} + { \Vert {\pi P_\epsilon^{n} - \pi_\epsilon} \Vert_{\text{TV}}}\\[3pt]
& \leq { \Vert {\pi_\epsilon - \pi P_\epsilon^{n-1}} \Vert_{\text{TV}}} + { \Vert {\pi P_\epsilon^{n} - \pi_\epsilon} \Vert_{\text{TV}}}\\[3pt] &
\leq \Vert {{\pi_\epsilon - \pi P_\epsilon^{n-1}}}\Vert_{L_2(\pi)} + \Vert {{\pi P_\epsilon^{n} - \pi_\epsilon}}\Vert_{L_2(\pi)} {\stackrel{{n\to\infty}}{\to}}{0};\end{align*}
thus we find that ![]() $\pi_\epsilon$ must be stationary for
$\pi_\epsilon$ must be stationary for ![]() $P_\epsilon$.
$P_\epsilon$.
It remains to verify that ![]() $\{\pi P_\epsilon^n\}_{n\in\mathbb{N}}$ is an
$\{\pi P_\epsilon^n\}_{n\in\mathbb{N}}$ is an ![]() $L_2(\pi)$-Cauchy sequence, and thus from completeness it must have an
$L_2(\pi)$-Cauchy sequence, and thus from completeness it must have an ![]() $L_2(\pi)$-limit. To this end, define
$L_2(\pi)$-limit. To this end, define ![]() $Q_\epsilon = (P_\epsilon - P)$. Let
$Q_\epsilon = (P_\epsilon - P)$. Let ![]() $\textbf{2}^k=\{0,1\}^k$ for all
$\textbf{2}^k=\{0,1\}^k$ for all ![]() $k\in\mathbb{N}$. We will expand
$k\in\mathbb{N}$. We will expand ![]() $\pi(P+Q_\epsilon)^n$ and use the following facts:
$\pi(P+Q_\epsilon)^n$ and use the following facts:
A.
 $\forall R\in\mathcal{B}(L_2(\pi))\ [\pi P^n R = \pi R]$.
$\forall R\in\mathcal{B}(L_2(\pi))\ [\pi P^n R = \pi R]$.-
B.
 $Q_\epsilon \,{:}\, L_2(\pi)\to L_{2,0}(\pi)$.
$Q_\epsilon \,{:}\, L_2(\pi)\to L_{2,0}(\pi)$. -
C.
 $P\vert_{L_{2,0}(\pi)}\in\mathcal{B}(L_{2,0}(\pi))$ and
$P\vert_{L_{2,0}(\pi)}\in\mathcal{B}(L_{2,0}(\pi))$ and  $ \Vert {{P\vert_{L_{2,0}(\pi)}}}\Vert_{L_{2,0}(\pi)} \leq (1-\alpha)$.
$ \Vert {{P\vert_{L_{2,0}(\pi)}}}\Vert_{L_{2,0}(\pi)} \leq (1-\alpha)$.
Since the operators P and ![]() $Q_\epsilon$ do not (necessarily) commute, when we expand
$Q_\epsilon$ do not (necessarily) commute, when we expand ![]() $(P+Q)^n$ we must have one distinct term per binary sequence of length n. We can then group terms by the number of leading Ps, and use (A) to cancel the leading terms.
$(P+Q)^n$ we must have one distinct term per binary sequence of length n. We can then group terms by the number of leading Ps, and use (A) to cancel the leading terms.
Let ![]() $m,n\in\textbf{N}$ be arbitrary with
$m,n\in\textbf{N}$ be arbitrary with ![]() $m\leq n$. Then
$m\leq n$. Then
 \begin{align*}& \Vert {{ \pi P_\epsilon^n -\pi P_\epsilon^m}}\Vert_{L_2(\pi)} \\[3pt] &= \Vert {{ \pi (P+Q_\epsilon)^n - \pi (P+Q_\epsilon)^m}}\Vert_{L_2(\pi)} \\[3pt]
&= \left\Vert {{\pi \left [{\left ({\sum_{\textbf{b}\in\textbf{2}^n}\prod_{j=1}^n P^{b_j} Q_\epsilon^{1-b_j} }\right)-\left ({\sum_{\textbf{b}\in\textbf{2}^m} \prod_{j=1}^m P^{b_j} Q_\epsilon^{1-b_j} }\right)}\right]}}\right\Vert_{L_2(\pi)} \\[3pt]
& =\Bigg \Vert\pi\Bigg[\left ({P^n+\sum_{k=0}^{n-1}P^{n-k-1}Q_\epsilon\sum_{\textbf{b}\in\textbf{2}^{k}}\prod_{j=1}^{k} P^{b_j} Q_\epsilon^{1-b_j}}\right) \\[3pt]&\qquad - \left ({P^m+\sum_{k=0}^{m-1}P^{m-k-1}Q_\epsilon\sum_{\textbf{b}\in\textbf{2}^{k}} \prod_{j=1}^{k} P^{b_j} Q_\epsilon^{1-b_j} }\right) \Bigg] \Bigg\Vert_{L_2(\pi)}\\[3pt]
& = \left \Vert{\left ({\pi+\sum_{k=0}^{n-1}\pi Q_\epsilon\sum_{\textbf{b}\in\textbf{2}^{k}} \prod_{j=1}^{k} P^{b_j} Q_\epsilon^{1-b_j} }\right) -\left ({\pi+\sum_{k=0}^{m-1}\pi Q_\epsilon\sum_{\textbf{b}\in\textbf{2}^{k}} \prod_{j=1}^{k} P^{b_j} Q_\epsilon^{1-b_j} }\right) } \right\Vert_{L_2(\pi)}\\[3pt]
& = \left\Vert {{\pi \sum_{k=m}^{n-1}Q_\epsilon\sum_{\textbf{b}\in\textbf{2}^{k}} \prod_{j=1}^{k} P^{b_j} Q_\epsilon^{1-b_j}}}\right\Vert_{L_2(\pi)} \\[3pt]
&\leq \epsilon \sum_{k=m}^{n-1}\sum_{\textbf{b}\in\textbf{2}^{k}} \prod_{j=1}^{k} (1-\alpha)^{b_j} \epsilon^{1-b_j}\\[3pt]
&=\epsilon \sum_{k=m}^{n-1}(1-\alpha+\epsilon)^{k}\\[3pt]
&\leq \frac{\epsilon}{\alpha-\epsilon} (1-\alpha+\epsilon)^m.\end{align*}
\begin{align*}& \Vert {{ \pi P_\epsilon^n -\pi P_\epsilon^m}}\Vert_{L_2(\pi)} \\[3pt] &= \Vert {{ \pi (P+Q_\epsilon)^n - \pi (P+Q_\epsilon)^m}}\Vert_{L_2(\pi)} \\[3pt]
&= \left\Vert {{\pi \left [{\left ({\sum_{\textbf{b}\in\textbf{2}^n}\prod_{j=1}^n P^{b_j} Q_\epsilon^{1-b_j} }\right)-\left ({\sum_{\textbf{b}\in\textbf{2}^m} \prod_{j=1}^m P^{b_j} Q_\epsilon^{1-b_j} }\right)}\right]}}\right\Vert_{L_2(\pi)} \\[3pt]
& =\Bigg \Vert\pi\Bigg[\left ({P^n+\sum_{k=0}^{n-1}P^{n-k-1}Q_\epsilon\sum_{\textbf{b}\in\textbf{2}^{k}}\prod_{j=1}^{k} P^{b_j} Q_\epsilon^{1-b_j}}\right) \\[3pt]&\qquad - \left ({P^m+\sum_{k=0}^{m-1}P^{m-k-1}Q_\epsilon\sum_{\textbf{b}\in\textbf{2}^{k}} \prod_{j=1}^{k} P^{b_j} Q_\epsilon^{1-b_j} }\right) \Bigg] \Bigg\Vert_{L_2(\pi)}\\[3pt]
& = \left \Vert{\left ({\pi+\sum_{k=0}^{n-1}\pi Q_\epsilon\sum_{\textbf{b}\in\textbf{2}^{k}} \prod_{j=1}^{k} P^{b_j} Q_\epsilon^{1-b_j} }\right) -\left ({\pi+\sum_{k=0}^{m-1}\pi Q_\epsilon\sum_{\textbf{b}\in\textbf{2}^{k}} \prod_{j=1}^{k} P^{b_j} Q_\epsilon^{1-b_j} }\right) } \right\Vert_{L_2(\pi)}\\[3pt]
& = \left\Vert {{\pi \sum_{k=m}^{n-1}Q_\epsilon\sum_{\textbf{b}\in\textbf{2}^{k}} \prod_{j=1}^{k} P^{b_j} Q_\epsilon^{1-b_j}}}\right\Vert_{L_2(\pi)} \\[3pt]
&\leq \epsilon \sum_{k=m}^{n-1}\sum_{\textbf{b}\in\textbf{2}^{k}} \prod_{j=1}^{k} (1-\alpha)^{b_j} \epsilon^{1-b_j}\\[3pt]
&=\epsilon \sum_{k=m}^{n-1}(1-\alpha+\epsilon)^{k}\\[3pt]
&\leq \frac{\epsilon}{\alpha-\epsilon} (1-\alpha+\epsilon)^m.\end{align*}
Since this upper bound on ![]() $ \Vert {{\pi P_\epsilon^n - \pi P_\epsilon^m}}\Vert_{L_2(\pi)} $ decreases to 0 monotonically in
$ \Vert {{\pi P_\epsilon^n - \pi P_\epsilon^m}}\Vert_{L_2(\pi)} $ decreases to 0 monotonically in ![]() $m=\textrm{min}(m,n)$, the sequence must be
$m=\textrm{min}(m,n)$, the sequence must be ![]() $L_2(\pi)$-Cauchy.
$L_2(\pi)$-Cauchy.
Now, to bound the norm of ![]() $\pi_\epsilon$, we take
$\pi_\epsilon$, we take ![]() $m=0$ and we get that for all
$m=0$ and we get that for all ![]() $n\in \mathbb{N}$,
$n\in \mathbb{N}$,
From the continuity of the norm, it must be the case that ![]() $ \Vert {{\pi_\epsilon- \pi}}\Vert_{L_2(\pi)} \leq \frac{\epsilon}{\alpha-\epsilon} $.
$ \Vert {{\pi_\epsilon- \pi}}\Vert_{L_2(\pi)} \leq \frac{\epsilon}{\alpha-\epsilon} $.
Lemma 6. Under the assumptions of Section 3.2, if in addition ![]() $\epsilon<\alpha$, then
$\epsilon<\alpha$, then
and
Proof. The two lower bounds are immediate from Lemma 3 and the positivity of norms:
To derive the first upper bound, we apply Lemma 3, our assumptions about the operators P and ![]() $P_\epsilon$, and the triangle inequality to
$P_\epsilon$, and the triangle inequality to ![]() $\Vert \pi-\pi_\epsilon\Vert_2$:
$\Vert \pi-\pi_\epsilon\Vert_2$:
 \begin{align*}\sqrt{ \Vert {{\pi_\epsilon}}\Vert_{L_2(\pi)} ^2-1}= \Vert {\pi-\pi_\epsilon}\Vert_{L_2(\pi)} &= \Vert {{\pi P - \pi_\epsilon P+ \pi_\epsilon P - \pi_\epsilon P_\epsilon}}\Vert_{L_2(\pi)} \\ &\leq \Vert {{\pi P - \pi_\epsilon P}}\Vert_{L_2(\pi)} + \Vert {{ \pi_\epsilon P - \pi_\epsilon P_\epsilon}}\Vert_{L_2(\pi)} \\ &\leq (1-\alpha) \Vert {\pi-\pi_\epsilon}\Vert_{L_2(\pi)} +\epsilon \Vert {{ \pi_\epsilon}}\Vert_{L_2(\pi)} \\ &= (1-\alpha)\sqrt{ \Vert {{ \pi_\epsilon}}\Vert_{L_2(\pi)} ^2-1}+\epsilon \Vert {{ \pi_\epsilon}}\Vert_{L_2(\pi)} .\end{align*}
\begin{align*}\sqrt{ \Vert {{\pi_\epsilon}}\Vert_{L_2(\pi)} ^2-1}= \Vert {\pi-\pi_\epsilon}\Vert_{L_2(\pi)} &= \Vert {{\pi P - \pi_\epsilon P+ \pi_\epsilon P - \pi_\epsilon P_\epsilon}}\Vert_{L_2(\pi)} \\ &\leq \Vert {{\pi P - \pi_\epsilon P}}\Vert_{L_2(\pi)} + \Vert {{ \pi_\epsilon P - \pi_\epsilon P_\epsilon}}\Vert_{L_2(\pi)} \\ &\leq (1-\alpha) \Vert {\pi-\pi_\epsilon}\Vert_{L_2(\pi)} +\epsilon \Vert {{ \pi_\epsilon}}\Vert_{L_2(\pi)} \\ &= (1-\alpha)\sqrt{ \Vert {{ \pi_\epsilon}}\Vert_{L_2(\pi)} ^2-1}+\epsilon \Vert {{ \pi_\epsilon}}\Vert_{L_2(\pi)} .\end{align*}
Collecting the square roots and squaring both sides yields
which implies that
Finally, the second upper bound is derived from the first one, again using Lemma 5.1:
We next observe that our assumptions imply that for small enough perturbations, the perturbed chain ![]() $P_\epsilon$ is geometrically ergodic in the
$P_\epsilon$ is geometrically ergodic in the ![]() $L_2(\pi)$ norm.
$L_2(\pi)$ norm.
Lemma 7. Under the assumptions of Section 3.2, if ![]() $\epsilon<\alpha$, then we have that
$\epsilon<\alpha$, then we have that ![]() $P_\epsilon$ is
$P_\epsilon$ is ![]() $L_2(\pi)$-GE, with factor
$L_2(\pi)$-GE, with factor ![]() $\leq 1-(\alpha-\epsilon)$.
$\leq 1-(\alpha-\epsilon)$.
Proof. Suppose that ![]() $\nu\in L_{2,0}(\pi)$. Then
$\nu\in L_{2,0}(\pi)$. Then
 \begin{align*} \Vert {{\nu P_\epsilon}}\Vert_{L_2(\pi)} & \leq \Vert {{\nu (P_\epsilon -P)}}\Vert_{L_2(\pi)} + \Vert {{\nu P}}\Vert_{L_2(\pi)} \\ & \leq \epsilon \Vert {{\nu}}\Vert_{L_2(\pi)} + (1-\alpha) \Vert {{\nu}}\Vert_{L_2(\pi)} \\ & =(1-\alpha+\epsilon) \Vert {{\nu}}\Vert_{L_2(\pi)} \, .\end{align*}
\begin{align*} \Vert {{\nu P_\epsilon}}\Vert_{L_2(\pi)} & \leq \Vert {{\nu (P_\epsilon -P)}}\Vert_{L_2(\pi)} + \Vert {{\nu P}}\Vert_{L_2(\pi)} \\ & \leq \epsilon \Vert {{\nu}}\Vert_{L_2(\pi)} + (1-\alpha) \Vert {{\nu}}\Vert_{L_2(\pi)} \\ & =(1-\alpha+\epsilon) \Vert {{\nu}}\Vert_{L_2(\pi)} \, .\end{align*}
Thus, for any probability measure ![]() $\mu\in L_2(\pi)$, since
$\mu\in L_2(\pi)$, since ![]() $\pi_\epsilon \in L_2(\pi)$ we have
$\pi_\epsilon \in L_2(\pi)$ we have
Combining Lemmas 5 to 7 together with the triangle inequality immediately yields combinedthm.
A.2. Proofs of Theorem 2, Theorem 3, and Corollary 1
Definition 3. Following [Reference Roberts and Rosenthal29], a subset ![]() $S\subset{\mathcal{X}}$ is called hyper-small for the
$S\subset{\mathcal{X}}$ is called hyper-small for the ![]() $\pi$-irreducible Markov kernel P with stationary measure
$\pi$-irreducible Markov kernel P with stationary measure ![]() $\pi$ if
$\pi$ if ![]() $\pi(S)>0$ and there exist
$\pi(S)>0$ and there exist ![]() $\delta_S>0$ and
$\delta_S>0$ and ![]() $k\in\mathbb{N}$ such that for all
$k\in\mathbb{N}$ such that for all ![]() $x,y\in\mathcal X$,
$x,y\in\mathcal X$,
or equivalently, if ![]() $P^k(x,A)\geq \delta_S\pi(A)$ for all
$P^k(x,A)\geq \delta_S\pi(A)$ for all ![]() $x\in S$ and
$x\in S$ and ![]() $A\subset S$ measurable.
$A\subset S$ measurable.
Lemma 4 of [Reference Jain and Jamison15] states that on a countably generated state space (as we have assumed herein), every set of positive ![]() $\pi$-measure contains a hyper-small subset.
$\pi$-measure contains a hyper-small subset.
Lemma 8. (Existence of hyper-small subsets from [Reference Jain and Jamison15].) Suppose that ![]() $({\mathcal{X}},\Sigma)$ is countably generated. Suppose that X is a
$({\mathcal{X}},\Sigma)$ is countably generated. Suppose that X is a ![]() $\phi$-irreducible Markov chain on
$\phi$-irreducible Markov chain on ![]() ${\mathcal{X}}$ with kernel P for some
${\mathcal{X}}$ with kernel P for some ![]() $\sigma$-finite measure
$\sigma$-finite measure ![]() $\phi$ on
$\phi$ on ![]() ${\mathcal{X}}$. Then any set
${\mathcal{X}}$. Then any set ![]() $K\subset {\mathcal{X}}$ with
$K\subset {\mathcal{X}}$ with ![]() $\phi(K)>0$ contains a set
$\phi(K)>0$ contains a set ![]() $S_K$ such that (for some
$S_K$ such that (for some ![]() $n_{K}\in\mathbb{N}$)
$n_{K}\in\mathbb{N}$)
In the case that a stationary distribution ![]() $\pi$ for P exists, without loss of generality we can take
$\pi$ for P exists, without loss of generality we can take ![]() $\phi=\pi$. In this case, it is immediate that any set
$\phi=\pi$. In this case, it is immediate that any set ![]() $(S_K, n_K)$ satisfying Lemma 8 also satisfies Definition 3.
$(S_K, n_K)$ satisfying Lemma 8 also satisfies Definition 3.
Also of importance to us is the following variant of Proposition 2.1 of [Reference Roberts and Rosenthal29], which provides a characterization of geometric ergodicity in terms of convergence to a hyper-small set.
Proposition 3. (Equivalent characterizations of ![]() $\pi$-a.e.-TV-GE from [Reference Nummelin and Tweedie27,Reference Roberts and Rosenthal29].) Suppose that
$\pi$-a.e.-TV-GE from [Reference Nummelin and Tweedie27,Reference Roberts and Rosenthal29].) Suppose that ![]() $(\Omega,\Sigma)$ is countably generated, and that X is a
$(\Omega,\Sigma)$ is countably generated, and that X is a ![]() $\phi$-irreducible Markov chain on
$\phi$-irreducible Markov chain on ![]() ${\mathcal{X}}$ with kernel P with stationary distribution
${\mathcal{X}}$ with kernel P with stationary distribution ![]() $\pi$. Then the following are equivalent:
$\pi$. Then the following are equivalent:
(i) There exists
 $\rho_{\text{TV}}\in(0,1)$ such that P is
$\rho_{\text{TV}}\in(0,1)$ such that P is  $\pi$-a.e.-TV-GE with factor
$\pi$-a.e.-TV-GE with factor  $\rho_{\text{TV}}$.
$\rho_{\text{TV}}$.-
(ii) There exist a hyper-small set
 $S\subset {\mathcal{X}}$ and constants
$S\subset {\mathcal{X}}$ and constants  $\rho_S<1$,
$\rho_S<1$,  $C_S\in\mathbb{R}_+$ such that
$C_S\in\mathbb{R}_+$ such that
 \begin{align*} { \left\Vert {\int \frac{\textbf{1}_S(y)\pi({\textrm{d}}y)}{\pi(S)} P^n(y,\cdot) -\pi}\right \Vert_{\text{TV}}} \leq C_S \rho_S^n \qquad \forall n\in\mathbb{N}. \end{align*}
\begin{align*} { \left\Vert {\int \frac{\textbf{1}_S(y)\pi({\textrm{d}}y)}{\pi(S)} P^n(y,\cdot) -\pi}\right \Vert_{\text{TV}}} \leq C_S \rho_S^n \qquad \forall n\in\mathbb{N}. \end{align*}
-
(iii) There exist a
 $\pi$-a.e. finite, measurable function
$\pi$-a.e. finite, measurable function  $V\,{:}\,{\mathcal{X}}\to[1,\infty]$ with
$V\,{:}\,{\mathcal{X}}\to[1,\infty]$ with  $\pi(V^2) <\infty$, and
$\pi(V^2) <\infty$, and  $\rho_V\in(0,1)$, and
$\rho_V\in(0,1)$, and  $C>0$ such that
where
$C>0$ such that
where \begin{align*} 2{ \Vert {\delta_x P^n -\pi} \Vert_{\text{TV}}}\leq \Vert {\delta_x P^n -\pi} \Vert_V \leq C V(x) \rho_V^n, \end{align*}
\begin{align*} 2{ \Vert {\delta_x P^n -\pi} \Vert_{\text{TV}}}\leq \Vert {\delta_x P^n -\pi} \Vert_V \leq C V(x) \rho_V^n, \end{align*}
 $ \Vert {\mu} \Vert_V = \sup\limits_{ \vert {{f}} \vert \leq V} \vert {{\mu(f)}} \vert $.
$ \Vert {\mu} \Vert_V = \sup\limits_{ \vert {{f}} \vert \leq V} \vert {{\mu(f)}} \vert $.
Proof of Theorem 2.
(i) Let S be a hyper-small set for
 $P_\epsilon$ (which must exist from Lemma 8, since
$P_\epsilon$ (which must exist from Lemma 8, since  $P_\epsilon$ is
$P_\epsilon$ is  $\pi_\epsilon$-irreducible). Then the measure
$\pi_\epsilon$-irreducible). Then the measure  $\mu_S$ defined by
satisfies (by Hölder’s inequality, and since
$\mu_S$ defined by
satisfies (by Hölder’s inequality, and since \begin{equation*}{\frac{{\textrm{d}}\mu_S}{\textrm{d} \pi}} = \frac{1_{S}}{\pi_\epsilon(S)} {\frac{\textrm{d} \pi_\epsilon}{\textrm{d} \pi}}\end{equation*}
\begin{equation*}{\frac{{\textrm{d}}\mu_S}{\textrm{d} \pi}} = \frac{1_{S}}{\pi_\epsilon(S)} {\frac{\textrm{d} \pi_\epsilon}{\textrm{d} \pi}}\end{equation*}
 $\pi_\epsilon\in L_2(\pi)$)
and hence
$\pi_\epsilon\in L_2(\pi)$)
and hence \begin{align*} \Vert {{\mu_S}}\Vert_{L_2(\pi)} ^2 \leq \Vert {{\pi_\epsilon}}\Vert_{L_2(\pi)} ^2 \pi_\epsilon(S)^{-2}<\infty, \end{align*}
\begin{align*} \Vert {{\mu_S}}\Vert_{L_2(\pi)} ^2 \leq \Vert {{\pi_\epsilon}}\Vert_{L_2(\pi)} ^2 \pi_\epsilon(S)^{-2}<\infty, \end{align*}
 $\mu_S\in L_2(\pi)$. Then (by Cauchy–Schwarz again)
which, along with Proposition 3, establishes that
$\mu_S\in L_2(\pi)$. Then (by Cauchy–Schwarz again)
which, along with Proposition 3, establishes that \begin{align*} { \left\Vert {\int \frac{\textbf{1}_S(y)\pi_\epsilon({\textrm{d}}y)}{\pi_\epsilon(S)} P_\epsilon^n(y,\cdot) -\pi_\epsilon} \right\Vert_{\text{TV}}} \leq \frac{1}{2} \Vert {{\mu_S P_\epsilon^n -\pi_\epsilon}}\Vert_{L_2(\pi)} \leq \Vert {{\mu_S - \pi_\epsilon}}\Vert_{L_2(\pi)} (1-\alpha +\epsilon)^n, \end{align*}
\begin{align*} { \left\Vert {\int \frac{\textbf{1}_S(y)\pi_\epsilon({\textrm{d}}y)}{\pi_\epsilon(S)} P_\epsilon^n(y,\cdot) -\pi_\epsilon} \right\Vert_{\text{TV}}} \leq \frac{1}{2} \Vert {{\mu_S P_\epsilon^n -\pi_\epsilon}}\Vert_{L_2(\pi)} \leq \Vert {{\mu_S - \pi_\epsilon}}\Vert_{L_2(\pi)} (1-\alpha +\epsilon)^n, \end{align*}
 $P_\epsilon$ is
$P_\epsilon$ is  $\pi_\epsilon$-a.e.-TV-GE with some factor
$\pi_\epsilon$-a.e.-TV-GE with some factor  $\rho_{\text{TV}}\in(0,1)$.
$\rho_{\text{TV}}\in(0,1)$.
-
(ii) Suppose that
 $\mu\in L_\infty(\pi_\epsilon)$. Then
$\mu\in L_\infty(\pi_\epsilon)$. Then  $\mu \in L_2(\pi)$ since
Since
$\mu \in L_2(\pi)$ since
Since \begin{equation*}{\frac{{\textrm{d}}\mu}{\textrm{d} \pi}} \leq \Vert {\mu} \Vert_{L_\infty(\pi_\epsilon)} {\frac{{\textrm{d}}\pi_\epsilon}{\textrm{d} \pi}}.\end{equation*}
\begin{equation*}{\frac{{\textrm{d}}\mu}{\textrm{d} \pi}} \leq \Vert {\mu} \Vert_{L_\infty(\pi_\epsilon)} {\frac{{\textrm{d}}\pi_\epsilon}{\textrm{d} \pi}}.\end{equation*}
 $\mu P_\epsilon^n - \pi_\epsilon \in L_1(\pi_\epsilon)\subset L_1(\pi)$,
(25)Applying this equality as well as Cauchy–Schwarz, we get
$\mu P_\epsilon^n - \pi_\epsilon \in L_1(\pi_\epsilon)\subset L_1(\pi)$,
(25)Applying this equality as well as Cauchy–Schwarz, we get \begin{equation}\begin{aligned} \Vert {\mu P_\epsilon^n - \pi_\epsilon} \Vert_{L_1(\pi_\epsilon)} = \Vert {\mu P_\epsilon^n - \pi_\epsilon} \Vert_{L_1(\pi)} = 2{ \Vert {\mu P_\epsilon^n - \pi_\epsilon} \Vert_{\text{TV}}}. \end{aligned}\end{equation}
(26)
\begin{equation}\begin{aligned} \Vert {\mu P_\epsilon^n - \pi_\epsilon} \Vert_{L_1(\pi_\epsilon)} = \Vert {\mu P_\epsilon^n - \pi_\epsilon} \Vert_{L_1(\pi)} = 2{ \Vert {\mu P_\epsilon^n - \pi_\epsilon} \Vert_{\text{TV}}}. \end{aligned}\end{equation}
(26) \begin{equation}\begin{aligned} \Vert {\mu P_\epsilon^n - \pi_\epsilon} \Vert_{L_1(\pi_\epsilon)} & = \Vert {\mu P_\epsilon^n - \pi_\epsilon} \Vert_{L_1(\pi)} \\[2pt] & \leq \Vert {\mu P_\epsilon^n - \pi_\epsilon} \Vert_{L_2(\pi)} \\[2pt] & \leq \Vert {{\mu-\pi_\epsilon}}\Vert_{L_2(\pi)} (1-\alpha-\epsilon)^n. \end{aligned}\end{equation}
\begin{equation}\begin{aligned} \Vert {\mu P_\epsilon^n - \pi_\epsilon} \Vert_{L_1(\pi_\epsilon)} & = \Vert {\mu P_\epsilon^n - \pi_\epsilon} \Vert_{L_1(\pi)} \\[2pt] & \leq \Vert {\mu P_\epsilon^n - \pi_\epsilon} \Vert_{L_2(\pi)} \\[2pt] & \leq \Vert {{\mu-\pi_\epsilon}}\Vert_{L_2(\pi)} (1-\alpha-\epsilon)^n. \end{aligned}\end{equation}
-
(iii) If
 $\pi\in L_\infty(\pi_\epsilon)$ and
$\pi\in L_\infty(\pi_\epsilon)$ and  $\mu\in L_2(\pi_\epsilon)$, then
(27)
$\mu\in L_2(\pi_\epsilon)$, then
(27) \begin{equation}\begin{aligned} \Vert {\mu P_\epsilon^n - \pi_\epsilon} \Vert_{L_2(\pi_\epsilon)}^2 & = \int \bigg ({{\frac{{\textrm{d}}\mu P_\epsilon^n - \pi_\epsilon}{{\textrm{d}}\pi_\epsilon}}}\bigg)^2 d \pi_\epsilon \\ & = \int \bigg({{\frac{{\textrm{d}}\mu P_\epsilon^n - \pi_\epsilon}{{\textrm{d}}\pi}}}\bigg)^2 {\frac{{\textrm{d}}\pi}{{\textrm{d}}\pi_\epsilon}} d \pi\\ &\leq \Vert {\pi} \Vert_{L_\infty(\pi_\epsilon)}\int \bigg({{\frac{{\textrm{d}}\mu P_\epsilon^n - \pi_\epsilon}{{\textrm{d}}\pi}}}\bigg)^2 d \pi\\ & = \Vert {\pi} \Vert_{L_\infty(\pi_\epsilon)} \Vert {{\mu P_\epsilon^n - \pi_\epsilon}}\Vert_{L_2(\pi)} ^2\\ & \leq \Vert {\pi} \Vert_{L_\infty(\pi_\epsilon)} \Vert {{\mu-\pi_\epsilon}}\Vert_{L_2(\pi)} ^2(1-(\alpha-\epsilon))^{2n}. \end{aligned}\end{equation}
\begin{equation}\begin{aligned} \Vert {\mu P_\epsilon^n - \pi_\epsilon} \Vert_{L_2(\pi_\epsilon)}^2 & = \int \bigg ({{\frac{{\textrm{d}}\mu P_\epsilon^n - \pi_\epsilon}{{\textrm{d}}\pi_\epsilon}}}\bigg)^2 d \pi_\epsilon \\ & = \int \bigg({{\frac{{\textrm{d}}\mu P_\epsilon^n - \pi_\epsilon}{{\textrm{d}}\pi}}}\bigg)^2 {\frac{{\textrm{d}}\pi}{{\textrm{d}}\pi_\epsilon}} d \pi\\ &\leq \Vert {\pi} \Vert_{L_\infty(\pi_\epsilon)}\int \bigg({{\frac{{\textrm{d}}\mu P_\epsilon^n - \pi_\epsilon}{{\textrm{d}}\pi}}}\bigg)^2 d \pi\\ & = \Vert {\pi} \Vert_{L_\infty(\pi_\epsilon)} \Vert {{\mu P_\epsilon^n - \pi_\epsilon}}\Vert_{L_2(\pi)} ^2\\ & \leq \Vert {\pi} \Vert_{L_\infty(\pi_\epsilon)} \Vert {{\mu-\pi_\epsilon}}\Vert_{L_2(\pi)} ^2(1-(\alpha-\epsilon))^{2n}. \end{aligned}\end{equation}
Proof of Theorem 3. From [Reference Baxter and Rosenthal4, Lemma 1], since ![]() $P_\epsilon$ has stationary measure
$P_\epsilon$ has stationary measure ![]() $\pi_\epsilon$, we have
$\pi_\epsilon$, we have ![]() $P_\epsilon\,{:}\, L_2(\pi_\epsilon)\to L_2(\pi_\epsilon)$. Since
$P_\epsilon\,{:}\, L_2(\pi_\epsilon)\to L_2(\pi_\epsilon)$. Since ![]() $P_\epsilon$ is
$P_\epsilon$ is ![]() $(L_\infty(\pi_\epsilon), \Vert {\cdot} \Vert_{L_1(\pi_\epsilon)})$-GE with factor
$(L_\infty(\pi_\epsilon), \Vert {\cdot} \Vert_{L_1(\pi_\epsilon)})$-GE with factor ![]() $\rho_1 \leq (1-(\alpha-\epsilon))$ (as established by Theorem 2) and
$\rho_1 \leq (1-(\alpha-\epsilon))$ (as established by Theorem 2) and ![]() $P_\epsilon$ is reversible, it must also be
$P_\epsilon$ is reversible, it must also be ![]() $L_2(\pi_\epsilon)$-GE with factor
$L_2(\pi_\epsilon)$-GE with factor ![]() $\rho =\rho_1$ by Lemma 2.
$\rho =\rho_1$ by Lemma 2.
Proof of Corollary 1. Note that the assumption that ![]() $ \Vert {{P-P_\epsilon}}\Vert_{L_2(\pi_\epsilon)} <\varphi$ implies
$ \Vert {{P-P_\epsilon}}\Vert_{L_2(\pi_\epsilon)} <\varphi$ implies ![]() $P-P_\epsilon \,{:}\, L_2(\pi_\epsilon)\to L_2(\pi_\epsilon)$.
$P-P_\epsilon \,{:}\, L_2(\pi_\epsilon)\to L_2(\pi_\epsilon)$.
(i) Since
 $P_\epsilon$ is
$P_\epsilon$ is  $L_2(\pi_\epsilon)$-GE with factor
$L_2(\pi_\epsilon)$-GE with factor  $(1-(\alpha-\epsilon))$ and
$(1-(\alpha-\epsilon))$ and  $\pi_\epsilon$-reversible, we can reverse the roles of P and
$\pi_\epsilon$-reversible, we can reverse the roles of P and  $P_\epsilon$, so the result follows by Theorem 1.
$P_\epsilon$, so the result follows by Theorem 1.-
(ii) Taking
 $\mu = \pi$ and
$\mu = \pi$ and  $n=1$ in Theorem(iii), we have
(28)Hence,
$n=1$ in Theorem(iii), we have
(28)Hence, \begin{equation}\begin{aligned} \Vert {\pi P_\epsilon - \pi_\epsilon} \Vert_{L_2(\pi_\epsilon)}^2 & \leq \Vert {\pi} \Vert_{L_\infty(\pi_\epsilon)} \Vert {\pi-\pi_\epsilon}\Vert_{L_2(\pi)} ^2(1-(\alpha-\epsilon))^2 \\ &\leq \Vert {\pi} \Vert_{L_\infty(\pi_\epsilon)}\frac{\epsilon^2}{\alpha^2-\epsilon^2}(1-(\alpha-\epsilon))^2.\end{aligned}\end{equation}
(29)Hence,
\begin{equation}\begin{aligned} \Vert {\pi P_\epsilon - \pi_\epsilon} \Vert_{L_2(\pi_\epsilon)}^2 & \leq \Vert {\pi} \Vert_{L_\infty(\pi_\epsilon)} \Vert {\pi-\pi_\epsilon}\Vert_{L_2(\pi)} ^2(1-(\alpha-\epsilon))^2 \\ &\leq \Vert {\pi} \Vert_{L_\infty(\pi_\epsilon)}\frac{\epsilon^2}{\alpha^2-\epsilon^2}(1-(\alpha-\epsilon))^2.\end{aligned}\end{equation}
(29)Hence, \begin{equation}\begin{aligned} \Vert {\pi - \pi_\epsilon} \Vert_{L_2(\pi_\epsilon)} &\leq \Vert {\pi P - \pi P_\epsilon} \Vert_{L_2(\pi_\epsilon)} + \Vert {\pi P_\epsilon - \pi_\epsilon} \Vert_{L_2(\pi_\epsilon)} \\[2pt] & \leq \varphi \Vert {{\pi}}\Vert_{L_2(\pi_\epsilon)} + \Vert {\pi} \Vert_{L_\infty(\pi_\epsilon)}^{1/2}\frac{\epsilon}{\sqrt{\alpha^2-\epsilon^2}}(1-(\alpha-\epsilon))\\[2pt] & = \varphi\sqrt{ \Vert {{\pi-\pi_\epsilon}}\Vert_{L_2(\pi_\epsilon)} ^2+1} + \Vert {\pi} \Vert_{L_\infty(\pi_\epsilon)}^{1/2}\frac{\epsilon}{\sqrt{\alpha^2-\epsilon^2}}(1-(\alpha-\epsilon))\\[2pt] & \leq \varphi( \Vert {{\pi-\pi_\epsilon}}\Vert_{L_2(\pi_\epsilon)} +1) + \Vert {\pi} \Vert_{L_\infty(\pi_\epsilon)}^{1/2}\frac{\epsilon}{\sqrt{\alpha^2-\epsilon^2}}(1-(\alpha-\epsilon)).\end{aligned}\end{equation}
(30)Finally,
\begin{equation}\begin{aligned} \Vert {\pi - \pi_\epsilon} \Vert_{L_2(\pi_\epsilon)} &\leq \Vert {\pi P - \pi P_\epsilon} \Vert_{L_2(\pi_\epsilon)} + \Vert {\pi P_\epsilon - \pi_\epsilon} \Vert_{L_2(\pi_\epsilon)} \\[2pt] & \leq \varphi \Vert {{\pi}}\Vert_{L_2(\pi_\epsilon)} + \Vert {\pi} \Vert_{L_\infty(\pi_\epsilon)}^{1/2}\frac{\epsilon}{\sqrt{\alpha^2-\epsilon^2}}(1-(\alpha-\epsilon))\\[2pt] & = \varphi\sqrt{ \Vert {{\pi-\pi_\epsilon}}\Vert_{L_2(\pi_\epsilon)} ^2+1} + \Vert {\pi} \Vert_{L_\infty(\pi_\epsilon)}^{1/2}\frac{\epsilon}{\sqrt{\alpha^2-\epsilon^2}}(1-(\alpha-\epsilon))\\[2pt] & \leq \varphi( \Vert {{\pi-\pi_\epsilon}}\Vert_{L_2(\pi_\epsilon)} +1) + \Vert {\pi} \Vert_{L_\infty(\pi_\epsilon)}^{1/2}\frac{\epsilon}{\sqrt{\alpha^2-\epsilon^2}}(1-(\alpha-\epsilon)).\end{aligned}\end{equation}
(30)Finally, \begin{equation}\begin{aligned} \Vert {{\pi-\pi_\epsilon}}\Vert_{L_2(\pi_\epsilon)} \leq \frac{\varphi + \Vert {\pi} \Vert_{L_\infty(\pi_\epsilon)}^{1/2}\frac{\epsilon}{\sqrt{\alpha^2-\epsilon^2}}(1-(\alpha-\epsilon))}{1-\varphi}.\end{aligned}\end{equation}
The first term is bounded by Theorem 2(iii), and the second term is bounded by (30).
\begin{equation}\begin{aligned} \Vert {{\pi-\pi_\epsilon}}\Vert_{L_2(\pi_\epsilon)} \leq \frac{\varphi + \Vert {\pi} \Vert_{L_\infty(\pi_\epsilon)}^{1/2}\frac{\epsilon}{\sqrt{\alpha^2-\epsilon^2}}(1-(\alpha-\epsilon))}{1-\varphi}.\end{aligned}\end{equation}
The first term is bounded by Theorem 2(iii), and the second term is bounded by (30). \begin{align*} \Vert {{\mu P_\epsilon^n -\pi}}\Vert_{L_2(\pi_\epsilon)} & \leq \Vert {{\mu P_\epsilon^n -\pi_\epsilon}}\Vert_{L_2(\pi_\epsilon)} + \Vert {{\pi_\epsilon - \pi}}\Vert_{L_2(\pi_\epsilon)} .\end{align*}
\begin{align*} \Vert {{\mu P_\epsilon^n -\pi}}\Vert_{L_2(\pi_\epsilon)} & \leq \Vert {{\mu P_\epsilon^n -\pi_\epsilon}}\Vert_{L_2(\pi_\epsilon)} + \Vert {{\pi_\epsilon - \pi}}\Vert_{L_2(\pi_\epsilon)} .\end{align*}
A.3. Proofs of Theorem 4 and Theorem 5
A.3.1 Time-averaging of marginal distributions
Proof of Theorem 4. The first result of Theorem 4 follows from the triangle inequality and Theorem 1:
 \begin{align*} \left\Vert {{\pi -\frac{1}{t}\sum_{k=0}^{t-1} \mu P_\epsilon^k}}\right\Vert_{L_2(\pi)} &\leq \frac{1}{t} \sum_{k=0}^{t-1} \left\Vert {{\pi - \mu P_\epsilon^k }}\right\Vert_{L_2(\pi)} \\[3pt] &\leq \frac{1}{t} \sum_{k=0}^{t-1}\left[(1-(\alpha-\epsilon))^k \Vert {{\pi_\epsilon-\mu}}\Vert_{L_2(\pi)} +\frac{\epsilon}{\sqrt{\alpha^2-\epsilon^2}}\right]\\[3pt] & \leq \frac{1-(1-(\alpha-\epsilon))^t}{t(\alpha-\epsilon)} \Vert {{ \pi_\epsilon-\mu}}\Vert_{L_2(\pi)} +\frac{\epsilon}{\sqrt{\alpha^2-\epsilon^2}} \ .\end{align*}
\begin{align*} \left\Vert {{\pi -\frac{1}{t}\sum_{k=0}^{t-1} \mu P_\epsilon^k}}\right\Vert_{L_2(\pi)} &\leq \frac{1}{t} \sum_{k=0}^{t-1} \left\Vert {{\pi - \mu P_\epsilon^k }}\right\Vert_{L_2(\pi)} \\[3pt] &\leq \frac{1}{t} \sum_{k=0}^{t-1}\left[(1-(\alpha-\epsilon))^k \Vert {{\pi_\epsilon-\mu}}\Vert_{L_2(\pi)} +\frac{\epsilon}{\sqrt{\alpha^2-\epsilon^2}}\right]\\[3pt] & \leq \frac{1-(1-(\alpha-\epsilon))^t}{t(\alpha-\epsilon)} \Vert {{ \pi_\epsilon-\mu}}\Vert_{L_2(\pi)} +\frac{\epsilon}{\sqrt{\alpha^2-\epsilon^2}} \ .\end{align*}
The subsequent results follow similarly via Theorems 2 and 3 and Corollary 1.
A.3.2 Covariance bounds
We turn our attention to the covariance structure of the original and perturbed chains. There is an obvious isometric isomorphism between the space of measures ![]() $L_2(\pi)$ and the function space
$L_2(\pi)$ and the function space
equipped with the norm ![]() $ \Vert {f} \Vert^2_{L^{\prime}_2(\pi)} = \int f(x)^2\pi(dx)$, where a measure
$ \Vert {f} \Vert^2_{L^{\prime}_2(\pi)} = \int f(x)^2\pi(dx)$, where a measure ![]() $\mu$ is mapped to its Radon–Nikodym derivative,
$\mu$ is mapped to its Radon–Nikodym derivative, ![]() $\mu\mapsto {\frac{{\textrm{d}}\mu}{{\textrm{d}}\pi}}$. For this reason, we need not distinguish between these spaces, and when dealing with a function
$\mu\mapsto {\frac{{\textrm{d}}\mu}{{\textrm{d}}\pi}}$. For this reason, we need not distinguish between these spaces, and when dealing with a function ![]() $f\in L^{\prime}_2(\pi)$ we may occasionally abuse notation and treat it as its associated measure. Let
$f\in L^{\prime}_2(\pi)$ we may occasionally abuse notation and treat it as its associated measure. Let ![]() $X_t$ and
$X_t$ and ![]() $X^\epsilon_t$ denote the original and perturbed chains run from some initial measure
$X^\epsilon_t$ denote the original and perturbed chains run from some initial measure ![]() $\mu\in L_2(\pi)$.
$\mu\in L_2(\pi)$.
Corollary 4. Under the assumptions of Section 3.2,
(a) if
 $X_0\sim\pi$ (the initial distribution is the stationary distribution), then for
$X_0\sim\pi$ (the initial distribution is the stationary distribution), then for  $f,g\in L^{\prime}_2(\pi)$,
(31)
$f,g\in L^{\prime}_2(\pi)$,
(31) \begin{equation}\begin{aligned} \textrm{Cov} [f(X_t),g(X_s)]\leq (1-\alpha)^{|t-s|} \Vert {{f-\pi f}}\Vert_{L^{\prime}_2(\pi)} \Vert {{g-\pi g}}\Vert_{L^{\prime}_2(\pi)} \ ;\end{aligned}\end{equation}
\begin{equation}\begin{aligned} \textrm{Cov} [f(X_t),g(X_s)]\leq (1-\alpha)^{|t-s|} \Vert {{f-\pi f}}\Vert_{L^{\prime}_2(\pi)} \Vert {{g-\pi g}}\Vert_{L^{\prime}_2(\pi)} \ ;\end{aligned}\end{equation}
-
(b) if
 $\epsilon<\alpha$, and
$\epsilon<\alpha$, and  $P_\epsilon$ is
$P_\epsilon$ is  $\pi_\epsilon$-reversible,
$\pi_\epsilon$-reversible,  $\rho_2 = (1-(\alpha-\epsilon))$, and
$\rho_2 = (1-(\alpha-\epsilon))$, and  $X^\epsilon_0\sim\pi_\epsilon$, then for
$X^\epsilon_0\sim\pi_\epsilon$, then for  $f,g\in L_2^{\prime}(\pi_\epsilon)$,
(32)
$f,g\in L_2^{\prime}(\pi_\epsilon)$,
(32) \begin{equation}\begin{aligned} \textrm{Cov} [f(X^\epsilon_t),g(X^\epsilon_s)]\leq \rho_2^{|t-s|} \Vert {{ f - \pi_\epsilon f}}\Vert_{L^{\prime}_2(\pi_\epsilon)} \Vert {{g - \pi_\epsilon g}}\Vert_{L^{\prime}_2(\pi_\epsilon)} \ ,\end{aligned}\end{equation}
\begin{equation}\begin{aligned} \textrm{Cov} [f(X^\epsilon_t),g(X^\epsilon_s)]\leq \rho_2^{|t-s|} \Vert {{ f - \pi_\epsilon f}}\Vert_{L^{\prime}_2(\pi_\epsilon)} \Vert {{g - \pi_\epsilon g}}\Vert_{L^{\prime}_2(\pi_\epsilon)} \ ,\end{aligned}\end{equation}
where for a function ![]() $h\,{:}\,{\mathcal{X}}\to\mathbb{R}$,
$h\,{:}\,{\mathcal{X}}\to\mathbb{R}$, ![]() $\pi h$ is the constant function equal to
$\pi h$ is the constant function equal to ![]() $\int h(s)\pi(ds)$ everywhere.
$\int h(s)\pi(ds)$ everywhere.
Proof. The proof of this result follows that of Corollary B.5 in [Reference Johndrow, Mattingly, Mukherjee and Dunson18]. We only show the proof for the original chain; however, the proof for the perturbed chain is the same, since it is reversible and ![]() $L_2(\pi_\epsilon)$-GE with the appropriate factor, from Theorem 3.
$L_2(\pi_\epsilon)$-GE with the appropriate factor, from Theorem 3.
Define the subspace
and define the operator ![]() $F \in \mathcal{B}(L^{\prime}_{2,0}(\pi))$ by
$F \in \mathcal{B}(L^{\prime}_{2,0}(\pi))$ by
From Lemma 12.6.4 of [Reference Liu21],
 \begin{align*} \sup\limits_{f,g\in L_2^{\prime}(\pi)} \text{corr}(f(X_0),g(X_t)) = \sup\limits_{\substack{ \Vert {{f}}\Vert_{L^{\prime}_2(\pi)} =1= \Vert {{g}}\Vert_{L^{\prime}_2(\pi)} \\f,g\in L^{\prime}_{2,0}(\pi)}} \langle f,F^t g\rangle = \Vert {F^t} \Vert_{L_{2,0}^{\prime}(\pi)}.\end{align*}
\begin{align*} \sup\limits_{f,g\in L_2^{\prime}(\pi)} \text{corr}(f(X_0),g(X_t)) = \sup\limits_{\substack{ \Vert {{f}}\Vert_{L^{\prime}_2(\pi)} =1= \Vert {{g}}\Vert_{L^{\prime}_2(\pi)} \\f,g\in L^{\prime}_{2,0}(\pi)}} \langle f,F^t g\rangle = \Vert {F^t} \Vert_{L_{2,0}^{\prime}(\pi)}.\end{align*}
Consider the canonical isomorphism between ![]() $L_2(\pi)$ and
$L_2(\pi)$ and ![]() $L^{\prime}_2(\pi)$. The restriction of this isomorphism (on the right) to elements of
$L^{\prime}_2(\pi)$. The restriction of this isomorphism (on the right) to elements of ![]() $L^{\prime}_{2,0}(\pi)$ yields
$L^{\prime}_{2,0}(\pi)$ yields ![]() $L_{2,0}(\pi)$ (on the left)—the signed measures with total measure 0. The image of F under the restricted isomorphism is the adjoint operator of P restricted to
$L_{2,0}(\pi)$ (on the left)—the signed measures with total measure 0. The image of F under the restricted isomorphism is the adjoint operator of P restricted to ![]() $L_{2,0}(\pi)$. Since P is
$L_{2,0}(\pi)$. Since P is ![]() $\pi$-reversible, it is self-adjoint in
$\pi$-reversible, it is self-adjoint in ![]() $L_2(\pi)$, so
$L_2(\pi)$, so ![]() $ \Vert {F} \Vert_{L_{2,0}^{\prime}(\pi)}= \Vert {P} \Vert_{L_{2,0}(\pi)}$. Thus
$ \Vert {F} \Vert_{L_{2,0}^{\prime}(\pi)}= \Vert {P} \Vert_{L_{2,0}(\pi)}$. Thus
Therefore
Since Cov is symmetric, the shifted and symmetrized result holds for any ![]() $f,g\in L^{\prime}_2(\pi)$:
$f,g\in L^{\prime}_2(\pi)$:
 \begin{equation}\begin{aligned} \textrm{Cov} [f(X_t),g(X_s)]\leq (1-\alpha)^{|t-s|} \Vert {{f -\pi f}}\Vert_{L^{\prime}_2(\pi)} \Vert {{ g - \pi g}}\Vert_{L^{\prime}_2(\pi)} .\end{aligned}\end{equation}
\begin{equation}\begin{aligned} \textrm{Cov} [f(X_t),g(X_s)]\leq (1-\alpha)^{|t-s|} \Vert {{f -\pi f}}\Vert_{L^{\prime}_2(\pi)} \Vert {{ g - \pi g}}\Vert_{L^{\prime}_2(\pi)} .\end{aligned}\end{equation}
We present further bounds for the case that the initial distribution is not the stationary distribution in Corollary 5.
Remark 8. Note in Corollary 4 that
Also note that
Corollary 5. Under the assumptions of Section 3.2,
(a) if
 $X_0\sim\mu$, then for
$X_0\sim\mu$, then for  $f,g\in L^{\prime}_4(\pi)$,
$f,g\in L^{\prime}_4(\pi)$,
 \begin{align*}&\textrm{Cov}(f(X_t),g(X_{t+s}))\\ &\qquad\leq (1-\alpha)^s \Vert {{f -\pi f}}\Vert_{L^{\prime}_2(\pi)} \Vert {{ g - \pi g}}\Vert_{L^{\prime}_2(\pi)} \\ &\qquad\qquad + 2^{3/2}(1-\alpha)^{t+s/2} \Vert {{\mu-\pi}}\Vert_{L_2(\pi)} \Vert {f -\pi f} \Vert_{L_4^{\prime}(\pi)} \Vert { g - \pi g} \Vert_{L_4^{\prime}(\pi)}\\ &\qquad\qquad -(\mu P^t f-\pi f)\left(\mu P^{t+s} g -\pi g\right);\end{align*}
\begin{align*}&\textrm{Cov}(f(X_t),g(X_{t+s}))\\ &\qquad\leq (1-\alpha)^s \Vert {{f -\pi f}}\Vert_{L^{\prime}_2(\pi)} \Vert {{ g - \pi g}}\Vert_{L^{\prime}_2(\pi)} \\ &\qquad\qquad + 2^{3/2}(1-\alpha)^{t+s/2} \Vert {{\mu-\pi}}\Vert_{L_2(\pi)} \Vert {f -\pi f} \Vert_{L_4^{\prime}(\pi)} \Vert { g - \pi g} \Vert_{L_4^{\prime}(\pi)}\\ &\qquad\qquad -(\mu P^t f-\pi f)\left(\mu P^{t+s} g -\pi g\right);\end{align*}
-
(b) if
 $\epsilon<\alpha$, and
$\epsilon<\alpha$, and  $P_\epsilon$ is
$P_\epsilon$ is  $\pi_\epsilon$-reversible,
$\pi_\epsilon$-reversible,  $\rho_2 = (1-(\alpha -\epsilon))$, and
$\rho_2 = (1-(\alpha -\epsilon))$, and  $X^\epsilon_0\sim\mu$, then for
$X^\epsilon_0\sim\mu$, then for  $f,g\in L^{\prime}_4(\pi_\epsilon)$,
$f,g\in L^{\prime}_4(\pi_\epsilon)$,
 \begin{align*}&\textrm{Cov}(f(X^\epsilon_t),g(X^\epsilon_{t+s}))\\ &\qquad\leq \rho_2^s \Vert {{f -\pi_\epsilon f}}\Vert_{L^{\prime}_2(\pi_\epsilon)} \Vert {{ g - \pi_\epsilon g}}\Vert_{L^{\prime}_2(\pi_\epsilon)} \\ &\qquad\qquad + 2^{3/2}\rho_2^{t+s/2} \Vert {{\mu-\pi}}\Vert_{L_2(\pi_\epsilon)} \Vert {f -\pi_\epsilon f} \Vert_{L_4^{\prime}(\pi_\epsilon)} \Vert { g - \pi_\epsilon g} \Vert_{L_4^{\prime}(\pi_\epsilon)}\\ &\qquad\qquad -(\mu P_\epsilon^t f-\pi_\epsilon f)\left(\mu P_\epsilon^{t+s} g -\pi_\epsilon g\right).\end{align*}
\begin{align*}&\textrm{Cov}(f(X^\epsilon_t),g(X^\epsilon_{t+s}))\\ &\qquad\leq \rho_2^s \Vert {{f -\pi_\epsilon f}}\Vert_{L^{\prime}_2(\pi_\epsilon)} \Vert {{ g - \pi_\epsilon g}}\Vert_{L^{\prime}_2(\pi_\epsilon)} \\ &\qquad\qquad + 2^{3/2}\rho_2^{t+s/2} \Vert {{\mu-\pi}}\Vert_{L_2(\pi_\epsilon)} \Vert {f -\pi_\epsilon f} \Vert_{L_4^{\prime}(\pi_\epsilon)} \Vert { g - \pi_\epsilon g} \Vert_{L_4^{\prime}(\pi_\epsilon)}\\ &\qquad\qquad -(\mu P_\epsilon^t f-\pi_\epsilon f)\left(\mu P_\epsilon^{t+s} g -\pi_\epsilon g\right).\end{align*}
Proof. This will use the following shorthand notation. Let
 \begin{align*}f_0 &= f-\pi f,\\g_0 &= g-\pi g,\\\Vert h\Vert_\star &= \left(\int (h(x)-\pi h)^2\pi(d x)\right)^{1/2},\\\Vert h\Vert_{{}_{\star\star}} &= \left(\int (h(x)-\pi h)^4\pi(d x)\right)^{1/4},\\C_\mu &= \Vert \mu -\pi\Vert_2.\end{align*}
\begin{align*}f_0 &= f-\pi f,\\g_0 &= g-\pi g,\\\Vert h\Vert_\star &= \left(\int (h(x)-\pi h)^2\pi(d x)\right)^{1/2},\\\Vert h\Vert_{{}_{\star\star}} &= \left(\int (h(x)-\pi h)^4\pi(d x)\right)^{1/4},\\C_\mu &= \Vert \mu -\pi\Vert_2.\end{align*}
We can interpret ![]() $\Vert\cdot\Vert_{{}_{\star\star}}$ as a centred 4-norm. It is certainly bounded above by
$\Vert\cdot\Vert_{{}_{\star\star}}$ as a centred 4-norm. It is certainly bounded above by ![]() $\Vert\cdot\Vert_4$, the norm on
$\Vert\cdot\Vert_4$, the norm on ![]() $L^{\prime}_4(\pi)$. For some results regarding the properties of a Markov transition kernel as an operator on
$L^{\prime}_4(\pi)$. For some results regarding the properties of a Markov transition kernel as an operator on ![]() $L^{\prime}_p(\pi)$ for general p given an
$L^{\prime}_p(\pi)$ for general p given an ![]() $L_2$-spectral gap (as is implied by
$L_2$-spectral gap (as is implied by ![]() $L_2$-GE), please refer to [Reference Rudolf34].
$L_2$-GE), please refer to [Reference Rudolf34].
We only show the proof for the original chain. The result for the perturbed chain has essentially the same proof.
By definition we can express the covariance by the triple integral below. We re-express this integral as a sum of two integrals involving the chain run from stationarity. This will allow us to apply Corollary 4. We have
 \begin{align*}&\textrm{Cov}(f(X_t),g(X_{t+s}))\\ &\ = \iiint (f(y)-\mu P^t f)(g(z)-\mu P^{t+s} g)\mu(d x)P^t(x,d y)P^s(y,dz)\\ &\ = \iiint (f(y)-\mu P^t f)(g(z)-\mu P^{t+s} g)\left[\frac{d\mu}{d\pi}(x)-1\right] \pi(d x)P^t(x,d y)P^s(y,dz)\\ &\ \quad +\iiint(f(y)-\mu P^t f)(g(z)-\mu P^{t+s} g)\pi(d x)P^t(x,d y)P^s(y,dz).\end{align*}
\begin{align*}&\textrm{Cov}(f(X_t),g(X_{t+s}))\\ &\ = \iiint (f(y)-\mu P^t f)(g(z)-\mu P^{t+s} g)\mu(d x)P^t(x,d y)P^s(y,dz)\\ &\ = \iiint (f(y)-\mu P^t f)(g(z)-\mu P^{t+s} g)\left[\frac{d\mu}{d\pi}(x)-1\right] \pi(d x)P^t(x,d y)P^s(y,dz)\\ &\ \quad +\iiint(f(y)-\mu P^t f)(g(z)-\mu P^{t+s} g)\pi(d x)P^t(x,d y)P^s(y,dz).\end{align*}
We will simplify each of these expressions separately, starting with the second term:
 \begin{align*}&\iiint(f(y)-\mu P^t f)(g(z)-\mu P^{t+s} g)\pi(d x)P^t(x,d y)P^s(y,dz)\\ &\qquad = \iint(f(y)-\mu P^t f)(g(z)-\mu P^{t+s} g)\pi(d y)P^s(y,dz)\\ &\qquad = \iint f(y)g(z)\pi(d y)P^s(y,dz) \\ &\qquad \qquad - (\mu P^t f)(\pi g)-(\pi f)(\mu P^{t+s} g)+(\mu P^t f)(\mu P^{t+s} g)\\ &\qquad = \iint f_0(y)g_0(z) \pi(d y)P^s(y,dz) +(\pi f)(\pi g)\\ &\qquad \qquad - (\mu P^t f)(\pi g)-(\pi f)(\mu P^{s+t} g)+(\mu P^t f)(\mu P^{t+s} g)\\ &\qquad = \left\langle f_0, F^s g_0 \right\rangle +(\mu P^t f-\pi f )(\mu P^{s+t} g - \pi g ).\end{align*}
\begin{align*}&\iiint(f(y)-\mu P^t f)(g(z)-\mu P^{t+s} g)\pi(d x)P^t(x,d y)P^s(y,dz)\\ &\qquad = \iint(f(y)-\mu P^t f)(g(z)-\mu P^{t+s} g)\pi(d y)P^s(y,dz)\\ &\qquad = \iint f(y)g(z)\pi(d y)P^s(y,dz) \\ &\qquad \qquad - (\mu P^t f)(\pi g)-(\pi f)(\mu P^{t+s} g)+(\mu P^t f)(\mu P^{t+s} g)\\ &\qquad = \iint f_0(y)g_0(z) \pi(d y)P^s(y,dz) +(\pi f)(\pi g)\\ &\qquad \qquad - (\mu P^t f)(\pi g)-(\pi f)(\mu P^{s+t} g)+(\mu P^t f)(\mu P^{t+s} g)\\ &\qquad = \left\langle f_0, F^s g_0 \right\rangle +(\mu P^t f-\pi f )(\mu P^{s+t} g - \pi g ).\end{align*}
For the first term we find that
 \begin{align*}&\iiint (f(y)-\mu P^t f)(g(z)-\mu P^{t+s} g)\left(\frac{d\mu}{d\pi}(x)-1\right)\pi(d x)P^t(x,d y)P^s(y,dz)\\ &\qquad = \iiint f(y)g(z)\left(\frac{d\mu}{d\pi}(x)-1\right)\pi(d x)P^t(x,d y)P^s(y,dz)\\ &\qquad\qquad-(\mu P^t f)\iint g(z)\left(\frac{d\mu}{d\pi}(x)-1\right)\pi(d x)P^{t+s}(x,dz)\\ &\qquad\qquad-(\mu P^{s+t} g)\iint f(y)\left(\frac{d\mu}{d\pi}(x)-1\right)\pi(d x)P^{t}(x,d y)\\ &\qquad\qquad+(\mu P^t f)(\mu P^{s+t} g)\int\left(\frac{d\mu}{d\pi}(x)-1\right)\pi(d x)\\ &\qquad = \iiint f_0(y) g_0(z)\left(\frac{d\mu}{d\pi}(x)-1\right)\pi(d x)P^t(x,d y)P^s(y,dz) \\ \end{align*}
\begin{align*}&\iiint (f(y)-\mu P^t f)(g(z)-\mu P^{t+s} g)\left(\frac{d\mu}{d\pi}(x)-1\right)\pi(d x)P^t(x,d y)P^s(y,dz)\\ &\qquad = \iiint f(y)g(z)\left(\frac{d\mu}{d\pi}(x)-1\right)\pi(d x)P^t(x,d y)P^s(y,dz)\\ &\qquad\qquad-(\mu P^t f)\iint g(z)\left(\frac{d\mu}{d\pi}(x)-1\right)\pi(d x)P^{t+s}(x,dz)\\ &\qquad\qquad-(\mu P^{s+t} g)\iint f(y)\left(\frac{d\mu}{d\pi}(x)-1\right)\pi(d x)P^{t}(x,d y)\\ &\qquad\qquad+(\mu P^t f)(\mu P^{s+t} g)\int\left(\frac{d\mu}{d\pi}(x)-1\right)\pi(d x)\\ &\qquad = \iiint f_0(y) g_0(z)\left(\frac{d\mu}{d\pi}(x)-1\right)\pi(d x)P^t(x,d y)P^s(y,dz) \\ \end{align*}
 \begin{align*} \\[-30pt] &\qquad\qquad-(\mu P^t f-\pi f)\iint g(z)\left(\frac{d\mu}{d\pi}(x)-1\right)\pi(d x)P^{t+s}(x,dz)\\ &\qquad\qquad-(\mu P^{s+t} g -\pi g)\iint f(y)\left(\frac{d\mu}{d\pi}(x)-1\right)\pi(d x)P^{t}(x,d y)\\ &\qquad\qquad -(\pi f)(\pi g)\int\left(\frac{d\mu}{d\pi}(x)-1\right)\pi(d x)\\ &\qquad =\left\langle\frac{d\mu}{d\pi}-1, F^t (f_0\otimes (F^s g_0))\right\rangle\\ &\qquad \qquad -(\mu P^t f-\pi f)\left\langle \frac{d\mu}{d\pi}-1,F^{t+s} g\right\rangle-(\mu P^{t+s} g -\pi g)\left\langle \frac{d\mu}{d\pi}-1,F^{t} f\right\rangle\\ &\qquad =\left\langle\frac{d\mu}{d\pi}-1, F^t (f_0\otimes (F^s g_0))\right\rangle-2(\mu P^t f-\pi f)\left(\mu P^{t+s} g -\pi g\right),\end{align*}
\begin{align*} \\[-30pt] &\qquad\qquad-(\mu P^t f-\pi f)\iint g(z)\left(\frac{d\mu}{d\pi}(x)-1\right)\pi(d x)P^{t+s}(x,dz)\\ &\qquad\qquad-(\mu P^{s+t} g -\pi g)\iint f(y)\left(\frac{d\mu}{d\pi}(x)-1\right)\pi(d x)P^{t}(x,d y)\\ &\qquad\qquad -(\pi f)(\pi g)\int\left(\frac{d\mu}{d\pi}(x)-1\right)\pi(d x)\\ &\qquad =\left\langle\frac{d\mu}{d\pi}-1, F^t (f_0\otimes (F^s g_0))\right\rangle\\ &\qquad \qquad -(\mu P^t f-\pi f)\left\langle \frac{d\mu}{d\pi}-1,F^{t+s} g\right\rangle-(\mu P^{t+s} g -\pi g)\left\langle \frac{d\mu}{d\pi}-1,F^{t} f\right\rangle\\ &\qquad =\left\langle\frac{d\mu}{d\pi}-1, F^t (f_0\otimes (F^s g_0))\right\rangle-2(\mu P^t f-\pi f)\left(\mu P^{t+s} g -\pi g\right),\end{align*}
where ![]() $f_0\otimes F^s g_0$ is defined by
$f_0\otimes F^s g_0$ is defined by
Putting these together,
 \begin{align*} &\textrm{Cov}(f(X_t),g(X_{t+s}))\\[2pt] &\qquad = \left\langle f_0, F^s g_0 \right\rangle +(\pi f -\mu P^t f)(\pi g - \mu P^{s+t} g)\\[2pt] &\qquad \qquad + \left\langle\frac{d\mu}{d\pi}-1, F^t (f_0\otimes (F^s g_0))\right\rangle-2(\mu P^t f-\pi f)\left(\mu P^{t+s} g -\pi g\right)\\[2pt] &\qquad = \left\langle f_0, F^s g_0 \right\rangle + \left\langle\frac{d\mu}{d\pi}-1, F^t (f_0\otimes (F^s g_0))\right\rangle -(\mu P^t f-\pi f)\left(\mu P^{t+s} g -\pi g\right)\\[2pt] &\qquad \leq (1-\alpha)^s \Vert f\Vert_\star \Vert g\Vert_\star + (1-\alpha)^{t}\Vert \mu-\pi\Vert_2 \Vert f_0\otimes F^s g_0\Vert_2\\[2pt] &\qquad\qquad -(\mu P^t f-\pi f)\left(\mu P^{t+s} g -\pi g\right)\\[2pt] &\qquad \leq (1-\alpha)^s \Vert f\Vert_\star \Vert g\Vert_\star + (1-\alpha)^{t}\Vert \mu-\pi\Vert_2 \Vert f_0 \Vert_4\Vert F^s g_0\Vert_4\\[2pt] &\qquad\qquad -(\mu P^t f-\pi f)\left(\mu P^{t+s} g -\pi g\right)\\[2pt] &\qquad \leq (1-\alpha)^s \Vert f\Vert_\star \Vert g\Vert_\star + (1-\alpha)^{t}\Vert \mu-\pi\Vert_2 \Vert f_0 \Vert_4\Vert g_0\Vert_4 \left\Vert F^s\big\vert_{L^{\prime}_{4,0}}\right\Vert_4\\[2pt] &\qquad\qquad -(\mu P^t f-\pi f)\left(\mu P^{t+s} g -\pi g\right)\\[2pt] &\qquad \leq (1-\alpha)^s \Vert f\Vert_\star \Vert g\Vert_\star + 2^{3/2}(1-\alpha)^{t+s/2}\Vert \mu-\pi\Vert_2 \Vert f \Vert_{{}_{\star\star}}\Vert g\Vert_{{}_{\star\star}}\\[2pt] &\qquad\qquad -(\mu P^t f-\pi f)\left(\mu P^{t+s} g -\pi g\right).\end{align*}
\begin{align*} &\textrm{Cov}(f(X_t),g(X_{t+s}))\\[2pt] &\qquad = \left\langle f_0, F^s g_0 \right\rangle +(\pi f -\mu P^t f)(\pi g - \mu P^{s+t} g)\\[2pt] &\qquad \qquad + \left\langle\frac{d\mu}{d\pi}-1, F^t (f_0\otimes (F^s g_0))\right\rangle-2(\mu P^t f-\pi f)\left(\mu P^{t+s} g -\pi g\right)\\[2pt] &\qquad = \left\langle f_0, F^s g_0 \right\rangle + \left\langle\frac{d\mu}{d\pi}-1, F^t (f_0\otimes (F^s g_0))\right\rangle -(\mu P^t f-\pi f)\left(\mu P^{t+s} g -\pi g\right)\\[2pt] &\qquad \leq (1-\alpha)^s \Vert f\Vert_\star \Vert g\Vert_\star + (1-\alpha)^{t}\Vert \mu-\pi\Vert_2 \Vert f_0\otimes F^s g_0\Vert_2\\[2pt] &\qquad\qquad -(\mu P^t f-\pi f)\left(\mu P^{t+s} g -\pi g\right)\\[2pt] &\qquad \leq (1-\alpha)^s \Vert f\Vert_\star \Vert g\Vert_\star + (1-\alpha)^{t}\Vert \mu-\pi\Vert_2 \Vert f_0 \Vert_4\Vert F^s g_0\Vert_4\\[2pt] &\qquad\qquad -(\mu P^t f-\pi f)\left(\mu P^{t+s} g -\pi g\right)\\[2pt] &\qquad \leq (1-\alpha)^s \Vert f\Vert_\star \Vert g\Vert_\star + (1-\alpha)^{t}\Vert \mu-\pi\Vert_2 \Vert f_0 \Vert_4\Vert g_0\Vert_4 \left\Vert F^s\big\vert_{L^{\prime}_{4,0}}\right\Vert_4\\[2pt] &\qquad\qquad -(\mu P^t f-\pi f)\left(\mu P^{t+s} g -\pi g\right)\\[2pt] &\qquad \leq (1-\alpha)^s \Vert f\Vert_\star \Vert g\Vert_\star + 2^{3/2}(1-\alpha)^{t+s/2}\Vert \mu-\pi\Vert_2 \Vert f \Vert_{{}_{\star\star}}\Vert g\Vert_{{}_{\star\star}}\\[2pt] &\qquad\qquad -(\mu P^t f-\pi f)\left(\mu P^{t+s} g -\pi g\right).\end{align*}
The ![]() $\left\langle f_0, F^s g_0 \right\rangle$ term is bounded using Corollary 4, where we have taken the result in its equivalent form using the
$\left\langle f_0, F^s g_0 \right\rangle$ term is bounded using Corollary 4, where we have taken the result in its equivalent form using the ![]() $\langle\cdot,\cdot\rangle$ notation and the forward operator F. The term
$\langle\cdot,\cdot\rangle$ notation and the forward operator F. The term
is bounded following the methodology of the proof of [Reference Rudolf34, Lemma 3.39] (in order, the inequalities are Cauchy–Schwarz, ![]() $\Vert F^s g_0\Vert \leq \Vert F^s\Vert\Vert g_0\Vert$ for any norm
$\Vert F^s g_0\Vert \leq \Vert F^s\Vert\Vert g_0\Vert$ for any norm ![]() $\Vert\cdot\Vert$, and Proposition 3.17 of [Reference Rudolf34]).
$\Vert\cdot\Vert$, and Proposition 3.17 of [Reference Rudolf34]).
The main motivation in establishing the covariance bounds in Corollaries 4 and 5 is that we will need to sum up covariances in order to establish bounds on the variance component of mean squared error for estimation of ![]() $\pi(f)$ via the dependent sample means
$\pi(f)$ via the dependent sample means
 \begin{equation*}\frac{1}{t}\sum_{j=0}^{t-1} f(X_j), \qquad \frac{1}{t}\sum_{j=0}^{t-1} f(X^\epsilon_j)\end{equation*}
\begin{equation*}\frac{1}{t}\sum_{j=0}^{t-1} f(X_j), \qquad \frac{1}{t}\sum_{j=0}^{t-1} f(X^\epsilon_j)\end{equation*}
for an arbitrary starting measure. To this end we will be interested in the following summation result.
Corollary 6. Under the assumptions of Section 3.2,
(a) if
 $X_0\sim\mu$, then for
$X_0\sim\mu$, then for  $f,g\in L^{\prime}_4(\pi)$,
$f,g\in L^{\prime}_4(\pi)$,
 \begin{align*}&\frac{1}{t^2}\sum_{m=0}^{t-1}\sum_{n=0}^{t-1} \textrm{Cov} (f(X_j),f(X_k)) \\ &\qquad\leq \frac{2 \Vert {{f - \pi f}}\Vert_{L^{\prime}_2(\pi)} ^2}{\alpha t} + \frac{2^{7/2} \Vert {{\mu -\pi}}\Vert_{L_2(\pi)} \Vert {f -\pi f} \Vert_{L_4^{\prime}(\pi)}^2}{\alpha^2 t^2} -\left(\frac{1}{t}\sum_{m=0}^{t-1}\mu P^m f-\pi f\right)^2;\end{align*}
\begin{align*}&\frac{1}{t^2}\sum_{m=0}^{t-1}\sum_{n=0}^{t-1} \textrm{Cov} (f(X_j),f(X_k)) \\ &\qquad\leq \frac{2 \Vert {{f - \pi f}}\Vert_{L^{\prime}_2(\pi)} ^2}{\alpha t} + \frac{2^{7/2} \Vert {{\mu -\pi}}\Vert_{L_2(\pi)} \Vert {f -\pi f} \Vert_{L_4^{\prime}(\pi)}^2}{\alpha^2 t^2} -\left(\frac{1}{t}\sum_{m=0}^{t-1}\mu P^m f-\pi f\right)^2;\end{align*}
-
(b) if
 $\epsilon<\alpha$, and
$\epsilon<\alpha$, and  $P_\epsilon$ is
$P_\epsilon$ is  $\pi_\epsilon$-reversible,
$\pi_\epsilon$-reversible,  $\rho_2 = (1-(\alpha-\epsilon))$, and
$\rho_2 = (1-(\alpha-\epsilon))$, and  $X^\epsilon_0\sim\mu$, then for
$X^\epsilon_0\sim\mu$, then for  $f,g\in$
$f,g\in$  $L^{\prime}_4(\pi_\epsilon)$,
$L^{\prime}_4(\pi_\epsilon)$,
 \begin{align*}&\frac{1}{t^2}\sum_{m=0}^{t-1}\sum_{n=0}^{t-1} \textrm{Cov} (f(X_j^\epsilon),f(X_k^\epsilon)) \\[3pt] &\qquad\leq \frac{2 \Vert {{f - \pi f}}\Vert_{L^{\prime}_2(\pi_\epsilon)} ^2}{(1-\rho_2) t} + \frac{2^{7/2} \Vert {{\mu -\pi}}\Vert_{L_2(\pi_\epsilon)} \Vert {f -\pi f} \Vert_{L_4^{\prime}(\pi_\epsilon)}^2}{(1-\rho_2)^2 t^2} -\left(\frac{1}{t}\sum_{m=0}^{t-1}\mu P_\epsilon^m f-\pi f\right)^2.\end{align*}
\begin{align*}&\frac{1}{t^2}\sum_{m=0}^{t-1}\sum_{n=0}^{t-1} \textrm{Cov} (f(X_j^\epsilon),f(X_k^\epsilon)) \\[3pt] &\qquad\leq \frac{2 \Vert {{f - \pi f}}\Vert_{L^{\prime}_2(\pi_\epsilon)} ^2}{(1-\rho_2) t} + \frac{2^{7/2} \Vert {{\mu -\pi}}\Vert_{L_2(\pi_\epsilon)} \Vert {f -\pi f} \Vert_{L_4^{\prime}(\pi_\epsilon)}^2}{(1-\rho_2)^2 t^2} -\left(\frac{1}{t}\sum_{m=0}^{t-1}\mu P_\epsilon^m f-\pi f\right)^2.\end{align*}
Proof. We only show the proof for the original chain. The results for the perturbed chain have essentially the same proof. The proof is largely an exercise in summation of geometric series and meticulous bookkeeping. The first inequality is due to Corollary 5. The second inequality makes use of the fact that ![]() $0<\alpha<1$. To simplify notation,
$0<\alpha<1$. To simplify notation, ![]() $C_\mu = \Vert {{\mu-\pi}}\Vert_{L_2(\pi)} $. We have
$C_\mu = \Vert {{\mu-\pi}}\Vert_{L_2(\pi)} $. We have
 \begin{align*} &\frac{1}{t^2}\sum_{m=0}^{t-1}\sum_{n=0}^{t-1} \textrm{Cov} (f(X_j),f(X_k))\\[2pt] &\qquad = \frac{\Vert f\Vert_\star^2}{t^2}\sum_{m=0}^{t-1}\sum_{n=0}^{t-1} (1-\alpha)^{\vert m - n\vert} -\frac{1}{t^2}\sum_{m=0}^{t-1}\sum_{n=0}^{t-1}(\mu P^m f-\pi f)\left(\mu P^n f -\pi f\right)\\[2pt] &\qquad\qquad + \frac{2^{3/2} C_\mu \Vert f \Vert_{{}_{\star\star}}^2}{t^2}\sum_{m=0}^{t-1}\sum_{n=0}^{t-1} (1-\alpha)^{(m+n)/2}\\[2pt] \end{align*}
\begin{align*} &\frac{1}{t^2}\sum_{m=0}^{t-1}\sum_{n=0}^{t-1} \textrm{Cov} (f(X_j),f(X_k))\\[2pt] &\qquad = \frac{\Vert f\Vert_\star^2}{t^2}\sum_{m=0}^{t-1}\sum_{n=0}^{t-1} (1-\alpha)^{\vert m - n\vert} -\frac{1}{t^2}\sum_{m=0}^{t-1}\sum_{n=0}^{t-1}(\mu P^m f-\pi f)\left(\mu P^n f -\pi f\right)\\[2pt] &\qquad\qquad + \frac{2^{3/2} C_\mu \Vert f \Vert_{{}_{\star\star}}^2}{t^2}\sum_{m=0}^{t-1}\sum_{n=0}^{t-1} (1-\alpha)^{(m+n)/2}\\[2pt] \end{align*}
 \begin{align*} &\qquad = \frac{\Vert f\Vert_\star^2}{t^2}\sum_{m=0}^{t-1} \left(1+2\sum_{s=1}^{t-m-1} (1-\alpha)^{s}\right) -\left(\frac{1}{t}\sum_{m=0}^{t-1}(\mu P^m f-\pi f)\right)^2\\[2pt] &\qquad\qquad+ \frac{2^{3/2} C_\mu \Vert f \Vert_{{}_{\star\star}}^2}{t^2}\sum_{m=0}^{t-1}(1-\alpha)^m\left(1+2\sum_{s=1}^{t-m-1} (1-\alpha)^{s/2}\right)\\[2pt] &\qquad = \frac{\Vert f\Vert_\star^2}{t^2}\sum_{m=0}^{t-1} \left(1+2\frac{(1-\alpha)-(1-\alpha)^{t-m}}{\alpha}\right) -\left(\frac{1}{t}\sum_{m=0}^{t-1}(\mu P^m f-\pi f)\right)^2\\[2pt] &\qquad\qquad+ \frac{2^{3/2} C_\mu \Vert f \Vert_{{}_{\star\star}}^2}{t^2}\sum_{m=0}^{t-1}(1-\alpha)^m\left(1+2\frac{\sqrt{1-\alpha}-\sqrt{1-\alpha}^{t-m}}{1-\sqrt{1-\alpha}}\right)\\[2pt] &\qquad = \frac{\Vert f\Vert_\star^2}{t^2}\sum_{m=0}^{t-1} \left(\frac{2-\alpha}{\alpha} -\frac{2}{\alpha}(1-\alpha)^{t-m}\right) -\left(\frac{1}{t}\sum_{m=0}^{t-1}(\mu P^m f-\pi f)\right)^2\\[2pt] &\qquad\qquad+ \frac{2^{3/2} C_\mu \Vert f \Vert_{{}_{\star\star}}^2}{t^2}\sum_{m=0}^{t-1}\left((1-\alpha)^m\frac{1+\sqrt{1-\alpha}}{1-\sqrt{1-\alpha}}-2\frac{\sqrt{1-\alpha}^{t+m}}{1-\sqrt{1-\alpha}}\right)\\[2pt] &\qquad = \frac{\Vert f\Vert_\star^2}{t^2} \left(\frac{2-\alpha}{\alpha}t -\frac{2}{\alpha}\frac{(1-\alpha) - (1-\alpha)^{t+1}}{\alpha}\right) -\left(\frac{1}{t}\sum_{m=0}^{t-1}(\mu P^m f-\pi f)\right)^2\\[2pt] &\qquad\qquad+ \frac{2^{3/2} C_\mu \Vert f \Vert_{{}_{\star\star}}^2}{t^2}\left(\left[\frac{1+\sqrt{1-\alpha}}{1-\sqrt{1-\alpha}}\right]\left[\frac{1-(1-\alpha)^t}{\alpha}\right]\right.\\ &\qquad\qquad\left.-\left[\frac{2\sqrt{1-\alpha}^t}{1-\sqrt{1-\alpha}}\right]\left[\frac{1-\sqrt{1-\alpha}^{t}}{1-\sqrt{1-\alpha}}\right]\right) \\ &\qquad = (2-\alpha)\frac{\Vert f\Vert_\star^2}{\alpha t} - 2(1-\alpha)\frac{1-(1-\alpha)^t}{\alpha^2 t^2} -\left(\frac{1}{t}\sum_{m=0}^{t-1}(\mu P^m f-\pi f)\right)^2\\ &\qquad\qquad+ \frac{2^{3/2} C_\mu \Vert f \Vert_{{}_{\star\star}}^2}{t^2}\left(\frac{1+\sqrt{1-\alpha}}{\alpha}\right)^2(1-(1-\alpha)^{t/2})^2\\ &\qquad \leq \frac{2\Vert f\Vert_\star^2}{\alpha t} + \frac{2^{7/2} C_\mu \Vert f \Vert_{{}_{\star\star}}^2}{\alpha^2 t^2} -\left(\frac{1}{t}\sum_{m=0}^{t-1}(\mu P^m f-\pi f)\right)^2. \end{align*}
\begin{align*} &\qquad = \frac{\Vert f\Vert_\star^2}{t^2}\sum_{m=0}^{t-1} \left(1+2\sum_{s=1}^{t-m-1} (1-\alpha)^{s}\right) -\left(\frac{1}{t}\sum_{m=0}^{t-1}(\mu P^m f-\pi f)\right)^2\\[2pt] &\qquad\qquad+ \frac{2^{3/2} C_\mu \Vert f \Vert_{{}_{\star\star}}^2}{t^2}\sum_{m=0}^{t-1}(1-\alpha)^m\left(1+2\sum_{s=1}^{t-m-1} (1-\alpha)^{s/2}\right)\\[2pt] &\qquad = \frac{\Vert f\Vert_\star^2}{t^2}\sum_{m=0}^{t-1} \left(1+2\frac{(1-\alpha)-(1-\alpha)^{t-m}}{\alpha}\right) -\left(\frac{1}{t}\sum_{m=0}^{t-1}(\mu P^m f-\pi f)\right)^2\\[2pt] &\qquad\qquad+ \frac{2^{3/2} C_\mu \Vert f \Vert_{{}_{\star\star}}^2}{t^2}\sum_{m=0}^{t-1}(1-\alpha)^m\left(1+2\frac{\sqrt{1-\alpha}-\sqrt{1-\alpha}^{t-m}}{1-\sqrt{1-\alpha}}\right)\\[2pt] &\qquad = \frac{\Vert f\Vert_\star^2}{t^2}\sum_{m=0}^{t-1} \left(\frac{2-\alpha}{\alpha} -\frac{2}{\alpha}(1-\alpha)^{t-m}\right) -\left(\frac{1}{t}\sum_{m=0}^{t-1}(\mu P^m f-\pi f)\right)^2\\[2pt] &\qquad\qquad+ \frac{2^{3/2} C_\mu \Vert f \Vert_{{}_{\star\star}}^2}{t^2}\sum_{m=0}^{t-1}\left((1-\alpha)^m\frac{1+\sqrt{1-\alpha}}{1-\sqrt{1-\alpha}}-2\frac{\sqrt{1-\alpha}^{t+m}}{1-\sqrt{1-\alpha}}\right)\\[2pt] &\qquad = \frac{\Vert f\Vert_\star^2}{t^2} \left(\frac{2-\alpha}{\alpha}t -\frac{2}{\alpha}\frac{(1-\alpha) - (1-\alpha)^{t+1}}{\alpha}\right) -\left(\frac{1}{t}\sum_{m=0}^{t-1}(\mu P^m f-\pi f)\right)^2\\[2pt] &\qquad\qquad+ \frac{2^{3/2} C_\mu \Vert f \Vert_{{}_{\star\star}}^2}{t^2}\left(\left[\frac{1+\sqrt{1-\alpha}}{1-\sqrt{1-\alpha}}\right]\left[\frac{1-(1-\alpha)^t}{\alpha}\right]\right.\\ &\qquad\qquad\left.-\left[\frac{2\sqrt{1-\alpha}^t}{1-\sqrt{1-\alpha}}\right]\left[\frac{1-\sqrt{1-\alpha}^{t}}{1-\sqrt{1-\alpha}}\right]\right) \\ &\qquad = (2-\alpha)\frac{\Vert f\Vert_\star^2}{\alpha t} - 2(1-\alpha)\frac{1-(1-\alpha)^t}{\alpha^2 t^2} -\left(\frac{1}{t}\sum_{m=0}^{t-1}(\mu P^m f-\pi f)\right)^2\\ &\qquad\qquad+ \frac{2^{3/2} C_\mu \Vert f \Vert_{{}_{\star\star}}^2}{t^2}\left(\frac{1+\sqrt{1-\alpha}}{\alpha}\right)^2(1-(1-\alpha)^{t/2})^2\\ &\qquad \leq \frac{2\Vert f\Vert_\star^2}{\alpha t} + \frac{2^{7/2} C_\mu \Vert f \Vert_{{}_{\star\star}}^2}{\alpha^2 t^2} -\left(\frac{1}{t}\sum_{m=0}^{t-1}(\mu P^m f-\pi f)\right)^2. \end{align*}
A.3.3 Mean squared error bounds
Theorem 7. Under the assumptions of Section 3.2, if ![]() $X_0\sim\mu\in L_2(\pi)$, then
$X_0\sim\mu\in L_2(\pi)$, then
 \begin{align*}&\mathbb{E}\left[\left(\pi(f) - \frac{1}{t}\sum_{k=0}^{t-1}f(X_k)\right)^2\right] \leq \frac{2\Vert f - \pi f\Vert_2^2}{\alpha t} + \frac{2^{7/2} \Vert \mu -\pi\Vert_2 \Vert f -\pi f \Vert_4^2}{\alpha^2 t^2}.\end{align*}
\begin{align*}&\mathbb{E}\left[\left(\pi(f) - \frac{1}{t}\sum_{k=0}^{t-1}f(X_k)\right)^2\right] \leq \frac{2\Vert f - \pi f\Vert_2^2}{\alpha t} + \frac{2^{7/2} \Vert \mu -\pi\Vert_2 \Vert f -\pi f \Vert_4^2}{\alpha^2 t^2}.\end{align*}
Proof. The proof proceeds by partitioning the mean squared error via the bias-variance decomposition, then bounding the variance term and noting that our bound for the variance contains an expression which exactly cancels the bias term. We compute that
 \begin{align*}& \mathbb{E}\left[\left(\pi(f) - \frac{1}{t}\sum_{k=0}^{t-1}f(X_k)\right)^2\right]\\ &=\mathbb{E}\left[\left(\pi(f) - \frac{1}{t}\sum_{k=0}^{t-1} [\mu P^k](f) - \frac{1}{t}\sum_{k=0}^{t-1} (f(X_k)-[\mu P^k](f))\right)^2\right]\\ &=\left(\pi(f) - \frac{1}{t}\sum_{k=0}^{t-1} [\mu P^k](f)\right)^2 +\mathbb{E}\left[\left(\frac{1}{t}\sum_{k=0}^{t-1} (f(X_k)-[\mu P^k](f))\right)^2\right]\\ &=\left(\pi(f) - \frac{1}{t}\sum_{k=0}^{t-1} [\mu P^k](f)\right)^2 +\frac{1}{t^2}\sum_{j=0}^{t-1}\sum_{k=0}^{t-1} \textrm{Cov} (f(X_j),f(X_k)).\end{align*}
\begin{align*}& \mathbb{E}\left[\left(\pi(f) - \frac{1}{t}\sum_{k=0}^{t-1}f(X_k)\right)^2\right]\\ &=\mathbb{E}\left[\left(\pi(f) - \frac{1}{t}\sum_{k=0}^{t-1} [\mu P^k](f) - \frac{1}{t}\sum_{k=0}^{t-1} (f(X_k)-[\mu P^k](f))\right)^2\right]\\ &=\left(\pi(f) - \frac{1}{t}\sum_{k=0}^{t-1} [\mu P^k](f)\right)^2 +\mathbb{E}\left[\left(\frac{1}{t}\sum_{k=0}^{t-1} (f(X_k)-[\mu P^k](f))\right)^2\right]\\ &=\left(\pi(f) - \frac{1}{t}\sum_{k=0}^{t-1} [\mu P^k](f)\right)^2 +\frac{1}{t^2}\sum_{j=0}^{t-1}\sum_{k=0}^{t-1} \textrm{Cov} (f(X_j),f(X_k)).\end{align*}
The variance term is bounded using Corollary 6:
 \begin{align*}&\frac{1}{t^2}\sum_{j=0}^{t-1}\sum_{k=0}^{t-1} \textrm{Cov} (f(X_j),f(X_k))\\ &\qquad\frac{2\Vert f - \pi f\Vert_2^2}{\alpha t} + \frac{2^{7/2} \Vert \mu -\pi\Vert_2 \Vert f -\pi f \Vert_4^2}{\alpha^2 t^2} -\left(\frac{1}{t}\sum_{m=0}^{t-1}\mu P^m f-\pi f\right)^2.\end{align*}
\begin{align*}&\frac{1}{t^2}\sum_{j=0}^{t-1}\sum_{k=0}^{t-1} \textrm{Cov} (f(X_j),f(X_k))\\ &\qquad\frac{2\Vert f - \pi f\Vert_2^2}{\alpha t} + \frac{2^{7/2} \Vert \mu -\pi\Vert_2 \Vert f -\pi f \Vert_4^2}{\alpha^2 t^2} -\left(\frac{1}{t}\sum_{m=0}^{t-1}\mu P^m f-\pi f\right)^2.\end{align*}
Putting these together yields the desired result.
Remark 9. We note that, as per Remark 8, ![]() $\Vert f - \pi f\Vert \leq \Vert f\Vert_2 $. Similarly
$\Vert f - \pi f\Vert \leq \Vert f\Vert_2 $. Similarly ![]() $\Vert f-\pi f\Vert_4\leq \Vert f\Vert_4$. Also, in the case that f is is
$\Vert f-\pi f\Vert_4\leq \Vert f\Vert_4$. Also, in the case that f is is ![]() $\pi$-essentially bounded,
$\pi$-essentially bounded, ![]() $\Vert f\Vert_2 \leq \Vert f\Vert_\infty$ and
$\Vert f\Vert_2 \leq \Vert f\Vert_\infty$ and ![]() $\Vert f\Vert_4 \leq \Vert f\Vert_\infty$. These alternative norms may be substituted into the result as necessary in order to make the bounds tractable for a given application.
$\Vert f\Vert_4 \leq \Vert f\Vert_\infty$. These alternative norms may be substituted into the result as necessary in order to make the bounds tractable for a given application.
Remark 10. Comparing our above geometrically ergodic results to the ![]() $L_1$ results of [Reference Johndrow, Mattingly, Mukherjee and Dunson18] in the uniformly ergodic case, we see that the
$L_1$ results of [Reference Johndrow, Mattingly, Mukherjee and Dunson18] in the uniformly ergodic case, we see that the ![]() $L_2$ and
$L_2$ and ![]() $L_1$ bounds we establish above differ from the corresponding
$L_1$ bounds we establish above differ from the corresponding ![]() $L_1$ bound of [Reference Johndrow, Mattingly, Mukherjee and Dunson18] only by a factor, which is constant in time, but varies with the initial distribution (as is to be expected when moving from uniform ergodicity to geometric ergodicity). For the mean squared error results, the
$L_1$ bound of [Reference Johndrow, Mattingly, Mukherjee and Dunson18] only by a factor, which is constant in time, but varies with the initial distribution (as is to be expected when moving from uniform ergodicity to geometric ergodicity). For the mean squared error results, the ![]() $\Vert\cdot\Vert_\star$-norm in that paper is based on the midrange-centred infinity norm, which as per Remark 9 is an upper bound on what we have.
$\Vert\cdot\Vert_\star$-norm in that paper is based on the midrange-centred infinity norm, which as per Remark 9 is an upper bound on what we have.
Proof of Theorem 5. For the first result, we proceed via bias-variance decomposition, as in the corresponding result for the exact chain. However, now the bias under consideration is itself decomposed as the square of a sum of two components. The squared sum is expanded simultaneously with the bias-variance expansion. We compute that
 \begin{align*}& \mathbb{E}\left[\left(\pi(f) - \frac{1}{t}\sum_{k=0}^{t-1}f(X^\epsilon_k)\right)^2\right]\\ &=\mathbb{E}\left[\left(\pi(f) - \pi_\epsilon(f) + \frac{1}{t}\sum_{k=0}^{t-1} \left[\pi_\epsilon - \mu P_\epsilon^k\right](f) - \frac{1}{t}\sum_{k=0}^{t-1} (f(X^\epsilon_k)-[\mu P_\epsilon^k](f))\right)^2\right] \end{align*}
\begin{align*}& \mathbb{E}\left[\left(\pi(f) - \frac{1}{t}\sum_{k=0}^{t-1}f(X^\epsilon_k)\right)^2\right]\\ &=\mathbb{E}\left[\left(\pi(f) - \pi_\epsilon(f) + \frac{1}{t}\sum_{k=0}^{t-1} \left[\pi_\epsilon - \mu P_\epsilon^k\right](f) - \frac{1}{t}\sum_{k=0}^{t-1} (f(X^\epsilon_k)-[\mu P_\epsilon^k](f))\right)^2\right] \end{align*}
 \begin{align*} \\[-25pt] &=\left([\pi-\pi_\epsilon](f)\right)^2 +2\left([\pi-\pi_\epsilon](f)\right)\left(\pi_\epsilon(f) - \frac{1}{t}\sum_{k=0}^{t-1} [\mu P_\epsilon^k](f)\right)\\[3pt] & + \left(\pi_\epsilon(f) - \frac{1}{t}\sum_{k=0}^{t-1} [\mu P_\epsilon^k](f)\right)^2 +\frac{1}{t^2}\sum_{j=0}^{t-1}\sum_{k=0}^{t-1} \textrm{Cov} (f(X^\epsilon_j),f(X^\epsilon_k)).\end{align*}
\begin{align*} \\[-25pt] &=\left([\pi-\pi_\epsilon](f)\right)^2 +2\left([\pi-\pi_\epsilon](f)\right)\left(\pi_\epsilon(f) - \frac{1}{t}\sum_{k=0}^{t-1} [\mu P_\epsilon^k](f)\right)\\[3pt] & + \left(\pi_\epsilon(f) - \frac{1}{t}\sum_{k=0}^{t-1} [\mu P_\epsilon^k](f)\right)^2 +\frac{1}{t^2}\sum_{j=0}^{t-1}\sum_{k=0}^{t-1} \textrm{Cov} (f(X^\epsilon_j),f(X^\epsilon_k)).\end{align*}
We bound the first component of the bias term using versions of Lemma 6:
 \begin{align*} \left([\pi-\pi_\epsilon](f)\right)^2 & = \left([\pi-\pi_\epsilon](f-\pi_\epsilon f)\right)^2 \\[3pt] & \leq \begin{cases} \Vert {\pi-\pi_\epsilon}\Vert_{L_2(\pi)} ^2 \Vert {{f-\pi_\epsilon f}}\Vert_{L^{\prime}_2(\pi)} ^2 & \\[3pt] \Vert {{\pi-\pi_\epsilon}}\Vert_{L_2(\pi_\epsilon)} ^2 \Vert {{f-\pi_\epsilon f}}\Vert_{L^{\prime}_2(\pi_\epsilon)} ^2 & \\[3pt] \end{cases}\\[3pt] & \leq \begin{cases} \frac{\epsilon^2}{\alpha^2 - \epsilon^2} \Vert {{f-\pi_\epsilon f}}\Vert_{L^{\prime}_2(\pi)} ^2 & \\[3pt] \frac{\varphi^2}{(1-\rho_2)^2 - \varphi^2} \Vert {{f-\pi_\epsilon f}}\Vert_{L^{\prime}_2(\pi_\epsilon)} ^2 &:\text{given } (*). \end{cases}\end{align*}
\begin{align*} \left([\pi-\pi_\epsilon](f)\right)^2 & = \left([\pi-\pi_\epsilon](f-\pi_\epsilon f)\right)^2 \\[3pt] & \leq \begin{cases} \Vert {\pi-\pi_\epsilon}\Vert_{L_2(\pi)} ^2 \Vert {{f-\pi_\epsilon f}}\Vert_{L^{\prime}_2(\pi)} ^2 & \\[3pt] \Vert {{\pi-\pi_\epsilon}}\Vert_{L_2(\pi_\epsilon)} ^2 \Vert {{f-\pi_\epsilon f}}\Vert_{L^{\prime}_2(\pi_\epsilon)} ^2 & \\[3pt] \end{cases}\\[3pt] & \leq \begin{cases} \frac{\epsilon^2}{\alpha^2 - \epsilon^2} \Vert {{f-\pi_\epsilon f}}\Vert_{L^{\prime}_2(\pi)} ^2 & \\[3pt] \frac{\varphi^2}{(1-\rho_2)^2 - \varphi^2} \Vert {{f-\pi_\epsilon f}}\Vert_{L^{\prime}_2(\pi_\epsilon)} ^2 &:\text{given } (*). \end{cases}\end{align*}
We bound the variance term using Corollary 6:
 \begin{align*}& \frac{1}{t^2}\sum_{j=0}^{t-1}\sum_{k=0}^{t-1} \textrm{Cov}(f(X^\epsilon_j),f(X^\epsilon_k))\\[3pt] &\qquad\leq \frac{2 \Vert {{ f - \pi_\epsilon f}}\Vert_{L^{\prime}_2(\pi_\epsilon)} ^2}{(1-\rho_2) t} + \frac{2^{7/2} \Vert {{ \mu -\pi_\epsilon}}\Vert_{L_2(\pi_\epsilon)} \Vert {f -\pi_\epsilon f } \Vert_{L_4^{\prime}(\pi_\epsilon)}}{(1-\rho_2)^2 t^2} -\left(\frac{1}{t}\sum_{m=0}^{t-1}\mu P_\epsilon^m f-\pi_\epsilon f\right)^2.\end{align*}
\begin{align*}& \frac{1}{t^2}\sum_{j=0}^{t-1}\sum_{k=0}^{t-1} \textrm{Cov}(f(X^\epsilon_j),f(X^\epsilon_k))\\[3pt] &\qquad\leq \frac{2 \Vert {{ f - \pi_\epsilon f}}\Vert_{L^{\prime}_2(\pi_\epsilon)} ^2}{(1-\rho_2) t} + \frac{2^{7/2} \Vert {{ \mu -\pi_\epsilon}}\Vert_{L_2(\pi_\epsilon)} \Vert {f -\pi_\epsilon f } \Vert_{L_4^{\prime}(\pi_\epsilon)}}{(1-\rho_2)^2 t^2} -\left(\frac{1}{t}\sum_{m=0}^{t-1}\mu P_\epsilon^m f-\pi_\epsilon f\right)^2.\end{align*}
The negative term in this expression exactly cancels out the third bias term in the expansion.
Finally, we bound the second bias term using Lemma 6 and Theorem 4:
 \begin{align*} & 2\left ({[\pi-\pi_\epsilon](f)}\right) \left ({\pi_\epsilon(f) -\frac{1}{t}\sum_{k=0}^{t-1} [\mu P_\epsilon^k](f)}\right)\\[3pt] & = 2\left ({[\pi-\pi_\epsilon](f-\pi_\epsilon f)}\right) \left ({\left [{\pi_\epsilon-\frac{1}{t}\sum_{k=0}^{t-1} \mu P_\epsilon^k }\right] (f-\pi_\epsilon f)}\right) \\[3pt] & \leq 2 \begin{cases} \frac{\varphi}{\sqrt{(1-\rho_2)^2 - \varphi^2}} \Vert {{f-\pi_\epsilon f}}\Vert_{L^{\prime}_2(\pi)} \frac{1-(1-(\alpha-\epsilon))^t}{t(\alpha-\epsilon)} \Vert {{ \pi_\epsilon-\mu}}\Vert_{L_2(\pi)} \Vert {{f-\pi_\epsilon f}}\Vert_{L^{\prime}_2(\pi)} & \\[3pt] \frac{\varphi^2}{(1-\rho_2)^2 - \varphi^2} \Vert {{f-\pi_\epsilon f}}\Vert_{L^{\prime}_2(\pi_\epsilon)} ^2 \frac{1-\rho_2^t}{t(1-\rho_2)} \Vert {{ \pi_\epsilon-\mu}}\Vert_{L_2(\pi_\epsilon)} \Vert {{f-\pi_\epsilon f}}\Vert_{L^{\prime}_2(\pi_\epsilon)} &:\,\text{given } (*) \end{cases} \\[3pt] & \leq 2 \begin{cases} \frac{\epsilon}{\sqrt{\alpha^2 - \epsilon^2}}\frac{1}{t(\alpha-\epsilon)} \Vert {{\pi_\epsilon-\mu}}\Vert_{L_2(\pi)} \Vert {{f-\pi_\epsilon f}}\Vert_{L^{\prime}_2(\pi)} ^2 & \\[3pt] \frac{\varphi}{\sqrt{(1-\rho_2)^2 - \varphi^2}} \frac{1}{t(1-\rho_2)} \Vert {{ \pi_\epsilon-\mu}}\Vert_{L_2(\pi_\epsilon)} \Vert {{f-\pi_\epsilon f}}\Vert_{L^{\prime}_2(\pi_\epsilon)} ^2 &:\text{given } (*). \end{cases}\end{align*}
\begin{align*} & 2\left ({[\pi-\pi_\epsilon](f)}\right) \left ({\pi_\epsilon(f) -\frac{1}{t}\sum_{k=0}^{t-1} [\mu P_\epsilon^k](f)}\right)\\[3pt] & = 2\left ({[\pi-\pi_\epsilon](f-\pi_\epsilon f)}\right) \left ({\left [{\pi_\epsilon-\frac{1}{t}\sum_{k=0}^{t-1} \mu P_\epsilon^k }\right] (f-\pi_\epsilon f)}\right) \\[3pt] & \leq 2 \begin{cases} \frac{\varphi}{\sqrt{(1-\rho_2)^2 - \varphi^2}} \Vert {{f-\pi_\epsilon f}}\Vert_{L^{\prime}_2(\pi)} \frac{1-(1-(\alpha-\epsilon))^t}{t(\alpha-\epsilon)} \Vert {{ \pi_\epsilon-\mu}}\Vert_{L_2(\pi)} \Vert {{f-\pi_\epsilon f}}\Vert_{L^{\prime}_2(\pi)} & \\[3pt] \frac{\varphi^2}{(1-\rho_2)^2 - \varphi^2} \Vert {{f-\pi_\epsilon f}}\Vert_{L^{\prime}_2(\pi_\epsilon)} ^2 \frac{1-\rho_2^t}{t(1-\rho_2)} \Vert {{ \pi_\epsilon-\mu}}\Vert_{L_2(\pi_\epsilon)} \Vert {{f-\pi_\epsilon f}}\Vert_{L^{\prime}_2(\pi_\epsilon)} &:\,\text{given } (*) \end{cases} \\[3pt] & \leq 2 \begin{cases} \frac{\epsilon}{\sqrt{\alpha^2 - \epsilon^2}}\frac{1}{t(\alpha-\epsilon)} \Vert {{\pi_\epsilon-\mu}}\Vert_{L_2(\pi)} \Vert {{f-\pi_\epsilon f}}\Vert_{L^{\prime}_2(\pi)} ^2 & \\[3pt] \frac{\varphi}{\sqrt{(1-\rho_2)^2 - \varphi^2}} \frac{1}{t(1-\rho_2)} \Vert {{ \pi_\epsilon-\mu}}\Vert_{L_2(\pi_\epsilon)} \Vert {{f-\pi_\epsilon f}}\Vert_{L^{\prime}_2(\pi_\epsilon)} ^2 &:\text{given } (*). \end{cases}\end{align*}
Putting these together yields the first and third results.
For the second and fourth results we use the fact that for any random variable Z and for any ![]() $a,b\in\mathbb{R}$ the following holds:
$a,b\in\mathbb{R}$ the following holds:
 \begin{align*}\mathbb{E}[(Z-a)^2] &= 2\mathbb{E}[(Z-b)^2]+2(a-b)^2 - \mathbb{E}[(Z+a-2 b)^2]\\ &\leq 2\mathbb{E}[(Z-b)^2]+2(a-b)^2.\end{align*}
\begin{align*}\mathbb{E}[(Z-a)^2] &= 2\mathbb{E}[(Z-b)^2]+2(a-b)^2 - \mathbb{E}[(Z+a-2 b)^2]\\ &\leq 2\mathbb{E}[(Z-b)^2]+2(a-b)^2.\end{align*}
We have
 \begin{align*}& \mathbb{E}\left [{\left ({\pi(f) - \frac{1}{t}\sum_{k=0}^{t-1}f(X^\epsilon_k)}\right)^2}\right]\\ &\qquad\leq 2([\pi-\pi_\epsilon](f))^2 +2 \mathbb{E}\left [{\left ({\pi_\epsilon(f) - \frac{1}{t}\sum_{k=0}^{t-1} f(X^\epsilon_k)}\right)^2}\right]\\ &\qquad= 2([\pi-\pi_\epsilon](f-\pi_\epsilon f))^2 \\ &\qquad\qquad+2 \mathbb{E}\left [{\left ({\pi_\epsilon(f)-\frac{1}{t}\sum_{k=0}^{t-1} [\mu P_\epsilon^k](f) - \frac{1}{t}\sum_{k=0}^{t-1} (f(X^\epsilon_k)-[\mu P_\epsilon^k](f))}\right)^2}\right] \end{align*}
\begin{align*}& \mathbb{E}\left [{\left ({\pi(f) - \frac{1}{t}\sum_{k=0}^{t-1}f(X^\epsilon_k)}\right)^2}\right]\\ &\qquad\leq 2([\pi-\pi_\epsilon](f))^2 +2 \mathbb{E}\left [{\left ({\pi_\epsilon(f) - \frac{1}{t}\sum_{k=0}^{t-1} f(X^\epsilon_k)}\right)^2}\right]\\ &\qquad= 2([\pi-\pi_\epsilon](f-\pi_\epsilon f))^2 \\ &\qquad\qquad+2 \mathbb{E}\left [{\left ({\pi_\epsilon(f)-\frac{1}{t}\sum_{k=0}^{t-1} [\mu P_\epsilon^k](f) - \frac{1}{t}\sum_{k=0}^{t-1} (f(X^\epsilon_k)-[\mu P_\epsilon^k](f))}\right)^2}\right] \end{align*}
 \begin{align*} \\[-35pt] &\qquad= 2([\pi-\pi_\epsilon](f-\pi_\epsilon f))^2 +2\left ({\pi_\epsilon(f)-\frac{1}{t}\sum_{k=0}^{t-1}[\mu P_\epsilon^k](f)}\right)^2\\ &\qquad\qquad+2\mathbb{E}\left [{\left ({\frac{1}{t}\sum_{k=0}^{t-1} (f(X^\epsilon_k)-[\mu P_\epsilon^k](f))}\right)^2}\right] \\ &\qquad= 2([\pi-\pi_\epsilon](f-\pi_\epsilon f))^2 +2\left ({\pi_\epsilon(f)-\frac{1}{t}\sum_{k=0}^{t-1}[\mu P_\epsilon^k](f)}\right) ^2\\ &\qquad\qquad+\frac{2}{t^2}\sum_{j=0}^{t-1}\sum_{k=0}^{t-1} \textrm{Cov} (f(X^\epsilon_j),f(X^\epsilon_k)).\end{align*}
\begin{align*} \\[-35pt] &\qquad= 2([\pi-\pi_\epsilon](f-\pi_\epsilon f))^2 +2\left ({\pi_\epsilon(f)-\frac{1}{t}\sum_{k=0}^{t-1}[\mu P_\epsilon^k](f)}\right)^2\\ &\qquad\qquad+2\mathbb{E}\left [{\left ({\frac{1}{t}\sum_{k=0}^{t-1} (f(X^\epsilon_k)-[\mu P_\epsilon^k](f))}\right)^2}\right] \\ &\qquad= 2([\pi-\pi_\epsilon](f-\pi_\epsilon f))^2 +2\left ({\pi_\epsilon(f)-\frac{1}{t}\sum_{k=0}^{t-1}[\mu P_\epsilon^k](f)}\right) ^2\\ &\qquad\qquad+\frac{2}{t^2}\sum_{j=0}^{t-1}\sum_{k=0}^{t-1} \textrm{Cov} (f(X^\epsilon_j),f(X^\epsilon_k)).\end{align*}
Applying Corollary 5 to bound the sum of covariances, we find that we are able to exactly cancel the second term in the final expression above. Using the same bound as before for the first expression, we get the final result.
Appendix B. Proof of Theorem 6
Let
 \begin{align*}\gamma(x) &= \mathbb{E}_{y\sim q(y|x)} r(y|x) = \int r(y|x)q(y|x) d y, \\ [\nu\Gamma]( d y ) &= \nu(y)\gamma(y) d y, \\ [\nu Z]( d y ) &= \left[\int r(y|x) q(y|x)\nu(x) d x \right] d y.\end{align*}
\begin{align*}\gamma(x) &= \mathbb{E}_{y\sim q(y|x)} r(y|x) = \int r(y|x)q(y|x) d y, \\ [\nu\Gamma]( d y ) &= \nu(y)\gamma(y) d y, \\ [\nu Z]( d y ) &= \left[\int r(y|x) q(y|x)\nu(x) d x \right] d y.\end{align*}
Lemma 9. ![]() $P-\hat P = Z -\Gamma$.
$P-\hat P = Z -\Gamma$.
Proof. We first give expressions for the elements of measure for transitions of the original chain. The first formula is the element of measure for transition from an arbitrary, fixed initial point. It is defined for us by the mechanics of the MH algorithm. The second expression is the element of measure for transition from a sample from an initial distribution, ![]() $\nu$. It is derived from the first expression by integrating over the sample from
$\nu$. It is derived from the first expression by integrating over the sample from ![]() $\nu$:
$\nu$:
 \begin{align*}P(x, d x^{\prime} ) &= \delta_x( d x' ) \left[1-\int({{a}}(y|x)q(y|x) d y \right] + {{a}}(x'|x) q(x'|x) d x', \\[3pt]\left[\nu P\right]( d x' ) &= \int\left[\delta_x( d x' ) \left[1-\int{{a}}(y|x)q(y|x) d y \right] + {{a}}(x'|x) q(x'|x) d x' \right]\nu(x) d x \\[3pt] &= \left[\left[1-\int{{a}}(y|x')q(y|x') d y \right]\nu(x') + \int{{a}}(x'|x) q(x'|x)\nu(x) d x \right] d x'. \end{align*}
\begin{align*}P(x, d x^{\prime} ) &= \delta_x( d x' ) \left[1-\int({{a}}(y|x)q(y|x) d y \right] + {{a}}(x'|x) q(x'|x) d x', \\[3pt]\left[\nu P\right]( d x' ) &= \int\left[\delta_x( d x' ) \left[1-\int{{a}}(y|x)q(y|x) d y \right] + {{a}}(x'|x) q(x'|x) d x' \right]\nu(x) d x \\[3pt] &= \left[\left[1-\int{{a}}(y|x')q(y|x') d y \right]\nu(x') + \int{{a}}(x'|x) q(x'|x)\nu(x) d x \right] d x'. \end{align*}
The second form of the second expression is an application of Fubini’s theorem. The exchange of the order of integration for the second term in the expression is immediate. For the first term, for an arbitrary non-negative function f,
 \begin{align*} \int_s\int_t f(s,t) \delta_t( d s ) d t =\int_t\int_s f(s,t)\delta_t( d s ) d t = \int_t f(t,t) d t =\int_s f(s,s) d s,\end{align*}
\begin{align*} \int_s\int_t f(s,t) \delta_t( d s ) d t =\int_t\int_s f(s,t)\delta_t( d s ) d t = \int_t f(t,t) d t =\int_s f(s,s) d s,\end{align*}
where the first equality is Fubini’s theorem, the second comes from integrating with respect to s, and the third comes from a change of dummy variable.
Similarly, the elements of measure for transitions from the approximating kernel are expressed below. The first expression, as above, is the element of measure for transition from an arbitrary, fixed initial point. It is defined for us by the mechanics of the nMH algorithm. The second expression is again derived by integrating the first against an initial measure, ![]() $\nu$:
$\nu$:
 \begin{align*}\hat P(x, d x' ) &= \delta_x( d x' ) \left[1-\iint{\hat{a}}(y|x,z)q(y|x)f_y(z) d z d y \right] \\[3pt] &\qquad\qquad + \int {\hat{a}}(x'|x,z) q(x'|x)f_{x'}(z) d z d x', \\[3pt]\left[\nu \hat P\right]( d x' ) &= \int\bigg(\delta_x( d x' ) \left[1-\iint{\hat{a}}(y|x,z)q(y|x)f_y(z) d z d y \right] \\[3pt]&\qquad\qquad\qquad\qquad + \int {\hat{a}}(x'|x,z) q(x'|x)f_{x'}(z) d z d x' \bigg)\nu(x) d x \\[3pt] &= \left[1-\iint{\hat{a}}(y|x',z)q(y|x')f_y(z) d z d y \right]\nu(x') d x' \\[3pt]&\qquad\qquad\qquad\qquad + \left[\iint {\hat{a}}(x'|x,z) q(x'|x)f_{x'}(z)\nu(x) d z d x \right] d x'.\end{align*}
\begin{align*}\hat P(x, d x' ) &= \delta_x( d x' ) \left[1-\iint{\hat{a}}(y|x,z)q(y|x)f_y(z) d z d y \right] \\[3pt] &\qquad\qquad + \int {\hat{a}}(x'|x,z) q(x'|x)f_{x'}(z) d z d x', \\[3pt]\left[\nu \hat P\right]( d x' ) &= \int\bigg(\delta_x( d x' ) \left[1-\iint{\hat{a}}(y|x,z)q(y|x)f_y(z) d z d y \right] \\[3pt]&\qquad\qquad\qquad\qquad + \int {\hat{a}}(x'|x,z) q(x'|x)f_{x'}(z) d z d x' \bigg)\nu(x) d x \\[3pt] &= \left[1-\iint{\hat{a}}(y|x',z)q(y|x')f_y(z) d z d y \right]\nu(x') d x' \\[3pt]&\qquad\qquad\qquad\qquad + \left[\iint {\hat{a}}(x'|x,z) q(x'|x)f_{x'}(z)\nu(x) d z d x \right] d x'.\end{align*}
The same applications of Fubini’s theorem occur as above.
We may now leverage our notation defined above to simplify the difference of these elements of measure:
 \begin{align*}&\left[\nu (P-\hat P)\right] ( d x'n )\\ &\qquad= \left[\iint\bigg({\hat{a}}(y|x',z)-{{a}}(y|x')\bigg)q(y|x')f_y(z) d z d y \right]\nu(x') d x' \\ &\qquad + \left[\iint \bigg({{a}}(x'|x)-{\hat{a}}(x'nnn|x,z)\bigg) q(x'|x)f_{x'}(z)\nu(x) d z d x \right] d x'n \\ &\qquad=\left[\int r(x'|x) q(x'|x)\nu(x) d x \right] d x' - \left[\int r(y|x') q(y|x') d y \right]\nu(x') d x' \\ &\qquad=[\nu(Z-\Gamma)]( d x' ).\end{align*}
\begin{align*}&\left[\nu (P-\hat P)\right] ( d x'n )\\ &\qquad= \left[\iint\bigg({\hat{a}}(y|x',z)-{{a}}(y|x')\bigg)q(y|x')f_y(z) d z d y \right]\nu(x') d x' \\ &\qquad + \left[\iint \bigg({{a}}(x'|x)-{\hat{a}}(x'nnn|x,z)\bigg) q(x'|x)f_{x'}(z)\nu(x) d z d x \right] d x'n \\ &\qquad=\left[\int r(x'|x) q(x'|x)\nu(x) d x \right] d x' - \left[\int r(y|x') q(y|x') d y \right]\nu(x') d x' \\ &\qquad=[\nu(Z-\Gamma)]( d x' ).\end{align*}
From this one may conclude that ![]() $\left(P- \hat P = Z - \Gamma\right)$ as operators.
$\left(P- \hat P = Z - \Gamma\right)$ as operators.
Proof of Theorem 6. It is obvious that if ![]() $ \vert {{r(y|x)}} \vert \leq R$ uniformly in
$ \vert {{r(y|x)}} \vert \leq R$ uniformly in ![]() $(x,y)\in {\mathcal{X}}^2$, then
$(x,y)\in {\mathcal{X}}^2$, then
and
By applying the previous lemma, given the assumptions stated, we have
Appendix C.  $(L_\infty(\pi), \Vert {{\cdot}}\Vert_{L_2(\pi)} )$-GE is distinct from
$(L_\infty(\pi), \Vert {{\cdot}}\Vert_{L_2(\pi)} )$-GE is distinct from  $L_2$-GE for non-reversible chains
$L_2$-GE for non-reversible chains
Let ![]() ${\mathcal{X}} = {\mathbb{N}\cup{0}}$, and let a be a probability mass function on
${\mathcal{X}} = {\mathbb{N}\cup{0}}$, and let a be a probability mass function on ![]() ${\mathcal{X}}$. Define transition probabilities by
${\mathcal{X}}$. Define transition probabilities by
 \begin{equation}\begin{aligned} p_{ij} & = \begin{cases} a_j &: i = 0, \\ 1 &: i>0,\ j=i-1, \\ 0 &: \text{otherwise}. \end{cases}\end{aligned}\end{equation}
\begin{equation}\begin{aligned} p_{ij} & = \begin{cases} a_j &: i = 0, \\ 1 &: i>0,\ j=i-1, \\ 0 &: \text{otherwise}. \end{cases}\end{aligned}\end{equation}
Let ![]() $b_j = \sum_{i=j}^\infty a_j$. It is easy to verify that if
$b_j = \sum_{i=j}^\infty a_j$. It is easy to verify that if ![]() $\sum_{j=1}^\infty b_j < \infty$ then
$\sum_{j=1}^\infty b_j < \infty$ then
is the unique stationary probability mass function for ![]() $P = [p_{ij}]_{ij\in{\mathcal{X}}^2}$.
$P = [p_{ij}]_{ij\in{\mathcal{X}}^2}$.
In the special case where ![]() $a_j = 2^{-j-1}$, we have
$a_j = 2^{-j-1}$, we have ![]() $\pi = a$. We continue this example working exclusively with this choice of a. Now,
$\pi = a$. We continue this example working exclusively with this choice of a. Now,
 \begin{equation}\begin{aligned} \delta_j P^n & = \begin{cases} \pi &:\, n\geq j+1, \\ \delta_{n-j} &:\, n\leq j. \end{cases}\end{aligned}\end{equation}
\begin{equation}\begin{aligned} \delta_j P^n & = \begin{cases} \pi &:\, n\geq j+1, \\ \delta_{n-j} &:\, n\leq j. \end{cases}\end{aligned}\end{equation}
Thus, for any initial probability mass function ![]() $\mu$,
$\mu$,
 \begin{equation}\begin{aligned} [\mu P^n]_j = \sum_{i=0}^{n-1} \mu_i \pi_j + \mu_{j+n}.\end{aligned}\end{equation}
\begin{equation}\begin{aligned} [\mu P^n]_j = \sum_{i=0}^{n-1} \mu_i \pi_j + \mu_{j+n}.\end{aligned}\end{equation}
If ![]() ${\frac{{\textrm{d}}\mu}{{\textrm{d}}\pi}}(j) = \frac{\mu_j}{\pi_j} \leq \Vert {{\mu}}_{L_\infty(\pi)} \Vert <\infty$ for all
${\frac{{\textrm{d}}\mu}{{\textrm{d}}\pi}}(j) = \frac{\mu_j}{\pi_j} \leq \Vert {{\mu}}_{L_\infty(\pi)} \Vert <\infty$ for all ![]() $j\in{\mathcal{X}}$, then
$j\in{\mathcal{X}}$, then
 \begin{equation}\begin{aligned} \Vert {{\mu P^n - \pi}}\Vert_{L_2(\pi)} ^2 & = \sum_{j=0}^\infty \pi_j \left ({\sum_{i=0}^{n-1} \mu_i + \frac{\mu_{j+n}}{\pi_j} -1 }\right) ^2 \\[3pt] & = \sum_{j=0}^\infty \pi_j \left ({-\sum_{i=n}^{\infty} \mu_i + \frac{\mu_{j+n}}{\pi_{j+n}} \frac{\pi_{j+n}}{\pi_j}}\right)^2\\[3pt] & = \sum_{j=0}^\infty \pi_j \left ({-\sum_{i=n}^{\infty} \frac{\mu_i}{\pi_i} \pi_i + \frac{\mu_{j+n}}{\pi_{j+n}} \frac{\pi_{j+n}}{\pi_j}}\right)^2\\[3pt] &\leq \sum_{j=0}^\infty \pi_j \left ({\sum_{i=n}^{\infty} \frac{\mu_i}{\pi_i} \pi_i + \frac{\mu_{j+n}}{\pi_{j+n}} \frac{\pi_{j+n}}{\pi_j}}\right)^2\\[3pt] &\leq \sum_{j=0}^\infty 2^{-j-1} \left ({\sum_{i=n}^{\infty} \Vert {{\mu}}_{L_\infty(\pi)} \Vert 2^{-i-1} + \Vert {{\mu}}_{L_\infty(\pi)} \Vert 2^{-n}}\right)^2\\[3pt] & = \Vert {{\mu}}\Vert_{L_\infty(\pi)} ^2 \sum_{j=0}^\infty 2^{-j-1} (2^{-n+1})^2\\[3pt] & = 4 \Vert {{\mu}}\Vert_{L_\infty(\pi)} ^2 (2^{-n})^2.\end{aligned}\end{equation}
\begin{equation}\begin{aligned} \Vert {{\mu P^n - \pi}}\Vert_{L_2(\pi)} ^2 & = \sum_{j=0}^\infty \pi_j \left ({\sum_{i=0}^{n-1} \mu_i + \frac{\mu_{j+n}}{\pi_j} -1 }\right) ^2 \\[3pt] & = \sum_{j=0}^\infty \pi_j \left ({-\sum_{i=n}^{\infty} \mu_i + \frac{\mu_{j+n}}{\pi_{j+n}} \frac{\pi_{j+n}}{\pi_j}}\right)^2\\[3pt] & = \sum_{j=0}^\infty \pi_j \left ({-\sum_{i=n}^{\infty} \frac{\mu_i}{\pi_i} \pi_i + \frac{\mu_{j+n}}{\pi_{j+n}} \frac{\pi_{j+n}}{\pi_j}}\right)^2\\[3pt] &\leq \sum_{j=0}^\infty \pi_j \left ({\sum_{i=n}^{\infty} \frac{\mu_i}{\pi_i} \pi_i + \frac{\mu_{j+n}}{\pi_{j+n}} \frac{\pi_{j+n}}{\pi_j}}\right)^2\\[3pt] &\leq \sum_{j=0}^\infty 2^{-j-1} \left ({\sum_{i=n}^{\infty} \Vert {{\mu}}_{L_\infty(\pi)} \Vert 2^{-i-1} + \Vert {{\mu}}_{L_\infty(\pi)} \Vert 2^{-n}}\right)^2\\[3pt] & = \Vert {{\mu}}\Vert_{L_\infty(\pi)} ^2 \sum_{j=0}^\infty 2^{-j-1} (2^{-n+1})^2\\[3pt] & = 4 \Vert {{\mu}}\Vert_{L_\infty(\pi)} ^2 (2^{-n})^2.\end{aligned}\end{equation}
Hence P is ![]() $(L_\infty(\pi), \Vert {{\cdot}}\Vert_{L_2(\pi)} )$-GE with optimal rate no larger than
$(L_\infty(\pi), \Vert {{\cdot}}\Vert_{L_2(\pi)} )$-GE with optimal rate no larger than ![]() $1/2$.
$1/2$.
For any ![]() $\alpha <\sqrt{0.5}$, let
$\alpha <\sqrt{0.5}$, let ![]() $\nu_j = (1-\alpha) (\alpha)^j$. Then
$\nu_j = (1-\alpha) (\alpha)^j$. Then ![]() $\nu\in L_2(\pi)$, since
$\nu\in L_2(\pi)$, since
 \begin{equation}\begin{aligned} \Vert {{\nu}}\Vert_{L_2(\pi)} ^2 & = \sum_{i=0}^\infty 0.5^{i+1} \left ({\frac{(1-\alpha)(\alpha)^i }{0.5^{i+1}}}\right)^2 \\[3pt] & = 2(1-\alpha)^2 \sum_{i=0}^\infty (2\alpha^2)^i = \frac{2(1-\alpha)^2}{1 - 2\alpha^2}.\end{aligned}\end{equation}
\begin{equation}\begin{aligned} \Vert {{\nu}}\Vert_{L_2(\pi)} ^2 & = \sum_{i=0}^\infty 0.5^{i+1} \left ({\frac{(1-\alpha)(\alpha)^i }{0.5^{i+1}}}\right)^2 \\[3pt] & = 2(1-\alpha)^2 \sum_{i=0}^\infty (2\alpha^2)^i = \frac{2(1-\alpha)^2}{1 - 2\alpha^2}.\end{aligned}\end{equation}
Moreover,
 \begin{equation}\begin{aligned} \Vert {{\nu P^n - \pi}}\Vert_{L_2(\pi)} ^2 & = \sum_{j=0}^\infty \pi_j \left ({\sum_{i=0}^{n-1} \nu_i + \frac{\nu_{j+n}}{\pi_j} -1 }\right)^2 \\[3pt] & = \sum_{j=0}^\infty 0.5^{j+1} \left ({-\sum_{i=n}^{\infty} (1-\alpha)\alpha^i + (1-\alpha)\alpha^{j+n} (0.5)^{-j-1} }\right)^2 \\[3pt] & = \alpha^{2n}\sum_{j=0}^\infty 0.5^{j+1} \left ({-1 + 2(1-\alpha)(2\alpha )^j}\right)^2 \\[3pt] & = \frac{\alpha^{2n}}{2} \sum_{j=0}^\infty ( 0.5^{j} -4(1-\alpha)\alpha^j +4(1-\alpha)^2 (2\alpha^2)^j) \\[3pt] \\[-35pt] & = \frac{\alpha^{2n}}{2} \left ({2 - \frac{4(1-\alpha)}{1-\alpha} + \frac{4(1-\alpha)^2}{1-2\alpha^2 }}\right) \\ & = \frac{(2\alpha-1)^2}{1-2\alpha^2} \alpha^{2n}. \end{aligned}\end{equation}
\begin{equation}\begin{aligned} \Vert {{\nu P^n - \pi}}\Vert_{L_2(\pi)} ^2 & = \sum_{j=0}^\infty \pi_j \left ({\sum_{i=0}^{n-1} \nu_i + \frac{\nu_{j+n}}{\pi_j} -1 }\right)^2 \\[3pt] & = \sum_{j=0}^\infty 0.5^{j+1} \left ({-\sum_{i=n}^{\infty} (1-\alpha)\alpha^i + (1-\alpha)\alpha^{j+n} (0.5)^{-j-1} }\right)^2 \\[3pt] & = \alpha^{2n}\sum_{j=0}^\infty 0.5^{j+1} \left ({-1 + 2(1-\alpha)(2\alpha )^j}\right)^2 \\[3pt] & = \frac{\alpha^{2n}}{2} \sum_{j=0}^\infty ( 0.5^{j} -4(1-\alpha)\alpha^j +4(1-\alpha)^2 (2\alpha^2)^j) \\[3pt] \\[-35pt] & = \frac{\alpha^{2n}}{2} \left ({2 - \frac{4(1-\alpha)}{1-\alpha} + \frac{4(1-\alpha)^2}{1-2\alpha^2 }}\right) \\ & = \frac{(2\alpha-1)^2}{1-2\alpha^2} \alpha^{2n}. \end{aligned}\end{equation}
Thus the convergence rate starting from this initial measure is ![]() $\alpha$.
$\alpha$.
Since this is true for any ![]() $\alpha <1/\sqrt{2}$, this shows that the
$\alpha <1/\sqrt{2}$, this shows that the ![]() $L_2(\pi)$-GE optimal rate is no smaller than
$L_2(\pi)$-GE optimal rate is no smaller than ![]() $\sqrt{0.5}$. Hence the
$\sqrt{0.5}$. Hence the ![]() $(L_\infty(\pi), \Vert {{\cdot}}\Vert_{L_2(\pi)} )$-GE and
$(L_\infty(\pi), \Vert {{\cdot}}\Vert_{L_2(\pi)} )$-GE and ![]() $L_2(\pi)$-GE optimal rates are different.
$L_2(\pi)$-GE optimal rates are different.
Appendix D. Proof of Proof of Lemma 2 and Lemma 1
Proof of Lemma 1. Let
 \begin{equation}\begin{aligned} \rho^\star & = \left \{{\rho>0: \exists C\,{:}\,V\to\mathbb{R}_+ \ \text{s.t.}\ \forall n\in\mathbb{N}, \nu\in V\cap \mathcal{M}_{+,1} \quad \vert{\kern-0.25ex{ \vert{\kern-0.25ex{ \vert {\nu P^n - \pi} \vert}\kern-0.25ex}\vert}\kern-0.25ex}\vert \leq C(\nu) \rho^n} \right\} \ , \\ \hat \rho & = \sup\limits_{\mu\in V\cap \mathcal{M}_{+,1}} \limsup_{n\to\infty} \vert{\kern-0.25ex{ \vert{\kern-0.25ex{ \vert {\mu P^n -\pi} \vert}\kern-0.25ex}\vert}\kern-0.25ex}\vert^{1/n}.\end{aligned}\end{equation}
\begin{equation}\begin{aligned} \rho^\star & = \left \{{\rho>0: \exists C\,{:}\,V\to\mathbb{R}_+ \ \text{s.t.}\ \forall n\in\mathbb{N}, \nu\in V\cap \mathcal{M}_{+,1} \quad \vert{\kern-0.25ex{ \vert{\kern-0.25ex{ \vert {\nu P^n - \pi} \vert}\kern-0.25ex}\vert}\kern-0.25ex}\vert \leq C(\nu) \rho^n} \right\} \ , \\ \hat \rho & = \sup\limits_{\mu\in V\cap \mathcal{M}_{+,1}} \limsup_{n\to\infty} \vert{\kern-0.25ex{ \vert{\kern-0.25ex{ \vert {\mu P^n -\pi} \vert}\kern-0.25ex}\vert}\kern-0.25ex}\vert^{1/n}.\end{aligned}\end{equation}
Proof that ![]() $\hat \rho \leq \rho^\star$: Let
$\hat \rho \leq \rho^\star$: Let ![]() $\epsilon>0$. We have
$\epsilon>0$. We have
 \begin{equation}\begin{aligned} \hat \rho & = \sup\limits_{\mu\in V\cap \mathcal{M}_{+,1}} \limsup_{n\to\infty} \vert{\kern-0.25ex{ \vert{\kern-0.25ex{ \vert {\mu P^n -\pi} \vert}\kern-0.25ex}\vert}\kern-0.25ex}\vert^{1/n} \\ & \leq \sup\limits_{\mu\in V\cap \mathcal{M}_{+,1}} \limsup_{n\to\infty} \vert{\kern-0.25ex{ \vert{\kern-0.25ex{ \vert {\mu P^n -\pi} \vert}\kern-0.25ex}\vert}\kern-0.25ex}\vert^{1/n} \\ & \leq \sup\limits_{\mu\in V\cap \mathcal{M}_{+,1}} \limsup_{n\to\infty} (C_\epsilon(\mu) (\rho^\star+\epsilon)^n)^{1/n}\\ & =\rho^\star +\epsilon . \end{aligned}\end{equation}
\begin{equation}\begin{aligned} \hat \rho & = \sup\limits_{\mu\in V\cap \mathcal{M}_{+,1}} \limsup_{n\to\infty} \vert{\kern-0.25ex{ \vert{\kern-0.25ex{ \vert {\mu P^n -\pi} \vert}\kern-0.25ex}\vert}\kern-0.25ex}\vert^{1/n} \\ & \leq \sup\limits_{\mu\in V\cap \mathcal{M}_{+,1}} \limsup_{n\to\infty} \vert{\kern-0.25ex{ \vert{\kern-0.25ex{ \vert {\mu P^n -\pi} \vert}\kern-0.25ex}\vert}\kern-0.25ex}\vert^{1/n} \\ & \leq \sup\limits_{\mu\in V\cap \mathcal{M}_{+,1}} \limsup_{n\to\infty} (C_\epsilon(\mu) (\rho^\star+\epsilon)^n)^{1/n}\\ & =\rho^\star +\epsilon . \end{aligned}\end{equation}
Since ![]() $\epsilon$ is arbitrary,
$\epsilon$ is arbitrary, ![]() $\hat \rho \leq \rho^\star$.
$\hat \rho \leq \rho^\star$.
Proof that ![]() $\hat \rho \geq \rho^\star$: For all
$\hat \rho \geq \rho^\star$: For all ![]() $\nu\in V\cap \mathcal{M}_{+,1}$,
$\nu\in V\cap \mathcal{M}_{+,1}$, ![]() $\limsup_{n\to\infty} \vert{\kern-0.25ex{ \vert{\kern-0.25ex{ \vert {\mu P^n -\pi} \vert}\kern-0.25ex}\vert}\kern-0.25ex}\vert^{1/n}\leq \hat\rho$. Let
$\limsup_{n\to\infty} \vert{\kern-0.25ex{ \vert{\kern-0.25ex{ \vert {\mu P^n -\pi} \vert}\kern-0.25ex}\vert}\kern-0.25ex}\vert^{1/n}\leq \hat\rho$. Let ![]() $\epsilon>0$. Then for all
$\epsilon>0$. Then for all ![]() $\mu\in V\cap \mathcal{M}_{+,1}$,
$\mu\in V\cap \mathcal{M}_{+,1}$, ![]() $ \vert{\kern-0.25ex{ \vert{\kern-0.25ex{ \vert {\mu P^n -\pi} \vert}\kern-0.25ex}\vert}\kern-0.25ex}\vert^{1/n}> \hat\rho+\epsilon$ for at most finitely many
$ \vert{\kern-0.25ex{ \vert{\kern-0.25ex{ \vert {\mu P^n -\pi} \vert}\kern-0.25ex}\vert}\kern-0.25ex}\vert^{1/n}> \hat\rho+\epsilon$ for at most finitely many ![]() $n\in \mathbb{N}$. Let
$n\in \mathbb{N}$. Let
 \begin{equation*}C_\epsilon(\mu) = \max_{n\in\mathbb{N}} ( {1\vee \frac{ \vert{\kern-0.25ex{ \vert{\kern-0.25ex{ \vert {\mu P^n -\pi} \vert}\kern-0.25ex}\vert}\kern-0.25ex}\vert}{(\rho+\epsilon)^n}} ) .\end{equation*}
\begin{equation*}C_\epsilon(\mu) = \max_{n\in\mathbb{N}} ( {1\vee \frac{ \vert{\kern-0.25ex{ \vert{\kern-0.25ex{ \vert {\mu P^n -\pi} \vert}\kern-0.25ex}\vert}\kern-0.25ex}\vert}{(\rho+\epsilon)^n}} ) .\end{equation*}
Then ![]() $C_\epsilon(\mu) <\infty$ since the maximum is over finitely many distinct elements. Therefore
$C_\epsilon(\mu) <\infty$ since the maximum is over finitely many distinct elements. Therefore ![]() $ \vert{\kern-0.25ex{ \vert{\kern-0.25ex{ \vert {\mu P^n - \pi } \vert}\kern-0.25ex}\vert}\kern-0.25ex}\vert \leq C_\epsilon(\mu) (\hat\rho+\epsilon)^n$ for all
$ \vert{\kern-0.25ex{ \vert{\kern-0.25ex{ \vert {\mu P^n - \pi } \vert}\kern-0.25ex}\vert}\kern-0.25ex}\vert \leq C_\epsilon(\mu) (\hat\rho+\epsilon)^n$ for all ![]() $n\in\mathbb{N}$. This implies that
$n\in\mathbb{N}$. This implies that ![]() $\hat\rho+\epsilon \geq \rho^\star$. Since
$\hat\rho+\epsilon \geq \rho^\star$. Since ![]() $\epsilon$ is arbitrary,
$\epsilon$ is arbitrary, ![]() $\hat\rho\geq \rho^\star$.
$\hat\rho\geq \rho^\star$.
Proof of Lemma 2. The equivalence [(iii) ![]() $\iff$ (iv)] is proven in [Reference Roberts and Rosenthal29, Theorem 2.1]. The implication [(iii)
$\iff$ (iv)] is proven in [Reference Roberts and Rosenthal29, Theorem 2.1]. The implication [(iii) ![]() $\implies$ (ii)] follows from the inclusion
$\implies$ (ii)] follows from the inclusion ![]() $L_\infty(\pi)\subset L_2(\pi)$, and [(ii)
$L_\infty(\pi)\subset L_2(\pi)$, and [(ii) ![]() $\implies$ (i)] follows from Cauchy–Schwarz.
$\implies$ (i)] follows from Cauchy–Schwarz.
Proof that [(ii) ![]() $\implies$ (iii)]:
$\implies$ (iii)]:
Without loss of generality, assume that ![]() $\rho$ is the optimal rate of
$\rho$ is the optimal rate of ![]() $(L_\infty(\pi_\epsilon), \Vert {\cdot} \Vert_{L_2(\pi)})$-GE:
$(L_\infty(\pi_\epsilon), \Vert {\cdot} \Vert_{L_2(\pi)})$-GE:
 \begin{equation}\begin{aligned} \rho = \sup\limits_{\nu\in L_{\infty,0}(\pi)} \limsup_{t\to\infty} \Vert {{\nu P^t}}\Vert_{L_2(\pi)} ^{1/t} \ . \end{aligned}\end{equation}
\begin{equation}\begin{aligned} \rho = \sup\limits_{\nu\in L_{\infty,0}(\pi)} \limsup_{t\to\infty} \Vert {{\nu P^t}}\Vert_{L_2(\pi)} ^{1/t} \ . \end{aligned}\end{equation}
From the proof of [Reference Roberts and Tweedie32, Theorem 1], P is ![]() $\pi$-a.e. geometrically ergodic with some unknown optimal rate. From [Reference Roberts and Rosenthal29, Theorem 2.1], P is
$\pi$-a.e. geometrically ergodic with some unknown optimal rate. From [Reference Roberts and Rosenthal29, Theorem 2.1], P is ![]() $L_2(\pi)$-GE with some unknown optimal rate
$L_2(\pi)$-GE with some unknown optimal rate ![]() $\rho_2$, which is equivalent to the spectral radius of
$\rho_2$, which is equivalent to the spectral radius of ![]() $P\vert_{L_{2,0}(\pi)}$:
$P\vert_{L_{2,0}(\pi)}$:
It remains to be shown that ![]() $\rho_2 \leq \rho$. We will use the spectral measure decomposition of P, as in [Reference Roberts and Rosenthal29]. Suppose, for a contradiction, that
$\rho_2 \leq \rho$. We will use the spectral measure decomposition of P, as in [Reference Roberts and Rosenthal29]. Suppose, for a contradiction, that ![]() $\rho_2 >\rho$. Let
$\rho_2 >\rho$. Let ![]() $\overline \rho = \frac{\rho+\rho_2}{2}$. Let
$\overline \rho = \frac{\rho+\rho_2}{2}$. Let ![]() $\mathcal{E}$ be the spectral measure of P, so that
$\mathcal{E}$ be the spectral measure of P, so that ![]() $\mu P^t = \int_{-1}^1 \lambda^t \mu \mathcal{E}(d\lambda)$. If
$\mu P^t = \int_{-1}^1 \lambda^t \mu \mathcal{E}(d\lambda)$. If ![]() $\rho_2 > \rho$ then either
$\rho_2 > \rho$ then either ![]() $\mathcal{E}([-\rho_2,-\overline \rho))\neq\textbf{0} $ or
$\mathcal{E}([-\rho_2,-\overline \rho))\neq\textbf{0} $ or ![]() $\mathcal{E}((\overline \rho,\rho_2]))\neq \textbf{0}$. Assume (replacing P by
$\mathcal{E}((\overline \rho,\rho_2]))\neq \textbf{0}$. Assume (replacing P by ![]() $P^2$,
$P^2$, ![]() $\rho$ by
$\rho$ by ![]() $\rho^2$, and
$\rho^2$, and ![]() $\rho_2$ by
$\rho_2$ by ![]() $\rho_2^2$ if necessary) that
$\rho_2^2$ if necessary) that ![]() $\mathcal{E}((\overline \rho,\rho_2])\neq \textbf{0}$ and
$\mathcal{E}((\overline \rho,\rho_2])\neq \textbf{0}$ and ![]() $\mathcal{E}((-1,0))= \textbf{0}$. Then there is some non-zero signed measure
$\mathcal{E}((-1,0))= \textbf{0}$. Then there is some non-zero signed measure ![]() $\nu$ in the range of
$\nu$ in the range of ![]() $\mathcal{E}((\overline \rho,\rho_2])$. Since the spectral projections are orthogonal and
$\mathcal{E}((\overline \rho,\rho_2])$. Since the spectral projections are orthogonal and ![]() $ \{ {1} \}\cap (\overline \rho,\rho_2] = \emptyset$, we have
$ \{ {1} \}\cap (\overline \rho,\rho_2] = \emptyset$, we have ![]() $\nu\perp \pi$, and hence
$\nu\perp \pi$, and hence ![]() $\nu({\mathcal{X}}) = 0$. Since
$\nu({\mathcal{X}}) = 0$. Since ![]() $L_{\infty,0}(\pi)$ is dense in
$L_{\infty,0}(\pi)$ is dense in ![]() $L_{2,0}(\pi)$, there is a
$L_{2,0}(\pi)$, there is a ![]() $\mu\in L_{\infty,0}(\pi)$ with
$\mu\in L_{\infty,0}(\pi)$ with ![]() $ \Vert {{\mu-\nu}}\Vert_{L_2(\pi)} < \Vert {{\nu}}\Vert_{L_2(\pi)} /2$. Then, from the polarization identity,
$ \Vert {{\mu-\nu}}\Vert_{L_2(\pi)} < \Vert {{\nu}}\Vert_{L_2(\pi)} /2$. Then, from the polarization identity,
 \begin{equation*} \langle {{\nu},\ {\mu}} \rangle_{L_2(\pi)} \geq \frac{3}{8} \Vert {{\nu}}\Vert_{L_2(\pi)} ^2 >0,\end{equation*}
\begin{equation*} \langle {{\nu},\ {\mu}} \rangle_{L_2(\pi)} \geq \frac{3}{8} \Vert {{\nu}}\Vert_{L_2(\pi)} ^2 >0,\end{equation*}
and ![]() $\mu\neq 0$.
$\mu\neq 0$.
Let ![]() $R = range(\int_{(\overline \rho,\rho_2]} \mathcal{E}(d \lambda))$. Then
$R = range(\int_{(\overline \rho,\rho_2]} \mathcal{E}(d \lambda))$. Then ![]() $\text{span}(\nu) \subset R$, so
$\text{span}(\nu) \subset R$, so
 \begin{equation}\begin{aligned} \Vert {{proj_{R}{\mu}}}\Vert_{L_2(\pi)} \geq \Vert {{proj_{\nu}{\mu}}}\Vert_{L_2(\pi)} \geq \frac{3}{8} \Vert {{\nu}}\Vert_{L_2(\pi)} . \\ \end{aligned}\end{equation}
\begin{equation}\begin{aligned} \Vert {{proj_{R}{\mu}}}\Vert_{L_2(\pi)} \geq \Vert {{proj_{\nu}{\mu}}}\Vert_{L_2(\pi)} \geq \frac{3}{8} \Vert {{\nu}}\Vert_{L_2(\pi)} . \\ \end{aligned}\end{equation}
Then
 \begin{equation}\begin{aligned} \Vert {{\mu P^k}}\Vert_{L_2(\pi)} ^2 & = \left\langle {{\mu P^k},\ {\mu P^k}} \right\rangle_{L_2(\pi)} \\ & = \left\langle {{\mu},\ {\mu P^{2k}}} \right\rangle_{L_2(\pi)} \\ & = \left\langle {{\mu},\ {\mu\int_{(0,\rho_2]} \lambda^{2k} \mathcal{E}(d \lambda)}} \right\rangle_{L_2(\pi)} \\ & \geq \left\langle {{\mu},\ {\mu\int_{(\overline \rho,\rho_2]} \lambda^{2k} \mathcal{E}(d \lambda)}} \right\rangle_{L_2(\pi)} \\ & \geq \left\langle {{\mu},\ {\mu\int_{(\overline \rho,\rho_2]} \overline \rho^{2k} \mathcal{E}(d \lambda)}} \right\rangle_{L_2(\pi)} \\ & = \overline\rho^{2k} \Vert {{proj_{R}{\mu}}}\Vert_{L_2(\pi)} ^2 \\ & \geq \overline\rho^{2k} \frac{9}{64} \Vert {{\nu}}\Vert_{L_2(\pi)} ^2 \ . \end{aligned}\end{equation}
\begin{equation}\begin{aligned} \Vert {{\mu P^k}}\Vert_{L_2(\pi)} ^2 & = \left\langle {{\mu P^k},\ {\mu P^k}} \right\rangle_{L_2(\pi)} \\ & = \left\langle {{\mu},\ {\mu P^{2k}}} \right\rangle_{L_2(\pi)} \\ & = \left\langle {{\mu},\ {\mu\int_{(0,\rho_2]} \lambda^{2k} \mathcal{E}(d \lambda)}} \right\rangle_{L_2(\pi)} \\ & \geq \left\langle {{\mu},\ {\mu\int_{(\overline \rho,\rho_2]} \lambda^{2k} \mathcal{E}(d \lambda)}} \right\rangle_{L_2(\pi)} \\ & \geq \left\langle {{\mu},\ {\mu\int_{(\overline \rho,\rho_2]} \overline \rho^{2k} \mathcal{E}(d \lambda)}} \right\rangle_{L_2(\pi)} \\ & = \overline\rho^{2k} \Vert {{proj_{R}{\mu}}}\Vert_{L_2(\pi)} ^2 \\ & \geq \overline\rho^{2k} \frac{9}{64} \Vert {{\nu}}\Vert_{L_2(\pi)} ^2 \ . \end{aligned}\end{equation}
Hence ![]() $\rho \geq \overline \rho$. This contradicts
$\rho \geq \overline \rho$. This contradicts ![]() $\rho_2 > \rho$.
$\rho_2 > \rho$.
Proof that [(i) ![]() $\implies$ (ii)]:
$\implies$ (ii)]:
Let the optimal rates of ![]() $(L_\infty(\pi_\epsilon), \Vert {\cdot} \Vert_{L_1(\pi)})$-GE and
$(L_\infty(\pi_\epsilon), \Vert {\cdot} \Vert_{L_1(\pi)})$-GE and ![]() $(L_\infty(\pi_\epsilon), \Vert {\cdot} \Vert_{L_2(\pi)})$-GE be (respectively)
$(L_\infty(\pi_\epsilon), \Vert {\cdot} \Vert_{L_2(\pi)})$-GE be (respectively)
 \begin{equation}\begin{aligned} \rho & = \sup\limits_{\mu\in L_{\infty,0}(\pi)}\limsup_{n\to\infty} \Vert {{\mu P^n}}\Vert_{L_1(\pi)} ^{1/n} \ , & \rho_2 & = \sup\limits_{\mu\in L_{\infty,0}(\pi)}\limsup_{n\to\infty} \Vert {{\mu P^n}}\Vert_{L_2(\pi)} ^{1/n} \ .\end{aligned}\end{equation}
\begin{equation}\begin{aligned} \rho & = \sup\limits_{\mu\in L_{\infty,0}(\pi)}\limsup_{n\to\infty} \Vert {{\mu P^n}}\Vert_{L_1(\pi)} ^{1/n} \ , & \rho_2 & = \sup\limits_{\mu\in L_{\infty,0}(\pi)}\limsup_{n\to\infty} \Vert {{\mu P^n}}\Vert_{L_2(\pi)} ^{1/n} \ .\end{aligned}\end{equation}
We want to show that ![]() $\rho_2 \leq \rho$.
$\rho_2 \leq \rho$.
Let ![]() $\epsilon>0$ be arbitrary. Let
$\epsilon>0$ be arbitrary. Let ![]() $\nu_\epsilon\in L_{\infty,0}(\pi)$ with
$\nu_\epsilon\in L_{\infty,0}(\pi)$ with
 \begin{equation}\begin{aligned} \limsup_{n\to\infty} \Vert {{\nu_\epsilon P^n}}\Vert_{L_2(\pi)} ^{1/n} & \geq \rho_2-\epsilon \ .\end{aligned}\end{equation}
\begin{equation}\begin{aligned} \limsup_{n\to\infty} \Vert {{\nu_\epsilon P^n}}\Vert_{L_2(\pi)} ^{1/n} & \geq \rho_2-\epsilon \ .\end{aligned}\end{equation}
Then, for some ![]() $c(\nu_\epsilon)>0$, for infinitely many
$c(\nu_\epsilon)>0$, for infinitely many ![]() $n\in\mathbb{N}$,
$n\in\mathbb{N}$,
 \begin{equation}\begin{aligned} \Vert {{\nu_\epsilon P^n}}\Vert_{L_2(\pi)} & \geq (\rho_2-2\epsilon)^n \ .\end{aligned}\end{equation}
\begin{equation}\begin{aligned} \Vert {{\nu_\epsilon P^n}}\Vert_{L_2(\pi)} & \geq (\rho_2-2\epsilon)^n \ .\end{aligned}\end{equation}
Using the fact that
 \begin{equation*} \Vert {{\mu}}\Vert_{L_1(\pi)} = \sup\limits_{\substack{f\in L'_\infty(\pi) \\ \Vert {f} \Vert_{L'_\infty(\pi)}}} \mu f,\end{equation*}
\begin{equation*} \Vert {{\mu}}\Vert_{L_1(\pi)} = \sup\limits_{\substack{f\in L'_\infty(\pi) \\ \Vert {f} \Vert_{L'_\infty(\pi)}}} \mu f,\end{equation*}
and using the self-adjointness of P in ![]() $L_2(\pi)$ (since P is reversible), as well as the fact that (a version of)
$L_2(\pi)$ (since P is reversible), as well as the fact that (a version of) ![]() ${\frac{{\textrm{d}}\nu_\epsilon}{{\textrm{d}}\pi}}$ is some bounded function with
${\frac{{\textrm{d}}\nu_\epsilon}{{\textrm{d}}\pi}}$ is some bounded function with
 \begin{equation*} \Vert {{\frac{\textrm{d} \nu_\epsilon}{\textrm{d} \pi}}} \Vert_{L'_\infty(\pi)} = \Vert {\nu_\epsilon} \Vert_{L_\infty(\pi)},\end{equation*}
\begin{equation*} \Vert {{\frac{\textrm{d} \nu_\epsilon}{\textrm{d} \pi}}} \Vert_{L'_\infty(\pi)} = \Vert {\nu_\epsilon} \Vert_{L_\infty(\pi)},\end{equation*}
we have the following for infinitely many ![]() $n\in\mathbb{N}$:
$n\in\mathbb{N}$:
 \begin{equation}\begin{aligned} \Vert {{\nu_\epsilon P^{2n}}}\Vert_{L_1(\pi)} & = \sup\limits_{ \Vert {f} \Vert_\infty\leq 1} \nu_\epsilon P^{2n} f \\& \geq \frac{1}{ \Vert {{\nu_\epsilon}}\Vert_{L_\infty(\pi)} } \nu_\epsilon P^{2n} {\frac{{\textrm{d}}\nu_\epsilon}{{\textrm{d}}\pi}} \\& = \frac{1}{ \Vert {{\nu_\epsilon}}\Vert_{L_\infty(\pi)} } \langle {{\nu_\epsilon P^{2n}},\ {\nu_\epsilon}} \rangle \\& = \frac{1}{ \Vert {{\nu_\epsilon}}\Vert_{L_\infty(\pi)} } \langle {{\nu_\epsilon P^{n}},\ {\nu_\epsilon P^n}} \rangle \\& = \frac{1}{ \Vert {{\nu_\epsilon}}\Vert_{L_\infty(\pi)} } \Vert {{\nu_\epsilon P^n}}\Vert_{L_2(\pi)} ^2 \\& \geq \frac{1}{ \Vert {{\nu_\epsilon}}\Vert_{L_\infty(\pi)} } (\rho_2-2\epsilon)^{2n}.\end{aligned}\end{equation}
\begin{equation}\begin{aligned} \Vert {{\nu_\epsilon P^{2n}}}\Vert_{L_1(\pi)} & = \sup\limits_{ \Vert {f} \Vert_\infty\leq 1} \nu_\epsilon P^{2n} f \\& \geq \frac{1}{ \Vert {{\nu_\epsilon}}\Vert_{L_\infty(\pi)} } \nu_\epsilon P^{2n} {\frac{{\textrm{d}}\nu_\epsilon}{{\textrm{d}}\pi}} \\& = \frac{1}{ \Vert {{\nu_\epsilon}}\Vert_{L_\infty(\pi)} } \langle {{\nu_\epsilon P^{2n}},\ {\nu_\epsilon}} \rangle \\& = \frac{1}{ \Vert {{\nu_\epsilon}}\Vert_{L_\infty(\pi)} } \langle {{\nu_\epsilon P^{n}},\ {\nu_\epsilon P^n}} \rangle \\& = \frac{1}{ \Vert {{\nu_\epsilon}}\Vert_{L_\infty(\pi)} } \Vert {{\nu_\epsilon P^n}}\Vert_{L_2(\pi)} ^2 \\& \geq \frac{1}{ \Vert {{\nu_\epsilon}}\Vert_{L_\infty(\pi)} } (\rho_2-2\epsilon)^{2n}.\end{aligned}\end{equation}
Thus ![]() $\rho_2-2\epsilon \leq \rho$. Since
$\rho_2-2\epsilon \leq \rho$. Since ![]() $\epsilon$ was arbitrary, we find that
$\epsilon$ was arbitrary, we find that ![]() $\rho_2\leq \rho$.
$\rho_2\leq \rho$.
Acknowledgements
We thank Daniel Rudolf for very helpful comments on the first version of our preprint. We also thank Gareth O. Roberts, Peter Rosenthal, and Don Hadwin for helpful discussions.