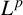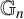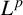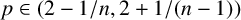1 Introduction
1.1 Szegö projection
Let
$\Omega $
be a domain in
$\mathbb {C}^{n}$
and
$\partial \Omega $
be the topological boundary of
$\Omega $
. We denote by
$d\sigma $
the Euclidean surface measure induced on
$\partial \Omega $
. Let
$\rho $
be a defining function for
$\Omega $
, that is,
$\Omega =\{z\in \mathbb {C}^{n}: \rho (z)<0\}, \nabla \rho \neq 0$
on
$\partial \Omega $
. Consider a family of approximating subdomains
$\Omega _{\varepsilon }\ (\varepsilon>0)$
as follows:
$\Omega _{\varepsilon }=\{z\in \mathbb {C}^{n}: \rho (z)<-\varepsilon \}$
. For
$1\leq p<\infty $
, there is a standard way to define the Hardy space
$\mathcal {H}^{p}(\Omega , d\sigma )$
. Namely,
$$ \begin{align*}\mathcal{H}^{p}(\Omega, d\sigma):=\bigg\{f\in \mathcal{O}(\Omega): \Vert f \Vert^{p}_{\mathcal{H}^{p}(\Omega, d\sigma)} =\sup_{\varepsilon>0}\int_{\partial\Omega_{\varepsilon}}\vert f(\zeta)\vert^{p}\,d\sigma_{\varepsilon}<\infty \bigg\}, \end{align*} $$
where
$\mathcal {O}(\Omega )$
is the set of all holomorphic functions on
$\Omega $
and
$d\sigma _{\varepsilon }$
is the Euclidean surface measure induced on the topological boundary
$\partial \Omega _{\varepsilon }$
.
Standard basic facts of Hardy space theory show that every function f in
$\mathcal {H}^{p}(\Omega , d\sigma )$
admits a boundary value function
$f^{*}$
almost everywhere on
$\partial \Omega $
with respect to the measure
$d\sigma $
. We denote by
$\mathcal {H}^{p}(\partial \Omega , d\sigma )$
the linear space of all these boundary value functions. It is a closed subspace of
$L^{p}(\partial \Omega , d\sigma )$
. The map
$f\rightarrow f^{*}$
is an isomorphism of
$\mathcal {H}^{p}(\Omega , d\sigma )$
onto
$\mathcal {H}^{p}(\partial \Omega , d\sigma )$
. We shall not make any distinction between these two spaces, including the corresponding projections and reproducing kernels. In particular, for
$p=2$
,
$\mathcal {H}^{2}(\Omega , d\sigma )$
is a Hilbert space under the inner product
$$ \begin{align*}\langle f, g \rangle_{\mathcal{H}^{2}(\Omega, d\sigma)}:=\int_{\partial\Omega}f^{*}\overline{g^{*}}\,d\sigma. \end{align*} $$
Sometimes we simply write
$\langle f, g \rangle _{\mathcal {H}^{2}(\Omega , d\sigma )}:=\int _{\partial \Omega }f\overline {g}\,d\sigma $
. The Szegö projection is the orthogonal projection,
$$ \begin{align*}\textbf{S}_{\Omega}: L^{2}(\partial\Omega, d\sigma)\rightarrow \mathcal{H}^{2}(\Omega, d\sigma)\cong \mathcal{H}^{2}(\partial\Omega, d\sigma). \end{align*} $$
It follows from the Riesz representation theorem that
$\textbf {S}_{\Omega }$
is an integral operator given by
$$ \begin{align*}\textbf{S}_{\Omega}f(z)=\langle f, S_{z} \rangle_{\mathcal{H}^{2}(\Omega, d\sigma)}:=\int_{\partial\Omega}f(\zeta)\overline{S_{z}(\zeta)}\,d\sigma(\zeta), \quad z\in \Omega, \end{align*} $$
where the reproducing kernel
$S_{\Omega }(z, \zeta ):=\overline {S_{z}(\zeta )}$
on
$\Omega \times \partial \Omega $
is called the Szegö kernel. For any orthonormal basis
$\{e_{n}(z)\}_{n=0}^{\infty }$
for
$\mathcal {H}^{2}(\Omega , d\sigma )$
,
$$ \begin{align*}S_{\Omega}(z, \zeta)=\sum_{n=0}^{\infty}e_{n}(z)\overline{e_{n}(\zeta)}. \end{align*} $$
We refer to Stein [Reference Stein20] for more information about the Hardy theory.
In the Hardy space setting, it is natural to study the
$L^{p}$
-regularity problem of the Szegö projection.
Question 1.1. For what
$p\in (1, \infty )$
is the Szegö projection
$\textbf {S}_{\Omega }$
bounded on
$L^{p}(\partial \Omega , d\sigma )$
?
If the projection
$\textbf {S}_{\Omega }$
is unbounded for all
$p\neq 2$
, we call it
$L^{p}$
-irregular. By analogy with the
$L^{p}$
-regularity of the Bergman projection, the
$L^{p}$
-regularity of the Szegö projection is also strongly dependent on the geometric properties of the domain
$\Omega $
. For example, if
$\Omega $
is a unit disc, a bidisc, a strongly pseudoconvex domain or some convex domains or pseudoconvex domains of finite type with locally diagonalisable Levi form, then the Szegö projection
$\textbf {S}_{\Omega }$
from
$L^{p}(\partial \Omega , d\sigma )$
to itself is bounded for all
$p\in (1, \infty )$
(see Charpentier–Dupain [Reference Charpentier and Dupain4], Grellier–Peloso [Reference Grellier and Peloso9], McNeal–Stein [Reference McNeal and Stein13], Phong–Stein [Reference Phong and Stein17]). In [Reference Munasinghe and Zeytuncu16], Munasinghe and Zeytuncu constructed a class of bounded pseudoconvex domains in
$\mathbb {C}^{2}$
on which the Szegö projection is
$L^{p}$
-irregular. There are domains, under different boundary conditions, on which the Szegö projection is bounded for different restricted ranges of p (see Lanzani–Stein [Reference Lanzani and Stein11]).
However, instead of the topological boundary, one may consider the Hardy space on the distinguished boundary. Békollé–Bonami [Reference Békollé and Bonami2] proved that, in the Hardy space setting defined on the distinguished boundary, the Szegö projection is
$L^{p}$
-irregular on the tube over an irreducible self-dual cone of rank greater than 1. Monguzzi–Peloso [Reference Monguzzi and Peloso15] obtained a sharp estimate for the Szegö projection on the distinguished boundary of model worm domains. One may also consider other measures on
$\partial \Omega $
(or on the distinguished boundary) in addition to the Euclidean surface measure, for example, Fefferman surface measure (see Barrett [Reference Barrett1]) and surface measure of the form
$\omega d\sigma $
, where
$\omega $
is a continuous and positive function on the boundary (see Lanzani–Stein [Reference Lanzani and Stein12]).
More recently, Chen et al. [Reference Chen, Krantz and Yuan5] discussed the
$L^{p}$
-regularity of the Bergman projection on the symmetrised polydisc. In fact, they dealt with more general bounded domains covered by the polydisc through a rational proper holomorphic mapping. Inspired by their work, it is of interest, as a model of a nonsmoothly bounded pseudoconvex domain without any strongly pseudoconvex boundary point, to consider the
$L^{p}$
-regularity problem of the Szegö projection on the symmetrised polydisc. The Szegö projection is very different to the Bergman projection because, in general, there is no transform formula for the Szegö projection under biholomorphic mappings in higher dimensions. Therefore, some methods in [Reference Chen, Krantz and Yuan5] for the Bergman projection cannot be applied to the Szegö projection directly, which makes it trickier to deal with this problem in the Hardy space setting.
In this paper, we focus on the
$L^{p}$
-regularity behaviour of the Szegö projection on the symmetrised polydisc with respect to the distinguished boundary.
1.2 Symmetrised polydisc
The symmetrised polydisc
$\mathbb {G}_{n}$
is defined as follows. Let
$\mathbb {D}$
be the unit disc in the complex plane
$\mathbb {C}$
and
$\lambda =(\lambda _{1}, \ldots , \lambda _{n})\in \mathbb {C}^{n}$
and let
$\pi _{n}=(\pi _{n,1}, \ldots , \pi _{n,n}): \mathbb {C}^{n}\longrightarrow \mathbb {C}^{n}$
be the symmetrisation map defined by
$$ \begin{align*} \pi_{n,k}(\lambda)=\sum_{1\leq j_{1} < \cdots < j_{k} \leq n}\lambda_{j_{1}} \cdots \lambda_{j_{k}}, \quad 1\leq k \leq n. \end{align*} $$
The image
$\mathbb {G}_{n}:=\pi _{n}(\mathbb {D}^{n})$
is known as the symmetrised polydisc. In particular,
$G_{1}=\mathbb {D}$
and
$G_{2}$
is the so-called symmetrised bidisc. It is easy to verify that
$\mathbb {G}_{n}$
is a bounded
$(1,2, \ldots , n)$
-circular domain. Let
$\partial _{0}\mathbb {G}_{n}$
be the distinguished boundary of the symmetrised polydisc
$\mathbb {G}_{n}$
. Then
$\partial _{0}\mathbb {G}_{n}=\{\pi _{n}(\lambda ): \lambda \in \mathbb {T}^{n}\}$
, where
$\mathbb {T}^{n}$
is the n-torus and
$\mathbb {T}=\{z\in \mathbb {C}: \vert z\vert =1\}$
(see Edigarian–Zwonek [Reference Edigarian and Zwonek7]). The restriction map
$\pi _{n}|_{\mathbb {D}^{n}}: \mathbb {D}^{n}\rightarrow \mathbb {G}_{n}$
is a proper holomorphic map (see Rudin [Reference Rudin19]). Thus, the symmetrised polydisc
$\mathbb {G}_{n}$
is a proper image of the bounded symmetric domain
$\mathbb {D}^{n}$
. For a general reference on the symmetrised polydisc, see the book by Jarnicki and Pflug [Reference Jarnicki and Pflug10, Ch. 7].
The symmetrised polydisc
$\mathbb {G}_{n}\ (n \geq 2)$
is a bounded inhomogeneous pseudoconvex domain without smooth boundary. In particular, it does not have any strongly pseudoconvex boundary point. It is important because the symmetrised bidisc is the first known example of a bounded pseudoconvex domain for which the Lempert function, the Kobayashi distance and the Carathéodory distance coincide, but which cannot be exhausted by domains biholomorphic to convex ones (see Costara [Reference Costara6]).
1.3 Hardy space on
$\mathbb {G}_{n}$
Next, we give a detailed description of the Hardy space corresponding to the distinguished boundary of the symmetrised polydisc.
Let
$d\Theta :=d\theta _{1}\cdots d\theta _{n}$
be the normalised Lebesgue measure on
$\mathbb {T}^{n}$
. We first recall the definition of the Hardy space
$\mathcal {H}^{p}(\mathbb {D}^{n}, d\Theta )$
and
$L^{p}(\mathbb {T}^{n}, d\Theta )$
with respect to the measure
$d\Theta $
on the distinguished boundary
$\mathbb {T}^{n}$
of the polydisc
$\mathbb {D}^{n}$
:
$$ \begin{align*}\mathcal{H}^{p}(\mathbb{D}^{n}, d\Theta):=\bigg\{f\in \mathcal{O}(\mathbb{D}^{n}): \Vert f\Vert^{p}_{\mathcal{H}^{p}(\mathbb{D}^{n}, d\Theta)}=\sup_{0<r<1}\int_{\mathbb{T}^{n}}f(re^{i\Theta})\,d\Theta<\infty\bigg\}, \end{align*} $$
and
$$ \begin{align*}L^{p}(\mathbb{T}^{n}, d\Theta):=\bigg\{f: \mathbb{T}^{n}\rightarrow \mathbb{C}~\text{is complex measurable}, \Vert f\Vert^{p}_{L^{p}(\mathbb{T}^{n}, d\Theta)}=\int_{\mathbb{T}^{n}}f(e^{i\Theta})\,d\Theta<\infty\bigg\}, \end{align*} $$
where
$e^{i\Theta }=(e^{i\theta _{1}}, \ldots , e^{i\theta _{n}})\in \mathbb {T}^{n}$
(see Rudin [Reference Rudin18]).
Following the definition of the Hardy space
$\mathcal {H}^{2}$
on the symmetric polydisc in Misra et al. [Reference Misra, Roy and Zhang14], we give the definition of the Hardy space
$\mathcal {H}^{p}$
on
$\mathbb {G}_{n}$
for
$1\leq p<\infty $
. It is natural that the symmetrisation map
$\pi _{n}$
induces a boundary measure
$d\Theta _{\pi _{n}}$
on
$\partial _{0}\mathbb {G}_{n}$
given by
$$ \begin{align*}\int_{\partial_{0}\mathbb{G}_{n}}f\,d\Theta_{\pi_{n}}:=\int_{\mathbb{T}^{n}}(f\circ\pi_{n})\vert J_{\pi_{n}}\vert^{2}\,d\Theta, \end{align*} $$
where
$\partial _{0}\mathbb {G}_{n}$
is defined as above and
$J_{\pi _{n}}:=\det \pi ^{\prime }_{n}$
is the complex Jacobian of the symmetrisation map
$\pi _{n}$
. Let
$\mathcal {O}(\mathbb {G}_{n})$
be the set of holomorphic functions on
$\mathbb {G}_{n}$
. For
$1\leq p<\infty $
, the Hardy space on the symmetrised polydisc
$\mathbb {G}_{n}$
is defined as
$$ \begin{align*}\mathcal{H}^{p}(\mathbb{G}_{n}, d\Theta_{\pi_{n}}):=\{f\in \mathcal{O}(\mathbb{G}_{n}): \Vert f\Vert_{\mathcal{H}^{p}(\mathbb{G}_{n}, d\Theta_{\pi_{n}})}<\infty\}, \end{align*} $$
where
$$ \begin{align} \Vert f\Vert^{p}_{\mathcal{H}^{p}(\mathbb{G}_{n}, d\Theta_{\pi_{n}})}:&=\Vert J_{\pi_{n}}\Vert^{-p}\sup_{0<r<1} \nonumber \int_{\partial_{0}\mathbb{G}_{n}}\vert f(rz_{1}, r^{2}z_{2},\ldots, r^{n}z_{n})\vert^{p}\,d\Theta_{\pi_{n}}\\[4pt] &=\Vert J_{\pi_{n}}\Vert^{-p}\sup_{0<r<1} \int_{\mathbb{T}^{n}}\vert f\circ\pi_{n}(re^{i\Theta})\vert^{p}\vert J_{\pi_{n}}(re^{i\Theta})\vert^{2}\,d\Theta \end{align} $$
and
$\Vert J_{\pi _{n}}\Vert = (\int _{\mathbb {T}^{n}}\vert J_{\pi _{n}}(e^{i\Theta })\vert ^{2}\,d\Theta )^{{1}/{2}}$
. The factor
$\Vert J_{\pi _{n}}\Vert ^{-p}$
is used to match the definition in Misra et al. [Reference Misra, Roy and Zhang14] in the case
$p=2$
, which ensures that
$\Vert 1 \Vert ^{2}_{\mathcal {H}^{2}(\mathbb {G}_{n}, d\Theta _{\pi _{n}})}=1$
.
The
$L^{p}$
space of the distinguished boundary
$\partial _{0}\mathbb {G}_{n}$
with respect to the boundary measure
$d\Theta _{\pi _{n}}$
is defined by
$$ \begin{align*}L^{p}(\partial_{0}\mathbb{G}_{n}, d\Theta_{\pi_{n}}):=\{f: \partial_{0}\mathbb{G}_{n}\rightarrow \mathbb{C}~\text{is complex measurable},\ \Vert f \Vert_{L^{p}(\partial_{0}\mathbb{G}_{n}, d\Theta_{\pi_{n}})}<\infty\}, \end{align*} $$
where
$$ \begin{align*} \Vert f\Vert^{p}_{L^{p}(\partial_{0}\mathbb{G}_{n}, d\Theta_{\pi_{n}})}:&=\Vert J_{\pi_{n}}\Vert^{-p} \int_{\partial_{0}\mathbb{G}_{n}}\vert f(z_{1}, z_{2},\ldots, z_{n})\vert^{p}\,d\Theta_{\pi_{n}}\\[4pt] &=\Vert J_{\pi_{n}}\Vert^{-p}\int_{\mathbb{T}^{n}}\vert f\circ\pi_{n}(e^{i\Theta})\vert^{p}\vert J_{\pi_{n}}(e^{i\Theta})\vert^{2}\,d\Theta. \end{align*} $$
In particular, for
$p=2$
,
$(\mathcal {H}^{2}(\mathbb {G}_{n}, d\Theta _{\pi _{n}}), \Vert \cdot \Vert _{\mathcal {H}^{2}(\mathbb {G}_{n}, d\Theta _{\pi _{n}})})$
is a Banach space and
$\mathcal {H}^{2}(\mathbb {G}_{n}, d\Theta _{\pi _{n}})$
can be isometrically embedded into
$L^{2}(\partial _{0}\mathbb {G}_{n}, d\Theta _{\pi _{n}})$
(see Misra et al. [Reference Misra, Roy and Zhang14]). Hence the Szegö projection
$$ \begin{align*}\textbf{S}_{\mathbb{G}_{n}}: L^{2}(\partial_{0}\mathbb{G}_{n}, d\Theta_{\pi_{n}})\rightarrow \mathcal{H}^{2}(\mathbb{G}_{n}, d\Theta_{\pi_{n}}) \end{align*} $$
exists. By constructing a complete orthonormal basis in
$\mathcal {H}^{2}(\mathbb {G}_{n}, d\Theta _{\pi _{n}})$
, Misra et al. [Reference Misra, Roy and Zhang14] defined the Szegö kernel
$S_{\mathbb {G}_{n}}(\cdot \,, \cdot )$
:
$$ \begin{align} S_{\mathbb{G}_{n}}(\pi_{n}(\lambda), \pi_{n}(\mu))=\prod_{j,k=1}^{n}(1-\lambda_{j}\bar{\mu}_{k})^{-1}, \quad (\lambda, \mu)\in \mathbb{D}^{n}\times \overline{\mathbb{T}^{n}}. \end{align} $$
The explicit formula (1.2) for the Szegö kernel
$S_{\mathbb {G}_{n}}(\cdot \,, \cdot )$
plays an important role in the study of the
$L^{p}$
-boundedness of the corresponding Szegö projection on the symmetrised polydisc.
In the Hardy space setting corresponding to the distinguished boundary of the symmetrised polydisc, we show that the restricted range of p for the Szegö projection on the symmetrised polydisc is larger than {2}. This gives an example of a nonsmoothly bounded pseudoconvex domain without any strongly pseudoconvex boundary point whose Szegö projection operator is not
$L^{p}$
-irregular.
1.4 Main results
More precisely, we obtain the following results.
Theorem 1.2. The Szegö projection
$\textbf {S}_{\mathbb {G}_{n}}: L^{p}(\partial _{0}\mathbb {G}_{n}, d\Theta _{\pi _{n}})\rightarrow \mathcal {H}^{p}(\mathbb {G}_{n}, d\Theta _{\pi _{n}})$
is bounded for
$p\in (2-{1}/{n}, 2+{1}/{(n-1)})$
.
As an immediate consequence, when
$n=2$
, we have the following regularity behaviour for the symmetric bidisc
$\mathbb {G}_{2}$
.
Corollary 1.3. The Szegö projection
$\textbf {S}_{\mathbb {G}_{2}}: L^{p}(\partial _{0}\mathbb {G}_{2}, d\Theta _{\pi _{2}})\rightarrow \mathcal {H}^{p}(\mathbb {G}_{2}, d\Theta _{\pi _{2}})$
is bounded for
$p\in (\tfrac 32, 3)$
.
Our starting point is the idea used in Lanzani–Stein [Reference Lanzani and Stein11] to study the
$L^{p}$
-regularity of the Bergman and Szegö projections on nonsmooth planar domains, adapted by Chen et al. [Reference Chen, Krantz and Yuan5] for the Bergman projection in higher dimensions. Their approach is to carry the problem back to a domain on which good analysis can be developed. More precisely, they pull back the Bergman projection on the base domain to the polydisc
$\mathbb {D}^{n}$
and then to the product of upper half planes
$\mathbb {U}^{n}$
. Here, we apply this technique to the Szegö projection in several complex variables. In [Reference Chen, Krantz and Yuan5], the proof is largely dependent on the Bergman projection transform which was used to derive the behaviour of the Bergman kernel under proper holomorphic mapping (see Bell [Reference Bell3]). However, in general, there is no similar transform for the Szegö projection. This makes it difficult to pull back the
$L^{p}$
regularity of the Szegö projection on
$\mathbb {G}_{n}$
to the polydisc
$\mathbb {D}^{n}$
. To remove this obstacle, we shall instead make use of the formula for the Szegö kernel
$S_{\mathbb {G}_{n}}$
given by (1.2) to derive a Szegö projection transform (see Lemma 2.7). By means of this transform, the Szegö projection on
$\mathbb {G}_{n}$
can be carried back to the polydisc
$\mathbb {D}^{n}$
. Moreover, we need not transfer it again to
$\mathbb {U}^{n}$
as Chen et al. did in [Reference Chen, Krantz and Yuan5].
2 Preliminaries
We first review some properties of the Szegö projection
$\textbf {S}_{\mathbb {D}}$
on the unit disc
$\mathbb {D}$
and the
$A_{p}(\mathbb {T})$
weights on the unit circle
$\mathbb {T}$
, which will be used in the subsequent section.
Definition 2.1 (Garnett [Reference Garnett8, page 247]).
Let
$p\in (1, \infty )$
. A weight
$\omega $
on the unit circle
$\mathbb {T}$
is said to be in
$A_{p}(\mathbb {T})$
if
$$ \begin{align*}\sup_{I\subseteq \mathbb{T}}\bigg(\frac{1}{\vert I\vert}\int_{I}\omega(\theta)\,d\theta\bigg) \bigg(\frac{1}{\vert I\vert}\int_{I}\omega(\theta)^{{1}/{(1-p)}}\,d\theta\bigg)^{p-1}<\infty, \end{align*} $$
where I denotes intervals in
$\mathbb {T}$
and
$\vert I\vert $
denotes arc-length.
Lemma 2.2. Assume that
$p\in (1, \infty )$
,
$\alpha \in [0,1]$
and
$\omega _{k}\in A_{p}(\mathbb {T})$
for
$k=1, 2$
. Then
$\omega _{1}^{\alpha }\omega _{2}^{1-\alpha }\in A_{p}(\mathbb {T})$
.
Remark 2.3. This result was already stated in Chen et al. [Reference Chen, Krantz and Yuan5] for the class
$A_{p}^{+}(\mathbb {U})$
on the upper plane. We will adapt the proof from [Reference Chen, Krantz and Yuan5] to the class
$A_{p}(\mathbb {T})$
.
Proof. Note that
$\alpha +(1-\alpha )=1$
. For any interval
$I\subseteq \mathbb {T}$
, by the Hölder inequality,
$$ \begin{align*} \frac{1}{\vert I\vert} \int_{I}\omega^{\alpha}_{1}(\theta)\omega^{1-\alpha}_{2}(\theta)\,d\theta \leq \bigg(\frac{1}{\vert I\vert}\int_{I}\omega_{1}(\theta)\,d\theta \bigg)^{\alpha}\bigg(\frac{1}{\vert I\vert}\int_{I}\omega_{2}(\theta)\,d\theta \bigg)^{1-\alpha} \end{align*} $$
and
$$ \begin{align*} \bigg(\frac{1}{\vert I\vert} \int_{I} & \omega^{{\alpha}/{(1-p)}}_{1}(\theta) \omega^{{(1-\alpha)}/{(1-p)}}_{2}(\theta)\,d\theta\bigg)^{p-1} \\[4pt] &\leq \bigg(\frac{1}{\vert I\vert}\int_{I}\omega^{{1}/{(1-p)}}_{1}(\theta)\,d\theta \bigg)^{\alpha(p-1)}\bigg(\frac{1}{\vert I\vert}\int_{I}\omega^{{1}/{(1-p)}}_{2}(\theta)\,d\theta \bigg)^{(1-\alpha)(p-1)}. \end{align*} $$
Since this inequality holds for any
$I\subseteq \mathbb {T}$
, we obtain the desired result.
Lemma 2.4 (Munasinghe–Zeytuncu [Reference Munasinghe and Zeytuncu16, Theorem 3]).
Let
$p\in (1, \infty )$
. The ordinary Szegö projection
$\textbf {S}_{\mathbb {D}}$
is bounded from
$L^{p}(\mathbb {T},\omega )$
to
$L^{p}(\mathbb {T},\omega )$
if and only if
$\omega \in A_{p}(\mathbb {T})$
.
Let f be a complex measurable function on
$\mathbb {C}^{n}$
. Misra et al. [Reference Misra, Roy and Zhang14] define an operator
$\Gamma $
by
$$ \begin{align*}\Gamma f:= \Vert J_{\pi_{n}} \Vert^{-1}J_{\pi_{n}} \cdot (f\circ\pi_{n}), \end{align*} $$
and prove that
$\Gamma : \mathcal {H}^{2}(\mathbb {G}_{n}, d\Theta _{\pi _{n}})\rightarrow \mathcal {H}^{2}(\mathbb {D}^{n}, d\Theta )$
is an isometry. Similarly,
$\Gamma $
is an isometry of the
$\mathcal {H}^{p}$
and
$L^{p}$
spaces for all
$p\in (1, \infty )$
. More precisely, we have the following result.
Lemma 2.5. For
$1< p<\infty $
, the operator
$\Gamma : L^{p}(\partial _{0}\mathbb {G}_{n}, d\Theta _{\pi _{n}})\rightarrow L^{p}(\mathbb {T}^{n}, \vert J_{\pi _{n}}\vert ^{2-p}d\Theta )$
(or
$\Gamma : \mathcal {H}^{p}(\mathbb {G}_{n}, d\Theta _{\pi _{n}})\rightarrow \mathcal {H}^{p}(\mathbb {D}^{n}, \vert J_{\pi _{n}}\vert ^{2-p}d\Theta )$
is an isometry, but not an isomorphism.
Remark 2.6. The function space
$L^{p}(\mathbb {T}^{n}, \vert J_{\pi _{n}}\vert ^{2-p}d\Theta )$
(or
$\mathcal {H}^{p}(\mathbb {D}^{n}, \vert J_{\pi _{n}}\vert ^{2-p}d\Theta $
)) is the weighted
$L^{p}$
(or
$\mathcal {H}^{p})$
space with weight
$\vert J_{\pi _{n}}\vert ^{2-p}$
. As p varies, the
$L^{p}$
(or
$\mathcal {H}^{p})$
space and also the weight change. If
$p=2$
, this weight degenerates to the identity.
Proof. We give the proof for one of the spaces; the other follows in an analogous manner.
For any
$f\in \mathcal {H}^{p}(\mathbb {G}_{n}, d\Theta _{\pi _{n}})$
, according to (1.1),
$$ \begin{align*} \Vert f \Vert^{p}_{\mathcal{H}^{p}(\mathbb{G}_{n}, d\Theta_{\pi_{n}})}&= \Vert J_{\pi_{n}}\Vert^{-p}\sup_{0<r<1} \int_{\mathbb{T}^{n}}\vert f\circ\pi_{n}(re^{i\Theta})\vert^{p}\vert J_{\pi_{n}}(re^{i\Theta})\vert^{2}\,d\Theta\\[4pt] &= \sup_{0<r<1} \int_{\mathbb{T}^{n}}|\,\Vert J_{\pi_{n}}\Vert^{-1}J_{\pi_{n}}(re^{i\Theta})\cdot (f\circ\pi_{n})(re^{i\Theta})\vert^{p}\vert J_{\pi_{n}}(re^{i\Theta})\vert^{2-p}\,d\Theta\\[4pt] &= \sup_{0<r<1} \int_{\mathbb{T}^{n}}\vert (\Gamma f)(r{e^{i\Theta}})\vert^{p}\vert J_{\pi_{n}}(re^{i\Theta})\vert^{2-p}\,d\Theta = \Vert \Gamma f \Vert^{p}_{\mathcal{H}^{p}(\mathbb{D}^{n}, \vert J_{\pi_{n}}\vert^{2-p}\,d\Theta)}. \end{align*} $$
This proves that
$\Gamma $
is an isometry from
$\mathcal {H}^{p}(\mathbb {G}_{n}, d\Theta _{\pi _{n}})$
to
$\mathcal {H}^{p}(\mathbb {D}^{n}, \vert J_{\pi _{n}}\vert ^{2-p}d\Theta )$
.
If
$1<p\leq 2$
, then
$\mathcal {H}^{p}(\mathbb {D}^{n}, \vert J_{\pi _{n}}\vert ^{2-p}d\Theta )$
contains the constant functions but
$\Gamma (\mathcal {H}^{p}(\mathbb {G}_{n}, d\Theta _{\pi _{n}}))$
does not, so
$\Gamma $
is not an isomorphism. For
$2<p<\infty $
, set
$g:= J_{\pi _{n}}^{2k}$
, where k is a positive integer. It is easy to verify that
$g\in \mathcal {H}^{p}(\mathbb {D}^{n}, \vert J_{\pi _{n}}\vert ^{2-p}d\Theta )$
, but g has no inverse image in
$\Gamma (\mathcal {H}^{p}(\mathbb {G}_{n}, d\Theta _{\pi _{n}}))$
. We conclude that
$\Gamma $
is not an isomorphism for
$p\in (1, \infty )$
. The lemma is proved.
In the Hardy space setting, in general, there is no Szegö projection transform under a biholomorphic mapping, let alone a proper holomorphic map. However, for the domains we considered here, we are able to obtain a transfer relationship between the Szegö projection
$\textbf {S}_{\mathbb {G}_{n}}$
and
$\textbf {S}_{\mathbb {D}^{n}}$
.
Lemma 2.7. Let
$\textbf {S}_{\mathbb {D}^{n}}: L^{2}(\mathbb {T}^{n}, d\Theta )\rightarrow \mathcal {H}^{2}(\mathbb {D}^{n}, d\Theta ) $
be the Szegö projection. Then
$$ \begin{align} \Gamma\circ\textbf{S}_{\mathbb{G}_{n}}=n!~\textbf{S}_{\mathbb{D}^{n}}\circ \Gamma, \end{align} $$
where
$\textbf {S}_{\mathbb {G}_{n}}$
is the Szegö projection from
$L^{2}(\partial _{0}\mathbb {G}_{n}, d\Theta _{\pi _{n}})$
to
$\mathcal {H}^{2}(\mathbb {G}_{n}, d\Theta _{\pi _{n}})$
.
Proof. It is well known (see Zhu [Reference Zhu21, page 163]) that the Szegö kernel with respect to the normalised arc-length measure on the unit circle
$\mathbb {T}$
is given by
$$ \begin{align*}S_{\mathbb{D}}(z, w)=\frac{1}{1-z\bar{w}}, \quad (z, w)\in \mathbb{D}\times \mathbb{T}. \end{align*} $$
It follows easily that on the polydisc
$\mathbb {D}^{n}$
, the Szegö kernel on the Hardy spaces corresponding to the distinguished boundary
$\mathbb {T}^{n}$
is
$$ \begin{align*}S_{\mathbb{D}^{n}}(\lambda, \mu)=\prod_{k=1}^{n}\frac{1}{1-\lambda_{k}\bar{\mu}_{k}}, \quad (\lambda, \mu)\in \mathbb{D}^{n}\times \mathbb{T}^{n}. \end{align*} $$
However, (1.2) may be rewritten as
$$ \begin{align} J_{ \pi_{n}}(\lambda)\overline{J_{\pi_{n}}(\mu)}S_{\mathbb{G}_{n}}(\pi_{n}(\lambda), {\pi_{n}(\mu)})=\det\bigg[\frac{1}{1-\lambda_{j}\bar{\mu}_{k}}\bigg]_{1 \leq j,k \leq n}, \quad (\lambda, \mu) \in \mathbb{D}^{n}\times \mathbb{T}^{n}. \end{align} $$
For the proper holomorphic mapping
$\pi _{n}: \mathbb {D}^{n}\rightarrow \mathbb {G}^{n}\;(n\geq 2)$
, define
$$ \begin{align*}\partial_{0}\Sigma_{n}:=\{\lambda \in \mathbb{T}^{n}: J_{\pi_{n}}(\lambda)=0\}, \end{align*} $$
where
$J_{\pi _{n}}(\lambda )= \det \pi ^{\prime }_{n}(\lambda )= \prod _{1\leq i<j\leq n}(\lambda _{i}- \lambda _{j})$
. Let
$\mathcal {P}_{n}$
be the set of all permutations of
$\{1,\ldots ,n\}$
. Set
$\lambda _{\sigma }=(\lambda _{\sigma (1)},\ldots , \lambda _{\sigma (n)})$
for
$\sigma \in \mathcal {P}_{n}$
. It is obvious that
$J_{\pi _{n}}(\lambda _{\sigma })=(-1)^{\tau (\sigma )}J_{\pi _{n}}(\lambda _{\sigma })$
, where
$\tau (\sigma )$
is the inverse order of the permutation
$\sigma $
. The form of (2.2) is similar to the expression of the Bergman kernel on the symmetric polydisc (see Edigarian–Zwonek [Reference Edigarian and Zwonek7]). So, for any
$\mu \in \mathbb {T}^{n}\backslash \partial _{0}\Sigma _{n}$
, by elementary calculations,
$$ \begin{align} \nonumber J_{ \pi_{n}}(\lambda)S_{\mathbb{G}_{n}} (\pi_{n}(\lambda), {\pi_{n}(\mu)}) &=\frac{1}{\overline{J_{\pi_{n}}(\mu)}}\det\bigg[\frac{1}{1-\lambda_{j}\bar{\mu}_{k}}\bigg]_{1 \leq j,k \leq n} \nonumber \\[4pt] &= \sum_{\sigma\in\mathcal{P}_{n}}\frac{1}{\overline{J_{\pi_{n}}(\mu_{\sigma})}} \bigg(\prod_{k=1}^{n}\frac{1}{1-\lambda_{j}\bar{\mu}_{\sigma_{(k)}}}\bigg) \nonumber \\[4pt] &= \sum_{\sigma\in\mathcal{P}_{n}}\frac{1}{\overline{J_{\pi_{n}}(\mu_{\sigma})}}S_{\mathbb{D}^{n}}(\lambda, \mu_{\sigma}). \end{align} $$
Therefore, for any
$f\in L^{2}(\partial _{0}\mathbb {G}_{n}, d\Theta _{\pi _{n}})$
,
$$ \begin{align*} \Gamma\circ(\textbf{S}_{\mathbb{G}_{n}}f)(\lambda) &=\Vert J_{\pi_{n}}\Vert^{-1}J_{\pi_{n}}(\lambda)\int_{\partial_{0}\mathbb{G}_{n}}S_{\mathbb{G}_{n}}(\pi_{n}(\lambda), \zeta)f(\zeta)\,d\Theta_{\pi_{n}}\\[4pt] &=\Vert J_{\pi_{n}}\Vert^{-1}J_{\pi_{n}}(\lambda)\int_{\mathbb{T}^{n}}S_{\mathbb{G}_{n}}(\pi_{n}(\lambda), \pi(\mu))(f\circ\pi)(\mu)\vert J_{\pi_{n}}(\mu)\vert^{2}\,d\Theta\\[4pt] &=\Vert J_{\pi_{n}}\Vert^{-1}\sum_{\sigma\in\mathcal{P}_{n}}\int_{\mathbb{T}^{n}\backslash \partial_{0}\Sigma_{n}}J_{\pi_{n}}(\mu_{\sigma})S_{\mathbb{D}^{n}}(\lambda, \mu_{\sigma})(f\circ\pi)(\mu_{\sigma})\,d\Theta\\[4pt] &= n!~\textbf{S}_{\mathbb{D}^{n}}\circ (\Gamma f)(\lambda). \end{align*} $$
For the third line, we apply (2.3) and the symmetrisation of the map
$\pi _{n}$
. This proves (2.1).
3 Proof of the main result
By Lemmas 2.5 and 2.7, we obtain the commutative diagram:
For
$1< p\leq 2$
, it is obvious that
$L^{p}(\mathbb {T}^{n}, \vert J_{\pi _{n}}\vert ^{2-p}d\Theta )\cap L^{2}(\mathbb {T}^{n}, d\Theta )=L^{2}(\mathbb {T}^{n}, d\Theta )\neq \emptyset $
. If
$2< p<\infty $
, we also have
$L^{p}(\mathbb {T}^{n}, \vert J_{\pi _{n}}\vert ^{2-p}d\Theta )\cap L^{2}(\mathbb {T}^{n}, d\Theta )\neq \emptyset $
, since
$\vert J_{\pi _{n}}\vert ^{(p-2)/{p}}$
is their common element. The preceding argument shows that (3.1) is well defined. Consequently,
$$ \begin{align*}\Vert \textbf{S}_{\mathbb{G}_{n}}\Vert\leq n!~\Vert \textbf{S}_{\mathbb{D}^{n}}\Vert. \end{align*} $$
Indeed, for any
$f\in L^{p}(\partial _{0}\mathbb {G}_{n}, d\Theta _{\pi _{n}})\cap L^{2}(\partial _{0}\mathbb {G}_{n}, d\Theta _{\pi _{n}})$
,
$$ \begin{align*} \Vert \textbf{S}_{\mathbb{G}_{n}} f\Vert_{\mathcal{H}^{p}(\mathbb{G}_{n}, d\Theta_{\pi_{n}})} &= \Vert \Gamma(\textbf{S}_{\mathbb{G}_{n}} f)\Vert_{\mathcal{H}^{p}(\mathbb{D}^{n}, \vert J_{\pi_{n}}\vert^{2-p}d\Theta)}\\[4pt] &= n!\Vert \textbf{S}_{\mathbb{D}^{n}} (\Gamma f)\Vert_{\mathcal{H}^{p}(\mathbb{D}^{n}, \vert J_{\pi_{n}}\vert^{2-p}d\Theta)}\\[4pt] &\leq n!\Vert \textbf{S}_{\mathbb{D}^{n}}\Vert \,\Vert\Gamma f\Vert_{L^{p}(\mathbb{T}^{n}, \vert J_{\pi_{n}}\vert^{2-p}d\Theta)}\\[4pt] &\leq n!\Vert \textbf{S}_{\mathbb{D}^{n}}\Vert \,\Vert f \Vert_{L^{p}(\partial_{0}\mathbb{G}_{n}, d\Theta_{\pi_{n}})}. \end{align*} $$
Since the operator
$\Gamma $
is not an isomorphism, these two Szegö projections, in general, are not equivalent.
To complete the proof, we only need to consider the
$L^{p}$
-regularity of the Szegö projection
$\textbf {S}_{\mathbb {D}^{n}}: L^{p}(\mathbb {T}^{n}, \vert J_{\pi _{n}}\vert ^{2-p}d\Theta )\rightarrow \mathcal {H}^{p}(\mathbb {D}^{n}, \vert J_{\pi _{n}}\vert ^{2-p}d\Theta )$
. It should be pointed out that
$\textbf {S}_{\mathbb {D}^{n}}$
is fixed, while the weighted function space changes as p changes.
For the polydisc in the Hardy space setting, we proceed in a similar manner to the proof in [Reference Chen, Krantz and Yuan5] for the product of the upper half planes in the Bergman space setting. Since we are working on the Hardy space with respect to the distinguished boundary
$\mathbb {T}^{n}$
, then
$\textbf {S}_{\mathbb {D}^{n}}=\bigotimes _{i=1}^{n} \textbf {S}_{\mathbb {D}}$
. This equality, in general, does not hold on the topological boundary of
$\mathbb {D}^{n}$
. Using Lemma 2.4, we only need to verify that, for all
$i=1, \ldots , n$
,
$\vert J_{\pi _{n}}(\lambda _{1},\ldots , \lambda _{n})\vert ^{2-p}$
as a weight in one variable
$\lambda _{i}$
is in
$A_{p}(\mathbb {T})$
with a uniform bound independent of the other variables.
By the symmetry, we may assume that
$i=1$
. Since
$$ \begin{align*} \vert J_{\pi_{n}}(\lambda)\vert^{2-p} = \prod_{1\leq i<j\leq n}(\lambda_{i}-\lambda_{j})^{2-p} =\prod_{k=2}^{n}(\lambda_{1}-\lambda_{k})^{2-p}\prod_{2\leq i<j\leq n}(\lambda_{i}-\lambda_{j})^{2-p}, \end{align*} $$
by Lemma 2.2, it is sufficient to check that
$$ \begin{align*}\vert \lambda_{1}-\lambda_{k}\vert^{(2-p)/\alpha_{k}}\in A_{p}(\mathbb{T}), \quad k=2, \ldots, n, \end{align*} $$
with a uniform bound independent of
$\lambda _{2}, \ldots , \lambda _{n}$
, where
$\alpha _{k} \in [0, 1]$
and
$\sum _{k=2}^{n}\alpha _{k}=1$
. According to the proof of [Reference Munasinghe and Zeytuncu16, Theorem 5], for
$\alpha \geq 0$
, the weight
$\vert z-1\vert ^{\alpha (2-p)}$
on
$\mathbb {T}$
is in
$ A_{p}(\mathbb {T})$
with a uniform upper bound if and only if
$p\in ({(2\alpha +1)}/({\alpha +1)}, {(2\alpha +1)}/{\alpha })$
. Since
$\lambda _{i}\in \mathbb {T}$
, it follows that
$\vert \lambda _{1}-\lambda _{k}\vert ^{{(2-p)}/{\alpha _{k}}}\in A_{p}(\mathbb {T})$
with a uniform bound independent of
$\lambda _{k}$
if and only if
$p\in ({(2+\alpha _{k})}/{(1+\alpha _{k})}, 2+\alpha _{k})$
. Thus the Szegö projection
$\textbf {S}_{\mathbb {D}^{n}}$
is bounded from
$L^{p}(\mathbb {T}^{n}, \vert J_{\pi _{n}}\vert ^{2-p}d\Theta )$
to
$ \mathcal {H}^{p}(\mathbb {D}^{n}, \vert J_{\pi _{n}}\vert ^{2-p}d\Theta )$
for
$p\in \bigcap _{k=2}^{n}({(2+\alpha _{k})}/{(1+\alpha _{k})}, 2+\alpha _{k})$
. As
$\alpha _{k}$
is arbitrary in
$[0,1]$
, the largest possible intersection occurs in the case
$\alpha _{k}={1}/{(n-1)}$
for all
$k=2, \ldots , n$
. Thus, we obtain the desired result.
