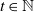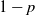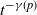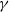1. Introduction
Empirical findings on properties of concrete networks have encouraged the proposal and investigation of nonhomogeneous random graph models. Data obtained from complex networks coming from distinct contexts has suggested that, although different in background, those networks share many special properties such as scale-freeness and small diameter. In this paper we are interested in the fact that such networks are highly clustered. We do not intend to survey the enormous amount of work done in the field, but the interested reader may find in [Reference van der Hofstad14] a complete overview as well as important rigorous results about many properties of the different models investigated so far, and a vast set of empirical properties can be found in [Reference Barabási and Albert2, Reference Strogatz and Watts13].
In this work we investigate two important graph observables known respectively as the global clustering coefficient (otherwise known as the transitivity coefficient) and the clique number, which are measurements of how agglomerated a graph is. We will discuss these quantities in more detail in Sections 1.1 and 1.2. We first highlight some important works in this area. The problem of understanding the global clustering coefficient in the context of the well-known Barabási–Álbert model [Reference Barabási and Albert2] is discussed in [Reference Bollobás, Riordan, Bronholdt, Schuster and Wiley4], obtaining estimates for the expected value of this observable, while [Reference Eggemann and Noble7] addressed the same problem for the affine version of the Barabási–Álbert model with positive constant, also obtaining estimates for the expected value of the clustering coefficient. Convergence of the probability of global clustering in a model which takes into account the distance between vertices in its dynamics was proved in [Reference Jacob and Mörters10].
In this paper we obtain concentration inequality results, proving the exact order, at the
![]() $\log$
scale, of the global clustering as well as the clique number for an instance of the model proposed in [Reference Cooper and Frieze5], which is a generalization of the Barabási–Álbert (BA) model. In the next subsection we define properly the model studied here.
$\log$
scale, of the global clustering as well as the clique number for an instance of the model proposed in [Reference Cooper and Frieze5], which is a generalization of the Barabási–Álbert (BA) model. In the next subsection we define properly the model studied here.
1.1. A preferential attachment dynamic with edge-steps
The model is defined inductively. At each step we decide according to a specific rule how to obtain the new graph from the previous one. There are two ways in which we modify the graphs:
-
Vertex-step: We add a new vertex v to the graph G and connect v to a vertex u in G selected according to the preferential attachment rule, i.e. u is selected with probability
 \begin{equation*} \mathbb{P} \left( u \text{ is chosen}\; \middle | \;G \right) = \frac{\text{degree of } u \text{ in }G}{\text{sum of the degrees of all vertices in } G };\end{equation*}
\begin{equation*} \mathbb{P} \left( u \text{ is chosen}\; \middle | \;G \right) = \frac{\text{degree of } u \text{ in }G}{\text{sum of the degrees of all vertices in } G };\end{equation*}
-
Edge-step: A new edge
 $\{u,w\}$
is added to G, where u and w are vertices in G chosen independently and also according to the preferential attachment rule described above.
$\{u,w\}$
is added to G, where u and w are vertices in G chosen independently and also according to the preferential attachment rule described above.
We point out that, in the edge-step, the vertices u and w may be the same; in this case we add a loop. Moreover, u and w may already be connected; in this case we allow multiple edges in the process.
The model evolves as follows. Given a parameter
![]() $p \in [0,1]$
, consider an initial graph
$p \in [0,1]$
, consider an initial graph
![]() $G_1$
and a collection of independent and identically distributed random variables
$G_1$
and a collection of independent and identically distributed random variables
![]() $\{ Z_t\}_{t \ge 2}$
following a Bernoulli distribution with parameter p. For each integer
$\{ Z_t\}_{t \ge 2}$
following a Bernoulli distribution with parameter p. For each integer
![]() $t\geq 2$
we obtain
$t\geq 2$
we obtain
![]() $G_{t+1}$
from
$G_{t+1}$
from
![]() $G_t$
by performing either a vertex-step on
$G_t$
by performing either a vertex-step on
![]() $G_t$
if
$G_t$
if
![]() $Z_{t+1} = 1$
, or an edge-step otherwise. In this setting we let
$Z_{t+1} = 1$
, or an edge-step otherwise. In this setting we let
![]() $\mathcal{F}_t$
denote the
$\mathcal{F}_t$
denote the
![]() $\sigma$
-algebra encoding all our knowledge about the process up to time t.
$\sigma$
-algebra encoding all our knowledge about the process up to time t.
We observe that when
![]() $p = 1$
this model corresponds to the BA model with
$p = 1$
this model corresponds to the BA model with
![]() $m=1$
. For general p, [Reference Cooper and Frieze5] shows that the degree distribution of the graphs generated by this model is close to a power-law distribution whose exponent is
$m=1$
. For general p, [Reference Cooper and Frieze5] shows that the degree distribution of the graphs generated by this model is close to a power-law distribution whose exponent is
![]() $2+p/(2-p)$
. For the sake of simplicity, throughout the paper we let
$2+p/(2-p)$
. For the sake of simplicity, throughout the paper we let
![]() $G_1$
be the graph with one vertex and one loop attached to it.
$G_1$
be the graph with one vertex and one loop attached to it.
The introduction of the edge-step has some advantages from the empirical and theoretical point of view. Using social-network terminology, we should expect that users already in the network may become friends eventually. And this is the kind of behavior the edge-step accommodates in the model. This advantage of the edge-step has been verified empirically: in [Reference Wang, Zhang and Zhou15] a statistical analysis is made comparing real-world prediction capabilities between a class of models with edge-step (called GLP in the paper) and other influential network models, such as Erdös–Rényi, Barabási–Álbert, and Tel Aviv Network Generator. Their results suggest that the process investigated here outperforms these popular models when the task is either to predict or to mimic real-world networks. Thus, the edge-step rule makes the model more realistic.
From the theoretical point of view, the edge-step rule makes the model richer in substructures and increases the combinatorial complexity of standard arguments. As we will see later, for any value of
![]() $p \in (0,1)$
, the number of triangles and paths of length 2 increases drastically when compared to the traditional BA model. The existence of complete subgraphs of polynomial order is also due to the edge-step rule.
$p \in (0,1)$
, the number of triangles and paths of length 2 increases drastically when compared to the traditional BA model. The existence of complete subgraphs of polynomial order is also due to the edge-step rule.
Although it has a simple statement, the edge-step rule prevents application of standard techniques such as Azuma’s inequality and combinatorial computation of the expected number of fixed subgraphs. The sort of issue imposed by this rule will be discussed in Section 1.4.
We would also like to stress that the model studied here is possibly the most straightforward way to allow edges between existing vertices to appear at any time while maintaining the preferential attachment rule. Even though the proposed change is simple, the consequences for the connectivity properties of the graph are substantial, and will be further outlined in the introduction.
1.2. Clustering coefficient
One of the common features of many concrete networks is clustering, i.e. the tendency that people with common friends tend to become friends. One way of quantifying this tendency for closing triangles is the global clustering coefficient (or transitivity),
![]() $\tau(G)$
, which is defined as
$\tau(G)$
, which is defined as
The observable
![]() $\tau(G)$
measures the probability of a uniformly chosen pair of vertices that have a common neighbor being connected.
$\tau(G)$
measures the probability of a uniformly chosen pair of vertices that have a common neighbor being connected.
It is important to point out here that we consider the number of triangles without multiplicities, which means three vertices form a triangle if, and only if, there exists at least one edge between each pair of vertices. The same goes for the number of paths of length 2; however, as we will see, the presence of multiple edges does not play an important role in the order of magnitude of this observable.
The traditional BA model with
![]() $m\ge 2$
, where at each step a new vertex with m randomly selected neighbors is added to the graph, was investigated in [Reference Bollobás, Riordan, Bronholdt, Schuster and Wiley4]. The authors showed that
$m\ge 2$
, where at each step a new vertex with m randomly selected neighbors is added to the graph, was investigated in [Reference Bollobás, Riordan, Bronholdt, Schuster and Wiley4]. The authors showed that
![]() $\mathbb{E}[\tau(G_t)]$
decays as
$\mathbb{E}[\tau(G_t)]$
decays as
![]() $\log^2(t)/t$
, and the expected number of triangles at time t is of order
$\log^2(t)/t$
, and the expected number of triangles at time t is of order
![]() $\log^3(t)$
. The same question was addressed in a variation of the BA model where vertices are selected with probability proportional to their degree plus a constant of attractiveness
$\log^3(t)$
. The same question was addressed in a variation of the BA model where vertices are selected with probability proportional to their degree plus a constant of attractiveness
![]() $\delta$
. Under this setup, called the affine version, [Reference Eggemann and Noble7] showed that for any positive
$\delta$
. Under this setup, called the affine version, [Reference Eggemann and Noble7] showed that for any positive
![]() $\delta$
the expected value of the number of triangles decreases and is of order
$\delta$
the expected value of the number of triangles decreases and is of order
![]() $\log^2(t)$
, and
$\log^2(t)$
, and
![]() $\mathbb{E}[\tau(G_t)]$
decays as
$\mathbb{E}[\tau(G_t)]$
decays as
![]() $\log(t)/t$
.
$\log(t)/t$
.
A different model for global clustering was investigated in [Reference Jacob and Mörters10]. In this case it was proved that
![]() $\tau(G_t)$
converges in probability to a constant whose positiveness depends on the choice of parameters. In our case, we prove a concentration inequality result for
$\tau(G_t)$
converges in probability to a constant whose positiveness depends on the choice of parameters. In our case, we prove a concentration inequality result for
![]() $\tau(G_t)$
, showing that it is, with high probability (w.h.p.), of order
$\tau(G_t)$
, showing that it is, with high probability (w.h.p.), of order
![]() $t^{-\gamma(p)}$
, where
$t^{-\gamma(p)}$
, where
![]() $\gamma(p)$
is a rational function of p.
$\gamma(p)$
is a rational function of p.
Theorem 1. (Global clustering coefficient.) For any
![]() $p\in (0,1)$
and positive
$p\in (0,1)$
and positive
![]() $\varepsilon < 1$
, there exist positive constants
$\varepsilon < 1$
, there exist positive constants
![]() $C_1$
,
$C_1$
,
![]() $C_2$
, and
$C_2$
, and
![]() $\delta$
, depending on
$\delta$
, depending on
![]() $\varepsilon$
and p only, such that, for large enough t,
$\varepsilon$
and p only, such that, for large enough t,
where
![]() $\gamma$
is the positive function
$\gamma$
is the positive function
At first glance we may think that the more edge-steps we take, the more clustered the graph, since the edge-step could close a lot of triangles. However, the edge-step also increases the number of paths of length 2. Thus it is not clear whether the clustering should be decreasing in p or not. As Theorem 1 states,
![]() $\tau(G_t)$
is largest when
$\tau(G_t)$
is largest when
![]() $\gamma(p)\in[0,1]$
is at its minimum. It turns out that this minimum is not achieved in the
$\gamma(p)\in[0,1]$
is at its minimum. It turns out that this minimum is not achieved in the
![]() $p=0$
case in which we only perform edge-steps. In fact, Theorem 1 shows that this model presents its highest global clustering when
$p=0$
case in which we only perform edge-steps. In fact, Theorem 1 shows that this model presents its highest global clustering when
![]() $p = 2 - \sqrt{3} \approx 0.26$
.
$p = 2 - \sqrt{3} \approx 0.26$
.
A consequence of the bounds given by Theorem 1 is convergence in log scale of the global clustering.
Corollary 1. (Convergence of the clustering.) Let
![]() $\tau(G_t)$
be the global clustering of
$\tau(G_t)$
be the global clustering of
![]() $G_t$
. Then, almost surely,
$G_t$
. Then, almost surely,
1.3. Clique number
The clique number of a graph G (denoted by
![]() $\omega(G)$
) is defined as the number of vertices in the largest complete subgraph (clique) in G. In the general context of random graphs, it has been studied extensively since the 1960s when [Reference Erdös and Renyi8] introduced the random graph model G(n,p). The problem of estimating the clique number of G(n,p) was addressed in [Reference Bollobás and Erdös3].
$\omega(G)$
) is defined as the number of vertices in the largest complete subgraph (clique) in G. In the general context of random graphs, it has been studied extensively since the 1960s when [Reference Erdös and Renyi8] introduced the random graph model G(n,p). The problem of estimating the clique number of G(n,p) was addressed in [Reference Bollobás and Erdös3].
To highlight some important works for less homogeneous random graph models, [Reference Devroye, György, Lugosi and Udina6] showed that for geometric random graphs in
![]() $\mathbb{R}^d $
, as the dimension grows the clique number behaves essentially as in the Erdös–Rényi model, whereas [Reference Janson, Luczak and Norros11] addressed the clique number problem for a random graph model whose degree distribution obeys a power law, showing how the clique number depends on the power-law exponent.
$\mathbb{R}^d $
, as the dimension grows the clique number behaves essentially as in the Erdös–Rényi model, whereas [Reference Janson, Luczak and Norros11] addressed the clique number problem for a random graph model whose degree distribution obeys a power law, showing how the clique number depends on the power-law exponent.
For the model investigated here, [Reference Alves, Ribeiro and Sanchis1] proved that for any
![]() $\varepsilon$
the graph
$\varepsilon$
the graph
![]() $G_t$
has w.h.p. a clique of order
$G_t$
has w.h.p. a clique of order
![]() $t^{(1-\varepsilon)(1-p)/(2-p)}$
, a power of the total number of vertices in
$t^{(1-\varepsilon)(1-p)/(2-p)}$
, a power of the total number of vertices in
![]() $G_t$
. As a byproduct of our results, we prove an upper bound for
$G_t$
. As a byproduct of our results, we prove an upper bound for
![]() $\omega(G_t)$
, proving that, at the
$\omega(G_t)$
, proving that, at the
![]() $\log$
scale, this is the right order of largest clique in
$\log$
scale, this is the right order of largest clique in
![]() $G_t$
. More precisely, we prove the following concentration inequality theorem for
$G_t$
. More precisely, we prove the following concentration inequality theorem for
![]() $\omega(G_t)$
.
$\omega(G_t)$
.
Theorem 2. (The clique number.) For any positive
![]() $\varepsilon <1$
, there exists a positive constant
$\varepsilon <1$
, there exists a positive constant
![]() $\delta$
depending on
$\delta$
depending on
![]() $\varepsilon$
and p only such that, for t large enough,
$\varepsilon$
and p only such that, for t large enough,
This theorem illustrates that the edge-step, even when taken in much smaller proportion than the vertex-step, is capable of producing robust substructures on the graphs that are not observed on the traditional BA model and many other modifications of it.
As in the case of the clustering, we do have convergence of the clique number in the log scale.
Corollary 2. (Convergence of the clique number.) Let
![]() $\omega(G_t)$
be the clique number of
$\omega(G_t)$
be the clique number of
![]() $G_t$
. Then, almost surely,
$G_t$
. Then, almost surely,
1.4. Technical ideas
The key steps in our proofs are: a sharp upper bound on the vertices’ degree, and a correlation estimate between the number of edges connecting three vertices.
Once we have at our disposal good control over the vertices’ degree, we can derive a concentration inequality for the number of paths of length 2. On the other hand, in our settings the upper bound for the number of triangles is somewhat more involved than in the proofs for models in which edge-steps are not allowed. The usual approach relies strongly on the absence of the edge-step (see [Reference Bollobás, Riordan, Bronholdt, Schuster and Wiley4, Reference Eggemann and Noble7]). More precisely, fixing three vertices i, j, and k such that
![]() $i<j<k$
, if the model does not allow an edge-step then, in order to form a triangle
$i<j<k$
, if the model does not allow an edge-step then, in order to form a triangle
![]() $\Delta_{i,j,k}$
, we necessarily have ‘one chance’ for each connection, i.e. the only possible way
$\Delta_{i,j,k}$
, we necessarily have ‘one chance’ for each connection, i.e. the only possible way
![]() $\Delta_{i,j,k}$
becomes a subgraph of
$\Delta_{i,j,k}$
becomes a subgraph of
![]() $G_t$
for large t is as follows: j is added to the graph and it sends one edge to i, then k is added to the graph and it sends one edge to i and one to j. Thus, by conditioning on the evolution of the degrees of i and j up to the time when k enters the graph, we can compute the probability that
$G_t$
for large t is as follows: j is added to the graph and it sends one edge to i, then k is added to the graph and it sends one edge to i and one to j. Thus, by conditioning on the evolution of the degrees of i and j up to the time when k enters the graph, we can compute the probability that
![]() $\Delta_{i,j,k}$
is included in
$\Delta_{i,j,k}$
is included in
![]() $G_t$
. However, in our case any pair of vertices can be connected at any time via the edge-step. This extra possibility increases the combinatorial complexity and prevents the application of the usual strategy seen in the literature.
$G_t$
. However, in our case any pair of vertices can be connected at any time via the edge-step. This extra possibility increases the combinatorial complexity and prevents the application of the usual strategy seen in the literature.
So, in order to obtain an upper bound for the number of triangles in
![]() $G_t$
,
$G_t$
,
![]() $\mathcal{T}(G_t)$
, we apply a correlation estimate together with a first moment estimate. If we let
$\mathcal{T}(G_t)$
, we apply a correlation estimate together with a first moment estimate. If we let
![]() $\textrm{edg}_t(i,j)$
be the integer random variable which counts the number of edges connecting vertices i and j at time t, then
$\textrm{edg}_t(i,j)$
be the integer random variable which counts the number of edges connecting vertices i and j at time t, then
![]() $\mathcal{T}(G_t)$
may be written as
$\mathcal{T}(G_t)$
may be written as
By the above identity, estimating the first moment of
![]() $\mathcal{T}(G_t)$
is the same as estimating the probability of the product
$\mathcal{T}(G_t)$
is the same as estimating the probability of the product
![]() $\textrm{edg}_t(i,j) \textrm{edg}_t(i,k)\textrm{edg}_t(j,k)$
being at least 1, which in turn is bounded from above by the expected value of the same product of random variables. Thus, our argument consists in bounding the expected value of a product of correlated random variables. This step in our proof requires bounds on the probability that the degree of a vertex eventually exceeds its expected value by a certain amount. Roughly speaking, given that vertices i and j already belong to
$\textrm{edg}_t(i,j) \textrm{edg}_t(i,k)\textrm{edg}_t(j,k)$
being at least 1, which in turn is bounded from above by the expected value of the same product of random variables. Thus, our argument consists in bounding the expected value of a product of correlated random variables. This step in our proof requires bounds on the probability that the degree of a vertex eventually exceeds its expected value by a certain amount. Roughly speaking, given that vertices i and j already belong to
![]() $G_t$
and that their degrees at time t have behaved properly, we could write
$G_t$
and that their degrees at time t have behaved properly, we could write
 \begin{equation*}\begin{split}\mathbb{P}\left( \textrm{edg}_{t+1}(i,j) = \textrm{edg}_t(i,j) +1 \mid G_t\right) & \approx \frac{{\rm degree}_{t}(i){\rm degree}_{t}(j)}{t^2}\\& \lessapprox \frac{\lambda^2\mathbb{E}\left[{\rm degree}_{t}(i)\right]\mathbb{E}\left[{\rm degree}_{t}(j)\right]}{t^2}.\end{split}\end{equation*}
\begin{equation*}\begin{split}\mathbb{P}\left( \textrm{edg}_{t+1}(i,j) = \textrm{edg}_t(i,j) +1 \mid G_t\right) & \approx \frac{{\rm degree}_{t}(i){\rm degree}_{t}(j)}{t^2}\\& \lessapprox \frac{\lambda^2\mathbb{E}\left[{\rm degree}_{t}(i)\right]\mathbb{E}\left[{\rm degree}_{t}(j)\right]}{t^2}.\end{split}\end{equation*}
The above domination holds as long as both degrees do not exceed their expected value by a factor of
![]() $\lambda$
. This leads us to pursue a result which says that w.h.p. we have that
$\lambda$
. This leads us to pursue a result which says that w.h.p. we have that
 \begin{equation*}\sup_{t \in \mathbb{N}} \left \lbrace \frac{{\rm degree}_{t}(i)}{\mathbb{E}\left[{\rm degree}_{t}(i)\right]} \right \rbrace \le \lambda.\end{equation*}
\begin{equation*}\sup_{t \in \mathbb{N}} \left \lbrace \frac{{\rm degree}_{t}(i)}{\mathbb{E}\left[{\rm degree}_{t}(i)\right]} \right \rbrace \le \lambda.\end{equation*}
The usual approach to obtain upper bounds for vertex degrees is applying Azuma’s inequality for a suitably constructed martingale. However, in our case, Azuma’s inequality does not lead to an upper bound as sharp as the one we need. To overcome this, we use a finer martingale inequality known as Freedman’s inequality in order to control the whole trajectory of the degree of a vertex.
1.5. Martingale concentration inequality
For convenience we provide here a more concise statement of Freedman’s inequality.
Theorem 3. (Freedman’s inequality [Reference Freedman9].) Let
![]() $(M_n, \mathcal{F}_n)_{n\ge 1}$
be a (super)martingale. Write
$(M_n, \mathcal{F}_n)_{n\ge 1}$
be a (super)martingale. Write
![]() $V_n \,:\!=\, \sum_{k=1}^{n-1}{\mathbb{E}}\left[(M_{k+1}-M_k)^2\mid \mathcal{F}_k\right]$
. Moreover, suppose that
$V_n \,:\!=\, \sum_{k=1}^{n-1}{\mathbb{E}}\left[(M_{k+1}-M_k)^2\mid \mathcal{F}_k\right]$
. Moreover, suppose that
![]() $M_0 =$
and
$M_0 =$
and
![]() $|M_{k+1}-M_k| \le R$
for all k. Then, for all
$|M_{k+1}-M_k| \le R$
for all k. Then, for all
![]() $A>0$
,
$A>0$
,
2. Bounds for the degree
This section is devoted to obtaining sharp upper bounds for the vertices’ degrees and guaranteeing the existence of at least one vertex with very high degree. These estimates will be needed to derive an upper bound for the number of triangles in
![]() $G_t$
and also to bound the number of paths of length 2.
$G_t$
and also to bound the number of paths of length 2.
Since the number of vertices is random, we use the letters i,j, k to express the ith, jth, and kth vertices added by the process. In this way, i will be used as an integer number and as a vertex itself. We let
![]() $d_t(i)$
be the degree of he ith vertex at time t, and define the following function of p that will appear several times in our proofs and results:
$d_t(i)$
be the degree of he ith vertex at time t, and define the following function of p that will appear several times in our proofs and results:
![]() $c_p \,:\!=\, 1 - \frac{p}{2}$
.
$c_p \,:\!=\, 1 - \frac{p}{2}$
.
2.1. Lower bound for the degree
In this part our aim is to ensure the existence of a vertex with very high degree. For this we apply [1, Theorem 2], which essentially states that when vertices are grouped in blocks of m vertices according to their time of appearance, the sum of the degree of the m vertices in the jth block cannot be too small when j is not too large. In other words, in the jth block of m vertices there must w.h.p. be at least one vertex with high degree.
Corollary 3. (of Theorem 2 in [Reference Alves, Ribeiro and Sanchis1].) Given
![]() $\varepsilon\in (0,1)$
, there exist positive constants
$\varepsilon\in (0,1)$
, there exist positive constants
![]() $C_1$
,
$C_1$
,
![]() $C_2$
, and a, depending on
$C_2$
, and a, depending on
![]() $\varepsilon$
and p only, such that
$\varepsilon$
and p only, such that
Proof. We will apply [1, Theorem 2]. In order to prove the result in a way that makes clear how
![]() $\delta$
may depend on
$\delta$
may depend on
![]() $\varepsilon$
and p, we will need to make some choices of parameters coming from results in [Reference Alves, Ribeiro and Sanchis1]. Set
$\varepsilon$
and p, we will need to make some choices of parameters coming from results in [Reference Alves, Ribeiro and Sanchis1]. Set
 \begin{equation*}\gamma = \frac{p}{2(2-p)} , \qquad m = \left \lceil \left( \frac{4\gamma(1-p)}{p\varepsilon} \right)^{1/\gamma} \right \rceil , \qquad R = mc_p(1-\varepsilon) , \qquad \beta = c_p(1-\varepsilon),\end{equation*}
\begin{equation*}\gamma = \frac{p}{2(2-p)} , \qquad m = \left \lceil \left( \frac{4\gamma(1-p)}{p\varepsilon} \right)^{1/\gamma} \right \rceil , \qquad R = mc_p(1-\varepsilon) , \qquad \beta = c_p(1-\varepsilon),\end{equation*}
where
![]() $\gamma$
is an auxiliary parameter coming from the statement of [1, Lemma 1], whereas m, R, and
$\gamma$
is an auxiliary parameter coming from the statement of [1, Lemma 1], whereas m, R, and
![]() $\beta$
come from [1, Theorem 2]. By our choice of m it follows that
$\beta$
come from [1, Theorem 2]. By our choice of m it follows that
![]() $\delta_m \leq \varepsilon/4$
. The term
$\delta_m \leq \varepsilon/4$
. The term
![]() $\delta_m$
is defined in [1, (3.4)]. Then, making
$\delta_m$
is defined in [1, (3.4)]. Then, making
![]() $j=t^{\varepsilon/4}$
again in the statement of [1, Theorem 2], it follows that there exists a constant
$j=t^{\varepsilon/4}$
again in the statement of [1, Theorem 2], it follows that there exists a constant
![]() $C_2$
depending on p and
$C_2$
depending on p and
![]() $\varepsilon$
such that
$\varepsilon$
such that
![]() $\mathbb{P}\left( d_{t,m}(t^{\varepsilon/4})<t^{\beta}\right) \le C_2t^{-a}$
, where
$\mathbb{P}\left( d_{t,m}(t^{\varepsilon/4})<t^{\beta}\right) \le C_2t^{-a}$
, where
![]() $d_{t,m}(j)$
denotes the sum of the degrees of the m vertices in the jth block of vertices and, because of our choices, a is strictly positive. Finally, using the fact that m is fixed, by the pigeonhole principle at least one vertex in the
$d_{t,m}(j)$
denotes the sum of the degrees of the m vertices in the jth block of vertices and, because of our choices, a is strictly positive. Finally, using the fact that m is fixed, by the pigeonhole principle at least one vertex in the
![]() $t^{\varepsilon/4}$
th block of m vertices has degree at least
$t^{\varepsilon/4}$
th block of m vertices has degree at least
![]() $t^{c_p(1-\varepsilon)}/m$
. This concludes the proof.
$t^{c_p(1-\varepsilon)}/m$
. This concludes the proof.
Observe that, due to the dynamics of this model, it could be the case that the degree of a vertex does not represent too well how many neighbors it has since its degree also counts multiple edges. Thus, for a fixed vertex j we let
![]() $\Gamma_t(j)$
be the number of neighboring vertices j has at time t. Notice that
$\Gamma_t(j)$
be the number of neighboring vertices j has at time t. Notice that
![]() $\Gamma_t(j) \le d_t(j)$
. In particular, it will be useful for us to estimate how many neighbors a vertex whose degree is at least
$\Gamma_t(j) \le d_t(j)$
. In particular, it will be useful for us to estimate how many neighbors a vertex whose degree is at least
![]() $C_1t^{c_p(1-\varepsilon)}$
has. For this, we prove the lemma below, which is essentially a statement of the above corollary for
$C_1t^{c_p(1-\varepsilon)}$
has. For this, we prove the lemma below, which is essentially a statement of the above corollary for
![]() $\Gamma_t(j)$
.
$\Gamma_t(j)$
.
Lemma 1. Given
![]() $\varepsilon >0$
, there exist positive constants
$\varepsilon >0$
, there exist positive constants
![]() $C^{\prime}_1$
,
$C^{\prime}_1$
,
![]() $C^{\prime}_2$
, and a depending on
$C^{\prime}_2$
, and a depending on
![]() $\varepsilon$
and p only such that
$\varepsilon$
and p only such that
![]() $\mathbb{P} \left( \text{there exists } j \in G_t, \Gamma_t(j) \ge C^{\prime}_1t^{c_p(1-\varepsilon)}\right) \ge 1 - C^{\prime}_2t^{-a}$
.
$\mathbb{P} \left( \text{there exists } j \in G_t, \Gamma_t(j) \ge C^{\prime}_1t^{c_p(1-\varepsilon)}\right) \ge 1 - C^{\prime}_2t^{-a}$
.
Proof. By Corollary 3 with probability at least
![]() $1 - C_2t^{-a}$
there exists in
$1 - C_2t^{-a}$
there exists in
![]() $G_t$
a vertex j with degree at least
$G_t$
a vertex j with degree at least
![]() $ C_1t^{c_p(1-\varepsilon)}$
. We claim that the number of neighbors of j at time 2t that connect to j between times t and 2t is at least
$ C_1t^{c_p(1-\varepsilon)}$
. We claim that the number of neighbors of j at time 2t that connect to j between times t and 2t is at least
![]() $C^{\prime}_1t^{c_p(1-\varepsilon)}$
w.h.p. To see this, consider the random variable
$C^{\prime}_1t^{c_p(1-\varepsilon)}$
w.h.p. To see this, consider the random variable
![]() $\zeta_s = \textbf{1} \lbrace \text{a vertex is added at step }s\text{ and it connects to }j \rbrace$
. Observe that for
$\zeta_s = \textbf{1} \lbrace \text{a vertex is added at step }s\text{ and it connects to }j \rbrace$
. Observe that for
![]() $s\in [t+1,2t]$
we have
$s\in [t+1,2t]$
we have
Notice that the random variable
![]() $N\,:\!=\, \sum_{s=t+1}^{2t} \zeta_s,$
which counts the number of neighbors j has gained between time t and 2t only by vertex-steps, conditioned on j having degree large enough, dominates a binomial random variable with parameter t and
$N\,:\!=\, \sum_{s=t+1}^{2t} \zeta_s,$
which counts the number of neighbors j has gained between time t and 2t only by vertex-steps, conditioned on j having degree large enough, dominates a binomial random variable with parameter t and
![]() $C_1 4^{-1}pt^{-\varepsilon - p2^{-1}(1-\varepsilon)}$
. Moreover,
$C_1 4^{-1}pt^{-\varepsilon - p2^{-1}(1-\varepsilon)}$
. Moreover,
![]() $\Gamma_{2t}(j) \ge N$
. Thus, setting
$\Gamma_{2t}(j) \ge N$
. Thus, setting
![]() $C^{\prime}_1 = C_1p/8$
and using Chernoff bounds and Corollary 3, it follows that
$C^{\prime}_1 = C_1p/8$
and using Chernoff bounds and Corollary 3, it follows that
 \begin{equation*}\begin{split}\mathbb{P} \left( \Gamma_{2t}(j) \le C^{\prime}_1t^{c_p(1-\varepsilon)}\right) & \le \mathbb{P} \left( N \le C^{\prime}_1 t^{c_p(1-\varepsilon)}, d_t(j) \ge C_1t^{c_p(1-\varepsilon)} \right) \\& \quad + \mathbb{P} \left( d_t(j) \le C_1t^{c_p(1-\varepsilon)} \right) \\& \le \mathbb{P} \left( \text{Bin} \left( t, \frac{C_1p}{4t^{\varepsilon + p(1-\varepsilon)/2}}\right) \le C^{\prime}_1 t^{c_p(1-\varepsilon)} \right) + C_2t^{-a} \\& \le \exp\left \lbrace-C_1pt^{c_p(1-\varepsilon)}/32 \right \rbrace + C_2t^{-a} \\& \le C^{\prime}_2 t^{-a} \end{split}\end{equation*}
\begin{equation*}\begin{split}\mathbb{P} \left( \Gamma_{2t}(j) \le C^{\prime}_1t^{c_p(1-\varepsilon)}\right) & \le \mathbb{P} \left( N \le C^{\prime}_1 t^{c_p(1-\varepsilon)}, d_t(j) \ge C_1t^{c_p(1-\varepsilon)} \right) \\& \quad + \mathbb{P} \left( d_t(j) \le C_1t^{c_p(1-\varepsilon)} \right) \\& \le \mathbb{P} \left( \text{Bin} \left( t, \frac{C_1p}{4t^{\varepsilon + p(1-\varepsilon)/2}}\right) \le C^{\prime}_1 t^{c_p(1-\varepsilon)} \right) + C_2t^{-a} \\& \le \exp\left \lbrace-C_1pt^{c_p(1-\varepsilon)}/32 \right \rbrace + C_2t^{-a} \\& \le C^{\prime}_2 t^{-a} \end{split}\end{equation*}
for a proper choice of
![]() $C^{\prime}_2$
, which proves the lemma.
$C^{\prime}_2$
, which proves the lemma.
2.2. Upper bound for the degree
In this part we obtain a sharp upper bound for the degree of a fixed vertex i. Since the proof relies on the fact that the degree of a vertex properly normalized is a martingale, we define below this normalizing factor:
 \begin{equation}\phi(t) \,:\!=\, \prod_{s=1}^{t-1} \left(1+\frac{c_p}{s} \right)=\frac{\Gamma(t+c_p)}{\Gamma(1+c_p)\Gamma(t)},\end{equation}
\begin{equation}\phi(t) \,:\!=\, \prod_{s=1}^{t-1} \left(1+\frac{c_p}{s} \right)=\frac{\Gamma(t+c_p)}{\Gamma(1+c_p)\Gamma(t)},\end{equation}
where
![]() $\Gamma(x)$
is the gamma function. A useful fact about
$\Gamma(x)$
is the gamma function. A useful fact about
![]() $\phi$
is that there exist
$\phi$
is that there exist
![]() $c_1,c_2 >0$
such that
$c_1,c_2 >0$
such that
![]() $c_2t^{c_p} \le \phi(t) \le c_1t^{c_p}$
for all t. The interested reader can check a formal proof of this fact in [12, Lemma A.5]. We will need this multiple times throughout the paper.
$c_2t^{c_p} \le \phi(t) \le c_1t^{c_p}$
for all t. The interested reader can check a formal proof of this fact in [12, Lemma A.5]. We will need this multiple times throughout the paper.
Now we go on to the proof of the main result of this section.
Theorem 4. (Upper bound for the degree.) There exist positive constants
![]() $C_1$
,
$C_1$
,
![]() $C_2$
, and
$C_2$
, and
![]() $C_3$
, depending on p only, such that for every vertex i and every number
$C_3$
, depending on p only, such that for every vertex i and every number
![]() $\lambda>C_3$
the following upper bound holds:
$\lambda>C_3$
the following upper bound holds:
Proof. The proof requires control over the degree of the ith vertex added by the process. Since the time at which the ith vertex is added to the graph is random, we will work with the process conditioned on the event that the ith vertex was added at time
![]() $t_i \ge i$
. More specifically, we let
$t_i \ge i$
. More specifically, we let
![]() $\mathbb{P}_{G_{t_i}}$
be the probability measure
$\mathbb{P}_{G_{t_i}}$
be the probability measure
![]() $\mathbb{P}$
conditioned on
$\mathbb{P}$
conditioned on
![]() $G_{t_i}$
, which is a realization of the process up to time
$G_{t_i}$
, which is a realization of the process up to time
![]() $t_i$
in which the ith vertex is added at time
$t_i$
in which the ith vertex is added at time
![]() $t_i$
. By [Reference Alves, Ribeiro and Sanchis1, Proposition 2.1], the sequence
$t_i$
. By [Reference Alves, Ribeiro and Sanchis1, Proposition 2.1], the sequence
![]() $\{X_{s,t_i}\}_{s \ge t_i}$
defined as
$\{X_{s,t_i}\}_{s \ge t_i}$
defined as
is a martingale with mean
![]() $\phi(t_i)^{-1}$
with respect to the natural filtration
$\phi(t_i)^{-1}$
with respect to the natural filtration
![]() $\{\mathcal{F}_s\}_{s\ge 1}$
and the measure
$\{\mathcal{F}_s\}_{s\ge 1}$
and the measure
![]() $\mathbb{P}_{G_{t_i}}$
. Recall that there exists a constant
$\mathbb{P}_{G_{t_i}}$
. Recall that there exists a constant
![]() $C_3$
such
$C_3$
such
![]() $\phi(t) \ge C_3t^{c_p}$
for all positive t. In this setting, for a fixed positive number
$\phi(t) \ge C_3t^{c_p}$
for all positive t. In this setting, for a fixed positive number
![]() $\lambda > C^{-1}_3$
, let
$\lambda > C^{-1}_3$
, let
![]() $\eta$
be the stopping time,
$\eta$
be the stopping time,
and let
![]() $\eta = \infty$
on the event
$\eta = \infty$
on the event
![]() $\{X_{s,t_i} <\lambda i^{-c_p}, \text{ for all } s\ge t_i\}$
. Then, we define the stopped martingale
$\{X_{s,t_i} <\lambda i^{-c_p}, \text{ for all } s\ge t_i\}$
. Then, we define the stopped martingale
![]() $X^{\prime}_s \,:\!=\, X_{s \wedge \eta,t_i}$
. Observe that the increment (
$X^{\prime}_s \,:\!=\, X_{s \wedge \eta,t_i}$
. Observe that the increment (
![]() $\Delta X^{\prime}_s \,:\!=\, X^{\prime}_{s+1} - X^{\prime}_s$
) of the stopped martingale satisfies, for
$\Delta X^{\prime}_s \,:\!=\, X^{\prime}_{s+1} - X^{\prime}_s$
) of the stopped martingale satisfies, for
![]() $s\ge t_i$
,
$s\ge t_i$
,
since
![]() $d_s(i) \le 2s$
for all s deterministically and
$d_s(i) \le 2s$
for all s deterministically and
![]() $\Delta d_s(i) \le 2\textbf{1}\{i$
is chosen at least once at step
$\Delta d_s(i) \le 2\textbf{1}\{i$
is chosen at least once at step
![]() $s+1\}$
. Combining the above bound with the second identity in (3), we also obtain, for
$s+1\}$
. Combining the above bound with the second identity in (3), we also obtain, for
![]() $s>t_i$
,
$s>t_i$
,
 \begin{equation*}\begin{split}{\mathbb{E}}_{G_{t_i}} \big[ \left(\Delta X^{\prime}_s\right)^2 \mid \mathcal{F}_{s} \big] & \le 2 {\mathbb{E}}_{G_{t_i}} \left[ \frac{(\Delta d_{s}(i))^2}{\phi^2(s+1)} \mid \mathcal{F}_{s} \right]\textbf{1}_{\{\eta > s \}} + \frac{2c^2_p d^2_{s}(i)}{s^2\phi^2(s+1)}\textbf{1}_{\{\eta > s \}} \\&\le\frac{2}{\phi^2(s+1)} {\mathbb{E}}_{G_{t_i}} [ 4\cdot\textbf{1}\{i\text{ chosen at least once at step }s+1\} | \mathcal{F}_{s} ]\textbf{1}_{\{\eta > s \}}\\&\quad + \frac{2c^2_p d^2_{s}(i)}{s^2\phi^2(s+1)}\textbf{1}_{\{\eta > s \}}\\& \le \left( \frac{8d_s(i)}{s\phi^2(s+1)} + \frac{2c^2_p d^2_{s}(i)}{s^2\phi^2(s+1)} \right)\textbf{1}_{\{\eta > s \}} \\& \le \frac{8\lambda }{i^{c_p}s\phi(s+1)} + \frac{4c^2_p\lambda}{i^{c_p}s\phi(s+1)} \le \frac{12\lambda}{i^{c_p}s\phi(s+1)}.\end{split}\end{equation*}
\begin{equation*}\begin{split}{\mathbb{E}}_{G_{t_i}} \big[ \left(\Delta X^{\prime}_s\right)^2 \mid \mathcal{F}_{s} \big] & \le 2 {\mathbb{E}}_{G_{t_i}} \left[ \frac{(\Delta d_{s}(i))^2}{\phi^2(s+1)} \mid \mathcal{F}_{s} \right]\textbf{1}_{\{\eta > s \}} + \frac{2c^2_p d^2_{s}(i)}{s^2\phi^2(s+1)}\textbf{1}_{\{\eta > s \}} \\&\le\frac{2}{\phi^2(s+1)} {\mathbb{E}}_{G_{t_i}} [ 4\cdot\textbf{1}\{i\text{ chosen at least once at step }s+1\} | \mathcal{F}_{s} ]\textbf{1}_{\{\eta > s \}}\\&\quad + \frac{2c^2_p d^2_{s}(i)}{s^2\phi^2(s+1)}\textbf{1}_{\{\eta > s \}}\\& \le \left( \frac{8d_s(i)}{s\phi^2(s+1)} + \frac{2c^2_p d^2_{s}(i)}{s^2\phi^2(s+1)} \right)\textbf{1}_{\{\eta > s \}} \\& \le \frac{8\lambda }{i^{c_p}s\phi(s+1)} + \frac{4c^2_p\lambda}{i^{c_p}s\phi(s+1)} \le \frac{12\lambda}{i^{c_p}s\phi(s+1)}.\end{split}\end{equation*}
Since
![]() $\phi(t) \ge C_3t^{c_p}$
, the above inequality implies that
$\phi(t) \ge C_3t^{c_p}$
, the above inequality implies that
 \begin{equation*}W^{\prime}_t \,:\!=\, \sum_{s=t_i}^{(t-1)\wedge \eta }{\mathbb{E}}_{G_{t_i}} \left[ \left(\Delta X^{\prime}_s\right)^2 \mid \mathcal{F}_{s} \right] \le \sum_{s=t_i}^{t-1} \frac{12 \lambda }{i^{c_p}s\phi(s+1)} \le \sum_{s=t_i}^{t-1}\frac{12 \lambda }{C_3i^{c_p}s^{1+c_p}} \le\frac{C_4\lambda}{i^{c_p}t^{c_p}_i} \end{equation*}
\begin{equation*}W^{\prime}_t \,:\!=\, \sum_{s=t_i}^{(t-1)\wedge \eta }{\mathbb{E}}_{G_{t_i}} \left[ \left(\Delta X^{\prime}_s\right)^2 \mid \mathcal{F}_{s} \right] \le \sum_{s=t_i}^{t-1} \frac{12 \lambda }{i^{c_p}s\phi(s+1)} \le \sum_{s=t_i}^{t-1}\frac{12 \lambda }{C_3i^{c_p}s^{1+c_p}} \le\frac{C_4\lambda}{i^{c_p}t^{c_p}_i} \end{equation*}
almost surely, where
![]() $C_4 = 12C_3^{-1}c_p^{-1}$
. Now we use Freedman’s inequality [Reference Freedman9] (Theorem 3) with
$C_4 = 12C_3^{-1}c_p^{-1}$
. Now we use Freedman’s inequality [Reference Freedman9] (Theorem 3) with
![]() $\sigma^2 = C_4\lambda i^{-c_p}t_i^{-c_p}$
and
$\sigma^2 = C_4\lambda i^{-c_p}t_i^{-c_p}$
and
![]() $R=4C_3^{-1}t_i^{-c_p}$
, which is possible due to (3), to obtain that, for any positive constant A,
$R=4C_3^{-1}t_i^{-c_p}$
, which is possible due to (3), to obtain that, for any positive constant A,
 \begin{equation}\mathbb{P}_{G_{t_i}} \left( X^{\prime}_t - \phi(t_i)^{-1} \ge A \right) \le \exp \left \lbrace - \frac{A^2}{\frac{2C_4\lambda}{i^{c_p}t^{c_p}_i}+\frac{ 8 A}{3C_3t_i^{c_p}}}\right \rbrace.\end{equation}
\begin{equation}\mathbb{P}_{G_{t_i}} \left( X^{\prime}_t - \phi(t_i)^{-1} \ge A \right) \le \exp \left \lbrace - \frac{A^2}{\frac{2C_4\lambda}{i^{c_p}t^{c_p}_i}+\frac{ 8 A}{3C_3t_i^{c_p}}}\right \rbrace.\end{equation}
Now, we would like to guarantee that the stopping time
![]() $\eta$
is not too small, i.e. that the martingales X
′ and X are essentially the same. To do this, observe that
$\eta$
is not too small, i.e. that the martingales X
′ and X are essentially the same. To do this, observe that
Also notice that since
![]() $\lambda > C^{-1}_3$
,
$\lambda > C^{-1}_3$
,
![]() $\phi(t_i)^{-1} \le C^{-1}_3t_i^{-c_p}$
,
$\phi(t_i)^{-1} \le C^{-1}_3t_i^{-c_p}$
,
![]() $i\leq t_i$
, and
$i\leq t_i$
, and
![]() $C_4 = 12C_3^{-1}c_p^{-1}$
, it follows that
$C_4 = 12C_3^{-1}c_p^{-1}$
, it follows that
which implies that
 \begin{equation}\begin{split}-\frac{(\lambda i^{-c_p} - \phi(t_i)^{-1})^2}{\frac{2C_4\lambda}{i^{c_p}t^{c_p}_i}+\frac{ 8(\lambda i^{-c_p} - \phi(t_i)^{-1})}{3C_3t_i^{c_p}}} & \le -\frac{(\lambda i^{-c_p} - \phi(t_i)^{-1})^2}{\frac{4C_4\lambda}{i^{c_p}t^{c_p}_i}} \\& = -\frac{t_i^{c_p}\lambda}{4C_4i^{c_p}} + \frac{t_i^{c_p}}{2C_4\phi(t_i)} - \frac{i^{c_p}t_i^{c_p}}{4C_4\lambda\phi(t_i)^2} \\& \le -\frac{t_i^{c_p}\lambda}{4C_4i^{c_p}} + \frac{1}{2C_3C_4}.\end{split}\end{equation}
\begin{equation}\begin{split}-\frac{(\lambda i^{-c_p} - \phi(t_i)^{-1})^2}{\frac{2C_4\lambda}{i^{c_p}t^{c_p}_i}+\frac{ 8(\lambda i^{-c_p} - \phi(t_i)^{-1})}{3C_3t_i^{c_p}}} & \le -\frac{(\lambda i^{-c_p} - \phi(t_i)^{-1})^2}{\frac{4C_4\lambda}{i^{c_p}t^{c_p}_i}} \\& = -\frac{t_i^{c_p}\lambda}{4C_4i^{c_p}} + \frac{t_i^{c_p}}{2C_4\phi(t_i)} - \frac{i^{c_p}t_i^{c_p}}{4C_4\lambda\phi(t_i)^2} \\& \le -\frac{t_i^{c_p}\lambda}{4C_4i^{c_p}} + \frac{1}{2C_3C_4}.\end{split}\end{equation}
Thus, setting
![]() $A = \lambda i^{-c_p} - \phi(t_i)^{-1}$
in (4) and using (6) yields
$A = \lambda i^{-c_p} - \phi(t_i)^{-1}$
in (4) and using (6) yields
 \begin{equation*}\begin{split}\mathbb{P}_{G_{t_i}} \left( X^{\prime}_t - \phi(t_i)^{-1} \ge \lambda i^{-c_p} - \phi(t_i)^{-1} \right) & \le \exp \left \lbrace - \frac{(\lambda i^{-c_p} - \phi(t_i)^{-1} )^2}{\frac{2C_4\lambda}{t^{c_p}_i}+\frac{4(\lambda - \phi(t_i)^{-1} )}{3t_i^{c_p}}}\right \rbrace \\[5pt]&\le \textrm{e}^{C_3^{-1}C_4^{-1}/2}\exp \left \lbrace -\frac{C_5t_i^{c_p}\lambda}{i^{c_p}} \right \rbrace,\end{split}\end{equation*}
\begin{equation*}\begin{split}\mathbb{P}_{G_{t_i}} \left( X^{\prime}_t - \phi(t_i)^{-1} \ge \lambda i^{-c_p} - \phi(t_i)^{-1} \right) & \le \exp \left \lbrace - \frac{(\lambda i^{-c_p} - \phi(t_i)^{-1} )^2}{\frac{2C_4\lambda}{t^{c_p}_i}+\frac{4(\lambda - \phi(t_i)^{-1} )}{3t_i^{c_p}}}\right \rbrace \\[5pt]&\le \textrm{e}^{C_3^{-1}C_4^{-1}/2}\exp \left \lbrace -\frac{C_5t_i^{c_p}\lambda}{i^{c_p}} \right \rbrace,\end{split}\end{equation*}
where
![]() $C_5 = 1/4C_4$
. Combining the above bound with (5), we obtain
$C_5 = 1/4C_4$
. Combining the above bound with (5), we obtain
 \begin{equation*}\mathbb{P}_{G_{t_i}} \left( \sup_{s \in \mathbb{N}} \left \lbrace \frac{d_s(i)}{\phi(s)}\right \rbrace \ge \frac{\lambda}{i^{c_p}}\right) = \mathbb{P}_{G_{t_i}} \left(\eta < \infty \right) \le C_6\exp \left \lbrace -\frac{C_5\lambda t_i^{c_p}}{i^{c_p}}\right \rbrace\end{equation*}
\begin{equation*}\mathbb{P}_{G_{t_i}} \left( \sup_{s \in \mathbb{N}} \left \lbrace \frac{d_s(i)}{\phi(s)}\right \rbrace \ge \frac{\lambda}{i^{c_p}}\right) = \mathbb{P}_{G_{t_i}} \left(\eta < \infty \right) \le C_6\exp \left \lbrace -\frac{C_5\lambda t_i^{c_p}}{i^{c_p}}\right \rbrace\end{equation*}
and, since
![]() $t_i \ge i$
, integrating over
$t_i \ge i$
, integrating over
![]() $G_{t_i}$
yields
$G_{t_i}$
yields
which proves the theorem.
3. Number of paths of length 2
In this section we combine the bounds obtained in the previous section to prove concentration inequalities for
![]() $\mathcal{C}(G_t)$
, i.e. the number of paths of length 2. Our aim is to prove the following theorem.
$\mathcal{C}(G_t)$
, i.e. the number of paths of length 2. Our aim is to prove the following theorem.
Theorem 5. (Concentration for paths of length 2.) Given
![]() $\varepsilon \in (0,1)$
, there exist positive constants
$\varepsilon \in (0,1)$
, there exist positive constants
![]() $C_1$
,
$C_1$
,
![]() $C_2$
,
$C_2$
,
![]() $C_3$
, and a, depending on
$C_3$
, and a, depending on
![]() $\varepsilon$
and p only, such that
$\varepsilon$
and p only, such that
Proof. We prove the lower bound first. Observe that for any given vertex
![]() $j\in G_t$
it follows that
$j\in G_t$
it follows that
where
![]() $\Gamma_t(j)$
is the number of vertices adjacent to j in
$\Gamma_t(j)$
is the number of vertices adjacent to j in
![]() $G_t$
. Thus, we have the following inclusion of events
$G_t$
. Thus, we have the following inclusion of events
where
![]() $C^{\prime}_1$
is chosen small enough that
$C^{\prime}_1$
is chosen small enough that
Thus, by Lemma 1 and (7) it follows that, for a given
![]() $\varepsilon>0$
, there exist positive constants a,
$\varepsilon>0$
, there exist positive constants a,
![]() $C^{\prime}_1$
, and
$C^{\prime}_1$
, and
![]() $C^{\prime}_2$
such that
$C^{\prime}_2$
such that
which proves the lower bound. For the upper bound, we begin by observing that
Then, in Theorem 4 take
![]() $\lambda = 10C_2^{-1}\log t$
. This particular choice of
$\lambda = 10C_2^{-1}\log t$
. This particular choice of
![]() $\lambda$
and a union bound lead to
$\lambda$
and a union bound lead to
 \begin{equation}\mathbb{P} \left( \bigcup_{i \in G_t} \left \lbrace d_t(i) \ge 10C_2^{-1}c_1\frac{t^{c_p}\log(t)}{i^{c_p}}\right \rbrace \right) \le C_1t^{-9} , \end{equation}
\begin{equation}\mathbb{P} \left( \bigcup_{i \in G_t} \left \lbrace d_t(i) \ge 10C_2^{-1}c_1\frac{t^{c_p}\log(t)}{i^{c_p}}\right \rbrace \right) \le C_1t^{-9} , \end{equation}
where we have used the fact that, for all t,
![]() $\phi(t) \le c_1t^{c_p}$
. Let
$\phi(t) \le c_1t^{c_p}$
. Let
![]() $A_t$
be the event
$A_t$
be the event
and observe that by (9), on
![]() $A_t^\textrm{c}$
the following upper bound holds:
$A_t^\textrm{c}$
the following upper bound holds:
 \begin{equation*}\begin{split}\mathcal{C}(G_t) \le \sum_{v \in G_t} \binom{d_t(v)}{2} \le 100C_2^{-2}c_1^2\sum_{i=1}^t\frac{t^{2-p}\log^2(t)}{i^{2-p}} \le C^{\prime}_3t^{2-p}\log^2(t) , \end{split}\end{equation*}
\begin{equation*}\begin{split}\mathcal{C}(G_t) \le \sum_{v \in G_t} \binom{d_t(v)}{2} \le 100C_2^{-2}c_1^2\sum_{i=1}^t\frac{t^{2-p}\log^2(t)}{i^{2-p}} \le C^{\prime}_3t^{2-p}\log^2(t) , \end{split}\end{equation*}
where
![]() $C^{\prime}_3 \,:\!=\, 100C_2^{-2}c_1^2(1-p)^{-1}$
. Thus, by (10),
$C^{\prime}_3 \,:\!=\, 100C_2^{-2}c_1^2(1-p)^{-1}$
. Thus, by (10),
![]() $\mathbb{P} \left(\mathcal{C}(G_t) > C^{\prime}_3t^{2-p}\log^2(t) \right) \le \mathbb{P} \left(A_t\right)\leq C_1t^{-9}$
. Finally, combining the above bound with (8) proves the result.
$\mathbb{P} \left(\mathcal{C}(G_t) > C^{\prime}_3t^{2-p}\log^2(t) \right) \le \mathbb{P} \left(A_t\right)\leq C_1t^{-9}$
. Finally, combining the above bound with (8) proves the result.
4. Decoupling the number of edges between vertices
Our results rely on a first moment argument in order to estimate the number of triangles in
![]() $G_t$
(counted without multiplicities), which we denote by
$G_t$
(counted without multiplicities), which we denote by
![]() $\mathcal{T}(G_t)$
. As discussed in Section 1.4, the first moment of
$\mathcal{T}(G_t)$
. As discussed in Section 1.4, the first moment of
![]() $\mathcal{T}(G_t)$
is bounded by the sum of a product of correlated random variables. Thus, in essence, this section is devoted to dealing with this correlation.
$\mathcal{T}(G_t)$
is bounded by the sum of a product of correlated random variables. Thus, in essence, this section is devoted to dealing with this correlation.
We will use i, j, and k to denote the ith, jth, and kth vertices added by
![]() $\{G_t\}_{t\ge 0}$
. Moreover, for a pair i and j and a specific time s, we let
$\{G_t\}_{t\ge 0}$
. Moreover, for a pair i and j and a specific time s, we let
![]() $e^{i,j}$
and
$e^{i,j}$
and
![]() $g_s^{i,j}$
be the following random variables:
$g_s^{i,j}$
be the following random variables:
Let
![]() $C_3 > 0$
be such that
$C_3 > 0$
be such that
We define, for
![]() $s \in \{1, \dots, t\}$
and
$s \in \{1, \dots, t\}$
and
![]() $i,j \in \{1, \dots, t\}$
, the functions
$i,j \in \{1, \dots, t\}$
, the functions
 \begin{alignat*}{3} p^{i,j}_s & \,:\!=\, C_p^2\frac{\log^2(t)}{i^{c_p}j^{c_p}s^{p}} \wedge 1, \quad & p^{i,k}_s & \,:\!=\, C_p^2\frac{\log^2(t)}{i^{c_p}k^{c_p}s^{p}}\wedge 1, \quad & p^{j,k}_s & \,:\!=\, C_p^2\frac{\log^2(t)}{j^{c_p}k^{c_p}s^{p}}\wedge 1, \\ q^{i,j} & \,:\!=\, C_p\frac{\log t }{i^{c_p} j^{\frac{p}{2}}}\wedge 1, & q^{i,k} & \,:\!=\, C_p\frac{\log t }{i^{c_p} k^{\frac{p}{2}}}\wedge 1, & q^{j,k} & \,:\!=\, C_p\frac{\log t }{j^{c_p} k^{\frac{p}{2}}}\wedge 1,\end{alignat*}
\begin{alignat*}{3} p^{i,j}_s & \,:\!=\, C_p^2\frac{\log^2(t)}{i^{c_p}j^{c_p}s^{p}} \wedge 1, \quad & p^{i,k}_s & \,:\!=\, C_p^2\frac{\log^2(t)}{i^{c_p}k^{c_p}s^{p}}\wedge 1, \quad & p^{j,k}_s & \,:\!=\, C_p^2\frac{\log^2(t)}{j^{c_p}k^{c_p}s^{p}}\wedge 1, \\ q^{i,j} & \,:\!=\, C_p\frac{\log t }{i^{c_p} j^{\frac{p}{2}}}\wedge 1, & q^{i,k} & \,:\!=\, C_p\frac{\log t }{i^{c_p} k^{\frac{p}{2}}}\wedge 1, & q^{j,k} & \,:\!=\, C_p\frac{\log t }{j^{c_p} k^{\frac{p}{2}}}\wedge 1,\end{alignat*}
where
![]() $C_p = 10C_2^{-1}C_3^{-1}$
, with
$C_p = 10C_2^{-1}C_3^{-1}$
, with
![]() $C_2$
the constant given by Theorem 4. The terms
$C_2$
the constant given by Theorem 4. The terms
![]() $p_s^{i,j}$
and
$p_s^{i,j}$
and
![]() $q^{i,j}$
are related to the random variables
$q^{i,j}$
are related to the random variables
![]() $g^{i,j}_{s}$
and
$g^{i,j}_{s}$
and
![]() $e^{i,j}$
as described by the following lemma.
$e^{i,j}$
as described by the following lemma.
Lemma 2. Given
![]() $t \ge 0$
, any triplet of vertices
$t \ge 0$
, any triplet of vertices
![]() $ i,j,k \in \{1, \dots, t\}$
, and times
$ i,j,k \in \{1, \dots, t\}$
, and times
![]() $r,s,s'\in \{1, \dots, t\}$
, there exists a positive constant
$r,s,s'\in \{1, \dots, t\}$
, there exists a positive constant
![]() $C_1$
such that
$C_1$
such that
![]() ${\mathbb{E}} \left[ e^{i,j}e^{i,k}g^{j,k}_{s'+1}\right] \le C_1 q^{i,j}q^{i,k}p^{j,k}_{s'}$
,
${\mathbb{E}} \left[ e^{i,j}e^{i,k}g^{j,k}_{s'+1}\right] \le C_1 q^{i,j}q^{i,k}p^{j,k}_{s'}$
,
![]() ${\mathbb{E}} \left[ e^{i,j}g^{i,k}_{s+1}g^{j,k}_{s'+1}\right] \le C_1 q^{i,j}p^{i,k}_sp^{j,k}_{s'}$
, and
${\mathbb{E}} \left[ e^{i,j}g^{i,k}_{s+1}g^{j,k}_{s'+1}\right] \le C_1 q^{i,j}p^{i,k}_sp^{j,k}_{s'}$
, and
![]() ${\mathbb{E}} \left[ g^{i,j}_{r+1}g^{i,k}_{s+1}g^{j,k}_{s'+1}\right] \le C_1 p^{i,j}_rp^{i,k}_sp^{j,k}_{s'}$
.
${\mathbb{E}} \left[ g^{i,j}_{r+1}g^{i,k}_{s+1}g^{j,k}_{s'+1}\right] \le C_1 p^{i,j}_rp^{i,k}_sp^{j,k}_{s'}$
.
Before we prove the above lemma, let us say something about its statement. Notice that, using the dynamics of the process
![]() $\{G_t\}_{t\ge 0}$
, we have
$\{G_t\}_{t\ge 0}$
, we have
Now, using (1) and the martingale associated with the degree
![]() $d_s(i)$
, we can show that there exist constants
$d_s(i)$
, we can show that there exist constants
![]() $c, c' > 0$
such that, uniformly over i and s,
$c, c' > 0$
such that, uniformly over i and s,
Observe that if the degree of the ith vertex behaves like its expectation, returning to (11), we would have that, up to multiplication by a power of
![]() $\log t$
,
$\log t$
,
![]() ${\mathbb{E}}[g^{i,j}_{s+1}]$
behaves like
${\mathbb{E}}[g^{i,j}_{s+1}]$
behaves like
![]() $p_s^{i,j}$
. The same reasoning could be carried over to
$p_s^{i,j}$
. The same reasoning could be carried over to
![]() ${\mathbb{E}}[e^{i,j}]$
, replacing
${\mathbb{E}}[e^{i,j}]$
, replacing
![]() $p_s^{i,j}$
by
$p_s^{i,j}$
by
![]() $q^{i,j}$
.
$q^{i,j}$
.
It may be instructive to think of
![]() $p_s^{i,j}$
(respectively
$p_s^{i,j}$
(respectively
![]() $q^{i,j}$
) as the expectation of
$q^{i,j}$
) as the expectation of
![]() $g^{i,j}_{s+1}$
(respectively
$g^{i,j}_{s+1}$
(respectively
![]() $e^{i,j}$
). From this perspective, the above lemma may be read as follows: up to a power of
$e^{i,j}$
). From this perspective, the above lemma may be read as follows: up to a power of
![]() $\log t$
, the random variables
$\log t$
, the random variables
![]() $g^{i,j}_{r}$
and
$g^{i,j}_{r}$
and
![]() $e^{i,j}$
are all negatively correlated. This approximated negative correlation will help us obtain a good upper bound for the expected number of triangles in
$e^{i,j}$
are all negatively correlated. This approximated negative correlation will help us obtain a good upper bound for the expected number of triangles in
![]() $G_t$
.
$G_t$
.
Now we can proceed to the proof of the result.
Proof of Lemma 2. As usual, we start by introducing some definitions and establishing some notation. Throughout this proof we will assume
![]() $i<j<k$
.
$i<j<k$
.
Recall the Bernoulli random variables
![]() $Z_s \stackrel{\textrm{d}}{=} \textrm{Ber}(p)$
from the definition of the random graph process
$Z_s \stackrel{\textrm{d}}{=} \textrm{Ber}(p)$
from the definition of the random graph process
![]() $\{G_t\}_{t\ge 0}$
. We define the filtration
$\{G_t\}_{t\ge 0}$
. We define the filtration
![]() $\mathcal{G}_s \,:\!=\, \sigma\left( \mathcal{F}_{s-1}, Z_s\right)$
, that is,
$\mathcal{G}_s \,:\!=\, \sigma\left( \mathcal{F}_{s-1}, Z_s\right)$
, that is,
![]() $\mathcal{G}_s$
carries information about all that happened up to time
$\mathcal{G}_s$
carries information about all that happened up to time
![]() $s-1$
, plus the knowledge about whether the step taken at time s was a vertex-step or an edge-step.
$s-1$
, plus the knowledge about whether the step taken at time s was a vertex-step or an edge-step.
Given a vertex i and a fixed time t, it will be useful to introduce the stopping time
and for a triplet of vertices
![]() $i<j<k$
we let
$i<j<k$
we let
![]() $\widetilde{\eta} = \eta_{i}\wedge\eta_{j}\wedge\eta_{k}$
. By the definition of
$\widetilde{\eta} = \eta_{i}\wedge\eta_{j}\wedge\eta_{k}$
. By the definition of
![]() $\widetilde{\eta}$
, the following bound holds:
$\widetilde{\eta}$
, the following bound holds:
For
![]() $e^{i,j}$
a similar bound holds under the proper conditioning. We let
$e^{i,j}$
a similar bound holds under the proper conditioning. We let
![]() $T_n$
denote the time at which the nth vertex is added to the process. Using the fact that
$T_n$
denote the time at which the nth vertex is added to the process. Using the fact that
![]() $T_n \geq n$
, we obtain
$T_n \geq n$
, we obtain
 \begin{equation}\begin{split}{\mathbb{E}}\left[ e^{i,j} \textbf{1}\{\widetilde{\eta} > T_j\} \mid \mathcal{G}_{T_j}\right] & \le \sum_{s=j-1}^{t-1} \frac{d_s(i)}{2s}\textbf{1}\{\widetilde{\eta} > s+1, T_j = s+1\} \\& \le \textbf{1}\{\widetilde{\eta} > T_j \}C_p\frac{\log t }{i^{c_p} j^{\frac{p}{2}}}\wedge 1\\& = q^{i,j}\textbf{1}\{\widetilde{\eta} > T_j \}.\end{split}\end{equation}
\begin{equation}\begin{split}{\mathbb{E}}\left[ e^{i,j} \textbf{1}\{\widetilde{\eta} > T_j\} \mid \mathcal{G}_{T_j}\right] & \le \sum_{s=j-1}^{t-1} \frac{d_s(i)}{2s}\textbf{1}\{\widetilde{\eta} > s+1, T_j = s+1\} \\& \le \textbf{1}\{\widetilde{\eta} > T_j \}C_p\frac{\log t }{i^{c_p} j^{\frac{p}{2}}}\wedge 1\\& = q^{i,j}\textbf{1}\{\widetilde{\eta} > T_j \}.\end{split}\end{equation}
Now we will prove the upper bounds given by the statement of the lemma. We will prove the more involved cases, but first we will derive some measurability results that will play important roles later in the proof.
Fix
![]() $i<j<k$
, and consider discrete times r, s, and s
′. Observe that since
$i<j<k$
, and consider discrete times r, s, and s
′. Observe that since
![]() $j<k$
we have
$j<k$
we have
![]() $T_j < T_k$
and then
$T_j < T_k$
and then
![]() $\mathcal{G}_{T_j} \subset \mathcal{G}_{T_k}$
. This implies that
$\mathcal{G}_{T_j} \subset \mathcal{G}_{T_k}$
. This implies that
![]() $e^{i,j} \in \mathcal{G}_{T_k}$
. Indeed, it is enough to notice that for a fixed r and
$e^{i,j} \in \mathcal{G}_{T_k}$
. Indeed, it is enough to notice that for a fixed r and
![]() $s > r$
, it follows that
$s > r$
, it follows that
 \begin{align*} { \{T_k = s\}\cap \left \lbrace e^{i,j}\textbf{1}\{T_j = r\} = 1\right \rbrace } = \underbrace{\{T_k = s\}}_{\in \mathcal{G}_s}\cap \underbrace{\{T_j = r\}}_{\in \mathcal{G}_r}\cap\underbrace{\Big\{\begin{array}{c}j \text{ is born at time }r \text{ and connects to}\\i \text{ via a vertex-step}\end{array}\Big\}}_{\in \mathcal{G}_{r+1}\subseteq \mathcal{G}_s},\end{align*}
\begin{align*} { \{T_k = s\}\cap \left \lbrace e^{i,j}\textbf{1}\{T_j = r\} = 1\right \rbrace } = \underbrace{\{T_k = s\}}_{\in \mathcal{G}_s}\cap \underbrace{\{T_j = r\}}_{\in \mathcal{G}_r}\cap\underbrace{\Big\{\begin{array}{c}j \text{ is born at time }r \text{ and connects to}\\i \text{ via a vertex-step}\end{array}\Big\}}_{\in \mathcal{G}_{r+1}\subseteq \mathcal{G}_s},\end{align*}
and, since
![]() $e^{i,j}\textbf{1}\{T_j = r\}$
takes values in
$e^{i,j}\textbf{1}\{T_j = r\}$
takes values in
![]() $\{0, 1\}$
,
$\{0, 1\}$
,
![]() $e^{i,j}\textbf{1}\{T_j = r\}$
is
$e^{i,j}\textbf{1}\{T_j = r\}$
is
![]() $\mathcal{G}_{T_k}$
-measurable. Consequently,
$\mathcal{G}_{T_k}$
-measurable. Consequently,
![]() $e^{i,j}$
is
$e^{i,j}$
is
![]() $\mathcal{G}_{T_k}$
-measurable as well. Applying the same reasoning as above, we also conclude that
$\mathcal{G}_{T_k}$
-measurable as well. Applying the same reasoning as above, we also conclude that
![]() $e^{i,j}\textbf{1}\{T_j = r\} \in \mathcal{F}_r$
. Considering
$e^{i,j}\textbf{1}\{T_j = r\} \in \mathcal{F}_r$
. Considering
![]() $r < s$
, we also have that
$r < s$
, we also have that
![]() $g^{i,j}_{r}\textbf{1}\{T_k = s\} \in \mathcal{G}_{T_k}$
. With all the above in mind, we can prove our bounds. Using (13) and the tower property of the conditional expectation, we deduce that
$g^{i,j}_{r}\textbf{1}\{T_k = s\} \in \mathcal{G}_{T_k}$
. With all the above in mind, we can prove our bounds. Using (13) and the tower property of the conditional expectation, we deduce that
 \begin{equation}\begin{split}{\mathbb{E}}\left[e^{i,j}e^{i,k}\textbf{1}\{\widetilde{\eta}>t\}\right] & = {\mathbb{E}}\left[ e^{i,j} {\mathbb{E}}\left[e^{i,k} \textbf{1}\{T_k \le t ,\widetilde{\eta}>t\}\middle | \mathcal{G}_{T_k}\right] \right]\\& \le q^{i,k}{\mathbb{E}}\left[e^{i,j}\textbf{1}\{\widetilde{\eta}>T_k\}\right] \\&\le q^{i,k}{\mathbb{E}}\left[e^{i,j}\textbf{1}\{\widetilde{\eta}>T_j\}\right]\le q^{i,j}q^{i,k}.\end{split}\end{equation}
\begin{equation}\begin{split}{\mathbb{E}}\left[e^{i,j}e^{i,k}\textbf{1}\{\widetilde{\eta}>t\}\right] & = {\mathbb{E}}\left[ e^{i,j} {\mathbb{E}}\left[e^{i,k} \textbf{1}\{T_k \le t ,\widetilde{\eta}>t\}\middle | \mathcal{G}_{T_k}\right] \right]\\& \le q^{i,k}{\mathbb{E}}\left[e^{i,j}\textbf{1}\{\widetilde{\eta}>T_k\}\right] \\&\le q^{i,k}{\mathbb{E}}\left[e^{i,j}\textbf{1}\{\widetilde{\eta}>T_j\}\right]\le q^{i,j}q^{i,k}.\end{split}\end{equation}
The same kind of reasoning for
![]() $r\leq s$
yields
$r\leq s$
yields
 \begin{align}\nonumber{\mathbb{E}}\left[e^{i,j}\textbf{1}\{T_j = r\}g^{l,j}_{s+1}\textbf{1}\{\widetilde{\eta}>t\}\right] & \le {\mathbb{E}}\left[e^{i,j}\textbf{1}\{T_j = r\}{\mathbb{E}}\left[g^{l,j}_{s+1}\textbf{1}\{\widetilde{\eta}>s\} \, \big | \, \mathcal{F}_s \right]\right] \\& \le p_s^{j,k}{\mathbb{E}}\left[e^{i,j}\textbf{1}\{T_j = r\}\textbf{1}\{\widetilde{\eta}>s\}\right] .\end{align}
\begin{align}\nonumber{\mathbb{E}}\left[e^{i,j}\textbf{1}\{T_j = r\}g^{l,j}_{s+1}\textbf{1}\{\widetilde{\eta}>t\}\right] & \le {\mathbb{E}}\left[e^{i,j}\textbf{1}\{T_j = r\}{\mathbb{E}}\left[g^{l,j}_{s+1}\textbf{1}\{\widetilde{\eta}>s\} \, \big | \, \mathcal{F}_s \right]\right] \\& \le p_s^{j,k}{\mathbb{E}}\left[e^{i,j}\textbf{1}\{T_j = r\}\textbf{1}\{\widetilde{\eta}>s\}\right] .\end{align}
For the case where
![]() $s+1\le r\le t$
, we have that
$s+1\le r\le t$
, we have that
![]() ${\mathbb{E}}\big[e^{i,j}\textbf{1}\{T_j = r\}g^{l,j}_{s+1}\big] = 0$
, since it is impossible for an edge-step to connect j and k before j is born or at the time when j is born. Then using
${\mathbb{E}}\big[e^{i,j}\textbf{1}\{T_j = r\}g^{l,j}_{s+1}\big] = 0$
, since it is impossible for an edge-step to connect j and k before j is born or at the time when j is born. Then using
![]() ${\mathbb{E}}\big[e^{i,j}g^{l,j}_{s+1}\textbf{1}\{\widetilde{\eta}>t\}\big] = \sum_{r=j}^{s}{\mathbb{E}}\big[e^{i,j}\textbf{1}\{T_j = r\}g^{l,j}_{s+1}\textbf{1}\{\widetilde{\eta}>t\}\big]$
together with (15), we obtain
${\mathbb{E}}\big[e^{i,j}g^{l,j}_{s+1}\textbf{1}\{\widetilde{\eta}>t\}\big] = \sum_{r=j}^{s}{\mathbb{E}}\big[e^{i,j}\textbf{1}\{T_j = r\}g^{l,j}_{s+1}\textbf{1}\{\widetilde{\eta}>t\}\big]$
together with (15), we obtain
![]() ${\mathbb{E}}\big[e^{i,j}g^{l,j}_{s+1}\textbf{1}\{\widetilde{\eta}>t\}\big] \le p_s^{j,k}{\mathbb{E}}\big[e^{i,j}\textbf{1}\{T_j \le s\}\textbf{1}\{\widetilde{\eta}>s\}\big]\le q^{i,j}p_s^{j,k}$
. Reasoning as above, we also obtain
${\mathbb{E}}\big[e^{i,j}g^{l,j}_{s+1}\textbf{1}\{\widetilde{\eta}>t\}\big] \le p_s^{j,k}{\mathbb{E}}\big[e^{i,j}\textbf{1}\{T_j \le s\}\textbf{1}\{\widetilde{\eta}>s\}\big]\le q^{i,j}p_s^{j,k}$
. Reasoning as above, we also obtain
The same general procedure of conditioning on the ‘last’ time also leads to
By (12) and (14), it follows that
 \begin{align*}{\mathbb{E}} \left[ e^{i,j}e^{i,k}g^{l,j}_{s+1} \textbf{1}\{\widetilde{\eta}>t\}\right] & = {\mathbb{E}} \left[ e^{i,j}e^{i,k}g^{l,j}_{s+1} \textbf{1}\{\widetilde{\eta}>t\}\textbf{1}\{T_k\le s\}\right] \\[4pt]& \le {\mathbb{E}} \left[ e^{i,j}e^{i,k} \textbf{1}\{\widetilde{\eta}>s\}\textbf{1}\{T_k\le s\}{\mathbb{E}} \left[ g^{l,j}_{s+1} \, \big | \, \mathcal{F}_s\right]\right] \\[4pt]& \le p_{s}^{j,k}{\mathbb{E}} \left[ e^{i,j}e^{i,k} \textbf{1}\{\widetilde{\eta}>s\}\textbf{1}\{T_k\le s\}\right] \\[4pt]& = p_{s}^{j,k}{\mathbb{E}} \left[ e^{i,j}e^{i,k} \textbf{1}\{\widetilde{\eta}>T_k\}\right] \\[4pt]& = p_{s}^{j,k}{\mathbb{E}}\left[ e^{i,j} \textbf{1}\{\widetilde{\eta}>T_k\}{\mathbb{E}}\left[e^{i,k} \mid \mathcal{G}_{T_k}\right] \right]\\[4pt]& \le p_{s}^{j,k}q^{i,k}q^{i,j},\end{align*}
\begin{align*}{\mathbb{E}} \left[ e^{i,j}e^{i,k}g^{l,j}_{s+1} \textbf{1}\{\widetilde{\eta}>t\}\right] & = {\mathbb{E}} \left[ e^{i,j}e^{i,k}g^{l,j}_{s+1} \textbf{1}\{\widetilde{\eta}>t\}\textbf{1}\{T_k\le s\}\right] \\[4pt]& \le {\mathbb{E}} \left[ e^{i,j}e^{i,k} \textbf{1}\{\widetilde{\eta}>s\}\textbf{1}\{T_k\le s\}{\mathbb{E}} \left[ g^{l,j}_{s+1} \, \big | \, \mathcal{F}_s\right]\right] \\[4pt]& \le p_{s}^{j,k}{\mathbb{E}} \left[ e^{i,j}e^{i,k} \textbf{1}\{\widetilde{\eta}>s\}\textbf{1}\{T_k\le s\}\right] \\[4pt]& = p_{s}^{j,k}{\mathbb{E}} \left[ e^{i,j}e^{i,k} \textbf{1}\{\widetilde{\eta}>T_k\}\right] \\[4pt]& = p_{s}^{j,k}{\mathbb{E}}\left[ e^{i,j} \textbf{1}\{\widetilde{\eta}>T_k\}{\mathbb{E}}\left[e^{i,k} \mid \mathcal{G}_{T_k}\right] \right]\\[4pt]& \le p_{s}^{j,k}q^{i,k}q^{i,j},\end{align*}
and analogous arguments also yield analogous bounds for
![]() ${\mathbb{E}} \left[ e^{i,j}g^{i,k}_{s+1}g^{j,k}_{s'+1}\textbf{1}\{\widetilde{\eta}>t\}\right]$
and
${\mathbb{E}} \left[ e^{i,j}g^{i,k}_{s+1}g^{j,k}_{s'+1}\textbf{1}\{\widetilde{\eta}>t\}\right]$
and
![]() ${\mathbb{E}} \left[ g^{i,j}_{r+1}g^{i,k}_{s+1}g^{j,k}_{s'+1}\textbf{1}\{\widetilde{\eta}>t\}\right] $
.
${\mathbb{E}} \left[ g^{i,j}_{r+1}g^{i,k}_{s+1}g^{j,k}_{s'+1}\textbf{1}\{\widetilde{\eta}>t\}\right] $
.
It remains to prove these bounds without the term
![]() $\textbf{1}\{\widetilde{\eta}>t\}$
inside the expectations above. To conclude this part of the proof, recall the definition of
$\textbf{1}\{\widetilde{\eta}>t\}$
inside the expectations above. To conclude this part of the proof, recall the definition of
![]() $\eta_i$
. Thus, by Theorem 4, with
$\eta_i$
. Thus, by Theorem 4, with
![]() $\lambda = C_p \log t$
it follows by the union bound that
$\lambda = C_p \log t$
it follows by the union bound that
![]() $\mathbb{P}\left( \widetilde{\eta} \le t \right) \le C_1 t^{-10}$
.
$\mathbb{P}\left( \widetilde{\eta} \le t \right) \le C_1 t^{-10}$
.
Then, for
![]() $s,r \in [1,t]$
and i, j, and k larger than
$s,r \in [1,t]$
and i, j, and k larger than
![]() $C_p \log t$
, it follows that, for large enough t,
$C_p \log t$
, it follows that, for large enough t,
![]() $C_1 t^{-10} \le \min\{q^{i,j}q^{i,k}p^{j,k}_{s'},\, q^{i,j}p^{i,k}_sp^{j,k}_{s'}, \, p^{i,j}_rp^{i,k}_sp^{j,k}_{s'}\}$
. This is enough to conclude the proof, since, for instance,
$C_1 t^{-10} \le \min\{q^{i,j}q^{i,k}p^{j,k}_{s'},\, q^{i,j}p^{i,k}_sp^{j,k}_{s'}, \, p^{i,j}_rp^{i,k}_sp^{j,k}_{s'}\}$
. This is enough to conclude the proof, since, for instance,
and the other bounds follow similarly.
5. The number of triangles
In this section we will use the estimates obtained in the previous section to prove an upper bound for the expected number of triangles at time t,
![]() $\mathcal{T}(G_t)$
, counted without multiplicities.
$\mathcal{T}(G_t)$
, counted without multiplicities.
Proposition 1. There exists a positive constant C, depending on p only, such that
![]() ${\mathbb{E}}[\mathcal{T}(G_t)]\leq C t^{3\alpha}(\log t)^8$
, where
${\mathbb{E}}[\mathcal{T}(G_t)]\leq C t^{3\alpha}(\log t)^8$
, where
![]() $\alpha$
is the function of p defined as
$\alpha$
is the function of p defined as
Proof. We begin by recalling that
![]() $\mathcal{T}(G_t)$
counts the number of triangles in
$\mathcal{T}(G_t)$
counts the number of triangles in
![]() $G_t$
disregarding the multiplicity of edges. Therefore, in order for the above discussion to be useful, it will be important to estimate the numbers of triangles formed by earlier vertices (which usually have high degree, corresponding to a high multiplicity of edges) and triangles formed by later vertices separately. We let
$G_t$
disregarding the multiplicity of edges. Therefore, in order for the above discussion to be useful, it will be important to estimate the numbers of triangles formed by earlier vertices (which usually have high degree, corresponding to a high multiplicity of edges) and triangles formed by later vertices separately. We let
 \begin{align*}\mathcal{T}_1(G_t)&\,:\!=\,\#\big\{\{i,j,k\}\subset\mathbb{N} ; i\cdot j \cdot k \leq t^{3\alpha} \big\},\nonumber\\[4pt]\mathcal{T}_2(G_t)&\,:\!=\,\#\left\{\begin{array}{c}\{i,j,k\}\subset\mathbb{N} ; i\cdot j \cdot k \geq t^{3\alpha};i<j<k;\\[4pt] \text{ and the vertices } i,j,k \text{ form a triangle in }G_t\end{array}\right\}.\end{align*}
\begin{align*}\mathcal{T}_1(G_t)&\,:\!=\,\#\big\{\{i,j,k\}\subset\mathbb{N} ; i\cdot j \cdot k \leq t^{3\alpha} \big\},\nonumber\\[4pt]\mathcal{T}_2(G_t)&\,:\!=\,\#\left\{\begin{array}{c}\{i,j,k\}\subset\mathbb{N} ; i\cdot j \cdot k \geq t^{3\alpha};i<j<k;\\[4pt] \text{ and the vertices } i,j,k \text{ form a triangle in }G_t\end{array}\right\}.\end{align*}
We then have
![]() $\mathcal{T}(G_t)\leq \mathcal{T}_1(G_t) + \mathcal{T}_2(G_t).$
Now,
$\mathcal{T}(G_t)\leq \mathcal{T}_1(G_t) + \mathcal{T}_2(G_t).$
Now,
![]() $\mathcal{T}_1(G_t)$
can be estimated in an elementary way:
$\mathcal{T}_1(G_t)$
can be estimated in an elementary way:
 \begin{equation*} \mathcal{T}_1(G_t)\leq \sum_{i=1}^{t^{3\alpha}}\sum_{j=1}^{\frac{t^{3\alpha}}{i}}\sum_{k=1}^{\frac{t^{3\alpha}}{ij}} 1 \leq Ct^{3\alpha}(\log t)^2.\end{equation*}
\begin{equation*} \mathcal{T}_1(G_t)\leq \sum_{i=1}^{t^{3\alpha}}\sum_{j=1}^{\frac{t^{3\alpha}}{i}}\sum_{k=1}^{\frac{t^{3\alpha}}{ij}} 1 \leq Ct^{3\alpha}(\log t)^2.\end{equation*}
But
![]() $\mathcal{T}_2(G_t)$
is more complicated. We have to break it into three distinct sets:
$\mathcal{T}_2(G_t)$
is more complicated. We have to break it into three distinct sets:
 \begin{align*}\mathcal{T}_2^0(G_t)&\,:\!=\,\#\left\{\begin{array}{c}\{i,j,k\}\subset\mathbb{N} ; i\cdot j \cdot k \geq t^{3\alpha};i<j<k;\\[4pt] \text{ and the vertices } i,j,k \text{ form a triangle in }\\[4pt] G_t \text{ with all edges coming from edge-steps}\end{array}\right\},\\[6pt] \mathcal{T}_2^1(G_t)&\,:\!=\,\#\left\{\begin{array}{c}\{i,j,k\}\subset\mathbb{N} ; i\cdot j \cdot k \geq t^{3\alpha};i<j<k;\\[4pt] \text{ and the vertices } i,j,k \text{ form a triangle in }G_t \text{ with two edges}\\[4pt] \text{ coming from edge-steps and one from a vertex-step}\end{array}\right\},\\[6pt] \mathcal{T}_2^2(G_t)&\,:\!=\,\#\left\{\begin{array}{c}\{i,j,k\}\subset\mathbb{N} ; i\cdot j \cdot k \geq t^{3\alpha};i<j<k;\\[4pt] \text{ and the vertices } i,j,k \text{ form a triangle in }G_t \text{ with one edge}\\[4pt] \text{ coming from an edge-step and two from vertex-steps}\end{array}\right\}.\end{align*}
\begin{align*}\mathcal{T}_2^0(G_t)&\,:\!=\,\#\left\{\begin{array}{c}\{i,j,k\}\subset\mathbb{N} ; i\cdot j \cdot k \geq t^{3\alpha};i<j<k;\\[4pt] \text{ and the vertices } i,j,k \text{ form a triangle in }\\[4pt] G_t \text{ with all edges coming from edge-steps}\end{array}\right\},\\[6pt] \mathcal{T}_2^1(G_t)&\,:\!=\,\#\left\{\begin{array}{c}\{i,j,k\}\subset\mathbb{N} ; i\cdot j \cdot k \geq t^{3\alpha};i<j<k;\\[4pt] \text{ and the vertices } i,j,k \text{ form a triangle in }G_t \text{ with two edges}\\[4pt] \text{ coming from edge-steps and one from a vertex-step}\end{array}\right\},\\[6pt] \mathcal{T}_2^2(G_t)&\,:\!=\,\#\left\{\begin{array}{c}\{i,j,k\}\subset\mathbb{N} ; i\cdot j \cdot k \geq t^{3\alpha};i<j<k;\\[4pt] \text{ and the vertices } i,j,k \text{ form a triangle in }G_t \text{ with one edge}\\[4pt] \text{ coming from an edge-step and two from vertex-steps}\end{array}\right\}.\end{align*}
Note that it is impossible for a triangle to be formed by three edges coming from vertex-steps. Therefore,
![]() $\mathcal{T}_2(G_t) \leq \mathcal{T}_2^0(G_t)+\mathcal{T}_2^1(G_t)+\mathcal{T}_2^2(G_t)$
. We bound the expectations of the variables on the right-hand side of this inequality separately, but before we go to the computations we introduce new notation in order to avoid clutter. We will need to sum over vertices’ indices as well as the time they became connected. Thus, we let I be the following region of
$\mathcal{T}_2(G_t) \leq \mathcal{T}_2^0(G_t)+\mathcal{T}_2^1(G_t)+\mathcal{T}_2^2(G_t)$
. We bound the expectations of the variables on the right-hand side of this inequality separately, but before we go to the computations we introduce new notation in order to avoid clutter. We will need to sum over vertices’ indices as well as the time they became connected. Thus, we let I be the following region of
![]() $\mathbb{Z}^3$
:
$\mathbb{Z}^3$
:
Observe that for
![]() $p\ge 1/2$
we have
$p\ge 1/2$
we have
![]() $3\alpha -1 \le 1$
. Also, for fixed (i,j,k) we let
$3\alpha -1 \le 1$
. Also, for fixed (i,j,k) we let
![]() $S_{i,j,k}$
be
$S_{i,j,k}$
be
![]() $S_{i,j,k} \,:\!=\, \left \lbrace (s_1,s_2,s_3) \in \mathbb{Z}^3 \, : \, s_1 \in [i,t];\, s_2 \in [j, t];\, s_3 \in [k, t] \right \rbrace$
whereas
$S_{i,j,k} \,:\!=\, \left \lbrace (s_1,s_2,s_3) \in \mathbb{Z}^3 \, : \, s_1 \in [i,t];\, s_2 \in [j, t];\, s_3 \in [k, t] \right \rbrace$
whereas
![]() $S_{i,j}$
denotes
$S_{i,j}$
denotes
![]() $S_{i,j} \,:\!=\, \left \lbrace (s_1,s_2) \in \mathbb{Z}^3 \, : \, s_1 \in [i,t];\, s_2 \in [j, t] \right \rbrace$
. We also use
$S_{i,j} \,:\!=\, \left \lbrace (s_1,s_2) \in \mathbb{Z}^3 \, : \, s_1 \in [i,t];\, s_2 \in [j, t] \right \rbrace$
. We also use
![]() $\vec{i}$
as a shorthand for (i,j,k) and
$\vec{i}$
as a shorthand for (i,j,k) and
![]() $\vec{s}$
for either
$\vec{s}$
for either
![]() $(s_1,s_2,s_3)$
when summing over
$(s_1,s_2,s_3)$
when summing over
![]() $S_{i,j,k}$
, or
$S_{i,j,k}$
, or
![]() $(s_1,s_2)$
when the summation is over
$(s_1,s_2)$
when the summation is over
![]() $S_{i,j}$
. Now we go to the remainder upper bound, recalling that
$S_{i,j}$
. Now we go to the remainder upper bound, recalling that
![]() $\alpha=\alpha(p)=(1-p)(2-p)^{-1}$
and bounding the summand by the integral, which yields
$\alpha=\alpha(p)=(1-p)(2-p)^{-1}$
and bounding the summand by the integral, which yields
 \begin{align}\nonumber{\mathbb{E}}[\mathcal{T}_2^0(G_t)]&\leq {\mathbb{E}}\left[ \sum_{\vec{i} \in I} \sum_{\vec{s} \in S_{i,j,k}}g^{i,j}_{s_1}g^{j,k}_{s_2}g^{i,k}_{s_3} \right]\nonumber\\[3pt] & \leq \sum_{\vec{i} \in I} \sum_{\vec{s} \in S_{i,j,k}}\frac{C_1 C_p^6 \log (t)^6}{(ijk)^{2-p}(s_1 s_2 s_3)^p} \qquad \text{[by Lemma 2]}\\[3pt] & \leq \frac{C_1C_p^6t^{3(1-p)}(\log t)^6}{(1-p)^3} \sum_{\vec{i} \in I} \frac{1}{(ijk)^{2-p}} \qquad \text{[by (2)].}\nonumber\end{align}
\begin{align}\nonumber{\mathbb{E}}[\mathcal{T}_2^0(G_t)]&\leq {\mathbb{E}}\left[ \sum_{\vec{i} \in I} \sum_{\vec{s} \in S_{i,j,k}}g^{i,j}_{s_1}g^{j,k}_{s_2}g^{i,k}_{s_3} \right]\nonumber\\[3pt] & \leq \sum_{\vec{i} \in I} \sum_{\vec{s} \in S_{i,j,k}}\frac{C_1 C_p^6 \log (t)^6}{(ijk)^{2-p}(s_1 s_2 s_3)^p} \qquad \text{[by Lemma 2]}\\[3pt] & \leq \frac{C_1C_p^6t^{3(1-p)}(\log t)^6}{(1-p)^3} \sum_{\vec{i} \in I} \frac{1}{(ijk)^{2-p}} \qquad \text{[by (2)].}\nonumber\end{align}
For the summation over I in the last inequality we bound the sum by the integral
 \begin{equation*}\begin{split}\sum_{\vec{i} \in I} \frac{1}{(ijk)^{2-p}} & \le \sum_{i=1}^{t}\sum_{j=1}^{t}\sum_{k=t^{3\alpha}/ij}^{t}\frac{1}{(ijk)^{2-p}} \\& \le \sum_{i=1}^{t}\sum_{j=i}^{t}\frac{1}{1-p}\frac{1}{(ij)^{2-p}}\frac{(ij)^{1-p}}{t^{3\alpha(1-p)}} \le \frac{(\log t)^2}{(1-p)t^{3\alpha(1-p)}}.\end{split}\end{equation*}
\begin{equation*}\begin{split}\sum_{\vec{i} \in I} \frac{1}{(ijk)^{2-p}} & \le \sum_{i=1}^{t}\sum_{j=1}^{t}\sum_{k=t^{3\alpha}/ij}^{t}\frac{1}{(ijk)^{2-p}} \\& \le \sum_{i=1}^{t}\sum_{j=i}^{t}\frac{1}{1-p}\frac{1}{(ij)^{2-p}}\frac{(ij)^{1-p}}{t^{3\alpha(1-p)}} \le \frac{(\log t)^2}{(1-p)t^{3\alpha(1-p)}}.\end{split}\end{equation*}
Replacing the above bound in (16) and using that
![]() $(1-p) - \alpha(1-p) = \alpha$
leads to
$(1-p) - \alpha(1-p) = \alpha$
leads to
![]() ${\mathbb{E}}[\mathcal{T}_2^0(G_t)] \le C_1C_p^6(1-p)^{-4}(\log t)^8 t^{3(1-p)(1-\alpha)} = C_1C_p^6(1-p)^{-4}(\log t)^8 t^{3\alpha}$
. For
${\mathbb{E}}[\mathcal{T}_2^0(G_t)] \le C_1C_p^6(1-p)^{-4}(\log t)^8 t^{3(1-p)(1-\alpha)} = C_1C_p^6(1-p)^{-4}(\log t)^8 t^{3\alpha}$
. For
![]() $\mathcal{T}_2^1(G_t)$
, using the bounds derived in Lemma 2 and the integral bound, we then obtain
$\mathcal{T}_2^1(G_t)$
, using the bounds derived in Lemma 2 and the integral bound, we then obtain
 \begin{align}\nonumber{\mathbb{E}}[\mathcal{T}_2^1(G_t)]&\leq {\mathbb{E}}\left[ \sum_{\vec{i} \in I} \sum_{\vec{s} \in S_{k,k}}e^{i,j}g^{j,k}_{s_1}g^{i,k}_{s_2} \right]+ {\mathbb{E}}\left[ \sum_{\vec{i} \in I} \sum_{\vec{s} \in S_{j,k}}g^{i,j}_{s_1}e^{j,k}g^{i,k}_{s_2} \right]\nonumber \\[4pt]&\quad +{\mathbb{E}}\left[ \sum_{\vec{i} \in I} \sum_{\vec{s} \in S_{j,k}}g^{i,j}_{s_1}g^{j,k}_{s_2}e^{i,k} \right]\\[4pt]& \leq C_1C_p^5(1-p)^{-2} t^{2(1-p)} (\log t)^5 \left(\sum_{\vec{i} \in I} \frac{1}{(ik)^{2-p}j} +\frac{2}{(ij)^{2-p}k} \right) \ \text{[by Lemma 2]}.\nonumber\end{align}
\begin{align}\nonumber{\mathbb{E}}[\mathcal{T}_2^1(G_t)]&\leq {\mathbb{E}}\left[ \sum_{\vec{i} \in I} \sum_{\vec{s} \in S_{k,k}}e^{i,j}g^{j,k}_{s_1}g^{i,k}_{s_2} \right]+ {\mathbb{E}}\left[ \sum_{\vec{i} \in I} \sum_{\vec{s} \in S_{j,k}}g^{i,j}_{s_1}e^{j,k}g^{i,k}_{s_2} \right]\nonumber \\[4pt]&\quad +{\mathbb{E}}\left[ \sum_{\vec{i} \in I} \sum_{\vec{s} \in S_{j,k}}g^{i,j}_{s_1}g^{j,k}_{s_2}e^{i,k} \right]\\[4pt]& \leq C_1C_p^5(1-p)^{-2} t^{2(1-p)} (\log t)^5 \left(\sum_{\vec{i} \in I} \frac{1}{(ik)^{2-p}j} +\frac{2}{(ij)^{2-p}k} \right) \ \text{[by Lemma 2]}.\nonumber\end{align}
We again bound the summation over I in the same way as before. We begin with the first sum, for which we obtain the following upper bound:
 \begin{equation}\begin{split}\sum_{\vec{i} \in I} \frac{1}{(ik)^{2-p}j} & \le \sum_{i=1}^{t}\sum_{j=1}^{t}\sum_{k=t^{3\alpha}/ij}^{t}\frac{1}{(ik)^{2-p}j} \\& \le \frac{1}{(1-p)} \sum_{i=1}^{t}\sum_{j=1}^{t}\frac{1}{ij^pt^{3\alpha(1-p)}} \le \frac{t^{1-p}\log t}{(1-p)^2t^{3\alpha(1-p)}}.\end{split}\end{equation}
\begin{equation}\begin{split}\sum_{\vec{i} \in I} \frac{1}{(ik)^{2-p}j} & \le \sum_{i=1}^{t}\sum_{j=1}^{t}\sum_{k=t^{3\alpha}/ij}^{t}\frac{1}{(ik)^{2-p}j} \\& \le \frac{1}{(1-p)} \sum_{i=1}^{t}\sum_{j=1}^{t}\frac{1}{ij^pt^{3\alpha(1-p)}} \le \frac{t^{1-p}\log t}{(1-p)^2t^{3\alpha(1-p)}}.\end{split}\end{equation}
The second summation over I in (17) is somewhat more involved. For this reason we will split it into two cases,
![]() $p\le 1/2$
and
$p\le 1/2$
and
![]() $p>1/2$
, in order to make clear the region over which we are integrating. For
$p>1/2$
, in order to make clear the region over which we are integrating. For
![]() $p>1/2$
we bound the second summation over I in the following way:
$p>1/2$
we bound the second summation over I in the following way:
 \begin{equation*} \begin{split}\sum_{\vec{i} \in I} \frac{2}{(ij)^{2-p}k} & \le \sum_{i=1}^{t}\sum_{j=1}^{t}\sum_{k=t^{3\alpha}/ij}^{t}\frac{2}{(ij)^{2-p}k} \le \frac{2\log t}{(1-p)^2}.\end{split}\end{equation*}
\begin{equation*} \begin{split}\sum_{\vec{i} \in I} \frac{2}{(ij)^{2-p}k} & \le \sum_{i=1}^{t}\sum_{j=1}^{t}\sum_{k=t^{3\alpha}/ij}^{t}\frac{2}{(ij)^{2-p}k} \le \frac{2\log t}{(1-p)^2}.\end{split}\end{equation*}
Then, replacing the above bound and (18) in (17) gives, for
![]() $p>1/2$
, the bound
$p>1/2$
, the bound
where
![]() $C= 3C_1C_p^5(1-p)^{-4}$
, since in this regime for p,
$C= 3C_1C_p^5(1-p)^{-4}$
, since in this regime for p,
![]() $2(1-p) \le 3\alpha$
. For
$2(1-p) \le 3\alpha$
. For
![]() $p\le 1/2$
we need to be more careful with our bounds. In this case we break up the sum depending on whether
$p\le 1/2$
we need to be more careful with our bounds. In this case we break up the sum depending on whether
We have
 \begin{equation*} \begin{split}\sum_{\vec{i} \in I} \frac{2}{(ij)^{2-p}k} & = \sum_{i=1}^{t^{(3\alpha-1)/2}}\sum_{j=t^{3\alpha - 1}/i}^{t}\sum_{k=t^{3\alpha}/ij}^{t}\frac{2}{(ij)^{2-p}k} + \sum_{i=t^{(3\alpha-1)/2}}^{t}\sum_{j=i}^{t}\sum_{k=t^{3\alpha}/ij}^{t}\frac{2}{(ij)^{2-p}k} \\& \le \sum_{i=1}^{t^{(3\alpha-1)/2}}\sum_{j=t^{3\alpha - 1}/i}^{t}\frac{2\log t}{(ij)^{2-p}} + \sum_{i=t^{(3\alpha-1)/2}}^{t}\sum_{j=i}^{t}\frac{2\log t}{(ij)^{2-p}} \\& \le \sum_{i=1}^{t^{(3\alpha-1)/2}}\frac{2(\log t)i^{1-p}}{(1-p)i^{2-p}t^{(3\alpha-1)(1-p)}} + \sum_{i=t^{(3\alpha-1)/2}}^{t}\frac{2\log t}{(1-p)i^{2-p}i^{1-p}} \\& \le \frac{2(\log t)^2}{(1-p)t^{(3\alpha-1)(1-p)}} + \frac{\log t}{(1-p)t^{(3\alpha-1)(1-p)}}.\end{split}\end{equation*}
\begin{equation*} \begin{split}\sum_{\vec{i} \in I} \frac{2}{(ij)^{2-p}k} & = \sum_{i=1}^{t^{(3\alpha-1)/2}}\sum_{j=t^{3\alpha - 1}/i}^{t}\sum_{k=t^{3\alpha}/ij}^{t}\frac{2}{(ij)^{2-p}k} + \sum_{i=t^{(3\alpha-1)/2}}^{t}\sum_{j=i}^{t}\sum_{k=t^{3\alpha}/ij}^{t}\frac{2}{(ij)^{2-p}k} \\& \le \sum_{i=1}^{t^{(3\alpha-1)/2}}\sum_{j=t^{3\alpha - 1}/i}^{t}\frac{2\log t}{(ij)^{2-p}} + \sum_{i=t^{(3\alpha-1)/2}}^{t}\sum_{j=i}^{t}\frac{2\log t}{(ij)^{2-p}} \\& \le \sum_{i=1}^{t^{(3\alpha-1)/2}}\frac{2(\log t)i^{1-p}}{(1-p)i^{2-p}t^{(3\alpha-1)(1-p)}} + \sum_{i=t^{(3\alpha-1)/2}}^{t}\frac{2\log t}{(1-p)i^{2-p}i^{1-p}} \\& \le \frac{2(\log t)^2}{(1-p)t^{(3\alpha-1)(1-p)}} + \frac{\log t}{(1-p)t^{(3\alpha-1)(1-p)}}.\end{split}\end{equation*}
Then, replacing the above bound and (18) in (17), and noticing that
![]() $2(1-p) - (3\alpha -1)(1-p) = (1-p)(2-3\alpha+1) = 3(1-p)(1-\alpha) = 3\alpha$
, gives us that for
$2(1-p) - (3\alpha -1)(1-p) = (1-p)(2-3\alpha+1) = 3(1-p)(1-\alpha) = 3\alpha$
, gives us that for
![]() $p>1/2$
and some constant depending on p only,
$p>1/2$
and some constant depending on p only,
![]() ${\mathbb{E}}[\mathcal{T}_2^1(G_t)] \le 4C_1C_p^5(1-p)^{-4}t^{3\alpha}(\log t)^7$
. We conclude by estimating the expectation of
${\mathbb{E}}[\mathcal{T}_2^1(G_t)] \le 4C_1C_p^5(1-p)^{-4}t^{3\alpha}(\log t)^7$
. We conclude by estimating the expectation of
![]() $\mathcal{T}_2^2(G_t)$
in a similar manner as above:
$\mathcal{T}_2^2(G_t)$
in a similar manner as above:
 \begin{align*}\nonumber{\mathbb{E}}[\mathcal{T}_2^2(G_t)]&\leq {\mathbb{E}}\left[ \sum_{\vec{i} \in I} \sum_{s = k}^te^{i,j}g^{j,k}_{s}e^{i,k} \right]+{\mathbb{E}}\left[ \sum_{\vec{i} \in I} \sum_{s = k}^te^{i,j}e^{j,k}g^{i,k}_{s} \right]\\& \leq 2\sum_{\vec{i} \in I} \sum_{s = k}^tC_1C_p^4 (\log t)^4 \frac{1}{i^{2-p}jks^{p}} \qquad \text{[by Lemma 2]}\\ \nonumber&\leq C_1C_p^4(1-p)^{-1}t^{1-p} (\log t)^4 \left(\sum_{\vec{i} \in I} \frac{2}{i^{2-p}jk} \right)\\& \nonumber\leq 2C_1C_p^4(1-p)^{-2} t^{1-p} (\log t)^6,\end{align*}
\begin{align*}\nonumber{\mathbb{E}}[\mathcal{T}_2^2(G_t)]&\leq {\mathbb{E}}\left[ \sum_{\vec{i} \in I} \sum_{s = k}^te^{i,j}g^{j,k}_{s}e^{i,k} \right]+{\mathbb{E}}\left[ \sum_{\vec{i} \in I} \sum_{s = k}^te^{i,j}e^{j,k}g^{i,k}_{s} \right]\\& \leq 2\sum_{\vec{i} \in I} \sum_{s = k}^tC_1C_p^4 (\log t)^4 \frac{1}{i^{2-p}jks^{p}} \qquad \text{[by Lemma 2]}\\ \nonumber&\leq C_1C_p^4(1-p)^{-1}t^{1-p} (\log t)^4 \left(\sum_{\vec{i} \in I} \frac{2}{i^{2-p}jk} \right)\\& \nonumber\leq 2C_1C_p^4(1-p)^{-2} t^{1-p} (\log t)^6,\end{align*}
which is enough to conclude the proof of Proposition 1.
The next lemma gives us concentration results for
![]() $\mathcal{T}(G_t)$
.
$\mathcal{T}(G_t)$
.
Lemma 3. Given
![]() $\varepsilon >0$
, there exist positive constants
$\varepsilon >0$
, there exist positive constants
![]() $C_1$
,
$C_1$
,
![]() $C_2$
,
$C_2$
,
![]() $C_3$
, and a, depending on
$C_3$
, and a, depending on
![]() $\varepsilon$
and p only, such that
$\varepsilon$
and p only, such that
![]() $\mathbb{P} \left( C_1t^{3\alpha(1-\varepsilon)} \le \mathcal{T}(G_t) \le C_2t^{3\alpha(1+\varepsilon)} \right) \ge 1-C_3t^{-a}$
.
$\mathbb{P} \left( C_1t^{3\alpha(1-\varepsilon)} \le \mathcal{T}(G_t) \le C_2t^{3\alpha(1+\varepsilon)} \right) \ge 1-C_3t^{-a}$
.
Proof. The upper bound for
![]() $\mathcal{T}(G_t)$
follows from Proposition 1 and Markov’s inequality, which yields
$\mathcal{T}(G_t)$
follows from Proposition 1 and Markov’s inequality, which yields
For the lower bound, we apply [Reference Alves, Ribeiro and Sanchis1, Theorem 1] (more specifically the polynomial bound given by (4.3)), which states that, with probability at least
![]() $1-t^{-a_2}$
,
$1-t^{-a_2}$
,
![]() $G_t$
contains a complete subgraph of order
$G_t$
contains a complete subgraph of order
![]() $t^{\alpha(1-\varepsilon)}$
. Notice that every three distinct vertices in this complete subgraph form a triangle. Thus, on the event that there exists a complete subgraph with at least
$t^{\alpha(1-\varepsilon)}$
. Notice that every three distinct vertices in this complete subgraph form a triangle. Thus, on the event that there exists a complete subgraph with at least
![]() $t^{\alpha(1-\varepsilon)}$
vertices in
$t^{\alpha(1-\varepsilon)}$
vertices in
![]() $G_t$
, the following lower bound holds:
$G_t$
, the following lower bound holds:
for some constant
![]() $C_4$
depending on p and
$C_4$
depending on p and
![]() $\varepsilon$
. This can be restated as
$\varepsilon$
. This can be restated as
The proof is finished by combining the inequalities (19) and (20), and choosing
![]() $a=\min\{\alpha\varepsilon,a_2\}$
.
$a=\min\{\alpha\varepsilon,a_2\}$
.
6. Proof of the main results
In this section we wrap up all the results we have proved so far in order to prove our two main results: Theorems 1 and 2, as well as their consequences, Corollaries 1 and 2.
Proof of Theorem 1: Clustering coefficient. We begin recalling the definition of some functions of p we have used throughout the paper, as well as the definition of
![]() $\tau(G_t)$
:
$\tau(G_t)$
:
Since p will be fixed, we simply write
![]() $\alpha$
and
$\alpha$
and
![]() $\gamma$
to avoid clutter. Let
$\gamma$
to avoid clutter. Let
![]() $\varepsilon'$
be
$\varepsilon'$
be
and consider the following events:
 \begin{align*}A & = \left \lbrace C_1t^{(2-p)(1-\varepsilon')} \le \mathcal{C}(G_t) \le C_2t^{(2-p)(1+\varepsilon')} \right \rbrace , \\B & = \left \lbrace C^{\prime}_1 t^{3\alpha(1-\varepsilon')}\le \mathcal{T}(G_t)\le C^{\prime}_2 t^{3\alpha(1+\varepsilon')}\right \rbrace.\end{align*}
\begin{align*}A & = \left \lbrace C_1t^{(2-p)(1-\varepsilon')} \le \mathcal{C}(G_t) \le C_2t^{(2-p)(1+\varepsilon')} \right \rbrace , \\B & = \left \lbrace C^{\prime}_1 t^{3\alpha(1-\varepsilon')}\le \mathcal{T}(G_t)\le C^{\prime}_2 t^{3\alpha(1+\varepsilon')}\right \rbrace.\end{align*}
By Theorem 5 and Lemma 3, we have that
![]() $\mathbb{P}\left(A^c\right) \le C_3t^{-a^{\prime}_1}$
and
$\mathbb{P}\left(A^c\right) \le C_3t^{-a^{\prime}_1}$
and
![]() $\mathbb{P}(B^c) \le C^{\prime}_3t^{-a^{\prime}_2}$
, where
$\mathbb{P}(B^c) \le C^{\prime}_3t^{-a^{\prime}_2}$
, where
![]() $a^{\prime}_1$
and
$a^{\prime}_1$
and
![]() $a^{\prime}_2$
are constants depending on p and
$a^{\prime}_2$
are constants depending on p and
![]() $\varepsilon'$
. Moreover, observe that on the event
$\varepsilon'$
. Moreover, observe that on the event
![]() $A\cap B$
the following bounds hold:
$A\cap B$
the following bounds hold:
since by the definition of
![]() $\varepsilon'$
,
$\varepsilon'$
,
![]() $\gamma$
, and
$\gamma$
, and
![]() $\alpha$
we have
$\alpha$
we have
![]() $(2-p)(1-\varepsilon') -3\alpha(1+\varepsilon') = \gamma(1-\varepsilon)$
,
$(2-p)(1-\varepsilon') -3\alpha(1+\varepsilon') = \gamma(1-\varepsilon)$
,
![]() $(2-p)(1+\varepsilon') -3\alpha(1-\varepsilon') = \gamma(1+\varepsilon)$
. Then, we conclude that
$(2-p)(1+\varepsilon') -3\alpha(1-\varepsilon') = \gamma(1+\varepsilon)$
. Then, we conclude that
where
![]() $a_3$
can be chosen as
$a_3$
can be chosen as
![]() $\min\{a^{\prime}_1,a^{\prime}_2\}$
, and
$\min\{a^{\prime}_1,a^{\prime}_2\}$
, and
![]() $C^{\prime\prime}_3=C_3+C^{\prime}_3$
. This concludes the proof.
$C^{\prime\prime}_3=C_3+C^{\prime}_3$
. This concludes the proof.
Now we use the bounds derived in the above proof to prove Corollary 1.
Proof of Corollary 1. Consider the sequence
![]() $t_k \,:\!=\, \textrm{e}^{k^2}$
and fix a positive
$t_k \,:\!=\, \textrm{e}^{k^2}$
and fix a positive
![]() $\varepsilon$
. For large enough k, Lemma 3 and Theorem 5 give us
$\varepsilon$
. For large enough k, Lemma 3 and Theorem 5 give us
Thus, the Borel–Cantelli lemma yields
![]() $\log \mathcal{T}(G_{t_k})/\log t_k \to 3\alpha$
and
$\log \mathcal{T}(G_{t_k})/\log t_k \to 3\alpha$
and
![]() $\log\mathcal{C}(G_{t_k})/\log t_k \to 2-p$
almost surely as k tends to infinity. Therefore, the definition of the global clustering
$\log\mathcal{C}(G_{t_k})/\log t_k \to 2-p$
almost surely as k tends to infinity. Therefore, the definition of the global clustering
![]() $\tau(G_{t_k})$
implies that
$\tau(G_{t_k})$
implies that
![]() $\log \tau(G_{t_k})/\log t_k \to 3\alpha-2+p$
almost surely. Now, since both quantities
$\log \tau(G_{t_k})/\log t_k \to 3\alpha-2+p$
almost surely. Now, since both quantities
![]() $\mathcal{T}(G_t)$
and
$\mathcal{T}(G_t)$
and
![]() $\mathcal{C}(G_t)$
are increasing on t, for any
$\mathcal{C}(G_t)$
are increasing on t, for any
![]() $t \in [t_k, t_{k+1}]$
we have
$t \in [t_k, t_{k+1}]$
we have
 \begin{align*}\log \left( \frac{3\mathcal{T}(G_{t_k})}{\mathcal{C}(G_{t_{k+1}})} \right) & \le \log \left( \frac{3\mathcal{T}(G_t)}{\mathcal{C}(G_t)} \right) \le \log \left( \frac{3\mathcal{T}(G_{t_{k+1}})}{\mathcal{C}(G_{t_{k}})} \right) , \\[4pt]\log \left( \frac{\tau(G_{t_k})\mathcal{C}(G_{t_k})}{\mathcal{C}(G_{t_{k+1}})} \right) & \le \log \tau(G_{t}) \le \log \left( \frac{\tau(G_{t_{k+1}})\mathcal{C}(G_{t_{k+1}})}{\mathcal{C}(G_{t_{k}})} \right).\end{align*}
\begin{align*}\log \left( \frac{3\mathcal{T}(G_{t_k})}{\mathcal{C}(G_{t_{k+1}})} \right) & \le \log \left( \frac{3\mathcal{T}(G_t)}{\mathcal{C}(G_t)} \right) \le \log \left( \frac{3\mathcal{T}(G_{t_{k+1}})}{\mathcal{C}(G_{t_{k}})} \right) , \\[4pt]\log \left( \frac{\tau(G_{t_k})\mathcal{C}(G_{t_k})}{\mathcal{C}(G_{t_{k+1}})} \right) & \le \log \tau(G_{t}) \le \log \left( \frac{\tau(G_{t_{k+1}})\mathcal{C}(G_{t_{k+1}})}{\mathcal{C}(G_{t_{k}})} \right).\end{align*}
Since
![]() $(t_k)_k$
is increasing in k as well, we obtain
$(t_k)_k$
is increasing in k as well, we obtain
 \begin{equation*}\frac{\log \left( \frac{\tau(G_{t_k})\mathcal{C}(G_{t_k})}{\mathcal{C}(G_{t_{k+1}})} \right)}{\log t_{k}} \cdot \frac{\log t_{k}}{\log t_{k+1}} \le \frac{\log \tau(G_{t})}{\log t} \le \frac{\log \left( \frac{\tau(G_{t_{k+1}})\mathcal{C}(G_{t_{k+1}})}{\mathcal{C}(G_{t_{k}})} \right)}{\log t_{k+1}} \cdot \frac{\log t_{k+1}}{\log t_k} ,\end{equation*}
\begin{equation*}\frac{\log \left( \frac{\tau(G_{t_k})\mathcal{C}(G_{t_k})}{\mathcal{C}(G_{t_{k+1}})} \right)}{\log t_{k}} \cdot \frac{\log t_{k}}{\log t_{k+1}} \le \frac{\log \tau(G_{t})}{\log t} \le \frac{\log \left( \frac{\tau(G_{t_{k+1}})\mathcal{C}(G_{t_{k+1}})}{\mathcal{C}(G_{t_{k}})} \right)}{\log t_{k+1}} \cdot \frac{\log t_{k+1}}{\log t_k} ,\end{equation*}
which are enough to conclude the proof, sending k to infinity and using the almost sure convergence of
![]() $(\log \tau(G_{t_k})/\log t_k )_{k\geq 1}$
and
$(\log \tau(G_{t_k})/\log t_k )_{k\geq 1}$
and
![]() $(\log \tau(G_{t_k})/\log t_k)_{k\geq 1}$
.
$(\log \tau(G_{t_k})/\log t_k)_{k\geq 1}$
.
Proof of Theorem 2. The existence of a clique of order
![]() $t^{\frac{(1-\varepsilon)(1-p)}{2-p}}$
in
$t^{\frac{(1-\varepsilon)(1-p)}{2-p}}$
in
![]() $G_t$
w.h.p. was proved by [Reference Alves, Ribeiro and Sanchis1, Theorem 1]. For the upper bound, observe that the existence of a complete subgraph of order
$G_t$
w.h.p. was proved by [Reference Alves, Ribeiro and Sanchis1, Theorem 1]. For the upper bound, observe that the existence of a complete subgraph of order
![]() $C^{1/3}t^{\frac{(1-p)}{2-p}}\log^3(t)$
in
$C^{1/3}t^{\frac{(1-p)}{2-p}}\log^3(t)$
in
![]() $G_t$
implies immediately that
$G_t$
implies immediately that
![]() $\mathcal{T}(G_t)$
is at least
$\mathcal{T}(G_t)$
is at least
![]() $C(\log t)^9t^{3\alpha}$
, which, by Proposition 1 and Markov’s inequality, occurs with probability at most
$C(\log t)^9t^{3\alpha}$
, which, by Proposition 1 and Markov’s inequality, occurs with probability at most
![]() $1/\log t$
. This proves the theorem.
$1/\log t$
. This proves the theorem.
The proof of Corollary 2 follows exactly the same reasoning, exploring monotonicity, given in the proof of Corollary 1, since polynomial bounds on the relevant probabilities are available (see [Reference Alves, Ribeiro and Sanchis1, (4.3)]). The proof is in fact simpler, since, unlike
![]() $\tau(G_t)$
,
$\tau(G_t)$
,
![]() $\omega(G_t)$
is itself increasing in t. For this reason we omit the proof.
$\omega(G_t)$
is itself increasing in t. For this reason we omit the proof.
Acknowledgements
We are grateful to Roberto Imbuzeiro Oliveira for the many inspiring conversations. C. A. was partially supported by FAPESP, grants 2013/24928-2 and 2015/18930-0, and by the DFG grant SA 3465/1-1. R. R. was partially supported by Conselho Nacional de Desenvolvimento Científicoe Tecnológico (CNPq) and by the project Stochastic Models of Disordered and Complex Systems. The Stochastic Models of Disordered and Complex Systems is a Millennium Nucleus (NC120062) supported by the Millenium Scientific Initiative of the Ministry of Science and Technology (Chile). R. S. has been partially supported by Conselho Nacional de Desenvolvimento Científicoe Tecnológico (CNPq) and by FAPEMIG (Programa Pesquisador Mineiro), grant PPM 00600/16.