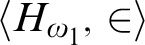1 Introduction
Set theory exhibits a robust mutual interpretability phenomenon: in a given model of set theory, we can define diverse other interpreted models of set theory. In any model of Zermelo–Fraenkel (ZF) set theory, for example, we can define an interpreted model of
![]() $\mathrm {ZFC}+\mathrm {GCH}$
, via the constructible universe, as well as definable interpreted models of
$\mathrm {ZFC}+\mathrm {GCH}$
, via the constructible universe, as well as definable interpreted models of
![]() $\mathrm {ZF}+\neg \mathrm {AC}$
, of
$\mathrm {ZF}+\neg \mathrm {AC}$
, of
![]() $\mathrm {ZFC}+\mathrm {MA}+\neg \mathrm {CH}$
, of
$\mathrm {ZFC}+\mathrm {MA}+\neg \mathrm {CH}$
, of
![]() $\mathrm {ZFC}+\mathfrak {b}<\mathfrak {d}$
, and so on for infinitely many theories. For these latter theories, set theorists often use forcing to construct outer models of the given model; but nevertheless the Boolean ultrapower method provides definable interpreted models of these theories inside the original model (see Theorem 7). Similarly, in models of ZFC with large cardinals, one can define fine-structural canonical inner models with large cardinals and models of ZF satisfying various determinacy principles, and vice versa. In this way, set theory exhibits an abundance of natural mutually interpretable theories.
$\mathrm {ZFC}+\mathfrak {b}<\mathfrak {d}$
, and so on for infinitely many theories. For these latter theories, set theorists often use forcing to construct outer models of the given model; but nevertheless the Boolean ultrapower method provides definable interpreted models of these theories inside the original model (see Theorem 7). Similarly, in models of ZFC with large cardinals, one can define fine-structural canonical inner models with large cardinals and models of ZF satisfying various determinacy principles, and vice versa. In this way, set theory exhibits an abundance of natural mutually interpretable theories.
Do these instances of mutual interpretation fulfill the more vigorous conception of bi-interpretation? Two models or theories are mutually interpretable, when merely each is interpreted in the other, whereas bi-interpretation requires that the interpretations are invertible in a sense after iteration, so that if one should interpret one model or theory in the other and then re-interpret the first theory inside that, then the resulting model should be definably isomorphic to the original universe (precise definitions in Sections 2 and 3). The interpretations mentioned above are not bi-interpretations, for if we start in a model of
![]() $\mathrm {ZFC}+\neg \mathrm {CH}$
and then go to L in order to interpret a model of
$\mathrm {ZFC}+\neg \mathrm {CH}$
and then go to L in order to interpret a model of
![]() $\mathrm {ZFC}+\mathrm {GCH}$
, then we’ve already discarded too much set-theoretic information to expect that we could get a copy of our original model back by interpreting inside L. This problem is inherent, in light of the following theorem of Ali Enayat, showing that indeed there is no nontrivial bi-interpretation phenomenon to be found amongst the set-theoretic models and theories satisfying ZF. In interpretation, one must inevitably discard set-theoretic information.
$\mathrm {ZFC}+\mathrm {GCH}$
, then we’ve already discarded too much set-theoretic information to expect that we could get a copy of our original model back by interpreting inside L. This problem is inherent, in light of the following theorem of Ali Enayat, showing that indeed there is no nontrivial bi-interpretation phenomenon to be found amongst the set-theoretic models and theories satisfying ZF. In interpretation, one must inevitably discard set-theoretic information.
Theorem 1 (Enayat [Reference Enayat, van Eijck, Iemhoff and Joosten3])
-
(1)
 $\mathrm {ZF}$
is tight: no two distinct theories extending
$\mathrm {ZF}$
is tight: no two distinct theories extending
 $\mathrm {ZF}$
are bi-interpretable.
$\mathrm {ZF}$
are bi-interpretable. -
(2) Indeed,
 $\mathrm {ZF}$
is semantically tight: no two non-isomorphic models of
$\mathrm {ZF}$
is semantically tight: no two non-isomorphic models of
 $\mathrm {ZF}$
are bi-interpretable.
$\mathrm {ZF}$
are bi-interpretable. -
(3) What is more,
 $\mathrm {ZF}$
is solid: if M and N are mutually interpretable models of
$\mathrm {ZF}$
is solid: if M and N are mutually interpretable models of
 $\mathrm {ZF}$
and the isomorphism of M with its copy inside the interpreted copy of N in M is M-definable, then M and N are isomorphic.
$\mathrm {ZF}$
and the isomorphism of M with its copy inside the interpreted copy of N in M is M-definable, then M and N are isomorphic.
We introduce the concept of semantic tightness in this paper, since we find it very natural; Enayat had proved statements (1) and (3); we provide proofs in Section 6. One should view solidity as a strengthening of semantic tightness—it amounts essentially to a one-sided version of semantic tightness, requiring the models to be isomorphic not only in instances of bi-interpretation, but also even in the case that only one of the two interpretation isomorphisms is definable, rather than both of them. Thus, statement (3) is a strengthening of statement (2). And statement (2) is an easy strengthening of statement (1), as we explain in Corollary 14.
The proofs of these theorems seem to use the full strength of
![]() $\mathrm {ZF}$
, and Enayat had consequently inquired whether the solidity/tightness phenomenon somehow required the strength of
$\mathrm {ZF}$
, and Enayat had consequently inquired whether the solidity/tightness phenomenon somehow required the strength of
![]() $\mathrm {ZF}$
set theory. In this paper, we shall find support for that conjecture by establishing nontrivial instances of bi-interpretation in various natural weak set theories, including Zermelo–Fraenkel theory
$\mathrm {ZF}$
set theory. In this paper, we shall find support for that conjecture by establishing nontrivial instances of bi-interpretation in various natural weak set theories, including Zermelo–Fraenkel theory
![]() $\mathrm {ZFC}^{-}$
, without the power set axiom, and Zermelo set theory Z, without the replacement axiom.
$\mathrm {ZFC}^{-}$
, without the power set axiom, and Zermelo set theory Z, without the replacement axiom.
-
(1)
 $\mathrm {ZFC}^{-}$
is not solid.
$\mathrm {ZFC}^{-}$
is not solid. -
(2)
 $\mathrm {ZFC}^{-}$
is not semantically tight, not even for well-founded models: there are well-founded models of
$\mathrm {ZFC}^{-}$
is not semantically tight, not even for well-founded models: there are well-founded models of
 $\mathrm {ZFC}^{-}$
that are bi-interpretable, but not isomorphic.
$\mathrm {ZFC}^{-}$
that are bi-interpretable, but not isomorphic. -
(3) Indeed, it is relatively consistent with
 $\mathrm {ZFC}$
that
$\mathrm {ZFC}$
that
 $\langle H_{\omega _1},\in \rangle $
and
$\langle H_{\omega _1},\in \rangle $
and
 $\langle H_{\omega _2},\in \rangle $
are bi-interpretable and indeed bi-interpretation synonymous.
$\langle H_{\omega _2},\in \rangle $
are bi-interpretable and indeed bi-interpretation synonymous. -
(4)
 $\mathrm {ZFC}^{-}$
is not tight: there are distinct bi-interpretable extensions of
$\mathrm {ZFC}^{-}$
is not tight: there are distinct bi-interpretable extensions of
 $\mathrm {ZFC}^{-}$
.
$\mathrm {ZFC}^{-}$
. -
(5)
 $\mathrm {Z}$
is not semantically tight (and hence not solid): there are well-founded models of
$\mathrm {Z}$
is not semantically tight (and hence not solid): there are well-founded models of
 $\mathrm {Z}$
that are bi-interpretable, but not isomorphic.
$\mathrm {Z}$
that are bi-interpretable, but not isomorphic. -
(6) Indeed, every model of
 $\mathrm {ZF}$
is bi-interpretable with a transitive inner model of
$\mathrm {ZF}$
is bi-interpretable with a transitive inner model of
 $\mathrm {Z}$
in which the replacement axiom fails.
$\mathrm {Z}$
in which the replacement axiom fails. -
(7)
 $\mathrm {Z}$
is not tight: there are distinct bi-interpretable extensions of Z.
$\mathrm {Z}$
is not tight: there are distinct bi-interpretable extensions of Z.
These claims are made and proved in Theorems 18, 19, and 21–23. We shall in addition prove the following theorems on this theme:
-
(7) Nonisomorphic well-founded models of
 $\mathrm {ZF}$
set theory are never mutually interpretable.
$\mathrm {ZF}$
set theory are never mutually interpretable. -
(8) The Väänänen internal categoricity theorem does not hold for
 $\mathrm {ZFC}^{-}$
, not even for well-founded models.
$\mathrm {ZFC}^{-}$
, not even for well-founded models.
These are Theorems 15 and 17. Statement (8) concerns the existence of a model
![]() $\langle M,\in\!,\overline{\in} \rangle $
satisfying
$\langle M,\in\!,\overline{\in} \rangle $
satisfying
![]() , meaning
, meaning
![]() $\mathrm {ZFC}^{-}$
in the common language with both predicates, using either
$\mathrm {ZFC}^{-}$
in the common language with both predicates, using either
![]() $\in $
or
$\in $
or
![]() as the membership relation, such that
as the membership relation, such that
![]() $\langle M,\in \rangle $
and
$\langle M,\in \rangle $
and
![]() are not isomorphic.
are not isomorphic.
2 Interpretability in models
Let us briefly review what interpretability means. The reader is likely familiar with the usual interpretation of the complex field
![]() $\langle {\mathbb C},+,\cdot ,0,1,i \rangle $
in the real field
$\langle {\mathbb C},+,\cdot ,0,1,i \rangle $
in the real field
![]() $\langle {\mathbb R},+,\cdot \rangle $
, where one represents the complex number
$\langle {\mathbb R},+,\cdot \rangle $
, where one represents the complex number
![]() $a+bi$
with the pair of real numbers
$a+bi$
with the pair of real numbers
![]() $(a,\,b)$
. The point is that complex number field operations are definable operations on these pairs in the real field. Conversely, it turns out that the real field is not actually interpreted in the complex field (see [Reference Hamkins15] for an elementary account), but it is interpreted in the complex field equipped also with the complex conjugate operation
$(a,\,b)$
. The point is that complex number field operations are definable operations on these pairs in the real field. Conversely, it turns out that the real field is not actually interpreted in the complex field (see [Reference Hamkins15] for an elementary account), but it is interpreted in the complex field equipped also with the complex conjugate operation
![]() $z\mapsto \bar z$
, for in this case you can define the real line as the class of z for which
$z\mapsto \bar z$
, for in this case you can define the real line as the class of z for which
![]() $z=\bar z$
. The reader is also likely familiar with the usual interpretation of the rational field
$z=\bar z$
. The reader is also likely familiar with the usual interpretation of the rational field
![]() $\langle {\mathbb Q},+,\cdot \rangle $
in the integer ring
$\langle {\mathbb Q},+,\cdot \rangle $
in the integer ring
![]() $\langle {\mathbb Z},+,\cdot \rangle $
, where one represents rational numbers as equivalence classes of integer pairs
$\langle {\mathbb Z},+,\cdot \rangle $
, where one represents rational numbers as equivalence classes of integer pairs
![]() $(p,\,q)$
, written more conveniently as fractions
$(p,\,q)$
, written more conveniently as fractions
![]() $\frac pq$
, with
$\frac pq$
, with
![]() $q\neq 0$
, considered under the equivalence relation
$q\neq 0$
, considered under the equivalence relation
 $\frac pq\equiv \frac rs\mathrel {\leftrightarrow } ps=qr$
; one then defines the rational field structure by means of the familiar fractional arithmetic. Another example would be the structure of hereditarily finite sets
$\frac pq\equiv \frac rs\mathrel {\leftrightarrow } ps=qr$
; one then defines the rational field structure by means of the familiar fractional arithmetic. Another example would be the structure of hereditarily finite sets
![]() $\langle \mathrm {HF},\in \rangle $
, which is interpreted in the standard model of arithmetic
$\langle \mathrm {HF},\in \rangle $
, which is interpreted in the standard model of arithmetic
![]() $\langle {\mathbb N},+,\cdot ,0,1,< \rangle $
by the Ackermann relation, the relation for which
$\langle {\mathbb N},+,\cdot ,0,1,< \rangle $
by the Ackermann relation, the relation for which
![]() $n\mathrel {E} m$
just in case the nth binary digit of m is
$n\mathrel {E} m$
just in case the nth binary digit of m is
![]() $1$
; this relation is definable in arithmetic and the reader may verify that
$1$
; this relation is definable in arithmetic and the reader may verify that
![]() $\langle \mathrm {HF},\in \rangle \cong \langle {\mathbb N},E \rangle $
.
$\langle \mathrm {HF},\in \rangle \cong \langle {\mathbb N},E \rangle $
.
More generally, we interpret one model in another as follows.
Definition 2. A model
![]() $N= \langle N,R,\ldots \rangle $
in a first-order language
$N= \langle N,R,\ldots \rangle $
in a first-order language
![]() $\mathcal {L}_N$
is interpreted in another model M in language
$\mathcal {L}_N$
is interpreted in another model M in language
![]() $\mathcal {L}_M$
, if for some finite k there is an M-definable (possibly with parameters) class
$\mathcal {L}_M$
, if for some finite k there is an M-definable (possibly with parameters) class
![]() $N^*\subseteq M^k$
of k-tuples and M-definable relations
$N^*\subseteq M^k$
of k-tuples and M-definable relations
![]() $R^{N^*}$
on
$R^{N^*}$
on
![]() $N^*$
for relation symbols R in
$N^*$
for relation symbols R in
![]() $\mathcal {L}_N$
, as well as functions (defined via their graphs) and constants, and an M-definable equivalence relation
$\mathcal {L}_N$
, as well as functions (defined via their graphs) and constants, and an M-definable equivalence relation
![]() $\simeq $
on
$\simeq $
on
![]() $N^*$
, which is a congruence with respect to those relations, for which there is an isomorphism j from N to the quotient structure
$N^*$
, which is a congruence with respect to those relations, for which there is an isomorphism j from N to the quotient structure
 $\langle N^*,R^{N^*},\ldots \rangle /\simeq $
.
$\langle N^*,R^{N^*},\ldots \rangle /\simeq $
.

Figure 1 Model N is interpreted in model M.
In models supporting an internal encoding of finite tuples, such as the models of arithmetic or set theory, there is no need for k-tuples and one may regard
![]() directly. In models of arithmetic or models of set theory with a definable global well-order, there is no need for the equivalence relation
directly. In models of arithmetic or models of set theory with a definable global well-order, there is no need for the equivalence relation
![]() $\simeq $
, since one can pick canonical least representatives from each class. Theorem 9 shows furthermore that in models of
$\simeq $
, since one can pick canonical least representatives from each class. Theorem 9 shows furthermore that in models of
![]() $\mathrm {ZF}$
, even when there isn’t a definable global well-order, one can still omit the need for the equivalence relation
$\mathrm {ZF}$
, even when there isn’t a definable global well-order, one can still omit the need for the equivalence relation
![]() $\simeq $
by means of Scott’s trick: replace every equivalence class with the set of its
$\simeq $
by means of Scott’s trick: replace every equivalence class with the set of its
![]() $\in $
-minimal rank elements. Thus, in the model-theoretic terminology, the theory
$\in $
-minimal rank elements. Thus, in the model-theoretic terminology, the theory
![]() $\mathrm {ZF}$
is said to eliminate imaginaries. This trick doesn’t necessarily work, however, in models of
$\mathrm {ZF}$
is said to eliminate imaginaries. This trick doesn’t necessarily work, however, in models of
![]() $\mathrm {ZFC}^{-}$
, without the power set axiom, since in this theory the class of minimal rank members could still be a proper class, although in
$\mathrm {ZFC}^{-}$
, without the power set axiom, since in this theory the class of minimal rank members could still be a proper class, although in
![]() $\mathrm {ZF}$
it is always a set.
$\mathrm {ZF}$
it is always a set.
Definition 3. Models M and N are mutually interpretable, if each of them is interpreted in the other.

Figure 2 Models M and N are mutually interpreted.
Since (the quotient of)
![]() $N^*$
is isomorphic to N, we may find the corresponding copy of M inside it, and similarly we may find the copy of N inside
$N^*$
is isomorphic to N, we may find the corresponding copy of M inside it, and similarly we may find the copy of N inside
![]() $M^*$
, as illustrated below, where we have now suppressed the representation of the equivalence relation.
$M^*$
, as illustrated below, where we have now suppressed the representation of the equivalence relation.

Figure 3 Iterating the interpretations of models M and N.
One may simply compose the isomorphisms i and j to form an isomorphism
![]() $ji$
between M and
$ji$
between M and
![]() , which is now a definable subset of M (although the map
, which is now a definable subset of M (although the map
![]() $ji$
may not be definable). Because in the general case these are quotient structures, one should think of the map
$ji$
may not be definable). Because in the general case these are quotient structures, one should think of the map
![]() $ji$
as a relation rather than literally a function, since each object a in M is in effect associated with an entire equivalence class
$ji$
as a relation rather than literally a function, since each object a in M is in effect associated with an entire equivalence class
![]() $\bar a$
in the quotient structure of
$\bar a$
in the quotient structure of
![]() . Similarly, the composition
. Similarly, the composition
![]() $ij$
is an isomorphism of the structure N with
$ij$
is an isomorphism of the structure N with
![]() , which is now definable in N.
, which is now definable in N.
It will be instructive to notice that we have little reason in general to expect the map
![]() $ji$
to be definable in M, and this issue is the key difference between the mutual interpretation of models and their bi-interpretation.
$ji$
to be definable in M, and this issue is the key difference between the mutual interpretation of models and their bi-interpretation.
Definition 4. Models M and N are bi-interpretable, if they are mutually interpretable in such a way that the isomorphisms
![]() and
and
![]() arising by composing the interpretation maps are definable in the original models M and N, respectively.
arising by composing the interpretation maps are definable in the original models M and N, respectively.

Figure 4 Models M and N are bi-interpreted.
A somewhat cleaner picture emerges if we should simply identify the model N with its isomorphic copy
![]() $N^*$
and
$N^*$
and
![]() $M^*$
with
$M^*$
with
![]() . Let us now use i to denote the isomorphism of M with its copy
. Let us now use i to denote the isomorphism of M with its copy
![]() inside N, and j is the isomorphism of N with its copy
inside N, and j is the isomorphism of N with its copy
![]() inside
inside
![]() . This picture applies with either mutual interpretation or bi-interpretation, the difference being that in the case of bi-interpretation, the isomorphisms i and j are definable in M and N, respectively. Furthermore, by iterating these interpretations, in the case either of mutual interpretation or bi-interpretation, one achieves a fractal-like nested sequence of definable structures, with isomorphisms at each level. In the case of bi-interpretation, all these maps are definable in M, and any of the later maps is definable inside any of the successive copies of M or N in which it resides.
. This picture applies with either mutual interpretation or bi-interpretation, the difference being that in the case of bi-interpretation, the isomorphisms i and j are definable in M and N, respectively. Furthermore, by iterating these interpretations, in the case either of mutual interpretation or bi-interpretation, one achieves a fractal-like nested sequence of definable structures, with isomorphisms at each level. In the case of bi-interpretation, all these maps are definable in M, and any of the later maps is definable inside any of the successive copies of M or N in which it resides.

Figure 5 Iterated bi-interpretations.
An even stronger connection between models is the notion of bi-interpretation synonymy. This relation was introduced by de Bouvère in [Reference de Bouvère2] and recently deepened by Friedman and Visser in [Reference Friedman and Visser7].
Definition 5. Models M and N are bi-interpretation synonymous, if there is a bi-interpretation for which (i) the domains of the interpreted structures are in each case the whole structure; and (ii) the equivalence relations used in the interpretation are the identity relations on M and N.
In remarks after Theorem 16, we explain how every instance of bi-interpretation between models of
![]() $\mathrm {ZF}$
can be transformed to an instance of bi-interpretation synonymy.
$\mathrm {ZF}$
can be transformed to an instance of bi-interpretation synonymy.
3 Interpretability in theories
Let us now explain how interpretability works in theories, as opposed to models. At bottom, an interpretation of one theory in another amounts to a uniform method of interpreting a model of the first theory in any model of the second theory. Specifically, we interpret one theory
![]() $T_1$
in another theory
$T_1$
in another theory
![]() $T_2$
by providing a way to translate the
$T_2$
by providing a way to translate the
![]() $T_1$
language and structure into the language and structure available in
$T_1$
language and structure into the language and structure available in
![]() $T_2$
, in such a way that the translation of every
$T_2$
, in such a way that the translation of every
![]() $T_1$
theorem is provable in
$T_1$
theorem is provable in
![]() $T_2$
.
$T_2$
.
In somewhat more detail, the interpretation I of theory
![]() $T_1$
in language
$T_1$
in language
![]() $\mathcal {L}_1$
into theory
$\mathcal {L}_1$
into theory
![]() $T_2$
in language
$T_2$
in language
![]() $\mathcal {L}_2$
should provide, first of all, an
$\mathcal {L}_2$
should provide, first of all, an
![]() $\mathcal {L}_2$
-formula
$\mathcal {L}_2$
-formula
![]() $U(\bar x)$
that will define the interpreted domain of k-tuples
$U(\bar x)$
that will define the interpreted domain of k-tuples
![]() $\bar x=(x_1,\dots ,x_k)$
and an
$\bar x=(x_1,\dots ,x_k)$
and an
![]() $\mathcal {L}_2$
-expressible relation
$\mathcal {L}_2$
-expressible relation
![]() $\bar x =^I\bar y$
, the interpretation of equality, that
$\bar x =^I\bar y$
, the interpretation of equality, that
![]() $T_2$
proves is an equivalence relation on tuples in U. Next, for each relation symbol R of
$T_2$
proves is an equivalence relation on tuples in U. Next, for each relation symbol R of
![]() $\mathcal {L}_1$
, the interpretation should provide a translation
$\mathcal {L}_1$
, the interpretation should provide a translation
![]() $R^I$
as an
$R^I$
as an
![]() $\mathcal {L}_2$
formula of the same arity on U as R has in
$\mathcal {L}_2$
formula of the same arity on U as R has in
![]() $\mathcal {L}_1$
, and
$\mathcal {L}_1$
, and
![]() $T_2$
should prove that this relation is well-defined modulo
$T_2$
should prove that this relation is well-defined modulo
![]() $=^I\!$
. Finally, functions are to be handled by considering their graphs
$=^I\!$
. Finally, functions are to be handled by considering their graphs
![]() $f(\bar x)=y$
as definable relations and interpreting these graph relations, but with the proviso that
$f(\bar x)=y$
as definable relations and interpreting these graph relations, but with the proviso that
![]() $T_2$
proves that the interpreted relation is indeed well-defined and functional on U modulo
$T_2$
proves that the interpreted relation is indeed well-defined and functional on U modulo
![]() $=^I\!$
. Ultimately, therefore, the theory
$=^I\!$
. Ultimately, therefore, the theory
![]() $T_2$
will prove that
$T_2$
will prove that
![]() $=^I$
is a congruence with respect to the interpreted relations
$=^I$
is a congruence with respect to the interpreted relations
![]() $R^I$
and functions
$R^I$
and functions
![]() $f^I\!$
.
$f^I\!$
.
Having thus interpreted the atomic
![]() $\mathcal {L}_1$
structure, one may naturally extend the interpretation to all
$\mathcal {L}_1$
structure, one may naturally extend the interpretation to all
![]() $\mathcal {L}_1$
assertions as follows.
$\mathcal {L}_1$
assertions as follows.
-
•
 $(\varphi \wedge \psi )^I=\varphi ^I\wedge \psi ^I$
.
$(\varphi \wedge \psi )^I=\varphi ^I\wedge \psi ^I$
. -
•
 $(\neg \varphi )^I=\neg \varphi ^I$
.
$(\neg \varphi )^I=\neg \varphi ^I$
. -
•
 $(\exists x\, \varphi (x))^I=\exists \bar x\ U(\bar x)\wedge \varphi ^I(\bar x)$
.
$(\exists x\, \varphi (x))^I=\exists \bar x\ U(\bar x)\wedge \varphi ^I(\bar x)$
.
Finally, for this to be an interpretation of
![]() $T_1$
in
$T_1$
in
![]() $T_2$
, we insist that
$T_2$
, we insist that
![]() $T_2$
proves that
$T_2$
proves that
![]() $T_1$
holds for the interpreted structure, or in other words, that
$T_1$
holds for the interpreted structure, or in other words, that
Because the interpretation preserves the Boolean and quantifier structure of interpreted formulas, it suffices that
![]() $T_2$
should prove the interpretation
$T_2$
should prove the interpretation
![]() $\varphi ^I$
of each axiom
$\varphi ^I$
of each axiom
![]() $\varphi $
of
$\varphi $
of
![]() $T_1$
. It is clear that if
$T_1$
. It is clear that if
![]() $T_1$
is interpreted in
$T_1$
is interpreted in
![]() $T_2$
by interpretation I, then in any model
$T_2$
by interpretation I, then in any model
![]() $M\models T_2$
we may use the interpretation to define a model
$M\models T_2$
we may use the interpretation to define a model
![]() $N= \langle U,R^I,f^I,\ldots \rangle /=^I$
of
$N= \langle U,R^I,f^I,\ldots \rangle /=^I$
of
![]() $T_1$
. The domain of N will consist of the quotient of U by
$T_1$
. The domain of N will consist of the quotient of U by
![]() $=^I$
as M sees it, and the relations R and functions f of N, if any, will be exactly those defined by
$=^I$
as M sees it, and the relations R and functions f of N, if any, will be exactly those defined by
![]() $R^I$
and
$R^I$
and
![]() $f^I$
via the interpretation.
$f^I$
via the interpretation.
-
(1) Two theories
 $T_1$
and
$T_1$
and
 $T_2$
are mutually interpretable, if each of them is interpretable in the other.
$T_2$
are mutually interpretable, if each of them is interpretable in the other. -
(2) Two theories
 $T_1$
and
$T_1$
and
 $T_2$
are bi-interpretable, in contrast, if they are mutually interpretable by interpretations I and J, respectively, which are provably invertible, in that the theory
$T_2$
are bi-interpretable, in contrast, if they are mutually interpretable by interpretations I and J, respectively, which are provably invertible, in that the theory
 $T_1$
proves that the universe is isomorphic, by a definable isomorphism map, to the model resulting by first interpreting via J to get a model of
$T_1$
proves that the universe is isomorphic, by a definable isomorphism map, to the model resulting by first interpreting via J to get a model of
 $T_2$
and then interpreting via I to get a model of
$T_2$
and then interpreting via I to get a model of
 $T_1$
inside that model; and similarly the theory
$T_1$
inside that model; and similarly the theory
 $T_2$
proves that its universe is definably isomorphic to the model obtained by first interpreting via I to get a model of
$T_2$
proves that its universe is definably isomorphic to the model obtained by first interpreting via I to get a model of
 $T_1$
and then inside that model via J to get a model of
$T_1$
and then inside that model via J to get a model of
 $T_2$
.
$T_2$
.
With mutual interpretation of theories, one can start with a model M of
![]() $T_1$
and then use J to define within it a model
$T_1$
and then use J to define within it a model
![]() $N=J^M$
of
$N=J^M$
of
![]() $T_2$
, which can then define a model
$T_2$
, which can then define a model
![]() $M'=I^N$
of
$M'=I^N$
of
![]() $T_1$
again. With mutual interpretability, there is no guarantee that
$T_1$
again. With mutual interpretability, there is no guarantee that
![]() $M'$
and M are isomorphic or even elementarily equivalent, beyond the basic requirement that both are models of
$M'$
and M are isomorphic or even elementarily equivalent, beyond the basic requirement that both are models of
![]() $T_1$
. The much stronger requirements of bi-interpretability, in contrast, ensure that
$T_1$
. The much stronger requirements of bi-interpretability, in contrast, ensure that
![]() $M'$
and M are isomorphic, and furthermore isomorphic by a definable isomorphism relation, which the theory
$M'$
and M are isomorphic, and furthermore isomorphic by a definable isomorphism relation, which the theory
![]() $T_1$
proves is an isomorphism. And similarly when interpreting in models of
$T_1$
proves is an isomorphism. And similarly when interpreting in models of
![]() $T_2$
. Thus, with bi-interpretation, each theory sees how its own structure is faithfully copied via the definable isomorphisms
$T_2$
. Thus, with bi-interpretation, each theory sees how its own structure is faithfully copied via the definable isomorphisms
![]() $f_1$
and
$f_1$
and
![]() $f_2$
under iterations of the interpretations. With bi-interpretability, it therefore follows that
$f_2$
under iterations of the interpretations. With bi-interpretability, it therefore follows that
-
(1) For every
 $\mathcal {L}_1$
assertion
$\mathcal {L}_1$
assertion
 $\alpha $
$\alpha $
 $$ \begin{align*} T_1 \vDash \forall\bar x\ \alpha(x_1,\ldots,x_n) \leftrightarrow {\alpha^J}^I(f_1(x_1), f_1(x_2), \ldots, f_1(x_n)). \end{align*} $$
$$ \begin{align*} T_1 \vDash \forall\bar x\ \alpha(x_1,\ldots,x_n) \leftrightarrow {\alpha^J}^I(f_1(x_1), f_1(x_2), \ldots, f_1(x_n)). \end{align*} $$
-
(2) For every
 $\mathcal {L}_2$
assertion
$\mathcal {L}_2$
assertion
 $\beta $
$\beta $
 $$ \begin{align*} T_2 \vDash \forall\bar y\ \beta(y_1,\ldots,y_m) \leftrightarrow {\beta^I}^J(f_2(\;y_1), f_2(y_2), \ldots, f_2(y_m)). \end{align*} $$
$$ \begin{align*} T_2 \vDash \forall\bar y\ \beta(y_1,\ldots,y_m) \leftrightarrow {\beta^I}^J(f_2(\;y_1), f_2(y_2), \ldots, f_2(y_m)). \end{align*} $$
In light of the quotients by the equivalence relations, the functions
![]() $f_1$
and
$f_1$
and
![]() $f_2$
are more properly thought of as relations
$f_2$
are more properly thought of as relations
![]() $f_1(x)=\bar y$
well-defined with respect to those relations; they need not be functional on points, but only in the quotient.
$f_1(x)=\bar y$
well-defined with respect to those relations; they need not be functional on points, but only in the quotient.
4 Mutual interpretation of diverse set theories
Let us briefly establish the mutual interpretability phenomenon in set theory.
Theorem 7. The following theories are pairwise mutually interpretable.
-
(1)
 $\mathrm {ZF}$
;
$\mathrm {ZF}$
; -
(2)
 $\mathrm {ZFC}$
;
$\mathrm {ZFC}$
; -
(3)
 $\mathrm {ZFC}+\mathrm {GCH}$
;
$\mathrm {ZFC}+\mathrm {GCH}$
; -
(4)
 $\mathrm {ZFC}+V=L$
;
$\mathrm {ZFC}+V=L$
; -
(5)
 $\mathrm {ZF}+\neg \mathrm {AC}$
;
$\mathrm {ZF}+\neg \mathrm {AC}$
; -
(6)
 $\mathrm {ZFC}+\neg \mathrm {CH}$
;
$\mathrm {ZFC}+\neg \mathrm {CH}$
; -
(7)
 $\mathrm {ZFC}+\mathrm {MA}+\neg \mathrm {CH}$
;
$\mathrm {ZFC}+\mathrm {MA}+\neg \mathrm {CH}$
; -
(8)
 $\mathrm {ZFC}+\mathfrak {b}<\mathfrak {d}$
;
$\mathrm {ZFC}+\mathfrak {b}<\mathfrak {d}$
; -
(9) Any extension of
 $\mathrm {ZF}$
provably holding in a definable inner model or provably forceable by set forcing over such an inner model.
$\mathrm {ZF}$
provably holding in a definable inner model or provably forceable by set forcing over such an inner model.
Proof. In many of these instances, the interpretation is obtained by defining a suitable inner model of the desired theory. For example, in any model of
![]() $\mathrm {ZF}$
, we can define the constructible universe, and thereby find an interpretation of
$\mathrm {ZF}$
, we can define the constructible universe, and thereby find an interpretation of
![]() $\mathrm {ZFC}+V=L$
and hence
$\mathrm {ZFC}+V=L$
and hence
![]() $\mathrm {ZFC}+\mathrm {GCH}$
and so forth in
$\mathrm {ZFC}+\mathrm {GCH}$
and so forth in
![]() $\mathrm {ZF}$
. Some of the interpretations involve forcing, however, which we usually conceive as a method for constructing outer models, rather than defining models inside the original model. Nevertheless, one can use forcing via the Boolean ultrapower method to define interpreted models of the forced theory inside the original model. Let us illustrate the general method by explaining how to interpret the theory
$\mathrm {ZF}$
. Some of the interpretations involve forcing, however, which we usually conceive as a method for constructing outer models, rather than defining models inside the original model. Nevertheless, one can use forcing via the Boolean ultrapower method to define interpreted models of the forced theory inside the original model. Let us illustrate the general method by explaining how to interpret the theory
![]() $\mathrm {ZFC}+\neg \mathrm {CH}$
in
$\mathrm {ZFC}+\neg \mathrm {CH}$
in
![]() $\mathrm {ZF}$
. In
$\mathrm {ZF}$
. In
![]() $\mathrm {ZF}$
, we may define L, and thereby define a model of
$\mathrm {ZF}$
, we may define L, and thereby define a model of
![]() $\mathrm {ZFC}$
with a definable global well-order. Inside that model, consider the forcing notion
$\mathrm {ZFC}$
with a definable global well-order. Inside that model, consider the forcing notion
![]() $\mathop {\mathrm {Add}}(\omega ,\omega _2)$
to add
$\mathop {\mathrm {Add}}(\omega ,\omega _2)$
to add
![]() $\omega _2$
many Cohen reals. Let
$\omega _2$
many Cohen reals. Let
![]() ${\mathbb B}$
be the Boolean completion of this forcing notion in L, and let
${\mathbb B}$
be the Boolean completion of this forcing notion in L, and let
![]() $U\subseteq {\mathbb B}$
be the L-least ultrafilter on this Boolean algebra. Using the Boolean ultrapower method, we define the quotient structure
$U\subseteq {\mathbb B}$
be the L-least ultrafilter on this Boolean algebra. Using the Boolean ultrapower method, we define the quotient structure
![]() $L^{\mathbb B}/U$
on the class of
$L^{\mathbb B}/U$
on the class of
![]() ${\mathbb B}$
-names by the relations:
${\mathbb B}$
-names by the relations:
 $$ \begin{align*} \begin{array}{rcl}\sigma=_U\tau & \mathrel{\Longleftrightarrow} & \mathopen{\lbrack\!\lbrack}\,\sigma=\tau\,\mathclose{\rbrack\!\rbrack}\in U; \\[6pt] \sigma\in_U\tau & \mathrel{\Longleftrightarrow} & \mathopen{\lbrack\!\lbrack}\,\sigma\in\tau\,\mathclose{\rbrack\!\rbrack}\in U. \end{array}\end{align*} $$
$$ \begin{align*} \begin{array}{rcl}\sigma=_U\tau & \mathrel{\Longleftrightarrow} & \mathopen{\lbrack\!\lbrack}\,\sigma=\tau\,\mathclose{\rbrack\!\rbrack}\in U; \\[6pt] \sigma\in_U\tau & \mathrel{\Longleftrightarrow} & \mathopen{\lbrack\!\lbrack}\,\sigma\in\tau\,\mathclose{\rbrack\!\rbrack}\in U. \end{array}\end{align*} $$
The model
![]() $L^{\mathbb B}/U$
consists of the
$L^{\mathbb B}/U$
consists of the
![]() $=_U$
equivalence classes of
$=_U$
equivalence classes of
![]() ${\mathbb B}$
-names in L under the membership relation
${\mathbb B}$
-names in L under the membership relation
![]() $\in _U$
. The Boolean ultrapower Łoś theorem shows that
$\in _U$
. The Boolean ultrapower Łoś theorem shows that
![]() $L^{\mathbb B}/U$
satisfies every statement
$L^{\mathbb B}/U$
satisfies every statement
![]() $\varphi $
whose Boolean value
$\varphi $
whose Boolean value
![]() $\mathopen {\lbrack \!\lbrack }\,\varphi \,\mathclose {\rbrack \!\rbrack }$
is in U, and so this is a model of
$\mathopen {\lbrack \!\lbrack }\,\varphi \,\mathclose {\rbrack \!\rbrack }$
is in U, and so this is a model of
![]() $\mathrm {ZFC}+\neg \mathrm {CH}$
. We should like to emphasize that there is no need in the Boolean ultrapower construction for the ultrafilter U to be generic in any sense, and
$\mathrm {ZFC}+\neg \mathrm {CH}$
. We should like to emphasize that there is no need in the Boolean ultrapower construction for the ultrafilter U to be generic in any sense, and
![]() $U\in L$
is completely fine (see extensive explanation in [Reference Hamkins and Seabold18, Section 2]). By using the L-least such ultrafilter U on
$U\in L$
is completely fine (see extensive explanation in [Reference Hamkins and Seabold18, Section 2]). By using the L-least such ultrafilter U on
![]() ${\mathbb B}$
, therefore, we eliminate the need for parameters—the Boolean ultrapower quotient
${\mathbb B}$
, therefore, we eliminate the need for parameters—the Boolean ultrapower quotient
![]() $L^{\mathbb B}/U$
is a definable interpreted model of
$L^{\mathbb B}/U$
is a definable interpreted model of
![]() $\mathrm {ZFC}+\neg \mathrm {CH}$
inside the original model, as desired.
$\mathrm {ZFC}+\neg \mathrm {CH}$
inside the original model, as desired.
The same method works generally. Any forceable theory will hold in an interpreted model, using the forcing notion and the ultrafilter U in the original model as parameters; when forcing over L or
![]() $\mathrm {HOD}$
one may use the corresponding definable well-order to eliminate the need for parameters, as we did above. Any theory that is provably forceable over a definable inner model will be forceable over L and therefore amenable to this parameter-elimination method. ⊣
$\mathrm {HOD}$
one may use the corresponding definable well-order to eliminate the need for parameters, as we did above. Any theory that is provably forceable over a definable inner model will be forceable over L and therefore amenable to this parameter-elimination method. ⊣
Apter, Gitman, and Hamkins [Reference Apter, Gitman and Hamkins1] similarly establish in numerous instances that one can find transitive inner models
![]() $ \langle M,\in \rangle $
of certain large cardinal theories usually obtained by forcing. For example, if there is a supercompact cardinal, then there is a definable transitive inner model with a Laver-indestructible supercompact cardinal, and another inner model with a non-indestructible supercompact cardinal, and another with a strongly compact cardinal that was also the least measurable cardinal, and so on.
$ \langle M,\in \rangle $
of certain large cardinal theories usually obtained by forcing. For example, if there is a supercompact cardinal, then there is a definable transitive inner model with a Laver-indestructible supercompact cardinal, and another inner model with a non-indestructible supercompact cardinal, and another with a strongly compact cardinal that was also the least measurable cardinal, and so on.
As we emphasized in the introduction of this article, Theorem 7 is concerned with mutual interpretation rather than bi-interpretation. The interpretation methods used in this theorem are not invertible, and when following an interpretation, one cannot in general get back to the original model. Every interpretation of one set theory in another will inevitably involve a loss of set-theoretic information in the models in which it is undertaken. The main lesson of Enayat’s theorem (Theorem 13) is that this problem is unavoidable: in fact, none of the theories above are bi-interpretable and there is no nontrivial bi-interpretation phenomenon to be found in set theory at the strength of
![]() $\mathrm {ZF}$
.
$\mathrm {ZF}$
.
One might have hoped to invert the forcing extension interpretations by means of the ground-model definability theorem ([Reference Laver19], see also [Reference Fuchs, Hamkins and Reitz8]), which asserts that every ground model M is definable (using parameters) in its forcing extensions
![]() $M[G]$
by set forcing. That is, since we have interpreted the theory of the forcing extension, can’t we reinterpret the ground model by means of the ground-model definability theorem? The problem with this idea is that the forcing Boolean ultrapower model
$M[G]$
by set forcing. That is, since we have interpreted the theory of the forcing extension, can’t we reinterpret the ground model by means of the ground-model definability theorem? The problem with this idea is that the forcing Boolean ultrapower model
![]() $M^{{\mathbb B}}/U$
that we used in Theorem 7 is not actually a forcing extension of M, but rather a forcing extension of its own ground model
$M^{{\mathbb B}}/U$
that we used in Theorem 7 is not actually a forcing extension of M, but rather a forcing extension of its own ground model
 $\check M/U$
, which in general is not the same as M, although it is an elementary extension of M by the Boolean ultrapower map
$\check M/U$
, which in general is not the same as M, although it is an elementary extension of M by the Boolean ultrapower map
 $i:M\to \check M/U$
. This map is an isomorphism only when U is M-generic, which is not true here for nontrivial forcing because
$i:M\to \check M/U$
. This map is an isomorphism only when U is M-generic, which is not true here for nontrivial forcing because
![]() $U\in M$
. Indeed, the Boolean ultrapower model
$U\in M$
. Indeed, the Boolean ultrapower model
 $\check M/U$
is usually ill-founded, even when M is well founded (although there can be instances of well-founded Boolean ultrapowers connected with very large cardinals; see [Reference Hamkins and Seabold18]). Nevertheless, the method does allow us to mutually interpret the theory of M with the theory of what it would be like in a forcing extension of M after forcing with
$\check M/U$
is usually ill-founded, even when M is well founded (although there can be instances of well-founded Boolean ultrapowers connected with very large cardinals; see [Reference Hamkins and Seabold18]). Nevertheless, the method does allow us to mutually interpret the theory of M with the theory of what it would be like in a forcing extension of M after forcing with
![]() ${\mathbb B}$
, as explained by the following theorem:
${\mathbb B}$
, as explained by the following theorem:
Theorem 8. For any model
![]() $M\models \mathrm {ZFC}$
and any notion of forcing
$M\models \mathrm {ZFC}$
and any notion of forcing
![]() ${\mathbb B}\in M$
, the theory of M with constants for every element of M is mutually interpretable with the theory, in the forcing language with constants for every
${\mathbb B}\in M$
, the theory of M with constants for every element of M is mutually interpretable with the theory, in the forcing language with constants for every
![]() ${\mathbb B}$
-name in M, asserting that the universe is a forcing extension via
${\mathbb B}$
-name in M, asserting that the universe is a forcing extension via
![]() ${\mathbb B}$
of a ground model with the theory of M.
${\mathbb B}$
of a ground model with the theory of M.
Proof. The latter theory, describing what it would be like in a forcing extension of M by
![]() ${\mathbb B}$
, is the same theory as used in the naturalist account of forcing in [Reference Hamkins12]. The theory has a predicate symbol
${\mathbb B}$
, is the same theory as used in the naturalist account of forcing in [Reference Hamkins12]. The theory has a predicate symbol
![]() $\check M$
for an inner model and asserts that this satisfies the same theory as M and that the universe is a forcing extension
$\check M$
for an inner model and asserts that this satisfies the same theory as M and that the universe is a forcing extension
![]() $\check M[G]$
for some
$\check M[G]$
for some
![]() $\check M$
-generic filter
$\check M$
-generic filter
![]() $G\subseteq \check {\mathbb B}$
. To be clear, we are not saying that the model M is mutually interpretable with some actual forcing extension model
$G\subseteq \check {\mathbb B}$
. To be clear, we are not saying that the model M is mutually interpretable with some actual forcing extension model
![]() $M[G]$
, but rather only that the theory of M is mutually interpretable with the theory expressing what it is like in such a forcing extension. We allow parameters in the interpretation definitions, although in many cases these are eliminable. Assume that
$M[G]$
, but rather only that the theory of M is mutually interpretable with the theory expressing what it is like in such a forcing extension. We allow parameters in the interpretation definitions, although in many cases these are eliminable. Assume that
![]() ${\mathbb B}$
is a complete Boolean algebra in M, and let
${\mathbb B}$
is a complete Boolean algebra in M, and let
![]() $U\subseteq {\mathbb B}$
be an ultrafilter in M. Inside M, we may define the forcing Boolean ultrapower
$U\subseteq {\mathbb B}$
be an ultrafilter in M. Inside M, we may define the forcing Boolean ultrapower
![]() $M^{{\mathbb B}}/U$
as described above, and this is a model of the theory asserting (in the forcing language) that the universe is a forcing extension of
$M^{{\mathbb B}}/U$
as described above, and this is a model of the theory asserting (in the forcing language) that the universe is a forcing extension of
![]() $\check M$
by
$\check M$
by
![]() $\check {\mathbb B}$
. That this is true is part of the theory of M, and so this interpretation works inside any model of the theory of M. Conversely, inside any model of the latter theory, we can define the ground model
$\check {\mathbb B}$
. That this is true is part of the theory of M, and so this interpretation works inside any model of the theory of M. Conversely, inside any model of the latter theory, we can define the ground model
![]() $\check M$
, which will be a model of the theory of M. ⊣
$\check M$
, which will be a model of the theory of M. ⊣
5 Further background on interpreting in models of set theory
Before getting to the main results, let us prove some further useful background material on interpretations in models of set theory. We have already mentioned in the remarks after Definition 2 that in models of set theory, we do not need to use k-tuples in interpretation, since we have definable pairing functions. But also, it turns out that when interpreting in a model of
![]() $\mathrm {ZF}$
, we do not need the equivalence relation:
$\mathrm {ZF}$
, we do not need the equivalence relation:
Theorem 9. If a structure A is interpreted in a model of
![]() $\mathrm {ZF}$
set theory, then there is an interpretation in which the equivalence relation is the identity.
$\mathrm {ZF}$
set theory, then there is an interpretation in which the equivalence relation is the identity.
This theorem appears as Exercise 2 of Section 4.4 of [Reference Hodges17].
Proof. The argument amounts to what is known as “Scott’s trick.” If
![]() $\simeq $
is a definable equivalence relation in a model
$\simeq $
is a definable equivalence relation in a model
![]() $M\models \mathrm {ZF}$
, then let us replace every equivalence class
$M\models \mathrm {ZF}$
, then let us replace every equivalence class
![]() $[a]_{\simeq }$
with the Scott class
$[a]_{\simeq }$
with the Scott class
![]() $[a]^{*}_{\simeq }$
, which consists of the elements of the equivalence class having minimal possible
$[a]^{*}_{\simeq }$
, which consists of the elements of the equivalence class having minimal possible
![]() $\in $
-rank in that class. This is a definable set in M, and from the Scott class one can identity the original
$\in $
-rank in that class. This is a definable set in M, and from the Scott class one can identity the original
![]() $\simeq $
equivalence class. So we can replace the original interpretation modulo
$\simeq $
equivalence class. So we can replace the original interpretation modulo
![]() $\simeq $
with the induced interpretation defined on the Scott classes. And since two Scott classes correspond to the same interpreted object if and only if they are equal, we have thereby eliminated the need for the equivalence relation. ⊣
$\simeq $
with the induced interpretation defined on the Scott classes. And since two Scott classes correspond to the same interpreted object if and only if they are equal, we have thereby eliminated the need for the equivalence relation. ⊣
This proof does not work in
![]() $\mathrm {ZFC}^{-}$
, that is, in set theory without the power set axiom, because the minimal rank instances from a class may still form a proper class, and so Scott’s trick doesn’t succeed in reducing the class to a set. And so we had asked the question, posting it on MathOverflow [Reference Hamkins14]:
$\mathrm {ZFC}^{-}$
, that is, in set theory without the power set axiom, because the minimal rank instances from a class may still form a proper class, and so Scott’s trick doesn’t succeed in reducing the class to a set. And so we had asked the question, posting it on MathOverflow [Reference Hamkins14]:
Question 10. Is there a structure that is interpretable in a model of
![]() $\mathrm {ZFC}^{-}$
, but only by means of a nontrivial equivalence relation?
$\mathrm {ZFC}^{-}$
, but only by means of a nontrivial equivalence relation?
The question was answered affirmative by Gabe Goldberg [Reference Goldberg11], assuming the consistency of large cardinals. He pointed out that if
![]() $\mathrm {AD}^{L({\mathbb R})}$
holds and
$\mathrm {AD}^{L({\mathbb R})}$
holds and
![]() $\delta ^1_2=\omega _2$
, there is a projectively definable prewellordering on the reals of order type
$\delta ^1_2=\omega _2$
, there is a projectively definable prewellordering on the reals of order type
![]() $\omega _2$
, and so the order structure
$\omega _2$
, and so the order structure
![]() $\langle \omega _2,< \rangle $
is interpretable in
$\langle \omega _2,< \rangle $
is interpretable in
![]() $ \langle H_{\omega _1},\in \rangle $
, but there is no definable order in this structure of type
$ \langle H_{\omega _1},\in \rangle $
, but there is no definable order in this structure of type
![]() $\omega _2$
, because there is, he proves, no injection of
$\omega _2$
, because there is, he proves, no injection of
![]() $\omega _2$
into
$\omega _2$
into
![]() $H_{\omega _1}$
in
$H_{\omega _1}$
in
![]() $L({\mathbb R})$
. Therefore, under these assumptions, we have a structure interpretable in a model of
$L({\mathbb R})$
. Therefore, under these assumptions, we have a structure interpretable in a model of
![]() $\mathrm {ZFC}^{-}$
, using a nontrivial equivalence relation, but not without. Can one produce an example in
$\mathrm {ZFC}^{-}$
, using a nontrivial equivalence relation, but not without. Can one produce an example in
![]() $\mathrm {ZFC}$
?
$\mathrm {ZFC}$
?
Next, we establish the phenomenon of automatic bi-interpretability for well-founded models of set theory.
Theorem 11. If a well-founded model M of
![]() $\mathrm {ZF}^-$
is interpreted in itself via
$\mathrm {ZF}^-$
is interpreted in itself via
![]() , then the interpretation isomorphism map i is unique and furthermore, it is definable in M.
, then the interpretation isomorphism map i is unique and furthermore, it is definable in M.
Proof. Assume that M is a well-founded model of
![]() $\mathrm {ZF}^-$
, which we may assume without loss to be transitive, and that
$\mathrm {ZF}^-$
, which we may assume without loss to be transitive, and that
![]() $\langle M,\in \rangle $
is interpreted in itself via the interpretation map
$\langle M,\in \rangle $
is interpreted in itself via the interpretation map
![]() , where
, where
![]() is a definable class in M with a definable relation
is a definable class in M with a definable relation
![]() , and
, and
![]() $\simeq $
is a definable equivalence relation on
$\simeq $
is a definable equivalence relation on
![]() , which is a congruence with respect to
, which is a congruence with respect to
![]() .
.

Figure 6 Self interpretation.
Since models of set theory admit pair functions, however, we may assume directly that
![]() rather than
rather than
![]() with k-tuples.
with k-tuples.
Let
![]() be the inverse map, viewed as a map on
be the inverse map, viewed as a map on
![]() . Since i is an isomorphism, it follows that
. Since i is an isomorphism, it follows that
![]() , and consequently,
, and consequently,
![]() . Thus,
. Thus,
![]() $\pi $
is precisely the Mostowski collapse of the relation
$\pi $
is precisely the Mostowski collapse of the relation
![]() on
on
![]() , which is well-founded precisely because it has a quotient that is isomorphic to
, which is well-founded precisely because it has a quotient that is isomorphic to
![]() $\langle M,\in \rangle $
. Thus, the map i is unique, for it is precisely the inverse of the Mostowski collapse of
$\langle M,\in \rangle $
. Thus, the map i is unique, for it is precisely the inverse of the Mostowski collapse of
 , as computed externally to M in the context where i exists.
, as computed externally to M in the context where i exists.
What remains is to show that M itself can undertake this Mostowski collapse. While the
![]() $\simeq $
-quotient of
$\simeq $
-quotient of
![]() is a well-founded extensional relation, the subtle issue is that
is a well-founded extensional relation, the subtle issue is that
![]() may not literally be set-like, since the
may not literally be set-like, since the
![]() $\simeq $
-equivalence classes themselves may be proper classes, and in
$\simeq $
-equivalence classes themselves may be proper classes, and in
![]() $\mathrm {ZF}^-$
we are not necessarily able to pick representatives globally from the equivalence classes. So it may not be immediately clear that M can undertake the Mostowski collapse. But, we show, it can.
$\mathrm {ZF}^-$
we are not necessarily able to pick representatives globally from the equivalence classes. So it may not be immediately clear that M can undertake the Mostowski collapse. But, we show, it can.
In M, let I be the class of pairs
![]() $(a,\bar a)$
where
$(a,\bar a)$
where
![]() $a\in M$
and
$a\in M$
and
![]() and there is a set
and there is a set
![]() with (i)
with (i)
![]() ; (ii)
; (ii)
![]() is transitive with respect to
is transitive with respect to
![]() modulo
modulo
![]() $\simeq $
, in the sense that if
$\simeq $
, in the sense that if
![]() , then there is some
, then there is some
![]() such that
such that
![]() $x\simeq x'$
; and (iii)
$x\simeq x'$
; and (iii)
 is isomorphic to
is isomorphic to
![]() $\left \langle \mathop {\mathrm {TC}}(\left \{{a}\right \}),\in \right \rangle $
. Note that if
$\left \langle \mathop {\mathrm {TC}}(\left \{{a}\right \}),\in \right \rangle $
. Note that if
![]() $(a,\bar a)$
are like this, then the isomorphism will be exactly the inverse of the Mostowski collapse of
$(a,\bar a)$
are like this, then the isomorphism will be exactly the inverse of the Mostowski collapse of
 .
.
We claim by
![]() -induction (externally to M) that every
-induction (externally to M) that every
![]() is associated in this way with some
is associated in this way with some
![]() $a\in M$
, and furthermore, the association I is simply the map
$a\in M$
, and furthermore, the association I is simply the map
![]() $i:a\mapsto \bar a$
. To see this, suppose
$i:a\mapsto \bar a$
. To see this, suppose
![]() and every
and every
![]() -element of
-element of
![]() $\bar a$
is associated via I. Since i is an isomorphism, there is some a such that
$\bar a$
is associated via I. Since i is an isomorphism, there is some a such that
![]() $i(a)=\bar a$
. Inductively, every
$i(a)=\bar a$
. Inductively, every
![]() is associated with some b for which
is associated with some b for which
![]() $i(b)=\bar b$
, and all such b are necessarily elements of a. So M can see that every
$i(b)=\bar b$
, and all such b are necessarily elements of a. So M can see that every
![]() is associated by the class I with a unique element
is associated by the class I with a unique element
![]() $b\in a$
. For each b, there are various sets
$b\in a$
. For each b, there are various sets
![]() with largest element
with largest element
![]() $\bar b$
realizing that
$\bar b$
realizing that
![]() $(b,\bar b)\in I$
. By the collection axiom, we can find a single set B containing such a set for every
$(b,\bar b)\in I$
. By the collection axiom, we can find a single set B containing such a set for every
![]() $b\in a$
, serving as a single witnessing set. Let
$b\in a$
, serving as a single witnessing set. Let
![]() , where
, where
![]() $\bar a$
is a representative of the
$\bar a$
is a representative of the
![]() $\simeq $
-class of
$\simeq $
-class of
![]() $i(a)$
. This is a set in M, it is contained in
$i(a)$
. This is a set in M, it is contained in
![]() , and it is transitive with respect to
, and it is transitive with respect to
![]() modulo
modulo
![]() $\simeq $
. Since
$\simeq $
. Since
![]() , the Mostowski collapse of
, the Mostowski collapse of
 agrees with the collapse of
agrees with the collapse of
 , and so sends
, and so sends
![]() $\bar b$
to b, for every
$\bar b$
to b, for every
![]() $b\in a$
. So this set
$b\in a$
. So this set
![]() witnesses that
witnesses that
![]() $(a,\bar a)\in I$
, and agrees with i on a. So the map i is definable in M, as desired. ⊣
$(a,\bar a)\in I$
, and agrees with i on a. So the map i is definable in M, as desired. ⊣
Notice that Theorem 11 is not true if one drops the well-foundedness assumption. For example, on general model-theoretic grounds there must be models
![]() $M\models \mathrm {ZF}^{-}$
with nontrivial automorphisms
$M\models \mathrm {ZF}^{-}$
with nontrivial automorphisms
![]() $i:M\to M$
, and any such map is an interpretation of M in itself (as itself), but such an automorphism can never be definable. Similarly, if
$i:M\to M$
, and any such map is an interpretation of M in itself (as itself), but such an automorphism can never be definable. Similarly, if
![]() $\mathrm {ZFC}$
is consistent, then there is a countable computably saturated model
$\mathrm {ZFC}$
is consistent, then there is a countable computably saturated model
 $\left \langle M,\in ^M\right \rangle \models \mathrm {ZFC}$
, and such a model contains an isomorphic copy of itself as an element m, an observation due to [Reference Schlipf21, Corollary 3.3]; see also [Reference Gitman and Hamkins9, Lemma 7]. This provides an interpretation of M in itself, using m as a parameter, but the isomorphism cannot be definable nor even amenable to M, since M cannot allow a definable injection from the universe to a set.
$\left \langle M,\in ^M\right \rangle \models \mathrm {ZFC}$
, and such a model contains an isomorphic copy of itself as an element m, an observation due to [Reference Schlipf21, Corollary 3.3]; see also [Reference Gitman and Hamkins9, Lemma 7]. This provides an interpretation of M in itself, using m as a parameter, but the isomorphism cannot be definable nor even amenable to M, since M cannot allow a definable injection from the universe to a set.
Corollary 12. Every instance of mutual interpretation amongst well-founded models of
![]() $\mathrm {ZF}^-$
is a bi-interpretation. Indeed, if M is a well-founded model of
$\mathrm {ZF}^-$
is a bi-interpretation. Indeed, if M is a well-founded model of
![]() $\mathrm {ZF}^-$
and mutually interpreted with any structure N of any theory, as in the Figure 7 below, then the isomorphism
$\mathrm {ZF}^-$
and mutually interpreted with any structure N of any theory, as in the Figure 7 below, then the isomorphism
![]() is definable in M.
is definable in M.

Figure 7 Mutual interpretation of well-founded models.
Proof. This follows immediately from Theorem 11, since any instance of mutual interpretation leads to an instance of a model being interpreted inside itself, and so by Theorem 11 the interpretation maps will be definable. ⊣
We are unsure whether we can achieve the half-way situation, where a transitive model
![]() $M\models \mathrm {ZF}^-$
is mutually interpreted with some nonstandard model
$M\models \mathrm {ZF}^-$
is mutually interpreted with some nonstandard model
![]() $N\models \mathrm {ZF}^-$
, without being bi-interpreted.
$N\models \mathrm {ZF}^-$
, without being bi-interpreted.
6 Bi-interpretation does not occur in models of
 $\mathrm {ZF}$
$\mathrm {ZF}$
Finally, we come to the heart of the paper, concerning the extent of bi-interpretation in set theory. Let us begin with Enayat’s theorem, which will show that distinct models of
![]() $\mathrm {ZF}$
are never bi-interpretable. As we mentioned earlier, a theory T is semantically tight, if any two bi-interpretable models of T are isomorphic. Strengthening this, a theory T is solid, if whenever M and N are mutually interpreted models of T and there is an M-definable isomorphism of M with its copy
$\mathrm {ZF}$
are never bi-interpretable. As we mentioned earlier, a theory T is semantically tight, if any two bi-interpretable models of T are isomorphic. Strengthening this, a theory T is solid, if whenever M and N are mutually interpreted models of T and there is an M-definable isomorphism of M with its copy
![]() inside the copy of N defined in M, then M and N are isomorphic. Thus, solidity strengthens semantic tightness, because it requires the models to be isomorphic even when one has essentially only half of a bi-interpretation, in that only one side of the interpretation needs to be definable in the model, rather than both.
inside the copy of N defined in M, then M and N are isomorphic. Thus, solidity strengthens semantic tightness, because it requires the models to be isomorphic even when one has essentially only half of a bi-interpretation, in that only one side of the interpretation needs to be definable in the model, rather than both.
Theorem 13 (Enayat [Reference Enayat, van Eijck, Iemhoff and Joosten3])
![]() $\mathrm {ZF}$
is solid.
$\mathrm {ZF}$
is solid.
Proof. Assume that M and N are mutually interpreted models of
![]() $\mathrm {ZF}$
, where N is definable in M and
$\mathrm {ZF}$
, where N is definable in M and
![]() is a definable copy of M inside N, with an isomorphism
is a definable copy of M inside N, with an isomorphism
![]() that is definable in M, as illustrated in the Figure 8.
that is definable in M, as illustrated in the Figure 8.

Figure 8 Bi-interpretation in a model of ZF.
Suppose that N thinks A is a nonempty subclass of
![]() . Consider the pre-image
. Consider the pre-image
![]() $A'=\{\,{i^{-1}(x)\mid x\in ^N A}\,\}$
, which is a nonempty class in M. So it must have an
$A'=\{\,{i^{-1}(x)\mid x\in ^N A}\,\}$
, which is a nonempty class in M. So it must have an
![]() $\in ^M$
-minimal element
$\in ^M$
-minimal element
![]() $a \in ^M A'$
. It follows that
$a \in ^M A'$
. It follows that
![]() $i(a)$
is an
$i(a)$
is an
![]() -minimal element of A, and so N sees
-minimal element of A, and so N sees
![]() as well founded. Because of this fact, the ordinals of the models will be comparable, and they will have some ordinals isomorphically in common. We claim that for these common ordinals, the rank-initial segments of M, N, and
as well founded. Because of this fact, the ordinals of the models will be comparable, and they will have some ordinals isomorphically in common. We claim that for these common ordinals, the rank-initial segments of M, N, and
![]() are isomorphic. Specifically, if
are isomorphic. Specifically, if
![]() $\alpha $
is an ordinal in M, which is isomorphic to the ordinal
$\alpha $
is an ordinal in M, which is isomorphic to the ordinal
![]() in
in
![]() , and this happens to be isomorphic in N to an ordinal
, and this happens to be isomorphic in N to an ordinal
![]() $\alpha ^*$
in N, then we claim that N can see that
$\alpha ^*$
in N, then we claim that N can see that
 ${\left \langle V_{\alpha ^*},\in \right \rangle }^N$
is isomorphic to
${\left \langle V_{\alpha ^*},\in \right \rangle }^N$
is isomorphic to
 , which we know is isomorphic to
, which we know is isomorphic to
 ${\left \langle V_\alpha ,\in \right \rangle }^M$
. This is certainly true when
${\left \langle V_\alpha ,\in \right \rangle }^M$
. This is certainly true when
![]() $\alpha =0$
, and if it is true at
$\alpha =0$
, and if it is true at
![]() $\alpha $
, then it will also be true at
$\alpha $
, then it will also be true at
![]() $\alpha +1$
, because every subset of
$\alpha +1$
, because every subset of
![]() $V_\alpha ^N$
exists also as a class in M and therefore can be pushed via i to the corresponding subset of
$V_\alpha ^N$
exists also as a class in M and therefore can be pushed via i to the corresponding subset of
 ; and conversely, every subset of
; and conversely, every subset of
 in
in
![]() exists also as a class in N and can be pulled back by the isomorphism with
exists also as a class in N and can be pulled back by the isomorphism with
![]() $V_{\alpha ^*}^N$
. So in N we may extend the isomorphism canonically from
$V_{\alpha ^*}^N$
. So in N we may extend the isomorphism canonically from
 to
to
 . Furthermore, because
. Furthermore, because
![]() $V_{\alpha ^*}^N$
is transitive in N and transitive sets are rigid, the isomorphisms must be unique, and so at limit stages the isomorphism will simply be the coherent union of the isomorphisms at the earlier stages.
$V_{\alpha ^*}^N$
is transitive in N and transitive sets are rigid, the isomorphisms must be unique, and so at limit stages the isomorphism will simply be the coherent union of the isomorphisms at the earlier stages.
If the ordinals of N run out before the ordinals of M, then
![]() ${\mathrm {Ord}}^N$
is isomorphic to an ordinal
${\mathrm {Ord}}^N$
is isomorphic to an ordinal
![]() $\lambda $
in M and hence to
$\lambda $
in M and hence to
![]() in
in
![]() . In this case, the isomorphism from the previous paragraph will mean that
. In this case, the isomorphism from the previous paragraph will mean that
 , which is isomorphic to
, which is isomorphic to
![]() $V_\lambda ^M$
. So M will see that N is bijective with a set. But M has a bijection of itself with
$V_\lambda ^M$
. So M will see that N is bijective with a set. But M has a bijection of itself with
![]() , which is contained in N. So M will think that the universe is bijective with a set, which is impossible in
, which is contained in N. So M will think that the universe is bijective with a set, which is impossible in
![]() $\mathrm {ZF}$
.
$\mathrm {ZF}$
.
If in contrast the ordinals of M and hence
![]() run out before the ordinals of N, then N would recognize that
run out before the ordinals of N, then N would recognize that
![]() is isomorphic to a transitive set
is isomorphic to a transitive set
![]() $V^N_{\alpha ^*}$
. Since it is a set, N has a truth predicate for it, and so N can define a truth predicate for
$V^N_{\alpha ^*}$
. Since it is a set, N has a truth predicate for it, and so N can define a truth predicate for
![]() . Since N and i are definable in M, we can pull this truth predicate back via i to produce an M-definable truth predicate on M, contrary to Tarski’s theorem on the nondefinability of truth.
. Since N and i are definable in M, we can pull this truth predicate back via i to produce an M-definable truth predicate on M, contrary to Tarski’s theorem on the nondefinability of truth.
So the ordinals of the three models must be exactly isomorphic, and so the isomorphisms of the rank-initial segments of the models in fact produce an isomorphism of
 $N=V_{{\mathrm {Ord}}}^N$
with
$N=V_{{\mathrm {Ord}}}^N$
with
 and hence with M, as desired. ⊣
and hence with M, as desired. ⊣
Albert Visser had initially proved a corresponding result in 2006 for Peano arithmetic
![]() $\mathrm {PA}$
in [Reference Visser22]. Ali Enayat had followed with a nice model-theoretic argument showing specifically that
$\mathrm {PA}$
in [Reference Visser22]. Ali Enayat had followed with a nice model-theoretic argument showing specifically that
![]() $\mathrm {ZF}$
and
$\mathrm {ZF}$
and
![]() $\mathrm {ZFC}$
are not bi-interpretable, using the fact that
$\mathrm {ZFC}$
are not bi-interpretable, using the fact that
![]() $\mathrm {ZFC}$
models can have no involutions in their automorphism groups, but
$\mathrm {ZFC}$
models can have no involutions in their automorphism groups, but
![]() $\mathrm {ZF}$
models can, before finally proving the general version of his theorem, for
$\mathrm {ZF}$
models can, before finally proving the general version of his theorem, for
![]() $\mathrm {ZF}$
, for second-order arithmetic
$\mathrm {ZF}$
, for second-order arithmetic
![]() $Z_2$
and for second-order set theory
$Z_2$
and for second-order set theory
![]() $\mathrm {KM}$
in [Reference Enayat, van Eijck, Iemhoff and Joosten3]. The ZF version was apparently also observed independently by Harvey Friedman and Albert Visser, by Fedor Pakhomov, as well as by ourselves [Reference Hamkins13], before we had realized that this was a rediscovery.
$\mathrm {KM}$
in [Reference Enayat, van Eijck, Iemhoff and Joosten3]. The ZF version was apparently also observed independently by Harvey Friedman and Albert Visser, by Fedor Pakhomov, as well as by ourselves [Reference Hamkins13], before we had realized that this was a rediscovery.
Enayat defines that a theory T is tight, if whenever two extensions of T are bi-interpretable, then they are the same theory.
Corollary 14.
![]() $\mathrm {ZF}$
is tight. That is, no two distinct set theories extending
$\mathrm {ZF}$
is tight. That is, no two distinct set theories extending
![]() $\mathrm {ZF}$
are bi-interpretable.
$\mathrm {ZF}$
are bi-interpretable.
This corollary follows from Theorem 13, because in fact every solid theory is tight. If T is solid, and
![]() $T_1$
and
$T_1$
and
![]() $T_2$
are distinct bi-interpretable extensions of T, then consider any model
$T_2$
are distinct bi-interpretable extensions of T, then consider any model
![]() $M\models T_1$
. By the bi-interpretability of the theories, M is bi-interpretable with a model
$M\models T_1$
. By the bi-interpretability of the theories, M is bi-interpretable with a model
![]() $N\models T_2$
. Since these are both models of T, it follows by the solidity of T that M and N are isomorphic, and so M is a model of
$N\models T_2$
. Since these are both models of T, it follows by the solidity of T that M and N are isomorphic, and so M is a model of
![]() $T_2$
. Since the argument also works conversely, the two theories are the same.
$T_2$
. Since the argument also works conversely, the two theories are the same.
In particular,
![]() $\mathrm {ZF}$
is not bi-interpretable with
$\mathrm {ZF}$
is not bi-interpretable with
![]() $\mathrm {ZFC}$
, nor with
$\mathrm {ZFC}$
, nor with
![]() $\mathrm {ZFC}+\mathrm {CH}$
, nor with
$\mathrm {ZFC}+\mathrm {CH}$
, nor with
![]() $\mathrm {ZFC}+\neg \mathrm {CH}$
, and so on. Theorem 7 therefore cannot be strengthened from mutual interpretation to bi-interpretation, and there is no nontrivial bi-interpretation phenomenon in set theory amongst the models or theories strengthening
$\mathrm {ZFC}+\neg \mathrm {CH}$
, and so on. Theorem 7 therefore cannot be strengthened from mutual interpretation to bi-interpretation, and there is no nontrivial bi-interpretation phenomenon in set theory amongst the models or theories strengthening
![]() $\mathrm {ZF}$
.
$\mathrm {ZF}$
.
Furthermore, we claim that there is no mutual interpretation phenomenon amongst the well-founded models of
![]() $\mathrm {ZF}$
.
$\mathrm {ZF}$
.
Theorem 15. Nonisomorphic well-founded models of
![]() $\mathrm {ZF}$
are never mutually interpretable.
$\mathrm {ZF}$
are never mutually interpretable.
Proof. Corollary 12 shows that every instance of mutual interpretation amongst the well-founded models of
![]() $\mathrm {ZF}$
is a bi-interpretation, but Theorem 13 shows that bi-interpretation amongst models of
$\mathrm {ZF}$
is a bi-interpretation, but Theorem 13 shows that bi-interpretation amongst models of
![]() $\mathrm {ZF}$
occurs only between isomorphic models. ⊣
$\mathrm {ZF}$
occurs only between isomorphic models. ⊣
Let us now explain how to deduce the tightness of
![]() $\mathrm {ZF}$
by means of the following “internal categoricity” theorem of Jouko Väänänen. He had stated the result in [Reference Väänänen23] for
$\mathrm {ZF}$
by means of the following “internal categoricity” theorem of Jouko Väänänen. He had stated the result in [Reference Väänänen23] for
![]() $\mathrm {ZFC}$
, but his argument did not use
$\mathrm {ZFC}$
, but his argument did not use
![]() $\mathrm {AC}$
, and so we state and prove it here for
$\mathrm {AC}$
, and so we state and prove it here for
![]() $\mathrm {ZF}$
.
$\mathrm {ZF}$
.
Theorem 16 (Väänänen [Reference Väänänen23])
Assume that
![]() is a model of
is a model of
![]() $\mathrm {ZF}$
with respect to both membership relations
$\mathrm {ZF}$
with respect to both membership relations
![]() $\in $
and
$\in $
and
![]() , in the common language. More precisely, it is a model of
, in the common language. More precisely, it is a model of
![]() , using
, using
![]() $\in $
as the membership relation and
$\in $
as the membership relation and
![]() as a class predicate and also of
as a class predicate and also of
![]() , using
, using
![]() as the membership relation and
as the membership relation and
![]() $\in $
as a class predicate. Then
$\in $
as a class predicate. Then
![]() , and furthermore, there is a unique definable isomorphism in
, and furthermore, there is a unique definable isomorphism in
![]() .
.
Proof. Let us begin by observing that by the foundation axiom, every nonempty definable
![]() $\in $
-class will admit an
$\in $
-class will admit an
![]() $\in $
-minimal element, and similarly every nonempty definable
$\in $
-minimal element, and similarly every nonempty definable
![]() -class will have an
-class will have an
![]() -minimal element. Thus, both
-minimal element. Thus, both
![]() $\in $
and
$\in $
and
![]() will be well-founded relations in this model, regardless of whether we use
will be well-founded relations in this model, regardless of whether we use
![]() $\in $
or
$\in $
or
![]() as the membership relation. In particular, the orders
as the membership relation. In particular, the orders
 $\langle {\mathrm {Ord}}^{\left \langle V,\in \right \rangle },\in \rangle $
and
$\langle {\mathrm {Ord}}^{\left \langle V,\in \right \rangle },\in \rangle $
and
 will be comparable well-ordered classes, and we may assume without loss that the former is isomorphic to an initial segment of the latter. Thus, for every
will be comparable well-ordered classes, and we may assume without loss that the former is isomorphic to an initial segment of the latter. Thus, for every
![]() $\in $
-ordinal
$\in $
-ordinal
![]() $\alpha $
, there is an
$\alpha $
, there is an
![]() -ordinal
-ordinal
![]() to which it is isomorphic, and furthermore this ordinal is unique, and the isomorphism is unique. We claim that
to which it is isomorphic, and furthermore this ordinal is unique, and the isomorphism is unique. We claim that
 , by induction on
, by induction on
![]() $\alpha $
. Since these are transitive sets and hence rigid, the isomorphism is unique. The claim is clearly true for
$\alpha $
. Since these are transitive sets and hence rigid, the isomorphism is unique. The claim is clearly true for
![]() $\alpha =0$
. It remains true through limit ordinals, since the isomorphism in that case is simply the union of the previous isomorphisms. At successor stages, we need only observe that any isomorphism of
$\alpha =0$
. It remains true through limit ordinals, since the isomorphism in that case is simply the union of the previous isomorphisms. At successor stages, we need only observe that any isomorphism of
![]() $\left \langle V_\alpha ,\in \right \rangle $
with
$\left \langle V_\alpha ,\in \right \rangle $
with
 extends to an isomorphism of the power set, since any
extends to an isomorphism of the power set, since any
![]() $\in $
-subset of
$\in $
-subset of
![]() $V_\alpha $
transfers to an
$V_\alpha $
transfers to an
![]() -subset of
-subset of
![]() by pointwise application of the isomorphism, and vice versa. If
by pointwise application of the isomorphism, and vice versa. If
![]() is taller than
is taller than
![]() ${\mathrm {Ord}}^{\left \langle V,\in \right \rangle }$
, then we can see that
${\mathrm {Ord}}^{\left \langle V,\in \right \rangle }$
, then we can see that
 , where
, where
 is the first
is the first
![]() -ordinal not arising from an
-ordinal not arising from an
![]() $\in $
-ordinal. But now
$\in $
-ordinal. But now
 , which is the
, which is the
![]() -power set of
-power set of
![]() , is a subclass of V and therefore injects into
, is a subclass of V and therefore injects into
![]() , contrary to Cantor’s theorem. So the ordinals are the same height, and thus we have achieved
, contrary to Cantor’s theorem. So the ordinals are the same height, and thus we have achieved
![]() . This isomorphism is definable, since every
. This isomorphism is definable, since every
![]() $V_\alpha $
is isomorphic to
$V_\alpha $
is isomorphic to
![]() by a unique isomorphism. ⊣
by a unique isomorphism. ⊣
Theorem 1, statements (1) and (2), can be seen as a consequence of this theorem—and indeed the proofs we gave are roughly analogous—because if two models of
![]() $\mathrm {ZF}$
are bi-interpretable, then by the results mentioned in Section 5, we do not need tuples or nonidentity equivalence relations. So the interpretations will interpret each model as a subclass of the other. By the class version of the Schröder–Cantor–Bernstein theorem, these injections can be transformed into bijection of the models, and in this way the bi-interpretation can be transformed into a bi-interpretation synonymy (see also [Reference Friedman and Visser7]). Thus, we reduce to the case of two membership relations
$\mathrm {ZF}$
are bi-interpretable, then by the results mentioned in Section 5, we do not need tuples or nonidentity equivalence relations. So the interpretations will interpret each model as a subclass of the other. By the class version of the Schröder–Cantor–Bernstein theorem, these injections can be transformed into bijection of the models, and in this way the bi-interpretation can be transformed into a bi-interpretation synonymy (see also [Reference Friedman and Visser7]). Thus, we reduce to the case of two membership relations
![]() on the whole universe, with each relation being definable when using the other as the membership relation. Because of this, the model will satisfy the theory
on the whole universe, with each relation being definable when using the other as the membership relation. Because of this, the model will satisfy the theory
![]() , and consequently the models will be isomorphic
, and consequently the models will be isomorphic
![]() by Väänänen’s theorem.
by Väänänen’s theorem.
7 Väänänen internal categoricity fails for
 $\mathrm {ZFC}^{-}$
$\mathrm {ZFC}^{-}$
Theorems 13 and 16 were both proved with arguments that made a fundamental use of the
![]() $V_\alpha $
hierarchy, thereby relying on the power set axiom. Was the use of the
$V_\alpha $
hierarchy, thereby relying on the power set axiom. Was the use of the
![]() $V_\alpha $
hierarchy significant? Can one prove the analogues of the theorems for
$V_\alpha $
hierarchy significant? Can one prove the analogues of the theorems for
![]() $\mathrm {ZFC}^{-}$
, that is, for set theory without the power set axiom? (See [Reference Gitman, Hamkins and Johnstone10] for a subtlety about exactly what the theory
$\mathrm {ZFC}^{-}$
, that is, for set theory without the power set axiom? (See [Reference Gitman, Hamkins and Johnstone10] for a subtlety about exactly what the theory
![]() $\mathrm {ZFC}^{-}$
is; one should include the collection axiom, and not just replacement.) The answer is negative. We shall prove that neither theorem is true for
$\mathrm {ZFC}^{-}$
is; one should include the collection axiom, and not just replacement.) The answer is negative. We shall prove that neither theorem is true for
![]() $\mathrm {ZFC}^{-}$
, not even in the case of well-founded models. Let us begin by proving that the Väänänen internal categoricity theorem fails for
$\mathrm {ZFC}^{-}$
, not even in the case of well-founded models. Let us begin by proving that the Väänänen internal categoricity theorem fails for
![]() $\mathrm {ZFC}^{-}$
.
$\mathrm {ZFC}^{-}$
.
Theorem 17. There is a transitive set M and an alternative well-founded membership relation
![]() on M, such that
on M, such that
![]() satisfies
satisfies
![]() , that is,
, that is,
![]() $\mathrm {ZFC}^{-}$
using either
$\mathrm {ZFC}^{-}$
using either
![]() $\in $
or
$\in $
or
![]() as the membership relation and allowing both as class predicates, such that
as the membership relation and allowing both as class predicates, such that
![]() $\left \langle M,\in \right \rangle $
is not isomorphic to
$\left \langle M,\in \right \rangle $
is not isomorphic to
![]() , although both are well-founded.
, although both are well-founded.
Proof. Let us argue first merely that the situation is consistent with
![]() $\mathrm {ZFC}$
. Assume that Luzin’s hypothesis holds, that is,
$\mathrm {ZFC}$
. Assume that Luzin’s hypothesis holds, that is,
![]() $2^\omega =2^{\omega _1}$
; for example, this holds after adding
$2^\omega =2^{\omega _1}$
; for example, this holds after adding
![]() $\omega _2$
many Cohen reals over a model of
$\omega _2$
many Cohen reals over a model of
![]() $\mathrm {GCH}$
, since in this case we would have
$\mathrm {GCH}$
, since in this case we would have
![]() $2^\omega =2^{\omega _1}=\omega _2$
. It follows that
$2^\omega =2^{\omega _1}=\omega _2$
. It follows that
![]() $H_{\omega _1}$
and
$H_{\omega _1}$
and
![]() $H_{\omega _2}$
are equinumerous, and so there is a bijection
$H_{\omega _2}$
are equinumerous, and so there is a bijection
![]() $\pi :H_{\omega _1}\to H_{\omega _2}$
. Let
$\pi :H_{\omega _1}\to H_{\omega _2}$
. Let
![]() $\tilde \in $
be the image of
$\tilde \in $
be the image of
![]() $\in \upharpoonright H_{\omega _1}$
under this bijection, and let
$\in \upharpoonright H_{\omega _1}$
under this bijection, and let
be the preimage of
![]() $\in \upharpoonright H_{\omega _2}$
. Thus,
$\in \upharpoonright H_{\omega _2}$
. Thus,
![]() $\pi $
is an isomorphism of the structures
$\pi $
is an isomorphism of the structures

The first of these is a model of
, using
![]() $\in $
as membership, since
$\in $
as membership, since
![]() $H_{\omega _1}$
is a model of
$H_{\omega _1}$
is a model of
![]() $\mathrm {ZFC}^{-}$
with respect to any predicate. Similarly, the second is a model of
$\mathrm {ZFC}^{-}$
with respect to any predicate. Similarly, the second is a model of
![]() $\mathrm {ZFC}^{-}(\tilde \in )$
, again using
$\mathrm {ZFC}^{-}(\tilde \in )$
, again using
![]() $\in $
as membership, since we can likewise augment
$\in $
as membership, since we can likewise augment
![]() $H_{\omega _2}$
with any predicate. By following the isomorphism, an equivalent way to say this is that
$H_{\omega _2}$
with any predicate. By following the isomorphism, an equivalent way to say this is that

is a model of
, using
![]() $\in $
as membership and
$\in $
as membership and
as predicate, and also a model of

, using
as membership this time and
![]() $\in $
as a class predicate. But
$\in $
as a class predicate. But
 $\left \langle H_{\omega _1},\in \right \rangle $
is not isomorphic to
$\left \langle H_{\omega _1},\in \right \rangle $
is not isomorphic to

, because the first thinks every set is countable and the second does not. So this model is just as desired.
To get outright existence of the models, observe first that by taking an elementary substructure, we can find a countable model of the desired form in the forcing extension. Furthermore, the existence of a countable well-founded model
![]() with the desired properties is a
with the desired properties is a
![]() $\Sigma ^1_2$
assertion, which is therefore absolute to the forcing extension by Shoenfield’s absoluteness theorem. And so therefore there must have already been such an example in the ground model, without need for any forcing. ⊣
$\Sigma ^1_2$
assertion, which is therefore absolute to the forcing extension by Shoenfield’s absoluteness theorem. And so therefore there must have already been such an example in the ground model, without need for any forcing. ⊣
8
 $\mathrm {ZFC}^{-}$
is neither solid nor tight
$\mathrm {ZFC}^{-}$
is neither solid nor tight
In order to show that
![]() $\mathrm {ZFC}^{-}$
is not solid, we need to provide different models of
$\mathrm {ZFC}^{-}$
is not solid, we need to provide different models of
![]() $\mathrm {ZFC}^{-}$
that are bi-interpretable, but not isomorphic. Let us begin by describing merely how this can happen in some models of set theory. For this, we shall employ a more refined version of the argument used to prove Theorem 17.
$\mathrm {ZFC}^{-}$
that are bi-interpretable, but not isomorphic. Let us begin by describing merely how this can happen in some models of set theory. For this, we shall employ a more refined version of the argument used to prove Theorem 17.
Theorem 18. In the Solovay–Tennenbaum model of
![]() $\mathrm {MA}+\neg \mathrm {CH}$
obtained by c.c.c. forcing over the constructible universe, the structures
$\mathrm {MA}+\neg \mathrm {CH}$
obtained by c.c.c. forcing over the constructible universe, the structures
 $\left \langle H_{\omega _1},\in \right \rangle $
and
$\left \langle H_{\omega _1},\in \right \rangle $
and
 $\left \langle H_{\omega _2},\in \right \rangle $
are bi-interpretable. Thus, there can be two well-founded models of
$\left \langle H_{\omega _2},\in \right \rangle $
are bi-interpretable. Thus, there can be two well-founded models of
![]() $\mathrm {ZFC}^{-}$
that are bi-interpretable, but not isomorphic.
$\mathrm {ZFC}^{-}$
that are bi-interpretable, but not isomorphic.
The features we require in the Solovay–Tennenbaum model are the following:
-
•
 $H_{\omega _1}$
has a definable almost disjoint
$H_{\omega _1}$
has a definable almost disjoint
 $\omega _1$
-sequence of reals;
$\omega _1$
-sequence of reals; -
• every subset
 $A\subseteq \omega _1$
is coded by a real via almost-disjoint coding with respect to this sequence.
$A\subseteq \omega _1$
is coded by a real via almost-disjoint coding with respect to this sequence.
In other words, there should be a definable
![]() $\omega _1$
-sequence
$\omega _1$
-sequence
![]() $\left \langle a_\alpha \mid \alpha <\omega _1\right \rangle $
of infinite subsets
$\left \langle a_\alpha \mid \alpha <\omega _1\right \rangle $
of infinite subsets
![]() $a_\alpha \subseteq \omega $
with any two having finite intersection; and for every
$a_\alpha \subseteq \omega $
with any two having finite intersection; and for every
![]() $A\subseteq \omega _1$
there should be
$A\subseteq \omega _1$
there should be
![]() $a\subseteq \omega $
for which
$a\subseteq \omega $
for which
![]() $\alpha \in A\mathrel {\leftrightarrow }\ a\cap a_\alpha $
is infinite. These properties are true in the Solovay–Tennenbaum model
$\alpha \in A\mathrel {\leftrightarrow }\ a\cap a_\alpha $
is infinite. These properties are true in the Solovay–Tennenbaum model
![]() $L[G]$
, because we can define the almost disjoint family in L, and by Martin’s axiom every subset of
$L[G]$
, because we can define the almost disjoint family in L, and by Martin’s axiom every subset of
![]() $\omega _1$
is coded with respect to it by almost-disjoint coding.
$\omega _1$
is coded with respect to it by almost-disjoint coding.
Proof. Let us assume we have the two properties isolated above. The structure
 $\left \langle H_{\omega _1},\in \right \rangle $
, of course, is a definable substructure of
$\left \langle H_{\omega _1},\in \right \rangle $
, of course, is a definable substructure of
 $\left \langle H_{\omega _2},\in \right \rangle $
, which gives one direction of the interpretation. It remains to interpret
$\left \langle H_{\omega _2},\in \right \rangle $
, which gives one direction of the interpretation. It remains to interpret
 $\left \langle H_{\omega _2},\in \right \rangle $
inside
$\left \langle H_{\omega _2},\in \right \rangle $
inside
 $\left \langle H_{\omega _1},\in \right \rangle $
and to prove that this is a bi-interpretation. The second assumption above implies, of course, that
$\left \langle H_{\omega _1},\in \right \rangle $
and to prove that this is a bi-interpretation. The second assumption above implies, of course, that
![]() $2^\omega =2^{\omega _1}$
, and so at least the two structures have the same cardinality. But more, because the almost-disjoint sequence is definable in
$2^\omega =2^{\omega _1}$
, and so at least the two structures have the same cardinality. But more, because the almost-disjoint sequence is definable in
![]() $H_{\omega _1}$
and all the reals are there, the structure
$H_{\omega _1}$
and all the reals are there, the structure
 $\left \langle H_{\omega _1},\in \right \rangle $
in effect has access to the full power set
$\left \langle H_{\omega _1},\in \right \rangle $
in effect has access to the full power set
![]() $P(\omega _1)$
; the subsets
$P(\omega _1)$
; the subsets
![]() $A\subseteq \omega _1$
are uniformly definable in the structure
$A\subseteq \omega _1$
are uniformly definable in the structure
 $\left \langle H_{\omega _1},\in \right \rangle $
from real parameters. And furthermore, every set in
$\left \langle H_{\omega _1},\in \right \rangle $
from real parameters. And furthermore, every set in
![]() $H_{\omega _2}$
is coded by a subset of
$H_{\omega _2}$
is coded by a subset of
![]() $\omega _1$
. Specifically, if
$\omega _1$
. Specifically, if
![]() $x\in H_{\omega _2}$
then x is an element of a transitive set t of size
$x\in H_{\omega _2}$
then x is an element of a transitive set t of size
![]() $\omega _1$
, with
$\omega _1$
, with
![]() $\left \langle t,\in \right \rangle \cong \left \langle \omega _1,E\right \rangle $
for some well-founded extensional relation E on
$\left \langle t,\in \right \rangle \cong \left \langle \omega _1,E\right \rangle $
for some well-founded extensional relation E on
![]() $\omega _1$
. The set x can be in effect coded by specifying E and the ordinal
$\omega _1$
. The set x can be in effect coded by specifying E and the ordinal
![]() $\alpha $
representing x in the structure
$\alpha $
representing x in the structure
![]() $\left \langle \omega _1,E\right \rangle $
. Since
$\left \langle \omega _1,E\right \rangle $
. Since
![]() $H_{\omega _1}$
contains all countable sequences of ordinals, it can correctly identify which relations E on
$H_{\omega _1}$
contains all countable sequences of ordinals, it can correctly identify which relations E on
![]() $\omega _1$
, as encoded by a real via the almost-disjoint coding, are well-founded and extensional. Let us define an equivalence relation
$\omega _1$
, as encoded by a real via the almost-disjoint coding, are well-founded and extensional. Let us define an equivalence relation
![]() $a\simeq a'$
for reals
$a\simeq a'$
for reals
![]() $a,a'\subseteq \omega $
coding such pairs
$a,a'\subseteq \omega $
coding such pairs
![]() $(\alpha ,E)$
and
$(\alpha ,E)$
and
![]() $(\alpha ',E')$
that represent the same set, which happens just in case there is an isomorphism of the hereditary E-predecessors of
$(\alpha ',E')$
that represent the same set, which happens just in case there is an isomorphism of the hereditary E-predecessors of
![]() $\alpha $
to the hereditary
$\alpha $
to the hereditary
![]() $E'$
-predecessors of
$E'$
-predecessors of
![]() $\alpha '$
; in other words, when the transitive closures of the corresponding encoded sets
$\alpha '$
; in other words, when the transitive closures of the corresponding encoded sets
![]() $\left \{{x}\right \}$
and
$\left \{{x}\right \}$
and
![]() $\left \{{x'}\right \}$
are isomorphic. The isomorphism itself is a map of size at most
$\left \{{x'}\right \}$
are isomorphic. The isomorphism itself is a map of size at most
![]() $\omega _1$
, which can therefore be seen definably in the structure
$\omega _1$
, which can therefore be seen definably in the structure
 $\left \langle H_{\omega _1},\in \right \rangle $
. And we can recognize when the set x coded by
$\left \langle H_{\omega _1},\in \right \rangle $
. And we can recognize when the set x coded by
![]() $(\alpha ,E)$
is an element of the set y coded by
$(\alpha ,E)$
is an element of the set y coded by
![]() $(\beta ,F)$
, since this just means that
$(\beta ,F)$
, since this just means that
![]() $(\alpha ,E)$
is equivalent to
$(\alpha ,E)$
is equivalent to
![]() $(\gamma ,F)$
for some
$(\gamma ,F)$
for some
![]() $\gamma \mathrel {F}\beta $
. Since every element of
$\gamma \mathrel {F}\beta $
. Since every element of
![]() $H_{\omega _2}$
is coded in this way by relations on
$H_{\omega _2}$
is coded in this way by relations on
![]() $\omega _1$
and hence ultimately by reals
$\omega _1$
and hence ultimately by reals
![]() $a\subseteq \omega $
, we see that
$a\subseteq \omega $
, we see that
 $\left \langle H_{\omega _2},\in \right \rangle $
is interpreted in
$\left \langle H_{\omega _2},\in \right \rangle $
is interpreted in
 $\left \langle H_{\omega _1},\in \right \rangle $
by the codes
$\left \langle H_{\omega _1},\in \right \rangle $
by the codes
![]() $(\alpha ,E)$
for well-founded extensional relations E on
$(\alpha ,E)$
for well-founded extensional relations E on
![]() $\omega _1$
, which are themselves coded by reals via almost-disjoint coding. Ultimately, objects
$\omega _1$
, which are themselves coded by reals via almost-disjoint coding. Ultimately, objects
![]() $x\in H_{\omega _2}$
are represented by a real
$x\in H_{\omega _2}$
are represented by a real
![]() $a\subseteq $
coding a pair
$a\subseteq $
coding a pair
![]() $(\alpha ,E)$
which codes a transitive set having x as an element at index
$(\alpha ,E)$
which codes a transitive set having x as an element at index
![]() $\alpha $
in that coding.
$\alpha $
in that coding.
This interpretation is a bi-interpretation, because
![]() $H_{\omega _1}$
can construct suitable codes for any object
$H_{\omega _1}$
can construct suitable codes for any object
![]() $x\in H_{\omega _1}$
, and thereby recognize how itself arises within the interpreted copy of
$x\in H_{\omega _1}$
, and thereby recognize how itself arises within the interpreted copy of
![]() $H_{\omega _2}$
. And conversely,
$H_{\omega _2}$
. And conversely,
![]() $H_{\omega _2}$
can define
$H_{\omega _2}$
can define
![]() $H_{\omega _1}$
as a submodel and it can see how the objects in
$H_{\omega _1}$
as a submodel and it can see how the objects in
![]() $H_{\omega _2}$
are represented inside that model via almost disjoint coding. The models
$H_{\omega _2}$
are represented inside that model via almost disjoint coding. The models
 $\left \langle H_{\omega _1},\in \right \rangle $
and
$\left \langle H_{\omega _1},\in \right \rangle $
and
 $\left \langle H_{\omega _2},\in \right \rangle $
are therefore well-founded models of
$\left \langle H_{\omega _2},\in \right \rangle $
are therefore well-founded models of
![]() $\mathrm {ZFC}^{-}$
that are bi-interpretable, but they are not isomorphic, because the first model thinks every set is countable and the second does not. ⊣
$\mathrm {ZFC}^{-}$
that are bi-interpretable, but they are not isomorphic, because the first model thinks every set is countable and the second does not. ⊣
We can improve the previous theorem to achieve an actual synonymy of the two structures as follows.
Theorem 19. If
![]() $\mathrm {ZFC}$
is consistent, then it is consistent that there is a membership relation
$\mathrm {ZFC}$
is consistent, then it is consistent that there is a membership relation
![]() definable in
definable in
 $\left \langle H_{\omega _1},\in \right \rangle $
such that
$\left \langle H_{\omega _1},\in \right \rangle $
such that
 , putting these structures into bi-interpretation synonymy.
, putting these structures into bi-interpretation synonymy.
Proof. The argument relies on a result of Leo Harrington [Reference Harrington16], showing that it is relatively consistent with
![]() $\mathrm {ZFC}$
that
$\mathrm {ZFC}$
that
![]() $\mathrm {MA}+\neg \mathrm {CH}$
hold, yet there is a projectively definable well-ordering of the reals; in fact, Harrington achieves this in a forcing extension of L. (Many thanks to Gabe Goldberg [Reference Goldberg11] for pointing out Harrington’s paper in response to our MathOverflow question concerning the possibility of this theorem.) In such a model, we can choose least elements within each equivalence class of reals in the interpretation used in the proof of Theorem 18, and thereby omit the need for an equivalence relation in the first place. So every element of
$\mathrm {MA}+\neg \mathrm {CH}$
hold, yet there is a projectively definable well-ordering of the reals; in fact, Harrington achieves this in a forcing extension of L. (Many thanks to Gabe Goldberg [Reference Goldberg11] for pointing out Harrington’s paper in response to our MathOverflow question concerning the possibility of this theorem.) In such a model, we can choose least elements within each equivalence class of reals in the interpretation used in the proof of Theorem 18, and thereby omit the need for an equivalence relation in the first place. So every element of
![]() $H_{\omega _2}$
will be coded by a real. Since the decoding of hereditarily countable sets can be undertaken inside
$H_{\omega _2}$
will be coded by a real. Since the decoding of hereditarily countable sets can be undertaken inside
![]() $H_{\omega _1}$
, we thereby have a definable injection of
$H_{\omega _1}$
, we thereby have a definable injection of
![]() $H_{\omega _1}$
into the coding reals, and so by the Cantor–Schröder–Bernstein theorem,
$H_{\omega _1}$
into the coding reals, and so by the Cantor–Schröder–Bernstein theorem,
![]() $H_{\omega _1}$
is bijective with the coding reals. Because the Cantor–Schröder–Bernstein theorem is sufficiently constructive, this bijection is definable inside
$H_{\omega _1}$
is bijective with the coding reals. Because the Cantor–Schröder–Bernstein theorem is sufficiently constructive, this bijection is definable inside
 $\left \langle H_{\omega _1},\in \right \rangle $
, and so we may pull back the interpreted membership relation on the coding reals to get a definable relation
$\left \langle H_{\omega _1},\in \right \rangle $
, and so we may pull back the interpreted membership relation on the coding reals to get a definable relation
![]() on all of
on all of
![]() $H_{\omega _1}$
, such that
$H_{\omega _1}$
, such that
 , as desired. This is a bi-interpretation synonymy, since
, as desired. This is a bi-interpretation synonymy, since
![]() $H_{\omega _1}$
can see how it is represented in that coding, and
$H_{\omega _1}$
can see how it is represented in that coding, and
![]() $H_{\omega _2}$
can define
$H_{\omega _2}$
can define
![]() $H_{\omega _1}$
and also see how its elements are coded. ⊣
$H_{\omega _1}$
and also see how its elements are coded. ⊣
We find it interesting to compare Theorems 18 and 19 with [Reference Enayat, van Eijck, Iemhoff and Joosten3, Corollary 2.5.1], which says that
![]() $\mathrm {ZFC}^{-}+$
“every set is countable” is solid, and similarly Corollary 2.7.1, which asserts that
$\mathrm {ZFC}^{-}+$
“every set is countable” is solid, and similarly Corollary 2.7.1, which asserts that
![]() for some inaccessible cardinal
for some inaccessible cardinal
![]() $\kappa $
” also is solid.
$\kappa $
” also is solid.
The following theorem explains somewhat the need in Theorem 18 for assuming that we were working close to L.
Theorem 20. If there is no projectively definable
![]() $\omega _1$
-sequence of distinct reals, then
$\omega _1$
-sequence of distinct reals, then
 $\left \langle H_{\omega _2},\in \right \rangle $
cannot be interpreted in
$\left \langle H_{\omega _2},\in \right \rangle $
cannot be interpreted in
 $\left \langle H_{\omega _1},\in \right \rangle $
. In particular, in this case the structures are not bi-interpretable nor even mutually interpretable.
$\left \langle H_{\omega _1},\in \right \rangle $
. In particular, in this case the structures are not bi-interpretable nor even mutually interpretable.
The hypothesis is a direct consequence of sufficient large cardinals, since it is a consequence of
![]() $\mathrm {AD}^{L({\mathbb R})}$
. But meanwhile, it can also be forced by the Lévy collapse of an inaccessible cardinal; and since it implies
$\mathrm {AD}^{L({\mathbb R})}$
. But meanwhile, it can also be forced by the Lévy collapse of an inaccessible cardinal; and since it implies
![]() $\omega _1$
is inaccessible to reals, it is equiconsistent with an inaccessible cardinal.
$\omega _1$
is inaccessible to reals, it is equiconsistent with an inaccessible cardinal.
Proof. If
![]() $H_{\omega _2}$
were interpreted in
$H_{\omega _2}$
were interpreted in
![]() $H_{\omega _1}\!$
, then since the former structure definitely has an
$H_{\omega _1}\!$
, then since the former structure definitely has an
![]() $\omega _1$
-sequence of distinct reals, such a sequence would be definable (from parameters) in the structure
$\omega _1$
-sequence of distinct reals, such a sequence would be definable (from parameters) in the structure
 $\left \langle H_{\omega _1},\in \right \rangle $
. But this latter structure is interpreted in the reals in second-order arithmetic, by coding hereditarily countable sets by relations on
$\left \langle H_{\omega _1},\in \right \rangle $
. But this latter structure is interpreted in the reals in second-order arithmetic, by coding hereditarily countable sets by relations on
![]() $\omega $
. By means of this interpretation, first-order assertions in
$\omega $
. By means of this interpretation, first-order assertions in
 $\left \langle H_{\omega _1},{\in }\right \rangle $
can be viewed as projective assertions. And so there would be a projectively definable
$\left \langle H_{\omega _1},{\in }\right \rangle $
can be viewed as projective assertions. And so there would be a projectively definable
![]() $\omega _1$
-sequence of distinct reals, contrary to our assumption. ⊣
$\omega _1$
-sequence of distinct reals, contrary to our assumption. ⊣
Meanwhile, we can extend Theorem 18 from the consistency result to prove outright in
![]() $\mathrm {ZFC}$
that there are always transitive counterexample models to be found.
$\mathrm {ZFC}$
that there are always transitive counterexample models to be found.
Theorem 21. The theory
![]() $\mathrm {ZFC}^{-}$
is not solid, and not even semantically tight, not even for well-founded models. Indeed, there are transitive models
$\mathrm {ZFC}^{-}$
is not solid, and not even semantically tight, not even for well-founded models. Indeed, there are transitive models
![]() $\left \langle M,\in \right \rangle $
and
$\left \langle M,\in \right \rangle $
and
![]() $\left \langle N,\in \right \rangle $
of
$\left \langle N,\in \right \rangle $
of
![]() $\mathrm {ZFC}^{-}$
that form a bi-interpretation synonymy, but are not isomorphic.
$\mathrm {ZFC}^{-}$
that form a bi-interpretation synonymy, but are not isomorphic.
Proof. By Theorem 19, there are such transitive sets in a forcing extension of L. In that model, by taking a countable elementary substructure, we can find countable transitive sets with the desired feature. And furthermore, the assertion that there are such countable transitive sets like that, for which the particular bi-interpretation definitions work and form a synonymy, is a statement of complexity
![]() $\Sigma ^1_2$
. By Shoenfield absoluteness, this statement must already be true in L, and hence also in V. So there are countable transitive models
$\Sigma ^1_2$
. By Shoenfield absoluteness, this statement must already be true in L, and hence also in V. So there are countable transitive models
![]() $\left \langle M,\in \right \rangle $
and
$\left \langle M,\in \right \rangle $
and
![]() $\left \langle N,\in \right \rangle $
of
$\left \langle N,\in \right \rangle $
of
![]() $\mathrm {ZFC}^{-}$
that form a bi-interpretation synonymy, but are not isomorphic. ⊣
$\mathrm {ZFC}^{-}$
that form a bi-interpretation synonymy, but are not isomorphic. ⊣
And we can also use the argument to show that
![]() $\mathrm {ZFC}^{-}$
is not tight.
$\mathrm {ZFC}^{-}$
is not tight.
Theorem 22.
![]() $\mathrm {ZFC}^{-}$
is not tight.
$\mathrm {ZFC}^{-}$
is not tight.
Proof. We shall find two extensions of
![]() $\mathrm {ZFC}^{-}$
that are bi-interpretable, but not the same theory. Let us take
$\mathrm {ZFC}^{-}$
that are bi-interpretable, but not the same theory. Let us take
![]() $T_1$
and
$T_1$
and
![]() $T_2$
be the theories describing the situation of
$T_2$
be the theories describing the situation of
 $\left \langle H_{\omega _1},\in \right \rangle $
and
$\left \langle H_{\omega _1},\in \right \rangle $
and
 $\left \langle H_{\omega _2},\in \right \rangle $
in Theorem 18. Specifically, let
$\left \langle H_{\omega _2},\in \right \rangle $
in Theorem 18. Specifically, let
![]() $T_2$
assert
$T_2$
assert
![]() $\mathrm {ZFC}^{-}$
plus the assertion that
$\mathrm {ZFC}^{-}$
plus the assertion that
![]() $\omega _1$
exists but not
$\omega _1$
exists but not
![]() $\omega _2$
, that
$\omega _2$
, that
![]() $\omega _1=\omega _1^L$
, that
$\omega _1=\omega _1^L$
, that
![]() $\omega _2=\omega _2^L$
, and that every subset of
$\omega _2=\omega _2^L$
, and that every subset of
![]() $\omega _1$
is coded by a real using the almost-disjoint coding with respect to the L-least almost-disjoint family
$\omega _1$
is coded by a real using the almost-disjoint coding with respect to the L-least almost-disjoint family
![]() $\left \langle a_\alpha \mid \alpha <\omega _1\right \rangle $
. Let
$\left \langle a_\alpha \mid \alpha <\omega _1\right \rangle $
. Let
![]() $T_1$
be the theory
$T_1$
be the theory
![]() $\mathrm {ZFC}^{-}$
plus the assertion that every set is countable and that the interpretation of
$\mathrm {ZFC}^{-}$
plus the assertion that every set is countable and that the interpretation of
![]() $H_{\omega _2}$
in
$H_{\omega _2}$
in
![]() $H_{\omega _1}$
used in the proof of Theorem 18 defines a model of
$H_{\omega _1}$
used in the proof of Theorem 18 defines a model of
![]() $T_2$
. That is,
$T_2$
. That is,
![]() $T_1$
asserts that the interpretation does indeed interpret a model of
$T_1$
asserts that the interpretation does indeed interpret a model of
![]() $T_2$
. These two theories are bi-interpretable, using the interpretations provided in the proof of Theorem 18, because any model of
$T_2$
. These two theories are bi-interpretable, using the interpretations provided in the proof of Theorem 18, because any model of
![]() $T_1$
interprets a model of
$T_1$
interprets a model of
![]() $T_2$
, and any model of
$T_2$
, and any model of
![]() $T_2$
can define its
$T_2$
can define its
![]() $H_{\omega _1}$
, which will be a model of
$H_{\omega _1}$
, which will be a model of
![]() $T_1$
, and the composition maps are definable just as before. ⊣
$T_1$
, and the composition maps are definable just as before. ⊣
9 Zermelo set theory is neither solid nor tight
We should like now to consider the case of Zermelo set theory. We shall prove that nontrivial instances of bi-interpretation occur in models of Zermelo set theory, and consequently Zermelo set theory is neither solid nor tight. Specifically, we shall prove the following:
-
(1)
 $\mathrm {Z}$
is not semantically tight (and hence not solid), not even for well-founded models: there are bi-interpretable well-founded models of Zermelo set theory that are not isomorphic.
$\mathrm {Z}$
is not semantically tight (and hence not solid), not even for well-founded models: there are bi-interpretable well-founded models of Zermelo set theory that are not isomorphic. -
(2) Every model of
 $\mathrm {ZF}$
is bi-interpretable with a transitive inner model of Zermelo set theory, in which the replacement axiom fails.
$\mathrm {ZF}$
is bi-interpretable with a transitive inner model of Zermelo set theory, in which the replacement axiom fails. -
(3)
 $\mathrm {Z}$
is not tight: there are distinct bi-interpretable strengthenings of Z.
$\mathrm {Z}$
is not tight: there are distinct bi-interpretable strengthenings of Z.
Our argument will make fundamental use of the model-construction method of Adrian Mathias [Reference Mathias20]. Mathias had used his methods to construct diverse interesting models of Zermelo set theory, some of them quite peculiar, such as a transitive inner model of Zermelo set theory containing all the ordinals, but not having
![]() $V_\omega $
as an element. Let us briefly review his method. The central definition is that a class C is fruitful, if
$V_\omega $
as an element. Let us briefly review his method. The central definition is that a class C is fruitful, if
-
(1) every
 $x\in C$
is transitive;
$x\in C$
is transitive; -
(2)
 ${\mathrm {Ord}}\subseteq C$
;
${\mathrm {Ord}}\subseteq C$
; -
(3)
 $x \in C$
and
$x \in C$
and
 $y \in C$
implies
$y \in C$
implies
 $x \cup y \in C$
;
$x \cup y \in C$
; -
(4)
 $x \in C$
and
$x \in C$
and
 $y \subseteq P(x)$
implies
$y \subseteq P(x)$
implies
 $x \cup y \in C$
.
$x \cup y \in C$
.
Fruitful classes, Mathias proves, lead to transitive models of Zermelo set theory as follows.
Theorem 24 (Mathias [Reference Mathias20, Proposition 1.2])
If C is fruitful, then
![]() $M=\bigcup C$
is a supertransitive model of Zermelo set theory with the foundation axiom.
$M=\bigcup C$
is a supertransitive model of Zermelo set theory with the foundation axiom.
A transitive set M is supertransitive, if it contains every subset of its elements, that is, if
![]() $x\subseteq y\in M\mathrel {\rightarrow } x\in M$
. In the context of Zermelo set theory, we take the foundation axiom in the form of the
$x\subseteq y\in M\mathrel {\rightarrow } x\in M$
. In the context of Zermelo set theory, we take the foundation axiom in the form of the
![]() $\in $
-induction scheme, which is equivalent over Z to the “transitive containment” assertion that every set is an element of a transitive set.
$\in $
-induction scheme, which is equivalent over Z to the “transitive containment” assertion that every set is an element of a transitive set.
The importance of the theorem is that Mathias explains how to construct a great variety of fruitful classes
![]() $T^{Q,G}$
, defined in terms of a function
$T^{Q,G}$
, defined in terms of a function
![]() $Q:\omega \to V_\omega $
and a family G of functions from
$Q:\omega \to V_\omega $
and a family G of functions from
![]() $\omega $
to
$\omega $
to
![]() $\omega $
, which specify rates of growth for the allowed sets. Namely, a transitive x is in
$\omega $
, which specify rates of growth for the allowed sets. Namely, a transitive x is in
![]() $T^{Q,G}$
just in case its rate-of-growth function
$T^{Q,G}$
just in case its rate-of-growth function
 $$ \begin{align*}f_x^Q(n)=|x\cap Q(n)|\end{align*} $$
$$ \begin{align*}f_x^Q(n)=|x\cap Q(n)|\end{align*} $$
is in G. Under general hypotheses, he proves,
![]() $T^{Q,G}$
is fruitful.
$T^{Q,G}$
is fruitful.
For our application, it will suffice to consider one of his key examples, described in [Reference Mathias20, Section 3]. Namely, we consider the case of
![]() $T^{R,F}$
, where
$T^{R,F}$
, where
![]() $R(n)=V_n$
is the rank-initial segment function and F is the collection of functions f bounded by one of the superexponential functions
$R(n)=V_n$
is the rank-initial segment function and F is the collection of functions f bounded by one of the superexponential functions
![]() $b_k$
of the form
$b_k$
of the form

for some
![]() $k\in \omega $
. Mathias proves in this instance that
$k\in \omega $
. Mathias proves in this instance that
![]() $T^{R,F}$
is fruitful, and therefore by Theorem 24 the class
$T^{R,F}$
is fruitful, and therefore by Theorem 24 the class
![]() $M=\bigcup T^{R,F}$
is a supertransitive model of Zermelo set theory. The elements of M are precisely those sets x whose transitive closure has a rate of growth in
$M=\bigcup T^{R,F}$
is a supertransitive model of Zermelo set theory. The elements of M are precisely those sets x whose transitive closure has a rate of growth in
![]() $V_n$
bounded by some
$V_n$
bounded by some
![]() $b_k$
.
$b_k$
.
Since each
![]() $b_k$
has a fixed superexponential depth k, it follows that each of them has strictly slower asymptotic growth than the full tetration function
$b_k$
has a fixed superexponential depth k, it follows that each of them has strictly slower asymptotic growth than the full tetration function

and therefore the set
![]() $V_\omega $
is not in M because it grows too quickly [Reference Mathias20, Theorem 3.8].
$V_\omega $
is not in M because it grows too quickly [Reference Mathias20, Theorem 3.8].
In order to prove the claims of Theorem 23, we shall show that the original
![]() $\mathrm {ZF}$
model
$\mathrm {ZF}$
model
![]() $\left \langle V,\in \right \rangle $
is bi-interpretable with the Zermelo model
$\left \langle V,\in \right \rangle $
is bi-interpretable with the Zermelo model
![]() $\left \langle M,\in \right \rangle $
defined by
$\left \langle M,\in \right \rangle $
defined by
![]() $M=\bigcup T^{R,F}$
above. We already have one direction of the interpretation, since we have defined M as a transitive inner model inside V. The difficult part will be conversely to provide an interpretation of
$M=\bigcup T^{R,F}$
above. We already have one direction of the interpretation, since we have defined M as a transitive inner model inside V. The difficult part will be conversely to provide an interpretation of
![]() $\left \langle V,\in \right \rangle $
inside
$\left \langle V,\in \right \rangle $
inside
![]() $\left \langle M,\in \right \rangle $
. For this, we shall make use of the Zermelo tower hierarchy, defined for any set a in V as follows:
$\left \langle M,\in \right \rangle $
. For this, we shall make use of the Zermelo tower hierarchy, defined for any set a in V as follows:
-
(1)
 $V^{(a)}_0 = \varnothing $
;
$V^{(a)}_0 = \varnothing $
; -
(2)
 $V^{(a)}_{\alpha + 1} = \{a\} \cup \bigl (P(V^{(a)}_{\alpha }) - \{\varnothing \}\bigr )$
, for successor ordinals;
$V^{(a)}_{\alpha + 1} = \{a\} \cup \bigl (P(V^{(a)}_{\alpha }) - \{\varnothing \}\bigr )$
, for successor ordinals; -
(3)
 $V^{(a)}_{\lambda } = \bigcup _{\alpha <\lambda } V^{(a)}_\alpha $
, for limit ordinals
$V^{(a)}_{\lambda } = \bigcup _{\alpha <\lambda } V^{(a)}_\alpha $
, for limit ordinals
 $\lambda $
.
$\lambda $
.
Mathias had introduced the Zermelo tower idea in [Reference Mathias20, Section 4], but defined and considered it only at finite stages and
![]() $\omega $
, whereas we continue the construction, crucially, through all the ordinals. Our reason for doing so is that the full Zermelo tower
$\omega $
, whereas we continue the construction, crucially, through all the ordinals. Our reason for doing so is that the full Zermelo tower
![]() $V^{(a)}$
is a definable copy of the original universe, as we prove here:
$V^{(a)}$
is a definable copy of the original universe, as we prove here:
Lemma 25. For any set a, the universe
![]() $\langle V,\in \rangle $
is definably isomorphic to the full Zermelo tower
$\langle V,\in \rangle $
is definably isomorphic to the full Zermelo tower
 $ \langle V^{(a)},\in \rangle $
.
$ \langle V^{(a)},\in \rangle $
.
Proof. The isomorphism from V to
![]() $V^{(a)}$
is simply the operation replacing every hereditary instance of
$V^{(a)}$
is simply the operation replacing every hereditary instance of
![]() $\varnothing $
in a set with a. Specifically, we define the replacing operation
$\varnothing $
in a set with a. Specifically, we define the replacing operation
![]() $x\mapsto x^{(a)}$
as follows:
$x\mapsto x^{(a)}$
as follows:
 $$ \begin{align*} \varnothing^{(a)} &= a.\\ x^{(a)} &= \{y^{(a)} \mid y\in x\}. \end{align*} $$
$$ \begin{align*} \varnothing^{(a)} &= a.\\ x^{(a)} &= \{y^{(a)} \mid y\in x\}. \end{align*} $$
A simple argument by transfinite induction now shows that this is an isomorphism of every
![]() $V_\alpha $
with
$V_\alpha $
with
 $V^{(a)}_\alpha $
, which establishes the theorem. ⊣
$V^{(a)}_\alpha $
, which establishes the theorem. ⊣
Next, we show that for suitable sets a, the Zermelo tower is contained within the Zermelo universe M we defined above.
Lemma 26. If a is any infinite transitive set in M, then
![]() $V^{(a)}\subseteq M$
.
$V^{(a)}\subseteq M$
.
Proof. Suppose that a is an infinite transitive set in M. It therefore obeys the growth rate requirement, and so there is some k for which
![]() $|a\cap V_n|\leq b_k(n)$
for every n. Notice that
$|a\cap V_n|\leq b_k(n)$
for every n. Notice that
 $a\cup V_\alpha ^{(a)}$
is a transitive set, and since (i)
$a\cup V_\alpha ^{(a)}$
is a transitive set, and since (i)
![]() $u^{(a)}$
is infinite for every set u, and (ii) every element of
$u^{(a)}$
is infinite for every set u, and (ii) every element of
![]() $V_n$
is hereditarily finite, it follows that
$V_n$
is hereditarily finite, it follows that
 $$ \begin{align*}(a\cup V_\alpha^{(a)})\cap V_n=a\cap V_n.\end{align*} $$
$$ \begin{align*}(a\cup V_\alpha^{(a)})\cap V_n=a\cap V_n.\end{align*} $$
Consequently,
 $a\cup V_\alpha ^{(a)}$
obeys the growth-rate requirement, and consequently every
$a\cup V_\alpha ^{(a)}$
obeys the growth-rate requirement, and consequently every
 $V^{(a)}_\alpha $
is in M. So
$V^{(a)}_\alpha $
is in M. So
![]() $V^{(a)}\subseteq M$
.⊣
$V^{(a)}\subseteq M$
.⊣
Lemma 27. For any set
![]() $a\in M$
, the class
$a\in M$
, the class
![]() $V^{(a)}$
is definable in M from parameter a.
$V^{(a)}$
is definable in M from parameter a.
Proof. One might naturally want to define
![]() $V^{(a)}$
in M by transfinite recursion, as we did in defining the hierarchy
$V^{(a)}$
in M by transfinite recursion, as we did in defining the hierarchy
 $V^{(a)}_\alpha $
above. The problem with this is that M is a model merely of Zermelo set theory, in which such definitions by transfinite recursion do not necessarily succeed. Nevertheless, in instances as here where we know independently that the recursion does have a solution in M, the recursive definition does in fact succeed in defining it.
$V^{(a)}_\alpha $
above. The problem with this is that M is a model merely of Zermelo set theory, in which such definitions by transfinite recursion do not necessarily succeed. Nevertheless, in instances as here where we know independently that the recursion does have a solution in M, the recursive definition does in fact succeed in defining it.
But instead of that definition, let us consider another simple definition. Define that a terminal
![]() $\in $
-descent from a set x is a finite
$\in $
-descent from a set x is a finite
![]() $\in $
-descending sequence of sets from x to
$\in $
-descending sequence of sets from x to
![]() $\varnothing $
$\varnothing $
We claim that
![]() $V^{(a)}$
consists in M precisely of those sets x for which every terminal
$V^{(a)}$
consists in M precisely of those sets x for which every terminal
![]() $\in $
-descent passes through the set a, in the sense that
$\in $
-descent passes through the set a, in the sense that
![]() $a=x_i$
for some i. Certainly every
$a=x_i$
for some i. Certainly every
![]() $x\in V^{(a)}$
is like this, since if
$x\in V^{(a)}$
is like this, since if
 $y\in x\in V^{(a)}_{\alpha +1}$
, then either
$y\in x\in V^{(a)}_{\alpha +1}$
, then either
![]() $x=a$
or
$x=a$
or
 $y\in V^{(a)}_\alpha $
, and by induction the terminal descents from y will pass through a. Conversely, assume that every terminal
$y\in V^{(a)}_\alpha $
, and by induction the terminal descents from y will pass through a. Conversely, assume that every terminal
![]() $\in $
-descent from x passes through a. So either
$\in $
-descent from x passes through a. So either
![]() $x=a$
, in which case it is in
$x=a$
, in which case it is in
![]() $V^{(a)}$
, or else the assumption about terminal descents is also true of the elements of x. By
$V^{(a)}$
, or else the assumption about terminal descents is also true of the elements of x. By
![]() $\in $
-induction, therefore, the elements of x are all in
$\in $
-induction, therefore, the elements of x are all in
![]() $V^{(a)}$
, and this implies that x is in
$V^{(a)}$
, and this implies that x is in
 $V^{(a)}_\gamma $
at an ordinal stage
$V^{(a)}_\gamma $
at an ordinal stage
![]() $\gamma $
beyond the stages where the elements of x are placed into
$\gamma $
beyond the stages where the elements of x are placed into
![]() $V^{(a)}$
.⊣
$V^{(a)}$
.⊣
If we take
![]() $a=\omega $
, or some other definable infinite transitive set in M, then we don’t need a as a parameter, and so we’ve proved that
$a=\omega $
, or some other definable infinite transitive set in M, then we don’t need a as a parameter, and so we’ve proved that
![]() $\langle V,\in \rangle $
and
$\langle V,\in \rangle $
and
![]() $ \langle M,\in \rangle $
are at least mutually interpretable; each has a definable copy in the other.
$ \langle M,\in \rangle $
are at least mutually interpretable; each has a definable copy in the other.
Lemma 28. The mutual interpretation of
![]() $ \langle V,\in \rangle $
and
$ \langle V,\in \rangle $
and
![]() $ \langle M,\in \rangle $
is a bi-interpretation.
$ \langle M,\in \rangle $
is a bi-interpretation.
Proof. We’ve seen already that M is a definable transitive inner model of V, and
![]() $ \langle V,\in \rangle $
is definably isomorphic to its copy
$ \langle V,\in \rangle $
is definably isomorphic to its copy
 $ \langle V^{(a)},\in \rangle $
in M, isomorphic by the map
$ \langle V^{(a)},\in \rangle $
in M, isomorphic by the map
![]() $x\mapsto x^{(a)}$
, which is definable in V, assuming as we have that we use
$x\mapsto x^{(a)}$
, which is definable in V, assuming as we have that we use
![]() $a=\omega $
or some other definable infinite transitive set in M.
$a=\omega $
or some other definable infinite transitive set in M.
Conversely, we’ve seen that M can define the model
 $ \langle V^{(a)},\in \rangle $
. Inside that model, we define the copy
$ \langle V^{(a)},\in \rangle $
. Inside that model, we define the copy
![]() $M^{(a)}$
of M, just as M is definable in V. For this to be a bi-interpretation, we need to show that the isomorphism of M with
$M^{(a)}$
of M, just as M is definable in V. For this to be a bi-interpretation, we need to show that the isomorphism of M with
![]() $M^{(a)}$
is definable in M. This isomorphism is precisely the function
$M^{(a)}$
is definable in M. This isomorphism is precisely the function
![]() $i:x\mapsto x^{(a)}$
, applied to
$i:x\mapsto x^{(a)}$
, applied to
![]() $x\in M$
. The problem again, however, is that M is not able in general to undertake recursive definitions, since it satisfies only Zermelo set theory, which does not prove that recursive definitions have solutions. Nevertheless, we claim that
$x\in M$
. The problem again, however, is that M is not able in general to undertake recursive definitions, since it satisfies only Zermelo set theory, which does not prove that recursive definitions have solutions. Nevertheless, we claim that
![]() $i\upharpoonright x\in M$
for any
$i\upharpoonright x\in M$
for any
![]() $x\in M$
. The reason is that the transitive closure of
$x\in M$
. The reason is that the transitive closure of
 $i\upharpoonright x=\{\,{(y,y^{(a)})\mid y\in x}\,\}$
can be seen to obey the growth-rate requirement, as x does with its transitive closure and the sets
$i\upharpoonright x=\{\,{(y,y^{(a)})\mid y\in x}\,\}$
can be seen to obey the growth-rate requirement, as x does with its transitive closure and the sets
![]() $y^{(a)}$
are either a or have no elements in any
$y^{(a)}$
are either a or have no elements in any
![]() $V_n$
, as in Lemma 26 above. Thus, M can see the isomorphism
$V_n$
, as in Lemma 26 above. Thus, M can see the isomorphism
![]() $i\upharpoonright x$
of
$i\upharpoonright x$
of
![]() $ \langle x,\in \rangle $
with
$ \langle x,\in \rangle $
with
 $ \langle x^{(a)},\in \rangle $
for any set
$ \langle x^{(a)},\in \rangle $
for any set
![]() $x\in M$
. If x is transitive, then since transitive sets are rigid, this isomorphism is unique, and since different transitive sets are never isomorphic,
$x\in M$
. If x is transitive, then since transitive sets are rigid, this isomorphism is unique, and since different transitive sets are never isomorphic,
![]() $ \langle x,\in \rangle $
will not be isomorphic to any
$ \langle x,\in \rangle $
will not be isomorphic to any
![]() $ \langle y,\in \rangle $
that
$ \langle y,\in \rangle $
that
![]() $M^{(a)}$
thinks is transitive. So M can define
$M^{(a)}$
thinks is transitive. So M can define
![]() $i\upharpoonright x$
for transitive sets x by the assertions that it is an isomorphism of
$i\upharpoonright x$
for transitive sets x by the assertions that it is an isomorphism of
![]() $ \langle x,\in \rangle $
with a set
$ \langle x,\in \rangle $
with a set
![]() $ \langle y,\in \rangle $
for a set y that
$ \langle y,\in \rangle $
for a set y that
![]() $M^{(a)}$
thinks is transitive. These maps all agree with and union up to the full isomorphism
$M^{(a)}$
thinks is transitive. These maps all agree with and union up to the full isomorphism
![]() $x\mapsto x^{(a)}$
of M with
$x\mapsto x^{(a)}$
of M with
![]() $M^{(a)}$
, which is therefore definable in M. So we have a bi-interpretation of
$M^{(a)}$
, which is therefore definable in M. So we have a bi-interpretation of
![]() $ \langle V,\in \rangle $
with
$ \langle V,\in \rangle $
with
![]() $ \langle M,\in \rangle $
. ⊣
$ \langle M,\in \rangle $
. ⊣
Let us now put all this together and explain how we have proved Theorem 23.
Proof of Theorem 23 The argument we have given shows that every model
![]() $V\models \mathrm {ZF}$
is bi-interpretable with a transitive inner model M of Zermelo set theory, which is not a model of
$V\models \mathrm {ZF}$
is bi-interpretable with a transitive inner model M of Zermelo set theory, which is not a model of
![]() $\mathrm {ZF}$
, because it does not even have
$\mathrm {ZF}$
, because it does not even have
![]() $V_\omega $
as an element. This establishes statement (2) of Theorem 23.
$V_\omega $
as an element. This establishes statement (2) of Theorem 23.
For statement (1), we can perform the construction inside a well-founded model of some sufficient fragment of
![]() $\mathrm {ZF}$
. For example, let us undertake the entire construction inside some
$\mathrm {ZF}$
. For example, let us undertake the entire construction inside some
![]() $V_\lambda $
, satisfying
$V_\lambda $
, satisfying
![]() $\Sigma _2$
-collection, say. We thereby get a transitive model
$\Sigma _2$
-collection, say. We thereby get a transitive model
![]() $M_\lambda \subseteq V_\lambda $
of Zermelo set theory, without
$M_\lambda \subseteq V_\lambda $
of Zermelo set theory, without
![]() $V_\omega $
, but with
$V_\omega $
, but with
![]() $\langle V_\lambda ,\in \rangle $
and
$\langle V_\lambda ,\in \rangle $
and
![]() $\left \langle M_\lambda ,\in \right \rangle $
bi-interpretable. So there are well-founded models of Zermelo set theory that are bi-interpretable, but not isomorphic.
$\left \langle M_\lambda ,\in \right \rangle $
bi-interpretable. So there are well-founded models of Zermelo set theory that are bi-interpretable, but not isomorphic.
Finally, let us consider statement (3). We consider the two extensions of Zermelo set theory describing the situation that enabled us to make the main example for statement (2). That is, the first theory is
![]() $\mathrm {ZF}$
itself; and the second theory, which we denote ZM, asserts Zermelo set theory Z, plus the assertion that the class
$\mathrm {ZF}$
itself; and the second theory, which we denote ZM, asserts Zermelo set theory Z, plus the assertion that the class
![]() $V^{(\omega )}$
, defined as in our main argument, is a model of
$V^{(\omega )}$
, defined as in our main argument, is a model of
![]() $\mathrm {ZF}$
, and the assertion that M is isomorphic to
$\mathrm {ZF}$
, and the assertion that M is isomorphic to
![]() $M^{(\omega )}$
inside that class by the isomorphism definition we provided. These two theories are different, but the argument that we gave above for the models shows that they are bi-interpretable. ⊣
$M^{(\omega )}$
inside that class by the isomorphism definition we provided. These two theories are different, but the argument that we gave above for the models shows that they are bi-interpretable. ⊣
Let us close this section by mentioning that the construction is quite malleable with respect to the instance of replacement we want to eliminate. Alternative versions of the construction will construct supertransitive inner models M that satisfy Zermelo set theory, and which have
![]() $V_\alpha $
as a set for every ordinal
$V_\alpha $
as a set for every ordinal
![]() $\alpha <\lambda $
, but do not have
$\alpha <\lambda $
, but do not have
![]() $V_\lambda $
as a set.
$V_\lambda $
as a set.
Theorem 29. For every limit ordinal
![]() $\lambda $
, the universe
$\lambda $
, the universe
![]() $\left \langle V,\in \right \rangle $
is bi-interpretable with a transitive inner model
$\left \langle V,\in \right \rangle $
is bi-interpretable with a transitive inner model
![]() $\left \langle M,\in \right \rangle $
satisfying Zermelo set theory with foundation, such that
$\left \langle M,\in \right \rangle $
satisfying Zermelo set theory with foundation, such that
![]() $V_\alpha \in M$
for every
$V_\alpha \in M$
for every
![]() $\alpha <\lambda $
, but
$\alpha <\lambda $
, but
![]() $V_\lambda \notin M$
.
$V_\lambda \notin M$
.
Proof. We use
![]() $M=\bigcup T^{Q,G}$
, where
$M=\bigcup T^{Q,G}$
, where
![]() $Q:\lambda \to V_\lambda $
is
$Q:\lambda \to V_\lambda $
is
![]() $Q(\alpha )=V_\alpha $
, and G consists of the functions f that are bounded by one of the functions
$Q(\alpha )=V_\alpha $
, and G consists of the functions f that are bounded by one of the functions
![]() $b_\beta $
, for some
$b_\beta $
, for some
![]() $\beta <\lambda $
, defined by
$\beta <\lambda $
, defined by
-
(1)
 $b_0(\alpha ) = \alpha $
;
$b_0(\alpha ) = \alpha $
; -
(2)
 $b_{\beta +1}(\alpha ) = 2^{b_\beta (\alpha )}$
;
$b_{\beta +1}(\alpha ) = 2^{b_\beta (\alpha )}$
; -
(3) if
 $\eta $
is a limit ordinal, then
$\eta $
is a limit ordinal, then
 $b_\eta (\alpha ) = {\text {sup}}_{\beta <\eta }b_\beta (\alpha )$
.
$b_\eta (\alpha ) = {\text {sup}}_{\beta <\eta }b_\beta (\alpha )$
.
This is defined with cardinal arithmetic, not ordinal arithmetic. The class
![]() $T^{Q,G}$
consists of all transitive sets x whose rate-of-growth function
$T^{Q,G}$
consists of all transitive sets x whose rate-of-growth function
 $$ \begin{align*} f_x^Q(\alpha)=|x\cap V_\alpha| \end{align*} $$
$$ \begin{align*} f_x^Q(\alpha)=|x\cap V_\alpha| \end{align*} $$
is bounded by one of the functions
![]() $b_\beta $
, for some
$b_\beta $
, for some
![]() $\beta <\lambda $
. It follows that
$\beta <\lambda $
. It follows that
![]() $T^{Q,G}$
is a fruitful class, and the resulting Zermelo model
$T^{Q,G}$
is a fruitful class, and the resulting Zermelo model
![]() $M=\bigcup T^{Q,G}$
is a transitive inner model of Zermelo set theory with foundation (in the form of the
$M=\bigcup T^{Q,G}$
is a transitive inner model of Zermelo set theory with foundation (in the form of the
![]() $\in $
-induction scheme). Every
$\in $
-induction scheme). Every
![]() $V_\alpha $
for
$V_\alpha $
for
![]() $\alpha <\lambda $
is in M, with growth rate bounded by
$\alpha <\lambda $
is in M, with growth rate bounded by
![]() $b_\alpha $
, but
$b_\alpha $
, but
![]() $V_\lambda $
is not in M, since this growth rate exceeds any given
$V_\lambda $
is not in M, since this growth rate exceeds any given
![]() $b_\beta $
for fixed
$b_\beta $
for fixed
![]() $\beta <\lambda $
. And
$\beta <\lambda $
. And
![]() $\left \langle V,\in \right \rangle $
is bi-interpretable with
$\left \langle V,\in \right \rangle $
is bi-interpretable with
![]() $\left \langle M,\in \right \rangle $
by analogous arguments to the above. ⊣
$\left \langle M,\in \right \rangle $
by analogous arguments to the above. ⊣
One can use this idea to produce many non-tight theories extending Zermelo set theory. For example, for any theory true in the model M that we produced in the proof of Theorem 23 will be bi-interpretable with
![]() $\mathrm {ZF}$
. For example, that model M satisfies the principle that every definable function from a set to the ordinals is bounded, which can be seen as a weak form of replacement not provable in Z, but true in M precisely because it is a transitive inner model (with all the ordinals) of a model of
$\mathrm {ZF}$
. For example, that model M satisfies the principle that every definable function from a set to the ordinals is bounded, which can be seen as a weak form of replacement not provable in Z, but true in M precisely because it is a transitive inner model (with all the ordinals) of a model of
![]() $\mathrm {ZF}$
. In Theorem 29 we similarly arranged that
$\mathrm {ZF}$
. In Theorem 29 we similarly arranged that
![]() $V_\alpha $
exists for all
$V_\alpha $
exists for all
![]() $\alpha $
up to some large definable limit ordinal
$\alpha $
up to some large definable limit ordinal
![]() $\lambda $
, which is itself another instance of replacement, and so this gives another extension of Zermelo set theory that is bi-interpretable with ZF.
$\lambda $
, which is itself another instance of replacement, and so this gives another extension of Zermelo set theory that is bi-interpretable with ZF.
Let us conclude the paper by distinguishing the theory form of bi-interpretation from a natural model-by-model form of bi-interpretation that might hold for the models of the theory. Specifically, we define that
Definition 30. Theories
![]() $T_1$
and
$T_1$
and
![]() $T_2$
are model-by-model bi-interpretable if every model of one of the theories is bi-interpretable with a model of the other.
$T_2$
are model-by-model bi-interpretable if every model of one of the theories is bi-interpretable with a model of the other.
The definition in effect drops the uniformity requirement for bi-interpretability of theories, since it could be a different interpretation that works in one model than in another, with perhaps no uniform definition that works in all models of the theory. This is precisely what we should like now to prove.
Theorem 31. There are theories
![]() $T_1$
and
$T_1$
and
![]() $T_2$
that are model-by-model bi-interpretable, but not bi-interpretable.
$T_2$
that are model-by-model bi-interpretable, but not bi-interpretable.
Proof. Consider the theories
-
(1)
 $T_1 = \mathrm {ZF}$
.
$T_1 = \mathrm {ZF}$
. -
(2)
 $T_2 = \{\alpha \lor \beta \mid \alpha \in \mathrm {ZF} \land \beta \in \mathrm {ZM}\}$
(That is,
$T_2 = \{\alpha \lor \beta \mid \alpha \in \mathrm {ZF} \land \beta \in \mathrm {ZM}\}$
(That is,
 $T_2 = \mathrm {ZM} \lor \mathrm {ZF}.$
),
$T_2 = \mathrm {ZM} \lor \mathrm {ZF}.$
),
where ZM is the theory used in the proof of Theorem 23. Observe that
![]() $M\models T_2$
if and only if
$M\models T_2$
if and only if
![]() $M\models \mathrm {ZF}$
or
$M\models \mathrm {ZF}$
or
![]() $M\models \mathrm {ZM}$
. The reverse implication is immediate, and if the latter fails, then
$M\models \mathrm {ZM}$
. The reverse implication is immediate, and if the latter fails, then
![]() $M\not \models \alpha $
and
$M\not \models \alpha $
and
![]() $M\not \models \beta $
for some
$M\not \models \beta $
for some
![]() $\alpha \in \mathrm {ZF}$
and
$\alpha \in \mathrm {ZF}$
and
![]() $\beta \in \mathrm {ZM}$
, which would mean
$\beta \in \mathrm {ZM}$
, which would mean
![]() $M\not \models \alpha \lor \beta $
, violating the former.
$M\not \models \alpha \lor \beta $
, violating the former.
Now observe simply that every model of
![]() $\mathrm {ZF}$
is bi-interpretable with itself, of course, and this is a model of
$\mathrm {ZF}$
is bi-interpretable with itself, of course, and this is a model of
![]() $T_2$
. And conversely, every model of
$T_2$
. And conversely, every model of
![]() $T_2$
is either a model of
$T_2$
is either a model of
![]() $\mathrm {ZF}$
already, or else a model of
$\mathrm {ZF}$
already, or else a model of
![]() $\mathrm {ZM}$
, which is bi-interpretable with a model of
$\mathrm {ZM}$
, which is bi-interpretable with a model of
![]() $\mathrm {ZF}$
. So these two theories are model-by-model bi-interpretable.
$\mathrm {ZF}$
. So these two theories are model-by-model bi-interpretable.
Let us now prove that the theories are not bi-interpretable. Suppose toward contradiction that
![]() $(I,J)$
form a bi-interpretation, so that I defines a model of
$(I,J)$
form a bi-interpretation, so that I defines a model of
![]() $T_1$
inside any model of
$T_1$
inside any model of
![]() $T_2$
and J defines a model of
$T_2$
and J defines a model of
![]() $T_2$
inside any model of
$T_2$
inside any model of
![]() $T_1$
, and the theories prove this and furthermore have definable isomorphisms of the original models with their successive double-interpreted copies. Let M be a model of
$T_1$
, and the theories prove this and furthermore have definable isomorphisms of the original models with their successive double-interpreted copies. Let M be a model of
![]() $\mathrm {ZM}$
that is not a model of
$\mathrm {ZM}$
that is not a model of
![]() $\mathrm {ZF}$
. Let
$\mathrm {ZF}$
. Let
![]() $I^M$
be the interpreted model of
$I^M$
be the interpreted model of
![]() $\mathrm {ZF}$
defined inside M. This is also a model of
$\mathrm {ZF}$
defined inside M. This is also a model of
![]() $\mathrm {ZM}$
, since
$\mathrm {ZM}$
, since
![]() $\mathrm {ZM}\subseteq \mathrm {ZF}$
, and so we may use I again to define
$\mathrm {ZM}\subseteq \mathrm {ZF}$
, and so we may use I again to define
![]() $I^{I^M}$
to get another model of
$I^{I^M}$
to get another model of
![]() $\mathrm {ZF}$
inside that model. Because we interpreted a model of
$\mathrm {ZF}$
inside that model. Because we interpreted a model of
![]() $T_2$
by I, it follows that
$T_2$
by I, it follows that
![]() $I^{I^M}$
and
$I^{I^M}$
and
![]() $I^M$
are bi-interpretable as models. But these are both models of
$I^M$
are bi-interpretable as models. But these are both models of
![]() $\mathrm {ZF}$
, and so by Theorem 13 they are isomorphic. By interpreting with J to get the corresponding interpreted
$\mathrm {ZF}$
, and so by Theorem 13 they are isomorphic. By interpreting with J to get the corresponding interpreted
![]() $\mathrm {ZM}$
models, it follows that
$\mathrm {ZM}$
models, it follows that
 $J^{I^{I^M}}$
and
$J^{I^{I^M}}$
and
![]() $J^{I^M}$
are isomorphic. Because
$J^{I^M}$
are isomorphic. Because
![]() $(I,J)$
form a bi-interpretation, the first of these is isomorphic to
$(I,J)$
form a bi-interpretation, the first of these is isomorphic to
![]() $I^M\!$
, which is a
$I^M\!$
, which is a
![]() $\mathrm {ZF}$
model, while the second is isomorphic to M, which is not. This is a contradiction, and so the theories are not bi-interpretable.⊣
$\mathrm {ZF}$
model, while the second is isomorphic to M, which is not. This is a contradiction, and so the theories are not bi-interpretable.⊣
The essence of the proof was that we had a theory
![]() $\mathrm {ZM}$
that was not solid, but it was a subtheory of a solid theory
$\mathrm {ZM}$
that was not solid, but it was a subtheory of a solid theory
![]() $\mathrm {ZF}$
, with which it was bi-interpretable.
$\mathrm {ZF}$
, with which it was bi-interpretable.
10 Final remarks
We have investigated the nature of mutual and bi-interpretation in set theory and the models of set theory. There is surely a vibrant mutual interpretation phenomenon in set theory, with numerous instances of mutual interpretation amongst diverse natural extensions of
![]() $\mathrm {ZF}$
set theory. This mutual-interpretation phenomenon, however, is less than fully robust in several respects. First, theories extending
$\mathrm {ZF}$
set theory. This mutual-interpretation phenomenon, however, is less than fully robust in several respects. First, theories extending
![]() $\mathrm {ZF}$
are never bi-interpretable, and indeed, there cannot be even a single nontrivial instance of models of
$\mathrm {ZF}$
are never bi-interpretable, and indeed, there cannot be even a single nontrivial instance of models of
![]() $\mathrm {ZF}$
set theory being bi-interpretable. Worse, amongst the well-founded models of
$\mathrm {ZF}$
set theory being bi-interpretable. Worse, amongst the well-founded models of
![]() $\mathrm {ZF}$
, there cannot even be nontrivial instances of mutual interpretation. The basic lesson of this is that, when one follows the mutual interpretations we mentioned above, there is no getting back. One cannot recover the original model. When you move from a well-founded model of
$\mathrm {ZF}$
, there cannot even be nontrivial instances of mutual interpretation. The basic lesson of this is that, when one follows the mutual interpretations we mentioned above, there is no getting back. One cannot recover the original model. When you move from a well-founded model of
![]() $\mathrm {ZFC}$
with large cardinals to the corresponding determinacy model, you cannot define a copy of the original model again, and the same when interpreting in the other direction. In this sense, interpretation in models of set theory inevitably involves and requires the loss of set-theoretic information.
$\mathrm {ZFC}$
with large cardinals to the corresponding determinacy model, you cannot define a copy of the original model again, and the same when interpreting in the other direction. In this sense, interpretation in models of set theory inevitably involves and requires the loss of set-theoretic information.
Meanwhile, we have showed that several natural weak set theories avoid this phenomenon, including Zermelo–Fraenkel set theory
![]() $\mathrm {ZFC}^{-}$
without the power set axiom and Zermelo set theory Z. It remains open just how strong the weak set theories can be, while still admitting non-trivial instances of bi-interpretation. In addition, there remain interesting open questions concerning the circumstances in which
$\mathrm {ZFC}^{-}$
without the power set axiom and Zermelo set theory Z. It remains open just how strong the weak set theories can be, while still admitting non-trivial instances of bi-interpretation. In addition, there remain interesting open questions concerning the circumstances in which
![]() $H_{\omega _1}$
and
$H_{\omega _1}$
and
![]() $H_{\omega _2}$
might be bi-interpretable or bi-interpretation synonymous.
$H_{\omega _2}$
might be bi-interpretable or bi-interpretation synonymous.
Acknowledgments
This research was supported by grant 2017/21020-0, São Paulo Research Foundation (FAPESP). The research project grew out of the first author’s Ph.D. dissertation [5], with related philosophical work in [Reference Freire and Peliš4, Reference Freire and de Alvarenga Freire6].