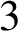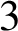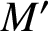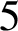1 Introduction
An open book decomposition of a closed connected oriented n-manifold M is a fibration
![]() $\pi :M\setminus B\to S^1$
, where B is a codimension-two oriented submanifold of M with a trivial normal bundle. The submanifold B is called the binding of the open book. The closure of each fibre of
$\pi :M\setminus B\to S^1$
, where B is a codimension-two oriented submanifold of M with a trivial normal bundle. The submanifold B is called the binding of the open book. The closure of each fibre of
![]() $\pi $
is called a page of the open book and each page is a codimension-one submanifold of M with boundary B. Alexander, in [Reference Alexander1], showed that every closed oriented
$\pi $
is called a page of the open book and each page is a codimension-one submanifold of M with boundary B. Alexander, in [Reference Alexander1], showed that every closed oriented
![]() $3$
-manifold admits an open book. For more details on open books, we refer to the survey [Reference Etnyre2].
$3$
-manifold admits an open book. For more details on open books, we refer to the survey [Reference Etnyre2].
Open book decomposition on odd-dimensional manifolds is an important tool in studying contact structures on manifolds. By a contact structure on a closed oriented
![]() $(2n+1)$
-manifold M, we mean a maximally nowhere integrable hyperplane field on
$(2n+1)$
-manifold M, we mean a maximally nowhere integrable hyperplane field on
![]() $M.$
Giroux, in [Reference Giroux4], showed that every co-oriented contact structure on a closed oriented
$M.$
Giroux, in [Reference Giroux4], showed that every co-oriented contact structure on a closed oriented
![]() $(2n+1)$
-manifold is supported by an open book. In [Reference Thurston and Winkelnkemper11], Thurston and Winkelnkemper constructed contact structures on closed oriented
$(2n+1)$
-manifold is supported by an open book. In [Reference Thurston and Winkelnkemper11], Thurston and Winkelnkemper constructed contact structures on closed oriented
![]() $3$
-manifolds using open books. In [Reference Giroux4], Giroux showed that there is a one-to-one correspondence between the isotopy classes of co-oriented contact structures on a closed oriented 3-manifold M and the open book decompositions of M up to positive stabilisations. By a positive stabilisation operation on an open book of
$3$
-manifolds using open books. In [Reference Giroux4], Giroux showed that there is a one-to-one correspondence between the isotopy classes of co-oriented contact structures on a closed oriented 3-manifold M and the open book decompositions of M up to positive stabilisations. By a positive stabilisation operation on an open book of
![]() $ M$
, we mean a plumbing of a positive Hopf band to the page of the open book. Open book decomposition is a useful tool in studying
$ M$
, we mean a plumbing of a positive Hopf band to the page of the open book. Open book decomposition is a useful tool in studying
![]() $3$
-manifolds. For instance, an open book decomposition of a manifold naturally gives a Heegaard splitting of the manifold, where the Heegaard surface is the closure of the union of two pages.
$3$
-manifolds. For instance, an open book decomposition of a manifold naturally gives a Heegaard splitting of the manifold, where the Heegaard surface is the closure of the union of two pages.
Open book embeddings of closed oriented
![]() $3$
-manifolds into the open books of
$3$
-manifolds into the open books of
![]() $S^2\times S^3$
as well as into
$S^2\times S^3$
as well as into
![]() $S^2 \,\tilde \times \, S^3$
with pages a
$S^2 \,\tilde \times \, S^3$
with pages a
![]() $2$
-disc bundle over
$2$
-disc bundle over
![]() $S^2$
and monodromy the identity map are studied in [Reference Pancholi, Pandit and Saha9]. Results in [Reference Pancholi, Pandit and Saha9] are extended for nonorientable closed
$S^2$
and monodromy the identity map are studied in [Reference Pancholi, Pandit and Saha9]. Results in [Reference Pancholi, Pandit and Saha9] are extended for nonorientable closed
![]() $3$
-manifolds in [Reference Ghanwat, Pandit and A3]. We say that a smooth manifold M with a given open book decomposition admits an open book embedding in an open book decomposition of a smooth manifold N if there exists an embedding of M in N such that, as a submanifold of N, the given open book decomposition on M is compatible with the open book decomposition of N. For the precise definition of an open book embedding, we refer to Definition 2.3. However, the existence of an open book for a closed oriented
$3$
-manifolds in [Reference Ghanwat, Pandit and A3]. We say that a smooth manifold M with a given open book decomposition admits an open book embedding in an open book decomposition of a smooth manifold N if there exists an embedding of M in N such that, as a submanifold of N, the given open book decomposition on M is compatible with the open book decomposition of N. For the precise definition of an open book embedding, we refer to Definition 2.3. However, the existence of an open book for a closed oriented
![]() $3$
-manifold, such that its open book embeds in the trivial open book of the
$3$
-manifold, such that its open book embeds in the trivial open book of the
![]() $5$
-sphere
$5$
-sphere
![]() $S^5$
with pages the
$S^5$
with pages the
![]() $4$
-disk
$4$
-disk
![]() $D^4$
and monodromy the identity map of
$D^4$
and monodromy the identity map of
![]() $D^4$
, is not known.
$D^4$
, is not known.
In this note, we study open book embeddings of closed oriented
![]() $3$
-manifolds in the
$3$
-manifolds in the
![]() $5$
-sphere
$5$
-sphere
![]() $S^5$
. We prove the following result.
$S^5$
. We prove the following result.
Theorem 1.1. Let M be a closed connected oriented
![]() $3$
-manifold. There exists a knot K in M such that the manifold
$3$
-manifold. There exists a knot K in M such that the manifold
![]() $M^{\prime }$
obtained from M, by performing an integer surgery, admits an open book decomposition and this open book embeds into the trivial open book of the
$M^{\prime }$
obtained from M, by performing an integer surgery, admits an open book decomposition and this open book embeds into the trivial open book of the
![]() $5$
-sphere
$5$
-sphere
![]() $S^5.$
$S^5.$
2 Preliminary
First, we recall the notions necessary for this note. All the manifolds and maps we consider are smooth.
Definition 2.1. An open book decomposition of a closed connected oriented manifold M is a pair
![]() $(B, \pi ),$
with the following properties.
$(B, \pi ),$
with the following properties.
-
(1) B is an oriented codimension-two submanifold in M with a trivial normal bundle called the binding of the open book.
-
(2)
 $ \pi : M \setminus B\rightarrow S^1$
is a locally trivial fibration such that the fibration
$ \pi : M \setminus B\rightarrow S^1$
is a locally trivial fibration such that the fibration
 $\pi $
in a tubular neighbourhood of B looks like the trivial fibration of
$\pi $
in a tubular neighbourhood of B looks like the trivial fibration of
 $(B\times D^2) \setminus B\times \{0\} \to S^1$
sending
$(B\times D^2) \setminus B\times \{0\} \to S^1$
sending
 $(x,r,\theta )$
to
$(x,r,\theta )$
to
 $\theta $
, where
$\theta $
, where
 $x\in B$
and
$x\in B$
and
 $(r,\theta )$
are polar coordinates on
$(r,\theta )$
are polar coordinates on
 $D^2$
.
$D^2$
. -
(3) For each
 $\theta \in S^1, \pi ^{-1}(\theta )$
is the interior of a compact codimension-one submanifold
$\theta \in S^1, \pi ^{-1}(\theta )$
is the interior of a compact codimension-one submanifold
 $N_{\theta }\subset M$
and
$N_{\theta }\subset M$
and
 $\partial N_\theta = B$
. The submanifold
$\partial N_\theta = B$
. The submanifold
 $N=N_\theta $
, for any
$N=N_\theta $
, for any
 $\theta $
, is called the page of the open book.
$\theta $
, is called the page of the open book.
The fibration
![]() $\pi :M\setminus B\to S^1$
with fibre N is determined by N and the monodromy
$\pi :M\setminus B\to S^1$
with fibre N is determined by N and the monodromy
![]() $\phi $
of the fibration up to conjugation by an orientation preserving diffeomorphism, that is, the fibre bundle
$\phi $
of the fibration up to conjugation by an orientation preserving diffeomorphism, that is, the fibre bundle
![]() $M\setminus B$
is canonically isomorphic to the mapping torus
$M\setminus B$
is canonically isomorphic to the mapping torus
where
![]() $\sim $
is the equivalence relation identifying
$\sim $
is the equivalence relation identifying
![]() $(x,1)$
with
$(x,1)$
with
![]() $(\varphi (x),0)$
. From the above definition, we can see that M is diffeomorphic to
$(\varphi (x),0)$
. From the above definition, we can see that M is diffeomorphic to
Thus, an open book decomposition of
![]() $M $
is determined, up to diffeomorphism of
$M $
is determined, up to diffeomorphism of
![]() $ M$
, by the topological type of the page N and the isotopy class of the monodromy which is an element of the mapping class group of N. The mapping class group of a manifold N with nonempty boundary is the group of isotopy classes of orientation-preserving diffeomorphisms of N which are the identity in a collar neighbourhood of the boundary.
$ M$
, by the topological type of the page N and the isotopy class of the monodromy which is an element of the mapping class group of N. The mapping class group of a manifold N with nonempty boundary is the group of isotopy classes of orientation-preserving diffeomorphisms of N which are the identity in a collar neighbourhood of the boundary.
This naturally leads to the notion called an abstract open book defined as follows.
Definition 2.2. An abstract open book associated with an n-manifold M is a pair
![]() $(\Sigma , \phi ),$
where
$(\Sigma , \phi ),$
where
![]() $\Sigma $
is a compact connected oriented
$\Sigma $
is a compact connected oriented
![]() $(n-1)$
-manifold with nonempty boundary and
$(n-1)$
-manifold with nonempty boundary and
![]() $\phi $
is an orientation-preserving diffeomorphism of
$\phi $
is an orientation-preserving diffeomorphism of
![]() $\Sigma $
such that M is diffeomorphic to
$\Sigma $
such that M is diffeomorphic to
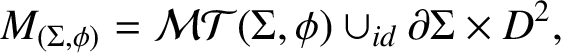 $$ \begin{align*}M_{(\Sigma,\phi)}=\mathcal{MT}(\Sigma, \phi) \cup_{id} \partial \Sigma \times D^2,\end{align*} $$
$$ \begin{align*}M_{(\Sigma,\phi)}=\mathcal{MT}(\Sigma, \phi) \cup_{id} \partial \Sigma \times D^2,\end{align*} $$
where
![]() $id$
denotes the identity map of
$id$
denotes the identity map of
![]() $\partial \Sigma \times S^1.$
$\partial \Sigma \times S^1.$
The map
![]() $\phi $
in the above definition is called the monodromy of the abstract open book. Note that the mapping class of
$\phi $
in the above definition is called the monodromy of the abstract open book. Note that the mapping class of
![]() $\phi $
determines M uniquely up to diffeomorphism. We will denote the manifold M with an abstract open book decomposition
$\phi $
determines M uniquely up to diffeomorphism. We will denote the manifold M with an abstract open book decomposition
![]() $(\Sigma ,\phi )$
by
$(\Sigma ,\phi )$
by
![]() $ \mathcal {A}ob(\Sigma ,\phi )$
. One can easily see that given an abstract open book decomposition of M, we can clearly associate an open book decomposition of M with pages
$ \mathcal {A}ob(\Sigma ,\phi )$
. One can easily see that given an abstract open book decomposition of M, we can clearly associate an open book decomposition of M with pages
![]() $\Sigma $
and vice versa. We will not generally distinguish between open books and abstract open books. For more details on open books, see [Reference Etnyre2].
$\Sigma $
and vice versa. We will not generally distinguish between open books and abstract open books. For more details on open books, see [Reference Etnyre2].
Let us recall the notion of an open book embedding.
Definition 2.3. Let
![]() $M^k$
and
$M^k$
and
![]() $N^l$
be manifolds with open book decompositions
$N^l$
be manifolds with open book decompositions
![]() $(B_1, \pi _1)$
and
$(B_1, \pi _1)$
and
![]() $(B_2, \pi _2)$
, respectively. We say an embedding
$(B_2, \pi _2)$
, respectively. We say an embedding
![]() $f: M \hookrightarrow N$
is an open book embedding of
$f: M \hookrightarrow N$
is an open book embedding of
![]() $(B_1, \pi _1)$
into
$(B_1, \pi _1)$
into
![]() $(B_2, \pi _2)$
if f embeds
$(B_2, \pi _2)$
if f embeds
![]() $B_1$
into
$B_1$
into
![]() $B_2$
such that
$B_2$
such that
![]() $\pi _2\circ f=\pi _1.$
$\pi _2\circ f=\pi _1.$
Similarly, we can also define an abstract open book embedding.
Definition 2.4. Let
![]() $M = \mathcal {A}ob (\Sigma _1, \phi _1)$
and
$M = \mathcal {A}ob (\Sigma _1, \phi _1)$
and
![]() $N = \mathcal {A}ob( \Sigma _2, \phi _2 )$
be two abstract open books. We say that there exists an abstract open book embedding of M into N if there exists a proper embedding f of
$N = \mathcal {A}ob( \Sigma _2, \phi _2 )$
be two abstract open books. We say that there exists an abstract open book embedding of M into N if there exists a proper embedding f of
![]() $\Sigma _1$
into
$\Sigma _1$
into
![]() $\Sigma _2$
such that
$\Sigma _2$
such that
![]() $\phi _1$
is isotopic to
$\phi _1$
is isotopic to
![]() $ f^{-1} \circ \phi _2 \circ f.$
$ f^{-1} \circ \phi _2 \circ f.$
It is clear from the definition that an abstract open book embedding produces an embedding for the associated open book and vice versa.
3 Proof of Theorem 1.1
In this section, we discuss our proof of Theorem 1.1. Recall that given an embedded circle c in the interior of a surface
![]() $\Sigma ,$
a Dehn twist
$\Sigma ,$
a Dehn twist
![]() $d_c$
(or
$d_c$
(or
![]() $d_c^{-1}$
) on
$d_c^{-1}$
) on
![]() $\Sigma $
along the circle c is a diffeomorphism which is the identity outside a neighbourhood of c and is a full twist on an annular neighbourhood of c. We begin by stating the following lemma, which is proved in [Reference Etnyre2].
$\Sigma $
along the circle c is a diffeomorphism which is the identity outside a neighbourhood of c and is a full twist on an annular neighbourhood of c. We begin by stating the following lemma, which is proved in [Reference Etnyre2].
Lemma 3.1. Let M be a closed oriented
![]() $3$
-manifold. Let
$3$
-manifold. Let
![]() $M=\mathcal Aob(\Sigma , \phi )$
. Suppose L is a knot sitting on a page
$M=\mathcal Aob(\Sigma , \phi )$
. Suppose L is a knot sitting on a page
![]() $\Sigma $
of the open book. Then, the new manifold
$\Sigma $
of the open book. Then, the new manifold
![]() $ M^{\prime }$
obtained by
$ M^{\prime }$
obtained by
![]() $\pm 1$
surgery along L, with respect to the page framing, admits an open book
$\pm 1$
surgery along L, with respect to the page framing, admits an open book
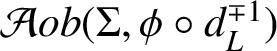 $\mathcal Aob(\Sigma ,\phi \circ d_L^{\mp 1})$
with pages
$\mathcal Aob(\Sigma ,\phi \circ d_L^{\mp 1})$
with pages
![]() $\Sigma $
and monodromy
$\Sigma $
and monodromy
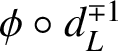 $\phi \circ d_L^{\mp 1}$
.
$\phi \circ d_L^{\mp 1}$
.
The following lemma will be needed in the proof of Theorem 1.1.
Lemma 3.2. Let M be a closed oriented
![]() $3$
-manifold. Let
$3$
-manifold. Let
![]() $M=\mathcal {A}ob(\Sigma , \phi )$
be an abstract open book of M. Suppose that K is a knot in M such that
$M=\mathcal {A}ob(\Sigma , \phi )$
be an abstract open book of M. Suppose that K is a knot in M such that
![]() $K=\{x\}\times [0,1]/(x,1)\sim (\phi (x),0)$
in M for some interior point
$K=\{x\}\times [0,1]/(x,1)\sim (\phi (x),0)$
in M for some interior point
![]() $x\in \Sigma $
. Let
$x\in \Sigma $
. Let
![]() $D_x$
be an open disc neighbourhood of x in
$D_x$
be an open disc neighbourhood of x in
![]() $ \Sigma $
such that
$ \Sigma $
such that
![]() $\phi |_{D_x}=id$
and let c be the curve parallel to
$\phi |_{D_x}=id$
and let c be the curve parallel to
![]() $\partial D_x$
in
$\partial D_x$
in
![]() $\Sigma \setminus D_x$
. Then, an integer n surgery along K gives a new manifold
$\Sigma \setminus D_x$
. Then, an integer n surgery along K gives a new manifold
![]() $M^{\prime }=\mathcal {A}ob(\Sigma ^{\prime },\phi ^\prime )$
with an open book decomposition having the surgery dual of K as one of the binding components, where the surface
$M^{\prime }=\mathcal {A}ob(\Sigma ^{\prime },\phi ^\prime )$
with an open book decomposition having the surgery dual of K as one of the binding components, where the surface
![]() $\Sigma ^\prime =\Sigma \setminus D_x$
is the page and the map
$\Sigma ^\prime =\Sigma \setminus D_x$
is the page and the map
![]() $\phi ^{\prime }=\phi |_{\Sigma ^{\prime }}\circ d_c^{-n}$
is the monodromy of the open book of
$\phi ^{\prime }=\phi |_{\Sigma ^{\prime }}\circ d_c^{-n}$
is the monodromy of the open book of
![]() $M^{\prime }$
.
$M^{\prime }$
.
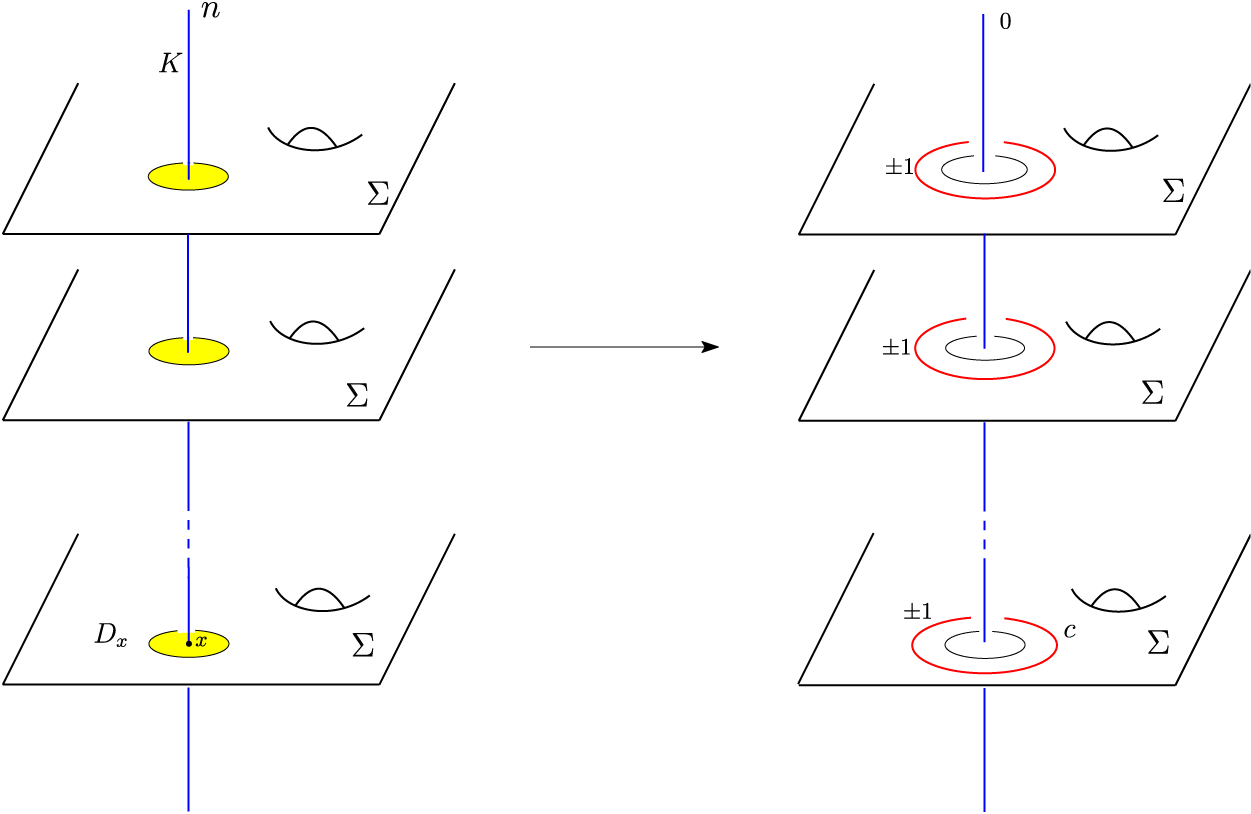
Proof. The knot K is transverse to each page of the open book
![]() $\mathcal Aob(\Sigma ,\phi )$
and intersects each page exactly once (see Figure 1). Suppose
$\mathcal Aob(\Sigma ,\phi )$
and intersects each page exactly once (see Figure 1). Suppose
![]() $n=0$
. Then, performing
$n=0$
. Then, performing
![]() $0$
surgery along K is equivalent to removing
$0$
surgery along K is equivalent to removing
![]() $D_x$
from each page and filling the resulting boundary
$D_x$
from each page and filling the resulting boundary
![]() $\partial D_x\times S^1$
of
$\partial D_x\times S^1$
of
![]() $M\setminus \mathcal N(K)$
by
$M\setminus \mathcal N(K)$
by
![]() $\partial D_x\times D^2$
using the identity map. Here,
$\partial D_x\times D^2$
using the identity map. Here,
![]() $\mathcal {N}(K)= D_x\times K$
denotes a tubular neighbourhood of K in
$\mathcal {N}(K)= D_x\times K$
denotes a tubular neighbourhood of K in
![]() $M.$
From this, one can easily see that the manifold
$M.$
From this, one can easily see that the manifold
![]() $M^{\prime }$
, obtained from M by performing
$M^{\prime }$
, obtained from M by performing
![]() $0$
surgery along K, admits an open book with pages
$0$
surgery along K, admits an open book with pages
![]() $\Sigma ^{\prime }=\Sigma \setminus D_x$
and monodromy
$\Sigma ^{\prime }=\Sigma \setminus D_x$
and monodromy
![]() $\phi ^{\prime }=\phi |_{\Sigma ^{\prime }}.$
$\phi ^{\prime }=\phi |_{\Sigma ^{\prime }}.$

Figure 1 Blowing up operations preformed on the knot K.
Suppose that n is a positive integer. From blowing up operations (see Figure 1), one can see that performing integer n surgery along K is equivalent to performing
![]() $-1$
surgery along n copies of a circle c parallel to
$-1$
surgery along n copies of a circle c parallel to
![]() $\partial D_x$
lying in n distinct pages of the open book
$\partial D_x$
lying in n distinct pages of the open book
![]() $\mathcal {A}ob(\Sigma ,\phi )$
and performing
$\mathcal {A}ob(\Sigma ,\phi )$
and performing
![]() $0$
surgery along K. Using Lemma 3.1, one can see that the manifold
$0$
surgery along K. Using Lemma 3.1, one can see that the manifold
![]() $M^{\prime }$
obtained from M by performing a positive integer n surgery along K admits an open book with pages
$M^{\prime }$
obtained from M by performing a positive integer n surgery along K admits an open book with pages
![]() $\Sigma ^{\prime }=\Sigma \setminus D_x$
and monodromy
$\Sigma ^{\prime }=\Sigma \setminus D_x$
and monodromy
![]() $\phi ^{\prime }=\phi |_{\Sigma ^{\prime }}\circ d_c^{-n}$
.
$\phi ^{\prime }=\phi |_{\Sigma ^{\prime }}\circ d_c^{-n}$
.
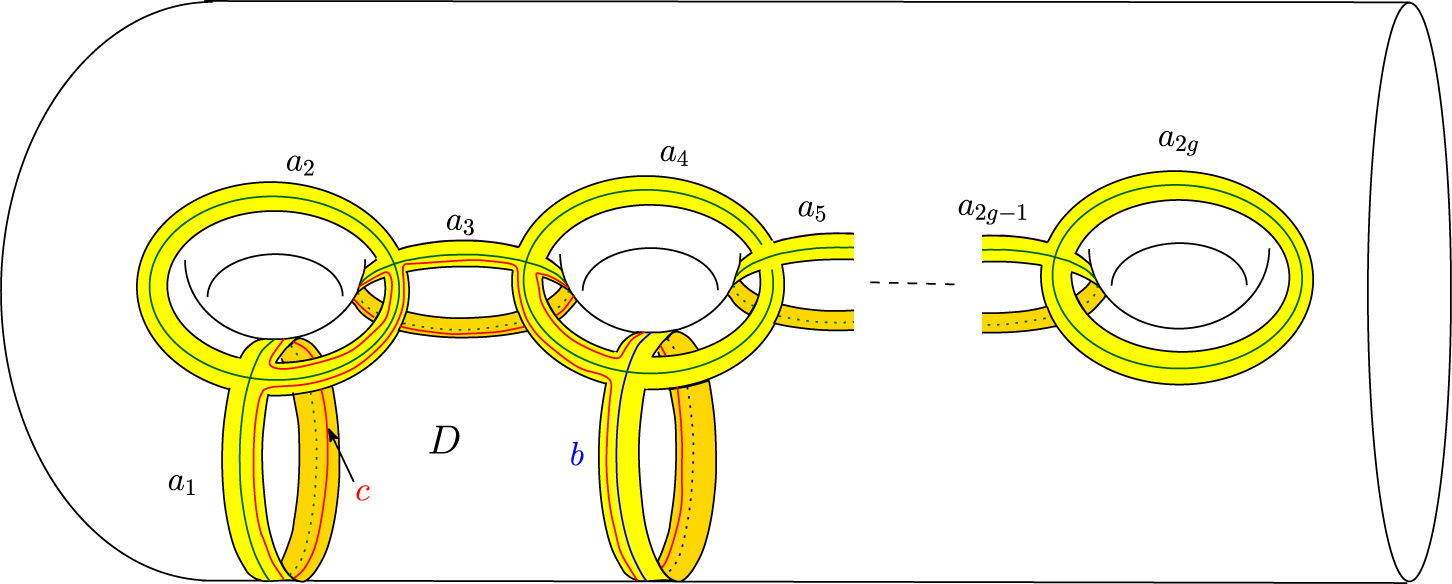
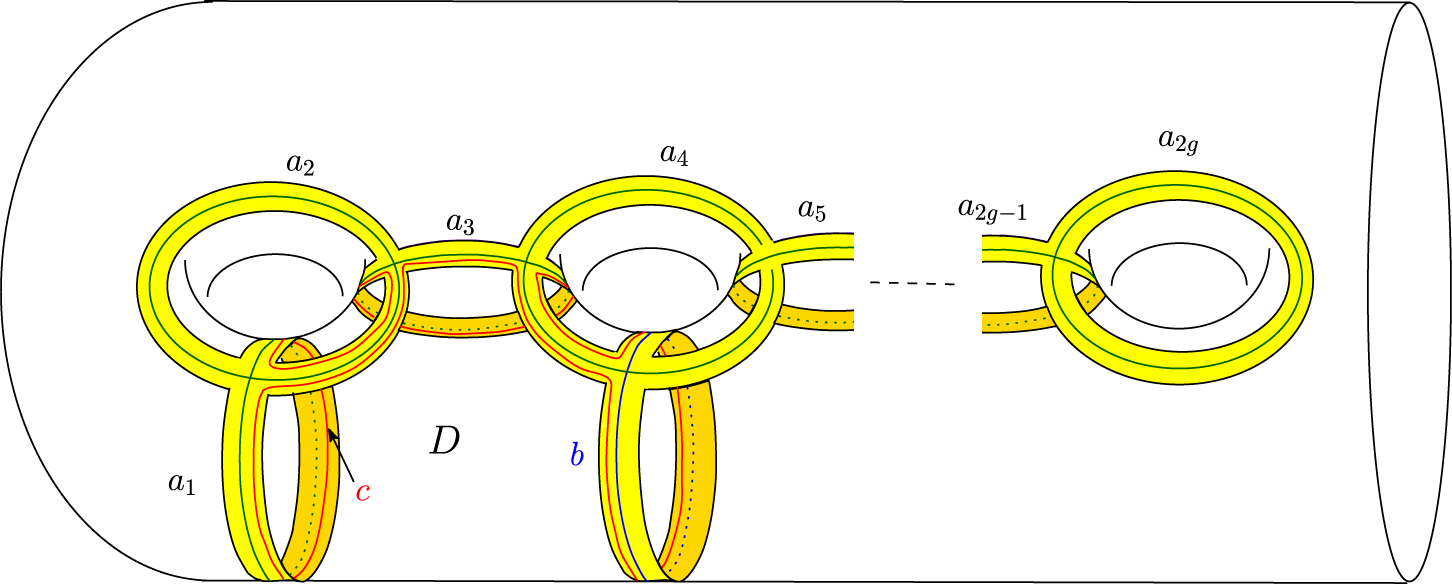
Figure 2 The Humphries generating curves
![]() $b,a_1,\ldots ,a_{2g}$
on the surface
$b,a_1,\ldots ,a_{2g}$
on the surface
![]() $\Sigma $
of genus g with connected boundary. The Dehn twist along these curves generates the mapping class group of
$\Sigma $
of genus g with connected boundary. The Dehn twist along these curves generates the mapping class group of
![]() $\Sigma $
. The union of the regular neighbourhoods of the Humphries generating curves is a subsurface S of
$\Sigma $
. The union of the regular neighbourhoods of the Humphries generating curves is a subsurface S of
![]() $\Sigma $
with two boundary components. One of the boundary components of S is parallel to
$\Sigma $
with two boundary components. One of the boundary components of S is parallel to
![]() $\partial \Sigma $
and the other boundary component bounds a disc D in
$\partial \Sigma $
and the other boundary component bounds a disc D in
![]() $\Sigma $
.
$\Sigma $
.
Similarly, when n is a negative integer, we can see that the surgered manifold
![]() $M^{\prime }$
admits an open book with pages
$M^{\prime }$
admits an open book with pages
![]() $\Sigma ^{\prime }=\Sigma \setminus D_x$
and monodromy
$\Sigma ^{\prime }=\Sigma \setminus D_x$
and monodromy
![]() $\phi ^{\prime }=\phi |_{\Sigma ^{\prime }}\circ d_c^{n}$
.
$\phi ^{\prime }=\phi |_{\Sigma ^{\prime }}\circ d_c^{n}$
.
Remark 3.3. Suppose that
![]() $\Sigma ^{\prime }$
has an arc
$\Sigma ^{\prime }$
has an arc
![]() $\alpha $
joining the boundary component
$\alpha $
joining the boundary component
![]() $\partial D_x$
to some component of
$\partial D_x$
to some component of
![]() $\partial \Sigma $
such that
$\partial \Sigma $
such that
![]() $\phi $
fixes
$\phi $
fixes
![]() $\alpha $
pointwise. Then, the open book
$\alpha $
pointwise. Then, the open book
![]() $\mathcal Aob(\Sigma ^{\prime }, \phi ^\prime )$
of
$\mathcal Aob(\Sigma ^{\prime }, \phi ^\prime )$
of
![]() $M^\prime $
, obtained from M by
$M^\prime $
, obtained from M by
![]() $\pm 1$
surgery along K, is just a stabilisation of
$\pm 1$
surgery along K, is just a stabilisation of
![]() $\mathcal Aob(\Sigma ,\phi )$
. In this case,
$\mathcal Aob(\Sigma ,\phi )$
. In this case,
![]() $M^\prime $
is diffeomorphic to
$M^\prime $
is diffeomorphic to
![]() $M.$
$M.$
Let M be a closed connected oriented
![]() $3$
-manifold. Recall that M admits an open book decomposition with connected binding (see [Reference Myers8]). Let
$3$
-manifold. Recall that M admits an open book decomposition with connected binding (see [Reference Myers8]). Let
![]() $M=\mathcal {A}ob(\Sigma ,\phi )$
, where
$M=\mathcal {A}ob(\Sigma ,\phi )$
, where
![]() $\Sigma $
is a compact connected oriented surface with connected boundary. By considering certain stabilisations of the abstract open book of
$\Sigma $
is a compact connected oriented surface with connected boundary. By considering certain stabilisations of the abstract open book of
![]() $\mathcal Aob(\Sigma ,\phi )$
if required, we can assume that
$\mathcal Aob(\Sigma ,\phi )$
if required, we can assume that
![]() $\Sigma $
has the genus
$\Sigma $
has the genus
![]() $g\geq 3$
. The monodromy
$g\geq 3$
. The monodromy
![]() $\phi $
of the open book is an element in the mapping class group of
$\phi $
of the open book is an element in the mapping class group of
![]() $\Sigma $
. Humphries [Reference Humphries and Fenn6] showed that the mapping class group of a closed surface
$\Sigma $
. Humphries [Reference Humphries and Fenn6] showed that the mapping class group of a closed surface
![]() $\tilde \Sigma $
of genus
$\tilde \Sigma $
of genus
![]() $g\geq 3$
is generated by the Dehn twist along
$g\geq 3$
is generated by the Dehn twist along
![]() $2g+1$
closed curves
$2g+1$
closed curves
![]() $b, a_1,a_2,\ldots ,a_{2g}$
, as shown in Figure 2, where the closed surface
$b, a_1,a_2,\ldots ,a_{2g}$
, as shown in Figure 2, where the closed surface
![]() $\tilde \Sigma $
is obtained from
$\tilde \Sigma $
is obtained from
![]() $\Sigma $
by gluing a disc along the boundary. We call these curves
$\Sigma $
by gluing a disc along the boundary. We call these curves
![]() $b, a_1,a_2,\ldots ,a_{2g}$
in
$b, a_1,a_2,\ldots ,a_{2g}$
in
![]() $\Sigma $
the Humphries generating curves and the corresponding Dehn twists the Humphries generators of the mapping class group of
$\Sigma $
the Humphries generating curves and the corresponding Dehn twists the Humphries generators of the mapping class group of
![]() $\Sigma $
. Johnson [Reference Johnson7] showed that the
$\Sigma $
. Johnson [Reference Johnson7] showed that the
![]() $2g+1$
Dehn twists about
$2g+1$
Dehn twists about
![]() $b,a_1,a_2,\ldots ,a_{2g}$
on
$b,a_1,a_2,\ldots ,a_{2g}$
on
![]() $\Sigma $
also generate the mapping class group of
$\Sigma $
also generate the mapping class group of
![]() $\Sigma $
.
$\Sigma $
.
Consider a regular neighbourhood of each Humphries generating curve in
![]() $\Sigma $
. The union S of the regular neighbourhoods of the Humphries generating curves can be considered as a surface obtained by plumbing
$\Sigma $
. The union S of the regular neighbourhoods of the Humphries generating curves can be considered as a surface obtained by plumbing
![]() $2g+1$
annuli, as shown in Figure 2. The surface S has two boundary components. One of the boundary components of S is parallel to
$2g+1$
annuli, as shown in Figure 2. The surface S has two boundary components. One of the boundary components of S is parallel to
![]() $\partial \Sigma $
, that is, they bound an annulus A in
$\partial \Sigma $
, that is, they bound an annulus A in
![]() $\Sigma $
, and the other boundary component of S bounds a disc
$\Sigma $
, and the other boundary component of S bounds a disc
![]() $D=\Sigma \setminus (S\cup A)$
in
$D=\Sigma \setminus (S\cup A)$
in
![]() $\Sigma $
, as shown in Figure 2. Note that
$\Sigma $
, as shown in Figure 2. Note that
![]() $\Sigma \setminus D$
is diffeomorphic to
$\Sigma \setminus D$
is diffeomorphic to
![]() $S.$
The monodromy
$S.$
The monodromy
![]() $\phi $
is supported in S and hence it is the identity on the disc D.
$\phi $
is supported in S and hence it is the identity on the disc D.
Let
![]() $x\in D$
be an interior point in
$x\in D$
be an interior point in
![]() $D\subset \Sigma .$
Consider the knot
$D\subset \Sigma .$
Consider the knot
![]() $K=\{x\}\times [0,1]/(x,1)\sim (\phi (x),0)$
in M. As discussed in Lemma 3.2, we get an open book
$K=\{x\}\times [0,1]/(x,1)\sim (\phi (x),0)$
in M. As discussed in Lemma 3.2, we get an open book
![]() $\mathcal Aob(\Sigma ^{\prime },\phi ^\prime )$
of
$\mathcal Aob(\Sigma ^{\prime },\phi ^\prime )$
of
![]() $M^\prime $
obtained by an integer n surgery along K in M. Here,
$M^\prime $
obtained by an integer n surgery along K in M. Here,
![]() $\Sigma ^\prime =S$
and
$\Sigma ^\prime =S$
and
![]() $\phi ^\prime =\phi \circ d_c^{-n}$
, where c is a curve in
$\phi ^\prime =\phi \circ d_c^{-n}$
, where c is a curve in
![]() $\Sigma ^\prime $
parallel to
$\Sigma ^\prime $
parallel to
![]() $\partial D.$
$\partial D.$
Now, we shall show that the open book
![]() $M^{\prime }=\mathcal Aob(\Sigma ^\prime ,\phi ^\prime )$
embeds into the trivial open book of
$M^{\prime }=\mathcal Aob(\Sigma ^\prime ,\phi ^\prime )$
embeds into the trivial open book of
![]() $S^5$
. We need to recall the following notion.
$S^5$
. We need to recall the following notion.
Definition 3.4. A diffeomorphism
![]() $\phi $
of a surface F is said to be a flexible diffeomorphism, with respect to a proper embedding f of
$\phi $
of a surface F is said to be a flexible diffeomorphism, with respect to a proper embedding f of
![]() $\Sigma $
in a
$\Sigma $
in a
![]() $4$
-manifold X, if there exists a diffeomorphism
$4$
-manifold X, if there exists a diffeomorphism
![]() $\Phi $
of X isotopic to the identity map of X (also the identity near the boundary if X has nonempty boundary) such that
$\Phi $
of X isotopic to the identity map of X (also the identity near the boundary if X has nonempty boundary) such that
![]() $\phi $
is isotopic to
$\phi $
is isotopic to
![]() $f^{-1} \circ \Phi \circ f$
.
$f^{-1} \circ \Phi \circ f$
.
One can easily observe that if a diffeomorphism
![]() $\phi $
of F is isotopic to a diffeomorphism
$\phi $
of F is isotopic to a diffeomorphism
![]() $\psi $
of F and
$\psi $
of F and
![]() $\phi $
is flexible with respect to an embedding f of F in X, then
$\phi $
is flexible with respect to an embedding f of F in X, then
![]() $\psi $
is also flexible in X with respect to f. To prove the existence of an (abstract) open book embedding of
$\psi $
is also flexible in X with respect to f. To prove the existence of an (abstract) open book embedding of
![]() $\mathcal Aob(\Sigma ^{\prime },\phi ^{\prime })$
in the trivial open book of
$\mathcal Aob(\Sigma ^{\prime },\phi ^{\prime })$
in the trivial open book of
![]() $S^5$
, we need to find an embedding f of
$S^5$
, we need to find an embedding f of
![]() $\Sigma ^{\prime }$
in
$\Sigma ^{\prime }$
in
![]() $D^4$
such that
$D^4$
such that
![]() $\phi ^{\prime }$
is flexible in
$\phi ^{\prime }$
is flexible in
![]() $D^4$
with respect to
$D^4$
with respect to
![]() $f.$
As
$f.$
As
![]() $\phi ^{\prime }$
is isotopic to a product of powers of Humphries generators and the Dehn twist
$\phi ^{\prime }$
is isotopic to a product of powers of Humphries generators and the Dehn twist
![]() $d_c$
, it is enough to construct a proper embedding f of
$d_c$
, it is enough to construct a proper embedding f of
![]() $\Sigma ^{\prime }$
in
$\Sigma ^{\prime }$
in
![]() $D^4$
such that the Humphries generators and the Dehn twist
$D^4$
such that the Humphries generators and the Dehn twist
![]() $d_c$
are flexible in
$d_c$
are flexible in
![]() $D^4$
with respect to
$D^4$
with respect to
![]() $f.$
$f.$
3.1 Construction of an embedding of
 ${\Sigma}^{\!\prime}$
in
${\Sigma}^{\!\prime}$
in
 $D^4$
$D^4$
A Dehn twist
![]() $d_\gamma $
along an embedded circle
$d_\gamma $
along an embedded circle
![]() $\gamma $
in
$\gamma $
in
![]() $\Sigma ^{\prime }$
is supported in an annular neighbourhood of
$\Sigma ^{\prime }$
is supported in an annular neighbourhood of
![]() $\gamma $
in
$\gamma $
in
![]() $\Sigma ^{\prime }$
. In [Reference Hirose and Yasuhara5], it is shown that there exists a (proper) embedding of an annulus
$\Sigma ^{\prime }$
. In [Reference Hirose and Yasuhara5], it is shown that there exists a (proper) embedding of an annulus
![]() $A=S^1\times [0,1]$
in
$A=S^1\times [0,1]$
in
![]() $D^4$
such that the Dehn twist along the central curve of A is flexible and hence so is each power of this Dehn twist. This follows from the fact that there exists a flow
$D^4$
such that the Dehn twist along the central curve of A is flexible and hence so is each power of this Dehn twist. This follows from the fact that there exists a flow
![]() $\Phi _t$
on the
$\Phi _t$
on the
![]() $3$
-sphere
$3$
-sphere
![]() $S^3$
associated to the open book decomposition of
$S^3$
associated to the open book decomposition of
![]() $S^3$
with pages a Hopf annulus and monodromy the Dehn twist along the central curve of the Hopf annulus such that the time
$S^3$
with pages a Hopf annulus and monodromy the Dehn twist along the central curve of the Hopf annulus such that the time
![]() $1$
map
$1$
map
![]() $\Phi _1$
on
$\Phi _1$
on
![]() $S^3$
induces the Dehn twist along the central curve on each page of the open book of
$S^3$
induces the Dehn twist along the central curve on each page of the open book of
![]() $S^3$
. We can choose any Hopf annulus page
$S^3$
. We can choose any Hopf annulus page
![]() $\mathcal A$
as an embedding of the annulus A in
$\mathcal A$
as an embedding of the annulus A in
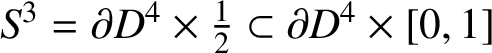 $S^3=\partial D^4\times \tfrac 12\subset \partial D^4\times [0,1]$
, where
$S^3=\partial D^4\times \tfrac 12\subset \partial D^4\times [0,1]$
, where
![]() $\partial D^4\times [0,1]$
is a collar of
$\partial D^4\times [0,1]$
is a collar of
![]() $\partial D^4$
in
$\partial D^4$
in
![]() $D^4$
. Using the flow
$D^4$
. Using the flow
![]() $\Phi _t$
, we can construct a diffeomorphism of
$\Phi _t$
, we can construct a diffeomorphism of
![]() $D^4$
which is isotopic to the identity and induces the Dehn twist along the central curve on the embedded Hopf annulus
$D^4$
which is isotopic to the identity and induces the Dehn twist along the central curve on the embedded Hopf annulus
![]() $\mathcal A$
. For more details, see [Reference Hirose and Yasuhara5, Reference Pancholi, Pandit and Saha9]. Note that
$\mathcal A$
. For more details, see [Reference Hirose and Yasuhara5, Reference Pancholi, Pandit and Saha9]. Note that
![]() $S^3$
admits an open book with pages a positive Hopf annulus as well as an open book with pages a negative Hopf annulus. So, we will construct a proper embedding of the surface
$S^3$
admits an open book with pages a positive Hopf annulus as well as an open book with pages a negative Hopf annulus. So, we will construct a proper embedding of the surface
![]() $\Sigma ^{\prime }$
in
$\Sigma ^{\prime }$
in
![]() $D^4$
such that each of the curves
$D^4$
such that each of the curves
![]() $b, a_1,\ldots ,a_{2g}$
and the boundary parallel curve c admits either a positive or a negative Hopf annulus regular neighbourhood in the embedded
$b, a_1,\ldots ,a_{2g}$
and the boundary parallel curve c admits either a positive or a negative Hopf annulus regular neighbourhood in the embedded
![]() $\Sigma ^{\prime }\subset D^4$
.
$\Sigma ^{\prime }\subset D^4$
.
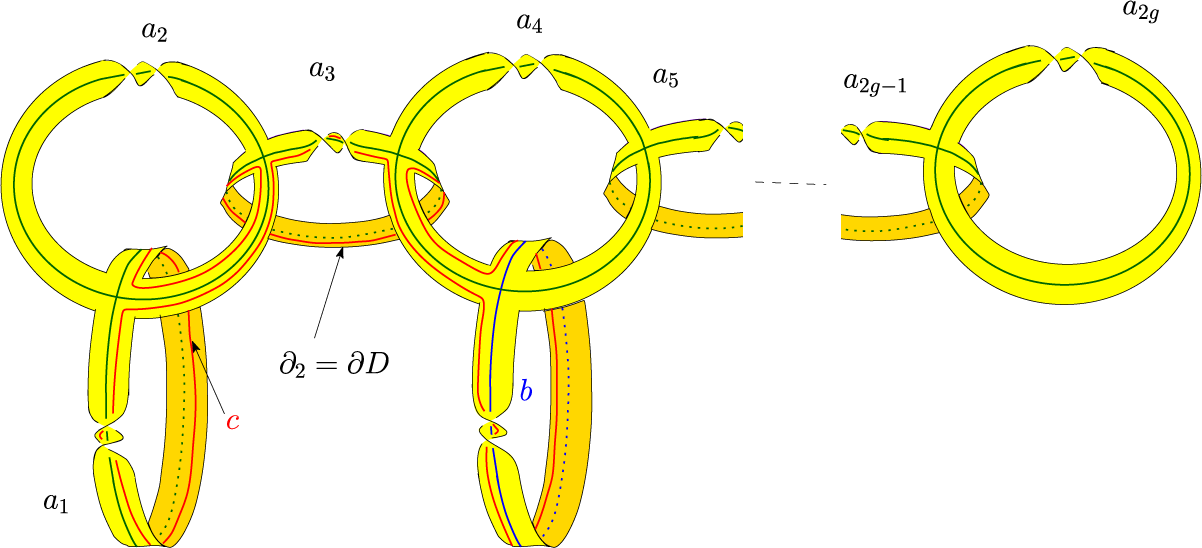
Consider a collar
![]() $S^3\times [0,1]$
of the
$S^3\times [0,1]$
of the
![]() $4$
-ball
$4$
-ball
![]() $D^4$
with
$D^4$
with
![]() $\partial D^4=S^3\times 0.$
Consider an embedding
$\partial D^4=S^3\times 0.$
Consider an embedding
![]() $S_1$
of the surface
$S_1$
of the surface
![]() $\Sigma ^{\prime }$
, which is obtained by plumbing
$\Sigma ^{\prime }$
, which is obtained by plumbing
![]() $2g$
positive Hopf annuli
$2g$
positive Hopf annuli
![]() $A_1,\ldots ,A_{2g}$
with central curves
$A_1,\ldots ,A_{2g}$
with central curves
![]() $a_1,a_2,\ldots ,a_{2g}$
and one negative Hopf annulus with central curve b in
$a_1,a_2,\ldots ,a_{2g}$
and one negative Hopf annulus with central curve b in
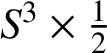 $S^3\times \tfrac 12$
, as shown in Figure 3. Recall that
$S^3\times \tfrac 12$
, as shown in Figure 3. Recall that
![]() $\Sigma ^{\prime }$
has two boundary components. We denote these components by
$\Sigma ^{\prime }$
has two boundary components. We denote these components by
![]() $\partial _1=\partial \Sigma $
and
$\partial _1=\partial \Sigma $
and
![]() $\partial _2=\partial D.$
We make this embedding a proper embedding f of
$\partial _2=\partial D.$
We make this embedding a proper embedding f of
![]() $\Sigma ^{\prime }$
by attaching cylinders
$\Sigma ^{\prime }$
by attaching cylinders
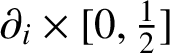 $\partial _i\times [0,\tfrac 12]$
to
$\partial _i\times [0,\tfrac 12]$
to
![]() $S_1$
along
$S_1$
along
![]() $\partial _i$
, for
$\partial _i$
, for
![]() $i=1,2$
, and smoothing out the corners to get a smooth embedding. By construction, we can see that a regular neighbourhood of each of the Humphries generating curves
$i=1,2$
, and smoothing out the corners to get a smooth embedding. By construction, we can see that a regular neighbourhood of each of the Humphries generating curves
![]() $a_1,\ldots ,a_{2g}$
in
$a_1,\ldots ,a_{2g}$
in
![]() $f(\Sigma ^{\prime })$
is a positive Hopf annulus in
$f(\Sigma ^{\prime })$
is a positive Hopf annulus in
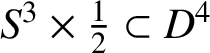 $S^3\times \tfrac 12\subset D^4$
and a regular neighbourhood of the Humphries generating curve b in
$S^3\times \tfrac 12\subset D^4$
and a regular neighbourhood of the Humphries generating curve b in
![]() $f(\Sigma ^{\prime })$
is a negative Hopf annulus
$f(\Sigma ^{\prime })$
is a negative Hopf annulus
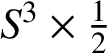 $S^3\times \tfrac 12$
. A regular neighbourhood of the curve c parallel to the boundary
$S^3\times \tfrac 12$
. A regular neighbourhood of the curve c parallel to the boundary
![]() $\partial _2$
in
$\partial _2$
in
![]() $f(\Sigma ^{\prime })$
has two positive full twists and one negative full twist. Two of the twists cancel each other to get a positive Hopf annulus neighbourhood for the curve c in
$f(\Sigma ^{\prime })$
has two positive full twists and one negative full twist. Two of the twists cancel each other to get a positive Hopf annulus neighbourhood for the curve c in
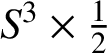 $S^3\times \tfrac 12$
(see Figure 3). From this, one can see that the Dehn twists along the curves
$S^3\times \tfrac 12$
(see Figure 3). From this, one can see that the Dehn twists along the curves
![]() $c,b,a_1,\ldots ,a_{2g}$
are flexible in
$c,b,a_1,\ldots ,a_{2g}$
are flexible in
![]() $D^4$
with respect to the embedding f of
$D^4$
with respect to the embedding f of
![]() $\Sigma ^{\prime }.$
For more details regarding the flexibility of the Dehn twists, see [Reference Pancholi, Pandit and Saha9]. An alternate argument for the flexibility of the Dehn twist along a simple closed curve in
$\Sigma ^{\prime }.$
For more details regarding the flexibility of the Dehn twists, see [Reference Pancholi, Pandit and Saha9]. An alternate argument for the flexibility of the Dehn twist along a simple closed curve in
![]() $\Sigma ^{\prime }$
admitting a Hopf annulus regular neighbourhood in
$\Sigma ^{\prime }$
admitting a Hopf annulus regular neighbourhood in
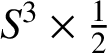 $S^3\times \tfrac 12$
is given in [Reference Pandit and A10]. For the sake of completeness, we summarise it here.
$S^3\times \tfrac 12$
is given in [Reference Pandit and A10]. For the sake of completeness, we summarise it here.

Figure 3 An embedding of the surface
![]() $\Sigma ^{\prime }=S$
in
$\Sigma ^{\prime }=S$
in
![]() $S^3$
, in which each Humphries generating curve as well as the boundary parallel curve c admits a Hopf annulus regular neighbourhood in
$S^3$
, in which each Humphries generating curve as well as the boundary parallel curve c admits a Hopf annulus regular neighbourhood in
![]() $S^3.$
$S^3.$
Observe that each curve
![]() $\alpha \in \{c, a_1,\ldots , a_{2g}\}$
bounds a disc
$\alpha \in \{c, a_1,\ldots , a_{2g}\}$
bounds a disc
![]() $D_\alpha $
in
$D_\alpha $
in
![]() $D^4$
which intersects
$D^4$
which intersects
![]() $f(\Sigma ^{\prime })$
in
$f(\Sigma ^{\prime })$
in
![]() $\alpha $
and a tubular neighbourhood
$\alpha $
and a tubular neighbourhood
![]() $\mathcal {N}(D_\alpha )=D^2\times D^2$
intersects
$\mathcal {N}(D_\alpha )=D^2\times D^2$
intersects
![]() $f(\Sigma ^{\prime })$
in a regular neighbourhood
$f(\Sigma ^{\prime })$
in a regular neighbourhood
![]() $\nu (\alpha )$
of
$\nu (\alpha )$
of
![]() $\alpha $
in
$\alpha $
in
![]() $f(\Sigma ^{\prime })$
. We can choose coordinates
$f(\Sigma ^{\prime })$
. We can choose coordinates
![]() $(z_1,z_2)$
on
$(z_1,z_2)$
on
![]() $\mathcal {N}(D_\alpha )$
such that
$\mathcal {N}(D_\alpha )$
such that
![]() $\nu (\alpha )=g^{-1}(1)\cap f(\Sigma ^{\prime })$
, where
$\nu (\alpha )=g^{-1}(1)\cap f(\Sigma ^{\prime })$
, where
![]() $g:\mathbb C^2\to \mathbb C$
is the map defined by
$g:\mathbb C^2\to \mathbb C$
is the map defined by
![]() $g(z_1,z_2)=z_1z_2$
. The monodromy of the singular fibration
$g(z_1,z_2)=z_1z_2$
. The monodromy of the singular fibration
![]() $g:\mathcal {N}(D_{\alpha })=\mathbb C^2\to \mathbb C= D^2$
with the singular point
$g:\mathcal {N}(D_{\alpha })=\mathbb C^2\to \mathbb C= D^2$
with the singular point
![]() $(0,0)$
is the positive Dehn twist
$(0,0)$
is the positive Dehn twist
![]() $d_{\alpha }$
along the curve
$d_{\alpha }$
along the curve
![]() $\alpha $
which lies in the regular fibre
$\alpha $
which lies in the regular fibre
![]() $g^{-1}(1)\cap \Sigma ^{\prime }=\nu (\alpha ).$
The isotopy of
$g^{-1}(1)\cap \Sigma ^{\prime }=\nu (\alpha ).$
The isotopy of
![]() $\mathcal {N}(D_{\alpha })$
, which produces the positive Dehn twist
$\mathcal {N}(D_{\alpha })$
, which produces the positive Dehn twist
![]() $d_{\alpha }$
on
$d_{\alpha }$
on
![]() $g^{-1}(1)\cap \Sigma ^{\prime }$
, can be extended to an isotopy
$g^{-1}(1)\cap \Sigma ^{\prime }$
, can be extended to an isotopy
![]() $\Psi _s$
,
$\Psi _s$
,
![]() $s\in [0,1]$
, of
$s\in [0,1]$
, of
![]() $D^4$
such that the isotopy is supported in the tubular neighbourhood
$D^4$
such that the isotopy is supported in the tubular neighbourhood
![]() $\mathcal {N}(D_{\alpha })$
. Then, we have
$\mathcal {N}(D_{\alpha })$
. Then, we have
![]() $f^{-1}\circ \Psi _1 \circ f=d_{\alpha }$
up to isotopy. We have an isotopy of
$f^{-1}\circ \Psi _1 \circ f=d_{\alpha }$
up to isotopy. We have an isotopy of
![]() $D^4$
supported in the tubular neighbourhood
$D^4$
supported in the tubular neighbourhood
![]() $\mathcal {N}(D_{\alpha })$
of
$\mathcal {N}(D_{\alpha })$
of
![]() $D_{\alpha }$
which produces the Dehn twist
$D_{\alpha }$
which produces the Dehn twist
![]() $d_\alpha $
on
$d_\alpha $
on
![]() $\Sigma ^{\prime }.$
From this, it follows that the Dehn twist
$\Sigma ^{\prime }.$
From this, it follows that the Dehn twist
![]() $d_{\alpha }$
is flexible in
$d_{\alpha }$
is flexible in
![]() $ D^4$
with respect to the embedding
$ D^4$
with respect to the embedding
![]() $f.$
$f.$
The curve b bounds a disc
![]() $D_b$
in
$D_b$
in
![]() $D^4$
which intersects
$D^4$
which intersects
![]() $f(\Sigma ^{\prime })$
in b and a tubular neighbourhood
$f(\Sigma ^{\prime })$
in b and a tubular neighbourhood
![]() $\mathcal {N}(D_b)=D^2\times D^2$
intersects
$\mathcal {N}(D_b)=D^2\times D^2$
intersects
![]() $f(\Sigma ^{\prime })$
in a regular neighbourhood
$f(\Sigma ^{\prime })$
in a regular neighbourhood
![]() $\nu (b)$
of b in
$\nu (b)$
of b in
![]() $f(\Sigma ^{\prime })$
. We can choose coordinates
$f(\Sigma ^{\prime })$
. We can choose coordinates
![]() $(z_1,z_2)$
on
$(z_1,z_2)$
on
![]() $\mathcal {N}(D_b)$
such that
$\mathcal {N}(D_b)$
such that
![]() $\nu (b)=g^{-1}(1)\cap f(\Sigma ^{\prime })$
, where
$\nu (b)=g^{-1}(1)\cap f(\Sigma ^{\prime })$
, where
![]() $g:\mathbb C^2\to \mathbb C$
is the map defined by
$g:\mathbb C^2\to \mathbb C$
is the map defined by
![]() $g(z_1,z_2)=z_1\bar {z}_2$
. The monodromy of the singular fibration
$g(z_1,z_2)=z_1\bar {z}_2$
. The monodromy of the singular fibration
![]() $g:\mathcal {N}(D_{b})=\mathbb C^2\to \mathbb C= D^2$
with the singular point
$g:\mathcal {N}(D_{b})=\mathbb C^2\to \mathbb C= D^2$
with the singular point
![]() $(0,0)$
is the negative Dehn twist
$(0,0)$
is the negative Dehn twist
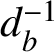 $d_{b}^{-1}$
along the curve b which lies in the regular fibre
$d_{b}^{-1}$
along the curve b which lies in the regular fibre
![]() $g^{-1}(1)\cap \Sigma ^{\prime }=\nu (b).$
By arguments similar to those above, there is an isotopy of
$g^{-1}(1)\cap \Sigma ^{\prime }=\nu (b).$
By arguments similar to those above, there is an isotopy of
![]() $D^4$
supported in the tubular neighbourhood
$D^4$
supported in the tubular neighbourhood
![]() $\mathcal {N}(D_{b})$
of
$\mathcal {N}(D_{b})$
of
![]() $D_{b}$
which produces the Dehn twist
$D_{b}$
which produces the Dehn twist
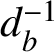 $d_b^{-1}$
on
$d_b^{-1}$
on
![]() $\Sigma ^{\prime }.$
Both
$\Sigma ^{\prime }.$
Both
![]() $d_b$
and
$d_b$
and
 $d_b^{-1}$
are flexible in
$d_b^{-1}$
are flexible in
![]() $D^4$
with respect to the embedding
$D^4$
with respect to the embedding
![]() $f.$
$f.$
It follows that the monodromy
![]() $\phi ^{\prime }$
is flexible in
$\phi ^{\prime }$
is flexible in
![]() $D^4$
with respect to the embedding f of
$D^4$
with respect to the embedding f of
![]() $\Sigma ^{\prime }$
, that is, there exists a diffeomorphism
$\Sigma ^{\prime }$
, that is, there exists a diffeomorphism
![]() $\Phi $
of
$\Phi $
of
![]() $D^4$
which is isotopic to the identity map of
$D^4$
which is isotopic to the identity map of
![]() $D^4$
and
$D^4$
and
![]() $f^{-1}\circ \Phi \circ f$
is isotopic to
$f^{-1}\circ \Phi \circ f$
is isotopic to
![]() $\phi ^{\prime }$
. This gives an abstract open book embedding of
$\phi ^{\prime }$
. This gives an abstract open book embedding of
![]() $M^{\prime }=\mathcal Aob(\Sigma ^{\prime },\phi ^{\prime })$
into
$M^{\prime }=\mathcal Aob(\Sigma ^{\prime },\phi ^{\prime })$
into
![]() $S^5=\mathcal {A}ob(D^4,\Phi ).$
This completes the proof of Theorem 1.1.
$S^5=\mathcal {A}ob(D^4,\Phi ).$
This completes the proof of Theorem 1.1.