Introduction
The role of irrigation management in the development of the first urban societies of Mesopotamia is still an important topic of discussion among philologists, archaeologists and historians.Footnote 1 Since the mid-twentieth century, the development of Mesopotamian civilization has been seen as being intrinsically linked to the building of water-related infrastructure such as dams and canals in order to tame the environment (see Postgate Reference Postgate1988). However, the importance of wetlands in the development of prehistoric communities in the Ubaid period has been emphasized by Oates (Reference Oates1960) and above all, more recently, by Pournelle (Reference Pournelle2003; Reference Pournelle and Stone2007). Their research has revealed that the life of these communities was closely linked to the “wet environment” and that many sites were probably islands within the marshes. From the third millennium b.c. the region of Sumer, just to the north, became an important area for the production of cereals and crops, irrigated by artificial canals, had probably developed more rapidly than the wetlands. This may have been due to the fact that, although the marshes represented a wealth of natural resources such as reeds, fish and shellfish, they could be over-exploited to the point of exhaustion, while the cultivation of cereals represented the economic foundation of the growing Sumerian civilization (Wilkinson Reference Wilkinson and Crawford2013: 38 with previous bibliography).
Earthwork projects and the building of reservoirs, dams and canals are closely related to the management of irrigation; several Ur III texts describe the building and repair of canals or their components. These works required the use of different materials, depending on the facilities to be built, but the most important was definitely earth. Civil (Reference Civil1994: 115) distinguishes two different categories of earthwork activity: earth moving (kin-sahar) and the reinforcement of levees (eg2-e u2-sag11-a).Footnote 2 Activities such as digging canals and piling up earth to build dams and dykes belong to the first category of works, which is the subject of this article. More specifically, as noted by Civil (Reference Civil1994: 115), works involving earth-moving can be divided into sahar si-ga, “to pile up earth”; sahar zi-ga, “to remove earth”; sahar šu-ti, “to collect earth”; and sahar šu bal-a, “to transport earth”. We must also add ba-al-la, “to dig”, and šu / šu2 luh… ak, “to clean” (the bed of a watercourse). These activities were necessary to build irrigation canals (pa4/pa5 or i7), banks (eg2), tanks and reservoirs for water control (kab2-ku5 or a-ga-am), barrages for waterways (a-igi), dams (giš-keš2) and mud walls (im-du8-a).
Several Old Babylonian mathematical problems highlight all the variables that had to be taken into account in order to carry out such works. Here, for example, is an excerpt from the text YBC 5037 (Neugebauer and Sachs Reference Neugebauer and Sachs1945: 59, Text F), a catalogue of problems that includes the excavation of earth as a common topic (Sumerian ki-la2, Akkadian kalakkum).Footnote 3 Obverse, 1-2 reads:
1. ki-la2 3½ nindan 3 kuš3-ta-am3 ib2-si8 2½ kuš3 bur3-bi 7½ gin2 eš2-gar3
2. 6 še a2-bi a-ša3 sahar erin2-ḫa2 u3 ku3-babbar en-nam
1. An excavation: 3½ nindan 3 kuš3 (c.22.5 m) is the length of each square-side; 2½ kuš3 (c.1.25 m) is its depth; 7½ gin2 (c.2.25 m3) is the (daily) work-load (for each worker);
2. 6 še (c.0.27 g) (of silver) is its wage. What are the area, the volume, the (number of) workers and the (total expenses in) silver?
As we can see from this excerpt, the variables to be taken into account are:Footnote 4
1. The length (in the example cited above 3½ nindan and 3 kuš3), the width (3½ nindan and 3 kuš3 – the text records that the length and the width are identical), and the depth of the earth to be excavated (2½ kuš3);
2. The daily quantity of earth to be excavated by each worker (7 ½ gin2);
3. The daily cost in silver (6 še);
4. The area of the base of excavation (to be found);
5. The total volume (to be found);
6. The total number of work-days (to be found);
7. The cost in silver (to be found).
The solution to the problem is therefore as follows:
The total area: 14 sar 3 ⅔ gin2 15 še (c.506 m2);
The total volume: 35 sar 9 ⅓ gin2 7 ½ še (c.633 m3);
The total number of work-days: 281 ¼;
The total cost in silver: 9 ⅔ gin2 7 ½ še (c.9.4 g).
It is clear from this typology of texts that there were challenges not only in the task itself but also in the practical procedure through which the measurements were obtained and calculated. From the point of view of the history of science and administration, it is fortunate that it is possible to identify, amongst the administrative texts of the Third Dynasty of Ur, documents that show how the Sumerians gathered this information.
All of the variables recorded in the Old Babylonian problem text shown above were necessary to complete the work; and they were the same as those used in daily practice by the officials of the Third Dynasty of Ur.Footnote 5 However, they never appear all together in a single document and so we need to study several different types of administrative text in order to throw light on the organization of such work.
The documentation
Calculations of the total amount of earth to be excavated
About twenty documentsFootnote 6 from Ur III Umma specifically measure the amount of earth to be excavated. As discussed further below, we should understand them as surveys and notes, probably made directly in the field, in order to estimate the amount of work required. We can divide them into two main types. In Type 1, all three measurements (length, width and depth) are recorded, while in Type 2 the scribe recorded only the length and the volume of earth to be removed per unit of length (Civil Reference Civil1994: 116).
Type 1 surveys, such as the undated text BPOA 7 2445, contain the following data:
• the measurements of the length (gid2), width (dagal) and depth (buru3);
• the calculation of the total volume (sahar-bi/kin-bi x sar), which results from the product of the length, width and depth recorded in the preceding line;Footnote 7
• the total sum of the lengths (šu-nigin2 x gid2);Footnote 8
• the total sum of the volumes (sahar-bi x sar);
• other administrative information, such as the kind of work, the place, the supervisors, etc.
Meanwhile Type 2 surveys, like the undated text AAICAB 1/3, Bod. S 157, give:
• The measurement of the length (gid2) and the volume of the earth to be excavated for every unit of length (x sar-ta);
• The calculation of the total volume of earth to be excavated (sahar-bi/kin-bi x sar), which results from the product of the unit volume and the length recorded in the preceding line;
• The total sum of the lengths (šu-nigin2 x gid2);Footnote 9
• The total sum of the volumes (sahar-bi x sar);
• Other administrative information, such as the kind of work, the place, the supervisors, etc.
Records of the daily quantity of earth to be excavated by each worker
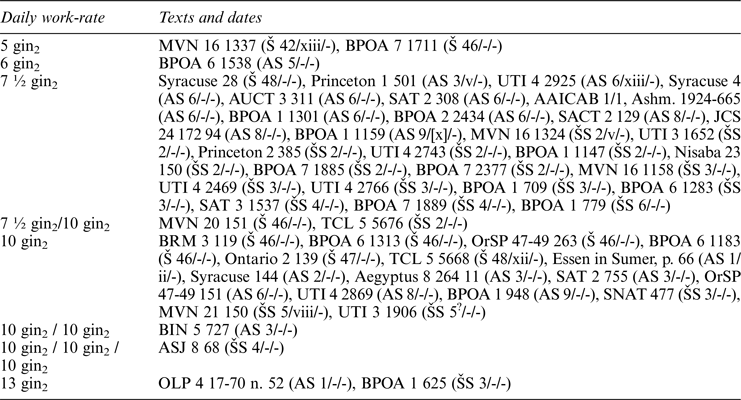
The amount of earth to be excavated by each individual worker is noted by the expression guruš-e x gin2-ta. It is explicitly recorded in some tablets from the city of Umma. See, for example, BPOA 1 1147 (ŠS 2/-/-):

Table 1 shows all the quantities of work-rates recorded, with texts given in chronological order.Footnote 10 As we can see, the two most frequently used values are 7 ½ and 10 gin2.Footnote 11 Indeed, 10 gin2 seems to have been the default value in the minds of the scribes, as in six texts it is not explicitly recorded on the tablet.Footnote 12 See, for example, Princeton 2466 (Š 47/-/-):

Table 1 Daily work-rates for excavating earth attested in Ur III Umma administrative records

If we divide the total amount of barley (11 gur and 2 ban2, i.e., 3,420 sila 3) by the daily expenditure on barley (6 sila3) we arrive at the number of workers: 3,420 ÷ 6 = 570 workers. If we now divide the total quantity of earth to be excavated (95 sar, i.e., 5,700 gin2, c.1,710 m3) by the total number of workers, we arrive at the quantity of earth to be excavated by each worker, namely 5700 ÷ 570 = 10 gin2, c.3 m3.
Eleanor Robson (Reference Robson1999: 158) has already identified this quantity as the value of an Old Babylonian mathematical “coefficient” (logogram igi.gub, Akkadian igigubbûm). Coefficients are numbers that represent a mathematical relationship or constant, and are used for solving particular types of mathematical problem. In Babylonian mathematics, Robson (Reference Robson1999: 14) distinguishes between “absolute constants”, such as, for example, that which links the diameter of a circle and its area; “metrological constants” between units of measure; and “empirical constants”, which represent a relationship fixed by convention, such as, for example, the work-rate for making bricks. Robson (Reference Robson1999: xiii) worked with twelve coefficient lists: eight Old Babylonian, two dating from some time in the first first millennium b.c., and two from the Late Babylonian period. They are clearly recognizable in both formal features and content and represent a distinct genre of mathematical text. Every number written on the tablet has a name or a brief description, which often helps us to understand the context in which a coefficient was used. Robson (Reference Robson1999: 158) identifies some coefficients recorded in the Old Babylonian lists that were already in use during the Ur III period. The volumes 20, 15, 10 and 7 ½ gin2 are recorded in the Old Babylonian coefficient lists and mathematical word problems, values which depend on the depth of the excavation to be made. Of these, Robson (Reference Robson1999: 139) remarks that 10 gin2 “is exactly the most commonly recorded work-rate for earth moving in both Ur III administrative records and OB school mathematics”. It is attested for instance in the coefficient list YBC 5022 (List F) obv. 43 as 10 gín éš.gàr lú 1, “10 shekels, the work-load of 1 man”, as well as in multiple problem texts and calculations (Robson Reference Robson1999: 96).
The total and daily cost in barley
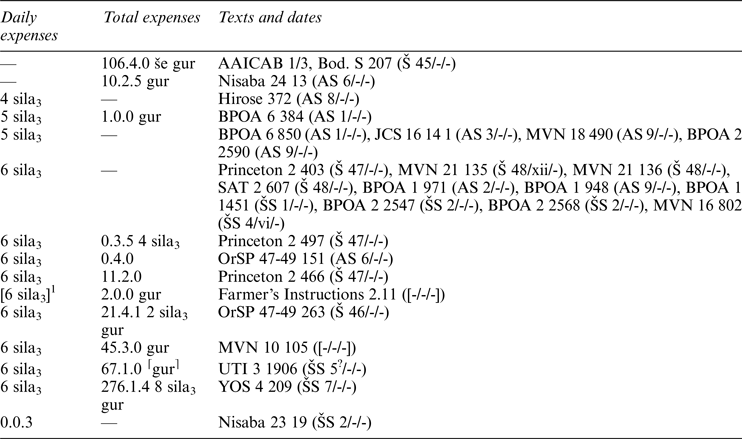
The daily expenditure on barley is defined in the Ur III texts by the expression a2 lu2 hun-ga2(-bi) x-sila3-ta, “x sila3 for the wages of hired men”. See, for example, BPOA 1 971 (AS 2/-/-):

The total cost is reported in the texts less frequently. An example is given in Princeton 2 497 (Š 47/-/-):

Table 2 shows the daily and the total expenses for earthwork activities. As one can see, the value is almost always 6 sila3. It is worth noting that, unlike the “coefficients” seen in the previous section, the values of the labour costs per day are almost always given explicitly in the Ur III administrative texts. If this value is not recorded it cannot be established, since the tablet does not contain all the data necessary to calculate it, starting from the total expenditure on barley.
Table 2 Daily and total expenses for earthwork activities in texts from Ur III Umma

1 It is possible to calculate this value as the text also records the total number of work-days (100).
The total number of workers and work-days
As one can see in Table 3, the total number of workers is not always recorded in the texts. Some documents record only the work-days. The challenge for the administration was thus to calculate the total amount of work. It did not matter whether the work was done, for example, by a single worker employed for ten days or ten workers employed for one day: the expenditure on barley would have been the same.
Table 3 Earthwork texts from Ur III Umma showing total number of workers and work-days

1 When the number of workers is provided, this column refers to the number of days. When the number of workers is not provided, the data in this column refers to the number of work-days (number of work-days = number of workers × number of days).
The combination of the information
As already stated above, there are no texts which record all the information needed to complete an earthwork project. More specifically, the combinations of the information recorded in the texts are shown in the Appendix.
To sum up, we can make the following observations:
• there are about twenty texts which measure only the quantity of earth to be excavated, based on linear measurements;
• there are about two hundred known documents which record, together with the volume of the earth already calculated, information on the quantity of work requested: the number of workers, work-days, the amount of earth to be excavated daily (Tables 1 and 3). These texts may also contain administrative information, such as the place where the work is to be carried out or the names of the officials;
• there are thirty identified texts that, together with the volume of earth already calculated, record the expenses incurred when undertaking the work (Table 2). As before, these texts may also contain administrative information, such as the place where the work is to be carried out or the names of the officials;
• finally, we have about twenty texts which record only the volume of the earth plus administrative information about the place where the work is to be carried out and the names of the officials in charge.Footnote 13
The procedure
We do not know who had the authority to commission a hydraulic project. As Stefanie Rost (Reference Rost and Selz2011: 123) has already pointed out, the dominant theory that there was a centralized irrigation management plan during the Third Dynasty of Ur has not been established with absolute certainty:Footnote 14
It is also evident that irrigation can be organized in many different ways and thus centralized management is just one possibility. In addition, many ethnographic case studies provide evidence for varying degrees of centralization as is seen when the state government only organizes a certain aspect of irrigation such as water distribution.
The most important information seems to be that which is related to the total volume of earth—which, in fact, is recorded in almost all the documents. Once this information had been obtained, the scribe could calculate the number of people needed to complete the work and therefore the total expense in barley. The calculations for the amount of work were based on two different coefficients, which represented the amount of earth that a typical worker was expected to dig in a day (10 and 7 ½ gin2);Footnote 15 the difference between them is probably due to the physical characteristics of the soil. The total expense mainly derived the daily cost of labour, which was commonly 6 sila3 of barley per worker. Using this data, the administration could quickly calculate expenditure of labour and wages. However, the scribe did not have to record all the information on the tablet: all that was needed was information about the total volume of earth to be excavated in order to calculate, first, the number of workers and then, the cost of the work.
Obviously, the first step in the process was to conduct a survey to gather the basic information needed. This information was recorded on a tablet (such as the texts in Table 1). It should be emphasised again that these texts never record the name of the person authorised to order the work to be done. The second step was to calculate how many workers were needed to complete the work (see the texts in Table 3). It was simple enough to do this by dividing the total volume by the coefficient representing the daily amount of earth to be excavated by one worker. At this point, a scribe had to simply multiply the number of workers by the amount of daily barley that each worker received in order to calculate the total cost of a particular project (texts in Table 2). We can summarise this sequence as follows:
Initial decision (?) → Survey to collect raw data → Calculation of volume to be excavated → Calculation of the total work → Calculation of the cost of the work.
It must be stressed that the sequence described above is inferred from administrative texts from Umma which show just the data and the results of the calculations: we do not have texts showing how the actual calculations were performed or the measurements taken. The linear measurements were probably taken by using a rope provided with knots at fixed lengths, whilst the calculations were probably performed with account tokens. After the intermediate results of the calculations were jotted down, either on tablets or on writing boards, they were probably erased by the scribe. As Robson (Reference Robson2008: 78) notes, “Good scribes never showed their working”.Footnote 16 What the tablets mostly show us are just the final results of all the operations.
Let us now compare the Old Babylonian problem texts introduced at the beginning of this paper with the Ur III documentation (Table 4). The relationship between Ur III administrative accounting practices and Old Babylonian mathematics was studied by Robson (Reference Robson1999: 165), who concluded that:
During the early Ur III period a sophisticated accounting procedure was developed for some sectors of the state economy, whereby the output of work-gangs could be monitored and compared to a theoretical maximum productivity. This overly bureaucratic system did not survive the end of Ur III empire, and records of production from the OB period reveal a truer picture of variable efficiency. Nevertheless, the rates of output deducible from the OB documents appear to cluster around the Ur III ideals. A few of the Ur III quotas appear in contemporary school practice texts, and many more seem to be the precursors to the OB quantity surveying coefficients.Footnote 17
Table 4 The structure of an Old Babylonian mathematical problem text compared to those of Ur III administrative texts about earthworks

To sum up, as evidenced by the mathematical text presented at the beginning of this paper, and others like it, Old Babylonian mathematical problems combined with a study of Ur III administrative documentation about earthworks allow us to reconstruct the practical procedure, used by Ur III officials, to prepare and complete earthworks. Moreover, it confirms the supposition that Old Babylonian mathematics about earthworks probably reflect Ur III procedures, while presenting the whole process in the form of a problem to be solved.
Appendix: Summary of the information included in the Ur III Umma texts about earthworks