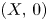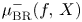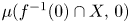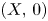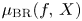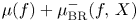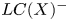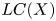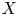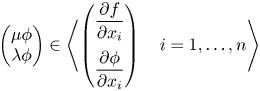1. Introduction
Let $(X,\,0)$![]() be a germ of complex analytic set in $\mathbb {C}^{n}$
be a germ of complex analytic set in $\mathbb {C}^{n}$![]() and $f:(\mathbb {C}^{n},\,0)\to (\mathbb {C},\,0)$
and $f:(\mathbb {C}^{n},\,0)\to (\mathbb {C},\,0)$![]() a holomorphic function germ. The Bruce–Roberts number of $f$
a holomorphic function germ. The Bruce–Roberts number of $f$![]() with respect to $(X,\,0)$
with respect to $(X,\,0)$![]() was introduced by Bruce and Roberts in [Reference Bruce and Roberts4] and is defined as
was introduced by Bruce and Roberts in [Reference Bruce and Roberts4] and is defined as
where $\mathcal {O}_n$![]() is the local ring of holomorphic functions $(\mathbb {C}^{n},\,0)\to \mathbb {C}$
is the local ring of holomorphic functions $(\mathbb {C}^{n},\,0)\to \mathbb {C}$![]() , $\textrm {d}f$
, $\textrm {d}f$![]() is the differential of $f$
is the differential of $f$![]() and $\Theta _X$
and $\Theta _X$![]() is the $\mathcal {O}_n$
is the $\mathcal {O}_n$![]() -submodule of $\Theta _n$
-submodule of $\Theta _n$![]() of vector fields on $(\mathbb {C}^{n},\,0)$
of vector fields on $(\mathbb {C}^{n},\,0)$![]() which are tangent to $(X,\,0)$
which are tangent to $(X,\,0)$![]() at its regular points. If $I_X$
at its regular points. If $I_X$![]() is the ideal of $\mathcal {O}_n$
is the ideal of $\mathcal {O}_n$![]() of functions vanishing on $(X,\,0)$
of functions vanishing on $(X,\,0)$![]() , then
, then
In particular, when $X=\mathbb {C}^{n}$![]() , $\textrm {d}f(\Theta _{X})$
, $\textrm {d}f(\Theta _{X})$![]() is the Jacobian ideal of $f$
is the Jacobian ideal of $f$![]() and thus, $\mu _{\textrm {BR}}(f,\,X)$
and thus, $\mu _{\textrm {BR}}(f,\,X)$![]() coincides with the classical Milnor number $\mu (f)$
coincides with the classical Milnor number $\mu (f)$![]() . We remark that $\Theta _X$
. We remark that $\Theta _X$![]() is also denoted in some papers by $\mbox {Der}(-\log X)$
is also denoted in some papers by $\mbox {Der}(-\log X)$![]() , following Saito's notation [Reference Saito11]. The main properties of $\mu _{\textrm {BR}}(f,\,X)$
, following Saito's notation [Reference Saito11]. The main properties of $\mu _{\textrm {BR}}(f,\,X)$![]() are the following (see [Reference Bruce and Roberts4]):
are the following (see [Reference Bruce and Roberts4]):
(a) $\mu _{\textrm {BR}}(f,\,X)$
 is invariant under the action of the group $\mathcal {R}_X$
is invariant under the action of the group $\mathcal {R}_X$ of diffeomorphisms $\phi :(\mathbb {C}^{n},\,0)\to (\mathbb {C}^{n},\,0)$
of diffeomorphisms $\phi :(\mathbb {C}^{n},\,0)\to (\mathbb {C}^{n},\,0)$ which preserve $(X,\,0)$
which preserve $(X,\,0)$ ;
;(b) $\mu _{\textrm {BR}}(f,\,X)<\infty$
 if and only if $f$
if and only if $f$ is finitely determined with respect to the $\mathcal {R}_X$
is finitely determined with respect to the $\mathcal {R}_X$ -equivalence;
-equivalence;(c) $\mu _{\textrm {BR}}(f,\,X)<\infty$
 if and only if $f$
if and only if $f$ restricted to each logarithmic stratum is a submersion in a punctured neighbourhood of the origin.
restricted to each logarithmic stratum is a submersion in a punctured neighbourhood of the origin.
In general, $\mu _{\textrm {BR}}(f,\,X)$![]() is not so easy to compute as the classical Milnor number. The main difficulty comes from the computation of the module $\Theta _X$
is not so easy to compute as the classical Milnor number. The main difficulty comes from the computation of the module $\Theta _X$![]() and most of the times, it is necessary to use a symbolic computer system like Singular [Reference Decker, Greuel, Pfister and Schönemann6]. If $(X,\,0)$
and most of the times, it is necessary to use a symbolic computer system like Singular [Reference Decker, Greuel, Pfister and Schönemann6]. If $(X,\,0)$![]() is an isolated complete intersection singularity (ICIS) and $\mu _{\textrm {BR}}(f,\,X)$
is an isolated complete intersection singularity (ICIS) and $\mu _{\textrm {BR}}(f,\,X)$![]() is finite, then $(f^{-1}(0)\cap X,\,0)$
is finite, then $(f^{-1}(0)\cap X,\,0)$![]() is an ICIS [Reference Biviá-Ausina and Ruas2, Proposition 2.8], therefore it has well-defined Milnor number. In a previous paper, [Reference Nuño-Ballesteros, Oréfice-Okamoto, Lima-Pereira and Tomazella9] we considered the case that $(X,\,0)$
is an ICIS [Reference Biviá-Ausina and Ruas2, Proposition 2.8], therefore it has well-defined Milnor number. In a previous paper, [Reference Nuño-Ballesteros, Oréfice-Okamoto, Lima-Pereira and Tomazella9] we considered the case that $(X,\,0)$![]() is an isolated hypersurface singularity (IHS). We showed that
is an isolated hypersurface singularity (IHS). We showed that
where $\mu$![]() and $\tau$
and $\tau$![]() are the Milnor and the Tjurina numbers, respectively. Thus, (1) gives an easy way to compute $\mu _{\textrm {BR}}(f,\,X)$
are the Milnor and the Tjurina numbers, respectively. Thus, (1) gives an easy way to compute $\mu _{\textrm {BR}}(f,\,X)$![]() in terms of well-known invariants. The formula (1) was also obtained independently in [Reference Kourliouros8] and previously in [Reference Nuño-Ballesteros, Oréfice-Okamoto and Tomazella10] when $(X,\,0)$
in terms of well-known invariants. The formula (1) was also obtained independently in [Reference Kourliouros8] and previously in [Reference Nuño-Ballesteros, Oréfice-Okamoto and Tomazella10] when $(X,\,0)$![]() is weighted homogeneous.
is weighted homogeneous.
An important application of (1) allowed us to conclude in [Reference Nuño-Ballesteros, Oréfice-Okamoto, Lima-Pereira and Tomazella9] that the logarithmic characteristic variety $LC(X)$![]() is Cohen–Macaulay. We recall that $LC(X)$
is Cohen–Macaulay. We recall that $LC(X)$![]() is the subvariety of the cotangent bundle $T^{*}\mathbb {C}^{n}$
is the subvariety of the cotangent bundle $T^{*}\mathbb {C}^{n}$![]() of pairs $(x,\,\alpha )$
of pairs $(x,\,\alpha )$![]() such that $\alpha (\xi _x)=0$
such that $\alpha (\xi _x)=0$![]() , for all $\xi \in \Theta _X$
, for all $\xi \in \Theta _X$![]() and for all $x$
and for all $x$![]() in a neighbourhood of $0$
in a neighbourhood of $0$![]() . When $(X,\,0)$
. When $(X,\,0)$![]() is holonomic, $LC(X)$
is holonomic, $LC(X)$![]() is Cohen–Macaulay if and only if for any Morsification $f_{t}$
is Cohen–Macaulay if and only if for any Morsification $f_{t}$![]() of $f$
of $f$![]() we have
we have
where $n_\alpha$![]() is the number of critical points of $f_t$
is the number of critical points of $f_t$![]() restricted to each logarithmic stratum $X_\alpha$
restricted to each logarithmic stratum $X_\alpha$![]() and $m_\alpha$
and $m_\alpha$![]() is the multiplicity of $LC(X)$
is the multiplicity of $LC(X)$![]() along the irreducible component $Y_\alpha$
along the irreducible component $Y_\alpha$![]() associated with $X_\alpha$
associated with $X_\alpha$![]() (see [Reference Bruce and Roberts4, Corollary 5.8]). When $(X,\,0)$
(see [Reference Bruce and Roberts4, Corollary 5.8]). When $(X,\,0)$![]() is an IHS, it always has a finite number of logarithmic strata (i.e., it is holonomic in Saito's terminology) given by $X_0=\mathbb {C}^{n}\setminus X$
is an IHS, it always has a finite number of logarithmic strata (i.e., it is holonomic in Saito's terminology) given by $X_0=\mathbb {C}^{n}\setminus X$![]() , $X_i\setminus \{0\}$
, $X_i\setminus \{0\}$![]() , with $i=1,\,\ldots ,\,k$
, with $i=1,\,\ldots ,\,k$![]() and $X_{k+1}=\{0\}$
and $X_{k+1}=\{0\}$![]() , where $X_1,\,\ldots ,\,X_k$
, where $X_1,\,\ldots ,\,X_k$![]() are the irreducible components of $X$
are the irreducible components of $X$![]() at $0$
at $0$![]() .
.
In this paper, we are interested in another important invariant introduced in [Reference Bruce and Roberts4],
which we call here the relative Bruce–Roberts number. This is an invariant of the restricted function $f:(X,\,0)\to (\mathbb {C},\,0)$![]() under the induced $\mathcal {R}_X$
under the induced $\mathcal {R}_X$![]() -action. In fact, as commented in [Reference Bruce and Roberts4], it is equal to the codimension of the $\mathcal {R}_X$
-action. In fact, as commented in [Reference Bruce and Roberts4], it is equal to the codimension of the $\mathcal {R}_X$![]() -orbit. Moreover, $\mu _{\textrm {BR}}^{-}(f,\,X)$
-orbit. Moreover, $\mu _{\textrm {BR}}^{-}(f,\,X)$![]() is finite if and only if $f$
is finite if and only if $f$![]() restricted to each logarithmic stratum (excluding $X_0$
restricted to each logarithmic stratum (excluding $X_0$![]() ) is a submersion in a punctured neighbourhood of the origin.
) is a submersion in a punctured neighbourhood of the origin.
A natural question is about the relationship between $\mu _{BR}(f,\,X)$![]() and $\mu _{BR}^{-}(f,\,X)$
and $\mu _{BR}^{-}(f,\,X)$![]() . It is shown in [Reference Bruce and Roberts4] that if $(X,\,0)$
. It is shown in [Reference Bruce and Roberts4] that if $(X,\,0)$![]() is a weighted homogeneous ICIS then
is a weighted homogeneous ICIS then
This, combined with (1) when $(X,\,0)$![]() is a weighted homogeneous IHS, gives that
is a weighted homogeneous IHS, gives that
Our main result in § 2 is that if $(X,\,0)$![]() is any IHS and $\mu _{BR}^{-}(f,\,X)$
is any IHS and $\mu _{BR}^{-}(f,\,X)$![]() is finite, then
is finite, then
In particular, (2) also holds when $\mu _{BR}(f,\,X)$![]() is finite, even when $(X,\,0)$
is finite, even when $(X,\,0)$![]() is not weighted homogeneous. We also show in Example 3.1 that (2) is not true for higher codimension ICIS.
is not weighted homogeneous. We also show in Example 3.1 that (2) is not true for higher codimension ICIS.
The relative logarithmic characteristic variety $LC(X)^{-}$![]() is obtained from $LC(X)$
is obtained from $LC(X)$![]() by eliminating the component $Y_0$
by eliminating the component $Y_0$![]() associated with the stratum $X_0=\mathbb {C}^{n}\setminus X$
associated with the stratum $X_0=\mathbb {C}^{n}\setminus X$![]() . In [Reference Bruce and Roberts4], they showed that $LC(X)$
. In [Reference Bruce and Roberts4], they showed that $LC(X)$![]() is never Cohen–Macaulay when $(X,\,0)$
is never Cohen–Macaulay when $(X,\,0)$![]() has codimension $>1$
has codimension $>1$![]() along the points on $X_0$
along the points on $X_0$![]() , but $LC(X)^{-}$
, but $LC(X)^{-}$![]() is always Cohen–Macaulay when $(X,\,0)$
is always Cohen–Macaulay when $(X,\,0)$![]() is a weighted homogeneous ICIS (of any codimension). Again, Cohen–Macaulayness of $LC(X)^{-}$
is a weighted homogeneous ICIS (of any codimension). Again, Cohen–Macaulayness of $LC(X)^{-}$![]() is interesting since it implies that
is interesting since it implies that
for any Morsification $f_t$![]() of $f$
of $f$![]() . As an application of (3), we show in § 3 that $LC(X)^{-}$
. As an application of (3), we show in § 3 that $LC(X)^{-}$![]() is also Cohen–Macaulay for any IHS $(X,\,0)$
is also Cohen–Macaulay for any IHS $(X,\,0)$![]() (not necessarily weighted homogeneous).
(not necessarily weighted homogeneous).
In § 4, we consider any holonomic variety $(X,\,0)$![]() and study characterizations of Cohen–Macaulayness of $LC(X)$
and study characterizations of Cohen–Macaulayness of $LC(X)$![]() and $LC(X)^{-}$
and $LC(X)^{-}$![]() in terms of the relative polar curve associated with a Morsification $f_t$
in terms of the relative polar curve associated with a Morsification $f_t$![]() of $f$
of $f$![]() . Finally, in § 5, we give a formula which generalizes the classical Thom–Sebastiani formula for the Milnor number of a function defined as a sum of functions with separated variables.
. Finally, in § 5, we give a formula which generalizes the classical Thom–Sebastiani formula for the Milnor number of a function defined as a sum of functions with separated variables.
2. The relative Bruce–Roberts number
The main goal of this section is to prove the equality (3). The next lemma is inspired by [Reference Biviá-Ausina and Ruas2, Proposition 2.8].
Lemma 2.1 Let $(X,\,0)$![]() be an IHS determined by $\phi :(\mathbb {C}^{n},\,0)\to (\mathbb {C},\,0)$
be an IHS determined by $\phi :(\mathbb {C}^{n},\,0)\to (\mathbb {C},\,0)$![]() and $f\in \mathcal {O}_{n}$
and $f\in \mathcal {O}_{n}$![]() . The map $(\phi ,\,f):(\mathbb {C}^{n},\,0)\to (\mathbb {C}^{2},\,0)$
. The map $(\phi ,\,f):(\mathbb {C}^{n},\,0)\to (\mathbb {C}^{2},\,0)$![]() defines an ICIS if and only if $\mu _{BR}^{-}(f,\,X)<\infty$
defines an ICIS if and only if $\mu _{BR}^{-}(f,\,X)<\infty$![]() .
.
Proof. If $(\phi ,\,f):(\mathbb {C}^{n},\,0)\to (\mathbb {C}^{2},\,0)$![]() defines an ICIS then $\mu _{BR}^{-}(f,\,X)$
defines an ICIS then $\mu _{BR}^{-}(f,\,X)$![]() is finite because
is finite because
For the converse, if $\mu _{BR}^{-}(f,\,X)<\infty$![]() then the restriction of $f$
then the restriction of $f$![]() to each logarithmic stratum, excluding $\mathbb {C}^{n}\setminus X$
to each logarithmic stratum, excluding $\mathbb {C}^{n}\setminus X$![]() is non-singular. The proof is now the same of Proposition 2.8 in [Reference Biviá-Ausina and Ruas2].
is non-singular. The proof is now the same of Proposition 2.8 in [Reference Biviá-Ausina and Ruas2].
The following technical lemma will be used in the proof of the next theorem. Given a matrix $A$![]() with entries in a ring $R$
with entries in a ring $R$![]() , we denote by $I_k(A)$
, we denote by $I_k(A)$![]() the ideal in $R$
the ideal in $R$![]() generated the $k\times k$
generated the $k\times k$![]() minors of $A$
minors of $A$![]() .
.
Lemma 2.2 Let $f,\,g\in \mathcal {O}_n$![]() be such that $\operatorname {dim} V(J(f,\,g))=1$
be such that $\operatorname {dim} V(J(f,\,g))=1$![]() and $V(Jf)=\{0\},$
and $V(Jf)=\{0\},$![]() and consider the following matrices
and consider the following matrices

where $\lambda ,\,\mu \in \mathcal {O}_n$![]() . Let $M,\,M'$
. Let $M,\,M'$![]() be the submodules of $\mathcal {O}_n^{2}$
be the submodules of $\mathcal {O}_n^{2}$![]() generated by the columns of $A,\,A'$
generated by the columns of $A,\,A'$![]() respectively. If $I_2(A)=I_2(A')$
respectively. If $I_2(A)=I_2(A')$![]() then $M=M'$
then $M=M'$![]() .
.
Proof. We see $A$![]() and $A'$
and $A'$![]() as homomorphims of modules over $R:=\mathcal {O}_n$
as homomorphims of modules over $R:=\mathcal {O}_n$![]() :
:
We consider the $R$![]() -module $R^{2}/M=\operatorname {coker}(A)$
-module $R^{2}/M=\operatorname {coker}(A)$![]() , which has support $V(I_2(A))=V(J(f,\,g))$
, which has support $V(I_2(A))=V(J(f,\,g))$![]() . Therefore, $\operatorname {dim}(R^{2}/M)=1=n-(n-2+1)$
. Therefore, $\operatorname {dim}(R^{2}/M)=1=n-(n-2+1)$![]() and hence it is Cohen–Macaulay (see [Reference Buchsbaum and Rim5]). In particular, it is unmixed. Now, $M'/M$
and hence it is Cohen–Macaulay (see [Reference Buchsbaum and Rim5]). In particular, it is unmixed. Now, $M'/M$![]() is a submodule of $R^{2}/M$
is a submodule of $R^{2}/M$![]() , so the associated primes $\operatorname {Ass} (M'/M)$
, so the associated primes $\operatorname {Ass} (M'/M)$![]() are included in $\operatorname {Ass}(R^{2}/M)$
are included in $\operatorname {Ass}(R^{2}/M)$![]() . If $M'/M\ne 0$
. If $M'/M\ne 0$![]() then $\operatorname {Ass} (M'/M)\ne \emptyset$
then $\operatorname {Ass} (M'/M)\ne \emptyset$![]() and it follows that $\operatorname {dim}(M'/M)=1$
and it follows that $\operatorname {dim}(M'/M)=1$![]() .
.
Let $U$![]() be a neighbourhood of $0$
be a neighbourhood of $0$![]() in $\mathbb {C}^{n}$
in $\mathbb {C}^{n}$![]() such that $0$
such that $0$![]() is the only critical point of $f$
is the only critical point of $f$![]() . For all $x\in U\setminus \{0\}$
. For all $x\in U\setminus \{0\}$![]() , there exist $i_{0}\in \{1,\,\ldots ,\,n\}$
, there exist $i_{0}\in \{1,\,\ldots ,\,n\}$![]() , such that $\partial f/\partial x_{i_{0}}(x)\neq 0$
, such that $\partial f/\partial x_{i_{0}}(x)\neq 0$![]() . We may suppose $i_{0}=1$
. We may suppose $i_{0}=1$![]() . Making elementary column operations in the matrices $A$
. Making elementary column operations in the matrices $A$![]() and $A'$
and $A'$![]() , we obtain
, we obtain
such that
By hypothesis $I_{2}(A)=I_{2}(A')$![]() and consequently $\langle c_{2},\,\ldots ,\,c_{n}\rangle =\langle \mu c_{1}-\lambda ,\,c_{2},\,\ldots ,\,c_{n}\rangle .$
and consequently $\langle c_{2},\,\ldots ,\,c_{n}\rangle =\langle \mu c_{1}-\lambda ,\,c_{2},\,\ldots ,\,c_{n}\rangle .$![]() This implies $\lambda =\mu c_{1}+\alpha _{2}c_{2}+\cdots +\alpha _{n}c_{n}$
This implies $\lambda =\mu c_{1}+\alpha _{2}c_{2}+\cdots +\alpha _{n}c_{n}$![]() , for some $\alpha _{2},\,\cdots ,\,\alpha _{n}\in R$
, for some $\alpha _{2},\,\cdots ,\,\alpha _{n}\in R$![]() . Thus,
. Thus,
and hence $(M'/M)_{x}=0$![]() . This shows that $\operatorname {Supp}(M'/M)\subset \{0\}$
. This shows that $\operatorname {Supp}(M'/M)\subset \{0\}$![]() and hence, $M'=M$
and hence, $M'=M$![]() .
.
Given an IHS $(X,\,0)$![]() defined by a holomorphic function germ $\phi :(\mathbb {C}^{n},\,0)\to (\mathbb {C},\,0),$
defined by a holomorphic function germ $\phi :(\mathbb {C}^{n},\,0)\to (\mathbb {C},\,0),$![]() we consider the $\mathcal {O}_{n}$
we consider the $\mathcal {O}_{n}$![]() -submodule of the trivial vectors fields, denoted by $\Theta _{X}^{T}$
-submodule of the trivial vectors fields, denoted by $\Theta _{X}^{T}$![]() , generated by
, generated by
This module was related to the Tjurina number of $(X,\,0)$![]() in [Reference Nuño-Ballesteros, Oréfice-Okamoto, Lima-Pereira and Tomazella9, Reference Tajima13]. By using different approaches, it is shown that $\tau (X,\,0)=\operatorname {dim}_{\mathbb {C}}\Theta _{X}/\Theta _{X}^{T}$
in [Reference Nuño-Ballesteros, Oréfice-Okamoto, Lima-Pereira and Tomazella9, Reference Tajima13]. By using different approaches, it is shown that $\tau (X,\,0)=\operatorname {dim}_{\mathbb {C}}\Theta _{X}/\Theta _{X}^{T}$![]() . Moreover, in [Reference Nuño-Ballesteros, Oréfice-Okamoto, Lima-Pereira and Tomazella9], we also proved that $\tau (X,\,0)=\operatorname {dim}_{\mathbb {C}}\textrm {d}f(\Theta _{X})/\textrm {d}f(\Theta _{X}^{T})$
. Moreover, in [Reference Nuño-Ballesteros, Oréfice-Okamoto, Lima-Pereira and Tomazella9], we also proved that $\tau (X,\,0)=\operatorname {dim}_{\mathbb {C}}\textrm {d}f(\Theta _{X})/\textrm {d}f(\Theta _{X}^{T})$![]() where $f$
where $f$![]() is any $\mathcal {R}_{X}$
is any $\mathcal {R}_{X}$![]() -finitely determined function germ. The following result generalizes this equality with a weaker hypothesis on $f$
-finitely determined function germ. The following result generalizes this equality with a weaker hypothesis on $f$![]() .
.
Theorem 2.3 Let $(X,\,0)$![]() be an IHS determined by $\phi :(\mathbb {C}^{n},\,0)\to (\mathbb {C},\,0)$
be an IHS determined by $\phi :(\mathbb {C}^{n},\,0)\to (\mathbb {C},\,0)$![]() and $f\in \mathcal {O}_{n}$
and $f\in \mathcal {O}_{n}$![]() such that $\mu _{BR}^{-}(f,\,X)<\infty ,$
such that $\mu _{BR}^{-}(f,\,X)<\infty ,$![]() then:
then:
(i) $\frac {\Theta _{X}}{\Theta _{X}^{T}}\approx \frac {\textrm {d}f(\Theta _{X})+I_{X}}{\textrm {d}f(\Theta _{X}^{T})+I_{X}};$

(ii) $\frac {\Theta _{X}}{\Theta _{X}^{T}}\approx \frac {\textrm {d}f(\Theta _{X})}{\textrm {d}f(\Theta _{X}^{T})};$

(iii) $\textrm {d}f(\Theta _{X})\cap I_{X}=JfI_{X};$

(iv) $\frac {\mathcal {O}_{n}}{Jf}\approx \frac {\textrm {d}f(\Theta _{X}^{-})}{\textrm {d}f(\Theta _{X})};$

(v) $\textrm {d}f(\Theta _{X}):I_{X}=Jf;$

(vi) $\textrm {d}f(\Theta _{X}^{T}):I_{X}=Jf,$

where $I_{X}$![]() is the ideal generated by $\phi$
is the ideal generated by $\phi$![]() .
.
Proof.
(i) The homomorphism $\Psi :\Theta _{X}\to \textrm {d}f(\Theta _{X})+I_{X}$
 defined by $\Psi (\xi )=\textrm {d}f(\xi )$
defined by $\Psi (\xi )=\textrm {d}f(\xi )$ induces the isomorphism
\[ \overline{\Psi}:\frac{\Theta_{X}}{\Theta_{X}^{T}}\to\frac{\textrm{d}f(\Theta_{X})+I_{X}}{\textrm{d}f(\Theta_{X}^{T})+I_{X}}. \]In fact, it is enough to show that $\Psi ^{-1}(\textrm {d}f(\Theta _{X}^{T})+I_{X})\subset \Theta _{X}^{T}.$
induces the isomorphism
\[ \overline{\Psi}:\frac{\Theta_{X}}{\Theta_{X}^{T}}\to\frac{\textrm{d}f(\Theta_{X})+I_{X}}{\textrm{d}f(\Theta_{X}^{T})+I_{X}}. \]In fact, it is enough to show that $\Psi ^{-1}(\textrm {d}f(\Theta _{X}^{T})+I_{X})\subset \Theta _{X}^{T}.$
 Let $\xi \in \Psi ^{-1}(\textrm {d}f(\Theta _{X}^{T})+I_{X})$
Let $\xi \in \Psi ^{-1}(\textrm {d}f(\Theta _{X}^{T})+I_{X})$ then $\Psi (\xi )\in \textrm {d}f(\Theta _{X}^{T})+I_{X}$
then $\Psi (\xi )\in \textrm {d}f(\Theta _{X}^{T})+I_{X}$ , that is, there exist $\eta \in \Theta _{X}^{T}$
, that is, there exist $\eta \in \Theta _{X}^{T}$ and $\mu ,\, \lambda \in \mathcal {O}_{n}$
and $\mu ,\, \lambda \in \mathcal {O}_{n}$ , such that
\[ \begin{cases} \textrm{d}f(\xi-\eta)=\mu\phi\\ \textrm{d}\phi(\xi-\eta)=\lambda\phi \end{cases}, \]then
, such that
\[ \begin{cases} \textrm{d}f(\xi-\eta)=\mu\phi\\ \textrm{d}\phi(\xi-\eta)=\lambda\phi \end{cases}, \]then \[ \left(\begin{array}{@{}c@{}} \mu\phi\\ \lambda\phi \end{array}\right)\in \left\langle \left(\begin{array}{@{}c@{}} \dfrac{\partial f}{\partial x_{i}}\\ \dfrac{\partial \phi}{\partial x_{i}} \end{array}\right) \quad i=1,\ldots,n \right\rangle \]and
\[ \left(\begin{array}{@{}c@{}} \mu\phi\\ \lambda\phi \end{array}\right)\in \left\langle \left(\begin{array}{@{}c@{}} \dfrac{\partial f}{\partial x_{i}}\\ \dfrac{\partial \phi}{\partial x_{i}} \end{array}\right) \quad i=1,\ldots,n \right\rangle \]and \[ I_{2}\begin{pmatrix}\mu\phi & \dfrac{\partial f}{\partial x_{1}} & \cdots & \dfrac{\partial f}{\partial x_{n}}\\ \lambda\phi & \dfrac{\partial \phi}{\partial x_{1}} & \cdots & \dfrac{\partial \phi}{\partial x_{n}} \end{pmatrix}=I_{2}\begin{pmatrix}\dfrac{\partial f}{\partial x_{1}} & \cdots & \dfrac{\partial f}{\partial x_{n}}\\ \dfrac{\partial \phi}{\partial x_{1}} & \cdots & \dfrac{\partial \phi}{\partial x_{n}} \end{pmatrix}=J(f,\phi). \]Therefore
\[ I_{2}\begin{pmatrix}\mu\phi & \dfrac{\partial f}{\partial x_{1}} & \cdots & \dfrac{\partial f}{\partial x_{n}}\\ \lambda\phi & \dfrac{\partial \phi}{\partial x_{1}} & \cdots & \dfrac{\partial \phi}{\partial x_{n}} \end{pmatrix}=I_{2}\begin{pmatrix}\dfrac{\partial f}{\partial x_{1}} & \cdots & \dfrac{\partial f}{\partial x_{n}}\\ \dfrac{\partial \phi}{\partial x_{1}} & \cdots & \dfrac{\partial \phi}{\partial x_{n}} \end{pmatrix}=J(f,\phi). \]Therefore \[ \left|\begin{array}{cc} \mu & \dfrac{\partial f}{\partial x_{i}} \\ \lambda & \dfrac{\partial \phi}{\partial x_{i}} \end{array}\right|\phi\in J(f,\phi) \]and since $\phi$
\[ \left|\begin{array}{cc} \mu & \dfrac{\partial f}{\partial x_{i}} \\ \lambda & \dfrac{\partial \phi}{\partial x_{i}} \end{array}\right|\phi\in J(f,\phi) \]and since $\phi$
 is regular in $\frac {\mathcal {O}_{n}}{J(f,\,\phi )}$
is regular in $\frac {\mathcal {O}_{n}}{J(f,\,\phi )}$ then
\[ \left|\begin{array}{cc} \mu & \dfrac{\partial f}{\partial x_{i}}\\ \lambda & \dfrac{\partial \phi}{\partial x_{i}} \end{array}\right|\in J(f,\phi),\quad i=1,\ldots,n. \]By Lemma 2.2, $\lambda \in J\phi$
then
\[ \left|\begin{array}{cc} \mu & \dfrac{\partial f}{\partial x_{i}}\\ \lambda & \dfrac{\partial \phi}{\partial x_{i}} \end{array}\right|\in J(f,\phi),\quad i=1,\ldots,n. \]By Lemma 2.2, $\lambda \in J\phi$
 and using [Reference Nuño-Ballesteros, Oréfice-Okamoto, Lima-Pereira and Tomazella9, Lemma 3.1], $\xi \in \Theta _{X}^{T}.$
and using [Reference Nuño-Ballesteros, Oréfice-Okamoto, Lima-Pereira and Tomazella9, Lemma 3.1], $\xi \in \Theta _{X}^{T}.$
(ii) This equality also was proved in [Reference Nuño-Ballesteros, Oréfice-Okamoto, Lima-Pereira and Tomazella9] with the additional hypothesis that $f$
 is $\mathcal {R}_{X}$
is $\mathcal {R}_{X}$ -finitely determined.
-finitely determined.The epimorphism $\psi :\Theta _{X}\to \textrm {d}f(\Theta _{X})$
 defined by $\psi (\xi )=\textrm {d}f(\xi )$
defined by $\psi (\xi )=\textrm {d}f(\xi )$ induces the isomorphism
\[ \overline{\psi}:\frac{\Theta_{X}}{\Theta_{X}^{T}}\to \frac{\textrm{d}f(\Theta_{X})}{\textrm{d}f(\Theta_{X}^{T})}. \]In fact, let $\xi \in \ker (\psi )$
induces the isomorphism
\[ \overline{\psi}:\frac{\Theta_{X}}{\Theta_{X}^{T}}\to \frac{\textrm{d}f(\Theta_{X})}{\textrm{d}f(\Theta_{X}^{T})}. \]In fact, let $\xi \in \ker (\psi )$
 , then there exist $\lambda \in \mathcal {O}_{n}$
, then there exist $\lambda \in \mathcal {O}_{n}$ , such that
\[ \begin{cases} \textrm{d}f(\xi)=0\\ \textrm{d}\phi(\xi)=\lambda\phi \end{cases} \]The rest is similar to the proof of (i).
, such that
\[ \begin{cases} \textrm{d}f(\xi)=0\\ \textrm{d}\phi(\xi)=\lambda\phi \end{cases} \]The rest is similar to the proof of (i).
(iii) Let $\xi \in \Theta _{X}$
 be such that $\textrm {d}f(\xi )\in I_{X}$
be such that $\textrm {d}f(\xi )\in I_{X}$ , then there exist $\mu ,\,\lambda \in \mathcal {O}_{n}$
, then there exist $\mu ,\,\lambda \in \mathcal {O}_{n}$ , such that
\[ \begin{cases} \textrm{d}f(\xi)=\mu\phi\\ \textrm{d}\phi(\xi)=\lambda\phi \end{cases} \]Using the same techniques of the proof of (i), we have
, such that
\[ \begin{cases} \textrm{d}f(\xi)=\mu\phi\\ \textrm{d}\phi(\xi)=\lambda\phi \end{cases} \]Using the same techniques of the proof of (i), we have \[ \textrm{d}f(\Theta_{X})\cap I_{X}\subset Jf I_{X}. \]The other inclusion is immediate.
\[ \textrm{d}f(\Theta_{X})\cap I_{X}\subset Jf I_{X}. \]The other inclusion is immediate.
(iv) It follows from the isomorphisms
\[ \frac{\textrm{d}f(\Theta_{X}^{-})}{\textrm{d}f(\Theta_{X})}=\frac{\textrm{d}f(\Theta_{X})+I_{X}}{\textrm{d}f(\Theta_{X})}\approx \frac{I_{X}}{\textrm{d}f(\Theta_{X})\cap I_{X}}\stackrel{(iii)}{=}\frac{I_{X}}{JfI_{X} }\approx\frac{\mathcal{O}_{n}}{Jf}. \]
(v) It follows from (iii).
(vi) It follows from (v) and $Jf\subset \textrm {d}f(\Theta _{X}^{T}):I_{X}$
 .
.
Remark 2.4 The items (ii) and (iv) of Theorem 2.3 seem a bit peculiar since from (iv) the quotient $\textrm {d}f(\Theta _{X}^{-})/\textrm {d}f(\Theta _{X})$![]() does not depend on $(X,\,0)$
does not depend on $(X,\,0)$![]() while from (ii), $\textrm {d}f(\Theta _{X})/\textrm {d}f(\Theta _{X}^{T})$
while from (ii), $\textrm {d}f(\Theta _{X})/\textrm {d}f(\Theta _{X}^{T})$![]() does not depend on $f$
does not depend on $f$![]() . Moreover by [Reference Nuño-Ballesteros, Oréfice-Okamoto, Lima-Pereira and Tomazella9, Reference Tajima13] if $(X,\,0)$
. Moreover by [Reference Nuño-Ballesteros, Oréfice-Okamoto, Lima-Pereira and Tomazella9, Reference Tajima13] if $(X,\,0)$![]() is an IHS determined by $\phi :(\mathbb {C}^{n},\,0)\to (\mathbb {C},\,0)$
is an IHS determined by $\phi :(\mathbb {C}^{n},\,0)\to (\mathbb {C},\,0)$![]() , then $\operatorname {dim}_{\mathbb {C}}\dfrac {\Theta _{X}}{\Theta _{X}^{T}}=\tau (X,\,0),$
, then $\operatorname {dim}_{\mathbb {C}}\dfrac {\Theta _{X}}{\Theta _{X}^{T}}=\tau (X,\,0),$![]() therefore
therefore
The next theorem is one of the main results of this work.
Theorem 2.5 Let $(X,\,0)$![]() is an IHS determined by $\phi :(\mathbb {C}^{n},\,0)\to (\mathbb {C},\,0)$
is an IHS determined by $\phi :(\mathbb {C}^{n},\,0)\to (\mathbb {C},\,0)$![]() and $f\in \mathcal {O}_{n}$
and $f\in \mathcal {O}_{n}$![]() be a function germ such that $\mu _{BR}^{-}(f,\,X)<\infty$
be a function germ such that $\mu _{BR}^{-}(f,\,X)<\infty$![]() . Then $(\phi ,\,f)$
. Then $(\phi ,\,f)$![]() defines an ICIS and
defines an ICIS and
Proof. We consider the exact sequence
Since $(X,\,0)$![]() is an IHS
is an IHS
hence

The last equality is a consequence of the Lê-Greuel formula [Reference Brieskorn and Greuel3] and Theorem 2.3 (i).
3. The relative Bruce–Roberts number of a function with isolated singularity
In this section, $(X,\,0)$![]() is an IHS and $f\in \mathcal {O}_{n}$
is an IHS and $f\in \mathcal {O}_{n}$![]() is a function germ $\mathcal {R}_{X}$
is a function germ $\mathcal {R}_{X}$![]() -finitely determined, then all the results in the previous section are true in this case. In particular from (iv) of Theorem 2.3
-finitely determined, then all the results in the previous section are true in this case. In particular from (iv) of Theorem 2.3
Therefore, by the exact sequence
we conclude that
The following example shows that the characterization of the Milnor number (4) is not true anymore when $(X,\,0)$![]() is an ICIS with codimension higher than one.
is an ICIS with codimension higher than one.
Example 3.1 Let $(X,\,0)$![]() be an ICIS determined by $\phi (x,\,y,\,z)=(x^{3}+x^{2}y^{2}+y^{7}+z^{3},\,xyz)$
be an ICIS determined by $\phi (x,\,y,\,z)=(x^{3}+x^{2}y^{2}+y^{7}+z^{3},\,xyz)$![]() , and $f(x,\,y,\,z)=xy-z^{4}$
, and $f(x,\,y,\,z)=xy-z^{4}$![]() , $f$
, $f$![]() is a $\mathcal {R}_{X}$
is a $\mathcal {R}_{X}$![]() -finitely determined and
-finitely determined and
As a consequence of the characterization of the Milnor number (4), we prove that $LC(X)^{-}$![]() is Cohen–Macaulay when $(X,\,0)$
is Cohen–Macaulay when $(X,\,0)$![]() is an IHS.
is an IHS.
The logarithmic characteristic variety, $LC(X)$![]() , is defined as follows. Suppose the vector fields $\delta _1,\,\ldots ,\,\delta _m$
, is defined as follows. Suppose the vector fields $\delta _1,\,\ldots ,\,\delta _m$![]() generate $\Theta _X$
generate $\Theta _X$![]() on some neighbourhood $U$
on some neighbourhood $U$![]() of $0$
of $0$![]() in $\mathbb {C}^{n}$
in $\mathbb {C}^{n}$![]() . Let $T^{*}_U\mathbb {C}^{n}$
. Let $T^{*}_U\mathbb {C}^{n}$![]() be the restriction of the cotangent bundle of $\mathbb {C}^{n}$
be the restriction of the cotangent bundle of $\mathbb {C}^{n}$![]() to $U$
to $U$![]() . We define $LC_U(X)$
. We define $LC_U(X)$![]() to be
to be
Then $LC(X)$![]() is the germ of $LC_U(X)$
is the germ of $LC_U(X)$![]() in $T^{*}\mathbb {C}^{n}$
in $T^{*}\mathbb {C}^{n}$![]() along $T^{*}_0\mathbb {C}^{n}$
along $T^{*}_0\mathbb {C}^{n}$![]() , the cotangent space to $\mathbb {C}^{n}$
, the cotangent space to $\mathbb {C}^{n}$![]() at $0$
at $0$![]() . As $LC(X)$
. As $LC(X)$![]() is independent of the choice of the vector fields $\delta _i$
is independent of the choice of the vector fields $\delta _i$![]() then it is a well-defined germ of analytic subvariety in $T^{*}\mathbb {C}^{n}$
then it is a well-defined germ of analytic subvariety in $T^{*}\mathbb {C}^{n}$![]() (see [Reference Bruce and Roberts4, Reference Saito11]).
(see [Reference Bruce and Roberts4, Reference Saito11]).
If $(X,\,0)$![]() is holonomic with logarithmic strata $X_0,\,\ldots ,\,X_k$
is holonomic with logarithmic strata $X_0,\,\ldots ,\,X_k$![]() then $LC(X)$
then $LC(X)$![]() has dimension $n$
has dimension $n$![]() , and its irreducible components are $Y_0,\,\ldots ,\,Y_k$
, and its irreducible components are $Y_0,\,\ldots ,\,Y_k$![]() , with $Y_i=\overline {N^{*}X_i}$
, with $Y_i=\overline {N^{*}X_i}$![]() as set-germs, where $\overline {N^{*}X_i}$
as set-germs, where $\overline {N^{*}X_i}$![]() is the closure of the conormal bundle $N^{*}X_i$
is the closure of the conormal bundle $N^{*}X_i$![]() of $X_i$
of $X_i$![]() in $\mathbb {C}^{n}$
in $\mathbb {C}^{n}$![]() (see [Reference Bruce and Roberts4, Proposition 1.14]).
(see [Reference Bruce and Roberts4, Proposition 1.14]).
When $(X,\,0)$![]() has codimension higher than one, Bruce and Roberts proved that $LC(X)$
has codimension higher than one, Bruce and Roberts proved that $LC(X)$![]() is not Cohen–Macaulay. Then they consider the subspace of $LC(X)$
is not Cohen–Macaulay. Then they consider the subspace of $LC(X)$![]() obtained by deleting the component $Y_{0}$
obtained by deleting the component $Y_{0}$![]() that corresponds to the stratum $X_0= \mathbb {C}^{n}\setminus X$
that corresponds to the stratum $X_0= \mathbb {C}^{n}\setminus X$![]() , that is
, that is

and as set-germs,

An interesting fact about $LC(X)^{-}$![]() is that it may be Cohen–Macaulay even when $LC(X)$
is that it may be Cohen–Macaulay even when $LC(X)$![]() is not Cohen–Macaulay, for example, if $(X,\,0)$
is not Cohen–Macaulay, for example, if $(X,\,0)$![]() is a weighted homogeneous ICIS, then $LC(X)^{-}$
is a weighted homogeneous ICIS, then $LC(X)^{-}$![]() is Cohen–Macaulay, [Reference Bruce and Roberts4].
is Cohen–Macaulay, [Reference Bruce and Roberts4].
Proposition 3.2 Let $(X,\,0)$![]() be an IHS, then $LC(X)^{-}$
be an IHS, then $LC(X)^{-}$![]() is Cohen–Macaulay.
is Cohen–Macaulay.
Proof. We consider $(0,\,p)\in LC(X)^{-}$![]() , then $(0,\,p)\in LC(X)$
, then $(0,\,p)\in LC(X)$![]() and there exists $f\in \mathcal {O}_{n}$
and there exists $f\in \mathcal {O}_{n}$![]() such that $\textrm {d}f(0)=p$
such that $\textrm {d}f(0)=p$![]() . In [Reference Nuño-Ballesteros, Oréfice-Okamoto, Lima-Pereira and Tomazella9], we proved that $LC(X)$
. In [Reference Nuño-Ballesteros, Oréfice-Okamoto, Lima-Pereira and Tomazella9], we proved that $LC(X)$![]() is Cohen–Macaulay. Therefore, by [Reference Bruce and Roberts4, Proposition 5.8],
is Cohen–Macaulay. Therefore, by [Reference Bruce and Roberts4, Proposition 5.8],

where $n_{i}$![]() is the number of critical points of a Morsification of $f$
is the number of critical points of a Morsification of $f$![]() in $X_{i}$
in $X_{i}$![]() and $m_{i}$
and $m_{i}$![]() is the multiplicity of irreducible component $Y_{i}$
is the multiplicity of irreducible component $Y_{i}$![]() . Thus,
. Thus,

and by [Reference Bruce and Roberts4, Proposition 5.11], we obtain that $LC(X)^{-}$![]() is Cohen–Macaulay.
is Cohen–Macaulay.
Remark 3.3 We remark that in the proof of the previous proposition, we just used that if $(X,\,0)\subset (\mathbb {C}^{n},\,0)$![]() is a hypersurface such that $\operatorname {dim}_{\mathbb {C}}\textrm {d}f(\Theta _{X}^{-})/\textrm {d}f(\Theta _{X})=\mu (f)$
is a hypersurface such that $\operatorname {dim}_{\mathbb {C}}\textrm {d}f(\Theta _{X}^{-})/\textrm {d}f(\Theta _{X})=\mu (f)$![]() for all $f$
for all $f$![]() $\mathcal {R}_{X}$
$\mathcal {R}_{X}$![]() -finitely determined then $LC(X)^{-}$
-finitely determined then $LC(X)^{-}$![]() is Cohen–Macaulay if and only if $LC(X)$
is Cohen–Macaulay if and only if $LC(X)$![]() is Cohen–Macaulay.
is Cohen–Macaulay.
4. Polar curves and logarithmic characteristic varieties
It is important to know whether the logarithmic characteristic variety of an analytic variety is Cohen–Macaulay. In [Reference Nuño-Ballesteros, Oréfice-Okamoto, Lima-Pereira and Tomazella9], we showed that this is the case for IHS. For non-isolated singularities, it is an open problem. In this section, we give one more step in order to solve it: we study the polar curve and the relative polar curve of a holomorphic function germ over a holonomic analytic variety. We show that these curves are Cohen–Macaulay if and only if the logarithmic characteristic variety and the relative logarithmic characteristic variety (respectively) are Cohen–Macaulay. As a consequence, we have the principle of conservation for the Bruce–Roberts number.
Definition 4.1 Let $f\in \mathcal {O}_{n}$![]() be a $\mathcal {R}_{X}$
be a $\mathcal {R}_{X}$![]() -finitely determined function germ and $F:(\mathbb {C}^{n}\times \mathbb {C},\,0)\to (\mathbb {C},\,0)$
-finitely determined function germ and $F:(\mathbb {C}^{n}\times \mathbb {C},\,0)\to (\mathbb {C},\,0)$![]() , $F(t,\,x)=f_t(x)$
, $F(t,\,x)=f_t(x)$![]() ,
,
a 1-parameter deformation of $f$![]() . The polar curve of $F$
. The polar curve of $F$![]() in $(X,\,0)$
in $(X,\,0)$![]() is
is
where $\Theta _{X}=\langle \delta _{1},\,\ldots ,\,\delta _{m}\rangle$![]() .
.
In [Reference Ahmed, Ruas and Tomazella1], it was proved that if $LC(X)$![]() is Cohen–Macaulay then the polar curve $C$
is Cohen–Macaulay then the polar curve $C$![]() is Cohen–Macaulay.
is Cohen–Macaulay.
Proposition 4.2 Let $(X,\,0)$![]() be a holonomic analytic variety. If any $\mathcal {R}_{X}$
be a holonomic analytic variety. If any $\mathcal {R}_{X}$![]() -finitely determined function germ has a Morsification whose polar curve is Cohen–Macaulay then $LC(X)$
-finitely determined function germ has a Morsification whose polar curve is Cohen–Macaulay then $LC(X)$![]() is Cohen–Macaulay.
is Cohen–Macaulay.
Proof. Let $(0,\,p)\in LC(X)$![]() , then there exists an $\mathcal {R}_{X}$
, then there exists an $\mathcal {R}_{X}$![]() -finitely determined function germ $f\in \mathcal {O}_{n},$
-finitely determined function germ $f\in \mathcal {O}_{n},$![]() such that $\textrm {d}f(0)=p$
such that $\textrm {d}f(0)=p$![]() . Let $F:(\mathbb {C}^{n}\times \mathbb {C})\to (\mathbb {C},\,0)$
. Let $F:(\mathbb {C}^{n}\times \mathbb {C})\to (\mathbb {C},\,0)$![]() , $F(x,\,t)=f_{t}(x)$
, $F(x,\,t)=f_{t}(x)$![]() ,
,
be a Morsification of $f$![]() . By hypothesis $\mathcal {O}_{n+1}/\textrm {d}f_{t}(\Theta _{X})$
. By hypothesis $\mathcal {O}_{n+1}/\textrm {d}f_{t}(\Theta _{X})$![]() is Cohen–Macaulay of dimension 1, then by the principle of conservation of number
is Cohen–Macaulay of dimension 1, then by the principle of conservation of number

because if $x\in X_{i}$![]() is a Morse critical point of $f_{t}$
is a Morse critical point of $f_{t}$![]() , then $\mu _{BR}(f_{t},\,X)_{x}=m_{i}$
, then $\mu _{BR}(f_{t},\,X)_{x}=m_{i}$![]() , and by [Reference Bruce and Roberts4, Proposition 5.8], $LC(X)$
, and by [Reference Bruce and Roberts4, Proposition 5.8], $LC(X)$![]() is Cohen–Macaulay.
is Cohen–Macaulay.
When $LC(X)$![]() is Cohen–Macaulay, we have
is Cohen–Macaulay, we have
where $f_{t}$![]() is any 1-parameter deformation of $f$
is any 1-parameter deformation of $f$![]() .
.
Our purpose now is to prove similar results for $LC(X)^{-}$![]() . We define the relative polar curve by
. We define the relative polar curve by
where $C$![]() is the polar curve of $F$
is the polar curve of $F$![]() in $(X,\,0).$
in $(X,\,0).$![]()
The proof of the next proposition is similar to the one of [Reference Ahmed, Ruas and Tomazella1, Theorem 3.7].
Proposition 4.3 Let $(X,\,0)$![]() be a holonomic analytic variety. If $LC(X)^{-}$
be a holonomic analytic variety. If $LC(X)^{-}$![]() is Cohen–Macaulay then the relative polar curve of every 1-parameter deformation of any $\mathcal {R}_{X}$
is Cohen–Macaulay then the relative polar curve of every 1-parameter deformation of any $\mathcal {R}_{X}$![]() -finitely determined function germ is Cohen–Macaulay.
-finitely determined function germ is Cohen–Macaulay.
For the converse, we need the following lemma, which is the analogous of [Reference Bruce and Roberts4, Proposition 5.12] for the relative Bruce–Roberts number.
Lemma 4.4 Let $(X,\,0)$![]() be a holonomic analytic variety and $f\in \mathcal {O}_{n}$
be a holonomic analytic variety and $f\in \mathcal {O}_{n}$![]() . We assume that $f$
. We assume that $f$![]() restricted to $(X,\,0)$
restricted to $(X,\,0)$![]() is a Morse function. If $x\in X$
is a Morse function. If $x\in X$![]() is a critical point of $f$
is a critical point of $f$![]() then $\mu _{BR}(f,\,X)_{x}^{-}=m_{\alpha },$
then $\mu _{BR}(f,\,X)_{x}^{-}=m_{\alpha },$![]() where $m_{\alpha }$
where $m_{\alpha }$![]() is the multiplicity of the irreducible component $Y_\alpha$
is the multiplicity of the irreducible component $Y_\alpha$![]() corresponding to the logarithmic stratum $X_\alpha$
corresponding to the logarithmic stratum $X_\alpha$![]() which contains $x$
which contains $x$![]() .
.
Proof. Let $Z_{i}=Y_{i}\setminus \bigcup _{j\neq i}Y_{j}$![]() where $Y_{i}$
where $Y_{i}$![]() are the irreducible components of $LC(X)$
are the irreducible components of $LC(X)$![]() . We know from [Reference Bruce and Roberts4, Proposition 5.12] that $LC(X)$
. We know from [Reference Bruce and Roberts4, Proposition 5.12] that $LC(X)$![]() is Cohen–Macaulay at points in $Z_{i}$
is Cohen–Macaulay at points in $Z_{i}$![]() , $i=1,\,\ldots ,\,k+1$
, $i=1,\,\ldots ,\,k+1$![]() . We see that $LC(X)^{-}$
. We see that $LC(X)^{-}$![]() coincides locally with $LC(X)$
coincides locally with $LC(X)$![]() and hence, $LC(X)^{-}$
and hence, $LC(X)^{-}$![]() is also Cohen–Macaulay at points in $Z_{i}$
is also Cohen–Macaulay at points in $Z_{i}$![]() , $i=1,\,\ldots ,\,k+1$
, $i=1,\,\ldots ,\,k+1$![]() .
.
In fact, let $(0,\,p)\in Z_{i}$![]() with $i\neq 0$
with $i\neq 0$![]() , then $(x,\,p)\not \in Y_{0}$
, then $(x,\,p)\not \in Y_{0}$![]() . Let $V:= T^{*}\mathbb {C}^{n}\setminus Y_{0}$
. Let $V:= T^{*}\mathbb {C}^{n}\setminus Y_{0}$![]() , which is an open neighbourhood of $(x,\,p)$
, which is an open neighbourhood of $(x,\,p)$![]() . Obviously, we have the equality of sets
. Obviously, we have the equality of sets
Moreover, let $I,\,\;I^{-}$![]() and $I_{j}$
and $I_{j}$![]() be the ideals which define $LC(X)$
be the ideals which define $LC(X)$![]() , $LC(X)^{-}$
, $LC(X)^{-}$![]() and $Y_{j}$
and $Y_{j}$![]() , $j=0,\,\ldots ,\,k+1$
, $j=0,\,\ldots ,\,k+1$![]() , respectively. Then,
, respectively. Then,
Since $p\neq 0$![]() , $I_{0}$
, $I_{0}$![]() is the total ring at $(x,\,p)$
is the total ring at $(x,\,p)$![]() , so we have an equality between germs of complex spaces.
, so we have an equality between germs of complex spaces.
Finally, we have

The equalities $(*)$![]() and $(**)$
and $(**)$![]() are consequences of [Reference Bruce and Roberts4, Propositions 5.11 and 5.2], respectively.
are consequences of [Reference Bruce and Roberts4, Propositions 5.11 and 5.2], respectively.
We are ready now to prove the converse of Proposition 4.3.
Proposition 4.5 Let $(X,\,0)$![]() be a holonomic analytic variety. If the relative polar curve of every 1-parameter deformation of any $\mathcal {R}_{X}$
be a holonomic analytic variety. If the relative polar curve of every 1-parameter deformation of any $\mathcal {R}_{X}$![]() -finitely determined function germ is Cohen–Macaulay then $LC(X)^{-}$
-finitely determined function germ is Cohen–Macaulay then $LC(X)^{-}$![]() is Cohen–Macaulay.
is Cohen–Macaulay.
Proof. Let $(0,\,p)\in LC(X)^{-}$![]() , then there exists an $\mathcal {R}_{X}$
, then there exists an $\mathcal {R}_{X}$![]() -finitely determined function germ $f\in \mathcal {O}_{n},$
-finitely determined function germ $f\in \mathcal {O}_{n},$![]() such that $\textrm {d}f(0)=p$
such that $\textrm {d}f(0)=p$![]() . Let $F:(\mathbb {C}^{n}\times \mathbb {C},\,0)\to (\mathbb {C},\,0)$
. Let $F:(\mathbb {C}^{n}\times \mathbb {C},\,0)\to (\mathbb {C},\,0)$![]() be a Morsification of $f$
be a Morsification of $f$![]() and set $f_{t}(x)=F(x,\,t)$
and set $f_{t}(x)=F(x,\,t)$![]() .
.
By hypothesis $\mathcal {O}_{n+1}/\textrm {d}f_{t}(\Theta _{X}^{-})$![]() is Cohen–Macaulay of dimension 1. By the principle of the conservation of the multiplicity,
is Cohen–Macaulay of dimension 1. By the principle of the conservation of the multiplicity,

because if $x\in X_{i}$![]() is a Morse critical point of $f_{t}$
is a Morse critical point of $f_{t}$![]() , then $\mu _{BR}(f_{t},\,X)^{-}_{x}=m_{i}$
, then $\mu _{BR}(f_{t},\,X)^{-}_{x}=m_{i}$![]() by Lemma 4.4. By [Reference Bruce and Roberts4, Proposition 5.11], $LC(X)^{-}$
by Lemma 4.4. By [Reference Bruce and Roberts4, Proposition 5.11], $LC(X)^{-}$![]() is Cohen–Macaulay.
is Cohen–Macaulay.
As a consequence of the previous result,
where $f_{t}$![]() is any 1-parameter deformation of $f$
is any 1-parameter deformation of $f$![]() .
.
5. An example with non-isolated singularities
Given natural numbers $0< k\leq n$![]() , we can see $\mathcal {O}_k$
, we can see $\mathcal {O}_k$![]() as a subring of $\mathcal {O}_n$
as a subring of $\mathcal {O}_n$![]() and $\Theta _{k}$
and $\Theta _{k}$![]() as a subset of $\Theta _{n}$
as a subset of $\Theta _{n}$![]() . We fix $(x_1,\,\ldots ,\,x_n)$
. We fix $(x_1,\,\ldots ,\,x_n)$![]() as the system of coordinates in $\mathcal {O}_n$
as the system of coordinates in $\mathcal {O}_n$![]() and we use $(x_1,\,\ldots ,\, x_k)$
and we use $(x_1,\,\ldots ,\, x_k)$![]() as the coordinate system of $\mathcal {O}_k$
as the coordinate system of $\mathcal {O}_k$![]() and $(x_{k+1},\,\ldots ,\,x_n)$
and $(x_{k+1},\,\ldots ,\,x_n)$![]() as the one in $\mathcal {O}_{n-k}$
as the one in $\mathcal {O}_{n-k}$![]() .
.
Let $(X,\,0)\subset (\mathbb {C}^{k},\,0)$![]() be an analytic variety. We denote by $(\tilde {X},\,0)\subset (\mathbb {C}^{n},\,0)$
be an analytic variety. We denote by $(\tilde {X},\,0)\subset (\mathbb {C}^{n},\,0)$![]() the inclusion of $(X,\,0)$
the inclusion of $(X,\,0)$![]() in $(\mathbb {C}^{n},\,0).$
in $(\mathbb {C}^{n},\,0).$![]() Then $\Theta _{\tilde {X}}=\mathcal {O}_{n}\Theta _{X}+\langle \tfrac {\partial }{\partial x_{k+1}},\ldots ,\tfrac {\partial }{\partial x_{n}}\rangle$
Then $\Theta _{\tilde {X}}=\mathcal {O}_{n}\Theta _{X}+\langle \tfrac {\partial }{\partial x_{k+1}},\ldots ,\tfrac {\partial }{\partial x_{n}}\rangle$![]() and $LC(\tilde {X})=LC(X)\times \mathbb {C}^{n-t}.$
and $LC(\tilde {X})=LC(X)\times \mathbb {C}^{n-t}.$![]()
Consequently, if $LC(X)$![]() is Cohen–Macaulay then $LC(\tilde {X})$
is Cohen–Macaulay then $LC(\tilde {X})$![]() is Cohen–Macaulay.
is Cohen–Macaulay.
In particular, if $(X,\,0)$![]() is an IHS then $LC(\tilde {X})$
is an IHS then $LC(\tilde {X})$![]() is Cohen–Macaulay.
is Cohen–Macaulay.
Let $F\in \mathcal {O}_{n}$![]() a function germ with isolated singularity such that $F=f+g$
a function germ with isolated singularity such that $F=f+g$![]() with $f\in \mathcal {O}_{k}$
with $f\in \mathcal {O}_{k}$![]() and $g\in \mathcal {O}_{n-k}$
and $g\in \mathcal {O}_{n-k}$![]() . It is known by Sebastiani and Thom [Reference Sebastiani and Thom12] that $\mu (F)=\mu (f)\mu (g)$
. It is known by Sebastiani and Thom [Reference Sebastiani and Thom12] that $\mu (F)=\mu (f)\mu (g)$![]() . We prove a similar result for the Bruce–Roberts number,
. We prove a similar result for the Bruce–Roberts number,
Proposition 5.1 Let $I$![]() and $J$
and $J$![]() be ideals in $\mathcal {O}_{k}$
be ideals in $\mathcal {O}_{k}$![]() and $\mathcal {O}_{n-k}$
and $\mathcal {O}_{n-k}$![]() , respectively. If we denote by $I'=I\mathcal {O}_n$
, respectively. If we denote by $I'=I\mathcal {O}_n$![]() and $J'=J\mathcal {O}_n$
and $J'=J\mathcal {O}_n$![]() the respective induced ideals in $\mathcal {O}_n$
the respective induced ideals in $\mathcal {O}_n$![]() , then
, then
Moreover, if these dimensions are finite then
Proof. The equivalence follows from
For the equality, by hypothesis there exist positive integer numbers $k',\,\;k_{i}$![]() and $k_{j}$
and $k_{j}$![]() such that
such that
where $\mathcal {M}_\ell$![]() is the maximal ideal of $\mathcal {O}_\ell$
is the maximal ideal of $\mathcal {O}_\ell$![]() . Let $r=\max \{k',\,\ k_{i},\, \ k_{j}\}$
. Let $r=\max \{k',\,\ k_{i},\, \ k_{j}\}$![]() , then
, then

where $z_1=(x_1,\,\ldots ,\,x_k)$![]() , $z_2=(x_{k+1},\,\ldots ,\,x_n)$
, $z_2=(x_{k+1},\,\ldots ,\,x_n)$![]() and $I''$
and $I''$![]() and $J''$
and $J''$![]() are the ideals in $\mathbb {C}[z_1,\,z_2]$
are the ideals in $\mathbb {C}[z_1,\,z_2]$![]() generated by the $r-1$
generated by the $r-1$![]() -jets of the generators of $I$
-jets of the generators of $I$![]() and $J$
and $J$![]() , respectively. Analogously,
, respectively. Analogously,
where $I'''$![]() and $J'''$
and $J'''$![]() are the ideals in $\mathbb {C}[z_1]$
are the ideals in $\mathbb {C}[z_1]$![]() and $\mathbb {C}[z_2]$
and $\mathbb {C}[z_2]$![]() generated by the $r-1$
generated by the $r-1$![]() -jets of the generators of $I$
-jets of the generators of $I$![]() and $J$
and $J$![]() , respectively. Finally, the equality follows from
, respectively. Finally, the equality follows from
where $\otimes _{\mathbb {C}}$![]() denotes the tensor product, see [Reference Greuel and Pfister7, Proposition 2.7.13].
denotes the tensor product, see [Reference Greuel and Pfister7, Proposition 2.7.13].
We observe that the previous result gives a simpler proof to the equality of [Reference Sebastiani and Thom12] about the Milnor numbers. Finally, we relate the Bruce–Roberts numbers $\mu _{BR}(F,\,\tilde {X})$![]() and $\mu _{BR}(f,\,X)$
and $\mu _{BR}(f,\,X)$![]() .
.
Corollary 5.2 Let $(\tilde {X},\,0),$![]() and $(X,\,0)$
and $(X,\,0)$![]() as before, and
as before, and
then:
(a) $F$
 is $\mathcal {R}_{\tilde {X}}$
is $\mathcal {R}_{\tilde {X}}$ -finitely determined if, and only if, $f$
-finitely determined if, and only if, $f$ is $\mathcal {R}_{X}$
is $\mathcal {R}_{X}$ -finitely determined and $g$
-finitely determined and $g$ has isolated singularity.
has isolated singularity.(b) If $F$
 is $\mathcal {R}_{\tilde {X}}$
is $\mathcal {R}_{\tilde {X}}$ -finitely determined, $\mu _{BR}(F,\,\tilde {X})=\mu (g)\mu _{BR}(f,\,X)$
-finitely determined, $\mu _{BR}(F,\,\tilde {X})=\mu (g)\mu _{BR}(f,\,X)$ .
.
Proof. It is a consequence of the characterization of $\Theta _{\tilde {X}}$![]() and the previous theorem.
and the previous theorem.
Acknowledgements
The first author was partially supported by CAPES. The second author was partially supported by MICINN Grant PGC2018–094889–B–I00 and by GVA Grant AICO/2019/024. The third and fourth authors were partially supported by FAPESP Grant 2019/07316-0.