I. INTRODUCTION
The objective of through-the-wall radar imaging (TWRI) is to obtain high-resolution images of obscured areas using electromagnetic (EM) waves. TWRI is useful in determining interior structures of buildings, in rescuing missions in fire and earthquakes, or in undergoing law enforcing [Reference Abdalla, Muqaibel and Al-Dharrab1–Reference Burchett6]. This technology has witnessed a tremendous growth and attracted the attention of many researchers lately.
When TWRI is used for imaging targets that are surrounded by walls, two major challenges are encountered: the effects of the front wall; and the multiple reflections from the side walls. The front wall, which is the wall standing between the targets and the radar, gives strong reflections, which weaken the signal reaching the targets behind the wall. Front wall causes multiple internal reflections, wall reverberation, leaving replicas of the wall and targets in the reconstructed image known as ghosts. The ghosts populate the scene and sometimes mask the targets especially those in the vicinity of the wall, which deteriorates the reconstruction and detection processes. Further, the front wall may reduce the receiver dynamic range and the risk of saturating and blocking the receiver [Reference Charvat, Kempel, Rothwell, Coleman and Mokole7].
The second challenge of TWRI is multipath stemming from multiple reflections of EM waves from the walls, floors, and ceilings, which also generate ghost targets [Reference Leigsnering, Ahmad, Amin and Zoubir8–Reference Krolik, Farrell and Steinhardt12]. In such scenarios, accurate target localization and tracking becomes difficult. In the literature, different techniques have been presented to suppress multipath ghosts, but their performance and/or practicability can be improved.
To obtain high-resolution images, we need wide bandwidth and large aperture. Consequently, huge amount of data need to be collected and processed [Reference Leigsnering, Ahmad, Amin and Zoubir8]. Yoon and Amin [Reference Yoon and Amin13] tackled this problem by applying compressive sensing (CS) techniques to TWRI assuming a sparse scene. As a result, only a small fraction of data is used to reconstruct the images with relatively good quality. Hence, multipath ghost suppression under CS framework inevitably becomes the preferred solution for sparse scene scenarios.
Multipath ghosts are aspect-dependent (AD), i.e. the location of the multipath ghost changes with the transceiver location. This feature has been successfully exploited to identify and suppress multipath ghosts from genuine targets [Reference Setlur, Amin, Ahmad and Member14–Reference Tan, Leung, Song and Wang17]. To the best of our knowledge, no research on ghost suppression has been presented employing AD under CS framework. In [Reference Tan15], the authors proposed a multipath ghost suppression method exploiting AD property of the ghost using full data set. The authors modeled the ghost positions as hidden Markov chain problem. However, their method shows some inherent challenges: it requires image decomposition into N subaperture images using directional filters; and complex advanced algorithms. In [Reference Li, Kong, Jia, Zhao and Lan16], the authors proposed a ghost suppression method exploiting AD feature without CS. The authors formed three images using back-projection method; the first two using extreme opposite subapertures and the rest using the whole aperture. The method involves tedious searching of appropriate subapertures and shifting of antenna array in two extreme ends of the room, which can mislaid the genuine targets particularly when using directional antennas. The authors in [Reference Gennarelli and Soldovieri18] proposed a suppression technique for ghosts originated from target-to-target interactions. They suggested different array configurations with image combining strategies to combat the effect of the ghosts. However, the effect of side walls was not addressed, which is unavoidable in TWRI. In [Reference Yan, Cui, Guo, Kong, Yang and Liu19], the author developed multipath model, which uses AD feature in conjunction with multipath exploitation. However, the model is limited to first-order multipath from single target only. Further it requires the knowledge of the reflecting geometry. Authors in [Reference Chen and Chen20] proposed a new multipath ghost suppression method, which cancels multipath components from the raw data. Though the method has the capability of preserving weak targets, it increases system complexity as the method does not employ CS.
On the other hand, there are few contributions for ghost suppressions based on CS but not employing AD feature [Reference Leigsnering, Ahmad, Amin and Zoubir8, Reference Leigsnering, Ahmad, Amin and Zoubir21, Reference Wang, Wang, Li, Song and Zhou22]. The authors in [Reference Leigsnering, Ahmad, Amin and Zoubir8] incorporated the wall reverberation effect of the front wall, which makes their approach more practical. They inverted multipath model assuming the knowledge of the reflecting geometry, which is not always available. Further, the effect of target-to-target interactions was not addressed.
This paper proposes a new multipath ghost suppression technique, which incorporates AD feature of the ghosts under CS framework. Contrary to the conventional CS-based TWRI, a fraction of J measurements is randomly collected from a given aperture of N locations. In this work, a pair of the same fraction is collected such that the AD feature is maximized and then their corresponding images are strategically combined to suppress the effect of the ghosts. Exploiting AD feature allows to simplify the existing image reconstruction problem significantly by reducing the size of the sensing matrix and eliminating the constraint of the knowledge of reflecting geometry. In this paper, we propose a new multipath ghost suppression method in TWRI, which exploit the AD feature under CS framework. We also extend the current received signal model based on point-target assumption to a more general model, which best reflect the real TWRI scenario. The model takes into account the front-wall reflections and reverberations, the side-wall reflections and target-to-target interaction as well. In CS-based approaches, the target-to-target interaction has been ignored due to non-linear behavior. In this work, we model the target-to-target interaction as a linear component by imposing additional but justifiable assumptions.
Further, the concept of synthetic aperture radar (SAR) is used to form large aperture, which can be achieved via mechanical scanning, or phased arrays. In the former, an antenna is physically moved over the desired aperture, while in the later, several antennas are physically stacked together with phase-shifted with respect to each other [Reference Ralston, Charvat and Peabody23]. For simplicity of design, we adapt the former approach in all our simulations and experiments. The paper investigates the influence of antenna configurations toward getting unambiguous images. In this regard, two array configurations were examined: multimonostatic and single-view bistatic configurations.
The effectiveness of the proposed method is shown using synthesized and experimental data.
The remainder of the paper is organized as follows: Section 2 introduces the TWRI signal and scene models. The effect of the front wall in the scene reconstruction and their commonly used mitigation techniques are highlighted. Proposed method is presented in Section 3 with sensing matrix design and its evaluation. Section 4 presents the results and discussion based on both synthesized and experimental data. Comparison with the recent work is tabulated herein, and Section 5 contains concluding remarks.
II. TWRI SIGNAL MODEL
Suppose there are N radar locations for the scene interrogation as in Fig. 1. At each location, M equally spaced monochromatic waves to realize an ultra-wideband (UWB) signal are transmitted and received. Similar signal was used by [Reference Leigsnering, Ahmad, Amin and Zoubir21, Reference Ahmed, Amin and Kassam24, Reference Gurbuz, McClellan and Scott25] in their analysis. The scene is divided into N x pixels in cross-range by N y pixels in downrange. The target reflectivity on a p th grid point is represented by σ p , with p = 0, 1, …, N x N y − 1 and the wall grid point reflectivity by σ w . If R target returns and R w wall returns are considered, the received signal, y[m, n], at the n th radar location when the m th frequency, f m , is transmitted is comprised of four main contributions: reflection from the front wall, target-to-side wall reflection, target-to-target reflection, and ambient noise, given by:
$$\eqalign{ y[m,n] &= \mathop \sum \limits_{r = 0}^{R - 1} \mathop \sum \limits_{p = 0}^{N_x N_y - 1} \sigma _p^{(r)} \exp \left( {-j2\pi f_m t_{pn}^{(r)}} \right) \cr & \quad + \mathop \sum \limits_{r_w = 0}^{R_w - 1} \sigma _w^{(r_w )} \exp \left( {-j2\pi f_m t_w^{(r_w )}} \right) \cr & \quad + \mathop \sum \limits_{r = 0}^{R - 1} \,\,\mathop \sum \limits_{{\scriptstyle p,\,q = 0 \hfill \atop \scriptstyle p \ne q \hfill}} ^{N_x N_y - 1} \sigma _{pq}^{(r)} \exp \left( {-j2\pi f_m t_{pqn}^{(r)}} \right) + v(m,n),} $$
where
$t_{pn}^{(r)} $
represents the round-trip delay between the p
th
target and the n
th
receiver due to the r
th
return,
$t_{pnq}^{(r)} $
is the round-trip delay between p
th
and q
th
targets with n
th
transceiver, and
$t_w^{(r_w )} $
is the time delay of the
$r_w^{th} $
front-wall return. While
$\sigma _p^{(r)} $
and
$\sigma _w^{r_w} $
are the target and wall pixel reflectivity, respectively, with respect to the r
th
return and v(m, n) is the noise sample.
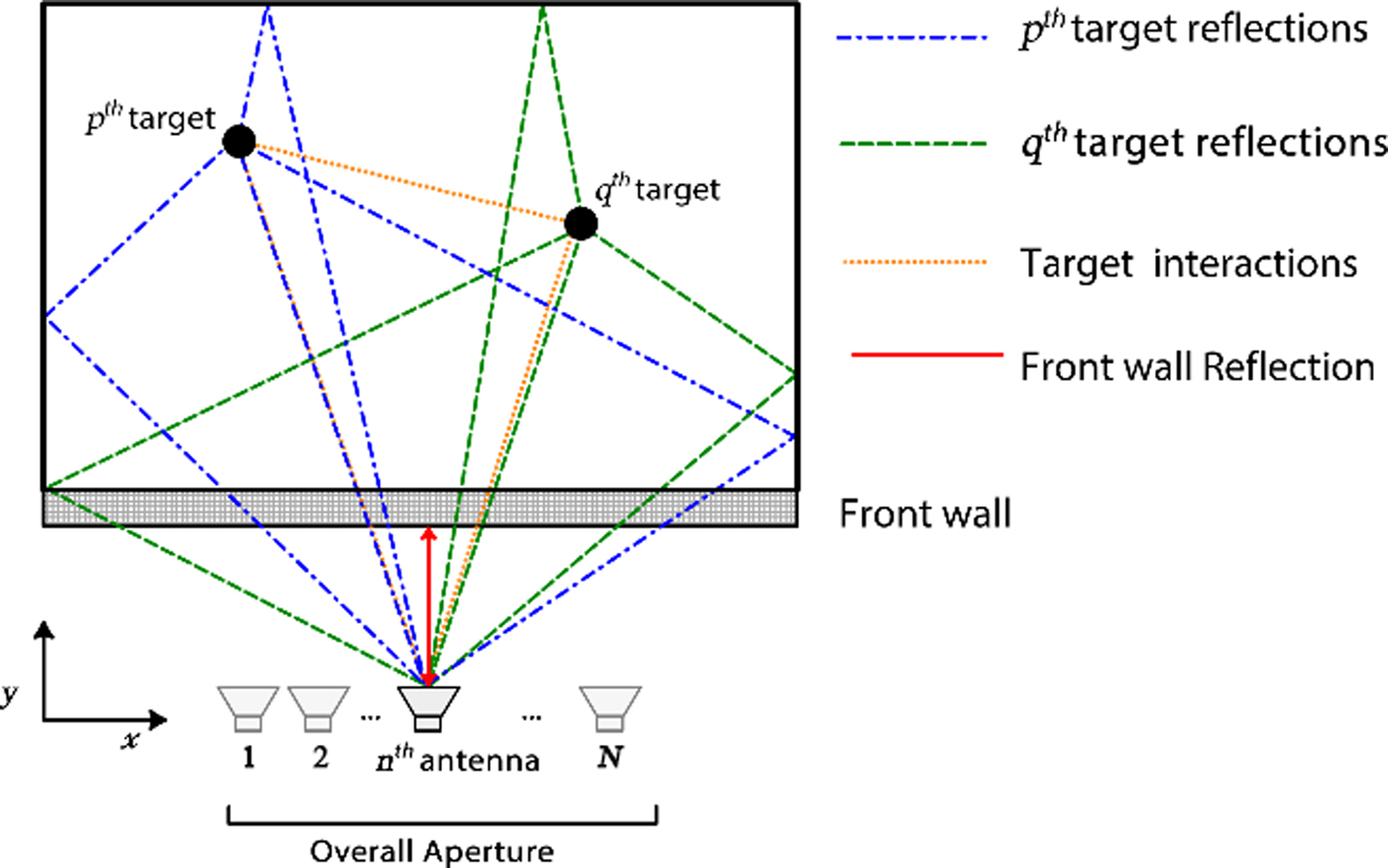
Fig. 1. TWR multipath scenario with first-order returns.
Since the contribution from target interactions in (1) is non-linear, we can assume that the overall signal reflectivity due to the target interactions,
$\sigma _{pq}^{(r)} $
, is dictated by the second target and first target is taken as perfect reflector. Then we can replace the term
$\sigma _{pq}^{(r)} $
in (1) by
$\beta _p^{(r)} $
.
Its corresponding matrix representation will be:
$${\rm \;} y = \mathop \sum \limits_{r = 0}^{R - 1} {\rm \Phi} ^{(r)} s^{(r)} + \mathop \sum \limits_{r_w = 0}^{R_w - 1} {\rm \Phi} _w^{(r)} s_w^{(r)} + \mathop \sum \limits_{r = 0}^{R - 1}\,\, \mathop \sum \limits_{{\scriptstyle p,\,q = 0 \hfill \atop \scriptstyle p \ne q \hfill}} ^{N_x N_y - 1} {\rm \Psi} _q^{(r)} s_q^{(r)} + v,$$
where
$s^{(r)}, s_q^{(r)} $
, and
$s_w^{(r_{\bi w} )} \in {\rm \open C}^{{\bi N}_{\bi x} {\bi N}_{\bi y} \times 1} $
, with r = 0, 1, … R − 1 and r
w
= 0, 1, … R
w
− 1 represents the vectors of reflectivities,
$\sigma _p^{(r)}, \beta _q^{(r)} $
, and
$\sigma _w^{r_w} $
, respectively. The entries of the matrices
$\Phi ^{(r)}, {\rm \;} \Phi _w^{(r)} {\rm, and\; \;} \Psi _q^{({\rm r})} \in {\rm \open C}^{MN \times N_x N_y} $
are defined as:
$$\eqalign{ \left[ {{\bf \Phi} ^{({\bi r})}} \right]_{ip} &= \exp \left( {-j2\pi f_m t_{pn}^{(r)}} \right),\; \left[ {{\bf \Psi} _q^{({\bi r})}} \right]_{ip} \cr &= \exp \left( {-j2\pi f_m t_{pnq}^{(r)}} \right){\rm \;}, \; \left[ {{\bf \Phi} _w^{({\bi r})}} \right]_{ip} \cr &= \exp \left( {-j2\pi f_m t_w^{(r)}} \right){\rm \;}} $$
$$m = i{\rm \;} mod{\rm \;} M,{\rm \; \;} n = \displaystyle{i \over M},{\rm \; \;} i = 0,{\rm \;} 1,{\rm \;} 2\,...\,MN - 1.$$
In TWRI, only first-order returns (involving single reflection) have significant effects. Returns involving multiple reflections will either be very weak due to strong attenuation when interacting with walls or their corresponding ghosts will reside outside the area of interest due to elongated time delays [Reference Setlur, Amin and Ahmad26]. Therefore, they are not considered in this work.
To correctly localize the targets during image reconstruction process, time delay caused by the front-wall reverberation needs to be properly taken into account, otherwise the target will be erroneously reconstructed.
A) Front-wall reverberation model
As the signal propagates through the front wall, part of it traverse and undergoes wall ringing or reverberation [Reference Leigsnering, Ahmad, Amin and Zoubir8, Reference Karousos, Koutitas and Tzaras27]. As a result, multipath ghosts are generated in the reconstructed image that are equally spaced in the radial direction from the array with exponentially reducing intensity [Reference Leigsnering, Ahmad, Amin and Zoubir8]. The wall reflections on the other hand, can be dealt with using available wall mitigation techniques [Reference Yoon and Amin28–Reference Lagunas, Amin, Ahmad and Nájar30].
The distance between the target and the array element in cross-range direction, Δx, in Fig. 2 can be expressed as:
$$\Delta x = (\Delta y - d)\tan \theta _{air} + d(1 + 2k)\tan \theta _{wall}, $$
where Δy is the distance between the target and the array element in downrange direction, θ air and θ wall , respectively, stand for the angles in the air and in the wall medium, d f is the standoff distance, d represents the thickness of the front wall and integer k is the number of wall reverberations. The two angles are related by famous Snell's law.
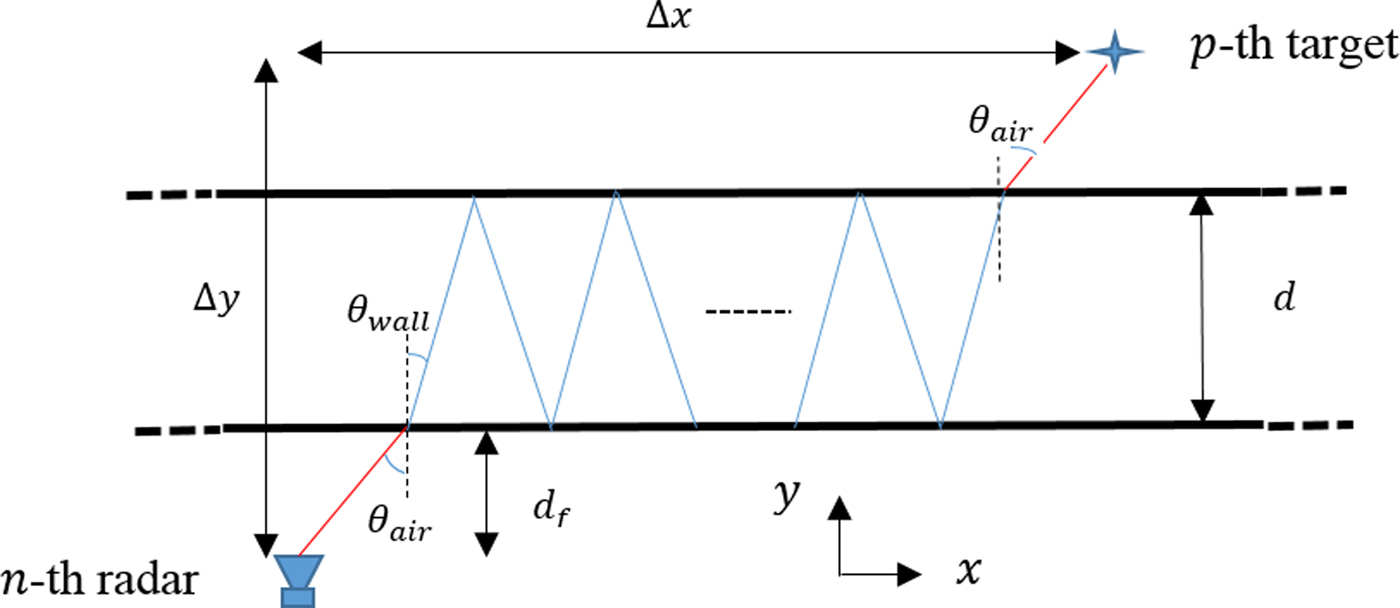
Fig. 2. Wall reverberation phenomenon.
The one-way time delay that a given return will undergo due to k wall reverberations will be [Reference Leigsnering, Amin, Ahmad and Zoubir31]:
$$\tau\,\, (\Delta x,{\rm \;} \Delta y,{\rm \;} k) = \displaystyle{{(\Delta y - d)} \over {c\cos \theta _{air}}} + \displaystyle{{d\sqrt {\varepsilon _r} (1 + 2k)} \over {c\cos \theta _{wall}}}, $$
where c is the speed of EM wave in free space and ε r represents the relative permittivity of the front wall. As the signal gets attenuated when it reflects within the wall, only few reverberations will be noticeable.
B) Front-wall mitigation under CS framework
Without an effective removal of the front-wall clutter, the targets hardly will be detected. For moving targets scenario, the wall effect can be alleviated by subtracting data acquired at different times. Though, this is not possible for stationary targets in which the front-wall reflections should be properly attenuated before image formation. Recently, the well-known wall mitigation techniques applicable under CS framework are spatial filtering and single-value decomposition-based approaches [Reference Lagunas, Amin, Ahmad and Nájar30, Reference Tivive, Bouzerdoum and Moeness32].
In spatial filtering, the zero spatial frequency of the wall contribution is used as peculiar characteristic to distinguish it from the target returns. Therefore, separating wall reflection from the target returns amounts to basically separating a zero-frequency signal from non-zero frequency-valued signals across antennas, which can be easily achieved using a proper spatial filter [Reference Yoon and Amin28, Reference Lagunas, Amin, Ahmad and Nájar30]. Mathematically, the spatial filter that notches out the constant component can be realized as the subtraction of the average value of the return across the antennas leaving the data free from front-wall clutters. The filtered signal
$\tilde y[m,n]$
is therefore given by [Reference Lagunas, Amin, Ahmad and Nájar30]:
$$\tilde y[m,n] = y[m,n] - \displaystyle{1 \over N}\mathop \sum \limits_{n = 0}^{N - 1} y[m,n].$$
In [Reference Lagunas, Amin, Ahmad and Nájar30], it was shown that both spatial filtering and subspace projection methods give better results when applied under CS framework. In this work, the former technique has been adopted.
III. PROPOSED GHOST SUPPRESSION METHODS
To address the challenges on the existing ghost suppression methods, we propose multipath ghost suppression technique, which incorporates AD feature of the multipath ghosts under CS framework. The introduction of AD feature simplifies the problem in terms of complexity and relaxes the requirement of knowing the reflecting geometry. In this case, we can reconstruct the scene without the complete knowledge of the location of the reflecting geometry.
In the reconstruction process, consider (2) as a perfect reverse model. Factorizing in (2) with respect to Φ(0) gives (7).
$$\eqalign{& y = \Phi ^{(0)}\left[ {s^{(0)} + \Phi ^{{(0)}{ - 1}}\sum\limits_{r = 1}^{R - 1} {\Phi ^{(r)}} s^{(r)} + \Phi ^{{(0)}{ - 1}}} \right. \cr & \quad \sum\limits_{r_w = 0}^{R - 1} {\Phi _w^{(r_w)} } s_w^{(r_w)} + \Phi ^{{(0)}{ - 1}}\sum\limits_{\scriptstyle p,\,q = 0 \hfill \atop \scriptstyle p \ne q \hfill} ^{N_xN_y - 1} {\sigma _q} \Psi _q^{(0)} s_q^{(0)} \cr & \quad \left. { + \ldots + \Phi ^{{(0)}{ - 1}}\sum\limits_{p,q = 0 \hfill \atop p \ne q \hfill} ^{N_xN_y - 1} {\sigma _q} \Psi _q^{(R - 1)} s_q^{(R - 1)} } \right] + v.} $$
If we define a residual column vector, w, which contains information from other subimages as:
$$\eqalign{{w} &= {\Phi} ^{({0}) {- 1}} \left[ {\mathop \sum \limits_{r = 1}^{R - 1} {\Phi} ^{(r)} {s}^{(r)} + \mathop \sum \limits_{r_w = 0}^{{R - 1}} {\Phi} _w^{(r_w )} {s}_w^{(r_w )} + \mathop \sum \limits_{{\scriptstyle p,\,q = 0 \hfill \atop \scriptstyle p \ne q \hfill}} ^{N_x N_y - 1} \sigma _q {\Psi} _q^{(0)} {s}_q^{(0)}} \right. \cr & \quad\left. {\quad + \ldots + \mathop \sum \limits_{{\scriptstyle p,\,q = 0 \hfill \atop \scriptstyle p \ne q \hfill}} ^{N_x N_y - 1} \sigma _q {{\Psi}_q^{(R - 1)}} {s}_q^{(R - 1)}} \right].}$$
Then (8) can be rewritten as:
$$y = \Phi ^{(0)} (s^{(0)} + w) + v.$$
Defining the transformed subimage,
$\check{s}^{(0)} = s^{(0)} + w$
, then (9) becomes:
$$y = \Phi ^{(0)} \check{s}^{(0)} + v.$$
Now, only direct path information, Φ(0), is used to reconstruct the modified scene. Since the reconstructed scene contains some contributions from other multipath returns, then it is populated by ghosts. We hypothesize that by properly shifting the array, the ghost locations can exhibit significant shifts enough to identify them from genuine targets.
By making independent sets of measurements using undersampling matrices D i ∈ {0, 1} J×MN with J ≪ M. The matrix D i is known to obey restricted isometry property [Reference Gurbuz, McClellan and Scott25, Reference Amin, Ahmad and Zhang33]. The optimum length of the subaperture, lN, for a given compressed frequency set is a function of the number of targets, P and surrounding scatters, where l is the ratio of the selected radar locations. In TWRI applications, this number is unknown beforehand. However, it can be estimated prior to running the actual measurement [Reference Donoho, Tsaig, Drori and Starck34].
$$J \ge CPR\log \left( {\displaystyle{{N_x N_y} \over {PR}}} \right),$$
where C is a positive constant defined in CS literature. Downsampling (10) gives:
$$\bar y_i = D_i \Phi ^{(0)} {\rm \;} \check{s} _i^{(0)} + \bar v_i, $$
where
$\bar v_i $
is the resulting noise vector. The compressed measurements,
$\bar y_i $
, are taken such that the corresponding subimages exhibit significant AD feature.
To exploit the AD feature, the given array is divided into subapertures. The images corresponding to these subapertures are sparsely reconstructed and then strategically combined to get a final image. A careful increase in the number of subarrays may increases the quality of the final image with the expense of computational cost. To overcome the challenge, we suggest duo-subaperture imaging with careful image fusion strategies to ameliorate the efficacy of the proposed method. Two random sets of locations, S i , i = 1, 2, are chosen from a linear array of N locations with interelement spacing of d units as shown in Fig. 3.
$$\eqalign{& S_1 = \left\{ {x:1 \le x \le \displaystyle{N \over 2}} \right\},\; S_2 = \left\{ {x:\displaystyle{N \over 2} \le x \le N} \right\}\;, \; \cr & \qquad \qquad \left \vert {S_1} \right \vert = \left \vert {S_2} \right \vert = lN.}$$
Fig. 3. Subarrays selection.
|S i | is the number of locations in the i th subarray and l denotes the ratio of the selected radar locations.
The selected subapertures (colored in blue) are then used to design the sensing matrices for image sensing and reconstruction.
A) Rationale of subarrays selection
The given array is subdivided into two halves making two subarrays with their centers separated by around N/2. It is desired to optimally decide the subarray separation to ensure maximum ghost suppression. To satisfy the desire, we perform correlation analysis of the received signals. Consider two observation vectors, y n and y n+k , when the subarrays are separated by kd units. It is hypothesized that the observed scenes will be different due to AD feature of the multipath contribution. From (12) we have:
$$\eqalign{\bar y_n = & \,\,A_n {\rm \;} \check{s} _n^{(0)} + \bar v_n \cr \bar y_{n + k} = &\,\, A_{n + k} {\rm \;} \check{s} _{n + k}^{(0)} + \bar v_{n + k}.} $$
The correlation of the received signals, R
n,n+k
is given by
$R_{n,n + k} = E\left\{ {\bar y_n, \bar y_{n + k}^H} \right\} = A_n R_{s_n s_{n + k}} A_{n + k}^H + R_v ;R_{s_n s_{n + k}} =\,\,E\left\{ {\check{s} _n^{(0)}, \check{s} _{n + k}^{(0)H}} \right\}$
. We need the value of k that minimizes the number of non-zero elements in
$R_{s_n s_{n + k}} $
. However, the matrix A
i
= D
i
Φ(0) is a function of the time delay, which also depends on the target location and it is unknown in priori. Hence, developing a closed form expression for the aperture separation is not feasible.
To overcome that challenge, a fairly exhaustive search of the acceptable subarray separation was conducted for random target locations placed in a room of 5 × 5 m2. Array of 2 m long and 77 locations, which conforms to most TWRI applications, was deployed. In each run, a different target location was assumed and their corresponding images were captured. The subarray was then linearly shifted along the cross-range direction and determine the cross-correlation between the current image vector, s k and the initial image, s 0. The normalized correlation value is given by:
$$R_k = \displaystyle{{s_k^H s_0} \over {\left \vert {s_k} \right \vert \left \vert {s_0} \right \vert}}.$$
The effective separation is determined when there is no significant change on the cross-correlation of the two images. The sample representation of the results for different target locations is shown in Fig. 4 where only five are displayed for clarity.
Fig. 4. (a) Scene with 10 random targets, (b) normalized correlation for five targets.
It can be concluded from Fig. 4 that the AD effect is more pronounced when the target is closer to the radar as the normalized correlation converges to a constant value after fewer subarray shifts. It is evident from Fig. 4(b) that the separation of N/2 may suffice. In other words, for all randomly selected target locations, the value of the correlation converges nearly to the same value after N/2, where N signifies the number of radar locations. We repeated the experiment using different room dimensions and we arrived at similar conclusions. The selected subarrays are then used to design the sensing matrices for image sensing and reconstruction.
B) Sensing matrix design and analysis
In TWRI, the sensing matrix can be viewed as the product of two matrices. The first is a predefined matrix describing the signal propagation model in (2), which is a function of the radar parameters and reflecting geometry. The second matrix is downsampling matrix, D, which compresses the data based on CS theories. Therefore, designing the sensing matrix in TWRI basically is designing the matrix D. The matrix D in this work consists of randomly chosen rows from an identity matrix as in [Reference Amin and Ahmad3, Reference Amin4, Reference Leigsnering35]. In stepped frequency radar, the downsampling occurs in the frequency and radar locations.
In CS theory, the sensing matrix plays an important role in the signal reconstruction process. To ensure the recoverability of the signal, the columns of the sensing matrix, A i = D i Φ(0), should have low correlation.
To analyze the recoverability of the sensing matrices, we evaluate the mutual coherence of the sensing matrix. The mutual coherence of the two columns is the normalized inner product between them, while the coherence of the matrix is the maximum absolute value of this inner product among all pairs of elements in the matrix [Reference Donoho, Tsaig, Drori and Starck34, Reference Li, Boufounos, Liu, Mansour and Sahinoglu36]:
$$\mu (A) = \mathop {{\rm max}}\limits_{i \ne j} \displaystyle{{\left \vert {a_i^H a_j} \right \vert} \over {a_i a_j}}. $$
When this metric returns a small value, it serves as sufficient condition to ensure sparse reconstruction. In classical algorithms, it may also provide useful information on the performance of the array including resolution, noise, and other interference robustness and ambiguity [Reference Vaidyanathan and Pal37].
The mutual coherence of the sensing matrix for various undersampling ratios and two image resolutions, averaged over 100 Monte-Carlo runs, are summarized in Table 1. The duo-subarray-based sensing matrix is compared with normal array sensing matrix. It is observed that the coherence increases with the image resolution. For subarray configuration discussed, the mutual coherence shows no significant change with data volume.
Table 1. Mutual coherence for full and subarray sensing matrices for two image resolutions.
Though, the coherence of the matrix is relatively high, but the mutual coherence is only a sufficient but not necessary condition to ensure perfect reconstruction. Using simulated and experimental data, we attained a very good image quality with similar measurement matrices.
Figure 5(a) shows a normalized correlation of the representative column for image resolution of 32 × 32 pixels, and Fig. 5(b) shows a correlation of a representative column for image resolution of 64 × 64 pixels when the undersampling ratio is
$6\% $
. The selected columns are column 500 for the case of 32 × 32 pixels and 2000 for the case of 64 × 64 pixels.
Fig. 5. Sample of normalized correlation of the proposed sensing matrix: (a) 500th column for 32 × 32 pixels, (b) 2000th column for 64 × 64 pixels.
C) Subimages sparse reconstruction
The modified subimage,
$\check{s} _i^{(0)}, $
in (12) can be reconstructed sequentially using conventional CS approach [Reference Donoho38, Reference Candès39] or concurrently to speed up the reconstruction process.
The reconstructed vectors,
$\check{s} _i^{(0)} $
, are obtained by solving optimization problem [Reference Donoho38, Reference Candès39]:
$$\eqalign{& \widetilde{{\check{s} _i^{(0)}}} = {\mathop{{\rm argmin}}\limits_{\check{\bf s}_i^{(0)}}} \ \vert \check{s}_i^{(0)}\vert_1 \cr & {\rm \; s}{\rm. t}{\rm. \; \; \; \;}\vert \bar y_i - D_i \Phi ^{(0)} {\rm \;} \check{s} _i^{(0)} \vert_2 \lt {\rm \varepsilon} {\rm.}} $$
The choice of ε is a function of noise power [Reference Huang, Qu, Wu and Fang40]. To eliminate the effect of the ghosts exploiting AD feature, the reconstructed subimages are strategically fused to yield a final image.
D) Image fusion strategies
When multiple and distinct compressed subapertures are considered as in Fig. 3, then the resulting ghosts in the respective subimages will be positioned differently following ghost AD feature. However, the true targets maintain the same location in all images. Therefore, a strategic fusion of the subimages is needed to suppress the effect of multipath ghosts.
The overall image is obtained by masking which involves pixel-wise multiplication of the individual subimages [Reference Li, Kong, Jia, Zhao and Lan16, Reference Gennarelli and Soldovieri18, Reference Setlur, Amin and Ahmad26].
Suppose there are L subimages, with s lp defines the image value at the p th pixel corresponding to the l th subimage, the overall image is obtained as:
$$s(p) = \mathop \prod \limits_{l = 1}^L \check{s} _{lp}^{(0)} $$
Masking sometimes tends to suppress the genuine targets or enhances the residual clutters [Reference Yan, Cui, Guo, Kong, Yang and Liu19]. In this work, we propose strategic image fusions, additive–multiplicative fusions, which can reduce this effect. In additive–multiplicative fusion, an intermediate image is first obtained as the strategic summation of the individual subimages. The summation is taken such that the magnitude of the true targets is preserved while minimizing the clutters. This helps to reduce the effect of the ghost and other clutters and hence increase target relative clutter peak (TRCP) at target locations. The intermediate image is then masked with the subimages to obtain the final image. We propose two subimage fusion strategies to enhance the image quality.
1) WEIGHTED SUM-BASED ADDITIVE–MULTIPLICATIVE FUSION (WSAM)
In this case, the intermediate image is the weighted sum, which minimizes the l
2 norm while maintaining the magnitudes of the true targets. Consider L subimages,
$\check{\rm s} _1^{(0)}, {\bi \;} \check{\rm s} _2^{(0)} \ldots\, \check{\rm s} _L^{(0)} $
, reconstructed from L compressed apertures. Their weighted mean is given by:
$$s_W (p) = \mathop \sum \limits_l^L \alpha _l \check{\rm s} _l^{(0)} (p),$$
where α l ∈ ℝ : 0 ≤ α l ≤ 1. The values of α l , which result in a minimum norm, are obtained using:
$$\min \vert\alpha _1 \check{s} _1^{(0)} + \ldots + \alpha _{\rm L} \check{s} _{\rm L}^{(0)}\vert {\rm \; \; subject\; to\;} \mathop \sum \limits_{l = 1}^L \alpha _l = 1.$$
2) HARMONIC MEAN-BASED ADDITIVE–MULTIPLICATIVE FUSION (HMAM)
The fact that harmonic mean of a list of non-negative numbers leans towards the least elements of the list while maintain the same value for equal elements can be utilized to suppress large clutters in TWRI while it maintains the true targets. For L subimages,
$\check{\rm s} _1^{(0)}, {\rm \;} \check{\rm s} _2^{(0)} \ldots \check{\rm s} _L^{(0)} $
, reconstructed from L compressed subaperture, the intermediate image,
s
H
, is defined as the harmonic mean of the corresponding subimages and is given by:
$$s_H (p) = \displaystyle{L \over {\mathop \sum \nolimits_{l = 1}^L (1/\check{s} _l^{(0)} (p))}}.$$
The overall image is obtained by masking the intermediate image with subimages.
For comparison, conventional delay and sum beamforming (DSBF) is used for image reconstruction. Given a set of measurements collected from N different transceiver locations with M monochromatic frequencies transmitted at every radar position. The complex image I(x p , y p ) of the p th grid point (x p , y p ) is obtained by summing phase-shifted copies of the available signals [Reference Leigsnering, Ahmad, Amin and Zoubir8, Reference Ahmed, Amin and Kassam24]:
$$I(x_p, y_p ) = \displaystyle{1 \over {MN}}\mathop \sum \limits_{n = 0}^{N - 1} \mathop \sum \limits_{m = 0}^{M - 1} y[m,n]\exp (j2\pi f_m \tau _{pn} ),$$
where τ pn is the focusing delay for the n th transceiver and the p th grid point.
IV. RESULTS AND DISCUSSION
A) Simulation results
A TWRI system was simulated using MATLAB®. For comparison, we adopt simulation parameters and setup as in [Reference Leigsnering, Ahmad, Amin and Zoubir8]. The left- and right-side walls of the room are at cross-range of − 1.8 m and 4 m, respectively, while the back wall resides at 6.37 m downrange. A SAR, which simulates a uniform linear monostatic array composed of 77 elements spaced out by 1.9 cm is used to capture the image. The center of the array is taken to be the origin of the system. The front wall parallel to the array is at 2.44 m downrange with thickness d = 20 cm and relative permittivity ε r = 7.67. A series of 201 monochromatic waves to realize a UWB signal occupying a spectrum between 1 and 3 GHz is employed for the scene interrogation.
The image of the scene was reconstructed with and without the front-wall mitigation. In this work, we define a path from the radar to the target or vice versa as partial path. A total of six multipath returns were considered in this work, where one partial path is always the direct path and the second partial path corresponds to: direct, back-wall multipath, left-side, right-side wall, and the wall reverberation multipath. A return due to the target interaction was also taken into account. We assume all side walls as perfect reflectors. When they are not perfect reflectors, then ghost targets will have less power, and hence, becomes relatively easy to be suppressed. During simulation, targets located at (0.31, 3.6) and (−0.62, 5.2) m were considered. White noise of 0 dB SNR was added to the simulated measurements. The DSBF image utilizing full available measurement is obtained for comparison. For the CS reconstructions, we use only
$10\% $
of the total measurement to reconstruct the corresponding images using Yall1 algorithm [Reference Yang and Zhang41].
The given array is divided into two halves, duo-subarray, to realize the AD effect of the resulting ghosts and then a fraction of the radar positions and frequency bins are selected from the two subarrays for sparse image reconstruction. We examine four different scenarios to evaluate the effectiveness of the proposed method under different data collocation modalities.
1) SCENARIO 1: WHOLE SUBARRAYS
In this case, we used only one-fifth of the frequency randomly selected and the same set is transmitted at each location of the given subarray. The radar locations represent one-half of the total available locations, which makes the compressed measurement 10% of the total data volume. The scene's layout and setup of this scenario is shown in Fig. 6.
Fig. 6. Scene's layout for scenario 1.
The subarray images are depicted in Fig. 7. The image quality using CS reconstruction is better than DSBF in spite of using entire measurement set. To obtain the final images, the two subimages were combined using proposed image combining techniques: WSAM fusion and HMAM fusion and are shown in Figs 7(d)–(f). Figure 7(d) is the final image using conventional masking for performance comparison. It is evident from Fig. 7 that the proposed fusion strategies perform better than conventional masking.
Fig. 7. Images with random frequency: (a) DSBF with full data, (b) subarray 1, (c) subarray 2, (d) final with masking, (e) final with WSAM 54% by 46%, (f) final with HMAM, (g) subarray 1 DSBF, (h) subarray 2 DSBF, and (i) final DSBF.
In the case of WSAM fusion, the intermediate image takes 54 and 46% of the intensity of first and second subimage, respectively, to minimize the clutter norm while maintaining the intensities of the true targets. The proposed image fusion techniques seem to have comparable performance and since the WSAM ensures the minimum clutter norm compared with HMAM, it is therefore preferred in practice and will be used to evaluate the final images in the coming scenarios.
To analyze the power of sparse reconstruction over DSBF algorithm, we generated DSBF images with the same reduced data volume as shown in Figs 7(g)–(i). Apparently from Fig. 7(i), DSBF showed inability to incorporate the AD feature for ghost suppression under reduced measurement scenario owing to its lower resolution caused by point spread function. Further, it suffers from increased level of unwanted clutters due to the violation on the required antenna spacing, and therefore, will not be compared in the proceeding results.
Using quantitative measures, we evaluated target signal-to-clutter ratio (TSCR) and TRCP and are summarized in Table 2.
Table 2. TSCR and TRCP for whole subarrays.
From Table 2 and Fig. 11(a), the method can dramatically attenuate the effect of the multipath ghosts. Only a threshold value of around 30% of the maximum can be used to isolate true targets from the surrounding clutters.
For target detection capability, the precisions of this scenario are demonstrated in Fig. 11(a). The precision metric used is defined as the ratio of the true positives “genuine targets” to the sum of the true positives and the false positives “false alarms”, where the false positives are the ghosts. Precision can be expressed by
$${\rm Precision} = \displaystyle{{TP} \over {TP + FP}}.$$
If there is no ghost for a given threshold value, the value of precision becomes unity. The metric will continue working even for extended targets.
2) SCENARIO 2: COMPRESSED SUBAPERTURES
One-half of the frequency bins were randomly chosen and the same set is transmitted at each selected location for design simplicity, and one-fifth of the radar locations were randomly selected from the given subarrays. The subaperture images are depicted in Figs 8(a) and 8(b), and their corresponding final image generated with WSAM fusion is depicted in Fig. 8(c). In WSAM, the fusion assumes 58% of the first subimage and 42% of the first second to effectively suppress the ghosts. In Fig. 8, the final image suppresses the multipath ghosts significantly and genuine targets can be detected. This observation is supported by numerical analysis using TSCR and TRCP, which show relatively good values enough to detect the targets as summarized in Table 3.
Fig. 8. Images: (a) subarray 1, (b) subarray 2, and (c) final with WSAM 58% by 42%.
Table 3. TSCR and TRCP for different scenarios.
The precision curves, which dictate the probability of correct detection, are plotted against the threshold values are shown in Fig. 11(b). The threshold of around 35% can correctly eradicate the surrounding clutters including ghosts.
3) SCENARIO 3: COMPRESSED SUBAPERTURES WITH SINGLE-VIEW BISTATIC CONFIGURATION
In the above setups, we considered monostatic radar system: transmitter and receiver are collocated. In this setup, we investigate the effect of bistatic radar configuration. The transmitter's location is fixed at the center of the array, then two receiver locations are selected randomly. The corresponding subimages are shown in Figs 9(a) and 9(b), and the corresponding final image with WSAM is depicted in Fig. 9(c) with its quality metrics summarized in Table 3.
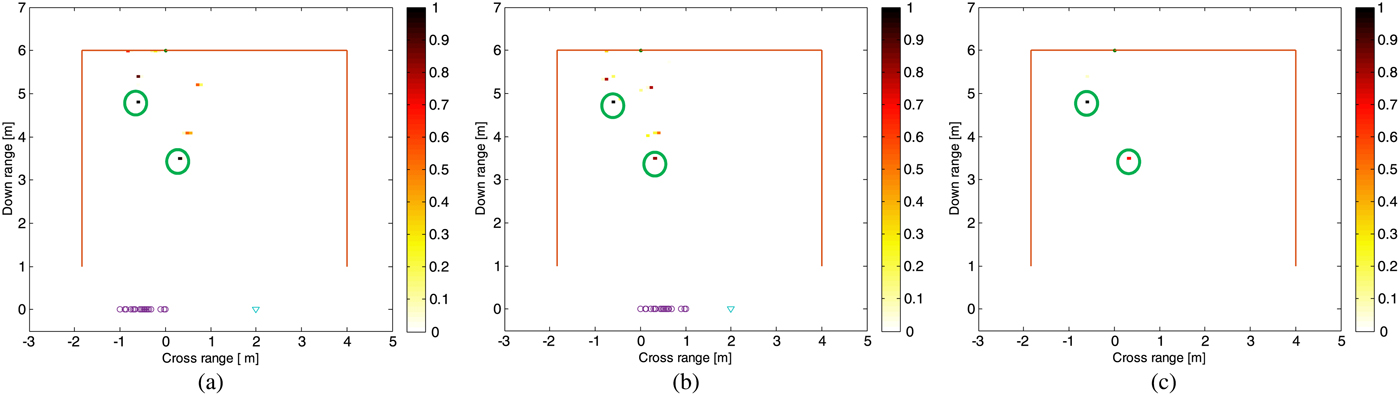
Fig. 9. Images for single-view bistatic: (a) subarray 1, (b) subarray 2, and (c) final with WSAM 44% by 56%.
The precision curves, which compare the number of true targets and the total number of available targets, are shown in Fig. 11(c). It is noted in Fig. 11(c) that the threshold of 15% suffices as detection threshold. This scenario shows a noticeable increase in the image quality compared with 35% threshold of its corresponding multi-view monostatic counterpart.
4) SCENARIO 4: SINGLE-VIEW BISTATIC WITH FRONT WALL
Using duo-subaperture, we can reconstruct the image without the need to mitigate the front wall. Applying the discussed fusion strategies, we can suppress the effect of the front wall, provided the measurement volume is adequate as recommended by the CS algorithms. The final image restores the intensities of the true targets and the wall is masked out as shown in Fig. 10.
Fig. 10. Image reconstruction with front wall: (a) subaperture 1, (b) subaperture 2, and (c) final with WSAM.
The precision in Fig. 11(d) demonstrates the effectiveness of the method even with front wall at the expense of increasing measurement volume as the scene becomes less sparse. With WSAM fusion, no postprocessing is needed to identify the true target as the ghosts are highly attenuated.
It should be pointed out that the target size will affect the aspect dependency and hence the suppression accuracy.
Fig. 11. Precision curves: (a) scenario 1, (b) scenario 2, (c) scenario 3, and (d) scenario 4.
B) Experimental results
A wideband SAR system was set up in a semicontrolled room at KFUPM-EE department for multipath analysis to validate the proposed ghost suppression method; a schematic sketch of the room as shown in Fig. 12. The SAR was deployed to cover 67 equally spaced locations with an interelement spacing of 2.5 cm along the X-axis. A stepped frequency signal occupying a spectrum between 1 and 3 GHz with 801 frequency points was used for scene interrogation. The background information was first captured for clutter suppression. Two metallic cylinders were placed at (−0.75, 2) and (0.5, 3) m as shown in the setup and room layout given by Fig. 12 with the origin taken at the center of the aperture. The room has two protruding corners of reinforced concrete pillars near the back side. The imaged region is chosen to be 4 × 5 m2.
Fig. 12. (a) The setup and room layout, (b) photograph of the scene setup.
To identify and suppress multipath ghosts, duo-subaperture with one-third of the radar locations are randomly selected and only one-eighth of the frequency bins were transmitted. Figures 12(a) and 12(b) show the images of selection of the duo-subaperture. The final image is obtained using WSAM fusion, which shows significant ghost reduction with all true targets correctly reconstructed despite the directivity challenge of the horn antenna as shown in Figs 13(a) and 13(b). This observation alludes that in real application, the subaperture need to be carefully chosen; otherwise, some real targets might be invisible by the radar system.
Fig. 13. Images: (a) subaperture 1, (b) subaperture 2, and (c) final with WSAM.
Quantitative performance measures, TSCR and TRCP defined in [Reference Abdalla, Muqaibel and Al-Dharrab1] summarized in Table 3, indicate the effectiveness of the suppression method.
The variation of the precision value with the possible threshold is given in the precision curves in Fig. 14, which indicates that the targets can be correctly detected without additional postprocessing.
Fig. 14. Precision curves under real data.
Comparison with related works
Comparing with recent works, our method shows satisfactory tradeoff between image quality improvement and complexity reduction. In [Reference Gennarelli and Soldovieri18], the authors achieved optimal tradeoff between improvement factor (IF) of 24.29 dB and target improvement factor (TIF) of 0.29 dB when using single-view multistatic radar with multiplicative–additive fusion of seven subarray images. The limited performance is due to point spread function in DSBF algorithm, which significantly lowers its resolution. In addition, the DSBF images suffer from increased level of unwanted clutters. In this work, we employed compressed duo-subaperture under CS framework and achieved 34.6 dB of IF and 21.7 dB of the TIF. Moreover, unlike in [Reference Gennarelli and Soldovieri18] where the authors tackled only multipath ghosts due to target interactions, this work considered multipath due to side-wall and front-wall reverberation as well.
In [Reference Leigsnering, Ahmad, Amin and Zoubir8], the presented method achieved the best suppression when using non-overlapping group sparse approach. It returned TSCR of 95 dB and TRCP of 25 dB with around 3% of the total measurement. Using nearly equal volume, the proposed method achieves TSCR of 97.3 dB and TRCP of 23.7 dB with WSAM image fusion strategy. In addition to front-wall and side-wall reflection considered in [Reference Leigsnering, Ahmad, Amin and Zoubir8], the work incorporated target-to-target interaction as well, which gives additional credit.
V. CONCLUSIONS
This paper proposed efficient multipath ghost suppression technique in TWRI exploiting the AD characteristic of the multipath ghosts under CS framework without the knowledge of the scene geometry. The method was scrutinized for different data collection modalities to evaluate its efficacy. New subimages combining strategies were proposed, which improves the TSCR at target locations. Further, two antenna deployments were studied using multiview monostatic and single-view bistatic configurations. The latter showed better results in both TSCR and TRCP, which increases the probability of correct detection.
As the extension of this work, the optimum subarrays separation can be investigated to ensure sufficient ghost suppression. Further, the proposed method is effective for pixel-sized targets; more analysis is required for extended targets scenarios (target occupying more than one pixel).
ACKNOWLEDGEMENTS
This work is funded by the National Plan for Science, Technology, and Innovation (Maarifah) – King AbdulAziz City for Technology – through the Science and Technology Unit at King Fahd University of petroleum and Minerals (KFUPM), The Kingdom of Saudi Arabia, award number 15-ELE4651-04.
Ali Hussein Muqaibel received the B.Sc. and M.Sc. degrees from King Fahd University of Petroleum and Minerals (KFUPM), Dhahran, Saudi Arabia, in 1996 and 1999, respectively, and the Ph.D. degree from Virginia Polytechnic Institute and State University (Virginia Tech), Blacksburg, in 2003. During his study at Virginia Tech, he was with both the Time Domain and RF Measurements Laboratory and the Mobile and Portable Radio Research Group. He is currently the Director of the Telecommunications Research Laboratory (TRL) and an Associate Professor with the Electrical Engineering Department, KFUPM. His main area of interest includes ultra-wideband (UWB) signal processing for localization and communications. He was a Visiting Scholar at both Georgia Institute of Technology, Georgia, USA and Villanova University, Villanova, Pennsylvania, USA. He is the author of two book chapters and more than 90 articles. Dr. Muqaibel received many awards in the excellence in teaching, advising, and instructional technology.
Abdi Talib Abdalla received the B.Sc. degree in Electronic Science and Communication and M.Sc. degree in Electronics Engineering and Information Technology from the University of Dar es Salaam, Tanzania, in 2006 and 2010, respectively, and the Ph.D. degree from King Fahd University of Petroleum and Minerals (KFUPM), Saudi Arabia, in 2016. Currently, he is a Lecturer at the Department of Electronics and Telecommunication Engineering of University of Dar es Salaam, Tanzania. His research interests include target localization, sparse arrays processing, through-the-wall radar imaging, and application of compressive sensing to radar signal processing.
Mohammad Tamim Alkhodary received his B.S. degree in Communication Engineering from the University of Science and Technology, Sana'a, Yemen, in 2008. He received his M.S. in Telecommunication Engineering in 2011 from KFUPM. He joined the Electrical Engineering Department at KFUPM as a Lecturer in 2012, and he is now working toward his Ph.D. degree in the Department of Electrical Engineering at the same institute. In 2015, he joined KAUST for 1-year research internship. His research interests include signal processing, UWB communication, compressive sensing theory and applications.
Suhail Al-Dharrab received his B.Sc. degree in Electrical Engineering from King Fahd University of Petroleum and Minerals, Dhahran, Saudi Arabia in 2005. He received the M.A.Sc. and Ph.D. degrees in Electrical and Computer Engineering from University of Waterloo, Waterloo, Canada, in 2009 and 2013, respectively. From 2005 to 2007, he worked as a Graduate Assistant in the Electrical Engineering Department at King Fahd University of Petroleum and Minerals. In 2015, he was a Visiting Scholar in the School of Electrical and Computer Engineering at the Georgia Institute of Technology, Atlanta, USA. He is currently an Assistant Professor in the Electrical Engineering Department and Assistant Director of the Center for Energy and Geo-Processing at King Fahd University of Petroleum and Minerals, Dhahran, Saudi Arabia. His research interests span topics in the areas of wireless communication systems, underwater acoustic communication, digital signal processing, and information theory.
