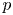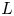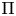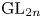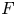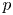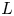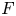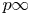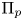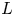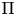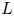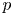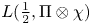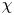Introduction
A crucial result in Shimura's work on the special values of ![]() $L$-functions of modular forms concerns the existence of a twisting character to ensure that a twisted
$L$-functions of modular forms concerns the existence of a twisting character to ensure that a twisted ![]() $L$-value is non-zero at the center of symmetry (see [Reference ShimuraShi77, Theorem 2]). Since then, it has been a very important problem in the analytic theory of automorphic
$L$-value is non-zero at the center of symmetry (see [Reference ShimuraShi77, Theorem 2]). Since then, it has been a very important problem in the analytic theory of automorphic ![]() $L$-functions to find characters to render a twisted
$L$-functions to find characters to render a twisted ![]() $L$-value non-zero. Rohrlich [Reference RohrlichRoh89] proved such a non-vanishing result in the context of cuspidal automorphic representations of
$L$-value non-zero. Rohrlich [Reference RohrlichRoh89] proved such a non-vanishing result in the context of cuspidal automorphic representations of ![]() $\operatorname {GL}_2$ over any number field. This was then generalized to
$\operatorname {GL}_2$ over any number field. This was then generalized to ![]() $\operatorname {GL}_N$ over any number field by Barthel and Ramakrishnan [Reference Barthel and RamakrishnanBR94] and further refined by Luo [Reference LuoLuo05]. However, neither [Reference Barthel and RamakrishnanBR94] nor [Reference LuoLuo05] can prove this at the center of symmetry if
$\operatorname {GL}_N$ over any number field by Barthel and Ramakrishnan [Reference Barthel and RamakrishnanBR94] and further refined by Luo [Reference LuoLuo05]. However, neither [Reference Barthel and RamakrishnanBR94] nor [Reference LuoLuo05] can prove this at the center of symmetry if ![]() $N \geqslant 4$ (for us the functional equation will be normalized so that
$N \geqslant 4$ (for us the functional equation will be normalized so that ![]() $s = \frac {1}{2}$ is the center of symmetry). There have been other types of analytic machinery that have been brought to bear on this problem, for example, see [Reference Chinta, Friedberg and HoffsteinCFH05]. Even for simple situations involving
$s = \frac {1}{2}$ is the center of symmetry). There have been other types of analytic machinery that have been brought to bear on this problem, for example, see [Reference Chinta, Friedberg and HoffsteinCFH05]. Even for simple situations involving ![]() $L$-functions of higher degree this problem is open. For example, suppose
$L$-functions of higher degree this problem is open. For example, suppose ![]() $\pi$ is the unitary cuspidal automorphic representation associated to a primitive holomorphic cusp form for
$\pi$ is the unitary cuspidal automorphic representation associated to a primitive holomorphic cusp form for ![]() $\operatorname {GL}_2/\mathbb {Q}$, then it has been an open problem to find a Dirichlet character
$\operatorname {GL}_2/\mathbb {Q}$, then it has been an open problem to find a Dirichlet character ![]() $\chi$ so that the twisted symmetric cube
$\chi$ so that the twisted symmetric cube ![]() $L$-function
$L$-function ![]() $L(\frac {1}{2}, (\operatorname {Sym}^{3}\pi ) \otimes \chi )$ is non-zero at the center.
$L(\frac {1}{2}, (\operatorname {Sym}^{3}\pi ) \otimes \chi )$ is non-zero at the center.
In this article, we prove the following result.
Theorem A Let ![]() $F$ be a totally real field and
$F$ be a totally real field and ![]() $\Sigma _\infty$ the set of all its real places. Let
$\Sigma _\infty$ the set of all its real places. Let ![]() $\Pi$ be a unitary cuspidal automorphic representation of
$\Pi$ be a unitary cuspidal automorphic representation of ![]() $\operatorname {GL}_{2n}/F$ admitting a Shalika model and such that
$\operatorname {GL}_{2n}/F$ admitting a Shalika model and such that ![]() $\Pi _\infty$ is cohomological with respect to a pure dominant integral weight
$\Pi _\infty$ is cohomological with respect to a pure dominant integral weight ![]() $\mu$ such that
$\mu$ such that
Assume that for all primes ![]() $\mathfrak {p}$ above a given prime number
$\mathfrak {p}$ above a given prime number ![]() $p$,
$p$, ![]() $\Pi _\mathfrak {p}$ is unramified and
$\Pi _\mathfrak {p}$ is unramified and ![]() $Q$-ordinary, where
$Q$-ordinary, where ![]() $Q$ is the parabolic of type
$Q$ is the parabolic of type ![]() $(n,n)$ of
$(n,n)$ of ![]() $\operatorname {GL}_{2n}/F$ (see (65)).
$\operatorname {GL}_{2n}/F$ (see (65)).
Then, for all but finitely many Dirichlet characters ![]() $\chi$ of
$\chi$ of ![]() $p$-power conductor we have
$p$-power conductor we have
For notions and notation that are not defined in the introduction, the reader should consult the main body of the paper. A more general statement is proven in Theorem 4.8. Furthermore, we can prove a stronger non-vanishing result covering the nearly ordinary case (see Corollary 4.9) as well as a simultaneous non-vanishing result (see Corollary 4.10). For example, with a classical normalization of ![]() $L$-functions, it follows from our results that there are infinitely many Dirichlet characters
$L$-functions, it follows from our results that there are infinitely many Dirichlet characters ![]() $\chi$ such that
$\chi$ such that
for the Ramanujan ![]() $\Delta$-function. Our methods are purely arithmetic and involve studying
$\Delta$-function. Our methods are purely arithmetic and involve studying ![]() $p$-adic distributions on
$p$-adic distributions on ![]() $\mathscr {C}\!\ell _F^{+}(p^{\infty })$, the Galois group of the maximal abelian extension of
$\mathscr {C}\!\ell _F^{+}(p^{\infty })$, the Galois group of the maximal abelian extension of ![]() $F$ unramified outside
$F$ unramified outside ![]() $p\infty$, that are attached to suitable eigenclasses in the cohomology of
$p\infty$, that are attached to suitable eigenclasses in the cohomology of ![]() $\operatorname {GL}_{2n}$.
$\operatorname {GL}_{2n}$.
Let us now describe our methods and results in greater detail. We begin with a purely cohomological situation, without any reference to automorphic forms or ![]() $L$-functions. Let
$L$-functions. Let ![]() $\mathcal {O}_{F}$ be the ring of integers of
$\mathcal {O}_{F}$ be the ring of integers of ![]() $F$ and
$F$ and ![]() $\mathfrak {d}$ its different. Take a pure dominant integral weight
$\mathfrak {d}$ its different. Take a pure dominant integral weight ![]() $\mu$ for
$\mu$ for ![]() $G = \operatorname {Res}_{\mathcal {O}_{F}/\mathbb {Z}}\operatorname {GL}_{2n},$ and let
$G = \operatorname {Res}_{\mathcal {O}_{F}/\mathbb {Z}}\operatorname {GL}_{2n},$ and let ![]() $V^{\mu }_{E}$ be the algebraic irreducible representation of
$V^{\mu }_{E}$ be the algebraic irreducible representation of ![]() $G(E)$, for some ‘large enough’
$G(E)$, for some ‘large enough’ ![]() $p$-adic field
$p$-adic field ![]() $E$. If
$E$. If ![]() $\mathcal {O}$ is the ring of integers of
$\mathcal {O}$ is the ring of integers of ![]() $E$, then we also consider an
$E$, then we also consider an ![]() $\mathcal {O}$-lattice
$\mathcal {O}$-lattice ![]() $V^{\mu }_{\mathcal {O}}$ stabilized by
$V^{\mu }_{\mathcal {O}}$ stabilized by ![]() $G(\mathcal {O})$. For any open compact subgroup
$G(\mathcal {O})$. For any open compact subgroup ![]() $K$ of
$K$ of ![]() $\operatorname {GL}_{2n}$ over the finite adeles of
$\operatorname {GL}_{2n}$ over the finite adeles of ![]() $F$, let
$F$, let ![]() $\mathcal {V}_{\mathcal {O}}^{\mu }$ be the associated sheaf on the locally symmetric space
$\mathcal {V}_{\mathcal {O}}^{\mu }$ be the associated sheaf on the locally symmetric space ![]() ${S^{G}_K}$ of
${S^{G}_K}$ of ![]() $G$ with level structure
$G$ with level structure ![]() $K$ and let us consider the compactly supported cohomology
$K$ and let us consider the compactly supported cohomology ![]() $\operatorname {H}^{q}_c ({S^{G}_K}, \mathcal {V}_{\mathcal {O}}^{\mu })$ endowed with the usual Hecke action. Assume that for
$\operatorname {H}^{q}_c ({S^{G}_K}, \mathcal {V}_{\mathcal {O}}^{\mu })$ endowed with the usual Hecke action. Assume that for ![]() $\mathfrak {p}$ dividing
$\mathfrak {p}$ dividing ![]() $p$,
$p$, ![]() $K_\mathfrak {p}$ is the parahoric subgroup corresponding to the parabolic
$K_\mathfrak {p}$ is the parahoric subgroup corresponding to the parabolic ![]() $Q$ and consider an eigenclass
$Q$ and consider an eigenclass ![]() $\phi \in \operatorname {H}^{t}_c({S^{G}_K}, \mathcal {V}_{\mathcal {O}}^{\mu })$ having a non-zero eigenvalue
$\phi \in \operatorname {H}^{t}_c({S^{G}_K}, \mathcal {V}_{\mathcal {O}}^{\mu })$ having a non-zero eigenvalue ![]() $\alpha _\mathfrak {p}$ for a particular Hecke operator
$\alpha _\mathfrak {p}$ for a particular Hecke operator ![]() $U_\mathfrak {p}$. Here and throughout the paper
$U_\mathfrak {p}$. Here and throughout the paper ![]() $t= |\Sigma _\infty |(n^{2}+n-1)$ denotes the top degree supporting cuspidal cohomology. The weight
$t= |\Sigma _\infty |(n^{2}+n-1)$ denotes the top degree supporting cuspidal cohomology. The weight ![]() $\mu$ determines a contiguous string of integers
$\mu$ determines a contiguous string of integers ![]() $\operatorname {Crit}(\mu )$, which would correspond to the set of critical points for an
$\operatorname {Crit}(\mu )$, which would correspond to the set of critical points for an ![]() $L$-function. For each
$L$-function. For each ![]() $j \in \operatorname {Crit}(\mu )$ we attach an
$j \in \operatorname {Crit}(\mu )$ we attach an ![]() $E$-valued distribution
$E$-valued distribution ![]() $\boldsymbol {\mu }_{\phi }^{j}$ on
$\boldsymbol {\mu }_{\phi }^{j}$ on ![]() $\mathscr {C}\!\ell _F^{+}(p^{\infty })$ and show that it is
$\mathscr {C}\!\ell _F^{+}(p^{\infty })$ and show that it is ![]() $\mathcal {O}$-valued when
$\mathcal {O}$-valued when ![]() $\phi$ is
$\phi$ is ![]() $Q$-ordinary, that is, it is a measure (see diagram (36) for a quick overview of the sheaf-theoretic maps that are involved in the construction). Most importantly we prove in Theorem 2.3 a Manin-type relation, namely for all
$Q$-ordinary, that is, it is a measure (see diagram (36) for a quick overview of the sheaf-theoretic maps that are involved in the construction). Most importantly we prove in Theorem 2.3 a Manin-type relation, namely for all ![]() $j,j' \in \operatorname {Crit}(\mu )$ we have
$j,j' \in \operatorname {Crit}(\mu )$ we have
where ![]() $\varepsilon : \mathscr {C}\!\ell _F^{+}(p^{\infty }) \to \mathbb {Z}_p^{\times }$ is the
$\varepsilon : \mathscr {C}\!\ell _F^{+}(p^{\infty }) \to \mathbb {Z}_p^{\times }$ is the ![]() $p$-adic cyclotomic character and
$p$-adic cyclotomic character and ![]() $\varepsilon _{\operatorname {cyc}}$ is the automorphism of
$\varepsilon _{\operatorname {cyc}}$ is the automorphism of ![]() $\mathcal {O}[[\mathscr {C}\!\ell _F^{+}(p^{\infty })]]$ sending
$\mathcal {O}[[\mathscr {C}\!\ell _F^{+}(p^{\infty })]]$ sending ![]() $[x]$ to
$[x]$ to ![]() $\varepsilon ([x])[x]$, allowing us to define a measure
$\varepsilon ([x])[x]$, allowing us to define a measure ![]() $\boldsymbol {\mu }_\phi = \varepsilon _{\operatorname {cyc}}^{-j}(\boldsymbol {\mu }^{j}_\phi )$ that is independent of
$\boldsymbol {\mu }_\phi = \varepsilon _{\operatorname {cyc}}^{-j}(\boldsymbol {\mu }^{j}_\phi )$ that is independent of ![]() $j$.
$j$.
Next we apply these considerations to the situation when ![]() $\phi$ is related to a cuspidal automorphic representation
$\phi$ is related to a cuspidal automorphic representation ![]() $\Pi$ of
$\Pi$ of ![]() $\operatorname {GL}_{2n}/F$ such that
$\operatorname {GL}_{2n}/F$ such that ![]() $\Pi _\infty$ is cohomological with respect to the weight
$\Pi _\infty$ is cohomological with respect to the weight ![]() $\mu$ (see § 4.1.3). Friedberg and Jacquet related the period integral of cusp forms in
$\mu$ (see § 4.1.3). Friedberg and Jacquet related the period integral of cusp forms in ![]() $\Pi$ over the Levi subgroup
$\Pi$ over the Levi subgroup ![]() $H$ of
$H$ of ![]() $Q$ to the standard
$Q$ to the standard ![]() $L$-function
$L$-function ![]() $L(s, \Pi )$, and for the unfolding of this integral to see the Eulerian property the representation is assumed to have a Shalika model (see § 4.1). Such a cohomological interpretation was used in [Reference Grobner and RaghuramGR14] to deduce algebraicity results for the critical values of
$L(s, \Pi )$, and for the unfolding of this integral to see the Eulerian property the representation is assumed to have a Shalika model (see § 4.1). Such a cohomological interpretation was used in [Reference Grobner and RaghuramGR14] to deduce algebraicity results for the critical values of ![]() $L(s, \Pi \otimes \chi )$. The following result further investigates their
$L(s, \Pi \otimes \chi )$. The following result further investigates their ![]() $p$-adic integrality properties. A more general
$p$-adic integrality properties. A more general ![]() $p$-adic interpolation statement is proven in Theorem 4.7 under the assumption that
$p$-adic interpolation statement is proven in Theorem 4.7 under the assumption that ![]() $\Pi _\mathfrak {p}$ admits a
$\Pi _\mathfrak {p}$ admits a ![]() $Q$-regular refinement
$Q$-regular refinement ![]() $\tilde \Pi _\mathfrak {p}$ for
$\tilde \Pi _\mathfrak {p}$ for ![]() $\mathfrak {p}\mid p$ (see Definition 3.5), which is shown to be always fulfilled when
$\mathfrak {p}\mid p$ (see Definition 3.5), which is shown to be always fulfilled when ![]() $\Pi _\mathfrak {p}$ is
$\Pi _\mathfrak {p}$ is ![]() $Q$-ordinary (see Lemma 4.4).
$Q$-ordinary (see Lemma 4.4).
Theorem 2 Let ![]() $\Pi$ be a cuspidal automorphic representation of
$\Pi$ be a cuspidal automorphic representation of ![]() $\operatorname {GL}_{2n}/F$ admitting a
$\operatorname {GL}_{2n}/F$ admitting a ![]() $(\psi ,\eta )$-Shalika model and such that
$(\psi ,\eta )$-Shalika model and such that ![]() $\Pi _\infty$ is cohomological of weight
$\Pi _\infty$ is cohomological of weight ![]() $\mu$. Assume that for all primes
$\mu$. Assume that for all primes ![]() $\mathfrak {p}$ above a given prime number
$\mathfrak {p}$ above a given prime number ![]() $p$,
$p$, ![]() $\Pi _\mathfrak {p}$ is spherical and
$\Pi _\mathfrak {p}$ is spherical and ![]() $Q$-ordinary, and let
$Q$-ordinary, and let ![]() $\alpha _{\mathfrak {p}}$ denote the corresponding
$\alpha _{\mathfrak {p}}$ denote the corresponding ![]() $U_{\mathfrak {p}}$-eigenvalue. Given any isomorphism
$U_{\mathfrak {p}}$-eigenvalue. Given any isomorphism ![]() $i_p: \mathbb {C} \xrightarrow {\sim } \bar {\mathbb {Q}}_p$, there exists a bounded
$i_p: \mathbb {C} \xrightarrow {\sim } \bar {\mathbb {Q}}_p$, there exists a bounded ![]() $p$-adic distribution
$p$-adic distribution ![]() $\boldsymbol {\mu }_{\tilde \Pi }$ on
$\boldsymbol {\mu }_{\tilde \Pi }$ on ![]() $\mathscr {C}\!\ell _F^{+}(p^{\infty })$ such that for any
$\mathscr {C}\!\ell _F^{+}(p^{\infty })$ such that for any ![]() $j\in \operatorname {Crit}(\mu )$ and for any finite order character
$j\in \operatorname {Crit}(\mu )$ and for any finite order character ![]() $\chi$ of
$\chi$ of ![]() $\mathscr {C}\!\ell _F^{+}(p^{\infty })$ of conductor
$\mathscr {C}\!\ell _F^{+}(p^{\infty })$ of conductor ![]() $\beta _\mathfrak {p} \geqslant 1$ at all
$\beta _\mathfrak {p} \geqslant 1$ at all ![]() $\mathfrak {p}\mid p$ one has
$\mathfrak {p}\mid p$ one has
 \begin{align*} &i_p^{-1}\bigg( \int_{\mathscr{C}\!\ell_F^{+}(p^{\infty})}\varepsilon^{j}(x) \chi(x) \, {d} \boldsymbol{\mu}_{\tilde\Pi}(x)\bigg)\nonumber\\
&\quad = \gamma \cdot \operatorname{N}^{jn}_{F/\mathbb{Q}}(\mathfrak{d}) \cdot \prod_{\mathfrak{p}\mid p} \big (\alpha_{\mathfrak{p}}^{-1} q_\mathfrak{p}^{n(j+1)}\big)^{\beta_\mathfrak{p}}
\cdot { \mathcal{G}(\chi_f)^{n} \cdot L\bigg(j+\dfrac{1}{2}, \Pi_f \otimes \chi_f\bigg) } \zeta_\infty\bigg(j+\dfrac{1}{2};W_{\Pi_\infty,j}^{(\varepsilon^{j}\chi\eta)_\infty}\bigg), \end{align*}
\begin{align*} &i_p^{-1}\bigg( \int_{\mathscr{C}\!\ell_F^{+}(p^{\infty})}\varepsilon^{j}(x) \chi(x) \, {d} \boldsymbol{\mu}_{\tilde\Pi}(x)\bigg)\nonumber\\
&\quad = \gamma \cdot \operatorname{N}^{jn}_{F/\mathbb{Q}}(\mathfrak{d}) \cdot \prod_{\mathfrak{p}\mid p} \big (\alpha_{\mathfrak{p}}^{-1} q_\mathfrak{p}^{n(j+1)}\big)^{\beta_\mathfrak{p}}
\cdot { \mathcal{G}(\chi_f)^{n} \cdot L\bigg(j+\dfrac{1}{2}, \Pi_f \otimes \chi_f\bigg) } \zeta_\infty\bigg(j+\dfrac{1}{2};W_{\Pi_\infty,j}^{(\varepsilon^{j}\chi\eta)_\infty}\bigg), \end{align*}
where ![]() $\mathcal {G}(\chi _f)$ is the Gauss sum, the zeta factor is non-zero by (76), and
$\mathcal {G}(\chi _f)$ is the Gauss sum, the zeta factor is non-zero by (76), and ![]() $\gamma \in \mathbb {Q}^{\times }$ is as in (77).
$\gamma \in \mathbb {Q}^{\times }$ is as in (77).
Let us hint on how we deduce Theorem A. Theorem B, the formulation of which implicitly uses the earlier established Manin relations, gives congruence relations between successive critical values, whereas (1) translates into ![]() $\frac {3}{2} \in \operatorname {Crit}(\mu )$. As the complex
$\frac {3}{2} \in \operatorname {Crit}(\mu )$. As the complex ![]() $L$-function of the unitary cuspidal automorphic representation
$L$-function of the unitary cuspidal automorphic representation ![]() $\Pi$ does not vanish for
$\Pi$ does not vanish for ![]() $\Re (s) \geqslant 1$ we deduce that
$\Re (s) \geqslant 1$ we deduce that ![]() $L(\frac {3}{2}, \Pi \otimes \chi )$ never vanishes, which, in turn, implies the non-vanishing of
$L(\frac {3}{2}, \Pi \otimes \chi )$ never vanishes, which, in turn, implies the non-vanishing of ![]() $L(\frac {1}{2}, \Pi \otimes (\chi \circ \operatorname {N}_{F/\mathbb {Q}}))$ for all but finitely many Dirichlet characters
$L(\frac {1}{2}, \Pi \otimes (\chi \circ \operatorname {N}_{F/\mathbb {Q}}))$ for all but finitely many Dirichlet characters ![]() $\chi$ (see the proof of Theorem 4.8).
$\chi$ (see the proof of Theorem 4.8).
Let us mention some relevant studies in the literature. First, Ash and Ginzburg [Reference Ash and GinzburgAG94] started the study of ![]() $p$-adic
$p$-adic ![]() $L$-functions for
$L$-functions for ![]() $\operatorname {GL}_{2n}$ over a totally real field by considering the analytic theory developed by Friedberg and Jacquet [Reference Friedberg and JacquetFJ93]. However, to quote the authors of [Reference Ash and GinzburgAG94], their results are definitive only for
$\operatorname {GL}_{2n}$ over a totally real field by considering the analytic theory developed by Friedberg and Jacquet [Reference Friedberg and JacquetFJ93]. However, to quote the authors of [Reference Ash and GinzburgAG94], their results are definitive only for ![]() $\operatorname {GL}_4$ over
$\operatorname {GL}_4$ over ![]() $\mathbb {Q}$ and for cohomology with constant coefficients. Furthermore, they constructed their distributions on local units while only suggesting that one should really work, as we do in this paper, on
$\mathbb {Q}$ and for cohomology with constant coefficients. Furthermore, they constructed their distributions on local units while only suggesting that one should really work, as we do in this paper, on ![]() $\mathscr {C}\!\ell _F^{+}(p^{\infty })$. This article uses the more recent techniques developed in independent papers by all three of the current authors; namely, [Reference DimitrovDim13], [Reference Grobner and RaghuramGR14], and [Reference JanuszewskiJan15]. Finally, we mention Gehrmann's thesis [Reference GehrmannGeh18], which also constructs
$\mathscr {C}\!\ell _F^{+}(p^{\infty })$. This article uses the more recent techniques developed in independent papers by all three of the current authors; namely, [Reference DimitrovDim13], [Reference Grobner and RaghuramGR14], and [Reference JanuszewskiJan15]. Finally, we mention Gehrmann's thesis [Reference GehrmannGeh18], which also constructs ![]() $p$-adic
$p$-adic ![]() $L$-functions in essentially a similar context, but his methods are entirely different from ours.
$L$-functions in essentially a similar context, but his methods are entirely different from ours.
To conclude the introduction, our emphasis is on the purely sheaf-theoretic nature of the construction of the distributions attached to eigenclasses in cohomology, which leads to a purely algebraic proof of Manin relations in a very general context. When specialized to a cohomology class related to a representation ![]() $\Pi$ of
$\Pi$ of ![]() $\operatorname {GL}_{2n}$, we obtain
$\operatorname {GL}_{2n}$, we obtain ![]() $p$-adic interpolation of the critical values of the standard
$p$-adic interpolation of the critical values of the standard ![]() $L$-function
$L$-function ![]() $L(s, \Pi )$, and Manin relations give non-vanishing of twists
$L(s, \Pi )$, and Manin relations give non-vanishing of twists ![]() $L(s, \Pi \otimes \chi )$ at the center of symmetry. A non-vanishing theorem in the realms of analytic number theory admitting a decidedly algebraic proof is philosophically piquant.
$L(s, \Pi \otimes \chi )$ at the center of symmetry. A non-vanishing theorem in the realms of analytic number theory admitting a decidedly algebraic proof is philosophically piquant.
1. Automorphic cohomology
Recall that ![]() $F$ is a totally real number field with ring of integers
$F$ is a totally real number field with ring of integers ![]() $\mathcal {O}_{F}$ and set of infinite places
$\mathcal {O}_{F}$ and set of infinite places ![]() $\Sigma _\infty$. For a set of places
$\Sigma _\infty$. For a set of places ![]() $\Sigma$, we denote by
$\Sigma$, we denote by ![]() $\mathbb {A}^{(\Sigma )}$ the topological ring of adeles of
$\mathbb {A}^{(\Sigma )}$ the topological ring of adeles of ![]() $\mathbb {Q}$ outside
$\mathbb {Q}$ outside ![]() $\Sigma$. Let
$\Sigma$. Let ![]() $\mathbb {A}_F=\mathbb {A}\otimes _{\mathbb {Q}} F$ (respectively,
$\mathbb {A}_F=\mathbb {A}\otimes _{\mathbb {Q}} F$ (respectively, ![]() $\mathbb {A}_{F,f}$) be the group of adeles (respectively, finite adeles) of
$\mathbb {A}_{F,f}$) be the group of adeles (respectively, finite adeles) of ![]() $F$.
$F$.
We consider ![]() $G=\operatorname {Res}_{\mathcal {O}_{F}/\mathbb {Z}}(\operatorname {GL}_{2n})$ as a reductive group scheme over
$G=\operatorname {Res}_{\mathcal {O}_{F}/\mathbb {Z}}(\operatorname {GL}_{2n})$ as a reductive group scheme over ![]() $\mathbb {Z}$, quasi-split over
$\mathbb {Z}$, quasi-split over ![]() $\mathbb {Q}$ and let
$\mathbb {Q}$ and let ![]() $Z=\operatorname {Res}_{\mathcal {O}_{F}/\mathbb {Z}}(\operatorname {GL}_1)$ be the center of
$Z=\operatorname {Res}_{\mathcal {O}_{F}/\mathbb {Z}}(\operatorname {GL}_1)$ be the center of ![]() $G$. The standard Borel subgroup
$G$. The standard Borel subgroup ![]() $B\subseteq G$ is defined as the restriction of scalars of the standard Borel subgroup of all upper triangular matrices in
$B\subseteq G$ is defined as the restriction of scalars of the standard Borel subgroup of all upper triangular matrices in ![]() $\operatorname {GL}_{2n}/\mathcal {O}_{F}$. We have
$\operatorname {GL}_{2n}/\mathcal {O}_{F}$. We have ![]() $B=TN$, where
$B=TN$, where ![]() $N$ is the unipotent radical of
$N$ is the unipotent radical of ![]() $B$ and
$B$ and ![]() $T$ is the standard torus of all diagonal matrices. Let
$T$ is the standard torus of all diagonal matrices. Let ![]() $H =\operatorname {Res}_{\mathcal {O}_{F}/\mathbb {Z}}(\operatorname {GL}_n \times \operatorname {GL}_n)$, and
$H =\operatorname {Res}_{\mathcal {O}_{F}/\mathbb {Z}}(\operatorname {GL}_n \times \operatorname {GL}_n)$, and ![]() $\iota : H \hookrightarrow G$ be the map that sends
$\iota : H \hookrightarrow G$ be the map that sends ![]() $(h_1,h_2)$ to
$(h_1,h_2)$ to ![]() $\big (\begin {smallmatrix} h_1 & 0 \\ 0 & h_2 \end {smallmatrix}\big )$. Let
$\big (\begin {smallmatrix} h_1 & 0 \\ 0 & h_2 \end {smallmatrix}\big )$. Let ![]() $Q=HU$ be the standard parabolic subgroup of type
$Q=HU$ be the standard parabolic subgroup of type ![]() $(n,n)$ whose Levi subgroup is
$(n,n)$ whose Levi subgroup is ![]() $H$ and unipotent radical is
$H$ and unipotent radical is ![]() $U$. Finally, the Shalika subgroup
$U$. Finally, the Shalika subgroup ![]() $S$ of
$S$ of ![]() $G$ is defined as
$G$ is defined as ![]() $S=\big \{ \big ( \begin {smallmatrix} h & 0 \\ 0 & h \end {smallmatrix}\big ) \big ( \begin {smallmatrix} 1 & X\\ 0 & 1 \end {smallmatrix}\big ) \mid h\in \operatorname {GL}_n, X\in {\rm M}_n \big \}$.
$S=\big \{ \big ( \begin {smallmatrix} h & 0 \\ 0 & h \end {smallmatrix}\big ) \big ( \begin {smallmatrix} 1 & X\\ 0 & 1 \end {smallmatrix}\big ) \mid h\in \operatorname {GL}_n, X\in {\rm M}_n \big \}$.
For any commutative ring ![]() $A$, we let
$A$, we let ![]() ${{\mathfrak {g}}}_A$,
${{\mathfrak {g}}}_A$, ![]() ${{\mathfrak {b}}}_A$,
${{\mathfrak {b}}}_A$, ![]() ${{\mathfrak {q}}}_A$,
${{\mathfrak {q}}}_A$, ![]() ${{\mathfrak {t}}}_A$,
${{\mathfrak {t}}}_A$, ![]() ${{\mathfrak {h}}}_A$,
${{\mathfrak {h}}}_A$, ![]() ${{\mathfrak {n}}}_A$, and
${{\mathfrak {n}}}_A$, and ![]() ${{\mathfrak {u}}}_A$ denote the Lie algebras of
${{\mathfrak {u}}}_A$ denote the Lie algebras of ![]() $G$,
$G$, ![]() $B$,
$B$, ![]() $Q$,
$Q$, ![]() $T$,
$T$, ![]() $H$,
$H$, ![]() $N$, and
$N$, and ![]() $U$ over
$U$ over ![]() $A$, respectively. For
$A$, respectively. For ![]() ${{\mathfrak {a}}}_A$ any amongst these, we let
${{\mathfrak {a}}}_A$ any amongst these, we let ![]() $\mathcal {U}({{\mathfrak {a}}}_A)$ denote the enveloping algebra over
$\mathcal {U}({{\mathfrak {a}}}_A)$ denote the enveloping algebra over ![]() $A$. In the particular case
$A$. In the particular case ![]() $A=\mathbb {R}$, let
$A=\mathbb {R}$, let ![]() ${{\mathfrak {g}}}_\infty ={{\mathfrak {g}}}_{\mathbb {R}} \otimes _{\mathbb {R}} \mathbb {C}$ denote the complexification and likewise for the other groups. The reader is referred to [Reference JantzenJan03] as a general reference for integral Lie algebras and their enveloping algebras.
${{\mathfrak {g}}}_\infty ={{\mathfrak {g}}}_{\mathbb {R}} \otimes _{\mathbb {R}} \mathbb {C}$ denote the complexification and likewise for the other groups. The reader is referred to [Reference JantzenJan03] as a general reference for integral Lie algebras and their enveloping algebras.
For any real reductive Lie group ![]() $\mathcal {G}$, we let
$\mathcal {G}$, we let ![]() $\mathcal {G}^{\circ }$ denote the connected component of the identity. Let
$\mathcal {G}^{\circ }$ denote the connected component of the identity. Let ![]() $G_\infty = G(\mathbb {R}),$ and similarly
$G_\infty = G(\mathbb {R}),$ and similarly ![]() $Z_{\infty } = Z(\mathbb {R})$.
$Z_{\infty } = Z(\mathbb {R})$.
1.1 Pure weights
We identify integral weights ![]() $\mu$ of
$\mu$ of ![]() $T$ with tuples of weights
$T$ with tuples of weights ![]() $\mu =(\mu _{\sigma })_{\sigma \in \Sigma _\infty },$
$\mu =(\mu _{\sigma })_{\sigma \in \Sigma _\infty },$ ![]() $\mu _{\sigma }=(\mu _{\sigma ,1},\ldots ,\mu _{\sigma ,2n})\in \mathbb {Z}^{2n}$. A weight
$\mu _{\sigma }=(\mu _{\sigma ,1},\ldots ,\mu _{\sigma ,2n})\in \mathbb {Z}^{2n}$. A weight ![]() $\mu$ is
$\mu$ is ![]() $B$-dominant if
$B$-dominant if
Let ![]() $X^{*}_+(T)$ be the set of all such dominant integral weights. For
$X^{*}_+(T)$ be the set of all such dominant integral weights. For ![]() $\mu \in X^{*}_+(T)$ denote by
$\mu \in X^{*}_+(T)$ denote by ![]() $V^{\mu }$ the unique algebraic irreducible rational representation of
$V^{\mu }$ the unique algebraic irreducible rational representation of ![]() $G$ of highest weight
$G$ of highest weight ![]() $\mu$. For any field
$\mu$. For any field ![]() $E$ over which
$E$ over which ![]() $\mu$ is defined, we denote by
$\mu$ is defined, we denote by ![]() $V^{\mu }_{E}$ its
$V^{\mu }_{E}$ its ![]() $E$-valued points. Denote by
$E$-valued points. Denote by ![]() $\mu ^{\vee }$ the highest weight of the contragredient
$\mu ^{\vee }$ the highest weight of the contragredient ![]() $(V^{\mu })^{\vee }$ of
$(V^{\mu })^{\vee }$ of ![]() $V^{\mu }$ which we consider as a rational character of
$V^{\mu }$ which we consider as a rational character of ![]() $B$.
$B$.
We call ![]() $\mu$ pure if there exists
$\mu$ pure if there exists ![]() ${{\sf w}}\in \mathbb {Z}$, called the purity weight of
${{\sf w}}\in \mathbb {Z}$, called the purity weight of ![]() $\mu$, such that
$\mu$, such that
where ![]() $\operatorname {N}_{F/\mathbb {Q}}:\operatorname {Res}_{F/\mathbb {Q}}(\operatorname {GL}_1)\to \operatorname {GL}_1$ denotes the norm homomorphism. If
$\operatorname {N}_{F/\mathbb {Q}}:\operatorname {Res}_{F/\mathbb {Q}}(\operatorname {GL}_1)\to \operatorname {GL}_1$ denotes the norm homomorphism. If ![]() $\mu$ is pure, then
$\mu$ is pure, then
In particular, ![]() $\sum _{i=1}^{2n} \mu _{\sigma ,i}={{\sf w}}n$ is independent of
$\sum _{i=1}^{2n} \mu _{\sigma ,i}={{\sf w}}n$ is independent of ![]() $\sigma$. We let
$\sigma$. We let ![]() $X^{*}_0(T)\subset X^{*}_+(T)$ denote the pure dominant integral weights of
$X^{*}_0(T)\subset X^{*}_+(T)$ denote the pure dominant integral weights of ![]() $T$. Given any
$T$. Given any ![]() $\mu \in X^{*}_0(T)$, define the set
$\mu \in X^{*}_0(T)$, define the set
It is well known that only pure weights support cuspidal cohomology, and the motivation for this definition comes from the fact proved in [Reference Grobner and RaghuramGR14, Proposition 6.1] that if ![]() $\Pi$ is a cuspidal automorphic representation of
$\Pi$ is a cuspidal automorphic representation of ![]() $G(\mathbb {A})$ that is cohomological with respect to
$G(\mathbb {A})$ that is cohomological with respect to ![]() $\mu$ (see § 4.1.3), then
$\mu$ (see § 4.1.3), then ![]() $\frac {1}{2}+j$ with
$\frac {1}{2}+j$ with ![]() $j \in \mathbb {Z}$ is critical for the standard
$j \in \mathbb {Z}$ is critical for the standard ![]() $L$-function
$L$-function ![]() $L(s, \Pi \otimes \chi )$ for any finite order character
$L(s, \Pi \otimes \chi )$ for any finite order character ![]() $\chi$ if and only if
$\chi$ if and only if ![]() $j \in \operatorname {Crit}(\mu )$. Note that the central point
$j \in \operatorname {Crit}(\mu )$. Note that the central point ![]() $({{{\sf w}}+1})/{2}$ of
$({{{\sf w}}+1})/{2}$ of ![]() $L(s, \Pi \otimes \chi )$ is critical (i.e.
$L(s, \Pi \otimes \chi )$ is critical (i.e. ![]() ${{{\sf w}}}/{2}\in \operatorname {Crit}(\mu )$) if and only if
${{{\sf w}}}/{2}\in \operatorname {Crit}(\mu )$) if and only if ![]() ${{\sf w}}$ is even.
${{\sf w}}$ is even.
1.2 Integral lattices
Let ![]() $E$ be a finite extension of
$E$ be a finite extension of ![]() $\mathbb {Q}_p$ and let
$\mathbb {Q}_p$ and let ![]() $\mathcal {O}$ be its ring of integers. Given
$\mathcal {O}$ be its ring of integers. Given ![]() $\mu \in X^{*}_+(T)$, we consider
$\mu \in X^{*}_+(T)$, we consider ![]() $V^{\mu }_{E}$ as a representation of
$V^{\mu }_{E}$ as a representation of ![]() $G(E)$.
$G(E)$.
Let ![]() $v_0 \in V^{\mu }_{E}$ be a non-zero lowest-weight vector. Then the unipotent radical
$v_0 \in V^{\mu }_{E}$ be a non-zero lowest-weight vector. Then the unipotent radical ![]() $N^{-}(E)$ of the Borel subgroup
$N^{-}(E)$ of the Borel subgroup ![]() $B^{-}(E)$ of lower triangular matrices fixes
$B^{-}(E)$ of lower triangular matrices fixes ![]() $v_0$, whereas
$v_0$, whereas ![]() $T(E)$ acts on
$T(E)$ acts on ![]() $v_0$ via the character
$v_0$ via the character ![]() $-\mu ^{\sf v} = w_{2n}(\mu )$ where
$-\mu ^{\sf v} = w_{2n}(\mu )$ where ![]() $w_{2n}$ is the Weyl group element of longest length.
$w_{2n}$ is the Weyl group element of longest length.
Observe that
is an ![]() $\mathcal {O}$-lattice
$\mathcal {O}$-lattice ![]() $V^{\mu }_{E}$ endowed with a natural action of
$V^{\mu }_{E}$ endowed with a natural action of ![]() $G(\mathcal {O})$.
$G(\mathcal {O})$.
We fix once and for all uniformizers ![]() $\varpi _{\mathfrak {p}}\in F_{\mathfrak {p}}$ and put
$\varpi _{\mathfrak {p}}\in F_{\mathfrak {p}}$ and put ![]() $t_{\mathfrak {p}} = \iota (\varpi _{\mathfrak {p}}\cdot \textbf {1}_n,\textbf {1}_n) \in \operatorname {GL}_{2n}(F_{\mathfrak {p}})$. Define for any integral multi-exponent
$t_{\mathfrak {p}} = \iota (\varpi _{\mathfrak {p}}\cdot \textbf {1}_n,\textbf {1}_n) \in \operatorname {GL}_{2n}(F_{\mathfrak {p}})$. Define for any integral multi-exponent ![]() $\beta =(\beta _{\mathfrak {p}})_{\mathfrak {p}\mid p}$ the element
$\beta =(\beta _{\mathfrak {p}})_{\mathfrak {p}\mid p}$ the element
and consider the semi-group
Then by our choice of dominance condition, we have for any ![]() $t\in \Delta _p^{+}$:
$t\in \Delta _p^{+}$:
Consider the standard maximal parahoric subgroup ![]() $J_p=\prod _{\mathfrak {p}\mid p} J_\mathfrak {p}\subset G(\mathbb {Z}_p)$, where
$J_p=\prod _{\mathfrak {p}\mid p} J_\mathfrak {p}\subset G(\mathbb {Z}_p)$, where
As ![]() $J_p \supset Q(\mathbb {Z}_p)$, the parahoric decomposition is given by
$J_p \supset Q(\mathbb {Z}_p)$, the parahoric decomposition is given by
Using (8) and (10) one sees that
is a semi-group. Moreover, because ![]() $U^{-}(\mathbb {Z}_p)\subset N^{-}(\mathbb {Z}_p)$ acts trivially on
$U^{-}(\mathbb {Z}_p)\subset N^{-}(\mathbb {Z}_p)$ acts trivially on ![]() $v_0$, the
$v_0$, the ![]() $J_p$-action on
$J_p$-action on ![]() $V^{\mu }_{\mathcal {O}}$ extends uniquely to an action
$V^{\mu }_{\mathcal {O}}$ extends uniquely to an action ![]() $\bullet$ of the semi-group
$\bullet$ of the semi-group ![]() $\Lambda _p$ by letting
$\Lambda _p$ by letting ![]() $\Delta _p^{+}$ act trivially on the lowest weight vector
$\Delta _p^{+}$ act trivially on the lowest weight vector ![]() $v_0$. Then for all
$v_0$. Then for all ![]() $t\in \Delta _p^{+}$ and
$t\in \Delta _p^{+}$ and ![]() $v\in V^{\mu }_{\mathcal {O}}$ one has
$v\in V^{\mu }_{\mathcal {O}}$ one has
In fact, by (5), one can write ![]() $v=m\cdot v_0$ for some
$v=m\cdot v_0$ for some ![]() $m\in \mathcal {U}({{\mathfrak {n}}}_\mathcal {O})$ and using (8) one finds
$m\in \mathcal {U}({{\mathfrak {n}}}_\mathcal {O})$ and using (8) one finds
1.3 Local systems on locally symmetric spaces for GL2n
The standard maximal compact subgroup of ![]() $G_\infty$ is denoted by
$G_\infty$ is denoted by ![]() $C_{\infty }=\prod _{\sigma \in \Sigma _\infty }C_\sigma$, where
$C_{\infty }=\prod _{\sigma \in \Sigma _\infty }C_\sigma$, where ![]() $C_{\sigma }\simeq {\rm O}_{2n}(\mathbb {R})$. The determinant identifies the group of connected components
$C_{\sigma }\simeq {\rm O}_{2n}(\mathbb {R})$. The determinant identifies the group of connected components ![]() $C_{\infty }/C_{\infty }^{\circ }$ with
$C_{\infty }/C_{\infty }^{\circ }$ with ![]() $F_{\infty }^{\times }/F_{\infty }^{\times \circ }\cong \{\pm 1\}^{\Sigma _\infty }$. Let
$F_{\infty }^{\times }/F_{\infty }^{\times \circ }\cong \{\pm 1\}^{\Sigma _\infty }$. Let ![]() $K_\infty =C_{\infty } Z_{\infty }$ and for any open compact subgroup
$K_\infty =C_{\infty } Z_{\infty }$ and for any open compact subgroup ![]() $K$ of
$K$ of ![]() $G(\mathbb {A}_f)$ consider the locally symmetric space:
$G(\mathbb {A}_f)$ consider the locally symmetric space:
Note that ![]() $K_{\infty }^{\circ } = C_{\infty }^{\circ } Z_{\infty }^{\circ }=C_{\infty }^{\circ } Z_{\infty }$ because
$K_{\infty }^{\circ } = C_{\infty }^{\circ } Z_{\infty }^{\circ }=C_{\infty }^{\circ } Z_{\infty }$ because ![]() $2n$ is even. In general,
$2n$ is even. In general, ![]() ${S^{G}_K}$ is only a real orbifold. In the sequel, we assume that
${S^{G}_K}$ is only a real orbifold. In the sequel, we assume that ![]() $K$ is sufficiently small in the sense that for all
$K$ is sufficiently small in the sense that for all ![]() $g\in G(\mathbb {A})$,
$g\in G(\mathbb {A})$,
which implies in particular that ![]() ${S^{G}_K}$ is a real manifold.
${S^{G}_K}$ is a real manifold.
Given a left ![]() $G(\mathbb {Q})$-module
$G(\mathbb {Q})$-module ![]() $V\!$, one can define
$V\!$, one can define ![]() $\mathcal {V}_K$ as the sheaf of locally constant sections of the local system:
$\mathcal {V}_K$ as the sheaf of locally constant sections of the local system:
where ![]() $\gamma (g,v)k=(\gamma g k,\gamma \cdot v)$ for all
$\gamma (g,v)k=(\gamma g k,\gamma \cdot v)$ for all ![]() $\gamma \in G(\mathbb {Q})$,
$\gamma \in G(\mathbb {Q})$, ![]() $k\in K K_{\infty }^{\circ }$. Consider the canonical fibration
$k\in K K_{\infty }^{\circ }$. Consider the canonical fibration ![]() $\pi : (G(\mathbb {R})/ K_{\infty }^{\circ } ) \times G(\mathbb {A}_f)/K \to {S^{G}_K}$ given by going modulo the left action of
$\pi : (G(\mathbb {R})/ K_{\infty }^{\circ } ) \times G(\mathbb {A}_f)/K \to {S^{G}_K}$ given by going modulo the left action of ![]() $G(\mathbb {Q})$. Then, for any open
$G(\mathbb {Q})$. Then, for any open ![]() $\mathcal {U} \subset {S^{G}_K}$, one has the sections
$\mathcal {U} \subset {S^{G}_K}$, one has the sections ![]() $\mathcal {V}_K(\mathcal {U})$ over
$\mathcal {V}_K(\mathcal {U})$ over ![]() $\mathcal {U}$ to be the set of all locally constant
$\mathcal {U}$ to be the set of all locally constant ![]() $s : \pi ^{-1}(\mathcal {U}) \to V$ such that
$s : \pi ^{-1}(\mathcal {U}) \to V$ such that ![]() $s(\gamma \cdot x) = \gamma \cdot s(x)$ for all
$s(\gamma \cdot x) = \gamma \cdot s(x)$ for all ![]() $\gamma \in G(\mathbb {Q}), x \in \pi ^{-1}(\mathcal {U}).$ We denote by
$\gamma \in G(\mathbb {Q}), x \in \pi ^{-1}(\mathcal {U}).$ We denote by ![]() $\mathcal {V}_{K,E}^{\mu }$ the sheaf associated to
$\mathcal {V}_{K,E}^{\mu }$ the sheaf associated to ![]() $V^{\mu }_{E}$. The sheaf
$V^{\mu }_{E}$. The sheaf ![]() $\mathcal {V}_{K,E}^{\mu }$ is non-trivial if and only if
$\mathcal {V}_{K,E}^{\mu }$ is non-trivial if and only if
Condition (15) is always satisfied if ![]() $\mu$ is pure, because
$\mu$ is pure, because ![]() $\det (F^{\times } \cap K K_{\infty }^{\circ } )\subset \mathcal {O}_{F}^{\times }\cap F_{\infty }^{\times \circ }$.
$\det (F^{\times } \cap K K_{\infty }^{\circ } )\subset \mathcal {O}_{F}^{\times }\cap F_{\infty }^{\times \circ }$.
In order to attach a sheaf to ![]() $V^{\mu }_{\mathcal {O}}$ we need a slightly different construction. Given a left
$V^{\mu }_{\mathcal {O}}$ we need a slightly different construction. Given a left ![]() $K$-module
$K$-module ![]() $V$ satisfying (15) define
$V$ satisfying (15) define ![]() $\mathcal {V}_K$ instead as the sheaf of locally constant sections of
$\mathcal {V}_K$ instead as the sheaf of locally constant sections of
with left ![]() $G(\mathbb {Q})$-action and right
$G(\mathbb {Q})$-action and right ![]() $K K_{\infty }^{\circ }$-action given by
$K K_{\infty }^{\circ }$-action given by ![]() $\gamma (g,v)k=(\gamma g k , k^{-1}\cdot v)$. As
$\gamma (g,v)k=(\gamma g k , k^{-1}\cdot v)$. As ![]() $K$ acts on
$K$ acts on ![]() $V^{\mu }_{\mathcal {O}}$ through its
$V^{\mu }_{\mathcal {O}}$ through its ![]() $p$-component
$p$-component ![]() $K_p\subset G(\mathbb {Z}_p)\subset G(\mathcal {O})$ we obtain a sheaf
$K_p\subset G(\mathbb {Z}_p)\subset G(\mathcal {O})$ we obtain a sheaf ![]() $\mathcal {V}_{\mathcal {O}}^{\mu }$ on
$\mathcal {V}_{\mathcal {O}}^{\mu }$ on ![]() ${S^{G}_K}$.
${S^{G}_K}$.
When the actions of ![]() $G(\mathbb {Q})$ and
$G(\mathbb {Q})$ and ![]() $K$ on
$K$ on ![]() $V$ extend compatibly into a left action of
$V$ extend compatibly into a left action of ![]() $G(\mathbb {A})$, the two resulting local systems are isomorphic by
$G(\mathbb {A})$, the two resulting local systems are isomorphic by ![]() $(g,v)\mapsto (g,g^{-1}\cdot v)$, justifying the abuse of notation.
$(g,v)\mapsto (g,g^{-1}\cdot v)$, justifying the abuse of notation.
1.4 Hecke operators
For any open compact subgroups ![]() $K'\subseteq K$ of
$K'\subseteq K$ of ![]() $G(\mathbb {A}_f)$ the natural map
$G(\mathbb {A}_f)$ the natural map ![]() $p_{K',K} : S^{G}_{K'}\to {S^{G}_K}$ induces an isomorphism of sheaves
$p_{K',K} : S^{G}_{K'}\to {S^{G}_K}$ induces an isomorphism of sheaves ![]() $p_{K',K}^{*}\mathcal {V}_K\overset {\sim }{\to } \mathcal {V}_{K'}$.
$p_{K',K}^{*}\mathcal {V}_K\overset {\sim }{\to } \mathcal {V}_{K'}$.
When the ![]() $K$-action on
$K$-action on ![]() $V$ extends to an action of a semi-group containing
$V$ extends to an action of a semi-group containing ![]() $K$ and
$K$ and ![]() $\gamma$, then one can define a Hecke operator
$\gamma$, then one can define a Hecke operator ![]() $[K\gamma K]$ as a composition of three maps:
$[K\gamma K]$ as a composition of three maps:
where ![]() $p_{K\cap \gamma ^{-1}K\gamma ,K}^{*}$ is the pull-back,
$p_{K\cap \gamma ^{-1}K\gamma ,K}^{*}$ is the pull-back, ![]() $\mathrm {Tr}(p_{\gamma K\gamma ^{-1}\cap K,K})$ is the finite flat trace and
$\mathrm {Tr}(p_{\gamma K\gamma ^{-1}\cap K,K})$ is the finite flat trace and
is induced by the morphism of local systems given by ![]() $(g,v)\mapsto (g\gamma ^{-1}, \gamma \cdot v)$ in the case of a right
$(g,v)\mapsto (g\gamma ^{-1}, \gamma \cdot v)$ in the case of a right ![]() $K$-action.
$K$-action.
When ![]() $K_p\subset J_p$, the above construction applies to
$K_p\subset J_p$, the above construction applies to ![]() $V^{\mu }_{\mathcal {O}}$ on which the semi-group
$V^{\mu }_{\mathcal {O}}$ on which the semi-group ![]() $\Lambda _p$ acts by the
$\Lambda _p$ acts by the ![]() $\bullet$-action (see (11)) yielding for each
$\bullet$-action (see (11)) yielding for each ![]() $t\in \Delta _p^{+}$ a Hecke operator
$t\in \Delta _p^{+}$ a Hecke operator ![]() $[KtK]$ on
$[KtK]$ on ![]() $\operatorname {H}_c^{q}({S^{G}_K},\mathcal {V}_{K,\mathcal {O}}^{\mu })$. Note that although the natural inclusion
$\operatorname {H}_c^{q}({S^{G}_K},\mathcal {V}_{K,\mathcal {O}}^{\mu })$. Note that although the natural inclusion ![]() $V^{\mu }_{\mathcal {O}}\subseteq V^{\mu }_{E}$ is
$V^{\mu }_{\mathcal {O}}\subseteq V^{\mu }_{E}$ is ![]() $K_p$-equivariant, it is not
$K_p$-equivariant, it is not ![]() $\Lambda _p$-equivariant (see (12)). As a consequence, the natural map
$\Lambda _p$-equivariant (see (12)). As a consequence, the natural map ![]() $\operatorname {H}_c^{q}({S^{G}_K},\mathcal {V}_{K,\mathcal {O}}^{\mu })\to \operatorname {H}_c^{q}({S^{G}_K},\mathcal {V}_{K,E}^{\mu })$ is equivariant for the
$\operatorname {H}_c^{q}({S^{G}_K},\mathcal {V}_{K,\mathcal {O}}^{\mu })\to \operatorname {H}_c^{q}({S^{G}_K},\mathcal {V}_{K,E}^{\mu })$ is equivariant for the ![]() $\bullet$-action of
$\bullet$-action of ![]() $[KtK]$ on the source and the action of the optimally integral Hecke operator
$[KtK]$ on the source and the action of the optimally integral Hecke operator ![]() $[KtK]^{\circ }=\mu ^{\vee }(t)[KtK]$ on the target. To ensure compatibility with extension of scalars, we also denote by
$[KtK]^{\circ }=\mu ^{\vee }(t)[KtK]$ on the target. To ensure compatibility with extension of scalars, we also denote by ![]() $[KtK]^{\circ }$ the Hecke operator
$[KtK]^{\circ }$ the Hecke operator ![]() $[KtK]$ acting (via the
$[KtK]$ acting (via the ![]() $\bullet$-action) on
$\bullet$-action) on ![]() $\operatorname {H}_c^{q}({S^{G}_K},\mathcal {V}_{K,\mathcal {O}}^{\mu })$.
$\operatorname {H}_c^{q}({S^{G}_K},\mathcal {V}_{K,\mathcal {O}}^{\mu })$.
For any prime ![]() $\mathfrak {p}\mid p$ of
$\mathfrak {p}\mid p$ of ![]() $F$, the following Hecke operators play an important role:
$F$, the following Hecke operators play an important role:
For ![]() $\beta =(\beta _\mathfrak {p})_{\mathfrak {p}\mid p}$ with
$\beta =(\beta _\mathfrak {p})_{\mathfrak {p}\mid p}$ with ![]() $\beta _\mathfrak {p}\in \mathbb {Z}_{\geqslant 0}$ we let
$\beta _\mathfrak {p}\in \mathbb {Z}_{\geqslant 0}$ we let ![]() $U_{p^{\beta }} = [K t_{p^{\beta }} K]$ and
$U_{p^{\beta }} = [K t_{p^{\beta }} K]$ and ![]() $U_{p^{\beta }}^{\circ }=\mu ^{\vee }(t_{p^{\beta }}) U_{p^{\beta }}.$
$U_{p^{\beta }}^{\circ }=\mu ^{\vee }(t_{p^{\beta }}) U_{p^{\beta }}.$
As the image of ![]() $\operatorname {H}^{q}_c({S^{G}_K}, \mathcal {V}_{\mathcal {O}}^{\mu })$ in
$\operatorname {H}^{q}_c({S^{G}_K}, \mathcal {V}_{\mathcal {O}}^{\mu })$ in ![]() $\operatorname {H}^{q}_c({S^{G}_K}, \mathcal {V}_{E}^{\mu })$ is a finitely generated
$\operatorname {H}^{q}_c({S^{G}_K}, \mathcal {V}_{E}^{\mu })$ is a finitely generated ![]() $\mathcal {O}$-module, we may assume that
$\mathcal {O}$-module, we may assume that ![]() $E$ is large enough so that all
$E$ is large enough so that all ![]() $U_{\mathfrak {p}}^{\circ }$-eigenvalues belong to
$U_{\mathfrak {p}}^{\circ }$-eigenvalues belong to ![]() $\mathcal {O}$.
$\mathcal {O}$.
2. Distributions attached to cohomology classes for GL2n
Let ![]() $F_p=F\otimes _\mathbb {Q}\mathbb {Q}_p=\prod _{\mathfrak {p} \mid p}F_{\mathfrak {p}}$. For a prime
$F_p=F\otimes _\mathbb {Q}\mathbb {Q}_p=\prod _{\mathfrak {p} \mid p}F_{\mathfrak {p}}$. For a prime ![]() $\mathfrak {p}\mid p$ of
$\mathfrak {p}\mid p$ of ![]() $F$ we denote by
$F$ we denote by ![]() $I_\mathfrak {p}$ (respectively,
$I_\mathfrak {p}$ (respectively, ![]() $J_\mathfrak {p}$) the standard Iwahori (respectively, parahoric) subgroup of
$J_\mathfrak {p}$) the standard Iwahori (respectively, parahoric) subgroup of ![]() $K_\mathfrak {p}^{\circ }=\operatorname {GL}_{2n}(\mathcal {O}_{F,\mathfrak {p}})$ consisting of elements whose reduction modulo the
$K_\mathfrak {p}^{\circ }=\operatorname {GL}_{2n}(\mathcal {O}_{F,\mathfrak {p}})$ consisting of elements whose reduction modulo the ![]() $\mathfrak {p}$ belongs to
$\mathfrak {p}$ belongs to ![]() $B(\mathcal {O}_{F}/{\mathfrak {p}})$ (respectively, to
$B(\mathcal {O}_{F}/{\mathfrak {p}})$ (respectively, to ![]() $Q(\mathcal {O}_{F}/{\mathfrak {p}})$).
$Q(\mathcal {O}_{F}/{\mathfrak {p}})$).
We let ![]() $K=K^{(p)}\times \prod _{\mathfrak {p}\mid p}K_\mathfrak {p}$ be an open compact subgroup of
$K=K^{(p)}\times \prod _{\mathfrak {p}\mid p}K_\mathfrak {p}$ be an open compact subgroup of ![]() $G(\mathbb {A}_f)$ such that:
$G(\mathbb {A}_f)$ such that:
(K1)
 $K^{(p)}$ is the principal congruence subgroup of modulus
$K^{(p)}$ is the principal congruence subgroup of modulus  $\mathfrak {m}$, an ideal of
$\mathfrak {m}$, an ideal of  $\mathcal {O}_F$ which is relatively prime to
$\mathcal {O}_F$ which is relatively prime to  $p$, and
$p$, and  $K^{(p)}G(\mathbb {Z}_p)$ satisfies (14);
$K^{(p)}G(\mathbb {Z}_p)$ satisfies (14);(K2)
 $\big (\begin {smallmatrix} T_n(\mathcal {O}_{F,\mathfrak {p}}) & M_n(\mathcal {O}_{F,\mathfrak {p}}) \\ \textbf {0}_n & T_n(\mathcal {O}_{F,\mathfrak {p}}) \end {smallmatrix}\big ) \subseteq K_\mathfrak {p} \subseteq J_\mathfrak {p}$ for all
$\big (\begin {smallmatrix} T_n(\mathcal {O}_{F,\mathfrak {p}}) & M_n(\mathcal {O}_{F,\mathfrak {p}}) \\ \textbf {0}_n & T_n(\mathcal {O}_{F,\mathfrak {p}}) \end {smallmatrix}\big ) \subseteq K_\mathfrak {p} \subseteq J_\mathfrak {p}$ for all  $\mathfrak {p} \mid p$.
$\mathfrak {p} \mid p$.
An important role will be played by the matrix ![]() $\xi \in \operatorname {GL}_{2n}(\mathbb {A}_F)$, where
$\xi \in \operatorname {GL}_{2n}(\mathbb {A}_F)$, where
Here ![]() $\textbf {1}_n$ and
$\textbf {1}_n$ and ![]() $\textbf {0}_n$ are the
$\textbf {0}_n$ are the ![]() $n \times n$ identity and zero matrices, respectively, and
$n \times n$ identity and zero matrices, respectively, and ![]() $w_n$ is the longest length element in the Weyl group of
$w_n$ is the longest length element in the Weyl group of ![]() $\operatorname {GL}_n,$ whose
$\operatorname {GL}_n,$ whose ![]() $(i,j)$-entry is
$(i,j)$-entry is ![]() $\delta _{i, n-j+1}$.
$\delta _{i, n-j+1}$.
We have ![]() $\xi _{\mathfrak {p}}^{-1} = \big (\begin {smallmatrix} \textbf {1}_n & -\textbf {1}_n\\ \textbf {0}_n & w_n \end {smallmatrix}\big )$. Once and for all we record the identities
$\xi _{\mathfrak {p}}^{-1} = \big (\begin {smallmatrix} \textbf {1}_n & -\textbf {1}_n\\ \textbf {0}_n & w_n \end {smallmatrix}\big )$. Once and for all we record the identities
 \begin{equation} \xi_{\mathfrak{p}}^{-1}\cdot\begin{pmatrix}A & B\\ C & D\end{pmatrix}\cdot\xi_{\mathfrak{p}} = \begin{pmatrix}A-C & (A-D+B-C)w_n \\ w_n C & w_n (C+D) w_n\end{pmatrix} \end{equation}
\begin{equation} \xi_{\mathfrak{p}}^{-1}\cdot\begin{pmatrix}A & B\\ C & D\end{pmatrix}\cdot\xi_{\mathfrak{p}} = \begin{pmatrix}A-C & (A-D+B-C)w_n \\ w_n C & w_n (C+D) w_n\end{pmatrix} \end{equation}and
 \begin{equation}\xi_{\mathfrak{p}}\cdot\begin{pmatrix}A & B\\ C & D\end{pmatrix}\cdot\xi_{\mathfrak{p}}^{-1} = \begin{pmatrix}A+w_nC & w_n D w_n-A+Bw_n-w_nC \\ w_n C & w_n D w_n-w_nC\end{pmatrix}. \end{equation}
\begin{equation}\xi_{\mathfrak{p}}\cdot\begin{pmatrix}A & B\\ C & D\end{pmatrix}\cdot\xi_{\mathfrak{p}}^{-1} = \begin{pmatrix}A+w_nC & w_n D w_n-A+Bw_n-w_nC \\ w_n C & w_n D w_n-w_nC\end{pmatrix}. \end{equation}2.1 Automorphic cycles
For any open-compact subgroup ![]() $L \subset H(\mathbb {A}_f)$ we consider the locally symmetric space:
$L \subset H(\mathbb {A}_f)$ we consider the locally symmetric space:
Note that for each ![]() $\sigma \in \Sigma _\infty$ one has
$\sigma \in \Sigma _\infty$ one has ![]() $L_\sigma ^{\circ } \simeq \big (\begin {smallmatrix}\operatorname {SO}_{n}(\mathbb {R}) & 0 \\ 0 & \operatorname {SO}_{n}(\mathbb {R}) \end {smallmatrix}\big )\mathbb {R}^{\times \circ }$. As in (14),
$L_\sigma ^{\circ } \simeq \big (\begin {smallmatrix}\operatorname {SO}_{n}(\mathbb {R}) & 0 \\ 0 & \operatorname {SO}_{n}(\mathbb {R}) \end {smallmatrix}\big )\mathbb {R}^{\times \circ }$. As in (14), ![]() $\tilde {S}^{H}_L$ is a real manifold when
$\tilde {S}^{H}_L$ is a real manifold when ![]() $L$ is sufficiently small in the sense that for all
$L$ is sufficiently small in the sense that for all ![]() $h\in H(\mathbb {A})$,
$h\in H(\mathbb {A})$,
Recall the notation ![]() $t_{\mathfrak {p}}= \iota (\varpi _{\mathfrak {p}}\cdot \textbf {1}_n,\textbf {1}_n)$ where
$t_{\mathfrak {p}}= \iota (\varpi _{\mathfrak {p}}\cdot \textbf {1}_n,\textbf {1}_n)$ where ![]() $\varpi _{\mathfrak {p}}$ is an uniformizer at
$\varpi _{\mathfrak {p}}$ is an uniformizer at ![]() $\mathfrak {p}\mid p$. Recall also that for
$\mathfrak {p}\mid p$. Recall also that for ![]() $\beta =(\beta _{\mathfrak {p}})_{\mathfrak {p}\mid p}$ with
$\beta =(\beta _{\mathfrak {p}})_{\mathfrak {p}\mid p}$ with ![]() $\beta _\mathfrak {p}\in \mathbb {Z}_{\geqslant 0}$ we let
$\beta _\mathfrak {p}\in \mathbb {Z}_{\geqslant 0}$ we let ![]() $p^{\beta }=\prod _{\mathfrak {p}\mid p}\varpi _{\mathfrak {p}}^{\beta _{\mathfrak {p}}}$ and
$p^{\beta }=\prod _{\mathfrak {p}\mid p}\varpi _{\mathfrak {p}}^{\beta _{\mathfrak {p}}}$ and ![]() $t_p^{\beta } = \prod _{\mathfrak {p}\mid p} t_{\mathfrak {p}}^{\beta _{\mathfrak {p}}} \in G(\mathbb {Q}_p)$.
$t_p^{\beta } = \prod _{\mathfrak {p}\mid p} t_{\mathfrak {p}}^{\beta _{\mathfrak {p}}} \in G(\mathbb {Q}_p)$.
For any ideal ![]() $\mathfrak {m}$ of
$\mathfrak {m}$ of ![]() $\mathcal {O}_F$, we denote by
$\mathcal {O}_F$, we denote by ![]() $I(\mathfrak {m})$ the open-compact subgroup of
$I(\mathfrak {m})$ the open-compact subgroup of ![]() $\mathbb {A}_{F,f}^{\times }$ of modulus
$\mathbb {A}_{F,f}^{\times }$ of modulus ![]() $\mathfrak {m}$, and we consider the strict idele class group:
$\mathfrak {m}$, and we consider the strict idele class group:
We let ![]() $L_\beta = L^{(p)} \prod _{\mathfrak {p}\mid p} L_\mathfrak {p}^{\beta _\mathfrak {p}}$ be an open compact subgroup of
$L_\beta = L^{(p)} \prod _{\mathfrak {p}\mid p} L_\mathfrak {p}^{\beta _\mathfrak {p}}$ be an open compact subgroup of ![]() $H(\mathbb {A}_f)$ such that:
$H(\mathbb {A}_f)$ such that:
(L1)
 $L^{(p)}=K^{(p)}\cap H$ is the principal congruence subgroup of modulus
$L^{(p)}=K^{(p)}\cap H$ is the principal congruence subgroup of modulus  $\mathfrak {m}$; and
$\mathfrak {m}$; and(L2)
 $L_\mathfrak {p}^{\beta _\mathfrak {p}}=H(F_\mathfrak {p})\cap K_\mathfrak {p}\cap \xi t_{\mathfrak {p}}^{\beta _\mathfrak {p}}K_\mathfrak {p} t_{\mathfrak {p}}^{-\beta _\mathfrak {p}}\xi ^{-1}$ for all
$L_\mathfrak {p}^{\beta _\mathfrak {p}}=H(F_\mathfrak {p})\cap K_\mathfrak {p}\cap \xi t_{\mathfrak {p}}^{\beta _\mathfrak {p}}K_\mathfrak {p} t_{\mathfrak {p}}^{-\beta _\mathfrak {p}}\xi ^{-1}$ for all  $\mathfrak {p} \mid p$.
$\mathfrak {p} \mid p$.
Note that conditions (K1) and (L1) imply (21), in particular that ![]() $\tilde {S}^{H}_{L_\beta }$ is a real manifold.
$\tilde {S}^{H}_{L_\beta }$ is a real manifold.
Lemma 2.1 ![]() $L_\mathfrak {p}^{\beta _\mathfrak {p}}$ consists of elements
$L_\mathfrak {p}^{\beta _\mathfrak {p}}$ consists of elements ![]() $(h_1 , h_2)\in \operatorname {GL}_n(\mathcal {O}_{F,\mathfrak {p}})\times \operatorname {GL}_n(\mathcal {O}_{F,\mathfrak {p}})$ such that
$(h_1 , h_2)\in \operatorname {GL}_n(\mathcal {O}_{F,\mathfrak {p}})\times \operatorname {GL}_n(\mathcal {O}_{F,\mathfrak {p}})$ such that
Proof. By (18) for all ![]() $(h_1,h_2) \in H(F_\mathfrak {p})\cap K_\mathfrak {p}=\operatorname {GL}_n(\mathcal {O}_{F,\mathfrak {p}})\times \operatorname {GL}_n(\mathcal {O}_{F,\mathfrak {p}})$ one has
$(h_1,h_2) \in H(F_\mathfrak {p})\cap K_\mathfrak {p}=\operatorname {GL}_n(\mathcal {O}_{F,\mathfrak {p}})\times \operatorname {GL}_n(\mathcal {O}_{F,\mathfrak {p}})$ one has
 \[ t_{\mathfrak{p}}^{-\beta_{\mathfrak{p}}} \xi^{-1} \begin{pmatrix}h_1 & \\ & h_2 \end{pmatrix}\xi t_{\mathfrak{p}}^{\beta_{\mathfrak{p}}}=\begin{pmatrix}h_1 & \varpi^{-\beta_{\mathfrak{p}}}(h_1 - h_2)w_n \\ & w_n h_2 w_n \end{pmatrix}. \]
\[ t_{\mathfrak{p}}^{-\beta_{\mathfrak{p}}} \xi^{-1} \begin{pmatrix}h_1 & \\ & h_2 \end{pmatrix}\xi t_{\mathfrak{p}}^{\beta_{\mathfrak{p}}}=\begin{pmatrix}h_1 & \varpi^{-\beta_{\mathfrak{p}}}(h_1 - h_2)w_n \\ & w_n h_2 w_n \end{pmatrix}. \]
Hence, ![]() $h_1- h_2 \in \varpi _\mathfrak {p}^{\beta _\mathfrak {p}}M_n(\mathcal {O}_{F,\mathfrak {p}})$, and as
$h_1- h_2 \in \varpi _\mathfrak {p}^{\beta _\mathfrak {p}}M_n(\mathcal {O}_{F,\mathfrak {p}})$, and as ![]() $\big (\begin {smallmatrix}\textbf {1}_n & M_n(\mathcal {O}_{F,\mathfrak {p}}) \\ \textbf {0}_n & \textbf {1}_n \end {smallmatrix}\big ) \subseteq K_\mathfrak {p}$, we obtain
$\big (\begin {smallmatrix}\textbf {1}_n & M_n(\mathcal {O}_{F,\mathfrak {p}}) \\ \textbf {0}_n & \textbf {1}_n \end {smallmatrix}\big ) \subseteq K_\mathfrak {p}$, we obtain ![]() $(h_1,w_n h_2 w_n)\in K_\mathfrak {p}$.
$(h_1,w_n h_2 w_n)\in K_\mathfrak {p}$.
Lemma 2.1 implies that the map ![]() $(1+ \varpi _\mathfrak {p}^{\beta _\mathfrak {p}}M_n(\mathcal {O}_{F,\mathfrak {p}}))\times \mathcal {O}_{F,\mathfrak {p}}^{\times } \to \det (L_\mathfrak {p}^{\beta _\mathfrak {p}})$ sending
$(1+ \varpi _\mathfrak {p}^{\beta _\mathfrak {p}}M_n(\mathcal {O}_{F,\mathfrak {p}}))\times \mathcal {O}_{F,\mathfrak {p}}^{\times } \to \det (L_\mathfrak {p}^{\beta _\mathfrak {p}})$ sending ![]() $(x,y)$ to
$(x,y)$ to ![]() $(xy,y)$ is an isomorphism. By the strong approximation theorem for
$(xy,y)$ is an isomorphism. By the strong approximation theorem for ![]() $\operatorname {SL}_{n}(\mathbb {A}_F)$ the map
$\operatorname {SL}_{n}(\mathbb {A}_F)$ the map
identifies the set of connected components of ![]() $\tilde {S}^{H}_{L_\beta }$ with a product of two idele class groups:
$\tilde {S}^{H}_{L_\beta }$ with a product of two idele class groups:
It is easy to see that the fiber ![]() $\tilde {S}^{H}_{L_\beta }[\delta ]$ of
$\tilde {S}^{H}_{L_\beta }[\delta ]$ of ![]() $[\delta ]\in \pi _0(\tilde {S}^{H}_{L_\beta })$ is connected of dimension
$[\delta ]\in \pi _0(\tilde {S}^{H}_{L_\beta })$ is connected of dimension
If we consider a cohomology class on ![]() ${S^{G}_K}$ in degree
${S^{G}_K}$ in degree ![]() $t$, and pull it back to
$t$, and pull it back to ![]() $\tilde {S}^{H}_{L_\beta }[\delta ]$, then we end up with a top-degree class. The degree
$\tilde {S}^{H}_{L_\beta }[\delta ]$, then we end up with a top-degree class. The degree ![]() $t$ happens to be the top-most degree with non-vanishing cuspidal cohomology of
$t$ happens to be the top-most degree with non-vanishing cuspidal cohomology of ![]() ${S^{G}_K}$. This magical numerology is at the heart of what ultimately permits us to give a cohomological interpretation to an integral representing an
${S^{G}_K}$. This magical numerology is at the heart of what ultimately permits us to give a cohomological interpretation to an integral representing an ![]() $L$-value (see [Reference Grobner and RaghuramGR14]) and allows us to study its
$L$-value (see [Reference Grobner and RaghuramGR14]) and allows us to study its ![]() $p$-adic properties.
$p$-adic properties.
2.2 Evaluation maps
Fix ![]() $\mu \in X^{*}_0(T)$.
$\mu \in X^{*}_0(T)$.
2.2.1 Automorphic symbols
By condition (L2), the map
is well-defined. As ![]() $\iota _\beta$ is proper by a well-known result of Borel and Prasad (see, for example, [Reference AshAsh80, Lemma 2.7]) one can consider the pull-back:
$\iota _\beta$ is proper by a well-known result of Borel and Prasad (see, for example, [Reference AshAsh80, Lemma 2.7]) one can consider the pull-back:
2.2.2 Twisting
By condition (L1), the map ![]() $\iota : \tilde {S}^{H}_{L_\beta } \to {S^{G}_K}$,
$\iota : \tilde {S}^{H}_{L_\beta } \to {S^{G}_K}$, ![]() $[h]\mapsto [\iota (h)]$ is well-defined and proper. As
$[h]\mapsto [\iota (h)]$ is well-defined and proper. As ![]() $\xi t_p^{\beta }\in \Lambda _p$, using the
$\xi t_p^{\beta }\in \Lambda _p$, using the ![]() $\bullet$-action from (12) one can consider the map
$\bullet$-action from (12) one can consider the map
inducing a homomorphism of sheaves ![]() $\tau _\beta ^{\circ } : \iota _\beta ^{*}\mathcal {V}_{\mathcal {O}}^{\mu } \longrightarrow \iota ^{*}\mathcal {V}_{\mathcal {O}}^{\mu }$, hence a map in cohomology
$\tau _\beta ^{\circ } : \iota _\beta ^{*}\mathcal {V}_{\mathcal {O}}^{\mu } \longrightarrow \iota ^{*}\mathcal {V}_{\mathcal {O}}^{\mu }$, hence a map in cohomology
Similarly, using the natural action of ![]() $G(E)$ on
$G(E)$ on ![]() $V_{E}^{\mu }$ instead of the
$V_{E}^{\mu }$ instead of the ![]() $\bullet$-action one defines a map
$\bullet$-action one defines a map
and ![]() $\tau _\beta =\mu ^{\vee }(t_p^{-\beta })\tau _\beta ^{\circ }$, because by (12) one has
$\tau _\beta =\mu ^{\vee }(t_p^{-\beta })\tau _\beta ^{\circ }$, because by (12) one has ![]() $(\xi t_p^{\beta }) \bullet v= \mu ^{\vee }(t_p^{\beta }) (\xi t_p^{\beta })\cdot v$ for all
$(\xi t_p^{\beta }) \bullet v= \mu ^{\vee }(t_p^{\beta }) (\xi t_p^{\beta })\cdot v$ for all ![]() $v\in V_{E}^{\mu }$.
$v\in V_{E}^{\mu }$.
2.2.3 Critical maps
For ![]() $j_1,j_2 \in \mathbb {Z}$ let
$j_1,j_2 \in \mathbb {Z}$ let ![]() $V^{(j_1,j_2)}$ be the
$V^{(j_1,j_2)}$ be the ![]() $1$-dimensional
$1$-dimensional ![]() $H$-representation
$H$-representation
Let ![]() $V^{(j_1,j_2)}_{\mathcal {O}}$ be a free rank one
$V^{(j_1,j_2)}_{\mathcal {O}}$ be a free rank one ![]() $\mathcal {O}$-module on which the previously defined natural
$\mathcal {O}$-module on which the previously defined natural ![]() $H(\mathbb {Z}_p)$-action is extended to a
$H(\mathbb {Z}_p)$-action is extended to a ![]() $H(\mathbb {Q}_p)$-action by letting
$H(\mathbb {Q}_p)$-action by letting ![]() $p\in \mathbb {Q}_p^{\times }$ act trivially. Note that this action is similar to the
$p\in \mathbb {Q}_p^{\times }$ act trivially. Note that this action is similar to the ![]() $\Lambda _p$-action on
$\Lambda _p$-action on ![]() $V^{\mu }_{\mathcal {O}}$ defined in § 1.2.
$V^{\mu }_{\mathcal {O}}$ defined in § 1.2.
It follows from [Reference Grobner and RaghuramGR14, Proposition 6.3] that ![]() $j \in \operatorname {Crit}(\mu )$ (see (4)) if and only if
$j \in \operatorname {Crit}(\mu )$ (see (4)) if and only if
Fix a non-zero ![]() $\kappa _j \in \operatorname {Hom}_H(V^{\mu }, V^{(j,{{\sf w}}-j)})$ normalized so as to obtain an integral map:
$\kappa _j \in \operatorname {Hom}_H(V^{\mu }, V^{(j,{{\sf w}}-j)})$ normalized so as to obtain an integral map:
Denoting by ![]() $\mathcal {V}^{(j,{{\sf w}}-j)}_{\mathcal {O}}$ the sheaf on
$\mathcal {V}^{(j,{{\sf w}}-j)}_{\mathcal {O}}$ the sheaf on ![]() $\tilde {S}^{H}_{L_\beta }$ attached to
$\tilde {S}^{H}_{L_\beta }$ attached to ![]() $V^{(j,{{\sf w}}-j)}_{\mathcal {O}}$ by the construction described in § 1.3, one obtains a homomorphism:
$V^{(j,{{\sf w}}-j)}_{\mathcal {O}}$ by the construction described in § 1.3, one obtains a homomorphism:
Putting (25), (26) and (29) together, for each ![]() $j \in \operatorname {Crit}(\mu )$, we obtain a map:
$j \in \operatorname {Crit}(\mu )$, we obtain a map:
2.2.4 Trivializations
Given any ![]() $\delta \in H(\mathbb {A}_f)$ the map
$\delta \in H(\mathbb {A}_f)$ the map
is well-defined because ![]() $H(\mathbb {Q})\cap L_\beta H_\infty ^{\circ }\subset \ker (\operatorname {N}_{F/\mathbb {Q}}\circ \det )$ acts trivially on
$H(\mathbb {Q})\cap L_\beta H_\infty ^{\circ }\subset \ker (\operatorname {N}_{F/\mathbb {Q}}\circ \det )$ acts trivially on ![]() $V^{(j,{{\sf w}}-j)}_{\mathcal {O}}$. An easy check shows that
$V^{(j,{{\sf w}}-j)}_{\mathcal {O}}$. An easy check shows that ![]() $\operatorname {triv}_\delta$ induces a homomorphism of local systems
$\operatorname {triv}_\delta$ induces a homomorphism of local systems
where ![]() $[\delta ]$ denotes the image of
$[\delta ]$ denotes the image of ![]() $\delta$ in
$\delta$ in ![]() $\pi _0(\tilde {S}^{H}_{L_\beta })$, hence yields a homomorphism:
$\pi _0(\tilde {S}^{H}_{L_\beta })$, hence yields a homomorphism:
We now render the trivializations independent of the choice of ![]() $\delta \in [\delta ]\in \pi _0(\tilde {S}^{H}_{L_\beta })$. By definition, for any
$\delta \in [\delta ]\in \pi _0(\tilde {S}^{H}_{L_\beta })$. By definition, for any ![]() $\delta '\in H(\mathbb {Q}) \delta l H_\infty$ one has
$\delta '\in H(\mathbb {Q}) \delta l H_\infty$ one has
The ![]() $p$-adic cyclotomic character
$p$-adic cyclotomic character ![]() $\varepsilon$ seen as idele class character
$\varepsilon$ seen as idele class character ![]() $F^{\times } \backslash \mathbb {A}_F^{\times } \to \mathbb {Z}_p^{\times }$ sends
$F^{\times } \backslash \mathbb {A}_F^{\times } \to \mathbb {Z}_p^{\times }$ sends ![]() $y$ to
$y$ to ![]() $\operatorname {N}_{F_p/\mathbb {Q}_p}(y_p)|y_f|_F\prod _{\sigma \in \Sigma _\infty } {\rm sgn}(y_\sigma )$, is trivial on
$\operatorname {N}_{F_p/\mathbb {Q}_p}(y_p)|y_f|_F\prod _{\sigma \in \Sigma _\infty } {\rm sgn}(y_\sigma )$, is trivial on ![]() $F_\infty ^{\times \circ }$ and given by
$F_\infty ^{\times \circ }$ and given by ![]() $\operatorname {N}_{F_p/\mathbb {Q}_p}$ on
$\operatorname {N}_{F_p/\mathbb {Q}_p}$ on ![]() $(\mathcal {O}_{F}\otimes \mathbb {Z}_p)^{\times }$. Hence,
$(\mathcal {O}_{F}\otimes \mathbb {Z}_p)^{\times }$. Hence,
is independent of the particular choice of ![]() $\delta \in [\delta ]\in \pi _0(\tilde {S}^{H}_{L_\beta })$.
$\delta \in [\delta ]\in \pi _0(\tilde {S}^{H}_{L_\beta })$.
2.2.5 Connected components and fundamental classes
Recall that for each ![]() $[\delta ]\in \pi _0(\tilde {S}^{H}_{L_\beta })$,
$[\delta ]\in \pi _0(\tilde {S}^{H}_{L_\beta })$, ![]() $\tilde {S}^{H}_{L_\beta }[\delta ]$ is a
$\tilde {S}^{H}_{L_\beta }[\delta ]$ is a ![]() $t$-dimensional connected orientable real manifold and that choosing an orientation amounts to choosing a fundamental class, that is, a basis
$t$-dimensional connected orientable real manifold and that choosing an orientation amounts to choosing a fundamental class, that is, a basis ![]() $\theta _{[\delta ]}$ of its Borel–Moore homology
$\theta _{[\delta ]}$ of its Borel–Moore homology ![]() $H_{t}^{\mathrm {BM}}(\tilde {S}^{H}_{L_\beta }[\delta ])\simeq \mathbb {Z}$. We choose such orientations in a consistent manner when
$H_{t}^{\mathrm {BM}}(\tilde {S}^{H}_{L_\beta }[\delta ])\simeq \mathbb {Z}$. We choose such orientations in a consistent manner when ![]() $\beta$ and
$\beta$ and ![]() $[\delta ]$ vary as follows. First, we fix, once and for all, an ordered basis on the tangent space of the symmetric space
$[\delta ]$ vary as follows. First, we fix, once and for all, an ordered basis on the tangent space of the symmetric space ![]() $H_\infty ^{\circ }/L_\infty ^{\circ }$ yielding fundamental classes
$H_\infty ^{\circ }/L_\infty ^{\circ }$ yielding fundamental classes ![]() $\theta _{\beta }$ of the connected components of identity
$\theta _{\beta }$ of the connected components of identity ![]() $\tilde {S}^{H}_{L_\beta }[1]$, when
$\tilde {S}^{H}_{L_\beta }[1]$, when ![]() $\beta$ varies. Then for each
$\beta$ varies. Then for each ![]() $[\delta ]\in \pi _0(\tilde {S}^{H}_{L_\beta })$, we consider the isomorphism
$[\delta ]\in \pi _0(\tilde {S}^{H}_{L_\beta })$, we consider the isomorphism ![]() $\tilde {S}^{H}_{L_\beta }[1]\underset {\sim }{\overset {\cdot \delta }{\longrightarrow }} \tilde {S}^{H}_{L_\beta }[\delta ]$ and define
$\tilde {S}^{H}_{L_\beta }[1]\underset {\sim }{\overset {\cdot \delta }{\longrightarrow }} \tilde {S}^{H}_{L_\beta }[\delta ]$ and define ![]() $\theta _{[\delta ]}=\delta _*\theta _{\beta }$, which is clearly independent of the particular choice of
$\theta _{[\delta ]}=\delta _*\theta _{\beta }$, which is clearly independent of the particular choice of ![]() $\delta \in [\delta ]$. Capping with
$\delta \in [\delta ]$. Capping with ![]() $\theta _{[\delta ]}$ and fixing a basis of
$\theta _{[\delta ]}$ and fixing a basis of ![]() $V^{(j,{{\sf w}}-j)}_{\mathcal {O}}$ (later in (40) we fix a particular basis in order to compare evaluations at different
$V^{(j,{{\sf w}}-j)}_{\mathcal {O}}$ (later in (40) we fix a particular basis in order to compare evaluations at different ![]() $j$) yields an isomorphism:
$j$) yields an isomorphism:
Combining this with (30) and (32) gives homomorphisms:
 \begin{align} \begin{aligned} \mathcal{E}^{j,{{\sf w}}}_{\beta,\delta}&=(\!\cap \theta_{[\delta]}) \circ\operatorname{triv}_\delta^{*}\circ\kappa_j \circ \tau_\beta^{\circ}\circ \iota_\beta^{*}: \operatorname{H}^{t}_c({S^{G}_K}, \mathcal{V}_{\mathcal{O}}^{\mu})\to \mathcal{O},\\ \mathcal{E}^{j,{{\sf w}}}_{\beta, [\delta]}&= \varepsilon \big(\det(\delta_{1}^{j}\delta_{2}^{{{\sf w}}-j})\big) \cdot \mathcal{E}^{j,{{\sf w}}}_{\beta,\delta}=(\!\cap \theta_{[\delta]}) \circ \operatorname{triv}_{[\delta]}^{*} \circ\kappa_j \circ \tau_\beta^{\circ}\circ \iota_\beta^{*} : \operatorname{H}^{t}_c({S^{G}_K}, \mathcal{V}_{\mathcal{O}}^{\mu})\to \mathcal{O}.\end{aligned} \end{align}
\begin{align} \begin{aligned} \mathcal{E}^{j,{{\sf w}}}_{\beta,\delta}&=(\!\cap \theta_{[\delta]}) \circ\operatorname{triv}_\delta^{*}\circ\kappa_j \circ \tau_\beta^{\circ}\circ \iota_\beta^{*}: \operatorname{H}^{t}_c({S^{G}_K}, \mathcal{V}_{\mathcal{O}}^{\mu})\to \mathcal{O},\\ \mathcal{E}^{j,{{\sf w}}}_{\beta, [\delta]}&= \varepsilon \big(\det(\delta_{1}^{j}\delta_{2}^{{{\sf w}}-j})\big) \cdot \mathcal{E}^{j,{{\sf w}}}_{\beta,\delta}=(\!\cap \theta_{[\delta]}) \circ \operatorname{triv}_{[\delta]}^{*} \circ\kappa_j \circ \tau_\beta^{\circ}\circ \iota_\beta^{*} : \operatorname{H}^{t}_c({S^{G}_K}, \mathcal{V}_{\mathcal{O}}^{\mu})\to \mathcal{O}.\end{aligned} \end{align}2.2.6 Summing over the second component
Consider a finite order ![]() $\mathcal {O}$-valued idele class character
$\mathcal {O}$-valued idele class character ![]() $\eta _0$ of
$\eta _0$ of ![]() $F$ that is trivial on
$F$ that is trivial on ![]() $I(\mathfrak {m})$, in particular unramified at all places above
$I(\mathfrak {m})$, in particular unramified at all places above ![]() $p$. The character
$p$. The character ![]() $\eta =\eta _0|\cdot |_F^{-{{\sf w}}}$ later plays a role when we discuss Shalika models for automorphic representations of
$\eta =\eta _0|\cdot |_F^{-{{\sf w}}}$ later plays a role when we discuss Shalika models for automorphic representations of ![]() $G$. The following map provides a section of (22):
$G$. The following map provides a section of (22):
When ![]() $(x,y)\in (\mathbb {A}_F^{\times })^{2}$ runs over a set of representatives of
$(x,y)\in (\mathbb {A}_F^{\times })^{2}$ runs over a set of representatives of ![]() $\mathscr {C}\!\ell _F^{+}(p^{\beta }\mathfrak {m})\times \mathscr {C}\!\ell _F^{+}(\mathfrak {m})$,
$\mathscr {C}\!\ell _F^{+}(p^{\beta }\mathfrak {m})\times \mathscr {C}\!\ell _F^{+}(\mathfrak {m})$, ![]() $\tilde {S}^{H}_{L_\beta }[\delta (x,y)]$ runs over the set of connected components of
$\tilde {S}^{H}_{L_\beta }[\delta (x,y)]$ runs over the set of connected components of ![]() $\tilde {S}^{H}_{L_\beta }.$ Define the level
$\tilde {S}^{H}_{L_\beta }.$ Define the level ![]() $\beta$ evaluation:
$\beta$ evaluation:
where the last sum runs over all ![]() $[x] \in \mathscr {C}\!\ell _F^{+}(p^{\beta }\mathfrak {m})$ mapping to
$[x] \in \mathscr {C}\!\ell _F^{+}(p^{\beta }\mathfrak {m})$ mapping to ![]() $[\bar x]$ under the natural projection.
$[\bar x]$ under the natural projection.
The following diagram recapitulates the steps in the construction of ![]() $\mathcal {E}^{j,\eta }_{\beta }$.
$\mathcal {E}^{j,\eta }_{\beta }$.

2.3 Distributions on  $\mathscr {C}\!\ell _F^{+}(p^{\infty })$
$\mathscr {C}\!\ell _F^{+}(p^{\infty })$
The object of this section is to relate when ![]() $\beta$ varies the evaluation maps
$\beta$ varies the evaluation maps ![]() $\mathcal {E}^{j,\eta }_{\beta }$ whose definition is summarized in (36).
$\mathcal {E}^{j,\eta }_{\beta }$ whose definition is summarized in (36).
2.3.1 The distributive property
Fix a ![]() $\beta =(\beta _{\mathfrak {p}})_{\mathfrak {p}\mid p}$ with
$\beta =(\beta _{\mathfrak {p}})_{\mathfrak {p}\mid p}$ with ![]() $\beta _{\mathfrak {p}}\in \mathbb {Z}_{>0}$ for all
$\beta _{\mathfrak {p}}\in \mathbb {Z}_{>0}$ for all ![]() $\mathfrak {p}\mid p$.
$\mathfrak {p}\mid p$.
Theorem 2.2 Given a prime ![]() $\mathfrak {p}\mid p$ we let
$\mathfrak {p}\mid p$ we let ![]() $p^{\beta '}=p^{\beta }\mathfrak {p}$ and consider the canonical projection
$p^{\beta '}=p^{\beta }\mathfrak {p}$ and consider the canonical projection ![]() $\operatorname {pr}_{\beta ',\beta } : \mathscr {C}\!\ell _F^{+}(p^{\beta '}) \to \mathscr {C}\!\ell _F^{+}(p^{\beta })$. For all
$\operatorname {pr}_{\beta ',\beta } : \mathscr {C}\!\ell _F^{+}(p^{\beta '}) \to \mathscr {C}\!\ell _F^{+}(p^{\beta })$. For all ![]() $[x] \in \mathscr {C}\!\ell _F^{+}(p^{\beta })$ we have
$[x] \in \mathscr {C}\!\ell _F^{+}(p^{\beta })$ we have ![]() $\mathcal {E}^{j,\eta }_{\beta }\circ U_\mathfrak {p}^{\circ }=\operatorname {pr}_{\beta ',\beta }\circ \mathcal {E}^{j,\eta }_{\beta '},$ that is,
$\mathcal {E}^{j,\eta }_{\beta }\circ U_\mathfrak {p}^{\circ }=\operatorname {pr}_{\beta ',\beta }\circ \mathcal {E}^{j,\eta }_{\beta '},$ that is,
 \[ \mathcal{E}^{j,\eta}_{\beta,[x]}\circ U_\mathfrak{p}^{\circ} = \sum_{[x'] \in \operatorname{pr}_{\beta',\beta}^{-1}([x])} \mathcal{E}^{j,\eta}_{\beta',[x']}. \]
\[ \mathcal{E}^{j,\eta}_{\beta,[x]}\circ U_\mathfrak{p}^{\circ} = \sum_{[x'] \in \operatorname{pr}_{\beta',\beta}^{-1}([x])} \mathcal{E}^{j,\eta}_{\beta',[x']}. \]Proof. Using (33), (34), and (35) one has to show that for all ![]() $[x] \in \mathscr {C}\!\ell _F^{+}(p^{\beta }\mathfrak {m}), [y]\in \mathscr {C}\!\ell _F^{+}(\mathfrak {m})$:
$[x] \in \mathscr {C}\!\ell _F^{+}(p^{\beta }\mathfrak {m}), [y]\in \mathscr {C}\!\ell _F^{+}(\mathfrak {m})$:
 \[ \mathcal{E}^{j,{{\sf w}}}_{\beta,\delta(x,y)}\circ U_\mathfrak{p}^{\circ} = \sum_{[x'] \in \operatorname{pr}_{\beta',\beta}^{-1}([x])} \operatorname{N}_{F_p/\mathbb{Q}_p}^{j}(u_{x'})\cdot \mathcal{E}^{j,{{\sf w}}}_{\beta',\delta(x',y)}, \]
\[ \mathcal{E}^{j,{{\sf w}}}_{\beta,\delta(x,y)}\circ U_\mathfrak{p}^{\circ} = \sum_{[x'] \in \operatorname{pr}_{\beta',\beta}^{-1}([x])} \operatorname{N}_{F_p/\mathbb{Q}_p}^{j}(u_{x'})\cdot \mathcal{E}^{j,{{\sf w}}}_{\beta',\delta(x',y)}, \]
where ![]() $u_{x'}\in I(p^{\beta })$ is such that
$u_{x'}\in I(p^{\beta })$ is such that ![]() $x'\in F^{\times } x u_{x'} F_\infty ^{\times \circ }$. We proceed as in the proof of [Reference Barrera, Dimitrov and JorzaBDJ, Proposition 3.4]. Pulling back the definition of the Hecke operator
$x'\in F^{\times } x u_{x'} F_\infty ^{\times \circ }$. We proceed as in the proof of [Reference Barrera, Dimitrov and JorzaBDJ, Proposition 3.4]. Pulling back the definition of the Hecke operator ![]() $U_\mathfrak {p}^{\circ }$ (see § 1.4) by the automorphic symbols (see § 2.2.1) and the twisting operators (see § 2.2.2) yields the following commutative diagram (we use implicitly that
$U_\mathfrak {p}^{\circ }$ (see § 1.4) by the automorphic symbols (see § 2.2.1) and the twisting operators (see § 2.2.2) yields the following commutative diagram (we use implicitly that ![]() $p_{K^{0}(\mathfrak {p}),K}$ and
$p_{K^{0}(\mathfrak {p}),K}$ and ![]() $\operatorname {pr}_{\beta ',\beta }$ have the same degree as
$\operatorname {pr}_{\beta ',\beta }$ have the same degree as ![]() $L_{\beta }/L_{\beta '}\simeq M_n(\mathcal {O}/\mathfrak {p})$)
$L_{\beta }/L_{\beta '}\simeq M_n(\mathcal {O}/\mathfrak {p})$)

where the upper ![]() $[t_\mathfrak {p}]$ is induced by the morphism
$[t_\mathfrak {p}]$ is induced by the morphism ![]() $(g,v)\mapsto (g\cdot t_\mathfrak {p}^{-1}, t_\mathfrak {p}\bullet v)$ of local systems, whereas the lower
$(g,v)\mapsto (g\cdot t_\mathfrak {p}^{-1}, t_\mathfrak {p}\bullet v)$ of local systems, whereas the lower ![]() $[t_\mathfrak {p}]$ is induced by the morphism
$[t_\mathfrak {p}]$ is induced by the morphism ![]() $(h,v)\mapsto (h, t_\mathfrak {p}\bullet v)$. Then
$(h,v)\mapsto (h, t_\mathfrak {p}\bullet v)$. Then

is another commutative diagram by (31), hence the claim.
2.3.2 Distributions for finite slope eigenvectors
Let ![]() $\phi \in \operatorname {H}^{t}_c({S^{G}_K}, \mathcal {V}_{\mathcal {O}}^{\mu })$ be an eigenvector for
$\phi \in \operatorname {H}^{t}_c({S^{G}_K}, \mathcal {V}_{\mathcal {O}}^{\mu })$ be an eigenvector for ![]() $U_{\mathfrak {p}}^{\circ }$ with eigenvalue
$U_{\mathfrak {p}}^{\circ }$ with eigenvalue ![]() $\alpha _\mathfrak {p}^{\circ }$ for all
$\alpha _\mathfrak {p}^{\circ }$ for all ![]() $\mathfrak {p}\mid p$. Then, for all
$\mathfrak {p}\mid p$. Then, for all ![]() $\beta =(\beta _\mathfrak {p})_{\mathfrak {p}\mid p}$, it is an eigenvector for
$\beta =(\beta _\mathfrak {p})_{\mathfrak {p}\mid p}$, it is an eigenvector for ![]() $U_{p^{\beta }}^{\circ }$ with eigenvalue
$U_{p^{\beta }}^{\circ }$ with eigenvalue ![]() $\alpha _{p^{\beta }}^{\circ }=\prod _{\mathfrak {p}\mid p}(\alpha _\mathfrak {p}^{\circ })^{\beta _\mathfrak {p}}$. We say that
$\alpha _{p^{\beta }}^{\circ }=\prod _{\mathfrak {p}\mid p}(\alpha _\mathfrak {p}^{\circ })^{\beta _\mathfrak {p}}$. We say that ![]() $\phi$ is of finite slope if
$\phi$ is of finite slope if ![]() $\alpha _{p}^{\circ } \neq 0$ and in which case we define its slope as
$\alpha _{p}^{\circ } \neq 0$ and in which case we define its slope as ![]() $v_p(\alpha _p^{\circ })$. A eigenvector
$v_p(\alpha _p^{\circ })$. A eigenvector ![]() $\phi$ of slope
$\phi$ of slope ![]() $0$ is called
$0$ is called ![]() $Q$-ordinary. Being
$Q$-ordinary. Being ![]() $Q$-ordinary is equivalent to saying that the
$Q$-ordinary is equivalent to saying that the ![]() $U_{\mathfrak {p}}$-eigenvalue
$U_{\mathfrak {p}}$-eigenvalue ![]() $\alpha _\mathfrak {p}$ satisfies
$\alpha _\mathfrak {p}$ satisfies ![]() $|\alpha _\mathfrak {p}|_p = |\mu ^{\vee }(t_\mathfrak {p})|_p^{-1}$ for all
$|\alpha _\mathfrak {p}|_p = |\mu ^{\vee }(t_\mathfrak {p})|_p^{-1}$ for all ![]() $\mathfrak {p}\mid p$ (see § 4.2 for more details).
$\mathfrak {p}\mid p$ (see § 4.2 for more details).
Given any ![]() $U_p$-eigenvector
$U_p$-eigenvector ![]() $\phi$ of finite slope and any
$\phi$ of finite slope and any ![]() $j\in \operatorname {Crit}(\mu )$ by Theorem 2.2 one has a well-defined element
$j\in \operatorname {Crit}(\mu )$ by Theorem 2.2 one has a well-defined element
which is thought of as an ![]() $E$-valued distribution on
$E$-valued distribution on ![]() $\mathscr {C}\!\ell _F^{+}(p^{\infty })$.
$\mathscr {C}\!\ell _F^{+}(p^{\infty })$.
We write ![]() $\operatorname {H}^{t}_c({S^{G}_K}, \mathcal {V}_{\mathcal {O}}^{\mu })^{Q-\mathrm {ord}}$ for the maximal
$\operatorname {H}^{t}_c({S^{G}_K}, \mathcal {V}_{\mathcal {O}}^{\mu })^{Q-\mathrm {ord}}$ for the maximal ![]() $\mathcal {O}$-submodule of
$\mathcal {O}$-submodule of ![]() $\operatorname {H}^{t}_c({S^{G}_K}, \mathcal {V}_{\mathcal {O}}^{\mu })$ on which the operators
$\operatorname {H}^{t}_c({S^{G}_K}, \mathcal {V}_{\mathcal {O}}^{\mu })$ on which the operators ![]() $U_{\mathfrak {p}}^{\circ }$ are invertible for all
$U_{\mathfrak {p}}^{\circ }$ are invertible for all ![]() $\mathfrak {p}\mid p$ (it is a direct
$\mathfrak {p}\mid p$ (it is a direct ![]() $\mathcal {O}$-factor). Given any (not necessarily
$\mathcal {O}$-factor). Given any (not necessarily ![]() $U_p^{\circ }$-eigen) non-torsion element
$U_p^{\circ }$-eigen) non-torsion element ![]() $\phi \in \operatorname {H}^{t}_c({S^{G}_K}, \mathcal {V}_{\mathcal {O}}^{\mu })^{Q-\mathrm {ord}}$ one defines
$\phi \in \operatorname {H}^{t}_c({S^{G}_K}, \mathcal {V}_{\mathcal {O}}^{\mu })^{Q-\mathrm {ord}}$ one defines
which can be reinterpreted as a measure (i.e. a bounded distribution) on ![]() $\mathscr {C}\!\ell _F^{+}(p^{\infty })$.
$\mathscr {C}\!\ell _F^{+}(p^{\infty })$.
2.4 Manin relations
Consider the ![]() $p$-adic cyclotomic character
$p$-adic cyclotomic character ![]() $\varepsilon : \mathscr {C}\!\ell _F^{+}(p^{\infty }) \to \mathbb {Z}_p^{\times }$ defined by composing the norm
$\varepsilon : \mathscr {C}\!\ell _F^{+}(p^{\infty }) \to \mathbb {Z}_p^{\times }$ defined by composing the norm ![]() $\operatorname {N}_{F/\mathbb {Q}}: \mathscr {C}\!\ell _F^{+}(p^{\infty })\to \mathcal {C}\ell _\mathbb {Q}^{+}(p^{\infty })$ with the
$\operatorname {N}_{F/\mathbb {Q}}: \mathscr {C}\!\ell _F^{+}(p^{\infty })\to \mathcal {C}\ell _\mathbb {Q}^{+}(p^{\infty })$ with the ![]() $p$-adic cyclotomic character over
$p$-adic cyclotomic character over ![]() $\mathbb {Q}$. In this section, we prove the following result.
$\mathbb {Q}$. In this section, we prove the following result.
Theorem 2.3 Let ![]() $\mu \in X^{*}_0(T)$ and suppose that
$\mu \in X^{*}_0(T)$ and suppose that ![]() $j$ and
$j$ and ![]() $j+1$ both belong to
$j+1$ both belong to ![]() $\operatorname {Crit}(\mu )$.
$\operatorname {Crit}(\mu )$.
For ![]() $\phi \in \operatorname {H}^{t}_c({S^{G}_K}, \mathcal {V}_{\mathcal {O}}^{\mu })^{Q-\mathrm {ord}}$ the following equality holds in
$\phi \in \operatorname {H}^{t}_c({S^{G}_K}, \mathcal {V}_{\mathcal {O}}^{\mu })^{Q-\mathrm {ord}}$ the following equality holds in ![]() $\mathcal {O}[[\mathscr {C}\!\ell _F^{+}(p^{\infty })]]$:
$\mathcal {O}[[\mathscr {C}\!\ell _F^{+}(p^{\infty })]]$:
where ![]() $\varepsilon _{\operatorname {cyc}}$ denotes the automorphism of
$\varepsilon _{\operatorname {cyc}}$ denotes the automorphism of ![]() $\mathcal {O}[[\mathscr {C}\!\ell _F^{+}(p^{\infty })]]$ sending
$\mathcal {O}[[\mathscr {C}\!\ell _F^{+}(p^{\infty })]]$ sending ![]() $[x]$ to
$[x]$ to ![]() $\varepsilon ([x])[x]$. Hence,
$\varepsilon ([x])[x]$. Hence,
is independent of ![]() $j\in \operatorname {Crit}(\mu )$.
$j\in \operatorname {Crit}(\mu )$.
The overdetermination of ![]() $\boldsymbol {\mu }^{\eta }_\phi$ in the
$\boldsymbol {\mu }^{\eta }_\phi$ in the ![]() $Q$-ordinary case, when there are at least two critical values, plays a pivotal role in the proof of main theorem. Before embarking on the proof of this theorem, we begin with some technical preparation (see [Reference JanuszewskiJan18, § 3]).
$Q$-ordinary case, when there are at least two critical values, plays a pivotal role in the proof of main theorem. Before embarking on the proof of this theorem, we begin with some technical preparation (see [Reference JanuszewskiJan18, § 3]).
2.4.1 Lie theoretic considerations
By the distributive property (see Theorem 2.2) we may reduce to strict ![]() $p^{\beta }$-power level with integral exponents
$p^{\beta }$-power level with integral exponents ![]() $\beta \in \mathbb {Z}_{>0},$ ignoring the finer components
$\beta \in \mathbb {Z}_{>0},$ ignoring the finer components ![]() $\mathfrak {p}\mid p$ for simplicity of notation. Recall that
$\mathfrak {p}\mid p$ for simplicity of notation. Recall that ![]() ${{\mathfrak {b}}}={{\mathfrak {t}}}\oplus {{\mathfrak {n}}}$ and
${{\mathfrak {b}}}={{\mathfrak {t}}}\oplus {{\mathfrak {n}}}$ and ![]() ${{\mathfrak {q}}}={{\mathfrak {h}}}\oplus {{\mathfrak {u}}}$. With the notation
${{\mathfrak {q}}}={{\mathfrak {h}}}\oplus {{\mathfrak {u}}}$. With the notation ![]() $t_p=\iota (p\textbf {1}_n,\textbf {1}_n)$, we observe for any
$t_p=\iota (p\textbf {1}_n,\textbf {1}_n)$, we observe for any ![]() $\beta \geqslant 0$ the relations
$\beta \geqslant 0$ the relations
Recall the matrix ![]() $\xi = \big (\begin {smallmatrix} \textbf {1}_n & w_n\\ \textbf {0}_n & w_n \end {smallmatrix}\big ).$ A superscript
$\xi = \big (\begin {smallmatrix} \textbf {1}_n & w_n\\ \textbf {0}_n & w_n \end {smallmatrix}\big ).$ A superscript ![]() ${}^{\xi }(-)$ denotes left conjugation action by
${}^{\xi }(-)$ denotes left conjugation action by ![]() $\xi$.
$\xi$.
Proposition 2.4 We have the relations:
(i)
 ${{\mathfrak {g}}}_\mathcal {O}={{\mathfrak {h}}}_\mathcal {O}+ {}^{\xi }\,{{\mathfrak {b}}}_\mathcal {O}^{-}$; and
${{\mathfrak {g}}}_\mathcal {O}={{\mathfrak {h}}}_\mathcal {O}+ {}^{\xi }\,{{\mathfrak {b}}}_\mathcal {O}^{-}$; and(ii)
 ${}^{\xi } \big ({{\mathfrak {n}}}_\mathcal {O}\cap {{\mathfrak {h}}}_\mathcal {O}\big ) \subseteq [{{\mathfrak {h}}},{{\mathfrak {h}}}]_\mathcal {O}+ {}^{\xi }\,{{\mathfrak {n}}}_\mathcal {O}^{-}$.
${}^{\xi } \big ({{\mathfrak {n}}}_\mathcal {O}\cap {{\mathfrak {h}}}_\mathcal {O}\big ) \subseteq [{{\mathfrak {h}}},{{\mathfrak {h}}}]_\mathcal {O}+ {}^{\xi }\,{{\mathfrak {n}}}_\mathcal {O}^{-}$.
Proof. (i) As ![]() $\xi \in G(\mathcal {O})$, it suffices to verify it over
$\xi \in G(\mathcal {O})$, it suffices to verify it over ![]() $E$, where it amounts to show that
$E$, where it amounts to show that ![]() $\dim _E({{\mathfrak {h}}}_E\cap {}^{\xi }\,{{\mathfrak {b}}}_E^{-}) = n$. To this end, let
$\dim _E({{\mathfrak {h}}}_E\cap {}^{\xi }\,{{\mathfrak {b}}}_E^{-}) = n$. To this end, let ![]() $l_1,l_2$ be lower triangular matrices in
$l_1,l_2$ be lower triangular matrices in ![]() $M_n(E)$ and
$M_n(E)$ and ![]() $u\in M_n(E)$. Then
$u\in M_n(E)$. Then
 \[ \xi\cdot \begin{pmatrix} l_1 & \\ u & l_2 \end{pmatrix}\cdot \xi^{-1} = \begin{pmatrix} l_1+w_nu & w_n l_2 w_n-l_1-w_nu\\ w_nu & w_n l_2 w_n-w_nu \end{pmatrix}, \]
\[ \xi\cdot \begin{pmatrix} l_1 & \\ u & l_2 \end{pmatrix}\cdot \xi^{-1} = \begin{pmatrix} l_1+w_nu & w_n l_2 w_n-l_1-w_nu\\ w_nu & w_n l_2 w_n-w_nu \end{pmatrix}, \]
lies in ![]() ${{\mathfrak {h}}}_E$ if and only if
${{\mathfrak {h}}}_E$ if and only if ![]() $u = 0$ and
$u = 0$ and ![]() $l_1 = w_n l_2 w_n$. Therefore,
$l_1 = w_n l_2 w_n$. Therefore, ![]() $l_1$ and
$l_1$ and ![]() $l_2$ are diagonal matrices determining each other uniquely.
$l_2$ are diagonal matrices determining each other uniquely.
(ii) Conjugation by ![]() $\xi ^{-1}$ reduces the claim to the problem of solving
$\xi ^{-1}$ reduces the claim to the problem of solving
 \[ \begin{pmatrix} n_1 & \\ & n_2 \end{pmatrix}= \begin{pmatrix} h_1 & (h_1-h_2)w_n\\ & w_n h_2 w_n \end{pmatrix} \;+\; \begin{pmatrix} \bar{n}_1 & \\ & \bar{n}_2 \end{pmatrix}, \]
\[ \begin{pmatrix} n_1 & \\ & n_2 \end{pmatrix}= \begin{pmatrix} h_1 & (h_1-h_2)w_n\\ & w_n h_2 w_n \end{pmatrix} \;+\; \begin{pmatrix} \bar{n}_1 & \\ & \bar{n}_2 \end{pmatrix}, \]
for given ![]() $\iota (n_1,n_2)\in {{\mathfrak {h}}}\cap {{\mathfrak {n}}}_\mathcal {O}$ and unknowns
$\iota (n_1,n_2)\in {{\mathfrak {h}}}\cap {{\mathfrak {n}}}_\mathcal {O}$ and unknowns ![]() $\iota (h_1,h_2)\in [{{\mathfrak {h}}}_\mathcal {O},{{\mathfrak {h}}}_\mathcal {O}]$ and
$\iota (h_1,h_2)\in [{{\mathfrak {h}}}_\mathcal {O},{{\mathfrak {h}}}_\mathcal {O}]$ and ![]() $\iota (\bar {n}_1,\bar {n}_2)\in {{\mathfrak {n}}}^{-}$. The choice
$\iota (\bar {n}_1,\bar {n}_2)\in {{\mathfrak {n}}}^{-}$. The choice
is a solution with the desired properties.
Corollary 2.5 For any ![]() $\beta \geqslant 0$, the following relations hold inside
$\beta \geqslant 0$, the following relations hold inside ![]() $\mathcal {U}({{\mathfrak {g}}}_\mathcal {O})$:
$\mathcal {U}({{\mathfrak {g}}}_\mathcal {O})$:
(i)
 $\mathcal {U}({{\mathfrak {g}}}_\mathcal {O})= \mathcal {U}({{\mathfrak {h}}}_\mathcal {O}) \cdot \mathcal {U}({}^{\xi } {{\mathfrak {b}}}_\mathcal {O}^{-})$; and
$\mathcal {U}({{\mathfrak {g}}}_\mathcal {O})= \mathcal {U}({{\mathfrak {h}}}_\mathcal {O}) \cdot \mathcal {U}({}^{\xi } {{\mathfrak {b}}}_\mathcal {O}^{-})$; and(ii)
 $\mathcal {U}({}^{\xi t_p^{\beta }}{{\mathfrak {n}}}_\mathcal {O})\subseteq \mathcal {U}([{{\mathfrak {h}}},{{\mathfrak {h}}}]_\mathcal {O}+p^{\beta }{{\mathfrak {h}}}_\mathcal {O})\cdot \mathcal {U}({}^{\xi }{{\mathfrak {n}}}_\mathcal {O}^{-} + p^{\beta } \, {}^{\xi }{{\mathfrak {b}}}_\mathcal {O}^{-})$.
$\mathcal {U}({}^{\xi t_p^{\beta }}{{\mathfrak {n}}}_\mathcal {O})\subseteq \mathcal {U}([{{\mathfrak {h}}},{{\mathfrak {h}}}]_\mathcal {O}+p^{\beta }{{\mathfrak {h}}}_\mathcal {O})\cdot \mathcal {U}({}^{\xi }{{\mathfrak {n}}}_\mathcal {O}^{-} + p^{\beta } \, {}^{\xi }{{\mathfrak {b}}}_\mathcal {O}^{-})$.
Proof. (i) This is a consequence of Proposition 2.4(i) and the Poincaré–Birkhoff–Witt theorem.
(ii) The decomposition ![]() ${{\mathfrak {n}}}_\mathcal {O} = ({{\mathfrak {h}}}_\mathcal {O}\cap {{\mathfrak {n}}}_\mathcal {O})\oplus {{\mathfrak {u}}}_\mathcal {O},$ gives
${{\mathfrak {n}}}_\mathcal {O} = ({{\mathfrak {h}}}_\mathcal {O}\cap {{\mathfrak {n}}}_\mathcal {O})\oplus {{\mathfrak {u}}}_\mathcal {O},$ gives ![]() $t_p^{\beta }{{\mathfrak {n}}}_\mathcal {O} t_p^{-\beta } = ({{\mathfrak {h}}}_\mathcal {O}\cap {{\mathfrak {n}}}_\mathcal {O})\oplus p^{\beta }{{\mathfrak {u}}}_\mathcal {O}$. Conjugating by
$t_p^{\beta }{{\mathfrak {n}}}_\mathcal {O} t_p^{-\beta } = ({{\mathfrak {h}}}_\mathcal {O}\cap {{\mathfrak {n}}}_\mathcal {O})\oplus p^{\beta }{{\mathfrak {u}}}_\mathcal {O}$. Conjugating by ![]() $\xi$, we obtain
$\xi$, we obtain
Applying Proposition 2.4(ii) to the first summand and Proposition 2.4(i) to the second we obtain
One concludes again by the Poincaré–Birkhoff–Witt theorem, because the sums within the parentheses on the right-hand side are Lie ![]() $\mathcal {O}$-algebras.
$\mathcal {O}$-algebras.
2.4.2 Lattices and the projection formula
Recall from (5) the lowest weight vector ![]() $v_0 \in V^{\mu }_{E}$ and the
$v_0 \in V^{\mu }_{E}$ and the ![]() $G(\mathcal {O})$-lattice
$G(\mathcal {O})$-lattice ![]() $V^{\mu }_{\mathcal {O}} = \mathcal {U}({{\mathfrak {g}}}_\mathcal {O})\cdot v_0 = \mathcal {U}({{\mathfrak {n}}}_\mathcal {O})\cdot v_0$. Recall also the
$V^{\mu }_{\mathcal {O}} = \mathcal {U}({{\mathfrak {g}}}_\mathcal {O})\cdot v_0 = \mathcal {U}({{\mathfrak {n}}}_\mathcal {O})\cdot v_0$. Recall also the ![]() $\bullet$-action of the semi-group
$\bullet$-action of the semi-group ![]() $\Lambda _p$ on
$\Lambda _p$ on ![]() $V^{\mu }_{\mathcal {O}}$ as in (12).
$V^{\mu }_{\mathcal {O}}$ as in (12).
Given ![]() $j \in \operatorname {Crit}(\mu )$ recall from § 2.2.3 the map
$j \in \operatorname {Crit}(\mu )$ recall from § 2.2.3 the map ![]() $\kappa _j: V^{\mu }_{\mathcal {O}} \to V^{(j,{{\sf w}}-j)}_{\mathcal {O}}$. By Corollary 2.5(i)
$\kappa _j: V^{\mu }_{\mathcal {O}} \to V^{(j,{{\sf w}}-j)}_{\mathcal {O}}$. By Corollary 2.5(i)
which implies that ![]() $\kappa _j(\xi v_0)$ is an
$\kappa _j(\xi v_0)$ is an ![]() $\mathcal {O}$-basis of
$\mathcal {O}$-basis of ![]() $V^{(j,{{\sf w}}-j)}_{\mathcal {O}}$ yielding a surjective
$V^{(j,{{\sf w}}-j)}_{\mathcal {O}}$ yielding a surjective ![]() $\mathcal {O}$-linear map
$\mathcal {O}$-linear map
It is independent from the choice of ![]() $\kappa _j$ because of (28), and
$\kappa _j$ because of (28), and ![]() $\kappa _j^{\circ }(\xi v_0)=1$. We now come to the main technical result that is at the heart of our proof of the Manin relations.
$\kappa _j^{\circ }(\xi v_0)=1$. We now come to the main technical result that is at the heart of our proof of the Manin relations.
Proposition 2.6 For any ![]() $\beta \geqslant 0$,
$\beta \geqslant 0$, ![]() $v\in (\xi t_p^{\beta })\bullet V^{\mu }_{\mathcal {O}} \subset V^{\mu }_{\mathcal {O}}$, and for all
$v\in (\xi t_p^{\beta })\bullet V^{\mu }_{\mathcal {O}} \subset V^{\mu }_{\mathcal {O}}$, and for all ![]() $j,j'\in \operatorname {Crit}(\mu )$, we have
$j,j'\in \operatorname {Crit}(\mu )$, we have
Proof. By (12) for ![]() $v\in (\xi t_p^{\beta })\bullet V^{\mu }_{\mathcal {O}}$ there exists
$v\in (\xi t_p^{\beta })\bullet V^{\mu }_{\mathcal {O}}$ there exists ![]() $m\in \mathcal {U}({{\mathfrak {n}}}_\mathcal {O})$ with
$m\in \mathcal {U}({{\mathfrak {n}}}_\mathcal {O})$ with
By Corollary 2.5(ii) we can write
Let ![]() $x_0, y_0 \in \mathcal {O}$ be the degree zero terms of
$x_0, y_0 \in \mathcal {O}$ be the degree zero terms of ![]() $x$ and
$x$ and ![]() $y$, respectively, and let
$y$, respectively, and let
 \begin{gather*} x_1 = x - x_0 \in ([{{\mathfrak{h}}},{{\mathfrak{h}}}]_\mathcal{O}+p^{\beta}{{\mathfrak{h}}})\cdot \mathcal{U}([{{\mathfrak{h}}},{{\mathfrak{h}}}]_\mathcal{O}+p^{\beta}{{\mathfrak{h}}}),\\ y_1 = y - y_0 \in ({}^{\xi}{{\mathfrak{n}}}_\mathcal{O}^{-}+p^{\beta}{}^{\xi}{{\mathfrak{b}}}_\mathcal{O}^{-})\cdot \mathcal{U}({}^{\xi}{{\mathfrak{n}}}_\mathcal{O}^{-}+p^{\beta}{}^{\xi}{{\mathfrak{b}}}_\mathcal{O}^{-}), \end{gather*}
\begin{gather*} x_1 = x - x_0 \in ([{{\mathfrak{h}}},{{\mathfrak{h}}}]_\mathcal{O}+p^{\beta}{{\mathfrak{h}}})\cdot \mathcal{U}([{{\mathfrak{h}}},{{\mathfrak{h}}}]_\mathcal{O}+p^{\beta}{{\mathfrak{h}}}),\\ y_1 = y - y_0 \in ({}^{\xi}{{\mathfrak{n}}}_\mathcal{O}^{-}+p^{\beta}{}^{\xi}{{\mathfrak{b}}}_\mathcal{O}^{-})\cdot \mathcal{U}({}^{\xi}{{\mathfrak{n}}}_\mathcal{O}^{-}+p^{\beta}{}^{\xi}{{\mathfrak{b}}}_\mathcal{O}^{-}), \end{gather*}be the higher degree terms in their respective enveloping algebras. Then
 \begin{align*} \begin{aligned} \kappa_j^{\circ}(v)&= \kappa_j^{\circ}(xy \cdot \xi v_0) = x \cdot \kappa_j^{\circ}(y \cdot \xi v_0)\quad \mbox{(because $\kappa_j^{\circ}$ is $H$-equivariant)}\\ &\equiv x \cdot \kappa_j^{\circ}(y_0 \cdot \xi v_0)\pmod{p^{\beta}} \qquad\mbox{(because ${}^{\xi}{{\mathfrak{n}}}_\mathcal{O}^{-}$ acts trivially on $\xi v_0$)}\\ &\equiv x_0 \cdot\kappa_j^{\circ}(y_0\cdot\xi v_0)\pmod{p^{\beta}} \quad\,\,\,\mbox{(because $[{{\mathfrak{h}}},{{\mathfrak{h}}}]_\mathcal{O}$ acts trivially on a line)}\\ &= x_0y_0\cdot\kappa_j^{\circ}(\xi v_0) = x_0y_0,\end{aligned}\end{align*}
\begin{align*} \begin{aligned} \kappa_j^{\circ}(v)&= \kappa_j^{\circ}(xy \cdot \xi v_0) = x \cdot \kappa_j^{\circ}(y \cdot \xi v_0)\quad \mbox{(because $\kappa_j^{\circ}$ is $H$-equivariant)}\\ &\equiv x \cdot \kappa_j^{\circ}(y_0 \cdot \xi v_0)\pmod{p^{\beta}} \qquad\mbox{(because ${}^{\xi}{{\mathfrak{n}}}_\mathcal{O}^{-}$ acts trivially on $\xi v_0$)}\\ &\equiv x_0 \cdot\kappa_j^{\circ}(y_0\cdot\xi v_0)\pmod{p^{\beta}} \quad\,\,\,\mbox{(because $[{{\mathfrak{h}}},{{\mathfrak{h}}}]_\mathcal{O}$ acts trivially on a line)}\\ &= x_0y_0\cdot\kappa_j^{\circ}(\xi v_0) = x_0y_0,\end{aligned}\end{align*}
which does not depend on ![]() $j$ as claimed.
$j$ as claimed.
2.4.3 Proof of Theorem 2.3
As ![]() $\mathcal {O}[[\mathscr {C}\!\ell _F^{+}(p^{\infty })]]= \varprojlim _{\beta }(\mathcal {O}/p^{\beta }\mathcal {O})[\mathscr {C}\!\ell _F^{+}(p^{\beta })]$ and because
$\mathcal {O}[[\mathscr {C}\!\ell _F^{+}(p^{\infty })]]= \varprojlim _{\beta }(\mathcal {O}/p^{\beta }\mathcal {O})[\mathscr {C}\!\ell _F^{+}(p^{\beta })]$ and because ![]() $\varepsilon \pmod {p^{\beta }}$ factors through
$\varepsilon \pmod {p^{\beta }}$ factors through ![]() $\mathscr {C}\!\ell _F^{+}(p^{\beta })$, it is enough to check that given
$\mathscr {C}\!\ell _F^{+}(p^{\beta })$, it is enough to check that given ![]() $\beta \geqslant 1$ and
$\beta \geqslant 1$ and ![]() $[x]\in \mathscr {C}\!\ell _F^{+}(p^{\beta })$ one has
$[x]\in \mathscr {C}\!\ell _F^{+}(p^{\beta })$ one has
As, by (32), one has ![]() $\operatorname {triv}_{[\delta (x,y)]}^{*}= \varepsilon (x^{j} y^{{{\sf w}}})\operatorname {triv}_{\delta (x,y)}^{*}$, it suffices to show that (see (36))
$\operatorname {triv}_{[\delta (x,y)]}^{*}= \varepsilon (x^{j} y^{{{\sf w}}})\operatorname {triv}_{\delta (x,y)}^{*}$, it suffices to show that (see (36))
Now, by definition, the homomorphism of sheaves ![]() $\tau _\beta ^{\circ }$ defined in § 2.2.2 factors as
$\tau _\beta ^{\circ }$ defined in § 2.2.2 factors as
Hence, Proposition 2.6 translates to the statement that (for the choice of basis of ![]() $V^{(j,{{\sf w}}-j)}_{\mathcal {O}}$ as in (40))
$V^{(j,{{\sf w}}-j)}_{\mathcal {O}}$ as in (40)) ![]() $(\!\cap \theta _{[\delta ]}) \circ \operatorname {triv}_\delta ^{*}\circ \kappa _j \circ \tau _\beta ^{\circ }\circ \iota _\beta ^{*}(\phi )\pmod {p^{\beta }}$ is independent of
$(\!\cap \theta _{[\delta ]}) \circ \operatorname {triv}_\delta ^{*}\circ \kappa _j \circ \tau _\beta ^{\circ }\circ \iota _\beta ^{*}(\phi )\pmod {p^{\beta }}$ is independent of ![]() $j\in \operatorname {Crit}(\mu )$.
$j\in \operatorname {Crit}(\mu )$.
3. Local considerations
We delineate some local calculations that are needed in the global considerations of the next section. For only this section, ![]() $F$ denotes a finite extension of
$F$ denotes a finite extension of ![]() $\mathbb {Q}_p$,
$\mathbb {Q}_p$, ![]() $\mathcal {O}$ its ring of integers,
$\mathcal {O}$ its ring of integers, ![]() $\mathcal {P}$ the maximal ideal,
$\mathcal {P}$ the maximal ideal, ![]() $\varpi \in \mathcal {P}$ a uniformizer,
$\varpi \in \mathcal {P}$ a uniformizer, ![]() $q=\#(\mathcal {O}/\mathcal {P})$, and
$q=\#(\mathcal {O}/\mathcal {P})$, and ![]() $\delta$ the valuation of the different. We use local notation corresponding to the global notation introduced at the beginning of § 1. For example,
$\delta$ the valuation of the different. We use local notation corresponding to the global notation introduced at the beginning of § 1. For example, ![]() $G=\operatorname {GL}_{2n}(F)\supset H=\operatorname {GL}_{n}(F)\times \operatorname {GL}_{n}(F)$.
$G=\operatorname {GL}_{2n}(F)\supset H=\operatorname {GL}_{n}(F)\times \operatorname {GL}_{n}(F)$.
3.1 Parahoric invariants
Let ![]() $K= \operatorname {GL}_{2n}(\mathcal {O})$ be the standard maximal compact subgroup of
$K= \operatorname {GL}_{2n}(\mathcal {O})$ be the standard maximal compact subgroup of ![]() $G$. Define the parahoric (respectively, Iwahori) subgroup
$G$. Define the parahoric (respectively, Iwahori) subgroup ![]() $J$ (respectively,
$J$ (respectively, ![]() $I$) of
$I$) of ![]() $K$ consisting of matrices whose reduction modulo
$K$ consisting of matrices whose reduction modulo ![]() $\mathcal {P}$ belongs to
$\mathcal {P}$ belongs to ![]() $Q(\mathcal {O}/\mathcal {P})$ (respectively, to
$Q(\mathcal {O}/\mathcal {P})$ (respectively, to ![]() $B(\mathcal {O}/\mathcal {P})$). One has
$B(\mathcal {O}/\mathcal {P})$). One has
Let ![]() $\Pi$ be an algebraic unramified and generic representation of
$\Pi$ be an algebraic unramified and generic representation of ![]() $G$. Then there exists an unramified character
$G$. Then there exists an unramified character ![]() $\lambda = \otimes _{i=1}^{2n} \lambda _i :T \to \bar {\mathbb {Q}}^{\times } \xrightarrow {i_\infty } \mathbb {C}^{\times }$ such that
$\lambda = \otimes _{i=1}^{2n} \lambda _i :T \to \bar {\mathbb {Q}}^{\times } \xrightarrow {i_\infty } \mathbb {C}^{\times }$ such that
where the right-hand side is the normalized parabolic induction, which differs from the usual induction by ![]() $\delta _B^{{1}/{2}}$ where
$\delta _B^{{1}/{2}}$ where
Recall Jacquet's exact functor sending an admissible ![]() $G$-representation
$G$-representation ![]() $V$ to the space of its co-invariants of
$V$ to the space of its co-invariants of ![]() $U$ defined as
$U$ defined as ![]() $V_U=V /\langle \{u\cdot v-v\mid u\in U, v\in V \} \rangle$, which is an admissible
$V_U=V /\langle \{u\cdot v-v\mid u\in U, v\in V \} \rangle$, which is an admissible ![]() $H$-representation. The Weyl groups of
$H$-representation. The Weyl groups of ![]() $G\supset H$ are given by
$G\supset H$ are given by ![]() $\mathfrak {S}_{2n} \simeq W_G \supset W_H\simeq (\mathfrak {S}_{n}\times \mathfrak {S}_{n})$. The group
$\mathfrak {S}_{2n} \simeq W_G \supset W_H\simeq (\mathfrak {S}_{n}\times \mathfrak {S}_{n})$. The group ![]() $W_G$ acts on the right on characters of
$W_G$ acts on the right on characters of ![]() $T$. There is a natural bijection:
$T$. There is a natural bijection:
Lemma 3.1 The semi-simplification of the Jacquet module ![]() $\Pi _U$ is isomorphic to
$\Pi _U$ is isomorphic to
where ![]() $\delta _Q(t_1,t_2,\ldots ,t_{2n})= |{t_1\ldots t_n}\cdot {t_{n+1}^{-1}\ldots t_{2n}^{-1}} |^{n}$. The semi-simplification can be omitted if
$\delta _Q(t_1,t_2,\ldots ,t_{2n})= |{t_1\ldots t_n}\cdot {t_{n+1}^{-1}\ldots t_{2n}^{-1}} |^{n}$. The semi-simplification can be omitted if ![]() $\Pi$ is regular in the sense that
$\Pi$ is regular in the sense that ![]() $\alpha _{i} = \lambda _i(\varpi )$ are pairwise distinct for
$\alpha _{i} = \lambda _i(\varpi )$ are pairwise distinct for ![]() $1\leqslant i\leqslant 2n$.
$1\leqslant i\leqslant 2n$.
The characteristic polynomial of the Hecke operator ![]() $U_\mathcal {P}=[J t_\varpi J ]$ acting on
$U_\mathcal {P}=[J t_\varpi J ]$ acting on ![]() $\Pi ^{J }$ equals
$\Pi ^{J }$ equals
 \[ \prod_{ \tau\in W_G / W_H}\bigg(X-q^{{n(1-n)}/{2}} \prod_{i\in \tau} \alpha_{i}\bigg). \]
\[ \prod_{ \tau\in W_G / W_H}\bigg(X-q^{{n(1-n)}/{2}} \prod_{i\in \tau} \alpha_{i}\bigg). \]Proof. The semi-simplification of the Jacquet module ![]() $\Pi _N$ with respect to
$\Pi _N$ with respect to ![]() $B$ is given by
$B$ is given by
As ![]() $\operatorname {Ind}_{B}^{G}= \operatorname {Ind}_{Q}^{G} \operatorname {Ind}_{B\cap H}^{H}$, Frobenius reciprocity implies that any irreducible sub-quotient of the Jacquet module of
$\operatorname {Ind}_{B}^{G}= \operatorname {Ind}_{Q}^{G} \operatorname {Ind}_{B\cap H}^{H}$, Frobenius reciprocity implies that any irreducible sub-quotient of the Jacquet module of ![]() $\Pi$ with respect to
$\Pi$ with respect to ![]() $Q$ is isomorphic to one of the summands in (45). The first claim then follows by a simple dimension count based on (46) and the transitivity of the Jacquet functors. By Bruhat decomposition,
$Q$ is isomorphic to one of the summands in (45). The first claim then follows by a simple dimension count based on (46) and the transitivity of the Jacquet functors. By Bruhat decomposition,
the dimension of ![]() $\Pi ^{J}$ is
$\Pi ^{J}$ is ![]() $\#(W_G/W_H)$. By the Iwasawa decomposition
$\#(W_G/W_H)$. By the Iwasawa decomposition ![]() $H= (B\cap H)\cdot (H\cap J)$,
$H= (B\cap H)\cdot (H\cap J)$,
is a line on which the central element ![]() $\iota (\textbf {1}_{n},\varpi \textbf {1}_{n})$ acts by
$\iota (\textbf {1}_{n},\varpi \textbf {1}_{n})$ acts by ![]() $q^{{n(1-n)}/{2}} \prod _{i\in \tau } \alpha _{i}$. Under the assumption that
$q^{{n(1-n)}/{2}} \prod _{i\in \tau } \alpha _{i}$. Under the assumption that ![]() $\Pi$ is regular, the image of
$\Pi$ is regular, the image of ![]() $\Pi ^{J }$ by the Jacquet functor equals the direct sum of the above lines when
$\Pi ^{J }$ by the Jacquet functor equals the direct sum of the above lines when ![]() $\tau$ runs over
$\tau$ runs over ![]() $W_G / W_H$, hence the second claim. The proof of the third claim is a standard double coset computation based on (47) (see also [Reference HidaHid98]).
$W_G / W_H$, hence the second claim. The proof of the third claim is a standard double coset computation based on (47) (see also [Reference HidaHid98]).
3.2 Twisted local Shalika integrals
We review the theory of global Shalika models and ![]() $L$-functions in § 4.1. The computations in this section are needed in § 4.3 to evaluate the twisted local zeta integral.
$L$-functions in § 4.1. The computations in this section are needed in § 4.3 to evaluate the twisted local zeta integral.
Fix an additive character ![]() $\psi :F\to \mathbb {C}^{\times }$ of conductor
$\psi :F\to \mathbb {C}^{\times }$ of conductor ![]() $\varpi ^{-\delta }$ and a multiplicative character
$\varpi ^{-\delta }$ and a multiplicative character ![]() $\eta : F^{\times } \to \mathbb {C}^{\times }$.
$\eta : F^{\times } \to \mathbb {C}^{\times }$.
Definition 3.2 We say that an admissible representation ![]() $\Pi$ of
$\Pi$ of ![]() $G$ has a local
$G$ has a local ![]() $(\eta ,\psi )$-Shalika model if there is a non-trivial (and, hence, injective) intertwining of
$(\eta ,\psi )$-Shalika model if there is a non-trivial (and, hence, injective) intertwining of ![]() $G=\operatorname {GL}_{2n}(F)$-modules
$G=\operatorname {GL}_{2n}(F)$-modules
For any ![]() $W\in \operatorname {Ind}_{S}^{G}(\eta \otimes \psi )$ and for any quasi-character
$W\in \operatorname {Ind}_{S}^{G}(\eta \otimes \psi )$ and for any quasi-character ![]() $\chi :F^{\times } \to \mathbb {C}^{\times }$ the zeta integral
$\chi :F^{\times } \to \mathbb {C}^{\times }$ the zeta integral
is absolutely convergent for ![]() $\Re (s)\gg 0$. The following result is due to Friedberg and Jacquet.
$\Re (s)\gg 0$. The following result is due to Friedberg and Jacquet.
Proposition 3.3 [FJ93, Propositions 3.1 and 3.2] Assume that ![]() $\Pi$ has an
$\Pi$ has an ![]() $(\eta ,\psi )$-Shalika model. Then for each
$(\eta ,\psi )$-Shalika model. Then for each ![]() $W\in \mathcal {S}^{\eta }_{\psi }(\Pi )$, there is a holomorphic function
$W\in \mathcal {S}^{\eta }_{\psi }(\Pi )$, there is a holomorphic function ![]() $P(s;W,\chi )$ such that
$P(s;W,\chi )$ such that
One may analytically continue ![]() $\zeta (s;W,\chi )$ by re-defining it as
$\zeta (s;W,\chi )$ by re-defining it as ![]() $L(s,\Pi \otimes \chi )P(s;W,\chi )$ for all
$L(s,\Pi \otimes \chi )P(s;W,\chi )$ for all ![]() $s\in \mathbb {C}$. Moreover, there exists a vector
$s\in \mathbb {C}$. Moreover, there exists a vector ![]() $W_{\Pi }\in \mathcal {S}^{\eta }_{\psi }(\Pi )$ such that all unramified quasi-characters
$W_{\Pi }\in \mathcal {S}^{\eta }_{\psi }(\Pi )$ such that all unramified quasi-characters ![]() $\chi :F^{\times }\to \mathbb {C}^{\times }$ and every
$\chi :F^{\times }\to \mathbb {C}^{\times }$ and every ![]() $s\in \mathbb {C}$ one has
$s\in \mathbb {C}$ one has
If ![]() $\Pi$ is spherical, then
$\Pi$ is spherical, then ![]() $W_{\Pi }$ can be taken to be the spherical vector
$W_{\Pi }$ can be taken to be the spherical vector ![]() $W_{\Pi }^{\circ }\in \mathcal {S}^{\eta }_{\psi }(\Pi )$ normalized by the condition
$W_{\Pi }^{\circ }\in \mathcal {S}^{\eta }_{\psi }(\Pi )$ normalized by the condition ![]() $W_{\Pi }^{\circ }(\mathbf {1}_{2n})=1$.
$W_{\Pi }^{\circ }(\mathbf {1}_{2n})=1$.
For ramified twists, we need the following refinement of Proposition 3.3.
Proposition 3.4 Let ![]() $W\in \mathcal {S}^{\eta }_{\psi }(\Pi )$ be a parahoric invariant vector, that is,
$W\in \mathcal {S}^{\eta }_{\psi }(\Pi )$ be a parahoric invariant vector, that is,
for all ![]() $h\in \operatorname {GL}_n(F),$
$h\in \operatorname {GL}_n(F),$ ![]() $X\in M_n(F),$
$X\in M_n(F),$ ![]() $g\in G$ and
$g\in G$ and ![]() $k\in J$. Then for every finite order character
$k\in J$. Then for every finite order character ![]() $\chi :F^{\times }\to \mathbb {C}^{\times }$ of conductor
$\chi :F^{\times }\to \mathbb {C}^{\times }$ of conductor ![]() $\beta \geqslant 1$, and for all
$\beta \geqslant 1$, and for all ![]() $s\in \mathbb {C}$ with
$s\in \mathbb {C}$ with ![]() $\Re (s)\gg 0$ one has
$\Re (s)\gg 0$ one has
Proof. For any ![]() $h\in \operatorname {GL}_{n}(F)$ and
$h\in \operatorname {GL}_{n}(F)$ and ![]() $X\in M_n(\mathcal {O})$, the Shalika property (49) implies that
$X\in M_n(\mathcal {O})$, the Shalika property (49) implies that
hence, the zeta integral is supported over ![]() $\operatorname {GL}_n(F)\cap \varpi ^{-\beta -\delta }M_n(\mathcal {O})$. In addition, for
$\operatorname {GL}_n(F)\cap \varpi ^{-\beta -\delta }M_n(\mathcal {O})$. In addition, for ![]() $h\in \operatorname {GL}_{n}(F)$:
$h\in \operatorname {GL}_{n}(F)$:
Using this and changing the variable ![]() $h\mapsto h \varpi ^{-\beta '}$ with
$h\mapsto h \varpi ^{-\beta '}$ with ![]() $\beta '=\beta +\delta$ yields
$\beta '=\beta +\delta$ yields
 \begin{align*} &\zeta(s; W(-\cdot \xi t_\varpi^{\beta}),\chi)\\
&\qquad= \int_{\operatorname{GL}_n(F)\cap M_n(\mathcal{O})} W\bigg(\begin{pmatrix}h\varpi^{-\delta} & \\ & \textbf{1}_n\end{pmatrix}\bigg) \psi(\operatorname{tr} (h\varpi^{-\beta'})) (\chi|\cdot|^{s-{1}/{2}})(\det (h\varpi^{-\beta'})) \, {d} h. \end{align*}
\begin{align*} &\zeta(s; W(-\cdot \xi t_\varpi^{\beta}),\chi)\\
&\qquad= \int_{\operatorname{GL}_n(F)\cap M_n(\mathcal{O})} W\bigg(\begin{pmatrix}h\varpi^{-\delta} & \\ & \textbf{1}_n\end{pmatrix}\bigg) \psi(\operatorname{tr} (h\varpi^{-\beta'})) (\chi|\cdot|^{s-{1}/{2}})(\det (h\varpi^{-\beta'})) \, {d} h. \end{align*} Denote by ![]() $(e_{ij})_{1\leqslant i,j\leqslant n}$ the standard basis of
$(e_{ij})_{1\leqslant i,j\leqslant n}$ the standard basis of ![]() $M_n(\mathcal {O})$. As
$M_n(\mathcal {O})$. As ![]() $W$ is parahoric invariant, for any
$W$ is parahoric invariant, for any ![]() $i\neq j$ and
$i\neq j$ and ![]() $c\in \mathcal {O}$, right translation by
$c\in \mathcal {O}$, right translation by ![]() $\textbf {1}_{n}+c e_{ij}\in \operatorname {SL}_n(\mathcal {O})$ in (50) yields
$\textbf {1}_{n}+c e_{ij}\in \operatorname {SL}_n(\mathcal {O})$ in (50) yields
 \begin{align*} &\zeta(s; W(-\cdot \xi t_\varpi^{\beta}),\chi)\\ &\qquad = \int dh\, W\bigg(\begin{pmatrix}h\varpi^{-\delta} & \\ & \textbf{1}_n\end{pmatrix}\bigg) \psi(\operatorname{tr} (h\varpi^{-\beta'})) (\chi|\cdot|^{s-{1}/{2}})(\det (h\varpi^{-\beta'})) \int_{\mathcal{O}} d c\, \psi(c h_{ji}\varpi^{-\beta'}), \end{align*}
\begin{align*} &\zeta(s; W(-\cdot \xi t_\varpi^{\beta}),\chi)\\ &\qquad = \int dh\, W\bigg(\begin{pmatrix}h\varpi^{-\delta} & \\ & \textbf{1}_n\end{pmatrix}\bigg) \psi(\operatorname{tr} (h\varpi^{-\beta'})) (\chi|\cdot|^{s-{1}/{2}})(\det (h\varpi^{-\beta'})) \int_{\mathcal{O}} d c\, \psi(c h_{ji}\varpi^{-\beta'}), \end{align*}
and observe that ![]() $\int _{\mathcal {O}} \psi (c h_{ji}\varpi ^{-\beta '})\,dc=0$ unless
$\int _{\mathcal {O}} \psi (c h_{ji}\varpi ^{-\beta '})\,dc=0$ unless ![]() $h_{ji}\in \mathcal {P}^{\beta }$.
$h_{ji}\in \mathcal {P}^{\beta }$.
Similarly, right translation by ![]() $\textbf {1}_{n}+ (c-1)e_{ii}$ with
$\textbf {1}_{n}+ (c-1)e_{ii}$ with ![]() $c\in \mathcal {O}^{\times }$ shows that (50) equals
$c\in \mathcal {O}^{\times }$ shows that (50) equals
and ![]() $\int _{\mathcal {O}^{\times }} \psi (c h_{ii} \varpi ^{-\beta '}) \chi (c)\,d^{\times } c =0$ unless
$\int _{\mathcal {O}^{\times }} \psi (c h_{ii} \varpi ^{-\beta '}) \chi (c)\,d^{\times } c =0$ unless ![]() $h_{ii}\in \mathcal {O}^{\times }$ as
$h_{ii}\in \mathcal {O}^{\times }$ as ![]() $\beta \geqslant 1$ equals the conductor of
$\beta \geqslant 1$ equals the conductor of ![]() $\chi$.
$\chi$.
Therefore, one can further restrict the domain of integration in (50) to the congruence subgroup ![]() $\ker (\operatorname {GL}_n(\mathcal {O})\to \operatorname {GL}_n(\mathcal {O}/\mathcal {P}^{\beta }))\cdot T_n(\mathcal {O}),$ which, by the Iwahori decomposition, may be identified to the product
$\ker (\operatorname {GL}_n(\mathcal {O})\to \operatorname {GL}_n(\mathcal {O}/\mathcal {P}^{\beta }))\cdot T_n(\mathcal {O}),$ which, by the Iwahori decomposition, may be identified to the product ![]() $N^{-}_n(\mathcal {P}^{\beta })\times T_n(\mathcal {O})\times N_n(\mathcal {P}^{\beta })$, where
$N^{-}_n(\mathcal {P}^{\beta })\times T_n(\mathcal {O})\times N_n(\mathcal {P}^{\beta })$, where ![]() $T_n$ denotes the diagonal subgroup of
$T_n$ denotes the diagonal subgroup of ![]() $\operatorname {GL}_n$ and
$\operatorname {GL}_n$ and ![]() $N_n$ denotes the unipotent radical of the standard Borel subgroup
$N_n$ denotes the unipotent radical of the standard Borel subgroup ![]() $B_n$. Hence,
$B_n$. Hence,
which can be simplified as
 \begin{align*} &q^{\beta n(1-n)+\beta' n(s-{1}/{2})} W(t_\varpi^{-\delta})\prod_{1\leqslant i\leqslant n} \int_{\mathcal{O}^{\times}} \psi(t_i \varpi^{-\beta'}) \chi(t_i \varpi^{-\beta'})\,d^{\times} t_i \\ &\quad = q^{\beta n(1-n)+(\beta+\delta) n(s-{1}/{2})} W(t_\varpi^{-\delta})\cdot \mathcal{G}(\chi)^{n}, \end{align*}
\begin{align*} &q^{\beta n(1-n)+\beta' n(s-{1}/{2})} W(t_\varpi^{-\delta})\prod_{1\leqslant i\leqslant n} \int_{\mathcal{O}^{\times}} \psi(t_i \varpi^{-\beta'}) \chi(t_i \varpi^{-\beta'})\,d^{\times} t_i \\ &\quad = q^{\beta n(1-n)+(\beta+\delta) n(s-{1}/{2})} W(t_\varpi^{-\delta})\cdot \mathcal{G}(\chi)^{n}, \end{align*}as desired.
3.3 Non-vanishing of a local twisted zeta integral
In order to ensure the non-vanishing of the local twisted Shalika integral in Proposition 3.4, which is crucial for our applications, one has to exhibit a parahoric-spherical Shalika function ![]() $W$ on
$W$ on ![]() $G$ such that
$G$ such that ![]() $W(t_\varpi ^{-\delta }) \neq 0$. Assume that
$W(t_\varpi ^{-\delta }) \neq 0$. Assume that ![]() $\Pi$ is a spherical representation isomorphic to
$\Pi$ is a spherical representation isomorphic to ![]() $\operatorname {Ind}_{B}^{G}(|\cdot |^{({2n-1})/{2}} \lambda )$ as in (43) and let
$\operatorname {Ind}_{B}^{G}(|\cdot |^{({2n-1})/{2}} \lambda )$ as in (43) and let ![]() $\alpha _{i}=\lambda _i(\varpi )$,
$\alpha _{i}=\lambda _i(\varpi )$, ![]() $1\leqslant i\leqslant 2n$. Consider an unramified character
$1\leqslant i\leqslant 2n$. Consider an unramified character ![]() $\eta$ of
$\eta$ of ![]() $F^{\times }$.
$F^{\times }$.
Definition 3.5 Let ![]() $\tau \in W_G/W_H$ thought of as an
$\tau \in W_G/W_H$ thought of as an ![]() $n$-element subset of
$n$-element subset of ![]() $\{1,\ldots , 2n\}$ (see (44)). We say that
$\{1,\ldots , 2n\}$ (see (44)). We say that ![]() $\tilde \Pi =(\Pi , \tau )$ is
$\tilde \Pi =(\Pi , \tau )$ is ![]() $Q$-regular if it satisfies the following two conditions:
$Q$-regular if it satisfies the following two conditions:
(i)
 $q^{{n(1-n)}/{2}} \prod _{i\in \tau } \alpha _{i}$ is a simple eigenvalue for
$q^{{n(1-n)}/{2}} \prod _{i\in \tau } \alpha _{i}$ is a simple eigenvalue for  $U_\mathcal {P}=[J t_\varpi J ]$ acting on
$U_\mathcal {P}=[J t_\varpi J ]$ acting on  $\Pi ^{J }$;
$\Pi ^{J }$;(ii) there exists
 $\rho \in \mathfrak {S}_{2n}$ such that for all
$\rho \in \mathfrak {S}_{2n}$ such that for all  $i\in \tau ,$
$i\in \tau ,$  $\rho (i)\notin \tau$ and
$\rho (i)\notin \tau$ and  $\alpha _{i} \alpha _{\rho (i)} = q^{2n-1} \eta (\varpi ).$
$\alpha _{i} \alpha _{\rho (i)} = q^{2n-1} \eta (\varpi ).$
Assume that ![]() $\tilde \Pi =(\Pi , \tau )$ is
$\tilde \Pi =(\Pi , \tau )$ is ![]() $Q$-regular. Then condition (i) together with Lemma 3.1 implies
$Q$-regular. Then condition (i) together with Lemma 3.1 implies
whereas condition (ii) implies by [Reference Ash and GinzburgAG94, Proposition 1.3] that ![]() $\Pi$ admits a
$\Pi$ admits a ![]() $(\eta ,\psi )$-Shalika model.
$(\eta ,\psi )$-Shalika model.
Without loss of generality assume from now on that ![]() $\tau =\{n+1,\ldots ,2n\}$ and that
$\tau =\{n+1,\ldots ,2n\}$ and that ![]() $\rho \in \mathfrak {S}_{2n}$ is the order
$\rho \in \mathfrak {S}_{2n}$ is the order ![]() $2$ element such that
$2$ element such that ![]() $\rho (i)=n+i$ for all
$\rho (i)=n+i$ for all ![]() $1\leqslant i\leqslant n$. In [Reference Ash and GinzburgAG94, (1.3)] the authors construct an
$1\leqslant i\leqslant n$. In [Reference Ash and GinzburgAG94, (1.3)] the authors construct an ![]() $(\eta , \psi )$-Shalika functional on
$(\eta , \psi )$-Shalika functional on ![]() $\Pi$ sending
$\Pi$ sending ![]() $f\in \operatorname {Ind}_{B_{2n}}^{\operatorname {GL}_{2n}}(|\cdot |^{({2n-1})/{2}} \lambda )$ to
$f\in \operatorname {Ind}_{B_{2n}}^{\operatorname {GL}_{2n}}(|\cdot |^{({2n-1})/{2}} \lambda )$ to
By [Reference Ash and GinzburgAG94, Lemma 1.5], this integral converges in a certain domain and, when multiplied by (51), can be analytically continued to ![]() $\mathbb {C}^{2n}$, thus makes sense whenever (51) is non-zero. Let
$\mathbb {C}^{2n}$, thus makes sense whenever (51) is non-zero. Let ![]() $f_0 \in \operatorname {Ind}_{B}^{G}(|\cdot |^{({2n-1})/{2}} \lambda )$ be the unique parahoric-spherical function supported on
$f_0 \in \operatorname {Ind}_{B}^{G}(|\cdot |^{({2n-1})/{2}} \lambda )$ be the unique parahoric-spherical function supported on ![]() $B w_{2n} J$ and characterized by
$B w_{2n} J$ and characterized by ![]() $f_0\big ( \big (\begin {smallmatrix} \textbf {1}_n & \\ & \varpi ^{-\delta }\textbf {1}_n \end {smallmatrix}\big ) w_{2n}\big ) = q^{-\delta n^{2}}$. The following analogue of [Reference Ash and GinzburgAG94, Lemma 1.4] holds.
$f_0\big ( \big (\begin {smallmatrix} \textbf {1}_n & \\ & \varpi ^{-\delta }\textbf {1}_n \end {smallmatrix}\big ) w_{2n}\big ) = q^{-\delta n^{2}}$. The following analogue of [Reference Ash and GinzburgAG94, Lemma 1.4] holds.
Lemma 3.6 Let ![]() $W=\mathcal {S}(f_0)$. Then
$W=\mathcal {S}(f_0)$. Then ![]() $W(t_\varpi ^{-\delta }) =1$. Moreover,
$W(t_\varpi ^{-\delta }) =1$. Moreover, ![]() $U_\mathcal {P}\cdot f_0= q^{{n(1-n)}/{2}}(\prod _{i=n+1}^{2n} \alpha _i) f_0$.
$U_\mathcal {P}\cdot f_0= q^{{n(1-n)}/{2}}(\prod _{i=n+1}^{2n} \alpha _i) f_0$.
Proof. By the Iwasawa decomposition ![]() $\operatorname {GL}_n = B_n K_n$ and as
$\operatorname {GL}_n = B_n K_n$ and as ![]() $\iota (K_n,K_n) \subset J$ we see that
$\iota (K_n,K_n) \subset J$ we see that
 \begin{align*} W(t_\varpi^{-\delta}) = \mathcal{S}(f_0)(t_\varpi^{-\delta}) & = \int_{M_n} f_0\bigg(\begin{pmatrix} & \textbf{1}_n \\ \textbf{1}_n & X \end{pmatrix} t_\varpi^{-\delta} \bigg) \bar\psi({\rm tr}(X)) \, dX \\ & = \int_{M_n} f_0\bigg( \begin{pmatrix} \textbf{1}_n & \\ & \varpi^{-\delta}\textbf{1}_n \end{pmatrix} \bigg( \begin{pmatrix} & \textbf{1}_n \\ \textbf{1}_n & \varpi^{\delta}X \end{pmatrix} \bigg) \bar\psi({\rm tr}(X)) \, dX \\ & = f_0 \bigg(\begin{pmatrix} \textbf{1}_n & \\ & \varpi^{-\delta}\textbf{1}_n \end{pmatrix} w_{2n}\bigg) q^{\delta n^{2}}\!\int_{M_n} \! f_0\bigg( \begin{pmatrix} & \textbf{1}_n \\ \textbf{1}_n & X \end{pmatrix} \bigg) \bar\psi({\rm tr}(\varpi^{-\delta}X)) \, dX=1. \end{align*}
\begin{align*} W(t_\varpi^{-\delta}) = \mathcal{S}(f_0)(t_\varpi^{-\delta}) & = \int_{M_n} f_0\bigg(\begin{pmatrix} & \textbf{1}_n \\ \textbf{1}_n & X \end{pmatrix} t_\varpi^{-\delta} \bigg) \bar\psi({\rm tr}(X)) \, dX \\ & = \int_{M_n} f_0\bigg( \begin{pmatrix} \textbf{1}_n & \\ & \varpi^{-\delta}\textbf{1}_n \end{pmatrix} \bigg( \begin{pmatrix} & \textbf{1}_n \\ \textbf{1}_n & \varpi^{\delta}X \end{pmatrix} \bigg) \bar\psi({\rm tr}(X)) \, dX \\ & = f_0 \bigg(\begin{pmatrix} \textbf{1}_n & \\ & \varpi^{-\delta}\textbf{1}_n \end{pmatrix} w_{2n}\bigg) q^{\delta n^{2}}\!\int_{M_n} \! f_0\bigg( \begin{pmatrix} & \textbf{1}_n \\ \textbf{1}_n & X \end{pmatrix} \bigg) \bar\psi({\rm tr}(\varpi^{-\delta}X)) \, dX=1. \end{align*}
One checks that ![]() $\big ( \begin {smallmatrix} & \textbf {1}_n \\ \textbf {1}_n & X \end {smallmatrix} \big ) \in Bw_{2n} J$ if and only if
$\big ( \begin {smallmatrix} & \textbf {1}_n \\ \textbf {1}_n & X \end {smallmatrix} \big ) \in Bw_{2n} J$ if and only if ![]() $X \in M_n(\mathcal {O})$, in which case
$X \in M_n(\mathcal {O})$, in which case ![]() $\psi ({\rm tr}(\varpi ^{-\delta }X))=1$. The parahoric decomposition of
$\psi ({\rm tr}(\varpi ^{-\delta }X))=1$. The parahoric decomposition of ![]() $J=(J\cap U^{-})(J \cap Q)=(J \cap U^{-})(J \cap Q)$ implies
$J=(J\cap U^{-})(J \cap Q)=(J \cap U^{-})(J \cap Q)$ implies
 \begin{equation} J t_\varpi J=\bigsqcup_{m\in M_n(\mathcal{O}/\mathcal{P})} \begin{pmatrix} \textbf{1}_n & m \\ & \textbf{1}_n \end{pmatrix} t_\varpi J. \end{equation}
\begin{equation} J t_\varpi J=\bigsqcup_{m\in M_n(\mathcal{O}/\mathcal{P})} \begin{pmatrix} \textbf{1}_n & m \\ & \textbf{1}_n \end{pmatrix} t_\varpi J. \end{equation}
By (47) it suffices to compute ![]() $(U_\mathcal {P}\cdot f_0)(\rho )$ for all
$(U_\mathcal {P}\cdot f_0)(\rho )$ for all ![]() $\rho \in W_G$. By the previous decomposition,
$\rho \in W_G$. By the previous decomposition,
 \[ (U_\mathcal{P}\cdot f_0)(\rho)=\sum_{m\in M_n(\mathcal{O})/M_n(\mathcal{P})} f_0\bigg(\rho \begin{pmatrix} \varpi\textbf{1}_n & m \\ & \textbf{1}_n \end{pmatrix}\bigg). \]
\[ (U_\mathcal{P}\cdot f_0)(\rho)=\sum_{m\in M_n(\mathcal{O})/M_n(\mathcal{P})} f_0\bigg(\rho \begin{pmatrix} \varpi\textbf{1}_n & m \\ & \textbf{1}_n \end{pmatrix}\bigg). \]
Note that ![]() $\rho \big (\begin {smallmatrix} \textbf {1}_n & m \\ & \textbf {1}_n \end {smallmatrix} \big )t_\varpi$ belongs to the support
$\rho \big (\begin {smallmatrix} \textbf {1}_n & m \\ & \textbf {1}_n \end {smallmatrix} \big )t_\varpi$ belongs to the support ![]() $B w_{2n} J = B w_{2n} t_\varpi J = B w_{2n} J^{-} t_\varpi$ of
$B w_{2n} J = B w_{2n} t_\varpi J = B w_{2n} J^{-} t_\varpi$ of ![]() $f_0$ if and only if
$f_0$ if and only if ![]() $\rho \big (\begin {smallmatrix} \textbf {1}_n & m \\ & \textbf {1}_n \end {smallmatrix} \big )\in K\cap B w_{2n} J^{-} = (K\cap B) w_{2n} J^{-}=w_{2n} J^{-}$ (see (47)), which implies
$\rho \big (\begin {smallmatrix} \textbf {1}_n & m \\ & \textbf {1}_n \end {smallmatrix} \big )\in K\cap B w_{2n} J^{-} = (K\cap B) w_{2n} J^{-}=w_{2n} J^{-}$ (see (47)), which implies ![]() $\rho =w_{2n}$ and
$\rho =w_{2n}$ and ![]() $m\in M_n(\mathcal {P})$. Hence,
$m\in M_n(\mathcal {P})$. Hence, ![]() $(U_\mathcal {P}\cdot f_0)(\rho )=0$ for all
$(U_\mathcal {P}\cdot f_0)(\rho )=0$ for all ![]() $\rho \neq w_{2n}$, while
$\rho \neq w_{2n}$, while ![]() $(U_\mathcal {P}\cdot f_0)(w_{2n})=f_0\big (w_{2n} \big (\begin {smallmatrix} \varpi \textbf {1}_n & \\ & \textbf {1}_n \end {smallmatrix} \big )\big ) =f_0\big (\big (\begin {smallmatrix} \textbf {1}_n & \\ & \varpi \textbf {1}_n \end {smallmatrix} \big )w_{2n} \big )= q^{{n(1-n)}/{2}}(\prod _{i=n+1}^{2n} \alpha _i) f_0(w_{2n})$.
$(U_\mathcal {P}\cdot f_0)(w_{2n})=f_0\big (w_{2n} \big (\begin {smallmatrix} \varpi \textbf {1}_n & \\ & \textbf {1}_n \end {smallmatrix} \big )\big ) =f_0\big (\big (\begin {smallmatrix} \textbf {1}_n & \\ & \varpi \textbf {1}_n \end {smallmatrix} \big )w_{2n} \big )= q^{{n(1-n)}/{2}}(\prod _{i=n+1}^{2n} \alpha _i) f_0(w_{2n})$.
4.  $L$-functions for
$L$-functions for  $\operatorname {GL}_{2n}$
$\operatorname {GL}_{2n}$
4.1 Global Shalika models and periods
This subsection contains a brief review of the necessary ingredients from [Reference Grobner and RaghuramGR14] and a discussion involving ![]() $p$-adically integrally refined Betti–Shalika periods. Henceforth,
$p$-adically integrally refined Betti–Shalika periods. Henceforth, ![]() $\Pi$ denotes a (not necessarily unitary) cuspidal automorphic representation of
$\Pi$ denotes a (not necessarily unitary) cuspidal automorphic representation of ![]() $G(\mathbb {A}) = \operatorname {GL}_{2n}(\mathbb {A}_F)$. Keeping multiplicity one for
$G(\mathbb {A}) = \operatorname {GL}_{2n}(\mathbb {A}_F)$. Keeping multiplicity one for ![]() $\operatorname {GL}_{2n}$ in mind, we let
$\operatorname {GL}_{2n}$ in mind, we let ![]() $\Pi$ also denote its representation space within the space of cusp forms for
$\Pi$ also denote its representation space within the space of cusp forms for ![]() $G(\mathbb {A})$. Fix the non-trivial additive unitary character
$G(\mathbb {A})$. Fix the non-trivial additive unitary character ![]() $\psi : \mathbb {A}_{F}/F\longrightarrow \mathbb {A}/\mathbb {Q} \longrightarrow \mathbb {C}^{\times }$ where the first map is the trace, whereas the second is the usual additive character
$\psi : \mathbb {A}_{F}/F\longrightarrow \mathbb {A}/\mathbb {Q} \longrightarrow \mathbb {C}^{\times }$ where the first map is the trace, whereas the second is the usual additive character ![]() $\psi _0$ on
$\psi _0$ on ![]() $\mathbb {A}/\mathbb {Q}$ characterized by
$\mathbb {A}/\mathbb {Q}$ characterized by ![]() $\ker (\psi _0|_{\mathbb {Q}_\ell })=\mathbb {Z}_\ell$ for every prime number
$\ker (\psi _0|_{\mathbb {Q}_\ell })=\mathbb {Z}_\ell$ for every prime number ![]() $\ell$ and
$\ell$ and ![]() $\psi _0|_{\mathbb {R}}(x)=\exp (2\pi ix)$. We remark that
$\psi _0|_{\mathbb {R}}(x)=\exp (2\pi ix)$. We remark that ![]() $(\varpi _{v}^{-\delta _v})$, where
$(\varpi _{v}^{-\delta _v})$, where ![]() $\delta _v$ is the valuation at
$\delta _v$ is the valuation at ![]() $v$ of the different
$v$ of the different ![]() $\mathfrak {d}$ of
$\mathfrak {d}$ of ![]() $F$, is the largest ideal contained in
$F$, is the largest ideal contained in ![]() $\ker (\psi _v)$. The discriminant of
$\ker (\psi _v)$. The discriminant of ![]() $F$ is
$F$ is ![]() $\operatorname {N}_{F/\mathbb {Q}}(\mathfrak {d})$.
$\operatorname {N}_{F/\mathbb {Q}}(\mathfrak {d})$.
4.1.1 Global Shalika models
Let ![]() $\eta : F^{\times } \backslash \mathbb {A}_F^{\times } \to \mathbb {C}^{\times }$ be a Hecke character such that
$\eta : F^{\times } \backslash \mathbb {A}_F^{\times } \to \mathbb {C}^{\times }$ be a Hecke character such that ![]() $\eta ^{n}$ equals the central character
$\eta ^{n}$ equals the central character ![]() $\omega _\Pi$ of
$\omega _\Pi$ of ![]() $\Pi$. We obtain an automorphic character:
$\Pi$. We obtain an automorphic character:
For a cusp form ![]() $\varphi \in \Pi$ and
$\varphi \in \Pi$ and ![]() $g\in G(\mathbb {A})$ consider the integral
$g\in G(\mathbb {A})$ consider the integral
where Haar measures are normalized as in [Reference Grobner and RaghuramGR14, § 2.8]. It is well-defined by the cuspidality of the function ![]() $\varphi$ (see [Reference Jacquet and ShalikaJS90, § 8.1]) and, hence, yields a function
$\varphi$ (see [Reference Jacquet and ShalikaJS90, § 8.1]) and, hence, yields a function ![]() $W^{\eta }_{\varphi }: G(\mathbb {A})\rightarrow \mathbb {C}$ such that
$W^{\eta }_{\varphi }: G(\mathbb {A})\rightarrow \mathbb {C}$ such that
for all ![]() $g\in G(\mathbb {A})$ and
$g\in G(\mathbb {A})$ and ![]() $s\in S(\mathbb {A})$. In particular, we obtain an intertwining of
$s\in S(\mathbb {A})$. In particular, we obtain an intertwining of ![]() $G(\mathbb {A})$-modules
$G(\mathbb {A})$-modules
The following theorem, due to Jacquet and Shalika, gives a necessary and sufficient conditions for the existence of a non-zero intertwining as in (55).
Theorem 4.1 [JS90, Theorem 1] The following assertions are equivalent.
(i) There exists
 $\varphi \in \Pi$ such that
$\varphi \in \Pi$ such that  $W^{\eta }_{\varphi } \neq 0$.
$W^{\eta }_{\varphi } \neq 0$.(ii) There exists an injection of
 $G(\mathbb {A})$-modules
$G(\mathbb {A})$-modules  $\Pi \hookrightarrow {\rm {Ind}}_{S(\mathbb {A})}^{G(\mathbb {A})}(\eta \otimes \psi )$.
$\Pi \hookrightarrow {\rm {Ind}}_{S(\mathbb {A})}^{G(\mathbb {A})}(\eta \otimes \psi )$.(iii) The twisted partial exterior square
 $L$-function
$L$-function  $\prod _{v\notin \Sigma _\Pi } L(s, \Pi _v, \wedge ^{2} \otimes \eta ^{-1}_v)$ has a pole at
$\prod _{v\notin \Sigma _\Pi } L(s, \Pi _v, \wedge ^{2} \otimes \eta ^{-1}_v)$ has a pole at  $s=1$, where
$s=1$, where  $\Sigma _\Pi$ is the set of places where
$\Sigma _\Pi$ is the set of places where  $\Pi$ is ramified.
$\Pi$ is ramified.
This is proved in [Reference Jacquet and ShalikaJS90] for unitary representations and its extension to the non-unitary case is easy. If ![]() $\Pi$ satisfies any one, and hence all, of the equivalent conditions of Theorem 4.1, then we say that
$\Pi$ satisfies any one, and hence all, of the equivalent conditions of Theorem 4.1, then we say that ![]() $\Pi$ has an
$\Pi$ has an ![]() $(\eta ,\psi )$-Shalika model, and we call the isomorphic image
$(\eta ,\psi )$-Shalika model, and we call the isomorphic image ![]() $\mathcal {S}^{\eta }_\psi (\Pi )$ of
$\mathcal {S}^{\eta }_\psi (\Pi )$ of ![]() $\Pi$ under (55) a global
$\Pi$ under (55) a global ![]() $(\eta ,\psi )$-Shalika model of
$(\eta ,\psi )$-Shalika model of ![]() $\Pi$. Then clearly
$\Pi$. Then clearly ![]() $\Pi \otimes \chi$ has an
$\Pi \otimes \chi$ has an ![]() $(\eta \chi ^{2},\psi )$-Shalika model for any Hecke character
$(\eta \chi ^{2},\psi )$-Shalika model for any Hecke character ![]() $\chi$, by keeping the same model and only twisting the action.
$\chi$, by keeping the same model and only twisting the action.
The following proposition (see [Reference Asgari and ShahidiAS14]) gives another equivalent condition for ![]() $\Pi$ to have a global Shalika model.
$\Pi$ to have a global Shalika model.
Proposition 4.2 Let ![]() $\Pi$ be a cuspidal automorphic representation of
$\Pi$ be a cuspidal automorphic representation of ![]() $\operatorname {GL}_{2n}(\mathbb {A}_F)$ with central character
$\operatorname {GL}_{2n}(\mathbb {A}_F)$ with central character ![]() $\omega _\Pi$. Then the following assertions are equivalent:
$\omega _\Pi$. Then the following assertions are equivalent:
(i)
 $\Pi$ has a global
$\Pi$ has a global  $(\eta ,\psi )$-Shalika model for some character
$(\eta ,\psi )$-Shalika model for some character  $\eta$ satisfying
$\eta$ satisfying  $\eta ^{n}=\omega _\Pi$;
$\eta ^{n}=\omega _\Pi$;(ii)
 $\Pi$ is the transfer of a globally generic cuspidal automorphic representation
$\Pi$ is the transfer of a globally generic cuspidal automorphic representation  $\pi$ of
$\pi$ of  ${\rm GSpin}_{2n+1}(\mathbb {A}_F)$.
${\rm GSpin}_{2n+1}(\mathbb {A}_F)$.
In particular, if any of these equivalent conditions is satisfied, then ![]() $\Pi$ is essentially self-dual, that is,
$\Pi$ is essentially self-dual, that is, ![]() $\Pi \cong \Pi ^{\vee }\otimes \eta$. The character
$\Pi \cong \Pi ^{\vee }\otimes \eta$. The character ![]() $\eta$ may be taken to be the central character of
$\eta$ may be taken to be the central character of ![]() $\pi$.
$\pi$.
4.1.2 Period integrals and  $L$-functions
$L$-functions
The following proposition, due to Friedberg and Jacquet, is crucial for much that follows. It relates the period integral over ![]() $H$ of a cusp form
$H$ of a cusp form ![]() $\varphi$ of
$\varphi$ of ![]() $G$ to a certain zeta integral of the function
$G$ to a certain zeta integral of the function ![]() $W^{\eta }_{\varphi }$ in the Shalika model corresponding to
$W^{\eta }_{\varphi }$ in the Shalika model corresponding to ![]() $\varphi$ over one copy of
$\varphi$ over one copy of ![]() $\operatorname {GL}_n$.
$\operatorname {GL}_n$.
Proposition 4.3 [FJ93, Proposition 2.3] Assume that ![]() $\Pi$ has an
$\Pi$ has an ![]() $(\eta ,\psi )$-Shalika model. For
$(\eta ,\psi )$-Shalika model. For ![]() $\varphi \in \Pi$,
$\varphi \in \Pi$,
converges absolutely for all ![]() $s\in \mathbb {C}$. For
$s\in \mathbb {C}$. For ![]() $\Re (s)\gg 0$ it is equal to
$\Re (s)\gg 0$ it is equal to
thus providing an analytic continuation of ![]() $\zeta (s;W^{\eta }_{\varphi },\chi )$ to all of
$\zeta (s;W^{\eta }_{\varphi },\chi )$ to all of ![]() $\mathbb {C}$.
$\mathbb {C}$.
Suppose the representation ![]() $\Pi$ of
$\Pi$ of ![]() $G(\mathbb {A}) = \operatorname {GL}_{2n}(\mathbb {A}_F)$ decomposes as
$G(\mathbb {A}) = \operatorname {GL}_{2n}(\mathbb {A}_F)$ decomposes as ![]() $\Pi = \otimes '_v \Pi _v$, where
$\Pi = \otimes '_v \Pi _v$, where ![]() $\Pi _v$ is an irreducible admissible representation of
$\Pi _v$ is an irreducible admissible representation of ![]() $\operatorname {GL}_{2n}(F_v)$.
$\operatorname {GL}_{2n}(F_v)$.
If ![]() $\Pi$ has a global Shalika model, then
$\Pi$ has a global Shalika model, then ![]() $\mathcal {S}^{\eta }_\psi$ defines local Shalika models at every place (see Definition 3.2). The corresponding local intertwining operators are denoted by
$\mathcal {S}^{\eta }_\psi$ defines local Shalika models at every place (see Definition 3.2). The corresponding local intertwining operators are denoted by ![]() $\mathcal {S}^{\eta _v}_{\psi _v}$ and their images by
$\mathcal {S}^{\eta _v}_{\psi _v}$ and their images by ![]() $\mathcal {S}^{\eta _v}_{\psi _v}(\Pi _v)$, whence
$\mathcal {S}^{\eta _v}_{\psi _v}(\Pi _v)$, whence ![]() $\mathcal {S}^{\eta }_\psi (\Pi )=\otimes '_v \mathcal {S}^{\eta _v}_{\psi _v}(\Pi _v)$. We can now consider cusp forms
$\mathcal {S}^{\eta }_\psi (\Pi )=\otimes '_v \mathcal {S}^{\eta _v}_{\psi _v}(\Pi _v)$. We can now consider cusp forms ![]() $\varphi$ such that the function
$\varphi$ such that the function ![]() $W_{\varphi }\in \mathcal {S}^{\eta }_\psi (\Pi )$ is factorizable as
$W_{\varphi }\in \mathcal {S}^{\eta }_\psi (\Pi )$ is factorizable as ![]() $W_\varphi =\otimes '_v W_{\varphi _v},$ where
$W_\varphi =\otimes '_v W_{\varphi _v},$ where
Then the following factorization holds for ![]() $\Re (s) \gg 0$:
$\Re (s) \gg 0$:
where the non-Archimedean local zeta integrals ![]() $\zeta _v(s;W_{\varphi _v},\chi _v)$ are related to
$\zeta _v(s;W_{\varphi _v},\chi _v)$ are related to ![]() $L$-functions in Proposition 3.3.
$L$-functions in Proposition 3.3.
Proposition 4.3 relates this Shalika zeta integral to a period integral over ![]() $H$, and the main thrust of [Reference Ash and GinzburgAG94], refined and generalized in [Reference Grobner and RaghuramGR14], is that the period integral over
$H$, and the main thrust of [Reference Ash and GinzburgAG94], refined and generalized in [Reference Grobner and RaghuramGR14], is that the period integral over ![]() $H$ admits a cohomological interpretation, provided that
$H$ admits a cohomological interpretation, provided that ![]() $\Pi$ is of cohomological type.
$\Pi$ is of cohomological type.
4.1.3 Shalika models and cuspidal cohomology
In this section, we recall some well-known facts from Clozel [Reference ClozelClo90, § 3] (see also [Reference Grobner and RaghuramGR14, § 3.4]). Assume from now on that the cuspidal automorphic representation ![]() $\Pi$ is cohomological with respect to a dominant integral weight
$\Pi$ is cohomological with respect to a dominant integral weight ![]() $\mu \in X_+^{*}(T)$ (see (3)), that is,
$\mu \in X_+^{*}(T)$ (see (3)), that is,
for some degree ![]() $q$. A necessary condition for the non-vanishing of this cohomology group is that the weight
$q$. A necessary condition for the non-vanishing of this cohomology group is that the weight ![]() $\mu$ is pure, that is,
$\mu$ is pure, that is, ![]() $\mu \in X_0^{*}(T)$. For each archimedean place
$\mu \in X_0^{*}(T)$. For each archimedean place ![]() $\sigma \in \Sigma _{\infty }$,
$\sigma \in \Sigma _{\infty }$, ![]() $\Pi _\sigma$ can be described explicitly as follows. For any integer
$\Pi _\sigma$ can be described explicitly as follows. For any integer ![]() $\ell \geqslant 1$ consider the unitary discrete series representation
$\ell \geqslant 1$ consider the unitary discrete series representation ![]() $D(\ell )$ of
$D(\ell )$ of ![]() $\operatorname {GL}_2(\mathbb {R})$ of lowest non-negative
$\operatorname {GL}_2(\mathbb {R})$ of lowest non-negative ![]() ${\rm SO}_2$-type
${\rm SO}_2$-type ![]() $\ell +1$ and central character
$\ell +1$ and central character ![]() $\mathrm {sgn}^{\ell +1}$. Let
$\mathrm {sgn}^{\ell +1}$. Let ![]() $P$ be the parabolic subgroup of
$P$ be the parabolic subgroup of ![]() $\operatorname {GL}_{2n}$ with Levi factor
$\operatorname {GL}_{2n}$ with Levi factor ![]() $\prod _{i=1}^{n} \operatorname {GL}_2$. Then
$\prod _{i=1}^{n} \operatorname {GL}_2$. Then
 \[ \Pi_\sigma\simeq{\rm Ind}^{\operatorname{GL}_{2n}(\mathbb{R})}_{P(\mathbb{R})} \bigg(\bigotimes_{i=1}^{n} D(2(\mu_{\sigma,i}+n-i)+ 1-{{\sf w}})\otimes |\!\det\!|^{-{{\sf w}}/2}\bigg), \]
\[ \Pi_\sigma\simeq{\rm Ind}^{\operatorname{GL}_{2n}(\mathbb{R})}_{P(\mathbb{R})} \bigg(\bigotimes_{i=1}^{n} D(2(\mu_{\sigma,i}+n-i)+ 1-{{\sf w}})\otimes |\!\det\!|^{-{{\sf w}}/2}\bigg), \]
in particular ![]() $\omega _{\Pi _\sigma }=|\cdot |^{-n {{\sf w}}}$. The highest degree supporting cuspidal cohomology of
$\omega _{\Pi _\sigma }=|\cdot |^{-n {{\sf w}}}$. The highest degree supporting cuspidal cohomology of ![]() $G$ is
$G$ is ![]() $t=|\Sigma _\infty |(n^{2}+n-1)$. For any character
$t=|\Sigma _\infty |(n^{2}+n-1)$. For any character ![]() $\epsilon$ of
$\epsilon$ of ![]() $K_{\infty }/K_\infty ^{\circ }$ the
$K_{\infty }/K_\infty ^{\circ }$ the ![]() $\epsilon$-eigenspace of
$\epsilon$-eigenspace of
is a line. If, in addition, ![]() $\Pi$ admits an
$\Pi$ admits an ![]() $(\eta ,\psi )$-Shalika model, then
$(\eta ,\psi )$-Shalika model, then ![]() $\eta$ is forced to be algebraic of the form
$\eta$ is forced to be algebraic of the form ![]() $\eta = \eta _0 | \cdot |_F^{-{{\sf w}}}$ with
$\eta = \eta _0 | \cdot |_F^{-{{\sf w}}}$ with ![]() $\eta _0$ of finite order,
$\eta _0$ of finite order, ![]() ${{\sf w}}$ is the purity weight of
${{\sf w}}$ is the purity weight of ![]() $\mu$ (see [Reference Gan and RaghuramGR13, Theorem 5.3]). Using the multiplicity one theorem for local Shalika models [Reference NienNie09] (see also [Reference Chen and SunCS20]), one deduces that, for any character
$\mu$ (see [Reference Gan and RaghuramGR13, Theorem 5.3]). Using the multiplicity one theorem for local Shalika models [Reference NienNie09] (see also [Reference Chen and SunCS20]), one deduces that, for any character ![]() $\epsilon$ of
$\epsilon$ of ![]() $K_{\infty }/K_\infty ^{\circ }$,
$K_{\infty }/K_\infty ^{\circ }$,
is a line, a basis ![]() $\Xi _\infty ^{\epsilon }$ of which we fix in way compatible with twisting (see [Reference Grobner and RaghuramGR14, Lemma 5.1.1]). The relative Lie algebra cohomology of
$\Xi _\infty ^{\epsilon }$ of which we fix in way compatible with twisting (see [Reference Grobner and RaghuramGR14, Lemma 5.1.1]). The relative Lie algebra cohomology of ![]() $\Pi$ as previously is a summand of the cuspidal cohomology, which, in turn, injects into the cohomology with compact supports (see [Reference Gan and RaghuramGR13, § 2])
$\Pi$ as previously is a summand of the cuspidal cohomology, which, in turn, injects into the cohomology with compact supports (see [Reference Gan and RaghuramGR13, § 2])
We define an isomorphism ![]() $\Theta ^{\epsilon }$ of
$\Theta ^{\epsilon }$ of ![]() $G(\mathbb {A}_f)$-modules as the composition
$G(\mathbb {A}_f)$-modules as the composition
 \begin{align} \mathcal{S}^{\eta_f}_{\psi_f}(\Pi_f) &\xrightarrow{\sim} \mathcal{S}^{\eta_f}_{\psi_f}(\Pi_f) \otimes \operatorname{H}^{t}({{\mathfrak{g}}}_\infty,K_{\infty}^{\circ} ; \mathcal{S}^{\eta_{\infty}}_{\psi_{\infty}}(\Pi_\infty) \otimes V^{\mu}_{\mathbb{C}})[\epsilon] \nonumber\\ &\xrightarrow{\sim} \operatorname{H}^{t}({{\mathfrak{g}}}_\infty,K_{\infty}^{\circ} ; \mathcal{S}^{\eta}_{\psi}(\Pi) \otimes V^{\mu}_{\mathbb{C}})[\epsilon] \xrightarrow{\sim} \operatorname{H}^{t}({{\mathfrak{g}}}_\infty,K_{\infty}^{\circ} ; \Pi \otimes V^{\mu}_{\mathbb{C}})[\epsilon], \end{align}
\begin{align} \mathcal{S}^{\eta_f}_{\psi_f}(\Pi_f) &\xrightarrow{\sim} \mathcal{S}^{\eta_f}_{\psi_f}(\Pi_f) \otimes \operatorname{H}^{t}({{\mathfrak{g}}}_\infty,K_{\infty}^{\circ} ; \mathcal{S}^{\eta_{\infty}}_{\psi_{\infty}}(\Pi_\infty) \otimes V^{\mu}_{\mathbb{C}})[\epsilon] \nonumber\\ &\xrightarrow{\sim} \operatorname{H}^{t}({{\mathfrak{g}}}_\infty,K_{\infty}^{\circ} ; \mathcal{S}^{\eta}_{\psi}(\Pi) \otimes V^{\mu}_{\mathbb{C}})[\epsilon] \xrightarrow{\sim} \operatorname{H}^{t}({{\mathfrak{g}}}_\infty,K_{\infty}^{\circ} ; \Pi \otimes V^{\mu}_{\mathbb{C}})[\epsilon], \end{align}
where the first map is ![]() $W_f \mapsto W_f \otimes \Xi _\infty ^{\epsilon }$, the second map is the natural one and the third map is the map induced in cohomology by
$W_f \mapsto W_f \otimes \Xi _\infty ^{\epsilon }$, the second map is the natural one and the third map is the map induced in cohomology by ![]() $(\mathcal {S}^{\eta }_\psi )^{-1}$ from (55). Taking
$(\mathcal {S}^{\eta }_\psi )^{-1}$ from (55). Taking ![]() $K$-invariants in (59) and composing with (58) yields a Hecke equivariant embedding
$K$-invariants in (59) and composing with (58) yields a Hecke equivariant embedding
The reader should appreciate that the analytic condition on ![]() $\Pi$ of admitting a Shalika model and the algebraic condition of contributing to the cuspidal cohomology of
$\Pi$ of admitting a Shalika model and the algebraic condition of contributing to the cuspidal cohomology of ![]() $G$ are of an entirely different nature. One may construct examples of representations satisfying only one of these conditions and not the other (see [Reference Grobner and RaghuramGR14, § 3.5]).
$G$ are of an entirely different nature. One may construct examples of representations satisfying only one of these conditions and not the other (see [Reference Grobner and RaghuramGR14, § 3.5]).
4.2 Ordinarity and regularity
For ![]() $\mathfrak {p}$ dividing
$\mathfrak {p}$ dividing ![]() $p$, we let
$p$, we let ![]() $\varpi _\mathfrak {p}$ denote a uniformizer of
$\varpi _\mathfrak {p}$ denote a uniformizer of ![]() $F_\mathfrak {p}$ and let
$F_\mathfrak {p}$ and let ![]() $q_\mathfrak {p}=|\varpi _\mathfrak {p} |_p^{-1}$ denote the cardinality of its residue field. Let
$q_\mathfrak {p}=|\varpi _\mathfrak {p} |_p^{-1}$ denote the cardinality of its residue field. Let ![]() $\Sigma _\infty =\coprod _{\mathfrak {p}\mid p} \Sigma _\mathfrak {p}$ be the partition induced by
$\Sigma _\infty =\coprod _{\mathfrak {p}\mid p} \Sigma _\mathfrak {p}$ be the partition induced by ![]() $i_p:\bar{\mathbb {Q}}\hookrightarrow \bar{\mathbb {Q}}_p$, where
$i_p:\bar{\mathbb {Q}}\hookrightarrow \bar{\mathbb {Q}}_p$, where ![]() $\Sigma _\mathfrak {p}=\{\sigma :F_\mathfrak {p}\hookrightarrow \bar{\mathbb {Q}}_p\}$.
$\Sigma _\mathfrak {p}=\{\sigma :F_\mathfrak {p}\hookrightarrow \bar{\mathbb {Q}}_p\}$.
Recall from § 1.1 that a weight ![]() $\mu \in X^{*}_+(T)$ yields a rational character
$\mu \in X^{*}_+(T)$ yields a rational character ![]() $\mu :T=\operatorname {Res}_{F/\mathbb {Q}}T_{2n}\to \operatorname {GL}_1$, therefore induces a character
$\mu :T=\operatorname {Res}_{F/\mathbb {Q}}T_{2n}\to \operatorname {GL}_1$, therefore induces a character ![]() $\mu _p=\otimes _{\mathfrak {p}\mid p}\mu _\mathfrak {p}$ of
$\mu _p=\otimes _{\mathfrak {p}\mid p}\mu _\mathfrak {p}$ of ![]() $T(\mathbb {Q}_p) = \prod _{\mathfrak {p} \mid p} T_{2n}(F_\mathfrak {p})$, where
$T(\mathbb {Q}_p) = \prod _{\mathfrak {p} \mid p} T_{2n}(F_\mathfrak {p})$, where
 \begin{equation} \begin{aligned} & \mu_\mathfrak{p}:T_{2n}(F_\mathfrak{p})\to \bar{\mathbb{Q}}_p^{\times} \text{ is given by } (\mu_{\sigma})_{\sigma\in \Sigma_\mathfrak{p}} \text{ subject to the dominance condition} \\ & \mu_{\sigma,1}\geqslant \mu_{\sigma,2}\geqslant \cdots \geqslant \mu_{\sigma,2n}, \text{ for all } \sigma\in \Sigma_\mathfrak{p}. \end{aligned} \end{equation}
\begin{equation} \begin{aligned} & \mu_\mathfrak{p}:T_{2n}(F_\mathfrak{p})\to \bar{\mathbb{Q}}_p^{\times} \text{ is given by } (\mu_{\sigma})_{\sigma\in \Sigma_\mathfrak{p}} \text{ subject to the dominance condition} \\ & \mu_{\sigma,1}\geqslant \mu_{\sigma,2}\geqslant \cdots \geqslant \mu_{\sigma,2n}, \text{ for all } \sigma\in \Sigma_\mathfrak{p}. \end{aligned} \end{equation} Recall the maximal ![]() $(n,n)$-parabolic subgroup
$(n,n)$-parabolic subgroup ![]() $Q\subseteq G$. Given a cuspidal automorphic representation
$Q\subseteq G$. Given a cuspidal automorphic representation ![]() $\Pi$ of
$\Pi$ of ![]() $G(\mathbb {A})$ that is cohomological with respect to the weight
$G(\mathbb {A})$ that is cohomological with respect to the weight ![]() $\mu \in X^{*}_+(T)$, we say that
$\mu \in X^{*}_+(T)$, we say that ![]() $\Pi _{\mathfrak {p}}$ is
$\Pi _{\mathfrak {p}}$ is ![]() $Q$-ordinary (respectively,
$Q$-ordinary (respectively, ![]() $B$-ordinary) as in [Reference HidaHid95, Reference HidaHid98].
$B$-ordinary) as in [Reference HidaHid95, Reference HidaHid98].
Assume from now on that ![]() $\Pi _\mathfrak {p}$ is unramified for all
$\Pi _\mathfrak {p}$ is unramified for all ![]() $\mathfrak {p}\mid p$. As
$\mathfrak {p}\mid p$. As ![]() $\Pi$ is cohomological, there exists an unramified algebraic character
$\Pi$ is cohomological, there exists an unramified algebraic character ![]() $\lambda _{\mathfrak {p}}:T_{2n}(F_\mathfrak {p})\to \bar{\mathbb {Q}}^{\times }\subset \mathbb {C}^{\times }$ such that (see (43))
$\lambda _{\mathfrak {p}}:T_{2n}(F_\mathfrak {p})\to \bar{\mathbb {Q}}^{\times }\subset \mathbb {C}^{\times }$ such that (see (43))
Using ![]() $i_p: \mathbb {C} \xrightarrow {\sim } \bar{\mathbb {Q}}_p$ allows us to see the Hecke parameters
$i_p: \mathbb {C} \xrightarrow {\sim } \bar{\mathbb {Q}}_p$ allows us to see the Hecke parameters ![]() $\alpha _{\mathfrak {p},i}=\lambda _{\mathfrak {p},i}(\varpi _\mathfrak {p}),\ 1\leqslant i\leqslant 2n$, as elements of
$\alpha _{\mathfrak {p},i}=\lambda _{\mathfrak {p},i}(\varpi _\mathfrak {p}),\ 1\leqslant i\leqslant 2n$, as elements of ![]() $\bar{\mathbb {Q}}_p^{\times }$. Then
$\bar{\mathbb {Q}}_p^{\times }$. Then ![]() $\Pi _\mathfrak {p}$ is
$\Pi _\mathfrak {p}$ is ![]() $B$-ordinary relative to an ordering of its Hecke parameters
$B$-ordinary relative to an ordering of its Hecke parameters ![]() $\alpha _{\mathfrak {p},i}$ if and only if
$\alpha _{\mathfrak {p},i}$ if and only if
where ![]() $|\cdot |_p$ denotes the
$|\cdot |_p$ denotes the ![]() $p$-adic norm. The
$p$-adic norm. The ![]() $B$-dominance condition (2) then implies that
$B$-dominance condition (2) then implies that
hence there exists at most one ordering of the Hecke parameters for which ![]() $\Pi _\mathfrak {p}$ is
$\Pi _\mathfrak {p}$ is ![]() $B$-ordinary. Moreover, this implies that a
$B$-ordinary. Moreover, this implies that a ![]() $B$-ordinary
$B$-ordinary ![]() $\Pi _\mathfrak {p}$ is necessarily regular, that is, the
$\Pi _\mathfrak {p}$ is necessarily regular, that is, the ![]() $\alpha _{\mathfrak {p},i}$ are pairwise distinct.
$\alpha _{\mathfrak {p},i}$ are pairwise distinct.
Similarly, ![]() $\Pi _\mathfrak {p}$ is
$\Pi _\mathfrak {p}$ is ![]() $Q$-ordinary relative to
$Q$-ordinary relative to ![]() $\tau \in W_G/W_H$ if and only if
$\tau \in W_G/W_H$ if and only if
We make a key observation that ![]() $Q$-ordinarity implies
$Q$-ordinarity implies ![]() $Q$-regularity (see Definition 3.5).
$Q$-regularity (see Definition 3.5).
Lemma 4.4 Assume that the cuspidal automorphic representation ![]() $\Pi$ of
$\Pi$ of ![]() $G(\mathbb {A})$ is cohomological with respect to
$G(\mathbb {A})$ is cohomological with respect to ![]() $\mu$ and admits an
$\mu$ and admits an ![]() $(\eta ,\psi )$-Shalika model. For
$(\eta ,\psi )$-Shalika model. For ![]() $\mathfrak {p}$ dividing
$\mathfrak {p}$ dividing ![]() $p$, if
$p$, if ![]() $\Pi _{\mathfrak {p}}$ is spherical and
$\Pi _{\mathfrak {p}}$ is spherical and ![]() $Q$-ordinary, then
$Q$-ordinary, then
In particular, ![]() $\Pi _{\mathfrak {p}}$ is
$\Pi _{\mathfrak {p}}$ is ![]() $Q$-ordinary only relative to
$Q$-ordinary only relative to ![]() $\tau$. Moreover,
$\tau$. Moreover, ![]() $\tilde \Pi _{\mathfrak {p}}=(\Pi _{\mathfrak {p}},\tau )$ is
$\tilde \Pi _{\mathfrak {p}}=(\Pi _{\mathfrak {p}},\tau )$ is ![]() $Q$-regular, that is,
$Q$-regular, that is, ![]() $q_\mathfrak {p}^{{n(1-n)}/{2}} \prod _{i\in \tau } \alpha _{\mathfrak {p},i}$ is a simple eigenvalue of
$q_\mathfrak {p}^{{n(1-n)}/{2}} \prod _{i\in \tau } \alpha _{\mathfrak {p},i}$ is a simple eigenvalue of ![]() $U_\mathfrak {p}$ acting on
$U_\mathfrak {p}$ acting on ![]() $\Pi _\mathfrak {p}^{J_\mathfrak {p}}$ and
$\Pi _\mathfrak {p}^{J_\mathfrak {p}}$ and ![]() $\lambda _{\mathfrak {p}, i}\neq \lambda _{\mathfrak {p}, i'}$ for all
$\lambda _{\mathfrak {p}, i}\neq \lambda _{\mathfrak {p}, i'}$ for all ![]() $i\in \tau , i'\notin \tau$.
$i\in \tau , i'\notin \tau$.
Proof. Consider the Hecke operators ![]() $U_{\mathfrak {p},n-1}=[I_{\mathfrak {p}}t_{\mathfrak {p},n-1} I_{\mathfrak {p}}]$ acting on
$U_{\mathfrak {p},n-1}=[I_{\mathfrak {p}}t_{\mathfrak {p},n-1} I_{\mathfrak {p}}]$ acting on ![]() $\Pi _{\mathfrak {p},N}^{I_\mathfrak {p}}$, where
$\Pi _{\mathfrak {p},N}^{I_\mathfrak {p}}$, where ![]() $t_{\mathfrak {p},n-1}=\operatorname {diag}(\varpi _\mathfrak {p}\textbf {1}_{n-1},\textbf {1}_{n+1})\in \operatorname {GL}_{2n}(F_\mathfrak {p})$. As
$t_{\mathfrak {p},n-1}=\operatorname {diag}(\varpi _\mathfrak {p}\textbf {1}_{n-1},\textbf {1}_{n+1})\in \operatorname {GL}_{2n}(F_\mathfrak {p})$. As ![]() $\mu _\mathfrak {p}^{\vee }(t_{\mathfrak {p},n-1})\cdot U_{\mathfrak {p},n-1}$ preserves
$\mu _\mathfrak {p}^{\vee }(t_{\mathfrak {p},n-1})\cdot U_{\mathfrak {p},n-1}$ preserves ![]() $p$-integrality its eigenvalues on
$p$-integrality its eigenvalues on ![]() $\Pi _{\mathfrak {p},N}^{I_\mathfrak {p}}$ are
$\Pi _{\mathfrak {p},N}^{I_\mathfrak {p}}$ are ![]() $p$-integral, in particular for any
$p$-integral, in particular for any ![]() $i\in \tau$ we have
$i\in \tau$ we have
Together with (65) this implies that ![]() $|\alpha _{\mathfrak {p},i} |_p \geqslant |\mu _{\mathfrak {p},n}^{\vee }(\varpi _{\mathfrak {p}}^{-1}) q_\mathfrak {p}^{n-1}|_p= |\mu _{\mathfrak {p},n+1}(\varpi _{\mathfrak {p}}) q_\mathfrak {p}^{n-1}|_p$, that is,
$|\alpha _{\mathfrak {p},i} |_p \geqslant |\mu _{\mathfrak {p},n}^{\vee }(\varpi _{\mathfrak {p}}^{-1}) q_\mathfrak {p}^{n-1}|_p= |\mu _{\mathfrak {p},n+1}(\varpi _{\mathfrak {p}}) q_\mathfrak {p}^{n-1}|_p$, that is,
The existence of ![]() $(\eta _\mathfrak {p},\psi _\mathfrak {p})$-Shalika model for
$(\eta _\mathfrak {p},\psi _\mathfrak {p})$-Shalika model for ![]() $\Pi _\mathfrak {p}$ gives by [Reference Ash and GinzburgAG94, Proposition 1.3] an
$\Pi _\mathfrak {p}$ gives by [Reference Ash and GinzburgAG94, Proposition 1.3] an ![]() $i'=\rho (i)$ so that
$i'=\rho (i)$ so that
The latter equality together with (3) and (67) yields, for all ![]() $i\in \tau$,
$i\in \tau$,
 \[ v_p( \alpha_{\mathfrak{p},i}) \leqslant \sum_{\sigma\in \Sigma_\mathfrak{p}} (n-1+ \mu_{\sigma,n+1})< |\Sigma_\mathfrak{p}|\frac{{{\sf w}}+2n-1}{2} < \sum_{\sigma\in \Sigma_\mathfrak{p}} (n+ \mu_{\sigma,n}) \leqslant v_p( \alpha_{\mathfrak{p},\rho(i)}). \]
\[ v_p( \alpha_{\mathfrak{p},i}) \leqslant \sum_{\sigma\in \Sigma_\mathfrak{p}} (n-1+ \mu_{\sigma,n+1})< |\Sigma_\mathfrak{p}|\frac{{{\sf w}}+2n-1}{2} < \sum_{\sigma\in \Sigma_\mathfrak{p}} (n+ \mu_{\sigma,n}) \leqslant v_p( \alpha_{\mathfrak{p},\rho(i)}). \]
All claims then follow easily as clearly ![]() $\rho (\tau )\cap \tau =\varnothing$ as required by Definition 3.5.
$\rho (\tau )\cap \tau =\varnothing$ as required by Definition 3.5.
4.3  $p$-adic interpolation of critical values
$p$-adic interpolation of critical values
We suppose in the sequel that ![]() $\Pi$ is a cuspidal automorphic representation of
$\Pi$ is a cuspidal automorphic representation of ![]() $G(\mathbb {A})$ that is cohomological with respect to a pure weight
$G(\mathbb {A})$ that is cohomological with respect to a pure weight ![]() $\mu \in X^{*}_0(T)$ and that
$\mu \in X^{*}_0(T)$ and that ![]() $\Pi$ admits an
$\Pi$ admits an ![]() $(\eta ,\psi )$-Shalika model. Assume further that for all
$(\eta ,\psi )$-Shalika model. Assume further that for all ![]() $\mathfrak {p}\mid p$,
$\mathfrak {p}\mid p$, ![]() $\Pi _\mathfrak {p}$ is spherical and that
$\Pi _\mathfrak {p}$ is spherical and that ![]() $\tilde \Pi _\mathfrak {p}=(\Pi _\mathfrak {p}, \tau )$ is
$\tilde \Pi _\mathfrak {p}=(\Pi _\mathfrak {p}, \tau )$ is ![]() $Q$-regular for
$Q$-regular for ![]() $\tau =\{n+1,\ldots , 2n\}$ in the sense of Definition 3.5.
$\tau =\{n+1,\ldots , 2n\}$ in the sense of Definition 3.5.
4.3.1 Choice of local Shalika vectors
For ![]() $v\nmid p\infty$ we recall the vector
$v\nmid p\infty$ we recall the vector ![]() $W_{\Pi _v}\in \mathcal {S}^{\eta _v}_{\psi _v}(\Pi _v)$ from Proposition 3.3.
$W_{\Pi _v}\in \mathcal {S}^{\eta _v}_{\psi _v}(\Pi _v)$ from Proposition 3.3.
For ![]() $\mathfrak {p} \mid p$,
$\mathfrak {p} \mid p$, ![]() $\Pi _\mathfrak {p}$ is spherical and
$\Pi _\mathfrak {p}$ is spherical and ![]() $\tilde \Pi _\mathfrak {p}=(\Pi _\mathfrak {p}, \{n+1,\ldots , 2n\})$ is
$\tilde \Pi _\mathfrak {p}=(\Pi _\mathfrak {p}, \{n+1,\ldots , 2n\})$ is ![]() $Q$-regular, in particular,
$Q$-regular, in particular, ![]() $\alpha _\mathfrak {p}=\prod _{n+1\leqslant i \leqslant 2n}\alpha _{\mathfrak {p},i}$ is a simple eigenvalue for the Hecke operator
$\alpha _\mathfrak {p}=\prod _{n+1\leqslant i \leqslant 2n}\alpha _{\mathfrak {p},i}$ is a simple eigenvalue for the Hecke operator ![]() $U_\mathfrak {p}$ acting on
$U_\mathfrak {p}$ acting on ![]() $\Pi _\mathfrak {p}^{J_\mathfrak {p}}$. By Lemma 3.6 there exists a unique
$\Pi _\mathfrak {p}^{J_\mathfrak {p}}$. By Lemma 3.6 there exists a unique ![]() $W_{\tilde \Pi _\mathfrak {p}}$ on the line
$W_{\tilde \Pi _\mathfrak {p}}$ on the line ![]() $\mathcal {S}^{\eta _\mathfrak {p}}_{\psi _\mathfrak {p}}(\Pi _\mathfrak {p})^{J_\mathfrak {p}}[U_\mathfrak {p}-\alpha _\mathfrak {p}]$ normalized so that
$\mathcal {S}^{\eta _\mathfrak {p}}_{\psi _\mathfrak {p}}(\Pi _\mathfrak {p})^{J_\mathfrak {p}}[U_\mathfrak {p}-\alpha _\mathfrak {p}]$ normalized so that ![]() $W_{\tilde \Pi _\mathfrak {p}}(t_\mathfrak {p}^{-\delta _\mathfrak {p}})=1$. Let
$W_{\tilde \Pi _\mathfrak {p}}(t_\mathfrak {p}^{-\delta _\mathfrak {p}})=1$. Let
In addition to conditions (K1) and (K2) on ![]() $K$ (see § 2), we henceforth assume that:
$K$ (see § 2), we henceforth assume that:
(K3)
 $K$ fixes
$K$ fixes  $W_{\tilde \Pi _f}$ and
$W_{\tilde \Pi _f}$ and  $\eta$ is trivial on
$\eta$ is trivial on  $I(\mathfrak {m})$, hence can be seen as a character of
$I(\mathfrak {m})$, hence can be seen as a character of  $\mathscr {C}\!\ell _F^{+}(\mathfrak {m})$.
$\mathscr {C}\!\ell _F^{+}(\mathfrak {m})$.
For the local vectors at infinity, given any character ![]() $\epsilon$ of
$\epsilon$ of ![]() $K_{\infty }/K_\infty ^{\circ }$ we recall the basis
$K_{\infty }/K_\infty ^{\circ }$ we recall the basis ![]() $\Xi _\infty ^{\epsilon }$ of the line
$\Xi _\infty ^{\epsilon }$ of the line ![]() $\operatorname {H}^{t}({{\mathfrak {g}}}_\infty ,K_{\infty }^{\circ }; \mathcal {S}^{\eta _\infty }_{\psi _\infty }(\Pi _\infty )\otimes V^{\mu }_{\mathbb {C}})[\epsilon ]$ from § 4.1.3. As in [Reference Grobner and RaghuramGR14, § 4.1], we define the following.
$\operatorname {H}^{t}({{\mathfrak {g}}}_\infty ,K_{\infty }^{\circ }; \mathcal {S}^{\eta _\infty }_{\psi _\infty }(\Pi _\infty )\otimes V^{\mu }_{\mathbb {C}})[\epsilon ]$ from § 4.1.3. As in [Reference Grobner and RaghuramGR14, § 4.1], we define the following.
Definition 4.5 Fix a basis ![]() $\{e_\alpha \}$ of
$\{e_\alpha \}$ of ![]() $V^{\mu }_{\mathbb {C}}$ and a basis
$V^{\mu }_{\mathbb {C}}$ and a basis ![]() $\{\omega _i\}$ of
$\{\omega _i\}$ of ![]() $\big ({{\mathfrak {g}}}_\infty /{{\mathfrak {k}}}_\infty \big )^{\vee }$. For
$\big ({{\mathfrak {g}}}_\infty /{{\mathfrak {k}}}_\infty \big )^{\vee }$. For ![]() $\underline i= (i_1,\ldots ,i_{t}),$ with
$\underline i= (i_1,\ldots ,i_{t}),$ with ![]() $1 \leqslant i_1 < \cdots < i_{t} \leqslant \dim \big ({{\mathfrak {g}}}_\infty /{{\mathfrak {k}}}_\infty \big )$, we let
$1 \leqslant i_1 < \cdots < i_{t} \leqslant \dim \big ({{\mathfrak {g}}}_\infty /{{\mathfrak {k}}}_\infty \big )$, we let ![]() $\omega _{\underline i}= \omega _{i_1}\wedge \cdots \wedge \omega _{i_{t}}\in \bigwedge ^{t} \big ({{\mathfrak {g}}}_\infty /{{\mathfrak {k}}}_\infty \big )^{\vee }.$
$\omega _{\underline i}= \omega _{i_1}\wedge \cdots \wedge \omega _{i_{t}}\in \bigwedge ^{t} \big ({{\mathfrak {g}}}_\infty /{{\mathfrak {k}}}_\infty \big )^{\vee }.$
Using (57), ![]() $\Xi _\infty ^{\epsilon }$ can be written as a
$\Xi _\infty ^{\epsilon }$ can be written as a ![]() $K_\infty ^{\circ }$-invariant element
$K_\infty ^{\circ }$-invariant element
for a unique choice of ![]() $W_{\infty , \underline i, \alpha }^{\epsilon } \in \mathcal {S}^{\eta _\infty }_{\psi _\infty }(\Pi _\infty )$ called ‘cohomological vectors at infinity’.
$W_{\infty , \underline i, \alpha }^{\epsilon } \in \mathcal {S}^{\eta _\infty }_{\psi _\infty }(\Pi _\infty )$ called ‘cohomological vectors at infinity’.
For ![]() $\underline i$ and
$\underline i$ and ![]() $\alpha$ as previously, let
$\alpha$ as previously, let ![]() $\varphi _{\underline i, \alpha }^{\epsilon } \in \Pi$ be the unique vector whose image under (55) equals
$\varphi _{\underline i, \alpha }^{\epsilon } \in \Pi$ be the unique vector whose image under (55) equals
For each character ![]() $\epsilon$ of
$\epsilon$ of ![]() $K_{\infty }/K_{\infty }^{\circ }$ the embedding
$K_{\infty }/K_{\infty }^{\circ }$ the embedding ![]() $\Theta ^{\epsilon }_K$ defined in (60) yields
$\Theta ^{\epsilon }_K$ defined in (60) yields
The image ![]() $\phi _{\tilde \Pi }^{\epsilon }$ of
$\phi _{\tilde \Pi }^{\epsilon }$ of ![]() $W_{\tilde \Pi _f}$ under the composition of these three maps belongs to
$W_{\tilde \Pi _f}$ under the composition of these three maps belongs to ![]() $\operatorname {H}^{t}_c({S^{G}_K}, \mathcal {V}_{E}^{\mu })[\epsilon ]$ for some finite extension
$\operatorname {H}^{t}_c({S^{G}_K}, \mathcal {V}_{E}^{\mu })[\epsilon ]$ for some finite extension ![]() $E$ of
$E$ of ![]() $\mathbb {Q}_p$, and after possibly rescaling the maps
$\mathbb {Q}_p$, and after possibly rescaling the maps ![]() $\Theta ^{\epsilon }$, that is, rescaling the basis elements
$\Theta ^{\epsilon }$, that is, rescaling the basis elements ![]() $\Xi _\infty ^{\epsilon }$, one can render the cohomology class
$\Xi _\infty ^{\epsilon }$, one can render the cohomology class ![]() $\mathcal {O}$-integral:
$\mathcal {O}$-integral:
Recall that the Hecke operator ![]() $U_{p^{\beta }}^{\circ }$ defines an endomorphism of
$U_{p^{\beta }}^{\circ }$ defines an endomorphism of ![]() $\operatorname {H}^{t}_c({S^{G}_K}, \mathcal {V}_{\mathcal {O}}^{\mu })[\epsilon ]$. As
$\operatorname {H}^{t}_c({S^{G}_K}, \mathcal {V}_{\mathcal {O}}^{\mu })[\epsilon ]$. As ![]() $W_{\tilde \Pi _f}$ is an
$W_{\tilde \Pi _f}$ is an ![]() $U_{p^{\beta }}$-eigenvector with eigenvalue
$U_{p^{\beta }}$-eigenvector with eigenvalue ![]() $\alpha _{p^{\beta }}=\prod _{\mathfrak {p}\mid p}\alpha _\mathfrak {p}^{\beta _\mathfrak {p}}$, it follows (after possibly additionally rescaling by a power of
$\alpha _{p^{\beta }}=\prod _{\mathfrak {p}\mid p}\alpha _\mathfrak {p}^{\beta _\mathfrak {p}}$, it follows (after possibly additionally rescaling by a power of ![]() $p$ killing the torsion in
$p$ killing the torsion in ![]() $\operatorname {H}^{t}_c({S^{G}_K}, \mathcal {V}_{\mathcal {O}}^{\mu })$) that one can assume
$\operatorname {H}^{t}_c({S^{G}_K}, \mathcal {V}_{\mathcal {O}}^{\mu })$) that one can assume ![]() $\phi _{\tilde \Pi }^{\epsilon }$ is an
$\phi _{\tilde \Pi }^{\epsilon }$ is an ![]() $U_{p^{\beta }}^{\circ }$-eigenvector with eigenvalue
$U_{p^{\beta }}^{\circ }$-eigenvector with eigenvalue ![]() $\alpha _{p^{\beta }}^{\circ }=\mu ^{\vee }(t_p^{\beta }) \alpha _{p^{\beta }}$.
$\alpha _{p^{\beta }}^{\circ }=\mu ^{\vee }(t_p^{\beta }) \alpha _{p^{\beta }}$.
4.3.2 Interpolation formula at critical points
In this section, we relate the image of ![]() $\phi _{\tilde \Pi }^{\epsilon }$ defined in (71) by the evaluation map
$\phi _{\tilde \Pi }^{\epsilon }$ defined in (71) by the evaluation map ![]() $\mathcal {E}^{j,\eta }_{\beta ,[\delta ]}$ from (33), to the Friedberg–Jacquet integral from Proposition 4.3.
$\mathcal {E}^{j,\eta }_{\beta ,[\delta ]}$ from (33), to the Friedberg–Jacquet integral from Proposition 4.3.
Proposition 4.6 For any character ![]() $\epsilon$ of
$\epsilon$ of ![]() $K_{\infty }/K_\infty ^{\circ }$ and any
$K_{\infty }/K_\infty ^{\circ }$ and any ![]() $[\delta ]\in \mathscr {C}\!\ell _F^{+}(p^{\beta }\mathfrak {m})\times \mathscr {C}\!\ell _F^{+}(\mathfrak {m})$ we have
$[\delta ]\in \mathscr {C}\!\ell _F^{+}(p^{\beta }\mathfrak {m})\times \mathscr {C}\!\ell _F^{+}(\mathfrak {m})$ we have
 \[ i_p^{-1}\big( \mu^{\vee}(t_p^{-\beta})\cdot \mathcal{E}^{j,{{\sf w}}}_{\beta,[\delta]}(\phi_{\tilde\Pi}^{\epsilon})\big)= \int_{\tilde{S}^{H}_{L_\beta}[\delta]} \varphi_{\tilde\Pi,j}^{\epsilon}(h \xi t_p^{\beta}) |\!\det(h_1^{j} h_2^{{{\sf w}}-j}) |_F \,d h, \]
\[ i_p^{-1}\big( \mu^{\vee}(t_p^{-\beta})\cdot \mathcal{E}^{j,{{\sf w}}}_{\beta,[\delta]}(\phi_{\tilde\Pi}^{\epsilon})\big)= \int_{\tilde{S}^{H}_{L_\beta}[\delta]} \varphi_{\tilde\Pi,j}^{\epsilon}(h \xi t_p^{\beta}) |\!\det(h_1^{j} h_2^{{{\sf w}}-j}) |_F \,d h, \]
where ![]() $\varphi _{\tilde \Pi ,j}^{\epsilon } = \sum _{\underline i} \sum _\alpha a_{\underline i, \alpha , j}^{\epsilon } \cdot \varphi _{\underline i, \alpha }^{\epsilon }$ for suitable
$\varphi _{\tilde \Pi ,j}^{\epsilon } = \sum _{\underline i} \sum _\alpha a_{\underline i, \alpha , j}^{\epsilon } \cdot \varphi _{\underline i, \alpha }^{\epsilon }$ for suitable ![]() $a_{\underline i, \alpha , j}^{\epsilon } \in \mathbb {C}$.
$a_{\underline i, \alpha , j}^{\epsilon } \in \mathbb {C}$.
In this proposition, and henceforth, ![]() $\sum _{\underline i}$ denotes summing over all
$\sum _{\underline i}$ denotes summing over all ![]() ${\underline i} = (i_1,\ldots ,i_{t})$ and
${\underline i} = (i_1,\ldots ,i_{t})$ and ![]() $\sum _\alpha$ denotes summing over all
$\sum _\alpha$ denotes summing over all ![]() $1 \leqslant \alpha \leqslant \dim (V^{\mu }),$ as in Definition 4.5. A more careful choice of the bases
$1 \leqslant \alpha \leqslant \dim (V^{\mu }),$ as in Definition 4.5. A more careful choice of the bases ![]() $\{e_\alpha \}$ and
$\{e_\alpha \}$ and ![]() $\{\omega _i\}$ as in [Reference JanuszewskiJan16, § 7] yields algebraic coefficients
$\{\omega _i\}$ as in [Reference JanuszewskiJan16, § 7] yields algebraic coefficients ![]() $a_{\underline i,\alpha ,j}^{\epsilon }\in \bar {\mathbb {Q}}$.
$a_{\underline i,\alpha ,j}^{\epsilon }\in \bar {\mathbb {Q}}$.
Proof. We follow closely the proof of [Reference Barrera, Dimitrov and JorzaBDJ, Proposition 4.1]. Consider the commutative diagram

where ![]() $\tau _\beta =\mu ^{\vee }(t_p^{-\beta })\tau _\beta ^{\circ }$ is defined in (27), the horizontal maps are induced from the morphisms of local systems written above them, the map
$\tau _\beta =\mu ^{\vee }(t_p^{-\beta })\tau _\beta ^{\circ }$ is defined in (27), the horizontal maps are induced from the morphisms of local systems written above them, the map ![]() $\mathcal {T}_{\beta }$ is induced from the morphisms of local systems
$\mathcal {T}_{\beta }$ is induced from the morphisms of local systems ![]() $(h,v)\mapsto (h\xi t_p^{\beta }, v)$, and
$(h,v)\mapsto (h\xi t_p^{\beta }, v)$, and ![]() $\operatorname {triv}'_\delta$ is induced from the morphisms of local systems:
$\operatorname {triv}'_\delta$ is induced from the morphisms of local systems:
As ![]() $\mathcal {E}^{j,{{\sf w}}}_{\beta , [\delta ]}= \varepsilon (\det (\delta _{1}^{j}\delta _{2}^{{{\sf w}}-j})) \mathcal {E}^{j,{{\sf w}}}_{\beta ,\delta }$, with
$\mathcal {E}^{j,{{\sf w}}}_{\beta , [\delta ]}= \varepsilon (\det (\delta _{1}^{j}\delta _{2}^{{{\sf w}}-j})) \mathcal {E}^{j,{{\sf w}}}_{\beta ,\delta }$, with ![]() $\varepsilon _f = |\cdot |_{F,f}\operatorname {N}_{F_p/\mathbb {Q}_p}$, the previous diagram shows that the proposition is equivalent to
$\varepsilon _f = |\cdot |_{F,f}\operatorname {N}_{F_p/\mathbb {Q}_p}$, the previous diagram shows that the proposition is equivalent to
 \begin{equation} |\!\det(\delta_{1,f}^{j}\delta_{2,f}^{{{\sf w}}-j})|_F \big(\!\cap \theta_{[\delta]})\circ\operatorname{triv}_\delta^{*}\circ\kappa_j\circ \mathcal{T}_{\beta}\big)(\phi_{\tilde\Pi}^{\epsilon}) = \int_{\tilde{S}^{H}_{L_\beta}[\delta]} \varphi_{\tilde\Pi,j}^{\epsilon}(h\xi t_p^{\beta}) |\!\det(h_1^{j} h_2^{{{\sf w}}-j}) |_F \,d h, \end{equation}
\begin{equation} |\!\det(\delta_{1,f}^{j}\delta_{2,f}^{{{\sf w}}-j})|_F \big(\!\cap \theta_{[\delta]})\circ\operatorname{triv}_\delta^{*}\circ\kappa_j\circ \mathcal{T}_{\beta}\big)(\phi_{\tilde\Pi}^{\epsilon}) = \int_{\tilde{S}^{H}_{L_\beta}[\delta]} \varphi_{\tilde\Pi,j}^{\epsilon}(h\xi t_p^{\beta}) |\!\det(h_1^{j} h_2^{{{\sf w}}-j}) |_F \,d h, \end{equation}
the left-hand side being considered over ![]() $\mathbb {C}$ via
$\mathbb {C}$ via ![]() $i_p^{-1}:\bar{\mathbb {Q}}_p \xrightarrow {\sim } \mathbb {C}$. By Definition 4.5
$i_p^{-1}:\bar{\mathbb {Q}}_p \xrightarrow {\sim } \mathbb {C}$. By Definition 4.5
yielding a ![]() $V^{\mu }_{\mathbb {C}}$-valued differential
$V^{\mu }_{\mathbb {C}}$-valued differential ![]() $t$-form on
$t$-form on ![]() $G_\infty ^{\circ }/K_\infty ^{\circ }$. Now, recall the basis
$G_\infty ^{\circ }/K_\infty ^{\circ }$. Now, recall the basis ![]() $\kappa _j$ of the one-dimensional
$\kappa _j$ of the one-dimensional ![]() $\operatorname {Hom}_H(V^{\mu }, V^{(j,{{\sf w}}-j)})$ from (28) and consider the map
$\operatorname {Hom}_H(V^{\mu }, V^{(j,{{\sf w}}-j)})$ from (28) and consider the map
We obtain
First, let ![]() $\kappa _j^{\circ }: V^{(j,{{\sf w}}-j)}_{\mathbb {C}}\xrightarrow {\sim } \mathbb {C}$ be the scalar extension of (40), and so
$\kappa _j^{\circ }: V^{(j,{{\sf w}}-j)}_{\mathbb {C}}\xrightarrow {\sim } \mathbb {C}$ be the scalar extension of (40), and so ![]() $\kappa _j(e_\alpha )$ corresponds to a complex number. Next, after the discussion in the paragraph following (23), we can fix a basis for the top exterior
$\kappa _j(e_\alpha )$ corresponds to a complex number. Next, after the discussion in the paragraph following (23), we can fix a basis for the top exterior ![]() $\wedge ^{t}({{\mathfrak {h}}}_\infty /{{\mathfrak {l}}}_\infty )^{\vee }$ corresponding to the Haar measure
$\wedge ^{t}({{\mathfrak {h}}}_\infty /{{\mathfrak {l}}}_\infty )^{\vee }$ corresponding to the Haar measure ![]() $dh_\infty$; hence
$dh_\infty$; hence ![]() $\iota ^{*} \omega _{\underline i}$ is a scalar multiple of
$\iota ^{*} \omega _{\underline i}$ is a scalar multiple of ![]() $dh_\infty$. Putting both together, the restriction to
$dh_\infty$. Putting both together, the restriction to ![]() $\tilde {S}^{H}_{L_\beta }[\delta ]$ of
$\tilde {S}^{H}_{L_\beta }[\delta ]$ of ![]() $\kappa _j( \mathcal {T}_{\beta }( \phi _{\tilde \Pi }^{\epsilon }))$ can be seen as
$\kappa _j( \mathcal {T}_{\beta }( \phi _{\tilde \Pi }^{\epsilon }))$ can be seen as ![]() $V^{(j,{{\sf w}}-j)}_{\mathbb {C}}$-valued top-degree differential form on
$V^{(j,{{\sf w}}-j)}_{\mathbb {C}}$-valued top-degree differential form on ![]() $H_\infty ^{\circ }/L_\infty ^{\circ }$ given by
$H_\infty ^{\circ }/L_\infty ^{\circ }$ given by
for suitable ![]() $a_{\underline i, \alpha , j}^{\epsilon }\in \mathbb {C}$. Writing
$a_{\underline i, \alpha , j}^{\epsilon }\in \mathbb {C}$. Writing ![]() $h=\gamma \delta l h'_\infty \in H(\mathbb {Q})\delta L_\beta H_\infty ^{\circ }\subset H(\mathbb {A})$, and using
$h=\gamma \delta l h'_\infty \in H(\mathbb {Q})\delta L_\beta H_\infty ^{\circ }\subset H(\mathbb {A})$, and using ![]() $\operatorname {triv}'_\delta (\gamma \delta \ell h'_\infty ,v)=(\gamma \delta \ell h'_\infty , \det (\gamma _{1,\infty }^{-j}\gamma _{2,\infty }^{j-{{\sf w}}}) v)$ one obtains (72) and the proposition from
$\operatorname {triv}'_\delta (\gamma \delta \ell h'_\infty ,v)=(\gamma \delta \ell h'_\infty , \det (\gamma _{1,\infty }^{-j}\gamma _{2,\infty }^{j-{{\sf w}}}) v)$ one obtains (72) and the proposition from
 \begin{align*} |\!\det(\delta_{1,f}^{j}\delta_{2,f}^{{{\sf w}}-j})|_F \det(\gamma_{1,\infty}^{-j}\gamma_{2,\infty}^{j-{{\sf w}}})\det(h_{1,\infty}^{ j} h_{2,\infty}^{ {{\sf w}}-j}) & = |\!\det(\delta_{1,f}^{j}\delta_{2,f}^{{{\sf w}}-j})|_F\det(h_{1,\infty}^{\prime j} h_{2,\infty}^{\prime {{\sf w}}-j})\\ & = |\!\det(h_1^{j} h_2^{{{\sf w}}-j})|_F. \end{align*}
\begin{align*} |\!\det(\delta_{1,f}^{j}\delta_{2,f}^{{{\sf w}}-j})|_F \det(\gamma_{1,\infty}^{-j}\gamma_{2,\infty}^{j-{{\sf w}}})\det(h_{1,\infty}^{ j} h_{2,\infty}^{ {{\sf w}}-j}) & = |\!\det(\delta_{1,f}^{j}\delta_{2,f}^{{{\sf w}}-j})|_F\det(h_{1,\infty}^{\prime j} h_{2,\infty}^{\prime {{\sf w}}-j})\\ & = |\!\det(h_1^{j} h_2^{{{\sf w}}-j})|_F. \end{align*}4.3.3  $p$-adic distributions attached to
$p$-adic distributions attached to  $\tilde \Pi$
$\tilde \Pi$
Recall that ![]() $\Pi$ is a cuspidal automorphic representation of
$\Pi$ is a cuspidal automorphic representation of ![]() $G(\mathbb {A})$ admitting a global
$G(\mathbb {A})$ admitting a global ![]() $(\psi ,\eta )$-Shalika model, which is cohomological with respect to a pure dominant integral weight
$(\psi ,\eta )$-Shalika model, which is cohomological with respect to a pure dominant integral weight ![]() $\mu$. Recall also that
$\mu$. Recall also that ![]() $\Pi _\mathfrak {p}$ is spherical for all
$\Pi _\mathfrak {p}$ is spherical for all ![]() $\mathfrak {p}\mid p$ and that
$\mathfrak {p}\mid p$ and that ![]() $\tilde \Pi _\mathfrak {p}=(\Pi _\mathfrak {p}, \{n+1,\ldots , 2n\})$ is
$\tilde \Pi _\mathfrak {p}=(\Pi _\mathfrak {p}, \{n+1,\ldots , 2n\})$ is ![]() $Q$-regular (see Definition 3.5), which by Lemma 4.4 is automatically fulfilled if
$Q$-regular (see Definition 3.5), which by Lemma 4.4 is automatically fulfilled if ![]() $\Pi _\mathfrak {p}$ is
$\Pi _\mathfrak {p}$ is ![]() $Q$-ordinary. In all cases
$Q$-ordinary. In all cases ![]() $\Pi _\mathfrak {p}^{J_\mathfrak {p}}$ contains a unique line on which
$\Pi _\mathfrak {p}^{J_\mathfrak {p}}$ contains a unique line on which ![]() $U_\mathfrak {p}$ acts by
$U_\mathfrak {p}$ acts by ![]() $\alpha _{\mathfrak {p}}$. Finally recall the
$\alpha _{\mathfrak {p}}$. Finally recall the ![]() $U_\mathfrak {p}^{\circ }$-eigenvectors
$U_\mathfrak {p}^{\circ }$-eigenvectors ![]() $\phi _{\tilde \Pi }^{\epsilon }$ constructed in (71). Then
$\phi _{\tilde \Pi }^{\epsilon }$ constructed in (71). Then
is an ![]() $U_\mathfrak {p}^{\circ }$-eigenvector with same eigenvalue. When
$U_\mathfrak {p}^{\circ }$-eigenvector with same eigenvalue. When ![]() $\tilde \Pi _p$ is
$\tilde \Pi _p$ is ![]() $Q$-ordinary, consider the element
$Q$-ordinary, consider the element
constructed in (37) and (39), which defines a measure ![]() $d\boldsymbol {\mu }_{\tilde \Pi }^{\eta }$ on
$d\boldsymbol {\mu }_{\tilde \Pi }^{\eta }$ on ![]() $\mathscr {C}\!\ell _F^{+}(p^{\infty })$.
$\mathscr {C}\!\ell _F^{+}(p^{\infty })$.
4.3.4 Main theorem on  $p$-adic interpolation
$p$-adic interpolation
Fix any character ![]() $\epsilon$ of
$\epsilon$ of ![]() $K_{\infty }/K_\infty ^{\circ }$ and any
$K_{\infty }/K_\infty ^{\circ }$ and any ![]() $j\in \operatorname {Crit}(\mu )$. Consider the following cohomological test vector:
$j\in \operatorname {Crit}(\mu )$. Consider the following cohomological test vector:
A crucial result of Sun [Reference SunSun19, Theorem 5.5] asserts the following non-vanishing:
Note that because ![]() $\Pi _\infty \otimes {\rm sgn} = \Pi _\infty$ we have suppressed
$\Pi _\infty \otimes {\rm sgn} = \Pi _\infty$ we have suppressed ![]() $\chi _\infty$ from the notation.
$\chi _\infty$ from the notation.
In fact, using Künneth's theorem, it is easy to see that ![]() $\zeta _\infty (j+\frac {1}{2};W_{\Pi _\infty ,j}^{\epsilon })$ is a product of similar quantities parsed over the archimedean places. As we have multiplicity one for cuspidal cohomology in top-degree (see (57)), we can only change the class
$\zeta _\infty (j+\frac {1}{2};W_{\Pi _\infty ,j}^{\epsilon })$ is a product of similar quantities parsed over the archimedean places. As we have multiplicity one for cuspidal cohomology in top-degree (see (57)), we can only change the class ![]() $\Xi _\infty ^{\epsilon }$ by a non-zero scalar, which correspondingly scales the cohomological test vector and so also the zeta integral. The variation of the complex period
$\Xi _\infty ^{\epsilon }$ by a non-zero scalar, which correspondingly scales the cohomological test vector and so also the zeta integral. The variation of the complex period ![]() $\zeta _\infty (j+\frac {1}{2};W_{\Pi _\infty ,j}^{\epsilon })$ in
$\zeta _\infty (j+\frac {1}{2};W_{\Pi _\infty ,j}^{\epsilon })$ in ![]() $j$ is studied in [Reference JanuszewskiJan16]. The reader is also referred to the discussion around [Reference Grobner and RaghuramGR14, Theorem 6.6.2].
$j$ is studied in [Reference JanuszewskiJan16]. The reader is also referred to the discussion around [Reference Grobner and RaghuramGR14, Theorem 6.6.2].
Recall the auxiliary ideal ![]() $\mathfrak {m}$ from (L1) in § 2.1 and, for brevity, let us define
$\mathfrak {m}$ from (L1) in § 2.1 and, for brevity, let us define
Theorem 4.7 Let ![]() $\Pi$ be a cuspidal automorphic representation of
$\Pi$ be a cuspidal automorphic representation of ![]() $\operatorname {GL}_{2n}/F$ admitting a
$\operatorname {GL}_{2n}/F$ admitting a ![]() $(\psi ,\eta )$-Shalika model and such that
$(\psi ,\eta )$-Shalika model and such that ![]() $\Pi _\infty$ is cohomological of weight
$\Pi _\infty$ is cohomological of weight ![]() $\mu$. Assume that for all
$\mu$. Assume that for all ![]() $\mathfrak {p}\mid p$,
$\mathfrak {p}\mid p$, ![]() $\Pi _\mathfrak {p}$ is spherical and admits a
$\Pi _\mathfrak {p}$ is spherical and admits a ![]() $Q$-regular refinement
$Q$-regular refinement ![]() $\tilde \Pi _{\mathfrak {p}}$. Then for any
$\tilde \Pi _{\mathfrak {p}}$. Then for any ![]() $j\in \operatorname {Crit}(\mu )$ and for any finite order character
$j\in \operatorname {Crit}(\mu )$ and for any finite order character ![]() $\chi$ of
$\chi$ of ![]() $\mathscr {C}\!\ell _F^{+}(p^{\infty })$ of conductor
$\mathscr {C}\!\ell _F^{+}(p^{\infty })$ of conductor ![]() $\beta _\mathfrak {p} \geqslant 1$ at
$\beta _\mathfrak {p} \geqslant 1$ at ![]() $\mathfrak {p}\mid p$:
$\mathfrak {p}\mid p$:
 \begin{align*} i_p^{-1}\bigg( \int_{\mathscr{C}\!\ell_F^{+}(p^{\infty})} \chi(x) \, d \boldsymbol{\mu}_{\phi_{\tilde\Pi}}^{\eta,j}(x) \bigg) &= \gamma \cdot \operatorname{N}^{jn}_{F/\mathbb{Q}}(\mathfrak{d}) \cdot \prod_{\mathfrak{p}\mid p}\big(\alpha_{\mathfrak{p}}^{-1} q_\mathfrak{p}^{n(j+1)}\big)^{\beta_\mathfrak{p}} \\ &\quad \cdot {\mathcal{G}(\chi_f)^{n} \cdot L\bigg(j+\frac{1}{2}, \Pi_f \otimes \chi_f\bigg) } \zeta_\infty\bigg(j+\frac{1}{2};W_{\Pi_\infty,j}^{(\varepsilon^{j}\chi\eta)_\infty}\bigg). \end{align*}
\begin{align*} i_p^{-1}\bigg( \int_{\mathscr{C}\!\ell_F^{+}(p^{\infty})} \chi(x) \, d \boldsymbol{\mu}_{\phi_{\tilde\Pi}}^{\eta,j}(x) \bigg) &= \gamma \cdot \operatorname{N}^{jn}_{F/\mathbb{Q}}(\mathfrak{d}) \cdot \prod_{\mathfrak{p}\mid p}\big(\alpha_{\mathfrak{p}}^{-1} q_\mathfrak{p}^{n(j+1)}\big)^{\beta_\mathfrak{p}} \\ &\quad \cdot {\mathcal{G}(\chi_f)^{n} \cdot L\bigg(j+\frac{1}{2}, \Pi_f \otimes \chi_f\bigg) } \zeta_\infty\bigg(j+\frac{1}{2};W_{\Pi_\infty,j}^{(\varepsilon^{j}\chi\eta)_\infty}\bigg). \end{align*}Proof. Using (37) and (35) we find that ![]() $\int _{\mathscr {C}\!\ell _F^{+}(p^{\infty })} \chi (x) \, d \boldsymbol {\mu }_{\phi _{\tilde \Pi }}^{\eta ,j}(x)$ equals
$\int _{\mathscr {C}\!\ell _F^{+}(p^{\infty })} \chi (x) \, d \boldsymbol {\mu }_{\phi _{\tilde \Pi }}^{\eta ,j}(x)$ equals
 \[ (\alpha_{p^{\beta}}^{\circ})^{-1} \sum_{[x]\in \mathscr{C}\!\ell_F^{+}(p^{\beta}\mathfrak{m})}\chi([x])\mathcal{E}^{j,\eta}_{\beta,[x]}(\phi_{\tilde\Pi}) \nonumber = \alpha_{p^{\beta}}^{-1} \cdot \mu^{\vee}(t_p^{-\beta}) \sum_{\substack{[x]\in \mathscr{C}\!\ell_F^{+}(p^{\beta}\mathfrak{m}) \\ [y]\in \mathscr{C}\!\ell_F^{+}(\mathfrak{m})}} \chi([x]) \eta_0([y]) \mathcal{E}^{j,{{\sf w}}}_{\beta,[\delta(x,y)]}(\phi_{\tilde\Pi}). \]
\[ (\alpha_{p^{\beta}}^{\circ})^{-1} \sum_{[x]\in \mathscr{C}\!\ell_F^{+}(p^{\beta}\mathfrak{m})}\chi([x])\mathcal{E}^{j,\eta}_{\beta,[x]}(\phi_{\tilde\Pi}) \nonumber = \alpha_{p^{\beta}}^{-1} \cdot \mu^{\vee}(t_p^{-\beta}) \sum_{\substack{[x]\in \mathscr{C}\!\ell_F^{+}(p^{\beta}\mathfrak{m}) \\ [y]\in \mathscr{C}\!\ell_F^{+}(\mathfrak{m})}} \chi([x]) \eta_0([y]) \mathcal{E}^{j,{{\sf w}}}_{\beta,[\delta(x,y)]}(\phi_{\tilde\Pi}). \]
As ![]() $\pi _0(\tilde {S}^{H}_{L_\beta })\simeq \mathscr {C}\!\ell _F^{+}(p^{\beta } \mathfrak {m})\times \mathscr {C}\!\ell _F^{+}(\mathfrak {m})$ by (73) and Proposition 4.6 the integral equals
$\pi _0(\tilde {S}^{H}_{L_\beta })\simeq \mathscr {C}\!\ell _F^{+}(p^{\beta } \mathfrak {m})\times \mathscr {C}\!\ell _F^{+}(\mathfrak {m})$ by (73) and Proposition 4.6 the integral equals
 \[ \alpha_{p^{\beta}}^{-1} \cdot \sum_{\epsilon: \{\pm 1\}^{\Sigma_\infty}\to \{\pm 1\}} \int_{\tilde{S}^{H}_{L_\beta}} \varphi_{\tilde\Pi,j}^{\epsilon}(h\xi t_p^{\beta}) \chi\bigg(\frac{\det(h_1)}{\det(h_2)}\bigg) \bigg| \frac{\det(h_1)}{\det(h_2)}\bigg|_F^{j} \eta^{-1}( \det(h_2)) \, d h. \]
\[ \alpha_{p^{\beta}}^{-1} \cdot \sum_{\epsilon: \{\pm 1\}^{\Sigma_\infty}\to \{\pm 1\}} \int_{\tilde{S}^{H}_{L_\beta}} \varphi_{\tilde\Pi,j}^{\epsilon}(h\xi t_p^{\beta}) \chi\bigg(\frac{\det(h_1)}{\det(h_2)}\bigg) \bigg| \frac{\det(h_1)}{\det(h_2)}\bigg|_F^{j} \eta^{-1}( \det(h_2)) \, d h. \]
Note that the integrand is ![]() $L_\infty ^{\circ } Z(\mathbb {A}_f)$-invariant and
$L_\infty ^{\circ } Z(\mathbb {A}_f)$-invariant and ![]() $L_\infty /L_\infty ^{\circ } Z_\infty$ acts on it by
$L_\infty /L_\infty ^{\circ } Z_\infty$ acts on it by ![]() $\epsilon \varepsilon _\infty ^{j}\chi _\infty \eta _\infty$, hence the integral vanishes unless
$\epsilon \varepsilon _\infty ^{j}\chi _\infty \eta _\infty$, hence the integral vanishes unless ![]() $\epsilon =(\varepsilon ^{j}\chi \eta )_\infty$. As
$\epsilon =(\varepsilon ^{j}\chi \eta )_\infty$. As ![]() $Z(\mathbb {A}_f)\cap L_\beta$ is independent of
$Z(\mathbb {A}_f)\cap L_\beta$ is independent of ![]() $\beta$, after some volume computation, one further finds
$\beta$, after some volume computation, one further finds
 \[ i_p^{-1}\bigg( \int_{\mathscr{C}\!\ell_F^{+}(p^{\infty})}\varepsilon^{j}(x) \chi(x) \, d \boldsymbol{\mu}_{\tilde\Pi}^{\eta}(x)\bigg) =\gamma \cdot \Psi\bigg(j+\frac{1}{2},\varphi_{\tilde\Pi,j}^{(\varepsilon^{j}\chi\eta)_\infty}(-\cdot \xi t_p^{\beta}),\chi,\eta\bigg) \prod_{\mathfrak{p}\mid p} (\alpha_{\mathfrak{p}}^{-1} q_\mathfrak{p}^{n^{2}})^{\beta_\mathfrak{p}}. \]
\[ i_p^{-1}\bigg( \int_{\mathscr{C}\!\ell_F^{+}(p^{\infty})}\varepsilon^{j}(x) \chi(x) \, d \boldsymbol{\mu}_{\tilde\Pi}^{\eta}(x)\bigg) =\gamma \cdot \Psi\bigg(j+\frac{1}{2},\varphi_{\tilde\Pi,j}^{(\varepsilon^{j}\chi\eta)_\infty}(-\cdot \xi t_p^{\beta}),\chi,\eta\bigg) \prod_{\mathfrak{p}\mid p} (\alpha_{\mathfrak{p}}^{-1} q_\mathfrak{p}^{n^{2}})^{\beta_\mathfrak{p}}. \]
By Proposition 4.3 the Friedberg–Jacquet integral has an Euler product for ![]() $\Re (s)\gg 0$:
$\Re (s)\gg 0$:
As ![]() $L(s, \Pi \otimes \chi )$ has trivial Euler factors at all places
$L(s, \Pi \otimes \chi )$ has trivial Euler factors at all places ![]() $\mathfrak {p}\mid p$ (as
$\mathfrak {p}\mid p$ (as ![]() $\Pi _\mathfrak {p}$ is spherical while
$\Pi _\mathfrak {p}$ is spherical while ![]() $\chi _\mathfrak {p}$ is ramified), Proposition 3.3 implies that
$\chi _\mathfrak {p}$ is ramified), Proposition 3.3 implies that
 \[ \prod_{v\nmid p\infty}\zeta_v\bigg(j+\frac{1}{2};W_{\Pi_v},\chi_v\bigg)= \operatorname{N}_{F/\mathbb{Q}}^{jn}(\mathfrak{d}^{(p)}) \chi(\mathfrak{d}^{-1})^{n} L\bigg(j+\frac{1}{2}, \Pi_f \otimes \chi_f\bigg). \]
\[ \prod_{v\nmid p\infty}\zeta_v\bigg(j+\frac{1}{2};W_{\Pi_v},\chi_v\bigg)= \operatorname{N}_{F/\mathbb{Q}}^{jn}(\mathfrak{d}^{(p)}) \chi(\mathfrak{d}^{-1})^{n} L\bigg(j+\frac{1}{2}, \Pi_f \otimes \chi_f\bigg). \]
The factor at ![]() $\mathfrak {p}\mid p$ is computed in Proposition 3.4, which together with Lemma 3.6 gives
$\mathfrak {p}\mid p$ is computed in Proposition 3.4, which together with Lemma 3.6 gives
As ![]() $\mathcal {G}(\chi _f)=\chi (\mathfrak {d}^{-1}) \prod _{\mathfrak {p}\mid p} \mathcal {G}(\chi _\mathfrak {p})$ and
$\mathcal {G}(\chi _f)=\chi (\mathfrak {d}^{-1}) \prod _{\mathfrak {p}\mid p} \mathcal {G}(\chi _\mathfrak {p})$ and ![]() $\mathfrak {d}=\mathfrak {d}_p\mathfrak {d}^{(p)}$ we obtain the desired formula.
$\mathfrak {d}=\mathfrak {d}_p\mathfrak {d}^{(p)}$ we obtain the desired formula.
Proof of Theorem 2 By Lemma 4.4, for each ![]() $\mathfrak {p}\mid p$, the
$\mathfrak {p}\mid p$, the ![]() $Q$-ordinary refinement
$Q$-ordinary refinement ![]() $\tilde \Pi _\mathfrak {p}$ of
$\tilde \Pi _\mathfrak {p}$ of ![]() $\Pi _\mathfrak {p}$ is
$\Pi _\mathfrak {p}$ is ![]() $Q$-regular, hence Theorem 4.7 applies. The interpolation formula in Theorem B then follows immediately because by Theorem 2.3 one has
$Q$-regular, hence Theorem 4.7 applies. The interpolation formula in Theorem B then follows immediately because by Theorem 2.3 one has
4.4 Non-vanishing of twists
4.4.1 The main theorem
Having established the Manin relations in our context (see Theorem 2.3), we can now prove a non-vanishing result for twisted ![]() $L$-functions using a method that goes back to Manin and Greenberg. Such a technique to prove non-vanishing of twists has also been used recently by Januszewski [Reference JanuszewskiJan18] for Rankin–Selberg
$L$-functions using a method that goes back to Manin and Greenberg. Such a technique to prove non-vanishing of twists has also been used recently by Januszewski [Reference JanuszewskiJan18] for Rankin–Selberg ![]() $L$-functions and Eischen [Reference EischenEis] for
$L$-functions and Eischen [Reference EischenEis] for ![]() $L$-functions of unitary groups. However, our results, Theorem 4.8 and Corollary 4.10, are not only independent of these other recent works but are also beyond the scope of results in both [Reference JanuszewskiJan18] and [Reference EischenEis] as well as previous results obtained by analytic number theoretic methods [Reference RohrlichRoh89, Reference Barthel and RamakrishnanBR94, Reference LuoLuo05, Reference Chinta, Friedberg and HoffsteinCFH05].
$L$-functions of unitary groups. However, our results, Theorem 4.8 and Corollary 4.10, are not only independent of these other recent works but are also beyond the scope of results in both [Reference JanuszewskiJan18] and [Reference EischenEis] as well as previous results obtained by analytic number theoretic methods [Reference RohrlichRoh89, Reference Barthel and RamakrishnanBR94, Reference LuoLuo05, Reference Chinta, Friedberg and HoffsteinCFH05].
Theorem 4.8 Let ![]() $\mu$ be a pure dominant integral weight such that
$\mu$ be a pure dominant integral weight such that
Let ![]() $\Pi$ be a cuspidal automorphic representation that is cohomological with respect to the weight
$\Pi$ be a cuspidal automorphic representation that is cohomological with respect to the weight ![]() $\mu$ and admitting an
$\mu$ and admitting an ![]() $(\eta ,\psi )$-Shalika model. Assume that for all primes
$(\eta ,\psi )$-Shalika model. Assume that for all primes ![]() $\mathfrak {p}$ above a prime number
$\mathfrak {p}$ above a prime number ![]() $p$,
$p$, ![]() $\Pi _\mathfrak {p}$ is unramified and
$\Pi _\mathfrak {p}$ is unramified and ![]() $Q$-ordinary. Then for all
$Q$-ordinary. Then for all ![]() $j\in \operatorname {Crit}(\mu )$ and for all but finitely many Dirichlet characters
$j\in \operatorname {Crit}(\mu )$ and for all but finitely many Dirichlet characters ![]() $\chi$ of
$\chi$ of ![]() $F$ of
$F$ of ![]() $p$-power conductor, we have
$p$-power conductor, we have
We begin with a few comments. As ![]() $\Pi ^{\circ } = \Pi \otimes |\cdot |^{{{\sf w}}/2}$ is a unitary cuspidal automorphic representation, we see that
$\Pi ^{\circ } = \Pi \otimes |\cdot |^{{{\sf w}}/2}$ is a unitary cuspidal automorphic representation, we see that ![]() $({1+{{\sf w}}})/{2}$ is the center of symmetry for the
$({1+{{\sf w}}})/{2}$ is the center of symmetry for the ![]() $L$-function of
$L$-function of ![]() $\Pi$:
$\Pi$:
By regularity one knows that ![]() $\operatorname {Crit}(\mu )$ is non-empty and condition (78) is equivalent to assuming that
$\operatorname {Crit}(\mu )$ is non-empty and condition (78) is equivalent to assuming that ![]() $\operatorname {Crit}(\mu )$ has at least two elements. If
$\operatorname {Crit}(\mu )$ has at least two elements. If ![]() $\Pi$ is unitary, then
$\Pi$ is unitary, then ![]() ${{\sf w}} = 0$ and
${{\sf w}} = 0$ and ![]() $\frac {1}{2} \in \operatorname {Crit}(\Pi \otimes \chi ) = \operatorname {Crit}(\mu )$, whence Theorem A is a particular case of Theorem 4.8.
$\frac {1}{2} \in \operatorname {Crit}(\Pi \otimes \chi ) = \operatorname {Crit}(\mu )$, whence Theorem A is a particular case of Theorem 4.8.
If Leopoldt's conjecture holds for ![]() $F$ at
$F$ at ![]() $p$, then one readily obtains a statement for all but finitely many
$p$, then one readily obtains a statement for all but finitely many ![]() $p$-power conductor Hecke characters, as opposed to Dirichlet characters.
$p$-power conductor Hecke characters, as opposed to Dirichlet characters.
We show non-vanishing of critical values of twisted ![]() $L$-functions by showing non-vanishing statement about distributions on the cyclotomic
$L$-functions by showing non-vanishing statement about distributions on the cyclotomic ![]() $\mathbb {Z}_p$-extension of
$\mathbb {Z}_p$-extension of ![]() $F$. Recall the
$F$. Recall the ![]() $p$-adic cyclotomic character
$p$-adic cyclotomic character
the first component of which is given by the Teichmüller character ![]() $\omega$, whereas the fixed field of the kernel of the second component
$\omega$, whereas the fixed field of the kernel of the second component ![]() $\varepsilon \omega ^{-1}$ is the cyclotomic
$\varepsilon \omega ^{-1}$ is the cyclotomic ![]() $\mathbb {Z}_p$-extension of
$\mathbb {Z}_p$-extension of ![]() $\mathbb {Q}$. Then by a well-known result due to Serre there is an isomorphism
$\mathbb {Q}$. Then by a well-known result due to Serre there is an isomorphism ![]() $\mathcal {O}[[1+2p\mathbb {Z}_p]]\simeq \mathcal {O}[[T]]$ sending
$\mathcal {O}[[1+2p\mathbb {Z}_p]]\simeq \mathcal {O}[[T]]$ sending ![]() $1+2p$ to
$1+2p$ to ![]() $1+T$. Composing with the norm map
$1+T$. Composing with the norm map ![]() $\operatorname {N}_{F/\mathbb {Q}}: \mathscr {C}\!\ell _F^{+}(p^{\infty })\to {\mathcal {C}\!\ell _{\mathbb {Q}}^{+}}(p^{\infty })$ allows us to lift Dirichlet characters to Hecke characters over
$\operatorname {N}_{F/\mathbb {Q}}: \mathscr {C}\!\ell _F^{+}(p^{\infty })\to {\mathcal {C}\!\ell _{\mathbb {Q}}^{+}}(p^{\infty })$ allows us to lift Dirichlet characters to Hecke characters over ![]() $F$, thus to push-forward of a measure on
$F$, thus to push-forward of a measure on ![]() $\mathscr {C}\!\ell _F^{+}(p^{\infty })$, such as
$\mathscr {C}\!\ell _F^{+}(p^{\infty })$, such as ![]() $\mu _{\tilde \Pi }$, to a measure on
$\mu _{\tilde \Pi }$, to a measure on ![]() ${\mathcal {C}\!\ell _{\mathbb {Q}}^{+}}(p^{\infty })$. Further composing with
${\mathcal {C}\!\ell _{\mathbb {Q}}^{+}}(p^{\infty })$. Further composing with ![]() $\omega ^{m}: \mu _{2p}\to \mathcal {O}^{\times }$ for
$\omega ^{m}: \mu _{2p}\to \mathcal {O}^{\times }$ for ![]() $0\leqslant m \leqslant p-1$ allows us to define a measure on
$0\leqslant m \leqslant p-1$ allows us to define a measure on ![]() $1+2p\mathbb {Z}_p$, that is, an element
$1+2p\mathbb {Z}_p$, that is, an element ![]() $\omega ^{m}(\mu _{\tilde \Pi })\in \mathcal {O}[[T]]$.
$\omega ^{m}(\mu _{\tilde \Pi })\in \mathcal {O}[[T]]$.
Proof. We first show that ![]() $\omega ^{m}(\mu _{\tilde \Pi }) \neq 0$ for all
$\omega ^{m}(\mu _{\tilde \Pi }) \neq 0$ for all ![]() $m\in \mathbb {Z}$. By the interpolation property in Theorem 4.7, the measure
$m\in \mathbb {Z}$. By the interpolation property in Theorem 4.7, the measure ![]() $\omega ^{m}(\mu _{\tilde \Pi })$ interpolates the algebraic parts of
$\omega ^{m}(\mu _{\tilde \Pi })$ interpolates the algebraic parts of ![]() $L(\frac {1}{2} + j, \Pi \otimes \omega ^{m-j}\chi )$ for
$L(\frac {1}{2} + j, \Pi \otimes \omega ^{m-j}\chi )$ for ![]() $j\in \operatorname {Crit}(\mu )$ and
$j\in \operatorname {Crit}(\mu )$ and ![]() $\chi$ runs over all Dirichlet characters of (non-trivial)
$\chi$ runs over all Dirichlet characters of (non-trivial) ![]() $p$-power order and conductor. Our hypothesis (78) implies that we find
$p$-power order and conductor. Our hypothesis (78) implies that we find ![]() $j\in \operatorname {Crit}(\mu )$ satisfying
$j\in \operatorname {Crit}(\mu )$ satisfying ![]() $j> {{{\sf w}}}/{2}$, hence
$j> {{{\sf w}}}/{2}$, hence ![]() $\frac {1}{2} + j$ lies outside the interior of the critical strip
$\frac {1}{2} + j$ lies outside the interior of the critical strip ![]() ${w}/{2} < \Re (s) < {w}/{2}+1$ for
${w}/{2} < \Re (s) < {w}/{2}+1$ for ![]() $L(s,\Pi )$ and, thus,
$L(s,\Pi )$ and, thus, ![]() $L(\frac {1}{2} + j, \Pi \otimes \omega ^{m-j}\chi )\neq 0$. Therefore,
$L(\frac {1}{2} + j, \Pi \otimes \omega ^{m-j}\chi )\neq 0$. Therefore, ![]() $\omega ^{m}(\mu _{\tilde \Pi }) \neq 0$ as claimed.
$\omega ^{m}(\mu _{\tilde \Pi }) \neq 0$ as claimed.
By the Weierstrass preparation theorem, a non-zero element of ![]() $\mathcal {O}[[T]]$ admits only finitely many zeros in
$\mathcal {O}[[T]]$ admits only finitely many zeros in ![]() $\bar{\mathbb {Z}}_p$. Again by Theorem 4.7 this means that, given any
$\bar{\mathbb {Z}}_p$. Again by Theorem 4.7 this means that, given any ![]() $j\in \operatorname {Crit}(\mu )$ and
$j\in \operatorname {Crit}(\mu )$ and ![]() $m$, there are at most finitely many Dirichlet characters
$m$, there are at most finitely many Dirichlet characters ![]() $\chi$ of
$\chi$ of ![]() $p$-power order and conductor such that
$p$-power order and conductor such that ![]() $L(\frac {1}{2} + j, \Pi \otimes \omega ^{m-j}\chi ) = 0$. As any
$L(\frac {1}{2} + j, \Pi \otimes \omega ^{m-j}\chi ) = 0$. As any ![]() $p$-power conductor Dirichlet character is of that form for some
$p$-power conductor Dirichlet character is of that form for some ![]() $0\leqslant m \leqslant p-1$, the theorem follows.
$0\leqslant m \leqslant p-1$, the theorem follows.
4.4.2 Variations
Corollary 4.9 Nearly ordinary case Under the hypotheses of Theorem 4.8, let ![]() $\nu$ be a finite order character of
$\nu$ be a finite order character of ![]() $\mathscr {C}\!\ell _F^{+}(p^{\infty })$. Then for all but finitely many Dirichlet characters
$\mathscr {C}\!\ell _F^{+}(p^{\infty })$. Then for all but finitely many Dirichlet characters ![]() $\chi$ of finite order and with
$\chi$ of finite order and with ![]() $p$-power conductor, we have
$p$-power conductor, we have
Proof. Use the twisted norm map ![]() $[x]\mapsto \nu (x) [\operatorname {N}_{F/\mathbb {Q}}x]$ to push-forward
$[x]\mapsto \nu (x) [\operatorname {N}_{F/\mathbb {Q}}x]$ to push-forward ![]() $\mu _{\tilde \Pi }$ to a measure on
$\mu _{\tilde \Pi }$ to a measure on ![]() ${\mathcal {C}\!\ell _{\mathbb {Q}}^{+}}(p^{\infty })$. Then proceed mutatis mutandis as in the proof of Theorem 4.8.
${\mathcal {C}\!\ell _{\mathbb {Q}}^{+}}(p^{\infty })$. Then proceed mutatis mutandis as in the proof of Theorem 4.8.
This result is slightly stronger because the representation ![]() $\Pi \otimes \nu$, even though of cohomological type and admitting a Shalika model, is no longer ordinary at
$\Pi \otimes \nu$, even though of cohomological type and admitting a Shalika model, is no longer ordinary at ![]() $p$, nor spherical.
$p$, nor spherical.
The following corollary of Theorem 4.8 follows from the fact that we have non-vanishing for all but finitely many Dirichlet characters ![]() $\chi$ of finite order and with
$\chi$ of finite order and with ![]() $p$-power conductor.
$p$-power conductor.
Corollary 4.10 Simultaneous non-vanishing For ![]() $1 \leqslant k \leqslant r$ fix
$1 \leqslant k \leqslant r$ fix ![]() $n_k\in \mathbb {Z}_{>0}$ and let
$n_k\in \mathbb {Z}_{>0}$ and let ![]() $\mu _k$ be a pure dominant integral weight for
$\mu _k$ be a pure dominant integral weight for ![]() $\operatorname {GL}_{2n_k}$ over
$\operatorname {GL}_{2n_k}$ over ![]() $F$. Suppose that each
$F$. Suppose that each ![]() $\mu _k$ satisfies the regularity condition in (78) and that its purity weight
$\mu _k$ satisfies the regularity condition in (78) and that its purity weight ![]() ${{\sf w}}_k$ is even. Let
${{\sf w}}_k$ is even. Let ![]() $\Pi _k$ be a cuspidal automorphic representation of
$\Pi _k$ be a cuspidal automorphic representation of ![]() $\operatorname {GL}_{2n_k}(\mathbb {A}_F)$ of cohomological weight
$\operatorname {GL}_{2n_k}(\mathbb {A}_F)$ of cohomological weight ![]() $\mu _k$ admitting a Shalika model. For a prime number
$\mu _k$ admitting a Shalika model. For a prime number ![]() $p$, suppose that each
$p$, suppose that each ![]() $\Pi _k$ is unramified and
$\Pi _k$ is unramified and ![]() $Q$-ordinary at
$Q$-ordinary at ![]() $p$. Then, for all but finitely many Dirichlet characters
$p$. Then, for all but finitely many Dirichlet characters ![]() $\chi$ of
$\chi$ of ![]() $p$-power conductor, we have
$p$-power conductor, we have
Let us note that this is a simultaneous non-vanishing result at the central point. We leave it to the reader to formulate the stronger version of simultaneous non-vanishing combining Corollaries 4.9 and 4.10.
As a very concrete example illustrating an application of simultaneous non-vanishing to algebraicity results, let us consider the unitary cuspidal automorphic representation ![]() $\pi (\Delta )$ of
$\pi (\Delta )$ of ![]() $\operatorname {GL}_2(\mathbb {A})$ associated to the Ramanujan
$\operatorname {GL}_2(\mathbb {A})$ associated to the Ramanujan ![]() $\Delta$-function. A particular case of Corollary 4.10 gives infinitely many Dirichlet characters
$\Delta$-function. A particular case of Corollary 4.10 gives infinitely many Dirichlet characters ![]() $\chi$ such that
$\chi$ such that
For such a character we obtain from [Reference RaghuramRag10, Corollary 5.2] the following identity of ![]() $L$-values:
$L$-values:
 \[ L\big(\tfrac{1}{2}, \operatorname{Sym}^{5}(\pi(\Delta))\otimes \chi\big) = \frac{L\big(\tfrac{1}{2}, \operatorname{Sym}^{3}(\pi(\Delta)) \times \operatorname{Sym}^{2}(\pi(\Delta))\big)} {L\big(\tfrac{1}{2}, \operatorname{Sym}^{3}(\pi(\Delta))\otimes \chi\big) L\big(\tfrac{1}{2}, \pi(\Delta)\otimes \chi\big)}. \]
\[ L\big(\tfrac{1}{2}, \operatorname{Sym}^{5}(\pi(\Delta))\otimes \chi\big) = \frac{L\big(\tfrac{1}{2}, \operatorname{Sym}^{3}(\pi(\Delta)) \times \operatorname{Sym}^{2}(\pi(\Delta))\big)} {L\big(\tfrac{1}{2}, \operatorname{Sym}^{3}(\pi(\Delta))\otimes \chi\big) L\big(\tfrac{1}{2}, \pi(\Delta)\otimes \chi\big)}. \]
Using the rationality result in [Reference RaghuramRag10, Theorem 1.1] for the ![]() $L$-value in the numerator of the right-hand side, and the [Reference RaghuramRag10, Theorem 1.3] for the
$L$-value in the numerator of the right-hand side, and the [Reference RaghuramRag10, Theorem 1.3] for the ![]() $L$-values in the denominator of the right-hand side, we obtain a new rationality result for
$L$-values in the denominator of the right-hand side, we obtain a new rationality result for
Similarly, using the results of [Reference RaghuramRag16], and simultaneous non-vanishing for the central values of the first and third symmetric power ![]() $L$-functions of a Hilbert cusp form, one may now generalize this to get new rationality results for the symmetric fifth power
$L$-functions of a Hilbert cusp form, one may now generalize this to get new rationality results for the symmetric fifth power ![]() $L$-functions of a Hilbert cusp form.
$L$-functions of a Hilbert cusp form.
Acknowledgements
This project started when the three authors met at a conference in July 2014 at IISER Pune on ![]() $p$-adic aspects of modular forms. Any subset of two of the authors is grateful to the host institute or university of the third author during various stages of this work. M.D. and A.R. thank the Indo-French research agency CEFIPRA that facilitated visits by each to the workplace of the other. A.R. is grateful to the Charles Simonyi Endowment that funded his stay at the Institute for Advanced Study, Princeton.
$p$-adic aspects of modular forms. Any subset of two of the authors is grateful to the host institute or university of the third author during various stages of this work. M.D. and A.R. thank the Indo-French research agency CEFIPRA that facilitated visits by each to the workplace of the other. A.R. is grateful to the Charles Simonyi Endowment that funded his stay at the Institute for Advanced Study, Princeton.
M.D. and A.R. acknowledge support from CEFIPRA project No. 5601-1. M.D. received partial support from ANR grants CEMPI (ANR-11-LABX-0007-01) and GALF (ANR-18-CE40-0029). A.R. received partial support from MATRICS grant MTR/2018/000918, from SERB, Department of Science and Technology, Government of India.