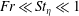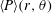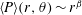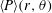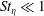1 Introduction
This paper presents a stochastic theory for the clustering of inertial particles that are settling rapidly in homogeneous isotropic turbulence. The theory focuses on the relative motion of low-Stokes-number pairs for sub-Kolmogorov separations. The study is principally motivated by the desire to understand the microphysical processes influencing the relative motion of water droplets in cumulus clouds.
Predicting the growth of droplets in a cloud from a radius of
$10{-}20~\unicode[STIX]{x03BC}\text{m}$
to raindrop size (radius
${>}100~\unicode[STIX]{x03BC}\text{m}$
) is a central problem in cloud physics. Cloud microphysical models describe droplet growth through two main mechanisms: (i) condensation, and (ii) droplet collision and coalescence. For radii
${<}20~\unicode[STIX]{x03BC}\text{m}$
, droplet growth is principally driven by condensation (Bartlett Reference Bartlett1966). For larger radii, collision and coalescence play an increasingly important role, eventually becoming the dominant mechanism for radii
${>}40~\unicode[STIX]{x03BC}\text{m}$
. Interestingly, in the
$15{-}40~\unicode[STIX]{x03BC}\text{m}$
radius range, droplet Stokes numbers
$St_{\unicode[STIX]{x1D702}}$
are in the 0.1–1 range. The relative motion of these droplet pairs is strongly susceptible to the effects of air turbulence. For instance, it is now well established that, for
$St_{\unicode[STIX]{x1D702}}<1$
, particles exhibit strong spatial clustering arising from the complex interactions between turbulent eddies and particle inertia (Chun et al.
Reference Chun, Koch, Rani, Ahluwalia and Collins2005; Bragg & Collins Reference Bragg and Collins2014a
,Reference Bragg and Collins
b
). Turbulence-induced clustering of droplets may lead to increased collision rates, and thereby to accelerated droplet growth. In addition to turbulence, differential gravitational settling among droplets is an important driver of collisions, particularly for pairs of larger drops whose size ratio departs substantially from one. Differential settling also reduces the clustering of particles with different radii, so that the most pronounced inertial clustering occurs in drops of nearly equal size (Ayala et al.
Reference Ayala, Rosa, Wang and Grabowski2008b
; Parishani et al.
Reference Parishani, Ayala, Rosa, Wang and Grabowski2015).
In cumulus and stratocumulus clouds, the Kolmogorov-scale fluid acceleration (
$a_{\unicode[STIX]{x1D702}}$
) is small relative to gravitational acceleration (
$g$
) so that the Froude number is
$Fr=a_{\unicode[STIX]{x1D702}}/g\sim 0.009{-}0.06$
(Ayala, Rosa & Wang Reference Ayala, Rosa and Wang2008a
; Fouxon et al.
Reference Fouxon, Park, Harduf and Lee2015). Therefore, the present study focuses on the relative motion of monodisperse, low-inertia particle pairs that are undergoing rapid settling in isotropic turbulence. While
$Fr$
characterizes fluid accelerations, the settling velocity parameter
$Sv_{\unicode[STIX]{x1D702}}$
is used to quantify particle settling, where
$Sv_{\unicode[STIX]{x1D702}}$
is defined as the ratio of particle terminal velocity to the Kolmogorov velocity scale. Therefore, by rapid settling, we mean
$Sv_{\unicode[STIX]{x1D702}}\gg 1$
. Recognizing that
$Sv_{\unicode[STIX]{x1D702}}=St_{\unicode[STIX]{x1D702}}/Fr$
, the current stochastic theory is derived in the parameter regime characterized by
$Fr\ll St_{\unicode[STIX]{x1D702}}\ll 1$
. Here Stokes number
$St_{\unicode[STIX]{x1D702}}$
is the ratio of the particle viscous relaxation time
$\unicode[STIX]{x1D70F}_{v}$
and the Kolmogorov time scale
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}$
. For
$St_{\unicode[STIX]{x1D702}}\ll 1$
particles, the transport equation for the probability density function (p.d.f.) of pair separations (
$\boldsymbol{r}$
) is of the drift–diffusion form (Chun et al.
Reference Chun, Koch, Rani, Ahluwalia and Collins2005). In this part I paper, we present the derivation of closures for the drift and diffusion fluxes. The p.d.f. equation is also solved analytically, giving rise to a p.d.f. with a power-law dependence on separation
$r$
with a negative exponent. An explicit expression is obtained for the exponent in terms of the drift and diffusion fluxes.
Turbulence-driven inhomogeneities in the spatial distribution of inertial particles are believed to play an important role in locally enhancing particle collision rates. Preferential concentration is one of the mechanisms of particle clustering, wherein inertial particles denser than the fluid are ejected out of vorticity-dominated regions, and accumulate in strain-dominated regions. Numerous computational, experimental and theoretical studies of aerosol dynamics in isotropic turbulence have established that inertial particles preferentially concentrate in regions of excess strain rate over rotation rate (Maxey Reference Maxey1987; Squires & Eaton Reference Squires and Eaton1991; Eaton & Fessler Reference Eaton and Fessler1994; Druzhinin Reference Druzhinin1995; Druzhinin & Elghobashi Reference Druzhinin and Elghobashi1999; Ferry, Rani & Balachandar Reference Ferry, Rani and Balachandar2003; Rani & Balachandar Reference Rani and Balachandar2003, Reference Rani and Balachandar2004; Chun et al. Reference Chun, Koch, Rani, Ahluwalia and Collins2005; Ray & Collins Reference Ray and Collins2011).
Since the characteristic length scales of strain rate and rotation rate in isotropic turbulence scale with the Kolmogorov length scale (
$\unicode[STIX]{x1D702}$
), it may be expected that preferential concentration enhances the probability of finding a pair of particles at separations comparable to
$\unicode[STIX]{x1D702}$
. However, Reade & Collins (Reference Reade and Collins2000) showed through direct numerical simulations (DNS) of particle-laden isotropic turbulence that inertial particles continued to exhibit clustering at separations much smaller than
$\unicode[STIX]{x1D702}$
. In fact, they found that for separations
$r\ll \unicode[STIX]{x1D702}$
, the radial distribution function (r.d.f.), an important measure of clustering, followed a power law given by
$$\begin{eqnarray}\displaystyle g(r)=c_{0}\left(\frac{\unicode[STIX]{x1D702}}{r}\right)^{c_{1}}, & & \displaystyle\end{eqnarray}$$
where
$g(r)$
is the r.d.f. The existence of a power-law r.d.f. for
$r/\unicode[STIX]{x1D702}\approx 10^{-3}$
in the DNS of Reade & Collins (Reference Reade and Collins2000) suggests that the mechanism of preferential concentration alone is insufficient to explain clustering at such small separations.
In Chun et al. (Reference Chun, Koch, Rani, Ahluwalia and Collins2005), we investigated the continued clustering of monodisperse particles at sub-Kolmogorov separations, and developed a theory for the r.d.f. of low-
$St_{\unicode[STIX]{x1D702}}$
, non-settling (i.e.
$Fr\rightarrow \infty$
) particle pairs. Motivated by the observation that much of the growth of the r.d.f. occurs for separations
$r<\unicode[STIX]{x1D702}$
, the Chun et al. (Reference Chun, Koch, Rani, Ahluwalia and Collins2005) study focused on the dynamics of pair separations in the dissipation regime of turbulence. Analytical closures were derived for the drift and diffusion fluxes in the p.d.f. equation of pair relative positions. The balance of these two fluxes determines the steady-state value of the r.d.f. at a given separation. Of particular interest in that theory is the closure form for the drift flux
$q_{i}^{d}(r)$
of monodisperse pairs, given by
$$\begin{eqnarray}\displaystyle q_{i}^{d}(r)=-\frac{St_{\unicode[STIX]{x1D702}}^{2}}{3}r_{i}\langle P\rangle (\boldsymbol{r})\int _{-\infty }^{t}\langle [S^{2}(t)-R^{2}(t)][S^{2}(t^{\prime })-R^{2}(t^{\prime })]\rangle \,\text{d}t^{\prime }, & & \displaystyle\end{eqnarray}$$
where
$S^{2}=S_{ij}S_{ij}$
and
$R^{2}=R_{ij}R_{ij}$
are the second invariants of the strain-rate and rotation-rate tensors, respectively, along particle paths.
It is evident from (1.2) that the net drift flux will be negative or radially inwards provided the primary particles sample more strain than rotation along their trajectories, a mechanism referred to as preferential concentration. One can also deduce from (1.2) a second mechanism of clustering that is particularly relevant for sub-Kolmogorov scale separations. We can see from (1.2) that the drift flux will continue to be negative even for
$r<\unicode[STIX]{x1D702}$
provided we have a positive two-time correlation of
$[S^{2}(t)-R^{2}(t)]$
along the trajectory of the primary particle. Thus, the sub-Kolmogorov scale clustering is driven by a path-history effect in that the pair separation at time
$t$
continues to be influenced by the preferential sampling of strain rate over rotation rate by the primary particle at earlier times (and at larger separations, on average). It is this path history effect that is responsible for the power-law behaviour of the r.d.f. at
$r\ll \unicode[STIX]{x1D702}$
. To the authors’ knowledge, the Chun et al. (Reference Chun, Koch, Rani, Ahluwalia and Collins2005) study is the first to provide an explicit relation for this effect through the integral in (1.2). Other mechanisms of particle clustering, such as caustics, have also been identified – a review of the various mechanisms may be found in Gustavsson & Mehlig (Reference Gustavsson and Mehlig2016).
Chun et al. (Reference Chun, Koch, Rani, Ahluwalia and Collins2005) also derived the drift–diffusion equation of the r.d.f. for bidisperse, non-settling pairs. Bidispersity, or more generally polydispersity, of the particle population is a key factor in determining clustering, and thereby the rate of particle collisions. Bidispersity is also important when considering the effects of gravitational settling, since differential sedimentation is thought to be a key contributing factor to enhanced collision frequency. In the current study, we consider a monodisperse population of settling particles. However, our theory accounts for the effects of gravity through the modified sampling of turbulence by the settling particles. Although cloud droplets would be polydisperse, it is noteworthy that: (a) condensation tends to narrow the size distribution; (b) turbulence-induced coalescence is most important for nearly equal-sized drops for which differential sedimentation is weak; and (c) clustering is strongest for nearly equal-sized drops. In the rapid settling limit, particles experience an essentially frozen turbulence, so that the flow time scales along particle trajectories may be approximated as the Eulerian correlation length scales divided by the particle terminal velocity.
Detailed reviews of stochastic theories for the relative motion of inertial particle pairs are provided in Rani, Dhariwal & Koch (Reference Rani, Dhariwal and Koch2014) and Dhariwal, Rani & Koch (Reference Dhariwal, Rani and Koch2017). An important study is that of Zaichik & Alipchenkov (Reference Zaichik and Alipchenkov2003), who developed a stochastic theory for describing the relative velocities and positions of monodisperse particle pairs. Their theory was conceived to be applicable for all Stokes numbers and for pair separations spanning all three regimes of turbulence, i.e. the integral, inertial and dissipation scale ranges. Zaichik & Alipchenkov (Reference Zaichik and Alipchenkov2003) derived a closure for the phase-space diffusion current by using the Furutsu–Novikov–Donsker (FND) formula. The FND formula relates the diffusion current to a series expansion in the cumulants of the fluid relative velocities seen by the pairs (
$\unicode[STIX]{x0394}\boldsymbol{u}$
) multiplied by the functional derivatives of the p.d.f. with respect to
$\unicode[STIX]{x0394}\boldsymbol{u}$
(Bragg & Collins Reference Bragg and Collins2014a
). Zaichik & Alipchenkov (Reference Zaichik and Alipchenkov2003) then computed the statistics of pair separation and relative velocity by solving the equations for the zeroth, first and second relative-velocity moments of the master p.d.f. equation.
Bragg & Collins (Reference Bragg and Collins2014a
) performed a rigorous, quantitative comparison of the Chun et al. (Reference Chun, Koch, Rani, Ahluwalia and Collins2005) and Zaichik & Alipchenkov (Reference Zaichik and Alipchenkov2007) stochastic models for inertial pair dynamics in isotropic turbulence. The focus of the Bragg & Collins study was to compare and analyse the predictions of particle clustering at sub-Kolmogorov scale separations by the two theories. The Zaichik & Alipchenkov (Reference Zaichik and Alipchenkov2007) study improved upon their earlier study (Zaichik & Alipchenkov Reference Zaichik and Alipchenkov2003) by accounting for the unequal Lagrangian correlation time scales of the strain-rate and rotation-rate tensors. Bragg & Collins (Reference Bragg and Collins2014a
) showed that the power-law exponents in the r.d.f.s predicted by the two theories were in good agreement for
$St_{\unicode[STIX]{x1D702}}\ll 1$
at
$r\ll \unicode[STIX]{x1D702}$
. Through a detailed theoretical analysis, they proved that this agreement was a consequence of the Chun et al. (Reference Chun, Koch, Rani, Ahluwalia and Collins2005) drift velocity being the same as the leading-order term in the Zaichik & Alipchenkov (Reference Zaichik and Alipchenkov2007) drift velocity. As is to be expected, for
$St_{\unicode[STIX]{x1D702}}\sim 1$
, the theories diverge.
Gustavsson, Vajedi & Mehlig (Reference Gustavsson, Vajedi and Mehlig2014) studied the clustering of settling particles in a two-dimensional random fluid velocity field. They developed a perturbation expansion for the divergence of the particle velocity field, with the Kubo number as the small parameter. Their theory shows that for
$St_{\unicode[STIX]{x1D702}}<1$
, settling attenuates particle clustering, but for
$St_{\unicode[STIX]{x1D702}}>1$
, gravity enhances clustering. In a recent analytical study, Fouxon et al. (Reference Fouxon, Park, Harduf and Lee2015) considered the clustering behaviour of fast-sedimenting particles in isotropic turbulence. For a broad range of Stokes numbers (
$St_{\unicode[STIX]{x1D702}}\gtrsim 1$
,
$St_{\unicode[STIX]{x1D702}}\ll 1$
) and small Froude numbers (
$Fr\ll 1$
), they derived the power-law exponents characterizing the dependence of pair clustering on separation
$r$
. The exponent that is applicable in the same parametric regime as in our study is (Fouxon et al.
Reference Fouxon, Park, Harduf and Lee2015)
$$\begin{eqnarray}\displaystyle D_{KY}=\frac{4\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}^{2}\displaystyle \int _{0}^{\infty }\unicode[STIX]{x1D705}^{3}E_{p}(\unicode[STIX]{x1D705})\,\text{d}\unicode[STIX]{x1D705}}{\displaystyle \int _{0}^{\infty }\unicode[STIX]{x1D705}E(\unicode[STIX]{x1D705})\,\text{d}\unicode[STIX]{x1D705}}\propto St_{\unicode[STIX]{x1D702}}^{2}, & & \displaystyle\end{eqnarray}$$
where
$D_{KY}$
is the Lyapunov power-law exponent (known as the Kaplan–Yorke codimension),
$E(\unicode[STIX]{x1D705})$
is the energy spectrum of isotropic turbulence, and
$E_{p}(\unicode[STIX]{x1D705})$
is the spectrum of pressure fluctuations. It may be noted that
$D_{KY}$
scales as
$St_{\unicode[STIX]{x1D702}}^{2}$
, and is independent of
$Fr$
. The exponent
$\unicode[STIX]{x1D6FD}$
derived in the current study also shows the same dependence on
$St_{\unicode[STIX]{x1D702}}$
. In our study, the first drift closure results in a
$\unicode[STIX]{x1D6FD}$
that is independent of
$Fr$
. However, the second drift closure can include the effects of
$Fr$
through the two-time correlations of dissipation rate and enstrophy along particle trajectories. Fouxon et al. (Reference Fouxon, Park, Harduf and Lee2015) did not quantify
$D_{KY}$
, as the spectrum
$E_{p}(\unicode[STIX]{x1D705})$
is not known. In our study, however,
$\unicode[STIX]{x1D6FD}_{2}$
is both quantified and compared with DNS data.
In this part 1 paper, we present the derivation of closures for the drift and diffusion fluxes in the p.d.f. equation for pair separations
$\boldsymbol{r}$
of rapidly settling, low-inertia, monodisperse particle pairs in isotropic turbulence. This study extends the Chun et al. (Reference Chun, Koch, Rani, Ahluwalia and Collins2005) work by including the effects of particle settling in high-gravity conditions. Motivated by the Chun et al. (Reference Chun, Koch, Rani, Ahluwalia and Collins2005) study, we approximate the fluid velocity field following the primary particle as locally linear. An additional assumption regarding the fluid velocity gradient ‘seen’ by the primary particle is also necessary to resolve the third and fourth moments of the velocity gradient that appear in the drift flux. Two types of assumption regarding the velocity gradient lead to two separate closures for the drift flux, while the diffusion flux has only one closure. The first closure of drift flux entails the assumption that the ‘seen’ fluid velocity gradient is Gaussian. Modelling the fluid velocity gradient as a single unit, however, does not capture the correlation times of the strain-rate and rotation-rate second invariants that are integral to the mechanisms driving particle clustering. This deficiency is addressed in the second drift closure by first decomposing the velocity gradient into the strain-rate and rotation-rate tensors scaled by the dissipation rate and enstrophy, respectively, and then assuming that the scaled tensors are normally distributed. In addition to the closures, an analytical solution is also derived for the p.d.f.
$\langle P\rangle (r,\unicode[STIX]{x1D703})$
, allowing us to quantify both the
$r$
dependence and the anisotropy of clustering due to gravity.
The organization of the paper is as follows. Section 2 presents the stochastic theory, including the derivation of the drift and diffusion flux closures. In § 3, an analytical solution to the p.d.f.
$\langle P\rangle (r,\unicode[STIX]{x1D703})$
is derived, with a power-law dependence on
$r$
. The results obtained from the first drift closure (in conjunction with the diffusion closure) are presented in § 4. These results are based on using the analytical form of the energy spectrum that is valid in the high-Reynolds-number limit. The advantages of using this spectrum are that it obviates the need for DNS inputs, and importantly allows us to quantify the drift and diffusion fluxes in a universal manner (i.e. independent of
$Re_{\unicode[STIX]{x1D706}}$
). Section 5 summarizes the key findings of this part 1 paper.
2 Stochastic theory
In this section, we derive closure approximations for the drift and diffusion fluxes in the p.d.f. equation for the relative positions
$\boldsymbol{r}$
of monodisperse, low-inertia particle pairs that are settling rapidly in stationary isotropic turbulence. The theory is applicable in the
$Fr\ll St_{\unicode[STIX]{x1D702}}\ll 1$
regime, and for pair separations in the dissipation regime of turbulence, i.e.
$r<\unicode[STIX]{x1D702}$
, where
$\unicode[STIX]{x1D702}$
is the Kolmogorov length scale. This restriction, however, allows us to approximate the fluid velocity field as being locally linear. The effects of hydrodynamic and interparticle interactions on pair probability are neglected.
We begin with the drift–diffusion equation derived by Chun et al. (Reference Chun, Koch, Rani, Ahluwalia and Collins2005) for the p.d.f.
$\langle P\rangle (\boldsymbol{r};t)$
:
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}\langle P\rangle }{\unicode[STIX]{x2202}t}+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}r_{i}}(q_{i}^{d}+q_{i}^{D})=0, & & \displaystyle\end{eqnarray}$$
where the drift flux is
$$\begin{eqnarray}\displaystyle q_{i}^{d}(\boldsymbol{r},t)=-\int _{-\infty }^{t}\left\langle w_{i}(\boldsymbol{r},\boldsymbol{x};t)\frac{\unicode[STIX]{x2202}w_{l}}{\unicode[STIX]{x2202}r_{l}}[\boldsymbol{r}(t^{\prime }),\boldsymbol{x}(t^{\prime });t^{\prime }]\right\rangle \langle P\rangle (\boldsymbol{r}^{\prime };t^{\prime })\,\text{d}t^{\prime } & & \displaystyle\end{eqnarray}$$
and the diffusive flux is
$$\begin{eqnarray}\displaystyle q_{i}^{D}(\boldsymbol{r},t)=-\int _{-\infty }^{t}\langle w_{i}(\boldsymbol{r},\boldsymbol{x};t)w_{j}[\boldsymbol{r}(t^{\prime }),\boldsymbol{x}(t^{\prime });t^{\prime }]\rangle \frac{\unicode[STIX]{x2202}\langle P\rangle }{\unicode[STIX]{x2202}r_{j}^{\prime }}(\boldsymbol{r}^{\prime };t^{\prime })\,\text{d}t^{\prime }. & & \displaystyle\end{eqnarray}$$
In (2.2) and (2.3),
$\boldsymbol{r}^{\prime }=\boldsymbol{r}(t^{\prime })$
is the pair separation at time
$t^{\prime }$
, and
$\boldsymbol{x}=\boldsymbol{x}(t)$
is the primary particle position at time
$t$
. As the drift and diffusion fluxes at
$\boldsymbol{r}$
depend on the pair probability and its derivative, respectively, at earlier pair separations
$\boldsymbol{r}^{\prime }$
, equation (2.1) is non-local and accounts for the path history effects.
The governing equations for the relative position (separation vector)
$r_{i}$
and relative velocity
$w_{i}$
of a settling, like-particle pair are
$$\begin{eqnarray}\displaystyle \frac{\text{d}r_{i}}{\text{d}t}=w_{i}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\text{d}w_{i}}{\text{d}t} & = & \displaystyle -\frac{1}{\unicode[STIX]{x1D70F}_{v}}\{w_{i}(t)-\unicode[STIX]{x0394}u_{i}[\boldsymbol{r}(t),\boldsymbol{x}(t);t]\}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & {\approx} & \displaystyle -\frac{1}{\unicode[STIX]{x1D70F}_{v}}\{w_{i}(t)-\unicode[STIX]{x1D6E4}_{ik}[\boldsymbol{x}(t);t]r_{k}\},\end{eqnarray}$$
where
$\boldsymbol{x}(t)$
is the location of the primary or reference particle, and
$\unicode[STIX]{x0394}u_{i}[\boldsymbol{r}(t),\boldsymbol{x}(t);t]$
is the difference in the fluid velocities seen by the secondary and primary particles of a pair. Using the approximation of a locally linear flow field, we write
$\unicode[STIX]{x0394}u_{i}\approx \unicode[STIX]{x1D6E4}_{ik}r_{k}$
, where
$\unicode[STIX]{x1D6E4}_{ik}=\unicode[STIX]{x2202}u_{i}/\unicode[STIX]{x2202}x_{k}$
is the fluid velocity gradient at the location of the primary particle,
$\boldsymbol{x}(t)$
. In the case of monodisperse particle pairs, gravity influences pair relative motion through the modified sampling of the fluid velocity gradient by the primary particle.
We now discuss the modelling of the drift and diffusion fluxes. Two separate closures will be considered for the drift flux, whereas a single closure is obtained for the diffusion flux. The two drift closures, DF1 and DF2, differ in the nature of the approximation made to analytically resolve the moments of the fluid velocity gradient tensor. It will be seen that DF2 has the advantage of capturing key mechanisms of particle clustering.
2.1 Drift flux closure 1 (DF1)
Based on Chun et al. (Reference Chun, Koch, Rani, Ahluwalia and Collins2005), we express the pair relative velocity
$w_{i}$
as a perturbation expansion with Stokes number
$St_{\unicode[STIX]{x1D702}}$
as the small parameter, as follows:
$$\begin{eqnarray}\displaystyle w_{i}=w_{i}^{[0]}+St_{\unicode[STIX]{x1D702}}w_{i}^{[1]}+\cdots \,. & & \displaystyle\end{eqnarray}$$
Substituting this expansion into (2.5) and equating terms of equal order in
$St_{\unicode[STIX]{x1D702}}$
yields
$$\begin{eqnarray}\displaystyle & \displaystyle w_{i}^{[0]}=\unicode[STIX]{x1D6E4}_{ik}r_{k}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle w_{i}^{[1]}=-\frac{1}{\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D702}}}\left[\frac{\text{d}\unicode[STIX]{x1D6E4}_{ik}}{\text{d}t}+\unicode[STIX]{x1D6E4}_{ij}\unicode[STIX]{x1D6E4}_{jk}\right]r_{k}, & \displaystyle\end{eqnarray}$$
where
$\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D702}}=1/\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}$
is the inverse of the Kolmogorov time scale
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}$
. We have also used
$\text{d}r_{k}/\text{d}t\approx w_{k}^{[0]}$
in deriving the expression for
$w_{i}^{[1]}$
. Thus, we can write
$$\begin{eqnarray}\displaystyle & \displaystyle w_{i}[\boldsymbol{r}(t),\boldsymbol{x}(t);t]=\unicode[STIX]{x1D6E4}_{ik}[\boldsymbol{x}(t);t]r_{k}-\frac{St_{\unicode[STIX]{x1D702}}}{\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D702}}}\left(\frac{\text{d}\unicode[STIX]{x1D6E4}_{ik}}{\text{d}t}+\unicode[STIX]{x1D6E4}_{ij}[\boldsymbol{x}(t);t]\unicode[STIX]{x1D6E4}_{jk}[\boldsymbol{x}(t);t]\right)r_{k}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \!\!\frac{\unicode[STIX]{x2202}w_{l}}{\unicode[STIX]{x2202}r_{l}}[\boldsymbol{r}(t^{\prime }),\boldsymbol{x}(t^{\prime });t^{\prime }]=\unicode[STIX]{x1D6E4}_{ll}-\frac{St_{\unicode[STIX]{x1D702}}}{\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D702}}}\left(\frac{\text{d}\unicode[STIX]{x1D6E4}_{ll}}{\text{d}t}+\unicode[STIX]{x1D6E4}_{lm}\unicode[STIX]{x1D6E4}_{ml}\right)=-\frac{St_{\unicode[STIX]{x1D702}}}{\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D702}}}\unicode[STIX]{x1D6E4}_{lm}[\boldsymbol{x}(t^{\prime });t^{\prime }]\unicode[STIX]{x1D6E4}_{ml}[\boldsymbol{x}(t^{\prime });t^{\prime }],\qquad \; & \displaystyle\end{eqnarray}$$
where
$\unicode[STIX]{x1D6E4}_{ll}=0$
due to continuity.
We now substitute (2.10) and (2.11) into the drift flux given by (2.2), yielding
$$\begin{eqnarray}\displaystyle q_{i}^{d}(\boldsymbol{r},t) & = & \displaystyle -\langle P\rangle (\boldsymbol{r};t)r_{k}\int _{-\infty }^{t}\left\{-\frac{St_{\unicode[STIX]{x1D702}}}{\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D702}}}\langle \unicode[STIX]{x1D6E4}_{ik}(t)\unicode[STIX]{x1D6E4}_{lm}(t^{\prime })\unicode[STIX]{x1D6E4}_{ml}(t^{\prime })\rangle \right.\nonumber\\ \displaystyle & & \displaystyle +\left.\frac{St_{\unicode[STIX]{x1D702}}^{2}}{\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D702}}^{2}}\left[\left\langle \frac{\text{d}\unicode[STIX]{x1D6E4}_{ik}}{\text{d}t}(t)\unicode[STIX]{x1D6E4}_{lm}(t^{\prime })\unicode[STIX]{x1D6E4}_{ml}(t^{\prime })\right\rangle +\langle \unicode[STIX]{x1D6E4}_{ij}(t)\unicode[STIX]{x1D6E4}_{jk}(t)\unicode[STIX]{x1D6E4}_{lm}(t^{\prime })\unicode[STIX]{x1D6E4}_{ml}(t^{\prime })\rangle \right]\right\}\text{d}t^{\prime },\qquad\end{eqnarray}$$
where
$\unicode[STIX]{x1D6E4}_{ij}(t)$
and
$\unicode[STIX]{x1D6E4}_{ij}(t^{\prime })$
are shorthand notations for the fluid velocity gradients at the locations
$\boldsymbol{x}(t)$
and
$\boldsymbol{x}(t^{\prime })$
along the trajectories of primary particles. In (2.12),
$r_{k}$
and
$\langle P\rangle$
have been brought out of the integral. This is reasonable under the parametric limits being considered, and can be explained as follows. In the rapid settling limit, the correlation times of
$\unicode[STIX]{x1D6E4}_{ij}$
along particle trajectories scale as
$\unicode[STIX]{x1D702}/g\unicode[STIX]{x1D70F}_{v}$
, whereas
$r_{k}$
evolves over
$\unicode[STIX]{x1D70F}_{v}\gg \unicode[STIX]{x1D702}/g\unicode[STIX]{x1D70F}_{v}$
. Thus, the pair separation remains essentially unchanged during the time the velocity gradient remains correlated. This allows us to pull
$r_{k}$
out of the ensemble averaging
$\langle \cdots \rangle$
, as well as the time integral. Further, we are able to write
$\langle P\rangle (\boldsymbol{r}^{\prime };t^{\prime })\approx \langle P\rangle (\boldsymbol{r};t)$
, and then bring the p.d.f. out of the time integral. In § 4.4, we will explicitly quantify the time over which the p.d.f.
$\langle P\rangle$
evolves, and show that this is
$\gg \unicode[STIX]{x1D702}/g\unicode[STIX]{x1D70F}_{v}$
, implying that the p.d.f. is relatively unchanged during the
$\unicode[STIX]{x1D6E4}_{ij}$
correlation times.
The drift flux in (2.12) contains the time integral of the third and fourth moments of the fluid velocity gradient along particle trajectories. To analytically resolve these moments, we apply the approximation that the velocity gradient tensor
$\unicode[STIX]{x1D71E}$
is Gaussian. The resulting closure is referred to as DF1. The fluid velocity gradient
$\unicode[STIX]{x1D6E4}_{ij}$
, determined primarily by small-scale turbulence, is known to be significantly non-Gaussian. However, the contribution of the tails of the
$\unicode[STIX]{x1D6E4}_{ij}$
p.d.f. to particle clustering quantified by the r.d.f. is not expected to be significant. This is because the r.d.f., being a lower- (zeroth-) order moment of the particle-pair probability, is expected to be less sensitive to the tails of the
$\unicode[STIX]{x1D6E4}_{ij}$
p.d.f. A similar argument was provided by Zaichik & Alipchenkov (Reference Zaichik and Alipchenkov2003) to assume that the p.d.f. of fluid relative velocities is Gaussian. Consequently, the two triple moment terms on the right-hand side (2.17) would drop out. Further, the fourth-moment term may be written in terms of second moments as follows:
$$\begin{eqnarray}\displaystyle & & \displaystyle \langle \unicode[STIX]{x1D6E4}_{ij}(t)\unicode[STIX]{x1D6E4}_{jk}(t)\unicode[STIX]{x1D6E4}_{lm}(t^{\prime })\unicode[STIX]{x1D6E4}_{ml}(t^{\prime })\rangle \nonumber\\ \displaystyle & & \displaystyle \quad =\langle \unicode[STIX]{x1D6E4}_{ij}(t)\unicode[STIX]{x1D6E4}_{jk}(t)\rangle \langle \unicode[STIX]{x1D6E4}_{lm}(t^{\prime })\unicode[STIX]{x1D6E4}_{ml}(t^{\prime })\rangle +2\langle \unicode[STIX]{x1D6E4}_{ij}(t)\unicode[STIX]{x1D6E4}_{lm}(t^{\prime })\rangle \langle \unicode[STIX]{x1D6E4}_{jk}(t)\unicode[STIX]{x1D6E4}_{ml}(t^{\prime })\rangle .\end{eqnarray}$$
The process for analytically resolving the two terms on the right-hand side of (2.13) is presented in appendix A. Substitution of the resulting expressions into (2.12) yields the following final form of drift flux in DF1:
$$\begin{eqnarray}\displaystyle q_{i}^{d}(\boldsymbol{r},t)=-\langle P\rangle (r,\unicode[STIX]{x1D703})2r_{k}\frac{St_{\unicode[STIX]{x1D702}}^{2}}{\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D702}}^{2}}[\unicode[STIX]{x1D706}_{1}(\unicode[STIX]{x1D6FF}_{ik}-\unicode[STIX]{x1D6FF}_{i3}\unicode[STIX]{x1D6FF}_{k3})+\unicode[STIX]{x1D706}_{2}\unicode[STIX]{x1D6FF}_{i3}\unicode[STIX]{x1D6FF}_{k3}]. & & \displaystyle\end{eqnarray}$$
Here
$\unicode[STIX]{x1D6FF}_{ik}$
is the Kronecker delta tensor, gravity acts along the
$-\boldsymbol{e}_{3}$
direction,
$\unicode[STIX]{x1D703}$
is the spherical polar angle that accounts for anisotropy in the r.d.f., and
$\unicode[STIX]{x1D706}_{1}$
and
$\unicode[STIX]{x1D706}_{2}$
are given by (A 18) and (A 19).
2.2 Drift flux closure 2 (DF2)
We now present the development of the second drift closure (DF2). In DF1, we modelled the velocity gradient as a whole, with the consequence that DF1 does not capture, as evident from (A 1), the two-time autocorrelations and cross-correlations of the strain-rate and rotation-rate invariants:
$\langle S^{2}(t)S^{2}(t^{\prime })\rangle$
,
$\langle R^{2}(t)R^{2}(t^{\prime })\rangle$
,
$\langle S^{2}(t)R^{2}(t^{\prime })\rangle$
and
$\langle R^{2}(t)S^{2}(t^{\prime })\rangle$
. As seen in (1.2), the drift flux of non-settling pairs involves the time integration of these correlations. We anticipate that the mechanism(s) driving the accumulation of pairs for
$Fr\ll 1$
will be related to those for
$Fr\gg 1$
(zero-gravity case), albeit modulated by gravity. Therefore, our objective is to derive a closure (DF2) that accounts for the above correlations.
Referring to the drift flux
$q_{i}^{d}$
in (2.12), we first decompose the velocity gradient tensor
$\unicode[STIX]{x1D6E4}_{ij}(t)$
into the sum of the strain-rate and rotation-rate tensors,
$S_{ij}(t)$
and
$R_{ij}(t)$
. Subsequently, we non-dimensionalize
$S_{ij}$
and
$R_{ij}$
using the instantaneous dissipation rate and enstrophy,
$\unicode[STIX]{x1D716}(t)$
and
$\unicode[STIX]{x1D701}(t)$
, respectively. These two steps allow us to write
$\unicode[STIX]{x1D6E4}_{ij}(t)$
as
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E4}_{ij}(t) & = & \displaystyle S_{ij}(t)+R_{ij}(t)\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & = & \displaystyle \frac{1}{\sqrt{2\unicode[STIX]{x1D708}}}[\sqrt{\unicode[STIX]{x1D716}(t)}\,\unicode[STIX]{x1D70E}_{ij}(t)+\sqrt{\unicode[STIX]{x1D701}(t)}\,\unicode[STIX]{x1D70C}_{ij}(t)],\end{eqnarray}$$
where
$\unicode[STIX]{x1D716}(t)=2\unicode[STIX]{x1D708}S_{ij}(t)S_{ij}(t)$
,
$\unicode[STIX]{x1D701}(t)=2\unicode[STIX]{x1D708}R_{ij}(t)R_{ij}(t)$
(where
$\unicode[STIX]{x1D708}$
is the kinematic viscosity), and
$\unicode[STIX]{x1D70E}_{ij}(t)$
and
$\unicode[STIX]{x1D70C}_{ij}(t)$
are the dimensionless strain-rate and rotation-rate tensors, respectively. Substituting (2.16) for
$\unicode[STIX]{x1D71E}$
in (2.12), and assuming
$\unicode[STIX]{x1D70E}_{ij}(t)$
and
$\unicode[STIX]{x1D70C}_{ij}(t)$
to be normally distributed, we can drop the third moments of
$\unicode[STIX]{x1D71E}$
as they, in turn, give rise to third moments of
$\unicode[STIX]{x1D748}$
and
$\unicode[STIX]{x1D746}$
and to cross-correlations of third order involving
$\unicode[STIX]{x1D748}$
and
$\unicode[STIX]{x1D746}$
. With these simplifications, the drift flux in (2.12) reduces to
$$\begin{eqnarray}\displaystyle q_{i}^{d}(\boldsymbol{r},t)=-\langle P\rangle (\boldsymbol{r};t)\frac{St_{\unicode[STIX]{x1D702}}^{2}}{\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D702}}^{2}}r_{k}\int _{-\infty }^{t}d_{ik}\,\text{d}t^{\prime }, & & \displaystyle\end{eqnarray}$$
where
$$\begin{eqnarray}\displaystyle \!\!\!\!d_{ik} & = & \displaystyle \langle \unicode[STIX]{x1D6E4}_{ij}(t)\unicode[STIX]{x1D6E4}_{jk}(t)\unicode[STIX]{x1D6E4}_{lm}(t^{\prime })\unicode[STIX]{x1D6E4}_{ml}(t^{\prime })\rangle \nonumber\\ \displaystyle & {\approx} & \displaystyle \frac{1}{4\unicode[STIX]{x1D708}^{2}}\{\langle \unicode[STIX]{x1D716}(t)\unicode[STIX]{x1D716}(t^{\prime })\rangle [\langle \unicode[STIX]{x1D70E}_{ij}(t)\unicode[STIX]{x1D70E}_{jk}(t)\rangle \langle \unicode[STIX]{x1D70E}_{lm}(t^{\prime })\unicode[STIX]{x1D70E}_{lm}(t^{\prime })\rangle +2\langle \unicode[STIX]{x1D70E}_{ij}(t)\unicode[STIX]{x1D70E}_{lm}(t^{\prime })\rangle \langle \unicode[STIX]{x1D70E}_{jk}(t)\unicode[STIX]{x1D70E}_{lm}(t^{\prime })\rangle ]\nonumber\\ \displaystyle & & \displaystyle -\,\langle \unicode[STIX]{x1D716}(t)\unicode[STIX]{x1D701}(t^{\prime })\rangle \langle \unicode[STIX]{x1D70E}_{ij}(t)\unicode[STIX]{x1D70E}_{jk}(t)\rangle \langle \unicode[STIX]{x1D70E}_{lm}(t^{\prime })\unicode[STIX]{x1D70E}_{lm}(t^{\prime })\rangle +\langle \unicode[STIX]{x1D701}(t)\unicode[STIX]{x1D716}(t^{\prime })\rangle \langle \unicode[STIX]{x1D70C}_{ij}(t)\unicode[STIX]{x1D70C}_{jk}(t)\rangle \langle \unicode[STIX]{x1D70E}_{lm}(t^{\prime })\unicode[STIX]{x1D70E}_{lm}(t^{\prime })\rangle \nonumber\\ \displaystyle & & \displaystyle -\,\langle \unicode[STIX]{x1D701}(t)\unicode[STIX]{x1D701}(t^{\prime })\rangle [\langle \unicode[STIX]{x1D70C}_{ij}(t)\unicode[STIX]{x1D70C}_{jk}(t)\rangle \langle \unicode[STIX]{x1D70C}_{lm}(t^{\prime })\unicode[STIX]{x1D70C}_{lm}(t^{\prime })\rangle +2\langle \unicode[STIX]{x1D70C}_{ij}(t)\unicode[STIX]{x1D70C}_{lm}(t^{\prime })\rangle \langle \unicode[STIX]{x1D70C}_{jk}(t)\unicode[STIX]{x1D70C}_{lm}(t^{\prime })\rangle ]\!\}.\qquad\end{eqnarray}$$
In (2.18), we have also assumed that
$\unicode[STIX]{x1D716}(t)$
and
$\unicode[STIX]{x1D748}(t)$
are weakly correlated, and so are
$\unicode[STIX]{x1D701}(t)$
and
$\unicode[STIX]{x1D746}(t)$
. This is a reasonable approximation since the dissipation rate and enstrophy vary over characteristic time scales that are quite different from those of strain-rate and rotation-rate tensors, respectively. The former two have scales of the order of large-eddy time scales (Chun et al.
Reference Chun, Koch, Rani, Ahluwalia and Collins2005). But, the components of strain rate have time scales
${\sim}2.3\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}$
and those of rotation rate
${\sim}7.2\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}$
(Chun et al.
Reference Chun, Koch, Rani, Ahluwalia and Collins2005; Zaichik & Alipchenkov Reference Zaichik and Alipchenkov2007), where
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}$
is the Kolmogorov time scale.
Owing to isotropy, the one-time correlations of the
$\unicode[STIX]{x1D748}$
and
$\unicode[STIX]{x1D746}$
tensors in (2.18) can be written as (Chun et al.
Reference Chun, Koch, Rani, Ahluwalia and Collins2005)
$$\begin{eqnarray}\displaystyle & \displaystyle \langle \unicode[STIX]{x1D70E}_{ij}(t)\unicode[STIX]{x1D70E}_{jk}(t)\rangle ={\textstyle \frac{1}{3}}\unicode[STIX]{x1D6FF}_{ik}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \langle \unicode[STIX]{x1D70E}_{lm}(t)\unicode[STIX]{x1D70E}_{lm}(t)\rangle =1, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \langle \unicode[STIX]{x1D70C}_{ij}(t)\unicode[STIX]{x1D70C}_{jk}(t)\rangle =-{\textstyle \frac{1}{3}}\unicode[STIX]{x1D6FF}_{ik}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \langle \unicode[STIX]{x1D70C}_{lm}(t)\unicode[STIX]{x1D70C}_{lm}(t)\rangle =1. & \displaystyle\end{eqnarray}$$
We now have
$$\begin{eqnarray}\displaystyle d_{ik} & = & \displaystyle \frac{1}{4\unicode[STIX]{x1D708}^{2}}\left\{\frac{1}{3}\unicode[STIX]{x1D6FF}_{ik}[\langle \unicode[STIX]{x1D716}(t)\unicode[STIX]{x1D716}(t^{\prime })\rangle +\langle \unicode[STIX]{x1D716}(t)\unicode[STIX]{x1D701}(t^{\prime })\rangle -\langle \unicode[STIX]{x1D701}(t)\unicode[STIX]{x1D716}(t^{\prime })\rangle -\langle \unicode[STIX]{x1D701}(t)\unicode[STIX]{x1D701}(t^{\prime })\rangle ]\right.\nonumber\\ \displaystyle & & \displaystyle +\,2\langle \unicode[STIX]{x1D716}(t)\unicode[STIX]{x1D716}(t^{\prime })\rangle \langle \unicode[STIX]{x1D70E}_{ij}(t)\unicode[STIX]{x1D70E}_{lm}(t^{\prime })\rangle \langle \unicode[STIX]{x1D70E}_{jk}(t)\unicode[STIX]{x1D70E}_{lm}(t^{\prime })\rangle \nonumber\\ \displaystyle & & \displaystyle -\left.2\langle \unicode[STIX]{x1D701}(t)\unicode[STIX]{x1D701}(t^{\prime })\rangle \langle \unicode[STIX]{x1D70C}_{ij}(t)\unicode[STIX]{x1D70C}_{lm}(t^{\prime })\rangle \langle \unicode[STIX]{x1D70C}_{jk}(t)\unicode[STIX]{x1D70C}_{lm}(t^{\prime })\rangle \right\}.\end{eqnarray}$$
In (2.23), we will express the two-time correlation of dissipation rate as (Chun et al. Reference Chun, Koch, Rani, Ahluwalia and Collins2005)
$$\begin{eqnarray}\displaystyle \langle \unicode[STIX]{x1D716}(t)\unicode[STIX]{x1D716}(t^{\prime })\rangle =\langle \unicode[STIX]{x1D716}^{2}\rangle \exp \left(-\frac{t-t^{\prime }}{T_{\unicode[STIX]{x1D716}\unicode[STIX]{x1D716}}}\right), & & \displaystyle\end{eqnarray}$$
so that
$$\begin{eqnarray}\displaystyle \int _{-\infty }^{t}\langle \unicode[STIX]{x1D716}(t)\unicode[STIX]{x1D716}(t^{\prime })\rangle \,\text{d}t^{\prime }=\langle \unicode[STIX]{x1D716}^{2}\rangle T_{\unicode[STIX]{x1D716}\unicode[STIX]{x1D716}}, & & \displaystyle\end{eqnarray}$$
where
$T_{\unicode[STIX]{x1D716}\unicode[STIX]{x1D716}}$
is the correlation time scale of
$\unicode[STIX]{x1D716}$
. In a similar manner, the correlations
$\langle \unicode[STIX]{x1D716}(t)\unicode[STIX]{x1D701}(t^{\prime })\rangle$
,
$\langle \unicode[STIX]{x1D701}(t)\unicode[STIX]{x1D716}(t^{\prime })\rangle$
and
$\langle \unicode[STIX]{x1D701}(t)\unicode[STIX]{x1D701}(t^{\prime })\rangle$
are expressed in terms of the correlation time scales
$T_{\unicode[STIX]{x1D716}\unicode[STIX]{x1D701}}$
,
$T_{\unicode[STIX]{x1D701}\unicode[STIX]{x1D716}}$
and
$T_{\unicode[STIX]{x1D701}\unicode[STIX]{x1D701}}$
, respectively. Thus, we have
$$\begin{eqnarray}\displaystyle \int _{-\infty }^{t}d_{ik}\,\text{d}t^{\prime } & = & \displaystyle \frac{1}{4\unicode[STIX]{x1D708}^{2}}\left\{\frac{1}{3}\unicode[STIX]{x1D6FF}_{ik}[\langle \unicode[STIX]{x1D716}^{2}\rangle T_{\unicode[STIX]{x1D716}\unicode[STIX]{x1D716}}+\langle \unicode[STIX]{x1D716}\unicode[STIX]{x1D701}\rangle T_{\unicode[STIX]{x1D716}\unicode[STIX]{x1D701}}-\langle \unicode[STIX]{x1D701}\unicode[STIX]{x1D716}\rangle T_{\unicode[STIX]{x1D701}\unicode[STIX]{x1D716}}-\langle \unicode[STIX]{x1D701}^{2}\rangle T_{\unicode[STIX]{x1D701}\unicode[STIX]{x1D701}}]\right.\nonumber\\ \displaystyle & & \displaystyle +\,2\langle \unicode[STIX]{x1D716}^{2}\rangle \int _{-\infty }^{t}\exp \left(-\frac{t-t^{\prime }}{T_{\unicode[STIX]{x1D716}\unicode[STIX]{x1D716}}}\right)\langle \unicode[STIX]{x1D70E}_{ij}(t)\unicode[STIX]{x1D70E}_{lm}(t^{\prime })\rangle \langle \unicode[STIX]{x1D70E}_{jk}(t)\unicode[STIX]{x1D70E}_{lm}(t^{\prime })\rangle \,\text{d}t^{\prime }\nonumber\\ \displaystyle & & \displaystyle -\left.2\langle \unicode[STIX]{x1D701}^{2}\rangle \int _{-\infty }^{t}\exp \left(-\frac{t-t^{\prime }}{T_{\unicode[STIX]{x1D701}\unicode[STIX]{x1D701}}}\right)\langle \unicode[STIX]{x1D70C}_{ij}(t)\unicode[STIX]{x1D70C}_{lm}(t^{\prime })\rangle \langle \unicode[STIX]{x1D70C}_{jk}(t)\unicode[STIX]{x1D70C}_{lm}(t^{\prime })\rangle \,\text{d}t^{\prime }\right\}.\qquad\end{eqnarray}$$
In the rapid settling limit, the time scales
$T_{\unicode[STIX]{x1D716}\unicode[STIX]{x1D716}}$
,
$T_{\unicode[STIX]{x1D716}\unicode[STIX]{x1D701}}$
,
$T_{\unicode[STIX]{x1D701}\unicode[STIX]{x1D716}}$
and
$T_{\unicode[STIX]{x1D701}\unicode[STIX]{x1D701}}$
can be approximated as the ratio of the corresponding Eulerian correlation length and the particle terminal velocity. For example,
$$\begin{eqnarray}\displaystyle T_{\unicode[STIX]{x1D716}\unicode[STIX]{x1D716}}\approx \frac{L_{\unicode[STIX]{x1D716}\unicode[STIX]{x1D716}}}{g\unicode[STIX]{x1D70F}_{v}}, & & \displaystyle\end{eqnarray}$$
where
$L_{\unicode[STIX]{x1D716}\unicode[STIX]{x1D716}}$
is the Eulerian length scale of
$\unicode[STIX]{x1D716}$
. The various Eulerian length scales are evaluated via DNS of isotropic turbulence.
To evaluate the two integrals on the right-hand side of (2.26), we need to resolve the two-time correlations of
$\unicode[STIX]{x1D748}$
and
$\unicode[STIX]{x1D746}$
, i.e.
$\langle \unicode[STIX]{x1D70E}_{ij}(t)\unicode[STIX]{x1D70E}_{lm}(t^{\prime })\rangle$
,
$\langle \unicode[STIX]{x1D70E}_{jk}(t)\unicode[STIX]{x1D70E}_{lm}(t^{\prime })\rangle$
,
$\langle \unicode[STIX]{x1D70C}_{ij}(t)\unicode[STIX]{x1D70C}_{lm}(t^{\prime })\rangle$
and
$\langle \unicode[STIX]{x1D70C}_{jk}(t)\unicode[STIX]{x1D70C}_{lm}(t^{\prime })\rangle$
. This is shown in appendix B.
The final form of drift flux for DF2 is analogous to that in (2.14) and is given by
$$\begin{eqnarray}\displaystyle q_{i}^{d}(\boldsymbol{r},t)=-\langle P\rangle (r,\unicode[STIX]{x1D703})2r_{k}\frac{St_{\unicode[STIX]{x1D702}}^{2}}{\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D702}}^{2}}[\unicode[STIX]{x1D706}_{1}^{\prime }(\unicode[STIX]{x1D6FF}_{ik}-\unicode[STIX]{x1D6FF}_{i3}\unicode[STIX]{x1D6FF}_{k3})+\unicode[STIX]{x1D706}_{2}^{\prime }\unicode[STIX]{x1D6FF}_{i3}\unicode[STIX]{x1D6FF}_{k3}], & & \displaystyle\end{eqnarray}$$
where
$\unicode[STIX]{x1D706}_{1}^{\prime }$
and
$\unicode[STIX]{x1D706}_{2}^{\prime }$
are the coefficients for DF2. The expressions for
$\unicode[STIX]{x1D706}_{1}^{\prime }$
and
$\unicode[STIX]{x1D706}_{2}^{\prime }$
are extremely involved and are not explicitly presented. As shown in appendix B, equation (B 6) gives rise to 13 separate integrations of the general form shown in (B 7), while (B 12) gives rise to three more such integrals. Each of these integrals is evaluated through numerical quadrature, and then assembled using (B 6) and (B 12) during runtime (of the computational code).
2.3 Diffusion flux
Applying (2.10) in the diffusion flux given by (2.3), and retaining only the leading-order term yields the following form of the diffusion flux (Chun et al. Reference Chun, Koch, Rani, Ahluwalia and Collins2005)
$$\begin{eqnarray}\displaystyle q_{i}^{D}(\boldsymbol{r})=-\mathscr{D}_{ij}\frac{\unicode[STIX]{x2202}\langle P\rangle }{\unicode[STIX]{x2202}r_{j}}, & & \displaystyle\end{eqnarray}$$
with the diffusivity tensor
$$\begin{eqnarray}\displaystyle \mathscr{D}_{ij}=r_{m}r_{n}\int _{-\infty }^{t}\langle \unicode[STIX]{x1D6E4}_{im}(t)\unicode[STIX]{x1D6E4}_{jn}(t^{\prime })\rangle \,\text{d}t^{\prime }=r_{m}r_{n}Q_{imjn}, & & \displaystyle\end{eqnarray}$$
where
$\unicode[STIX]{x1D6E4}_{im}(t)=\unicode[STIX]{x1D6E4}_{im}(\boldsymbol{x}(t),t)$
and
$\unicode[STIX]{x1D6E4}_{jn}(t^{\prime })=\unicode[STIX]{x1D6E4}_{jn}(\boldsymbol{x}(t^{\prime }),t^{\prime })$
.
In writing (2.29), we have invoked the assumption that the pair separation does not change appreciably over the correlation time for the ‘seen’ fluid velocity gradient. Such an approximation has been referred to as the local diffusion analysis in the Chun et al. (Reference Chun, Koch, Rani, Ahluwalia and Collins2005) study, and is particularly suitable for the case of rapidly settling particle pairs. As noted by Ireland, Bragg & Collins (Reference Ireland, Bragg and Collins2016), gravity reduces the Lagrangian time scales of strain rate and rotation rate along the particle trajectories. Therefore, in the rapid settling limit, one would anticipate these time scales to be significantly smaller than those in the zero-gravity case. Thus, it is reasonable to assume the pair separation to be essentially constant in these reduced correlation times of the fluid velocity gradient.
Analogous to the drift analysis, we can express the two-time correlation
$\langle \unicode[STIX]{x1D6E4}_{im}(t)\unicode[STIX]{x1D6E4}_{jn}(t^{\prime })\rangle$
in terms of two-point Eulerian correlation as
$$\begin{eqnarray}\displaystyle \langle \unicode[STIX]{x1D6E4}_{im}(t)\unicode[STIX]{x1D6E4}_{jn}(t^{\prime })\rangle & = & \displaystyle \langle \unicode[STIX]{x1D6E4}_{im}(\boldsymbol{x};t)\unicode[STIX]{x1D6E4}_{jn}[\boldsymbol{x}+\boldsymbol{g}\unicode[STIX]{x1D70F}_{v}(t^{\prime }-t);t]\rangle \nonumber\\ \displaystyle & = & \displaystyle \int \text{d}\unicode[STIX]{x1D73F}\,\unicode[STIX]{x1D705}_{m}\unicode[STIX]{x1D705}_{n}\unicode[STIX]{x1D6F7}_{ij}(\unicode[STIX]{x1D73F})\text{e}^{\text{i}\unicode[STIX]{x1D73F}\boldsymbol{\cdot }\boldsymbol{g}\unicode[STIX]{x1D70F}_{v}(t^{\prime }-t)}\nonumber\\ \displaystyle & = & \displaystyle \int \text{d}\unicode[STIX]{x1D73F}\,\unicode[STIX]{x1D705}_{m}\unicode[STIX]{x1D705}_{n}\frac{E(\unicode[STIX]{x1D705})}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D705}^{2}}\left(\unicode[STIX]{x1D6FF}_{ij}-\frac{\unicode[STIX]{x1D705}_{i}\unicode[STIX]{x1D705}_{j}}{\unicode[STIX]{x1D705}^{2}}\right)\text{e}^{\text{i}\unicode[STIX]{x1D73F}\boldsymbol{\cdot }\boldsymbol{g}\unicode[STIX]{x1D70F}_{v}(t^{\prime }-t)}.\end{eqnarray}$$
Thus, the diffusivity tensor may be written as
$$\begin{eqnarray}\displaystyle \mathscr{D}_{ij}(\boldsymbol{r}) & = & \displaystyle r_{m}r_{n}\int \text{d}\unicode[STIX]{x1D73F}\,\unicode[STIX]{x1D705}_{m}\unicode[STIX]{x1D705}_{n}\frac{E(\unicode[STIX]{x1D705})}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D705}^{2}}\left(\unicode[STIX]{x1D6FF}_{ij}-\frac{\unicode[STIX]{x1D705}_{i}\unicode[STIX]{x1D705}_{j}}{\unicode[STIX]{x1D705}^{2}}\right)\int _{-\infty }^{0}\text{e}^{\text{i}\unicode[STIX]{x1D73F}\boldsymbol{\cdot }\boldsymbol{g}\unicode[STIX]{x1D70F}_{v}t}\,\text{d}t\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2}r_{m}r_{n}\int \text{d}\unicode[STIX]{x1D73F}\,\unicode[STIX]{x1D705}_{m}\unicode[STIX]{x1D705}_{n}\frac{E(\unicode[STIX]{x1D705})}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D705}^{2}}\left(\unicode[STIX]{x1D6FF}_{ij}-\frac{\unicode[STIX]{x1D705}_{i}\unicode[STIX]{x1D705}_{j}}{\unicode[STIX]{x1D705}^{2}}\right)\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D73F}\boldsymbol{\cdot }\boldsymbol{g}\unicode[STIX]{x1D70F}_{v})\nonumber\\ \displaystyle & = & \displaystyle r_{m}r_{n}\frac{1}{2g\unicode[STIX]{x1D70F}_{v}}\int \text{d}\unicode[STIX]{x1D743}\,\unicode[STIX]{x1D709}_{m}\unicode[STIX]{x1D709}_{n}\frac{E(\unicode[STIX]{x1D709})}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D709}^{2}}\left(\unicode[STIX]{x1D6FF}_{ij}-\frac{\unicode[STIX]{x1D709}_{i}\unicode[STIX]{x1D709}_{j}}{\unicode[STIX]{x1D709}^{2}}\right),\end{eqnarray}$$
where
$\unicode[STIX]{x1D743}=(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2},0)$
is the wavenumber vector in the homogeneous
$x_{1}{-}x_{2}$
plane.
Using (2.30) and (2.32), and applying the tensor constraints on the fourth-order tensor
$Q_{imjn}$
, yields (details of the tensor analysis are in appendix F)
$$\begin{eqnarray}\displaystyle Q_{imjn} & = & \displaystyle \frac{1}{2g\unicode[STIX]{x1D70F}_{v}}\int \text{d}\unicode[STIX]{x1D743}\,\unicode[STIX]{x1D709}_{m}\unicode[STIX]{x1D709}_{n}\frac{E(\unicode[STIX]{x1D709})}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D709}^{2}}\left(\unicode[STIX]{x1D6FF}_{ij}-\frac{\unicode[STIX]{x1D709}_{i}\unicode[STIX]{x1D709}_{j}}{\unicode[STIX]{x1D709}^{2}}\right)\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D706}_{5}(\unicode[STIX]{x1D6FF}_{i3}\unicode[STIX]{x1D6FF}_{m3}\unicode[STIX]{x1D6FF}_{j3}\unicode[STIX]{x1D6FF}_{n3}-\unicode[STIX]{x1D6FF}_{i3}\unicode[STIX]{x1D6FF}_{j3}\unicode[STIX]{x1D6FF}_{mn})\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D706}_{6} (\!\unicode[STIX]{x1D6FF}_{in}\unicode[STIX]{x1D6FF}_{mj}+\unicode[STIX]{x1D6FF}_{im}\unicode[STIX]{x1D6FF}_{jn}-3\unicode[STIX]{x1D6FF}_{ij}\unicode[STIX]{x1D6FF}_{mn}-\unicode[STIX]{x1D6FF}_{i3}\unicode[STIX]{x1D6FF}_{n3}\unicode[STIX]{x1D6FF}_{mj}-\unicode[STIX]{x1D6FF}_{j3}\unicode[STIX]{x1D6FF}_{n3}\unicode[STIX]{x1D6FF}_{im}-\unicode[STIX]{x1D6FF}_{i3}\unicode[STIX]{x1D6FF}_{m3}\unicode[STIX]{x1D6FF}_{jn}\nonumber\\ \displaystyle & & \displaystyle -\,\unicode[STIX]{x1D6FF}_{m3}\unicode[STIX]{x1D6FF}_{j3}\unicode[STIX]{x1D6FF}_{in}+2\unicode[STIX]{x1D6FF}_{i3}\unicode[STIX]{x1D6FF}_{j3}\unicode[STIX]{x1D6FF}_{mn}+3\unicode[STIX]{x1D6FF}_{m3}\unicode[STIX]{x1D6FF}_{n3}\unicode[STIX]{x1D6FF}_{im}\! ),\end{eqnarray}$$
which gives
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D706}_{5}=-\frac{3\unicode[STIX]{x03C0}}{16g\unicode[STIX]{x1D70F}_{v}}\int _{\unicode[STIX]{x1D709}=0}^{\infty }\unicode[STIX]{x1D709}E(\unicode[STIX]{x1D709})\,\text{d}\unicode[STIX]{x1D709}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D706}_{6}=\frac{\unicode[STIX]{x1D706}_{5}}{3}. & \displaystyle\end{eqnarray}$$
Therefore,
$$\begin{eqnarray}\displaystyle \mathscr{D}_{ij}(\boldsymbol{r}) & = & \displaystyle r_{m}r_{n}A_{imjn}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D706}_{6}[(3r_{3}^{2}-r^{2})\unicode[STIX]{x1D6FF}_{i3}\unicode[STIX]{x1D6FF}_{j3}+2r_{i}r_{j}+3(r_{3}^{2}-r^{2})\unicode[STIX]{x1D6FF}_{ij}-2r_{3}(r_{j}\unicode[STIX]{x1D6FF}_{i3}+r_{i}\unicode[STIX]{x1D6FF}_{j3})].\end{eqnarray}$$
Having derived closures for the drift and diffusion fluxes, we present the analytical solution to the p.d.f. equation (2.1).
3 Solution of the probability density function equation
We will solve the p.d.f. equation (2.1) in spherical coordinates. At steady state, the governing equation for
$\langle P\rangle (r,\unicode[STIX]{x1D703})$
is given by
$$\begin{eqnarray}\displaystyle \frac{1}{r^{2}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}r}(r^{2}q_{r})+\frac{1}{r\sin \unicode[STIX]{x1D703}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}(\sin \unicode[STIX]{x1D703}q_{\unicode[STIX]{x1D703}})=0, & & \displaystyle\end{eqnarray}$$
where
$q_{r}$
and
$q_{\unicode[STIX]{x1D703}}$
are fluxes along the radial and polar directions. These contain both the drift and diffusion fluxes, and are given by
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle q_{r}=v_{r}\langle P\rangle -\mathscr{D}_{rr}\frac{\unicode[STIX]{x2202}\langle P\rangle }{\unicode[STIX]{x2202}r}-\mathscr{D}_{r\unicode[STIX]{x1D703}}\frac{1}{r}\frac{\unicode[STIX]{x2202}\langle P\rangle }{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}},\\ \displaystyle q_{\unicode[STIX]{x1D703}}=v_{\unicode[STIX]{x1D703}}\langle P\rangle -\mathscr{D}_{r\unicode[STIX]{x1D703}}\frac{\unicode[STIX]{x2202}\langle P\rangle }{\unicode[STIX]{x2202}r}-\mathscr{D}_{\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}}\frac{1}{r}\frac{\unicode[STIX]{x2202}\langle P\rangle }{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}},\\ v_{r}=-2r(\unicode[STIX]{x1D706}_{1}\sin ^{2}\unicode[STIX]{x1D703}+\unicode[STIX]{x1D706}_{2}\cos ^{2}\unicode[STIX]{x1D703})St_{\unicode[STIX]{x1D702}}^{2},\\ v_{\unicode[STIX]{x1D703}}=-2r(\unicode[STIX]{x1D706}_{1}-\unicode[STIX]{x1D706}_{2})St_{\unicode[STIX]{x1D702}}^{2}\sin \unicode[STIX]{x1D703}\cos \unicode[STIX]{x1D703},\\ \mathscr{D}_{rr}=\unicode[STIX]{x1D706}_{6}r^{2}(3\sin ^{4}\unicode[STIX]{x1D703}-4\sin ^{2}\unicode[STIX]{x1D703}),\\ \mathscr{D}_{r\unicode[STIX]{x1D703}}=3\unicode[STIX]{x1D706}_{6}r^{2}\sin ^{3}\unicode[STIX]{x1D703}\cos \unicode[STIX]{x1D703},\\ \mathscr{D}_{\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}}=-\unicode[STIX]{x1D706}_{6}r^{2}(\sin ^{2}\unicode[STIX]{x1D703}+3\sin ^{4}\unicode[STIX]{x1D703}).\end{array}\right\} & & \displaystyle\end{eqnarray}$$
The coefficients
$\unicode[STIX]{x1D706}_{1}$
,
$\unicode[STIX]{x1D706}_{2}$
and
$\unicode[STIX]{x1D706}_{6}$
in the above equations are given in (A 18), (A 19) and (2.35) respectively, while
$\mathscr{D}_{rr}$
,
$\mathscr{D}_{r\unicode[STIX]{x1D703}}$
and
$\mathscr{D}_{\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}}$
are the components in spherical coordinates of the diffusivity tensor
$\mathscr{D}_{ij}(\boldsymbol{r})$
in (2.36). When applying DF2, we use
$\unicode[STIX]{x1D706}_{1}^{\prime }$
and
$\unicode[STIX]{x1D706}_{2}^{\prime }$
in place of
$\unicode[STIX]{x1D706}_{1}$
and
$\unicode[STIX]{x1D706}_{2}$
.
It is evident from the
$q_{r}$
and
$q_{\unicode[STIX]{x1D703}}$
equations that the variables
$r$
and
$\unicode[STIX]{x1D703}$
are separable. Also, the form of the p.d.f. equation (3.1) suggests a solution with a power-law dependence on separation
$r$
. Accordingly, we write
$\langle P\rangle (r,\unicode[STIX]{x1D703})=r^{\unicode[STIX]{x1D6FD}}f(\unicode[STIX]{x1D703})$
and substitute this form into (3.1). A change of variable
$\unicode[STIX]{x1D707}=\cos \unicode[STIX]{x1D703}$
leads to the following equation for
$f(\unicode[STIX]{x1D707})$
:
$$\begin{eqnarray}\displaystyle a(\unicode[STIX]{x1D707})\frac{\text{d}^{2}f}{\text{d}\unicode[STIX]{x1D707}^{2}}+b(\unicode[STIX]{x1D707})\frac{\text{d}f}{\text{d}\unicode[STIX]{x1D707}}+c(\unicode[STIX]{x1D707})f=0, & & \displaystyle\end{eqnarray}$$
where
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}rcl@{}}a(\unicode[STIX]{x1D707})\; & =\; & \unicode[STIX]{x1D706}_{6}(3\unicode[STIX]{x1D707}^{2}-4)(1-\unicode[STIX]{x1D707}^{2})^{2},\\ b(\unicode[STIX]{x1D707})\; & =\; & 2(\unicode[STIX]{x1D706}_{2}-\unicode[STIX]{x1D706}_{1})St^{2}\unicode[STIX]{x1D707}(1-\unicode[STIX]{x1D707}^{2})-3\unicode[STIX]{x1D706}_{6}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D707}(1-\unicode[STIX]{x1D707}^{2})^{2}\\ \; & \; & -\,\unicode[STIX]{x1D706}_{6}\unicode[STIX]{x1D707}(18\unicode[STIX]{x1D707}^{2}-22)(1-\unicode[STIX]{x1D707}^{2})-3\unicode[STIX]{x1D706}_{6}(\unicode[STIX]{x1D6FD}+3)\unicode[STIX]{x1D707}(1-\unicode[STIX]{x1D707}^{2})^{2},\\ c(\unicode[STIX]{x1D707})\; & =\; & 2(\unicode[STIX]{x1D706}_{2}-\unicode[STIX]{x1D706}_{1})St^{2}(1-3\unicode[STIX]{x1D707}^{2})-3\unicode[STIX]{x1D706}_{6}\unicode[STIX]{x1D6FD}(1-\unicode[STIX]{x1D707}^{2})(1-5\unicode[STIX]{x1D707}^{2})\\ \; & \; & +\,(\unicode[STIX]{x1D6FD}+3)\{2[\unicode[STIX]{x1D706}_{1}(1-\unicode[STIX]{x1D707}^{2})+\unicode[STIX]{x1D706}_{2}\unicode[STIX]{x1D707}^{2}]St^{2}-\unicode[STIX]{x1D706}_{6}\unicode[STIX]{x1D6FD}(1+3\unicode[STIX]{x1D707}^{2})(1-\unicode[STIX]{x1D707}^{2})\}.\end{array}\right\} & & \displaystyle\end{eqnarray}$$
3.1 Power-law exponent
$\unicode[STIX]{x1D6FD}$
To find the power-law exponent, we apply the constraint that, at steady state, the net radial flux through a spherical surface of radius
$r$
is zero, given by
$$\begin{eqnarray}\displaystyle \int _{-1}^{1}q_{r}\,\text{d}\unicode[STIX]{x1D707}=0, & & \displaystyle\end{eqnarray}$$
leading to
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FD}=\frac{\displaystyle \int _{-1}^{1}\left(A_{r}\,f(\unicode[STIX]{x1D707})+B_{r\unicode[STIX]{x1D703}}\sqrt{1-\unicode[STIX]{x1D707}^{2}}\frac{\text{d}f}{\text{d}\unicode[STIX]{x1D707}}\right)\text{d}\unicode[STIX]{x1D707}}{\int _{-1}^{1}B_{rr}\,f(\unicode[STIX]{x1D707})\,\text{d}\unicode[STIX]{x1D707}}, & & \displaystyle\end{eqnarray}$$
where
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}A_{r}=-2[\unicode[STIX]{x1D706}_{1}(1-\unicode[STIX]{x1D707}^{2})+\unicode[STIX]{x1D706}_{2}\unicode[STIX]{x1D707}^{2}]St_{\unicode[STIX]{x1D702}}^{2},\\ B_{rr}=-\unicode[STIX]{x1D706}_{6}(1-\unicode[STIX]{x1D707}^{2})(1+3\unicode[STIX]{x1D707}^{2}),\\ B_{r\unicode[STIX]{x1D703}}=3\unicode[STIX]{x1D706}_{6}\unicode[STIX]{x1D707}(1-\unicode[STIX]{x1D707}^{2})\sqrt{1-\unicode[STIX]{x1D707}^{2}}.\end{array}\right\} & & \displaystyle\end{eqnarray}$$
Since the drift flux scales as
$St_{\unicode[STIX]{x1D702}}^{2}$
, we seek
$\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D6FD}_{2}St_{\unicode[STIX]{x1D702}}^{2}$
(
$\unicode[STIX]{x1D6FD}_{2}>0$
), which then means that the numerator of (3.6),
$\int _{-1}^{1}(A_{r}\,f(\unicode[STIX]{x1D707})+B_{r\unicode[STIX]{x1D703}}\sqrt{1-\unicode[STIX]{x1D707}^{2}}\,\text{d}f/\text{d}\unicode[STIX]{x1D707})\,\text{d}\unicode[STIX]{x1D707}$
, should also scale as
$St_{\unicode[STIX]{x1D702}}^{2}$
. With these arguments, we seek a perturbation solution to (3.3) of the form
$$\begin{eqnarray}\displaystyle f(\unicode[STIX]{x1D707})=f_{0}(\unicode[STIX]{x1D707})+St_{\unicode[STIX]{x1D702}}^{2}\,f_{2}(\unicode[STIX]{x1D707}). & & \displaystyle\end{eqnarray}$$
3.2 Perturbation solution for
$f(\unicode[STIX]{x1D707})$
Substitution of
$f(\unicode[STIX]{x1D707})=f_{0}(\unicode[STIX]{x1D707})+St_{\unicode[STIX]{x1D702}}^{2}\,f_{2}(\unicode[STIX]{x1D707})$
into (3.3) and gathering terms that are
$O(St^{0})$
gives
$$\begin{eqnarray}\displaystyle a_{0}(\unicode[STIX]{x1D707})\frac{\text{d}^{2}f_{0}}{\text{d}\unicode[STIX]{x1D707}^{2}}+b_{0}(\unicode[STIX]{x1D707})\frac{\text{d}f_{0}}{\text{d}\unicode[STIX]{x1D707}}=0, & & \displaystyle\end{eqnarray}$$
where
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}a_{0}(\unicode[STIX]{x1D707})=\unicode[STIX]{x1D706}_{6}(3\unicode[STIX]{x1D707}^{2}-4)(1-\unicode[STIX]{x1D707}^{2})^{2},\\ b_{0}(\unicode[STIX]{x1D707})=-\unicode[STIX]{x1D706}_{6}\unicode[STIX]{x1D707}(18\unicode[STIX]{x1D707}^{2}-22)(1-\unicode[STIX]{x1D707}^{2})-9\unicode[STIX]{x1D706}_{6}\unicode[STIX]{x1D707}(1-\unicode[STIX]{x1D707}^{2})^{2}.\end{array}\right\} & & \displaystyle\end{eqnarray}$$
Equation (3.9) can be integrated to give
$$\begin{eqnarray}\displaystyle \frac{\text{d}f_{0}}{\text{d}\unicode[STIX]{x1D707}}=k_{1}\frac{(4-3\unicode[STIX]{x1D707}^{2})^{1/2}}{(1-\unicode[STIX]{x1D707}^{2})^{2}}, & & \displaystyle\end{eqnarray}$$
which upon further integration leads to
$$\begin{eqnarray}\displaystyle f_{0}(\unicode[STIX]{x1D707})=k_{2}+k_{1}\left[\frac{1}{2}\frac{\unicode[STIX]{x1D707}(4-3\unicode[STIX]{x1D707}^{2})^{1/2}}{(1-\unicode[STIX]{x1D707}^{2})}+2\tanh ^{-1}\unicode[STIX]{x1D707}+\ln \left(\frac{4-3\unicode[STIX]{x1D707}+\sqrt{4-3\unicode[STIX]{x1D707}^{2}}}{4+3\unicode[STIX]{x1D707}+\sqrt{4-3\unicode[STIX]{x1D707}^{2}}}\right)\right].\qquad & & \displaystyle\end{eqnarray}$$
Recalling that
$\unicode[STIX]{x1D707}=\cos \unicode[STIX]{x1D703}\in [-1,1]$
, it can be seen that
$f_{0}\rightarrow \infty$
as
$\unicode[STIX]{x1D707}\rightarrow \pm 1$
. These singularities prevent the normalization of the probability density
$f_{0}$
, suggesting that the integration constant
$k_{1}=0$
. Hence, we have
$f_{0}(\unicode[STIX]{x1D707})=k_{2}$
. Using the normalization constraint
$\int _{0}^{1}f_{0}\,\text{d}\unicode[STIX]{x1D707}=1/(4\unicode[STIX]{x03C0})$
leads to
$f_{0}=1/(4\unicode[STIX]{x03C0})$
.
Having determined
$f_{0}$
, we now gather terms that are
$O(St^{2})$
as well as use
$f_{0}=1/(4\unicode[STIX]{x03C0})$
, giving us
$$\begin{eqnarray}\displaystyle a_{0}(\unicode[STIX]{x1D707})\frac{\text{d}^{2}f_{2}}{\text{d}\unicode[STIX]{x1D707}^{2}}+b_{0}(\unicode[STIX]{x1D707})\frac{\text{d}f_{2}}{\text{d}\unicode[STIX]{x1D707}}+\frac{c_{2}(\unicode[STIX]{x1D707})}{4\unicode[STIX]{x03C0}}=0, & & \displaystyle\end{eqnarray}$$
where
$$\begin{eqnarray}\displaystyle c_{2}(\unicode[STIX]{x1D707}) & = & \displaystyle 2(\unicode[STIX]{x1D706}_{2}-\unicode[STIX]{x1D706}_{1})(1-3\unicode[STIX]{x1D707}^{2})-3\unicode[STIX]{x1D706}_{6}\unicode[STIX]{x1D6FD}_{2}(1-\unicode[STIX]{x1D707}^{2})(1-5\unicode[STIX]{x1D707}^{2})\nonumber\\ \displaystyle & & \displaystyle +\,6[\unicode[STIX]{x1D706}_{1}(1-\unicode[STIX]{x1D707}^{2})+\unicode[STIX]{x1D706}_{2}\unicode[STIX]{x1D707}^{2}]-3\unicode[STIX]{x1D706}_{6}\unicode[STIX]{x1D6FD}_{2}(1+3\unicode[STIX]{x1D707}^{2})(1-\unicode[STIX]{x1D707}^{2}).\end{eqnarray}$$
Equation (3.14) is a linear, inhomogeneous first-order ordinary differential equation in
$\text{d}f_{2}/\text{d}\unicode[STIX]{x1D707}$
, and can be integrated using the integrating factor
$I$
:
$$\begin{eqnarray}\displaystyle I=\exp \left[\int \frac{Q_{0}(\unicode[STIX]{x1D707})}{P_{0}(\unicode[STIX]{x1D707})}\,\text{d}\unicode[STIX]{x1D707}\right]=\frac{(1-\unicode[STIX]{x1D707}^{2})^{2}}{(4-3\unicode[STIX]{x1D707}^{2})^{1/2}}. & & \displaystyle\end{eqnarray}$$
Thus, we have
$$\begin{eqnarray}\displaystyle I\frac{\text{d}f_{2}}{\text{d}\unicode[STIX]{x1D707}}=\int I\frac{-R_{2}(\unicode[STIX]{x1D707})}{P_{0}(\unicode[STIX]{x1D707})4\unicode[STIX]{x03C0}}\,\text{d}\unicode[STIX]{x1D707}+k_{3}, & & \displaystyle\end{eqnarray}$$
where
$k_{3}$
is a constant of integration. To find
$k_{3}$
, we enforce symmetry
$\text{d}f/\text{d}\unicode[STIX]{x1D707}=0$
at
$\unicode[STIX]{x1D707}=0$
. Since the first term on the right-hand side of (3.16) is zero at
$\unicode[STIX]{x1D707}=0$
, it follows that
$k_{3}=0$
in order to satisfy the symmetry requirement. Thus
$$\begin{eqnarray}\displaystyle \frac{\text{d}f_{2}}{\text{d}\unicode[STIX]{x1D707}}=\frac{1}{4\unicode[STIX]{x03C0}}\frac{\unicode[STIX]{x1D707}[\unicode[STIX]{x1D706}_{2}+2\unicode[STIX]{x1D706}_{1}+\unicode[STIX]{x1D706}_{6}\unicode[STIX]{x1D6FD}_{2}(-3+2\unicode[STIX]{x1D707}^{2})]}{2\unicode[STIX]{x1D706}_{6}(1-\unicode[STIX]{x1D707}^{2})^{2}}. & & \displaystyle\end{eqnarray}$$
Referring to (3.6), in order for
$\unicode[STIX]{x1D6FD}$
to scale as
$St_{\unicode[STIX]{x1D702}}^{2}$
, we use
$f(\unicode[STIX]{x1D707})=f_{0}=1/(4\unicode[STIX]{x03C0})$
and
$\text{d}f/\text{d}\unicode[STIX]{x1D707}=\text{d}f_{2}/\text{d}\unicode[STIX]{x1D707}$
in the numerator of (3.6), giving us
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FD}_{2}=\frac{\displaystyle \int _{0}^{1}\left(\displaystyle \frac{a_{r}}{4\unicode[STIX]{x03C0}}+b_{r\unicode[STIX]{x1D703}}\frac{\text{d}f_{2}}{\text{d}\unicode[STIX]{x1D707}}\right)\text{d}\unicode[STIX]{x1D707}}{\displaystyle \int _{0}^{1}\frac{B_{rr}}{4\unicode[STIX]{x03C0}}\,\text{d}\unicode[STIX]{x1D707}}, & & \displaystyle\end{eqnarray}$$
where
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}a_{r}=-2[\unicode[STIX]{x1D706}_{1}(1-\unicode[STIX]{x1D707}^{2})+\unicode[STIX]{x1D706}_{2}\unicode[STIX]{x1D707}^{2}],\\ B_{rr}=-\unicode[STIX]{x1D706}_{6}(1-\unicode[STIX]{x1D707}^{2})(1+3\unicode[STIX]{x1D707}^{2}),\\ b_{r\unicode[STIX]{x1D703}}=3\unicode[STIX]{x1D706}_{6}\unicode[STIX]{x1D707}(1-\unicode[STIX]{x1D707}^{2})^{2}.\end{array}\right\} & & \displaystyle\end{eqnarray}$$
Substitution of (3.17) into (3.18) and simplification thereafter leads to
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FD}_{2}=\frac{\unicode[STIX]{x1D706}_{2}+2\unicode[STIX]{x1D706}_{1}}{\unicode[STIX]{x1D706}_{6}}. & & \displaystyle\end{eqnarray}$$
It may noted that
$\unicode[STIX]{x1D6FD}_{2}<0$
as both
$\unicode[STIX]{x1D706}_{1}$
and
$\unicode[STIX]{x1D706}_{2}$
are less than
$0$
.
Using the above form of
$\unicode[STIX]{x1D6FD}_{2}$
in (3.17) we get
$$\begin{eqnarray}\displaystyle \frac{\text{d}f_{2}}{\text{d}\unicode[STIX]{x1D707}}=-\frac{1}{4\unicode[STIX]{x03C0}}\frac{\unicode[STIX]{x1D707}\unicode[STIX]{x1D6FD}_{2}}{(1-\unicode[STIX]{x1D707}^{2})}, & & \displaystyle\end{eqnarray}$$
which leads to
$$\begin{eqnarray}\displaystyle f_{2}=\frac{\unicode[STIX]{x1D6FD}_{2}}{8\unicode[STIX]{x03C0}}\ln (1-\unicode[STIX]{x1D707}^{2})+k_{4}. & & \displaystyle\end{eqnarray}$$
The unknown constant
$k_{4}$
may be determined using
$\int _{0}^{1}f_{2}\,\text{d}\unicode[STIX]{x1D707}=0$
, yielding
$$\begin{eqnarray}\displaystyle k_{4}=-\frac{1}{4\unicode[STIX]{x03C0}}\unicode[STIX]{x1D6FD}_{2}(\ln 2-1). & & \displaystyle\end{eqnarray}$$
Thus the complete solution for
$f(\unicode[STIX]{x1D707})$
is given by
$$\begin{eqnarray}\displaystyle f(\unicode[STIX]{x1D707})=\frac{1}{4\unicode[STIX]{x03C0}}\left[1+St_{\unicode[STIX]{x1D702}}^{2}\unicode[STIX]{x1D6FD}_{2}\left(\frac{1}{2}\ln (1-\unicode[STIX]{x1D707}^{2})-(\ln 2-1)\right)\right]. & & \displaystyle\end{eqnarray}$$
Therefore
$\langle P\rangle (r,\unicode[STIX]{x1D707})$
is given by
$$\begin{eqnarray}\displaystyle \langle P\rangle (r,\unicode[STIX]{x1D707})=r^{\unicode[STIX]{x1D6FD}_{2}St^{2}}\frac{1}{4\unicode[STIX]{x03C0}}\left[1+St_{\unicode[STIX]{x1D702}}^{2}\unicode[STIX]{x1D6FD}_{2}\left(\frac{1}{2}\ln (1-\unicode[STIX]{x1D707}^{2})-(\ln 2-1)\right)\right], & & \displaystyle\end{eqnarray}$$
where
$\unicode[STIX]{x1D6FD}_{2}$
is given by (3.20).
4 Results
4.1 Discussion of the p.d.f. solution
The p.d.f. solution
$\langle P\rangle (r,\unicode[STIX]{x1D707})$
in (3.25) quantifies the dependence of particle clustering on separation
$r$
and direction cosine
$\unicode[STIX]{x1D707}~(=\cos \unicode[STIX]{x1D703})$
, the latter describing the anisotropy due to particle settling. In the DNS by Ireland et al. (Reference Ireland, Bragg and Collins2016), they referred to
$\langle P\rangle$
as the angular distribution function (a.d.f.)
$g(\boldsymbol{r})$
, and expressed it in terms of the Legendre spherical harmonic functions, as below:
$$\begin{eqnarray}\displaystyle \frac{g(\boldsymbol{r})}{g(r)}=\mathop{\sum }_{l=1}^{\infty }\frac{\mathscr{C}_{2l}^{0}(r)}{\mathscr{C}_{0}^{0}(r)}Y_{2l}^{0}(\cos \unicode[STIX]{x1D703}), & & \displaystyle\end{eqnarray}$$
where
$$\begin{eqnarray}\displaystyle g(r)=\mathscr{C}_{0}^{0}(r)=\int _{0}^{\unicode[STIX]{x03C0}}\text{d}\unicode[STIX]{x1D703}\sin \unicode[STIX]{x1D703}\,g(\boldsymbol{r}). & & \displaystyle\end{eqnarray}$$
Applying the orthogonality of Legendre polynomials to (4.1), we get the leading-order coefficient for anisotropy to be
$$\begin{eqnarray}\displaystyle \frac{\mathscr{C}_{2}^{0}(r)}{\mathscr{C}_{0}^{0}(r)}=\frac{5}{2}\frac{\displaystyle \int _{0}^{\unicode[STIX]{x03C0}}\text{d}\unicode[STIX]{x1D703}\sin \unicode[STIX]{x1D703}\,g(\boldsymbol{r})Y_{2}^{0}(\cos \unicode[STIX]{x1D703})}{g(r)}. & & \displaystyle\end{eqnarray}$$
The corresponding coefficient from the theory is
$$\begin{eqnarray}\displaystyle \left[\frac{\mathscr{C}_{2}^{0}(r)}{\mathscr{C}_{0}^{0}(r)}\right]_{theory}=\frac{5\unicode[STIX]{x1D6FD}_{2}St_{\unicode[STIX]{x1D702}}^{2}}{12}. & & \displaystyle\end{eqnarray}$$
Ireland et al. (Reference Ireland, Bragg and Collins2016) plotted the ratio
$\mathscr{C}_{2}^{0}(r)/\mathscr{C}_{0}^{0}(r)$
as a function of
$r$
for
$St_{\unicode[STIX]{x1D702}}\geqslant 0.3$
. These curves show that for
$r\ll \unicode[STIX]{x1D702}$
, the coefficient ratio becomes independent of
$r$
, suggesting that both
$g(\boldsymbol{r})$
and
$g(r)$
have the same functionality in
$r$
for sub-Kolmogorov separations. It was seen that the smaller the
$St_{\unicode[STIX]{x1D702}}$
, the quicker the plateauing began, i.e. the spherical harmonic coefficient began flattening at larger separations. For instance, for
$St_{\unicode[STIX]{x1D702}}=0.3$
, the plateauing seemed to occur for
$r\lesssim \unicode[STIX]{x1D702}$
, while for larger
$St_{\unicode[STIX]{x1D702}}$
this occurred at much smaller separations. The current theory also predicts that, for
$r\ll \unicode[STIX]{x1D702}$
, the coefficient ratio is independent of
$r$
. However, we could not directly compare the DNS and theory values of the coefficient ratio, as the theory is applicable for
$St_{\unicode[STIX]{x1D702}}\ll 1$
, while Ireland et al. (Reference Ireland, Bragg and Collins2016) gave the DNS values only for
$St_{\unicode[STIX]{x1D702}}\geqslant 0.3$
. It is evident from (4.4) that anisotropy due to gravity is small for
$St_{\unicode[STIX]{x1D702}}\ll 1$
. A similar trend is noticed in the DNS of Ireland et al. (Reference Ireland, Bragg and Collins2016).
4.2 Time scale of p.d.f.
$\langle P\rangle$
We have seen in § 3 that the radial component,
$\mathscr{D}_{rr}$
, of the diffusivity tensor scales as
$\unicode[STIX]{x1D706}_{6}r^{2}$
, where
$\unicode[STIX]{x1D706}_{6}$
has the dimensions of inverse time. Thus, a good estimate of the characteristic time over which the p.d.f.
$\langle P\rangle$
evolves is given by
$1/\unicode[STIX]{x1D706}_{6}$
. To calculate
$\unicode[STIX]{x1D706}_{6}$
from (2.35), we need the energy spectrum
$E(\unicode[STIX]{x1D705})$
. A fully analytical and universal result for
$\unicode[STIX]{x1D706}_{6}$
may be obtained by using the following dimensionless form of
$E(\unicode[STIX]{x1D705})$
, which is valid in the limit
$Re_{\unicode[STIX]{x1D706}}\rightarrow \infty$
, and follows from Kolmogorov’s first similarity hypothesis (Pope Reference Pope2000):
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{E(\unicode[STIX]{x1D705}\unicode[STIX]{x1D702})}{\unicode[STIX]{x1D702}u_{\unicode[STIX]{x1D702}}^{2}}=1.5(\unicode[STIX]{x1D705}\unicode[STIX]{x1D702})^{-5/3}f_{\unicode[STIX]{x1D702}}(\unicode[STIX]{x1D705}\unicode[STIX]{x1D702}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle f_{\unicode[STIX]{x1D702}}(\unicode[STIX]{x1D705}\unicode[STIX]{x1D702})=\text{exp}\{-5.2([(\unicode[STIX]{x1D705}\unicode[STIX]{x1D702})^{4}+c_{\unicode[STIX]{x1D702}}^{4}]^{1/4}-c_{\unicode[STIX]{x1D702}})\}, & \displaystyle\end{eqnarray}$$
where
$c_{\unicode[STIX]{x1D702}}\approx 0.4$
for
$Re_{\unicode[STIX]{x1D706}}\rightarrow \infty$
, and
$\unicode[STIX]{x1D702}$
and
$u_{\unicode[STIX]{x1D702}}$
are the Kolmogorov length and velocity scales. The integral in (2.35) is then evaluated through numerical quadrature. The characteristic time scale of
$\langle P\rangle$
is obtained to be
$=1.43118\times (St_{\unicode[STIX]{x1D702}}/Fr)\times \unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}\gg \unicode[STIX]{x1D702}/g\unicode[STIX]{x1D70F}_{v}$
. Thus, the p.d.f. evolves over time scales that are much longer than the settling time of a particle through a Kolmogorov-scale eddy.
4.3 Mechanism for clustering of rapidly settling particles
Gustavsson et al. (Reference Gustavsson, Vajedi and Mehlig2014) raised the question that, since rapidly settling particles fall too quickly through eddies for preferential sampling to be a clustering mechanism, what then is the mechanism of clustering for rapidly settling particles? They went on to provide a qualitative explanation for this phenomenon. However, the drift closure(s) developed in this study provide a clear and quantitative explanation for the clustering of rapidly settling particles. As discussed in § A.2, particles experience frozen turbulence, with the implication that the spatial correlations of eddies give rise to temporal correlations in the frame of settling particles. Temporal correlations of fluid velocity gradients contribute to the drift flux driving the clustering. More specifically, DF2 shows us that the temporal autocorrelations and cross-correlations of the strain-rate and rotation-rate second invariants are responsible for clustering.
4.4 Prediction of clustering through universal scaling
The first drift closure DF1 and the diffusion flux have the advantage that the only statistical input they require is the energy spectrum
$E(\unicode[STIX]{x1D705})$
. In contrast, DF2 additionally requires the correlation length scales of dissipation rate and enstrophy. The spectrum in (4.5) allows us to obtain universal values of the DF1 drift flux, as well as the diffusion flux. To determine the power-law exponent
$\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D6FD}_{2}St_{\unicode[STIX]{x1D702}}^{2}$
for the spatial clustering of particles, we first non-dimensionalize the drift and diffusion fluxes using the Kolmogorov length and time scales. We then substitute (4.5) into the dimensionless forms of (A 18) and (A 19) for
$\unicode[STIX]{x1D706}_{1}$
and
$\unicode[STIX]{x1D706}_{2}$
of DF1, and also into the dimensionless forms of (2.33) and (2.35) for the diffusion flux. Finally, the integrals are evaluated through numerical quadrature. These integrals converge as the energy spectrum in (4.5) has an inertial-range dependence of the form
$\unicode[STIX]{x1D705}^{-\unicode[STIX]{x1D6FE}}$
with
$\unicode[STIX]{x1D6FE}>1$
, along with a dissipation-range dependence given by
$f_{\unicode[STIX]{x1D702}}$
. The
$\unicode[STIX]{x1D705}^{-\unicode[STIX]{x1D6FE}}$
functionality of
$E(\unicode[STIX]{x1D705})$
dominates in the inertial range, and
$f_{\unicode[STIX]{x1D702}}$
dominates for
$\unicode[STIX]{x1D705}\rightarrow \infty$
in the dissipation range, both contributing to the convergence of the integrals.
The
$\unicode[STIX]{x1D6FD}$
values obtained using the above process are shown as a function of Stokes number in figure 1. Also included are the DNS data from Ireland et al. (Reference Ireland, Bragg and Collins2016) with and without gravity (
$Fr=0.052$
and
$Fr=\infty$
, respectively) at
$Re_{\unicode[STIX]{x1D706}}=398$
. We see that the theory-predicted
$\unicode[STIX]{x1D6FD}$
values are lower than the DNS values for both
$Fr=0.052$
and
$Fr=\infty$
. This is probably because the theory is derived for
$Fr\ll 1$
, while the DNS runs are for larger
$Fr$
. Another contributing factor is that DF1 does not capture the two-time auto- and cross-correlations of the strain-rate and rotation-rate invariants, which are key to predicting particle clustering (Chun et al.
Reference Chun, Koch, Rani, Ahluwalia and Collins2005).
In the part 2 paper (Rani, Dhariwal & Koch Reference Rani, Dhariwal and Koch2019), we shall present a direct comparison of the theory predictions of particle clustering with our DNS data for the same Stokes numbers. Results obtained using both DF1 and DF2 will be presented. Turbulence and particle statistics needed as inputs to the theory will be obtained from the DNS runs. The dependence of clustering on both separation and angular direction will be quantified.
Figure 1. Power-law exponent
$\unicode[STIX]{x1D6FD}$
obtained from DF1 based on the universal energy spectrum (referred to as theory 1 in the plot legend). Also shown are the DNS data of Ireland et al. (Reference Ireland, Bragg and Collins2016) for
$Fr=\infty$
and
$Fr=0.052$
at
$Re_{\unicode[STIX]{x1D706}}=398$
.
5 Conclusions
In this part 1 of this two-part study, we presented the derivation of closures for the drift and diffusion fluxes in the p.d.f. equation for the pair relative positions
$\boldsymbol{r}$
. The theory focuses on pair separations smaller than the Kolmogorov length scale, at which separations the theory approximates the fluid velocity field as being locally linear. This allows us to express the fluid velocity difference between the secondary and primary particles of a pair in terms of the fluid velocity gradient at the location of the primary particle and their relative position. Drift flux closures are obtained by expressing the pair relative velocity
$w_{i}$
as a perturbation expansion in the Stokes number
$St_{\unicode[STIX]{x1D702}}$
.
The drift flux contains the time integral of the third and fourth moments of the ‘seen’ fluid velocity gradients along the trajectories of primary particles. These moments are analytically resolved by making approximations regarding the velocity gradient. Accordingly, two closure forms, DF1 and DF2, are derived specifically for the drift flux. DF1 is based on the assumption that the fluid velocity gradient ‘seen’ by the primary particle has a Gaussian distribution. In DF2, instead of modelling the velocity gradient as a whole, we decompose it into the ‘seen’ strain-rate and rotation-rate tensors scaled by the dissipation rate and enstrophy, respectively. The scale strain rate and rotation rate are then assumed to be normally distributed. This decomposition followed by normalization enable DF2 to capture the two-time autocorrelations and cross-correlations of the strain-rate and rotation-rate invariants. Time integrals of these correlations form a key contribution to the radially inward drift flux responsible for particle clustering. An analytical form of the p.d.f.
$\langle P\rangle (r,\unicode[STIX]{x1D703})$
is then obtained with a power-law dependence on separation
$r$
. Analogous to the theoretical result of Chun et al. (Reference Chun, Koch, Rani, Ahluwalia and Collins2005) for non-settling pairs, and that of Fouxon et al. (Reference Fouxon, Park, Harduf and Lee2015) for rapidly settling pairs, the power-law exponent scales as
$St_{\unicode[STIX]{x1D702}}^{2}$
. The anisotropy in clustering due to gravity is also quantified by deriving an analytical expression for the leading-order coefficient of anisotropy in the spherical harmonics expansion of the p.d.f. As observed in the DNS of Ireland et al. (Reference Ireland, Bragg and Collins2016), when
$St_{\unicode[STIX]{x1D702}}<1$
, the p.d.f. obtained from the theory is only weakly anisotropic. Predictions of particle clustering obtained from DF1 in conjunction with the universal Kolmogorov energy spectrum are presented, and compared with the DNS data of Ireland et al. (Reference Ireland, Bragg and Collins2016). A more detailed and rigorous comparison of theory and DNS results is presented in the part 2 paper.
Acknowledgements
S.L.R. and V.K.G. gratefully acknowledge NSF support through the grant CBET-1436100.
Appendix A. Drift flux closure 1 (DF1)
A.1 First term on the right-hand side of (2.13)
We resolve this term by writing
$\unicode[STIX]{x1D6E4}_{lm}=S_{lm}+R_{lm}$
, where
$S_{lm}$
and
$R_{lm}$
are the fluid strain-rate and rotation-rate tensors. Thus, we have
$$\begin{eqnarray}\displaystyle \langle \unicode[STIX]{x1D6E4}_{ij}(t)\unicode[STIX]{x1D6E4}_{jk}(t)\rangle \langle \unicode[STIX]{x1D6E4}_{lm}(t^{\prime })\unicode[STIX]{x1D6E4}_{ml}(t^{\prime })\rangle =\langle \unicode[STIX]{x1D6E4}_{ij}(t)\unicode[STIX]{x1D6E4}_{jk}(t)\rangle \langle S^{2}(t^{\prime })-R^{2}(t^{\prime })\rangle =0, & & \displaystyle\end{eqnarray}$$
where
$S^{2}=S_{lm}S_{lm}$
and
$R^{2}=R_{lm}R_{lm}$
. The steps for showing that
$\langle \unicode[STIX]{x1D6E4}_{ij}(t)\unicode[STIX]{x1D6E4}_{jk}(t)\rangle =0$
are presented below (
$\langle S^{2}(t^{\prime })-R^{2}(t^{\prime })\rangle \neq 0$
since the strain rate and rotation rate are along inertial particle trajectories).
Consider
$$\begin{eqnarray}\displaystyle \langle \unicode[STIX]{x1D6E4}_{ij}(t)\unicode[STIX]{x1D6E4}_{jk}(t)\rangle =\left\langle \frac{\unicode[STIX]{x2202}u_{i}}{\unicode[STIX]{x2202}x_{j}}(\boldsymbol{x},t)\frac{\unicode[STIX]{x2202}u_{j}}{\unicode[STIX]{x2202}x_{k}}(\boldsymbol{x},t)\right\rangle . & & \displaystyle\end{eqnarray}$$
Expressing the fluid velocities
$u_{i}$
and
$u_{j}$
in terms of Fourier coefficients in the wavenumber space yields
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}u_{i}}{\unicode[STIX]{x2202}x_{j}}(\boldsymbol{x},t)=\int \text{i}\unicode[STIX]{x1D705}_{j}\hat{u} _{i}(\unicode[STIX]{x1D73F},t)\text{e}^{\text{i}\unicode[STIX]{x1D73F}\boldsymbol{\cdot }\boldsymbol{x}}\,\text{d}\unicode[STIX]{x1D73F}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}u_{j}}{\unicode[STIX]{x2202}x_{k}}(\boldsymbol{x},t)=\int \text{i}\unicode[STIX]{x1D705}_{k}^{\prime }\hat{u} _{j}(\unicode[STIX]{x1D73F}^{\prime },t)\text{e}^{\text{i}\unicode[STIX]{x1D73F}^{\prime }\boldsymbol{\cdot }\boldsymbol{x}}\,\text{d}\unicode[STIX]{x1D73F}^{\prime }, & \displaystyle\end{eqnarray}$$
where
$\text{i}=\sqrt{-1}$
,
$\unicode[STIX]{x1D73F}$
and
$\unicode[STIX]{x1D73F}^{\prime }$
are both wavenumber vectors, and
$\hat{u} _{i}(\unicode[STIX]{x1D73F},t)$
is a Fourier component of the fluid velocity corresponding to the wavenumber
$\unicode[STIX]{x1D73F}$
.
Since the covariance
$\langle \unicode[STIX]{x1D6E4}_{ij}(t)\unicode[STIX]{x1D6E4}_{jk}(t)\rangle$
consists of velocity gradients at the same time
$t$
, it is homogeneous and isotropic. Therefore, using spatial homogeneity, we can further average the covariance over
$\boldsymbol{x}$
-space giving (Pope Reference Pope2000)
$$\begin{eqnarray}\displaystyle \left\langle \left\langle \frac{\unicode[STIX]{x2202}u_{i}}{\unicode[STIX]{x2202}x_{j}}(\boldsymbol{x},t)\frac{\unicode[STIX]{x2202}u_{j}}{\unicode[STIX]{x2202}x_{k}}(\boldsymbol{x},t)\right\rangle _{\!{\mathcal{L}}}\right\rangle & = & \displaystyle -\iint \text{d}\unicode[STIX]{x1D73F}\,\text{d}\unicode[STIX]{x1D73F}^{\prime }\,\unicode[STIX]{x1D705}_{j}\unicode[STIX]{x1D705}_{k}^{\prime }\langle \hat{u} _{i}(\unicode[STIX]{x1D73F},t)\hat{u} _{j}(\unicode[STIX]{x1D73F}^{\prime },t)\rangle \langle \text{e}^{\text{i}(\unicode[STIX]{x1D73F}+\unicode[STIX]{x1D73F}^{\prime })\boldsymbol{\cdot }\boldsymbol{x}}\rangle _{{\mathcal{L}}}\nonumber\\ \displaystyle & = & \displaystyle -\iint \text{d}\unicode[STIX]{x1D73F}\,\text{d}\unicode[STIX]{x1D73F}^{\prime }\unicode[STIX]{x1D705}_{j}\unicode[STIX]{x1D705}_{k}^{\prime }\langle \hat{u} _{i}(\unicode[STIX]{x1D73F},t)\hat{u} _{j}(\unicode[STIX]{x1D73F}^{\prime },t)\rangle \unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D73F}+\unicode[STIX]{x1D73F}^{\prime })\nonumber\\ \displaystyle & = & \displaystyle \int \text{d}\unicode[STIX]{x1D73F}\,\unicode[STIX]{x1D705}_{j}\unicode[STIX]{x1D705}_{k}\langle \hat{u} _{i}(\unicode[STIX]{x1D73F},t)\hat{u} _{j}^{\ast }(\unicode[STIX]{x1D73F},t)\rangle \nonumber\\ \displaystyle & = & \displaystyle \int \text{d}\unicode[STIX]{x1D73F}\,\unicode[STIX]{x1D705}_{j}\unicode[STIX]{x1D705}_{k}\unicode[STIX]{x1D6F7}_{ij}(\unicode[STIX]{x1D73F}),\end{eqnarray}$$
where
$\langle \cdots \rangle _{{\mathcal{L}}}$
denotes the averaging over
$\boldsymbol{x}$
,
$\unicode[STIX]{x1D6FF}(\cdots )$
denotes the Dirac delta function, and
$\hat{u} _{j}^{\ast }$
is the complex conjugate of
$\hat{u} _{j}$
. The velocity spectrum tensor
$\unicode[STIX]{x1D6F7}_{ij}(\unicode[STIX]{x1D73F})$
can be written in terms of the energy spectrum
$E(\unicode[STIX]{x1D705})$
as (Pope Reference Pope2000)
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}_{ij}(\unicode[STIX]{x1D73F})=\frac{E(\unicode[STIX]{x1D705})}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D705}^{2}}\left(\unicode[STIX]{x1D6FF}_{ij}-\frac{\unicode[STIX]{x1D705}_{i}\unicode[STIX]{x1D705}_{j}}{\unicode[STIX]{x1D705}^{2}}\right). & & \displaystyle\end{eqnarray}$$
It is now straightforward to show that
$\unicode[STIX]{x1D705}_{j}\unicode[STIX]{x1D705}_{k}\unicode[STIX]{x1D6F7}_{ij}(\unicode[STIX]{x1D73F})=0$
. Thus, the first term on the right-hand side of (2.13) = 0, and thereby makes no contribution to the first drift closure DF1.
A.2 Second term on the right-hand side of (2.13)
Let us now consider the second term on the right-hand side of (2.13):
We will consider the correlations 
and 
separately. In the rapid settling limit, particles fall through Kolmogorov-scale eddies in the time
$\unicode[STIX]{x1D702}/(g\unicode[STIX]{x1D70F}_{v})\ll \unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}$
. Thus, during the settling times through the smaller eddies, particles experience frozen turbulence, enabling us to express the two-time correlation of fluid velocity gradients as a two-point correlation with a spatial separation of
$\boldsymbol{x}_{g}=\boldsymbol{g}\unicode[STIX]{x1D70F}_{v}(t^{\prime }-t)$
. Therefore,
We now use the process presented in § A.1 to resolve 
. This involves: (1) expressing the fluid velocities
$u_{i}$
and
$u_{l}$
in terms of Fourier coefficients in the wavenumber space, and (2) using the spatial homogeneity of the one-time, two-point correlations. These steps give us
Similarly,
The time integral of the product of 
and 
is
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{-\infty }^{0}\text{d}t\,\langle \unicode[STIX]{x1D6E4}_{ij}[\boldsymbol{x}(0),0]\unicode[STIX]{x1D6E4}_{lm}[\boldsymbol{x}(0)+\boldsymbol{x}_{g},0]\rangle \langle \unicode[STIX]{x1D6E4}_{jk}[\boldsymbol{x}(0),0]\unicode[STIX]{x1D6E4}_{ml}[\boldsymbol{x}(0)+\boldsymbol{x}_{g},0]\rangle \nonumber\\ \displaystyle & & \displaystyle \quad =\iint \text{d}\unicode[STIX]{x1D73F}\,\text{d}\unicode[STIX]{x1D73F}^{\prime }\,\unicode[STIX]{x1D705}_{j}\unicode[STIX]{x1D705}_{m}\unicode[STIX]{x1D6F7}_{il}(\unicode[STIX]{x1D73F})\unicode[STIX]{x1D705}_{k}^{\prime }\unicode[STIX]{x1D705}_{l}^{\prime }\unicode[STIX]{x1D6F7}_{jm}(\unicode[STIX]{x1D73F}^{\prime })\int _{-\infty }^{0}\,\text{d}t\,\text{e}^{-\text{i}(\unicode[STIX]{x1D73F}+\unicode[STIX]{x1D73F}^{\prime })\boldsymbol{\cdot }\boldsymbol{g}\unicode[STIX]{x1D70F}_{v}t}\nonumber\\ \displaystyle & & \displaystyle \quad =\iint \text{d}\unicode[STIX]{x1D73F}\,\text{d}\unicode[STIX]{x1D73F}^{\prime }\,\unicode[STIX]{x1D705}_{j}\unicode[STIX]{x1D705}_{m}\unicode[STIX]{x1D6F7}_{il}(\unicode[STIX]{x1D73F})\unicode[STIX]{x1D705}_{k}^{\prime }\unicode[STIX]{x1D705}_{l}^{\prime }\unicode[STIX]{x1D6F7}_{jm}(\unicode[STIX]{x1D73F}^{\prime })\left\{\frac{1}{2}\unicode[STIX]{x1D6FF}\left[-\frac{(\unicode[STIX]{x1D73F}+\unicode[STIX]{x1D73F}^{\prime })\boldsymbol{\cdot }\boldsymbol{g}\unicode[STIX]{x1D70F}_{v}}{2\unicode[STIX]{x03C0}}\right]-\frac{1}{\text{i}(\unicode[STIX]{x1D73F}+\unicode[STIX]{x1D73F}^{\prime })\boldsymbol{\cdot }\boldsymbol{g}\unicode[STIX]{x1D70F}_{v}}\right\}.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
where we have used the Fourier transform identity for the time integral
$\int _{-\infty }^{0}\text{d}t\,\text{e}^{-\text{i}(\unicode[STIX]{x1D73F}+\unicode[STIX]{x1D73F}^{\prime })\boldsymbol{\cdot }\boldsymbol{g}\unicode[STIX]{x1D70F}_{v}t}$
. Let us consider the two terms in the above integral separately. The first term given by the integral
$$\begin{eqnarray}\displaystyle \frac{1}{2}\iint \text{d}\unicode[STIX]{x1D73F}\,\text{d}\unicode[STIX]{x1D73F}^{\prime }\,\unicode[STIX]{x1D705}_{j}\unicode[STIX]{x1D705}_{m}\unicode[STIX]{x1D6F7}_{il}(\unicode[STIX]{x1D73F})\unicode[STIX]{x1D705}_{k}^{\prime }\unicode[STIX]{x1D705}_{l}^{\prime }\unicode[STIX]{x1D6F7}_{jm}(\unicode[STIX]{x1D73F}^{\prime })\unicode[STIX]{x1D6FF}\left[-\frac{(\unicode[STIX]{x1D73F}+\unicode[STIX]{x1D73F}^{\prime })\boldsymbol{\cdot }\boldsymbol{g}\unicode[STIX]{x1D70F}_{v}}{2\unicode[STIX]{x03C0}}\right] & & \displaystyle\end{eqnarray}$$
is non-zero only when
$(\unicode[STIX]{x1D73F}+\unicode[STIX]{x1D73F}^{\prime })\boldsymbol{\cdot }\boldsymbol{g}=0$
, or
$(\unicode[STIX]{x1D73F}+\unicode[STIX]{x1D73F}^{\prime })$
is perpendicular to
$\boldsymbol{g}=-g\hat{\boldsymbol{e}}_{3}$
. Let
$(\unicode[STIX]{x1D73F}+\unicode[STIX]{x1D73F}^{\prime })=\unicode[STIX]{x1D743}=(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2},0)$
such that this property is satisfied. Using the sifting property of the Dirac delta function, as well as the identity
$\unicode[STIX]{x1D6FF}(ax)=(1/|a|)\unicode[STIX]{x1D6FF}(x)$
, the integral in (A 12) now becomes
$$\begin{eqnarray}\displaystyle \frac{1}{2}\frac{2\unicode[STIX]{x03C0}}{g\unicode[STIX]{x1D70F}_{v}}\iint \text{d}\unicode[STIX]{x1D73F}\,\text{d}\unicode[STIX]{x1D709}_{1}\,\text{d}\unicode[STIX]{x1D709}_{2}\,\unicode[STIX]{x1D705}_{j}\unicode[STIX]{x1D705}_{m}\unicode[STIX]{x1D6F7}_{il}(\unicode[STIX]{x1D73F})(\unicode[STIX]{x1D709}_{k}-\unicode[STIX]{x1D705}_{k})(\unicode[STIX]{x1D709}_{l}-\unicode[STIX]{x1D705}_{l})\unicode[STIX]{x1D6F7}_{jm}(\unicode[STIX]{x1D743}-\unicode[STIX]{x1D73F}). & & \displaystyle\end{eqnarray}$$
Next, we consider the second term in the integral in the last line of (A 11). Unlike the first term, it will be seen subsequently that this term does not make any contribution to the drift.
Recognizing that the particles preferentially sample the velocity gradients along the
$-\boldsymbol{e}_{3}$
or gravity direction, we apply the tensorial constraints for a field that is homogeneous along the
$x_{1}$
and
$x_{2}$
directions. Expressing the integral in (A 13) in terms of these tensor constraints, we have
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x03C0}}{g\unicode[STIX]{x1D70F}_{v}}\iint \text{d}\unicode[STIX]{x1D73F}\,\text{d}\unicode[STIX]{x1D709}_{1}\,\text{d}\unicode[STIX]{x1D709}_{2}\,\unicode[STIX]{x1D705}_{j}\unicode[STIX]{x1D705}_{m}\unicode[STIX]{x1D6F7}_{il}(\unicode[STIX]{x1D73F})(\unicode[STIX]{x1D709}_{k}-\unicode[STIX]{x1D705}_{k})(\unicode[STIX]{x1D709}_{l}-\unicode[STIX]{x1D705}_{l})\unicode[STIX]{x1D6F7}_{jm}(\unicode[STIX]{x1D743}-\unicode[STIX]{x1D73F})\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D706}_{1}(\unicode[STIX]{x1D6FF}_{ik}-\unicode[STIX]{x1D6FF}_{i3}\unicode[STIX]{x1D6FF}_{k3})+\unicode[STIX]{x1D706}_{2}\unicode[STIX]{x1D6FF}_{i3}\unicode[STIX]{x1D6FF}_{k3}.\end{eqnarray}$$
Multiplying the above equation with
$(\unicode[STIX]{x1D6FF}_{ik}-\unicode[STIX]{x1D6FF}_{i3}\unicode[STIX]{x1D6FF}_{k3})$
gives
$\unicode[STIX]{x1D706}_{1}$
and with
$\unicode[STIX]{x1D6FF}_{i3}\unicode[STIX]{x1D6FF}_{k3}$
gives
$\unicode[STIX]{x1D706}_{2}$
:
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D706}_{1}=\frac{\unicode[STIX]{x03C0}}{2g\unicode[STIX]{x1D70F}_{v}}\iint \text{d}\unicode[STIX]{x1D73F}\,\text{d}\unicode[STIX]{x1D709}_{1}\,\text{d}\unicode[STIX]{x1D709}_{2}\,\unicode[STIX]{x1D705}_{j}\unicode[STIX]{x1D705}_{m}\unicode[STIX]{x1D6F7}_{jm}(\unicode[STIX]{x1D743}-\unicode[STIX]{x1D73F})(\unicode[STIX]{x1D709}_{l}-\unicode[STIX]{x1D705}_{l})[\unicode[STIX]{x1D6F7}_{il}(\unicode[STIX]{x1D73F})(\unicode[STIX]{x1D709}_{i}-\unicode[STIX]{x1D705}_{i})+\unicode[STIX]{x1D6F7}_{3l}(\unicode[STIX]{x1D73F})\unicode[STIX]{x1D705}_{3}],\qquad & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D706}_{2}=-\frac{\unicode[STIX]{x03C0}}{g\unicode[STIX]{x1D70F}_{v}}\iint \text{d}\unicode[STIX]{x1D73F}\,\text{d}\unicode[STIX]{x1D709}_{1}\,\text{d}\unicode[STIX]{x1D709}_{2}\,\unicode[STIX]{x1D705}_{j}\unicode[STIX]{x1D705}_{m}\unicode[STIX]{x1D6F7}_{3l}(\unicode[STIX]{x1D73F})\unicode[STIX]{x1D705}_{3}(\unicode[STIX]{x1D709}_{l}-\unicode[STIX]{x1D705}_{l})\unicode[STIX]{x1D6F7}_{jm}(\unicode[STIX]{x1D743}-\unicode[STIX]{x1D73F}). & \displaystyle\end{eqnarray}$$
Using spherical coordinates to represent the
$\unicode[STIX]{x1D73F}$
vector and cylindrical coordinates to represent
$\unicode[STIX]{x1D743}$
, we have
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\unicode[STIX]{x1D73F}=(\unicode[STIX]{x1D705}_{1},\unicode[STIX]{x1D705}_{2},\unicode[STIX]{x1D705}_{3})=(\unicode[STIX]{x1D705}\sin \unicode[STIX]{x1D703}\cos \unicode[STIX]{x1D719},\unicode[STIX]{x1D705}\sin \unicode[STIX]{x1D703}\sin \unicode[STIX]{x1D719},\unicode[STIX]{x1D705}\cos \unicode[STIX]{x1D703}),\\ \unicode[STIX]{x1D743}=(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2},0)=(\unicode[STIX]{x1D709}\cos \unicode[STIX]{x1D713},\unicode[STIX]{x1D709}\sin \unicode[STIX]{x1D713},0).\end{array}\right\} & & \displaystyle\end{eqnarray}$$
Using (A 17) in the equations for
$\unicode[STIX]{x1D706}_{1}$
and
$\unicode[STIX]{x1D706}_{2}$
, i.e. (A 15) and (A 16),
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D706}_{1}=\frac{\unicode[STIX]{x03C0}}{2g\unicode[STIX]{x1D70F}_{v}}\int _{\unicode[STIX]{x1D719}=0}^{2\unicode[STIX]{x03C0}}\text{d}\unicode[STIX]{x1D719}\int _{\unicode[STIX]{x1D703}=0}^{\unicode[STIX]{x03C0}}\text{d}\unicode[STIX]{x1D703}\int _{\unicode[STIX]{x1D705}=0}^{\infty }\text{d}\unicode[STIX]{x1D705}\int _{\unicode[STIX]{x1D713}=0}^{2\unicode[STIX]{x03C0}}\text{d}\unicode[STIX]{x1D713}\int _{\unicode[STIX]{x1D709}=0}^{\infty }\text{d}\unicode[STIX]{x1D709}\times [\text{integrand}~\unicode[STIX]{x2460}], & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D706}_{2}=\frac{\unicode[STIX]{x03C0}}{g\unicode[STIX]{x1D70F}_{v}}\int _{\unicode[STIX]{x1D719}=0}^{2\unicode[STIX]{x03C0}}\text{d}\unicode[STIX]{x1D719}\int _{\unicode[STIX]{x1D703}=0}^{\unicode[STIX]{x03C0}}\text{d}\unicode[STIX]{x1D703}\int _{\unicode[STIX]{x1D705}=0}^{\infty }\text{d}\unicode[STIX]{x1D705}\int _{\unicode[STIX]{x1D713}=0}^{2\unicode[STIX]{x03C0}}\text{d}\unicode[STIX]{x1D713}\int _{\unicode[STIX]{x1D709}=0}^{\infty }\text{d}\unicode[STIX]{x1D709}\times [\text{integrand}~\unicode[STIX]{x2461}], & \displaystyle\end{eqnarray}$$
where
$$\begin{eqnarray}\displaystyle \text{integrand}~\unicode[STIX]{x2460} & = & \displaystyle \frac{E(|\unicode[STIX]{x1D743}-\unicode[STIX]{x1D73F}|)}{4\unicode[STIX]{x03C0}[\unicode[STIX]{x1D709}^{2}+\unicode[STIX]{x1D705}^{2}-2\unicode[STIX]{x1D709}\unicode[STIX]{x1D705}\sin \unicode[STIX]{x1D703}\cos (\unicode[STIX]{x1D713}-\unicode[STIX]{x1D719})]}\frac{\unicode[STIX]{x1D709}^{3}\unicode[STIX]{x1D705}^{4}[1-\sin ^{2}\unicode[STIX]{x1D703}\cos ^{2}(\unicode[STIX]{x1D713}-\unicode[STIX]{x1D719})]\sin \unicode[STIX]{x1D703}}{\unicode[STIX]{x1D709}^{2}+\unicode[STIX]{x1D705}^{2}-2\unicode[STIX]{x1D709}\unicode[STIX]{x1D705}\sin \unicode[STIX]{x1D703}\cos (\unicode[STIX]{x1D713}-\unicode[STIX]{x1D719})}\nonumber\\ \displaystyle & & \displaystyle \times \,\frac{E(\unicode[STIX]{x1D705})}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D705}^{2}}\left\{\unicode[STIX]{x1D709}^{2}[1-\sin ^{2}\unicode[STIX]{x1D703}\cos ^{2}(\unicode[STIX]{x1D713}-\unicode[STIX]{x1D719})]-\frac{\unicode[STIX]{x1D709}\unicode[STIX]{x1D705}\cos \unicode[STIX]{x1D703}}{2}\sin 2\unicode[STIX]{x1D703}\cos (\unicode[STIX]{x1D713}-\unicode[STIX]{x1D719})\right\},\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{integrand}~\unicode[STIX]{x2461} & = & \displaystyle \frac{E(|\unicode[STIX]{x1D743}-\unicode[STIX]{x1D73F}|)}{4\unicode[STIX]{x03C0}[\unicode[STIX]{x1D709}^{2}+\unicode[STIX]{x1D705}^{2}-2\unicode[STIX]{x1D709}\unicode[STIX]{x1D705}\sin \unicode[STIX]{x1D703}\cos (\unicode[STIX]{x1D713}-\unicode[STIX]{x1D719})]}\frac{\unicode[STIX]{x1D709}^{3}\unicode[STIX]{x1D705}^{4}[1-\sin ^{2}\unicode[STIX]{x1D703}\cos ^{2}(\unicode[STIX]{x1D713}-\unicode[STIX]{x1D719})]\sin \unicode[STIX]{x1D703}}{\unicode[STIX]{x1D709}^{2}+\unicode[STIX]{x1D705}^{2}-2\unicode[STIX]{x1D709}\unicode[STIX]{x1D705}\sin \unicode[STIX]{x1D703}\cos (\unicode[STIX]{x1D713}-\unicode[STIX]{x1D719})}\nonumber\\ \displaystyle & & \displaystyle \times \,\frac{E(\unicode[STIX]{x1D705})}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D705}^{2}}\frac{\unicode[STIX]{x1D709}\unicode[STIX]{x1D705}\cos \unicode[STIX]{x1D703}}{2}\sin 2\unicode[STIX]{x1D703}\cos (\unicode[STIX]{x1D713}-\unicode[STIX]{x1D719}).\end{eqnarray}$$
Let us now consider the second term in the integral of (A 11) (it has already been mentioned earlier that this term goes to zero), given by
$$\begin{eqnarray}\displaystyle & & \displaystyle -\iint \text{d}\unicode[STIX]{x1D73F}\,\text{d}\unicode[STIX]{x1D73F}^{\prime }\,\unicode[STIX]{x1D705}_{j}\unicode[STIX]{x1D705}_{m}\unicode[STIX]{x1D6F7}_{il}(\unicode[STIX]{x1D73F})\unicode[STIX]{x1D705}_{k}^{\prime }\unicode[STIX]{x1D705}_{l}^{\prime }\unicode[STIX]{x1D6F7}_{jm}(\unicode[STIX]{x1D73F}^{\prime })\frac{1}{\text{i}(\unicode[STIX]{x1D73F}+\unicode[STIX]{x1D73F}^{\prime })\boldsymbol{\cdot }\boldsymbol{g}\unicode[STIX]{x1D70F}_{v}}\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D706}_{3}(\unicode[STIX]{x1D6FF}_{ik}-\unicode[STIX]{x1D6FF}_{i3}\unicode[STIX]{x1D6FF}_{k3})+\unicode[STIX]{x1D706}_{4}\unicode[STIX]{x1D6FF}_{i3}\unicode[STIX]{x1D6FF}_{k3}=\unicode[STIX]{x1D706}_{3}\left(\unicode[STIX]{x1D6FF}_{ik}-\frac{g_{i}g_{k}}{g^{2}}\right)+\unicode[STIX]{x1D706}_{4}\frac{g_{i}g_{k}}{g^{2}},\end{eqnarray}$$
where
$g_{i}$
is the gravity vector that is non-zero only when
$i=3$
. The integral on the left-hand side of (A 22) is odd in
$\boldsymbol{g}$
, but the right-hand side is even in
$\boldsymbol{g}$
. Hence the integral will be zero.
Appendix B. Drift flux closure 2 (DF2)
In this appendix, we evaluate the two integrals on the right-hand side of (2.26) that contain the two-time correlations of
$\unicode[STIX]{x1D748}$
and
$\unicode[STIX]{x1D746}$
, i.e.
$\langle \unicode[STIX]{x1D70E}_{ij}(t)\unicode[STIX]{x1D70E}_{lm}(t^{\prime })\rangle$
,
$\langle \unicode[STIX]{x1D70E}_{jk}(t)\unicode[STIX]{x1D70E}_{lm}(t^{\prime })\rangle$
,
$\langle \unicode[STIX]{x1D70C}_{ij}(t)\unicode[STIX]{x1D70C}_{lm}(t^{\prime })\rangle$
and
$\langle \unicode[STIX]{x1D70C}_{jk}(t)\unicode[STIX]{x1D70C}_{lm}(t^{\prime })\rangle$
. Analogous to the process leading to (A 9), we will transform the two-time correlations of
$\unicode[STIX]{x1D748}$
and
$\unicode[STIX]{x1D746}$
into two-point correlations with a spatial separation of
$\boldsymbol{x}_{g}=\boldsymbol{g}\unicode[STIX]{x1D70F}_{v}(t^{\prime }-t)$
, and express the two-point correlations as Fourier integrals. Subsequently, we apply the tensorial constraints arising from the particles sampling the flow field preferentially along the
$x_{3}$
direction, but homogeneously in the
$x_{1}{-}x_{2}$
plane. Accordingly,
$\langle \unicode[STIX]{x1D70E}_{ij}(t)\unicode[STIX]{x1D70E}_{lm}(t^{\prime })\rangle$
can be expressed as
$$\begin{eqnarray}\displaystyle & & \displaystyle \langle \unicode[STIX]{x1D70E}_{ij}(\boldsymbol{x},t)\unicode[STIX]{x1D70E}_{lm}(\boldsymbol{x}^{\prime },t^{\prime })\rangle \nonumber\\ \displaystyle & & \displaystyle \quad =\int \text{d}\unicode[STIX]{x1D73F}\,\langle \hat{\unicode[STIX]{x1D70E}}_{ij}(\unicode[STIX]{x1D73F},t)\hat{\unicode[STIX]{x1D70E}}_{lm}^{\ast }(\unicode[STIX]{x1D73F},t)\rangle \text{e}^{-\text{i}\unicode[STIX]{x1D73F}\boldsymbol{\cdot }\boldsymbol{x}_{g}}=\mathscr{L}_{ijlm}\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FF}_{ij}\unicode[STIX]{x1D6FF}_{lm}+\unicode[STIX]{x1D6FC}_{2}(\unicode[STIX]{x1D6FF}_{im}\unicode[STIX]{x1D6FF}_{jl}+\unicode[STIX]{x1D6FF}_{il}\unicode[STIX]{x1D6FF}_{jm})+\unicode[STIX]{x1D6FC}_{4}\unicode[STIX]{x1D6FF}_{i3}\unicode[STIX]{x1D6FF}_{j3}\unicode[STIX]{x1D6FF}_{l3}\unicode[STIX]{x1D6FF}_{m3}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\unicode[STIX]{x1D6FC}_{5}(\unicode[STIX]{x1D6FF}_{i3}\unicode[STIX]{x1D6FF}_{j3}\unicode[STIX]{x1D6FF}_{lm}+\unicode[STIX]{x1D6FF}_{ij}\unicode[STIX]{x1D6FF}_{l3}\unicode[STIX]{x1D6FF}_{m3})+\unicode[STIX]{x1D6FC}_{6}(\unicode[STIX]{x1D6FF}_{i3}\unicode[STIX]{x1D6FF}_{l3}\unicode[STIX]{x1D6FF}_{jm}+\unicode[STIX]{x1D6FF}_{i3}\unicode[STIX]{x1D6FF}_{m3}\unicode[STIX]{x1D6FF}_{jl}+\unicode[STIX]{x1D6FF}_{j3}\unicode[STIX]{x1D6FF}_{l3}\unicode[STIX]{x1D6FF}_{im}+\unicode[STIX]{x1D6FF}_{j3}\unicode[STIX]{x1D6FF}_{m3}\unicode[STIX]{x1D6FF}_{il}),\qquad\end{eqnarray}$$
where
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\unicode[STIX]{x1D6FC}_{1}=-{\textstyle \frac{1}{8}}(2B_{1}-B_{2}-4B_{3}),\quad \unicode[STIX]{x1D6FC}_{2}={\textstyle \frac{1}{8}}(2B_{1}+B_{2}-4B_{3}),\\ \unicode[STIX]{x1D6FC}_{4}={\textstyle \frac{1}{8}}(2B_{1}+35B_{2}-20B_{3}),\quad \unicode[STIX]{x1D6FC}_{5}={\textstyle \frac{1}{8}}(2B_{1}-5B_{2}-4B_{3}),\\ \unicode[STIX]{x1D6FC}_{6}=-{\textstyle \frac{1}{8}}(2B_{1}+5B_{2}-8B_{3}),\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle B_{1}=\frac{\unicode[STIX]{x1D708}}{2\langle \unicode[STIX]{x1D716}\rangle }\left[\frac{1}{\unicode[STIX]{x03C0}}\int \text{d}\unicode[STIX]{x1D73F}\,E(\unicode[STIX]{x1D705})\text{e}^{-\text{i}\unicode[STIX]{x1D73F}\boldsymbol{\cdot }\boldsymbol{x}_{g}}\right], & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle B_{2}=\frac{\unicode[STIX]{x1D708}}{2\langle \unicode[STIX]{x1D716}\rangle }\left[4\int \text{d}\unicode[STIX]{x1D73F}\,\unicode[STIX]{x1D705}_{3}^{2}\frac{E(\unicode[STIX]{x1D705})}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D705}^{2}}\left(1-\frac{\unicode[STIX]{x1D705}_{3}^{2}}{\unicode[STIX]{x1D705}^{2}}\right)\text{e}^{-\text{i}\unicode[STIX]{x1D73F}\boldsymbol{\cdot }\boldsymbol{x}_{g}}\right], & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle B_{3}=\frac{\unicode[STIX]{x1D708}}{2\langle \unicode[STIX]{x1D716}\rangle }\left[\int \text{d}\unicode[STIX]{x1D73F}\,\unicode[STIX]{x1D705}_{j}\unicode[STIX]{x1D705}_{j}\frac{E(\unicode[STIX]{x1D705})}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D705}^{2}}\left(1+\frac{\unicode[STIX]{x1D705}_{3}^{2}}{\unicode[STIX]{x1D705}^{2}}\right)\text{e}^{-\text{i}\unicode[STIX]{x1D73F}\boldsymbol{\cdot }\boldsymbol{x}_{g}}\right]. & \displaystyle\end{eqnarray}$$
In (B 3)–(B 5),
$E(\unicode[STIX]{x1D705})$
is the energy spectrum of isotropic turbulence, and
$\unicode[STIX]{x1D705}_{3}$
is the component of
$\unicode[STIX]{x1D73F}$
along the
$x_{3}$
direction. Appendix C presents the process for determining the form of the tensorial constraints in (B 1), as well as the coefficients
$\unicode[STIX]{x1D6FC}_{1},~\unicode[STIX]{x1D6FC}_{2}$
and others. Appendix D presents the evaluation of
$\langle \hat{\unicode[STIX]{x1D70E}}_{ij}(\unicode[STIX]{x1D73F},t)\hat{\unicode[STIX]{x1D70E}}_{lm}^{\ast }(\unicode[STIX]{x1D73F},t)\rangle$
.
The term
$\langle \unicode[STIX]{x1D70E}_{jk}(\boldsymbol{x},t)\unicode[STIX]{x1D70E}_{lm}(\boldsymbol{x}^{\prime },t^{\prime })\rangle$
may also be expressed analogously to (B 1). Thus, the product
$\langle \unicode[STIX]{x1D70E}_{ij}(t)\unicode[STIX]{x1D70E}_{lm}(t^{\prime })\rangle \langle \unicode[STIX]{x1D70E}_{jk}(t)\unicode[STIX]{x1D70E}_{lm}(t^{\prime })\rangle$
in (2.26) can now be written as
$$\begin{eqnarray}\displaystyle & & \displaystyle \langle \unicode[STIX]{x1D70E}_{ij}(t)\unicode[STIX]{x1D70E}_{lm}(t^{\prime })\rangle \langle \unicode[STIX]{x1D70E}_{jk}(t)\unicode[STIX]{x1D70E}_{lm}(t^{\prime })\rangle \nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D6FF}_{ik}(3\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{1}+4\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}+2\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{5}+8\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FC}_{2}+4\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FC}_{6}+\unicode[STIX]{x1D6FC}_{5}\unicode[STIX]{x1D6FC}_{5}+2\unicode[STIX]{x1D6FC}_{6}\unicode[STIX]{x1D6FC}_{6})\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\unicode[STIX]{x1D6FF}_{i3}\unicode[STIX]{x1D6FF}_{k3} (\!2\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{4}+6\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{5}+8\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{6}+4\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FC}_{4}+8\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FC}_{5}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,20\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FC}_{6}+\unicode[STIX]{x1D6FC}_{4}\unicode[STIX]{x1D6FC}_{4}+4\unicode[STIX]{x1D6FC}_{4}\unicode[STIX]{x1D6FC}_{5}+8\unicode[STIX]{x1D6FC}_{4}\unicode[STIX]{x1D6FC}_{6}+5\unicode[STIX]{x1D6FC}_{5}\unicode[STIX]{x1D6FC}_{5}+16\unicode[STIX]{x1D6FC}_{5}\unicode[STIX]{x1D6FC}_{6}+18\unicode[STIX]{x1D6FC}_{6}\unicode[STIX]{x1D6FC}_{6}\! )\!.\end{eqnarray}$$
Terms such as
$\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{1}$
,
$\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}$
and others give rise to wavenumber integration of the form
$\int \text{d}\unicode[STIX]{x1D73F}\,\text{d}\unicode[STIX]{x1D73F}^{\prime }\,\text{e}^{-\text{i}(\unicode[STIX]{x1D73F}+\unicode[STIX]{x1D73F}^{\prime })\boldsymbol{\cdot }\boldsymbol{x}_{g}}\times (\cdots \,)$
, which upon substitution into (2.26) leads to time integrals of the following form:
$$\begin{eqnarray}\displaystyle \int _{-\infty }^{t}\exp \left(-\frac{t-t^{\prime }}{T_{\unicode[STIX]{x1D716}\unicode[STIX]{x1D716}}}\right)\text{e}^{-\text{i}(\unicode[STIX]{x1D73F}+\unicode[STIX]{x1D73F}^{\prime })\boldsymbol{\cdot }\boldsymbol{x}_{g}}\,\text{d}t^{\prime } & = & \displaystyle \frac{1}{\left(\displaystyle \frac{1}{T_{\unicode[STIX]{x1D716}\unicode[STIX]{x1D716}}}\right)-\text{i}(\unicode[STIX]{x1D73F}+\unicode[STIX]{x1D73F}^{\prime })\boldsymbol{\cdot }\boldsymbol{g}\unicode[STIX]{x1D70F}_{v}}\nonumber\\ \displaystyle & = & \displaystyle \frac{\left(\displaystyle \frac{1}{T_{\unicode[STIX]{x1D716}\unicode[STIX]{x1D716}}}\right)+\text{i}(\unicode[STIX]{x1D73F}+\unicode[STIX]{x1D73F}^{\prime })\boldsymbol{\cdot }\boldsymbol{g}\unicode[STIX]{x1D70F}_{v}}{\left(\displaystyle \frac{1}{T_{\unicode[STIX]{x1D716}\unicode[STIX]{x1D716}}}\right)^{2}+[(\unicode[STIX]{x1D73F}+\unicode[STIX]{x1D73F}^{\prime })\boldsymbol{\cdot }\boldsymbol{g}\unicode[STIX]{x1D70F}_{v}]^{2}}.\end{eqnarray}$$
It may be noted that in (B 7), the imaginary part on the right-hand side is odd in
$\boldsymbol{g}$
, whereas the drift flux is tensorially constrained to be even in
$\boldsymbol{g}$
. Thus, the imaginary part does not contribute to the overall drift flux. Further details of the evaluation of the right-hand side of (B 6) are presented in appendix E.
Next we evaluate the term
$\langle \unicode[STIX]{x1D70C}_{ij}(t)\unicode[STIX]{x1D70C}_{lm}(t^{\prime })\rangle \langle \unicode[STIX]{x1D70C}_{jk}(t)\unicode[STIX]{x1D70C}_{lm}(t^{\prime })\rangle$
in (2.26). This again involves applying the appropriate tensorial constraints on each of the two correlations as follows:
$$\begin{eqnarray}\displaystyle & & \displaystyle \langle \unicode[STIX]{x1D70C}_{ij}(\boldsymbol{x},t)\unicode[STIX]{x1D70C}_{lm}(\boldsymbol{x}^{\prime },t^{\prime })\rangle =\int \text{d}\unicode[STIX]{x1D73F}\langle \hat{\unicode[STIX]{x1D70C}}_{ij}(\unicode[STIX]{x1D73F},t)\hat{\unicode[STIX]{x1D70C}}_{lm}^{\ast }(\unicode[STIX]{x1D73F},t)\rangle \text{e}^{-\text{i}\unicode[STIX]{x1D73F}\boldsymbol{\cdot }\boldsymbol{x}_{g}}=\mathscr{M}_{ijlm}\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D6FD}_{2}(\unicode[STIX]{x1D6FF}_{im}\unicode[STIX]{x1D6FF}_{jl}-\unicode[STIX]{x1D6FF}_{il}\unicode[STIX]{x1D6FF}_{jm})+\unicode[STIX]{x1D6FD}_{6}(\unicode[STIX]{x1D6FF}_{i3}\unicode[STIX]{x1D6FF}_{l3}\unicode[STIX]{x1D6FF}_{jm}-\unicode[STIX]{x1D6FF}_{i3}\unicode[STIX]{x1D6FF}_{m3}\unicode[STIX]{x1D6FF}_{jl}-\unicode[STIX]{x1D6FF}_{j3}\unicode[STIX]{x1D6FF}_{l3}\unicode[STIX]{x1D6FF}_{im}+\unicode[STIX]{x1D6FF}_{j3}\unicode[STIX]{x1D6FF}_{m3}\unicode[STIX]{x1D6FF}_{il}).\qquad\end{eqnarray}$$
The criteria for determining
$\unicode[STIX]{x1D6FD}$
values – provided in appendix C – yield
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FD}_{2}={\textstyle \frac{1}{2}}(2C_{2}-C_{1}),\quad \unicode[STIX]{x1D6FD}_{6}={\textstyle \frac{1}{2}}(3C_{2}-C_{1}), & & \displaystyle\end{eqnarray}$$
where
$$\begin{eqnarray}\displaystyle & \displaystyle C_{1}=\frac{\unicode[STIX]{x1D708}}{2\langle \unicode[STIX]{x1D701}\rangle }\left[\frac{1}{\unicode[STIX]{x03C0}}\int \text{d}\unicode[STIX]{x1D73F}\,E(\unicode[STIX]{x1D705})\text{e}^{-\text{i}\unicode[STIX]{x1D73F}\boldsymbol{\cdot }\boldsymbol{x}_{g}}\right], & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle C_{2}=\frac{\unicode[STIX]{x1D708}}{2\langle \unicode[STIX]{x1D701}\rangle }\left[\int \text{d}\unicode[STIX]{x1D73F}\,\unicode[STIX]{x1D705}_{j}\unicode[STIX]{x1D705}_{j}\frac{E(\unicode[STIX]{x1D705})}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D705}^{2}}\left(1+\frac{\unicode[STIX]{x1D705}_{3}^{2}}{\unicode[STIX]{x1D705}^{2}}\right)\text{e}^{-\text{i}\unicode[STIX]{x1D73F}\boldsymbol{\cdot }\boldsymbol{x}_{g}}\right]. & \displaystyle\end{eqnarray}$$
Thus, the product
$\langle \unicode[STIX]{x1D70C}_{ij}(t)\unicode[STIX]{x1D70C}_{lm}(t^{\prime })\rangle \langle \unicode[STIX]{x1D70C}_{jk}(t)\unicode[STIX]{x1D70C}_{lm}(t^{\prime })\rangle$
in (2.26) can now be written as
$$\begin{eqnarray}\displaystyle \langle \unicode[STIX]{x1D70C}_{ij}(t)\unicode[STIX]{x1D70C}_{lm}(t^{\prime })\rangle \langle \unicode[STIX]{x1D70C}_{jk}(t)\unicode[STIX]{x1D70C}_{lm}(t^{\prime })\rangle =\unicode[STIX]{x1D6FF}_{ik}(-4\unicode[STIX]{x1D6FD}_{2}\unicode[STIX]{x1D6FD}_{2}+4\unicode[STIX]{x1D6FD}_{2}\unicode[STIX]{x1D6FD}_{6}-2\unicode[STIX]{x1D6FD}_{6}\unicode[STIX]{x1D6FD}_{6})+\unicode[STIX]{x1D6FF}_{i3}\unicode[STIX]{x1D6FF}_{k3}(4\unicode[STIX]{x1D6FD}_{2}\unicode[STIX]{x1D6FD}_{6}-2\unicode[STIX]{x1D6FD}_{6}\unicode[STIX]{x1D6FD}_{6}). & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
Terms on the right-hand side of (B 12) such as
$\unicode[STIX]{x1D6FD}_{2}\unicode[STIX]{x1D6FD}_{2}$
,
$\unicode[STIX]{x1D6FD}_{2}\unicode[STIX]{x1D6FD}_{6}$
and
$\unicode[STIX]{x1D6FD}_{6}\unicode[STIX]{x1D6FD}_{6}$
contain wavenumber integration of the form
$\int \text{d}\unicode[STIX]{x1D73F}\,\text{d}\unicode[STIX]{x1D73F}^{\prime }\,\text{e}^{-\text{i}(\unicode[STIX]{x1D73F}+\unicode[STIX]{x1D73F}^{\prime })\boldsymbol{\cdot }\boldsymbol{x}_{g}}\times (\cdots \,)$
, which upon substitution into (2.26) leads to a time integration similar to that in (B 7), with the
$T_{\unicode[STIX]{x1D716}\unicode[STIX]{x1D716}}$
replaced by
$T_{\unicode[STIX]{x1D701}\unicode[STIX]{x1D701}}$
.
Recalling the integral
$\int _{-\infty }^{t}\text{d}_{ik}\,\text{d}t^{\prime }$
in (2.26), we can evaluate terms such as
$$\begin{eqnarray}\displaystyle \int _{-\infty }^{t}\,\text{d}t^{\prime }\,\langle \unicode[STIX]{x1D716}(t)\unicode[STIX]{x1D716}(t^{\prime })\rangle \langle \unicode[STIX]{x1D70E}_{ij}(t)\unicode[STIX]{x1D70E}_{lm}(t^{\prime })\rangle \langle \unicode[STIX]{x1D70E}_{jk}(t)\unicode[STIX]{x1D70E}_{lm}(t^{\prime })\rangle & & \displaystyle\end{eqnarray}$$
by applying the time integral in (B 7) along with (B 1)–(B 6).
Appendix C. Tensorial constraints
C.1 The tensor
$\langle \unicode[STIX]{x1D70E}_{ij}(t)\unicode[STIX]{x1D70E}_{lm}(t^{\prime })\rangle =\mathscr{L}_{ijlm}$
Gravitational acceleration induces anisotropy along the
$x_{3}$
direction, but homogeneity is satisfied along the
$x_{1}$
and
$x_{2}$
directions. Accordingly, the fourth-order tensor
$A_{ijlm}$
in (B 1) may be represented as
$$\begin{eqnarray}\displaystyle \mathscr{L}_{ijlm} & = & \displaystyle \unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FF}_{ij}\unicode[STIX]{x1D6FF}_{lm}+\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FF}_{im}\unicode[STIX]{x1D6FF}_{jl}+\unicode[STIX]{x1D6FC}_{3}\unicode[STIX]{x1D6FF}_{il}\unicode[STIX]{x1D6FF}_{jm}+\unicode[STIX]{x1D6FC}_{4}\unicode[STIX]{x1D6FF}_{i3}\unicode[STIX]{x1D6FF}_{j3}\unicode[STIX]{x1D6FF}_{l3}\unicode[STIX]{x1D6FF}_{m3}+\unicode[STIX]{x1D6FC}_{5}\unicode[STIX]{x1D6FF}_{i3}\unicode[STIX]{x1D6FF}_{j3}\unicode[STIX]{x1D6FF}_{lm}\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D6FC}_{6}\unicode[STIX]{x1D6FF}_{i3}\unicode[STIX]{x1D6FF}_{l3}\unicode[STIX]{x1D6FF}_{jm}+\unicode[STIX]{x1D6FC}_{7}\unicode[STIX]{x1D6FF}_{i3}\unicode[STIX]{x1D6FF}_{m3}\unicode[STIX]{x1D6FF}_{jl}+\unicode[STIX]{x1D6FC}_{8}\unicode[STIX]{x1D6FF}_{j3}\unicode[STIX]{x1D6FF}_{l3}\unicode[STIX]{x1D6FF}_{im}+\unicode[STIX]{x1D6FC}_{9}\unicode[STIX]{x1D6FF}_{j3}\unicode[STIX]{x1D6FF}_{m3}\unicode[STIX]{x1D6FF}_{il}+\unicode[STIX]{x1D6FC}_{10}\unicode[STIX]{x1D6FF}_{l3}\unicode[STIX]{x1D6FF}_{m3}\unicode[STIX]{x1D6FF}_{ij},\qquad\end{eqnarray}$$
where
$$\begin{eqnarray}\displaystyle \mathscr{L}_{ijlm}=\int \text{d}\unicode[STIX]{x1D73F}\,\langle \hat{\unicode[STIX]{x1D70E}}_{ij}(\unicode[STIX]{x1D73F},t)\hat{\unicode[STIX]{x1D70E}}_{lm}^{\ast }(\unicode[STIX]{x1D73F},t)\rangle \text{e}^{-\text{i}\unicode[STIX]{x1D73F}\boldsymbol{\cdot }\boldsymbol{x}_{g}}. & & \displaystyle\end{eqnarray}$$
Evaluation of the correlation
$\langle \hat{\unicode[STIX]{x1D70E}}_{ij}(\unicode[STIX]{x1D73F},t)\hat{\unicode[STIX]{x1D70E}}_{lm}^{\ast }(\unicode[STIX]{x1D73F},t)\rangle$
is presented in appendix D. The coefficients
$\unicode[STIX]{x1D6FC}_{1}$
through
$\unicode[STIX]{x1D6FC}_{10}$
in (C 1) are determined using the following criteria.
(i) Continuity:
$\mathscr{L}_{iilm}=0$
;
$\mathscr{L}_{ijmm}=0$
.(ii) Symmetry:
$\mathscr{L}_{ijlm}=\mathscr{L}_{ijml}$
;
$\mathscr{L}_{jilm}=\mathscr{L}_{lmij}$
.(iii) Additional independent equations:
(C 3)where$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\mathscr{L}_{ijij}=B_{1},\\ \mathscr{L}_{3333}=B_{2},\\ \mathscr{L}_{3j3j}=B_{3},\end{array}\right\} & & \displaystyle\end{eqnarray}$$
(C 4)$$\begin{eqnarray}\displaystyle & \displaystyle B_{1}=\frac{\unicode[STIX]{x1D708}}{2\langle \unicode[STIX]{x1D716}\rangle }\left[\frac{1}{\unicode[STIX]{x03C0}}\int \text{d}\unicode[STIX]{x1D73F}\,E(\unicode[STIX]{x1D705})\text{e}^{-\text{i}\unicode[STIX]{x1D73F}\boldsymbol{\cdot }\boldsymbol{x}_{g}}\right], & \displaystyle\end{eqnarray}$$
(C 5)$$\begin{eqnarray}\displaystyle & \displaystyle B_{2}=\frac{\unicode[STIX]{x1D708}}{2\langle \unicode[STIX]{x1D716}\rangle }\left[4\int \text{d}\unicode[STIX]{x1D73F}\,\unicode[STIX]{x1D705}_{3}^{2}\frac{E(\unicode[STIX]{x1D705})}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D705}^{2}}\left(1-\frac{\unicode[STIX]{x1D705}_{3}^{2}}{\unicode[STIX]{x1D705}^{2}}\right)\text{e}^{-\text{i}\unicode[STIX]{x1D73F}\boldsymbol{\cdot }\boldsymbol{x}_{g}}\right], & \displaystyle\end{eqnarray}$$
(C 6)$$\begin{eqnarray}\displaystyle & \displaystyle B_{3}=\frac{\unicode[STIX]{x1D708}}{2\langle \unicode[STIX]{x1D716}\rangle }\left[\int \text{d}\unicode[STIX]{x1D73F}\,\unicode[STIX]{x1D705}_{j}\unicode[STIX]{x1D705}_{j}\frac{E(\unicode[STIX]{x1D705})}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D705}^{2}}\left(1+\frac{\unicode[STIX]{x1D705}_{3}^{2}}{\unicode[STIX]{x1D705}^{2}}\right)\text{e}^{-\text{i}\unicode[STIX]{x1D73F}\boldsymbol{\cdot }\boldsymbol{x}_{g}}\right]. & \displaystyle\end{eqnarray}$$
C.2 The tensor
$\langle \unicode[STIX]{x1D70C}_{ij}(t)\unicode[STIX]{x1D70C}_{lm}(t^{\prime })\rangle =\mathscr{M}_{ijlm}$
The tensor
$\mathscr{M}_{ijlm}$
may be represented as
$$\begin{eqnarray}\displaystyle \mathscr{M}_{ijlm} & = & \displaystyle \unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FF}_{ij}\unicode[STIX]{x1D6FF}_{lm}+\unicode[STIX]{x1D6FD}_{2}\unicode[STIX]{x1D6FF}_{im}\unicode[STIX]{x1D6FF}_{jl}+\unicode[STIX]{x1D6FD}_{3}\unicode[STIX]{x1D6FF}_{il}\unicode[STIX]{x1D6FF}_{jm}+\unicode[STIX]{x1D6FD}_{4}\unicode[STIX]{x1D6FF}_{i3}\unicode[STIX]{x1D6FF}_{j3}\unicode[STIX]{x1D6FF}_{l3}\unicode[STIX]{x1D6FF}_{m3}+\unicode[STIX]{x1D6FD}_{5}\unicode[STIX]{x1D6FF}_{i3}\unicode[STIX]{x1D6FF}_{j3}\unicode[STIX]{x1D6FF}_{lm}\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D6FD}_{6}\unicode[STIX]{x1D6FF}_{i3}\unicode[STIX]{x1D6FF}_{l3}\unicode[STIX]{x1D6FF}_{jm}+\unicode[STIX]{x1D6FD}_{7}\unicode[STIX]{x1D6FF}_{i3}\unicode[STIX]{x1D6FF}_{m3}\unicode[STIX]{x1D6FF}_{jl}+\unicode[STIX]{x1D6FD}_{8}\unicode[STIX]{x1D6FF}_{j3}\unicode[STIX]{x1D6FF}_{l3}\unicode[STIX]{x1D6FF}_{im}+\unicode[STIX]{x1D6FD}_{9}\unicode[STIX]{x1D6FF}_{j3}\unicode[STIX]{x1D6FF}_{m3}\unicode[STIX]{x1D6FF}_{il}+\unicode[STIX]{x1D6FD}_{10}\unicode[STIX]{x1D6FF}_{l3}\unicode[STIX]{x1D6FF}_{m3}\unicode[STIX]{x1D6FF}_{ij},\qquad\end{eqnarray}$$
where
$$\begin{eqnarray}\displaystyle \mathscr{M}_{ijlm}=\int \text{d}\unicode[STIX]{x1D73F}\,\langle \hat{\unicode[STIX]{x1D70C}}_{ij}(\unicode[STIX]{x1D73F},t)\hat{\unicode[STIX]{x1D70C}}_{lm}^{\ast }(\unicode[STIX]{x1D73F},t)\rangle \text{e}^{-\text{i}\unicode[STIX]{x1D73F}\boldsymbol{\cdot }\boldsymbol{x}_{g}}. & & \displaystyle\end{eqnarray}$$
The unknown
$\unicode[STIX]{x1D6FD}$
coefficients are determined using the following constraints.
(i) Continuity:
$\mathscr{M}_{iilm}=0$
;
$\mathscr{M}_{ijmm}=0$
.(ii) Symmetry:
$\mathscr{M}_{ijlm}=\mathscr{M}_{lmij}$
;
$\mathscr{M}_{lmij}=-\mathscr{M}_{ijml}$
.(iii) Additional independent equations:
(C 9)$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\mathscr{M}_{ijij}=C_{1},\\ \mathscr{M}_{3j3j}=C_{2},\end{array}\right\} & & \displaystyle\end{eqnarray}$$
where
$$\begin{eqnarray}\displaystyle & \displaystyle C_{1}=\frac{\unicode[STIX]{x1D708}}{2\langle \unicode[STIX]{x1D701}\rangle }\left[\frac{1}{\unicode[STIX]{x03C0}}\int \text{d}\unicode[STIX]{x1D73F}\,E(\unicode[STIX]{x1D705})\text{e}^{-\text{i}\unicode[STIX]{x1D73F}\boldsymbol{\cdot }\boldsymbol{x}_{g}}\right], & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle C_{2}=\frac{\unicode[STIX]{x1D708}}{2\langle \unicode[STIX]{x1D701}\rangle }\left[\int \text{d}\unicode[STIX]{x1D73F}\,\unicode[STIX]{x1D705}_{j}\unicode[STIX]{x1D705}_{j}\frac{E(\unicode[STIX]{x1D705})}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D705}^{2}}\left(1+\frac{\unicode[STIX]{x1D705}_{3}^{2}}{\unicode[STIX]{x1D705}^{2}}\right)\text{e}^{-\text{i}\unicode[STIX]{x1D73F}\boldsymbol{\cdot }\boldsymbol{x}_{g}}\right]. & \displaystyle\end{eqnarray}$$
Appendix D. Evaluation of
$\langle \hat{\unicode[STIX]{x1D70E}}_{ij}(\unicode[STIX]{x1D73F},t)\hat{\unicode[STIX]{x1D70E}}_{lm}^{\ast }(\unicode[STIX]{x1D73F},t)\rangle$
Using the normalization of the strain-rate tensor defined in (2.16), we can write
$\hat{\unicode[STIX]{x1D70E}}_{ij}$
in terms of the Fourier coefficients of the fluid velocity as
$$\begin{eqnarray}\displaystyle \hat{\unicode[STIX]{x1D70E}}_{ij}(\unicode[STIX]{x1D73F},t)=\sqrt{\frac{2\unicode[STIX]{x1D708}}{\unicode[STIX]{x1D716}(t)}}\frac{1}{2}[\text{i}\unicode[STIX]{x1D705}_{j}\hat{u} _{i}(\unicode[STIX]{x1D73F},t)+\text{i}\unicode[STIX]{x1D705}_{i}\hat{u} _{j}(\unicode[STIX]{x1D73F},t)], & & \displaystyle\end{eqnarray}$$
where
$i=\sqrt{-1}$
. We now have
$$\begin{eqnarray}\displaystyle \langle \hat{\unicode[STIX]{x1D70E}}_{ij}(\unicode[STIX]{x1D73F},t)\hat{\unicode[STIX]{x1D70E}}_{lm}^{\ast }(\unicode[STIX]{x1D73F},t)\rangle & = & \displaystyle -\frac{\unicode[STIX]{x1D708}}{2}\left\langle \frac{1}{\unicode[STIX]{x1D716}(t)}(\text{i}\unicode[STIX]{x1D705}_{j}\hat{u} _{i}+\text{i}\unicode[STIX]{x1D705}_{i}\hat{u} _{j})(\text{i}\unicode[STIX]{x1D705}_{m}\hat{u} _{l}^{\ast }+\text{i}\unicode[STIX]{x1D705}_{l}\hat{u} _{m}^{\ast })\right\rangle \nonumber\\ \displaystyle & {\approx} & \displaystyle \frac{\unicode[STIX]{x1D708}}{2\langle \unicode[STIX]{x1D716}\rangle }[\unicode[STIX]{x1D705}_{j}\unicode[STIX]{x1D705}_{m}\langle \hat{u} _{i}\hat{u} _{l}^{\ast }\rangle +\unicode[STIX]{x1D705}_{j}\unicode[STIX]{x1D705}_{l}\langle \hat{u} _{i}\hat{u} _{m}^{\ast }\rangle +\unicode[STIX]{x1D705}_{i}\unicode[STIX]{x1D705}_{m}\langle \hat{u} _{j}\hat{u} _{l}^{\ast }\rangle +\unicode[STIX]{x1D705}_{i}\unicode[STIX]{x1D705}_{l}\langle \hat{u} _{j}\hat{u} _{m}^{\ast }\rangle ]\nonumber\\ \displaystyle & = & \displaystyle \frac{\unicode[STIX]{x1D708}}{2\langle \unicode[STIX]{x1D716}\rangle }[\unicode[STIX]{x1D705}_{j}\unicode[STIX]{x1D705}_{m}\unicode[STIX]{x1D6F7}_{il}(\unicode[STIX]{x1D73F},t)+\unicode[STIX]{x1D705}_{j}\unicode[STIX]{x1D705}_{l}\unicode[STIX]{x1D6F7}_{im}(\unicode[STIX]{x1D73F},t)+\unicode[STIX]{x1D705}_{i}\unicode[STIX]{x1D705}_{m}\unicode[STIX]{x1D6F7}_{jl}(\unicode[STIX]{x1D73F},t)+\unicode[STIX]{x1D705}_{i}\unicode[STIX]{x1D705}_{l}\unicode[STIX]{x1D6F7}_{jm}(\unicode[STIX]{x1D73F},t)],\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
where we have applied
$\hat{\unicode[STIX]{x1D70E}}_{lm}^{\ast }(\unicode[STIX]{x1D73F},t)=\hat{\unicode[STIX]{x1D70E}}_{lm}(-\unicode[STIX]{x1D73F},t)$
, and
$\unicode[STIX]{x1D6F7}_{il}(\unicode[STIX]{x1D73F},t)=\langle \hat{u} _{i}(\unicode[STIX]{x1D73F},t)\hat{u} _{l}^{\ast }(\unicode[STIX]{x1D73F},t)\rangle$
is the velocity spectrum tensor (see (A 6)).
The constraint
$\mathscr{L}_{ijij}=B_{1}$
can now be obtained from (D 2) as follows:
$$\begin{eqnarray}\displaystyle B_{1} & = & \displaystyle \int \text{d}\unicode[STIX]{x1D73F}\,\langle \hat{\unicode[STIX]{x1D70E}}_{ij}(\unicode[STIX]{x1D73F},t)\hat{\unicode[STIX]{x1D70E}}_{ij}^{\ast }(\unicode[STIX]{x1D73F},t)\rangle \text{e}^{-\text{i}\unicode[STIX]{x1D73F}\boldsymbol{\cdot }\boldsymbol{x}_{g}}\nonumber\\ \displaystyle & = & \displaystyle \frac{\unicode[STIX]{x1D708}}{2\langle \unicode[STIX]{x1D716}\rangle }\int \text{d}\unicode[STIX]{x1D73F}\,[\unicode[STIX]{x1D705}_{j}\unicode[STIX]{x1D705}_{j}\unicode[STIX]{x1D6F7}_{ii}(\unicode[STIX]{x1D73F},t)+\unicode[STIX]{x1D705}_{j}\unicode[STIX]{x1D705}_{i}\unicode[STIX]{x1D6F7}_{ij}(\unicode[STIX]{x1D73F},t)+\unicode[STIX]{x1D705}_{i}\unicode[STIX]{x1D705}_{j}\unicode[STIX]{x1D6F7}_{ji}(\unicode[STIX]{x1D73F},t)+\unicode[STIX]{x1D705}_{i}\unicode[STIX]{x1D705}_{i}\unicode[STIX]{x1D6F7}_{jj}(\unicode[STIX]{x1D73F},t)]\text{e}^{-\text{i}\unicode[STIX]{x1D73F}\boldsymbol{\cdot }\boldsymbol{x}_{g}}.\qquad \;\;\end{eqnarray}$$
Using in (D 3) the velocity spectrum tensor
$\unicode[STIX]{x1D6F7}_{ij}(\unicode[STIX]{x1D73F},t)$
(see (A 6)), it is relatively straightforward to show that
$\unicode[STIX]{x1D705}_{j}\unicode[STIX]{x1D705}_{i}\unicode[STIX]{x1D6F7}_{ij}(\unicode[STIX]{x1D73F},t)=0$
, and the remaining terms together are equal to
$B_{1}$
in (C 4). The integrals contained in
$B_{2}$
and
$B_{3}$
((C 5) and (C 6)) can be arrived at in a similar manner.
Analogous to (D 2), we can also write
$$\begin{eqnarray}\displaystyle & & \displaystyle \langle \hat{\unicode[STIX]{x1D70E}}_{jk}(\unicode[STIX]{x1D73F},t)\hat{\unicode[STIX]{x1D70E}}_{lm}^{\ast }(\unicode[STIX]{x1D73F},t)\rangle \nonumber\\ \displaystyle & & \displaystyle \quad =\frac{\unicode[STIX]{x1D708}}{2\langle \unicode[STIX]{x1D716}\rangle }[\unicode[STIX]{x1D705}_{k}\unicode[STIX]{x1D705}_{m}\langle \unicode[STIX]{x1D6F7}_{jl}(\unicode[STIX]{x1D73F},t)\rangle +\unicode[STIX]{x1D705}_{k}\unicode[STIX]{x1D705}_{l}\langle \unicode[STIX]{x1D6F7}_{jm}(\unicode[STIX]{x1D73F},t)\rangle +\unicode[STIX]{x1D705}_{j}\unicode[STIX]{x1D705}_{m}\langle \unicode[STIX]{x1D6F7}_{kl}(\unicode[STIX]{x1D73F},t)\rangle +\unicode[STIX]{x1D705}_{j}\unicode[STIX]{x1D705}_{l}\langle \unicode[STIX]{x1D6F7}_{km}(\unicode[STIX]{x1D73F},t)\rangle ],\qquad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \langle \hat{\unicode[STIX]{x1D70C}}_{ij}(\unicode[STIX]{x1D73F},t)\hat{\unicode[STIX]{x1D70C}}_{lm}^{\ast }(\unicode[STIX]{x1D73F},t)\rangle \nonumber\\ \displaystyle & & \displaystyle \quad =\frac{\unicode[STIX]{x1D708}}{2\langle \unicode[STIX]{x1D716}\rangle }[\unicode[STIX]{x1D705}_{j}\unicode[STIX]{x1D705}_{m}\langle \unicode[STIX]{x1D6F7}_{il}(\unicode[STIX]{x1D73F},t)\rangle -\unicode[STIX]{x1D705}_{j}\unicode[STIX]{x1D705}_{l}\langle \unicode[STIX]{x1D6F7}_{im}(\unicode[STIX]{x1D73F},t)\rangle -\unicode[STIX]{x1D705}_{i}\unicode[STIX]{x1D705}_{m}\langle \unicode[STIX]{x1D6F7}_{jl}(\unicode[STIX]{x1D73F},t)\rangle +\unicode[STIX]{x1D705}_{i}\unicode[STIX]{x1D705}_{l}\langle \unicode[STIX]{x1D6F7}_{jm}(\unicode[STIX]{x1D73F},t)\rangle ],\quad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \langle \hat{\unicode[STIX]{x1D70C}}_{jk}(\unicode[STIX]{x1D73F},t)\hat{\unicode[STIX]{x1D70C}}_{lm}^{\ast }(\unicode[STIX]{x1D73F},t)\rangle \nonumber\\ \displaystyle & & \displaystyle \quad =\frac{\unicode[STIX]{x1D708}}{2\langle \unicode[STIX]{x1D716}\rangle }[\unicode[STIX]{x1D705}_{k}\unicode[STIX]{x1D705}_{m}\langle \unicode[STIX]{x1D6F7}_{jl}(\unicode[STIX]{x1D73F},t)\rangle -\unicode[STIX]{x1D705}_{k}\unicode[STIX]{x1D705}_{l}\langle \unicode[STIX]{x1D6F7}_{jm}(\unicode[STIX]{x1D73F},t)\rangle -\unicode[STIX]{x1D705}_{j}\unicode[STIX]{x1D705}_{m}\langle \unicode[STIX]{x1D6F7}_{kl}(\unicode[STIX]{x1D73F},t)\rangle +\unicode[STIX]{x1D705}_{j}\unicode[STIX]{x1D705}_{l}\langle \unicode[STIX]{x1D6F7}_{km}(\unicode[STIX]{x1D73F},t)\rangle ].\qquad\end{eqnarray}$$
Appendix E. Evaluation of time integrals containing
$\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{1}$
,
$\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2},\ldots$
Reproducing (2.26)
$$\begin{eqnarray}\displaystyle \int _{-\infty }^{t}d_{ik}\,\text{d}t^{\prime } & = & \displaystyle \frac{1}{4\unicode[STIX]{x1D708}^{2}}\left\{\frac{1}{3}\unicode[STIX]{x1D6FF}_{ik}[\langle \unicode[STIX]{x1D716}^{2}\rangle T_{\unicode[STIX]{x1D716}\unicode[STIX]{x1D716}}+\langle \unicode[STIX]{x1D716}\unicode[STIX]{x1D701}\rangle T_{\unicode[STIX]{x1D716}\unicode[STIX]{x1D701}}-\langle \unicode[STIX]{x1D701}\unicode[STIX]{x1D716}\rangle T_{\unicode[STIX]{x1D701}\unicode[STIX]{x1D716}}-\langle \unicode[STIX]{x1D701}\unicode[STIX]{x1D701}\rangle T_{\unicode[STIX]{x1D701}\unicode[STIX]{x1D701}}]\right.\nonumber\\ \displaystyle & & \displaystyle +\,2\langle \unicode[STIX]{x1D716}^{2}\rangle \int _{-\infty }^{t}\exp \left(-\frac{t-t^{\prime }}{T_{\unicode[STIX]{x1D716}\unicode[STIX]{x1D716}}}\right)\langle \unicode[STIX]{x1D70E}_{ij}(t)\unicode[STIX]{x1D70E}_{lm}(t^{\prime })\rangle \langle \unicode[STIX]{x1D70E}_{jk}(t)\unicode[STIX]{x1D70E}_{lm}(t^{\prime })\rangle \,\text{d}t^{\prime }\nonumber\\ \displaystyle & & \displaystyle -\left.2\langle \unicode[STIX]{x1D701}^{2}\rangle \int _{-\infty }^{t}\exp \left(-\frac{t-t^{\prime }}{T_{\unicode[STIX]{x1D701}\unicode[STIX]{x1D701}}}\right)\langle \unicode[STIX]{x1D70C}_{ij}(t)\unicode[STIX]{x1D70C}_{lm}(t^{\prime })\rangle \langle \unicode[STIX]{x1D70C}_{jk}(t)\unicode[STIX]{x1D70C}_{lm}(t^{\prime })\rangle \,\text{d}t^{\prime }\right\},\end{eqnarray}$$
the term
$\int _{-\infty }^{t}\exp (-(t-t^{\prime })/T_{\unicode[STIX]{x1D716}\unicode[STIX]{x1D716}})\langle \unicode[STIX]{x1D70E}_{ij}(t)\unicode[STIX]{x1D70E}_{lm}(t^{\prime })\rangle \langle \unicode[STIX]{x1D70E}_{jk}(t)\unicode[STIX]{x1D70E}_{lm}(t^{\prime })\rangle \,\text{d}t^{\prime }$
, in turn, contains integrals such as (see (C 1) and (C 2))
$$\begin{eqnarray}\displaystyle \int _{-\infty }^{t}\exp \left(-\frac{t-t^{\prime }}{T_{\unicode[STIX]{x1D716}\unicode[STIX]{x1D716}}}\right)\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{1}, & & \displaystyle\end{eqnarray}$$
which leads to integrals of the form
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \int _{-\infty }^{t}\exp \left(-\frac{t-t^{\prime }}{T_{\unicode[STIX]{x1D716}\unicode[STIX]{x1D716}}}\right)\text{e}^{-\text{i}(\unicode[STIX]{x1D73F}+\unicode[STIX]{x1D73F}^{\prime })\boldsymbol{\cdot }\boldsymbol{x}_{g}}\,\text{d}t^{\prime }\int \text{d}\unicode[STIX]{x1D73F}\,\text{d}\unicode[STIX]{x1D73F}^{\prime }\,E(\unicode[STIX]{x1D705})E(\unicode[STIX]{x1D705}^{\prime })\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \quad \displaystyle =\int \text{d}\unicode[STIX]{x1D73F}\,\text{d}\unicode[STIX]{x1D73F}^{\prime }\,E(\unicode[STIX]{x1D705})E(\unicode[STIX]{x1D705}^{\prime })\frac{\left(\displaystyle \frac{1}{T_{\unicode[STIX]{x1D716}\unicode[STIX]{x1D716}}}\right)}{\left(\displaystyle \frac{1}{T_{\unicode[STIX]{x1D716}\unicode[STIX]{x1D716}}}\right)^{2}+[(\unicode[STIX]{x1D73F}+\unicode[STIX]{x1D73F}^{\prime })\boldsymbol{\cdot }\boldsymbol{g}\unicode[STIX]{x1D70F}_{v}]^{2}}.\end{eqnarray}$$
The integral
$\int \text{d}\unicode[STIX]{x1D73F}\,\text{d}\unicode[STIX]{x1D73F}^{\prime }\,E(\unicode[STIX]{x1D705})E(\unicode[STIX]{x1D705}^{\prime })\times (\cdots \,)$
is then evaluated in spherical coordinates through numerical quadrature.
Appendix F. Diffusion flux tensor constraints
The fourth-order tensor
$Q_{imjn}$
may be represented as
$$\begin{eqnarray}\displaystyle Q_{imjn} & = & \displaystyle \unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FF}_{im}\unicode[STIX]{x1D6FF}_{jn}+\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FF}_{in}\unicode[STIX]{x1D6FF}_{mj}+\unicode[STIX]{x1D6FC}_{3}\unicode[STIX]{x1D6FF}_{ij}\unicode[STIX]{x1D6FF}_{mn}+\unicode[STIX]{x1D6FC}_{4}\unicode[STIX]{x1D6FF}_{i3}\unicode[STIX]{x1D6FF}_{m3}\unicode[STIX]{x1D6FF}_{j3}\unicode[STIX]{x1D6FF}_{n3}+\unicode[STIX]{x1D6FC}_{5}\unicode[STIX]{x1D6FF}_{i3}\unicode[STIX]{x1D6FF}_{m3}\unicode[STIX]{x1D6FF}_{jn}\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D6FC}_{6}\unicode[STIX]{x1D6FF}_{i3}\unicode[STIX]{x1D6FF}_{j3}\unicode[STIX]{x1D6FF}_{mn}+\unicode[STIX]{x1D6FC}_{7}\unicode[STIX]{x1D6FF}_{i3}\unicode[STIX]{x1D6FF}_{n3}\unicode[STIX]{x1D6FF}_{mj}+\unicode[STIX]{x1D6FC}_{8}\unicode[STIX]{x1D6FF}_{in}\unicode[STIX]{x1D6FF}_{m3}\unicode[STIX]{x1D6FF}_{j3}+\unicode[STIX]{x1D6FC}_{9}\unicode[STIX]{x1D6FF}_{ij}\unicode[STIX]{x1D6FF}_{m3}\unicode[STIX]{x1D6FF}_{n3}+\unicode[STIX]{x1D6FC}_{10}\unicode[STIX]{x1D6FF}_{im}\unicode[STIX]{x1D6FF}_{j3}\unicode[STIX]{x1D6FF}_{n3},\quad\end{eqnarray}$$
where the coefficients
$\unicode[STIX]{x1D6FC}_{1}$
through
$\unicode[STIX]{x1D6FC}_{10}$
are determined using the following criteria.
(i) Continuity:
$Q_{iijn}=0$
,
$Q_{imjj}=0$
,
$Q_{iijj}=0$
.(ii) Symmetry:
$Q_{imjn}=Q_{jmin}$
,
$Q_{imjn}=Q_{jnim}$
.(iii) Additional independent equations:
(F 2)$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle Q_{3m3m}=\frac{\unicode[STIX]{x03C0}}{2g\unicode[STIX]{x1D70F}_{v}}\int _{\unicode[STIX]{x1D709}=0}^{\infty }\unicode[STIX]{x1D709}E(\unicode[STIX]{x1D709})\,\text{d}\unicode[STIX]{x1D709},\\ \displaystyle Q_{imim}=\frac{\unicode[STIX]{x03C0}}{g\unicode[STIX]{x1D70F}_{v}}\int _{\unicode[STIX]{x1D709}=0}^{\infty }\unicode[STIX]{x1D709}E(\unicode[STIX]{x1D709})\,\text{d}\unicode[STIX]{x1D709}.\end{array}\right\} & & \displaystyle\end{eqnarray}$$
