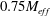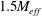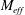1. Introduction
Recently, laboratory and computational works by Hurst & Vassilicos (Reference Hurst and Vassilicos2007), Suzuki et al. (Reference Suzuki, Nagata, Sakai and Ukai2010), Nicolleau, Salim & Nowakowski (Reference Nicolleau, Salim and Nowakowski2011), Gomes-Fernandes, Ganapathisubramani & Vassilicos (Reference Gomes-Fernandes, Ganapathisubramani and Vassilicos2012), Laizet & Vassilicos (Reference Laizet and Vassilicos2012), Nagata et al. (Reference Nagata, Sakai, Inaba, Suzuki, Terashima and Suzuki2013) and Nedić, Vassilicos & Ganapathisubramani (Reference Nedić, Vassilicos and Ganapathisubramani2013) have used multiscale/fractal objects to generate turbulence in wind and water tunnels (either in the laboratory or virtually in the computer) and have shown that complex multiscale boundary/initial conditions can drastically influence the behaviour of a turbulent flow. Fractal geometry is a concept in which a given pattern is repeated and split into parts, each being a reduced copy of the whole. Multiscale (fractal) objects can be designed to be immersed in any fluid flow where there is a need to passively control and design the turbulence generated by the object. The experiments and simulations have shown that, unlike regular objects (where the turbulence is generated by only one scale), a slight modification of one of the multiscale object parameters can very significantly modify the turbulent flow. Multiscale objects offer the opportunity to discover new complex flow effects/interactions that can help in understanding how to control and/or manage complex fluid flows. Furthermore, such multiscale objects can be designed as energy-efficient mixers with high turbulent intensities and no penalty in pressure drop, see Laizet & Vassilicos (Reference Laizet and Vassilicos2012). Coffey et al. (Reference Coffey, Hunt, Seoud and Vassilicos2007) have shown experimentally that fractal grids can be designed as stirring elements for inline static mixers and, as such, that they compare favourably with commercially available state-of-the-art stirring elements.
In this computational study we calculate and compare the effects of various fractal and regular grids on scalar fluxes and turbulent stirring in a mean scalar gradient configuration. This particular configuration has been widely studied in the past, following the theoretical work of Corrsin (Reference Corrsin1952). Tavoularis & Corrsin (Reference Tavoularis and Corrsin1981b ,Reference Tavoularis and Corrsin a ) and more recently Ferchichi & Tavoularis (Reference Ferchichi and Tavoularis2002) carried out wind tunnel experiments in a turbulent shear flow with a uniform mean temperature gradient. Mydlarski & Warhaft (Reference Mydlarski and Warhaft1998a ,Reference Mydlarski and Warhaft b ) generated turbulence in their wind tunnel by means of an active grid and the passive temperature fluctuations were generated by a mean transverse temperature gradient, formed at the entrance of the wind tunnel by an array of differentially heated elements. One important finding of these works was the highly intermittent nature of small-scale scalar fluctuations in the form of a ramp–cliff morphology, a feature which is ubiquitous in all flows with mean gradients of a passive scalar and which was already observed in the heated turbulent jet experiments of Sreenivasan, Antonia & Britz (Reference Sreenivasan, Antonia and Britz1979) and in the direct numerical simulations (DNS) of fully periodic turbulence by Pumir (Reference Pumir1994).
The vast majority of DNS of fluctuating passive scalars sustained by a mean scalar gradient have been carried out for fully periodic turbulence and concentrated on two-point and gradient statistics. For example, Pumir (Reference Pumir1994) studied the probability distribution function (PDF) of the scalar gradients parallel and perpendicular to the direction of the mean gradient; Yeung, Xu & Sreenivasan (Reference Yeung, Xu and Sreenivasan2002) investigated the effects of very high Schmidt numbers on scalar spectra, structure functions, and various quantities that characterise local isotropy and intermittency; most recently Yeung & Sreenivasan (Reference Yeung and Sreenivasan2014) investigated the spectral properties of the fluctuating scalar field at very low Schmidt numbers. To our knowledge, only two DNS studies to this date (Suzuki et al. Reference Suzuki, Nagata, Sakai and Ukai2010; Laizet & Vassilicos Reference Laizet and Vassilicos2012) have focused on the spatial development of a passive scalar with a mean gradient in a grid-generated non-homogeneous turbulent flow. They have both concentrated on one-point statistics which are the most basic statistics to study in such a setting, thus paving the way for future DNS studies of two-point statistics in such spatially developing turbulent flows. In this paper we follow Suzuki et al. (Reference Suzuki, Nagata, Sakai and Ukai2010) and Laizet & Vassilicos (Reference Laizet and Vassilicos2012) and carry out such DNS for the widest range yet of turbulence-generating grids, mean scalar gradients and scalar diffusivities. We are therefore able to make meaningful comparisons between different turbulence-generating grids (see the summary of results in § 6), a very first issue which needs to be addressed before anything else.
The paper is organised as follows. In the next section, we present the DNS methodology, the turbulence-generating grids and the numerical parameters of each simulation. Results on the turbulence and the flow field downstream of the grid are discussed in the following section. Then, passive scalar results are presented, followed by the results of a planar model problem which demonstrate the importance of the fractal nature of the grids, followed by a conclusion.
2. Flow parameters and numerical modelling
2.1. Governing equations
The governing equations are the forced incompressible Navier–Stokes equations
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial \boldsymbol{u}}{\partial t}=-\boldsymbol{{\rm\nabla}}p-\frac{1}{2}\left[\boldsymbol{{\rm\nabla}}\left(\boldsymbol{u}\otimes \boldsymbol{u}\right)+(\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}})\boldsymbol{u}\right]+{\it\nu}{\rm\nabla}^{2}\boldsymbol{u}+\boldsymbol{f}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{u}=0, & \displaystyle\end{eqnarray}$$
$p(\boldsymbol{x},t)$
is the pressure field (for a fluid with a constant density
${\it\rho}=1$
),
$\boldsymbol{u}$
the velocity field and
${\it\nu}$
the kinematic viscosity of the fluid. In this work, we use an immersed boundary method (IBM) which is based on a forcing field
$\boldsymbol{f}(\boldsymbol{x},t)$
in order to take into account the turbulence-generating grid inside the computational domain. Note that the convective terms are written in skew-symmetric form. This form reduces aliasing errors while remaining energy conserving for the type of spatial discretisation considered here.
The equation that describes the advection of a diffusive passive scalar field
${\it\theta}(\boldsymbol{x},t)$
by the velocity field
$\boldsymbol{u}$
is
$$\begin{eqnarray}\frac{\partial {\it\theta}}{\partial t}+\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\theta}={\it\kappa}{\rm\nabla}^{2}{\it\theta},\end{eqnarray}$$
with molecular diffusivity
${\it\kappa}={\it\nu}/Sc$
,
$Sc$
being the Schmidt number.
The initial condition for the velocity field is
$\boldsymbol{u}(\boldsymbol{x},t=0)=(U_{\infty },0,0)$
and for the scalar field it is
${\it\theta}(\boldsymbol{x},t=0)=Sy$
where
$S$
is a constant scalar gradient and
$y$
is a transverse spatial coordinate. The coordinate system is orthonormal with coordinate
$x$
in the streamwise direction and coordinates
$(y,z)$
in the transverse plane such that
$y=z=0$
on the centreline. In relation to the turbulence-generating grids, the transverse coordinate
$y$
is vertical and the transverse coordinate
$z$
is horizontal in figure 1. The boundary conditions are of inflow/outflow type in the streamwise direction (coordinate
$x$
) and periodic in the transverse direction along the spatial coordinate
$z$
. In the
$y$
transverse direction the boundary condition is periodic for the velocity field but anti-symmetric for the scalar field so as to ensure continuity of the scalar gradient across computational domain boundaries in the
$y$
direction. The inflow conditions are
$\boldsymbol{u}\,(x=x_{in},y,z,t)=(U_{\infty },0,0)$
and
${\it\theta}\,(x=x_{in},y,z,t)=Sy$
, and the outflow conditions are
$\partial \boldsymbol{u}/\partial t+U_{\infty }(\partial \boldsymbol{u}/\partial x)=0$
and
$\partial {\it\theta}/\partial t+U_{\infty }(\partial {\it\theta}/\partial x)=0$
at
$x=x_{out}$
(
$x=x_{in}$
and
$x=x_{out}$
correspond to the first and last planes of the computational domain). The pressure field is treated as in Laizet & Lamballais (Reference Laizet and Lamballais2009) (see also the next section).
Figure 1. Diagrams of the six grids used in this study. From left to right: fractal square grid with three fractal iterations, I grid with three fractal iterations, fractal square grid with four fractal iterations (top) and the three regular grids (bottom) with a blockage ratio of 0.54, 0.42 and 0.32 (left to right).
The generation of a passive scalar flux is done through a constant scalar gradient
$S$
. It should be noted that the fact that
$S$
is independent of position in space simplifies comparisons between grids as there is no distribution of length scales inherent to the initial scalar field to take into account.
2.2. Numerical methods
To solve the incompressible Navier–Stokes equations and the scalar transport equations, we use the in-house numerical code Incompact3d which is based on sixth-order compact schemes for spatial discretisation on a Cartesian mesh and a third-order Adams–Bashforth scheme for time advancement. To treat the incompressibility condition, a fractional step method requires the solution of a Poisson equation. For efficiency reasons, this equation is solved in spectral space using appropriate three-dimensional fast Fourier transforms (FFT). In order to have a strict equivalence between finite-difference operators in physical space and spectral operators, we use the concept of modified wavenumber introduced by Lele (Reference Lele1992) which allows the accuracy of the spectral operators to be reduced to sixth-order accuracy. Note that the divergence-free condition is ensured up to machine accuracy.
The modelling of the turbulence-generating grids is performed with an IBM. Following the procedure proposed by Parnaudeau et al. (Reference Parnaudeau, Carlier, Heitz and Lamballais2008), the present IBM is a direct forcing approach that ensures the no-slip boundary condition at the wall of the grid. The idea is to force the velocity to zero at the wall and inside the grids as our mesh is Cartesian and therefore conforms with the geometry of the grids because they consist of right angles and are placed normal to the mean flow. Finally, the pressure mesh is staggered from the velocity one by half a mesh to avoid spurious pressure oscillations introduced by the IBM. More details about the present code and its validation, especially the original treatment of the pressure in spectral space, can be found in Laizet & Lamballais (Reference Laizet and Lamballais2009).
Because of the size of the simulations, the parallel version of Incompact3d has been used for this numerical work. Based on a highly scalable two-dimensional decomposition library and a distributed FFT interface, it is possible to use the code on thousands of computational cores. More details about this efficient parallel strategy can be found in Laizet & Li (Reference Laizet and Li2011).
2.3. Description of the grids
As shown in figure 1, six different grids are used in this numerical work to investigate the streamwise evolution of the transport, stirring and mixing of a passive scalar in the presence of a mean scalar gradient. We consider two families of fractal grids, each based on a different fractal-generating pattern. The two patterns can be distinguished by the number of rectangular bars they require, three for the I grid and four for the square grids (see Hurst & Vassilicos Reference Hurst and Vassilicos2007 for descriptions of fractal I and fractal square grids). These fractal grids are completely characterised by the choice of the pattern and: (i) the number of fractal iterations
$N$
, here
$N=3$
for the fractal I grid and
$N=3,4$
for the fractal square grids; (ii) the bar lengths
$L_{j}=R_{L}^{\,j}L_{0}$
and lateral thicknesses
$t_{j}=R_{t}^{\,j}t_{0}$
(in the plane of the grid, normal to the mean flow) at iteration
$j$
,
$j=0,\dots ,N-1$
(here,
$R_{L}=1/2$
,
$L_{0}=0.5L_{y}$
for all the fractal grids, where
$L_{y}$
and
$L_{z}$
are the lateral sizes of the computational domain); (iii) the number
$4^{\,j}$
of patterns (square or I) at iteration
$j$
; (iv) the thickness ratio
$t_{r}\equiv t_{max}/t_{min}$
, i.e. the ratio between the lateral thickness of the bars making the largest pattern and the lateral thickness of the smallest.
By definition,
$L_{0}=L_{max}$
,
$L_{N-1}=L_{min}$
,
$t_{0}=t_{max}$
and
$t_{N-1}=t_{min}$
. Note that
$t_{min}$
is set to the same value (
$=1$
) for all fractal grids and is therefore the spatial unit for all our simulations;
$t_{r}=8.67$
for the fractal square grid with three iterations,
$t_{r}=10.5$
for the fractal I grid and
$t_{r}=8.5$
for the fractal square grid with four fractal iterations.
The blockage ratio
${\it\sigma}$
of our turbulence-generating grids is defined as the ratio of their total area in the transverse plane to the area
$T^{2}=L_{y}\times L_{z}$
. This total area was approximately calculated for fractal grids by neglecting the overlap areas between different sized bars in Laizet & Vassilicos (Reference Laizet and Vassilicos2012). However, we do not make such an approximation in the present paper and the blockage ratio
${\it\sigma}$
is therefore more accurately calculated here than in Laizet & Vassilicos (Reference Laizet and Vassilicos2012). This blockage ratio is determined by our choice of the previously mentioned parameters and is given in table 1 for the different grids.
Table 1. Grid lengths and thicknesses and effective mesh size
$M_{eff}$
, all normalized by
$t_{min}$
(the lateral thickness of the smallest bars on the fractal grids), and blockage ratio
${\it\sigma}$
for the six grids used here. Table 2 shows which grid (fractal square, fractal I or regular) corresponds to which DNS.
Unlike regular grids, multiscale/fractal grids do not have a well-defined mesh size. This is why Hurst & Vassilicos (Reference Hurst and Vassilicos2007) introduced an effective mesh size for multiscale grids,
$M_{eff}=(4T^{2}/L_{TG})\sqrt{1-{\it\sigma}}$
, where
$L_{TG}$
is the total perimeter length in the
$(y{-}z)$
plane of the fractal grid (note that Laizet & Vassilicos Reference Laizet and Vassilicos2012 used the alternative definition
$M_{eff}=(4T^{2}/L_{G})\sqrt{1-{\it\sigma}}$
where
$L_{G}$
is the total length of the grid when it has been stripped of its thickness). The present definition of
$M_{eff}$
is the one in Hurst & Vassilicos (Reference Hurst and Vassilicos2007) and it returns the usual mesh size when applied to regular grids. The multiscale nature of multiscale/fractal grids influences
$M_{eff}$
via the perimeter length
$L_{TG}$
which can be extremely long in spite of being constrained to fit within the area
$T^{2}=L_{y}\times L_{z}$
. As with the blockage ratio
${\it\sigma}$
, the effective mesh sizes of our turbulence-generating grids are fully determined by our choice of parameters characterising the grids and are given in table 1. Note finally that the streamwise thickness of the bars is
$3.2t_{min}$
for all the grids used in this numerical study.
Table 2. Numerical parameters of the simulations and characteristics of the grids, whether fractal square grids (
$\Box$
), fractal I grids (I) or regular grids (Reg.).
2.4. Numerical parameters
The computational domain and number of mesh nodes for each simulation are given in table 2. For the fractal grids with three iterations (DNS1 to DNS8), the computational domain is split into 2304 computational cores. It is split into 8100 computational cores for the fractal square grid with four fractal iterations (DNS9) and into 7200 computational cores for the regular grids (DNS10 to DNS12). For each turbulence-generating grid, the simulation is performed with a global Reynolds number
$\mathit{Re}_{t_{min}}=300$
(based on the streamwise upstream velocity
$U_{\infty }$
and the smallest lateral thickness
$t_{min}$
of the fractal grids, which we use as a length unit for all simulations) and a time step
${\rm\Delta}t=0.01t_{min}/U_{\infty }$
. In terms of the effective mesh size
$M_{eff}$
, the Reynolds number
$\mathit{Re}_{M}$
is equal to 4110 for DNS1 to DNS5, 6300 for DNS6 to DNS8, 2610 for DNS9 and DNS11, 1950 for DNS10 and 3600 for DNS12. In terms of the Kolmogorov microscale
${\it\eta}$
(the smallest length scale of the turbulence evaluated locally), the spatial resolution for more than 95 % of the computational domain is at worst
${\rm\Delta}x={\rm\Delta}y={\rm\Delta}z\leqslant 2{\it\eta}$
for all the simulations. Where the turbulence is at its most intense, i.e. around the location where the turbulence intensity takes its greatest values (which represents less than 5 % of the entire computational domain),
${\rm\Delta}x={\rm\Delta}y={\rm\Delta}z\leqslant 8{\it\eta}$
. Such a resolution justifies the need of a numerical procedure with a small-scale-localised extra dissipation introduced artificially via the viscous term (Lamballais, Fortune & Laizet Reference Lamballais, Fortune and Laizet2011). This procedure is of course only active for the unresolved smallest scales of the flow around the location where the turbulence intensity takes its greatest values.
The streamwise position of the grid at
$x=0$
has been carefully chosen in relation to the inflow position so as to avoid any spurious interactions between the modelling of the grid and the inflow boundary condition:
$x_{in}=-100t_{min}$
for DNS9 to DNS12 and
$x_{in}=-30t_{min}$
for DNS1 to DNS8. (Note also that
$x=0$
coincides with the downstream side of the grid.)
2.5. Collection time for statistics
The collection time for the statistics presented in this paper is
$T=1000t_{min}/U_{\infty }$
for the twelve simulations. During this collection time, 100 three-dimensional snapshots at full resolution of the velocity, pressure and scalar fields have been randomly collected. This is may not seem much but it is already extremely demanding in terms of data storage by today’s standards. In the next paragraph we argue that it may be just about enough for the present study, which is mostly concerned with first- and second-order moments.
We define the fluctuating velocity field
$\boldsymbol{u}^{\prime }(\boldsymbol{x},t)=\boldsymbol{ u}(\boldsymbol{x},t)-\overline{\boldsymbol{u}}(\boldsymbol{x})$
and the fluctuating scalar field
${\it\theta}^{\prime }(\boldsymbol{x},t)={\it\theta}(\boldsymbol{x},t)-\overline{{\it\theta}}(\boldsymbol{x})$
where the overbar signifies an average over time (specifically over the 100 snapshots). Using the notation
$\boldsymbol{u}^{\prime }=(u^{\prime },v^{\prime },w^{\prime })$
in a coordinate system aligned with
$(x,y,z)$
, we have calculated (for DNS1)
$\overline{u^{\prime 2}}/U_{\infty }^{2}$
and
$-\overline{v^{\prime }{\it\theta}^{\prime }}/{\it\kappa}S$
and their respective 95 % confidence intervals along the centreline
$y=z=0$
for
$N_{s}=100$
, assuming that the 100 random snapshots are statistically independent. These confidence intervals turn out to be significantly larger than the statistics they correspond to, mainly because they converge to zero as slowly as
$N_{s}^{-1/2}$
, and it is impossible to collect orders of magnitude more snapshots with currently available technology.
However, the statistics we mostly concentrate on in this paper are averaged over both time (number
$N_{s}$
of snapshots) and
$y$
,
$z$
. Different samples at different
$y$
,
$z$
positions cannot be considered independent and therefore it does not make sense to calculate the usual confidence intervals. Nevertheless, we checked statistical convergence of the streamwise evolution of
$\langle u^{\prime 2}\rangle ^{0.5}/U_{\infty }$
and of
$-\langle v^{\prime }{\it\theta}^{\prime }\rangle /{\it\kappa}S$
for DNS1 where
$\langle \cdot \rangle$
signifies an average over
$y$
,
$z$
and the number
$N_{s}$
of snapshots. Figure 2 shows that these streamwise profiles do not significantly depend on
$N_{s}$
for
$N_{s}=50,75,100$
. (The non-dimensionalisation by
${\it\kappa}S$
is not important here but is used in § 4 to compare turbulent scalar fluxes resulting from different turbulence-generating grids at the same
${\it\kappa}$
and the same
$S$
.)
Figure 2. Verification of the level of convergence for the statistics for DNS1. Streamwise evolution of
$\langle u^{\prime 2}\rangle ^{0.5}/U_{\infty }$
(a) and
$-\langle v^{\prime }{\it\theta}^{\prime }\rangle /{\it\kappa}S$
(b), where
$\langle \cdot \rangle$
denotes an average over
$y$
,
$z$
and a number
$N_{s}$
of snapshots (see § 2.5).
The maximum deviation between
$N_{s}=50$
and
$N_{s}=100$
is 6.5 % for the
$\langle u^{\prime 2}\rangle ^{0.5}/U_{\infty }$
statistic and 15 % for
$-\langle v^{\prime }{\it\theta}^{\prime }\rangle /{\it\kappa}S$
. For
$N_{s}=75$
and
$N_{s}=100$
the maximum deviation is 2.5 % for
$\langle u^{\prime 2}\rangle ^{0.5}/U_{\infty }$
and 3.5 % for
$-\langle v^{\prime }{\it\theta}^{\prime }\rangle /{\it\kappa}S$
. The difference between
$\langle u^{\prime 2}\rangle ^{0.5}/U_{\infty }$
for
$N_{s}=75$
and
$\langle u^{\prime 2}\rangle ^{0.5}/U_{\infty }$
for
$N_{s}=100$
is less than 2 % over 80 % of the entire streamwise extent of our computational domain and the same holds true for
$-\langle v^{\prime }{\it\theta}^{\prime }\rangle /{\it\kappa}S$
.
We end this section by pointing out that we find
$\langle \boldsymbol{u}\rangle =(U_{\infty },0,0)$
to good approximation at all streamwise positions
$x$
for all our DNS cases, DNS1 to DNS12.
3. Flow fields, turbulence intensities and pressure drops
With the single exception of Hurst & Vassilicos (Reference Hurst and Vassilicos2007), there have been no comparisons of the turbulent flows generated by fractal I grids and fractal square grids to date. In fact, even Hurst & Vassilicos (Reference Hurst and Vassilicos2007), who did compare centreline statistics of these two type of flows, did not compare full velocity fields and their statistics as we do in this section and did not compare scalar statistics either as we do in the next section.
For the sake of comparison (see table 2), DNS1 to DNS3 and DNS6 to DNS8 are DNS of turbulent flows generated by fractal square grids (DNS1 to DNS3) and fractal I grids (DNS6 to DNS8) all with the same blockage ratio
${\it\sigma}=0.3$
and same number of fractal iterations
$N=3$
. They also all have the same value of
${\it\kappa}/{\it\nu}=10$
and the same
$\mathit{Re}_{t_{min}}=300$
but different though comparable values of
$\mathit{Re}_{M}$
(
$\mathit{Re}_{M}=4110$
for DNS1 to DNS3,
$\mathit{Re}_{M}=6300$
for DNS6 to DNS8). In this section we compare average turbulence intensities and normalised pressure drops, which are not expected to depend too sensitively on global Reynolds number. In the next section we compare scalar statistics for which DNS1 has been designed to correspond to DNS6 as they both have the same
$St_{min}=1/16$
, DNS2 to DNS7 with the same
$St_{min}=1/32$
and DNS3 to DNS8 with the same
$St_{min}=1/64$
(see table 2).
Figures 3 and 4 show snapshots of instantaneous streamwise velocity components of the flows generated by DNS1 and DNS6. One can clearly see the impact on the flow of the wakes generated by the various bars making the grids. The actual large-scale shape of the grid remains present in the flow till about
$x=8M_{eff}$
in the case of the I grid and till about
$x=10M_{eff}$
in the case of the square grid. In both cases, the memory of the grid seems to disappear, at least visually on the plots of figure 4, at
$x$
larger than
$20M_{eff}$
.
Figure 3. Instantaneous streamwise velocity component of the flow in the
$(xy)$
plane for the fractal I grid (a) and the fractal square grid (b) with three fractal iterations. The visualisations cover 50 % of the computational domain at locations
$z/t_{min}=0,L_{y}/4$
and
$3L_{y}/8$
from top to bottom respectively. The grid location is clear in the plots.
Figure 4. Instantaneous streamwise velocity component of the flow in the
$(zy)$
plane for the fractal I grid (a) and the fractal square grid (b) with three fractal iterations. The visualisations are at streamwise locations
$x/t_{min}=0,40,80,160,320$
and 640 from left to right respectively (which correspond to
$x/M_{eff}=0,1.9,3.81,7.62,15.24$
and 30.48 for the I grid and
$x/M_{eff}=0,2.9,5.84,11.68,23.36$
and 46.7 for the square grid).
Given that the size of the largest bars making the fractal grids is about half the size of the lateral periodic computational domain, one can expect correlations between one end of the domain and the other in the periodic directions. However, based on the fact that the integral scale is one order of magnitude smaller than the domain size in our simulations (see below), one can expect the contribution of these long-range correlations to be negligible for one-point statistics, in which case one-point statistics are mostly unaffected by the periodic boundary conditions and the size of the fractal grid. A laboratory experiment with the same or similar grid and domain size but different boundary conditions in the lateral directions would then return the same or similar statistics, as is indeed the case. DNS of fractal-generated turbulence employing periodic cross-stream boundary conditions and grids very similar in size to the present ones have already been published by Laizet & Vassilicos (Reference Laizet and Vassilicos2011) and have shown good qualitative agreement with wind tunnel experiments on such flows (various one-point profiles and even turbulence decay exponents). Similar DNS have now been shown to quantitatively agree with experiments up to fourth-order one-point statistics (see Laizet, Nedić & Vassilicos Reference Laizet, Nedić and Vassilicos2014). Zhou et al. (Reference Zhou, Nagata, Sakai, Suzuki, Ito, Terashima and Hayase2014) carried out very similar DNS with periodic cross-stream boundary conditions and a single square grid that is half the cross-stream domain size. As they report in their paper, their results also compare well with wind tunnel experiments. Furthermore, D’Addio et al. (Reference D’Addio, Sassun, Flores and Orlandi2014) performed DNS of turbulence generated by various grids (fractal and regular) similar in size to ours with various boundary conditions and showed that the influence of the cross-stream boundary conditions is negligible in most of the flow. Even so, to ensure that our simulations reproduce the new physics observed in the recent laboratory experiments of Seoud & Vassilicos (Reference Seoud and Vassilicos2007), Mazellier & Vassilicos (Reference Mazellier and Vassilicos2010), Gomes-Fernandes et al. (Reference Gomes-Fernandes, Ganapathisubramani and Vassilicos2012), Valente & Vassilicos (Reference Valente and Vassilicos2012), Nagata et al. (Reference Nagata, Sakai, Inaba, Suzuki, Terashima and Suzuki2013) and Hearst & Lavoie (Reference Hearst and Lavoie2014) we plot in figure 5(a) the ratio
$L/{\it\lambda}$
of the longitudinal integral length scale
$L$
to the Taylor microscale
${\it\lambda}$
and
$\mathit{Re}_{{\it\lambda}}=\langle u^{\prime 2}\rangle ^{1/2}{\it\lambda}/{\it\nu}$
as functions of streamwise distance from the turbulence-generating grid along the centreline. The constancy of
$L/{\it\lambda}$
whilst
$\mathit{Re}_{{\it\lambda}}$
decays is exactly the behaviour observed by the aforementioned experimental works, which also reported power-law energy spectra with exponents close to
$-5/3$
accompanying this behaviour. We plot a longitudinal energy spectrum
$E_{u}(\,f)$
in figure 5(b) along with a scalar energy spectrum
$E_{{\it\theta}}(\,f)$
for completeness, both compensated by
$f^{-5/3}$
where
$f$
stands for frequency, as these spectra are evaluated in time at a given location in the flow.
Figure 5. (a) Streamwise evolution along the centreline of
$\mathit{Re}_{{\it\lambda}}$
and
$L/{\it\lambda}$
for DNS9. (b) Streamwise velocity and scalar spectra at
$x/M_{eff}=5$
on the centreline for DNS1. The spectra are compensated by
$f^{-5/3}$
and plotted against the non-dimensional frequency
$f\,M_{eff}/U_{\infty }$
.
Figures 6 and 7 show the streamwise evolution of
$\langle u^{\prime 2}\rangle ^{0.5}/U_{\infty }$
for the six different grids with respect to
$x/t_{min}$
and
$x/M_{eff}$
. The regular grids generate a much higher peak average turbulence intensity than the three fractal grids with values of approximately 55 %, 42 % and 32 % for the regular grids with blockage ratio
${\it\sigma}=$
54 %, 42 % and 32 % (see figure 7
a in particular). (We note in passing that the maximum values of the peak average turbulence intensities are about equal, in the case of our regular grids, to the blockage ratios of these grids.)
Figure 6. Streamwise evolution of
$\langle u^{\prime 2}\rangle ^{0.5}/U_{\infty }$
where
$\langle \cdot \rangle$
denotes an average over
$y$
and
$z$
and over the collection time
$T$
(i.e. over 100 random snapshots taken during this collection time). Streamwise distance normalised by
$t_{min}$
.
Figure 7. Streamwise evolution of
$\langle u^{\prime 2}\rangle ^{0.5}/U_{\infty }$
where
$\langle \cdot \rangle$
denotes an average over
$y$
and
$z$
and over the collection time
$T$
(i.e. over 100 random snapshots taken during this collection time). Streamwise distance normalised by
$M_{eff}$
.
On the other hand, in the spatial units chosen for the plots in figures 6 and 7, the average turbulence decay appears much slower for the fractal grids than for our regular grids. The fractal grids, both I and square, can sustain the turbulence much further than the regular grids in
$M_{eff}$
and
$t_{min}$
units. This is particularly clear in figure 6(a) where all grids have the same blockage ratio
${\it\sigma}\approx 0.3$
and where DNS1 and DNS6 correspond to fractal square and fractal I grids respectively whereas DNS12 corresponds to a regular grid. As shown in figure 6(b) and figure 7(b), this is even more so for our fractal square grid with
$N=4$
and
${\it\sigma}=0.41$
(both higher than for our I grid), whereas the average turbulence intensities generated by all our three regular grids reach about same low levels by
$x\approx 8M_{eff}$
irrespective of the blockage ratio of these regular grids which ranges between 0.3 and 0.54. Note finally that at
$x/M_{eff}\geqslant 10$
the average turbulence decay exponents obtained from figure 7(b) in those cases where a long enough streamwise range permits a reasonable fit (all except DNS6) lie between 1.2 and 1.4 (by setting the virtual origin to zero).
The spatial location of the peak of average turbulence intensity is approximately located at a distance from the grids which is commensurate with
$M_{eff}$
(see figure 7
b). This observation was also made by Laizet & Vassilicos (Reference Laizet and Vassilicos2012) but with not as good a definition of
$M_{eff}$
as the one here (see § 2.3) and without including I grids which we do here. For the fractal square grid with three iterations, the peak of turbulence is located at a distance of
$1.45M_{eff}$
from the grid, for the I grid it is located at
$0.76M_{eff}$
, for the fractal square grid with four iterations and the regular grid with a blockage ratio of 0.42 it is located at
$0.73M_{eff}$
, for the regular grid with a blockage ratio of 0.32 it is located at
$0.8M_{eff}$
and finally for the regular grid with a blockage ratio of 0.54 it is located at
$1.23M_{eff}$
.
In relation to potential mixing and heat transfer applications, note that the highest average turbulence intensities are obtained with the
$N=4$
fractal square grid (see figure 7) which also has the highest blockage ratio of all our fractal grids. Then come the
${\it\sigma}=0.3$
fractal I and fractal square grids which are comparable in turbulence intensities. Still, it may be useful in applications to know that at
$x<20M_{eff}$
the highest turbulence intensities are achieved with the fractal square grid whereas they are achieved with the fractal I grid at
$x>20M_{eff}$
. Note, in particular, the significant difference in average turbulence intensity, with a value of 7.7 % for the I grid (DNS6) and only 4.8 % for the square grid (DNS1) at the end of the computational domain even though they have the same
${\it\sigma}$
. Note also that near the end of the computational domain, i.e. at
$x=600t_{min}$
, DNS9 and DNS6 return the same average turbulence intensity of 8 % even though the fractal square grid in DNS9 has a higher blockage ratio than the fractal I grid in DNS6. It makes sense for applications to measure distances in terms of units such as
$t_{min}$
which are not closely related to the flow but are related to the dimensions of the technological application in mind.
The blockage ratio
${\it\sigma}$
turns out, in fact, to be a good predictor of the normalised average pressure drop across the grid. The normalised average pressure drop
$\langle P\rangle /0.5{\it\rho}U_{\infty }^{2}$
(where
$P$
is the pressure drop divided by the fluid mass density) is plotted as a function of streamwise distance in figure 8. The results show that the far-field normalised pressure drop is about the same for different grids if they have the same blockage ratio. For example, the regular grid with the highest blockage ratio,
${\it\sigma}=0.54$
, also has the highest overall pressure drop whereas the grids with the lowest blockage ratio,
${\it\sigma}\approx 0.3$
, have the lowest overall pressure drop. The fractal square grid with
${\it\sigma}=0.41$
and the regular grid with
${\it\sigma}=0.42$
have very comparable pressure drops in between the previous two. The fractal I grid seems to have slightly less overall (long-range) average pressure drop than all other grids and also one of the highest average turbulence intensity behaviours over an extended streamwise distance. Finally note, as also observed by Laizet & Vassilicos (Reference Laizet and Vassilicos2012), that the fractal grids have a much slower pressure recovery than the regular grids.
Figure 8. Streamwise evolution of
$\langle P\rangle /0.5{\it\rho}U_{\infty }^{2}$
where
$\langle \cdot \rangle$
denotes an average over
$y$
and
$z$
and over the collection time
$T$
(i.e. over 100 random snapshots taken during this collection time). Streamwise distance normalised by
$t_{min}$
in (a) and
$M_{eff}$
in (b).
It was claimed by Laizet & Vassilicos (Reference Laizet and Vassilicos2012) that fractal square grids return a much lower pressure drop than regular grids of same blockage ratio. Our present results invalidate their conclusion on the pressure drop, which was due to an inaccurate calculation of
${\it\sigma}$
as they did not take into account the overlap areas between the bars which, as it turns out, are significant (see also § 2.3).
4. Passive scalar statistics
4.1. Mean scalar field
Our first observation is that
$\overline{{\it\theta}}=Sy+{\it\theta}_{r}(\boldsymbol{x})$
, where
${\it\theta}_{r}$
is a random scalar field independent of time but varying in space around 0, see figure 9 where it is also shown that
$\langle {\it\theta}_{r}\rangle$
oscillates around 0 for all cases (the definitions of our two averaging operations are given in § 2.5 and are repeated in the first sentence of § 4.2). This result has already been claimed by Laizet & Vassilicos (Reference Laizet and Vassilicos2012) and is here generalised to a wider range of grids including, in particular, fractal I grids which have never been considered in this context previously. The result is non-trivial and is reminiscent of a previous one by Corrsin (Reference Corrsin1952) for homogeneous isotropic turbulence (see also Mydlarski & Warhaft Reference Mydlarski and Warhaft1998a
).
Figure 9. (a) Profiles in the
$y$
direction of
$\overline{{\it\theta}}$
at
$x=600t_{min}$
. The line termed ‘Corrsin’ is
$Sy$
. (b) Streamwise evolution of
$\langle {\it\theta}_{r}\rangle$
. Data extracted for the six different grids (see figure 1) from DNS1, DNS6, DNS9, DNS10, DNS11 and DNS12.
4.2. Scalar variance and flux
From (2.3) combined with
${\it\theta}=\overline{{\it\theta}}+{\it\theta}^{\prime }$
and
$\overline{{\it\theta}}=Sy+{\it\theta}_{r}$
(where the overbar signifies an average over time, in our case over 100 random snapshots) we can now obtain an equation for the fluctuating scalar variance
$\langle {\it\theta}^{\prime 2}\rangle$
(where the angle brackets signify an average over
$y$
,
$z$
and time). Defining
$\overline{\boldsymbol{u}}(\boldsymbol{x})=\langle \boldsymbol{u}\rangle +\tilde{\boldsymbol{u}}(\boldsymbol{x})$
, where
$\langle \tilde{\boldsymbol{u}}(\boldsymbol{x})\rangle =0$
by construction and
$\langle \boldsymbol{u}\rangle =(U_{\infty },0,0)$
by observation in all our simulations, standard mathematical manipulations lead to:
$$\begin{eqnarray}\frac{U_{\infty }}{2}\frac{\text{d}}{\text{d}x}\langle {\it\theta}^{\prime 2}\rangle +\frac{1}{2}[\tilde{\boldsymbol{u}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\overline{{\it\theta}^{\prime 2}}]+S\langle v^{\prime }{\it\theta}^{\prime }\rangle +[\overline{{\it\theta}^{\prime }\boldsymbol{u}^{\prime }}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\theta}_{r}]+\frac{1}{2}\langle \boldsymbol{u}^{\prime }\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\theta}^{\prime 2}\rangle =-{\it\kappa}\langle |\boldsymbol{{\rm\nabla}}{\it\theta}^{\prime }|^{2}\rangle +\frac{{\it\kappa}}{2}\langle {\rm\nabla}^{2}{\it\theta}^{\prime 2}\rangle\end{eqnarray}$$
where the square brackets
$[\cdots ]$
signify an average over
$y$
and
$z$
but not over time and where it was taken for granted that
$\overline{(\partial /\partial t){\it\theta}^{\prime 2}}=0$
(otherwise the term
$\langle (\partial /\partial t){\it\theta}^{\prime 2}\rangle /2$
should be added to the left-hand side).
This equation shows how the fluctuating scalar variance evolves in the streamwise direction
$\langle {\it\theta}^{\prime 2}\rangle$
as a result of various terms, in particular the transverse scalar flux term
$S\langle v^{\prime }{\it\theta}^{\prime }\rangle$
, which is negative and is therefore the term whereby the mean scalar profile produces scalar fluctuations. Other notable terms are the spatial transport term
$\langle \boldsymbol{u}^{\prime }\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\theta}^{\prime 2}\rangle /2$
, which vanishes in homogeneous incompressible turbulence, and the scalar dissipation term
$-{\it\kappa}\langle |\boldsymbol{{\rm\nabla}}{\it\theta}^{\prime }|^{2}\rangle$
, which destroys scalar fluctuations by molecular smearing. Before assessing in § 4.3 the relative importance of each of the terms in (4.1), we first describe the salient properties of the fluctuating scalar variance and the scalar flux as obtained from our simulations (figures 9–17).
Figure 10. Streamwise evolution of the variance
$\langle {\it\theta}^{\prime 2}\rangle /2$
(a) and of
$-\langle v^{\prime }{\it\theta}^{\prime }\rangle /{\it\kappa}S$
(b). Data for the four different grids corresponding to simulations DNS1, DNS6, DNS9, DNS10, DNS11 and DNS12 all of which have the same values of
$St_{min}$
and
${\it\kappa}/{\it\nu}$
.
Firstly,
$\langle {\it\theta}^{\prime 2}\rangle$
is a monotonically increasing function of streamwise distance for all the present grids (see figure 10
a), a result perhaps reminiscent of the decaying grid-generated turbulence experiments of Sullivan (Reference Sullivan1976) and Sirivat & Warhaft (Reference Sirivat and Warhaft1983) where a linear scalar variance growth with streamwise distance was reported. It should be noted that the antisymmetric boundary condition for the scalar field along the
$y$
-axis (see § 2.3) means that there is no wall effect on the scalar and therefore the isotropic turbulence treatment in Corrsin (Reference Corrsin1952), which implies a monotonic linear scalar variance growth, may be, to some extent, applicable here, at least where the turbulence is approximately homogeneous and isotropic.
Secondly, the fluctuating scalar variance
$\langle {\it\theta}^{\prime 2}\rangle$
is much greater and grows much faster for the fractal than for the regular grids (see figure 10
a and the caption) at equal values of
$St_{min}$
,
$ST$
and
${\it\kappa}/{\it\nu}$
(which is the case for DNS1, DNS6, DNS11 and DNS12). In fact,
$\langle {\it\theta}^{\prime 2}\rangle$
grows to be between factors and an order of magnitude larger with the fractal grids than with the regular ones.
Note that we have chosen
$t_{min}$
as our length unit for the streamwise distance in figure 10 as in all subsequent figures in this paper. We take the engineering point of view that we may need to tailor a grid for a particular static inline mixer or a heat transfer/cooling application, in which case lengths and distances need to be comparable to installation dimensions and therefore measured in terms of an arbitrary unit:
$t_{min}$
serves here as such a non-flow-specific unit. Flow-specific units were proposed in previous works, namely the effective mesh size in Hurst & Vassilicos (Reference Hurst and Vassilicos2007) and the wake-interaction length scale in Mazellier & Vassilicos (Reference Mazellier and Vassilicos2010) and Gomes-Fernandes et al. (Reference Gomes-Fernandes, Ganapathisubramani and Vassilicos2012). The wake-interaction length scale was shown to be appropriate for predicting properties of scalar variance and flux streamwise profiles by Laizet & Vassilicos (Reference Laizet and Vassilicos2012) but only for fractal square and regular grids. The question of how to define an appropriate such flow-specific length scale for fractal I grids remains open and is not addressed here.
We now turn our attention to the scalar flux, which we normalise in terms of properties of the scalar, namely the molecular diffusivity
${\it\kappa}$
and the mean scalar gradient
$S$
. This normalisation is not necessarily physically meaningful but it facilitates comparisons between different set-ups which use the same scalar and the same mean scalar gradient. Again, such comparisons are of potential relevance to technological applications.
Streamwise evolution of
$-\langle v^{\prime }{\it\theta}^{\prime }\rangle /{\it\kappa}S$
are plotted in figure 10(b). Firstly, at equal values of
$St_{min}$
,
$ST$
and
${\it\kappa}/{\it\nu}$
(which is the case for DNS1, DNS6, DNS11 and DNS12),
$-\langle v^{\prime }{\it\theta}^{\prime }\rangle /{\it\kappa}S$
is between factors and an entire order of magnitude greater for the fractal grids than for the regular ones in most of the flow. For example, the ratio of
$-\langle {\it\theta}^{\prime }v^{\prime }\rangle$
for the fractal grid with four fractal iterations (DNS9) to
$\langle {\it\theta}^{\prime }v^{\prime }\rangle$
for the regular grid (DNS10) is oscillating between 19 at
$x=200t_{min}$
and 32 by the end of our computational domain.
Secondly, along the downstream streamwise direction measured in
$t_{min}$
spatial units,
$-\langle v^{\prime }{\it\theta}^{\prime }\rangle /{\it\kappa}S$
grows, then peaks then decays for the regular grids, whereas it grows, peaks much further downstream from the grid and then either remains about constant or slowly decays for the fractal grids. Specifically, for the fractal square grid with four fractal iterations (DNS9) and for the fractal I grid (DNS6), the normalised transverse turbulent scalar flux peaks just before
$200t_{min}$
and then remains approximately constant until the end of the computational domain with a value of 16 for DNS9 and around 10 for DNS6. For the fractal square grid with three fractal iterations (DNS1), the normalised transverse turbulent scalar flux peaks also at approximately
$200t_{min}$
but then decays from a value of approximately 15 to a value of approximately 7 by the end of our computational domain.
Figure 11. Two-dimensional visualisations in the
$z=0~(x,y)$
plane of the instantaneous passive scalar field for various values of
$S$
but the same
${\it\kappa}$
: (a) DNS1 with
$St_{min}=1/16$
, (b) DNS2 with
$St_{min}=1/32$
and (c) DNS3 with
$St_{min}=1/64$
. The visualisations are in the region
$3L_{y}\leqslant x\leqslant 4L_{y}$
,
$-L_{y}/2\leqslant y\leqslant L_{y}/2$
. Values lower than
$-0.5$
are in blue and values higher than 0.5 are in red.
Figure 12. Two-dimensional visualisations in the
$z=0~(x,y)$
plane of the instantaneous passive scalar field for various Schmidt numbers but for the same
$S$
(
$St_{min}=1/32$
): (a) DNS2 with
${\it\kappa}=10{\it\nu}$
, (b) DNS4 with
${\it\kappa}=5{\it\nu}$
and (c) DNS5 with
${\it\kappa}=2.5{\it\nu}$
. The visualisations are in the region
$3L_{y}\leqslant x\leqslant 4L_{y}$
,
$-L_{y}/2\leqslant y\leqslant L_{y}/2$
. Values lower than
$-0.5$
are in blue and values higher than 0.5 are in red.
Figure 13. (a) Streamwise evolution of the variance
$\langle {\it\theta}^{\prime 2}\rangle /2$
for the fractal square grid with three fractal iterations, the same
${\it\kappa}/{\it\nu}=10$
but different values of
$St_{min}$
(DNS1, DNS2 and DNS3). (b) Streamwise evolution of the variance
$\langle {\it\theta}^{\prime 2}\rangle /2$
for the fractal square grid with three fractal iterations, the same value of
$St_{min}=1/32$
but different molecular diffusivities
${\it\kappa}/{\it\nu}=10,5,2.5$
(DNS2, DNS4 and DNS5).
Figure 14. (a) Streamwise evolution of
$-\langle v^{\prime }{\it\theta}^{\prime }\rangle$
for the fractal grids with three fractal iterations, different values of
$St_{min}$
but the same
${\it\kappa}/{\it\nu}$
(DNS1, DNS2, DNS3, DNS6, DNS7 and DNS8). (b) Streamwise evolution of
$-\langle v^{\prime }{\it\theta}^{\prime }\rangle /{\it\kappa}S$
for the fractal grids with three fractal iterations, different values of
$St_{min}$
and
${\it\kappa}/{\it\nu}$
(DNS1 to DNS8).
As might be expected from the presence of the terms
$S\langle v^{\prime }{\it\theta}^{\prime }\rangle$
and
$-{\it\kappa}\langle |\boldsymbol{{\rm\nabla}}{\it\theta}^{\prime }|^{2}\rangle$
in (4.1), the fluctuating scalar variance
$\langle {\it\theta}^{\prime 2}\rangle$
is an increasing function of the dimensionless parameter
$St_{min}$
and a decreasing function of
${\it\kappa}/{\it\nu}$
(see figures 11–13). Figures 11 and 12 illustrate these dependences in terms of scalar visualisations obtained at exactly the same time for different simulations as per the figure captions. Ceteris paribus plots of the streamwise evolution of
$\langle {\it\theta}^{\prime 2}\rangle /2$
are shown in figure 13 for the fractal square grid with three fractal iterations by varying only
$St_{min}$
(a) or only
${\it\kappa}/{\it\nu}$
(b). The data in figure 13(a) can be collapsed exactly by plotting
$(\langle {\it\theta}^{\prime 2}\rangle /(St_{min})^{2})/2$
as a function of
$x/t_{min}$
. If (4.1) is rewritten for
${\it\theta}^{\prime }/S$
and
${\it\theta}_{r}/S$
it then becomes an equation independent of
$S$
, which agrees with the
$(\langle {\it\theta}^{\prime 2}\rangle /(St_{min})^{2})/2$
collapse in figure 13 and also suggests that
$-\langle v^{\prime }{\it\theta}^{\prime }\rangle$
should increase linearly with
$St_{min}$
. This is indeed the case and is demonstrated for both fractal square and I grids in of figure 14
b), which shows
$\langle v^{\prime }{\it\theta}^{\prime }\rangle /{\it\kappa}S$
versus
$x/t_{min}$
. Note the very good collapse of the DNS1, DNS2 and DNS3 data (square grid, same
${\it\kappa}/{\it\nu}$
but different
$St_{min}$
) on the one hand and the DNS6, DNS7 and DNS8 data (I grid, same
${\it\kappa}/{\it\nu}$
but different
$St_{min}$
) on the other, both of which appear as single curves on the plot (the two lowest ones on the plot). (Figure 14
a shows the DNS1 to DNS3 and DNS6 to DNS8 data prior to collapse for reference and more detailed comparisons.) These, perhaps trivial, observations are confirmed in the collapses of the scalar flux coefficient
$\langle v^{\prime }{\it\theta}^{\prime }\rangle /\sqrt{\langle v^{\prime 2}\rangle \langle {\it\theta}^{\prime 2}\rangle }$
shown in figure 15.
Having turned our attention again to the scalar flux, we note in figure 16(a) that
$\langle u^{\prime }{\it\theta}^{\prime }\rangle$
and
$\langle w^{\prime }{\it\theta}^{\prime }\rangle$
can be neglected by comparison to
$\langle v^{\prime }{\it\theta}^{\prime }\rangle$
and can be assumed to effectively vanish (this is shown for DNS1 in figure 16 but is also observed in all our other simulations). The same conclusion was reached in Laizet & Vassilicos (Reference Laizet and Vassilicos2012) but only for the fractal square grid and one regular grid, whereas it covers six different grids in the present paper including, for the first time, a fractal I grid which is not symmetric with respect to the
$y$
and
$z$
directions.
Figure 16(b) shows that
${\it\kappa}/{\it\nu}$
has a very small influence on
$\langle v^{\prime }{\it\theta}^{\prime }\rangle$
:
$\langle v^{\prime }{\it\theta}^{\prime }\rangle$
very slowly decreases with increasing
${\it\kappa}/{\it\nu}$
, in fact at a significantly slower rate than the decrease of
$\langle {\it\theta}^{\prime 2}\rangle$
with increasing
${\it\kappa}/{\it\nu}$
(figure 13) as confirmed by the clear if weak increasing dependence of the scalar flux coefficient in figure 17(a). This observation illustrates, in particular, the well-known fact that the scaling
$-\langle v^{\prime }{\it\theta}^{\prime }\rangle /{\it\kappa}S$
is of limited physical significance for
${\it\kappa}$
even though it may be of use in specific engineering contexts.
Figure 15. Streamwise evolution of
$-\langle v^{\prime }{\it\theta}^{\prime }\rangle /\sqrt{\langle v^{\prime 2}\rangle \langle {\it\theta}^{\prime 2}\rangle }$
for (a) DNS1, DNS2 and DNS3 (fractal square grid, all parameters same but for
$St_{min}$
) and (b) DNS6, DNS7 and DNS8 (fractal I grid, all parameters same but for
$St_{min}$
).
Figure 16. (a) Streamwise evolution of
$-\langle u^{\prime }{\it\theta}^{\prime }\rangle$
,
$-\langle v^{\prime }{\it\theta}^{\prime }\rangle$
and
$-\langle w^{\prime }{\it\theta}^{\prime }\rangle$
for DNS1. (b) Streamwise evolution of
$-\langle v^{\prime }{\it\theta}^{\prime }\rangle$
for the fractal square grid with three fractal iterations, the same value of
$St_{min}=1/32$
but different
${\it\kappa}/{\it\nu}=10,5,2.5$
(DNS2, DNS4 and DNS5).
Figure 17. (a) Streamwise evolution of
$-\langle v^{\prime }{\it\theta}^{\prime }\rangle /\langle v^{\prime 2}\rangle ^{0.5}\langle {\it\theta}^{\prime 2}\rangle ^{0.5}$
for the fractal square grid with three fractal iterations when varying
${\it\kappa}/{\it\nu}$
while keeping all other parameters constant (DNS2,
${\it\kappa}=10{\it\nu}$
; DNS4,
${\it\kappa}=5{\it\nu}$
; DNS5,
${\it\kappa}=2.5{\it\nu}$
). (b) Streamwise evolution of
$-\langle v^{\prime }{\it\theta}^{\prime }\rangle /\langle v^{\prime 2}\rangle ^{0.5}\langle {\it\theta}^{\prime 2}\rangle ^{0.5}$
for all our six grids in six different simulations where
$St_{min}=1/16$
and
${\it\kappa}/{\it\nu}=10$
(DNS1, DNS6, DNS9, DNS10, DNS11 and DNS12).
We end this section with figure 17(b) which shows how the scalar flux coefficient depends on inlet conditions (specifically on the type and details of the turbulence-generating grid) even though, as shown in figure 15, it does not depend on the mean scalar gradient. The scalar variance coefficient rises within the first approximately 100
$t_{min}$
length units from each grid towards a constant value between 0.45 and 0.7 around which it fluctuates. Even though the regular grids produce the weakest turbulence and weakest and less self-sustained fluctuating scalar variance growth and scalar flux, they achieve the largest values of
$-\langle v^{\prime }{\it\theta}^{\prime }\rangle /\langle v^{\prime 2}\rangle ^{0.5}\langle {\it\theta}^{\prime 2}\rangle ^{0.5}$
, between 0.6 and 0.7. The three-iteration fractal square grid follows with
$-\langle v^{\prime }{\it\theta}^{\prime }\rangle /\langle v^{\prime 2}\rangle ^{0.5}\langle {\it\theta}^{\prime 2}\rangle ^{0.5}$
between 0.5 and 0.6 and the lowest values of
$-\langle v^{\prime }{\it\theta}^{\prime }\rangle /\langle v^{\prime 2}\rangle ^{0.5}\langle {\it\theta}^{\prime 2}\rangle ^{0.5}$
are returned by the three-iteration fractal I grid and the four-iteration fractal square grid. A complete collapse of
$-\langle v^{\prime }{\it\theta}^{\prime }\rangle /\langle v^{\prime 2}\rangle ^{0.5}\langle {\it\theta}^{\prime 2}\rangle ^{0.5}$
for different grids will therefore require appropriately quantified information concerning the turbulence-generating grid, an interesting and important problem which we must leave for future investigation.
4.3. The scalar variance equation
The dominance of the scalar flux term in the dependence of
$\langle {\it\theta}^{\prime 2}\rangle$
on
$St_{min}$
suggests that
$S\langle v^{\prime }{\it\theta}^{\prime }\rangle$
may also dominate (4.1), at least in the flow configurations and parameter ranges considered in this paper. We therefore now study the relative contributions of each term in the integral form of this equation, as the integral form smooths out fluctuations and allows clear conclusions.
Integrating (4.1) over the streamwise distance from 0 to
$x$
yields
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{U_{\infty }}{2}\langle {\it\theta}^{\prime 2}\rangle +\int _{0}^{x}\text{d}x\frac{1}{2}[\tilde{\boldsymbol{u}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\overline{{\it\theta}^{\prime 2}}]+S\int _{0}^{x}\text{d}x\langle v^{\prime }{\it\theta}^{\prime }\rangle +\int _{0}^{x}\text{d}x[\overline{{\it\theta}^{\prime }\boldsymbol{u}^{\prime }}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\theta}_{r}]\nonumber\\ \displaystyle & & \displaystyle \quad +\,\int _{0}^{x}\frac{1}{2}\langle \boldsymbol{u}^{\prime }\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\theta}^{\prime 2}\rangle =-{\it\kappa}\int _{0}^{x}\text{d}x\langle |\boldsymbol{{\rm\nabla}}{\it\theta}^{\prime }|^{2}\rangle +\frac{{\it\kappa}}{2}\int _{0}^{x}\text{d}x\langle {\rm\nabla}^{2}{\it\theta}^{\prime 2}\rangle .\end{eqnarray}$$
We refer to the five terms on the left-hand side of (4.2) as terms 1 to 5 in order from left to right and to the two terms on the right-hand side as terms 6 and 7. Term 3 is the integral of the transverse scalar flux multiplied by
$S$
and term 6 is the integral of the dissipation rate of scalar fluctuations. Both these terms are negative. At low enough diffusivity values, one expects term 7 to be negligible and definitely much smaller than term 6. If the correction terms 2 and 4 (which involve the square bracket averaging operation) and the turbulent transport term 5 are also negligibly small, then term 1 may be approximated by
$$\begin{eqnarray}\frac{U_{\infty }}{2}\langle {\it\theta}^{\prime 2}\rangle \approx -{\it\kappa}\int _{0}^{x}\text{d}x\langle |\boldsymbol{{\rm\nabla}}{\it\theta}^{\prime }|^{2}\rangle -S\int _{0}^{x}\langle v^{\prime }{\it\theta}^{\prime }\rangle ,\end{eqnarray}$$
meaning that the mean scalar gradient and the turbulent scalar flux cause the fluctuating scalar variance to grow with
$x$
while the scalar dissipation dampens that growth.
This is indeed what happens qualitatively, though not quite quantitatively, in all our simulations (see the examples plotted in figures 18 and 19). In the fractal grid cases, term 4 is responsible for much, though not all, of the discrepancy between the right- and left-hand sides of (4.3) and taking into account all terms in (4.2) generally reduces this discrepancy a little further. In the regular grid cases, the balance (4.3) holds within approximately 10 % for most of the streamwise extent of the simulation and no significant improvements are brought to this balance by the other terms in (4.2). This discrepancy must be accountable to various integration and numerical errors and to the absence of
$\langle (\partial /\partial t){\it\theta}^{\prime 2}\rangle /2$
in (4.1).
Figure 18. Streamwise evolution of the different terms of (4.2) for DNS1 (a) and DNS6 (b).
Figure 19. Streamwise evolution of the different terms of (4.2) for DNS9 (a) and DNS10 (b).
5. The importance of the fractal nature of the grids
As we have seen, fractal grids, irrespective of their particular nature (whether I or square), return much greater scalar fluxes and, as a result, much greater fluctuating scalar variances than regular grids of the same or even higher blockage ratios. This suggests a fractal mechanism of scalar flux enhancement which relies mainly on the fractality of the grid and less on the details of this fractality. Such a mechanism has been proposed by Laizet & Vassilicos (Reference Laizet and Vassilicos2012) but its validity has never been verified. This is the space-scale unfolding (SSU) mechanism, which we now briefly describe. We then use the Lagrangian approach of the SSU mechanism to verify that it is the fractality of the grid which is responsible for the enhanced scalar fluxes.
In the presence of a mean scalar gradient, the SSU mechanism is based on the relation between scalar flux and turbulent diffusivity which follows from
$\overline{{\it\theta}}=Sy+{\it\theta}_{r}(\boldsymbol{x})$
(see § 4.1) when advection dominates over molecular diffusion. The transverse scalar flux is effectively proportional to the transverse turbulent diffusivity (see Corrsin Reference Corrsin1952 and Laizet & Vassilicos Reference Laizet and Vassilicos2012) and the turbulent diffusivity can be understood in Lagrangian terms as follows. Defining
$y_{0}$
to be the initial transverse position of a fluid element and
$y(t)$
the same fluid element transverse coordinate at time
$t$
, the turbulent diffusivity is the time derivative of the average of
$(y(t)-y_{0})^{2}$
. The faster this average square transverse displacement grows, the greater the scalar flux. The SSU mechanism is predicated on the expectation that a fluid element in a turbulent flow generated by a fractal grid will have opportunities to progressively move from wakes of small bars to wakes of larger bars and therefore be convected by increasingly larger scale eddies as it moves away from the grid. As a result the average square transverse displacement should increase faster with streamwise distance and be larger than if the grid were just regular and not fractal.
Figure 20. The four sets of obstacles. The thickness of all obstacles in the streamwise direction is
$D/2$
. RG1 consists of 20 square obstacles of lateral size
$D$
; RG2 of 10 square obstacles of lateral size
$2D$
; RG4 of 5 square obstacles of lateral size
$4D$
; and the fractal arrangement FSG consists of 2 square obstacles of lateral size
$4D$
, 4 square obstacles of lateral size
$2D$
and 8 square obstacles of lateral size
$D$
. All four obstacle arrangements have the same 50 % blockage and they are all placed at a distance
$5D$
from the inlet of the computational domain.
This idea being generic, and in fact independent of the presence of a scalar gradient which simply acts to mark the imprint of the SSU mechanism on the scalar flux, we use it to test the fractality’s effect on stirring in a simplified two-dimensional setting without mean scalar gradient. We run simulations of four different planar turbulent flows generated by four different sets of obstacles, RG1, RG2, RG4 and FSG (see figure 20). These four sets of obstacles have the same 50 % blockage ratio in the plane of the flow and can be viewed as cuts through four different grids. FSG is a fractal set of obstacles and comprises two obstacles of size
$4D$
, four obstacles of size
$2D$
and eight obstacles of size
$D$
. One might think that the higher scalar fluxes and fluctuating scalar variances reported for fractal grids in § 4 have their origin in the larger and more intense eddies resulting from the bigger bars or obstacles in the grid. If so, RG4 which consists of five obstacles of size
$4D$
should produce similar, if not even larger, transverse turbulent diffusion compared to FSG. RG4 should also return larger transverse turbulent diffusion than RG2, which in turn should return larger transverse turbulent diffusion than RG1. However, if the transverse turbulent diffusion is higher with FSG than with any RG set of obstacles then it is the fractal nature of the sets which must be responsible for the enhancement.
We use our code Incompact3d to compute the planar flows generated by the sets of obstacles shown in figure 20, with a domain size that is
$L_{x}=30D$
long in the streamwise and
$L_{y}=40D$
long in the transverse directions. The number of mesh nodes is
$n_{x}\times n_{y}=901\times 1200$
. The uniform and constant inlet velocity
$U_{\infty }$
upstream of the obstacles is in the streamwise direction and is such that the Reynolds number
$U_{\infty }D/{\it\nu}=600$
. The time step is
$0.00025D/U_{\infty }$
. The obstacles are placed at a distance
$5D$
from the inlet, which consists of a uniform flow field free from any perturbation, and there is an outflow boundary condition at the outlet. In the transverse direction the boundary conditions are periodic. Fluid element trajectories are integrated using a second-order Adams–Bashforth scheme and a bi-linear interpolation in space for the estimation of the velocities at the fluid element positions. The fluid elements are released at 160 different equally spaced transverse positions
$y_{0}$
at a streamwise distance
$D$
from the obstacles. The 160 different initial coordinates
$y_{0}$
span the entire extent of the transverse domain
$L_{y}=40D$
. Such sets of 160 fluid elements are repeatedly released with a time period equal to
$0.6D/U_{\infty }$
. We therefore integrate 25 600 fluid element trajectories over a total duration of 400 000 time steps so that the vast majority of them have the time to cross the entire domain. We then use these statistics to calculate the transverse position
$y$
of each of our fluid elements when it reaches a given streamwise position
$x$
and calculate
$\langle (y-y_{0})^{2}\rangle _{0}$
as a function of
$x$
, where the averaging operation
$\langle \,\rangle _{0}$
is over all 25 600 fluid elements. The results are plotted in figure 21.
Figure 21.
$\langle (y-y_{0})^{2}\rangle _{0}/D^{2}$
versus
$x/D$
for all four obstacle arrangements.
Figure 21 shows clearly that
$\langle (y-y_{0})^{2}\rangle _{0}$
grows much faster and is much larger for the FSG flow than for the RG flows. The idea that higher transverse turbulent diffusion is caused by larger and more intense eddies is definitely consistent with the RG results as
$\langle (y-y_{0})^{2}\rangle _{0}$
grows faster and is larger for RG4 than for RG2 and also grows faster and is larger for RG2 than for RG1. However, this classical idea cannot explain our result that
$\langle (y-y_{0})^{2}\rangle _{0}$
is dramatically larger for the FSG than for all RG arrangements, a result as dramatic as that for the scalar flux and the fluctuating scalar variance in § 4. This clearly demonstrates that the effect must have its cause in the fractality of the obstacle arrangements in this section and of the grids in § 4.
We end this section with some suggestive visualisations in figure 22 which show that the flow consists of small-scale eddies in the lee of RG1, intermediate-scale eddies in the lee of RG2 and large-scale eddies in the lee of RG4. The FSG visualisation shows that the FSG flow consists of small and intermediate size eddies and that the eddies are more numerous than in the RG flows. Furthermore, the FSG flow appears more chaotic than the RG flows. The larger number and the more chaotic nature of multiscale eddies produced by the FSG arrangement is consistent with our observation of enhanced transverse turbulent diffusion by this FSG arrangement.
Figure 22. Vorticity visualisations for all four obstacle arrangements. The mean flow is from left to right. (a) RG1, (b) RG2, (c) RG4, (d) FSG. Plotted are isovalues of vorticity between
$-25U_{\infty }/D$
in blue to
$+25U_{\infty }/D$
in red (green is zero).
6. Conclusion
Twelve three-dimensional spatially developing turbulent velocity and scalar fields generated by three different fractal grids (two fractal square grids which differ in number of fractal iterations and blockage ratio and one fractal I grid) and three different regular grids have been investigated by means of DNS in a computational virtual wind tunnel. This is the first time that fractal I grids have been considered in this context. The twelve simulations cover different sustained mean scalar gradients and different molecular diffusivities. In our simulations the fluctuating scalar variance is dominated by the sustained mean scalar gradient, which persistently generates scalar fluctuations, and by the scalar dissipation, which persistently smooths them out. However, these two terms are not in balance and the mean scalar gradient forces the fluctuating scalar variance to consistently grow in the streamwise extent of the flow region considered here.
For all these grids, the turbulence intensity averaged over time and over a plane parallel to the grid takes its maximum (peak) value when the streamwise position of this plane is between
$0.75M_{eff}$
and
$1.5M_{eff}$
, where
$M_{eff}$
is the effective mesh size introduced by Hurst & Vassilicos (Reference Hurst and Vassilicos2007). Downstream of the location of this maximum (peak) value, the turbulence intensity averaged in this way is greatly enhanced by the fractal grids by comparison to the regular grids even though the fractal grids have comparable or lower blockage ratios. The pressure drop is about the same across grids of same blockage ratio irrespective of whether they are fractal or not (with the proviso that the pressure recovery is longer for the fractal grids). Even so, the fractal grids enhance turbulent scalar fluxes by up to an order of magnitude in the region downstream of the aforementioned peak and they also greatly enhance the streamwise growth of the fluctuating scalar variance in that region. The cause of this phenomenon lies in the fractality of the grid. When averaged over lateral planes, the turbulent scalar flux scales with the mean scalar gradient and the turbulent scalar variance with the square of this mean scalar gradient. The turbulence scalar flux coefficient is constant far enough downstream of all the present grids and is independent of the mean scalar gradient but significantly dependent on the nature and details of the turbulence-generating grid.
Acknowledgements
The authors are grateful to Dr N. Li for helping with the parallel version of Incompact3d and to Dr G. Papadakis for his helpful comments on an early version of the paper. We acknowledge support from EPSRC Research grants EP/E008475/1 and EP/L000261/1 (UK Turbulence Consortium) and PRACE for awarding us access to resource SUPERMUC based in Germany at Leibniz-Rechenzentrum (Leibniz Supercomputing Centre).
