Published online by Cambridge University Press: 19 July 2005
We discuss the effects of temporal aggregation on the estimation of cointegrating vectors and on testing linear restrictions on this vector. We adopt a discrete time approach and demonstrate, in contrast with the findings of Chambers (2003, Econometric Theory 19, 49–77), who adopts a continuous time approach, that in some situations, when the regressand must be aggregated, systematic sampling is preferable to average sampling for estimation purposes. Like Chambers, we show that the best aggregation scheme for regressors, in terms of asymptotic estimation efficiency, is always average sampling. We also show that different types of aggregation have no influence on the relative size of tests of linear restrictions on the cointegration vector.We thank Soren Johansen, Niels Haldrup, Raquel Waters, the associate editor, and two anonymous referees for their helpful comments. Of course, any remaining error is the responsibility of the authors. The first author gratefully acknowledges the financial support of a Marie Curie Fellowship of the European Community Programme “Improving the Human Research Potential and the Socio-Economic Knowledge Base” under contract HPMF-CT-2002-01662 and the Danish Research Council. The second author gratefully acknowledges the financial support of the Spanish Ministry of Science and Technology SEC2002-01512.
Economic theories are frequently tested not with data measured at their generating time interval, but with temporally aggregated time series because most economic time series are measured at a lower sampling frequency than economic agents make decisions. Temporal aggregation changes many time series properties such as weak exogeneity or Granger causality and in some cases deteriorates statistical inference because valuable information is lost with such data transformation and cannot be recovered with the observable data (see Wei, 1989; Marcellino, 1999). However, the estimation of cointegrating vectors does not fit into this pessimistic picture because an estimator of cointegrating vectors constructed with temporally aggregated data is consistent (see Granger, 1990; Phillips, 1991a) and, when all the variables of the cointegrated system are flows, asymptotically as efficient as the estimator based on disaggregated time series (see Chambers, 2003).1
The invariance of cointegrating vectors with the sampling interval holds whenever the seasonal unit roots do not alias into the zero frequency (see Granger and Siklos, 1995).
Chambers (2003) shows that when both the regressand and the regressor are temporally aggregated by average sampling there is no loss of asymptotic efficiency for the estimation of the cointegrating vectors.
There are different methodological approaches to discuss the effects of temporal aggregation on cointegrated systems. The continuous time aggregation analysis (see Phillips, 1991a; Comte, 1999; Chambers, 2003) assumes that the long-run dynamics evolves in continuous time. This assumption is not realistic for some cointegrating relations because the continuous approach imposes that the markets react instantaneously to a long-run disequilibrium, but in practice many cointegrating relations, such as the purchasing power parity (PPP) (see Johansen and Juselius, 1992), correct a situation of long-run disequilibrium very slowly as a result of information costs or barriers to trade. Another approximation to the issue is the discrete time aggregation that considers that the long-run dynamics are generated at equally spaced time intervals (see Granger, 1990; Granger and Siklos, 1995; Marcellino, 1999). This approach also can be considered an approximation to discuss temporal aggregation of cointegrating relations because it assumes an equally spaced time interval between shocks and long-run reactions, and in practice the time interval between the shock and the long-run reaction may vary along the sample period.2
A recently developed approach, the random time aggregation (see Jordà, 1999), allows the dynamics to be generated at random time intervals.
The aim of this paper is an in-depth examination of the theory of the effects that discrete time aggregation has on inference on cointegrating vectors. We consider the effects of different types of aggregation on the estimation of cointegrating relations with I(1) and I(2) variables and on hypothesis testing on cointegrating vectors. As stressed by Johansen (1994, 1995) the marginal distribution of the estimator is not relevant for inference on cointegrating vectors. What is of interest is the joint distribution of the estimator and the observed information. We provide evidence from a simulation study to confirm this statement for our specific aggregation scenario. More specifically, we show that the aggregation scheme most able to guarantee the estimation's precision is not necessarily the best suited for testing a hypothesis on the cointegrating vector and, in addition, although different aggregation schemes have different effects on the estimator, they have similar effects on the test.
This paper is organized as follows. In Section 2 we present a representation of the cointegrated system with a varying, but equally spaced, sampling interval. The dependency of the optimal regression-type estimators and the observed information on temporal aggregation are discussed in Section 3. Next, we evaluate the finite-sample effects of temporal aggregation on the Phillips and Hansen (1990) fully modified ordinary least squares (FM-OLS) estimator. Finally, Section 5 concludes the paper. The Appendix contains the proofs of a lemma and theorems.
We shall use the following notation: B denotes a vector of Brownian motions, Ω the long-run variance matrix, and W a vector of standardized independent Brownian motions; CI(d,b) stands for a cointegrated process of orders (d,b); [·] denotes the integer part and ⇒ weak convergence; zt represents a k-dimensional disaggregated time series; T ≡ [t/m] denotes the aggregated time unit; N ≡ [n/m] is the aggregated sample size, t is the disaggregated time unit; m is a finite positive integer that determines the length of the sampling interval; and n denotes the span of the sample measured in t-periods. The k-dimensional temporally aggregated time series is defined as

where sm(L) = 1 + L + ··· + Lm−1 is the summation filter. More specifically, ZT(0) denotes a systematically sampled time series and ZT(1) an average sampled time series.3
Systematic sampling is typically applied to stock variables such as prices or population, and average sampling is applied to flow variables such as consumption or income and to stock variables also.

where YT(j0) is temporally aggregated by scheme j0 and XT(j1) is temporally aggregated by a different scheme j1 (≠j0).
In this section we present a representation of the cointegrated system where the length of the sampling interval m is not fixed. This representation is used to discuss the problem of temporal aggregation that occurs when a practitioner makes inference on cointegration with data measured at a longer sampling interval than the long-run dynamics are generated. Hence, we use the term disaggregated model to describe the cointegrated system measured at the frequency where the long-run dynamics are generated, i.e., the time interval between a shock that alters the equilibrium and the moment the markets react to the disequilibrium. We use the triangular system representation of Phillips (1991b) to do so, because this model avoids having to specify the short-run dynamics and the aggregation effect on the long-run variance can be determined exactly.
Suppose that the long-run dynamics of a k-dimensional I(1) time series zt = (yt′,x1,t′)′ were generated at time interval Δt by the process
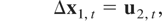
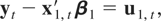
where yt is k0-dimensional, x1,t is k1-dimensional, and ut ≡ (u1,t′,u2,t′)′ is a stationary process that satisfies the invariance principle
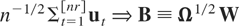
for r ∈ [0,1] as n → ∞, where W denotes a k-dimensional standardized Brownian motion with variance matrix Ω ≡ limn→∞ n−1E [(Σ1nuj)(Σ1nuj)′], the long-run variance of ut. Let us partition Ω according to ut:
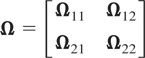
and define the conditional long-run variance Ω11.2 ≡ Ω11 − Ω12Ω22−1Ω21. We assume that the matrix Ω22 is positive definite in such a way that x1,t is individually I(1) but not CI(1,1). Under these assumptions, the process zt is a CI(1,1) process with k0 cointegrating relations and k1 common stochastic trends.
Representation (1)–(3) has been used to analyze optimal inference on cointegrating vectors (see Phillips, 1991b) and to design a number of optimal regression-type estimators. Phillips and Hansen (1990) and Park (1992) propose semiparametric methods, Saikkonen (1991) and Stock and Watson (1993) dynamic regression methods, and Phillips (1991c) a frequency domain method. A very important property of optimal estimators of cointegrating vectors is their asymptotic mixed Gaussian distribution, meaning that a test for g restrictions on β1 is χg2 distributed (Phillips, 1991b). However, regression-type methods are not very well suited to model building because they impose the location and number of unit roots on the model rather than testing them. This has two important consequences. First, it is not possible to test sequentially for the number of cointegration relations, because a triangular model with k0′ cointegrating relations is not nested into a triangular model with k0′′ (>k0′) cointegrating relations (see Johansen, 1994). Second, regression-type estimators impose normalization restrictions on cointegrating vectors, and this may lead to inconsistent inference if such restrictions do not hold. In addition, these methods were originally designed to test for a single cointegrating relation (k0 = 1), and this restricts their applicability to very small systems. However, even small systems can be governed by more than one cointegrating relation, and although it is possible to estimate more than one cointegrating relation with regression methods, the properties of the estimator and tests for the extra cointegrating relations are not clear (see Hargreaves, 1994). For all these reasons, system methods that test for the dimension of the cointegrating space and do not impose normalization restrictions, such as the full maximum likelihood analysis of cointegrated vector autoregression (VAR) (see Johansen, 1991), are commonly used for model building.
The aim of this paper is to study the effects of different aggregation options on inference rather than on model building, and the triangular model is more suitable for this purpose than other representations of the cointegrated system, such as the VAR model or the moving average (MA) model, because of its nonparameterization of the short-run dynamics.
The main focus of the paper is CI(1,1) relations, but we consider two particular cases of cointegration with I(2) variables. To do so, let us suppose that the long-run dynamics of a k-dimensional time series zt ≡ (yt′,x1,t′,x2,t′)′ are generated by the following model:
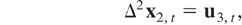
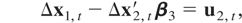
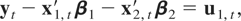
where x2,t is k2-dimensional (k0 + k1 + k2 = k), ut = (u1,t′,u2,t′,u3,t′)′ satisfies (3), and Ω22 and Ω33 are positive definite. This is a very general model that allows for many different cointegrating relationships. Matrix [Ik1,−β3] denotes the CI(2,1) cointegrating vectors of (x1,t′,x2,t′)′, matrix [Ik0,−β2] contains CI(2,2) cointegrating vectors of (yt′,x2,t′)′ when some or all the elements of β1 are zero, and matrix [Ik0,−β1] contains the CI(1,1) cointegrating vectors of (yt′,x1,t′)′ when some or all the vectors of matrix β2 are zero. For the nonrestricted case, [Ik0,−β2] denotes the CI(2,1) cointegrating vectors of (yt′,x2,t′)′, and [Ik0,−β1] denotes the CI(1,1) vectors of (yt′ − x2,t′ β2,x1,t′)′. In this general setting, Stock and Watson (1993) proposed dynamic optimal inference methods and Kitamura (1995) full and partial information maximum likelihood methods. Under the very restrictive assumption that Ω12 = Ω13 = Ω23 = 0, the ordinary least squares (OLS) estimator is optimal in the sense that it has a mixed Gaussian distribution allowing for a standard χ2 inference (see Haldrup, 1994).
Let us use ZT(j0,j1,j2) (with j0,j1,j2 = {0,1}) to denote the observable vector time series that is measured at a longer sampling interval ΔmT = mΔt than zt. The representation of this temporally aggregated process is given in the following lemma.
LEMMA 2.1. If zt is generated by (3)–(6), the observable temporally aggregated time series ZT(j0,j1,j2) can be represented as

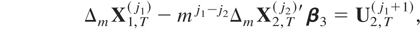
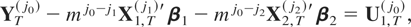
where LmZT(j0,j1,j2) = ZT−1(j0,j1,j2) , Δm ≡ 1 − Lm, and UT(j0,j1+1,j2+2) ≡ (U1,T(j0)′,U2,T(j1+1)′,U3,T(j2+2)′)′ satisfies the multivariate invariance principle

where Ω11(0) = m−1(Ω11 + Λ(m)), Ω11(1) = mΩ11, Λ(m) = 4πΣj=1m−1F11(2πj/m), and F11(ω) is the spectral density matrix of u1,t.
Proof. See the Appendix.
From Lemma 2.1, the number of cointegrating relations is invariant with any of the different combinations of aggregation schemes. However, the cointegrating spaces are not generally invariant with temporal aggregation. More specifically, when the aggregation schemes applied to the regressand and the respective regressors are the same (jl = jh), the cointegrating relations are invariant. If not, when some of the variables are aggregated with systematic sampling and others with average sampling, the cointegrating space changes with m. The weights mjl−jh capture this change in cointegrating relations, which is exclusively attributable to a change in the unit of measurement. Ericsson, Hendry, and Tran (1994) analyze the effects of linear filters, zta = g(L)zt, on cointegrating vectors. They show that when all the filtered time series are measured by the same units, g(1) = I, then the filtered series zta and the original series zt have the same cointegrating space. This condition does not hold for mixed sampling, because the flow variables are measured in relation to the sampling interval, i.e., that month's income but not the stocks, i.e., money supply.
The second main effect of temporal aggregation on the cointegrated system is a change in the short-run dynamics. The different effects of temporal aggregation on the error terms of the cointegrated system change the short-run dynamics and also their contribution to the long run, represented by the aggregated long-run variance Ω(j0,j1+1,j3+2) . For any possible combination of aggregation schemes, the short-run dynamics will always vary. For example, when the aggregation schemes are the same (j0 = j1 = j3 = j), the long-run variance of U2,T(j+1) increases in relation to the long-run variance of U1,T(j), and the long-run variance of U3,T(j+2) increases in relation to the long-run variances of the other errors. Note that when the regressand is systematically sampled, YT(0), the long-run variance of U1,T(0) is an average of the disaggregated long-run variance Ω11 and the variance of those seasonal cycles that emerge as a result of the aliasing effect, Λ(m). For instance, a quarterly stock variable with an important semiannual seasonal cycle (F11(π)) systematically sampled as a semiannual variable (m = 2) will experience a substantial increase in the long-run variance of the semiannual systematically sampled cointegrating error U1,T(0). As discussed in the next section, this type of aggregation will make the mixed normal distribution of the estimator of the cointegrating vectors more disperse.
Let us focus on the CI(1,1) model. The following corollary particularizes the previous results to this situation.
COROLLARY 2.2. If zt is generated by (1)–(3), the temporally aggregated time series ZT(j0,j1) can be represented as
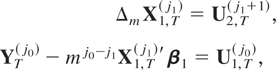
where UT(j0,j1+1) ≡ (U1,T(j0),U2,T(j1+1)) satisfies the multivariate invariance principle
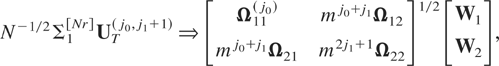
where Ω11(j0) is defined as before.
Proof. It follows from Lemma 2.1.
In this case, we can differentiate four different temporal aggregation situations. We use the same classification as Chambers (2003) and identify the pure systematic sampling situation as aggregation type I (ZT(0) = (YT(0)′,X1,T(0)′)′), the mixed sampled process ZT(01) = (YT(0)′,X1,T(1)′)′ as aggregation type II, the other mixed sampled situation ZT(10) = (YT(1)′,X1,T(0)′)′ as aggregation type III, and finally the pure average sampled process (ZT(11) = (YT(1)′,X1,T(1)′)′) as aggregation type IV. Table 1 shows the aggregation effect of these different aggregation schemes for m = 3 on the long-run variances Ω11.2(j0), Ω22(j1+1), and on Ξi(m) ≡ mj0−j1(Ω11.2 + (1 − j0)Λ(m))1/2 (i = I, II, III, IV), which, as shown in the next section, is the relative dispersion of the mixed normal distribution across m for the different aggregation schemes.
Temporally aggregated long-run variances of the CI(1,1) model for m = 3

Let us consider a particular case of the I(1) cointegrated model. Assume that k0 = k1 = 1, u1,t = ρu1,t−1 + ε1,t with |ρ| < 1, ε1,t is i.i.d.N(0,1), u2,t = ε2,t is i.i.d.N(0,σ2), and E(ε1,tε2,t−j) = 0 for all j. The systematically sampled model is given by
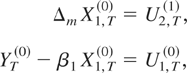
where U2,T(1) = E2,T(1) = sm(L)ε2,mT, and U1,T(0) = ρmU1,T−1(0) + E1,T(0), E1,T(0) = [(1 − ρmLm)/(1 − ρL)]ε1,mT is serially uncorrelated and not correlated with E2,T(1) for all lags and leads. From Pesaran and Shin (1996) the impact of a unit shock to the variable YT(0) on the cointegrating relation after one T-period is given by the autoregressive coefficient ρm. Then, given |ρ| < 1, the longer the sampling interval with respect to the long-run dynamics generating time interval, the faster the adjustment of the system to a disequilibrium. Let us consider the two limiting aggregation cases. In the maximum aggregation case, i.e., when m → ∞, all the adjustment takes place in one period (limm→∞ ρm = 0), whereas for the maximum disaggregation case, when m → 0, no adjustment takes place (limm→0 ρm = 1). Therefore, the finer the sampling interval the closer the cointegrated model is to a noncointegrated system.
This example illustrates that when the long-run dynamics are measured at a much longer sampling interval than their generating time interval, then the speed of adjustment of the cointegrating relation should be very fast. In practice, for many cointegrated relations the estimated speed of adjustment with monthly or quarterly time series is low, and this suggests that the long-run dynamics for many cointegrated systems are not generated at a much shorter time interval.
We will now discuss the asymptotic effects of different types of aggregation on the estimation of β1, β2, and β3 and on the observed information. Even though we focus on optimal CI(1,1) regressions we also provide theoretical results for two examples of CI(2,2) and CI(2,1) processes.
Suppose that a k-dimensional time series zt = {(yt,x1,t′)′}t=1n, where yt is a scalar time series4 and x1,t is a k1-dimensional time series, is generated by
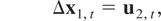
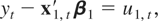
where ut = (u1,t,u2,t′)′ is a stationary process that satisfies (3). Let
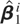
denote an optimal regression-type estimator of β1 using the time series ZT(j0,j1) where i = I for ZT(0), i = II for ZT(01), i = III for ZT(10), and i = IV for ZT(1). The following theorem presents its limiting distribution.
THEOREM 3.1. The asymptotic distribution of the optimal regression-type estimator of β1 in model (10) and (11) with temporally aggregated time series is
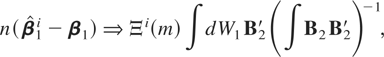
where the relative dispersion across the sampling interval Ξi(m) is ΞI(m) = (Ω11.2 + Λ(m))1/2, ΞII(m) = m−1(Ω11.2 + Λ(m))1/2, ΞIII(m) = mΩ11.21/2, and ΞIV(m) = Ω11.21/2.
Proof. See the Appendix.
From Theorem 3.1, comparing these asymptotic distributions with the one for an optimal estimator of the disaggregated model, Ω11.21/2 ∫dW1B2′(∫B2B2′)−1, there is no loss of efficiency when the regressand and the regressor are average sampled (aggregation IV), whereas there is a loss of efficiency when the regressors are systematically sampled, i.e., aggregation schemes I and III. These results are in keeping with those of Chambers (2003), who considers a similar scenario where the disaggregated model is a continuous time cointegrated model.
However, in contrast with Chambers (2003), in case II three situations are possible depending on the relative size of the aliasing component Λ(m) in relation to the conditional long-run variance Ω11.2. To be more specific, when Λ(m) = (m2 − 1)Ω11.2, which implies that 2Σj=1m−1F11(2πj/m) = (m2 − 1)F11.2(0), there is no loss of efficiency, whereas for 2Σj=1m−1F11(2πj/m) > (m2 − 1)F11.2(0), there is a loss of asymptotic efficiency, and when 2Σj=1m−1F11(2πj/m) < (m2 − 1)F11.2(0) there is a gain in asymptotic efficiency. In any case ΞII(m) < ΞI(m), and when Λ(m) < (m4 − 1)Ω11.2, then ΞII(m) < ΞIII(m).
To summarize, type II aggregation is always more efficient than type I aggregation, and type IV aggregation is always more efficient than types I and III aggregation. When Λ(m) < (m2 − 1)Ω11.2 type II is more efficient than IV aggregation and therefore is the most efficient option.
Continuing with the example of Section 2.2 and for m = 3, a situation of no loss of asymptotic efficiency with aggregation II occurs when ρ = −0.27, for −1 < ρ < −0.27 there is a loss of efficiency, whereas for −0.27 < ρ < −1 there is a gain of efficiency.
Let us compare the relative dispersions Ξi(m) with those derived with the continuous time aggregation approach (see Chambers, 2003), which we denote as ΞCi. To do so, let us consider a bivariate triangular continuous time cointegrated model:
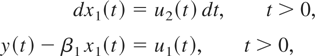
where (u1(t),u2(t))′ is a stationary continuous time process with spectral density function FC(ω) with −∞ < ω < ∞. From Chambers (2003, p. 59) and given that for j ≠ 0 h(2πij) = (2πij)−1, h(2πij) + h(−2πij) = 0 and |h(2πij)|2 = (4π2j2)−1, we obtain the expressions

There are important differences between ΞCi and Ξi(m). First of all, in the continuous time setting, type II aggregation is the most inefficient option for any FC(ω), a result that contrasts with the findings obtained in the discrete time approach where type II aggregation may be the most efficient way to aggregate the time series and in any case is less efficient than schemes I. Second, the cointegration coefficient β1 appears at the limiting distributions of the discrete time optimal estimator derived from the continuous time cointegrated system, a result that is in contradiction with the optimal theory of estimation of cointegrating vectors (see Saikkonen, 1991; Phillips, 1991b). Finally, in the continuous time approach, the aliasing affects the distributions through the error process of the cointegrated relations (2πΣj≠0 FC,11(2πj)), and through the error process of the common stochastic trends (2πβ12Σj≠0(4π2j2)−1FC,22(2πj)), a surprising result because for both types of aggregation the process u2(t) is at least cumulated once ∫u2(t − s) ds, a transformation that eliminates the components FC,22(2πj) in scheme IV of continuous time aggregation for the errors of the cointegrating relations. Thus, the continuous time aggregation fails to explain the discrete time aggregation results.
Theorem 3.1 has practical implications. If we consider the common situation where the practitioner may decide how to aggregate a stock time series, then we have two different situations depending on whether it is the regressand or the regressor that is temporally aggregated. When a practitioner has to aggregate a stock regressand and the regressor is a stock, the best aggregation option depends on the sign of Λ(m) − (m2 − 1)Ω11.2. If this magnitude is negative, the best option, in terms of estimation efficiency, is to use systematic sampling (aggregation I), whereas if it is positive, the optimal choice is average sampling (aggregation III). When the regressor is a flow, the best option depends on Λ(m) − (m2 − 1)Ω11.2, in the sense that when this parameter is positive the stock regressand should be aggregated by average sampling (aggregation IV), whereas when it is negative the regressand should be aggregated by systematic sampling (aggregation II). When a practitioner has to aggregate a stock regressor, the best option, in terms of the asymptotic dispersion of the estimator, is always to apply average sampling to the regressor because aggregations II and IV are superior in efficiency to aggregations I and III, respectively. Therefore, the picture that emerges from the discrete time aggregation analysis is more complex than the one obtained from the continuous time approach where the best option seems to be in any situation to apply average sampling. We provide finite-sample evidence favoring our theoretical findings in Section 4.
In practice, when deciding whether to aggregate the stock regressand by systematic or average sampling, we need to compare Λ(m) with (m2 − 1)Ω11.2. However, because the flow variables are observable at a longer sampling interval than the stock variables, it is necessary to get Ω12Ω22−1Ω21 from the observable Ω12(j0,2)Ω22(3)−1Ω21(2,j1). Then, from the relation

we can estimate Ω12Ω22−1Ω21 and Ω11.2 and compare the estimations of Λ(m) and (m2 − 1)Ω11.2.
To summarize, when a stock regressand must be temporally aggregated because some of the regressors are not available at the finest sampling interval, then depending on the magnitudes Λ(m) and (m2 − 1)Ω11.2 systematic or average sampling are the best aggregation options in terms of the dispersion of the mixed normal distribution. When a practitioner has to choose an aggregation option for the stock regressor, the best choice is always to apply average sampling.
The main results found for case CI(1,1) can be extended to models with I(2) variables. We do not aim to cover all possible situations of cointegration in models with I(2) variables but to show the robustness of the aggregation theory for some relevant examples. First, let us assume the following disaggregated model:
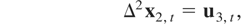

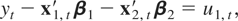
where ut = (u1,t,u2,t′,u3,t′)′ satisfies the assumptions described in Section 2 and the long-run covariances are zero Ω12 = Ω13 = Ω23 = 0. For this model the optimal estimator is the OLS estimator. Theorem 3.2 shows the asymptotic distribution of the optimal estimator of β1 and β2 for the aggregation schemes ZT(0) (aggregation I), ZT(011) (aggregation II), ZT(100) (aggregation III), and ZT(1) (aggregation IV).
THEOREM 3.2. The asymptotic distribution of the optimal regression-type estimator of β = (β1′, β2′)′ in model (12)–(14) with temporally aggregated time series is

Proof. See the Appendix.
From Theorem 3.2, temporal aggregation has the same effect on the separate distribution of the estimator of β1 as on the separate distribution of the estimator of β2, and this effect is exactly like that found for case CI(1,1).
Now consider the estimation of CI(2,1) relations, which we assume are generated by the following model:
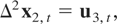
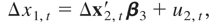
where ut = (u2,t,u3,t′)′ satisfies the general assumptions for the cointegrated model with I(2) variables described in Section 2. In this situation, the optimal regression-type estimators of β3 are those estimators for the CI(1,1) model with differenced variables. The limiting distribution for the different aggregation schemes is given in the next corollary.
COROLLARY 3.3. The asymptotic distribution of the optimal regression-type estimator of β3 in model (15) and (16) with temporally aggregated time series is
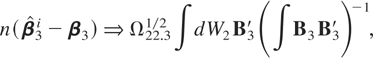
where ΞI(m) = Ω22.31/2, ΞII(m) = m−1Ω22.31/2, ΞIII(m) = mΩ22.31/2, and ΞIV(m) = Ω22.31/2.
In this case, as a result of the absence of the aliasing effect because the errors are average and double-average sampled, we find slightly different results. Now, for pure aggregation schemes I and IV the limiting distribution remains invariant despite the sampling interval, whereas in the case of mixed sampling the dispersion is reduced with m for aggregation II, and it increases with m for aggregation III.
Now, when a practitioner has to aggregate a stock regressand, the best option is always to apply systematic sampling. This is slightly different from case CI(1,1) where in some situations the best way to aggregate the regressand was average sampling when the regressor was a flow. When it is the stock regressor that needs to be aggregated, the practitioner has to apply average sampling in all cases, in keeping with case CI(1,1).
The limiting properties of the optimal estimator of β1 are derived under the assumption that the long-run variance Ω must be consistently estimated, and there may be a loss of valuable information when this matrix is estimated with temporally aggregated time series. Consequently, the aggregation effects on the estimation of Ω may alter the preceding conclusions reached on the best aggregation option for the estimation of long-run relations in finite samples. However, the Monte Carlo evidence provided in Section 4 shows that the estimation of Ω does not make any significant difference to the order in which the types of aggregation are ranked.
When the purpose of the analysis is to test a hypothesis on the cointegrating vectors, such as the PPP theory or permanent income hypothesis, the aggregation effect on the marginal distribution of the estimator provides us with half the story, because for nonstationary cointegrating regressions, the observed information Jn(β1) ≡ −∂2 log L(β1)/∂β1∂β1 where log L(β1) is the log likelihood function, and not the variance of
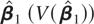
, is used as the normalizing matrix of the χ2-distributed Wald test (see Johansen, 1995):
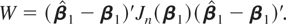
This situation is different from a stationary regression where
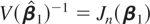
, and the marginal distribution of the estimator is sufficient to discuss the aggregation effect. However, the observed information in a cointegrated model is different from the inverse of the variance of the estimator, and the aggregation effect must be considered on both the estimator and the information. This task is straightforward when we only consider the asymptotic properties, because the χ2 distribution of the Wald test implies that the aggregation effect on the observed information should neutralize the aggregation effect on the estimator. Thus, an increase in the dispersion of the asymptotic distribution of the estimator due to aggregation should be counterbalanced by a reduction in the dispersion of the distribution of the information. For example, for Λ(m) = (m2 − 1)Ω11.2, the asymptotic dispersion of the observed information increases for cases I and III, whereas it is invariant for cases II and IV. Therefore, in asymptotic terms it is not relevant which type of aggregation we select to test restrictions on β1.
However, this asymptotic result may be different when we consider the more realistic finite-sample framework. In such a setting, as shown by Johansen (2002), the distribution of the test is slightly different from the χ2 distribution, depending not only on the number of observations but also on the parameters of the model. As shown in Section 2, different combinations of aggregation schemes have different effects on the short-run dynamics, and therefore in finite samples one aggregation scheme may be clearly superior to another for hypothesis testing. Moreover, the faster convergence of the observed information n−2Jni(β1) than the estimator
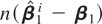
may contribute to the fact that the aggregation effect on Jn(β1) has a bigger influence on the finite-sample properties of the test than the aggregation effect on

. However, the Monte Carlo experiment in Section 4 shows that, for the selected model, all the aggregation options have similar effects on the size of the test.
In this section we study the finite-sample aggregation effect on the FM-OLS.5
We use the FM-OLS routine available at the COINT Gauss library, programmed by Sam Ouliaris and Peter Phillips. More specifically, the long-run variance is estimated with the Parzen spectral window, AR(1) prewhitening, and automatic bandwidth selection. We also considered the dynamic ordinary least squares estimator, which led to qualitatively similar results that are not reported here to save space.
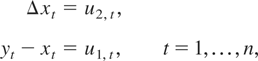
where u1,t = ρu1,t−1 + ε1,t, u2,t = ε2,t, and
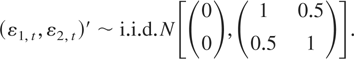
The length of the sampling interval was fixed as m = 3. The relevant magnitudes for the aggregation effect are the aliasing component, Λ(3), and the conditional long-run variance of the cointegrating errors, Ω11.2. This very simple model allows us to control these magnitudes through parameter ρ. More specifically, we consider three sizes for the aliasing effect, so that for ρ = −0.5 the aliasing component is very big in comparison with 8Ω11.2 (Λ(3) = 4.54 and 8Ω11.2 = 2.64); for ρ = 0 the aliasing component is slightly smaller than 8Ω11.2 (Λ(3) = 4 and 8Ω11.2 = 6), and for ρ = 0.5 the aliasing component is much bigger than 8Ω11.2 (Λ(3) = 2.28 and 8Ω11.2 = 24).
The experiment is performed with two spans, n = 120 and n = 360. We only present the results for the shorter span, n = 120, to compare the different aggregation effects on the estimator and test (see Table 2) because a comparison of the aggregation schemes is not (qualitatively) affected by the size of the span. As a measure of the aggregation effect on the precision of the estimator, we provide the ratio of the mean square error (MSE) of the aggregated estimator in relation to the disaggregated estimator, denoted M(i) where i ∈ {I, II, III, IV} is an aggregation scheme. As a measure of the aggregation effect on the test, we compute the variation of the size of the test for H0 : β = 1 based on the 5% level, denoted S(i) with i ∈ {I, II, III, IV}. That is, S(i) stands for the difference between the size of the test in the aggregated models and the size in the disaggregated model. Three thousand replications of the experiment are used to obtain Monte Carlo estimations of the MSE and 10,000 for the size of the test. We also compare the aggregation effect with the span effect. To do so, with the disaggregated model we compute the variation in the MSE (M(n)) and size (S(n)) for a small sample n = 120 and a big sample n = 360. To avoid the influence of initial conditions, a constant is estimated together with the cointegrating coefficient and the first 50 observations are discarded.6
Additionally we considered many other values for the parameters, i.e., different correlations between the errors (δ = 0 and δ = −0.5 instead of δ = 0.5) and different values for the variance of u2,t (σ2 = 2). However, the aggregation effect does not depend on the value of these parameters, and therefore we do not present all these results here. Tables with the additional results are available upon request.
Comparison of the different temporal aggregation effects

Table 2 shows the variation in the MSE and the size of the test when different types of aggregation are applied to the DGP described previously for n = 120. When 8Ω11.2 > Λ(3), the best aggregation scheme, in terms of the precision of the estimator, is aggregation type II, with a lower MSE than the disaggregated estimator. The second best aggregation option is aggregation type IV. With this data transformation, the MSE hardly varies in comparison with the disaggregated estimator. Much less precise estimations of the cointegrated vector are obtained when the regressor is systematically sampled, with aggregation III being the worst option and there being a tremendous relative increase in the dispersion of the estimator. The performance of the estimator, when both variables are systematically sampled (i = I), is largely dependent on the relative size of the aliasing component, with the result that when the aliasing component is smaller than the long-run conditional variance, the precision of the estimator is closer to the precision of the estimator with aggregation IV.
If we look at the aggregation effect on the test, we find a different story. In this case, all the aggregation schemes increase the distortion of the test by approximately 3 to 5 points. The main difference, when compared with the aggregation effect on the precision of the estimator, is that now the different types of aggregation all share a very similar effect. The few differences that can be observed reveal that the aggregation effect on the test cannot be explained by the aggregation effect on the estimator. The most significant example is the case ρ = 0.5, where the least distorted test is obtained with aggregation III, the worst aggregation option in terms of the MSE. However, we cannot infer from this that the worst aggregation for estimation purposes is the best one for testing, because if we look at case III for ρ = −0.5, where there is the biggest loss in estimator precision (22.9), it is not the one with the least size distortion.
It is interesting to compare the aggregation effect with the effect of the span on the estimator and the test. In Table 3 we present the variation in the MSE and size when the sample is reduced from 360 to 120 observations, either by reducing the span by 3 (M(n) and S(n)), or by temporal aggregation (M(i) and S(i), i ∈ {I, II, III, IV}). If we examine the effects on the precision of the estimators, the reduction of the span has similar repercussions to the worst aggregation schemes (I, III), a situation similar to that one expects to find with a stationary regression. However, the reduction of the span clearly has worse consequences than aggregation schemes II and IV, which shows that the aggregation effect on the estimation of cointegrating regressions is not as important as the aggregation effect on stationary regressions.
Comparison between the span effect and the temporal aggregation effect

Focusing on the test, reducing the span has a slightly bigger impact on size than aggregation. However, once again the few exceptions that can be observed show how the effects on the test are different than on the estimator. For example, when ρ = 0, the size distortion of aggregation II is practically the same (2.2) as the distortion caused by the reduction of the span (2.1). However, for this case, if we consider the effect on the precision of the estimator, the reduction of the span affects the quality of the estimation far more than aggregation with scheme II.
To summarize the Monte Carlo results, different aggregation schemes have very different effects on the precision of the estimator, thus confirming the asymptotic theory derived in the paper. More specifically, when the regressor is average sampled, the precision is not affected or even improved by temporal aggregation, whereas when the regressor is systematically sampled the estimator is clearly less precise, especially when the regressand is average sampled. The aggregation effects on the test are very different from the effects on the estimator. In this case, there are no significant differences among the different aggregation options. Finally, we found that reducing the span has a similar effect on precision to those aggregation schemes where the regressor is systematically sampled (I, III) and a much greater effect than those aggregations where the regressor is average sampled (II, IV). Also, a reduction in the span has a slightly greater effect on size than the temporal aggregation of the variables.
We have discussed the effects of different types of discrete time aggregation on the regression-type optimal inference on cointegrating vectors and have shown how different types of aggregation have different effects on the limiting properties and finite-sample properties of optimal estimators but similar effects on the hypothesis test. The theoretical aggregation results have potential empirical implications, because in many situations, a practitioner decides how to temporally aggregate certain variables before making inferences on the cointegrating vectors, because stock variables such as exchange rates, interest rates, or the money supply can be temporally aggregated either by systematic sampling or by average sampling. As for the practical implications of our study, if a stock regressand must be temporally aggregated, because some of the regressors are not available at the finest sampling interval, then when Λ(m) < (m2 − 1)Ω11.2 the best aggregation scheme is systematic sampling whereas otherwise average sampling is the best option in terms of estimation precision. When a practitioner has to choose an aggregation option for the regressor, the best choice is always to apply average sampling. These results only partially corroborate those of Chambers (2003), where the main recommendation was always to use average sampling. From our conclusions it seems that, as long as the aliasing effect is not very important, it is a very bad idea to apply average sampling to a regressand when the regressor is a stock, because this combination of aggregations leads to the highest increase in the noise-to-signal ratio. These differences are discussed theoretically and illustrated with a Monte Carlo study where aggregation type II outperforms aggregation type IV for the situation predicted by the discrete time aggregation theory.
It is a very different story when a practitioner plans to test a long-term theory, rather than just estimating a long-run relation. In this case the different aggregation options have a very similar effect on the test, and none of them, whatever the situation, leads to a least size-distorted test.
We have also compared the effect of the span with the effect of temporal aggregation, and the main conclusion is that the span has a greater effect on inference than temporal aggregation. To be more precise, the span has a much greater impact on the estimator than the best aggregation schemes, II and IV, and a slightly bigger effect on the test than any of the aggregation schemes.
As a further research issue it would be interesting to analyze which aggregation option is best suited for other purposes such as prediction, because in this case the relevant aggregation effects are not those on the cointegrating vector but on the adjusting vector (see Johansen, 1994).
Proof of Lemma 2.1.
(a) Temporally Aggregated Triangular Representation. Let us consider the representation of the systematically sampled process ZT(0). To apply systematic sampling to equations (4)–(6), we need to express the model in such a way that the variables are observable every m t-period. This is the case of all the variables in equation (6) but not in (4) or (5) because of the presence of differenced (Δx1,t, Δx2,t) and double-differenced variables Δ2x2,t. Because Δm = Δsm(L), we multiply both sides of (5) by the summation filter and both sides of (4) by [sm(L)]2 to get the following representation:
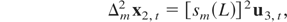
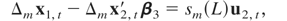
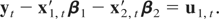
Now this representation of the disaggregated cointegrated model is observable at the longer sampling interval mΔt, and so we just apply systematic sampling to (A.1)–(A.3), thus obtaining the representation of ZT(0):

where U3,T(2) = [sm(L)]2u3,mT, U2,T(1) = sm(L)u2,mT, and U1,T(0) = u1,mT.
To obtain the representation of the pure average sampled process ZT(1), we just need to apply the summation polynomial to equations (A.1)–(A.3) and then apply systematic sampling. The aggregated model for mixed sampling is obtained by similar transformations to the two preceding cases. Let us focus on equation (A.3) and consider the cases ZT(010) and ZT(110). For the first case, we multiply x1,t in (A.3) by sm(L)−1sm(L):
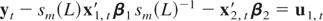
and then apply systematic sampling, thereby obtaining
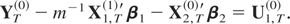
For the case ZT(110), we apply the summation polynomial to both sides of (A.3):
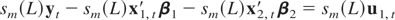
and then, through sampling, obtain

The remaining cases are obtained in a similar way.
(b) Temporally Aggregated Multivariate Invariance Principle. Given the fact that m is finite, the application of any of the temporal aggregation schemes as a linear filter does not alter the multivariate invariance principle, but rather the variance of the Brownian motion, the long-run variance of ut. Consequently, we derive the aggregation effects on the long-run variance, and for this purpose we determine the effects of the different aggregation filters on the covariance function.
Let Γ(k) ≡ E(utut−k′) denote the covariance function of the stationary process ut. The effect of systematic sampling on the covariance function is
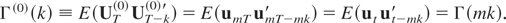
Any combination of aggregation schemes implies the application of a specific lag polynomial to the covariance function before applying systematic sampling. Thus, the effect of the lag operator on the displacement k of the covariance function (see other examples from literature on temporal aggregation such as Telser, 1967; Stram and Wei, 1986) is
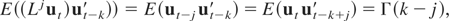
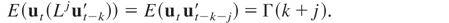
From (A.4)–(A.6) it is straightforward to determine the effect of the different combinations of aggregations on the covariance matrix function. All possible combinations are given by

Thus, the temporally aggregated long-run variances are obtained from the definition of long-run variance:
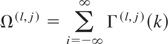
in such a way that, with the exception of Ω(0), they are

For the systematically sampled long-run variance Ω(0), we use the result reached by Niemi (1984), who obtains F(0)(ω), the spectrum of a systematically sampled process, and the fact that Ω(0) = 2πF(0)(0), getting

Proof of Theorem 3.1. To obtain the asymptotic distribution of the different combinations of aggregations, we replace the expressions for the temporally aggregated long-run variances presented in Lemma 2.1 in the formulation of the mixed normal distribution of Theorem 1 of Phillips (1991b, p. 299), so that, after some manipulation of the sampling interval, we get

These expressions cannot be compared with the disaggregated mixed normal distribution because they are normalized by a different sample size. So, to get comparable distributions, we must obtain the expression for the distribution where the span normalizes the estimator bias:

Proof of Theorem 3.2. The proof of this theorem is very similar to the preceding one, and therefore we have not presented the details. It is only necessary to replace the expressions for the different long-run variances cited in Lemma 2.2 in Haldrup's Theorem 2 (Haldrup, 1994, p. 163). █

Temporally aggregated long-run variances of the CI(1,1) model for m = 3

Comparison of the different temporal aggregation effects

Comparison between the span effect and the temporal aggregation effect