1 Introduction
Solutions to the Stokes equation can be constructed by combining suitably placed Stokeslets (the Green function of the Stokes equation) and other singular solutions, that simultaneously satisfy the equation of motion and the boundary conditions (Happel & Brenner Reference Happel and Brenner1983). This approach has proven especially fruitful in describing the motion of small solid bodies (Chwang & Wu Reference Chwang and Wu1975). In recent years, methods of Stokesian dynamics have been widely employed in studies of active matter systems and self-propelled particles (Lauga & Powers Reference Lauga and Powers2009; Spagnolie & Lauga Reference Spagnolie and Lauga2012). Such systems often possess unique mechanical properties, with a vanishingly small shear viscosity observed in suspensions of swimming bacteria (López et al. Reference López, Gachelin, Douarche, Auradou and Clément2015; Saintillan Reference Saintillan2018) and a recent debate on the pressure exerted by microswimmers on the walls of the enclosing container (Takatori, Yan & Brady Reference Takatori, Yan and Brady2014; Yang, Manning & Marchetti Reference Yang, Manning and Marchetti2014; Solon et al. Reference Solon, Fily, Baskaran, Cates, Kafri, Kardar and Tailleur2015) being just a few examples. Most of the macroscopic properties predicted for active matter systems still await experimental confirmation. When designing such experiments, which typically include measurements of the forces that the system in question exerts on confining boundaries, as in the cases of shear viscosity and pressure, one often seeks to estimate the order of magnitude of the potential effect. Since the velocity fields generated by self-propelled particles can be constructed from the fundamental solutions of the Stokes equation, it is sufficient to consider the forces exerted on solid boundaries due to the latter. Surprisingly, there are no results available in the literature for the forces exerted on solid boundaries, even by the simplest of singularities, and here we seek to fill this gap.
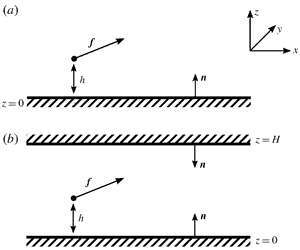
We study two archetypal problems: a Stokeslet next to a single flat boundary, and a Stokeslet confined in between two parallel walls, see figure 1. Both problems are solved in a Cartesian coordinate system
$\{x,y,z\}$
, with the
$z$
-direction selected perpendicular to the boundaries. The velocity field
$\boldsymbol{v}(\boldsymbol{r})$
at a position
$\boldsymbol{r}$
satisfies the incompressible Stokes equation
$$\begin{eqnarray}\displaystyle & \displaystyle -\unicode[STIX]{x2202}_{i}p(\boldsymbol{r})+\unicode[STIX]{x1D707}\unicode[STIX]{x2202}^{2}v_{i}(\boldsymbol{r})+f_{i}\unicode[STIX]{x1D6FF}(\boldsymbol{r}-\boldsymbol{r}_{\mathbf{0}})=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x2202}_{i}v_{i}(\boldsymbol{r})=0, & \displaystyle\end{eqnarray}$$
where
$p$
is the pressure, and
$\unicode[STIX]{x1D707}$
is the viscosity of the fluid;
$\unicode[STIX]{x2202}_{i}$
denotes the spatial derivative in the
$i$
th direction,
$i=\{x,y,z\}$
, while
$\unicode[STIX]{x2202}^{2}$
denotes the Laplacian. The point force
$\boldsymbol{f}$
is applied to the fluid at a position
$\boldsymbol{r}_{\mathbf{0}}$
, which, without loss of generality, is chosen to be
$(0,0,h)$
. The fluid is assumed to satisfy the no-slip condition at all boundaries. The solution to (1.1) and (1.2) has been obtained by Blake (Reference Blake1971), for the case of a single boundary, and by Liron & Mochon (Reference Liron and Mochon1976) and Daddi-Moussa-Ider et al. (Reference Daddi-Moussa-Ider, Lisicki, Mathijssen, Hoell, Goh, Bławzdziewicz, Menzel and Löwen2018) for two confining walls. Here, we use these results to evaluate the associated forces applied by the fluid on the enclosing boundaries.
Figure 1. Geometries used in this note. (a) A point force applied to a fluid next to a wall. (b) A point force applied in between two parallel walls. The unit vector
$\boldsymbol{n}$
gives the direction of the outer normal to each boundary.
2 A point force next to a single boundary
In this problem, we consider a semi-infinite fluid bounded by an infinite, flat solid boundary at
$z=0$
(see figure 1
a). The solution to (1.1) and (1.2) in this case has been obtained by Blake (Reference Blake1971), and reads
$$\begin{eqnarray}\displaystyle v_{j} & = & \displaystyle \frac{f_{k}}{8\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}}\left[\left(\frac{1}{r}-\frac{1}{R}\right)\unicode[STIX]{x1D6FF}_{jk}+\frac{r_{j}r_{k}}{r^{3}}-\frac{R_{j}R_{k}}{R^{3}}\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,2h\left(\unicode[STIX]{x1D6FF}_{k1}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R_{1}}+\unicode[STIX]{x1D6FF}_{k2}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R_{2}}-\unicode[STIX]{x1D6FF}_{k3}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R_{3}}\right)\left\{\frac{hR_{j}}{R^{3}}-\frac{\unicode[STIX]{x1D6FF}_{j3}}{R}-\frac{R_{j}R_{3}}{R^{3}}\right\}\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle p=\frac{f_{k}}{8\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}}\left[\frac{r_{k}}{r^{3}}-\frac{R_{k}}{R^{3}}-2h\left(\unicode[STIX]{x1D6FF}_{k1}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R_{1}}+\unicode[STIX]{x1D6FF}_{k2}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R_{2}}-\unicode[STIX]{x1D6FF}_{k3}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}R_{3}}\right)\left(\frac{R_{3}}{R^{3}}\right)\right], & & \displaystyle\end{eqnarray}$$
where
$\boldsymbol{r}=(x,y,z-h)$
and
$\boldsymbol{R}=(x,y,z+h)$
. An infinitesimal force exerted on the boundary by this velocity field is given by Landau & Lifshitz (Reference Landau and Lifshitz1987),
$$\begin{eqnarray}\displaystyle \text{d}F_{i}=\unicode[STIX]{x1D6F4}_{ij}|_{z=0}\,n_{j}\,\text{d}x\,\text{d}y, & & \displaystyle\end{eqnarray}$$
where
$\boldsymbol{n}$
is the outer normal to the solid boundary, and
$\unicode[STIX]{x1D6F4}_{ij}$
is the stress tensor
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F4}_{ij}=-p\unicode[STIX]{x1D6FF}_{ij}+\unicode[STIX]{x1D707}(\unicode[STIX]{x2202}_{j}v_{i}+\unicode[STIX]{x2202}_{i}v_{j}). & & \displaystyle\end{eqnarray}$$
Using
$n_{j}=\unicode[STIX]{x1D6FF}_{jz}$
, we obtain for the total force on the boundary
$$\begin{eqnarray}\displaystyle & \displaystyle F_{x}=\unicode[STIX]{x1D707}\int _{-\infty }^{\infty }\text{d}x\,\text{d}y\unicode[STIX]{x2202}_{z}v_{x}\biggm\vert_{z=0}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle F_{z}=-\int _{-\infty }^{\infty }\text{d}x\,\text{d}y\,p\biggm\vert_{z=0}, & \displaystyle\end{eqnarray}$$
where we used
$\unicode[STIX]{x2202}_{x}v_{z}|_{z=0}=\unicode[STIX]{x2202}_{y}v_{z}|_{z=0}=0$
, since the operations of taking a derivative with respect to
$x$
or
$y$
and evaluating these velocity components at
$z=0$
commute, and
$v_{i}$
vanish at the boundary. In a similar fashion, we set
$\unicode[STIX]{x2202}_{z}v_{z}|_{z=0}=0$
in (2.6), which follows from the incompressibility condition, equation (1.2), and the argument above. The expression for the
$y$
-component of the force is obtained by replacing the subscripts
$x$
with
$y$
in (2.5).
Explicit evaluation using (2.1) and (2.2) yields
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D707}\unicode[STIX]{x2202}_{z}v_{x}|_{z=0}=\frac{3hx}{2\unicode[STIX]{x03C0}}\frac{f_{x}x+f_{y}y-f_{z}h}{(h^{2}+x^{2}+y^{2})^{5/2}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle p|_{z=0}=\frac{3h^{2}}{2\unicode[STIX]{x03C0}}\frac{f_{x}x+f_{y}y-f_{z}h}{(h^{2}+x^{2}+y^{2})^{5/2}}, & \displaystyle\end{eqnarray}$$
which, upon integration in (2.5) and (2.6), give
$$\begin{eqnarray}\displaystyle F_{i}=f_{i}. & & \displaystyle\end{eqnarray}$$
The same conclusion can be reached by observing that the image system of a point force next to a flat no-slip boundary includes a Stokeslet of an equal and opposite strength and higher-order flow singularities (Blake Reference Blake1971; Cichocki & Jones Reference Cichocki and Jones1998; Bhattacharya & Bławzdziewicz Reference Bhattacharya and Bławzdziewicz2002). The force on the wall is, therefore, equal to the force applied to the fluid. In § 4, we provide an intuitive argument for their equality.
3 A point force in a plane channel
In the second problem we consider a fluid confined in between two infinite parallel walls placed at
$z=0$
and
$z=H$
(see figure 1
b). The flow field
$v_{i}(\boldsymbol{r})$
satisfies (1.1) and (1.2) with the boundary conditions
$v_{i}(z=0)=v_{i}(z=H)=0$
. The solution to this problem was first reported by Liron & Mochon (Reference Liron and Mochon1976), who used a method similar to that of Blake (Reference Blake1971). An alternative approach was developed by Bickel (Reference Bickel2007), and by Daddi-Moussa-Ider and co-workers (Daddi-Moussa-Ider & Gekle Reference Daddi-Moussa-Ider and Gekle2018; Daddi-Moussa-Ider et al.
Reference Daddi-Moussa-Ider, Lisicki, Mathijssen, Hoell, Goh, Bławzdziewicz, Menzel and Löwen2018), which is more convenient for evaluating the force applied to the boundaries. In what follows, we use the method of Daddi-Moussa-Ider et al. (Reference Daddi-Moussa-Ider, Lisicki, Mathijssen, Hoell, Goh, Bławzdziewicz, Menzel and Löwen2018), and repeat the main steps of their derivation for completeness. Since the result of Liron & Mochon (Reference Liron and Mochon1976) is probably better known, in appendix A we repeat the same derivation using their method. We note here that the results of this analysis can also be deduced from the lubrication theory used to describe highly bidisperse colloidal suspensions (Bhattacharya & Blawzdziewicz Reference Bhattacharya and Blawzdziewicz2008; Navardi & Bhattacharya Reference Navardi and Bhattacharya2010).
We start by introducing a two-dimensional Fourier transform for the velocity
$$\begin{eqnarray}\displaystyle v_{i}(x,y,z)=\frac{1}{(2\unicode[STIX]{x03C0})^{2}}\int _{-\infty }^{\infty }\text{d}k_{x}\,\text{d}k_{y}\text{e}^{\text{i}(k_{x}x+k_{y}y)}\hat{v}_{i}(k_{x},k_{y},z), & & \displaystyle\end{eqnarray}$$
and a similar transform for the pressure. Upon inserting these expressions into (1.1) and (1.2), we obtain
$$\begin{eqnarray}\displaystyle & \displaystyle -\text{i}k_{\unicode[STIX]{x1D6FC}}\hat{p}+\unicode[STIX]{x1D707}(\unicode[STIX]{x2202}_{z}^{2}-k^{2})\hat{v}_{\unicode[STIX]{x1D6FC}}+f_{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FF}(z-h)=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle -\unicode[STIX]{x2202}_{z}\hat{p}+\unicode[STIX]{x1D707}(\unicode[STIX]{x2202}_{z}^{2}-k^{2})\hat{v}_{z}+f_{z}\unicode[STIX]{x1D6FF}(z-h)=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \text{i}k_{x}\hat{v}_{x}+\text{i}k_{y}\hat{v}_{y}+\unicode[STIX]{x2202}_{z}\hat{v}_{z}=0, & \displaystyle\end{eqnarray}$$
where
$\unicode[STIX]{x1D6FC}=\{x,y\}$
, and
$k^{2}=k_{x}^{2}+k_{y}^{2}$
. To proceed, we introduce the longitudinal and transverse components of the in-plane velocity
$$\begin{eqnarray}\displaystyle \hat{v}_{x}=\frac{k_{x}}{k}\hat{v}_{l}+\frac{k_{y}}{k}\hat{v}_{t},\quad \hat{v}_{y}=\frac{k_{y}}{k}\hat{v}_{l}-\frac{k_{x}}{k}\hat{v}_{t}, & & \displaystyle\end{eqnarray}$$
and a similar transformation for the longitudinal
$f_{l}$
and transverse
$f_{t}$
components of the point force. Applying this transformation to (3.2)–(3.4), we obtain
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D707}(\unicode[STIX]{x2202}_{z}^{2}-k^{2})\hat{v}_{t}+f_{t}\unicode[STIX]{x1D6FF}(z-h)=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle -\text{i}k\hat{p}+\unicode[STIX]{x1D707}(\unicode[STIX]{x2202}_{z}^{2}-k^{2})\hat{v}_{l}+f_{l}\unicode[STIX]{x1D6FF}(z-h)=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle -\unicode[STIX]{x2202}_{z}\hat{p}+\unicode[STIX]{x1D707}(\unicode[STIX]{x2202}_{z}^{2}-k^{2})\hat{v}_{z}+f_{z}\unicode[STIX]{x1D6FF}(z-h)=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \text{i}k\hat{v}_{l}+\unicode[STIX]{x2202}_{z}\hat{v}_{z}=0. & \displaystyle\end{eqnarray}$$
These equations decouple the transverse component from the rest, and below we solve the associated problems separately.
3.1 Transverse velocity component
To solve (3.6), we observe that its solution can be split into two parts,
$\hat{v}_{t}^{+}$
for
$z>h$
, and
$\hat{v}_{t}^{-}$
for
$z<h$
, that satisfy that same equation
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D707}(\unicode[STIX]{x2202}_{z}^{2}-k^{2})\hat{v}_{t}^{\pm }=0, & & \displaystyle\end{eqnarray}$$
and the boundary conditions
$$\begin{eqnarray}\displaystyle \hat{v}_{t}^{-}(0)=\hat{v}_{t}^{+}(H)=0. & & \displaystyle\end{eqnarray}$$
The matching condition at
$z=h$
is obtained by integrating (3.6) from
$z=h-\unicode[STIX]{x1D700}$
to
$z=h+\unicode[STIX]{x1D700}$
, which, in the limit
$\unicode[STIX]{x1D700}\rightarrow 0$
, yields
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x2202}_{z}\hat{v}_{t}^{+}(h)-\unicode[STIX]{x2202}_{z}\hat{v}_{t}^{-}(h)=-f_{t}/\unicode[STIX]{x1D707}. & & \displaystyle\end{eqnarray}$$
Together with the requirement that the velocity is continuous,
$v_{t}^{+}(h)=v_{t}^{-}(h)$
, this fully specifies the solution, which is given by
$$\begin{eqnarray}\displaystyle & \displaystyle \hat{v}_{t}^{-}(z)=\frac{f_{t}}{k\unicode[STIX]{x1D707}}\frac{\sinh (k(H-h))}{\sinh (kH)}\sinh (kz), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \hat{v}_{t}^{+}(z)=\frac{f_{t}}{k\unicode[STIX]{x1D707}}\frac{\sinh (kh)}{\sinh (kH)}\sinh (k(H-z)). & \displaystyle\end{eqnarray}$$
3.2 Longitudinal and vertical velocity components
Excluding the pressure from (3.7) and (3.8), and using the incompressibility condition, equation (3.9), we obtain for the vertical velocity
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D707}(\unicode[STIX]{x2202}_{z}^{2}-k^{2})^{2}\hat{v}_{z}-k^{2}f_{z}\unicode[STIX]{x1D6FF}(z-h)-\text{i}kf_{l}\unicode[STIX]{x2202}_{z}\unicode[STIX]{x1D6FF}(z-h)=0. & & \displaystyle\end{eqnarray}$$
Similar to the transverse case, this equation is solved by splitting its solution into two components,
$\hat{v}_{z}^{\pm }$
, that satisfy
$$\begin{eqnarray}\displaystyle & \displaystyle (\unicode[STIX]{x2202}_{z}^{2}-k^{2})^{2}\hat{v}_{z}^{\pm }=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \hat{v}_{z}^{-}(0)=\unicode[STIX]{x2202}_{z}\hat{v}_{z}^{-}(0)=\hat{v}_{z}^{+}(H)=\unicode[STIX]{x2202}_{z}\hat{v}_{z}^{+}(H)=0. & \displaystyle\end{eqnarray}$$
Repeated integration of (3.15) in a small vicinity of
$z=h$
yields the following matching conditions
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x2202}_{z}^{3}\hat{v}_{z}^{+}(h)-\unicode[STIX]{x2202}_{z}^{3}\hat{v}_{z}^{-}(h)=k^{2}\unicode[STIX]{x1D707}^{-1}f_{z}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x2202}_{z}^{2}\hat{v}_{z}^{+}(h)-\unicode[STIX]{x2202}_{z}^{2}\hat{v}_{z}^{-}(h)=\text{i}k\unicode[STIX]{x1D707}^{-1}f_{l}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x2202}_{z}\hat{v}_{z}^{+}(h)-\unicode[STIX]{x2202}_{z}\hat{v}_{z}^{-}(h)=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \hat{v}_{z}^{+}(h)-\hat{v}_{z}^{-}(h)=0. & \displaystyle\end{eqnarray}$$
The solution to (3.16)–(3.21) is given by
$$\begin{eqnarray}\displaystyle v_{z}^{\pm }=\frac{T_{zz}^{\pm }f_{z}+T_{zl}^{\pm }\text{i}kf_{l}}{4k\unicode[STIX]{x1D707}(1+2H^{2}k^{2}-\cosh (2Hk))}, & & \displaystyle\end{eqnarray}$$
where
$$\begin{eqnarray}\displaystyle T_{zz}^{-}(z,h) & = & \displaystyle -(2Hk^{2}(-h+H+z)+1)\sinh (k(h-z))\nonumber\\ \displaystyle & & \displaystyle +\,k(z(4Hk^{2}(h-H)-1)+h-2H)\cosh (k(h-z))\nonumber\\ \displaystyle & & \displaystyle +\,(2k^{2}(H-h)(H-z)+1)\sinh (k(h+z))\nonumber\\ \displaystyle & & \displaystyle -\,k(h-2H+z)\cosh (k(h+z))\nonumber\\ \displaystyle & & \displaystyle -\,(2hk^{2}z+1)\sinh (k(h-2H+z))\nonumber\\ \displaystyle & & \displaystyle +\,k(h+z)\cosh (k(h-2H+z))\nonumber\\ \displaystyle & & \displaystyle +\,\sinh (k(h-2H-z))\nonumber\\ \displaystyle & & \displaystyle +\,k(z-h)\cosh (k(h-2H-z)),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle T_{zl}^{-}(z,h) & = & \displaystyle (4Hk^{2}z(H-h)+(z-h))\sinh (k(h-z))\nonumber\\ \displaystyle & & \displaystyle -\,2Hk(h-H+z)\cosh (k(h-z))\nonumber\\ \displaystyle & & \displaystyle +\,(h-z)\sinh (k(h+z))\nonumber\\ \displaystyle & & \displaystyle +\,2k(h-H)(H-z)\cosh (k(h+z))\nonumber\\ \displaystyle & & \displaystyle +\,(z-h)\sinh (k(h-2H+z))\nonumber\\ \displaystyle & & \displaystyle +\,2hkz\cosh (k(h-2H+z))\nonumber\\ \displaystyle & & \displaystyle +\,(h-z)\sinh (k(h-2H-z)),\end{eqnarray}$$
and
$$\begin{eqnarray}\displaystyle & \displaystyle T_{zz}^{+}(z,h)=T_{zz}^{-}(H-z,H-h), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle T_{zl}^{+}(z,h)=-T_{zl}^{-}(H-z,H-h). & \displaystyle\end{eqnarray}$$
The longitudinal component
$\hat{v}_{l}$
can now be obtained from (3.9), while the pressure is given by (3.7).
3.3 Forces exerted on the boundaries
The forces applied by the flow determined above can now be calculated in a manner similar to § 2, and are given by
$$\begin{eqnarray}\displaystyle & \displaystyle F_{x}^{\pm }=\mp \unicode[STIX]{x1D707}\int _{-\infty }^{\infty }\text{d}x\,\text{d}y\,\unicode[STIX]{x2202}_{z}v_{x}^{\pm }, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle F_{z}^{\pm }=\pm \int _{-\infty }^{\infty }\text{d}x\,\text{d}y\,p^{\pm }, & \displaystyle\end{eqnarray}$$
evaluated at
$z=H$
and
$z=0$
, respectively. Here,
$v_{x}^{\pm }$
and
$p^{\pm }$
are the inverse transforms of the corresponding Fourier components, and we used the fact that the outer normal at the
$z=H$
boundary is pointing in the negative
$z$
-direction. The integrals in (3.27) and (3.28) can, in fact, be obtained from the Fourier transform introduced in (3.1). Indeed, if we put
$k_{x}=k\cos \unicode[STIX]{x1D703}$
and
$k_{y}=k\sin \unicode[STIX]{x1D703}$
, for an arbitrary function
$\unicode[STIX]{x1D719}$
that depends on
$x$
and
$y$
in a symmetric manner we obtain
$$\begin{eqnarray}\displaystyle \int _{-\infty }^{\infty }\text{d}x\,\text{d}y\unicode[STIX]{x1D719}(x,y)=\frac{1}{2\unicode[STIX]{x03C0}}\lim _{k\rightarrow 0}\int _{0}^{2\unicode[STIX]{x03C0}}\text{d}\unicode[STIX]{x1D703}\hat{\unicode[STIX]{x1D719}}(k,\unicode[STIX]{x1D703}). & & \displaystyle\end{eqnarray}$$
Therefore, the forces on the boundaries are readily obtained by integrating
$\mp \unicode[STIX]{x1D707}\unicode[STIX]{x2202}_{z}\hat{v}_{x}^{\pm }$
and
$\pm \hat{p}^{\pm }$
over
$\unicode[STIX]{x1D703}$
, taking the limit
$k\rightarrow 0$
and evaluating the result at the appropriate
$z$
. The final results then read
$$\begin{eqnarray}\displaystyle F_{\unicode[STIX]{x1D6FC}}^{-}=(1-\unicode[STIX]{x1D6E5})(1-{\textstyle \frac{3}{2}}\unicode[STIX]{x1D6E5})f_{\unicode[STIX]{x1D6FC}},\quad F_{z}^{-}=(1-\unicode[STIX]{x1D6E5})^{2}(1+2\unicode[STIX]{x1D6E5})f_{z}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{\unicode[STIX]{x1D6FC}}^{+}={\textstyle \frac{1}{2}}\unicode[STIX]{x1D6E5}(3\unicode[STIX]{x1D6E5}-1)f_{\unicode[STIX]{x1D6FC}},\quad F_{z}^{+}=\unicode[STIX]{x1D6E5}^{2}(3-2\unicode[STIX]{x1D6E5})f_{z}, & & \displaystyle\end{eqnarray}$$
where
$\unicode[STIX]{x1D6E5}=h/H$
, and
$\unicode[STIX]{x1D6FC}=\{x,y\}$
.
4 Discussion
Equations (2.9) and (3.30)–(3.31) constitute the main results of this work. The first case corresponds to a Stokeslet near an infinite plane wall and implies that the whole force applied to the fluid is transmitted to the wall, independent of the Stokeslet’s distance to the wall. While appearing surprising, this result can be understood from a simple argument. Due to the linearity of the Stokes equation, we expect the force on the wall to be proportional to the strength of the force applied to the fluid,
$F_{i}=g(h)f_{i}$
, where
$g(h)$
is an unknown function of the distance between the Stokeslet and the wall. Since
$g(h)$
should be dimensionless, it can only depend on a ratio between
$h$
and another length scale. However, there are no other length scales in the problem, and
$g$
is constant, independent of
$h$
. Considering the case when the Stokeslet is applied directly to the interface between the wall and the fluid fixes
$g=1$
, giving the result in (2.9). An interesting consequence of this result is that an arbitrary force distribution applied to the fluid next to a single wall exerts no force on the wall, as long as the total force applied to the fluid is zero, as in the case of a collection of force-free self-propelled particles. In a similar fashion, a force-free microswimmer stalled by the wall, exerts no total force on it. Indeed, the propulsive force generated by the swimmer is directly transmitted to the wall through the action of the interaction potential between the wall and the swimmer. To generate this propulsive force, the swimmer applies the equal and opposite force on the fluid some distance away from the wall, which is fully transmitted to the wall, as (2.9) suggests. The total sum is zero for any orientation of the swimmer in contact with the wall. Therefore, there is no hydrodynamic contribution to the pressure from a suspension of force-free swimmers next to a single boundary.
When the Stokeslet is confined between two parallel walls, the argument above yields
$F_{i}=g(h/H)f_{i}$
, since there are now two length scales in the problem. The corresponding functions
$g$
are non-trivial and different for the force components perpendicular and parallel to the wall, see (3.30) and (3.31). First, we observe that these expressions are symmetric with respect to
$\unicode[STIX]{x1D6E5}\rightarrow 1-\unicode[STIX]{x1D6E5}$
, as expected. Next, in the limit of
$H\rightarrow \infty$
, keeping
$h$
finite, we recover (2.9) for the force on the lower wall, while
$F_{i}^{+}=0$
; the same holds for
$h\rightarrow \infty$
, keeping
$H-h$
finite, with
$F_{i}^{+}=f_{i}$
and
$F_{i}^{-}=0$
. Finally, the correct behaviour is also recovered in the limits of
$h\rightarrow 0$
and
$h\rightarrow H$
.
Equations (3.30) and (3.31) also allow us to make an interesting observation regarding the total force applied to both boundaries. While the total vertical force on the walls is equal to the vertical force applied to the fluid,
$F_{z}^{-}+F_{z}^{+}=f_{z}$
, the horizontal components give
$F_{\unicode[STIX]{x1D6FC}}^{-}+F_{\unicode[STIX]{x1D6FC}}^{+}=(1-3\unicode[STIX]{x1D6E5}(1-\unicode[STIX]{x1D6E5}))f_{\unicode[STIX]{x1D6FC}}$
, with
$\unicode[STIX]{x1D6FC}=\{x,y\}$
. The latter result implies that
$F_{\unicode[STIX]{x1D6FC}}^{-}+F_{\unicode[STIX]{x1D6FC}}^{+}\leqslant f_{i}$
, where the equality only applies when
$\unicode[STIX]{x1D6E5}=0$
or
$1$
. To understand the origin of the ‘missing’ force, we consider an imaginary box around the Stokeslet and calculate the forces applied to the planes
$x=\pm L$
and
$y=\pm L$
, where
$L\gg H$
. Far away from the Stokeslet, the velocity field is given by equation (51) of Liron & Mochon (Reference Liron and Mochon1976), and has only the in-plane components, while the far-field behaviour of the pressure can be deduced from equation (56) of the same reference. Calculating the forces exerted by this velocity field in the
$x$
-direction on the fictitious surfaces as
$L\rightarrow \infty$
, we obtain that the forces at
$y=\pm L$
are zero, while the forces at
$x=\pm L$
are the same and equal to
$(3/2)\unicode[STIX]{x1D6E5}(1-\unicode[STIX]{x1D6E5})f_{x}$
, where only the pressure term contributes to this result. An identical expression is, of course, obtained for the
$y$
-component of the force, where only the fictitious surfaces perpendicular to the
$y$
-axis experience non-zero forces. Together with (3.30) and (3.31), this gives the total force applied to the boundaries enclosing the Stokeslet being equal to
$f_{i}$
, as it should.
We conclude by observing that our results can be trivially generalised for an arbitrary distribution of point forces applied to the fluid due to linearity of the Stokes equation. In particular, we consider a force dipole, which is relevant for force-free self-propelled microswimmers (Lauga & Powers Reference Lauga and Powers2009). The dipole consists of two equal and opposite point forces,
$-f\boldsymbol{e}$
and
$f\boldsymbol{e}$
, applied to the fluid at
$(0,0,h)$
and
$(0,0,h)+l\boldsymbol{e}$
, respectively, where
$f$
is the magnitude of the force,
$\boldsymbol{e}$
is a unit vector along the direction of the dipole and
$l$
is its length. From (3.31), the vertical component force on the upper boundary due to the dipole is given by
$$\begin{eqnarray}\displaystyle F_{d}(h)=\frac{fl}{H}\left[-2\frac{l^{2}}{H^{2}}e_{z}^{4}+6e_{z}^{2}\unicode[STIX]{x1D6E5}(1-\unicode[STIX]{x1D6E5})+3e_{z}^{3}\frac{l}{H}(1-2\unicode[STIX]{x1D6E5})\right], & & \displaystyle\end{eqnarray}$$
where
$e_{z}$
denotes the
$z$
-component of
$\boldsymbol{e}$
. An equal and opposite force is applied to the lower boundary. Next, we consider a collection of such dipoles at a number density
$n$
. Although it has been demonstrated that suspensions of dipolar microswimmers exhibit significant correlations even at low densities (Stenhammar et al.
Reference Stenhammar, Nardini, Nash, Marenduzzo and Morozov2017), here we assume the suspension to be homogeneous and isotropic, for simplicity. The pressure on the upper wall (a force per unit area) can then be calculated as the following average
$$\begin{eqnarray}\displaystyle p_{d}=\frac{n}{2}\int _{0}^{\unicode[STIX]{x03C0}}\text{d}\unicode[STIX]{x1D703}\sin \unicode[STIX]{x1D703}\int _{0}^{H}\text{d}hF_{d}(h)\approx \frac{1}{3}fln, & & \displaystyle\end{eqnarray}$$
where we used
$e_{z}=\cos \unicode[STIX]{x1D703}$
in spherical coordinates, and neglected terms of order
$l/H$
. Apart from a numerical factor, this result can be readily obtained from dimensional analysis. Using the dipolar strength
$fl\sim 8\times 10^{-19}~\text{N}~\text{s}$
as measured by Drescher et al. (Reference Drescher, Dunkel, Cisneros, Ganguly and Goldstein2011) for E.coli bacteria, and setting
$n\sim 10^{9}~\text{ml}^{-1}$
, as in typical experiments with dilute bacterial suspensions (Jepson et al.
Reference Jepson, Martinez, Schwarz-Linek, Morozov and Poon2013; López et al.
Reference López, Gachelin, Douarche, Auradou and Clément2015), we obtain
$p_{d}\sim 10^{-4}~\text{Pa}$
. Such pressures are too small to be measured by conventional rheometry but, perhaps, can be observed in an appropriate microfluidic experiment. We would like to note that the pressure calculated above is due to the velocity fields generated by the swimmers, and does not contain the osmotic contribution (Takatori et al.
Reference Takatori, Yan and Brady2014; Yang et al.
Reference Yang, Manning and Marchetti2014; Solon et al.
Reference Solon, Fily, Baskaran, Cates, Kafri, Kardar and Tailleur2015).
Acknowledgements
Discussions with M. Cates, W. Poon, S. Spagnolie and J. Tailleur are gratefully acknowledged.
Appendix A. Alternative derivation of (3.30)–(3.31)
Here we demonstrate that the forces exerted on the walls of a plane channel by a Stokeslet can also be derived with the help of the velocity field obtained by Liron & Mochon (Reference Liron and Mochon1976), which is probably the most famous treatment of that problem.
Their solution for the
$j$
th component of the velocity field due to the
$k$
th component of the point force,
$u_{j}^{k}$
, is decomposed into two parts
$$\begin{eqnarray}\displaystyle u_{j}^{k}=v_{j}^{k}+w_{j}^{k}, & & \displaystyle\end{eqnarray}$$
where
$v_{j}^{k}$
is the contribution due to the original free-space Stokeslet, together with an infinite number of its images, and
$w_{j}^{k}$
is an auxiliary solution that ensures the no-slip boundary conditions at the walls. The Fourier transform of the auxiliary solution is given by equations (26) and (31) of Liron & Mochon (Reference Liron and Mochon1976); note that their Fourier transform convention differs from ours, equation (3.1), by
$2\unicode[STIX]{x03C0}$
. Using the same argument as in § 3.3, we express the contribution of the auxiliary solution to the forces on the upper boundary as
$$\begin{eqnarray}\displaystyle & \displaystyle F_{w,\unicode[STIX]{x1D6FC}}^{+}=-\unicode[STIX]{x1D707}f^{k}\lim _{\unicode[STIX]{x1D701}\rightarrow \infty }\int _{0}^{2\unicode[STIX]{x03C0}}\text{d}\unicode[STIX]{x1D703}\unicode[STIX]{x2202}_{z}{\hat{w}}_{\unicode[STIX]{x1D6FC}}^{k}(\unicode[STIX]{x1D706}_{x}=\unicode[STIX]{x1D701}\cos \unicode[STIX]{x1D703},\unicode[STIX]{x1D706}_{y}=\unicode[STIX]{x1D701}\sin \unicode[STIX]{x1D703},z=H), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle F_{w,z}^{+}=f^{k}\lim _{\unicode[STIX]{x1D701}\rightarrow \infty }\int _{0}^{2\unicode[STIX]{x03C0}}\text{d}\unicode[STIX]{x1D703}\hat{p}^{k}(\unicode[STIX]{x1D706}_{x}=\unicode[STIX]{x1D701}\cos \unicode[STIX]{x1D703},\unicode[STIX]{x1D706}_{y}=\unicode[STIX]{x1D701}\sin \unicode[STIX]{x1D703},z=H), & \displaystyle\end{eqnarray}$$
where
$\unicode[STIX]{x1D706}_{x}$
and
$\unicode[STIX]{x1D706}_{y}$
are the analogues of
$k_{x}$
and
$k_{y}$
used in the main text, and
$\unicode[STIX]{x1D701}^{2}=\unicode[STIX]{x1D706}_{x}^{2}+\unicode[STIX]{x1D706}_{y}^{2}$
, as in Liron & Mochon (Reference Liron and Mochon1976). Here,
$\unicode[STIX]{x1D6FC}=\{x,y\}$
, and
${\hat{w}}_{\unicode[STIX]{x1D6FC}}^{k}$
and
$\hat{p}^{k}$
denote the Fourier transforms of the auxiliary velocity and pressure, respectively. Performing the integrals and taking the limit yields
$$\begin{eqnarray}\displaystyle & \displaystyle F_{w,\unicode[STIX]{x1D6FC}}^{+}=-{\textstyle \frac{3}{2}}\unicode[STIX]{x1D6E5}(1-\unicode[STIX]{x1D6E5})f_{\unicode[STIX]{x1D6FC}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle F_{w,z}^{+}=-\unicode[STIX]{x1D6E5}(1-\unicode[STIX]{x1D6E5})(1-2\unicode[STIX]{x1D6E5})f_{z}. & \displaystyle\end{eqnarray}$$
The velocity and pressure fields due to the original free-space Stokeslet and its images are given in equations (15) and (16) of Liron & Mochon (Reference Liron and Mochon1976), and are conveniently expressed in terms of the infinite series from equations (43) and (44) ibid. Using (3.27) and (3.28), we obtain
$$\begin{eqnarray}\displaystyle F_{v,\unicode[STIX]{x1D6FC}}^{+} & = & \displaystyle -\frac{f_{\unicode[STIX]{x1D6FC}}}{2\unicode[STIX]{x03C0}H^{2}}\int _{-\infty }^{\infty }\text{d}x\,\text{d}y\nonumber\\ \displaystyle & & \displaystyle \times \mathop{\sum }_{n=1}^{\infty }(-1)^{n}\unicode[STIX]{x03C0}n\sin (\unicode[STIX]{x03C0}n\unicode[STIX]{x1D6E5})\left[\text{K}_{0}\left(\frac{\unicode[STIX]{x03C0}n\unicode[STIX]{x1D70C}}{H}\right)+\frac{x^{2}}{\unicode[STIX]{x1D70C}}\frac{\unicode[STIX]{x03C0}n}{H}\text{K}_{1}\left(\frac{\unicode[STIX]{x03C0}n\unicode[STIX]{x1D70C}}{H}\right)\right]=f_{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6E5},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{v,z}^{+}=-\frac{f_{z}}{\unicode[STIX]{x03C0}H^{2}}\int _{-\infty }^{\infty }\text{d}x\,\text{d}y\mathop{\sum }_{n=1}^{\infty }(-1)^{n}\unicode[STIX]{x03C0}n\sin (\unicode[STIX]{x03C0}n\unicode[STIX]{x1D6E5})\text{K}_{0}\left(\frac{\unicode[STIX]{x03C0}n\unicode[STIX]{x1D70C}}{H}\right)=f_{z}\unicode[STIX]{x1D6E5}, & & \displaystyle\end{eqnarray}$$
where
$\unicode[STIX]{x1D70C}^{2}=x^{2}+y^{2}$
,
$\text{K}_{0}$
and
$\text{K}_{1}$
denote the zeroth- and first-order modified Bessel functions of the second kind, and we dropped the terms that do not contribute to the force. Combining these expressions with (A 4) and (A 5), we arrive at (3.31). The force on the lower boundary is obtained by replacing
$\unicode[STIX]{x1D6E5}$
with
$1-\unicode[STIX]{x1D6E5}$
in (3.31), as can be seen from (3.30).
