Introduction
Multihead placement machines, which can be adapted to process various components, are the most flexible machines for assembling printed circuit boards (PCBs). However, the production efficiency of multihead placement machines is limited. Problems in the related optimization of production efficiency can be classified into three typical subproblems:
(1) Auto nozzle changer (ANC) assembly problem;
(2) Nozzle setup problem;
(3) Component pick-and-place sequence problem.
Various optimization methods have been developed to address these subproblems. For example, Grunow et al. (Reference Grunow, Günther, Schleusener and Yilmaz2004) proposed a three-step heuristic algorithm to solve the pick-and-place problem. For multihead placement machines with a specific place sequence, Knuutila et al. (Reference Knuutila, Pyöttiälä and Nevalainen2007) employed a greedy algorithm to optimize nozzle assignment and reduce the number of picks. The concept of component batches was employed by Ashayeri et al. (Reference Ashayeri, Ma and Sotirov2011) to formulate a multihead placement optimization problem for a mixed integer program designed to balance placement head loadings and reduce the number of nozzle changes. Ball and Magazine (Reference Ball and Magazine1998) defined the place sequence for a multihead machine as a postman problem. Leipälä and Nevalainen (Reference Leipälä and Nevalainen1989) considered a place sequence for a multihead machine to be a traveling salesman problem. Kumar and Li (Reference Kumar and Li1995) used linear programming for feeder assignment and place sequence, where the local search was accompanied by 2 and 3 changes. Recently, meta-algorithms, including greedy algorithms, genetic algorithms (GAs), and particle swarm optimization (PSO), have been successfully applied to multihead machine problems. For example, Fu and Su (Reference Fu and Su2000) employed a GA, simulated annealing algorithm, and Tabu search-based algorithm to solve a dynamically combinatorial problem. Moreover, Loh et al. (2007) applied a GA to auto nozzle changer (ANC) assignment and place sequence for a placement machine. Jiang et al. (Reference Jiang, Chen, Zang, Wang and Tan2010a, Reference Jiang, Du, Liu and Zhang2010b, Reference Jiang, Liu, Zhang, Wang, Tan and Chen2010c) employed an improved ant colony algorithm to optimize place sequence and minimize nozzle changes. A memetic algorithm was proposed to solve a placement machine scheduling problem (Neammanee and Reodecha, Reference Neammanee and Reodecha2009). For PCB assembly, Du et al., focused on feeder assignment and component pick-and-place sequence problems and presented a hybrid GA combining heuristic and genetic algorithms for evaluating the performance of feasible solutions (Du and Li, Reference Du and Li2008). In another study of multihead placement machines, a GA with a distinct crossover operation and mutation operators was applied to yield satisfactory results on robot assembly time by reducing movement distance of a feeder carrier and PCB table (Lin and Zhu, Reference Lin and Zhu2008). An efficient neural network approach was presented to minimize the cycle time of a schedule for a cyclic job shop problem (Kechadi et al., Reference Kechadi, Low and Goncalves2013). Al-Anzi and Allahverdi focused on modeling a two-stage multimachine assembly scheduling problem by employing an artificial immune system to minimize total assembly time (Al-Anzi and Allahverdi, Reference Al-Anzi and Allahverdi2013). Other related studies include Smed et al., Reference Smed, Johnsson, Puranen, Leipala and Nevalainen1999; Chen et al., Reference Chen, Luo and Hu2011; Chen and Shen, Reference Chen and Shen2010; Jiang et al., Reference Jiang, Chen, Zang, Wang and Tan2010a, Reference Jiang, Du, Liu and Zhang2010b, Reference Jiang, Liu, Zhang, Wang, Tan and Chen2010c; Luo et al., Reference Luo, Li, Liu and Hu2010; Zhang et al., Reference Zhang, Li and Du2010; Alkaya and Duman, Reference Alkaya and Duman2013; Chen et al., Reference Chen, Luo, Du and Hu2012a, Reference Chen, Wang, Zou, Hou and Zhao2012b; Csaba and Nevalainen, Reference Csaba and Nevalainen2015; Jensen, Reference Jensen2003; Chen and Chang, Reference Chen and Chang1995; Park et al., Reference Park, Lee, Shin and Lee2005.
Kim et al., developed an ontology-based model representing morphological characteristics related to assembly joints (Kim et al., Reference Kim, Chin, Kwon and Ellis2009). A two-phase automatic generation of assembly plans was designed. First, a graph-based procedure with topological and geometric description provided a layout of an assembled product. Second, heuristic knowledge of mechanical components and assembly processes were used to plan selected assembly sequences (Kroll et al., Reference Kroll, Lenz and Wolberg1989). A new GA encoding scheme and selection criteria were proposed for automatic generation of electromechanical engineering designs (Peysakhov and Regli, Reference Peysakhov and Regli2003). Zeng et al. developed probability increment-based swarm optimization (PIBSO) through roulette wheel selection and probability updating to solve a PCB assembly optimization problem. PIBSO provides improved tour length and CPU running time (Zeng et al., Reference Zeng, Tan, Dong and Yang2014). Chen and Wichman (Reference Chen and Wichman1993) developed a novel system that integrated neural networks to capture a design concept and instigated a rule-based system for automatically generating an assembly plan. Intelligent selective disassembly with an ant colony algorithm has been used to solve combinatorial optimization problems (Wang et al., Reference Wang, Liu, Li and Zhong2003).
To simplify the investigated problems, the aforementioned studies have ignored some practical limitations of placement machines. This study aimed to overcome these limitations and the following hardware constraints: (1) component height restrictions, (2) time consumption for nozzle changes, (3) picking restrictions, (4) placing restrictions, (5) simultaneous pickup restrictions, and (6) component shape restrictions. Moreover, a hybrid group search optimizer (HGSO) is proposed to generate feasible and efficient scheduling solutions for PCB assembly.
Machine description
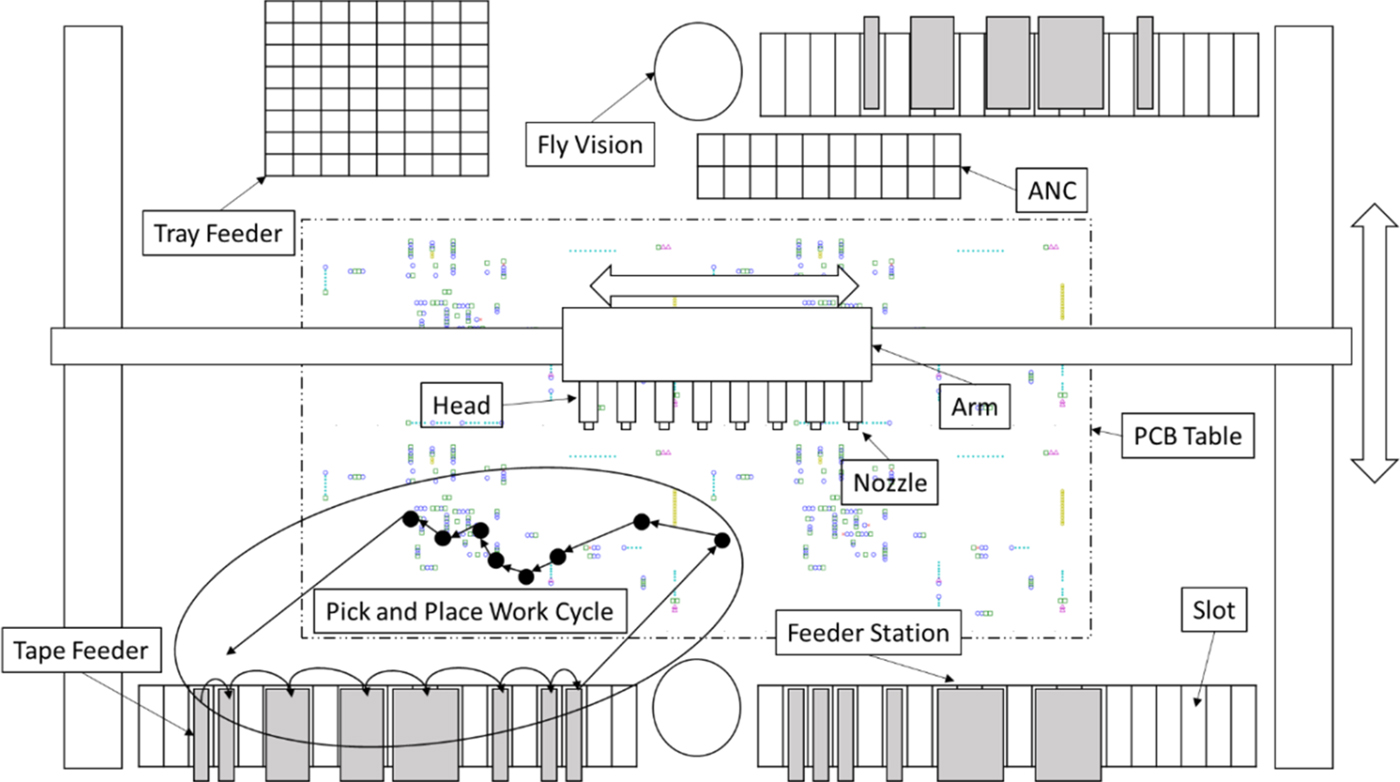
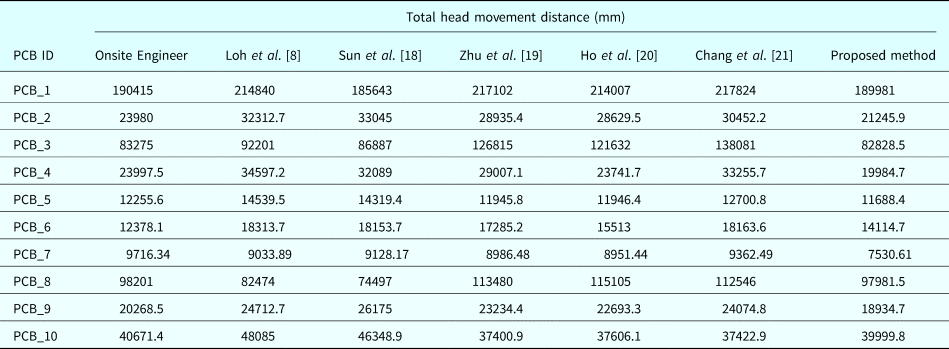
Surface mount technology (SMT) equipment, also termed placement machines, are the most crucial and complex equipment in SMT production. Figure 1 presents the multihead placement machine examined in this study. The machine has eight heads for eight nozzles, and different nozzles can be selected according to the shape of the component to be installed. One ANC accommodates 16 small nozzles and 4 large nozzles. For continuous assembly of components, 90 feeder slots are integrated using tape or stick feeders. The head moves along the X–Y axis to pick components from a feeder slot and place them at appropriate positions on the PCB. A pick-and-place cycle is completed when all the picked components are placed at their appropriate positions.
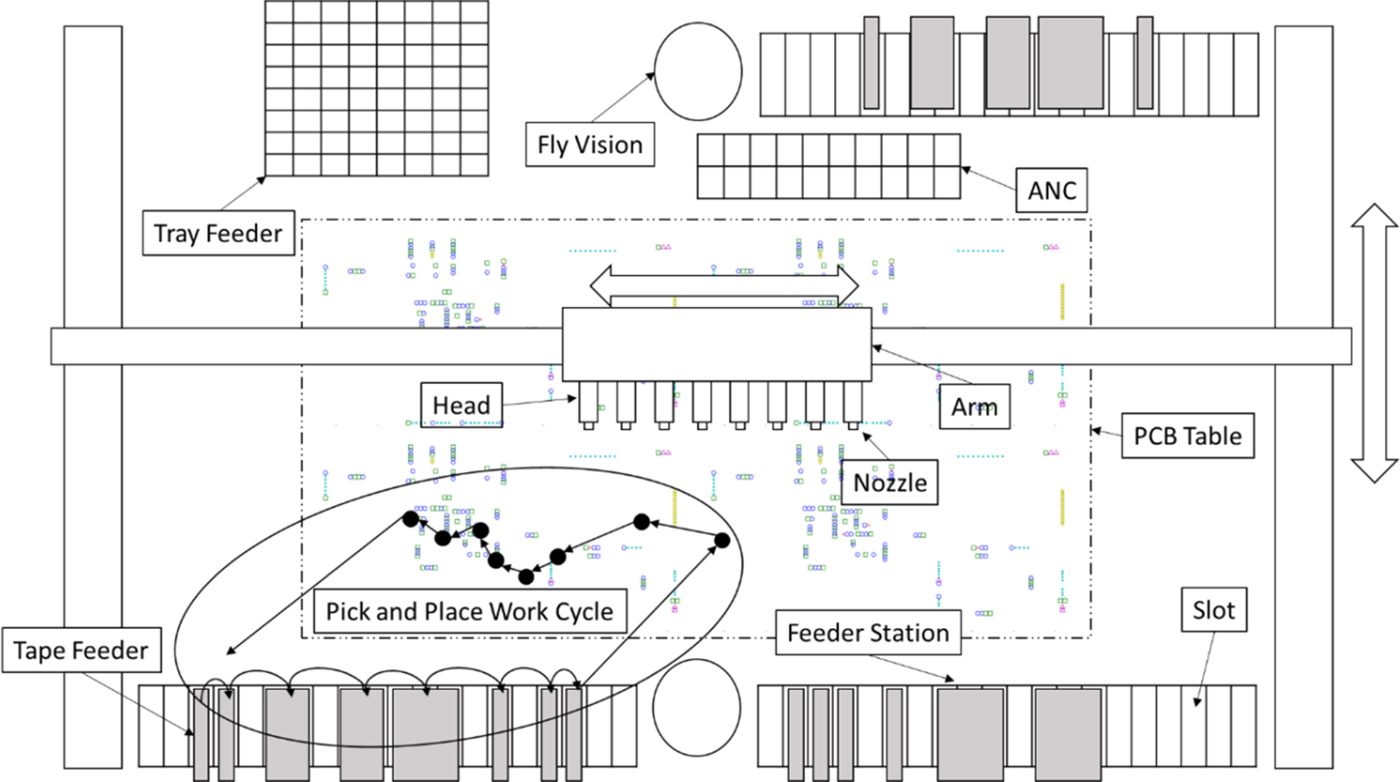
Fig. 1. Schematic of the multihead placement machine used in this study
The primary parts of a placement machine are as follows:
(1) Head: Each head has one nozzle that can pick one component.
(2) Nozzle: A nozzle is installed on a head and used to pick components. A nozzle of a specified shape can only pick up components of the same shape.
(3) ANC: An ANC is designed for holding and exchanging nozzles.
(4) Feeder: A feeder stores and supplies components. Each feeder can store one component.
(5) Slot: A slot is designed for feeder insertion.
(6) Feeder station: A feeder station holds feeders.
(7) PCB table: A PCB table is designed to fix PCBs.
(8) Arm: An arm moves the heads in an X–Y axis direction to appropriate positions for picking and placing components.
(9) Fly vision: This is designed to ensure that the components are correct and defect-free and to relocate X–Y coordinates.
Problem definition
Restrictions of placement machine
To generate an efficient schedule for the placement machine in this study, the following restrictions were considered:
(1) Component height: The component heights are different. To avoid collisions with already installed components, components with lower heights should be placed with higher priority.
(2) Nozzle setup: Components with different shapes require nozzles with the corresponding shapes, but changing the nozzles increases production time and cost.
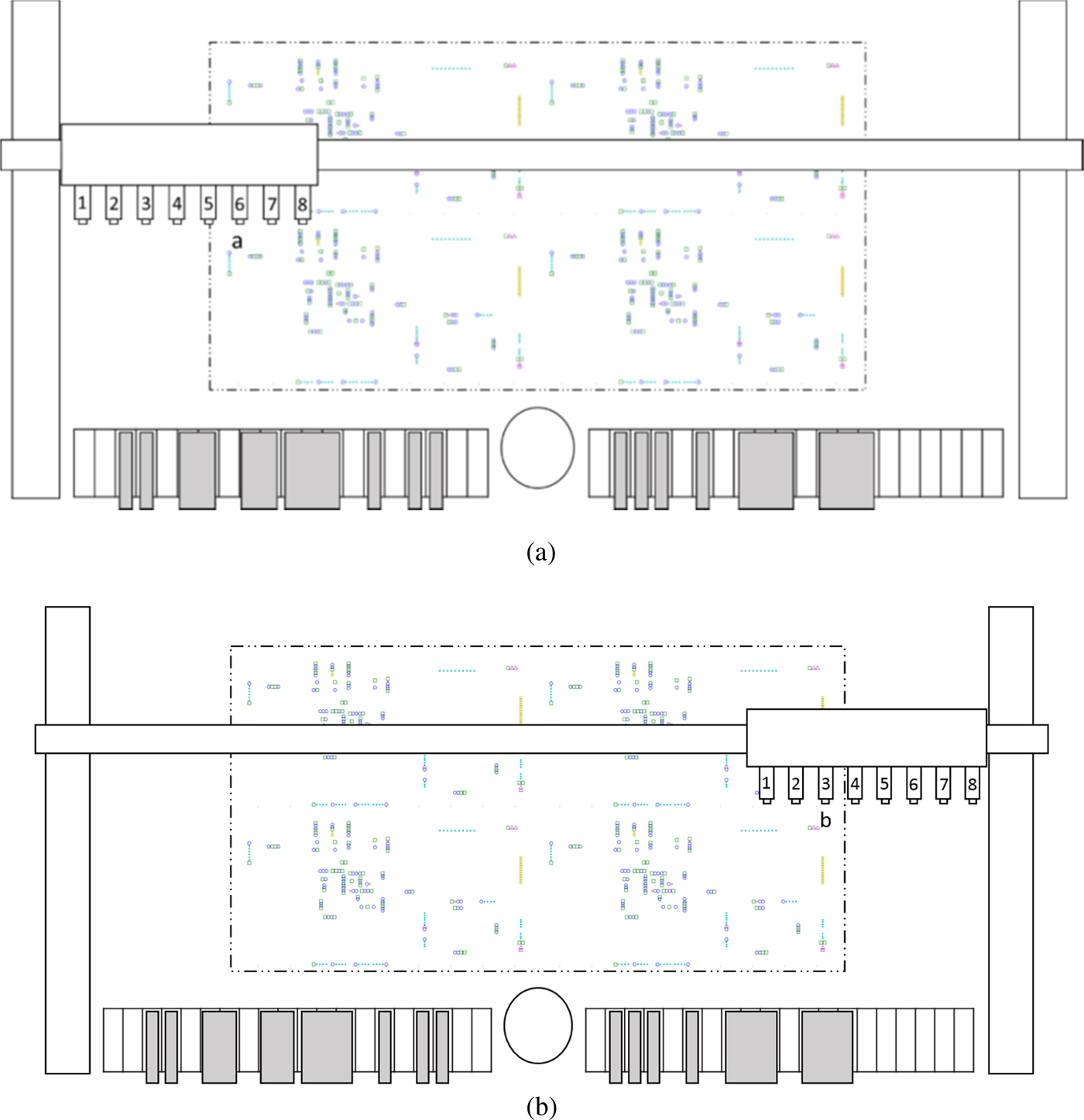
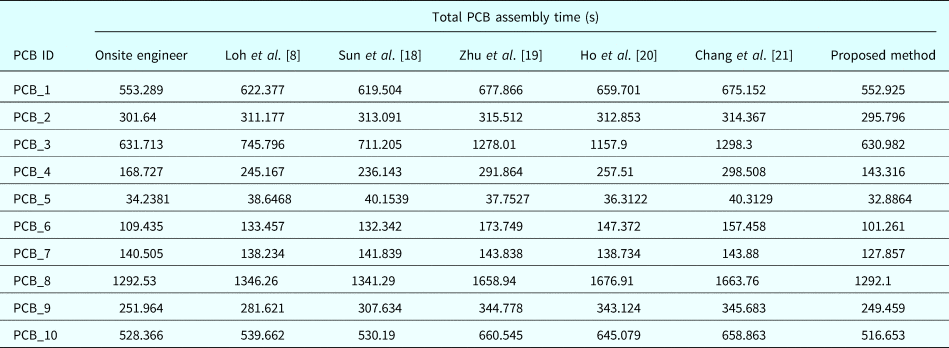
(3) Picking restrictions: The moving distance of each head is practically limited. For example, in Figure 2a, b, heads 3–8 cannot reach components in slot c, and heads 1–2 cannot pick components in slot d, respectively.
(4) Placing restrictions: Not all heads can place components in all slots. For example, in Figure 3a, heads 7–8 cannot place components at position a, and in Figure 3b, heads 1–2 cannot place components at position b.
(5) Simultaneous pickup restrictions: Simultaneous pickup is essential for reducing the number of pickups and therefore production time. The following conditions are necessary for simultaneous pickup:
a. Components are stored in the tape feeder.
b. One feeder slot between component feeders.
c. Picking angles for all components are the same.
d. The same camera is used for fly vision.
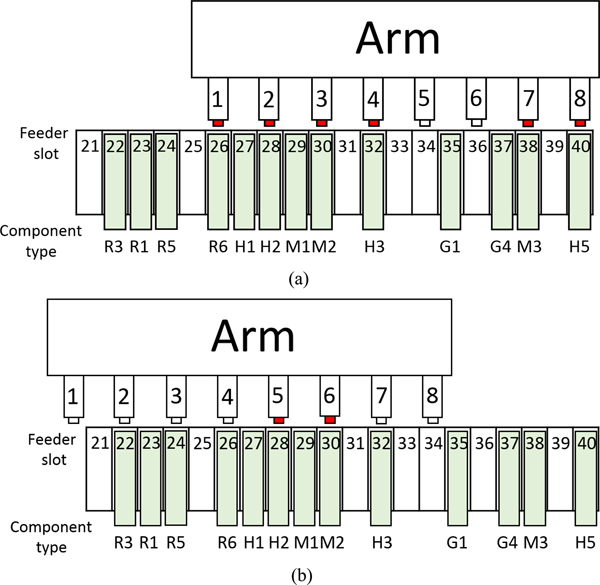
In the first run, eight heads, excluding heads #5 and #6, can simultaneously pick components R6, H2, M2, H3, M3, and H5 (Fig. 4a). In the second run, components H2 and M2 can be picked by heads #5 and #6 (Fig. 4b). The increased number of simultaneously picked components reduces the number of pickups required.
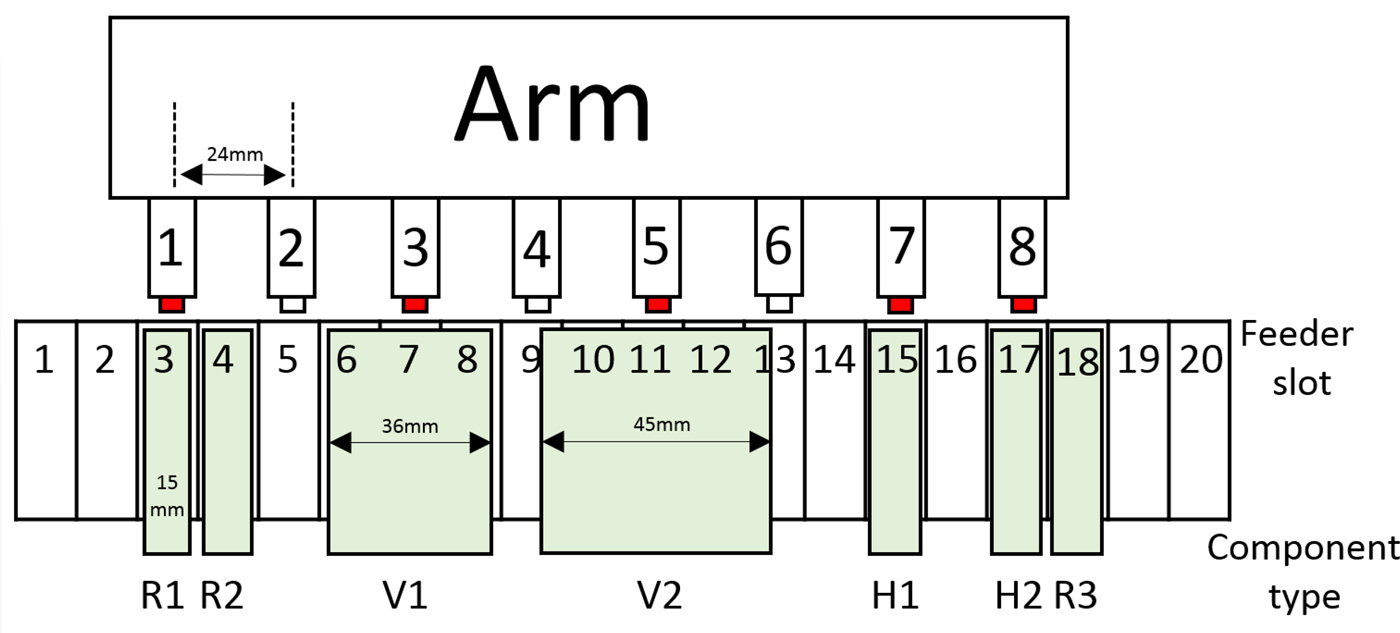
(6) Component shape restrictions: When a component is larger than 15 mm, it requires the space of more than one head. In such cases, the adjacent head cannot be used. In our example in Figure 5, the sizes for components V1 and V2 are 36 and 45 mm, respectively; therefore, heads #2, #4, and #6 are idle when heads #3 and #5 are used (Fig. 5).
Fig. 2. Picking restrictions
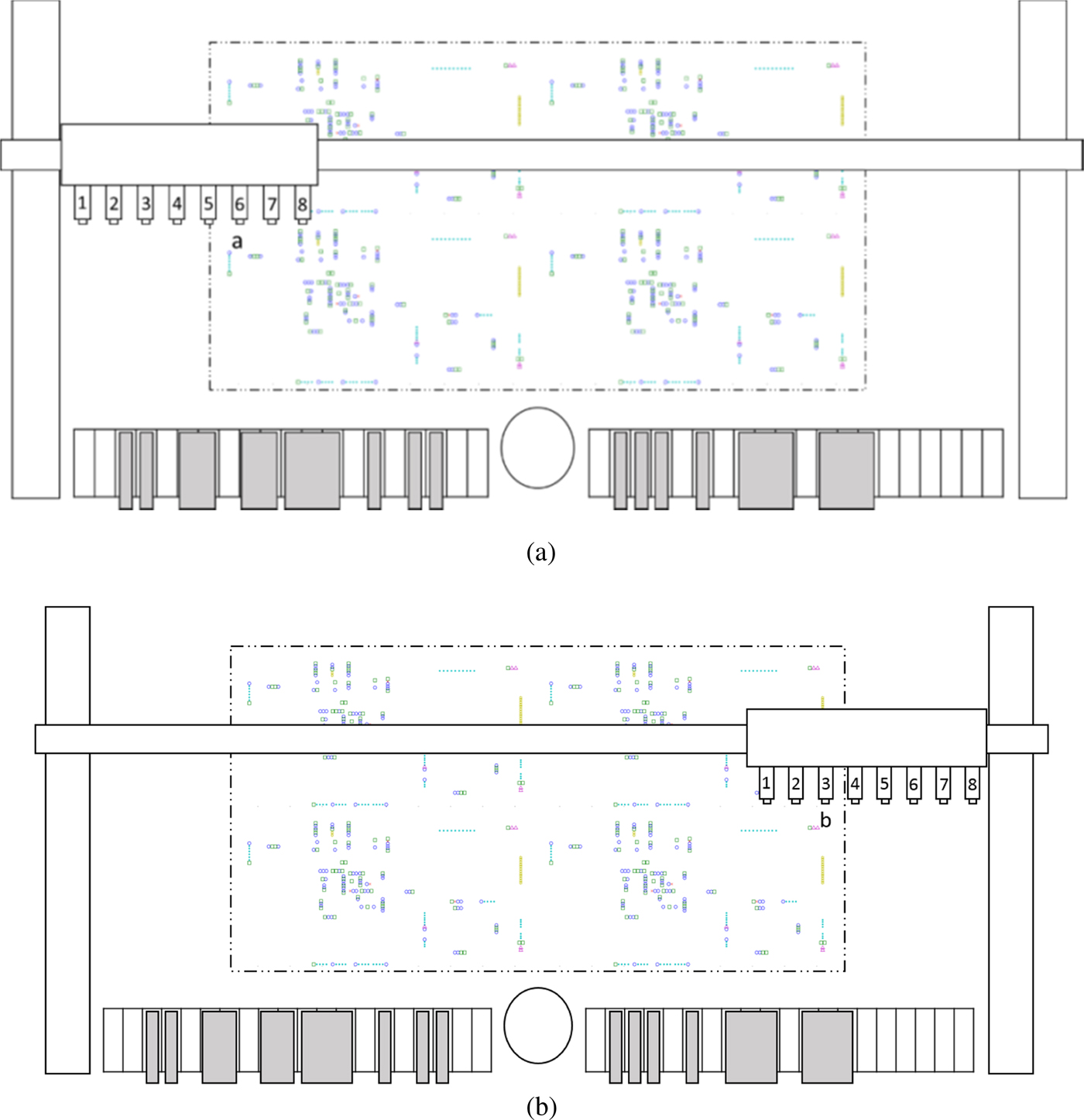
Fig. 3. Placing restrictions
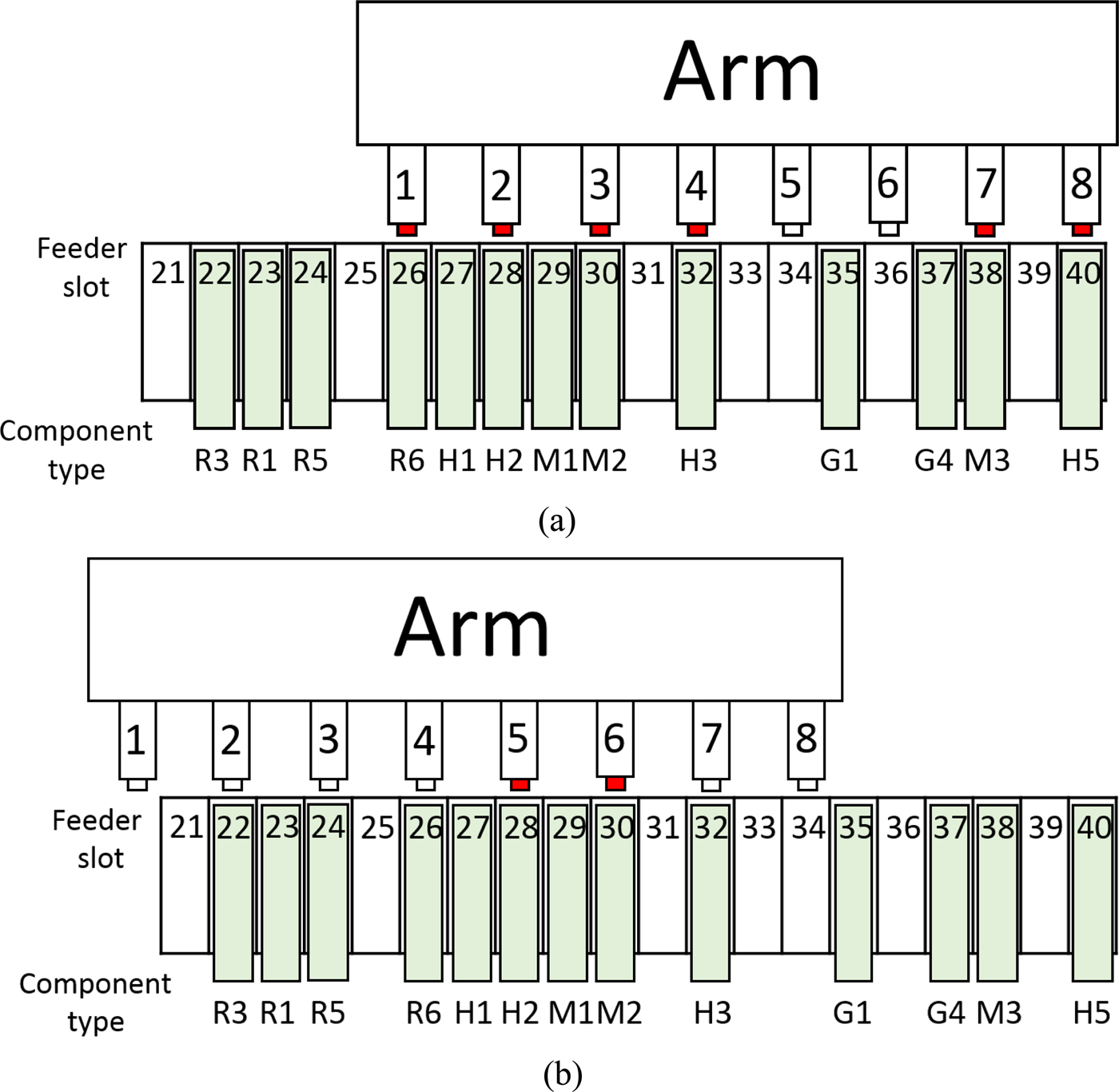
Fig. 4. Simultaneous pickups
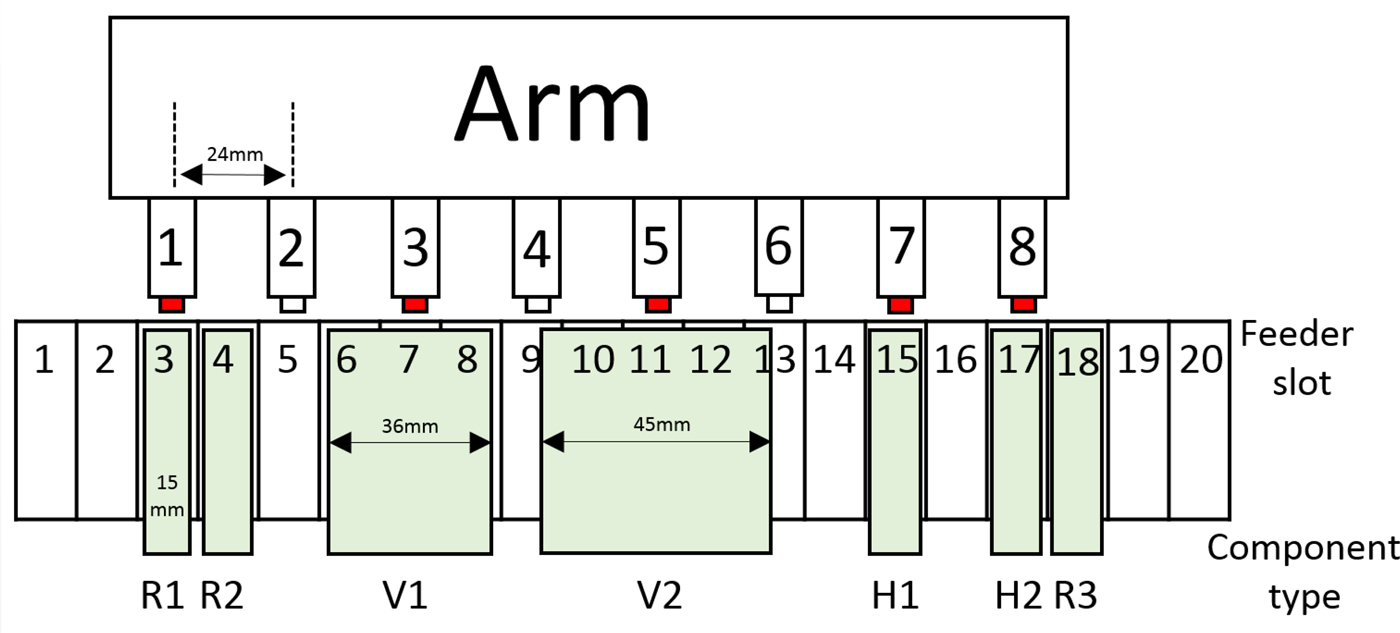
Fig. 5. Component shape restrictions
Problem statement
This study aimed to provide efficient scheduling with minimum production time for assembling PCBs. An interview with the site engineer responsible for the placement machine revealed that although the component positions in the feeders are not fixed, the arrangement seldom varies in practice. If the same components are used in different PCBs, their positions in the feeders are generally retained. The following three interacting problems are discussed herein:
(1) ANC assignment: component pick-and-place sequences interact with each other to enable determination of the optimal ANC.
(2) Nozzle assignment: The nozzle must be assigned by considering the pick, place, component height, and simultaneous pickup restrictions to reduce the number of pickups and nozzle changes, thereby reducing the total assembly time.
(3) Component pick-and-place sequence: The component pick-and-place sequence must be optimized so that head movement for pick-and-place operations uses the shortest path.
Problem formulation
Considering limitations in the practical operation of a multihead placement machine, a mathematical model is proposed for optimizing the total assembly time, which includes pick time, place time, and ANC time. Eq. (1) can be applied to minimize the total assembly time for PCB production.
$$T_{{\rm total}} = \mathop \sum \limits_{c = 1}^{NC} (T_{{\rm pick}}(c))( + T_{{\rm place}} + T_{{\rm change}})$$where T total, T pick, T place, and T change are the total production time for PCB assembly, total pick time, total placing time, and total nozzle change time, respectively. T pick, T place, and T changeare given as follows:
$$\eqalign{&T_{{\rm pick}} \cr &= \left\{ {\matrix{ {\mathop \sum \limits_{i = 1}^{NP-1} (T{\rm (}d{\rm (}S_i\comma \,S_{i + 1}{\rm )}) + T_z({\rm i} + 1) + {\rm T}{\rm D}_{i + 1} + {\rm T}{\rm P}_{i + 1})\;\comma \, \; \; c = 1} \cr {T(d({\rm P}{\rm C}_N\comma \,S_1)) + T_z(1) + {\rm T}{\rm D}_1 + {\rm T}{\rm P}_1 + } \cr {\mathop \sum \limits_{i = 1}^{NP-1} (T(d(S_i\comma \,S_{i + 1})) \!+\1 T_z(i + 1) \!+\! {\rm T}{\rm D}_{i + 1} \!+\! {\rm T}{\rm P}_{i + 1})\comma \,{\rm \;\ otherwise}} \cr}} \right.} $$
$$\eqalign{T_{{\rm place}} & = T(d{\rm (}S_N\comma \,{\rm P}{\rm C}_1{\rm )}) + T_z(1) + {\rm T}{\rm B}_1 + {\rm T}{\rm L}_1 + \cr & \quad \mathop \sum \limits_{\,j = 2}^N (T{\rm (}d{\rm (P}{\rm C}_{\,j-1}\comma \,{\rm P}{\rm C}_j{\rm ))} + T_z({\rm j}) + {\rm T}{\rm B}_j + {\rm T}{\rm L}_j)} $$
$$\eqalign{T_{{\rm change}} & = T({\rm d(}PC_N\comma \,A_1{\rm )}) + T(d(A_{CN}\comma \,S_1)) \cr & \quad + \mathop \sum \limits_{k = 1}^{{\rm CN}} ' {T(d{\rm (}A_k\comma \,A_{k + 1}{\rm )}) + {\rm T}{\rm N}_k} \rsqb } $$where Min(T total) indicates that the objective is to minimize the total assembly time; NC, N, and NP are the total number of cycles in the assembly, heads in the placement machine, and pickups in the assembly, respectively; and TD, TP, TB, and TN are the vacuum on delay time, total waiting time for picking components, total waiting time for placing components, load wait time, and total time for changing nozzles, respectively. Furthermore, CN is the total number of nozzle changes; PC is the component picking position; S is the position of the active slot; A is the position of nozzle change in the ANC; d() is the movement distance of the head; T() is the time required for head movement; andT z(c) is the movement time in both directions along the Z axis.
HGSO for scheduling optimization
The GSO is a heuristic algorithm that was developed in 2009 (He et al., Reference He, Wu and Saunders2009). The SO mimics the behavior of animals searching for food, resources, and places. The GSO reaches global optimum through a local search of team members. It involves few control parameters, and the associated calculations are easy. Under most circumstances, only slight adjustments are required to both parameters and team members in order to apply the GSO to different optimization problems.
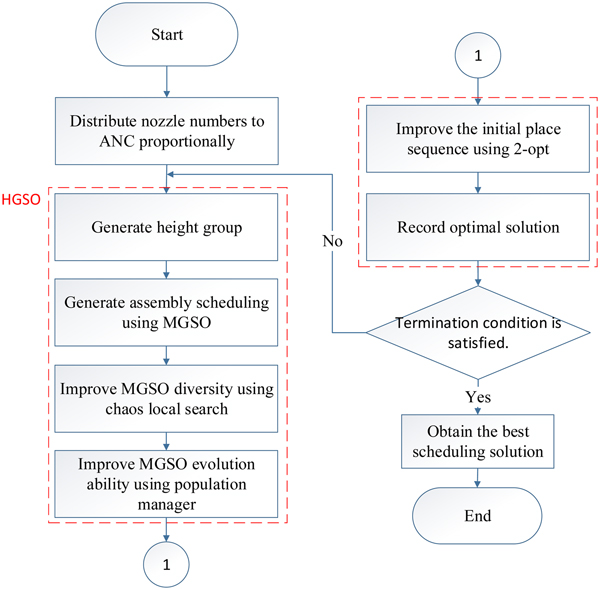
Based on the GSO, an HGSO algorithm is proposed herein for optimizing PCB assembly time. The proposed HGSO overcomes several hardware limitations, including (1) component height restrictions, (2) time consuming nozzle changes, (3) picking restrictions, (4) placing restrictions, (5) simultaneous pickup restrictions, and (6) component shape restrictions. The proposed HGSO divides PCB assembly into three problems: the (1) ANC assembly problem, (2) nozzle setup problem, and (3) component pick-and-place sequence problem. The first step of the HGSO is to proportionally distribute nozzles to the ANC according to required nozzle usage, which is determined by the component picking sequence. The component heights must be considered to avoid collision (i.e., shorter components must be placed earlier). Then, the HGSO generates an efficient picking schedule by considering picking, simultaneous picking, component shape, and placing restrictions. Chaos local search and a population manager are utilized to increase the diversity of placing routes and reduce total PCB assembly time. Figure 6 presents the procedures of the proposed method.
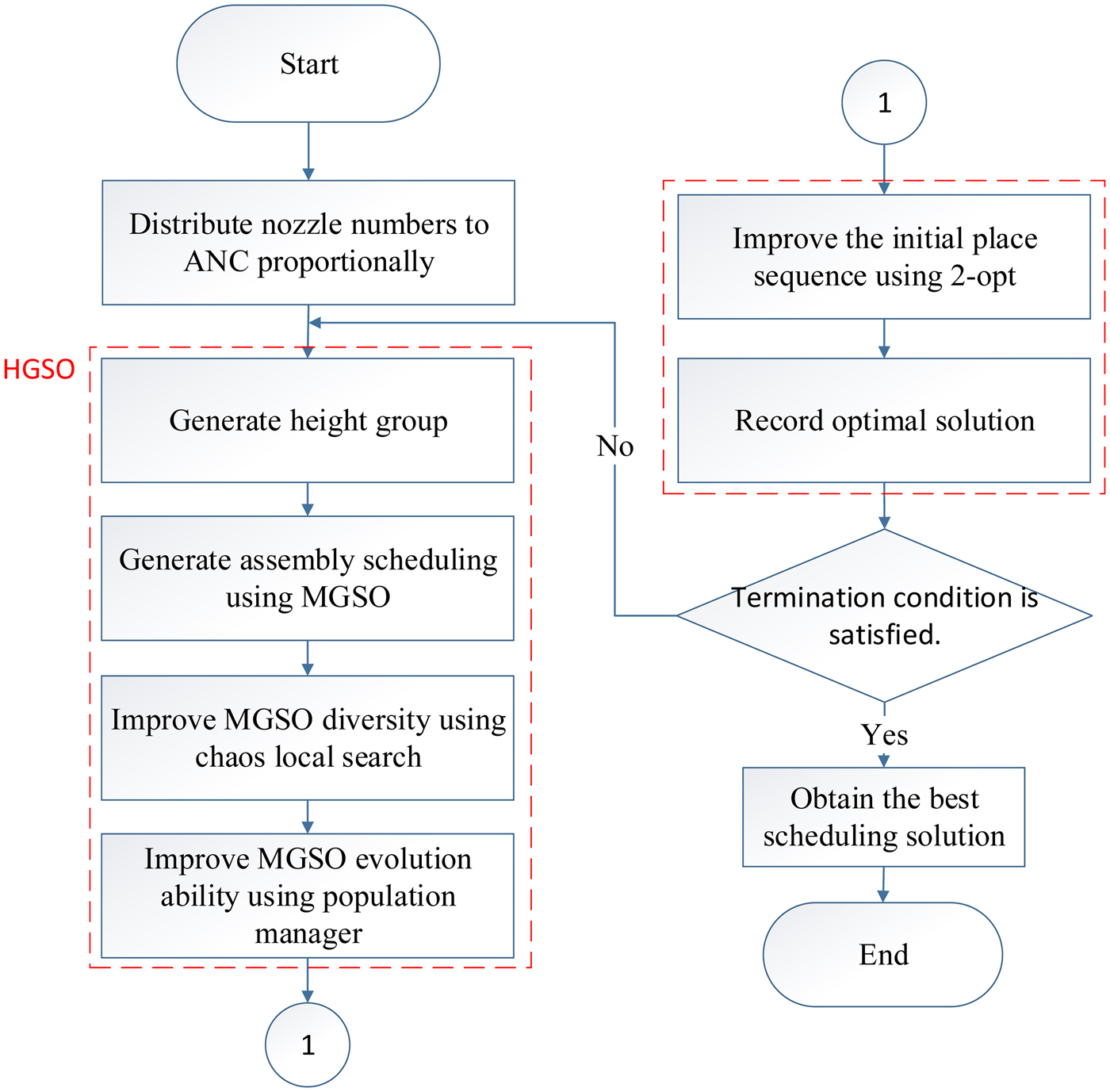
Fig. 6. Systematic procedures within HGSO
Proportional distribution of nozzles to the ANC
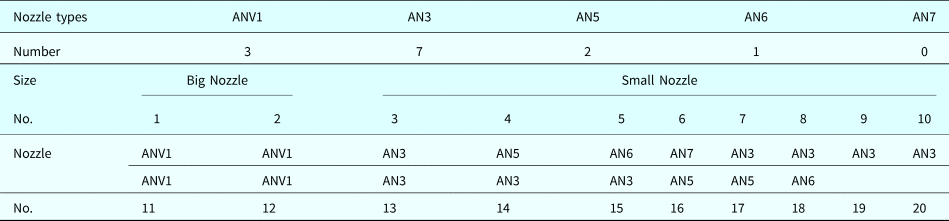
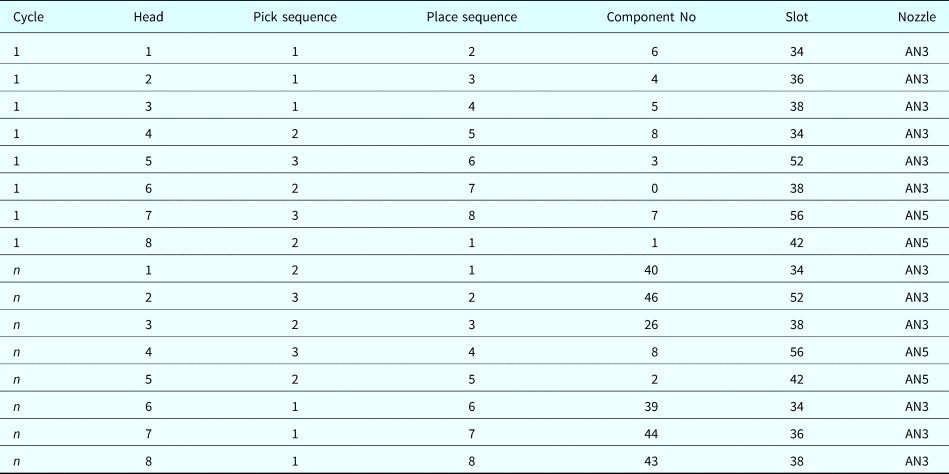
During production, any head in the placement machine may require nozzle change to pick the subsequent component. The ANC has 20 cells, with 16 small and 4 large cells (Table 1). PCBs are different with different numbers of components. For efficient production, the nozzles must be assigned to the ANC before commencing operation. In this study, the nozzles were distributed to the ANC according to the number of pickups by each nozzle. Table 1 presents nozzle arrangement involving one large nozzle (ANV1) and four small nozzles (AN3, AN5, AN6, and AN7).
Step 1: Ensure that at least one nozzle is assigned in the ANC to each component in Table 2, namely ANV1, AN3, AN5, AN6, and AN7.
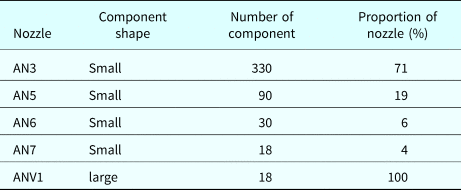
Step 2: Subtract the number of cells that have been occupied in step 1 (i.e., 20−5 = 15). Compute the number of nozzles required for each nozzle type (Table 3) according to the components to be picked up (Table 6).
Step 3: Ensure that the number of nozzles assigned for each type is not higher than the number of heads. For example, if the number of nozzles assigned for type AN3 exceeds the number of heads, reduce the number of nozzles to the maximum number of heads (Table 4).
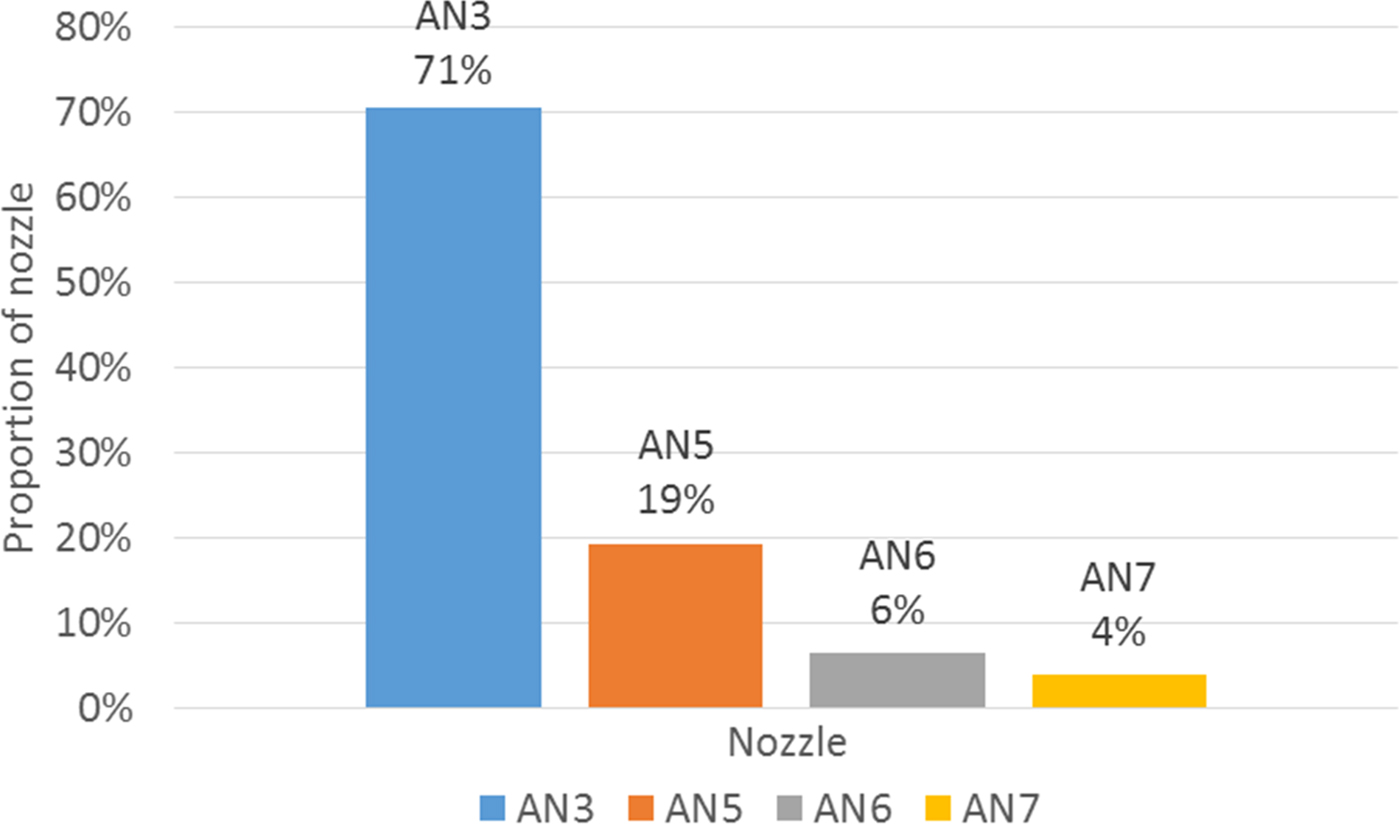
Step 4: Repeat steps 2 and 3 until all cells in the ANC are occupied (Tables 5 and 6, Fig. 7).
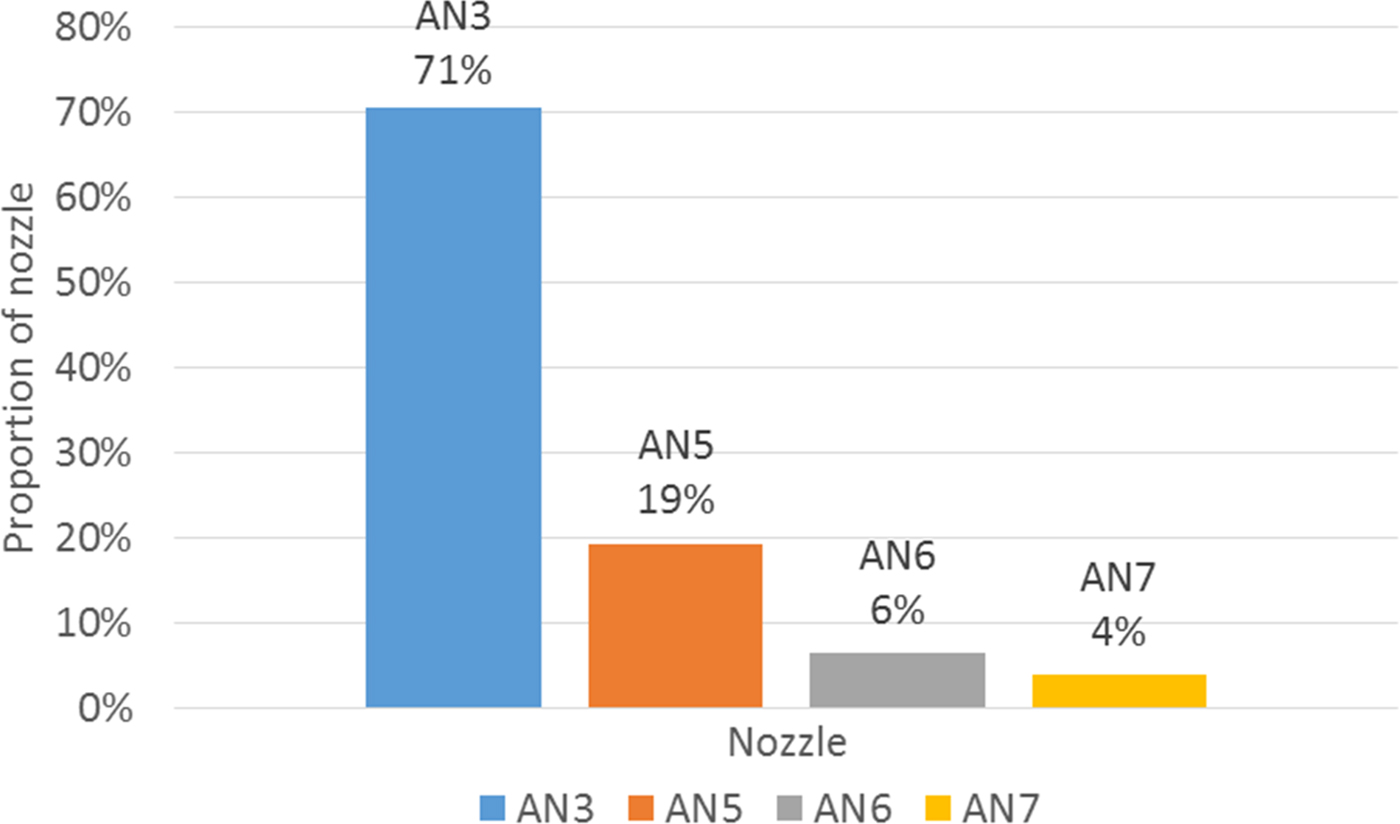
Fig. 7. Proportion of small nozzles
Table 1. Nozzle arrangement in ANC
Table 2. ANC arrangement step 1
Table 3. Number of nozzles per type
Table 4. Nozzle arrangement checklist
Table 5. Final nozzle arrangement
Table 6. Components per nozzle type
HGSO algorithm
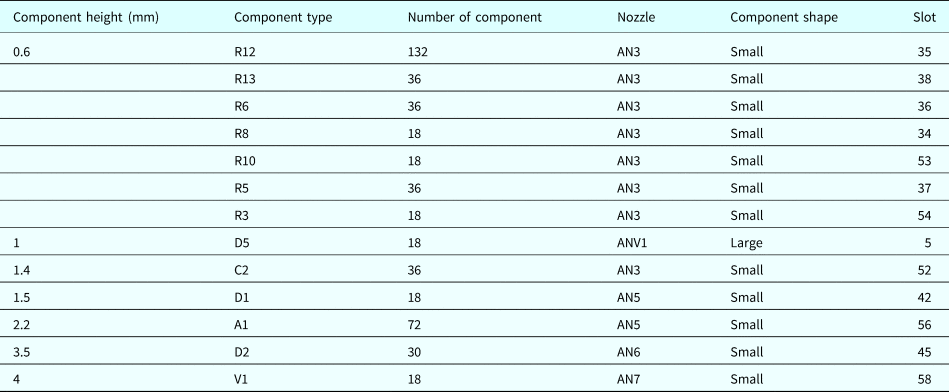
To avoid collision during component placement, shorter components must be placed earlier. In the following example, components with a height of 0.6–2.6 mm (see Table 7) are grouped together and can be arbitrarily placed if height restriction is 2 mm.
Table 7. Component information
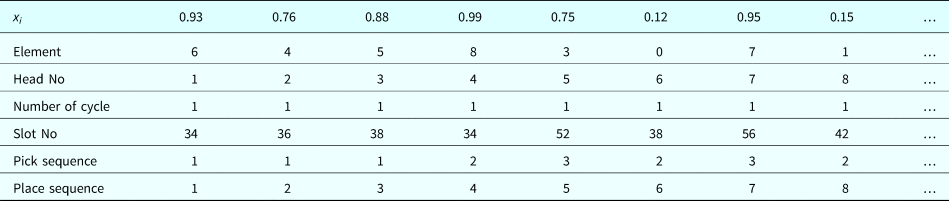
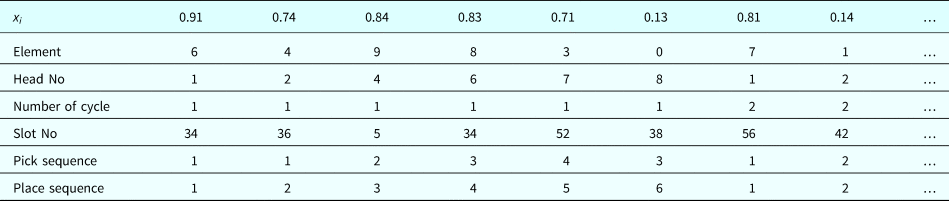
A random number between 0 and 1 is generated and assigned to each member for executing the GSO algorithm (Table 8). N and x i are the total number of components and the i th member in the GSO, respectively. Each member represents a scheduling solution.
Table 8. Coding method for GSO members
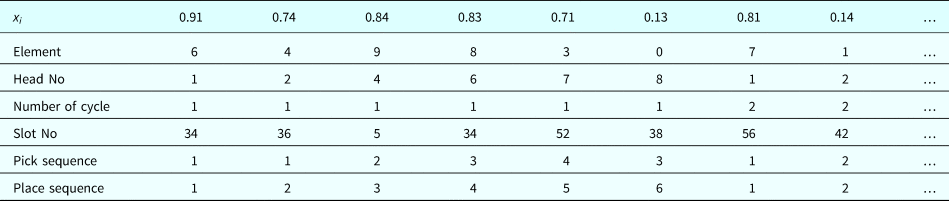
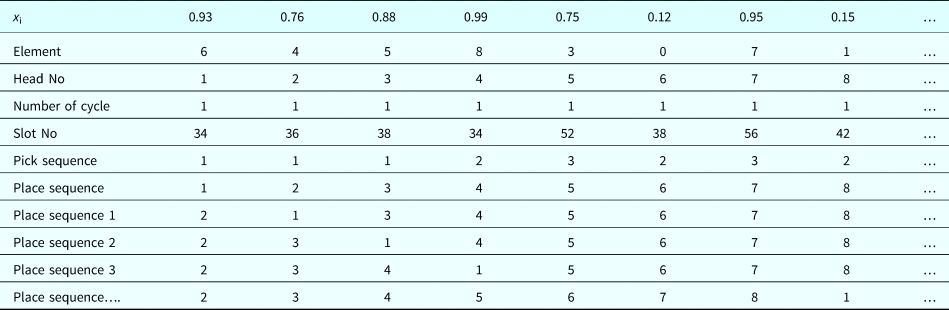
The traditional GSO cannot be employed to schedule placement machines because this problem is a type of integer optimization. In this study, an MGSO with an added random key (Snyder and Daskin, Reference Snyder and Daskin2006) was proposed for scheduling optimization of PCB assembly. Tables 9–11 illustrates the procedure. The first random number in Table 9 is 0.95. Component 6 is assigned to the first cell after considering component height, component shape, nozzle assignment, and picking restrictions. In Table 10, the initial solution with random numbers in Table 9 is adjusted by placing the elements in an ascending order: 0.12, 0.15, 0.75, 0.76, 0.88, 0.93, 0.95, and 0.99. Element 0 is assigned to the lowest random number (0.12), element 1 is assigned to the subsequent number (0.15), and so on (Table 11). Table 12 presents the solutions for the large components, where head #3 and #5 are idle in the first cycle because component 9 occupies the space beneath them.
Table 9. Initial solution: random numbers
Table 10. Members arranged in ascending order
Table 11. Final solution of members
Table 12. MGSO of large components
The 2-opt method is employed to the solution of the initial path derived from Table 12. Table 13 presents the improved solution. A mathematical model that calculates the total assembly time is then applied to evaluate the performance of the probable solutions. Table 14 presents the final result.
Table 13. The 2-opt method
Table 14. Final scheduling results
Chaos local search
Chaos local search (Liu et al., Reference Liu, Wang, Jin, Tang and Huang2005), which is a new optimization technique, is applied to improve MGSO evolution performance. Chaos local search has several advantages for obtaining the initial solution, such as sensitivity and dependence, which ensure the diversity and appropriate search behavior of the entire space. The chaos search formula is as follows:
$$x_{n + 1} = \mu \times x_n(1-x_n)\comma \,\; 0 \le x_0 \le 1$$where μ and x are a control parameter and a random variable, respectively, with n = 0, 1, 2, … However, when μ = 4, x 0{0, 0.25, 0.5, 0.75, 1} can be applied to Eq. (5). Chaos is sensitive and dependent on initial conditions, and a slight initial difference can generate considerable variances given a long enough timeframe. The MGSO searches the entire space by using particular characteristics of chaos [Eq. (6)]:
$$cx_i^{(k + 1)} = 4cx_i^{(k)} (1-cx_i^{(k)} )\comma \,\; i = 1\comma \,\; 2\comma \,\; \ldots \ldots\comma \, N$$where cx i and k are a chaos variable and the number of iterations, respectively. 
$cx_i^{\lpar k \rpar } \; $ has a range of [0, 1] and satisfies
${\rm \;} cx_i^{(0)} \in (0\comma \,1)$, 
$cx_i^{(0)} \not\subset \lcub {0.25\comma \,{\rm \;} 0.5\comma \,{\rm \;} 0.75} \rcub $. The procedure of chaos search is as follows:
Step 1: Use Eq. (6) to produce chaos variables for the subsequent generation.
(7)
$$cx_i^{(k + 1)}\comma \,cx_i^{(k)} = x_i$$Step 2: Compare the new solution
$cx_i^{(k + 1)} $ with the original solution $cx_i^{(k)} $. Use the more favorable solution.(8)$$x_i = cx_i^{(k + 1)} $$Step 3: Repeat steps 1 and 2 until i = N.
Population manager
Because similar subjects have similar fitness values and converge to likely positions, the worse subjects must be eliminated to improve efficiency and reduce computation. Similarity is evaluated as follows (Liang and Lee, Reference Liang and Lee2015):
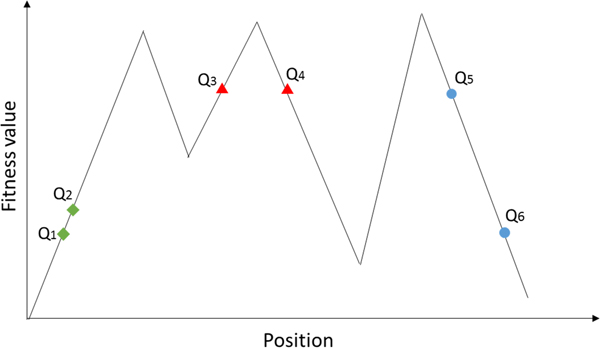
$$\left \vert {\displaystyle{{\,f\,(x_i)-f\,(x_j)} \over {\,f\,(x_j)}}} \right \vert \lt \delta _{\rm m}{\rm \;\comma \,} \,{\rm \;} x_{\rm i}-x_{\rm j} \lt r_{\rm m}$$where δ m and r m are threshold values, representing the average fitness value and average distance of the entire space, respectively; 
${\left\Vert \cdot \right\Vert} $ denotes the distance betweenx i and x j. Figure 8 illustrates this concept. Subjects Q3 and Q4 have similar fitness values (less than δ m); however, the distance is larger than r m. The positions for Q5 and Q6 are close (less than r m); however, the fitness values are considerably different. The fitness values and positions for Q1 and Q2 are similar, which satisfy Eq. (9), and the lower value (Q1) can be deleted.
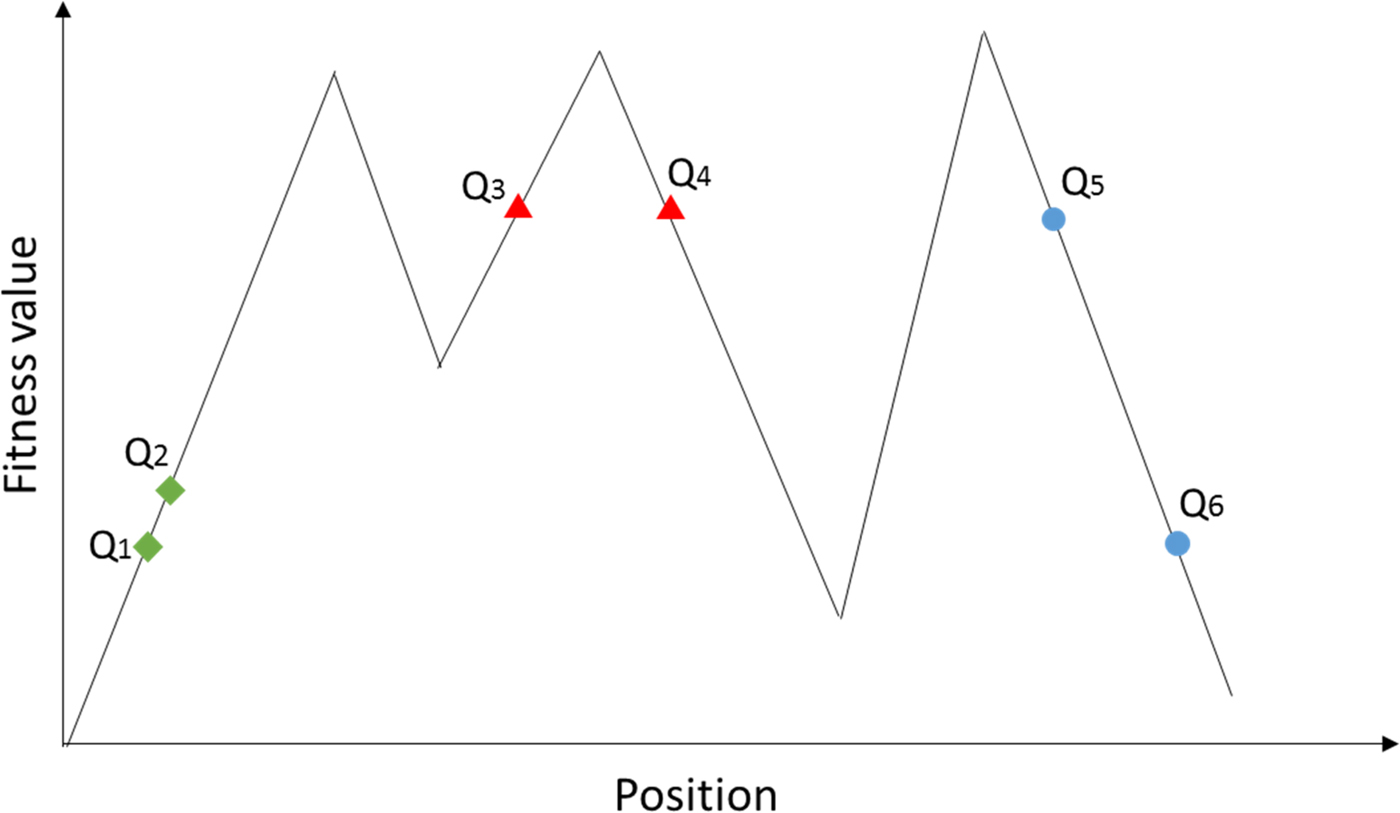
Fig. 8. Fitness value and position
Experimental results and comparisons
The real-time data from a placement machine (EM-780, Evest Corporation, Taoyuan, Taiwan; Figure 9) were used to evaluate the feasibility of the proposed method. In this study, 10 PCBs with different numbers and types of components, nozzle types, and feeders (Table 15) were assembled.
Fig. 9. Placement machine EM-780
Table 15. PCB information
According to Section ‘GSO for scheduling optimization’, the initial settings are as follows: N = 100, iterations = 3000, scroungers = 80%, rangers = 20%, and head angle = 0.25π. The maximum iteration is 
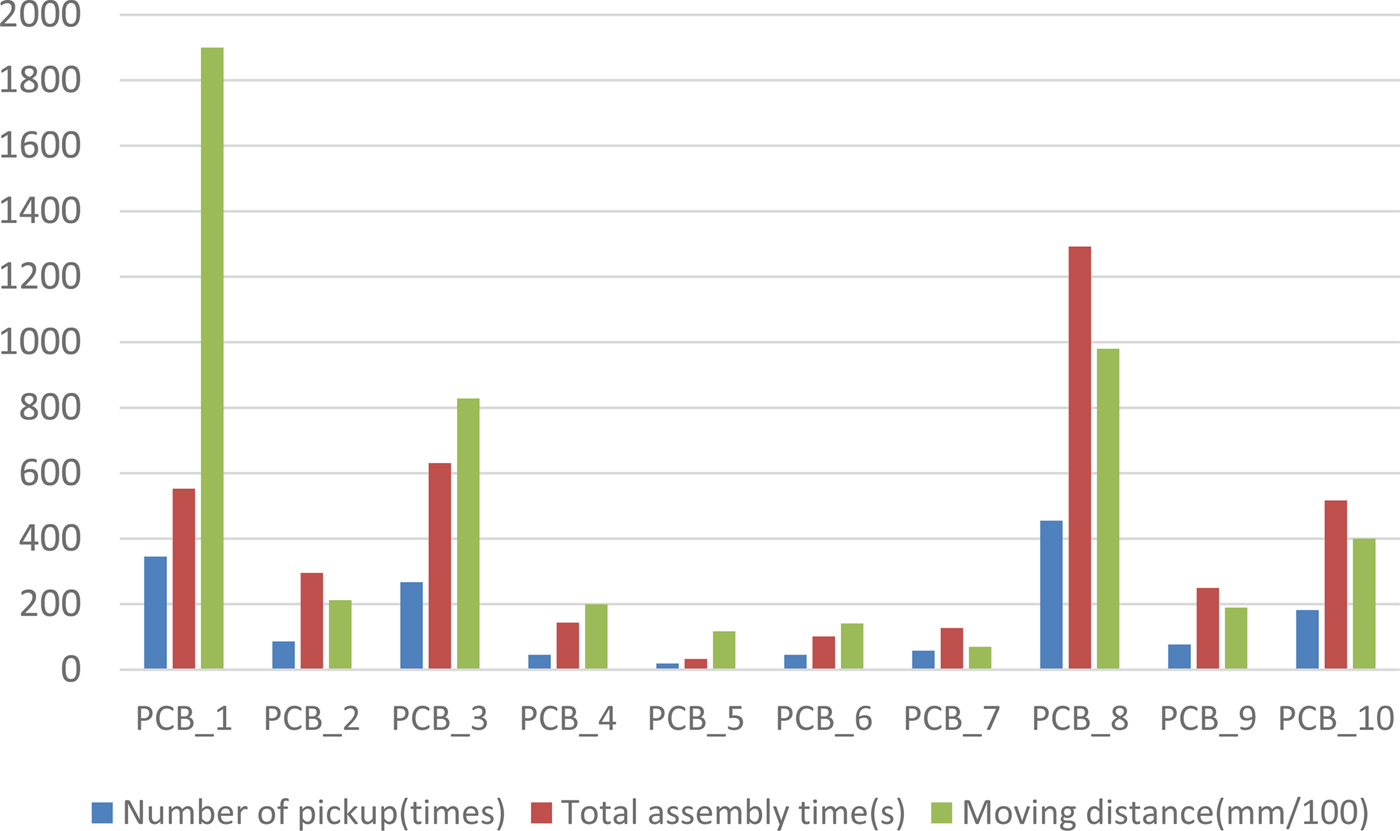
$a = {\rm round}\sqrt {n + 1} $. If the producer cannot determine the improved area after a iterations, U i and L i are equal to 1 and −1. Here, n and 
$l_{{\rm max}} = \sqrt {\mathop \sum \limits_{i = 1}^N {(U_{\rm i}-L_{\rm i})}^2} $ are the number of components and maximum pursuit distance, respectively. Figure 10 displays the number of pickups, total assembly time, and moving distance obtained using the proposed method.
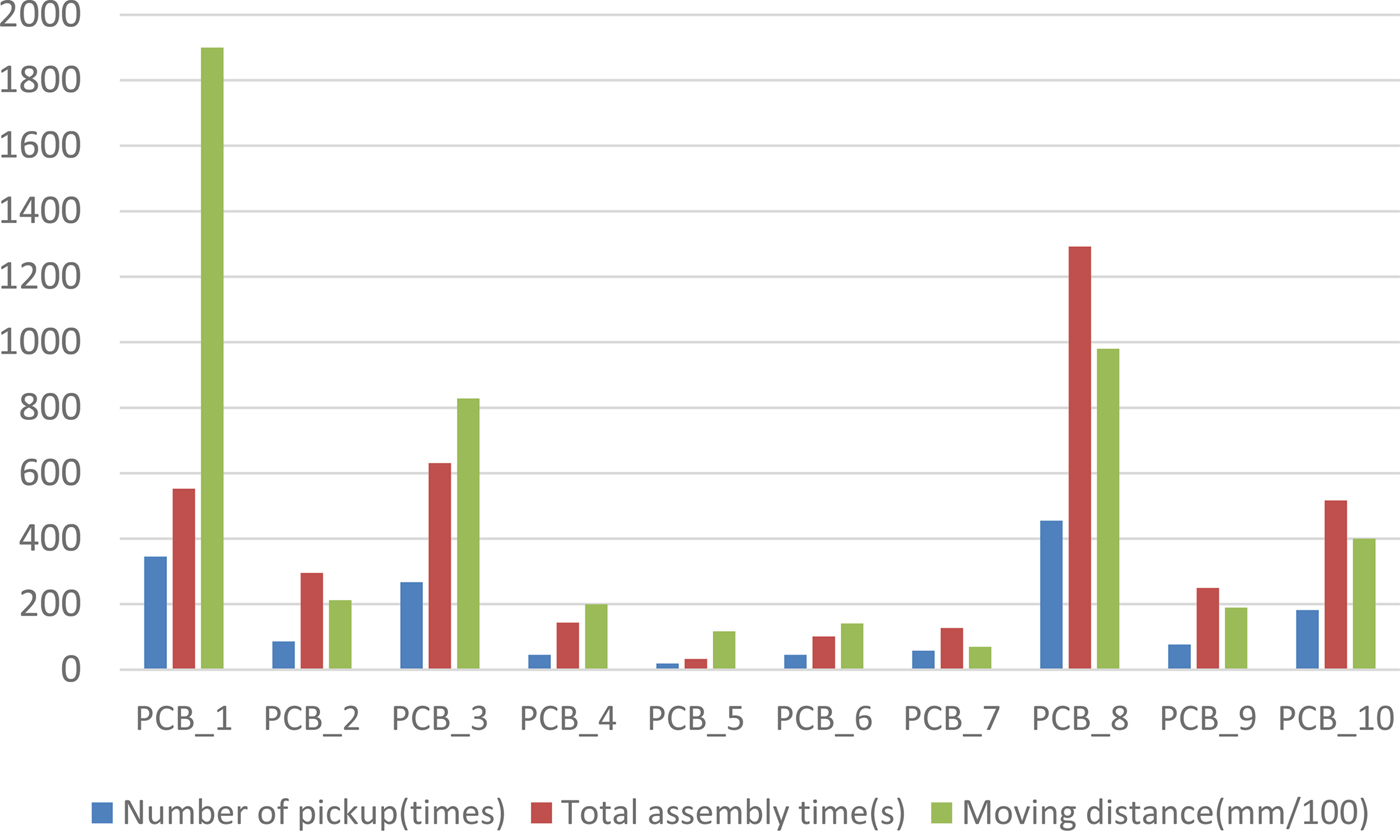
Fig. 10. Number of pickups, total assembly time, and moving distance obtained through the proposed method
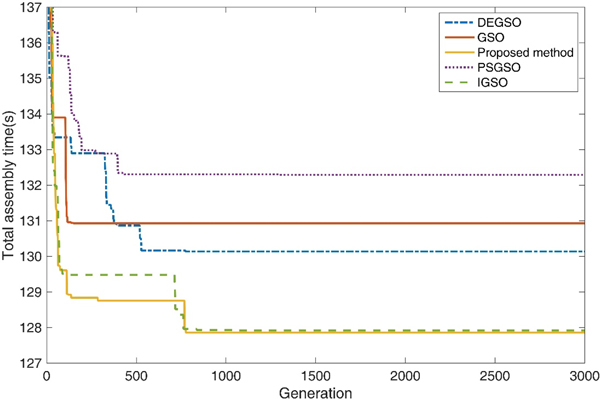
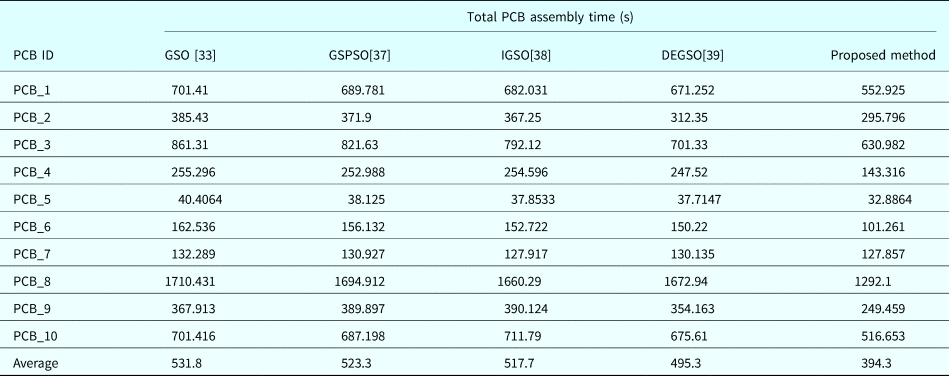
Yan et al. (2011) proposed GSPSO, which integrates high-speed computation in PSO with the favorable high-dimensional performance of GSO. Chen et al. (Reference Chen, Luo, Du and Hu2012a, Reference Chen, Wang, Zou, Hou and Zhao2012b) presented an improved group search optimizer (IGSO) with a quantum-behaved operator for scroungers according to a certain probability of improving GSO convergence performance. In this method, the scroungers are categorized into two types: the scroungers that update their positions with quantum PSO operators and those that search for opportunities to join the resources found by the producer. Nian et al. (Reference Nian, Wang and Qian2013) proposed a differential evolution (DE) GSO, which is a hybrid of DE and GSO. DE prevents traditional GSO from falling into local optimal and enhances its accuracy. Table 16 compares the proposed method and related algorithms. The proposed method required the least total PCB assembly time for the 10 PCBs out of the compared algorithms. Figure 11 shows the learning curve for PCB_7, revealing that the total assembly times of PCB_7 using the proposed method and IGSO are similar [38]. Table 16 shows that the total average assembly times for the 10 PCBs (i.e., PCB_1–PCB_10) were 531.8, 523.3, 517.7, 495.3, and 394.3 s for the GSO (He et al., Reference He, Wu and Saunders2009), GSPSO (Yan and Shi, Reference Yan and Shi2011), IGSO (Chen et al., Reference Chen, Luo, Du and Hu2012a, Reference Chen, Wang, Zou, Hou and Zhao2012b), DEGSO (Nian et al., Reference Nian, Wang and Qian2013), and proposed method, respectively. Therefore, the total average assembly time of the proposed method is superior to that of other methods (He et al., Reference He, Wu and Saunders2009; Yan and Shi, Reference Yan and Shi2011; Chen et al., Reference Chen, Luo, Du and Hu2012a, Reference Chen, Wang, Zou, Hou and Zhao2012b; Nian et al., Reference Nian, Wang and Qian2013).
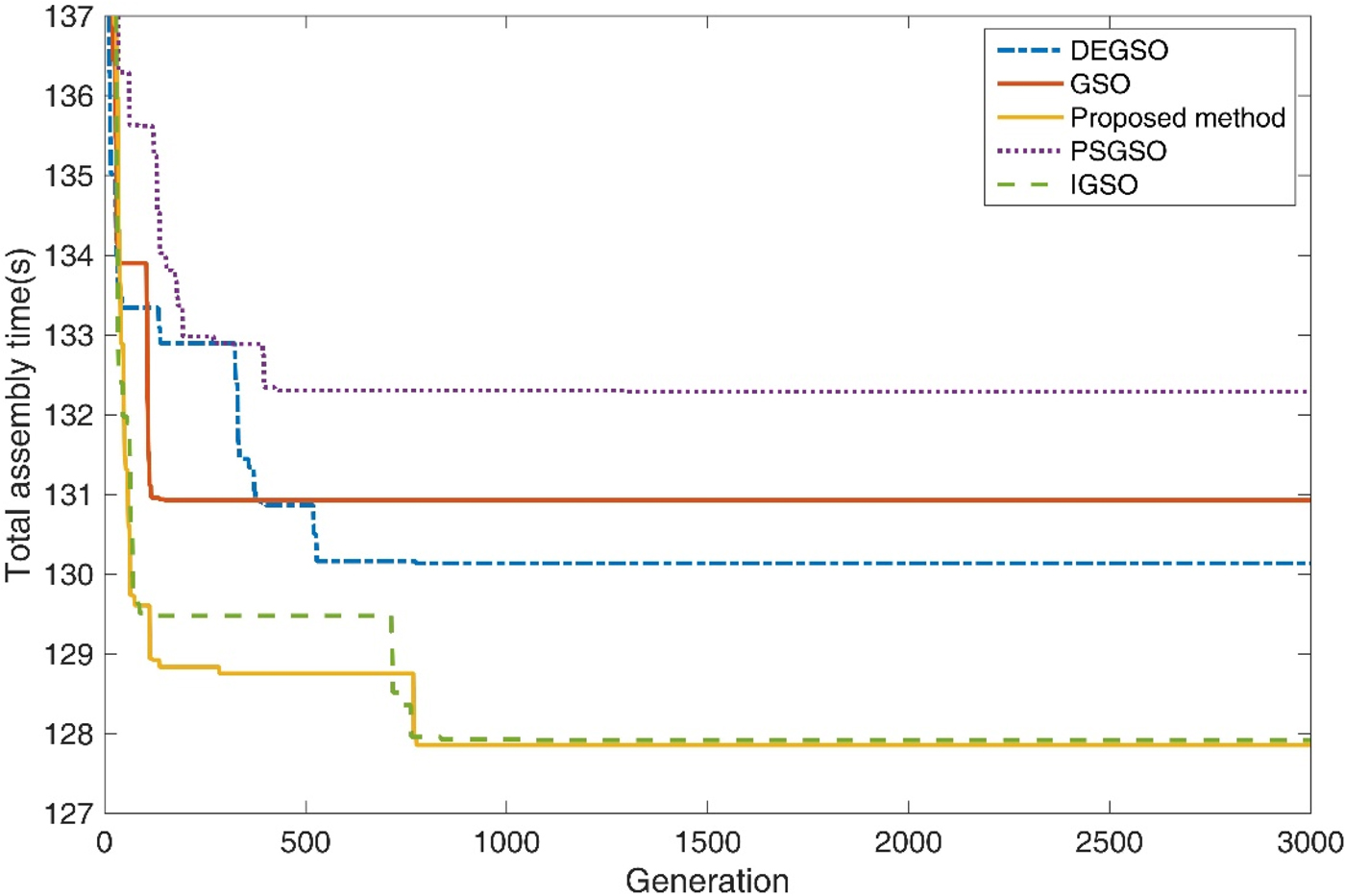
Fig. 11. Learning curve of PCB_7
Table 16. Total assembly time in the proposed method and related GSOs
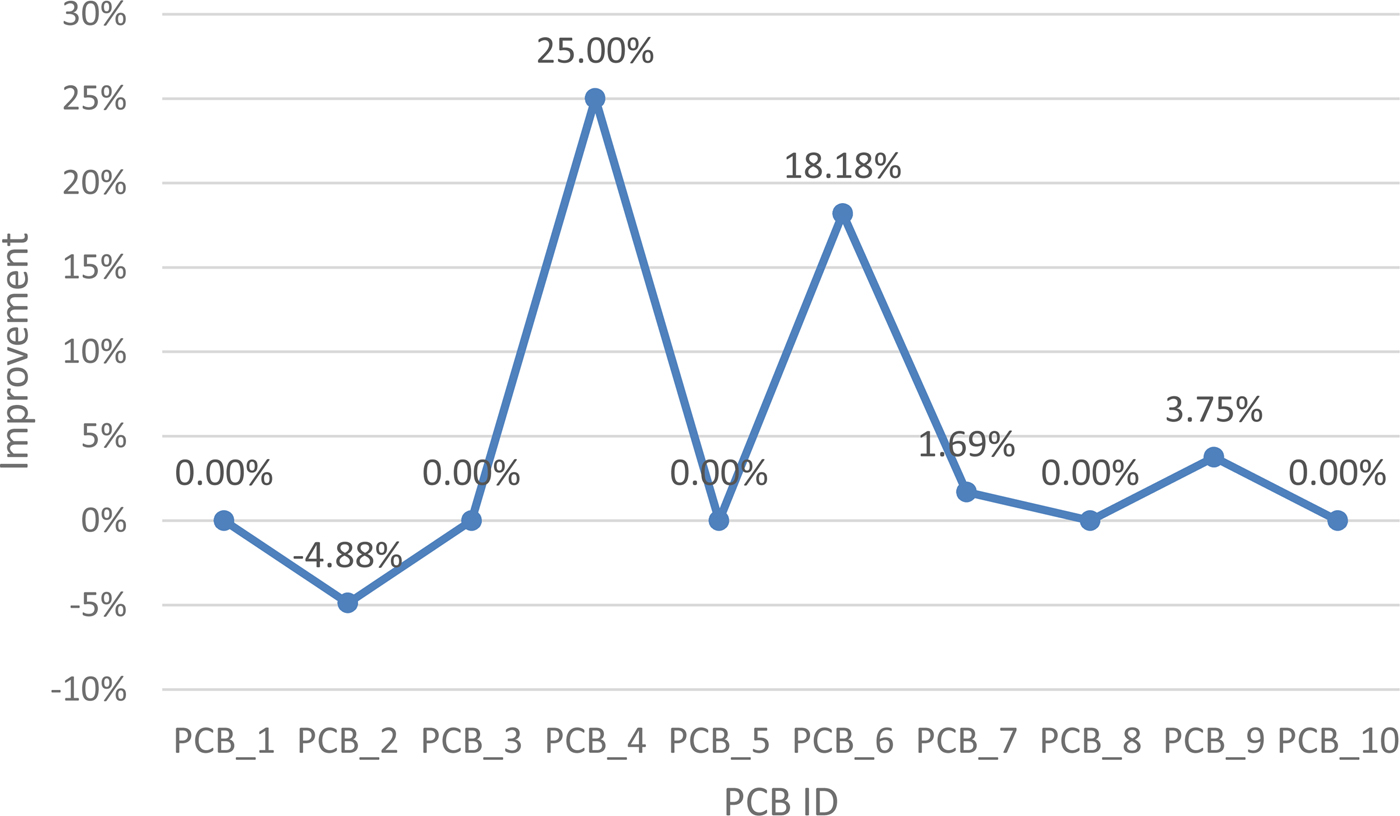
Algorithm performance in this study is determined in terms of the (1) total number of pickups, (2) total head movement distance, and (3) total assembly time. The results of the proposed method were compared with those of related algorithms, such as GAs or the improved shuffled frog leaping algorithm (Loh et al., Reference Loh, Bukkapatnam, Medeiros and Kwon2001; Sun et al., Reference Sun, Lee and Kim2005; Chang et al., Reference Chang, Hsieh and Wang2007; Ho and Ji, Reference Ho and Ji2010; Zhu and Zhang, Reference Zhu and Zhang2014). The number of pickups considerably influences PCB assembly, with total assembly time reducing with decreasing number of pickups. The proposed method required the least number of pickups for all experimental PCBs, excluding PCB_2 (Table 17). Figures 12–14 exhibit improvements calculated using the following equation:
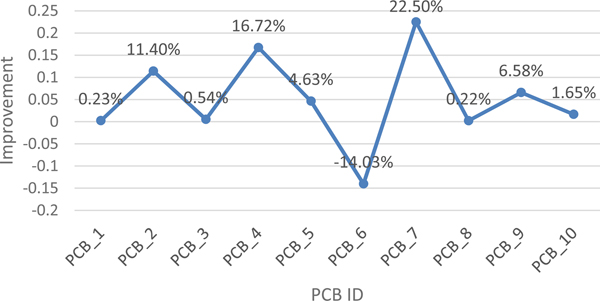
$${\rm Improvement} = \displaystyle{{{\rm Onsite}\_{\rm Engineer}-{\rm Our}\_{\rm method}} \over {{\rm Onsite}\_{\rm Engineer}}} \times 100\% $$Assembly time reduces with decreasing total head movement distance. Table 18 presents the experimental results, which indicate that the proposed algorithm can effectively reduce total head movement distance. Table 18 outlines the operation for PCB_6, showing that the head movement distance generated by the proposed algorithm is longer than that produced by an onsite engineer. Figure 13 reveals improvement in the total head movement distance achieved using the proposed algorithm.
Fig. 12. Improvement in total number of pickups
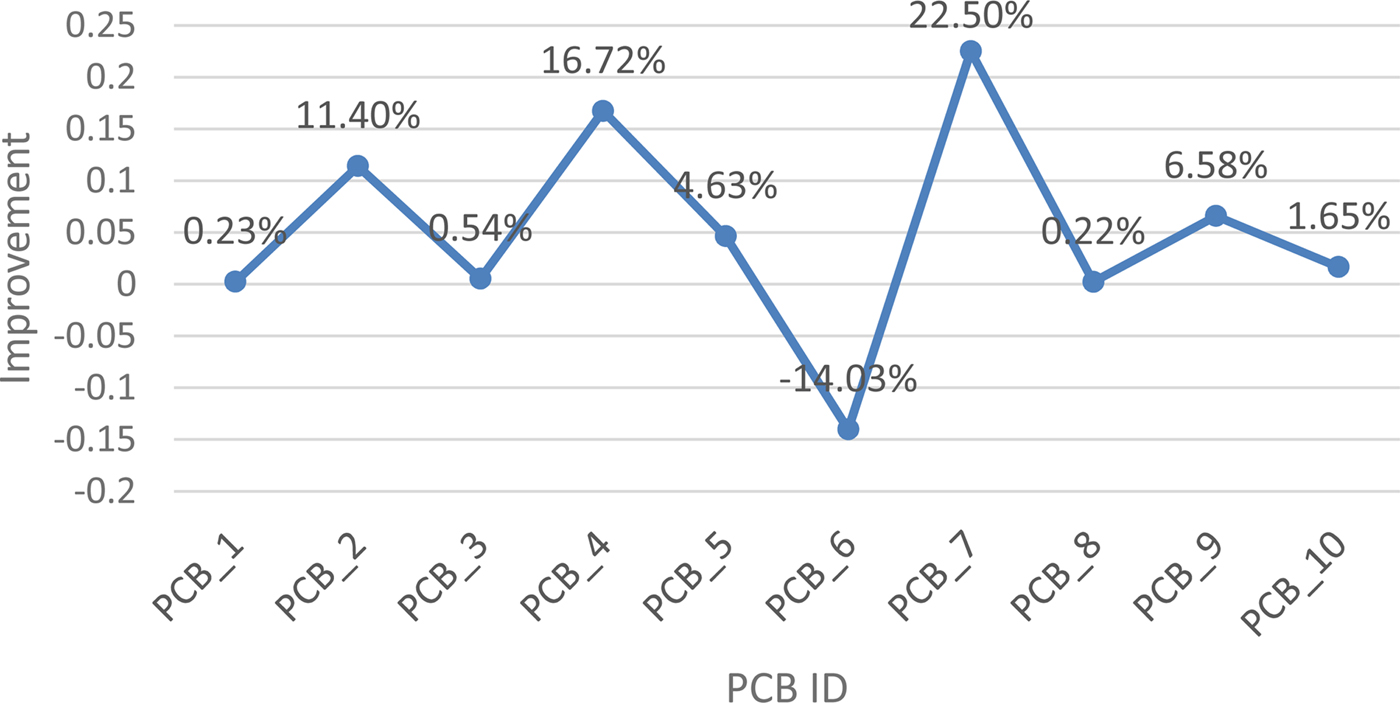
Fig. 13. Improvement in total head movement distance
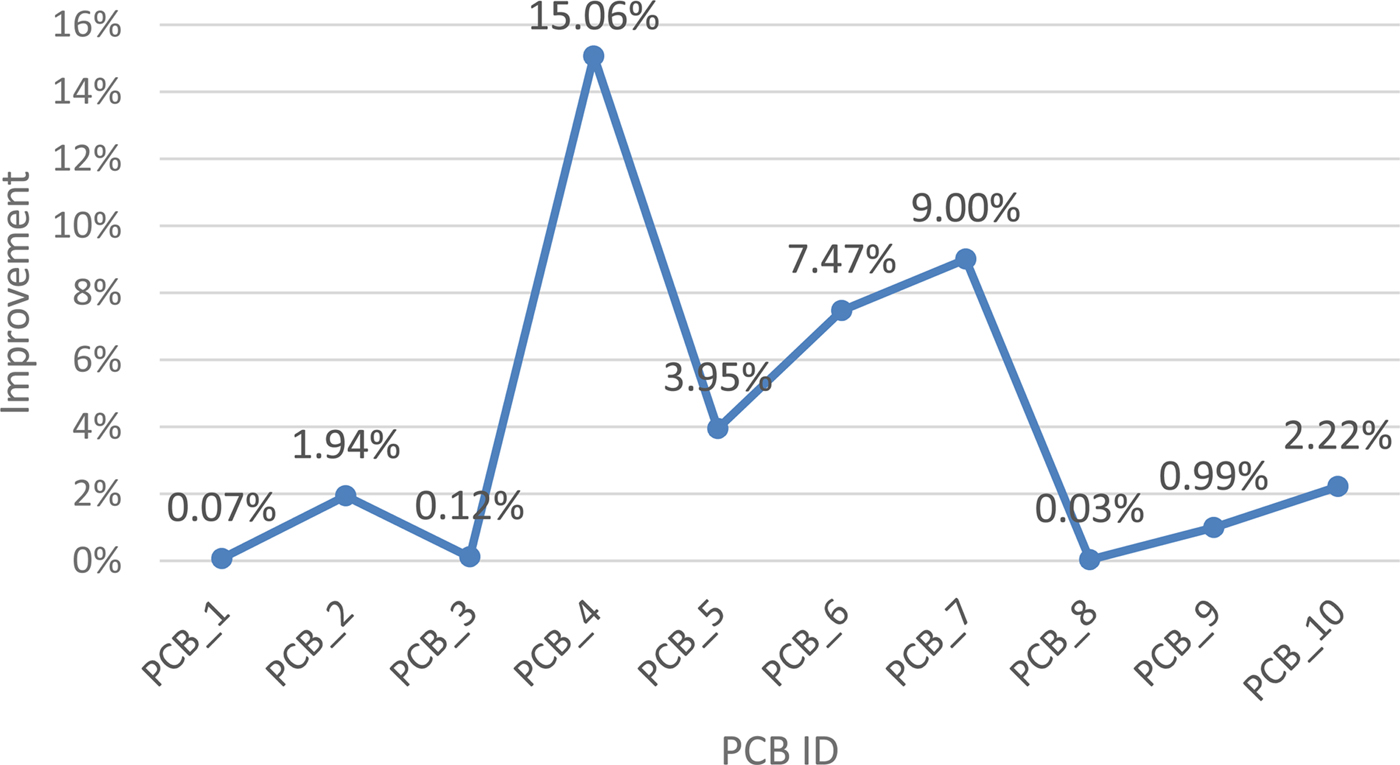
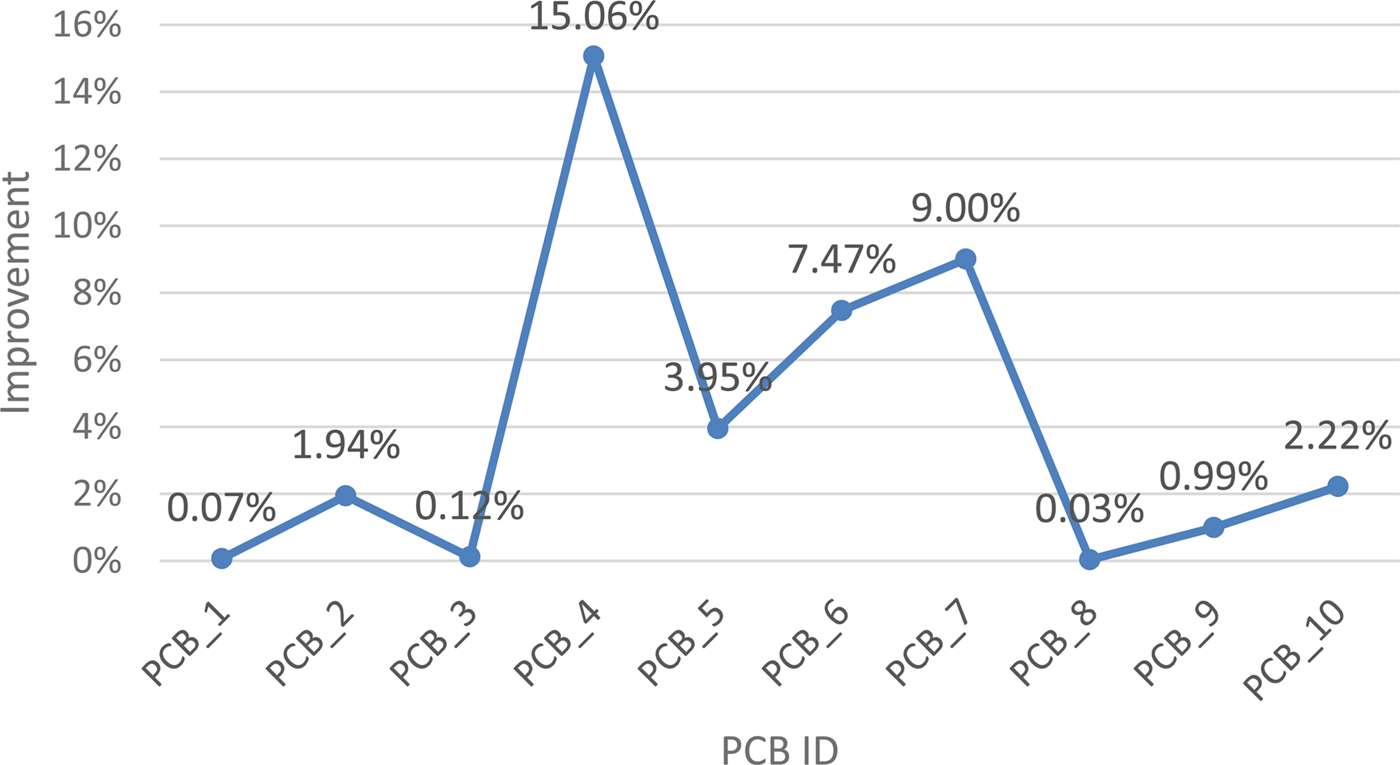
Fig. 14. Improvement in total assembly time
Table 17. Comparison of total number of pickups
Table 18. Total head movement distance
From Table 19 and Figure 14, the proposed HGSO algorithm outperforms other algorithms and the onsite engineer in terms of assembly time. Although the total number of pickups for PCB_1, PCB_3, and PCB_8 in Table 17 did not differ substantially, the total head movement distances (Table 18) were clearly different. Figure 14 shows the excellent performance of the proposed HGSO in terms of total assembly time. In practice, onsite engineers can appropriately design optimal pickup sequences but not path optimization. The proposed HGSO considers the total number of pickups and the total head movement distance to reduce the total assembly time. In the total assembly time, considerably more time is spent on pickups than it is on head movement. Table 20 presents the percentages of pickup time, placing time, and ANC time. To reduce total assembly time, a higher head movement distance is traded off for fewer pickups. Studies (Loh et al., Reference Loh, Bukkapatnam, Medeiros and Kwon2001) and (Jiang et al., Reference Jiang, Chen, Zang, Wang and Tan2010a, Reference Jiang, Du, Liu and Zhang2010b, Reference Jiang, Liu, Zhang, Wang, Tan and Chen2010c) have decomposed the scheduling problem into two stages: optimization (minimization) of (1) the number of pickups and (2) the place movement based on the results of stage one. The proposed HGSO is less complicated than the two-stage method.
Table 19. Total assembly time
Table 20. Total assembly time
Discussion and conclusions
This study aimed to perform scheduling optimization for reducing total PCB assembly time. Scheduling for a placement machine is a highly comprehensive task. Several studies have overlooked machine limitations to simplify the problem. However, the generated schedules produced by these studies cannot be practically applied to production lines. By contrast, this study proposed an HGSO that considers the limitations of placement machines to generate an applicable schedule are summarized as follows.
(1) Component height: The height of each component could be different, and the components are picked and placed in the ascending order of the height to avoid collision, i.e., The component with the lowest height must be placed first at the beginning of the placement machine during work.
(2) The Time consuming of nozzle changes: shapes of the components are different, and each matches a unique corresponding nozzle. When the nozzle is not applicable, the head need to exchange the nozzle. The process of nozzle changes takes time. Some scholars ignore the time consuming of nozzle changes.
(3) Picking restrictions: In the placement machine, not every head can pick up component in all feeders because there are some positions that the head cannot reach.
(4) Placing restrictions: As above, there are some destinations that head cannot arrive.
(5) Simultaneous pickup restrictions: Simultaneous pickup is important in the placement machine process. Practically, we want to simultaneously pick up components as many as possible to reduce the time consuming on picking components. The restrictions of the head pitch and the feeder pitch should be under consideration.
(6) Component-shape restrictions: the components differ in shape and size. If the component shape is larger than the limit, the adjacent head cannot pick up the component.
Compared with the related works in this field, this study considers more restrictions than others. This is the first study includes component heights and component shapes in the scheduling problem of a placement machine. In addition, this study modified the traditional group search optimizer for the possible usage for PCB assembly. The results indicate that the proposed HGSO is superior to related algorithms and an onsite engineer in terms of total assembly time. Although the diversity of placement machines for PCB assembly is many, the key structures of placement machines are the same. The proposed hybrid group search optimizer possesses flexibility on adjusting the parameters according to the head numbers, number of nozzle types, etc. and can be widely applied to general multihead placement machines.
Acknowledgments
This study was partially supported by the Ministry of Science and Technology, Taiwan, ROC, under the grant MOST 105-2221-E-167-012.
Cheng-Jian Lin received the Ph.D. degree in electrical and control engineering from the National Chiao-Tung University, Taiwan, R.O.C., in 1996. Currently, he is a Distinguished Professor of Computer Science and Information Engineering Department, National Chin-Yi University of Technology, Taichung County, Taiwan, R.O.C. His current research interests are artificial intelligent, machine learning, intelligent control, evolutionary robotic, image processing, and pattern recognition.
Mei-Ling Huang received her M.S. and Ph.D. in Industrial Engineering from University of Wisconsin - Madison and National Chiao-Tung University. Now, she is affiliated with the Department of Industrial Engineering & Management at National Chin-Yi University of Technology. Her research interests include quality management, quality engineering, data mining, and assisted medical diagnosis.
