It is frequently supposed that the residual variance is homogeneous in linear models used in the field of animal breeding. But, distinctions in the residual variance among animals are completely usual and it would be necessary to comprise heteroscedastic residual effects in the models used for estimation of customary breeding values (Hill, Reference Hill1984; Felleki et al., Reference Felleki, Lee, Lee, Gilmour and Rönnegård2012). The homogeneity of animals or their products is mostly an appropriate breeding objective. Therefore, methods are required to estimate breeding values and variance components for the residual variance section of the model. This provides the possibility to select animals which can fulfill this objective (Felleki et al., Reference Felleki, Lee, Lee, Gilmour and Rönnegård2012). In addition, use of routine methods/models for the prediction of genetic selection response is deceptive when heterogeneity of variance is present (Hill and Zhang, Reference Hill and Zhang2004; Mulder et al., Reference Mulder, Bijma and Hill2007; Felleki et al., Reference Felleki, Lee, Lee, Gilmour and Rönnegård2012).
In the present dairy enterprise, it is important that dairy cows are resistant to environmental fluctuations for important characters (Vandenplas et al., Reference Vandenplas, Bastin, Gengler and Mulder2013). Uniformity variations between animals for a given character may be depicted based on distinctions in residual variance (Rönnegård et al., Reference Rönnegård, Felleki, Fikse, Mulder and Strandberg2013). Some environmental factors are recognizable and can be classified or measured and therefore are called macro-environmental variables. The remaining environmental variables are unknown and regarded as micro-environmental variables (Falconer and Mackay, Reference Falconer and Mackay1996). Therefore, genetic variance for macro-environmental sensitivity is the genetic variance because of identified environmental effects and can be declared as the slope of a reaction norm genetic variance when environments can be measured on a continuous scale. When environments are classifiable, then phenotypes in various environments are assumed as distinct characters and a criterion for determining genetic variability in macro-environmental sensitivity is the genetic covariance between different environments. Genetic heterogeneity of residual variance defined as the existence of genetic variation in micro-environmental sensitivity or phenotypic plasticity because of the heterogeneous residual variance between animals. This heterogeneity would be regarded as a character with low heritability and applied to ameliorate robustness through selection (Mulder et al., Reference Mulder, Bijma and Hill2007, Reference Mulder, Bijma and Hill2008). Genetics of micro-environmental sensitivity, which is called environmental variance, has been examined less substantially than the genetic perspective of macro-environmental sensitivity (Mulder et al., Reference Mulder, Rönnegård, Fikse, Veerkamp and Strandberg2013).
The double hierarchical generalized linear model (DHGLM) was proposed by Rönnegård et al. (Reference Rönnegård, Felleki, Fikse, Mulder and Strandberg2010) and Felleki et al. (Reference Felleki, Lee, Lee, Gilmour and Rönnegård2012), concurrently correcting two sets of mixed model equations (on levels of the mean and residual variance). Rönnegård et al. (Reference Rönnegård, Felleki, Fikse, Mulder and Strandberg2010) observed the model used has the possibility to apply on large data sets in dairy industry. An adjustment for correcting the erroneousness of applying estimated residual effects as a representative for the residual variance for each individual is conducted in some studies (Iung et al., Reference Iung, Neves, Mulder and Carvalheiro2017). Using DHGLM, selection for uniformity character would be possible in dairy herds through using these models because breeding values would justify genetic heterogeneity of residual variance (Vandenplas et al., Reference Vandenplas, Bastin, Gengler and Mulder2013).
Different studies reported the estimates of genetic variation in heterogeneity of residual variance for various character sets in farm animals (Sorensen and Waagepetersen, Reference Sorensen and Waagepetersen2003; Damgaard et al., Reference Damgaard, Rydhmer, Lovendahl and Grandinson2003; Mulder et al., Reference Mulder, Hill, Vereijken and Veerkamp2009; Janhunen et al., Reference Janhunen, Kause, Vehvilainen and Jarvisalo2012; Rönnegård et al., Reference Rönnegård, Felleki, Fikse, Mulder and Strandberg2013). In general, these studies obtained considerable genetic variation for heterogeneity of residual variance but low heritability for individual dispersion (Mulder et al., Reference Mulder, Bijma and Hill2007). The existence of genetic heterogeneity of residual variance indicated the possibility of selection for modifying residual variance (Sonesson et al., Reference Sonesson, Ødegård and Rönnegård2013) To our knowledge, there are few studies of milk yield and no reports of milk fat and protein yield to study the genetic heterogeneity of residual variance in the first three lactations of dairy cows. In addition, milk components are highly correlated to economic performance and even energetic efficiency. Therefore, the objective of this study was to estimate genetic parameters for environmental sensitivities in milk yield and composition of Iranian Holstein cows using DHGLM method.
Materials and methods
Data
The data set included test-day productive records of cows which were provided by the Animal Breeding Center and Promotion of Animal Products of Iran during 1983 to 2014. A pedigree file was constructed for all animals in the dataset. Detailed description of pedigree file was reported in a previous study (Ehsaninia et al., Reference Ehsaninia, Ghavi Hossein-Zadeh and Shadparvar2016). Descriptive statistics for test-day productive records over the first three parities are shown in Table 1. For editing data, records within herd-year classes comprising more than five observations were kept. Data edition was applied in which records on daughters of bulls with at least 10 records in at least five herds were retained. Only herds containing ≥10 cows and sires having ≥5 progenies were considered.
Table 1. Descriptive statistics for test-day productive records in different lactation stages of the first three parities of Holstein cows
Also, data were edited for errors, redundancy, and incomplete observations and missing cow identification. Records were eliminated if no registration number was present for a given cow. Age at calving was limited to be between 18–40 months, 28–49 months, and 40–68 months in the first three parities, respectively. A record was included in the final dataset if it also contained information on pedigree, season and year of calving, parity and herd for each cow. Four seasons were defined based on calving month classes: April through June (spring), July through September (summer), October through December (fall) and January through March (winter).
For considering heterogeneous residual variance in the models of analysis, test-day records were classified into 10 groups according to days in milk: 5–35, 36–65, 66–95, 96–125, 126–155, 156–185, 186–215, 216–245, 255–285 and 286–305 d in milk. Individual daily milk yield, milk fat yield and milk protein yield should be between 5–55, 5–65 and 5–64 kg; 0.2–2, 0.2–2.4 and 0.2–3 kg; 0.2–1.8, 0.2–2.2 and 0.2–2.3 kg over the first three parities, respectively. Each individual should have at least eight test-day records to include in the final data set.
Double hierarchical generalized linear models (DHGLM)
Test-day productive records were analyzed using the DHGLM model, proposed by Rönnegård et al. (Reference Rönnegård, Felleki, Fikse, Mulder and Strandberg2010), to estimate variance components for micro-environmental sensitivities. In the DHGLM method, fitted animal model included two parts of mean and residual variance. A random regression model (mean model) and a residual variance model were used to study the genetic variation of micro-environmental sensitivities. Legendre polynomial functions were chosen to fit the lactation curves in the framework of a random regression test day model for estimating (co)variance components. In order to obtain the appropriate random regression test day model for the genetic analysis of test day records, different orders of fit for random regression coefficients of additive genetic and permanent environmental effects were evaluated. The difference of these models was based on the Legendre polynomials applied to fit the covariance functions for additive genetic and permanent environmental effects. Maximum logarithm likelihood of the models was compared and models with the lowest values of this criterion were selected for further analysis. The order of fit for fixed regression coefficients was considered to be five for all models. Based on the selected models, orders of fit for additive genetic and permanent environmental effects of milk yield, fat yield and protein yield were (4,4), (4,4) and (5,3); (4,3), (5,4) and (4,4); (4,4), (5,3) and (5,3) in the first three lactations, respectively. The fitted random regression model was as follows:
$${\bf y} = {\bf X\beta} + {\bf Z}_{\bf u}{\bf u} + {\bf Z}_{\bf p}{\bf p} + {\bf e}$$where y = vector of test day records; β = vector of fixed effects for the mean including herd-test date, year-season of calving, days in milk and age of animal at calving; u = vector of additive genetic random regression coefficients for the mean; p = vector of permanent environmental random regression coefficients for the mean and e = vector of random residual effects. X, 
${\bf Z}_{\bf u}$ and 
${\bf Z}_{\bf p}$ are design matrices associating the records to fixed, random and permanent environmental effects, respectively. Then residual variance model was fitted as follows:
$${\rm V(}{\bf e}{\rm )} = {\rm exp}({\bf X}_{\bf v}{\bf \beta} _{\bf v} + {\bf Z}_{{\bf u}_{\bf v}}{\bf u}_{\bf v} + {\bf Z}_{{\bf p}_{\bf v}}{\bf p}_{\bf v}{\rm )}$$where 
${\bf \beta} _{\bf v}$ = vector of fixed effects for residual variance including the effects of herd-test date, year-season of calving, days in milk and age of animal at calving; 
${\bf u}_{\bf v}$ and 
${\bf p}_{\bf v}$ = vectors of random additive genetic and permanent environmental effects for residual variance, respectively; 
${\bf X}_{\bf v}$, 
${\bf Z}_{{\bf u}_{\bf v}}$ and 
${\bf Z}_{{\bf p}_{\bf v}}$ = design matrices associating the records to fixed, random and permanent environmental effects, respectively. It was assumed that 
${\bf u}_{\bf v}$ and 
${\bf p}_{\bf v}$ had multivariate normal distributions:
$${\bf p}_{\bf v} \sim N{\rm (}0, {\bf I}{\rm \sigma} _{{\bf p}_{\bf v}}^2 {\rm )}$$
$${\bf u}_{\bf v} \sim N{\rm (}0, {\bf A}{\rm \sigma} _{{\bf u}_{\bf v}}^2 {\rm )}$$where 
${\rm \sigma} _{{\bf u}_{\bf v}}^2 $ = additive genetic variance for residual variance and 
${\rm \sigma} _{{\bf p}_{\bf v}}^2 $ = permanent environmental variance for residual variance. Also, it was assumed that there was no correlation between u and uv or between p and pv (Mulder et al., Reference Mulder, Rönnegård, Fikse, Veerkamp and Strandberg2013; Rönnegård et al., Reference Rönnegård, Felleki, Fikse, Mulder and Strandberg2013; Vandenplas et al., Reference Vandenplas, Bastin, Gengler and Mulder2013).
In order to consider macro-environmental sensitivities, DHGLM was extended using a reaction norm model, and a sire model was used in spite of an animal model because DHGLM in the context of animal model provided biased estimates of variance components (Mulder et al., Reference Mulder, Rönnegård, Fikse, Veerkamp and Strandberg2013). In the reaction norm models, it was assumed that environmental parameters which cause response of genotypes to different environments are known without error and there is no need to estimate them from data. The statistical model used for estimating genetic parameters and genetic correlations of micro- and macro-environmental sensitivities was a bivariate sire model as follows:
$$\left[ {\matrix{ {\rm y} \cr {{\rm \psi }_{\rm s}} \cr } } \right] = {\rm \; }\left[ {\matrix{ {\rm X} & 0 \cr 0 & {{\rm X}_{\rm v}} \cr } } \right]\left[ {\matrix{ {\rm b} \cr {{\rm b}_{\rm v}} \cr } } \right] + \left[ {\matrix{ {{\rm Z}_{\rm s}} & {{\rm Z}_{\rm x}} & 0 \cr 0 & 0 & {{\rm Z}_{{\rm sv}}} \cr } } \right] \times \left[ {\matrix{ {{\rm S}_{{\rm int}}} \cr {{\rm S}_{{\rm sl}}} \cr {{\rm S}_{\rm v}} \cr } } \right] + \left[ {\matrix{ {{\rm e}_{\rm s}} \cr {{\rm e}_{{\rm sv}}} \cr } } \right]$$where 
${\bf y}$ and ψs = vectors of response variables for the mean and residual variance models, respectively; 
${\bf Z}_{\bf s}$ and 
${\bf Z}_{{\bf sv}}$ = design matrices of sire effects for the intercept of the reaction norm and for the environmental variance, respectively; 
${\bf Z}_{\bf x}$ = is the matrix with the environmental parameter x as a covariate for the sire effects for the slope of the reaction norm; Sint, Ssl and Sv = vectors including estimated effects of sires for intercept, macro-environmental sensitivities and environmental variance (micro-environmental sensitivities), respectively. It was assumed that sire effects of Sint, Ssl and Sv had trivariate normal distributions of 
${\it N}\left( {{\rm 0,}\displaystyle{{\rm 1} \over {\rm 4}}{\bf G}\otimes {\bf A}} \right)$, assuming that sire (co)variances are a quarter of the additive genetic variance. Also, it was assumed that residuals of es and esv were independent and had normal distribution because Cov(e, e2) = 0 (Mulder et al., Reference Mulder, Rönnegård, Fikse, Veerkamp and Strandberg2013):
$$\left( {\left[ {\matrix{ {{\rm e}_{\rm s}} \cr {{\rm e}_{{\rm sv}}} \cr } } \right] \sim {\it N}\left( {\matrix{ 0 \cr 0 \cr }, {\rm \; }\left[ {\matrix{ {{\rm W}_{\rm s}^{-1} {\rm \sigma }_\in ^2 } & 0 \cr 0 & {{\rm W}_{{\rm sv}}^{-1} {\rm \sigma }{_\in ^2 }_{s{\rm v}}} \cr } } \right]} \right)} \right)$$where 
${\rm \sigma}_{\in}^{2} $ and 
${\rm \sigma}_{\in \rm sv}^{2}$ = are scaling variances for residual variances in the sire model which their expectations are equal to one because 
${\bf W}_{\bf s}$ = diag
$\lpar {\widehat{{{\rm \psi}_{\rm s}}}} \rpar ^{-1}$and 
${\bf W}_{{\bf sv}}$ = diag
$\left( {\displaystyle{{1-{\rm h}} \over 2}} \right)$ already contain the reciprocals of the estimated residual variances per record. Also, h is the diagonal element of the hat matrix corresponding to the same individual. All genetic analyses were conducted using the ASReml 4.0 program (Gilmour et al., Reference Gilmour, Gogel, Cullis and Thompson2009) to obtain estimates of variance components for the studied traits. In each ASReml run, REML-estimates of the variance components were obtained for the current values of ψs, 
${\bf W}_{\bf s}$ and 
${\bf W}_{{\bf sv}}$. The vector ψs and the diagonals of 
${\bf W}_{\bf s}$ and 
${\bf W}_{{\bf sv}}$ were updated after each run of ASReml. Genetic correlation between micro- and macro-environmental sensitivities estimated through iterative reweighted least square (IRWLS) algorithm and in the basis of mean and residual variance models.
Four statistical models were fitted to estimate and compare the genetic parameters for micro- and macro-environmental sensitivities: a combined micro—macro environmental sensitivity model ‘Micro—macro’, a macro-environmental sensitivity model ‘Macro’, a micro-environmental sensitivity model ‘Micro’ and a simple model ‘Simple’ with only one additive genetic effect for the phenotype. Micro—macro model is a model accounting for both macro- and micro-environmental sensitivities; Macro model is a model with only macro environmental sensitivity; Micro model is a model with only micro-environmental sensitivity, and Simple model is a model without macro- and micro environmental sensitivities:
Simple model: y = μ + Aint + e
Micro model:
${\rm y} = {\mu} + {\rm A}_{{\rm int}} + {\rm exp}\lpar {0.5\,{\rm ln}\lpar {{\rm \sigma}_{\rm E}^2} \rpar + 0.5{\rm A}_{\rm v}} \rpar {\rm \varepsilon} $Macro model: y = μ + Aint + Aslx + ε
Micro–macro model:
${\rm y} = {\mu} + {\rm A}_{{\rm int}} + {\rm A}_{{\rm sl}}{\rm x} + {\rm exp}\lpar {0.5{\rm ln}\lpar {{\rm \sigma}_{\rm E}^2} \rpar + 0.5{\rm A}_{\rm v}} \rpar {\rm \varepsilon} $
where y = vector of records; μ = population mean for productive traits; x = environmental parameter (continuous or discrete) which cause response of genotypes to different environments (herd-year-season and age at calving); Aint, Asl and Av = additive genetic effects for the intercept of the reaction norm, for the slope of the reaction norm (macro-environmental sensitivities) and for the environmental variance (micro-environmental sensitivities), respectively; 
${\rm \sigma} _{\rm E}^2 $ = environmental variance of exponential model, and ε = environmental deviation with variance one. The basic for these statistical models were DHGLM algorithm which iterates between linear mixed models for phenotypic observations and Gamma linear models for residual variance. After convergence, variance components for corresponding traits, micro- and macro-environmental sensitivities were estimated. These four statistical models were examined for goodness of fit using Akaike's information criterion (AIC), Bayesian's information criterion (BIC) and adjusted profile h-likelihood (APHL). The AIC is a good statistic for comparison of models of different complexity and calculated as follows:
$${\rm AIC} = -2\log \lpar {{\rm M}{\rm L}_k} \rpar + 2p_k$$where MLk is the maximum likelihood of k th model and p k is the number of model parameters. Bayesian's information criterion (BIC), a criterion for model selection among parametric models with different numbers of parameters, was estimated as follows:
$${\rm BIC} = -2\log \lpar {{\rm M}{\rm L}_k} \rpar + k\,{\rm log}\lpar n \rpar $$where k is the model parameters and n is the number of observations. The adjusted profile h-likelihood (APHL) can be approximated from the log REML-likelihood (log L) of the bivariate model taking into account the fact that the adjusted squared residuals from the mean model were fitted for the residual variance model (Felleki et al., Reference Felleki, Lee, Lee, Gilmour and Rönnegård2012; Mulder et al., Reference Mulder, Rönnegård, Fikse, Veerkamp and Strandberg2013):
$${\rm APHL} = -2{\rm logL}-\sum {\rm e}_{{\rm v}_{\rm i}}^2 {\rm w}_{{\rm v}_{\rm i}}{\rm \sigma} _{{\rm e}_{\rm v}}^{-2} -\sum \ln \left( {\displaystyle{{{\rm \sigma}_{{\rm e}_{\rm v}}^2} \over {{\rm w}_{{\rm v}_{\rm i}}}}} \right)$$where 
${\rm w}_{{\rm v}_i}$ and 
${\rm e}_{{\rm v}_i}$ are weight (i.e. the i th diagonal of 
${\bf W}_{{\bf sv}}$) and residual for the variance model for the i th observation, respectively, and 
${\rm \sigma} _{{\rm e}_{\rm v}}^2 $ is the scaling residual variance for the residual variance model.
Results
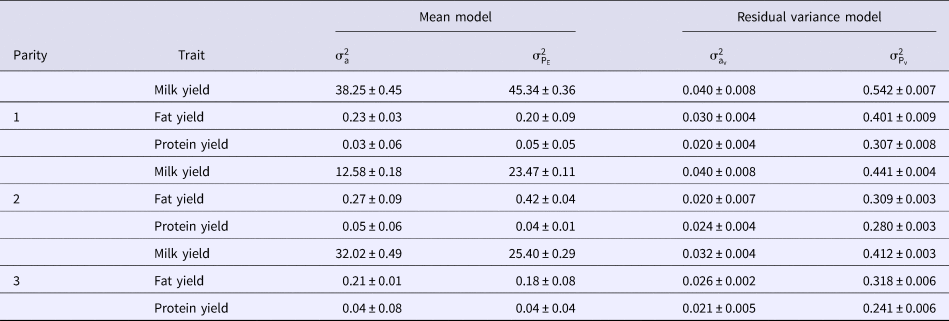
Variance components of micro-environmental sensitivities for milk yield and composition based on DHGLM method in the first three parities of Holstein cows are shown in Table 2. Additive genetic and permanent environmental variances for the mean and residual variance of milk yield were generally the greatest in the first lactation cows. Additive genetic and permanent environmental variances for the mean of fat yield increased from first to second lactation, and then decreased to third lactation. Additive genetic variance of the mean for protein yield had similar variation to fat yield but, permanent environmental variance of the mean for protein yield was the greatest in the first lactation. The greatest additive genetic and permanent environmental variances for the residual variance of fat yield were observed in the first lactation. The additive genetic variance of the residual variance for protein yield had the same variation as its counterpart in the mean model, but permanent environmental variance of the residual model for protein yield had decreasing trend over the first three lactations (Table 2).
Table 2. Variance components of micro-environmental sensitivities for milk yield and composition based on DHGLM method in the first three parities of Holstein cows
${\rm \sigma} _{\rm a}^2 $, additive genetic variance for mean; 
${\rm \sigma} _{{\rm P}_{\rm E}}^2 $, permanent environmental variance for mean; 
${\rm \sigma} _{{\rm a}_{\rm v}}^2 $, additive genetic variance for residual variance; 
${\rm \sigma} _{{\rm P}_{\rm v}}^2 $, permanent environmental variance for residual variance.
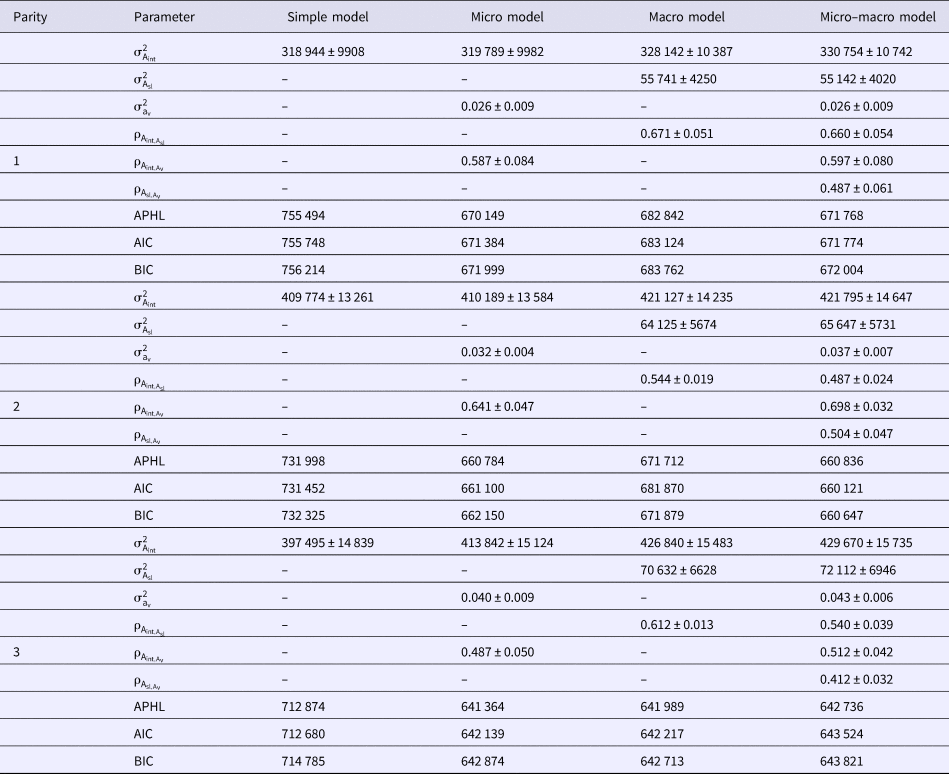
Estimates of genetic parameters for micro- and macro-environmental sensitivities of milk yield, fat yield and protein yield in the first three parities of Holstein cows using different models are shown in Tables 3–5, respectively. To this end, Simple, Micro, Macro and Micro-macro models were fitted to analyze milk yield and composition. The results indicated considerably better fit of Micro-macro, Micro and Macro models compared with Simple model. The Micro model was the best fitted model according to the AIC statistic. The lowest values of BIC and APHL statistics also were for Micro model. Genetic variance of micro-environmental sensitivities for milk yield and composition increased considerably from the first through third lactation. Difference of comparison criteria in Simple model was very large in comparison with other models, but the difference of BIC between Micro and Micro-macro models was very low. Estimated genetic variance of macro-environmental sensitivities was low compared with the genetic variance of trait.
Table 3. Estimates of genetic parameters for micro- and macro-environmental sensitivities of milk yield in the first three parities of Holstein cows using different models
${\rm \sigma }_{{\rm A}_{{\rm int}}}^2 $, additive genetic variance; 
${\rm \sigma }_{{\rm A}_{{\rm sl}}}^2 $, additive genetic variance of macro environmental sensitivities; 
${\rm \sigma }_{{\rm a}_{\rm v}}^2 $, additive genetic variance of micro environmental sensitivities; 
${\rm \rho }_{{\rm A}_{{\rm int},{\rm A}_{\rm v}}}$, genetic correlation between additive genetic variance and micro environmental sensitivities; 
${\rm \rho }_{{\rm A}_{{\rm int},{\rm A}_{{\rm sl}}}}$, genetic correlation between additive genetic variance and macro environmental sensitivities; 
${\rm \rho }_{{\rm A}_{{\rm sl},{\rm A}_{\rm v}}}$, genetic correlation between micro- and macro environmental sensitivities; AIC, Akaike's information criterion; BIC, Bayesian information criterion; APHL, Adjusted profile hierarchical-likelihood.
Table 4. Estimates of genetic parameters for micro- and macro-environmental sensitivities of milk fat yield in the first three parities of Holstein cows using different models
${\rm \sigma }_{{\rm A}_{{\rm int}}}^2 $, additive genetic variance; 
${\rm \sigma }_{{\rm A}_{{\rm sl}}}^2 $, additive genetic variance of macro environmental sensitivities; 
${\rm \sigma }_{{\rm a}_{\rm v}}^2 $, additive genetic variance of micro environmental sensitivities; 
${\rm \rho }_{{\rm A}_{{\rm int},{\rm A}_{\rm v}}}$, genetic correlation between additive genetic variance and micro environmental sensitivities; 
${\rm \rho }_{{\rm A}_{{\rm int},{\rm A}_{{\rm sl}}}}$, genetic correlation between additive genetic variance and macro environmental sensitivities; 
${\rm \rho }_{{\rm A}_{{\rm sl},{\rm A}_{\rm v}}}$, genetic correlation between micro- and macro environmental sensitivities; AIC, Akaike's information criterion; BIC, Bayesian information criterion; APHL, Adjusted profile hierarchical-likelihood.
Table 5. Estimates of genetic parameters for micro- and macro-environmental sensitivities of milk protein yield in the first three parities of Holstein cows using different models
${\rm \sigma }_{{\rm A}_{{\rm int}}}^2 $, additive genetic variance; 
${\rm \sigma }_{{\rm A}_{{\rm sl}}}^2 $, additive genetic variance of macro environmental sensitivities; 
${\rm \sigma }_{{\rm a}_{\rm v}}^2 $, additive genetic variance of micro environmental sensitivities; 
${\rm \rho }_{{\rm A}_{{\rm int},{\rm A}_{\rm v}}}$, genetic correlation between additive genetic variance and micro environmental sensitivities; 
${\rm \rho }_{{\rm A}_{{\rm int},{\rm A}_{{\rm sl}}}}$, genetic correlation between additive genetic variance and macro environmental sensitivities; 
${\rm \rho }_{{\rm A}_{{\rm sl},{\rm A}_{\rm v}}}$, genetic correlation between micro- and macro environmental sensitivities; AIC, Akaike's information criterion; BIC, Bayesian information criterion; APHL, Adjusted profile hierarchical-likelihood.
Estimates of genetic correlations between milk yield and macro- and micro-environmental sensitivities were high and varied from 0.487–0.660 and 0.512–0.698 over the lactations, respectively. These correlations varied from 0.503–0.595 and 0.307–0.553 for fat yield, and ranged from 0.474–0.623 and from 0.468–0.543 for protein yield over the lactations, respectively. Genetic correlations between macro- and micro-environmental sensitivities varied from 0.412–0.504 for milk yield, 0.321–0.412 for fat yield, and 0.412–0.567 for protein yield in the first three lactations, respectively (Tables 3–5).
Discussion
This study is the first report on the estimation of genetic parameters for environmental sensitivities of milk composition in dairy cows. Genetic variation in environmental sensitivities indicated the differences between animals based on their response to environmental variables from the genetic perspective. Animals with greater resistance to environmental fluctuations are more appropriate in the dairy production industry. Therefore, genetic heterogeneity of residual variance could be considered as a character with low heritability and useful for improving the general potential of animals to environmental sensitivities via selection.
In some breeding programs and selection experiments, considerable genetic responses were reported for characters with low heritability (Mulder et al., Reference Mulder, Bijma and Hill2007; Neves et al., Reference Neves, Carvalheiro, Roso and Queiroz2011; Formoso-Rafferty et al., Reference Formoso-Rafferty, Cervantes, Ibáñez-Escriche and Gutiérrez2016). Mulder et al. (Reference Mulder, Bijma and Hill2008) reported that considering residual variance in the breeding goal is crucial only when the profit equation is non-linear. Even so, in most conditions the optimal index puts more selection pressure on the mean so that changes in residual variance are minor. Selection based on the genetic variation of micro-environmental sensitivities will be important in cases that have individuals with low variation, and optimum level of the traits would be economically influential. Considerable levels of genetic variation for residual variance in different animal species were reported which would be in the range from 20% or greater (Mulder et al., Reference Mulder, Hill, Vereijken and Veerkamp2009; Neves et al., Reference Neves, Carvalheiro and Queiroz2012). When the genetic variation for residual variance and also number of records per sire is large, it appears that selection for residual variance would be suitable. In addition, low heterogeneity of residual variance indicated that cows in their productive environment had lower sensitivity to unfavorable environmental situations and this truly could be considered as a uniformity criterion. Therefore, it is clear that decrease of residual variance for milk traits through genetic selection and breeding would be useful (Mulder et al., Reference Mulder, Rönnegård, Fikse, Veerkamp and Strandberg2013).
Existence of genetic variation in the level of environmental variance provides the possibility for modifying it through selection. Unknown environmental factors are described as micro-environmental sensitivities. Genetic variance of micro-environmental sensitivities or genetic heterogeneity of environmental variance is known as the genetic variance arising from unknown environmental variables. Genetic differences in micro-environmental sensitivities could be studied through heterogeneity of residual variance among animals. Recent studies showed that part of environmental variance is under control of genetic factors and would be heritable (Hill and Mulder, 2010; Rönnegård et al., Reference Rönnegård, Felleki, Fikse, Mulder and Strandberg2010; Felleki et al., Reference Felleki, Lee, Lee, Gilmour and Rönnegård2012). Therefore, selection produces changes in the environmental variability (Formoso-Rafferty et al., Reference Formoso-Rafferty, Cervantes, Ibáñez-Escriche and Gutiérrez2016). Selection according to micro-environmental sensitivities is important when low variation between animals and also breeding values close to optimum level are economically critical. For example, broilers with the same carcass weight and close to average limit are very important in slaughterhouses. Permanent variations in micro-environmental sensitivities are possible when genetic variation exists for residual variance.
The results of this study indicated the possibility of fitting a model for studying the genetic heterogeneity of residual variance for a large data set of dairy cows. Existence of greater genetic variation in environmental sensitivities of milk yield compared with other productive traits showed better modification of environmental sensitivities for milk yield through selection. In general, DHGLM method provided useful information for dairy practitioners regarding to the herd management and uniformity of milk traits through studying the genetic variation of residual variance and selection for decreased micro-environmental sensitivities. Therefore, selection for improved potential of animals to micro-environmental sensitivities is likely.
Reaction norm models combined with DHGLM method were used to estimate simultaneously the macro- and micro-environmental sensitivities in the context of a sire model because the animal model provided greatly biased estimates of variance components due to the high dependence of the estimated breeding values and residuals on the variance ratio applied in the mixed model equations (Mulder et al., Reference Mulder, Rönnegård, Fikse, Veerkamp and Strandberg2013). Sire models are commonly applied in combination with reaction norm models (Windig et al., Reference Windig, Mulder, Bohthe-Wilhelmus and Veerkamp2011; Mulder et al., Reference Mulder, Rönnegård, Fikse, Veerkamp and Strandberg2013). In addition, an animal model with heterogeneous residual variance (in DHGLM method) produced a poorer APHL statistic than an animal model without homogenous residual variance which indicated the first model in a scenario with the consideration of both macro- and micro-environmental sensitivities did not provide better fit (Mulder et al., Reference Mulder, Rönnegård, Fikse, Veerkamp and Strandberg2013). Because of the abovementioned reasons, sire model was used for the estimation of macro- and micro-environmental sensitivities. Lillehammer et al. (Reference Lillehammer, Odegard and Meuwissen2009) showed that when heterogeneity of residual variance was ignored, sire models produced biased estimates of genetic variance for micro-environmental sensitivities.
Consistent with the results of this study, Rönnegård et al. (Reference Rönnegård, Felleki, Fikse, Mulder and Strandberg2013) reported the lowest value of APHL was for Micro model in Swedish Holsteins. Also, Vandenplas et al. (Reference Vandenplas, Bastin, Gengler and Mulder2013) reported lower values of AIC, BIC and APHL for milk yield in heterogeneous model compared with homogenous model in Walloon Holstein cows. One unit change in genetic standard deviation of environmental variance modified the micro-environmental sensitivities of first lactation milk yield, fat yield and protein yield as 0.16, 0.18 and 0.19, respectively, but these values were generally lower than those in other studies (Hill and Mulder, 2010; Mulder et al., Reference Mulder, Rönnegård, Fikse, Veerkamp and Strandberg2013).
Estimates of genetic correlation between milk yield and macro- and micro-environmental sensitivities indicated that selection for more milk yield could increase both macro- and micro-environmental sensitivities. Therefore, because of the positive correlation between milk production traits and environmental sensitivities, selection of animals with higher estimated breeding values for traits of interest would increase the residual variance of macro-environmental sensitivities. Similar to the current study, Rönnegård et al. (Reference Rönnegård, Felleki, Fikse, Mulder and Strandberg2013) obtained positive genetic correlations between breeding values of milk yield and residual variance. Some studies reported negative correlations between mean and residual variance (Mulder et al., Reference Mulder, Hill, Vereijken and Veerkamp2009; Wolc et al., Reference Wolc, White, Avendano and Hill2009), and some recent studies reported positive correlations (Sae-Lim et al., Reference Sae-Lim, Mulder, Gjerde, Koskinen, Lillehammer and Kause2015; Formoso-Rafferty et al., Reference Formoso-Rafferty, Cervantes, Ibáñez-Escriche and Gutiérrez2016; Marjanovic et al., Reference Marjanovic, Mulder, Khaw and Bijma2016). When the breeding objective is the concurrent improvement of trait mean and increase in the uniformity of end products, positive genetic correlation between mean and residual variance would not be appropriate. Vandenplas et al. (Reference Vandenplas, Bastin, Gengler and Mulder2013) estimated the correlation between breeding values of milk yield and residual variance as 0.47 and 0.41 in bulls and cows, respectively.
The results of this study showed that macro- and micro-environmental sensitivities were present for milk production traits of Iranian Holsteins. There was positive genetic correlation between macro- and micro-environmental sensitivities so that selection for each source of sensitivity would influence the other in similar direction. Paying attention to macro- and micro-environmental sensitivities is very important in animal breeding. Therefore, breeding and selection of animals which had suitable performance and limited environmental sensitivities in a broad spectrum of environmental conditions is necessary. Reduction of environmental sensitivities would increase the predicted performance of animals and decreased corresponding threats for dairy farmers.
Acknowledgements
The authors wish to acknowledge National Animal Breeding Center and Promotion of Animal Products of Iran for providing the data used in the current study.
