1. INTRODUCTION
The problem of a solid being ablated by a laser light has been
studied in the past from different points of view (Max et al., 1980; Sanz
et al., 1981), mostly in the context of inertial
confinement fusion studies (laser driven) and different geometries
(one-dimensional [1D] to three-dimensional [3D]).
Several ablative models have been proposed on which to base
Rayleigh–Taylor instability analysis (Takabe
et al., 1983; Kull & Anisimov,
1986; Kull, 1989, 1991; Sanz, 1996), a key
problem in achieving ignition of implosion targets. Here we approach
the problem in a somewhat different way.
Let us consider a solid slab with initial temperature
T0 and density ρ0 being thermally
ablated by a laser. After a short transient period of time, a certain
(high) temperature Tb is assumed to
stabilize at a certain distance (critical surface) L from the
slab surface (Fig. 1) that is now at
temperature Ta <<
Tb and density ρa.
Heat conduction moves the energy from the critical surface to the slab
and a (supposed) constant mass flow rate
is ablated from the slab mass M0. The high ablation
pressure Pa moves the slab with
acceleration
.
The process is analyzed using a reference attached to the slab surface.
2. HYDRODYNAMIC EQUATIONS
Continuity, momentum, and energy Navier–Stokes equations read
as follows:
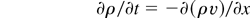
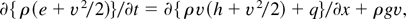
where the acceleration g has been included in the momentum
and energy equations, and v is velocity, x is the
distance from the slab surface (positive toward the incoming laser),
p is pressure, e is specific energy, h is
specific enthalpy, and q is the heat flux.
For simplicity, the ablated plasma will be taken as an ideal
mono-atomic gas with equations of state (EOS): p =
ρT, h = (5/2)T, and e =
(3/2)T. Also we will assume classical (Spitzer) heat flux
with q = −KT5/2
dT/dx.
The basic initial and boundary conditions, at any time, will be
T = Tb at x = L
and T = Ta at x = 0.
Other variables will be discussed later in consistency with above
equations and assumptions to be made.
3. THE QUASI STEADY 1D MODEL FOR THE PLASMA
CORONA
Although a real problem is not steady and requires solving fully Eqs.
(1)–(3), we think a quasisteady approximation, valid on a time
scale when the slab mass change is not too big, can shed some light
onto the problem. Then, neglecting temporal derivatives, a constant
mass flow rate
is ablated at the slab surface x = 0 by the energy flux coming
from the right (x > 0 region). Integrating (1)–(3) from
x = 0 we have
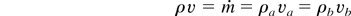
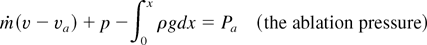
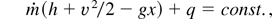
where, in consistency with the previous assumption
Ta <<
Tb, we will put
Ta = va = 0,
and then const. = 0, as a convenient first approximation in
our model.
The exact solution to the complete model in Eqs.
(4)–(6) is discussed later in Appendix B; briefly, the eigenvalues
get determined, as functions of the boundary conditions and profiles of
the different variables, only when the complete solution of the problem
has been obtained. As we will confirm later, a good approximation
appears, in a simplified model, neglecting velocity and
gravity terms v2/2 − gx <<
h in (6); then, we have
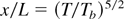
with
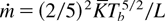
for the temperature profile and the eigenvalue mass flow for all
g values in terms of physical quantities.
Using dimensionless variables x′ =
x/L, T′ =
T/Tb, v′ =
v/Tb1/2, and
the EOS we have for the momentum equation
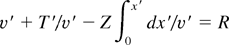
with
the normalized gravity acceleration and the normalized ablation
pressure, respectively.
In the case of no gravity, g = 0, and assuming sonic flow in
x = L, we have the solution T′ =
x′(2/5), and v′ = 1 −
(1 − T′)1/2, where T′
and v′ grow from zero in x′ = 0, to sonic
conditions v′2 = T′ = 1 in
x′ = 1, included in Figure 2. The
eigenvalue ablation pressure is now
.
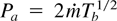
Solution with subsonic conditions in x′ = 1 are also
possible; then, the ablation pressure increases to
with Mb = vb
/Tb1/2 ≤ 1, the Mach
number at x = L. Continuous solutions, supersonic in
x′ = 1, are not allowed in this case.
Pressure, temperature, and velocity profiles for Z ≤ 0.4
(note Pa is Z
dependent).
For every nonzero value of the gravity g, Eq. (8) admits
phase variables η,ξ discussed in Appendix A. Here, we
summarize the results. For every Z, a singular (saddle) sonic
point
(xs′,vs′)
=
((0.4/Z)5/3,(0.4/Z)1/3)
permits crossing from subsonic conditions, near x = 0, to
supersonic ones, far from the origin, traveling along the integral line
v′(x′) that links the origin with the
saddle point.
For a certain characteristic value
(the inverse number of the exponent in the Spitzer law), the saddle locates
exactly at x′ = 1, where sonic conditions are allowed (point
B in Fig. A1 in Appendix A). The eigenvalue ablation pressure is now
,
being
,
a numerical value that appears (see Table 1) after
integrating along the above mentioned integral line (note the ablation
pressure is reduced about 36% in comparison with the g = 0
case).
The integral
in Eq. (8) for some Z values (simplified model)
For
(low Z), the saddle point locates at
xs′ > 1 (point A in Fig. A1; note that
Z approaching zero gives xs′
going to infinity, and then ηs =
1/xs′ < 1). Both sonic or
subsonic conditions are possible now in x′ = 1; we are
only interested in the sonic case. The solution for (8) can easily be
obtained through an iterative process, if we start with the solution
for g = 0 (with R0 = 2) and use the
recursive formula vi+1′ =
Ai −
(Ai2 −
x′(2/5))1/2, and new variable
Ai = 1 −
0.5Z(Ii(1) −
Ii(x′)), with
.
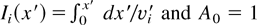
The numerical convergence of the iterations is fast (three or four cycles
are enough to get a stable graphical result; the use of absolute value inside
the square root may be convenient through the calculations, and it does not
influence the final true solution). The eigenvalue ablation pressure is, in
this case
where I(1) is a function tabulated in Table
1 for some Z values.
For
(high Z) the saddle sonic point locates at
xs′ < 1 (i.e.,
ηs =
1/xs′ > 1, point C in Fig.
A1). In x′ = 1 only certain supersonic conditions are
allowed (the ones given by the mentioned integral line at that
position), and the ablation pressure is now
where the factor (0.4/Z)1/3 can also be read
as vs′, or
Ts′1/2, or
xs′1/5 (note that Z
approaching infinity gives Pa going to zero).
In Figure 2, the corresponding profiles for
pressure, temperature, and velocity are given for some Z
values (0, 0.1, 0.2, 0.3, and 0.4). Also, in Figure
3, we show the normalized ablation pressure R as a
function of the normalized gravity acceleration Z for a
moderate range of Z values.
Normalized ablation pressure R versus normalized
acceleration Z.
4. THE NONSTEADY EVOLUTION OF THE SLAB
At every instant time, the slab mass
is accelerated by the ablation pressure
and this allows us, in a first approximation, to couple the corona
model and the slab evolution in a consistent manner. In terms of a
characteristic burning time
with
from (7) and a characteristic fluid time tc =
L/Tb1/2, we
found the simple expression
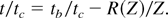
At t = 0 we have
(R(Z)/Z)0 =
tb /tc.
In Figure 4, it is given
R(Z)/Z, nearly a straight line in
logarithmic scale, for a wide range of Z values. For every
practical case (given Tb, L,
K, and M0), entering with
tb /tc in
the vertical axis, we can read the normalized initial acceleration
Z0 in the horizontal one.
Although Eq. (9) and Figure 4 provide a
useful tool to evaluate the function Z(t), taking
into account that for Z > 0.4 is R/Z
= const./Z4/3 and Z
necessarily increases with time, for practical purposes, we propose the
simple analytical formula
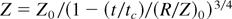
for the normalized slab acceleration due to the ablation pressure.
5. THE MODEL AND THE NUMERICAL SIMULATION
Two kinds of problems have been studied numerically, using computer
code Multi2D (Ramis & Meyer-ter-Vehn,
1992), to test and validate the above simplified model. First, a
plane target with initial velocity V0 is
decelerated by a laser until the target is completely ablated.
Typically, we have used Ta
/Tb around
and an initial normalized deceleration in the range of 0.05 to 0.15. Computed
temperature, velocity, and pressure profiles have been followed along
the time and compared to the ones in the model. In velocity and
pressure the agreement has been found good, except that numerical
values for the ablation pressure Pa are
typically around 90% the ones provided in the model. The neglecting of
the velocity and gravity terms in the energy equation (6), to solve the
model in Section 3, has been found responsible for half of this
disagreement. The other part may be due to the fact that numerical
simulations are really nonsteady whereas the model is quasisteady and,
obviously, they must show differences. Regarding the temperature
profiles, the fitting has been found very good.
Second, both the simplified and the complete models for the plasma
region x > xa, besides the
isentropic approximation with g nonzero (v =
va(Ta
/T)3/2, T =
Ta + 0.4Z(x −
xa)) for the slab region x <
xa, up to a position where profiles get
multivalued (Mach number (5/3)1/2), have been used
as initial solution to build “indefinitely steady numerical
profiles” on which to study numerically the evolution of
fundamental Rayleigh–Taylor instability problems in ablation
fronts (Sanz et al., 2002; including
single and multimode evolution in 2D and 3D axisymmetrical geometries,
cutoff wave length determination, etc.) in a wide range of values for
the parameters Ta
/Tb and Z. No special
advantage has been found in using the complete model instead of the
simplified one. Results of these studies will be published shortly,
elsewhere.
6. CONCLUSIONS
From fundamental laws we have developed a 1D model for a
laser-ablated slab under acceleration g. The assumption of a
quasisteady problem, although strictly valid only for short periods of
time or low mass ablation rates, has been found useful to close the
nonsteady problem. A simple law for the acceleration
g(t) of the nonsteady laser-ablated slab is proposed.
In the quasisteady approximation, a characteristic acceleration
gc is identified; above this value, a
sonic point appears between the slab and the critical surface; the
ablation pressure is strongly reduced
∝1/g1/3. The hydrodynamic profiles in
the simplified model have been proved a key step in the numerical
analysis of basic Rayleigh–Taylor instability problems in
ablation fronts.
ACKNOWLEDGMENTS
This research was supported by the CICYT of Spain (C97010502, FTN
2000-2048-C0301), and by the EURATOM/CIEMAT association in the
framework of the “IFE Keep-in-Touch Activities.”
APPENDIX A: THE PHASE PLANE IN THE
SIMPLIFIED MODEL
The complete discussion of the solutions in Eqs. (7)–(8)
appears analyzing the corresponding phase plane. Using (7) in (8) and
after derivation we have
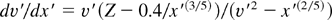
that shows, in the physical plane
(x′,v′) a singular (node) critical point
at the origin (0,0), a singular (saddle) critical point at
(xs′,vs′)
=
((0.4/Z)5/3,(0.4/Z)1/3),
and a sonic line v′2 =
x′(2/5) (with
T′ = x′(2/5)) where the Mach
number is unity. Normalizing position and velocity with corresponding values
at this saddle point we have, for the new phase variables η =
x′/xs′ and ξ
= v′/vs′, the
normalized equation
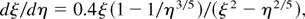
with the singular points at (0,0) and (1,1), and the sonic line
(ξ = η1/5), all of them represented in Figure
A1; also some integral lines coming from the node and others
approaching the saddle are drawn.
The normalized phase plane (η, ξ) (dashed, the sonic
line).
The characteristic value Zc = 0.4 (i.e.,
g = 0.4Tb /L) plays
an important role in the solutions of Eq. (A1). For Z =
Zc, both the physical
(x′,v′) and the normalized (η,ξ)
phase planes are identical; only one integral line is allowed to go
continuously from the origin x′ = 0 to sonic conditions
in x′ = 1 (point B in Fig. A1); supersonic conditions
are not possible there. For Z > 0.4 (high g)
xs′ < 1 (thus
ηb =
1/xs′ > 1, point C in Fig.
A1) and only specific supersonic conditions are allowed in
x′ = 1 when coming from x′ = 0 (the ones
fixed by the mentioned integral line at that point). For Z
< 0.4 (low g) xs′ > 1
(thus ηb =
1/xs′ < 1, point A in Fig.
A1) and only a specific sonic solution is possible in x′
= 1 (also several subsonic ones, or supersonic multivalued, which we
are not interested in).
APPENDIX B: THE COMPLETE MODEL
As we advanced in Section 3, in the case of g = 0, in the
simplified model, we neglect v2/2
<< h; then the solution of Eq. (4)–(6) with
Ta = va = 0
leads to
the condition of the sonic point in x = L giving
eigenvalues
in terms of the physical quantities K,
Tb, and L.
Using dimensionless variables
,
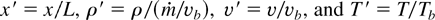
we have the normalized solution
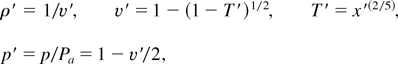
which is represented in Figure B1.
The normalized profiles for g = 0.
As we are interested here in the complete model, the energy
equation (6) can be put in differential form
.
Using the above dimensionless variables and integrating from
x′ = 0 we have
with
.
Evaluating the above equation in x′ = 1 gives the
eigenvalue mass flow
In the same manner, the dimensionless momentum equation is
with
,
and, after evaluation in x′ = 1, with Mach unity there for
moderate Z values, we have the other eigenvalue
The quantities I(1), J(1), and K(1) for
every Z appear after the complete integration of the problem
has been done, and are given in Table B1 for
some Z values of interest.
The integrals I,J,K for some Z values
(complete model)
The complete analysis of Eqs. (B3)–(B6) leads to a phase plane
similar to the one considered in Appendix A. For every Z, a
(saddle) critical sonic point is found in
(xs′,vs′)
at the xs′ value that is solution of
the equation dT′/dx′ = Z and
is numerically obtained after integrating the solution
T′(x′). We have found that for a certain
characteristic value Zc = 0.4027…
xs′ = 1.
For Z below this Zc value,
sonic solutions in x′ = 1 are possible, and can be
obtained as follows: Using (B4) and (B6) in (B3) and (B5), we have
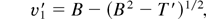
with B = 1 − 0.5Z[I(1) −
I(x′)] , which can be solved numerically.
Starting with the universal solution (B2) T0′
= x′0.4, v0′ = 1
− (1 − T0′)1/2, we
evaluate the integrals I, J, K, and the auxiliary
variable B; with (B7) we get T1′ and
with (B8) also v1′ and so on for the
following steps (three or four cycles are enough for good graphical
results). In Figure B2 we show the obtained v′ profiles
for some Z values; to compare, dashed lines show the
corresponding ones using the simplified model described in Section 3.
We see that the simplified model represents quite well the complete
one.
Velocity profiles for some Z values in the complete model
(dashed lines represent the simplified one).
For Z above Zc, the saddle
sonic point xs′ moves toward the
origin (and this distance becomes the convenient normalizer, instead of
L, for the subsonic part of the plasma region). Figure B3
shows xs′ as function of Z
(dashed line represents the simplified model). We also see both models
fit quite well.
Sonic point location versus acceleration (dashed line represents the
simplified model).
Finally Figure B4 compares both models as far as both eigenvalues,
the ablation pressure, and the mass flow is concerned. Typically, the
complete model proposes around 6–8% less flow mass and more
ablation pressure.
Ablation pressure and mass flow versus acceleration (dashed lines
represent the simplified model).
