1. INTRODUCTION
Autonomous Underwater Vehicles (AUVs) have been used increasingly in a variety of applications, such as long range underwater survey, exploitation of underwater resources and underwater pipeline tracking (Ataei and Yousefi-Koma, Reference Ataei and Yousefi-Koma2015; Sun et al., Reference Sun, Zhu and Yang2016). A trajectory tracking controller with reliability and robustness is of great importance to perform a successful mission in the unknown and complicated ocean environment (Fossen et al., Reference Fossen, Pettersen and Galeazzi2015; Lekkas and Fossen, Reference Lekkas and Fossen2014). Therefore, it is crucial to develop a robust and reliable trajectory tracking controller for AUVs.
The main challenges in trajectory tracking control arise from the inherent nonlinearity, serious multivariate coupling and model parameter variation of an AUV subject to external disturbance (Koofigar, Reference Koofigar2014). In order to deal with these problems, numerous control methodologies have been proposed, including backstepping control (Bing et al., Reference Bing, Daqi and Yang2014; Morishita and Souza, Reference Morishita and Souza2014), sliding mode control (Bessa et al., Reference Bessa, Dutra and Kreuzer2010; Soylu et al., Reference Soylu, Buckham and Podhorodeski2008), H infinity control (Slotine and Li, Reference Slotine and Li1991; You et al., Reference You, Lim and Jeong2010) and artificial intelligence control (Chu et al., Reference Chu, Zhu and Yang2016; Seok Park, Reference Seok Park2014). In the above cited references, the controller's goal is to acquire high tracking precision, which would result in more energy consumption. However, in some special applications, such as underwater pipeline tracking, underwater searching and plume tracking, the users pay more attention to energy consumption. In other words, they expect longer missions as long as the tracking error is within the desired region. Since the energy carried by an AUV is limited, any reductions in the energy consumption can prolong the time of AUV operation (Zhang and Chu, Reference Zhang and Chu2014). As for these special applications, an adaptive region tracking method was proposed for AUV based on the concept of region potential function (Li et al., Reference Li, Hou and Cheah2010). Ismail and Dunnigan (Reference Ismail and Dunnigan2011) applied the method in tracking control of an underwater vehicle-manipulator system. On the basis of the concept of region potential function, Zhang and Chu (Reference Zhang and Chu2014) developed an adaptive region tracking control based on Radial Basis Function (RBF) neural network and sliding mode control. Mukherjee et al. (Reference Mukherjee, Kat and Bhatt2015) took input delay into consideration in the region tracking control. The references do not involve fault tolerant control, so these methods cannot be directly applied in cases where thruster faults occur.
During long missions in special applications, an AUV is liable to suffer from faults in the unknown and complicated ocean environment. In fact thrusters are some of the most important and common fault sources (Omerdic and Roberts, Reference Omerdic and Roberts2004). In order to accomplish fault tolerant control for an AUV with a thruster fault, Ismail et al. (Reference Ismail, Faudzi and Dunnigan2014) developed a region tracking fault tolerant control method based on weighted pseudo-inverse. Thrust reallocation is a common technique to deal with thruster faults using fault information provided by the Fault Detection and Diagnosis (FDD) module in the process of mapping the given control demand into the individual thruster forces (Johansen and Fossen; Reference Johansen and Fossen2013, Soylu et al., Reference Soylu, Buckham and Podhorodeski2008). The accuracy and time taken for FDD should satisfy the requirement of fault tolerant control (Jiang and Yu, Reference Jiang and Yu2012). Due to the features of incipient thruster fault and the ocean current disturbance, more time would be taken to acquire fault information in the FDD module, and sometimes false alarms, including missing faults, would occur. Therefore, an adaptive fault tolerant control strategy may be more suitable for cases with an incipient thruster fault. Hu et al. (Reference Hu, Xiao and Friswell2011) achieved adaptive fault tolerant control by assuming that the upper and lower bounds of an actuator fault were known in advance. Wang et al. (Reference Wang, Xie and Zhang2012) investigated adaptive fault tolerant control based on an adaptive linear sliding mode algorithm.
The region tracking concept leads to energy saving but does not provide a solution to the problem of thruster amplitude and rate saturation constraints, especially in the initial period, due to the inevitable initial errors of the AUV. Ismail et al. (Reference Ismail, Faudzi and Dunnigan2014) adopted the joint limit concept to keep the thruster force within the saturation limits. Thrust allocation can also be used to keep the thruster force within saturation limits, such as infinity-norm based techniques (Soylu et al., Reference Soylu, Buckham and Podhorodeski2008). These references investigated thrust amplitude saturation constraints from the view of passive adjustment and ignored thruster rate saturation constraints, but in practical applications, the thruster rate constraint has a great effect on tracking performance. In other fields, such as spacecraft, in order to tackle the actuator constraints, another strategy has been studied using the adjustment of the desired trajectory or reference trajectory (Leonessa et al., Reference Leonessa, Haddad, Hayakawa and Morel2009). A pseudo-control hedging scheme was proposed by modifying the reference command to prevent the adaptive element from adapting to these actuator saturations (Lombaerts et al., Reference Lombaerts, Looye, Chu and Mulder2012; Simplício et al., Reference Simplício, Pavel, Van Kampen and Chu2013). A trajectory re-planning methodology was proposed based on differential flatness to protect the control command from violating the systems constraints (Chamseddine et al., Reference Chamseddine, Join and Theilliol2013; Reference Chamseddine, Theilliol, Zhang, Join and Rabbath2015). A reference governor approach was proposed by computing a feasible reference signal to guarantee the constraints are always satisfied (Aghaei et al., Reference Aghaei, Sheikholeslam, Farina and Scattolini2013; Boussaid et al., Reference Boussaid, Aubrun, Jiang and Abdelkrim2014).
Motivated by the above considerations, region tracking fault tolerant control is investigated for AUV subject to ocean current disturbance, modelling uncertainty, unknown thruster fault and thruster amplitude and rate saturation constraints. The main contributions and novelties of the present work are presented as follows. Firstly, in the frame of backstepping technique, the paper constructs a novel types of Lyapunov functions to deal with region tracking, which is different from the concept of region potential function. In contrast to the previous results, the paper analyses the bound structures of the lumped uncertainty and the variation of the thruster distribution matrix resulting from unknown thruster faults. In order to not require the knowledge of the lumped uncertainty and thruster fault in advance, an adaptive technique is adopted to estimate the coefficients of the bounds. In addition, inspired by Leonessa et al. (Reference Leonessa, Haddad, Hayakawa and Morel2009), the paper develops a desired trajectory adjustment method to tackle thruster amplitude and rate saturation constraints by transforming these two constraints into one. Barbalat's lemma is applied to verify that the tracking errors can be reached and maintained in the designed region based on the proposed method. Finally, simulations and pool experiments are carried out to demonstrate the effectiveness of the proposed methodology.
The paper is organised as follows. Section 2 briefly describes a general model of autonomous underwater vehicles in ocean environments and formulates the control objective. Backstepping-based adaptive region tracking fault tolerant control for AUV is proposed in Section 3. Then, Section 4 studies region tracking fault tolerant control with thruster amplitude and rate saturation constraints. In Section 5, two examples are presented to illustrate the effectiveness of the proposed controller. Finally, conclusions are drawn in Section 6.
2. AUV DYNAMIC MODEL
The nonlinear dynamic equations of AUV with six degrees of freedom in an ocean environment can be expressed as (Fossen, Reference Fossen2011):
$$\eqalign{& \dot \eta = J(\eta )v \cr & M \dot v + C_{RB} (v)v + C_A (v_r )v_r + D(v_r )v_r + g(\eta ) = \tau} $$
where J(η) ∈ R 6×6 is a spatial transformation matrix from the body fixed frame to the earth fixed frame. η ∈ R 6×1 is the position and orientation vector of the vehicle with respect to the earth fixed frame. v ∈ R 6×1 is the linear and angular velocity of the vehicle with respect to the body fixed frame. v r = v − v c . v c is the vector of ocean current with respect to the body fixed frame. M ∈ R 6×6 is the inertia matrix including added mass. C RB (v) ∈ R 6×6 is the rigid-body Coriolis and centripetal matrix. C A (v r ) ∈ R 6×6 is the hydrodynamic Coriolis and centripetal matrix. D(v r ) ∈ R 6×6 is the drag matrix. g(η) ∈ R 6×1 are the restoring forces and moments due to gravity and buoyancy. τ ∈ R 6×1 is the vector of forces and moments acting on the centroid of vehicle resulting from thrusters. The detailed expressions of these above matrixes/vectors can be seen in Podder and Sarkar (Reference Podder and Sarkar2001).
Equation (1) can be represented in the inertial fixed frame as
$$M_\eta (\eta )\ddot \eta + C_{RB\eta} (v,\eta )\dot \eta + C_{A\eta} (v_r, \eta )\dot \eta _r + D_\eta (v_r, \eta )\dot \eta _r + g_\eta (\eta ) = J^{ - T} \tau $$
where M
η
(η) = J−TMJ−1, C
RBη
(v,η) = J−T(C
RB
-MJ−1
$\dot J$
)J−1, C
Aη
(vr,η) = J−TC
A
J−1, Dη(vr,η) = J−TD
A
J−1, gη(η) = J−Tg,
$\dot \eta _r $
= Jv
r
.
The control objective is to design an adaptive region tracking fault tolerant controller for AUV described as Equation (2) in order to guarantee that all the closed-loop signals are bounded and the tracking error could reach and maintain into the desired region despite being in the presence of the lumped uncertainty, unknown thruster fault and thruster amplitude and rate saturation constraints.
3. BACKSTEPPING-BASED ADAPTIVE REGION TRACKING FAULT TOLERANT CONTROL
This section sets out to design the region tracking fault tolerant controller based on the backstepping technique. First, in order to manage tracking error to reach into the desired region, a type of piecewise and continuous function is developed to construct the Lyapunov function. Then, the paper analyses the bound structures of the lumped uncertainty and variation of thruster distribution matrix caused by thruster fault, respectively. Finally, in the frame of backstepping technique, the control law and adaptive law are derived by the constructed Lyapunov function.
3.1. Piecewise Lyapunov function
The aim of a controller based on the traditional Lyapunov function is to force the tracking error to converge to zero. In order to achieve region tracking control, Li et al. (Reference Li, Hou and Cheah2010) proposed the concept of region potential function. Unlike the previous work, this paper investigates a region tracking controller from the view of piecewise Lyapunov function. Inspired by Wu et al. (Reference Wu, Li and Chen2014), who constructed a Cm -class switching function based on power function, to avoid discontinuity caused by the breaking point in the traditional piecewise function, a type of piecewise, continuous and (n-1) order differentiable function is constructed by taking advantage of the features of exponential function and power function. The detailed expression is given as Equation (3).
$$P_{n,\varepsilon }(z) = \left\{ {\matrix{ {\exp (k(\left\vert z \right\vert - \varepsilon )) \times \displaystyle{{{(\left\vert z \right\vert - \varepsilon )}^n} \over {n!}}, \left\vert z \right\vert \ge \varepsilon } \cr {0, \left\vert z \right\vert \lt \varepsilon } \cr } } \right.$$
where, z is variable, described in the latter; k and ε are positive constants; n is an integer and larger than one, and the detailed selection will be given later; | z| denotes to take the absolute value of variable z.
As can be seen from Equation (3), P n,ε (z) is not less than zero. Meanwhile, according to the derivative of the generalised function (Gel'fand and Shilov, Reference Gel'fand and Shilov1964), it is easy to prove the continuity and (n−1) order differentiable features of the constructed function. In the latter part of this paper, the piecewise Lyapunov function will be constructed based on the proposed function P n,ε (z).
3.2. Bound structure
In the process of deriving a control law based on the constructed piecewise Lyapunov function, we should take the lumped uncertainty and unknown thruster faults into consideration. This paper deals with the effects of lumped uncertainty and thruster fault from the view of bound structure.
The considered fault is the loss of effectiveness in a thruster, which can be modelled as the variation of thruster distribution matrix B. Therefore, when thrusters are faulty, the force/torque caused by thrusters is changed from τ to τ f .
$$\tau _f = Bu - BKu = (B + {\tilde B})u $$
where, u is the control input of thrusters. K is a diagonal matrix, and its diagonal element k ii ∈[0,1]; k ii = 0 denotes the ith thruster is healthy; k ii = 1 denotes the ith thruster is failing; k ii ∈(0,1) denotes the ith thruster has a partial loss fault.
Due to the property of K, namely
$\left\Vert K \right\Vert \lt 1$
, it can be derived from
$\left\Vert {\tilde BB^ + } \right\Vert \lt \left\Vert K \right\Vert\left\Vert {BB^ + } \right\Vert$
. Hence, there exists an unknown constant L ∈ (0, 1), so the following inequality holds
$$\left \Vert {\tilde B}B^{+} \right \Vert \lt L $$
where, B
+denotes the pseudo-inverse of matrix B, and
$\left\Vert {} \right\Vert$
denotes Euclidean norm.
Due to the inherent nonlinearity and serious multivariate coupling, an AUV dynamic model based on the dynamic modelling technique has great uncertainty (Zhang et al., Reference Zhang, Liu, Yin and Liu2015). In this paper, the modelling uncertainty is expressed as follows:
$$\eqalign{M_{\eta} =& {\hat M}_{\eta} + {\tilde M}_{\eta} ;\,C_{RB\eta} = {\hat C}_{RB\eta} + C_{RB\eta} ;\,C_{A\eta} = {\hat C}_{A\eta} + {\tilde C}_{A\eta} ;\,D_{\eta} = {\hat D}_{\eta} + {\tilde D}_{\eta} ;\, \cr g_{\eta} = & {\hat g}_{\eta} + {\tilde g}_{\eta}}$$
According to the analysis presented above, the model of an AUV with lumped uncertainty and thruster fault can be described as
$$\ddot \eta = \hat M_\eta ^{ - 1} \left[ {J^{ - T} \left( {B + \tilde B} \right)u - \hat C_{RB\eta} \dot \eta - \hat C_{A\eta} \dot \eta - \hat D_\eta \dot \eta - \hat g_\eta} \right] - H $$
where,
$H = \hat M_\eta ^{ - 1} (\tilde M_\eta \ddot \eta + \tilde C_{RB\eta} \dot \eta + \tilde C_{A\eta} \dot \eta _r - C_{A\eta} Jv_c + \tilde D_\eta \dot \eta _r - D_\eta Jv_c + \tilde g_\eta )$
.
In general, the amplitude of ocean current is bounded. From the structure of the AUV dynamic model in Podder and Sarkar (Reference Podder and Sarkar2001), it has the following inequalities:
$$\eqalign{& \left \Vert {\hat M_\eta ^{ - 1} \tilde M_\eta \ddot \eta} \right \Vert \lt b_0 + b_1 \left \Vert {\dot \eta} \right \Vert + b_2 \left \Vert {\dot \eta} \right \Vert ^2 ;\,\left \Vert {\hat M_\eta ^{ - 1} \tilde C_{RB\eta} \dot \eta} \right \Vert \lt c_0 \left \Vert {\dot \eta} \right \Vert ^2 ;\,\cr & \left \Vert {\hat M_\eta ^{ - 1} \tilde C_{A\eta} \dot \eta _r} \right \Vert = \left \Vert {\hat M_\eta ^{ - 1} \tilde C_{A\eta} (\dot \eta - Jv_c )} \right \Vert \lt c_1 \left \Vert {\dot \eta} \right \Vert ^2 + c_2 \left \Vert {\dot \eta} \right \Vert ;\, \cr & \left \Vert {\hat M_\eta ^{ - 1} C_{A\eta} Jv_c} \right \Vert \lt c_3 \left \Vert {\dot \eta} \right \Vert ;\,\left \Vert {\hat M_\eta ^{ - 1} \tilde D_\eta (\dot \eta - Jv_c )} \right \Vert \lt d_0 \left \Vert {\dot \eta} \right \Vert ^2 + d_1 \left \Vert {\dot \eta} \right \Vert ;\, \cr & \left \Vert {\hat M_\eta ^{ - 1} D_\eta Jv_c} \right \Vert \lt d_2 \left \Vert {\dot \eta} \right \Vert ;\left \Vert {\hat M_\eta ^{ - 1} \tilde g_\eta} \right \Vert \lt d_3} $$
where b i , ci, di (i = 0,1,2,3) are all positive constants.
Consequently, according to the structure of inequalities presented above, it can be concluded that there exist unknown and constant vectors ϕ i > 0, i = 0,1,2, so the following inequality holds
$$\left \Vert H \right \Vert \lt \varphi _0 + \varphi _1 \left \Vert {\dot \eta} \right \Vert + \varphi _2 \left \Vert {\dot \eta} \right \Vert ^2 $$
3.3. Control law formulation
According to the above-presented piecewise Lyapunov function Equation (3), the bound structures of the variation of thruster distribution matrix caused by thruster fault Equation (5), and the bound structure of the lumped uncertainty Equation (8), this paper derives the control law.
At first, the desired trajectory is transferred as a reference trajectory, so as to acquire the position/orientation, velocity and acceleration of the reference trajectory which are required to construct the controller. The following second-order system is adopted as the trajectory reference model, given by
$$\left( {\matrix{ {\dot \eta _R} \cr {\ddot \eta _R} \cr}} \right) = \left( {\matrix{ {0_{6 \times 6}} & {I_{6 \times 6}} \cr { - \omega _n ^2 I_{6 \times 6}} & { - 2\omega _n \xi I_{6 \times 6}} \cr}} \right)\left( {\matrix{ {\eta _R} \cr {\dot \eta _R} \cr}} \right) + \left( {\matrix{ {0_{6 \times 6}} \cr {\omega _n ^2 I_{6 \times 6}} \cr}} \right)\eta _d $$
where, η d ∈ R 6×1 is the desired trajectory, η R ∈ R 6×1 is the reference state vector. ω n and ξ are positive constants.
Before designing the adaptive region tracking fault tolerant controller based on the backstepping technique, we define the following variables z 1 and z 2
$$\eqalign{& z_1 = \eta - \eta _R \cr & z_2 = \dot \eta - \alpha} $$
where, α is the virtual variable and will be designed later.
According to the above-presented piecewise function Equation (3), we define a Lyapunov function in terms of tracking error z 1
$$V_1 = \sum\limits_{i = 1}^6 {P_{3,\varepsilon _1 (i)} (z_1 (i))} $$
where, ε 1 is the desired tracking error region; ε 1(i) is the ith element of vector ε 1; z 1(i) is the ith element of vector z 1; V 1 ≥ 0.
The time derivative of Equation (11) is presented as follows:
$$\dot V_1 = \sum\limits_{i = 1}^6 {(kP_{3,\varepsilon _1 (i)} (z_1 (i)) + P_{2,\varepsilon _1 (i)} (z_1 (i)))sign(z_1 (i))\dot z_1 (i)} $$
Apparently, discontinuity may exist in the latter derivative due to the sign function in Equation (12). However, after further analysing the property of function as Equation (3), it can be found that sign(z
1) could not affect the continuity of V
1, since function P
3,ε1 (i) (z
1 (i)) equals zero in the interval of [−ε
1(i), ε
1(i)], but it would affect the continuity of the virtual variable α and control law. Based on the fact that the value of sign(z
1) on the interval of [−ε
1(i), ε
1(i)] does not change the value of
$\dot V_1 $
, another sign-like function takes the place of sign(z
1) in this paper, shown as Equation (13) so as to not introduce the sign(z
1) in the latter control law. Specifically, in the interval of [-ε
1(i), ε
1(i)], trigonometric functions are adopted to avoid the breaking point in the traditional sign function.
$${\mathop{\rm sgn}} _{\varepsilon _1 (i)} (z_1 (i)) = \left\{ {\matrix{ {sign(z_1 (i)), \left \vert {z_1} \right \vert \ge \varepsilon _1 (i)} \cr {\sin \left(\displaystyle{\pi \over 2}\cos \left(\displaystyle{\pi \over 2}\displaystyle{{z_1 (i) - \varepsilon _1 (i)} \over {\varepsilon _1 (i)}}\right)\right), \left \vert {z_1} \right \vert \lt \varepsilon _1 (i)} \cr}} \right.$$
where,
${\mathop{\rm sgn}} _{\varepsilon _1 \left( i \right)} (z_1 \left( i \right))$
is continuous and the derivative can be calculated by treating it as generalised function.
Using Equations (10) and (13), Equation (12) can be represented by vector form as Equation (14)
$$\dot V_1 = \Sigma (kP_{3,\varepsilon _1} (z_1 ) + P_{2,\varepsilon _1} (z_1 )){\mathop{\rm sgn}} _{\varepsilon _1} (z_1 )(z_2 + \alpha - \dot \eta _R ) $$
where,
$P_{3,\varepsilon _1} (z_1 ) = [P_{3,\varepsilon _1 (1)} (z_1 (1)),P_{3,\varepsilon _1 (2)} (z_1 (2)), \cdots, P_{3,\varepsilon _1 (6)} (z_1 (6))]^T $
; vector
${\mathop{\rm sgn}} _{\varepsilon _1} (z_1 )$
and
$P_{2,\varepsilon _1} (z_1 )$
are similar as
$P_{3,\varepsilon _1} (z_1 )$
.
$\Sigma X$
denotes to calculate the sum of all elements in vector X. We note that the product of vectors with the same dimensions should be operated as a product of the corresponding elements in the vectors. For example, the product of [x
1,x
2,x
3]
T
and [y
1,y
2,y
3]
T
is [x
1
y
1, x
2
y
2, x
3
y
3]
T
.
We design the virtual variable α
$$\alpha = - \left(g_1 + \displaystyle{1 \over 4}\right)(kP_{3,\varepsilon _1} (z_1 ) + P_{2,\varepsilon _1} (z_1 )){\mathop{\rm sgn}} _{\varepsilon _1} (z_1 ) + \dot \eta _R - (\varepsilon _2 + \sigma ){\mathop{\rm sgn}} _{\varepsilon _1} (z_1 ) $$
where, g 1 is positive constant; σ is positive vector. It can be simply verified that the virtual variable α is continuous and differentiable based on the generalised function.
Next, according to the above-presented function, we define a Lyapunov function in terms of the variable z 2
$$V_2 = V_1 + \Sigma P_{2,\varepsilon _2} (z_2 ) $$
The time derivative of V 2 is
$$\dot V_2 = \dot V_1 + \Sigma (kP_{2,\varepsilon _2} (z_2 ) + P_{1,\varepsilon _2} (z_2 )){\mathop{\rm sgn}} _{\varepsilon _2} (z_2 )(\ddot \eta - \dot \alpha ) $$
Substituting Equation (7) into Equation (17), yields
$$\eqalign{& \dot V_2 = \dot V_1 + \Sigma (kP_{2,\varepsilon _2} (z_2 ) + P_{1,\varepsilon _2} (z_2 )){\mathop{\rm sgn}} _{\varepsilon _2} (z_2 )\cr & \left(\hat M_\eta ^{ - 1} \left[ {J^{ - T} \left( {B + \tilde B} \right)u - \dot \eta - \hat C_{A\eta} \dot \eta - \hat D_\eta \dot \eta - \hat g_\eta} \right] - H - \dot \alpha \right)} $$
The first main result of this paper is given in the following.
Theorem 1: Consider an AUV described as in Equation (7) subject to the lumped uncertainty and unknown thruster faults, all the closed-loop signals are bounded and the tracking error could reach into the desired region with the action of the control law, expressed as Equations (19a)–(19c) and adaptive law, expressed as Equations (20a)–(20d).
$$\eqalign{u &= B^ + J^T [(\hat C_{RB\eta} \dot \eta + \hat C_{A\eta} \dot \eta + \hat D_\eta \dot \eta + \hat g_\eta ) + \hat M_\eta \dot \alpha _1 \cr & \quad- (g_2 + 1) \hat M_\eta P_{1,\varepsilon _2} (z_2 ){\mathop{\rm sgn}} _{\varepsilon 2} (z_2 )] + u_1 + u_2 }$$
$$u_1 = - B^ + J^T \hat M_\eta (\hat \rho _0 + \hat \rho _1 \left \Vert {\dot \eta} \right \Vert + \hat \rho _2 \left \Vert {\dot \eta} \right \Vert ^2 ){\rm sgn}_{\varepsilon _2} (z_2 ) $$
$$ \eqalign{u_2 =& - B^ + J^T \hat \rho _3 \Vert [(\hat C_{RB\eta} \dot \eta + \hat C_{A\eta} \dot \eta + \hat D_\eta \dot \eta + \hat g_\eta ) + \hat M_\eta \dot \alpha _1 \cr & - (g_2 + 1)\hat M_\eta P_{1,\varepsilon _2} (z_2 ){\mathop{\rm sgn}} _{\varepsilon _2} (z_2 )] \Vert {\rm sgn}_{\varepsilon _2} (z_2 )} $$
$${\dot {\hat \rho}} _0 = \Gamma _0 (kP_{2,\varepsilon _2} (z_2 ) + P_{1,\varepsilon _2} (z_2 )) $$
$${\dot {\hat \rho}} _1 = \Gamma _1 (kP_{2,\varepsilon _2} (z_2 ) + P_{1,\varepsilon _2} (z_2 ))\left \Vert {\dot \eta} \right \Vert $$
$${\dot {\hat \rho}} _2 = \Gamma _2 (kP_{2,\varepsilon _2} (z_2 ) + P_{1,\varepsilon _2} (z_2 ))\left \Vert {\dot \eta} \right \Vert ^2 $$
$$\eqalign{&{\dot {\hat \rho}} _3 = \Gamma _3 \hat M_\eta ^{ - 1} (kP_{2,\varepsilon _2} (z_2 ) + P_{1,\varepsilon _2} (z_2 )) \cr & \left \Vert {[(\hat C_{RB\eta} \dot \eta + \hat C_{A\eta} \dot \eta + \hat D_\eta \dot \eta + \hat g_\eta ) + \hat M_\eta \dot \alpha _1 - (g_2 + 1)\hat M_\eta P_{1,\varepsilon _2} (z_2 ){\mathop{\rm sgn}} _{\varepsilon _2} (z_2 )]} \right \Vert} $$
where, g
2 is positive constant; ρ
i
= ϕ
i
/(1 − L) i = 0,1,2.;
$\hat \rho _k $
is the estimation of ρ
k
, k = 0,1,2,3. ρ
3 = [L/(1 − L), L/(1 − L), L/(1 − L)]
T
; Γ
j
(j = 0,1,2,3) are diagonal and positive definite matrix.
The proof of Theorem 1 is given in Appendix A.
From the derivation and analysis procedure presented above, the proposed region tracking fault tolerant control algorithm is robust to ocean current disturbance and model uncertainty due to its adaptive term. It could also compensate unknown thruster faults, independent of the FDD.
4. REGION TRACKING FAULT TOLERANT CONTROL WITH THRUSTER AMPLITUDE AND RATE SATURATION CONSTRAINTS
This section extends the proposed region tracking fault tolerant controller described in Section 3 to region tracking fault tolerant control with thruster amplitude and rate saturation constraints.
With respect to control input constraints, the strategies based on adjustment of the desired trajectory have been investigated in recent years, including pseudo-control hedging, trajectory re-planning and reference governors. In contrast to the technique in Leonessa et al. (Reference Leonessa, Haddad, Hayakawa and Morel2009), which was accomplished in the respect of the derivative of control law, we investigate thruster amplitude and rate saturation constraints based on thruster constraints transfer and the relationship between the controller output and the desired trajectory.
4.1. Constraints Transfer
At first, the thruster amplitude and rate saturation constraints can be described as
$$\eqalign{& u_{\min} \le u \le u_{\max} \cr & \gamma _{\min} \le \dot u \le \gamma _{\max}} $$
where, u max and u min are the upper and lower limits of thruster amplitude. γ max and γ min are the upper and lower limits of thruster rate.
Thruster amplitude and rate saturation constraints can be transferred to a single constraint, namely Equation (21) can be approximately transformed as
$$\underline{u} \le u \le \bar u $$
where,
${\underline u} = \max \left\{{\matrix{ {u_{\min}} & {u(t - T) + T\gamma_{\min}} \cr}} \right\}$
;
${\bar u} = \min \left\{{\matrix{ {u_{\max}} & {u(t - T) + T{\gamma}_{\max}} \cr}} \right\}$
; Equation (22) can be derived based on the approximation relationship
${\dot u} \approx \left({u(t) - u(t - T)}\right)/T \cdot u(t)$
and u(t − T) are the present and previous step of thruster output, respectively. T is the control interval.
4.2. Desired trajectory adjustment
Recalling the control law in Equation (19a) and Equation (15), the controller output u explicitly depends on the desired trajectory.
Using Equations (9), (15) and (19a)–(19c), the desired trajectory can be expressed as
$$\eqalign{ \eta _d &= (w_n^2 J^T \hat M_\eta )^{ - 1} B(u - B^ + J^T [(\hat C_{RB\eta} \dot \eta + \hat C_{A\eta} \dot \eta + \hat D_\eta \dot \eta + \hat g_\eta ) \cr & \quad+ \hat M_\eta \left(\displaystyle{{df\,(z_1 )} \over {dt}} - \omega _n^2 \eta _R - 2\omega _n \xi \dot \eta _R \right) - (g_2 + 1)\hat M_\eta P_{1,\varepsilon _2} (z_2 ){\mathop{\rm sgn}} _{\varepsilon _2} (z_2 )] + u_1 + u_2 )} $$
where,
$f(z_1 ) = - (g_1 + \displaystyle{1 \over 4})(kP_{3,\varepsilon _1} (z_1 ) + P_{2,\varepsilon _1} (z_1 )){\mathop{\rm sgn}} _{\varepsilon _1} (z_1 ) - (\varepsilon _2 + \sigma ){\mathop{\rm sgn}} _{\varepsilon _1} (z_1 )$
.
To deal with thruster amplitude and rate saturation constraints, the desired trajectory should be shaped to guarantee the control output u in Equation (23) to satisfy Equation (22).
Next, another important result is presented:
Theorem 2: Consider an AUV described as per Equation (1) with the lumped uncertainty, unknown thruster fault and thruster amplitude and rate saturation constraints, control laws designed as Equations (19a)–(19c) and adaptive laws expressed as Equations (20a)–(20d). The desired trajectory is modified as follows
$$\eta _d^{\prime} = \eta _d + (\omega _n^2 J^T \hat M_\eta )^{ - 1} Bu^{\ast} (\delta (u^{\ast} ) - 1) $$
where,
$\delta (u^{\ast}) = \left\{ {\matrix{ {\bar u} \big/ u^{\ast} &u^{\ast} \gt {\bar u} \cr 1 &\underline{u} \le u^{\ast} \le {\bar u} \cr {\underline{u}} \big/ u^{\ast} &u^{\ast} \lt \underline{u} }} \right.$
; u* is the control output without considering thruster constraints in Section 3. Then, the following statements hold:
-
(i) The tracking error could be reached in the designed region ε1;
(ii) The control output would satisfy Equation (22).
The proof of Theorem 2 is given in Appendix B.
From the above design and analysis, it can be concluded that the proposed method could deal with thruster amplitude and rate saturation constraints by locally modifying the desired trajectory. Thus we have tracking fault tolerant control for an AUV with lumped uncertainty, unknown thruster faults and thruster amplitude and rate saturation constraints.
5. SIMULATIONS AND POOL EXPERIMENTS
In this section, simulation and experiment results are presented to demonstrate the feasibility and effectiveness of the proposed method. For this purpose, two examples are considered. In the first example, a series of simulations of an ODIN AUV are performed. In the second example, the proposed region tracking fault tolerant controller is used to experiment on Beaver 2 AUV, designed by the authors' laboratory.
5.1. Simulations on ODIN AUV
In order to verify the effectiveness of the proposed region tracking fault tolerant controller, a serial of simulations were conducted on an ODIN AUV subject to ocean current disturbance, modelling uncertainty, unknown thruster fault, and thruster amplitude and rate saturation constraints. The parameters of the ODIN AUV can be seen in Podder and Sarkar (Reference Podder and Sarkar2001). The thruster distribution matrix in the considered ODIN AUV is expressed as follows.
$$B = \left[ {\matrix{ s & { - s} & { - s} & s & 0 & 0 & 0 & 0 \cr s & s & { - s} & { - s} & 0 & 0 & 0 & 0 \cr 0 & 0 & 0 & 0 & { - 1} & { - 1} & { - 1} & { - 1} \cr 0 & 0 & 0 & 0 & {Rs} & {Rs} & { - Rs} & { - Rs} \cr 0 & 0 & 0 & 0 & {Rs} & { - Rs} & { - Rs} & {Rs} \cr {R_z} & { - R_z} & {R_z} & { - R_z} & 0 & 0 & 0 & 0 \cr}} \right]$$
where s = sin(pi/4); R = 0·381; R z = 0·508.
In this section, 30% model uncertainty is set for each of the parameters in the ODIN AUV, which means the nominal system dynamics used in the controller is 70%. The ocean current speed V c is generated using a first-order Gauss-Markov process, expressed as Equation (25) (Fossen, Reference Fossen2011).
$$\dot V_c + \mu V_c = \omega $$
where ω is Gaussian white noise with mean −1·5 and variance 1; μ = 3; two angles concerning the direction of ocean current: β c (sideslip angle) and α c (angle of attack); β c is generated by the sum of Gaussian noise with mean 0 and variance 50; and α c = β c /2.
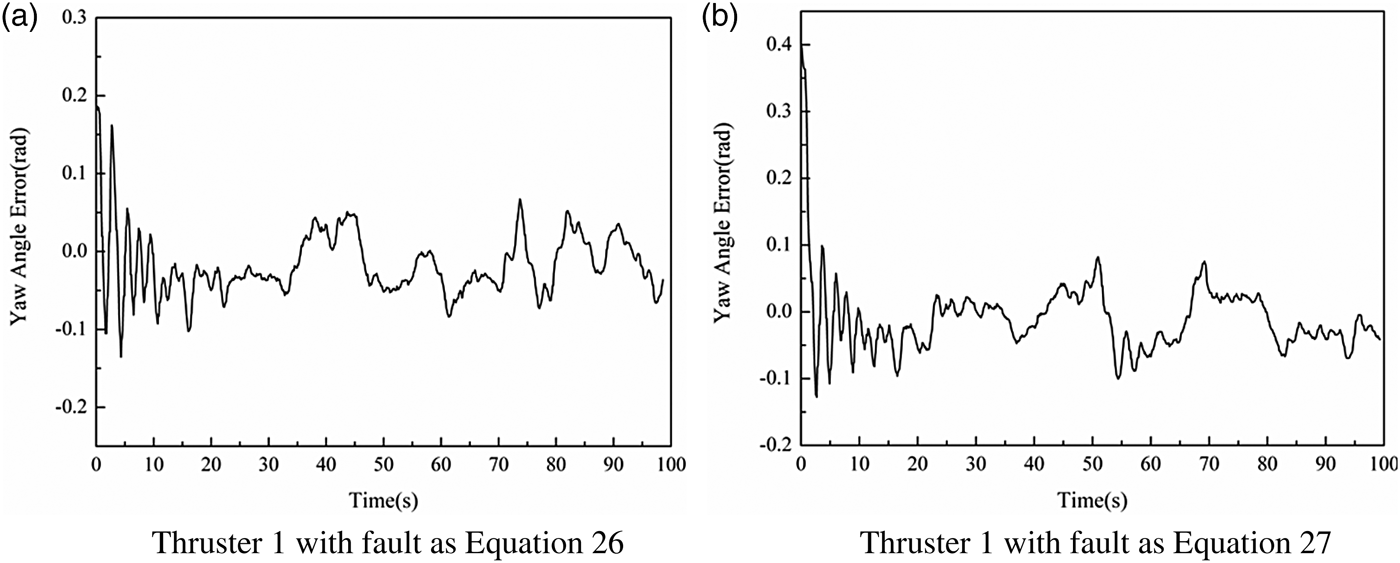
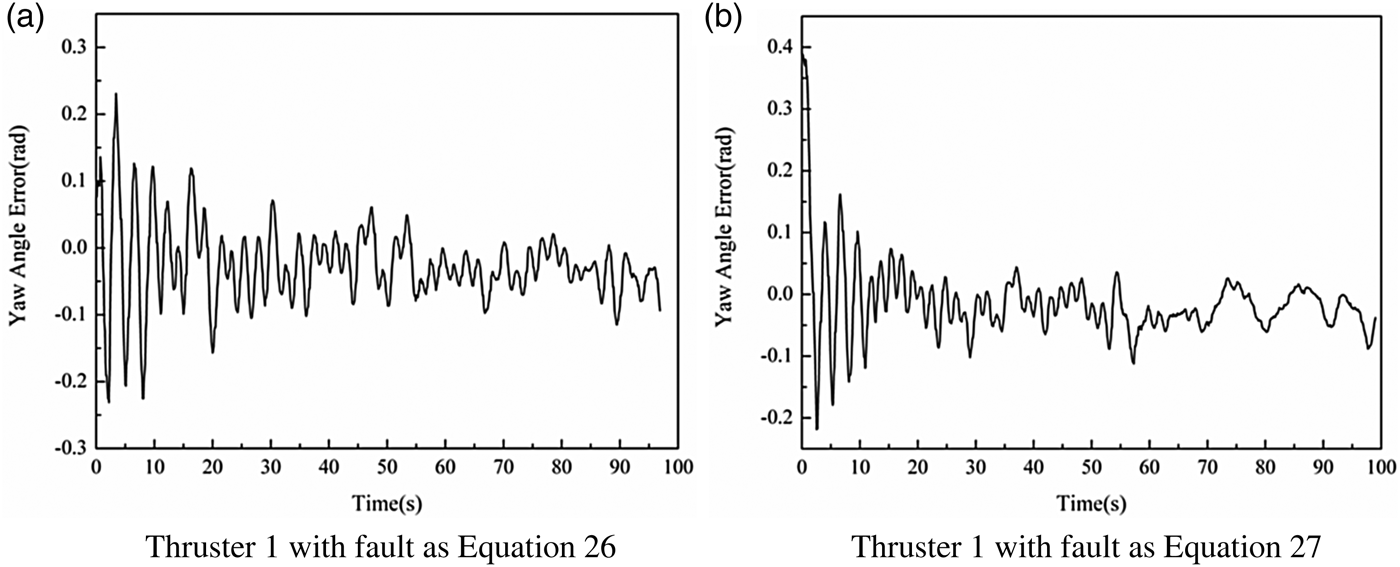
There are two kinds of incipient thruster faults considered in this paper, shown as Equations (26) and (27).
$$k_{11} = \left\{ {\matrix{ { 0, t \lt 20} \cr {\displaystyle{{0\!\cdot\!29} \over {30}}(t - 20) + 0\!\cdot\!01\sin \left(\displaystyle{\pi \over 5}(t - 20)\right),{\rm 20} \le t \lt 50} \cr {\displaystyle{{0\!\cdot\!29} \over {30}} + 0\!\cdot\!01\sin \left(\displaystyle{\pi \over {10}}(t - 50)\right), t \ge 50} \cr}} \right. $$
$$k_{11} = \left\{ {\matrix{ {0, t \lt 20} \cr {0\!\cdot\!5\Bigg(1 - \exp \left(\displaystyle{{ - (t - 20)} \over {10}}\Bigg)\right), t \ge 50} \cr}} \right. $$
The initial position of the ODIN AUV is η 0 = [0·4; 0·4;−0·4; pi/18; pi/18; pi/9] and its initial velocity is zero. Furthermore, it is assumed that the thruster amplitude limits are ±200N, and the thruster rate limits are ±100N/s, namely, u max = 200; u min = −200; γ max = 100 and γ min = −100.
The parameters in the proposed method in Section 3 are given as follows:
$$\varepsilon _1 = \left[ {0 \!\cdot\! 3,0 \!\cdot\! 3,0 \!\cdot\! 3,0 \!\cdot\! 15,0 \!\cdot\! 15,0 \!\cdot\! 15} \right]^{\prime};\varepsilon _2 = \left[ {0 \!\cdot\! 5,0 \!\cdot\! 5,0 \!\cdot\! 5,0 \!\cdot\! 25,0 \!\cdot\! 25,0 \!\cdot\! 25} \right]^{\prime};$$
$$g_1 = 2;g_2 = 5;k = 1;w_n = 3;\xi = 0 \!\cdot\! 7;\sigma = \left[ {0 \!\cdot\! 1,0 \!\cdot\! 1,0 \!\cdot\! 1,0 \!\cdot\! 1,0 \!\cdot\! 1,0 \!\cdot\! 1} \right]^{\prime};$$
$$\eqalign{{\bi \Gamma} _{\bi 0} = {\rm diag}\left( {0 \!\cdot\! 5;0 \!\cdot\! 5;0 \!\cdot\! 5;0 \!\cdot\! 05;0 \!\cdot\! 05;0 \!\cdot\! 05} \right);\cr {\bi \Gamma} _{\bi 1} = {\rm diag}\left( {0 \!\cdot\! 5;0 \!\cdot\! 5;0 \!\cdot\! 5;0 \!\cdot\! 05;0 \!\cdot\! 05;0 \!\cdot\! 05} \right);}$$
$$\eqalign{{\bi \Gamma} _{\bi 2} = {\rm diag}\left( {0 \!\cdot\! 5;0 \!\cdot\! 5;0 \!\cdot\! 5;0 \!\cdot\! 05;0 \!\cdot\! 05;0 \!\cdot\! 05} \right);\,\cr{\bi \Gamma} _{\bi 3} = {\rm diag}\left( {0 \!\cdot\! 5;0 \!\cdot\! 5;0 \!\cdot\! 5;0 \!\cdot\! 05;0 \!\cdot\! 05;0 \!\cdot\! 05} \right);}$$
Now, the proposed method is used to track two kinds of trajectories: an ellipse shape and a figure of eight curve shape.
5.1.1. An ellipse shape trajectory
The ellipse shape desired trajectory is given by
$$x_d = 6\left( {1 - {\rm cos}\left( {0 \!\cdot\! 15t} \right)} \right);y_d = 3{\rm sin}\left( {0 \!\cdot\! 15t} \right);z_d = - 0 \!\cdot\! 2x_d ;\eta _d = \left[ {x_d, y_d, z_d, 0, 0, 0} \right]$$
The following three cases are considered.
Case 1: No thruster fault occurs;
Case 2: The first thruster fault occurs as Equation (26); and the fifth thruster completely fails after the 20th second;
Case 3: The first thruster fault occurs as Equation (27); and the fifth thruster completely fails after the 20th second.
Figures 1 and 2 illustrate the simulation results about path, tracking error and control output for Case 1, Case 2 and Case 3, respectively.
Figure 1. Simulation results for Case 1 of the ellipse shape trajectory.
Figure 2. Simulation results for Case 2 and Case 3 of the ellipse shape trajectory.
As can be seen from Figures 1 and 2, no matter whether thruster faults occur, the tracking error could be reached and maintained into the desired region based on the developed region tracking controller, while tracking the ellipse shape trajectory. Moreover, in these cases, affected by the thruster rate saturation constraint, the control outputs do not change abruptly in the initial period, although there exists the initial error. The control outputs do not violate the thruster constraints in the whole process.
5.1.2. Figure of eight curve shape trajectory
In a similar way, a different desired trajectory is considered in the paper, given by
$$x_d = 4\left( {1 - {\rm cos}\left( {0 \!\cdot\! 10t} \right)} \right);y_d = 2{\rm sin}\left( {0 \!\cdot\! 20t} \right);z_d = - 0 \!\cdot\! 2x_d ;\eta _d = \left[ {x_d, y_d, z_d, 0, 0, 0} \right]$$
In this subsection, simulation is carried out in the condition of Case 2. The simulation result is shown in Figure 3.
Figure 3. Simulation results of the figure of eight curve shape trajectory.
As shown in Figure 3, although the tracking error is outside of the desired region in the initial period, after about 10 seconds, the tracking error could be in the desired region based on the proposed region tracking controller, even after thruster faults have occurred.
In addition, in order to further demonstrate the effectiveness of the proposed method, the simulations with another new desired region (ε 1) are performed. The new desired region is set as ε 1 = [0·1,0·1,0·1,0·05,0·05,0·05]’, and the other parameters are the same as those in Case 2.
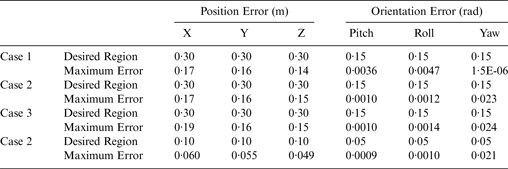
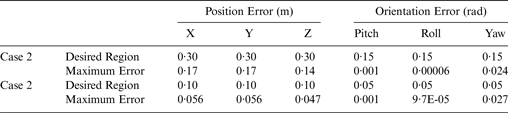
Figure 4 shows the tracking errors for the two tracking cases. According to Figure 4, the tracking errors could be reached and maintained in the new desired region after about 5 seconds. The simulation results are tabulated in Tables 1 and 2.
Figure 4. Simulation results for another desired region.
Table 1. Region tracking performance of the ellipse shape trajectory after 10 seconds.
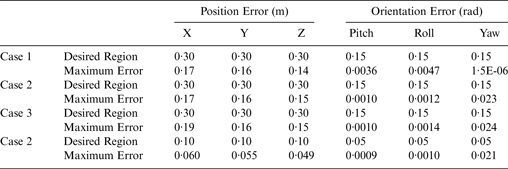
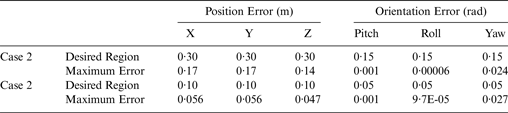
Table 2. Region tracking performance of the figure of eight curve shape trajectory after 10 seconds.
5.1.3. Comparative simulation studies
In order to demonstrate the efficacy of the proposed region tracking method, comparative simulation studies were performed based on the concept of region potential function. The comparative simulations are divided into two parts, that is, one is the case without ocean current disturbance, and the other is the case with ocean current disturbance after the 50th second simulated as Equation (25). In the comparative simulations, the desired region ε1 = [0·3,0·3,0·3,0·15,0·15,0·15]’. The initial position and orientation η 0 = [0·04;0·04;−0·04; pi/360;pi/360;pi/180]’. The controller parameters K p = 500*diag (5,5,5,3,3,3); L d = 20I 13×13; K v = diag(500,500,500,30,30,30). The detailed controller expression was given in Ismail et al. (Reference Ismail, Faudzi and Dunnigan2014).
Figure 5 shows the tracking errors for tracking the ellipse shape trajectory with/without ocean current disturbance while Figure 6 shows the results of tracking another trajectory.
Figure 5. Comparative simulation results for the ellipse shape trajectory.
Figure 6. Comparative simulation results for the figure of eight curve shape trajectory.
From Figures 5 and 6, in the case of no ocean current disturbance, the tracking errors could be maintained in the desired regions for the two desired trajectories. This indicates that the concept of region potential function can be adopted to achieve region tracking control without external disturbance. However, in the presence of ocean current disturbance, the tracking errors obtained from the comparative method are out of the desired region. Therefore, in comparison with the concept of region potential function, the simulation results demonstrate the efficacy of the proposed region tracking method.
5.2. Experiments on Beaver 2 AUV
Another example is considered in the paper to verify the efficacy of the proposed method. In the example, experiments are performed on the Beaver 2 AUV, designed by the authors' laboratory in 2014 (thrusters were changed in 2015), shown in Figure 7(a). The Beaver 2 AUV was 0·8 m × 0·5 m × 0·4 m. Its dry weight was 50 kg and slightly positively buoyant. The left and right thrusters were configured in Beaver 2, which can provide a maximum thrust of approximately 30N. Figure 7(b) describes the hardware architecture of Beaver 2.
Figure 7. Beaver 2 AUV and its hardware architecture.
It should be explained that in order to conduct experiments conveniently, the power of Beaver 2 comes from outside by the umbilical cable, but the controller algorithm runs in the PC104 working with Vxworks embedded control system inside Beaver 2. The host computer is in charge of sending only Start/Stop commands and receiving and saving experiment data. The sensor system was composed of HMR3000 digital compass (measuring roll, pitch and yaw angles), and Mini-Avatar (measuring angular velocities).
In this section, the yaw angle tracking is considered. The yaw model of Beaver 2 used to synthesize controller is described as follows (Zhang et al., Reference Zhang, Liu, Yin and Liu2015).
$$M_\psi \dot r + D_{\psi 1} r + D_{\psi 2} r\left \vert r \right \vert + g_\psi = T_r $$
where M ψ = 22·0753; D ψ1 = 4·4458; D ψ2 = 15·4308; g ψ = 0·5828; T r is the torque generated by thrusters.
In the experiments, two desired yaw angles are considered, shown as follows.
$$\psi _{d1} = 0 \!\cdot\! 75\pi (1 - \exp ( - 0 \!\cdot\! \!1t)) $$
$$\psi _{d2} = \left\{ {\matrix{ {0 \!\cdot\! 45\pi (1 - \exp ( - 0 \!\cdot\! 1t)){\rm 0} \le {\rm t} \le {\rm 50}} \cr {0 \!\cdot\! 45\pi + 0 \!\cdot\! 3\pi (1 - \exp ( - 0 \!\cdot\! 1(t - 50))) 50 \lt {\rm t}} \cr}} \right. $$
Similar to Section 5.1, two kinds of thruster faults are taken into account in the experiments. The expressions of thruster faults are the same as Equations (26) and (27). The thruster distribution matrix is expressed as B = [−0·74,0·74].
The parameters in the controller are given in the following:
$$\eqalign{& \varepsilon _1 = 0 \!\cdot\! 1;\varepsilon _2 = 0 \!\cdot\! 3;c_1 = 2;c_2 = 5;k = 1;w_n = 3;\xi = 0 \!\cdot\! 7; \cr & \sigma = 0 \!\cdot\! 1;\,\Gamma _0 = 0 \!\cdot\! 001;\,\Gamma _1 = 0 \!\cdot\! 001;\,\Gamma _2 = 0 \!\cdot\! 001;\,\Gamma _3 = 0 \!\cdot\! 005;}$$
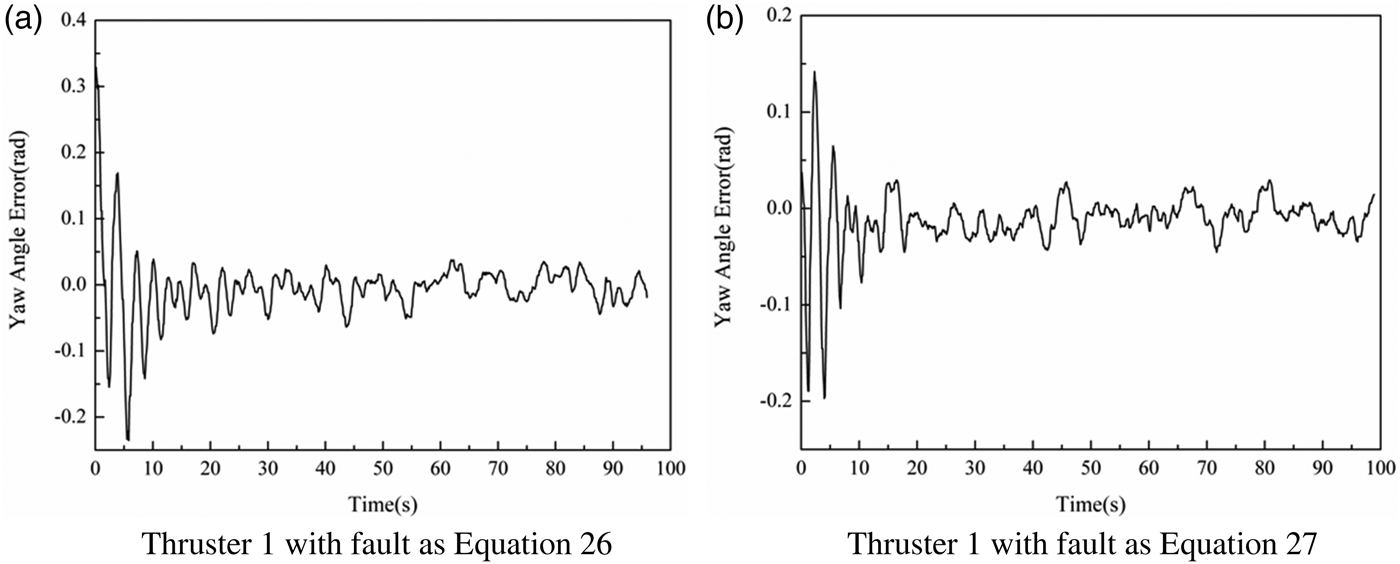
Figures 8 and 9 illustrate the tracking errors for the above desired yaw angles, when the two kinds of faults occur in the first thruster, respectively. As can be seen from Figures 8 and 9, although the tracking errors are outside of the desired region in the initial period, it reached the desired region after about 10 seconds based on the developed region tracking controller.
Figure 8. Experiments results for Yaw Angle 1.
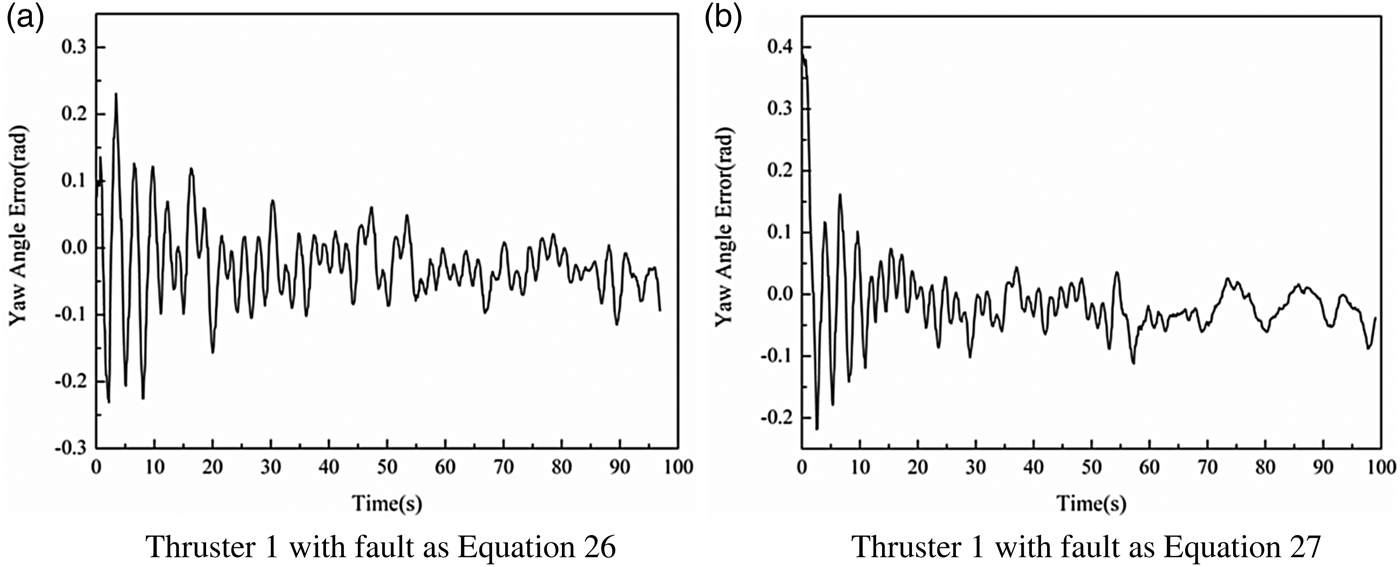
Figure 9. Experiments results for Yaw Angle 2.
In addition, similar to Section 5.1, another desired region is used when tracking the first desired yaw angle, in the experiments with the above two kinds of different thruster faults, respectively. The new desired region: ε 1 = 0·05, and the other parameters are not changed.
Figure 10 describes the experiments results for the two tracking cases. It can be seen from Figure 10 that the tracking error could reach the new desired region, no matter what kind of thruster fault occurs during the mission.
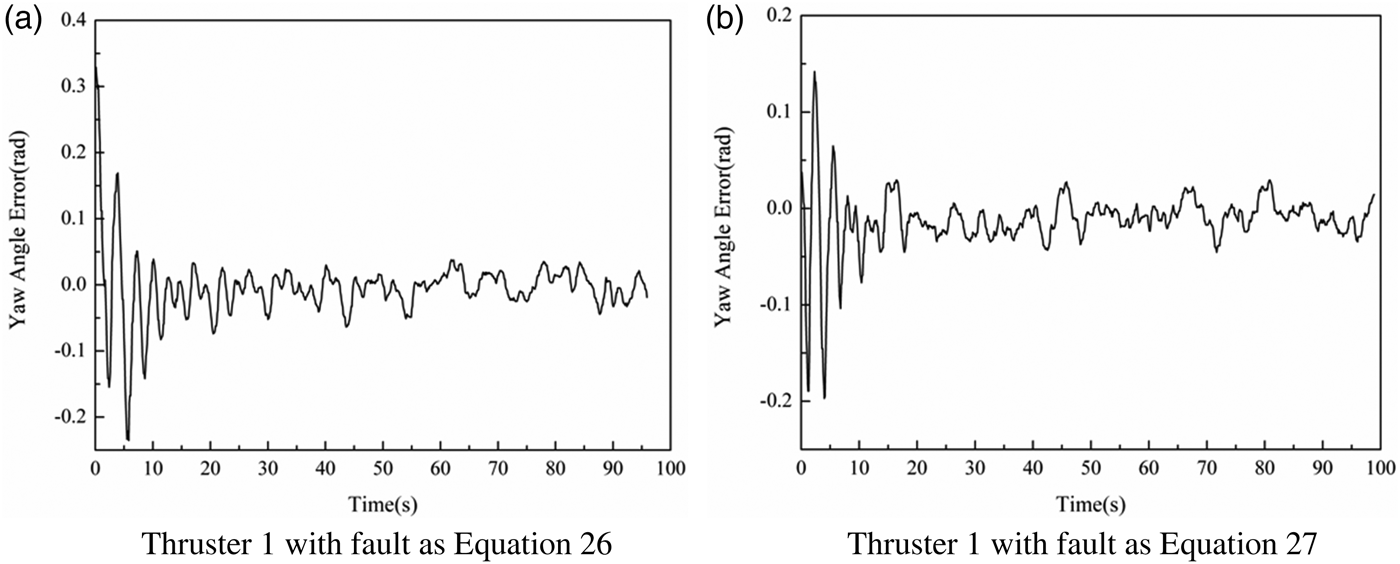
Figure 10. Experiments results for Yaw Angle 1 with another desired region.
6. CONCLUSIONS
Adaptive region tracking fault tolerant control method is proposed for AUV while taking modelling uncertainty, ocean current disturbance, unknown thruster fault and thruster amplitude and rate saturation constraints into account simultaneously. The developed method is based on the backstepping technique. Information about thruster fault and ocean current disturbance is not required. Region tracking is achieved by constructing a continuous and piecewise Lyapunov function. Based on Barbalat's lemma, it demonstrates that the tracking errors could reach the designed region. Thruster amplitude and rate saturation constraints are transformed to a single constraint, and it is dealt with by locally modifying the desired trajectory. Simulation and pool experiments results illustrate the effectiveness of the proposed method.
ACKNOWLEDGMENTS
This work is supported by the National Natural Science Foundation of China (51279040) and Basic Research Program of Ministry of Industry and Information Technology of People's Republic of China (B2420133003).
APPENDIX A. PROOF OF THEOREM 1
Define estimation error
$$\tilde {\rho _i} = \rho _i - \hat \rho _i $$
Choose the following Lyapunov function
$$V_3 = V_2 + \displaystyle{{1 - L} \over 2}{\tilde {\rho} _0}^T \Gamma _0 {\tilde \rho} _0 + \displaystyle{{1 - L} \over 2}{\tilde \rho} _1^T \Gamma _1 {\tilde \rho} _1 + \displaystyle{{1 - L} \over 2}{\tilde \rho} _2^T \Gamma _2 {\tilde \rho} _2 + \displaystyle{{1 - L} \over 2}{\tilde \rho} _3^T \Gamma _3 {\tilde \rho} _3 $$
The derivative of Equation (A2) is
$$\dot V_3 = \dot V_2 - (1 - L){\tilde \rho} _0^T \Gamma _0 {\dot {\hat \rho}} _0 - (1 - L){\tilde \rho} _1^T \Gamma _1 {\dot {\hat \rho}} _1 - (1 - L){\tilde \rho} _2^T \Gamma _2 {\dot {\hat \rho}} _2 - (1 - L){\tilde \rho} _3^T \Gamma _3 {\dot {\hat \rho}} _3 $$
Substituting Control law Equation (19) and adaptive law Equation (20) into Equation (A3), yielding
$$\eqalign{& \dot V_3 \le \Sigma ( - g_1 (kP_{3,\varepsilon _1} (z_1 ) + P_{2,\varepsilon _1} (z_1 ))^2 - g_2 (kP_{2,\varepsilon _2} (z_2 ) + P_{1,\varepsilon _2} (z_2 ))P_{1,\varepsilon _2} (z_2 ) + W \cr & + (kP_{2,\varepsilon _2} (z_2 ) + P_{1,\varepsilon _2} (z_2 ))( - (1 - L)(\hat \rho _0 + \hat \rho _1 \left \Vert {\dot \eta} \right \Vert + \hat \rho _2 \left \Vert {\dot \eta} \right \Vert ^2 ) + H) \cr & - (kP_{2,\varepsilon _2} (z_2 ) + P_{1,\varepsilon _2} (z_2 ))(\hat M_\eta ^{ - 1} (1 - L)\hat \rho _3 - [L,L,L]^T )\phi \cr & - (1 - L){\tilde \rho} _0^T (kP_{2,\varepsilon _2} (z_2 ) + P_{1,\varepsilon 2} (z_2 )) - (1 - L){\tilde \rho} _1^T (kP_{2,\varepsilon _2} (z_2 ) \cr & + P_{1,\varepsilon _2} (z_2 ))\left \Vert {\dot \eta} \right \Vert - (1 - L){\tilde \rho} _2^T (kP_{2,\varepsilon _2} (z_2 ) + P_{1,\varepsilon _2} (z_2 ))\left \Vert {\dot \eta} \right \Vert ^2 \cr & - (1 - L){\tilde \rho} _3^T \hat M_\eta ^{ - 1} (kP_{2,\varepsilon _2} (z_2 ) + P_{1,\varepsilon _2} (z_2 ))\phi )} $$
where,
$\phi = \left\Vert {[(\hat C_{RB\eta} \dot \eta + \hat C_{A\eta} \dot \eta + \hat D_\eta \dot \eta + \hat g_\eta ) + \hat M_\eta \dot \alpha _1 - (g_2 + 1)\hat M_\eta P_{1,\varepsilon _2} (z_2 ){\mathop{\rm sgn}} _{\varepsilon _2} (z_2 )]} \right\Vert$
;
$$W = \Sigma ( - \displaystyle{1 \over 4}(kP_{3,\varepsilon _1} (z_1 ) + P_{2,\varepsilon _1} (z_1 ))^2 + (kP_{3,\varepsilon _1} (z_1 ) + P_{2,\varepsilon _1} (z_1 ))(\left \vert {z_2} \right \vert - (\varepsilon _2 + \sigma )) - (kP_{2,\varepsilon _2} (z_2 ) + P_{1,\varepsilon _2} (z_2 ))P_{1,\varepsilon _2} (z_2 )).$
When |z 2| < (ε2 + σ), it is straightforward that W <0. And when |z 2| ≥ (ε 2 + σ), integrating with Young's Inequality, we can derive the following inequality
$$\eqalign{& W \le \Sigma ((\left \vert {z_2} \right \vert - (\varepsilon _2 + \sigma ))^2 - (kP_{2,\varepsilon _2} (z_2 ) + P_{1,\varepsilon _2} (z_2 ))P_{1,\varepsilon _2} (z_2 )) \cr &\quad \le \Sigma ((\left \vert {z_2} \right \vert - (\varepsilon _2 + \sigma ))^2 - P_{\varepsilon 2,1} (z_2 )^2 = (\left \vert {z_2} \right \vert - (\varepsilon _2 + \sigma ))^2 \cr &\quad - \exp (k(\left \vert {z_2} \right \vert - \varepsilon _2 )) \times (\left \vert {z_2} \right \vert - \varepsilon _2 )^2 ) \cr &\quad \le \Sigma (\left \vert {z_2} \right \vert - (\varepsilon _2 + \sigma ))^2 - \Sigma (\left \vert {z_2} \right \vert - \varepsilon _2 )^2 \lt 0} $$
Therefore, according to Equations (5) and (8), Inequality (A4) can be presented
$$\eqalign{& \dot V_3 \le \Sigma ( - g_1 (kP_{3,\varepsilon _1} (z_1 ) + P_{2,\varepsilon _1} (z_1 ))^2 - g_2 (kP_{2,\varepsilon _2} (z_2 ) + P_{1,\varepsilon _2} (z_2 ))P_{1,\varepsilon _2} (z_2 )) \cr & \le \Sigma ( - g_1 (kP_{3,\varepsilon _1} (z_1 ) + P_{2,\varepsilon _1} (z_1 ))^2 )} $$
Since Lyapunov function V
3 > 0 and
$\dot V_3 \le 0$
, V
3 is bounded. So z
1, z
2 and
${\tilde \rho} _i $
, i = 0,1,2,3 are bounded. And since the reference states η
r
$\dot \eta _r $
and
$\ddot \eta _r $
are bounded, the virtual variable α is bounded from Equation (15).
Let
$\Delta = \Sigma (g_1 (kP_{3,\varepsilon _1} (z_1 ) + P_{2,\varepsilon _1} (z_1 ))^2 )$
. Integrating Inequality Equation (A6) at the interval of [0, t], we have
$\int_0^t {\Delta (\vartheta )} d\vartheta \le V_3 (0)$
, which means
$\int_0^t {\Delta (\vartheta )} d\vartheta $
has a finite limit as t → ∞. According to Equation (3), we can see that Δ is differentiable, and the derivative of Δ is a function of
$\dot z_1 $
. From Equation (10), the boundedness of
$\dot z_1 $
can be ensured. So we can prove that the derivative of Δ is bounded. Thus, we conclude that Δ is uniformly continuous.
Consequently, according to the facts that
$\int_0^t {\Delta (\vartheta )} d\vartheta $
has a finite limit as t → ∞ and Δ is uniformly continuous, it can be concluded that Δ equals to zero, as t → ∞ based on Barbalat's lemma, which means z
1 ≤ ε1 as t → ∞. This completes the proof.
APPENDIX B. PROOF OF THEOREM 2
Statement (i) can be directly proved according to Appendix A.
In order to prove statement (ii), substituting Equations (23) and (24) into Equation (19), we can derive
$$\eqalign{& u = B^ + J^T [(\hat C_{RB\eta} \dot \eta + \hat C_{A\eta} \dot \eta + \hat D_\eta \dot \eta + \hat g_\eta ) \cr &\quad + \hat M_\eta \Big(\displaystyle{{df\,(z_1 )} \over {dt}} - \omega _n^2 \eta _R - 2\omega _n \xi \dot \eta _R \cr & \quad + \omega _n^2 (\eta _d + (\omega _n^2 J^T \hat M_\eta )^{ - 1} Bu^{\ast} (\delta (u^{\ast} ) - 1))\Big) \cr & \quad - (c_2 + 1)\hat M_\eta P_{\varepsilon 2,1} (z_2 ){\mathop{\rm sgn}} _{\varepsilon 2} (z_2 )] + u_1 + u_2 \cr & = u^{\ast} + u^{\ast} (\delta (u^{\ast} ) - 1) \cr & = u^{\ast} \delta (u^{\ast} )} $$
From the property of δ(u*) and Equation (B1), it is implied that the control outputs after modifying the desired trajectory as Equation (24) are guaranteed to satisfy the thruster amplitude and rate saturation constraints as Equation (22). This completes the proof.
