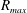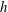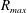2 Experimental set-up

Two $5~\text{cm}$ diameter optical lenses are placed horizontally and separated by a gap with controlled thickness $h$ , varied from 0.9 mm to 3.6 mm. The bottom lens is plano convex (the convex face placed upward) while the upper one is plano concave (the concave face placed downward) and both lenses have an equal curvature radius (38.6 cm). One thus obtains a Hele-Shaw cell of homogeneous thickness with a very slight curvature (figure 1). This cell is immersed in a large tank (20 cm sided) filled with tap water, which has been previously degassed by pumping its vapour for about ten minutes in order to prevent any spurious nucleation in the liquid during the bubble expansion and collapse. Finally, the ambient pressure is restored so that during experiments the external pressure is $P_{atm}=1~\text{bar}$ .

A stoichiometric mixture of $\text{H}_{2}$ and $\text{O}_{2}$ is prepared by electrolysing water and is injected in the gap separating the two lenses in order to form a bubble. Because of the gravity and of the Hele-Shaw cell profile, the bubble is centred with respect to the system. Soap dissolved in the water with a $5:10^{6}$ dilution prevents the bubble triple line pinning on the glass and allows for a perfect centring of the bubble.

One ground electrode is immersed in the liquid (which is equipotential as the liquid is sufficiently conductive) while a high voltage electrode is put in contact with the bubble. This electrode is insulated everywhere except at its tip. At the initial instant, a high voltage ( ${\approx}5$  kV) is delivered so that a spark is formed in the gas bubble between the electrode tip and the bubble wall. This ignites the reactive mixture, which leads to the explosion of the bubble. The reaction produces water vapour that condenses on the walls. Consequently, the vapour is drained from the bubble so that the cavity pressure decreases and the bubble finally implodes (see figure 2). After the system has relaxed, it may remain in some cases a small bubble that contains the unburnt gas (hydrogen or oxygen in excess or contaminant present in the initial bubble). The final bubble volume is smaller than 1 % of the initial bubble volume, proving that the initial bubble contains at least 99 % of a stoichiometric hydrogen–oxygen mixture.

Figure 1. Experimental set-up: a hydrogen–oxygen bubble is trapped between two curved glass walls which form a curved Hele-Shaw cell. An electrode delivers a high voltage at an initial time, igniting the reactive mixture. The experiment is observed by a high-speed camera placed above the cell.

Figure 2. Sequence of the explosion and collapse of a hydrogen–oxygen bubble. The gap thickness is $h=1.6$  mm. First snapshot, initial condition ( $t_{0}$ ). Second snapshot, maximal expansion $R_{max}=6.5$  mm ( $t_{m}$ ). Last snapshot, final collapse ( $t_{f}$ ). See movie 1 in supplementary material (https://doi.org/10.1017/jfm.2018.804). The dotted red rectangle on the first snapshot represents the restricted field of view for acquisition at $10^{6}$ frames per second.

The full scene is recorded with a fast camera running at 60 000 frames per second, with an exposure time $10^{-6}$  s and $320\times 320~\text{pixels}^{2}$ resolution (see the field of view on figure 2). Some experiments focused on a partial view field with resolution $8\times 320~\text{pixels}^{2}$ and recorded at a higher frame rate ( $10^{6}$ frames per second) are dedicated to the fine description of the trajectory $R(t)$ in the first instants. In the latter case, the bubble contour can not be observed in its whole, but only along a single diameter.

3 Cavity formation

After the reactive mixture is ignited, the bubble expands and forms a cylindrical cavity of radius $R_{max}$ . In this section, we describe this expansion process and discuss how the maximal radius depends on the bubble’s initial radius $R_{0}$ and on the gap thickness $h$ . Energy is transformed throughout the process. Initially, energy is stored in chemical form, then it is transformed into kinetic energy of the surrounding liquid, and finally used to increase the pressure and the temperature within the bubble.

The initial chemical energy contained within the bubble is

(3.1) $$\begin{eqnarray}\displaystyle E_{\unicode[STIX]{x1D712}}=\frac{2}{3}\frac{\unicode[STIX]{x03C0}R_{0}^{2}h}{v_{m}}\unicode[STIX]{x0394}H, & & \displaystyle\end{eqnarray}$$

with $v_{m}=RT/P_{atm}$ the molar volume of the initial mixture at ambient pressure and temperature and $\unicode[STIX]{x0394}H=-243~\text{kJ}~\text{mol}^{-1}$ the molar reaction heat of water vapour (Lide Reference Lide2005). The combustion transforms this potential chemical energy into potential mechanical energy, leading to a pressure increase. This, in turn, forces the bubble to expand and the outer liquid to flow away, so that the potential mechanical energy is converted into kinetic energy. Because of the condensation, the pressure inside the bubble vanishes rapidly. However, due to the liquid inertia, the bubble keeps expanding until it reaches its maximal radius $R_{max}$ . At this stage, the system is out of equilibrium and its potential energy is

(3.2) $$\begin{eqnarray}\displaystyle E_{P}=\unicode[STIX]{x03C0}R_{max}^{2}hP_{atm}. & & \displaystyle\end{eqnarray}$$

One defines the efficiency $\unicode[STIX]{x1D702}$ of the chemical to mechanical energy conversion as

(3.3) $$\begin{eqnarray}\displaystyle E_{P}=E_{0}+\unicode[STIX]{x1D702}E_{\unicode[STIX]{x1D712}}, & & \displaystyle\end{eqnarray}$$

where $E_{0}=\unicode[STIX]{x03C0}R_{0}^{2}hP_{atm}$ is the work used to form the initial reactant bubble.

We observe that the efficiency of the energy conversion is very small ( $\unicode[STIX]{x1D702}$ ranges from 0.5 % to 8 % in our experiments) and that it depends on the gap thickness $h$ . For extremely thin gaps, the efficiency is vanishingly small. However, the mechanical dissipation of energy by viscosity is negligible here: viscous boundary layers’ thickness grows as $\unicode[STIX]{x1D6FF}\sim \sqrt{\unicode[STIX]{x1D708}\unicode[STIX]{x1D70F}}$ . The time scales $\unicode[STIX]{x1D70F}$ of the experiments are of the order of a few tenths of ms, $\unicode[STIX]{x1D6FF}$ varying from 0.02 to 0.05 mm. This length scale is small in comparison with the gap thickness $h$ of the cell and more than 96 % of the mechanical energy is conserved. This low efficiency is a consequence of both the vapour condensation process and the poor conversion from chemical to mechanical energy.

Figure 3. Evolution of bubble radius (a) and inner pressure (b), deduced from (3.4), for a gap thickness $h=2.3~\text{mm}$ and initial radius $R_{0}=3.8$ , 6.9 and 9.1 mm (respectively, black continuous line, red dashed line, and orange loosely dashed line). The radius evolution of the largest bubble is not represented as it becomes larger than the camera view field. Note that the overpressure (thick lines) period is short in comparison with the bubble expansion period. Because of the liquid inertia, the bubble continues to expand even after the pressure has vanished (thin lines). The transition between the overpressure period and the depressurization period is set arbitrarily.

3.1 Combustion process and pressure increasing

Dedicated experiments are performed to measure in great detail the evolution of the instantaneous bubble radius $R(t)$ during the first instants. Pictures are acquired at $10^{6}$ frames per seconds, allowing for the computation of the bubble inner pressure (see figure 3). The Rayleigh–Plesset equation describes the evolution of spherical bubbles. A similar equation may be derived for the cylindrical case (Oguz & Prosperetti Reference Oguz and Prosperetti1993; Séon & Antkowiak Reference Séon and Antkowiak2012): introducing $P_{\infty }$ and $u_{\infty }$ , the pressure, respectively, the velocity at the Hele-Shaw cell border, and $P_{atm}$ the ambient pressure, $P_{atm}-P_{\infty }=\unicode[STIX]{x1D6FC}(1/2)\unicode[STIX]{x1D70C}u_{\infty }^{2}$ , with $\unicode[STIX]{x1D6FC}$ a numerical coefficient. During the explosion, the fluid is expulsed from the Hele-Shaw cell and a jet is formed in the outer tank. Consequently, during this stage, $P_{\infty }=P_{atm}$ and $\unicode[STIX]{x1D6FC}=0$ . During the bubble implosion, the fluid is sucked inside the Hele-Shaw cell and $P_{\infty }=P_{atm}-(1/2)\unicode[STIX]{x1D70C}u_{\infty }^{2}$ and $\unicode[STIX]{x1D6FC}=1$ . Finally, one obtains

(3.4) $$\begin{eqnarray}\displaystyle (R\ddot{R}+{\dot{R}}^{2})\log \frac{R}{R_{\infty }}+\left(1-(1-\unicode[STIX]{x1D6FC})\frac{R^{2}}{R_{\infty }^{2}}\right)\frac{{\dot{R}}^{2}}{2}=-\frac{P_{b}-P_{atm}}{\unicode[STIX]{x1D70C}}, & & \displaystyle\end{eqnarray}$$

where $P_{b}$ is the bubble inner pressure, $\unicode[STIX]{x1D70C}$ is the water density, and $R_{\infty }=2.5~\text{cm}$ is the radius of the spherical lens that delimits the Hele-Shaw cell.

The bubble inner pressure rises after the ignition, reaches its maximal value $P_{max}$ , and then vanishes in a short time compared to the bubble growth duration. During this short time lapse, the bubble does not significantly grow and the reaction may be considered isochoric. In the meantime, the surrounding liquid is significantly accelerated and accumulates some kinetic energy. Figure 3 shows the typical evolution of the bubble radius and pressure.

The combustion of a stoichiometric mixture of hydrogen and oxygen at ambient pressure and temperature in an adiabatic vessel of constant volume leads to the formation of water vapour $\text{H}_{2}\text{O}_{(v)}$ at high temperature ( $T\approx 3500$  K). At such a high temperature, many chemical species, named intermediate products (IP) hereafter (including free radicals $\text{O}^{\bullet }$ , $\text{H}^{\bullet }$ and $\text{OH}^{\bullet }$ ), coexist with water and the reaction is not complete: only a fraction $\unicode[STIX]{x1D709}_{comb}=0.68$ of the initial mixture is converted into water. In this case, the pressure rise is expected to be $P_{comb}=9.6~\text{atm}$ (Morley Reference Morley2005). In our experiment, the bubble walls are not adiabatic and water vapour condenses, allowing for the further transformation of IP and the reaction to go forward until it is completed.

The combustion process involves the propagation of a flame travelling from the ignition point through the whole volume. The flame progresses at constant velocity $u_{f}\approx 3.6~\text{m}~\text{s}^{-1}$ in the reference frame of the fresh gas (Zeldovich & Frank-Kamenetskii Reference Zeldovich and Frank-Kamenetskii1938; Landau & Lifshitz Reference Landau and Lifshitz1987). It transforms reactants into IP and delimits a cylinder with radius $r_{f}(t)$ of burnt gas that expands pushing the fresh gas. Consequently, the flame velocity $c$ is much larger than $u_{f}$ , and we observe, with our experimental parameters, that $c\approx 50~\text{m}~\text{s}^{-1}$ (see figure 4).

Figure 4. (a) Flame propagation through the initial bubble, by time steps of $1/15\,000$  s. The flame front is underlined in red to be visible in the pictures. See movie 2 in supplementary material. The whole frame is 2.9 cm wide. (b) Spatio-temporal view of the flame propagation. The separation line between the fresh and burnt gas is straight, which indicates that the flame propagates at constant velocity ( $c\approx 50~\text{m}~\text{s}^{-1}$ ). The flame front propagation is indicated by two red arrows.

By taking into account the flame propagation timescale $\unicode[STIX]{x1D70F}_{1}=2R_{0}/c$ , of the fast chemical reaction timescales $\unicode[STIX]{x1D70F}_{2}$ and $\unicode[STIX]{x1D70F}_{-2}$ (for the forward and backward reaction, respectively) and of the condensation timescale $\unicode[STIX]{x1D70F}_{3}$ , and introducing $\unicode[STIX]{x1D709}_{0,1,2,3}(t)$ the mass fraction for each state of matter (respectively, fresh gas, IP, $\text{H}_{2}\text{O}_{(v)}$ , $\text{H}_{2}\text{O}_{(\ell )}$ ), one may represent the process with the following simplified first-order kinetic scheme (a much more detailed scheme has been analysed, see e.g., Li et al. (Reference Li, Zhao, Kazakov and Dryer2004)):

(3.5) $$\begin{eqnarray}\displaystyle \begin{array}{@{}ccccccc@{}} & \text{Flame propagation} & & & & \text{Condensation} & \\ \text{H}_{2}+\frac{1}{2}\text{O}_{2} & \longrightarrow & \text{IP} & \longleftrightarrow & \text{H}_{2}\text{O}_{(v)} & \longrightarrow & \text{H}_{2}\text{O}_{(\ell )}\\ & \unicode[STIX]{x1D70F}_{1} & & \unicode[STIX]{x1D70F}_{2},\unicode[STIX]{x1D70F}_{-2} & & \unicode[STIX]{x1D70F}_{3}\\ \unicode[STIX]{x1D709}_{0}(t) & & \unicode[STIX]{x1D709}_{1}(t) & & \unicode[STIX]{x1D709}_{2}(t) & & \unicode[STIX]{x1D709}_{3}(t),\end{array} & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$

whose dynamics is given by:

(3.6) $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}l@{}}\dot{\unicode[STIX]{x1D709}_{0}}=-1/\unicode[STIX]{x1D70F}_{1}\quad ~(\text{for}~t<\unicode[STIX]{x1D70F}_{1}),0~(t>\unicode[STIX]{x1D70F}_{1}),\\ \dot{\unicode[STIX]{x1D709}_{1}}=-\dot{\unicode[STIX]{x1D709}_{0}}-\unicode[STIX]{x1D709}_{1}/\unicode[STIX]{x1D70F}_{2}+\unicode[STIX]{x1D709}_{2}/\unicode[STIX]{x1D70F}_{-2},\\ \dot{\unicode[STIX]{x1D709}_{2}}=\unicode[STIX]{x1D709}_{1}/\unicode[STIX]{x1D70F}_{2}-\unicode[STIX]{x1D709}_{2}/\unicode[STIX]{x1D70F}_{-2}-\unicode[STIX]{x1D709}_{2}/\unicode[STIX]{x1D70F}_{3},\\ \dot{\unicode[STIX]{x1D709}_{3}}=\unicode[STIX]{x1D709}_{2}/\unicode[STIX]{x1D70F}_{3},\end{array}\right\} & & \displaystyle\end{eqnarray}$$

with $\unicode[STIX]{x1D709}_{0}(0)=1$ and $\unicode[STIX]{x1D709}_{1}(0)=\unicode[STIX]{x1D709}_{2}(0)=\unicode[STIX]{x1D709}_{3}(0)=0$ . The typical evolution of $\unicode[STIX]{x1D709}_{0,1,2,3}$ is given in figure 5.

Figure 5. Typical evolution of $\unicode[STIX]{x1D709}_{0}$ (continuous black line), $\unicode[STIX]{x1D709}_{1}$ (dotted red line), $\unicode[STIX]{x1D709}_{2}$ (dotted orange line), and $\unicode[STIX]{x1D709}_{3}$ (dashed blue line) as a solution of (3.6), for $\unicode[STIX]{x1D70F}_{3}=\unicode[STIX]{x1D70F}_{1}/2$ .

As the transformation of IP into water vapour is fast and reversible, these species are in chemical equilibrium, so that $\unicode[STIX]{x1D709}_{1}(t)/\unicode[STIX]{x1D709}_{2}(t)$ is constant. In the absence of condensation, all explosive reactants are transformed into IP or into water vapour so that $\unicode[STIX]{x1D709}_{1}/\unicode[STIX]{x1D709}_{2}=(1-\unicode[STIX]{x1D709}_{comb})/\unicode[STIX]{x1D709}_{comb}=\unicode[STIX]{x1D70F}_{2}/\unicode[STIX]{x1D70F}_{-2}\approx 0.47$ . During this combustion process, heat is released when water molecules are formed, i.e., at the second step of the proposed simplified scheme and the temperature and pressure rise. When the water molecules condense, they transport their own energy into the liquid and heat is extracted. Thus, the bubble inner pressure is approximately proportional to $\unicode[STIX]{x1D709}_{2}$ and $P(t)\approx (\unicode[STIX]{x1D709}_{2}(t)/\unicode[STIX]{x1D709}_{comb})P_{comb}$ . It is maximal at $t=\unicode[STIX]{x1D70F}_{1}$ and

(3.7) $$\begin{eqnarray}\displaystyle P_{max}=P(\unicode[STIX]{x1D70F}_{1})=P_{comb}\frac{\unicode[STIX]{x1D70F}_{3}^{\star }}{\unicode[STIX]{x1D70F}_{1}}[1-\exp (-\unicode[STIX]{x1D70F}_{1}/\unicode[STIX]{x1D70F}_{3}^{\star })], & & \displaystyle\end{eqnarray}$$

where $\unicode[STIX]{x1D70F}_{3}^{\star }=\unicode[STIX]{x1D70F}_{3}(1+\unicode[STIX]{x1D70F}_{2}/\unicode[STIX]{x1D70F}_{-2})=\unicode[STIX]{x1D70F}_{3}/\unicode[STIX]{x1D709}_{comb}$ . When the inner pressure exceeds the ambient pressure, the bubble expands with increasing velocity. The bubble expansion transmits some work,

(3.8) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}W=\int (P-P_{atm})\,\text{d}V, & & \displaystyle\end{eqnarray}$$

to the external fluid. Let us introduce $\unicode[STIX]{x1D70F}_{p}$ , a phenomenological parameter such that (3.8) can be written in a very simple form:

(3.9) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}W=2\unicode[STIX]{x03C0}R_{0}h(P_{max}-P_{atm}){\dot{R}}_{max}\unicode[STIX]{x1D70F}_{p}, & & \displaystyle\end{eqnarray}$$

with ${\dot{R}}_{max}$ the bubble wall maximal velocity. $\unicode[STIX]{x1D70F}_{p}$ scales with the overpressure period duration. During the very short overpressure period, the bubble radius is nearly constant (see, for example, figure 3), although the wall velocity ${\dot{R}}_{max}$ is large. The fluid maximal kinetic energy is

(3.10) $$\begin{eqnarray}\displaystyle E_{k,max}=\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}R_{0}^{2}{\dot{R}}_{max}^{2}h\log (R_{\infty }/R_{0}). & & \displaystyle\end{eqnarray}$$

Balancing the work produced by the bubble with the kinetic energy accumulated in the liquid, $\unicode[STIX]{x1D6FF}W=E_{k,max}$ , we show that $R_{0}{\dot{R}}_{max}=2\unicode[STIX]{x1D70F}_{p}(P(\unicode[STIX]{x1D70F}_{1})-P_{atm})/(\unicode[STIX]{x1D70C}\log (R_{\infty }/R_{0}))$ , and finally that

(3.11) $$\begin{eqnarray}\displaystyle E_{k,max}=4\unicode[STIX]{x03C0}h\unicode[STIX]{x1D70F}_{p}^{2}(P(\unicode[STIX]{x1D70F}_{1})-P_{atm})^{2}/\unicode[STIX]{x1D70C}\log (R_{\infty }/R_{0}). & & \displaystyle\end{eqnarray}$$

Figure 6. Maximal inner pressure as a function of $\unicode[STIX]{x1D70F}_{1}/\unicode[STIX]{x1D70F}_{3}^{\ast }$ , with $\unicode[STIX]{x1D70F}_{1}=2R_{0}/c$ the combustion time and $\unicode[STIX]{x1D70F}_{3}^{\ast }=h^{2}/4D\unicode[STIX]{x1D709}_{c}$ the typical diffusion time of water vapour through the gap. ▫  $h=1.25$  mm, ▪ (blue) $h=1.4$  mm, ▫ (blue) $h=1.6$  mm, ▫ (purple) $h=2.3$  mm, and ▫ (orange) $h=3.6$  mm. Continuous line represents (3.7), with $D$ a free parameter ( $D=3\times 10^{-3}~\text{m}^{2}~\text{s}^{-1}$ ).

Because of the liquid inertia, the bubble expands even after condensation has occurred. It finally reaches its maximal radius $R_{max}$ . Assuming that the inner pressure is zero during this second stage of the expansion, the accumulated kinetic energy $E_{k,max}$ is converted into potential energy:

(3.12) $$\begin{eqnarray}\displaystyle E_{k,max}=P_{atm}h\unicode[STIX]{x03C0}(R_{max}^{2}-R_{0}^{2}). & & \displaystyle\end{eqnarray}$$

Combining equations (3.11) and (3.12), and remembering that $\unicode[STIX]{x1D70F}_{1}=2R_{0}/c$ , one obtains

(3.13) $$\begin{eqnarray}\displaystyle \frac{R_{max}^{2}-R_{0}^{2}}{R_{0}^{2}}\log \left(\frac{R_{\infty }}{R_{0}}\right)=\frac{P_{atm}}{\unicode[STIX]{x1D70C}c^{2}}\left(\frac{P(\unicode[STIX]{x1D70F}_{1})}{P_{atm}}-1\right)^{2}\left(\frac{\unicode[STIX]{x1D70F}_{p}}{\unicode[STIX]{x1D70F}_{1}}\right)^{2}. & & \displaystyle\end{eqnarray}$$

Figure 6 shows the maximal pressure in the bubble at $t=\unicode[STIX]{x1D70F}_{1}$ , while figure 7 shows the maximal expansion of the bubble. The bubble inner pressure is obtained by the double derivation of $R(t)$ . The accuracy of this measurement is necessarily limited, and figure 6 by itself hardly discriminates the nature of the condensation process. However, for all gap thicknesses, figures 6 and 7 collapse on a single master curve for $\unicode[STIX]{x1D70F}_{3}$ scaling with $h^{2}$ . This indicates that the condensation process is limited by the diffusion of water vapour through the gap.

Now, using $\unicode[STIX]{x1D70F}_{3}=h^{2}/4D$ with $D$ , a free parameter, we find that the maximal pressure is well predicted by (3.7) for $D\approx 3\times 10^{-3}~\text{m}^{2}~\text{s}^{-1}$ . This indirect measurement of the water vapour diffusion coefficient has an order of magnitude, which is in agreement with computed values for water vapour diffusion in oxygen (Walker & Westenberg Reference Walker and Westenberg1960).

Figure 7. Maximal bubble area $\unicode[STIX]{x03C0}R_{max}^{2}$ as a function of initial radius $R_{0}$ and gap thickness $h$ . ▪  $h=0.92$  mm, ▫  $h=1.25$  mm, ▪ (purple) $h=1.7$  mm, ▪ (red) $h=2.7$  mm, and ▫ (red) $h=3.2$  mm. Continuous line represents (3.13) with $\unicode[STIX]{x1D70F}_{p}=1.\unicode[STIX]{x1D70F}_{1}+0.1\unicode[STIX]{x1D70F}_{3}^{\ast }$ . (The two numerical factors are fitting parameters.)

The maximal expansion of the bubble (figure 7) increases for larger gaps. This is expected, as for larger gaps the condensation process is slower and the pressure $P_{max}$ induced by the combustion is higher and is maintained for a longer time. The duration of the overpressure period $\unicode[STIX]{x1D70F}_{p}$ (introduced in (3.9)) depends on the characteristic times $\unicode[STIX]{x1D70F}_{1}$ and $\unicode[STIX]{x1D70F}_{3}$ of each reaction step ( $\unicode[STIX]{x1D70F}_{2}$ is negligible). Experimental data are in agreement with the (3.13) for $\unicode[STIX]{x1D70F}_{p}=1.0\unicode[STIX]{x1D70F}_{1}+0.1\unicode[STIX]{x1D70F}_{3}^{\ast }$ , where the two numerical coefficients are fitting parameters.

For the experiments shown in figure 3, the computed values of $\unicode[STIX]{x1D70F}_{p}$ are, respectively, 0.21 ms, 0.33 ms, and 0.42 ms for $R_{0}=3.8$  mm, 6.9 mm, and 9.1 mm. This agrees with the observed overpressure duration, and thus confirms the physical meaning of the phenomenological parameter $\unicode[STIX]{x1D70F}_{p}$ .

The flame propagation time $\unicode[STIX]{x1D70F}_{1}$ and the condensation time $\unicode[STIX]{x1D70F}_{3}$ determine the maximal pressure $P_{max}$ reached during the combustion process and the duration of the overpressure period. These two parameters determine the efficiency of the conversion of chemical energy to mechanical energy, and finally determine the bubble maximal expansion.

4 Collapse dynamics

After the bubble has expanded and reached its maximal radius $R_{max}$ , the bubble inner pressure is close to zero: water vapour is at equilibrium with the surrounding liquid and is at saturation pressure $P=P_{sat}\approx 25~\text{hPa}$ . Then the bubble collapses in a finite time $\unicode[STIX]{x1D70F}$ that grows with increasing $R_{max}$ . For a strictly void bubble, the work produced by the outer pressure is converted into kinetic energy of the water flow, and for any intermediate radius $R$ :

(4.1) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x03C0}h(R_{max}^{2}-R^{2})P_{atm}\approx \unicode[STIX]{x1D70C}\unicode[STIX]{x03C0}hR^{2}{\dot{R}}^{2}\log (R_{\infty }/R), & & \displaystyle\end{eqnarray}$$

if the kinetic energy of the fluid outside the Hele-Shaw cell is neglected. The collapse time $\unicode[STIX]{x1D70F}$ is

(4.2) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70F}=\int _{R_{max}}^{0}\frac{\text{d}R}{{\dot{R}}}=\sqrt{\frac{\unicode[STIX]{x1D70C}R_{max}^{2}}{P_{atm}}}\int _{0}^{1}\sqrt{\frac{x^{2}}{1-x^{2}}\log \frac{R_{\infty }}{xR_{max}}}\,\text{d}x. & & \displaystyle\end{eqnarray}$$

This integral expression (4.2) admits no analytical explicit form. It is, however, very well approximated by

(4.3) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70F}\approx R_{max}\sqrt{\frac{\unicode[STIX]{x1D70C}}{P_{atm}}}\sqrt{0.444^{2}+\log \left(\frac{R_{\infty }}{R_{max}}\right)}, & & \displaystyle\end{eqnarray}$$

within our experimental parameter range. Experimental data are in agreement with the exact theoretical prediction ((4.2), see figure 8).

Figure 8. Bubble collapse duration, defined as the delay between the instant when the radius is maximal and the instant of maximal compression, as a function of the maximal radius $R_{max}$ , for several bubble thicknesses (▪  $h=0.92$  mm, ▫ (blue) $h=1.6$  mm and ▪ (red) $h=2.7$  mm). A continuous line is given by (4.2) without any adjustable parameter. The dotted line is the approximated expression (4.3).

The very last stage of the collapse process is singular: when the bubble radius vanishes, the interface velocity ${\dot{R}}$ becomes infinitely large in order to preserve the fluid kinetic energy. Equation (4.1) shows

(4.4) $$\begin{eqnarray}\displaystyle \frac{1}{2}\left(\frac{R}{R_{max}}\right)^{2}\sqrt{\log \left(\frac{R_{\infty }}{R_{max}}\frac{R_{max}}{R}\right)}=\left(\frac{\unicode[STIX]{x1D70F}^{\ast }-t}{R_{max}\sqrt{\unicode[STIX]{x1D70C}/P_{atm}}}\right), & & \displaystyle\end{eqnarray}$$

as an approximate solution for $R\xrightarrow[{}]{}0$ . It is singular for $t$ close to $\unicode[STIX]{x1D70F}$ , and one has $R\sim \sqrt{(\unicode[STIX]{x1D70F}^{\ast }-t)/\unicode[STIX]{x1D70F}}$ for the range of observable values of $R(t)$ , as the logarithmic correction is weak. Experimental observations are in excellent agreement with this prediction (see figure 9).

Figure 9. Bubble collapse dynamics for various initial radii $R_{0}$ and gap heights $h$ . ( $h=0.92$  mm: ▪  $R_{max}=2.3$  mm, ▫  $R_{max}=3.8$  mm;  $h=1.6$  mm: ▫ (blue) $R_{max}=4.7$  mm;  $h=2.7$  mm: ▫ (red) $R_{max}=7$  mm, ▪ (red) $R_{max}=9.3$  mm, ○ (red) $R_{max}=11$  mm.)

5 Comparison with 3D case and concluding remarks

The amplitude of the explosion of 2D bubbles is analysed: it is shown that the amplitude is determined by the amount of available chemical energy and is limited by the condensation process. When an inert gas (argon or air) is introduced into the bubble prior to its ignition, it is observed that the expansion of the bubble is larger, although the amount of chemical energy is unchanged. Significant effects are observed if the concentration of inert gas exceeds 10 %–20 % in volume. This case is not discussed in this paper, but an example is available in the supplementary material (see movies 3 and 4). Contrary to water vapour, this inert gas does not condense. As it is warmed up by the combustion of hydrogen, its partial pressure increases. This contributes to the larger expansion of the bubble.

For spherical bubbles, similar experiments were previously performed in water or glycerol with centimetric stoichiometric hydrogen–oxygen 3D bubbles (Duplat & Villermaux Reference Duplat and Villermaux2015). Classical observations of underwater explosion (Blaik & Christian Reference Blaik and Christian1965; Chapman Reference Chapman1988) report on the ‘first bubble period’ caused by the explosion, and allow for an indirect estimation of the bubble maximal size using the Rayleigh time. Extrapolating their observation to the hydrogen–oxygen bubble, it is predicted that $R_{max}/R_{0}=3.2$ . However, this classical prediction overestimates the expansion for hydrogen–oxygen bubbles, for which we observe that $R_{max}/R_{0}=2.2$ .

As discussed in this paper, the expansion of an explosive bubble (either in 2D or in 3D) depends on the evolution of its inner pressure. We show here that the condensation of water vapour is crucial for the dynamics of hydrogen–oxygen bubbles. For ‘classical’ explosives, the combustion reaction produces water vapour and carbon dioxide. While the former condenses, the latter remains gaseous and the bubble is never empty. The prediction by Chapman (Reference Chapman1988) or by Blaik & Christian (Reference Blaik and Christian1965) applies in this classical situation, but fails to describe the explosion of hydrogen–oxygen bubbles for which all reaction products condense. Although the flame temperature of the stoichiometric hydrogen–oxygen mixture is higher than most of the other fuel-comburant mixtures, it leads to a weaker underwater explosion.

The present study for 2D bubbles allows for quantitatively describing the condensation process. For the 3D case, water vapour is produced at the bubble centre and condenses at the bubble wall. The condensation process is thus limited by the transport of water vapour over a distance of the order of $R_{0}$ , which is much larger than the gap $h$ of the present experiments. Surprisingly, the energetic efficiency for 3D experiments ( $\unicode[STIX]{x1D702}_{3D}\approx 0.1$ ) is not much larger than that for 2D experiments (Duplat & Villermaux Reference Duplat and Villermaux2015). This suggests that the condensation process in spherical bubbles is much more efficient than it is in cylindrical bubbles and is not driven by a diffusive process. In the 3D case, the transport of water vapour toward the bubble wall is assisted by a strong mixing process inside the bubble, visible during the flame propagation. While the flame front is smooth and propagates at constant velocity in the present study, it is rough and very irregular in the 3D experiments. This intensely stirred flow inside the bubble also accelerates the transport of water vapour toward the bubble walls. Note that the origin of this agitation is very unclear: in very similar conditions, the flame propagation in a stoichiometric hydrogen–oxygen mixture inside a 3D centimetric soap bubble is smooth (Vledouts et al. Reference Vledouts, Quinard, Vandenberghe and Villermaux2016). This discussion is beyond the scope of the present paper.

We also analyse the bubble collapse, and we show that the radius vanishes in the last instants ( $R(t)\sim (\unicode[STIX]{x1D70F}^{\ast }-t)^{1/2}$ ). The collapse of a spherical bubble is even more singular: for a void bubble the radius vanishes as $R(t)\sim (\unicode[STIX]{x1D70F}^{\ast }-t)^{2/5}$ (Rayleigh Reference Rayleigh1917), and the bubble wall velocity diverges. In real experiments, however, the bubble is not strictly void (either because the initial mixture is not strictly stoichiometric or as a consequence of the presence of some inert gas). The bubble collapse dynamics is affected very little by the presence of residual gas, except at the very last instant of the collapse, when the gases are strongly compressed and prevent the bubble radius annihilation. As for the sonoluminescence experiment, the collapse of 3D hydrogen–oxygen bubbles leads to some light emission at the instant of maximal compression. The compression process induces the temperature elevation of the residual gas. For 3D experiments, it is observed that the compression factor $V_{max}/V_{min}\approx 125$ . Assuming an isentropic process, one predicts that the final temperature is close to 30 000 K, which is in qualitative agreement with the experimental observation (Duplat & Villermaux Reference Duplat and Villermaux2015). For the present 2D experiments, similar compression ratios are observed ( $V_{max}/V_{min}>100$ ). Although the compression is at least as efficient for 2D as that for 3D, no light emission is observed, which suggests that the temperature elevation is weaker in the 2D case.

One might be tempted to attribute the weaker temperature elevation to the weaker singularity of the flow. However, this is not the case. The maximal compression state is predicted by balancing the outer liquid mechanical energy with the bubble work. When the bubble has a maximal volume $V_{max}$ , the inner pressure is $P=\unicode[STIX]{x1D716}P_{atm}$ with $\unicode[STIX]{x1D716}<1$ , and the outer liquid is at rest. The bubble collapses and the outer liquid accumulates kinetic energy before the bubble inner pressure increases and becomes larger than $P_{atm}$ . Then, the outer liquid kinetic energy decreases and vanishes when the bubble volume is minimal $V_{min}$ . By conservation of the mechanical energy, one obtains

(5.1) $$\begin{eqnarray}\displaystyle \int _{V_{max}}^{V_{min}}\left(P_{atm}-P\right)\,\text{d}V=0. & & \displaystyle\end{eqnarray}$$

Assuming $\unicode[STIX]{x1D716}\ll 1$ and that the compression process is polytropic, i.e., $PV^{k}=C$ , the compression ratio is given by

(5.2) $$\begin{eqnarray}\displaystyle \frac{V_{min}}{V_{max}}\approx \left(\frac{\unicode[STIX]{x1D716}}{k-1}\right)^{1/(k-1)} & & \displaystyle\end{eqnarray}$$

and thus, a temperature at maximal compression such that

(5.3) $$\begin{eqnarray}\displaystyle \frac{T_{max}}{T_{min}}\approx \frac{k-1}{\unicode[STIX]{x1D716}}. & & \displaystyle\end{eqnarray}$$

These predictions are independent of the temporal evolution of the bubble volume. We observe that 2D bubbles collapse with a weaker singularity than do 3D bubbles. This fact, however, has no direct impact on the efficiency of the compression process by inertial confinement. As suggested by the experimental observations, the temperature reached by the bubble is weaker for the 2D case. In 3D experiments, the heat transfer is weak because of the geometry, and the compression process is nearly adiabatic. On the contrary, for 2D experiments, heat is transferred to the horizontal walls, and energy loss can not be neglected. The process of inertial confinement is thus probably more efficient in 3D geometry than in 2D. The singularity of the collapse is also stronger for the 3D case than for the 2D case. However, these two statements are independent of one another, as the larger efficiency of 3D confinement is the consequence of a better adiabaticity and not of a stronger collapse.