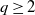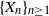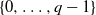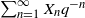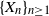1. Introduction
Consider a random variable X on the unit interval [0, 1] which is given by the base-q expansion
where
![]() $q\in\mathbb N$
(the set of natural numbers), and where the digits
$q\in\mathbb N$
(the set of natural numbers), and where the digits
![]() $\{X_n\}_{n\ge1}$
form a stochastic process with values in
$\{X_n\}_{n\ge1}$
form a stochastic process with values in
![]() $\{0,\ldots,q-1\}$
. The case where the
$\{0,\ldots,q-1\}$
. The case where the
![]() $X_n$
are independent and identically distributed (i.i.d.) has been much studied in the literature (see Sections 1.1 and 1.3). The present paper deals with the more general case where
$X_n$
are independent and identically distributed (i.i.d.) has been much studied in the literature (see Sections 1.1 and 1.3). The present paper deals with the more general case where
![]() $\{X_n\}_{n\geq 1}$
is stationary, i.e. when
$\{X_n\}_{n\geq 1}$
is stationary, i.e. when
![]() $\{X_n\}_{n\ge1}$
and
$\{X_n\}_{n\ge1}$
and
![]() $\{X_n\}_{n\ge2}$
are identically distributed – for short we refer to this setting as stationarity. As we will see, under stationarity there is almost surely a one-to-one correspondence between
$\{X_n\}_{n\ge2}$
are identically distributed – for short we refer to this setting as stationarity. As we will see, under stationarity there is almost surely a one-to-one correspondence between
![]() $\{X_n\}_{n\ge1}$
and X, and we will study various properties of the cumulative distribution function (CDF) of X given by
$\{X_n\}_{n\ge1}$
and X, and we will study various properties of the cumulative distribution function (CDF) of X given by
and its associated probability measure
![]() $\mathrm d F$
.
$\mathrm d F$
.
1.1. Background
Assuming the
![]() $X_n$
are i.i.d., the stochastic process
$X_n$
are i.i.d., the stochastic process
![]() $\{X_n\}_{n\geq 1}$
is a so-called Bernoulli scheme. Then, in the dyadic case
$\{X_n\}_{n\geq 1}$
is a so-called Bernoulli scheme. Then, in the dyadic case
![]() $q=2$
, ignoring the trivial case with
$q=2$
, ignoring the trivial case with
![]() $\mathbb P(X_1=0)=1$
or
$\mathbb P(X_1=0)=1$
or
![]() $\mathbb P(X_1=1)=1$
, only two different things can happen: if the digits 0 and 1 are equally likely, then F is the uniform CDF (on [0, 1]); otherwise, F is singular (i.e. F is non-constant and differentiable almost everywhere with
$\mathbb P(X_1=1)=1$
, only two different things can happen: if the digits 0 and 1 are equally likely, then F is the uniform CDF (on [0, 1]); otherwise, F is singular (i.e. F is non-constant and differentiable almost everywhere with
![]() $F^{\prime}(x)=0$
), continuous, and strictly increasing on [0, 1], cf. [Reference Riesz and Sz.-Nagy20, Reference Salem22, Reference Takács24]. In the triadic case
$F^{\prime}(x)=0$
), continuous, and strictly increasing on [0, 1], cf. [Reference Riesz and Sz.-Nagy20, Reference Salem22, Reference Takács24]. In the triadic case
![]() $q=3$
, if 0 and 2 are equally likely and
$q=3$
, if 0 and 2 are equally likely and
![]() $\mathbb P(X_1 = 1) = 0$
, then F is the Cantor function, cf. [Reference Billingsley3, Problem 31.2]. This function is also singular continuous, but piecewise constant and only increasing on the Cantor set. In fact, interestingly, the measures
$\mathbb P(X_1 = 1) = 0$
, then F is the Cantor function, cf. [Reference Billingsley3, Problem 31.2]. This function is also singular continuous, but piecewise constant and only increasing on the Cantor set. In fact, interestingly, the measures
![]() $\mathrm d F$
in all the Bernoulli schemes for any q are again all singular with respect to one another (this seems to be a folk theorem, but see [Reference Billingsley2, Section 14]) and only one is absolutely continuous relative to Lebesgue measure, and that is the one where all
$\mathrm d F$
in all the Bernoulli schemes for any q are again all singular with respect to one another (this seems to be a folk theorem, but see [Reference Billingsley2, Section 14]) and only one is absolutely continuous relative to Lebesgue measure, and that is the one where all
![]() $j \in \{0,\dots, q-1\}$
are equally likely. In the latter case,
$j \in \{0,\dots, q-1\}$
are equally likely. In the latter case,
![]() $\mathrm d F$
is Lebesgue measure itself on [0, 1].
$\mathrm d F$
is Lebesgue measure itself on [0, 1].
Harris in [Reference Harris8] considered the case where
![]() $q\geq 2$
and
$q\geq 2$
and
![]() $\{X_n\}_{n\geq 1}$
is stationary and of a mixing type. He showed that either F is the uniform CDF, or F has a single jump of magnitude 1 at one of the points
$\{X_n\}_{n\geq 1}$
is stationary and of a mixing type. He showed that either F is the uniform CDF, or F has a single jump of magnitude 1 at one of the points
![]() ${k}/{(q-1)}$
,
${k}/{(q-1)}$
,
![]() $k=0,\dots,q-1$
, or F is singular continuous. A similar result has been shown in [Reference Dym6] under the assumption that
$k=0,\dots,q-1$
, or F is singular continuous. A similar result has been shown in [Reference Dym6] under the assumption that
![]() $\{X_n\}_{n\geq 1}$
is stationary and ergodic, namely that either F is the uniform CDF, or F has k jumps of magnitude
$\{X_n\}_{n\geq 1}$
is stationary and ergodic, namely that either F is the uniform CDF, or F has k jumps of magnitude
![]() $k^{-1}$
, or F is singular continuous.
$k^{-1}$
, or F is singular continuous.
It is well known that if the
![]() $X_n$
are i.i.d., then F is the uniform CDF if and only if
$X_n$
are i.i.d., then F is the uniform CDF if and only if
![]() $\mathrm{d} F$
is a Rajchman measure [Reference Hu9, Reference Reese18, Reference Salem22]. Recall that a Rajchman measure is a finite measure whose characteristic function
$\mathrm{d} F$
is a Rajchman measure [Reference Hu9, Reference Reese18, Reference Salem22]. Recall that a Rajchman measure is a finite measure whose characteristic function
![]() $\mathbb{E} \mathrm{e}^{itX}$
tends to zero as
$\mathbb{E} \mathrm{e}^{itX}$
tends to zero as
![]() $t \to\pm\infty$
. Rajchman measures have received much attention in the Fourier analysis community (see the review article [Reference Lyons13]) and the behavior of the characteristic function of singular continuous probability measures at infinity are of general interest in quantum mechanics (see [Reference Barbaroux, Combes and Montcho1] and references therein). To the best of our knowledge it has yet not been clarified in the literature whether, under stationarity and when F is not the uniform CDF on [0, 1], there is a case where
$t \to\pm\infty$
. Rajchman measures have received much attention in the Fourier analysis community (see the review article [Reference Lyons13]) and the behavior of the characteristic function of singular continuous probability measures at infinity are of general interest in quantum mechanics (see [Reference Barbaroux, Combes and Montcho1] and references therein). To the best of our knowledge it has yet not been clarified in the literature whether, under stationarity and when F is not the uniform CDF on [0, 1], there is a case where
![]() $\mathrm d F$
is a Rajchman measure.
$\mathrm d F$
is a Rajchman measure.
1.2. Our results
In this paper, Theorem 2.1 provides a complete characterization of stationarity in terms of a functional equation for F without using the extra assumptions of [Reference Harris8] and [Reference Dym6]. This leads to Theorem 2.2, which characterizes stationarity in terms of the characteristic function of X, and the asymptotic behavior of the characteristic function at
![]() $\pm \infty$
is treated in the stationary case. In particular, we show that none of the measures
$\pm \infty$
is treated in the stationary case. In particular, we show that none of the measures
![]() $\mathrm{d} F$
arising are Rajchman measures, except when
$\mathrm{d} F$
arising are Rajchman measures, except when
![]() $\mathrm{d} F$
is Lebesgue measure on [0, 1]. Furthermore, Theorem 2.3 describes stationarity in terms of a Lebesgue decomposition result for F. Here, it is known that the absolutely continuous component of F can only be the uniform CDF (see [Reference Parry15, Theorems 1 and 2]), but we give a simpler proof (see Proposition 2.2). In addition, we prove that the atomic component of F can only be a countable convex combination of certain explicitly computable CDFs for probability distributions with finite support.
$\mathrm{d} F$
is Lebesgue measure on [0, 1]. Furthermore, Theorem 2.3 describes stationarity in terms of a Lebesgue decomposition result for F. Here, it is known that the absolutely continuous component of F can only be the uniform CDF (see [Reference Parry15, Theorems 1 and 2]), but we give a simpler proof (see Proposition 2.2). In addition, we prove that the atomic component of F can only be a countable convex combination of certain explicitly computable CDFs for probability distributions with finite support.
For ease of presentation, the proofs of our theorems and propositions are deferred to Section 3. Moreover, Section 3 provides an interesting example of a function not belonging to
![]() $L^1$
(Example 3.1) and another interesting example of a non-measurable function (Example 3.2), both of which satisfy an important requirement (but not all requirements) of a putative probability density function for X in the stationary case.
$L^1$
(Example 3.1) and another interesting example of a non-measurable function (Example 3.2), both of which satisfy an important requirement (but not all requirements) of a putative probability density function for X in the stationary case.
1.3. Future work
From Theorem 2.3 it is reasonable to expect that many well-known stationary stochastic processes with a finite state space correspond to singular continuous F. Assuming that the
![]() $X_n$
only take values 0 and 1, a natural generalization of (1.1) would be to consider
$X_n$
only take values 0 and 1, a natural generalization of (1.1) would be to consider
![]() $X=\sum_{n=1}^\infty X_n \lambda^n$
, where
$X=\sum_{n=1}^\infty X_n \lambda^n$
, where
![]() $\lambda\in (0, 1)$
. Let
$\lambda\in (0, 1)$
. Let
![]() $\nu_\lambda$
denote the probability distribution of the affine transformation
$\nu_\lambda$
denote the probability distribution of the affine transformation
![]() $\sum_{n=1}^\infty\! (2X_n-1) \lambda^{n-1}=(2/\lambda)X-1/(1-\lambda)$
. If the
$\sum_{n=1}^\infty\! (2X_n-1) \lambda^{n-1}=(2/\lambda)X-1/(1-\lambda)$
. If the
![]() $X_n$
are i.i.d.,
$X_n$
are i.i.d.,
![]() $\nu_{\lambda}$
is a Bernoulli convolution. This is a much studied case in the literature, and in particular the absolute continuity or singularity and the Hausdorff dimension of the support of
$\nu_{\lambda}$
is a Bernoulli convolution. This is a much studied case in the literature, and in particular the absolute continuity or singularity and the Hausdorff dimension of the support of
![]() $\nu_\lambda$
as a function of
$\nu_\lambda$
as a function of
![]() $\lambda$
have been of interest (see [Reference Peres, Schlag and Solomyak16, Reference Varjú25] and references therein). We leave it as an open problem to study the absolute continuity or singularity of
$\lambda$
have been of interest (see [Reference Peres, Schlag and Solomyak16, Reference Varjú25] and references therein). We leave it as an open problem to study the absolute continuity or singularity of
![]() $\nu_\lambda$
in the more general case where
$\nu_\lambda$
in the more general case where
![]() $\{X_n\}_{n\geq 1}$
is stationary and
$\{X_n\}_{n\geq 1}$
is stationary and
![]() $1/\lambda$
is not an integer (the present paper covers only the case where
$1/\lambda$
is not an integer (the present paper covers only the case where
![]() $q=1/\lambda$
is an integer). Also, in the stationary case and for any
$q=1/\lambda$
is an integer). Also, in the stationary case and for any
![]() $\lambda\in (0, 1)$
, it would be interesting to study the Hausdorff dimension of the support of
$\lambda\in (0, 1)$
, it would be interesting to study the Hausdorff dimension of the support of
![]() $\nu_\lambda$
.
$\nu_\lambda$
.
Define the function
![]() $f(x_1,x_2,\ldots)\,:\!=\,\sum_{n\geq 1} x_n\lambda^n=x$
with
$f(x_1,x_2,\ldots)\,:\!=\,\sum_{n\geq 1} x_n\lambda^n=x$
with
![]() $x_1,x_2,\ldots\in \{0,1\}$
, and for
$x_1,x_2,\ldots\in \{0,1\}$
, and for
![]() $m=1,2,\ldots$
, consider the
$m=1,2,\ldots$
, consider the
![]() $2^m$
closed intervals of length
$2^m$
closed intervals of length
![]() $\lambda^{m+1}/(1-\lambda)$
and having left end points
$\lambda^{m+1}/(1-\lambda)$
and having left end points
![]() $\sum_{n=1}^m x_n\lambda^n$
with
$\sum_{n=1}^m x_n\lambda^n$
with
![]() $x_1,\ldots,x_m\in \{0,1\}$
. These
$x_1,\ldots,x_m\in \{0,1\}$
. These
![]() $2^m$
intervals cover the range of f, which contains the state space of X. For
$2^m$
intervals cover the range of f, which contains the state space of X. For
![]() $0<\lambda<\frac{1}{2}$
the
$0<\lambda<\frac{1}{2}$
the
![]() $2^m$
intervals are disjoint, so it follows that f is injective and the range of f has Lebesgue measure zero, since
$2^m$
intervals are disjoint, so it follows that f is injective and the range of f has Lebesgue measure zero, since
![]() $2^m\lambda^{m+1}/(1-\lambda)\rightarrow0$
as
$2^m\lambda^{m+1}/(1-\lambda)\rightarrow0$
as
![]() $m\rightarrow\infty$
. Consequently, if
$m\rightarrow\infty$
. Consequently, if
![]() $0<\lambda<\frac{1}{2}$
, the CDF of X is purely singular (no matter whether
$0<\lambda<\frac{1}{2}$
, the CDF of X is purely singular (no matter whether
![]() $\{X_n\}_{n\ge1}$
is stationary or not). Thus, the case with
$\{X_n\}_{n\ge1}$
is stationary or not). Thus, the case with
![]() $\frac{1}{2} < \lambda < 1$
is more interesting and difficult, but a good starting point could be to study the stationary case.
$\frac{1}{2} < \lambda < 1$
is more interesting and difficult, but a good starting point could be to study the stationary case.
In a follow-up paper we will consider the categorization of Markov chain models, renewal processes, and mixtures of these in terms of the Lebesgue decomposition of the corresponding F. Furthermore, in some examples of that paper we will derive closed-form expressions for F.
2. Main results
2.1. Characterization of stationarity by a functional equation for F
Recall that any number
![]() $x\in[0, 1]$
has a base-q expansion
$x\in[0, 1]$
has a base-q expansion
![]() $x=(0.x_1x_2\ldots)_q$
with
$x=(0.x_1x_2\ldots)_q$
with
![]() $x_1,x_2,\ldots\in\{0,\ldots,q-1\}$
. This expansion is unique except when x is a base-q fraction in (0, 1), that is, when for some (necessarily unique)
$x_1,x_2,\ldots\in\{0,\ldots,q-1\}$
. This expansion is unique except when x is a base-q fraction in (0, 1), that is, when for some (necessarily unique)
![]() $n\in\mathbb N$
we have either
$n\in\mathbb N$
we have either
![]() $x_n<x_{n+1}=x_{n+2}=\cdots=q-1$
or
$x_n<x_{n+1}=x_{n+2}=\cdots=q-1$
or
![]() $x_n>x_{n+1}=x_{n+2}=\cdots=0$
; we refer to n as the order of x and denote the set of all base-q fractions in (0, 1) by
$x_n>x_{n+1}=x_{n+2}=\cdots=0$
; we refer to n as the order of x and denote the set of all base-q fractions in (0, 1) by
![]() $\mathbb{Q}_q$
.
$\mathbb{Q}_q$
.
Here is the first main result of our paper.
Theorem 2.1. We have the following:
-
(I) Stationarity of
 $\{X_n\}_{n\geq 1}$
holds if and only if, for all
$\{X_n\}_{n\geq 1}$
holds if and only if, for all
 $x \in \mathbb{Q}_q$
, we have (2.1)
$x \in \mathbb{Q}_q$
, we have (2.1) \begin{equation} F(x) = F(0)+\sum_{j=0}^{q-1} [F((x+j)/q)-F(j/q)]. \end{equation}
\begin{equation} F(x) = F(0)+\sum_{j=0}^{q-1} [F((x+j)/q)-F(j/q)]. \end{equation}
-
(II) Suppose that
 $\tilde F$
is a CDF for a probability distribution on
$\tilde F$
is a CDF for a probability distribution on
 $[0, 1]$
such that
$[0, 1]$
such that
 $\tilde F$
satisfies (2.1) for all
$\tilde F$
satisfies (2.1) for all
 $x \in \mathbb{Q}_q$
. Then there exists a unique stationary stochastic process
$x \in \mathbb{Q}_q$
. Then there exists a unique stationary stochastic process
 $\{\tilde X_n\}_{n\geq 1}$
on
$\{\tilde X_n\}_{n\geq 1}$
on
 $\{0,\ldots,q-1\}$
such that
$\{0,\ldots,q-1\}$
such that
 $(0.\tilde X_1\tilde X_2\ldots)_q$
follows
$(0.\tilde X_1\tilde X_2\ldots)_q$
follows
 $\tilde F$
. Furthermore,
$\tilde F$
. Furthermore,
 $\tilde F$
is continuous at all
$\tilde F$
is continuous at all
 $x \in \mathbb{Q}_q$
, and
$x \in \mathbb{Q}_q$
, and
 $\tilde F$
satisfies the functional equation in (2.1) for all
$\tilde F$
satisfies the functional equation in (2.1) for all
 $x\in[0, 1]$
(not just for
$x\in[0, 1]$
(not just for
 $x \in \mathbb{Q}_q$
).
$x \in \mathbb{Q}_q$
).
Remark 2.1. Functional equations for the characterization of singular functions have been used in various non-probabilistic contexts, cf. [Reference Kairies12]. Our stationarity equation (2.1) is equivalent to special cases noticed in [Reference Kairies12], namely in connection to the de Rham–Takács (see the last sentence in [Reference Kairies12, Section 5C]) and the Cantor function (see the last sentence in [Reference Kairies12, Section 5A]); however, it was not noticed in [Reference Kairies12] that (2.1) provides a characterization of stationarity as we show in Theorem 2.1.
Remark 2.2. Clearly, when the
![]() $X_n$
are i.i.d., (2.1) is satisfied, and for the examples of i.i.d.
$X_n$
are i.i.d., (2.1) is satisfied, and for the examples of i.i.d.
![]() $X_n$
discussed in Section 1.1, F was either the uniform CDF on [0, 1] or a singular continuous function.
$X_n$
discussed in Section 1.1, F was either the uniform CDF on [0, 1] or a singular continuous function.
Apart from these examples, the best-known example of a singular continuous CDF is probably Minkowski’s question-mark function (Fragefunktion ?(x)) restricted to [0, 1]; see, e.g., [Reference Denjoy4, Reference Denjoy5, Reference Kairies12, Reference Minkowski14]. Recall that for two reduced fractions
![]() $p/q>r/s$
such that
$p/q>r/s$
such that
![]() $ ps-rq =1$
(i.e. two consecutive Farey fractions), Minkowski’s question-mark function is recursively defined by
$ ps-rq =1$
(i.e. two consecutive Farey fractions), Minkowski’s question-mark function is recursively defined by
and extended to any
![]() $x\in [0, 1]$
by continuity. As later shown in Corollary 2.1, the ?-function does not satisfy (2.1) for any
$x\in [0, 1]$
by continuity. As later shown in Corollary 2.1, the ?-function does not satisfy (2.1) for any
![]() $q\geq 2$
. Hence, if the ?-function is studied in the framework of (1.1) and (1.2), the process
$q\geq 2$
. Hence, if the ?-function is studied in the framework of (1.1) and (1.2), the process
![]() $\{X_n\}_{n\geq 1}$
would not be stationary.
$\{X_n\}_{n\geq 1}$
would not be stationary.
In the case of a Bernoulli scheme it is well known that
![]() $\mathrm{d}F$
is self-similar in the sense of Hutchinson, see [Reference Hu9, Reference Hutchinson10, Reference Strichartz23]. For completeness we remind the reader that
$\mathrm{d}F$
is self-similar in the sense of Hutchinson, see [Reference Hu9, Reference Hutchinson10, Reference Strichartz23]. For completeness we remind the reader that
![]() $\mathrm{d}F$
is self-similar if there exist
$\mathrm{d}F$
is self-similar if there exist
![]() $p_0,\dots, p_n>0$
with
$p_0,\dots, p_n>0$
with
![]() $\sum_{j=0}^n p_j=1$
and contractions
$\sum_{j=0}^n p_j=1$
and contractions
![]() $S_0,\dots,S_n$
on
$S_0,\dots,S_n$
on
![]() $\mathbb{R}$
such that
$\mathbb{R}$
such that
![]() $\mathrm{d}F(E)=\sum_{j=0}^n p_j \mathrm{d} F(S_j^{-1}(E))$
, for all Borel sets
$\mathrm{d}F(E)=\sum_{j=0}^n p_j \mathrm{d} F(S_j^{-1}(E))$
, for all Borel sets
![]() $E\subset \mathbb{R}$
. When
$E\subset \mathbb{R}$
. When
![]() $n=q-1$
and
$n=q-1$
and
![]() $S_j(x)=(x+j)/q$
for
$S_j(x)=(x+j)/q$
for
![]() $j=0,\dots,q-1$
, we show in the next proposition that self-similarity occurs if and only if the
$j=0,\dots,q-1$
, we show in the next proposition that self-similarity occurs if and only if the
![]() $X_n$
are i.i.d.
$X_n$
are i.i.d.
Proposition 2.1. Under stationarity the
![]() $X_n$
are i.i.d. if and only if
$X_n$
are i.i.d. if and only if
 \begin{equation} F(x)=\sum_{j=0}^{q-1} \mathbb{P}(X_1=j) F(qx-j), \qquad x\in [0, 1]. \end{equation}
\begin{equation} F(x)=\sum_{j=0}^{q-1} \mathbb{P}(X_1=j) F(qx-j), \qquad x\in [0, 1]. \end{equation}
As any CDF is differentiable almost everywhere, we next consider the derivative of F when F satisfies (2.1). As usual, we let
![]() $L^1([0, 1])$
be the set of complex absolutely integrable Borel functions defined on [0, 1]. Note that F
′(x) exists outside a set of Lebesgue measure zero,
$L^1([0, 1])$
be the set of complex absolutely integrable Borel functions defined on [0, 1]. Note that F
′(x) exists outside a set of Lebesgue measure zero,
![]() $M\subset [0, 1]$
, and, for all x not belonging to
$M\subset [0, 1]$
, and, for all x not belonging to
![]() $M\cup \{ x\in [0, 1] \,:\, x\in qM-j$
for some
$M\cup \{ x\in [0, 1] \,:\, x\in qM-j$
for some
![]() $j\in \{0,\dots, q-1\} \}$
, it follows from (2.1) that
$j\in \{0,\dots, q-1\} \}$
, it follows from (2.1) that
![]() $F^{\prime}(x)=q^{-1} \sum_{j=0}^{q-1} F^{\prime}((x+j)/q)$
, for almost all
$F^{\prime}(x)=q^{-1} \sum_{j=0}^{q-1} F^{\prime}((x+j)/q)$
, for almost all
![]() $x\in [0, 1]$
. Proposition 2.2 shows that F
′ is almost everywhere on [0, 1] equal to a constant
$x\in [0, 1]$
. Proposition 2.2 shows that F
′ is almost everywhere on [0, 1] equal to a constant
![]() $c\in[0, 1]$
(with
$c\in[0, 1]$
(with
![]() $c=1$
if and only if F is absolutely continuous), and hence that the only purely absolutely continuous
$c=1$
if and only if F is absolutely continuous), and hence that the only purely absolutely continuous
![]() $\mathrm dF$
is Lebesgue measure. Proposition 2.2 is a consequence of [Reference Parry15, Theorems 1 and 2], where the author considers absolutely continuous measures which are invariant under the transformation
$\mathrm dF$
is Lebesgue measure. Proposition 2.2 is a consequence of [Reference Parry15, Theorems 1 and 2], where the author considers absolutely continuous measures which are invariant under the transformation
![]() $T(x)=\beta x\pmod 1$
where
$T(x)=\beta x\pmod 1$
where
![]() $\beta>1$
. In Section 3.3 we give a proof for Proposition 2.2 which is simpler than the one in [Reference Parry15] due to the fact that q is integer.
$\beta>1$
. In Section 3.3 we give a proof for Proposition 2.2 which is simpler than the one in [Reference Parry15] due to the fact that q is integer.
Proposition 2.2. Let
![]() $f\in L^1([0, 1])$
be such that, for almost all
$f\in L^1([0, 1])$
be such that, for almost all
![]() $x\in [0, 1] $
(with respect to Lebesgue measure),
$x\in [0, 1] $
(with respect to Lebesgue measure),
 \begin{equation} f(x)=q^{-1}\sum_{j=0}^{q-1}f((x+j)/q). \end{equation}
\begin{equation} f(x)=q^{-1}\sum_{j=0}^{q-1}f((x+j)/q). \end{equation}
Then f is almost everywhere a (complex) constant equal to
![]() $\int_0^1 f(x)\,\mathrm{d} x$
.
$\int_0^1 f(x)\,\mathrm{d} x$
.
In Section 3.3 we construct remarkable examples of functions
![]() $f\not\in L^1([0, 1])$
where (2.3) is satisfied, but in one case f is not absolutely integrable and in another case f is not measurable.
$f\not\in L^1([0, 1])$
where (2.3) is satisfied, but in one case f is not absolutely integrable and in another case f is not measurable.
2.2. Characterization of stationarity by the characteristic function of X
Next, we characterize stationarity of
![]() $\{X_n\}_{n\geq 1}$
in terms of the characteristic function of X given by
$\{X_n\}_{n\geq 1}$
in terms of the characteristic function of X given by
![]() $f(t)\,:\!=\, \int \mathrm{e}^{itx} \, \mathrm{d} F(x)$
,
$f(t)\,:\!=\, \int \mathrm{e}^{itx} \, \mathrm{d} F(x)$
,
![]() $t\in \mathbb{R}$
. In particular, we discuss when
$t\in \mathbb{R}$
. In particular, we discuss when
![]() $\mathrm{d} F$
is a Rajchman measure, meaning that
$\mathrm{d} F$
is a Rajchman measure, meaning that
![]() $f(t)\rightarrow 0$
as
$f(t)\rightarrow 0$
as
![]() $t\to \pm\infty$
, cf. Section 1.1.
$t\to \pm\infty$
, cf. Section 1.1.
Theorem 2.2.
-
(I) Let
 $\tilde X$
be a random variable on
$\tilde X$
be a random variable on
 $[0, 1]$
with CDF
$[0, 1]$
with CDF
 $\tilde{F}$
and characteristic function
$\tilde{F}$
and characteristic function
 $\tilde f$
. Then
$\tilde f$
. Then
 $\tilde{F}$
satisfies (2.1) if and only if, for all
$\tilde{F}$
satisfies (2.1) if and only if, for all
 $k\in \mathbb{Z}$
,
$k\in \mathbb{Z}$
,
 $\tilde f(2\pi k q)=\tilde f(2\pi k)$
.
$\tilde f(2\pi k q)=\tilde f(2\pi k)$
. -
(II) If F satisfies (2.1), then
 $\lim _{t \to \infty} f(t)$
exists if and only if there exists
$\lim _{t \to \infty} f(t)$
exists if and only if there exists
 $c\in [0, 1]$
such that, for all
$c\in [0, 1]$
such that, for all
 $x\in [0, 1]$
,
$x\in [0, 1]$
,
 $F(x)=(1-c)x+c H(x)$
. In this case,
$F(x)=(1-c)x+c H(x)$
. In this case,
 $c=\lim_{t\to \infty} f(t)$
. In particular,
$c=\lim_{t\to \infty} f(t)$
. In particular,
 $\mathrm{d} F$
is a Rajchman measure if and only if F is the uniform CDF on
$\mathrm{d} F$
is a Rajchman measure if and only if F is the uniform CDF on
 $[0, 1]$
.
$[0, 1]$
.
By the Riemann–Lebesgue lemma, if
![]() $\mathrm{d} F$
is absolutely continuous relative to Lebesgue measure, then it is also a Rajchman measure. Thus, a corollary to Theorem 2.2(II) is that if F is a CDF satisfying (2.1), then
$\mathrm{d} F$
is absolutely continuous relative to Lebesgue measure, then it is also a Rajchman measure. Thus, a corollary to Theorem 2.2(II) is that if F is a CDF satisfying (2.1), then
![]() $\mathrm{d} F$
is absolutely continuous with respect to Lebesgue measure if and only if F is the uniform CDF on [0, 1]. But a more direct argument for this is to apply Proposition 2.2; see the beginning of Section 3.5.
$\mathrm{d} F$
is absolutely continuous with respect to Lebesgue measure if and only if F is the uniform CDF on [0, 1]. But a more direct argument for this is to apply Proposition 2.2; see the beginning of Section 3.5.
Salem in [Reference Salem22] asked whether the measure
![]() $\mathrm{d} ?$
corresponding to Minkowski’s question-mark function restricted to [0, 1] is a Rajchman measure. It has recently been shown that
$\mathrm{d} ?$
corresponding to Minkowski’s question-mark function restricted to [0, 1] is a Rajchman measure. It has recently been shown that
![]() $\mathrm{d} ?$
is indeed a Rajchman measure [Reference Jordan and Sahlsten11, Reference Persson17]. Combining this with Theorem 2.2(II), we obtain the following corollary.
$\mathrm{d} ?$
is indeed a Rajchman measure [Reference Jordan and Sahlsten11, Reference Persson17]. Combining this with Theorem 2.2(II), we obtain the following corollary.
2.3. Characterization of stationarity by a decomposition result for F
The theorem below characterizes stationarity of
![]() $\{X_n\}_{n\geq 1}$
by properties of each part of the Lebesgue decomposition of F. It is a generalization of results obtained in [Reference Harris8] and [Reference Dym6]; our proof in Section 3.5 is based on Theorem 2.1, Proposition 2.2, Theorem 2.2, and a technical result (Lemma 3.3).
$\{X_n\}_{n\geq 1}$
by properties of each part of the Lebesgue decomposition of F. It is a generalization of results obtained in [Reference Harris8] and [Reference Dym6]; our proof in Section 3.5 is based on Theorem 2.1, Proposition 2.2, Theorem 2.2, and a technical result (Lemma 3.3).
Table 1. All cycles up to equivalence when
![]() $q\in\{2,3\}$
and
$q\in\{2,3\}$
and
![]() $n\in\{1,2,3\}$
.
$n\in\{1,2,3\}$
.

We need the following notation and concepts. We call
![]() $s\in[0, 1]$
a purely repeating base-q number of order n if the base-q expansion of s is of the form
$s\in[0, 1]$
a purely repeating base-q number of order n if the base-q expansion of s is of the form
![]() $s=(0.\overline{t_1\dots t_n})_q\,:\!=\,(0.t_1 \ldots t_n t_1\ldots t_n\ldots)_q =\sum_{j=1}^n t_jq^{-j}/(1-q^{-n})$
, where n is the smallest possible positive integer and
$s=(0.\overline{t_1\dots t_n})_q\,:\!=\,(0.t_1 \ldots t_n t_1\ldots t_n\ldots)_q =\sum_{j=1}^n t_jq^{-j}/(1-q^{-n})$
, where n is the smallest possible positive integer and
![]() $t_1,\ldots,t_n\in\{0,\ldots,q-1\}$
. A purely repeating base-q number cannot be a base-q fraction; if
$t_1,\ldots,t_n\in\{0,\ldots,q-1\}$
. A purely repeating base-q number cannot be a base-q fraction; if
![]() $S_j(x)\,:\!=\,(x+j)/q$
then the purely repeating number
$S_j(x)\,:\!=\,(x+j)/q$
then the purely repeating number
![]() $(0.\overline{t_1\dots t_n})_q$
is the unique fixed point of the function
$(0.\overline{t_1\dots t_n})_q$
is the unique fixed point of the function
![]() $S_{t_1}\circ\dots \circ S_{t_n}$
. For any
$S_{t_1}\circ\dots \circ S_{t_n}$
. For any
![]() $n\in\mathbb N$
we call
$n\in\mathbb N$
we call
![]() $(s_1,\ldots,s_n)$
a cycle of order
$(s_1,\ldots,s_n)$
a cycle of order
![]() $n\in\mathbb N$
if, for some integers
$n\in\mathbb N$
if, for some integers
![]() $t_1,\dots,t_n\in \{0,\ldots,q-1\}$
,
$t_1,\dots,t_n\in \{0,\ldots,q-1\}$
,
and
![]() $s_1,\dots,s_n$
are pairwise distinct. Note that for two cycles
$s_1,\dots,s_n$
are pairwise distinct. Note that for two cycles
![]() $(s_1,\dots,s_n)$
and
$(s_1,\dots,s_n)$
and
![]() $(s^{\prime}_1,\dots,s^{\prime}_m)$
, the sets
$(s^{\prime}_1,\dots,s^{\prime}_m)$
, the sets
![]() $\{s_1,\dots, s_n\}$
and
$\{s_1,\dots, s_n\}$
and
![]() $\{s^{\prime}_1,\dots, s^{\prime}_m\}$
are either equal or disjoint. Table 1 shows the cycles up to the order of elements for
$\{s^{\prime}_1,\dots, s^{\prime}_m\}$
are either equal or disjoint. Table 1 shows the cycles up to the order of elements for
![]() $q=2,3$
and
$q=2,3$
and
![]() $n=1,2,3$
. Moreover, let H be the Heaviside function defined by
$n=1,2,3$
. Moreover, let H be the Heaviside function defined by
![]() $H(x)=0$
for
$H(x)=0$
for
![]() $x<0$
and
$x<0$
and
![]() $H(x)=1$
for
$H(x)=1$
for
![]() $x\ge0$
. Finally, we say that F is a mixture of an at most countable number of CDFs if there exist CDFs
$x\ge0$
. Finally, we say that F is a mixture of an at most countable number of CDFs if there exist CDFs
![]() $F_1,F_2,\ldots$
and a discrete probability distribution
$F_1,F_2,\ldots$
and a discrete probability distribution
![]() $(\theta_1,\theta_2,\ldots)$
such that
$(\theta_1,\theta_2,\ldots)$
such that
![]() $\tilde F=\sum_{i}\theta_iF_i$
.
$\tilde F=\sum_{i}\theta_iF_i$
.
Theorem 2.3.
F satisfies the stationarity equation (2.1) if and only if F is a mixture of three CDFs
![]() $F_1,F_2,F_3$
whose corresponding probability distributions are mutually singular measures concentrated on
$F_1,F_2,F_3$
whose corresponding probability distributions are mutually singular measures concentrated on
![]() $[0, 1]$
such that
$[0, 1]$
such that
![]() $F_1,F_2,F_3$
satisfy the following statements (I)–(III):
$F_1,F_2,F_3$
satisfy the following statements (I)–(III):
-
(I)
 $F_1$
is the uniform CDF on
$F_1$
is the uniform CDF on
 $[0, 1]$
, that is,
$[0, 1]$
, that is,
 $F_1(x)=x$
for
$F_1(x)=x$
for
 $x\in[0, 1]$
.
$x\in[0, 1]$
. -
(II)
 $F_2$
is a mixture of an at most countable number of CDFs of the form (2.5)where
$F_2$
is a mixture of an at most countable number of CDFs of the form (2.5)where \begin{equation} F_{s_1,\ldots,s_n}(x)\,:\!=\,\frac{1}{n}\sum_{j=1}^{n} H(x-s_j),\qquad x\in\mathbb R, \end{equation}
\begin{equation} F_{s_1,\ldots,s_n}(x)\,:\!=\,\frac{1}{n}\sum_{j=1}^{n} H(x-s_j),\qquad x\in\mathbb R, \end{equation}
 $(s_1,\ldots,s_n)$
is a cycle of order n.
$(s_1,\ldots,s_n)$
is a cycle of order n.
-
(III)
 $F_3$
is singular continuous and satisfies (2.1) (with F replaced by
$F_3$
is singular continuous and satisfies (2.1) (with F replaced by
 $F_3$
).
$F_3$
).
Moreover, we have:
-
(IV)
 $F_1$
and
$F_1$
and
 $F_2$
also satisfy (2.1) (with F replaced by
$F_2$
also satisfy (2.1) (with F replaced by
 $F_1$
and
$F_1$
and
 $F_2$
, respectively).
$F_2$
, respectively).
The CDF
![]() $F_{s_1,\ldots,s_n}$
given by (2.5) is just the empirical CDF at the points in the cycle
$F_{s_1,\ldots,s_n}$
given by (2.5) is just the empirical CDF at the points in the cycle
![]() $(s_1,\ldots,s_n)$
. Thus, the following corollary follows immediately from (2.5).
$(s_1,\ldots,s_n)$
. Thus, the following corollary follows immediately from (2.5).
Corollary 2.2. Let
![]() $(s_1,\dots, s_n)$
be a cycle of order n, defined by
$(s_1,\dots, s_n)$
be a cycle of order n, defined by
![]() $t_1,\ldots,t_n\in\{0,\ldots,q-1\}$
as given in (2.4), and assume that X follows
$t_1,\ldots,t_n\in\{0,\ldots,q-1\}$
as given in (2.4), and assume that X follows
![]() $F_{s_1,\ldots,s_n}$
given by (2.5).
$F_{s_1,\ldots,s_n}$
given by (2.5).
-
(I) If
 $n=1$
, then
$n=1$
, then
 $X_1=X_2=\cdots=t_1$
almost surely.
$X_1=X_2=\cdots=t_1$
almost surely. -
(II) If
 $n\ge2$
, then the distribution of
$n\ge2$
, then the distribution of
 $\{X_m\}_{m\ge1}$
is completely determined by the fact that
$\{X_m\}_{m\ge1}$
is completely determined by the fact that
 $(X_1,\ldots,X_{n-1})$
is uniformly distributed on
$(X_1,\ldots,X_{n-1})$
is uniformly distributed on
 $\{(t_1,\ldots,t_{n-1})$
,
$\{(t_1,\ldots,t_{n-1})$
,
 $(t_n,t_1,\ldots,t_{n-2})$
, …,
$(t_n,t_1,\ldots,t_{n-2})$
, …,
 $(t_{2},\ldots,t_n)\}$
, since almost surely
$(t_{2},\ldots,t_n)\}$
, since almost surely
 $\{X_m\}_{m\ge1}$
is in a one-to-one correspondence with X and
$\{X_m\}_{m\ge1}$
is in a one-to-one correspondence with X and  \begin{eqnarray*} (X_1,\ldots,X_{n-1})=(t_1,\ldots,t_{n-1})\ &\quad \Rightarrow\quad &\ X=s_1=(0.\overline{t_1\ldots t_n})_q , \\ (X_1,\ldots,X_{n-1})=(t_n,t_1,\ldots,t_{n-2})\ &\quad \Rightarrow\quad &\ X=s_2=(0.\overline{t_nt_1\ldots t_{n-1}})_q , \\ & \vdots & \\ (X_1,\ldots,X_{n-1})=(t_{2},\ldots,t_n)\ &\quad \Rightarrow\quad &\ X=s_n=(0.\overline{t_2\ldots t_{n}t_1})_q. \end{eqnarray*}
\begin{eqnarray*} (X_1,\ldots,X_{n-1})=(t_1,\ldots,t_{n-1})\ &\quad \Rightarrow\quad &\ X=s_1=(0.\overline{t_1\ldots t_n})_q , \\ (X_1,\ldots,X_{n-1})=(t_n,t_1,\ldots,t_{n-2})\ &\quad \Rightarrow\quad &\ X=s_2=(0.\overline{t_nt_1\ldots t_{n-1}})_q , \\ & \vdots & \\ (X_1,\ldots,X_{n-1})=(t_{2},\ldots,t_n)\ &\quad \Rightarrow\quad &\ X=s_n=(0.\overline{t_2\ldots t_{n}t_1})_q. \end{eqnarray*}
Remark 2.3. Corollary 2.2 shows that the stochastic process corresponding to a CDF as in (2.5) is a Markov chain of order
![]() $n-1$
, but essentially it is equivalent to a uniform distribution on n elements. Thus, a stationary stochastic process
$n-1$
, but essentially it is equivalent to a uniform distribution on n elements. Thus, a stationary stochastic process
![]() $\{X_n\}_{n\ge1}$
corresponding to a mixture of CDFs as in (2.5) will be rather trivial. Hence, by Theorem 2.3, it only remains to understand those stationary stochastic processes
$\{X_n\}_{n\ge1}$
corresponding to a mixture of CDFs as in (2.5) will be rather trivial. Hence, by Theorem 2.3, it only remains to understand those stationary stochastic processes
![]() $\{X_n\}_{n\ge1}$
which generate a singular continuous CDF F. This will be the topic of our follow-up paper mentioned at the very end of Section 1.
$\{X_n\}_{n\ge1}$
which generate a singular continuous CDF F. This will be the topic of our follow-up paper mentioned at the very end of Section 1.
3. Proofs and further results
3.1. Proof of Theorem 2.1
Before proving Theorem 2.1, we need the following two lemmas.
Lemma 3.1. Suppose that
![]() $\{X_n\}_{n\geq 1}$
is stationary. Then the probability of all
$\{X_n\}_{n\geq 1}$
is stationary. Then the probability of all
![]() $X_n$
having the same value starting from some
$X_n$
having the same value starting from some
![]() $n_0>1$
and at least one
$n_0>1$
and at least one
![]() $X_m$
having a different value for some
$X_m$
having a different value for some
![]() $m<n_0$
is zero:
$m<n_0$
is zero:
 \begin{equation} \mathbb P\Bigg(\bigcup_{0<m<n_0<\infty}\{X_m\not= X_{n_0}=X_{n_0+1}=\cdots\}\Bigg)=0. \end{equation}
\begin{equation} \mathbb P\Bigg(\bigcup_{0<m<n_0<\infty}\{X_m\not= X_{n_0}=X_{n_0+1}=\cdots\}\Bigg)=0. \end{equation}
Proof. It suffices to verify that, for integers
![]() $0<m<n_0<\infty$
,
$0<m<n_0<\infty$
,
where, without loss of generality, we may assume that
![]() $m=n_0-1$
. For any
$m=n_0-1$
. For any
![]() $k\in\{0,\ldots,q-1\}$
, we have, by the law of total probability for two events, that
$k\in\{0,\ldots,q-1\}$
, we have, by the law of total probability for two events, that
Then (3.2) follows, since by stationarity of
![]() $\{X_n\}_{n\geq 1}$
we have
$\{X_n\}_{n\geq 1}$
we have
![]() $\mathbb P(X_{n_0}=X_{n_0+1}=\cdots=k)=\mathbb P(X_{n_0-1}=X_{n_0}=\ldots=k)$
. Thereby, (3.1) is verified.
$\mathbb P(X_{n_0}=X_{n_0+1}=\cdots=k)=\mathbb P(X_{n_0-1}=X_{n_0}=\ldots=k)$
. Thereby, (3.1) is verified.
Lemma 3.2. If
![]() $\tilde{F}$
is the CDF for a probability distribution on
$\tilde{F}$
is the CDF for a probability distribution on
![]() $[0, 1]$
which obeys (2.1), then
$[0, 1]$
which obeys (2.1), then
![]() $\tilde{F}$
is continuous at every
$\tilde{F}$
is continuous at every
![]() $x \in \mathbb{Q}_q$
.
$x \in \mathbb{Q}_q$
.
Proof. Clearly, (2.1) is also true for
![]() $\tilde{F}(x)$
if
$\tilde{F}(x)$
if
![]() $x=1$
, so using (2.1) we have, for any
$x=1$
, so using (2.1) we have, for any
![]() $\delta \in \mathbb{Q}_q$
and for any base-q fraction
$\delta \in \mathbb{Q}_q$
and for any base-q fraction
![]() $x\in(\delta,1)$
or for
$x\in(\delta,1)$
or for
![]() $x=1$
, that
$x=1$
, that
 \begin{equation} \tilde{F}(x)-\tilde{F}(x-\delta)=\sum_{j=0}^{q-1} [\tilde{F}((j+x)/q)-\tilde{F}((j+x)/q -\delta/q)]. \end{equation}
\begin{equation} \tilde{F}(x)-\tilde{F}(x-\delta)=\sum_{j=0}^{q-1} [\tilde{F}((j+x)/q)-\tilde{F}((j+x)/q -\delta/q)]. \end{equation}
Now, we prove the lemma by induction, considering first base-q fractions of order one. Letting
![]() $x=1$
gives
$x=1$
gives
![]() $\tilde{F}(1)-\tilde{F}(1-\delta) = \tilde{F}(1)-\tilde{F}(1-\delta/q)+ \sum_{j=0}^{q-2} [\tilde{F}((j+1)/q)-\tilde{F}((j+1)/q -\delta/q)]$
, and letting
$\tilde{F}(1)-\tilde{F}(1-\delta) = \tilde{F}(1)-\tilde{F}(1-\delta/q)+ \sum_{j=0}^{q-2} [\tilde{F}((j+1)/q)-\tilde{F}((j+1)/q -\delta/q)]$
, and letting
![]() $\delta\downarrow 0$
we see that all the jumps of
$\delta\downarrow 0$
we see that all the jumps of
![]() $\tilde{F}$
at
$\tilde{F}$
at
![]() $1/q, \ldots, (q-1)/q$
must be zero, so
$1/q, \ldots, (q-1)/q$
must be zero, so
![]() $\tilde{F}$
is continuous at these points, which are first-order base-q fractions. Next, let us assume that, for a given order
$\tilde{F}$
is continuous at these points, which are first-order base-q fractions. Next, let us assume that, for a given order
![]() $n \geq 1$
,
$n \geq 1$
,
![]() $\tilde{F}$
is continuous at all base-q fractions of order n. Let
$\tilde{F}$
is continuous at all base-q fractions of order n. Let
![]() $x=(0.k_1k_2\ldots k_n)_q$
with
$x=(0.k_1k_2\ldots k_n)_q$
with
![]() $k_n \neq 0$
. By using (3.3) and taking
$k_n \neq 0$
. By using (3.3) and taking
![]() $\delta \downarrow 0$
, we obtain that
$\delta \downarrow 0$
, we obtain that
![]() $\tilde{F}$
is continuous at all numbers of the form
$\tilde{F}$
is continuous at all numbers of the form
![]() $(x+j)/q=(0.jk_1,\ldots k_n)_q$
for all
$(x+j)/q=(0.jk_1,\ldots k_n)_q$
for all
![]() $j \in \{0,\ldots,q-1\}$
. This shows that
$j \in \{0,\ldots,q-1\}$
. This shows that
![]() $\tilde{F}$
is continuous at all base-q fractions of order
$\tilde{F}$
is continuous at all base-q fractions of order
![]() $n+1$
, which completes the proof.
$n+1$
, which completes the proof.
Now, to prove Theorem 2.1 we need the following notation and observations. Let
![]() $(x_1,\ldots,x_n)$
,
$(x_1,\ldots,x_n)$
,
![]() $(t_1,\ldots,t_n)\in\{0,\ldots,q-1\}^n$
. We write
$(t_1,\ldots,t_n)\in\{0,\ldots,q-1\}^n$
. We write
![]() $(x_1,\ldots,x_n)\le(t_1,\ldots,t_n)$
if
$(x_1,\ldots,x_n)\le(t_1,\ldots,t_n)$
if
![]() $\sum_{k=1}^n x_kq^{-k}\le\sum_{k=1}^n t_kq^{-k}$
. Define
$\sum_{k=1}^n x_kq^{-k}\le\sum_{k=1}^n t_kq^{-k}$
. Define
![]() $t\,:\!=\,\sum_{j=1}^nt_jq^{-j}$
. Note that
$t\,:\!=\,\sum_{j=1}^nt_jq^{-j}$
. Note that
![]() $x=\sum_{i=1}^\infty x_i q^{-i}\in [0, 1]$
satisfies
$x=\sum_{i=1}^\infty x_i q^{-i}\in [0, 1]$
satisfies
![]() $x\leq t+q^{-n}$
if and only if one of the following two statements holds true:
$x\leq t+q^{-n}$
if and only if one of the following two statements holds true:
-
The first n digits of x obey
 $(x_1,\ldots,x_n)\le(t_1,\ldots,t_n)$
(regardless of the values of the next digits
$(x_1,\ldots,x_n)\le(t_1,\ldots,t_n)$
(regardless of the values of the next digits
 $x_{n+1}, x_{n+2},\ldots$
).
$x_{n+1}, x_{n+2},\ldots$
). -
We have
 $x_1=t_1,\ldots,x_{n-1}=t_{n-1},x_n=t_n+1,x_{n+1}=x_{n+2}=\cdots=0$
.
$x_1=t_1,\ldots,x_{n-1}=t_{n-1},x_n=t_n+1,x_{n+1}=x_{n+2}=\cdots=0$
.
Define
 \begin{align*} \mathcal{F}_1(t_1,\dots,t_n) & \,:\!=\, \mathbb P((X_1,\ldots, X_n)\leq {(t_1,\dots,t_n)}) \\ & = \sum_{(x_1,\ldots,x_n)\leq (t_1,\ldots,t_n)}\mathbb P(X_1=x_1,\dots,X_n=x_n).\end{align*}
\begin{align*} \mathcal{F}_1(t_1,\dots,t_n) & \,:\!=\, \mathbb P((X_1,\ldots, X_n)\leq {(t_1,\dots,t_n)}) \\ & = \sum_{(x_1,\ldots,x_n)\leq (t_1,\ldots,t_n)}\mathbb P(X_1=x_1,\dots,X_n=x_n).\end{align*}
Stationarity of
![]() $\{X_n\}_{n\geq 1}$
is equivalent to that for every
$\{X_n\}_{n\geq 1}$
is equivalent to that for every
![]() $(t_1,\ldots,t_n)\in \{0,\ldots,q-1\}^n$
, so
$(t_1,\ldots,t_n)\in \{0,\ldots,q-1\}^n$
, so
![]() $\mathcal{F}_1(t_1,\ldots,t_n)$
equals
$\mathcal{F}_1(t_1,\ldots,t_n)$
equals
cf. Kolmogorov’s extension theorem. Furthermore, by (1.1) and (1.2) we have
Proof of Theorem
2.1(I).Assume that
![]() $\{X_n\}_{n\geq 1}$
is stationary. Using (3.4) together with Lemma 3.1 we obtain
$\{X_n\}_{n\geq 1}$
is stationary. Using (3.4) together with Lemma 3.1 we obtain
Furthermore, stationarity of
![]() $\{X_n\}_{n\geq 1}$
implies that X and the ‘left-shifted’ stochastic variable
$\{X_n\}_{n\geq 1}$
implies that X and the ‘left-shifted’ stochastic variable
![]() $\sum_{n=1}^\infty X_{n+1}q^{-n}=qX-X_1$
are identically distributed. Thus,
$\sum_{n=1}^\infty X_{n+1}q^{-n}=qX-X_1$
are identically distributed. Thus,
![]() $F(x)=\mathbb P(qX-X_1\leq x)=\sum_{j=0}^{q-1}\mathbb P(X_1=j,\,X\le (x+j)/q)$
. We see that
$F(x)=\mathbb P(qX-X_1\leq x)=\sum_{j=0}^{q-1}\mathbb P(X_1=j,\,X\le (x+j)/q)$
. We see that
![]() $\mathbb P(X_1=0,\,X\le x/q) = \mathbb P(X=0)+\mathbb P(0<\,X\le x/q) = F(0)+(F(x/q)-F(0))$
. Further, for
$\mathbb P(X_1=0,\,X\le x/q) = \mathbb P(X=0)+\mathbb P(0<\,X\le x/q) = F(0)+(F(x/q)-F(0))$
. Further, for
![]() $j\in\{1,\ldots, q-1\}$
,
$j\in\{1,\ldots, q-1\}$
,
where we used (3.1) in order to get the second identity. This leads to (2.1).
Conversely, assume that F satisfies (2.1). Then, since F is right continuous and
![]() $\mathbb{Q}_q$
constitutes a dense subset of [0, 1], (2.1) holds for all
$\mathbb{Q}_q$
constitutes a dense subset of [0, 1], (2.1) holds for all
![]() $x\in[0, 1]$
. Further, by Kolmogorov’s extension theorem we can define the distribution of
$x\in[0, 1]$
. Further, by Kolmogorov’s extension theorem we can define the distribution of
![]() $\{X_n\}_{n\geq 1}$
on
$\{X_n\}_{n\geq 1}$
on
![]() $\{0,\ldots,q-1\}$
by specifying the finite-dimensional distribution
$\{0,\ldots,q-1\}$
by specifying the finite-dimensional distribution
![]() $\mathcal{F}_1$
o f
$\mathcal{F}_1$
o f
![]() $( X_1,\dots, X_n)$
for every integer
$( X_1,\dots, X_n)$
for every integer
![]() $n\ge1$
in a consistent way, setting
$n\ge1$
in a consistent way, setting
Furthermore, for any
![]() $\epsilon>0$
and
$\epsilon>0$
and
![]() $x_1,\dots, x_n\in \{0,\dots,q-1\}$
, the inequality
$x_1,\dots, x_n\in \{0,\dots,q-1\}$
, the inequality
![]() $\mathbb{P}(X_1=x_1,\ldots, $
$\mathbb{P}(X_1=x_1,\ldots, $
![]() $X_n=x_n,X_{n+1}=\cdots=0) + \mathbb P(X_1=x_1,\ldots,X_{n-1}=x_{n-1}, X_n=x_n-1,X_{n+1}=\cdots=q-1) \leq$
$X_n=x_n,X_{n+1}=\cdots=0) + \mathbb P(X_1=x_1,\ldots,X_{n-1}=x_{n-1}, X_n=x_n-1,X_{n+1}=\cdots=q-1) \leq$
![]() $\mathbb P(x-\epsilon<X\leq x)=F(x)-F(x-\epsilon)$
holds, and hence by Lemma 3.2 the probability of realizing a base-q fraction is 0. Hence, the second term on the right-hand side of (3.4) is 0, and so (3.5) again holds true. Consequently, for any
$\mathbb P(x-\epsilon<X\leq x)=F(x)-F(x-\epsilon)$
holds, and hence by Lemma 3.2 the probability of realizing a base-q fraction is 0. Hence, the second term on the right-hand side of (3.4) is 0, and so (3.5) again holds true. Consequently, for any
![]() $n\in\mathbb N$
and
$n\in\mathbb N$
and
![]() $(t_1,\ldots,t_n)\in\{0,\ldots,q-1\}^n$
,
$(t_1,\ldots,t_n)\in\{0,\ldots,q-1\}^n$
,
 \begin{align*} \mathcal{F}_2(t_1,\dots,t_n)&=\sum_{j=0}^{q-1}\sum_{(x_2,\ldots,x_{n+1})\leq (t_1,\ldots,t_n)}\mathbb P(X_1=j,X_2=x_2,\dots,X_{n+1}=x_{n+1}) \\ &=\mathbb P(X=0)+\sum_{j=0}^{q-1} \mathbb P(j/q<X\leq j/q + t/q +q^{-n-1})\\ &=F(0)+\sum_{j=0}^{q-1} (F((t+q^{-n}+j)/q)-F(j/q)) \\ &=F(t+q^{-n}), \end{align*}
\begin{align*} \mathcal{F}_2(t_1,\dots,t_n)&=\sum_{j=0}^{q-1}\sum_{(x_2,\ldots,x_{n+1})\leq (t_1,\ldots,t_n)}\mathbb P(X_1=j,X_2=x_2,\dots,X_{n+1}=x_{n+1}) \\ &=\mathbb P(X=0)+\sum_{j=0}^{q-1} \mathbb P(j/q<X\leq j/q + t/q +q^{-n-1})\\ &=F(0)+\sum_{j=0}^{q-1} (F((t+q^{-n}+j)/q)-F(j/q)) \\ &=F(t+q^{-n}), \end{align*}
using in the first identity the law of total probability, in the second that the probability of realizing a base-q point is zero, in the third (1.2), and in the last (2.1). Thereby, (3.6) gives that
![]() $\mathcal{F}_1(t_1,\dots,t_n)=\mathcal{F}_2(t_1,\dots,t_n)$
for every
$\mathcal{F}_1(t_1,\dots,t_n)=\mathcal{F}_2(t_1,\dots,t_n)$
for every
![]() $n\in\mathbb N$
and every
$n\in\mathbb N$
and every
![]() $(t_1,\ldots,t_n)\in\{0,\ldots,q-1\}^n$
, so
$(t_1,\ldots,t_n)\in\{0,\ldots,q-1\}^n$
, so
![]() $\{X_n\}_{n\geq 1}$
is stationary.
$\{X_n\}_{n\geq 1}$
is stationary.
Proof of Theorem
2.1(II).Let
![]() $\phi(x)= \{x_n\}_{n\ge1}$
be the one-to-one mapping on
$\phi(x)= \{x_n\}_{n\ge1}$
be the one-to-one mapping on
![]() $[0, 1]\setminus\mathbb Q_q$
corresponding to mapping x into its base-q digits
$[0, 1]\setminus\mathbb Q_q$
corresponding to mapping x into its base-q digits
![]() $x_1,x_2,\ldots$
, i.e.
$x_1,x_2,\ldots$
, i.e.
![]() $x=\sum_{n=1}^\infty x_nq^{-n}$
. Further, let
$x=\sum_{n=1}^\infty x_nq^{-n}$
. Further, let
![]() $\tilde F$
be a CDF for a random variable
$\tilde F$
be a CDF for a random variable
![]() $\tilde X$
on [0, 1] such that
$\tilde X$
on [0, 1] such that
![]() $\tilde F$
satisfies (2.1) for all
$\tilde F$
satisfies (2.1) for all
![]() $x\in \mathbb Q_q$
. By Lemma 3.2, and since
$x\in \mathbb Q_q$
. By Lemma 3.2, and since
![]() $\mathbb Q_q$
is countable, we can assume that
$\mathbb Q_q$
is countable, we can assume that
![]() $\tilde X\not\in\mathbb Q_q$
. Then
$\tilde X\not\in\mathbb Q_q$
. Then
![]() $\tilde X$
is in a one-to-one correspondence with
$\tilde X$
is in a one-to-one correspondence with
![]() $\{\tilde X_n\}_{n\ge1}\,:\!=\,\phi(\tilde X)$
, and
$\{\tilde X_n\}_{n\ge1}\,:\!=\,\phi(\tilde X)$
, and
![]() $\tilde X=\sum_{n=1}^\infty \tilde X_nq^{-n}$
follows
$\tilde X=\sum_{n=1}^\infty \tilde X_nq^{-n}$
follows
![]() $\tilde F$
. We conclude from Theorem 2.1(I) that the stochastic process
$\tilde F$
. We conclude from Theorem 2.1(I) that the stochastic process
![]() $\{\tilde X_n\}_{n\ge1}$
is stationary. Since the distribution of
$\{\tilde X_n\}_{n\ge1}$
is stationary. Since the distribution of
![]() $\{\tilde X_n\}_{n\ge1}$
is induced by that of
$\{\tilde X_n\}_{n\ge1}$
is induced by that of
![]() $\tilde X$
and the one-to-one mapping
$\tilde X$
and the one-to-one mapping
![]() $\phi$
, let us show that
$\phi$
, let us show that
![]() $\{\tilde X_n\}_{n\ge1}$
is the unique (up to its distribution) stationary stochastic process on
$\{\tilde X_n\}_{n\ge1}$
is the unique (up to its distribution) stationary stochastic process on
![]() $\{0,\ldots,q-1\}$
so that
$\{0,\ldots,q-1\}$
so that
![]() $\sum_{n=1}^\infty \tilde X_nq^{-n}$
follows
$\sum_{n=1}^\infty \tilde X_nq^{-n}$
follows
![]() $\tilde F$
: if
$\tilde F$
: if
![]() $\{\bar X_n\}_{n\ge1}$
is another stationary stochastic process on
$\{\bar X_n\}_{n\ge1}$
is another stationary stochastic process on
![]() $\{0,\ldots,q-1\}$
so that
$\{0,\ldots,q-1\}$
so that
![]() $\sum_{n=1}^\infty \bar X_nq^{-n}$
follows
$\sum_{n=1}^\infty \bar X_nq^{-n}$
follows
![]() $\tilde F$
, then, for any event G of sequences
$\tilde F$
, then, for any event G of sequences
![]() $\{x_n\}_{n\ge1}$
such that each
$\{x_n\}_{n\ge1}$
such that each
![]() $x_n\in\{0,\ldots,q-1\}$
and
$x_n\in\{0,\ldots,q-1\}$
and
![]() $\sum_{n=1}^\infty x_nq^{-n}\not\in\mathbb Q_q$
, we have
$\sum_{n=1}^\infty x_nq^{-n}\not\in\mathbb Q_q$
, we have
![]() $\mathbb P(\{\bar X_n\}_{n\ge1}\in G)=\mathbb P(\tilde X\in\phi^{-1}(G))=\mathbb P(\{\tilde X_n\}_{n\ge1}\in G)$
. Furthermore, by right continuity of
$\mathbb P(\{\bar X_n\}_{n\ge1}\in G)=\mathbb P(\tilde X\in\phi^{-1}(G))=\mathbb P(\{\tilde X_n\}_{n\ge1}\in G)$
. Furthermore, by right continuity of
![]() $\tilde F$
and since
$\tilde F$
and since
![]() $\mathbb{Q}_q$
is dense on (0, 1),
$\mathbb{Q}_q$
is dense on (0, 1),
![]() $\tilde F$
satisfies (2.1) for all
$\tilde F$
satisfies (2.1) for all
![]() $x\in(0, 1)$
. Finally,
$x\in(0, 1)$
. Finally,
![]() $\tilde F$
obviously satisfies (2.1) for
$\tilde F$
obviously satisfies (2.1) for
![]() $x=0$
and
$x=0$
and
![]() $x=1$
.
$x=1$
.
3.2. Proof of Proposition 2.1
Suppose that the
![]() $X_n$
are i.i.d. Since (2.2) holds for
$X_n$
are i.i.d. Since (2.2) holds for
![]() $x=1$
, F is right continuous, and
$x=1$
, F is right continuous, and
![]() $\mathbb{Q}_q$
is dense on (0, 1), it suffices to show that (2.2) holds for all
$\mathbb{Q}_q$
is dense on (0, 1), it suffices to show that (2.2) holds for all
![]() $x \in \mathbb{Q}_q$
. Let
$x \in \mathbb{Q}_q$
. Let
![]() $x=(0.x_1\dots x_n)_q$
with
$x=(0.x_1\dots x_n)_q$
with
![]() $x_1,\dots,x_n\in \{0,\dots,q-1\}$
where
$x_1,\dots,x_n\in \{0,\dots,q-1\}$
where
![]() $x_n \neq 0$
. By Lemma 3.1,
$x_n \neq 0$
. By Lemma 3.1,
![]() $\mathbb{P}(X_1=x_1,\dots, X_n=x_n, X_{n+1}=X_{n+2}=\cdots=0)=0$
. Hence, setting
$\mathbb{P}(X_1=x_1,\dots, X_n=x_n, X_{n+1}=X_{n+2}=\cdots=0)=0$
. Hence, setting
![]() $\sum_{j=0}^{-1} \dots =0$
,
$\sum_{j=0}^{-1} \dots =0$
,
 \begin{align*} F(x)&=\sum_{j=0}^{x_1-1}\mathbb{P}(X_1=j)+\mathbb{P}(X_1=x_1)\sum_{j=0}^{x_2-1}\mathbb{P}(X_2=j)\\ &\quad+\dots+\mathbb{P}(X_1=x_1)\sum_{j=0}^{x_n-1} \mathbb{P}(X_2=x_2,\dots, X_{n-1}=x_{n-1},X_n=j) \\ &=\sum_{j=0}^{x_1-1} \mathbb{P}(X_1=j)+\mathbb{P}(X_1=x_1)F(qx-x_1),\end{align*}
\begin{align*} F(x)&=\sum_{j=0}^{x_1-1}\mathbb{P}(X_1=j)+\mathbb{P}(X_1=x_1)\sum_{j=0}^{x_2-1}\mathbb{P}(X_2=j)\\ &\quad+\dots+\mathbb{P}(X_1=x_1)\sum_{j=0}^{x_n-1} \mathbb{P}(X_2=x_2,\dots, X_{n-1}=x_{n-1},X_n=j) \\ &=\sum_{j=0}^{x_1-1} \mathbb{P}(X_1=j)+\mathbb{P}(X_1=x_1)F(qx-x_1),\end{align*}
using that the
![]() $X_n$
are independent in the first identity and identically distributed in the second. Furthermore, for
$X_n$
are independent in the first identity and identically distributed in the second. Furthermore, for
![]() $j\in \{0,\dots,q-1\}$
,
$j\in \{0,\dots,q-1\}$
,
 \begin{equation} F(qx-j)= \begin{cases} 0 & \textrm{if } x_1<j, \\[4pt] 1 & \textrm{if } x_1>j, \\[4pt] F((0.x_2\ldots,x_n)_q) & \textrm{if } x_1=j, \end{cases}\end{equation}
\begin{equation} F(qx-j)= \begin{cases} 0 & \textrm{if } x_1<j, \\[4pt] 1 & \textrm{if } x_1>j, \\[4pt] F((0.x_2\ldots,x_n)_q) & \textrm{if } x_1=j, \end{cases}\end{equation}
and so we conclude that (2.2) holds at x.
Conversely, suppose that (2.2) holds. Then
![]() $F(0)=\mathbb{P}(X_1=0)F(0)$
, so either
$F(0)=\mathbb{P}(X_1=0)F(0)$
, so either
![]() $\mathbb{P}(X_1=0)=1$
or
$\mathbb{P}(X_1=0)=1$
or
![]() $F(0)=0$
. In the first case, since by stationarity the
$F(0)=0$
. In the first case, since by stationarity the
![]() $X_n$
are identically distributed, we obtain immediately that the
$X_n$
are identically distributed, we obtain immediately that the
![]() $X_n$
are i.i.d. So, assume that
$X_n$
are i.i.d. So, assume that
![]() $F(0)=0$
and let
$F(0)=0$
and let
![]() $x=(0.x_1\dots x_n)_q$
with
$x=(0.x_1\dots x_n)_q$
with
![]() $x_1,\dots,x_n\in \{0,\dots,q-1\}$
. Then
$x_1,\dots,x_n\in \{0,\dots,q-1\}$
. Then
![]() $\mathbb{P}(X_1=x_1,\dots, X_n=x_n)=\mathbb{P}(x\leq X\leq x+q^{-n})=F(x+q^{-n})-F(x)$
, using in the last identity that
$\mathbb{P}(X_1=x_1,\dots, X_n=x_n)=\mathbb{P}(x\leq X\leq x+q^{-n})=F(x+q^{-n})-F(x)$
, using in the last identity that
![]() $\mathbb{P}(X=x)=0$
, cf. Lemma 3.1. Thus,
$\mathbb{P}(X=x)=0$
, cf. Lemma 3.1. Thus,
 \begin{align*} \mathbb{P}(X_1=x_1,\dots, &\,X_n=x_n)=F(x+q^{-n}) - F(x) \\ &=\sum_{j=0}^{q-1}\mathbb{P}(X_1=j) \big (F(q(x+q^{-n})-j)-F(qx-j)\big )\\ &=\mathbb{P}(X_1=x_1) \big (F((0.x_2\dots x_n)_q+q^{-n+1})-F((0.x_2\dots x_n)_q)\big ),\end{align*}
\begin{align*} \mathbb{P}(X_1=x_1,\dots, &\,X_n=x_n)=F(x+q^{-n}) - F(x) \\ &=\sum_{j=0}^{q-1}\mathbb{P}(X_1=j) \big (F(q(x+q^{-n})-j)-F(qx-j)\big )\\ &=\mathbb{P}(X_1=x_1) \big (F((0.x_2\dots x_n)_q+q^{-n+1})-F((0.x_2\dots x_n)_q)\big ),\end{align*}
where in the second equality we use (2.2) and in the third we use (3.7). The dependence on
![]() $x_1$
has now been isolated in the factor
$x_1$
has now been isolated in the factor
![]() $\mathbb{P}(X_1=x_1)$
, and using the same method for the other variables
$\mathbb{P}(X_1=x_1)$
, and using the same method for the other variables
![]() $x_2,\ldots,x_n$
we obtain
$x_2,\ldots,x_n$
we obtain
 \begin{align*} \mathbb{P}(&X_1=x_1,\dots,X_n=x_n)\\ &=\mathbb{P}(X_1=x_1)\sum_{j=0}^{q-1}\mathbb{P}(X_1=j) \big (F(x_2-j+(0.x_3\dots x_n)_q+q^{-n+2})\\ &\phantom{=\mathbb{P}(X_1=x_1)\sum\mathbb{P}(X_1=j) \big (}-F(x_2-j+(0.x_3\dots x_n)_q)\big ) \end{align*}
\begin{align*} \mathbb{P}(&X_1=x_1,\dots,X_n=x_n)\\ &=\mathbb{P}(X_1=x_1)\sum_{j=0}^{q-1}\mathbb{P}(X_1=j) \big (F(x_2-j+(0.x_3\dots x_n)_q+q^{-n+2})\\ &\phantom{=\mathbb{P}(X_1=x_1)\sum\mathbb{P}(X_1=j) \big (}-F(x_2-j+(0.x_3\dots x_n)_q)\big ) \end{align*}
 \begin{align*} &=\mathbb{P}(X_1=x_1)\mathbb{P}(X_1=x_2) \big (F((0.x_3\dots x_n)_q+q^{-n+2})-F((0.x_3\dots x_n)_q)\big )\\ &\;\,\vdots\\ &=\mathbb{P}(X_1=x_1)\cdots\mathbb{P}(X_1=x_{n-1})\sum_{j=0}^{q-1}\mathbb{P}(X_1=j) \big (F(x_n-j+1)-F(x_n-j)\big )\\ &=\mathbb{P}(X_1=x_1)\cdots \mathbb{P}(X_{1}=x_{n-1})\big (\mathbb{P}(X_1=x_n)(1-F(0))+\mathbb{P}(X_1=x_{n}+1)F(0)\big ).\end{align*}
\begin{align*} &=\mathbb{P}(X_1=x_1)\mathbb{P}(X_1=x_2) \big (F((0.x_3\dots x_n)_q+q^{-n+2})-F((0.x_3\dots x_n)_q)\big )\\ &\;\,\vdots\\ &=\mathbb{P}(X_1=x_1)\cdots\mathbb{P}(X_1=x_{n-1})\sum_{j=0}^{q-1}\mathbb{P}(X_1=j) \big (F(x_n-j+1)-F(x_n-j)\big )\\ &=\mathbb{P}(X_1=x_1)\cdots \mathbb{P}(X_{1}=x_{n-1})\big (\mathbb{P}(X_1=x_n)(1-F(0))+\mathbb{P}(X_1=x_{n}+1)F(0)\big ).\end{align*}
Consequently, since
![]() $F(0)=0$
and by stationarity the
$F(0)=0$
and by stationarity the
![]() $X_n$
are identically distributed,
$X_n$
are identically distributed,
![]() $\mathbb{P}(X_1=x_1,\dots, X_n=x_n)=\mathbb{P}(X_1=x_1)\cdots \mathbb{P}(X_{1}=x_{n})=\mathbb{P}(X_n=x_1)\cdots \mathbb{P}(X_{n}=x_{n})$
. Therefore, the
$\mathbb{P}(X_1=x_1,\dots, X_n=x_n)=\mathbb{P}(X_1=x_1)\cdots \mathbb{P}(X_{1}=x_{n})=\mathbb{P}(X_n=x_1)\cdots \mathbb{P}(X_{n}=x_{n})$
. Therefore, the
![]() $X_n$
are i.i.d.
$X_n$
are i.i.d.
3.3. Proof of Proposition 2.2 and related examples
Proof of Proposition
2.2.We first claim that for every
![]() $n\in\mathbb N$
, there exists a Borel set
$n\in\mathbb N$
, there exists a Borel set
![]() $A_n\subseteq [0, 1]$
of Lebesgue measure 1 such that, for all
$A_n\subseteq [0, 1]$
of Lebesgue measure 1 such that, for all
![]() $x\in A_n$
,
$x\in A_n$
,
 \begin{equation} f(x)=q^{-n}\sum_{j=0}^{q^n-1} f((x+j)/q^n). \end{equation}
\begin{equation} f(x)=q^{-n}\sum_{j=0}^{q^n-1} f((x+j)/q^n). \end{equation}
The case
![]() $n=1$
follows by the assumption in Proposition 2.2. Define
$n=1$
follows by the assumption in Proposition 2.2. Define
 \begin{equation*} \tilde{A}_2\,:\!=\, \bigcup_{j=0}^{q-1} \frac{A_1+j}{q},\qquad A_2\,:\!=\, A_1 \cap \tilde{A}_2. \end{equation*}
\begin{equation*} \tilde{A}_2\,:\!=\, \bigcup_{j=0}^{q-1} \frac{A_1+j}{q},\qquad A_2\,:\!=\, A_1 \cap \tilde{A}_2. \end{equation*}
Since the Lebesgue measure of
![]() $({A_1+j})/{q} \cap ({A_1+k})/{q}$
is 0 for
$({A_1+j})/{q} \cap ({A_1+k})/{q}$
is 0 for
![]() $j \neq k$
,
$j \neq k$
,
![]() $\tilde{A}_2$
and hence
$\tilde{A}_2$
and hence
![]() $A_2$
have Lebesgue measure 1. For every
$A_2$
have Lebesgue measure 1. For every
![]() $x\in A_2$
we have
$x\in A_2$
we have
![]() $(x+j)/q\in A_1$
and hence, using (2.3) for
$(x+j)/q\in A_1$
and hence, using (2.3) for
![]() $f((x+j)/q)$
, we obtain
$f((x+j)/q)$
, we obtain
 \begin{align*} f(x)=q^{-2} \sum_{j=0}^{q-1} \sum_{k=0}^{q-1} f\bigg( \frac{x+j}{q^2} + \frac{k}{q} \bigg) = q^{-2} \sum_{j=0}^{q^2-1} f\bigg( \frac{x+j}{q^2}\bigg). \end{align*}
\begin{align*} f(x)=q^{-2} \sum_{j=0}^{q-1} \sum_{k=0}^{q-1} f\bigg( \frac{x+j}{q^2} + \frac{k}{q} \bigg) = q^{-2} \sum_{j=0}^{q^2-1} f\bigg( \frac{x+j}{q^2}\bigg). \end{align*}
Continuing in this way the claim is verified. Define
![]() $\mathcal{I}\,:\!=\,\int_0^1 f(t) \, \mathrm{d} t\in \mathbb{C}$
and
$\mathcal{I}\,:\!=\,\int_0^1 f(t) \, \mathrm{d} t\in \mathbb{C}$
and
![]() $I_{j,n}\,:\!=\,(jq^{-n},jq^{-n}+q^{-n})$
. Then (3.8) gives, for all
$I_{j,n}\,:\!=\,(jq^{-n},jq^{-n}+q^{-n})$
. Then (3.8) gives, for all
![]() $x\in A_n$
,
$x\in A_n$
,
![]() $f(x)-\mathcal{I}=\sum_{j=0}^{q^n-1} \int_{I_{j,n}} \{ f((x+j)/q^n) -f(y) \}\,\mathrm{d} y$
, so
$f(x)-\mathcal{I}=\sum_{j=0}^{q^n-1} \int_{I_{j,n}} \{ f((x+j)/q^n) -f(y) \}\,\mathrm{d} y$
, so
![]() $|f(x)-\mathcal{I}|\leq \sum_{j=0}^{q^n-1} \int_{I_{j,n}} \vert f((x+j)/q^n) -f(y) \vert \,\mathrm{d} y$
. Integrating with respect to
$|f(x)-\mathcal{I}|\leq \sum_{j=0}^{q^n-1} \int_{I_{j,n}} \vert f((x+j)/q^n) -f(y) \vert \,\mathrm{d} y$
. Integrating with respect to
![]() $x\in[0, 1]$
and making the change of variable
$x\in[0, 1]$
and making the change of variable
![]() $t =(x+j)/q^n\in I_{j,n}$
, we obtain
$t =(x+j)/q^n\in I_{j,n}$
, we obtain
 \begin{equation} \int_0^1|f(x)-\mathcal{I}|\,\mathrm{d} x\leq q^n\sum_{j=0}^{q^n-1} \int_{I_{j,n}}\int_{I_{j,n}}|f(t) -f(y)|\,\mathrm{d} y\,\mathrm{d} t. \end{equation}
\begin{equation} \int_0^1|f(x)-\mathcal{I}|\,\mathrm{d} x\leq q^n\sum_{j=0}^{q^n-1} \int_{I_{j,n}}\int_{I_{j,n}}|f(t) -f(y)|\,\mathrm{d} y\,\mathrm{d} t. \end{equation}
Now, for any
![]() $\varepsilon>0$
, there exists a uniformly continuous function
$\varepsilon>0$
, there exists a uniformly continuous function
![]() $g_\varepsilon \,:\, [0, 1]\to\mathbb R$
such that
$g_\varepsilon \,:\, [0, 1]\to\mathbb R$
such that
![]() $\Vert f-g_\varepsilon\Vert_{L^1}\leq \varepsilon /3$
, where we consider the usual
$\Vert f-g_\varepsilon\Vert_{L^1}\leq \varepsilon /3$
, where we consider the usual
![]() $L^1$
-norm. Writing
$L^1$
-norm. Writing
![]() $|f(t)-f(y)|\leq |f(t)-g_\varepsilon(t)|+| f(y)-g_\varepsilon(y)|+|g_\varepsilon (t)-g_\varepsilon(y)|$
, we obtain from (3.9) that
$|f(t)-f(y)|\leq |f(t)-g_\varepsilon(t)|+| f(y)-g_\varepsilon(y)|+|g_\varepsilon (t)-g_\varepsilon(y)|$
, we obtain from (3.9) that
![]() $\int_0^1|f(x)-\mathcal{I}|\,\mathrm{d} x\leq 2\varepsilon/3 +\sup_{|t-y|\leq q^{-n}} |g_\varepsilon (t)-g_\varepsilon(y)|$
. Since
$\int_0^1|f(x)-\mathcal{I}|\,\mathrm{d} x\leq 2\varepsilon/3 +\sup_{|t-y|\leq q^{-n}} |g_\varepsilon (t)-g_\varepsilon(y)|$
. Since
![]() $g_\varepsilon$
is uniformly continuous, for any sufficiently large
$g_\varepsilon$
is uniformly continuous, for any sufficiently large
![]() $n=n(\varepsilon)\in\mathbb N$
we have
$n=n(\varepsilon)\in\mathbb N$
we have
![]() $\sup_{|t-y|\leq q^{-n(\varepsilon)}} |g_\varepsilon (t)-g_\varepsilon(y)|\leq \varepsilon/3$
. Thus,
$\sup_{|t-y|\leq q^{-n(\varepsilon)}} |g_\varepsilon (t)-g_\varepsilon(y)|\leq \varepsilon/3$
. Thus,
![]() $\int_0^1|f(x)-\mathcal{I}|\,\mathrm{d} x\leq \varepsilon$
. Consequently,
$\int_0^1|f(x)-\mathcal{I}|\,\mathrm{d} x\leq \varepsilon$
. Consequently,
![]() $f=\mathcal{I}$
almost everywhere on [0, 1].
$f=\mathcal{I}$
almost everywhere on [0, 1].
We end this section by presenting two examples of functions
![]() $f\not\in L^1([0, 1])$
where (2.3) is satisfied but in one case f is not absolutely integrable and in the other case f is not measurable.
$f\not\in L^1([0, 1])$
where (2.3) is satisfied but in one case f is not absolutely integrable and in the other case f is not measurable.
Example 3.1. (A solution to (2.3) which is not in
![]() $L^1([0, 1])$
.) Let
$L^1([0, 1])$
.) Let
![]() $q=2$
. Below we construct a solution to (2.3) which is piecewise smooth on [0, 1], has finite jumps at all dyadic fractions
$q=2$
. Below we construct a solution to (2.3) which is piecewise smooth on [0, 1], has finite jumps at all dyadic fractions
![]() $1-2^{-n}$
with
$1-2^{-n}$
with
![]() $n\in\mathbb N$
, but whose integral diverges.
$n\in\mathbb N$
, but whose integral diverges.
For this, we notice the following. For any function
![]() $f\,:\,[0, 1]\rightarrow\mathbb R$
, define
$f\,:\,[0, 1]\rightarrow\mathbb R$
, define
![]() $g(x)\,:\!=\,f(x)-1/(1-x)$
for
$g(x)\,:\!=\,f(x)-1/(1-x)$
for
![]() $x\in[0, 1)$
, and let g(1) be any number. Then f satisfies (2.3) if and only if g satisfies the equation
$x\in[0, 1)$
, and let g(1) be any number. Then f satisfies (2.3) if and only if g satisfies the equation
To construct a particular solution g to (3.10), we start by setting
![]() $g(x)\,:\!=\,0$
for all
$g(x)\,:\!=\,0$
for all
![]() $x\in \big[0,\frac12\big)$
. Then
$x\in \big[0,\frac12\big)$
. Then
![]() $g(x/2)=0$
for all
$g(x/2)=0$
for all
![]() $x\in [0, 1)$
, and in accordance with (3.10) we should have
$x\in [0, 1)$
, and in accordance with (3.10) we should have
which is possible because of the following observations. For each
![]() $n\in\mathbb N\cup\{0\}$
, the map
$n\in\mathbb N\cup\{0\}$
, the map
![]() $[1-2^{-n},1-2^{-n-1})\ni {\color{black}x\mapsto (x+1)/2}\in [1-2^{-n-1},1-2^{-n-2})$
is a bijection. Thus, for
$[1-2^{-n},1-2^{-n-1})\ni {\color{black}x\mapsto (x+1)/2}\in [1-2^{-n-1},1-2^{-n-2})$
is a bijection. Thus, for
![]() $n=1,2,\ldots$
, we can inductively use (3.11) to compute g(x) for all
$n=1,2,\ldots$
, we can inductively use (3.11) to compute g(x) for all
![]() $x\in [1-2^{-n},1-2^{-n-1})$
. We see that g becomes more and more negative near 1. Now, the function
$x\in [1-2^{-n},1-2^{-n-1})$
. We see that g becomes more and more negative near 1. Now, the function
![]() $f(x)=g(x)+1/(1-x)$
is not constant on [0, 1), since
$f(x)=g(x)+1/(1-x)$
is not constant on [0, 1), since
![]() $f(x)=1/(1-x)$
on
$f(x)=1/(1-x)$
on
![]() $[0,\frac12)$
. Although f satisfies (2.3) and is smooth on each interval
$[0,\frac12)$
. Although f satisfies (2.3) and is smooth on each interval
![]() $[1-2^{-n},1-2^{-n-1})$
with
$[1-2^{-n},1-2^{-n-1})$
with
![]() $n\in\mathbb N$
, f cannot have a finite integral due to Proposition 2.2. Figure 1 shows a plot of f.
$n\in\mathbb N$
, f cannot have a finite integral due to Proposition 2.2. Figure 1 shows a plot of f.

Figure 1. The function
![]() $f(x)=g(x)+1/(1-x)$
for
$f(x)=g(x)+1/(1-x)$
for
![]() $x\in[0,1-2^{-4}]$
, where g is given in Example 3.1.
$x\in[0,1-2^{-4}]$
, where g is given in Example 3.1.
Example 3.2. (A non-measurable solution to (2.3).) Let
![]() $q=2$
. Below we construct a solution to (2.3) which is bounded but cannot be measurable.
$q=2$
. Below we construct a solution to (2.3) which is bounded but cannot be measurable.
Define
![]() $G\,:\!=\,\{(2^n,r) \mid n\in\mathbb Z,\,r\in\mathbb D\}$
, where
$G\,:\!=\,\{(2^n,r) \mid n\in\mathbb Z,\,r\in\mathbb D\}$
, where
![]() $\mathbb D\,:\!=\,\{{m}2^{-n} \mid m\in\mathbb Z,\,n\in\mathbb N\}$
. Then G is a group with product
$\mathbb D\,:\!=\,\{{m}2^{-n} \mid m\in\mathbb Z,\,n\in\mathbb N\}$
. Then G is a group with product
![]() $(2^m,p)(2^n,r)=(2^{m+n},p+2^mr)$
for
$(2^m,p)(2^n,r)=(2^{m+n},p+2^mr)$
for
![]() $(2^m,p),(2^n,r)\in G$
, and G acts on
$(2^m,p),(2^n,r)\in G$
, and G acts on
![]() $\mathbb R$
by
$\mathbb R$
by
![]() $(2^n,r)x\,:\!=\,2^nx+r$
for
$(2^n,r)x\,:\!=\,2^nx+r$
for
![]() $(2^n,r)\in G$
,
$(2^n,r)\in G$
,
![]() $x\in\mathbb R$
. For any
$x\in\mathbb R$
. For any
![]() $x\in [0, 1]$
, let
$x\in [0, 1]$
, let
![]() $M_x$
be the restriction of the orbit
$M_x$
be the restriction of the orbit
![]() $\{2^nx+r \mid n\in\mathbb Z,\,r\in\mathbb D\}$
to [0, 1] (this is a countable dense set in [0, 1]). Given any
$\{2^nx+r \mid n\in\mathbb Z,\,r\in\mathbb D\}$
to [0, 1] (this is a countable dense set in [0, 1]). Given any
![]() $x\in [0, 1]$
, then both
$x\in [0, 1]$
, then both
![]() $x/2$
and
$x/2$
and
![]() $(x+1)/2$
belong to
$(x+1)/2$
belong to
![]() $M_x$
.
$M_x$
.
By the axiom of choice, given any orbit restriction
![]() $M\cap [0, 1]$
, we can pick a representative
$M\cap [0, 1]$
, we can pick a representative
![]() $C(M)\in [0, 1]$
and thus construct a function
$C(M)\in [0, 1]$
and thus construct a function
![]() $f(x)\,:\!=\,C(M_x)\in [0, 1]$
,
$f(x)\,:\!=\,C(M_x)\in [0, 1]$
,
![]() $x\in [0, 1]$
. Then f is constant on each orbit, though with different constants on different orbits. Since x,
$x\in [0, 1]$
. Then f is constant on each orbit, though with different constants on different orbits. Since x,
![]() $x/2$
, and
$x/2$
, and
![]() $(x+1)/2$
always belong to the same orbit, (2.3) is satisfied everywhere. We now show that this (bounded) function cannot be measurable due to Proposition 2.2. Indeed, if f was measurable, it would be integrable and equal to a constant on [0, 1] outside some set A of zero Lebesgue measure. Since f has different (constant) values on different orbits and because f is constant on
$(x+1)/2$
always belong to the same orbit, (2.3) is satisfied everywhere. We now show that this (bounded) function cannot be measurable due to Proposition 2.2. Indeed, if f was measurable, it would be integrable and equal to a constant on [0, 1] outside some set A of zero Lebesgue measure. Since f has different (constant) values on different orbits and because f is constant on
![]() $[0, 1]\setminus A$
, it implies that
$[0, 1]\setminus A$
, it implies that
![]() $[0, 1]\setminus A$
is a subset of exactly one orbit. As the orbit is countable and has Lebesgue measure zero, it follows that the Lebesgue measure of [0, 1] is zero. Hence we have a contradiction.
$[0, 1]\setminus A$
is a subset of exactly one orbit. As the orbit is countable and has Lebesgue measure zero, it follows that the Lebesgue measure of [0, 1] is zero. Hence we have a contradiction.
3.4. Proof of Theorem 2.2
First, we prove Theorem 2.2(I) with
![]() $\tilde X$
,
$\tilde X$
,
![]() $\tilde{F}$
, and
$\tilde{F}$
, and
![]() $\tilde{f}$
as in the theorem and
$\tilde{f}$
as in the theorem and
![]() $S_j(x)=(x+j)/q$
as in Section 2.3. Note that, for any
$S_j(x)=(x+j)/q$
as in Section 2.3. Note that, for any
![]() $k\in\mathbb{Z}$
,
$k\in\mathbb{Z}$
,
 \begin{align} \tilde{f}(2\pi k q)&=\int_0^1 \exp\!(2\pi \mathrm{i} x kq)\, \mathrm{d} \tilde F(x)\nonumber =\sum_{j=0}^{q-1}\int_{j/q}^{(j+1)/q} \exp\!(2\pi \mathrm{i} x k q)\, \mathrm{d} \tilde F(x)\\\nonumber&=\sum_{j=0}^{q-1}\int_{0}^{1} \exp\!(2\pi \mathrm{i} (x+j) k)\, \mathrm{d} (\tilde F\circ S_j)(x)\\&=\int_{0}^{1} \exp\!(2\pi \mathrm{i} x k) \,\mathrm{d} \Bigg(\sum_{j=0}^{q-1}\tilde F\circ S_j\Bigg)(x).\end{align}
\begin{align} \tilde{f}(2\pi k q)&=\int_0^1 \exp\!(2\pi \mathrm{i} x kq)\, \mathrm{d} \tilde F(x)\nonumber =\sum_{j=0}^{q-1}\int_{j/q}^{(j+1)/q} \exp\!(2\pi \mathrm{i} x k q)\, \mathrm{d} \tilde F(x)\\\nonumber&=\sum_{j=0}^{q-1}\int_{0}^{1} \exp\!(2\pi \mathrm{i} (x+j) k)\, \mathrm{d} (\tilde F\circ S_j)(x)\\&=\int_{0}^{1} \exp\!(2\pi \mathrm{i} x k) \,\mathrm{d} \Bigg(\sum_{j=0}^{q-1}\tilde F\circ S_j\Bigg)(x).\end{align}
If
![]() $\tilde F$
satisfies (2.1) then
$\tilde F$
satisfies (2.1) then
![]() $\mathrm{d} \tilde F=\sum_{j=0}^{q-1} \mathrm{d} (\tilde F\circ S_j)$
, which, combined with (3.12), shows that
$\mathrm{d} \tilde F=\sum_{j=0}^{q-1} \mathrm{d} (\tilde F\circ S_j)$
, which, combined with (3.12), shows that
for all
![]() $k\in \mathbb Z$
.
$k\in \mathbb Z$
.
Now, suppose that (3.13) holds for all
![]() $k\in \mathbb{Z}$
. Define
$k\in \mathbb{Z}$
. Define
![]() $\mathrm{d} \tilde G\,:\!=\,\mathrm{d} \big(\sum_{j=0}^{q-1} \tilde F\circ S_j\big)$
and
$\mathrm{d} \tilde G\,:\!=\,\mathrm{d} \big(\sum_{j=0}^{q-1} \tilde F\circ S_j\big)$
and
![]() $\tilde g(t)\,:\!=\,\int \mathrm{e}^{\mathrm{i}xt} \, \mathrm{d} \tilde G(x)$
. From (3.12) we have that
$\tilde g(t)\,:\!=\,\int \mathrm{e}^{\mathrm{i}xt} \, \mathrm{d} \tilde G(x)$
. From (3.12) we have that
![]() $\tilde{f}(2\pi kq)=\tilde{g}(2\pi k)$
which, together with (3.13), implies
$\tilde{f}(2\pi kq)=\tilde{g}(2\pi k)$
which, together with (3.13), implies
![]() $\tilde f(2\pi k)=\tilde g(2\pi k)$
for all
$\tilde f(2\pi k)=\tilde g(2\pi k)$
for all
![]() $k\in \mathbb{Z}$
. Recall that any continuous
$k\in \mathbb{Z}$
. Recall that any continuous
![]() $\mathbb{Z}$
-periodic function
$\mathbb{Z}$
-periodic function
![]() $\varphi\,:\, \mathbb{R}\to \mathbb{C}$
is a uniform limit of trigonometric polynomials
$\varphi\,:\, \mathbb{R}\to \mathbb{C}$
is a uniform limit of trigonometric polynomials
![]() $\sum_{k=- N}^N c_k^N\mathrm{e}^{2\pi \mathrm{i} kx}$
, where each
$\sum_{k=- N}^N c_k^N\mathrm{e}^{2\pi \mathrm{i} kx}$
, where each
![]() $c_k^N\in \mathbb{C}$
and
$c_k^N\in \mathbb{C}$
and
![]() $N\in \mathbb{N}$
[Reference Rudin21]. Taking the limit
$N\in \mathbb{N}$
[Reference Rudin21]. Taking the limit
![]() $N\to \infty$
and using Lebesgue’s dominated convergence theorem, we get
$N\to \infty$
and using Lebesgue’s dominated convergence theorem, we get
The remaining part of this proof consists of verifying (3.14) when
![]() $\varphi$
is merely continuous and then applying the Riesz–Markov theorem, which implies that a positive linear functional on
$\varphi$
is merely continuous and then applying the Riesz–Markov theorem, which implies that a positive linear functional on
![]() $C_0([0, 1])$
can be represented by a unique measure (see [Reference Riesz19]). First, we establish equality of
$C_0([0, 1])$
can be represented by a unique measure (see [Reference Riesz19]). First, we establish equality of
![]() $\mathrm{d} \tilde F$
and
$\mathrm{d} \tilde F$
and
![]() $\mathrm{d} \tilde G$
at the endpoints of the interval [0, 1]. Since the indicator function of
$\mathrm{d} \tilde G$
at the endpoints of the interval [0, 1]. Since the indicator function of
![]() $\mathbb{Z}$
can be pointwise approximated by uniformly bounded continuous
$\mathbb{Z}$
can be pointwise approximated by uniformly bounded continuous
![]() $\mathbb{Z}$
-periodic functions, another application of Lebesgue’s dominated convergence theorem in (3.14) gives
$\mathbb{Z}$
-periodic functions, another application of Lebesgue’s dominated convergence theorem in (3.14) gives
![]() $\mathrm{d}\tilde F(\{0\})+\mathrm{d}\tilde F(\{1\})=\mathrm{d}\tilde G(\{0\})+\mathrm{d}\tilde G(\{1\})$
, where, by the definition of
$\mathrm{d}\tilde F(\{0\})+\mathrm{d}\tilde F(\{1\})=\mathrm{d}\tilde G(\{0\})+\mathrm{d}\tilde G(\{1\})$
, where, by the definition of
![]() $\mathrm d\tilde G$
,
$\mathrm d\tilde G$
,
![]() $\mathrm{d}\tilde G(\{0\})=\mathrm{d} \tilde F(\{0\}+\mathrm{d} \tilde F(\{1/q\})+\dots+\mathrm{d} \tilde F(\{(q-1)/q\})$
and
$\mathrm{d}\tilde G(\{0\})=\mathrm{d} \tilde F(\{0\}+\mathrm{d} \tilde F(\{1/q\})+\dots+\mathrm{d} \tilde F(\{(q-1)/q\})$
and
![]() $\mathrm{d}\tilde G(\{1\})=\mathrm{d} \tilde F(\{1/q\})+\dots+\mathrm{d} \tilde F(\{(q-1)/q\})+\mathrm{d}\tilde F(\{1\})$
. From this, it immediately follows that
$\mathrm{d}\tilde G(\{1\})=\mathrm{d} \tilde F(\{1/q\})+\dots+\mathrm{d} \tilde F(\{(q-1)/q\})+\mathrm{d}\tilde F(\{1\})$
. From this, it immediately follows that
![]() $\mathrm{d} \tilde{F}(\{j/q\})=0$
for
$\mathrm{d} \tilde{F}(\{j/q\})=0$
for
![]() $j=1,\ldots, q-1$
, which leads to
$j=1,\ldots, q-1$
, which leads to
![]() $\mathrm{d}\tilde F(\{0\})=\mathrm{d} \tilde G(\{0\})$
and
$\mathrm{d}\tilde F(\{0\})=\mathrm{d} \tilde G(\{0\})$
and
![]() $\mathrm{d}\tilde F(\{1\})=\mathrm{d} \tilde G(\{1\})$
. Second, we extend (3.14) to all continuous functions on [0, 1] in the following way. If
$\mathrm{d}\tilde F(\{1\})=\mathrm{d} \tilde G(\{1\})$
. Second, we extend (3.14) to all continuous functions on [0, 1] in the following way. If
![]() $\psi\,:\, [0, 1]\to \mathbb{C}$
is continuous, define, for
$\psi\,:\, [0, 1]\to \mathbb{C}$
is continuous, define, for
![]() $n=1,2,\dots$
,
$n=1,2,\dots$
,
 \begin{equation*}\varphi_n(x)\,:\!=\, \begin{cases} \psi(x)& \textrm{ for } x\in \big[0,1-\frac 1 n\big], \\[7pt] n\big[\psi(0)-\psi\big(1-\frac{1}{n}\big)\big]\big(x-\big(1-\frac 1 n\big)\big)+\psi\big(1-\frac{1}{n}\big)& \textrm{ for } x\in \big(1-\frac{1}{n},1\big]. \end{cases}\end{equation*}
\begin{equation*}\varphi_n(x)\,:\!=\, \begin{cases} \psi(x)& \textrm{ for } x\in \big[0,1-\frac 1 n\big], \\[7pt] n\big[\psi(0)-\psi\big(1-\frac{1}{n}\big)\big]\big(x-\big(1-\frac 1 n\big)\big)+\psi\big(1-\frac{1}{n}\big)& \textrm{ for } x\in \big(1-\frac{1}{n},1\big]. \end{cases}\end{equation*}
This is a uniformly bounded sequence of continuous and
![]() $\mathbb{Z}$
-periodic functions converging pointwise to
$\mathbb{Z}$
-periodic functions converging pointwise to
![]() $\psi$
on [0, 1). Since
$\psi$
on [0, 1). Since
![]() $\mathrm{d} \tilde F(\{1\})=\mathrm{d} \tilde G(\{1\})$
, it follows from Lebesgue’s dominated convergence theorem that
$\mathrm{d} \tilde F(\{1\})=\mathrm{d} \tilde G(\{1\})$
, it follows from Lebesgue’s dominated convergence theorem that
 \begin{align*}\int_{[0, 1]} \psi(x) \,\mathrm{d} \tilde F(x)&= \mathrm{d} \tilde F(\{1\})\psi(1)+\lim_{n\to \infty} \int_{[0, 1)}\varphi_n(x) \,\mathrm{d} \tilde F(x)\\&=\mathrm{d} \tilde G(\{1\})\psi(1)+\lim_{n\to \infty} \int_{[0, 1)}\varphi_n(x) \,\mathrm{d} \tilde G(x)\\&=\int_{[0, 1]} \psi(x) \,\mathrm{d} \tilde G(x).\end{align*}
\begin{align*}\int_{[0, 1]} \psi(x) \,\mathrm{d} \tilde F(x)&= \mathrm{d} \tilde F(\{1\})\psi(1)+\lim_{n\to \infty} \int_{[0, 1)}\varphi_n(x) \,\mathrm{d} \tilde F(x)\\&=\mathrm{d} \tilde G(\{1\})\psi(1)+\lim_{n\to \infty} \int_{[0, 1)}\varphi_n(x) \,\mathrm{d} \tilde G(x)\\&=\int_{[0, 1]} \psi(x) \,\mathrm{d} \tilde G(x).\end{align*}
The maps
![]() $C_0([0, 1])\ni\psi \mapsto \int_{[0, 1]} \psi(x) \, \mathrm{d}\tilde{F}(x) \in \mathbb{C}$
$C_0([0, 1])\ni\psi \mapsto \int_{[0, 1]} \psi(x) \, \mathrm{d}\tilde{F}(x) \in \mathbb{C}$
![]() $C_0([0, 1])\ni\psi \mapsto \int_{[0, 1]} \psi(x) \, \mathrm{d}\tilde{G}(x) \in \mathbb{C}$
are positive linear functionals and can be represented by a unique measure according to the Riesz–Markov theorem (see [Reference Riesz19]), thus
$C_0([0, 1])\ni\psi \mapsto \int_{[0, 1]} \psi(x) \, \mathrm{d}\tilde{G}(x) \in \mathbb{C}$
are positive linear functionals and can be represented by a unique measure according to the Riesz–Markov theorem (see [Reference Riesz19]), thus
![]() $\mathrm{d}\tilde F=\mathrm{d} \tilde G$
on [0, 1]. Equivalently,
$\mathrm{d}\tilde F=\mathrm{d} \tilde G$
on [0, 1]. Equivalently,
![]() $\tilde F$
satisfies (2.1) and the proof of Theorem 2.2(I) is complete.
$\tilde F$
satisfies (2.1) and the proof of Theorem 2.2(I) is complete.
Next, we prove Theorem 2.2(II). As the ‘if’ part of the proof follows from a direct calculation, we only prove that if
![]() $c\,:\!=\,\lim_{t\to \infty}f(t)\in \mathbb{C}$
exists, then
$c\,:\!=\,\lim_{t\to \infty}f(t)\in \mathbb{C}$
exists, then
![]() $0\leq c\leq 1$
and, for every
$0\leq c\leq 1$
and, for every
![]() $x\in[0, 1]$
,
$x\in[0, 1]$
,
where H is the Heaviside function. Since
![]() $\lim_{t \to \infty} f(t) = c$
, for any
$\lim_{t \to \infty} f(t) = c$
, for any
![]() $a\in \mathbb{R}$
a straightforward calculation gives
$a\in \mathbb{R}$
a straightforward calculation gives
 \begin{equation*} \lim_{T \to \infty} T^{-1}\int_0^T f(t)\mathrm{e}^{-\mathrm{i}ta}\,\mathrm{d} t =\left\{\begin{matrix}c\quad {\rm if}\; a=0, \\[4pt]0\quad {\rm if}\; a\neq 0.\end{matrix}\right .\end{equation*}
\begin{equation*} \lim_{T \to \infty} T^{-1}\int_0^T f(t)\mathrm{e}^{-\mathrm{i}ta}\,\mathrm{d} t =\left\{\begin{matrix}c\quad {\rm if}\; a=0, \\[4pt]0\quad {\rm if}\; a\neq 0.\end{matrix}\right .\end{equation*}
Define
 \begin{align*} f_T (x) \,:\!=\, \frac{1}{T}\int_0^T \mathrm e^{\mathrm{i}t(x-a)} \, \mathrm{d}t = \begin{cases} 1 & \textrm{ if } x=a, \\[4pt] (\mathrm{i}(x-a)T)^{-1}(\mathrm e^{\mathrm{i}T(x-a)}-1) & \textrm{ if } x \neq a.\end{cases}\end{align*}
\begin{align*} f_T (x) \,:\!=\, \frac{1}{T}\int_0^T \mathrm e^{\mathrm{i}t(x-a)} \, \mathrm{d}t = \begin{cases} 1 & \textrm{ if } x=a, \\[4pt] (\mathrm{i}(x-a)T)^{-1}(\mathrm e^{\mathrm{i}T(x-a)}-1) & \textrm{ if } x \neq a.\end{cases}\end{align*}
Using Fubini’s theorem we obtain
![]() $\frac{1}{T}\int_0^T f(t)\mathrm e^{-\mathrm{i}ta} \, \mathrm{d} t = \int_{[0, 1]} f_T(x) \, \mathrm{d} F(x)$
. Since
$\frac{1}{T}\int_0^T f(t)\mathrm e^{-\mathrm{i}ta} \, \mathrm{d} t = \int_{[0, 1]} f_T(x) \, \mathrm{d} F(x)$
. Since
![]() $\vert f_T(x)\vert \leq 1$
and
$\vert f_T(x)\vert \leq 1$
and
![]() $f_T(x)$
converges pointwise to the indicator function of the set
$f_T(x)$
converges pointwise to the indicator function of the set
![]() $\{a\}$
, an application of Lebesgue’s dominated convergence theorem shows that the above limit equals
$\{a\}$
, an application of Lebesgue’s dominated convergence theorem shows that the above limit equals
![]() $\mathrm{d} F(\{a\})$
. Consequently,
$\mathrm{d} F(\{a\})$
. Consequently,
![]() $c=F(0)\in[0, 1]$
and F is continuous on (0, 1).
$c=F(0)\in[0, 1]$
and F is continuous on (0, 1).
It remains to verify (3.15). If
![]() $c=1$
, then
$c=1$
, then
![]() $F=H$
and (3.15) follows. Assume
$F=H$
and (3.15) follows. Assume
![]() $c<1$
. Then
$c<1$
. Then
![]() $G(x)\,:\!=\,(F(x) - cH(x))/(1-c)$
is a continuous CDF that also satisfies the stationarity condition (2.1). Thus, defining
$G(x)\,:\!=\,(F(x) - cH(x))/(1-c)$
is a continuous CDF that also satisfies the stationarity condition (2.1). Thus, defining
![]() $g(t)\,:\!=\,\int \mathrm{e}^{\mathrm{i}tx} \, \mathrm{d} G(x)$
, we obtain the identity
$g(t)\,:\!=\,\int \mathrm{e}^{\mathrm{i}tx} \, \mathrm{d} G(x)$
, we obtain the identity
![]() $g(2\pi kq)=g(2\pi k)$
for all
$g(2\pi kq)=g(2\pi k)$
for all
![]() $k\in \mathbb{Z}$
. A repeated use of this identity gives, for any
$k\in \mathbb{Z}$
. A repeated use of this identity gives, for any
![]() $m\in\mathbb N$
and
$m\in\mathbb N$
and
![]() $k\in\mathbb{Z}$
,
$k\in\mathbb{Z}$
,
From the definition of G it follows that
![]() $\lim_{t \to \infty} g(t) = 0$
, and since c is real we also obtain
$\lim_{t \to \infty} g(t) = 0$
, and since c is real we also obtain
![]() $\lim_{t \to -\infty} g(t) = 0$
. Combining this with (3.16) where we take m to infinity, we conclude that
$\lim_{t \to -\infty} g(t) = 0$
. Combining this with (3.16) where we take m to infinity, we conclude that
![]() $g(2\pi k)=0$
for all
$g(2\pi k)=0$
for all
![]() $k\in\mathbb{Z}\setminus\{ 0\}$
. If
$k\in\mathbb{Z}\setminus\{ 0\}$
. If
![]() $h(t)\,:\!=\,\int_0^1 \mathrm{e}^{\mathrm{i}tx} \, \mathrm{d} x$
, then also
$h(t)\,:\!=\,\int_0^1 \mathrm{e}^{\mathrm{i}tx} \, \mathrm{d} x$
, then also
![]() $h(2\pi k)=0$
for all
$h(2\pi k)=0$
for all
![]() $k\in \mathbb{Z}\setminus\{0\}$
, and since
$k\in \mathbb{Z}\setminus\{0\}$
, and since
![]() $\mathrm{d} G(\{1\})=0$
it follows from the same arguments as in the proof of Theorem 2.2(I) that
$\mathrm{d} G(\{1\})=0$
it follows from the same arguments as in the proof of Theorem 2.2(I) that
![]() $\mathrm{d} G=\mathrm{d} x$
on [0, 1]. Consequently,
$\mathrm{d} G=\mathrm{d} x$
on [0, 1]. Consequently,
![]() $F(x)=(1-c)x+cH(x)$
for all
$F(x)=(1-c)x+cH(x)$
for all
![]() $x\in[0, 1]$
.
$x\in[0, 1]$
.
3.5. Proof of Theorem 2.3
The Lebesgue–Radon–Nikodym theorem [Reference Billingsley3, Reference Folland7] leads to the decomposition
![]() $F(x) = \theta_1 F_1(x) + \theta_2 F_2(x) + \theta_3 F_3(x)$
for
$F(x) = \theta_1 F_1(x) + \theta_2 F_2(x) + \theta_3 F_3(x)$
for
![]() $x\in [0, 1]$
, where
$x\in [0, 1]$
, where
![]() $\theta_1,\theta_2,\theta_3\geq 0$
and
$\theta_1,\theta_2,\theta_3\geq 0$
and
![]() $\theta_1 + \theta_2 + \theta_3 = 1$
,
$\theta_1 + \theta_2 + \theta_3 = 1$
,
![]() $F_1$
is an absolutely continuous CDF on [0, 1],
$F_1$
is an absolutely continuous CDF on [0, 1],
![]() $F_2$
is a discrete CDF on [0, 1], and
$F_2$
is a discrete CDF on [0, 1], and
![]() $F_3$
is singular continuous CDF on [0, 1]. Proposition 2.2 implies that
$F_3$
is singular continuous CDF on [0, 1]. Proposition 2.2 implies that
![]() $F^{\prime}_1 =1$
almost everywhere on [0, 1], and so since
$F^{\prime}_1 =1$
almost everywhere on [0, 1], and so since
![]() $F_1$
is absolutely continuous,
$F_1$
is absolutely continuous,
![]() $F_1(x)=x$
for all
$F_1(x)=x$
for all
![]() $x\in [0, 1]$
. Thus,
$x\in [0, 1]$
. Thus,
![]() $F_1$
satisfies (2.1) and it only remains to show that
$F_1$
satisfies (2.1) and it only remains to show that
![]() $F_2$
is as claimed in Theorem 2.3(II) and satisfies (2.1).
$F_2$
is as claimed in Theorem 2.3(II) and satisfies (2.1).
3.5.1. Proof of Theorem 2.3(II)
Lemma 3.3. Suppose that F satisfies (2.1) and
![]() $s\in[0, 1]$
is a discontinuity of F. Then there exists
$s\in[0, 1]$
is a discontinuity of F. Then there exists
![]() $n\in\mathbb{N}$
and a cycle
$n\in\mathbb{N}$
and a cycle
![]() $(s_1,\ldots,s_n)$
in the sense of (2.4) such that
$(s_1,\ldots,s_n)$
in the sense of (2.4) such that
![]() $s=s_1$
and
$s=s_1$
and
![]() $s_1,\ldots,s_n$
are discontinuities of F. Furthermore, the jumps of F at these n discontinuities are all equal.
$s_1,\ldots,s_n$
are discontinuities of F. Furthermore, the jumps of F at these n discontinuities are all equal.
Proof. We start by investigating what can happen at 0 and 1. Both
![]() $0=(0.\overline{0})_q$
and
$0=(0.\overline{0})_q$
and
![]() $1=(0.\overline{q-1})_q$
are purely repeating base-q numbers of order 1, and they can be discontinuity points because both H(x) and
$1=(0.\overline{q-1})_q$
are purely repeating base-q numbers of order 1, and they can be discontinuity points because both H(x) and
![]() $H(x-1)$
satisfy (2.1). Therefore, in the following we will only consider possible discontinuities at
$H(x-1)$
satisfy (2.1). Therefore, in the following we will only consider possible discontinuities at
![]() $x\in (0, 1)$
. Our idea is then to show that each point of discontinuity belongs to a ‘cycle’ of finitely many points which are all discontinuities and the jump at each point is the same.
$x\in (0, 1)$
. Our idea is then to show that each point of discontinuity belongs to a ‘cycle’ of finitely many points which are all discontinuities and the jump at each point is the same.
As in Section 2.3, define
![]() $S_j(x)\,:\!=\,(x+j)/q$
for
$S_j(x)\,:\!=\,(x+j)/q$
for
![]() $x\in (0, 1)$
and
$x\in (0, 1)$
and
![]() $j=0,\dots,q-1$
. Then, by Theorem 2.1, it follows that, for any
$j=0,\dots,q-1$
. Then, by Theorem 2.1, it follows that, for any
![]() $x\in (0, 1)$
, there exists a sufficiently small
$x\in (0, 1)$
, there exists a sufficiently small
![]() $\delta_0>0$
such that, for all
$\delta_0>0$
such that, for all
![]() $\delta\in (0,\delta_0)$
,
$\delta\in (0,\delta_0)$
,
 \begin{equation} F(x)-F(x-\delta)=\sum_{j=0}^{q-1}[F(S_j(x))-F(S_j(x-\delta))].\end{equation}
\begin{equation} F(x)-F(x-\delta)=\sum_{j=0}^{q-1}[F(S_j(x))-F(S_j(x-\delta))].\end{equation}
For
![]() $x\in (0, 1)$
, define
$x\in (0, 1)$
, define
![]() $L_0(x)\,:\!=\,\{x\}$
and
$L_0(x)\,:\!=\,\{x\}$
and
![]() $L_n(x)\,:\!=\,\bigcup_{j=0}^{q-1}S_j(L_{n-1}(x))$
,
$L_n(x)\,:\!=\,\bigcup_{j=0}^{q-1}S_j(L_{n-1}(x))$
,
![]() $n=1,2,\ldots$
Furthermore, let
$n=1,2,\ldots$
Furthermore, let
![]() $J_x\,:\!=\,\lim_{\delta\downarrow 0} [F(x)-F(x-\delta)]$
denote the jump of F at
$J_x\,:\!=\,\lim_{\delta\downarrow 0} [F(x)-F(x-\delta)]$
denote the jump of F at
![]() $x\in (0, 1)$
. Taking
$x\in (0, 1)$
. Taking
![]() $\delta\downarrow 0$
in (3.17) shows that
$\delta\downarrow 0$
in (3.17) shows that
Suppose
![]() $s\in (0, 1)$
is a discontinuity of F with jump
$s\in (0, 1)$
is a discontinuity of F with jump
![]() $J_s>0$
, and let
$J_s>0$
, and let
![]() $k>1/J_s$
be an integer. First, we show that the sets
$k>1/J_s$
be an integer. First, we show that the sets
![]() $L_0(s), \dots, L_k(s)$
are not pairwise disjoint. For the purpose of a contradiction assume that
$L_0(s), \dots, L_k(s)$
are not pairwise disjoint. For the purpose of a contradiction assume that
![]() $L_0(s), \dots, L_k(s)$
are pairwise disjoint. By assumption
$L_0(s), \dots, L_k(s)$
are pairwise disjoint. By assumption
![]() $s\not \in L_1(s)$
, thus replacing
$s\not \in L_1(s)$
, thus replacing
![]() $x=s$
in (3.18) shows that F has a total jump of at least
$x=s$
in (3.18) shows that F has a total jump of at least
![]() $2J_s$
: one
$2J_s$
: one
![]() $J_s$
from s, and the other
$J_s$
from s, and the other
![]() $J_s$
from the accumulated contribution of all the points of
$J_s$
from the accumulated contribution of all the points of
![]() $L_1(s)$
. Using (3.18) for
$L_1(s)$
. Using (3.18) for
![]() $x=S_j(s)$
with
$x=S_j(s)$
with
![]() $j=0,\ldots,q-1$
, we see that the possible jump at each
$j=0,\ldots,q-1$
, we see that the possible jump at each
![]() $S_j(s)$
equals the total accumulated jump at the points of
$S_j(s)$
equals the total accumulated jump at the points of
![]() $L_1(S_j(s))$
. Hence, by assumption, the total jump of F at the points of
$L_1(S_j(s))$
. Hence, by assumption, the total jump of F at the points of
![]() $L_2(s)$
is again
$L_2(s)$
is again
![]() $J_s$
. Continuing this way we obtain that
$J_s$
. Continuing this way we obtain that
![]() $\sum_{x\in L_j(s)} J_x =J_s$
for
$\sum_{x\in L_j(s)} J_x =J_s$
for
![]() $j=0,1,\dots, k$
. By the choice of k this contradicts
$j=0,1,\dots, k$
. By the choice of k this contradicts
![]() $F\leq 1$
and hence the sets
$F\leq 1$
and hence the sets
![]() $L_0(s), \dots, L_k(s)$
are not pairwise disjoint.
$L_0(s), \dots, L_k(s)$
are not pairwise disjoint.
Next, let n denote the smallest integer (not necessarily larger than
![]() $1/J_s$
) such that
$1/J_s$
) such that
![]() $L_0(s),\dots,L_n(s)$
are not pairwise disjoint. We will show that
$L_0(s),\dots,L_n(s)$
are not pairwise disjoint. We will show that
![]() $s\in L_n(s)$
. Suppose this is not the case. Then by the choice of n there exist an integer m with
$s\in L_n(s)$
. Suppose this is not the case. Then by the choice of n there exist an integer m with
![]() $1\leq m<n$
and
$1\leq m<n$
and
![]() $j_1,\dots,j_{m},j^{\prime}_1,\dots,j^{\prime}_{n}\in \{0,\dots,q-1\}$
such that
$j_1,\dots,j_{m},j^{\prime}_1,\dots,j^{\prime}_{n}\in \{0,\dots,q-1\}$
such that
If
![]() $s=(0.t_1 t_2\dots)_q$
, then from (3.19) it follows that
$s=(0.t_1 t_2\dots)_q$
, then from (3.19) it follows that
![]() $(0.j_1\dots j_m t_1t_2\dots)_q=S_{j_1}\circ \dots \circ S_{j_m}(s)=S_{j^{\prime}_1}\circ \dots \circ S_{j^{\prime}_{n}}(s)=(0.j^{\prime}_1\dots j^{\prime}_{n} t_1t_2\dots)_q$
, and thus
$(0.j_1\dots j_m t_1t_2\dots)_q=S_{j_1}\circ \dots \circ S_{j_m}(s)=S_{j^{\prime}_1}\circ \dots \circ S_{j^{\prime}_{n}}(s)=(0.j^{\prime}_1\dots j^{\prime}_{n} t_1t_2\dots)_q$
, and thus
![]() $S_{j^{\prime}_{m+1}}\circ\dots \circ S_{j^{\prime}_{n}}(s)=s$
, contradicting the minimality of n. Hence,
$S_{j^{\prime}_{m+1}}\circ\dots \circ S_{j^{\prime}_{n}}(s)=s$
, contradicting the minimality of n. Hence,
![]() $s\in L_n(s)$
, which implies that there exist
$s\in L_n(s)$
, which implies that there exist
![]() $i_1,\dots,i_n\in\{0,\dots,q-1\}$
such that
$i_1,\dots,i_n\in\{0,\dots,q-1\}$
such that
![]() $S_{i_1}\circ \dots \circ S_{i_n}(s)=s$
. Note that
$S_{i_1}\circ \dots \circ S_{i_n}(s)=s$
. Note that
![]() $(0.\overline{i_1\dots i_n})_q$
is also a fixed point of
$(0.\overline{i_1\dots i_n})_q$
is also a fixed point of
![]() $S_{i_1}\circ\dots S_{i_n}$
, but since
$S_{i_1}\circ\dots S_{i_n}$
, but since
![]() $S_{i_1}\circ\dots S_{i_n}$
is a contraction on [0, 1] (with Lipschitz constant
$S_{i_1}\circ\dots S_{i_n}$
is a contraction on [0, 1] (with Lipschitz constant
![]() $q^{-n}$
) it has a unique fixed point and we must have
$q^{-n}$
) it has a unique fixed point and we must have
![]() $s=(0.\overline{i_1\dots i_n})_q$
.
$s=(0.\overline{i_1\dots i_n})_q$
.
By definition
![]() $S_{i_n}(s)\in L_1(s)$
, and from (3.18) we deduce that
$S_{i_n}(s)\in L_1(s)$
, and from (3.18) we deduce that
![]() $J_s\geq J_{S_{i_n}(s)}$
. Letting
$J_s\geq J_{S_{i_n}(s)}$
. Letting
![]() $x=S_{i_n}(s)$
in the left-hand side of (3.18) we have that
$x=S_{i_n}(s)$
in the left-hand side of (3.18) we have that
![]() $J_s\geq J_{S_{i_n}(s)}\geq J_{S_{i_{n-1}}\circ S_{i_n}(s)}$
. Continuing in this way we see that
$J_s\geq J_{S_{i_n}(s)}\geq J_{S_{i_{n-1}}\circ S_{i_n}(s)}$
. Continuing in this way we see that
![]() $J_s\geq J_{S_{i_n}(s)}\geq \dots\geq J_{S_{i_2}\circ \dots \circ S_{i_n}(s)}\geq J_{S_{i_1}\circ \dots \circ S_{i_n}(s)}=J_{s}$
. This shows that the numbers
$J_s\geq J_{S_{i_n}(s)}\geq \dots\geq J_{S_{i_2}\circ \dots \circ S_{i_n}(s)}\geq J_{S_{i_1}\circ \dots \circ S_{i_n}(s)}=J_{s}$
. This shows that the numbers
![]() $s,S_{i_n}(s),\dots, S_{i_2}\circ \dots \circ S_{i_n}(s)$
are discontinuities of F with the same jump. By the minimality of n these points are distinct and hence constitute a cycle.
$s,S_{i_n}(s),\dots, S_{i_2}\circ \dots \circ S_{i_n}(s)$
are discontinuities of F with the same jump. By the minimality of n these points are distinct and hence constitute a cycle.
Now, Theorem 2.3(II) follows from Lemma 3.3 and the fact that F has countably many points of discontinuity.
3.5.2. Proof that
 $F_2$
satisfies (2.1)
$F_2$
satisfies (2.1)
Because of Theorem 2.3(II), in order to show that
![]() $F_2$
satisfies (2.1), without loss of generality we may assume that
$F_2$
satisfies (2.1), without loss of generality we may assume that
![]() $F_2(x)=\frac{1}{n}\sum_{j=1}^n H(x-s_j)$
, where
$F_2(x)=\frac{1}{n}\sum_{j=1}^n H(x-s_j)$
, where
![]() $(s_1,\ldots,s_n)$
is a cycle. For each
$(s_1,\ldots,s_n)$
is a cycle. For each
![]() $j \in \{1,\dots,n\}$
, let
$j \in \{1,\dots,n\}$
, let
![]() $s_{j}(1)$
denote the first digit in the base-q expansion of
$s_{j}(1)$
denote the first digit in the base-q expansion of
![]() $s_j$
and note that
$s_j$
and note that
![]() $qs_j=s_{j-1}+s_{j}(1)$
, where we define
$qs_j=s_{j-1}+s_{j}(1)$
, where we define
![]() $s_0\,:\!=\,s_n$
. Hence, for any
$s_0\,:\!=\,s_n$
. Hence, for any
![]() $k\in \mathbb{Z}$
, the characteristic function
$k\in \mathbb{Z}$
, the characteristic function
![]() $f_2$
of
$f_2$
of
![]() $F_2$
satisfies
$F_2$
satisfies
 \begin{equation*} f_2(2\pi k q)=\frac{1}{n}\sum_{j=1}^n \mathrm{e}^{2\pi \mathrm{i} k q s_j} =\frac{1}{n}\sum_{j=1}^n \mathrm{e}^{2\pi \mathrm{i} k s_{j-1}}= f_2(2\pi k).\end{equation*}
\begin{equation*} f_2(2\pi k q)=\frac{1}{n}\sum_{j=1}^n \mathrm{e}^{2\pi \mathrm{i} k q s_j} =\frac{1}{n}\sum_{j=1}^n \mathrm{e}^{2\pi \mathrm{i} k s_{j-1}}= f_2(2\pi k).\end{equation*}
Then, by Theorem 2.2(I) it follows that
![]() $F_2$
satisfies (2.1).
$F_2$
satisfies (2.1).
Funding information
JM and HC are supported in part by The Danish Council for Independent Research | Natural Sciences, grant 7014-00074B, ‘Statistics for point processes in space and beyond’. JM, BS, and KSS are supported in part by the Centre for Stochastic Geometry and Advanced Bioimaging, funded by grant 8721 from the Villum Foundation. This work was supported by The Danish Council for Independent Research | Natural Sciences, grant DFF – 10.46540/2032-00005B.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.