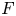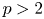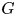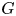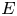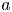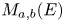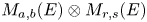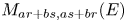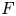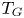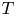1. Introduction
The term “verbally prime algebra” was introduced by A. Kemer [Reference Kemer23] in his solution to the Specht problem. These algebras play a crucial role in the theory developed by Kemer. An algebra $A$![]() is verbally prime if, whenever $f(x_1,\ldots, x_r)$
is verbally prime if, whenever $f(x_1,\ldots, x_r)$![]() and $g(x_{r+1},\ldots, x_s)$
and $g(x_{r+1},\ldots, x_s)$![]() are two polynomials in distinct variables and $f\cdot g$
are two polynomials in distinct variables and $f\cdot g$![]() is an identity for $A$
is an identity for $A$![]() , then either $f$
, then either $f$![]() or $g$
or $g$![]() is an identity for $A$
is an identity for $A$![]() , or both are. Roughly speaking, $A$
, or both are. Roughly speaking, $A$![]() is verbally prime if its T-ideal (the ideal of all polynomial identities satisfied by $A$
is verbally prime if its T-ideal (the ideal of all polynomial identities satisfied by $A$![]() ) is prime inside the class of all T-ideals. Kemer proved that, in characteristic 0, every non-trivial verbally prime PI algebra is PI equivalent to one of the algebras $M_n(F)$
) is prime inside the class of all T-ideals. Kemer proved that, in characteristic 0, every non-trivial verbally prime PI algebra is PI equivalent to one of the algebras $M_n(F)$![]() , $M_n(E)$
, $M_n(E)$![]() or certain subalgebras $M_{a,b}(E)$
or certain subalgebras $M_{a,b}(E)$![]() of $M_{a+b}(E)$
of $M_{a+b}(E)$![]() . This latter algebra consists of all matrices of the form
. This latter algebra consists of all matrices of the form
where $A\in M_{a}(E_{(0)})$![]() , $D\in M_{b}(E_{(0)})$
, $D\in M_{b}(E_{(0)})$![]() , $B\in M_{a\times b}(E_{(1)})$
, $B\in M_{a\times b}(E_{(1)})$![]() , $C\in M_{b\times a}(E_{(1)})$
, $C\in M_{b\times a}(E_{(1)})$![]() . Here and in what follows $E$
. Here and in what follows $E$![]() stands for the Grassmann algebra of an infinite-dimensional vector space, $E=E_{(0)}\oplus E_{(1)}$
stands for the Grassmann algebra of an infinite-dimensional vector space, $E=E_{(0)}\oplus E_{(1)}$![]() , where $E_{(0)}$
, where $E_{(0)}$![]() is the centre of $E$
is the centre of $E$![]() , and $E_{(1)}$
, and $E_{(1)}$![]() is the “anticommuting” part of $E$
is the “anticommuting” part of $E$![]() .
.
As a consequence of his structure theory, Kemer described the PI equivalences of the tensor products of verbally prime algebras. This description is given below; it is known as the Tensor Product Theorem.
Theorem 1.1 Tensor Product Theorem
Let $F$![]() be a field of characteristic zero. Then the class of verbally prime algebras is closed under tensor products. Moreover one has the following PI equivalences (meaning the corresponding algebras satisfy the same polynomial identities):
be a field of characteristic zero. Then the class of verbally prime algebras is closed under tensor products. Moreover one has the following PI equivalences (meaning the corresponding algebras satisfy the same polynomial identities):
(1) $M_{a,b}(E)\otimes E\sim M_{a+b}(E)$
 ;
;(2) $M_{a,b}(E)\otimes M_{c,d}(E)\sim M_{ac+bd,ad+bc}(E)$
 ;
;(3) $M_{1,1}(E)\sim E\otimes E$
 .
.
The remaining tensor products of verbally prime algebras can be deduced from the above and easy isomorphisms.
Here and in what follows, all tensor products are supposed to be over $F$![]() .
.
This theorem admits proofs that do not depend on the structure theory developed by Kemer. The first such proof was given by Regev in [Reference Regev28]. Regev used implicitly adequate gradings on the corresponding algebras. Later on, Di Vincenzo in [Reference Di Vincenzo13] gave a proof of the third statement by using gradings by the cyclic group of order 2. Di Vincenzo's results concerning the graded identities for $M_{1,1}(E)$![]() and $E\otimes E$
and $E\otimes E$![]() were extended in [Reference Koshlukov and Azevedo26] where it was proved that in positive characteristics the graded identities of these two algebras differ. By using appropriate gradings and graded identities, the second statement of the previous theorem was proved in [Reference Di Vincenzo and Nardozza15, Reference Di Vincenzo and Nardozza16]. In [Reference Azevedo, Fidelis and Koshlukov5, Reference Azevedo, Fidelis and Koshlukov6], the authors proved that Regev's results hold over an arbitrary infinite field of characteristic $p\ne 2$
were extended in [Reference Koshlukov and Azevedo26] where it was proved that in positive characteristics the graded identities of these two algebras differ. By using appropriate gradings and graded identities, the second statement of the previous theorem was proved in [Reference Di Vincenzo and Nardozza15, Reference Di Vincenzo and Nardozza16]. In [Reference Azevedo, Fidelis and Koshlukov5, Reference Azevedo, Fidelis and Koshlukov6], the authors proved that Regev's results hold over an arbitrary infinite field of characteristic $p\ne 2$![]() but only at multilinear level, and consequently, they showed that if $p>2$
but only at multilinear level, and consequently, they showed that if $p>2$![]() then the third statement of the Tensor Product Theorem fails. Moreover, they showed that in positive characteristic, the algebras $M_2(E)$
then the third statement of the Tensor Product Theorem fails. Moreover, they showed that in positive characteristic, the algebras $M_2(E)$![]() and $M_{1,1}(E)\otimes E$
and $M_{1,1}(E)\otimes E$![]() are not PI equivalent. We refer the reader to the monograph [Reference Kemer24] for details about the important structure theory of PI algebras and Kemer's contributions to it.
are not PI equivalent. We refer the reader to the monograph [Reference Kemer24] for details about the important structure theory of PI algebras and Kemer's contributions to it.
Graded polynomial identities play an important role in the study of PI algebras. When the grading group is $\mathbb {Z}_2$![]() they were used in the theory developed by Kemer. This should not be surprising as the Grassmann algebra $E$
they were used in the theory developed by Kemer. This should not be surprising as the Grassmann algebra $E$![]() possesses a natural grading by this group, and this grading is essential in obtaining the verbally prime algebras. Another motivation that favours the graded identities and their usage is that they are easier to describe in many important cases and are related to the ordinary ones. We recall as an example that if two graded algebras share the same graded identities, then they share the same ordinary identities. Let us also recall that the polynomial identities of the $n\times n$
possesses a natural grading by this group, and this grading is essential in obtaining the verbally prime algebras. Another motivation that favours the graded identities and their usage is that they are easier to describe in many important cases and are related to the ordinary ones. We recall as an example that if two graded algebras share the same graded identities, then they share the same ordinary identities. Let us also recall that the polynomial identities of the $n\times n$![]() matrix algebra $M_n(F)$
matrix algebra $M_n(F)$![]() are not known whenever $n>2$
are not known whenever $n>2$![]() . On the other hand, $M_n(F)$
. On the other hand, $M_n(F)$![]() admits a natural $\mathbb {Z}_n$
admits a natural $\mathbb {Z}_n$![]() -grading by assuming the elementary matrix $E_{ij}$
-grading by assuming the elementary matrix $E_{ij}$![]() of degree $j-i\pmod {n}$
of degree $j-i\pmod {n}$![]() . The graded identities for this grading on $M_n(F)$
. The graded identities for this grading on $M_n(F)$![]() are well known, see [Reference Azevedo4, Reference Vasilovsky31]. In [Reference Di Vincenzo, Koshlukov and Santulo18], the authors studied the graded identities of the algebras $M_{a,b}(E)\otimes M_{c,d}(E)$
are well known, see [Reference Azevedo4, Reference Vasilovsky31]. In [Reference Di Vincenzo, Koshlukov and Santulo18], the authors studied the graded identities of the algebras $M_{a,b}(E)\otimes M_{c,d}(E)$![]() and $M_{ac+bd,ad+bc}(E)$
and $M_{ac+bd,ad+bc}(E)$![]() , and they proved that $T_G( M_{ac+bd,ad+bc}(E))\subseteq T_G(M_{a,b}(E)\otimes M_{c,d}(E))$
, and they proved that $T_G( M_{ac+bd,ad+bc}(E))\subseteq T_G(M_{a,b}(E)\otimes M_{c,d}(E))$![]() . As a consequence, they obtained the inclusion for ordinary polynomial identities. On that occasion, the authors considered $G$
. As a consequence, they obtained the inclusion for ordinary polynomial identities. On that occasion, the authors considered $G$![]() as the group $\mathbb {Z}_{mn}\times \mathbb {Z}_2$
as the group $\mathbb {Z}_{mn}\times \mathbb {Z}_2$![]() , $a+b=m$
, $a+b=m$![]() and $c+d=n$
and $c+d=n$![]() . Here and in what follows we denote by $T(A)$
. Here and in what follows we denote by $T(A)$![]() and by $T_G(A)$
and by $T_G(A)$![]() the ideal of the ordinary, respectively $G$
the ideal of the ordinary, respectively $G$![]() -graded identities for the algebra $A$
-graded identities for the algebra $A$![]() .
.
However, over an infinite field of positive characteristic, very little is as yet known about the concrete description of ordinary or graded identities apart from some particular cases. It should be noted that the information on the verbally prime algebras in positive characteristic is very far from complete. It is known that there exist other verbally prime algebras but the complete classification seems to be out of reach at present. The interested reader can consult the monograph [Reference Razmyslov27, Section 33.2], and also [Reference Kemer25] for more details.
Let $F$![]() be an infinite field of positive characteristic $p>2$
be an infinite field of positive characteristic $p>2$![]() . The paper is organized as follows. In § 2, we give the necessary background on associative algebras, elementary gradings and graded identities. The usage of gradings on algebras possessing a multiplicative basis is essential. The interested reader may consult [Reference Bemm, Fornaroli and Santulo9] for more details about this topic. Considering graded algebras with multiplicative basis, in § 3, we exhibit a set of generators of degrees 2 and 3, up to graded monomial identities, that form a basis for the set of all graded identities for these algebras. As a consequence, we exhibit a basis for the graded identities of the algebras $M_{a,b}(E)$
. The paper is organized as follows. In § 2, we give the necessary background on associative algebras, elementary gradings and graded identities. The usage of gradings on algebras possessing a multiplicative basis is essential. The interested reader may consult [Reference Bemm, Fornaroli and Santulo9] for more details about this topic. Considering graded algebras with multiplicative basis, in § 3, we exhibit a set of generators of degrees 2 and 3, up to graded monomial identities, that form a basis for the set of all graded identities for these algebras. As a consequence, we exhibit a basis for the graded identities of the algebras $M_{a,b}(E)$![]() with respect to these elementary gradings, as well as their tensor products, once again up to graded monomial identities. The problem of describing these monomial identities is still open even in characteristic zero, and it is still far from being understood, although it was done in several particular cases, see [Reference Fidelis, Diniz, Bernardo and Koshlukov20].
with respect to these elementary gradings, as well as their tensor products, once again up to graded monomial identities. The problem of describing these monomial identities is still open even in characteristic zero, and it is still far from being understood, although it was done in several particular cases, see [Reference Fidelis, Diniz, Bernardo and Koshlukov20].
However, in § 4, we obtain an upper bound on the degrees of these monomial identities, and moreover, we prove that all graded monomial identities of an algebra with elementary $G$![]() -grading, under a technical condition, follow from those of bounded degree.
-grading, under a technical condition, follow from those of bounded degree.
Finally, in § 5, an alternative proof that the inclusion $T(M_{ac+bd,ad+bc}(E))\subseteq T(M_{a,b}(E)\otimes M_{c,d}(E))$![]() holds, for the ordinary polynomial identities, is presented. To this end, we make use of a generic construction similar to the one given in [Reference Di Vincenzo, Koshlukov and Santulo18, Section 2].
holds, for the ordinary polynomial identities, is presented. To this end, we make use of a generic construction similar to the one given in [Reference Di Vincenzo, Koshlukov and Santulo18, Section 2].
2. Preliminaries
All algebras and vector spaces, as well as their tensor products, will be considered over a fixed infinite field $F$![]() of characteristic $p\ne 2$
of characteristic $p\ne 2$![]() .
.
Let $G$![]() be a group with identity element $\epsilon$
be a group with identity element $\epsilon$![]() and $A$
and $A$![]() an algebra. A grading by the group $G$
an algebra. A grading by the group $G$![]() on $A$
on $A$![]() is a vector space decomposition $A=\oplus _{g\in G} A_g$
is a vector space decomposition $A=\oplus _{g\in G} A_g$![]() such that $A_{g}A_{h}\subseteq A_{gh}$
such that $A_{g}A_{h}\subseteq A_{gh}$![]() for every $g$
for every $g$![]() , $h$
, $h$![]() in $G$
in $G$![]() . The subspaces $A_{g}$
. The subspaces $A_{g}$![]() are called the homogeneous components of $A$
are called the homogeneous components of $A$![]() . A non-zero element $a\in A$
. A non-zero element $a\in A$![]() is homogeneous of degree $g$
is homogeneous of degree $g$![]() if $a\in A_{g}$
if $a\in A_{g}$![]() and we denote it by $|a|_G=g$
and we denote it by $|a|_G=g$![]() or $\alpha _G(a)=g$
or $\alpha _G(a)=g$![]() (or simply $|a|=g$
(or simply $|a|=g$![]() or $\alpha (a)=g$
or $\alpha (a)=g$![]() when the group $G$
when the group $G$![]() is inferred from the context). If the grading group is the direct product $G\times H$
is inferred from the context). If the grading group is the direct product $G\times H$![]() of the groups $G$
of the groups $G$![]() and $H$
and $H$![]() we denote the entries, in $G$
we denote the entries, in $G$![]() and $H$
and $H$![]() , of degree $\alpha _{G\times H} (a)$
, of degree $\alpha _{G\times H} (a)$![]() of the homogeneous element $a$
of the homogeneous element $a$![]() , by $\alpha _G (a)$
, by $\alpha _G (a)$![]() and $\alpha _H(a)$
and $\alpha _H(a)$![]() , respectively. The support of $A$
, respectively. The support of $A$![]() in the $G$
in the $G$![]() -grading is the set $\mathrm {supp}\ A=\{g\in G\mid A_g\neq 0\}$
-grading is the set $\mathrm {supp}\ A=\{g\in G\mid A_g\neq 0\}$![]() . A vector subspace (subalgebra, ideal) $B$
. A vector subspace (subalgebra, ideal) $B$![]() of $A$
of $A$![]() is said to be graded or homogeneous if $B=\oplus _{g\in G} A_{g}\cap B$
is said to be graded or homogeneous if $B=\oplus _{g\in G} A_{g}\cap B$![]() . Let $A=\oplus _{g\in G}A_g$
. Let $A=\oplus _{g\in G}A_g$![]() and $B=\oplus _{h\in H}B_h$
and $B=\oplus _{h\in H}B_h$![]() be algebras graded by the groups $G$
be algebras graded by the groups $G$![]() and $H$
and $H$![]() , respectively. The tensor product $A\otimes B$
, respectively. The tensor product $A\otimes B$![]() has a canonical $G\times H$
has a canonical $G\times H$![]() -grading where $(A\otimes B)_{(g,h)} = A_g\otimes B_h$
-grading where $(A\otimes B)_{(g,h)} = A_g\otimes B_h$![]() , $g\in G$
, $g\in G$![]() , $h\in H$
, $h\in H$![]() . If $A$
. If $A$![]() , $B$
, $B$![]() are $G$
are $G$![]() -graded algebras, an algebra homomorphism $\varphi \colon A\to B$
-graded algebras, an algebra homomorphism $\varphi \colon A\to B$![]() is a homomorphism of graded algebras if $\varphi (A_g)\subseteq B_g$
is a homomorphism of graded algebras if $\varphi (A_g)\subseteq B_g$![]() for all $g\in G$
for all $g\in G$![]() . Such homomorphisms are called $G$
. Such homomorphisms are called $G$![]() -graded ones.
-graded ones.
An important example of a graded algebra is the Grassmann algebra. Kemer proved that every associative PI algebra over a field of characteristic zero is PI equivalent to the Grassmann envelope of a finite-dimensional associative superalgebra. (Here, we deal with associative algebras, and in this setting, a superalgebra is the same as a $\mathbb {Z}_2$![]() -graded algebra.) Let $L$
-graded algebra.) Let $L$![]() be a vector space with a basis $\mathcal {B}=\{e_{1}, e_{2},\ldots \}$
be a vector space with a basis $\mathcal {B}=\{e_{1}, e_{2},\ldots \}$![]() . The infinite-dimensional Grassmann (or exterior) algebra $E$
. The infinite-dimensional Grassmann (or exterior) algebra $E$![]() of $L$
of $L$![]() has a basis $\mathcal {B}_E$
has a basis $\mathcal {B}_E$![]() consisting of 1 and all monomials $e_{i_1}e_{i_2}\cdots e_{i_k}$
consisting of 1 and all monomials $e_{i_1}e_{i_2}\cdots e_{i_k}$![]() , where $i_1 < i_2 <\ldots < i_k$
, where $i_1 < i_2 <\ldots < i_k$![]() for every $k\geq 1$
for every $k\geq 1$![]() . The multiplication in $E$
. The multiplication in $E$![]() is induced by $e_ie_j =-e_je_i$
is induced by $e_ie_j =-e_je_i$![]() for all $i$
for all $i$![]() and $j$
and $j$![]() . Hence $E=E_{(0)}\oplus E_{(1)}$
. Hence $E=E_{(0)}\oplus E_{(1)}$![]() , where $E_{(0)}$
, where $E_{(0)}$![]() is the subspace spanned by 1 and all monomials of even length while $E_{(1)}$
is the subspace spanned by 1 and all monomials of even length while $E_{(1)}$![]() is spanned by the monomials of odd length. This decomposition gives the natural (or canonical) $\mathbb {Z}_2$
is spanned by the monomials of odd length. This decomposition gives the natural (or canonical) $\mathbb {Z}_2$![]() -grading on $E$
-grading on $E$![]() , denoted by $E_{can}$
, denoted by $E_{can}$![]() . Recall that the Grassmann algebra has other gradings by the group $\mathbb {Z}_2$
. Recall that the Grassmann algebra has other gradings by the group $\mathbb {Z}_2$![]() . Here we are not going to discuss these constructions (since we will not need them here) but instead, we refer the reader to [Reference Di Vincenzo and da Silva14, Reference Guimarães and Koshlukov22].
. Here we are not going to discuss these constructions (since we will not need them here) but instead, we refer the reader to [Reference Di Vincenzo and da Silva14, Reference Guimarães and Koshlukov22].
Another example of graded algebras is the so-called $\beta$![]() -colour commutative algebras (or simply colour commutative algebras). The case of $\beta$
-colour commutative algebras (or simply colour commutative algebras). The case of $\beta$![]() -colour Lie superalgebras was treated extensively in the monograph [Reference Bahturin, Mikhalev, Petrogradsky and Zaicev8]. Let $H$
-colour Lie superalgebras was treated extensively in the monograph [Reference Bahturin, Mikhalev, Petrogradsky and Zaicev8]. Let $H$![]() be an abelian group with the additive notation, and let $\beta \colon H\times H \to F^{\times }$
be an abelian group with the additive notation, and let $\beta \colon H\times H \to F^{\times }$![]() be a skew-symmetric bicharacter. This means $\beta$
be a skew-symmetric bicharacter. This means $\beta$![]() is a function in two arguments from $H$
is a function in two arguments from $H$![]() taking values in the multiplicative group $F^{\times }$
taking values in the multiplicative group $F^{\times }$![]() of $F$
of $F$![]() with the properties
with the properties

for all $g$![]() , $h$
, $h$![]() , $k\in H$
, $k\in H$![]() . Define the $\beta$
. Define the $\beta$![]() -commutator in $R =\oplus _{g\in H}R_g$
-commutator in $R =\oplus _{g\in H}R_g$![]() by $[a,\, b]_\beta = ab-\beta (g,\, h)ba$
by $[a,\, b]_\beta = ab-\beta (g,\, h)ba$![]() where $a\in R_g$
where $a\in R_g$![]() , $b\in R_h$
, $b\in R_h$![]() , and then extend it by linearity. We call $R$
, and then extend it by linearity. We call $R$![]() a $H$
a $H$![]() -graded colour $\beta$
-graded colour $\beta$![]() -commutative algebra whenever $[a,\,b]_\beta =0$
-commutative algebra whenever $[a,\,b]_\beta =0$![]() for every $a$
for every $a$![]() , $b\in R$
, $b\in R$![]() . We draw the reader's attention that $\beta$
. We draw the reader's attention that $\beta$![]() can be omitted when it is inferred from the context. A particularly interesting case of a colour commutative algebra is the Grassmann algebra. According to [Reference Aljadeff and Ofir1, Reference Regev and Seeman29], an $H$
can be omitted when it is inferred from the context. A particularly interesting case of a colour commutative algebra is the Grassmann algebra. According to [Reference Aljadeff and Ofir1, Reference Regev and Seeman29], an $H$![]() -graded colour commutative algebra $R$
-graded colour commutative algebra $R$![]() is called regular if it satisfies the following property: for every integer $n>0$
is called regular if it satisfies the following property: for every integer $n>0$![]() and every $n$
and every $n$![]() -tuple $(h_1,\,\ldots, h_n)$
-tuple $(h_1,\,\ldots, h_n)$![]() of elements of $H$
of elements of $H$![]() , there exist $r_1$
, there exist $r_1$![]() , …, $r_n$
, …, $r_n$![]() with $r_j\in R_{h_j}$
with $r_j\in R_{h_j}$![]() such that $r_1\cdots r_n\neq 0$
such that $r_1\cdots r_n\neq 0$![]() .
.
Let $\{X_g\}_{g\in G}$![]() be a family of pairwise disjoint sets $X_g = \{x_{1}^{g},\, x_{2}^{g},\, \ldots \}$
be a family of pairwise disjoint sets $X_g = \{x_{1}^{g},\, x_{2}^{g},\, \ldots \}$![]() . We denote by $F\langle X_G \rangle$
. We denote by $F\langle X_G \rangle$![]() the free $G$
the free $G$![]() -graded algebra, freely generated by the set $X_{G}=\cup _{g\in G}X_g$
-graded algebra, freely generated by the set $X_{G}=\cup _{g\in G}X_g$![]() . This algebra has a natural grading by $G$
. This algebra has a natural grading by $G$![]() assuming the elements of $X_g$
assuming the elements of $X_g$![]() homogeneous of degree $g$
homogeneous of degree $g$![]() . Hence the homogeneous component $(F\langle X_G \rangle )_g$
. Hence the homogeneous component $(F\langle X_G \rangle )_g$![]() is the subspace spanned by all monomials $x_{i_1}^{g_1}\cdots x_{i_m}^{g_m}$
is the subspace spanned by all monomials $x_{i_1}^{g_1}\cdots x_{i_m}^{g_m}$![]() such that $g_{1}\cdots g_m=g$
such that $g_{1}\cdots g_m=g$![]() . The elements in $F\langle X_G\rangle$
. The elements in $F\langle X_G\rangle$![]() are called graded polynomials (or simply polynomials). Let $f(x_{1}^{g_1},\ldots, x_{m}^{g_m})$
are called graded polynomials (or simply polynomials). Let $f(x_{1}^{g_1},\ldots, x_{m}^{g_m})$![]() be a polynomial in $F\langle X_G \rangle$
be a polynomial in $F\langle X_G \rangle$![]() . The degree of $f$
. The degree of $f$![]() in $x_i^{g_i}$
in $x_i^{g_i}$![]() , denoted by $\deg _{x_i^{g_i}}f$
, denoted by $\deg _{x_i^{g_i}}f$![]() , counts how many times the variable $x_i^{g_i}$
, counts how many times the variable $x_i^{g_i}$![]() appears in the monomial of largest degree in $x_i^{g_i}$
appears in the monomial of largest degree in $x_i^{g_i}$![]() with a non-zero coefficient in $f$
with a non-zero coefficient in $f$![]() , and it is defined in the usual way. The definitions of multilinear and multihomogeneous polynomials are the natural ones.
, and it is defined in the usual way. The definitions of multilinear and multihomogeneous polynomials are the natural ones.
We will omit the upper indices of the free generators $x_i^{g}$![]() and we will write instead $x_i$
and we will write instead $x_i$![]() if these are clear from the context.
if these are clear from the context.
Let $A=\oplus _{g\in G}A_g$![]() be a $G$
be a $G$![]() -graded algebra. An $m$
-graded algebra. An $m$![]() -tuple $(a_1,\ldots, a_m)$
-tuple $(a_1,\ldots, a_m)$![]() such that $a_i\in A_{g_i}$
such that $a_i\in A_{g_i}$![]() , for $i=1$
, for $i=1$![]() , …, $m$
, …, $m$![]() , is called $f$
, is called $f$![]() -admissible substitution (or simply admissible substitution). The polynomial $f$
-admissible substitution (or simply admissible substitution). The polynomial $f$![]() is called a graded polynomial identity for $A$
is called a graded polynomial identity for $A$![]() if $f(a_1,\ldots,a_m)=0$
if $f(a_1,\ldots,a_m)=0$![]() for every admissible substitution $(a_1,\ldots, a_m)$
for every admissible substitution $(a_1,\ldots, a_m)$![]() . We denote by $T_G(A)\subseteq F\langle X_G \rangle$
. We denote by $T_G(A)\subseteq F\langle X_G \rangle$![]() the set of all graded identities for a given $G$
the set of all graded identities for a given $G$![]() -grading on $A$
-grading on $A$![]() . If $A$
. If $A$![]() and $B$
and $B$![]() are $G$
are $G$![]() -graded algebras we say that $A$
-graded algebras we say that $A$![]() and $B$
and $B$![]() are PI equivalent as $G$
are PI equivalent as $G$![]() -graded algebras if $T_{G}(A)=T_{G}(B)$
-graded algebras if $T_{G}(A)=T_{G}(B)$![]() .
.
Let $A$![]() be an algebra graded by the group $G$
be an algebra graded by the group $G$![]() . It is clear that $T_G(A)$
. It is clear that $T_G(A)$![]() is an ideal of $F\langle X_G \rangle$
is an ideal of $F\langle X_G \rangle$![]() , moreover it is invariant under all $G$
, moreover it is invariant under all $G$![]() -graded endomorphisms of $F\langle X_G \rangle$
-graded endomorphisms of $F\langle X_G \rangle$![]() . Such ideals are called $T_G$
. Such ideals are called $T_G$![]() -ideals. The intersection of $T_G$
-ideals. The intersection of $T_G$![]() -ideals of $F\langle X_G \rangle$
-ideals of $F\langle X_G \rangle$![]() is also a $T_G$
is also a $T_G$![]() -ideal. A subset $\mathcal {P}\subset F\langle X_G \rangle$
-ideal. A subset $\mathcal {P}\subset F\langle X_G \rangle$![]() is a basis for the $T_G$
is a basis for the $T_G$![]() -ideal $T_G(A)$
-ideal $T_G(A)$![]() if $T_G(A)$
if $T_G(A)$![]() is the intersection of all $T_G$
is the intersection of all $T_G$![]() -ideals in $F\langle X_G \rangle$
-ideals in $F\langle X_G \rangle$![]() which contain $\mathcal {P}$
which contain $\mathcal {P}$![]() ; this $T_G$
; this $T_G$![]() -ideal is denoted by $\langle \mathcal {P}\rangle ^{T_G}$
-ideal is denoted by $\langle \mathcal {P}\rangle ^{T_G}$![]() . If $G=\{\epsilon \}$
. If $G=\{\epsilon \}$![]() we recover the definition of ordinary polynomial identities; in this case, we use the notation $F\langle X \rangle$
we recover the definition of ordinary polynomial identities; in this case, we use the notation $F\langle X \rangle$![]() for the free-associative algebra and $x_{i}$
for the free-associative algebra and $x_{i}$![]() for the variables. It is well known that if $A$
for the variables. It is well known that if $A$![]() is a $G$
is a $G$![]() -graded algebra over a field of characteristic 0, the ideal $T_G(A)$
-graded algebra over a field of characteristic 0, the ideal $T_G(A)$![]() is generated, as a $T_G$
is generated, as a $T_G$![]() -ideal, by its multilinear polynomials. Over an infinite field of positive characteristic, one has to take into account the multihomogeneous polynomials instead of the multilinear ones. Recall that if $f$
-ideal, by its multilinear polynomials. Over an infinite field of positive characteristic, one has to take into account the multihomogeneous polynomials instead of the multilinear ones. Recall that if $f$![]() is a multihomogeneous graded polynomial one can, by linearization (or polarization), obtain a multilinear polynomial in $\langle f\rangle ^{T_G}$
is a multihomogeneous graded polynomial one can, by linearization (or polarization), obtain a multilinear polynomial in $\langle f\rangle ^{T_G}$![]() . If the characteristic is 0 one can recover $f$
. If the characteristic is 0 one can recover $f$![]() by symmetrization (or restitution) but in positive characteristic, this may be impossible.
by symmetrization (or restitution) but in positive characteristic, this may be impossible.
The next definition will be very important in what follows. It can be found in [Reference Di Vincenzo and Nardozza17], we recall it here for the readers’ convenience.
Definition 2.1 [Reference Di Vincenzo and Nardozza17, Definition 1]
Let $\mathcal {B}$![]() be a basis for the vector space of an algebra $A$
be a basis for the vector space of an algebra $A$![]() . We say $\mathcal {B}$
. We say $\mathcal {B}$![]() is a multiplicative basis for $A$
is a multiplicative basis for $A$![]() if it satisfies the following condition. For every $b_1$
if it satisfies the following condition. For every $b_1$![]() , $b_2\in \mathcal {B}$
, $b_2\in \mathcal {B}$![]() such that $b_1b_2\neq 0$
such that $b_1b_2\neq 0$![]() there exists a non-zero scalar $\lambda =\lambda (b_1,\,b_2)$
there exists a non-zero scalar $\lambda =\lambda (b_1,\,b_2)$![]() in $F$
in $F$![]() such that $\lambda b_1b_2\in \mathcal {B}$
such that $\lambda b_1b_2\in \mathcal {B}$![]() .
.
Let $G$![]() be a group. Suppose that there is a multiplicative basis $\mathcal {B}$
be a group. Suppose that there is a multiplicative basis $\mathcal {B}$![]() for $A$
for $A$![]() , and there is a map $|\cdot |\colon \mathcal {B}\to G$
, and there is a map $|\cdot |\colon \mathcal {B}\to G$![]() satisfying
satisfying
Then we can endow $A$![]() with a $G$
with a $G$![]() -grading. More precisely, $A_g=\mathrm {sp}\,\{ b\in \mathcal {B}\mid |b|=g\}$
-grading. More precisely, $A_g=\mathrm {sp}\,\{ b\in \mathcal {B}\mid |b|=g\}$![]() for every $g\in G$
for every $g\in G$![]() . Then $\mathcal {B}$
. Then $\mathcal {B}$![]() is a basis of homogeneous elements. We shall express this by calling $\mathcal {B}$
is a basis of homogeneous elements. We shall express this by calling $\mathcal {B}$![]() a $G$
a $G$![]() -multiplicative basis for the $G$
-multiplicative basis for the $G$![]() -graded algebra $A$
-graded algebra $A$![]() .
.
Definition 2.2 Bemm et al. [Reference Bemm, Fornaroli and Santulo9]
A multiplicative basis $\mathcal {B}$![]() for an algebra $A$
for an algebra $A$![]() is called an elementary basis if there exists a set of pairwise orthogonal idempotents $I\subset \mathcal {B}$
is called an elementary basis if there exists a set of pairwise orthogonal idempotents $I\subset \mathcal {B}$![]() such that for every $u\in \mathcal {B}$
such that for every $u\in \mathcal {B}$![]() there exist idempotents $a_u$
there exist idempotents $a_u$![]() , $b_u\in I$
, $b_u\in I$![]() such that the equality $u=a_uub_u$
such that the equality $u=a_uub_u$![]() holds. Moreover, we say that $I$
holds. Moreover, we say that $I$![]() is an elementary set of idempotents of $B$
is an elementary set of idempotents of $B$![]() .
.
The idempotents $a_u$![]() and $b_u$
and $b_u$![]() in the above definition are uniquely determined by the element $u$
in the above definition are uniquely determined by the element $u$![]() . It is immediate that the canonical bases of the verbally prime algebras $M_n(F)$
. It is immediate that the canonical bases of the verbally prime algebras $M_n(F)$![]() , $M_n(E)$
, $M_n(E)$![]() and $M_{a,b}(E)$
and $M_{a,b}(E)$![]() are elementary ones. Moreover, if $\mathcal {B}_A$
are elementary ones. Moreover, if $\mathcal {B}_A$![]() , $\mathcal {B}_{A^{\prime }}$
, $\mathcal {B}_{A^{\prime }}$![]() are elementary bases for the algebras $A$
are elementary bases for the algebras $A$![]() , $A^{\prime }$
, $A^{\prime }$![]() , respectively, then $\mathcal {B}_{A\otimes A^{\prime }}=\{u\otimes u^{\prime }\mid u\in \mathcal {B}_{A},\, u^{\prime }\in \mathcal {B}_{A^{\prime }}\}$
, respectively, then $\mathcal {B}_{A\otimes A^{\prime }}=\{u\otimes u^{\prime }\mid u\in \mathcal {B}_{A},\, u^{\prime }\in \mathcal {B}_{A^{\prime }}\}$![]() is an elementary basis for $A\otimes A^{\prime }$
is an elementary basis for $A\otimes A^{\prime }$![]() . Therefore, the canonical basis for the algebra $M_{a,b}(E)\otimes M_{r,s}(E)$
. Therefore, the canonical basis for the algebra $M_{a,b}(E)\otimes M_{r,s}(E)$![]() is also an elementary one. Finally, if an algebra admits a multiplicative basis $\mathcal {B}$
is also an elementary one. Finally, if an algebra admits a multiplicative basis $\mathcal {B}$![]() we say that a $G$
we say that a $G$![]() -grading of $A$
-grading of $A$![]() is a $\mathcal {B}$
is a $\mathcal {B}$![]() -good grading if all elements of $\mathcal {B}$
-good grading if all elements of $\mathcal {B}$![]() are homogeneous.
are homogeneous.
Definition 2.3 Let $A$![]() be an algebra with an elementary basis $\mathcal {B}$
be an algebra with an elementary basis $\mathcal {B}$![]() and let $I$
and let $I$![]() be the corresponding elementary set of idempotents. Let $G$
be the corresponding elementary set of idempotents. Let $G$![]() be a group. A $G$
be a group. A $G$![]() -grading of $A$
-grading of $A$![]() is said to be a $\mathcal {B}$
is said to be a $\mathcal {B}$![]() -elementary grading if it is a $\mathcal {B}$
-elementary grading if it is a $\mathcal {B}$![]() -good grading such that there exists $f\colon I\to G$
-good grading such that there exists $f\colon I\to G$![]() with the property $|u| =[f(a_u)]^{-1}f(b_u)$
with the property $|u| =[f(a_u)]^{-1}f(b_u)$![]() , for all $u\in \mathcal {B}$
, for all $u\in \mathcal {B}$![]() .
.
Let $\mathcal {B}$![]() be an elementary basis of $A$
be an elementary basis of $A$![]() and let $I$
and let $I$![]() be its elementary set of idempotents. For each $f\colon I\to G$
be its elementary set of idempotents. For each $f\colon I\to G$![]() , there exists a $\mathcal {B}$
, there exists a $\mathcal {B}$![]() -elementary $G$
-elementary $G$![]() -grading of $A$
-grading of $A$![]() such that $|u| =[f(a_u)]^{-1}f(b_u)$
such that $|u| =[f(a_u)]^{-1}f(b_u)$![]() , for all $u\in \mathcal {B}$
, for all $u\in \mathcal {B}$![]() . Moreover, according to [Reference Bemm, Fornaroli and Santulo9, Remark 2.2], the set $I$
. Moreover, according to [Reference Bemm, Fornaroli and Santulo9, Remark 2.2], the set $I$![]() is finite and $1=\sum \nolimits _{u\in I}u$
is finite and $1=\sum \nolimits _{u\in I}u$![]() .
.
Now let $A$![]() , $A^{\prime }$
, $A^{\prime }$![]() be two algebras equipped with elementary gradings relative to the bases $\mathcal {B}$
be two algebras equipped with elementary gradings relative to the bases $\mathcal {B}$![]() and $\mathcal {B}^{\prime }$
and $\mathcal {B}^{\prime }$![]() , respectively. Furthermore, we suppose that the elements of $\mathrm {supp}\ A$
, respectively. Furthermore, we suppose that the elements of $\mathrm {supp}\ A$![]() commute with the elements of $\mathrm {supp}\ A^{\prime }$
commute with the elements of $\mathrm {supp}\ A^{\prime }$![]() . Then the tensor product grading on $A\otimes A^{\prime }$
. Then the tensor product grading on $A\otimes A^{\prime }$![]() is a $\mathcal {B}^{\prime \prime }$
is a $\mathcal {B}^{\prime \prime }$![]() -elementary grading where $\mathcal {B}^{\prime \prime }=\{b\otimes b^{\prime }\mid b\in \mathcal {B},\, b^{\prime }\in \mathcal {B}^{\prime }\}$
-elementary grading where $\mathcal {B}^{\prime \prime }=\{b\otimes b^{\prime }\mid b\in \mathcal {B},\, b^{\prime }\in \mathcal {B}^{\prime }\}$![]() . The canonical basis of $E$
. The canonical basis of $E$![]() , and more generally of $E^{\otimes n}$
, and more generally of $E^{\otimes n}$![]() , is an elementary basis with a set of idempotents $I$
, is an elementary basis with a set of idempotents $I$![]() consisting of the unit element, hence the only elementary grading on such algebras is the trivial grading.
consisting of the unit element, hence the only elementary grading on such algebras is the trivial grading.
We draw the readers’ attention that for the algebras $M_n(F)$![]() , $M_n(E)$
, $M_n(E)$![]() , $M_{a,b}(E)$
, $M_{a,b}(E)$![]() equipped with their canonical (multiplicative) bases, the corresponding set $I$
equipped with their canonical (multiplicative) bases, the corresponding set $I$![]() is non-trivial, that is, it contains at least two elements, as long as $n>1$
is non-trivial, that is, it contains at least two elements, as long as $n>1$![]() , or $a+b>1$
, or $a+b>1$![]() , respectively.
, respectively.
3. Graded identities for algebras with elementary gradings
Let $A$![]() be an algebra with a $\mathcal {B}$
be an algebra with a $\mathcal {B}$![]() -elementary grading, here we describe a basis for the graded identities of $A$
-elementary grading, here we describe a basis for the graded identities of $A$![]() provided it satisfies the following graded identities of degrees $2$
provided it satisfies the following graded identities of degrees $2$![]() and $3$
and $3$![]() :
:
Here $\lambda _g$![]() is a non-zero scalar in $F$
is a non-zero scalar in $F$![]() . Note that if the monomial $x_1x_2x_3$
. Note that if the monomial $x_1x_2x_3$![]() in (3.2) is not an identity for $A$
in (3.2) is not an identity for $A$![]() then $\lambda _g=\pm 1$
then $\lambda _g=\pm 1$![]() .
.
Let $\mathcal {I}$![]() be the $T_{G}$
be the $T_{G}$![]() -ideal generated by the identities from (3.1) and (3.2). Variants of the following lemma were proved in various situations, to the best of our knowledge, a similar statement first appeared in [Reference Vasilovsky30, Lemma 6]. In our case, the proof of the lemma follows word by word the one of [Reference Fidelis, Diniz, Bernardo and Koshlukov20, Lemma 6.4], and that is why we omit it here.
-ideal generated by the identities from (3.1) and (3.2). Variants of the following lemma were proved in various situations, to the best of our knowledge, a similar statement first appeared in [Reference Vasilovsky30, Lemma 6]. In our case, the proof of the lemma follows word by word the one of [Reference Fidelis, Diniz, Bernardo and Koshlukov20, Lemma 6.4], and that is why we omit it here.
Lemma 3.1 Let $A$![]() be an algebra with a $\mathcal {B}$
be an algebra with a $\mathcal {B}$![]() -elementary grading such that $\mathcal {I}\subset T_{G}(A)$
-elementary grading such that $\mathcal {I}\subset T_{G}(A)$![]() . Let $m,$
. Let $m,$![]() $n$
$n$![]() be multilinear monomials in the same set of variables and let $S$
be multilinear monomials in the same set of variables and let $S$![]() be an admissible substitution in $A$
be an admissible substitution in $A$![]() by elements of $\mathcal {B}$
by elements of $\mathcal {B}$![]() such that $n_S=cm_S\neq 0$
such that $n_S=cm_S\neq 0$![]() for some $c\in F$
for some $c\in F$![]() . Then $n\equiv cm\pmod {\mathcal {I}}$
. Then $n\equiv cm\pmod {\mathcal {I}}$![]() .
.
The previous lemma justifies our interest in investigating more closely the result for any admissible substitution. We introduce the following notation: Let $m$![]() be a graded monomial and $S$
be a graded monomial and $S$![]() an admissible substitution in $A$
an admissible substitution in $A$![]() . Consider $\mathcal {B}=\{b_i\mid i\in \Lambda \}$
. Consider $\mathcal {B}=\{b_i\mid i\in \Lambda \}$![]() , a $G$
, a $G$![]() -multiplicative basis of $A$
-multiplicative basis of $A$![]() . We denote
. We denote
the element of $A$![]() obtained from $m$
obtained from $m$![]() by the admissible substitution $S$
by the admissible substitution $S$![]() where $(m|_S)_i$
where $(m|_S)_i$![]() are scalars in $F$
are scalars in $F$![]() almost all equal to 0 (that is all but finitely many of these scalars are equal to 0).
almost all equal to 0 (that is all but finitely many of these scalars are equal to 0).
Definition 3.2 Let $A$![]() be an algebra with an elementary basis $\mathcal {B}$
be an algebra with an elementary basis $\mathcal {B}$![]() , and with the corresponding set of idempotents $I\subset \mathcal {B}$
, and with the corresponding set of idempotents $I\subset \mathcal {B}$![]() . The $(n+1)$
. The $(n+1)$![]() -tuple $(a_0,\,a_1,\,\ldots,\, a_n)$
-tuple $(a_0,\,a_1,\,\ldots,\, a_n)$![]() of elements in $I$
of elements in $I$![]() is called a good sequence if there exist $u_1$
is called a good sequence if there exist $u_1$![]() , $u_2$
, $u_2$![]() , …, $u_n$
, …, $u_n$![]() in $\mathcal {B}$
in $\mathcal {B}$![]() such that $a_{i-1}u_ia_{i}=u_i$
such that $a_{i-1}u_ia_{i}=u_i$![]() , for each $i=1$
, for each $i=1$![]() , …, $n$
, …, $n$![]() , and $u_1 u_2 \cdots u_n\neq 0$
, and $u_1 u_2 \cdots u_n\neq 0$![]() .
.
We will assume, until the end of this paper that our $G$![]() -graded algebras are finite dimensional. In fact, $M_n(F)$
-graded algebras are finite dimensional. In fact, $M_n(F)$![]() is finite dimensional while $M_{a,b}(E)$
is finite dimensional while $M_{a,b}(E)$![]() and $M_n(E)$
and $M_n(E)$![]() are not. We draw the readers’ attention to the fact that our arguments do apply to the latter two algebras as well, see Remark 3.14. On the other hand, working with finite-dimensional algebras simplifies the exposition. Let $A$
are not. We draw the readers’ attention to the fact that our arguments do apply to the latter two algebras as well, see Remark 3.14. On the other hand, working with finite-dimensional algebras simplifies the exposition. Let $A$![]() be a $G$
be a $G$![]() -graded algebra of dimension $n$
-graded algebra of dimension $n$![]() with $G$
with $G$![]() -multiplicative basis $\mathcal {B}$
-multiplicative basis $\mathcal {B}$![]() . For each $g\in \mathrm {supp}\ A$
. For each $g\in \mathrm {supp}\ A$![]() , we consider $\{u_1^{g},\,\ldots,\, u_{n_g}^{g}\}\subseteq \mathcal {B}$
, we consider $\{u_1^{g},\,\ldots,\, u_{n_g}^{g}\}\subseteq \mathcal {B}$![]() , a basis for the vector space $A_g$
, a basis for the vector space $A_g$![]() . Moreover, we define a countable set $T^{g}=\{t^{g}_{i,j}\mid 1\leq j\leq \dim _FA_g,\,~j\geq 1 \}$
. Moreover, we define a countable set $T^{g}=\{t^{g}_{i,j}\mid 1\leq j\leq \dim _FA_g,\,~j\geq 1 \}$![]() of commuting variables. Let $T=\cup _{g\in \mathrm {supp}\ A} T^{g}$
of commuting variables. Let $T=\cup _{g\in \mathrm {supp}\ A} T^{g}$![]() and denote $\Gamma =F[T]$
and denote $\Gamma =F[T]$![]() the polynomial ring in the commuting variables $T$
the polynomial ring in the commuting variables $T$![]() .
.
Let $A$![]() be an algebra with a $\mathcal {B}$
be an algebra with a $\mathcal {B}$![]() -elementary grading. The algebra $A\otimes \Gamma$
-elementary grading. The algebra $A\otimes \Gamma$![]() has an elementary grading induced by the elements of set $I$
has an elementary grading induced by the elements of set $I$![]() , the elementary set of idempotents of $B$
, the elementary set of idempotents of $B$![]() , which we denote by $I=\{u_1,\,\ldots,\,u_l\}$
, which we denote by $I=\{u_1,\,\ldots,\,u_l\}$![]() . Given $h\in G$
. Given $h\in G$![]() , we are interested in determining the elements $u_{i,j}^{h}$
, we are interested in determining the elements $u_{i,j}^{h}$![]() of $\mathcal {B}$
of $\mathcal {B}$![]() whose $G$
whose $G$![]() -degree equals $h$
-degree equals $h$![]() . Here we consider, without loss of generality, that $u_{i,j}^{h}=u_iu_{i,j}^{h}u_j$
. Here we consider, without loss of generality, that $u_{i,j}^{h}=u_iu_{i,j}^{h}u_j$![]() where $u_i$
where $u_i$![]() , $u_j\in I$
, $u_j\in I$![]() . Fixed $i$
. Fixed $i$![]() , $1\le i\le l$
, $1\le i\le l$![]() , there exists an element $u_{i,j}^{h}$
, there exists an element $u_{i,j}^{h}$![]() if and only if there exists $u_j\in I$
if and only if there exists $u_j\in I$![]() such that $u_{i,j}^{h}=u_iu_{i,j}^{h}u_j$
such that $u_{i,j}^{h}=u_iu_{i,j}^{h}u_j$![]() and $f(u_i)h=f(u_j)$
and $f(u_i)h=f(u_j)$![]() . Here $f$
. Here $f$![]() stands for the function given in Definition 2.3.
stands for the function given in Definition 2.3.
Put $f(I)=\{f(u)\mid u\in I\}$![]() . For each $h\in G$
. For each $h\in G$![]() we denote by $L_h$
we denote by $L_h$![]() the set of all indices $k$
the set of all indices $k$![]() , $1\le k\le l$
, $1\le k\le l$![]() , such that $f(u_k)h\in f(I)$
, such that $f(u_k)h\in f(I)$![]() , and by $s_h^{k}$
, and by $s_h^{k}$![]() , $1\le s_h^{k}\le l$
, $1\le s_h^{k}\le l$![]() , an index satisfying $f(u_k)h=f(u_{s_h^{k}})$
, an index satisfying $f(u_k)h=f(u_{s_h^{k}})$![]() . It is easy to see that $(A\otimes \Gamma )_h =0$
. It is easy to see that $(A\otimes \Gamma )_h =0$![]() if and only if $L_h =\emptyset$
if and only if $L_h =\emptyset$![]() , moreover if $L_h\neq \emptyset$
, moreover if $L_h\neq \emptyset$![]() then $\{u_{k,s_h^{k}}\mid k\in L_h\}$
then $\{u_{k,s_h^{k}}\mid k\in L_h\}$![]() is the set of all elements in $\mathcal {B}$
is the set of all elements in $\mathcal {B}$![]() of degree $h$
of degree $h$![]() . The algebra $A\otimes \Gamma$
. The algebra $A\otimes \Gamma$![]() has a grading induced by the one on $A$
has a grading induced by the one on $A$![]() . We consider, in $A\otimes \Gamma$
. We consider, in $A\otimes \Gamma$![]() , the homogeneous elements
, the homogeneous elements
Clearly, the element $Y^{h}_i$![]() is homogeneous of degree $h$
is homogeneous of degree $h$![]() . Denote by $\mathcal {R}$
. Denote by $\mathcal {R}$![]() the $G$
the $G$![]() -graded subalgebra of $A\otimes \Gamma$
-graded subalgebra of $A\otimes \Gamma$![]() generated by the generic elements $Y^{h}_i$
generated by the generic elements $Y^{h}_i$![]() , for every $h\in G$
, for every $h\in G$![]() and $i>0$
and $i>0$![]() .
.
Remark 3.3 The previous construction can be performed on a free colour commutative algebra graded by an abelian group $H$![]() . Consider the $H$
. Consider the $H$![]() -graded set $T_H=\cup _{g\in supp A}( \cup _{h\in H}T_h^{g})$
-graded set $T_H=\cup _{g\in supp A}( \cup _{h\in H}T_h^{g})$![]() where $T_h^{g}=\{t^{g,h}_{i,j}\mid 1\leq j\leq \dim _FA_g,\,~i\geq 1\}$
where $T_h^{g}=\{t^{g,h}_{i,j}\mid 1\leq j\leq \dim _FA_g,\,~i\geq 1\}$![]() for each $h\in H$
for each $h\in H$![]() and $g\in \mathrm {supp}\ A\subseteq G$
and $g\in \mathrm {supp}\ A\subseteq G$![]() . We construct the free $H$
. We construct the free $H$![]() -colour commutative algebra on $T_H$
-colour commutative algebra on $T_H$![]() determined by a skew-symmetric bicharacter $\beta \colon H\times H\to F^{\times }$
determined by a skew-symmetric bicharacter $\beta \colon H\times H\to F^{\times }$![]() . Here and in what follows we denote this free algebra by $\Gamma ^{\beta }=F^{\beta }[T_H]$
. Here and in what follows we denote this free algebra by $\Gamma ^{\beta }=F^{\beta }[T_H]$![]() . The relations it satisfies are $xy=\beta (h_1,\,h_2)yx$
. The relations it satisfies are $xy=\beta (h_1,\,h_2)yx$![]() for all $x\in T^{g_1}_{h_1}$
for all $x\in T^{g_1}_{h_1}$![]() and $y\in T^{g_2}_{h_2}$
and $y\in T^{g_2}_{h_2}$![]() . Note that if $a_1$
. Note that if $a_1$![]() , …, $a_n$
, …, $a_n$![]() are homogeneous elements of $\Gamma ^{\beta }$
are homogeneous elements of $\Gamma ^{\beta }$![]() with non-zero product $a_1\cdots a_n\ne 0$
with non-zero product $a_1\cdots a_n\ne 0$![]() and $\sigma \in S_n$
and $\sigma \in S_n$![]() then there exists $\lambda \in F^{\times }$
then there exists $\lambda \in F^{\times }$![]() depending only on the degrees of each $a_i$
depending only on the degrees of each $a_i$![]() and on the permutation $\sigma$
and on the permutation $\sigma$![]() such that
such that
Such construction can be found in [Reference Berele11]. Although our results will hold for the types of algebras as in [Reference Berele11], we will only study free colour commutative algebras as in the general case the arguments and notation become quite clumsy. In the next subsection, we will display the free $\mathbb {Z}_2$![]() -colour Lie algebra for $\beta (0,\,1)=\beta (0,\,0)=1$
-colour Lie algebra for $\beta (0,\,1)=\beta (0,\,0)=1$![]() and $\beta (1,\,1)=-1$
and $\beta (1,\,1)=-1$![]() .
.
Lemma 3.4 The relatively free $G$![]() -graded algebra $F\langle X_G\rangle /T_G(A)$
-graded algebra $F\langle X_G\rangle /T_G(A)$![]() is isomorphic to the algebra $\mathcal {R}$
is isomorphic to the algebra $\mathcal {R}$![]() .
.
Proof. The proof is standard. The map $\varphi \colon F\langle X_G\rangle \to \mathcal {R}$![]() defined by $\varphi (x_{i,g})=Y_{i}^{g}$
defined by $\varphi (x_{i,g})=Y_{i}^{g}$![]() , is a $G$
, is a $G$![]() -graded homomorphism. Clearly $\varphi$
-graded homomorphism. Clearly $\varphi$![]() is onto. Moreover, a standard argument shows that $\ker \varphi =T_G(A)$
is onto. Moreover, a standard argument shows that $\ker \varphi =T_G(A)$![]() and the result follows, as required.
and the result follows, as required.
Thus, we can work in the graded algebra $\mathcal {R}$![]() instead of the graded relatively free algebra $F\langle X_G\rangle /T_G(A)$
instead of the graded relatively free algebra $F\langle X_G\rangle /T_G(A)$![]() .
.
Definition 3.5 Let ${\bf h}=(h_1,\,\ldots,\,h_q)\in G^{q}$![]() , the set
, the set
is the set associated with ${\bf h}$![]() . For each $k\in L_{\bf h}$
. For each $k\in L_{\bf h}$![]() , we define the $(q+1)$
, we define the $(q+1)$![]() -tuples $s_k =(s_0^{k},\,s_1^{k},\,\ldots,\, s_q^{k})$
-tuples $s_k =(s_0^{k},\,s_1^{k},\,\ldots,\, s_q^{k})$![]() , inductively by setting:
, inductively by setting:
(i) $s_0^{k}=k$
 ,
,(ii) for $1\le i\le q$
 we choose the index $s^{k}_{i}$
we choose the index $s^{k}_{i}$ , $1\le s_i^{k}\le l$
, $1\le s_i^{k}\le l$ such that $f(u_{s_i^{k}})=f(u_{s_{i-1}^{k}})h_i$
such that $f(u_{s_i^{k}})=f(u_{s_{i-1}^{k}})h_i$ ,
,(iii) $(u_{s_0^{k}},\,u_{s_1^{k}},\,\ldots,\, u_{s_q^{k}})$
 is a good sequence in the sense of Definition 3.2.
is a good sequence in the sense of Definition 3.2.
Remark 3.6 Let $(a_{i_0},\,a_{i_1},\,a_{i_2},\,\ldots,\, a_{i_q})$![]() be a good sequence of elements in $I$
be a good sequence of elements in $I$![]() , as in Definition 3.2. In this case, $i_0\in L_{\bf h}$
, as in Definition 3.2. In this case, $i_0\in L_{\bf h}$![]() for ${\bf h}=(|u_{i_1}|,\,|u_{i_2}|,\,\ldots,\, |u_{i_{q-1}}|)$
for ${\bf h}=(|u_{i_1}|,\,|u_{i_2}|,\,\ldots,\, |u_{i_{q-1}}|)$![]() where $|u_{i_l}|=[f(a_{i_{l-1}})]^{-1}f(a_{i_{l}})$
where $|u_{i_l}|=[f(a_{i_{l-1}})]^{-1}f(a_{i_{l}})$![]() , for every $l$
, for every $l$![]() , $1\le l\le q-1$
, $1\le l\le q-1$![]() .
.
The following statements deal with an algebra $A$![]() which is equipped with a $\mathcal {B}$
which is equipped with a $\mathcal {B}$![]() -elementary grading such that $\mathcal {I}\subset T_{G}(A)$
-elementary grading such that $\mathcal {I}\subset T_{G}(A)$![]() .
.
Lemma 3.7 If $L$![]() is the set of indices associated with the $q$
is the set of indices associated with the $q$![]() -tuple $(h_1,\,\ldots,\, h_q)$
-tuple $(h_1,\,\ldots,\, h_q)$![]() in $G^{q}$
in $G^{q}$![]() and $s_k =(s_0^{k},\,s_1^{k},\,\ldots,\, s_q^{k})$
and $s_k =(s_0^{k},\,s_1^{k},\,\ldots,\, s_q^{k})$![]() denotes the corresponding sequence determined by $k\in L$
denotes the corresponding sequence determined by $k\in L$![]() then
then
where $w_k=t^{h_1}_{i_1,s_1^{k}}t^{h_2}_{i_2,s_2^{k}}\cdots t^{h_q}_{i_q,s_q^{k}}$![]() .
.
Proof. From Definition 3.5, we conclude that
if and only if $k_1\in L$![]() and for every $i$
and for every $i$![]() , $1\le i\le q$
, $1\le i\le q$![]() , we have $k_i=s_{h_{i-1}}^{k_{i-1}}$
, we have $k_i=s_{h_{i-1}}^{k_{i-1}}$![]() . From Eq. (3.3), we have
. From Eq. (3.3), we have
and the result follows.
The following consequence of the above lemma will be useful in the next section. We recall that given a monomial $m = x_{i_1}\cdots x_{i_q}$![]() of length $q$
of length $q$![]() , the sequence $(h_1,\,\ldots,\, h_q)$
, the sequence $(h_1,\,\ldots,\, h_q)$![]() , where $h_k$
, where $h_k$![]() is the $G$
is the $G$![]() -degree of the variable $x_{i_k}$
-degree of the variable $x_{i_k}$![]() , is denoted by $h(m)$
, is denoted by $h(m)$![]() .
.
Corollary 3.8 Let $m_1,$![]() $m_2$
$m_2$![]() be monomials such that $h(m_1) = h(m_2),$
be monomials such that $h(m_1) = h(m_2),$![]() then $m_1 \in T_G(A)$
then $m_1 \in T_G(A)$![]() if and only if $m_2 \in T_G(A)$
if and only if $m_2 \in T_G(A)$![]() .
.
Proof. It follows directly from the above lemma, since $m_i\in T_G(A)$![]() if and only if the set associated with $h(m_i)$
if and only if the set associated with $h(m_i)$![]() is empty.
is empty.
The product $Y_{i_1}Y_{i_2}\cdots Y_{i_r}$![]() is a linear combination of the elements $u=a_uub_u\in \mathcal {B}$
is a linear combination of the elements $u=a_uub_u\in \mathcal {B}$![]() . Here $a_u$
. Here $a_u$![]() , $b_u\in I\subseteq \mathcal {B}$
, $b_u\in I\subseteq \mathcal {B}$![]() are the corresponding idempotents. Since the elements $u$
are the corresponding idempotents. Since the elements $u$![]() are linearly independent, the coefficients of the combination are determined uniquely. We shall refer to these coefficients as the entries of the product.
are linearly independent, the coefficients of the combination are determined uniquely. We shall refer to these coefficients as the entries of the product.
Lemma 3.9 If $m=x_{i_1}x_{i_2}\cdots x_{i_r}$![]() and $n=x_{j_1}x_{j_2}\cdots x_{j_s}$
and $n=x_{j_1}x_{j_2}\cdots x_{j_s}$![]() are graded monomials such that the elements $Y_{i_1}Y_{i_2}\cdots Y_{i_r}$
are graded monomials such that the elements $Y_{i_1}Y_{i_2}\cdots Y_{i_r}$![]() and $Y_{j_1}Y_{j_2}\cdots Y_{j_s}$
and $Y_{j_1}Y_{j_2}\cdots Y_{j_s}$![]() have in the same position the same non-zero entry, up to a scalar multiple, then $r=s$
have in the same position the same non-zero entry, up to a scalar multiple, then $r=s$![]() and there exists $\sigma \in S_r$
and there exists $\sigma \in S_r$![]() such that
such that
Proof. Let us assume $Y_{i_1}Y_{i_2}\cdots Y_{i_r}$![]() and $Y_{j_1}Y_{j_2}\cdots Y_{j_s}$
and $Y_{j_1}Y_{j_2}\cdots Y_{j_s}$![]() have the same non-zero entry in the basis element $u=a_uub_u\in \mathcal {B}$
have the same non-zero entry in the basis element $u=a_uub_u\in \mathcal {B}$![]() . Such entries are polynomials in $\Gamma$
. Such entries are polynomials in $\Gamma$![]() . By our hypothesis, there exist monomials with variables in $T$
. By our hypothesis, there exist monomials with variables in $T$![]() , such that
, such that
and
are equal. Here the $r$![]() -tuple $(a_1,\,\ldots,\,a_r)$
-tuple $(a_1,\,\ldots,\,a_r)$![]() and the $s$
and the $s$![]() -tuple $(a^{\prime }_1,\,\ldots,\,a^{\prime }_s)$
-tuple $(a^{\prime }_1,\,\ldots,\,a^{\prime }_s)$![]() denote the good sequences associated with the monomials $m$
denote the good sequences associated with the monomials $m$![]() and $n$
and $n$![]() , respectively, whose entry is equal and non-zero. From the equality of the monomials in $\Gamma$
, respectively, whose entry is equal and non-zero. From the equality of the monomials in $\Gamma$![]() , and by homogeneity, we conclude that $r = s$
, and by homogeneity, we conclude that $r = s$![]() and there exists $\sigma \in S_r$
and there exists $\sigma \in S_r$![]() such that $j_l = i_{\sigma (l)}$
such that $j_l = i_{\sigma (l)}$![]() , for every $l$
, for every $l$![]() , $1\le l\le r$
, $1\le l\le r$![]() . Thus the proof is complete.
. Thus the proof is complete.
Lemma 3.10 Let $m$![]() and $n$
and $n$![]() be two graded monomials in the same set of variables and of the same multidegree in $F\langle X_G\rangle$
be two graded monomials in the same set of variables and of the same multidegree in $F\langle X_G\rangle$![]() . Suppose that there exist an admissible substitution $S$
. Suppose that there exist an admissible substitution $S$![]() in $\mathcal {R}$
in $\mathcal {R}$![]() and a non-zero $c\in F$
and a non-zero $c\in F$![]() such that, for some $r\in I,$
such that, for some $r\in I,$![]() $(m|_S)_r$
$(m|_S)_r$![]() and $c(n|_S)_r$
and $c(n|_S)_r$![]() are non-zero, and they share, in the same position, at least one common monomial, in $T$
are non-zero, and they share, in the same position, at least one common monomial, in $T$![]() . Then $m\equiv c n\pmod {\mathcal {I}}$
. Then $m\equiv c n\pmod {\mathcal {I}}$![]() .
.
Proof. If $m$![]() and $n$
and $n$![]() are multilinear, then the result follows from Lemma 3.1. Therefore, we can consider only the case when $m$
are multilinear, then the result follows from Lemma 3.1. Therefore, we can consider only the case when $m$![]() (and consequently $n$
(and consequently $n$![]() ) is not multilinear. Notice that for every monomial
) is not multilinear. Notice that for every monomial
in $F\langle X_G\rangle$![]() with $l< q$
with $l< q$![]() , which is not an identity for $A$
, which is not an identity for $A$![]() , there exists a multilinear monomial
, there exists a multilinear monomial
which is not an identity for $A$![]() either, and such that $h(m)=h(m^{\prime })$
either, and such that $h(m)=h(m^{\prime })$![]() .
.
Now we consider the specialization $\varphi _m\colon F\langle y_1,\,\ldots,\,y_q\rangle \to F\langle x_1,\,\ldots,\,x_l\rangle$![]() given by $\varphi _m(y_k)=x_{i_k}$
given by $\varphi _m(y_k)=x_{i_k}$![]() . It is clear that $\varphi _m$
. It is clear that $\varphi _m$![]() is onto and a $G$
is onto and a $G$![]() -homomorphism of algebras. Let $n$
-homomorphism of algebras. Let $n$![]() be a monomial in the same set of variables and of the same multidegree as $m$
be a monomial in the same set of variables and of the same multidegree as $m$![]() . In this case, there exists a multilinear graded monomial $n^{\prime }=z_1z_2\cdots z_q\in F\langle X_G\rangle$
. In this case, there exists a multilinear graded monomial $n^{\prime }=z_1z_2\cdots z_q\in F\langle X_G\rangle$![]() such that $\varphi _n(n^{\prime })=n$
such that $\varphi _n(n^{\prime })=n$![]() . By hypothesis $(m|_S)_r=c(n|_S)_r\neq 0$
. By hypothesis $(m|_S)_r=c(n|_S)_r\neq 0$![]() . Then Lemma 3.9 implies that
. Then Lemma 3.9 implies that
for some $\sigma \in S_q$![]() , and consequently $\varphi _m(n^{\prime })=\varphi _n(n^{\prime })=n$
, and consequently $\varphi _m(n^{\prime })=\varphi _n(n^{\prime })=n$![]() . On the other hand, Lemma 3.1 implies that
. On the other hand, Lemma 3.1 implies that
Hence,
This concludes the proof of the lemma.
The next proposition is a variation of [Reference Di Vincenzo and Nardozza17, Proposition 8]. It can be traced back to the papers by Vasilovsky [Reference Vasilovsky31] and later on Azevedo [Reference Azevedo4].
Proposition 3.11 Let $A$![]() be a $G$
be a $G$![]() -graded algebra equipped with a $\mathcal {B}$
-graded algebra equipped with a $\mathcal {B}$![]() -elementary grading and let $\mathcal {I}$
-elementary grading and let $\mathcal {I}$![]() be the $T_{G}$
be the $T_{G}$![]() -ideal generated by the identities in (3.1) and (3.2) such that $\mathcal {I}\subseteq T_G(A)$
-ideal generated by the identities in (3.1) and (3.2) such that $\mathcal {I}\subseteq T_G(A)$![]() . Let $\mathfrak {M}$
. Let $\mathfrak {M}$![]() denote the set of all monomials in $F\langle X_G \rangle$
denote the set of all monomials in $F\langle X_G \rangle$![]() . Assume that for every $m,$
. Assume that for every $m,$![]() $m^{\prime }\in \mathfrak {M}\setminus T_G(A)$
$m^{\prime }\in \mathfrak {M}\setminus T_G(A)$![]() there exists an admissible substitution $S$
there exists an admissible substitution $S$![]() in $\mathcal {R}$
in $\mathcal {R}$![]() (as in Lemma 3.4) and a non-zero scalar $c\in F$
(as in Lemma 3.4) and a non-zero scalar $c\in F$![]() such that, for some $r=1,$
such that, for some $r=1,$![]() …, $n,$
…, $n,$![]() satisfying the property
satisfying the property
$(m|_S)_r$
 and $c(m'|_S)_r$
and $c(m'|_S)_r$ are non-zero and they share at least one monomial, in $T,$
are non-zero and they share at least one monomial, in $T,$ if and only if $m\equiv c m^{\prime } \pmod {\mathcal {I}}$
if and only if $m\equiv c m^{\prime } \pmod {\mathcal {I}}$ .
.
Then $T_G(A)$![]() is generated by the identities in (3.1) and (3.2) together with the graded monomial identities from $(\mathfrak {M}\cap T_G(A))$
is generated by the identities in (3.1) and (3.2) together with the graded monomial identities from $(\mathfrak {M}\cap T_G(A))$![]() .
.
Proof. Let $J$![]() be the $T_G$
be the $T_G$![]() -ideal generated by (3.1) and (3.2) together with $(\mathfrak {M}\cap T_G(A))$
-ideal generated by (3.1) and (3.2) together with $(\mathfrak {M}\cap T_G(A))$![]() . One has $\mathcal {I} \subseteq J\subseteq T_G(A)$
. One has $\mathcal {I} \subseteq J\subseteq T_G(A)$![]() . Therefore, we have to prove that every multihomogeneous graded identity for $A$
. Therefore, we have to prove that every multihomogeneous graded identity for $A$![]() lies in $J$
lies in $J$![]() . We consider a multihomogeneous polynomial $f = f(x_1,\,\ldots,\, x_n)\in T_G(A)$
. We consider a multihomogeneous polynomial $f = f(x_1,\,\ldots,\, x_n)\in T_G(A)$![]() . We write,
. We write,

for some monomials $m_i\in \mathfrak {M}$![]() of the same multidegree, non-zero scalars $c_i\in F$
of the same multidegree, non-zero scalars $c_i\in F$![]() , and a positive integer $t$
, and a positive integer $t$![]() . Choose $t$
. Choose $t$![]() minimal with respect to this property. Clearly $t\ge 2$
minimal with respect to this property. Clearly $t\ge 2$![]() , and hence, for each $i$
, and hence, for each $i$![]() , we have $m_i\notin T_G(A)$
, we have $m_i\notin T_G(A)$![]() . Pay attention that if $t=2$
. Pay attention that if $t=2$![]() then $m_1-cm_2\in \mathcal {I}$
then $m_1-cm_2\in \mathcal {I}$![]() thus $f=(c_1c-c_2)m_2\in \mathcal {I}\subseteq J$
thus $f=(c_1c-c_2)m_2\in \mathcal {I}\subseteq J$![]() . We obtain $c_1c-c_2=0$
. We obtain $c_1c-c_2=0$![]() and $f\in \mathcal {I}$
and $f\in \mathcal {I}$![]() . This says we can in fact suppose without loss of generality that $t>2$
. This says we can in fact suppose without loss of generality that $t>2$![]() .
.
We have an admissible substitution $S$![]() of elements in $\mathcal {R}$
of elements in $\mathcal {R}$![]() such that $m_1|_S\neq 0$
such that $m_1|_S\neq 0$![]() . This implies
. This implies

By Lemma 3.7, there exists some $h$![]() , $2\leq h\leq t$
, $2\leq h\leq t$![]() such that $(m_1|_S)_r$
such that $(m_1|_S)_r$![]() and $c(m_h|_S)_r$
and $c(m_h|_S)_r$![]() are non-zero and they have at least one monomial, in $T$
are non-zero and they have at least one monomial, in $T$![]() , which are equal, for some $c\in F$
, which are equal, for some $c\in F$![]() and $r=1$
and $r=1$![]() , …, $n$
, …, $n$![]() . We can assume, without loss of generality, that $h=2$
. We can assume, without loss of generality, that $h=2$![]() . According to Property ($\mathcal {P}$
. According to Property ($\mathcal {P}$![]() ), we have $m_1\equiv c m_2\pmod {\mathcal {I}}$
), we have $m_1\equiv c m_2\pmod {\mathcal {I}}$![]() . Therefore, $f$
. Therefore, $f$![]() can be represented as
can be represented as

Obviously, this contradicts the minimality of $t$![]() , therefore $f\in J$
, therefore $f\in J$![]() and we are done.
and we are done.
As a consequence of Lemma 3.10 and Proposition 3.11, we obtain the following theorem.
Theorem 3.12 Let $A$![]() be a $G$
be a $G$![]() -graded algebra with a $\mathcal {B}$
-graded algebra with a $\mathcal {B}$![]() -elementary grading relative to the $G$
-elementary grading relative to the $G$![]() -multiplicative finite basis $\mathcal {B}$
-multiplicative finite basis $\mathcal {B}$![]() such that $\mathcal {I}\subset T_{G}(A)$
such that $\mathcal {I}\subset T_{G}(A)$![]() . The $T_{G}$
. The $T_{G}$![]() -ideal of the graded identities of $A$
-ideal of the graded identities of $A$![]() is generated by (3.1) and (3.2), together with all monomials which are graded identities of $A$
is generated by (3.1) and (3.2), together with all monomials which are graded identities of $A$![]() .
.
We recall that the graded identities in (3.1) and (3.2) do not depend on the characteristic of the base field. On the other hand, the monomial identities satisfied by $A$![]() might depend on the characteristic of $F$
might depend on the characteristic of $F$![]() .
.
The problem of describing the monomial identities that appear in Theorem 3.12 is still open even in characteristic zero. The nature of these monomial identities is still far from being understood, although they were described in several particular cases. The next result will give us a bound on the length of monomials which are needed in the basis in the theorem above.
Lemma 3.13 If a monomial $x_{i_1}x_{i_2}\cdots x_{i_q}$![]() in $F\langle X_G\rangle$
in $F\langle X_G\rangle$![]() is a graded identity for $A,$
is a graded identity for $A,$![]() then it is a consequence of a monomial $x_{i_1}x_{i_2}\cdots x_{i_l}$
then it is a consequence of a monomial $x_{i_1}x_{i_2}\cdots x_{i_l}$![]() in $T_G(A)$
in $T_G(A)$![]() . Here $\alpha _G (x_{i_r})\in \mathrm {supp}\ A,$
. Here $\alpha _G (x_{i_r})\in \mathrm {supp}\ A,$![]() and the degree $l$
and the degree $l$![]() is bounded by a function of $|\mathrm {supp}\ A|=s$
is bounded by a function of $|\mathrm {supp}\ A|=s$![]() .
.
Proof. If $s=1$![]() then our grading is trivial, hence we suppose $s> 1$
then our grading is trivial, hence we suppose $s> 1$![]() . By Corollary 3.8, we can consider that the monomial $x_{i_1}x_{i_2}\cdots x_{i_q}$
. By Corollary 3.8, we can consider that the monomial $x_{i_1}x_{i_2}\cdots x_{i_q}$![]() , in $T_G(A)$
, in $T_G(A)$![]() , is multilinear. Assume also that if $x_1\cdots x_k\notin T_G(A)$
, is multilinear. Assume also that if $x_1\cdots x_k\notin T_G(A)$![]() then $x_1\cdots x_k x_{k+1}\cdots x_{2k}\notin T_G(A)$
then $x_1\cdots x_k x_{k+1}\cdots x_{2k}\notin T_G(A)$![]() where $\alpha _G(x_{k+i})=\alpha _G(x_i)$
where $\alpha _G(x_{k+i})=\alpha _G(x_i)$![]() , for every $i=1$
, for every $i=1$![]() , …, $k$
, …, $k$![]() . In this case, the proof of [Reference Bahturin and Drensky7, Proposition 4.2] yields that the set $\mathfrak {M}\cap T_G(A)$
. In this case, the proof of [Reference Bahturin and Drensky7, Proposition 4.2] yields that the set $\mathfrak {M}\cap T_G(A)$![]() in Theorem 3.12 may be replaced by finitely many elements in $\mathfrak {M}\cap T_G(A)$
in Theorem 3.12 may be replaced by finitely many elements in $\mathfrak {M}\cap T_G(A)$![]() whose degrees are bounded by a function of the number of elements in $\mathrm {supp}\ A$
whose degrees are bounded by a function of the number of elements in $\mathrm {supp}\ A$![]() .
.
We point out that, in some cases, it is possible to find a better bound but the one we find here is sufficient for the proof of the previous lemma, see the next section.
Remark 3.14 The conclusions of Lemmas 3.4, 3.9, 3.10, Proposition 3.11, and Theorem 3.12 still hold if we change the polynomial ring $\Gamma$![]() by the ring $\Gamma ^{\beta }$
by the ring $\Gamma ^{\beta }$![]() given in Remark 3.3.
given in Remark 3.3.
As a consequence, we obtain an alternative proof of the description of a basis for the $G$![]() -graded polynomial identities of the algebra of upper block-triangular matrices, denoted by $UT(d_1,\,\ldots,\, d_n)$
-graded polynomial identities of the algebra of upper block-triangular matrices, denoted by $UT(d_1,\,\ldots,\, d_n)$![]() , with an elementary grading induced by an $n$
, with an elementary grading induced by an $n$![]() -tuple of elements of a group $G$
-tuple of elements of a group $G$![]() such that the neutral component corresponds to the diagonal of $UT(d_1,\,\ldots,\, d_n)$
such that the neutral component corresponds to the diagonal of $UT(d_1,\,\ldots,\, d_n)$![]() , see for example [Reference Diniz and de Mello19, Theorem 3.7].
, see for example [Reference Diniz and de Mello19, Theorem 3.7].
4. Monomial identities for algebras with elementary gradings
Here we use the notation adopted in the preceding section. We consider $A$![]() as a finite-dimensional algebra with $\mathcal {B}$
as a finite-dimensional algebra with $\mathcal {B}$![]() -elementary grading. We draw the readers’ attention that we do not require the inclusion $\mathcal {I}\subset T_{G}(A)$
-elementary grading. We draw the readers’ attention that we do not require the inclusion $\mathcal {I}\subset T_{G}(A)$![]() (recall that $\mathcal {I}$
(recall that $\mathcal {I}$![]() is the $T_{G}$
is the $T_{G}$![]() -ideal generated by the identities from (3.1) and (3.2). This means that our results from this section are in rather general form.
-ideal generated by the identities from (3.1) and (3.2). This means that our results from this section are in rather general form.
We shall show that, under an additional restriction, all graded monomial identities in $T_G(A)$![]() of length larger than $|I|=n$
of length larger than $|I|=n$![]() are consequences of those of length at most $n$
are consequences of those of length at most $n$![]() . Recall that $I$
. Recall that $I$![]() is the corresponding elementary set of idempotents of $\mathcal {B}$
is the corresponding elementary set of idempotents of $\mathcal {B}$![]() .
.
We consider a basis element $u=a_uub_u\in \mathcal {B}$![]() , where $a_u$
, where $a_u$![]() , $b_u\in I\subset \mathcal {B}$
, $b_u\in I\subset \mathcal {B}$![]() are the corresponding idempotents. We write
are the corresponding idempotents. We write
an element of $A$![]() . We say that $\alpha _u$
. We say that $\alpha _u$![]() is the entry $(a_u,\,b_u)$
is the entry $(a_u,\,b_u)$![]() , if $u=a_uub_u$
, if $u=a_uub_u$![]() . Moreover, $a_u$
. Moreover, $a_u$![]() will denote the row of $\alpha _u$
will denote the row of $\alpha _u$![]() while $b_u$
while $b_u$![]() the column of $\alpha _u$
the column of $\alpha _u$![]() . Clearly, this terminology is influenced by matrix algebras.
. Clearly, this terminology is influenced by matrix algebras.
Given an entry $(a_u,\,b_u)$![]() , there may be no element $u$
, there may be no element $u$![]() in $\mathcal {B}$
in $\mathcal {B}$![]() such that $u=a_uub_u$
such that $u=a_uub_u$![]() . For example, if we consider the canonical basis of $UT_{n}(F)$
. For example, if we consider the canonical basis of $UT_{n}(F)$![]() , then, for every $i< j$
, then, for every $i< j$![]() , there will be no corresponding $E_{ji}$
, there will be no corresponding $E_{ji}$![]() , since $I=\{E_{ii}\mid i=1,\,\ldots,\, n\}$
, since $I=\{E_{ii}\mid i=1,\,\ldots,\, n\}$![]() . This motivates our next definition.
. This motivates our next definition.
Definition 4.1 Let $A$![]() be an algebra with an elementary basis $\mathcal {B}$
be an algebra with an elementary basis $\mathcal {B}$![]() and let $I$
and let $I$![]() be the corresponding elementary set of idempotents. We say that $\mathcal {B}$
be the corresponding elementary set of idempotents. We say that $\mathcal {B}$![]() is complete if every sequence $(u_1,\,\ldots,\, u_q)$
is complete if every sequence $(u_1,\,\ldots,\, u_q)$![]() of elements of $I$
of elements of $I$![]() is good in the sense of Definition 3.2.
is good in the sense of Definition 3.2.
It is easy to see that the standard bases of the algebras $M_n(F)$![]() , $M_n(E)$
, $M_n(E)$![]() and $M_{a,b}(E)$
and $M_{a,b}(E)$![]() are complete. We shall use this fact in the next section in order to describe a basis of the graded identities for the latter algebra.
are complete. We shall use this fact in the next section in order to describe a basis of the graded identities for the latter algebra.
The next result, concerning graded monomial identities, is a key step in the proof of the main theorem of this section.
Lemma 4.2 Let $A$![]() be a $G$
be a $G$![]() -graded algebra with a $\mathcal {B}$
-graded algebra with a $\mathcal {B}$![]() -elementary grading relative to the $G$
-elementary grading relative to the $G$![]() -multiplicative finite basis $\mathcal {B}$
-multiplicative finite basis $\mathcal {B}$![]() . For $h\in \mathrm {supp}\ A,$
. For $h\in \mathrm {supp}\ A,$![]() let us denote
let us denote
Let $h_1,\,\ldots,\,h_k$![]() be elements of $\mathrm {supp}\ A$
be elements of $\mathrm {supp}\ A$![]() . If $h_1\cdots h_k = \epsilon,$
. If $h_1\cdots h_k = \epsilon,$![]() then the number of non-zero rows in $M_1 = Y^{h_1}_{i_1}Y^{h_2}_{i_2}\cdots Y^{h_q}_{i_q}$
then the number of non-zero rows in $M_1 = Y^{h_1}_{i_1}Y^{h_2}_{i_2}\cdots Y^{h_q}_{i_q}$![]() and $M_2= Y^{h_2}_{i_2}\cdots Y^{h_q}_{i_q}$
and $M_2= Y^{h_2}_{i_2}\cdots Y^{h_q}_{i_q}$![]() is the same.
is the same.
Proof. By Lemma 3.7, we have
Let $a_1$![]() , …, $a_r$
, …, $a_r$![]() be the indices of the rows of $M_1$
be the indices of the rows of $M_1$![]() which are non-zero. It is clear those rows are also non-zero ones in $Y^{h_1}_{i_1}$
which are non-zero. It is clear those rows are also non-zero ones in $Y^{h_1}_{i_1}$![]() . Define $j_1=s_{h_1}^{a_1}$
. Define $j_1=s_{h_1}^{a_1}$![]() , …, $j_r=s_{h_1}^{a_r}$
, …, $j_r=s_{h_1}^{a_r}$![]() . The claim follows once we prove $j_1$
. The claim follows once we prove $j_1$![]() , …, $j_r$
, …, $j_r$![]() are exactly the non-zero rows of $M_2$
are exactly the non-zero rows of $M_2$![]() .
.
Since $Y^{h_1}_{i_1}$![]() is homogeneous of degree $h_1$
is homogeneous of degree $h_1$![]() , we have $M_2$
, we have $M_2$![]() is homogeneous of degree $h_1^{-1}$
is homogeneous of degree $h_1^{-1}$![]() . If the $j$
. If the $j$![]() -th row of $M_2$
-th row of $M_2$![]() is non-zero, then there exists $i$
is non-zero, then there exists $i$![]() such that $u=a_jua_i$
such that $u=a_jua_i$![]() has degree $h^{-1}_1$
has degree $h^{-1}_1$![]() . Of course, there exists an element $u_1\in \mathcal {B}$
. Of course, there exists an element $u_1\in \mathcal {B}$![]() of $Y^{h_1}_{i_1}$
of $Y^{h_1}_{i_1}$![]() such that $|u_1u|=\epsilon$
such that $|u_1u|=\epsilon$![]() . In this case, $u_1=a_iu_1a_j$
. In this case, $u_1=a_iu_1a_j$![]() . Hence $j=s_{h_1}^{i}$
. Hence $j=s_{h_1}^{i}$![]() where $i$
where $i$![]() is a non-zero row of $M_1$
is a non-zero row of $M_1$![]() , since $u_1M_2\neq 0$
, since $u_1M_2\neq 0$![]() . Hence the result follows.
. Hence the result follows.
Lemma 4.3 Let $m = x_{i_1}x_{i_2}\cdots x_{i_k}$![]() be a graded monomial identity of homogeneous degree $\epsilon$
be a graded monomial identity of homogeneous degree $\epsilon$![]() of $A,$
of $A,$![]() where $\alpha _G(x_{i_1})\in \mathrm {supp}\ A$
where $\alpha _G(x_{i_1})\in \mathrm {supp}\ A$![]() . Then it is a consequence of the graded monomial identity $m^{\prime } = x_{i_2}\cdots x_{i_k}$
. Then it is a consequence of the graded monomial identity $m^{\prime } = x_{i_2}\cdots x_{i_k}$![]() .
.
Proof. The statement follows immediately from the previous lemma.
Now we have all the ingredients for the proof of the main result of the section.
Theorem 4.4 Let $A$![]() be a $G$
be a $G$![]() -graded algebra with a $\mathcal {B}$
-graded algebra with a $\mathcal {B}$![]() -elementary grading relative to the $G$
-elementary grading relative to the $G$![]() -multiplicative complete finite basis $\mathcal {B}$
-multiplicative complete finite basis $\mathcal {B}$![]() . Let $I$
. Let $I$![]() be the corresponding elementary set of idempotents of $\mathcal {B}$
be the corresponding elementary set of idempotents of $\mathcal {B}$![]() with $|I|=n$
with $|I|=n$![]() . If $m = x_{i_1}\cdots x_{i_k}$
. If $m = x_{i_1}\cdots x_{i_k}$![]() is a graded monomial identity for $A$
is a graded monomial identity for $A$![]() and $k > n$
and $k > n$![]() then $m$
then $m$![]() is a consequence of a graded monomial identity of $A$
is a consequence of a graded monomial identity of $A$![]() of degree at most $n$
of degree at most $n$![]() .
.
Proof. Suppose $k > n$![]() . According to Corollary 3.8, there exists a multilinear monomial
. According to Corollary 3.8, there exists a multilinear monomial
with $h(m)=h(m^{\prime })$![]() , and such that $m\in T_G(A)$
, and such that $m\in T_G(A)$![]() if and only if $m^{\prime }\in T_G(A)$
if and only if $m^{\prime }\in T_G(A)$![]() . Hence it is enough to prove the theorem for multilinear monomials. If $x_{1}\cdots x_{n}$
. Hence it is enough to prove the theorem for multilinear monomials. If $x_{1}\cdots x_{n}$![]() is a graded monomial identity for $A$
is a graded monomial identity for $A$![]() we are done. Assume that $x_{1}\cdots x_{n}$
we are done. Assume that $x_{1}\cdots x_{n}$![]() is not a graded identity for $A$
is not a graded identity for $A$![]() . In this case, there are indices $i_1$
. In this case, there are indices $i_1$![]() , $j_1$
, $j_1$![]() , …, $i_n$
, …, $i_n$![]() , $j_n$
, $j_n$![]() such that $u_r=a_{i_r}u_ra_{j_r}\in \mathcal {B}$
such that $u_r=a_{i_r}u_ra_{j_r}\in \mathcal {B}$![]() with $\alpha _G(u_r)=\alpha _G(x_{r})=h_r$
with $\alpha _G(u_r)=\alpha _G(x_{r})=h_r$![]() , for each $r=1$
, for each $r=1$![]() , 2, …, $n$
, 2, …, $n$![]() , and $u_{1}u_{2}\cdots u_{n}\neq 0$
, and $u_{1}u_{2}\cdots u_{n}\neq 0$![]() . Then $j_r=i_{r+1}$
. Then $j_r=i_{r+1}$![]() for every $r< n$
for every $r< n$![]() . Defining $j_n=i_{n+1}$
. Defining $j_n=i_{n+1}$![]() since $i_r\in \{1,\,\ldots,\, n\}$
since $i_r\in \{1,\,\ldots,\, n\}$![]() , for every $r$
, for every $r$![]() , at least two among the indices $i_1$
, at least two among the indices $i_1$![]() , $i_2$
, $i_2$![]() , …, $i_{n+1}$
, …, $i_{n+1}$![]() are equal. Let $i_s$
are equal. Let $i_s$![]() and $i_{t+1}=j_t$
and $i_{t+1}=j_t$![]() be such indices. Then $\alpha _G(x_{s}\cdots x_{t}) =\epsilon$
be such indices. Then $\alpha _G(x_{s}\cdots x_{t}) =\epsilon$![]() . In other words $m$
. In other words $m$![]() has a submonomial $m^{\prime } = x_{s}\cdots x_{t}$
has a submonomial $m^{\prime } = x_{s}\cdots x_{t}$![]() of degree $\epsilon$
of degree $\epsilon$![]() .
.
Suppose first $s = 1$![]() , that is $m^{\prime }$
, that is $m^{\prime }$![]() is at the beginning of the monomial $m$
is at the beginning of the monomial $m$![]() . Then Lemma 4.2 shows that $m$
. Then Lemma 4.2 shows that $m$![]() is a consequence of $x_{2}\cdots x_{k}$
is a consequence of $x_{2}\cdots x_{k}$![]() , and the result follows by the induction hypothesis.
, and the result follows by the induction hypothesis.
Suppose now $s > 1$![]() . If $m^{[s,t]}=x_{s}\cdots x_{t}$
. If $m^{[s,t]}=x_{s}\cdots x_{t}$![]() is a graded identity for $A$
is a graded identity for $A$![]() then the result follows again by the induction hypothesis. Therefore, we assume $m^{[s,t]}$
then the result follows again by the induction hypothesis. Therefore, we assume $m^{[s,t]}$![]() is not a graded identity for $A$
is not a graded identity for $A$![]() . We claim the monomial
. We claim the monomial
is a graded monomial identity for $A$![]() where $\alpha _G(y)=h_{s-1}h_{s}=g_s$
where $\alpha _G(y)=h_{s-1}h_{s}=g_s$![]() . To this end, it is enough to show that the non-zero rows of $Y^{h_{s-1}}Y^{h_{s}}\cdots Y^{h_t}$
. To this end, it is enough to show that the non-zero rows of $Y^{h_{s-1}}Y^{h_{s}}\cdots Y^{h_t}$![]() and $Y^{g_{s}}Y^{h_{s+1}}\cdots Y^{h_t}$
and $Y^{g_{s}}Y^{h_{s+1}}\cdots Y^{h_t}$![]() are the same. In order to prove this claim, we notice that every non-zero row of the former product is a non-zero rowof the latter.
are the same. In order to prove this claim, we notice that every non-zero row of the former product is a non-zero rowof the latter.
Now, let $i$![]() be a non-zero row of $Y^{g_{s}}Y^{h_{s+1}}\cdots Y^{h_t}$
be a non-zero row of $Y^{g_{s}}Y^{h_{s+1}}\cdots Y^{h_t}$![]() . As before, there are elements $u_r=a_{i_r}u_ra_{j_r}$
. As before, there are elements $u_r=a_{i_r}u_ra_{j_r}$![]() , for $r\in \{s + 1,\,\ldots,\, t\}$
, for $r\in \{s + 1,\,\ldots,\, t\}$![]() , such that $\alpha _G(u_r)=h_r$
, such that $\alpha _G(u_r)=h_r$![]() and $uu_{s+1}\cdots u_{t}\neq 0$
and $uu_{s+1}\cdots u_{t}\neq 0$![]() where $\alpha _G(u)=h_{s-1}h_s$
where $\alpha _G(u)=h_{s-1}h_s$![]() . Since $h_s\cdots h_t=\epsilon$
. Since $h_s\cdots h_t=\epsilon$![]() , we have $h_s=|f(a_{j_t})|^{-1}|f(a_{i_{s+1}})|$
, we have $h_s=|f(a_{j_t})|^{-1}|f(a_{i_{s+1}})|$![]() with $f\colon I\to G$
with $f\colon I\to G$![]() .
.
By comparing degrees, one gets $\bar {u}\in \mathcal {B}$![]() with $\alpha _{G}(\bar {u})=|f(a_{i})|^{-1}|f(a_{j_t})|$
with $\alpha _{G}(\bar {u})=|f(a_{i})|^{-1}|f(a_{j_t})|$![]() . Hence
. Hence
and this means $i$![]() is a non-zero row of $Y^{h_{s-1}}Y^{h_{s}}Y^{h_{s+1}}\cdots Y^{h_{t}}$
is a non-zero row of $Y^{h_{s-1}}Y^{h_{s}}Y^{h_{s+1}}\cdots Y^{h_{t}}$![]() . The latter claim holds since the basis is complete.
. The latter claim holds since the basis is complete.
In order to finish the proof, we apply induction on $k \geq n+1$![]() . If $k = n+1$
. If $k = n+1$![]() , the discussion above shows that $m$
, the discussion above shows that $m$![]() is a consequence of a graded monomial of degree $n$
is a consequence of a graded monomial of degree $n$![]() and we are done. Suppose the result holds for $k -1 \geq n + 1$
and we are done. Suppose the result holds for $k -1 \geq n + 1$![]() , we shall prove it for $k \geq n + 2$
, we shall prove it for $k \geq n + 2$![]() . As above, $m$
. As above, $m$![]() is a consequence of a graded identity of degree less than $k$
is a consequence of a graded identity of degree less than $k$![]() . Hence, by induction, it is a consequence of a graded monomial of degree $\le n$
. Hence, by induction, it is a consequence of a graded monomial of degree $\le n$![]() and now the proof is complete.
and now the proof is complete.
The latter theorem generalizes [Reference Centrone, Diniz and de Mello12, Theorem 3.5.]. In that paper, the authors proved that all multilinear graded monomial identities of the full matrix algebra of order $n$![]() follow from those of degree $n$
follow from those of degree $n$![]() provided the grading is elementary. In the next section, we consider elementary gradings on $M_{a,b}(E)$
provided the grading is elementary. In the next section, we consider elementary gradings on $M_{a,b}(E)$![]() , as well as their tensor product.
, as well as their tensor product.
5. Graded polynomial identities of $M_{a,b}(E)$ and $M_{a,b}(E)\otimes M_{r,s}(E)$
and $M_{a,b}(E)\otimes M_{r,s}(E)$
In this section, we study concrete algebras that satisfy the graded identities (3.1) and (3.2). We denote by $E_{ij}$![]() the elementary matrix having 1 at position $(i,\,j)$
the elementary matrix having 1 at position $(i,\,j)$![]() and 0 elsewhere.
and 0 elsewhere.
5.1. Graded identities for ${\bf M_{a,b}(E)}$
The main result in this subsection is the description of a basis for the graded polynomial identities of $M_{a,b}(E)$![]() equipped with certain $\mathcal {B}$
equipped with certain $\mathcal {B}$![]() -elementary grading.
-elementary grading.
Definition 5.1 Let $m$![]() , $n$
, $n$![]() , and $a\geq b$
, and $a\geq b$![]() be positive integers such that $a+b=mn$
be positive integers such that $a+b=mn$![]() . Let $G$
. Let $G$![]() be a group and $\varphi \colon \{1,\,\ldots,\, m\}\times \{1,\,\ldots,\, n\}\to G$
be a group and $\varphi \colon \{1,\,\ldots,\, m\}\times \{1,\,\ldots,\, n\}\to G$![]() an injective function. Given $1\leq i \leq mn$
an injective function. Given $1\leq i \leq mn$![]() there exists a unique pair $(a_i,\, b_i)\in \{1,\,\ldots,\, m\}\times \{1,\,\ldots,\, n\}$
there exists a unique pair $(a_i,\, b_i)\in \{1,\,\ldots,\, m\}\times \{1,\,\ldots,\, n\}$![]() such that $i=n(a_i-1)+b_i$
such that $i=n(a_i-1)+b_i$![]() . For every $\mathfrak {a}E_{ij}$
. For every $\mathfrak {a}E_{ij}$![]() in the canonical basis of $M_{a,b}(E)$
in the canonical basis of $M_{a,b}(E)$![]() we set
we set
The map $|\cdot |$![]() satisfies Condition (2.1); therefore, it determines a $G^{\ast }$
satisfies Condition (2.1); therefore, it determines a $G^{\ast }$![]() -grading on $M_{a,b}(E)$
-grading on $M_{a,b}(E)$![]() . This $G^{\ast }$
. This $G^{\ast }$![]() -grading is called the grading induced by $\varphi$
-grading is called the grading induced by $\varphi$![]() .
.
The grading introduced in the previous definition is a $\mathcal {B}$![]() -elementary grading relative to the canonical basis $\mathcal {B}$
-elementary grading relative to the canonical basis $\mathcal {B}$![]() and the set of idempotents $I=\{E_{ii}\otimes 1_E\mid 1\leq i\leq a+b\}$
and the set of idempotents $I=\{E_{ii}\otimes 1_E\mid 1\leq i\leq a+b\}$![]() . It is induced by the function $f\colon I\to G^{\ast }$
. It is induced by the function $f\colon I\to G^{\ast }$![]() given by $f(E_{ii})=(\varphi (a_i,\,b_i),\,0)$
given by $f(E_{ii})=(\varphi (a_i,\,b_i),\,0)$![]() if $i\leq a$
if $i\leq a$![]() and $f(E_{ii})=(\varphi (a_i,\,b_i),\,1)$
and $f(E_{ii})=(\varphi (a_i,\,b_i),\,1)$![]() , otherwise. Here we observe that $m$
, otherwise. Here we observe that $m$![]() can be equal to 1 and $\mathcal {B}$
can be equal to 1 and $\mathcal {B}$![]() is complete in sense of Definition 4.1. The identities for $M_{a,b}(E)$
is complete in sense of Definition 4.1. The identities for $M_{a,b}(E)$![]() with the elementary $\mathbb {Z}_{a+b}\times \mathbb {Z}_2$
with the elementary $\mathbb {Z}_{a+b}\times \mathbb {Z}_2$![]() -grading induced by $\varphi (u,\,1)=-\overline {u}$
-grading induced by $\varphi (u,\,1)=-\overline {u}$![]() were described in [Reference Di Vincenzo and Nardozza17], over a field of characteristic zero, and in [Reference Di Vincenzo, Koshlukov and Santulo18] when the ground field is infinite of characteristic different from 2. Here $\overline {u}$
were described in [Reference Di Vincenzo and Nardozza17], over a field of characteristic zero, and in [Reference Di Vincenzo, Koshlukov and Santulo18] when the ground field is infinite of characteristic different from 2. Here $\overline {u}$![]() stands for $u\pmod {a+b}$
stands for $u\pmod {a+b}$![]() . Moreover, in [Reference Fidelis, Diniz, Bernardo and Koshlukov20], over a field of characteristic zero, it was provided a basis of the graded identities for $M_{a,b}(E)$
. Moreover, in [Reference Fidelis, Diniz, Bernardo and Koshlukov20], over a field of characteristic zero, it was provided a basis of the graded identities for $M_{a,b}(E)$![]() when equipped with the grading given in the above definition.
when equipped with the grading given in the above definition.
Lemma 5.2 Let $G$![]() be an arbitrary group, let $a,$
be an arbitrary group, let $a,$![]() $b$
$b$![]() be positive integers such that $a+b=n,$
be positive integers such that $a+b=n,$![]() and $\varphi \colon \{1,\,\ldots,\, n\}=\{1,\,\ldots,\, n\}\times \{1\}\to G$
and $\varphi \colon \{1,\,\ldots,\, n\}=\{1,\,\ldots,\, n\}\times \{1\}\to G$![]() be an injective function. Considering $M_{a,b}(E)$
be an injective function. Considering $M_{a,b}(E)$![]() equipped with the elementary grading induced by $\varphi,$
equipped with the elementary grading induced by $\varphi,$![]() the graded polynomials
the graded polynomials
are graded identities of $M_{a,b}(E)$![]() .
.
Proof. The proof of this lemma is well known, see for example [Reference Fidelis, Diniz, Bernardo and Koshlukov20, Theorem 4.6].
The next theorem then follows as a direct consequence of the previous lemma, Remark 3.14 and Theorem 4.4.
Theorem 5.3 Let $G$![]() be an arbitrary group, let $a$
be an arbitrary group, let $a$![]() , $b$
, $b$![]() be positive integers such that $a+b=n,$
be positive integers such that $a+b=n,$![]() and $\varphi \colon \{1,\,\ldots,\, n\}\to G$
and $\varphi \colon \{1,\,\ldots,\, n\}\to G$![]() be an injective function. Consider $M_{a,b}(E)$
be an injective function. Consider $M_{a,b}(E)$![]() with the elementary grading induced by $\varphi$
with the elementary grading induced by $\varphi$![]() . Over an infinite field of characteristic different from 2, the $T_{G^{\ast }}$
. Over an infinite field of characteristic different from 2, the $T_{G^{\ast }}$![]() -ideal $T_{G^{\ast }}(M_{a,b}(E))$
-ideal $T_{G^{\ast }}(M_{a,b}(E))$![]() is generated by the graded identities (5.1)–(5.3), together with its graded monomial identities of degree at most $n$
is generated by the graded identities (5.1)–(5.3), together with its graded monomial identities of degree at most $n$![]() .
.
5.2. Graded identities for $M_{a,b}(E)\otimes M_{r,s}(E)$
Here we consider the counterpart of the previous subsection for the graded identities of the tensor product $M_{a,b}(E)\otimes M_{r,s}(E)$![]() .
.
Definition 5.4 Let $G$![]() be a group and let $\varphi \colon \{1,\, \ldots,\, a+b\}\times \{1,\, \ldots,\, r+s\}\rightarrow G$
be a group and let $\varphi \colon \{1,\, \ldots,\, a+b\}\times \{1,\, \ldots,\, r+s\}\rightarrow G$![]() be an injective function. For every $(aE_{ij},\,bE_{uv})\in \mathcal {B}_1\times \mathcal {B}_2=\mathcal {B}$
be an injective function. For every $(aE_{ij},\,bE_{uv})\in \mathcal {B}_1\times \mathcal {B}_2=\mathcal {B}$![]() we set
we set
The map $|\cdot |$![]() satisfies Condition (2.1). Therefore, it determines a $G^{\ast }$
satisfies Condition (2.1). Therefore, it determines a $G^{\ast }$![]() -grading on $M_{a,b}(E)\otimes M_{r,s}(E)$
-grading on $M_{a,b}(E)\otimes M_{r,s}(E)$![]() . It is called the grading induced by $\varphi$
. It is called the grading induced by $\varphi$![]() .
.
We assume that the elements of $\mathrm {supp}\ M_{a,b}(E)$![]() commute with the elements of $\mathrm {supp}\ M_{r,s}(E)$
commute with the elements of $\mathrm {supp}\ M_{r,s}(E)$![]() . Then the comments stated after Definition 2.3 imply that the tensor product grading on $M_{a,b}(E)\otimes M_{r,s}(E)$
. Then the comments stated after Definition 2.3 imply that the tensor product grading on $M_{a,b}(E)\otimes M_{r,s}(E)$![]() given in the previous definition is an elementary grading relative to the canonical basis and set of idempotents, on $M_{a,b}(E)\otimes M_{r,s}(E)$
given in the previous definition is an elementary grading relative to the canonical basis and set of idempotents, on $M_{a,b}(E)\otimes M_{r,s}(E)$![]() . Moreover, this basis is complete.
. Moreover, this basis is complete.
The graded identities of $M_{a,b}(E)\otimes M_{r,s}(E)$![]() endowed with the elementary $\mathbb {Z}_{mn}\times \mathbb {Z}_2$
endowed with the elementary $\mathbb {Z}_{mn}\times \mathbb {Z}_2$![]() -grading, where $m=a+b$
-grading, where $m=a+b$![]() , $n=r+s$
, $n=r+s$![]() , induced by $\varphi (i,\,u)=-(\overline {ni+u})$
, induced by $\varphi (i,\,u)=-(\overline {ni+u})$![]() , were studied in [Reference Di Vincenzo and Nardozza17, Reference Di Vincenzo, Koshlukov and Santulo18]. Furthermore, over a field of characteristic zero, a description for the graded identities discussed above was provided in [Reference Fidelis, Diniz, Bernardo and Koshlukov20].
, were studied in [Reference Di Vincenzo and Nardozza17, Reference Di Vincenzo, Koshlukov and Santulo18]. Furthermore, over a field of characteristic zero, a description for the graded identities discussed above was provided in [Reference Fidelis, Diniz, Bernardo and Koshlukov20].
Lemma 5.5 Let $\mathcal {I}$![]() be the $T_{G\times \mathbb {Z}_2}$
be the $T_{G\times \mathbb {Z}_2}$![]() -ideal in $F\langle X_{G\times \mathbb {Z}_2}\rangle$
-ideal in $F\langle X_{G\times \mathbb {Z}_2}\rangle$![]() generated by the polynomials (5.1)–(5.3). Let $G$
generated by the polynomials (5.1)–(5.3). Let $G$![]() be a group such that the elements of $\mathrm {supp}\ M_{a,b}(E)$
be a group such that the elements of $\mathrm {supp}\ M_{a,b}(E)$![]() commute with the elements of $\mathrm {supp}\ M_{r,s}(E)$
commute with the elements of $\mathrm {supp}\ M_{r,s}(E)$![]() . Denote by $A$
. Denote by $A$![]() the algebra $M_{a,b}(E)\otimes M_{r,s}(E)$
the algebra $M_{a,b}(E)\otimes M_{r,s}(E)$![]() equipped with the elementary grading given in Definition 5.4. Then the $T_{G\times \mathbb {Z}_2}$
equipped with the elementary grading given in Definition 5.4. Then the $T_{G\times \mathbb {Z}_2}$![]() -ideal $\mathcal {I}$
-ideal $\mathcal {I}$![]() is contained in $T_{G\times \mathbb {Z}}(A)$
is contained in $T_{G\times \mathbb {Z}}(A)$![]() .
.
Proof. It is clear that the polynomial in (5.1) is a graded identity for $M_{a,b}(E)\otimes M_{r,s}(E)$![]() . Let $w_h = a_hE_{i_hj_h}\otimes b_hE_{u_hv_h}\in \mathcal {B}$
. Let $w_h = a_hE_{i_hj_h}\otimes b_hE_{u_hv_h}\in \mathcal {B}$![]() , for $h = 1$
, for $h = 1$![]() , 2, 3, and assume that $\alpha _{G\times \mathbb {Z}_2}( w_1)=\alpha _{G\times \mathbb {Z}_2}(w_3)=\alpha _{G\times \mathbb {Z}_2}(w_2)^{-1}$
, 2, 3, and assume that $\alpha _{G\times \mathbb {Z}_2}( w_1)=\alpha _{G\times \mathbb {Z}_2}(w_3)=\alpha _{G\times \mathbb {Z}_2}(w_2)^{-1}$![]() . If $w_1w_2w_3\neq 0$
. If $w_1w_2w_3\neq 0$![]() then $|w_1w_2|=(\epsilon,\,0)$
then $|w_1w_2|=(\epsilon,\,0)$![]() and $w_1w_2\neq 0$
and $w_1w_2\neq 0$![]() . We have $j_1=i_2$
. We have $j_1=i_2$![]() , $v_1=u_2$
, $v_1=u_2$![]() , and, since the function $f$
, and, since the function $f$![]() is injective, $j_2=i_1$
is injective, $j_2=i_1$![]() , $v_2=u_1$
, $v_2=u_1$![]() . Similarly $j_2 = i_3$
. Similarly $j_2 = i_3$![]() , $v_2 = u_3$
, $v_2 = u_3$![]() , and $j_3 = i_2$
, and $j_3 = i_2$![]() , $v_3 = u_2$
, $v_3 = u_2$![]() . Therefore, $w_1 = a_1E_{ij}\otimes b_1E_{uv}$
. Therefore, $w_1 = a_1E_{ij}\otimes b_1E_{uv}$![]() , $w_2 = a_2E_{ji}\otimes b_2E_{vu}$
, $w_2 = a_2E_{ji}\otimes b_2E_{vu}$![]() , and $w_3 = a_3E_{ij}\otimes b_2E_{uv}$
, and $w_3 = a_3E_{ij}\otimes b_2E_{uv}$![]() for some $1\leq i,\, j\leq a+b$
for some $1\leq i,\, j\leq a+b$![]() and $1\leq u,\, v\leq r+s$
and $1\leq u,\, v\leq r+s$![]() . Hence we obtain $w_1w_2w_3= a_1a_2a_3E_{ij}\otimes b_1b_2b_3E_{uv}$
. Hence we obtain $w_1w_2w_3= a_1a_2a_3E_{ij}\otimes b_1b_2b_3E_{uv}$![]() and $w_3w_2w_1= a_3a_2a_1E_{ij}\otimes b_3b_2b_1E_{uv}$
and $w_3w_2w_1= a_3a_2a_1E_{ij}\otimes b_3b_2b_1E_{uv}$![]() . In this way, we conclude the proof since the $a_i$
. In this way, we conclude the proof since the $a_i$![]() and $b_j$
and $b_j$![]() are elements in the canonical basis of $E$
are elements in the canonical basis of $E$![]() .
.
The previous lemma, Theorem 3.12, Remark 3.14 and Theorem 4.4 imply the proof of the next theorem.
Theorem 5.6 Assume the base field is infinite and of characteristic different from 2. Let $G$![]() be a group such that the elements of $\mathrm {supp}\ M_{a,b}(E)$
be a group such that the elements of $\mathrm {supp}\ M_{a,b}(E)$![]() commute with the elements of $\mathrm {supp}\ M_{r,s}(E)$
commute with the elements of $\mathrm {supp}\ M_{r,s}(E)$![]() . The $T_{G\times \mathbb {Z}_2}$
. The $T_{G\times \mathbb {Z}_2}$![]() -ideal of the graded identities of the algebra $M_{a,b}(E)\otimes M_{r,s}(E),$
-ideal of the graded identities of the algebra $M_{a,b}(E)\otimes M_{r,s}(E),$![]() equipped with the grading given in Definition 5.4, is generated by (5.1)–(5.3), together with its graded monomial identities of degree at most $(a+b)(r+s)$
equipped with the grading given in Definition 5.4, is generated by (5.1)–(5.3), together with its graded monomial identities of degree at most $(a+b)(r+s)$![]() .
.
5.3. Models for the relatively free graded algebras
Now we have all the ingredients in order to study the relationship between the graded identities for the algebras $M_{ar+bs,as+br}(E)$![]() and $M_{a,b}(E)\otimes M_{r,s}(E)$
and $M_{a,b}(E)\otimes M_{r,s}(E)$![]() . In this section, our main goal will be to deduce that the $T_{G}$
. In this section, our main goal will be to deduce that the $T_{G}$![]() -ideal of the former algebra is contained in the $T_G$
-ideal of the former algebra is contained in the $T_G$![]() -ideal of the latter. The intriguing fact that this inclusion, over an infinite field of positive characteristic $p > 2$
-ideal of the latter. The intriguing fact that this inclusion, over an infinite field of positive characteristic $p > 2$![]() , is proper, follows directly from the results obtained by Alves in [Reference Alves2, Theorem 13].
, is proper, follows directly from the results obtained by Alves in [Reference Alves2, Theorem 13].
The construction of appropriate generic models for the relatively free graded algebras for $M_{a,b}(E)\otimes M_{r,s}(E)$![]() and $M_{ar+bs,as+br}(E)$
and $M_{ar+bs,as+br}(E)$![]() is essential. We relate these generic models to the corresponding graded identities.
is essential. We relate these generic models to the corresponding graded identities.
Let $m$![]() , $n$
, $n$![]() , $a\geq b$
, $a\geq b$![]() , and $r\geq s$
, and $r\geq s$![]() be positive integers such that $a+b=m$
be positive integers such that $a+b=m$![]() and $r+s= n$
and $r+s= n$![]() . Let $G$
. Let $G$![]() be a group and let $\varphi \colon \{1,\,\ldots,\, m\}\times \{1,\,\ldots,\, n\}\rightarrow G$
be a group and let $\varphi \colon \{1,\,\ldots,\, m\}\times \{1,\,\ldots,\, n\}\rightarrow G$![]() be an injective function. We consider a grading on the full matrix algebra $M_{mn}(F)$
be an injective function. We consider a grading on the full matrix algebra $M_{mn}(F)$![]() defined in the following way: Given $1\leq i \leq mn$
defined in the following way: Given $1\leq i \leq mn$![]() , there exists unique pair $(a_i,\, b_i)\in \{1,\,\ldots,\, m\}\times \{1,\,\ldots,\, n\}$
, there exists unique pair $(a_i,\, b_i)\in \{1,\,\ldots,\, m\}\times \{1,\,\ldots,\, n\}$![]() such that $i=n(a_i-1)+b_i$
such that $i=n(a_i-1)+b_i$![]() . For every $E_{ij}$
. For every $E_{ij}$![]() , in the canonical basis of $M_{mn}(F)$
, in the canonical basis of $M_{mn}(F)$![]() , we set $\alpha _G(E_{ij})=\varphi (a_i,\,b_i)\varphi (a_j,\,b_j)^{-1}$
, we set $\alpha _G(E_{ij})=\varphi (a_i,\,b_i)\varphi (a_j,\,b_j)^{-1}$![]() . This function satisfies Condition (2.1), hence it determines an elementary $G$
. This function satisfies Condition (2.1), hence it determines an elementary $G$![]() -grading on $M_{mn}(F)$
-grading on $M_{mn}(F)$![]() . Furthermore, if $R$
. Furthermore, if $R$![]() is a $\mathbb {Z}_2$
is a $\mathbb {Z}_2$![]() -graded algebra, we consider the $G\times \mathbb {Z}_2$
-graded algebra, we consider the $G\times \mathbb {Z}_2$![]() -grading on $M_{mn}(R) \simeq M_{mn}(F) \otimes R$
-grading on $M_{mn}(R) \simeq M_{mn}(F) \otimes R$![]() defined over the tensor product of graded algebras. Now we define the function $\gamma _{a,b}\colon \{1,\, \ldots,\, m\}\to \mathbb {Z}_2$
defined over the tensor product of graded algebras. Now we define the function $\gamma _{a,b}\colon \{1,\, \ldots,\, m\}\to \mathbb {Z}_2$![]() by $\gamma _{a,b}(i) = 0$
by $\gamma _{a,b}(i) = 0$![]() when $1\leq i\leq a$
when $1\leq i\leq a$![]() , and $\gamma _{a,b}(i) = 1$
, and $\gamma _{a,b}(i) = 1$![]() otherwise. We define similarly the function $\gamma _{r,s}\colon \{1,\,\ldots,\, n\}\to \mathbb {Z}_2$
otherwise. We define similarly the function $\gamma _{r,s}\colon \{1,\,\ldots,\, n\}\to \mathbb {Z}_2$![]() .
.
Consider the following sets of variables:
where $k = 1$![]() , 2, … Notice that $F\langle Y\cup Z\rangle$
, 2, … Notice that $F\langle Y\cup Z\rangle$![]() is the free algebra and define a $\mathbb {Z}_2$
is the free algebra and define a $\mathbb {Z}_2$![]() -grading on it by putting $|y_{ij}^{k}|_{2} = \gamma _{a,b}(i) + \gamma _{a,b}(j)$
-grading on it by putting $|y_{ij}^{k}|_{2} = \gamma _{a,b}(i) + \gamma _{a,b}(j)$![]() and $| z_{ij}^{k}|_{2} = \gamma _{r,s}(i) + \gamma _{r,s}(j)$
and $| z_{ij}^{k}|_{2} = \gamma _{r,s}(i) + \gamma _{r,s}(j)$![]() . Let $P_1$
. Let $P_1$![]() be the ideal in $F\langle Y\cup Z\rangle$
be the ideal in $F\langle Y\cup Z\rangle$![]() determined by the relations:
determined by the relations:

for every $k_1$![]() , $k_2$
, $k_2$![]() , $i_1$
, $i_1$![]() , $i_2$
, $i_2$![]() , $j_1$
, $j_1$![]() , $j_2$
, $j_2$![]() . Here and in what follows $[a,\, b] = ab-ba$
. Here and in what follows $[a,\, b] = ab-ba$![]() is the commutator of $a$
is the commutator of $a$![]() and $b$
and $b$![]() , and $a \circ b = ab + ba$
, and $a \circ b = ab + ba$![]() is the Jordan product of $a$
is the Jordan product of $a$![]() and $b$
and $b$![]() . Define $R_1 = F\langle Y \cup Z \rangle /P_1$
. Define $R_1 = F\langle Y \cup Z \rangle /P_1$![]() . We shall use the same letters $y_{ij}^{k}$
. We shall use the same letters $y_{ij}^{k}$![]() and $z_{ij}^{k}$
and $z_{ij}^{k}$![]() for the images of $y_{ij}^{k}$
for the images of $y_{ij}^{k}$![]() and $z_{ij}^{k}$
and $z_{ij}^{k}$![]() under the projection $F\langle Y \cup Z\rangle \to R_1$
under the projection $F\langle Y \cup Z\rangle \to R_1$![]() . It follows from the above relations that $R_1$
. It follows from the above relations that $R_1$![]() is a $\mathbb {Z}_2$
is a $\mathbb {Z}_2$![]() -graded algebra. Moreover, the set $Y$
-graded algebra. Moreover, the set $Y$![]() generates a free supercommutative algebra (see, for example, [Reference Berele10] for a precise definition) as well as the set $Z$
generates a free supercommutative algebra (see, for example, [Reference Berele10] for a precise definition) as well as the set $Z$![]() does, and the elements of $Y$
does, and the elements of $Y$![]() commute with those of $Z$
commute with those of $Z$![]() .
.
Let $(g,\, \mathfrak {a}) \in G^{\ast } = G\times \mathbb {Z}_2$![]() and define the following matrices in $M_{mn}(R_1)$
and define the following matrices in $M_{mn}(R_1)$![]() :
:
where $\gamma =\gamma _{a,b}(a_i) + \gamma _{a,b}(a_j)+\gamma _{r,s}(b_i) + \gamma _{r,s}(b_j)$![]() . Here $\delta$
. Here $\delta$![]() is the usual Kronecker symbol and, as above, $E_{v,w}$
is the usual Kronecker symbol and, as above, $E_{v,w}$![]() stands for the corresponding elementary matrices. Clearly $A^{(g,\mathfrak {a})}_k$
stands for the corresponding elementary matrices. Clearly $A^{(g,\mathfrak {a})}_k$![]() is a homogeneous element in the $G\times \mathbb {Z}_2$
is a homogeneous element in the $G\times \mathbb {Z}_2$![]() -graded algebra $M_{mn}(R_1)$
-graded algebra $M_{mn}(R_1)$![]() .
.
Put $\mathcal {G}^{(g,\mathfrak {a})}$![]() to be the set of all matrices $A^{(g,\mathfrak {a})}_k$
to be the set of all matrices $A^{(g,\mathfrak {a})}_k$![]() , $k\geq 1$
, $k\geq 1$![]() , and $\mathcal {G} = \cup _{(g,\mathfrak {a})\in G^{\ast }} \mathcal {G}^{(g,\mathfrak {a})}$
, and $\mathcal {G} = \cup _{(g,\mathfrak {a})\in G^{\ast }} \mathcal {G}^{(g,\mathfrak {a})}$![]() . Finally define the algebra $F_{a,b,r,s}$
. Finally define the algebra $F_{a,b,r,s}$![]() as the one generated by the set $\mathcal {G}$
as the one generated by the set $\mathcal {G}$![]() . Then the algebra $F_{a,b,r,s}$
. Then the algebra $F_{a,b,r,s}$![]() is a $G^{\ast }$
is a $G^{\ast }$![]() -graded subalgebra of $M_{mn}(R_1)$
-graded subalgebra of $M_{mn}(R_1)$![]() . Here we recall that $R_1 = F\langle Y \cup Z \rangle /P_1$
. Here we recall that $R_1 = F\langle Y \cup Z \rangle /P_1$![]() .
.
Now we will construct the algebra $L_{a,b,r,s}$![]() . Considering Definition 5.1, for every $w\in \{1,\, \ldots,\, mn\}$
. Considering Definition 5.1, for every $w\in \{1,\, \ldots,\, mn\}$![]() , we write $w=n(a_1-1)+b_1$
, we write $w=n(a_1-1)+b_1$![]() where $a_1\in \{1,\, \ldots,\, m\}$
where $a_1\in \{1,\, \ldots,\, m\}$![]() and $b_1\in \{1,\,\ldots,\, n\}$
and $b_1\in \{1,\,\ldots,\, n\}$![]() . Thus, we denote $\xi (w) = \gamma _{a,b}(a_1) +\gamma _{r,s}(b_1)$
. Thus, we denote $\xi (w) = \gamma _{a,b}(a_1) +\gamma _{r,s}(b_1)$![]() . Observe that $\xi (w)$
. Observe that $\xi (w)$![]() is well defined since $a_1$
is well defined since $a_1$![]() and $b_1$
and $b_1$![]() are determined uniquely by $w$
are determined uniquely by $w$![]() . Set $P_2$
. Set $P_2$![]() the ideal in the free associative algebra $F\langle U\rangle$
the ideal in the free associative algebra $F\langle U\rangle$![]() determined by the relations
determined by the relations

Let $R_2 = F\langle U\rangle /P_2$![]() , it is clear that $R_2$
, it is clear that $R_2$![]() is a $\mathbb {Z}_2$
is a $\mathbb {Z}_2$![]() -graded algebra which is free supercommutative; its even variables are all $u_{ij}^{k}$
-graded algebra which is free supercommutative; its even variables are all $u_{ij}^{k}$![]() such that $\xi (i) + \xi (j) = 0$
such that $\xi (i) + \xi (j) = 0$![]() ; the variables with $\xi (i) + \xi (j) = 1$
; the variables with $\xi (i) + \xi (j) = 1$![]() are odd. (As above, in order to keep the notation as simple as possible, we use the same letters $u_{ij}^{k}$
are odd. (As above, in order to keep the notation as simple as possible, we use the same letters $u_{ij}^{k}$![]() for the generators of $F\langle U\rangle$
for the generators of $F\langle U\rangle$![]() and for their images in $R_2$
and for their images in $R_2$![]() .)
.)
Denoting $p = ar + bs\geq q = as + br$![]() and fixing $(g,\, \mathfrak {c})\in G^{\ast }$
and fixing $(g,\, \mathfrak {c})\in G^{\ast }$![]() , we define $\mathcal {H}^{(g, \mathfrak {c})}$
, we define $\mathcal {H}^{(g, \mathfrak {c})}$![]() as the set of all matrices
as the set of all matrices
in $M_{mn}(R_2)$![]() . Hence we put $\mathcal {H} = \cup _{(g,\mathfrak {c})\in G^{\ast }}\mathcal {H}^{(g, \mathfrak {c})}$
. Hence we put $\mathcal {H} = \cup _{(g,\mathfrak {c})\in G^{\ast }}\mathcal {H}^{(g, \mathfrak {c})}$![]() . Let $L_{a,b,r,s}$
. Let $L_{a,b,r,s}$![]() be the algebra generated by the set $\mathcal {H}$
be the algebra generated by the set $\mathcal {H}$![]() . It is immediate that $L_{a,b,r,s}$
. It is immediate that $L_{a,b,r,s}$![]() is a $G^{\ast }$
is a $G^{\ast }$![]() -graded subalgebra of $M_{mn}(R_2)$
-graded subalgebra of $M_{mn}(R_2)$![]() in a natural way.
in a natural way.
Remark 5.7 We have $(g,\, \mathfrak {a})\in G^{\ast }$![]() . Fix $a$
. Fix $a$![]() , $b$
, $b$![]() , $r$
, $r$![]() , $s$
, $s$![]() . Then due to the gradings on $F_{a,b,r,s}$
. Then due to the gradings on $F_{a,b,r,s}$![]() and $L_{a,b,r,s}$
and $L_{a,b,r,s}$![]() the positions of the non-zero entries of the matrix $B_k^{(g,\mathfrak {c})}$
the positions of the non-zero entries of the matrix $B_k^{(g,\mathfrak {c})}$![]() are the same as those of $A_k^{(g,\mathfrak {c})}$
are the same as those of $A_k^{(g,\mathfrak {c})}$![]() .
.
Lemma 5.8 The algebra $F_{a,b,r,s}$![]() is relatively free in the variety of $G^{\ast }$
is relatively free in the variety of $G^{\ast }$![]() -graded algebras determined by $M_{a,b}(E)\otimes M_{r,s}(E)$
-graded algebras determined by $M_{a,b}(E)\otimes M_{r,s}(E)$![]() in Definition 5.4. The algebra $L_{a,b,r,s}$
in Definition 5.4. The algebra $L_{a,b,r,s}$![]() is relatively free in the variety of $G^{\ast }$
is relatively free in the variety of $G^{\ast }$![]() -graded algebras determined by $M_{p,q}(E)$
-graded algebras determined by $M_{p,q}(E)$![]() in the Definition 5.1 where $p=ar+bs$
in the Definition 5.1 where $p=ar+bs$![]() and $q=as+br$
and $q=as+br$![]() .
.
Proof. One repeats verbatim the proofs from [Reference Di Vincenzo, Koshlukov and Santulo18, Lemma 3 and Lemma 4].
Thus we generalize the models constructed in [Reference Di Vincenzo, Koshlukov and Santulo18].
If $M = M(x_1,\,\ldots,\, x_d)$![]() is a graded monomial, we define the density of $M$
is a graded monomial, we define the density of $M$![]() in $L_{a,b,r,s}$
in $L_{a,b,r,s}$![]() as the number of non-zero entries of the matrix $M(\tilde {B}_1,\,\ldots,\,\tilde {B}_d)$
as the number of non-zero entries of the matrix $M(\tilde {B}_1,\,\ldots,\,\tilde {B}_d)$![]() . Here $\tilde {B}$
. Here $\tilde {B}$![]() stands for the matrix of the same size as $B$
stands for the matrix of the same size as $B$![]() , as given in (5.4), and obtained from $B$
, as given in (5.4), and obtained from $B$![]() by substituting all non-zero entries of $B$
by substituting all non-zero entries of $B$![]() by $1\in F$
by $1\in F$![]() , while preserving the zero entries.
, while preserving the zero entries.
Definition 5.9 The graded monomial $M$![]() is said to be sparse in $L_{a,b,r,s}$
is said to be sparse in $L_{a,b,r,s}$![]() if its density in $L_{a,b,r,s}$
if its density in $L_{a,b,r,s}$![]() equals $0$
equals $0$![]() .
.
The notion of sparse monomials in $F_{a,b,r,s}$![]() is defined analogously. The next lemma follows from Remark 5.7.
is defined analogously. The next lemma follows from Remark 5.7.
Lemma 5.10 A monomial is sparse in $F_{a,b,r,s}$![]() if and only if it is sparse in $L_{a,b,r,s}$
if and only if it is sparse in $L_{a,b,r,s}$![]() .
.
Over a field of characteristic zero, it was proved in [Reference Fidelis, Diniz, Bernardo and Koshlukov20, Theorem 6.11] that the sets $T_{G^{\ast }}(M_{ar+bs,as+br}(E))$![]() and $T_{G^{\ast }}( M_{a,b}(E)\otimes M_{r,s}(E))$
and $T_{G^{\ast }}( M_{a,b}(E)\otimes M_{r,s}(E))$![]() coincide. Such a condition may fail when the field is infinite of positive characteristic $p$
coincide. Such a condition may fail when the field is infinite of positive characteristic $p$![]() . In [Reference Alves and Koshlukov3], whenever $p>2$
. In [Reference Alves and Koshlukov3], whenever $p>2$![]() , the authors constructed an ordinary polynomial identity for $M_{a,b}(E)\otimes M_{r,s}(E)$
, the authors constructed an ordinary polynomial identity for $M_{a,b}(E)\otimes M_{r,s}(E)$![]() which is not one for $M_{ar+bs,as+br}(E)$
which is not one for $M_{ar+bs,as+br}(E)$![]() , in the case $(r,\, s) = (1,\, 1)$
, in the case $(r,\, s) = (1,\, 1)$![]() . We also mention that a generalization of the latter result was obtained in [Reference Alves2, Theorem 13].
. We also mention that a generalization of the latter result was obtained in [Reference Alves2, Theorem 13].
Theorem 5.11 Let $G$![]() be a group and consider the gradings by the group $G^{\ast }=G\times \mathbb {Z}_2$
be a group and consider the gradings by the group $G^{\ast }=G\times \mathbb {Z}_2$![]() given in Definitions 5.4 and 5.1 such that the elements of $\mathrm {supp}\ M_{a,b}(E)$
given in Definitions 5.4 and 5.1 such that the elements of $\mathrm {supp}\ M_{a,b}(E)$![]() commute with the elements of $\mathrm {supp}\ M_{r,s}(E)$
commute with the elements of $\mathrm {supp}\ M_{r,s}(E)$![]() . Then $T_{G^{\ast }}(M_{ar+bs,as+br}(E))\subseteq T_{G^{\ast }}( M_{a,b}(E)\otimes M_{r,s}(E))$
. Then $T_{G^{\ast }}(M_{ar+bs,as+br}(E))\subseteq T_{G^{\ast }}( M_{a,b}(E)\otimes M_{r,s}(E))$![]() . Furthermore, over an infinite field of characteristic $p>2,$
. Furthermore, over an infinite field of characteristic $p>2,$![]() the latter inclusion is proper.
the latter inclusion is proper.
Proof. Denote $A=M_{ar+bs,as+br}(E)$![]() and $A^{\prime }=M_{a,b}(E)\otimes M_{r,s}(E)$
and $A^{\prime }=M_{a,b}(E)\otimes M_{r,s}(E)$![]() . By Theorems 5.3 and 5.6, it is enough to prove that all graded monomial identities for $A$
. By Theorems 5.3 and 5.6, it is enough to prove that all graded monomial identities for $A$![]() are graded identities for $A^{\prime }$
are graded identities for $A^{\prime }$![]() as well. By [Reference Fidelis, Diniz, Bernardo and Koshlukov20, Theorem 6.11], we can consider monomials with at least one variable which appears at least twice. Let $\mathfrak {m}=\mathfrak {m}(x_1,\,\ldots,\,x_d)$
as well. By [Reference Fidelis, Diniz, Bernardo and Koshlukov20, Theorem 6.11], we can consider monomials with at least one variable which appears at least twice. Let $\mathfrak {m}=\mathfrak {m}(x_1,\,\ldots,\,x_d)$![]() be such a monomial identity for $A$
be such a monomial identity for $A$![]() . If $\mathfrak {m}$
. If $\mathfrak {m}$![]() is sparse then the result follows from Lemma 5.10. Thus we can consider that $\mathfrak {m}$
is sparse then the result follows from Lemma 5.10. Thus we can consider that $\mathfrak {m}$![]() is not sparse. In this case there exist matrices $\tilde {B}_{1}$
is not sparse. In this case there exist matrices $\tilde {B}_{1}$![]() , …, $\tilde {B}_d$
, …, $\tilde {B}_d$![]() in $M_n(\mathbb {Z}_p)$
in $M_n(\mathbb {Z}_p)$![]() such that $\mathfrak {m}(\tilde {B}_{1},\, \ldots,\, \tilde {B}_d)\neq 0$
such that $\mathfrak {m}(\tilde {B}_{1},\, \ldots,\, \tilde {B}_d)\neq 0$![]() . Hence some variable $u^{k}_{ij}$
. Hence some variable $u^{k}_{ij}$![]() appears at least twice among the non-zero entries of the element $\mathfrak {m}(B_{1},\, \ldots,\, B_d)$
appears at least twice among the non-zero entries of the element $\mathfrak {m}(B_{1},\, \ldots,\, B_d)$![]() in $A$
in $A$![]() . Suppose that all variables that appear at least twice in $\mathfrak {m}$
. Suppose that all variables that appear at least twice in $\mathfrak {m}$![]() have even degrees. We make a substitution by elements of the basis of $E$
have even degrees. We make a substitution by elements of the basis of $E$![]() such that it respects the $G^{\ast }$
such that it respects the $G^{\ast }$![]() -grading given in Definition 5.4, and moreover, we require that $m_1^{\alpha _1}\cdots m_d^{\alpha _d}$
-grading given in Definition 5.4, and moreover, we require that $m_1^{\alpha _1}\cdots m_d^{\alpha _d}$![]() is non-zero. This implies that $\mathfrak {m}$
is non-zero. This implies that $\mathfrak {m}$![]() is not an identity for $T_{G^{\ast }}(A)$
is not an identity for $T_{G^{\ast }}(A)$![]() , which is impossible. Therefore, we can suppose that there exists at least one odd variable $u^{k}_{ij}$
, which is impossible. Therefore, we can suppose that there exists at least one odd variable $u^{k}_{ij}$![]() , in $\mathfrak {m}$
, in $\mathfrak {m}$![]() . Thus
. Thus
with $\alpha _{G^{\ast }}(m_1)=\alpha _{G^{\ast }}(m_1x_{k}^{(g,1)}m_2)$![]() . But this implies $\alpha _{G^{\ast }}(x_{k}^{(g,1)}m_2)=(\epsilon,\,0)$
. But this implies $\alpha _{G^{\ast }}(x_{k}^{(g,1)}m_2)=(\epsilon,\,0)$![]() , since if $\alpha _{G^{\ast }}(x_{k}^{(g,1)}m_2)=(\epsilon,\,1)$
, since if $\alpha _{G^{\ast }}(x_{k}^{(g,1)}m_2)=(\epsilon,\,1)$![]() then, by induction hypothesis, $\mathfrak {m}$
then, by induction hypothesis, $\mathfrak {m}$![]() lies in $T_{G^{\ast }}( M_{a,b}(E)\otimes M_{r,s}(E))$
lies in $T_{G^{\ast }}( M_{a,b}(E)\otimes M_{r,s}(E))$![]() . Therefore, we obtain $\alpha _{G^{\ast }}(m_2)=(g^{-1},\,1)$
. Therefore, we obtain $\alpha _{G^{\ast }}(m_2)=(g^{-1},\,1)$![]() and hence
and hence
Thus $2\mathfrak {m}\in \mathcal {I}\subseteq T_{G^{\ast }}(A^{\prime })$![]() and since $char K\neq 2$
and since $char K\neq 2$![]() , we obtain that $\mathfrak {m}\in T_{G^{\ast }}(A^{\prime })$
, we obtain that $\mathfrak {m}\in T_{G^{\ast }}(A^{\prime })$![]() .
.
The latter claim of the theorem is in fact [Reference Alves2, Theorem 13].
Acknowledgements
The authors thank the Referee for her/his valuable comments and suggestions helped us in making the exposition more attractive.C. Fidelis was supported by FAPESP grant No. 2019/12498-0, D. Diniz was supported by CNPq grants No. 301704/2019-8, P. Koshlukov was partially supported by FAPESP grant No. 2018/23690-6 and by CNPq grant No. 302238/2019-0