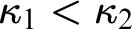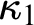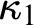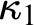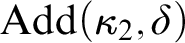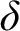1 Introduction and preliminaries
The study of indestructibility properties that non-supercompact strongly compact cardinals may possess has been carried out in several papers, including [Reference Apter and Gitik3, Reference Apter and Sargsyan5, Reference Sargsyan17]. In particular, [Reference Sargsyan17, Question 5] asks whether it is possible for the first two strongly compact cardinals
![]() $\kappa _1$
and
$\kappa _1$
and
![]() $\kappa _2$
to be the first two measurable cardinals, with the second strongly compact cardinal (
$\kappa _2$
to be the first two measurable cardinals, with the second strongly compact cardinal (
![]() $\kappa _2$
) having its strong compactness indestructible under
$\kappa _2$
) having its strong compactness indestructible under
![]() $\mathrm {Add}(\kappa _2, \kappa ^{++}_2)$
(where for
$\mathrm {Add}(\kappa _2, \kappa ^{++}_2)$
(where for
![]() $\kappa \ge \aleph _0$
a regular cardinal and
$\kappa \ge \aleph _0$
a regular cardinal and
![]() $\lambda $
an ordinal,
$\lambda $
an ordinal,
![]() $\mathrm {Add}(\kappa , \lambda )$
is the standard partial ordering for adding
$\mathrm {Add}(\kappa , \lambda )$
is the standard partial ordering for adding
![]() $\lambda $
many Cohen subsets of
$\lambda $
many Cohen subsets of
![]() $\kappa $
).
$\kappa $
).
The purpose of this paper is to answer [Reference Sargsyan17, Question 5] in the affirmative, and also prove a theorem showing that the first two strongly compact cardinals
![]() $\kappa _1$
and
$\kappa _1$
and
![]() $\kappa _2$
can be the first two measurable cardinals, where in addition, each
$\kappa _2$
can be the first two measurable cardinals, where in addition, each
![]() $\kappa _i$
(for
$\kappa _i$
(for
![]() $i = 1,2$
) is
$i = 1,2$
) is
![]() $\kappa ^+_i$
supercompact and also exhibits certain indestructibility properties. Specifically, we will prove the following two theorems, where we take as terminology for the rest of this paper that a supercompact cardinal
$\kappa ^+_i$
supercompact and also exhibits certain indestructibility properties. Specifically, we will prove the following two theorems, where we take as terminology for the rest of this paper that a supercompact cardinal
![]() $\kappa $
has its supercompactness indestructible under forcing with a class of partial orderings
$\kappa $
has its supercompactness indestructible under forcing with a class of partial orderings
![]() ${\mathcal C}$
if
${\mathcal C}$
if
![]() $\kappa $
remains supercompact after forcing with members of
$\kappa $
remains supercompact after forcing with members of
![]() ${\mathcal C}$
.
${\mathcal C}$
.
Theorem 1.1. Suppose
![]() $V \vDash $
“ZFC
$V \vDash $
“ZFC
![]() $+\ \kappa _1 < \kappa _2$
are supercompact.” There is then a partial ordering
$+\ \kappa _1 < \kappa _2$
are supercompact.” There is then a partial ordering
![]() ${\mathbb P} \subseteq V$
such that
${\mathbb P} \subseteq V$
such that
![]() $V^{\mathbb P} \vDash $
“ZFC
$V^{\mathbb P} \vDash $
“ZFC
![]() $+ \kappa _1$
and
$+ \kappa _1$
and
![]() $\kappa _2$
are both the first two strongly compact and first two measurable cardinals.” In
$\kappa _2$
are both the first two strongly compact and first two measurable cardinals.” In
![]() $V^{\mathbb P}$
,
$V^{\mathbb P}$
,
![]() $\kappa _1$
’s strong compactness is indestructible under arbitrary
$\kappa _1$
’s strong compactness is indestructible under arbitrary
![]() $\kappa _1$
-directed closed forcing, and
$\kappa _1$
-directed closed forcing, and
![]() $\kappa _2$
’s strong compactness is indestructible under forcing with
$\kappa _2$
’s strong compactness is indestructible under forcing with
![]() $\mathrm {Add}(\kappa _2, \delta )$
for any ordinal
$\mathrm {Add}(\kappa _2, \delta )$
for any ordinal
![]() $\delta $
.
$\delta $
.
Theorem 1.2. Suppose
![]() $V \vDash $
“ZFC
$V \vDash $
“ZFC
![]() $+ \kappa _1 < \kappa _2$
are supercompact.” There is then a partial ordering
$+ \kappa _1 < \kappa _2$
are supercompact.” There is then a partial ordering
![]() ${\mathbb P} \subseteq V$
such that
${\mathbb P} \subseteq V$
such that
![]() $V^{\mathbb P} \vDash $
“ZFC
$V^{\mathbb P} \vDash $
“ZFC
![]() $+ \kappa _1$
and
$+ \kappa _1$
and
![]() $\kappa _2$
are both the first two strongly compact and first two measurable cardinals.” Further, in
$\kappa _2$
are both the first two strongly compact and first two measurable cardinals.” Further, in
![]() $V^{\mathbb P}$
, the following properties hold.
$V^{\mathbb P}$
, the following properties hold.
-
1. Each
 $\kappa _i \ ($
for
$\kappa _i \ ($
for
 $i = 1,2)$
is
$i = 1,2)$
is
 $\kappa ^+_i$
supercompact and satisfies
$\kappa ^+_i$
supercompact and satisfies
 $2^{\kappa _i} = 2^{\kappa ^+_i} = \kappa ^{++}_i$
.
$2^{\kappa _i} = 2^{\kappa ^+_i} = \kappa ^{++}_i$
. -
2.
 $2^\delta = \delta ^+$
for every
$2^\delta = \delta ^+$
for every
 $\delta \ge \kappa ^{++}_2$
.
$\delta \ge \kappa ^{++}_2$
. -
3.
 $\kappa _1$
’s strong compactness is indestructible under arbitrary
$\kappa _1$
’s strong compactness is indestructible under arbitrary
 $\kappa _1$
-directed closed forcing.
$\kappa _1$
-directed closed forcing. -
4.
 $\kappa _2$
’s strong compactness is indestructible under
$\kappa _2$
’s strong compactness is indestructible under
 $\kappa _2$
-directed closed,
$\kappa _2$
-directed closed,
 $(\kappa ^+_2, \infty )$
-distributive forcing.
$(\kappa ^+_2, \infty )$
-distributive forcing. -
5. Let
 $\lambda = (\kappa ^+_2)^{V^{\mathbb P}}$
. Then the
$\lambda = (\kappa ^+_2)^{V^{\mathbb P}}$
. Then the
 $\lambda $
supercompactness of
$\lambda $
supercompactness of
 $\kappa _2$
is indestructible under
$\kappa _2$
is indestructible under
 $\kappa _2$
-directed closed forcing having size at most
$\kappa _2$
-directed closed forcing having size at most
 $\lambda $
.
$\lambda $
.
We take this opportunity to make a few remarks concerning Theorems 1.1 and 1.2. We note that Theorem 1.1 provides a model witnessing a strengthened version of [Reference Sargsyan17, Question 5], in that the first strongly compact and measurable cardinal
![]() $\kappa _1$
is fully indestructible, and the second strongly compact cardinal
$\kappa _1$
is fully indestructible, and the second strongly compact cardinal
![]() $\kappa _2$
has its strong compactness indestructible under
$\kappa _2$
has its strong compactness indestructible under
![]() $\mathrm {Add}(\kappa _2, \delta )$
for arbitrary
$\mathrm {Add}(\kappa _2, \delta )$
for arbitrary
![]() $\delta $
, rather than being indestructible only under
$\delta $
, rather than being indestructible only under
![]() $\mathrm {Add}(\kappa _2, \kappa ^{++}_2)$
. In addition, Theorem 1.2 provides a generalization of both [Reference Apter and Gitik3, Theorem 1] and [Reference Apter and Sargsyan5, Theorem 2]. Also, in Theorem 1.2, it is impossible for
$\mathrm {Add}(\kappa _2, \kappa ^{++}_2)$
. In addition, Theorem 1.2 provides a generalization of both [Reference Apter and Gitik3, Theorem 1] and [Reference Apter and Sargsyan5, Theorem 2]. Also, in Theorem 1.2, it is impossible for
![]() $i = 1,2$
to have that
$i = 1,2$
to have that
![]() $\kappa _i$
is
$\kappa _i$
is
![]() $2^{\kappa _i} = \kappa ^{++}_i$
supercompact. This is since
$2^{\kappa _i} = \kappa ^{++}_i$
supercompact. This is since
![]() $\kappa _1$
and
$\kappa _1$
and
![]() $\kappa _2$
are the first two measurable cardinals, and it is a well-known fact (see [Reference Jech13, Lemma 20.16]) that if
$\kappa _2$
are the first two measurable cardinals, and it is a well-known fact (see [Reference Jech13, Lemma 20.16]) that if
![]() $\kappa $
is
$\kappa $
is
![]() $2^\kappa $
supercompact, then
$2^\kappa $
supercompact, then
![]() $\kappa $
is a limit of measurable cardinals. Further, because for
$\kappa $
is a limit of measurable cardinals. Further, because for
![]() $i = 1,2$
, any partial ordering which is
$i = 1,2$
, any partial ordering which is
![]() $(\kappa ^+_i, \infty )$
-distributive adds no new subsets of
$(\kappa ^+_i, \infty )$
-distributive adds no new subsets of
![]() $\kappa ^+_i$
and hence also adds no new subsets of
$\kappa ^+_i$
and hence also adds no new subsets of
![]() $P_{\kappa _i}(\kappa ^+_i)$
, each
$P_{\kappa _i}(\kappa ^+_i)$
, each
![]() $\kappa _i$
automatically has its
$\kappa _i$
automatically has its
![]() $\kappa ^+_i$
supercompactness indestructible under every
$\kappa ^+_i$
supercompactness indestructible under every
![]() $(\kappa ^+_i, \infty )$
-distributive forcing notion. However, unlike the situation with
$(\kappa ^+_i, \infty )$
-distributive forcing notion. However, unlike the situation with
![]() $\kappa _2$
, the current state of forcing technology doesn’t appear to provide a way for one to force the
$\kappa _2$
, the current state of forcing technology doesn’t appear to provide a way for one to force the
![]() $\kappa ^+_1$
supercompactness of
$\kappa ^+_1$
supercompactness of
![]() $\kappa _1$
to be indestructible under
$\kappa _1$
to be indestructible under
![]() $\kappa _1$
-directed closed forcing having size at most
$\kappa _1$
-directed closed forcing having size at most
![]() $\kappa ^+_1$
. We will discuss this issue in greater detail towards the end of the paper.
$\kappa ^+_1$
. We will discuss this issue in greater detail towards the end of the paper.
Before continuing, we mention the overall structure of this paper. Section 1 contains our introductory comments. Section 2 contains the proofs of Theorems 1.1 and 1.2. Section 3 contains our concluding remarks.
We now briefly mention some preliminary information and terminology. Essentially, our notation and terminology are standard, and when this is not the case, this will be clearly noted. When forcing,
![]() $q \ge p$
will mean that q is stronger than p. If G is V-generic over
$q \ge p$
will mean that q is stronger than p. If G is V-generic over
![]() ${\mathbb P}$
, we will abuse notation slightly and use both
${\mathbb P}$
, we will abuse notation slightly and use both
![]() $V[G]$
and
$V[G]$
and
![]() $V^{{\mathbb P}}$
to indicate the universe obtained by forcing with
$V^{{\mathbb P}}$
to indicate the universe obtained by forcing with
![]() ${\mathbb P}$
. If
${\mathbb P}$
. If
![]() $x \in V[G]$
, then
$x \in V[G]$
, then
![]() $\dot x$
will be a term in V for x. We may, from time to time, confuse terms with the sets they denote and write x when we actually mean
$\dot x$
will be a term in V for x. We may, from time to time, confuse terms with the sets they denote and write x when we actually mean
![]() $\dot x$
or
$\dot x$
or
![]() $\check x$
, especially when x is some variant of the generic set G, or x is in the ground model V. The abuse of notation mentioned above will be compounded by writing
$\check x$
, especially when x is some variant of the generic set G, or x is in the ground model V. The abuse of notation mentioned above will be compounded by writing
![]() $x \in V^{\mathbb P}$
instead of
$x \in V^{\mathbb P}$
instead of
![]() $\dot x \in V^{\mathbb P}$
. Any term for trivial forcing will always be taken as a term for the partial ordering
$\dot x \in V^{\mathbb P}$
. Any term for trivial forcing will always be taken as a term for the partial ordering
![]() $\{\emptyset \}$
. If
$\{\emptyset \}$
. If
![]() $\varphi $
is a formula in the forcing language with respect to
$\varphi $
is a formula in the forcing language with respect to
![]() ${\mathbb P}$
and
${\mathbb P}$
and
![]() $p \in {\mathbb P}$
, then
$p \in {\mathbb P}$
, then
![]() $p \parallel \varphi $
means that p decides
$p \parallel \varphi $
means that p decides
![]() $\varphi $
.
$\varphi $
.
If
![]() ${\mathbb P}$
is an arbitrary partial ordering and
${\mathbb P}$
is an arbitrary partial ordering and
![]() $\kappa $
is a regular cardinal,
$\kappa $
is a regular cardinal,
![]() ${\mathbb P}$
is
${\mathbb P}$
is
![]() $(\kappa , \infty )$
-distributive if for every sequence
$(\kappa , \infty )$
-distributive if for every sequence
![]() $\langle D_\alpha \mid \alpha < \kappa \rangle $
of dense open subsets of
$\langle D_\alpha \mid \alpha < \kappa \rangle $
of dense open subsets of
![]() ${\mathbb P}$
,
${\mathbb P}$
,
![]() $\bigcap _{\alpha < \kappa } D_\alpha $
is dense open.
$\bigcap _{\alpha < \kappa } D_\alpha $
is dense open.
![]() ${\mathbb P}$
is
${\mathbb P}$
is
![]() $\kappa $
-directed closed if for every cardinal
$\kappa $
-directed closed if for every cardinal
![]() $\delta < \kappa $
and every directed set
$\delta < \kappa $
and every directed set
![]() $\langle p_\alpha \mid \alpha < \delta \rangle $
of elements of
$\langle p_\alpha \mid \alpha < \delta \rangle $
of elements of
![]() ${\mathbb P}$
${\mathbb P}$
![]() $($
where
$($
where
![]() $\langle p_\alpha \mid \alpha < \delta \rangle $
is directed if every two elements
$\langle p_\alpha \mid \alpha < \delta \rangle $
is directed if every two elements
![]() $p_\rho $
and
$p_\rho $
and
![]() $p_\nu $
have a common upper bound of the form
$p_\nu $
have a common upper bound of the form
![]() $p_\sigma )$
, there is an upper bound
$p_\sigma )$
, there is an upper bound
![]() $p \in {\mathbb P}$
.
$p \in {\mathbb P}$
.
![]() ${\mathbb P}$
is
${\mathbb P}$
is
![]() $\kappa $
-strategically closed if in the two person game of length
$\kappa $
-strategically closed if in the two person game of length
![]() $\kappa + 1$
in which the players construct an increasing sequence
$\kappa + 1$
in which the players construct an increasing sequence
![]() $\langle p_\alpha \mid \alpha \le \kappa \rangle $
, where Player I plays odd stages and Player II plays even stages
$\langle p_\alpha \mid \alpha \le \kappa \rangle $
, where Player I plays odd stages and Player II plays even stages
![]() $($
choosing the trivial condition at stage 0
$($
choosing the trivial condition at stage 0
![]() $)$
, Player II has a strategy which ensures the game can always be continued.
$)$
, Player II has a strategy which ensures the game can always be continued.
![]() ${\mathbb P}$
is
${\mathbb P}$
is
![]() ${\prec }\kappa $
-strategically closed if in the two person game in which the players construct an increasing sequence
${\prec }\kappa $
-strategically closed if in the two person game in which the players construct an increasing sequence
![]() $\langle p_\alpha \mid \alpha < \kappa \rangle $
, where Player I plays odd stages and Player II plays even and limit stages
$\langle p_\alpha \mid \alpha < \kappa \rangle $
, where Player I plays odd stages and Player II plays even and limit stages
![]() $($
again choosing the trivial condition at stage 0
$($
again choosing the trivial condition at stage 0
![]() $)$
, then Player II has a strategy which ensures the game can always be continued. Note that if
$)$
, then Player II has a strategy which ensures the game can always be continued. Note that if
![]() ${\mathbb P}$
is
${\mathbb P}$
is
![]() $\kappa ^+$
-directed closed, then
$\kappa ^+$
-directed closed, then
![]() ${\mathbb P}$
is
${\mathbb P}$
is
![]() ${\prec } \kappa ^+$
-strategically closed.
${\prec } \kappa ^+$
-strategically closed.
An example of a partial ordering which is
![]() ${\prec } \kappa $
-strategically closed and which will be used in the proof of Theorem 1.2 is the partial ordering
${\prec } \kappa $
-strategically closed and which will be used in the proof of Theorem 1.2 is the partial ordering
![]() ${\mathbb P}$
for adding a nonreflecting stationary set of ordinals of cofinality
${\mathbb P}$
for adding a nonreflecting stationary set of ordinals of cofinality
![]() $\lambda $
to
$\lambda $
to
![]() $\kappa $
, where
$\kappa $
, where
![]() $\lambda < \kappa $
is a regular cardinal. Specifically,
$\lambda < \kappa $
is a regular cardinal. Specifically,
![]() ${\mathbb P} = \{p \mid $
For some
${\mathbb P} = \{p \mid $
For some
![]() $\alpha < \kappa $
,
$\alpha < \kappa $
,
![]() $p : \alpha \to \{0, 1\}$
is a characteristic function of
$p : \alpha \to \{0, 1\}$
is a characteristic function of
![]() $S_p$
, a subset of
$S_p$
, a subset of
![]() $\alpha $
not stationary at its supremum nor having any initial segment which is stationary at its supremum, such that
$\alpha $
not stationary at its supremum nor having any initial segment which is stationary at its supremum, such that
![]() $\beta \in S_p$
implies
$\beta \in S_p$
implies
![]() $\beta> \lambda $
and
$\beta> \lambda $
and
![]() $\mathrm {cof}(\beta ) = \lambda \}$
, ordered by
$\mathrm {cof}(\beta ) = \lambda \}$
, ordered by
![]() $q \ge p$
iff
$q \ge p$
iff
![]() $q \supseteq p$
and
$q \supseteq p$
and
![]() $S_p = S_q \cap \sup (S_p)$
, i.e.,
$S_p = S_q \cap \sup (S_p)$
, i.e.,
![]() $S_q$
is an end extension of
$S_q$
is an end extension of
![]() $S_p$
. It is virtually immediate that
$S_p$
. It is virtually immediate that
![]() ${\mathbb P}$
is
${\mathbb P}$
is
![]() $\lambda $
-directed closed. For additional details, readers are urged to consult [Reference Apter and Shelah6, second paragraph of Section 1, p. 106].
$\lambda $
-directed closed. For additional details, readers are urged to consult [Reference Apter and Shelah6, second paragraph of Section 1, p. 106].
We recall for the benefit of readers the definition given by Hamkins in [Reference Hamkins11, Section 3] of the lottery sum of a collection of partial orderings. If
![]() ${\mathfrak A}$
is a collection of partial orderings, then the lottery sum is the partial ordering
${\mathfrak A}$
is a collection of partial orderings, then the lottery sum is the partial ordering
![]() $\oplus {\mathfrak A} = \{\langle {\mathbb P}, p \rangle \mid {\mathbb P} \in {\mathfrak A}$
and
$\oplus {\mathfrak A} = \{\langle {\mathbb P}, p \rangle \mid {\mathbb P} \in {\mathfrak A}$
and
![]() $p \in {\mathbb P}\} \cup \{0\}$
, ordered with
$p \in {\mathbb P}\} \cup \{0\}$
, ordered with
![]() $0$
below everything and
$0$
below everything and
![]() $\langle {\mathbb P}, p \rangle \le \langle {\mathbb P}', p' \rangle $
iff
$\langle {\mathbb P}, p \rangle \le \langle {\mathbb P}', p' \rangle $
iff
![]() ${\mathbb P} = {\mathbb P}'$
and
${\mathbb P} = {\mathbb P}'$
and
![]() $p \le p'$
. Intuitively, if G is V-generic over
$p \le p'$
. Intuitively, if G is V-generic over
![]() $\oplus {\mathfrak A}$
, then G first selects an element of
$\oplus {\mathfrak A}$
, then G first selects an element of
![]() ${\mathfrak A}\ ($
or as Hamkins says in [Reference Hamkins11], “holds a lottery among the posets in
${\mathfrak A}\ ($
or as Hamkins says in [Reference Hamkins11], “holds a lottery among the posets in
![]() ${\mathfrak A}$
”
${\mathfrak A}$
”
![]() $)$
and then forces with it.Footnote
1
$)$
and then forces with it.Footnote
1
A corollary of Hamkins’ work on gap forcing found in [Reference Hamkins10, Reference Hamkins12] will be employed in the proof of Theorems 1.1 and 1.2. We therefore state as a separate theorem what is relevant for this paper, along with some associated terminology, quoting from [Reference Hamkins10, Reference Hamkins12] when appropriate. Suppose
![]() ${\mathbb P}$
is a partial ordering which can be written as
${\mathbb P}$
is a partial ordering which can be written as
![]() ${\mathbb Q} \ast \dot {\mathbb R}$
, where
${\mathbb Q} \ast \dot {\mathbb R}$
, where
![]() ${\vert {\mathbb Q} \vert } < \delta $
,
${\vert {\mathbb Q} \vert } < \delta $
,
![]() ${\mathbb Q}$
is nontrivial, and
${\mathbb Q}$
is nontrivial, and
 $\Vdash _{\mathbb Q} ``\dot {\mathbb R}$
is
$\Vdash _{\mathbb Q} ``\dot {\mathbb R}$
is
![]() $\delta ^+$
-directed closed.” In Hamkins’ terminology of [Reference Hamkins10, Reference Hamkins12],
$\delta ^+$
-directed closed.” In Hamkins’ terminology of [Reference Hamkins10, Reference Hamkins12],
![]() ${\mathbb P}$
admits a gap at
${\mathbb P}$
admits a gap at
![]() $\delta $
. Also, as in the terminology of [Reference Hamkins10, Reference Hamkins12] and elsewhere, an embedding
$\delta $
. Also, as in the terminology of [Reference Hamkins10, Reference Hamkins12] and elsewhere, an embedding
![]() $j : V \to M$
is amenable to V when
$j : V \to M$
is amenable to V when
![]() $j \restriction A \in V$
for any
$j \restriction A \in V$
for any
![]() $A \in V$
. The specific corollary of Hamkins’ work from [Reference Hamkins10, Reference Hamkins12] we will be using is then the following.
$A \in V$
. The specific corollary of Hamkins’ work from [Reference Hamkins10, Reference Hamkins12] we will be using is then the following.
Theorem 1.3 (Hamkins).
Suppose that
![]() $V[G]$
is a generic extension obtained by forcing with
$V[G]$
is a generic extension obtained by forcing with
![]() ${\mathbb P}$
that admits a gap at some regular
${\mathbb P}$
that admits a gap at some regular
![]() $\delta < \kappa $
. Suppose further that
$\delta < \kappa $
. Suppose further that
![]() $j: V[G] \to M[j(G)]$
is an elementary embedding with critical point
$j: V[G] \to M[j(G)]$
is an elementary embedding with critical point
![]() $\kappa $
for which
$\kappa $
for which
![]() $M[j(G)] \subseteq V[G]$
and
$M[j(G)] \subseteq V[G]$
and
 ${M[j(G)]}^\delta \subseteq M[j(G)]$
in
${M[j(G)]}^\delta \subseteq M[j(G)]$
in
![]() $V[G]$
. Then
$V[G]$
. Then
![]() $M \subseteq V;$
indeed,
$M \subseteq V;$
indeed,
![]() $M = V \cap M[j(G)]$
. If the full embedding j is amenable to
$M = V \cap M[j(G)]$
. If the full embedding j is amenable to
![]() $V[G]$
, then the restricted embedding
$V[G]$
, then the restricted embedding
![]() $j \restriction V : V \to M$
is amenable to V. If j is definable from parameters
$j \restriction V : V \to M$
is amenable to V. If j is definable from parameters
![]() $($
such as a measure or extender
$($
such as a measure or extender
![]() $)$
in
$)$
in
![]() $V[G]$
, then the restricted embedding
$V[G]$
, then the restricted embedding
![]() $j \restriction V$
is definable from the names of those parameters in V.
$j \restriction V$
is definable from the names of those parameters in V.
Theorem 1.3 immediately implies that if
![]() $\kappa $
is measurable in a generic extension by a partial ordering admitting a gap at
$\kappa $
is measurable in a generic extension by a partial ordering admitting a gap at
![]() $\delta < \kappa $
, then
$\delta < \kappa $
, then
![]() $\kappa $
had to have been measurable in the ground model V.
$\kappa $
had to have been measurable in the ground model V.
Finally, we mention that we are assuming familiarity with the large cardinal notions of measurability, strong compactness, and supercompactness. Interested readers may consult [Reference Jech13] for further details.
2 The proofs of Theorems 1.1 and 1.2
We turn now to the proof of Theorem 1.1.
Proof. Suppose
![]() $V \vDash ``$
ZFC
$V \vDash ``$
ZFC
![]() $+ \kappa _1 < \kappa _2$
are supercompact.” Without loss of generality, by first doing a preliminary forcing and truncating the universe if necessary, we assume in addition that
$+ \kappa _1 < \kappa _2$
are supercompact.” Without loss of generality, by first doing a preliminary forcing and truncating the universe if necessary, we assume in addition that
![]() $V \vDash ``\mathrm {GCH}\ +$
No cardinal
$V \vDash ``\mathrm {GCH}\ +$
No cardinal
![]() $\lambda> \kappa _2$
is measurable.”
$\lambda> \kappa _2$
is measurable.”
The proof of Theorem 1.1 may now be divided into four modules, as follows
![]() $:$
$:$
Module 1
![]() $:$
Let
$:$
Let
![]() ${\mathbb P}^0 \in V$
be the partial ordering used in the proof of [Reference Apter and Gitik3, Theorem 1] defined with respect to
${\mathbb P}^0 \in V$
be the partial ordering used in the proof of [Reference Apter and Gitik3, Theorem 1] defined with respect to
![]() $\kappa _1$
. Set
$\kappa _1$
. Set
 $V_1 = V^{{\mathbb P}^0}$
. It is then the case that
$V_1 = V^{{\mathbb P}^0}$
. It is then the case that
![]() $V_1 \vDash ``\kappa _1$
is both the least strongly compact and least measurable cardinal
$V_1 \vDash ``\kappa _1$
is both the least strongly compact and least measurable cardinal
![]() $+$
$+$
![]() $\kappa _1$
’s strong compactness is indestructible under arbitrary
$\kappa _1$
’s strong compactness is indestructible under arbitrary
![]() $\kappa _1$
-directed closed forcing.” Since
$\kappa _1$
-directed closed forcing.” Since
![]() ${\mathbb P}^0$
may be defined so that
${\mathbb P}^0$
may be defined so that
![]() ${\vert {\mathbb P}^0 \vert } = \kappa _1$
, standard arguments in conjunction with the Lévy–Solovay results [Reference Lévy and Solovay15] yield that
${\vert {\mathbb P}^0 \vert } = \kappa _1$
, standard arguments in conjunction with the Lévy–Solovay results [Reference Lévy and Solovay15] yield that
![]() $V_1 \vDash ``$
GCH holds at and above
$V_1 \vDash ``$
GCH holds at and above
![]() $\kappa _1 + \kappa _2$
is supercompact
$\kappa _1 + \kappa _2$
is supercompact
![]() $+$
No cardinal
$+$
No cardinal
![]() $\lambda> \kappa _2$
is measurable.”
$\lambda> \kappa _2$
is measurable.”
Module 2
![]() $:$
Let
$:$
Let
![]() ${\mathbb P}^1 \in V_1$
be the Easton support iteration of length
${\mathbb P}^1 \in V_1$
be the Easton support iteration of length
![]() $\kappa _2$
which adds, to every measurable cardinal
$\kappa _2$
which adds, to every measurable cardinal
![]() $\delta \in (\kappa _1, \kappa _2)$
, a nonreflecting stationary set of ordinals of cofinality
$\delta \in (\kappa _1, \kappa _2)$
, a nonreflecting stationary set of ordinals of cofinality
![]() $\kappa _1$
. Set
$\kappa _1$
. Set
 $V_2 = V^{{\mathbb P}^1}_1$
. Since
$V_2 = V^{{\mathbb P}^1}_1$
. Since
![]() $V_1 \vDash ``$
No cardinal
$V_1 \vDash ``$
No cardinal
![]() $\lambda> \kappa _2$
is measurable,” by an argument due to Magidor
$\lambda> \kappa _2$
is measurable,” by an argument due to Magidor
![]() $($
unpublished by him, but given in the proof of [Reference Apter and Cummings1, Theorem 2]
$($
unpublished by him, but given in the proof of [Reference Apter and Cummings1, Theorem 2]
![]() $)$
,
$)$
,
![]() $V_2 \vDash ``\kappa _2$
is both the least measurable and least strongly compact cardinal greater than
$V_2 \vDash ``\kappa _2$
is both the least measurable and least strongly compact cardinal greater than
![]() $\kappa _1$
.” Because
$\kappa _1$
.” Because
![]() $V_1 \vDash ``\kappa _1$
is both the least strongly compact and least measurable cardinal
$V_1 \vDash ``\kappa _1$
is both the least strongly compact and least measurable cardinal
![]() $+$
$+$
![]() $\kappa _1$
’s strong compactness is indestructible under arbitrary
$\kappa _1$
’s strong compactness is indestructible under arbitrary
![]() $\kappa _1$
-directed closed forcing
$\kappa _1$
-directed closed forcing
![]() $+$
$+$
![]() ${\mathbb P}^1$
is
${\mathbb P}^1$
is
![]() $\kappa _1$
-directed closed,” it consequently follows that
$\kappa _1$
-directed closed,” it consequently follows that
![]() $V_2 \vDash ``\kappa _1$
and
$V_2 \vDash ``\kappa _1$
and
![]() $\kappa _2$
are both the first two strongly compact and first two measurable cardinals
$\kappa _2$
are both the first two strongly compact and first two measurable cardinals
![]() $+\ \kappa _1$
’s strong compactness is indestructible under arbitrary
$+\ \kappa _1$
’s strong compactness is indestructible under arbitrary
![]() $\kappa _1$
-directed closed forcing.”
$\kappa _1$
-directed closed forcing.”
Module 3
![]() $:$
Working in
$:$
Working in
![]() $V_2$
, let
$V_2$
, let
![]() $\kappa ^{\prime }_1$
be the least inaccessible cardinal greater than
$\kappa ^{\prime }_1$
be the least inaccessible cardinal greater than
![]() $\kappa _1$
. Let
$\kappa _1$
. Let
![]() ${\mathbb P}^2 \in V_2$
be
${\mathbb P}^2 \in V_2$
be
 $\mathrm {Add}(\kappa _1, 1) \ast \dot {\mathbb F}_{\kappa ^{\prime }_1, \kappa _2}$
, where
$\mathrm {Add}(\kappa _1, 1) \ast \dot {\mathbb F}_{\kappa ^{\prime }_1, \kappa _2}$
, where
 ${\mathbb F}_{\kappa ^{\prime }_1, \kappa _2}$
is Hamkins’ presentation from [Reference Hamkins11, Section 1] of Woodin’s notion of fast function forcing defined using functions whose domain lies in the half-open interval
${\mathbb F}_{\kappa ^{\prime }_1, \kappa _2}$
is Hamkins’ presentation from [Reference Hamkins11, Section 1] of Woodin’s notion of fast function forcing defined using functions whose domain lies in the half-open interval
![]() $[\kappa ^{\prime }_1, \kappa _2)$
.
$[\kappa ^{\prime }_1, \kappa _2)$
.
 $({\mathbb F}_{\kappa ^{\prime }_1, \kappa _2} = \{p \mid p : \kappa _2 \to \kappa _2$
is a function such that
$({\mathbb F}_{\kappa ^{\prime }_1, \kappa _2} = \{p \mid p : \kappa _2 \to \kappa _2$
is a function such that
![]() ${\vert \mathrm {dom}(p) \vert } < \kappa _2$
,
${\vert \mathrm {dom}(p) \vert } < \kappa _2$
,
![]() $\mathrm {dom}(p) \subseteq [\kappa ^{\prime }_1, \kappa _2)$
,
$\mathrm {dom}(p) \subseteq [\kappa ^{\prime }_1, \kappa _2)$
,
![]() $\delta \in \mathrm {dom}(p)$
implies that
$\delta \in \mathrm {dom}(p)$
implies that
![]() $\delta $
is inaccessible, and if
$\delta $
is inaccessible, and if
![]() $\delta \in \mathrm {dom}(p)$
, then
$\delta \in \mathrm {dom}(p)$
, then
![]() $p '' \delta \subseteq \delta $
and
$p '' \delta \subseteq \delta $
and
![]() ${\vert p \restriction \delta \vert } < \delta \}$
, ordered by inclusion.
${\vert p \restriction \delta \vert } < \delta \}$
, ordered by inclusion.
![]() $)$
Set
$)$
Set
 $V_3 = V^{{\mathbb P}^2}_2$
. By [Reference Hamkins11, Section 1, paragraph 3],
$V_3 = V^{{\mathbb P}^2}_2$
. By [Reference Hamkins11, Section 1, paragraph 3],
 $\Vdash _{\mathrm {Add}(\kappa _1, 1)} ``\dot {\mathbb F}_{\kappa ^{\prime }_1, \kappa _2}$
is
$\Vdash _{\mathrm {Add}(\kappa _1, 1)} ``\dot {\mathbb F}_{\kappa ^{\prime }_1, \kappa _2}$
is
![]() $\kappa ^{\prime }_1$
-directed closed.” Thus,
$\kappa ^{\prime }_1$
-directed closed.” Thus,
![]() ${\mathbb P}^2$
is
${\mathbb P}^2$
is
![]() $\kappa _1$
-directed closed, from which it immediately follows that
$\kappa _1$
-directed closed, from which it immediately follows that
![]() $V_3 \vDash ``\kappa _1$
is both the least strongly compact and least measurable cardinal
$V_3 \vDash ``\kappa _1$
is both the least strongly compact and least measurable cardinal
![]() $+$
$+$
![]() $\kappa _1$
’s strong compactness is indestructible under arbitrary
$\kappa _1$
’s strong compactness is indestructible under arbitrary
![]() $\kappa _1$
-directed closed forcing.” By [Reference Hamkins11, Theorem 1.7],
$\kappa _1$
-directed closed forcing.” By [Reference Hamkins11, Theorem 1.7],
![]() $V_3 \vDash ``\kappa _2$
is strongly compact
$V_3 \vDash ``\kappa _2$
is strongly compact
![]() $($
and hence measurable
$($
and hence measurable
![]() $)$
.” In addition, since
$)$
.” In addition, since
![]() ${\vert \mathrm {Add}(\kappa _1, 1) \vert } = \kappa _1 < \kappa ^{+}_1 < \kappa _1'$
and
${\vert \mathrm {Add}(\kappa _1, 1) \vert } = \kappa _1 < \kappa ^{+}_1 < \kappa _1'$
and
 $\Vdash _{\mathrm {Add}(\kappa _1, 1)} ``\dot {\mathbb F}_{\kappa ^{\prime }_1, \kappa _2}$
is
$\Vdash _{\mathrm {Add}(\kappa _1, 1)} ``\dot {\mathbb F}_{\kappa ^{\prime }_1, \kappa _2}$
is
![]() $\kappa ^{\prime }_1$
-directed closed,”
$\kappa ^{\prime }_1$
-directed closed,”
![]() ${\mathbb P}^2$
admits a gap at
${\mathbb P}^2$
admits a gap at
![]() $\kappa ^+_1$
. Consequently, by our remarks immediately following the statement of Theorem 1.3, any cardinal greater than
$\kappa ^+_1$
. Consequently, by our remarks immediately following the statement of Theorem 1.3, any cardinal greater than
![]() $\kappa ^+_1$
which is measurable in
$\kappa ^+_1$
which is measurable in
![]() $V_3$
had to have been measurable in
$V_3$
had to have been measurable in
![]() $V_2$
. Because
$V_2$
. Because
![]() $V_2 \vDash ``\kappa _2$
is the second measurable cardinal,” it therefore follows that
$V_2 \vDash ``\kappa _2$
is the second measurable cardinal,” it therefore follows that
![]() $V_3 \vDash ``\kappa _2$
is the second measurable cardinal” as well.
$V_3 \vDash ``\kappa _2$
is the second measurable cardinal” as well.
Module 4
![]() $:$
We will now use methods from a theorem due to Usuba
$:$
We will now use methods from a theorem due to Usuba
![]() $($
specifically, [Reference Apter, Dimopoulos and Usuba2, Theorem 3.1] and the techniques in its proof
$($
specifically, [Reference Apter, Dimopoulos and Usuba2, Theorem 3.1] and the techniques in its proof
![]() $)$
to force over
$)$
to force over
![]() $V_3$
in order to create a model
$V_3$
in order to create a model
![]() $V_4$
witnessing the conclusions of Theorem 1.1. Since Usuba’s theorem and proof have only recently appeared in print, we will provide a detailed exposition of his arguments, feeling free to quote verbatim when appropriate from [Reference Apter, Dimopoulos and Usuba2].
$V_4$
witnessing the conclusions of Theorem 1.1. Since Usuba’s theorem and proof have only recently appeared in print, we will provide a detailed exposition of his arguments, feeling free to quote verbatim when appropriate from [Reference Apter, Dimopoulos and Usuba2].
By our work from Module 3, we can assume that there is a fast function
![]() $f:\kappa _2\to \kappa _2$
in
$f:\kappa _2\to \kappa _2$
in
![]() $V_3$
. Define
$V_3$
. Define
![]() ${\mathbb P}^3=\langle \langle {\mathbb P}_\alpha ,\dot {\mathbb Q}_\alpha \rangle \mid \alpha < \kappa _2\rangle $
, an Easton support iteration of length
${\mathbb P}^3=\langle \langle {\mathbb P}_\alpha ,\dot {\mathbb Q}_\alpha \rangle \mid \alpha < \kappa _2\rangle $
, an Easton support iteration of length
![]() $\kappa _2$
, as follows. Let
$\kappa _2$
, as follows. Let
![]() ${\mathbb P}_0 = \mathrm {Add}(\kappa _1, 1)$
.
${\mathbb P}_0 = \mathrm {Add}(\kappa _1, 1)$
.
![]() $\dot {\mathbb Q}_\alpha $
is then a name for the trivial forcing notion, unless
$\dot {\mathbb Q}_\alpha $
is then a name for the trivial forcing notion, unless
![]() $\alpha \in \mathrm {dom}(f)$
. In this case,
$\alpha \in \mathrm {dom}(f)$
. In this case,
![]() $\dot {\mathbb Q}_\alpha $
is a name for the lottery sum
$\dot {\mathbb Q}_\alpha $
is a name for the lottery sum
 $\oplus _{\beta <f(\alpha )} \mathrm {Add}(\alpha ,\beta ),$
as defined in
$\oplus _{\beta <f(\alpha )} \mathrm {Add}(\alpha ,\beta ),$
as defined in
 $V_3^{{\mathbb P}_\alpha }$
, where by convention, we take
$V_3^{{\mathbb P}_\alpha }$
, where by convention, we take
![]() $\mathrm {Add}(\alpha , 0)$
to be trivial forcing.
$\mathrm {Add}(\alpha , 0)$
to be trivial forcing.
Let
![]() $G\subseteq {\mathbb P}^3$
be
$G\subseteq {\mathbb P}^3$
be
![]() $V_3$
-generic. Set
$V_3$
-generic. Set
![]() $V_4 = V_3[G]$
. The arguments of [Reference Hamkins11, Theorem 3.7] show that
$V_4 = V_3[G]$
. The arguments of [Reference Hamkins11, Theorem 3.7] show that
![]() $\kappa _2$
remains strongly compact in
$\kappa _2$
remains strongly compact in
![]() $V_4$
. We wish to show that in
$V_4$
. We wish to show that in
![]() $V_4$
, the strong compactness of
$V_4$
, the strong compactness of
![]() $\kappa _2$
is indestructible under
$\kappa _2$
is indestructible under
![]() $\mathrm {Add}(\kappa _2,\delta )$
for all
$\mathrm {Add}(\kappa _2,\delta )$
for all
![]() $\delta $
. Fix
$\delta $
. Fix
![]() $\delta $
, and let
$\delta $
, and let
![]() $g\subseteq \mathrm {Add}(\kappa _2,\delta )$
be
$g\subseteq \mathrm {Add}(\kappa _2,\delta )$
be
![]() $V_4$
-generic. If we let
$V_4$
-generic. If we let
![]() $Q=\bigcup g$
, then
$Q=\bigcup g$
, then
![]() $Q : \kappa _2\times \delta \to 2$
is a function.
$Q : \kappa _2\times \delta \to 2$
is a function.
Let
![]() $\lambda>\max (\kappa _2, \delta )$
be a regular cardinal, and fix a cardinal
$\lambda>\max (\kappa _2, \delta )$
be a regular cardinal, and fix a cardinal
![]() $\theta \ge 2^{\lambda ^{< \kappa _2}}$
. By [Reference Hamkins11, Theorem 1.12], let
$\theta \ge 2^{\lambda ^{< \kappa _2}}$
. By [Reference Hamkins11, Theorem 1.12], let
![]() $j:V_3\to M$
be an ultrapower embedding by a
$j:V_3\to M$
be an ultrapower embedding by a
![]() $\kappa _2$
-complete, fine ultrafilter
$\kappa _2$
-complete, fine ultrafilter
![]() ${\cal U} \in V_3$
over
${\cal U} \in V_3$
over
![]() $P_{\kappa _2}(\theta )$
with
$P_{\kappa _2}(\theta )$
with
![]() $\mathrm {crit}(j)=\kappa _2$
such that
$\mathrm {crit}(j)=\kappa _2$
such that
![]() $|[\mathrm {id}]_{\cal U}|^M<j(f)(\kappa _2)$
. Since there is no source of confusion, we will drop the subscript from elements of M and denote them as
$|[\mathrm {id}]_{\cal U}|^M<j(f)(\kappa _2)$
. Since there is no source of confusion, we will drop the subscript from elements of M and denote them as
![]() $[h]$
. As usual,
$[h]$
. As usual,
![]() $j''\theta \subseteq [\mathrm {id}]$
, so
$j''\theta \subseteq [\mathrm {id}]$
, so
![]() $|\theta |^M \le |[\mathrm {id}]|^M$
.
$|\theta |^M \le |[\mathrm {id}]|^M$
.
Claim 2.1. There is in M a function
![]() $\pi :[\mathrm {id}]\to \theta $
such that for all
$\pi :[\mathrm {id}]\to \theta $
such that for all
![]() $\alpha <\theta $
,
$\alpha <\theta $
,
![]() $\pi (j(\alpha ))=\alpha $
.
$\pi (j(\alpha ))=\alpha $
.
Proof. For each
![]() $\alpha <\theta $
, let
$\alpha <\theta $
, let
![]() $g_\alpha :P_{\kappa _2}(\theta )\to V_3$
be a function such that
$g_\alpha :P_{\kappa _2}(\theta )\to V_3$
be a function such that
![]() $[g_\alpha ]=\alpha $
. Without loss of generality, we can assume that
$[g_\alpha ]=\alpha $
. Without loss of generality, we can assume that
![]() $g_\alpha (p)$
is defined for every
$g_\alpha (p)$
is defined for every
![]() $p \in P_{\kappa _2}(\theta )$
. Let
$p \in P_{\kappa _2}(\theta )$
. Let
![]() $h:P_{\kappa _2}(\theta )\to V_3$
be so that for each
$h:P_{\kappa _2}(\theta )\to V_3$
be so that for each
![]() $p \in P_{\kappa _2}(\theta )$
,
$p \in P_{\kappa _2}(\theta )$
,
![]() $h(p)$
is the function having domain p such that for every
$h(p)$
is the function having domain p such that for every
![]() $\alpha \in p$
,
$\alpha \in p$
,
![]() $h(\alpha ) = g_\alpha (p)$
. It follows that
$h(\alpha ) = g_\alpha (p)$
. It follows that
![]() $[h]$
is a function with domain
$[h]$
is a function with domain
![]() $[\mathrm {id}]$
, and by the fineness of
$[\mathrm {id}]$
, and by the fineness of
![]() ${\cal U}$
, for each
${\cal U}$
, for each
![]() $\alpha <\theta $
, on a measure
$\alpha <\theta $
, on a measure
![]() $1$
subset of
$1$
subset of
![]() $\{p \mid \alpha \in p\}$
,
$\{p \mid \alpha \in p\}$
,
![]() $[h](j(\alpha ))=[g_\alpha ]=\alpha $
. This completes the proof, since we can easily use
$[h](j(\alpha ))=[g_\alpha ]=\alpha $
. This completes the proof, since we can easily use
![]() $[h]$
to define a function
$[h]$
to define a function
![]() $\pi $
with the desired properties by setting
$\pi $
with the desired properties by setting
![]() $\pi = [h]$
.⊣
$\pi = [h]$
.⊣
We now proceed by liftingjthrough
![]() ${\mathbb P}^3\ast \dot {\mathrm {Add}}(\kappa _2,\delta )$
. As usual,
${\mathbb P}^3\ast \dot {\mathrm {Add}}(\kappa _2,\delta )$
. As usual,
![]() $j({\mathbb P}^3)$
can be factorized as
$j({\mathbb P}^3)$
can be factorized as
![]() ${\mathbb P}^3\ast \dot {\mathbb Q} \ast \dot {\mathbb P}_{\mathrm {tail}}$
, where
${\mathbb P}^3\ast \dot {\mathbb Q} \ast \dot {\mathbb P}_{\mathrm {tail}}$
, where
![]() $\dot {\mathbb Q}$
is a name for the lottery sum
$\dot {\mathbb Q}$
is a name for the lottery sum
 $\oplus _{\beta <j(f)(\kappa _2)}\mathrm {Add}(\kappa _2,\beta )$
, and
$\oplus _{\beta <j(f)(\kappa _2)}\mathrm {Add}(\kappa _2,\beta )$
, and
![]() $\dot {\mathbb P}_{\mathrm {tail}}$
is a name for the remaining stages through
$\dot {\mathbb P}_{\mathrm {tail}}$
is a name for the remaining stages through
![]() $j(\kappa _2)$
. Using G as an M-generic filter for
$j(\kappa _2)$
. Using G as an M-generic filter for
![]() ${\mathbb P}^3$
, we can form
${\mathbb P}^3$
, we can form
![]() $M[G]$
. Also, since
$M[G]$
. Also, since
![]() $\delta < \theta \le |[\mathrm {id}]|^M < j(f)(\kappa _2)$
, we can choose to force above a condition in
$\delta < \theta \le |[\mathrm {id}]|^M < j(f)(\kappa _2)$
, we can choose to force above a condition in
![]() ${\mathbb Q}=\mathrm {int}_G(\dot {\mathbb Q})$
that opts for
${\mathbb Q}=\mathrm {int}_G(\dot {\mathbb Q})$
that opts for
![]() $\mathrm {Add}(\kappa _2,\delta )$
. Thus, we can use g as an
$\mathrm {Add}(\kappa _2,\delta )$
. Thus, we can use g as an
![]() $M[G]$
-generic filter for
$M[G]$
-generic filter for
![]() ${\mathbb Q}$
. Furthermore, note that since
${\mathbb Q}$
. Furthermore, note that since
![]() $j(f)(\kappa _2)>|[\mathrm {id}]|^M$
,
$j(f)(\kappa _2)>|[\mathrm {id}]|^M$
,
 ${\mathbb P}_{\mathrm {tail}} = \mathrm {int}_{G * g}(\dot {\mathbb P}_{\mathrm {tail}})$
is at least
${\mathbb P}_{\mathrm {tail}} = \mathrm {int}_{G * g}(\dot {\mathbb P}_{\mathrm {tail}})$
is at least
![]() $(|[\mathrm {id}]|^+)^M$
-directed closed in
$(|[\mathrm {id}]|^+)^M$
-directed closed in
![]() $M[G][g]$
.
$M[G][g]$
.
Force over
![]() $V_4[g]$
to add a generic filter
$V_4[g]$
to add a generic filter
![]() $G_{\mathrm {tail}}$
for
$G_{\mathrm {tail}}$
for
![]() ${\mathbb P}_{\mathrm {tail}}$
. Using
${\mathbb P}_{\mathrm {tail}}$
. Using
![]() $G_{\mathrm {tail}}$
as an
$G_{\mathrm {tail}}$
as an
![]() $M[G][g]$
-generic filter for
$M[G][g]$
-generic filter for
![]() ${\mathbb P}_{\mathrm {tail}}$
, since
${\mathbb P}_{\mathrm {tail}}$
, since
![]() $j '' G \subseteq G$
, we can lift j in
$j '' G \subseteq G$
, we can lift j in
![]() $V_4[g][G_{\mathrm {tail}}]$
to
$V_4[g][G_{\mathrm {tail}}]$
to
![]() $j:V_4\to M[j(G)],$
where
$j:V_4\to M[j(G)],$
where
![]() $j(G)=G\ast g \ast G_{\mathrm {tail}}$
. In order to further lift j through
$j(G)=G\ast g \ast G_{\mathrm {tail}}$
. In order to further lift j through
![]() $\mathrm {Add}(\kappa _2,\delta )$
, we will use a master condition argument. Consider the function
$\mathrm {Add}(\kappa _2,\delta )$
, we will use a master condition argument. Consider the function
![]() $\pi $
given by Claim 2.1, and note that
$\pi $
given by Claim 2.1, and note that
![]() $|[\mathrm {id}]\cap j(\delta )|^M\leq |[\mathrm {id}]|^M<j(\kappa _2)$
. Define in
$|[\mathrm {id}]\cap j(\delta )|^M\leq |[\mathrm {id}]|^M<j(\kappa _2)$
. Define in
![]() $M[j(G)]$
a function
$M[j(G)]$
a function
![]() $q:\kappa _2\times ([\mathrm {id}]\cap j(\delta ))\to 2$
given by
$q:\kappa _2\times ([\mathrm {id}]\cap j(\delta ))\to 2$
given by
![]() $q(\langle \beta ,\gamma \rangle )= Q(\langle \beta ,\pi (\gamma ) \rangle )$
if
$q(\langle \beta ,\gamma \rangle )= Q(\langle \beta ,\pi (\gamma ) \rangle )$
if
![]() $\pi (\gamma ) < \delta $
, and
$\pi (\gamma ) < \delta $
, and
![]() $0$
otherwise. Clearly, q is a condition in
$0$
otherwise. Clearly, q is a condition in
![]() $j(\mathrm {Add}(\kappa _2,\delta ))$
.
$j(\mathrm {Add}(\kappa _2,\delta ))$
.
Claim 2.2.
![]() $q\geq j(p)$
for all
$q\geq j(p)$
for all
![]() $p\in g$
.
$p\in g$
.
Proof. By elementarity and the fact that
![]() $\mathrm {crit}(j)=\kappa _2$
, for each
$\mathrm {crit}(j)=\kappa _2$
, for each
![]() $p\in g$
,
$p\in g$
,
![]() $j(p)$
is a function with domain
$j(p)$
is a function with domain
![]() $j''\mathrm {dom}(p)=\{\langle \beta ,j(\gamma )\rangle \mid \langle \beta ,\gamma \rangle \in \mathrm {dom}(p)\}$
. Hence,
$j''\mathrm {dom}(p)=\{\langle \beta ,j(\gamma )\rangle \mid \langle \beta ,\gamma \rangle \in \mathrm {dom}(p)\}$
. Hence,
![]() $\mathrm {dom}(j(p))\subseteq \mathrm {dom}(q)$
. For
$\mathrm {dom}(j(p))\subseteq \mathrm {dom}(q)$
. For
![]() $\langle \beta ,j(\gamma )\rangle \in \mathrm {dom}(j(p))$
, we have
$\langle \beta ,j(\gamma )\rangle \in \mathrm {dom}(j(p))$
, we have
![]() $j(p)(\langle \beta ,j(\gamma ) \rangle )= p(\langle \beta ,\gamma \rangle )= Q(\langle \beta ,\gamma \rangle )= Q(\langle \beta ,\pi (j(\gamma )) \rangle )=q(\langle \beta , j(\gamma ) \rangle )$
.⊣
$j(p)(\langle \beta ,j(\gamma ) \rangle )= p(\langle \beta ,\gamma \rangle )= Q(\langle \beta ,\gamma \rangle )= Q(\langle \beta ,\pi (j(\gamma )) \rangle )=q(\langle \beta , j(\gamma ) \rangle )$
.⊣
Force over
![]() $V_4[g][G_{\mathrm {tail}}]$
to add a generic filter
$V_4[g][G_{\mathrm {tail}}]$
to add a generic filter
![]() $h^*\subseteq j(\mathrm {Add}(\kappa _2,\delta ))$
containing q. By Claim 2.2, we can lift j in
$h^*\subseteq j(\mathrm {Add}(\kappa _2,\delta ))$
containing q. By Claim 2.2, we can lift j in
![]() $V_4[g][G_{\mathrm {tail}}][h^*]$
to
$V_4[g][G_{\mathrm {tail}}][h^*]$
to
![]() $j:V_4[g]\to M[j(G)][h^*].$
$j:V_4[g]\to M[j(G)][h^*].$
Let
 $\vec {X}=\langle X_\xi \mid \xi < 2^{[\lambda ]^{<\kappa _2}}\rangle \in V_4[g]$
be an enumeration of
$\vec {X}=\langle X_\xi \mid \xi < 2^{[\lambda ]^{<\kappa _2}}\rangle \in V_4[g]$
be an enumeration of
 ${\wp }(P_{\kappa _2}(\lambda ))^{V_4[g]}$
. In
${\wp }(P_{\kappa _2}(\lambda ))^{V_4[g]}$
. In
![]() $M[j(G)][h^*]$
, consider the set
$M[j(G)][h^*]$
, consider the set
 $B=\{\xi \in [\mathrm {id}]\mid [\mathrm {id}]\cap j(\lambda )\in j(\vec {X})_\xi \}$
. Since
$B=\{\xi \in [\mathrm {id}]\mid [\mathrm {id}]\cap j(\lambda )\in j(\vec {X})_\xi \}$
. Since
![]() ${\mathbb P}_{\mathrm {tail}}\ast j(\dot {\mathrm {Add}}(\kappa _2,\delta ))$
is at least
${\mathbb P}_{\mathrm {tail}}\ast j(\dot {\mathrm {Add}}(\kappa _2,\delta ))$
is at least
![]() $(|[\mathrm {id}]|^+)^M$
-directed closed in
$(|[\mathrm {id}]|^+)^M$
-directed closed in
![]() $M[G][g]$
,
$M[G][g]$
,
![]() $B\in M[G][g]\subseteq V_4[g]$
. Hence,
$B\in M[G][g]\subseteq V_4[g]$
. Hence,
 ${\cal W} = \{X_\xi \in {\wp } (P_{\kappa _2}(\lambda ))^{V_4[g]} \mid j(\xi )\in B\} \in V_4[g]$
, and since
${\cal W} = \{X_\xi \in {\wp } (P_{\kappa _2}(\lambda ))^{V_4[g]} \mid j(\xi )\in B\} \in V_4[g]$
, and since
![]() $\theta \ge 2^{[\lambda ]^{< \kappa _2}}$
,
$\theta \ge 2^{[\lambda ]^{< \kappa _2}}$
,
![]() ${\cal W}$
is easily seen to be a
${\cal W}$
is easily seen to be a
![]() $\kappa _2$
-complete, fine ultrafilter over
$\kappa _2$
-complete, fine ultrafilter over
![]() $P_{\kappa _2}(\lambda )$
. Thus,
$P_{\kappa _2}(\lambda )$
. Thus,
![]() $\kappa _2$
is
$\kappa _2$
is
![]() $\lambda $
strongly compact in
$\lambda $
strongly compact in
![]() $V_4[g]$
. Since
$V_4[g]$
. Since
![]() $\lambda $
can be chosen arbitrarily large, we have shown that
$\lambda $
can be chosen arbitrarily large, we have shown that
![]() $\kappa _2$
remains strongly compact in
$\kappa _2$
remains strongly compact in
![]() $V_4[g]$
, from which we immediately infer that
$V_4[g]$
, from which we immediately infer that
![]() $V_4 \vDash ``\kappa _2$
’s strong compactness is indestructible under forcing with
$V_4 \vDash ``\kappa _2$
’s strong compactness is indestructible under forcing with
![]() $\mathrm {Add}(\kappa _2, \delta )$
for any ordinal
$\mathrm {Add}(\kappa _2, \delta )$
for any ordinal
![]() $\delta $
.”
$\delta $
.”
We finish the proof of Theorem 1.1 by combining the work of Modules 1–4. Because
![]() $V_3 \vDash ``{\mathbb P}^3$
is
$V_3 \vDash ``{\mathbb P}^3$
is
![]() $\kappa _1$
-directed closed,”
$\kappa _1$
-directed closed,”
![]() $V_4 \vDash ``\kappa _1$
is both the least strongly compact and least measurable cardinal
$V_4 \vDash ``\kappa _1$
is both the least strongly compact and least measurable cardinal
![]() $+$
$+$
![]() $\kappa _1$
’s strong compactness is indestructible under arbitrary
$\kappa _1$
’s strong compactness is indestructible under arbitrary
![]() $\kappa _1$
-directed closed forcing.” By the arguments of Module 4, since we have taken
$\kappa _1$
-directed closed forcing.” By the arguments of Module 4, since we have taken
![]() $\mathrm {Add}(\kappa _2, 0)$
to be trivial forcing,
$\mathrm {Add}(\kappa _2, 0)$
to be trivial forcing,
![]() $V_4 \vDash ``\kappa _2$
is strongly compact and hence measurable.” In addition, by its definition,
$V_4 \vDash ``\kappa _2$
is strongly compact and hence measurable.” In addition, by its definition,
![]() ${\mathbb P}^3 = \mathrm {Add}(\kappa _1, 1) \ast \dot {\mathbb Q}$
, where
${\mathbb P}^3 = \mathrm {Add}(\kappa _1, 1) \ast \dot {\mathbb Q}$
, where
![]() ${\vert \mathrm {Add}(\kappa _1, 1) \vert } = \kappa _1$
and
${\vert \mathrm {Add}(\kappa _1, 1) \vert } = \kappa _1$
and
 $\Vdash _{\mathrm {Add}(\kappa _1, 1)} ``\dot {\mathbb Q}$
is
$\Vdash _{\mathrm {Add}(\kappa _1, 1)} ``\dot {\mathbb Q}$
is
![]() $\kappa _1'$
-directed closed.” This means that as in Module 3,
$\kappa _1'$
-directed closed.” This means that as in Module 3,
![]() $V_4 \vDash ``\kappa _2$
is the second measurable cardinal.” It consequently follows that
$V_4 \vDash ``\kappa _2$
is the second measurable cardinal.” It consequently follows that
![]() $V_4$
is the desired model witnessing the conclusions of Theorem 1.1. By writing
$V_4$
is the desired model witnessing the conclusions of Theorem 1.1. By writing
![]() ${\mathbb P} = {\mathbb P}^0 \ast \dot {\mathbb P}^1 \ast \dot {\mathbb P}^2 \ast \dot {\mathbb P}^3$
, we have completed the proof of Theorem 1.1.⊣
${\mathbb P} = {\mathbb P}^0 \ast \dot {\mathbb P}^1 \ast \dot {\mathbb P}^2 \ast \dot {\mathbb P}^3$
, we have completed the proof of Theorem 1.1.⊣
We turn now to the proof of Theorem 1.2.
Proof. Suppose
![]() $V \vDash ``$
ZFC
$V \vDash ``$
ZFC
![]() $+ \kappa _1 < \kappa _2$
are supercompact.” Without loss of generality, by truncating the universe if necessary, we assume in addition that
$+ \kappa _1 < \kappa _2$
are supercompact.” Without loss of generality, by truncating the universe if necessary, we assume in addition that
![]() $V \vDash ``$
No cardinal
$V \vDash ``$
No cardinal
![]() $\lambda> \kappa _2$
is inaccessible.” We explicitly mention it will of course be the case that in any of our generic extensions of V, there will be no inaccessible cardinals greater than
$\lambda> \kappa _2$
is inaccessible.” We explicitly mention it will of course be the case that in any of our generic extensions of V, there will be no inaccessible cardinals greater than
![]() $\kappa _2$
.
$\kappa _2$
.
Lemma 2.3. There is a partial ordering
![]() ${\mathbb P}^* \subseteq V$
such that
${\mathbb P}^* \subseteq V$
such that
![]() $V^{{\mathbb P}^*} \vDash \textit{``}$
For
$V^{{\mathbb P}^*} \vDash \textit{``}$
For
![]() $i = 1,2$
,
$i = 1,2$
,
 $2^{\kappa _i} = 2^{\kappa ^+_i} = \kappa ^{++}_i$
and
$2^{\kappa _i} = 2^{\kappa ^+_i} = \kappa ^{++}_i$
and
![]() $\kappa _i$
is supercompact
$\kappa _i$
is supercompact
![]() $+$
There are supercompact ultrafilters
$+$
There are supercompact ultrafilters
![]() ${\cal U}_i$
over
${\cal U}_i$
over
![]() $P_{\kappa _i}(\kappa ^+_i)$
such that
$P_{\kappa _i}(\kappa ^+_i)$
such that
![]() $\kappa _i$
isn’t measurable in the ultrapower by
$\kappa _i$
isn’t measurable in the ultrapower by
![]() ${\cal U}_i + 2^\delta = \delta ^+$
for every cardinal
${\cal U}_i + 2^\delta = \delta ^+$
for every cardinal
![]() $\delta \ge \kappa ^{++}_2$
.”
$\delta \ge \kappa ^{++}_2$
.”
Proof. To prove Lemma 2.3, begin by forcing GCH using the partial ordering
![]() ${\mathbb Q}^0$
. Next, force indestructibility for
${\mathbb Q}^0$
. Next, force indestructibility for
![]() $\kappa _1$
’s supercompactness as in [Reference Laver14], using a partial ordering
$\kappa _1$
’s supercompactness as in [Reference Laver14], using a partial ordering
![]() ${\mathbb Q}^1$
having cardinality
${\mathbb Q}^1$
having cardinality
![]() $\kappa _1$
. Since
$\kappa _1$
. Since
![]() ${\vert {\mathbb Q}^1 \vert } = \kappa _1$
,
${\vert {\mathbb Q}^1 \vert } = \kappa _1$
,
![]() $2^\delta = \delta ^+$
for every
$2^\delta = \delta ^+$
for every
![]() $\delta \ge \kappa _1$
, and by the results of [Reference Lévy and Solovay15],
$\delta \ge \kappa _1$
, and by the results of [Reference Lévy and Solovay15],
![]() $\kappa _2$
remains supercompact after forcing with
$\kappa _2$
remains supercompact after forcing with
![]() ${\mathbb Q}^1$
. Now, force with the partial ordering
${\mathbb Q}^1$
. Now, force with the partial ordering
![]() ${\mathbb Q}^2$
used in the proof of [Reference Apter and Cummings1, Lemma 2] defined with respect to
${\mathbb Q}^2$
used in the proof of [Reference Apter and Cummings1, Lemma 2] defined with respect to
![]() $\kappa _2$
and acting nontrivially only on inaccessible cardinals in the open interval
$\kappa _2$
and acting nontrivially only on inaccessible cardinals in the open interval
![]() $(\kappa _1, \kappa _2)$
. Since this definition ensures that
$(\kappa _1, \kappa _2)$
. Since this definition ensures that
![]() ${\mathbb Q}^2$
is
${\mathbb Q}^2$
is
![]() $\kappa _1$
-directed closed,
$\kappa _1$
-directed closed,
![]() $\kappa _1$
remains supercompact after forcing with
$\kappa _1$
remains supercompact after forcing with
![]() ${\mathbb Q}^2$
. In addition, after forcing with
${\mathbb Q}^2$
. In addition, after forcing with
![]() ${\mathbb Q}^2$
, as in [Reference Apter and Cummings1],
${\mathbb Q}^2$
, as in [Reference Apter and Cummings1],
![]() $\kappa _2$
remains supercompact,
$\kappa _2$
remains supercompact,
 $2^{\kappa _2} = 2^{\kappa ^+_2} = \kappa ^{++}_2$
,
$2^{\kappa _2} = 2^{\kappa ^+_2} = \kappa ^{++}_2$
,
![]() $2^\delta = \delta ^+$
for every cardinal
$2^\delta = \delta ^+$
for every cardinal
![]() $\delta \ge \kappa ^{++}_2$
, and there is a supercompact ultrafilter
$\delta \ge \kappa ^{++}_2$
, and there is a supercompact ultrafilter
![]() ${\cal U}_2$
over
${\cal U}_2$
over
![]() $P_{\kappa _2}(\kappa ^+_2)$
such that
$P_{\kappa _2}(\kappa ^+_2)$
such that
![]() $\kappa _2$
isn’t measurable in the ultrapower by
$\kappa _2$
isn’t measurable in the ultrapower by
![]() ${\cal U}_2$
. Finally, force with the partial ordering
${\cal U}_2$
. Finally, force with the partial ordering
![]() ${\mathbb Q}^3$
used in the proof of [Reference Apter and Cummings1, Lemma 2] defined with respect to
${\mathbb Q}^3$
used in the proof of [Reference Apter and Cummings1, Lemma 2] defined with respect to
![]() $\kappa _1$
on inaccessible cardinals
$\kappa _1$
on inaccessible cardinals
![]() $\delta < \kappa _1$
such that
$\delta < \kappa _1$
such that
![]() $2^\delta = \delta ^+$
. Let
$2^\delta = \delta ^+$
. Let
![]() ${\mathbb P}^* = {\mathbb Q}^0 \ast \dot {\mathbb Q}^1 \ast \dot {\mathbb Q}^2 \ast \dot {\mathbb Q}^3$
. Because
${\mathbb P}^* = {\mathbb Q}^0 \ast \dot {\mathbb Q}^1 \ast \dot {\mathbb Q}^2 \ast \dot {\mathbb Q}^3$
. Because
![]() ${\mathbb Q}^3$
can be defined so as to have cardinality
${\mathbb Q}^3$
can be defined so as to have cardinality
![]() $\kappa _1$
, our previous work, [Reference Apter and Cummings1, Lemma 2] applied to
$\kappa _1$
, our previous work, [Reference Apter and Cummings1, Lemma 2] applied to
![]() ${\mathbb Q}^3$
, another application of the results of [Reference Lévy and Solovay15], and standard arguments for calculating the size of power sets in generic extensions yield that
${\mathbb Q}^3$
, another application of the results of [Reference Lévy and Solovay15], and standard arguments for calculating the size of power sets in generic extensions yield that
![]() $V^{{\mathbb P}^*} \vDash ``$
For
$V^{{\mathbb P}^*} \vDash ``$
For
![]() $i = 1,2$
,
$i = 1,2$
,
 $2^{\kappa _i} = 2^{\kappa ^+_i} = \kappa ^{++}_i$
and
$2^{\kappa _i} = 2^{\kappa ^+_i} = \kappa ^{++}_i$
and
![]() $\kappa _i$
is supercompact
$\kappa _i$
is supercompact
![]() $+$
There are supercompact ultrafilters
$+$
There are supercompact ultrafilters
![]() ${\cal U}_i$
over
${\cal U}_i$
over
![]() $P_{\kappa _i}(\kappa ^+_i)$
such that
$P_{\kappa _i}(\kappa ^+_i)$
such that
![]() $\kappa _i$
isn’t measurable in the ultrapower by
$\kappa _i$
isn’t measurable in the ultrapower by
![]() ${\cal U}_i + $
${\cal U}_i + $
![]() $2^\delta = \delta ^+$
for every cardinal
$2^\delta = \delta ^+$
for every cardinal
![]() $\delta \ge \kappa ^{++}_2$
.” This completes the proof of Lemma 2.3.⊣
$\delta \ge \kappa ^{++}_2$
.” This completes the proof of Lemma 2.3.⊣
With a slight abuse of notation, we relabel
![]() $V^{{\mathbb P}^*}$
as V. Now, as in the proof of Theorem 1.1, let
$V^{{\mathbb P}^*}$
as V. Now, as in the proof of Theorem 1.1, let
![]() ${\mathbb P}^0 \in V$
be the partial ordering used in the proof of [Reference Apter and Gitik3, Theorem 1] defined with respect to
${\mathbb P}^0 \in V$
be the partial ordering used in the proof of [Reference Apter and Gitik3, Theorem 1] defined with respect to
![]() $\kappa _1$
. Set
$\kappa _1$
. Set
 $V_1 = V^{{\mathbb P}^0}$
. Since
$V_1 = V^{{\mathbb P}^0}$
. Since
![]() ${\mathbb P}^0$
is an Easton support iteration of length
${\mathbb P}^0$
is an Easton support iteration of length
![]() $\kappa _1$
such that
$\kappa _1$
such that
![]() ${\vert {\mathbb P}^0 \vert } = \kappa _1$
, standard arguments in conjunction with the results of [Reference Lévy and Solovay15] and Lemma 2.3 yield that
${\vert {\mathbb P}^0 \vert } = \kappa _1$
, standard arguments in conjunction with the results of [Reference Lévy and Solovay15] and Lemma 2.3 yield that
![]() $V_1 \vDash ``$
For
$V_1 \vDash ``$
For
![]() $i = 1, 2$
,
$i = 1, 2$
,
 $2^{\kappa _i} = 2^{\kappa ^+_i} = \kappa ^{++}_i + 2^\delta = \delta ^+$
for every cardinal
$2^{\kappa _i} = 2^{\kappa ^+_i} = \kappa ^{++}_i + 2^\delta = \delta ^+$
for every cardinal
![]() $\delta \ge \kappa ^{++}_2$
+
$\delta \ge \kappa ^{++}_2$
+
![]() $\kappa _2$
is supercompact
$\kappa _2$
is supercompact
![]() $+$
There is a supercompact ultrafilter
$+$
There is a supercompact ultrafilter
![]() ${\cal U}^*_2$
over
${\cal U}^*_2$
over
![]() $P_{\kappa _2}(\kappa ^+_2)$
such that
$P_{\kappa _2}(\kappa ^+_2)$
such that
![]() $\kappa _2$
isn’t measurable in the ultrapower by
$\kappa _2$
isn’t measurable in the ultrapower by
![]() ${\cal U}^*_2$
.” Because [Reference Gitik9, Lemmas 1.2 and 1.4] require no GCH assumptions, and because the proof of [Reference Apter and Gitik3, Lemma 2] only requires that
${\cal U}^*_2$
.” Because [Reference Gitik9, Lemmas 1.2 and 1.4] require no GCH assumptions, and because the proof of [Reference Apter and Gitik3, Lemma 2] only requires that
![]() $2^\delta = \delta ^+$
holds for sufficiently large
$2^\delta = \delta ^+$
holds for sufficiently large
![]() $\delta $
, it is then the case that
$\delta $
, it is then the case that
![]() $V_1 \vDash ``\kappa _1$
is both the least strongly compact and least measurable cardinal
$V_1 \vDash ``\kappa _1$
is both the least strongly compact and least measurable cardinal
![]() $+$
$+$
![]() $\kappa _1$
’s strong compactness is indestructible under arbitrary
$\kappa _1$
’s strong compactness is indestructible under arbitrary
![]() $\kappa _1$
-directed closed forcing.”
$\kappa _1$
-directed closed forcing.”
Lemma 2.4.
![]() $V_1 \vDash \textit{``}\kappa _1$
is
$V_1 \vDash \textit{``}\kappa _1$
is
![]() $\kappa ^+_1$
supercompact.”
$\kappa ^+_1$
supercompact.”
Proof. We will follow to a certain extent the proofs of [Reference Gitik9, Lemma 1.5] and [Reference Magidor16, Theorem 2.5]. Let G be V-generic over
![]() ${\mathbb P}^0$
. By Lemma 2.3, let
${\mathbb P}^0$
. By Lemma 2.3, let
![]() $j : V \to M$
be an elementary embedding
$j : V \to M$
be an elementary embedding
![]() $($
which we take to be generated by the ultrafilter
$($
which we take to be generated by the ultrafilter
![]() ${\cal U}_1$
over
${\cal U}_1$
over
![]() $P_{\kappa _1}(\kappa ^+_1)$
witnessing the
$P_{\kappa _1}(\kappa ^+_1)$
witnessing the
![]() $\kappa ^+_1$
supercompactness of
$\kappa ^+_1$
supercompactness of
![]() $\kappa _1)$
such that
$\kappa _1)$
such that
![]() $M \vDash ``\kappa _1$
isn’t measurable.” Because we may assume that
$M \vDash ``\kappa _1$
isn’t measurable.” Because we may assume that
![]() ${\mathbb P}^0$
does nontrivial forcing only at V-measurable cardinals,
${\mathbb P}^0$
does nontrivial forcing only at V-measurable cardinals,
![]() $j({\mathbb P}^0) = {\mathbb P}^0 \ast \dot {\mathbb Q}$
, where the first nontrivial stage in
$j({\mathbb P}^0) = {\mathbb P}^0 \ast \dot {\mathbb Q}$
, where the first nontrivial stage in
![]() $\dot {\mathbb Q}$
is forced to be well above
$\dot {\mathbb Q}$
is forced to be well above
![]() $\kappa ^+_1$
. In addition, because
$\kappa ^+_1$
. In addition, because
 $2^{\kappa ^+_1} = \kappa ^{++}_1$
, we may let
$2^{\kappa ^+_1} = \kappa ^{++}_1$
, we may let
 $\langle \dot A_\alpha \mid \alpha < \kappa ^{++}_1 \rangle \in V$
be an enumeration of all of the canonical
$\langle \dot A_\alpha \mid \alpha < \kappa ^{++}_1 \rangle \in V$
be an enumeration of all of the canonical
![]() ${\mathbb P}^0$
-names for subsets of
${\mathbb P}^0$
-names for subsets of
 $(P_{\kappa _1}(\kappa ^+_1))^{V[G]}$
. Also, as
$(P_{\kappa _1}(\kappa ^+_1))^{V[G]}$
. Also, as
![]() ${\mathbb P}^0$
is an Easton support iteration of length
${\mathbb P}^0$
is an Easton support iteration of length
![]() $\kappa _1$
and is thus
$\kappa _1$
and is thus
![]() $\kappa _1$
-c.c.,
$\kappa _1$
-c.c.,
![]() $M[G]$
remains
$M[G]$
remains
![]() $\kappa ^+_1$
-closed with respect to
$\kappa ^+_1$
-closed with respect to
![]() $V[G]$
. We now use terminology and results from [Reference Gitik9], to which we refer readers for further details and explanations. Specifically, since
$V[G]$
. We now use terminology and results from [Reference Gitik9], to which we refer readers for further details and explanations. Specifically, since
![]() ${\mathbb P}^0$
is an Easton support iteration of partial orderings satisfying the Prikry property and
${\mathbb P}^0$
is an Easton support iteration of partial orderings satisfying the Prikry property and
![]() ${\mathbb Q} = j({\mathbb P}^0)/G$
is
${\mathbb Q} = j({\mathbb P}^0)/G$
is
![]() $\kappa ^{++}_1$
-weakly closed, we may define in
$\kappa ^{++}_1$
-weakly closed, we may define in
![]() $V[G]$
an increasing sequence of Easton extensions
$V[G]$
an increasing sequence of Easton extensions
![]() $\langle p_\alpha \mid \alpha < \kappa ^{++}_1 \rangle $
of members of
$\langle p_\alpha \mid \alpha < \kappa ^{++}_1 \rangle $
of members of
![]() ${\mathbb Q}$
such that in
${\mathbb Q}$
such that in
![]() $M[G]$
, for every
$M[G]$
, for every
![]() $\alpha < \kappa ^{++}_1$
,
$\alpha < \kappa ^{++}_1$
,
 $p_{\alpha + 1} \parallel _{{\mathbb Q}} ``\langle j(\beta ) \mid \beta < \kappa ^+_1 \rangle \in j(\dot A_\alpha )$
.”Footnote
2
Note that because
$p_{\alpha + 1} \parallel _{{\mathbb Q}} ``\langle j(\beta ) \mid \beta < \kappa ^+_1 \rangle \in j(\dot A_\alpha )$
.”Footnote
2
Note that because
 $M[G]^{\kappa ^+_1} \subseteq M[G]$
,
$M[G]^{\kappa ^+_1} \subseteq M[G]$
,
![]() $\langle p_\alpha \mid \alpha < \kappa ^{++}_1 \rangle $
is well defined, and every initial segment of this sequence is a member of
$\langle p_\alpha \mid \alpha < \kappa ^{++}_1 \rangle $
is well defined, and every initial segment of this sequence is a member of
![]() $M[G]$
. In analogy to the proof of [Reference Gitik9, Lemma 1.5], this now allows us to define
$M[G]$
. In analogy to the proof of [Reference Gitik9, Lemma 1.5], this now allows us to define
![]() ${\cal U}^*_1 \in V_1$
by
${\cal U}^*_1 \in V_1$
by
![]() $A \in {\cal U}^*_1$
iff for some
$A \in {\cal U}^*_1$
iff for some
![]() $\alpha < \kappa ^{++}_1$
and some
$\alpha < \kappa ^{++}_1$
and some
![]() ${\mathbb P}^0$
-name
${\mathbb P}^0$
-name
![]() $\dot A$
for A, in
$\dot A$
for A, in
![]() $M[G]$
,
$M[G]$
,
 $p_\alpha \Vdash _{{\mathbb Q}} ``\langle j(\beta ) \mid \beta < \kappa ^+_1 \rangle \in j(\dot A)$
.” Because
$p_\alpha \Vdash _{{\mathbb Q}} ``\langle j(\beta ) \mid \beta < \kappa ^+_1 \rangle \in j(\dot A)$
.” Because
![]() $j '' G = G$
, as in [Reference Gitik9, Lemma 1.5], the definition of
$j '' G = G$
, as in [Reference Gitik9, Lemma 1.5], the definition of
![]() ${\cal U}^*_1$
doesn’t depend on a particular name for A, and so
${\cal U}^*_1$
doesn’t depend on a particular name for A, and so
![]() ${\cal U}^*_1$
is well defined. The arguments given on [Reference Apter and Gitik3, proof of Lemma 2, p. 1408]
${\cal U}^*_1$
is well defined. The arguments given on [Reference Apter and Gitik3, proof of Lemma 2, p. 1408]
![]() $($
suitably modified
$($
suitably modified
![]() $)$
then allow us to infer that
$)$
then allow us to infer that
![]() $V_1 = V[G] \vDash ``\kappa _1$
is
$V_1 = V[G] \vDash ``\kappa _1$
is
![]() $\kappa ^+_1$
strongly compact.”
$\kappa ^+_1$
strongly compact.”
To show that
![]() $V_1 \vDash ``\kappa _1$
is
$V_1 \vDash ``\kappa _1$
is
![]() $\kappa ^+_1$
supercompact”
$\kappa ^+_1$
supercompact”
![]() $($
i.e., that
$($
i.e., that
![]() $V_1 \vDash ``{\cal U}^*_1$
is normal”
$V_1 \vDash ``{\cal U}^*_1$
is normal”
![]() $)$
, we modify Magidor’s argument found in the proof of [Reference Magidor16, Theorem 2.5, pp. 47–48]. Specifically, suppose
$)$
, we modify Magidor’s argument found in the proof of [Reference Magidor16, Theorem 2.5, pp. 47–48]. Specifically, suppose
 $\Vdash _{{\mathbb P}^0} ``\dot f : \dot P_{\kappa _1}(\kappa ^+_1) \to \kappa ^+_1$
is such that
$\Vdash _{{\mathbb P}^0} ``\dot f : \dot P_{\kappa _1}(\kappa ^+_1) \to \kappa ^+_1$
is such that
![]() $\dot f(p) \in p$
for every
$\dot f(p) \in p$
for every
 $p \in \dot P_{\kappa _1}(\kappa ^+_1)$
.” It is then the case that
$p \in \dot P_{\kappa _1}(\kappa ^+_1)$
.” It is then the case that
 $\Vdash _{j({\mathbb P}^0)} ``j(\dot f) : \dot P_{j(\kappa _1)}(j(\kappa ^+_1)) \to j(\kappa _1)$
is such that
$\Vdash _{j({\mathbb P}^0)} ``j(\dot f) : \dot P_{j(\kappa _1)}(j(\kappa ^+_1)) \to j(\kappa _1)$
is such that
![]() $j(\dot f)(p) \in p$
for every
$j(\dot f)(p) \in p$
for every
 $p \in \dot P_{j(\kappa _1)}(j(\kappa ^+_1))$
.” Let
$p \in \dot P_{j(\kappa _1)}(j(\kappa ^+_1))$
.” Let
![]() $ \Phi = \langle \varphi _\alpha \mid \alpha < \kappa ^+_1 \rangle \in V[G]$
be the sequence where each
$ \Phi = \langle \varphi _\alpha \mid \alpha < \kappa ^+_1 \rangle \in V[G]$
be the sequence where each
![]() $\varphi _\alpha $
is the statement “
$\varphi _\alpha $
is the statement “
 $j(\dot f)(\langle j(\beta ) \mid \beta < \kappa ^+_1 \rangle ) = j(\alpha )$
.” Since
$j(\dot f)(\langle j(\beta ) \mid \beta < \kappa ^+_1 \rangle ) = j(\alpha )$
.” Since
 $M[G]^{\kappa ^+_1} \subseteq M[G]$
,
$M[G]^{\kappa ^+_1} \subseteq M[G]$
,
![]() $\Phi \in M[G]$
. And, working in V, for each
$\Phi \in M[G]$
. And, working in V, for each
![]() $\alpha < \kappa ^+_1$
, let
$\alpha < \kappa ^+_1$
, let
![]() $\gamma _\alpha $
be the least ordinal such that
$\gamma _\alpha $
be the least ordinal such that
 $\dot A_{\gamma _\alpha }$
is a term for
$\dot A_{\gamma _\alpha }$
is a term for
![]() $\{p \in P_{\kappa _1}(\kappa ^+_1) \mid f(p) = \alpha \}$
. By the regularity of
$\{p \in P_{\kappa _1}(\kappa ^+_1) \mid f(p) = \alpha \}$
. By the regularity of
![]() $\kappa ^{++}_1$
in V,
$\kappa ^{++}_1$
in V,
 $\gamma = \sup _{\alpha < \kappa ^+_1} (\gamma _\alpha + 1) < \kappa ^{++}_1$
. Working for the rest of the proof of Lemma 2.4 in
$\gamma = \sup _{\alpha < \kappa ^+_1} (\gamma _\alpha + 1) < \kappa ^{++}_1$
. Working for the rest of the proof of Lemma 2.4 in
![]() $M[G]$
, we may define the increasing sequence of Easton extensions
$M[G]$
, we may define the increasing sequence of Easton extensions
![]() $\langle q_\alpha \mid \alpha < \kappa ^+_1 \rangle $
of members of
$\langle q_\alpha \mid \alpha < \kappa ^+_1 \rangle $
of members of
![]() ${\mathbb Q}$
such that
${\mathbb Q}$
such that
![]() $q_0 = p_\gamma $
and for every
$q_0 = p_\gamma $
and for every
![]() $\alpha < \kappa ^+_1$
,
$\alpha < \kappa ^+_1$
,
![]() $q_{\alpha + 1} \parallel _{{\mathbb Q}} \varphi _\alpha $
. Let q be an upper bound to
$q_{\alpha + 1} \parallel _{{\mathbb Q}} \varphi _\alpha $
. Let q be an upper bound to
![]() $\langle q_\alpha \mid \alpha < \kappa ^+_1 \rangle $
. If
$\langle q_\alpha \mid \alpha < \kappa ^+_1 \rangle $
. If
![]() $q' \ge q$
and
$q' \ge q$
and
![]() $\delta < \kappa ^+_1$
are such that
$\delta < \kappa ^+_1$
are such that
 $q' \Vdash _{{\mathbb Q}} ``j(\dot f)(\langle j(\beta ) \mid \beta < \kappa ^+_1 \rangle ) = j(\delta )$
,” then since by construction
$q' \Vdash _{{\mathbb Q}} ``j(\dot f)(\langle j(\beta ) \mid \beta < \kappa ^+_1 \rangle ) = j(\delta )$
,” then since by construction
![]() $q \ge q_{\delta + 1}$
,
$q \ge q_{\delta + 1}$
,
![]() $q' \ge q_{\delta + 1}$
. Because
$q' \ge q_{\delta + 1}$
. Because
![]() $q_{\delta + 1} \parallel _{{\mathbb Q}} \varphi _\delta $
, it consequently follows that
$q_{\delta + 1} \parallel _{{\mathbb Q}} \varphi _\delta $
, it consequently follows that
 $q_{\delta + 1} \Vdash _{{\mathbb Q}} ``j(\dot f)(\langle j(\beta ) \mid \beta < \kappa ^+_1 \rangle ) = j(\delta )$
,” i.e., that
$q_{\delta + 1} \Vdash _{{\mathbb Q}} ``j(\dot f)(\langle j(\beta ) \mid \beta < \kappa ^+_1 \rangle ) = j(\delta )$
,” i.e., that
 $q_{\delta + 1} \Vdash _{\mathbb Q} ``\langle j(\beta ) \mid \beta < \kappa ^+_1 \rangle \in j(\dot A_{\gamma _\delta })$
.” As again by construction,
$q_{\delta + 1} \Vdash _{\mathbb Q} ``\langle j(\beta ) \mid \beta < \kappa ^+_1 \rangle \in j(\dot A_{\gamma _\delta })$
.” As again by construction,
![]() $q_{\delta + 1} \ge p_\gamma \ge p_{\gamma _\delta + 1}$
and
$q_{\delta + 1} \ge p_\gamma \ge p_{\gamma _\delta + 1}$
and
 $p_{\gamma _\delta + 1} \parallel _{{\mathbb Q}} ``\langle j(\beta ) \mid \beta < \kappa ^+_1 \rangle \in j(\dot A_{\gamma _\delta })$
,”
$p_{\gamma _\delta + 1} \parallel _{{\mathbb Q}} ``\langle j(\beta ) \mid \beta < \kappa ^+_1 \rangle \in j(\dot A_{\gamma _\delta })$
,”
 $p_{\gamma _\delta + 1} \Vdash _{{\mathbb Q}} ``\langle j(\beta ) \mid \beta < \kappa ^+_1 \rangle \in j(\dot A_{\gamma _\delta })$
.” Thus,
$p_{\gamma _\delta + 1} \Vdash _{{\mathbb Q}} ``\langle j(\beta ) \mid \beta < \kappa ^+_1 \rangle \in j(\dot A_{\gamma _\delta })$
.” Thus,
![]() $A_{\gamma _\delta } = \{p \in P_{\kappa _1}(\kappa ^+_1) \mid f(p) = \delta \} \in {\cal U}^*_1$
. This completes the proof of Lemma 2.4.⊣
$A_{\gamma _\delta } = \{p \in P_{\kappa _1}(\kappa ^+_1) \mid f(p) = \delta \} \in {\cal U}^*_1$
. This completes the proof of Lemma 2.4.⊣
Working now in
![]() $V_1$
, let
$V_1$
, let
![]() $\langle \delta _\alpha \mid \alpha < \kappa _2 \rangle $
enumerate the inaccessible cardinals in the open interval
$\langle \delta _\alpha \mid \alpha < \kappa _2 \rangle $
enumerate the inaccessible cardinals in the open interval
![]() $(\kappa _1, \kappa _2)$
. We define an Easton support iteration of length
$(\kappa _1, \kappa _2)$
. We define an Easton support iteration of length
![]() $\kappa _2$
,
$\kappa _2$
,
![]() ${\mathbb P}^1 = \langle \langle {\mathbb P}_\alpha , \dot {\mathbb Q}_\alpha \rangle \mid \alpha < \kappa _2 \rangle $
, as follows:
${\mathbb P}^1 = \langle \langle {\mathbb P}_\alpha , \dot {\mathbb Q}_\alpha \rangle \mid \alpha < \kappa _2 \rangle $
, as follows:
-
1.
 ${\mathbb P}_0 = \mathrm {Add}(\kappa ^{+3}_1, 1)$
.
${\mathbb P}_0 = \mathrm {Add}(\kappa ^{+3}_1, 1)$
. -
2. If
 $V_1 \vDash ``\delta _\alpha $
is inaccessible but not measurable,” then
$V_1 \vDash ``\delta _\alpha $
is inaccessible but not measurable,” then
 $\dot {\mathbb Q}_\alpha $
is a term for the lottery sum of all
$\dot {\mathbb Q}_\alpha $
is a term for the lottery sum of all
 $\delta _\alpha $
-directed closed partial orderings in
$\delta _\alpha $
-directed closed partial orderings in
 $V^{{\mathbb P}_\alpha } \ ($
including trivial forcing
$V^{{\mathbb P}_\alpha } \ ($
including trivial forcing
 $)$
having size at most
$)$
having size at most
 $\delta ^+_\alpha $
.
$\delta ^+_\alpha $
. -
3. If
 $V_1 \vDash ``\delta _\alpha $
is measurable,” then
$V_1 \vDash ``\delta _\alpha $
is measurable,” then
 ${\mathbb P}_{\alpha + 1} = {\mathbb P}_\alpha \ast \dot {\mathbb Q}' \ast \dot {\mathbb R}$
, where
${\mathbb P}_{\alpha + 1} = {\mathbb P}_\alpha \ast \dot {\mathbb Q}' \ast \dot {\mathbb R}$
, where
 $\dot {\mathbb Q}'$
is a term for the lottery sum of all
$\dot {\mathbb Q}'$
is a term for the lottery sum of all
 $\delta _\alpha $
-directed closed partial orderings in
$\delta _\alpha $
-directed closed partial orderings in
 $V^{{\mathbb P}_\alpha }$
$V^{{\mathbb P}_\alpha }$
 $($
again including trivial forcing
$($
again including trivial forcing
 $)$
having rank below
$)$
having rank below
 $\delta _{\alpha + 1}$
, and
$\delta _{\alpha + 1}$
, and
 $\dot {\mathbb R}$
is a term for the partial ordering which adds a nonreflecting stationary set of ordinals of cofinality
$\dot {\mathbb R}$
is a term for the partial ordering which adds a nonreflecting stationary set of ordinals of cofinality
 $\kappa _1$
to
$\kappa _1$
to
 $\delta _\alpha $
.
$\delta _\alpha $
.
Let
 $V_2 = V^{{\mathbb P}^1}_1$
. Because
$V_2 = V^{{\mathbb P}^1}_1$
. Because
![]() $V_1 \vDash ``{\mathbb P}^1$
is a
$V_1 \vDash ``{\mathbb P}^1$
is a
 $\kappa ^{+3}_1$
-directed closed,
$\kappa ^{+3}_1$
-directed closed,
![]() $\kappa _2$
-c.c
$\kappa _2$
-c.c
![]() $.$
partial ordering having size
$.$
partial ordering having size
![]() $\kappa _2$
,”
$\kappa _2$
,”
![]() $V_2 \vDash ``\kappa _1$
is both the least strongly compact and least measurable cardinal
$V_2 \vDash ``\kappa _1$
is both the least strongly compact and least measurable cardinal
![]() $+$
$+$
![]() $\kappa _1$
is
$\kappa _1$
is
![]() $\kappa ^+_1$
supercompact
$\kappa ^+_1$
supercompact
![]() $+$
For
$+$
For
![]() $i = 1,2$
,
$i = 1,2$
,
 $2^{\kappa _i} = 2^{\kappa ^+_i} = \kappa ^{++}_i +$
Cardinals and cofinalities at and above
$2^{\kappa _i} = 2^{\kappa ^+_i} = \kappa ^{++}_i +$
Cardinals and cofinalities at and above
![]() $\kappa _2$
are the same as in
$\kappa _2$
are the same as in
![]() $V_1$
+
$V_1$
+
![]() $2^\delta = \delta ^+$
for every
$2^\delta = \delta ^+$
for every
![]() $\delta \ge \kappa ^{++}_2 + \kappa _1$
’s strong compactness is indestructible under arbitrary
$\delta \ge \kappa ^{++}_2 + \kappa _1$
’s strong compactness is indestructible under arbitrary
![]() $\kappa _1$
-directed closed forcing.”
$\kappa _1$
-directed closed forcing.”
Lemma 2.5.
![]() $V_2 \vDash $
“No cardinal
$V_2 \vDash $
“No cardinal
![]() $\delta \in (\kappa _1, \kappa _2)$
is measurable.”
$\delta \in (\kappa _1, \kappa _2)$
is measurable.”
Proof. Since
 ${\mathbb P}^1 = \mathrm {Add}(\kappa ^{+3}_1, 1) \ast \dot {\mathbb Q}$
,
${\mathbb P}^1 = \mathrm {Add}(\kappa ^{+3}_1, 1) \ast \dot {\mathbb Q}$
,
 ${\vert \mathrm {Add}(\kappa ^{+3}_1, 1) \vert } = \kappa ^{+3}_1 < \kappa ^{+ 4}_1 < \delta _0$
, and
${\vert \mathrm {Add}(\kappa ^{+3}_1, 1) \vert } = \kappa ^{+3}_1 < \kappa ^{+ 4}_1 < \delta _0$
, and
 $\Vdash _{\mathrm {Add}(\kappa ^{+3}_1, 1)} \text{``}\dot {\mathbb Q}$
is
$\Vdash _{\mathrm {Add}(\kappa ^{+3}_1, 1)} \text{``}\dot {\mathbb Q}$
is
![]() $\delta _0$
-directed closed,”
$\delta _0$
-directed closed,”
![]() ${\mathbb P}^1$
admits a gap at
${\mathbb P}^1$
admits a gap at
 $\kappa ^{+ 4}_1$
. As in Module 3, by our remarks immediately following the statement of Theorem 1.3, any
$\kappa ^{+ 4}_1$
. As in Module 3, by our remarks immediately following the statement of Theorem 1.3, any
![]() $\delta \in (\kappa _1, \kappa _2)$
which is measurable in
$\delta \in (\kappa _1, \kappa _2)$
which is measurable in
![]() $V_2$
had to have been measurable in
$V_2$
had to have been measurable in
![]() $V_1$
. However, by the definition of
$V_1$
. However, by the definition of
![]() ${\mathbb P}^1$
,
${\mathbb P}^1$
,
![]() $V_2 \vDash ``$
Any
$V_2 \vDash ``$
Any
![]() $\delta \in (\kappa _1, \kappa _2)$
which is measurable in
$\delta \in (\kappa _1, \kappa _2)$
which is measurable in
![]() $V_1$
contains a nonreflecting stationary set of ordinals of cofinality
$V_1$
contains a nonreflecting stationary set of ordinals of cofinality
![]() $\kappa _1$
and hence is not measurable
$\kappa _1$
and hence is not measurable
![]() $($
or even weakly compact
$($
or even weakly compact
![]() $)$
.” This completes the proof of Lemma 2.5.⊣
$)$
.” This completes the proof of Lemma 2.5.⊣
Lemma 2.6. For
![]() $\lambda = (\kappa ^+_2)^{V_2} = (\kappa ^+_2)^{V_1}$
,
$\lambda = (\kappa ^+_2)^{V_2} = (\kappa ^+_2)^{V_1}$
,
![]() $V_2 \vDash \textit{``}\kappa _2$
is
$V_2 \vDash \textit{``}\kappa _2$
is
![]() $\lambda $
supercompact and has its
$\lambda $
supercompact and has its
![]() $\lambda $
supercompactness indestructible under
$\lambda $
supercompactness indestructible under
![]() $\kappa _2$
-directed closed forcing having size at most
$\kappa _2$
-directed closed forcing having size at most
![]() $\lambda $
.”
$\lambda $
.”
Proof. Let
![]() ${\mathbb Q} \in V_2$
be any partial ordering
${\mathbb Q} \in V_2$
be any partial ordering
![]() $($
including trivial forcing
$($
including trivial forcing
![]() $)$
such that
$)$
such that
![]() $V_2 \vDash ``{\mathbb Q}$
is a
$V_2 \vDash ``{\mathbb Q}$
is a
![]() $\kappa _2$
-directed closed partial ordering such that
$\kappa _2$
-directed closed partial ordering such that
![]() ${\vert {\mathbb Q} \vert } \le \lambda $
,” with
${\vert {\mathbb Q} \vert } \le \lambda $
,” with
![]() $\dot {\mathbb Q}$
a canonical term for
$\dot {\mathbb Q}$
a canonical term for
![]() ${\mathbb Q}$
. By our remarks in the paragraph immediately following the proof of Lemma 2.3, let
${\mathbb Q}$
. By our remarks in the paragraph immediately following the proof of Lemma 2.3, let
![]() $j : V_1 \to M$
be an elementary embedding
$j : V_1 \to M$
be an elementary embedding
![]() $($
which we take to be generated by the supercompact ultrafilter
$($
which we take to be generated by the supercompact ultrafilter
![]() ${\cal U}^*_2$
over
${\cal U}^*_2$
over
![]() $P_{\kappa _2}(\kappa ^+_2))$
such that
$P_{\kappa _2}(\kappa ^+_2))$
such that
![]() $M \vDash ``\kappa _2$
isn’t measurable.” By forcing in M above a condition opting for
$M \vDash ``\kappa _2$
isn’t measurable.” By forcing in M above a condition opting for
![]() ${\mathbb Q}$
in the stage
${\mathbb Q}$
in the stage
![]() $\kappa _2$
lottery held in M in the definition of
$\kappa _2$
lottery held in M in the definition of
![]() $j({\mathbb P}^1)$
, we may assume that
$j({\mathbb P}^1)$
, we may assume that
![]() $j({\mathbb P}^1 \ast \dot {\mathbb Q})$
is forcing equivalent in M to
$j({\mathbb P}^1 \ast \dot {\mathbb Q})$
is forcing equivalent in M to
![]() ${\mathbb P}^1 \ast \dot {\mathbb Q} \ast \dot {\mathbb R} \ast j(\dot {\mathbb Q})$
, where
${\mathbb P}^1 \ast \dot {\mathbb Q} \ast \dot {\mathbb R} \ast j(\dot {\mathbb Q})$
, where
![]() $\dot {\mathbb R}$
is a term for the portion of
$\dot {\mathbb R}$
is a term for the portion of
![]() $j({\mathbb P}^1)$
acting on ordinals in the open interval
$j({\mathbb P}^1)$
acting on ordinals in the open interval
![]() $(\kappa _2, j(\kappa _2))$
.
$(\kappa _2, j(\kappa _2))$
.
Let
![]() $G_0$
be
$G_0$
be
![]() $V_1$
-generic over
$V_1$
-generic over
![]() ${\mathbb P}^1$
and
${\mathbb P}^1$
and
![]() $G_1$
be
$G_1$
be
![]() $V_1[G_0]$
-generic over
$V_1[G_0]$
-generic over
![]() ${\mathbb Q}$
. Because
${\mathbb Q}$
. Because
![]() $M[G_0][G_1] \vDash ``{\vert {\mathbb R} \vert } = j({\kappa _2})$
,”
$M[G_0][G_1] \vDash ``{\vert {\mathbb R} \vert } = j({\kappa _2})$
,”
![]() $\kappa _2$
is inaccessible, and
$\kappa _2$
is inaccessible, and
 $2^{\kappa _2} = 2^{\kappa ^+_2} = 2^\lambda = \kappa ^{++}_2 = \lambda ^+$
,
$2^{\kappa _2} = 2^{\kappa ^+_2} = 2^\lambda = \kappa ^{++}_2 = \lambda ^+$
,
 $V_1 \vDash ``{\vert j(\kappa ^{++}_2) \vert } = {\vert j(\lambda ^+) \vert } = {\vert j(2^{\kappa _2}) \vert } = {\vert \{f \mid f : P_{\kappa _2}(\lambda ) \to \kappa ^{++}_2\} \vert } = \vert \{f \mid f : \lambda \to \kappa ^{++}_2\} \vert = {\vert \{f \mid f : \lambda \to \lambda ^+\} \vert } = {\vert [\lambda ^+]^\lambda \vert } = 2^\lambda = \lambda ^+$
.” Consequently,
$V_1 \vDash ``{\vert j(\kappa ^{++}_2) \vert } = {\vert j(\lambda ^+) \vert } = {\vert j(2^{\kappa _2}) \vert } = {\vert \{f \mid f : P_{\kappa _2}(\lambda ) \to \kappa ^{++}_2\} \vert } = \vert \{f \mid f : \lambda \to \kappa ^{++}_2\} \vert = {\vert \{f \mid f : \lambda \to \lambda ^+\} \vert } = {\vert [\lambda ^+]^\lambda \vert } = 2^\lambda = \lambda ^+$
.” Consequently,
![]() $V_1[G_0][G_1] \vDash ``$
There are
$V_1[G_0][G_1] \vDash ``$
There are
![]() $($
at most
$($
at most
![]() $) \ \lambda ^+ = 2^\lambda = {\vert j(\kappa ^{++}_2) \vert } = {\vert j(2^{\kappa _2}) \vert } $
many dense open subsets of
$) \ \lambda ^+ = 2^\lambda = {\vert j(\kappa ^{++}_2) \vert } = {\vert j(2^{\kappa _2}) \vert } $
many dense open subsets of
![]() ${\mathbb R}$
present in
${\mathbb R}$
present in
![]() $M[G_0][G_1]$
.” It is therefore possible to let
$M[G_0][G_1]$
.” It is therefore possible to let
![]() $\langle D_\alpha \mid \alpha < \lambda ^+ \rangle $
enumerate the dense open subsets of
$\langle D_\alpha \mid \alpha < \lambda ^+ \rangle $
enumerate the dense open subsets of
![]() ${\mathbb R}$
which are members of
${\mathbb R}$
which are members of
![]() $M[G_0][G_1]$
. Since standard arguments show that
$M[G_0][G_1]$
. Since standard arguments show that
![]() $M[G_0][G_1]$
remains
$M[G_0][G_1]$
remains
![]() $\lambda $
-closed with respect to
$\lambda $
-closed with respect to
![]() $V_1[G_0][G_1]$
and
$V_1[G_0][G_1]$
and
![]() ${\mathbb R}$
is
${\mathbb R}$
is
![]() ${\prec } \lambda ^+$
-strategically closed in both
${\prec } \lambda ^+$
-strategically closed in both
![]() $M[G_0][G_1]$
and
$M[G_0][G_1]$
and
![]() $V_1[G_0][G_1]$
, working in
$V_1[G_0][G_1]$
, working in
![]() $V_1[G_0][G_1]$
, we may then meet all of these sets in order to build an
$V_1[G_0][G_1]$
, we may then meet all of these sets in order to build an
![]() $M[G_0][G_1]$
-generic object
$M[G_0][G_1]$
-generic object
![]() $G_2$
over
$G_2$
over
![]() ${\mathbb R}$
such that
${\mathbb R}$
such that
![]() $j '' G_0 \subseteq G_0 \ast G_1 \ast G_2$
. Still working in
$j '' G_0 \subseteq G_0 \ast G_1 \ast G_2$
. Still working in
![]() $V_1[G_0][G_1]$
, j lifts to
$V_1[G_0][G_1]$
, j lifts to
![]() $j : V_1[G_0] \to M[G_0][G_1][G_2]$
. Since
$j : V_1[G_0] \to M[G_0][G_1][G_2]$
. Since
![]() $M[G_0][G_1][G_2]$
remains
$M[G_0][G_1][G_2]$
remains
![]() $\lambda $
-closed with respect to
$\lambda $
-closed with respect to
![]() $V_1[G_0][G_1][G_2] = V_1[G_0][G_1]$
,
$V_1[G_0][G_1][G_2] = V_1[G_0][G_1]$
,
![]() $V_1[G_0] \vDash ``{\vert {\mathbb Q} \vert } \le \lambda $
,”
$V_1[G_0] \vDash ``{\vert {\mathbb Q} \vert } \le \lambda $
,”
![]() $j(\kappa _2)> \lambda $
, and
$j(\kappa _2)> \lambda $
, and
![]() $M[G_0][G_1][G_2] \vDash ``j({\mathbb Q})$
is
$M[G_0][G_1][G_2] \vDash ``j({\mathbb Q})$
is
![]() $j(\kappa _2)$
-directed closed,” there is a master condition
$j(\kappa _2)$
-directed closed,” there is a master condition
![]() $q \in V_1[G_0][G_1]$
for
$q \in V_1[G_0][G_1]$
for
![]() $\{j(p) \mid p \in G_1\}$
. Because
$\{j(p) \mid p \in G_1\}$
. Because
![]() $V_1 \vDash ``{\vert j(\lambda ^+) \vert } = {\vert j(2^\lambda ) \vert } = \lambda ^+$
” and
$V_1 \vDash ``{\vert j(\lambda ^+) \vert } = {\vert j(2^\lambda ) \vert } = \lambda ^+$
” and
![]() $M[G_0][G_1][G_2] \vDash ``{\vert j({\mathbb Q}) \vert } \le j(\lambda )$
,” there are
$M[G_0][G_1][G_2] \vDash ``{\vert j({\mathbb Q}) \vert } \le j(\lambda )$
,” there are
![]() $($
at most
$($
at most
![]() $) \ \lambda ^+$
many dense open subsets of
$) \ \lambda ^+$
many dense open subsets of
![]() $j({\mathbb Q})$
present in
$j({\mathbb Q})$
present in
![]() $V_1[G_0][G_1]$
. As
$V_1[G_0][G_1]$
. As
![]() $j({\mathbb Q})$
is
$j({\mathbb Q})$
is
![]() $\lambda ^+$
-directed closed and hence
$\lambda ^+$
-directed closed and hence
![]() ${\prec } \lambda ^+$
-strategically closed in both
${\prec } \lambda ^+$
-strategically closed in both
![]() $M[G_0][G_1][G_2]$
and
$M[G_0][G_1][G_2]$
and
![]() $V_1[G_0][G_1]$
, we may thus as was done for
$V_1[G_0][G_1]$
, we may thus as was done for
![]() $G_2$
build in
$G_2$
build in
![]() $V_1[G_0][G_1]$
an
$V_1[G_0][G_1]$
an
![]() $M[G_0][G_1][G_2]$
-generic object
$M[G_0][G_1][G_2]$
-generic object
![]() $G_3$
for
$G_3$
for
![]() $j({\mathbb Q})$
containing q. It is then the case that
$j({\mathbb Q})$
containing q. It is then the case that
![]() $j '' (G_0 \ast G_1) \subseteq G_0 \ast G_1 \ast G_2 \ast G_3$
, so we may fully lift j in
$j '' (G_0 \ast G_1) \subseteq G_0 \ast G_1 \ast G_2 \ast G_3$
, so we may fully lift j in
![]() $V_1[G_0][G_1]$
to a
$V_1[G_0][G_1]$
to a
![]() $\lambda $
supercompactness embedding
$\lambda $
supercompactness embedding
![]() $j : V_1[G_0][G_1] \to M[G_0][G_1][G_2][G_3]$
. This completes the proof of Lemma 2.6.⊣
$j : V_1[G_0][G_1] \to M[G_0][G_1][G_2][G_3]$
. This completes the proof of Lemma 2.6.⊣
Lemma 2.7.
![]() $V_2 \vDash \text{``}\kappa _2$
is a strongly compact cardinal whose strong compactness is indestructible under
$V_2 \vDash \text{``}\kappa _2$
is a strongly compact cardinal whose strong compactness is indestructible under
![]() ${} \kappa _2$
-directed closed forcing which is also
${} \kappa _2$
-directed closed forcing which is also
![]() $(\kappa ^+_2, \infty )$
-distributive.”
$(\kappa ^+_2, \infty )$
-distributive.”
Proof. We mimic to a certain extent the proof of [Reference Apter and Sargsyan5, Lemma 3], once again feeling free to quote verbatim as appropriate. We begin as in the proof of Lemma 2.6. Let
![]() ${\mathbb Q} \in V_2$
be any partial ordering
${\mathbb Q} \in V_2$
be any partial ordering
![]() $($
including trivial forcing
$($
including trivial forcing
![]() $)$
such that
$)$
such that
![]() $V_2 \vDash ``{\mathbb Q}$
is both
$V_2 \vDash ``{\mathbb Q}$
is both
![]() $\kappa _2$
-directed closed and
$\kappa _2$
-directed closed and
![]() $(\kappa ^+_2, \infty )$
-distributive,” with
$(\kappa ^+_2, \infty )$
-distributive,” with
![]() $\dot {\mathbb Q}$
a canonical term for
$\dot {\mathbb Q}$
a canonical term for
![]() ${\mathbb Q}$
. Let
${\mathbb Q}$
. Let
 $\gamma = (\max ({\vert \mathrm {TC}(\dot {\mathbb Q}) \vert } , \kappa ^{++}_2))^{+ \omega }$
, and let
$\gamma = (\max ({\vert \mathrm {TC}(\dot {\mathbb Q}) \vert } , \kappa ^{++}_2))^{+ \omega }$
, and let
![]() $\lambda> \gamma $
be a regular cardinal. Take
$\lambda> \gamma $
be a regular cardinal. Take
![]() $j : V_1 \to M$
to be an elementary embedding witnessing the
$j : V_1 \to M$
to be an elementary embedding witnessing the
![]() $\lambda $
supercompactness of
$\lambda $
supercompactness of
![]() $\kappa _2$
generated by a supercompact ultrafilter over
$\kappa _2$
generated by a supercompact ultrafilter over
![]() $P_{\kappa _2}(\lambda )$
. By forcing in M above a condition opting for
$P_{\kappa _2}(\lambda )$
. By forcing in M above a condition opting for
![]() ${\mathbb Q}$
in the stage
${\mathbb Q}$
in the stage
![]() $\kappa _2$
lottery held in M in the definition of
$\kappa _2$
lottery held in M in the definition of
![]() $j({\mathbb P}^1)$
, we may assume that
$j({\mathbb P}^1)$
, we may assume that
![]() $j({\mathbb P}^1 \ast \dot {\mathbb Q})$
is forcing equivalent in M to
$j({\mathbb P}^1 \ast \dot {\mathbb Q})$
is forcing equivalent in M to
![]() ${\mathbb P}^1 \ast \dot {\mathbb Q} \ast \dot {\mathbb R}' \ast \dot {\mathbb S} \ast j(\dot {\mathbb Q})$
, where
${\mathbb P}^1 \ast \dot {\mathbb Q} \ast \dot {\mathbb R}' \ast \dot {\mathbb S} \ast j(\dot {\mathbb Q})$
, where
![]() $\dot {\mathbb Q} \ast \dot {\mathbb R}'$
is a term for the forcing taking place at stage
$\dot {\mathbb Q} \ast \dot {\mathbb R}'$
is a term for the forcing taking place at stage
![]() $\kappa _2$
in M,
$\kappa _2$
in M,
![]() $\dot {\mathbb R}'$
is a term for the partial ordering which adds a nonreflecting stationary set of ordinals of cofinality
$\dot {\mathbb R}'$
is a term for the partial ordering which adds a nonreflecting stationary set of ordinals of cofinality
![]() $\kappa _1$
to
$\kappa _1$
to
![]() $\kappa _2$
, and
$\kappa _2$
, and
![]() $\dot {\mathbb S}$
is a term for the portion of
$\dot {\mathbb S}$
is a term for the portion of
![]() $j({\mathbb P}^1)$
acting on ordinals in the open interval
$j({\mathbb P}^1)$
acting on ordinals in the open interval
![]() $(\kappa _2, j(\kappa _2))$
.
$(\kappa _2, j(\kappa _2))$
.
Because
![]() $\lambda $
has been chosen large enough
$\lambda $
has been chosen large enough
![]() $($
so that in particular,
$($
so that in particular,
 $\lambda> 2^{[\kappa ^+_2]^{< \kappa _2}} = 2^{\kappa ^+_2} = \kappa ^{++}_2)$
,
$\lambda> 2^{[\kappa ^+_2]^{< \kappa _2}} = 2^{\kappa ^+_2} = \kappa ^{++}_2)$
,
![]() ${\cal U}^*_2 \in M$
. Let
${\cal U}^*_2 \in M$
. Let
![]() $k : M \to N$
be the elementary embedding generated by the ultrapower via
$k : M \to N$
be the elementary embedding generated by the ultrapower via
![]() ${\cal U}^*_2$
. It is then true that
${\cal U}^*_2$
. It is then true that
![]() $N \vDash ``\kappa _2$
isn’t measurable.” It is the case that if
$N \vDash ``\kappa _2$
isn’t measurable.” It is the case that if
![]() $i : V_1 \to N$
is an elementary embedding having critical point
$i : V_1 \to N$
is an elementary embedding having critical point
![]() $\kappa _2$
and for any
$\kappa _2$
and for any
![]() $x \subseteq N$
with
$x \subseteq N$
with
![]() ${\vert x \vert } \le \lambda $
, there is some
${\vert x \vert } \le \lambda $
, there is some
![]() $y \in N$
such that
$y \in N$
such that
![]() $x \subseteq y$
and
$x \subseteq y$
and
![]() $N \vDash ``{\vert y \vert } < i(\kappa _2)$
,” then i witnesses the
$N \vDash ``{\vert y \vert } < i(\kappa _2)$
,” then i witnesses the
![]() $\lambda $
strong compactness of
$\lambda $
strong compactness of
![]() $\kappa _2$
. Using this fact, it is easily verifiable that
$\kappa _2$
. Using this fact, it is easily verifiable that
![]() $i = k \circ j$
is an elementary embedding witnessing the
$i = k \circ j$
is an elementary embedding witnessing the
![]() $\lambda $
strong compactness of
$\lambda $
strong compactness of
![]() $\kappa _2$
. We show that i lifts in
$\kappa _2$
. We show that i lifts in
 $V_1^{{\mathbb P}^1 \ast \dot {\mathbb Q}}$
to
$V_1^{{\mathbb P}^1 \ast \dot {\mathbb Q}}$
to
 $i : V_1^{{\mathbb P}^1 \ast \dot {\mathbb Q}} \to N^{i({\mathbb P}^1 \ast \dot {\mathbb Q})}$
. Since this lifted embedding witnesses the
$i : V_1^{{\mathbb P}^1 \ast \dot {\mathbb Q}} \to N^{i({\mathbb P}^1 \ast \dot {\mathbb Q})}$
. Since this lifted embedding witnesses the
![]() $\lambda $
strong compactness of
$\lambda $
strong compactness of
![]() $\kappa _2$
in
$\kappa _2$
in
 $V_1^{{\mathbb P}^1 \ast \dot {\mathbb Q}}$
and
$V_1^{{\mathbb P}^1 \ast \dot {\mathbb Q}}$
and
![]() $\lambda $
was arbitrarily chosen, this completes the proof of Lemma 2.7.
$\lambda $
was arbitrarily chosen, this completes the proof of Lemma 2.7.
Let
![]() $G_0$
be
$G_0$
be
![]() $V_1$
-generic over
$V_1$
-generic over
![]() ${\mathbb P}^1$
, and let H be
${\mathbb P}^1$
, and let H be
![]() $V_1[G_0]$
-generic over
$V_1[G_0]$
-generic over
![]() ${\mathbb Q}$
. By forcing in N above a condition opting for trivial forcing in the stage
${\mathbb Q}$
. By forcing in N above a condition opting for trivial forcing in the stage
![]() $\kappa _2$
lottery held in N in the definition of
$\kappa _2$
lottery held in N in the definition of
![]() $i({\mathbb P}^1)$
, we may assume that
$i({\mathbb P}^1)$
, we may assume that
![]() $i({\mathbb P}^1)$
is forcing equivalent in N to
$i({\mathbb P}^1)$
is forcing equivalent in N to
![]() ${\mathbb P}^1 \ast \dot {\mathbb Q}^1 \ast \dot {\mathbb Q}^2 \ast \dot {\mathbb Q}^3$
, where
${\mathbb P}^1 \ast \dot {\mathbb Q}^1 \ast \dot {\mathbb Q}^2 \ast \dot {\mathbb Q}^3$
, where
![]() $\dot {\mathbb Q}^1$
is a term for the portion of the forcing acting on ordinals in the open interval
$\dot {\mathbb Q}^1$
is a term for the portion of the forcing acting on ordinals in the open interval
![]() $(\kappa _2, k(\kappa _2))$
,
$(\kappa _2, k(\kappa _2))$
,
![]() $\dot {\mathbb Q}^2$
is a term for the forcing done at stage
$\dot {\mathbb Q}^2$
is a term for the forcing done at stage
![]() $k(\kappa _2)$
, and
$k(\kappa _2)$
, and
![]() $\dot {\mathbb Q}^3$
is a term for the remainder of the forcing, i.e., the portion acting on ordinals in the half-open interval
$\dot {\mathbb Q}^3$
is a term for the remainder of the forcing, i.e., the portion acting on ordinals in the half-open interval
![]() $(k(\kappa _2), k(j(\kappa _2))]$
$(k(\kappa _2), k(j(\kappa _2))]$
![]() $($
inclusive of the term
$($
inclusive of the term
![]() $i(\dot {\mathbb Q})$
for the forcing done at stage
$i(\dot {\mathbb Q})$
for the forcing done at stage
![]() $k(j(\kappa _2)) = i(\kappa _2))$
. We will build in
$k(j(\kappa _2)) = i(\kappa _2))$
. We will build in
![]() $V_1[G_0][H]$
generic objects for the different portions of
$V_1[G_0][H]$
generic objects for the different portions of
![]() $i({\mathbb P}^1)$
.
$i({\mathbb P}^1)$
.
To do this, we use a modification of an argument initially due to Magidor, unpublished by him but presented in, among other places, [Reference Apter and Cummings1, Theorem 2]. The modification is due to Sargsyan and is found in [Reference Apter and Sargsyan5, Lemma 3]. In particular, we begin by constructing an
![]() $N[G_0]$
-generic object
$N[G_0]$
-generic object
![]() $G_1$
for
$G_1$
for
![]() ${\mathbb Q}^1$
. The argument used will be carried out in
${\mathbb Q}^1$
. The argument used will be carried out in
![]() $M[G_0] \subseteq V_1[G_0] \subseteq V_1[G_0][H]$
. Specifically, since we are assuming that
$M[G_0] \subseteq V_1[G_0] \subseteq V_1[G_0][H]$
. Specifically, since we are assuming that
![]() $\dot {\mathbb Q}^1$
is forced to act nontrivially only on ordinals in the open interval
$\dot {\mathbb Q}^1$
is forced to act nontrivially only on ordinals in the open interval
![]() $(\kappa _2, k(\kappa _2))$
, we may therefore build in
$(\kappa _2, k(\kappa _2))$
, we may therefore build in
![]() $M[G_0]$
an
$M[G_0]$
an
![]() $N[G_0]$
-generic object
$N[G_0]$
-generic object
![]() $G_1$
for
$G_1$
for
![]() ${\mathbb Q}^1$
in the same manner as the construction of the generic object
${\mathbb Q}^1$
in the same manner as the construction of the generic object
![]() $G_2$
given in the proof of Lemma 2.6.
$G_2$
given in the proof of Lemma 2.6.
We next analyze the exact nature of
![]() $\dot {\mathbb Q}^2$
. As we have already observed, we may assume that
$\dot {\mathbb Q}^2$
. As we have already observed, we may assume that
![]() $j({\mathbb P}^1 \ast \dot {\mathbb Q})$
is forcing equivalent in M to
$j({\mathbb P}^1 \ast \dot {\mathbb Q})$
is forcing equivalent in M to
![]() ${\mathbb P}^1 \ast \dot {\mathbb Q} \ast \dot {\mathbb R}' \ast \dot {\mathbb S} \ast j(\dot {\mathbb Q})$
, where
${\mathbb P}^1 \ast \dot {\mathbb Q} \ast \dot {\mathbb R}' \ast \dot {\mathbb S} \ast j(\dot {\mathbb Q})$
, where
![]() $\dot {\mathbb Q} \ast \dot {\mathbb R}'$
is a term for the forcing taking place at stage
$\dot {\mathbb Q} \ast \dot {\mathbb R}'$
is a term for the forcing taking place at stage
![]() $\kappa _2$
in M,
$\kappa _2$
in M,
![]() $\dot {\mathbb R}'$
is a term for the partial ordering which adds a nonreflecting stationary set of ordinals of cofinality
$\dot {\mathbb R}'$
is a term for the partial ordering which adds a nonreflecting stationary set of ordinals of cofinality
![]() $\kappa _1$
to
$\kappa _1$
to
![]() $\kappa _2$
, and
$\kappa _2$
, and
![]() $\dot {\mathbb S}$
is a term for the portion of
$\dot {\mathbb S}$
is a term for the portion of
![]() $j({\mathbb P}^1)$
acting on ordinals in the open interval
$j({\mathbb P}^1)$
acting on ordinals in the open interval
![]() $(\kappa _2, j(\kappa _2))$
. By elementarity, since
$(\kappa _2, j(\kappa _2))$
. By elementarity, since
![]() $\dot {\mathbb Q}^2$
is a term for the forcing which takes place at stage
$\dot {\mathbb Q}^2$
is a term for the forcing which takes place at stage
![]() $k(\kappa _2)$
in N, we may write
$k(\kappa _2)$
in N, we may write
![]() $\dot {\mathbb Q}^2 = k(\dot {\mathbb Q}) \ast k(\dot {\mathbb R}')$
. We will construct in
$\dot {\mathbb Q}^2 = k(\dot {\mathbb Q}) \ast k(\dot {\mathbb R}')$
. We will construct in
![]() $M[G_0][H]$
generic objects for
$M[G_0][H]$
generic objects for
![]() $k({\mathbb Q})$
and
$k({\mathbb Q})$
and
![]() $k({\mathbb R}')$
.
$k({\mathbb R}')$
.
For
![]() $k({\mathbb Q})$
, we use an argument containing ideas due to Woodin. First, note that since N is given by an ultrapower,
$k({\mathbb Q})$
, we use an argument containing ideas due to Woodin. First, note that since N is given by an ultrapower,
![]() $N = \{k(h)(\langle k(\beta ) \mid \beta < \kappa ^+_2 \rangle ) \mid h : P_{\kappa _2}(\kappa ^+_2) \to M$
is a function in
$N = \{k(h)(\langle k(\beta ) \mid \beta < \kappa ^+_2 \rangle ) \mid h : P_{\kappa _2}(\kappa ^+_2) \to M$
is a function in
![]() $M\}$
. Further, since by the definition of
$M\}$
. Further, since by the definition of
![]() $G_1$
,
$G_1$
,
![]() $k '' G_0 \subseteq G_0 \ast G_1$
, k lifts in both
$k '' G_0 \subseteq G_0 \ast G_1$
, k lifts in both
![]() $M[G_0]$
and
$M[G_0]$
and
![]() $M[G_0][H]$
to
$M[G_0][H]$
to
![]() $k : M[G_0] \to N[G_0][G_1]$
. From these facts, we may now show that
$k : M[G_0] \to N[G_0][G_1]$
. From these facts, we may now show that
![]() $k '' H \subseteq k({\mathbb Q})$
generates an
$k '' H \subseteq k({\mathbb Q})$
generates an
![]() $N[G_0][G_1]$
-generic object
$N[G_0][G_1]$
-generic object
![]() $G_2$
over
$G_2$
over
![]() $k({\mathbb Q})$
. Specifically, given a dense open subset
$k({\mathbb Q})$
. Specifically, given a dense open subset
![]() $D \subseteq k({\mathbb Q})$
,
$D \subseteq k({\mathbb Q})$
,
![]() $D \in N[G_0][G_1]$
,
$D \in N[G_0][G_1]$
,
 $D = \mathrm {int}_{G_0 \ast G_1}(\dot D)$
for some N-name
$D = \mathrm {int}_{G_0 \ast G_1}(\dot D)$
for some N-name
 $\dot D = k(\vec D)(\langle k(\beta ) \mid \beta < \kappa ^+_2 \rangle )$
, where
$\dot D = k(\vec D)(\langle k(\beta ) \mid \beta < \kappa ^+_2 \rangle )$
, where
 $\vec D = \langle D_p \mid p \in P_{\kappa _2}(\kappa ^+_2) \rangle $
is a function in M. We may assume that every
$\vec D = \langle D_p \mid p \in P_{\kappa _2}(\kappa ^+_2) \rangle $
is a function in M. We may assume that every
![]() $D_p$
is a dense open subset of
$D_p$
is a dense open subset of
![]() ${\mathbb Q}$
. Since
${\mathbb Q}$
. Since
![]() ${\mathbb Q}$
is
${\mathbb Q}$
is
![]() $(\kappa ^+_2, \infty )$
-distributive and
$(\kappa ^+_2, \infty )$
-distributive and
![]() ${\vert P_{\kappa _2}(\kappa ^+_2) \vert } = \kappa ^+_2$
, it follows that
${\vert P_{\kappa _2}(\kappa ^+_2) \vert } = \kappa ^+_2$
, it follows that
 $D' = \bigcap _{p \in P_{\kappa _2}(\kappa ^+_2)} D_p$
is also a dense open subset of
$D' = \bigcap _{p \in P_{\kappa _2}(\kappa ^+_2)} D_p$
is also a dense open subset of
![]() ${\mathbb Q}$
. As
${\mathbb Q}$
. As
![]() $k(D') \subseteq D$
and
$k(D') \subseteq D$
and
![]() $H \cap D' \neq \emptyset $
,
$H \cap D' \neq \emptyset $
,
![]() $k '' H \cap D \neq \emptyset $
. Thus,
$k '' H \cap D \neq \emptyset $
. Thus,
![]() $G_2 = \{p \in k({\mathbb Q}) \mid \exists q \in k '' H [q \ge p]\}$
, which is definable in
$G_2 = \{p \in k({\mathbb Q}) \mid \exists q \in k '' H [q \ge p]\}$
, which is definable in
![]() $M[G_0][H]$
, is our desired
$M[G_0][H]$
, is our desired
![]() $N[G_0][G_1]$
-generic object over
$N[G_0][G_1]$
-generic object over
![]() $k({\mathbb Q})$
. Then, since
$k({\mathbb Q})$
. Then, since
![]() $k({\mathbb R}')$
is in
$k({\mathbb R}')$
is in
![]() $N[G_0][G_1][G_2]$
the partial ordering which adds a nonreflecting stationary set of ordinals of cofinality
$N[G_0][G_1][G_2]$
the partial ordering which adds a nonreflecting stationary set of ordinals of cofinality
![]() $k(\kappa _1)$
to
$k(\kappa _1)$
to
![]() $k(\kappa _2)$
, we know that
$k(\kappa _2)$
, we know that
![]() $N[G_0][G_1][G_2] \vDash ``{\vert k({\mathbb R}') \vert } = k(\kappa _2)$
and
$N[G_0][G_1][G_2] \vDash ``{\vert k({\mathbb R}') \vert } = k(\kappa _2)$
and
 ${\vert \wp (k({\mathbb R}')) \vert } = 2^{k(\kappa _2)} = k(\kappa ^{++}_2)$
.” Hence, since
${\vert \wp (k({\mathbb R}')) \vert } = 2^{k(\kappa _2)} = k(\kappa ^{++}_2)$
.” Hence, since
![]() $N[G_0][G_1][G_2]$
remains
$N[G_0][G_1][G_2]$
remains
![]() $\kappa ^+_2$
-closed with respect to
$\kappa ^+_2$
-closed with respect to
![]() $M[G_0][H]$
, which means
$M[G_0][H]$
, which means
![]() $k({\mathbb R}')$
is
$k({\mathbb R}')$
is
![]() ${\prec } \kappa ^{++}_2$
-strategically closed in
${\prec } \kappa ^{++}_2$
-strategically closed in
![]() $N[G_0][G_1][G_2]$
and
$N[G_0][G_1][G_2]$
and
![]() $M[G_0][H]$
, the same argument used in the construction of
$M[G_0][H]$
, the same argument used in the construction of
![]() $G_1$
allows us to build in
$G_1$
allows us to build in
![]() $M[G_0][H]$
an
$M[G_0][H]$
an
![]() $N[G_0][G_1][G_2]$
-generic object
$N[G_0][G_1][G_2]$
-generic object
![]() $G_3$
for
$G_3$
for
![]() $k({\mathbb R}')$
.
$k({\mathbb R}')$
.
We construct now (in
![]() $V_1[G_0][H]$
) an
$V_1[G_0][H]$
) an
![]() $N[G_0][G_1][G_2][G_3]$
-generic object for
$N[G_0][G_1][G_2][G_3]$
-generic object for
![]() ${\mathbb Q}^3$
. As in the proof of [Reference Apter and Sargsyan5, Lemma 3], we do this by combining the term forcing argument found in [Reference Apter and Cummings1, Theorem 2] with the argument for the creation of a “master condition” found in [Reference Apter and Gitik3, Lemma 2]. Specifically, we begin by showing the existence of a term
${\mathbb Q}^3$
. As in the proof of [Reference Apter and Sargsyan5, Lemma 3], we do this by combining the term forcing argument found in [Reference Apter and Cummings1, Theorem 2] with the argument for the creation of a “master condition” found in [Reference Apter and Gitik3, Lemma 2]. Specifically, we begin by showing the existence of a term
![]() $\tau \in M$
for a “master condition” for
$\tau \in M$
for a “master condition” for
![]() $j(\dot {\mathbb Q})$
, i.e., we show the existence of a term
$j(\dot {\mathbb Q})$
, i.e., we show the existence of a term
![]() $\tau \in M$
in the language of forcing with respect to
$\tau \in M$
in the language of forcing with respect to
![]() $j({\mathbb P}^1)$
such that in M,
$j({\mathbb P}^1)$
such that in M,
 $\Vdash _{j({\mathbb P}^1)} ``\tau \in j(\dot {\mathbb Q})$
extends every
$\Vdash _{j({\mathbb P}^1)} ``\tau \in j(\dot {\mathbb Q})$
extends every
![]() $j(\dot q)$
for
$j(\dot q)$
for
![]() $\dot q \in \dot H$
.” We first note that since
$\dot q \in \dot H$
.” We first note that since
![]() ${\mathbb P}^1$
is
${\mathbb P}^1$
is
![]() $\kappa _2$
-c.c
$\kappa _2$
-c.c
![]() $.$
in both
$.$
in both
![]() $V_1$
and M, as
$V_1$
and M, as
![]() $\Vdash _{{\mathbb P}^1} ``\dot {\mathbb Q}$
is
$\Vdash _{{\mathbb P}^1} ``\dot {\mathbb Q}$
is
![]() ${} \kappa _2$
-directed closed and
${} \kappa _2$
-directed closed and
![]() ${\vert \dot {\mathbb Q} \vert } < \lambda $
,” the usual arguments show
${\vert \dot {\mathbb Q} \vert } < \lambda $
,” the usual arguments show
![]() $M[G_0][H]$
remains
$M[G_0][H]$
remains
![]() $\lambda $
-closed with respect to
$\lambda $
-closed with respect to
![]() $V_1[G_0][H]$
. This means
$V_1[G_0][H]$
. This means
![]() $T = \{j(\dot q) \mid \exists r \in G_0 [\langle r, \mathrm {int}_{G_0 * H}(\dot q) \rangle \in G_0 \ast H]\} \in M[G_0][H]$
, so T has a name
$T = \{j(\dot q) \mid \exists r \in G_0 [\langle r, \mathrm {int}_{G_0 * H}(\dot q) \rangle \in G_0 \ast H]\} \in M[G_0][H]$
, so T has a name
![]() $\dot T \in M$
such that in M,
$\dot T \in M$
such that in M,
 $\Vdash _{j({\mathbb P}^1)} ``{\vert \dot T \vert } < \lambda < j(\kappa _2)$
, any two elements of
$\Vdash _{j({\mathbb P}^1)} ``{\vert \dot T \vert } < \lambda < j(\kappa _2)$
, any two elements of
![]() $\dot T$
are compatible, and
$\dot T$
are compatible, and
![]() $\dot T$
is a subset of a partial ordering (namely
$\dot T$
is a subset of a partial ordering (namely
![]() $j(\dot {\mathbb Q}))$
which is
$j(\dot {\mathbb Q}))$
which is
![]() ${} j(\kappa _2)$
-directed closed.” Thus, in M, since
${} j(\kappa _2)$
-directed closed.” Thus, in M, since
![]() $j(\kappa _2)> \lambda $
, and
$j(\kappa _2)> \lambda $
, and
![]() $M^\lambda \subseteq M$
,
$M^\lambda \subseteq M$
,
![]() $\Vdash _{j({\mathbb P}^1)} ``$
There is a condition in
$\Vdash _{j({\mathbb P}^1)} ``$
There is a condition in
![]() $j(\dot {\mathbb Q})$
extending each element of
$j(\dot {\mathbb Q})$
extending each element of
![]() $\dot T$
.” A term
$\dot T$
.” A term
![]() $\tau $
for this common extension is as desired.
$\tau $
for this common extension is as desired.
We work for the time being in M. Consider the “term forcing” partial ordering
![]() ${\mathbb S}^*$
(see [Reference Foreman8] for the first published account of term forcing or [Reference Cummings7, Section 1.2.5, p. 8]—the notion is originally due to Laver) associated with
${\mathbb S}^*$
(see [Reference Foreman8] for the first published account of term forcing or [Reference Cummings7, Section 1.2.5, p. 8]—the notion is originally due to Laver) associated with
![]() $\dot {\mathbb S} \ast j(\dot {\mathbb Q})$
, i.e.,
$\dot {\mathbb S} \ast j(\dot {\mathbb Q})$
, i.e.,
![]() $\sigma \in {\mathbb S}^*$
iff
$\sigma \in {\mathbb S}^*$
iff
![]() $\sigma $
is a term in the forcing language with respect to
$\sigma $
is a term in the forcing language with respect to
![]() ${\mathbb P}^1 \ast \dot {\mathbb Q} \ast \dot {\mathbb R}'$
and
${\mathbb P}^1 \ast \dot {\mathbb Q} \ast \dot {\mathbb R}'$
and
 $\Vdash _{{\mathbb P}^1 \ast \dot {\mathbb Q} \ast \dot {\mathbb R}'} ``\sigma \in \dot {\mathbb S} \ast j(\dot {\mathbb Q})$
,” ordered by
$\Vdash _{{\mathbb P}^1 \ast \dot {\mathbb Q} \ast \dot {\mathbb R}'} ``\sigma \in \dot {\mathbb S} \ast j(\dot {\mathbb Q})$
,” ordered by
![]() $\sigma _1 \ge \sigma _0$
iff
$\sigma _1 \ge \sigma _0$
iff
![]() $\Vdash _{{\mathbb P}^1 \ast \dot {\mathbb Q} \ast \dot {\mathbb R}'} ``\sigma _1 \ge \sigma _0$
.” Note that
$\Vdash _{{\mathbb P}^1 \ast \dot {\mathbb Q} \ast \dot {\mathbb R}'} ``\sigma _1 \ge \sigma _0$
.” Note that
![]() $\tau '$
defined as the term in the language of forcing with respect to
$\tau '$
defined as the term in the language of forcing with respect to
![]() ${\mathbb P}^1 \ast \dot {\mathbb Q} \ast \dot {\mathbb R}'$
composed of the tuple all of whose members are forced to be the trivial condition, with the exception of the last member, which is
${\mathbb P}^1 \ast \dot {\mathbb Q} \ast \dot {\mathbb R}'$
composed of the tuple all of whose members are forced to be the trivial condition, with the exception of the last member, which is
![]() $\tau $
, is an element of
$\tau $
, is an element of
![]() ${\mathbb S}^*$
.
${\mathbb S}^*$
.
Clearly,
![]() ${\mathbb S}^* \in M$
. In addition, since
${\mathbb S}^* \in M$
. In addition, since
![]() $V_1 \vDash ``$
No cardinal above
$V_1 \vDash ``$
No cardinal above
![]() $\kappa _2$
is inaccessible,” because
$\kappa _2$
is inaccessible,” because
![]() $M^\lambda \subseteq M$
,
$M^\lambda \subseteq M$
,
![]() $M \vDash ``$
The first stage at which
$M \vDash ``$
The first stage at which
![]() $\dot {\mathbb S} \ast j(\dot {\mathbb Q})$
is forced to do nontrivial forcing is above
$\dot {\mathbb S} \ast j(\dot {\mathbb Q})$
is forced to do nontrivial forcing is above
![]() $\lambda $
.” Thus,
$\lambda $
.” Thus,
 $\Vdash _{{\mathbb P}^1 \ast \dot {\mathbb Q} \ast \dot {\mathbb R}'} ``\dot {\mathbb S} \ast j(\dot {\mathbb Q})$
is
$\Vdash _{{\mathbb P}^1 \ast \dot {\mathbb Q} \ast \dot {\mathbb R}'} ``\dot {\mathbb S} \ast j(\dot {\mathbb Q})$
is
![]() ${\prec } \lambda ^+$
-strategically closed,” which, since
${\prec } \lambda ^+$
-strategically closed,” which, since
![]() $M^\lambda \subseteq M$
, immediately implies that
$M^\lambda \subseteq M$
, immediately implies that
![]() ${\mathbb S}^*$
itself is
${\mathbb S}^*$
itself is
![]() ${\prec } \lambda ^+$
-strategically closed in both
${\prec } \lambda ^+$
-strategically closed in both
![]() $V_1$
and M. Further, since
$V_1$
and M. Further, since
![]() $\Vdash _{{\mathbb P}^1} ``{\vert \dot {\mathbb Q} \vert } < \gamma < \lambda $
,” in M,
$\Vdash _{{\mathbb P}^1} ``{\vert \dot {\mathbb Q} \vert } < \gamma < \lambda $
,” in M,
 $\Vdash _{{\mathbb P}^1 \ast \dot {\mathbb Q} \ast \dot {\mathbb R}'} ``{\vert \dot {\mathbb S} \ast j(\dot {\mathbb Q}) \vert } < j(\gamma ) < j(\lambda )$
.” We also have that
$\Vdash _{{\mathbb P}^1 \ast \dot {\mathbb Q} \ast \dot {\mathbb R}'} ``{\vert \dot {\mathbb S} \ast j(\dot {\mathbb Q}) \vert } < j(\gamma ) < j(\lambda )$
.” We also have that
![]() $2^\delta = \delta ^+$
for
$2^\delta = \delta ^+$
for
![]() $\delta \ge \kappa ^+_2$
in
$\delta \ge \kappa ^+_2$
in
![]() $V_1$
and
$V_1$
and
![]() $\delta \ge j(\kappa ^+_2)$
in M. Consequently, as j is given via an ultrapower embedding by a normal measure over
$\delta \ge j(\kappa ^+_2)$
in M. Consequently, as j is given via an ultrapower embedding by a normal measure over
![]() $P_{\kappa _2}(\lambda )$
,
$P_{\kappa _2}(\lambda )$
,
 ${\vert j(\lambda ^+) \vert } = {\vert \{f \mid f : P_{\kappa _2}(\lambda ) \to \lambda ^+ \vert } = {\vert {[\lambda ^+]}^{\lambda } \vert } = \lambda ^+$
and
${\vert j(\lambda ^+) \vert } = {\vert \{f \mid f : P_{\kappa _2}(\lambda ) \to \lambda ^+ \vert } = {\vert {[\lambda ^+]}^{\lambda } \vert } = \lambda ^+$
and
 $\Vdash _{{\mathbb P}^1 \ast \dot {\mathbb Q} \ast \dot {\mathbb R}'} ``{\vert \wp (\dot {\mathbb S} \ast j(\dot {\mathbb Q})) \vert } < 2^{j(\gamma )} = j(\gamma ^+) \le j(\lambda ) < 2^{j(\lambda )} = j(\lambda ^+)$
.” Therefore, since as in the footnote given in the proof of [Reference Apter and Hamkins4, Lemma 8], we may assume that
$\Vdash _{{\mathbb P}^1 \ast \dot {\mathbb Q} \ast \dot {\mathbb R}'} ``{\vert \wp (\dot {\mathbb S} \ast j(\dot {\mathbb Q})) \vert } < 2^{j(\gamma )} = j(\gamma ^+) \le j(\lambda ) < 2^{j(\lambda )} = j(\lambda ^+)$
.” Therefore, since as in the footnote given in the proof of [Reference Apter and Hamkins4, Lemma 8], we may assume that
![]() ${\mathbb S}^*$
has cardinality below
${\mathbb S}^*$
has cardinality below
![]() $j(\gamma )$
in M, we may once again build in
$j(\gamma )$
in M, we may once again build in
![]() $V_1$
an M-generic object
$V_1$
an M-generic object
![]() $G^*_4$
for
$G^*_4$
for
![]() ${\mathbb S}^*$
containing
${\mathbb S}^*$
containing
![]() $\tau '$
as in the construction of the generic object
$\tau '$
as in the construction of the generic object
![]() $G_1$
of this lemma.
$G_1$
of this lemma.
Note now that since N is given by an ultrapower of M via a normal measure over
![]() $P_{\kappa _2}(\kappa ^+_2)$
, [Reference Cummings7, Section 1.2.2, Fact 2] tells us that
$P_{\kappa _2}(\kappa ^+_2)$
, [Reference Cummings7, Section 1.2.2, Fact 2] tells us that
![]() $k '' G^*_4$
generates an N-generic object
$k '' G^*_4$
generates an N-generic object
![]() $G^{**}_4$
over
$G^{**}_4$
over
![]() $k({\mathbb S}^*)$
containing
$k({\mathbb S}^*)$
containing
![]() $k(\tau ')$
. By elementarity,
$k(\tau ')$
. By elementarity,
![]() $k({\mathbb S}^*)$
is the term forcing in N defined with respect to
$k({\mathbb S}^*)$
is the term forcing in N defined with respect to
 $k(j({\mathbb P}^1_{})_{\kappa _2 + 1})$
, which is forcing equivalent to
$k(j({\mathbb P}^1_{})_{\kappa _2 + 1})$
, which is forcing equivalent to
![]() ${\mathbb P}^1 \ast \dot {\mathbb Q}^1 \ast \dot {\mathbb Q}^2$
. Therefore, since
${\mathbb P}^1 \ast \dot {\mathbb Q}^1 \ast \dot {\mathbb Q}^2$
. Therefore, since
![]() $i({\mathbb P}^1 \ast \dot {\mathbb Q}) = k(j({\mathbb P}^1 \ast \dot {\mathbb Q}))$
is forcing equivalent to
$i({\mathbb P}^1 \ast \dot {\mathbb Q}) = k(j({\mathbb P}^1 \ast \dot {\mathbb Q}))$
is forcing equivalent to
![]() ${\mathbb P}^1 \ast \dot {\mathbb Q}^1 \ast \dot {\mathbb Q}^2 \ast \dot {\mathbb Q}^3$
,
${\mathbb P}^1 \ast \dot {\mathbb Q}^1 \ast \dot {\mathbb Q}^2 \ast \dot {\mathbb Q}^3$
,
![]() $G^{**}_4$
is N-generic over
$G^{**}_4$
is N-generic over
![]() $k({\mathbb S}^*)$
, and
$k({\mathbb S}^*)$
, and
![]() $G_0 \ast G_1 \ast G_2 \ast G_3$
is
$G_0 \ast G_1 \ast G_2 \ast G_3$
is
![]() $k({\mathbb P}^1 \ast \dot {\mathbb Q} \ast \dot {\mathbb R}')$
-generic over N, [Reference Cummings7, Section 1.2.5, Fact 1] (see also [Reference Foreman8]) tells us that for
$k({\mathbb P}^1 \ast \dot {\mathbb Q} \ast \dot {\mathbb R}')$
-generic over N, [Reference Cummings7, Section 1.2.5, Fact 1] (see also [Reference Foreman8]) tells us that for
![]() $G_4 = \{\mathrm {int}_{G_0 \ast G_1 \ast G_2 \ast G_3}(\sigma ) \mid \sigma \in G^{**}_4\}$
,
$G_4 = \{\mathrm {int}_{G_0 \ast G_1 \ast G_2 \ast G_3}(\sigma ) \mid \sigma \in G^{**}_4\}$
,
![]() $G_4$
is
$G_4$
is
![]() $N[G_0][G_1][G_2][G_3]$
-generic over
$N[G_0][G_1][G_2][G_3]$
-generic over
![]() ${\mathbb Q}^3$
. In addition, since the definition of
${\mathbb Q}^3$
. In addition, since the definition of
![]() $\tau $
tells us that in M, the statement “
$\tau $
tells us that in M, the statement “
![]() $\langle p, \dot q \rangle \in j({\mathbb P}^1 \ast \dot {\mathbb Q})$
implies that
$\langle p, \dot q \rangle \in j({\mathbb P}^1 \ast \dot {\mathbb Q})$
implies that
 $\langle p, \dot q \rangle \Vdash _{j({\mathbb P}^1 \ast \dot {\mathbb Q})} `\tau $
extends
$\langle p, \dot q \rangle \Vdash _{j({\mathbb P}^1 \ast \dot {\mathbb Q})} `\tau $
extends
![]() $\dot q$
’ ” is true, by elementarity, in N, the statement “
$\dot q$
’ ” is true, by elementarity, in N, the statement “
![]() $\langle p, \dot q \rangle \in k(j({\mathbb P}^1 \ast \dot {\mathbb Q}))$
implies that
$\langle p, \dot q \rangle \in k(j({\mathbb P}^1 \ast \dot {\mathbb Q}))$
implies that
 $\langle p, \dot q \rangle \Vdash _{k(j({\mathbb P}^1 \ast \dot {\mathbb Q}))} `k(\tau )$
extends
$\langle p, \dot q \rangle \Vdash _{k(j({\mathbb P}^1 \ast \dot {\mathbb Q}))} `k(\tau )$
extends
![]() $\dot q$
’ ” is true. In other words, since
$\dot q$
’ ” is true. In other words, since
![]() $k \circ j = i$
, in N, the statement “
$k \circ j = i$
, in N, the statement “
![]() $\langle p, \dot q \rangle \in i({\mathbb P}^1 \ast \dot {\mathbb Q})$
implies that
$\langle p, \dot q \rangle \in i({\mathbb P}^1 \ast \dot {\mathbb Q})$
implies that
 $\langle p, \dot q \rangle \Vdash _{i({\mathbb P}^1 \ast \dot {\mathbb Q})} `k(\tau )$
extends
$\langle p, \dot q \rangle \Vdash _{i({\mathbb P}^1 \ast \dot {\mathbb Q})} `k(\tau )$
extends
![]() $\dot q$
’ ” is true. Thus, in N,
$\dot q$
’ ” is true. Thus, in N,
![]() $k(\tau )$
functions as a term for a “master condition” for
$k(\tau )$
functions as a term for a “master condition” for
![]() $i(\dot {\mathbb Q})$
, so since
$i(\dot {\mathbb Q})$
, so since
![]() $G^{**}_4$
contains
$G^{**}_4$
contains
![]() $k(\tau ')$
, the construction of all of the above generic objects immediately yields that
$k(\tau ')$
, the construction of all of the above generic objects immediately yields that
![]() $i '' (G_0 \ast H) \subseteq G_0 \ast G_1 \ast G_2 \ast G_3 \ast G_4$
. This means that i lifts in
$i '' (G_0 \ast H) \subseteq G_0 \ast G_1 \ast G_2 \ast G_3 \ast G_4$
. This means that i lifts in
 $V_1^{{\mathbb P}^1 \ast \dot {\mathbb Q}}$
to
$V_1^{{\mathbb P}^1 \ast \dot {\mathbb Q}}$
to
 $i : V_1^{{\mathbb P}^1 \ast \dot {\mathbb Q}} \to N^{i({\mathbb P}^1 \ast \dot {\mathbb Q})}$
. This completes the proof of Lemma 2.7.⊣
$i : V_1^{{\mathbb P}^1 \ast \dot {\mathbb Q}} \to N^{i({\mathbb P}^1 \ast \dot {\mathbb Q})}$
. This completes the proof of Lemma 2.7.⊣
Let
![]() ${\mathbb P} = {\mathbb P}^* \ast \dot {\mathbb P}^0 \ast \dot {\mathbb P}^1$
. Lemmas 2.3–2.7 and the intervening remarks then complete the proof of Theorem 1.2.⊣
${\mathbb P} = {\mathbb P}^* \ast \dot {\mathbb P}^0 \ast \dot {\mathbb P}^1$
. Lemmas 2.3–2.7 and the intervening remarks then complete the proof of Theorem 1.2.⊣
3 Concluding remarks
We conclude this paper with several remarks, noting that in what we are about to say, we always assume that we begin with a model V of ZFC in which
![]() $\kappa _1 < \kappa _2$
are both supercompact. First, we note that it is possible to obtain a version of Theorem 1.1 where
$\kappa _1 < \kappa _2$
are both supercompact. First, we note that it is possible to obtain a version of Theorem 1.1 where
![]() $2^{\kappa _2} = \kappa ^{++}_2$
,
$2^{\kappa _2} = \kappa ^{++}_2$
,
![]() $\kappa _2$
is strongly compact,
$\kappa _2$
is strongly compact,
![]() $\kappa _2$
is
$\kappa _2$
is
![]() $\kappa ^+_2$
supercompact, and the indestructibility property for
$\kappa ^+_2$
supercompact, and the indestructibility property for
![]() $\kappa _2$
is that
$\kappa _2$
is that
![]() $\kappa _2$
’s strong compactness is indestructible under forcing with
$\kappa _2$
’s strong compactness is indestructible under forcing with
![]() $\mathrm {Add}(\kappa _2, \delta )$
for any ordinal
$\mathrm {Add}(\kappa _2, \delta )$
for any ordinal
![]() $\delta $
and for
$\delta $
and for
 $\lambda = (\kappa ^+_2)^{V^{\mathbb P}}$
, the
$\lambda = (\kappa ^+_2)^{V^{\mathbb P}}$
, the
![]() $\lambda $
supercompactness of
$\lambda $
supercompactness of
![]() $\kappa _2$
is indestructible under
$\kappa _2$
is indestructible under
![]() $\kappa _2$
-directed closed forcing having size at most
$\kappa _2$
-directed closed forcing having size at most
![]() $\lambda $
. We present a brief sketch of how this is done, and leave it to interested readers to provide any missing details. Specifically, we may assume from the proof of Theorem 1.2 that we are forcing over a ground model V in which
$\lambda $
. We present a brief sketch of how this is done, and leave it to interested readers to provide any missing details. Specifically, we may assume from the proof of Theorem 1.2 that we are forcing over a ground model V in which
![]() $\kappa _1$
is both the first strongly compact and first measurable cardinal and has its strong compactness indestructible under arbitrary
$\kappa _1$
is both the first strongly compact and first measurable cardinal and has its strong compactness indestructible under arbitrary
![]() $\kappa _1$
-directed closed forcing,
$\kappa _1$
-directed closed forcing,
![]() $\kappa _2$
is supercompact,
$\kappa _2$
is supercompact,
 $2^{\kappa _2} = 2^{\kappa ^+_2} = \kappa ^{++}_2$
,
$2^{\kappa _2} = 2^{\kappa ^+_2} = \kappa ^{++}_2$
,
![]() $2^\delta = \delta ^{+}$
for every
$2^\delta = \delta ^{+}$
for every
![]() $\delta \ge \kappa ^{++}_2$
, and
$\delta \ge \kappa ^{++}_2$
, and
![]() $\kappa _2$
carries a supercompact ultrafilter
$\kappa _2$
carries a supercompact ultrafilter
![]() ${\cal U}_2$
such that
${\cal U}_2$
such that
![]() $\kappa _2$
isn’t measurable in the ultrapower by
$\kappa _2$
isn’t measurable in the ultrapower by
![]() ${\cal U}_2$
. We then force as in Modules 2 and 3 of the proof of Theorem 1.1. By the proofs of [Reference Apter and Cummings1, Lemma 5], [Reference Hamkins11, Theorems 1.7 and 1.8], and Theorem 1.1, we are now in a new ground model V in which
${\cal U}_2$
. We then force as in Modules 2 and 3 of the proof of Theorem 1.1. By the proofs of [Reference Apter and Cummings1, Lemma 5], [Reference Hamkins11, Theorems 1.7 and 1.8], and Theorem 1.1, we are now in a new ground model V in which
![]() $\kappa _1$
is both the first strongly compact and first measurable cardinal and has its strong compactness indestructible under arbitrary
$\kappa _1$
is both the first strongly compact and first measurable cardinal and has its strong compactness indestructible under arbitrary
![]() $\kappa _1$
-directed closed forcing,
$\kappa _1$
-directed closed forcing,
![]() $\kappa _2$
is both the second strongly compact and second measurable cardinal,
$\kappa _2$
is both the second strongly compact and second measurable cardinal,
![]() $\kappa _2$
is
$\kappa _2$
is
![]() $\kappa ^+_2$
supercompact, and there is a fast function
$\kappa ^+_2$
supercompact, and there is a fast function
![]() $f : \kappa _2 \to \kappa _2$
for
$f : \kappa _2 \to \kappa _2$
for
![]() $\kappa _2$
. We then force with the lottery preparation defined as on [Reference Hamkins11, p. 127] using f, where the partial orderings allowed in the lottery sum at a nontrivial stage of forcing
$\kappa _2$
. We then force with the lottery preparation defined as on [Reference Hamkins11, p. 127] using f, where the partial orderings allowed in the lottery sum at a nontrivial stage of forcing
![]() $\alpha $
all must be
$\alpha $
all must be
![]() $\alpha $
-directed closed. Since the proof found in Module 4 of Theorem 1.1 requires no GCH assumptions about
$\alpha $
-directed closed. Since the proof found in Module 4 of Theorem 1.1 requires no GCH assumptions about
![]() $\kappa _2$
, the arguments of Module 4 and Lemma 2.6 now show that we have constructed our desired model.
$\kappa _2$
, the arguments of Module 4 and Lemma 2.6 now show that we have constructed our desired model.
We next observe that with slight modifications to our proofs, it is possible to change the assumption in the proof of Theorem 1.2 that
![]() $V \vDash ``$
No cardinal
$V \vDash ``$
No cardinal
![]() $\lambda> \kappa _2$
is inaccessible” to, e.g.,
$\lambda> \kappa _2$
is inaccessible” to, e.g.,
![]() $V \vDash ``$
No cardinal
$V \vDash ``$
No cardinal
![]() $\lambda> \kappa _2$
is Mahlo.” This is accomplished by letting
$\lambda> \kappa _2$
is Mahlo.” This is accomplished by letting
![]() $\langle \delta _\alpha \mid \alpha < \kappa _2 \rangle $
enumerate the Mahlo cardinals in the open interval
$\langle \delta _\alpha \mid \alpha < \kappa _2 \rangle $
enumerate the Mahlo cardinals in the open interval
![]() $(\kappa _1, \kappa _2)$
and replacing “inaccessible” with “Mahlo” in clause (2) in the definition of
$(\kappa _1, \kappa _2)$
and replacing “inaccessible” with “Mahlo” in clause (2) in the definition of
![]() ${\mathbb P}^1$
. It is in addition possible to have in Theorem 1.2 that, e.g.,
${\mathbb P}^1$
. It is in addition possible to have in Theorem 1.2 that, e.g.,
 $2^{\kappa _1} = \kappa ^{+38}_1$
,
$2^{\kappa _1} = \kappa ^{+38}_1$
,
![]() $\kappa _1$
is
$\kappa _1$
is
 $\kappa ^{+37}_1$
supercompact,
$\kappa ^{+37}_1$
supercompact,
 $2^{\kappa _2} = \kappa^{+75}_2$
,
$2^{\kappa _2} = \kappa^{+75}_2$
,
![]() $\kappa _2$
is
$\kappa _2$
is
 $\kappa ^{+74}_2$
supercompact,
$\kappa ^{+74}_2$
supercompact,
![]() $2^\delta = \delta ^+$
for every
$2^\delta = \delta ^+$
for every
 $\delta \ge \kappa ^{+ 75}_2$
,
$\delta \ge \kappa ^{+ 75}_2$
,
![]() $\kappa _1$
’s strong compactness is indestructible under arbitrary
$\kappa _1$
’s strong compactness is indestructible under arbitrary
![]() $\kappa _1$
-directed closed forcing,
$\kappa _1$
-directed closed forcing,
![]() $\kappa _2$
’s strong compactness is indestructible under
$\kappa _2$
’s strong compactness is indestructible under
![]() $\kappa _2$
-directed closed,
$\kappa _2$
-directed closed,
 $(\kappa ^{+ 74}_2, \infty )$
-distributive forcing, and for
$(\kappa ^{+ 74}_2, \infty )$
-distributive forcing, and for
 $\lambda = (\kappa ^{+ 74}_2)^{V^{\mathbb P}}$
, the
$\lambda = (\kappa ^{+ 74}_2)^{V^{\mathbb P}}$
, the
![]() $\lambda $
supercompactness of
$\lambda $
supercompactness of
![]() $\kappa _2$
is indestructible under
$\kappa _2$
is indestructible under
![]() $\kappa _2$
-directed closed forcing having size at most
$\kappa _2$
-directed closed forcing having size at most
![]() $\lambda $
. Other variations for Theorems 1.1 and 1.2 along these same lines (including versions of Theorem 1.1 where
$\lambda $
. Other variations for Theorems 1.1 and 1.2 along these same lines (including versions of Theorem 1.1 where
![]() $\kappa _1$
exhibits nontrivial degrees of supercompactness) are possible as well. We leave it to readers to fill in the details for themselves.
$\kappa _1$
exhibits nontrivial degrees of supercompactness) are possible as well. We leave it to readers to fill in the details for themselves.
We also return to the issue (first raised in Section 1) of why in Theorem 1.2, the current state of forcing technology doesn’t appear to provide a way for one to force the
![]() $\kappa ^+_1$
supercompactness of
$\kappa ^+_1$
supercompactness of
![]() $\kappa _1$
to be indestructible under
$\kappa _1$
to be indestructible under
![]() $\kappa _1$
-directed closed forcing having size at most
$\kappa _1$
-directed closed forcing having size at most
 $(\kappa ^+_1)^{V^{\mathbb P}}$
. This is since
$(\kappa ^+_1)^{V^{\mathbb P}}$
. This is since
![]() ${\mathbb P}^0$
is not an iteration of the type considered in [Reference Hamkins10, Reference Hamkins12], and so no analogue of Theorem 1.3 is presently known which allows us to establish the appropriate version of Lemma 2.5.
${\mathbb P}^0$
is not an iteration of the type considered in [Reference Hamkins10, Reference Hamkins12], and so no analogue of Theorem 1.3 is presently known which allows us to establish the appropriate version of Lemma 2.5.
We finally ask the very broad and general question of what other sorts of indestructibility theorems are possible when considering the class of strongly compact cardinals. As examples, can the first i strongly compact cardinals
![]() $\kappa _i$
(for
$\kappa _i$
(for
![]() $i> 1$
an ordinal) be the first i measurable cardinals, and also have their strong compactness indestructible under arbitrary
$i> 1$
an ordinal) be the first i measurable cardinals, and also have their strong compactness indestructible under arbitrary
![]() $\kappa _i$
-directed closed forcing? Since the proof of Theorem 1.1 doesn’t seem to have a generalization beyond
$\kappa _i$
-directed closed forcing? Since the proof of Theorem 1.1 doesn’t seem to have a generalization beyond
![]() $i = 2$
, is it even possible for the first i strongly compact cardinals
$i = 2$
, is it even possible for the first i strongly compact cardinals
![]() $\kappa _i$
(for
$\kappa _i$
(for
![]() $i> 2$
a natural number) to have their strong compactness indestructible under
$i> 2$
a natural number) to have their strong compactness indestructible under
![]() $\mathrm {Add}(\kappa _i, \delta )$
for any ordinal
$\mathrm {Add}(\kappa _i, \delta )$
for any ordinal
![]() $\delta $
? These are the questions with which we end this paper.
$\delta $
? These are the questions with which we end this paper.