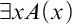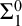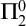In contrast to what seems to be the case today, in the early part of the twentieth century, many leading mathematicians were very concerned with problems in the foundations of mathematics. They thought there was a great problem awaiting their contributions. Hilbert was no exception. The main idea of what has become known as the Hilbert program was of course to prove the consistency of various systems of mathematics by “finitary” means. He and his followers thought that this would show that a very narrow class of statements—those that they regarded as having a finitary meaning—would therefore be shown to be provable by finitary “metamathematical” means, even though they were proved in systems that we must consider too “infinitistic” to regard as true.

The antagonism between Hilbert and Brouwer in much of the foundational debate of this period is famous.Footnote ¹ Yet, it is worth remarking that Hilbert’s actual program in the 1920s advocated an official “finitism” which, though never fully defined, seems to have found valid a much narrower class of arguments than those admitted by Brouwer. The class of statements that had a clear finitary meaning was also narrow. (Hilbert had little interest in the mathematical statements and arguments accepted by Brouwer.) A system containing infinitary mathematics was supposed to be justified by a finitary metamathematical argument that would show that all statements provable in the system in the narrowly meaningful class can be proved without resort to the dubious statements used in the proof.

Now, Hilbert’s interests are only partially described by the formulation of the Hilbert program in the 1920s. They actually progressed to that position. In the preceding years, for example, he was interested in the approach of Principia Mathematica and wished to have Russell come to Göttingen (see [Reference Sieg28] for a history).Footnote ² But although he oscillated in his views, he really seemed to have hankered after a position in which classical mathematics will really be true, even though officially it largely consists only of “ideal” statements used to prove “contentual” statements. And his famous slogan, “No one shall be able to drive us from the Paradise that Cantor created for us” in his relatively late (and rather obscure in his claim to have solved the continuum problem) paper “On the Infinite” [Reference Hilbert and Bernays19, p. 376], seems to confirm that this was a long-held position.

We all know that the story of Hilbert’s program doesn’t have a happy ending, but we should also remember that it did not “collapse” (as I say in my title) without a legacy—both in the notion of a formal system as rigorously formulated and independent of its interpretation, and in the subject of proof theory (in which a lot of Hilbert’s standards have had to be relaxed to carry some goals of the program through). Unlike Principia Mathematica, Hilbert and his followers rigorously separated the purely formal, syntactic, formulation of a system, from its interpretation. As Gödel has remarked, Principia was a considerable backwards step from Frege’s work in the rigor of its formalization.Footnote ³ Frege’s standards of formalization were in fact the modern ones, even though (as far as I know) he did not emphasize what the standards should be. Hilbert and his school did so.

Hilbert and Ackermann’s famous textbook [Reference Hilbert and Ackermann18] formulates, among other things, first-order logic without identity (really already known to Hilbert much earlier), and the problems of completeness and decidability with respect to validity in any non-empty domain are clearly stated. In other lectures Hilbert did include identity as a part of first-order logic. Gödel [Reference Gödel13] proved completeness for both systems without and with identity.Footnote ⁴ Regarding proof theory, Hilbert formulated an approach to the subject, as well as the subject itself. This subject is still alive today, and is even related to some current problems in computer science and other formal disciplines. But the complete realization of Hilbert’s original program of the 1920s is usually thought to have been shown to be impossible.Footnote ⁵

The details of Hilbert’s approach, and the reasons it convinced a generation of logicians to believe that it obviously must succeed and that only technical work remained to finish it, are generally left to more specialized textbooks. As we will see, the “Hilbertians” had ample reason to assume that it would succeed. Indeed, Gödel’s incompleteness theorems came as a shock to them—especially the second incompleteness theorem, in which he gave a rigorous proof that a reasonably strong consistent formal system cannot prove its own consistency. Gödel himself wrote that his work did not disprove the viability of the Hilbert program. Perhaps there are finitary methods that cannot be formalized in the system discussed.Footnote ⁶ But most people believed that since finitary methods are supposed to be rather weak, however they are to be delineated, they must be formalizable within any reasonably strong system. In particular, the program is supposed to be formalizable in the very system discussed. So most people concluded that Gödel had shown that Hilbert’s program was hopeless. Throughout the present paper, we will ourselves assume that the consequences of the program are formalizable in the very system being discussed.

There are two relevant questions here. First, why were the Hilbertians so convinced that the program would work? And, second, why wasn’t it eventually noted that if the program really succeeded in the way it was actually proposed in detail, it would imply its own collapse (assuming its detailed claims could be carried out in the very system discussed )?Footnote ⁷

For our purposes, we will apply the Hilbert approach to systems formulated only with quantification over the natural numbers in the usual first-order logic with identity. We assume that the system—call it S—contains symbols for the numerals (standing for 0 and a successor function). It is also convenient to suppose that it contains function symbols for arbitrary primitive recursive functions, where the axioms imply the ordinary recursion equations. Arbitrary primitive recursive predicates can then be defined as simply predicates of the form f(x) = 1. Note that the proof predicate of the system, supposed to be formalized in ordinary first-order logic with identity, will itself be primitive recursive, as long as the non-logical axioms are primitive recursive. The system S could simply amount to the usual first-order Peano arithmetic, or it could be something stronger. (It could also be weaker. Anything containing a weak theory adequate for primitive recursion would work for this version of the argument.) The arithmetical statements provable in set theory would be much stronger, but can be separately axiomatized in accordance with these requirements using Craig’s device.Footnote ⁸ The Hilbert approach (or Ansatz) was meant to apply to these stronger systems also.

The basic ideas of the program are two. Hilbert’s first main idea was that quantifiers are to be eliminated, so the system will consist only of quantifier-free statements. Instead of writing $\exists xA(x)$ , write A(εxA(x)), where εxA(x) denotes some true instance of A(x), and is arbitrary if there is no such instance. In terms of the ε symbol, (x)A(x) can be defined as A(εx∼A(x)). When all quantifiers have been eliminated in this way, one needs only the axiom scheme A(t) ⊃ A(εxA(x)), where t is any term.Footnote ⁹ Terms can be formed using the constant and function symbols of the original language, but we must also allow new terms formed using the ε symbol itself. One then needs only propositional logic and identityFootnote ¹⁰ to deduce theorems from the axioms. Moreover, when particular values are assigned to each ε term, it is always decidable whether a given formula is true.

Then we take A(t) ⊃ A(εxA(x)) as an axiom for the ε symbol, where $t$ is any term of the language denoting a number. t can be as simple as a numeral or a primitive recursive function symbol applied to numerals, but it must be allowed to contain ε symbols itself for the idea to work out. Conditionals of this form, taken as axioms, replace the whole of quantification theory. Thus, we need only propositional logic and identity to make inferences from the axioms. But all the axioms have to be rewritten in terms of these ε symbols. Now, stated this way, the whole thing looks pretty easy. But in fact anything written out in terms of ε symbols, as people who have studied this know, is a mess because there are quantifiers embedded inside of other quantifiers, leading to ε-terms embedded in ε-terms.

So, while these formulae are a mess, everything else is very simple because all inferences are a matter of pure propositional logic and identity without need of quantification theory. To the Hilbertians that was important because in the intellectual atmosphere of the time (which is not today’s) quantification even over all the natural numbers was—at least in classical logic, and maybe even in intuitionistic logic—a dubious idea. When they were pursuing the Hilbert program, with its restriction to finitary arguments, the Hilbert school officially had therefore to regard infinitary model theory as meaningless. This is so even though in the book by Hilbert and Ackermann the question of the completeness of quantification theory was raised, and Ackermann and Bernays used model theory to show that some subclasses of first-order logic were decidable.Footnote ¹¹

Hilbert’s second main idea was that you couldn’t get a contradiction from these axioms as long as all the ε-terms have true numerical values. Then, ordinary numerals for natural numbers when substituted for them will make them true. So their truth under such a substitution would show the consistency of mathematics. No contradiction could be derived from true axioms with only propositional (truth-functional) inferences. Identity statements must also be used.

Now, since there are no quantifiers in these formulae, whether a given substitution of natural numbers for a set of ε-terms makes a formula true or false is actually decidable. Of course, they didn’t have a formal theory of decidability at the time, but they knew intuitively that it was checkable. The simplest way would be to set every ε term occurring in a given formula—or throughout the proof—to zero. Then you could say whether any of the given formulae was true or false simply by deciding the zero case. Now, supposing we were lucky enough that that worked, we could not possibly deduce a contradiction like 0 = 1, because everything is checkable in propositional logic, and identity statements. Of course, it is unlikely that we will be that lucky: that all the ε-terms will be satisfied by the number 0. But this circumstance gave rise to the idea of another kind of interpretation, different from conventional model-theoretic interpretation; that is, a proof that is interpreted by giving values to the ε-terms.

How can we see whether a given assignment works? Well, first we try all zeros. Probably that fails, and the formulae in the proof do not all come out true. Next, we follow a systematic procedure that the Hilbert school prescribed to allow one to change one’s mind; so a $0$ can change to $1$ and so on.Footnote ¹² Now since, as I said, ε-terms may involve other ε-terms, changes in the values of some ε-terms intuitively ought to effect changes in the other involved ones. On the other hand, if a given ε term was free of any dependence on other ε-terms, you could change it without affecting anything else. So they set up the idea of a priority ordering of substitutions; that is, some changes will affect others, while other changes allow you to stick to what you already have. Now, this is more or less the idea that was rediscovered by Friedberg [Reference Friedberg10] and Muchnik [Reference Muchnik27] in recursion theory (computability theory): a priority ordering in which you keep on changing your mind, but which is supposed to terminate. (See also footnote 25 to Remark 4).

Hilbert and his followers tried to show that after a finite number of changes of mind, you would eventually get it right. That is, you can find values for the ε-terms that will make the axioms, and hence, by propositional logic and identity, all formulae in the proof, true. Most members of the school were convinced throughout the 1920s that this procedure just had to work; it is just a matter of ingenuity and detail to do it. But why were they so convinced? Well, because really, in the back of their minds, they thought that the axioms (and hence the theorems) of first-order Peano arithmetic—or whatever the fundamental mathematical practice with numbers was—were true. And that would imply that there are true values for these ε-terms.Footnote ¹³

That is, if the existential statement $\exists xA(x)$ is true, then there is a numeral which if it replaces εxA(x) in A(εxA(x)), the result will be true. So, therefore, they really thought it was only a matter of combinatorial work to change this into an argument that doesn’t officially appeal to the model but shows that everything will terminate in values for the terms that will make the axioms true.Footnote ¹⁴ And papers were published that purported to do this; only they contained errors. ([Reference Ackermann1], as described by Zach [Reference Zach35], is a system of a second-order version of primitive recursive arithmetic that was stated to have been proved consistent. But the paper was also believed to have proved the consistency of first-order Peano arithmetic.)

The method was supposed to be completely “finitary,” but exactly what the Hilbert school meant by this is not so clear. Two clarifications have been proposed. One is Tait’s [Reference Tait30, Reference Tait31]—identifying finitary arguments with those that can be carried out in Skolem’s [Reference Skolem29] primitive recursive arithmetic—but historically it appears that the Hilbert school wanted to go beyond this version, though nowadays it has been widely used as a finitary or combinatory standard. Another one is by Gödel [Reference Gödel16] and Kreisel [Reference Kreisel23], who seem to believe that induction up to any fixed ordinal <ε₀ is finitary, but not ε₀ induction itself.Footnote ¹⁵

The main requirement here is simply that the means by which the combinatorial argument is carried out be formalizable within the system itself. This requirement is much weaker than what the Hilbert school intended. It is only in virtue of our contemporary sophistication that we know that we can’t give a consistency proof of a reasonably strong system within the system itself.

But the Hilbertian way of looking at things actually influenced me, because, as I said, I started all this with model theory and only afterward translated it into proof theory. The proof-theoretic argument was rather complicated at first, but finally, motivated by the Hilbert Ansatz, a very simple argument emerged.

Well, again, what shows that this program must come to an end? I was trying to say why everyone thought it must work. But as is well known Gödel showed that, at least if we retain the requirement that it be carried out within the system itself, it does not, in fact, work. Gödel’s famous argument is in one sense a “deus ex machina.” It has no direct relation to the Hilbert program or whether it can succeed. Originally Gödel wasn’t looking for such a result. His argument for the first incompleteness theorem has no direct relation to this, and he himself didn’t originally realize that it was connected to the Hilbert program.Footnote ¹⁶

At this point let’s note that the Hilbert program had, as a corollary, a much stronger result than the mere consistency of mathematics. The latter would merely mean that you couldn’t prove false equations like 0 = 1 or other false equations within the system where the identities are of arbitrary terms (not containing the ε symbol). To put it in more positive terms, any provable equations within the system will have been proved by finitary metamathematical means to be true. It will follow that any universal statement whose instances are calculable within the system must actually be true. And in most reports of the Hilbert program, either simple consistency is all that is stated, or the consequence that any ${\Pi}_1^0$ statement that is proved within the system must be true.

But the Hilbert program or approach (Ansatz) actually implied something much stronger. Here’s the idea. Whenever a statement like A(εxA(x)) is provable (remember, there are no quantifiers) there actually will be a value of the term εxA(x) that is true and provable in the system, because quantifier-free calculations can be carried out within the system. This in turn implies, if we rewrite it in terms of ordinary quantification theory, that if you prove $\exists xA(x)$ and A(x) is itself free of quantifiers (say, a primitive recursive predicate), some numerical instance must be provable. Therefore, we obtain something much stronger, using the details of the Hilbert program, than the mere consistency of mathematics. In contemporary consistency jargon, it would be called the 1-consistency of mathematics, which is a special case of what Gödel called ω-consistency (the only ω-consistency notion he actually used).Footnote ¹⁷ But we could also call this the ${\Sigma}_1^0$ -correctness of the system—that is, if it can prove a ${\Sigma}_1^0$ statement, that statement is true. Moreover, the ${\Sigma}_1^0$ -correctness would hold in a constructive sense. One could actually calculate a true instance. Further, that instance would have to be provable in the system.Footnote ¹⁸ Thus, the Hilbertian idea would have shown not merely that every ${\Pi}_1^0$ statement that is provable has a finitary proof (as stated above), but even that the same result holds for ${\Pi}_2^0$ statements. For if a ${\Pi}_2^0$ statement is provable, each numerical instance is a provable ${\Sigma}_1^0$ statement, which by hypothesis must be true.Footnote ¹⁹

The goal of the Hilbert program was to show that at least each of the narrower class of meaningful statements which are proved using resources that appeared to be highly infinitistic—i.e., resources that involved quantifiers over infinite totalities, which were therefore supposed to be suspect—would in fact have a so-called finitary proof (whatever precisely that meant).

As I have said, what I am trying to show here is that although Gödel’s work (independently) led to the collapse of the Hilbert program, if the Hilbertians had really thought through what they were claiming, they should have seen that their own demands were impossible. It is strange to me that nobody appears to have noticed this, either immediately or in the following decades. Perhaps people just regarded Gödel’s work as a sufficient refutation and stopped thinking further about it. (I am struck that I myself took a surprisingly long time to see this, and only came to see it eventually via a complicated route. See footnote 7.)

Let’s return to the question: What, therefore, is being claimed by the Hilbertians? Well, they claim that, given any proof p of a ${\Pi}_2^0$ statement— $(x)\!\left(\exists y\right)A(x,y)$ —where A(x, y) is a simple, decidable formula not involving quantifiers, say a primitive recursive formula, and for any number $m$ , there is a proof p ₁—remember, this can be a different proof and even longer than the proof p, so that p ₁ may exceed p—of some particular instance $A({0}^{(m)},{0}^{(n)})$ . Now, first, intuitively—and reasoning infinitistically, so to speak—this is a true statement. In fact, we can eventually say something stronger than that, but at any rate this formulation is a true statement. The question is whether it is formalizable within the system. If you state this claim within the system, it says that for every proof p and any number m there is another proof p ₁ and a number $n$ making an instance of this true. Notice that this statement is itself a ${\Pi}_2^0$ statement making a general statement about all ${\Pi}_2^0$ statements provable in the system.

The Gödel theorem has sometimes been compared to the Liar paradox. In our case we again have something like “All Cretans are liars”—only here it may seem more positive than negative. We are saying that every ${\Pi}_2^0$ statement has a certain property, and the statement is itself a ${\Pi}_2^0$ statement. So, whatever is self-referential here has not been introduced by some ingenious external argument—a deus ex machina, as I would characterize Gödel’s famous argument—but rather arises from within the Hilbert program itself. They are making a ${\Pi}_2^0$ statement about all ${\Pi}_2^0$ statements, including, of course, that very statement itself.

However, we have to allow for the possibility that the Hilbertians might have realized the reflexiveness of this statement while thinking of it as merely analogous to a Cretan saying, “All Cretans tell the truth.” For the property they were talking about was good; it wasn’t quite like “All Cretans are liars.”

Consider the two statements:Footnote ²⁰

(*) (x ₁)(x ₂)((x ₁ proves a ${\Pi}_2^0$ statement ⌜(x)(∃y)A(x,y)⌝) ⊃ (∃y)(y proves an instance ⌜ $A({0}^{\left({x}_2\right)},{0}^{(n)})$ ⌝)) $.$

(**) (x)((x proves a ${\Pi}_2^0$ statement ⌜(x)(∃y)A(x,y)⌝) ⊃ (∃y)(y proves an instance ⌜A(0^(x), 0⁽ⁿ⁾)⌝)).

Here (*) is the general claim to be made. (**) is the special case where x ₁ = x ₂.

Now (**) is a ${\Pi}_2^0$ statement, but to put it in an appropriate normal form with one universal quantifier and one existential quantifier, we must write it as:

(***) (x)(∃y)((x proves a ${\Pi}_2^0$ statement ⌜(x)(∃y)A(x,y))⌝ ⊃ (y proves an instance ⌜A(0^(x), 0⁽ⁿ⁾)⌝).

(***) is clearly equivalent to (**). One must note here that the predicates involved are all primitive recursive. In spite of their verbal form, they need not involve quantifiers to be eliminated in the ε-calculus (since bounded quantification is primitive recursive).

Recall that we have formulated our system S to be strong enough that primitive recursive predicates are correctly decidable within S and are quantifier-free.

(***) is a sweeping statement about the provability of ${\Pi}_2^0$ statements in the system. Yet it itself is a ${\Pi}_2^0$ statement. Note also that it does involve the notion of Gödel numbering, assumed to be done in some standard way. Note also that the quantifier-free part of (***) is the conditional given. Call it A*** (x, y). Now, suppose (***) were provable. Then it has a proof with Gödel number p. Since p does prove (***) and true primitive recursive statements are all provable in S, the antecedent of A*** (x, y) is provable, with the variable x replaced by 0^(p).

Assume also that the system S is 1-consistent ( ${\Sigma}_1^0$ -correct). Given this assumption, there must be a number p ₁ instantiating the variable y of A*** (x, y). Since the antecedent of the conditional is true, the consequent must be true also. So there is a number p ₁ that is the Gödel number of a proof of an instance of A*** (x, y). Hence, there must be a least such p ₁.

Now p ₁ is supposed to be a proof of an instance of A*** (0^(p), y). But if that instance is, say, A*** (0^(p), 0⁽ⁿ⁾) for some particular n, clearly, in any standard Gödel numbering, n < p ₁. But n is supposed to be an instance of the existential quantifier in (***). This is clearly impossible if p ₁ is chosen to be an instance as small as possible.

(***) is therefore unprovable if the system is 1-consistent ( ${\Sigma}_1^0$ -correct).

Now if S is inconsistent, (***) is true, since every formula is provable. On the other hand, if S is 1-consistent ( ${\Sigma}_1^0$ -correct), (***) is also true, as we have just argued. In this latter case, the situation is just like Gödel’s formula: (***) is true but unprovable.

In either case (whether S is inconsistent or 1-consistent), every numerical instance of (***) is provable, being a true ${\Sigma}_1^0$ statement. Hence, as in the case of Gödel’s formula, (***) cannot be refuted if S is ω-consistent (in fact, 2-consistency suffices).

As in the case of Gödel’s second incompleteness theorem, as long as the argument just stated can be formalized within the system S, it shows that “S is inconsistent or 1-consistent” or equivalently, the material conditional “if S is consistent, it is 1-consistent” cannot be proved in S if S itself is 1-consistent. (Here, however, unlike the Gödel case, the original statement (***) comes close to being a 1-consistency statement itself.)Footnote ²¹

Note that the original statement (*) also has the properties ascribed to (***). It is true if S is inconsistent, and true but unprovable if S is 1-consistent. Also, in either case, every numerical instance (substituting for both variables x ₁ and x ₂) is provable. Here again (*) is not refutable, hence undecidable if S is ω-consistent (even 2-consistent).Footnote ²² In this argument, unlike Gödel’s original, the undecidability result comes from a natural statement that will be believed true by anyone who believes S to be 1-consistent. The “self-referential” aspect comes simply from the fact that it is a sweeping ${\Pi}_2^0$ statement about the provability of ${\Pi}_2^0$ statements in the system, not from an ingenious diagonalization. The statement was suggested by the Hilbert Ansatz, but the result and its naturalness are independent of the Hilbert program itself.Footnote ²³