2.1 Facility

The measurements are performed in an open return boundary-layer wind tunnel in the Walter Basset Aerodynamics Laboratory at the University of Melbourne. A complete description of this facility is given in Harun et al. (Reference Harun, Monty, Mathis and Marusic2013). The test section has the dimensions of $6.7~\text{m}\times 0.94~\text{m}\times 0.38~\text{m}$ (length $\times$ width $\times$ height), with measurements made in the turbulent boundary layer developing over the lower surface. The free-stream turbulence level is ${\approx}0.3\,\%$. The boundary layer is tripped by a strip of P-40 sandpaper (length 115 mm) at the beginning of the test section.

The streamwise pressure coefficient $C_{p}\equiv 2\unicode[STIX]{x0394}P/\unicode[STIX]{x1D70C}U_{\infty }^{2}$ is measured for each surface in this study using 11 static pressure taps located at the roof of the tunnel, spaced approximately by 0.5 m in $x$, from $x=0$ to 5.5 m ($x=0$ is at the end of the trip, at the inlet of the working section); $\unicode[STIX]{x0394}P$ is the difference between the static pressure measured on each tap and the reference tap above the trip, $\unicode[STIX]{x1D70C}$ is the density of air and $U_{\infty }$ is the free-stream velocity. For all heterogeneous surfaces, the magnitude of $C_{p}$ varies within $\pm 0.013$ along the length of the test section. This range is very close to the $C_{p}$ variation ($C_{p}\pm 0.01$) observed for the zero-pressure-gradient smooth-wall cases conducted in the same facility previously by Harun et al. (Reference Harun, Monty, Mathis and Marusic2013).

2.2 Spanwise heterogeneous cases

Spanwise heterogeneous surfaces are constructed from strips of P-36 grit sandpaper (rough patch) and 2 mm thick cardboard (smooth patch) of equal width $S$, as shown in figure 4(b). These strips are assembled in a spanwise-alternating pattern, covering the first 5.6 m of the test section after the trip (from $x=0$ and extending to $x=5.6~\text{m}$), such that the surfaces have periodic rough and smooth patches of wavelength $\unicode[STIX]{x1D6EC}=2S$. The use of the 2 mm thick cardboard strips for the smooth patches ensures, as far as possible, that the heterogeneity is imposed by the spanwise shear stress variation between the cardboard and sandpaper strips rather than any mismatch in virtual origin (strip- rather than ridge-type heterogeneity, figure 1). The thickness of the cardboard is selected to minimise variation in the virtual origin between the rough and smooth strips. A laser scan of a $60~\text{mm}\times 20~\text{mm}$ sample of this surface (figure 4a) reveals that the cardboard surface is close to the maximum height of the sand grains, with the average height of the sandpaper grain 0.728 mm lower than the cardboard, and the maximum peak height of the sandpaper approximately 0.324 mm above the cardboard. The mean grain size of the sandpaper roughness is $k=0.902~\text{mm}$ with $k_{s}=1.96~\text{mm}$ (Squire et al. Reference Squire, Morrill-Winter, Hutchins, Schultz, Klewicki and Marusic2016), which corresponds to $\unicode[STIX]{x1D6FF}_{s}/k\approx 63$ for the wind tunnel conditions used here (where $\unicode[STIX]{x1D6FF}_{s}$ is the smooth wall boundary layer at $x=4~\text{m}$ and $k$ is the mean grain size of the sandpaper strip). For the spanwise heterogeneous surfaces, the equivalent sand grain roughness $k_{s}$ and the true virtual origin are unknown and, in fact, not well defined.

Figure 4. (a) Magnified view of $20~\text{mm}\times 20~~\text{mm}$ sample of the spanwise heterogeneous surface. Rough patch profile is obtained from a laser profilometer. (b) Spanwise heterogenous surface and measurement plane at 4 m downstream of the inlet to the working section. The white and black patches correspond to strips of cardboard and sandpaper, respectively. (c) Hot-wire anemometry measurement grid. Measurements start at the centre of a smooth patch (——, blue) and end at the centre of the adjacent rough patch (——, red). $S$ is the width of the roughness strips.

Table 1. Summary of spanwise heterogeneous roughness cases and the reference smooth- and rough-wall cases. The statistics are obtained from HWA: $\overline{\unicode[STIX]{x1D6FF}}$ is the spanwise-averaged 98 % boundary-layer thickness of the surface with spanwise heterogeneity, while $\unicode[STIX]{x1D6FF}_{s}$ and $\unicode[STIX]{x1D6FF}_{r}$ are the 98 % boundary-layer thickness of the reference smooth- and rough-wall cases, respectively; $\overline{\unicode[STIX]{x1D703}}$ is the spanwise-averaged momentum thickness of the spanwise heterogeneous surfaces, while $\unicode[STIX]{x1D703}_{s}$ and $\unicode[STIX]{x1D703}_{r}$ are the momentum thickness of the reference smooth- and rough-wall cases, respectively. Reynolds number definitions are: $Re_{x}\equiv xU_{\infty }/\unicode[STIX]{x1D708}$, $Re_{\unicode[STIX]{x1D6FF}}\equiv \unicode[STIX]{x1D6FF}U_{\infty }/\unicode[STIX]{x1D708}$, and $Re_{\unicode[STIX]{x1D703}}\equiv \unicode[STIX]{x1D703}U_{\infty }/\unicode[STIX]{x1D708}$. The last three columns show the availability of data from all measurement methods: HWA, SPIV and WPPIV.

Table 1 describes all spanwise heterogeneous roughness (‘SR’) cases in this study. Five surfaces with varying $S$ are constructed for this study to achieve a range of $S/\overline{\unicode[STIX]{x1D6FF}}=0.32{-}6.81$. Here, $S$ is normalised by the spanwise-averaged boundary-layer thickness $\overline{\unicode[STIX]{x1D6FF}}$. The variation of boundary-layer thickness $\unicode[STIX]{x1D6FF}(y)$ across the span is under $\pm 20\,\%$ of its mean.

All SR cases, except for SR250-1, are carried out at matched free-stream velocity $U_{\infty }\approx 15~\text{m}~\text{s}^{-1}$ at $x=4~\text{m}$. Due to the limited test section width (0.94 m), measurements are carried out at $x=1.85~\text{m}$ for SR250-1 to achieve $S/\overline{\unicode[STIX]{x1D6FF}}=6.81$.

2.3 Reference cases

Two reference cases for spanwise homogeneous conditions are included in table 1 for comparison to SR cases. The first is the reference smooth-wall case (‘SW’) and the second is the reference rough-wall case (‘RW’), where the surface is constructed entirely from a sheet of P-36 grit sandpaper (the same sandpaper used to form the roughness strips for the SR cases). HWA measurements for these reference cases are taken at similar $Re_{x}\equiv xU_{\infty }/\unicode[STIX]{x1D708}$ to their spanwise heterogeneous counterparts, that is, SW-1 and RW-1 for case SR250-1 at $x=1.85~\text{m}$, SW-2 and RW-2 for all other cases at $x=4~\text{m}$.

Table 2. Summary of reference smooth- and rough-wall cases in viscous-scaled units. $\unicode[STIX]{x1D6FF}_{s}$ and $\unicode[STIX]{x1D6FF}_{r}$ are the 98 % boundary-layer thickness for the smooth- and rough-wall reference cases, respectively, and $\unicode[STIX]{x1D6FF}_{s}^{+}\equiv \unicode[STIX]{x1D6FF}_{s}U_{\unicode[STIX]{x1D70F}}/\unicode[STIX]{x1D708}$, $\unicode[STIX]{x1D6FF}_{r}^{+}\equiv \unicode[STIX]{x1D6FF}_{r}U_{\unicode[STIX]{x1D70F}}/\unicode[STIX]{x1D708}$. $l^{+}$ is the viscous-scaled length of the etched portion of the hot-wire. Coefficient of friction is defined as $C_{f}\equiv 2(U_{\unicode[STIX]{x1D70F}}/U_{\infty })^{2}$.

Figure 5. Boundary-layer profiles from hot-wire measurements of reference smooth- and rough-wall cases, SW-1, SW-2, RW-1 and RW-2 (legend in table 2). (a) Mean streamwise velocity profile $U^{+}$; - - -, $(1/0.384)\log z^{+}+4.17$. (b) Turbulence intensity $\overline{u^{\prime }u^{\prime }}^{+}$; DNS (Sillero, Jiménez & Moser Reference Sillero, Jiménez and Moser2014), filtered according to the spatial resolution $l^{+}$ for SW-1 (——, grey) and SW-2 (——, black). (c) Velocity defect profile $U_{\infty }^{+}-U^{+}$; - - -,$2.3-(1/0.384)\log (z/\unicode[STIX]{x1D6FF}_{99})$, where $\unicode[STIX]{x1D6FF}_{99}$ is the 99 % boundary-layer thickness. Data points are downsampled for clarity.

For the SW cases, the wall friction velocity $U_{\unicode[STIX]{x1D70F}}$ is determined by fitting the mean velocity profile from HWA measurements to the composite profile of Chauhan, Monkewitz & Nagib (Reference Chauhan, Monkewitz and Nagib2009). In the outer region, the smooth-wall turbulent boundary-layer profile follows

(2.1)$$\begin{eqnarray}U^{+}=\frac{1}{\unicode[STIX]{x1D705}}\log z^{+}+A+\frac{2\unicode[STIX]{x1D6F1}}{\unicode[STIX]{x1D705}}{\mathcal{W}}\left(\frac{z}{\unicode[STIX]{x1D6FF}}\right),\end{eqnarray}$$

where subscript ‘$+$’ denotes viscous scaling of velocity and length $U^{+}\equiv U/U_{\unicode[STIX]{x1D70F}}$, $z^{+}\equiv zU_{\unicode[STIX]{x1D70F}}/\unicode[STIX]{x1D708}$, where $\unicode[STIX]{x1D705}$ is the von Kármán constant, $\unicode[STIX]{x1D6F1}$ is the wake parameter and ${\mathcal{W}}$ is the modified wake function (Chauhan et al. Reference Chauhan, Monkewitz and Nagib2009). Here, $\unicode[STIX]{x1D705}=0.384$ and $A=4.17$, following Marusic et al. (Reference Marusic, Chauhan, Kulandaivelu and Hutchins2015). The viscous-scaled parameters for the reference cases are summarised in table 2.

For the RW cases, the profile is shifted from (2.1) according to the Hama roughness function (Hama Reference Hama1954),

(2.2)$$\begin{eqnarray}\unicode[STIX]{x0394}U^{+}=\frac{1}{\unicode[STIX]{x1D705}}\log k_{s}^{+}+A-A_{FR},\end{eqnarray}$$

where $k_{s}^{+}\equiv k_{s}U_{\unicode[STIX]{x1D70F}}/\unicode[STIX]{x1D708}$ and $A_{FR}$ is 8.5, following Nikuradse (Reference Nikuradse1933). As shown in table 2, $k_{s}\approx 2~\text{mm}$ for both RW-1 and RW-2, close to that obtained by Squire et al. (Reference Squire, Morrill-Winter, Hutchins, Schultz, Klewicki and Marusic2016) for the same P-36 sandpaper surface. This value translates to 98 and 91 viscous units for RW-1 and RW-2, respectively.

HWA-measured boundary-layer profiles for these reference cases are shown in figure 5. Figure 5(a) shows that $U^{+}$ for the smooth-wall reference cases SW-1 and SW-2 collapses to the log law $\unicode[STIX]{x1D705}^{-1}\log z^{+}+A$, while $U^{+}$ for the rough-wall cases RW-1 and RW-2 is shifted by $\unicode[STIX]{x0394}U^{+}\approx 7.5$ from this line. Viscous-scaled turbulence intensities $\overline{u^{\prime }u^{\prime }}^{+}$ are shown in figure 5(b). Reasonable collapse is observed for SW-1 and SW-2 to the direct numerical simulation (DNS) results of Sillero et al. (Reference Sillero, Jiménez and Moser2014) at matched $Re_{\unicode[STIX]{x1D703}_{s}}\equiv \unicode[STIX]{x1D703}_{s}U_{\infty }/\unicode[STIX]{x1D708}$, where $\unicode[STIX]{x1D703}_{s}$ is the momentum thickness of the reference smooth-wall cases. It should be noted that the $\overline{u^{\prime }u^{\prime }}$ attributed to the DNS results have been modified to account for the expected attenuation due to the hot-wire spatial resolution $l^{+}\equiv lU_{\unicode[STIX]{x1D70F}}/\unicode[STIX]{x1D708}$ (table 2) utilised in this study. That is, the missing energy, which is assumed to be function of $l^{+}$, has been subtracted from the original DNS statistics, following the approach of Lee, Kevin & Hutchins (Reference Lee, Monty and Hutchins2016). A measure of outer-layer similarity for these reference cases is given in figure 5(c), where velocity defect profiles $U_{\infty }^{+}-U^{+}$ for all cases collapse to the line $2.3-\unicode[STIX]{x1D705}^{-1}\log (z/\unicode[STIX]{x1D6FF}_{99})$, consistent with Marusic et al. (Reference Marusic, Chauhan, Kulandaivelu and Hutchins2015).

2.4 Hot-wire anemometry

Two sets of hot-wire measurements of streamwise velocity are performed for each case of spanwise heterogeneity in table 1. The first is a wall-normal traverse at 40 logarithmically spaced $z$ locations over the centre of the smooth patch to obtain the near-wall profile. The second is a measurement over a spanwise–wall-normal grid, in which profiles are obtained at 11 (cases SR25–SR160) and 15 (cases SR250-1 and SR250-2) spanwise locations over one half-wavelength $S$. The grid spans from the midpoint of the smooth patch to the midpoint of the adjacent rough patch (figure 4c). At each spanwise location, the boundary layer is traversed at 30 logarithmically spaced wall-normal locations. For both smooth- and rough-wall reference cases (SW and RW), only the wall-normal traverse is conducted at the spanwise centre of the test section.

Hot-wire measurements are carried out using a modified Dantec 55P05 single-sensor boundary-layer probe attached to a Dantec 55H21 probe support. The sensor is made by soldering a Woolaston wire with a $5~\unicode[STIX]{x03BC}\text{m}$ diameter platinum core to the tip of the probe. A 1 mm long portion of the wire is etched with nitric acid solution to remove the silver coating, yielding the recommended wire length-to-diameter ratio of 200 (Ligrani & Bradshaw Reference Ligrani and Bradshaw1987). The viscous-scaled etched lengths $l^{+}$ for the reference cases are shown in table 2. The anemometer used in this study is an in-house constant-temperature anemometer (MUCTA) with a fixed overheat ratio of 1.8. The output signal from the constant-temperature anemometer (CTA) is sampled at 30 kHz and low-pass filtered at the cutoff frequency of 15 kHz, corresponding to $t^{+}\sim O(1)$. Sampling time $T$ is set to maintain turnover times $TU_{\infty }/\unicode[STIX]{x1D6FF}\geqslant 20\,000$ (Hutchins et al. Reference Hutchins, Nickels, Marusic and Chong2009), thus allowing the convergence of energy spectra.

The hot-wire probe is calibrated before and after each measurement to obtain the output voltage and streamwise velocity relationship, which is fitted with a third-order polynomial. For the wall-normal traverse, time-based interpolation is applied between pre- and post-calibration curves to compensate for a slight sensor drift. For the spanwise–wall-normal grid measurements, which take longer times, the hot-wire voltage in the free stream is monitored after each wall-normal traverse to account for sensor drift using a modified version of the methodology suggested by Talluru et al. (Reference Talluru, Kulandaivelu, Hutchins and Marusic2014).

Figure 6. (a) Field of view of stereoscopic PIV measurements, stitched from front camera (C$_{F}$) and rear camera (C$_{R}$). (b) Schematic of stereoscopic PIV set-up.

Figure 7. (a) Field of view of wall-parallel PIV measurements, stitched from 3 cameras: C$_{1}$, C$_{2}$ and C$_{3}$. (b) Schematic of wall-parallel PIV set-up. $z_{sheet}$ is the distance between the laser sheet and the wall.

Figure 8. Contours of mean streamwise velocity $U/U_{\infty }$ for reference smooth-wall case SW-2 (a) and spanwise heterogeneous (SR) cases (b–g). All data are obtained from SPIV measurements except for (b), which data are obtained from HWA measurements. The white and black patches correspond to smooth and rough strips, respectively. Vectors indicate $V$ and $W$, downsampled for clarity. Solid white lines mark the three spanwise locations related to the mean secondary flows: common flow up (ⓤ), centre of a mean secondary flow (ⓒ) and common flow down (ⓓ). White dashed lines are the 98 % boundary-layer thickness $\unicode[STIX]{x1D6FF}$ as a function of $y$.

2.5 Stereoscopic PIV

Non-time-resolved cross-stream plane ($y$–$z$) stereoscopic PIV experiments are performed at $x=4$ m. As shown in table 1, SPIV data are available for all spanwise heterogeneous cases and the reference smooth wall, except for cases located at $x=1.85~\text{m}$ (SR250-1 and SW-1) due to limited optical access. SPIV measurements are also not conducted on the reference rough-wall cases (RW-1 and RW-2).

The complete description of the experimental set-up and PIV parameters are given in appendix A. SPIV images are captured from two pco.4000 cameras positioned upstream and downstream of the $y$–$z$-plane (figure 6b). The current set-up gives a field of view (FOV) of approximately $4\unicode[STIX]{x1D6FF}_{s}\times 3\unicode[STIX]{x1D6FF}_{s}$ (figure 6a), where $\unicode[STIX]{x1D6FF}_{s}$ corresponds to the SW-2 case. The FOV width is 240 mm or ${\geqslant}2S$ for SR25, SR50, and SR100, but ${<}2S$ for case SR160 and SR250-2. For these two cases, the FOV is limited to the region near to the rough-to-smooth interface and a complete pair of roll modes is not captured. Furthermore, since a full wavelength is not captured for these two cases, the global mean $\langle \boldsymbol{U}\rangle _{\unicode[STIX]{x1D6EC}}$ and the time-averaged, spanwise variations $\widetilde{\boldsymbol{U}}$ in (1.2) are obtained by reflecting the FOV about the centre of a smooth strip ($y=0$).

2.6 Wall-parallel PIV

In order to more fully capture the spatio-temporal variation of the roll modes, PIV measurements are performed on streamwise–spanwise ($x$–$y$) planes, parallel to the surfaces and non-simultaneous with the SPIV measurements. As with the SPIV, WPPIV measurements are not conducted for cases located at 1.85 m downstream of the trip (SR250-1 and SW-1, table 1) or for the reference rough-wall cases (RW-1 and RW-2).

The complete description of the experimental set-up and PIV parameters are given in appendix B. The streamwise extent of the FOV (figure 7a) extends from $x=3.5~\text{m}$ to $x=4.01~\text{m}$, covering approximately $9\unicode[STIX]{x1D6FF}_{s}$ in the streamwise direction, and is constructed by stitching together three pco.4000 cameras (figure 7b). The spanwise width of the FOV is 270 mm or ${\geqslant}2S$ for SR25, SR50 and SR100, but ${<}2S$ for case SR160 and SR250-2. Similar to the SPIV measurements, the FOV is limited to the region close to the rough-to-smooth interface for case SR160 and SR250-2 and a complete pair of roll modes is not captured for these cases. To capture the roll modes forming above the spanwise heterogeneous roughness surfaces, the WPPIV laser sheet is set at some distance $z_{sheet}$ from the wall (figure 7b), approximately at the centre of the mean secondary flows (figure 8). For the reference smooth-wall case SW-2, the laser sheet is set at $z_{sheet}/\unicode[STIX]{x1D6FF}_{s}=0.5$.

3.1 Mean streamwise velocity

Figure 8 shows the contours of mean streamwise velocity profiles $U$ for the reference smooth-wall case SW-2 (figure 8a) and all spanwise heterogeneous (SR) cases in table 1 (figure 8b–g). Contours are obtained from SPIV measurements, except for case SR250-1 (figure 8b) due to limited optical access at the streamwise location where the measurements are taken. For this case, the contours are constructed from the spanwise–wall-normal grid of HWA measurements. Since no attempt is made to measure $U_{\unicode[STIX]{x1D70F}}$ for these cases, we present $U$ normalised by the free-stream velocity $U_{\infty }$ as a function of outer-scaled wall location $z/\overline{\unicode[STIX]{x1D6FF}}$ and spanwise location $y/S$. The origin of $z$ is at the smooth strips, whereas the virtual origin for the rough strips remains unknown. The contours are presented in the same spatial extent (see ordinate and abscissa on the right-hand sides and figure 8a,b). It should be noted that for cases SR250-1, SR250-2 and SR160 (figure 8b–d), the FOV is ${<}2S$, hence only one half-pair of secondary flows is shown, whereas for cases SR100, SR50 and SR25 (figure 8e–g), at least a complete pair of secondary flows is captured in the FOV.

Figure 9. (a) Mean wall-normal velocity $W$ of case SR50 ($S/\overline{\unicode[STIX]{x1D6FF}}=0.62$) at $z/S=0.5$ obtained from SPIV data (——, grey), smoothed (——, black). The maximum of $W$ is the common flow up (ⓤ), minimum is the common flow down (ⓓ) and $W\approx 0$ is the centre of the secondary flow (ⓒ). (b) Mean secondary flows width $l_{y}$ normalised by $\overline{\unicode[STIX]{x1D6FF}}$ as a function of $S/\overline{\unicode[STIX]{x1D6FF}}$.

The mean secondary flows are shown in figure 8 as vectors of $V$ and $W$ (mean spanwise and wall-normal velocity, respectively). As expected, large-scale mean secondary flows do not exist in the reference smooth-wall case SW-2 (figure 8a). Where spanwise heterogeneity exists, however, large-scale secondary flows are apparent near the roughness transition between the smooth and rough patches. The direction of the secondary flows, for all SR cases, is consistent with that shown in Hinze (Reference Hinze1967, Reference Hinze1973), where turbulent flows are transferred from the high shear stress patch (rough strip) to the low shear stress patch (smooth strip). The resulting mean secondary flows are characterised with regions of upwelling ($W>0$) and downwelling ($W<0$) over the smooth and rough strips, respectively. The spanwise locations of common flow up is identified as the maximum of $W$ at a given wall-normal location (see for example figure 9a), while the common flow down is the minimum. The maxima and minima of $W$ are computed at $z/\overline{\unicode[STIX]{x1D6FF}}=0.35$ for cases SR250–SR100 (figure 8c–e) and $z/S=0.5$ for cases SR50 and SR25 (figure 8f,g) due to the decreasing size of the mean secondary flows. Between common flow up and down, the spanwise location where $W\approx 0$ is the centre of the secondary flows. The spanwise locations of common flow up, centre of the secondary flow and common flow down in figure 8 are marked by symbols ⓤ, ⓒ and ⓓ, respectively. These regions are marked in figure 8 (for clarity only a single secondary flow is annotated in this manner). The local boundary-layer thickness $\unicode[STIX]{x1D6FF}(y)$ is shown by the white dashed line. It is observed in figure 8(c–g) that within the common flow up regions, positive $W$ locally corresponds to a thickening of the boundary layers, whereas within the common flow down regions, negative $W$ drives the flows towards the wall, corresponding to a local thinning of the boundary layers. Based on this observation of local thickening and thinning of the boundary layers, the locations of common flow up and down for case SR250-1 (figure 8b) can be estimated even though the vectors of $V$ and $W$ are not available for this case.

Figure 8 also shows how the size of the secondary flows vary with the roughness patch size. We define $l_{y}$ as the width of the secondary flow, measured from the spanwise location of the common flow up to down (ⓤ and ⓓ in figure 8). $l_{y}$ for various $S/\overline{\unicode[STIX]{x1D6FF}}$ can be approximated as

(3.1)$$\begin{eqnarray}l_{y}\approx \left\{\begin{array}{@{}ll@{}}C\overline{\unicode[STIX]{x1D6FF}}, & S/\overline{\unicode[STIX]{x1D6FF}}\geqslant C\\ S, & S/\overline{\unicode[STIX]{x1D6FF}}<C.\end{array}\right.\end{eqnarray}$$

The precise value of the constant $C$ in (3.1) will vary according to the assessment method. An assessment of figure 8 and the extent of non-zero swirl strength in figure 11 suggest that $C\approx 0.7$ is a good approximation for the present data (figure 9b). Regardless of the assessment method, the overall trend shown by figure 9(b) holds; when $S/\overline{\unicode[STIX]{x1D6FF}}$ is small, the size of the secondary flow is a function of $S$, but when $S$ becomes comparable to $\overline{\unicode[STIX]{x1D6FF}}$, the size of the secondary flow seems to asymptote to a constant. The effect of patch size (and consequently the size of the secondary flows) on $U$ is discussed in the following.

Figure 10. Mean streamwise velocity $U/U_{\infty }$ for SR cases. Red curves show centre of the rough patch, blue curves show centre of the smooth patch and grey curves show all intermediate positions. Reference SW and RW case data are plotted for comparison using symbols defined in table 2, normalised by $\unicode[STIX]{x1D6FF}_{s}$ and $\unicode[STIX]{x1D6FF}_{r}$. The legend is given schematically at the top of the figure.

Figure 11. Large-scale secondary flows shown by the mean swirl strength $\unicode[STIX]{x1D6EC}_{ci}$ multiplied by the sign of vorticity $\unicode[STIX]{x1D6FA}_{x}/|\unicode[STIX]{x1D6FA}_{x}|$. Red and blue indicate counterclockwise (CCW) and clockwise (CW) secondary flows, respectively. In (b), —— illustrates the area of integration in (3.2).

The largest $S/\overline{\unicode[STIX]{x1D6FF}}$ cases correspond to SR250-1 ($S/\overline{\unicode[STIX]{x1D6FF}}=6.81$) and SR250-2 ($S/\overline{\unicode[STIX]{x1D6FF}}=3.63$). These cases (figure 8b,c) exhibit a thicker boundary layer above the rough patch than that above the smooth patch, with the exception of the area surrounding the secondary flows. For these largest $S/\overline{\unicode[STIX]{x1D6FF}}$ cases, $U$ is slower above the centre of a rough patch than above the centre of a smooth patch at any $z/\overline{\unicode[STIX]{x1D6FF}}$. This is consistent with observations from either a homogeneous rough- or smooth-wall flow at a matched free-stream velocity. Figure 10 shows the profiles of $U$ in various spanwise locations as a function of $z/\overline{\unicode[STIX]{x1D6FF}}$. For the largest spanwise wavelengths (SR250-1 and SR250-2, figures 10a and 10b, respectively), the profiles at the centres of the smooth and rough strips nearly collapse to the corresponding homogeneous smooth and rough reference cases (SW and RW, respectively), suggesting that for these largest $S/\overline{\unicode[STIX]{x1D6FF}}$, the centre of the rough and smooth strips are in near equilibrium with their local boundary conditions, as observed by Chung et al. (Reference Chung, Monty and Hutchins2018). Hinze (Reference Hinze1967) suggests that secondary flows occur where the production–dissipation imbalance occurs, i.e. somewhere near the spanwise roughness transition. When $S$ is larger than $\overline{\unicode[STIX]{x1D6FF}}$, the secondary flows have approximate diameter $\overline{\unicode[STIX]{x1D6FF}}$ and are confined near the transition between smooth–rough patch (figure 2a). Sufficiently far removed in the span from these secondary flows, the flow becomes locally homogeneous in accord with the local surface conditions and therefore the smooth and rough patches approach the reference SW and RW cases, respectively. In these regions, we would expect outer-layer similarity to be preserved. In figures 8 and 10, we observe locally homogeneous conditions for $S/\overline{\unicode[STIX]{x1D6FF}}\gtrsim 3$, which is comparable to the limit found in other studies, such as $S/\unicode[STIX]{x1D6FF}\gtrsim 6$ (Chung et al. Reference Chung, Monty and Hutchins2018) for strip-type roughness, and $L/(2\unicode[STIX]{x1D6FF})>1.6$ (Medjnoun et al. Reference Medjnoun, Vanderwel and Ganapathisubramani2018), $L/(2\unicode[STIX]{x1D6FF})\gtrsim 1$ (Yang & Anderson Reference Yang and Anderson2018) for ridge-type roughness.

The intermediate case of $S/\overline{\unicode[STIX]{x1D6FF}}\approx 1$ is approximately attained for cases SR100 and SR50, which correspond to $S/\overline{\unicode[STIX]{x1D6FF}}=1.35$ and 0.62, respectively (figure 8e,f). For these cases, the boundary layer is thicker above the smooth patch than above the rough patch. The velocity profiles in figure 10(d,e) show that, away from the immediate near-wall region ($z/\overline{\unicode[STIX]{x1D6FF}}\gtrsim 0.05$), the flow slows down above the centres of the smooth strips and speeds up above the centres of the rough strips. This is the opposite behaviour to that observed for $S/\overline{\unicode[STIX]{x1D6FF}}\gg 1$ (figures 10a,b and 8b,c). We attribute the switch in this behaviour to the secondary flows at the limit of $S/\overline{\unicode[STIX]{x1D6FF}}\approx 1$. At this limit of $S/\overline{\unicode[STIX]{x1D6FF}}\approx 1$, the secondary flows fill the space inside the boundary layer such that in this case the centres of the smooth strips are characterised by common flow up, where the flow is pushed upward, thickening the boundary layers above the smooth strips (ⓤ in figure 8e,f). Common flow down is observed somewhere nearby the roughness transitions (ⓓ in figure 8e) or at the centres of the rough strips (ⓓ in figure 8f), leading to the thinning of the boundary layers above the rough strips. A similar switch in the isovels (a switch in whether low or high speed occurs above the rough or smooth strips) is also documented in other studies, with the range where behaviour switches estimated as $S/\unicode[STIX]{x1D6FF}\approx$ 0.8–3 (Chung et al. Reference Chung, Monty and Hutchins2018), $L/(2\unicode[STIX]{x1D6FF})\approx 0.5$ (Medjnoun et al. Reference Medjnoun, Vanderwel and Ganapathisubramani2018), $0.5\lesssim L/(2\unicode[STIX]{x1D6FF})\lesssim 1$ (Yang & Anderson Reference Yang and Anderson2018). It should be noted that this behaviour is expected as $S/\overline{\unicode[STIX]{x1D6FF}}$ continues to decrease. As the strips become narrower, a secondary cell is restricted by its spanwise-adjacent secondary cell such that the common flow up occurs above the centre of smooth strips and common flow down above the centre of rough strips.

The limiting case $S/\overline{\unicode[STIX]{x1D6FF}}\ll 1$ is represented by case SR25 ($S/\overline{\unicode[STIX]{x1D6FF}}=0.32$) in figure 8(g). Since $S<\overline{\unicode[STIX]{x1D6FF}}$, the diameter of secondary flows is limited by $S$ instead of $\overline{\unicode[STIX]{x1D6FF}}$ and hence these secondary flows are confined closer to the wall. The contour in figure 8(g) shows that for wall-normal distances beyond the influence of the secondary flows, the boundary layer approaches a spanwise homogeneous condition, as illustrated in figure 2(c), and the boundary-layer thickness is approximately constant across the spanwise extent. In figure 10(f), it is noted that $U/U_{\infty }$ collapses at all spanwise positions for $z/\overline{\unicode[STIX]{x1D6FF}}\gtrsim 0.32=S/\overline{\unicode[STIX]{x1D6FF}}$, suggesting spanwise homogeneity. We note that this homogeneous outer velocity profile for $z/\overline{\unicode[STIX]{x1D6FF}}>0.32$ falls somewhere between the reference SW and RW cases. This limiting case is documented in other studies as $L/(2\unicode[STIX]{x1D6FF})\leqslant 0.23$ (Vanderwel & Ganapathisubramani Reference Vanderwel and Ganapathisubramani2015), $S/\unicode[STIX]{x1D6FF}<0.4$ (Chung et al. Reference Chung, Monty and Hutchins2018) and $L/(2\unicode[STIX]{x1D6FF})\lesssim 0.5$ (Yang & Anderson Reference Yang and Anderson2018). We also note certain parallels with the study of homogeneous sinusoidal egg-carton type roughness by Chan et al. (Reference Chan, Chung, MacDonald, Hutchins and Ooi2018), which showed that spanwise homogeneity is attained when $z\gtrsim 0.5\unicode[STIX]{x1D706}$, where $\unicode[STIX]{x1D706}$ is the spanwise wavelength of the sinusoids.

3.2 Time-averaged strength of the secondary flows: mean swirl

Figure 11 shows the swirl strength $\unicode[STIX]{x1D6EC}_{ci}$ for all of the cases in table 1 (where SPIV data are available). The swirl strength is defined as the imaginary part of the complex eigenvalue of the mean velocity gradient tensor (Tomkins & Adrian Reference Tomkins and Adrian2003). The direction of the swirl, either clockwise (CW) or counterclockwise (CCW), is obtained by multiplying the swirl strength by the sign of mean vorticity, $\unicode[STIX]{x1D6FA}_{x}/|\unicode[STIX]{x1D6FA}_{x}|$, $\unicode[STIX]{x1D6FA}_{x}\equiv \unicode[STIX]{x2202}W/\unicode[STIX]{x2202}y-\unicode[STIX]{x2202}V/\unicode[STIX]{x2202}z$. The quantity $\unicode[STIX]{x1D6EC}_{ci}\unicode[STIX]{x1D6FA}_{x}/|\unicode[STIX]{x1D6FA}_{x}|$ in figure 11 is normalised by the free-stream velocity and the boundary-layer thickness of the reference smooth-wall case SW-2, $U_{\infty }/\unicode[STIX]{x1D6FF}_{s}$.

Figure 12. Integrated mean swirl strength $I_{\unicode[STIX]{x1D6EC}_{ci}}$ as a function of $S/\overline{\unicode[STIX]{x1D6FF}}$. $I_{\unicode[STIX]{x1D6EC}_{ci}}$ of counterclockwise (–▪–, red) and clockwise (–▪–, blue) roll modes inside the FOV (if any). Dashed line (- - -) is the reference smooth-wall case (SW-2).

In figure 11(b–f), regions of non-zero swirl strength clearly show the counter-rotating large-scale mean secondary flows due to spanwise heterogeneity. The strength of the swirl appears to be dependent on $S/\overline{\unicode[STIX]{x1D6FF}}$, with the strongest swirl at case SR50 ($S/\overline{\unicode[STIX]{x1D6FF}}=0.62$, figure 11e). The mean swirl then decays in strength and size as $S/\overline{\unicode[STIX]{x1D6FF}}$ decreases further to SR25 ($S/\overline{\unicode[STIX]{x1D6FF}}=0.32$, figure 11f). To investigate this further, the strength of the mean secondary flows is quantified for every case by integrating $\unicode[STIX]{x1D6EC}_{ci}\unicode[STIX]{x1D6FA}_{x}/|\unicode[STIX]{x1D6FA}_{x}|$ across a span $\pm 0.5l_{y}$ about the spanwise location of the centre of the secondary flows $y_{c}$ (ⓒ in figure 8), and the wall-normal location, $0<z\leqslant l_{y}$

(3.2)$$\begin{eqnarray}I_{\unicode[STIX]{x1D6EC}_{ci}}=\frac{1}{N}\mathop{\sum }^{N}\frac{1}{l_{y}^{2}}\int _{0}^{l_{y}}\int _{y_{c}-l_{y}/2}^{y_{c}+l_{y}/2}\left|\unicode[STIX]{x1D6EC}_{ci}\frac{\unicode[STIX]{x1D6FA}_{x}}{|\unicode[STIX]{x1D6FA}_{x}|}\frac{\unicode[STIX]{x1D6FF}_{s}}{U_{\infty }}\right|\,\text{d}y\,\text{d}z,\end{eqnarray}$$

where $l_{y}^{2}$ is the area of integration marked by —— in figure 11(b). For cases where a number ($N$) of roll modes are present in the FOV (cases SR25 and SR50), the integrated swirl is averaged over $N$. For the reference smooth-wall SW-2 case, $\unicode[STIX]{x1D6EC}_{ci}\unicode[STIX]{x1D6FA}_{x}/|\unicode[STIX]{x1D6FA}_{x}|$ is integrated over the entire FOV, $-2\unicode[STIX]{x1D6FF}_{s}\leqslant y\leqslant 2\unicode[STIX]{x1D6FF}_{s}$ and $0\leqslant z\leqslant \unicode[STIX]{x1D6FF}_{s}$. The integrated swirl strength $I_{\unicode[STIX]{x1D6EC}_{ci}}$ as a function of $S/\overline{\unicode[STIX]{x1D6FF}}$ in figure 12 confirms the observation from figure 11 and preliminary results in Wangsawijaya et al. (Reference Wangsawijaya, de Silva, Baidya, Chung, Marusic and Hutchins2019). The value of $I_{\unicode[STIX]{x1D6EC}_{ci}}$ is close to zero over a smooth wall (case SW-2, dashed line in figure 12), peaks at case SR50 ($S/\overline{\unicode[STIX]{x1D6FF}}\approx 1$) and decays as $S/\overline{\unicode[STIX]{x1D6FF}}$ increases further.

4.1 Turbulence energy spectra

To further explore the nature of the turbulence under the imposed spanwise heterogeneities, the energy spectrograms (constructed from hot-wire measurements) of all SR cases are presented and discussed in the following. The power spectral density of the streamwise turbulent fluctuations $\unicode[STIX]{x1D6F7}_{u^{\prime }u^{\prime }}$ in the streamwise direction is defined as

(4.1)$$\begin{eqnarray}\overline{u^{\prime }u^{\prime }}=\int _{0}^{\infty }\unicode[STIX]{x1D6F7}_{u^{\prime }u^{\prime }}\,\text{d}(k_{x}).\end{eqnarray}$$

Here, $k_{x}\equiv 2\unicode[STIX]{x03C0}/\unicode[STIX]{x1D706}_{x}$ is defined as the streamwise wavenumber and $\unicode[STIX]{x1D706}_{x}\equiv U(y,z)/f$ is the streamwise wavelength, where $f$ is the sampling frequency and $U(y,z)$ is the mean streamwise velocity at each spanwise–wall-normal grid data point. We assume Taylor’s hypothesis (Taylor Reference Taylor1938) to project time-series data spatially, with the local mean $U(y,z)$ as the assumed convection velocity. Specifically, here we are focussing on energetic signatures that are in the range of $\unicode[STIX]{x1D706}_{x}/\overline{\unicode[STIX]{x1D6FF}}=3{-}6$. The limitation of Taylor’s hypothesis over large projected streamwise distance was investigated by Dennis & Nickels (Reference Dennis and Nickels2008). They confirmed the accuracy of Taylor’s approximation for projection distances up to 6$\unicode[STIX]{x1D6FF}$, which covers the range of events investigated here. Furthermore, we show later in § 4.2 that the results from energy spectra are supported by true spatial measurements from WPPIV. The premultiplied energy spectrograms are normalised by free-stream velocity $U_{\infty }^{2}$, since $U_{\unicode[STIX]{x1D70F}}$ is not available for the spanwise heterogeneous cases.

Figure 13. Premultiplied 1-D streamwise energy spectra $k_{x}\unicode[STIX]{x1D6F7}_{u^{\prime }u^{\prime }}$ as a function of streamwise wavelength $\unicode[STIX]{x1D706}_{x}$ and wall location $z$ of (a) reference homogeneous cases (SW-2 and RW-2) and (b–f) SR cases: (i) is the spectrogram at the centre of the smooth patch and (ii) is at the centre of the rough patch (legends are at the top of the page). Label Ⓘ indicates the energetic peak associated with the secondary flow. Inner-scaled axis are available for (a) at the right and side and top, where $U_{\unicode[STIX]{x1D70F}}$ is obtained by composite fit described in § 2.3. Dashed line in (f) is $z/\overline{\unicode[STIX]{x1D6FF}}=0.32$.

Figure 14. Isosurface of 1-D streamwise energy spectra $k_{x}\unicode[STIX]{x1D6F7}_{u^{\prime }u^{\prime }}$ across half-wavelength $S$ for cases (a) SR250-1, (b) SR250-2, (c) SR160, (d) SR100, (e) SR50, (f) SR25. Colour level: blue ($k_{x}\unicode[STIX]{x1D6F7}_{u^{\prime }u^{\prime }}/U_{\infty }^{2}=0.001$), yellow (0.0015) and red (0.002). Label Ⓘ denotes the peak associated with the secondary flows exist. The red box in (e) is the integration domain in (4.2).

Figure 13(a) shows the premultiplied energy spectrograms $k_{x}\unicode[STIX]{x1D6F7}_{u^{\prime }u^{\prime }}$ for the homogeneous smooth- and rough-wall reference cases (SW-2 and RW-2). The premultiplied energy spectrograms are shown as a function of $\unicode[STIX]{x1D706}_{x}$ and $z$, normalised by $\unicode[STIX]{x1D6FF}_{s}$ (SW-2) or $\unicode[STIX]{x1D6FF}_{r}$ (RW-2) at the left-hand side and bottom axis. The inner-scaled $\unicode[STIX]{x1D706}_{x}$ and $z$ ($\unicode[STIX]{x1D706}_{x}^{+}$ and $z^{+}$) are shown in the right-hand side and top axis for the reference cases only. The inner peak representing the viscous near-wall cycle (Hutchins & Marusic Reference Hutchins and Marusic2007b) of SW-2 ($\unicode[STIX]{x1D6FF}_{s}^{+}=2030$), marked by ‘$+$’ in figure 13(a), is captured at $z/\unicode[STIX]{x1D6FF}_{s}\approx 0.01$ and $\unicode[STIX]{x1D706}_{x}/\unicode[STIX]{x1D6FF}_{s}\approx 0.5$, which correspond to $z^{+}\approx 15$ and $\unicode[STIX]{x1D706}_{x}^{+}\approx 1000$. A smaller outer peak (also marked by ‘$+$’) emerges at $z/\unicode[STIX]{x1D6FF}_{s}\approx 0.1$, whose wavelength is $\unicode[STIX]{x1D706}_{x}/\unicode[STIX]{x1D6FF}_{s}\approx 6$, consistent with that of long, meandering large-scale structures observed in the logarithmic region by Hutchins & Marusic (Reference Hutchins and Marusic2007a,Reference Hutchins and Marusicb), Mathis, Hutchins & Marusic (Reference Mathis, Hutchins and Marusic2009) and others. The reference rough-wall case RW-2 in figure 13(a) has overall higher energy than that of SW-2. A peak (marked by ‘$+$’) is detected within the logarithmic region at $z/\unicode[STIX]{x1D6FF}_{r}\approx 0.1$, $\unicode[STIX]{x1D706}_{x}/\unicode[STIX]{x1D6FF}_{r}\approx 3$.

The energy spectrograms of the spanwise heterogeneous cases are shown for the cases measured at $x=4$ m: SR250-2 ($S/\overline{\unicode[STIX]{x1D6FF}}=3.63$, figure 13b), SR160 ($S/\overline{\unicode[STIX]{x1D6FF}}=2.28$, figure 13c), SR100 ($S/\overline{\unicode[STIX]{x1D6FF}}=1.35$, figure 13d), SR50 ($S/\overline{\unicode[STIX]{x1D6FF}}=0.62$, figure 13e) and SR25 ($S/\overline{\unicode[STIX]{x1D6FF}}=0.32$, figure 13f), plotted as a function of $\unicode[STIX]{x1D706}_{x}/\overline{\unicode[STIX]{x1D6FF}}$ and $z/\overline{\unicode[STIX]{x1D6FF}}$. For each case, the spectrogram is shown at two spanwise locations: the centre of a smooth strip (marked by (i) in figure 13) and the centre of a rough strip (marked by (ii) in figure 13).

Comparisons are drawn between the spectrograms of the reference smooth-wall case SW-2 and the spanwise heterogeneous roughness cases. In terms of the viscous near-wall cycle, the reference smooth-wall case SW-2 and all of the spanwise heterogeneous cases over the centre of a smooth strip show a nearly constant location of the inner peak (marked by ‘$+$’) at $z/\overline{\unicode[STIX]{x1D6FF}}\approx 0.01$, $\unicode[STIX]{x1D706}_{x}/\overline{\unicode[STIX]{x1D6FF}}\approx 0.5$ (figure 13b (i)–f (i)). Later, we show that the increasing strength of secondary flows and increasing meandering are observed for $\unicode[STIX]{x1D706}_{y}/\overline{\unicode[STIX]{x1D6FF}}\approx 2$, which roughly corresponds to $\unicode[STIX]{x1D706}_{y}^{+}\approx 4000$ wall units or 40 times the Kline spacing (${\approx}100U_{\unicode[STIX]{x1D70F}}/\unicode[STIX]{x1D708}$) of the near-wall streaks (Kline et al. Reference Kline, Reynolds, Schraub and Runstadlers1967). This supports the observation in Stroh et al. (Reference Stroh, Hasegawa, Kriegseis and Frohnapfel2016) and Vanderwel et al. (Reference Vanderwel, Stroh, Kriegseis, Frohnapfel and Ganapathisubramani2019), that outer scaling is more relevant than inner scaling in the formation of secondary flows. The spectrograms in the outer layer, however, differ between the reference smooth-wall and spanwise heterogeneous cases. In case SR250-2 (the limit where $S/\overline{\unicode[STIX]{x1D6FF}}\gg 1$, figure 13b), we observe that the energy spectrograms over the centre of the smooth and the rough strips best resemble the homogeneous reference cases (figure 13a) as compared to other cases. This observation from the spectra is in line with that from the mean velocity profiles of figures 10 and 8 for $S/\overline{\unicode[STIX]{x1D6FF}}\gg 1$. The outer peak for SW-2 (figure 13a) occurs at $\unicode[STIX]{x1D706}_{x}/\unicode[STIX]{x1D6FF}_{s}\approx 6$, $z/\unicode[STIX]{x1D6FF}_{s}\approx 0.1$ and is associated with the large-/very large-scale motions (LSM/VLSM) in the log region. For SR250-2, this peak (marked by ‘$+$’ in figure 13b (i)) is still present over the centre of the smooth strip but is now supplemented with additional energy at $\unicode[STIX]{x1D706}_{x}/\overline{\unicode[STIX]{x1D6FF}}\approx 3$, $z/\overline{\unicode[STIX]{x1D6FF}}\approx 0.2$ (labelled Ⓘ in figure 13). The additional energetic sites labelled Ⓘ in these figures are presumed to be related to the secondary flows formed over these surfaces. As $S/\overline{\unicode[STIX]{x1D6FF}}$ decreases to 2.28 (figure 13c (i)), this additional outer bump of energy at $\unicode[STIX]{x1D706}_{x}/\overline{\unicode[STIX]{x1D6FF}}\approx 3$ is pushed outwards towards $z/\overline{\unicode[STIX]{x1D6FF}}\approx 0.5$, which approximately coincides with the wall-normal location of the centre of the secondary flow (figure 8d). The relation between the peak associated with LSM/VLSM and secondary flows due to heterogeneity is discussed further in § 5. Meanwhile, the energy spectra above the rough strips (figure 13b (ii), c (ii)) still resemble those above the reference rough wall RW-2 (figure 13a), which is expected since the counter-rotating pairs of secondary flows tend to move towards the centres of the smooth strips (instead of rough strips) as $S/\overline{\unicode[STIX]{x1D6FF}}$ decreases (figure 8).

The spectrograms for cases where $S/\overline{\unicode[STIX]{x1D6FF}}\approx 1$ (figure 13d,e) offer a new insight. In this case, the spectrogram above the smooth strip exhibits a strong additional energetic site at a wavelength of $\unicode[STIX]{x1D706}_{x}/\overline{\unicode[STIX]{x1D6FF}}\approx 3$ at a wall-normal location of $z/\overline{\unicode[STIX]{x1D6FF}}\approx 0.5$ for SR100 (figure 13d (i)) and $z/\overline{\unicode[STIX]{x1D6FF}}\approx 0.3$ for SR50 (figure 13e (i)), roughly corresponding to the wall-normal location of the centre of the secondary flows for these configurations (figure 8e,f). As this additional outer peak above the centre of a smooth strip becomes stronger in case SR50 ($S/\overline{\unicode[STIX]{x1D6FF}}=0.62$, figure 13e (i)), the energy in the outer layer of the rough strip becomes less prominent (figure 13e (ii)).

As $S/\overline{\unicode[STIX]{x1D6FF}}$ decreases further to the small limit where $S/\overline{\unicode[STIX]{x1D6FF}}\ll 1$ (SR25, figure 13f), the energy levels over the smooth and rough strips appear more equal, and no longer resemble the reference cases. We note that the outer peak over the centre of a smooth and a rough strip is now located at $z/\overline{\unicode[STIX]{x1D6FF}}\approx 0.1$ (close to the location in the reference cases). For $z/\overline{\unicode[STIX]{x1D6FF}}>0.32$ (corresponding to $z>S$, marked by the dashed line in figure 13f), the energy spectrograms over the rough and smooth strips are almost the same, indicating a return to spanwise homogeneity in the outer region for this case.

In figure 14, the 3-D isosurfaces of streamwise energy spectrograms are plotted for all SR cases to show the complete spanwise variation in energy. The isosurfaces are plotted as a function of the streamwise wavelength $\unicode[STIX]{x1D706}_{x}/\overline{\unicode[STIX]{x1D6FF}}$, spanwise location $y/S$ and wall-normal location $z/\overline{\unicode[STIX]{x1D6FF}}$. The isosurfaces span one half-wavelength $S$, where $y/S=0$ is the centre of a smooth strip, $y/S=0.5$ is the roughness transition and $y/S=1$ is the centre of the adjacent rough strip. For clarity, only three levels are shown. Note that the aspect ratio of spanwise to wall-normal axes is not preserved between plots in figure 14. For example, figure 13(a) covers a much wider spanwise domain ($6.81\overline{\unicode[STIX]{x1D6FF}}$) than figure 14(f) ($0.32\overline{\unicode[STIX]{x1D6FF}}$).

At the limit where $S/\overline{\unicode[STIX]{x1D6FF}}\gg 1$, the energy spectrograms of SR250-1 ($S/\overline{\unicode[STIX]{x1D6FF}}=6.81$) in figure 14(a) exhibit the expected behaviour. The rough patch has higher energy than the smooth patch and the behaviour is relatively homogeneous across the rough and smooth strips. A small bulge of energy in the outer layer is noticeable near the roughness transition, at $y/S\approx 0.4$ (visible in the blue isosurface and labelled Ⓘ). As $S/\overline{\unicode[STIX]{x1D6FF}}$ reduces through figure 14(b,c), the degree of spanwise uniformity over either the rough or smooth patches diminishes. The bulge remains as $S/\overline{\unicode[STIX]{x1D6FF}}$ decreases and extends towards the centre of the smooth patch. This bulge is centred at $y/S\approx 0.3$ in case SR250-2 (figure 14b) and nearly throughout the spanwise extent of the smooth patch for case SR160 (figure 14c), appearing to be related to the regions of common flow up (figure 8b–d) due to the secondary flows, where the boundary layer thickens and there is a local low momentum pathway.

As $S/\overline{\unicode[STIX]{x1D6FF}}$ decreases to the intermediate case where $S/\overline{\unicode[STIX]{x1D6FF}}\approx 1$ in figure 14(d) (SR100, $S/\overline{\unicode[STIX]{x1D6FF}}=1.35$), the counter-rotating secondary flows fill the entire spanwise and wall-normal extent of the boundary layer and common flow up occurs over the centre of smooth strips. The extra bulge of energy now becomes stronger still (yellow isosurface) and is approximately centred at $z/\overline{\unicode[STIX]{x1D6FF}}\approx 0.5$ and with a characteristic length scale of $\unicode[STIX]{x1D706}_{x}/\overline{\unicode[STIX]{x1D6FF}}\approx 3$. The bulge is even stronger (red isosurface) as $S/\overline{\unicode[STIX]{x1D6FF}}$ decreases to 0.62 (SR50, figure 14e), appearing over the roughness transition ($y/S=0.5$) and spanning the wall-normal location $0.1\lesssim z/\overline{\unicode[STIX]{x1D6FF}}\lesssim 0.5$. The streamwise wavelength of the bulge is roughly unchanged from the previous case at $\unicode[STIX]{x1D706}_{x}/\overline{\unicode[STIX]{x1D6FF}}\approx 3$.

In the limit where $S/\overline{\unicode[STIX]{x1D6FF}}\ll 1$, figure 14(f) shows that the energy spectrograms of the smooth and rough strips approach spanwise homogeneity. The two roughness strips have similar energy spectrograms in the outer layer. Closer to the surface, energy spectrograms are governed by their respective wall conditions, notably with high energy above the rough patch. An energy bulge is detected above the roughness transition ($y/S=0.5$) at $\unicode[STIX]{x1D706}_{x}/\overline{\unicode[STIX]{x1D6FF}}\approx 3$ and $z/\overline{\unicode[STIX]{x1D6FF}}\approx 0.1$. However, the main observation from figure 14(f) is that beyond the expected secondary flows, i.e. $z/\overline{\unicode[STIX]{x1D6FF}}\gtrsim 0.32$, the energy across the rough and smooth strips is homogeneous, marking the return to spanwise homogeneity as suggested by Chung et al. (Reference Chung, Monty and Hutchins2018) and Medjnoun et al. (Reference Medjnoun, Vanderwel and Ganapathisubramani2018), and as illustrated in figure 2(c).

Figure 15. Integrated energy spectra $I_{\unicode[STIX]{x1D6F7}_{u^{\prime }u^{\prime }}}$ as a function of $S/\overline{\unicode[STIX]{x1D6FF}}$ for SR cases (–▪–). Dashed line (- - -) is reference smooth wall SW-1 and dash-dot line (– ⋅ – ⋅ –) is reference rough wall RW-2.

The additional information provided by the energy spectra in figures 13 and 14 is the presence of an additional outer energetic peak approximately above the roughness transition, where secondary flows occur. We quantify the strength of this emergent peak in the energy spectra by integrating $k_{x}\unicode[STIX]{x1D6F7}_{u^{\prime }u^{\prime }}$ within the volume in figure 14, in which this emergent peak resides. The integration volume (figure 14e) comprises a range of streamwise wavelengths encompassing a region in the spectrograms where the energy peak is observed ($1\leqslant \unicode[STIX]{x1D706}_{x}/\overline{\unicode[STIX]{x1D6FF}}\leqslant 10$), the wall-normal extent up to the boundary-layer height ($0<z\leqslant \overline{\unicode[STIX]{x1D6FF}}$), and a span $\pm 0.5l_{y}$ about the spanwise location of the centre of the secondary flows $y_{c}$ (ⓒ in figure 8), $l_{y}$ is the width of the mean secondary flows defined in (3.1). The integrated energy is given by

(4.2)$$\begin{eqnarray}I_{\unicode[STIX]{x1D6F7}_{u^{\prime }u^{\prime }}}=\frac{1}{\overline{\unicode[STIX]{x1D6FF}}l_{y}}\int _{0}^{\overline{\unicode[STIX]{x1D6FF}}}\;\int _{y_{c}-l_{y}/2}^{y_{c}+l_{y}/2}\;\int _{2\unicode[STIX]{x03C0}/\overline{\unicode[STIX]{x1D6FF}}}^{2\unicode[STIX]{x03C0}/(10\overline{\unicode[STIX]{x1D6FF}})}\frac{\unicode[STIX]{x1D6F7}_{u^{\prime }u^{\prime }}}{U_{\infty }^{2}}\,\text{d}k_{x}\,\text{d}y\,\text{d}z.\end{eqnarray}$$

For comparison, the integrated energy is also calculated for the reference smooth- and rough-wall cases

(4.3)$$\begin{eqnarray}I_{\unicode[STIX]{x1D6F7}_{u^{\prime }u^{\prime }}}=\frac{1}{\unicode[STIX]{x1D6FF}}\int _{0}^{\unicode[STIX]{x1D6FF}}\int _{2\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FF}}^{2\unicode[STIX]{x03C0}/(10\unicode[STIX]{x1D6FF})}\frac{\unicode[STIX]{x1D6F7}_{u^{\prime }u^{\prime }}}{U_{\infty }^{2}}\,\text{d}k_{x}\,\text{d}z,\end{eqnarray}$$

where $\unicode[STIX]{x1D6FF}$ is either $\unicode[STIX]{x1D6FF}_{s}$ for the reference smooth-wall cases (SW-1 and SW-2) or $\unicode[STIX]{x1D6FF}_{r}$ for the reference rough-wall cases (RW-1 and RW-2).

The magnitude of $I_{\unicode[STIX]{x1D6F7}_{u^{\prime }u^{\prime }}}$ as a function of $S/\overline{\unicode[STIX]{x1D6FF}}$ is shown in figure 15, along with the integrated energy from both smooth and rough reference cases. In the limit where $S/\overline{\unicode[STIX]{x1D6FF}}\gg 1$, the integrated energy of case SR250-1 ($S/\overline{\unicode[STIX]{x1D6FF}}=6.81$) approaches its reference smooth-wall counterpart (SW-1, dashed line in figure 15). In the other limit, as$S/\overline{\unicode[STIX]{x1D6FF}}\ll 1$, we would expect the energy within the integral bounds to asymptote to some value between the reference SW and RW cases. This case is represented by SR25 ($S/\overline{\unicode[STIX]{x1D6FF}}=0.32$), whose integrated energy falls below its reference rough-wall counterpart (RW-2, dash-dot line in figure 15). Clearly, figure 15 indicates that there is an $S/\overline{\unicode[STIX]{x1D6FF}}$ dependency in the energy within the integral limits, with a clear peak occurring at $S/\overline{\unicode[STIX]{x1D6FF}}\approx 1$. The peak in the energy indicates an additional periodicity that becomes prominent at case SR50 ($S/\overline{\unicode[STIX]{x1D6FF}}=0.62$, $S/\overline{\unicode[STIX]{x1D6FF}}\approx 1$) and seems to be related to the location of the secondary flows. This suggests that there is some time-varying dependence or instability of the secondary flows that emerges at these spanwise wavelengths. We also note that the trend shown in figure 15 is similar to that of the mean secondary flow strength in figure 12. At this point, with only hot-wire time-series data, we lack the ability to reconstruct a view of the flow structure that leads to these features in the energy spectra. We are able, however, to view the flow structure through the instantaneous velocity fields in the $x$–$y$-plane taken from the WPPIV measurements.

Figure 16. Snapshot of $\widetilde{u}^{\prime }$ (turbulent fluctuations and mean spanwise variation) for (a) the reference smooth-wall case SW-2, (b) SR100 and (c) SR50, taken from WPPIV measurements. Dashed lines are the spanwise locations related to the common flow up (ⓤ) and common flow down (ⓓ) of the mean secondary flows.

Figure 16 shows the instantaneous velocity fields for the reference smooth-wall case SW-2 (figure 16a) and the intermediate cases, $S/\overline{\unicode[STIX]{x1D6FF}}\approx 1$, where a strong outer peak in the energy spectra is observed (SR100 and SR50, figures 16b and 16c, respectively). It should be noted that the HWA-measured energy spectrograms are constructed from the turbulent fluctuations $u^{\prime }$, while the velocity fields in figure 16 are shown as $\widetilde{u}^{\prime }$ (these two quantities are equal in the reference smooth-wall case). Long, large-scale structures, spanning the entire streamwise extent of the FOV, can be observed clearly in the intermediate cases (figure 16b,c), but less so in the reference smooth-wall case SW-2 (figure 16a). These PIV planes slice the centre of the mean secondary flows for the spanwise heterogeneous cases, hence we believe that we capture the instantaneous flow fields of the secondary flows in figure 16(b,c). These flow fields suggest that the secondary flows are not a time-invariant feature, and instead exhibit a prominent spatial meandering.

4.2 Turbulent fluctuation velocity fields

To further examine the meandering behaviour of the secondary flows shown by the HWA-measured energy spectrograms, two-point correlations of the velocity fields obtained from SPIV and WPPIV measurements are computed. The correlations are computed for the streamwise turbulent fluctuations $u^{\prime }$ (figure 3). To limit the observations to the large-scale structures which are approximately the scale of the secondary flows induced by spanwise heterogeneity, the velocity fields are filtered with a box filter of $0.1\unicode[STIX]{x1D6FF}_{s}\times 0.1\unicode[STIX]{x1D6FF}_{s}$ size for case SW-2 and $0.1\overline{\unicode[STIX]{x1D6FF}}\times 0.1\overline{\unicode[STIX]{x1D6FF}}$ for the SR cases. The filtered streamwise turbulent fluctuations are denoted by $u_{f}^{\prime }$.

Figure 17. Contours of the normalised one-sided two-point correlation coefficient $R_{u_{f}^{\prime }u_{f}^{\prime }}$ computed for low-speed events only ($u_{f}^{\prime }<0$), where $u_{f}^{\prime }$ is the filtered streamwise velocity fluctuations, for (a) reference smooth-wall case SW-2, (b) SR250-2, (c) SR160, (d) SR100, (e)  SR50 and (f) SR25. For heterogeneous cases, correlations are computed at a spanwise location corresponding to the common flow up of the secondary flow (ⓤ in figure 8). Symbol ‘$+$’ indicates the reference wall height $z_{ref}/\unicode[STIX]{x1D6FF}_{s}=0.1$ (a) and $z_{ref}/\overline{\unicode[STIX]{x1D6FF}}=0.1$ (b–f). Red and blue solid contour lines are $R_{u_{f}^{\prime }u_{f}^{\prime }}=0.1,0.2,\ldots ,0.9$, further conditioned based on the sign of filtered spanwise velocity fluctuations at the reference location: $v_{f}^{\prime }>0$ (——, red) and $v_{f}^{\prime }<0$ (——, blue). Dashed line (- - -) shows the inclination of the $v_{f}^{\prime }$-conditioned correlation maps. In (e), ${\hat{y}}$ is the distance between $v_{f}^{\prime }$-conditioned correlation maps measured at $z/\overline{\unicode[STIX]{x1D6FF}}=0.5$ and $\unicode[STIX]{x1D713}$ is the angle between the inclination of correlation maps.

For the reference smooth-wall case SW-2 in the $y$–$z$-plane, the two-point correlation coefficient of $u_{f}^{\prime }$ taken at a wall-normal reference point $z_{ref}$ and normalised by the standard deviation, $\unicode[STIX]{x1D70E}_{u_{f}^{\prime }}$, is defined as

(4.4)$$\begin{eqnarray}R_{u_{f}^{\prime }u_{f}^{\prime }}(z_{ref})=\frac{\overline{u_{f}^{\prime }(y,z_{ref})u_{f}^{\prime }(y+\unicode[STIX]{x0394}y,z)}}{\unicode[STIX]{x1D70E}_{u_{f}^{\prime }}(z_{ref})\unicode[STIX]{x1D70E}_{u_{f}^{\prime }}(z)},\end{eqnarray}$$

while for the heterogeneous (SR) cases, where the flow is heterogeneous in the spanwise direction,

(4.5)$$\begin{eqnarray}R_{u_{f}^{\prime }u_{f}^{\prime }}(y_{ref},z_{ref})=\frac{\overline{u_{f}^{\prime }(y_{ref},z_{ref})u_{f}^{\prime }(y_{ref}+\unicode[STIX]{x0394}y,z)}}{\unicode[STIX]{x1D70E}_{u_{f}^{\prime }}(y_{ref},z_{ref})\unicode[STIX]{x1D70E}_{u_{f}^{\prime }}(y_{ref}+\unicode[STIX]{x0394}y,z)},\end{eqnarray}$$

where $\unicode[STIX]{x0394}y$ is the spanwise separation between $u_{f}^{\prime }$. Figure 17 shows the contours of $R_{u_{f}^{\prime }u_{f}^{\prime }}$ in the cross-plane computed at a reference wall height $z_{ref}/\unicode[STIX]{x1D6FF}_{s}=0.1$ for case SW-2 and $z_{ref}/\overline{\unicode[STIX]{x1D6FF}}=0.1$ for SR cases. The one-sided correlations are conditioned on low-speed events, $u_{f}^{\prime }<0$, which is approximately 50 % of available vectors for all cases. For SR cases in figure 17(b–f), the correlations are taken at the spanwise location of the common flow up (ⓤ in figure 8). For the intermediate case, where $S/\overline{\unicode[STIX]{x1D6FF}}\approx 1$, the instantaneous velocity fields in figure 16(b,c) show that the occurrence of long, persistent low-speed streaks coincides with this spanwise location. It should be noted that figure 17(a–f) is shown within the same spatial extent in mm (see ordinate and abscissa on the right-hand side and top). Within this spatial extent, the positive correlation map (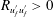$R_{u_{f}^{\prime }u_{f}^{\prime }}>0$, red-filled contour) in all SR cases is taller than that in the SW-2 case. This is expected since the structures scale with the locally thickening boundary layer in the common flow up regions (ⓤ in figure 8).

Aside from these differences in scale (resulting from spanwise variations in local $\unicode[STIX]{x1D6FF}$), no marked difference is observed in the overall shape of the $R_{u_{f}^{\prime }u_{f}^{\prime }}>0$ contours between the reference smooth-wall (SW-2) and SR cases. However, as shown in Kevin et al. (Reference Monty, Bai, Pathikonda, Nugroho, Barros, Christensen and Hutchins2017), the shape of ensemble-averaged correlation maps might result from the superposition of two opposing events. To investigate this, we further condition the events in the velocity fields based on the sign of the filtered spanwise turbulent fluctuations $v_{f}^{\prime }$ at the reference point. Note that with this additional condition, we are now looking at two-point correlation coefficients of negative $u_{f}^{\prime }$ fluctuations, further conditioned on the sign of $v_{f}^{\prime }$. Hence, each case (either $u_{f}^{\prime }<0$, $v_{f}^{\prime }<0$ or $u_{f}^{\prime }<0$, $v_{f}^{\prime }>0$) will occur for approximately 25 % of snapshots at a given reference location. The correlation maps for this additional $v_{f}^{\prime }>0$ and $v_{f}^{\prime }<0$ condition are shown by the solid red and blue contour lines. Only contour lines for $R_{u_{f}^{\prime }u_{f}^{\prime }}>0$ are shown for clarity. The contours depict a large-scale structure leaning sideways to the left or right depending on the sign of $v_{f}^{\prime }$. The standard one-sided two-point correlation results in the superposition of these two events, shown as the red filled contours in figure 17. We can relate this spanwise-leaning motion to the time-varying behaviour of the secondary flows inferred from the energy spectrograms of figures 13 and 14 and also from the instantaneous WPPIV shown in figure 16. The red and blue contours in figure 17 show that an ejection ($u^{\prime }<0$) event, which is associated with the low-speed streak, has a possibility of either leaning left ($v^{\prime }<0$) or right ($v^{\prime }>0$) depending on the sign of the local spanwise fluctuation. When projected into the wall-parallel plane, this left- and right-leaning tendency will give rise to long, meandering low-speed sinusoidal-like structures (as evident from blue-coloured contours in the instantaneous WPPIV shown in figure 16).

Figure 17(d,e) shows that the spanwise-leaning tendency becomes somewhat more prominent in the intermediate cases ($S/\overline{\unicode[STIX]{x1D6FF}}\approx 1$) compared to other SR cases (figure 17b,c,f) and the reference smooth-wall case (figure 17a). This spanwise-leaning tendency is quantifiable, as shown in the preliminary results in Wangsawijaya et al. (Reference Wangsawijaya, de Silva, Baidya, Chung, Marusic and Hutchins2019). We attempt to measure the magnitude of leaning by fitting a major axis of the $v_{f}^{\prime }$ conditioned correlation contours, drawn by taking the linear trend of maximum $R_{u_{f}^{\prime }u_{f}^{\prime }}$ at every wall-normal location (dashed lines in figure 17). Spanwise distance between two major axes of $v_{f}^{\prime }$-conditioned correlation maps ${\hat{y}}$ is measured at $z/\unicode[STIX]{x1D6FF}_{s}=0.5$ for SW and $z/\overline{\unicode[STIX]{x1D6FF}}=0.5$ for spanwise heterogeneous cases. Figure 17(e) shows a visual representation of ${\hat{y}}$ extraction from the conditional correlation maps. An alternative method to quantify the leaning tendency is by measuring the angle $\unicode[STIX]{x1D713}$ between the two major axes of the $v_{f}^{\prime }$-conditioned correlation maps (figure 17e). Figure 18 shows the amplitude of spanwise leaning, normalised by $\unicode[STIX]{x1D6FF}_{s}$ or $\overline{\unicode[STIX]{x1D6FF}}$ for each case, and the spanwise leaning angle $\unicode[STIX]{x1D713}$ as a function of $S/\overline{\unicode[STIX]{x1D6FF}}$. This trend is maximum when $S/\overline{\unicode[STIX]{x1D6FF}}\approx 1$ and decays as $S/\overline{\unicode[STIX]{x1D6FF}}$ increases, similar to that obtained from integrated energy spectrograms in figure 15 and the integrated mean swirl strength in figure 12. So far, these results (from HWA and SPIV) suggest that the secondary flows meander, and the behaviour of the meandering is dependent of the roughness patch width $S/\overline{\unicode[STIX]{x1D6FF}}$. Both results also show that the meandering is most prominent when $S/\overline{\unicode[STIX]{x1D6FF}}\approx 1$. The HWA-measured data, however, are converted from time series to space with the assumption that Taylor’s hypothesis holds. It is not possible to extract information on the streamwise wavelength of meandering from the statistically independent non-time-resolved instantaneous cross-plane snapshots obtained from the SPIV measurements. Hence, to complete the analysis on the meandering of the secondary flows, we compute the two-point correlations of the velocity fluctuation $R_{u_{f}^{\prime }u_{f}^{\prime }}$ in the $xy$-plane using the WPPIV data.

Figure 18. Spanwise distance between $v_{f}^{\prime }$-conditioned correlation maps in figure 17 ${\hat{y}}$, normalised by the boundary-layer thickness of each case $\overline{\unicode[STIX]{x1D6FF}}$. Right hand-side axis: the angle between the inclination of correlation maps $\unicode[STIX]{x1D713}$ in figure 17.

Figure 19. Contours of normalised two-point correlation coefficient $R_{u_{f}^{\prime }u_{f}^{\prime }}$ in $x$–$y$-plane. Correlations are taken at the centre of secondary flows (ⓒ in figure 8). Symbol ‘$+$’ indicates the reference point. Contour levels: $R_{u_{f}^{\prime }u_{f}^{\prime }}=0.05$ (——) and $R_{u_{f}^{\prime }u_{f}^{\prime }}=-0.025$ (– ⋅ – ⋅ –). Dash-dot lines (- - -) are the spanwise locations related to the mean secondary flows, the symbols are previously defined in figure 8.

For the reference smooth-wall case, where the flow is homogeneous in both $x$ and $y$, the two-point correlation of the filtered streamwise velocity fluctuations $R_{u_{f}^{\prime }u_{f}^{\prime }}$ in the $x$–$y$-plane is defined as

(4.6)$$\begin{eqnarray}R_{u_{f}^{\prime }u_{f}^{\prime }}=\frac{\overline{u_{f}^{\prime }(x,y)u_{f}^{\prime }(x+\unicode[STIX]{x0394}x,y+\unicode[STIX]{x0394}y)}}{\unicode[STIX]{x1D70E}_{u_{f}^{\prime }}\unicode[STIX]{x1D70E}_{u_{f}^{\prime }}},\end{eqnarray}$$

while for the SR cases, due to heterogeneity in $y$,

(4.7)$$\begin{eqnarray}R_{u_{f}^{\prime }u_{f}^{\prime }}(y_{ref})=\frac{\overline{u_{f}^{\prime }(x,y_{ref})u_{f}^{\prime }(x+\unicode[STIX]{x0394}x,y_{ref}+\unicode[STIX]{x0394}y)}}{\unicode[STIX]{x1D70E}_{u_{f}^{\prime }}(y_{ref})\unicode[STIX]{x1D70E}_{u_{f}^{\prime }}(y_{ref}+\unicode[STIX]{x0394}y)},\end{eqnarray}$$

where $\unicode[STIX]{x0394}x$ is the streamwise separation between $u_{f}^{\prime }$. Figure 19 shows the contours of $R_{u_{f}^{\prime }u_{f}^{\prime }}$ in the $x$–$y$-plane for the reference smooth-wall case (a) and SR cases (b–f); $R_{u_{f}^{\prime }u_{f}^{\prime }}$ is computed without conditions in both $u_{f}^{\prime }$ and $v_{f}^{\prime }$. The contours in figure 19 are presented in the same spatial extent (see ordinate and abscissa on the right-hand side and top of panels). For the SR cases, the two-point correlations are computed at the spanwise location that corresponds to the centre of the secondary flows (ⓒ in figure 8), which is approximately where the energetic peak is observed in the intermediate cases (figure 14d,e). This spanwise location is approximately midway between the high- and low-speed streaks formed by the secondary flow (see for example figure 16c). Contours of $R_{u_{f}^{\prime }u_{f}^{\prime }}>0$ and $R_{u_{f}^{\prime }u_{f}^{\prime }}<0$ are shown by the solid and dashed black lines, respectively. Dash-dot lines in figure 19(b–f) show the three spanwise locations of the upwelling, downwelling and centre of the secondary flows (symbols are defined in figure 8). The contours of $R_{u_{f}^{\prime }u_{f}^{\prime }}$ for the reference smooth-wall case SW-2 in $x$–$y$- and $y$–$z$-planes (figures 19a and 17a, respectively) depict the high- and low-speed large-scale structures in the canonical spanwise homogeneous turbulent boundary layers, where a streamwise elongated region of positive correlation is flanked by two negative (anticorrelated) lobes. A largely similar pattern is observed in the cases where $S/\overline{\unicode[STIX]{x1D6FF}}\gtrsim 1$ (SR250-2 and SR160, figure 19b,c) and $S/\overline{\unicode[STIX]{x1D6FF}}\ll 1$ (SR25, figure 19f).

However, a distinctly different pattern in $R_{u_{f}^{\prime }u_{f}^{\prime }}$ is observed for the intermediate cases (SR100 and SR50, figures 19d and 19e, respectively). Here, a pronounced anticorrelated pattern emerges in $x$ (a streamwise alternating pattern of positive and negative correlation, with antiphase behaviour to the span). It is noted that a similar anticorrelated pattern was also observed above the yawed region of C-D riblets in Kevin & Hutchins (Reference Monty and Hutchins2019b), where $S/\overline{\unicode[STIX]{x1D6FF}}\approx 1$. This pattern suggests a strong periodicity in the flow field for the turbulent fluctuations $u^{\prime }$. The distance between two $R_{u_{f}^{\prime }u_{f}^{\prime }}>0$ regions in $x$ can be used to estimate the streamwise wavelength of this flow periodicity (in figure 19e this can also be estimated from the separation between consecutive $R_{u_{f}^{\prime }u_{f}^{\prime }}<0$ regions). The streamwise wavelength is estimated at $\unicode[STIX]{x1D706}_{x}/\overline{\unicode[STIX]{x1D6FF}}\approx 4$. The time-series hot-wire data, when converted to space using Taylor’s hypothesis, also show an energetic peak at $\unicode[STIX]{x1D706}_{x}/\overline{\unicode[STIX]{x1D6FF}}\approx 3{-}4$ in the premultiplied energy spectrograms of $u^{\prime }$ for the same cases (SR100 and SR50, figures 14d and 14e, respectively), at spanwise and wall-normal locations that approximately correspond to the centre of the secondary flows. Taken together, the extra bump of energy evident in the pre-multiplied energy spectrograms, along with the side-to-side leaning apparent in the cross-plane SPIV, and now the anticorrelated behaviour observed in the wall-parallel plane, together strongly suggest that the secondary flows meander in the streamwise direction. Such meandering is also evident in the instantaneous WPPIV snapshots shown in figure 16. This meandering is masked by the tendency to consider secondary flows in only a time-averaged sense. Further, it is observed that the degree of meandering is strongly dependent on the size of the roughness patches ($S/\overline{\unicode[STIX]{x1D6FF}}$), with the most prominent meandering modes occurring when $S/\overline{\unicode[STIX]{x1D6FF}}\approx 1$. This also corresponds to the spanwise heterogeneous wavelength at which the strongest secondary flows are observed for a given heterogeneity condition, and where the secondary flows are approximately space filling within the turbulent boundary layer.