I. INTRODUCTION
One particularly simple device for generating an atmospheric or higher pressure RF or microwave plasma is the quarter wave coaxial cavity resonator (QWCCR). As an alternative to a traditional sparkplug used for initiating combustion, such a device has been studied by researchers at the West Virginia University's Mechanical and Aerospace Engineering Department for a number of years [Reference Nash1–Reference Lowery, Pertl and Smith10]. A recent publication [Reference Wilhelm, Pertl, Wildfire and Smith8] shows that the minimum required ignition energy of the QWCCR is comparable to that of a sparkplug. Numerical simulations and experimental investigations of various cavity geometries have been performed in [Reference Pertl, Lowery and Smith6, Reference Lowery11]. An analytic approach relating cavity parameters to the developed electric field strengths that lead to gas breakdown and plasma formation have been published in [Reference Pertl and Smith12].
The losses in the cavity, in particular the aperture radiation losses, can substantially lower the resonant step-up potential of the device as characterized by the quality factor, Q, of the cavity. This is especially true when the aperture size is not negligible with respect to the operating wavelength λ. This has lead to empirical geometries which reduce the aperture through tapering of the cavity, an example of which is shown in Fig. 1. Such tapered and straight cavity designs are, at a minimum, approximately a quarter wavelength (λ/4) in physical size. Naturally, larger odd multiples of λ/4 could also be used to make longer devices. Using the shortest λ/4 size, at a frequency of 2.45 GHz the approximate cavity length is 3 cm. To make the physical size of these resonators practical, and comparable to sparkplugs, such GHz range frequency have been used, but this is not necessarily desirable from a cavity wall conduction loss point of view, since conduction losses increase with operating frequency.

Fig. 1. Cross sectional view of small aperture 2.45 GHz tapered cavity design.
The current document makes use of the previous work presented in [Reference Pertl and Smith12] to approximately characterize more compact, shorter, nested QWCCR designs with a smaller aperture-to-wavelength ratio. Additionally, these designs are of practical length even at lower frequencies; and a reduction in cavity wall surface resistance, R s, is beneficial for maintaining a high Q factor. Note reduction of operating frequency can also be accomplished through reactive loading of the cavity, or by filling the interior with a dielectric. However, these approaches add additional Q lowering losses, especially if the loss tangent of the material and its dielectric constant are relatively large.
II. SHORTENED CONCENTRICALLY NESTED DESIGN
The folded design consists of concentrically connected segments of coaxial transmission line. The radial dimensions have been chosen to maintain a uniform transmission line impedance from the RF input end of the cavity to the discharge end. While it may be practical, as mentioned above, to fill the entire interior of the igniter with a dielectric to reduce its electrical length, z, the disadvantage is again the additional dielectric loss incurred. For this reason, only very short dielectric washers have been employed in the folded design to seal the device from the combustion chamber. This also avoids potential thermal expansion rate differences between metal and dielectric which in the case of ceramics may lead to cracking. A 3D view of a potential design showing the concentric coaxial segments is given in Fig. 2.

Fig. 2. 3D view of folded QWCCR design concept.
The dimension of this design target is 433 MHz. The 2D view in Fig. 3 shows more clearly the manner in which the transmission line segments are connected. RF feeds in via the N-type connector on the left, couples into the cavity with a loop structure, and then travels to the right in the outer most space until it is reflected by the short circuit on the right-hand side into the volume of the structure that formed the center conductor of the outer most section. The wave then switches direction and travels to the left until the end of this inner volume, where the previous process is repeated, until the open end of the cavity is reached. The entire path is electrically one-quarter wavelength long. As mentioned previously, higher odd multiples of quarter wavelength could also be used. The portions of the inner section contain low-loss dielectric disks to seal the resonator from the combustion and to maintain impedance as the geometry changes. An approximately equivalent unfolded structure is shown in Fig. 4. Note that the shorting plates are now sandwiched between dielectric regions for an overall length that is twice the dielectric washer length compared to Fig. 3. The transmission line sections’ radii were chosen to have an outer to inner radius ratio, b/a, approximately equal to 1.88. This was done to exploit conveniently available tube sizes, but other ratios could be used. Explicit values for the dimension of this design are given in Table 1. With a free-space intrinsic impedance of ![]() , this resulting transmission line impedance,
, this resulting transmission line impedance, ![]() equals 38 Ω, a reasonable value considering the theoretical optimums for the lowest loss is 77 Ω, and for highest field handling capabilities is 30 Ω [Reference Gilmour13].
equals 38 Ω, a reasonable value considering the theoretical optimums for the lowest loss is 77 Ω, and for highest field handling capabilities is 30 Ω [Reference Gilmour13].

Fig. 3. 2D view of folded QWCCR design, see Table 1 for dimension values.

Fig. 4. 2D view of unfolded equivalent structure.
Table 1. Dimension and properties of coaxial line sections.

III. ANALYSIS OF NESTED DESIGN
Ultimately, whether plasma is formed or not, depends on the breakdown strength of the gas mixture and the field strength at the discharge electrode tip. The developed electric field, E a-tip, at the tip of the quarter wave cavity can be related to the power, P, fed into the cavity, its quality factor, and the tip geometry [Reference Pertl and Smith12]. Assuming an unsharpened rounded tip with a spherical radius of curvature equal to the electrode radius, a tip, at a potential, V o, the tip field can be approximated by
At resonance, the tip potential, V o, is proportional to the time average energy, U, stored in the cavity, volume that is related to the quality factor, Q, is given by
where ω is the angular resonant frequency. The time average energy stored in the cavity can be found from
This is the integration of the energy density of the electric field E and the magnetic field H, over the volume of the cavity. Note that at resonance the magnetic and electric stored time average energies are equal. The energy stored per unit length is not directly dependent of the actual radii of the coaxial line section, but is a function of the line's characteristic impedance, i.e. the radius ratio. This means that the equations for stored energy in a quarter wave resonant section do not change even if parts of the line are reduced in diameter, provided the characteristic impedance is preserved. The equations for the tip electric field magnitude, (4), and the equation for the cavity stored energy as given in [Reference Pertl and Smith12] are still applicable:
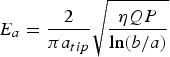
and
Using the relation between wavelength, λ, frequency, f, and propagation velocity, ![]() , these equations can also be expressed in terms of the characteristic impedance of the line, Z o, by
, these equations can also be expressed in terms of the characteristic impedance of the line, Z o, by

and
This shows that stored energy increases with line impedance, Z o, and decreases with frequency, f. What remains is to examine the losses of the transmission line sections. This can be done by assuming the field fringing at the internal corners of the line junction points are negligible, and that the fields of the resonance are approximately transverse electromagnetic mode (TEM) standing quarter wave sinusoids such that
and
where β = 2π/λ and I o is some assumed amplitude. For a cylindrical conductor surface, with surface resistance R s, and radius r o, the time average power dissipated is given by the surface integral

where dimensions along the line have been recast in terms of electrical angles so that ![]() . Considering an area interpretation of the integral over
. Considering an area interpretation of the integral over ![]() , it can be seen that losses per unit length decrease as the open end of the cavity is approached. This suggests that using large radii toward the short-circuited end of the resonant line is more important in reducing losses than using them toward the open-circuited end. If constant power dissipation per unit length is desired, the radii could vary as
, it can be seen that losses per unit length decrease as the open end of the cavity is approached. This suggests that using large radii toward the short-circuited end of the resonant line is more important in reducing losses than using them toward the open-circuited end. If constant power dissipation per unit length is desired, the radii could vary as ![]() resulting in a tapered shape shown in Fig. 5. The sidewall surface loss of (10) would then reduce to
resulting in a tapered shape shown in Fig. 5. The sidewall surface loss of (10) would then reduce to

Fig. 5. Cos2 tapered geometry for constant loss per unit length.
Through a similar area integration the ohmic power losses for a circular annulus with inner and outer radius a′ and b, respectively, at a distance z along the line is determined as
Placing annuli close to the short-circuited end of the transmission line, where the magnetic fields are higher, will result in larger losses. The power dissipated by the standing wave in a low-loss dielectric filling, with effective conductivity, ![]() , in the coaxial line with inner radius, a, and outer radius, b, extending between distances z 1 and z 2 along the line is
, in the coaxial line with inner radius, a, and outer radius, b, extending between distances z 1 and z 2 along the line is

for the sinusoidal resonant field distribution. Considering the integral over ![]() in (13), the closer a dielectric filling is placed to the open end of the resonator, the higher the losses will be. The quality factors, Q, of the resonator can now be estimated as
in (13), the closer a dielectric filling is placed to the open end of the resonator, the higher the losses will be. The quality factors, Q, of the resonator can now be estimated as

Prior to analyzing any design, the section lengths of the resonator have to be converted to electrical degrees so the integrals can be evaluated. The dielectric constant of the transition regions will affect the angular electrical line length. The relative dielectric constant required to maintain the same line impedance when the conductor radius ratio changes from b 0/a 0 to b 1/a 1 is given by
![\varepsilon _r=\left[{{{\ln \lpar {b_1 /a_1 } \rpar } \over {\ln \lpar {b_0 /a_0 } \rpar }}} \right]^2 .](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151022075450975-0612:S1759078711000493_eqn15.gif?pub-status=live)
For an initial test case, the structure shown in Fig. 4 was assembled out of commercially available brass tubing sizes targeting a resonance frequency of 433 MHz (69.3 cm wavelength) with dimensions as given in Tables 1 and 2. The value 0.0104 Ω was used as the surface resistance, R s, of brass at 433 MHz. Note that the impedance matching dielectric at the first junction, which should have had a relative dielectric constant of 4.7, was omitted. Provided the length of the mismatch is short with respect to wavelength, no serious reflections will occur, and instead the junction steps will appear as small shunt capacitances. The magnitude of these capacitances can be estimated by the method outlined in chapter 6 of [Reference Moreno14] and their combination is on the order of 0.2 pF which is located in a region of relatively low electric field magnitudes. For the purpose of this analysis, this shunt capacitance will be ignored (Fig. 6).

Fig. 6. Electrical angular lengths along unfolded equivalent structure.
Table 2. Dimensions and location of annuli.

The calculated combined unloaded quality factor is 414. This is about 2.5 times greater than if the resonator had been made out of the smallest diameter section, c5, for the entire length, but naturally lower than if the larger diameters of section, c1, had been used throughout. It is apparent from the calculated Q i, that the annuli losses are insignificant. However, the dielectric losses should not be discounted, despite the fact that the dielectric is set back from the maximum electric fields by 33.8°. Also of note is the fact that despite having the largest radii, the cylinders of the c1 section contribute the largest losses as it experiences the strongest magnetic fields.
As a figure of merit, that can be used to compare the transmission line sections, ΔzQ i was also computed. This metric highlights the dielectric losses. Had the section not been kept short, the overall quality factor of the cavity would be drastically lowered. Improvements in the resonator's Q can therefore be achieved by further increasing these radii. For the analysis to hold, the radii cannot be increased beyond the point where higher order modes start to appear in the cavity. This indicates that an upper limit should be set as 2π(b + a) < λ/2 [Reference Clayton15]. A compact cavity with larger radii, and assembled as shown in Fig. 7, was designed with dimensions given in Tables 3 and 4. The calculated, combined unloaded quality factor for this second design is 834, twice the small radii design quality factor. Note that an additional reduction in radii in going from c5 to c7 was included without a reversal in direction, and without accounting for the annuli losses in the reduction as the losses on the annuli are very low, i.e. their Q's are very high.

Fig. 7. 2D view of large radii folded QWCCR design.
Table 3. Dimension and properties of coaxial line sections.

Table 4. Dimensions and location of annuli.

As a comparison and using the same TEM assumptions, the quality factor of a ![]() tapered, unfolded cavity of quarter wavelength using air as a dielectric was derived using: (7) for the energy stored, (11) for the tapered side conductors, and (12) for the base conductor annulus at the shorting end. The result without accounting for the dielectric is given by
tapered, unfolded cavity of quarter wavelength using air as a dielectric was derived using: (7) for the energy stored, (11) for the tapered side conductors, and (12) for the base conductor annulus at the shorting end. The result without accounting for the dielectric is given by
![Q_{\cos ^2 }=\left[{{{{\lambda R_s } \over {2\pi^2 Z_o }}}\left({{1 \over a} + {1 \over b}} \right)+{{4R_s } \over {\pi \eta }}} \right]^{ - 1} .](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151022075450975-0612:S1759078711000493_eqn16.gif?pub-status=live)
The dielectric losses increase dramatically toward the open-circuited end of the cavity in such a tapered design since the ![]() term under the integral in (13) is turned into a
term under the integral in (13) is turned into a ![]() term by the tapering:
term by the tapering:

In an actual implementation, the length would be slightly shorter than λ/4, to allow an aperture that would have capacitance. Nevertheless, filling the entire cavity would create excessive losses. Since the previous two example cavities were mostly hollow, the tapered cavity will be assumed to be made of brass with an air dielectric throughout. The resulting quality factors of the tapered design using the same radii at the shorted base as the two sectioned cavities are: 418 for the initial and 927 for the enlarged radii, respectively. These values are quite similar to the values calculated for the discretely sectioned designs; depending on how well the step tapered sections fit the ![]() distribution, a first cut estimate of a sectioned design could be obtained using the tapered results. One could also construct such a tapered cavity by approximating the
distribution, a first cut estimate of a sectioned design could be obtained using the tapered results. One could also construct such a tapered cavity by approximating the ![]() taper with a straight line, thereby making a conical similar to Fig. 1.
taper with a straight line, thereby making a conical similar to Fig. 1.
IV. SOME DESIGN IMPLEMENTATIONS
To check how valid the approximate analysis is, both designs were implemented with available brass tubing. The larger radii cavity is shown below in Fig. 8, at various stages of implementation.

Fig. 8. Large radii cavity at various stages of implementation.
Measurement of the quality factor and the degree of coupling on a HP8753D network analyzer resulted in an unloaded Q of 340 at a resonance frequency of 425.75 MHz for the small radii geometry. The larger radii geometry resulted in an unloaded Q of 760 with a resonance frequency of 439.87 MHz. The two assembled implementations are shown in Figs 9 and 10, respectively. A conical brass resonator had been constructed some time ago with a base radius of 1.5″ and a b/a ratio of 6 for an approximate line impedance of 108 Ω. Its resonance frequency had been measured at 960 MHz with an unloaded Q of 1800 [16]. Calculations using the ![]() taper results would predict a quality factor of 2100, with a 17% difference from the conical measured result. For the folded cavities constructed, the frequencies of the implementations of the first and second cavity differ from the design frequencies by 1.7 and 1.6%, respectively. As is generally the case, the measured quality factors were both lower than the theoretically calculated values. The respective differences for the small and large radii cavities were 18 and 9%. Note that disturbance of the electromagnetic fields at the base of the cavity due to the coupling structure have been ignored in the analysis. There is also potential for error due to conductivity differences, surface imperfections, solder joints, and uncertainty in the dielectric parameters.
taper results would predict a quality factor of 2100, with a 17% difference from the conical measured result. For the folded cavities constructed, the frequencies of the implementations of the first and second cavity differ from the design frequencies by 1.7 and 1.6%, respectively. As is generally the case, the measured quality factors were both lower than the theoretically calculated values. The respective differences for the small and large radii cavities were 18 and 9%. Note that disturbance of the electromagnetic fields at the base of the cavity due to the coupling structure have been ignored in the analysis. There is also potential for error due to conductivity differences, surface imperfections, solder joints, and uncertainty in the dielectric parameters.

Fig. 9. Completed initial test case cavity.

Fig. 10. Completed second test case cavity.
V. CONCLUSION
The feasibility of shortening the QWCCR by step tapering, and then concentrically nesting cylindrical structure inside of itself has been demonstrated. This allows more compact implementations of QWCCR and operation at lower frequencies where longer designs may be physically undesirable. When considering cavities designs that use odd multiples of λ/4 larger than one, the quality factor can be enhanced by making the high magnetic field sections along the cavity length have large radii.
An approximate analysis procedure to estimate the performance of such nested and tapered designs has been outlined. Despite considerable simplifications, the presented method can be used to estimate quality factors of the tapered and nested designs. More accurate results can be obtained with exact field distributions including fringing and capacitive loading at the step discontinuities. The approximate results suffice to allow the estimation of the approximate power requirements, P, in order to achieve breakdown and plasma formation for a given tip radius via (6). The folded cavity design performance is comparable with the performance of tapered design.
 Franz A. Pertl received his Bachelor of Science degrees in Electrical and Computer Engineering from West Virginia University (WVU), Morgantown, West Virginia, USA in 1994, and his Master of Science degree in Electrical Engineering from West Virginia University in 1996 and his Ph.D. in Mechanical Engineering from West Virginia University in 2008. He currently holds a program coordinator position with the mechanical and aerospace engineering department at West Virginia University and works as a Research Engineer for the Center of Industrial Research Applications (CIRA). He has also worked for the Engine and Emissions Research Center at West Virginia University and taught summer courses at the University. His areas of expertise include software design, data acquisition, microprocessor applications, color machine vision, controls, wind turbines and other areas of electrical engineering. He has published 26 conference papers, 8 journal papers and has been awarded 5 United States Patents to date and has been principal or co-principal investigator on several research projects. His current interests include electromagnetic and microwave plasma ignition. Dr. Pertl is a member of Sigma Xi Scientific Research Society and the Society of Automotive Engineers (SAE) International.
Franz A. Pertl received his Bachelor of Science degrees in Electrical and Computer Engineering from West Virginia University (WVU), Morgantown, West Virginia, USA in 1994, and his Master of Science degree in Electrical Engineering from West Virginia University in 1996 and his Ph.D. in Mechanical Engineering from West Virginia University in 2008. He currently holds a program coordinator position with the mechanical and aerospace engineering department at West Virginia University and works as a Research Engineer for the Center of Industrial Research Applications (CIRA). He has also worked for the Engine and Emissions Research Center at West Virginia University and taught summer courses at the University. His areas of expertise include software design, data acquisition, microprocessor applications, color machine vision, controls, wind turbines and other areas of electrical engineering. He has published 26 conference papers, 8 journal papers and has been awarded 5 United States Patents to date and has been principal or co-principal investigator on several research projects. His current interests include electromagnetic and microwave plasma ignition. Dr. Pertl is a member of Sigma Xi Scientific Research Society and the Society of Automotive Engineers (SAE) International.
 Mary Ann Clarke assistant professor of mathematics at West Virginia University, is an applied mathematician with particular interests in scientific programming and engineering problem solving. Trained in materials engineering, classical mathematics, and numerical methods, she offers researchers in scientific disciplines a segue into physical modeling through the adaptation of empirical relationships and descriptive equations into computer codes. Winner of the 2010 WVU Foundation Award for Outstanding Teaching, she imparts to her students the utility of mathematics as an investigative tool as well as the importance of conceptual understanding and application of mathematical ideas to science and engineering.
Mary Ann Clarke assistant professor of mathematics at West Virginia University, is an applied mathematician with particular interests in scientific programming and engineering problem solving. Trained in materials engineering, classical mathematics, and numerical methods, she offers researchers in scientific disciplines a segue into physical modeling through the adaptation of empirical relationships and descriptive equations into computer codes. Winner of the 2010 WVU Foundation Award for Outstanding Teaching, she imparts to her students the utility of mathematics as an investigative tool as well as the importance of conceptual understanding and application of mathematical ideas to science and engineering.
 James E. Smith received his Bachelor of Science and Master of Science degrees in Aerospace Engineering and Doctor of Philosophy degree in Mechanical Engineering from West Virginia University (WVU), Morgantown, West Virginia, USA in 1972, 1974, and 1984, respectively. He is currently the Director of the Center for Industrial Research Applications (CIRA) at West Virginia University, where he is also a Professor in the Mechanical and Aerospace Engineering (MAE) Department. He has taught at the University since 1976, before which he was a Research Engineer for the Department of Energy (DOE). During his 30-plus-year scientific career, he has been the principal and/or co-principal investigator for various projects funded by federal agencies (Tank-Automotive Armaments Command (TACOM), Department of Defense (DOD), HEW, Department of Transportation (DOT), US Navy, Defense Advanced Research Projects Agency (DARPA), and Department of Energy (DOE)), international corporations, and numerous US corporations. The work in these projects has resulted in the publication of 164 conference papers and 50 journal or bound transaction papers. This work has resulted in the granting of 31 United States Patents and numerous foreign patents on mechanical and energy-related devices. Dr. Smith is a member of American Institute of Aeronautics and Astronautics (AIAA), Society of Automotive Engineers (SAE) International, American Society of Mechanical Engineers (ASME), International Society for Computers and Applications (ISCA), American Society for Engineering Education (ASEE), and International Society for Instrumentation Engineers (SPIE).
James E. Smith received his Bachelor of Science and Master of Science degrees in Aerospace Engineering and Doctor of Philosophy degree in Mechanical Engineering from West Virginia University (WVU), Morgantown, West Virginia, USA in 1972, 1974, and 1984, respectively. He is currently the Director of the Center for Industrial Research Applications (CIRA) at West Virginia University, where he is also a Professor in the Mechanical and Aerospace Engineering (MAE) Department. He has taught at the University since 1976, before which he was a Research Engineer for the Department of Energy (DOE). During his 30-plus-year scientific career, he has been the principal and/or co-principal investigator for various projects funded by federal agencies (Tank-Automotive Armaments Command (TACOM), Department of Defense (DOD), HEW, Department of Transportation (DOT), US Navy, Defense Advanced Research Projects Agency (DARPA), and Department of Energy (DOE)), international corporations, and numerous US corporations. The work in these projects has resulted in the publication of 164 conference papers and 50 journal or bound transaction papers. This work has resulted in the granting of 31 United States Patents and numerous foreign patents on mechanical and energy-related devices. Dr. Smith is a member of American Institute of Aeronautics and Astronautics (AIAA), Society of Automotive Engineers (SAE) International, American Society of Mechanical Engineers (ASME), International Society for Computers and Applications (ISCA), American Society for Engineering Education (ASEE), and International Society for Instrumentation Engineers (SPIE).
















