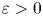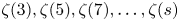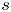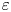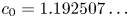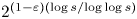1. Introduction
The Riemann zeta function ![]() $\zeta (s)$ is one of the most fascinating objects in mathematics. Due to the work of Euler and Lindemann, it is well known that for any positive integer
$\zeta (s)$ is one of the most fascinating objects in mathematics. Due to the work of Euler and Lindemann, it is well known that for any positive integer ![]() $k$, the Riemann zeta value
$k$, the Riemann zeta value ![]() $\zeta (2k)$ is a (non-zero) rational multiple of
$\zeta (2k)$ is a (non-zero) rational multiple of ![]() $\pi ^{2k}$; therefore, is transcendental. One may want to further investigate the odd zeta values, i.e., the numbers
$\pi ^{2k}$; therefore, is transcendental. One may want to further investigate the odd zeta values, i.e., the numbers ![]() $\zeta (2k+1)$. It is conjectured that
$\zeta (2k+1)$. It is conjectured that ![]() $\pi , \zeta (3), \zeta (5),\zeta (7),\ldots$ are algebraically independent over
$\pi , \zeta (3), \zeta (5),\zeta (7),\ldots$ are algebraically independent over ![]() $\mathbb {Q}$, but very little is known.
$\mathbb {Q}$, but very little is known.
We mention a few works on this subject. In 1978, Apéry proved that ![]() $\zeta (3)$ is irrational [Reference ApéryApé79]. (See also van der Poorten's report [Reference van der PoortenPoo79] and Beukers’ alternative proof [Reference BeukersBeu79]. For a survey, see [Reference FischlerFis04].) In 2000, Ball and Rivoal [Reference Ball and RivoalBR01] (see also Rivoal [Reference RivoalRiv00]) showed that for all odd integers
$\zeta (3)$ is irrational [Reference ApéryApé79]. (See also van der Poorten's report [Reference van der PoortenPoo79] and Beukers’ alternative proof [Reference BeukersBeu79]. For a survey, see [Reference FischlerFis04].) In 2000, Ball and Rivoal [Reference Ball and RivoalBR01] (see also Rivoal [Reference RivoalRiv00]) showed that for all odd integers ![]() $s \geqslant 3$, we have the following asymptotics as
$s \geqslant 3$, we have the following asymptotics as ![]() $s \rightarrow +\infty$:
$s \rightarrow +\infty$:
The proof of Ball and Rivoal makes use of Nesterenko's linear independence criterion [Reference NesterenkoNes85] and the following auxiliary rational functions:
 \[ R_{n}^{(\rm{BR})}(t) = n!^{s-2r} \frac{\prod_{j=0}^{(2r+1)n}(t-rn+j)}{\prod_{j=0}^{n}(t+j)^{s+1}}. \]
\[ R_{n}^{(\rm{BR})}(t) = n!^{s-2r} \frac{\prod_{j=0}^{(2r+1)n}(t-rn+j)}{\prod_{j=0}^{n}(t+j)^{s+1}}. \]
As a corollary, there are infinitely many irrational numbers among odd zeta values. In 2018, Zudilin [Reference ZudilinZud18] studied the following rational functions (with ![]() $s = 25$):
$s = 25$):
 \[ R_n^\textrm{(Z)}(t) = 2^{6n} n!^{s-5} \frac{\prod_{j=0}^{6n} (t-n + j/2)}{ \prod_{j=0}^{n} (t+j)^{s+1}} \]
\[ R_n^\textrm{(Z)}(t) = 2^{6n} n!^{s-5} \frac{\prod_{j=0}^{6n} (t-n + j/2)}{ \prod_{j=0}^{n} (t+j)^{s+1}} \]
and proved that both series ![]() $\sum _{t=1}^{\infty } R_n^\textrm {(Z)}(t)$ and
$\sum _{t=1}^{\infty } R_n^\textrm {(Z)}(t)$ and ![]() $\sum _{t=1}^{\infty } R_n^\textrm {(Z)}(t+\frac {1}{2})$ are
$\sum _{t=1}^{\infty } R_n^\textrm {(Z)}(t+\frac {1}{2})$ are ![]() $\mathbb {Q}$-linear combinations of odd zeta values with related coefficients; it provides a new elimination procedure. Zudilin's new idea inspired many works afterwards (see Sprang [Reference SprangSpr18] and Fischler [Reference FischlerFis20]). Based on further developments in [Reference ZudilinZud18] and an important arithmetic observation of Sprang [Reference SprangSpr18, Lemma 1.4], in 2018, Fischler, Sprang and Zudilin [Reference Fischler, Sprang and ZudilinFSZ19] proved for all
$\mathbb {Q}$-linear combinations of odd zeta values with related coefficients; it provides a new elimination procedure. Zudilin's new idea inspired many works afterwards (see Sprang [Reference SprangSpr18] and Fischler [Reference FischlerFis20]). Based on further developments in [Reference ZudilinZud18] and an important arithmetic observation of Sprang [Reference SprangSpr18, Lemma 1.4], in 2018, Fischler, Sprang and Zudilin [Reference Fischler, Sprang and ZudilinFSZ19] proved for all ![]() $\varepsilon >0$, for any odd integer
$\varepsilon >0$, for any odd integer ![]() $s$ which is sufficiently large with respect to
$s$ which is sufficiently large with respect to ![]() $\varepsilon$, with the help of the following rational functions:
$\varepsilon$, with the help of the following rational functions:
 \[ R_{n}^{(\textrm{FSZ})}(t) = D^{3Dn} n!^{s+1-3D} \frac{ \prod_{j=0}^{3Dn}(t-n+j/D)}{ \prod_{j=0}^{n}(t+j)^{s+1}}, \]
\[ R_{n}^{(\textrm{FSZ})}(t) = D^{3Dn} n!^{s+1-3D} \frac{ \prod_{j=0}^{3Dn}(t-n+j/D)}{ \prod_{j=0}^{n}(t+j)^{s+1}}, \]
that the number of irrationals in the set ![]() $\{\zeta (3),\zeta (5),\zeta (7),\ldots ,\zeta (s)\}$ is at least
$\{\zeta (3),\zeta (5),\zeta (7),\ldots ,\zeta (s)\}$ is at least ![]() $2^{(1-\varepsilon )({\log s}/{\log \log s})}$. (See also [Reference Fischler, Sprang and ZudilinFSZ18].)
$2^{(1-\varepsilon )({\log s}/{\log \log s})}$. (See also [Reference Fischler, Sprang and ZudilinFSZ18].)
In the current work, we prove the following result.
Theorem 1.1 For any small ![]() $\varepsilon > 0$ and for all odd integers
$\varepsilon > 0$ and for all odd integers ![]() $s$ sufficiently large with respect to
$s$ sufficiently large with respect to ![]() $\varepsilon$, there are at least
$\varepsilon$, there are at least
 \[ \left(c_0 - \varepsilon\right) \frac{s^{{1}/{2}}}{\log^{{1}/{2}} s} \]
\[ \left(c_0 - \varepsilon\right) \frac{s^{{1}/{2}}}{\log^{{1}/{2}} s} \]
irrational numbers among ![]() $\{\zeta (3),\zeta (5),\zeta (7),\ldots ,\zeta (s)\}$, where the constant
$\{\zeta (3),\zeta (5),\zeta (7),\ldots ,\zeta (s)\}$, where the constant
 \[ c_0 = \sqrt{\frac{4\zeta(2)\zeta(3)}{\zeta(6)} \biggl( 1 - \log \frac{\sqrt{4e^2+1}-1}{2} \biggr) } = 1.192507\ldots. \]
\[ c_0 = \sqrt{\frac{4\zeta(2)\zeta(3)}{\zeta(6)} \biggl( 1 - \log \frac{\sqrt{4e^2+1}-1}{2} \biggr) } = 1.192507\ldots. \]The proof is a natural extension to the original ideas of Zudilin [Reference ZudilinZud18] and Sprang [Reference SprangSpr18]. Our main strategies are exactly the same as [Reference Fischler, Sprang and ZudilinFSZ19], though an amount of small technical modifications is involved. The major new ingredient of our work is an asymptotically optimal design for the rational zeros of the auxiliary rational functions. In an earlier version of this note,Footnote 1 we made use of the rational functions
 \[ \biggl( \prod_{d=1}^{D} d^{3dn+1} \biggr)n!^{s+D-({3}/{2})D(D+1)}\frac{\prod_{d=1}^{D}\prod_{j=0}^{3dn}(t-n+{j}/{d})}{\prod_{j=0}^{n} (t+j)^{s+D}} \]
\[ \biggl( \prod_{d=1}^{D} d^{3dn+1} \biggr)n!^{s+D-({3}/{2})D(D+1)}\frac{\prod_{d=1}^{D}\prod_{j=0}^{3dn}(t-n+{j}/{d})}{\prod_{j=0}^{n} (t+j)^{s+D}} \]
and proved that the number of irrationals in the set ![]() $\{\zeta (3),\zeta (5),\ldots ,\zeta (s)\}$ is at least
$\{\zeta (3),\zeta (5),\ldots ,\zeta (s)\}$ is at least ![]() $\frac {1}{10} s^{1/2} / \log ^{1/2} s$ for any odd integer
$\frac {1}{10} s^{1/2} / \log ^{1/2} s$ for any odd integer ![]() $s \geqslant 10^4$. In order to improve the constant
$s \geqslant 10^4$. In order to improve the constant ![]() $\frac {1}{10}$, we need to consider more technical modifications; see Definition 2.3. Since our constructions inherit the spirit of
$\frac {1}{10}$, we need to consider more technical modifications; see Definition 2.3. Since our constructions inherit the spirit of ![]() $R_{n}^{(\textrm {FSZ})}(t)$, we refer to them (and a class of similar constructions) as FSZ constructions. It turns out that the optimal design for the zeros of FSZ constructions is in connection with the inverse totient problem.
$R_{n}^{(\textrm {FSZ})}(t)$, we refer to them (and a class of similar constructions) as FSZ constructions. It turns out that the optimal design for the zeros of FSZ constructions is in connection with the inverse totient problem.
The structure of this note is as follows: in § 2, we introduce the auxiliary rational functions ![]() $R_n(t)$ and related linear forms. In § 3, we study the arithmetic of the denominators appearing in the linear forms. In § 4, we bound the growth of the linear forms. In § 5, we prove Theorem 1.1. Finally, in § 6, we show that under certain constraints, the FSZ auxiliary functions constructed in this note are the most economical ones (up to an
$R_n(t)$ and related linear forms. In § 3, we study the arithmetic of the denominators appearing in the linear forms. In § 4, we bound the growth of the linear forms. In § 5, we prove Theorem 1.1. Finally, in § 6, we show that under certain constraints, the FSZ auxiliary functions constructed in this note are the most economical ones (up to an ![]() $o(1)$ term).
$o(1)$ term).
2. Auxiliary functions and linear forms
Let ![]() $r = {\textrm {num}{(r)}}/{\textrm {den}{(r)}}$ be a positive rational number, where
$r = {\textrm {num}{(r)}}/{\textrm {den}{(r)}}$ be a positive rational number, where ![]() $\textrm {num}{(r)}$ and
$\textrm {num}{(r)}$ and ![]() $\textrm {den}{(r)}$ are the numerator and denominator of
$\textrm {den}{(r)}$ are the numerator and denominator of ![]() $r$ in reduced form, respectively. We refer to
$r$ in reduced form, respectively. We refer to ![]() $r$ as the Ball–Rivoal length parameter [Reference Ball and RivoalBR01]. Eventually we will take the rational number
$r$ as the Ball–Rivoal length parameter [Reference Ball and RivoalBR01]. Eventually we will take the rational number ![]() $r$ arbitrarily close to
$r$ arbitrarily close to ![]() $r_0 = {(\sqrt {4e^2+1}-1)}/{2} \approx 2.26388$ in order to maximize a certain quantity.
$r_0 = {(\sqrt {4e^2+1}-1)}/{2} \approx 2.26388$ in order to maximize a certain quantity.
Let ![]() $s$ be a positive odd integer and
$s$ be a positive odd integer and ![]() $B$ be a positive real number. We will always assume that:
$B$ be a positive real number. We will always assume that:
(1) both
 $s$ and
$s$ and  $B$ are larger than some absolute constant;
$B$ are larger than some absolute constant;(2)
 $s \geqslant 10(2r+1)B^2$.
$s \geqslant 10(2r+1)B^2$.
Eventually we will take ![]() $B = cs^{1/2}/\log ^{1/2} s$ for some constant
$B = cs^{1/2}/\log ^{1/2} s$ for some constant ![]() $c$.
$c$.
Definition 2.1 We define the following two sets which depend only on ![]() $B$:
$B$:
(1) the denominator set
where \[ {\Psi}_B = \{ b \in \mathbb{N} \mid \varphi(b) \leqslant B \}, \]
\[ {\Psi}_B = \{ b \in \mathbb{N} \mid \varphi(b) \leqslant B \}, \] $\varphi (\cdot )$ is the Euler totient function;
$\varphi (\cdot )$ is the Euler totient function;(2) the zero set
 \[ \mathcal{F}_{B} = \left\{ \left.\frac{a}{b} \in \mathbb{Q}\ \right|\, b \in {\Psi}_B, 1 \leqslant a \leqslant b\ \text{and}\ \gcd(a,b) = 1 \right\}. \]
\[ \mathcal{F}_{B} = \left\{ \left.\frac{a}{b} \in \mathbb{Q}\ \right|\, b \in {\Psi}_B, 1 \leqslant a \leqslant b\ \text{and}\ \gcd(a,b) = 1 \right\}. \]
The zero set ![]() $\mathcal {F}_B$ consists of the zeros in the interval
$\mathcal {F}_B$ consists of the zeros in the interval ![]() $(0,1]$ of our auxiliary rational functions, and the denominator set
$(0,1]$ of our auxiliary rational functions, and the denominator set ![]() ${\Psi }_B$ consists of different denominators of the zeros. We collect some properties of these two sets. The first property is known in the topic about the inverse totient problem.
${\Psi }_B$ consists of different denominators of the zeros. We collect some properties of these two sets. The first property is known in the topic about the inverse totient problem.
Proposition 2.2
(1) The size of the set
 ${\Psi }_B$ is
${\Psi }_B$ is
 \[ \left| {\Psi}_B \right| = \left( \frac{\zeta(2)\zeta(3)}{\zeta(6)} + o_{B \rightarrow +\infty}(1) \right) B. \]
\[ \left| {\Psi}_B \right| = \left( \frac{\zeta(2)\zeta(3)}{\zeta(6)} + o_{B \rightarrow +\infty}(1) \right) B. \](2) For any
 $b \in {\Psi }_B$, we have
$b \in {\Psi }_B$, we have
 \[ \left\{ \frac{1}{b},\frac{2}{b},\ldots,\frac{b}{b} \right\} \subset \mathcal{F}_{B}. \]
\[ \left\{ \frac{1}{b},\frac{2}{b},\ldots,\frac{b}{b} \right\} \subset \mathcal{F}_{B}. \](3) If
 $B$ is larger than some absolute constant, then
$B$ is larger than some absolute constant, then
 \[ \left| \mathcal{F}_{B} \right| \leqslant B^2. \]
\[ \left| \mathcal{F}_{B} \right| \leqslant B^2. \]
Proof. For the first proposition, we refer the reader to [Reference DresslerDre70] or [Reference BatemanBat72]. Since
 \[ \left|\mathcal{F}_{B}\right| = \sum_{b \in {\Psi}_B} \varphi(b) = \sum_{m=1}^{\lfloor B \rfloor } m\left( \left| {\Psi}_m \right| - \left| {\Psi}_{m-1} \right| \right) = \lfloor B \rfloor \left| {\Psi}_{\lfloor B \rfloor} \right| - \sum_{m=1}^{\lfloor B \rfloor -1} \left| {\Psi}_m \right|, \]
\[ \left|\mathcal{F}_{B}\right| = \sum_{b \in {\Psi}_B} \varphi(b) = \sum_{m=1}^{\lfloor B \rfloor } m\left( \left| {\Psi}_m \right| - \left| {\Psi}_{m-1} \right| \right) = \lfloor B \rfloor \left| {\Psi}_{\lfloor B \rfloor} \right| - \sum_{m=1}^{\lfloor B \rfloor -1} \left| {\Psi}_m \right|, \]
the first proposition implies that ![]() $|\mathcal {F}_{B}| =(\frac {1}{2}({\zeta (2)\zeta (3)}/{\zeta (6)})+o(1))B^2$. Now,
$|\mathcal {F}_{B}| =(\frac {1}{2}({\zeta (2)\zeta (3)}/{\zeta (6)})+o(1))B^2$. Now, ![]() ${\zeta (2)\zeta (3)}/{\zeta (6)} = 1.94\ldots < 2$ and the third proposition follows. For the second proposition, note that if
${\zeta (2)\zeta (3)}/{\zeta (6)} = 1.94\ldots < 2$ and the third proposition follows. For the second proposition, note that if ![]() $b \in {\Psi }_B$ and
$b \in {\Psi }_B$ and ![]() $b'$ is any divisor of
$b'$ is any divisor of ![]() $b$, then
$b$, then ![]() $\varphi (b') \leqslant \varphi (b) \leqslant B$, so
$\varphi (b') \leqslant \varphi (b) \leqslant B$, so ![]() $b' \in {\Psi }_B$. Therefore, for any
$b' \in {\Psi }_B$. Therefore, for any ![]() $k \in \{ 1,2,\ldots ,b \}$, we have
$k \in \{ 1,2,\ldots ,b \}$, we have ![]() ${k}/{b} = ({k/\gcd (k,b)})/({b/\gcd (k,b)}) \in \mathcal {F}_{B}$.
${k}/{b} = ({k/\gcd (k,b)})/({b/\gcd (k,b)}) \in \mathcal {F}_{B}$.
We define the integer
where ![]() $\text {LCM}$ means taking the least common multiple. As a convention, the letter
$\text {LCM}$ means taking the least common multiple. As a convention, the letter ![]() $p$ always denotes prime numbers.
$p$ always denotes prime numbers.
For given ![]() $r$,
$r$, ![]() $s$ and
$s$ and ![]() $B$, we define the following auxiliary rational functions.
$B$, we define the following auxiliary rational functions.
Definition 2.3 (FSZ constructions) For any positive integer ![]() $n$ which is a multiple of
$n$ which is a multiple of ![]() $P_{B,\textrm {den}(r)}$, we define the rational function
$P_{B,\textrm {den}(r)}$, we define the rational function
 \[ R_n(t) = A_1(B)^n A_2(B)^n \frac{n!^{s+1}}{( {n}/{\textrm{den}(r)})!~^{\textrm{den}(r)(2r+1)|\mathcal{F}_B|}} \frac{(t-rn)\prod_{\theta \in \mathcal{F}_{B}} \prod_{j=0}^{(2r+1)n-1} \left( t-rn+j+\theta \right) }{\prod_{j=0}^{n}(t+j)^{s+1}}, \]
\[ R_n(t) = A_1(B)^n A_2(B)^n \frac{n!^{s+1}}{( {n}/{\textrm{den}(r)})!~^{\textrm{den}(r)(2r+1)|\mathcal{F}_B|}} \frac{(t-rn)\prod_{\theta \in \mathcal{F}_{B}} \prod_{j=0}^{(2r+1)n-1} \left( t-rn+j+\theta \right) }{\prod_{j=0}^{n}(t+j)^{s+1}}, \]where
we refer to ![]() $A_1(B)^n$ the major arithmetic (wasting) factor, and
$A_1(B)^n$ the major arithmetic (wasting) factor, and
we refer to ![]() $A_2(B)^n$ the minor arithmetic (wasting) factor.
$A_2(B)^n$ the minor arithmetic (wasting) factor.
Notice that by (2.1), both ![]() $A_1(B)^n$ and
$A_1(B)^n$ and ![]() $A_2(B)^n$ are integers; also,
$A_2(B)^n$ are integers; also, ![]() ${n}/{\textrm {den}(r)}$,
${n}/{\textrm {den}(r)}$, ![]() $rn$ and
$rn$ and ![]() $(2r+1)n$ are integers. The factors
$(2r+1)n$ are integers. The factors ![]() $A_1(B)^n$ and
$A_1(B)^n$ and ![]() $A_2(B)^n$ are technical: approximately speaking, they are designed to remedy the arithmetic loss from the denominators of rational zeros (it will be clear later in § 3). In the following lemma we estimate
$A_2(B)^n$ are technical: approximately speaking, they are designed to remedy the arithmetic loss from the denominators of rational zeros (it will be clear later in § 3). In the following lemma we estimate ![]() $A_1(B)$ and
$A_1(B)$ and ![]() $A_2(B)$.
$A_2(B)$.
Lemma 2.4 We have
and, for any ![]() $B$ larger than some absolute constant,
$B$ larger than some absolute constant,
Proof. We start by ![]() $\log A_1(B) = (2r+1)\sum _{b \in {\Psi }_B} \varphi (b)\log b$. Firstly,
$\log A_1(B) = (2r+1)\sum _{b \in {\Psi }_B} \varphi (b)\log b$. Firstly,
 \begin{align*} \log A_1(B) &\geqslant (2r+1)\sum_{b \in {\Psi}_B} \varphi(b)\log \varphi(b) \\ &= (2r+1) \int_{1^{-}}^{B} x\log x \,{d}|{\Psi}_x|; \end{align*}
\begin{align*} \log A_1(B) &\geqslant (2r+1)\sum_{b \in {\Psi}_B} \varphi(b)\log \varphi(b) \\ &= (2r+1) \int_{1^{-}}^{B} x\log x \,{d}|{\Psi}_x|; \end{align*}
an integration by parts argument with the fact that ![]() $| {\Psi }_x| = (({\zeta (2)\zeta (3)}/{\zeta (6)})+o_{x \rightarrow +\infty }(1)) x$ (see Proposition 2.2(1)) gives
$| {\Psi }_x| = (({\zeta (2)\zeta (3)}/{\zeta (6)})+o_{x \rightarrow +\infty }(1)) x$ (see Proposition 2.2(1)) gives ![]() $\log A_1(B) \geqslant (2r+1)(\frac {1}{2} ({\zeta (2)\zeta (3)}/{\zeta (6)}) + o_{B \rightarrow + \infty }(1) ) B^2 \log B$. On the other hand, it is well known (see, for instance, [Reference Montgomery and VaughanMV06, Theorem 2.9]) that
$\log A_1(B) \geqslant (2r+1)(\frac {1}{2} ({\zeta (2)\zeta (3)}/{\zeta (6)}) + o_{B \rightarrow + \infty }(1) ) B^2 \log B$. On the other hand, it is well known (see, for instance, [Reference Montgomery and VaughanMV06, Theorem 2.9]) that
where ![]() $\gamma = 0.577\ldots$ is Euler's constant. For any
$\gamma = 0.577\ldots$ is Euler's constant. For any ![]() $b \in {\Psi }_B$, since
$b \in {\Psi }_B$, since ![]() $\varphi (b) \leqslant B$, we derive that
$\varphi (b) \leqslant B$, we derive that
thus, ![]() $\log A_1(B) \leqslant (2r+1)(1+o_{B\rightarrow +\infty }(1))\log B \sum _{b \in {\Psi }_B} \varphi (b)$ and a summation by parts argument as above gives
$\log A_1(B) \leqslant (2r+1)(1+o_{B\rightarrow +\infty }(1))\log B \sum _{b \in {\Psi }_B} \varphi (b)$ and a summation by parts argument as above gives ![]() $\log A_1(B) \leqslant (2r+1)( \frac {1}{2} ({\zeta (2)\zeta (3)}/{\zeta (6)}) + o_{B \rightarrow + \infty }(1) ) B^2 \log B$. Combining the two parts, we obtain the estimate for
$\log A_1(B) \leqslant (2r+1)( \frac {1}{2} ({\zeta (2)\zeta (3)}/{\zeta (6)}) + o_{B \rightarrow + \infty }(1) ) B^2 \log B$. Combining the two parts, we obtain the estimate for ![]() $A_1(B)$.
$A_1(B)$.
Now, for ![]() $A_2(B)$, by (2.2) and
$A_2(B)$, by (2.2) and ![]() $e^{\gamma } = 1.78\ldots < 2$, when
$e^{\gamma } = 1.78\ldots < 2$, when ![]() $B$ is larger than some absolute constant, we have
$B$ is larger than some absolute constant, we have
 \begin{align*} \log A_2(B) &\leqslant (2r+1) \sum_{b \leqslant 2B\log\log B} \varphi(b) \sum_{p \mid b} \frac{\log p}{p-1} \\ &= (2r+1) \sum_{p \leqslant 2B\log\log B} \frac{\log p}{p-1} \sum_{\substack{b \leqslant 2B\log\log B \\ p \mid b}} \varphi(b). \end{align*}
\begin{align*} \log A_2(B) &\leqslant (2r+1) \sum_{b \leqslant 2B\log\log B} \varphi(b) \sum_{p \mid b} \frac{\log p}{p-1} \\ &= (2r+1) \sum_{p \leqslant 2B\log\log B} \frac{\log p}{p-1} \sum_{\substack{b \leqslant 2B\log\log B \\ p \mid b}} \varphi(b). \end{align*}
Since ![]() $\sum _{\substack {b \leqslant 2B\log \log B \\ p \mid b}} \varphi (b) \leqslant \sum _{\substack {b \leqslant 2B\log \log B \\ p \mid b}} b \leqslant {4B^2 (\log \log B)^2}/{p}$, it implies that
$\sum _{\substack {b \leqslant 2B\log \log B \\ p \mid b}} \varphi (b) \leqslant \sum _{\substack {b \leqslant 2B\log \log B \\ p \mid b}} b \leqslant {4B^2 (\log \log B)^2}/{p}$, it implies that
 \[ \log A_2(B) \leqslant 4(2r+1) B^2 (\log\log B)^2 \sum_{p} \frac{\log p}{p(p-1)}. \]
\[ \log A_2(B) \leqslant 4(2r+1) B^2 (\log\log B)^2 \sum_{p} \frac{\log p}{p(p-1)}. \]
Because ![]() $\sum _{p} (({\log p)}/{p(p-1)}) \leqslant \sum _{p \leqslant 5} (({\log p})/{p(p-1)}) + \sum _{p \geqslant 7} ({1}/{p^{1.5}}) \leqslant 2$, the estimate for
$\sum _{p} (({\log p)}/{p(p-1)}) \leqslant \sum _{p \leqslant 5} (({\log p})/{p(p-1)}) + \sum _{p \geqslant 7} ({1}/{p^{1.5}}) \leqslant 2$, the estimate for ![]() $A_2(B)$ follows.
$A_2(B)$ follows.
We proceed to construct linear forms in Hurwitz zeta values. Since the numerator and denominator of ![]() $R_{n}(t)$ have a common factor
$R_{n}(t)$ have a common factor ![]() $\prod _{j=0}^{n} (t+j)$, it can be rewritten as
$\prod _{j=0}^{n} (t+j)$, it can be rewritten as ![]() $R_{n}(t) = {Q_{n}(t)}/{\prod _{j=0}^{n} (t+j)^{s}}$, where
$R_{n}(t) = {Q_{n}(t)}/{\prod _{j=0}^{n} (t+j)^{s}}$, where ![]() $Q_{n}(t)$ is a polynomial in
$Q_{n}(t)$ is a polynomial in ![]() $t$ with rational coefficients. Since
$t$ with rational coefficients. Since ![]() $\deg R_n <0$ (see below), we know that
$\deg R_n <0$ (see below), we know that ![]() $R_n(t)$ has a (unique) partial fraction expansion
$R_n(t)$ has a (unique) partial fraction expansion
 \begin{equation} R_n(t) = \sum_{i=1}^{s}\sum_{k=0}^{n} \frac{a_{i,k}}{(t+k)^i} \end{equation}
\begin{equation} R_n(t) = \sum_{i=1}^{s}\sum_{k=0}^{n} \frac{a_{i,k}}{(t+k)^i} \end{equation}
with coefficients ![]() $a_{i,k} \in \mathbb {Q}$. Note that these coefficients
$a_{i,k} \in \mathbb {Q}$. Note that these coefficients ![]() $a_{i,k}$ also depend on
$a_{i,k}$ also depend on ![]() $n$,
$n$, ![]() $r$,
$r$, ![]() $s$ and
$s$ and ![]() $B$.
$B$.
We list two properties of ![]() $R_n(t)$ and
$R_n(t)$ and ![]() $a_{i,k}$ which will be used later in Lemma 2.5.
$a_{i,k}$ which will be used later in Lemma 2.5.
(1) As a rational function, the degree of ![]() $R_{n}(t)$ is
$R_{n}(t)$ is
This is due to ![]() $|\mathcal {F}_B| \leqslant B^2$ and
$|\mathcal {F}_B| \leqslant B^2$ and ![]() $s \geqslant 10(2r+1)B^2$.
$s \geqslant 10(2r+1)B^2$.
(2) The auxiliary function ![]() $R_{n}(t)$ has the following symmetry:
$R_{n}(t)$ has the following symmetry:
In fact, if we substitute ![]() $t$ by
$t$ by ![]() $-t-n$ in the definition of
$-t-n$ in the definition of ![]() $R_n(t)$ (see Definition 2.3), the factor
$R_n(t)$ (see Definition 2.3), the factor
 \[ \frac{(t-rn)\prod_{\theta \in \mathcal{F}_{B}} \prod_{j=0}^{(2r+1)n-1} \left( t-rn+j+\theta \right) }{\prod_{j=0}^{n}(t+j)^{s+1}} \]
\[ \frac{(t-rn)\prod_{\theta \in \mathcal{F}_{B}} \prod_{j=0}^{(2r+1)n-1} \left( t-rn+j+\theta \right) }{\prod_{j=0}^{n}(t+j)^{s+1}} \]becomes
 \begin{align*} & \frac{(-t-(r+1)n)\prod_{\theta \in \mathcal{F}_{B}} \prod_{j=0}^{(2r+1)n-1} \left( -t-(r+1)n+j+\theta \right) }{\prod_{j=0}^{n}(-t-n+j)^{s+1}} \\ &\quad = (-1)^{1+(2r+1)n|\mathcal{F}_B|-(s+1)(n+1)} \times \frac{(t+(r+1)n)\prod_{\theta \in \mathcal{F}_{B}} \prod_{j=0}^{(2r+1)n-1} \left( t+(r+1)n-j-\theta \right) }{\prod_{j=0}^{n}(t+n-j)^{s+1}} \\ &\quad = (-1) \times \prod_{j=-rn}^{(r+1)n}(t+j) \times \frac{\prod_{\theta \in \mathcal{F}_{B} \setminus \{ 1\}} \prod_{j=0}^{(2r+1)n-1} \left( t- rn +j + 1-\theta \right) }{\prod_{j=0}^{n}(t+j)^{s+1}}. \end{align*}
\begin{align*} & \frac{(-t-(r+1)n)\prod_{\theta \in \mathcal{F}_{B}} \prod_{j=0}^{(2r+1)n-1} \left( -t-(r+1)n+j+\theta \right) }{\prod_{j=0}^{n}(-t-n+j)^{s+1}} \\ &\quad = (-1)^{1+(2r+1)n|\mathcal{F}_B|-(s+1)(n+1)} \times \frac{(t+(r+1)n)\prod_{\theta \in \mathcal{F}_{B}} \prod_{j=0}^{(2r+1)n-1} \left( t+(r+1)n-j-\theta \right) }{\prod_{j=0}^{n}(t+n-j)^{s+1}} \\ &\quad = (-1) \times \prod_{j=-rn}^{(r+1)n}(t+j) \times \frac{\prod_{\theta \in \mathcal{F}_{B} \setminus \{ 1\}} \prod_{j=0}^{(2r+1)n-1} \left( t- rn +j + 1-\theta \right) }{\prod_{j=0}^{n}(t+j)^{s+1}}. \end{align*}
We have used the facts that ![]() $(2r+1)n$ is even and
$(2r+1)n$ is even and ![]() $s$ is odd in the above computation. By observing that
$s$ is odd in the above computation. By observing that
we obtain ![]() $R_{n}(-t-n) = - R_{n}(t)$. In particular, since the partial fraction expansion for
$R_{n}(-t-n) = - R_{n}(t)$. In particular, since the partial fraction expansion for ![]() $R_n(t)$ is unique, we derive that
$R_n(t)$ is unique, we derive that
for all ![]() $1\leqslant i\leqslant s$,
$1\leqslant i\leqslant s$, ![]() $0 \leqslant k \leqslant n$.
$0 \leqslant k \leqslant n$.
For all ![]() $\theta \in \mathcal {F}_B$, we define the following quantities:
$\theta \in \mathcal {F}_B$, we define the following quantities:
 \begin{equation} r_{n,\theta} = \sum_{m=1}^{\infty} R_{n}(m+\theta). \end{equation}
\begin{equation} r_{n,\theta} = \sum_{m=1}^{\infty} R_{n}(m+\theta). \end{equation}
The notation ![]() $r_{n,\theta }$ is adopted to keep pace with that in [Reference Fischler, Sprang and ZudilinFSZ19]. There is no risk for it to be confused with the Ball–Rivoal length parameter
$r_{n,\theta }$ is adopted to keep pace with that in [Reference Fischler, Sprang and ZudilinFSZ19]. There is no risk for it to be confused with the Ball–Rivoal length parameter ![]() $r$.
$r$.
We recall the definition of the Hurwitz zeta values:
 \[ \zeta(i,\alpha) = \sum_{m=0}^{\infty} \frac{1}{(m+\alpha)^i}, \]
\[ \zeta(i,\alpha) = \sum_{m=0}^{\infty} \frac{1}{(m+\alpha)^i}, \]
where ![]() $i\geqslant 2$ is an integer and
$i\geqslant 2$ is an integer and ![]() $\alpha$ is a positive real number.
$\alpha$ is a positive real number.
The following lemma is the same as [Reference Fischler, Sprang and ZudilinFSZ19, Lemma 1] (for a proof, see therein).
Lemma 2.5 (Linear forms) For all ![]() $\theta \in \mathcal {F}_B$, we have
$\theta \in \mathcal {F}_B$, we have
 \[ r_{n,\theta} = \rho_{0,\theta} + \sum_{\substack{3 \leqslant i \leqslant s \\ i \ \textrm{odd}}} \rho_{i} \zeta\left(i,\theta \right), \]
\[ r_{n,\theta} = \rho_{0,\theta} + \sum_{\substack{3 \leqslant i \leqslant s \\ i \ \textrm{odd}}} \rho_{i} \zeta\left(i,\theta \right), \]where the rational coefficient
 \[ \rho_{i} = \sum_{k=0}^{n} a_{i,k} \quad \text{for } 3 \leqslant i \leqslant s, i \ {\rm odd} , \]
\[ \rho_{i} = \sum_{k=0}^{n} a_{i,k} \quad \text{for } 3 \leqslant i \leqslant s, i \ {\rm odd} , \]
does not depend on ![]() $\theta \in \mathcal {F}_B$, and
$\theta \in \mathcal {F}_B$, and
 \[ \rho_{0,\theta} = - \sum_{k=0}^{n}\sum_{\ell=0}^{k}\sum_{i=1}^{s} \frac{a_{i,k}}{\left( \ell+\theta \right)^i}. \]
\[ \rho_{0,\theta} = - \sum_{k=0}^{n}\sum_{\ell=0}^{k}\sum_{i=1}^{s} \frac{a_{i,k}}{\left( \ell+\theta \right)^i}. \]3. Arithmetic lemma
The following proposition is elementary; we omit the proof.
Proposition 3.1 Let ![]() $L \in \mathbb {N} \cup \{ 0 \}$. Suppose that
$L \in \mathbb {N} \cup \{ 0 \}$. Suppose that ![]() $x_1,x_2,\ldots ,x_L$ are any
$x_1,x_2,\ldots ,x_L$ are any ![]() $L$ consecutive terms in an integer arithmetic progression with common difference
$L$ consecutive terms in an integer arithmetic progression with common difference ![]() $b \in \mathbb {N}$; then, for any prime
$b \in \mathbb {N}$; then, for any prime ![]() $q \nmid b$, we have
$q \nmid b$, we have
 \[ v_q(x_1x_2\ldots x_L) \geqslant \sum_{i=1}^{\infty} \left\lfloor \frac{L}{q^i} \right\rfloor . \]
\[ v_q(x_1x_2\ldots x_L) \geqslant \sum_{i=1}^{\infty} \left\lfloor \frac{L}{q^i} \right\rfloor . \]
In the degenerate case of ![]() $L=0$, we view
$L=0$, we view ![]() $x_1x_2\ldots x_L = 1$.
$x_1x_2\ldots x_L = 1$.
For any ![]() ${a}/{b} \in \mathcal {F}_{B}$ with
${a}/{b} \in \mathcal {F}_{B}$ with ![]() $\gcd (a,b)=1$, we define the following polynomials:
$\gcd (a,b)=1$, we define the following polynomials:
 \begin{align} F_{b,a}(t) &= \frac{\prod_{p \mid b} p^{{(2r+1)n}/({p-1})}}{( {n}/{\textrm{den}(r)})!^{\,\textrm{den}(r)(2r+1)}}\cdot b^{(2r+1)n} \prod_{j=0}^{(2r+1)n -1} \left( t-rn + j + \frac{a}{b} \right) \nonumber\\ &= \frac{\prod_{p \mid b} p^{{(2r+1)n}/({p-1})}}{( {n}/{\textrm{den}(r)})!^{\,\textrm{den}(r)(2r+1)}} \prod_{j=0}^{(2r+1)n -1} \left( bt-brn + a + bj \right). \end{align}
\begin{align} F_{b,a}(t) &= \frac{\prod_{p \mid b} p^{{(2r+1)n}/({p-1})}}{( {n}/{\textrm{den}(r)})!^{\,\textrm{den}(r)(2r+1)}}\cdot b^{(2r+1)n} \prod_{j=0}^{(2r+1)n -1} \left( t-rn + j + \frac{a}{b} \right) \nonumber\\ &= \frac{\prod_{p \mid b} p^{{(2r+1)n}/({p-1})}}{( {n}/{\textrm{den}(r)})!^{\,\textrm{den}(r)(2r+1)}} \prod_{j=0}^{(2r+1)n -1} \left( bt-brn + a + bj \right). \end{align}Then we define
 \[ \widetilde{F}_{b,a}(t) = \begin{cases} F_{b,a}(t) & \text{if}\ {a}/{b} \neq 1, \\ (t-rn)F_{1,1}(t) & \text{if}\ {a}/{b} = 1. \end{cases} \]
\[ \widetilde{F}_{b,a}(t) = \begin{cases} F_{b,a}(t) & \text{if}\ {a}/{b} \neq 1, \\ (t-rn)F_{1,1}(t) & \text{if}\ {a}/{b} = 1. \end{cases} \]
Notice that since ![]() $n \in P_{B,\textrm {den}(r)}\mathbb {N}$, by (2.1), all of
$n \in P_{B,\textrm {den}(r)}\mathbb {N}$, by (2.1), all of ![]() ${(2r+1)n}/({p-1})$,
${(2r+1)n}/({p-1})$, ![]() ${n}/{\textrm {den}(r)}$,
${n}/{\textrm {den}(r)}$, ![]() $rn$ and
$rn$ and ![]() $(2r+1)n$ are integers. By Definition 2.3, we have
$(2r+1)n$ are integers. By Definition 2.3, we have
 \begin{equation} R_n(t) = n!^{s+1} \frac{\prod_{{a}/{b} \in \mathcal{F}_{B}}\widetilde{F}_{b,a}(t)}{\prod_{j=0}^{n}(t+j)^{s+1}}. \end{equation}
\begin{equation} R_n(t) = n!^{s+1} \frac{\prod_{{a}/{b} \in \mathcal{F}_{B}}\widetilde{F}_{b,a}(t)}{\prod_{j=0}^{n}(t+j)^{s+1}}. \end{equation} For a formal series ![]() $U(t) = \sum _{\ell =0}^{\infty } u_{\ell } t^{\ell } \in \mathbb {Q}[[t]]$, we denote by
$U(t) = \sum _{\ell =0}^{\infty } u_{\ell } t^{\ell } \in \mathbb {Q}[[t]]$, we denote by ![]() $[t^{\ell }](U(t))$ the
$[t^{\ell }](U(t))$ the ![]() $\ell$th coefficient of
$\ell$th coefficient of ![]() $U(t)$, i.e.,
$U(t)$, i.e., ![]() $[t^{\ell }](U(t)) = u_{\ell }$.
$[t^{\ell }](U(t)) = u_{\ell }$.
As usual, we denote by ![]() $d_n=\text {LCM}\{1,2,\ldots ,n\}$ the least common multiple of the first
$d_n=\text {LCM}\{1,2,\ldots ,n\}$ the least common multiple of the first ![]() $n$ positive integers. By the prime number theorem, we have
$n$ positive integers. By the prime number theorem, we have ![]() $\lim _{n \rightarrow +\infty } d_n^{1/n} = e$. We first establish the following arithmetic property of
$\lim _{n \rightarrow +\infty } d_n^{1/n} = e$. We first establish the following arithmetic property of ![]() $\widetilde {F}_{b,a}(t)$.
$\widetilde {F}_{b,a}(t)$.
Proposition 3.2 For any non-negative integers ![]() $\ell$ and
$\ell$ and ![]() $k$, we have
$k$, we have
Proof. Note that we only need to prove the proposition with ![]() $\widetilde {F}_{b,a}$ replaced by
$\widetilde {F}_{b,a}$ replaced by ![]() $F_{b,a}$. If
$F_{b,a}$. If ![]() $\ell > \deg F_{b,a} =(2r+1)n$, the proposition trivially holds. In the rest of the proof, we assume that
$\ell > \deg F_{b,a} =(2r+1)n$, the proposition trivially holds. In the rest of the proof, we assume that ![]() $\ell \leqslant \deg F_{b,a}$.
$\ell \leqslant \deg F_{b,a}$.
For a prime ![]() $q \mid b$, the
$q \mid b$, the ![]() $q$-adic order of the factor
$q$-adic order of the factor ![]() ${\prod _{p \mid b} p^{{(2r+1)n}/({p-1})}}/{({n}/{\textrm {den}(r)} )!^{\,\textrm {den}(r)(2r+1)}}$ is non-negative (recall that
${\prod _{p \mid b} p^{{(2r+1)n}/({p-1})}}/{({n}/{\textrm {den}(r)} )!^{\,\textrm {den}(r)(2r+1)}}$ is non-negative (recall that ![]() $v_q(m!) \leqslant {m}/({q-1})$). So, by (3.1), the
$v_q(m!) \leqslant {m}/({q-1})$). So, by (3.1), the ![]() $q$-adic order of every coefficient of
$q$-adic order of every coefficient of ![]() $F_{b,a}(t-k)$ is non-negative. Therefore, for any prime
$F_{b,a}(t-k)$ is non-negative. Therefore, for any prime ![]() $q \mid b$, we have
$q \mid b$, we have ![]() $v_q( d_{n}^{\ell } \cdot [t^{\ell }](F_{b,a}(t-k))) \geqslant 0$.
$v_q( d_{n}^{\ell } \cdot [t^{\ell }](F_{b,a}(t-k))) \geqslant 0$.
Now consider a prime ![]() $q \nmid b$. Notice that
$q \nmid b$. Notice that ![]() $[t^{\ell }](\prod _{j=0}^{(2r+1)n -1} ( b(t-k)-brn + a + bj ))$ is a sum of finitely many terms all of the form
$[t^{\ell }](\prod _{j=0}^{(2r+1)n -1} ( b(t-k)-brn + a + bj ))$ is a sum of finitely many terms all of the form
 \begin{equation} b^{\ell} \prod_{i=1}^{\ell + 1}\prod_{j \in J_i} \left( -bk-brn + a + bj \right), \end{equation}
\begin{equation} b^{\ell} \prod_{i=1}^{\ell + 1}\prod_{j \in J_i} \left( -bk-brn + a + bj \right), \end{equation}
where ![]() $J_i$ is a set consisting of
$J_i$ is a set consisting of ![]() $L_i \in \mathbb {N} \cup \{ 0 \}$ consecutive integers such that
$L_i \in \mathbb {N} \cup \{ 0 \}$ consecutive integers such that ![]() $L_1 + L_2 + \cdots + L_{\ell + 1} = (2r+1)n - \ell$. By Proposition 3.1, we derive that the
$L_1 + L_2 + \cdots + L_{\ell + 1} = (2r+1)n - \ell$. By Proposition 3.1, we derive that the ![]() $q$-adic order of the expression (3.3) is
$q$-adic order of the expression (3.3) is
 \[ v_q(\hbox{Equation (3.3)}) \geqslant \sum_{i=1}^{\infty} \sum_{j=1}^{\ell + 1} \left\lfloor \frac{L_j}{q^i} \right\rfloor. \]
\[ v_q(\hbox{Equation (3.3)}) \geqslant \sum_{i=1}^{\infty} \sum_{j=1}^{\ell + 1} \left\lfloor \frac{L_j}{q^i} \right\rfloor. \]
For a fixed ![]() $i \geqslant 1$, we have
$i \geqslant 1$, we have
 \begin{align*} \sum_{j=1}^{\ell + 1} \biggl\lfloor \frac{L_j}{q^i} \biggr\rfloor \geqslant \sum_{j=1}^{\ell + 1} \frac{L_j - (q^i - 1)}{q^i} = \frac{(2r+1)n+1}{q^i} - \ell - 1 > \biggl\lfloor \frac{(2r+1)n}{q^i} \biggr\rfloor - \ell - 1, \end{align*}
\begin{align*} \sum_{j=1}^{\ell + 1} \biggl\lfloor \frac{L_j}{q^i} \biggr\rfloor \geqslant \sum_{j=1}^{\ell + 1} \frac{L_j - (q^i - 1)}{q^i} = \frac{(2r+1)n+1}{q^i} - \ell - 1 > \biggl\lfloor \frac{(2r+1)n}{q^i} \biggr\rfloor - \ell - 1, \end{align*}
but the left-hand side is a non-negative integer, so we obtain that ![]() $\sum _{j=1}^{\ell + 1} \lfloor {L_j}/{q^i} \rfloor \geqslant \max (0, \lfloor {(2r+1)n}/{q^i} \rfloor - \ell )$. Therefore,
$\sum _{j=1}^{\ell + 1} \lfloor {L_j}/{q^i} \rfloor \geqslant \max (0, \lfloor {(2r+1)n}/{q^i} \rfloor - \ell )$. Therefore,
 \begin{align} v_q(\hbox{Equation (3.3)}) &\geqslant \sum_{i=1}^{\lfloor \log_q n \rfloor} \left( \left\lfloor \frac{(2r+1)n}{q^i} \right\rfloor - \ell \right) \nonumber\\ &\geqslant \sum_{i=1}^{\lfloor \log_q n \rfloor} \left( \textrm{den}(r)(2r+1) \left\lfloor \frac{n/\textrm{den}(r)}{q^i} \right\rfloor - \ell \right) \nonumber\\ &= v_q\left( \left( \frac{n}{\textrm{den}(r)} \right)!^{\,\textrm{den}(r)(2r+1)} \right) - \ell v_q(d_n). \end{align}
\begin{align} v_q(\hbox{Equation (3.3)}) &\geqslant \sum_{i=1}^{\lfloor \log_q n \rfloor} \left( \left\lfloor \frac{(2r+1)n}{q^i} \right\rfloor - \ell \right) \nonumber\\ &\geqslant \sum_{i=1}^{\lfloor \log_q n \rfloor} \left( \textrm{den}(r)(2r+1) \left\lfloor \frac{n/\textrm{den}(r)}{q^i} \right\rfloor - \ell \right) \nonumber\\ &= v_q\left( \left( \frac{n}{\textrm{den}(r)} \right)!^{\,\textrm{den}(r)(2r+1)} \right) - \ell v_q(d_n). \end{align}
(The non-trivial part is for cases ![]() $q\leqslant n$; for
$q\leqslant n$; for ![]() $q>n$, the above derivation is also valid but degenerates to trivial results.) In conclusion, for any prime
$q>n$, the above derivation is also valid but degenerates to trivial results.) In conclusion, for any prime ![]() $q \nmid b$, by (3.1) and inequality (3.4), we find that
$q \nmid b$, by (3.1) and inequality (3.4), we find that ![]() $d_{n}^{\ell } \cdot [t^{\ell }](F_{b,a}(t-k))$ is a sum of finitely many terms, each of these terms having non-negative
$d_{n}^{\ell } \cdot [t^{\ell }](F_{b,a}(t-k))$ is a sum of finitely many terms, each of these terms having non-negative ![]() $q$-adic order; this completes the proof of Proposition 3.2.
$q$-adic order; this completes the proof of Proposition 3.2.
We prove the following arithmetic lemma, which corresponds to [Reference Fischler, Sprang and ZudilinFSZ19, Lemma 2]. In our situation, the Ball–Rivoal length parameter ![]() $r$ is just a rational number (not necessarily an integer or a half integer), so we have to modify the proof for
$r$ is just a rational number (not necessarily an integer or a half integer), so we have to modify the proof for ![]() $d_n^{s+1-i} a_{i,k} \in \mathbb {Z}$, but the rest of proof is the same as [Reference Fischler, Sprang and ZudilinFSZ19, Lemma 2].
$d_n^{s+1-i} a_{i,k} \in \mathbb {Z}$, but the rest of proof is the same as [Reference Fischler, Sprang and ZudilinFSZ19, Lemma 2].
Lemma 3.3 (Arithmetic lemma) We have
for all odd integers ![]() $i$ with
$i$ with ![]() $3 \leqslant i \leqslant s$, and we have
$3 \leqslant i \leqslant s$, and we have
for all ![]() $\theta \in \mathcal {F}_B$.
$\theta \in \mathcal {F}_B$.
Proof. For any ![]() $k \in \{ 0,1,\ldots ,n \}$ and any
$k \in \{ 0,1,\ldots ,n \}$ and any ![]() $i \in \{ 1,2,\ldots ,s \}$, by comparing (3.2) with the partial fraction expansion (2.3) of
$i \in \{ 1,2,\ldots ,s \}$, by comparing (3.2) with the partial fraction expansion (2.3) of ![]() $R_n(t)$, and by viewing
$R_n(t)$, and by viewing ![]() $t^{s+1}R_n(t-k) \in \mathbb {Q}[[t]]$ as a formal series, we have
$t^{s+1}R_n(t-k) \in \mathbb {Q}[[t]]$ as a formal series, we have
 \begin{align*} a_{i,k} &= [t^{s+1-i}]\big( t^{s+1}R_{n}(t-k) \big) \\ &= (-1)^{(s+1)k}\frac{n!^{s+1}}{k!^{s+1}(n-k)!^{s+1}} [t^{s+1-i}]\biggl( \prod_{{a}/{b} \in \mathcal{F}_{B}} \widetilde{F}_{b,a}(t-k) \prod_{\substack{0 \leqslant j \leqslant n \\ j \neq k}} (1+ \frac{t}{j-k} )^{-s-1} \biggr) \\ &= \binom{n}{k}^{s+1} \sum_{\substack{\underline{\ell} \\ \textrm{sum}(\underline{\ell}) = s+1-i}} \prod_{{a}/{b} \in \mathcal{F}_{B}} [t^{\ell_{b,a}}]( \widetilde{F}_{b,a}(t-k) ) \prod_{\substack{0 \leqslant j \leqslant n \\ j \neq k}} \frac{(-1)^{\ell_j}\binom{s+\ell_j}{\ell_j}}{(j-k)^{\ell_j}}, \end{align*}
\begin{align*} a_{i,k} &= [t^{s+1-i}]\big( t^{s+1}R_{n}(t-k) \big) \\ &= (-1)^{(s+1)k}\frac{n!^{s+1}}{k!^{s+1}(n-k)!^{s+1}} [t^{s+1-i}]\biggl( \prod_{{a}/{b} \in \mathcal{F}_{B}} \widetilde{F}_{b,a}(t-k) \prod_{\substack{0 \leqslant j \leqslant n \\ j \neq k}} (1+ \frac{t}{j-k} )^{-s-1} \biggr) \\ &= \binom{n}{k}^{s+1} \sum_{\substack{\underline{\ell} \\ \textrm{sum}(\underline{\ell}) = s+1-i}} \prod_{{a}/{b} \in \mathcal{F}_{B}} [t^{\ell_{b,a}}]( \widetilde{F}_{b,a}(t-k) ) \prod_{\substack{0 \leqslant j \leqslant n \\ j \neq k}} \frac{(-1)^{\ell_j}\binom{s+\ell_j}{\ell_j}}{(j-k)^{\ell_j}}, \end{align*}
where the sum is taken for all tuples ![]() $\underline {\ell }$ consisting of non-negative integers
$\underline {\ell }$ consisting of non-negative integers ![]() $\ell _{b,a}$ and
$\ell _{b,a}$ and ![]() $\ell _j$ such that
$\ell _j$ such that
 \[ \textrm{sum}(\underline{\ell}) = \sum_{{a}/{b} \in \mathcal{F}_{B}} \ell_{b,a} + \sum_{\substack{0 \leqslant j \leqslant n \\ j \neq k}} \ell_j = s+1-i. \]
\[ \textrm{sum}(\underline{\ell}) = \sum_{{a}/{b} \in \mathcal{F}_{B}} \ell_{b,a} + \sum_{\substack{0 \leqslant j \leqslant n \\ j \neq k}} \ell_j = s+1-i. \]
By Proposition 3.2 and the fact that ![]() $d_n^{\ell _j} ({1}/{(j-k)^{\ell _j}}) \in \mathbb {Z}$, we derive that
$d_n^{\ell _j} ({1}/{(j-k)^{\ell _j}}) \in \mathbb {Z}$, we derive that
Once ![]() $d_{n}^{s+1-i} a_{i,k} \in \mathbb {Z}$ is established, the rest of the arguments are the same as [Reference Fischler, Sprang and ZudilinFSZ19, Lemma 2]. We only outline the proof as follows:
$d_{n}^{s+1-i} a_{i,k} \in \mathbb {Z}$ is established, the rest of the arguments are the same as [Reference Fischler, Sprang and ZudilinFSZ19, Lemma 2]. We only outline the proof as follows: ![]() $d_n^{s+1-i}\rho _i \in \mathbb {Z}$ follows immediately from the expression of
$d_n^{s+1-i}\rho _i \in \mathbb {Z}$ follows immediately from the expression of ![]() $\rho _i$. The proof for
$\rho _i$. The proof for ![]() $d_{n+1}^{s+1} \rho _{0,\theta } \in \mathbb {Z}$ is more involved; it is proved by showing that
$d_{n+1}^{s+1} \rho _{0,\theta } \in \mathbb {Z}$ is more involved; it is proved by showing that
 \[ \sum_{i=1}^{s} \frac{d_{n+1}^{s+1} a_{i,k}}{(\ell + \theta)^{i}} \]
\[ \sum_{i=1}^{s} \frac{d_{n+1}^{s+1} a_{i,k}}{(\ell + \theta)^{i}} \]
is an integer for any ![]() $0 \leqslant \ell \leqslant k \leqslant n$ and
$0 \leqslant \ell \leqslant k \leqslant n$ and ![]() $\theta \in \mathcal {F}_B$. In order to do this, we will use the fact that
$\theta \in \mathcal {F}_B$. In order to do this, we will use the fact that ![]() $R_n(t)$ has zeros
$R_n(t)$ has zeros ![]() $-n+\theta , -n+1+\theta , -n+2 +\theta ,\ldots , \theta$ for
$-n+\theta , -n+1+\theta , -n+2 +\theta ,\ldots , \theta$ for ![]() $\theta \in \mathcal {F}_B \setminus \{1\}$.
$\theta \in \mathcal {F}_B \setminus \{1\}$.
4. Analysis lemma
Under our assumptions that ![]() $s \geqslant 10(2r+1)B^2$ and
$s \geqslant 10(2r+1)B^2$ and ![]() $B$ is larger than some absolute constant, we have the following result.
$B$ is larger than some absolute constant, we have the following result.
Lemma 4.1 (Analysis lemma) We have
where
and ![]() $x_0$ is the unique positive real solution of the equation
$x_0$ is the unique positive real solution of the equation
 \[ f(X) = \left( \frac{X+2r+1}{X} \right)^{|\mathcal{F}_B|} \left( \frac{X+r}{X+r+1} \right)^{s+1} = 1. \]
\[ f(X) = \left( \frac{X+2r+1}{X} \right)^{|\mathcal{F}_B|} \left( \frac{X+r}{X+r+1} \right)^{s+1} = 1. \]
Moreover, for any ![]() $\theta \in \mathcal {F}_B$, we have
$\theta \in \mathcal {F}_B$, we have
Before proving the analysis lemma, we first collect some properties of the functions ![]() $f$ and
$f$ and ![]() $g$. Note that these two functions depend only on
$g$. Note that these two functions depend only on ![]() $r,s$ and
$r,s$ and ![]() $B$.
$B$.
Proposition 4.2 Let ![]() $f(x)$ and
$f(x)$ and ![]() $g(x)$ be the functions in Lemma 4.1 (defined on
$g(x)$ be the functions in Lemma 4.1 (defined on ![]() $x \in (0,+\infty )$). Then:
$x \in (0,+\infty )$). Then:
(1) there exists a unique
 $x_0 \in (0,+\infty )$ such that
$x_0 \in (0,+\infty )$ such that  $f(x_0) = 1$,
$f(x_0) = 1$,  $f(x) > 1$ on
$f(x) > 1$ on  $(0,x_0)$ and
$(0,x_0)$ and  $f(x) < 1$ on
$f(x) < 1$ on  $(x_0,+\infty )$; moreover,
$(x_0,+\infty )$; moreover,
 \[ x_0 < \frac{r(r+1)|\mathcal{F}_B|}{s+1 - (2r+1)|\mathcal{F}_B|}; \]
\[ x_0 < \frac{r(r+1)|\mathcal{F}_B|}{s+1 - (2r+1)|\mathcal{F}_B|}; \](2) if we fix
 $r \in \mathbb {Q}_{+}$ and assume in addition that
$r \in \mathbb {Q}_{+}$ and assume in addition that  $B = cs^{1/2}/\log ^{1/2} s$ for some positive constant
$B = cs^{1/2}/\log ^{1/2} s$ for some positive constant  $c$, when
$c$, when  $s \rightarrow +\infty$, we have
$s \rightarrow +\infty$, we have
 \[ \lim_{\substack{s \rightarrow +\infty \\ B = cs^{1/2}/\log^{1/2} s}} g(x_0)^{{1}/({s+1})} = \exp\left( \frac{\zeta(2)\zeta(3)}{4\zeta(6)}(2r+1)c^2 \right) \frac{r^r}{(r+1)^{r+1}}. \]
\[ \lim_{\substack{s \rightarrow +\infty \\ B = cs^{1/2}/\log^{1/2} s}} g(x_0)^{{1}/({s+1})} = \exp\left( \frac{\zeta(2)\zeta(3)}{4\zeta(6)}(2r+1)c^2 \right) \frac{r^r}{(r+1)^{r+1}}. \]
Proof. For the first proposition, by calculating ![]() ${f'(x)}/{f(x)}$, we find that
${f'(x)}/{f(x)}$, we find that ![]() $f'(x) = 0$ has a unique positive solution
$f'(x) = 0$ has a unique positive solution ![]() $x_1$ which satisfies
$x_1$ which satisfies
and ![]() $f$ is decreasing on
$f$ is decreasing on ![]() $(0,x_1)$, increasing on
$(0,x_1)$, increasing on ![]() $(x_1,+\infty )$. Since
$(x_1,+\infty )$. Since ![]() $f(0^{+}) = +\infty$ and
$f(0^{+}) = +\infty$ and ![]() $f(+\infty ) = 1$, there exists a unique
$f(+\infty ) = 1$, there exists a unique ![]() $x_0$ satisfying all the requirements. The last (very weak) bound for
$x_0$ satisfying all the requirements. The last (very weak) bound for ![]() $x_0$ comes from
$x_0$ comes from ![]() $x_0 < x_1$ and (4.1).
$x_0 < x_1$ and (4.1).
The second proposition follows from the estimates for ![]() $A_1(B)$,
$A_1(B)$, ![]() $A_2(B)$,
$A_2(B)$, ![]() $|\mathcal {F}_B|$ (see Proposition 2.2 and Lemma 2.4) and
$|\mathcal {F}_B|$ (see Proposition 2.2 and Lemma 2.4) and ![]() $x_0 \rightarrow 0$.
$x_0 \rightarrow 0$.
Now we prove Lemma 4.1. We claim that it can be proved by the same strategy in [Reference Fischler, Sprang and ZudilinFSZ19, Lemma 3], but we give a slightly modified proof.
Proof Proof of Lemma 4.1 For any ![]() $\theta \in \mathcal {F}_B$, since
$\theta \in \mathcal {F}_B$, since ![]() $R_n(m+\theta ) = 0$ for
$R_n(m+\theta ) = 0$ for ![]() $m=1,2,\ldots ,rn-1$, we define the shift version of the auxiliary rational functions:
$m=1,2,\ldots ,rn-1$, we define the shift version of the auxiliary rational functions:
then, by (2.4), we have
 \begin{equation} r_{n,\theta} = \sum_{k=0}^{\infty} \widehat{R}_{n}(k+\theta). \end{equation}
\begin{equation} r_{n,\theta} = \sum_{k=0}^{\infty} \widehat{R}_{n}(k+\theta). \end{equation} We have the following two expressions for ![]() $\widehat {R}_{n}(t)$:
$\widehat {R}_{n}(t)$:
 \begin{align} \widehat{R}_{n}(t) &= A_1(B)^n A_2(B)^n \frac{n!^{s+1}}{( {n}/{\textrm{den}(r)})!^{\,\textrm{den}(r)(2r+1)|\mathcal{F}_B|}} \frac{ t\prod_{\theta' \in \mathcal{F}_B} \prod_{j=0}^{(2r+1)n-1} \left(t+j+\theta' \right)}{ \prod_{j=0}^{n} (t+rn+j)^{s+1}} \end{align}
\begin{align} \widehat{R}_{n}(t) &= A_1(B)^n A_2(B)^n \frac{n!^{s+1}}{( {n}/{\textrm{den}(r)})!^{\,\textrm{den}(r)(2r+1)|\mathcal{F}_B|}} \frac{ t\prod_{\theta' \in \mathcal{F}_B} \prod_{j=0}^{(2r+1)n-1} \left(t+j+\theta' \right)}{ \prod_{j=0}^{n} (t+rn+j)^{s+1}} \end{align} \begin{align} &= A_1(B)^n A_2(B)^n \frac{n!^{s+1}}{( {n}/{\textrm{den}(r)})!^{\,\textrm{den}(r)(2r+1)|\mathcal{F}_B|}} \nonumber\\ &\quad \times t \biggl( \prod_{\theta' \in \mathcal{F}_B } \frac{\Gamma(t+(2r+1)n+\theta')}{\Gamma(t+\theta')} \biggr) \left( \frac{\Gamma(t+rn)}{\Gamma(t+(r+1)n+1)} \right)^{s+1} . \end{align}
\begin{align} &= A_1(B)^n A_2(B)^n \frac{n!^{s+1}}{( {n}/{\textrm{den}(r)})!^{\,\textrm{den}(r)(2r+1)|\mathcal{F}_B|}} \nonumber\\ &\quad \times t \biggl( \prod_{\theta' \in \mathcal{F}_B } \frac{\Gamma(t+(2r+1)n+\theta')}{\Gamma(t+\theta')} \biggr) \left( \frac{\Gamma(t+rn)}{\Gamma(t+(r+1)n+1)} \right)^{s+1} . \end{align} We define ![]() $c_1 = \min (\frac {1}{2}e^{-10s/r},{x_0}/{2})$, which is independent of
$c_1 = \min (\frac {1}{2}e^{-10s/r},{x_0}/{2})$, which is independent of ![]() $n$. To estimate the series (4.2) for
$n$. To estimate the series (4.2) for ![]() $r_{n,\theta }$, we divide it into three parts:
$r_{n,\theta }$, we divide it into three parts:
 \[ r_{n,\theta} = \biggl( \sum_{0 \leqslant k < c_1n} + \sum_{c_1 n \leqslant k \leqslant n^{10}} + \sum_{k>n^{10}} \biggr) ( \widehat{R}_{n}(k+\theta)). \]
\[ r_{n,\theta} = \biggl( \sum_{0 \leqslant k < c_1n} + \sum_{c_1 n \leqslant k \leqslant n^{10}} + \sum_{k>n^{10}} \biggr) ( \widehat{R}_{n}(k+\theta)). \] For the first part, by (4.3), for all ![]() $t \in (0,2c_1 n]$, we have
$t \in (0,2c_1 n]$, we have
 \begin{align*} \frac{\widehat{R}_{n}^{\prime}(t)}{\widehat{R}_{n}(t)} &> \sum_{j=0}^{(2r+1)n} \frac{1}{t+j} - (s+1) \sum_{j=0}^{n} \frac{1}{t+rn+j} \\ &> \log\left( \frac{t +(2r+1)n}{t} \right) - (s+1) \frac{n+1}{rn} \\ &> \log\left(\frac{1}{2c_1}\right) - 4s/r \\ &> 0. \end{align*}
\begin{align*} \frac{\widehat{R}_{n}^{\prime}(t)}{\widehat{R}_{n}(t)} &> \sum_{j=0}^{(2r+1)n} \frac{1}{t+j} - (s+1) \sum_{j=0}^{n} \frac{1}{t+rn+j} \\ &> \log\left( \frac{t +(2r+1)n}{t} \right) - (s+1) \frac{n+1}{rn} \\ &> \log\left(\frac{1}{2c_1}\right) - 4s/r \\ &> 0. \end{align*}
So, ![]() $\widehat {R}_{n}(t)$ is increasing on
$\widehat {R}_{n}(t)$ is increasing on ![]() $t \in (0,2c_1 n]$; we derive that (when
$t \in (0,2c_1 n]$; we derive that (when ![]() $n > c_1^{-1}$)
$n > c_1^{-1}$)
To deal with the middle part, for all ![]() $c_1 n \leqslant k \leqslant n^{10}$, we denote
$c_1 n \leqslant k \leqslant n^{10}$, we denote ![]() $\kappa = \kappa (k,n) = {k}/{n} \in [c_1, +\infty )$. By applying Stirling's formula in the weak form
$\kappa = \kappa (k,n) = {k}/{n} \in [c_1, +\infty )$. By applying Stirling's formula in the weak form
for the equation (4.4), a calculation shows that as ![]() $n \rightarrow +\infty$,
$n \rightarrow +\infty$,
 \begin{align} \widehat{R}_{n}(k+\theta) &= n^{O(1)} \cdot A_1(B)^n A_2(B)^n \frac{(n/e)^{(s+1)n}}{(( {n}/{\textrm{den}(r)})/e)^{(2r+1)|\mathcal{F}_B|n}} \nonumber\\ &\quad \times \biggl( \frac{( (k+(2r+1)n)/e )^{k+(2r+1)n}}{(k/e)^{k}} \biggr)^{\left| \mathcal{F}_B \right|} \frac{\left( (k+rn)/e \right)^{(s+1)(k+rn)}}{\left( (k+(r+1)n)/e \right)^{(s+1)(k+(r+1)n)}} \nonumber \\ &= n^{O(1)} \cdot A_1(B)^n A_2(B)^n \textrm{den}(r)^{(2r+1)|\mathcal{F}_B|n} \nonumber\\ &\quad \times \left( \frac{(\kappa + 2r + 1)^{\kappa + 2r + 1}}{\kappa^\kappa} \right)^{|\mathcal{F}_B|n} \left( \frac{(\kappa + r)^{\kappa + r}}{(\kappa + r + 1)^{\kappa + r + 1}} \right)^{(s+1)n} \nonumber\\ &= n^{O(1)} \cdot \left( f(\kappa)^{\kappa} g(\kappa) \right)^n \nonumber\\ &= n^{O(1)} \cdot h(\kappa)^n \end{align}
\begin{align} \widehat{R}_{n}(k+\theta) &= n^{O(1)} \cdot A_1(B)^n A_2(B)^n \frac{(n/e)^{(s+1)n}}{(( {n}/{\textrm{den}(r)})/e)^{(2r+1)|\mathcal{F}_B|n}} \nonumber\\ &\quad \times \biggl( \frac{( (k+(2r+1)n)/e )^{k+(2r+1)n}}{(k/e)^{k}} \biggr)^{\left| \mathcal{F}_B \right|} \frac{\left( (k+rn)/e \right)^{(s+1)(k+rn)}}{\left( (k+(r+1)n)/e \right)^{(s+1)(k+(r+1)n)}} \nonumber \\ &= n^{O(1)} \cdot A_1(B)^n A_2(B)^n \textrm{den}(r)^{(2r+1)|\mathcal{F}_B|n} \nonumber\\ &\quad \times \left( \frac{(\kappa + 2r + 1)^{\kappa + 2r + 1}}{\kappa^\kappa} \right)^{|\mathcal{F}_B|n} \left( \frac{(\kappa + r)^{\kappa + r}}{(\kappa + r + 1)^{\kappa + r + 1}} \right)^{(s+1)n} \nonumber\\ &= n^{O(1)} \cdot \left( f(\kappa)^{\kappa} g(\kappa) \right)^n \nonumber\\ &= n^{O(1)} \cdot h(\kappa)^n \end{align}
uniformly for any ![]() $k \in [c_1n,n^{10}]$ and any
$k \in [c_1n,n^{10}]$ and any ![]() $\theta \in \mathcal {F}_B$ (the absolute bound for
$\theta \in \mathcal {F}_B$ (the absolute bound for ![]() $O(1)$ depends only on
$O(1)$ depends only on ![]() $s,B,r$ and
$s,B,r$ and ![]() $\textrm {den}(r)$); here the function
$\textrm {den}(r)$); here the function ![]() $h(x)$ is defined for
$h(x)$ is defined for ![]() $x>0$ as
$x>0$ as ![]() $h(x)= f(x)^x g(x)$ and a direct computation shows that
$h(x)= f(x)^x g(x)$ and a direct computation shows that ![]() ${h'(x)}/{h(x)} = \log f(x)$. Hence,
${h'(x)}/{h(x)} = \log f(x)$. Hence, ![]() $h(x)$ achieves its maximum only at
$h(x)$ achieves its maximum only at ![]() $x = x_0$ with maximal value
$x = x_0$ with maximal value ![]() $h(x_0) = g(x_0)$.
$h(x_0) = g(x_0)$.
In particular, we have the following bound for each ![]() $k \in [c_1 n , n^{10}]$:
$k \in [c_1 n , n^{10}]$:
Finally, we treat the tail part. For any ![]() $k > n^{10}$, when
$k > n^{10}$, when ![]() $n$ is sufficiently large in terms of
$n$ is sufficiently large in terms of ![]() $r,s$ and
$r,s$ and ![]() $B$ (more precisely, when
$B$ (more precisely, when ![]() $n \geqslant \max (10(2r+1), 10A_1(B)A_2(B), {10}/{g(x_0)})$), by (4.3) and our assumption that
$n \geqslant \max (10(2r+1), 10A_1(B)A_2(B), {10}/{g(x_0)})$), by (4.3) and our assumption that ![]() $s \geqslant 10(2r+1)B^2$, we have
$s \geqslant 10(2r+1)B^2$, we have
 \begin{align*} \widehat{R}_{n}(k+\theta) &< A_1(B)^n A_2(B)^n n^{(s+1)n} \cdot \frac{(2k)\prod_{\theta' \in \mathcal{F}_B}\prod_{j=0}^{(2r+1)n-1} (2k)}{\prod_{j=0}^{n}(k)^{s+1}} \\ &< \frac{(2A_1(B)A_2(B)n)^{(s+1)n}}{k^{({9}/{10})(s+1)n + 2}} \\ &< \left( \frac{2A_1(B)A_2(B)}{n^8}\right)^{(s+1)n}\frac{1}{k^2} \\ &< \left( \frac{g(x_0)}{2} \right)^n \frac{1}{k^2}. \end{align*}
\begin{align*} \widehat{R}_{n}(k+\theta) &< A_1(B)^n A_2(B)^n n^{(s+1)n} \cdot \frac{(2k)\prod_{\theta' \in \mathcal{F}_B}\prod_{j=0}^{(2r+1)n-1} (2k)}{\prod_{j=0}^{n}(k)^{s+1}} \\ &< \frac{(2A_1(B)A_2(B)n)^{(s+1)n}}{k^{({9}/{10})(s+1)n + 2}} \\ &< \left( \frac{2A_1(B)A_2(B)}{n^8}\right)^{(s+1)n}\frac{1}{k^2} \\ &< \left( \frac{g(x_0)}{2} \right)^n \frac{1}{k^2}. \end{align*}
As a conclusion, we obtain the following bound for the tail part for all sufficiently large ![]() $n$:
$n$:
 \begin{equation} \sum_{k> n^{10}} \widehat{R}_{n}(k+\theta) \leqslant \left( \frac{g(x_0)}{2} \right)^n. \end{equation}
\begin{equation} \sum_{k> n^{10}} \widehat{R}_{n}(k+\theta) \leqslant \left( \frac{g(x_0)}{2} \right)^n. \end{equation} Now, in view of the estimates (4.5), (4.7) and (4.8), we have ![]() $r_{n,1} \leqslant n^{O(1)} g(x_0)^n$. On the other hand, (4.6) implies that
$r_{n,1} \leqslant n^{O(1)} g(x_0)^n$. On the other hand, (4.6) implies that ![]() $r_{n,1} \geqslant \widehat {R}_{n}(\lfloor x_0n \rfloor ) = n^{O(1)}h(x_0 + o(1))^n$. Therefore,
$r_{n,1} \geqslant \widehat {R}_{n}(\lfloor x_0n \rfloor ) = n^{O(1)}h(x_0 + o(1))^n$. Therefore,
To prove the last statement in the lemma, we first fix an arbitrary (sufficiently) small ![]() $\varepsilon _0 > 0$. For all
$\varepsilon _0 > 0$. For all ![]() $\theta \in \mathcal {F}_B$, we have
$\theta \in \mathcal {F}_B$, we have
In view of the estimates (4.5), (4.6) and (4.8), we also have
 \begin{align} r_{n,\theta} &\leqslant n^{O(1)}\max ( h(x_0 - \varepsilon_0), h(x_0 + \varepsilon_0))^n \quad + \quad \sum_{(x_0 - \varepsilon_0)n \leqslant k \leqslant (x_0 + \varepsilon_0)n} \widehat{R}_{n}(k+\theta) \nonumber\\ &< (1+\varepsilon_0) \sum_{(x_0 - \varepsilon_0)n \leqslant k \leqslant (x_0 + \varepsilon_0)n} \widehat{R}_{n}(k+\theta), \end{align}
\begin{align} r_{n,\theta} &\leqslant n^{O(1)}\max ( h(x_0 - \varepsilon_0), h(x_0 + \varepsilon_0))^n \quad + \quad \sum_{(x_0 - \varepsilon_0)n \leqslant k \leqslant (x_0 + \varepsilon_0)n} \widehat{R}_{n}(k+\theta) \nonumber\\ &< (1+\varepsilon_0) \sum_{(x_0 - \varepsilon_0)n \leqslant k \leqslant (x_0 + \varepsilon_0)n} \widehat{R}_{n}(k+\theta), \end{align}
provided ![]() $n$ is sufficiently large with respect to
$n$ is sufficiently large with respect to ![]() $\varepsilon _0$, i.e.,
$\varepsilon _0$, i.e., ![]() $n \geqslant n_0(\varepsilon _0)$. For all
$n \geqslant n_0(\varepsilon _0)$. For all ![]() $k$ with
$k$ with ![]() $(x_0 - \varepsilon _0)n \leqslant k \leqslant (x_0 + \varepsilon _0)n$, let
$(x_0 - \varepsilon _0)n \leqslant k \leqslant (x_0 + \varepsilon _0)n$, let ![]() $\kappa = \kappa (n,k) = {k}/{n}$ as before. We now use the fact that, for any fixed real number
$\kappa = \kappa (n,k) = {k}/{n}$ as before. We now use the fact that, for any fixed real number ![]() $\tau$,
$\tau$,
Applying (4.11) to (4.4), we derive that
 \begin{align} \frac{\widehat{R}_{n}(k+1)}{\widehat{R}_{n}(k+\theta)} &= \left( 1+o(1) \right) \left( \frac{\kappa + 2r + 1}{\kappa} \right)^{|\mathcal{F}_B| (1-\theta)}\left( \frac{\kappa + r}{\kappa + r+1} \right)^{(s+1)(1-\theta)} \nonumber\\ &= \left( 1+o(1) \right) f(\kappa)^{1 - \theta} \end{align}
\begin{align} \frac{\widehat{R}_{n}(k+1)}{\widehat{R}_{n}(k+\theta)} &= \left( 1+o(1) \right) \left( \frac{\kappa + 2r + 1}{\kappa} \right)^{|\mathcal{F}_B| (1-\theta)}\left( \frac{\kappa + r}{\kappa + r+1} \right)^{(s+1)(1-\theta)} \nonumber\\ &= \left( 1+o(1) \right) f(\kappa)^{1 - \theta} \end{align}
uniformly for ![]() $k \in [(x_0 - \varepsilon _0)n , (x_0 + \varepsilon _0)n]$ as
$k \in [(x_0 - \varepsilon _0)n , (x_0 + \varepsilon _0)n]$ as ![]() $n \rightarrow +\infty$. By (4.9), (4.10) and (4.12), we find that
$n \rightarrow +\infty$. By (4.9), (4.10) and (4.12), we find that
thus,
It is true for all sufficiently small ![]() $\varepsilon _0>0$. Letting
$\varepsilon _0>0$. Letting ![]() $\varepsilon _0 \rightarrow 0^+$, we deduce that
$\varepsilon _0 \rightarrow 0^+$, we deduce that
This completes the proof of Lemma 4.1.
5. Elimination procedure and proof of the theorem
We prove Theorem 1.1 in this section. We will use the same strategy as [Reference Fischler, Sprang and ZudilinFSZ19, § 5], namely, an elimination procedure. So, we only give an outline of this elimination procedure.
We denote ![]() $I_s = \{ 3,5,7,\ldots ,s \}$. For any subset
$I_s = \{ 3,5,7,\ldots ,s \}$. For any subset ![]() $J \subset I_s$ with
$J \subset I_s$ with ![]() $|J| = |{\Psi }_B| -1$, since the following general Vandermonde matrix (see, for instance, [Reference Gantmacher and KreinGK02, pp. 76–77]):
$|J| = |{\Psi }_B| -1$, since the following general Vandermonde matrix (see, for instance, [Reference Gantmacher and KreinGK02, pp. 76–77]):
is invertible, there exist integers ![]() $w_b \in \mathbb {Z}$ for all
$w_b \in \mathbb {Z}$ for all ![]() $b \in {\Psi }_B$ such that
$b \in {\Psi }_B$ such that ![]() $\sum _{b \in {\Psi }_B} w_{b} b^{j} = 0$ for any
$\sum _{b \in {\Psi }_B} w_{b} b^{j} = 0$ for any ![]() $j \in J$ and
$j \in J$ and ![]() $\sum _{b \in {\Psi }_B} w_{b} b \neq 0$. (Note that these
$\sum _{b \in {\Psi }_B} w_{b} b \neq 0$. (Note that these ![]() $w_b$ depend only on
$w_b$ depend only on ![]() $J$ and
$J$ and ![]() ${\Psi }_B$.) Since
${\Psi }_B$.) Since
 \begin{equation} \sum_{k=1}^{b} \zeta\left(i,\frac{k}{b}\right) = \sum_{k=1}^{b} \sum_{m=0}^{\infty} \frac{b^i}{(mb+k)^i} = b^i \zeta(i), \end{equation}
\begin{equation} \sum_{k=1}^{b} \zeta\left(i,\frac{k}{b}\right) = \sum_{k=1}^{b} \sum_{m=0}^{\infty} \frac{b^i}{(mb+k)^i} = b^i \zeta(i), \end{equation}
we derive that (recall Proposition 2.2(2), ![]() ${k}/{b} \in \mathcal {F}_B$)
${k}/{b} \in \mathcal {F}_B$)
 \[ \widehat{r}_{n,b} := \sum_{k=1}^{b} r_{n,{k}/{b}} = \sum_{k=1}^{b} \rho_{0,{k}/{b}} + \sum_{i \in I_s} \rho_{i} b^i \zeta(i) \]
\[ \widehat{r}_{n,b} := \sum_{k=1}^{b} r_{n,{k}/{b}} = \sum_{k=1}^{b} \rho_{0,{k}/{b}} + \sum_{i \in I_s} \rho_{i} b^i \zeta(i) \]
is a linear combination of ![]() $1$ and odd zeta values. By Lemma 4.1, we have
$1$ and odd zeta values. By Lemma 4.1, we have ![]() $\widehat {r}_{n,b} = (b+o(1))r_{n,1}$ as
$\widehat {r}_{n,b} = (b+o(1))r_{n,1}$ as ![]() $n \rightarrow +\infty$. Let
$n \rightarrow +\infty$. Let
then
 \begin{equation} \widetilde{r}_{n} = \sum_{b \in {\Psi}_B} w_b \sum_{k=1}^{b} \rho_{0,{k}/{b}} + \sum_{i \in I_s \setminus J} \biggl( \sum_{b \in {\Psi}_B} w_b b^i \biggr) \rho_{i} \zeta(i) \end{equation}
\begin{equation} \widetilde{r}_{n} = \sum_{b \in {\Psi}_B} w_b \sum_{k=1}^{b} \rho_{0,{k}/{b}} + \sum_{i \in I_s \setminus J} \biggl( \sum_{b \in {\Psi}_B} w_b b^i \biggr) \rho_{i} \zeta(i) \end{equation}
and, as ![]() $n \rightarrow +\infty$,
$n \rightarrow +\infty$,
 \begin{equation} \widetilde{r}_{n} = \biggl( \sum_{b \in {\Psi}_B} w_{b} b + o(1)\biggr) r_{n,1} \quad \text{with}\ \sum_{b \in {\Psi}_B} w_{b} b \neq 0. \end{equation}
\begin{equation} \widetilde{r}_{n} = \biggl( \sum_{b \in {\Psi}_B} w_{b} b + o(1)\biggr) r_{n,1} \quad \text{with}\ \sum_{b \in {\Psi}_B} w_{b} b \neq 0. \end{equation}
Equation (5.2) shows that we can eliminate any ![]() $|{\Psi }_B|-1$ odd zeta values.
$|{\Psi }_B|-1$ odd zeta values.
Proposition 5.1 If ![]() $g(x_0) < e^{-(s+1)}$, then the number of irrationals in the odd zeta values set
$g(x_0) < e^{-(s+1)}$, then the number of irrationals in the odd zeta values set ![]() $\{ \zeta (i) \}_{i \in I_s}$ is at least
$\{ \zeta (i) \}_{i \in I_s}$ is at least ![]() $|{\Psi }_B|$.
$|{\Psi }_B|$.
Proof. We argue by contradiction. Suppose that the number of irrationals in ![]() $\{ \zeta (i) \}_{i \in I_s}$ is less than
$\{ \zeta (i) \}_{i \in I_s}$ is less than ![]() $|{\Psi }_B|$; then we can take a subset
$|{\Psi }_B|$; then we can take a subset ![]() $J \subset I_s$ with
$J \subset I_s$ with ![]() $|J| = |{\Psi }_B| -1$ such that
$|J| = |{\Psi }_B| -1$ such that ![]() $\zeta (i) \in \mathbb {Q}$ for all
$\zeta (i) \in \mathbb {Q}$ for all ![]() $I_s \setminus J$; let
$I_s \setminus J$; let ![]() $A$ be the common denominator of these rational zeta values. Define
$A$ be the common denominator of these rational zeta values. Define ![]() $\widetilde {r}_{n}$ as above for this
$\widetilde {r}_{n}$ as above for this ![]() $J$; then, by (5.2) and Lemma 3.3, for all
$J$; then, by (5.2) and Lemma 3.3, for all ![]() $n \in P_{B,\textrm {den}(r)}\mathbb {N}$, we derive that
$n \in P_{B,\textrm {den}(r)}\mathbb {N}$, we derive that
But by (5.3), Lemma 4.1 and the hypothesis ![]() $g(x_0) < e^{-(s+1)}$, we have
$g(x_0) < e^{-(s+1)}$, we have
This is a contradiction.
So, we seek parameters ![]() $r$,
$r$, ![]() $s$ and
$s$ and ![]() $B$ to meet the requirement that
$B$ to meet the requirement that ![]() $g(x_0) < e^{-(s+1)}$, and at the same time to make
$g(x_0) < e^{-(s+1)}$, and at the same time to make ![]() $|{\Psi }_B| \sim ({\zeta (2)\zeta (3)}/{\zeta (6)}) B$ as large as possible. By Proposition 4.2(2), for a fixed
$|{\Psi }_B| \sim ({\zeta (2)\zeta (3)}/{\zeta (6)}) B$ as large as possible. By Proposition 4.2(2), for a fixed ![]() $r$ (such that
$r$ (such that ![]() ${r^r}/{(r+1)^{r+1}} < e^{-1}$), if we take
${r^r}/{(r+1)^{r+1}} < e^{-1}$), if we take ![]() $B = cs^{1/2} / \log ^{1/2} s$ for some constant
$B = cs^{1/2} / \log ^{1/2} s$ for some constant ![]() $c$, then
$c$, then ![]() $\lim _{s \rightarrow +\infty } g(x_0)^{{1}/({s+1})} < e^{-1}$ if and only if
$\lim _{s \rightarrow +\infty } g(x_0)^{{1}/({s+1})} < e^{-1}$ if and only if
 \[ c < \sqrt{ \frac{4\zeta(6)}{\zeta(2)\zeta(3)} \frac{(r+1)\log(r+1)-r\log(r)-1}{2r+1}}. \]
\[ c < \sqrt{ \frac{4\zeta(6)}{\zeta(2)\zeta(3)} \frac{(r+1)\log(r+1)-r\log(r)-1}{2r+1}}. \]
The maximum point of the function ![]() $r \mapsto ({(r+1)\log (r+1)-r\log (r)-1})/({2r+1})$ is
$r \mapsto ({(r+1)\log (r+1)-r\log (r)-1})/({2r+1})$ is
with maximal value ![]() $1 - \log r_0$. The constant
$1 - \log r_0$. The constant ![]() $c_0$ in Theorem 1.1 is designed by
$c_0$ in Theorem 1.1 is designed by
 \[ c_0 = \sqrt{\frac{4\zeta(2)\zeta(3)}{\zeta(6)}\left( 1 -\log r_0 \right)}. \]
\[ c_0 = \sqrt{\frac{4\zeta(2)\zeta(3)}{\zeta(6)}\left( 1 -\log r_0 \right)}. \]This leads to the following proof.
Proof Proof of Theorem 1.1 Given any small ![]() $\varepsilon > 0$, we first fix a rational number
$\varepsilon > 0$, we first fix a rational number ![]() $r = r(\varepsilon )$ sufficiently close to
$r = r(\varepsilon )$ sufficiently close to ![]() $r_0$ such that
$r_0$ such that
 \[ \frac{c_0 - \varepsilon/10}{\zeta(2)\zeta(3)/\zeta(6)} < \sqrt{ \frac{4\zeta(6)}{\zeta(2)\zeta(3)} \frac{(r+1)\log(r+1)-r\log(r)-1}{2r+1}}. \]
\[ \frac{c_0 - \varepsilon/10}{\zeta(2)\zeta(3)/\zeta(6)} < \sqrt{ \frac{4\zeta(6)}{\zeta(2)\zeta(3)} \frac{(r+1)\log(r+1)-r\log(r)-1}{2r+1}}. \]
Take ![]() $B = cs^{1/2}/\log ^{1/2} s$ with constant
$B = cs^{1/2}/\log ^{1/2} s$ with constant ![]() $c = ({c_0 - \varepsilon /10})/{(\zeta (2)\zeta (3)/\zeta (6))}$; by Propositions 4.2(2) and 2.2(1), there exists
$c = ({c_0 - \varepsilon /10})/{(\zeta (2)\zeta (3)/\zeta (6))}$; by Propositions 4.2(2) and 2.2(1), there exists ![]() $s_0(r,\varepsilon )$ such that for any odd integer
$s_0(r,\varepsilon )$ such that for any odd integer ![]() $s \geqslant s_0(r,\varepsilon )$, we have
$s \geqslant s_0(r,\varepsilon )$, we have ![]() $g(x_0) < e^{-(s+1)}$ and
$g(x_0) < e^{-(s+1)}$ and ![]() $|{\Psi }_B| > (\zeta (2)\zeta (3)/\zeta (6) - \varepsilon /10)B$. Therefore, by Proposition 5.1, the number of irrationals among
$|{\Psi }_B| > (\zeta (2)\zeta (3)/\zeta (6) - \varepsilon /10)B$. Therefore, by Proposition 5.1, the number of irrationals among ![]() $\zeta (3),\zeta (5),\ldots , \zeta (s)$ is at least
$\zeta (3),\zeta (5),\ldots , \zeta (s)$ is at least
 \[ |{\Psi}_B| > (c_0 - \varepsilon) \frac{s^{1/2}}{\log^{1/2} s}. \]
\[ |{\Psi}_B| > (c_0 - \varepsilon) \frac{s^{1/2}}{\log^{1/2} s}. \]6. Remarks on FSZ constructions
If we choose a general finite set ![]() $\mathcal {F} \subset (0,1]$ of rational numbers to be the zero set of the auxiliary function
$\mathcal {F} \subset (0,1]$ of rational numbers to be the zero set of the auxiliary function ![]() $R(t)$, like [Reference Fischler, Sprang and ZudilinFSZ19] and this note, we design the factor
$R(t)$, like [Reference Fischler, Sprang and ZudilinFSZ19] and this note, we design the factor
to remedy the arithmetic loss from the denominators of rational zeros. Suppose that our goal is to prove that there exist ![]() $D$ irrational numbers among
$D$ irrational numbers among ![]() $\zeta (3), \zeta (5), \ldots , \zeta (s)$. In order to eliminate
$\zeta (3), \zeta (5), \ldots , \zeta (s)$. In order to eliminate ![]() $D-1$ zeta values, in view of (5.1), we assume that there exist
$D-1$ zeta values, in view of (5.1), we assume that there exist ![]() $D$ pairwise different positive integers
$D$ pairwise different positive integers ![]() $b_1, b_2 , \ldots , b_D$ such that
$b_1, b_2 , \ldots , b_D$ such that
for any ![]() $i=1,2,\ldots ,D$. Then
$i=1,2,\ldots ,D$. Then ![]() $\mathcal {F}$ contains the following disjoint union:
$\mathcal {F}$ contains the following disjoint union:
 \[ \mathcal{F} \supset \bigcup_{i=1}^{D} \left\{ \left.\frac{a}{b_i} \,\right| 1 \leqslant a \leqslant b_i, \gcd(a,b_i) = 1 \right\}. \]
\[ \mathcal{F} \supset \bigcup_{i=1}^{D} \left\{ \left.\frac{a}{b_i} \,\right| 1 \leqslant a \leqslant b_i, \gcd(a,b_i) = 1 \right\}. \]Hence, we have
 \[ A_1(\mathcal{F}) \geqslant \prod_{i=1}^{D} b_i^{(2r+1)\varphi(b_i)}. \]
\[ A_1(\mathcal{F}) \geqslant \prod_{i=1}^{D} b_i^{(2r+1)\varphi(b_i)}. \]
Now we consider the minimal magnitude of ![]() $A_1(\mathcal {F})$.
$A_1(\mathcal {F})$.
Proposition 6.1 We have
 \[ \min \prod_{i=1}^{D} b_i^{\varphi(b_i)} = \exp\left( \left( \frac{1}{2}\frac{\zeta(6)}{\zeta(2)\zeta(3)} +o_{D \rightarrow +\infty}(1)\right) D^2\log D \right), \]
\[ \min \prod_{i=1}^{D} b_i^{\varphi(b_i)} = \exp\left( \left( \frac{1}{2}\frac{\zeta(6)}{\zeta(2)\zeta(3)} +o_{D \rightarrow +\infty}(1)\right) D^2\log D \right), \]
where the minimum is taken for all ![]() $D$-tuples
$D$-tuples ![]() $(b_1,\ldots ,b_D)$ such that
$(b_1,\ldots ,b_D)$ such that ![]() $b_1,b_2,\ldots ,b_D$ are
$b_1,b_2,\ldots ,b_D$ are ![]() $D$ pairwise distinct positive integers.
$D$ pairwise distinct positive integers.
Proof. We have
 \begin{align*} \log \prod_{i=1}^{D} b_i^{\varphi(b_i)} &\geqslant \sum_{i=1}^{D} \varphi(b_i)\log \varphi(b_i) \\ &\geqslant \sum_{i=1}^{D} \varphi(b'_i)\log \varphi(b'_i), \end{align*}
\begin{align*} \log \prod_{i=1}^{D} b_i^{\varphi(b_i)} &\geqslant \sum_{i=1}^{D} \varphi(b_i)\log \varphi(b_i) \\ &\geqslant \sum_{i=1}^{D} \varphi(b'_i)\log \varphi(b'_i), \end{align*}
where ![]() $b'_1,b'_2,\ldots ,b'_D$ are the
$b'_1,b'_2,\ldots ,b'_D$ are the ![]() $D$ smallest positive integers in the linear order
$D$ smallest positive integers in the linear order ![]() $\prec$ defined by
$\prec$ defined by
Recall that for any positive real number ![]() $x$, we define
$x$, we define ![]() ${\Psi }_x = \{ b \in \mathbb {N} \mid \varphi (b) \leqslant x \}$. Then there exists an integer
${\Psi }_x = \{ b \in \mathbb {N} \mid \varphi (b) \leqslant x \}$. Then there exists an integer ![]() $B$ such that
$B$ such that ![]() ${\Psi }_{B-1} \subset \{ b'_1,\ldots ,b'_D \} \subset {\Psi }_{B}$. By Proposition 2.2(1), we have the asymptotical relation
${\Psi }_{B-1} \subset \{ b'_1,\ldots ,b'_D \} \subset {\Psi }_{B}$. By Proposition 2.2(1), we have the asymptotical relation ![]() $B = ({\zeta (6)}/{\zeta (2)\zeta (3)} + o_{D \rightarrow +\infty }(1) ) D$. Following the first paragraph in the proof of Lemma 2.4, we derive that
$B = ({\zeta (6)}/{\zeta (2)\zeta (3)} + o_{D \rightarrow +\infty }(1) ) D$. Following the first paragraph in the proof of Lemma 2.4, we derive that
 \begin{align*} \sum_{i=1}^{D} \varphi(b'_i)\log \varphi(b'_i) &\geqslant \sum_{b \in {\Psi}_{B-1}} \varphi(b)\log \varphi(b) \\ &\geqslant \left( \frac{1}{2} \frac{\zeta(2)\zeta(3)}{\zeta(6)} +o_{B \rightarrow +\infty}(1) \right) B^2 \log B \\ &= \left( \frac{1}{2}\frac{\zeta(6)}{\zeta(2)\zeta(3)} +o_{D \rightarrow +\infty}(1)\right) D^2\log D. \end{align*}
\begin{align*} \sum_{i=1}^{D} \varphi(b'_i)\log \varphi(b'_i) &\geqslant \sum_{b \in {\Psi}_{B-1}} \varphi(b)\log \varphi(b) \\ &\geqslant \left( \frac{1}{2} \frac{\zeta(2)\zeta(3)}{\zeta(6)} +o_{B \rightarrow +\infty}(1) \right) B^2 \log B \\ &= \left( \frac{1}{2}\frac{\zeta(6)}{\zeta(2)\zeta(3)} +o_{D \rightarrow +\infty}(1)\right) D^2\log D. \end{align*}This shows that
 \[ \prod_{i=1}^{D} b_i^{\varphi(b_i)} \geqslant \exp\left( \left( \frac{1}{2}\frac{\zeta(6)}{\zeta(2)\zeta(3)} +o_{D \rightarrow +\infty}(1)\right) D^2\log D \right) \]
\[ \prod_{i=1}^{D} b_i^{\varphi(b_i)} \geqslant \exp\left( \left( \frac{1}{2}\frac{\zeta(6)}{\zeta(2)\zeta(3)} +o_{D \rightarrow +\infty}(1)\right) D^2\log D \right) \]
for any pairwise distinct positive integers ![]() $b_1,b_2,\ldots ,b_D$. On the other hand, if we take
$b_1,b_2,\ldots ,b_D$. On the other hand, if we take ![]() $(b'_1, \ldots , b'_D)$ as defined above, then Lemma 2.4 also implies that
$(b'_1, \ldots , b'_D)$ as defined above, then Lemma 2.4 also implies that
 \begin{align*} \prod_{i=1}^{D} b_i^{\prime\varphi(b'_i)} &\leqslant \prod_{b \in {\Psi}_{B}} b^{\varphi(b)} \\ &= \exp\left( \left( \frac{1}{2}\frac{\zeta(2)\zeta(3)}{\zeta(6)} +o_{B \rightarrow +\infty}(1)\right) B^2\log B \right) \\ &= \exp\left( \left( \frac{1}{2}\frac{\zeta(6)}{\zeta(2)\zeta(3)} +o_{D \rightarrow +\infty}(1)\right) D^2\log D \right). \end{align*}
\begin{align*} \prod_{i=1}^{D} b_i^{\prime\varphi(b'_i)} &\leqslant \prod_{b \in {\Psi}_{B}} b^{\varphi(b)} \\ &= \exp\left( \left( \frac{1}{2}\frac{\zeta(2)\zeta(3)}{\zeta(6)} +o_{B \rightarrow +\infty}(1)\right) B^2\log B \right) \\ &= \exp\left( \left( \frac{1}{2}\frac{\zeta(6)}{\zeta(2)\zeta(3)} +o_{D \rightarrow +\infty}(1)\right) D^2\log D \right). \end{align*}We complete the proof of Proposition 6.1.
Proposition 6.1 shows that, under the constraints (6.1) and (6.2), the choice ![]() $\mathcal {F} = \mathcal {F}_B$ in Definition 2.1 is optimal up to an
$\mathcal {F} = \mathcal {F}_B$ in Definition 2.1 is optimal up to an ![]() $o(1)$ term for minimizing the major arithmetic wasting factor
$o(1)$ term for minimizing the major arithmetic wasting factor ![]() $A_1(\mathcal {F})$. We do not need to consider the minor arithmetic wasting factor
$A_1(\mathcal {F})$. We do not need to consider the minor arithmetic wasting factor ![]() $A_2(\mathcal {F})$ for general
$A_2(\mathcal {F})$ for general ![]() $\mathcal {F}$, since
$\mathcal {F}$, since ![]() $A_2(\mathcal {F}_B)$ is asymptotically negligible with respect to
$A_2(\mathcal {F}_B)$ is asymptotically negligible with respect to ![]() $A_1(\mathcal {F}_B)$ (see Lemma 2.4); we already have that
$A_1(\mathcal {F}_B)$ (see Lemma 2.4); we already have that
For the factorial factor
comparing to the corresponding factor ![]() $n!^{s+1-(2r+1)|\mathcal {F}|}$ in [Reference Ball and RivoalBR01] or [Reference Fischler, Sprang and ZudilinFSZ19], we have an extra waste of
$n!^{s+1-(2r+1)|\mathcal {F}|}$ in [Reference Ball and RivoalBR01] or [Reference Fischler, Sprang and ZudilinFSZ19], we have an extra waste of
 \[ \binom{n}{ \underbrace{\frac{n}{\textrm{den}(r)},\ldots,\frac{n}{\textrm{den}(r)}}_{\textrm{den}(r)\ \text{in number}}}^{(2r+1)|\mathcal{F}|} \leqslant \textrm{den}(r)^{(2r+1)|\mathcal{F}|n}, \]
\[ \binom{n}{ \underbrace{\frac{n}{\textrm{den}(r)},\ldots,\frac{n}{\textrm{den}(r)}}_{\textrm{den}(r)\ \text{in number}}}^{(2r+1)|\mathcal{F}|} \leqslant \textrm{den}(r)^{(2r+1)|\mathcal{F}|n}, \]
which is asymptotically negligible with respect to ![]() $A_1(\mathcal {F})^n$ (at least for
$A_1(\mathcal {F})^n$ (at least for ![]() $\mathcal {F} = \mathcal {F}_B$). Usually the Ball–Rivoal length parameter
$\mathcal {F} = \mathcal {F}_B$). Usually the Ball–Rivoal length parameter ![]() $r$ is taken to be an integer in the literature, since in the case that
$r$ is taken to be an integer in the literature, since in the case that ![]() $r$ is integral, the corresponding arithmetic lemmas (see [Reference Ball and RivoalBR01, Lemme 5] and [Reference Fischler, Sprang and ZudilinFSZ19, Lemma 2]) can be proved in a simpler way. We need to take non-integral rational
$r$ is integral, the corresponding arithmetic lemmas (see [Reference Ball and RivoalBR01, Lemme 5] and [Reference Fischler, Sprang and ZudilinFSZ19, Lemma 2]) can be proved in a simpler way. We need to take non-integral rational ![]() $r$ in order to let it be arbitrarily close to
$r$ in order to let it be arbitrarily close to ![]() $r_0$. The idea of taking non-integral
$r_0$. The idea of taking non-integral ![]() $r$ is not new: it has appeared in the literature (for example, [Reference ZudilinZud01]), but in a different form.
$r$ is not new: it has appeared in the literature (for example, [Reference ZudilinZud01]), but in a different form.
There exist some arithmetic saving factors known as ![]() $\Phi _n$ factors. They are certain products over primes in the range
$\Phi _n$ factors. They are certain products over primes in the range ![]() $C_{B,r} \sqrt {n} \leqslant p \leqslant n$ (here we can take
$C_{B,r} \sqrt {n} \leqslant p \leqslant n$ (here we can take ![]() $C_{B,r} = \sqrt {2(r+1)B\log \log B}$). We mention that the saving from
$C_{B,r} = \sqrt {2(r+1)B\log \log B}$). We mention that the saving from ![]() $\Phi _n^{-1}$ plays an important role in small cases for the odd zeta problem; see, for instance, [Reference ZudilinZud01, Reference Rivoal and ZudilinRZ20], [Reference ZudilinZud02, § 4] or [Reference Krattenthaler and RivoalKR07, Chapitre 11]. However, like [Reference Fischler, Sprang and ZudilinFSZ19, Remark 2], the known types of
$\Phi _n^{-1}$ plays an important role in small cases for the odd zeta problem; see, for instance, [Reference ZudilinZud01, Reference Rivoal and ZudilinRZ20], [Reference ZudilinZud02, § 4] or [Reference Krattenthaler and RivoalKR07, Chapitre 11]. However, like [Reference Fischler, Sprang and ZudilinFSZ19, Remark 2], the known types of ![]() $\Phi _n$ factors have no effect on asymptotics. The reason is that, by Definition 2.3, (2.3) and (3.2), for any
$\Phi _n$ factors have no effect on asymptotics. The reason is that, by Definition 2.3, (2.3) and (3.2), for any ![]() $k \in \{ 0,1,\ldots ,n \}$,
$k \in \{ 0,1,\ldots ,n \}$,
 \begin{align*} a_{s,k} &= \left( (t+k)^s R_n(t) \right) |_{t=-k} \\ &= (-1)^{k}\binom{n}{k}^s \frac{n!(k+1)_{rn}(-k+n+1)_{rn}}{ ( {n}/{ \textrm{den}(r)})!^{\,\textrm{den}(r)(2r+1)} } \prod_{{a}/{b} \in \mathcal{F}_B \setminus \{1\} } F_{b,a}(-k), \end{align*}
\begin{align*} a_{s,k} &= \left( (t+k)^s R_n(t) \right) |_{t=-k} \\ &= (-1)^{k}\binom{n}{k}^s \frac{n!(k+1)_{rn}(-k+n+1)_{rn}}{ ( {n}/{ \textrm{den}(r)})!^{\,\textrm{den}(r)(2r+1)} } \prod_{{a}/{b} \in \mathcal{F}_B \setminus \{1\} } F_{b,a}(-k), \end{align*}
where ![]() $(x)_{m} := x(x+1)\cdots (x+m-1)$. For any prime
$(x)_{m} := x(x+1)\cdots (x+m-1)$. For any prime ![]() $p$ with
$p$ with ![]() $C_{B,r} \sqrt {n} \leqslant p \leqslant n$, the
$C_{B,r} \sqrt {n} \leqslant p \leqslant n$, the ![]() $p$-adic order of
$p$-adic order of ![]() $a_{s,0}$ is relatively small. If we define
$a_{s,0}$ is relatively small. If we define
then we can show that ![]() $\widetilde {\Phi }_n \leqslant A_2(B)^n \cdot d_n^{(\textrm {den}(r)(2r+1) + 1)|\mathcal {F}_B|}$, which is asymptotically negligible with respect to
$\widetilde {\Phi }_n \leqslant A_2(B)^n \cdot d_n^{(\textrm {den}(r)(2r+1) + 1)|\mathcal {F}_B|}$, which is asymptotically negligible with respect to ![]() $A_1(\mathcal {F}_B)^n$. One may want to directly save the common divisor of
$A_1(\mathcal {F}_B)^n$. One may want to directly save the common divisor of ![]() $d_{n+1}^{s+1}\rho _{0, \theta }$ and
$d_{n+1}^{s+1}\rho _{0, \theta }$ and ![]() $d_{n+1}^{s+1}\rho _i$, but it is out of current research. The small cases are more difficult to study; up to now, besides Apéry's theorem [Reference ApéryApé79] that
$d_{n+1}^{s+1}\rho _i$, but it is out of current research. The small cases are more difficult to study; up to now, besides Apéry's theorem [Reference ApéryApé79] that ![]() $\zeta (3)$ is irrational, the most remarkable result is that at least one of
$\zeta (3)$ is irrational, the most remarkable result is that at least one of ![]() $\zeta (5),\zeta (7),\zeta (9),\zeta (11)$ is irrational, due to Zudilin [Reference ZudilinZud01] in 2001. The question whether
$\zeta (5),\zeta (7),\zeta (9),\zeta (11)$ is irrational, due to Zudilin [Reference ZudilinZud01] in 2001. The question whether ![]() $\zeta (5)$ is irrational remains open.
$\zeta (5)$ is irrational remains open.
Acknowledgements
The authors would like to thank Stéphane Fischler, Johannes Sprang and Wadim Zudilin for their valuable comments and discussions on an early version of this note. The authors are indebted to the referee; his or her comments improved the presentation of this note. L.L. wishes to thank Jianyuan Bai for her support. P.Y. is supported by NSFC11825103.