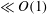1 Introduction
Density stratification in oceans and lakes occurs due to gradients in temperature or salinity. This affects the swimming behaviour and the migration patterns of organisms living in these environments (Doostmohammadi, Stocker & Ardekani Reference Doostmohammadi, Stocker and Ardekani2012; Ardekani, Doostmohammadi & Desai Reference Ardekani, Doostmohammadi and Desai2017). An example of this includes the accumulation of dinoflagellates at thermoclines caused by restriction to propulsion due to steep thermal gradients (Heaney & Eppley Reference Heaney and Eppley1981). Planktonic species of copepods have been observed to migrate towards higher salinity gradients and eventually concentrate at haloclines (Heuch Reference Heuch1995). Temperature-induced stratification has been shown to influence the distribution of the phytoplankton community (Arrigo et al. Reference Arrigo, Robinson, Worthen, Dunbar, DiTullio, VanWoert and Lizotte1999) and even enhance the period of phytoplankton blooms (Sherman et al. Reference Sherman, Webster, Jones and Oliver1998; Mahadevan et al. Reference Mahadevan, Dasaro, Lee and Perry2012).
The swimming of organisms in homogeneous fluids has been studied for over five decades (see Brennen & Winet Reference Brennen and Winet1977; Lauga & Powers Reference Lauga and Powers2009; Elgeti, Winkler & Gompper Reference Elgeti, Winkler and Gompper2015; Lauga Reference Lauga2016) and significant progress has been made. Theoretical work in this direction was started by Taylor (Reference Taylor1951) who derived an analytical expression for the swimming velocity of a thin waving sheet immersed in a homogeneous fluid at low Reynolds numbers. Later, Reynolds (Reference Reynolds1965) derived an expression for the sheet’s swimming velocity by including the effect of inertia in his analysis. The formula was corrected by Tuck (Reference Tuck1968), who showed that contrary to the observations made by Reynolds, the sheet swimming velocity decreases with inertia.
In the present work, we provide a theoretical analysis of the swimming velocity of a Taylor sheet in a density-stratified fluid. The theoretical approach used in this study has been applied by researchers in a wide range of physical scenarios. This includes locomotion in complex fluids (Chaudhury Reference Chaudhury1979; Lauga Reference Lauga2007; Elfring & Goyal Reference Elfring and Goyal2016), in a gel (Leshansky Reference Leshansky2009; Fu, Shenoy & Powers Reference Fu, Shenoy and Powers2010), in two-phase viscous fluids (Du et al. Reference Du, Keener, Guy and Fogelson2012), in a liquid crystal (Krieger, Dias & Powers Reference Krieger, Dias and Powers2015) and near solid boundaries (Reynolds Reference Reynolds1965; Katz Reference Katz1974). Hydrodynamic interaction between multiple sheets is also studied using this methodology (Elfring & Lauga Reference Elfring and Lauga2009). Despite the numerous ecological implications of stratification, there are limited theoretical studies which shed light on the swimming behaviour of microorganisms in a density-stratified environment.
Ardekani & Stocker (Reference Ardekani and Stocker2010) quantified the effect of stratification on the swimming of organisms by means of singularity solutions at low Reynolds numbers. They identified the appropriate length scale to quantify the role of stratification and showed that stratification has a significant influence on the hydrodynamics of aquatic organisms. Point-force singularities, however, only give knowledge about the far-field flow generated by a swimmer at low Reynolds and Péclet numbers.
Numerical models were further developed for a more accurate representation of swimming organisms in density-stratified fluids. Doostmohammadi et al. (Reference Doostmohammadi, Stocker and Ardekani2012) carried out a detailed numerical analysis of the motion of a spherical squirmer swimming in a stratified fluid at low Reynolds numbers. They observed that buoyancy forces induced by density stratification have a significant impact on the flow field of the swimmer and its energy expenditure. They found the propulsion speed of the swimmer to be dependent on the direction of the thrust generation by the swimmer, which is generally not the case in homogeneous fluids. Wang & Ardekani (Reference Wang and Ardekani2015) performed three-dimensional fully resolved simulations of a suspension of squirmers in a density-stratified environment to study the mixing induced by organisms in aquatic environments.
Swimmers create a local disruption in the surrounding fluid during their locomotion. Biogenic mixing has been extensively studied in the literature (Katija Reference Katija2012; Simoncelli, Thackeray & Wain Reference Simoncelli, Thackeray and Wain2017). There are arguments both in support of the importance of biogenic mixing (Dewar et al. Reference Dewar, Bingham, Iverson, Nowacek, St Laurent and Wiebe2006) and against it (Visser Reference Visser2007). An understanding of the influence of stratification on the hydrodynamics of swimming is crucial for making reliable predictions about biogenic mixing.
In this work, we analytically derive an expression for the swimming velocity in a density-stratified fluid. We model the swimmer as a two-dimensional infinitely long sheet that propels by passing waves of small amplitude along its surface. This model can be used to represent the tail of a human spermatozoon (Taylor Reference Taylor1951), flat ciliated Paramecium, Opalina (Blake Reference Blake1971) or Caenorhabditis elegans (Sznitman et al.
Reference Sznitman, Purohit, Krajacic, Lamitina and Arratia2010). We analyse the effects of stratification on swimmer propulsion. We divide our analysis into two regimes of low (
$\ll O(1)$
) and finite Reynolds numbers. This will help us understand how inertia affects the locomotion in a stratified fluid. Furthermore, we make predictions about the hydrodynamic power, swimming efficiency and the mixing induced by the swimmer in a stratified fluid.
2 Problem formulation
Figure 1 shows a schematic of a swimmer immersed in a linearly density-stratified fluid in the undisturbed state. The ambient or the undisturbed density variations in the fluid are given by
$$\begin{eqnarray}\unicode[STIX]{x1D70C}_{0}=\unicode[STIX]{x1D70C}_{\infty }-\unicode[STIX]{x1D6FE}y.\end{eqnarray}$$
Here,
$\unicode[STIX]{x1D70C}_{\infty }$
is the reference fluid density and
$\unicode[STIX]{x1D6FE}({>}0)$
is the density gradient in the vertical direction.
We consider the swimmer to be neutrally buoyant with respect to the surrounding fluid. The swimmer is thus stationary when it does not propagate waves along its surface. This is a good assumption since marine organisms have been observed to regulate their density and remain neutrally buoyant in deep waters. For example, aquatic copepods, which are the dominant members of the zooplankton biomass, change their lipid concentration during winter to remain neutrally buoyant (Visser & Jónasdóttir Reference Visser and Jónasdóttir1999; Campbell & Dower Reference Campbell and Dower2003). Several species of notothenoid fishes in the mid-water community have been observed to be neutrally buoyant (Eastman Reference Eastman1985; Phleger Reference Phleger1998).
The swimmer propels by beating its flagella periodically, generating a travelling wave along its surface. This mechanism creates a disturbance in the surrounding fluid. The surface of the swimmer is assumed to deform according to the travelling wave
$x=b\sin (ky+\unicode[STIX]{x1D70E}t)$
, where
$b$
is the wave amplitude which is assumed to be small compared to the wavelength
$2\unicode[STIX]{x03C0}/k$
(Taylor Reference Taylor1951) and
$\unicode[STIX]{x1D70E}$
is the angular frequency of the wave.
Figure 1. Swimming sheet immersed in a density-stratified fluid with ambient density
$\unicode[STIX]{x1D70C}_{0}=\unicode[STIX]{x1D70C}_{\infty }-\unicode[STIX]{x1D6FE}y$
, where gravity
$\boldsymbol{g}$
points in the negative
$y$
direction. The swimmer propels in the
$y$
direction by generating a travelling wave in the negative
$y$
direction with a speed
$\unicode[STIX]{x1D70E}/k$
. Parameters
$b$
and
$\unicode[STIX]{x1D706}$
are the wave amplitude and wavelength, respectively.
2.1 Governing equations
Using the Bousinessq approximation (Doostmohammadi et al. Reference Doostmohammadi, Stocker and Ardekani2012; Ardekani et al. Reference Ardekani, Doostmohammadi and Desai2017), we begin by writing the equations of motion for the fluid:
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}x}+\frac{\unicode[STIX]{x2202}v}{\unicode[STIX]{x2202}y}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D70C}_{\infty }\left(\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}t}+u\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}x}+v\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}y}\right)=-\frac{\unicode[STIX]{x2202}p}{\unicode[STIX]{x2202}x}+\unicode[STIX]{x1D707}\left(\frac{\unicode[STIX]{x2202}^{2}u}{\unicode[STIX]{x2202}x^{2}}+\frac{\unicode[STIX]{x2202}^{2}u}{\unicode[STIX]{x2202}y^{2}}\right), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D70C}_{\infty }\left(\frac{\unicode[STIX]{x2202}v}{\unicode[STIX]{x2202}t}+u\frac{\unicode[STIX]{x2202}v}{\unicode[STIX]{x2202}x}+v\frac{\unicode[STIX]{x2202}v}{\unicode[STIX]{x2202}y}\right)=-\frac{\unicode[STIX]{x2202}p}{\unicode[STIX]{x2202}y}-\unicode[STIX]{x1D70C}g+\unicode[STIX]{x1D707}\left(\frac{\unicode[STIX]{x2202}^{2}v}{\unicode[STIX]{x2202}x^{2}}+\frac{\unicode[STIX]{x2202}^{2}v}{\unicode[STIX]{x2202}y^{2}}\right)-\unicode[STIX]{x1D70C}_{\infty }\frac{\text{d}V}{\text{d}t}. & \displaystyle\end{eqnarray}$$
Equations (2.2)–(2.4) represent the continuity equation and the momentum conservation equations in the
$x$
and
$y$
directions, respectively. Here,
$u$
and
$v$
are the velocity fields in the
$x$
and
$y$
directions, respectively, in the frame of reference translating with the swimming velocity of the sheet given by
$V$
. Note that, in this frame of reference, the ambient density of the fluid (
$\unicode[STIX]{x1D70C}_{0}$
) will depend on time.
When the changes in the concentration/temperature are linearly related to the changes in the density, one can solve for the advection–diffusion equation for the density (2.5), instead of such an equation for the temperature or concentration:
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}}{\unicode[STIX]{x2202}t}+\frac{\unicode[STIX]{x2202}(\unicode[STIX]{x1D70C}u)}{\unicode[STIX]{x2202}x}+\frac{\unicode[STIX]{x2202}(\unicode[STIX]{x1D70C}v)}{\unicode[STIX]{x2202}y}=c\left(\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D70C}}{\unicode[STIX]{x2202}x^{2}}+\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D70C}}{\unicode[STIX]{x2202}y^{2}}\right).\end{eqnarray}$$
Here,
$c$
is the diffusivity coefficient. The density and pressure fields can be expressed as a combination of disturbed and undisturbed fields:
$\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}_{0}+\unicode[STIX]{x1D70C}^{\prime }$
and
$p=p_{0}+p^{\prime }$
. Here,
$\unicode[STIX]{x1D70C}^{\prime }$
and
$p^{\prime }$
are the disturbed density and pressure fields generated because of the deformation of the swimmer. The contribution of the undisturbed density to the buoyancy force term is balanced by the undisturbed pressure. Hence, we obtain the equations governing the flow and density in terms of the disturbance density and pressure as follows:
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}x}+\frac{\unicode[STIX]{x2202}v}{\unicode[STIX]{x2202}y}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D70C}_{\infty }\left(\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}t}+u\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}x}+v\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}y}\right)=-\frac{\unicode[STIX]{x2202}p^{\prime }}{\unicode[STIX]{x2202}x}+\unicode[STIX]{x1D707}\left(\frac{\unicode[STIX]{x2202}^{2}u}{\unicode[STIX]{x2202}x^{2}}+\frac{\unicode[STIX]{x2202}^{2}u}{\unicode[STIX]{x2202}y^{2}}\right), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D70C}_{\infty }\left(\frac{\unicode[STIX]{x2202}v}{\unicode[STIX]{x2202}t}+u\frac{\unicode[STIX]{x2202}v}{\unicode[STIX]{x2202}x}+v\frac{\unicode[STIX]{x2202}v}{\unicode[STIX]{x2202}y}\right)=-\frac{\unicode[STIX]{x2202}p^{\prime }}{\unicode[STIX]{x2202}y}-\unicode[STIX]{x1D70C}^{\prime }g+\unicode[STIX]{x1D707}\left(\frac{\unicode[STIX]{x2202}^{2}v}{\unicode[STIX]{x2202}x^{2}}+\frac{\unicode[STIX]{x2202}^{2}v}{\unicode[STIX]{x2202}y^{2}}\right)-\unicode[STIX]{x1D70C}_{\infty }\frac{\text{d}V}{\text{d}t}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \left(\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}^{\prime }}{\unicode[STIX]{x2202}t}-\unicode[STIX]{x1D6FE}V\right)+\frac{\unicode[STIX]{x2202}(\unicode[STIX]{x1D70C}^{\prime }u)}{\unicode[STIX]{x2202}x}+\frac{\unicode[STIX]{x2202}(\unicode[STIX]{x1D70C}^{\prime }v)}{\unicode[STIX]{x2202}y}-\unicode[STIX]{x1D6FE}v=c\left(\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D70C}^{\prime }}{\unicode[STIX]{x2202}x^{2}}+\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D70C}^{\prime }}{\unicode[STIX]{x2202}y^{2}}\right). & \displaystyle\end{eqnarray}$$
Next, we non-dimensionalize the problem by using the following scales: length scale
$l_{c}=1/k$
, velocity scale
$u_{c}=\unicode[STIX]{x1D70E}/k$
, time scale
$t_{c}=1/\unicode[STIX]{x1D70E}$
, pressure scale
$p_{c}=\unicode[STIX]{x1D707}\unicode[STIX]{x1D70E}$
, density scale
$\unicode[STIX]{x1D70C}_{c}=\unicode[STIX]{x1D6FE}/k$
. The term
$\unicode[STIX]{x2202}V/\unicode[STIX]{x2202}t$
will be non-dimensionalized later and is retained in its dimensional form for now. We use the same variables to denote the dimensionless variables. The governing equations are thus written as follows:
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}x}+\frac{\unicode[STIX]{x2202}v}{\unicode[STIX]{x2202}y}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle Re\left(\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}t}+u\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}x}+v\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}y}\right)=-\frac{\unicode[STIX]{x2202}p^{\prime }}{\unicode[STIX]{x2202}x}+\frac{\unicode[STIX]{x2202}^{2}u}{\unicode[STIX]{x2202}x^{2}}+\frac{\unicode[STIX]{x2202}^{2}u}{\unicode[STIX]{x2202}y^{2}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle Re\left(\frac{\unicode[STIX]{x2202}v}{\unicode[STIX]{x2202}t}+u\frac{\unicode[STIX]{x2202}v}{\unicode[STIX]{x2202}x}+v\frac{\unicode[STIX]{x2202}v}{\unicode[STIX]{x2202}y}\right)=-\frac{\unicode[STIX]{x2202}p^{\prime }}{\unicode[STIX]{x2202}y}-Ri\unicode[STIX]{x1D70C}^{\prime }+\frac{\unicode[STIX]{x2202}^{2}v}{\unicode[STIX]{x2202}x^{2}}+\frac{\unicode[STIX]{x2202}^{2}v}{\unicode[STIX]{x2202}y^{2}}-\frac{\unicode[STIX]{x1D70C}_{\infty }}{\unicode[STIX]{x1D707}\unicode[STIX]{x1D70E}k}\frac{\text{d}V}{\text{d}t}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle Pe\left(\left(\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}^{\prime }}{\unicode[STIX]{x2202}t}-V\right)+\frac{\unicode[STIX]{x2202}(\unicode[STIX]{x1D70C}^{\prime }u)}{\unicode[STIX]{x2202}x}+\frac{\unicode[STIX]{x2202}(\unicode[STIX]{x1D70C}^{\prime }v)}{\unicode[STIX]{x2202}y}-v\right)=\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D70C}^{\prime }}{\unicode[STIX]{x2202}x^{2}}+\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D70C}^{\prime }}{\unicode[STIX]{x2202}y^{2}}. & \displaystyle\end{eqnarray}$$
Here,
$Re=\unicode[STIX]{x1D70C}_{\infty }\unicode[STIX]{x1D70E}/k^{2}\unicode[STIX]{x1D707}$
represents the Reynolds number, the ratio of the inertial to the viscous forces,
$Pe=\unicode[STIX]{x1D70E}/k^{2}c$
is the Péclet number, the ratio of the advective to the diffusive transport rates of density, and
$Ri=\unicode[STIX]{x1D6FE}g/\unicode[STIX]{x1D707}\unicode[STIX]{x1D70E}k^{2}$
is the viscous Richardson number, which is the ratio of the buoyancy to the viscous forces. The magnitude of the Richardson number represents the extent of stratification in the fluid.
The term
$\unicode[STIX]{x2202}V/\unicode[STIX]{x2202}t$
denotes the dimensional acceleration of the swimmer. We expect the swimming velocity to change with time, because of the time-varying fluid density encountered by the translating sheet which is caused by the stratification gradient. The time-varying buoyancy force per unit volume experienced by the sheet (
$F_{B}$
) scales as
$$\begin{eqnarray}F_{B}\sim \frac{\unicode[STIX]{x1D6FE}g}{k}.\end{eqnarray}$$
If the density of the sheet is assumed to be
$\unicode[STIX]{x1D70C}_{p}$
, the acceleration of the swimmer due to this buoyancy force will scale as
$$\begin{eqnarray}\frac{\text{d}V}{\text{d}t}\sim \frac{\unicode[STIX]{x1D6FE}g}{\unicode[STIX]{x1D70C}_{p}k}.\end{eqnarray}$$
If we now substitute this scale for the sheet’s acceleration in (2.12), we find that the unsteady force exerted on the fluid due to the translating swimming sheet satisfies
$$\begin{eqnarray}\frac{\unicode[STIX]{x1D70C}_{\infty }}{\unicode[STIX]{x1D707}\unicode[STIX]{x1D70E}k}\frac{\text{d}V}{\text{d}t}=\frac{\unicode[STIX]{x1D70C}_{\infty }}{\unicode[STIX]{x1D70C}_{p}}Ri(a_{s}),\end{eqnarray}$$
where
$a_{s}$
denotes the non-dimensional acceleration of the sheet. As a result, for steady motion of the sheet, the following condition must be satisfied:
$$\begin{eqnarray}\frac{\unicode[STIX]{x1D70C}_{\infty }}{\unicode[STIX]{x1D70C}_{p}}Ri(a_{s})\ll 1.\end{eqnarray}$$
As we have assumed the swimmer to be neutrally buoyant with respect to the surrounding fluid (density of the swimmer changes appropriately to ensure the net force acting on the swimmer is zero), we have
$$\begin{eqnarray}a_{s}\ll 1.\end{eqnarray}$$
This implies that the unsteady contribution due to the sheet’s translational velocity can be neglected and the motion of the sheet can be considered as steady. If the density of the swimmer remains constant with time, then the steady-state assumption is only valid if
$Ri\ll 1$
. We note that this assumption does not affect the calculation and analysis presented here as
$\unicode[STIX]{x2202}V/\unicode[STIX]{x2202}t$
does not appear in the equation governing stream function. We expect, however, that the neutrally buoyant assumption is necessary to yield a consistent force balance condition.
We further simplify these expressions by representing the velocity fields in terms of the stream function (
$\unicode[STIX]{x1D713}$
) as follows:
$$\begin{eqnarray}u=-\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}{\unicode[STIX]{x2202}y},\quad v=\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}{\unicode[STIX]{x2202}x}.\end{eqnarray}$$
Next, we eliminate the unknown pressure field by combining equations (2.11) and (2.12) to obtain a single equation in terms of the stream function. We make another simplification by introducing a variable transformation given by
$z=y+t$
(Reynolds Reference Reynolds1965; Lauga Reference Lauga2007). This allows us to express the derivatives with respect to
$y$
and
$t$
in terms of a single variable
$z$
. We note that the wave appears to be steady in this transformed frame of reference. This allows us to express the governing equations with no dependence on the time variable. After performing these calculations, we finally obtain the equations of motion for the disturbances generated by the swimmer as follows:
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6FB}^{4}\unicode[STIX]{x1D713}-Ri\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}^{\prime }}{\unicode[STIX]{x2202}x}=Re\left(\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}{\unicode[STIX]{x2202}x}\left(\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}z}\unicode[STIX]{x1D6FB}^{2}\unicode[STIX]{x1D713}\right)-\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}{\unicode[STIX]{x2202}z}\left(\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}\unicode[STIX]{x1D6FB}^{2}\unicode[STIX]{x1D713}\right)+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}z}\unicode[STIX]{x1D6FB}^{2}\unicode[STIX]{x1D713}\right), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle Pe\left(\left(\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}^{\prime }}{\unicode[STIX]{x2202}z}-V\right)\!+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}\left(-\unicode[STIX]{x1D70C}^{\prime }\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}{\unicode[STIX]{x2202}z}\right)\!+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}z}\left(\unicode[STIX]{x1D70C}^{\prime }\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}{\unicode[STIX]{x2202}x}\right)-\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}{\unicode[STIX]{x2202}x}\right)=\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D70C}^{\prime }}{\unicode[STIX]{x2202}x^{2}}+\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D70C}^{\prime }}{\unicode[STIX]{x2202}z^{2}}. & \displaystyle\end{eqnarray}$$
Note that we have obtained a system of two differential equations in terms of two unknowns, the density field and the stream function.
2.2 Boundary conditions
We apply a no-slip and no-penetration boundary condition at the surface of the sheet which can be written as follows:
$$\begin{eqnarray}u|_{x=bk\sin (z)}=bk\cos (z),\quad v|_{x=bk\sin (z)}=0.\end{eqnarray}$$
Far away from the sheet, the fluid velocity should be the negative of the sheet’s swimming velocity:
$$\begin{eqnarray}u|_{x\rightarrow \infty }=0,\quad v|_{x\rightarrow \infty }=-V.\end{eqnarray}$$
For the density field, we apply a no-flux boundary condition at the surface of the swimmer. For stratification induced due to gradients in concentration, this implies that the surface of the swimmer is impermeable; whereas it implies an adiabatic boundary condition at the surface in the case of thermal gradients. Hence we obtain
$$\begin{eqnarray}\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}\boldsymbol{\cdot }\boldsymbol{n}|_{x=bk\text{sin(z)}}=0.\end{eqnarray}$$
Here,
$\boldsymbol{n}$
represents the normal vector at the surface of the swimmer.
The disturbance density should vanish far away from the swimmer, which implies
$$\begin{eqnarray}\unicode[STIX]{x1D70C}^{\prime }|_{x\rightarrow \infty }=0.\end{eqnarray}$$
3 Solution
In order to solve equations (2.20) and (2.21), we expand the stream function and the density in the form of a regular perturbation series. We introduce the small parameter
$\unicode[STIX]{x1D716}=bk$
and express the variables in the following form:
$$\begin{eqnarray}\unicode[STIX]{x1D713}=\unicode[STIX]{x1D716}\unicode[STIX]{x1D713}_{1}+\unicode[STIX]{x1D716}^{2}\unicode[STIX]{x1D713}_{2}+O(\unicode[STIX]{x1D716}^{3}),\quad \unicode[STIX]{x1D70C}^{\prime }=\unicode[STIX]{x1D716}\unicode[STIX]{x1D70C}_{1}+\unicode[STIX]{x1D716}^{2}\unicode[STIX]{x1D70C}_{2}+O(\unicode[STIX]{x1D716}^{3}).\end{eqnarray}$$
We express the swimming velocity of the sheet as
$$\begin{eqnarray}V=\unicode[STIX]{x1D716}V_{1}+\unicode[STIX]{x1D716}^{2}V_{2}+O(\unicode[STIX]{x1D716}^{3}).\end{eqnarray}$$
Next, we substitute these expansions in the boundary conditions and governing equations and solve at each order of
$\unicode[STIX]{x1D716}$
.
3.1 Boundary conditions for successive approximations
We seek to transform the velocity boundary conditions at the surface to obtain conditions at
$x=0$
. Hence, we first expand the velocity boundary conditions at the surface of the swimmer about
$x=0$
using Taylor series representation. We thus obtain
$$\begin{eqnarray}\left.\begin{array}{@{}l@{}}\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}{\unicode[STIX]{x2202}z}\bigg|_{x=\unicode[STIX]{x1D716}\sin (z)}=\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}{\unicode[STIX]{x2202}z}\bigg|_{x=0}+\unicode[STIX]{x1D716}\sin (z)\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D713}}{\unicode[STIX]{x2202}z\unicode[STIX]{x2202}x}\bigg|_{x=0}+\cdots \,,\\ \displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}{\unicode[STIX]{x2202}x}\bigg|_{x=\unicode[STIX]{x1D716}\sin (z)}=\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}{\unicode[STIX]{x2202}x}\bigg|_{x=0}+\unicode[STIX]{x1D716}\sin (z)\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D713}}{\unicode[STIX]{x2202}x^{2}}\bigg|_{x=0}+\cdots \,.\end{array}\right\}\end{eqnarray}$$
Next, we substitute the perturbation expansion for the stream function in the above expression and collect the terms at various powers of
$\unicode[STIX]{x1D716}$
. We obtain the following boundary conditions at
$x=0$
at the first and second order:
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{1}}{\unicode[STIX]{x2202}x}=0,\quad \displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{1}}{\unicode[STIX]{x2202}z}=-\cos (z)\quad \text{at }x=0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{2}}{\unicode[STIX]{x2202}x}=-\sin (z)\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D713}_{1}}{\unicode[STIX]{x2202}x^{2}},\quad \displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{2}}{\unicode[STIX]{x2202}z}=-\sin (z)\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D713}_{1}}{\unicode[STIX]{x2202}x\unicode[STIX]{x2202}z}\quad \text{at }x=0.\end{eqnarray}$$
The no-flux boundary condition for density can be written as
$$\begin{eqnarray}\unicode[STIX]{x1D735}(\unicode[STIX]{x1D70C}_{0}+\unicode[STIX]{x1D70C}^{\prime })\boldsymbol{\cdot }\boldsymbol{n}|_{x=\unicode[STIX]{x1D716}\sin (z)}=0.\end{eqnarray}$$
Using a similar procedure to that described for the velocity boundary conditions, we expand the above equation about
$x=0$
to obtain
$$\begin{eqnarray}\unicode[STIX]{x1D735}(\unicode[STIX]{x1D70C}_{0}+\unicode[STIX]{x1D70C}^{\prime })\boldsymbol{\cdot }\boldsymbol{n}|_{x=\unicode[STIX]{x1D716}\sin (z)}=\unicode[STIX]{x1D735}(\unicode[STIX]{x1D70C}_{0}+\unicode[STIX]{x1D70C}^{\prime })\boldsymbol{\cdot }\boldsymbol{n}|_{x=0}+\unicode[STIX]{x1D716}\sin (z)\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}(\unicode[STIX]{x1D735}(\unicode[STIX]{x1D70C}_{0}+\unicode[STIX]{x1D70C}^{\prime })\boldsymbol{\cdot }\boldsymbol{n})|_{x=0}.\end{eqnarray}$$
The normal vector can also be represented by the Taylor series approximation to obtain
$$\begin{eqnarray}n_{x}=-1+\frac{\unicode[STIX]{x1D716}^{2}\cos ^{2}(z)}{2}+O(\unicode[STIX]{x1D716}^{3}),\quad n_{y}=\unicode[STIX]{x1D716}\cos (z)+O(\unicode[STIX]{x1D716}^{3}).\end{eqnarray}$$
Next, we substitute the density perturbation expansion in (3.7) and use the normal vector approximation to obtain the density boundary conditions at
$x=0$
at the first and second order:
$$\begin{eqnarray}\begin{array}{@{}l@{}}\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}_{1}}{\unicode[STIX]{x2202}x}=-\cos (z)\quad \text{at }x=0,\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}_{2}}{\unicode[STIX]{x2202}x}=-\sin (z)\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D70C}_{1}}{\unicode[STIX]{x2202}x^{2}}+\cos (z)\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}_{1}}{\unicode[STIX]{x2202}z}\quad \text{at }x=0.\end{eqnarray}$$
Finally, the boundary condition for the vanishing disturbance density far away from the swimmer simplifies to
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D70C}_{1}\rightarrow 0,\quad \text{as }x\rightarrow \infty , & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D70C}_{2}\rightarrow 0,\quad \text{as }x\rightarrow \infty . & \displaystyle\end{eqnarray}$$
Next, we substitute the perturbation expansions of the velocity and the density fields in the equations of motion (equations (2.20) and (2.21)), and obtain the governing equations at various orders of
$\unicode[STIX]{x1D716}$
.
3.2 Solution at
$O(\unicode[STIX]{x1D716})$
The equations governing the stream function and the density disturbance at
$O(\unicode[STIX]{x1D716})$
are given by
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6FB}^{4}\unicode[STIX]{x1D713}_{1}-Ri\left(\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}_{1}}{\unicode[STIX]{x2202}x}\right)=Re\left(\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}z}\unicode[STIX]{x1D6FB}^{2}\unicode[STIX]{x1D713}_{1}\right), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle Pe\left(\left(\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}_{1}}{\unicode[STIX]{x2202}z}-V_{1}\right)-\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{1}}{\unicode[STIX]{x2202}x}\right)=\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D70C}_{1}}{\unicode[STIX]{x2202}x^{2}}+\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D70C}_{1}}{\unicode[STIX]{x2202}z^{2}}. & \displaystyle\end{eqnarray}$$
These equations are subjected to the boundary conditions at the first order (equations (3.4), (3.9) and (3.11a )). The first-order velocity averaged over the vertical direction at the sheet surface is zero (equation (3.4)). Thus, we expect the first-order solution to be periodic in the vertical direction. This allows us to express the stream function and the density in the following form:
$$\begin{eqnarray}\unicode[STIX]{x1D713}_{1}=f(x)\text{e}^{\text{i}z},\quad \unicode[STIX]{x1D70C}_{1}=g(x)\text{e}^{\text{i}z}.\end{eqnarray}$$
Consequently, we note that, in (3.13), the mean value of all the terms involving density (
$\unicode[STIX]{x1D70C}_{1}$
) or the stream function (
$\unicode[STIX]{x1D713}_{1}$
) is zero. This implies that the first-order swimming velocity should be zero. Hence we get
$V_{1}=0$
. We thus conclude that stratification does not induce any velocity at the first order. Note that Taylor (Reference Taylor1951) made a similar prediction for a sheet immersed in a homogeneous fluid.
Substituting these expressions in the governing equations at the first order and solving for
$f(x),g(x)$
, we get the first-order fields as follows:
$$\begin{eqnarray}\displaystyle \hspace{-12.0pt} & \displaystyle \unicode[STIX]{x1D713}_{1}={\mathcal{R}}((s_{1}\text{e}^{m_{1}x}+s_{2}\text{e}^{m_{2}x}+s_{3}\text{e}^{m_{3}x})\text{e}^{\text{i}z}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \hspace{-12.0pt} & \displaystyle \unicode[STIX]{x1D70C}_{1}={\mathcal{R}}\left(\left(s_{1}\frac{Pem_{1}}{1-m_{1}^{2}+\text{i}Pe}\text{e}^{m_{1}x}+s_{2}\frac{Pem_{2}}{1-m_{2}^{2}+\text{i}Pe}\text{e}^{m_{2}x}+s_{3}\frac{Pem_{2}}{1-m_{3}^{2}+\text{i}Pe}\text{e}^{m_{3}x}\right)\text{e}^{\text{i}z}\right). & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
Here
${\mathcal{R}}$
denotes the real part;
$m_{1},m_{2}$
and
$m_{3}$
are the roots of the equation
$m^{6}+m^{4}(-3-\text{i}Pe-\text{i}Re)+m^{2}(3-PeRe+PeRi+\text{i}(2Pe+2Re))-(1+\text{i}Pe)(1+\text{i}Re)=0$
having a negative real part. Enforcing the boundary conditions at first order, we obtain the following equations whose solution determines
$s_{1},s_{2}$
and
$s_{3}$
:
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle s_{1}+s_{2}+s_{3}=\text{i},\\ \displaystyle s_{1}m_{1}+s_{2}m_{2}+s_{3}m_{3}=0,\\ \displaystyle s_{1}(m_{1}^{2}-1)^{2}+s_{2}(m_{2}^{2}-1)^{2}+s_{3}(m_{3}^{2}-1)^{2}=Ri.\end{array}\right\}\end{eqnarray}$$
Hence,
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle s_{1}=\frac{\left|\begin{array}{@{}ccc@{}}\text{i} & 1 & 1\\ 0 & m_{2} & m_{3}\\ Ri & (m_{2}^{2}-1)^{2} & (m_{3}^{2}-1)^{2}\\ \end{array}\right|}{D},\quad s_{2}=\frac{\left|\begin{array}{@{}ccc@{}}1 & \text{i} & 1\\ m_{1} & 0 & m_{3}\\ (m_{1}^{2}-1)^{2} & Ri & (m_{3}^{2}-1)^{2}\\ \end{array}\right|}{D},\\ \displaystyle s_{3}=\frac{\left|\begin{array}{@{}ccc@{}}1 & 1 & \text{i}\\ m_{1} & m_{2} & 0\\ (m_{1}^{2}-1)^{2} & (m_{2}^{2}-1)^{2} & Ri\\ \end{array}\right|}{D},\end{array}\right\}\end{eqnarray}$$
where
$$\begin{eqnarray}D=\left|\begin{array}{@{}ccc@{}}1 & 1 & 1\\ m_{1} & m_{2} & m_{3}\\ (m_{1}^{2}-1)^{2} & (m_{2}^{2}-1)^{2} & (m_{3}^{2}-1)^{2}\\ \end{array}\right|.\end{eqnarray}$$
3.3 Solution at
$O(\unicode[STIX]{x1D716}^{2})$
The equations governing the stream function and the density disturbance at
$O(\unicode[STIX]{x1D716}^{2})$
are given by
$$\begin{eqnarray}\displaystyle \hspace{-12.0pt} & \displaystyle \unicode[STIX]{x1D6FB}^{4}\unicode[STIX]{x1D713}_{2}-Ri\left(\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}_{2}}{\unicode[STIX]{x2202}x}\right)=Re\left(\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{1}}{\unicode[STIX]{x2202}x}\left(\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}z}\unicode[STIX]{x1D6FB}^{2}\unicode[STIX]{x1D713}_{1}\right)-\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{1}}{\unicode[STIX]{x2202}z}\left(\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}\unicode[STIX]{x1D6FB}^{2}\unicode[STIX]{x1D713}_{1}\right)+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}z}\unicode[STIX]{x1D6FB}^{2}\unicode[STIX]{x1D713}_{2}\right), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \hspace{-12.0pt} & \displaystyle Pe\left(-V_{2}+\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}_{2}}{\unicode[STIX]{x2202}z}+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}\left(-\unicode[STIX]{x1D70C}_{1}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{1}}{\unicode[STIX]{x2202}z}\right)+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}z}\left(\unicode[STIX]{x1D70C}_{1}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{1}}{\unicode[STIX]{x2202}x}\right)-\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{2}}{\unicode[STIX]{x2202}x}\right)=\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D70C}_{2}}{\unicode[STIX]{x2202}x^{2}}+\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D70C}_{2}}{\unicode[STIX]{x2202}z^{2}}. & \displaystyle\end{eqnarray}$$
From the boundary conditions at the second order (equations (3.5), (3.10) and (3.11b )), we find that second-order vertical velocity and the density gradient averaged in the vertical direction at the surface of the sheet are non-zero. Hence, the velocity and density fields must have a non-zero mean component to satisfy the boundary conditions. In order to obtain these mean components, we define the vertical averaged density and stream function in the domain as follows:
$$\begin{eqnarray}\langle \unicode[STIX]{x1D713}_{2}\rangle =\frac{1}{2\unicode[STIX]{x03C0}}\int _{0}^{2\unicode[STIX]{x03C0}}\unicode[STIX]{x1D713}_{2}(x,z)\,\text{d}z,\quad \langle \unicode[STIX]{x1D70C}_{2}\rangle =\frac{1}{2\unicode[STIX]{x03C0}}\int _{0}^{2\unicode[STIX]{x03C0}}\unicode[STIX]{x1D70C}_{2}(x,z)\,\text{d}z.\end{eqnarray}$$
We now average over the vertical direction on both sides of (3.20) and (3.21) to obtain
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}^{4}\langle \unicode[STIX]{x1D713}_{2}\rangle }{\text{d}x^{4}}=Ri\frac{\text{d}\langle \unicode[STIX]{x1D70C}_{2}\rangle }{\text{d}x}+Rek_{1}(x), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle Pe\left(-V_{2}+k_{2}(x)-\frac{\text{d}\langle \unicode[STIX]{x1D713}_{2}\rangle }{\text{d}x}\right)=\frac{\text{d}^{2}\langle \unicode[STIX]{x1D70C}_{2}\rangle }{\text{d}x^{2}}. & \displaystyle\end{eqnarray}$$
Here,
$k_{1}(x)=\langle \unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{1}/\unicode[STIX]{x2202}x(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}z\unicode[STIX]{x1D6FB}^{2}\unicode[STIX]{x1D713}_{1})-\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{1}/\unicode[STIX]{x2202}z(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x\unicode[STIX]{x1D6FB}^{2}\unicode[STIX]{x1D713}_{1})\rangle$
and
$k_{2}(x)=\langle \unicode[STIX]{x2202}/\unicode[STIX]{x2202}x(-\unicode[STIX]{x1D70C}_{1}\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{1}/\unicode[STIX]{x2202}z)+\unicode[STIX]{x2202}/\unicode[STIX]{x2202}z(\unicode[STIX]{x1D70C}_{1}\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{1}/\unicode[STIX]{x2202}x)\rangle$
, where
$\langle .\rangle$
represents the average in the vertical direction. These can be easily obtained from the first-order velocity and density fields.
We define
$\langle \unicode[STIX]{x1D713}_{2}\rangle =-V_{2}x+\unicode[STIX]{x1D713}_{2s}$
, where
$\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{2s}/\unicode[STIX]{x2202}x$
is the vertically averaged
$y$
-direction velocity field in the fluid domain measured in a stationary frame of reference. We substitute this expression in (3.23) and (3.24) to obtain the following differential equation for
$\unicode[STIX]{x1D713}_{2s}$
after some algebraic manipulations:
$$\begin{eqnarray}\frac{\text{d}^{5}\unicode[STIX]{x1D713}_{2s}}{\text{d}x^{5}}+(RiPe)\frac{\text{d}\unicode[STIX]{x1D713}_{2s}}{\text{d}x}=(RiPe)k_{2}(x)+Re\frac{\text{d}}{\text{d}x}k_{1}(x).\end{eqnarray}$$
We can now find the contribution of the mean velocity field at
$x=0$
, which is given by
$$\begin{eqnarray}\frac{\text{d}\langle \unicode[STIX]{x1D713}_{2}\rangle }{\text{d}x}(x=0)=-V_{2}+\frac{\text{d}\unicode[STIX]{x1D713}_{2s}}{\text{d}x}(x=0).\end{eqnarray}$$
We equate this contribution to the mean value of the second-order boundary condition at the sheet surface (equation (3.5a )) to obtain
$$\begin{eqnarray}V_{2}=\left\langle \sin (z)\frac{\text{d}^{2}\unicode[STIX]{x1D713}_{1}}{\text{d}x^{2}}(x=0)\right\rangle +\frac{\text{d}\unicode[STIX]{x1D713}_{2s}}{\text{d}x}(x=0).\end{eqnarray}$$
Here,
$\unicode[STIX]{x1D713}_{1}$
and
$\unicode[STIX]{x1D713}_{2s}$
are obtained by solving equations (3.15) and (3.25), respectively. We solve equations (3.25) and (3.27) to obtain the velocity of the sheet which is given by
$$\begin{eqnarray}V_{2}=\frac{1}{2}\text{Im}\left(\mathop{\sum }_{i=1}^{3}\mathop{\sum }_{j=1}^{3}\frac{s_{i}\overline{s_{j}}(m_{i}^{2}-1)(m_{i}+\overline{m_{j}})}{RiPe+(m_{i}+\overline{m_{j}})^{4}}\left(Pe\frac{(m_{i}^{2}-1)^{2}}{m_{i}}-Re(m_{i}+\overline{m_{j}})\right)-\mathop{\sum }_{i=1}^{3}m_{i}^{2}s_{i}\right),\end{eqnarray}$$
where
$\overline{s_{i}}$
and
$\overline{m_{i}}$
represent the complex conjugates of
$s_{i}$
and
$m_{i}$
, respectively, Im is the imaginary part and
$\text{i}^{2}=-1$
. The dimensional swimming velocity of the sheet is given by
$$\begin{eqnarray}V_{s}=\left(\frac{\unicode[STIX]{x1D70E}}{k}\right)b^{2}k^{2}V_{2}.\end{eqnarray}$$
From the above expression, we observe that the velocity of a swimmer immersed in density-stratified fluid is proportional to the wave speed, the square of the wave amplitude and the wavenumber. By substituting
$Ri=0$
in (3.28), we obtain the expression for the sheet’s swimming velocity in a homogeneous fluid as follows:
$$\begin{eqnarray}V_{s}=\left(\frac{\unicode[STIX]{x1D70E}}{k}\right)b^{2}k^{2}\left(\frac{1}{2}\sqrt{\frac{1+\sqrt{1+Re^{2}}}{2}}\right).\end{eqnarray}$$
We note that this expression matches with the formula derived by Tuck (Reference Tuck1968), thus verifying the theoretical procedure used in our analysis.
4 Results and discussion
We divide our analysis into two regimes. We first discuss the low-Reynolds-number regime, where the inertial forces acting on the swimmer are negligible (
$Re\ll 1$
). In this case, the swimmer is propelled only by the viscous forces acting on its surface. The second regime is that of a swimmer having a finite
$Re$
. Here, inertial forces can no longer be neglected and will contribute to the propulsion of the swimmer. Owing to the dearth of theoretical studies conducted in both these regimes, we expect our results to provide a fundamental understanding about the effect of stratification on the swimming of microorganisms.
Henceforth, we will express the Péclet number in terms of the Prandtl number (
$Pr=Pe/Re$
) which is defined as the ratio of the momentum diffusivity to the thermal diffusivity. We use the same number for salt transport as well, even though such a number is the Schmidt number when mass transfer occurs. Typical values of Prandtl number for some practically relevant stratification conditions are
$Pr=700$
for salt stratification in water and
$Pr=7$
for temperature-stratified water. The magnitude of stratification is often represented by the Brunt–Väisälä frequency (
$N=\sqrt{\unicode[STIX]{x1D6FE}g/\unicode[STIX]{x1D70C}_{\infty }}$
). The typical values of
$N$
range from
$10^{-4}$
to
$0.3~\text{s}^{-1}$
(Thorpe Reference Thorpe2005). Using this estimate, in density-stratified water (
$\unicode[STIX]{x1D70C}_{\infty }\approx 1000~\text{kg}~\text{m}^{-3}$
,
$\unicode[STIX]{x1D707}\approx 10^{-3}~\text{kg}~\text{m}^{-1}~\text{s}^{-1}$
), we find that
$\unicode[STIX]{x1D6FE}\approx 10^{-6}$
–
$10~\text{kg}~\text{m}^{-4}$
. We can use these parameter values to determine typical values of
$Re=\unicode[STIX]{x1D70C}_{\infty }u_{c}l_{c}/\unicode[STIX]{x1D707}$
and
$Ri=\unicode[STIX]{x1D6FE}gl_{c}^{3}/(\unicode[STIX]{x1D707}u_{c})$
for various motile organisms in stratified water with
$\unicode[STIX]{x1D6FE}=1~\text{kg}~\text{m}^{-4}$
. Examples include Escherichia coli, Salmonella typhimurium (
$l_{c}\approx 1~\unicode[STIX]{x03BC}\text{m}$
,
$u_{c}\approx 20{-}30~\unicode[STIX]{x03BC}\text{m}~\text{s}^{-1}$
) (Lauga & Powers Reference Lauga and Powers2009):
$Re\approx 10^{-5}$
–
$10^{-4},Ri\approx 10^{-8}$
; copepods (
$l_{c}\approx 0.05$
–0.3 cm,
$u_{c}\approx 0.1$
–
$0.5~\text{cm}~\text{s}^{-1}$
) (Strickler Reference Strickler1975):
$Re\approx 10^{-2}$
–
$10^{3},Ri\approx 0.01$
–
$0.05$
; Euphausia pacifica (krills) (
$l_{c}\approx 1$
cm,
$u_{c}\approx 5~\text{mm}~\text{s}^{-1}$
) (Yen, Brown & Webster Reference Yen, Brown and Webster2003):
$Re\approx 175,Ri\approx 1$
–
$5$
.
Figure 2. First-order flow field (
$\unicode[STIX]{x1D713}_{1}$
) induced by the swimmer in (a) homogeneous fluid and (b) stratified fluid (
$Pr=7,Ri=5$
). Contours are the streamlines and colours show the value of the stream function. (c) Isopycnals (
$\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}_{0}+\unicode[STIX]{x1D70C}^{\prime }$
) for
$Pr=7,Ri=5$
. Vertical arrows represent the direction of isopycnal retreat and solid black lines represent the swimming sheet. (d) Comparison of streamline of a stratified fluid (dashed line) with a homogeneous fluid (solid line). Black arrows represent the direction of the first-order velocity and blue arrows represent additional vertical velocities due to isopycnal retreat. Here
$Re=0.001$
is chosen for all the subplots.
4.1 Low-Reynolds-number regime (
$Re\ll 1$
)
4.1.1 Effect of stratification on swimming velocity
We first analyse the first-order flow field generated by the propelling sheet in the presence of stratification. We observe that stratification markedly changes the flow pattern in comparison with the homogeneous fluid (figure 2
a,b). The flow field generated by the sheet is vertically biased as the streamlines bend towards the denser portion of the fluid. This observation can be understood by considering that the motion of the swimmer disturbs the density field in its proximity. This causes the isopycnals to deform and assume a configuration which is no longer horizontal. Note that the isopycnals deform such that they are oriented in a direction normal to the surface of the swimmer, so as to satisfy the no-flux boundary condition. Consequently, the isopycnals near the lower (upper) end of the sheet’s crest deflect in the positive (negative)
$y$
direction. This is clearly shown in figure 2(c) which depicts the displaced isopycnals close to the sheet. The tendency of the displaced density layers to return to their original position creates additional vertical velocities in the fluid domain (shown by vertical arrows in figure 2
c), in a direction which is opposite to the deformation of isopycnals. We note that this velocity acts in the negative
$y$
direction near the lower end of the sheet’s crest (
$0\leqslant y<\unicode[STIX]{x03C0}/2$
) and in the positive
$y$
direction near the upper end (
$\unicode[STIX]{x03C0}/2<y\leqslant \unicode[STIX]{x03C0}$
). One can add this stratification-induced velocity to the flow field in a homogeneous fluid to determine the flow field in a stratified fluid. If we consider a streamline in a homogeneous fluid which is directed from
$y\approx 0.5$
to
$y\approx 2.5$
as shown by the solid curve in figure 2(d), the effect of stratification-induced velocity is to decrease the slope of this curve near
$y\approx 0.5$
and to increase this slope near
$y\approx 2.5$
, due to which the streamline in a stratified fluid appears to be bent in the negative
$y$
direction. This flow pattern has a significant influence on the hydrodynamics of the sheet propulsion, which is discussed in later sections. The effect of stratification on swimming can be characterized by
$Ri$
which depends on the strength of the density stratification and
$Pr$
which depends on the diffusivity of the stratifying agent. We now analyse the effect of both of these parameters on the swimming velocity.
Figure 3. Variation of the swimming velocity with (a) Richardson number and (b) Prandtl number, for
$Re=0.001$
, normalized with respect to the velocity in a homogeneous fluid in the Stokes regime. First order vorticity field at (c)
$Ri=0$
and (d)
$Ri=5$
, for
$Re=0.001,Pr=700$
.
Figure 4. Decomposition of the swimming velocity for (a)
$Pr=700$
and (b)
$Ri=1.5$
, for
$Re=0.001.$
Figure 3(a) shows the variation of the swimming velocity with
$Ri$
normalized with respect to the velocity in a homogeneous fluid (
$Ri=0,Re=0$
). We observe that the velocity decreases with stratification for all values of
$Pr$
. This implies that an increase in stratification hampers the vertical motion of swimmers. We now observe the effect of diffusion on the swimming velocity (see figure 3
b). For smaller levels of stratification, we see that the velocity initially decreases with
$Pr$
, and then increases after reaching a minimum (see figure 3
b (
$Ri=1.5$
)). Thus, for small
$Ri$
, diffusivity of the stratifying agent plays a key role in determining the swimming behaviour. For higher levels of stratification, we find that the velocity monotonically decreases with
$Pr$
(see figure 3
b (
$Ri=5$
)). Additionally, we observe that, for very high values of diffusion (
$Pr\ll 1$
), the swimmer moves with the same velocity as that in a homogeneous fluid (see figure 3
b). This is mainly because the density disturbance becomes negligible for very high values of diffusion. We further find that, for small values of
$Ri$
and
$Pe$
, the velocity decreases linearly with respect to these parameters. By using a numerical fit to the velocity curves in figure 3(a,b) for small
$Ri$
and
$Pe$
, the mathematical form of the velocity variation is obtained as follows:
$$\begin{eqnarray}V=V_{H}(1-0.46RiPe).\end{eqnarray}$$
The sheet swimming velocity can be decomposed into two contributions (refer to (3.27)). The first term signifies the second-order vertical velocity at the sheet boundary because of the no-slip condition at the sheet surface. In the case of a homogeneous fluid, this is the only contribution to the sheet propulsion. We can rewrite this term as follows:
$$\begin{eqnarray}\left\langle \sin (z)\frac{\text{d}^{2}\unicode[STIX]{x1D713}_{1}}{\text{d}x^{2}}(x=0)\right\rangle =\frac{1}{2}(\unicode[STIX]{x1D714}_{1}(0,\unicode[STIX]{x03C0}/2)-1).\end{eqnarray}$$
Here,
$\unicode[STIX]{x1D714}_{1}(0,\unicode[STIX]{x03C0}/2)$
represents the value of first-order vorticity in the fluid at the sheet crests. We thus find that this contribution to the swimming velocity is directly proportional to the magnitude of the vorticity generated in the fluid at the sheet crests. Lauga & Powers (Reference Lauga and Powers2009) explained that the vortices are caused due to the opposite direction of longitudinal displacement of the fluid particles close to the sheet’s crests. The second contribution is caused by the mean second-order velocity field which is induced in the fluid when density stratification is taken into account (refer to (3.25)). For a stratified fluid without inertia this contribution is completely governed by
$k_{2}(x)$
. Physically, this quantity signifies average rate of mass transfer due to advection across the fluid volume.
Figure 4 shows the reconstruction of the velocity from both these contributions. We observe that the second-order vertical velocity at the sheet boundary (represented by the propulsion component) is positive for all
$Ri,Pr$
, which causes the sheet to propel. Furthermore, this propulsion component of the velocity decreases with
$Ri$
. We rationalize this observation by considering that the propulsion component is generated due to the vortices developed in the fluid at the sheet crests (refer to (4.2)). Figure 3(c,d) shows the modification in the vorticity field when stratification is taken into account. We find that the vorticity peak is no longer aligned with the sheet crests in the presence of stratification. Consequently, the magnitude of the vorticity at the sheet crests decreases, which ultimately causes the propulsion component to decrease with
$Ri$
.
From figure 4(a), we also find that the contribution of the mean second-order velocity field developed in the fluid due to stratification is negative. In order to understand this observation, we first note that, as the swimmer translates in the positive
$y$
direction, it pulls the surrounding fluid with itself. If we now consider a fixed control volume inside the fluid, we deduce that its mass is increasing with time, as the fluid is being replaced by a heavier fluid. If we further assume that diffusion is not very large, then mass conservation dictates that the rate of mass transfer due to advection across the control volume should be negative. Consequently, we note that the quantity that governs the mean second-order velocity field (refer to
$k_{2}(x)$
in (3.25)) is negative everywhere in the fluid domain. This causes the contribution of the mean second-order velocity field to oppose the propulsion of the swimmer. Furthermore, if the ambient density gradient is increased, the mass of the control volume will increase at a faster rate, causing
$k_{2}(x)$
to become more negative in the fluid. Consequently, we find that increasing stratification leads to an increase in the opposition caused by the mean second-order velocity field (see figure 4
a). After analysing the variations of both of the velocity contributions, we infer that increasing stratification restricts the vertical motion of swimmers. From figure 4(b), we observe that, for low stratification strengths, the propulsion component decreases with
$Pr$
; however, the resistance to propulsion increases with
$Pr$
and then decreases, eventually supporting the propulsion for high
$Pr$
. This trend is consequently reflected in the velocity of the swimmer (see figure 3
b,
$Ri=1.5$
). Interestingly, if the density gradient is small, for low levels of diffusion, the swimmer can even propel faster than in a homogeneous fluid (see figure 3
b,
$Ri=1.5,Pr=1000$
).
To summarize, we find that higher stratification strengths mostly hamper the swimming velocity of the sheet in a low-Reynolds-number regime. This result is expected from an intuitive standpoint, because for the class of problems involving particles settling in a density-stratified Newtonian fluid, it is well known that an increased drag force inhibits their vertical motion (Yick et al. Reference Yick, Torres, Peacock and Stocker2009; Candelier, Mehaddi & Vauquelin Reference Candelier, Mehaddi and Vauquelin2014; Doostmohammadi, Dabiri & Ardekani Reference Doostmohammadi, Dabiri and Ardekani2014). However, in the narrow regime of lower stratification strengths and negligible diffusion, we find that stratification supports the swimming motion of the sheet.
4.1.2 Effect of stratification on power expenditure and swimming efficiency
In this section, we analyse the influence of stratification on the power expended by the swimmer to achieve propulsion. This depends on the work done by the hydrodynamic stresses acting on its surface. Ardekani & Stocker (Reference Ardekani and Stocker2010) predicted that point forces acting on a stratified fluid generate a flow field around the swimmer which augments its power expenditure. Later, Doostmohammadi et al. (Reference Doostmohammadi, Stocker and Ardekani2012) analysed the power expended by squirmers suspended in a density-stratified fluid. By conducting a series of numerical studies, they came to the same conclusion that stratification magnifies the energy required for swimming.
The power expended by the swimmer is given by
$$\begin{eqnarray}P=\int _{S(t)}\boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D748}\boldsymbol{\cdot }\boldsymbol{u}\,\text{d}S=\int _{{\mathcal{V}}(t)}(\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D748})\boldsymbol{\cdot }\boldsymbol{u}\,\text{d}{\mathcal{V}}+2\unicode[STIX]{x1D707}\int _{V(t)}\unicode[STIX]{x1D640}\boldsymbol{ : }\unicode[STIX]{x1D640}\,\text{d}{\mathcal{V}}.\end{eqnarray}$$
Here,
$\unicode[STIX]{x1D748}$
and
$\unicode[STIX]{x1D640}$
are the stress tensor and the rate-of-strain tensor, respectively,
$S(t)$
represents the surface of the swimmer and
${\mathcal{V}}$
represents the fluid volume which is bounded by the sheet surface and extends to infinity. The first term on the right-hand side indicates the work done to move the isopycnals against gravity, while the second term indicates the viscous energy dissipation in the fluid. The rate-of-strain tensor can be written as
$\unicode[STIX]{x1D640}={\textstyle \frac{1}{2}}(\unicode[STIX]{x1D735}\boldsymbol{u}+\unicode[STIX]{x1D735}\boldsymbol{u}^{\text{T}})$
, where
$\boldsymbol{u}=(u_{1},v_{1})$
represents the first-order velocity field. The divergence of the stress tensor is
$$\begin{eqnarray}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D748}=-\unicode[STIX]{x1D70C}^{\prime }\boldsymbol{g}.\end{eqnarray}$$
We non-dimensionalize the above quantities and obtain the following expression for the power dissipation at low Reynolds numbers:
$$\begin{eqnarray}P=\int _{{\mathcal{V}}(t)}\!\unicode[STIX]{x1D707}\unicode[STIX]{x1D70E}^{2}\!\left(\unicode[STIX]{x1D716}^{2}\!\left(Ri(\unicode[STIX]{x1D70C}_{1}v_{1})+2\!\left(\!\!\left(\frac{\unicode[STIX]{x2202}u_{1}}{\unicode[STIX]{x2202}x}\right)^{2}\!+\left(\frac{\unicode[STIX]{x2202}v_{1}}{\unicode[STIX]{x2202}z}\right)^{2}\!+\frac{1}{2}\!\left(\frac{\unicode[STIX]{x2202}u_{1}}{\unicode[STIX]{x2202}z}+\frac{\unicode[STIX]{x2202}v_{1}}{\unicode[STIX]{x2202}x}\right)^{2}\right)\!\right)\!+O(\unicode[STIX]{x1D716}^{3})\!\right)\text{d}{\mathcal{V}}.\end{eqnarray}$$
Here,
$u_{1}$
and
$v_{1}$
are the first-order velocity fields in the
$x$
and
$y$
directions, respectively. We observe that, in addition to the viscous dissipation, stratification induces an additional contribution from the buoyancy force generated by the first-order disturbance density field.
We calculate the mean power over one time period and compare it with the power expended by the swimmer in a homogeneous fluid by varying the stratification magnitude (see figure 5
a). We observe that stratification augments the power expenditure at all values of
$Pr$
considered. We previously noted that the streamlines surrounding the swimmer become more tilted in the presence of stratification (figure 2
b). Similar to the streamlines, we find that the velocity contours also become vertically skewed due to stratification effects. The skewed velocity contours augment the velocity gradients generated in the fluid domain. This enhances the shear stresses developed in the fluid, and consequently the viscous dissipation in the fluid increases. Moreover, the swimmer consumes more energy in mixing the fluid as well. As a result, we find that swimming becomes more energetically expensive in a density-stratified fluid. This result matches with the predictions made by Ardekani & Stocker (Reference Ardekani and Stocker2010) and Doostmohammadi et al. (Reference Doostmohammadi, Stocker and Ardekani2012), even though the geometry of the swimmer is different in each case. We further observe that an increase in diffusion decreases the power expenditure of the swimmer. This can be understood by considering that stronger diffusion counteracts the effect of buoyancy more effectively by restricting the tilting of the density contours. As a result, the work done by buoyancy forces is mitigated which consequently decreases the power expenditure. This analysis is shown in figure 5(c,d) which compares the isopyncal deflections for
$Pr=7$
and
$Pr=700$
. In order to understand the deflection of isopycnals for low values of diffusion, we note that, far away from the swimmer, the vertically averaged mass flux developed in the fluid due to the deformation of the swimmer is positive for smaller values of diffusion. This implies that, as the swimmer propels, fluid mass is migrating in the positive
$y$
direction. To account for this mass transport, the isopycnals can no longer be horizontal and are bent upwards. However, for high values of diffusion, we find that there is no mass transport across the isopycnals and hence they retain their undisturbed position.
We seek to analyse the effect of stratification on the hydrodynamic efficiency of the swimmer. Efficiency depends on the fraction of the available power used for locomotion. Lighthill (Reference Lighthill1952) defined swimming efficiency as the ratio of external power required to move the swimmer at a constant velocity to the power expended by the swimmer. This definition is commonly used to represent the hydrodynamic efficiency of undulating sheets. We use this definition to quantify the hydrodynamic efficiency in a stratified fluid. Hence, we obtain
$$\begin{eqnarray}\unicode[STIX]{x1D702}\propto \frac{V^{2}}{P}.\end{eqnarray}$$
Here,
$V$
is the swimming velocity and
$P$
is the mean power expended by the swimmer over one time period. We compare this efficiency with that in the homogeneous fluid and observe the variation with the stratification strength (see figure 5
b). We observe that an increase in
$Ri$
decreases the efficiency of the swimmer. This is expected because with increasing
$Ri$
, the power expenditure of the swimmer is increasing (see figure 5
a), while the swimming velocity is decreasing (see figure 3
a). Hence, the swimmer is converting less fraction of the available power into locomotion. For the values of
$Pr$
considered for the efficiency analysis, we have seen that with increasing diffusion, the swimming velocity increases, while the power expenditure of the sheet decreases. This causes the swimming efficiency to increase with diffusion for a fixed
$Ri$
.
Figure 5. Effect of stratification on (a) power expenditure and (b) swimming efficiency, normalized with respect to that in a homogeneous fluid in the Stokes regime. First-order density field (
$\unicode[STIX]{x1D70C}_{1}$
) contours for (c)
$Ri=5,Pr=7$
and (d)
$Ri=5,Pr=700$
. Here
$Re=0.001$
is chosen for all the subplots.
4.1.3 Effect of stratification on mixing
Biogenic mixing has been studied via experimental and numerical studies (Katija & Dabiri Reference Katija and Dabiri2009; Katija Reference Katija2012; Wang & Ardekani Reference Wang and Ardekani2015). Mixing efficiency can be defined as the fraction of mechanical energy converted to change the potential energy of the fluid by the mixing process. It is represented by the following formula:
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}=\frac{\unicode[STIX]{x0394}PE}{\unicode[STIX]{x0394}KE}=\frac{Ri\int _{{\mathcal{V}}}\unicode[STIX]{x1D70C}^{\prime }v\,\text{d}{\mathcal{V}}}{Ri\int _{{\mathcal{V}}}\unicode[STIX]{x1D70C}^{\prime }v\,\text{d}{\mathcal{V}}+2\int _{{\mathcal{V}}}\unicode[STIX]{x1D640}\boldsymbol{ : }\unicode[STIX]{x1D640}\,\text{d}{\mathcal{V}}}.\end{eqnarray}$$
Here,
$\unicode[STIX]{x1D70C}^{\prime }$
and
$v$
denote the disturbance density field and the vertical velocity field, respectively. The numerator denotes the potential energy change in the fluid induced by the swimming organism, while the denominator indicates the total mechanical energy of the fluid. From the above expression, it is evident that mixing efficiency depends on the ratio of the change in the potential energy of the fluid to the viscous dissipation.
Figure 6. Variation of the mixing efficiency with Richardson number for
$Re=0.001$
.
Figure 6 shows the variation of mixing efficiency with
$Ri$
. Wagner, Young & Lauga (Reference Wagner, Young and Lauga2014) showed that the vertical mixing induced by an ensemble of microorganisms, represented by force dipoles, at small Reynolds and Péclet numbers is very small (
${\approx}8\,\%$
). Here we consider the mixing induced by a Taylor swimming sheet. Interestingly, our results show that the mixing efficiencies can reach up to
$40\,\%$
for thermally stratified water. Although the viscous dissipation increases with stratification as mentioned before, the bending of the streamlines induces additional vertical velocities in the fluid domain (see figure 2
b). This causes the mass flux to increase, which consequently increases the potential energy of the fluid. As a result, we observe that the mixing efficiency increases with
$Ri$
. Wang & Ardekani (Reference Wang and Ardekani2015) also observed that mixing efficiency increases with stratification strength at low Reynolds numbers by performing fully resolved three-dimensional simulations on a suspension of squirmers swimming in thermally stratified water (
$Pr=7$
). In addition to this, we observe that for lower values of diffusion (
$Pr=700$
), which is the case for salt-stratified water, the mixing efficiency increases with stratification and then saturates for higher values of
$Ri$
. This indicates that the change in potential energy balances the viscous dissipation for low diffusion and higher stratification strength. The maximum mixing efficiency for salt-stratified water is about
$15\,\%$
. We find that the mixing efficiency is highest when the diffusion of the stratifying agent is very high (
$Pr\approx 0$
). We thus infer that, at low Reynolds number, a swimmer immersed in thermally stratified water will induce more mixing compared to salt-stratified water.
4.2 Finite inertia analysis
Next, we discuss the effect of inertia in our analysis. We will analyse the effect of stratification on the same parameters that were considered for the low-Reynolds-number regime. Although our procedure is applicable for any arbitrary value of
$Pr$
, we focus our attention on the cases where diffusion is not significantly large (
$Pr>1$
). These are the problems which are typically encountered in practice as mentioned before (salt-stratified water (
$Pr=700$
); temperature-stratified water (
$Pr=7$
)). Analysis of the influence of stratification on swimming in high-diffusion scenarios is given briefly in the Appendix.
4.2.1 Effect of stratification on swimming velocity
Figure 7. Variation of swimming velocity with (a) Richardson number and (b) Prandtl number, for
$Re=5$
, normalized with that in a homogeneous fluid at the same
$Re$
. (c) Decomposition of the swimming velocity into two components for
$Pr=700$
,
$Re=5$
. (d) Variation of swimming velocity with Reynolds number.
Figure 7(a) shows the effect of stratification on the swimming velocity for
$Re=5$
. We observe that inclusion of inertia augments the swimmer’s velocity for low stratification strength. For thermally induced stratification (
$Pr=7$
), the maximum velocity increase is almost five times that of the homogeneous case. Further increase in stratification strength causes the velocity to decrease, ultimately leading to a direction reversal for a sufficiently high
$Ri$
. Even higher values of
$Ri$
induce a nominal increase in the velocity with the opposite swimming direction maintained. For low values of diffusion (
$Pr=700$
), the velocity of the swimmer is almost zero for most values of
$Ri$
considered. This implies that strong salt stratification inhibits the vertical migration of the swimmer causing it to remain essentially stationary. Variation with
$Pr$
also follows a similar trend, comprising a velocity peak followed by a motion reversal, eventually leading to saturation (see figure 7
b). Interestingly, higher stratification strengths tend to completely hamper the velocity of the sheet. We thus conclude that, for moderately small values of
$Re$
, if the diffusion of the stratifying agent is very low or the stratification strength of the fluid is high, then the swimmer will not propel (see figure 7
a,b). This observation is similar to the preferential aggregation of marine organisms at pycnoclines at steep density gradients reported by Harder (Reference Harder1968).
Similar to the Stokes regime, we find that the swimming velocity follows a trend similar to the contribution of the mean second-order velocity field developed in the fluid domain (see figure 7
c). We also observe that the propulsion component of the velocity is almost independent of
$Ri$
. As discussed before, we know that the propulsion component of the velocity is governed by the vorticity generated in the fluid. We note that, when inertial effects are considered, the inertia-induced vorticity near the sheet crests dominates the vorticity induced due to the density gradients. Consequently, we find that stratification has a negligible influence on the propulsion component of the velocity. For a homogeneous fluid, Tuck (Reference Tuck1968) noted that inclusion of inertia creates a second-order mean convective velocity which opposes propulsion. However, for a density-stratified fluid, we find that the second-order velocity field supports propulsion for smaller
$Ri$
, and opposes propulsion for higher density gradients (see figure 7
c). We see that, for higher
$Ri$
, the resistance to motion dominates over the propulsion component causing the swimmer to reverse its direction of motion.
Next, we quantify the variation of the swimming velocity with Reynolds number for the cases of both temperature and salt stratification (figure 7
d). We find that, in contrast to a homogeneous fluid, the presence of stratification causes the swimming velocity to become more sensitive to inertial effects. For thermally stratified water, the swimming velocity is independent of
$Re$
for higher Reynolds numbers and only increases with stratification. The saturation of swimming velocity at higher
$Re$
is also seen for a homogeneous fluid. This is not the case for salt stratification, where we observe that higher stratification strengths cause the swimming velocity to increase with
$Re$
, with the swimmer reversing its direction of motion for all Reynolds numbers. As explained before (figure 7
c), this is mainly because of the dominance of the mean second-order velocity component which becomes negative for higher stratification strengths.
4.2.2 Effect of stratification on power expenditure and swimming efficiency
In the case of finite
$Re$
, we have
$$\begin{eqnarray}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D70E}=(Ri\unicode[STIX]{x1D70C}^{\prime })\boldsymbol{e}_{\boldsymbol{ y}}+Re\frac{\text{D}\boldsymbol{u}}{\text{D}t}.\end{eqnarray}$$
Here,
$\text{D}/\text{D}t$
represents the material derivative and
$\boldsymbol{u}=(u,v)$
is the fluid velocity vector. Thus, unlike the Stokes regime, the work done by the fluid inertia will add to the power expended by the swimmer (see (4.3)).
Figure 8. (a) Power expenditure and (b) hydrodynamic efficiency for
$Re=5$
, normalized with respect to that in a homogeneous fluid at the same
$Re$
.
As in the case of the Stokes regime, we find that with increasing stratification, the viscous dissipation in the fluid increases and the swimmer does more work in changing the potential energy of the fluid as well. Consequently, we observe that the swimmer consumes more power with increasing stratification (see figure 8
a). We thus infer that stratification augments the power expenditure of swimmers irrespective of the importance of inertia. Figure 8(b) shows the effect of stratification on the swimming efficiency for finite fluid inertia. For all values of
$Pr$
considered, the efficiency increases with
$Ri$
, reaches a peak value and then decreases. For thermal stratification, the peak efficiency is 20 times that for the homogeneous case. The trend of the swimming efficiency closely matches that for the swimmer’s velocity (see figure 7
a). This directly follows from the definition of the swimming efficiency (see (4.6)). As discussed before, for lower values of diffusion, stratification severely hampers the vertical migration of swimmers for finite fluid inertia. Consequently, we find that, for high
$Pr$
, the efficiency is zero for most values of stratification.
4.3 Effect of stratification on mixing
Figure 9. Variation of the mixing efficiency with (a) Richardson number (
$Re=5$
) and (b) Reynolds number. (c) Spatial variation of vertical averaged viscous dissipation energy (
$Pr=7,Ri=5$
);
$\unicode[STIX]{x1D640}$
is the rate-of-strain tensor. (d) Variation of diapycnal eddy diffusivity with Reynolds number.
In this section, we quantify the mixing induced by a swimmer at finite
$Re$
. This analysis is relevant for the zooplankton community in oceans, which have
$Re\approx O(1{-}100)$
. We first focus on the mixing efficiency of the swimmer (refer to (4.7)). We observe that, as in the case of the Stokes regime, an increase in stratification enhances mixing efficiency of the swimmer (see figure 9
a). However, the mixing efficiency follows a fast decay with
$Re$
(see figure 9
b). This observation can be rationalized by considering that the viscous dissipation in the fluid increases rapidly with
$Re$
, dominating any variations in the potential energy, and ultimately leading to the decay in the mixing efficiency. This can be seen from figure 9(c) which shows the mean vertical viscous dissipation energy per unit volume. This observation is consistent with our knowledge derived from application of the Helmoltz minimum energy dissipation theorem, that Stokes solution has the smallest rate of viscous dissipation as compared to solutions obtained by considering finite inertia. For high Reynolds numbers (
$Re>200$
), the mixing induced by the sheet is negligible for both salt and temperature stratifications. In addition to this, for salt stratification (
$Pr=700$
), the mixing is insignificant for low
$Re$
as well. This implies that, for salt-stratified water, most of the power expended by the swimmer is dissipated as viscous heat for all Reynolds numbers. However, for stratification induced by temperature gradients, we find that the swimmer converts a higher fraction of the power to change the potential energy of the fluid at low Reynolds numbers, which consequently leads to higher mixing efficiencies.
Another parameter which is often used to characterize mixing is the diapycnal eddy diffusivity (
$K_{v}$
), which is a measure of the vertical mass flux in the fluid. The dimensionless diapycnal eddy diffusivity is defined as (Osborn Reference Osborn1980)
$$\begin{eqnarray}\frac{K_{v}}{\unicode[STIX]{x1D708}}=-Re\langle \langle \unicode[STIX]{x1D70C}^{\prime }v\rangle \rangle .\end{eqnarray}$$
Here,
$\unicode[STIX]{x1D70C}^{\prime }$
is the disturbed density field,
$v$
is the vertical velocity field,
$\unicode[STIX]{x1D708}$
is the kinematic viscosity and
$\langle \langle \cdot \rangle \rangle$
represents the average in the entire fluid domain. We calculated
$K_{v}$
for density-stratified water and observed the variation with Reynolds number (see figure 9
d). We observe that the vertical mass flux induced by the swimmer due to salt stratification is negligible. For thermally stratified water (
$Pr=700,\unicode[STIX]{x1D708}=10^{-6}~\text{m}^{2}~\text{s}^{-1}$
), we find that for higher Reynolds numbers (
$Re>50$
),
$K_{v}>10^{-7}~\text{m}^{2}~\text{s}^{-1}$
which is the molecular temperature diffusivity in water. This implies that, for higher
$Re$
, stratification has potential to enhance mixing in the fluid. Additionally, we find that
$K_{v}$
increases with Reynolds number. A similar trend was observed by Wang & Ardekani (Reference Wang and Ardekani2015), by performing simulations on a suspension of squirmers in a stratified fluid by considering a volume fraction of
$4\,\%$
. They also noted that the vertical mass flux is independent of stratification for
$Fr\approx 20$
, where
$Fr$
is the Froude number. Our results match with this observation, as it can be seen from figure 9(d) that increasing stratification has a negligible influence on the diapycnal eddy diffusivity at all Reynolds numbers.
5 Conclusion
We analytically obtained the swimming velocity for a self-propelling sheet immersed in a density-stratified fluid. We performed a regular perturbation to obtain this velocity up to second order of the undulation amplitude (
$bk$
). We found that, as in the case of a homogeneous fluid (Taylor Reference Taylor1951), the first-order component of the velocity is zero and the swimming velocity only depends on the square of the wave amplitude and the wavenumber. We analysed the influence of stratification on the swimming behaviour by considering cases of both small and finite
$Re$
.
For low
$Re$
, we found that a large density stratification in the fluid mostly hampers the vertical motion of the swimmers. This results in a swimming velocity which is less than that in a homogeneous fluid. We interestingly found that, in cases where both stratification strength and the diffusivity of the stratifying agent are low, the swimming speed is magnified and stratification supports the propulsion of the swimmer. The results in the Stokes regime are relevant for small-scale organisms in stratified environments; for example, motion of organisms such as bacteria (e.g. Escherichia coli, Salmonella typhimurium), small plankton, larvae of marine organisms and smaller sized copepods in oceanic waters. For finite inertia, we found that the swimming velocity behaviour is highly sensitive to the stratification strength, diffusion in the fluid and Reynolds number. We found that, for higher stratification strengths or low values of diffusion, the motion of the swimmer is highly restricted and it essentially remains stationary. We elucidated the similarity between this observation and the experimentally observed phenomenon of preferential aggregation of swimmers at pycnoclines for steep density gradients. The observations in the regime of finite inertia are particularly relevant for moderately sized swimmers such as zooplankton, e.g. Euphausia pacifica (krills) and larger sized copepods, for which the Reynolds number can be much greater than unity. The velocity behaviour in both regimes of Reynolds number is primarily governed by the mean second-order field developed in the fluid.
Stratification causes the streamlines to become vertically biased and tilt towards the denser portion of the fluid. This results in enhanced shear stresses generated in the fluid which consequently leads to an increased power expenditure by the swimmer. Moreover, the skewed streamlines cause additional vertical velocities to be developed in the fluid domain which increases the vertical mass flux. Consequently, the mixing efficiency induced by the swimmer increases with stratification. We also found that diffusion plays an important role in influencing the motility characteristics of the swimmer. A more diffusive fluid will prevent the tilting of the density contours in the presence of stratification, which more effectively counteracts the buoyancy-induced disturbances. This results in a decreased power expenditure by the swimmer and consequently leads to a higher swimming efficiency.
Increase in inertia causes a higher fraction of the power consumed by the swimmer to be expended in the form of viscous dissipation in the fluid. This leads to a decreased mixing efficiency and consequently we observe a fast decay of the mixing efficiency with Reynolds number. However, the diapycnal eddy diffusivity, which is a measure of the vertical mass flux, increases with inertia. Additionally, we found that, in both regimes of Reynolds number, a swimmer immersed in thermally stratified water leads to higher mixing efficiency and diapycnal eddy diffusivity as compared to salt-stratified water, which has negligible mixing efficiency and diapycnal eddy diffusivity in the inertial regime.
Acknowledgement
This publication was made possible due to support from NSF (grant nos 1700961, 1604423, and 1705371).
Appendix. Effect of stratification on swimming velocity for high diffusion, finite inertia (
$Pr<1$
)
Here, we analyse the case of swimmers immersed in a highly diffusive environment (see figure 10). For
$Pr=0.001$
, we see that the swimming velocity increases with stratification strength. However, with further increase in
$Pr$
, the curve becomes flatter, ultimately with the trend reversing for
$Pr=0.1$
.
Figure 10. Effect of stratification on swimming velocity at high values of diffusion for
$Re=5$
.
