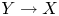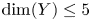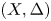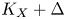1. Introduction
Smooth varieties with trivial canonical bundle constitute one of the fundamental building blocks in the birational classification of algebraic varieties. Hence, it is an important problem to understand their possible algebraic and topological structures. By a well-known result of Beauville and Bogomolov [Reference BeauvilleBea83], every smooth variety with trivial canonical bundle can be decomposed (after a finite étale cover) as a product of abelian, hyperkähler or Calabi–Yau varieties. A smooth projective variety 
$Y$ with trivial canonical bundle is Calabi–Yau if it is simply connected and 
$H^{i}(Y, \mathcal {O}_Y)=0$ for 
$0<i<\dim Y$.
While we have a clear understanding of the algebraic and topological structures of abelian varieties, the situation is far from being settled in the other two cases. In dimension two, Calabi–Yau surfaces are K3 surfaces and admit a unique topological model, though in order to show this one has to take into account non-projective models. In higher dimension the problem of determining the number of deformation types of Calabi–Yau manifolds is wide open; nonetheless, every Calabi–Yau manifold of dimension at least three is automatically projective.
The problem of understanding whether there are finitely many algebraic families of Calabi–Yau varieties for each fixed dimension 
$n\geq 3$ is the main motivation of this paper. A class of varieties that can be described by finitely many families is said to be bounded; see § 2.3. In particular, we study the boundedness of those Calabi–Yau varieties admitting an elliptic fibration, that is, a projective morphism with connected fibres, whose general fibre is one-dimensional of genus one. This class of varieties has already been understood in dimension 
$\leq 3$ and it is of particular interest for its applications in theoretical physics, as we explain below.
In dimension two, the question of boundedness has a negative answer, since there are infinitely many algebraic families of projective elliptic K3 surfaces. On the other hand, if we consider elliptic K3 surfaces admitting a section, it is not hard to show that boundedness holds for this class of varieties.
Surprisingly, the lack of boundedness for general Calabi–Yau elliptic fibrations appears to be a behaviour peculiar to surfaces only: M. Gross showed that there are indeed finitely many families, up to birational equivalence, of Calabi–Yau 
$3$-folds possessing a non-isotrivial elliptic fibration over a rational base; see [Reference GrossGro94]. In the three-dimensional case, when the base of the fibration is not rational, then it is an Enriques surface and the total space behaves like a product, the fibration being isotrivial. In his work, Gross showed that the problem of boundedness can be split into two steps: studying the boundedness of those surfaces that appear as bases of elliptic fibrations together with the study of elliptic curves defined over the function field of the possible bases. A similar behaviour is expected to hold in higher dimension.
The main result of this paper is a generalization of Gross’s theorem to elliptic varieties of dimension at most five with terminal singularities and numerically trivial canonical class, provided that the fibration admits a rational section.
Theorem 1.1 Let 
$2\leq n\leq 5$ be an integer. Then there are finitely many families, up to isomorphism in codimension one, of elliptic fibrations 
$Y\rightarrow X$ such that
(i)
$Y$ is terminal projective of dimension $n$ and $K_Y \equiv 0$,(ii)
$Y$ is not of product type, and(iii) there exists a rational section
$X\dashrightarrow Y$.
The condition that 
$Y$ be not of product type should be thought as an analogue of the non-isotriviality required in Gross’s theorem. For a precise definition we refer the reader to Definition 2.24. If 
$Y$ is of product type, then 
$Y$ is birationally isomorphic to the quotient of a product; cf. Theorem 2.22.
Once we require the existence of a section, our proof shows that even elliptic K3 surfaces are bounded. The proof of Theorem 1.1 heavily relies on the existence of a section to produce a suitably positive divisor, more precisely a big and nef divisor, on the total space with bounded volume; see §§ 4 and 5. The need for a section is the main reason why we are not able to recover the full statement proved by Gross in dimension three, although we expect Gross’s result to generalize to higher dimension. After the completion of this work, Birkar and the authors obtained an extension of Theorem 1.1 to any dimension (see [Reference Birkar, Di Cerbo and SvaldiBDS20]), while Filipazzi and the second named author [Reference Filipazzi and SvaldiFS20] extended the ideas contained in this paper to the case of 
$n$-dimensional varieties of Kodaira dimension 
$n-1$; cf. also [Reference FilipazziFil20c].
Theorem 1.1, combined with results from motivic integration, implies uniform boundedness of Hodge numbers for elliptic Calabi–Yau manifolds.
Corollary 1.2 Let 
$2 \leq n\leq 5$ be an integer. Then there exists a positive integer 
$M_n$ such that 
$h^{p,q}(Y)\leq M_n$ for any 
$p,q$, where 
$Y$ is a smooth manifold satisfying the conditions of Theorem 1.1.
Elliptic Calabi–Yau 
$4$-folds with a section seem to be the most relevant in F-theory and bounding their Hodge numbers is a central problem in string theory; see, for example, [Reference Taylor and WangTW15].
The key ingredient in the proof of Theorem 1.1 is a boundedness statement for the base of an elliptic fibration. If 
$Y$ has an elliptic fibration 
$Y \rightarrow X$ then, by a general version of Kodaira's canonical bundle formula, 
$X$ carries the structure of a Calabi–Yau pair, which means that there exists an effective divisor 
$\Delta$ such that 
$(X,\Delta )$ is Kawamata log terminal (klt) and 
$K_X +\Delta$ is numerically trivial; see § 2.5. In order to understand boundedness of elliptic Calabi–Yau varieties, we first need to understand if those Calabi–Yau pairs appearing as the base of such fibrations indeed belong to a bounded family. One crucial observation is that we have some control on the coefficients of 
$\Delta$, as was already clear to Kodaira; indeed, the coefficients vary in a finite set, which is the first fundamental hint and step towards boundedness; cf. Section 2.3.
Let us observe that the set of 
$3$-folds of the form 
$S\times \mathbb {P}^{1}$, where 
$S$ is a K3 surface, forms an unbounded family of Calabi–Yau pairs. On the other hand, a result of Kollár and Larsen in [Reference Kollár and LarsenKL09] implies that the base of an elliptic Calabi–Yau manifold 
$Y$ is rationally connected when 
$Y$ is not a product. A conjecture of McKernan and Prokhorov [Reference McKernan and ProkhorovMP04, Conjecture 3.9] predicts that the set of rationally connected varieties 
$X$ admitting a Calabi–Yau pair structure 
$(X, \Delta )$ is bounded in any fixed dimension if we restrict the type of singularities of the pair; see also [Reference Chen, Di Cerbo, Han, Jiang and SvaldiCDHJS21, Conjecture 1.3]. Our next result offers a first important piece of evidence for this conjecture in dimension up to four.
Theorem 1.3 Fix a positive integer 
$n\leq 4$ and a finite set 
$I \subset [0,1]$. Then the set 
$\mathfrak {D}$ of pairs 
$(X,\Delta )$ such that
(i)
$X$ is a projective variety of dimension $n$,(ii)
$(X,\Delta )$ is klt with coefficients of $\Delta$ in $I$ and $\Delta \neq 0$,(iii)
$K_X+\Delta$ is numerically trivial, and(iv)
$(X,\Delta )$ is not of product type
forms a log birationally bounded family. More precisely, there exists a bounded family of Calabi–Yau pairs 
$\mathfrak {D}'$ such that each pair in 
$\mathfrak {D}$ is isomorphic in codimension one to a pair in 
$\mathfrak {D}'$.
The condition that 
$(X,\Delta )$ is not of product type is analogous to that of Theorem 1.1 and is necessary in order to avoid the examples of unbounded Calabi–Yau pairs from the previous paragraph. We can show that this condition can be characterized by studying possible outcomes of runs of the minimal model program (MMP), as shown in Theorem 1.8. Roughly speaking, 
$(X,\Delta )$ is of product type if a run of the MMP ends with a special type of generically isotrivial fibration. Let us also point out that the condition that 
$(X,\Delta )$ is klt cannot be relaxed, as shown in Example 1.11.
An immediate corollary of what we have discussed so far is the birational boundedness of bases of elliptic Calabi–Yau manifolds in low dimension. We have already seen that this is a fundamental step in the proof of Theorem 1.1.
Corollary 1.4 Let 
$n\leq 5$ be an integer. Then there are finitely many families, up to birational equivalence, of bases 
$X$ of elliptic fibrations 
$Y \to X$ such that
(i)
$Y$ is terminal projective of dimension $n$ and $K_Y \equiv 0$, and(ii)
$Y$ is not of product type.
Combining the previous results, we get effective control of the torsion index for the canonical class 
$K_Y$ of 
$Y$.
Corollary 1.5 Fix a positive integer 
$n\leq 5$. Then there exists a positive integer 
$m_0=m_0(n)$ such that if
(i)
$Y$ is a terminal projective of dimension $n$ and $K_Y \equiv 0$,(ii) there exists an elliptic fibration
$Y\rightarrow X$, and(iii)
$Y$ is not of product type,
then 
$h^{0}(Y,\mathcal {O}_Y (m(K_Y)))\neq 0$ for any 
$m$ divisible by 
$m_0$.
Theorem 1.3 implies also uniform boundedness of the Picard number and effective non-vanishing of the log plurigenera of Calabi–Yau pairs.
Corollary 1.6 Fix a positive integer 
$n\leq 4$ and a finite set 
$I \subset [0,1]\cap \mathbb {Q}$. Then there are integers 
$\rho$ and 
$m_0$ depending on 
$n$ and 
$I$ such that for any 
$(X,\Delta )$ as in Theorem 1.3, we have 
$\rho (X)\leq \rho$ and 
$h^{0}(X,\mathcal {O}_X (m(K_X +\Delta )))\neq 0$ for any 
$m$ divisible by 
$m_0$.
All of the statements illustrated so far follow from the main technical result of this paper, Theorem 1.9. Roughly speaking, this result shows that a family of Calabi–Yau pairs is bounded provided that each pair is endowed with a Mori fibration whose base also varies in a bounded family. It is not hard to see, thanks to standard results in the MMP [Reference Birkar, Cascini, Hacon and McKernanBCHM10], that, given a Calabi–Yau pair, it is always possible to pass to a birational one that is endowed with a Mori fibration. Hence, in view of this result, the original boundedness problem for Calabi–Yau pairs is turned into a boundedness problem for the bases of Mori fibrations for which the total space admits a Calabi–Yau pair structure. The bases of such fibrations are, in turn, Calabi–Yau pairs, although we lack control on the coefficients of the possible boundaries.
Theorem 1.9 holds in any dimension and hence might constitute a possible inductive step in the generalization of this paper's main results to dimension greater than five. In fact, it is not unreasonable to expect that the approach we employed to prove Theorem 1.3 extends to higher dimension. Indeed, this holds true automatically if we assume a well-known conjecture in birational geometry: after Birkar's proof of the Borisov–Alexeev–Borisov (BAB) conjecture (cf. Theorem 2.12), assuming the effective base-point freeness conjecture [Reference Prokhorov and ShokurovPS09, Conjecture 7.13.3] would immediately imply Theorem 1.3 in any dimension. Theorem 1.9 has recently been refined by Birkar [Reference BirkarBir18] using slightly different techniques to generalize the strategy formulated in this paper and extend Theorem 1.3 to higher dimension.
We expect Theorem 1.9 to have a wide range of applications. For example, combining it with the main theorem in [Reference Hacon and XuHX15], we obtain the following result.
Corollary 1.7 Fix a positive integer 
$n$ and a finite set 
$I\subset [0,1]\cap \mathbb {Q}$. Let 
$\mathfrak {D}$ the set of pairs 
$(X, \Delta )$ satisfying the following conditions:
(i)
$(X, \Delta )$ is a projective klt pair of dimension $n$;(ii) the coefficients of
$\Delta$ belong to $I$;(iii)
$K_X+\Delta \equiv 0$;(iv) there exists a contraction morphism
$f\colon X\to Z$ with $\dim Z < \dim X$;(v)
$\Delta$ is big over $Z$; and(vi)
$f$ has maximal variation.
Then there exists a bounded family of Calabi–Yau pairs 
$\mathfrak {D}'$ such that each pair in 
$\mathfrak {D}$ is isomorphic in codimension one to a pair in 
$\mathfrak {D}'$.
The variation of 
$f$ is said to be maximal if there is a non-empty open set of 
$Z$ over which the isomorphism equivalence classes of pairs given by a fibre 
$F$ and the restriction of 
$\Delta$ to 
$F$ are finite. Intuitively, 
$f$ has maximal variation if the image of the rational map from the base of the fibration to the moduli space of the fibres 
$(F,\Delta |_F)$ has maximal dimension. In particular, the moduli part in the canonical bundle formula is a big divisor; see § 2.5 for more details, in particular Remark 2.20.
Let us conclude with a remark. In all statements of this Introduction, the assumption of the existence of a finite set in which the coefficients for the divisor 
$\Delta$ may vary can be weakened to the existence of a set of coefficients satisfying the descending chain condition; see § 2 for the definition. This is a now standard reduction in view of the fundamental results of [Reference Hacon, McKernan and XuHMX14]. In particular, all the results of this paper work in this more general setting and their proofs will accordingly reflect this.
1.1 Strategy of the proof
The proof of Theorem 1.3 consists of three main steps which we now proceed to summarize. The first two steps work in any dimension, and only to complete the final one do we need to impose the extra condition that the dimension of the Calabi–Yau pairs be at most four.
The first step of the proof is to show that, given a Calabi–Yau pair, we can find a suitable birational model that allows us to adopt an inductive strategy of proof. This is done by deriving the following structure theorem for Calabi–Yau pairs.
Theorem 1.8 Let 
$(X,\Delta )$ be a projective klt Calabi–Yau pair not of product type with 
$\Delta \neq 0$. Then there exists a birational contraction
\[ \pi \colon X \dashrightarrow X' \]
to a 
$\mathbb {Q}$-factorial projective klt Calabi–Yau pair 
$(X', \Delta ' := \pi _\ast \Delta )$ with 
$\Delta ' \neq 0$ and a tower of morphisms
such that each morphism 
$p_i\colon Y_i \to Y_{i+1}$ is a 
$K_{Y_i}$-Mori fibre space and 
$Y_k$ is Fano with klt singularities.
Once we are in this framework, we proceed to prove that the set of Calabi–Yau pairs endowed with a Mori fibre space structure where the base belongs to a bounded family is also bounded. This is in fact our second step.
Theorem 1.9 Fix a positive integer 
$n$, a descending chain condition (DCC) set 
$I\subset [0,1]$ and a bounded family 
$\mathfrak {F}$ of projective varieties. Then the set of pairs 
$(X, \Delta )$ satisfying
(i)
$(X, \Delta )$ is a projective klt pair of dimension $n$,(ii) the coefficients of
$\Delta$ belong to $I$,(iii)
$K_X+\Delta \equiv 0$,(iv) there exists a contraction
$f\colon X\to Z$ with $\dim Z < \dim X$,(v)
$-K_X$ is $f$-ample, and(vi)
$Z \in \mathfrak {F}$
forms a bounded family.
As 
$\Delta$ is relatively ample over 
$Z$, it is natural to consider ample divisors of the form 
$\delta \Delta + f^{\ast } H$, 
$0<\delta \ll 1$, where 
$H$ is a very ample Cartier divisor with bounded volume, coming from the boundedness of 
$Z$. In order to prove boundedness for the pairs 
$(X, \Delta )$ in the statement of Theorem 1.9, by results of Hacon, McKernan and Xu (see §§ 2.2 and 2.3), it suffices to show that we can choose a value of 
$\delta$ for which we can control the singularities of 
$(X, (1+\delta )\Delta + f^{\ast } H)$ as well as bound the volume of 
$\delta \Delta + f^{\ast } H$ uniformly on all the pairs. Control on the singularities follows from the fact that we are working with Calabi–Yau pairs and the coefficients of 
$\Delta$ vary in a DCC set; cf. Theorem 2.8 and Corollary 2.9. Instead, the volume estimate is achieved by reducing inductively to estimating the volume of the restriction of 
$\Delta$ to the general fibre 
$F$ of 
$f$ (cf. Proposition 4.7); as 
$F$ is Fano and 
$(F, \Delta |_F)$ is klt Calabi–Yau with DCC coefficients, the boundedness of the volume of 
$\Delta |_F$ is just Theorem 2.7.
It is well understood that Theorem 1.9 fails without the klt assumption. For example, Hirzebruch surfaces give an example of an unbounded family of log canonical (lc) Calabi–Yau pairs admitting Mori fibre space structures over 
$\mathbb {P}^{1}$. Hence, in these hypotheses, we cannot admit singularities worse than klt, as shown in Example 1.11. In the case of 
$3$-folds, a similar boundedness result has been obtained by Jiang [Reference JiangJia18] under slightly different assumptions.
The final step is to run induction on the number of factors appearing in Theorem 1.8. The base case can be done in any dimension using the BAB conjecture proved for surfaces by Alexeev [Reference AlexeevAle94], and in general by Birkar [Reference BirkarBir21].
Corollary 1.10 Fix a DCC set 
$I\subset [0,1]$ and a positive integer 
$n$. Then the set 
$\mathfrak D$ of pairs 
$(X, \Delta )$ satisfying
(i)
$(X, \Delta )$ is a projective klt pair of dimension $n$,(ii) the coefficients of
$\Delta$ belong to $I$,(iii)
$K_X+\Delta \equiv 0$,(iv) there exists a contraction
$f\colon X\to Z$ with $\dim Z < \dim X$,(v)
$-K_X$ is $f$-ample, and(vi)
$Z$ is normal and $-K_Z$ is big,
forms a bounded family.
Unfortunately, the final inductive step in the proof of Theorem 1.3 can be carried out only in low dimension. The main issue here arises when the tower of Mori fibre spaces constructed in Theorem 1.8 contains more than one step and the relative dimension of the morphism is 
$>1$. In this case we are not able to conclude that the intermediate varieties appearing in the tower carry a structure of Calabi–Yau pair with DCC coefficients (a condition which would allow us to run our argument inductively). As the effective base-point freeness conjecture has been verified for morphisms of relative dimension one by Prokhorov and Shokurov [Reference Prokhorov and ShokurovPS09], this does not constitute an issue in dimension up to four.
Let us conclude this section by showing by means of a simple example that Theorem 1.3 cannot be generalized to lc pairs.
Example 1.11 Let 
$X=\mathbb {F}_e$ be the 
$e$th Hirzebruch surface and let 
$\Delta =\sum _{i\geq 0} \delta _i \Delta _i$ be an effective divisor such that 
$K_X+\Delta \equiv 0$. We can assume that 
$\Delta _0= C_0$, where 
$C_0$ is the section with 
$C_0^{2} = -e$. By [Reference HartshorneHar77, Proposition V.2.20], for 
$i\geq 1$, we have that 
$\Delta _i \equiv a_i C_0 + b_i f$ with 
$a_i \geq 0$ and 
$b_i \geq a_i e$, where 
$f$ is the generic fibre. The Calabi–Yau condition implies that
\[ \begin{cases} \displaystyle\delta_{0}+\sum_{i\geq 1}\delta_{i}a_{i}=2, \\ \displaystyle\sum_{i\geq 1}\delta_{i}b_{i}=e+2. \end{cases} \]Then
\[ e+2=\sum_{i\geq 1}\delta_{i}b_{i}\geq \sum_{i\geq 1}\delta_{i}a_{i}e=e(2-\delta_{0}). \]
In particular, 
$(1-\delta _0)e\leq 2$. If we allow 
$\delta _0$ to be 
$1$, the family of Hirzebruch surfaces is an unbounded family of Calabi–Yau pairs with lc singularities. On the other hand, if we impose that 
$\delta _0$ is uniformly bounded away from 
$1$, the family is bounded. We remark that we are only requiring that 
$(X,\Delta )$ is klt along the generic fibre and as, we will see later, this is a very important property for our strategy; cf. § 4.
The paper is organized as follows. In § 2 we introduce the basic definitions and preliminary results that will be used in the rest of the paper. In § 3 we prove Theorem 1.8. In § 4 we study Mori fibrations with bounded bases and prove those results that are needed for the proof Theorem 1.9. Finally, the proofs of the results of the paper appear in §§ 5 and 6.
2. Preliminaries
Let 
$I \subset \mathbb {R}$ be a subset of the real numbers. We say that 
$I$ satisfies the descending (ascending) chain condition if any non-increasing (non-decreasing) subsequence of numbers in 
$I$ is eventually constant.
2.1 Minimal model program
We follow the notation and definitions used in [Reference Kollár and MoriKM98]. Moreover, we will make use of the minimal model program (MMP) mostly for varieties with non-pseudo-effective canonical class. In this case, the existence and termination of the MMP have been established by Birkar, Cascini, Hacon and McKernan.
Theorem 2.1 [Reference Birkar, Cascini, Hacon and McKernanBCHM10, Corollary 1.3.3]
Let 
$(X,\Delta )$ be a 
$\mathbb {Q}$-factorial klt pair. Assume 
$K_{X}+\Delta$ is not pseudo-effective. Then we may run a 
$(K_{X}+\Delta )$-MMP 
$g \colon X \dashrightarrow X'$ that terminates with a Mori fibre space 
$f\colon X' \rightarrow Z$.
Let us recall the definition of a Mori fibre space.
Definition 2.2 Let 
$(X,\Delta )$ be a klt pair and 
$f \colon X\rightarrow Z$ be a projective morphism of normal varieties with 
$\dim Z <\dim (X)$ and 
$f_\ast \mathcal {O}_X=\mathcal {O}_Z$. Then 
$f$ is a 
$(K_X+\Delta )$-Mori fibre space if
(i)
$X$ is $\mathbb {Q}$-factorial,(ii)
$f$ is a primitive contraction (i.e. the relative Picard number $\rho (X/Z)=1$) and(iii)
$-(K_{X}+\Delta )$ is $f$-ample.
The conditions that 
$\rho (X/Z)=1$ and 
$X$ is 
$\mathbb {Q}$-factorial readily imply that 
$Z$ is also 
$\mathbb {Q}$-factorial; see [Reference Kollár and MoriKM98, Proposition 3.36].
2.2 Boundedness of pairs
We recall important definitions and results related to the notion of boundedness for log pairs; cf. [Reference Hacon, McKernan and XuHMX14, Definition 3.5.1].
Definition 2.3 A set 
$\mathfrak {D}$ of projective log pairs is bounded if there exist a pair 
$(Z,B)$ and a projective morphism 
$f\colon Z \rightarrow T$ with 
$T$ of finite type such that any 
$(X,\Delta ) \in \mathfrak {D}$ is isomorphic to the fibre 
$(Z_t, B_t)$ of 
$f$ for some closed point 
$t\in T$.
A set 
$\mathfrak {D}$ of log pairs is log birationally bounded if there exists a pair 
$(Z,B)$, where the coefficients of 
$B$ are all 
$1$, and a projective morphism 
$f \colon Z \rightarrow T$ with 
$T$ of finite type, such that for any 
$(X,\Delta ) \in \mathfrak {D}$, there exist a closed point 
$t\in T$ and a birational map 
$g\colon Z_t \dashrightarrow X$ such that the support of 
$B_t$ contains the support of the strict transform of 
$\Delta$ and any 
$g$-exceptional divisor.
To show that a given set of log pairs is log birationally bounded, we will mainly use the following theorem which is a combination of results in [Reference Hacon, McKernan and XuHMX13, Reference Hacon, McKernan and XuHMX14].
Theorem 2.4 [Reference Hacon, McKernan and XuHMX13, Theorem 3.1], [Reference Hacon, McKernan and XuHMX14, Theorem 1.3]
Fix two positive integers 
$n$ and 
$V$ and a DCC set 
$I\subset [0,1]$. Then the set of pairs 
$(X,\Delta )$ satisfying
(i)
$X$ is a projective variety of dimension $n$,(ii)
$(X, \Delta )$ is lc,(iii) the coefficients of
$\Delta$ belong to $I$, and(iv)
$0<\operatorname {\mathrm {Vol}}(K_X+\Delta )\leq V$,
is log birationally bounded.
The reader can find the definition of the volume 
$\operatorname {\mathrm {Vol}}(D)$ of a divisor 
$D$ in [Reference LazarsfeldLaz04, Definition 2.2.31].
In certain special cases it is possible to deduce boundedness from log birational boundedness.
Theorem 2.5 [Reference Hacon, McKernan and XuHMX14, Thorem 1.6]
Fix a positive integer 
$n$ and two positive real numbers 
$\delta$ and 
$\epsilon$. Let 
$\mathfrak {D}$ be a set of log pairs 
$(X,\Delta )$ such that:
(i)
$X$ is a projective variety of dimension $n$;(ii)
$K_{X}+\Delta$ is ample;(iii) the coefficients of
$\Delta$ are at least $\delta$; and(iv) the log discrepancy of
$(X,\Delta )$ is greater than $\epsilon$.
If 
$\mathfrak {D}$ is log birationally bounded then 
$\mathfrak {D}$ is a bounded set of log pairs.
2.3 Boundedness of Calabi–Yau pairs
In this subsection we recall some of the results on boundedness of log pairs that we will need in the rest of this paper.
A first key result in [Reference Hacon, McKernan and XuHMX14] is the following lemma which will play a fundamental role in § 4.
Lemma 2.6 [Reference Hacon, McKernan and XuHMX14, Lemma 6.1]
Fix a positive integer 
$n$ and a set 
$I \subset [0,1]$ satisfying the DCC. Then there exists a constant 
$\epsilon =\epsilon (n, I)>0$ satisfying the following property. Let 
$(X,\Delta )$ be a pair such that
(i)
$X$ is a projective variety of dimension $n$,(ii)
$(X, \Delta )$ is klt,(iii) the coefficients of
$\Delta$ belong to $I$,(iv)
$\Delta$ is a big divisor, and(v)
$K_X+\Delta$ is numerically trivial.
If 
$\Phi$ is a divisor with 
$K_{X}+\Phi \equiv 0$ and 
$\Phi \geq (1-\delta )\Delta$ for some 
$\delta <\epsilon$, then 
$(X,\Phi )$ is klt.
A generalization of this result appeared in [Reference Chen, Di Cerbo, Han, Jiang and SvaldiCDHJS21, Lemma 4.3].
Lemma 2.6 easily implies that the boundary divisor of any klt Calabi–Yau pair has bounded volume, once its coefficients belong to a DCC subset of 
$[0,1]$.
Theorem 2.7 [Reference Hacon, McKernan and XuHMX14, Theorem B]
Fix a positive integer 
$n$ and a set 
$I \subset [0,1]$ satisfying the DCC. Then there exists a positive integer 
$M=M(n, I)$ such that if 
$(X,\Delta )$ is a pair with
(i)
$X$ is a projective variety of dimension $n$,(ii)
$(X, \Delta )$ is klt,(iii) the coefficients of
$\Delta$ belong to $I$, and(iv)
$K_X+\Delta$ is numerically trivial,
then 
$\operatorname {\mathrm {Vol}}(X,\Delta )\leq M$.
As a consequence of these results, we can even bound the singularities of Calabi–Yau pairs, by showing that the coefficients of Calabi–Yau pairs actually belong to a finite set.
Theorem 2.8 [Reference Hacon, McKernan and XuHMX14, Theorem 1.5]
Fix a positive integer 
$n$ and a set 
$I \subset [0,1]$ satisfying the DCC. Then there is a finite subset 
$I_0 \subseteq I$ with the following properties. If 
$(X, \Delta )$ is a log pair such that
(i)
$X$ is a projective variety of dimension $n$,(ii)
$(X, \Delta )$ is lc,(iii) the coefficients of
$\Delta$ belong to $I$, and(iv)
$K_X+\Delta$ is numerically trivial,
then the coefficients of 
$\Delta$ belong to 
$I_0$.
We will need the following well known generalization of the above theorem; see, for example, [Reference BirkarBir19, Lemma 2.48].
Corollary 2.9 Fix a positive integer 
$n$ and a set 
$I \subset [0,1]$ satisfying the DCC. Then there exists a positive real number 
$\epsilon =\epsilon (n, I)$ such that any 
$n$-dimensional projective klt Calabi–Yau pair 
$(X,\Delta )$ is 
$\epsilon$-lc.
Imposing more conditions on the set of pairs, it is possible to deduce stronger boundedness statements. For example, in [Reference Hacon, McKernan and XuHMX14], the following result is proved.
Theorem 2.10 [Reference Hacon, McKernan and XuHMX14, Theorem 1.7]
Fix a positive integer 
$n$, a real number 
$\epsilon >0$ and a set 
$I \subset [0,1]$ satisfying the DCC. Let 
$\mathfrak {D}$ be the set of all pairs 
$(X, \Delta )$ such that
(i)
$X$ is a projective variety of dimension $n$,(ii) the coefficients of
$\Delta$ belong to $I$,(iii) the total log discrepancy of
$(X, \Delta )$ is greater than $\epsilon$,(iv)
$K_X+\Delta$ is numerically trivial, and(v)
$-K_X$ is ample.
Then 
$\mathfrak {D}$ forms a bounded family.
In a similar fashion, Hacon and Xu proved the following result.
Theorem 2.11 [Reference Hacon and XuHX15, Theorem 1.3]
Fix a positive integer 
$n$ and a DCC set 
$I \subset [0,1]\cap \mathbb {Q}$. Let 
$\mathfrak {D}$ be the set of all pairs 
$(X, \Delta )$ such that
(i)
$X$ is a projective variety of dimension $n$,(ii)
$(X,\Delta )$ is klt with coefficients of $\Delta$ in $I$,(iii)
$K_X+\Delta$ is numerically trivial, and(iv)
$\Delta$ is big.
Then 
$\mathfrak {D}$ forms a bounded family.
The above theorems can be thought as a first step towards results predicted by the famous BAB conjecture, which has recently been solved by Birkar.
Theorem 2.12 [Reference BirkarBir21, Corollary 1.2]
Fix a positive integer 
$n$ and a positive real number 
$\epsilon$. Then the set of 
$n$-dimensional projective varieties 
$X$ such that
(i) there exists an effective divisor
$\Delta$ such that the pair $(X, \Delta )$ is an $\epsilon$-lc Calabi–Yau pair, and(ii)
$\Delta$ is big
forms a bounded family.
In dimension two, Alexeev proved a more general statement, which we will use in § 5.
Theorem 2.13 [Reference AlexeevAle94, Theorem 6.8]
Let 
$\epsilon$ be a positive real number. Let 
$\mathfrak D$ be the set of projective surfaces 
$X$ such that there exists an 
$\mathbb {R}$-divisor 
$\Delta$ on 
$X$ with 
$(X,\Delta )$ 
$\epsilon$-klt and 
$-(K_X + \Delta )$ is nef, where we exclude those surfaces 
$X$ for which at the same time 
$K_X$ is numerically trivial and 
$X$ has at worst Du Val singularities. Then 
$\mathfrak D$ is bounded.
2.4 Generalized pairs
For the definition of b-divisor and related notions, we refer the reader to [Reference Birkar and ZhangBZ16]. There, the authors also introduced the notion of generalized pairs. Let us recall that a b-
$\mathbb {R}$-divisor 
$\mathbf {N}$ is said to descend to the divisor 
$N'$ on a model 
$X'$ if 
$\mathbf {N}$ equals the Cartier closure of its trace 
$\mathbf {N}_{X'}$ on 
$X'$ and 
$\mathbf {N}_{X'}=N'$.
Definition 2.14 Let 
$T$ be a variety. A generalized polarized pair over 
$T$ is a tuple 
$(X' \to X, B, M')$ consisting of the following data:
(i) a normal variety
$X \to T$ projective over $T$ equipped with a projective birational morphism $\phi \colon X' \rightarrow X$;(ii) an effective
$\mathbb {R}$-Weil divisor $B$ on $X$;(iii) a b-
$\mathbb {R}$-Cartier b-divisor $\mathbf {M}$ over $X$ which descends on $X'$ such that $M':=\mathbf {M}_{X'}$ is nef over $T$; and(iv)
$K_X +B+ M$ is $\mathbb {R}$-Cartier, where $M := \phi _\ast M'$.
When no confusion arises, we refer to the pair by saying that 
$(X, B+M)$ is a generalized pair with data 
$X' \rightarrow X \rightarrow T$ and 
$M'$. We call 
$M'$ the nef part of the generalized pair.
Similarly to log pairs, we can define discrepancies and singularities for generalized pairs; cf. [Reference Birkar and ZhangBZ16, Definition 4.1].
2.5 Log canonical trivial fibrations
Since in this paper we deal mostly with Mori fibrations of Calabi–Yau pairs, in this subsection we collect some specific results about lc-trivial fibrations which can be applied to our setting.
An lc-trivial fibration is a contraction 
$f \colon X\rightarrow Z$ of normal varieties, with 
$\dim Z >0$, for which there is an effective divisor 
$\Delta$ on 
$X$ such that the pair 
$(X,\Delta )$ is klt over the generic point of 
$Z$ and 
$K_{X}+\Delta \sim _{f,\mathbb {R}} 0$. We will denote this by saying that 
$f \colon (X, \Delta ) \to Z$ is an lc-trivial fibration. For more details, we refer to [Reference AmbroAmb04, Reference AmbroAmb05], and to [Reference Fujino and GongyoFG12, Theorem 3.1] for the case of real coefficients. The main result which we will need is the following theorem, also known as the canonical bundle formula.
Theorem 2.15 Let 
$f \colon (X, \Delta )\rightarrow Z$ be an lc-trivial fibration. Then there exist an effective divisor 
$B_{Z}$ on 
$Z$ and a b-divisor 
$\mathbf {M}$ descending to a nef divisor 
$M':=\mathbf {M}_{Z'}$ on a higher model 
$Z' \to Z$ such that the tuple 
$(Z' \to Z, B_Z, \mathbf {M})$ is a generalized pair. Moreover, if 
$(X,\Delta )$ is klt then there exists an effective divisor 
$0 \leq \bar {M} \sim _\mathbb {R} M_Z$ such that 
$(Z,B_{Z} +\bar {M})$ is klt.
In the rest of the paper we will refer to 
$B_Z$ (respectively, 
$M_Z$) as the boundary part (respectively, the moduli part) of the fibration 
$f$. It is actually possible to define divisors 
$B_{Z'}, M_{Z'}$ on every birational model 
$Z' \to Z$ over 
$Z$ that are analogues of 
$B_Z, M_Z$ and that capture the behaviour of the pullback of the fibration 
$f$ to 
$Z'$. Moreover, the collection of all 
$B_{Z'}$ (respectively, 
$M_{Z'}$) fit together to form a so-called b-divisor; see [Reference AmbroAmb04, § 2] for more details.
We quickly recall the definition of 
$B_Z$: we set
\begin{equation} B_Z := \sum (1-l_D) D, \end{equation}
where the sum is taken over every prime divisor 
$D$ on 
$Z$, and 
$l_D$ is the lc threshold of 
$f^{*}D$ with respect to 
$(X,\Delta )$ over the generic point of 
$D$.
The following lemma shows that in many cases we can control the coefficients of the boundary part.
Lemma 2.16 Let 
$I$ be a DCC set. Let 
$(X, \Delta )$ be a pair such that the coefficients of 
$\Delta$ are contained in 
$I$. Let 
$f \colon (X, \Delta ) \to Z$ be an lc-trivial fibration with 
$K_X+ \Delta \sim _{f, \mathbb {R}}0$. Then there exists a DCC set 
$J$ such that the coefficients of the boundary part 
$B_Z$ are contained in 
$J$.
Proof. Given a prime divisor 
$D$ on 
$Z$, the coefficient 
$\mu _D B_Z$ of 
$D$ in 
$B_Z$ satisfies 
$\mu _D B_Z = 1 -l_D$, where 
$l_D$ is the lc threshold of 
$f^{\ast } D$ with respect to 
$(X,\Delta )$ over the generic point of 
$D$; see (1). As 
$l_D$ is computed over the generic point of 
$D$, we can assume that the coefficients of 
$f^{\ast } D$ belong to 
$\mathbb {N}_{>0}$. Since also the coefficients of 
$\Delta$ belong to a DCC set, [Reference Hacon, McKernan and XuHMX14, Theorem 1.1] implies that there exists an ascending chain condition set 
$J'=J'(\dim X, I, \mathbb {N}_{>0})$ such that 
$l_D$ belongs to 
$J'$. Defining 
$J:=\{1-t \ \vert \ t \in J'\}$, then 
$J$ is a DCC set and 
$\mu _D B_Z$ belongs to 
$J$.
It is important for induction purposes to be able to control the singularities of the base of an lc-trivial fibration. By a theorem of Birkar, it is possible to do so under some conditions on the singularities of the generic fibre.
Theorem 2.17 [Reference BirkarBir16, Theorem 1.4]
Let 
$n$ be a positive integer, 
$\epsilon >0$ be a real number and let 
$\mathfrak {D}$ be a bounded set of pairs. Then there is a real number 
$\delta =\delta (n,\epsilon,\mathfrak {D})>0$ satisfying the following assertion. Let 
$(X,\Delta )$ be a projective log pair and 
$f\colon X \rightarrow Z$ be a contraction such that:
(i)
$(X,\Delta )$ is $\epsilon$-lc of dimension $n$;(ii)
$K_X+\Delta \sim _{f, \mathbb {R}} 0$;(iii) the general fibre
$F$ of $f$ is of Fano type; and(iv)
$(F,\Delta \vert _F)\in \mathfrak {D}$.
Then we can choose an 
$\mathbb {R}$-divisor 
$M_{Z}\geq 0$ representing the moduli part so that 
$(Z, B_Z+M_Z)$ is 
$\delta$-lc.
Remark 2.18 Birkar's solution of the BAB conjecture [Reference BirkarBir19, Reference BirkarBir21] implies that for a fixed positive integer 
$n$, and fixed positive real numbers 
$\epsilon$, 
$\eta$, the set 
$\mathfrak {D}_{n, \epsilon, \eta }$ of pairs 
$(Z, \Gamma )$ such that
(i)
$(Z,\Gamma )$ is $\epsilon$-lc of dimension $n$,(ii)
$K_Z+\Gamma \sim _{\mathbb {R}} 0$, and(iii)
$Z$ is projective of Fano type and the coefficients of $\Gamma$ are $\geq \eta$
is bounded. Hence, Theorem 2.17 holds for 
$\mathfrak {D}=\mathfrak {D}_{n, \epsilon, \eta }$. The positive real number 
$\delta$ whose existence is claimed in the theorem will then depend on 
$n, \epsilon, \eta$.
It is conjectured in [Reference Prokhorov and ShokurovPS09] that, after passing to a birational model 
$Z' \to Z$ of the base, a fixed power of the moduli part 
$M_{Z'}$, only depending on the coefficients of 
$\Delta$, is base-point-free. In the same paper, the authors prove the conjecture in the special case where the relative dimension of the lc-trivial fibration is one.
Theorem 2.19 [Reference Prokhorov and ShokurovPS09, Theorem 8.1]
Fix two positive integers 
$n$ and 
$r$ and a DCC set of rational coefficients 
$I \subset \mathbb {Q} \cap (0,1)$. Let 
$(X, \Delta )$ be a projective klt pair with coefficients in 
$I$ and assume that there exists an lc-trivial fibration 
$f\colon X \rightarrow Z$ with 
$n=\dim X =\dim Z +1$ and 
$r(K_X+\Delta )|_F \sim 0$, where 
$F$ is the generic fibre of 
$f$. Then there exist a positive integer 
$m=m(n,r, I)$ and a birational morphism 
$Z' \rightarrow Z$ with 
$|mM_{Z'}|$ base-point-free.
Both the boundary and moduli part reflect the geometry of the fibration and can be used to deduce important information about the total space and the variation of the fibres. In general, we can use the moduli part to measure the variation of the fibres. More precisely, let 
$f\colon (X,\Delta )\rightarrow Z$ be an lc-trivial fibration. By [Reference AmbroAmb05, Theorem 3.3], there exists a diagram
where 
$\tau$ is generically finite and surjective, 
$\rho$ is surjective, and 
$f^{!}$ is an lc-trivial fibration such that there exists a non-empty open set 
$U\subseteq \bar {Z}$ over which
where the top horizontal arrow is an isomorphism of pairs; furthermore, the moduli part 
$M_{Z^{!}}$ of 
$f^{!}$ is big and nef and 
$\tau ^{*} (M_Z)=\rho ^{*}(M_{Z^{!}})$. The variation of 
$f$ is defined to be the dimension of 
$Z^{!}$ in (
).
Remark 2.20 We say that the morphism 
$f$ has maximal variation if the map 
$\rho$ in (2) is quasi-finite, that is, if 
$Z$, 
$Z^{!}$ have the same dimension. By the above discussion, if 
$f$ has maximal variation then 
$M_{\bar Z}$ is big and the same holds for 
$M_Z$, since 
$\tau _\ast M_{\bar {Z}}$ is a multiple of 
$M_Z$, by construction.
Definition 2.21 Let 
$(X,\Delta )$ be a klt pair. Let 
$f\colon (X, \Delta )\rightarrow Z$ be an lc-trivial fibration.
(i) We say that
$f$ is generically isotrivial if there exists a non-empty open set $U \subset Z$ over which the pairs $(X_z, \Delta \vert _{X_z})$, $z \in U$, are all isomorphic and $Z^{!}$ is a point in (2).(ii) We say that
$f$ is strongly generically isotrivial if it is generically isotrivial and, moreover, we can take the map $\tau$ in the diagram in (2) to be étale in codimension one.
Being generically isotrivial immediately implies that the moduli part is numerically trivial, in view of the diagram in (3). On the other hand, the notion of strong generic isotriviality of an lc-trivial fibration is more rigid and can be characterized through the following result which is a simple extension of [Reference AmbroAmb05, Theorem 4.7].
Theorem 2.22 Let 
$f \colon (X,\Delta )\rightarrow Z$ be an lc-trivial fibration. Assume that 
$B_{Z}=0$ and 
$M_{Z}\sim_\mathbb{R}\,0$. We denote by 
$F$ a general fibre of 
$f$. Then the morphism 
$\tau \colon \bar {Z} \rightarrow Z$ in (2) can be taken to be a finite Galois covering satisfying the following properties:
(i)
$\tau$ is étale in codimension one; and(ii) there exist a non-empty open subset
$U\subset \bar {Z}$ and an isomorphism
over\[ (X,\Delta)\times_Z \bar{Z}\vert_U \rightarrow (F,\Delta\vert_F) \times \bar{Z}\vert_U \]$U$.
Proof. If 
$\Delta$ is a 
$\mathbb {Q}$-divisor and 
$M_Z \sim _\mathbb {Q} 0$, then the statement of the theorem is implied by [Reference AmbroAmb05, Theorem 4.7] and there is nothing prove.
We then assume that 
$\Delta$ is an 
$\mathbb {R}$-divisor. Following the proof of [Reference Fujino and GongyoFG12, Theorem 3.1], it is possible to find effective 
$\mathbb {Q}$-divisors 
$\Delta _1, \ldots, \Delta _k$ such that for any 
$i$, 
$(X, \Delta _i)$ is klt over the generic point of 
$Z$, and there exists 
$0<r_i<1$, 
$r_i \in \mathbb {R}$, such that
\begin{equation} K_X+\Delta = \sum_{i=1}^{k} r_i (K_X+\Delta_i) \quad \text{and} \quad \sum_{i=1}^{k} r_i=1. \end{equation}
Moreover, the divisors 
$\Delta _i$ can be chosen so that for any 
$i$, 
$f \colon (X, \Delta _i) \to Z$ is an lc trivial fibration.
Claim For all 
$i=1, 2, \ldots, k$, 
$K_X+\Delta _i \sim _\mathbb {Q} f^{\ast } K_Z$.
Proof. By Theorem 2.15, for all 
$i=1, 2, \ldots, k$, there exist an effective 
$\mathbb {Q}$-divisor 
$B_{Z, i}$ and a pseudo-effective 
$\mathbb {Q}$-divisor 
$M_{Z, i}$ such that
\begin{equation} K_X+\Delta \sim_\mathbb{Q} f^{{\ast}} (K_Z+B_{Z, i}+M_{Z, i}). \end{equation}
\[ f^{{\ast}} K_Z \sim_\mathbb{R} K_X+\Delta = \sum_{i=1}^{k} r_i (K_X+\Delta_i) \sim_\mathbb{Q} f^{{\ast}} \bigg(K_Z+\sum_{i=1}^{k} r_i B_{Z, i}+\sum_{i=1}^{k} r_iM_{Z, i}\bigg). \]
As 
$\sum _{i=1}^{k} r_i B_{Z, i}$ is effective and 
$\sum _{i=1}^{k} r_iM_{Z, i}$ is pseudo-effective, this implies that for all 
$i$, 
$M_{Z, i} \equiv 0 = B_{Z, i}$. Finally, [Reference FlorisFlo14, Theorem 1.3] implies that 
$M_{Z, i} \sim _\mathbb {Q} 0$, which concludes the proof of the claim.
Applying [Reference AmbroAmb05, Theorem 4.7] to 
$f \colon (X, \Delta _i) \to Z$, it follows that for any 
$i$ there exists a finite Galois covering 
$\tau _i \colon \bar {Z}_i \to Z$ satisfying the following properties:
(i)
$\tau _i$ is étale in codimension one; and(ii) there exist a non-empty open subset
$U_i\subset \bar {Z}_i$ and an isomorphism
over\[ (X,\Delta_i)\times_Z \bar{Z}_i \vert_{U_i} \rightarrow (F,\Delta_i\vert_F) \times \bar{Z}_i\vert_{U_i} \]$U_i$.
By passing to the simultaneous Galois closure of the composition of the Galois field extensions induced by the morphisms 
$\tau _i$, there exists a finite Galois covering 
$\tau \colon \bar {Z} \to Z$ such that:
(i)
$\tau$ is étale in codimension one;(ii) for any
$i$, $\tau$ factors through $\tau _i$; and(iii) there exist a non-empty open subset
$U\subset \bar {Z}$ and isomorphisms
over\[ (X,\Delta_i)\times_Z \bar{Z} \vert_{U} \rightarrow (F,\Delta_i\vert_F) \times \bar{Z}\vert_{U} \]$U$.
By the diagram in property (3) above and by (4), it then follows that over 
$U$ the morphism
\[ (X,\Delta)\times_Z \bar{Z} \vert_{U} \rightarrow (F,\Delta\vert_F) \times \bar{Z}\vert_{U} \]is an isomorphism, which concludes the proof.
Remark 2.23 (i) Theorem 2.22 implies that under the condition of the theorem 
$f\colon (X, \Delta )\rightarrow Z$ is a strongly birationally isotrivial lc-trivial fibration; cf. Definition 2.21. In fact, property (ii) in the statement of Theorem 2.22 implies that in the diagram (2) 
$Z^{!}$ can be taken to be a point, as it suffices to define 
$(X^{!}, \Delta ^{!}):=(F, \Delta \vert _F)$.
(ii) It follows from (1)–(3) that the converse of the statement of Theorem 2.22 holds as well: namely, given a pair 
$(X, \Delta )$ and an lc-trivial fibration 
$f \colon (X, \Delta ) \to Z$, for which conditions (i)–(ii) of Theorem 2.22 hold, 
$B_Z=0$ by the definition in (1), and 
$M_Z\sim _\mathbb {R} 0$ by (3) and condition (ii).
Theorem 2.22 motivates the following definition.
Definition 2.24 Let 
$X$ be a normal variety.
(i) Let
$(X,\Delta )$ be a klt pair. We say that $(X,\Delta )$ is of product type if there exists a birational contraction $\pi \colon X \dashrightarrow X'$ such that $(X', \pi _* \Delta )$ admits a strongly generically isotrivial lc-trivial fibration.(ii) We say that
$X$ is of product type if there exists an effective divisor $\Delta$ such that $(X, \Delta )$ is a klt pair which is of product type.
By Theorem 2.22, if 
$(X,\Delta )$ is of product type then 
$X$ is birational to a quotient of a product.
2.6 Birational transformations of fibred Calabi–Yau manifolds
In § 5 we will be interested in modifying the base 
$X$ of an elliptic fibration 
$f \colon Y \to X$ by means of a birational contraction 
$X \dashrightarrow X'$ and show that 
$X'$ is also the base of a terminal elliptic variety with numerically trivial canonical class. To this end, we prove the following result.
Proposition 2.25 Let 
$Y$ be a projective terminal variety with 
$K_Y \equiv 0$. Let 
$f \colon Y \to X$ be a contraction of terminal varieties. Let 
$s \colon X' \to X$ be a small morphism. Then there exist a 
$\mathbb {Q}$-factorial terminal Calabi–Yau variety 
$Y'$ and a surjective morphism 
$f' \colon Y' \to X'$. In particular, 
$Y'$ is isomorphic to 
$Y$ in codimension one.
Proof. We denote by 
$T$ (respectively, 
$T'$) the exceptional locus of 
$s^{-1}$ (respectively, 
$s$) on 
$X$ (respectively, 
$X'$), so that 
$X \setminus T$ is isomorphic to 
$X' \setminus T'$.
Claim There exist a terminal 
$\mathbb {Q}$-factorial variety 
$\bar Y$, a birational contraction 
$p \colon \bar {Y} \to Y$, and a contraction 
$\bar {f} \colon \bar {Y} \to X'$ for which the following diagram commutes.
Moreover, 
$\bar {f}(\bar E) \subset T'$, where 
$\bar E$ is the divisorial part of the exceptional locus of 
$p$.
Proof of the claim Let 
$\Gamma \subset Y \times X'$ be normalization of the main component of the Zariski closure of the graph of the morphism 
$s^{-1} \circ f \colon Y \dashrightarrow X'$. We denote by
the restrictions of the projections to the two factors of 
$Y \times X'$. By construction, 
$p_1$ is birational and it is an isomorphism over the Zariski open set 
$X\setminus T \subset X$.
Let 
$\tilde Y$ be a resolution of 
$\Gamma$. Then we can run the 
$K_{\tilde Y}$-MMP relatively over 
$\Gamma$ with scaling of an ample divisor which terminates with a relatively minimal model 
$\pi \colon \bar {Y} \to \Gamma$, where 
$\bar {Y}$ is a terminal 
$\mathbb {Q}$-factorial projective variety. We denote 
$p:=p_1 \circ \pi$, 
$\bar f := p_2 \circ \pi$. As 
$Y$ is terminal and 
$p_1$ is an isomorphism over 
$X \setminus T$, then defining 
$U := f^{-1}(X \setminus T)$, it follows that 
$p\vert _{p^{-1}(U)} \colon p^{-1}(U) \to U$ is a small 
$\mathbb {Q}$-factorial model, by minimality of 
$\bar {Y}$ over 
$\Gamma$. Hence, the centre on 
$Y$ of all 
$p$-exceptional divisors is contained in 
$Y \setminus U=f^{-1}(T)$, which then implies the second part of the statement.
Since 
$Y$ is terminal, it follows that
\begin{equation} K_{\bar{Y}}= p^{{\ast}} K_Y + E \sim_\mathbb{Q} E, \end{equation}
where 
$E$ is an effective divisor whose support coincides with 
$\bar E$. By the claim, 
$E$ is 
$f'$-exceptional in the sense of [Reference LaiLai11, Definition 2.9], since 
$\bar {f}(E)$ has codimension 
$\geq 2$ in 
$X'$, as 
$\bar {f}(E) \subset T'$. By construction, the general fibre 
$F'$ of 
$f'$ has a good minimal model, by (7) and since 
$K_F \sim _\mathbb {Q}0$ on a general fibre 
$F$ of 
$f$; and 
$F$ is terminal by adjunction. Hence, by [Reference Hacon and XuHX13, Theorem 1.1], it follows that there is a good minimal model for 
$K_{\bar {Y}}$ over 
$X'$. Then [Reference Hacon and XuHX13, Corollary 2.9] implies that any run of the relative 
$K_{\bar {Y}}$-MMP with scaling of an ample divisor terminates. Running one such MMP, we can assume that there exists a minimal model 
$Y' \to X'$. By [Reference LaiLai11, Lemma 2.10], as 
$E$ is 
$f'$-exceptional, it follows that the relative 
$K_{\bar {Y}}$-MMP over 
$X'$ contracts 
$E$ and hence it terminates with a variety 
$Y'$ such that 
$K_{Y'} \equiv 0$ and 
$Y'$ is terminal.
The final claim in the statement of the proposition follows from the fact that we have contracted all and only the divisors in the support of 
$E$ whose support coincided with the exceptional locus of 
$p$.
A similar result holds if we modify the base of an elliptic fibration by means of a birational contraction.
Proposition 2.26 Let 
$Y$ be a projective terminal variety with 
$K_Y \equiv 0$. Let 
$f \colon Y \to X$ be a contraction of normal varieties. Assume that 
$X$ is a 
$\mathbb {Q}$-factorial variety and let 
$t\colon X \dashrightarrow X'$ be a birational contraction to a normal projective variety 
$X'$. Then there exist a 
$\mathbb {Q}$-factorial terminal Calabi–Yau variety 
$Y'$ and a surjective morphism 
$f' \colon Y' \to X'$. In particular, 
$Y'$ is isomorphic to 
$Y$ in codimension one.
Proof. Let 
$H'$ be an ample Cartier divisor on 
$X'$, so that 
$X'=\textrm {Proj}\; R(X', H')$, where 
$R(X', H')$ is the ring of section of 
$H'$. Let 
$H$ be the pullback of 
$H'$ on 
$X$.Footnote 1 As 
$t$ is a birational contraction, we have that 
$R(X', H') = R(X, H)$. As 
$f$ has connected fibres, 
$R(X', H') = R(X, H)= R(Y, f^{\ast } H)$.
If we consider the pair 
$(Y, \epsilon f^{\ast } H)$, 
$0<\epsilon \ll 1$, then 
$K_Y+f^{\ast } H$ is abundant since 
$H$ is big on 
$X$ and 
$K_Y \sim _ \mathbb {Q} 0$. By [Reference Gongyo and LehmannGL13, Theorem 4.3], 
$(Y, \epsilon f^{\ast } H)$ has a good minimal model, and [Reference Hacon and XuHX13, Corollary 2.9] implies that any run of the 
$(K_Y+\epsilon f^{\ast } H)$-MMP with scaling of an ample divisor terminates. Hence, running one such MMP, we can assume that there exists a minimal model 
$Y\dashrightarrow Y''$ for 
$(Y, \epsilon f^{\ast } H)$. Denoting by 
$G''$ the strict transform of 
$f^{\ast } H$ on 
$Y''$, 
$G''$ is nef on 
$Y''$, and moreover, by [Reference Gongyo and LehmannGL13, Proposition 3.13, Corollary 3.14], it is also abundant. Hence, as 
$K_Y \sim _ \mathbb {Q} 0$, [Reference FujinoFuj11a, Theorem 1.1] implies that 
$G''$ is semiample on 
$Y''$. As by construction 
$R(Y'', G'')= R(Y, f^{\ast } H) = R(X', H')$, there exists a morphism 
$Y'' \to X'$. Passing to a terminalization 
$Y' \to Y''$ of 
$(Y'', 0)$ yields the desired model.
The final claim follows from [Reference Kollár and MoriKM98, Corollary 3.54], as 
$Y'$ is also terminal projective with 
$K_{Y'} \equiv 0$ since in going from 
$Y''$ to 
$Y'$ we only extracted divisors of discrepancy 
$0$ with respect to 
$K_{Y''}$.
We complete this section by proving a result that illustrates a criterion to determine when a projective terminal variety with trivial canonical class is of product type.
Lemma 2.27 Let 
$Y$ be a terminal projective variety with 
$K_Y \equiv 0$. Let 
$f \colon Y \to Z$ be a contraction of normal projective varieties.
(i) If
$0< \dim Z < \dim Y$ and $K_Z \equiv 0$, then $Y$ is of product type.(ii) If
$Z$ is of product type, then $Y$ is also of product type.
Proof. (i) As 
$K_Y\equiv 0$, the canonical bundle formula 
$K_Y \sim _\mathbb {Q} 0$. Hence, by the canonical bundle formula (Theorem 2.15), 
$B_Z=0$ and 
$M_Z\sim _\mathbb {Q} 0$. But this implies that 
$f$ is strongly generically isotrivial by Theorem 2.22 (see Remark 2.23), and 
$Y$ is of product type by Definition 2.24.
(ii) As 
$Z$ is of product type, there exists a boundary 
$\Delta$ such that 
$(Z, \Delta )$ is of product type. Hence, there exist a birational contraction 
$Z \dashrightarrow Z'$ and a contraction 
$Z' \to W'$ which is strongly generically isotrivial, by Definition 2.24. In particular, 
$K_{W'} \sim _\mathbb {Q} 0$.
By Proposition 2.25, we can assume that 
$Z$ is 
$\mathbb {Q}$-factorial. Hence, by Proposition 2.26 there exist a birational terminal projective variety 
$Y'$ with 
$K_{Y'}\equiv 0$, and a contraction 
$f \colon Y' \to W'$. But then part (i) implies that 
$Y'$ is product type and the same holds for 
$Y$ since it is isomorphic in codimension one to 
$Y'$.
3. A structure theorem for Calabi–Yau pairs
We would like to characterize Calabi–Yau pairs which behave like a product of lower-dimensional varieties. In this section we prove a structure theorem for Calabi–Yau pairs which is inspired by the following theorem of Kollár and Larsen.
Theorem 3.1 [Reference Kollár and LarsenKL09, Theorem 3]
Let 
$X$ be a smooth, simply connected projective Calabi–Yau variety and 
$f \colon X\dashrightarrow Y$ a dominant map such that 
$Y$ is not uniruled. Then one can write
where 
$\pi$ is a projection to a direct factor of 
$X\cong X_1 \times X_2$ and 
$g\colon X_1 \dashrightarrow Y$ is generically finite.
Any run of a 
$K_X$-MMP with scaling of an ample divisor on a Calabi–Yau pair 
$(X, \Delta )$, with 
$\Delta > 0$, terminates with a Mori fibre space structure. If the base of this fibration is a variety with trivial canonical class then the pair 
$(X, \Delta )$ is of product type by Definition 2.24. If that is not the case, we can repeat the same procedure on the base of the Mori fibre space.
By iterating this procedure, we can obtain the following description of Calabi–Yau pairs which is the main result of this section.
Theorem 3.2 Let 
$(X, \Delta )$ be a projective klt Calabi–Yau pair with 
$\Delta \neq 0$. Then there exists a birational contraction
\[ \pi \colon X \dashrightarrow X' \]
to a projective Calabi–Yau pair 
$(X', \Delta ' =\pi _\ast \Delta )$, 
$\Delta '\neq 0$, and a tower of morphisms
such that:
(i) for any
$i$, $Y_i$ is $\mathbb {Q}$-factorial;(ii) for any
$1 \leq i < k$, there exists a boundary $\Delta _i \neq 0$ on $Y_i$ such that $(Y_i, \Delta _i)$ is a projective klt Calabi–Yau pair;(iii) for any
$0 \leq i \leq k$ the morphism $p_i\colon Y_i \to Y_{i+1}$ is a $K_{Y_i}$-Mori fibre space (in particular, $\rho (Y_i/Y_{i+1})=1$); and(iv)
$Y_k$ is a projective klt Calabi–Yau variety, that is, $K_{Y_k} \equiv 0$ and $Y_k$ has klt singularities.
If 
$\dim Y_k >0$, then 
$(X, \Delta )$ is of product type.
Moreover, if 
$X$ is 
$\mathbb {Q}$-factorial, then the birational contraction 
$X \dashrightarrow X'$ is a composition of divisorial contractions and 
$(K_X+\Delta )$-flops.
Proof. We prove the statement of the theorem by induction on the dimension of 
$X$, which we denote by 
$n$.
When 
$n=1$, we have that 
$X=\mathbb {P}^{1}$ and it suffices to consider the constant morphism to a point. Let us now assume that 
$n>1$ and that the theorem holds for any pair of dimension 
$<n$ satisfying the hypotheses of the statement.
By [Reference KollárKol13, Corollary 1.37], we can replace 
$(X,\Delta )$ with a small 
$\mathbb {Q}$-factorial model without losing the klt Calabi–Yau condition; it suffices to prove the result for this new pair, as it is isomorphic in codimension one to 
$(X, \Delta )$. Abusing notation, we denote this new model by 
$(X, \Delta )$, so that we can assume that the pair 
$(X, \Delta )$ is 
$\mathbb {Q}$-factorial. Since 
$\Delta \neq 0$, 
$K_{X}$ is not pseudo-effective and, by Theorem 2.1, we can run a 
$K_X$-MMP with scaling of an ample divisor
which terminates with a 
$K_{\bar {X}}$-Mori fibre space 
$\bar {m} \colon \bar {X} \to Y$.
Let us note that since 
$X$ is 
$\mathbb {Q}$-factorial, the same holds for 
$\bar {X}$ and 
$Y$ as they are outcomes of a run of the MMP. Furthermore, 
$\bar {\Delta }=\pi _\ast \Delta \neq 0$ because we are running a 
$K_X$-MMP and 
$K_X +\Delta \sim _\mathbb {R} 0$. Hence, 
$K_{\bar {X}}+\bar {\Delta } \sim _\mathbb {R} 0$ and 
$(\bar {X}, \bar {\Delta })$ is klt, and Theorem 2.15 implies that there exists an effective divisor 
$\Gamma$ on 
$Y$ such that 
$(Y, \Gamma )$ is klt and 
$K_{Y} +\Gamma \sim _\mathbb {R} 0$.
If 
$\Gamma =0$ then 
$K_{Y} \equiv 0$ and we are done, by taking 
$Y_0=\bar {X}$, 
$Y_1=Y$. Otherwise, 
$\Gamma \neq 0$ and by inductive hypothesis there exists a diagram
such that 
$q_0$ is a birational contraction and the tower of morphisms
satisfies conditions (i)–(iv) in the statement of the theorem.
The statement of the theorem then follows if we show that there exist a 
$\mathbb {Q}$-factorial klt Calabi–Yau pair 
$(X', \Delta ')$ with 
$\Delta ' \neq 0$, a birational contraction 
$\pi ' \colon \bar {X} \dashrightarrow X'$ which is a composition of divisorial contractions and 
$(K_{\bar {X}}+\bar {\Delta })$-flops, and a 
$K_{X'}$-Mori fibre space 
$m' \colon X' \to Y_1$ such that the following diagram commutes.
By inductive hypothesis, as 
$Y$ is 
$\mathbb {Q}$-factorial, the birational contraction 
$q_0$ can be decomposed as a sequence of divisorial contractions and 
$(K_Y+\Gamma )$-flops
Thus, it suffices to prove the following claim. We will use the notation 
$(X^{(0)}, \Delta ^{(0)}):= (\bar {X}, \bar {\Delta })$.
Claim For any 
$0\leq t \leq j$, there exist a 
$\mathbb {Q}$-factorial klt Calabi–Yau pair 
$(X^{(t)}, \Delta ^{(t)})$, with 
$\Delta ^{(t)} \neq 0$, and a 
$K_{X^{(t)}}$-Mori fibre space 
$m'_t \colon X^{(t)} \to Y^{(t)}$ such that the following diagram commutes:
and also 
$\Delta ^{(t)}:=r_{t\ast } \Delta ^{(t-1)}$ and 
$r_t$ is a birational contraction that is a composition of divisorial contractions and 
$(K_{X^{(t-1)}}+\Delta ^{(t-1)})$-flops.
Proof of the claim We use induction on 
$t \in \{0, 1, \ldots, j\}$.
For 
$t=0$, there is nothing to prove. Thus, we can assume that the statement of the claim holds up to 
$t-1$ and we shall prove that it holds for 
$t$ as well. By inductive hypothesis, we can assume that the diagram
exists and satisfies the conditions in the statement of the claim.
Hence it suffices to show that the diagram
can be completed to give a diagram
where 
$r_t$ is a composition of divisorial contractions and 
$(K_{X^{(t-1)}}+\Delta ^{(t-1)})$-flops and 
$m'_t$ is a 
$K_{X^{(t)}}$-Mori fibre space. Since 
$s_t$ is either a divisorial contraction or a 
$(K_{Y^{(t-1)}} + \Gamma ^{(t-1)})$-flop by inductive hypothesis, where 
$\Gamma ^{(t-1)}$ is the strict transform of 
$\Gamma$ on 
$Y^{(t-1)}$, the existence of the diagram in (
If 
$\dim Y_k >0$ then Definition 2.24 immediately implies that 
$(X, \Delta )$ is of product type; in fact, as 
$K_{Y^{k}} \sim _\mathbb {Q} 0$, the lc-fibration 
$(X', \Delta ') \to Y^{k}$ that we have constructed is strongly birationally isotrivial by Theorem 2.22 (see Remark 2.23), and 
$\pi ' \circ \pi$ is a birational contraction.
If 
$X$ is 
$\mathbb {Q}$-factorial, then the birational contraction 
$\pi ' \circ \pi \colon X \dashrightarrow X'$ is a composition of divisorial contraction and 
$(K_X+\Delta )$-flops. The map 
$\pi \colon X \dashrightarrow \bar {X}$ in (9) is constructed by running a 
$K_X$-MMP, hence it is a composition of divisorial contractions and 
$K_X$-flips; as 
$K_X+\Delta \sim _\mathbb {R} 0$, those 
$K_X$-flips are also 
$(K_X+\Delta )$-flops. On the other hand, 
$\pi ' \colon \bar {X} \to Y_0$ in (10) is in turn a composition of divisorial contractions and 
$(K_{\bar {X}}+\bar {\Delta })$-flops, as shown in the proof of the claim. As 
$\pi$ is crepant with respect to 
$(X, \Delta )$, then those 
$(K_{\bar {X}}+\bar {\Delta })$-flops are also 
$(K_{X}+\Delta )$- flops.
In the previous proof we used the following two lemmas.
Lemma 3.3 Let 
$(X,\Delta )$ be a projective klt Calabi–Yau pair with 
$\Delta \neq 0$. Let 
$p \colon X\rightarrow Y$ be a 
$K_X$-Mori fibre space of 
$\mathbb {Q}$-factorial varieties. Let 
$q \colon Y \rightarrow Y'$ be a divisorial contraction. Then there exist a 
$\mathbb {Q}$-factorial projective klt Calabi–Yau pair 
$(X',\Delta ')$, with 
$\Delta ' \neq 0$, a 
$K_{X'}$-Mori fibre space 
$p' \colon X'\rightarrow Y'$, and a birational contraction 
$f\colon X\dashrightarrow X'$ which is a composition of a finite number of 
$(K_X+\Delta )$-flops followed by a divisorial contraction, such that the following diagram commutes.
Proof. Since 
$p$ is a 
$K_X$-Mori fibre space, we have that 
$\dim \operatorname {N^{1}}(X/Y')=2$. Let 
$F$ be the irreducible divisor contracted by 
$q$ on 
$Y$ and let 
$E=p^{\ast }(F)$. As, for 
$0<\epsilon \ll 1$, 
$(X, \Delta +\epsilon E)$ is klt, 
$K_X+\Delta + \epsilon E\sim _\mathbb {R} \epsilon E$, and 
$\Delta$ is relatively big, we can run the 
$E$-MMP with scaling relatively over 
$Y'$ and this must terminate. But then, as 
$E$ is effective and 
$q(p(E))$ has codimension 
$\geq 2$ in 
$Y'$, [Reference LaiLai11, Lemma 2.10] implies that this run of the relative 
$E$-MMP must terminate by contracting 
$E$ to a 
$\mathbb {Q}$-factorial model 
$X'$ of 
$X$, and 
$E$ is irreducible since 
$\rho (X'/Y')=1$. Hence, the birational contraction 
$f \colon X \to X'$ is a composition of 
$E$-flips, followed by a divisorial contraction. As 
$K_X+\Delta \sim _\mathbb {R} 0$, those 
$E$-flips are also 
$(K_X+\Delta )$-flops.
Finally, the claim that 
$\Delta ' \neq 0$ follows because 
$\Delta$ is relatively big over 
$Y'$, hence, 
$0\neq f_\ast \Delta =\Delta '$.
Lemma 3.4 Let 
$(X,\Delta )$ be a projective klt Calabi–Yau pair with 
$\Delta \neq 0$. Let 
$p \colon X\rightarrow Y$ be a 
$K_X$-Mori fibre space of 
$\mathbb {Q}$-factorial varieties with 
$K_X+\Delta \sim _{\mathbb {R}} p^{\ast }(K_Y+G)$, and 
$(Y, G)$ is a klt pair. Let 
$q \colon Y \dashrightarrow Y'$ be a 
$(K_Y+G)$-flop. Then there exist a projective klt Calabi–Yau pair 
$(X',\Delta ')$, with 
$\Delta '\neq 0$, a 
$K_{X'}$-Mori fibre space 
$p' : X'\rightarrow Y'$, and an isomorphism 
$f\colon X\dashrightarrow X'$ in codimension one such that the following diagram commutes.
Proof. Let 
$\pi \colon Y\rightarrow Z$, 
$\pi ' \colon Y'\rightarrow Z$ be the flopping contractions associated to 
$q$ and let 
$H$ be an effective relatively anti-ample Cartier divisor on 
$Y$ over 
$Z$. We denote 
$\bar {H}:=p^{\ast } H$. We want to produce a map 
$f$ which is an isomorphism in codimension one and that makes the following diagram commute.
As, for 
$0<\epsilon \ll 1$, 
$(X, \Delta +\epsilon \bar {H})$ is klt, 
$K_X+\Delta + \epsilon \bar {H}\sim _\mathbb {R} \epsilon \bar {H}$, and 
$\Delta$ is relatively big, we can run the 
$\bar {H}$-MMP with scaling of an ample divisor relatively over 
$Z$, and this must terminate with a 
$\mathbb {Q}$-factorial relatively minimal model
The strict transform 
$\bar {H}'$ of 
$\bar {H}$ on 
$X'$ is semiample since 
$\Delta '$ is big over 
$Z$, where 
$\Delta ':=f_\ast \Delta$. As
\[ Y'={\rm Proj}_{\mathcal{O}_{Z}}(\oplus_{n \geq 0} \pi_\ast \mathcal{O}_Y(nH))= {\rm Proj}_{\mathcal{O}_{Z}}(\oplus_{n \geq 0} (\pi \circ p)_\ast \mathcal{O}_X(n\bar{H})), \]
the relative Iitaka fibration of 
$\bar {H}'$ over 
$Z$ induces a morphism 
$p' \colon X' \to Y'$, since, for any 
$n \geq 0$,
\[ \pi_\ast \mathcal{O}_Y(nH) = (\pi \circ p)_\ast \mathcal{O}_X(n\bar{H})) = s'_\ast \mathcal{O}_{X'}(n\bar{H}'), \]
as 
$f$ is constructed as the run of an 
$\bar {H}$-MMP and 
$f_\ast \bar {H}=\bar {H}'$.
We have that 
$\rho (X'/Z) \leq 2$ since 
$f$ is a birational contraction and 
$q$ is an isomorphism in codimension one of 
$\mathbb {Q}$-factorial varieties. Since also 
$\rho (Y'/Z)=1\leq \rho (X'/Y')$, we have that 
$\rho (X'/Z)=2$; moreover, as 
$X'$ is 
$\mathbb {Q}$-factorial we have that 
$X$, 
$X'$ are again isomorphic in codimension one, as 
$f$ by construction is a birational contraction and 
$\rho (X'/Z)= \rho (X/Z)$.
Finally the claim that 
$\Delta ' \neq 0$ follows because 
$\Delta$ is relatively big over 
$Y'$, hence, 
$0<f_\ast \Delta =\Delta '$.
We conclude this section with a remark on the differences between the property of being rationally connected and the property of having product type.
Remark 3.5 If 
$(X,\Delta )$ is a projective klt Calabi–Yau pair not of product type then Theorem 3.2 proves that 
$X$ is rationally connected, as 
$X$ is decomposed into a tower of morphisms with rationally connected fibres. On the other hand, if 
$(X,\Delta )$ is of product type and 
$X$ is not rationally connected, then Theorem 3.2 provides the maximally rationally connected fibration. Let us point out that if 
$(X,\Delta )$ is of product type it is not always the case that 
$X$ is not rationally connected; there are examples of rationally connected varieties 
$Y$ with klt singularities and 
$K_Y\equiv 0$ (see [Reference Oguiso and TruongOT15]).
As we saw in the Introduction, log birational boundedness of Calabi–Yau pairs does not hold if we allow ourselves also to consider product-type pairs. Nonetheless, it is possible that the boundedness can still be proven if we consider 
$n$-dimensional product-type pairs 
$(X, \Delta )$ with 
$X$ rationally connected and the coefficients of 
$\Delta$ vary in a fixed DCC set; see [Reference Chen, Di Cerbo, Han, Jiang and SvaldiCDHJS21, Conjecture 1.3]. A proof of this fact appears in [Reference Birkar, Di Cerbo and SvaldiBDS20, Theorem 1.4].
4. Boundedness of Mori fibre spaces
In this section we prove the main technical result needed for Theorem 1.3. More precisely, we show that if we fix a bounded set of varieties 
$\mathfrak {D}$, then the set of klt Calabi–Yau pairs endowed with a Mori fibre space structure mapping to one of the varieties in 
$\mathfrak {D}$ is bounded as well. The strategy is to lift a very ample divisor with bounded volume from the base to the total space, suitably perturb it by means of the boundary of the klt Calabi–Yau pair and then use the results from § 2.2 to show that boundedness must hold for the Calabi–Yau pairs.
4.1 Boundedness of volume for Mori fibre spaces of generalized pairs
The main aim of this subsection is to prove Theorem 4.3 which represents a first step towards proving the boundedness of Calabi–Yau pairs endowed with a Mori fibre space whose base belongs to a bounded family. Here, we will work in the more comprehensive setting of generalized pairs. For the definition and basic properties of generalized pairs, the interested reader can check [Reference Birkar and ZhangBZ16, § 4].
We start by first recalling the following theorem of Birkar which is one of the fundamental tools in his proof of Theorem 2.12.
Theorem 4.1 [Reference BirkarBir21, Theorem 1.6]
Let 
$n,r$ be positive integers and 
$\epsilon$ a positive real number. Then there exists a positive real number 
$t= t(n,r,\epsilon )$ satisfying the following assertion. Assume that:
•
$(F,B)$ is a projective $\epsilon$-lc pair of dimension $n$;•
$A$ is a very ample divisor on $F$ with $A^{n}\le r$;•
$A-B$ is ample; and•
$M\ge 0$ is an $\mathbb {R}$-Cartier $\mathbb {R}$-divisor with $|A-M|_\mathbb {R}\neq \emptyset$.
Then
\[ \operatorname{\mathrm{lct}}(F,B,|M|_\mathbb{R})\ge \operatorname{\mathrm{lct}}(F,B,|A|_\mathbb{R})\ge t. \]Let us also recall the following immediate consequence of Birkar's proof of the BAB conjecture; see [Reference BirkarBir19, Reference BirkarBir21].
Lemma 4.2 Fix a positive integer 
$n$ and a positive real number 
$\epsilon$. Then, there exist positive integers 
$m_{n, \epsilon }=m(n, \epsilon )$, 
$s_{n, \epsilon }=s(n, \epsilon )$ such that, for any 
$n$-dimensional 
$\epsilon$-lc Fano variety 
$X$, 
$-m_{n, \epsilon } K_X$ is a very ample Cartier divisor on 
$X$ of degree at most 
$s_{n, \epsilon }$.
In particular, 
$s_{n, \epsilon }$ also provides a bound for the volume of 
$-m_{n, \epsilon } K_X$. We can always assume that 
$m_{n, \epsilon } \geq 2$.
Proof. Theorem 2.12 and [Reference BirkarBir19, Lemma 2.24] imply that there exists 
$t=t(n, \epsilon )$ such that 
$-tK_X$ is Cartier. As 
$-K_X$ is ample, [Reference KollárKol93, Theorem 1.1 and Lemma 1.2] imply that there exists 
$l=l(n, \epsilon )$ such that 
$-ltK_X$ is very ample. Hence, we can define 
$m_{n, \epsilon }:=ln$.
The existence of 
$s_{n, \epsilon }$ follows from the previous part and the bound on the volume of 
$-K_X$ that was established in [Reference BirkarBir21, Theorem 2.11].
We are now ready to state the main result of this section. We remind the reader that the definition of generalized pair can be found in § 2.4
Theorem 4.3 Fix a positive real number 
$\epsilon$, a DCC set 
$I$, and positive integers 
$n, p, d, l$. Let 
$\mathfrak {D}$ be the set of pairs 
$(X', \Delta '+(1/l) G)$ satisfying the following properties:
(i) there exists an
$n$-dimensional projective generalized klt pair $(X \to X', \Delta ', M)$;(ii) the coefficients of
$\Delta '$ belong to $I$, and $pM$ is Cartier;(iii)
$K_{X'}+\Delta '+M' \equiv 0$;(iv) there exists
$\Gamma \sim _\mathbb {R} M$ such that $(X', \Delta '+\Gamma ')$ is $\epsilon$-klt;(v) there exists a contraction
$f\colon X' \to Z$ on $X'$, with $\dim Z < \dim X'$;(vi)
$-K_{X'}$ is $f$-ample;(vii) there exists a very ample Cartier divisor
$H$ such that $\operatorname {\mathrm {Vol}}(Z,H)\leq d$; and(viii)
$G \sim l f^{\ast } H$ and the coefficients of $(1/ l) G$ are in $[0, 1]$.
Then 
$\mathfrak {D}$ forms a log birationally bounded family.
We postpone the proof of Theorem 4.3 to the end of this subsection.
Theorem 4.3 can be deduced from [Reference Birkar and ZhangBZ16, Theorem 1.3] together with the following technical result which shows for suitable generalized pairs of Calabi–Yau type, endowed with a fibration, that the volume of the anticanonical class is bounded from above, thus generalizing the result of Theorem 2.7.
Proposition 4.4 Fix a DCC set 
$I$, a positive real number 
$\epsilon$ and positive integers 
$n, p$. If 
$(X \to X', \Delta ', M)$ is a projective 
$n$-dimensional generalized klt pair such that
(i) the coefficients of
$\Delta '$ are in $I$ and $pM$ is Cartier,(ii) there exists a morphism
$f\colon X' \to Z$, $0< \dim Z < \dim X'$, and $-K_{X'}$ is $f$-ample,(iii) there exists a very ample Cartier divisor
$H$ on $Z$ such that
\[ K_{X'}+\Delta'+M' \sim_\mathbb{Q} f^{{\ast}} H, \quad \textrm{and} \ K_Z+H\ \textrm{is big}, \](iv) there exists
$0 \leq \Gamma \sim _\mathbb {R} M$ such that $(F, (\Delta '+\Gamma ')\vert _F)$ is $\epsilon$-klt where $F$ is a general fibre of $f$ and $\Gamma '$ is the pushforward of $\Gamma$ on $X'$,
then there exists a constant 
$k=k(I, \epsilon, p, n)$ such that
\[ \operatorname{\mathrm{Vol}}(X', \Delta'+M') \leq k \operatorname{\mathrm{Vol}}(Z, H). \]Proof. If 
$\operatorname {\mathrm {Vol}}(X', \Delta '+M')=0$ there is nothing to prove. Hence, we can assume that 
$\Delta '+M'$ is big and consequently that also its restriction to a general fibre of 
$f$ is big. We can also assume that 
$X'$ is 
$\mathbb {Q}$-factorial by passing to a small 
$\mathbb {Q}$-factorial modification as that does not alter any of the hypotheses in the statement of the proposition.
We will prove that there exists a constant 
$k'=k'(I, \epsilon, p, n, j)$ such that the conclusion of the proposition holds for 
$k'$ instead of 
$k$, where 
$j=\dim Z$. The statement of the theorem then follows by taking
\[ k(I, \epsilon, p, n):= \max_{0<j<n} k'(I, \epsilon, p, n, j). \]
To define 
$k'$, we will work by induction on the set of ordered pairs of integers 
$(n, j)$, 
$n>j>0$, with the lexicographic order.
The pair 
$(F, \Delta _F :=(\Delta ' + \Gamma ')|_F)$ is generalized 
$\epsilon$-klt and 
$K_F + \Delta _F \sim _\mathbb {R} 0$, by adjunction. In particular, 
$F$ belongs to a bounded family, by Theorem 2.12. Let us also fix 
${m_{\dim F, \epsilon }}={m_{n-j, \epsilon }}=m(n-j, \epsilon ), \; {s_{\dim F, \epsilon }}={s_{n-j, \epsilon }}=s(n-j, \epsilon )$, the two natural numbers defined in Lemma 4.2. Apply Theorem 4.1 to the pair 
$(F, \Delta _F)$ with 
$A:=-m_{\dim F, \epsilon }K_F$, 
$r:=s_{\dim F, \epsilon }$. Then we define 
$t=t(n-j, {s_{n-j, \epsilon }}, \epsilon )$. In particular, for any effective divisor 
$G \in |-K_F|_{\mathbb {R}}$, 
$(F, \Delta _F+tG)$ is klt. We define 
$\bar {t}:= \min \{\frac 1 2, t/ 2\}$.
Claim 
${\rm Vol}(X',\bar {t}(\Delta '+\Gamma ')-2f^{*}H)=0$.
Proof. In fact, if that is not the case, then 
$\bar {t}(\Delta '+\Gamma ')-2f^{*}H$ is big. Thus, there exists an effective 
$\mathbb {R}$-divisor 
$E\sim _{\mathbb {R}} \bar {t}(\Delta '+\Gamma ')-2f^{*}H$. Let us define
\[ \Theta:=(1-\bar{t})(\Delta'+\Gamma')+E, \]
so that 
$K_{X'}+\Theta \sim _{\mathbb {R}} -f^{*}H$. Since 
$E\vert _F \sim _{\mathbb {R}} -\bar {t}K_F$ by construction, by the above discussion 
$(F, \Theta \vert _F)$ is klt. Hence, 
$(X',\Theta )$ is klt over the generic point of 
$Z$, and, by Theorem 2.15, there exists an effective divisor 
$\Gamma _Z$ on 
$Z$ such that
\[ - f^{*}H \sim_{\mathbb{R}} K_{X'}+\Theta \sim_{\mathbb{R}} f^{*}(K_Z+\Gamma_Z). \]
This immediately gives a contradiction since 
$K_Z+H$ is supposed to be big, while we have just proved that 
$K_Z+\Gamma _Z+H \sim _{\mathbb {R}} 0$.
We fix a general element 
$H' \in |H|$ and define 
$H'':=f^{-1}H'$, so that 
$H'' \sim f^{\ast } H$.
Lemma 4.6 implies that
\[ {\rm Vol}(X',\bar{t}(\Delta'+\Gamma')) \leq {\rm Vol}(X',\bar{t}(\Delta'+\Gamma')-2f^{{\ast}} H)+2n{\rm Vol}(H'',\bar{t}(\Delta'+\Gamma')|_{H''}). \]
Hence, as 
$\textrm {Vol}(X',\bar {t}(\Delta '+\Gamma ')-2f^{\ast } H)=0$ and 
$\Gamma ' \sim M'$
\[ {\rm Vol}(X',\Delta'+M')\leq 2n \bar{t}^{{-}1} {\rm Vol}(H'',(\Delta'+M')|_{H''}). \]
If 
$j=1$, then 
$H''=\sum _{i=1}^{h}F_i$ where 
$h=\deg _Z(H)=\textrm {Vol}(Z, H)$ and 
$F_i$ is a general fibre of 
$f$ for each 
$i$. Hence, 
$(F_i, (\Delta '+\Gamma ')|_{F_i})$ is 
$\epsilon$-klt log Calabi–Yau pair of dimension 
$\dim X-1$. By Theorem 2.12,
\[ {\rm Vol}(H'',(\Delta'+M')|_{H''})=\sum_{i=1}^{h}{\rm Vol}(F_i, -K_{F_i})\leq \frac{s_{n-1, \epsilon}}{m_{n-1, \epsilon}^{n-1}} {\rm Vol}(Z, H). \]Hence, we may take
\[ k'(I,\epsilon, p, n, 1):=2n \bar{t}^{{-}1} \frac{s_{n-1, \epsilon}}{m_{n-1, \epsilon}^{n-1}}, \]
thus proving the starting step of the induction, as 
$j=1$.
When 
$j >1$, let us consider the map 
$g:=f|_{H''}$: 
$H''\rightarrow H'$. Then, by adjunction, 
$H''$ supports a generalized klt pair 
$(H''' \to H'', \Delta '\vert _{H''}, M\vert _{H'''})$, such that:
•
$H'''$ is a divisor in $X$, by possibly passing to a higher model of $X$;•
$\dim H'=j-1 >0$;• the coefficients of
$\Delta '\vert _{H''}$ are in $I$ which is DCC, by adjunction and freeness of $|g^{\ast } H|$;•
$pM\vert _{H'''}$ is Cartier and $\Gamma \vert _{H'''}\sim _\mathbb {R} M\vert _{H'''}$, by restricting;•
$(\Delta '+\Gamma ')|_{H''}$ is $\epsilon$-klt along the general fibre of $g$, by adjunction and freeness of $|f^{\ast } H|$;•
$K_{H''}= (K_{X'}+H'')\vert _{H''}$ by adjunction, since $H''$ is Cartier and general in a base-point-free linear system;•
$-K_{H''}$ is $g$-ample since $H'' \sim _{g} 0$; and•
$K_{H''}+\Delta |_{H''}\sim _{\mathbb {R}}2g^{*}(H|_{H'})$, and $K_{H'} \sim (K_Z+H)|_{H'}$ is big.
Thus, by inductive hypothesis, since 
$\dim H'' =\dim X -1$,
\begin{align*} {\rm Vol}(H'',(\Delta'+M')|_{H''}) & \leq k'(I,\epsilon, p, n-1, j-1){\rm Vol}(H',2H|_{H'})\\ &=2^{j-1}k'(I, \epsilon, p, n-1, j-1){\rm Vol}(Z,H). \end{align*}Taking
\[ k'(I,\epsilon, p, n,j):=2^{j}n \bar{t}^{{-}1} k'(I,\epsilon, p, n-1, j-1), \]the proof is complete.
Remark 4.5 From the point of view of the proof of Proposition 4.4 there seem to be quite a few points where the strategy could be improved if we had better knowledge and understanding of the features of generalized pairs.
For example, it would be nice to show that it is possible to write down a canonical bundle formula for generalized pairs that would make it possible to drop hypothesis (iv) on the existence of an effective member of the linear system 
$|M|$ with bounded singularities.
For instance, for the purpose of the above proof, it would be enough to know that for a generalized klt pair 
$(X \to X', \Delta ', M)$ and a morphisms 
$f \colon X' \to Z$ such that 
$K_{X'}+\Delta '+M' \sim _{f, \mathbb {R}} 0$, there exist a klt pair 
$(Z, \Gamma )$ and a pseudo-effective divisor 
$P$ for which
\[ K_{X'}+\Delta'+M' \sim_{\mathbb{R}} f^{{\ast}}(K_Z+ \Gamma+P). \]After the completion of this paper, it was shown in [Reference FilipazziFil20a, Reference Han and LiuHL19] that a canonical bundle formula exists for generalized pairs in full generality.
In the course of the proof of Proposition 4.4 we used the following easy generalization of [Reference JiangJia18, Lemma 2.5].
Lemma 4.6 Let 
$X$ be a projective normal variety and let 
$D$ be an 
$\mathbb {R}$-Cartier 
$\mathbb {R}$-divisor on 
$X$. Let 
$S$ be a base-point-free Cartier prime divisor on 
$X$. Then for any rational number 
$q>0$,
\[ \operatorname{\mathrm{Vol}}(X, D+qS) \leq \operatorname{\mathrm{Vol}}(X, D) + q\cdot \dim X \cdot \operatorname{\mathrm{Vol}}(S, D|_S+qS|_S). \]Proof. When 
$D$ is a 
$\mathbb {Q}$-Cartier 
$\mathbb {Q}$-divisor on 
$X$, this is the original statement of [Reference JiangJia18, Lemma 2.5].
When 
$D$ instead is an 
$\mathbb {R}$-Cartier 
$\mathbb {R}$-divisor, then it suffices to choose a sequence of 
$\mathbb {Q}$-Cartier 
$\mathbb {Q}$-divisors approximating 
$D$ in the Néron–Severi group and notice that by virtue of continuity of the volume function the inequality in the statement of the Lemma is preserved in the limit.
When working with log pairs, rather than generalized ones (i.e. when 
$M = 0$), the statement of Proposition 4.4 can be immediately reduced to the following one.
Proposition 4.7 Fix a DCC set 
$I \subset [0, 1)$ and an integer 
$n$. If 
$(X, \Delta )$ is a pair such that
(i)
$X$ is a projective variety of dimension $n$,(ii)
$(X, \Delta )$ is klt and the coefficients of $\Delta$ are in $I$,(iii) there exists a morphism
$f\colon X \to Z$, $0< \dim Z< \dim X$, and $-K_X$ is $f$-ample, and(iv) there exists a very ample Cartier divisor
$H$ on $Z$ such that $K_X+\Delta \sim _\mathbb {R} f^{\ast } H$ and $K_Z+H$ is big,
then there exists a constant 
$k=k(I, n)$ such that
\[ \operatorname{\mathrm{Vol}}(X, \Delta) \leq k \operatorname{\mathrm{Vol}}(Z, H). \]Proof. Hypotheses (i)–(iii) of Proposition 4.4 are automatically satisfied. Corollary 2.9 then implies that there exists 
$0<\epsilon =\epsilon (\dim X -\dim Y, I)$ such that 
$(F, \Delta \vert _F)$ is 
$\epsilon$-klt and this implies that condition (iv) in Proposition 4.4 is satisfied as well, by adjunction to a general fibre of 
$f$.
Proof of Theorem 4.3 Given a pair 
$(X',\Delta ' + (1 /l) G) \in \mathfrak {D}$, let us consider the generalized pair
\[ (X \to X', \Delta', M + \bar{H}), \]
where 
$\bar {H}$ is the pullback of 
$H$ to 
$X$. Since 
$(X \to X', \Delta ', M)$ is generalized klt, the same holds for 
$(X \to X', \Delta ', M + \bar {H})$. Moreover, we can assume that 
$X$ is a log resolution of 
$(X', \Delta ' + \Gamma )$ where 
$M$ descends. We will denote by 
$\widetilde G$ (respectively, 
$\widetilde{\Delta'}$) the strict transform of 
$G$ (respectively, 
$\Delta '$) on 
$X$, and 
$\bar {G}:= \mathrm {Supp}(\widetilde G)$. In particular, since 
$G \sim l f^{\ast } H$ and the coefficients of 
$(1 /l) G$ are in 
$[0, 1]$,
\begin{equation} \bar{G} \leq l\bar{H}. \end{equation}
Let us fix 
$H_1 \in |H|$ sufficiently general. Let us define 
$H':=f^{-1} H_1$ on 
$X'$ and let 
$H''$ be the strict transform of 
$H'$ on 
$X$. Thus, 
$H'' \in |\bar {H}|$, for a sufficiently general element.
By adjunction, up to choosing a sufficiently high model 
$X \to X'$, there exists a generalized pair structure 
$(H'' \to H',\Delta '\vert _{H'}, (M+\bar {H})\vert _{H''})$ satisfying the following conditions:
(i) the coefficients of
$\Delta '\vert _{H'}$ are in the DCC set $I$, since $H'$ is a general element of a base-point-free linear system;(ii)
$p(M +l\bar {H})\vert _{H''}$ is Cartier, for all $l \in \mathbb {N}$;(iii)
$\Gamma \vert _{H''} \sim _{\mathbb {R}} M\vert _{H''}$;(iv)
$(H', (\Delta '+\Gamma ')\vert _{H'})$ is $\epsilon$-klt by Bertini's theorem for log pairs;(v) the restriction of
$f$ to $H'$ gives a morphism $f_{H'}\colon H' \to H_1$, $\dim H_1 < \dim H'$;(vi) the trace of
$\bar {H}\vert _{H''}$ on $H'$ is just $f_{H'}^{\ast } (H\vert _{H_1})$, by construction; and(vii) for all
$l \in \mathbb {N}$ and for the very ample Cartier divisor $H\vert _{H_1}$ on $H_1$, $K_{H'}+(\Delta '+\Gamma '+ l\bar {H})\vert _{H'} \sim _\mathbb {Q} (1+l)f^{\ast }_{H'} (H\vert _{H_1})$.
As 
$f$ is a 
$K_{X'}$-Mori fibre space, then for 
$0< \lambda \ll 1$, 
$K_{X'}+(1+\lambda )(\Delta '+M')+f^{\ast } H$ is ample. Hence, the divisor
\[ K_X+E +\lceil \widetilde{\Delta'} \rceil+ 2M + \bar{H} \]
is big, where 
$E$ is the exceptional divisor of the birational morphism 
$X \to X'$. By [Reference Birkar and ZhangBZ16, Theorem 1.3], there exists a positive integer 
$m=m(I, n, p)$ such that, for any 
$m'$ divisible by 
$m$, the linear system 
$|m'(K_X+E +\lceil \widetilde{\Delta'} \rceil + 2M + \bar {H})|$ defines a birational map. Up to passing to a higher birational model of 
$X$, we can assume that on 
$X$,
\begin{equation} |m(K_X+E +\lceil \widetilde{\Delta'} \rceil+ 2M + \bar{H})|= |N| + F, \end{equation}
where 
$|N|$ is a base-point-free linear system inducing a birational morphism and 
$F$ the effective fixed part of the linear system.
As the coefficients of 
$\Delta '$ vary in the DCC set 
$I$, there exists a positive integer 
$c=c(I)$ such that the coefficients of the divisor 
$c\Delta '$ are 
$\geq 1$ for any 
$(X', \Delta ')$ in 
$\mathfrak {D}$. Thus,
\begin{align} \operatorname{Vol}(X', c\Delta'+ M'+ f^{{\ast}} H) & = c^{n}\operatorname{Vol}\biggl(X', \Delta'+ \frac{M'+ f^{{\ast}} H}{c}\biggr) \nonumber\\ &\leq c^{n}\operatorname{\mathrm{Vol}}(X', \Delta'+ M' + f^{{\ast}} H). \end{align}Lemma 4.6 implies that
\begin{align} \operatorname{\mathrm{Vol}}(X', \Delta'+ M' + f^{{\ast}} H) &\leq \operatorname{\mathrm{Vol}}(X', \Delta'+M')+ n \cdot \operatorname{\mathrm{Vol}}(H', (\Delta' +M')|_{H'}+f^{*} H|_{H'})\nonumber\\ &= \operatorname{\mathrm{Vol}}(X', \Delta'+M')+ n \cdot \operatorname{\mathrm{Vol}}(H', (\Delta' +M')|_{H'}+f^{*}_{H'} (H|_{H_1})). \end{align}Hence,
\begin{equation}\begin{aligned} &\operatorname{Vol}(X, K_X+E +\lceil \widetilde{\Delta'} \rceil+ 2M + \bar{H}) \\ &\quad\leq\operatorname{Vol}(X', K_{X'}+\lceil \widetilde{\Delta'} \rceil+ 2M' + H') & \hfill(\text{using $f_{\ast}$})\\ &\quad\leq \operatorname{Vol}(X', c\Delta'+ M'+H') & \hfill(K_{X'} + \Delta'+M' \equiv 0)\\ &\quad\leq c^n \operatorname{Vol}(X', \Delta'+M'+H') & \hfill({\rm by}\ (14))\\ &\quad\leq c^{n} [\operatorname{Vol}(X', \Delta'+M') \\ &\qquad +n \cdot \operatorname{Vol}(H', (\Delta'+M')|_{H'}+ f^*_{H'} (H|_{H_1})], \end{aligned}\end{equation}where the last inequality follows from (15).
cla There exists a positive real number 
$C_1=C_1(n, \epsilon )$ such that
\[ \operatorname{\mathrm{Vol}}(X', \Delta'+M') \leq C_1. \]Proof. We can assume that 
$\operatorname {\mathrm {Vol}}(X', \Delta '+M') >0$, otherwise there is nothing to prove. We can also assume that 
$X'$ is 
$\mathbb {Q}$-factorial, as passing to a small 
$\mathbb {Q}$-factorialization does not change volumes.
Hence, for 
$0<\eta \ll 1$, 
$(X', (1+\eta )(\Delta ' + \Gamma '))$ is klt and 
$K_{X'}+(1+\eta )(\Delta ' + \Gamma ') \sim _\mathbb {R} \eta (\Delta ' + \Gamma ')$ is big. Thus, we can run the 
$(\eta (\Delta ' + \Gamma '))$-MMP with scaling of an ample divisor which terminates with a birational model 
$\psi \colon X' \dashrightarrow X''$ such that 
$\Delta '' + \Gamma ''$ is ample on 
$X''$ and 
$\operatorname {\mathrm {Vol}}(X'', \Delta '' + \Gamma '') = \operatorname {\mathrm {Vol}}(X', \Delta ' + \Gamma ')$, where 
$\Delta '' := \psi _\ast \Delta '$, 
$\Gamma '':=\psi _\ast \Gamma '$. On the other hand, as 
$K_{X'}+\Delta ' + \Gamma ' \sim _\mathbb {R} 0$ and 
$(X', \Delta ' + \Gamma ')$ is 
$\epsilon$-klt, 
$X''$ is an 
$\epsilon$-klt Fano variety and 
$\operatorname {\mathrm {Vol}}(X'', \Delta '' + \Gamma '') = \operatorname {\mathrm {Vol}}(X'', -K_{X''})$. Hence, it suffices to take 
$C_1$ to be the constant whose existence is implied by [Reference BirkarBir21, Theorem 2.11].
cla There exists a positive real number 
$C_2=C_2(I, \epsilon, p, n)$ such that
\[ \operatorname{\mathrm{Vol}}(H', (\Delta'+M')\vert_{H'} + f^{{\ast}} H\vert_{H'}) \leq C_2. \]Proof. We can assume that 
$\operatorname {\mathrm {Vol}}(H', (\Delta '+M')\vert _{H'} + f^{\ast } H\vert _{H'}) >0$, otherwise there is nothing to prove. We can assume that 
$H'$ is 
$\mathbb {Q}$-factorial, as passing to a small 
$\mathbb {Q}$-factorialization does not change volumes. We distinguish two cases.
If 
$\dim H_1=0$, then 
$H'$ is the disjoint union of 
$s$ fibres of 
$f_{H'}$, 
$F_1, \ldots, F_s$, where 
$s:=\operatorname {\mathrm {Vol}}(Z, H)\leq d$. Furthermore, in this case 
$f^{\ast }_{H'} (H|_{H_1}) = 0$ so that
\begin{align*} \operatorname{\mathrm{Vol}}(H', (\Delta'+M')\vert_{H'} + f^{{\ast}}_{H'} (H|_{H_1})) &=\operatorname{\mathrm{Vol}}(H', (\Delta'+M')\vert_{H'})\\ &= \sum_{i=1}^{s}(\Delta'+M')^{\dim X'-\dim Z} \cdot F_i = s (\Delta'+M')^{\dim F} \cdot F, \end{align*}
where 
$F$ is a general fibre of 
$f\vert _{H'}$ (equivalently, of 
$f$). By hypotheses (iii)–(vi) in the statement of the theorem, 
$F$ is an 
$\epsilon$-klt Fano and 
$K_{F} \sim _\mathbb {R} (\Delta '+M')\vert _{F}$; hence, by [Reference BirkarBir21, Theorem 2.11] there exists a constant 
$\bar {C}=\bar {C}(\epsilon, \dim F)$ such that
\[ (\Delta'+M')\vert_{H'}^{\dim F} \cdot F = \operatorname{\mathrm{Vol}}(F, (\Delta'+M')\vert_{F}) = \operatorname{\mathrm{Vol}}(F, -K_F) \leq \bar{C}. \]
We define 
$C_{2, a}:=\max _{0<i<\dim X'} \bar {C}(\epsilon, i)$.
If 
$\dim H_1> 0$, by properties (vi) and (vii) in the proof of Theorem 4.3,
\[ K_{H'}+(\Delta'+M')\vert_{H'} + l f_{H'}^{{\ast}} (H\vert_{H_1}) \sim_\mathbb{R} f_{H'}^{{\ast}} ((1+ l)H\vert_{H_1}), \quad \forall \, l \geq 0. \]
Moreover, Kawamata–Viehweg vanishing and the fact that 
$H\vert _{H_1}$ is very ample imply that 
$K_{H_1}+(n+1)H\vert _{H_1}$ is big; in fact, for some 
$m \in \{1, \ldots, n\}$, 
$h^{0}(H_1, K_{H_1}+mH\vert _{H_1}) \neq 0$ as 
$\chi (H_1, K_{H_1}+mH\vert _{H_1})= h^{0}(H_1, K_{H_1}+mH\vert _{H_1})$ by Kawamata–Viehweg vanishing. Hence, by properties (i)–(vii) in the proof of the theorem, using Proposition 4.4, we conclude that there exists 
$k=k(I, \epsilon, p, n-1)$ such that
\begin{align*} \operatorname{\mathrm{Vol}}(H', (\Delta'+M')\vert_{H'}+ f_{H_1}^{{\ast}} (H\vert_{H_1})) &\leq \operatorname{\mathrm{Vol}}(H', (\Delta'+M')\vert_{H'}+ n f_{H'}^{{\ast}} (H\vert_{H'}) )\\ &\leq k (n+1)^{n-1} \operatorname{\mathrm{Vol}}(H_1, H\vert_{H_1})\\ &\leq k (n+1)^{n-1} d, \end{align*}
as 
$\operatorname {\mathrm {Vol}}(H_1, H\vert _{H_1}) = \operatorname {\mathrm {Vol}}(Z, H) \leq d$ since 
$H_1 \in |H|$. We define 
$C_{2, b}:=k (n+1)^{n-1} d$.
To complete the proof of the claim, it suffices to take 
$C_2:= \max \{C_{2, a}, C_{2, b}\}$.
By [Reference Hacon, McKernan and XuHMX13, Lemma 2.4.2(3)], to show that 
$\mathfrak {D}$ forms a log birationally bounded family, it suffices to show that the set of pairs 
$(X, \lceil \widetilde{\Delta'} + \tilde {G} \rceil + E)$ is log birationally bounded. Since 
$|N|$ in (13) is a base-point-free linear system that induces a birational morphism, by [Reference Hacon, McKernan and XuHMX13, Lemma 2.4.2(4)] it suffices to show that there exist positive real numbers 
$C_3=C_3(I, \epsilon, p, n)$, 
$C_4=C_4(I, \epsilon, p, n)$ such that
\[ \operatorname{\mathrm{Vol}}(X, N) \leq C_3 \quad {\rm and} \quad (\lceil \widetilde{\Delta'}\rceil+ E+\bar G) \cdot N^{n-1} \leq C_4. \]Claims 1 and 2 and (16) imply that
\begin{equation} \operatorname{\mathrm{Vol}}(X, K_X+E +\lceil \widetilde{\Delta'} \rceil+ 2M + \bar{H}) \leq c^{n}(C_1+C_2). \end{equation}By construction and (17),
\[ \operatorname{\mathrm{Vol}}(X, N) \leq m^{n}\operatorname{\mathrm{Vol}}(X, K_X+E +\lceil \widetilde{\Delta'} \rceil+ 2M + \bar{H}) \leq (cm)^{n} (C_1+C_2). \]
Thus, it suffices to take 
$C_3:=(cm)^{n} (C_1+C_2)$.
By [Reference Hacon, McKernan and XuHMX13, Lemma 3.2], denoting 
$N'=2(2n+1)N$,
\begin{align} (\lceil \widetilde{\Delta'}\rceil+ E + \bar G) \cdot N^{n-1} &\leq (\lceil \widetilde{\Delta'}\rceil+ E+\bar G) \cdot (N')^{n-1}\nonumber\\ &\leq 2^{n} \operatorname{\mathrm{Vol}}(X, K_X+\lceil \widetilde{\Delta'}\rceil+ E+\bar G+ N'). \end{align}
Since 
$|m(K_X+\lceil \widetilde{\Delta'}\rceil + E+ 2M + \bar {H}))| = |N| + F$ and 
$F \geq 0$, it follows, using (12), that
\begin{align} &\operatorname{\mathrm{Vol}}(X, K_X+\lceil \widetilde{\Delta'}\rceil+ E+ \bar G+ N')\nonumber\\ &\quad \leq \operatorname{\mathrm{Vol}}(X, K_X+\lceil \widetilde{\Delta'}\rceil+ E+ \bar G+ 2(2n+1) (K_X+\lceil \widetilde{\Delta'}\rceil+ E+ 2M + \bar{H}))\nonumber\\ &\quad \leq \operatorname{\mathrm{Vol}}(X, K_X+\lceil \widetilde{\Delta'}\rceil+ E+ l\bar{H}+ 2(2n+1) (K_X+\lceil \widetilde{\Delta'}\rceil+ E+ 2M + \bar{H})). \end{align}Thus, (18) and (19) imply that
\begin{align*} &(\lceil \widetilde{\Delta'}\rceil+ E + \bar G) \cdot N^{n-1}\\ & \quad \leq 2^{n} \operatorname{\mathrm{Vol}}(X, K_X+\lceil \widetilde{\Delta'}\rceil+ E+l\bar{H} + 2(2n+1) m(K_X+\lceil \widetilde{\Delta'}\rceil+ E+ 2M + \bar{H})) \\ & \quad \leq 2^{n} \operatorname{\mathrm{Vol}}(X, (2(2n+1)m+l) (K_X+ \lceil\widetilde{\Delta'}\rceil+ E+ 2M + \bar{H})), \end{align*}
where the last inequality follows from the fact that 
$M$ and 
$K_X+ \lceil \widetilde{\Delta'}\rceil + E+ 2M$ are pseudo-effective. By (17) it suffices to take 
$C_4:= 2^{n}(2(2n+1)m+l)^{n}c^{n} (C_1+C_2)$.
4.2 Boundedness for Mori fibre spaces of log Calabi–Yau type
We can now use the results from the previous subsection to show that, in the case of klt Calabi–Yau pairs endowed with a Mori fibre space structure with bounded base and singularities, we can produce a very ample divisor with bounded volume on the total space using the one on the base.
After the completion of this paper, a generalization of this result appeared in [Reference Chen, Di Cerbo, Han, Jiang and SvaldiCDHJS21, Theorem 4.6] which was later further improved in [Reference BirkarBir18, Theorem 1.2].
Theorem 4.8 Fix a DCC set 
$I\subset [0,1]$ and positive integers 
$n, d$. Then the set 
$\mathfrak {D}$ of log pairs 
$(X, \Delta )$ satisfying
(i)
$(X, \Delta )$ is a projective klt pair of dimension $n$,(ii) the coefficients of
$\Delta$ belong to $I$,(iii)
$K_X+\Delta \equiv 0$,(iv) there exists a contraction
$f\colon X\to Z$ with $\dim Z < \dim X$,(v)
$-K_X$ is $f$-ample, and(vi) there exists a very ample Cartier divisor
$H$ on $Z$ with $\operatorname {\mathrm {Vol}}(Z,H)\leq d$,
forms a bounded family.
Proof. By Theorem 2.8, we can assume that 
$I$ is finite. By Corollary 2.9, there exists 
$\epsilon (n, I) >0$ such that 
$(X, \Delta )$ is 
$\epsilon$-lc. As 
$f^{*} H$ is base-point-free, by Bertini's theorem for log pairs (cf. [Reference KollárKol97, Theorem 4.8]), there exists an effective prime divisor 
$0 \leq G\sim 2f^{*} H$ such that 
$(X,\Delta +\frac 1 2 G)$ is 
$\epsilon '$-lc, where 
$\epsilon '=\min \{\frac 1 2, \epsilon \}$; furthermore, the coefficients of 
$\Delta +\frac 1 2 G$ are contained in 
$I'=I \cup \{\frac 1 2\}$ which is still a DCC set. For any pair 
$(X, \Delta ) \in \mathfrak {D}$, we fix such a choice of 
$G=G(X, \Delta )$.
We define the set of pairs
\[ \mathfrak{D'}:=\{ (X, \Delta+\tfrac 1 2 G) \mid (X, \Delta) \in \mathfrak{D}, \ G\ {\rm is\ the\ divisor\ defined\ above}\}. \]
The set 
$\mathfrak {D}'$ is log birationally bounded: in fact, pairs 
$(X, \Delta +\frac 1 2 G) \in \mathfrak {D}'$ satisfy the hypotheses of Theorem 4.3, since:
•
$(X,\Delta )$ is trivially a generalized pair by imposing $M=0$;• it suffices to fix the integer
$l$ in the statement of Theorem 4.3 to be $2$;•
$I$ is a DCC set;•
$-K_X$ is $f$-ample; and•
$(X, \Delta )$ is $\epsilon$-lc.
Since 
$-K_X$ is 
$f$-ample, for any 
$0<\eta \ll 1$,
\[ K_X + (1+\eta) \Delta+\tfrac 1 2 G \sim_\mathbb{R} \eta \Delta + \tfrac 1 2 G \]
is an ample divisor and the pair 
$(X, (1+\eta ) \Delta +\frac 1 2 G)$ is 
${\epsilon '}/{2}$-klt. For any pair 
$(X, \Delta + \frac 1 2 G) \in \mathfrak {D}'$, we fix such a choice of 
$\eta =\eta (X, \Delta, G)$.
We define the set of pairs
\begin{align*} \mathfrak{D}'' :=\{ (X, (1+\eta)\Delta+\tfrac 1 2 G) \mid (X, \Delta+\tfrac 1 2 G) \in \mathfrak{D}',\ \eta\ {\rm is\ the\ positive\ real\ number\ defined\ above}\}. \end{align*}
As 
$\mathfrak {D}'$ is log birationally bounded, and the notion of log birational boundedness does not depend on the coefficients of the divisor of the pairs in 
$\mathfrak {D}'$ (see Definition 2.3), 
$\mathfrak {D}''$ is also log birationally bounded.
Claim The set 
$\mathfrak {D}''$ satisfies the hypotheses of Theorem 2.5.
Proof. As the coefficients of 
$\Delta +\frac 1 2 G$ are contained in a DCC set, there exists 
$\delta =\delta (I) >0$ such that the coefficients of 
$\Delta +\frac 1 2 G$ are 
$\geq \delta$; a fortiori, the same must hold for the coefficients of 
$(1+\eta )\Delta +\frac 1 2 G$. By construction 
$K_X+(1+\eta )\Delta +\frac 1 2 G$ is ample, and by construction 
$(X, (1+\eta )\Delta +\frac 1 2 G)$ is 
${\epsilon '}/{2}$-klt for 
$\epsilon '=\epsilon '(n, I)$.
Applying Theorem 2.5, 
$\mathfrak {D}''$ is a bounded set of pairs. In particular, 
$X$ belongs to a bounded family: by the definition of boundedness of 
$\mathfrak {D}''$ (see Definition 2.3), in particular, there exists a projective morphism 
$f \colon Z \to T$ such that 
$T$ is of finite type and any variety 
$X \in \mathfrak {D}''$ appears also as one of the fibres of 
$f$. Hence, up to decomposing 
$T$ as a finite disjoint union of locally closed subsets, we can assume that 
$Z \subset \mathbb {P}^{n} \times T$, which implies, by generic flatness, that there exists a positive integer 
$d=d(\mathfrak {D}'')$ such that for any 
$X \in \mathfrak {D}''$ one can find a very ample Cartier divisor 
$H_X$ on 
$X$ satisfying 
$H_X^{\dim X} \leq d$. Since the coefficients of 
$\Delta$ belong to the finite set 
$I$ and 
$\Delta \equiv -K_X$, the set 
$\mathfrak {D}$ is a bounded set, again, by the existence of Chow varieties [Reference KollárKol96, Theorem 3.12], since the degree with respect to 
$H_X$ of each component of 
$\Delta$ is bounded.
5. Proof of the theorems
In this section we prove the theorems stated in the Introduction.
Proof of Theorem 1.8 From Theorem 3.2, after a birational contraction, we obtain a tower of Mori fibre spaces
Since 
$X$ is not of product type, then the same theorem implies that the variety 
$Y_{k+1}$ is a point and, thus, 
$Y_k$ must be Fano.
Proof of Theorem 1.9 By Theorem 2.8, we can assume that the coefficients of 
$\Delta$ belong to a finite set 
$I_0 \subset I$.
As the set of varieties 
$Z$ in the statement forms the bounded family 
$\mathfrak {F}$, there exists a projective morphism 
$f \colon \mathcal {Z} \to T$ such that 
$T$ is of finite type and any variety 
$Z \in \mathfrak F$ appears as one of the fibres of 
$f$. Hence, up to decomposing 
$T$ as a finite disjoint union of locally closed subsets, we can assume that 
$\mathcal {Z} \subset \mathbb {P}^{n} \times T$, for some fixed 
$n=n(\mathfrak F)$; thus, by generic flatness, that there exists a positive integer 
$d=d(\mathfrak {F})$ such that for any 
$Z \in \mathfrak F$ there exists a very ample Cartier divisor 
$H_Z$ on 
$Z$ satisfying 
$H_Z^{\dim Z} \leq d$.
Then the theorem follows from Theorems 4.8.
Proof of Theorem 1.3 We prove the theorem by induction on 
$n \leq 4$. By Theorem 2.8, we can assume that the set 
$I$ is finite.
The case 
$n=1$ is immediate as 
$X$ can only be 
$\mathbb {P}^{1}$ and 
$I$ is finite.
Let us assume that the theorem holds for 
$n-1$. Let 
$(X, \Delta )$ be a pair in 
$\mathfrak {D}$. By Theorem 3.2, 
$X$ is birational to the following tower of Mori fibre spaces.
For 
$i>0$, if 
$\dim Y_i>0$, then by Theorem 2.15, there exists an effective divisor 
$\Delta _i$ on 
$Y_i$ such that 
$(Y_i, \Delta _i)$ is a klt Calabi–Yau pair. The divisor 
$\Delta _i \neq 0$, otherwise the lc-trivial contraction 
$p_{i-1} \circ \dots \circ p_1\circ p_0 \colon (X', \Delta ') \to Y_i$ would be strongly generically isotrivial by Theorem 2.22 (cf. Remark 2.23); by Definition 2.24, the rational contraction 
$p_0 \circ r \colon X \to Y_1$ would contradict the assumption that 
$(X, \Delta )$ is not of product type.
We denote by 
$\mathfrak {F}$ the set of pairs 
$(X',\Delta '=r_\ast \Delta )$ just constructed. We first prove that the set 
$\mathfrak {F}$ forms a bounded family. By Theorem 1.9, it suffices to show that the set 
$\mathfrak {F}_1$ given by varieties 
$Y_1$ appearing in (20) forms a bounded family, since the morphism 
$p_0$ in (20) is a 
$K_{X'}$-Mori fibre space. To this end, we distinguish several cases depending on the dimension of 
$Y_1$.
If 
$Y_1$ is a point, then 
$Y_1$ is certainly bounded.
If 
$\dim Y_1 =1$, then 
$Y_1 = \mathbb {P}^{1}$, since 
$\Delta _1 \neq 0$; thus, 
$Y_1$ is bounded.
If 
$\dim Y_1 =2$, then by Theorem 2.17 there exist an effective divisor 
$\Delta _1 \neq 0$ on 
$Y_1$ and a positive real number 
$\epsilon =\epsilon (N, I)$ such that 
$(Y_1, \Delta _1)$ is an 
$\epsilon$-lc Calabi–Yau surface pair. Then boundedness of 
$Y_1$ then follows from Theorem 2.13.
If 
$\dim Y_1=3$, then by Theorem 2.19 and Lemma 2.16 we can assume that 
$\Delta _1$ is a divisor on 
$Y_1$ with coefficients in a DCC set 
$J=J(n, I)$. Furthermore, by Theorem 2.8, we can assume that the set 
$J$ is finite. If 
$Y_2$ is a point, then 
$Y_1$ is bounded by Corollary 2.9 and Theorem 2.10. If 
$\dim Y_2 =1$, then 
$Y_2 = \mathbb {P}^{1}$ as 
$\Delta _2 \neq 0$. Hence, 
$Y_2$ is bounded. If 
$\dim Y_2=2$, by Theorem 2.17 we can assume that there exists a positive real number 
$\epsilon$ such that 
$(Y_2, \Delta _2)$ is an 
$\epsilon$-lc Calabi–Yau surface pair; as 
$\Delta _2 \neq 0$, boundedness of 
$Y_2$ follows from Theorem 2.13. In both cases 
$\dim Y_2=1, 2$, boundedness of 
$Y_1$ follows from Theorem 1.9 as 
$Y_2$ belongs to a bounded family.
As the set 
$\mathfrak {F}$ forms a bounded family, [Reference Hacon and XuHX15, Proposition 2.5] implies that there exists a bounded family 
$(Z,D)\rightarrow T$ such that, for any pair 
$(X',\Delta ') \in \mathfrak {F}$ and for any set 
$\{E_1, \ldots, E_k\}$ of exceptional divisors of discrepancy at most zero over 
$(X', \Delta ')$, there exist 
$t\in T$ and a birational morphism 
$\mu _t : Z_t \rightarrow X'$ which extracts precisely 
$\{E_1, \ldots, E_k\}$ and 
$K_{Z_t}+D_t=\mu _t^{*} (K_{X'} +\Delta ')$. We define the set 
$\mathfrak {D}'$ to be the set of klt Calabi–Yau pairs 
$(Z_t, D_t)$ just constructed. Given 
$(X, \Delta ) \in \mathfrak {D}'$ and the corresponding pair 
$(X', \Delta ') \in \mathfrak {F}$ constructed in (20), since 
$K_X +\Delta \sim _\mathbb {R} 0$ and 
$K_{X'} +\Delta ' \sim _\mathbb {R} 0$, all the exceptional divisors 
$E_1, \ldots, E_l$ for 
$r \colon X \dashrightarrow X'$ have discrepancy 
$\leq 0$ with respect to 
$(X', \Delta ')$. Hence, by the above construction, there exists 
$(Z_t, D_t) \in \mathfrak {D}'$ crepantly extracting the divisors 
$E_1, \ldots, E_l$; hence, by construction, 
$(Z_t, D_t)$ is isomorphic in codimension one to 
$(X, \Delta )$, which proves the second part of the statement of the theorem. As 
$\mathfrak {D}'$ forms a bounded family and pairs in 
$\mathfrak {D}$ are isomorphic in codimension one to pairs in 
$\mathfrak {D}'$, [Reference Hacon, McKernan and XuHMX13, Lemma 2.4.2(3)] implies that 
$\mathfrak {D}$ is log birationally bounded.
Proof of Theorem 1.1 For the sake of presentation we divide this proof into steps.
For 
$2\leq n \leq 5$, we denote by 
$\mathfrak {E}_n$ the set of 
$n$-dimensional elliptic fibrations 
$f \colon Y \to X$ satisfying the hypotheses in the statement of the theorem. We fix the value of 
$n$. We denote by 
$S$ the Zariski closure of the rational section of 
$f$ whose existence is assumed in the statement of the theorem.
Step 0. In this step we show that there exists a finite set 
$I \subset [0, 1) \cap \mathbb {Q}$ which only depends on 
$n$ such that, for any normal variety 
$X$ that is the base of an elliptic fibrations 
$f \colon Y \to X$ in 
$\mathfrak {E}_n$, there exists an effective divisor 
$\Delta$ on 
$X$ with coefficients in 
$I$ and 
$(X, \Delta )$ is a klt Calabi–Yau pair.
Given an elliptic fibration 
$f \colon Y \to X \in \mathfrak {E}_n$, as 
$K_Y \sim _\mathbb {Q} 0$ and 
$Y$ is terminal, the canonical bundle formula (see Theorem 2.15) implies that
\[ K_Y \sim_\mathbb{Q} f^{{\ast}}(K_X+B_X+M_X), \]
where 
$B_X$ is the boundary part and 
$M_X$ is the moduli part. As the generic fibre of 
$f$ has dimension and genus one, Theorem 2.19 implies that there exists 
$m=m(n)$ for which the moduli part 
$|mM_{\hat {X}}|$ becomes base-point-free, on a suitable birational model 
$\hat {X} \to X$ of the base of the elliptic fibration. By Lemma 2.16, the coefficients of 
$B_X$ in turn belong to a DCC set 
$I'=I'(n) \subset \mathbb {Q}$. By choosing a sufficiently general member 
$\hat {M} \in |mM_{\hat {X}}|$, we can assume that the pair 
$(X, \Delta )$, 
$\Delta := B_X+({1}/{m})M$ is a klt Calabi–Yau pair, where 
$M$ is the pushforward of 
$\hat {M}$ on 
$X$; moreover, as the coefficients of 
$\Delta$ belong to the DCC set 
$I' \cup \{ 1/ m\}$, Theorem 2.8 implies that those actually lie in a finite set 
$I \subset I' \cup \{1 /m\}$. As 
$X$ is not of product type, Lemma 2.27 implies that 
$K_X \not \sim _\mathbb {Q} 0$, hence, 
$\Delta \neq 0$.
We denote by 
$\mathfrak {D}_n$ the set of 
$(n-1)$-dimensional klt Calabi–Yau pairs 
$(X, \Delta )$ that we have just constructed.
Step 1. In this step we prove that there exists a bounded set of pairs 
$\mathfrak {D}'_n$ such that any pair 
$(X, \Delta ) \in \mathfrak {D}_n$ is isomorphic in codimension one to a 
$\mathbb {Q}$-factorial klt Calabi–Yau pair 
$(X', \Delta ') \in \mathfrak {D}'_n$. The hypothesis on the 
$\mathbb {Q}$-factoriality of the 
$X'$ will be used in step 5.
Since for any Calabi–Yau pair 
$(X, \Delta ) \in \mathfrak {D}_n$, 
$X$ is not of product type and the coefficients of 
$\Delta$ lie in a finite set 
$I$, by step 0, Theorem 1.3 implies that there exists a bounded set of pairs 
$\bar {\mathfrak {D}}_n$ such that any 
$(X, \Delta ) \in \mathfrak {D}_n$ is isomorphic in codimension one to a klt Calabi–Yau pair 
$(\bar {X}, \bar {\Delta }) \in \bar {\mathfrak {D}}_n$. Hence, by definition of boundedness there exist a positive integer 
$\bar {C} = \bar {C}(n, I)$ and a very ample Cartier divisor 
$\bar {H}$ on 
$\bar {X}$ such that 
$\bar {H}^{\dim \bar {X}} \leq \bar {C}$. Given a pair 
$(X, \Delta ) \in \mathfrak {D}_n$, we define a pair 
$(X', \Delta ') \in \mathfrak {D}'_n$ as follows:
(a) if the variety
$\bar {X}$ defined above is $\mathbb {Q}$-factorial, we take $(X', \Delta ') := (\bar {X}, \bar {\Delta })$;(b) otherwise, we consider a small
$\mathbb {Q}$-factorialization $\bar {\pi } \colon X' \to \bar {X}$ of $\bar {X}$ together with the strict transform $\Delta '$ of $\bar {\Delta }$ on $X'$.
By construction, we know that the varieties from (a) belong to a bounded set. To show boundedness for the pairs 
$(X', \Delta ')$ in case (b), let 
$H_1 \in |2\bar {\pi }^{\ast }\bar {H}|$ be a sufficiently general member of the base-point-free linear system of 
$2\bar {\pi }^{\ast }\bar {H}$. The pair 
$(X', \Delta ' + \frac 1 2 H_1)$ is klt by Bertini's theorem and 
$K_{X'} +\Delta ' + \frac 1 2 H_1$ is big and nef. The volume of 
$K_{X'} +\Delta ' + \frac 1 2 H_1$ coincides with the volume of 
$\bar {H}$, hence it is an integer that is at most 
$\bar {C}$. Thus, [Reference Martinelli, Schreieder and TasinMST20, Theorem 6] implies that the pair 
$(X', \Delta ' + \frac 1 2 H_1)$ and thus also the pair 
$(X', \Delta ')$ belong to a bounded family of pairs. Hence, for any pair 
$(X', \Delta ') \in \mathfrak {D}'_n$ there exist a positive integer 
$C' = C'(n, I)$ and a very ample Cartier divisor 
$H'$ on 
$X'$ such that 
$H'^{n-1} \leq C'$.
Step 2. In this step we show that for any elliptic fibration 
$f \colon Y \to X$ in 
$\mathfrak {E}_n$ there exists an elliptic fibration 
$f' \colon Y' \to X'$ satisfying the following properties:
(i) there exists
$\Delta '$ such that $(X', \Delta ') \in \mathfrak {D}'_n$;(ii)
$Y'$ is projective, $\mathbb {Q}$-factorial, terminal, $K_{Y'} \sim _\mathbb {Q} 0$, and $Y'$ is isomorphic to $Y$ in codimension one.
Given 
$f \colon Y \to X$ in 
$\mathfrak {E}_n$, there exists a 
$\mathbb {Q}$-factorial klt Calabi–Yau pair 
$(X', \Delta ')$ in 
$\mathfrak {D}'_n$ isomorphic in codimension one to the pair 
$(X, \Delta )$ constructed in step 1. By Proposition 2.25, given a small 
$\mathbb {Q}$-factorialization 
$\tilde {X} \to X$ of 
$X$, there exists a terminal 
$\mathbb {Q}$-factorial projective elliptic variety 
$\tilde {f} \colon \tilde {Y} \to \tilde {X}$, and 
$\tilde {Y}$ is isomorphic to 
$Y$ in codimension one. As 
$\tilde {X}$ and 
$X'$ are isomorphic in codimension one and 
$\tilde {X}$ is 
$\mathbb {Q}$-factorial by construction, the existence of a fibration 
$f' \colon Y' \to X'$ satisfying (ii) is guaranteed by Proposition 2.26. In particular, 
$K_{Y'} \sim _{\mathbb {Q}} 0$.
We denote by 
$\mathfrak {E}'_n$ the set of elliptic Calabi–Yau fibrations 
$f' \colon Y' \to X'$ just constructed. Given any 
$f \colon Y \to X \in \mathfrak {E}_n$ and the corresponding 
$f' \colon Y' \to X' \in \mathfrak {E}'_n$, we will denote by 
$S'$ the strict transform of 
$S$ on 
$Y'$. The irreducible divisor 
$S'$ is still a rational section for the elliptic fibration 
$f' \colon Y' \to X'$ since 
$f'$ is isomorphic to 
$f$ over a dense open set of 
$X'$ by construction.
Step 3. In this step we show that for any elliptic fibration 
$f'\colon Y' \to X'$ in 
$\mathfrak {E}'_n$ we can run an 
$S'$-MMP over 
$X'$ with scaling of an ample divisor. We show that this MMP terminates with a relatively minimal model 
$f_m \colon Y^{m} \to X'$. Moreover, we show that 
$Y^{m}$ is terminal, 
$\mathbb {Q}$-factorial and isomorphic to 
$Y'$ in codimension one.
Given an elliptic fibration 
$f'\colon Y' \to X'$ in 
$\mathfrak {E}'_n$, as 
$S'$ is a rational section for 
$f'$ and 
$Y'$ is 
$\mathbb {Q}$-factorial, 
$S'$ is relatively big over 
$X'$. As 
$K_{Y'} \sim _\mathbb {Q} 0$, for any positive real 
$\gamma$,
\begin{equation} K_{Y'} + \gamma S' \sim_\mathbb{R} \gamma S'. \end{equation}
Since for a general fibre 
$F$ of 
$f'$, 
$S'\cdot F=1$, it follows that 
$K_{Y'} + \gamma S'$ is big over 
$X'$, and for any 
$0 < \gamma \ll 1$, 
$(Y', \gamma S')$ is klt. Thus, we can run the 
$(K_{Y'} + \gamma S')$-MMP with scaling of an ample divisor over 
$X'$ and by (21) this is also a run of the 
$S'$-MMP. By [Reference Birkar, Cascini, Hacon and McKernanBCHM10, Corollary 1.4.2], this run of the MMP terminates with a relatively minimal model 
$Y' \dashrightarrow Y^{m}$ since 
$S'$ is relatively big. The strict transform 
$S_m$ of 
$S'$ on 
$Y^{m}$ is big and nef over 
$X'$. As 
$Y^{m}$ is a relatively minimal model, it follows that it is 
$\mathbb {Q}$-factorial.
By (21), any extremal ray that is contracted in the run of the MMP in this step has negative intersection with the strict transform of 
$S'$. As 
$S'$ is irreducible, each step of the MMP must be a flip. In fact, if that were not the case, then there would be some step of the MMP which is a divisorial contraction and the exceptional divisor would then be the strict transform of 
$S'$; this is not possible since 
$S'$ is big over 
$X'$ and it is irreducible. Hence, 
$K_{Y^{m}}\sim _\mathbb {Q} 0$, and 
$Y'$ and 
$Y^{m}$ are isomorphic in codimension one. Since the relative dimension of 
$f' \colon Y' \to X'$ is one and the birational map 
$Y' \dashrightarrow Y^{m}$ is the outcome of the run of a relative MMP over 
$X'$, the exceptional locus of 
$Y' \dashrightarrow Y^{m}$ is vertical over 
$X'$; in particular, 
$f'$ and 
$f^{m}$ are isomorphic over a dense open set of 
$X'$, by construction. Hence, as 
$S'$ is a rational section for 
$f'$, the strict transform 
$S^{m}$ of 
$S'$ on 
$Y^{m}$ will be a rational section for 
$f^{m} \colon Y^{m} \to X'$.
We denote by 
$\mathfrak {E}^{m}_n$ the set of elliptic fibrations 
$f^{m} \colon Y^{m} \to X'$ that we have just constructed. We define the set
\[ \mathfrak{L}_n :=\{ Y_m \mid \exists f^{m} \colon Y^{m} \to X' \in \mathfrak{E}^{m}_n \}. \] Step 4. In this step we show that to prove the theorem it suffices to prove that 
$\mathfrak {L}_n$ is bounded.
Given any elliptic fibration 
$f \colon Y \to X$ in 
$\mathfrak {E}_n$, we have constructed an elliptic fibration 
$f^{m} \colon Y^{m} \to X'$ in 
$\mathfrak {E}^{m}_n$ such that 
$Y^{m}$ is isomorphic to 
$Y$ in codimension one, by steps 2 and 3. By construction, 
$Y^{m}$ is isomorphic to 
$Y'$ in codimension one, which is in turn isomorphic to 
$Y$ in codimension one. If 
$\mathfrak {L}_n$ is bounded, then the set of the 
$Y$ in 
$\mathfrak {E}_n$ is bounded up to isomorphisms in codimension one, which is what we wish to prove.
For the remainder of the proof, we fix an elliptic fibration 
$f^{m} \colon Y^{m} \to X'$ in 
$\mathfrak {E}^{m}_n$. We remind the reader that 
$S_m$ denotes the rational section of 
$f^{m}$ constructed in step 3 as the strict transform of the section 
$S$ of the corresponding fibration 
$f \colon Y \to X$.
Step 5. In this step we show that 
$(Y^{m}, S_m)$ is a purely log terminal pair.
By adjunction, it suffices to show that 
$(Y^{m}, S_m)$ is lc and 
$S_m$ is the only lc centre. Let us consider the normalization of 
$S_m$, 
$\nu \colon S_m^{\nu } \to S_m$. On 
$S_m^{\nu }$ there is a canonically defined effective divisor 
$\operatorname {\mathrm {Diff}}(0)$ such that 
$K_{S_m^{\nu }}+\operatorname {\mathrm {Diff}}(0)=\nu ^{\ast }((K_{Y^{m}}+S_m)|_{S_m})$; see [Reference KollárKol13, § 4.1]. In particular, 
$K_{S_m^{\nu }}+\operatorname {\mathrm {Diff}}(0)$ is relatively big and nef over 
$X'$. As 
$Y^{m}$ is terminal and 
$\mathbb {Q}$-factorial, Lemma 5.1 implies that
\begin{equation} (f^{m} \circ \nu)_\ast \operatorname{\mathrm{Diff}}(0)=0. \end{equation}
Thus, 
$(f^{m} \circ \nu )_\ast (K_{\bar {S}_m^{\nu }} + \operatorname {\mathrm {Diff}}(0))=K_{X'}$. As, by step 1, 
$X'$ is 
$\mathbb {Q}$-factorial, the negativity lemma [Reference Kollár and MoriKM98, Lemma 3.39] implies that
\[ K_{S_m^{\nu}}+\operatorname{\mathrm{Diff}}(0)=(f_m \circ \nu)^{{\ast}}(K_{X'}) -E, \]
where 
$E$ is an effective divisor exceptional over 
$X'$. Thus, the pair 
$(S_m^{\nu }, \operatorname {\mathrm {Diff}}(0))$ is klt, since 
$(X', 0)$ is. Hence, by inversion of adjunction [Reference Kollár and MoriKM98, Theorem 5.50], 
$S_m$ is the only lc centre of the pair 
$(Y^{m}, S_m)$ which in turn implies that 
$S_m$ is normal; see [Reference Kollár and MoriKM98, Proposition 5.51].
Step 6. In this step we fix a general member 
$G \in |f_m^{\ast }(2n+1) H'|$ and we show that 
$(Y^{m}, \frac 1 2 S_m+\frac 1 2 G)$ is 
$\frac 1 2$-klt and 
$K_{Y^{m}}+\frac 1 2 S_m+\frac 1 2 G$ is nef and big. Here 
$H'$ is the very ample divisor of bounded volume on 
$X'$ that was constructed at the end of step 1.
Since 
$|f_m^{\ast } (2n+1)H'|$ is base-point-free, Bertini's theorem implies that 
$(Y^{m}, S_m+G)$ is lc. On the other hand, 
$(Y^{m}, 0)$ is terminal, by step 3. As discrepancies of valuations are linear functions of the boundary divisor of a pair, it follows that 
$(Y^{m}, \frac 1 2 S_m+\frac 1 2 G)$ is 
$\frac 1 2$-klt. As 
$K_{Y^{m}} \sim _\mathbb {Q} 0$ and 
$S_m$ is relatively big, it follows immediately that 
$K_{Y^{m}}+\frac 1 2 S_m+\frac 1 2 G$ is big. As, for any 
$t \in \mathbb {R}$, 
$K_{Y^{m}}+t S_m+t G \sim _\mathbb {R} tS_m+tG$, showing nefness of 
$K_{Y^{m}}+\frac 1 2 S_m+\frac 1 2 G$ is equivalent to showing nefness of 
$K_{Y^{m}}+S_m+G$. Let us assume that 
$K_{Y^{m}}+S_m+G$ is not nef. Then the cone theorem for lc pairs [Reference FujinoFuj11b, Theorem 1.4] implies the existence of a 
$(K_{Y^{m}}+S_m+G)$-negative extremal ray 
$R \subset \overline {\mathrm {NE}}(X)$ which is spanned by the class of a curve 
$C \subset Y^{m}$ such that 
$0 <-((K_{Y^{m}}+S_m+G) \cdot C) \leq 2n$. As 
$G \sim f_m^{\ast } (2n+1) H'$ and 
$H'$ is ample and Cartier, 
$G \cdot C$ is either 
$0$ or 
$\geq 2n+1$ and, consequently, 
$(K_{Y^{m}} + S_m) \cdot C < 0$; moreover, as 
$K_{Y^{m}} + S_m$ is nef over 
$X'$, it follows that 
$C$ is not contained in a fibre of 
$f^{m}$, thus, 
$G \cdot C \geq 2n+1$. As the class of 
$C$ spans the extremal ray 
$R$, applying the cone theorem with the pair 
$(Y^{m}, S_m)$, there exists another curve 
$C'$ whose class spans 
$R$, 
$0< -(K_{Y^{m}} + S_m) \cdot C) \leq 2n$, and 
$G \cdot C' \geq 2n+1$. This leads to a contradiction, as then 
$(K_{Y^{m}} + S_m+G) \cdot C'> 0$ while the class of 
$C'$ was assumed to span a 
$(K_{Y^{m}} + S_m+G)$-negative extremal ray.
Step 7. In this step we show that there exist positive integers 
$C_i= C_i(n, I)$, 
$i=1, 2$, such that 
$C_1 \leq (K_{Y^{m}}+\frac 1 2 S_m+\frac 1 2 G)^{n} \leq C_2$.
As 
$K_{Y^{m}}+\frac 1 2 S_m+\frac 1 2 G$ is big, the existence of a positive lower bound only depending on 
$n$ and 
$I$ for 
$\operatorname {\mathrm {vol}}(Y^{m}, K_{Y^{m}}+\frac 1 2 S_m+\frac 1 2 G)$ follows from step 6 and [Reference Hacon, McKernan and XuHMX14, Theorem 1.3]. In step 6 we have shown that 
$S_m+G$ is big and nef. As 
$G$ is nef, it follows that for any 
$t \in [0, 1]$, 
$G+tS_m$ is nef. Hence, 
$(G+tS_m)^{n} \geq 0$ for any 
$t \in [0, 1]$, and since 
$G \sim f^{\ast }_m (2n+1) H'$ it follows that 
$G^{n} =0$ and
\[ (S_m+G)^{n}=S_m \cdot (S_m+G)^{n-1} + G \cdot (S_m+G)^{n-1}. \]
The adjunction formula for 
$S_m$ yields (cf. step 5),
\[ (K_{Y^{m}} + S_m)\vert_{S_m} = S_m\vert_{S_m} = K_{S_m} + \operatorname{\mathrm{Diff}}(0) = (f_m \circ \nu)^{{\ast}} (K_{X'}) - E, \quad E, \operatorname{\mathrm{Diff}}(0) \geq 0. \]
By the canonical bundle formula (cf. Theorem 2.15), 
$-K_{X'}$ is effective, thus, 
$L:=-((f_m \circ \nu )^{\ast } (K_{X'}) - E)$ is effective, so that
\begin{align*} S_m \cdot (S_m+G)^{n-1} &= (S_m\vert_{S_m}+G\vert_{S_m})^{n-1} = \operatorname{\mathrm{vol}}(S_m, G\vert_{S_m} - L) \leq \operatorname{\mathrm{vol}}(S_m, G\vert_{S_m}) \\ &= \operatorname{\mathrm{vol}}(S_m, f_m\vert_{S_m}^{{\ast}} (2n+1)H')\\ &= \operatorname{\mathrm{vol}}(X',(2n+1)H') \leq (2n+1)^{n-1} C', \end{align*}
where 
$C'= C'(n, I)$ is the positive integer whose existence has been shown in step 1, and for which 
$H'^{n-1} \leq C'$.
In order to bound 
$G \cdot (S_m+G)^{n-1}$ we prove the following claim.
Claim For any 
$0<k \leq n$,
\[ \ G^{k}\cdot (S_m+G)^{n-k}\leq (n-k)(2n+1)^{n-1} C'. \]Proof We prove the claim by descending induction on 
$k$.
The claim holds for 
$k=n$, as 
$G^{n}=0$. Hence we can assume that 
$k<n$ and that the claim holds for 
$k+1$.
Then, as in the previous paragraph, we have that
\begin{align*} G^{k}\cdot (S_m+G)^{n-k} &= G^{k}\cdot (S_m+G) \cdot (S_m+G)^{n-k-1} \\ &=G^{k+1} \cdot (S_m+G)^{n-k-1} + S_m \cdot G^{k} \cdot (S_m+G)^{n-k-1} \\ &\leq (n-k-1)(2n+1)^{n-1} C' + S_m \cdot G^{k} \cdot (S_m+G)^{n-k-1}, \end{align*}where the final inequality follows from inductive hypothesis. Hence, to prove the claim, it suffices to show that
\[ S_m \cdot G^{k} \cdot (S_m+G)^{n-k-1} \leq (2n+1)^{n-1} C'. \]As above,
\[ S_m \cdot G^{k} \cdot (S_m+G)^{n-k-1} = G\vert_{S_m}^{k} \cdot (G\vert_{S_m} - L)^{n-k-1} \leq G\vert_{S_m}^{n-1}, \]
where the last inequality follows from the fact that 
$G\vert _{S_m}$ is a semiample divisor and 
$L$ is effective. Finally, as we have already seen above, 
$G\vert _{S_m}^{n-1} \leq (2n+1)^{n-1} C'$.
Thus, to conclude the proof of this step, it suffices to take 
$C_2 := n(2n+1)^{n-1} H'^{n-1}$.
Step 8. In this step, the proof is concluded.
For any 
$Y^{m} \in \mathfrak {L}_n$, we have constructed a pair 
$(Y^{m}, \frac 1 2 S_m+\frac 1 2 G)$ which is 
$\frac 1 2$-klt. The set of coefficients of the boundaries of such pairs is the set 
$\{\frac 1 2\}$. By steps 6 and 7 and [Reference FilipazziFil20b, Theorem 1.3], 
$K_{Y^{m}}+\frac 1 2 S_m+\frac 1 2 G$ is nef and big and its volume lies in a discrete set 
$J$ of 
$[C_1, C_2] \subset \mathbb {R}_{>0}$, where 
$C_i=C_i(n, I)$. The set 
$J$ is discrete and limited in a closed interval, hence finite. Thus, the set of pairs 
$(Y^{m}, \frac 1 2 S_m+\frac 1 2 G)$ constructed in step 6, where 
$Y^{m} \in \mathfrak {L}_n$, is bounded by [Reference Martinelli, Schreieder and TasinMST20, Theorem 6]. In particular, the set 
$\mathfrak {L}_n$ itself is bounded and, by step 4, this concludes the proof.
Lemma 5.1 Let 
$g \colon T \to B$ be a surjective morphism of normal quasi-projective varieties with 
$\dim T -\dim B=1$. Assume that 
$(T, 0)$ is terminal and that there exists a rational section 
$s \colon B \dashrightarrow T$. Let 
$S$ be the Zariski closure of 
$s(B)$ and let 
$\nu \colon S^{\nu } \to S$ be the normalization of 
$S$. Then 
$\operatorname {\mathrm {Diff}}_{S^{\nu }}(0)$ is exceptional over 
$B$.
Proof. Since 
$s$ is a rational section, the finite part in the Stein factorization of 
$g$ is an isomorphism. Hence we can assume that 
$g$ is a contraction.
Since 
$T$ is terminal, it is smooth in codimension two. In particular, 
$\omega _T(S)$ is locally free at each codimension-one point of 
$S$. Let 
$P \in S$ be a codimension-one point such that 
$g\vert _S(P)=Q \in B$ and 
$Q$ is codimension one. As 
$T$ is smooth at 
$P$, it suffices to show that 
$S$ is normal at 
$P$, since then 
$\nu$ would be an isomorphism locally around 
$P$ and the coefficient of 
$\operatorname {\mathrm {Diff}}_{S^{\nu }}(0)$ at the codimension-one point 
$\nu ^{-1}(P)$ would be 
$0$.
Considering the birational morphism 
$g\vert _S \circ \nu \colon S^{\nu } \to B$, the generic point 
$P'$ of the strict transform of the closure of 
$Q$ on 
$S^{\nu }$ is the unique codimension-one point which is mapped to 
$Q$. Hence, 
$g\vert _S^{-1}(Q)=P$ and, furthermore, 
$\nu ^{-1}(P)=P'$. Since 
$B$ is normal quasi-projective, the map 
$s$ is well defined at 
$Q$, and 
$s(Q)=P$ since 
$g\vert _S\circ s$ is the identity around 
$Q$ and 
$P$ is the only point above 
$Q$. Then there exists a lift 
$s_\nu \colon B \dashrightarrow S^{\nu }$ which is well defined at 
$Q$ and such that 
$\nu \circ s_\nu =s$ and 
$s_\nu (Q)=P'$ by construction. But then, since 
$S^{\nu }$ is smooth at 
$P'$ and 
$g\vert _S \circ \nu \circ s_\nu$ is the identity of 
$B$ and a morphism around 
$P$, it follows that 
$s_\nu$ is an isomorphism locally around 
$P$ and the same holds for 
$s$, which implies that normality of 
$S$ at 
$P$.
6. Proof of the corollaries
In this section we prove the corollaries stated in the Introduction.
Proof of Corollary 1.10 The canonical bundle formula and Theorem 2.17 imply that there exist a positive real number 
$\delta =\delta (n, I) >0$ an effective divisor 
$\Gamma _Z$ on 
$Z$ such that 
$(Z, \Gamma _Z)$ is a 
$\delta$-klt Calabi–Yau pair. As 
$-K_Z$ is big, Theorem 2.12 implies that 
$Z$ belongs to a bounded family. Finally, Theorem 1.9 concludes the proof.
Proof of Corollary 1.6 Let 
$\mathfrak {D}$ be the set of pairs 
$(X, \Delta )$ satisfying the hypotheses of the statement of the corollary. By Theorem 1.3, there exists a bounded set of pairs 
$\mathfrak {D}'$ such that for any pair 
$(X, \Delta ) \in \mathfrak {D}$ there exists a pair 
$(X', \Delta ') \in \mathfrak {D}'$ such that 
$(X, \Delta )$, 
$(X', \Delta ')$ are isomorphic in codimension one, so that 
$\rho (X)=\rho (X')$, and for any 
$m \in \mathbb {N}$, 
$h^{0}(X, m(K_X+\Delta ))= h^{0}(X, m(K_{X'}+\Delta '))$. Moreover, by [Reference Martinelli, Schreieder and TasinMST20, Theorem 6], we can assume that the pairs in 
$\mathfrak {D}'$ are 
$\mathbb {Q}$-factorial, so that 
$\rho (X') \leq h^{2}(X', \mathbb {Q})$. Hence, it suffices to show that the conclusion in the statement of the corollary holds for the pairs in 
$\mathfrak {D}''$. Furthermore, since 
$(X, \Delta ) \in \mathfrak {D}$ are not of product type, Definition 2.24 readily implies that the same holds for 
$(X', \Delta ')\in \mathfrak {D}'$, as these pairs are isomorphic in codimension one.
By definition of boundedness, there exists a pair 
$(Z, D) \to T$ over a base 
$T$ of finite type such that for any pair 
$(X', \Delta ') \in \mathfrak {D}''$, there exists 
$t \in T$ such that the pair 
$(Z_t, D_t)$ is isomorphic to 
$(X', \Delta ')$. By substituting 
$T$ with the Zariski closure of the set of points 
$t \in T$ for which 
$(Z_t, D_t)$ is isomorphic to a pair 
$(X', \Delta ') \in \mathfrak {D}'$, we can then assume that the set of such 
$t$ is Zariski dense in 
$T$.
Up to decomposing 
$T$ into a finite union of locally closed subsets, we may assume that there exists a log resolution 
$\psi \colon (Z', D') \to Z$ of 
$(Z, D)$, where 
$D'$ is the sum of the strict transform of 
$D$ and the exceptional divisor of 
$\psi$. Furthermore, up to decomposing 
$T$ further into a finite union of locally closed subsets, we may also assume that, for any 
$t \in T$, 
$(Z'_t, D'\vert _{Z'_t})$ is a log resolution of 
$(Z_t, D\vert _{Z_t})$. In particular, for any 
$t \in T$, for all 
$m > 0$,
\[ H^{0}(Z_t, \mathcal{O}_{Z_t}(m(K_{Z_t}+D\vert_{Z_t}))) = H^{0}(Z'_t, \mathcal{O}_{Z'_t}(m(K_{Z'_t}+D'\vert_{Z'_t}))). \]
Then [Reference Hacon, McKernan and XuHMX18, Theorem 4.2] implies that, for any connected component 
$\bar {T}$ of 
$T$, 
$h^{0}(Z_t, \mathcal {O}_{Z_t}(m(K_{Z_t}+D\vert _{Z_t})))$ is independent of 
$t \in \bar {T}$, for all 
$m >0$. At this point, we discard those connected components of 
$T$ such that 
$(Z_t, D_t)$ is isomorphic to one of the pairs in 
$\mathfrak {D}'$. By construction, then, for a connected component 
$\bar {T}_i$ of 
$T$, there exist 
$\bar {t}_i \in \bar {T}_i$ and a positive integer 
$\bar {m}_i$ such that 
$\bar {m}_i(K_{Z_{\bar {t}_i}} + D\vert _{Z_{\bar {t}_i}}) \sim 0$; thus, by construction,
\begin{equation} h^{0}(Z_{\bar{t}_i}, \mathcal{O}_{Z_{\bar{t}_i}}(\bar{m}_i(K_{Z_{\bar{t}_i}} + D\vert_{Z_{\bar{t}_i}}))=1, \quad \forall \,\bar{t}_i \in \bar{T}_i. \end{equation}
Hence, it suffices to define 
$m_0$ to be the maximum of the positive integers 
$\bar {m}_i$ just defined; 
$m_0$ is well defined as 
$T$ has only finitely many connected components, being of finite type, by definition of boundedness.
We turn now to showing that the Picard ranks of the fibres of 
$(Z, D) \to T$ are bounded. Since for any 
$(X', \Delta ') \in \mathfrak {D}'$, 
$\rho (X') \leq h^{2}(X', \mathbb {Q})$, it suffices to show that there exists a positive integer 
$\rho$ such that 
$h^{2}(Z_t, \mathbb {Q}) \leq \rho$ for any 
$t \in T$. By Verdier's generalization of Ehresmann's theorem [Reference VerdierVer76, Corollaire 5.1], up to decomposing 
$T$ into a disjoint union of finitely many locally closed subvarieties, we can assume that 
$Z \to T$ is a locally trivial topological fibration. Hence, on each connected component 
$\bar {T}_i$ of 
$T$, there exists 
$\bar {\rho }_i$ such that
\[ h^{2}(Z_t, \mathbb{Q})=\bar{\rho}_i, \quad \forall \, t \in \bar{T}_i. \]
Hence, it suffices to define 
$\rho$ to be the maximum of the positive integers 
$\bar {\rho }_i$ just defined.
Proof of Corollary 1.4 Let 
$\pi \colon Y \rightarrow X$ be an elliptic fibration satisfying the hypotheses of the statement of the corollary. Using the canonical bundle formula (cf. Theorem 2.15), by Theorem 2.19 and Lemma 2.16 there exists a divisor 
$\Delta$ on 
$X$ such that 
$(X, \Delta )$ is a klt Calabi–Yau pair and the coefficients of 
$\Delta$ are in a DCC set 
$J=J(n, I)$; by Theorem 2.8, we can assume that the set 
$J$ is finite. By Lemma 2.27, as 
$Y$ is not of product type, 
$\Delta \neq 0$ and 
$(X, \Delta )$ is not of product type. The result then follows from Theorem 1.3.
Proof of Corollary 1.7 By Theorem 2.8, we can assume that the coefficients of 
$\Delta$ belong to a finite set 
$I_0 \subset I$.
As 
$f$ has maximal variation, then the moduli part 
$M_Z$ induced by the canonical bundle formula (Theorem 2.15) for 
$(X, \Delta )$ is big; see Remark 2.20. In particular, 
$-K_Z$ is big, because 
$K_Z+B_Z+M_Z \sim _{\mathbb {R}}0$ and 
$B_Z$ is effective.
As 
$\Delta$ is big over 
$Z$, for 
$0< \eta \ll 1$ we can run the relative 
$(K_X+(1+\eta )\Delta )$-MMP, and this terminates with an ample model 
$f' \colon X' \to Z$ on which the strict transform 
$\Delta '$ of 
$\Delta$ is ample over 
$Z$. We first show that the set of pairs 
$(X', \Delta ')$ forms a bounded family.
As the coefficients of 
$\Delta '$ belong to 
$I_0$, given a general fibre 
$F'$ of 
$f'$, the pair 
$(F', \Delta '\vert _{F'})$ belongs to a bounded family by Corollary 2.9 and Theorem 2.12. Theorem 2.17 together with Remark 2.18 implies that there exist 
$\delta =\delta (n, I_0)$ and a big effective divisor 
$\Gamma _Z$ on 
$Z$ such that 
$(Z, \Gamma _Z)$ is a 
$\delta$-klt Calabi–Yau pair and 
$\Gamma _Z$ is big, since 
$-K_Z$ is big. Thus, Theorem 2.12 implies that the set 
$\mathfrak {F}$ of varieties 
$Z$ forms a bounded family. As 
$-K_{X'}$ is 
$f'$-ample and 
$\mathfrak {F}$ forms a bounded family, Theorem 1.9 implies that the set 
$\mathfrak {D}''$ of pairs 
$(X', \Delta ')$ forms a bounded family.
As the set of pairs 
$(X', \Delta ')$ forms the bounded family 
$\mathfrak {D}''$, [Reference Hacon and XuHX15, Proposition 2.5] implies that there exists a bounded family 
$(Z,D)\rightarrow T$ such that, for any pair 
$(X',\Delta ')$ and for any set 
$\{E_1, \ldots, E_k\}$ of exceptional divisors of discrepancy at most zero over 
$(X', \Delta ')$, there exist 
$t\in T$ and a birational morphism 
$\mu _t : Z_t \rightarrow X'$ which extracts precisely 
$\{E_1, \ldots, E_k\}$ and 
$K_{Z_t}+D_t=\mu _t^{*} (K_{X'} +\Delta ')$. Since 
$K_X +\Delta \sim _\mathbb {R} 0$ and 
$K_{X'} +\Delta ' \sim _\mathbb {R} 0$, all the exceptional divisors for 
$r \colon X \dashrightarrow X'$ have discrepancy 
$\leq 0$ with respect to 
$(X', \Delta ')$. In particular, 
$(X, \Delta )$ is birational in codimension one to a pair 
$(Z_s, D_s)$ for some closed point 
$s \in T$. Defining 
$\mathfrak {D}'$ to be the set of pairs 
$(Z_s, D_s)$ just constructed completes the proof.
Proof Corollary 1.2 By Theorem 1.1 there exists a family 
$\mathcal {X}\rightarrow \mathcal {T}$ such that any elliptic Calabi–Yau manifold with a section is birational in codimension one to a fibre 
$\mathcal {X}_s$ of the family. Let 
$\mathcal {Y}\rightarrow \mathcal {X}$ be a log resolution. Since the generic fibre of 
$\mathcal {Y}$ is smooth, there exists a Zariski open subset 
$U$ of 
$\mathcal {T}$ such that the 
$E(\mathcal {Y}_s)$ does not depend on 
$s\in U$, where 
$E$ is the Euler function of a smooth variety. By the definition of the stringy 
$E$-function [Reference BatyrevBat99], we have that 
$E(\mathcal {X}_s)$ is constant over 
$U$ as well. By Noetherian induction, it follows that we obtain only a finite number of stringy 
$E$-functions from the fibres of 
$\mathcal {X}\rightarrow \mathcal {T}$.
Let 
$X$ be a smooth elliptic Calabi–Yau with a section. By Theorem 1.1, 
$X$ is K-equivalent to 
$\mathcal {X}_s$ for some 
$s$, and [Reference VeysVey01, Theorem 2.7] implies that they have the same 
$E$-function. In particular, there are finitely many possibilities for the 
$E$-function of an elliptic Calabi–Yau with a section. The Hodge numbers are precisely the coefficients of those functions, and thus they are uniformly bounded. See [Reference VeysVey01] for more details.
Acknowledgements
We would like to thank Paolo Cascini, Johan de Jong, Antonella Grassi, Christopher Hacon, János Kollár, James McKernan, Edward Witten and Chenyang Xu for many valuable conversations, suggestions and comments. We wish to thank the anonymous referees for many corrections, improvements, and suggestions regarding the paper.
