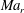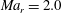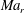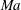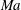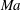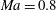1 Introduction
Understanding high-speed transitional wakes is of great interest in scramjet engines, aero-optic laser diffraction and transonic turbomachinery. At the heart of this interest lies the desire to modify, predict and/or control the large-scale coherent structures originating during transition. This is especially important as wakes interact with other canonical flows in most applications (Wu et al. Reference Wu, Jacobs, Hunt and Durbin1999; Wu & Hickey Reference Wu and Hickey2012). From an engineering perspective, these highly anisotropic transitional structures are important for their mixing enhancement potential as they are the main contributors to the large-scale entrainment (Brown & Roshko Reference Brown and Roshko1974), a generally desired attribute for fuel injector systems. At the same time, these structures are one of the primary sources of aeroacoustic disturbances resulting from the large pressure gradients and vortical reconnection (Sandham Reference Sandham1994; Virk, Hussain & Kerr Reference Virk, Hussain and Kerr1995; Bastin, Lafon & Candel Reference Bastin, Lafon and Candel1997; Hussain & Duraisamy Reference Hussain and Duraisamy2011) which, downstream, may lead to combustion oscillations in supersonic propulsion systems (Choi, Ma & Yang Reference Choi, Ma and Yang2005). In order to control these conflicting characteristics, the effects of compressibility on the transitional high-speed wake need to be much better understood.
Characterizing compressibility effects. Insight into compressibility effects (understood herein as Mach number effects) in free-shear flows has historically been gained through the study of the high-speed mixing layer – a simple and ubiquitous free shear flow. The most intriguing effect is the reduced lateral spreading with increased convective Mach number,
![]() $Ma_{c}$
. From early experiments, the reduced turbulent kinetic energy (TKE) could qualitatively explain the lower spread rate; density variations only have a second-order effect (Brown & Roshko Reference Brown and Roshko1974). What is less clear is the exact mechanism by which compressibility limits TKE growth. From the governing equations, the evolution of TKE for a compressible flow is written as
$Ma_{c}$
. From early experiments, the reduced turbulent kinetic energy (TKE) could qualitatively explain the lower spread rate; density variations only have a second-order effect (Brown & Roshko Reference Brown and Roshko1974). What is less clear is the exact mechanism by which compressibility limits TKE growth. From the governing equations, the evolution of TKE for a compressible flow is written as
where
![]() $P$
,
$P$
,
![]() ${\it\Sigma}^{d}$
,
${\it\Sigma}^{d}$
,
![]() $\overline{{\it\epsilon}}_{s}$
and
$\overline{{\it\epsilon}}_{s}$
and
![]() $\overline{{\it\epsilon}}_{d}$
are respectively the production, pressure-dilatation correlation, solenoidal dissipation and dilatational dissipation. Early works attributed the lower turbulent kinetic energy to a negative pressure–dilatational and dilatational dissipation terms in shear flows (Zeman Reference Zeman1990; Sarkar, Erlebacher & Hussaini Reference Sarkar, Erlebacher and Hussaini1991). But the dilatation alone cannot account for the extent of the TKE reduction as the increased dilatation with
$\overline{{\it\epsilon}}_{d}$
are respectively the production, pressure-dilatation correlation, solenoidal dissipation and dilatational dissipation. Early works attributed the lower turbulent kinetic energy to a negative pressure–dilatational and dilatational dissipation terms in shear flows (Zeman Reference Zeman1990; Sarkar, Erlebacher & Hussaini Reference Sarkar, Erlebacher and Hussaini1991). But the dilatation alone cannot account for the extent of the TKE reduction as the increased dilatation with
![]() $Ma$
is modest apart from a very limited region of the flow found within a shock wave. Breidenthal (Reference Breidenthal1992) proposed a novel structural explanation for the reduced spread rate using a sonic-eddy model to account for the reduced entrainment of high-speed flows. Numerical simulations have led us to conclude that the reduction of the pressure–strain term implicitly inhibits the turbulence production by reducing the transfer among velocity components (Blaisdell, Mansour & Reynolds Reference Blaisdell, Mansour and Reynolds1993; Vreman, Sandham & Luo Reference Vreman, Sandham and Luo1996; Pantano & Sarkar Reference Pantano and Sarkar2002; Foysi & Sarkar Reference Foysi and Sarkar2010). Naturally, the delayed return to isotropy caused by the finite propagation speed of the acoustic waves modifies the near-field anisotropy of the flow (Pantano & Sarkar Reference Pantano and Sarkar2002). Pantano & Sarkar (Reference Pantano and Sarkar2002) showed, using an analysis based on the wave equation of a pressure perturbation, that the pressure–strain term decreases monotonically with increasing
$Ma$
is modest apart from a very limited region of the flow found within a shock wave. Breidenthal (Reference Breidenthal1992) proposed a novel structural explanation for the reduced spread rate using a sonic-eddy model to account for the reduced entrainment of high-speed flows. Numerical simulations have led us to conclude that the reduction of the pressure–strain term implicitly inhibits the turbulence production by reducing the transfer among velocity components (Blaisdell, Mansour & Reynolds Reference Blaisdell, Mansour and Reynolds1993; Vreman, Sandham & Luo Reference Vreman, Sandham and Luo1996; Pantano & Sarkar Reference Pantano and Sarkar2002; Foysi & Sarkar Reference Foysi and Sarkar2010). Naturally, the delayed return to isotropy caused by the finite propagation speed of the acoustic waves modifies the near-field anisotropy of the flow (Pantano & Sarkar Reference Pantano and Sarkar2002). Pantano & Sarkar (Reference Pantano and Sarkar2002) showed, using an analysis based on the wave equation of a pressure perturbation, that the pressure–strain term decreases monotonically with increasing
![]() $Ma$
as the acoustic interaction time increases.
$Ma$
as the acoustic interaction time increases.
Fewer studies have specifically tackled compressibility effects in the planar wake. This is partly because the compressibility effects, characterized by the relative Mach number
![]() $Ma_{r}=U_{o}/c_{\infty }$
(where
$Ma_{r}=U_{o}/c_{\infty }$
(where
![]() $U_{o}$
is the centreline velocity defect and
$U_{o}$
is the centreline velocity defect and
![]() $c_{\infty }$
the free-stream speed of sound), are not constant and, therefore, more difficult to isolate than in the mixing layer. As
$c_{\infty }$
the free-stream speed of sound), are not constant and, therefore, more difficult to isolate than in the mixing layer. As
![]() $Ma_{r}$
monotonically decreases with the wake evolution, so does the influence of compressibility. The coupling between the compressibility and the wake evolution raises an important question on the scaling of the wake. On one hand, if compressibility inhibits the spread rate through reduction of the pressure–strain term, as is the case for the mixing layer, the wake half-width appears to be an ill-suited non-dimensionalization parameter, as the spread rate would reduce with reducing compressibility as the wake evolves. On the other hand, if the spread rate remains invariant to the decreasing
$Ma_{r}$
monotonically decreases with the wake evolution, so does the influence of compressibility. The coupling between the compressibility and the wake evolution raises an important question on the scaling of the wake. On one hand, if compressibility inhibits the spread rate through reduction of the pressure–strain term, as is the case for the mixing layer, the wake half-width appears to be an ill-suited non-dimensionalization parameter, as the spread rate would reduce with reducing compressibility as the wake evolves. On the other hand, if the spread rate remains invariant to the decreasing
![]() $Ma_{r}$
with the wake evolution (in the mid- and far-wake when compressibility may still be non-negligible), a structure-based explanation must be sought for the contrast with the mixing layer results. Even though the wake tends toward a fully incompressible state as the velocity defect becomes null, it does not necessarily mean that the self-similar states of the incompressible and high-speed wakes are identical. Since free-shear flows maintain a ‘memory’ of their origin, it can be inferred that a differing far-wake structural organization and statistics found by Bonnet et al. (Reference Bonnet, Delville, Sapin, Sullivan and Yeru1991) and Hickey, Hussain & Wu (Reference Hickey, Hussain and Wu2013) may be related to the near-wake and/or transitional evolution.
$Ma_{r}$
with the wake evolution (in the mid- and far-wake when compressibility may still be non-negligible), a structure-based explanation must be sought for the contrast with the mixing layer results. Even though the wake tends toward a fully incompressible state as the velocity defect becomes null, it does not necessarily mean that the self-similar states of the incompressible and high-speed wakes are identical. Since free-shear flows maintain a ‘memory’ of their origin, it can be inferred that a differing far-wake structural organization and statistics found by Bonnet et al. (Reference Bonnet, Delville, Sapin, Sullivan and Yeru1991) and Hickey, Hussain & Wu (Reference Hickey, Hussain and Wu2013) may be related to the near-wake and/or transitional evolution.
Transition of planar wakes. As for all shear flows, the compressibility has a stabilizing effect in the wake (Behrens Reference Behrens1968; Demetriades Reference Demetriades1971), a finding confirmed by hydrodynamic stability calculations (Chen, Cantwell & Mansour Reference Chen, Cantwell and Mansour1990; Watanabe & Maekawa Reference Watanabe and Maekawa2004). In contrast to the obliquity of the primary instability mode in the high-speed mixing layer (above
![]() $Ma_{c}=0.6$
), a two-dimensional anti-symmetric mode is found to be dominant for all Mach numbers in the planar wake (Chen et al.
Reference Chen, Cantwell and Mansour1990). This result was nuanced by Papageorgiou (Reference Papageorgiou1990) who questioned the validity of the parallel flow assumption inherent in the temporal stability calculations and showed that a three-dimensional wave inclined at
$Ma_{c}=0.6$
), a two-dimensional anti-symmetric mode is found to be dominant for all Mach numbers in the planar wake (Chen et al.
Reference Chen, Cantwell and Mansour1990). This result was nuanced by Papageorgiou (Reference Papageorgiou1990) who questioned the validity of the parallel flow assumption inherent in the temporal stability calculations and showed that a three-dimensional wave inclined at
![]() $60^{\circ }$
has the highest growth rate for spatially evolving wakes with a Gaussian velocity profile at
$60^{\circ }$
has the highest growth rate for spatially evolving wakes with a Gaussian velocity profile at
![]() $Ma_{\infty }=3.0$
. The obliquity of the transitional mode was experimentally observed by Lysenko (Reference Lysenko1999) by artificially forcing a splitter-plate wake at
$Ma_{\infty }=3.0$
. The obliquity of the transitional mode was experimentally observed by Lysenko (Reference Lysenko1999) by artificially forcing a splitter-plate wake at
![]() $Ma_{\infty }=2.0$
. It is unclear why the observed oblique perturbation undergoes the largest growth. It could be related to one of the following reasons: (i) the growth of the most unstable oblique mode, as found by Papageorgiou (Reference Papageorgiou1990); (ii) as hypothesized by Lysenko (Reference Lysenko1999), a receptivity of an inclined symmetric mode which emerges for
$Ma_{\infty }=2.0$
. It is unclear why the observed oblique perturbation undergoes the largest growth. It could be related to one of the following reasons: (i) the growth of the most unstable oblique mode, as found by Papageorgiou (Reference Papageorgiou1990); (ii) as hypothesized by Lysenko (Reference Lysenko1999), a receptivity of an inclined symmetric mode which emerges for
![]() $Ma_{r}>1.2$
(Watanabe & Maekawa Reference Watanabe and Maekawa2004); (iii) a secondary acoustic mode which resonates between the sonic lines of the wake as in the boundary layer (Mack Reference Mack1990); or (iv) a triadic nonlinear interaction as observed in the
$Ma_{r}>1.2$
(Watanabe & Maekawa Reference Watanabe and Maekawa2004); (iii) a secondary acoustic mode which resonates between the sonic lines of the wake as in the boundary layer (Mack Reference Mack1990); or (iv) a triadic nonlinear interaction as observed in the
![]() $H$
-type transition in the boundary layer (Hebert Reference Hebert1988). The debate surrounding the origin of the three-dimensional modes remains open and central to the understanding of the transitional mechanism of the planar wake.
$H$
-type transition in the boundary layer (Hebert Reference Hebert1988). The debate surrounding the origin of the three-dimensional modes remains open and central to the understanding of the transitional mechanism of the planar wake.
Structures in high-speed flows. There has been some debate on the presence (or absence) of transitional spanwise coherent rollers in the planar wake. Kendall (cited in Laufer (Reference Laufer1975)) noted a clear absence of structures in the transitional region. More recently, experiments by Clemens & Smith (Reference Clemens and Smith1998) found that the high-speed wake shares many structural similarities with its incompressible counterpart, most importantly in terms of the two-dimensionality of the transitional rollers connected by rib-like structures. From experiments, it is difficult to establish the origin of the transitional structures, as they may emerge due to linear growth of an unstable mode or due to the receptivity of the unsteady Kutta condition (Barone & Lele Reference Barone and Lele2005). Alternatively, the structures may also originate from the two-dimensional convective instability in the base flow (Sandham & Sandberg Reference Sandham and Sandberg2009). What is clear, is that the wake and the transitional structures are highly sensitive to the splitter-plate design (Althaus Reference Althaus1990). In the intermediate and far wake, the two-dimensionality of the structures has been well established (Bonnet & Chaput Reference Bonnet and Chaput1986; Nakagawa & Dahm Reference Nakagawa and Dahm2006) having a Strouhal number of 0.3 (Behrens & Ko Reference Behrens and Ko1971; Gai, Hughes & Perry Reference Gai, Hughes and Perry2002).
Direct numerical simulations of idealized wakes help clarify the transitional mechanisms and structures. Using a laminar base flow with eigenmode perturbations, Chen et al. (Reference Chen, Cantwell and Mansour1990) and Watanabe & Maekawa (Reference Watanabe and Maekawa2004) showed many qualitative similarities with the low-speed wake: two-dimensional and staggered spanwise rollers connected by rib-like structures. This apparent structural invariance to
![]() $Ma$
contrasts the emergence of
$Ma$
contrasts the emergence of
![]() ${\it\Lambda}$
-type structures in the high-speed mixing layer (Kourta & Sauvage Reference Kourta and Sauvage2002). When the base flow was perturbed with broadband random fluctuations (Watanabe & Maekawa Reference Watanabe and Maekawa2004), an oblique mode briefly dominates the early wake evolution before being overtaken by the growth of the primary two-dimensional mode: clearly an unexpected finding based on linear stability results. Unfortunately, the available direct numerical simulations of high-speed planar wakes (Chen et al.
Reference Chen, Cantwell and Mansour1990; Watanabe & Maekawa Reference Watanabe and Maekawa2004) are inadequate to fully understand the origin of the three-dimensional modes. More specifically, it is unclear if they are caused by an oblique principal mode, or by the receptivity of a secondary symmetric mode. The reasons for the inadequacy of existing DNS simulations are: (i) the limited streamwise and spanwise computational domains (
${\it\Lambda}$
-type structures in the high-speed mixing layer (Kourta & Sauvage Reference Kourta and Sauvage2002). When the base flow was perturbed with broadband random fluctuations (Watanabe & Maekawa Reference Watanabe and Maekawa2004), an oblique mode briefly dominates the early wake evolution before being overtaken by the growth of the primary two-dimensional mode: clearly an unexpected finding based on linear stability results. Unfortunately, the available direct numerical simulations of high-speed planar wakes (Chen et al.
Reference Chen, Cantwell and Mansour1990; Watanabe & Maekawa Reference Watanabe and Maekawa2004) are inadequate to fully understand the origin of the three-dimensional modes. More specifically, it is unclear if they are caused by an oblique principal mode, or by the receptivity of a secondary symmetric mode. The reasons for the inadequacy of existing DNS simulations are: (i) the limited streamwise and spanwise computational domains (
![]() $L_{x}$
twice the most unstable wavelength (Chen et al.
Reference Chen, Cantwell and Mansour1990)) cannot capture the symmetric instability mode which is over twice the streamwise wavelength at
$L_{x}$
twice the most unstable wavelength (Chen et al.
Reference Chen, Cantwell and Mansour1990)) cannot capture the symmetric instability mode which is over twice the streamwise wavelength at
![]() $Ma=2.0$
, (ii) the low Reynolds number of the simulations (
$Ma=2.0$
, (ii) the low Reynolds number of the simulations (
![]() $Re=300$
in Chen et al. (Reference Chen, Cantwell and Mansour1990) and up to
$Re=300$
in Chen et al. (Reference Chen, Cantwell and Mansour1990) and up to
![]() $Re=1000$
in Watanabe & Maekawa (Reference Watanabe and Maekawa2004)) limits the growth of the oblique instability mode, which is shown herein to be very sensitive to viscous effects at low Reynolds numbers. These shortcomings invite a closer investigation of transitional mechanisms with modern day computational resources with a canonical set-up, free of trailing edge effects.
$Re=1000$
in Watanabe & Maekawa (Reference Watanabe and Maekawa2004)) limits the growth of the oblique instability mode, which is shown herein to be very sensitive to viscous effects at low Reynolds numbers. These shortcomings invite a closer investigation of transitional mechanisms with modern day computational resources with a canonical set-up, free of trailing edge effects.
In this work, we seek to elucidate the influence of compressibility on the transitional structures of the planar high-speed wake. We shed light on some lingering questions: what is the effect of compressibility on the structures in the transitional flow? How does the
![]() $Ma$
influence the structural pairing of rollers? What is the effect on the turbulence anisotropy? What is the influence of compressibility on the three-dimensionality of the wake? The present investigation rests on a combined study using linear stability analysis, vortex dynamics and direct numerical simulations of the transitional high-speed wake to gain insight into the flow physics. The paper is organized as follows. The details of the linear stability analysis and numerical simulations are presented in the § 2. The stability results are detailed in § 3. Based on these findings and an idealized understanding of the wake, we infer the structural features of the nonlinear stage of transition in § 4. These theoretical results are supplemented by direct numerical simulations of the transitional high-speed wakes in which the statistics and structural evolution are respectively presented in §§ 5 and 6.
$Ma$
influence the structural pairing of rollers? What is the effect on the turbulence anisotropy? What is the influence of compressibility on the three-dimensionality of the wake? The present investigation rests on a combined study using linear stability analysis, vortex dynamics and direct numerical simulations of the transitional high-speed wake to gain insight into the flow physics. The paper is organized as follows. The details of the linear stability analysis and numerical simulations are presented in the § 2. The stability results are detailed in § 3. Based on these findings and an idealized understanding of the wake, we infer the structural features of the nonlinear stage of transition in § 4. These theoretical results are supplemented by direct numerical simulations of the transitional high-speed wakes in which the statistics and structural evolution are respectively presented in §§ 5 and 6.
2 Numerical details
2.1 Viscous linear stability theory
A viscous, compressible linear stability analysis tool was developed to study the transitional characteristics of the high-speed planar wake based on the previous work by Chen et al. (Reference Chen, Cantwell and Mansour1990) and Watanabe & Maekawa (Reference Watanabe and Maekawa2004). A periodic disturbance, with given streamwise and spanwise wavelengths, is applied to a laminar base flow. The temporal growth of the perturbation is computed from the linearized three-dimensional Navier–Stokes equations (conservation of mass and momentum) and the energy equation in non-conservative form. To assure the validity of the linear assumption, we impose a very low-amplitude perturbation to the base flow of the form:
![]() $\unicode[STIX]{x1D731}=\hat{\unicode[STIX]{x1D731}}\exp (\text{i}({\it\alpha}x+{\it\beta}y-{\it\omega}t))$
, where
$\unicode[STIX]{x1D731}=\hat{\unicode[STIX]{x1D731}}\exp (\text{i}({\it\alpha}x+{\it\beta}y-{\it\omega}t))$
, where
![]() $\unicode[STIX]{x1D731}$
represents a vector of the primitive variables:
$\unicode[STIX]{x1D731}$
represents a vector of the primitive variables:
![]() $[{\it\rho},u,v,w,T]$
. For a temporal stability calculation,
$[{\it\rho},u,v,w,T]$
. For a temporal stability calculation,
![]() ${\it\alpha}$
and
${\it\alpha}$
and
![]() ${\it\beta}$
are real and respectively the streamwise and spanwise wavenumbers, while
${\it\beta}$
are real and respectively the streamwise and spanwise wavenumbers, while
![]() ${\it\omega}$
is complex with the imaginary part being the temporal growth rate of the given perturbation. Assuming a parallel flow, we consider the stability characteristics of an initial Gaussian velocity profile:
${\it\omega}$
is complex with the imaginary part being the temporal growth rate of the given perturbation. Assuming a parallel flow, we consider the stability characteristics of an initial Gaussian velocity profile:
![]() $U(y)=U_{\infty }-U_{0}\exp (-\text{ln}(2)y^{2})$
, where
$U(y)=U_{\infty }-U_{0}\exp (-\text{ln}(2)y^{2})$
, where
![]() $U_{\infty }$
and
$U_{\infty }$
and
![]() $U_{0}$
are respectively the free-stream velocity and centreline defect. These values are chosen to compare our results with the previous investigations (Chen et al.
Reference Chen, Cantwell and Mansour1990; Watanabe & Maekawa Reference Watanabe and Maekawa2004). The thermodynamic quantities are related through the ideal gas equation of state where the non-dimensionalized static pressure was assumed to be constant across the wake. The initial temperature and density profiles were determined using the Crocco–Busseman relation with a unitary Prandtl value. In the cross-wake direction, a hyperbolic tangent stretching was used to convert the doubly infinite domain to a finite computational domain defined on
$U_{0}$
are respectively the free-stream velocity and centreline defect. These values are chosen to compare our results with the previous investigations (Chen et al.
Reference Chen, Cantwell and Mansour1990; Watanabe & Maekawa Reference Watanabe and Maekawa2004). The thermodynamic quantities are related through the ideal gas equation of state where the non-dimensionalized static pressure was assumed to be constant across the wake. The initial temperature and density profiles were determined using the Crocco–Busseman relation with a unitary Prandtl value. In the cross-wake direction, a hyperbolic tangent stretching was used to convert the doubly infinite domain to a finite computational domain defined on
![]() ${\it\zeta}=[0,1]$
using the spectral mapping techniques by Cain, Ferziger & Reynolds (Reference Cain, Ferziger and Reynolds1984). The linearized equation set can be solved as a simple eigenvalue problem of the form
${\it\zeta}=[0,1]$
using the spectral mapping techniques by Cain, Ferziger & Reynolds (Reference Cain, Ferziger and Reynolds1984). The linearized equation set can be solved as a simple eigenvalue problem of the form
![]() ${\mathcal{L}}\hat{\unicode[STIX]{x1D731}}={\it\omega}\hat{\unicode[STIX]{x1D731}}$
where
${\mathcal{L}}\hat{\unicode[STIX]{x1D731}}={\it\omega}\hat{\unicode[STIX]{x1D731}}$
where
![]() ${\mathcal{L}}$
is a linear operator acting on the eigenvector
${\mathcal{L}}$
is a linear operator acting on the eigenvector
![]() $\hat{\unicode[STIX]{x1D731}}=[\hat{{\it\rho}},\hat{u} ,\hat{v},{\hat{w}},\hat{T}]$
for a given eigenvalue,
$\hat{\unicode[STIX]{x1D731}}=[\hat{{\it\rho}},\hat{u} ,\hat{v},{\hat{w}},\hat{T}]$
for a given eigenvalue,
![]() ${\it\omega}$
. The eigenvalue with the largest imaginary part represents the maximal growth of the imposed perturbations. By investigating the resulting real part of the eigenvectors of the equation, we distinguish between the symmetric (varicose) and anti-symmetric (sinuous) modes. The complete mathematical formulation of the problem can be found in Watanabe & Maekawa (Reference Watanabe and Maekawa2004) and is not repeated. Numerically, the eigenvalue calculations are performed using the LAPACK scientific library. A gradient-based sequential least-squares programming algorithm (SLSQP), implemented through the pyOpt package (Perez, Jansen & Martins Reference Perez, Jansen and Martins2012), was used to reduce the computational time required to identify the optimal growth over the solution domain. We confirmed the validity of our linear stability code by comparing our results with previously calculated linear stability statistics from Chen et al. (Reference Chen, Cantwell and Mansour1990) and Watanabe & Maekawa (Reference Watanabe and Maekawa2004). The linear stability source code can be found in Hickey (Reference Hickey2012).
${\it\omega}$
. The eigenvalue with the largest imaginary part represents the maximal growth of the imposed perturbations. By investigating the resulting real part of the eigenvectors of the equation, we distinguish between the symmetric (varicose) and anti-symmetric (sinuous) modes. The complete mathematical formulation of the problem can be found in Watanabe & Maekawa (Reference Watanabe and Maekawa2004) and is not repeated. Numerically, the eigenvalue calculations are performed using the LAPACK scientific library. A gradient-based sequential least-squares programming algorithm (SLSQP), implemented through the pyOpt package (Perez, Jansen & Martins Reference Perez, Jansen and Martins2012), was used to reduce the computational time required to identify the optimal growth over the solution domain. We confirmed the validity of our linear stability code by comparing our results with previously calculated linear stability statistics from Chen et al. (Reference Chen, Cantwell and Mansour1990) and Watanabe & Maekawa (Reference Watanabe and Maekawa2004). The linear stability source code can be found in Hickey (Reference Hickey2012).
2.2 Direct numerical simulation details
2.2.1 Governing equations
The solved equation set for direct numerical simulation, written in conservative form, consists of the equations for mass, momentum and total energy along with an additional passive scalar equation. The equations are non-dimensionalized by the free-stream velocity,
![]() $\boldsymbol{U}=U_{\infty }$
and the initial wake half-width,
$\boldsymbol{U}=U_{\infty }$
and the initial wake half-width,
![]() $\boldsymbol{L}=b_{0}$
. The other parameters are non-dimensionalized with the free-stream values. The corresponding non-dimensional pressure and energy are respectively
$\boldsymbol{L}=b_{0}$
. The other parameters are non-dimensionalized with the free-stream values. The corresponding non-dimensional pressure and energy are respectively
![]() $p=p^{\ast }{\it\rho}_{0}c_{0}^{2}/{\it\gamma}$
and
$p=p^{\ast }{\it\rho}_{0}c_{0}^{2}/{\it\gamma}$
and
![]() $E=E^{\ast }/{\it\rho}_{0}\boldsymbol{U}^{2}$
, while the Reynolds, Prandtl and Mach numbers are
$E=E^{\ast }/{\it\rho}_{0}\boldsymbol{U}^{2}$
, while the Reynolds, Prandtl and Mach numbers are
The non-dimensionalized governing equations are
 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \frac{\partial {\it\rho}}{\partial t}+\frac{\partial ({\it\rho}u_{i})}{\partial x_{i}}=0\\ \displaystyle \frac{\partial ({\it\rho}u_{i})}{\partial t}+\frac{\partial }{\partial x_{j}}({\it\rho}u_{i}u_{j}+p/({\it\gamma}Ma^{2}){\it\delta}_{ij})=\frac{1}{Re}\frac{\partial {\it\sigma}_{ij}}{\partial x_{j}},\\ \displaystyle \frac{\partial E}{\partial t}+\frac{\partial }{\partial x_{i}}[(Eu_{i}+p/({\it\gamma}Ma^{2}))]=\frac{1}{PrRe({\it\gamma}-1)Ma^{2}}\frac{\partial }{\partial x_{i}}\left({\it\kappa}\frac{\partial T}{\partial x_{i}}\right)+\frac{1}{Re}\frac{\partial u_{j}{\it\sigma}_{ij}}{\partial x_{i}},\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \frac{\partial {\it\rho}}{\partial t}+\frac{\partial ({\it\rho}u_{i})}{\partial x_{i}}=0\\ \displaystyle \frac{\partial ({\it\rho}u_{i})}{\partial t}+\frac{\partial }{\partial x_{j}}({\it\rho}u_{i}u_{j}+p/({\it\gamma}Ma^{2}){\it\delta}_{ij})=\frac{1}{Re}\frac{\partial {\it\sigma}_{ij}}{\partial x_{j}},\\ \displaystyle \frac{\partial E}{\partial t}+\frac{\partial }{\partial x_{i}}[(Eu_{i}+p/({\it\gamma}Ma^{2}))]=\frac{1}{PrRe({\it\gamma}-1)Ma^{2}}\frac{\partial }{\partial x_{i}}\left({\it\kappa}\frac{\partial T}{\partial x_{i}}\right)+\frac{1}{Re}\frac{\partial u_{j}{\it\sigma}_{ij}}{\partial x_{i}},\end{array}\right\} & & \displaystyle\end{eqnarray}$$
where
![]() ${\it\sigma}_{ij}={\it\mu}(\partial u_{i}/\partial x_{j}+\partial u_{j}/\partial x_{i}-(2/3)(u_{k}/x_{k}){\it\delta}_{ij})$
. The above equation set is closed with the normalized equation of state:
${\it\sigma}_{ij}={\it\mu}(\partial u_{i}/\partial x_{j}+\partial u_{j}/\partial x_{i}-(2/3)(u_{k}/x_{k}){\it\delta}_{ij})$
. The above equation set is closed with the normalized equation of state:
![]() $p={\it\rho}T$
. The energy term represents the total energy, which is the sum of the internal and kinetic energies, such that
$p={\it\rho}T$
. The energy term represents the total energy, which is the sum of the internal and kinetic energies, such that
![]() $E=p/(({\it\gamma}-1){\it\gamma}Ma^{2})+(1/2){\it\rho}(u_{i}u_{i})$
. The normalized viscosity is uniquely a function of temperature and follows a power law of the form
$E=p/(({\it\gamma}-1){\it\gamma}Ma^{2})+(1/2){\it\rho}(u_{i}u_{i})$
. The normalized viscosity is uniquely a function of temperature and follows a power law of the form
![]() ${\it\mu}=T^{0.76}$
.
${\it\mu}=T^{0.76}$
.
2.2.2 Numerical scheme
We developed and validated a high-order predictor/corrector finite difference solver, which was used to compute the compressible Navier–Stokes equations. The spatial scheme is fourth-order accurate inside the domain with a one-sided third-order scheme at the finite boundaries. The high-order MacCormack-like scheme was chosen as the biased stencil on the convective terms provides a robust and efficient method to deal with the high gradients (without adding artificial viscosity) while offering acceptable dispersion and dissipative qualities (see Hickey (Reference Hickey2012) for details). The greater resolution required to account for the slightly inferior numerical qualities compared to spectral or Padé schemes, for example, is offset by the computational efficiency, parallelisability and small memory footprint. The time-dependent compressible Navier–Stokes equations are solved in conservative form with skew-symmetric convective terms for robustness and reduced aliasing errors. The time was advanced using a second-order explicit scheme in which the time step was set by an imposed acoustic Courant number. The numerical code was extensively verified against the analytical solution of a viscous shock, Taylor–Green vortex and decaying compressible isotropic turbulence. Validation with experimental wake data in the incompressible limit was performed in Hickey et al. (Reference Hickey, Hussain and Wu2013).
2.2.3 Grid, boundary and initials conditions
A homogeneous grid was used in the streamwise and spanwise directions. In the cross-wake direction, the grid was clustered about the centreline using a hyperbolic tangent mapping. The grid resolution was chosen to resolve down to the Kolmogorov scale for the entire evolution of the wake. As the flow is temporally evolving, periodic boundary conditions were set in the streamwise (
![]() $x$
) and spanwise (
$x$
) and spanwise (
![]() $z$
) directions. In the cross-wake direction (
$z$
) directions. In the cross-wake direction (
![]() $y$
), non-reflecting boundary conditions (Thompson Reference Thompson1990), supplemented with sponge layers, were used to attenuate spurious numerical oscillations at the boundaries. The domain size was selected to be at least eight times the most unstable anti-symmetric wavelength in the streamwise direction and four times the most unstable oblique symmetric mode in the spanwise direction. Consequently, the domain sizes are Mach number dependent. In the cross-wake, the domain height was chosen large enough to accommodate at least six wake half-widths at all times during the simulation. The very large computational domain was justified by the need to enhance the sampling of higher-order statistics, to reduce the dependence of the domain size on the developing instability modes and to allow the growth of the long-wavelength, oblique varicose mode.
$y$
), non-reflecting boundary conditions (Thompson Reference Thompson1990), supplemented with sponge layers, were used to attenuate spurious numerical oscillations at the boundaries. The domain size was selected to be at least eight times the most unstable anti-symmetric wavelength in the streamwise direction and four times the most unstable oblique symmetric mode in the spanwise direction. Consequently, the domain sizes are Mach number dependent. In the cross-wake, the domain height was chosen large enough to accommodate at least six wake half-widths at all times during the simulation. The very large computational domain was justified by the need to enhance the sampling of higher-order statistics, to reduce the dependence of the domain size on the developing instability modes and to allow the growth of the long-wavelength, oblique varicose mode.
The simulations are temporally evolving. Although temporal simulations remain of great scientific interest, they fall short in faithfully reproducing the transition of wake flows. On the one hand, the temporal simulations require a parallel flow assumption, which is not entirely valid in the case of transitional wakes. In addition, the instability modes are unable to spatially grow, as would occur in a spatial simulation or experimental set-up, and are constrained by the computational domain. A final issue concerns the infinite propagation in the streamwise and spanwise direction of acoustical, vortical and entropic perturbations. These perturbations then recontaminate the computational domain, whereas in the spatial case, they are simply advected out of the domain. Despite these valid concerns, the study of temporal transition of free-shear flow remains valuable in understanding transitional mechanism. Many temporal studies of high-speed free-shear flows have shown convincing quantitative matching of experimental results (e.g. Pantano & Sarkar Reference Pantano and Sarkar2002). Furthermore, the correct physical mechanisms of the temporally evolving simulations are extensively reported (Rempfer Reference Rempfer2003). In addition, the temporal wake evolves without a receptive trailing edge and therefore we are able to isolate the intrinsic wake transition from the wake generating body. Furthermore, given the lengthy transition caused by the increasing stability of the high-speed wake, we are able to simulate higher Reynolds number flows than could be afforded by a spatial simulation.
Table 1. Characteristics of the numerical simulations of the transitional wake. The
![]() ${\it\eta}/{\rm\Delta}x|_{min}$
represents the minimal value over the domain, during the entire transitional simulation.
${\it\eta}/{\rm\Delta}x|_{min}$
represents the minimal value over the domain, during the entire transitional simulation.
The wakes were simulated at a constant Reynolds number of 3000, based on the initial wake half-width and initial velocity defect, at two different initial relative Mach numbers:
![]() $Ma=0.8$
and 2.0 (herein, the wakes are identified by their initial
$Ma=0.8$
and 2.0 (herein, the wakes are identified by their initial
![]() $Ma_{r}$
; for clarity, the subscript ‘
$Ma_{r}$
; for clarity, the subscript ‘
![]() $r$
’ from
$r$
’ from
![]() $Ma_{r}$
is dropped). To fully resolve all the scales of turbulence, a grid of 473 and 619 million nodes, respectively, was needed, see the numerical details in table 1. A laminar initial velocity profile was used:
$Ma_{r}$
is dropped). To fully resolve all the scales of turbulence, a grid of 473 and 619 million nodes, respectively, was needed, see the numerical details in table 1. A laminar initial velocity profile was used:
![]() $\langle u(y)\rangle =U_{\infty }-U_{d}\exp (-\text{ln}(2)y/b)^{2}$
where
$\langle u(y)\rangle =U_{\infty }-U_{d}\exp (-\text{ln}(2)y/b)^{2}$
where
![]() $U_{\infty }$
,
$U_{\infty }$
,
![]() $U_{d}$
and
$U_{d}$
and
![]() $b$
are respectively the free-stream velocity, the initial deficit velocity and the initial wake half-width. Admittedly, the choice of a Gaussian, instead of a double Blasius profile, may inhibit the development of near-wake instability modes originating from a double boundary layer profile (Papageorgiou & Smith Reference Papageorgiou and Smith1989; Papageorgiou Reference Papageorgiou1990). In Hickey et al. (Reference Hickey, Hussain and Wu2013), the evolution of a Gaussian and double Blasius wake profile were compared in the incompressible limit; other than a delayed transition, the main characteristic structures and statistics remain surprisingly similar. Based on these conclusions, we deemed that an initial Gaussian profile allows the greatest generality for the study of the temporally evolving wake. The laminar base flow velocity and temperature fields were related through the Crocco–Busemann relationship. The initial wake profile is perturbed by broadband velocity fluctuations for the components in
$b$
are respectively the free-stream velocity, the initial deficit velocity and the initial wake half-width. Admittedly, the choice of a Gaussian, instead of a double Blasius profile, may inhibit the development of near-wake instability modes originating from a double boundary layer profile (Papageorgiou & Smith Reference Papageorgiou and Smith1989; Papageorgiou Reference Papageorgiou1990). In Hickey et al. (Reference Hickey, Hussain and Wu2013), the evolution of a Gaussian and double Blasius wake profile were compared in the incompressible limit; other than a delayed transition, the main characteristic structures and statistics remain surprisingly similar. Based on these conclusions, we deemed that an initial Gaussian profile allows the greatest generality for the study of the temporally evolving wake. The laminar base flow velocity and temperature fields were related through the Crocco–Busemann relationship. The initial wake profile is perturbed by broadband velocity fluctuations for the components in
![]() $x$
- and
$x$
- and
![]() $y$
-directions with an r.m.s. value of 1.5 % of the velocity deficit, in order to break the symmetry about the centreline. The broadband perturbations have a greater generality but result in a longer transition compared to specific mode forcing. The initial wake half-width was unity resulting in a constant mass flux defect of
$y$
-directions with an r.m.s. value of 1.5 % of the velocity deficit, in order to break the symmetry about the centreline. The broadband perturbations have a greater generality but result in a longer transition compared to specific mode forcing. The initial wake half-width was unity resulting in a constant mass flux defect of
![]() ${\dot{m}}\approx 1$
. The computations were conducted at the High Performance Computing Virtual Laboratory (HPCVL) in Kingston, Ontario using 128 processors and required a wall clock time of approximately 45 days per simulation. In addition to these computations, we conducted numerous lower Reynolds number simulations at
${\dot{m}}\approx 1$
. The computations were conducted at the High Performance Computing Virtual Laboratory (HPCVL) in Kingston, Ontario using 128 processors and required a wall clock time of approximately 45 days per simulation. In addition to these computations, we conducted numerous lower Reynolds number simulations at
![]() $Re=1500$
on a fixed computational domain (
$Re=1500$
on a fixed computational domain (
![]() $L_{x}$
,
$L_{x}$
,
![]() $L_{y}$
,
$L_{y}$
,
![]() $L_{z}=50$
, 25, 12.5) and grid (56 million grid points) for
$L_{z}=50$
, 25, 12.5) and grid (56 million grid points) for
![]() $Ma=0.3$
, 0.8, 1.2 and 2.0. These fully resolved simulations are used to validate the generality of our results at different relative Mach numbers. Grid convergence and resolution tests are presented in the Appendix.
$Ma=0.3$
, 0.8, 1.2 and 2.0. These fully resolved simulations are used to validate the generality of our results at different relative Mach numbers. Grid convergence and resolution tests are presented in the Appendix.
3 Linear stability of high-speed wakes
Given the symmetry of the laminar base flow, two classes of instability modes arise. The anti-symmetric (or sinuous) mode is defined at the centreline as
![]() $\hat{u} =0$
and
$\hat{u} =0$
and
![]() $\text{d}\hat{v}/\text{d}y=0$
while the symmetric (or varicose) mode is defined as
$\text{d}\hat{v}/\text{d}y=0$
while the symmetric (or varicose) mode is defined as
![]() $\hat{v}=0$
and
$\hat{v}=0$
and
![]() $\text{d}\hat{u} /\text{d}y=0$
. Both modes have exponentially unstable components in the two-dimensional planar wake.
$\text{d}\hat{u} /\text{d}y=0$
. Both modes have exponentially unstable components in the two-dimensional planar wake.

Figure 1. Influence of compressibility and viscosity on the maximal growth rate of the instability modes (two-dimensional, anti-symmetric mode). The maximal exponential growth for Reynolds numbers of 500, 1000, 2000 and 4000 are compared with the inviscid results by Chen et al. (Reference Chen, Cantwell and Mansour1990). The streamwise wavenumber of the most unstable mode (squares) is shown on the right-hand side.
3.1 Sinuous instability mode
As in the incompressible wake, the highest exponential growth is achieved for a purely two-dimensional, anti-symmetric (sinuous) perturbation for all Mach numbers. This perturbation results in the formation of two rows of staggered spanwise coherent rollers, sharing many characteristics with the classical Kármán vortex street in the wake of a bluff body. From previous investigations (Chen et al.
Reference Chen, Cantwell and Mansour1990; Watanabe & Maekawa Reference Watanabe and Maekawa2004), an increasing Mach number decreases the maximal exponential growth of the primary disturbance. Between free-stream Mach numbers of
![]() $Ma=0.01$
and 2.0, the exponential growth rate is reduced by approximately 30 %, see figure 1; a modest decrease compared with the very drastic drop in growth rates observed in the mixing layer (a reduction of approximately 18 % from the incompressible growth rate at
$Ma=0.01$
and 2.0, the exponential growth rate is reduced by approximately 30 %, see figure 1; a modest decrease compared with the very drastic drop in growth rates observed in the mixing layer (a reduction of approximately 18 % from the incompressible growth rate at
![]() $Ma_{c}=0.4\,\%$
and 72 % at
$Ma_{c}=0.4\,\%$
and 72 % at
![]() $Ma_{c}=1.2$
(Sandham & Reynolds Reference Sandham and Reynolds1990)). The viscosity has a slightly stabilizing effect on the high-speed wake. Although the stabilizing effect of viscosity is minimal compared with the inflectional instability of the mean profile. As noted by Watanabe & Maekawa (Reference Watanabe and Maekawa2004), there is less than 2 % difference between growth rate at
$Ma_{c}=1.2$
(Sandham & Reynolds Reference Sandham and Reynolds1990)). The viscosity has a slightly stabilizing effect on the high-speed wake. Although the stabilizing effect of viscosity is minimal compared with the inflectional instability of the mean profile. As noted by Watanabe & Maekawa (Reference Watanabe and Maekawa2004), there is less than 2 % difference between growth rate at
![]() $\mathit{Re}=1000$
and the fully inviscid case for all Mach numbers studied, see figure 1. Overshadowed in the previous studies is the striking correlation between the growth rate and the wavelength of the most unstable mode. The wavelength of the most unstable mode is similarly approximately 18 % longer at a Mach number of 2.0 compared to the incompressible baseline. The concomitant effects of an increased wavelength are discussed in the following sections and are central to our understanding of high-speed wake transition.
$\mathit{Re}=1000$
and the fully inviscid case for all Mach numbers studied, see figure 1. Overshadowed in the previous studies is the striking correlation between the growth rate and the wavelength of the most unstable mode. The wavelength of the most unstable mode is similarly approximately 18 % longer at a Mach number of 2.0 compared to the incompressible baseline. The concomitant effects of an increased wavelength are discussed in the following sections and are central to our understanding of high-speed wake transition.

Figure 2. Eigenvectors of the most unstable mode at
![]() $Re=10\,000$
at
$Re=10\,000$
at
![]() $Ma=1.92$
(
$Ma=1.92$
(
![]() ${\it\alpha}=0.239$
,
${\it\alpha}=0.239$
,
![]() ${\it\beta}=0.264$
). The real (red line, dashed-dot), imaginary (blue line, dashed) and the magnitude (black line, full) are presented for
${\it\beta}=0.264$
). The real (red line, dashed-dot), imaginary (blue line, dashed) and the magnitude (black line, full) are presented for
![]() $\hat{u}$
(a),
$\hat{u}$
(a),
![]() $\hat{v}$
(b) and
$\hat{v}$
(b) and
![]() $\hat{{\it\rho}}$
(c).
$\hat{{\it\rho}}$
(c).

Figure 3. Influence of compressibility and viscosity on the varicose (two- and three-dimensional, symmetric perturbation) mode in the high-speed wake. The viscosity has a strong stabilizing effect on the growth (top). The streamwise and spanwise wavenumbers of the most unstable symmetric mode for
![]() $Re=10\,000$
are presented along with the corresponding angle of the optimal disturbance.
$Re=10\,000$
are presented along with the corresponding angle of the optimal disturbance.
3.2 Varicose instability mode
The symmetric (varicose) mode plays a secondary role in the transitional mechanism of the high-speed wake, as the growth rate is less than a third of the primary anti-symmetric instability. Nonetheless, the importance of the symmetric mode cannot be neglected as it may modulate the anti-symmetric mode, as noted in the incompressible case by Wygnanski, Champagne & Marasli (Reference Wygnanski, Champagne and Marasli1986). For completeness, figure 2 shows the eigenvectors of the most unstable varicose mode. The influence of this mode is particularly important for high-speed wakes as it shifts from a purely two-dimensional to an oblique perturbation at approximately
![]() $Ma=1.2$
(see figure 3) as previously observed by Chen et al. (Reference Chen, Cantwell and Mansour1990) and Watanabe & Maekawa (Reference Watanabe and Maekawa2004). This raises the question of why the symmetric mode has a drastic jump in the appearance of a cross-wise component to the instability. This observation recalls the onset of three-dimensionality in the transitional high-speed mixing layer above a convective Mach number of 0.6. To the best of the authors’ knowledge the exact physical mechanism of this jump in the mixing layer remains elusive. Similar to the primary mode, the symmetric instability mode is damped by both viscous and compressibility effects. The viscous effects play an important role in impeding the growth of this mode. Figure 3 shows that at
$Ma=1.2$
(see figure 3) as previously observed by Chen et al. (Reference Chen, Cantwell and Mansour1990) and Watanabe & Maekawa (Reference Watanabe and Maekawa2004). This raises the question of why the symmetric mode has a drastic jump in the appearance of a cross-wise component to the instability. This observation recalls the onset of three-dimensionality in the transitional high-speed mixing layer above a convective Mach number of 0.6. To the best of the authors’ knowledge the exact physical mechanism of this jump in the mixing layer remains elusive. Similar to the primary mode, the symmetric instability mode is damped by both viscous and compressibility effects. The viscous effects play an important role in impeding the growth of this mode. Figure 3 shows that at
![]() $Re=1000$
, the exponential growth rate is 10 % lower than the inviscid case at
$Re=1000$
, the exponential growth rate is 10 % lower than the inviscid case at
![]() $Ma=0.001$
– at Mach number 2.0, it is 30 % lower. The varicose mode is nearly completely suppressed for Reynolds numbers under 250. In addition to the stabilizing effect of viscosity, the wavelength of the symmetric mode is over twice that the anti-symmetric mode over all the Mach numbers investigated. The combined effects of an inhibited growth rate caused by viscosity and the longer instability wavelength may have hindered the observation of the emergence of this three-dimensional mode in the previous direct numerical simulations of transitioning high-speed wakes. Those simulations at
$Ma=0.001$
– at Mach number 2.0, it is 30 % lower. The varicose mode is nearly completely suppressed for Reynolds numbers under 250. In addition to the stabilizing effect of viscosity, the wavelength of the symmetric mode is over twice that the anti-symmetric mode over all the Mach numbers investigated. The combined effects of an inhibited growth rate caused by viscosity and the longer instability wavelength may have hindered the observation of the emergence of this three-dimensional mode in the previous direct numerical simulations of transitioning high-speed wakes. Those simulations at
![]() $Re=300$
(Chen et al.
Reference Chen, Cantwell and Mansour1990) and 1000 (Watanabe & Maekawa Reference Watanabe and Maekawa2004) were on computational domains clearly too small to capture the varicose modes. As a result, the effects of the three-dimensional symmetric mode were probably inhibited. These observations invite a new investigation, at higher Reynolds number and on a larger domain in order to accommodate the longer wavelengths.
$Re=300$
(Chen et al.
Reference Chen, Cantwell and Mansour1990) and 1000 (Watanabe & Maekawa Reference Watanabe and Maekawa2004) were on computational domains clearly too small to capture the varicose modes. As a result, the effects of the three-dimensional symmetric mode were probably inhibited. These observations invite a new investigation, at higher Reynolds number and on a larger domain in order to accommodate the longer wavelengths.
4 Domain of influence in the transitional wake
In free-shear flows, the wavelength imposed by the fastest growing instability mode characterizes the length scale of the emerging transitional structures. Based on the results from linear stability theory § 3 (assuming no external forcing), it comes as no surprise that the rollers emerge as purely two-dimensional structures with an increasing wavelength with increasing
![]() $Ma$
number. The increased wavelength of the primary instability mode leads to two, seemingly trivial, features of the high-speed wake transition: (i) increased streamwise separation between neighbouring rollers on the same row; and hence (ii) increased circulation of each roller. For a fixed wake half-width of the base flow,
$Ma$
number. The increased wavelength of the primary instability mode leads to two, seemingly trivial, features of the high-speed wake transition: (i) increased streamwise separation between neighbouring rollers on the same row; and hence (ii) increased circulation of each roller. For a fixed wake half-width of the base flow,
![]() $b$
, compressibility decreases the ratio of the cross-wake to streamwise separation,
$b$
, compressibility decreases the ratio of the cross-wake to streamwise separation,
![]() $h/{\it\lambda}$
, where
$h/{\it\lambda}$
, where
![]() $h$
represents the cross-wake separation between rows (which is, to a close approximation, a function of the wake half-width,
$h$
represents the cross-wake separation between rows (which is, to a close approximation, a function of the wake half-width,
![]() $b$
) and
$b$
) and
![]() ${\it\lambda}$
the streamwise separation between neighbouring rollers (being related the most unstable wavelength). In the present section, we consider the compressibility effects on the acoustic propagation and the domain of influence in the laminar base state of the high-speed planar wake.
${\it\lambda}$
the streamwise separation between neighbouring rollers (being related the most unstable wavelength). In the present section, we consider the compressibility effects on the acoustic propagation and the domain of influence in the laminar base state of the high-speed planar wake.
4.1 Domain of influence in the transitional compressible wake
The staggered array of spanwise vortices, forming a Kármán vortex-like street, has been shown to be unstable to infinitesimal perturbations for two-dimensional vortex filaments in the inviscid case, except for the well-known neutrally stable configuration of
![]() $h/{\it\lambda}=0.28055$
. Using an inviscid hollow vortex model, Crowdy & Green (Reference Crowdy and Green2011) showed a cross-over point at an aspect ratio of
$h/{\it\lambda}=0.28055$
. Using an inviscid hollow vortex model, Crowdy & Green (Reference Crowdy and Green2011) showed a cross-over point at an aspect ratio of
![]() $h/{\it\lambda}=0.34{-}0.36$
. Above this threshold, pairing occurs between neighbouring rollers on the same side, as typically observed in most low-speed transitioning wakes. Below this threshold, it occurs between rollers from across the centreplane (merger between rollers with opposite circulation, clearly breaking up and then decimating both rollers due to cross-diffusion of vorticity). The stability properties of such flows were considered in Llewellyn Smith & Crowdy (Reference Llewellyn Smith and Crowdy2012).
$h/{\it\lambda}=0.34{-}0.36$
. Above this threshold, pairing occurs between neighbouring rollers on the same side, as typically observed in most low-speed transitioning wakes. Below this threshold, it occurs between rollers from across the centreplane (merger between rollers with opposite circulation, clearly breaking up and then decimating both rollers due to cross-diffusion of vorticity). The stability properties of such flows were considered in Llewellyn Smith & Crowdy (Reference Llewellyn Smith and Crowdy2012).
Although it is tempting to infer the stability features from incompressible vortex dynamics, this approach is invalid for high-speed flows as the domain of influence of each roller is no longer global. The classic Biot–Savart induction law is not directly applicable to compressible flows, partly because of the dilatational component of the flow, but more importantly, because the induced velocity follows the characteristic lines (Smits & Dussauge Reference Smits and Dussauge2006) which are modified by the gradient of the mean flow. To address this issue, we approximate the characteristic lines (which we assume to be the communication path) of a single point within a laminar wake profile in order to infer the domain of influence of a compact roller.
The path of communication in compressible flows follows the characteristic lines. In a high-speed free-shear flow, the mean Mach gradient modifies the path of the characteristic wavefronts. As a result, communication between two neighbouring rollers may be hindered, possibly even completely cutoff. Despite the simplicity of the approach, the geometric evaluation of the ray paths have been shown by Papamoschou (Reference Papamoschou1994) to offer a good qualitative and quantitative comparison with the characteristic-based computations from the linearized equations of motion. In order to investigate the compressibility effects on the communication paths in the high-speed wake, we extend the analysis of the mixing layer (Papamoschou Reference Papamoschou1993, Reference Papamoschou1994; Papamoschou & Lele Reference Papamoschou and Lele1993) to consider the symmetric profile of the high-speed wake. Assuming a constant speed of sound, the generalized form of Snell’s law relating the direction of acoustic propagation to the local
![]() $Ma$
is
$Ma$
is
where
![]() ${\it\theta}$
is the angle from the vertical and the subscript ‘
${\it\theta}$
is the angle from the vertical and the subscript ‘
![]() $_{o}$
’ represents the Mach number and angle at the origin
$_{o}$
’ represents the Mach number and angle at the origin
![]() $(Ma_{o},{\it\theta}_{o})$
. Based on classical ray tracing theory, the trajectory can be defined as a simple ordinary differential equation in two dimensions:
$(Ma_{o},{\it\theta}_{o})$
. Based on classical ray tracing theory, the trajectory can be defined as a simple ordinary differential equation in two dimensions:
Herein, we are interested in understanding the path of information propagation. For simplicity, we assume a laminar Gaussian distribution of velocity: a valid assumption even during emergence of transitional spanwise rollers. We developed a two-dimensional ray tracing tool using an explicit time advancement based on a fourth-order Runge–Kutta scheme, similar to Papamoschou (Reference Papamoschou1993); the source code can be found in Hickey (Reference Hickey2012). Figure 4 shows the path of propagation of a perturbation emitted from a source at the wake half-width (a,c,e) and at the centreplane (b,d,f). For the computations, we neglect the effect of wave dispersion or attenuation.

Figure 4. Propagation path of an omnidirectional acoustic disturbance in laminar wake (Gaussian profile shown in a,b) at
![]() $Ma_{r}=0.0$
, 0.5 and 1.0 (rows top to bottom) for a source at the upper inflection point of the mean velocity profile (a,c,e) and at the centreline (b,d,f). The contour lines represent the wavefronts. The dashed vertical lines represent the streamwise locations of signal intensity measurements in figure 5.
$Ma_{r}=0.0$
, 0.5 and 1.0 (rows top to bottom) for a source at the upper inflection point of the mean velocity profile (a,c,e) and at the centreline (b,d,f). The contour lines represent the wavefronts. The dashed vertical lines represent the streamwise locations of signal intensity measurements in figure 5.
The path of communication is greatly influenced by the Mach number gradient of the base flow. If we approximate a single roller as a compact vortical source at the wake half-width (figure 4
a,c,e), a clear increased cross-wake information is observed with increasing
![]() $Ma$
; simultaneously, the streamwise communication is inhibited. An important region of near-silence develops upstream (to the left) of the source, while a region of weak acoustic intensity develops downstream of the source (to the right). The increased cross-wake influence can also be seen in the increasing inclination of the wavefronts with
$Ma$
; simultaneously, the streamwise communication is inhibited. An important region of near-silence develops upstream (to the left) of the source, while a region of weak acoustic intensity develops downstream of the source (to the right). The increased cross-wake influence can also be seen in the increasing inclination of the wavefronts with
![]() $Ma$
. The constitutive shear layers of the wake act as a waveguide, as such, the perturbations within the wake are internally reflected, raising the possibility of the emergence of an acoustic instability modes as in the boundary layer (Mack Reference Mack1975, Reference Mack1990). Interestingly, the information which does exit the waveguide is preferentially inclined to the free stream with an increasing streamwise orientation with Mach number, recalling the findings of acoustic waves in the free stream by Watanabe & Maekawa (Reference Watanabe and Maekawa2004) and Maekawa, Takiguchi & Watanabe (Reference Maekawa, Takiguchi and Watanabe2006).
$Ma$
. The constitutive shear layers of the wake act as a waveguide, as such, the perturbations within the wake are internally reflected, raising the possibility of the emergence of an acoustic instability modes as in the boundary layer (Mack Reference Mack1975, Reference Mack1990). Interestingly, the information which does exit the waveguide is preferentially inclined to the free stream with an increasing streamwise orientation with Mach number, recalling the findings of acoustic waves in the free stream by Watanabe & Maekawa (Reference Watanabe and Maekawa2004) and Maekawa, Takiguchi & Watanabe (Reference Maekawa, Takiguchi and Watanabe2006).

Figure 5. Relative intensity profile of an omnidirectional acoustic source at
![]() $(x/b,y/b)=(0,0.5)$
at various streamwise locations for a free-stream Mach number of 0 (solid line), 0.5 (dashed line) and 1.0 (dotted line): (a)
$(x/b,y/b)=(0,0.5)$
at various streamwise locations for a free-stream Mach number of 0 (solid line), 0.5 (dashed line) and 1.0 (dotted line): (a)
![]() $x/b=0.5$
; (b)
$x/b=0.5$
; (b)
![]() $x/b=1.25$
; (c)
$x/b=1.25$
; (c)
![]() $x/b=2.0$
. The streamwise locations are identified in figure 4(a,c,e) by dashed vertical lines.
$x/b=2.0$
. The streamwise locations are identified in figure 4(a,c,e) by dashed vertical lines.
We recall that the acoustic intensity is proportional to the separation between two adjacent traces for an omnidirectional acoustic source (Papamoschou Reference Papamoschou1993): the closer two adjacent traces are to each other, the stronger the signal (valid under the assumption of zero wave dispersion or attenuation). Hayes (Reference Hayes1968) formalized the energy conservation law for geometric acoustics in a moving medium. From figure 4 at
![]() $Ma=0.5$
and 1.0, we can infer the important effect of compressibility on the intensity of the acoustic disturbance. A very weak acoustic signal is found between 1.5 and 3.5 wake half-widths downstream (to the right of the source), which represents the typical streamwise separation between adjacent rollers in the transitional high-speed wakes. To quantify this effect, the intensity of the acoustic signal is computed at three streamwise locations (shown as vertical dashed lines in figure 4
a,c,e) for an acoustic source at the inflection point of the wake. The relative acoustic intensity profile is shown in figure 5. For the fully incompressible case, the relative intensity of the signal is directly proportional to the distance from the source which can be seen in the Gaussian distribution of the acoustic intensity at various streamwise locations. As the free-stream Mach number increases, the relative intensity of the acoustic signal along the same row (
$Ma=0.5$
and 1.0, we can infer the important effect of compressibility on the intensity of the acoustic disturbance. A very weak acoustic signal is found between 1.5 and 3.5 wake half-widths downstream (to the right of the source), which represents the typical streamwise separation between adjacent rollers in the transitional high-speed wakes. To quantify this effect, the intensity of the acoustic signal is computed at three streamwise locations (shown as vertical dashed lines in figure 4
a,c,e) for an acoustic source at the inflection point of the wake. The relative acoustic intensity profile is shown in figure 5. For the fully incompressible case, the relative intensity of the signal is directly proportional to the distance from the source which can be seen in the Gaussian distribution of the acoustic intensity at various streamwise locations. As the free-stream Mach number increases, the relative intensity of the acoustic signal along the same row (
![]() $y/b=0.5$
) decreases with respect to the incompressible baseline. Simultaneously, the signal strength increases on the opposite side of the wake (
$y/b=0.5$
) decreases with respect to the incompressible baseline. Simultaneously, the signal strength increases on the opposite side of the wake (
![]() $y/b=-0.5$
).
$y/b=-0.5$
).

Figure 6. Integrated acoustic energy crossing the wake centreplane and angle with the centreplane of the peak intensity (a). Normalized acoustic intensity distribution along the centreplane (b) from an omnidirectional source located at the wake half-width.
Following the approach by Papamoschou (Reference Papamoschou1993), the integrated intensity of the acoustic signal crossing the centreplane of the wake is shown in figure 6(a). Similar to the shear layer, the integrated acoustic intensity crossing the wake centreplane decreases monotonically with the free-stream
![]() $Ma$
(for an omnidirectional source located at the wake half-width). But compressibility effects modify the distribution of the acoustic intensity along the centreplane. The acoustic intensity becomes increasingly localized with increasing compressibility of the base flow. Figure 6(b) shows the normalized acoustic energy distribution along the centreplane. The angle of the peak acoustic intensity varies from
$Ma$
(for an omnidirectional source located at the wake half-width). But compressibility effects modify the distribution of the acoustic intensity along the centreplane. The acoustic intensity becomes increasingly localized with increasing compressibility of the base flow. Figure 6(b) shows the normalized acoustic energy distribution along the centreplane. The angle of the peak acoustic intensity varies from
![]() $90^{\circ }$
in the incompressible case to below 50
$90^{\circ }$
in the incompressible case to below 50
![]() $^{\circ }$
at
$^{\circ }$
at
![]() $Ma=2.0$
. The zone of influence of a receiver located on the centreplane of a wake is shown in figure 7. As the emerging instability modes in the wake are anti-symmetric, the increasing obliquity of the zone of influence promotes a cross-wake communication between the emerging coherent structures.
$Ma=2.0$
. The zone of influence of a receiver located on the centreplane of a wake is shown in figure 7. As the emerging instability modes in the wake are anti-symmetric, the increasing obliquity of the zone of influence promotes a cross-wake communication between the emerging coherent structures.

Figure 7. The Mach number effect on the zone of influence for a receiver located at (0,0): (a)
![]() $Ma=0$
; (b)
$Ma=0$
; (b)
![]() $Ma=0.5$
; (c)
$Ma=0.5$
; (c)
![]() $Ma=2.0$
. The isocontour lines represent the intensity of the acoustic signal at the receiver point.
$Ma=2.0$
. The isocontour lines represent the intensity of the acoustic signal at the receiver point.
5 Numerical simulation: transitional statistics
5.1 Defining compressibility effects
The global compressibility effect is characterized by the relative Mach number
![]() $Ma_{r}$
, which is the ratio of the centreline velocity defect to the free-stream speed of sound:
$Ma_{r}$
, which is the ratio of the centreline velocity defect to the free-stream speed of sound:
![]() $Ma_{r}=Ma_{\infty }-Ma_{o}=(U_{\infty }-U_{0})/c_{\infty }$
. Unlike the mixing layer case, the level of compressibility in the wake decays with its evolution; the decay in time of
$Ma_{r}=Ma_{\infty }-Ma_{o}=(U_{\infty }-U_{0})/c_{\infty }$
. Unlike the mixing layer case, the level of compressibility in the wake decays with its evolution; the decay in time of
![]() $Ma_{r}$
is shown in figure 8. Given a long enough evolution, the relative Mach number, as well as the velocity defect, asymptotically tend toward zero and the wake essentially becomes incompressible. This is not to say that the far wake of the compressible and incompressible wakes are identical. Bonnet et al. (Reference Bonnet, Delville, Sapin, Sullivan and Yeru1991) and Gatski & Bonnet (Reference Gatski and Bonnet2009) noted clear differences in turbulence statistics in the far field between low- and high-speed wakes, the most notable difference is the peak turbulence intensity which is located further from the centreplane with increasing compressibility. Since the mean compressibility is small in the far wake, the differences are most likely caused by the ‘memory effects’ which are imparted to the flow in the near wake. A comprehensive study of the memory effects in incompressible wakes can be found in Hickey et al. (Reference Hickey, Hussain and Wu2013).
$Ma_{r}$
is shown in figure 8. Given a long enough evolution, the relative Mach number, as well as the velocity defect, asymptotically tend toward zero and the wake essentially becomes incompressible. This is not to say that the far wake of the compressible and incompressible wakes are identical. Bonnet et al. (Reference Bonnet, Delville, Sapin, Sullivan and Yeru1991) and Gatski & Bonnet (Reference Gatski and Bonnet2009) noted clear differences in turbulence statistics in the far field between low- and high-speed wakes, the most notable difference is the peak turbulence intensity which is located further from the centreplane with increasing compressibility. Since the mean compressibility is small in the far wake, the differences are most likely caused by the ‘memory effects’ which are imparted to the flow in the near wake. A comprehensive study of the memory effects in incompressible wakes can be found in Hickey et al. (Reference Hickey, Hussain and Wu2013).
During the pre-transitional evolution, the centreline defect decreases faster, the lower the Reynolds number and the greater the initial Mach number. In the early nonlinear stage of transition, which roughly corresponds to the abrupt change of slope in figure 8(a) at the time
![]() $[40{-}50]$
(
$[40{-}50]$
(
![]() $Ma=0.8$
) and
$Ma=0.8$
) and
![]() $[70{-}85]$
(
$[70{-}85]$
(
![]() $Ma=2.0$
), the relative Mach number decays at an increasing rate with the Mach number. The maximum slope of the relative Mach number with respect to time is
$Ma=2.0$
), the relative Mach number decays at an increasing rate with the Mach number. The maximum slope of the relative Mach number with respect to time is
![]() $-$
0.035 (
$-$
0.035 (
![]() $Ma=0.8$
) and
$Ma=0.8$
) and
![]() $-$
0.057 (
$-$
0.057 (
![]() $Ma=2.0$
). The trend is consistent in the lower Reynolds number simulations:
$Ma=2.0$
). The trend is consistent in the lower Reynolds number simulations:
![]() $-$
0.012 (
$-$
0.012 (
![]() $Ma=0.3$
),
$Ma=0.3$
),
![]() $-$
0.028 (
$-$
0.028 (
![]() $Ma=0.8$
),
$Ma=0.8$
),
![]() $-$
0.035 (
$-$
0.035 (
![]() $Ma=1.2$
) and
$Ma=1.2$
) and
![]() $-$
0.036 (
$-$
0.036 (
![]() $Ma=2.0$
), although it is unclear why the
$Ma=2.0$
), although it is unclear why the
![]() $Ma$
should have an effect on the viscous dissipation caused by the mean flow gradient.
$Ma$
should have an effect on the viscous dissipation caused by the mean flow gradient.
The turbulent Mach number characterizes the compressibility effects due to turbulent fluctuations and is defined as:
![]() $Ma_{t}=\langle u^{\prime }\rangle _{max}/c_{\infty }$
. The maximum turbulent Mach number is reached during transition and corresponds to: 0.1396 (
$Ma_{t}=\langle u^{\prime }\rangle _{max}/c_{\infty }$
. The maximum turbulent Mach number is reached during transition and corresponds to: 0.1396 (
![]() $Ma=0.8$
) and 0.307 (
$Ma=0.8$
) and 0.307 (
![]() $Ma=2.0$
). For the low-
$Ma=2.0$
). For the low-
![]() $Re$
cases: 0.049, 0.128, 0.183 and 0.250 respectively for
$Re$
cases: 0.049, 0.128, 0.183 and 0.250 respectively for
![]() $Ma=0.3$
, 0.8, 1.2 and 2.0. In the far wake the turbulent Mach number monotonically decreases and follows a decay law, as in the incompressible case of
$Ma=0.3$
, 0.8, 1.2 and 2.0. In the far wake the turbulent Mach number monotonically decreases and follows a decay law, as in the incompressible case of
![]() $O(t^{-1/2})$
. Given the initial level of compressibility of the flow, these turbulent Mach numbers are rather small, and a priori, should not promote the formation of any shocklets (discussed in more detail in § 5.7). To put this into context, Sandham & Reynolds (Reference Sandham and Reynolds1990) did not observe any shocklets for three-dimensional mixing layers with a unitary convective Mach number. Passot & Pouquet (Reference Passot and Pouquet1987) noted that a turbulent Mach number of 0.3 was the approximate threshold for shocklet formation in decaying isotropic turbulence in two-dimensional simulations; higher turbulence Mach numbers are needed for three-dimensional simulations (Lee, Lele & Moin Reference Lee, Lele and Moin1991; Samtaney, Pullin & Kosovic Reference Samtaney, Pullin and Kosovic2001). Note that careful checks of
$O(t^{-1/2})$
. Given the initial level of compressibility of the flow, these turbulent Mach numbers are rather small, and a priori, should not promote the formation of any shocklets (discussed in more detail in § 5.7). To put this into context, Sandham & Reynolds (Reference Sandham and Reynolds1990) did not observe any shocklets for three-dimensional mixing layers with a unitary convective Mach number. Passot & Pouquet (Reference Passot and Pouquet1987) noted that a turbulent Mach number of 0.3 was the approximate threshold for shocklet formation in decaying isotropic turbulence in two-dimensional simulations; higher turbulence Mach numbers are needed for three-dimensional simulations (Lee, Lele & Moin Reference Lee, Lele and Moin1991; Samtaney, Pullin & Kosovic Reference Samtaney, Pullin and Kosovic2001). Note that careful checks of
![]() $Ma$
contours failed to reveal the presence of any shocklets in the flow domain.
$Ma$
contours failed to reveal the presence of any shocklets in the flow domain.

Figure 8. Evolution of the relative Mach number (a) and of the maximal turbulent Mach number (b). The dashed lines represent the
![]() $Re=1500$
simulations.
$Re=1500$
simulations.

Figure 9. Evolution of the maximal Favre-averaged normalized Reynolds stresses. The dashed lines represent
![]() $Re=1500$
cases for
$Re=1500$
cases for
![]() $Ma=0.3$
, 0.8, 1.2 and 2.0.
$Ma=0.3$
, 0.8, 1.2 and 2.0.
5.2 Evolution of Reynolds stresses and energy budgets
The maximal Favre-averaged turbulence statistics in the cross-wake direction (data is averaged over the periodic directions) at each time step are presented in figure 9. Other than the delayed transition, the qualitative evolution of all curves remains similar. Viscous effects are small but non-negligible when comparing
![]() $\mathit{Re}=1500$
(dashed lines) and 3000 (full lines), although the relative difference between both
$\mathit{Re}=1500$
(dashed lines) and 3000 (full lines), although the relative difference between both
![]() $Re$
increases with
$Re$
increases with
![]() $Ma$
. All wakes show a well-defined peak in
$Ma$
. All wakes show a well-defined peak in
![]() $vv$
and
$vv$
and
![]() $uv$
during the nonlinear stage of the transition; the peak is attributable to the roll-up process during transition. As for the incompressible cases, the peaks in the streamwise and spanwise normal stresses are rather blunt, and slowly decay to a far-field plateau which is approximately half of the peak value (Hickey et al.
Reference Hickey, Hussain and Wu2013). One of the principal quantitative differences in the turbulence statistics is found in the peak values reached during transition. A 53 % relative difference in the normalized cross-wake peak is observed between
$uv$
during the nonlinear stage of the transition; the peak is attributable to the roll-up process during transition. As for the incompressible cases, the peaks in the streamwise and spanwise normal stresses are rather blunt, and slowly decay to a far-field plateau which is approximately half of the peak value (Hickey et al.
Reference Hickey, Hussain and Wu2013). One of the principal quantitative differences in the turbulence statistics is found in the peak values reached during transition. A 53 % relative difference in the normalized cross-wake peak is observed between
![]() $Ma=0.8$
and 2.0. Interestingly, at lower
$Ma=0.8$
and 2.0. Interestingly, at lower
![]() $Re$
, the peak value is approximately constant (and shows no clear monotonic trend) for
$Re$
, the peak value is approximately constant (and shows no clear monotonic trend) for
![]() $Ma$
between 0.3 and 1.2, while the peak at
$Ma$
between 0.3 and 1.2, while the peak at
![]() $Ma=2.0$
is almost 19 % higher. As will be discussed in the next sections, this discrepancy between the low and high
$Ma=2.0$
is almost 19 % higher. As will be discussed in the next sections, this discrepancy between the low and high
![]() $Ma$
peaks is related to the slightly different structural mechanisms of transition compounded with the increased anisotropy of turbulent statistics with
$Ma$
peaks is related to the slightly different structural mechanisms of transition compounded with the increased anisotropy of turbulent statistics with
![]() $Ma$
.
$Ma$
.
Figure 10 shows the normalized profiles of production, dissipation and transport at characteristic times during transition. The normalized production profiles nearly overlap, with identical peaks located at
![]() $y/b=\pm 0.45$
, at both Mach numbers. A large discrepancy is found in the transport term which is very sensitive to the compressibility effects. For the higher
$y/b=\pm 0.45$
, at both Mach numbers. A large discrepancy is found in the transport term which is very sensitive to the compressibility effects. For the higher
![]() $Ma$
, the centreplane transport term remains a significant positive contributor to the TKE at both chosen times during transition. A discussion on the statistics of the transitional wake in the incompressible limit was undertaken in Hickey et al. (Reference Hickey, Hussain and Wu2013).
$Ma$
, the centreplane transport term remains a significant positive contributor to the TKE at both chosen times during transition. A discussion on the statistics of the transitional wake in the incompressible limit was undertaken in Hickey et al. (Reference Hickey, Hussain and Wu2013).

Figure 10. Normalized turbulent kinetic energy budget terms during transition at the peak
![]() $\langle vv\rangle$
((a)
$\langle vv\rangle$
((a)
![]() $Ma=0.8$
at
$Ma=0.8$
at
![]() $t=50$
;
$t=50$
;
![]() $Ma=2.0$
at
$Ma=2.0$
at
![]() $t=80$
) and at the approximate peak
$t=80$
) and at the approximate peak
![]() $\langle uu\rangle$
((b)
$\langle uu\rangle$
((b)
![]() $Ma=0.8$
at
$Ma=0.8$
at
![]() $t=80$
;
$t=80$
;
![]() $Ma=2.0$
at
$Ma=2.0$
at
![]() $t=122$
). The normalization parameter is
$t=122$
). The normalization parameter is
![]() $U_{0}^{3}/b$
. Since the flow is not in an equilibrium state, the sum of the energy budget is not expected to be null. The figures provide a snapshot-averaged value of the energy budget, the lack of time averaging results in the non-smooth profile of the transport term.
$U_{0}^{3}/b$
. Since the flow is not in an equilibrium state, the sum of the energy budget is not expected to be null. The figures provide a snapshot-averaged value of the energy budget, the lack of time averaging results in the non-smooth profile of the transport term.
5.3 Location of the maximal turbulence intensity
The far-wake turbulence statistics by Bonnet et al. (Reference Bonnet, Delville, Sapin, Sullivan and Yeru1991) and Gatski & Bonnet (Reference Gatski and Bonnet2009) show a clear outward shift of the location of the normalized TKE peak with increasing
![]() $Ma$
. The peak shifts from approximately
$Ma$
. The peak shifts from approximately
![]() $y(TKE_{max})/b=0.34$
in an incompressible far wake up to
$y(TKE_{max})/b=0.34$
in an incompressible far wake up to
![]() $y(TKE_{max})/b=0.51$
at
$y(TKE_{max})/b=0.51$
at
![]() $Ma=2.0$
, where
$Ma=2.0$
, where
![]() $b$
is the wake half-width. Since the effects of compressibility are negligible in the far wake, these statistical features must be imparted to the flow in the near field (where the compressibility effects are important) and maintained through the memory effects imparted by the structures. During the early stages leading up to transition, the normalized TKE peak location remains approximately constant until transition. The cross-wake location of the normalized TKE peak increases with increasing
$b$
is the wake half-width. Since the effects of compressibility are negligible in the far wake, these statistical features must be imparted to the flow in the near field (where the compressibility effects are important) and maintained through the memory effects imparted by the structures. During the early stages leading up to transition, the normalized TKE peak location remains approximately constant until transition. The cross-wake location of the normalized TKE peak increases with increasing
![]() $Ma$
(see figure 11); a similarly increasing monotonic trend in the peak location is observed in lower-
$Ma$
(see figure 11); a similarly increasing monotonic trend in the peak location is observed in lower-
![]() $Re$
simulations. As rollers develop, the typical double peaks of the TKE profile is lost and the maximum turbulence intensity is located about the centreplane, as seen in figure 12; the double peak is soon regained after transition, see Hickey et al. (Reference Hickey, Hussain and Wu2013) for similar profiles for the incompressible wake. The centreline peak of the TKE profile during transition is the result of the induced cross-wake velocity (caused by the coherent spanwise rollers), see the time evolution of
$Re$
simulations. As rollers develop, the typical double peaks of the TKE profile is lost and the maximum turbulence intensity is located about the centreplane, as seen in figure 12; the double peak is soon regained after transition, see Hickey et al. (Reference Hickey, Hussain and Wu2013) for similar profiles for the incompressible wake. The centreline peak of the TKE profile during transition is the result of the induced cross-wake velocity (caused by the coherent spanwise rollers), see the time evolution of
![]() $\langle {\it\rho}vv\rangle$
in figure 9. The large cross-wake-induced velocity leads to a strong
$\langle {\it\rho}vv\rangle$
in figure 9. The large cross-wake-induced velocity leads to a strong
![]() $u_{rms}$
component along the centreplane and thus a TKE peak to shift from the outer edge of the wake to the centreline. In order to understand the structural features of transition, we investigate the location of the maximum density fluctuation, which can be considered to be an approximate surrogate for the average cross-wake location of the spanwise rollers during transition. Figure 11(b) shows a very distinct peak at
$u_{rms}$
component along the centreplane and thus a TKE peak to shift from the outer edge of the wake to the centreline. In order to understand the structural features of transition, we investigate the location of the maximum density fluctuation, which can be considered to be an approximate surrogate for the average cross-wake location of the spanwise rollers during transition. Figure 11(b) shows a very distinct peak at
![]() $t=50$
and 83 for
$t=50$
and 83 for
![]() $Ma=0.8$
and 2.0 respectively. These peaks correspond to the exact time of the peak in
$Ma=0.8$
and 2.0 respectively. These peaks correspond to the exact time of the peak in
![]() $\langle {\it\rho}vv\rangle /\langle {\it\rho}\rangle U_{0}^{2}$
, see figure 9. The larger the Mach number of the wake, the farther this peak is located from the centreplane (
$\langle {\it\rho}vv\rangle /\langle {\it\rho}\rangle U_{0}^{2}$
, see figure 9. The larger the Mach number of the wake, the farther this peak is located from the centreplane (
![]() $y_{peak}=1.35$
(
$y_{peak}=1.35$
(
![]() $Ma=0.8$
) and 1.85 (
$Ma=0.8$
) and 1.85 (
![]() $Ma=2.0$
)). The structural understanding of these statistical features will be more thoroughly addressed in § 6.
$Ma=2.0$
)). The structural understanding of these statistical features will be more thoroughly addressed in § 6.

Figure 11. Evolution of the normalized cross-wake location of the maximum turbulent kinetic energy (a). The horizontal lines correspond to the far-wake locations of the maximum TKE for
![]() $Ma=0.8$
and 2.0 which was interpolated from the experimental data by Bonnet et al. (Reference Bonnet, Delville, Sapin, Sullivan and Yeru1991, figure 3). The evolution of the location of the maximum density fluctuations (b).
$Ma=0.8$
and 2.0 which was interpolated from the experimental data by Bonnet et al. (Reference Bonnet, Delville, Sapin, Sullivan and Yeru1991, figure 3). The evolution of the location of the maximum density fluctuations (b).

Figure 12. Profile of the normalized turbulent kinetic energy at three instances during the early stages of transition for
![]() $Ma=0.8$
(a) and 2.0 (b).
$Ma=0.8$
(a) and 2.0 (b).
5.4 Spectral distribution of TKE
The evolution of the spectral distribution of the TKE at the wake half-width is shown in figure 13. The peaks are visible in all the velocity components to a varying degree. The spectral peaks are found at
![]() ${\it\kappa}=1.46$
, 3.12 and 4.87 and 1.26, 2.26, 3.46 and 5.68, respectively for
${\it\kappa}=1.46$
, 3.12 and 4.87 and 1.26, 2.26, 3.46 and 5.68, respectively for
![]() $Ma=0.8$
and 2.0 (we recall that
$Ma=0.8$
and 2.0 (we recall that
![]() ${\it\kappa}^{2}={\it\alpha}^{2}+{\it\beta}^{2}$
). The primary wavenumbers correspond acceptably well to the theoretical results obtained from linear stability analysis (note that wavenumber of the linear stability results must be multiplied by two given the different definition of the wake half-width) which are
${\it\kappa}^{2}={\it\alpha}^{2}+{\it\beta}^{2}$
). The primary wavenumbers correspond acceptably well to the theoretical results obtained from linear stability analysis (note that wavenumber of the linear stability results must be multiplied by two given the different definition of the wake half-width) which are
![]() ${\it\kappa}=1.50$
(
${\it\kappa}=1.50$
(
![]() $Ma=0.8$
) and 1.30 (
$Ma=0.8$
) and 1.30 (
![]() $Ma=2.0$
). Interestingly, the secondary peaks are not exact integers of the primary modes suggesting that they may be the result of secondary instability modes of the wake. Note that they do not correspond to the most unstable sinuous perturbation, which has a lower wavenumber than the primary anti-symmetric instability mode. The energetic modes diffuse and the wavelength increases as the wake undergoes transition. For
$Ma=2.0$
). Interestingly, the secondary peaks are not exact integers of the primary modes suggesting that they may be the result of secondary instability modes of the wake. Note that they do not correspond to the most unstable sinuous perturbation, which has a lower wavenumber than the primary anti-symmetric instability mode. The energetic modes diffuse and the wavelength increases as the wake undergoes transition. For
![]() $Ma=0.8$
, the secondary peaks are completely lost between
$Ma=0.8$
, the secondary peaks are completely lost between
![]() $t=42$
and 50. Between
$t=42$
and 50. Between
![]() $t=50$
and 62, only the primary rollers can be identified in the spectrum and, once the wake transitions, the primary peak is completely lost. At
$t=50$
and 62, only the primary rollers can be identified in the spectrum and, once the wake transitions, the primary peak is completely lost. At
![]() $Ma=2.0$
, the rollers are more resilient to the scrambling of the turbulent fluctuations occurring during transition. A clear peak is observed until approximately
$Ma=2.0$
, the rollers are more resilient to the scrambling of the turbulent fluctuations occurring during transition. A clear peak is observed until approximately
![]() $t=115$
, which corresponds to a very late stage of transition, recall figure 9. Although not presented, the spectral energy distribution in the spanwise direction is void of any energetic peak during transition.
$t=115$
, which corresponds to a very late stage of transition, recall figure 9. Although not presented, the spectral energy distribution in the spanwise direction is void of any energetic peak during transition.

Figure 13. Spectral distribution of the turbulent kinetic energy at the wake half-width. The spectra are offset by two decades between each line: (a)
![]() $Ma=0.8$
; (b)
$Ma=0.8$
; (b)
![]() $Ma=2.0$
.
$Ma=2.0$
.
5.5 Evolution of Reynolds stress anisotropies
The explanation for reduced turbulence production in compressible flows has often been tied to the reduction of the pressure–strain term which imposes a finite time scale (related to the acoustic propagation speed in compressible flows) to the redistribution of the TKE among the various turbulent components. As a result, the increased compressibility leads to an increased anisotropy, which we investigate during the transition of the wake. The Reynolds stress anisotropy tensor is defined as
where
![]() $\unicode[STIX]{x1D619}_{ij}$
represents the
$\unicode[STIX]{x1D619}_{ij}$
represents the
![]() $ij$
component of the Favre-averaged Reynolds stress which is integrated in the cross-wake direction. In the high-speed mixing layer, Pantano & Sarkar (Reference Pantano and Sarkar2002) showed a monotonic increase of the magnitude of the normal terms with increasing convective Mach number, but only in the near field. A similar result is observed for the transitional wake, see figure 14 and table 2. Unlike the mixing layer, the wake undergoes a return to isotropy after transition. The anisotropy in the far wake becomes negligible as the centreline defect, hence, the mean shear, tends toward zero. In the transitional region, all the peak values of the normal terms show a slight monotonic increase in magnitude with
$ij$
component of the Favre-averaged Reynolds stress which is integrated in the cross-wake direction. In the high-speed mixing layer, Pantano & Sarkar (Reference Pantano and Sarkar2002) showed a monotonic increase of the magnitude of the normal terms with increasing convective Mach number, but only in the near field. A similar result is observed for the transitional wake, see figure 14 and table 2. Unlike the mixing layer, the wake undergoes a return to isotropy after transition. The anisotropy in the far wake becomes negligible as the centreline defect, hence, the mean shear, tends toward zero. In the transitional region, all the peak values of the normal terms show a slight monotonic increase in magnitude with
![]() $Ma$
, while
$Ma$
, while
![]() $\unicode[STIX]{x1D623}_{12}$
shows a clear decrease; a similar trend is observed among the lower-
$\unicode[STIX]{x1D623}_{12}$
shows a clear decrease; a similar trend is observed among the lower-
![]() $Re$
simulations. The most significant effect of compressibility is noted in the pre-transitional anisotropy where the difference between
$Re$
simulations. The most significant effect of compressibility is noted in the pre-transitional anisotropy where the difference between
![]() $\unicode[STIX]{x1D623}_{11}$
and
$\unicode[STIX]{x1D623}_{11}$
and
![]() $\unicode[STIX]{x1D623}_{22}$
increases, rather significantly, with the Mach number of the flow. As the pre-transitional flow is primarily two-dimensional
$\unicode[STIX]{x1D623}_{22}$
increases, rather significantly, with the Mach number of the flow. As the pre-transitional flow is primarily two-dimensional
![]() $\unicode[STIX]{x1D619}_{33}\approx 0$
, it is expected that
$\unicode[STIX]{x1D619}_{33}\approx 0$
, it is expected that
![]() $\unicode[STIX]{x1D623}_{11}$
and
$\unicode[STIX]{x1D623}_{11}$
and
![]() $\unicode[STIX]{x1D623}_{22}$
have a similar but opposite behaviour and that
$\unicode[STIX]{x1D623}_{22}$
have a similar but opposite behaviour and that
![]() $\unicode[STIX]{x1D619}_{11}$
is largest contributor to
$\unicode[STIX]{x1D619}_{11}$
is largest contributor to
![]() $\unicode[STIX]{x1D619}_{kk}$
(since it is normal to the gradient of the mean flow). The cross-over between
$\unicode[STIX]{x1D619}_{kk}$
(since it is normal to the gradient of the mean flow). The cross-over between
![]() $\unicode[STIX]{x1D623}_{11}$
and
$\unicode[STIX]{x1D623}_{11}$
and
![]() $\unicode[STIX]{x1D623}_{22}$
occurs as the spanwise coherent rollers emerge in the transitional wake and contributes to important cross-wake mixing. These general results are very similar to those in the high-speed mixing layer (Pantano & Sarkar Reference Pantano and Sarkar2002). The importance of the anisotropy can be seen in the recent advances in turbulence modelling for second-order closure. Recent three-equation turbulence models (Yoshizawa et al.
Reference Yoshizawa, Abe, Matsuo, Fujiwara and Mizobuchi2012) have attempted to capture the Reynolds stress anisotropy through the formation of a supersonic non-equilibrium parameters (which is a function of
$\unicode[STIX]{x1D623}_{22}$
occurs as the spanwise coherent rollers emerge in the transitional wake and contributes to important cross-wake mixing. These general results are very similar to those in the high-speed mixing layer (Pantano & Sarkar Reference Pantano and Sarkar2002). The importance of the anisotropy can be seen in the recent advances in turbulence modelling for second-order closure. Recent three-equation turbulence models (Yoshizawa et al.
Reference Yoshizawa, Abe, Matsuo, Fujiwara and Mizobuchi2012) have attempted to capture the Reynolds stress anisotropy through the formation of a supersonic non-equilibrium parameters (which is a function of
![]() $Ma_{t}$
), which in turn results in a reduced spread rate in the high-speed mixing layer.
$Ma_{t}$
), which in turn results in a reduced spread rate in the high-speed mixing layer.

Figure 14. Evolution of the integrated Favre-averaged anisotropy for
![]() $Ma_{r}=0.8$
(a) and 2.0 (b).
$Ma_{r}=0.8$
(a) and 2.0 (b).
Table 2. Peak values of the Favre-averaged Reynolds stress anisotropy for the near-wake evolution. The mixing layer results are obtained from Pantano & Sarkar (Reference Pantano and Sarkar2002).

5.6 Transitional convection velocity
The velocity of convecting structures in free-shear flows plays a central role in the entrainment of ambient fluid into the turbulent flow. In bluff-body wakes, any modification to the convective velocity is therefore tied to the base pressure (Kastengren, Dutton & Elliot Reference Kastengren, Dutton and Elliot2007) and, consequently, the total drag of a body. The effects of compressibility on the convection velocity of free-shear flows have been subject to much debate, especially for the mixing layer. It has been suggested that at high convective Mach numbers, the isentropic approximation does not capture the velocity of convecting structures (Clemens & Mungal Reference Clemens and Mungal1995): the convection velocity is either higher or lower depending on the sub or supersonic nature of the co-flowing streams. Other workers have suggested that the experimental difficulties of computing this velocity may explain the non-isotropic convection velocity results (Thurow et al. Reference Thurow, Jiang, Kim, Lempert and Samimy2008).

Figure 15. Convection velocity at various temporal locations during transition of the wake: (a)
![]() $Ma_{r}=0.8$
; (b)
$Ma_{r}=0.8$
; (b)
![]() $Ma_{r}=2.0$
. A fourth-order polynomial is used to interpolate all the discrete convective velocity profiles for clarity. The convection velocity is based on the separation distance which maximizes the two-point correlation of density,
$Ma_{r}=2.0$
. A fourth-order polynomial is used to interpolate all the discrete convective velocity profiles for clarity. The convection velocity is based on the separation distance which maximizes the two-point correlation of density,
![]() ${\it\rho}$
, with
${\it\rho}$
, with
![]() ${\it\tau}=4$
.
${\it\tau}=4$
.
Any modification to the convection velocity caused by the compressibility effects in the transitioning wake would greatly modify the dynamics of the flow and this issue needs to be addressed for completeness. Different approaches to the computation of the convective velocity have been proposed. To investigate Taylor’s hypothesis, del Alamo & Jimenez (Reference del Alamo and Jimenez2009) computed the convective velocity in spectral space, Hussain & Clark (Reference Hussain and Clark1981) proposed a method based on the frequency–wavenumber spectrum peak while Demetriades (Reference Demetriades1976) suggested a spatio-temporal correlation approach. In the present work, the latter approach is used by finding the streamwise separation,
![]() ${\it\delta}x$
, which maximizes the peak cross-correlation coefficient for a given temporal separation
${\it\delta}x$
, which maximizes the peak cross-correlation coefficient for a given temporal separation
![]() ${\it\tau}$
; a similar approach was also used by Kim & Hussain (Reference Kim and Hussain1993). Therefore, the convection velocity of the structures is defined as
${\it\tau}$
; a similar approach was also used by Kim & Hussain (Reference Kim and Hussain1993). Therefore, the convection velocity of the structures is defined as
As the
![]() ${\it\delta}x$
is confined to a finite grid, we must judiciously choose a minimal temporal separation,
${\it\delta}x$
is confined to a finite grid, we must judiciously choose a minimal temporal separation,
![]() ${\it\tau}$
, which allows enough resolution to adequately determine the convection velocity. If
${\it\tau}$
, which allows enough resolution to adequately determine the convection velocity. If
![]() ${\it\tau}$
is too small, the convection velocity becomes limited by the spatial resolution of the simulation. Alternatively, if
${\it\tau}$
is too small, the convection velocity becomes limited by the spatial resolution of the simulation. Alternatively, if
![]() ${\it\tau}$
is too large, the convection velocity becomes an average value of little physical interest and the inherent parallel flow assumption in this approach becomes questionable. For the current cases,
${\it\tau}$
is too large, the convection velocity becomes an average value of little physical interest and the inherent parallel flow assumption in this approach becomes questionable. For the current cases,
![]() ${\it\tau}=4$
was chosen as a baseline, it should be noted that the results remain unchanged for
${\it\tau}=4$
was chosen as a baseline, it should be noted that the results remain unchanged for
![]() ${\it\tau}=8$
. The density is used to identify the maximal cross-correlation coefficient, although other variables such as velocity, pressure and scalar field have also been used employing the same procedure and yielded very similar results.
${\it\tau}=8$
. The density is used to identify the maximal cross-correlation coefficient, although other variables such as velocity, pressure and scalar field have also been used employing the same procedure and yielded very similar results.
Figure 15 presents the difference between the local convection and mean velocity normalized by the centreline defect. As the instantaneous convection velocity represents an averaged value over a finite time window (
![]() ${\it\tau}=4$
), the mean and centreline velocities are computed over the same temporal span. The convection velocity at the centreline differs drastically from the mean flow, the identified structures convect at significantly faster speed than the mean centreline velocity. This result should come as no surprise since any structure which drifts toward the centreplane will naturally have a higher velocity. Similarly, the structures drifting outside the wake have a lower velocity than the local mean flow. After transition, the convection velocity outside the wake (
${\it\tau}=4$
), the mean and centreline velocities are computed over the same temporal span. The convection velocity at the centreline differs drastically from the mean flow, the identified structures convect at significantly faster speed than the mean centreline velocity. This result should come as no surprise since any structure which drifts toward the centreplane will naturally have a higher velocity. Similarly, the structures drifting outside the wake have a lower velocity than the local mean flow. After transition, the convection velocity outside the wake (
![]() ${\approx}y/b>1.0$
) becomes equal to the mean. Interestingly, the convection velocity is invariant to the
${\approx}y/b>1.0$
) becomes equal to the mean. Interestingly, the convection velocity is invariant to the
![]() $Ma$
of the wake, a result which comes as a surprise given the large centreplane discrepancy between the magnitude of the transport term, recall figure 10.
$Ma$
of the wake, a result which comes as a surprise given the large centreplane discrepancy between the magnitude of the transport term, recall figure 10.
5.7 Shocklet formation
Shocklets is the term used to describe a localized discontinuity caused by fluctuating fields of turbulent eddies (Lee et al.
Reference Lee, Lele and Moin1991). They are known to occur in decaying isotropic turbulence (Lee et al.
Reference Lee, Lele and Moin1991; Samtaney et al.
Reference Samtaney, Pullin and Kosovic2001) and in mixing layers (Sandham & Yee Reference Sandham and Yee1989; Papamoschou Reference Papamoschou1995; Vreman et al.
Reference Vreman, Sandham and Luo1996; Freund, Lele & Moin Reference Freund, Lele and Moin2000a
,Reference Freund, Lele and Moin
b
). In the two-dimensional mixing layer simulations, the shocklets appear at
![]() $Ma_{c}=0.7$
(Sandham & Yee Reference Sandham and Yee1989); for three-dimensional simulations, a higher convective Mach number is needed, approximately
$Ma_{c}=0.7$
(Sandham & Yee Reference Sandham and Yee1989); for three-dimensional simulations, a higher convective Mach number is needed, approximately
![]() $Ma_{c}=1.2$
(Vreman et al.
Reference Vreman, Sandham and Luo1996). In the case of the wake, Clemens & Smith (Reference Clemens and Smith1998) observed eddy-induced shocklets in the near-field wake (
$Ma_{c}=1.2$
(Vreman et al.
Reference Vreman, Sandham and Luo1996). In the case of the wake, Clemens & Smith (Reference Clemens and Smith1998) observed eddy-induced shocklets in the near-field wake (
![]() $Ma_{r}>0.9$
). These observations were primarily based on the inspection of PLS images from a free-stream transitioning wake at
$Ma_{r}>0.9$
). These observations were primarily based on the inspection of PLS images from a free-stream transitioning wake at
![]() $Ma_{\infty }=3$
. The presence of shocklets in the transitioning wake has the potential of greatly modifying the dynamics of the flow, as shocks promote a rapid change from kinetic to internal energy (i.e. dissipation) and also alters the eddies and turbulence via vorticity–shocklet interactions. Given the low relative and turbulent Mach numbers during the nonlinear stage of transition, it comes as no surprise that shocklets are not observed in the present transitioning wakes. Nonetheless, the evolution of the maximum local pressure,
$Ma_{\infty }=3$
. The presence of shocklets in the transitioning wake has the potential of greatly modifying the dynamics of the flow, as shocks promote a rapid change from kinetic to internal energy (i.e. dissipation) and also alters the eddies and turbulence via vorticity–shocklet interactions. Given the low relative and turbulent Mach numbers during the nonlinear stage of transition, it comes as no surprise that shocklets are not observed in the present transitioning wakes. Nonetheless, the evolution of the maximum local pressure,
![]() $(\partial p/\partial x_{i}\cdot \partial p/\partial x_{i})^{1/2}$
, and density,
$(\partial p/\partial x_{i}\cdot \partial p/\partial x_{i})^{1/2}$
, and density,
![]() $(\partial {\it\rho}/\partial x_{i}\cdot \partial {\it\rho}/\partial x_{i})^{1/2}$
, derivatives are shown in figure 16. Despite an important peak at
$(\partial {\it\rho}/\partial x_{i}\cdot \partial {\it\rho}/\partial x_{i})^{1/2}$
, derivatives are shown in figure 16. Despite an important peak at
![]() $t=100$
(for
$t=100$
(for
![]() $Ma=2.0$
), no clear evidence of a shocklet was observed in the instantaneous velocity field. The turbulent Mach number peaks at 0.3, which is far below the minimum value for shocklets to appear in decaying isotropic turbulence.
$Ma=2.0$
), no clear evidence of a shocklet was observed in the instantaneous velocity field. The turbulent Mach number peaks at 0.3, which is far below the minimum value for shocklets to appear in decaying isotropic turbulence.

Figure 16. Evolution of the magnitude of the maximum pressure and density gradient (a) and the minimum and maximum pressure (b).
6 Numerical simulation: structural eduction
6.1 Formation and shape of rollers
Based on the flow visualization, Clemens & Mungal (Reference Clemens and Mungal1995) showed that the compressibility effects modify the shape of the rollers in the mixing layer; as the
![]() $Ma$
increased, the rollers change from a circular to polygonal shape. Messersmith & Dutton (Reference Messersmith and Dutton1996) showed, using a more rigorous statistical approach, that the structures become elongated and compressed with increasing compressibility. In the wake, the experimental (Clemens & Smith Reference Clemens and Smith1998) and numerical (Chen et al.
Reference Chen, Cantwell and Mansour1990; Watanabe & Maekawa Reference Watanabe and Maekawa2004) visualizations show initially circular rollers which deform and tend toward an elliptical shape, although from the results, it is difficult to assess if it is a transitional, a compressibility or purely shearing effect. To gain an overall understanding of the transitional structures in the planar wake, a slice of the magnitude of the density gradient, at various times, is shown in figures 17 and 18. These figures, especially figure 18, highlight some of the limitations of temporal simulations. The primary instability wavelength, as computed from the linear stability theory, dictates the streamwise extent of the computational domain. As the flow evolves and the principal wavelength becomes longer, the domain can no longer support an integer number of structures and localized cross-wake pairing may arise (see figure 18 at
$Ma$
increased, the rollers change from a circular to polygonal shape. Messersmith & Dutton (Reference Messersmith and Dutton1996) showed, using a more rigorous statistical approach, that the structures become elongated and compressed with increasing compressibility. In the wake, the experimental (Clemens & Smith Reference Clemens and Smith1998) and numerical (Chen et al.
Reference Chen, Cantwell and Mansour1990; Watanabe & Maekawa Reference Watanabe and Maekawa2004) visualizations show initially circular rollers which deform and tend toward an elliptical shape, although from the results, it is difficult to assess if it is a transitional, a compressibility or purely shearing effect. To gain an overall understanding of the transitional structures in the planar wake, a slice of the magnitude of the density gradient, at various times, is shown in figures 17 and 18. These figures, especially figure 18, highlight some of the limitations of temporal simulations. The primary instability wavelength, as computed from the linear stability theory, dictates the streamwise extent of the computational domain. As the flow evolves and the principal wavelength becomes longer, the domain can no longer support an integer number of structures and localized cross-wake pairing may arise (see figure 18 at
![]() $t=93$
and 109). These localized events should not limit the generality of our findings but need to be considered in the analysis.
$t=93$
and 109). These localized events should not limit the generality of our findings but need to be considered in the analysis.

Figure 17. Magnitude of the density gradient (at the middle of the spanwise computational domain) for
![]() $Ma_{r}=0.8$
at times (top to bottom) 41, 46, 51, 56, 62 and 76.
$Ma_{r}=0.8$
at times (top to bottom) 41, 46, 51, 56, 62 and 76.
The two-dimensional slice provides a local and instantaneous representation of the roller shape. Although the rollers are predominantly two-dimensional, there is a non-negligible variation of the shape at different spanwise locations (this will become obvious while discussing the three-dimensional structural visualizations in figures 25 and 26). These spanwise variations are attributable to the internal core dynamic instabilities of the rollers (Melander & Hussain Reference Melander and Hussain1994) and to local inhomogeneities (Pradeep & Hussain Reference Pradeep and Hussain2001) in the spanwise direction. Therefore, we seek to generalize the effect of compressibility on the evolution of a prototypical roller during transition. To this effect, an eduction technique based on the
![]() ${\it\lambda}_{2}$
-criteria was developed (results are very similar when using density or
${\it\lambda}_{2}$
-criteria was developed (results are very similar when using density or
![]() $Q$
-criteria to identify the structures).
$Q$
-criteria to identify the structures).

Figure 18. Magnitude of the density gradient (at the middle of the spanwise computational domain) for
![]() $Ma_{r}=2.0$
at times (top to bottom) 66, 78, 93, 109 and 122.
$Ma_{r}=2.0$
at times (top to bottom) 66, 78, 93, 109 and 122.
In the first step, we agnostically average the flow in the spanwise direction and locate the mean vortex axis location by identifying the local peaks in the averaged
![]() ${\it\lambda}_{2}$
. We visually confirm that these peaks correspond to the approximate axis of the rollers. In the second step, the rollers are extracted in the spanwise direction using a window of
${\it\lambda}_{2}$
. We visually confirm that these peaks correspond to the approximate axis of the rollers. In the second step, the rollers are extracted in the spanwise direction using a window of
![]() $b/2\times b/2$
(in the
$b/2\times b/2$
(in the
![]() $x$
–
$x$
–
![]() $y$
plane) around each identified peak. Each roller is remapped, using a second-order Lagrangian polynomial, onto a homogeneous grid (in the
$y$
plane) around each identified peak. Each roller is remapped, using a second-order Lagrangian polynomial, onto a homogeneous grid (in the
![]() $x$
–
$x$
–
![]() $y$
plane;
$y$
plane;
![]() $z$
is already homogeneous) with a higher resolution (
$z$
is already homogeneous) with a higher resolution (
![]() $71\times 71$
for a computational domain of
$71\times 71$
for a computational domain of
![]() $b\times b$
). The
$b\times b$
). The
![]() $x{-}y$
slices at each
$x{-}y$
slices at each
![]() $z$
location are first correlated to the spanwise-averaged slice. By offsetting the slice by up to 12 grid points in each direction (which represents a maximal offset of approximately
$z$
location are first correlated to the spanwise-averaged slice. By offsetting the slice by up to 12 grid points in each direction (which represents a maximal offset of approximately
![]() $b/6$
in
$b/6$
in
![]() $x$
and
$x$
and
![]() $y$
-directions), we identify the offset which maximizes the autocorrelation coefficient. The spanwise average, with the optimal offset, is computed with the slices which have an above average correlation coefficient. The remaining slices are discarded and a bootstrapping technique is used. The new spanwise-averaged roller (with optimal offset) is used to re-correlate all the slices, which are once more offset to maximize the correlation; again, only the above average correlation coefficient slices are used for the spanwise average. After 3 loops, we obtain a highly correlated coherent structure (a similar approach has been proposed by Jeong et al. (Reference Jeong, Hussain, Schoppa and Kim1997)). The evolution of the prototypical rollers during transition is unambiguously educed and presented in figures 19 and 21. In order to confirm the validity of the educed features, figures 20 and 22 show the evolution of a typical roller from a single slice of spanwise vorticity.
$y$
-directions), we identify the offset which maximizes the autocorrelation coefficient. The spanwise average, with the optimal offset, is computed with the slices which have an above average correlation coefficient. The remaining slices are discarded and a bootstrapping technique is used. The new spanwise-averaged roller (with optimal offset) is used to re-correlate all the slices, which are once more offset to maximize the correlation; again, only the above average correlation coefficient slices are used for the spanwise average. After 3 loops, we obtain a highly correlated coherent structure (a similar approach has been proposed by Jeong et al. (Reference Jeong, Hussain, Schoppa and Kim1997)). The evolution of the prototypical rollers during transition is unambiguously educed and presented in figures 19 and 21. In order to confirm the validity of the educed features, figures 20 and 22 show the evolution of a typical roller from a single slice of spanwise vorticity.

Figure 19. Evolution of the spanwise educed structure for
![]() $Ma=0.8$
(at approximately
$Ma=0.8$
(at approximately
![]() $x=46$
) at times 46 (a), 48 (b), 52 (c), 54 (d) and 56 (e).
$x=46$
) at times 46 (a), 48 (b), 52 (c), 54 (d) and 56 (e).

Figure 20. Formation of a roller from an instantaneous slice of the spanwise vorticity for the low Mach number case (
![]() $Ma=0.8$
). Contour lines are
$Ma=0.8$
). Contour lines are
![]() ${\it\omega}_{z}=\pm 0.25$
, 0.5, 0.75 and 1.0.
${\it\omega}_{z}=\pm 0.25$
, 0.5, 0.75 and 1.0.

Figure 21. Evolution of the spanwise educed structure for
![]() $Ma=2.0$
(at around
$Ma=2.0$
(at around
![]() $x=42$
) at times 76 (a), 84 (b), 88 (c), 90 (d) and 92 (e).
$x=42$
) at times 76 (a), 84 (b), 88 (c), 90 (d) and 92 (e).
The effects of compressibility on the roller formation of the planar wakes is illustrated in figure 23. The increased ellipticity is a consequence of the combined effects of an increased wavelength and a reduced growth rate with increasing Mach number. Given an infinitesimal sinusoidal perturbation within a shear layer, shown in figure 23,
![]() $\text{Im}({\it\omega})$
defines the linear grow of a perturbation in time. As the perturbation grows, the shear pushes the vorticity toward the centrepoint of the sinusoidal perturbation, hence forming the rollers. Naturally, the larger the growth rate, the faster the roll-up process. In transitional wakes, the growth rate of the most unstable mode is proportional to the conjugate diameter of the resulting elliptical structure, while the transverse diameter is characterized by the wavelength of the instability. Since the growth rate and wavelength are negatively coupled with varying Mach number (recall the linear stability theory and figure 1), it comes as no surprise that the higher Mach number (hence lower growth and longer wavelength of the most unstable mode) leads to an increased ellipticity of the transitional structures.
$\text{Im}({\it\omega})$
defines the linear grow of a perturbation in time. As the perturbation grows, the shear pushes the vorticity toward the centrepoint of the sinusoidal perturbation, hence forming the rollers. Naturally, the larger the growth rate, the faster the roll-up process. In transitional wakes, the growth rate of the most unstable mode is proportional to the conjugate diameter of the resulting elliptical structure, while the transverse diameter is characterized by the wavelength of the instability. Since the growth rate and wavelength are negatively coupled with varying Mach number (recall the linear stability theory and figure 1), it comes as no surprise that the higher Mach number (hence lower growth and longer wavelength of the most unstable mode) leads to an increased ellipticity of the transitional structures.

Figure 22. Formation of a roller from an instantaneous slice of the spanwise vorticity for the higher Mach number case (
![]() $Ma=2.0$
). Contour lines are
$Ma=2.0$
). Contour lines are
![]() ${\it\omega}_{z}=\pm 0.05$
, 0.15, 0.3, 0.45 0.6 and 0.75. The approximate rotation angle of the principal axis of the elliptical rollers is shown: (a)
${\it\omega}_{z}=\pm 0.05$
, 0.15, 0.3, 0.45 0.6 and 0.75. The approximate rotation angle of the principal axis of the elliptical rollers is shown: (a)
![]() $35^{\circ }$
; (b)
$35^{\circ }$
; (b)
![]() $50^{\circ }$
; (c)
$50^{\circ }$
; (c)
![]() $95^{\circ }$
; (d)
$95^{\circ }$
; (d)
![]() $120^{\circ }$
; (e)
$120^{\circ }$
; (e)
![]() $145^{\circ }$
.
$145^{\circ }$
.

Figure 23. Conceptual sketch of the growth of a sinusoidal perturbation in a shear layer. The wavelength,
![]() ${\it\lambda}$
, increases and the growth
${\it\lambda}$
, increases and the growth
![]() $\text{Im}({\it\omega})$
decreases with
$\text{Im}({\it\omega})$
decreases with
![]() $Ma$
. In a shear flow, the perturbations in a low-speed wake (denoted
$Ma$
. In a shear flow, the perturbations in a low-speed wake (denoted
![]() $ls$
, (a)) will have a more circular while the high-speed wake (denoted
$ls$
, (a)) will have a more circular while the high-speed wake (denoted
![]() $hs$
, (b)) will be more elliptical. The lines correspond to the temporal evolution of a sinusoidal perturbation.
$hs$
, (b)) will be more elliptical. The lines correspond to the temporal evolution of a sinusoidal perturbation.
The increasing ellipticity with Mach number is evidenced by the educed rollers in figures 19 and 21 as well as by the two-dimensional slices of vorticity in figures 20 and 22. The present findings are in agreement with Messersmith & Dutton (Reference Messersmith and Dutton1996) who suggested that compressibility elongates the coherent structures in the mixing layer. In contrast to our conceptual understanding of the roll up, the rollers show a clear asymmetry with vorticity initially congregating towards the outer-wake side of the rollers, see figures 20 and 22. As the roll-up process evolves, the point of the largest vorticity rotates at the outer radius of the roller. Interestingly, the rotation of the maximum vorticity mirrors the local peak in the location of the maximum density fluctuations (at times
![]() $t=50$
and 83 for
$t=50$
and 83 for
![]() $Ma=0.8$
and 2.0, respectively) in figure 11. This result entails that the evolution of the roll-up process can be inferred from the average statistics in the wake.
$Ma=0.8$
and 2.0, respectively) in figure 11. This result entails that the evolution of the roll-up process can be inferred from the average statistics in the wake.
6.2 Evolution of roller configuration during transition
The effects of compressibility on the structural configuration of the rollers is investigated. The evolution of the streamwise separation of the rollers,
![]() ${\it\lambda}$
, is presented in figure 24(a). It is defined as the first positive peak of the two-point correlation with streamwise separation of the cross-wake velocity (
${\it\lambda}$
, is presented in figure 24(a). It is defined as the first positive peak of the two-point correlation with streamwise separation of the cross-wake velocity (
![]() ${\it\lambda}$
is also invariant to the use of other velocity or thermodynamic components for the correlation) at the wake half-width. In order to unambiguously identify the first positive peak, the minimal correlation coefficient was set to
${\it\lambda}$
is also invariant to the use of other velocity or thermodynamic components for the correlation) at the wake half-width. In order to unambiguously identify the first positive peak, the minimal correlation coefficient was set to
![]() $-$
0.15 for the first negative peak and 0.1 for the first positive peak. For that reason, the values for
$-$
0.15 for the first negative peak and 0.1 for the first positive peak. For that reason, the values for
![]() $t>76$
(
$t>76$
(
![]() $Ma=0.8$
) and
$Ma=0.8$
) and
![]() $t>98$
(
$t>98$
(
![]() $Ma=2.0$
) are not presented as the peaks in the streamwise correlation are too weak. As expected from the linear stability theory, the increasing Mach number results in a longer streamwise separation of the rollers. The plateau of
$Ma=2.0$
) are not presented as the peaks in the streamwise correlation are too weak. As expected from the linear stability theory, the increasing Mach number results in a longer streamwise separation of the rollers. The plateau of
![]() ${\it\lambda}$
during linear stage and the roller formation stage, conforms surprisingly well with the calculated wavelength of the primary instability mode from § 3.2 (recall that the wake half-width of the linear stability calculations is twice that of the DNS):
${\it\lambda}$
during linear stage and the roller formation stage, conforms surprisingly well with the calculated wavelength of the primary instability mode from § 3.2 (recall that the wake half-width of the linear stability calculations is twice that of the DNS):
![]() ${\it\lambda}_{linear}=4.18$
compared with
${\it\lambda}_{linear}=4.18$
compared with
![]() ${\it\lambda}_{DNS}=4.12$
for
${\it\lambda}_{DNS}=4.12$
for
![]() $Ma=0.8$
. For the higher Mach number case, the difference is slightly greater (
$Ma=0.8$
. For the higher Mach number case, the difference is slightly greater (
![]() ${\it\lambda}_{linear}=4.83$
compared with
${\it\lambda}_{linear}=4.83$
compared with
![]() ${\it\lambda}_{DNS}=5.24$
). It should be noted that the monotonically increasing wavelength with
${\it\lambda}_{DNS}=5.24$
). It should be noted that the monotonically increasing wavelength with
![]() $Ma$
is also observed for the lower-
$Ma$
is also observed for the lower-
![]() $Re$
despite the constant computational domain size. The pairing of rollers can be seen in the increase of the streamwise separation in
$Re$
despite the constant computational domain size. The pairing of rollers can be seen in the increase of the streamwise separation in
![]() $Ma=0.8$
. As pairing does not occur simultaneously for all rollers, there is an incremental roller separation from
$Ma=0.8$
. As pairing does not occur simultaneously for all rollers, there is an incremental roller separation from
![]() $t>60$
(
$t>60$
(
![]() $Ma=0.8$
). Interestingly, there is no noticeable increase in the length scale for
$Ma=0.8$
). Interestingly, there is no noticeable increase in the length scale for
![]() $Ma=2.0$
(and, thus, no pairing): a result corroborated by the spectral analysis in figure 13.
$Ma=2.0$
(and, thus, no pairing): a result corroborated by the spectral analysis in figure 13.

Figure 24. Evolution of the size of the spanwise rollers during transition. The separation length of the first positive peak in the two-point correlation of the cross-wake velocity was used to estimate the size of the rollers (a). Evolution of the ratio of the cross-wake to streamwise separation of rollers with comparative line of the neutrally stable configuration (b).
The evolution of the wake half-width,
![]() $b$
, is also shown in figure 24(a). The initial linear stage of the wake evolution is characterized by low spread rates (up to
$b$
, is also shown in figure 24(a). The initial linear stage of the wake evolution is characterized by low spread rates (up to
![]() $t=40$
for
$t=40$
for
![]() $Ma=0.8$
and
$Ma=0.8$
and
![]() $t=65$
for
$t=65$
for
![]() $Ma=2.0$
). At the start of the nonlinear stage, a very rapid lateral spreading occurs during which the rollers form and rotate; recall figures 19 and 21. The spread rate during the roller formation stage decreases, albeit very slightly, with Mach number (
$Ma=2.0$
). At the start of the nonlinear stage, a very rapid lateral spreading occurs during which the rollers form and rotate; recall figures 19 and 21. The spread rate during the roller formation stage decreases, albeit very slightly, with Mach number (
![]() $\text{d}b/\text{d}t=0.1155$
and 0.1058; for
$\text{d}b/\text{d}t=0.1155$
and 0.1058; for
![]() $Ma=0.8$
and 2.0, respectively). It should be noted that the lower-
$Ma=0.8$
and 2.0, respectively). It should be noted that the lower-
![]() $Re$
cases did not reveal a clear monotonic trend with Mach number. After the rollers form and rotate
$Re$
cases did not reveal a clear monotonic trend with Mach number. After the rollers form and rotate
![]() $180^{\circ }$
(see figure 22 for the roller rotation), the lateral spreading levels off. For
$180^{\circ }$
(see figure 22 for the roller rotation), the lateral spreading levels off. For
![]() $Ma=2.0$
, there is even a slight, temporary decrease in the lateral length scale of the wake caused by the rotation of the elliptical rollers. As the transverse axis of the roller is oriented in the cross-wake direction (
$Ma=2.0$
, there is even a slight, temporary decrease in the lateral length scale of the wake caused by the rotation of the elliptical rollers. As the transverse axis of the roller is oriented in the cross-wake direction (
![]() $90^{\circ }$
rotation), the wake half-width is maximized; as
$90^{\circ }$
rotation), the wake half-width is maximized; as
![]() $180^{\circ }$
rotation is completed and the transverse axis becomes parallel to the streamwise direction, the wake half-width is reduced, albeit temporarily.
$180^{\circ }$
rotation is completed and the transverse axis becomes parallel to the streamwise direction, the wake half-width is reduced, albeit temporarily.
The ratio of the cross-wake to streamwise roller separation,
![]() $h/{\it\lambda}$
, (discussed in § 4) is shown in figure 24(b). For the cross-wake separation, we use the location of the maximum density fluctuations (figure 11) as a proxy. As expected, the ratio of
$h/{\it\lambda}$
, (discussed in § 4) is shown in figure 24(b). For the cross-wake separation, we use the location of the maximum density fluctuations (figure 11) as a proxy. As expected, the ratio of
![]() $h/{\it\lambda}$
decreases with increasing Mach number during the roller formation stage. As the rollers rotate, the peak density fluctuations gets pushed to the outer edge of the wake, resulting in an increasing ratio of
$h/{\it\lambda}$
decreases with increasing Mach number during the roller formation stage. As the rollers rotate, the peak density fluctuations gets pushed to the outer edge of the wake, resulting in an increasing ratio of
![]() $h/{\it\lambda}$
.
$h/{\it\lambda}$
.
6.3 Visualization of the rollers and ribs

Figure 25. Top view of the transition of
![]() $Ma=0.8$
during transition at
$Ma=0.8$
during transition at
![]() $t=50$
(a), 54 (b), 56 (c), 58 (d), 60 (e), 62 (f), 64 (g), 66 (h) and 68 (i). Isosurfaces of
$t=50$
(a), 54 (b), 56 (c), 58 (d), 60 (e), 62 (f), 64 (g), 66 (h) and 68 (i). Isosurfaces of
![]() ${\it\lambda}_{2}$
coloured by the streamwise velocity. Each panel corresponds to
${\it\lambda}_{2}$
coloured by the streamwise velocity. Each panel corresponds to
![]() $3/16$
of the total streamwise domain (
$3/16$
of the total streamwise domain (
![]() $L_{x}\approx 12.7$
).
$L_{x}\approx 12.7$
).

Figure 26. Top view of the transition of
![]() $Ma=2.0$
during transition at
$Ma=2.0$
during transition at
![]() $t=90$
(a), 94 (b), 96 (c), 98 (d), 100 (e), 104 (f) and 108 (g). Isosurfaces of
$t=90$
(a), 94 (b), 96 (c), 98 (d), 100 (e), 104 (f) and 108 (g). Isosurfaces of
![]() ${\it\lambda}_{2}$
coloured by the streamwise velocity. Each panel corresponds to
${\it\lambda}_{2}$
coloured by the streamwise velocity. Each panel corresponds to
![]() ${\approx}3/18$
of the total streamwise domain (
${\approx}3/18$
of the total streamwise domain (
![]() $Lx\approx 13.1$
).
$Lx\approx 13.1$
).

Figure 27. Illustrative effects of compressibility on the domain of influence of the rollers. In typical low-speed wakes (
![]() $ls$
), communication occurs primarily between neighbouring vortices along the same row (a). In higher-speed wakes (
$ls$
), communication occurs primarily between neighbouring vortices along the same row (a). In higher-speed wakes (
![]() $hs$
), the domain of influence is predominantly in the cross-wake direction (b).
$hs$
), the domain of influence is predominantly in the cross-wake direction (b).

Figure 28. Organization of the rib vortices (isosurface of
![]() $Q=0.5$
) with respect to the spanwise rollers at
$Q=0.5$
) with respect to the spanwise rollers at
![]() $Ma=2.0$
at
$Ma=2.0$
at
![]() $t=92$
. The rollers are identified by a two-dimensional contour plot of the
$t=92$
. The rollers are identified by a two-dimensional contour plot of the
![]() ${\it\lambda}_{2}$
-criteria.
${\it\lambda}_{2}$
-criteria.
The top-view visualization of the rollers, in figures 25 and 26, offers a different perspective to understand the effects of compressibility on the vortex array configuration. The cumulative effects of the increased streamwise roller separation (§ 3 and previous subsection) and an inhibited streamwise communication between rollers on the same row (§ 4) drastically modifies the interaction between the rollers. As the compressibility effects become more important, there is an increasing cross-wake and reduced streamwise interaction, see illustration 27, which eventually impedes the pairing of rollers, as the roller pairing implies a mutual induction between neighbouring coherent structures. This inhibited pairing is observed in figure 26 and in the corresponding statistics of the streamwise separation figure 24(a). Presumably, in the fully turbulent region, pairing or amalgamation of turbulent rollers occurs but, unlike the
![]() $Ma=0.8$
case in figure 25, it is not a transitional feature.
$Ma=0.8$
case in figure 25, it is not a transitional feature.
The increased cross-wake communication, longer roll-up time and the inhibited structural pairing in the high-speed wake promotes the formation of well-organized rib structures which connect rollers on the opposite side of the centreplane. Figure 28 shows the organization of the rib structures with respect to the primarily two-dimensional rollers in the case of
![]() $Ma=2.0$
. The rib-structures are highly organized and survive throughout transition: a clear contrast to the incompressible and low-speed wakes. The very-well-organized rib structures are a striking feature of the experimental work by Clemens & Smith (Reference Clemens and Smith1998), shown in figure 29. The increased stability of the high-speed rollers results in the transition of the secondary rib structures before the principal rollers become fully turbulent. Signs of rib breakdown events can be inferred from experimental visualizations by Clemens & Smith (Reference Clemens and Smith1998) and from the numerical work by Watanabe & Maekawa (Reference Watanabe and Maekawa2004). The breakdown of the rib structures of the high-speed planar wake was recently reported in a complementary study by Hickey & Wu (Reference Hickey and Wu2015).
$Ma=2.0$
. The rib-structures are highly organized and survive throughout transition: a clear contrast to the incompressible and low-speed wakes. The very-well-organized rib structures are a striking feature of the experimental work by Clemens & Smith (Reference Clemens and Smith1998), shown in figure 29. The increased stability of the high-speed rollers results in the transition of the secondary rib structures before the principal rollers become fully turbulent. Signs of rib breakdown events can be inferred from experimental visualizations by Clemens & Smith (Reference Clemens and Smith1998) and from the numerical work by Watanabe & Maekawa (Reference Watanabe and Maekawa2004). The breakdown of the rib structures of the high-speed planar wake was recently reported in a complementary study by Hickey & Wu (Reference Hickey and Wu2015).

Figure 29. Experimental roller visualization for a planar wake at
![]() $Ma=3.0$
(reproduced with permission from Clemens & Smith Reference Clemens and Smith1998).
$Ma=3.0$
(reproduced with permission from Clemens & Smith Reference Clemens and Smith1998).
7 Discussion and conclusions
Many previous investigations have downplayed the importance of the compressibility effects in high-speed wake flows. It is true, at least qualitatively, that the increasing
![]() $Ma$
does little to modify the general features of transition (e.g. two-dimensionality of primary instability modes, rib-structure formation), especially in comparison with the drastic changes observed in the transitioning high-speed mixing layer. In the present work, we highlight the insidious effects of compressibility on the emerging structures, along with the concomitant changes to the statistics during the transition of plane wakes. The structural modification is caused by two important features: (i) modification of the time and length scales imposed by the most unstable linear mode (recall figure 1), and (ii) alteration of the communication paths between neighbouring coherent structures (recall figure 4). These features modify the emerging rollers, their staggered spatial arrangement and their ability to merge during transition (recall figures 17 and 18). The effects of the structural changes on the transitional turbulence statistics are explored in the present work.
$Ma$
does little to modify the general features of transition (e.g. two-dimensionality of primary instability modes, rib-structure formation), especially in comparison with the drastic changes observed in the transitioning high-speed mixing layer. In the present work, we highlight the insidious effects of compressibility on the emerging structures, along with the concomitant changes to the statistics during the transition of plane wakes. The structural modification is caused by two important features: (i) modification of the time and length scales imposed by the most unstable linear mode (recall figure 1), and (ii) alteration of the communication paths between neighbouring coherent structures (recall figure 4). These features modify the emerging rollers, their staggered spatial arrangement and their ability to merge during transition (recall figures 17 and 18). The effects of the structural changes on the transitional turbulence statistics are explored in the present work.
The cause of the structural differences in the emerging transitional rollers stems from a reduced exponential growth rate and an increased wavelength of the primary instability mode with increasing
![]() $Ma_{r}$
. The most unstable spectral mode imposes a time and a length scale to the laminar base wake flow. Two direct consequences of the increased wavelength are: an increased streamwise separation between adjacent rollers; and an obviously increased circulation of the individual rollers. Based on a geometric interpretation of the characteristic lines in the wake, we show that with an increasing
$Ma_{r}$
. The most unstable spectral mode imposes a time and a length scale to the laminar base wake flow. Two direct consequences of the increased wavelength are: an increased streamwise separation between adjacent rollers; and an obviously increased circulation of the individual rollers. Based on a geometric interpretation of the characteristic lines in the wake, we show that with an increasing
![]() $Ma$
, communication between neighbouring rollers is reduced along the same row but enhanced in cross-wake direction.
$Ma$
, communication between neighbouring rollers is reduced along the same row but enhanced in cross-wake direction.
Direct numerical simulations support our claims inferred from theoretical considerations. Our work sheds light on the increasing ellipticity of the transitional structures in the high-speed free-shear flows. The ellipticity is a result of length and time scales imposed by the linear stability characteristics. As the exponential growth rate is reduced (slower roll up and reduced minor axis of the ellipse) and the wavelength increased (stretched major axis of the ellipse), the resulting structures become increasingly elliptical. The eduction technique clearly shows the rotation of the elliptical rollers during transition. As the highly elliptical rollers complete a
![]() $180^{\circ }$
rotation and the transverse axis is parallel to the streamwise direction (see figure 18 at time
$180^{\circ }$
rotation and the transverse axis is parallel to the streamwise direction (see figure 18 at time
![]() $t=93$
) the wake spreading is temporally hindered as the contribution of the rollers to the mean velocity is located closer to the centreplane. For the
$t=93$
) the wake spreading is temporally hindered as the contribution of the rollers to the mean velocity is located closer to the centreplane. For the
![]() $Ma=2.0$
case, there is even a temporary decrease of the wake half-width. The increased ellipticity of the rotating rollers acts to push the structures further away from the centreplane. It can be inferred that the structures, located farther from the centreplane, impart a memory to the wake which results in the outward drift of the maximum TKE location with increasing Mach number experimentally observed by Bonnet et al. (Reference Bonnet, Delville, Sapin, Sullivan and Yeru1991) and Gatski & Bonnet (Reference Gatski and Bonnet2009). A far-wake compressible planar wake simulation would be necessary to unequivocally confirm this hypothesis.
$Ma=2.0$
case, there is even a temporary decrease of the wake half-width. The increased ellipticity of the rotating rollers acts to push the structures further away from the centreplane. It can be inferred that the structures, located farther from the centreplane, impart a memory to the wake which results in the outward drift of the maximum TKE location with increasing Mach number experimentally observed by Bonnet et al. (Reference Bonnet, Delville, Sapin, Sullivan and Yeru1991) and Gatski & Bonnet (Reference Gatski and Bonnet2009). A far-wake compressible planar wake simulation would be necessary to unequivocally confirm this hypothesis.
The simulation results also revealed that the increased streamwise separation and inhibited streamwise communication eventually limit the roller pairing: an important feature of low-speed wake transition. The lack of pairing is clearly highlighted by our structural visualization between the
![]() $Ma=0.8$
(figure 25) and 2.0 (figure 26) cases. Interestingly, the lack of roller pairing means that there is an increased two-dimensionality during transition with increasing
$Ma=0.8$
(figure 25) and 2.0 (figure 26) cases. Interestingly, the lack of roller pairing means that there is an increased two-dimensionality during transition with increasing
![]() $Ma$
, a result which is also evident in the experimental visualizations of bluff-body wakes (see Nakagawa & Dahm (Reference Nakagawa and Dahm2006), figures 2 and 3). The three-dimensional varicose mode (for
$Ma$
, a result which is also evident in the experimental visualizations of bluff-body wakes (see Nakagawa & Dahm (Reference Nakagawa and Dahm2006), figures 2 and 3). The three-dimensional varicose mode (for
![]() $Ma>1.2$
), found in the linear stability analysis, plays a negligible role in the wake transition. This is an expected result, since the growth rate of the primary, sinuous mode is approximately three times larger at all investigated Mach numbers. The reduced growth of the primary instability mode combined with the increased stability of the roller arrays (due to the lack of structural pairing) with increasing compressibility mean that the connecting ribs have a drastically longer life time and develop intricate structures which are very stable and well defined.
$Ma>1.2$
), found in the linear stability analysis, plays a negligible role in the wake transition. This is an expected result, since the growth rate of the primary, sinuous mode is approximately three times larger at all investigated Mach numbers. The reduced growth of the primary instability mode combined with the increased stability of the roller arrays (due to the lack of structural pairing) with increasing compressibility mean that the connecting ribs have a drastically longer life time and develop intricate structures which are very stable and well defined.
A closer look at the transitional statistics reveals that shocklets do not play a significant role in the transition of planar wake up to an initial relative Mach number of
![]() $Ma=2.0$
. Furthermore, the anisotropy of the Reynolds stress tensor is increased by the compressibility effects through an impeded pressure redistribution term, although the greatest variability is observed in the linear regime of the wake. As the wake transitions, there is a return to isotropy which is invariant to the initial level of compressibility in the wake. Finally, the convection velocity is independent of the initial Mach number during the entire transitional wake evolution.
$Ma=2.0$
. Furthermore, the anisotropy of the Reynolds stress tensor is increased by the compressibility effects through an impeded pressure redistribution term, although the greatest variability is observed in the linear regime of the wake. As the wake transitions, there is a return to isotropy which is invariant to the initial level of compressibility in the wake. Finally, the convection velocity is independent of the initial Mach number during the entire transitional wake evolution.
The present work contributes to a better understanding of high-speed wake transition. Some questions raised will require further studies. Some of the unresolved are: (i) effect of ellipticity on the induced flow; (ii) stability of compressible staggered vortex array; and (iii) characterization of the maximal Mach number for roller pairing. Studies of these questions will contribute to a more comprehensive understanding of wake transition mechanisms and potentially open new paths for the control of these high-speed free-shear flows.
Acknowledgements
This work was supported by an NSERC Discovery Grant, the Department of Defence Academic Research Program (ARP), and the Canada Research Chair Program (CRC). J.P.H. would like to acknowledge the financial support of the NSERC PGS. The simulations were performed at the High Performance Computing Virtual Laboratory (HPCVL). The kind assistance of the HPCVL staff is gratefully acknowledged.
Appendix
Care was taken to resolve all scales of turbulence during transition. Figure 30(a) shows the evolution of the minimal ratio of the Kolmogorov length scale to the grid spacing during the entire simulation. For all simulations, the coarsest resolution is only slightly below unity; therefore we can confidently state that all the scales of turbulence are adequately resolved by our simulations. A grid convergence study was done by comparing the evolution of the maximal turbulent kinetic energy and the streamwise dissipation for three different grid resolutions (all other parameters remained unchanged, see table 1):
![]() $77\times 10^{6}$
(
$77\times 10^{6}$
(
![]() $1/2$
grid in each direction),
$1/2$
grid in each direction),
![]() $413\times 10^{6}$
(
$413\times 10^{6}$
(
![]() $1/\sqrt{2}$
grid in each direction) and
$1/\sqrt{2}$
grid in each direction) and
![]() $619\times 10^{6}$
. The grid convergence is shown in figure 30(b,c); other statistical parameters such as integrated production show a similarly good agreement (less than 1.6 % of the peak production value). Needless to say that the agreement of the mean profiles are nearly perfectly captured among the different grid resolutions.
$619\times 10^{6}$
. The grid convergence is shown in figure 30(b,c); other statistical parameters such as integrated production show a similarly good agreement (less than 1.6 % of the peak production value). Needless to say that the agreement of the mean profiles are nearly perfectly captured among the different grid resolutions.

Figure 30. Evolution of the minimal ratio of
![]() ${\it\eta}/{\rm\Delta}x$
during transition (a); simulations at
${\it\eta}/{\rm\Delta}x$
during transition (a); simulations at
![]() $Re=1500$
(dashed lines) and
$Re=1500$
(dashed lines) and
![]() $Re=3000$
(full lines). Grid convergence test based on the evolution of the peak turbulent kinetic energy for the wake at
$Re=3000$
(full lines). Grid convergence test based on the evolution of the peak turbulent kinetic energy for the wake at
![]() $Ma=2.0$
(b) and the streamwise dissipation (c) using three different grid densities: 77, 413 and 619 million nodes.
$Ma=2.0$
(b) and the streamwise dissipation (c) using three different grid densities: 77, 413 and 619 million nodes.