The Dielectric Function

Following Sodha et al. (Reference Sodha, Tripathi and Ghatak1976), the variation of the dielectric function of air due to thermal self-action at a temperature T may be expressed as,

(1a)$${\rm \varepsilon} \lpar r\comma z\rpar = {\rm \varepsilon} _r \lpar T_0 \rpar + \left[T\lpar r\comma z\rpar - T_0 \right]{\left.{d{\rm \varepsilon} _r \over dT}\right\vert_{T = 0}} - i{\rm \varepsilon} _i\comma$$

where ɛ_r is the real part of the dielectric function, T₀ is the maximum temperature on the wave-front of the beam, and ɛ_i is the imaginary part of the dielectric function and is practically independent of temperature; for air $d{\rm \varepsilon} _r / dT$ is negative. Since T is a function of r and z, Eq. (1a) may be written as

(1b)$${\rm \varepsilon} \lpar r\comma z\rpar = {\rm \varepsilon} _R \lpar r\comma \; z\rpar - i{\rm \varepsilon} _i\comma$$

where R = g, n for Gaussian and Hollow Gaussian beam, respectively, in this analysis.

Propagation

Consider the propagation of a linearly polarized radially symmetric electromagnetic beam with its electric vector polarized along the y-axis, propagating in air along the z-axis. The amplitude of the electric field vector E satisfies the scalar wave equation for such a beam, which may be expressed in a cylindrical coordinate system with azimuthal symmetry as

(2)$${\partial ^2 {E} \over \partial z^2} + \left({\partial ^2 \over \partial r^2 } + {1 \over r} {\partial \over \partial r} \right)E + {{\rm \omega}^2 \over c^2} {\rm \varepsilon} \lpar r\comma z\rpar \;E =0\comma$$

where c is the speed of light in vacuum. Eq. (2) can be solved in the paraxial approximation by following the analysis of Akhmanov et al. (Reference Akhmanov, Sukhorukov and Khokhlov1968a; Reference Akhmanov, Krindach, Migulier, Sukhorukov and Khokhlov1968b) and its extension by Sodha et al. (Reference Sodha, Ghatak and Tripathi1974; Reference Sodha, Tripathi and Ghatak1976) for Gaussian beam and the work of Sodha et al. (Reference Sodha, Mishra and Misra2009a; Reference Sodha, Mishra and Misra2009b) and Misra and Mishra (Reference Misra and Mishra2009) on nonlinear propagation of hollow Gaussian beams in plasmas.

The starting point is a solution of the form

(3)$$E\lpar r\comma z\rpar = A\lpar r\comma z\rpar \exp \left(- i \int_0^z k\lpar z\rpar dz \right)\comma$$

where A(r,z) is the complex amplitude of the electric field, $k\lpar z\rpar = {{\rm \omega} / c}\sqrt {{\rm \varepsilon} _{R0} \lpar z\rpar }$, ɛ_R0 (z) is the dielectric function, corresponding to the maximum electric field on the wave-front of the electromagnetic beam. Substituting for E(r,z) from Eq. (3) in Eq. (2) and neglecting ∂²A/∂z ² (in the Jeffreys-Wentzel-Kramers-Brillouin approximation) one obtains

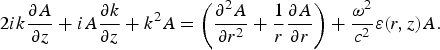(4)$$2ik{\partial A \over \partial z} + iA{\partial k \over \partial z} + k^2 A = \left({{\partial ^2 A \over \partial r^2} + {1 \over r}{\partial A \over \partial r}}\right)+ {{\rm \omega}^2 \over c^2}{\rm \varepsilon}\lpar r\comma z\rpar A.$$

For a nearly spherical wave front (a valid assumption in the paraxial approximation), the complex amplitude A(r,z) may be expressed as,

(5)$$A\lpar r\comma z\rpar = A_0 \lpar r\comma z\rpar \exp \left(- ik\lpar z\rpar S\lpar r\comma z\rpar \right)\comma$$

where S(r,z) is the eikonal associated with the electromagnetic beam and A ₀(r,z) is the real amplitude of the electromagnetic beam. The propagation of the Gaussian beam and various orders HGBs in air has been analyzed separately as follows.

The Gaussian Beam

The electric field distribution for the Gaussian beam may be expressed as

(6)$$\lpar E_{0g} \rpar _{z = 0} = E_{00g} \exp \left(- {r^2 \over 2r_{0g}^2 } \right)\comma$$

where r _0g is the initial beam width of the Gaussian beam.

Following the paraxial approach the relevant parameters (i.e., dielectric function ɛ(r,z), eikonal and irradiance) may be expanded around the maximum of the Gaussian electromagnetic beam, i.e., around r = 0. Thus, one can express the dielectric function ɛ_g(r,z) as

(7)$${\rm \varepsilon} _g \lpar r\comma z\rpar = {\rm \varepsilon} _{0g} \lpar z\rpar - \lpar r^2 /r_{0g}^2 \rpar {\rm \varepsilon} _{2g} \lpar z\rpar - i{\rm \varepsilon} _i \comma$$

where ɛ_0g(z) and ɛ_2g(z) are the coefficients associated with r ⁰ and r ² in the expansion of ɛ_g(r,z) around r = 0. The expressions for these coefficients (all real) have been derived later.

Substitution for A(r,z) from Eq. (5) and ɛ(r,z) from Eqs. (1b) and (7) in Eq. (4) and equating the real and imaginary parts on both sides of the resulting equation one obtains

(8a)$$\eqalign{& \displaystyle{{2S_g } \over k}\displaystyle{{\partial k} \over {\partial z}} + 2\displaystyle{{\partial S_g } \over {\partial z}} + \left({\displaystyle{{\partial S_g } \over {\partial r}}} \right)^2 \cr & \quad= \displaystyle{1 \over {k^2 A_{0g} }}\left({\displaystyle{{\partial ^2 A_{0g} } \over {\partial r^2 }} + \displaystyle{1 \over r}\displaystyle{{\partial A_{0g} } \over {\partial r}}} \right) - \displaystyle{{r^2 } \over {r_{0g}^2 }}\displaystyle{{{\rm \varepsilon} _{2g} \lpar z\rpar } \over {{\rm \varepsilon} _{0g} \lpar z\rpar }}\comma \;}$$

and

(8b)$$\eqalign{&\displaystyle{{\partial A_{0g}^2 } \over {\partial z}} + A_{0g}^2 \left({\displaystyle{{\partial ^2 S_g } \over {\partial r^2 }} + \displaystyle{1 \over r}\displaystyle{{\partial S_g } \over {\partial r}}} \right)+ \displaystyle{{\partial A_{0g}^2 } \over {\partial r}}\displaystyle{{\partial S_g } \over {\partial r}} \cr & \quad + A_{0g}^2 \left({\displaystyle{1 \over {k\lpar z\rpar }}\displaystyle{{\partial k\lpar z\rpar } \over {\partial z}} + k\lpar z\rpar \displaystyle{{{\rm \varepsilon} _i \lpar z\rpar } \over {{\rm \varepsilon} _{0g} \lpar z\rpar }}} \right)= 0\comma \; }$$

where ɛ_i(z) is the imaginary part of the dielectric function.

One can express the solution of Eq. (8b) (in the paraxial approximation r/r ₀ ≪ 1) as

(9a)$$\eqalign{A_{0g}^2 & = \displaystyle{{E_{0g}^2 } \over {\,f_0^2 }}\left({\displaystyle{{{\rm \varepsilon} _{0g} \lpar 0\rpar } \over {{\rm \varepsilon} _{0g} \lpar z\rpar }}} \right)^{1/2} {\rm exp}\left({ - \displaystyle{{r^2 } \over {r_{0g}^2 f_0^2 }}} \right)\cr & \quad \times {\rm exp}\left[{ - \int_0^z {\displaystyle{{{\rm \varepsilon} _i \lpar {\rm \omega} /c\rpar dz} \over {\sqrt {{\rm \varepsilon} _{0g} \lpar z\rpar } }}} } \right]\comma \; \cr & \quad \approx \displaystyle{{E_{0g}^2 } \over {\,f_0^2 }}\left({\displaystyle{{{\rm \varepsilon} _{0g} \lpar 0\rpar } \over {{\rm \varepsilon} _{0g} \lpar z\rpar }}} \right)^{1/2} {\rm exp}\left({ - \displaystyle{{r^2 } \over {r_{0g}^2 f_0^2 }}} \right)\times {\rm exp}\lpar\! -\! {\rm \delta} z\rpar \comma \; }$$

where

(9b)$$\eqalign{& S_g \lpar r\comma \; z\rpar =\displaystyle{{r^2 } \over 2}{\rm \beta} _g \lpar z\rpar +{\rm \varphi} _g \lpar z\rpar \comma \; \cr & {\rm \beta} _g \lpar z\rpar =\displaystyle{1 \over {\,f_0 }}\displaystyle{{df_0 } \over {dz}}\comma \; \cr & {\rm \varepsilon} _{0g} \lpar z\rpar \approx 1 \hbox{for air}\comma \; \cr & {\rm \delta}= \varepsilon_i({\rm \omega}/c) \;\hbox{may be recognized as the irradiation} \cr & \hbox{attenuation constant in the medium}, \cr & {\rm \varphi}_g(z) \;\hbox{is an arbitrary function of} \;z,}$$

and

$${f}_0(z) \hbox{is the beam width parameter, associated with the Gaussian beam.}$$

On substituting for A _0g² and S _g from Eqs. (9a) and (9b) in Eq. (8a) and equating the coefficient of r ² on both sides of the resulting equation, one obtains

(10)$$\,f_0 \displaystyle{{d^2 f_0 } \over {dz^2 }} =\displaystyle{1 \over {k^2 r_{0g}^2 f_0^2 }} - \displaystyle{1 \over {r_{0g}^2 }}\displaystyle{{{\rm \varepsilon} _{2g} } \over {{\rm \varepsilon} _{0g} }}.$$

The dependence of the beam width parameter f ₀ on z can be obtained by the numerical solution of Eq. (10) after putting suitable expressions for ɛ_0g and ɛ_2g, with the initial boundary conditions f ₀ = 1, ${{df_0 \over dz} = B^{ - 1}}$ at z = 0, where B is the initial radius of curvature of the beam.

The Hollow Gaussian Beam

The amplitude of the electric field associated with a hollow Gaussian electromagnetic beam (HGB) having zero irradiance along the axis r = 0 and a maximum away from the axis, can be expressed as

(11)$$\lpar E_{0n} \rpar _{z =0} {\bi \;=\;}E_{00n} \left({\displaystyle{{r^2 } \over {2r_{0n}^2 }}} \right)^n \exp \left({ - \displaystyle{{r^2 } \over {2r_{0n}^2 }}} \right)\comma$$

where r _0n is the initial beam width of the HGB, n is the order of the HGB and a positive integer, characterizing the shape of the HGB and position of its maximum and |E ₀| is maximum at r ² = r _max² = 2nr _0n².

To proceed further one can adopt a paraxial like approach (Sodha et al., Reference Sodha, Mishra and Misra2009a; Reference Sodha, Mishra and Misra2009b; Misra & Mishra, Reference Misra and Mishra2009), analogous to the paraxial approximation. Thus, one may start by expressing Eq. (4) in terms of variables η and z, where η is defined as

(12)$${\rm \eta}^2 = \left[\left(r / r_{0n} f_n \right)^2 -\, 2n \right]\comma \;$$

r _0nf _n (z) is the width of the beam, and r ² = 2nr _0n²f _n² is the position of the maximum irradiance of the propagating beam. It is shown later that in the paraxial like approximation, i.e., when η² ≪ 2n, the beam retains its profile.

In the paraxial like approximation the relevant parameters (i.e., dielectric function ɛ(r,z), eikonal and irradiance) may be expanded around the maximum of the HGB, i.e., around η = 0. Thus, one can express the dielectric function ɛ_n(η,z) around the maximum (η = 0) of the HGB as

(13)$${\rm \varepsilon} _n \lpar {\rm \eta} \comma \; z\rpar ={\rm \varepsilon} _{0n} \lpar z\rpar - {\rm \eta} ^2 {\rm \varepsilon} _{2n} \lpar z\rpar - i{\rm \varepsilon} _i\comma \;$$

where ɛ_0n(z) and ɛ_2n(z) are the coefficients (both real) associated with η⁰ and η² in the expansion of ɛ_n(η ,z) around η = 0. The expressions for these coefficients have been derived later.

Substitution for A(r,z) from Eq. (5) and ɛ(r,z) from Eq. (1b) and ɛ_n(η,z) from Eq. (13) in Eq. (4) by using the transformation Eq. (12) and the separation of the real and imaginary parts on both side of the resulting equation leads to

(14a)$$\eqalign{& \displaystyle{{2S_g } \over k}\displaystyle{{\partial k} \over {\partial z}} +2\left({\displaystyle{{\partial S_n } \over {\partial z}} - \displaystyle{{\lpar \sqrt {2n} +{\rm \eta} \rpar } \over f}\displaystyle{{\partial f} \over {\partial z}}\displaystyle{{\partial S_n } \over {\partial {\rm \eta} }}} \right)\cr & \quad +\displaystyle{1 \over {r_{0n}^2 f_n^2 }}\left({\displaystyle{{2n +{\rm \eta} ^2 } \over {{\rm \eta} ^2 }}} \right)\left({\displaystyle{{\partial S_n } \over {\partial {\rm \eta} }}} \right)^2 \cr & \quad =\left[{\left({\displaystyle{2 \over {\rm \eta} } - \displaystyle{{2n +{\rm \eta} ^2 } \over {{\rm \eta} ^3 }}} \right)\displaystyle{{\partial A_{0n} } \over {\partial {\rm \eta} }} +\displaystyle{{2n +{\rm \eta} ^2 } \over {{\rm \eta} ^2 }}\displaystyle{{\partial ^2 A_{0n} } \over {\partial {\rm \eta} ^2 }}} \right]\cr &\qquad - {\rm \eta} ^2 \displaystyle{{{\rm \varepsilon} _{2n} \lpar z\rpar } \over {{\rm \varepsilon} _{0n} \lpar z\rpar }}\comma \; }$$

and

(14b)$$\eqalign{& \left({\displaystyle{{\partial A_{0n}^2 } \over {\partial z}} - \displaystyle{{\lpar \sqrt {2n} +{\rm \eta} \rpar } \over f}\displaystyle{{\partial f} \over {\partial z}}\displaystyle{{\partial A_{0n}^2 } \over {\partial {\rm \eta} }}} \right)+\displaystyle{{A_{0n}^2 } \over {r_{0n}^2 f_n^2 }}\cr & \quad \times \left[{\left({\displaystyle{{\partial ^2 S_n } \over {\partial {\rm \eta} ^2 }} +\displaystyle{1 \over {\rm \eta} }\displaystyle{{\partial S_n } \over {\partial {\rm \eta} }}} \right)+\displaystyle{{2n} \over {{\rm \eta} ^2 }}\left({\displaystyle{{\partial ^2 S_n } \over {\partial {\rm \eta} ^2 }} - \displaystyle{1 \over {\rm \eta} }\displaystyle{{\partial S_n } \over {\partial {\rm \eta} }}} \right)} \right]\cr & \quad +\displaystyle{1 \over {r_{0n}^2 f_n^2 }}\displaystyle{{\lpar 2n +{\rm \eta} ^2 \rpar } \over {{\rm \eta} ^2 }}\displaystyle{{\partial A_{0n}^2 } \over {\partial {\rm \eta} }}\displaystyle{{\partial S_n } \over {\partial {\rm \eta} }} \cr & \quad +A_{0n}^2 \left({\displaystyle{1 \over {k\lpar z\rpar }}\displaystyle{{\partial k\lpar z\rpar } \over {\partial z}} +k\lpar z\rpar \displaystyle{{{\rm \varepsilon} _{i0} \lpar z\rpar } \over {{\rm \varepsilon} _{0n} \lpar z\rpar }}} \right)=0.}$$

One can express the solution of Eq. (14b) (in the paraxial like approximation η² ≪ 2n) as

(15a)$$\eqalign{A_{0n}^2 & = \displaystyle{{E_{0n}^2 } \over {2^{2n} f_n^2 }}\left({\displaystyle{{{\rm \varepsilon} _{0n} \lpar 0\rpar } \over {{\rm \varepsilon} _{0n} \lpar z\rpar }}} \right)^{1/2} \left({2n + {\rm \eta} ^2 } \right)^{2n} \cr & \quad \times \exp \left({ - \left({2n + {\rm \eta} ^2 } \right)} \right)\times \exp\lpar \! - {\rm \delta} z\rpar \comma \;}$$

where

(15b)$$\eqalign{& S_n \lpar {\rm \eta} \comma \; z\rpar = \displaystyle{{{\rm \eta} ^2 } \over 2}{\rm \beta} _n \lpar z\rpar + {\rm \varphi} _n \lpar z\rpar \;\hbox{is the eikonal term} \cr & \qquad \qquad\quad\hbox{corresponding to HGB}\comma \; \cr & {\rm \beta} _n \lpar z\rpar = r_{0n}^2 f_n \displaystyle{{df_n } \over {dz}}\comma \; \cr & {\rm \varphi} _n \lpar z\rpar \;\hbox{is an arbitrary function of z}\comma \;}$$

and

$$\,f_{n}(z) \;\hbox{is the beam width parameter for the HGB.}$$

On substituting for A _0n² and S _n from Eqs. (15a) and (15b) in Eq. (14a) and equating the coefficients of η² on both sides of the resulting equation, one obtains

(16)$${\rm \varepsilon} _{0n} f_n \displaystyle{{d^2 f_n } \over {dz^2 }} = \displaystyle{{\lpar 12n^2 - 2n - 13/4\rpar } \over {k^2 r_{0n}^2 f_n^2 }} - \displaystyle{{{\rm \varepsilon} _{2n} } \over {r_{0n}^2 }}.$$

The variation of the beam width parameter f _n with z can be obtained by the numerical integration of Eq. (16) after putting suitable expressions for ɛ_0n and ɛ_2n, with appropriate initial boundary conditions viz. f _n = 1, $\displaystyle{{df_n } \over {dz}} = B^{ - 1}$ at z = 0.

The Nonlinear Term

Consider a cylindrical shell of thickness dr (with radius r), whose axis is coincident with the beam. Neglecting convection effects the steady state thermal balance may be expressed as

(17a)$${\rm \chi} {\partial \over \partial r} \left(r{\partial T \over \partial r} \right)= r{dI\lpar r\comma \; z\rpar \over dz}\comma \;$$

where

(17b)$$\eqalign{& I\lpar r\comma \; z\rpar = \lpar c/4{\rm \pi} \rpar A_0^2 \lpar r\comma \; z\rpar \comma \; \cr & {A_0^2}\ \hbox{is given by Eqs. (9a) and (15a) with}\ \varepsilon_{0r}\approx 1,}$$

and

$${\rm \chi} \;\hbox{is the thermal conductivity of the medium.}$$

The attenuation coefficient δ is the sum of the absorption (α_a) and scattering (α_s) coefficients, i.e.,

(17c)$${\rm \delta} = {\rm \alpha} _a + {\rm \alpha} _s .$$

Gaussian Beam

In the paraxial approximation (r/r ₀ ≪ 1), one can expand T(r,z) around the maximum viz. r = 0, as

(18)$$T\lpar r\comma \; z\rpar = T_{0g} - \lpar r^2 /r_0^2 \rpar T_{2g}.$$

Substituting for T(r,z) from Eq. (18) in Eq. (1) and comparing the coefficient of r ⁰ and r ² in the resulting equation with Eq. (7) one obtains,

(18a)$${\rm \varepsilon} _{0g} = {\rm \varepsilon} _0 + \left[{T_{0g} - T_0 } \right]\displaystyle{{d{\rm \varepsilon} } \over {dT}}\comma \;$$

and

(18b)$${\rm \varepsilon} _{2g} = T_{2g} \displaystyle{{d{\rm \varepsilon} } \over {dT}}.$$

On substituting for T(r,z) from Eq. (18) in Eq. (17a) and comparing the r independent terms on both side of the resulting equation one obtains,

(19)$$T_{2g} = \displaystyle{{{\rm \alpha} _a cr_{0g}^2 } \over {16{\rm \pi} {\rm \chi} }}\displaystyle{{E_{0g}^2 } \over {\,f_0^2 }}\exp \left({ - \lpar {\rm \alpha} _a + {\rm \alpha} _s \rpar z} \right)$$

Substituting for T _2g from Eq. (19) in Eq. (7)

$${\rm \varepsilon} _{2g} = \displaystyle{{{\rm \alpha} _a cr_{0g}^2 } \over {16{\rm \pi} {\rm \chi} }}\displaystyle{{E_{0g}^2 } \over {\,f_0^2 }}\exp \left({ - \lpar {\rm \alpha} _a + {\rm \alpha} _s \rpar z} \right)\displaystyle{{d{\rm \varepsilon} } \over {dT}}$$

or

(20a)$${\rm \varepsilon} _{2g} = \displaystyle{{{\rm \alpha} _a } \over {4{\rm \pi} {\rm \chi} }}\displaystyle{{P_{0g}^{} } \over {\,f_0^2 }}\exp \left({ - \lpar {\rm \alpha} _a + {\rm \alpha} _s \rpar z} \right)\displaystyle{{d{\rm \varepsilon} } \over {dT}}\comma$$

where

(20b)$${P}_{0g} = cr_0^2 E_{0g}^2 /4 \hbox{is the initial power of the Gaussian electromagnetic beam.}$$

On substituting for ɛ_2g from Eq. (20a) in Eq. (10) and remembering that ɛ_0g ≈1 one obtains,

$$\,f_0 \displaystyle{{d^2 f_0 } \over {dz^2 }} = \displaystyle{1 \over {r_{0g}^4 k^2 f_0^2 }} - \displaystyle{{{\rm \alpha} _a } \over {r_{0g}^2 4{\rm \pi} {\rm \chi} }}P_{0g}^{} \exp \left({ - \lpar {\rm \alpha} _a + {\rm \alpha} _s \rpar z} \right)\displaystyle{{d{\rm \varepsilon} } \over {dT}}\comma \;$$

or

(10a)$$\,f_0 \displaystyle{{d^2 f_0 } \over {d{\rm \xi} ^2 }} = \displaystyle{1 \over {\,f_0^2 {\rm \rho} _{0g}^2 }} + \Pi _{0g} \exp \left({ - {\rm \beta} {\rm \xi} } \right)\comma$$

where $\Pi _{0g} = \Lambda = - \left({\displaystyle{{{\rm \alpha} _a P_{0g}} / {4{\rm \pi} {\rm \chi} }}\displaystyle{{d{\rm \varepsilon} } / {dT}}} \right)$ is proportional to the product of the initial power of the Gaussian electromagnetic beam and the absorption coefficient, ρ_0g= (r _0gω/c) is the dimensionless beam width, β = r _0g (α_a + α_s) and ξ = z/r ₀.

Hollow Gaussian Beam

Following the paraxial like approach (i.e., η² ≪ 2n), the radial dependence of the electron temperature T(η,z), can be expanded around the maximum of the irradiance of the beam; thus,

(21)$$T \lpar {\rm \eta} \comma \; z\rpar = T_{0n} - {\rm \eta} ^2 T_{2n} .$$

Substituting for T(η,z) from Eq. (21) in Eq. (1) and comparing the coefficient of r ⁰ and r ² in the resulting equation with Eq. (13) one obtains,

(22a)$${\rm \varepsilon} _{0n} = {\rm \varepsilon} _0 + \left[{T_{0n} - T_0 } \right]\displaystyle{{d{\rm \varepsilon} } \over {dT}}\comma \;$$

and

(22b)$${\rm \varepsilon} _{2n} = T_{2n} \displaystyle{{d{\rm \varepsilon} } \over {dT}}.$$

The thermal balance (Eq. (17a)) may be expressed in terms of variables (η,z) as follows,

(23)$$\displaystyle{{\rm \chi} \over {r_{0n}^2 f_n^2 }}\left[{\left({\displaystyle{{\partial ^2 T} \over {\partial {\rm \eta} ^2 }} + \displaystyle{1 \over {\rm \eta} }\displaystyle{{\partial T} \over {\partial {\rm \eta} }}} \right)+ \displaystyle{{2n} \over {{\rm \eta} ^2 }}\left({\displaystyle{{\partial ^2 T} \over {\partial {\rm \eta} ^2 }} - \displaystyle{1 \over {\rm \eta} }\displaystyle{{\partial T} \over {\partial {\rm \eta} }}} \right)} \right]= \displaystyle{{dI} \over {dz}}\comma$$

where

$${\rm \beta} = r_{0g} \lpar {\rm \alpha} _a + {\rm \alpha} _s \rpar .$$

Substituting for T(η,z) from Eq. (21) in Eq. (23) and comparing the η independent terms on both sides in the resulting equation one gets,

(24)$$T_{2n} =\displaystyle{c \over {4{\rm \pi} }}\displaystyle{{{\rm \alpha} _a r_{0n}^2 } \over {4{\rm \chi} f_n^2 }}E_{0n}^2 \exp \left({ - 2n} \right)n^{2n} \exp \left({ - \lpar {\rm \alpha} _a + {\rm \alpha} _s \rpar z} \right).$$

From Eqs. (22b) and (24) one obtains,

$${\rm \varepsilon} _{2n} = \displaystyle{c \over {4{\rm \pi} }}\displaystyle{{{\rm \alpha} _a r_{0n}^2 } \over {4{\rm \chi} f_n^2 }}E_{0n}^2 \exp \left({ - 2n} \right)n^{2n} \exp \left({ - \lpar {\rm \alpha} _a + {\rm \alpha} _s \rpar z} \right)\displaystyle{{d{\rm \varepsilon} } \over {dT}}\comma \;$$

or

(25a)$${\rm \varepsilon} _{2n} = \displaystyle{{{\rm \alpha} _a } \over {4{\rm \pi} {\rm \chi} f_n^2 }}\left({\displaystyle{{2^{2n} } \over {2n!}}} \right)P_{0n} \exp \left({ - 2n} \right)n^{2n} \exp \left({ - \lpar {\rm \alpha} _a + {\rm \alpha} _s \rpar z} \right)\displaystyle{{d{\rm \varepsilon} } \over {dT}}\comma$$

where

(25b)$$P_{0n} = \displaystyle{{cr_{0n}^2 E_{0n}^2 } \over 4}\left({\displaystyle{{2n!} \over {2^{2n} }}} \right)\;\hbox{is the initial power of the HGB.}$$

On substituting for ɛ_2n from Eq. (25a) in Eq. (16) and remembering that ɛ_0n ≈ 1 the equation for beam width parameter f _n is

$$\eqalign{\,f_n \displaystyle{{d^2 f_n } \over {dz^2 }} = & \displaystyle{{\lpar 12n^2 - 2n - 13/4\rpar } \over {k^2 r_{0n}^4 f_n^2 }} - \displaystyle{{{\rm \alpha} _a } \over {4{\rm \pi} {\rm \chi} }}\displaystyle{{P_{0n} } \over {r_{0n}^2 }}\displaystyle{{d{\rm \varepsilon} } \over {dT}}\left({\displaystyle{{2^{2n} } \over {2n!}}} \right)n^{2n} \cr & \quad \times \exp \left({ - 2n} \right)\exp \left({ - \lpar {\rm \alpha} _a + {\rm \alpha} _s \rpar z} \right)\comma \; }$$

or

(16a)$$\,f_n \displaystyle{{d^2 f_n } \over {d{\rm \xi} ^2 }} = \displaystyle{{\lpar 12n^2 - 2n - 13/4\rpar } \over {\,f_n^2 {\rm \rho} _{0n}^2 }} + \Pi _{0n} \exp \left({ - {\rm \beta} {\rm \xi} } \right)\comma$$

where

$$\eqalign{\Pi _{0n} &= - \left({\displaystyle{{{\rm \alpha} _a } \over {4{\rm \pi} {\rm \chi} _e }}\displaystyle{{d{\rm \varepsilon} } \over {dT}}P_{0n}^{} \left({\displaystyle{{2^{2n} } \over {2n!}}} \right)n^{2n} \exp \left({ - 2n} \right)} \right)\cr&\quad= \left({\left({\displaystyle{{2^{2n} } \over {2n!}}} \right)n^{2n} \exp \left({ - 2n} \right)} \right)\Lambda \;\lpar \hbox{with}\ P_{og} = P_{on} \rpar \comma}$$

corresponds to initial dimensionless power of the HGB, ρ_0n = (r _0n ω/c) is the dimensionless beam width and β_n = r _0n (α_a + α_s ); for n = 1, Π_on = 2exp(−2)Λ.

Atmospheric Parameters

The absorption (α_a) and scattering (α_s) coefficients for four environments, arrived at by Spangle et al. (2005) are given in Table 1.

Table 1. Absorption and scattering coefficients of laser beams in air (Sprangle et al., Reference Sprangle, Penaus and Hafizi2005)

Thermal conductivity of air χ = 2.5 × 10³erg/s cmK

Rate of change of dielectric function with temperature $\displaystyle{{d{\rm \varepsilon} } \over {dT}} = - 8.7 \times 10^{ - 7} /K$

Laser Parameters

r ₀ (r _0g = r _0n) = 50 to 100 cm, initial power P ₀ = 0.5 to 5.0 MW and wavelengths 1.045 μm, 1.625 μm and 2.141 μm (water absorption windows).

Dimensionless Parameters

With the above data the relevant dimensionless parameters lie in the ranges indicated as follows;

$$\Lambda = \displaystyle{{{\rm \alpha} _a } \over {4{\rm \pi} {\rm \chi} }}\displaystyle{{P_0^{} } \over {r_{0n}^2 }}\displaystyle{{d{\rm \varepsilon} } \over {dT}}\semicolon \; 10^{ - 6} \;to\; 5 \times 10^{ - 4}\comma \;$$

$${\rm \beta} = r_0 \lpar {\rm \alpha} _a + {\rm \alpha} _s \rpar \semicolon \; 2.5 \times 10^{ - 5} \;to\; 2 \times 10^{ - 4}\comma \;$$

and

$${\rm \rho} _0 = \lpar r_0 {\rm \omega} /c\rpar = \lpar 2{\rm \pi} r_0 /{\rm \lambda} \rpar \semicolon \; 1.5 \times 10^6 \;to\; 6 \times 10^6.$$

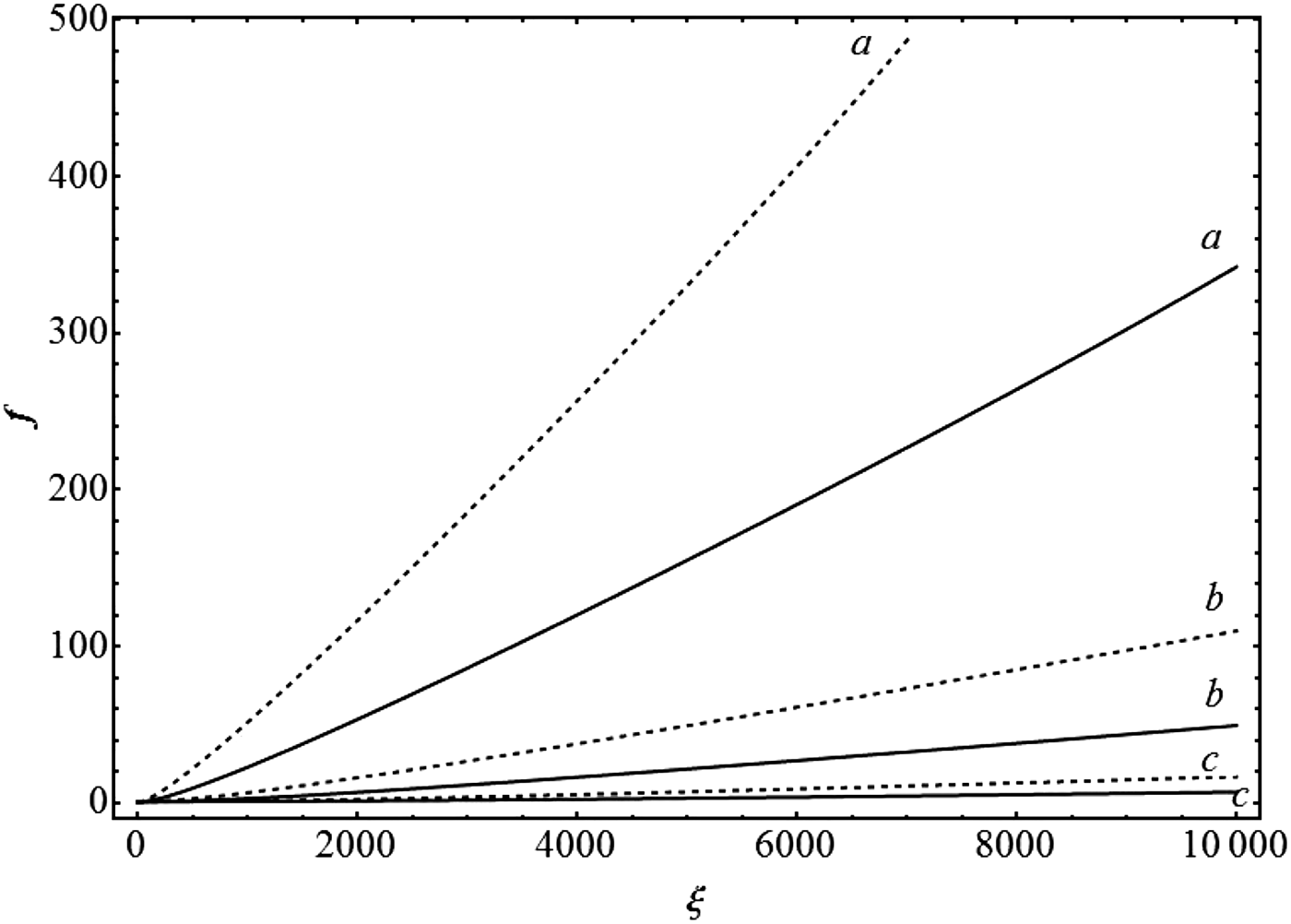
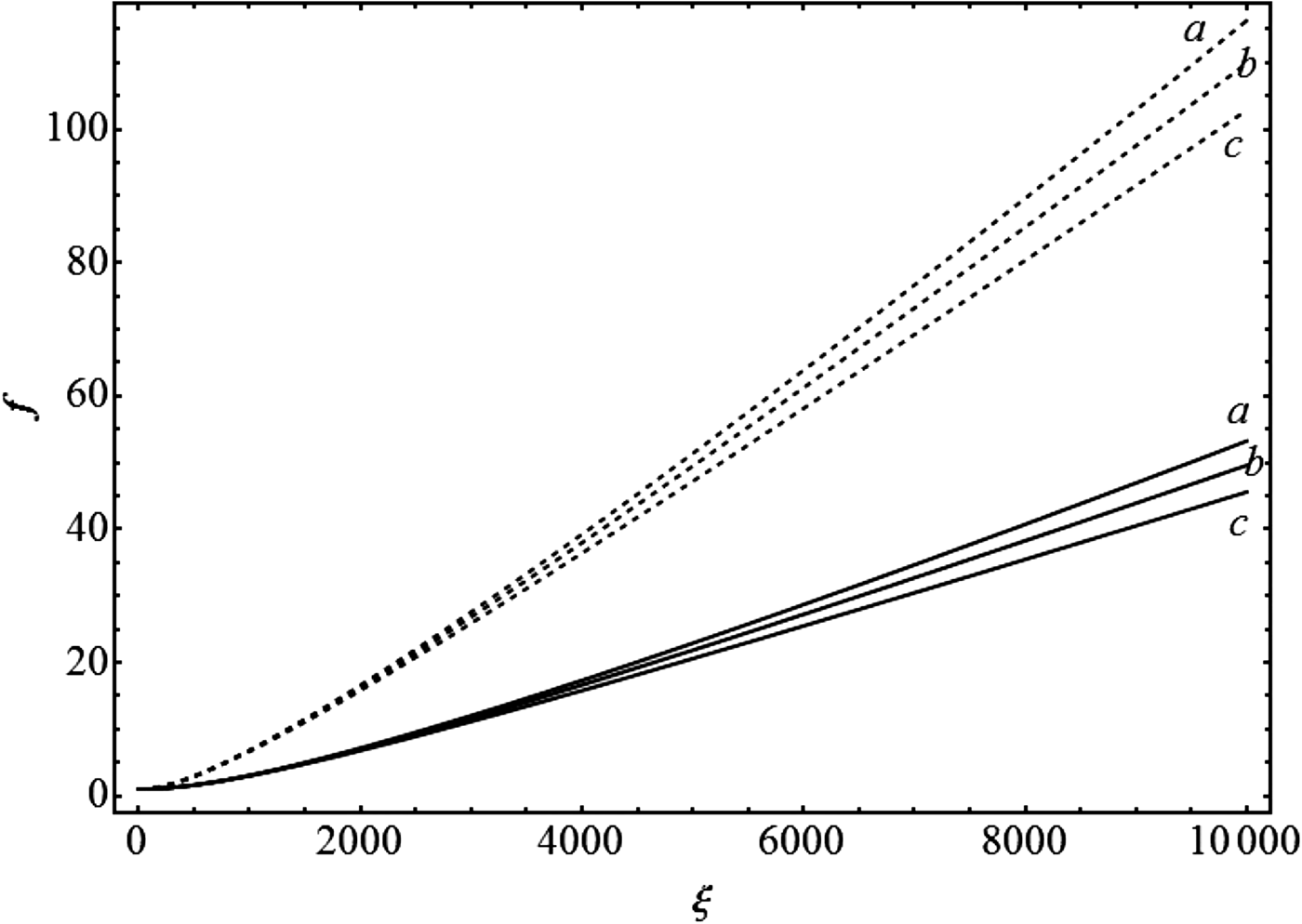
Figure 1 illustrates the dependence of the focusing parameter f on dimensionless distance of propagation ξ for different values of Λ (proportional to the product of initial beam power and the absorption coefficient). It is seen that f (or defocusing) increases with increasing Λ and that it is very much less for a hollow Gaussian beam as compared to that for a Gaussian beam; the physical reasoning for this fact is rather simple. In the central portion of a dark hollow beam 0 < r < r _m the temperature increases radially, while in the peripheral region the temperature decreases radially; the maximum irradiance of the beam occurs at r = r _m. Hence the dielectric function decreases radially in the central r < r _m portion of beam which tends to focus the beam, while the peripheral portion of the beam (in which ɛ increases with r) defocuses. Hence in contrast to a Gaussian beam the central r <r _m portion of HGB tends to focus the beam, while the peripheral portion of the beam defocuses. As a result the defocusing in case of HGB is much less than that in case of Gaussian beams, where all portions of the beam defocus. Fig. 2 indicates the dependence of f on ξ for different values of β. It is seen that f or defocusing decreases with increasing β this is due to the fact that the thermal effect decreases as the beam propagates due to decrease in the beam power, corresponding to enhanced absorption. Fig. 2 also indicates much reduced defocusing for the hollow Gaussian beam, as compared to a Gaussian beam. Computations also lead to an interesting conclusion that f – ξ relationship is independent of ρ₀ and to a good approximation f ∝ ξ (=z/r ₀) and hence inversely proportional to r ₀ at a given position (value of z).

Fig. 1. Dependence of beam width parameter f on dimensionless distance of propagation ξ for different values of Λ (proportional to the product of initial beam power and the absorption coefficient) for β = 10^{− 4} and ρ = 4.5 × 10⁶; where a, b and c refer to Λ = 5 × 10^{− 4}, 2 × 10^{− 5} and 10^{− 5} respectively. The broken and full curves correspond to Gaussian and hollow Gaussian beams, respectively.

Fig. 2. Dependence of beam width parameter f on dimensionless distance of propagation ξ for different values of attenuation constant β = r ₀ (α_a + α_s ) for Λ = 2 × 10^{− 5} and ρ = 4.5 × 10⁶; where a, b and c refer to β = 5 × 10^{− 4}, 2 × 10^{− 5}and 10⁻⁵ respectively. The broken and full curves correspond to Gaussian and hollow Gaussian beams, respectively.

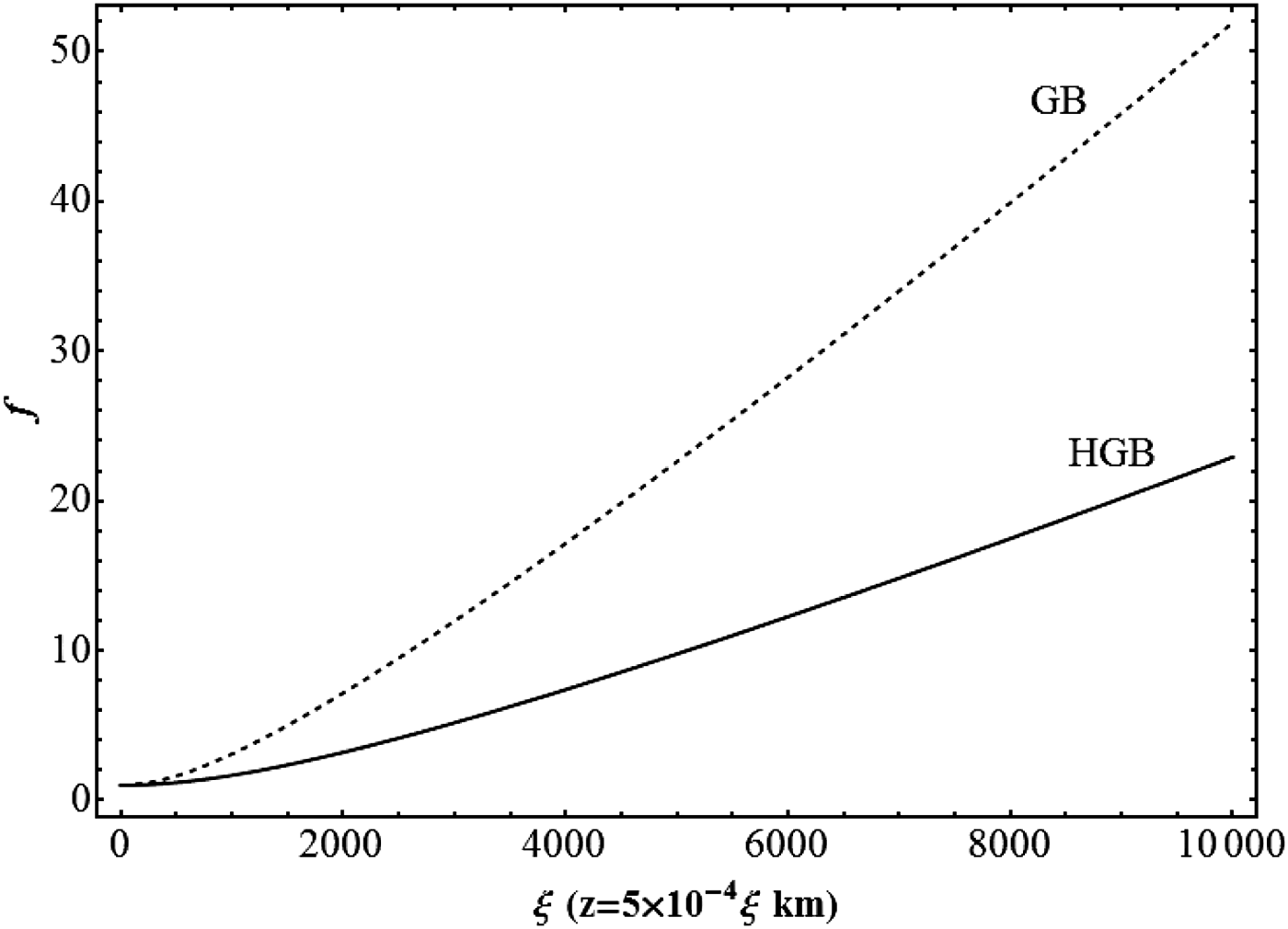
In addition to the dimensionless discussion (Figs. 1 and 2), it will also be of general interest to consider a specific case of propagation (in maritime environment) viz. λ = 1.045 μm, P₀ = 1 MW, α_a = 2 × 10⁻³ km⁻¹, α_s = 1.2 × 10⁻¹ km⁻¹ and r ₀ = 50 cm; the dependence of the beam width parameter f on the distance of propagation z in km is shown in Figure 3. This figure also highlights the fact that an HGB defocuses significantly less than a corresponding Gaussian beam of same radius and power.

Fig. 3. Dependence of beam width parameter f on dimensionless distance of propagation ξ(=z/r ₀) in maritime environment; λ = 1.045 μm, P ₀ = 1 MW, α_a = 2 × 10⁻³km ⁻¹, α_s = 1.2 × 10⁻¹km ⁻¹ and r ₀ = 50 cm. The broken and full curves correspond to Gaussian and hollow Gaussian beams, respectively.