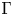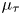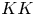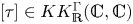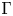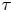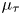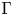1. Introduction
The Baum–Connes conjecture [Reference Baum and ConnesBC00] predicts an isomorphism between two abelian groups naturally associated with a discrete group 
$\Gamma$. More precisely, an assembly map
\[ \mu:K^{\textrm{top}}_*(\Gamma) \longrightarrow K_*(C^*_r\Gamma) \]
is constructed and is conjectured to be an isomorphism. The left-hand side is a topological object, based on the 
$K$-homology of proper 
$\Gamma$-spaces with compact quotient; the right-hand side is analytic, the 
$K$-theory of the reduced 
$C^*$-algebra of 
$\Gamma$.
We refer to the vast literature on the subject (see [Reference Baum and ConnesBC00, Reference Baum, Connes and HigsonBCH93], the book [Reference ValetteVal02] and the recent articles [Reference Baum, Guentner and WillettBGW16, Reference Buss, Echterhoff and WillettBEW18, Reference Gomez Aparicio, Julg and ValetteGJV19] and the references therein). One of the main motivations for the conjecture is that the injectivity of 
$\mu$ implies the Novikov conjecture.
In fact, the Novikov conjecture is implied by the rational injectivity of the Mishchenko–Kasparov assembly map [Reference KasparovKas88, Reference Mishchenko and FomenkoMF80]
\[ \tilde \mu: K_*(B\Gamma) \longrightarrow K_*(C^*_r\Gamma) \]
and the Baum–Connes map incorporates the Mishchenko–Kasparov assembly in the sense that 
$\tilde \mu =\mu \circ \sigma$, where 
$\sigma :K_*(B\Gamma )\to K^{\textrm {top}}_*(\Gamma )$ is a natural, rationally injective ‘forgetful’ map. When 
$\Gamma$ is torsion free, one simply has 
$\mu =\tilde \mu$. In general, the left-hand side 
$K^{\textrm {top}}_*(\Gamma )$ of the Baum–Connes map also contains information coming from finite-order elements of 
$\Gamma$ [Reference Baum, Connes and HigsonBCH93].
The more general formulation of the Baum–Connes conjecture is the one called ‘with coefficients’, which involves the action of a discrete group 
$\Gamma$ on a 
$C^*$-algebra 
$A$. In this case, the conjecture about the bijectivity of the map
\[ \mu^A:K^{\textrm{top}}_*(\Gamma;A) \longrightarrow K(A\rtimes_r\Gamma) \]is known to admit counterexamples [Reference Higson, Lafforgue and SkandalisHLS02].
In the present paper, we apply the model of 
$KK$-theory with real coefficients developed in [Reference Antonini, Azzali and SkandalisAAS16] to study the properties of the assembly maps. We explain how adding coefficients in 
${\mathbin {{\mathbb {R}}}}$ provides a way to localise at the unit element of 
$\Gamma$. The upshot is a localised form of the Baum–Connes conjecture that we relate to the classical Baum–Connes and Novikov conjectures.
In [Reference Antonini, Azzali and SkandalisAAS16] we identified a distinguished idempotent element 
$[\tau ]$ of the commutative ring 
$KK_{\mathbin {{\mathbb {R}}}}^\Gamma (\mathbb {C},\mathbb {C})$ that is canonically associated to the group 
$\Gamma$ via its group trace. If the group 
$\Gamma$ acts freely and properly on a locally compact space 
$Y$, then 
$[\tau ]$ acts as the identity element on the 
$\Gamma$-algebra of functions 
$C_0(Y)$, that is, it defines the unit element of the ring 
$KK_{{\mathbin {{\mathbb {R}}}}}^\Gamma (C_0(Y),C_0(Y))$.
Via the action of the idempotent 
$[\tau ]$ we define for 
$\Gamma$-algebras 
$A$, 
$B$ the 
$\tau$-part of 
$KK^\Gamma _{\mathbin {{\mathbb {R}}}}(A, B)$ to be the subgroup
\[ KK^\Gamma_{\mathbin{{\mathbb{R}}}}(A, B)_{\tau}:=\{x\otimes [\tau]; \ x\in KK^\Gamma_{\mathbin{{\mathbb{R}}}}(A, B)\}=\{x\in KK^\Gamma_{\mathbin{{\mathbb{R}}}}(A, B): x\otimes [\tau]=x\} \]
on which 
$[\tau ]$ acts as the identity.
The map 
$\mu _\tau$ that we construct is defined on 
$KK$-theory with real coefficients and relates the 
$\tau$-parts of the left- and right-hand side of the Baum–Connes assembly map.
(i) The left-hand side of the
$\tau$-assembly morphism will be $K^{\textrm {top}}_{*, {\mathbin {{\mathbb {R}}}}}(\Gamma ;A)_{\tau }$.(ii) For the right-hand side, it is natural to define the
$\tau$-part of $K_{\mathbin {{\mathbb {R}}}}(A\rtimes _r \Gamma )$ letting $[\tau ]$ act via descent, that is, by right multiplication with the idempotent element $J^\Gamma _r(1_A\otimes [\tau ])$ of the ring $KK_{\mathbin {{\mathbb {R}}}}(A\rtimes _r \Gamma , A\rtimes _r \Gamma )$. We thus set
\[ K_{*,{\mathbin{{\mathbb{R}}}}}(A\rtimes_r \Gamma)_{\tau}:=\{\xi\in K_{*,{\mathbin{{\mathbb{R}}}}}(A\rtimes_r \Gamma):\, \xi\otimes J^\Gamma_r(1_A\otimes [\tau])=\xi\}. \](iii) The assembly morphism defines a map
\[ \mu_\tau: K^{\textrm{top}}_{*, {\mathbin{{\mathbb{R}}}}}(\Gamma;A)_{\tau}\longrightarrow K_{\mathbin{{\mathbb{R}}}}(A\rtimes_r \Gamma)_{\tau} . \]
The 
$\tau$-form of the Baum–Connes conjecture with coefficients in a 
$\Gamma$-algebra 
$A$ is then the statement that 
$\mu _\tau$ is an isomorphism.
We show that the 
$\tau$-form of the Baum–Connes conjecture is weaker than the Baum–Connes conjecture, in the sense that, if the Baum–Connes assembly map is injective (respectively, surjective) for 
$A\otimes N$ for every 
$\textrm {II}_1$-factor 
$N$, then 
$\mu _\tau$ is injective (respectively, surjective) for 
$A$ (Theorem 3.10).
Moreover, the 
$\tau$-form of Baum–Connes is ‘closer’ to the Novikov conjecture, because it is only concerned with the part of 
$K_*^{top}(\Gamma )$ corresponding to free and proper actions. We show the following result.
Theorem 6.2 If 
$\mu _\tau : K^{\textrm {top}}_{*, {\mathbin {{\mathbb {R}}}}}(\Gamma )_{\tau }\longrightarrow K_{\mathbin {{\mathbb {R}}}}(C^*_r \Gamma )_{\tau }$ is injective, then the Mishchenko–Kasparov assembly map 
$K_*(B\Gamma )\to K_*(C_r^*\Gamma )$ is rationally injective.
To do so, exploiting the properties of 
$KK$-theory with real coefficients, we prove (Theorem 5.4) that the 
$\tau$-part of 
$K^{\textrm {top}}_{*, {\mathbin {{\mathbb {R}}}}}(\Gamma )$ identifies with 
$K_{*,\mathbb {R}}(B\Gamma )$ and, more generally, the 
$\tau$-part of 
$K^{\textrm {top}}_{*, {\mathbin {{\mathbb {R}}}}}(\Gamma ;A)$ identifies with 
$K^\Gamma _{*,\mathbb {R}}(E\Gamma ; A)$.
We already know from [Reference Antonini, Azzali and SkandalisAAS16] that the idempotent 
$[\tau ]$ acts as the identity on 
$K^\Gamma _{*,\mathbb {R}}(E\Gamma ; A)$.
To show that the 
$\tau$-part of 
$K^{\textrm {top}}_{*, {\mathbin {{\mathbb {R}}}}}(\Gamma ;A)$ is contained in 
$K^\Gamma _{*,\mathbb {R}}(E\Gamma ; A)$, we construct a compact 
$\Gamma$-space 
$X$ with an invariant probability measure on which each torsion subgroup of 
$\Gamma$ acts freely. In particular, this provides an inverse 
$t$ to the map 
$\sigma : K_{*,\mathbb {R}}(B\Gamma )\to K^{\textrm {top}}_{*, {\mathbin {{\mathbb {R}}}}}(\Gamma )_\tau$ on the 
$\tau$-part.
The relation between the localised Baum–Connes assembly map 
$\mu _\tau$ and the Mishchenko–Kasparov assembly 
$\tilde \mu$ is summarised by the following commutative diagram (Remark 6.3).
This also provides information about the image of the assembly map 
$\tilde \mu \otimes 1$. More precisely, applying the natural map 
$\beta$, the image of 
$\tilde \mu \otimes 1$ is in the 
$\tau$-part of 
$K_{*,{\mathbin {{\mathbb {R}}}}}(C_r^*\Gamma )$.
Let us also mention some other potentially important features of our construction. First, the localised map 
$\mu _\tau$ does not distinguish between full and reduced group 
$C^*$-algebra: in fact, we observe (Proposition 3.3) that
\[ K_{*,{\mathbin{{\mathbb{R}}}}}(C^*\Gamma)_\tau\simeq K_{*,{\mathbin{{\mathbb{R}}}}}(C_r^*\Gamma)_\tau . \]
The second feature is related to functoriality. It is known that the reduced 
$C^*$-algebra of groups is not functorial with respect to (non-injective) morphisms 
$\Gamma _1\to \Gamma _2$ of countable groups, unlike the left-hand side of 
$K_*^\textrm {top}(\Gamma )$. On the other hand, we show that the group 
$K_{*,{\mathbin {{\mathbb {R}}}}}(C^*\Gamma )_\tau$ is functorial (see § 3.2).
From the properties given previously, arguing that the Baum–Connes conjecture holds for hyperbolic groups [Reference LafforgueLaf12], one could hope to be able to establish bijectivity of 
$\mu _\tau$ in a great generality.
For the case with coefficients in a 
$\Gamma$-algebra this is unfortunately not the case: in § 7 we show that the construction of [Reference Higson, Lafforgue and SkandalisHLS02] for group actions using the ‘Gromov monster’ still provides counterexamples to the bijectivity of the localised Baum–Connes assembly 
$\mu _\tau : K^{\textrm {top}}_{*, {\mathbin {{\mathbb {R}}}}}(\Gamma ;A)_{\tau }\longrightarrow K_{\mathbin {{\mathbb {R}}}}(A\rtimes _r \Gamma )_{\tau }$ for a suitable choice of coefficients 
$A$. Again the failure of exactness is the source of counterexamples. In fact, using the properties of a Gromov monster group 
$\Gamma$ [Reference Arzhantseva and DelzantAD08, Reference GromovGro03], and letting 
$A:=\ell ^{\infty }(\mathbb {N};c_0(\Gamma ))$ we show that the sequence of the 
$\tau$-parts
is not exact in the middle. This proves that 
$\mu _\tau$ cannot be an isomorphism for every 
$\Gamma$-algebra.
1.0.1 On the terminology
Let us say in what sense the element 
$\tau$ localises at the unit element.
(i) Naively,
$\tau$ really takes the value of a function at the unit element.(ii) In a more sophisticated sense, we know from [Reference Baum, Connes and HigsonBCH93] that the left-hand side
$K^{\textrm {top}}_{*}(\Gamma )$ rationally breaks into contributions of the various conjugacy classes of $\Gamma$. In the same way, it is known from [Reference BurgheleaBur85] that the cyclic cohomology of the group algebra $\mathbb {C}\Gamma$ breaks into contributions of the various conjugacy classes of the group; the one associated to the unit element is equal to the cohomology group $H^*(\Gamma ;\mathbb {C})=H^*(B\Gamma ;\mathbb {C})$. The idempotent $[\tau ]$ isolates this component at the level of the ‘right-hand side’ $K_*(C_r^*\Gamma )$.
1.0.2 Notation
All the tensor products considered here are minimal tensor products and will be just written with the sign ‘
$\otimes$’.
We use the sign ‘
$\otimes _D$’ for the Kasparov product of 
$KK$-elements over a 
$C^*$-algebra 
$D$ in the sense of [Reference KasparovKas81, Reference KasparovKas88]. When 
$x\in KK(A,D)$ and 
$y\in KK(D,B)$ we sometimes drop the subscript 
$D$ and write 
$x\otimes y$ instead of 
$x\otimes _D y$.
Throughout the paper, when dealing with classifying spaces 
$E\Gamma$ and 
$B\Gamma$, we always use the notation 
$K_*(B\Gamma )$ and or 
$K_*^\Gamma (E\Gamma )$ to mean the 
$K$-homology with compact supports (or 
$\Gamma$-compact supports), which are often denoted by 
$RK_*$ and 
$RK_*^\Gamma$ in the literature.
2. $KK$-theory with real coefficients
In this section we briefly recall some constructions we will need later.
2.1 Non-separable $C^*$-algebras and $K$-theory
Let us recall some material from [Reference SkandalisSka85b]. One shows that, when 
$A$ is a separable 
$C^*$-algebra, then for every 
$C^*$-algebra 
$B$, the group 
$KK(A,B)$ is the inductive limit over all the separable subalgebras of 
$B$. Based on this, one constructs a new group 
$KK_{sep}(A,B)$ for not-necessarily separable 
$A$ and 
$B$; it is defined as the projective limit of the groups 
$KK(A_1,B)$ where 
$A_1$ runs over all the separable subalgebras 
$A_1 \subset A$. It enjoys two important properties:
(i) the familiar Kasparov group maps to this new
$KK(A,B)$;(ii) in the new
$KK(A,B)$, the Kasparov product
is always defined without separability assumptions; this follows from the naturality of the Kasparov product in the separable case.\[ \otimes_D:KK_{\textrm{sep}}(A_1,B_1\otimes D) \times KK_{\textrm{sep}}(D\otimes A_2,B_2) \longrightarrow KK_{\textrm{sep}}(A_1\otimes A_2, B_1 \otimes B_2) \]
One may note that all these facts can immediately be extended to the equivariant case: with respect to a second countable group 
$\Gamma$.
We have the following result.
Lemma 2.1 Let 
$\Gamma$ be a countable discrete group, and 
$B$ a 
$\Gamma$-algebra.
(i) For every separable
$\Gamma$ algebra $A$, the group $KK^\Gamma (A,B)$ is the inductive limit of $KK^\Gamma (A,B_1)$ where $B_1$ runs over separable $\Gamma$-subalgebras $B_1 \subset B$.(ii) For every separable algebra
$A$, the group $KK(A;B\rtimes _r \Gamma )$ is the inductive limit of $KK(A,B_1\rtimes _r \Gamma )$ where $B_1$ runs over separable $\Gamma$-subalgebras $B_1 \subset B$.
The proof of statement (i) goes as in [Reference SkandalisSka85b, Remark 3.2], by using that 
$\Gamma$ is a countable group.
Statement (ii) follows from the fact that every separable subalgebra of 
$B\rtimes _r \Gamma$ is contained in a 
$B_1\rtimes _r \Gamma$.
Note that the same remarks hold also for full crossed products.
2.2 $KK$-theory with real coefficients
In [Reference Antonini, Azzali and SkandalisAAS16], we constructed the functor 
$KK^G_{{\mathbin {{\mathbb {R}}}}}$ by taking an inductive limit over 
$\textrm {II}_1$-factors. More precisely, given a locally compact group(oid) and two 
$G$-algebras 
$A$ and 
$B$, we defined 
$KK^G_{\mathbin {{\mathbb {R}}}}(A,B)$ as the limit of 
$KK^G(A,B\otimes M)$ where 
$M$ runs over 
$\textrm {II}_1$-factors with trivial 
$G$ action and unital embeddings.
An equivalent definition of 
$KK^G_{\mathbin {{\mathbb {R}}}}(A, B)$ can be given by taking limits of 
$KK^G_{\mathbin {{\mathbb {R}}}}(A, B\otimes D)$ over pairs 
$(D,\lambda )$ where 
$D$ is a unital 
$C^*$-algebra with trivial 
$G$-action, and 
$\lambda$ is a tracial state on 
$D$ [Reference Antonini, Azzali and SkandalisAAS16, Remarks 1.6].
2.3 The Kasparov product in $KK^G_{{\mathbin {{\mathbb {R}}}}}$
Let 
$x_1\in KK^G_{{\mathbin {{\mathbb {R}}}}}(A_1,B_1\otimes D)$ and 
$x_2\in KK^G_{{\mathbin {{\mathbb {R}}}}}(D\otimes A_2,B_2)$; represent them as elements 
$y_1\in KK^G_{{\mathbin {{\mathbb {R}}}}}(A_1,B_1\otimes M_1\otimes D)$ and 
$y_2\in KK^G(D\otimes A_2,M_2\otimes B_2)$ where 
$M_1$ and 
$M_2$ are 
$\rm {II}_1$-factors. The Kasparov product 
$(y_1\otimes 1_{A_2})\otimes _D (1_{B_1\otimes M_1}\otimes y_2)$ is an element in 
$KK^G(A_1\otimes A_2,B_1\otimes M_1\otimes M_2\otimes B_2)$. Finally, using the canonical morphism 
$M_1\otimes M_2\to M_1\bar {\otimes } M_2$ to the von Neumann tensor product, we obtain an element 
$x_1\otimes _Dx_2\in KK^G_{{\mathbin {{\mathbb {R}}}}}(A_1\otimes A_2,B_1\otimes B_2)$.
The Kasparov product in 
$KK^G_{{\mathbin {{\mathbb {R}}}}}$ has all the usual properties (bilinearity, associativity, functoriality, etc.). In particular, we have the following result.
Lemma 2.2 The exterior product in 
$KK^G_{{\mathbin {{\mathbb {R}}}}}$ is commutative.
Proof. Let 
$A_1, A_2, B_1, B_2$ be 
$G$-algebras, 
$x_i\in KK_{\mathbin {{\mathbb {R}}}}^G(A_i,B_i)$. There exist 
$\textrm {II}_1$-factors 
$M_1, M_2$ with trivial 
$G$-action such that 
$x_i$ are images of 
$y_i\in KK^G(A_i,B_i\otimes M_i)$. By [Reference KasparovKas88, Theorem 2.14 (8)], the exterior Kasparov products 
$y_1\otimes _\mathbb {C} y_2$ and 
$y_2\otimes _\mathbb {C} y_1$ coincide (under the natural flip isomorphisms) in 
$KK^G(A_1\otimes A_2,B_1\otimes M_1\otimes B_2\otimes M_2)$. The Kasparov products 
$x_1\otimes _\mathbb {C} x_2$ and 
$x_2\otimes _\mathbb {C} x_1$ are, by definition, the images of 
$y_1\otimes _\mathbb {C} y_2$ and 
$y_2\otimes _\mathbb {C} y_1$, respectively, in the group 
$KK_{\mathbin {{\mathbb {R}}}}^G(A_1\otimes A_2,B_1\otimes B_2)$ through a morphism from 
$M_1\otimes M_2$ to a 
$\textrm {II}_1$-factor (e.g. their von Neumann tensor product) and then passing to the inductive limit. They coincide.
As a direct consequence, we find the following.
Proposition 2.3 For every pair 
$(A,B)$ of 
$G$-algebras, 
$KK^G_{{\mathbin {{\mathbb {R}}}}}(A,B)$ is a module over the ring 
$KK^G_{{\mathbin {{\mathbb {R}}}}}(\mathbb {C},\mathbb {C})$ and the Kasparov product is 
$KK^G_{{\mathbin {{\mathbb {R}}}}}(\mathbb {C},\mathbb {C})$-bilinear. In particular, 
$KK^G_{{\mathbin {{\mathbb {R}}}}}(A,A)$ is an algebra over this ring.
Remarks 2.4 (i) Note also that using the group morphism 
$G\to \{1\}$, we obtain a ring morphism 
${\mathbin {{\mathbb {R}}}}=KK_{\mathbin {{\mathbb {R}}}}(\mathbb {C},\mathbb {C})\to KK^G_{{\mathbin {{\mathbb {R}}}}}(\mathbb {C},\mathbb {C})$ and it follows that the groups 
$KK^G_{{\mathbin {{\mathbb {R}}}}}(A,B)$ are real vector spaces and 
$KK^G_{{\mathbin {{\mathbb {R}}}}}(A,A)$ is an algebra over 
${\mathbin {{\mathbb {R}}}}$ (see also [Reference Antonini, Azzali and SkandalisAAS16, Remark 1.9]).
(ii) Let 
$M$ be a 
$\textrm {II}_1$-factor with trivial 
$G$-action. The identity of 
$M$ defines an element 
$[\textrm {id}_M]\in KK^{G}_{{\mathbin {{\mathbb {R}}}}}(M,\mathbb {C})$. We have a canonical map 
$KK^G_{{\mathbin {{\mathbb {R}}}}}(A,B\otimes M ) \to KK^G_{{\mathbin {{\mathbb {R}}}}}(A,B)$ by Kasparov product with this element. Let us describe it.
Let 
$N$ be a 
$\rm {II}_1$-factor and 
$x \in KK^G(A,B\otimes M\otimes N)$ representing in the limit an element in 
$KK^G_{{\mathbin {{\mathbb {R}}}}}(A,B\otimes M )$. Denote by 
$M\bar {\otimes } N$ the von Neumann tensor product of 
$M$ and 
$N$. Using the embedding 
$B\otimes M\otimes N\to B\otimes (M\bar {\otimes } N)$ we obtain a morphism 
$KK^G(A,B\otimes M\otimes N)\to KK_{\mathbin {{\mathbb {R}}}}^G(A,B)$.
Let 
$\iota :\mathbb {C}\to M$ denote the unital inclusion. The element 
$\iota ^*[\textrm {id}_M]$ is the unit element of the ring 
$KK^{G}_{{\mathbin {{\mathbb {R}}}}}(\mathbb {C},\mathbb {C})$. The element 
$\iota _*[\textrm {id}_M]$ is therefore an idempotent in 
$KK^{G}_{{\mathbin {{\mathbb {R}}}}}(M,M)$. It is not clear what this idempotent is.
(iii) The exterior product map 
$KK^G(A, B)\times KK^G(C,D\otimes M)\to KK^G(A\otimes C, B\otimes D\otimes M)$ induces an ‘inhomogeneous product’ map
\begin{equation} \otimes:KK^G(A, B)\otimes KK^G_{\mathbin{{\mathbb{R}}}}(C,D)\longrightarrow KK^G_{\mathbin{{\mathbb{R}}}}(A\otimes C, B\otimes D) . \end{equation}
Clearly this is the same as computing the product in 
$KK_{\mathbin {{\mathbb {R}}}}$ after applying the change of coefficient map 
$KK^G(A, B)\to KK^G_{\mathbin {{\mathbb {R}}}}(A, B)$ (see also [Reference Antonini, Azzali and SkandalisAAS16, § 1.5]).
(iv) Real 
$KK$ for non-separable algebras. We adapt the discussion given in § 2.1 to define 
$KK_{\mathbin {{\mathbb {R}}}}^G(A,B)$ when 
$G$ is second countable locally compact, and 
$A,B$ are generally non-separable 
$C^*$-algebras.
(a) To begin with let us take
$A$ as separable, $B$ as any $C^*$-algebra and $G$ as any locally compact group. Then there exists the inductive limit $\displaystyle \varinjlim _N KK^G(A,B\otimes N)$ with $N$ running over the space of all $\rm {II}_1$-factors (acting on a fixed separable Hilbert space) with tracial embeddings as morphisms. The existence of the limit is given by exactly the same proof in [Reference Antonini, Azzali and SkandalisAAS16] where only the general properties of the space of $\textrm {II}_1$-factors are used and there is no need for separability assumptions on $B$. We can thus put
\[ KK_{\mathbb{R}}^G(A,B):= \varinjlim_N KK^G(A,B \otimes N). \](b) Assume
$A$ is separable; start with any element in $KK_{{\mathbin {{\mathbb {R}}}}}^{G}(A,B)$ represented by some $x \in KK^{G}(A,B \otimes N)$, then we can find a separable subalgebra $D \subset B\otimes N$ whose image in $KK^G(A, B\otimes N)$ is $x$. We can then also find a separable $C^*$-subalgebra $B_1 \subset B$ and an element $x_1 \in KK^{G}(A,B_1 \otimes N)$ representing $x$. This implies
\[ KK^G_{{\mathbin{{\mathbb{R}}}}}(A,B)= \varinjlim_{\substack{B' \subset B\\ B' {\textrm{separable}} } } KK^{G}_{{\mathbin{{\mathbb{R}}}}}(A,B). \](c) By the above remark we can define
$KK^G_{{\mathbin {{\mathbb {R}}}}}(A,B)$ for not necessarily separable $A$ and $B$ and countable $G$. It is analogous to $KK_{sep}^G(A,B)$ of § 2.1:
(2)and is also given with a well-defined Kasparov product.\begin{equation} KK^G_{sep,{\mathbin{{\mathbb{R}}}}}(A,B):= \varprojlim_{\substack{A' \subset A\\ A' \textrm{separable} } } KK^{G}_{{\mathbin{{\mathbb{R}}}}}(A',B)=\varprojlim_{\substack{A' \subset A\\ A' \textrm{separable} } }\varinjlim_N KK^G(A',B\otimes N), \end{equation}
2.4 $KK$-elements associated with traces
If 
$D$ is a 
$C^*$-algebra (with trivial 
$G$-action) and 
$\lambda$ is a tracial state on 
$D$, we may map 
$D$ in a trace-preserving way into a II
$_1$-factor and, thus, 
$\lambda$ gives rise to a natural 
$KK$-class with real coefficients 
$[\lambda ]\in KK_{{\mathbin {{\mathbb {R}}}}}(D,\mathbb {C})$.
Let us make some remarks.
Remarks 2.5 Let 
$D$ be a 
$G$-algebra and 
$\lambda$ a tracial state on 
$D$.
(i) If the action of 
$G$ on 
$D$ is inner, that is, through a continuous morphism of 
$G$ into the set of unitary elements of 
$D$, then 
$D$ with the 
$G$ action is Morita equivalent to the algebra 
$D$ with trivial 
$G$ action and, thus, 
$[\lambda ]\in KK^G_{{\mathbin {{\mathbb {R}}}}}(D,\mathbb {C})$ is still well defined.
(ii) Recall that when 
$G$ is discrete and acts trivially on 
$B$ the groups 
$KK^G(A, B)$ and 
$KK(A\rtimes G, B)$ coincide (the crossed product 
$A\rtimes G$ is the maximal one). The same isomorphism holds at the 
$KK_{\mathbin {{\mathbb {R}}}}^G$ level.
(iii) If 
$G$ is discrete and 
$\lambda$ is invariant, then the crossed product algebra 
$D\rtimes G$ carries the natural (dual) trace associated with 
$\lambda$. We have an equivariant inclusion 
$D\to D\rtimes G$ where the action of 
$G$ is now inner on 
$D\rtimes G$. We thus still obtain an element 
$[\lambda ]\in KK^G_{{\mathbin {{\mathbb {R}}}}}(D,\mathbb {C})$.
(iv) Let 
$\Gamma$ be a discrete group. Then by the previous discussion, every tracial state on 
$C^*\Gamma$ defines an element of 
$KK_{\mathbin {{\mathbb {R}}}}(C^*\Gamma ,\mathbb {C})=KK_{\mathbin {{\mathbb {R}}}}^{\Gamma }(\mathbb {C},\mathbb {C})$. Let 
$\sigma ,\sigma '$ be tracial states on 
$C^*\Gamma$. Let 
$\delta :C^*\Gamma \longrightarrow C^*\Gamma \otimes C^*\Gamma$ denote the coproduct; then we can write 
$[\sigma ]\otimes [\sigma '] = [\sigma .\sigma ']$ where 
$\sigma .\sigma '$ is the tracial state 
$\sigma .\sigma ':=(\sigma \otimes \sigma ') \circ \delta$. We have 
$\sigma .\sigma '(g)=\sigma (g)\sigma '(g)$ on every 
$g\in \Gamma$.
In particular, the canonical group trace 
$\textrm {tr}_\Gamma$ that satisfies 
$\textrm {tr}_\Gamma (e)=1$ and 
$\textrm {tr}_\Gamma (g)=g$ for 
$g\ne e$ absorbs every tracial state: 
$[\sigma ]\otimes [\textrm {tr}_\Gamma ]= [\textrm {tr}_\Gamma ]$.
2.5 Descent morphism
Let us describe the descent morphism in 
$KK_{\mathbin {{\mathbb {R}}}}$.
Let 
$\Gamma$ be a discrete group, then there is a descent map
\begin{equation} J^{\Gamma}: KK^\Gamma_{{\mathbin{{\mathbb{R}}}}}(A,B) \longrightarrow KK_{{\mathbin{{\mathbb{R}}}}}(A \rtimes \Gamma,B \rtimes \Gamma), \end{equation}
with respect to the maximal crossed product, which is induced by the classical Kasparov descent map on 
$KK^\Gamma$. It is natural with respect to the Kasparov product and satisfies 
$J^{\Gamma }(1_A)=1_{A \rtimes \Gamma }$.
Indeed let 
$M \to N$ be a morphism of 
$C^*$-algebras, both with trivial 
$\Gamma$ action, and let 
$B$ a 
$\Gamma$-algebra; we have a commutative diagram
which follows from the universal properties of the full crossed product and the fact that 
$\Gamma$ acts trivially on 
$M$ and 
$N$. When 
$M \hookrightarrow N$ is a unital embedding of 
$\textrm {II}_1$-factors, applying the 
$KK$ functor and the Kasparov descent map before passing to the limit defines (3).
We have a commutative diagram similar to (4) involving reduced crossed products. Actually, when taking reduced crossed products (and minimal tensor products) the vertical arrows are isomorphisms: let 
$B$ be acting faithfully on the Hilbert space 
$H_1$ and 
$M$ on the Hilbert space 
$H_2$; then both 
$(B\otimes M) \rtimes _{r} \Gamma$ and 
$(B\rtimes _{r} \Gamma )\otimes M$ are canonically and faithfully represented in the Hilbert space 
$H_1\otimes H_2 \otimes \ell ^2\Gamma$, and the same with 
$N$ instead of 
$M$.
Therefore, in the same way, we define a reduced descent morphism
\begin{equation} J^\Gamma_r :KK_{{\mathbin{{\mathbb{R}}}}}^\Gamma(A,B) \longrightarrow KK_{{\mathbin{{\mathbb{R}}}}}(A \rtimes_r \Gamma, B\rtimes_r \Gamma) . \end{equation}3. The $\tau$-element and the $\tau$-part
Let 
$\Gamma$ be a discrete group; the 
$\tau$-element of 
$\Gamma$ is associated to 
$\Gamma$ by means of its canonical trace 
$\operatorname {tr}_\Gamma :C^*\Gamma \rightarrow \mathbb {C}$. Indeed applying point (iv) of Remark 2.5 to 
$\operatorname {tr}_\Gamma$ we obtain a natural class that we call 
$[\tau ]\in KK^\Gamma _{{\mathbin {{\mathbb {R}}}}}(\mathbb {C},\mathbb {C})$.
Two algebraic properties of 
$[\tau ]$ are immediate to check: 
$[\tau ]$ is an idempotent, that is, 
$[\tau ]\otimes [\tau ]=[\tau ]$ (see [Reference Antonini, Azzali and SkandalisAAS16]); furthermore, 
$[\tau ]$ is central in 
$KK_{{\mathbin {{\mathbb {R}}}}}^\Gamma$, that is, for any 
$\Gamma$-algebras 
$A,B$ and any 
$[x] \in KK_{{\mathbin {{\mathbb {R}}}}}^\Gamma (A;B)$, then 
$[x]\otimes [\tau ]= [\tau ]\otimes [x]$, as follows by Lemma 2.2.
As 
$\tau$ is fundamental for what follows, it is worth giving a more detailed description.
(i) One starts with any trace-preserving morphism
$\varphi _N:C^*\Gamma \longrightarrow N$ to a $\textrm {II}_1$-factor that defines a class in $KK(C^*\Gamma ,N)$ and in the limit a class $[\varphi _N]\in KK_{{\mathbin {{\mathbb {R}}}}}(C^*\Gamma ;\mathbb {C}).$(ii) Consider
$\Gamma$ acting trivially on $\mathbb {C}$ and apply the canonical isomorphism $KK_{{\mathbin {{\mathbb {R}}}}}(C^*\Gamma ,\mathbb {C})\simeq KK_{{\mathbin {{\mathbb {R}}}}}^\Gamma (\mathbb {C},\mathbb {C})$ to the class $[\varphi _N]$. The element we obtain is $[\tau ]$.(iii) Concretely
$[\tau ]$ is represented in the limit by the class in $KK^\Gamma (\mathbb {C},N)$ of the $\Gamma$-$(\mathbb {C},N)$ bimodule that is $N$ (considered as a Hilbert $N$-module) with the $\Gamma$-action $\gamma \cdot n= \varphi _N(\gamma ) n$. If $\Gamma$ is an infinite conjugacy class (i.c.c.) group, one can take $N=L\Gamma$ to be the group von Neumann algebra of $\Gamma$. More generally, one can, for instance, embed $\Gamma$ in an i.c.c. group $\Gamma '$ and take $N$ to be the group von Neumann algebra of $\Gamma '$.
3.1 The $\tau$-part of $K$-theory
3.1.1 The $\tau$-part of $KK_{\mathbin {{\mathbb {R}}}}^\Gamma$ and of crossed products
The action of the idempotent 
$[\tau ]$ suggests the following definition.
Definition 3.1 We denote by 
$KK_{{\mathbin {{\mathbb {R}}}}}^\Gamma (A,B)_{\tau }$ the image of the idempotent 
$[\tau ]$ acting on 
$KK_{{\mathbin {{\mathbb {R}}}}}^\Gamma (A,B)$ and call it the 
$\tau$-part of 
$KK_{\mathbin {{\mathbb {R}}}}^\Gamma (A,B)$.
It is natural to define the 
$\tau$-part also for the 
$K$-theory of group 
$C^*$-algebras (or, more generally, crossed products). To do so, we consider the action of the element 
$J^\Gamma ([\tau ])$ obtained by applying the descent morphisms, as follows.
Definition 3.2 {(
$\tau$-part of crossed products)}
Let 
$J^\Gamma$ and 
$J^\Gamma _r$ be the descent maps defined in (3) and (5). Let 
$A$ be a 
$\Gamma$-
$C^*$-algebra. Let 
$1_A$ denote the unit of 
$KK^\Gamma (A,A)$. We set
\begin{gather} {[}\tau^A]_{\text{max}}:=J^\Gamma(1_A\otimes [\tau])\in KK_{\mathbin{{\mathbb{R}}}}(A\rtimes \Gamma, A\rtimes\Gamma) \end{gather}
\begin{gather} {[}\tau^A]_{r}:=J^\Gamma_r(1_A\otimes [\tau])\in KK_{\mathbin{{\mathbb{R}}}}(A\rtimes_r\Gamma, A\rtimes_r\Gamma) . \end{gather}
When 
$A=\mathbb {C}$ we simply write 
$[\tau ]_{\text {max}}$ and 
$[\tau ]_{r}$.
Let now 
$D$ be any 
$C^*$-algebra. We call the 
$\tau$-part of 
$KK_{\mathbin {{\mathbb {R}}}}(D,A\rtimes _r\Gamma )$ the image of the idempotent 
$[\tau ^A]_{r}$ acting by right multiplication on 
$KK_{{\mathbin {{\mathbb {R}}}}}(D,A\rtimes _r\Gamma )$:
\[ KK_{\mathbin{{\mathbb{R}}}}(D,A\rtimes_r\Gamma)_{\tau}:=\textrm{Image} \big{\{} \cdot{\otimes} [\tau^A]_{r}: KK_{{\mathbin{{\mathbb{R}}}}}(D,A\rtimes_r\Gamma) \longrightarrow KK_{{\mathbin{{\mathbb{R}}}}}(D,A\rtimes_r\Gamma) \big{\}}. \]
Analogously, the 
$\tau$-part of 
$KK_{\mathbin {{\mathbb {R}}}}(D,A\rtimes \Gamma )$, denoted by 
$KK_{\mathbin {{\mathbb {R}}}}(D,A\rtimes \Gamma )_{\tau }$, is the image of 
$\,[\tau ^A]_{\text {max}}$ acting by left multiplication on 
$KK_{{\mathbin {{\mathbb {R}}}}}(D,A\rtimes \Gamma )$. When 
$D=\mathbb {C}$ we abbreviate with 
$K_{*,{\mathbin {{\mathbb {R}}}}}(C^*\Gamma )_{\tau }$ and 
$K_{*,{\mathbin {{\mathbb {R}}}}}(C_r^*\Gamma )_{\tau }$.
3.1.2 Reduced versus maximal crossed products
The name 
$\tau$-part is unambiguous; indeed the following proposition shows that 
$KK_{\mathbin {{\mathbb {R}}}}(D,A\rtimes \Gamma )_{\tau }$ and 
$KK_{\mathbin {{\mathbb {R}}}}(D,A\rtimes _r\Gamma )_{\tau }$ are canonically isomorphic.
Let 
$\lambda ^A:A\rtimes \Gamma \to A\rtimes _r \Gamma$ be the natural morphism and denote by 
$[\lambda ^A]\in KK(A\rtimes \Gamma , A\rtimes _r \Gamma )$ its class.
There is also a natural morphism 
$\Delta ^A:A\rtimes _r\Gamma \to (A\rtimes \Gamma )\otimes C^*_r\Gamma$ induced by the coproduct. Indeed, the coproduct gives a morphism 
$\Delta _{\max }^A:A\rtimes \Gamma \to (A\rtimes \Gamma )\otimes C^*_r(\Gamma )$ defined by the covariant morphism 
$a\mapsto a\otimes 1$ and 
$g\mapsto g\otimes \lambda _g$. Let 
$A\rtimes \Gamma$ be faithfully represented on a Hilbert space 
$H$. Then we obtain a faithful representation 
$\pi$ of 
$(A\rtimes \Gamma )\otimes C^*_r(\Gamma )$ on 
$H\otimes \ell ^2(\Gamma )$. The composition 
$\pi \circ \Delta _{\max }^A$ is the canonical faithful representation of the reduced crossed product. It follows that the morphism 
$\Delta _{\max }^A$ factors through 
$A\rtimes _r \Gamma$: there is a (faithful) morphism 
$\Delta ^A:A\rtimes _r\Gamma \to (A\rtimes \Gamma )\otimes C^*_r\Gamma$ such that 
$\Delta _{\max }^A=\Delta ^A\circ \lambda ^A$.
Composing with a trace-preserving embedding of 
$C^*_r\Gamma$ in a 
$\textrm {II}_1$-factor 
$N$, we thus obtain a class 
$[\Delta _\tau ^A]=[\Delta ^A]\otimes _{C^*_r\Gamma }[\tau ]\in KK_{\mathbin {{\mathbb {R}}}}(A\rtimes _r\Gamma , A\rtimes \Gamma )$.
Proposition 3.3 (Cf. [AAS16, Proof of Remark 2.4]) We have
\begin{equation} \begin{aligned} & [\lambda^A]\otimes [\Delta^A_\tau] =[\tau^A]_{\operatorname{max}}\in KK_{\mathbin{{\mathbb{R}}}}(A\rtimes\Gamma, A\rtimes\Gamma), \\ & [\Delta^A_\tau]\otimes [\lambda^A] = [\tau^A]_{r} \;\;\;\;\in KK_{\mathbin{{\mathbb{R}}}}(A\rtimes_r\Gamma, A\rtimes_r\Gamma) . \end{aligned} \end{equation}
Then, for every 
$C^*$-algebra 
$D$, the product with 
$[\Delta ^A_\tau ]$ induces a canonical isomorphism
Proof. Represent 
$[\tau ]$ using a trace-preserving morphism 
$\varphi : C_r^*\Gamma \longrightarrow N$. Then 
$[\tau ^A]_{\operatorname {max}}$ is given by the composition 
$(\textrm {id}\otimes \varphi )\circ \Delta _{\max }^A=(\textrm {id}\otimes \varphi )\circ \Delta ^A\circ \lambda ^A$. The first equality follows.
In the same way, 
$[\tau ^A]_r$ is given by the composition 
$(\textrm {id}\otimes \varphi )\circ \Delta _{r}^A$, where 
$\Delta _{r}^A$ is the usual coproduct 
$A\rtimes _r\Gamma \to (A\rtimes _r\Gamma )\otimes C^*_r\Gamma$. The second equality follows because 
$\Delta _r^A=(\lambda ^A\otimes \textrm {id})\circ \Delta ^A$.
We can interpret this fact by saying that 
$[\tau ]$ belongs to the ‘
$K$-amenable part of 
$KK^\Gamma _{\mathbin {{\mathbb {R}}}}(\mathbb {C},\mathbb {C})$’ in the spirit of [Reference CuntzCun83].
3.1.3 Functoriality
We remark here a functoriality property of the 
$\tau$-parts that we need later.
Let 
$A$ and 
$B$ be 
$\Gamma$-algebras and 
$x\in KK_{{\mathbin {{\mathbb {R}}}}}^\Gamma (A,B)$.
Proposition 3.4 The map 
$\cdot \otimes _{J_r(x)}:KK_{{\mathbin {{\mathbb {R}}}}}(\mathbb {C}, A\rtimes _r \Gamma ) \longrightarrow KK_{{\mathbin {{\mathbb {R}}}}}(\mathbb {C}, B\rtimes _r \Gamma )$ preserves the 
$\tau$-parts inducing a map 
$KK_{{\mathbin {{\mathbb {R}}}}}(D, A\rtimes _r \Gamma )_\tau \longrightarrow KK_{{\mathbin {{\mathbb {R}}}}}(D, B\rtimes _r \Gamma )_\tau$. In particular, if 
$f:A\to B$ is an equivariant morphism, the induced map 
$f_*:KK_{{\mathbin {{\mathbb {R}}}}}(\mathbb {C}, A\rtimes _r \Gamma ) \longrightarrow KK_{{\mathbin {{\mathbb {R}}}}}(\mathbb {C}, B\rtimes _r \Gamma )$ preserves the 
$\tau$-parts.
Proof. Let 
$y\in KK_{{\mathbin {{\mathbb {R}}}}}(D; A\rtimes _r \Gamma )_\tau$. Then 
$y=y\otimes J_r(1_A\otimes [\tau ])$ and 
$y\otimes J_r(x)=y\otimes J_r([\tau ]\otimes x)=y\otimes J_r(x\otimes [\tau ])\in KK_{{\mathbin {{\mathbb {R}}}}}(D; B\rtimes _r \Gamma )_\tau .$
This discussion holds of course also for the full crossed product.
3.2 Naturality of the $\tau$-part of $KK_{\mathbin {{\mathbb {R}}}}(\mathbb {C}, C^*_r\Gamma )$ with respect to group morphisms
Let 
$\varphi :\Gamma _1 \to \Gamma _2$ be a morphism of groups. It defines a morphism 
$\varphi :C^*\Gamma _1\to C^*\Gamma _2$ and therefore an element 
$[\varphi ]\in KK(C^*\Gamma _1,C^*\Gamma _2)$. This morphism is not defined in general at the level of reduced 
$C^*$-algebras (if 
$\ker \varphi$ is not amenable) unlike the left-hand side 
$K_*^\textrm {top}(\Gamma )$ of the Baum–Connes assembly map.
Using the 
$\tau$ elements, we can easily bypass this difficulty.
We denote by 
$[\tau _1]\in KK^{\Gamma _1}_{\mathbin {{\mathbb {R}}}}(\mathbb {C},\mathbb {C})$ and 
$[\tau _2]\in KK^{\Gamma _2}_{\mathbin {{\mathbb {R}}}}(\mathbb {C},\mathbb {C})$ the corresponding 
$\tau$-elements.
Define 
$[\varphi ]_r\in KK_{\mathbin {{\mathbb {R}}}}(C_r^*\Gamma _1,C_r^*\Gamma _2)$ by putting 
$[\varphi ]_r=(\lambda _2\circ \varphi )_*[\Delta _{\tau _1}]$ where 
$[\Delta _{\tau _1}]=[\Delta ^\mathbb {C}_{\tau _1}]\in KK_{\mathbin {{\mathbb {R}}}}(C_r^*\Gamma _1,C^*\Gamma _1)$ was defined in § 3.1.2.
By the Kasparov product by 
$[\varphi ]_r$, we obtain a linear map 
$KK_{{\mathbin {{\mathbb {R}}}}}(\mathbb {C},C_r^*\Gamma _1)\overset {\otimes [\varphi ]_r}{\longrightarrow } KK_{{\mathbin {{\mathbb {R}}}}}(\mathbb {C},C_r^*\Gamma _2)$.
Claim 3.5 We have 
$[\varphi ]_r=J_r^{\Gamma _1}([\tau _1])\otimes [\varphi ]_r\otimes J_r^{\Gamma _2}([\tau _2])$. In particular, the map 
$\otimes [\varphi ]_r$ preserves the 
$\tau$-parts.
Indeed,
(i)
$[\Delta _{\tau _1}]=J_r^{\Gamma _1}([\tau _1])\otimes [\Delta _{\tau _1}]$, and thus $[\varphi ]_r=J_r^{\Gamma _1}([\tau _1])\otimes [\varphi ]_r$.(ii) The element
$[\varphi ]_r$ is the class of a morphism $C^*_r(\Gamma _1)\to C^*_r(\Gamma _2)\otimes N_1$ given by $\delta _{g_1}\mapsto \delta _{\varphi ({g_1})}\otimes j_1(\delta _{g_1})$ (for ${g_1}\in \Gamma _1$) where $N_1$ is any $\textrm {II}_1$-factor and $j_1:C^*_r\Gamma _1\to N_1$ is any trace-preserving morphism.Let
$j_1:C^*_r\Gamma _1\to N_1$ and $j_2:C^*_r\Gamma _2\to N_2$ be trace-preserving inclusions into $\textrm {II}_1$-factors. The element $[\varphi ]_r\otimes J_r^{\Gamma _2}([\tau _2])$ corresponds to the morphism $C^*_r(\Gamma _1)\to C^*_r(\Gamma _2)\otimes N_2\bar \otimes N_1$, given by $\delta _{g_1}\mapsto \delta _{\varphi ({g_1})}\otimes j_2(\delta _{\varphi ({g_1})})\otimes j_1(\delta _{g_1})$. But the map $\delta _{g_1}\mapsto j_2(\delta _{\varphi ({g_1})})\otimes j_1(\delta _{g_1})$ is a trace-preserving inclusion of $C^*_r\Gamma _1$ into the $\textrm {II}_1$-factor $N_2\bar \otimes N_1$, and thus $[\varphi ]_r\otimes J_r^{\Gamma _2}([\tau _2])=[\varphi ]_r$.
Hence, we have shown the following result.
Proposition 3.6 A morphism of discrete groups 
$\varphi :\Gamma _1 \to \Gamma _2$ naturally induces a linear map
\[ K_{*,{\mathbin{{\mathbb{R}}}}}(C_r^*\Gamma_1)_\tau\longrightarrow K_{*,{\mathbin{{\mathbb{R}}}}}(C_r^*\Gamma_2)_\tau\ . \]3.3 The $\tau$-Baum–Connes map
3.3.1 Classifying spaces
Let 
$\Gamma$ be a discrete group and let 
$A$ be a 
$\Gamma$-algebra. The group 
$K_{*}^{\textrm {top}}(\Gamma ; A)$ is defined [Reference Baum, Connes and HigsonBCH93] by
\[ K_{*}^{\textrm{top}}(\Gamma; A)=\varinjlim_{Y }KK_*^\Gamma(C_0(Y), A). \]
In this direct limit of Kasparov equivariant homology groups, all the proper cocompact 
$\Gamma$-invariant subspaces 
$Y\subset \underline E\Gamma$ of the classifying space for proper actions 
$\underline {E}\Gamma$ are taken into account.
The universal property of 
$\underline E\Gamma$ ensures that every proper 
$\Gamma$-space 
$Z$ has a 
$\Gamma$-map to 
$\underline E\Gamma$ that is unique up to homotopy. Therefore, 
$K_{*}^\Gamma (\underline E\Gamma ; A)$ is the limit of the inductive system 
$KK_{*}^\Gamma (C_0(Z), A)$ where 
$Z$ runs over proper and cocompact 
$\Gamma$-spaces. We can therefore use the following notation: for a pair 
$(Y, y)$ where 
$Y$ is a proper and cocompact 
$\Gamma$-space and 
$y\in KK^\Gamma (C_0(Y), A)$, we denote by 
$[\kern-1pt[ \, Y, y\, ]\kern-1pt]$ its associated class in the inductive limit.
Concerning real coefficients, we define
\[ K_{*,\mathbb{R}}^{\textrm{top}}(\Gamma; A)=\varinjlim_{\substack{Y\subset \underline E\Gamma\\ Y \;\Gamma\text{-compact}}} KK_{*,{\mathbin{{\mathbb{R}}}}}^\Gamma(C_0(Y), A). \]
Note this is an iterated limit, first over factors, then on subsets 
$Y$. It exists because 
$Y \longmapsto KK^{\Gamma }_{{\mathbin {{\mathbb {R}}}}}(C_0(Y),A)$ is a directed system with values groups. In addition, by Remark 1.6 (4) of [Reference Antonini, Azzali and SkandalisAAS16], the opposite iterated limit
\[ \varinjlim_N \varinjlim_{\substack{Y\subset \underline E\Gamma\\ Y \;\Gamma\text{-compact}}} KK_{*}^\Gamma(C_0(Y), A\otimes N)=\varinjlim_N K_{*}^{\operatorname{top}}(\Gamma,A\otimes N) \]
exists. Here 
$N$ ranges over a fixed space of 
$\textrm {II}_1$-factors acting on a separable Hilbert space and with morphisms 
$N \longrightarrow M$ that are trace-preserving embeddings. We can show that these two limits coincide and give a well-defined group 
$K^{\operatorname {top}}_{*,{\mathbin {{\mathbb {R}}}}}(\Gamma ;A)$. Indeed, we are just taking the limits in the two entries of the covariant bifunctor 
$(Y,N) \mapsto KK^\Gamma (C_0(Y), A\otimes N)$ defined on the corresponding product category. Generalising the notation given previously, we are thus allowed to represent elements in 
$K_{*,{\mathbin {{\mathbb {R}}}}}^{\operatorname {top}}(\Gamma ;A)$ as classes 
$[\kern-1pt[ \, Y, y\, ]\kern-1pt]$ with 
$Y$ proper 
$\Gamma$-compact 
$\Gamma$-space and 
$y \in KK^\Gamma (C_0(Y),A \otimes N)$.
3.3.2 The Baum–Connes map with real coefficients
Let 
$A$ a be 
$\Gamma$-algebra. Recall that the Baum–Connes assembly map 
$\mu ^A: K^{\textrm {top}}_*(\Gamma ;A)\longrightarrow K_{*}(A\rtimes _r \Gamma )$ assigns to 
$[\kern-1pt[ \,Y, \xi \,]\kern-1pt] \in K^{\textrm {top}}_*(\Gamma ;A)$, as previously, the element
\[ \mu^A([\kern-1pt[ \,Y, \xi\,]\kern-1pt])=p_Y \otimes j_r^\Gamma (\xi) \]
where 
$p_Y\in KK(\mathbb {C}, C_0(Y)\rtimes _r \Gamma )$ is the Kasparov projector.
The map 
$\mu ^A$ factors through the 
$K$-theory of the maximal crossed product 
$K_{*}(A\rtimes \Gamma )$. We sometimes write just 
$\mu$ instead of 
$\mu ^A$ if 
$A=\mathbb {C}$ or when there is no ambiguity on the 
$\Gamma$-algebra 
$A$.
Replacing 
$A$ with 
$A\otimes N$ for a 
$\rm {II}_1$-factor 
$N$ (with trivial 
$\Gamma$-action), and using the isomorphism 
$(A\otimes N) \rtimes _r \Gamma \simeq (A\rtimes _r \Gamma )\otimes N$ defines a collection of assembly maps 
$K^{\operatorname {top}}_{*}(\Gamma ; A\otimes N) \longrightarrow K_*((A\rtimes _r \Gamma )\otimes N)$ passing to the limit to an assembly map in 
$K_{{\mathbin {{\mathbb {R}}}}}$:
\begin{equation} \mu_{{\mathbin{{\mathbb{R}}}}}:K^\textrm{top}_{*,{\mathbin{{\mathbb{R}}}}}(\Gamma;A) \longrightarrow K_{{\mathbin{{\mathbb{R}}}}}(A \rtimes_r \Gamma). \end{equation}
By construction, 
$\mu _{{\mathbin {{\mathbb {R}}}}}$ is formally defined by the same recipe as 
$\mu .$
Lemma 3.7 The assembly map 
$\mu _{{\mathbin {{\mathbb {R}}}}}$ is given by first applying the real reduced descent map and then taking the 
$KK_{{\mathbin {{\mathbb {R}}}}}$-product with 
$p_Y\in KK(\mathbb {C}, C_0(Y)\rtimes _r \Gamma )$ followed by the direct limit on 
$Y$:
Proof. We know that we can interchange the limits in our definition of 
$K^\textrm {top}_{{\mathbin {{\mathbb {R}}}}}(\Gamma ;A)$. Then the lemma follows immediately by the definition of the descent morphism in 
$KK_{{\mathbin {{\mathbb {R}}}}}$ (3) and of the 
$KK_{{\mathbin {{\mathbb {R}}}}}$-Kasparov product. Indeed, starting from (9), and with self-explanatory notation:
\[ \mu_{{\mathbin{{\mathbb{R}}}}} = \varinjlim_N \mu^{A \otimes N} = \varinjlim_N \varinjlim_Y p_Y \otimes J^\Gamma_r =\varinjlim_Y p_Y \otimes \varinjlim_N J^\Gamma_r. \]3.3.3 The $\tau$-Baum–Connes map
We now define a map 
$\mu _\tau : K^{\textrm {top}}_{{\mathbin {{\mathbb {R}}}},*}(\Gamma ;A)_{\tau }\longrightarrow K_{{\mathbin {{\mathbb {R}}}},*}(A\rtimes _r \Gamma )_{\tau }$ between the corresponding 
$\tau$-parts of the real 
$K$-theory.
Let us remark that if 
$A,B$ are 
$\Gamma$-algebras, 
$z\in K^{\textrm {top}}_{{\mathbin {{\mathbb {R}}}},*}(\Gamma ;A)$ and 
$y\in KK^\Gamma _{\mathbin {{\mathbb {R}}}}(A,B)$, then we have 
$\mu ^B_{\mathbin {{\mathbb {R}}}}(z\otimes y)=\mu ^{A}_{{\mathbin {{\mathbb {R}}}}}(z)\otimes J_r^\Gamma (y)$. Taking 
$B=A$, we find that the real assembly map 
$\mu ^A_{{\mathbin {{\mathbb {R}}}}}$ is 
$KK^\Gamma _{\mathbin {{\mathbb {R}}}}(A,A)$ linear from the right 
$KK^\Gamma _{\mathbin {{\mathbb {R}}}}(A,A)$-module 
$K^{\textrm {top}}_{{\mathbin {{\mathbb {R}}}},*}(\Gamma ;A)$ to the right 
$KK^\Gamma _{\mathbin {{\mathbb {R}}}}(A,A)$-module 
$KK_{\mathbin {{\mathbb {R}}}}(\mathbb {C},A\rtimes _r \Gamma )$ (where 
$KK^\Gamma _{\mathbin {{\mathbb {R}}}}(A,A)$ acts via the ring morphism 
$J^\Gamma _r:KK^\Gamma _{\mathbin {{\mathbb {R}}}}(A,A)\to KK_{\mathbin {{\mathbb {R}}}}(A\rtimes _r \Gamma ,A\rtimes _r \Gamma )$. In particular, using the morphism 
$y\mapsto 1_A\otimes y$ from 
$KK^\Gamma _{\mathbin {{\mathbb {R}}}}(\mathbb {C},\mathbb {C})\to KK^\Gamma _{\mathbin {{\mathbb {R}}}}(A,A)$, it follows that 
$\mu ^A_{\mathbin {{\mathbb {R}}}}$ is 
$KK^\Gamma _{\mathbin {{\mathbb {R}}}}(\mathbb {C},\mathbb {C})$-linear.
We therefore find a map 
$\mu _{\tau }$ filling the following commutative diagram.
Here on the right vertical arrow there is the product with 
$[\tau ]_r:=J_r^\Gamma (1_A\otimes [\tau ])$. It is straightforward to check directly the existence of 
$\mu _{\tau }$; indeed using Lemma 3.7 we compute for every 
$z \in K_{*,{\mathbin {{\mathbb {R}}}}}^{\operatorname {top}}(\Gamma ; A)$ represented as a class 
$[\kern-1pt[ Y,y ]\kern-1pt]$ with 
$y \in KK_{{\mathbin {{\mathbb {R}}}}}^{\Gamma }(C_0(Y),A)$:
\[ \mu_{{\mathbin{{\mathbb{R}}}}}(z) \otimes [\tau]_r = p_Y \otimes J^{\Gamma}_r (y \otimes [\tau]) = p_Y \otimes J^{\Gamma}_r ([\tau] \otimes y ) = \mu_{{\mathbin{{\mathbb{R}}}}}([\tau]\otimes z) . \]
It follows that 
$\mu _{{\mathbin {{\mathbb {R}}}}}$ descends to a map on the 
$\tau$-parts simply given by
\[ \mu_\tau(x \otimes [\tau]):=\mu_{{\mathbin{{\mathbb{R}}}}}(x) \otimes [\tau]_r, \quad x \in K^{\textrm{top}}_{*,{\mathbin{{\mathbb{R}}}}}(\Gamma;A). \]Definition 3.8 We call 
$\mu _\tau : K^{\textrm {top}}_{*,{\mathbin {{\mathbb {R}}}}}(\Gamma ;A)_{\tau }\longrightarrow K_{*,{\mathbin {{\mathbb {R}}}}}(A\rtimes _r \Gamma )_{\tau }$ the 
$\tau$-Baum–Connes map.
We can state the following 
$\tau$-form of the Baum–Connes conjecture with coefficients.
Conjecture 3.9 The map 
$\mu _\tau : K^{\textrm {top}}_{*,{\mathbin {{\mathbb {R}}}}}(\Gamma ;A)_{\tau }\longrightarrow K_{*,{\mathbin {{\mathbb {R}}}}}(A\rtimes _r \Gamma )_\tau$ is bijective.
Theorem 3.10 Fix a 
$\Gamma\text{-}C^*$-algebra 
$A$; if the Baum–Connes map
\[ \mu:K^\textrm{top}_*(\Gamma;A\otimes N) \longrightarrow K_*(A\rtimes_r \Gamma \otimes N) \]
with coefficients in 
$A\otimes N$ is injective (surjective) for any choice of a 
$\textrm {II}_1$-factor 
$N$, then:
(i) the corresponding
$\mu _{\mathbin {{\mathbb {R}}}}: K^{\textrm {top}}_{*,{\mathbin {{\mathbb {R}}}}}(\Gamma ;A) \longrightarrow K_{{\mathbin {{\mathbb {R}}}}}(A\rtimes _r \Gamma )$ is injective (surjective);(ii) the corresponding
$\mu _\tau : K^{\textrm {top}}_{*,{\mathbin {{\mathbb {R}}}}}(\Gamma ;A)_{\tau }\longrightarrow K_{{\mathbin {{\mathbb {R}}}}}(A\rtimes _r \Gamma )_\tau$ is injective (surjective).
Proof. We prove statement (ii). Statement (ii) follows because the morphism 
$\mu _{\mathbin {{\mathbb {R}}}}$ is 
$KK_{\mathbin {{\mathbb {R}}}}^\Gamma (\mathbb {C},\mathbb {C})$ linear.
To establish the surjectivity statement just note that every element of 
$K_{*,{\mathbin {{\mathbb {R}}}}}(A\rtimes _r \Gamma )$ is the image of an element of 
$K_*((A\rtimes _r \Gamma ) \otimes N)=K_*((A\otimes N)\rtimes _r \Gamma )$ and, thus, by surjectivity of 
$\mu ^{A\otimes N}$, from an element in 
$K_*^\textrm {top}(\Gamma ;A\otimes N)$.
Let us now establish the injectivity statement. Let 
$x \in K^{\textrm {top}}_{*,{\mathbin {{\mathbb {R}}}}}(\Gamma ;A)$ be such that 
$\mu _{{\mathbin {{\mathbb {R}}}}}^A(x) =0 \in K_{*,{\mathbin {{\mathbb {R}}}}}(A \rtimes _r \Gamma ).$
The element 
$x$ comes from an element 
$x_0\in K^{\textrm {top}}_{*}(\Gamma ;A\otimes N_0)$. The fact that 
$x\in \ker \mu _{\mathbin {{\mathbb {R}}}}$ means that 
$\mu (x_0)$ is zero in some 
$K_*((A \rtimes _r \Gamma )\otimes N_2)$, where 
$N_1\subset N_2$. By injectivity of 
$\mu ^{A\otimes N_2}$ it follows that the image of 
$x_0\in K_*^\textrm {top}(\Gamma ;A\otimes N_2)$ is 
$0$ and therefore 
$x=0.$
4. Action of $[\tau ]$ on the classifying space
4.1 The group $K_{*}^\Gamma (E\Gamma ; A)$.
Replacing 
$\underline E\Gamma$ by the usual classifying space 
$E\Gamma$ in the definition of 
$K^{\operatorname {top}}_{*}(\Gamma ;A)$ we obtain the construction of the group 
$K_{*}^\Gamma (E\Gamma ; A)$:
Definition 4.1 The equivariant 
$K$-homology with 
$\Gamma$-compact supports of the standard classifying space for free and proper actions is the group
\[ K_{*}^\Gamma(E\Gamma; A)=\varinjlim_{\substack{Y\subset E\Gamma\\ Y \;\Gamma\text{-compact}}} KK_{*}^\Gamma(C_0(Y), A). \] In the same way as for 
$\underline E\Gamma$, the universal property of 
$E\Gamma$ ensures that every free and proper 
$\Gamma$-space 
$Z$ has a 
$\Gamma$-map to 
$E\Gamma$ that is unique up to homotopy. Therefore, 
$K_{*}^\Gamma (E\Gamma ; A)$ is the limit of the inductive system 
$KK_{*}^\Gamma (C_0(Y), A)$ where 
$Y$ runs over free, proper and cocompact 
$\Gamma$-spaces.
We denote by 
$\langle\!\langle Y,y\rangle\!\rangle$ the class in 
$K_{*}^\Gamma (E\Gamma ; A)$ of a pair 
$(Y, y)$ where Y is a free proper and cocompact 
$\Gamma$-space and 
$y\in KK^\Gamma (C_0(Y), A)$.
4.2 Atiyah's theorem and $B\Gamma$
In [Reference Antonini, Azzali and SkandalisAAS14] we proved that Atiyah's theorem for a covering space 
$\tilde {V} \rightarrow V$ with deck group 
$\Gamma$ is equivalent to the triviality in 
$K$-theory of the Mishchenko bundle 
$\tilde {V} \times _{\Gamma } N$ constructed from a morphism 
$\Gamma \rightarrow U(N)$ into a 
$\textrm {II}_1$-factor 
$N$ (see also the recent article [Reference Kaad and ProiettiKP18]). This inspired the definition of ‘
$K$-theoretically free and proper’ (KFP) algebras as the 
$\Gamma$-algebras where 
$[\tau ]$ acts as the identity [Reference Antonini, Azzali and SkandalisAAS16].
Definition 4.2 For a 
$\Gamma$-algebra 
$A$ we say that it has the KFP property if the equation 
$1_A^\Gamma \otimes [\tau ]=1_{A,{\mathbin {{\mathbb {R}}}}}^\Gamma$ holds in 
$KK^\Gamma _{{\mathbin {{\mathbb {R}}}}}(A,A)$.
Here 
$1_A^\Gamma$ and 
$1_{A,{\mathbin {{\mathbb {R}}}}}^{\Gamma }$ are the units of the rings 
$KK^\Gamma (A,A)$ and 
$KK^{\Gamma }_{{\mathbin {{\mathbb {R}}}}}(A,A)$, respectively.
Remark 4.3 Note that 
$A$ has the KFP property if and only if 
$KK_{*,{\mathbin {{\mathbb {R}}}}}^\Gamma (A, A)_{\tau }=KK_{*,{\mathbin {{\mathbb {R}}}}}^\Gamma (A, A)$. In addition, if 
$A$ has the KFP property, then by Lemma 2.2 we know that 
$[\tau ]$ acts as the unit element also on 
$KK^{\Gamma }_{{\mathbin {{\mathbb {R}}}}}(A,B)$ and 
$KK^{\Gamma }_{{\mathbin {{\mathbb {R}}}}}(B,A)$ for every 
$C^*$-algebra 
$B$.
The main examples of KFP algebras are the free and proper ones in the language of Kasparov [Reference KasparovKas88] (see [Reference Antonini, Azzali and SkandalisAAS16, Theorem 3.10]). Of course 
$C_0(Y)$ for a cocompact free and proper 
$\Gamma$-space 
$Y$ is KFP. We can put this in another way as follows.
Proposition 4.4 Let 
$A$ be any 
$\Gamma$-
$C^*$-algebra. The action of 
$[\tau ]$ on 
$K_{*,\mathbb {R}}^\Gamma (E\Gamma ; A)$ is the identity. In particular,
\[ K_{*,\mathbb{R}}^\Gamma(E\Gamma;A)_{\tau}=K_{*,\mathbb{R}}^\Gamma(E\Gamma;A). \]Proof. The 
$K$-homology group 
$K_{*,\mathbb {R}}^\Gamma (E\Gamma ;A)$ is defined as a limit over all the cocompact 
$\Gamma$-invariant pieces. It is thus sufficient to prove that for every cocompact free and proper 
$\Gamma$-space 
$Y$, the element 
$[\tau ]$ acts as the identity on 
$KK^{\Gamma }_{{\mathbin {{\mathbb {R}}}}}(C_0(Y),A)$. This is true because 
$C_0(Y)$ is KFP and by Remark 4.3.
5. Comparison between $K^\Gamma _{*,{\mathbin {{\mathbb {R}}}}}(E\Gamma ;A)$ and $K^{\operatorname {top}}_{*,{\mathbin {{\mathbb {R}}}}}(\Gamma ;A)$
In this section we use 
$[\tau ]$ to compare the 
$K$-homology of 
$E\Gamma$ with the one of 
$\underline {E}\Gamma$ at the level of real coefficients. In particular, for any 
$\Gamma$-algebra 
$A$ we show that the natural map 
$\sigma :E\Gamma \longrightarrow \underline {E}\Gamma$ induces an isomorphism
In the case 
$A=\mathbb {C}$ this will be used in § 6 and implies an isomorphism
Note that 
$\sigma _*(\langle\!\langle Y,y\rangle\!\rangle )=[\kern-1pt[ Y,y]\kern-1pt]$ for every free, proper cocompact 
$\Gamma$-space 
$Y$ and every 
$y\in KK_{*,{\mathbin {{\mathbb {R}}}}}^\Gamma (C_0(Y), A)$.
We construct the inverse of 
$\sigma _*$ using any compact probability space where 
$\Gamma$ acts probability measure preserving (p.m.p.) and sufficiently freely.
Proposition 5.1 Let 
$(X,m)$ be any compact p.m.p. 
$\Gamma$-space. The invariant measure 
$m$ defines a dual trace 
$t_{m} : C(X)\rtimes \Gamma \longrightarrow \mathbb {C}$, hence an element 
$[t_{m}] \in KK^\Gamma _{{\mathbin {{\mathbb {R}}}}}(C(X),\mathbb {C})$. We have 
$i_X^*[t_m]=[\tau ]$ where 
$i_X: \mathbb {C}\hookrightarrow C(X)$ is the unital inclusion and 
$[t_m]\otimes [\tau ]= [t_m]$.
Proof. The first point is an immediate consequence of Remark 2.5. By definition of a dual trace, we have 
$t_m\circ i_X=\tau$. Finally, 
$[t_m]\otimes [\tau ]$ is the class of the trace 
$(t_m\otimes \tau )\circ \,\delta _X$ on 
$C(X)\rtimes \Gamma$, where 
$\delta _X:C(X)\rtimes \Gamma \to (C(X)\rtimes \Gamma )\otimes C^*\Gamma$ is the coaction. Obviously 
$(t_m\otimes \tau )\circ \delta _X=t_m$ because 
$t_m$ is a dual trace.
5.1 Property TAF
Definition 5.2 A compact space 
$X$ with an action of 
$\Gamma$ such that every torsion element acts freely is said to have property torsion acts freely (TAF).
Note that if 
$X$ is TAF and 
$Y$ is a proper 
$\Gamma$-space, then 
$Y\times X$ is free and proper with respect to the diagonal action. We use this simple remark to map naturally 
$K^{\textrm {top}}_{*,{\mathbin {{\mathbb {R}}}}}(\Gamma ;A)$ to the ‘free and proper part’ 
$\;K_{*, {\mathbin {{\mathbb {R}}}}}^\Gamma (E\Gamma ; A)$, for every 
$\Gamma$-algebra 
$A$.
Proposition 5.3 Let 
$(X,m)$ be any compact p.m.p. 
$\Gamma$-space with the TAF property, and 
$[t_m]\in KK^\Gamma _{{\mathbin {{\mathbb {R}}}}}(C(X),\mathbb {C})$ the class constructed previously.
(i) The product by
$[t_m]$ induces a well-defined map
(10)given at the level of cycles by\begin{equation} t_{(X,m)}:K^{\textrm{top}}_{*,{\mathbin{{\mathbb{R}}}}}(\Gamma;A)\longrightarrow K_{*,{\mathbin{{\mathbb{R}}}}}^\Gamma(E\Gamma; A), \end{equation}$t_{(X,m)}([\kern-1pt[ \, Y, y\,]\kern-1pt] )= \langle\!\langle \,Y\times X, y\otimes [t_m]\,\rangle\!\rangle$ (where $Y$ is a proper $\Gamma$-compact space and $y\in KK^\Gamma _{\mathbin {{\mathbb {R}}}}(C_0(Y),A)$).(ii) The composition
$t_{(X,m)}\circ \sigma _*$ is the identity of $K_{*,{\mathbin {{\mathbb {R}}}}}^\Gamma (E\Gamma ; A)$.(iii) The map
$t_{(X,m)}$ does not depend on the choice of $(X,m)$. We will denote it by $t$.
Proof. Let 
$[\kern-1pt[ \, Y, y\, ]\kern-1pt] \in K_{*,{\mathbin {{\mathbb {R}}}}}^{\textrm {top}}(\Gamma ; A)$. Then 
$y \otimes [t_m]\in KK^\Gamma _{{\mathbin {{\mathbb {R}}}}}(C_0(Y\times X),A)$ and 
$Y \times X$ maps to 
$E\Gamma$ because it is free and proper.
If 
$Z$ is another proper 
$\Gamma$-compact space and 
$f:Y\to Z$ is a 
$\Gamma$-equivariant map, then 
$(f\times \operatorname {id}_X)_*(y\otimes [t_m])= f_*y\otimes [t_m]$. This shows that 
$t_{(X,m)}$ is well defined in the limit.
If the action of 
$\Gamma$ on 
$Y$ is free and proper, using the map of free and proper 
$\Gamma$-spaces 
$q:Y\times X\to Y$, it follows that the class 
$\langle\!\langle \,Y\times X, w\,\rangle\!\rangle$ in 
$K_{*,{\mathbin {{\mathbb {R}}}}}^\Gamma (E\Gamma ; A)$ of an element 
$w\in KK_{*,{\mathbin {{\mathbb {R}}}}}^\Gamma (C_0(Y\times X), A)$ is equal to 
$\langle\!\langle \,Y, q_*(w)\,\rangle\!\rangle$. In particular, 
$\langle\!\langle \,Y\times X, y\otimes [t_m]\,\rangle\!\rangle =\langle\!\langle \,Y, y\otimes i_X^*[t_m]\,\rangle\!\rangle =\langle\!\langle \,Y, y\otimes [\tau ]\rangle\!\rangle =\langle\!\langle \,Y, y\rangle\!\rangle$. Thus, statement (ii) follows.
Given 
$(X_1,m_1)$ and 
$(X_2,m_2)$, put 
$X=X_1\times X_2$ and 
$m=m_1\times m_2$. Then, for every cycle 
$[Y,y]$, we have 
$\langle\!\langle Y\times X,y\otimes [t_m]\rangle\!\rangle =t_{(X_2,m_2)}([\kern-1pt[ Y\times X_1,y\otimes [t_{m_1}]]\kern-1pt] )$. As the action of 
$\Gamma$ on 
$Y\times X_1$ is free and proper, it follows that 
$t_{(X_2,m_2)}([\kern-1pt[ Y\times X_1,y\otimes [t_{m_1}]]\kern-1pt] )=\langle\!\langle Y\times X_1,y\otimes [t_{m_1}]\rangle\!\rangle$ from part (ii), that is, 
$t_{(X,m)}([\kern-1pt[ Y,y]\kern-1pt] )=t_{(X_1,m_1)}([\kern-1pt[ Y,y]\kern-1pt] )$.
In the same way 
$t_{(X,m)}([\kern-1pt[ Y,y]\kern-1pt] )=t_{(X_2,m_2)}([\kern-1pt[ Y,y]\kern-1pt] )$.
We show in the following (Theorem 5.7) that every discrete countable 
$\Gamma$ admits a compact TAF p.m.p. space. We use this space in the next theorem. Let 
$\sigma _{*}: K^{\Gamma }_{*,{\mathbin {{\mathbb {R}}}}}(E\Gamma ; A)\to K_{*,{\mathbin {{\mathbb {R}}}}}^{\textrm {top}}(\Gamma ; A)$ be induced by the natural map 
$\sigma : E\Gamma \to \underline E\Gamma$.
Theorem 5.4 The morphism 
$t$ is a left inverse of 
$\sigma _*$. More precisely:
(i)
$t\circ \sigma _*=\tau$ and $\sigma _{*}\circ t=\tau$, that is, the following diagram commutes.
(ii) as a consequence we have an induced isomorphism
(11)
Proof. We already proved in Proposition 5.3(ii) that 
$t\circ \sigma _*$ is the identity of 
$K^\Gamma _{*,{\mathbin {{\mathbb {R}}}}}(E\Gamma ; A)$.
Let 
$Y$ be a free proper and cocompact 
$\Gamma$-space and 
$y\in KK^\Gamma (C_0(Y), A)$. Then
\begin{align*} (\sigma_* \circ t)([\kern-1pt[ \, Y, y\, ]\kern-1pt])&= \sigma_*(\langle\!\langle \,Y\times X, y\otimes [t_m]\,\rangle\!\rangle)= [\kern-1pt[ Y\times X, y\otimes [t_m]]\kern-1pt]\\ & =[\kern-1pt[\, Y , (y\otimes i_X(t_m))\,]\kern-1pt]= [\tau][\kern-1pt[ \,Y, y\,]\kern-1pt] \end{align*}
by Proposition 5.1. (iii) Note that the third equality here follows from the defining property of 
$\underline {E}\Gamma$ as a direct limit over all the proper 
$\Gamma$-spaces.
A model of TAF space
We construct a natural TAF space associated to the discrete group 
$\Gamma$. Let 
$F \subset \Gamma$ be a finite subgroup; define 
$X_F$ to be the space of all the (set-theoretical) sections of the projection 
$\pi :\Gamma \longrightarrow \Gamma /F$:
\[ X_F:= \{s:\Gamma/F \longrightarrow \Gamma, \ \pi \circ s=\operatorname{Id}\}. \]Note that we can write it as the direct product of all the cosets:
\[ X_F=\prod_{[g] \in \Gamma/F}gF. \]
We give 
$X_F$ the natural topological product structure. In particular, it is a compact (Cantor) metrisable space. Let us consider on every coset 
$gF$ the counting measure normalised by 
${\#(F)}^{-1}$. Then we define 
$m^F$ to be the product measure on 
$X_F$. Thanks to the normalisation, 
$m^F$ is a probability measure.
The group 
$\Gamma$ naturally acts on the left on 
$\Gamma$ and on 
$\Gamma /F$, then also on 
$X_F$ by setting
Indeed (because 
$\pi$ is equivariant), 
$\gamma \cdot s$ is a section.
Lemma 5.5 Properties of 
$X_F$:
(i)
$F$ acts freely on $X_F$;(ii) the product measure
$m^F$ is $\Gamma$-invariant.
Proof. (i) If 
$a\in F$ fixes 
$s$, because 
$aF=F$, 
$s(F)=s(aF)=as(F)$ and, thus, 
$a=e$.
(ii) By definition, 
$m^F$ is the normalised counting measure on every cylindrical set. These cylindrical sets generate the Borel structure and are in the form 
$C_T$ where for a finite subset 
$T\subset \Gamma$ we put
\[ C_T=\{s\in X_F;\ s(\pi(x))=x,\ \hbox{for all}\ x\in T\}. \]
If 
$C_T\ne \emptyset$, that is, if 
$\pi$ is injective on 
$T$, we have 
$m^F(C_T)=\#(F)^{-\# (T)}$. As 
$g(C_T)=C_{g(T)}$, invariance of 
$m_F$ follows.
Definition 5.6 We define
\[ X\Gamma:=\prod_{ F \in \mathscr{F} } X_F,\quad \mathscr{F}:=\{ \textrm{finite subgroups } F \subset \Gamma\}, \]
endowed with the product topology, with the product probability measure 
$m:=\prod m^F$ and, with the diagonal action of 
$\Gamma$.
Then 
$X\Gamma$ is Hausdorff, compact and second-countable; 
$m$ is 
$\Gamma$-invariant and, by construction, every finite subgroup 
$F\subset \Gamma$ acts freely on one of the components, and thus on 
$X\Gamma$. We have shown the following.
Theorem 5.7 The compact (Cantor) space 
$X\Gamma$ has property TAF and 
$\Gamma$ preserves its probability measure.
Remark 5.8 It is also possible, although not needed in our construction, to construct a free compact 
$\Gamma$-space with a probability measure preserved.
Indeed, let 
$g\in \Gamma \setminus \{e\}$, let 
${\langle g \rangle }$ be the subgroup of 
$\Gamma$ it generates, and let 
$Y_g$ be a free compact 
${\langle g\rangle }$-space with a probability measure preserved. Let 
$X_g=(Y_g^\Gamma )^g$ be the subset of 
$Y_g^\Gamma$ of 
$f:\Gamma \to Y_g$ such that 
$f(hg)=g^{-1}f(h)$ for all 
$h\in \Gamma$. The space 
$X_g$ identifies with 
$Y_g^{\Gamma /{\langle g\rangle }}$ thanks to any cross-section 
$s:\Gamma /{\langle g\rangle }\to \Gamma$ and therefore carries a natural product probability measure (independent of this cross-section). In addition, 
$\Gamma$ acts on 
$X_g$ by putting 
$(h.f)(k)=f(h^{-1}k)$ for every 
$h,k\in \Gamma$ and fixes this product measure.
Note that the map 
$f\mapsto f(e)$ is 
${\langle g\rangle }$-equivariant from 
$X_g$ to 
$Y_g$, and therefore 
$X_g$ has no 
$g$ fixed points.
The product 
$\prod _g X_g$ is the desired space.
6. Relation with the Novikov conjecture
In this section we prove that the injectivity of 
$\mu _{\tau }$ implies the rational injectivity of the Mishchenko–Kasparov assembly map 
$\tilde \mu :K_*(B\Gamma ) \longrightarrow K_*(C^*_r\Gamma )$ and a fortiori the Novikov conjecture. First, we need a simple observation.
Remark 6.1 We use the fact that for 
$B\Gamma$, at the level of 
$K$-homology, adding real coefficients only discards torsion. In other words there is a canonical isomorphism
\begin{equation} K^\Gamma_{*,{\mathbin{{\mathbb{R}}}}}(E\Gamma)\simeq K_{*,{\mathbin{{\mathbb{R}}}}}(B\Gamma)\simeq K_*(B\Gamma) \otimes {\mathbin{{\mathbb{R}}}} . \end{equation}
This identification follows immediately starting from the definition of the compactly supported 
$K$-homology of 
$B\Gamma$ as a direct limit of 
$K$-homology groups of finite complexes 
$Z$. For each of these compact pieces, the group 
$KK(C(Z),\mathbb {C})$ is finitely generated and the analogous isomorphism 
$KK_{{\mathbin {{\mathbb {R}}}}}(C(Z),\mathbb {C})\simeq KK(C(Z),\mathbb {C})\otimes {\mathbin {{\mathbb {R}}}}$ holds. By the flatness of 
${\mathbin {{\mathbb {R}}}}$, the isomorphism is preserved by the direct limit.
The Mishchenko–Kasparov assembly map is denoted 
$\tilde \mu :K_*^\Gamma (E\Gamma )\longrightarrow K_*(C^*_r\Gamma )$. It is given by 
$\tilde \mu =\mu \circ \sigma _*$. The corresponding map with values in 
$K_*(C^*\Gamma )$ is denoted 
$\tilde \mu _{\textrm {max}}: K_*^\Gamma (E\Gamma )\longrightarrow K_*(C^*\Gamma )$.
Theorem 6.2 If 
$\mu _\tau : K^{\textrm {top}}_{*, {\mathbin {{\mathbb {R}}}}}(\Gamma )_{\tau }\longrightarrow K_{\mathbin {{\mathbb {R}}}}(C^*_r \Gamma )_{\tau }$ is injective, then the Mishchenko–Kasparov assembly map 
$\tilde \mu : K_*^\Gamma (E\Gamma )\longrightarrow K_*(C^*_r\Gamma )$ is rationally injective.
Proof. It is enough to show that, under the assumption of injectivity of 
$\mu _\tau$, the kernel of 
$\tilde \mu$ consists only of torsion elements. Let 
$x\in K^{\Gamma }_{*}( E\Gamma )$ such that 
$\mu (\sigma _*(x))=0$ in 
$K_*(C_r^*\Gamma )$. By the definition of 
$\mu _\tau$, we deduce that the element 
$\sigma _*(x)=\sigma _*(x)\otimes [\tau ]$ is in the kernel of 
$\mu _\tau$, so that 
$\sigma _*(x)\otimes [\tau ]=0$ in 
$K_{*,{\mathbin {{\mathbb {R}}}}}^{\textrm {top}}(\Gamma )_{\tau }$. Applying the map 
$t$ and using that by Theorem 5.4 
$t\circ \sigma =\tau$, we have
\[ 0=t(\sigma_*(x)\otimes [\tau])=t(\sigma_*(x))=x\otimes [\tau] \quad\text{in}\ K_{*, {\mathbin{{\mathbb{R}}}}}^\Gamma(E\Gamma) . \]
By Remark 6.1, we conclude that 
$x$ is torsion in 
$K_{*}^\Gamma (E\Gamma )$.
Remark 6.3 For every 
$C^*$-algebra 
$A$ there is a map 
$\beta : K_{*}(A)\otimes \mathbb {R}\longrightarrow K_{*,\mathbb {R}}(A)$ induced by the exterior Kasparov product.
The relation between 
$\mu _\tau$ and 
$\tilde \mu \otimes 1$ used in the proof is summarised in the following commutative diagram.
The injectivity of the map 
$\sigma _{*}: K^{\Gamma }_{*,\mathbb {R}}(E\Gamma )\longrightarrow K_{*,\mathbb {R}}^{\textrm {top}}(\Gamma )$ (Theorem 5.4) has recently been used in [Reference Gong, Wu and YuGWY18] to show that the Novikov conjecture holds for any discrete group admitting an isometric and metrically proper action on an admissible Hilbert–Hadamard space.
7. Exactness and monster-based counterexamples
We show that the construction of the counterexamples for group actions in [Reference Higson, Lafforgue and SkandalisHLS02] still provides a counterexample to the bijectivity of the 
$\tau$-Baum–Connes map 
$\mu _\tau$.
We know from § 3.1.3 that the 
$\tau$-parts are functorial. In particular, an exact sequence 
$I \rightarrow A \rightarrow Q$ of 
$\Gamma\text{-}C^*$-algebras induces a sequence
We show that with exactly the same Gromov's group 
$\Gamma$ and the same 
$C^*$-algebras 
$A$ and 
$I$ as in [Reference Higson, Lafforgue and SkandalisHLS02], this is not exact. This is in spite of the fact that the 
$\tau$-parts for the maximal and the reduced algebras are the same, and that we could think of (
) as induced by the full crossed product exact sequence
\[ I \rtimes \Gamma \longrightarrow A\rtimes \Gamma \longrightarrow Q\rtimes \Gamma . \] In fact, we show that taking the minimal tensor product with a 
$\textrm {II}_1$-factor destroys exactness and this is why the sequence (13) fails exactness.
We briefly recall the construction of [Reference Higson, Lafforgue and SkandalisHLS02].
Let 
$\Gamma$ be a Gromov monster group (see [Reference Arzhantseva and DelzantAD08, Reference GromovGro03] and, more recently, [Reference CoulonCou14, Reference OsajdaOsa14]). This is a finitely generated, discrete group and one can map (in the sense of Cayley graphs) an expanding sequence of finite graphs 
$X_n$ to 
$\Gamma$ in a controlled and ‘essentially injective’ way. Call 
$\varphi _n:X_n^0 \longrightarrow \Gamma$ such a collection of maps from the corresponding object spaces 
$X_n^0$.
Given that, one can find a compact metrisable 
$\Gamma$-space 
$Z$ such that the Baum–Connes map with coefficients in 
$C(Z)\rtimes _r \Gamma$ is not an isomorphism. To do so, two passages are needed.
(i) The construction of a sequence of
$C^*$-algebras (involving non-separable ones) that is not exact in the middle. This is done by considering $\Gamma$ acting by translation on the (non-separable) $C^*$-algebra $A:=\ell ^{\infty }(\mathbb {N};c_0(\Gamma ))$: then the sequence
(14)is non-exact in the middle. This happens even at level of$K$-theory. We recall later why the sequence:
(15)is not exact in the middle.(ii) Building on
$A$, an argument of direct limits and Gel'fand duality produces the compact $\Gamma$-space $Z$. This is the separable counterexample.
The middle non-exactness of (15) is shown directly: there is a class 
$[\,p]\in K_0(A\rtimes _r \Gamma )$ mapping to zero that cannot come from 
$K_0(c_0(\mathbb {N}\times \Gamma ) \rtimes _r \Gamma )$. The projection
\[ p \in A \rtimes_r \Gamma \subset \ell^{\infty}(\mathbb{N};\mathbb{K}(\ell^2(\Gamma)) \]
is constructed using the spectral properties of the expander. First, one represents faithfully 
$A\rtimes _r \Gamma$ on 
$\ell ^2(\mathbb {N}\times \Gamma )$, then using the maps 
$\varphi _n$ and the graph Laplacians on each 
$X_n$, a bounded operator 
$D \in \widetilde {C_c(\Gamma ;A)}$ (unitalisation) is constructed. Zero is isolated in the spectrum of 
$D$ and 
$[\,p]$ is exactly the projection on the kernel. Seeing 
$p$ as a sequence of infinite matrices 
$p_n$, it is easy to check that
\[ p_{n,y,z}=\dfrac{ \sqrt{ \# (\varphi_n^{{-}1}(y) ) \# (\varphi_n^{{-}1}(z)) } } {\#({X_n^0})}, \quad y,z \in \Gamma, \ n \in \mathbb{N}. \] By the essential injectivity of the maps 
$\varphi _n$, the coefficients of 
$p_n$ tend to 
$0$ when 
$n\to \infty$. It then follows that the image of 
$p\in {(}A/c_0(\mathbb {N}\times \Gamma ) {)}\rtimes _r \Gamma$ is 
$0$.
The evaluation morphisms 
$\pi _n : \ell ^\infty (\mathbb {N};c_0(\Gamma )) \rtimes _r \Gamma \longrightarrow c_0(\Gamma )\rtimes \Gamma$ induce maps
\[ \pi_n: K_0(A\rtimes_r \Gamma) \longrightarrow K_0(c_0(\Gamma)\rtimes_r \Gamma) \cong \mathbb{Z} \]
such that 
$\pi _n([\,p])=[\,p_n]=1$ because 
$p_n$ is a rank-one projection. It follows immediately that 
$[\,p]$ cannot be the image of an element in 
$K_0(c_0(\mathbb {N}\times \Gamma ) \rtimes _r \Gamma )$ (15) because this is isomorphic to an algebraic direct sum 
$\bigoplus _{n\in \mathbb {N}}\mathbb {Z}$.
Let us now pass to the 
$\tau$-parts.
Proof. Let 
$[\,p]_{\mathbin {{\mathbb {R}}}}\in K_{0,{\mathbin {{\mathbb {R}}}}}(A \rtimes _r \Gamma )$ be the image of the class 
$[\,p]$ of the projection given previously via the change of coefficients. We show that the element 
$P:=[\,p]_{\mathbin {{\mathbb {R}}}}\otimes [\tau ^A]_r=[\,p]_{\mathbin {{\mathbb {R}}}}\otimes J^\Gamma _r(1_A\otimes [\tau ])$ in the middle group of the sequence is mapped to zero but does not come from the first group.
As the image of 
$p$ vanishes already in 
${(}A/c_0(\mathbb {N}\times \Gamma ) {)}\rtimes _r \Gamma$ the first assertion follows immediately.
Note that 
$K_{0, {\mathbin {{\mathbb {R}}}}}(c_0(\Gamma )\rtimes _r \Gamma ) \cong \mathbb {R}$: indeed 
$c_0(\Gamma )\rtimes _r \Gamma$ and 
$\mathbb {C}$ are Morita equivalent (before tensoring with a 
$\textrm {II}_1$-factor). In the same way, one sees that 
$K_{0, {\mathbin {{\mathbb {R}}}}}(c_0(\mathbb {N}\times \Gamma )\rtimes _r \Gamma )$ is the algebraic direct sum 
$\bigoplus _{n\in \mathbb {N}}\mathbb {R}$.
Now for every 
$n\in \mathbb {N}$, the morphism induced by the evaluation 
$\pi _n$ on the 
$\tau$-parts acts on 
$P$ as
\[ \pi_n(P)=\pi_n([\,p]_{\mathbin{{\mathbb{R}}}}\otimes [\tau^A]_r)=[\,p_n]_{\mathbin{{\mathbb{R}}}}\otimes [\tau^{C_0(\Gamma)}]_r=[\,p_n]_{{\mathbin{{\mathbb{R}}}}} \]
where we have applied that 
$[\tau ]$ acts as the identity on the KFP algebra 
$C_0(\Gamma )$. In particular, 
$\pi _n(P)$ is non-zero for every 
$n\in \mathbb {N}$. This implies that 
$P$ does not come from 
$K_{0,{\mathbin {{\mathbb {R}}}}}(c_0(\mathbb {N}\times \Gamma )=\bigoplus _{n\in \mathbb {N}}\mathbb {R}.$
Proposition 7.2 Let 
$A=\ell ^\infty (\mathbb {N}, c_0(\Gamma ))$ and 
$I=c_0(\mathbb {N}\times \Gamma )$. Consider the exact sequence of 
$\Gamma$-algebras 
$I\to A\to A/I$. Then the corresponding sequence
is exact.
To show Proposition 7.2, first recall that by (11) the isomorphism 
$K^{\textrm {top}}_{*,{\mathbin {{\mathbb {R}}}}}(\Gamma ;A)_{\tau }\simeq K^\Gamma _{*,{\mathbin {{\mathbb {R}}}}}(E\Gamma ; A)$ holds true and commutes with the morphisms induced by the sequence 
$I\to A\to A/I$, so that it is enough to show the following.
Lemma 7.3 Let 
$Y$ be a free and proper, cocompact 
$\Gamma$-space. Let 
$I\to A\to A/I$ be the exact sequence of 
$\Gamma$-algebras appearing in (14). Then the sequence
is exact.
To show Lemma 7.3, let 
$N$ be any 
$\textrm {II}_1$-factor with trivial 
$\Gamma$-action. Nuclearity of 
$A$ and 
$I$ implies that the sequence
\begin{equation} I\otimes N\longrightarrow A\otimes N\longrightarrow (A/I)\otimes N \end{equation}
is still exact. A completely positive cross-section of 
$A \longrightarrow A/I$ induces a completely positive cross-section of (17), which thus remains semi-split. We now show the following fact in the slightly more general case of any proper 
$\Gamma$-algebra 
$D$. In our application it will be 
$D=C_0(Y)$, which is free and proper.
Lemma 7.4 Let 
$D$ be a separable proper 
$\Gamma$-algebra. Let 
be a semi-split exact sequence of (possibly non-separable) 
$\Gamma$-
$C^*$-algebras. Then the sequence
is exact.
Once Lemma 7.4 is proved, we shall apply it to 
$D=C_0(Y)$ and to the exact sequence 
$I\otimes N\to A\otimes N\to (A/I)\otimes N$. The exactness of
will follow. Finally, taking the limit over 
$N$ of the groups in the exact sequence given previously, we prove Lemma 7.3. We are hence left with the following proof.
Proof of Lemma 7.4 If 
$B$ and 
$J$ are separable, the statement is proved in [Reference El MorsliEM06, Proposition 2.3]. Let us discuss the generalisation to the non-separable case, for which we follow closely [Reference SkandalisSka85b, Proof of Proposition 3.1]. More precisely, we assume that (18) is middle exact in the separable case and we show that it is middle exact in full generality.
Let 
$x\in KK^\Gamma (D,B)$ such that 
$q_*(x)=0$ in 
$KK^\Gamma (D, B/J)$. As 
$KK^\Gamma (D,B)$ is the inductive limit over separable subalgebras of 
$B$ (cf. [Reference SkandalisSka85b] and Lemma 2.1), there exists a separable 
$\Gamma$-invariant subalgebra 
$B_1$ of 
$B$ and an element 
$x_1\in KK^\Gamma (D,B_1)$ whose image by the inclusion 
$j_1:B_1\to B$ is 
$x$. Let 
$q_1:B_1\to q(B_1)$ be the restriction of 
$q$ to 
$B_1$ and 
$\ell _1:q(B_1)\to B/J$ be the inclusion. As 
$q\circ j_1=\ell _1\circ q_1$, we find that 
$(\ell _1)_*((q_1)_*(x))=0$.
As 
$KK^\Gamma (D,B/J)$ is the inductive limit over separable 
$\Gamma$-invariant subalgebras of 
$B/J$, there exists a separable 
$\Gamma$-invariant subalgebra 
$Q_2\subset B/J$, containing 
$q(B_1)$, such that the image of 
$(q_1)_*(x)$ in 
$Q_2$ through the inclusion 
$\ell :q(B_1)\to Q_2$ is the 
$0$ element of 
$KK^\Gamma (D,Q_2)$. Let 
$s$ be a completely positive section of 
$q$ and then let 
$B_2$ be the (separable) 
$\Gamma$-invariant subalgebra of 
$B$ generated by 
$s(Q_2)$, its 
$\Gamma$-translates, and 
$B_1$. Denote by 
$j:B_1\to B_2$ the inclusion. Note that 
$q(B_2)=Q_2$ and put 
$q_2:B_2\to Q_2$. We then have 
$(q_2)_*(j_*(x_1))=\ell _*((q_1)_*(x_1))=0$.
Now set 
$x_2=j_*(x_1)$ and let 
$j_2:B_2\to B$ and 
$\ell _2:Q_2\to B/J$ be the inclusions.
As 
$j_1=j_2\circ j$, we have 
$(j_2)_*(x_2)=(j_1)_*(x_1)$.
Applying [Reference El MorsliEM06, Proposition 2.3] to the exact sequence of separable 
$\Gamma$-algebras
\[ 0\to J\cap B_2\to B_2\to Q_2\to 0, \]
we find that 
$x_2$ is the image of an element 
$y_2\in KK^\Gamma (D,J\cap B_2)$ whose image in 
$B_2$ is 
$x_2$, whence its image in 
$B$ is 
$x$.
This argument provides a (non-separable) counterexample to the bijectivity of 
$\mu _\tau$, as stated more precisely in the following.
Proposition 7.5 Let 
$A=\ell ^\infty (\mathbb {N}, c_0(\Gamma ))$, 
$I=c_0(\mathbb {N}\times \Gamma )$ as before. If 
$\mu ^{A/I}_\tau$ is injective, then 
$\mu ^{A}_\tau$ is not surjective.
Proof. Let 
$x\in K_{0,{\mathbin {{\mathbb {R}}}}}(A\rtimes _r \Gamma )_{\tau }$ be the element that fails exactness in the second line of the following commutative diagram.
Suppose 
$\mu ^{A/I}_\tau$ is injective and by contradiction that 
$\mu ^{A}_\tau$ is surjective. Then the preimage 
$y\in K_{0,{\mathbin {{\mathbb {R}}}}}^{\textrm {top}}(\Gamma , A)_{\tau }$ of 
$x$ is mapped to zero in 
$K_{0,{\mathbin {{\mathbb {R}}}}}^{\textrm {top}}(\Gamma , A/I)$ by the injectiviy assumption. As the second line is exact, 
$y$ comes from an element in 
$K_{0,{\mathbin {{\mathbb {R}}}}}^{\textrm {top}}(\Gamma , I)_{\tau }$, which then provides the contradiction.
Remarks 7.6 (i) Using the argument in [Reference Higson, Lafforgue and SkandalisHLS02, Remark 12] based on double mapping cones, one may construct an abelian 
$C^*$-algebra 
$B$ such that 
$K^{top}_{{\mathbin {{\mathbb {R}}}},*}(\Gamma ;B)=0$ and 
$K_{{\mathbin {{\mathbb {R}}}},*}(B\rtimes \Gamma )_{\tau }\ne 0$, whence 
$\mu _\tau$ is not surjective.
(ii) We further show that we can pass to a separable counterexample. Assume that for an algebra 
$B$ the map 
$\mu ^{B}_\tau$ is not surjective. Then there exists a (commutative) separable 
$\Gamma$-subalgebra 
$D\subset B$ such that 
$\mu ^{D}_\tau$ is not surjective.
Indeed, let 
$y\in K_{{\mathbin {{\mathbb {R}}}},*}(B\rtimes _r\Gamma )_{\tau }$. By functoriality of the assembly 
$\mu _\tau$, it is enough to show that there exists a separable 
$\Gamma$-invariant subalgebra 
$B'\subset B$ and 
$y_1\in K_{{\mathbin {{\mathbb {R}}}},*}(B'\rtimes _r\Gamma )_{\tau }$ such that 
$y=i_*(y_1)$, where 
$i:B'\to B$ is the inclusion. In other words, it is enough to show that
\begin{equation} K_{{\mathbin{{\mathbb{R}}}},*}(B\rtimes_r\Gamma)_{\tau}=\lim_{\substack{B' \subset B\\ B'\textrm{separable}\\ \Gamma-\textrm{invariant}}}K_{{\mathbin{{\mathbb{R}}}},*}(B'\rtimes_r\Gamma)_{\tau} . \end{equation}
Let 
$y=[\tau ]\otimes w$, for 
$w\in K_{{\mathbin {{\mathbb {R}}}},*}(B\rtimes _r\Gamma )$. Then there exists a 
$\textrm {II}_1$-factor 
$N$ such that 
$w \in K_*((B\rtimes _r\Gamma )\otimes N)$. We apply now Lemma 2.1: there exists a separable 
$B'\subset B$ such that 
$w=(i\otimes 1)_*(z_1)$ for a 
$z_1\in K_*((B'\rtimes _r\Gamma )\otimes N)$, and where 
$i:B'\to B$ is the inclusion. Hence, 
$y=[\tau ]\otimes w=[\tau ]\otimes (i\otimes 1)_*(z_1)=(i\otimes 1)_*([\tau ]\otimes z_1)$, which shows (19).
(iii) By Lafforgue's work [Reference LafforgueLaf12], the Baum–Connes conjecture with coefficients for hyperbolic groups holds. Now, Gromov's monster is an inductive limit of hyperbolic groups. Despite the functoriality of our 
$\mu _\tau$, the failure of the bijectivity of 
$\mu _\tau$ of Proposition 7.5 shows that the group 
$K_{\mathbin {{\mathbb {R}}}}(A\rtimes _r\Gamma )_\tau$ is not compatible with inductive limits of groups. It may be worth noting that the difficulty comes from the fact that the group morphisms in this inductive limit are onto but not one-to-one. In other words, passing from one step to the next we add relations, not generators.
Let us finally comment on a possibility of fixing the non-exactness of our construction along the lines of the recent papers of Baum et al. [Reference Baum, Guentner and WillettBGW16] and of Buss et al. [Reference Buss, Echterhoff and WillettBEW18].
A modified assembly map involving a minimal exact and Morita compatible crossed product functor has been proposed in [Reference Baum, Guentner and WillettBGW16], as the ‘right-hand side’ that should be considered in the Baum–Connes conjecture (see also [Reference Antonini, Buss, Engel and SiebenandABES20] for some relations with the strong Novikov conjecture for low degree classes).
One may try to correct the non-exactness in our context by correcting the right-hand side for the 
$KK$-theory with real coefficients. One could, for instance, think of replacing the minimal tensor product with 
$\textrm {II}_1$-factors by a tensor product with 
$\textrm {II}_1$-factors which is minimal exact (and Morita compatible).
Acknowledgements
The authors wish to thank the referee for many helpful suggestions that greatly improved the paper.
