INTRODUCTION
A number of studies have documented statistically significant nonlinearities in the dynamics of several macroeconomic time-series (Lee, White, and Granger 1993). Within a univariate setting, nonlinearities in U.S. aggregate income-series have been reported in Neftci (1984), Hamilton (1989), Potter (1995), Bidarkota (2000), and several others. Although statistical tests widely reject linearity in macroeconomic series, nonetheless, out-of-sample forecasts obtained from nonlinear models are generally not superior to those from linear models. For instance, Ramsey (1996) asks, “If nonlinear models cannot forecast, what use are they?”
This paper is an attempt to address whether nonlinear time-series models, despite their documented lack of superiority in out-of-sample forecasting, can be useful in macroeconomic modeling. We address this issue by exploring to what extent the equilibrium implications of macro models differ quantitatively when the exogenous variables in these models are characterized alternatively as linear and nonlinear processes. This exercise provides a metric for determining the economic costs of ignoring nonlinearities in macroeconomic models.
Although nonlinearities have been extensively documented in macroeconomic series, nonetheless, most macroeconomic studies utilize simple, invariably linear, stochastic processes for characterizing exogenous variables in the models. For instance, much of the real business cycle literature uses simple autoregressive technology processes for driving economic fluctuations. Under special circumstances, such simplicity affords tractable exact analytical solutions to the endogenous variables of the model.
Nonlinear forcing processes have been used to a limited extent in macroeconomic models. Most applications, however, involve nonlinearities arising from conditional heteroskedasticity as modeled by ARCH/GARCH type processes. An important application of nonlinear forcing processes in macro models (not involving conditional heteroskedasticity) pertains to the use of Hamilton's (1989) Markov switching process. This nonlinear process has been used extensively in various theoretical macro models, including models of asset pricing, exchange rate determination, and so forth. An important reason for the use of Hamilton's model to characterize the exogenous driving processes in macro models is the analytical tractability it affords in finding solutions to these models (Cecchetti, Lam, and Mark 1993, Bonomo and Garcia 1994). However, in general, most nonlinear forcing processes typically prelude the possibility of finding exact analytical solutions to macro models in most settings.
In this paper, we address the issue of nonlinearities in macro models in the specific context of the consumption-based asset pricing model of Lucas (1978). Our main focus is in characterizing the effects of nonzlinearities in the conditional mean dynamics of exogenous dividends in the model. Accordingly, we solve the model under two alternative assumptions on the exogenous dividend process. In the benchmark case, dividends are modeled as a simple autoregression (AR). In the nonlinear case, dividends are modeled as threshold autoregressive processes (Tong and Lim, 1980). In the benchmark case, an exact solution to the model is available (Burnside 1998). In the nonlinear case, an exact analytical solution is not tractable. In this case, we solve the model numerically, by first using Markov chain approximations for the dividends process (Tauchen, 1986) and subsequently solving the Euler equations of the model by quadrature techniques (Tauchen and Hussey, 1991). Moments of the model-implied endogenous variables, including rates of return, are then compared across the two cases to evaluate the economic impact of modeling nonlinearities.
A few other studies on asset pricing have utilized nonlinear driving processes. For instance, Kandel and Stambaugh (1990), Tauchen and Hussey (1991), and, more recently, Ebell (2001) use an AR process with autoregressive conditional heteroskedasticty (ARCH) to model dividends. However, although the focus of the work in Tauchen and Hussey is to illustrate the quadrature solution technique, the focus of the work in the other two studies is on drawing out the implications of ARCH on the conditional moments of asset return dynamics.
A systematic evaluation of the effects of nonlinearities on the economic implications of macro models has so far not been undertaken. We use the standard asset-pricing model here to analyze the economic impact of nonlinearities because of the simplicity that the model affords (it has only one state variable) and because exact analytical solutions to the equilibrium quantities of interest are available at least in the benchmark linear endowment case. Our efforts are not to be viewed as a test of this asset-pricing model. The failure of the standard version of this model in replicating the empirical features of observed data on equity and bond returns has been thoroughly established. See Kocherlakota (1996) for a survey of this literature.
This paper is organized as follows. In Section 2, we briefly sketch the asset pricing model, outline its solution under a linear endowment process, and describe the solution under a nonlinear endowment process. In Section 3, we evaluate the accuracy of discrete-valued Markov chains in approximating continuous-valued linear and nonlinear stochastic processes with a simulation study. In Section 4, we evaluate the accuracy of the numerical solution to the asset pricing model and also undertake an empirical analysis of the asset pricing model with linear and nonlinear endowment processes. We also evaluate the impact of nonlinearities on model-implied rates of return. In Section 5, we explore the robustness of our findings in Section 4 to conditional heteroskedasticity in the forcing process, to alternative functional forms for nonlinearity, and to alternative data proxies. In the final section, we conclude with a summary of the implications of nonlinearities emerging from our study.
THE MODEL AND ITS SOLUTIONS
Subsection 2.1 sketches the asset pricing model, Subsection 2.2 outlines the exact solution to the model with a linear autoregressive endowment process, and Subsection 2.3 describes a numerical solution to the model with a nonlinear threshold autoregressive endowment process.
The Asset Pricing Model
In a single good Lucas (1978) economy, with a representative maximizing agent and a single asset that pays exogenous dividends of nonstorable consumption goods, the first-order Euler condition is:
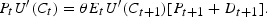
Here,
- Pt is the real price of the single asset in terms of the consumption good
- U′(C) is the marginal utility of consumption C for the representative agent
- θ is a subjective discount factor, assumed nonstochastic and constant
- D is the dividend from the single productive unit
- Et is the mathematical expectation, conditioned on information available at time t.
Assume a constant relative risk aversion (CRRA) utility function:
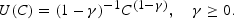
Since consumption simply equals dividends in this simple model, that is, C=D every period, (1) reduces to:
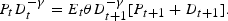
On rearranging, this yields:
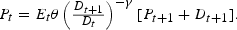
Let vt denote the price-dividend ratio, that is, vt=Pt/Dt. Then, we can rewrite (4) in terms of vt as:
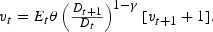
Thus, this equation implicitly defines the solution to the asset pricing problem in this model. One specifies an exogenous stochastic process for dividends and solves for the price dividend ratio vt.
Using yt=ln(Dt/Dt−1) to denote the dividend growth rate, we can express (5) as:
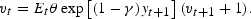
Defining mt+1≡θexp [(1−γ)yt+1], we can rewrite (6) as:
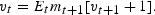
Thus, (7) is the first order Euler condition for the asset pricing problem. In the following subsections, we show how to solve this equation under alternative assumptions about the evolution of exogenous dividends.
Asset Pricing Solution under AR(1) Dividend Growth Rates
As a benchmark case, we assume that the dividend growth rates stochastically evolve according to:
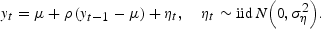
Here, |ρ|<1 to impose stationarity of the dividends process.
Under such an AR(1) endowment process, Burnside (1998) derives an exact analytical solution to the price-dividend ratio in the asset pricing model. On forward iteration, the first-order Euler condition in (7) yields:
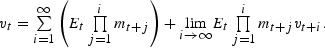
One solution to the above difference equation in vt is obtained by imposing the transversality condition:
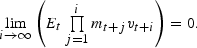
This condition rules out solutions to the asset pricing model that imply intrinsic bubbles (Froot and Obstfeld 1991). Imposing the transversality condition on (9) gives:
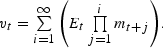
Burnside (1998) shows that under an AR(1) process for dividend growth rates, the price-dividend ratio is given by:

In this solution, the constants ai and bi are given by:

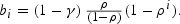
Burnside (1998) further shows that the infinite series in (12) converges if and only if
.
A Nonlinear Model—SETAR(1,1) Process
To assess the impact of nonlinearities, we assume that the dividend growth rates stochastically evolve as a self-exciting threshold autoregressive (SETAR) process. Threshold autoregressions were introduced in Tong and Lim (1980), and versions of these models were fit to U.S. GNP series by Potter (1995), Bidarkota (2000), and others.
A SETAR(1,1) process can be written as follows. In regime 1, the process evolves as the following first-order autoregression:
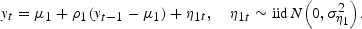
In regime 2, the process evolves as the following alternative first-order autoregression:
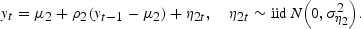
In order to facilitate comparison with the linear AR(1) process and a statistical test for linearity later, we use first-order autoregressions in the two regimes.
The switch between the two regimes is governed by past values of yt. This feature makes these processes self-exciting. For instance, the switch could be governed by the criterion yt−l > s, and l and s estimated along with other parameters of the model. Potter (1995) reports estimates of the delay parameter l and the threshold parameter s of 2 and 0, respectively, for quarterly U.S. GNP series. As discussed by him, these estimates closely match those obtained by other scholars. We therefore simply set l=2 and s=0 in our empirical work that follows. Thus, we get regime 1 whenever yt−2>0, and we get regime 2 whenever yt−2[les ]0.
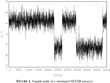
Figure 1 shows simulated realizations from such a SETAR(1,1) process. The mean in regime 1 is 5 and in regime 2 is −5. The AR coefficients and error standard deviations in the two regimes are identical and equal to 0.5 and 1.5, respectively. The figure clearly shows a readily interpretable type of nonlinearity captured by this version of a SETAR process. The sample skewness for the simulated data is estimated to be −0.52, with a p-value of 1 indicating strong asymmetries. If the AR coefficients and error variances also differ across the two regimes in addition to the mean, further nonlinearities are generated by such a process.

Sample path of a simulated SETAR process.
In order to further demonstrate that the SETAR(1,1) process can exhibit significant nonlinearities, we undertake the following exercise. We fit by maximum likelihood the AR(1) process given in (8) and a SETAR(1,1) process given in Equations (15.1) and (15.2), assuming that the correct switching criterion between regimes is known, to the simulated data plotted in Figure 1. The maximized log-likelihood value in the AR(1) and SETAR(1,1) cases is −9929.29 and −9244.13, respectively. Thus, the SETAR(1,1) model shows large improvement in the maximized log-likelihood value. Values of the Akaiki Information Criterion (AIC) in the two cases are 19864.59 and 18500.27, respectively. Values of the Schwarz Bayesian Criterion (SBC) in the two cases are 19884.14 and 18539.37, respectively. Thus, both model selection criteria pick the SETAR model over the linear AR(1).
The null hypothesis of a single regime (the null of linearity) can be tested by testing for equality of the parameter values in the two regimes. The likelihood ratio (LR) test statistic shows a p-value of 0.000 for the test. Thus, single regime (linearity) is overwhelmingly rejected in favor of a two regime nonlinear process.
Asset Pricing Solution under SETAR(1,1) Dividend Growth Rates
Exact analytical solutions to the Lucas (1978) asset pricing model are available only in a handful of special cases, typically with a simple endowment process (Burnside 1998, Bidarkota and McCulloch 2003, Tsionas 2003). When an exact analytical solution is not tractable, we need to resort to numerical techniques for finding approximate solutions to the model-implied price-dividend ratio. This involves solving the integral (7).
Tauchen and Hussey (1991) provide one method for finding an approximate solution to (7). Intuitively, their method is simple and very appealing. The method involves first approximating the (typically) continuous-valued state vector in the model by a discrete-valued Markov chain. Once the Markov chain approximation is found, the integral asset pricing (7) reduces to a system of linear simultaneous equations. The solution to these equations gives the price-dividend ratios at the discretized state space of the approximating Markov chain. The solution can then be extended to the entire continuous-valued domain of the true state vector using techniques such as Nystrom's extension (see Tauchen and Hussey, 1991).
A Markov Chain approximation can be found to any continuous-valued process (linear or nonlinear) in the following way. Let yt follow an arbitrary continuous-valued process:
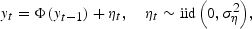
where Φ(.) is some continuous function, and the error term has the distribution
with F(.) being the cumulative distribution function with unit variance.
Let
be a discrete-valued approximating process to (16). Let
be the values taken by
. For instance, we could choose
for some m>0 and
. The rest of the nodes could be equispaced on the interval
. Let w denote the interval between any two nodes.
Tauchen (1986) provides a simple method for finding the transition probabilities of the approximating Markov chain. Let
be a typical element of the transition matrix. Then, one could choose

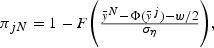
and for 2[les ]k[les ]N−1
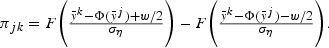
Once an approximating Markov chain is found to the continuous-valued process, Tauchen and Hussey (1991) provide a way to obtain a solution to the first-order Euler equation in the asset pricing model. Consider the Euler equation (7) at time t−1:
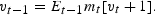
Let x≡{yt−1, yt−2, …, yt−L} denote the state vector at time t−1. Let x−≡{yt−1, yt−2, …, yt−L+1} and y≡{yt}. Then the state vector at time t is {yt, x−}. The first-order Euler condition can then be written as
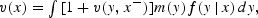
where f(.|x) is the conditional density given the state vector x.
Let
be the approximate solution. Then the first-order condition can be approximated with
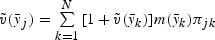
Let
be the values of
at each of the abscissa. The first-order condition can be written as
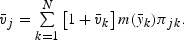
These are N linear equations in
. Solving these N equations gives the values of the price-dividend ratios at the discretized values of the state space. We can then extend the solution
to the entire domain of the state space through some interpolation techniques.
One can gauge the accuracy of the approximate solution by comparing it to the exact solution available under special cases. For instance, we can solve the asset pricing model for the price-dividend ratio when the dividend growth rates evolve as a first-order autoregression using Burnside's (1998) exact solution and Tauchen and Hussey's (1991) approximate solution, and compare the two to get a sense of the approximation errors.
ASSESSING THE ACCURACY OF MARKOV CHAINS APPROXIMATIONS
In this section, we provide a measure of the accuracy involved in approximating a continuous-valued stochastic process with a discrete-valued Markov chain. We do this for two different stochastic processes. One is a linear first-order Gaussian autoregression and the second is a nonlinear conditionally Gaussian SETAR(1,1) process.
In order to assess the accuracy of the Markov chain approximation technique, we conducted the following two exercises. First, we simulated a simple first-order Gaussian autoregressive process and obtained a sample of 5,000 observations. We estimated an AR(1) process by maximum likelihood (ML) with this simulated data. We then fit a Markov chain approximation to the simulated AR process using Tauchen's (1986) approximation method, using 75 nodes. Subsequently, we obtained a simulated sample of 5,000 observations from this approximating Markov chain. We then estimated an AR(1) process by maximum likelihood with this simulated data. The ML estimates of the AR(1) process obtained with the two simulated samples are reported in Table 1, along with the true parameters values. The table shows that the Markov chain approximates an AR(1) process quite well.

In the second exercise, we repeated the above with a Gaussian SETAR(1,1) process. The switch is governed by the value of the variable two periods earlier. If it is positive, the process is in regime 1, otherwise the process is in regime 2. We first simulated 5,000 observations from such a SETAR(1,1) process, and estimated a similar SETAR(1,1) model by ML with the simulated data. We then obtained a Markov chain approximation to the SETAR(1,1) process, simulated 5,000 observations from this approximating process, and then fit a SETAR(1,1) model by ML to this data. The ML estimates of the SETAR(1,1) process fit to the two simulated samples are presented in Table 2, along with the true parameter values. Once again, this table shows that the ML estimates from the two samples are quite close to their true parameter values.

Thus, the Markov chain with 75 nodes seems to approximate both a linear AR(1) and a nonlinear SETAR(1,1) process quite well.
ASSET PRICING
In Subsection 4.1, we present empirical results using an AR(1) endowment process. In Subsection 4.2, we present results using SETAR(1,1) process. In Subsec- tion 4.3, we compare model-implied rates of return obtained in the two cases.
Asset Pricing with Linear AR(1) Endowment
In this section, we first describe the data used to proxy for the endowment in the model, and provide maximum likelihood estimates obtained by fitting an AR(1) process to this data series. We then evaluate the model-implied price-dividend ratios obtained from the exact solution to the model under the AR(1) endowment process. We go on to compare these price-dividend ratios with those obtained by solving the model numerically, using the techniques in Tauchen and Hussey (1991), in order to get a sense of the accuracy of the numerical solution method.
In the standard Lucas (1978) model, because consumption, dividends, and output are identical, we could estimate our endowment process with observed data on any of these three variables as proxies for the endowment in the model. In this study we use GNP. This is primarily because several studies, including Potter (1995) and Bidarkota (2000), have fit SETAR processes to this version of the aggregate income series. We use quarterly U.S. real GNP data obtained from the Survey of Current Business. The dataset spans the period 1947:1–1996:4.
The discount factor θ was set to 0.97 and the risk aversion coefficient γ to 1.5 throughout the empirical analysis in the rest of the paper.
Table 3 presents ML estimates of a simple first-order Gaussian autoregression fit to the GNP growth rates. The mean growth rate is estimated to be 0.008 per quarter (or, 3.2 percent per annum). The persistence is quite strong, with the AR(1) parameter estimated at 0.36 and strongly statistically significant. The second-order partial autocorrelation coefficient of the growth rates is 0.07. Thus, an AR(1) process seems adequate for capturing the bulk of the persistence in the growth rates.

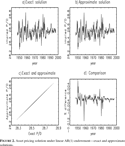
Figure 2a shows the model-implied price-dividend (P/D) ratios obtained from the asset pricing model with a linear AR(1) endowment process. The P/D ratios were computed using the exact solution given by Burnside (1998), reproduced in (12). The infinite summation was truncated to the first 10,000 terms. We verified that the P/D ratios were indistinguishable at truncations of 1,000 and 10,000 terms, indicating that the infinite summation had converged by the first 1,000 terms.

Asset pricing solution under linear AR(1) endowment—exact and approximate solutions.
The mean P/D ratio is about 28.55, and it varies within a range of only about 0.6 of its mean value. This inability of the consumption-based asset pricing model to generate sufficient variation in the implied P/D ratios is well known in the literature.
Figure 2b shows the P/D ratios computed using the approximate solution method of Tauchen and Hussey (1991), after fitting an approximate Markov chain to the linear AR(1) endowment process using techniques in Tauchen (1986). Comparing the approximate P/D ratios to their exact values in Figure 2a suggests that the approximation is generally quite good. The exact and approximate P/D ratios plotted in Figure 2c are virtually indistinguishable, as they lie almost exactly on a 45-degree line. Their differences, approximate minus exact P/D ratios as a percentage of exact P/D ratios, plotted in Figure 2d show a maximum approximation error of less than 0.12 percent in absolute value. Compared to the mean P/D ratio of 28.55, the approximation error is quite small.
Asset Pricing with Nonlinear SETAR(1,1) Endowment
In this section, we first provide ML estimates obtained by fitting a SETAR(1,1) process to the endowment data. We then evaluate the model-implied P/D ratios in the asset pricing model driven by the estimated SETAR(1,1) endowment process. Finally, we compare these P/D ratios with those obtained with the linear endowment process discussed in Subsection 4.1.
Table 4 presents ML estimates of a SETAR(1,1) process fit to the GNP growth rates. The difference in the mean growth rates in the two regimes is only 0.0008 per quarter (or, 0.32 percent per annum). The second regime (corresponding to lower growth rates) is more volatile but less persistent than the first regime (corresponding to higher growth rates). Overall, the nonlinear effects are quantitatively weak. This, of course, has an important bearing on the overall impact of nonlinearities, as we shall see subsequently.

The null hypothesis of a single regime (the null of linearity) can be tested by testing for equality of the parameter values in the two regimes. In general SETAR models, the switch between regimes is governed by yt−l > s, and l and s are estimated along with other parameters of the model. In such a case, under the null hypothesis of a single regime, the parameters l and s are not identified. Standard asymptotic distribution theory does not go through (Hansen 1996). In our paper, because we do not estimate the parameters l and s but instead set l=2 and s=0 in accordance with the findings in previous studies, our tests do not suffer from this problem. Our test here is, therefore, carried out with the LR test statistic and critical values are drawn from the χ2 distribution with appropriate degrees of freedom.
The likelihood ratio (LR) test statistic, reported in Table 4, shows a p-value of 0.054 for the test. Thus, linearity is not rejected (barely) at the 5 percent significance level, but it can be rejected at the 6 percent level.
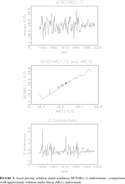
Figure 3a plots the model-implied P/D ratios in the asset pricing model with SETAR(1,1) endowment. The P/D ratios are computed using the approximate solution method in Tauchen and Hussey (1991), after approximating the SETAR(1,1) process with discrete Markov chains using the techniques in Tauchen (1986). The mean P/D ratio is once again about 28.55, the value obtained under AR(1) endowment.

Asset pricing solution under nonlinear SETAR(1,1)endowment—comparison with approximate solution under linear AR(1) endowment.
Figure 3b plots the P/D ratios under SETAR(1,1) endowment, against the values obtained under AR(1) endowment using the approximate solution method. This figure summarizes the effects of modeling nonlinearities in the dividend growth rates on the equilibrium implications of the asset pricing model. Any deviations from a 45-degree line in the figure can be attributed solely to nonlinearities in the driving process. The figure shows that the variation in the P/D ratios under SETAR(1,1) endowment is largely similar to that under AR(1) endowment. Although small deviations are noticeable, the implied P/D ratios largely lie along the 45 degree line for the most part. SETAR(1,1) minus AR(1) P/D ratios as a percentage of AR(1) P/D ratios, plotted in Figure 3c, show a maximum difference of less than 0.5 percent. Compared to the mean P/D ratio of 28.55, this difference is quite small.
Implications of Nonlinearities for Model-Implied Rates of Return
Given the model-implied P/D ratios, it is straightforward to compute the model-implied rate of return on risky assets with both linear and nonlinear endowment. This will not be derived here but the reader can refer, for instance, to Bidarkota and McCulloch (2003). Similarly, the rate of return on risk-free assets also can be easily evaluated. However, although an exact closed-form solution can be easily derived for the risk-free rate with linear endowment, such a solution is not tractable with nonlinear endowment. The discretization of the state vector involved in the Tauchen and Hussey (1991) numerical solution permits computation of the risk free returns with nonlinear endowment.
Table 5 presents the means and standard deviations of the model-implied rates of return with both SETAR(1,1) and AR(1) endowments. The table reports statistics for the implied risk free returns, equity returns, and equity premia. The model predicts a mean risk free rate of 17.31 percent per annum with the SETAR(1,1) endowment and an equity return of 17.36 percent per annum. Thus, the equity premium predicted by the model is only 0.05 percent per annum. This low equity premium, as compared to the U.S. average in excess of 7 percent per annum over the last 100 years, is the well-known equity premium puzzle of Mehra and Prescott (1985).

The model with a linear AR(1) endowment implies mean rates of return that are within 0.01 percent of those from the model with the nonlinear SETAR(1,1) endowment. The approximation errors on the rates of return in the linear AR(1) case associated with the numerical solution techniques of Tauchen (1986) and Tauchen and Hussey (1991) are even smaller, as evident from the first two rows of Table 5. The biggest impact of the approximate solution appears to be in the standard deviation of the equity premium. The model with linear endowment implies a standard deviation of the equity premium of 3.07 percent per annum with the exact solution and only 1.76 with the numerical solution.
Overall, it appears that in the context of the consumption-based asset-pricing model of Lucas (1978), the effects of modeling nonlinearities in the endowment process on the model-implied rates of return are miniscule. The mean implied rates of return in the model with linear and nonlinear endowment are within 0.01 percent per annum of each other.
EXPLORING ROBUSTNESS OF RESULTS
In this Section, we explore robustness of our results with respect to conditional heteroskedasticity in Subsection 5.1, with respect to alternative functional forms for nonlinearity in Subsection 5.2, and with respect to alternative data proxies for dividends in Subsection 5.3.
Conditional Heteroskedasticity
In order to explore the sensitivity of our results to conditional heteroskedasticity, we extend the homoskedastic linear and nonlinear dividend processes to incorporate ARCH effects. In order to keep the dimension of the state vector small, we model conditional heteroskedasticity simply as an ARCH(1) process. This specification is used in Tauchen and Hussey (1991) as well.
The AR(1) process with ARCH(1) errors is given by:
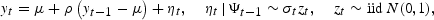
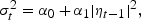
where α0>0 and 0[les ]α1<1 and Ψt denotes the information set available at time t comprising of {yt, yt−1, …, y1}.
The SETAR(1,1) process with ARCH(1) errors can be written as follows:
In regime 1,
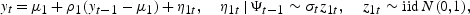
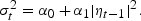
In regime 2,
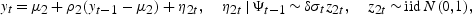
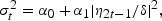
where δ>0 is the ratio of error standard deviation in regime 2 versus regime 1. As in Section 2, we get regime 1 when yt−2>0, and regime 2 when yt−2[les ]0.
We estimated both the AR and SETAR models with ARCH effects using the real GNP data from Section 4. ML estimates are presented in Table 6. The ARCH parameter is estimated to be 0.23 with the AR model and 0.28 with the SETAR model. A likelihood ratio test would reject homoskedasticity in favor of ARCH effects.

With ARCH effects, exact analytical solution to the Euler equation does not exist even in the AR case. The asset pricing model needs to solved using the Markov chain approximation technique. Table 7 presents model-implied rates of return for the AR and SETAR models with ARCH effects. When comparing with the implied rates of return in the homoskedastic case, the most notable difference is the near doubling of the implied mean equity premium. However, once again, comparing the rates of return across the AR and SETAR models, differences in the mean rates of return are less than 0.1 percent per annum. Thus, effects of nonlinearities in the conditional mean remain small.

Alternative Functional Forms
In order to explore the sensitivity of our results to alternative functional forms for modeling nonlinearity in the conditional mean, we entertain two further specifications of nonlinear dividends process.
The first is a neural network model. We know from the literature on neural networks that these are universal approximators, that is, they are capable of capturing nonlinearity of any form that may exist in a data series (Stinchcombe and White 1989). A neural network model, augmented with ARCH(1) errors, takes the form
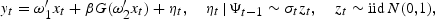
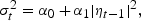
where xt≡{1, yt−1}′, G(.) is the logistic function G(x)=1/{1+exp(−x)}, and ωj≡{ωj1, ωj2}′, j=1, 2 is a vector of unknown parameters.
The second nonlinear model is motivated by the neural network literature. This can be viewed as an ad hoc nonlinear model. It can be represented as follows:
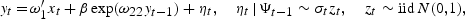
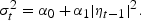
ML estimates of the two models are presented in Table 8. Parameter estimates common with the AR(1)–ARCH(1) model are very similar. The coefficient on the nonlinear term (logistic or exponential) is estimated to be small (0.007 in the ANN model and −0.007 in the Ad hoc model). The maximized log-likelihood value shows no increase compared to the value in the AR(1)–ARCH(1) case.

Model-implied rates of return from solving the Euler equation in the two cases are presented in Table 9. Once again, comparing these rates of return with those under AR(1)–ARCH(1) process shows insignificant effects of nonlinearities.

Alternative Data Proxies for Dividends
Because the Lucas (1978) asset pricing model has dividends being equal to consumption and income, we could proxy the exogenous dividends in the model with any of these three variables from data. Therefore, we carried out the empirical analysis described in Sections 4 through 5.2 using annual per capita real consumption data on nondurables and services in the United States from 1889 to 1997 as well. This data series is commonly used in the equity premium literature (see, for instance, Campbell and Cochrane 1999).
For the sake of brevity, we only summarize the main results obtained from the analysis using consumption data. ML estimates indicate negative first-order autocorrelation in consumption growth rates. Mean consumption growth rate is twice, and its volatility thrice as much, as that of GNP. A comparison of the maximized log-likelihood values in the homoskedastic AR and SETAR models indicates no statistically significant nonlinearities in the conditional mean (p-value for the LR test statistic is 0.264). Model-implied rates of return differ by less than 0.25 percent per annum in the two cases.
Consumption growth rates exhibit stronger ARCH effects. The ARCH parameter is estimated to be 0.363. An LR test for homoskedasticity would reject in favor of ARCH(1) effects. Unlike with GNP data, the implied equity premium declines, and is in fact driven to −0.22 percent per annum, in the AR, ANN, and Ad hoc models once ARCH effects are incorporated. In the SETAR case, the implied premium rises by 0.15 percent per annum with the introduction of ARCH. Comparing across the conditionally linear in the mean and conditionally nonlinear in the mean models with ARCH effects, the effects of nonlinearities are negligible in the case of ANN and Ad hoc nonlinear models. The SETAR–ARCH model shows implied rates of return that differ from the AR–ARCH case by as much as 1.15 percent per annum. In the AR–ARCH case, the AR coefficient is estimated to be −0.179. In the SETAR–ARCH case, the AR coefficient is estimated to be 0.315 in regime 1 and 0.072 in regime 2. This accounts for the larger effects of nonlinearities in this case.
CONCLUSIONS
In this study, we analyzed the economic importance of modeling nonlinearities in the conditional mean dynamics of exogenous forcing processes on the moments of endogenous variables in the context of a macroeconomic model. We used the popular consumption-based asset pricing model of Lucas (1978) for our analysis. A linear AR(1) process and a nonlinear SETAR(1,1) process were used alternatively to model the exogenous endowment sequence. Exact solution to the model with a linear endowment was used to solve for endogenous quantities of interest, including the model-implied price-dividend ratio, and risk-free and risky rates of return. A numerical solution of Tauchen and Hussey (1991) was used to solve the model with a nonlinear endowment.
Our analysis suggests that the overall impact of modeling nonlinearities in the conditional mean dynamics of the exogenous endowment sequence on the implied rates of return in this model is small.
Our finding of weak effects of nonlinearities is in part a result of weak nonlinearities in the conditional mean dynamics of GNP data, as noted in Section 4.2. It is conceivable that in other contexts where the underlying nonlinearities are stronger, the overall impact of such nonlinearities on the implications of models may be stronger.
This paper was presented at the 12th Annual Symposium of the Society for Non-Linear Dynamics and Econometrics (Atlanta Fed), at the Departments of Economics at the University of Miami and Florida International University. I would like to thank participants at these presentations, two anonymous referees, Jonathan Hill, and Prasad Bhattacharya for several comments that led to substantial improvements in the paper. None of these individuals are responsible for errors, if any.