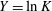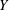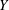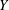1. Introduction
Water-retaining structures, such as dams or sheet pile walls, may fail due to several causes. Some of these, like erosion or heaving, depend to a large extent upon the seepage through the porous formation underlying the structure. Understanding how seepage influences the occurrence of such failures is of paramount importance for a safe design. In the traditional approach, which regards the porous formation as a homogeneous unit, this is achieved by computing the total volumetric flow rate
$Q$
downstream of the structure, and subsequently by applying a safety factor
$s_{f}=2{-}5$
. The reason for this ‘conservative’ approach is twofold. First, erosion and heaving may lead to a complete (and very rapid) failure of a civil engineering structure with (in most of the cases) little advanced warning (Fraccarollo & Capart Reference Fraccarollo and Capart2002; Ferrari et al.
Reference Ferrari, Fraccarollo, Dumbser, Toro and Armanini2010). Second, flow underneath a wall is very variable due to the spatial variability (heterogeneity) of the hydraulic conductivity
$K$
. The present paper aims at tackling this second issue by relating
$Q$
to the heterogeneity of
$K$
.
Figure 1. Sketch of seepage underneath a vertical wall (of thickness
$b$
) induced by a water-level drop
${\rm\Delta}H$
much larger than
$b$
. Continuous lines are the streamlines pertaining to a heterogeneous medium, whereas dashed lines represent streamlines in a homogeneous medium.
The impact of spatial variability of the hydraulic conductivity on flow in porous formations represents a very active research field. Over the past few years, it has been recognized that the stochastic approach represents an appropriate tool to model such a variability (an exhaustive exposition on the topic can be found in Dagan Reference Dagan1987, Reference Dagan1989; Rubin Reference Rubin2003). Basically, this approach recognizes that, owing to its erratic variations,
$K$
is affected by uncertainty and regards it as a random space function (hereafter also denoted as RSF). As a consequence, the flow variables become RSFs as well, so that a solution of any seepage problem should be represented by means of all the statistical moments of the flow variables. However, such solutions are generally limited to the derivation of the first two moments, which both have practical significance and are often the only measurable quantities.
In the present study we consider steady seepage induced by a head drop
${\rm\Delta}H$
applied upstream/downstream of a water-retaining wall (figure 1). Seepage occurs in the half-space
${\rm\Omega}\equiv \{(x_{1},x_{2},x_{3}):x_{1}\geqslant 0,(x_{2},x_{3})\in \mathbb{R}^{2}\}$
. The thickness
$b$
of the wall is assumed to be much smaller than
${\rm\Delta}H$
. Since
$b=O(1~\text{m})$
and
${\rm\Delta}H=O(10{-}100~\text{m})$
, the condition
$b/{\rm\Delta}H\ll 1$
is met in the majority of real cases. Although simplified, such a formulation enables one to grasp the main features of a very complex problem by means of simple (i.e. analytical) results, therefore providing useful insights for both theoretical purposes and practical applications. The classical approach to the problem at stake is to consider the medium
${\rm\Omega}$
as homogeneous (constant hydraulic conductivity). Within this framework, an analytical solution is available (Bruggeman Reference Bruggeman1999), and the subject has stimulated intense research activity in view of its importance for engineering applications (see e.g. Lancellotta Reference Lancellotta1993; Fenton & Griffiths Reference Fenton and Griffiths2008). On the contrary, little work has been done to account for the impact of spatial variability of the hydraulic properties of porous formations. All the studies relating spatial variability of the hydraulic properties to the failure probability of water-retaining structures are purely numerical (an exhaustive review can be found in Fenton & Griffiths Reference Fenton and Griffiths2008, and references therein). In particular, Griffiths & Fenton (Reference Griffiths and Fenton1997) have shown (by means of Monte Carlo simulations) that the critical value of the volumetric flow rate determining the failure of the wall has an upper bound which depends upon the domain dimensionality, as well as on the statistical moments of the log-conductivity
$Y=\ln K$
. Numerical approaches can handle a large variety of boundary conditions and complex geometries, but they are computationally intensive and prone to numerical inaccuracies (especially when computing high-order moments). Moreover, this computational complexity increases tremendously when dealing with three-dimensional domains. On the contrary, analytical results (although mathematically cumbersome) are very simple to implement for the subsequent analysis/discussion, and provide explicit relationships between input parameters and model output. In addition, analytical results represent a benchmark to validate more involved numerical codes.
In the present study we analytically solve, for the first time, steady seepage underneath a water-retaining wall where
$Y=\ln K$
is modelled as a stationary, normally distributed, RSF with given mean
$\langle Y\rangle$
and covariance (here and in what follows
$\langle \,\rangle$
denotes the ensemble-average operator). Within a homogeneous medium the problem under consideration is characterized by streamlines which are semi-circles originating upstream and ending downstream of the wall. The ‘distortion effect’ due to the heterogeneity of
$Y$
causes the streamlines to fluctuate around the ones pertaining to a homogeneous medium (figure 1), similarly to a vortex-type flow where the fluctuations are due to the uncertainty of the hydrodynamical coefficient(s) (Landau & Lifshitz Reference Landau and Lifshitz1959). To obtain simple expressions for the second-order moments of the flow variables, we derive an approximate solution for the flow field that is sufficiently accurate for small variance
${\it\sigma}_{Y}^{2}$
(weak heterogeneity), i.e. the heterogeneous flow slightly differs from the homogeneous (mean) one, similarly to the ‘frozen field’ approximation in turbulent flows.
Generally, modelling
$Y$
(and consequently the resulting flow field) as an RSF is equivalent to the approach adopted in a large variety of turbulent flows, such as flow in pipelines, density-driven flows, flow through pumps and turbines, and reactive flows (a wide review can be found in Pope Reference Pope2010). The difference is that in turbulent flows the random nature of the dependent scalar field(s) is due to the velocity, which is regarded as a given random field, whereas in the present case the random nature of the flow variables (i.e. pressure head and specific discharge) stems from the spatial variability of
$Y$
.
The paper is organized as follows: we begin by formulating the mathematical problem in the context of a stochastic framework, and derive general results (§ 2). Second-order moments of the head are analyzed in § 3. To highlight the potential use of our results for a reliability-based design, we discuss how the spatial variability of
$Y$
affects the risk of failure (§ 4). Concluding remarks are reported in § 5.
2. Problem formulation and general results
Steady seepage takes place in a semi-bounded domain
${\rm\Omega}$
, and it is induced by a head-drop
${\rm\Delta}H$
upstream/downstream of a water-retaining wall (figure 1). Seepage is modelled by: (i) the Darcy’s (constitutive) law, i.e.
$\mathbf{q}(\boldsymbol{x})=-K(\boldsymbol{x})\boldsymbol{{\rm\nabla}}h(\boldsymbol{x})$
, relating the gradient of the hydraulic head
$h$
to the flux
$\mathbf{q}$
via the conductivity
$K$
; and (ii) the continuity equation
$\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\mathbf{q}(\boldsymbol{x})=0$
. The combination of (i)–(ii) leads to the following equation:
$$\begin{eqnarray}\displaystyle {\rm\nabla}^{2}h(\boldsymbol{x})+\boldsymbol{{\rm\nabla}}Y^{\prime }(\boldsymbol{x})\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}h(\boldsymbol{x})=0, & & \displaystyle\end{eqnarray}$$
which is solved subjected to the boundary conditions:
$$\begin{eqnarray}\displaystyle h(\boldsymbol{x})|_{x_{1}=0}=\left\{\begin{array}{@{}ll@{}}H_{1}\quad & \text{for }x_{2}<0,\\ H_{1}-{\rm\Delta}H\quad & \text{for }x_{2}>0,\end{array}\right.\quad \lim _{x\rightarrow \infty }|h(\boldsymbol{x})|<\infty & & \displaystyle\end{eqnarray}$$
(figure 1). In line with most of the field investigations (Rubin Reference Rubin2003), and in agreement with similar studies (e.g. Indelman Reference Indelman1996; Indelman & Dagan Reference Indelman and Dagan1999), the fluctuation
$Y^{\prime }=Y-\langle Y\rangle$
is regarded as a zero-mean stationary RSF completely characterized by the (constant) variance
${\it\sigma}_{Y}^{2}\equiv \langle Y^{\prime 2}\rangle$
, and the two-point autocorrelation function
${\it\rho}_{Y}(\boldsymbol{x}-\boldsymbol{y})\equiv \langle Y^{\prime }(\boldsymbol{x})Y^{\prime }(\boldsymbol{y})\rangle$
. The random nature of the fluctuation
$Y^{\prime }$
greatly complicates the mathematical problem, such that no analytical solution is achievable. Simple results can be obtained by adopting an asymptotic expansion similarly to Indelman & Dagan (Reference Indelman and Dagan1999) and Tartakovsky, Guadagnini & Riva (Reference Tartakovsky, Guadagnini and Riva2003). Thus, the head field is sought as
$$\begin{eqnarray}\displaystyle h(\boldsymbol{x})=\mathop{\sum }_{n}h^{(n)}(\boldsymbol{x}),\quad h^{(n)}=O(Y^{\prime n}). & & \displaystyle\end{eqnarray}$$
Substitution into (2.1), and collecting terms of the same order, yields
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}ll@{}}\displaystyle {\rm\nabla}^{2}h^{(0)}(\boldsymbol{x})=0 & \\ {\rm\nabla}^{2}h^{(n)}(\boldsymbol{x})=-\boldsymbol{{\rm\nabla}}Y^{\prime }(\boldsymbol{x})\displaystyle \boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}h^{(n-1)}(\boldsymbol{x}), & n=1,2,\dots .\end{array}\right\} & & \displaystyle\end{eqnarray}$$
The leading-order term
$h^{(0)}$
(valid for a medium of constant conductivity) is
$$\begin{eqnarray}\displaystyle h^{(0)}(\boldsymbol{x}^{\star })=\frac{{\rm\Delta}H}{{\rm\pi}}\arctan \left(\frac{x_{2}}{x_{1}}\right) & & \displaystyle\end{eqnarray}$$
(Bruggeman Reference Bruggeman1999), whereas the head fluctuation
$h^{(1)}$
is the solution of the following problem:
$$\begin{eqnarray}\displaystyle {\rm\nabla}^{2}h^{(1)}(\boldsymbol{x})=-\boldsymbol{{\rm\nabla}}Y^{\prime }(\boldsymbol{x})\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}h^{(0)}(\boldsymbol{x}^{\star }),\quad h^{(1)}(\boldsymbol{x})|_{x_{1}=0}=0. & & \displaystyle\end{eqnarray}$$
Here and hereafter, the ‘star’ symbol denotes any point belonging to the half-plane
${\rm\Omega}^{\star }\equiv \{(x_{1},x_{2}):x_{1}\geqslant 0,x_{2}\in \mathbb{R}\}$
. The fluctuation
$\mathbf{q}^{(1)}\equiv (q_{1}^{(1)},q_{2}^{(1)},q_{3}^{(1)})$
of the flux is obtained from Darcy’s law by employing the same asymptotic expansion as before. This yields
$$\begin{eqnarray}\displaystyle q_{l}^{(1)}(\boldsymbol{x})=-K_{G}\left[Y^{\prime }(\boldsymbol{x})\frac{\partial }{\partial x_{l}}h^{(0)}(\boldsymbol{x}^{\star })+\frac{\partial }{\partial x_{l}}h^{(1)}(\boldsymbol{x})\right]\quad (l=1,2,3), & & \displaystyle\end{eqnarray}$$
where
$K_{G}=\exp (\langle Y\rangle )$
is the geometric mean of
$Y$
. Equations (2.6)–(2.7) represent the starting point for the next developments. In particular, we aim to compute the second-order moments of the head and the volumetric rate, since these statistical quantities are of main interest for the present study.
Hereafter, we deal with an axisymmetric anisotropic porous medium characterized by a horizontal correlation integral scale,
$I_{\infty }$
, of
$Y$
that is much larger than the vertical one,
$I$
. This allows one to regard the
$Y$
-field as perfectly correlated in the horizontal plane, and consequently the autocorrelation
${\it\rho}_{Y}$
depends upon the vertical distance solely, i.e.
${\it\rho}_{Y}(\boldsymbol{x})\equiv {\it\rho}_{Y}(x_{1})$
. In other words, we regard
$Y$
as: (i) random along the vertical direction; and (ii) deterministic in the horizontal plane. Such a statistical correlation structure is typical of formations wherein the fluctuation of
$Y/\langle Y\rangle$
along the vertical direction is much larger than that in the horizontal plane (see e.g. Sudicky Reference Sudicky1986; Zinn & Harvey Reference Zinn and Harvey2003). It is worth noting here that such a geological structure is also typical of formations made up by strata of significantly different conductivities (Dagan Reference Dagan1989) for which other approaches have been employed (see e.g. Guadagnini et al.
Reference Guadagnini, Guadagnini, Tartakovsky and Winter2003). With the details reported in appendix A, the covariance
$C_{h}(\boldsymbol{x},\boldsymbol{y})\equiv \langle h^{(1)}(\boldsymbol{x})h^{(1)}(\boldsymbol{y})\rangle$
of the head is given by
$$\begin{eqnarray}\displaystyle C_{h}(\boldsymbol{x}^{\star },\boldsymbol{y}^{\star })=\frac{{\it\sigma}_{Y}^{2}}{4}\bar{c}(\boldsymbol{x}^{\star },\boldsymbol{y}^{\star }), & & \displaystyle\end{eqnarray}$$
where
$\bar{c}\equiv \bar{c}(\boldsymbol{x}^{\star },\boldsymbol{y}^{\star })$
is given by (A 29) in appendix A. Hereafter, lengths are scaled by the integral scale
$I$
(although for simplicity we retain the same notation). The result (2.8) represents a general expression for the head covariance, and it can be straightforwardly computed after specifying the shape of
${\it\rho}_{Y}$
. Furthermore, one can easily check (see (A 21) in appendix A) that
$C_{h}$
vanishes for either
$x_{1}=0$
or
$y_{1}=0$
due to the deterministic nature of the head there, which requires:
$h^{(1)}(\boldsymbol{x})|_{x_{1}=0}=h^{(1)}(\boldsymbol{y})|_{y_{1}=0}=0$
.
At the second order in
${\it\sigma}_{Y}^{2}$
the mean head
$\langle h\rangle$
is given by
$\langle h\rangle =h^{(0)}+\langle h^{(2)}\rangle$
with
$h^{(2)}$
computed from (2.4) for
$n\equiv 2$
. It is convenient to represent
$\langle h\rangle$
as
$$\begin{eqnarray}\displaystyle \langle h(\boldsymbol{x}^{\star })\rangle ={\rm\Psi}(\boldsymbol{x}^{\star })h^{(0)}(\boldsymbol{x}^{\star }),\quad {\rm\Psi}(\boldsymbol{x}^{\star })=1-{\it\sigma}_{Y}^{2}{\it\psi}(\boldsymbol{x}^{\star }),\quad {\it\psi}(\boldsymbol{x}^{\star })=-{\it\sigma}_{Y}^{-2}\frac{\langle h^{(2)}(\boldsymbol{x}^{\star })\rangle }{h^{(0)}(\boldsymbol{x}^{\star })},\qquad \quad & & \displaystyle\end{eqnarray}$$
i.e. the mean head is expressed as the product between
$h^{(0)}$
(valid for a homogeneous formation) and a characteristic function
${\rm\Psi}$
which ‘adjusts’
$h^{(0)}$
according to the medium heterogeneity. One advantage of the representation (2.9) is that it is useful to identify the statistical properties of the porous formation. Indeed, once
$\langle h\rangle$
has been estimated by the head measurements, one can determine the variance and the integral scale of the RSF
$Y$
by matching with (2.9). The function
${\it\psi}\equiv {\it\psi}(\boldsymbol{x}^{\star })$
is determined by computing the quantity
${\it\sigma}_{Y}^{-2}\langle h^{(2)}(\boldsymbol{x}^{\star })\rangle$
. The final result is (appendix B)
$$\begin{eqnarray}\displaystyle {\it\psi}(\boldsymbol{x}^{\star })=\frac{x_{2}{\rm\Lambda}(\boldsymbol{x}^{\star })}{\arctan \left({\displaystyle \frac{x_{2}}{x_{1}}}\right)}, & & \displaystyle\end{eqnarray}$$
where
$$\begin{eqnarray}\displaystyle & & \displaystyle {\rm\Lambda}(\boldsymbol{x}^{\star })=\frac{x_{1}}{x_{1}^{2}+x_{2}^{2}}+\int _{0}^{x_{1}}\frac{\text{d}u{\it\rho}_{Y}(u)}{(3x_{1}-u)^{2}+x_{2}^{2}}-2\int _{0}^{x_{1}}\frac{\text{d}u{\it\rho}_{Y}(u)}{(u+x_{1})^{2}+x_{2}^{2}}+\int _{0}^{\infty }\frac{\text{d}u{\it\rho}_{Y}(u)}{(u+3x_{1})^{2}+x_{2}^{2}}\nonumber\\ \displaystyle & & \displaystyle \quad +\,2\int _{x_{1}}^{\infty }\frac{\text{d}u{\it\rho}_{Y}(u)}{(2u-x_{1})^{2}+x_{2}^{2}}-\int _{0}^{\infty }\frac{\text{d}u{\it\rho}_{Y}(u)}{(u+x_{1})^{2}+x_{2}^{2}}-2\int _{0}^{\infty }\frac{\text{d}u{\it\rho}_{Y}(u)}{(2u+x_{1})^{2}+x_{2}^{2}}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\int _{0}^{\infty }\frac{\text{d}u{\it\rho}_{Y}(u)}{(3u+x_{1})^{2}+x_{2}^{2}}-\int _{x_{1}}^{\infty }\frac{\text{d}u{\it\rho}_{Y}(u)}{(3u-x_{1})^{2}+x_{2}^{2}}-x_{1}\int _{0}^{\infty }\frac{\text{d}u(u+x_{1}){\it\rho}_{Y}(u)}{[(u+x_{1})^{2}+x_{2}^{2}]^{2}}.\end{eqnarray}$$
The normalized correction (2.10) allows one to investigate the flow in the far field. Thus, it yields
$$\begin{eqnarray}\displaystyle \lim _{x^{\star }\rightarrow \infty }{\it\psi}(\boldsymbol{x}^{\star })=\frac{\sin 2{\it\theta}}{2{\it\theta}}\quad (\text{any }{\it\rho}_{Y}), & & \displaystyle\end{eqnarray}$$
where we have introduced polar coordinates
$\boldsymbol{x}^{\star }\equiv x^{\star }(\cos {\it\theta},\sin {\it\theta})$
. The limit (2.12) suggests that at large distances from the wall the mean flow behaves like a homogeneous one driven by
$$\begin{eqnarray}\displaystyle \langle h({\it\theta})\rangle _{\infty }=\left(1-{\it\sigma}_{Y}^{2}\frac{\sin 2{\it\theta}}{2{\it\theta}}\right)h^{(0)}(x^{\star },{\it\theta})=\frac{{\rm\Delta}H}{{\rm\pi}}({\it\theta}-{\it\sigma}_{Y}^{2}\sin {\it\theta}\cos {\it\theta})\quad \text{for }x^{\star }\gg I.\quad & & \displaystyle\end{eqnarray}$$
The asymptotic equation (2.13), whose dependence upon the polar angle
${\it\theta}$
is depicted in figure 2, represents a useful benchmark to validate numerical codes.
Figure 2. Dependence of the scaled asymptotic head
$\langle h({\it\theta})\rangle _{\infty }/{\rm\Delta}H$
on the polar angle
${\it\theta}\in [-{\rm\pi}/2,{\rm\pi}/2]$
for some values of the variance
${\it\sigma}_{Y}^{2}$
of the log-conductivity
$Y=\ln K$
.
3. Discussion
Besides being of definite theoretical interest, the statistical moments of the head obtained so far may serve: (i) in field applications for the purpose of carrying out proper head measurements; and (ii) as a benchmark to validate numerical codes.
The head variance
${\it\sigma}_{h}^{2}(\boldsymbol{x}^{\star })=C_{h}(\boldsymbol{x}^{\star },\boldsymbol{x}^{\star })$
is computed from (2.8) by carrying out a single numerical quadrature as shown in appendix A. However, a simpler (closed-form) expression for
${\it\sigma}_{h}^{2}$
is obtained by approximating the fluctuation
$Y^{\prime }=Y-\langle Y\rangle$
of the log-conductivity by a Gaussian white noise (in analogy to the
${\it\delta}$
-approximation of the energy spectrum in the theory of homogeneous turbulence), i.e.
${\it\rho}_{Y}(x_{1})\approx I{\it\delta}(x_{1})$
. The result (in dimensional form) is
$$\begin{eqnarray}\displaystyle \frac{{\it\sigma}_{h}^{2}(\boldsymbol{x}^{\star })}{({\rm\Delta}H{\it\sigma}_{Y})^{2}} & = & \displaystyle \frac{I\sin {\it\theta}}{x^{\star }{\rm\pi}^{2}}\left\{{\it\theta}-\arctan \left(\frac{\tan {\it\theta}}{2}\right)\right.\nonumber\\ \displaystyle & & \displaystyle +\,\sin {\it\theta}\cos {\it\theta}\left[\frac{f_{1}(\tan ^{2}{\it\theta})}{1+8\sin ^{2}{\it\theta}}+\frac{f_{2}(\tan ^{2}{\it\theta})}{3(1+8\cos ^{2}{\it\theta})}\right.\nonumber\\ \displaystyle & & \displaystyle +\,\left.\left.\frac{f_{3}(\tan ^{2}{\it\theta})}{(1+24\cos ^{2}{\it\theta})(9+16\cos ^{2}{\it\theta})}\right]\right\},\quad -\frac{{\rm\pi}}{2}\leqslant {\it\theta}\leqslant \frac{{\rm\pi}}{2},\end{eqnarray}$$
where
$$\begin{eqnarray}\displaystyle & \displaystyle f_{1}(a)=\frac{1+3a}{\sqrt{a}}\left[\arctan \left(\frac{3}{\sqrt{a}}\right)-\arctan \left(\frac{1}{\sqrt{a}}\right)\right]+\ln \left[\frac{(9+a)}{16(1+a)}\right], & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle f_{2}(a)=\frac{a-3}{2\sqrt{a}}\arctan \left(\frac{2}{\sqrt{a}}\right)-\frac{a+3}{\sqrt{a}}\arctan \left(\frac{1}{\sqrt{a}}\right)+\ln \left[\frac{(1+a)}{4(4+a)}\right]+{\rm\pi}\frac{9+a}{4\sqrt{a}},\quad & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle f_{3}(a) & = & \displaystyle \frac{125+9a}{2\sqrt{a}}\arctan \left(\frac{1}{\sqrt{a}}\right)-\frac{25-3a}{2\sqrt{a}}\arctan \left(\frac{2}{\sqrt{a}}\right)\nonumber\\ \displaystyle & & \displaystyle -\,\frac{25+9a}{2\sqrt{a}}\arctan \left(\frac{3}{\sqrt{a}}\right)+5\ln \left[\frac{4(1+a)}{4+a}\right]-3{\rm\pi}\frac{25+a}{4\sqrt{a}}.\end{eqnarray}$$
Before going on, it is worth noting that one can replace
${\it\rho}_{Y}$
with a white noise when the
$\log$
-conductivity
$Y$
is correlated over a very short vertical scale. However, within the context of hydrological applications it has been shown (see e.g. Fiori, Indelman & Dagan Reference Fiori, Indelman and Dagan1998; Indelman & Dagan Reference Indelman and Dagan1999; Severino & Coppola Reference Severino and Coppola2012) that this becomes a reasonable working assumption when
$I/I_{\infty }\ll 1$
(in line with the assumption of a highly anisotropic porous formation). From the practical point of view, the white-noise approximation has already been found to be in good agreement with field findings (Sudicky Reference Sudicky1986; Zinn & Harvey Reference Zinn and Harvey2003) and Monte Carlo simulations (e.g. Indelman, Or & Rubin Reference Indelman, Or and Rubin1993) for
$I/I_{\infty }\lesssim 0.05$
.
For comparison purposes, we have also conducted Monte Carlo simulations (MCS) using the code RFLOW (freely available at: http://courses.engmath.dal.ca/rfem/). For the sake of completeness, we briefly describe the algorithm here (a detailed description can be found in Fenton & Griffiths Reference Fenton and Griffiths2008). Any realization of the random field
$K$
, which is generated by the local average subdivision method (chapter 6.4.6 in Fenton & Griffiths Reference Fenton and Griffiths2008), is mapped upon a regular mesh (step 1). The elliptic-type equation (2.1) is then discretized (by means of the finite-elements method) into a system of linear algebraic equations. The latter is solved for the nodal
$h$
-values by using the Gaussian elimination algorithm (step 2). Steps 1 and 2 are iterated
$\mathscr{N}_{r}$
times (with
$\mathscr{N}_{r}\gg 1$
) to obtain a set of realizations at each node for any flow variable that is used to evaluate moments (for details, see chapter 8 in Fenton & Griffiths Reference Fenton and Griffiths2008). In the present study, the numerical mesh consisted of
$100\times 40\times 40$
elements. The boundary conditions at
$x_{1}=0$
were such that the head drop
${\rm\Delta}H$
across the wall (of zero thickness) was set to unity, whereas the outer boundary of the mesh was assigned a ‘no-flow’ boundary condition. The vertical and horizontal integral scales were taken such that
$I/I_{\infty }=0.001$
. Finally,
$\mathscr{N}_{r}=5000$
realizations were performed for each case.
Figure 3. Sketch of a horizontally elongated inclusion of conductivity
$K_{0}$
imbedded in a matrix
${\rm\Omega}_{eff}$
of effective conductivity
$K^{eff}$
such that the homogeneous flow field coincides with that generated by
$h^{(0)}$
in (2.5).
Figure 4. Contour plot of the scaled head variance
${\it\sigma}_{h}^{2}(\boldsymbol{x}^{\star })/({\it\sigma}_{Y}{\rm\Delta}H)^{2}$
computed with the analytical expression (3.1) (black lines), and the MCS (red lines).
To discuss the behaviour of the head variance
${\it\sigma}_{h}^{2}$
to be shown in figures 4 and 5, it is convenient to focus upon the head pattern in the vicinity of an inclusion of conductivity
$K_{0}$
embedded into a matrix
${\rm\Omega}_{eff}$
. The latter is homogenized (to ensure the same flux) with the effective conductivity
$K^{eff}$
(details on how to compute
$K^{eff}$
in this case can be found in Indelman Reference Indelman1996; Severino, Santini & Sommella Reference Severino, Santini and Sommella2008; Severino Reference Severino2011; Severino & Coppola Reference Severino and Coppola2012). The variance
${\it\sigma}_{h}^{2}$
is obtained by ensemble averaging the square of the head fluctuation,
$h^{(1)}(\boldsymbol{x})=h(\boldsymbol{x})-\langle h(\boldsymbol{x})\rangle$
, as computed by several such single realizations. Toward this end, we have depicted in figure 3 an horizontally elongated (large
$I_{\infty }$
and small
$I$
) inclusion to mimic the statistical structure of a highly anisotropic formation. We start by analyzing the disturbance in the flow field when such an inclusion is close to the upper boundary
$x_{1}=0$
. In this case one has
$$\begin{eqnarray}\displaystyle q_{1}\approx K^{eff}\frac{{\rm\Delta}H}{{\rm\pi}x_{2}}\quad \text{and}\quad q_{2}\approx 0\quad (\text{for }x_{1}\rightarrow 0). & & \displaystyle\end{eqnarray}$$
As a consequence, the flux close to
$x_{1}$
is mainly vertical. Therefore any fluid particle will be ‘forced to pass through’ the inclusion, thus causing a variation (i.e. a fluctuation) of the head with respect to the mean one. More precisely, depending upon the contrast ratio
${\it\kappa}=K_{0}/K^{eff}$
and due to the mass-conservation law, streamlines will: (i) be attracted by the inclusion (similarly to the channelling mechanism) for
${\it\kappa}>1$
; or (ii) try to circumvent the inclusion for
${\it\kappa}<1$
. The deformation of the streamlines in the vicinity of the inclusion determines steeper gradients above/below it, and consequently the heads in the close vicinity of the inclusion are higher (
${\it\kappa}<1$
) or lower (
${\it\kappa}>1$
) than the mean. Hence, the variance
${\it\sigma}_{h}^{2}\equiv \langle h^{(1)2}\rangle$
increases in this zone (figure 4). Such a physical explanation applies to both upstream (
$x_{2}<0$
) and downstream (
$x_{2}>0$
) of the wall. This explains the symmetry of
${\it\sigma}_{h}^{2}$
depicted in figures 4 and 5, as well as the fact that the main source of uncertainty is concentrated below the wall (figure 4).
Figure 5. Dependence of: (i) the normalized variance
${\it\sigma}_{h}^{2}/({\rm\Delta}H{\it\sigma}_{Y})^{2}$
(continuous line), and (ii) the coefficient of variation
$\mathtt{CV}_{h}/{\it\sigma}_{Y}$
(dash-dot line) of the RSF
$h$
upon the polar angle
${\it\theta}\in [-{\rm\pi}/2,{\rm\pi}/2]$
, for some values of the dimensionless distance
$x^{\star }/I$
from the vortex
$\boldsymbol{x}^{\star }\equiv (0,0)$
.
As the flux becomes horizontal, a smaller and smaller amount of fluid particles passes through the inclusion. Indeed, unlike the previous case, the horizontal flux (and consequently the head) is not affected by the elongated shape of the inclusion (see figure 3), and thus the head variance decreases as
${\it\theta}\rightarrow 0$
(figure 5). In the case of a ‘purely horizontal’ flow (i.e.
${\it\theta}\equiv 0$
), the head field is not influenced at all by the perturbation generated by the inclusion, and therefore
${\it\sigma}_{h}^{2}$
vanishes (see figure 5). As the distance
$x^{\star }$
increases (along a given direction
${\it\theta}$
), the head fluctuation (and consequently
${\it\sigma}_{h}^{2}$
) increases, reaching its a maximum at a certain distance. By this distance, the head starts to behave like the mean one (see (2.13)), and consequently the head variance decays with increasing
$x^{\star }$
(see figure 4). Unlike the variance, the coefficient of variation
$\mathtt{CV}_{h}$
(dash-dot lines in the figure 5) reveals that the more uncertain head values (as compared with the mean (2.5)) are those beneath the wall (
${\it\theta}=0$
). The same conclusions can be drawn for either the exponential or the Gaussian model for
${\it\rho}_{Y}$
. An improvement in the agreement between the analytical expression (3.1) and the MCS (see figure 4) can be obtained by using a more accurate (higher-order) finite-difference scheme in the numerical simulations.
Figure 6. (a) Contour lines of the correction function
${\it\psi}\equiv {\it\psi}(\boldsymbol{x}^{\star })$
for exponential
${\it\rho}_{Y}$
. (b) Contour lines of the normalized mean head
$\langle h(\boldsymbol{x}^{\star })\rangle /{\rm\Delta}H$
for
${\it\sigma}_{Y}^{2}=0.5$
computed with: (i) MCS (dashed black thick lines), and (ii) the analytical model (2.10) (blue continuous lines) with exponential
${\it\rho}_{Y}$
. Red dash-dot lines refer to the normalized leading-order term:
$h^{(0)}(\boldsymbol{x}^{\star })/{\rm\Delta}H$
.
In order to show how the heterogeneity affects the spatial distribution of the mean head, in figure 6(a) we have depicted a few contour levels of the function
${\it\psi}$
(see (2.9)–(2.10)). Up to depths smaller than three integral scales (i.e. for
$x_{1}\leqslant 3I$
), the
${\it\psi}$
distribution upstream of the wall (corresponding to
$x_{2}<0$
) is negative, and therefore
${\rm\Psi}>1$
(see (2.9a
)). The consequence is that within such a zone the mean head
$\langle h\rangle$
is larger than
$h^{(0)}$
, which is obtained by assuming
$K\equiv K_{G}$
throughout the domain
${\rm\Omega}$
. Instead, for
$x_{1}>3I$
(and
$x_{2}\leqslant 0$
),
${\rm\Psi}<1$
and, therefore,
$\langle h\rangle <h^{(0)}$
(in agreement with the asymptotic equation (2.13)). The situation is completely reversed downstream of the wall (
$x_{2}>0$
). Such a behaviour is visualized in figure 6(b), wherein we compare the isolines of the mean head computed by the MCS and the analytical model (2.10) for exponential
${\it\rho}_{Y}$
(the same conclusions are drawn for a Gaussian
${\it\rho}_{Y}$
) against the leading-order term (2.5).
4. Analysis of the failure probability: risk quantification
The majority of the engineering analyses aimed at the design of water-retaining structures are deterministic in that the hydraulic conductivity
$K$
is regarded as uniformly distributed over the entire flow domain. Spatial variations of
$K$
are subsequently accounted for by applying (often rather arbitrarily) a safety factor
$s_{f}$
to the exit volumetric flow rate
$Q$
downstream of the wall (see e.g. Lancellotta Reference Lancellotta1993). Such an approach suffers from many flaws (a wide-ranging discussion can be found in Fenton & Griffiths Reference Fenton and Griffiths2008), the most important of which is the total lack of the associated risk. In fact, even if the deterministically predicted
$Q$
is amplified by
$s_{f}$
, there is no a priori guarantee that for the ‘upscaled’ value
$Q_{f}=s_{f}Q$
the probability of failure (due to the well-known piping effect) will be small enough to be tolerated. On the contrary, the stochastic approach provides a way to estimate the probability of failure (risk quantification), therefore leading to a reliability-based design. More precisely, the risk quantification enables one to compute the probability that the actual volumetric flow rate will exceed a certain value (see e.g. Tartakovsky Reference Tartakovsky2013).
In order to compute the probability associated with the RSF
$Q$
, we adopt the log-normal distribution. The feasibility of such a hypothesis has been tested in several studies (see Fenton & Griffiths Reference Fenton and Griffiths2008, and references therein), and it will also be checked in the present study. As a consequence, to determine the probability associated with
$Q$
it suffices to compute the mean
${\it\mu}_{Q}$
and the variance
${\it\sigma}_{Q}^{2}$
of the total flow rate
$Q$
(hereafter per unit transverse length). Thus, we expand the RSF
$Q$
into an asymptotic sequence to obtain
$$\begin{eqnarray}\displaystyle {\it\mu}_{Q}\equiv Q^{(0)}=-\int _{{\it\varrho}}^{x^{\star }}\text{d}s\,q_{1}^{(0)}(0,s)=K_{G}\frac{{\rm\Delta}H}{{\rm\pi}}\ln \left(\frac{x^{\star }}{{\it\varrho}}\right),\quad Q^{(1)}=-\int _{{\it\varrho}}^{x^{\star }}\text{d}s\,q_{1}^{(1)}(0,s). & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
The flux
$\mathbf{q}$
(unlike the hydraulic head
$h$
) is singular at the vortex
$x^{\star }=0$
, and therefore to guarantee the integrability of the second term in (4.1) we have excluded from
${\rm\Omega}^{\star }$
the (very tiny) semi-circle
$\mathscr{C}({\it\varrho})\equiv \{(x_{1},x_{2})\in {\rm\Omega}^{\star }:x_{1}^{2}+x_{2}^{2}\leqslant {\it\varrho}^{2}\}$
of radius
${\it\varrho}=b/2$
. Thus, the variance of the total flow rate is given by
$$\begin{eqnarray}\displaystyle {\it\sigma}_{Q}^{2}=\langle Q^{(1)2}\rangle =\int _{{\it\varrho}}^{x^{\star }}\int _{{\it\varrho}}^{x^{\star }}\text{d}s^{\prime }\,\text{d}s^{\prime \prime }\langle q_{1}^{(1)}(0,s^{\prime })q_{1}^{(1)}(0,s^{\prime \prime })\rangle . & & \displaystyle\end{eqnarray}$$
In particular, to evaluate the variance (4.2) one has to compute the covariance
$$\begin{eqnarray}\displaystyle \langle q_{1}^{(1)}(0,x_{2})q_{1}^{(1)}(0,y_{2})\rangle \equiv C_{q_{1}}(\boldsymbol{x}^{\star };\boldsymbol{y}^{\star })|_{x_{1}=y_{1}=0}=\frac{({\it\sigma}_{Y}K_{G}{\rm\Delta}H)^{2}}{{\rm\pi}^{2}}\mathscr{C}_{q_{1}}(x_{2},y_{2}) & & \displaystyle\end{eqnarray}$$
of the vertical flux downstream of the wall. The scaled covariance
$\mathscr{C}_{q_{1}}$
is expressed in terms of a single quadrature (for details, see appendix C), and consequently the variance
${\it\sigma}_{Q}^{2}$
is obtained from (4.2) by a triple numerical quadrature. For simplicity, we approximate
${\it\rho}_{Y}$
by white noise which leads to a very simple (closed-form) result for the coefficient of variation
$\mathtt{CV}_{Q}={\it\sigma}_{Q}/|{\it\mu}_{Q}|$
, i.e.
$$\begin{eqnarray}\displaystyle \left(\frac{\mathtt{CV}_{Q}}{{\it\sigma}_{Y}}\right)^{2}=1+\frac{{\rm\pi}(x^{\star }-{\it\varrho})^{2}}{2{\it\varrho}x^{\star }(x^{\star }+{\it\varrho})\ln ^{2}(x^{\star }/{\it\varrho})}. & & \displaystyle\end{eqnarray}$$
From (4.4) it is seen that
$\mathtt{CV}_{Q}^{2}$
decays monotonically (for given
${\it\varrho}$
) with the distance
$x^{\star }$
, ranging from the very high values attained in the neighbourhood of the wall (
$x^{\star }\simeq {\it\varrho}$
) to
$\mathtt{CV}_{Q}^{2}\equiv {\it\sigma}_{Y}^{2}$
corresponding to the large-distance value. The highest values of
$\mathtt{CV}_{Q}$
are due to the fact that close to the wall the local vertical flux
$q_{1}(0,x_{2})$
(and consequently
$Q$
) undergoes very large fluctuations. Instead, for
$x^{\star }\gg I$
the flow behaves as a mean uniform one (see (2.13)), and therefore one recovers
$\mathtt{CV}_{Q}^{2}\simeq O({\it\sigma}_{Y}^{2})$
in agreement with previous studies (see e.g. Dagan Reference Dagan1987; Indelman Reference Indelman1996). The property
$\mathtt{CV}_{Q}(\infty )<\mathtt{CV}_{Q}(x^{\star })<\mathtt{CV}_{Q}({\it\varrho})$
is of utility for both design (as will be shown later on) and numerical (to validate/check more involved codes) purposes.
For a reliability-based design, a major goal is to estimate the probability that a ‘given’ design value of the flow rate (say
$Q_{d}$
) underestimates the current one. Such an event implies an unsafe design, and therefore it would be desirable to attach it to a low (failure) probability. The probability that
$Q$
exceeds the value
$Q_{d}$
is computed as
$$\begin{eqnarray}\displaystyle \mathtt{P}_{d}\equiv \mathtt{P}[Q>Q_{d}]=1-F(Q_{d})=\frac{1}{2}\;\text{erfc}\left\{\frac{\ln \left[(Q_{d}/{\it\mu}_{Q})\sqrt{1+\mathtt{CV }_{Q}^{2}}\,\right]}{\sqrt{2\ln (1+\mathtt{CV }_{Q}^{2})}}\right\}, & & \displaystyle\end{eqnarray}$$
where
${\it\mu}_{Q}$
and
$\mathtt{CV}_{Q}$
are given by (4.1) and (4.4), respectively. The probability (4.5) evaluated at
$x^{\star }=I$
and
$x^{\star }=10I$
is depicted in figure 7 along with the failure probability obtained with the MCS, figure 8, and the failure probability (dash-dot lines) corresponding to
$\mathtt{CV}_{Q}\equiv 0$
(homogeneous formation). In the second case, the failure probability is
$1$
as long as the design value
$Q_{d}$
does not exceed
${\it\mu}_{Q}$
; otherwise it is zero, i.e.
$\mathtt{P}_{d}\equiv {\it\chi}({\it\mu}_{Q}-Q_{d})$
. Thus,
$Q_{d}\ll {\it\mu}_{Q}$
means that within almost all the
$K$
-field realizations the flow rates (even those attached to the highest values of
$\mathtt{CV}_{Q}$
, and therefore significantly different from the mean
${\it\mu}_{Q}$
) are greater than
$Q_{d}$
. This explains why
$\mathtt{P}_{d}\sim 1$
for
$Q_{d}\ll {\it\mu}_{Q}$
. As
$Q_{d}$
increases (but still being less than
${\it\mu}_{Q}$
) the outcome depends on whether
$\mathtt{CV}_{Q}$
is small or large. In the first case, most of the flow rates do not differ significantly from
${\it\mu}_{Q}$
, and therefore the majority of them are higher than
$Q_{d}$
. As a consequence, this case is close to the previous one, and therefore
$\mathtt{P}_{d}$
is still approximately
$1$
. On the other hand, a large coefficient of variation
$\mathtt{CV}_{Q}$
results in numerous events where the flow rate does not exceed
$Q_{d}$
, and consequently the failure probability is significantly smaller than
$1$
. Since the coefficient of variation (4.4) is a decreasing function of the distance
$x^{\star }$
, one detects a smaller
$\mathtt{P}_{d}$
for the smaller distance (black lines) downstream of the wall (figure 7).
Figure 7. Probability of the dimensionless volumetric flow rate
$Q/(K_{G}{\rm\Delta}H)$
exceeding a certain design value
$Q_{d}$
. Continuous lines represent the analytical model (4.5), whereas circles pertain to the MCS. Parameter values:
$x^{\star }=I$
(black),
$x^{\star }=10I$
(blue),
${\it\varrho}=0.002I$
, and
${\it\sigma}_{Y}^{2}=0.50$
. The dash-dot lines correspond to a homogeneous (
${\it\sigma}_{Y}^{2}\equiv 0$
) aquifer
${\rm\Omega}$
. In the inset, the horizontal and vertical scales are both expressed in logarithmic scale.
Figure 8. Probability density function of the volumetric flow rate
$Q/(\langle K\rangle {\rm\Delta}H)$
obtained with the MCS (dotted line), along with the fitted log-normal model (continuous line). Parameter values are the same as in figure 7. The
$p$
-value (i.e. the smallest value of the significance level 5 % at which the hypothesis of log-normal distribution would be rejected) for the
${\it\chi}^{2}$
-test of fitting is 68 % and 13 % for
$x^{\star }=I$
and
$x^{\star }=10I$
, respectively.
The case
$Q_{d}>{\it\mu}_{Q}$
is much more interesting from the application point of view. While for a homogeneous medium (dashed-dot lines) the failure probability is zero (therefore leading to a safe design), the medium heterogeneity clearly makes it possible to have
$Q>Q_{d}$
with a probability
$\mathtt{P}_{d}\neq 0$
. This unwarranted event may be associated with an unacceptable result from the safety stand-point. More precisely, even if one amplifies
${\it\mu}_{Q}$
by a safety factor
$s_{f}$
(as is routinely done in the classical approach), there is no a priori guarantee that the failure probability will be small enough to consider the design acceptable. A very simple manner to illustrate such an unwarranted outcome is to provide an answer to the following question: What reliability-based safety factor
$s_{f}^{\star }$
does one have to adopt within a classical design procedure in order to have a failure probability less than a certain value
${\it\alpha}$
?
To answer this question, we define
$Q_{d}^{{\it\alpha}}$
as the design volumetric flow rate corresponding to a failure probability
${\it\alpha}$
, and seek
$s_{f}^{\star }$
so that
$Q_{d}^{{\it\alpha}}=s_{f}^{\star }{\it\mu}_{Q}$
. Here
${\it\mu}_{Q}$
is the volumetric flow rate that a designer would use if, according to the classical approach, the aquifer is regarded as homogeneous. Hence, the answer to the above question is straightforwardly found from figure 7. Indeed, let us assume that
${\it\alpha}=1\,\%$
, then from the inset one recovers
$Q_{d}^{0.01}/(K_{G}{\rm\Delta}H)\approx 30$
for
$x^{\star }=I$
. Then (4.1) gives
$s_{f}^{\star }\approx 30{\rm\pi}/\ln (10^{3})\approx 14$
. This value, which is far beyond the commonly accepted range for
$s_{f}^{\star }$
, clearly demonstrates that the heterogeneity may lead to predictions which are significantly different from those obtained by classical methods. Such a difference is magnified further if one aims to increase the safety level (for instance, when potential risks for human lives are directly/indirectly involved into the design) by requiring that
${\it\alpha}=1$
‰. In these cases some additional devices (such as the insertion of a cut off) would be worth adopting.
5. Concluding remarks
We have developed a procedure to model seepage underneath a water-retaining wall (figure 1) in heterogeneous formations of stationary log-conductivity
$Y$
. Unlike the previous (numerical) studies (see e.g. Griffiths & Fenton Reference Griffiths and Fenton2007; Fenton & Griffiths Reference Fenton and Griffiths2008), here the problem is tackled by means of analytical methods. By dealing with a highly anisotropic porous formation and by adopting a first-order expansion in the variance
${\it\sigma}_{Y}^{2}$
of the RSF
$Y$
, closed-form expressions for the second-order moments of the head
$h$
, and the volumetric flow rate
$Q$
are derived.
The main theoretical achievements of the present paper can be summarized as follows. (i) We have demonstrated that large uncertainty in the head sampling is confined to the close vicinity of the water-retaining wall. This result can be used as a benchmark to check more involved numerical codes, as well as to design proper sampling strategies to monitor the head distribution surrounding the water-retaining structure. (ii) We have derived a general representation of the mean head
$\langle h\rangle =(1-{\it\sigma}_{Y}^{2}{\it\psi})h^{(0)}$
, where
${\it\psi}$
is a characteristic heterogeneity function that can be easily computed after specifying the autocorrelation function
${\it\rho}_{Y}$
. (iii) We have shown that at large distances from the wall the flow behaves as a mean uniform one driven by a mean head, which does not depend upon the shape of the autocorrelation
${\it\rho}_{Y}$
.
Apart from the theoretical interest, the present analysis enables one to assess the risk of occurrence of flow events which may cause the failure (e.g. piping and/or erosion) of civil structures. We found that the probability of failure may be unacceptable even when a relatively large safety factor is applied.
Although the present study shows how the stochastic approach can be successfully applied to solve practical problems, there are still many topics (such as accounting for highly heterogeneous formations or unsteady flow conditions) which remain unresolved and require future investigations.
Acknowledgements
This research was supported by: (i) ‘Programma di scambi internazionali per mobilità di breve durata’ (University of Naples, Italy), (ii) ‘OECD Cooperative Research Programme: Biological Resource Management for Sustainable Agricultural Systems’ (contract: no. JA00073336), (iii) PRIN-project ‘I paesaggi tradizionali dell’agricoltura italiana: definizione di un modello interpretativo multidisciplinare e multiscala finalizzato alla pianificazione e alla gestione’ (contract: no. 2010LE4NBM_007), and (iv) ‘Solute Transport in Heterogeneous Media: Modelling and Computational Aspects’ (Departmental funds). The constructive comments from the three anonymous referees are deeply appreciated.
Appendix A. Computation of the head covariance
In order to compute the head covariance
$C_{h}$
, we preliminarily derive (by the method of moment equations) the cross-covariance
$C_{hY}(\boldsymbol{x},\boldsymbol{y})\equiv \langle h^{(1)}(\boldsymbol{x})Y^{\prime }(\boldsymbol{y})\rangle$
. Thus, we multiply (2.6) by
$Y^{\prime }$
evaluated at
$\boldsymbol{y}\neq \boldsymbol{x}$
, and then take the ensemble average to get
$$\begin{eqnarray}\displaystyle {\rm\nabla}^{2}C_{hY}(\boldsymbol{x},\boldsymbol{y})=-{\it\sigma}_{Y}^{2}\boldsymbol{{\rm\nabla}}{\it\rho}_{Y}(\boldsymbol{x}-\boldsymbol{y})\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}h^{(0)}(\boldsymbol{x}^{\star }), & & \displaystyle\end{eqnarray}$$
the differentiations in (A 1) being in terms of
$\boldsymbol{x}$
. Similarly, we multiply (2.6) by
$h^{(1)}(\boldsymbol{y})$
and average to yield
$$\begin{eqnarray}\displaystyle {\rm\nabla}^{2}C_{h}(\boldsymbol{x},\boldsymbol{y})=-\boldsymbol{{\rm\nabla}}C_{Yh}(\boldsymbol{x},\boldsymbol{y})\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}h^{(0)}(\boldsymbol{x}^{\star }). & & \displaystyle\end{eqnarray}$$
The covariances
$C_{hY}$
–
$C_{h}$
are not stationary in the domain
${\rm\Omega}^{\star }$
due to the non-uniformity of the mean flow there. Instead, they are stationary along the (perpendicular to
${\rm\Omega}^{\star }$
)
$x_{3}$
-axis. It is therefore convenient to take the Fourier transform (FT), i.e.
$$\begin{eqnarray}\displaystyle \text{FT}[f(\boldsymbol{x})]_{\boldsymbol{k}}\equiv \tilde{f}(\boldsymbol{k})=(2{\rm\pi})^{-d/2}\int \text{d}\boldsymbol{x}\,f(\boldsymbol{x})\exp (\jmath \boldsymbol{x}\boldsymbol{\cdot }\boldsymbol{k}) & & \displaystyle\end{eqnarray}$$
(
$d$
being the dimensionality of the Fourier space) along
$r=x_{3}-y_{3}$
(
$d\equiv 1$
in this case). As a consequence, (A 1) is transformed into the following Helmholtz-type equation:
$$\begin{eqnarray}\displaystyle {\rm\nabla}^{2}\tilde{C}_{hY}(\boldsymbol{x}^{\star },\boldsymbol{y}^{\star };k)-k^{2}\tilde{C}_{hY}(\boldsymbol{x}^{\star },\boldsymbol{y}^{\star };k)=-{\it\sigma}_{Y}^{2}\boldsymbol{{\rm\nabla}}\tilde{{\it\rho}}_{Y}(\boldsymbol{x}^{\star }-\boldsymbol{y}^{\star };k)\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}h^{(0)}(\boldsymbol{x}^{\star }). & & \displaystyle\end{eqnarray}$$
The FT
$\tilde{C}_{hY}$
is obtained by means of the Green’s function
$$\begin{eqnarray}\displaystyle G_{k}(\boldsymbol{x}^{\star };{\bf\xi}^{\star })=\frac{1}{2{\rm\pi}}[\text{K}_{0}(|k|r_{-})-\text{K}_{0}(|k|r_{+})],\quad r_{\mp }^{2}=(x_{1}\mp {\it\xi}_{1})^{2}+(x_{2}-{\it\xi}_{2})^{2}, & & \displaystyle\end{eqnarray}$$
solution of the equation
${\rm\nabla}^{2}G_{k}-k^{2}G_{k}=-{\it\delta}(\boldsymbol{x}^{\star }-{\bf\xi}^{\star })$
. Thus, it yields (after integrating by parts, and by accounting for the fact that
$h^{(0)}$
is harmonic)
$$\begin{eqnarray}\displaystyle \tilde{C}_{hY}(\boldsymbol{x}^{\star },\boldsymbol{y}^{\star };k)=-{\it\sigma}_{Y}^{2}\int _{{\rm\Omega}^{\star }}\text{d}{\bf\xi}^{\star }\,\tilde{{\it\rho}}_{Y}({\bf\xi}^{\star }-\boldsymbol{y}^{\star };k)\boldsymbol{{\rm\nabla}}G_{k}(\boldsymbol{x}^{\star };{\bf\xi}^{\star })\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}h^{(0)}({\bf\xi}^{\star }). & & \displaystyle\end{eqnarray}$$
Insertion of FT
$$\begin{eqnarray}\displaystyle \mathtt{FT}[{\it\rho}_{Y}(x_{1})]=\frac{{\it\rho}_{Y}(x_{1})}{(2{\rm\pi})^{1/2}}\int _{-\infty }^{+\infty }\text{d}x_{3}\exp (\jmath kx_{3})=(2{\rm\pi})^{1/2}{\it\rho}_{Y}(x_{1}){\it\delta}(k) & & \displaystyle\end{eqnarray}$$
into (A 6), and recalling that
$$\begin{eqnarray}\displaystyle \mathtt{FT}^{-1}[{\it\delta}(k)G_{k}(\boldsymbol{x}^{\star };{\bf\xi}^{\star })]=-(2{\rm\pi})^{-3/2}\ln \left(\frac{r_{-}}{r_{+}}\right)\equiv (2{\rm\pi})^{-1/2}G^{\star }(\boldsymbol{x}^{\star };{\bf\xi}^{\star }) & & \displaystyle\end{eqnarray}$$
(
$G^{\star }$
being the Green’s function pertaining to
${\rm\Omega}^{\star }$
) leads to
$$\begin{eqnarray}\displaystyle C_{hY}(\boldsymbol{x}^{\star };\boldsymbol{y}^{\star })={\it\sigma}_{Y}^{2}\int _{{\rm\Omega}^{\star }}\text{d}{\bf\xi}^{\star }{\it\rho}_{Y}({\it\xi}_{1}-y_{1})\frac{\partial }{\partial {\it\xi}_{m}}h^{(0)}({\bf\xi}^{\star })\frac{\partial }{\partial {\it\xi}_{m}}G^{\star }(\boldsymbol{x}^{\star };{\bf\xi}^{\star }) & & \displaystyle\end{eqnarray}$$
(summation convention over
$m=1,2$
has been adopted). Hence, integration by parts yields
$$\begin{eqnarray}\displaystyle \frac{C_{hY}}{{\it\sigma}_{Y}^{2}}=[{\it\rho}_{Y}(y_{1})-{\it\rho}_{Y}(x_{1}-y_{1})]h^{(0)}(\boldsymbol{x}^{\star })-\int _{{\rm\Omega}^{\star }}\text{d}{\bf\xi}^{\star }\frac{\partial }{\partial {\it\xi}_{1}}{\it\rho}_{Y}({\it\xi}_{1}-y_{1})h^{(0)}({\bf\xi}^{\star })\frac{\partial }{\partial {\it\xi}_{1}}G^{\star }(\boldsymbol{x}^{\star };{\bf\xi}^{\star }), & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
where we have used the property
${\rm\nabla}^{2}G^{\star }(\boldsymbol{x}^{\star };{\bf\xi}^{\star })={\it\delta}(\boldsymbol{x}^{\star }-{\bf\xi}^{\star })$
. The quadrature over
${\it\xi}_{2}$
appearing in the integral on the right-hand side of (A 10) is easily computed by combining the definition of FT and convolution as follows:
$$\begin{eqnarray}\displaystyle \mathscr{I}(\boldsymbol{x}^{\star };{\it\xi}_{1}) & = & \displaystyle \int _{-\infty }^{+\infty }\text{d}{\it\xi}_{2}\,h^{(0)}({\bf\xi}^{\star })\frac{\partial }{\partial {\it\xi}_{1}}G^{\star }(\boldsymbol{x}^{\star };{\bf\xi}^{\star })=(2{\rm\pi})^{1/2}\lim _{k\rightarrow 0}\mathtt{FT}\left[h^{(0)}({\bf\xi}^{\star })\frac{\partial }{\partial {\it\xi}_{1}}G^{\star }(\boldsymbol{x}^{\star };{\bf\xi}^{\star })\right]_{k}\nonumber\\ \displaystyle & = & \displaystyle \lim _{k\rightarrow 0}\int _{-\infty }^{+\infty }\text{d}p\,\tilde{h}^{(0)}({\it\xi}_{1},k-p)\frac{\partial }{\partial {\it\xi}_{1}}\tilde{G}^{\star }(\boldsymbol{x}^{\star };{\it\xi}_{1},p).\end{eqnarray}$$
By recalling that
$$\begin{eqnarray}\displaystyle & \displaystyle \mathtt{FT}[h^{(0)}({\bf\xi}^{\star })]_{k}=\frac{\jmath {\rm\Delta}H}{(2{\rm\pi})^{1/2}}\frac{\exp (-|k|{\it\xi}_{1})}{k}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \mathtt{FT}[G^{\star }(\boldsymbol{x}^{\star };{\bf\xi}^{\star })]_{k}=\frac{\exp (\jmath kx_{2})}{2|k|(2{\rm\pi})^{1/2}}\{\exp [-(x_{1}+{\it\xi}_{1})|k|]-\exp (-|x_{1}-{\it\xi}_{1}||k|)\}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 2\mathscr{I}(\boldsymbol{x}^{\star };{\it\xi})=-h^{(0)}(2x_{1}+{\it\xi},x_{2})-[{\it\chi}(x_{1}-{\it\xi})-{\it\chi}({\it\xi}-x_{1})]h^{(0)}(x_{1}+|x_{1}-{\it\xi}|,x_{2}),\qquad & & \displaystyle\end{eqnarray}$$
where
${\it\chi}\equiv {\it\chi}(\cdot )$
is the Heaviside step function. Insertion of (A 14) into (A 10) gives
$$\begin{eqnarray}\displaystyle C_{hY}(\boldsymbol{x}^{\star };y_{1})=\frac{{\it\sigma}_{Y}^{2}}{2}{\rm\Psi}_{hY}(\boldsymbol{x}^{\star };y_{1}), & & \displaystyle\end{eqnarray}$$
with
$$\begin{eqnarray}\displaystyle & & \displaystyle {\rm\Psi}_{hY}(\boldsymbol{x}^{\star };y_{1})=2[{\it\rho}_{Y}(y_{1})-{\it\rho}_{Y}(x_{1}-y_{1})]h^{(0)}(\boldsymbol{x}^{\star })+\int _{0}^{x_{1}}\text{d}{\it\xi}h^{(0)}(2x_{1}-{\it\xi},x_{2})\frac{\partial }{\partial {\it\xi}}{\it\rho}_{Y}({\it\xi}-y_{1})\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\int _{0}^{\infty }\text{d}{\it\xi}h^{(0)}(2x_{1}+{\it\xi},x_{2})\frac{\partial }{\partial {\it\xi}}{\it\rho}_{Y}({\it\xi}-y_{1})-\int _{x_{1}}^{\infty }\text{d}{\it\xi}h^{(0)}({\it\xi},x_{2})\frac{\partial }{\partial {\it\xi}}{\it\rho}_{Y}({\it\xi}-y_{1})\nonumber\\ \displaystyle & & \displaystyle \quad =2{\it\rho}_{Y}(y_{1})[h^{(0)}(\boldsymbol{x}^{\star })-h^{(0)}(2x_{1},x_{2})]-\int _{0}^{x_{1}}\text{d}{\it\xi}{\it\rho}_{Y}({\it\xi}-y_{1})\frac{\partial }{\partial {\it\xi}}h^{(0)}(2x_{1}-{\it\xi},x_{2})\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\int _{x_{1}}^{\infty }\text{d}{\it\xi}{\it\rho}_{Y}({\it\xi}-y_{1})\frac{\partial }{\partial {\it\xi}}h^{(0)}({\it\xi},x_{2})-\int _{0}^{\infty }\text{d}{\it\xi}{\it\rho}_{Y}({\it\xi}-y_{1})\frac{\partial }{\partial {\it\xi}}h^{(0)}(2x_{1}+{\it\xi},x_{2}).\qquad \quad\end{eqnarray}$$
For
$x_{1}=0$
the cross-covariance (A 15) vanishes due to the fact that the boundary condition requires a given (i.e. deterministic) head, and therefore the head fluctuation there is zero.
The head covariance is obtained from (A 2) by means of the Green’s function
$$\begin{eqnarray}\displaystyle G(\boldsymbol{x};{\bf\xi})=\frac{1}{4{\rm\pi}}\left(\frac{1}{{\it\rho}_{-}}-\frac{1}{{\it\rho}_{+}}\right),\quad {\it\rho}_{\mp }=\sqrt{(x_{1}\mp {\it\xi}_{1})^{2}+(x_{2}-{\it\xi}_{2})^{2}+(x_{3}-{\it\xi}_{3})^{2}}\qquad \quad & & \displaystyle\end{eqnarray}$$
pertaining to
${\rm\Omega}$
, and integrating by parts, i.e.
$$\begin{eqnarray}\displaystyle C_{h}(\boldsymbol{x},\boldsymbol{y})=\int _{0}^{\infty }\text{d}{\it\xi}_{1}C_{hY}(\boldsymbol{y}^{\star },{\it\xi}_{1})\int _{-\infty }^{+\infty }\int _{-\infty }^{+\infty }\text{d}{\it\xi}_{2}\,\text{d}{\it\xi}_{3}\frac{\partial }{\partial {\it\xi}_{m}}h^{(0)}({\bf\xi}^{\star })\frac{\partial }{\partial {\it\xi}_{m}}G(\boldsymbol{x};{\bf\xi}). & & \displaystyle\end{eqnarray}$$
The double quadrature over
${\bf\xi}_{h}\equiv ({\it\xi}_{2},{\it\xi}_{3})\in \mathbb{R}^{2}$
is evaluated in analogy to (A 11) as
$$\begin{eqnarray}\displaystyle & & \displaystyle \int \text{d}{\bf\xi}_{h}\frac{\partial }{\partial {\it\xi}_{m}}G(\boldsymbol{x};{\bf\xi})\frac{\partial }{\partial {\it\xi}_{m}}h^{(0)}({\bf\xi}^{\star })=2{\rm\pi}\lim _{k_{h}\rightarrow 0}\mathtt{FT}\left[\frac{\partial }{\partial {\it\xi}_{m}}G(\boldsymbol{x};{\bf\xi})\frac{\partial }{\partial {\it\xi}_{m}}h^{(0)}({\bf\xi}^{\star })\right]_{\boldsymbol{ k}_{h}}\nonumber\\ \displaystyle & & \displaystyle \quad =\lim _{k_{h}\rightarrow 0}\int \text{d}\boldsymbol{p}_{h}\,\mathtt{FT}\left[\frac{\partial }{\partial {\it\xi}_{m}}G(\boldsymbol{x};{\bf\xi})\right]_{\boldsymbol{p}_{h}}\mathtt{FT}\left[\frac{\partial }{\partial {\it\xi}_{m}}h^{(0)}({\bf\xi}^{\star })\right]_{\boldsymbol{k}_{h}-\boldsymbol{p}_{h}}\quad (m=1,2).\end{eqnarray}$$
On skipping the algebraic derivations, one comes up with
$$\begin{eqnarray}\displaystyle 2\int \text{d}{\bf\xi}_{h}\frac{\partial }{\partial {\it\xi}_{m}}G(\boldsymbol{x};{\bf\xi})\frac{\partial }{\partial {\it\xi}_{m}}h^{(0)}({\bf\xi}^{\star })={\it\chi}({\it\xi}_{1}-x_{1})\frac{\partial }{\partial {\it\xi}_{1}}h^{(0)}(2{\it\xi}_{1}-x_{1},x_{2})\!-\!\frac{\partial }{\partial {\it\xi}_{1}}h^{(0)}(2{\it\xi}_{1}+x_{1},x_{2}).\hspace{-12.0pt} & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
Substitution into (A 18) leads to
$$\begin{eqnarray}\displaystyle C_{h} & = & \displaystyle \frac{1}{2}\int _{x_{1}}^{\infty }\text{d}{\it\xi}C_{hY}(\boldsymbol{y}^{\star },{\it\xi})\frac{\partial }{\partial {\it\xi}}h^{(0)}(2{\it\xi}-x_{1},x_{2})-\frac{1}{2}\int _{0}^{\infty }\text{d}{\it\xi}C_{hY}(\boldsymbol{y}^{\star },{\it\xi})\frac{\partial }{\partial {\it\xi}}h^{(0)}(2{\it\xi}+x_{1},x_{2})\nonumber\\ \displaystyle & = & \displaystyle \frac{{\it\sigma}_{Y}^{2}}{4}\int _{x_{1}}^{\infty }\text{d}{\it\xi}\left[{\rm\Psi}_{hY}\left(\boldsymbol{y}^{\star },\frac{{\it\xi}+x_{1}}{2}\right)-{\rm\Psi}_{hY}\left(\boldsymbol{y}^{\star },\frac{{\it\xi}-x_{1}}{2}\right)\right]\frac{\partial }{\partial {\it\xi}}h^{(0)}({\it\xi},x_{2}),\end{eqnarray}$$
where we have accounted for (A 15). To reduce the computation of
$C_{h}$
to the evaluation of a single quadrature, we insert (A 16) into (A 21) to give
$$\begin{eqnarray}\displaystyle C_{h}(\boldsymbol{x}^{\star },\boldsymbol{y}^{\star })={\displaystyle \frac{{\it\sigma}_{Y}^{2}}{4}}\mathop{\sum }_{k=1}^{4}\mathscr{C}_{k}(\boldsymbol{x}^{\star },\boldsymbol{y}^{\star }), & & \displaystyle\end{eqnarray}$$
where we have set
$$\begin{eqnarray}\displaystyle & \displaystyle \mathscr{C}_{1}(\boldsymbol{x}^{\star },\boldsymbol{y}^{\star })=2h^{(0)}(\boldsymbol{y}^{\star })\int _{x_{1}}^{\infty }\text{d}{\it\xi}[\mathscr{R}_{0}({\it\xi})-\mathscr{R}_{y_{1}}({\it\xi})]\frac{\partial }{\partial {\it\xi}}h^{(0)}({\it\xi},x_{2}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \mathscr{C}_{2}(\boldsymbol{x}^{\star },\boldsymbol{y}^{\star })=\int _{x_{1}}^{\infty }\int _{0}^{y_{1}}\text{d}{\it\xi}^{\prime }{\it\xi}^{\prime \prime }h^{(0)}(2y_{1}-{\it\xi}^{\prime \prime },y_{2})\frac{\partial }{\partial {\it\xi}^{\prime }}h^{(0)}({\it\xi}^{\prime },x_{2})\frac{\partial }{\partial {\it\xi}^{\prime \prime }}\mathscr{R}_{{\it\xi}^{\prime \prime }}({\it\xi}^{\prime }), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \mathscr{C}_{3}(\boldsymbol{x}^{\star },\boldsymbol{y}^{\star })=\int _{x_{1}}^{\infty }\int _{0}^{\infty }\text{d}{\it\xi}^{\prime }{\it\xi}^{\prime \prime }h^{(0)}(2y_{1}+{\it\xi}^{\prime \prime },y_{2})\frac{\partial }{\partial {\it\xi}^{\prime }}h^{(0)}({\it\xi}^{\prime },x_{2})\frac{\partial }{\partial {\it\xi}^{\prime \prime }}\mathscr{R}_{{\it\xi}^{\prime \prime }}({\it\xi}^{\prime }), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \mathscr{C}_{4}(\boldsymbol{x}^{\star },\boldsymbol{y}^{\star })=-\int _{x_{1}}^{\infty }\int _{y_{1}}^{\infty }\text{d}{\it\xi}^{\prime }{\it\xi}^{\prime \prime }h^{(0)}({\it\xi}^{\prime \prime },y_{2})\frac{\partial }{\partial {\it\xi}^{\prime }}h^{(0)}({\it\xi}^{\prime },x_{2})\frac{\partial }{\partial {\it\xi}^{\prime \prime }}\mathscr{R}_{{\it\xi}^{\prime \prime }}({\it\xi}^{\prime }), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathscr{R}_{{\it\alpha}}({\it\beta})\equiv {\it\rho}_{Y}\left({\it\alpha}-\frac{{\it\beta}+x_{1}}{2}\right)-{\it\rho}_{Y}\left({\it\alpha}-\frac{{\it\beta}-x_{1}}{2}\right)\!. & & \displaystyle\end{eqnarray}$$
Integration by parts over
${\it\xi}^{\prime \prime }$
leads to
$$\begin{eqnarray}\displaystyle \bar{c} & = & \displaystyle \mathop{\sum }_{k=1}^{4}\mathscr{C}_{k}(\boldsymbol{x}^{\star },\boldsymbol{y}^{\star })=2[h^{(0)}(\boldsymbol{y}^{\star })-h^{(0)}(2y_{1},y_{2})]\int _{x_{1}}^{\infty }\text{d}{\it\xi}\mathscr{R}_{0}({\it\xi})\frac{\partial }{\partial {\it\xi}}h^{(0)}({\it\xi},x_{2})\nonumber\\ \displaystyle & & \displaystyle -\,\int _{x_{1}}^{\infty }\text{d}{\it\xi}^{\prime }\frac{\partial }{\partial {\it\xi}^{\prime }}h^{(0)}({\it\xi}^{\prime },x_{2})\left[\int _{0}^{y_{1}}\text{d}{\it\xi}^{\prime \prime }\mathscr{R}_{{\it\xi}^{\prime \prime }}({\it\xi}^{\prime })\frac{\partial }{\partial {\it\xi}^{\prime \prime }}h^{(0)}(2y_{1}-{\it\xi}^{\prime \prime },y_{2})\right.\nonumber\\ \displaystyle & & \displaystyle +\,\left.\int _{0}^{\infty }\text{d}{\it\xi}^{\prime \prime }\mathscr{R}_{{\it\xi}^{\prime \prime }}({\it\xi}^{\prime })\frac{\partial }{\partial {\it\xi}^{\prime \prime }}h^{(0)}(2y_{1}+{\it\xi}^{\prime \prime },y_{2})-\int _{y_{1}}^{\infty }\text{d}{\it\xi}^{\prime \prime }\mathscr{R}_{{\it\xi}^{\prime \prime }}({\it\xi}^{\prime })\frac{\partial }{\partial {\it\xi}^{\prime \prime }}h^{(0)}({\it\xi}^{\prime \prime },y_{2})\right]\!.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
We now change the order of integration in the double quadratures appearing in (A 28), and compute one integral to get
$$\begin{eqnarray}\displaystyle & & \displaystyle \bar{c}=2[h^{(0)}(\boldsymbol{y}^{\star })-h^{(0)}(2y_{1},y_{2})]\int _{x_{1}}^{+\infty }\text{d}v\mathscr{R}_{0}(v)\frac{\partial }{\partial v}h^{(0)}(v,x_{2})+x_{2}y_{2}\left(\frac{{\rm\Delta}H}{{\rm\pi}}\right)^{2}{\it\Phi}(\boldsymbol{x}^{\star },\boldsymbol{y}^{\star }),\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{{\it\Phi}(\boldsymbol{x}^{\star },\boldsymbol{y}^{\star })}{4}=\int _{-\infty }^{+\infty }\text{d}v{\it\rho}_{Y}(v)\mathscr{F}(2v+x_{1};\infty )-\int _{-\infty }^{y_{1}-x_{1}}\text{d}v{\it\rho}_{Y}(v)\mathscr{F}(2v+x_{1};2y_{1}-x_{1}-2v)\nonumber\\ \displaystyle & & \displaystyle \quad -\,\int _{y_{1}-x_{1}}^{+\infty }\text{d}v{\it\rho}_{Y}(v)\mathscr{F}(2v+x_{1};x_{1})+\int _{-\infty }^{+\infty }\text{d}v{\it\rho}_{Y}(v)\mathscr{F}(2v-x_{1}+4y_{1};\infty )\nonumber\\ \displaystyle & & \displaystyle \quad -\,\int _{-\infty }^{0}\text{d}v{\it\rho}_{Y}(v)\mathscr{F}(2v-x_{1}+4y_{1};x_{1}-2v)-\int _{0}^{+\infty }\text{d}v{\it\rho}_{Y}(v)\mathscr{F}(2v-x_{1}+4y_{1};x_{1})\nonumber\\ \displaystyle & & \displaystyle \quad +\,\int _{-\infty }^{y_{1}}\text{d}v{\it\rho}_{Y}(v)\mathscr{F}(2v-x_{1}-4y_{1};x_{1}+2y_{1})-\int _{-\infty }^{0}\text{d}v{\it\rho}_{Y}(v)\mathscr{F}(2v-x_{1}-4y_{1};x_{1}-2v)\nonumber\\ \displaystyle & & \displaystyle \quad -\,\int _{0}^{y_{1}}\text{d}v{\it\rho}_{Y}(v)\mathscr{F}(2v-x_{1}-4y_{1};x_{1})-\int _{-\infty }^{+\infty }\text{d}v{\it\rho}_{Y}(v)\mathscr{F}(2v-x_{1};\infty )\nonumber\\ \displaystyle & & \displaystyle \quad +\,\int _{-\infty }^{y_{1}}\text{d}v{\it\rho}_{Y}(v)\mathscr{F}(2v-x_{1};2y_{1}+x_{1}-2v)+\int _{y_{1}}^{+\infty }\text{d}v{\it\rho}_{Y}(v)\mathscr{F}(2v-x_{1};x_{1})\nonumber\\ \displaystyle & & \displaystyle \quad -\,\int _{-\infty }^{+\infty }\text{d}v{\it\rho}_{Y}(v)\mathscr{F}(2v+x_{1}+4y_{1};\infty )+\int _{-\infty }^{-x_{1}}\text{d}v{\it\rho}_{Y}(v)\mathscr{F}(2v+x_{1}+4y_{1};-2v-x_{1})\nonumber\\ \displaystyle & & \displaystyle \quad +\,\int _{-x_{1}}^{+\infty }\text{d}v{\it\rho}_{Y}(v)\mathscr{F}(2v+x_{1}+4y_{1};x_{1})-\int _{-\infty }^{y_{1}-x_{1}}\text{d}v{\it\rho}_{Y}(v)\mathscr{F}(2v+x_{1}-4y_{1};\infty )\nonumber\\ \displaystyle & & \displaystyle \quad +\,\int _{-\infty }^{-x_{1}}\text{d}v{\it\rho}_{Y}(v)\mathscr{F}(2v+x_{1}-4y_{1};-2v-x_{1})+\int _{-x_{1}}^{y_{1}-x_{1}}\text{d}v{\it\rho}_{Y}(v)\mathscr{F}(2v+x_{1}-4y_{1};x_{1}),\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathscr{F}({\it\alpha};u) & = & \displaystyle \frac{1}{[{\it\alpha}^{2}+(x_{2}+2y_{2})^{2}][{\it\alpha}^{2}+(x_{2}-2y_{2})^{2}]}\nonumber\\ \displaystyle & & \displaystyle \times \,\left\{\frac{{\it\alpha}^{2}-(x_{2}^{2}-4y_{2}^{2})}{x_{2}}\arctan \left(\frac{u}{x_{2}}\right)\right.\nonumber\\ \displaystyle & & \displaystyle +\,\left.\frac{{\it\alpha}^{2}+(x_{2}^{2}-4y_{2}^{2})}{2y_{2}}\arctan \left(\frac{u+{\it\alpha}}{2y_{2}}\right)+{\it\alpha}\ln \left[\frac{({\it\alpha}+u)^{2}+4y_{2}^{2}}{u^{2}+x_{2}^{2}}\right]\right\}\!.\quad\end{eqnarray}$$
Appendix B. Computation of the normalized correction (2.10)
To compute it, we first derive the second-order correction
$h^{(2)}$
to the head. This is obtained from (2.4) for
$n=2$
, and it is as follows:
$$\begin{eqnarray}\displaystyle & & \displaystyle h^{(2)}(\boldsymbol{x})=-\int _{{\rm\Omega}}\text{d}{\bf\xi}G(\boldsymbol{x};{\bf\xi})\frac{\partial }{\partial {\it\xi}_{m}}Y^{\prime }({\bf\xi})\frac{\partial }{\partial {\it\xi}_{m}}h^{(1)}({\bf\xi})\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{{\rm\Omega}}\text{d}{\bf\xi}Y^{\prime }({\bf\xi})\frac{\partial }{\partial {\it\xi}_{m}}h^{(1)}({\bf\xi})\frac{\partial }{\partial {\it\xi}_{m}}G(\boldsymbol{x};{\bf\xi})-\frac{1}{2}\int _{{\rm\Omega}}\text{d}{\bf\xi}G(\boldsymbol{x};{\bf\xi})\frac{\partial }{\partial {\it\xi}_{m}}Y^{\prime 2}({\bf\xi})\frac{\partial }{\partial {\it\xi}_{m}}h^{(0)}({\bf\xi})\qquad\end{eqnarray}$$
(the last part has been obtained by virtue of (2.6)). Then, taking the expectation into (B 1) and using the stationarity of
$Y$
, leads to
$$\begin{eqnarray}\displaystyle \langle h^{(2)}(\boldsymbol{x})\rangle =\int _{{\rm\Omega}^{\star }}\text{d}{\bf\xi}^{\star }{\it\sigma}_{E_{m}Y}({\bf\xi}^{\star })\frac{\partial }{\partial {\it\xi}_{m}}\int _{-\infty }^{+\infty }\text{d}{\it\xi}_{3}G(\boldsymbol{x};{\bf\xi})\quad (m=1,2), & & \displaystyle\end{eqnarray}$$
the cross-variance appearing in (B 2) being obtained from (A 15) in appendix A as
$$\begin{eqnarray}\displaystyle {\it\sigma}_{E_{m}Y}(\boldsymbol{x}^{\star })=\lim _{y_{1}\rightarrow x_{1}}\frac{\partial }{\partial x_{m}}C_{hY}(\boldsymbol{x}^{\star },y_{1}). & & \displaystyle\end{eqnarray}$$
In (B 2) the quadrature over
${\it\xi}_{3}$
is easily carried out after noting that
$$\begin{eqnarray}\displaystyle \int _{-\infty }^{+\infty }\text{d}{\it\xi}_{3}G(\boldsymbol{x};{\bf\xi})=(2{\rm\pi})^{1/2}\lim _{k\rightarrow 0}G_{k}(\boldsymbol{x}^{\star };{\bf\xi}^{\star })=G^{\star }(\boldsymbol{x}^{\star };{\bf\xi}^{\star }). & & \displaystyle\end{eqnarray}$$
Hence, the
${\it\sigma}_{Y}^{2}$
-order correction to the mean head is
$$\begin{eqnarray}\displaystyle \langle h^{(2)}(\boldsymbol{x}^{\star })\rangle =\int _{{\rm\Omega}^{\star }}\text{d}{\bf\xi}^{\star }{\it\sigma}_{E_{m}Y}({\bf\xi}^{\star })\frac{\partial }{\partial {\it\xi}_{m}}G^{\star }(\boldsymbol{x}^{\star };{\bf\xi}^{\star }). & & \displaystyle\end{eqnarray}$$
Insertion of (A 15)–(A 16) into (B 5) provides
$$\begin{eqnarray}\displaystyle & & \displaystyle {\it\sigma}_{Y}^{-2}\langle h^{(2)}(\boldsymbol{x}^{\star })\rangle =\int _{-x_{1}}^{0}\text{d}u{\it\rho}_{Y}(u)\frac{\partial }{\partial u}h^{(0)}(x_{1}-u,x_{2})+\int _{-x_{1}}^{\infty }\text{d}u{\it\rho}_{Y}(u)\frac{\partial }{\partial u}h^{(0)}(u+3x_{1},x_{2})\nonumber\\ \displaystyle & & \displaystyle \quad -\,\frac{x_{1}}{{\rm\pi}}\int _{{\rm\Omega}^{\star }}\frac{\text{d}{\bf\xi}^{\star }{\it\rho}_{Y}({\it\xi}_{1})}{x_{1}^{2}+(x_{2}-{\it\xi}_{2})^{2}}\frac{\partial }{\partial {\it\xi}_{1}}h^{(0)}({\bf\xi}^{\star })+2\int _{{\rm\Omega}^{\star }}\text{d}{\bf\xi}^{\star }{\it\rho}_{Y}({\it\xi}_{1})\frac{\partial }{\partial {\it\xi}_{m}}G^{\star }(\boldsymbol{x}^{\star };{\bf\xi}^{\star })\frac{\partial }{\partial {\it\xi}_{m}}h^{(0)}({\bf\xi}^{\star })\nonumber\\ \displaystyle & & \displaystyle \quad -\,2\int _{{\rm\Omega}^{\star }}\text{d}{\bf\xi}^{\star }\frac{\partial }{\partial {\it\xi}_{1}}G^{\star }(\boldsymbol{x}^{\star };{\bf\xi}^{\star })\frac{\partial }{\partial {\it\xi}_{1}}h^{(0)}({\bf\xi}^{\star })-2\int _{{\rm\Omega}^{\star }}\text{d}{\bf\xi}^{\star }{\it\rho}_{Y}({\it\xi}_{1})\frac{\partial }{\partial {\it\xi}_{2}}G^{\star }(\boldsymbol{x}^{\star };{\bf\xi}^{\star })\frac{\partial }{\partial {\it\xi}_{2}}h^{(0)}(2{\it\xi}_{1},{\it\xi}_{2})\nonumber\\ \displaystyle & & \displaystyle \quad +\,\int _{0}^{\infty }\text{d}u{\it\rho}_{Y}(u)\frac{\partial }{\partial u}\int _{{\rm\Omega}^{\star }}\text{d}{\bf\xi}^{\star }\frac{\partial }{\partial {\it\xi}_{2}}G^{\star }(\boldsymbol{x}^{\star };{\bf\xi}^{\star })\frac{\partial }{\partial {\it\xi}_{2}}h^{(0)}(u+{\it\xi}_{1},{\it\xi}_{2}).\end{eqnarray}$$
Finally, carrying out the inner quadratures and dividing the result by the zero-order approximation (2.5) leads to (2.10).
Appendix C. Covariance of the vertical flux downstream the wall
To compute the covariance
$C_{q_{1}}(\boldsymbol{x},\boldsymbol{y})=\langle q^{(1)}(\boldsymbol{x})q^{(1)}(\boldsymbol{y})\rangle$
of
$q_{1}$
, we represent the flux fluctuation (2.7) as
$$\begin{eqnarray}\displaystyle -\frac{q_{\ell }^{(1)}(\boldsymbol{x})}{K_{G}}=Y^{\prime }(\boldsymbol{x})\frac{\partial }{\partial x_{\ell }}h^{(0)}(\boldsymbol{x}^{\star })+\frac{\partial }{\partial x_{\ell }}\int _{{\rm\Omega}}\text{d}{\bf\xi}Y^{\prime }({\bf\xi})\frac{\partial }{\partial {\it\xi}_{m}}G(\boldsymbol{x};{\bf\xi})\frac{\partial }{\partial {\it\xi}_{m}}h^{(0)}({\bf\xi}^{\star })\quad (m=1,2), & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
where we have expressed the head fluctuation
$h^{(1)}$
, the solution of (2.6), by means of the Green’s function (A 17) pertaining to the half-space
${\rm\Omega}$
. Hence, the covariance of the vertical flux is written
$$\begin{eqnarray}\displaystyle & & \displaystyle C_{q_{1}}(\boldsymbol{x}^{\star },\boldsymbol{y}^{\star })=(K_{G}{\it\sigma}_{Y})^{2}\left[{\it\rho}_{Y}(x_{1}-y_{1})\frac{\partial }{\partial x_{1}}h^{(0)}(\boldsymbol{x}^{\star })\frac{\partial }{\partial y_{1}}h^{(0)}(\boldsymbol{y}^{\star })\right.\nonumber\\ \displaystyle & & \displaystyle \quad +\,\frac{1}{2}\frac{\partial }{\partial x_{1}}h^{(0)}(\boldsymbol{x}^{\star })\int _{0}^{\infty }\text{d}{\it\xi}{\it\rho}_{Y}({\it\xi}-x_{1})\mathscr{T}(\boldsymbol{y}^{\star };{\it\xi})+\frac{1}{2}\frac{\partial }{\partial y_{1}}h^{(0)}(\boldsymbol{y}^{\star })\int _{0}^{\infty }\text{d}{\it\xi}{\it\rho}_{Y}({\it\xi}-y_{1})\mathscr{T}(\boldsymbol{x}^{\star };{\it\xi})\nonumber\\ \displaystyle & & \displaystyle \quad +\,\left.\frac{1}{4}\int _{0}^{\infty }\int _{0}^{\infty }\text{d}{\it\xi}_{1}^{\prime }\,\text{d}{\it\xi}_{1}^{\prime \prime }{\it\rho}_{Y}({\it\xi}_{1}^{\prime }-{\it\xi}_{1}^{\prime \prime })\mathscr{T}(\boldsymbol{x}^{\star };{\it\xi}_{1}^{\prime })\mathscr{T}(\boldsymbol{y}^{\star };{\it\xi}_{1}^{\prime \prime })\right],\end{eqnarray}$$
where we have set
$$\begin{eqnarray}\displaystyle \mathscr{T}(\boldsymbol{x}^{\star };{\it\xi}_{1}) & = & \displaystyle \frac{\partial }{\partial x_{1}}\int \text{d}{\bf\xi}_{h}\frac{\partial }{\partial {\it\xi}_{m}}G(\boldsymbol{x};{\bf\xi})\frac{\partial }{\partial {\it\xi}_{m}}h^{(0)}({\bf\xi}^{\star })=-{\it\delta}({\it\xi}_{1}-x_{1})\frac{\partial }{\partial {\it\xi}_{1}}h^{(0)}(2{\it\xi}_{1}-x_{1},x_{2})\nonumber\\ \displaystyle & & \displaystyle +\,{\it\chi}({\it\xi}_{1}-x_{1})\frac{\partial ^{2}}{\partial x_{1}\partial {\it\xi}_{1}}h^{(0)}(2{\it\xi}_{1}-x_{1},x_{2})-\frac{\partial ^{2}}{\partial x_{1}\partial {\it\xi}_{1}}h^{(0)}(2{\it\xi}_{1}+x_{1},x_{2})\end{eqnarray}$$
(the last part has been obtained by carrying out the derivative of the second of (A 20) with respect to
$x_{1}$
). Hence, the scaled covariance
$\mathscr{C}_{q_{1}}$
in (4.3) can be written (after reducing the double quadrature appearing in (C 2) to a single one) as
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathscr{C}_{q_{1}}(x_{2},y_{2})=\frac{1}{x_{2}y_{2}}+\frac{4}{x_{2}y_{2}}\int _{0}^{\infty }\frac{\text{d}u\,u}{(1+4u^{2})^{2}}[2{\it\rho}_{Y}(y_{2}u)+{\it\rho}_{Y}(x_{2}u)]\nonumber\\ \displaystyle & & \displaystyle \quad +\,\frac{\partial ^{2}}{\partial x_{2}\partial y_{2}}\int _{0}^{\infty }\frac{\text{d}u{\it\rho}_{Y}(u)}{4u^{2}+(x_{2}+y_{2})^{2}}\left[2{\rm\pi}(x_{2}+y_{2})-\frac{\mathscr{A}(u;x_{2},y_{2})+\mathscr{A}(u;y_{2},x_{2})+\mathscr{B}(u;x_{2},y_{2})}{4u^{2}+(x_{2}-y_{2})^{2}}\right]\!,\hspace{-10.00002pt}\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
where
$$\begin{eqnarray}\displaystyle & \displaystyle \mathscr{A}(u;x_{2},y_{2})=y_{2}(4u^{2}+y_{2}^{2}-x_{2}^{2})\arctan \left(\frac{2u}{y_{2}}\right), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \mathscr{B}(u;x_{2},y_{2})=u(4u^{2}+y_{2}^{2}+x_{2}^{2})\ln \frac{(x_{2}y_{2})^{2}}{(4u^{2}+x_{2}^{2})(4u^{2}+y_{2}^{2})}. & \displaystyle\end{eqnarray}$$
