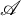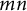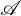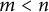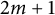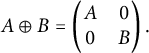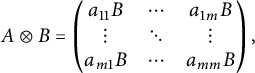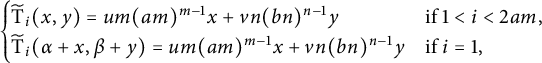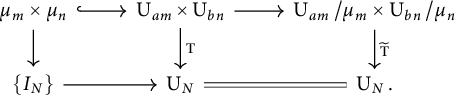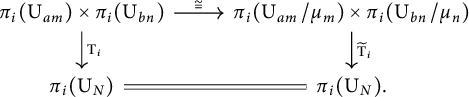1 Introduction
The classical theory of central simple algebras over a field was generalized by Azumaya [Reference Azumaya5] and Auslander–Goldman [Reference Auslander and Goldman4] by introducing the concept of an Azumaya algebra over a local commutative ring and over an arbitrary commutative ring, respectively. This concept was generalized by Grothendieck [Reference Grothendieck7, 1.1] to the notion of a topological Azumaya algebra.
Grothendieck [Reference Grothendieck7, Section 2] defined the notion of an Azumaya algebra over any locally-ringed topos
$(X_{\operatorname {\mathrm {\text {\'et}}}}, \mathscr {O}_{X})$
where
$X_{\operatorname {\mathrm {\text {\'et}}}}$
is an étale topos of a scheme X, and the local ring
$\mathscr {O}_{X}$
is the structure sheaf of X.
Definition 1.1 A topological Azumaya algebra of degree n over a topological space X is a bundle of associative and unital complex algebras over X that is locally isomorphic to the matrix algebra
$\operatorname {\mathrm {M}}_{n \times n}({\mathbb {C}})$
where
${\mathbb {C}}$
has its ordinary topology, [Reference Grothendieck7, 1.1].
Topological Azumaya algebras are classified by pointed homotopy classes of maps to
$\operatorname {\mathrm {B}}\operatorname {\mathrm {PGL}}_{n}({\mathbb {C}})$
, as there is a bijective correspondence
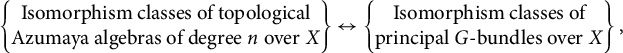$$ \begin{align*} \begin{Bmatrix} \text{Isomorphism classes of topological}\\ \text{Azumaya algebras of degree } n \text { over } X \end{Bmatrix} \leftrightarrow \begin{Bmatrix} \text{Isomorphism classes of}\\ \text{principal } G\text{-bundles over } X \end{Bmatrix}, \end{align*} $$
where G is the topological group of automorphisms of
$\operatorname {\mathrm {M}}_{n \times n} ({\mathbb {C}})$
as an algebra, [Reference Steenrod12, 8.2]. The Skolem–Noether theorem asserts that this is
$\operatorname {\mathrm {PGL}}_{n}({\mathbb {C}})$
; i.e., matrices acting by conjugation.
For brevity of notation, we work with
$\operatorname {\mathrm {U}}_{n}$
instead of
$\operatorname {\mathrm {GL}}_{n}({\mathbb {C}})$
. Our choice of notation does not affect our results because
$\operatorname {\mathrm {U}}_{n}$
included in
$\operatorname {\mathrm {GL}}_{n}({\mathbb {C}})$
as the maximal compact Lie subgroup is a deformation retract, in particular the inclusion is a weak equivalence. Hence, the homotopy type of
$\operatorname {\mathrm {U}}_{n}$
is that of
$\operatorname {\mathrm {GL}}_{n}({\mathbb {C}})$
. The homotopy equivalence is more than an equivalence of spaces, it upgrades to one of topological groups, hence of classifiying spaces.
Let a and m be positive integers. Let
$\mu _{m}\subset \operatorname {\mathrm {U}}_{am}$
be the cyclic subgroup of order m consisting of scalar matrices
$\zeta I_{am}$
for
$\zeta $
an mth root of unity. If we have a principal
$\operatorname {\mathrm {U}}_{am}/\mu _{m}$
-bundle on a topological space X, then the quotient map
$q:\operatorname {\mathrm {U}}_{am}/\mu _{m}\rightarrow \operatorname {\mathrm {PU}}_{am}$
gives rise by an extension of structure group to a principal
$\operatorname {\mathrm {PU}}_{am}$
-bundle and therefore a topological Azumaya algebra of degree
$am$
.
The tensor product of complex algebras can be extended to topological Azumaya algebras by performing the operation fiberwise. The Brauer group of a topological space X classifies topological Azumaya algebras on X up to Brauer equivalence:
$\mathscr {A}$
and
$\mathscr {A}^{\prime }$
are Brauer equivalent if there exist complex vector bundles
$\mathscr {V}$
and
$\mathscr {V}^{\prime }$
, and an isomorphism
$\mathscr {A} \otimes \operatorname {\mathrm {End}}(\mathscr {V}) \cong \mathscr {A}^{\prime } \otimes \operatorname {\mathrm {End}}(\mathscr {V}^{\prime })$
of bundles of
${\mathbb {C}}$
-algebras. If X is a finite dimensional CW complex, then
$\operatorname {\mathrm {Br}}(X)\cong \operatorname {\mathrm {H}}^{3}(X;{\mathbb {Z}})_{\operatorname {\mathrm {tors}}}$
the torsion part of the cohomology group
$\operatorname {\mathrm {H}}^{3}(X;{\mathbb {Z}})$
[Reference Grothendieck7]. The order of a class
$\alpha \in \operatorname {\mathrm {Br}}(X)$
is called the period of
$\alpha $
, and it is denoted by
$\operatorname {\mathrm {per}}(\alpha )$
.
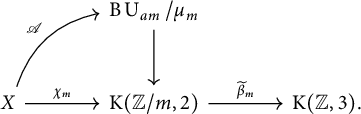
The Brauer class of a map
$\mathscr {A}:X \longrightarrow \operatorname {\mathrm {B}}\operatorname {\mathrm {U}}_{am}/\mu _{m}$
is an element in
$\operatorname {\mathrm {Br}}(X)$
which will be denoted by
$\operatorname {\mathrm {cl}}(\mathscr {A})$
. It is defined as follows. Let
$\chi _{m}$
denote the composite of the projection of
$\operatorname {\mathrm {B}}\operatorname {\mathrm {U}}_{am}/\mu _{m}$
on the the first nontrivial stage of its Postnikov tower,
$\operatorname {\mathrm {B}}\operatorname {\mathrm {U}}_{am}/\mu _{m} \rightarrow \operatorname {\mathrm {K}}({\mathbb {Z}}/m,2)$
, and the unreduced Bockstein map,
$\widetilde{\beta}_{m}:\operatorname {\mathrm {K}}({\mathbb {Z}}/m,2)\rightarrow \operatorname {\mathrm {K}}({\mathbb {Z}},3)$
, as illustrated in the diagram above. Then
$\operatorname {\mathrm {cl}}(\mathscr {A})$
is equal to the composite
$\widetilde{\beta}_{m}\circ \chi _{m}$
.
Remark 1.1 For a deeper discussion on topological Azumaya algebras and the Brauer group of a topological space, we refer the reader to [Reference Antieau and Williams3].
Saltman asked in [Reference Saltman10, p. 35] whether there is prime decomposition for Azumaya algebras under the tensor product operation, as there is for central simple algebras over a field. Antieau–Williams answered this question for topological Azumaya algebras in [Reference Antieau and Williams2, Corollary 1.3] by showing the following result:
Theorem 1.2 For
$n>1$
an odd integer, there exist a six-dimensional CW complex X and a topological Azumaya algebra
$\mathscr {A}$
on X of degree
$2n$
and period
$2$
such that
$\mathscr {A}$
has no decomposition
$\mathscr {A}\cong \mathscr {A}_{2}\otimes \mathscr {A}_{n}$
for topological Azumaya algebras of degrees
$2$
and n, respectively.
The aim of this paper is to provide conditions on a positive integer n and a topological space X such that a topological Azumaya algebra of degree n on X has a tensor product decomposition. The main result of this paper is the following theorem:
Theorem 1.3 Let m and n be positive integers such that m and n are relatively prime and
$m<n$
. Let X be a CW complex such that
$\dim (X)\leq 2m+1$
.
If
$\mathscr {A}$
is a topological Azumaya algebra of degree
$mn$
over X, then there exist topological Azumaya algebras
$\mathscr {A}_{m}$
and
$\mathscr {A}_{n}$
of degrees m and n, respectively, such that
$\mathscr {A}\cong \mathscr {A}_{m}\otimes \mathscr {A}_{n}$
.
Theorem 1.3 is a corollary of a more general result. We prove in Theorem 3.3 that a map
$X\rightarrow \operatorname {\mathrm {B}}\operatorname {\mathrm {U}}_{abmn}/\mu _{mn}$
can be lifted to
$\operatorname {\mathrm {B}}\operatorname {\mathrm {U}}_{am}/\mu _{m}\times \operatorname {\mathrm {B}}\operatorname {\mathrm {U}}_{bn}/\mu _{n}$
when the dimension of X is less than
$2am+2$
, the positive integers a, b, m and n are such that
$am$
is relatively prime to
$bn$
, and
$am<bn$
. The proof of Theorem 3.3 relies significantly in the description of the homomorphisms induced on homotopy groups by the r-fold direct sum of matrices
$\oplus ^{r}:\operatorname {\mathrm {U}}_{n} \longrightarrow \operatorname {\mathrm {U}}_{rn}$
in the range
$\{0,1,\dots ,2n+1\}$
. We call this set “the stable range” for
$\operatorname {\mathrm {U}}_{n}$
.
This paper is organized as follows. The Section 2 presents preliminaries on the effect of direct sum and tensor product operations on homotopy groups of compact Lie groups related to the unitary groups
$\operatorname {\mathrm {U}}_{n}$
. The Section 3 is devoted to the proof of Theorem 3.3. We explain in Remark 3.7 why the decomposition in Theorem 1.3 is not unique up to isomorphism.
2 Stabilization of operations on
$\operatorname {\mathrm {U}}_{n}$
Let
$m, n \in {\mathbb {N}}$
, we consider the following matrix operations:
-
(1) The direct sum of matrices,
$\oplus :\operatorname {\mathrm {U}}_{m}\times \operatorname {\mathrm {U}}_{n} \longrightarrow \operatorname {\mathrm {U}}_{m+n}$
defined by
$$ \begin{align*} A\oplus B= \begin{pmatrix} A & 0\\ 0 & B \end{pmatrix}. \end{align*} $$
-
(2) The r-fold direct sum,
$\oplus ^{r}:\operatorname {\mathrm {U}}_{n} \longrightarrow \operatorname {\mathrm {U}}_{rn}$
given by
$A^{\oplus r}=\underbrace {A\oplus \cdots \oplus A}_{r\text {-times}}$
. -
(3) The tensor product of matrices,
$\otimes :\operatorname {\mathrm {U}}_{m}\times \operatorname {\mathrm {U}}_{n} \longrightarrow \operatorname {\mathrm {U}}_{mn}$
defined by for
$$ \begin{align*} A\otimes B = \begin{pmatrix} a_{11}B & \cdots & a_{1m}B\\ \vdots & \ddots & \vdots \\ a_{m1}B & \cdots & a_{mm}B \end{pmatrix}, \end{align*} $$
$A=(a_{ij}) \in \operatorname {\mathrm {U}}_{m}$
.
-
(4) The r-fold tensor product,
$\otimes ^{r}:\operatorname {\mathrm {U}}_{n} \longrightarrow \operatorname {\mathrm {U}}_{n^{r}}$
given by
$A^{\otimes r} =\underbrace {A\otimes \cdots \otimes A}_{r\text {-times}}$
.
The homomorphisms of homotopy groups induced by the operations above will be denoted by
$\oplus _{*}$
,
$\oplus ^{r}_{*}$
,
$\otimes _{*}$
, and
$\otimes ^{r}_{*}$
, respectively.
We begin by recalling low degree homotopy groups of the unitary groups and the special unitary groups. The first homotopy groups of
$\operatorname {\mathrm {U}}_{n}$
can be calculated by using Bott periodicity. Bott proves in [Reference Bott6] that
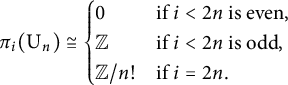$$ \begin{align*} \pi_{i}(\operatorname{\mathrm{U}}_{n})\cong \begin{cases} 0 &\text{if } i<2n \text{ is even,}\\ {\mathbb{Z}} &\text{if } i<2n \text{ is odd,}\\ {\mathbb{Z}}/n! &\text{if } i=2n. \end{cases} \end{align*} $$
Since
$\operatorname {\mathrm {SU}}_{n}$
is the universal cover of
$\operatorname {\mathrm {U}}_{n}$
, and there is a fibration
$\operatorname {\mathrm {SU}}_{n}\hookrightarrow \operatorname {\mathrm {U}}_{n} \xrightarrow {\det } S^{1}$
, it follows that
$$ \begin{align*} \pi_{i}(\operatorname{\mathrm{SU}}_{n})\cong \begin{cases} 0 &\text{if } i=1,\\ \pi_{i}(\operatorname{\mathrm{U}}_{n}) &\text{otherwise.} \end{cases} \end{align*} $$
We now compute the low degree homotopy groups of
$\operatorname {\mathrm {U}}_{am}/\mu _{m}$
and
$\operatorname {\mathrm {SU}}_{am}/\mu _{m}$
. As
$\operatorname {\mathrm {SU}}_{am}$
is a simply connected m-cover of
$\operatorname {\mathrm {SU}}_{am}/\mu _{m}$
we have
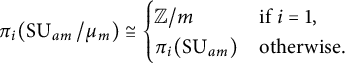$$ \begin{align*} \pi_{i}(\operatorname{\mathrm{SU}}_{am}/\mu_{m})\cong \begin{cases} {\mathbb{Z}}/m &\text{if } i=1,\\ \pi_{i}(\operatorname{\mathrm{SU}}_{am}) &\text{otherwise}. \end{cases} \end{align*} $$
All columns as well as the two top rows of diagram (2.1) are short exact. The nine-lemma implies that the bottom row is also short exact.
Therefore,
$\pi _{i}(\operatorname {\mathrm {U}}_{am}/\mu _{m})\cong \pi _{i}(\operatorname {\mathrm {SU}}_{am}/\mu _{m})$
for all
$i>1$
. It remains to compute the fundamental group of
$\operatorname {\mathrm {U}}_{am}/\mu _{m}$
.
By exactness of the bottom row of diagram (2.1), the induced sequence on fundamental groups is exact,
The map
$\det :\operatorname {\mathrm {U}}_{am}\rightarrow S^{1}$
has a section
$t:S^{1}\rightarrow \operatorname {\mathrm {U}}_{am}$
defined by
$$ \begin{align*} t(\omega)= \begin{pmatrix} \omega & 0 \\ 0 & I_{am-1} \end{pmatrix}. \end{align*} $$
The section t is one of groups; in fact
$\operatorname {\mathrm {U}}_{n}$
is a semi-direct product of
$S^{1}$
by
$\operatorname {\mathrm {SU}}_{n}$
. This section induces a section of
$\det :\operatorname {\mathrm {U}}_{am}/\mu _{m}\rightarrow S^{1}$
, which we also denote by t,
Since
$\pi _{1}\left (S^{1}\right )\cong {\mathbb {Z}}$
, sequence (2.2) splits. We describe
$\pi _{1}\left (\operatorname {\mathrm {U}}_{am}/\mu _{m}\right )$
in terms of
$i_{*}:\pi _{1}\left (\operatorname {\mathrm {SU}}_{am}/\mu _{m}\right ) \rightarrow \pi _{1}\left (\operatorname {\mathrm {U}}_{am}/\mu _{m}\right )$
and
$t_{*}:\pi _{1}\left (S^{1}\right ) \rightarrow \pi _{1}\left (\operatorname {\mathrm {U}}_{am}/\mu _{m}\right )$
as
$\pi _{1}\left (\operatorname {\mathrm {U}}_{am}/\mu _{m}\right )= \operatorname {\mathrm {Im}} i_{*} \oplus \operatorname {\mathrm {Im}} t_{*} \cong {\mathbb {Z}}/m \oplus {\mathbb {Z}}$
.
2.1 Stabilization
Let
$m,n \in {\mathbb {N}}$
and
$m \leq n$
. Define the map
The standard inclusion of unitary groups
$\operatorname {\mathrm {U}}_{n} \hookrightarrow \operatorname {\mathrm {U}}_{n+1}$
is
$2n$
-connected. Since the map
$\operatorname {\mathrm {s}}$
is equal to the consecutive composite of standard inclusions, it follows that
$\operatorname {\mathrm {s}}$
is
$2m$
-connected. Hence,
$\operatorname {\mathrm {s}}$
induces a surjection in degree
$2m$
and an isomorphism on homotopy groups in degrees less than
$2m$
.
Notation 2.1 Let
$\operatorname {\mathrm {stab}}$
denote
$\pi _{i}(\operatorname {\mathrm {s}})$
, the homomorphism
$\operatorname {\mathrm {s}}$
induces on homotopy groups. Henceforth, the following isomorphism for
$i<2m$
will be needed throughout the paper
to identify
$\pi _{i}(\operatorname {\mathrm {U}}_{m})$
with
$\pi _{i}(\operatorname {\mathrm {U}}_{m+n})$
for all
$i<2m$
.
Lemma 2.2 Let
$r:\operatorname {\mathrm {U}}_{m}\rightarrow \operatorname {\mathrm {U}}_{m}$
be conjugation by
$P \in \operatorname {\mathrm {U}}_{m}$
. There is a basepoint preserving homotopy H from r to
$\operatorname {\mathrm {id}}_{\operatorname {\mathrm {U}}_{m}}$
such that for all
$t \in [0,1]$
,
$H(-,t)$
is a homomorphism.
Proof Since
$\operatorname {\mathrm {U}}_{m}$
is path-connected, there exists a path
$\alpha $
from P to
$I_{m}$
in
$\operatorname {\mathrm {U}}_{m}$
. Define
$H:\operatorname {\mathrm {U}}_{m}\times [0,1] \rightarrow \operatorname {\mathrm {U}}_{m}$
by
$H(A,t)=\alpha (t)A\alpha (t)^{-1}$
. Observe that
$H(-,t):\operatorname {\mathrm {U}}_{m}\to \operatorname {\mathrm {U}}_{m}$
,
$A\mapsto H(A,t)$
is a homomorphism. Moreover, H is such that
$$ \begin{align*} H(I_{m},t)=I_{m}, \;\; H(A,0)=r(A) \;\text{ and }\; H(A,1)=A. \end{align*} $$
Therefore, the result follows.▪
Lemma 2.3 Let
$n,r \in {\mathbb {N}}$
. For all
$j=1,\dots ,r$
define
$\operatorname {\mathrm {s}}_{j}:\operatorname {\mathrm {U}}_{n} \longrightarrow \operatorname {\mathrm {U}}_{rn}$
by
$$ \begin{align*} \operatorname{\mathrm{s}}_{j}(A)=\operatorname{\mathrm{diag}}(I_{n},\dots,I_{n},A,I_{n},\dots,I_{n}), \end{align*} $$
where A is in the jth position. The maps
$\operatorname {\mathrm {s}}_{j}$
and
$\operatorname {\mathrm {s}}_{j+1}$
are pointed homotopic for all
$j=1,\dots ,r-1$
.
Proof The block matrix
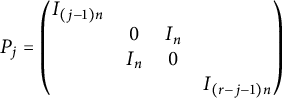$$ \begin{align*} P_{j}= \begin{pmatrix} I_{(j-1)n} & & & \\ & 0 & I_{n} & \\ & I_{n} & 0 & \\ & & & I_{(r-j-1)n} \end{pmatrix} \end{align*} $$
is such that
$P_{j}P_{j}=I_{rn}$
for
$j=1,\dots ,r-1$
. Moreover, if
$A, B \in \operatorname {\mathrm {U}}_{n}$
, then
$$ \begin{align*} P_{j}\operatorname{\mathrm{diag}}(I_{n},\dots,I_{n},A,B,I_{n},\dots,I_{n})P_{j}=\operatorname{\mathrm{diag}}(I_{n},\dots,I_{n},B,A,I_{n},\dots,I_{n}), \end{align*} $$
where A and B are in positions
$(j,j)$
,
$(j+1,j+1)$
, and
$(j+1,j+1)$
,
$(j,j)$
, respectively.
From Lemma 2.2,
$\operatorname {\mathrm {s}}_{j}$
and
$\operatorname {\mathrm {s}}_{j+1}$
are pointed homotopic.▪
Notation 2.4 We call the
$\operatorname {\mathrm {s}}_{j}$
maps stabilization maps. As
$\operatorname {\mathrm {s}}_{1}$
is equal to
$\operatorname {\mathrm {s}}:\operatorname {\mathrm {U}}_{n} \to \operatorname {\mathrm {U}}_{n+(r-1)n}$
, it follows that
$\operatorname {\mathrm {s}}_{j}$
is
$2n$
-connected for all
$j=1,\dots ,r$
. From Lemma 2.3 the homomorphisms induced on homotopy groups by the stabilization maps are equal, hence
$\operatorname {\mathrm {stab}}$
also denotes
$\pi _{i}(\operatorname {\mathrm {s}}_{1})=\cdots =\pi _{i}(\operatorname {\mathrm {s}}_{r})$
. Thus we identify
$\pi _{i}(\operatorname {\mathrm {U}}_{n})$
with
$\pi _{i}(\operatorname {\mathrm {U}}_{rn})$
for
$i<2n$
through
$\operatorname {\mathrm {stab}}$
. The identification allows one to introduce a slight abuse of notation, namely to identify x and
$\operatorname {\mathrm {stab}}(x)$
for
$x\in \pi _{i}(\operatorname {\mathrm {U}}_{n})$
and
$i<2n$
.
2.2 Operations
Proposition 2.5 Let
$i\in {\mathbb {N}}$
, the homomorphism
$\oplus _{*}:\pi _{i}(\operatorname {\mathrm {U}}_{m})\times \pi _{i}(\operatorname {\mathrm {U}}_{n}) \longrightarrow \pi _{i}(\operatorname {\mathrm {U}}_{m+n})$
is given by
$$ \begin{align*} \oplus_{*}(x,y)=\operatorname{\mathrm{stab}}(x)+\operatorname{\mathrm{stab}}(y) \end{align*} $$
for
$x \in \pi _{i}(\operatorname {\mathrm {U}}_{m})$
and
$y \in \pi _{i}(\operatorname {\mathrm {U}}_{n})$
.
Proof It is enough to observe that the direct sum factors as
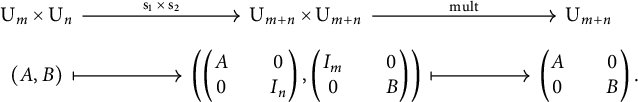
Thus
$\oplus _{*}(x,y)=\operatorname {\mathrm {mult}}_{*}\circ (\operatorname {\mathrm {stab}}\times \operatorname {\mathrm {stab}})(x,y)=\operatorname {\mathrm {stab}}(x)+\operatorname {\mathrm {stab}}(y)$
, where the last equality is true by the Eckmann–Hilton argument, [Reference Spanier11, Theorem 1.6.8].▪
Corollary 2.6 If
$m<n$
and
$i<2m$
, then
$\oplus _{*}(x,y)=x+y$
for
$x \in \pi _{i}(\operatorname {\mathrm {U}}_{m})$
and
$y \in \pi _{i}(\operatorname {\mathrm {U}}_{n})$
.
Proof Since
$\operatorname {\mathrm {s}}_{1}$
and
$\operatorname {\mathrm {s}}_{2}$
are
$2m$
-connected, the homomorphisms
$\operatorname {\mathrm {stab}}:\pi _{i}(\operatorname {\mathrm {U}}_{m}) \longrightarrow \pi _{i}(\operatorname {\mathrm {U}}_{m+n})$
and
$\operatorname {\mathrm {stab}}:\pi _{i}(\operatorname {\mathrm {U}}_{n}) \longrightarrow \pi _{i}(\operatorname {\mathrm {U}}_{m+n})$
are isomorphisms
$i<2m$
and
$i<2n$
, respectively. We use these isomorphisms to identify source and target.
From Proposition 2.5,
$\oplus _{*}(x,y)=\operatorname {\mathrm {stab}}(x)+\operatorname {\mathrm {stab}}(y)=x+y$
for
$i<2m$
.▪
Proposition 2.7 Let
$i\in {\mathbb {N}}$
, the homomorphism
$\oplus ^{r}_{*}:\pi _{i}(\operatorname {\mathrm {U}}_{n}) \longrightarrow \pi _{i}(\operatorname {\mathrm {U}}_{rn})$
is given by
$$ \begin{align*} \oplus^{r}_{*}(x)=r\operatorname{\mathrm{stab}}(x) \end{align*} $$
for
$x \in \pi _{i}(\operatorname {\mathrm {U}}_{n})$
.
Proof Let
$\Delta :\operatorname {\mathrm {U}}_{n} \rightarrow (\operatorname {\mathrm {U}}_{n})^{\times r}$
denote the diagonal map. The r-block summation factors as
By the Eckmann–Hilton argument
$\operatorname {\mathrm {mult}}_{*}:\pi _{i}(\operatorname {\mathrm {U}}_{rn})^{r} \longrightarrow \pi _{i}(\operatorname {\mathrm {U}}_{rn})$
is given by
$$ \begin{align*} \operatorname{\mathrm{mult}}_{*}(x_{1},\dots,x_{r})=x_{1}+\cdots+x_{r} \end{align*} $$
for
$x_{j} \in \pi _{i}(\operatorname {\mathrm {U}}_{rn})$
and
$j=1,\dots ,r$
. From this
$\oplus _{*}^{r}$
takes the form
This proves the statement.▪
Corollary 2.8 If
$i<2n$
, then
$\oplus _{*}^{r}(x)=rx$
for
$x \in \pi _{i}(\operatorname {\mathrm {U}}_{n})$
.
Proof The homomorphism
$\operatorname {\mathrm {stab}}^{\times r}:\pi _{i}(\operatorname {\mathrm {U}}_{n})^{\times r} \longrightarrow \pi _{i}(\operatorname {\mathrm {U}}_{rn})^{\times r}$
is an isomorphism for all
$i<2n$
because so is
$\operatorname {\mathrm {stab}}:\pi _{i}(\operatorname {\mathrm {U}}_{n}) \longrightarrow \pi _{i}(\operatorname {\mathrm {U}}_{rn})$
. By Proposition 2.7, we conclude
$\oplus _{*}^{r}(x)=r\operatorname {\mathrm {s}}_{*}(x)=rx$
for
$i<2n$
.▪
Lemma 2.9 Let
$L, R: \operatorname {\mathrm {U}}_{m}\rightarrow \operatorname {\mathrm {U}}_{mn}$
be the maps
$L(A)=A\otimes I_{n}$
and
$R(A)=I_{n}\otimes A$
. There is a basepoint preserving homotopy H from L to R such that for all
$t \in [0,1]$
,
$H(-,t)$
is a homomorphism.
Proof Let
$A\in \operatorname {\mathrm {U}}_{m}$
.
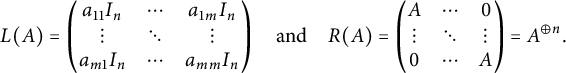$$ \begin{align*} L(A)= \begin{pmatrix} a_{11}I_{n}& \cdots & a_{1m}I_{n}\\ \vdots& \ddots & \vdots\\ a_{m1}I_{n}& \cdots & a_{mm}I_{n} \end{pmatrix} \quad \text{and} \quad R(A)= \begin{pmatrix} A& \cdots & 0\\ \vdots& \ddots & \vdots\\ 0& \cdots & A \end{pmatrix}=A^{\oplus n}. \end{align*} $$
Let
$P_{m,n}$
be the permutation matrix
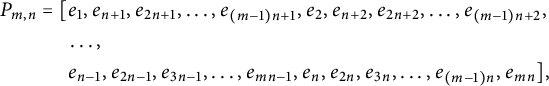$$ \begin{align*} P_{m,n}=[&e_{1},e_{n+1},e_{2n+1},\dots, e_{(m-1)n+1}, e_{2},e_{n+2},e_{2n+2},\dots, e_{(m-1)n+2},\\ &\dots,\\ &e_{n-1},e_{2n-1},e_{3n-1},\dots,e_{mn-1}, e_{n},e_{2n},e_{3n},\dots, e_{(m-1)n},e_{mn}], \end{align*} $$
where,
$e_{i}$
is the ith standard basis vector of
${\mathbb {C}}^{mn}$
written as a column vector. Observe that
$L(A)=P_{m,n}R(A)P_{m,n}^{-1}$
. The result follows from Lemma 2.2.▪
Proposition 2.10 Let
$i\in {\mathbb {N}}$
, the homomorphism
$\otimes _{*}:\pi _{i}(\operatorname {\mathrm {U}}_{m})\times \pi _{i}(\operatorname {\mathrm {U}}_{n}) \longrightarrow \pi _{i}(\operatorname {\mathrm {U}}_{mn})$
is given by
$$ \begin{align*} \otimes_{*}(x,y)=n\operatorname{\mathrm{stab}}(x)+m\operatorname{\mathrm{stab}}(y) \end{align*} $$
for
$x \in \pi _{i}(\operatorname {\mathrm {U}}_{m})$
and
$y\in \pi _{i}(\operatorname {\mathrm {U}}_{n})$
.
Proof By the mixed-product property of the tensor product of matrices
$$ \begin{align*} A\otimes B=(A\otimes I_{n})(I_{m}\otimes B)=L(A)R(B). \end{align*} $$
Lemma 2.9 gives
$L_{*}=\oplus _{*}^{n}:\pi _{i}(\operatorname {\mathrm {U}}_{m})\rightarrow \pi _{i}(\operatorname {\mathrm {U}}_{mn})$
. Proposition 2.7 now yields
$\otimes _{*}(x,y)=n\operatorname {\mathrm {stab}}(x)+m\operatorname {\mathrm {stab}}(y)$
.▪
Corollary 2.11 If
$m<n$
and
$i<2m$
, then
$\otimes _{*}(x,y)=nx+my$
for
$x \in \pi _{i}(\operatorname {\mathrm {U}}_{m})$
and
$y\in \pi _{i}(\operatorname {\mathrm {U}}_{n})$
.
Proposition 2.12 Let
$i\in {\mathbb {N}}$
, the homomorphism
$\otimes ^{r}_{*}:\pi _{i}(\operatorname {\mathrm {U}}_{n}) \longrightarrow \pi _{i}(\operatorname {\mathrm {U}}_{n^{r}})$
is given by
$$ \begin{align*} \otimes^{r}_{*}(x)=rn^{r-1}\operatorname{\mathrm{stab}}(x) \end{align*} $$
for
$x\in \pi _{i}(\operatorname {\mathrm {U}}_{n})$
.
Corollary 2.13 If
$i<2n$
, then
$\otimes ^{r}_{*}(x)=rn^{r-1}x$
for
$x\in \pi _{i}(\operatorname {\mathrm {U}}_{n})$
.
2.2.1 Tensor product on the quotient
Let a, b, m and n be positive integers so that
$m<n$
. The tensor product operation
$\otimes :\operatorname {\mathrm {U}}_{am}\times \operatorname {\mathrm {U}}_{bn} \longrightarrow \operatorname {\mathrm {U}}_{abmn}$
sends the group
$\mu _{m}\times \mu _{n}$
to
$\mu _{mn}$
. In consequence, the operation descends to the quotient
$$ \begin{align} \otimes:\operatorname{\mathrm{U}}_{am}/\mu_{m}\times\operatorname{\mathrm{U}}_{bn}/\mu_{n} \longrightarrow \operatorname{\mathrm{U}}_{abmn}/\mu_{mn}. \end{align} $$
Proposition 2.14 If
$i>1$
, the homomorphism
$$ \begin{align*} \otimes_{*}:\pi_{i}(\operatorname{\mathrm{U}}_{am}/\mu_{m})\times\pi_{i}(\operatorname{\mathrm{U}}_{bn}/\mu_{n}) \longrightarrow \pi_{i}(\operatorname{\mathrm{U}}_{abmn}/\mu_{mn}) \end{align*} $$
is given by
$$ \begin{align*} \otimes_{*}(x,y)=bn\operatorname{\mathrm{stab}}(x)+am\operatorname{\mathrm{stab}}(y) \end{align*} $$
for
$x \in \pi _{i}(\operatorname {\mathrm {U}}_{am}/\mu _{m})$
and
$y \in \pi _{i}(\operatorname {\mathrm {U}}_{bn}/\mu _{n})$
.
Proof There is a map of fibrations
From the homomorphism of long exact sequences associated to the fibrations in diagram (2.6), we obtain a commutative square
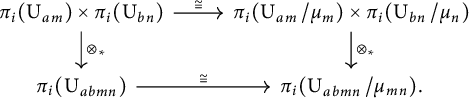
for
$i>1$
. This diagram and Proposition 2.10 gives
$\otimes _{*}(x,y)=\oplus ^{bn}_{*}(x)+\oplus ^{am}_{*}(y)=bn\operatorname {\mathrm {stab}}(x)+am\operatorname {\mathrm {stab}}(y)$
for all
$i>1$
.▪
In the following proposition, we identify
$\pi _{1}(\operatorname {\mathrm {U}}_{am}/\mu _{m})$
with
$\operatorname {\mathrm {Im}} i_{*}\oplus \operatorname {\mathrm {Im}} t_{*}\cong {\mathbb {Z}}/m \oplus {\mathbb {Z}}$
, where i and t are the maps in diagram (2.3). We also identify
${\mathbb {Z}}/m$
and
${\mathbb {Z}}/n$
with the subgroups
$\{0,n,2n,\dots ,(m-1)n\}\subset {\mathbb {Z}}/mn$
and
$\{0,m,2m,\dots ,(n-1)m\}\subset {\mathbb {Z}}/mn$
, respectively.
Proposition 2.15 The homomorphism
$$ \begin{align*} \otimes_{*}:\pi_{1}(\operatorname{\mathrm{U}}_{am}/\mu_{m})\times\pi_{1}(\operatorname{\mathrm{U}}_{bn}/\mu_{n}) \longrightarrow \pi_{1}(\operatorname{\mathrm{U}}_{abmn}/\mu_{mn}) \end{align*} $$
is given by
$$ \begin{align*} \otimes_{*}(\alpha+x,\beta+y)=(\alpha+\beta)+(bnx+amy) \end{align*} $$
for
$\alpha \in {\mathbb {Z}}/m \subset {\mathbb {Z}}/mn$
,
$\beta \in {\mathbb {Z}}/n \subset {\mathbb {Z}}/mn$
, and
$x, y \in {\mathbb {Z}}$
.
Proof Since the determinant of a tensor product is the product of powers of the determinants, we define
$\phi :S^{1}\times S^{1} \rightarrow S^{1}$
by
$\phi (\upsilon ,\omega )=\upsilon ^{bn}\omega ^{am}$
so that the diagram below is a map of fibrations.
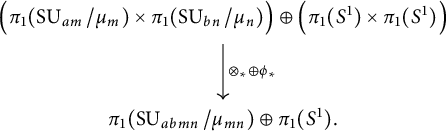
This map of fibrations induces a homomorphism of short exact sequences
We want to determine the homomorphism
$\otimes _{*}$
in the middle of diagram (2.7). In order to do this, we will determine
$\otimes _{*}:\pi _{1}(\operatorname {\mathrm {SU}}_{am}/\mu _{m})\times \pi _{1}(\operatorname {\mathrm {SU}}_{bn}/\mu _{n}) \longrightarrow \pi _{1}(\operatorname {\mathrm {SU}}_{abmn}/\mu _{mn})$
, and show that the short exact sequences in diagram (2.7) split compatibly so that
$\otimes _{*}:\pi _{1}(\operatorname {\mathrm {U}}_{am}/\mu _{m})\times \pi _{1}(\operatorname {\mathrm {U}}_{bn}/\mu _{n}) \longrightarrow \pi _{1}(\operatorname {\mathrm {U}}_{abmn}/\mu _{mn})$
is equal to
We begin by observing that there exists a similar map of fibrations to the one in diagram (2.6), but with the spaces
$\operatorname {\mathrm {SU}}_{am}$
and
$\operatorname {\mathrm {SU}}_{bn}$
instead of
$\operatorname {\mathrm {U}}_{am}$
and
$\operatorname {\mathrm {U}}_{bn}$
, respectively. In this case, we obtain the commutative square,
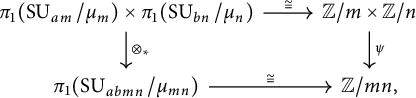
where
${\mathbb {Z}}/m$
and
${\mathbb {Z}}/n$
are considered as subgroups of
${\mathbb {Z}}/mn$
, and
$\psi :{\mathbb {Z}}/m \times {\mathbb {Z}}/n \to {\mathbb {Z}}/mn$
is addition. From this
$\otimes _{*}:\pi _{1}(\operatorname {\mathrm {SU}}_{am}/\mu _{m})\times \pi _{1}(\operatorname {\mathrm {SU}}_{bn}/\mu _{n})\rightarrow \pi _{1}(\operatorname {\mathrm {SU}}_{abmn}/\mu _{mn})$
is equal to the addition.
In order to prove the compatibility, we observe that even though diagram (2.8) below does not commute, Claim 2.16 implies that it is commutative up to a pointed homotopy. Therefore, the induced diagram on homotopy groups does commute
Consequently, the diagram below commutes
this is,
$\otimes _{*}(\alpha +x,\beta +y)=\psi (\alpha ,\beta )+\phi _{*}(x,y)$
for
$\alpha +x \in {\mathbb {Z}}/m\oplus {\mathbb {Z}}$
and
$\beta +y \in {\mathbb {Z}}/n\oplus {\mathbb {Z}}$
. By the Eckmann–Hilton argument and Corollary 2.11,
$\otimes _{*}(\alpha +x,\beta +y)=\psi (\alpha ,\beta )+(bnx+amy)$
.▪
Claim 2.16 Diagram (2.8) commutes up to a pointed homotopy,
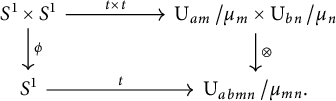
Proof Consider the stabilization maps
$\operatorname {\mathrm {s}}_{j}:\operatorname {\mathrm {U}}_{1} \to \operatorname {\mathrm {U}}_{abmn}$
for
$j=1,\dots ,abmn$
. Let
$\upsilon , \omega \in S^{1}$
, then
$$ \begin{align*} t(\phi(\upsilon,\omega))= \begin{pmatrix} \upsilon^{bn}\omega^{am} & 0 \\ 0 & I_{abmn-1} \end{pmatrix} \;\; \text{and} \;\; t(\upsilon)\otimes t(\omega)= \begin{pmatrix} \upsilon t(\omega) & 0 & \cdots & 0\\ 0 & t(\omega) & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots\\ 0 & 0 & \cdots & t(\omega) \end{pmatrix}. \end{align*} $$
Observe that
$t\circ \phi $
is equal to the composite
where
$g=(\operatorname {\mathrm {s}}_{1}\times \cdots \times \operatorname {\mathrm {s}}_{1},\operatorname {\mathrm {s}}_{1}\times \cdots \times \operatorname {\mathrm {s}}_{1})$
, and
$t\otimes t$
is equal to
where
$h=(\operatorname {\mathrm {s}}_{1}\times \operatorname {\mathrm {s}}_{2}\times \cdots \times \operatorname {\mathrm {s}}_{bn},\operatorname {\mathrm {s}}_{1}\times \operatorname {\mathrm {s}}_{bn+1}\times \cdots \times \operatorname {\mathrm {s}}_{(am-1)bn+1})$
. By Lemma 2.3,
$t\circ \phi $
and
$t\otimes t$
are pointed homotopic.▪
3 Proof of Theorem 1.3
Proposition 3.1 Let a, b, m and n be positive integers such that
$am$
and
$bn$
are relatively prime and
$am<bn$
. Then there exist positive integers u and v satisfying
$|vn(bn)^{n}-um(am)^{m}|=1$
, so that there exist a positive integer N and a homomorphism
$\operatorname {\mathrm {T}}:\operatorname {\mathrm {U}}_{am}\times \operatorname {\mathrm {U}}_{bn} \longrightarrow \operatorname {\mathrm {U}}_{N}$
such that
-
(1) the homomorphism
$\operatorname {\mathrm {T}}$
factors through
$\widetilde {\operatorname {\mathrm {T}}}:\operatorname {\mathrm {U}}_{am}/\mu _{m}\times \operatorname {\mathrm {U}}_{bn}/\mu _{n} \longrightarrow \operatorname {\mathrm {U}}_{N}$
, and -
(2) the homomorphisms induced on homotopy groups
are given by
$$ \begin{align*} \widetilde{\operatorname{\mathrm{T}}}_{i}:\pi_{i}(\operatorname{\mathrm{U}}_{am}/\mu_{m})\times \pi_{i}(\operatorname{\mathrm{U}}_{bn}/\mu_{n}) \longrightarrow \pi_{i}(\operatorname{\mathrm{U}}_{N}) \end{align*} $$
where
$$ \begin{align*} \begin{cases} \widetilde{\operatorname{\mathrm{T}}}_{i}(x,y)=um(am)^{m-1}x+vn(bn)^{n-1}y & \text{if } 1<i<2am,\\ \widetilde{\operatorname{\mathrm{T}}}_{i}(\alpha+x,\beta+y)=um(am)^{m-1}x+vn(bn)^{n-1}y & \text{if } i=1, \end{cases} \end{align*} $$
$\alpha \in {\mathbb {Z}}/m$
,
$\beta \in {\mathbb {Z}}/n$
and
$x,y \in {\mathbb {Z}}$
.
Proof We first construct
$\operatorname {\mathrm {T}}$
.
Since
$am$
and
$bn$
are relatively prime, so are
$m(am)^{m}$
and
$n(bn)^{n}$
. Hence there exist positive integers u and v such that
$vn(bn)^{n}-um(am)^{m}=\pm 1$
. Let N denote
$u(am)^{m}+v(bn)^{n}$
. We define
$\operatorname {\mathrm {T}}$
using the operations described in Section 2, as the composite
-
(1) We must show that
$\mu _{m}\times \mu _{n}$
is contained in
$\operatorname {\mathrm {Ker}}(\operatorname {\mathrm {T}})$
. Let
$\alpha $
and
$\beta $
be mth and nth roots of unity, respectively. Note that the element
$\bigl (\alpha I_{am},\beta I_{bn}\bigr )$
is sent to
$\bigl (I_{u(am)^{m}},I_{v(bn)^{n}}\bigr )$
by
$(\otimes ^{m},\otimes ^{n})$
, hence to the identity by the composite
$\operatorname {\mathrm {T}}$
defined above. -
(2) We observe that Corollaries 2.6, 2.8, and 2.13 imply
for all
$i<2am$
.
From part (1) there is a map of fibrations
Case 1. Let
$i>1$
. From the long exact sequence, diagram (3.1) commutes.(3.1)Thus,
$\widetilde {\operatorname {\mathrm {T}}}_{i}(x,y)=\operatorname {\mathrm {T}}_{i}(x,y)=um(am)^{m-1}x+vn(bn)^{n-1}y$
for
$1<i<2m$
.
Case 2. Let
$i=1$
. From the long exact sequence there is a homomorphism of short exact sequencesThe top short exact sequence splits. By direct inspection, we obtain
$\widetilde {\operatorname {\mathrm {T}}}_{1}(\alpha +x,\beta +y)=\operatorname {\mathrm {T}}_{1}(x,y)=um(am)^{m-1}x+vn(bn)^{n-1}y$
.▪
3.1 A left homotopy inverse
Let a, b, m and n be positive integers. By applying the classifying-space functor to the homomorphism (2.5), we obtain a map
$$ \begin{align} F_{\otimes}: \operatorname{\mathrm{B}}\operatorname{\mathrm{U}}_{am}/\mu_{m}\times\operatorname{\mathrm{B}}\operatorname{\mathrm{U}}_{bn}/\mu_{n} \rightarrow \operatorname{\mathrm{B}}\operatorname{\mathrm{U}}_{abmn}/\mu_{mn}. \end{align} $$
If we take the quotient by
$\mu _{am}$
and
$\mu _{bn}$
in (3.2), we write
$f_{\otimes }$
instead of
$F_{\otimes }$
.
Let J be the map
where the integer N is the one provided by Proposition 3.1.
Proposition 3.2 Let a, b, m and n be positive integers such that
$am$
and
$bn$
are relatively prime and
$am<bn$
. The map J is
$(2am+1)$
-connected.
Proof We want to prove that the induced homomorphism on homotopy groups
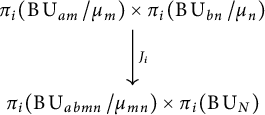
is an isomorphism for all
$i<2am+1$
and an epimorphism for
$i=2am+1$
.
Observe that the homotopy groups of the spaces involved are trivial in odd degrees below
$2am+2$
, hence it suffices to prove that
$J_{i}$
is an isomorphism for all i even and
$i<2am+1$
.
We divide the proof into two cases.
Case 1. Let
$i<2am+1$
and
$i\neq 2$
. For this case computations can be done at the level of the universal covers of the groups
$\operatorname {\mathrm {U}}_{am}/\mu _{m}, \operatorname {\mathrm {U}}_{bn}/\mu _{n}$
, and
$\operatorname {\mathrm {U}}_{abmn}/\mu _{mn}$
.
The homomorphism (3.3) takes the form
$$ \begin{align*} J_{i}:{\mathbb{Z}}\times{\mathbb{Z}} \longrightarrow {\mathbb{Z}}\times{\mathbb{Z}}. \end{align*} $$
Propositions 2.15 and 3.1 yield
$$ \begin{align*} J_{i}(x,y) =\Bigl(bnx+amy,um(am)^{m-1}x+vn(bn)^{n-1}y\Bigr). \end{align*} $$
Thereby, the homomorphism (3.3) is represented by the matrix
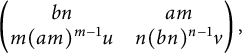$$ \begin{align*} \begin{pmatrix} bn & am\\ m(am)^{m-1}u & n(bn)^{n-1}v \end{pmatrix}, \end{align*} $$
which is invertible. This proves
$J_{i}$
is an isomorphism.
Case 2. Let
$i=2$
. The homomorphism (3.3) takes the form
$$ \begin{align*} J_{2}:({\mathbb{Z}}/m\oplus{\mathbb{Z}})\times({\mathbb{Z}}/n\oplus{\mathbb{Z}}) \longrightarrow ({\mathbb{Z}}/mn\oplus{\mathbb{Z}})\times{\mathbb{Z}}. \end{align*} $$
Propositions 2.15 and 3.1 yield
$$ \begin{align*} J_{2}(x+\alpha,y+\beta) &= \Bigl(\psi(\alpha,\beta)+(bnx+amy),um(am)^{m-1}x+vn(bn)^{n-1}y\Bigr). \end{align*} $$
Recall that
$\psi :{\mathbb {Z}}/m \times {\mathbb {Z}}/n \to {\mathbb {Z}}/mn$
is addition where
${\mathbb {Z}}/m$
and
${\mathbb {Z}}/n$
are considered as subgroups of
${\mathbb {Z}}/mn$
, see proof of Proposition 2.15. The homomorphism
$\psi $
is an isomorphism. From this and the invertibility of the matrix above,
$J_{2}$
is an isomorphism.▪
3.2 Factorization through
$F_{\otimes }: \operatorname {\mathrm {B}}\operatorname {\mathrm {U}}_{am}/\mu _{m}\times \operatorname {\mathrm {B}}\operatorname {\mathrm {U}}_{bn}/\mu _{b} \rightarrow \operatorname {\mathrm {B}}\operatorname {\mathrm {U}}_{abmn}/\mu _{mn}$
Theorem 3.3 Let a, b, m and n be positive integers such that
$am$
and
$bn$
are relatively prime and
$am<bn$
. Let X be a topological space with the homotopy type of a finite dimensional CW complex such that
$\dim (X)\leq 2am+1$
.
Every map
$\mathscr {A}:X \rightarrow \operatorname {\mathrm {B}}\operatorname {\mathrm {U}}_{abmn}/\mu _{mn}$
can be lifted to
$\operatorname {\mathrm {B}}\operatorname {\mathrm {U}}_{am}/\mu _{m}\times \operatorname {\mathrm {B}}\operatorname {\mathrm {U}}_{bn}/\mu _{n}$
along the map
$F_{\otimes }$
up to a pointed homotopy.
Proof Diagramatically speaking, we want to find a map
$$ \begin{align*} \mathscr{A}_{m}\times\mathscr{A}_{n}:X \rightarrow \operatorname{\mathrm{B}}\operatorname{\mathrm{U}}_{am}/\mu_{m}\times\operatorname{\mathrm{B}}\operatorname{\mathrm{U}}_{bn}/\mu_{n} \end{align*} $$
such that diagram (3.4) commutes up to homotopy
Proposition 3.2 yields a map
$J:\operatorname {\mathrm {B}}\operatorname {\mathrm {U}}_{am}/\mu _{m}\times \operatorname {\mathrm {B}}\operatorname {\mathrm {U}}_{bn}/\mu _{n} \longrightarrow \operatorname {\mathrm {B}}\operatorname {\mathrm {U}}_{abmn}/\mu _{mn}\times \operatorname {\mathrm {B}}\operatorname {\mathrm {U}}_{N}$
where N is some positive integer. Observe that
$F_{\otimes }$
factors through
$\operatorname {\mathrm {B}}\operatorname {\mathrm {U}}_{abmn}/\mu _{mn}\times \operatorname {\mathrm {B}}\operatorname {\mathrm {U}}_{N}$
, so we can write
$F_{\otimes }$
as the composite of J and the projection
$\operatorname {\mathrm {proj}}_{1}$
shown in diagram (3.5).
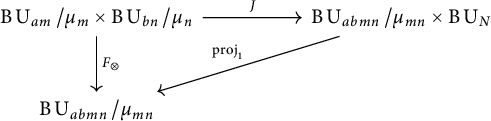
Since J is
$(2am+1)$
-connected and
$\dim (X)\leq 2am+1$
, then by Whitehead’s theorem
$$ \begin{align*} J_{\#}:[X, \operatorname{\mathrm{B}}\operatorname{\mathrm{U}}_{am}/\mu_{m}\times\operatorname{\mathrm{B}}\operatorname{\mathrm{U}}_{bn}/\mu_{n}] \rightarrow [X,\operatorname{\mathrm{B}}\operatorname{\mathrm{U}}_{abmn}/\mu_{mn}\times\operatorname{\mathrm{B}}\operatorname{\mathrm{U}}_{N}] \end{align*} $$
is a surjection, [Reference Spanier11, Corollary 7.6.23].
Let s denote a section of
$\operatorname {\mathrm {proj}}_{1}$
. The surjectivity of
$J_{\#}$
implies
$s\circ \mathscr {A}$
has a preimage
$\mathscr {A}_{m}\times \mathscr {A}_{n}:X \rightarrow \operatorname {\mathrm {B}}\operatorname {\mathrm {U}}_{am}/\mu _{m}\times \operatorname {\mathrm {B}}\operatorname {\mathrm {U}}_{bn}/\mu _{n}$
such that
$J\circ (\mathscr {A}_{m}\times \mathscr {A}_{n})\simeq s\circ \mathscr {A}$
.
The commutativity of diagram (3.4) follows from commutativity of diagram (3.5). Thus, the result follows.▪
3.3 Factorization through
$f_{\otimes }: \operatorname {\mathrm {B}}\operatorname {\mathrm {PU}}_{am}\times \operatorname {\mathrm {B}}\operatorname {\mathrm {PU}}_{bn} \rightarrow \operatorname {\mathrm {B}}\operatorname {\mathrm {PU}}_{abmn}$
Proposition 3.4 Let X be a finite CW complex. Let
$\alpha \in \operatorname {\mathrm {Br}}(X)$
be a class of period m. There exists a lifting
$\mathscr {A}^{\prime }$
of
$\alpha $
if and only if
$\alpha $
is represented by a topological Azumaya algebra
$\mathscr {A}$
of degree
$am$
.
Proof Let
$\alpha \in \operatorname {\mathrm {Br}}(X)$
be a Brauer class of period m. There exists a lifting
$\xi \in \operatorname {\mathrm {H}}^{2}(X;{\mathbb {Z}}/m)$
such that
$\widetilde{\beta}_{m}(\xi )=\alpha $
. Diagrammatically,
The map of fibrations below
induces a commutative diagram
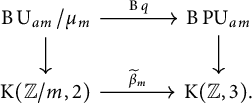
In order to prove the proposition, we show that there exists a lifting
$\mathscr {A}^{\prime }$
of
$\xi $
if and only if there exists a lifting
$\mathscr {A}$
of
$\xi $
, see diagram (3.6) below.
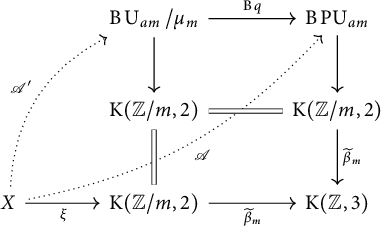
If there exists a lifting
$\mathscr {A}^{\prime }:X \longrightarrow \operatorname {\mathrm {B}}\operatorname {\mathrm {U}}_{am}/\mu _{m}$
, then the composite
$\operatorname {\mathrm {B}} q\circ \mathscr {A}^{\prime }$
is a topological Azumaya algebra of degree
$am$
that represents the Brauer class
$\alpha $
.
Conversely, suppose there exists an Azumaya algebra
$\mathscr {A}$
of degree
$am$
making the outer square in the diagram below commute up to homotopy.
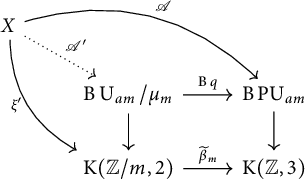
In the inner square, the induced map on the homotopy fibers of
$\operatorname {\mathrm {B}} q$
and
$\widetilde{\beta}_{m}$
is a homotopy equivalence. An application of the five-lemma implies that the inner square is a homotopy pullback square. Therefore, there exists a lifting
$\mathscr {A}^{\prime }$
representing
$\alpha $
.▪
Theorem 3.5 Let a, b, m and n be positive integers such that
$am$
and
$bn$
are relatively prime and
$am<bn$
. Let X be a CW complex such that
$\dim (X)\leq 2am+1$
.
If
$\mathscr {A}$
is a topological Azumaya algebra of degree
$abmn$
such that
$\operatorname {\mathrm {cl}}(\mathscr {A})$
has period
$mn$
, then there exist topological Azumaya algebras
$\mathscr {A}_{m}$
and
$\mathscr {A}_{n}$
of degrees
$am$
and
$bn$
, respectively, such that
$\operatorname {\mathrm {per}}(\operatorname {\mathrm {cl}}(\mathscr {A}_{m}))=m$
,
$\operatorname {\mathrm {per}}(\operatorname {\mathrm {cl}}(\mathscr {A}_{n}))=n$
and
$\mathscr {A}\cong \mathscr {A}_{m}\otimes \mathscr {A}_{n}$
.
Proof In this case, we want to solve the lifting problem shown in diagram (3.7) up to homotopy, with
$\operatorname {\mathrm {per}}(\operatorname {\mathrm {cl}}(\mathscr {A}_{m}))=m$
,
$\operatorname {\mathrm {per}}(\operatorname {\mathrm {cl}}(\mathscr {A}_{n}))=n$
.
By Proposition 3.4, there exists a map
$\mathscr {A}^{\prime }:X \rightarrow \operatorname {\mathrm {B}}\operatorname {\mathrm {U}}_{abmn}/\mu _{mn}$
such that
$\operatorname {\mathrm {per}}(\operatorname {\mathrm {cl}}(\mathscr {A}^{\prime }))=\operatorname {\mathrm {per}}(\operatorname {\mathrm {cl}}(\mathscr {A}))=mn$
. Then, by Theorem 3.3, there exists a map
$\mathscr {A}^{\prime }_{m}\times \mathscr {A}^{\prime }_{n}:X \longrightarrow \operatorname {\mathrm {B}}\operatorname {\mathrm {U}}_{am}/\mu _{m}\times \operatorname {\mathrm {B}}\operatorname {\mathrm {U}}_{bn}/\mu _{n}$
such that
$F_{\otimes }\circ (\mathscr {A}^{\prime }_{m}\times \mathscr {A}^{\prime }_{n})\simeq \mathscr {A}^{\prime }$
.
Since
$\operatorname {\mathrm {cl}}(\mathscr {A}^{\prime }_{m})\operatorname {\mathrm {cl}}(\mathscr {A}^{\prime }_{n})=\operatorname {\mathrm {cl}}(\mathscr {A}^{\prime }_{mn})$
, m and n are relatively prime, and
$\operatorname {\mathrm {per}}(\operatorname {\mathrm {cl}}(\mathscr {A}^{\prime }))=mn$
then
$\operatorname {\mathrm {per}}(\operatorname {\mathrm {cl}}(\mathscr {A}^{\prime }_{m}))=m$
and
$\operatorname {\mathrm {per}}(\operatorname {\mathrm {cl}}(\mathscr {A}^{\prime }_{n}))=n$
.
By Proposition 3.4, there exists a map
$\mathscr {A}_{m}\times \mathscr {A}_{n}:X \longrightarrow \operatorname {\mathrm {B}}\operatorname {\mathrm {PU}}_{am}\times \operatorname {\mathrm {B}}\operatorname {\mathrm {PU}}_{bn}$
such that
$\operatorname {\mathrm {per}}(\operatorname {\mathrm {cl}}(\mathscr {A}_{m}))=\operatorname {\mathrm {per}}(\operatorname {\mathrm {cl}}(\mathscr {A}^{\prime }_{m}))$
and
$\operatorname {\mathrm {per}}(\operatorname {\mathrm {cl}}(\mathscr {A}_{n}))=\operatorname {\mathrm {per}}(\operatorname {\mathrm {cl}}(\mathscr {A}^{\prime }_{n}))$
.
It remains to show that diagram (3.7) commutes. Consider the diagram below
Observe that the square, as well as top, bottom and left triangles, of diagram (3.8) commute. Hence, the right triangle commutes.▪
Theorem 1.3 is a corollary of Theorem 3.5.
Theorem 3.6 Let a, b, m and n be positive integers such that
$am$
and
$bn$
are relatively prime and
$am<bn$
. The map
$F_{\otimes }: \operatorname {\mathrm {B}}\operatorname {\mathrm {U}}_{am}/\mu _{m}\times \operatorname {\mathrm {B}}\operatorname {\mathrm {U}}_{bn}/\mu _{n} \rightarrow \operatorname {\mathrm {B}}\operatorname {\mathrm {U}}_{abmn}/\mu _{mn}$
does not have any section.
Proof Suppose there exists a section
$\sigma $
of
$F_{\otimes }$
.
By Proposition 2.15, the map
$F_{\otimes }$
induces a homomorphism on homotopy groups which is given by
$(x,y)\mapsto bn\operatorname {\mathrm {stab}}(x)+am\operatorname {\mathrm {stab}}(y)$
for
$i>2$
. In degree
$2am+2$
the homomorphism
$(F_{\otimes })_{*}$
takes the form
$(F_{\otimes })_{*}:\pi _{2am+2}(\operatorname {\mathrm {B}}\operatorname {\mathrm {U}}_{am}/\mu _{m})\times {\mathbb {Z}} \rightarrow {\mathbb {Z}}$
, where
$\pi _{2am+2}(\operatorname {\mathrm {B}}\operatorname {\mathrm {U}}_{am}/\mu _{m})\cong \pi _{2am+2}(\operatorname {\mathrm {B}}\operatorname {\mathrm {U}}_{am})$
and
$\pi _{2am+2}(\operatorname {\mathrm {B}}\operatorname {\mathrm {U}}_{am})$
is trivial when
$am$
is odd, and
${\mathbb {Z}}/2$
when
$am$
is even, see [Reference Mimura and James9, p. 971]. Therefore,
$(F_{\otimes })_{*}(x,y)=am\operatorname {\mathrm {stab}}(y)$
. Thus
$\operatorname {\mathrm {Im}}(F_{\otimes })_{*}=am{\mathbb {Z}}$
.
On the other side, since
$\sigma $
is a section of
$F_{\otimes }$
, the composite
$(F_{\otimes })_{*}\circ \sigma _{*}:\pi _{2am+2} (\operatorname {\mathrm {B}}\operatorname {\mathrm {U}}_{abmn}/\mu _{mn})\ \rightarrow\ \pi _{2am+2}(\operatorname {\mathrm {B}}\operatorname {\mathrm {U}}_{am}/\mu _{m})\times \pi _{2am+2}(\operatorname {\mathrm {B}}\operatorname {\mathrm {U}}_{bn}/\mu _{n})\ \rightarrow\ \pi _{2am+2} (\operatorname {\mathrm {B}}\operatorname {\mathrm {U}}_{abmn}/ \mu _{mn})$
is the identity. This contradicts the fact that
$\operatorname {\mathrm {Im}}( (F_{\otimes })_{*}\circ \sigma _{*}) \subset am{\mathbb {Z}}$
.▪
In Theorem 1.3, it is proven that there exists a tensor product decomposition for topological Azumaya algebras over low dimensional CW complexes, and that such decomposition does not exist for topological Azumaya algebras over an arbitrary CW complex. The proof of Theorem 3.6 implies that for positive integers m and n where
$m<n$
, if
$\mathscr {A}$
is a topological Azumaya algebra of degree
$mn$
over a finite CW complex of dimension higher than
$2m+1$
, then
$\mathscr {A}$
may not be decomposable as
$\mathscr {A}_{m}\otimes \mathscr {A}_{n}$
. In fact, consider the unit
$(2m+2)$
-sphere, and let
$\mathscr {S}:S^{2m+2}\to \operatorname {\mathrm {B}}\operatorname {\mathrm {PU}}_{mn}$
be a topological Azumaya algebra of degree
$mn$
on
$S^{2m+2}$
such that
$\mathscr {S}$
generates
$\pi _{2m+2}(\operatorname {\mathrm {B}}\operatorname {\mathrm {PU}}_{mn})$
, then
$\mathscr {S}$
cannot be decomposed as the tensor product of topological Azumaya algebras of degrees m and n.
Remark 3.7 Under the hypotheses of Theorem 1.3, the topological Azumaya algebras
$\mathscr {A}_{m}$
and
$\mathscr {A}_{n}$
are not neccesarily unique up to isomorphism. In order to see this, we consider the Moore–Postnikov tower for
$f_{\otimes }$
:
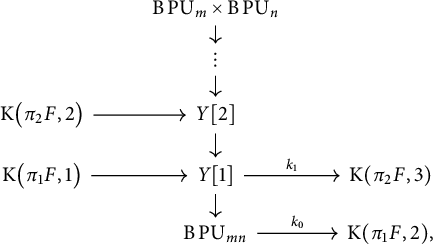
where F is the homotopy fiber of
$f_{\otimes }$
, and
$k_{i-1}:Y[i-1]\rightarrow \operatorname {\mathrm {K}}\bigl (\pi _{i}F,i+1\bigr )$
is the k-invariant that classifies the fiber sequence
$Y[i] \rightarrow Y[i-1]$
, for
$i>0$
, [Reference Hatcher8, Theorem 4.71].
Since the map
$f_{\otimes }$
induces an isomorphism on
$\pi _{2}$
, and
$\pi _{2i+1}$
for
$0<i<m$
, it follows that
$\operatorname {\mathrm {B}}\operatorname {\mathrm {PU}}_{mn} \simeq Y[i]$
for
$i=1,2,3$
, and
$Y[2i]\simeq Y[2i+1]$
for
$1<i<m$
.
The long exact sequence of
$F\to \operatorname {\mathrm {B}}\operatorname {\mathrm {PU}}_{m}\times \operatorname {\mathrm {B}}\operatorname {\mathrm {PU}}_{n} \to \operatorname {\mathrm {B}}\operatorname {\mathrm {PU}}_{mn}$
yields
$$ \begin{align*} \pi_{i}F\cong \begin{cases} 0 & \text{if } i=2 \text{ or } i \text{ is odd and } i<2m+1,\\ {\mathbb{Z}} & \text{if } i\neq2, i \text{ is even and } i<2m+1. \end{cases} \end{align*} $$
Hence, the Moore–Postnikov tower of
$f_{\otimes }$
takes the form
Let X be a CW complex of
$\dim (X)\leq 6$
. Let m and n be as in the hypothesis of Theorem 1.3, and
$m>3$
. Let
$\mathscr {A}$
be a topological Azumaya algebra of degree
$mn$
.
Observe that the k-invariant
$k_{3}$
is trivial because
$\operatorname {\mathrm {H}}^{5}(\operatorname {\mathrm {B}}\operatorname {\mathrm {PU}}_{mn};{\mathbb {Z}})$
is trivial, [Reference Antieau and Williams1, Proposition 4.1]. Hence, there is no obstruction to lift
$\mathscr {A}$
to
$Y[4]$
. Similarly, we can lift the identity map
$\operatorname {\mathrm {id}}_{\operatorname {\mathrm {B}}\operatorname {\mathrm {PU}}_{mn}}$
to
$Y[4]$
, in this case, we obtain the splitting
$Y[4]\simeq \operatorname {\mathrm {B}}\operatorname {\mathrm {PU}}_{mn}\times \operatorname {\mathrm {K}}({\mathbb {Z}},4)$
. Then the lifting of
$\mathscr {A}$
takes the form
$(\mathscr {A},\xi ):X\rightarrow \operatorname {\mathrm {B}}\operatorname {\mathrm {PU}}_{mn}\times \operatorname {\mathrm {K}}({\mathbb {Z}},4)$
.
The cohomology groups of X vanish for all degrees greater than 6, given that X is six-dimensional. Thus
$(\mathscr {A},\xi )$
can be lifted up the Moore–Postnikov tower to
$\operatorname {\mathrm {B}}\operatorname {\mathrm {PU}}_{m}\times \operatorname {\mathrm {B}}\operatorname {\mathrm {PU}}_{n}$
. See diagram (3.9).
This proves that
$\mathscr {A}$
can be decomposed as
$\mathscr {A}_{m}\otimes \mathscr {A}_{n}$
. The lifting
$(\mathscr {A},\xi )$
is not necessarily unique. In fact, every cohomology class
$\xi \in \operatorname {\mathrm {H}}^{4}(X;{\mathbb {Z}})$
gives rise to a lifting
$(\mathscr {A},\xi )$
.
Acknowledgement
The author would like to express her deep gratitude to Ben Williams, her thesis advisor, for having proposed this research topic, pointing out relevant references, and having devoted a great deal of time to discuss details of the research with the author. The author gratefully acknowledges the anonymous referee for reading the paper carefully and providing thoughtful comments, many of which have resulted in changes to the revised version of the manuscript.
