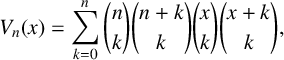1 Introduction
In his ingenious proof of the irrationality of
$\zeta (2)$
and
$\zeta (3)$
, Apéry [Reference Apéry1] introduced the numbers
$$ \begin{align*} A_n=\sum_{k=0}^n{n\choose k}^2{n+k\choose k}^2\quad \text{and}\quad A_n'=\sum_{k=0}^n{n\choose k}^2{n+k\choose k}, \end{align*} $$
which are now known as the Apéry numbers. Since the appearance of the Apéry numbers, some interesting arithmetic properties have been gradually discovered. For instance, Sun [Reference Sun8, formula (1.6)] showed that for any prime
$p\ge 5$
,
$$ \begin{align*} \sum_{k=0}^{p-1}(2k+1)A_k\equiv p+\frac{7}{6}p^4B_{p-3}\pmod{p^5}, \end{align*} $$
where
$B_n$
denotes the nth Bernoulli number. In 2012, Guo and Zeng [Reference Guo and Zeng3, Theorem 1.3] proved that
$$ \begin{align*} \sum_{k=0}^{p-1}(2k+1)^3A_k\equiv p^3\pmod{2p^6}. \end{align*} $$
In 2012, Sun [Reference Sun8] introduced the Apéry polynomials,
$$ \begin{align*} A_n(x)=\sum_{k=0}^n{n\choose k}^2{n+k\choose k}^2x^k, \end{align*} $$
and conjectured that
$$ \begin{align*} \sum_{k=0}^{n-1}\epsilon^k(2k+1)A_k(x)^m\equiv 0\pmod{n}, \end{align*} $$
where
$\epsilon =\pm 1$
and
$n,m$
are positive integers. This conjectural divisibility result was confirmed by Pan [Reference Pan5, Theorem 1.1].
In 2020, Sun [Reference Sun7, formula (1.8)] introduced the Apéry-like polynomials
$$ \begin{align*} V_n(x)=\sum_{k=0}^n {n\choose k}{n+k\choose k}{x\choose k}{x+k\choose k}. \end{align*} $$
Note that
$V_n(n)=A_n$
and
$$ \begin{align*} V_n\bigg(-\frac{1}{2}\bigg)=\frac{1}{16^n}\sum_{k=0}^n{2k\choose k}^2{2n-2k\choose n-k}^2. \end{align*} $$
Let
$p\ge 5$
be a prime and, for
$x\in \mathbb {Z}_p$
, let
$\langle x\rangle _p$
denote the least nonnegative integer a with
$a\equiv x \pmod {p}$
. Sun [Reference Sun7, Theorem 4.5] also showed that for
$x\not \equiv 0,-1\pmod {p}$
and
$x'=(x-\langle x\rangle _p)/p$
,
$$ \begin{align*} \sum_{k=0}^{p-1}(2k+1)V_k(x)\equiv p^3\frac{x'(x'+1)}{x(x+1)}+2p^4\frac{x'(x'+1)+1}{x(x+1)}H_{\langle x\rangle_p}\pmod{p^5}, \end{align*} $$
where
$H_n=\sum _{i=1}^n1/i$
denotes the nth harmonic number.
Recently, Wang [Reference Wang10, Theorem 1.1] proved that for any prime
$p\ge 5$
,
$$ \begin{align*} \sum_{k=0}^{p-1}(-1)^k(2k+1)V_n\bigg(-\frac{1}{2}\bigg) &\equiv (-1)^{{(p-1)}/{2}}p+3p^3E_{p-3}\pmod{p^4},\\[10pt] \sum_{k=0}^{p-1}2^k(k+1)V_n\bigg(-\frac{1}{2}\bigg) &\equiv (-1)^{{(p-1)}/{2}}p+5p^3E_{p-3}\pmod{p^4}, \end{align*} $$
which confirm two supercongruence conjectures due to Sun [Reference Sun9, Conjecture 33].
In his talk at the 7th Chinese National Conference on Combinatorial Number Theory, Z.-H. Sun discussed the sums of squares of the Apéry-like polynomials
$V_n(x)$
and proposed the following divisibility conjecture.
Conjecture 1.1. Let
$p\ge 5$
be a prime. For
$x\in \mathbb {Z}_p$
and
$x\not \equiv -1/2\pmod {p}$
,
$$ \begin{align*} \sum_{n=0}^{p-1}(2n+1)V_n(x)^2\equiv 0\pmod{p^2}. \end{align*} $$
The aim of this note is to give a positive answer to this problem as follows.
Theorem 1.2. Let
$p\ge 5$
be a prime. For
$x\in \mathbb {Z}_p$
,
$$ \begin{align*} \sum_{n=0}^{p-1}(2n+1)V_n(x)^2\equiv \frac{p^2}{2\langle x\rangle_p+1}\pmod{p^2}. \end{align*} $$
2 Proof of Theorem 1.2
We begin with the following identity [Reference Guo2, formula (2.5)]:
$$ \begin{align} {x\choose j}{x+j\choose j}{x\choose k}{x+k\choose k}=\sum_{s=0}^{j+k}{j+k\choose s}{s\choose j}{s\choose k}{x\choose s}{x+s\choose s}. \end{align} $$
Using (2.1) twice, we obtain
$$ \begin{align*} V_n(x)^2&=\sum_{j=0}^n\sum_{k=0}^n {n\choose j}{n+j\choose j}{n\choose k}{n+k\choose k}{x\choose j}{x+j\choose j}{x\choose k}{x+k\choose k}\\[2pt] &=\sum_{j=0}^n\sum_{k=0}^n \sum_{r=0}^{j+k}\sum_{s=0}^{j+k}{n\choose r}{n+r\choose r}{x\choose s}{x+s\choose s}{j+k\choose r}{r\choose j}{r\choose k}{j+k\choose s}{s\choose j}{s\choose k}. \end{align*} $$
It follows that
$$ \begin{align} \sum_{n=0}^{p-1}(2n+1)V_n(x)^2 & =\sum_{j=0}^{p-1}\sum_{k=0}^{p-1} \sum_{r=0}^{j+k}\sum_{s=0}^{j+k}{x\choose s}{x+s\choose s}{j+k\choose r}{r\choose j}{r\choose k}{j+k\choose s}{s\choose j}{s\choose k} \notag\\[2pt] &\quad \times\sum_{n=0}^{p-1}(2n+1){n\choose r}{n+r\choose r}. \end{align} $$
Since
$$ \begin{align*} \sum_{n=0}^{N-1}(2n+1){n\choose r}{n+r\choose r} =\frac{N^2}{r+1}{N+r\choose r}{N-1\choose r}, \end{align*} $$
which can be easily proved by induction on N, we deduce that for
$0\le r\le 2p-2$
,
$$ \begin{align} \sum_{n=0}^{p-1}(2n+1){n\choose r}{n+r\choose r} &=\frac{p^2}{r+1}{p+r\choose r}{p-1\choose r}\notag\\[2pt] &=\frac{p^2(p^2-1^2)\cdots(p^2-r^2)}{(r+1)r!^2}\notag\\[2pt] &\equiv \frac{(-1)^rp^2}{r+1}\pmod{p^2}. \end{align} $$
Substituting (2.3) into the right-hand side of (2.2) gives
$$ \begin{align} \sum_{n=0}^{p-1}(2n+1)V_n(x)^2 &\equiv p^2\sum_{j=0}^{p-1}\sum_{k=0}^{p-1} \sum_{s=0}^{j+k}{x\choose s}{x+s\choose s}{j+k\choose s}{s\choose j}{s\choose k}\notag \\[2pt] &\quad \times\sum_{r=0}^{j+k}\frac{(-1)^r}{r+1}{j+k\choose r}{r\choose j}{r\choose k}\pmod{p^2}. \end{align} $$
Using the identity,
$$ \begin{align*} \sum_{r=0}^{j+k}\frac{(-1)^{r}}{r+1}{r\choose j}{j\choose r-k}=\frac{(-1)^{j+k}}{(j+k+1){j+k\choose j}}, \end{align*} $$
from [Reference Liu4, formula (2.2)], we get
$$ \begin{align} \sum_{r=0}^{j+k}\frac{(-1)^r}{r+1}{j+k\choose r}{r\choose j}{r\choose k}={j+k\choose j}\sum_{r=0}^{j+k}\frac{(-1)^r}{r+1}{r\choose j}{j\choose r-k}=\frac{(-1)^{j+k}}{j+k+1}. \end{align} $$
Combining (2.4) and (2.5), we obtain
$$ \begin{align} \sum_{n=0}^{p-1}(2n+1)V_n(x)^2 &\equiv p^2\sum_{j=0}^{p-1}\sum_{k=0}^{p-1} \sum_{s=0}^{j+k}\frac{(-1)^{j+k}}{j+k+1}{x\choose s}{x+s\choose s}{j+k\choose s}{s\choose j}{s\choose k}\pmod{p^2}\notag\\[2pt] &=p^2\sum_{s=0}^{2p-2}\sum_{j=0}^{p-1}\sum_{k=0}^{p-1} \frac{(-1)^{j+k}}{j+k+1}{x\choose s}{x+s\choose s}{j+k\choose s}{s\choose j}{s\choose k}. \end{align} $$
Since the summands on the right-hand side of (2.6) are congruent to
$0$
modulo
$p^2$
except for
$j+k=p-1$
, we conclude that
$$ \begin{align*} \sum_{n=0}^{p-1}(2n+1)V_n(x)^2 &\equiv p\sum_{s=0}^{p-1}{x\choose s}{x+s\choose s}{p-1\choose s}\sum_{j+k=p-1}{s\choose j}{s\choose k}\pmod{p^2}\\[2pt] &=p\sum_{s=0}^{p-1}{x\choose s}{x+s\choose s}{p-1\choose s}{2s\choose p-1}, \end{align*} $$
where we have used the Chu–Vandermonde identity in the last step.
Furthermore, we have
${p-1\choose s}\equiv (-1)^s\pmod {p}$
and
${2s\choose p-1}\equiv p/(2s+1)\pmod {p}$
for
$0\le s\le p-1$
. It follows that
$$ \begin{align} \sum_{n=0}^{p-1}(2n+1)V_n(x)^2 &\equiv p^2\sum_{s=0}^{p-1}\frac{(-1)^s}{2s+1}{x\choose s}{x+s\choose s}\notag\\[2pt] &\equiv p^2\sum_{s=0}^{\langle x\rangle_p}\frac{(-1)^s}{2s+1}{\langle x\rangle_p\choose s}{\langle x\rangle_p+s\choose s}\pmod{p^2}. \end{align} $$
Next, we recall the identity [Reference Prodinger6, formula (2.1)],
$$ \begin{align} \sum_{s=0}^n\frac{(-1)^s}{z+s}{n\choose s}{n+s\choose s}=\frac{(1-z)_n}{z(1+z)_n}. \end{align} $$
The case
$z=1/2$
in (2.8) reads
$$ \begin{align} \sum_{s=0}^n\frac{(-1)^s}{2s+1}{n\choose s}{n+s\choose s}=\frac{1}{2n+1}. \end{align} $$
Finally, combining (2.7) and (2.9), we obtain
$$ \begin{align*} \sum_{n=0}^{p-1}(2n+1)V_n(x)^2\equiv \frac{p^2}{2\langle x\rangle_p+1}\pmod{p^2}, \end{align*} $$
as desired.
