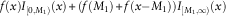1. Introduction
Designing an optimal reinsurance policy, in some sense, is one of the most attractive aspects in actuarial science. Reinsurance is a form of an insurance contract, according to which the reinsurer accepts to cover a portion of an insurer’s risk by receiving a reinsurance premium. Therefore, both reinsurance and insurance companies try to design an optimal reinsurance policy to improve their ability to managing their risks under a certain criteria, e.g., increasing their surplus/wealth of company, decreasing the ruin probability, etc.
Several authors considered the problem of designing an optimal reinsurance policy under a certain optimal criteria. Surprisingly, in most of the studies the stop-loss reinsurance policy (or some its modification) is established as an optimal policy. For instance, Borch (Reference Borch1960) proved that, under the variance retained risk optimal criteria and in the class of reinsurance policies with an equal reinsurance premium, the stop-loss reinsurance minimises such variance. Under Borch’s (Reference Borch1960) class of reinsurance policies, Hesselager (Reference Hesselager1990) showed that the stop-loss reinsurance is an optimal policy which provides the smallest Lundberg’s upper bound for the ruin probability. Optimality of the one-layer stop-loss contract under the minimisation of the ruin probability criteria and several premium principles has been established by Kaluszka (Reference Kaluszka2005). Passalacqua (Reference Passalacqua2007) studied the impacts of multi-layer stop-loss reinsurance contract on the valuation of risk capital (assessed under the Solvency II framework) for credit insurance. Cai et al. (Reference Chi2008) showed that the one-layer stop-loss contract is optimal whenever either both the ceded and the retained loss functions are increasing or the retained loss function is increasing and left-continuous. Kaluszka & Okolewski (Reference Kaluszka and Okolewski2008) established that the one-layer stop-loss contract is an optimal contract under the maximisation of the expected utility, the stability and the survival probability of the cedent. Tan et al. (2011) and Chi & Tan (Reference Chi2011) showed that under the expectation premium principle assumption and the Conditional Tail Expectation (CTE) minimisation criteria the stop-loss reinsurance contract is optimal. Porth et al. (Reference Porth, Seng Tan and Weng2013) employed an empirical reinsurance model (introduced by Weng, Reference Weng2009) to show that, under the standard deviation premium principle and consistency with market practice, a one-layer stop-loss reinsurance contract is optimal. In a situation that both the ceded and the retained loss functions are constrained to be increasing and under the variance premium principle assumption, Chi (2012a, Reference Cai, Tan, Weng and Zhang2012 b) showed that one-layer stop-loss reinsurance is always optimal over both the Value-at-Risk (VaR) and the Conditional Value-at-Risk (CVaR) criteria. Ouyang & Li (Reference Ouyang and Li2010) constructed a multi-layer reinsurance policy to achieve sustainable development of an agricultural insurance policy in the sense of adverse selection and mortal hazard problems. In 2012, Dedu generalised the stop-loss reinsurance to a multi-layer reinsurance policy. In the first step, she considered a certain class of multi-layer reinsurance policies with some unknown parameters. An optimal reinsurance policy, in such class, have been obtained by estimating unknown parameters such that the VaR and the CTE of the insurer’s total risk have been minimised. Chi (2012a, Reference Cai, Tan, Weng and Zhang2012 b) showed that under minimising the risk-adjusted value of an insurer’s liability and the VaR (or the CVaR) criteria the two-layer reinsurance contract is optimal under the Dutch premium principle assumption. Cortes et al. (Reference Cortes, Rau-Chaplin, Wilson, Cook and Gaiser-Porter2013) considered a multi-layer reinsurance contract consisting of a fixed number of layers. Then, they determined an optimal multi-layer contract such that for a given expected return the associated risk value is minimised. Chi & Tan (Reference Chi and Tan2013) established that a one-layer stop-loss contract is always optimal over both the VaR and the CVaR criteria and the prescribed premium principles. Cai & Weng (Reference Chi and Tan2014) showed that under risk margin associated with an expectile risk measure criteria, a two-layer reinsurance contract minimises the liability of an insurer for a general class of reinsurance premium principles. Panahi Bazaz & Payandeh Najafabadi (Reference Panahi Bazaz and Payandeh Najafabadi2015) estimated parameters of a one-layer reinsurance policy such that a convex combination of the CTE of both the insurer’s and reinsurer’s random risks is minimised. Optimality of the stop-loss contract under distortion risk measures and premiums has been established by Assa (Reference Assa2015). Zhuang et al. (Reference Zhuang, Weng, Tan and Assa2016) showed that in a situation that the premium budget is not sufficiently high enough, under the CVaR optimality criteria, the optimal reinsurance policy will change from the stop-loss contract to a one-layer stop-loss. Payandeh Najafabadi & Panahi Bazaz (Reference Payandeh Najafabadi and Qazvini2016) considered a co-reinsurance contract which is a combination of several reinsurance contracts. Using a Bayesian approach parameters of co-reinsurance contract have been estimated.
In order to exclude the moral hazard, an appropriate reinsurance contract has to assign increasing functions to both insurer and reinsurer portions. On the other hand, reported claims in insurance industry have the property that higher claim size is less frequent with more severe probability of loss, whereas lower claim sizes are more frequent with less severe probability of loss. Unfortunately, the stop-loss reinsurance contract despite several well-known properties does not consider these two important facts.
This article considers minimising the CTE risk measure of the insurer’s total risk as an optimal criterion to design an optimal reinsurance contract. Then, it introduces an algorithm which generalises a given optimal stop-loss policy to a multi-layer optimal reinsurance policy. To achieve such optimal multi-layer reinsurance policy, this article starts from a given optimal stop-loss reinsurance policy f(⋅). In the first step, it cuts down the interval [0, ∞) into intervals [0, M
1) and [M
1, ∞). By shifting the origin of Cartesian coordinate system to (M
1, f(M
1)), it shows that under the CTE criteria,
$$f\left( x \right)I_{{[0,M_{{\rm 1}} )}} \left( x \right){\plus}\left( {f\left( {M_{{\rm 1}} } \right){\plus}f\left( {x{\minus}M_{{\rm 1}} } \right)} \right)I_{{[M_{{\rm 1}} ,{\rm }\infty)}} \left( x \right)$$
is, again, an optimal policy. This extension procedure can be repeated to obtain an optimal k-layer reinsurance policy. Finally, unknown parameters of the multi-layer reinsurance policy are estimated using some additional appropriate criteria. Practical application of our findings have been shown through a simulation study. The multi-layer reinsurance policy, similar to the original stop-loss reinsurance policy is optimal, in a same sense. Moreover, it involves some other optimal criteria which the original policy does not have. Under optimality criterion of minimising a general translative and monotone risk measure ρ(⋅) of either the insurer’s total risk or both the insurer’s and the reinsurer’s total risks, this article (in its discussion) also extends an optimal reinsurance contract f(⋅) to an optimal multi-layer and continuous reinsurance policy.
This article is organised as the following. Section 2 collects some elements that play vital roles in the rest of this article. Moreover, section 2 presents an algorithm that extends a given optimal stop-loss reinsurance policy to an optimal multi-layer policy. Section 3 describes three simulation-based studies illustrating the practical application of our results. Parameters of the optimal multi-layer contract, for each simulation study, have been estimated using an additional appropriate criteria. In discussioning results of this article (from two different senses) extends an optimal reinsurance contract f(⋅), under a general translative and monotone risk measure ρ(⋅), to an optimal multi-layer and continuous reinsurance policy.
2. Preliminary
Suppose continuous and non-negative random variable X stands for the aggregate claim initially assumed by an insurer. In addition, suppose that random claim X with a cumulative distribution function F
X
(t) and a survival function
$\bar{F}_{X} (t)$
, and a density function f
X
defines on the probability space
$(\Omega ,{\cal F},P),$
where Ω=[0, ∞) and
${\cal F}$
is the Borel σ-field on Ω. Now, let X
I
and X
R
(or X
R
=h(X)), respectively, stand for the insurer’s and the reinsurer’s risk portions from random claim X, such that X=X
I
+X
R
and 0≤X
I
& X
R
=h(X)≤X. Under this presentation, the total risk of the insurance company can be restated as
$$\eqalignno{ T_{h} (X) & \, {\equals}\, X_{I} {\plus}\pi _{h}^{X} \cr & \, {\equals}\, X\, {\minus}\, h(X){\plus}\pi _{h}^{X} $$
where h(⋅) is a functional form of a reinsurance contract and
$\pi _{h}^{X} $
stands for a reinsurance premium.
Now, we collect some elements that play vital roles in the rest of this article.
Definition 1 The risk measure ρ(⋅) is called translative and monotone if and only if ρ(X+c)=ρ(X)+c and ρ(X)≤ρ(Y) whenever P(X≤Y)=1 and
$c\in{\Bbb R}$
.
In the sense of the above definition a wide class of risk measures, such as coherent, spectral, distortion, Quantile-based and Wang, are translative and monotone risk measures, see Denuit et al. (Reference Denuit, Dhaene, Goovaerts and Kaas2006) for other possible classes of translative and monotone risk measures.
Consider the following class of reinsurance policies:
$$\eqalignno{ {\cal C}\, {\equals}\, & \left\{ {h(X)\,\,\colon\,\,{\rm both}\;h(X)\;{\rm and}\;X\, {\minus}\, h(X)\;{\rm are}\;{\rm non {\hbox - } decreasing}\;{\rm in}\;X;} \right. \cr& \left. { \quad \quad 0\leq h(X)\leq X\,; \ {\rm and}\,\pi _{h}^{X} \, {\equals}\, \:{\rm constant}\:} \right\} $$
where
$\pi _{h}^{X} $
stands for the reinsurance premium under a reinsurance contract h(⋅).
Suppose that f(⋅) in class of reinsurer contracts
${\cal C}$
, given by (2), minimises a given translative and monotone risk measure ρ(⋅) of the total risk of insurance company, i.e.,
$f(X)\,\equiv\,\mathop{{{\rm argmin}}}\limits_{{h\in{\cal C}}} \rho \left( {T_{h} (X)} \right)$
. Now one may cut down the interval [0, ∞) into intervals [0, M
1) and [M
1, ∞) and shift the origin of Cartesian coordinate system to (M
1, f(M
1)), see Figure 1(a) for an illustration. Again, in the new Cartesian coordinate system, the shifted reinsurance contract f(⋅) is an optimal contract and, in the old Cartesian coordinate system, the reinsurance contract g(x)=f(x)I
[0,M
1)(x)+
$$\left( {f\left( {M_{{\rm 1}} } \right){\plus}f\left( {x\, {\minus}\, M_{{\rm 1}} } \right)} \right)I_{{[M_{{\rm 1}} ,{\rm }\infty)}} \left( x \right)$$
is an appropriate contract. Since f(⋅) is an optimal contract, optimality of g(⋅) arrives by showing that ρ(T
g
(X))≡ρ(T
f
(X)). Unfortunately proof of such identity is not available for general translative and monotone risk measures. Hopefully, Tan et al. (2011, theorem 3.1) showed that under the CTE criteria as far as
$g( \cdot )\in{\cal C}$
and 0≤g(x)≤f*(x)=max{x−d
α
, 0}, for a given α∈(0, 1) and all x≥0, any contract g(⋅) is again optimal, i.e.,
$\rho (T_{g} (X))\,\equiv\,\rho (T_{{f^{{\asterisk}} }} (X))$
. Using such seminal result, we can conclude that under the CTE minimisation criteria, the new contract
$g(x)\, {\equals}\, f^{{\asterisk}} (x)I_{{[0,M_{1} )}} (x){\plus}(f^{{\asterisk}} (M_{1} ){\plus}f^{{\asterisk}} (x\, {\minus}\, M_{1} ))I_{{[M_{1} ,\infty)}} (x)$
is optimal. Again cutting down the interval [M
1, ∞) into intervals [M
1, M
2) and [M
2, ∞) and shifting the origin of Cartesian coordinate system to (M
2, f*(M
2−M
1)), we can obtain new contract f*(x)I
[0,M
1)(x)+
$(f^{{\asterisk}} (M_{1} ){\plus}f^{{\asterisk}} (x\, {\minus}\, M_{1} ))I_{{[M_{1} ,M_{2} )}} (x){\plus}(f^{{\asterisk}} (M_{2} ){\plus}f^{{\asterisk}} (x\, {\minus}\, M_{2} ))I_{{[M_{2} ,\infty)}} (x)$
which Tan et al. (2011, theorem 3.1) warranties its optimality. Several implementation of the above procedure leads to an optimal multi-layer reinsurance contract, under the CTE minimisation criteria. The following algorithm provides such multi-layer contract.
Algorithm 1. Suppose X R stands for the reinsurer’s risk portion from random claim X. The following steps design a multi-layer reinsurance policy which minimises the CTE of the insurer’s total risk.
Figure 1 (a) Shifting the Cartesian coordinate system and finding the optimal contract in the new Cartesian coordinate system and (b) stop-loss and an optimal and k-layer reinsurance strategies.
Step (1): A multi-layer reinsurance policy is obtained by the following iterative algorithm:
Part (1): For k≥2; cut down the interval [M k , ∞) into intervals [M k , M k+1) and [M k+1, ∞) and define the reinsurer’s risk portion by
$$f_{k} (X)\, {\equals}\, f_{{k\, {\minus}\, 1}} (X)I_{{[0,\,M_{k} )}} (X){\plus}\left[ {f_{{k\, {\minus}\, 1}} (M_{k} ){\plus}f(X\, {\minus}\, M_{k} )} \right]I_{{[M_{k} ,\,\infty)}} (X)$$
where f 0(X)=f(X)=max{X−d α , 0};
Part (2): Go to Step 2 if a given stop criteria is met, otherwise set k=k+1 and go to Part (1)
Step (2) Part (1): The reinsurer’s risk portion under the k-layer reinsurance policy is
$X_{R} \, {\equals}\, f(X)I_{{[0,\,M_{1} )}} (X){\plus}\mathop{\sum}\nolimits_{j\, {\equals}\, 1}^{k\, {\minus}\, 1} {f_{j} (X)I_{{[M_{j} ,\,M_{{j{\plus}1}} )}} (X){\plus}\left[ {f_{{k\, {\minus}\, 1}} (M_{k} ){\plus}f(X\, {\minus}\, M_{k} )} \right]I_{{[M_{k} ,\,\infty)}} (X)} .$
Part (2): Now estimate unknown parameters by some additional appropriate criteria (or estimation methods) along the fact that the fact that E(max{X−d α , 0})=E(X R ).
Closeness to an appropriate criteria (such as an optimal ruin probability) can be considered, in advance, as a stopping criteria in the above algorithm.
Algorithm (1) designs an optimal multi-layer reinsurance policy which the insurer’s and the reinsurer’s portion of both companies are increasing functions in the initial insurer claim X. Moreover it provides a sharing system such that its higher layer works appropriately for large reported claim size.
Application of Algorithm (1) leads to the following optimal k-layer reinsurance policy.
$$\matrix{ {X_{R}^{{{\rm opt}}} } & {\, {\equals}\, \left\{ {\matrix{ 0 & {X\,\lt\,d_{\alpha } } \cr {X\, {\minus}\, d_{\alpha } } & {d_{\alpha } \leq X\,\lt\,M_{1} } \cr {M_{1} \, {\minus}\, d_{\alpha } } & {M_{1} \leq X\,\lt\,M_{1} {\plus}d_{\alpha } } \cr {X\, {\minus}\, 2d_{\alpha } } & {M_{1} {\plus}d_{\alpha } \leq X\,\lt\,M_{2} } \cr \vdots & {} \cr {M_{k} \, {\minus}\, kd_{\alpha } } & {M_{k} \leq X\,\lt\,M_{k} {\plus}d_{\alpha } } \cr {X\, {\minus}\, kd_{\alpha } } & {M_{k} {\plus}d_{\alpha } \leq X} \cr } } \right.} \cr } $$
Figure 1(b) illustrates optimal multi-layer reinsurance policy (4).
For the sake of simplicity, hereafter now, we set
$M_{0}^{{\asterisk}} \,\colon\,\, {\equals}\, d_{\alpha } ,\,M_{1}^{{\asterisk}} \,\colon\,\, {\equals}\, M_{1} ,\,M_{2}^{{\asterisk}} \,\colon\,\, {\equals}\, M_{1} {\plus}d_{\alpha } $
and so on.
The cumulative distribution function for optimal k-layer reinsurance policy (4) can be restated as
$$\eqalignno{ F_{{X_{R}^{{{\rm opt}}} }} \left( t \right)\, {\equals}\, & F_{X} \left( {t_{\, {\minus}\, } {\plus}M_{0}^{{\asterisk}} } \right)I_{{\left[ {0,M_{1}^{{\asterisk}} \, {\minus}\, M_{0}^{{\asterisk}} } \right)}} \left( t \right){\plus}F_{X} \left( {t{\plus}M_{2}^{{\asterisk}} \, {\minus}\, \left( {M_{1}^{{\asterisk}} \, {\minus}\, M_{0}^{{\asterisk}} } \right)} \right)I_{{\left[ {M_{1}^{{\asterisk}} \, {\minus}\, M_{0}^{{\asterisk}} ,\,\left( {M_{3}^{{\asterisk}} \, {\minus}\, M_{2}^{{\asterisk}} } \right){\plus}\left( {M_{1}^{{\asterisk}} \, {\minus}\, M_{0}^{{\asterisk}} } \right)} \right)}} \left( t \right) \cr & {\plus}F_{X} \left( {t{\plus}M_{4}^{{\asterisk}} \, {\minus}\, \left( {M_{3}^{{\asterisk}} \, {\minus}\, M_{2}^{{\asterisk}} } \right)\, {\minus}\, \left( {M_{1}^{{\asterisk}} \, {\minus}\, M_{0}^{{\asterisk}} } \right)} \right)I_{{\left[ {\left( {M_{3}^{{\asterisk}} \, {\minus}\, M_{2}^{{\asterisk}} } \right){\plus}\left( {M_{1}^{{\asterisk}} \, {\minus}\, M_{0}^{{\asterisk}} } \right),\,\left( {M_{5}^{{\asterisk}} \, {\minus}\, M_{4}^{{\asterisk}} } \right){\plus}\left( {M_{3}^{{\asterisk}} \, {\minus}\, M_{2}^{{\asterisk}} } \right){\plus}\left( {M_{1}^{{\asterisk}} \, {\minus}\, M_{0}^{{\asterisk}} } \right)} \right)}} (t) \cr & {\plus} \cdots {\plus}F_{X} \left( {t{\plus}M_{{m\, {\minus}\, 2}}^{{\asterisk}} \, {\minus}\, \mathop{\sum}\limits_{j\, {\equals}\, 1}^{k\,/\,2\, {\minus}\, 2} {\left( {M_{{2j{\plus}1}}^{{\asterisk}} \, {\minus}\, M_{{2j}}^{{\asterisk}} } \right)\, {\minus}\, \left( {M_{1}^{{\asterisk}} \, {\minus}\, M_{0}^{{\asterisk}} } \right)} } \right)I_{{\left[ {\mathop{\sum}\limits_{j\, {\equals}\, 1}^{k\,/\,2\, {\minus}\, 2} {\left( {M_{{2j{\plus}1}}^{{\asterisk}} \, {\minus}\, M_{{2j}}^{{\asterisk}} } \right)} {\plus}\left( {M_{1}^{{\asterisk}} \, {\minus}\, M_{0}^{{\asterisk}} } \right),\infty} \right)}} (t) $$
The following provides the moment generating function for the reinsurer’s risk portion from random claim X, under optimal k-layer reinsurance policy (4).
Proposition 1.
Suppose X
R
stands for the reinsurer’s risk portion from random claim X, under an optimal k-layer reinsurance policy which minimises the CTE of the insurer’s total risk. Then, the moment generating function for the reinsurer’s risk portion
$X_{R}^{{{\rm opt}}} $
under an optimal k-layer reinsurance policy:
$$\eqalignno{ M_{{X_{R}^{{{\rm opt}}} }} (t) \, {\equals}\, & 1\, {\minus}\, {\rm e}^{{t\left( {\left( {M_{1}^{{\asterisk}} \, {\minus}\, M_{0}^{{\asterisk}} } \right)} \right.{\plus}\mathop{\sum}\limits_{j\, {\equals}\, 1}^{k\,/\,2\, {\minus}\, 1} {\left. {\left( {M_{{2j{\plus}1}}^{{\asterisk}} \, {\minus}\, M_{{2j}}^{{\asterisk}} } \right)} \right)} }} \bar{F}_{X} \left( {M_{{k\, {\minus}\, 2}}^{{\asterisk}} } \right){\plus}{\int}_{M_{0}^{{\asterisk}} }^{M_{1}^{{\asterisk}} } {t{\rm e}^{{t\left( {X\, {\minus}\, M_{0}^{{\asterisk}} } \right)}} \bar{F}_{X} \left( x \right)dx} \cr& {\plus}\mathop{\sum}\limits_{j\, {\equals}\, 1}^{k\,/\,2\, {\minus}\, 1} {{\int}_{M_{{2j}}^{{\asterisk}} }^{M_{{2j{\plus}1}}^{{\asterisk}} } {t{\rm e}^{{t\left( {x{\plus}} \right.\left( {M_{1}^{{\asterisk}} \, {\minus}\, M_{0}^{{\asterisk}} } \right){\plus}\mathop{\sum}\limits_{i\, {\equals}\, 1}^{j\, {\minus}\, 1} {\left( {M_{{2i{\plus}1}}^{{\asterisk}} \, {\minus}\, M_{{2i}}^{{\asterisk}} } \right)\left. {\, {\minus}\, M_{{2j}}^{{\asterisk}} } \right)} }} \bar{F}_{X} \left( x \right)dx} } \cr & {\plus}{\int}_{M_{{k\, {\minus}\, 2}}^{{\asterisk}} }^\infty {{\rm e}^{{t\left( {X{\plus}} \right.\mathop{\sum}\limits_{j\, {\equals}\, 1}^{k\,/\,2\, {\minus}\, 1} {\left( {M_{{2j{\plus}1}}^{{\asterisk}} \, {\minus}\, M_{{2j}}^{{\asterisk}} } \right)} {\plus}\left( {M_{1}^{{\asterisk}} \, {\minus}\, M_{0}^{{\asterisk}} } \right)\left. {\, {\minus}\, M_{{k\, {\minus}\, 2}}^{{\asterisk}} } \right)}} dF_{X} \left( x \right)} $$
where
$\mathop{\sum}\nolimits_{j\, {\equals}\, a}^b {c_{j} \, {\equals}\, 0} $
whenever b<a.
Proof
Observe that the moment generating function of
$X_{R}^{{{\rm opt}}} $
, given by equation (4) can be calculated as follows:
$$M_{{X_{R}^{{{\rm opt}}} }} \left( t \right)\, {\equals}\, {\int}_0^{M_{0}^{{\asterisk}} } {dF_{X} \left( x \right)} {\plus}{\int}_{M_{0}^{{\asterisk}} }^{M_{1}^{{\asterisk}} } {{\rm e}^{{t\left( {x\, {\minus}\, M_{0}^{{\asterisk}} } \right)}} dF_{X} \left( x \right)} {\plus} \cdots {\plus}{\int}_{M_{{m\, {\minus}\, 2}}^{{\asterisk}} }^\infty {{\rm e}^{{t\left( {X{\plus}} \right.\mathop{\sum}\limits_{j\, {\equals}\, 1}^{k\,/\,2\, {\minus}\, 1} {\left( {M_{{2j{\plus}1}}^{{\asterisk}} \, {\minus}\, M_{{2j}}^{{\asterisk}} } \right)} {\plus}\left( {M_{1}^{{\asterisk}} \, {\minus}\, M_{0}^{{\asterisk}} } \right)\left. {\, {\minus}\, M_{{k\, {\minus}\, 2}}^{{\asterisk}} } \right)}} } $$
The odd terms can be evaluated directly. The following calculation represents that how one can evaluate other terms:
$$\eqalignno{ {\int}_{M_{2}^{{\asterisk}} }^{M_{3}^{{\asterisk}} } {{\rm e}^{{t\left( {x{\plus}\left( {M_{1}^{{\asterisk}} \, {\minus}\, M_{0}^{{\asterisk}} } \right)\, {\minus}\, M_{2}^{{\asterisk}} } \right)}} dF_{X} \left( x \right)} & \, {\equals}\, \left. {{\rm e}^{{t\left( {x{\plus}\left( {M_{1}^{{\asterisk}} \, {\minus}\, M_{0}^{{\asterisk}} } \right)\, {\minus}\, M_{2}^{{\asterisk}} } \right)}} F_{X} \left( x \right)} \right|_{{M_{2}^{{\asterisk}} }}^{{M_{3}^{{\asterisk}} }} \, {\minus}\, {\int}_{M_{2}^{{\asterisk}} }^{M_{3}^{{\asterisk}} } {t{\rm e}^{{t\left( {x{\plus}\left( {M_{1}^{{\asterisk}} \, {\minus}\, M_{0}^{{\asterisk}} } \right)\, {\minus}\, M_{2}^{{\asterisk}} } \right)}} F_{X} \left( x \right)dx} \cr & \, {\equals}\, {\rm e}^{{t\left( {M_{3}^{{\asterisk}} {\plus}\left( {M_{1}^{{\asterisk}} \, {\minus}\, M_{0}^{{\asterisk}} } \right)\, {\minus}\, M_{2}^{{\asterisk}} } \right)}} F_{X} \left( {M_{3}^{{\asterisk}} } \right)\, {\minus}\, {\rm e}^{{t\left( {M_{2}^{{\asterisk}} {\plus}\left( {M_{1}^{{\asterisk}} \, {\minus}\, M_{0}^{{\asterisk}} } \right)\, {\minus}\, M_{2}^{{\asterisk}} } \right)}} F_{X} \left( {M_{2}^{{\asterisk}} } \right) \cr & \, \quad {\minus}\, {\int}_{M_{2}^{{\asterisk}} }^{M_{3}^{{\asterisk}} } {t{\rm e}^{{t\left( {x{\plus}\left( {M_{1}^{{\asterisk}} \, {\minus}\, M_{0}^{{\asterisk}} } \right)\, {\minus}\, M_{4}^{{\asterisk}} } \right)}} F_{X} \left( x \right)dx} \cr & \, {\equals}\, {\rm e}^{{t\left( {M_{3}^{{\asterisk}} {\plus}\left( {M_{1}^{{\asterisk}} \, {\minus}\, M_{0}^{{\asterisk}} } \right)\, {\minus}\, M_{2}^{{\asterisk}} } \right)}} F_{X} \left( {M_{3}^{{\asterisk}} } \right)\, {\minus}\, {\rm e}^{{t\left( {M_{1}^{{\asterisk}} \, {\minus}\, M_{0}^{{\asterisk}} } \right)}} F_{X} \left( {M_{2}^{{\asterisk}} } \right) \cr & \, \quad {\minus}\, {\int}_{M_{2}^{{\asterisk}} }^{M_{3}^{{\asterisk}} } {t{\rm e}^{{t\left( {x{\plus}\left( {M_{1}^{{\asterisk}} \, {\minus}\, M_{0}^{{\asterisk}} } \right)\, {\minus}\, M_{2}^{{\asterisk}} } \right)}} dx} {\plus}{\int}_{M_{2}^{{\asterisk}} }^{M_{3}^{{\asterisk}} } {t{\rm e}^{{t\left( {x{\plus}\left( {M_{1}^{{\asterisk}} \, {\minus}\, M_{0}^{{\asterisk}} } \right)\, {\minus}\, M_{2}^{{\asterisk}} } \right)}} \bar{F}_{X} \left( x \right)dx}} $$
$$\eqalignno{ & \, {\equals}\, {\rm e}^{{t\left( {M_{3}^{{\asterisk}} {\plus}\left( {M_{1}^{{\asterisk}} \, {\minus}\, M_{0}^{{\asterisk}} } \right)\, {\minus}\, M_{2}^{{\asterisk}} } \right)}} F_{X} \left( {M_{3}^{{\asterisk}} } \right)\, {\minus}\, {\rm e}^{{t\left( {M_{1}^{{\asterisk}} \, {\minus}\, M_{0}^{{\asterisk}} } \right)}} F_{X} \left( {M_{2}^{{\asterisk}} } \right) \cr & \, \quad {\minus}\, {\rm e}^{{t\left( {M_{3}^{{\asterisk}} {\plus}\left( {M_{1}^{{\asterisk}} \, {\minus}\, M_{0}^{{\asterisk}} } \right)\, {\minus}\, M_{2}^{{\asterisk}} } \right)}} {\plus}{\rm e}^{{t\left( {M_{1}^{{\asterisk}} \, {\minus}\, M_{0}^{{\asterisk}} } \right)}} {\plus}{\int}_{M_{2}^{{\asterisk}} }^{M_{3}^{{\asterisk}} } {t{\rm e}^{{t\left( {x{\plus}\left( {M_{1}^{{\asterisk}} \, {\minus}\, M_{0}^{{\asterisk}} } \right)\, {\minus}\, M_{2}^{{\asterisk}} } \right)}} \bar{F}_{X} \left( x \right)dx} $$
The desired proof arrives by a straightforward calculation.□
Similar to Proposition (1), one may show that under the optimal k-layer reinsurance contract, the moment generating function for the insurer’s risk portion,
$X_{I} \, {\equals}\, X\, {\minus}\, X_{R}^{{{\rm opt}}} ,$
from random claim X, is
$$\eqalignno{ M_{{X\, {\minus}\, X_{R}^{{{\rm opt}}} }} \left( t \right) & \, {\equals}\, \bar{F}_{X} \left( 0 \right)\, {\minus}\, {\rm e}^{{t\Big( {M_{{k\, {\minus}\, 2}} \, {\minus}\, \mathop{\sum}\limits_{j\, {\equals}\, 1}^{k\,/\,2\, {\minus}\, 2} {\left( {M_{{2j{\plus}1}} \, {\minus}\, M_{{2j}} } \right)\, {\minus}\, \left( {M_{1} \, {\minus}\, M_{0} } \right)} } \Big)}} \bar{F}_{X} \left( {M_{{k\, {\minus}\, 2}} } \right){\plus}{\int}_0^{M_{0} } {t{\rm e}^{{tx}} \bar{F}_{X} \left( x \right)dx} \cr & \quad {\plus}\mathop{\sum}\limits_{j\, {\equals}\, 1}^{k\,/\,2\, {\minus}\, 1} {{\int}_{M_{{2j\, {\minus}\, 1}} }^{M_{{2j}} } {t{\rm e}^{{t\Big( {x\, {\minus}\, \left( {M_{1} \, {\minus}\, M_{0} } \right)\, {\minus}\, \mathop{\sum}\limits_{i\, {\equals}\, 1}^{j\, {\minus}\, 1} {\left( {M_{{2i{\plus}1}} \, {\minus}\, M_{{2i}} } \right)} } \Big)}} \bar{F}_{X} \left( x \right)dx} } \cr & \quad {\plus}{\rm e}^{{t\Big( {M_{{k\, {\minus}\, 2}} \, {\minus}\, \left( {M_{1} \, {\minus}\, M_{0} } \right)\, {\minus}\, \mathop{\sum}\limits_{j\, {\equals}\, 1}^{k\,/\,2\, {\minus}\, 2} {\left( {M_{{2j{\plus}1}} \, {\minus}\, M_{{2j}} } \right)} } \Big)}} \bar{F}_{X} \left( {M_{{k\, {\minus}\, 2}} } \right) $$
where
$\mathop{\sum}\nolimits_{j\, {\equals}\, a}^b c_{j} \, {\equals}\, 0$
whenever b<a.
Using Proposition (1) the expectation of the reinsurer’s risk portion
$X_{R}^{{{\rm opt}}} $
, under an optimal k-layer reinsurance can be evaluated as
$$\eqalignno{ E\left( {X_{R}^{{{\rm opt}}} } \right) & \, {\equals}\, M_{0}^{{\asterisk}} \left( {F_{X} \left( {M_{1}^{{\asterisk}} } \right)\, {\minus}\, F_{X} \left( {M_{0}^{{\asterisk}} } \right)} \right){\plus}{\int}_{M_{0}^{{\asterisk}} }^{M_{1}^{{\asterisk}} } {\bar{F}_{X} \left( x \right)dx} {\plus}\mathop{\sum}\limits_{j\, {\equals}\, 1}^{k\,/\,2\, {\minus}\, 2} {{\int}_{2j}^{2j{\plus}1} {\bar{F}_{X} \left( x \right)dx} } \cr & \quad {\plus}{\int}_{M_{{k\, {\minus}\, 2}}^{{\asterisk}} }^\infty {xdF_{X} \left( x \right)\, {\minus}\, M_{{k\, {\minus}\, 2}}^{{\asterisk}} \left( {1\, {\minus}\, F_{X} \left( {M_{{k\, {\minus}\, 2}}^{{\asterisk}} } \right)} \right)} $$
The next section conducts several simulation-based studies, to show “how one can employ some other appropriate criteria to fully determine an optimal k-layer reinsurance contract”.
3. Simulation Study
This section provides four numerical examples to show how the above findings, along with some other additional appropriate criteria, can be applied in practice. These examples consider a given multi-layer reinsurance policy which arrives by an extension of the optimal stop-loss reinsurance policy. Unknown parameters of each multi-layer reinsurance policy are estimated using an additional appropriate criteria.
Borch (Reference Borch1960) showed that, under the variance retained risk optimal criteria, in the class of reinsurance contracts
${\cal C},$
given by equation (2), the stop-loss reinsurance is optimal. The following proposition shows that the proportional reinsurance contract minimises a convex combination of variance of the insurer’s and the reinsurer’s risk portions from random claim X.
Proposition 2.
Suppose X
R
=h(X) and X
I
=X−h(X), respectively, stand for the reinsurer’s and the insurer’s risk portions from random claim X. Then, in the class of reinsurance contracts
${\cal C},$
given by equation (2), proportional contract
$h^{{\asterisk}} (X)\, {\equals}\, {1 \over {1{\plus}\omega }}X$
minimises the following convex combination of variance of X
R
=h(X) and X
I
=X−h(X)
$$Q_{h} \, {\equals}\, \omega {\rm Var}\left( {h\left( X \right)} \right){\plus}\left( {1\, {\minus}\, \omega } \right){\rm Var}\left( {X\, {\minus}\, h\left( X \right)} \right)$$
where ω∈[0, 1].
Proof The above convex combination of two variances can be restated as
$$\eqalignno{ \mathop{{{\rm argmin} }}\limits_{{h\in{\cal C}}} Q_{h} & \, {\equals}\, \mathop{{\rm argmin}}\limits_{{h\in{\cal C}}} \,\left\{ {\omega {\rm Var}\left( {h\left( X \right)\, {\minus}\, X{\plus}X} \right){\plus}\left( {1\, {\minus}\, \omega } \right){\rm Var}\left( {X\, {\minus}\, h\left( X \right)} \right)} \right\} \cr & \, {\equals}\, \mathop{{\rm argmin}}\limits_{{h\in{\cal C}}} \,\left\{ {\omega {\rm Var}\left( {X\, {\minus}\, \left( {X\, {\minus}\, h\left( x \right)} \right)} \right){\plus}\left( {1\, {\minus}\, \omega } \right)Var\left( {X\, {\minus}\, h\left( X \right)} \right)} \right\} \cr & \, {\equals}\, \mathop{{\rm argmin}}\limits_{{h\in{\cal C}}} \,\left\{ {\omega {\rm Var}\left( X \right){\plus}{\rm Var}\left( {X\, {\minus}\, h\left( X \right)} \right)\, {\minus}\, 2\omega {\rm Cov}\left( {X,X\, {\minus}\, h\left( X \right)} \right)} \right\} \cr & \, {\equals}\, \mathop{{\rm argmin}}\limits_{{h\in{\cal C}}} \,\left\{ {{\rm Var}\left( {X\, {\minus}\, h\left( X \right)} \right)\, {\minus}\, 2\omega {\rm Cov}\left( {X,X\, {\minus}\, h\left( X \right)} \right)} \right\} \cr & \, {\equals}\, \mathop{{\rm argmin}}\limits_{{h\in{\cal C}}} \,\left\{ {E\left[ {\left( {X\, {\minus}\, h\left( X \right)} \right)^{2} } \right]\, {\minus}\, E\left[ {\left( {X\, {\minus}\, h\left( X \right)} \right)} \right]^{2} \, {\minus}\, 2\omega E\left[ {\left( {X\, {\minus}\, h\left( X \right)} \right)X} \right]{\plus}2\omega E\left[ {\left( {X\, {\minus}\, h\left( X \right)} \right)} \right]E\left[ X \right]} \right\} \cr & \, {\equals}\, \mathop{{\rm argmin}}\limits_{{h\in{\cal C}}} \,\left\{ {E\left[ {\left( {X\, {\minus}\, h\left( X \right)} \right)^{2} \, {\minus}\, 2\omega \left( {X\, {\minus}\, h\left( X \right)} \right)X} \right]\, {\minus}\, E\left[ {\left( {X\, {\minus}\, h\left( X \right)} \right)} \right]\left[ {E\left[ {\left( {X\, {\minus}\, h\left( X \right)} \right)} \right]\, {\minus}\, 2\omega E\left( X \right)} \right]} \right\} \cr & \, {\equals}\, \mathop{{\rm argmin}}\limits_{{h\in{\cal C}}} \,\left\{ {E\left[ {\left[ {\left( {X\, {\minus}\, h\left( X \right)} \right)} \right]\left[ {\left( {X\, {\minus}\, h\left( X \right)} \right)\, {\minus}\, 2\omega X} \right]} \right]\, {\minus}\, E\left[ {\left( {X\, {\minus}\, h\left( X \right)} \right)} \right]E\left[ {\left( {1\, {\minus}\, 2\omega } \right)X\, {\minus}\, h\left( X \right)} \right]} \right\} \cr & \, {\equals}\, \mathop{{\rm argmin}}\limits_{{h\in{\cal C}}} \,\left\{ {{\rm Cov}\left[ {\left( {X\, {\minus}\, h\left( X \right)} \right),\,\left( {1\, {\minus}\, 2\omega } \right)X\, {\minus}\, h\left( X \right)} \right]} \right\} $$
Therefore, one may conclude that the above convex combination is minimal whenever (X−h(X)) and (1−2ω)X−h(X)] are linearly dependent. Choosing (1−2ω)X−h(X)=β 0+β 1(X−h(X)) leads to h(X)=(1−2ω−β 1)X/(1−β 1)−β 0/(1−β 1) The fact that 0≤h(X)≤X implies that β 0=0. Now by substituting back h(X)=(1−2ω−β 1)X/(1−β 1) in the above convex combination, we have
$$Q_{I} \, {\equals}\, \left[ {\omega {{\left( {1\, {\minus}\, 2\omega \, {\minus}\, \beta _{1} } \right)^{2} } \over {\left( {1\, {\minus}\, \beta _{1} } \right)^{2} }}{\plus}\left( {1\, {\minus}\, \omega } \right){{\left( {2\omega } \right)^{2} } \over {\left( {1\, {\minus}\, \beta _{1} } \right)^{2} }}} \right]{\rm Var}\left( X \right)$$
Minimising this expression, with respect to β 1, leads to desired result.□
Proposition (2) shows that the proportional reinsurance the contract minimises a convex combination of variance of X R and X−X R . The following example considers this observation as an appropriate criteria to estimate unknown parameters of an optimal two-layer contract.
Example 1. Suppose that random claim X has been distributed according to one of the distributions given in the first column of Table 1. Moreover suppose that the optimal multi-layer contract has two layers and restated as
$$\matrix{ {X_{R}^{{2\, {\minus}\, {\rm layer}}} \left( X \right)} & {\, {\equals}\, \left\{ {\matrix{ {0\quad \:\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad X\,\lt\,d_{\alpha } } \hfill \cr {X\, {\minus}\, d_{\alpha } \quad \quad \quad \quad \quad \quad \quad d_{\alpha } \leq X\,\lt\,M_{1} } \hfill \cr {M_{1} \, {\minus}\, d_{\alpha } \:\quad \quad \quad \quad \quad \quad \quad M_{1} \leq X\,\lt\,M_{1} {\plus}d_{\alpha } } \hfill \cr {X\, {\minus}\, 2d_{\alpha } \:\quad \quad \quad \quad M_{1} {\plus}d_{\alpha } \leq X\,\lt\,M_{2} } \hfill \cr {M_{2} \, {\minus}\, 2d_{\alpha } \quad \quad \quad \quad M_{2} \leq X\,\lt\,M_{2} {\plus}d_{\alpha } } \hfill \cr {X\, {\minus}\, 3d_{\alpha } \:\quad \quad \quad \quad M_{2} {\plus}d_{\alpha } \leq X} \hfill \cr } } \right.} \cr } $$
Table 1 Estimation for unknown parameters of the optimal two-layer contract under variance optimal criteria, whenever ω=0.1 and α=0.1.
Note: Q
h
and h
*
are given in Proposition (2), h
SL
(X)=max{X−d
α
, 0} and
$h^{{2{\minus}{\rm layer}}} (X)\, {\equals}\, X_{R}^{{2{\minus}{\rm layer}}} (X)$
.
For the sake of simplicity, we set M
1=d
α
+d
1 and M
2=2d
α
+d
1+d
2. Now M
0
has been estimated such that E(X
R
)=E(max{X−d
α
, 0}). Other two parameters d
1 and d
2 have been estimated such that the square distance
$\big[ {Q_{{X_{R}^{{2\, {\minus}\, {\rm layer}}} }} \, {\minus}\, Q_{{h^{{\asterisk}} }} } \big]^{2} $
is minimised, where Q
h
and h
* are given in Proposition (2).
Table 1 shows estimation for unknown parameters of the above optimal two-layer
$X_{R}^{{2\, {\minus}\, {\rm layer}}} $
.
The last three columns of Table 1 show the convex combination of variance of X R =h(X) and X I =X−h(X) for optimal stop-loss, optimal two-layer and proportional (given by Proposition (2)) contracts, respectively. As one may observe that, under the optimal two-layer contract such convex combination of variances, compare to optimal stop-loss, has been improved. We conjecture that by increasing number of layer such convex combination of variances will be improved.
Under criteria of maximising the expected utility, one may either determine an optimal reinsurance contract (see Kaluszka & Okolewski, Reference Kaluszka and Okolewski2008, for more details) or estimate unknown parameters of an optimal reinsurance contract (see Dickson, Reference Dickson2005: §9.2, for more details).
The following example considers criteria of maximising of convex combination of the expected exponential utility of X R and X−X R as an additional appropriate criteria to estimate unknown parameters of a two-layer optimal reinsurance contract.
Example 2. Suppose that random claim X has been distributed according to one of the distributions given in the first column of Table 2. Moreover consider the optimal two-layer contract given in Example (1).
Table 2 Estimation for unknown parameters of the optimal two-layer contract under minimisation U h as an optimal criteria, whenever ω=0.2 and α=0.1.
Note: Q
h
and h
* are given by equation (5), h
SL
(X)=max{X−d
α
, 0} and
$h^{{2{\minus}{\rm layer}}} (X){\equals}X_{R}^{{2{\minus}{\rm layer}}} (X)$
.
Similar to Example (1), for the sake of simplicity, we set M 1=d α +d 1 and M 2=2d α +d 1+d 2. Now M 0 has been estimated such that E(X R )=E(max{X−d α , 0}). Other two parameters d 1 and d 2 are estimated such that the following convex combination of the expected exponential utilities of X R and X−X R has been minimised.
$$U_{h} \, {\equals}\, \omega E\left( {{\rm exp}\left( {\, {\minus}\, \beta \left( {h\left( X \right)} \right)} \right)} \right){\plus}\left( {1\, {\minus}\, \omega } \right)E\left( {{\rm exp}\left( {\, {\minus}\, \beta \left( {X\, {\minus}\, h\left( X \right)} \right)} \right)} \right)$$
where we set ω=0.2 and β 1=β 2=1.
Table 2 shows estimation for unknown parameters of the optimal two-layer
$X_{R}^{{2\, {\minus}\, {\rm layer}}} $
.
The last two columns of Table 2 show the convex combination of expected exponential utility of X R =h(X) and X I =X−h(X) for the optimal stop-loss and the optimal two-layer contracts, respectively. As one may observe, under the optimal two-layer contract such convex combination of utilities, compare to optimal stop-loss contract, is improved.
The Bayesian method under name of the credibility method is well-known in various areas of the actuarial sciences. For instance see: Whitney (Reference Whitney1918) and Payandeh Najafabadi & Qazvini (Reference Payandeh Najafabadi and Panahi Bazaz2015) for its application in the experience rating system; Bailey (Reference Bailey1950), Payandeh Najafabadi (Reference Payandeh Najafabadi2010) and Payandeh Najafabadi et al. (Reference Payandeh Najafabadi, Hatami and Omidi Najafabadi2012) for its application in evaluating insurance premium; Hesselager & Witting (Reference Hesselager and Witting1988) and England & Verrall (Reference Fang and Qu2002) for its application in the IBNR claims reserving system; and see Makov et al. (Reference Makov, Smith and Liu1996), Makov (Reference Makov2001), and Hossack et al. (Reference Hossack, Pollard and Zenwirth1999) for its general applications in actuarial science.
Now we employ the Bayesian estimation method as an appropriate method to estimate unknown parameters of an optimal multi-layer reinsurance contract.
To derive any Bayes estimator for
$M_{0}^{{\asterisk}} , \cdots ,M_{{m\, {\minus}\, 2}}^{{\asterisk}} ,$
based upon identically independent random claim
$X^{{(1)}} , \cdots ,X^{{(n)}} $
, one has to consider initial values for
$M_{0}^{{\asterisk}} , \cdots ,M_{{m\, {\minus}\, 2}}^{{\asterisk}} .$
Then, using such initial values, he/she can define i.i.d reinsurer’s random claim
$X_{R}^{{(1)}} , \cdots ,X_{R}^{{(n)}} .$
Now, using information given by
$X_{R}^{{(1)}} , \cdots ,X_{R}^{{(n)}} $
accompanied with prior information on parameters
$M_{0}^{{\asterisk}} , \cdots ,M_{{m\, {\minus}\, 2}}^{{\asterisk}} $
and other unknown parameters, the Bayes estimators for parameters
$M_{0}^{{\asterisk}} , \cdots ,M_{{m\, {\minus}\, 2}}^{{\asterisk}} ,$
under an appropriate loss function, say
$\hat{M}_{0}^{{\asterisk}} , \cdots ,\hat{M}_{{m\, {\minus}\, 2}}^{{\asterisk}} ,$
can be obtained. Certainly, such Bayes estimator may be, iteratively, improved by using
$\hat{M}_{0}^{{\asterisk}} , \cdots ,\hat{M}_{{m\, {\minus}\, 2}}^{{\asterisk}} $
as a new initial estimator for
$M_{0}^{{\asterisk}} , \cdots ,M_{{m\, {\minus}\, 2}}^{{\asterisk}} ,$
then determining
$X_{R}^{{(1)}} , \cdots ,X_{R}^{{(n)}} ,$
and finally reevaluating the Bayes estimator
$\hat{M}_{0}^{{\asterisk}} , \cdots ,\hat{M}_{{m\, {\minus}\, 2}}^{{\asterisk}} ,$
again.
Suppose
$X^{{(1)}} , \cdots ,X^{{(n)}} ,$
given parameter θ, are i.i.d. random claims with a common density function f
X
and a distribution function F
X
. Moreover, suppose that
$m_{0}^{{\asterisk}} , \cdots ,m_{{k\, {\minus}\, 2}}^{{\asterisk}} $
stand for the initial values for
$$M_{0}^{{\asterisk}} , \cdots ,M_{{k\, {\minus}\, 2}}^{{\asterisk}} .$$
Using a straightforward calculation, the density function for random variable
$$X_{R}^{{(i)}} ,$$
for
$i\, {\equals}\, 1, \cdots ,n,$
given parameters
$\Theta \,\colon\,\, {\equals}\, (\theta ,M_{0}^{{\asterisk}} , \cdots ,M_{{k\, {\minus}\, 2}}^{{\asterisk}} )$
at observed value y
(i), is equal to
$$\eqalignno{ g_{{X_{R}^{{(i)}} \,\mid\,\Theta }} \big( {y^{{(i)}} } \big) & \, {\equals}\, \left( {F_{X} \left( {M_{0}^{{\asterisk}} } \right)\, {\minus}\, F_{X} \left( 0 \right)} \right)I_{{\{ 0\} }} \big( {y^{{(i)}} } \big){\plus}f_{X} \big( {y^{{(i)}} {\plus}M_{0}^{{\asterisk}} } \big)I_{{\left( {0,M_{1}^{{\asterisk}} \, {\minus}\, M_{0}^{{\asterisk}} } \right)}} \big( {y^{{(i)}} } \big) \cr & \quad {\plus}\left( {F_{X} \left( {M_{2}^{{\asterisk}} } \right)\, {\minus}\, F_{X} \left( {M_{1}^{{\asterisk}} } \right)} \right)I_{{\left\{ {M_{1}^{{\asterisk}} \, {\minus}\, M_{0}^{{\asterisk}} } \right\}}} \big( {y^{{(i)}} } \big) } $$
$$\eqalignno{ \cr & \quad {\plus}f_{X} \big( {y^{{(i)}} {\plus}M_{2}^{{\asterisk}} \, {\minus}\, \big( {M_{1}^{{\asterisk}} \, {\minus}\, M_{0}^{{\asterisk}} } \big)} \big)I_{{\big( {M_{1}^{{\asterisk}} \, {\minus}\, M_{0}^{{\asterisk}} ,M_{3}^{{\asterisk}} \, {\minus}\, M_{2}^{{\asterisk}} {\plus}M_{1}^{{\asterisk}} \, {\minus}\, M_{0}^{{\asterisk}} } \big)}} \big( {y^{{(i)}} } \big)\cr & \quad {\plus}\big( {F_{X} \big( {M_{4}^{{\asterisk}} } \big)\, {\minus}\, F_{X} \big( {M_{3}^{{\asterisk}} } \big)} \big)I_{{\big\{ {M_{3}^{{\asterisk}} \, {\minus}\, M_{2}^{{\asterisk}} {\plus}M_{1}^{{\asterisk}} \, {\minus}\, M_{0}^{{\asterisk}} } \big\}}} \big( {y^{{(i)}} } \big){\plus} \cdots \cr & \quad {\plus}f_{X} \big( {y^{{(i)}} {\plus}M_{{k\, {\minus}\, 2}}^{{\asterisk}} \, {\minus}\, \mathop{\sum}\limits_{j\, {\equals}\, 1}^{k\,/\,2\, {\minus}\, 2} {\big( {M_{{2j{\plus}1}}^{{\asterisk}} \, {\minus}\, M_{{2j}}^{{\asterisk}} } \big)\, {\minus}\, \big( {M_{1}^{{\asterisk}} \, {\minus}\, M_{0}^{{\asterisk}} } \big)} } \big)I_{{\big( {\mathop{\sum}\limits_{j\, {\equals}\, 1}^{k\,/\,2\, {\minus}\, 2} \big( {M_{{2j{\plus}1}}^{{\asterisk}} \, {\minus}\, M_{{2j}}^{{\asterisk}} } \big){\plus}\big( {M_{1}^{{\asterisk}} \, {\minus}\, M_{0}^{{\asterisk}} } \big),\infty} \big)}} \big( {y^{{(i)}} } \big) $$
Using the fact that random variables
$$X_{R}^{{(1)}} , \cdots ,X_{R}^{{(n)}} $$
are i.i.d., it follows that the joint density function for
$X_{R}^{{(1)}} , \cdots ,X_{R}^{{(n)}} ,$
given parameters
$\Theta \,\colon\,\, {\equals}\, (\theta ,M_{0}^{{\asterisk}} , \cdots ,M_{{k\, {\minus}\, 2}}^{{\asterisk}} ),$
can be restated as
$$\eqalignno{ f_{{X_{R}^{{(1)}} , \cdots ,X_{R}^{{(n)}} }} \big( {y^{{(1)}} , \cdots ,y^{{(n)}} \!\mid\!\Theta } \big) & \, {\equals}\, \left[ {F_{X} \left( {M_{0}^{{\asterisk}} } \right)\, {\minus}\, F_{X} \left( 0 \right)} \right]^{{n_{0} }} \prod\limits_{i\, {\equals}\, 1}^{n_{1} } {f_{X} \big( {y^{{(i)}} {\plus}M_{0}^{{\asterisk}} } \big)\left[ {F_{X} (M_{2}^{{\asterisk}} )\, {\minus}\, F_{X} (M_{1}^{{\asterisk}} )} \right]^{{n_{2} }} \cdots } \cr & \quad {\times}\prod\limits_{i\, {\equals}\, n_{0} {\plus} \cdots n_{{(k\, {\minus}\, 2)}} }^n {f_{X} \left( {y^{{(i)}} {\plus}M_{{k\, {\minus}\, 2}}^{{\asterisk}} \, {\minus}\, \mathop{\sum}\limits_{i\, {\equals}\, 1}^{k\,/\,2\, {\minus}\, 2} {\left( {M_{{2i{\plus}1}}^{{\asterisk}} \, {\minus}\, M_{{2i}}^{{\asterisk}} } \right)\, {\minus}\, \left( {M_{1}^{{\asterisk}} \, {\minus}\, M_{0}^{{\asterisk}} } \right)} } \right)} $$
where n
0:=#(y
(i)=0),
$n_{1} \,\colon\,\, {\equals}\, \,\#\,(0\,\lt\,y^{{(i)}} \,\lt\,(M_{1}^{{\asterisk}} \, {\minus}\, M_{0}^{{\asterisk}} )),\ $
$n_{2} \,\colon\,\, {\equals}\, \,\#\,(y^{{(i)}} \, {\equals}\, (M_{1}^{{\asterisk}} \, {\minus}\, M_{0}^{{\asterisk}} )),\cdots \,n_{{k\, {\minus}\, 2}} \colon\,= $
$ \#\,\left( {\mathop{\sum}\nolimits_{i\, {\equals}\, 1}^{k\,/\,2\, {\minus}\, 2} {(M_{{2i{\plus}1}}^{{\asterisk}} \, {\minus}\, M_{{2i}}^{{\asterisk}} )\,\lt\,y^{{(i)}} } } \right)$
Assuming
$\pi (\theta ,M_{0}^{{\asterisk}} , \cdots ,M_{{k\, {\minus}\, 2}}^{{\asterisk}} )$
is the prior distribution for vector
$(\theta ,M_{0}^{{\asterisk}} , \cdots ,M_{{m\, {\minus}\, 2}}^{{\asterisk}} )$
, the joint posterior distribution for vector
$\Theta \,\colon\,\, {\equals}\, (\theta ,M_{0}^{{\asterisk}} , \cdots ,M_{{k\, {\minus}\, 2}}^{{\asterisk}} )$
is
$$\eqalignno{ & \pi \left( {\theta ,\,M_{0}^{{\asterisk}} , \cdots ,M_{{m\, {\minus}\, 2}}^{{\asterisk}} \!\mid\!y^{{(1)}} , \cdots ,y^{{(n)}} } \right)\, {\equals}\, \cr & {{f_{{X_{R}^{{(1)}} , \cdots ,X_{R}^{{(n)}} }} \left( {y^{{(1)}} , \cdots ,y^{{(n)}} \!\mid\!\theta ,M_{0}^{{\asterisk}} , \cdots ,M_{{k\, {\minus}\, 2}}^{{\asterisk}} } \right)\pi \left( {\theta ,M_{0}^{{\asterisk}} , \cdots ,M_{{k\, {\minus}\, 2}}^{{\asterisk}} } \right)} \over {\mathop{\int}_{{\cal M}{\asterisk}_{{_{{k\, {\minus}\, 2}} }} } { \cdots \mathop{\int}_\Theta {f_{{X_{R}^{{(1)}} , \cdots ,X_{R}^{{(n)}} }} \left( {y^{{(1)}} , \cdots ,y^{{(n)}} \!\mid\!\theta ,M_{0}^{{\asterisk}} , \cdots ,M^{{\asterisk}} {(}\left. {k\, {\minus}\, 2} \right)} \right)\pi \left( {\theta ,M_{0}^{{\asterisk}} , \cdots ,M_{{k\, {\minus}\, 2}}^{{\asterisk}} } \right)d\theta dM_{0}^{{\asterisk}} , \cdots ,dM_{{k\, {\minus}\, 2}}^{{\asterisk}} } } }} $$
Using the above joint posterior distribution, the Bayes estimator for each
$$M_{0}^{{\asterisk}} ,_{ \cdots } ,M_{{k\, {\minus}\, 2}}^{{\asterisk}} $$
under the square error loss function, is
$$\hat{M}^{{\asterisk}} _{i} \, {\equals}\, \mathop{\int}_{{\cal M}{\asterisk}_{{k\, {\minus}\, 2}} } \,\ldots\, \mathop{\int}_\Theta {M_{i}^{{\asterisk}} \pi \left( {\theta ,M_{0}^{{\asterisk}} ,\, \cdots ,\,M_{{k\, {\minus}\, 2}}^{{\asterisk}} \!\mid\!y^{{(1)}} ,\, \cdots \,,y^{{(n)}} } \right)d\theta dM_{0}^{{\asterisk}} \cdots dM_{{k\, {\minus}\, 2}}^{{\asterisk}} } $$
for
$i\, {\equals}\, 0, \cdots ,k\, {\minus}\, 2.$
Now as an application of the above findings, we consider the following example.
Example 3. Suppose that random claim X has been distributed according to one of the distributions given in the first column of Table 3. Moreover, suppose that the optimal multi-layer contract has one layer and restated as
$$X_{R}^{{1\, {\minus}\, {\rm layer}}} \, {\equals}\, \left\{ {\matrix{ {0\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \ \,X\,\lt\,M_{0} } \hfill \cr {X\, {\minus}\, M_{0} \:\quad \quad \quad \quad \quad \quad \quad \quad \ \,M_{0} \leq X\,\lt\,M_{1} } \hfill \cr {M_{1} \, {\minus}\, M_{0} \quad \quad \quad \quad \quad \quad \quad \quad M_{1} \leq X\,\lt\,M_{2} } \hfill \cr {X{\plus}\left( {M_{1} \, {\minus}\, M_{0} } \right)\, {\minus}\, M_{2} \:\quad \quad \quad M_{2} \leq X} \hfill \cr } } \right.$$
Table 3 Mean (standard deviation) of Bayes estimator for d 0, d 1 and d 2 based upon 100 sample size and 100 iterations, whenever α=0.1.
Note: h
SL
(X)=max{X−d
α
, 0} and
$h^{{1{\minus}{\rm layer}}} (X){\equals}X_{R}^{{1{\minus}{\rm layer}}} (X)$
.
For the sake of simplicity, we set d 0=M 0, d 1=M 1−M 0 and d 2=M 2−M 1. Now, suppose that the prior distributions of the unknown parameters d 0, d 1 and d 2 are independent and given in the second, third and fourth columns of Table 3, respectively.
To construct a Bayes estimator for unknown parameters, we employed d 0=0.20, d 1=0.15 and d 2=0.02 as initial values.
The three last columns of Table 3 represent the mean and the standard deviation, respectively, of the Bayes estimator for d 0, d 1 and d 2, which generates 100 random numbers from a given distribution. This estimators were derived using equation (6) when the mean of 100 iterations of the Bayes estimator for d 0, d 1 and d 2 was used as an estimator for d 0, d 1 and d 2.
The small variance of these estimators shows that the estimation method is an appropriate method to use with the different samples.
4. Conclusion and Suggestions
This article generalises the stop-loss reinsurance policy to a new continuous multi-layer reinsurance policy which minimises the CTE risk measure of the insurer’s total risk. Unknown parameters of the new optimal multi-layer reinsurance policy can be estimated using other additional appropriate criteria. Therefore, the new multi-layer reinsurance policy not only similar to the original stop-loss reinsurance policy is optimal, in a same sense, but also it has some other appropriate criteria which the original stop-loss policy does not have. Estimation method of this article can be generalised to the other appropriate criteria such as the ruin probability (Fang & Qu, Reference England and Verrall2014), percentile matching estimating method (Teugels & Sundt, Reference Teugels and Sundt2004), etc.
The following two propositions are generalised result of this article under the general translative and monotone risk measure ρ(⋅).
The following suppose that under minimisation criteria of a translative and monotone risk measure ρ(⋅) of the insurer’s total risk reinsurance contract f(⋅) is optimal. Then, it provides a multi-layer reinsurance contract which its corresponding risk measure coincides with the insurer’s total risk under contract f(⋅), see Figure 2(a) for an illustration.
Proposition 3.
Suppose ρ(⋅) is a translative and monotone risk measure. Moreover, suppose that f(⋅) in the class of reinsurance strategies
${\cal C}$
minimises risk measure of the total risk of insurance company. Then, reinsurance g(⋅) also minimises the risk measure of total risk of insurance company:
$$\eqalignno{ g\left( X \right) & \, {\equals}\, f\left( X \right)I_{{\left[ {0,M_{1} } \right)}} \left( X \right){\plus}\left( {X\, {\minus}\, M_{1} {\plus}f\left( {M_{1} } \right)} \right)I_{{\left[ {M_{1} ,M_{2} } \right)}} \left( X \right){\plus}f\left( {M_{2}^{{\asterisk}} } \right)I_{{\left[ {M_{2} ,M_{2}^{{\asterisk}} } \right)}} \left( X \right) \cr & \quad {\plus}\left( {X\, {\minus}\, M_{2}^{{\asterisk}} {\plus}f\left( {M_{2}^{{\asterisk}} } \right)} \right)I_{{\left[ {M_{2}^{{\asterisk}} ,M_{3} } \right)}} \left( X \right){\plus} \cdots {\plus}\left( {X\, {\minus}\, M_{k}^{{\asterisk}} {\plus}f\left( {M_{k}^{{\asterisk}} } \right)} \right)I_{{\left[ {M_{k}^{{\asterisk}} ,\infty} \right)}} \left( X \right) $$
where
$M_{1} ,M_{2} , \cdots ,M_{k} $
are unknown parameters of the new optimal reinsurance and
$M_{1}^{{\asterisk}} ,M_{2}^{{\asterisk}} , \cdots ,M_{k}^{{\asterisk}} $
have to be evaluated using equation
$f(M_{2}^{{\asterisk}} )\, {\equals}\, M_{2} \, {\minus}\, M_{1} {\plus}f(M_{1} )$
and
$f(M_{i}^{{\asterisk}} )\, {\equals}\, M_{i} \, {\minus}\, M_{{i\, {\minus}\, 1}}^{{\asterisk}} {\plus}f(M_{{i\, {\minus}\, 1}}^{{\asterisk}} )$
for
$$i\, {\equals}\, 3, \cdots ,k.$$
Proof Since ρ(⋅) is a translative risk measure, one may write that
$$\eqalignno{ \rho \left( {X\, {\minus}\, g\left( X \right){\plus}\pi _{g}^{X} } \right) & \, {\equals}\, \rho \left( {X\, {\minus}\, g\left( X \right)} \right){\plus}\pi _{g}^{X} \cr & \, {\equals}\, \rho \left[ {\left( {X\, {\minus}\, f\left( X \right)} \right)I_{{\left[ {0,M_{1} } \right)}} \left( X \right){\plus}\left( {M_{1} \, {\minus}\, f\left( {M_{1} } \right)} \right)I_{{[M_{1} ,M_{2} )}} \left( X \right)} \right. \cr & \quad {\plus}\left( {X\, {\minus}\, f\left( {M_{2}^{{\asterisk}} } \right)I_{{\left[ {M_{2} ,M_{2}^{{\asterisk}} } \right)}} \left( X \right)} \right){\plus}\left( {M_{2}^{{\asterisk}} \, {\minus}\, f\left( {M_{2}^{{\asterisk}} } \right)} \right)I_{{\left[ {M_{2}^{{\asterisk}} ,M_{3} } \right)}} \left( X \right) \cr & \left. \quad {{\plus}\left( {X\, {\minus}\, f\left( {M_{3}^{{\asterisk}} } \right)} \right)I_{{\left[ {M_{3} ,M_{3}^{{\asterisk}} } \right)}} {\plus} \cdots {\plus}\left( {M_{k}^{{\asterisk}} \, {\minus}\, f\left( {M_{k}^{{\asterisk}} } \right)} \right)I_{{\left[ {M_{k}^{{\asterisk}} ,\infty} \right)}} \left( X \right)} \right]{\plus}\pi _{g}^{X} \cr & \leq \rho \left( {X\, {\minus}\, f\left( X \right)} \right){\plus}\pi _{g}^{X} \cr & \, {\equals}\, \rho \left( {X\, {\minus}\, f\left( X \right){\plus}\pi _{g}^{X} } \right) \cr & \, {\equals}\, \rho \left( {X\, {\minus}\, f\left( X \right){\plus}\pi _{f}^{X} } \right) $$
Figure 2 (a) The optimal multi-layer reinsurance contract, given by Proposition (3) whenever
$f(X)\, {\equals}\, {\rm argmin}_{{h\in{\cal C}}} \{ \rho (X{\minus}h(X){\plus}\pi _{h}^{X} )\} $
and (b) the optimal multi-layer reinsurance contract, given by Proposition (4), whenever
$f(X)\, {\equals}\, {\rm argmin}_{{h\in{\cal C}}} \{ \omega \rho _{1} (X{\minus}h(X){\plus}\pi _{h}^{X} ){\plus}(1{\minus}\omega )\rho _{2} (h(X){\minus}\pi _{h}^{X} )\} $
and ω∈[0, 1].
The above inequality arrives from the fact that ρ(⋅) is a monotone risk measure and X−g(X)≤X−f(X) with probability 1. Now using the fact that
$\rho (X\, {\minus}\, f(X))\, {\equals}\, \mathop {{\rm min}}\limits_{h\in{\cal C}} \rho (X\, {\minus}\, h(X){\plus}\pi _{h}^{X} )$
we conclude that the above inequality has to be changed to an equality.□
Now we provide an optimal multi-layer reinsurance contract, for a situation that the optimal reinsurance f(⋅) arrives by minimising a convex combination of two translative and monotone risk measures ρ
1(⋅) and ρ
2(⋅) of the insurer’s total risk, X
R
=h(X), and the reinsurer’s total risk X
I
=X−h(X), i.e.,
$f(X)\, {\equals}\, {\rm argmin}_{{h\in{\cal C}}} \{ \omega \rho _{1} (X\, {\minus}\, h(X){\plus}\pi _{h}^{X} ){\plus}(1\, {\minus}\, \omega )\rho _{2} (h(X)\, {\minus}\, \pi _{h}^{X} )\} ,$
where ω∈[0, 1], see Figure 2(b) for an illustration.
As an example for such optimal reinsurance f(⋅), under such the convex combination of two distortion risk measures, see Assa (Reference Assa2015).
Proposition 4.
Suppose ρ
1
(⋅) and ρ
2
(⋅) are two translative and monotone risk measures. Moreover, suppose that f(⋅) in the class of reinsurance strategies
${\cal C}$
minimises a convex combination of two risk measures ρ
1
(⋅) and ρ
2
(⋅), i.e.,
$f(X)\, {\equals}\, {\rm argmin}_{{h\in{\cal C}}} \{ \omega \rho _{1} (X\, {\minus}\, h(X){\plus}\pi _{h}^{X} ){\plus}(1\, {\minus}\, \omega )\rho _{2} (h(X)\, {\minus}\, \pi _{h}^{X} )\} ,$
where ω∈[0, 1]. Then, for ω*∈(0, a
min
/(a
min
+a
max)), the following k-layer reinsurance g(⋅) also minimises such the convex combination of two risk measures ρ
1
(⋅) and ρ
2
(⋅).
$$\eqalignno{ g(X) & \, {\equals}\, f\left( X \right)I_{{\left[ {0,M_{1} } \right)}} \left( X \right){\plus}\left( {X\, {\minus}\, M_{1} {\plus}f\left( {M_{1} } \right)} \right)I_{{\left[ {M_{1} ,M_{2} } \right)}} \left( X \right){\plus}f\left( {M_{2}^{{\asterisk}} } \right)I_{{\left[ {M_{2} ,M_{3} } \right)}} \left( X \right) \cr & \quad {\plus}\left( {X\, {\minus}\, M_{3} {\plus}f\left( {M_{2}^{{\asterisk}} } \right)} \right)I_{{\left[ {M_{3} ,M_{4} } \right)}} \left( X \right){\plus} \cdots {\plus}f\left( X \right)I_{{\left[ {M_{{2k{\plus}1}}^{{\asterisk}} ,\infty} \right)}} \left( X \right) $$
where
$M_{1} ,M_{2} , \cdots ,M_{k} $
are unknown parameters of the new optimal reinsurance and
$M_{1}^{{\asterisk}} ,M_{2}^{{\asterisk}} , \cdots ,M_{k}^{{\asterisk}} $
have to be evaluated using equation:
$f(M_{2}^{{\asterisk}} ){\equals}M_{2} \, {\minus}\, M_{2} {\plus}f(M_{1} ),\,f(M_{{2j\, {\minus}\, 1}}^{{\asterisk}} ){\equals} M_{{2j\, {\minus}\, 1}}^{{\asterisk}} \, {\minus}\, M_{{2j\, {\minus}\, 1}}{\plus} $
$f(M_{{2(j\, {\minus}\, 1)}}^{{\asterisk}} ),\,f(M_{{2j}}^{{\asterisk}} )\, {\equals}\, f(M_{{2(j\, {\minus}\, 1)}}^{{\asterisk}} ){\plus}M_{{2j}} \, {\minus}\, M_{{2j\, {\minus}\, 1}} ,$
for
$j\, {\equals}\, 2, \cdots ,k,\,a_{{\min }} \,\colon\,{\equals} \min _{{x \in A}} \{ \!\mid\!2f(x)\, {\minus}\! x\!\mid\,\} ,\,a_{{\max }} \,\colon\,{\equals}$
$\max _{{x \in A}} \{ \!\mid\!2f(x)\, {\minus}\, x\!\mid\!\} $
and
$A\,\colon\,{\equals}[M^{1} ,M_{2}^{{\asterisk}} ){\cup}_{{j{\equals}2}}^{k} [M_{{2j\, {\minus}\, 1}}^{{\asterisk}} ,M_{{2j}}^{{\asterisk}} ].$
Proof
Set
$\pi _{g}^{{\asterisk}} \,\colon\,\, {\equals}\, \omega ^{{\asterisk}} \pi _{g}^{X} \, {\minus}\, (1\, {\minus}\, \omega ^{{\asterisk}} )\pi _{g}^{X} .$
Since ρ
1(⋅) and ρ
2(⋅) are a translative risk measures, one may write that
$$\eqalignno{ \omega ^{{\asterisk}} \rho _{1} \left( {X\, {\minus}\, g\left( X \right){\plus}\pi _{g}^{X} } \right){\plus}\left( {1\, {\minus}\, \omega ^{{\asterisk}} } \right)\rho _{2} \left( {g\left( X \right)\, {\minus}\, \pi _{g}^{X} } \right) \, &{\equals}\, \pi _{g}^{{\asterisk}} {\plus}\omega ^{{\asterisk}} \rho _{1} \left( {X\, {\minus}\, g\left( X \right)} \right){\plus}\left( {1\, {\minus}\, \omega ^{{\asterisk}} } \right)\rho _{2} \left( {g\left( X \right)} \right. \cr & \leq \pi _{g}^{{\asterisk}} {\plus}\omega ^{{\asterisk}} \rho _{1} \left[ {\left( {X\, {\minus}\, f\left( X \right)} \right)I_{{\left[ {0,M_{1} } \right)}} \left( X \right){\plus}f\left( X \right)I_{{_{{\left[ {M_{1} ,M_{2}^{{\asterisk}} } \right)}} }} \left( X \right)} \right. \cr & \quad \left. {{\plus}\left( {X\, {\minus}\, f\left( X \right)} \right)I_{{_{{\left[ {M_{2}^{{\asterisk}} ,M_{3}^{{\asterisk}} } \right)}} }} \left( X \right){\plus} \cdots {\plus}\left( {X\, {\minus}\, f\left( X \right)} \right)I_{{\left[ {M_{{2k{\plus}1}}^{{\asterisk}} ,\infty} \right)}} (X)} \right] \cr &\quad {\plus}\left( {1\, {\minus}\, \omega ^{{\asterisk}} } \right)\rho _{2} \left[ {f\left( X \right)I_{{[0,M_{1} )}} \left( X \right){\plus}\left( {X\, {\minus}\, f(X)} \right)I_{{\left[ {M_{1} ,M_{2}^{{\asterisk}} } \right)}} \left( X \right)} \right. \cr & \left. { \quad {\plus}f\left( X \right)I_{{\left[ {M_{2}^{{\asterisk}} ,M_{3}^{{\asterisk}} } \right)}} \left( X \right){\plus} \cdots {\plus}f\left( X \right)I_{{\left[ {M_{{2k{\plus}1}}^{{\asterisk}} ,\infty} \right)}} \left( X \right)} \right] \cr & \ {\equals}\ \pi _{g}^{{\asterisk}} {\plus}\omega ^{{\asterisk}} \rho _{1} \left[ {\left( {X\, {\minus}\, f\left( X \right)} \right)I_{{\left[ {0,\infty} \right)}} \left( X \right){\plus}\left( {2f\left( X \right)\, {\minus}\, X} \right)I_{{\left[ {M^{1} ,M_{2}^{{\asterisk}} } \right)}} \left. {\left( X \right)} \right)} \right. \cr & \quad {\plus}\left( {2f\left( X \right)\, {\minus}\, X} \right)\mathop{\sum}\limits_{j\, {\equals}\, 2}^k {I_{{\left[ {M_{{2j\, {\minus}\, 1}}^{{\asterisk}} ,M_{{2j}}^{{\asterisk}} } \right)}} \left. {\left. {\left( X \right)} \right)} \right]} \cr & \quad {\plus}\left( {1\, {\minus}\, \omega ^{{\asterisk}} } \right)\rho _{2} \left[ {f\left( X \right)I_{{[0,\infty)}} \left( X \right){\plus}\left( {X\, {\minus}\, 2f\left( X \right)} \right)I_{{\left[ {M^{1} ,M_{2}^{{\asterisk}} } \right)}} \left. {\left( X \right)} \right)} \right. \cr & \quad {\plus}\left( {X\, {\minus}\, 2f\left( X \right)} \right)\mathop{\sum}\limits_{j\, {\equals}\, 2}^k {I_{{\left[ {M_{{2j\, {\minus}\, 1}}^{{\asterisk}} ,M_{{2j}}^{{\asterisk}} } \right)}} \left. {\left. {\left( X \right)} \right)} \right]} \cr & \leq \pi _{g}^{{\asterisk}} {\plus}\omega ^{{\asterisk}} \rho _{1} \left[ {\left( {X\, {\minus}\, f\left( X \right)} \right)I_{{\left[ {0,\infty} \right)}} \left( X \right)} \right]{\plus}\left( {1\, {\minus}\, \omega ^{{\asterisk}} } \right)\rho _{2} \left[ {f\left( X \right)} \right] \cr & \quad {\plus}\omega ^{{\asterisk}} ka_{{{\rm max}}} \, {\minus}\, \left( {1\, {\minus}\, \omega ^{{\asterisk}} } \right)ka_{{{\rm min}}} \cr & \leq \pi _{g}^{{\asterisk}} {\plus}\omega ^{{\asterisk}} \rho _{1} \left[ {\left( {X\, {\minus}\, f\left( X \right)} \right)I_{{\left[ {0,\infty} \right)}} \left( X \right)} \right]{\plus}\left( {1\, {\minus}\, \omega ^{{\asterisk}} } \right)\rho _{2} \left[ {f\left( X \right)} \right] \cr & \, {\equals}\, \omega ^{{\asterisk}} \rho _{1} \left( {X\, {\minus}\, f\left( X \right){\plus}\pi _{g}^{X} } \right){\plus}\left( {1\, {\minus}\, \omega ^{{\asterisk}} } \right)\rho _{2} \left( {f\left( X \right)\, {\minus}\, \pi _{g}^{X} } \right) \cr & \, {\equals}\, \omega ^{{\asterisk}} \rho _{1} \left( {X\, {\minus}\, f\left( X \right){\plus}\pi _{f}^{X} } \right){\plus}\left( {1\, {\minus}\, \omega ^{{\asterisk}} } \right)\rho _{2} \left( {f\left( X \right)\, {\minus}\, \pi _{f}^{X} } \right) $$
The last inequality arrives from the fact that
$\omega ^{{\asterisk}} \in[0,a_{{{\rm min}}} \,/\,(a_{{{\rm min}}} {\plus}a_{{{\rm max}}} ).$
Now using the fact that
$\omega ^{{\asterisk}} \rho _{1} (X\, {\minus}\, f(X){\plus}\pi _{f}^{X} ){\plus}(1\, {\minus}\, \omega ^{{\asterisk}} )\rho _{2} (f(X)\, {\minus}\, \pi _{f}^{X} )\, {\equals}\, \mathop {{\rm min}}\limits_{h\in{\cal C}} \left\{ {\omega ^{{\asterisk}} \rho _{1} (X\, {\minus}\, h(X){\plus}\pi _{h}^{X} ){\plus}(1\, {\minus}\, \omega ^{{\asterisk}} )\rho _{2} (h(X)\, {\minus}\, \pi _{h}^{X} )} \right\},$
we conclude that the k-layer reinsurance g(⋅) also minimises such the convex combination.□
Acknowledgements
The authors thank Dr Hirbod Assa for his useful comments and suggestions on an earlier version of this manuscript. Thanks are due to the Editor and anonymous Reviewer for his/her useful comments and suggestions on an earlier version of this manuscript which led to this improved version. The second author also would like thanks support of the Central Insurance of the Islamic Republic of Iran.
